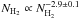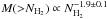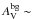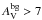| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A91 | |
| Number of page(s) | 33 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201525861 | |
| Published online | 26 November 2015 | |
A census of dense cores in the Aquila cloud complex: SPIRE/PACS observations from the Herschel Gould Belt survey⋆,⋆⋆,⋆⋆⋆
1 Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot, IRFU/Service d’Astrophysique, CEA Saclay, 91191 Gif-sur-Yvette, France
e-mail: vera.konyves@cea.fr; pandre@cea.fr
2 Institut d’Astrophysique Spatiale, UMR8617, CNRS/Université Paris-Sud 11, 91405 Orsay, France
3 Univ. Bordeaux, LAB, UMR5804, 33270 Floirac, France
4 CNRS, LAB, UMR5804, 33270 Floirac, France
5 Department of Physics and Astronomy, University of Victoria, PO Box 355, STN CSC, Victoria, BC, V8W 3P6, Canada
6 National Research Council Canada, 5071 West Saanich Road, Victoria, BC, V9E 2E7, Canada
7 School of Physics & Astronomy, Cardiff University, The Parade, Cardiff CF24 3AA, UK
8 Istituto di Astrofisica e Planetologia Spaziali-INAF, via Fosso del Cavaliere 100, 00133 Roma, Italy
9 CNRS, IRAP, 9 Av. colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
10 Université de Toulouse, UPS-OMP, IRAP, 31028 Toulouse Cedex 4, France
11 Joint ALMA Observatory, Alonso de Cordova 3107, Vitacura, Santiago, Chile
12 Jeremiah Horrocks Institute, University of Central Lancashire, Preston, Lancashire, PR1 2HE, UK
13 Canadian Institute for Theoretical Astrophysics, University of Toronto, 60 St. George Street, Toronto, ON M5S 3H8, Canada
14 National Astronomical Observatory of Japan, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
15 Institut d’Astrophysique de Paris, Sorbonne Universités, UPMC Univ. Paris 06, CNRS UMR 7095, 75014 Paris, France
16 Scientific Support Office, Directorate of Science and Robotic Exploration, European Space Research and Technology Centre (ESA/ESTEC), Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
17 INAF-IRA, Via P. Gobetti 101, 40129 Bologna, Italy
18 Max-Planck-Institut für Astronomie (MPIA), Königstuhl 17, 69117 Heidelberg, Germany
19 RALSpace, The Rutherford Appleton Laboratory, Chilton, Didcot, Oxfordshire, OX11 0QX, England
20 Department of Physics and Astronomy, The Open University, Walton Hall, Milton Keynes, MK7 6AA, England
Received: 10 February 2015
Accepted: 13 July 2015
We present and discuss the results of the Herschel Gould Belt survey (HGBS) observations in an ~11 deg2 area of the Aquila molecular cloud complex at d ~ 260 pc, imaged with the SPIRE and PACS photometric cameras in parallel mode from 70 μm to 500 μm. Using the multi-scale, multi-wavelength source extraction algorithm getsources, we identify a complete sample of starless dense cores and embedded (Class 0-I) protostars in this region, and analyze their global properties and spatial distributions. We find a total of 651 starless cores, ~60% ± 10% of which are gravitationally bound prestellar cores, and they will likely form stars inthe future. We also detect 58 protostellar cores. The core mass function (CMF) derived for the large population of prestellar cores is very similar in shape to the stellar initial mass function (IMF), confirming earlier findings on a much stronger statistical basis and supporting the view that there is a close physical link between the stellar IMF and the prestellar CMF. The global shift in mass scale observed between the CMF and the IMF is consistent with a typical star formation efficiency of ~40% at the level of an individual core. By comparing the numbers of starless cores in various density bins to the number of young stellar objects (YSOs), we estimate that the lifetime of prestellar cores is ~1 Myr, which is typically ~4 times longer than the core free-fall time, and that it decreases with average core density. We find a strong correlation between the spatial distribution of prestellar cores and the densest filaments observed in the Aquila complex. About 90% of the Herschel-identified prestellar cores are located above a background column density corresponding to AV ~ 7, and ~75% of them lie within filamentary structures with supercritical masses per unit length ≳16 M⊙/pc. These findings support a picture wherein the cores making up the peak of the CMF (and probably responsible for the base of the IMF) result primarily from the gravitational fragmentation of marginally supercritical filaments. Given that filaments appear to dominate the mass budget of dense gas at AV> 7, our findings also suggest that the physics of prestellar core formation within filaments is responsible for a characteristic “efficiency” 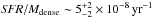 for the star formation process in dense gas.
for the star formation process in dense gas.
Key words: ISM: individual objects: Aquila Rift complex / stars: formation / ISM: clouds / ISM: structure / submillimeter: ISM
Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
Figures 18, 19, and Appendices are available in electronic form at http://www.aanda.org
Herschel column density and temperature maps (FITS format) and full Tables A.1 and A.2 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/584/A91
© ESO, 2015
1. Introduction: The Herschel Gould Belt survey
Understanding how dense cloud cores and protostars form out of the diffuse interstellar medium (ISM) is a fundamental question in contemporary astrophysics (e.g., McKee & Ostriker 2007; and other recent reviews in Beuther et al. 2014). Much progress is being made on this front thanks to imaging surveys with the Herschel Space Observatory (Pilbratt et al. 2010). Its far-infrared and submillimeter cameras PACS (Poglitsch et al. 2010) and SPIRE (Griffin et al. 2010) provide unprecedented sensitivity and dynamic range at wavelengths around the peak of the spectral energy distributions (SEDs) of starless cores and protostars.
In particular, the bulk of nearby (d ≲ 500 pc) molecular clouds, mostly located in the Gould Belt (e.g., Guillout 2001; Perrot & Grenier 2003), have been imaged at five wavelengths between 70 μm and 500 μm as part of the Herschel Gould Belt survey (HGBS; André et al. 2010). Observationally, the molecular clouds of the Gould Belt are the best laboratories at our disposal for investigating the star formation process in detail, at least as far as low-mass stars are concerned. They are the only clouds for which the ~15″ angular resolution of Herschel around λ ~ 200 μm is sufficient to resolve the typical Jeans length ~0.03 pc in cluster-forming clumps (e.g., Larson 1985; Myers 1998).
The 15 or so nearby clouds covered by the HGBS span a wide range of physical and environmental conditions, from very active, cluster-forming complexes such as the Orion A & B giant molecular clouds (GMCs) or the Aquila Rift cloud complex (e.g., Dame et al. 2001; Gutermuth et al. 2008) to quiescent regions with no star formation activity whatsoever, such as the Polaris flare translucent cloud (e.g., Heithausen et al. 2002; Ward-Thompson et al. 2010). The total surface area covered by the survey1 exceeds 160 deg2. The HGBS will eventually provide an essentially complete census of (solar-type) prestellar cores and Class 0 protostars with well-characterized luminosity and mass functions in most nearby star-forming regions.
The main scientific goals of the HGBS are to clarify the nature of the relationship between the prestellar core mass function (CMF) and the stellar initial mass function (IMF) and to elucidate the physical mechanisms responsible for the growth of structure in the cold ISM, leading to the formation of prestellar cores and protostars in molecular clouds.
Initial results from the HGBS have already been presented in several “first-look” papers and may be summarized as follows. The HGBS observations confirm the omnipresence of filaments in nearby molecular clouds and suggest an intimate connection between the filamentary structure of the cold ISM and the formation process of prestellar cores (André et al. 2010; Men’shchikov et al. 2010). While molecular clouds were already known to exhibit large-scale filamentary structures long before Herschel (e.g., Schneider & Elmegreen 1979; Hartmann 2002; Myers 2009), the Herschel observations from the HGBS (e.g., Men’shchikov et al. 2010; Miville-Deschênes et al. 2010) and other imaging surveys such as HiGAL (Molinari et al. 2010; Schisano et al. 2014), HOBYS (Motte et al. 2010; Hill et al. 2011), and EPoS (Henning et al. 2010) now demonstrate that these filaments are truly ubiquitous in the cold ISM, present a high degree of universality (e.g., Arzoumanian et al. 2011), and likely play a central role in the star formation process (see André et al. 2014, for a recent review). In any given cloud, Herschel imaging reveals a whole network of filaments, and a detailed analysis of the radial column density profiles of the nearby, resolved filaments observed in the HGBS shows that they are characterized by a very narrow distribution of central widths with a typical full width at half maximum (FWHM) value ~0.1 pc and a dispersion of less than a factor of 2 (Arzoumanian et al. 2011; Palmeirim et al. 2013; Alves de Oliveira et al. 2014). Other groups have reported results in broad agreement with our HGBS finding of a common filament width. Juvela et al. (2012) found a typical FWHM width of ~0.2−0.3 pc for a number of filaments mapped as part of the Herschel “Galactic Cold Cores” project in clouds with (rather uncertain) distances ranging from ~100 pc to a few kpc. Ysard et al. (2013) reported a mean FWHM width ~0.1 pc for the L1506 filament in Taurus but found significant variations – by up to a factor of ~2 on either side of the mean width – along the length of the filament. Smith et al. (2014) explored filament properties in a set of numerical hydrodynamic simulations and found a range of filament widths rather than a constant value. Recent magneto-hydrodynamic (MHD) simulations by Ntormousi et al. (2015), however, suggest that non-ideal MHD turbulence can account for the properties of observed filaments much better than hydrodynamic turbulence does (see also Hennebelle 2013).
The origin of the common inner width of interstellar filaments in nearby clouds is not yet well understood. A possible interpretation is that filaments result from planar intersecting shock waves due to supersonic interstellar turbulence (e.g. Pudritz & Kevlahan 2013), and that the filament width corresponds to the sonic scale below which the turbulence becomes subsonic in diffuse, non-star-forming molecular gas (cf. Padoan et al. 2001). Alternatively, a characteristic width may arise if interstellar filaments are formed as quasi-equilibrium structures in pressure balance with a typical ambient ISM pressure Pext ~ 2−5 × 104 K cm-3 (Fischera & Martin 2012, S. Inutsuka, priv. comm.). Yet another possibility is that the filament inner width may be set by the dissipation mechanism of MHD waves due to ion-neutral friction (Hennebelle 2013).
The early results from the HGBS further suggest that prestellar cores and protostars form primarily in the densest filaments (e.g., André et al. 2010; Polychroni et al. 2013), for which the mass per unit length exceeds the critical line mass of nearly isothermal, long cylinders (e.g., Inutsuka & Miyama 1997), 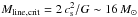 /pc, where cs ~ 0.2 km s-1 is the isothermal sound speed for molecular gas at T ~ 10 K. They also confirm the existence of a close relationship between the prestellar CMF and the stellar IMF in the regime of low to intermediate stellar masses (~0.1–5M⊙ – Könyves et al. 2010). These Herschel findings support a scenario according to which the formation of solar-type stars occurs in two main steps (André et al. 2014): first, the dissipation of kinetic energy in large-scale magneto-hydrodynamic (MHD) flows (turbulent or not) generates a quasi-universal web-like filamentary structure in the ISM; second, the densest filaments fragment into prestellar cores (and ultimately protostars) by gravitational instability.
/pc, where cs ~ 0.2 km s-1 is the isothermal sound speed for molecular gas at T ~ 10 K. They also confirm the existence of a close relationship between the prestellar CMF and the stellar IMF in the regime of low to intermediate stellar masses (~0.1–5M⊙ – Könyves et al. 2010). These Herschel findings support a scenario according to which the formation of solar-type stars occurs in two main steps (André et al. 2014): first, the dissipation of kinetic energy in large-scale magneto-hydrodynamic (MHD) flows (turbulent or not) generates a quasi-universal web-like filamentary structure in the ISM; second, the densest filaments fragment into prestellar cores (and ultimately protostars) by gravitational instability.
In this paper, we present the “first-generation” catalog of dense cores obtained from HGBS data in the Aquila Rift cloud complex and discuss the global properties of these dense cores in relation to the filamentary structure of the complex. In particular, we use these results to quantify the role of filaments in the star formation process. The present study extends and reinforces our early Herschel findings in Aquila (Könyves et al. 2010; André et al. 2010) on the basis of a more advanced examination of the data with improved data reduction, source extraction, and source characterization. The paper is organized as follows. Section 2 introduces the Aquila Rift region. Section 3 provides details about the Herschel imaging observations and the data reduction. Section 4 presents the dust temperature and column density maps derived from Herschel data, describes the filamentary structure seen in these maps, and explains how dense cores were extracted, prestellar cores selected, and their properties measured from the maps. In Sect. 5, we discuss estimates of prestellar core lifetimes, the observational evidence of a column density threshold for prestellar core formation, the spatial distribution of extracted dense cores, and the strong connection with the filamentary structure of the Aquila cloud. We also compare the CMF of the Aquila sample of prestellar cores with the IMF, and link the global star formation rate of the complex with the total mass of dense gas above the column density threshold for star formation. Finally, Sect. 6 concludes the paper by summarizing the HGBS results in the Aquila region and discussing possible implications for our understanding of star formation on GMC scales.
2. The Aquila Rift region
The Aquila Rift molecular cloud complex corresponds to a large extinction feature (see Prato et al. 2008), located above the Galactic plane (b ≲ 4°) at galactic longitudes between l = 30° and l = 50°. The portion of the cloud complex mapped with Herschel as part of the HGBS corresponds to the western high-extinction area of the Aquila Rift at l< 35° (see Bontemps et al. 2010).
While the northern part of the Aquila high-extinction area harbors the well-documented Serpens Main star-forming region, the properties of the southern part (the focus of the present paper) remained largely unexplored until Spitzer infrared observations (e.g., Gutermuth et al. 2008). This extinction-defined area (see Bontemps et al. 2010), rich in gas but initially thought to be almost devoid of star formation (Prato et al. 2008), is now known to harbor two cluster-forming clumps (Maury et al. 2011): Serpens South, a young protostellar cluster showing very active recent star formation and embedded in a dense filamentary cloud (Gutermuth et al. 2008; Bontemps et al. 2010; Nakamura et al. 2011; Teixeira et al. 2012; Friesen et al. 2013; Kirk et al. 2013a; Tanaka et al. 2013), and W40 a young star cluster associated with the eponymous HII region, also known as Sharpless 2-64 (Smith et al. 1985; Vallee 1987; Kuhn et al. 2010; Pirogov et al. 2013).
Whether or not the southern part of the Aquila high-extinction region and the Serpens Main cloud are at the same distance is still a matter of debate (Bontemps et al. 2010; Maury et al. 2011; Loinard 2013). Based on stellar photometry, Straižys et al. (2003) concluded that the front edge of the Aquila molecular cloud was at 255±55 pc. Using VLBI observations, however, Dzib et al. (2010) measured the trigonometric parallax of the binary system EC95 in the Serpens Main region and obtained a distance of 415±15 pc. From the extinction maps obtained by Bontemps et al. (2010), the respective extinction features toward the eastern Aquila Rift region (containing Serpens South, W40, and Sh2-62) and the Serpens Main cloud are seen as clearly distinct regions. It is therefore possible that the two clouds are not physically associated, but located along neighboring lines of sight. While the method used by Straižys et al. (2003, 1996) would naturally be sensitive to the first dust extinction screen along the line of sight, the larger VLBI-based distance of the Serpens Main core by Dzib et al. (2010) suggests that Serpens Main is located behind the extinction wall associated with the Aquila clouds (Serpens South being the highest extinction region found inside the Aquila Rift complex). A distance of 260 pc for the Aquila Rift complex also suits the MWC297/Sh2-62 region since the young star MWC297 itself has an accepted distance of 250 pc (Drew et al. 1997). It is finally worth noting that the visual extinction map derived by Cambrésy (1999) from optical star counts and only tracing the first layer of the extinction wall has exactly the same global aspect as the 2MASS extinction map of Bontemps et al. (2010), suggesting that both Serpens South and the W40/Aquila Rift/MWC297 region are associated with this extinction wall at 260 pc. We will thus adopt a distance d = 260 pc for the entire Aquila complex, throughout this paper (see Appendix C, however, for a brief discussion of how our results would change had we adopted a distance of 415 pc instead).
Rescaled to our adopted distance, the molecular mass of the entire Aquila Rift has been estimated from CO and extinction data to be 2−5 × 105M⊙ within a 25 pc-radius region (Dame et al. 1987; Straižys et al. 2003). Rescaled to the same distance, the virial mass for the entire Aquila Rift estimated by Dame & Thaddeus (1985) is ~3.3 × 105M⊙, suggesting that the whole complex is close to virial balance on large scales. More recently, Tanaka et al. (2013) obtained a virial parameter ~0.08–0.24 for the Serpens South filament (again rescaled to a distance of 260 pc) on ~0.5 pc scales (see also Kirk et al. 2013a), and Maury et al. (2011) derived a high star formation rate of ~23 M⊙ Myr-1 pc-2 for the protocluster associated with the filament (of total mass ~610 M⊙, also using d = 260 pc). Altogether, these results suggest that the Aquila Rift complex is globally gravitationally bound on scales of ~25 pc and includes a few highly unstable (sub-virial) clumps on the verge of forming rich star clusters on sub-parsec scales.
3. Observations and data reduction
The Herschel Gould Belt survey observations of the Aquila Rift complex were taken on 24 October 2009 during the Science Demonstration Phase of Herschel (Pilbratt et al. 2010). The SPIRE/PACS parallel-mode scan maps covered a common ~11 deg2 area with both SPIRE (Griffin et al. 2010) and PACS (Poglitsch et al. 2010). With one repetition in two orthogonal observing directions (OBSIDs: 1342186277, 1342186278), the scanning speed was 60″s-1, and the total duration of the mapping was ~12 h. The above strategy is similar for all the parallel-mode SPIRE/PACS observations of the HGBS.
PACS data reduction The individual scan directions of the parallel-mode PACS data at 70 μm and 160 μm were reduced with HIPE (Ott 2011) version 9.0.3063, provided by the Herschel Science Center.
Starting from the raw data (level-0) and up to the level-1 stage, standard steps of the default pipeline were applied. The PACS photometer flux calibration scheme was applied using the up-to-date responsivity and correction factors (PACS ICC report, Balog et al.)2 of the executed HIPE version with the calibration file set PACS_CAL_45_0. During the actual processing of the data, we created masks to avoid bad and saturated pixels, calibration blocks and their unexpected transient effect on the subsequent frames. Besides the flat-field correction, we applied a non-linearity correction to the data (PACS ICC report, Billot et al.)2. The PACS bolometers enter a non-linear regime for point sources above ~100 Jy/beam in all bands (70–160 μm), and the flux densities of brighter targets are underestimated by typically a few percent. The applied non-linearity correction of the PACS bolometer signal had a very minor effect on the Aquila data. Cosmic ray hits on the detectors were removed with the “second-level deglitching” method of HIPE. To make best use of the deglitcher, we took special care to prepare its input data. First, a high-pass filtering with a scan-leg length outside of a protective object mask was performed. Next, the second-level deglitching was then applied on these temporary data. Baseline subtraction was only used for deglitching purposes, but not on the resulting level-1 frames. The slew/turn-around data at the end of the scan legs were also preserved in the processing.
Further treatment of the flux- and pointing-calibrated level-1 time series and the projection of the combined scans were performed with an IDL-based map-maker, Scanamorphos, version 20 (Roussel 2013)3. The processing is fully automated with some user-defined options. It consists of the main functionalities of subtracting both the thermal and non-thermal components of the brightness drifts, as well as detecting and masking remaining glitches and brightness discontinuities in the PACS data. In the final map projection, we adopted a spatial grid of 3″/pixel. Scanamorphos also provides associated maps of error, total drift, and weight (see Sect. 3.7 of Roussel 2013, for details). The error map provides the error on the mean brightness in each pixel. In the case of two scan directions, an additional “clean” map is produced, which is a signal map weighted so that noisy scans are excluded for each pixel. The clean map is only used for diagnostic purposes. In the PACS map processing, a final step was performed to remove long artifact glitches, which remained mainly in the 70 μm map, due to a jump in the brightness of the PACS data that could affect whole array rows. Thanks to the various planes of the output map, we could replace only affected pixels by “clean map” pixels. Our PACS output (level-2) fits files were produced in Jy/3′′-pixel units.
For PACS data, the absolute flux accuracy of point sources is 3% in the blue band (70 μm) and better than 5% in the red band (160 μm) (cf. PACS ICC report by Müller et al.2). The extended source calibration is more uncertain. In this paper, we conservatively adopted 10% and 20% absolute calibration uncertainties for the integrated source flux densities measured in the 70 μm and 160 μm bands, respectively (see also Sect. 4.6 below).
SPIRE data reduction The SPIRE 250 μm, 350 μm, and 500 μm data were reduced with HIPE version 10.0.2751 using modified pipeline scripts. The nominal and orthogonal scan directions were processed individually, and combined in a second step. Data taken during the turnarounds of the satellite were not included in the final maps.
The raw level-0 data (in engineering units) were processed to level-0.5 (in physical units) using the relevant calibration trees (SPIRE_CAL_10_1) built in HIPE. The following pipeline steps to level-1 (cf. Dowell et al. 2010) consist of: 1) converting detector timelines to angles on the sky; 2) creating the pointing product for the observation; 3) correcting for thermistor-bolometer electrical crosstalk; 4) correcting temperature drifts and detecting temperature jumps; 5) identifying glitches caused by cosmic rays, for which the assumption was that all glitches affect all bolometers of SPIRE simultaneously; 6) applying the low-pass filter response correction; 7) applying the flux conversion; and 8) searching and correcting for cooler burps by recalculating the temperature drift calibration table. (A cooler burp is a steep temperature rise which reaches a stable plateau ~6–7 h after the cooler recycle ends.)
As the Aquila region is dominated by extended emission from the ISM, relative gain factors appropriate to extended sources were applied to the bolometer timelines. These gains, determined by the SPIRE ICC, represent the ratio between the response of each bolometer to the extended emission and the average response. Variations in the specific response of each bolometer arise due to variations in the beam area among bolometers.
The destriper module of the pipeline was used in an iterative manner. The iterative process starts with level-1 timelines for both scan directions, and reconstructs an initial naïve map which is only corrected for a median offset. The destriper then fits a constant level to the difference between each input timeline and the corresponding map timeline, subtracts the fit from the original timeline, and reconstructs another map. By default, bright sources are excluded during baseline fitting. These steps are iterated until convergence. We adopted default grid pixel sizes of 6′′, 10′′, 14′′ for the SPIRE 250 μm, 350 μm, 500 μm wavelengths, respectively. The output (level-2) fits files for each SPIRE wavelength were in Jy/beam units. For SPIRE data, the absolute flux accuracy is better than ~5% for point sources (Bendo et al. 2013) and better than ~10% for extended sources (cf. Griffin et al. 2013) in the three bands.
 |
Fig. 1 a) H2 column density map of the Aquila region at 18.2″ angular resolution, as derived from HGBS data using the method described in Sect. 4.1. b) Same map as in the left panel with the positions of the 446 candidate prestellar cores and 58 protostellar cores identified in the Herschel images with getsources (see Sects. 4.4 and 4.5) shown as black and magenta triangles, respectively. Yellow triangles locate additional prestellar and protostellar cores which were excluded from the analysis and discussion of this paper, due to likely contamination by more distant objects belonging to background CO clouds at significantly higher LSR velocities than the bulk of the Aquila complex (cf. Sect. 4.3). The orientation of the galactic coordinate axes is indicated at the lower right of each panel. The lower left edge of the map is oriented almost parallel to the galactic longitude axis at Gb ~ 2° above the Galactic plane. (Color figure is available in the online version.) |
Map-making tests and consistency of the SPIRE vs. PACS maps SPIRE and PACS map-making tests and benchmarks were carried out in early 2012 by SPIRE/PACS ICC members, map-maker developers, and Herschel key program representatives. The public SPIRE4 and PACS5 results of this test campaign, which compared the performance of several publicly available map-making methods, justify our choice of the destriper pipeline with 0th-order baseline removal (P0) for SPIRE data reduction and the choice of Scanamorphos for PACS map-making. In particular, the destriper P0, the default map-maker in the SPIRE scan-map pipeline since HIPE v9, performed remarkably well and compared favorably among all map makers in all test cases except for those suffering from the “cooler burp” effect. Furthermore, the destriper can handle observations with complex extended emission structures and with large-scale background gradients very well. Power-spectrum tests carried out on SPIRE scan maps by the SPIRE ICC (see also Miville-Deschênes et al. 2010, for the case of the HGBS images of the Polaris flare cirrus cloud) demonstrate that large SPIRE maps such as the HGBS maps trace a wide range of angular scales reliably, from ≳30′ or more down to the SPIRE angular resolution (e.g. ~18″ at 250 μm). This high spatial dynamic range is a key advantage of the Herschel/SPIRE images (compared to, e.g., ground-based submillimeter continuum data), which makes our Herschel survey simultaneously sensitive to both large-scale structures in molecular clouds (e.g. filaments) and small-scale structures such as individual prestellar and protostellar cores. As for PACS maps, comparison metrics showed that the photometry of both point-like and extended sources carried out on Scanamorphos maps is highly consistent with the results obtained on maps produced with other map-makers.
The relative astrometry between the SPIRE and PACS images was tested by cross-correlating the various maps after reprojecting them on the same grid. Using the evolved pointing products in the Herschel system, a good match was found between the intensity peaks seen in the SPIRE and PACS maps on a resampled 2′′/pixel scale grid. The 3′′/pixel maps used in the present analysis are thus well registered and have a relative astrometric consistency better than 2′′. The absolute astrometry of the Herschel images was also compared with publicly-available Spitzer data, as well as high-positional accuracy (<1″) 3 mm IRAM Plateau de Bure observations of a small field at the center of the Serpens South filament (Maury et al. 2011). The final absolute astrometric accuracy of the Herschel maps is estimated to be better than 3′′.
The parallel-mode PACS and SPIRE maps used in this paper were all converted to MJy/sr units and reprojected to a common 3″ pixel grid. The conversion of the PACS maps from Jy/3′′-pixel units to MJy/sr units was obtained using a square pixel area of 9 arcsec2. For the SPIRE unit conversion from Jy/beam to MJy/sr units, we assumed the beam areas measured in 1′′-pixel beam maps by the SPIRE ICC, as given in Table 5.2 of the SPIRE Observer’s Manual v.2.2 (29 Nov. 2010), namely 426 arcsec2, 771 arcsec2, 1626 arcsec2 at 250 μm, 350 μm, 500 μm, respectively. The half-power beam width (HPBW) resolutions of the maps are 8.4″, 13.5″, 18.2″, 24.9″, and 36.3″ at 70 μm, 160 μm, 250 μm, 350 μm, and 500 μm, respectively. These high-quality maps are publicly available from the Herschel Gould Belt Survey Archive6.
4. Results and analysis
4.1. Dust temperature and column density maps
We used the Herschel images to construct an H2 column density map (NH2, Fig. 1) and a dust temperature map (Td, Fig. 2) of the Aquila field. We first smoothed all Herschel images (reprojected to the same 3″ pixel grid – see above) to the 36.3′′ HPBW resolution of the SPIRE 500 μm data.
 |
Fig. 2 Dust temperature map of the Aquila region at 36.3′′resolution, as derived from HGBS data (see Sect. 4.1). The white contour outlines the W40 HII region which has Td> 17 K. (Color figure is available in the online version.) |
A zero-level offset, obtained by correlating the Herschel data with Planck and IRAS data (cf. Bernard et al. 2010), was also added at this stage to each Herschel map. The added offset values were 27.7, 159.9, 169.7, 94.4, and 41.5 MJy/sr at 70, 160, 250, 350, and 500 μm, respectively. Assuming optically thin dust emission at a single temperature Td for each map pixel, we then fitted a modified blackbody function of the form Iν = Bν(Td)κνΣ to the four observed data points from 160 μm to 500 μm on a pixel-by-pixel basis, where Iν is the surface brightness at frequency ν and Bν(Td) is the Planck blackbody function. Each SED data point was weighted by 1/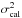 , where σcal corresponds to the absolute calibration error (20% of the intensity at 160 μm and 10% for the SPIRE bands). We adopted a power law approximation to the dust opacity law per unit mass (of dust+gas) at submillimeter wavelengths, namely κλ = 0.1 × (λ/ 300 μm)− β cm2/g, and fixed the dust emissivity index β to 2 (cf. Hildebrand 1983). Based on a detailed comparison of the Herschel results with the near-infrared extinction study of Alves et al. (2001) for the starless core B68, Roy et al. (2014) concluded that these dust opacity assumptions are likely appropriate to better than 50% accuracy over the whole range of H2 column densities between ~3 × 1021 cm-2 and ~1023 cm-2.
, where σcal corresponds to the absolute calibration error (20% of the intensity at 160 μm and 10% for the SPIRE bands). We adopted a power law approximation to the dust opacity law per unit mass (of dust+gas) at submillimeter wavelengths, namely κλ = 0.1 × (λ/ 300 μm)− β cm2/g, and fixed the dust emissivity index β to 2 (cf. Hildebrand 1983). Based on a detailed comparison of the Herschel results with the near-infrared extinction study of Alves et al. (2001) for the starless core B68, Roy et al. (2014) concluded that these dust opacity assumptions are likely appropriate to better than 50% accuracy over the whole range of H2 column densities between ~3 × 1021 cm-2 and ~1023 cm-2.
In the SED fitting procedure, the gas surface density distribution (Σ) and the dust temperature were left as two free parameters. The H2 column density (NH2) was then calculated from Σ = μH2mHNH2, adopting a mean molecular weight per hydrogen molecule μH2 = 2.8 (e.g., Kauffmann et al. 2008). Based on this SED-fitting method, we derived both a standard column density map at the ~36.3″ resolution of the SPIRE 500 μm data and a “high-resolution” column density map at the ~18.2″ resolution of the SPIRE 250 μm data. The procedure used to construct the “high-resolution” column density map is based on a multi-scale decomposition of the imaging data and described in detail in Appendix A of Palmeirim et al. (2013).
Both the standard and the high-resolution column density maps were tested against a near-infrared extinction map of the Aquila/Serpens region derived from 2MASS data (see Bontemps et al. 2010; Schneider et al. 2011), the latter with a FWHM spatial resolution of ~120″. To do this, the Herschel column density maps were smoothed to 120″ and converted to visual extinction units assuming NH2 (cm-2) = 0.94 × 1021AV (mag) (Bohlin et al. 1978). We then derived ratio maps of the converted Herschel maps to the AV map from 2MASS on the same grid. In most of the field covered by Fig. 1, the ratio maps are within ~10% of unity, indicating excellent agreement (see also Appendix of Könyves et al. 2010).
 |
Fig. 3 Left: network of filaments in the Aquila cloud complex as traced by the curvelet transform component (cf. Starck et al. 2003) of the Herschel high-resolution column density map shown in Fig. 1. Given the typical filament width Wfil ~ 0.1 pc (see Arzoumanian et al. 2011 and Fig. 18) and the relation Mline ≈ Σ0 × Wfil between the central gas surface density Σ0 of a filament, this curvelet column density map provides information on the mass per unit length along the filaments (cf. André et al. 2010), as indicated by the color bar on the right. The white areas highlight regions of the map where Σ × Wfil exceeds half the critical mass per unit length |
 |
Fig. 4 Left: mask of the filamentary network traced by getfilaments (Men’shchikov 2013) in the Herschel high-resolution column density map of the Aquila cloud complex. For better visualization, only angular scales up to 320″ (i.e., ~0.4 pc at d = 260 pc) are shown. The color scale displayed within the filamentary mask corresponds to column density values in the column density map (Fig. 1). The crests of the filaments traced by DisPerSE (Sousbie 2011) are overlaid in blue (see Sect. 4.2 for details). Right: blow-up of the subfield marked by the white square in the left panel, using the same color scale. (Color figure is available in the online version.) |
4.2. Filamentary structure of the Aquila cloud complex
As emphasized by Men’shchikov et al. (2010) and André et al. (2010) and mentioned in Sect. 1, filaments are widespread in the Herschel images of the Aquila region. Conceptually, an interstellar filament may be defined as any elongated structure in the ISM which is significantly denser than its surroundings. For the purposes of this paper, we adopt a minimum aspect ratio of ~3 and a minimum column density excess of ~10% with respect to the local background, i.e., 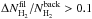 , when averaged along the length of the structure. For more mathematical and algorithmic definitions of a filament, the reader is referred to Sousbie (2011) and Men’shchikov (2013), respectively.
, when averaged along the length of the structure. For more mathematical and algorithmic definitions of a filament, the reader is referred to Sousbie (2011) and Men’shchikov (2013), respectively.
In order to identify filaments in the high-resolution column density map of the Aquila field, several methods were employed and compared. First, the contrast of elongated features was enhanced using a “morphological component analysis” (MCA) decomposition of the map on a basis of curvelets and wavelets (e.g., Starck et al. 2003). In such a decomposition, filamentary features are contained in the curvelet components, while roundish structures (e.g. dense cores) are contained in the wavelet components. Summing up all curvelet components led to the image shown in Fig. 3, which provides a high-contrast view of the filaments after subtraction of core-like and other non-elongated structures (e.g. non-filamentary background). Given the typical filament width Wfil ~ 0.1 pc (Arzoumanian et al. 2011) and the relation Mline ≈ Σ0 × Wfil between the central gas surface density Σ0 of a filament and its mass per unit length Mline (cf. Appendix A of André et al. 2010), this curvelet component of the column density map is equivalent to a map of mass per unit length along the filaments. The white areas trace regions of the map where Σ × Wfil is larger than half the critical value 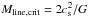 (cf. Inutsuka & Miyama 1997) and the filaments are likely to be gravitationally unstable, i.e., supercritical7 with Mline ~ Σ0 × Wfil>Mline,crit on the filament crest.
(cf. Inutsuka & Miyama 1997) and the filaments are likely to be gravitationally unstable, i.e., supercritical7 with Mline ~ Σ0 × Wfil>Mline,crit on the filament crest.
 |
Fig. 5 a) Probability density function of column density (N-PDF) in the Aquila cloud, derived from the 18.2′′-resolution column density image shown in Fig. 1. The left and right axes give the actual and normalized numbers of independent beams per logarithmic bin in the column density map, respectively. (The right axis thus provides an estimate of a proper N-PDF whose integral is 1.) A power-law fit to the high column density tail at AV> 7 gives dN/dlog |
A second, independent method used to trace filamentary structures in the mapped region was the multi-scale algorithm getfilaments (Men’shchikov 2013). Instead of tracing filaments directly in the observed images, getfilaments analyzes highly-filtered spatial decompositions of them (called “single-scale” images) across a wide range of scales (Sect. 2.3 of Men’shchikov 2013). Using an automated iterative thresholding algorithm (Sect. 2.4.1 of Men’shchikov 2013), getfilaments analyzes single-scale images and finds 1σ intensity levels (on each spatial scale) that separate significant elongated structures from noise and background fluctuations. Setting to zero those pixels whose intensities are below the thresholds, the algorithm effectively “cleans” the single-scale images from noise and background. Fine spatial decomposition allows the algorithm to identify filaments as significantly elongated clusters of connected pixels on each spatial scale (Sect. 2.4.2 of Men’shchikov 2013), separating them from other (roundish) clusters of non-filamentary nature (e.g. sources or cores, noise peaks, isotropic backgrounds). Having produced the clean single-scale images of filamentary structures on each spatial scale, getfilaments reconstructs the intrinsic intensity distribution of the filamentary component of the images (largely free of sources, noise, and background) by accumulating the clean decomposed images over all (or a range of) spatial scales (Sect. 2.4.3 of Men’shchikov 2013). Finally, the algorithm generates mask images of filaments up to various transverse angular scales, as well as skeletons of the filament spines in the format of fits images (see Sect. 2.4.4 of Men’shchikov 2013). Filament extraction with getfilaments is fully automated and there are no free parameters involved. Figure 4 displays the filamentary network obtained by applying getfilaments to the high-resolution column density map shown in Fig. 1. For better visualization, Fig. 4 shows a mask image corresponding to elongated structures with transverse angular scales up to 320′′, equivalent to ~0.4 pc at d = 260 pc. The color scale displayed within the filamentary mask corresponds to the column density values in the input column density map (i.e., Fig. 1). The network of filaments outlined in this way (Fig. 4) is very similar to that traced by the curvelet transform (Fig. 3).
As a third, independent method to trace filaments, we also applied the DisPerSE algorithm8 (Sousbie 2011). DisPerSE is a general tool to identify persistent topological features such as peaks, voids, and filamentary structures in astrophysical data sets. It traces filaments by connecting saddle points to maxima with integral lines, following the gradient in a map. This method has already been used successfully to trace filamentary networks in Herschel images of nearby star-forming clouds (e.g., Arzoumanian et al. 2011; Hill et al. 2011; Peretto et al. 2012; Schneider et al. 2012; Palmeirim et al. 2013). To trace filaments in the Aquila field, DisPerSE was run on the standard column density map (at 36.3′′ resolution) on a 6′′/pixel scale where this pixel scale sets the resolution of the filament skeleton sampling. We used DisPerSE with a relative “persistence” threshold of 4.8 × 1020 cm-2, which corresponds to ~3 times the rms level of background column density fluctuations in the low density portion (AV ~ 2) of the column density image. “Persistence” is a measure of the robustness of topological features in the map (see Sousbie 2011, for details). Segments of filaments found by DisPerSE were assembled into longer filaments, with the constraint that assembled segments did not form an angle larger than 65°.
The DisPerSE filaments were also trimmed to ensure that the minimum column density along the resulting skeleton was 5 × 1021 cm-2 everywhere. This choice of DisPerSE parameters was adopted to facilitate the clean identification of dense, supercritical filaments, which are most relevant to the problem of core formation and the present paper (see André et al. 2010, and Sect. 5.3 below). From the output of DisPerSE, we then built a 1-pixel-wide mask or skeleton image of the filament crests in the same way as Arzoumanian et al. (2011) did, after removing filamentary features shorter than 3 × 0.1 pc long (or ~80 pixels of 3″). The resulting DisPerSE skeleton, which comprises a total of 90 filaments, is overlaid in blue in both Figs. 3 and 4. Owing to the adopted minimum column density, this DisPerSE skeleton is biased toward filaments which are either entirely or at least partly supercritical along their length. It nevertheless contains a dozen subcritical filaments. As can be seen by comparing Figs. 3 and 4, the three above-mentioned methods trace very similar sets of filamentary structures. The agreement is particularly good in the case of supercritical filaments going over white areas in the image panels.
The same filament profile analysis as described in Arzoumanian et al. (2011) was performed on the sample of filaments identified here with DisPerSE, resulting in the distribution of filament inner widths shown in Fig. 18. A median FWHM width of 0.12 ± 0.04 pc was found, which is very similar to the median width reported by Arzoumanian et al. (2011) for a smaller sample of 32 filaments in Aquila.
4.3. Distribution of mass in the Aquila cloud
Figure 5a shows the probability density function (PDF) of column density in the Aquila cloud complex as derived from the high-resolution column density map displayed in Fig. 1. (Likewise, the distribution of dust temperatures corresponding to the dust temperature map in Fig. 2 is shown in Fig. 19a.) The column density PDF is well fit by a log-normal distribution at low column densities (i.e., 3 ≲ AV ≲ 7) and by a power-law distribution at high column densities (i.e., AV ≳ 7). Similar column density PDFs have already been reported in the literature for other star-forming complexes based on near-infrared extinction data (e.g., Kainulainen et al. 2009) and Herschel observations (e.g., Schneider et al. 2013). As discussed by, e.g., Kainulainen et al. (2011), column density PDFs are a powerful tool to characterize molecular cloud structure and the transition from turbulence-dominated to collapsing, star-forming gas. The slope of the power-law distribution at high column densities can be readily related to the logarithmic slope of the equivalent radial density profile expected in cloud collapse models (see, e.g., Federrath & Klessen 2013). The power-law tail of the PDF is particularly well developed in the case of the Aquila complex (see Fig. 5a). The best power-law fit for AV> 7 corresponds to dN/d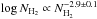 .
.
The total mass of the Aquila cloud imaged with Herschel was derived from the column density map (Fig. 1) as:
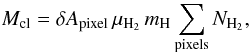 where δApixel is the surface area subtended by one pixel at the adopted distance d = 260 pc of the cloud, μH2 = 2.8 is the mean molecular weight, mH is the hydrogen atom mass, and the column density values in the map are summed up over all pixels. This procedure gave a total cloud mass of ~2.4 × 104M⊙. This estimate of the total cloud mass from Herschel data is in very good agreement with the total mass of ~2.0 × 104M⊙ derived from the extinction map of Bontemps et al. (2010) and with the total gas mass of ~2.5 × 104M⊙ derived from the CO(1–0) observations of Dame et al. (2001) over the same area.
where δApixel is the surface area subtended by one pixel at the adopted distance d = 260 pc of the cloud, μH2 = 2.8 is the mean molecular weight, mH is the hydrogen atom mass, and the column density values in the map are summed up over all pixels. This procedure gave a total cloud mass of ~2.4 × 104M⊙. This estimate of the total cloud mass from Herschel data is in very good agreement with the total mass of ~2.0 × 104M⊙ derived from the extinction map of Bontemps et al. (2010) and with the total gas mass of ~2.5 × 104M⊙ derived from the CO(1–0) observations of Dame et al. (2001) over the same area.
The same mass calculation was repeated for the pixels above a given column density, which led to the cumulative mass fraction of gas mass in the cloud as a function of column density shown in Fig. 5b. For future reference, the fraction of dense gas mass above AV = 7–8 mag in visual extinction represents only ~24–17% (5800–4200 M⊙) of the total cloud mass, respectively. A similar fraction of cloud mass at AV> 7 mag was reported by Johnstone et al. (2004) in the case of the Ophiuchus main cloud. Clearly, the low (column) density regions in the map shown in Fig. 1 account for most of the cloud mass.
As the Aquila Rift lies quite close to the Galactic Plane, we have to consider the potential contamination of the column density map (Fig. 1) by background clouds along some lines of sight. To assess the importance of this potential contamination, we used the CO database of Dame et al. (2001). Throughout the whole field shown in Fig. 1, the most significant CO(1–0) emission was found in the same 5–7 kms-1 LSR velocity range. This correspondence suggests that the bulk of the CO emission comes from the same cloud complex at d ~ 260 pc. Two isolated patches with significantly higher LSR velocities (30–40 km s-1), however, are present in the CO data of Dame et al. (2001), in the eastern corner and the relatively empty central part of the Herschel field of Fig. 1, respectively. Given that these patches are very local and contribute only modest CO emission, their influence on the above column density and mass estimates is minor. Based on the fraction of CO emission observed at high LSR velocities and the column densities derived from Herschel data, we estimate that the background patches cannot change the value of the total cloud mass given above – which excludes these patches – by more than 4%. We also stress that the exclusion of the CO high-VLSR areas from the distributions shown in Fig. 5 has very little impact on the power-law slopes of the N-PDF and cumulative mass fraction plots since the background patches occupy only a small surface area. (Including the patches in the N-PDF would change the power-law slope of −2.9 ± 0.1 by much less than the quoted error bar.) The presence of these background clouds will nevertheless be taken into account when selecting dense cores belonging to the Aquila complex in Sect. 4.5.
4.4. Multiwavelength core extraction with getsources
Conceptually, a dense core is a single star-forming entity which may potentially form a star or a multiple system by gravitational collapse (e.g., Myers 1983; Ward-Thompson et al. 1994; André et al. 2000; Di Francesco et al. 2007). In practice, a core can be defined as the immediate vicinity of a local peak in the Herschel column density maps. In more mathematical terms, a dense core corresponds to a “descending 2-manifold” (cf. Sousbie 2011) associated with a local peak in column density. This manifold defines a region in projection to the plane of sky whose map pixels are connected to the peak by lines following the gradient of the column density distribution.
To generate an extensive catalog of dense cores from HGBS data in the Aquila region, the parallel-mode SPIRE/PACS images were processed with getsources, a multi-scale, multi-wavelength source extraction algorithm (Men’shchikov et al. 2012)9. This algorithm was designed primarily for extracting dense cores and young stellar objects (YSOs) in far-infrared/submillimeter surveys of Galactic molecular clouds with Herschel. The main features of the source extraction method, which may be conveniently divided into a detection and a measurement stage, can be summarized as follows (see Men’shchikov et al. 2012, for full details).
At the detection stage, in contrast to the usual approach of detecting sources directly in the observed images, getsources analyzes “single-scale” images (i.e., fine spatial decompositions of the original images – cf. Sect. 4.2) across a wide range of scales and across all observed wavebands. This decomposition filters out irrelevant spatial scales and improves source detectability, especially in crowded regions and for extended sources. Using an automated iterative thresholding method (see Sect. 2.3 of Men’shchikov et al. 2012), getsources analyzes single-scale images and finds 3σ to 6σ intensity levels (on each spatial scale) that separate signals of significant sources from noise and background fluctuations. Setting to zero those pixels whose intensities are below the thresholds, the algorithm effectively “cleans” the single-scale images from noise and background (including the filamentary component of the images). For detecting sources, getsources constructs a set of wavelength-independent single-scale detection images that preserve information in both spatial and wavelength dimensions (Sect. 2.4 of Men’shchikov et al. 2012). This multi-wavelength design combines data over all wavebands and thus naturally produces a wavelength-independent detection catalog with invariant source positions for all wavebands. Besides eliminating the need and problems of matching independent monochromatic extraction catalogs, the method also improves the detectability of weak sources and enables substantial super-resolution at wavelengths with lower spatial resolution. Sources are detected by getsources in the combined single-scale detection images by analyzing the evolution of their peak intensities and segmentation masks across all spatial scales (Sect. 2.5 of Men’shchikov et al. 2012). The spatial scale on which a source is brightest determines its characteristic size and corresponding footprint size. The latter is defined as the entire area that would give a non-negligible contribution to the integrated flux. The peak position of each source is determined from the wavelength-combined single-scale detection images using the first moments of intensity (Appendix F of Men’shchikov et al. 2012) measured over a range of spatial scales between the smallest scale on which the source appears and the characteristic scale on which the source is brightest. In effect, source coordinates are largely determined by the wavebands with higher angular resolution and unaffected by large-scale emission.
At the measurement stage, properties of detected sources are measured in the original observed images at each wavelength. These measurements go beyond simple aperture photometry since they are done together with background subtraction and deblending of overlapping sources (Sect. 2.6 of Men’shchikov et al. 2012). Background is subtracted by linear interpolation under the source footprints found at the detection stage, constrained by different angular resolutions in each waveband. The footprints must be at least as large as the beam size and their elongation must correspond to that of the source intensity distribution at that wavelength (Eq. (20) of Men’shchikov et al. 2012). Overlapping sources are deblended in an iterative procedure that splits pixel intensity between blended sources, assuming a simple shape for their intensity distributions. The deblending shape has a Gaussian-like circular profile with somewhat stronger power-law wings (see Eq. (14) of Men’shchikov et al. 2012) that should approximate the intensity profiles of observed sources. Local uncertainties of the peak intensities and integrated fluxes are given by the standard deviations estimated in elliptical annuli (covering areas of 20 observational beams) just outside the footprints. In crowded areas, the standard deviations are estimated in expanded annuli outside of any of the overlapping sources (see Sect. 2.6 of Men’shchikov et al. 2012). Aperture corrections are applied by getsources using tables of the encircled energy fraction values for the actual point spread functions (PSFs) provided by the PACS and SPIRE ICCs (Balog et al. 2014; Bendo et al. 2013).
Source extraction with getsources is fully automated and there are no free parameters involved: default configuration parameters have been extensively tested and fine-tuned to work in most practical cases. For the production of the “first-generation” catalogs of starless and protostellar cores from the HGBS, the following two-pronged extraction strategy has been adopted. Two sets of dedicated getsources extractions are performed, optimized for the detection of dense cores and YSOs/protostars, respectively.
In the first set, all of the Herschel data tracing column density are combined at the detection stage, to improve the detectability of dense cores. The detection image is thus combined from the clean 160 μm, 250 μm, 350 μm, and 500 μm maps, together with the high-resolution column density image (see Sect. 4.1) used as an additional “wavelength”. The latter is added to the combined detection image to ensure that detected sources correspond to genuine column density peaks. Furthermore, the 160 μm component to the detection image is “temperature-corrected” to reduce the effects of strong, anisotropic temperature gradients present in parts of the observed fields, such as in the vicinity of the W40 HII region in Aquila10. The temperature-corrected 160 μm map is obtained by converting the original observed 160 μm map (13.5″ resolution) to an approximate column density image, using the color-temperature map derived from the intensity ratio between 160 μm and 250 μm (at the 18.2″ resolution of the 250 μm map). Simulations on synthetic emission maps including model cores (see, e.g., Sect. 4.8 below and Appendix B.1) confirm the validity of this approach to detecting dense cores.
A second set of getsources extractions is performed to trace the presence of self-luminous YSOs/protostars and discriminate between protostellar and starless cores. Here, the only Herschel data used at the detection stage come from the 70 μm image. Indeed, the presence of point-like 70 μm emission traces the internal luminosity of a protostar very well (e.g., Dunham et al. 2008), and Herschel/PACS observations of nearby (d< 500 pc) clouds even have the sensitivity to detect candidate “first hydrostatic cores”, the very first and lowest-luminosity stage of protostars (cf. Pezzuto et al. 2012).
At the measurement stage of both sets of extractions, source properties are measured at the detected positions of either cores or YSOs/protostars, using the observed, background-subtracted, and deblended images at all five Herschel wavelengths, plus the high-resolution column density map. The advantage of this two-pronged extraction strategy is that it provides more reliable detections and measurements of column-density cores and 70 μm luminous YSOs/protostars, respectively.
4.5. Selection and classification of reliable core detections
Here, we summarize the criteria adopted to select various types of dense cores from the raw source lists produced by the two sets of multi-wavelength getsources extractions described at the end of Sect. 4.4. For each source type, the following prescribed criteria should be met at the same time.
Selection of candidate dense cores (either starless or protostellar) from the “core” set of extractions
-
Column density detection significance greater than 5, wheredetection significance here refers to a single-scale analog to aclassical signal-to-noise ratio (S/N) (see Eq. (17)of Men’shchikov et al. 2012) in the high-resolution columndensity map;
-
Global detection significance over all wavelengths (see Eq. (18) of Men’shchikov et al. 2012) greater than 10;
-
Global “goodness” ≥ 1, where goodness is an output quality parameter of getsources, combining global S/N and source reliability, and defined in Eq. (19) of Men’shchikov et al. (2012);
-
Column density measurement S/N11 greater than 1 in the high-resolution column density map;
-
Monochromatic detection significance greater than 5 in at least two bands between 160 μm and 500 μm; and
-
Flux measurement with S/N> 1 in at least one band between 160 μm and 500 μm for which the monochromatic detection significance is simultaneously greater than 5.
Selection of candidate YSOs from the “protostellar” set of extractions
-
Monochromatic detection significance greater than 5 in the70 μm band;
-
Positive peak and integrated flux densities at 70 μm;
-
Global “goodness” greater than or equal to 1;
-
Flux measurement with S/N> 1.5 in the 70 μm band;
-
FWHM source size at 70 μm smaller than 1.5 times the 70 μm beam size (i.e., <1.5 × 8.4″ or <12.6″); and
-
Estimated source elongation <1.30 at 70 μm, where source elongation is defined as the ratio of the major and minor FWHM sizes.
The discussion of the Herschel-identified sample of protostars and YSOs in Aquila will be presented in a complementary paper (Könyves et al., in prep.; see Maury et al. 2011 for a preliminary subsample around W40 and Serpens-South).
Selection of candidate starless cores and protostellar cores
-
After cross-matching the selected dense cores with the candidate YSOs/protostars, a selected dense core is classified as “starless” if there is no candidate 70 μm YSO within its half-power (high-resolution) column density contour.
-
Conversely, a selected dense core is classified as “protostellar” if there is a candidate 70 μm YSO within its half-power column density contour.
-
The most reliable SED of a selected protostellar core is obtained by combining the 70 μm flux density from the “protostellar” extractions with the 160 μm, 250 μm, 350 μm, and 500 μm flux densities from the “core” extractions.
Post-selection checks All of the cores automatically selected according to the above criteria were visually inspected in the SPIRE/PACS and column density images (see blow-up maps in Figs. A.3 and A.4). Any dubious source was removed from the final catalog of cores presented in Table A.1 (see below).
To eliminate from our discussion of Aquila cores extragalactic contaminants that may be misidentified as cores or YSOs, we also cross-matched all selected sources with the NASA Extragalactic Database12 (NED), but no close match (within 6′′) was found.
Likewise, we checked likely associations between the selected Herschel cores and objects in the SIMBAD database or the combined c2d and Gould Belt Spitzer database (Dunham et al. 2013; Allen et al., in prep.). Any matches are reported in the catalog (Table A.1). In particular, 27 associations with a Spitzer source were found using a 6″ matching radius.
In the eastern corner of the field shown in Fig. 1, there are two known dense clumps (ISOSS J18364-0221 SMM1/SMM2) with >30 km s-1 LSR velocities from molecular line measurements (Birkmann et al. 2006). Their LSR velocities correspond to a kinematical distance of ~2.2 kpc. We therefore excluded from our Aquila discussion 23 candidate prestellar cores and 6 protostellar cores (shown as yellow triangles in Fig. 1) lying in the high-VLSR CO area of the Herschel field mentioned at the end of Sect. 4.3. These cores are nevertheless listed (with appropriate comments) in the catalogs (Tables A.1 and A.2).
In the post-selection phase, we also used another source extraction method to generate an “alternative-algorithm” flag for our getsources master source catalog entries. For this purpose, we used CSAR (Cardiff Sourcefinding AlgoRithm – Kirk et al. 2013b), a hierarchical source-finding algorithm, which we applied to the high-resolution column density map. In the Aquila entire field, the fraction of matches between selected starless cores and CSAR-detected sources is ~45%, adopting a matching separation of less than 6″ between peak positions. The resulting “CSAR”-flag appears in the catalogs to indicate if a given getsources core was independently detected by CSAR. Several reasons explain the relatively low fraction of matches with CSAR-detected sources based on peak positions. First, CSAR is a very conservative source-finding algorithm, especially in crowded areas where the multi-scale nature of getsources makes it easier to detect blended objects. Second, CSAR is a “monochromatic” algorithm which detects sources in a single observed image (here the column density map, intrinsically noisier than the Herschel images) and does not benefit from the multi-wavelength design of getsources (significantly improving the detectability of weak sources). Third, the present core sample is dominated by starless cores which tend to have flat-topped density profiles (Ward-Thompson et al. 1994) and whose peak positions are not as well defined as the peak positions of YSOs. Relaxing our matching condition somewhat, we note that ~65% of all selected cores include the peak position of a CSAR source within their FWHM contours. Moreover, as much as ~ 85% of the surface area occupied by the FWHM ellipses of our selected cores in the high-resolution column density map is also covered by the outer footprints of CSAR sources. Based on our visual inspection checks, we are confident that all getsources detections reported in Table A.1 are robust. (The reader can judge by looking at the blow-up maps provided on http://gouldbelt-herschel.cea.fr/archives for each source – see examples in Figs. A.3 and A.4). For the sake of robustness at this “first-generation” stage, ~20% of the automatically-selected getsources cores were visually rejected for reasons such as map artifacts, sources seen only at some Herschel bands but not in the column density image, or sources seen only in the column density map but not at any of the Herschel bands.
Our getsources selection and classification procedure resulted in a final sample of 709 Aquila cores (not counting 40 objects – 34 starless cores, including 23 candidate prestellar cores, and 6 protostellar cores – in the high-VLSR CO area), comprising 651 starless cores and 58 protostellar cores. A total of 446 starless cores were classified as candidate prestellar cores on the basis of their locations in a mass versus size diagram (see Sect. 4.7 and Fig. 7 below). The spatial distribution of the prestellar and protostellar cores is shown in Fig. 1, overplotted on the high-resolution column density map of the cloud.
 |
Fig. 6 Distributions of beam-averaged column densities a) and beam-averaged volume densities b) at the resolution of the SPIRE 500 μm observations for the population of 446 candidate prestellar cores in Aquila (solid curves). In both panels, the dashed curves show the corresponding distributions for all 651 selected starless cores. (Color figure is available in the online version.) |
The observed properties of all selected cores are given in the accompanying catalog (cf. Table A.1). The contents of Table A.1 are as follows: core running number (Col. 1), HGBS source name (Col. 2), J2000 equatorial coordinates (Cols. 3 and 4), then, for each Herschel wavelength, detection significance (Cols. 5, 15, 25, 35, 45), peak flux density and error ((6)±(7), (16)±(17), (26)±(27), (36)±(37), (46)±(47)), contrast over local background (Cols. 8, 18, 28, 38, 48), peak flux density in a 36.3″ beam (9, 19, 29, 39), total integrated flux density and error ((10)±(11), (20)±(21), (30)±(31), (40)±(41), (49)±(50)), major & minor FWHM diameters ((12)–(13), (22)–(23), (32)–(33), (42)–(43), (51)–(52)), and position angle of the major axis (Cols. 14, 24, 34, 44, 53), followed by detection significance in the high-resolution column density map (54), peak H2 column density at 18.2″ resolution (55), column density contrast over local background (56), peak column density in a 36.3″ beam (57), column density of local background (58), major & minor FWHM diameters and position angle of the major axis in the high-resolution column density map ((59)–(61)), number of Herschel bands at which the core is significant (62), “CSAR”-flag (63), core type (64), closest SIMBAD counterpart if any (65), closest Spitzer-c2d counterpart if any (66), and comments (67).
4.6. Derived core properties
The SED fitting procedure used to derive core properties was similar to the procedure described in Sect. 4.1 for the production of the column density map. Here, the SEDs were constructed from the integrated flux densities measured by getsources for each extracted core (see Fig. A.1) and the SED data points were weighted by 1/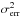 , where σerr corresponds to the flux measurement error estimated by getsources for each point. (In contrast to Sect. 4.1 where the dominant source of error was the calibration uncertainty, the errors on source flux estimates are primarily driven by uncertain background subtraction.) The modified blackbody fits to the observed SEDs were performed with the MPCURVEFIT routine (Markwardt 2009) in IDL. These SED fits provided direct estimates of the mass and line-of-sight-averaged (SED) dust temperature for most of the selected cores. The core masses were derived assuming the same dust opacity law as in Sect. 4.1 and a distance d = 260 pc for the Aquila complex. The angular FWHM size estimate returned by getsources for each core (as measured at 18.2″ resolution in the high-resolution column density map) was converted to a physical core radius assuming the same distance. Two estimates of the core radius are provided (see Table A.2). The first estimate is a deconvolved radius, calculated as
, where σerr corresponds to the flux measurement error estimated by getsources for each point. (In contrast to Sect. 4.1 where the dominant source of error was the calibration uncertainty, the errors on source flux estimates are primarily driven by uncertain background subtraction.) The modified blackbody fits to the observed SEDs were performed with the MPCURVEFIT routine (Markwardt 2009) in IDL. These SED fits provided direct estimates of the mass and line-of-sight-averaged (SED) dust temperature for most of the selected cores. The core masses were derived assuming the same dust opacity law as in Sect. 4.1 and a distance d = 260 pc for the Aquila complex. The angular FWHM size estimate returned by getsources for each core (as measured at 18.2″ resolution in the high-resolution column density map) was converted to a physical core radius assuming the same distance. Two estimates of the core radius are provided (see Table A.2). The first estimate is a deconvolved radius, calculated as 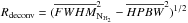 , where
, where 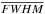 and
and 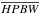 denote the physical sizes corresponding to the FWHM angular size of the core and the HPBW resolution of the high-resolution column density map, respectively. The second estimate simply corresponds to the observed average FWHM size of the core (geometrical average between the major and minor FWHM sizes). In principle the first value provides a more accurate estimate of the intrinsic core radius, but it is affected by significantly larger uncertainties than the second value in the case of marginally resolved cores. In the case of a self-gravitating prestellar core, both values provide estimates of the core outer radius under the assumption that such a core can be approximately described as a critical Bonnor-Ebert (BE) sphere (e.g., Bonnor 1956). (Indeed, a critical BE sphere of outer radius RBE has a column density profile approaching that of a Gaussian distribution of FWHM diameter ~RBE.) A peak (or central beam) column density, an average column density, a central-beam volume density, and an average volume density were also derived for each core based on its estimated mass and radius. The central-beam column density was estimated from the peak flux densities of the core at the resolution of the SPIRE 500 μm observations (HPBW = 36.3″ or ~0.046 pc at d = 260 pc) using an SED fitting procedure similar to that described in Sect. 4.1. The central-beam volume density n0 (at the same resolution) was derived from the central-beam column density N0 assuming a Gaussian spherical distribution, for which
denote the physical sizes corresponding to the FWHM angular size of the core and the HPBW resolution of the high-resolution column density map, respectively. The second estimate simply corresponds to the observed average FWHM size of the core (geometrical average between the major and minor FWHM sizes). In principle the first value provides a more accurate estimate of the intrinsic core radius, but it is affected by significantly larger uncertainties than the second value in the case of marginally resolved cores. In the case of a self-gravitating prestellar core, both values provide estimates of the core outer radius under the assumption that such a core can be approximately described as a critical Bonnor-Ebert (BE) sphere (e.g., Bonnor 1956). (Indeed, a critical BE sphere of outer radius RBE has a column density profile approaching that of a Gaussian distribution of FWHM diameter ~RBE.) A peak (or central beam) column density, an average column density, a central-beam volume density, and an average volume density were also derived for each core based on its estimated mass and radius. The central-beam column density was estimated from the peak flux densities of the core at the resolution of the SPIRE 500 μm observations (HPBW = 36.3″ or ~0.046 pc at d = 260 pc) using an SED fitting procedure similar to that described in Sect. 4.1. The central-beam volume density n0 (at the same resolution) was derived from the central-beam column density N0 assuming a Gaussian spherical distribution, for which 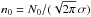 , where σ is the standard deviation of the Gaussian distribution. The distributions of column densities and volume densities for the population of starless cores are shown in Fig. 6.
, where σ is the standard deviation of the Gaussian distribution. The distributions of column densities and volume densities for the population of starless cores are shown in Fig. 6.
All of the derived properties are provided in Table A.2 for the whole sample of selected Herschel cores. The contents of Table A.2 are as follows: core running number (Col. 1), HGBS core name (Col. 2), J2000 equatorial coordinates (Cols. 3 and 4), deconvolved and observed core radii (Cols. 5 and 6), estimated core mass and corresponding error (Cols. 7 and 8), SED dust temperature and corresponding error (Cols. 9 and 10), peak column density at 36.3″ resolution (Col. 11), average column density measured before and after deconvolution (Cols. 12 and 13), beam-averaged peak volume density at 36.3″ resolution (Col. 14), average volume density derived before and after deconvolution (Cols. 15 and 16), Bonnor-Ebert mass ratio (Col. 17 – see Sect. 4.7), core type (Col. 18), and comments (Col. 19).
Since color correction factors are usually small, we did not apply any color corrections to the measured flux densities. Instead, like Kelly et al. (2012), we adopted an elevated calibration uncertainty representing multiple sources of uncertainties. Our adopted calibration uncertainties for the SED data points were 10–20% for the PACS 70–160 μm bands and 10% for the SPIRE 250/350/500 μm bands, respectively, which are conservative values compared to the HSC-recommended point source calibration uncertainties13.
 |
Fig. 7 Mass versus size diagram for the entire population of 651 starless cores identified with Herschel in the Aquila cloud. The core FWHM sizes were measured with getsources in the high-resolution column density map (Fig. 1) and deconvolved from an 18.2″ (HPBW) Gaussian beam; the vertical dashed line marks the corresponding physical |
The robustness of the SED fits was assessed by using and comparing two successive runs of the fitting routine with slightly different weighting schemes for each source. In the first run the 70 μm data point was included in the fit and the getsources detection errors were used to weigh the SED data points, while in the second run the 70 μm point was not fitted and the (more conservative) measurement errors were used to weigh the SED data points. The detection errors on significant data points were typically ~15% (comparable to the absolute calibration uncertainty), while the median measurement errors ranged from ~30% to ~70% depending on wavelength (being typically higher at 160 μm). The results of the SED fits were accepted for a given source if 1) significant flux measurements exist for this source in at least three Herschel bands; 2) the source has a larger integrated flux density at 350 μm than at 500 μm; and 3) there was less than a factor of 2 difference between the core mass estimates derived from the two fit runs. About 68% of the starless cores had reliable SED fits. The corresponding distribution of SED dust temperatures is shown in Fig. 19b. Comparison with the distribution of dust temperatures in the background cloud (Fig. 19a) indicates that the Aquila starless cores are somewhat colder than the parent cloud, as expected (cf. Roy et al. 2014).
The masses of the starless cores for which the SED fit results were rejected were directly estimated from the measured integrated flux density at the longest significant wavelength in each case, assuming optically thin dust emission at the median dust temperature found for starless cores with reliable SED fits (i.e., 11.5 ± 2 K outside the W40/Sh62 areas and 14.5 ± 3 K within the higher radiation field areas W40 and Sh62). The corresponding cores have more uncertain properties and are marked as having “no SED fits” in the last column of Table A.2.
Accuracy of the core mass estimates Uncertainties in the dust opacity law alone induce uncertainties of up to a factor ~1.5–2 in the core mass estimates. As mentioned in Sect. 4.1, the dust opacity law adopted here and in other HGBS papers, namely κλ = 0.1 × (λ/ 300 μm)− β cm2/g, is likely appropriate to better than 50% in the 160–500 μm range for column densities between ~3 × 1021 cm-2 and ~1023 cm-2 (cf. Roy et al. 2014).
In addition to the dust opacity, another systematic effect affects the accuracy of our simple SED mass estimates. A single-temperature graybody fit to the integrated flux densities can only provide an average value of the dust temperature for each source and neglects any variation in dust temperature within the source. In reality, starless dense cores, which are externally heated objects, are known from both radiative transfer calculations (e.g., Evans et al. 2001; Stamatellos et al. 2007) and, e.g., Herschel observations (e.g., Nielbock et al. 2012; Roy et al. 2014) to have a stratified temperature structure with a significant drop in dust temperature toward core center. In such a situation, the average dust temperature derived from a global SED fit can sometimes significantly overestimate the mass-averaged dust temperature within a starless core, leading to an underestimate of the core mass. The magnitude of this effect is very modest (<20%) for low column density cores such as B68 (Roy et al. 2014) but increases to up to a factor of ~2 for high-density cores with average column densities ≳1023 cm-2. In the case of spatially-resolved cores with good S/N data, techniques such as the Abel-inversion method (Roy et al. 2014) or the COREFIT method (Marsh et al. 2014) can help to retrieve the intrinsic temperature structure and derive more accurate mass estimates. We did not attempt to use such techniques here. Based on the results of the simulations performed to estimate the completeness of the survey (see Sect. 4.8 below and Appendix B.1), however, we estimate that the SED masses listed in Table A.2 for starless cores are likely underestimated by ~20–30% on average compared to the intrinsic core masses, mainly due to the fact that the SED dust temperatures tend to slightly overestimate the intrinsic mass-averaged temperatures of starless cores. The column densities and volume densities listed in Table A.2 and used in Fig. 6 (see also Fig. 9 below) have not been corrected for this small effect.
4.7. Selecting self-gravitating prestellar cores
Conceptually, a dense core is deemed to be prestellar if it is both starless and self-gravitating (cf. André et al. 2000; Di Francesco et al. 2007; Ward-Thompson et al. 2007). Such starless cores will most likely form (proto)stars in the future. Lacking spectroscopic observations for most of the Herschel cores, we used the thermal value of the critical Bonnor-Ebert (BE) mass (MBE,crit – Bonnor 1956) to assess whether a starless core was self-gravitating or not based on the value of its BE mass ratio αBE = MBE,crit/Mobs. The critical BE mass can be expressed as
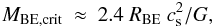 where RBE is the BE radius, cs the isothermal sound speed, and G the gravitational constant. In the presence of significant nonthermal motions, the thermal BE mass should be replaced by a modified BE mass obtained by substituting the total (thermal + non thermal) one-dimensional velocity dispersion for the isothermal sound speed in the above formula. The simplified approach adopted here, where the nonthermal component of the velocity dispersion is neglected, is justified by observations of nearby cores in dense gas molecular tracers such as NH3 and N2H+ lines, which show that nonthermal motions are negligible in low-mass (and intermediate-mass) starless cores (e.g., Myers 1983; André et al. 2007). For each object, we estimated the thermal BE mass, MBE, from the deconvolved core radius Rdeconv measured in the high-resolution column density map (see Sect. 4.6) assuming a typical gas temperature of 10 K.
where RBE is the BE radius, cs the isothermal sound speed, and G the gravitational constant. In the presence of significant nonthermal motions, the thermal BE mass should be replaced by a modified BE mass obtained by substituting the total (thermal + non thermal) one-dimensional velocity dispersion for the isothermal sound speed in the above formula. The simplified approach adopted here, where the nonthermal component of the velocity dispersion is neglected, is justified by observations of nearby cores in dense gas molecular tracers such as NH3 and N2H+ lines, which show that nonthermal motions are negligible in low-mass (and intermediate-mass) starless cores (e.g., Myers 1983; André et al. 2007). For each object, we estimated the thermal BE mass, MBE, from the deconvolved core radius Rdeconv measured in the high-resolution column density map (see Sect. 4.6) assuming a typical gas temperature of 10 K.
In practice, we used the positions of the Herschel cores in a mass versus size diagram (Fig. 7) to distinguish between candidate prestellar cores and unbound starless cores, after deriving a reasonable lower envelope for self-gravitating cores in such a diagram. In our first-look papers (Könyves et al. 2010; André et al. 2010), the criterion adopted to define this lower envelope was simply αBE ≤ 2, by analogy with the usual criterion to select self-gravitating objects based on the virial mass ratio (αvir = Mvir/Mobs ≤ 2 – e.g., Bertoldi & McKee 1992). Adopting the same criterion here led to a first sample of 292 robust prestellar cores, shown as filled blue triangles in Fig. 7. However, the Monte-Carlo simulations performed in Sect. 4.8 below to assess the completeness of the survey suggest that this criterion may be too restrictive, in the sense that it selects only ~85% of the simulated BE cores detected by getsources after source classification. For this reason, we also derived a less restrictive lower envelope (shown as a red curve in Fig. 7) based on the results of our Monte-Carlo simulations. This second, empirical lower envelope contains >95% of the simulated BE cores after getsources extraction, and corresponds to the following, size-dependent limiting BE mass ratio: αBE ≤ 5 × (HPBWNH2/FWHMNH2)0.4, where FWHMNH2 is the measured FWHM source diameter in the high-resolution column density map and HPBWNH2 = 18.2″ is the HPBW resolution of the map. The limiting BE mass ratio varies from ~2 for well-resolved cores with 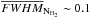 pc to ~5 for unresolved cores with
pc to ~5 for unresolved cores with 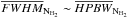 . The reason why one has to be more flexible and use a larger limiting BE mass ratio for unresolved or marginally resolved cores is that the intrinsic core radius (and therefore the intrinsic BE mass) is more uncertain for such cores.
. The reason why one has to be more flexible and use a larger limiting BE mass ratio for unresolved or marginally resolved cores is that the intrinsic core radius (and therefore the intrinsic BE mass) is more uncertain for such cores.
Based on the latter criterion, 446 of the 651 starless cores in the Aquila entire field were classified as candidate prestellar cores. All of the 292 robust prestellar cores belong to the wider sample of 446 candidate prestellar cores. These two samples of cores reflect the uncertainties in the classification of detected starless cores as gravitationally bound or unbound objects, which are fairly large for marginally-resolved cores. In the absence of higher-resolution observations, the status of the 155 candidate prestellar cores which do not match the first criterion (αBE ≤ 2) is more uncertain (these cores are marked as “tentative bound” in the last column of Table A.2). We will thus consider both samples of prestellar cores in the discussion presented in Sect. 5 below.
The mass vs. size distribution of the entire population of selected starless cores (Fig. 7) shows a spread of deconvolved 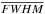 sizes between ~0.01 pc and ~0.1 pc and a range in core mass between ~0.03 M⊙ and ~10 M⊙. The high fraction of self-gravitating cores (~45% or ~69%, depending on whether the robust or the candidate sample is adopted) is reflected in the locations of the Aquila starless cores in this mass vs. size diagram. The selected robust prestellar cores are clustered around (or above) the mass–size relations expected for critical BE isothermal spheres with gas temperatures between 7 K and 20 K (parallel black solid lines in Fig. 7). Besides, they are more than an order of magnitude denser than typical CO clumps (yellow band in Fig. 7), which are mostly unbound structures (e.g., Elmegreen & Falgarone 1996; Kramer et al. 1998).
sizes between ~0.01 pc and ~0.1 pc and a range in core mass between ~0.03 M⊙ and ~10 M⊙. The high fraction of self-gravitating cores (~45% or ~69%, depending on whether the robust or the candidate sample is adopted) is reflected in the locations of the Aquila starless cores in this mass vs. size diagram. The selected robust prestellar cores are clustered around (or above) the mass–size relations expected for critical BE isothermal spheres with gas temperatures between 7 K and 20 K (parallel black solid lines in Fig. 7). Besides, they are more than an order of magnitude denser than typical CO clumps (yellow band in Fig. 7), which are mostly unbound structures (e.g., Elmegreen & Falgarone 1996; Kramer et al. 1998).
4.8. Completeness of the prestellar core survey
To estimate the completeness of our census of prestellar cores in Aquila, we performed Monte-Carlo simulations (see Appendix B.1). We first constructed clean maps of the background emission at all Herschel wavelengths (including a column density plane), by subtracting the emission of the compact sources identified with getsources. We then inserted a population of ~5600 model Bonnor-Ebert-like14 cores throughout the clean-background images to generate a full set of synthetic Herschel and column density images of the region. The model cores were given a flat mass distribution (dN/dlogM ∝ M-0.7) from 0.02 M⊙ to ~30 M⊙ and were assumed to follow a M ∝ R mass versus size relation appropriate for isothermal spheres. The dust continuum emission from the synthetic Bonnor-Ebert cores in all Herschel bands was simulated using an extensive grid of spherical dust radiative transfer models constructed by us with the MODUST code (e.g., Bouwman et al. 2000; Bouwman 2001). Compact source extraction for several sets of such synthetic skies was performed with getsources in the same way as for the observed images.
Based on the results of these simulations (see Appendix B.1 for further details), we estimate that our Herschel census of candidate prestellar cores is >90% complete above a true core mass of ~0.3 M⊙ which corresponds to an observed core mass of ~0.2 M⊙ on average, given that observed masses are typically underestimated by ~20–30% due to the internal temperature structure of starless cores (see end of Sect. 4.6 and Fig. B.2a). Likewise, our sample of robust prestellar cores is estimated to be ~80% complete above a true core mass of ~0.3 M⊙ or an observed core mass of ~0.2 M⊙. The completeness curve of the Aquila core survey as a function of true core mass is plotted in Fig. 8.
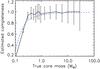 |
Fig. 8 Completeness curve of our Herschel sample of candidate prestellar cores as a function of true core mass (solid line), as estimated from the Monte-Carlo simulations described in Sect. 4.8 and Appendix B.1. For comparison, the dashed line shows the global completeness curve predicted by the model discussed in Appendix B.2. (Color figure is available in the online version.) |
In reality, the completeness level of the core survey is expected to be background dependent. In an effort to assess the magnitude of this dependence, we constructed a simple model of the prestellar core population and core extraction process described in Appendix B.2. This model shows that the completeness of prestellar core extractions does decrease as background cloud column density and cirrus noise increase (see Fig. B.6) but suggests that the global completeness curve of the prestellar core survey in Aquila is consistent with that inferred from our Monte-Carlo simulations (compare the dashed and the solid line in Fig. 8).
Armed with a good understanding of the completeness of the core survey, we discuss in Sect. 5 below the global properties of the dense core population and their connection with the filamentary structure of the cloud complex on the basis of statistically representative observational results.
5. Discussion
5.1. Lifetimes of Herschel prestellar cores
As our Herschel survey provides an essentially complete census of prestellar cores in the Aquila cloud, the core statistics can be used to set constraints on the typical lifetime of prestellar cores and the timescale of the core formation process. Following a technique introduced by Beichman et al. (1986) in the context of IRAS data, a rough estimate of the lifetime of prestellar cores can be obtained by comparing the number of starless cores found with Herschel to the number of Class II YSOs detected by Spitzer in the same region. The underlying assumptions are 1) that all starless cores will evolve into YSOs in the future; and 2) that star formation proceeds at a roughly constant rate, at least when averaged over an entire cloud. In the ~3° × 3° field covered by Herschel, and excluding the dubious, small area with higher LSR velocities in the eastern corner of the column density map (see Fig. 1 and Sect. 4.3), our survey revealed a total of 651 starless cores, including 446 candidate and 292 robust prestellar cores, while the combined c2d and Gould Belt Spitzer surveys detected 622 Class II YSOs (Dunham et al. 2013, Allen et al., in prep.). Adopting a reference lifetime of 2 Myr for Class II YSOs (Evans et al. 2009), these numbers lead to typical lifetimes of ~ 2 Myr, ~1.4 Myr, and ~0.9 Myr for the global populations of Herschel starless cores15, candidate prestellar cores, and robust prestellar cores, respectively. Given the large sizes of the populations of starless cores and YSOs in Aquila, the main sources of error in these estimates come from the fact that some starless or even candidate prestellar cores may never evolve into YSOs, as they may be “failed cores” that will disperse before collapsing (e.g. Vázquez-Semadeni et al. 2005), and from the uncertainty in the number and lifetime of Class II YSOs in Aquila. Combining the constraints coming from the two samples of observed prestellar cores, our best estimate of the global lifetime of the prestellar core phase is tpre = 1.2 ± 0.3 Myr.
 |
Fig. 9 Estimated lifetime against minimum average volume density (blue solid line and filled triangles) for the population of 446 candidate prestellar cores identified with Herschel in the Aquila cloud (blue triangles), similar to the “JWT” plot introduced by Jessop & Ward-Thompson (2000). The error bars only reflect |
We have a large enough sample of cores in Aquila to investigate a possible trend between core lifetime and core density. Figure 9 shows a plot of estimated core lifetime versus average volume density, similar to that introduced by Jessop & Ward-Thompson (2000), but for the sample of Herschel-identified candidate prestellar cores in Aquila. In this plot, the Aquila data are represented by blue triangles and compared to literature data (black crosses) from Ward-Thompson et al. (2007). The blue solid line and filled triangles represent the estimated trend between core lifetime and average core density, where the latter quantity was obtained by dividing the observed mass of each core by the deconvolved estimate of its volume (i.e., core density reported in Col. 16 of Table A.2). As can be seen, the plot suggests that the typical lifetime of prestellar cores decreases from ~1.4 Myr for cores with average volume density ≳104 cm-3 to a few times 104 yr for cores with average volume density ≳105–106 cm-3. Moreover, the estimated core lifetimes lie between one free-fall time (tff, lower dashed line in Fig. 9), the timescale expected in free-fall collapse, and 10 × tff (upper dashed line in Fig. 9), roughly the timescale expected for highly subcritical cores undergoing ambipolar diffusion (e.g., Mouschovias 1991). At the median average volume density ~4 × 104 cm-3 of the candidate prestellar cores identified with Herschel, the estimated core lifetime is ~0.75 Myr or ~4–5tff. The densest cores in our sample, which have beam-averaged volume densities ≳2 × 105 cm-3 at the resolution of the 500 μm data and average deconvolved volume densities ≳106 cm-3, have a much shorter lifetime ~0.02–0.05 Myr or ~tff, suggesting they may evolve essentially on a free-fall timescale. Indeed, the tentative presence of a power-law tail in the distribution of beam-averaged core densities above ~105 cm-3 (see Fig. 6b) suggests that these cores may be undergoing nearly free-fall collapse.
In this context, it is worth pointing out that density may not be the only relevant parameter and that core evolution may also be mass dependent as suggested by, e.g., Hatchell & Fuller (2008). Indeed, we observe a weak positive correlation between core density and core mass above ~2–3M⊙ (see Fig. 10), indicating that the most massive prestellar cores in our sample tend to be the densest objects. Assuming that the lifetime of a core is proportional to its free-fall time, the correlation in Fig. 10 suggests that prestellar cores more massive than ~2–3M⊙ may evolve on significantly shorter timescales than the majority of the cores in our sample, which have masses ~0.1–2M⊙ (see Fig. 16 below). This finding would be consistent with the results of earlier searches for high-mass prestellar cores (i.e., precursors to stars >8 M⊙) in massive star-forming regions which have shown that such cores, if they exist at all, are extremely rare with lifetimes comparable to (or shorter than) the free-fall timescale (Motte et al. 2007).
 |
Fig. 10 Average volume density versus observed core mass for the sample of 446 candidate prestellar cores. The blue solid triangles mark the median deconvolved volume density for each mass bin. (For comparison, the black open triangles show the median 36.3′′-beam-averaged densities for the upper three mass bins.) The error bars correspond to the interquartile range of densities in each mass bin. The data points become very uncertain at the high-mass end due to the small number of cores in the higher mass bins (see core mass function in Fig. 16 below). (No interquartile range can be plotted for the last bin which contains only two cores.) Note the weak, but significant, correlation between core density and core mass above ~2–3M⊙. The red curve represents a parabolic fit to the data points. (Color figure is available in the online version.) |
 |
Fig. 11 a) Distribution of background cloud column densities for the population of 446 candidate prestellar cores identified with Herschel in the whole Aquila field. The vertical dashed line marks a fiducial threshold at an equivalent visual extinction level |
5.2. Evidence of a column density threshold for prestellar core formation
Figure 11a shows the distribution of background cloud column densities (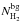 ) for the entire population of 446 candidate prestellar cores identified with Herschel in the Aquila cloud (see Sects. 4.4 & 4.7). This distribution shows a steep rise above
) for the entire population of 446 candidate prestellar cores identified with Herschel in the Aquila cloud (see Sects. 4.4 & 4.7). This distribution shows a steep rise above 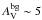 and is such that most (~90%)16 prestellar cores are found above a background column density corresponding to
and is such that most (~90%)16 prestellar cores are found above a background column density corresponding to 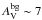 or a background gas surface density Σbg ~ 150 M⊙/pc2. As already emphasized by André et al. (2010, 2014), the shape of the distribution shown in Fig. 11a strongly supports the existence of a column density threshold for the formation of prestellar cores. The existence of such a threshold had been suspected for a long time, based on the results of ground-based millimeter and submillimeter surveys for cores in, e.g., the Taurus, Ophiuchus, and Perseus clouds (e.g., Onishi et al. 1998; Johnstone et al. 2004; Kirk et al. 2006). These early claims, however, were not completely convincing due to the limited column density sensitivity and spatial dynamic range of ground-based observations, hence their limited capability to probe prestellar cores and the parent background cloud simultaneously. The Herschel results presented in this paper provide a much stronger case for a (column) density threshold. We stress that the distribution of cloud mass as a function of column density (see Fig. 5b in Sect. 4.3) and the background-dependent completeness level of our survey for prestellar cores make the threshold even more significant than Fig. 11a suggests. Indeed, ~85% of the mass in the Aquila cloud is at column densities lower than AV ~ 7 (see Fig. 5b) and ~95% of the surface area covered by the Herschel survey is below AV ~ 7. Furthermore, the completeness level of our Herschel census for prestellar cores is not limited by sensitivity (as was typically the case for earlier ground-based surveys), but by “cirrus confusion noise” (see Appendix B), and is better in AV< 7 areas than in AV> 7 areas (see Fig. B.6). Therefore, if prestellar cores were distributed randomly in the cloud, we would be much more likely to detect prestellar cores in AV< 7 areas than in higher column density regions. Figure 11a already shows that this is clearly not the case. To further strengthen the point, we plot in Fig. 11b a probability function of finding a prestellar core as a function of background column density, obtained by normalizing the number of prestellar cores detected below a given background column density by the total surface area imaged by Herschel below the same background column density level (for a related probability function in the case of the submm continuum cores detected by SCUBA in Perseus, see Hatchell et al. 2005). The probability function,
or a background gas surface density Σbg ~ 150 M⊙/pc2. As already emphasized by André et al. (2010, 2014), the shape of the distribution shown in Fig. 11a strongly supports the existence of a column density threshold for the formation of prestellar cores. The existence of such a threshold had been suspected for a long time, based on the results of ground-based millimeter and submillimeter surveys for cores in, e.g., the Taurus, Ophiuchus, and Perseus clouds (e.g., Onishi et al. 1998; Johnstone et al. 2004; Kirk et al. 2006). These early claims, however, were not completely convincing due to the limited column density sensitivity and spatial dynamic range of ground-based observations, hence their limited capability to probe prestellar cores and the parent background cloud simultaneously. The Herschel results presented in this paper provide a much stronger case for a (column) density threshold. We stress that the distribution of cloud mass as a function of column density (see Fig. 5b in Sect. 4.3) and the background-dependent completeness level of our survey for prestellar cores make the threshold even more significant than Fig. 11a suggests. Indeed, ~85% of the mass in the Aquila cloud is at column densities lower than AV ~ 7 (see Fig. 5b) and ~95% of the surface area covered by the Herschel survey is below AV ~ 7. Furthermore, the completeness level of our Herschel census for prestellar cores is not limited by sensitivity (as was typically the case for earlier ground-based surveys), but by “cirrus confusion noise” (see Appendix B), and is better in AV< 7 areas than in AV> 7 areas (see Fig. B.6). Therefore, if prestellar cores were distributed randomly in the cloud, we would be much more likely to detect prestellar cores in AV< 7 areas than in higher column density regions. Figure 11a already shows that this is clearly not the case. To further strengthen the point, we plot in Fig. 11b a probability function of finding a prestellar core as a function of background column density, obtained by normalizing the number of prestellar cores detected below a given background column density by the total surface area imaged by Herschel below the same background column density level (for a related probability function in the case of the submm continuum cores detected by SCUBA in Perseus, see Hatchell et al. 2005). The probability function, 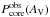 , shown in Fig. 11b increases by more than an order of magnitude between AV ~ 4 and AV ~ 10, and looks like a smooth step function. It is very well fit by the simple exponential step function Pcore(AV) = 1 − exp(−0.17 × AV + 0.86).
, shown in Fig. 11b increases by more than an order of magnitude between AV ~ 4 and AV ~ 10, and looks like a smooth step function. It is very well fit by the simple exponential step function Pcore(AV) = 1 − exp(−0.17 × AV + 0.86).
5.2.1. Comparison with models of the star formation rate
There is some debate in the literature as to whether the kind of results shown in Fig. 11 reflect a true column density threshold for star formation or whether the efficiency of the star formation process simply increases gradually with (column) density (cf. Hatchell et al. 2005). Starting with the work of Krumholz & McKee (2005), a number of theoretical models of the star formation rate (SFR) in molecular clouds have been proposed based on the general idea that star formation is regulated by interstellar turbulence and that clouds typically convert ϵff ~ 1% of their molecular gas mass into stars per (local) free-fall time (e.g., Padoan & Nordlund 2011; Hennebelle & Chabrier 2011; Krumholz et al. 2012 – see also Federrath & Klessen 2012 and Padoan et al. 2014, for overviews and comparisons of the models). In the “multi-freefall” versions of these theoretical models, which are most appropriate to fit real observations17 (cf., Hennebelle & Chabrier 2011; Federrath & Klessen 2012), there is not necessarily any sharp (column) density threshold, but the SFR drops significantly at low densities because of a significant increase in the local free-fall time (see also the related discussion by Burkert & Hartmann 2013). In Fig. 12, we compare the observed core formation efficiency (CFE) as a function of background column density with the prediction of the simplified multi-freefall model of Hennebelle & Chabrier (2011). Here, we define the observed core formation efficiency as CFEobs(AV) = ΔMcores(AV)/ΔMcloud(AV) where ΔMcores(AV) is the mass of the prestellar cores18 identified with Herschel in a given bin of background AV values and ΔMcloud(AV) is the cloud mass estimated from the Herschel column density map in the same AV bin. In the multi-freefall model, the fraction of gas mass converted into core mass per unit time is simply 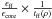 , where ϵff ~ 1% (see above), ϵcore ~ 40% is the star formation efficiency at the level of an individual prestellar core (see Sect. 5.5 below), and tff(ρ) is the local free-fall time at the local gas density ρ. Over the typical lifetime of prestellar cores tpre ~ 1 Myr (see Sect. 5.1), the expected core formation efficiency is thus:
, where ϵff ~ 1% (see above), ϵcore ~ 40% is the star formation efficiency at the level of an individual prestellar core (see Sect. 5.5 below), and tff(ρ) is the local free-fall time at the local gas density ρ. Over the typical lifetime of prestellar cores tpre ~ 1 Myr (see Sect. 5.1), the expected core formation efficiency is thus:
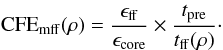 In order to use this formula, we had to estimate the local gas density and free-fall time in the Aquila cloud. To do so, we made use of the fact that the cloud surface area above a given column density level S( >NH2) scales as the column density PDF shown in Fig. 5a and in particular features a well-defined power-law tail
In order to use this formula, we had to estimate the local gas density and free-fall time in the Aquila cloud. To do so, we made use of the fact that the cloud surface area above a given column density level S( >NH2) scales as the column density PDF shown in Fig. 5a and in particular features a well-defined power-law tail 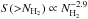 at high column densities (AV> 5–7).
at high column densities (AV> 5–7).
 |
Fig. 12 Observed differential core formation efficiency (CFE) as a function of background column density expressed in AV units (blue histogram with error bars), obtained by dividing the mass in the form of prestellar cores in a given column density bin by the cloud mass observed in the same column density bin. The right axis gives the corresponding star formation rate per unit gas mass (in units of yr-1), estimated assuming a local star formation efficiency ϵcore = 0.4 at the core level and a prestellar core lifetime tpre = 1.2 Myr (see text). For comparison, the black curve shows the prediction of the multi-freefall version of the turbulence regulated model of the star formation rate initially proposed by Krumholz & McKee (2005) (see Hennebelle & Chabrier 2011). The vertical dashed line marks the same fiducial threshold at |
 |
Fig. 13 Comparison of the spatial distribution of the prestellar core population identified in Sect. 4.7 using getsources (blue triangles) with the footprints of all the filaments traced with DisPerSE (red contours), both overlaid on the curvelet component of the high-resolution column density map (cf. Fig. 3). The gray scale corresponds to the color scale of Fig. 3. The red contours outline 0.1 pc–wide footprints around the crests of filaments. The green contours correspond to AV = 7 in the column density map smoothed to a resolution of 5′. (Color figure is available in the online version.) |
In spherical geometry, this is indicative19 of a power-law density distribution ρ ∝ r-1.7 for the dense gas and is consistent with large-scale cloud contraction above AV> 5–7. Under the assumption of a roughly spheroidal ambient cloud, we then derived the effective volume density, nH2(AV), and effective free-fall time, tff(AV), of the gas as a function of background cloud density expressed in AV units. Applying the above multi-freefall formula, this allowed us to obtain the core formation efficiency, 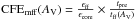 , predicted by the multi-freefall model as a function of AV, for direct comparison with CFEobs(AV). As can be seen in Fig. 12, the Herschel observations indicate a much sharper transition than the multi-freefall model does, between a regime of negligible prestellar core formation efficiency at AV< 5 and a regime of roughly constant CFE ~15% at AV> 15. Furthermore, we stress that differential completeness between low and high column density areas (see Fig. B.6) implies that the real transition between the two regimes is in fact somewhat sharper than indicated by the blue histogram in Fig. 12. On this basis, we argue for the presence of a true physical threshold for prestellar core formation around a fiducial value AV ~ 7, although the observed transition is clearly not infinitely sharp like a true Heaviside step function.
, predicted by the multi-freefall model as a function of AV, for direct comparison with CFEobs(AV). As can be seen in Fig. 12, the Herschel observations indicate a much sharper transition than the multi-freefall model does, between a regime of negligible prestellar core formation efficiency at AV< 5 and a regime of roughly constant CFE ~15% at AV> 15. Furthermore, we stress that differential completeness between low and high column density areas (see Fig. B.6) implies that the real transition between the two regimes is in fact somewhat sharper than indicated by the blue histogram in Fig. 12. On this basis, we argue for the presence of a true physical threshold for prestellar core formation around a fiducial value AV ~ 7, although the observed transition is clearly not infinitely sharp like a true Heaviside step function.
Interestingly, a very similar extinction threshold at 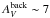 has independently been observed with Spitzer in the spatial distribution of YSOs in nearby clouds (Heiderman et al. 2010; Lada et al. 2010; Evans et al. 2014 – see also Sect. 5.6 below). Following André et al. (2010, 2014), we interpret this star formation threshold in terms of the quasi-universal filamentary structure of molecular clouds in Sect. 5.4 below.
has independently been observed with Spitzer in the spatial distribution of YSOs in nearby clouds (Heiderman et al. 2010; Lada et al. 2010; Evans et al. 2014 – see also Sect. 5.6 below). Following André et al. (2010, 2014), we interpret this star formation threshold in terms of the quasi-universal filamentary structure of molecular clouds in Sect. 5.4 below.
5.3. Spatial distribution of Herschel cores and connection with filaments
As already pointed out in earlier HGBS papers (e.g., André et al. 2010; Men’shchikov et al. 2010), there is a very close correspondence between the spatial distribution of compact dense cores and the network of filaments identified in the Herschel column density map of the Aquila cloud. Furthermore, candidate prestellar cores and embedded protostars are preferentially found within the densest filaments with supercritical masses per unit length (i.e., 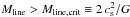 – see Sects. 1 and 4.2) (e.g., André et al. 2010, 2014).
– see Sects. 1 and 4.2) (e.g., André et al. 2010, 2014).
 |
Fig. 14 Upper: curvelet component (cf. Starck et al. 2003) of a portion of the Herschel high-resolution column density map shown in Fig. 1. Given the typical filament width of ~0.1 pc (Arzoumanian et al. 2011), this map is equivalent to a map of the mass per unit length along the filaments (cf. André et al. 2010), as indicated by the color bar on the right. The white areas highlight regions of the map where the filaments have a mass per unit length larger than half the critical value |
The connection between cores and filaments is illustrated in Figs. 13 and 14 and can be quantified in detail based on the census of cores presented in Sects. 4.4, 4.5, and 4.7 and the census of filaments described in Sect. 4.2. To this end, a mask image of the filament “footprints” was constructed by convolving the filamentary skeleton traced with DisPerSE and shown in Figs. 3 and 4 with a Gaussian kernel corresponding to a typical filament inner width ~0.1 pc (Arzoumanian et al. 2011), i.e., an angular width ~80″ at the distance of Aquila. An alternative mask image of the filaments, similar to that shown in Fig. 4, was created by considering all transverse angular scales up to 80″ in the multi-scale decomposition performed by getfilaments (see Sect. 4.2). The core positions were then compared with these two sets of 0.1-pc filament footprints to estimate the fraction of cores associated with filaments. The results of this comparison, summarized in Table 1, indicate that a very high fraction (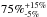 ) of prestellar cores are closely associated with filaments, i.e., lie within 0.1-pc filament footprints. This correspondence is illustrated in Fig. 13, where the 0.1-pc footprints of the filaments traced with DisPerSE (cf. Fig. 3) are outlined by red contours and the population of 446 candidate prestellar cores identified with getsources in Sect. 4 are superimposed as blue triangles. It can be seen that most (~70%) of the candidate prestellar cores lie within the red filament footprints. Likewise, ~80% of the robust prestellar cores lie within the red filament footprints. A more detailed view of this connection in the Aquila “main subfield”, including Serpens-South and W40, is provided by Fig. 14 which shows the locations of candidate prestellar cores overlaid on the curvelet component (cf. Starck et al. 2003) of the high-resolution column density map (see André et al. 2010, for an early version of the same view). It is important to stress that the connection between cores and filaments does not strongly depend on the precise definition adopted for a filament or on the algorithm used to trace filaments. In particular, as can be seen in Table 1, the values found for the fractions of cores associated with filaments using getfilaments footprints are very similar to the values found using DisPerSE footprints.
) of prestellar cores are closely associated with filaments, i.e., lie within 0.1-pc filament footprints. This correspondence is illustrated in Fig. 13, where the 0.1-pc footprints of the filaments traced with DisPerSE (cf. Fig. 3) are outlined by red contours and the population of 446 candidate prestellar cores identified with getsources in Sect. 4 are superimposed as blue triangles. It can be seen that most (~70%) of the candidate prestellar cores lie within the red filament footprints. Likewise, ~80% of the robust prestellar cores lie within the red filament footprints. A more detailed view of this connection in the Aquila “main subfield”, including Serpens-South and W40, is provided by Fig. 14 which shows the locations of candidate prestellar cores overlaid on the curvelet component (cf. Starck et al. 2003) of the high-resolution column density map (see André et al. 2010, for an early version of the same view). It is important to stress that the connection between cores and filaments does not strongly depend on the precise definition adopted for a filament or on the algorithm used to trace filaments. In particular, as can be seen in Table 1, the values found for the fractions of cores associated with filaments using getfilaments footprints are very similar to the values found using DisPerSE footprints.
Fractions of cores associated with filaments in Aquila.
Table 1 also reports the fractions of cores found within supercritical portions of filaments. For the sake of simplicity, in the present paper focusing primarily on cores, our classification of filament segments as either supercritical or subcritical relies on the assumption of a constant filament width ~0.1 pc (Arzoumanian et al. 2011) and is based on the local column density measured in the clean background column density image (after subtracting the contribution of cores with getsources). To take into account the fact that the transverse column density profiles of supercritical filaments feature power-law wings which extend beyond the 0.1 pc inner width (Arzoumanian et al. 2011; Palmeirim et al. 2013), we also considered 0.2 pc-wide filament footprints and provide corresponding core fractions in Table 1. For example, the well-studied Serpens South and Taurus-B211/B213 filaments have transverse column density profiles which extend up to ~0.4–0.5 pc in radius on average and equivalent widths20 of ~0.2 pc (Hill et al. 2012; Palmeirim et al. 2013). While a detailed discussion of the radial column density profiles of the present filament sample is out of the scope of this paper, simple comparison of the line masses obtained by integration over the filament profiles with the line masses derived from the central column densities of the filaments using a characteristic inner width of 0.1 pc suggests that the equivalent width20 of the supercritical filaments traced here with DisPerSE (see end of Sect. 4.2) is also typically ~0.2 pc.
5.4. Mass budget in the cloud and interpretation of the star formation threshold in terms of the filamentary structure
Our Herschel census of prestellar cores and filaments allows us to derive a detailed mass budget in the Aquila cloud. Below the fiducial column density threshold at 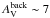 , ~10%–20% of the gas mass is in the form of (mostly subcritical) filaments and <1% of the cloud mass is in the form of prestellar cores. Above
, ~10%–20% of the gas mass is in the form of (mostly subcritical) filaments and <1% of the cloud mass is in the form of prestellar cores. Above 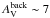 , ~50%–60% of the cloud mass is in the form of (mostly supercritical) filaments and a fraction fpre ~ 15% ± 5% of the mass is in the form of prestellar cores. We note that fpre roughly corresponds to the asymptotic core formation efficiency value reached at
, ~50%–60% of the cloud mass is in the form of (mostly supercritical) filaments and a fraction fpre ~ 15% ± 5% of the mass is in the form of prestellar cores. We note that fpre roughly corresponds to the asymptotic core formation efficiency value reached at 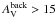 in Fig. 12. The fraction of cloud mass in the form of filaments reaches a very high value ~75% above
in Fig. 12. The fraction of cloud mass in the form of filaments reaches a very high value ~75% above 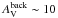 . In attempt to quantify further the relative contributions of cores and filaments to the cloud material as a function of column density, we compare in Fig. 15 the column density PDFs observed for the cloud before any component subtraction (blue histogram, identical to the PDF shown in Fig. 5a), after subtraction of dense cores (red solid line), and after subtraction of both dense cores and filaments (black solid line). To generate this plot, we used getsources to create a column density map of the cloud after subtracting the contribution of all compact cores, and getfilaments to construct another column density map after also subtracting the contribution of filaments. Although there are admittedly rather large uncertainties involved in this two-step subtraction process, the result clearly suggests that filaments dominate the mass budget of the Aquila cloud at high densities.
. In attempt to quantify further the relative contributions of cores and filaments to the cloud material as a function of column density, we compare in Fig. 15 the column density PDFs observed for the cloud before any component subtraction (blue histogram, identical to the PDF shown in Fig. 5a), after subtraction of dense cores (red solid line), and after subtraction of both dense cores and filaments (black solid line). To generate this plot, we used getsources to create a column density map of the cloud after subtracting the contribution of all compact cores, and getfilaments to construct another column density map after also subtracting the contribution of filaments. Although there are admittedly rather large uncertainties involved in this two-step subtraction process, the result clearly suggests that filaments dominate the mass budget of the Aquila cloud at high densities.
 |
Fig. 15 Comparison of the global column density PDF in the Aquila cloud (blue histogram with statistical error bars, identical to that shown in Fig. 5a) to the column density PDF measured after subtraction of dense cores (red solid line) and the PDF measured after subtraction of both dense cores and filaments (black solid line with statistical error bars). The vertical dashed line marks the same fiducial threshold at |
Since filaments appear to make up a dominant fraction of the dense gas material at 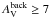 within which the vast majority of prestellar cores are observed (see Fig. 11), and since the spatial distribution of prestellar cores is strongly correlated with filaments (see Sect. 5.3), it is tempting to interpret the star formation threshold discussed in Sect. 5.2 in terms of the quasi-universal filamentary structure of molecular clouds (cf. André et al. 2014). Given the typical width Wfil ~ 0.1 pc measured for filaments (Arzoumanian et al. 2011) and the relation Mline ≈ Σ0 × Wfil between the central gas surface density Σ0 and the mass per unit length Mline of a filament (cf. Appendix A of André et al. 2010), the threshold at
within which the vast majority of prestellar cores are observed (see Fig. 11), and since the spatial distribution of prestellar cores is strongly correlated with filaments (see Sect. 5.3), it is tempting to interpret the star formation threshold discussed in Sect. 5.2 in terms of the quasi-universal filamentary structure of molecular clouds (cf. André et al. 2014). Given the typical width Wfil ~ 0.1 pc measured for filaments (Arzoumanian et al. 2011) and the relation Mline ≈ Σ0 × Wfil between the central gas surface density Σ0 and the mass per unit length Mline of a filament (cf. Appendix A of André et al. 2010), the threshold at 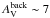 or
or 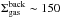 M⊙ pc-2 corresponds to within a factor21 of <2 to the critical mass per unit length
M⊙ pc-2 corresponds to within a factor21 of <2 to the critical mass per unit length 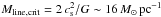 of nearly isothermal, long cylinders (see Inutsuka & Miyama 1997) for a typical gas temperature T ~ 10 K. Thus, the prestellar core formation threshold approximately corresponds to the threshold above which interstellar filaments become gravitationally unstable (André et al. 2010).
of nearly isothermal, long cylinders (see Inutsuka & Miyama 1997) for a typical gas temperature T ~ 10 K. Thus, the prestellar core formation threshold approximately corresponds to the threshold above which interstellar filaments become gravitationally unstable (André et al. 2010).
5.5. Prestellar CMF and link with the IMF
The prestellar CMF derived from the samples of 446 candidate and 292 robust prestellar cores identified in the whole Aquila cloud (see Sect. 4.7), excluding the CO high-VLSR area in the eastern corner of the field (see Sects. 4.3 and 4.5), is shown in the form of a differential mass distribution in Fig. 16 (see dark blue histograms and light blue shade). The mass distribution of the wider sample of 651 starless cores selected in Sect. 4.5 is plotted as a green histogram for comparison. The 90% completeness level of our Herschel census of prestellar cores, as estimated from both Monte-Carlo simulations (Sect. 4.8) and the simple model described in Appendix B.2, is marked by the vertical dashed line. We stress that the differential CMF presented here (see Könyves et al. 2010; André et al. 2010, for preliminary versions of this CMF) is based on a core sample ~2–9 times larger than the CMFs derived from earlier ground-based studies (e.g., Motte et al. 1998; Johnstone et al. 2000; Stanke et al. 2006; Alves et al. 2007; Enoch et al. 2008) and that its shape is therefore much more robustly defined. In particular, it suffers very little from the arbitrary choice of mass bins, a well-known disadvantage of differential mass functions (e.g., Reid & Wilson 2006), except perhaps at the very high mass end (e.g. at M ≳ 5 M⊙, where the number of cores per mass bin drops to less than 10 in Fig. 16). Note also that, while we preferred to display the differential form of the CMF in Fig. 16 because it is more intuitive and easier to compare with the IMF, we used the cumulative form – which is independent of binning and thus amenable to cleaner statistical tests – to quantify the resemblance of the observed CMF to several well-known functional forms.
 |
Fig. 16 Differential core mass function (dN/dlogM) of the 651 starless cores (dark green histogram), 446 candidate prestellar cores (upper blue histogram and open triangles), and 292 robust prestellar cores (lower blue histogram and filled triangles) identified with Herschel in the whole Aquila field. The error bars correspond to |
As can be seen in Fig. 16, the Aquila prestellar CMF is well fit by a lognormal distribution (solid and dashed red curves for the samples of robust and candidate prestellar cores, respectively) and very similar in shape to the system IMF advocated by Chabrier (2005). Performing a non-parametric Kolmogorov-Smirnov (K-S) test (see, e.g. Press et al. 1992) on the corresponding cumulative mass distributions N(>M) indicates that the observed prestellar CMF is statistically indistinguishable at the 97% confidence level from a lognormal mass function with central mass 0.45 ± 0.2 M⊙ and standard deviation 0.52 ± 0.05 above the completeness mass limit ~0.2 M⊙. For comparison, the lognormal part of the Chabrier (2005) system IMF has a central mass of 0.25 M⊙ and a standard deviation of 0.55 in log10M. The error on the two parameters of the lognormal fit to the prestellar CMF (i.e., central mass and standard deviation) are mainly driven by the uncertain classification of observed starless cores as gravitationally bound or unbound objects, which leads to two slightly different CMF shapes for the samples of robust and candidate prestellar cores (blue shaded area in Fig. 16). The high-mass end of the Aquila CMF above 1 M⊙ is also consistent with a power-law mass function, dN/dlogM∝M− 1.33 ± 0.06, at a K-S significance level of 87%. Here, the error bar on the power-law exponent was derived from the range of values for which the K-S significance level is larger than 68% (corresponding to 1σ in Gaussian statistics). This function is very similar to the Salpeter power-law IMF which is dN/dlogM∝M-1.35 in this format. (We note, however, that given the limited range of core masses probed by our data a power law does not provide a significantly better fit to the high-mass end of the CMF than a pure lognormal fit.) In contrast, the CMF observed above 1 M⊙ differs from the shallower power-law mass distribution of CO clumps and clouds (dN/dlogM∝M-0.7 – e.g. Blitz 1993; Kramer et al. 1998) at a very high confidence level. The probability that the CMF can be consistent with dN/dlogM∝M-0.7 is only PK−S ~ 7.7 × 10-7.
A possible caveat to the similarity between the Salpeter IMF and the prestellar CMF at the high-mass end should be mentioned, however. As pointed out by Clark et al. (2007), if cores of different mass evolve on different timescales, then the observed CMF may not be representative of the intrinsic prestellar CMF. This is because an observer is more likely to detect long-lived cores than short-lived cores. Therefore, if there is a correlation between core lifetime and core mass, then the observed CMF can be significantly distorted compared to the “initial” prestellar core mass distribution. In the present sample of prestellar cores, there is essentially no correlation between core density and core mass below ~2 M⊙ but a weak positive correlation above ~2–3M⊙ (Fig. 10), suggesting that prestellar cores more massive than ~2–3M⊙ may evolve to protostars somewhat faster than lower mass cores do (see end of Sect. 5.1). To quantify the importance of this potential differential timescale bias on the CMF, we have overplotted in Fig. 16 a weighted version of the observed CMF (blue open squares and dashed histogram), obtained by weighting the number of prestellar cores observed in each mass bin by a factor inversely proportional to a mass-dependent free-fall time. The latter was estimated for each mass bin by using the parabolic fit to the observed correlation between core density and core mass shown by the red curve in Fig. 10. As can be seen in Fig. 16, the weighted CMF is indistinguishable from the unweighted CMF for M< 2 M⊙, but somewhat shallower above ~2 M⊙. (A K-S analysis indicates that the high-mass end of the weighted CMF above 2 M⊙ is consistent with a power-law mass function, dN/dlogM∝M− 1.0 ± 0.2, at a K-S significance level of 90%.) The main effect of the differential timescale correction is to broaden the prestellar CMF, leaving the peak mass at ~0.5 M⊙ essentially unchanged22.
As already discussed by André et al. (2010) and Könyves et al. (2010) (see also Alves et al. 2007), the observed CMF is consistent with an essentially one-to-one mapping between prestellar core mass and stellar system mass23, i.e., M⋆ sys = ϵcore × Mcore, where ϵcore represents the efficiency of the conversion process from core mass to stellar system mass, i.e., the star formation efficiency within an individual prestellar core. The peak of the prestellar CMF is at 0.45 ± 0.2 M⊙ in observed core mass, suggesting a real peak at 0.6 ± 0.2 M⊙ in terms of intrinsic prestellar core mass, after correcting the observed masses upward by ~25% due to the fact that the SED mass values tend to slightly underestimate the intrinsic core masses according to our simulations (see Sect. 4.6 and Appendix B.1). Our data therefore suggest that 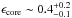 .
.
 |
Fig. 17 Comparison of the CMF observed for the majority (~81%) of candidate prestellar cores lying within the 0.2 pc-wide footprints of the DisPerSE-detected filaments (light blue histogram) to that observed for the minority (~19%) of prestellar cores lying outside these filaments (magenta histogram). The upper dark blue histogram and the other lines are the same as in Fig. 16. (Color figure is available in the online version.) |
It is also interesting to investigate possible variations in the CMF as a function of local cloud environment, in particular depending on whether the cores lie within or outside dense filaments. In L1641 (Orion A), for instance, Polychroni et al. (2013) reported that the cores lying on filaments were generally more massive than those lying off filaments. Figure 17 compares the CMF derived for the candidate prestellar cores lying on filaments (light blue histogram) to the CMF of the candidate prestellar cores lying off filaments (magenta histogram) and to the global prestellar CMF in Aquila (upper dark blue histogram). It can be seen that the prestellar CMF observed on filaments is very similar to the global prestellar CMF. A two-sample K-S test confirms that these two CMFs are indistinguishable at a >95% confidence level. On the other hand, there is a marginal indication that the prestellar CMF observed off filaments may peak at a somewhat lower mass. A two-sample K-S test indicates that the probability that the CMFs observed on and off filaments above 0.2 M⊙ are drawn from the same intrinsic distribution is only ~2% (equivalent to a ~2.3σ result in Gaussian statistics). This is not a very strong conclusion, however. First, there are only 54 candidate prestellar cores with masses >0.2 M⊙ lying outside the 0.2 pc-wide filament footprints, implying that our estimate of the prestellar CMF off filaments suffers from small-number statistics. In fact, we cannot even exclude the possibility that some of the prestellar cores presently classified as lying off filaments may be associated with faint filaments not identified with DisPerSE in Sect. 4.2. Second, the median background cloud column density observed off filaments is lower (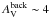 ) than the median background cloud column density observed on filaments (
) than the median background cloud column density observed on filaments (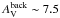 ). Accordingly, the completeness level of our Herschel survey for prestellar cores is expected to be somewhat better off filaments than on filaments (see Fig. B.6), which may slightly bias the direct comparison of the two CMFs.
). Accordingly, the completeness level of our Herschel survey for prestellar cores is expected to be somewhat better off filaments than on filaments (see Fig. B.6), which may slightly bias the direct comparison of the two CMFs.
5.6. A quasi-universal efficiency of the star formation process in dense gas?
Our Herschel results on the prestellar core formation efficiency (CFE) as a function of column density in the Aquila cloud (see Sect. 5.2 and Fig. 12) connect very well with recent near-/mid-infrared studies of the star formation rate (SFR) as a function of gas surface density in nearby molecular clouds (e.g., Heiderman et al. 2010; Lada et al. 2010, 2012; Evans et al. 2014). These infrared studies show that the global SFR derived from direct YSO counting (as opposed to the prestellar core counting used in the present study) tends to be linearly proportional to the mass of dense gas above a surface density threshold corresponding to 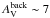 –8, and drops to much lower values below the threshold. This column density threshold is essentially the same as that found with Herschel for the formation of prestellar cores in the Aquila cloud (cf. Figs. 11 and 12). Moreover, the star formation rate per unit mass of dense gas above the threshold found by infrared studies of nearby clouds, namely SFR/Mdense ~ 4.6 × 10-8 yr-1 (Lada et al. 2010, 2012) or
–8, and drops to much lower values below the threshold. This column density threshold is essentially the same as that found with Herschel for the formation of prestellar cores in the Aquila cloud (cf. Figs. 11 and 12). Moreover, the star formation rate per unit mass of dense gas above the threshold found by infrared studies of nearby clouds, namely SFR/Mdense ~ 4.6 × 10-8 yr-1 (Lada et al. 2010, 2012) or 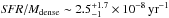 (Evans et al. 2014), is entirely consistent with the roughly constant prestellar CFE derived for AV> 7 in Aquila, which corresponds to
(Evans et al. 2014), is entirely consistent with the roughly constant prestellar CFE derived for AV> 7 in Aquila, which corresponds to 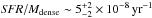 (see horizontal dotted line in Fig. 12) adopting a typical prestellar core lifetime tpre = 1.2 Myr (see Sect. 5.1) and a local star formation efficiency ϵcore = 0.4 at the core level (see Sect. 5.5).
(see horizontal dotted line in Fig. 12) adopting a typical prestellar core lifetime tpre = 1.2 Myr (see Sect. 5.1) and a local star formation efficiency ϵcore = 0.4 at the core level (see Sect. 5.5).
As pointed out by Lada et al. (2010, 2012), the nearby cloud value of the “efficiency” of the star formation process in dense gas is also very similar to the efficiency value SFR/Mdense ~ 2 × 10-8 yr-1 found by Gao & Solomon (2004) for external galaxies, using HCN observations of dense gas and far-infrared (IRAS) estimates of the SFR in galaxies. While direct comparison between the Galactic and extragalactic values is affected by large uncertainties because different tracers of dense gas and star formation were used by Lada et al. (2010) on the one hand and Gao & Solomon (2004) on the other, these results suggest that there may be a quasi-universal “star formation law” within dense gas above the (column) density threshold. Equivalently, in terms of a concept often used in the extragalactic community, this means that there may be a quasi-universal depletion time, tdep ≡ Mdense/SFR ~ 20−50 Myr, for the dense gas above the threshold. This “star formation law” is not strictly universal since it does not seem to apply to the extreme environmental conditions of the central molecular zone near the Galactic center, for instance, where star formation is observed to be more inefficient above the same density threshold, by more than an order of magnitude (Longmore et al. 2013).
Our Herschel findings in the Aquila cloud allow us to go one step further and link this quasi-universal efficiency of the star formation process in dense gas to three parameters characterizing the physics of prestellar cores, i.e., the core formation efficiency in supercritical filaments, fpre, the lifetime of prestellar cores, tpre, and the efficiency of the conversion from prestellar core mass to stellar system mass, ϵcore, i.e., 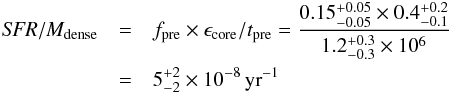 (see André et al. 2014).
(see André et al. 2014).
6. Summary and conclusions
We used the SPIRE and PACS parallel-mode maps taken as part of the Herschel Gould Belt survey to obtain an extensive census of dense cores and their connection with molecular cloud structure in the Aquila star-forming region. Our main results and conclusions may be summarized as follows:
-
1.
The high-resolution (~18″ or ~0.02 pc) column density map that we derived from the Herschel photometric data shows that the Aquila cloud is highly filamentary and features a column density probability density function (PDF) with a prominent power-law tail above AV ~ 5–7. About 10%–20% of the gas mass is in the form of filaments below AV ~ 7, while as much as ~50%–75% of the gas mass is in the form of filamentary structures above AV ~ 7–10.
-
2.
In the ~11 deg2 field imaged with both SPIRE and PACS at five wavelengths from 70 μm to 500 μm, we identified 651 starless cores, 446 candidate and 292 robust prestellar cores, and 58 protostellar cores (such as Class 0 objects), based on multi-scale, multi-wavelength core extraction with the getsources algorithm. The samples of candidate and robust prestellar cores were estimated to be ~90% and ~80% complete, respectively, down to an observed core mass ~0.2 M⊙. The candidate prestellar cores have estimated median mass ~0.45 M⊙, median deconvolved FWHM diameter ~0.03 pc, median average column density ~7 × 1021 cm-3 and median average volume density ~4 × 104 cm-3.
-
3.
The typical lifetime of the Herschel prestellar cores was estimated to be tpre = 1.2 ± 0.3 Myr or ~4 free-fall times (tff) and to decrease from tpre ~1.4 Myr for cores with average volume density ≳104 cm-3 to a few times 104 yr for cores with average volume density ≳106 cm-3. The densest prestellar cores in the sample appear to have a lifetime comparable to their free-fall timescale and may be collapsing.
-
4.
There is strong evidence of a column density threshold for the formation of prestellar cores, at an equivalent visual extinction level
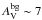 , in the sense that the probability function of finding a prestellar core increases by more than an order of magnitude from
, in the sense that the probability function of finding a prestellar core increases by more than an order of magnitude from 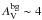 to
to 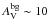 and is well fit by a smooth exponential step function. Likewise, the prestellar core formation efficiency (CFE) or fraction of cloud mass in the form of prestellar cores was found to increase by about two orders of magnitude between
and is well fit by a smooth exponential step function. Likewise, the prestellar core formation efficiency (CFE) or fraction of cloud mass in the form of prestellar cores was found to increase by about two orders of magnitude between 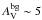 and
and 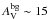 and to reach a roughly constant value CFEmax ≡ fpre ~ 15% at higher column densities. This reflects a significantly sharper transition than predicted by “multi-freefall” models of the star formation rate in molecular clouds, and argues for the presence of a true physical (column) density threshold for prestellar core formation.
and to reach a roughly constant value CFEmax ≡ fpre ~ 15% at higher column densities. This reflects a significantly sharper transition than predicted by “multi-freefall” models of the star formation rate in molecular clouds, and argues for the presence of a true physical (column) density threshold for prestellar core formation. -
5.
The compact dense cores are closely associated with the filamentary structure, and preferentially the densest filaments. In particular, a very high fraction (
 ) of prestellar cores were found to lie within supercritical filaments with masses per unit length Mline>Mline,crit, where
) of prestellar cores were found to lie within supercritical filaments with masses per unit length Mline>Mline,crit, where 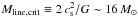 /pc is the critical mass per unit length of nearly isothermal, long cylinders at T ~ 10 K (see Inutsuka & Miyama 1997).
/pc is the critical mass per unit length of nearly isothermal, long cylinders at T ~ 10 K (see Inutsuka & Miyama 1997). -
6.
The prestellar CMF derived using the samples of 446 candidate and 292 robust prestellar cores is well fit by a lognormal distribution, peaks at ~0.4–0.6M⊙, and is very similar in shape to the system IMF. This CMF is consistent with an essentially one-to-one mapping between prestellar core mass and stellar system mass with a local star formation efficiency
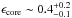 within an individual prestellar core.
within an individual prestellar core. -
7.
Our Herschel findings in the Aquila cloud connect very well with recent Spitzer studies of the star formation rate in nearby molecular clouds. They support the view that there may be a quasi-universal “efficiency” of the star formation process in dense gas,
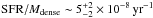 , and that this quasi-universal “efficiency” may be closely linked to the physics of prestellar core formation within filaments: SFR /Mdense = fpre × ϵcore/tpre.
, and that this quasi-universal “efficiency” may be closely linked to the physics of prestellar core formation within filaments: SFR /Mdense = fpre × ϵcore/tpre.
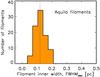 |
Fig. 18 Distribution of mean FWHM inner widths for the 90 filaments traced with DisPerSE in the Aquila entire field (see blue skeleton in Figs. 3 and 4 and Sect. 4.2). These widths result from a filament profile analysis similar to that described in Arzoumanian et al. (2011) and were deconvolved from the 18.2″ HPBW resolution of the high-resolution column density map used to construct the radial profiles of the filaments. The median filament width is 0.12 pc, as marked by the vertical dotted line, and the standard deviation of the distribution is 0.04 pc. |
Online material
Appendix A: A catalog of dense cores identified with Herschel in the Aquila cloud complex
Based on our Herschel SPIRE/PACS parallel-mode imaging survey of the Aquila cloud complex, we identified a total of 749 dense cores, including 685 starless cores and 64 protostellar cores. (Among these, 34 starless cores shown as yellow triangles in Fig. 1, as well as 6 protostellar cores, were excluded from the scientific discussion of Sect. 5 due to likely contamination by more distant, background objects – see Sect. 4.3.) The master
catalog listing the observed properties of all of these Herschel cores is available in Table A.1. A template of this online catalog is provided below to illustrate its form and content.
The derived properties (physical radius, mass, SED dust temperature, peak column density at the resolution of the 500 μm data, average column density, peak volume density, and average density) are given in Table A.2 for each core. A portion of this online table is also provided below. The derived properties of the Herschel-detected protostars and YSOs will be published in a forthcoming paper.
Catalog of dense cores identified in the HGBS maps of the Aquila complex (the full catalog is at the CDS).
Derived properties of the dense cores identified in the HGBS maps of the Aquila region (the full table is at the CDS).
 |
Fig. A.1 Examples of Herschel spectral energy distributions (SEDs) for a prestellar core (left, see Fig. A.3 for the corresponding image cutouts) and a protostellar core (right, see Fig. A.4 for the corresponding image cutouts). These SEDs were constructed from the background-subtracted integrated flux densities (cross symbols) measured by getsources. A graybody fit to the SED observed longward of 160 μm is superimposed as a blue curve in both panels. Only upper limits are available at 70 μm and 160 μm for the prestellar core shown in the left panel. A single-temperature graybody rarely provides a good fit to the overall SED of a protostellar core but can nevertheless describe the SED longward of 160 μm reasonably well (cf. right panel). Similar SED plots are provided on http://gouldbelt-herschel.cea.fr/archives for all selected cores. |
 |
Fig. A.2 Blow-up column density images of two Aquila subfields at 18.2″ resolution. Black and red ellipses mark the FWHM sizes of the starless cores and protostellar cores, respectively, selected from getsources extractions in these two subfields. Green ellipses show the FWHM sizes of the sources independently detected with CSAR (Kirk et al. 2013b) in the high-resolution column density image. |
 |
Fig. A.3 Example blow-up Herschel images at 70/160/250/350/500 μm and high-resolution column density map for a (bound) prestellar core. Ellipses represent the estimated major and minor FWHM sizes of the core at each wavelength; they are shown as solid or dashed curves depending on whether the core is significantly detected or not, respectively, at a particular wavelength. See Table A.2 for the physical radius of the core and other derived properties. An angular scale of 30″ (i.e., ~ 0.038 pc at d = 260 pc) is shown at the bottom right. North is up, east is left. Similar image cutouts are provided on http://gouldbelt-herschel.cea.fr/archives for all selected starless cores. |
 |
Fig. A.4 Same as Fig. A.3 for a protostellar core. Similar image cutouts are provided on http://gouldbelt-herschel.cea.fr/archives for all selected protostellar cores. |
Appendix B: Completeness of HGBS prestellar core extractions in Aquila
To estimate the completeness of our census of prestellar cores in Aquila, we used several sets of simulated data on the one hand (Appendix B.1), and a simple model of the core extraction process and completeness problem on the other (Appendix B.2).
Appendix B.1: Monte-Carlo simulations
To simulate real core extractions, we first constructed clean maps of the background emission at all Herschel wavelengths (including a column density plane), by subtracting the emission of the compact cores identified with getsources in the observed data (cf. Sects. 4.4 and 4.5). We then inserted several sets of model Bonnor-Ebert-like cores throughout the clean-background images in order to generate a full set of synthetic Herschel and column density images of the region. In the example illustrated in Figs. B.1 and B.2, for instance, we used a population of 5622 model starless cores with a flat input mass distribution (dN/dlog M ∝ M-0.7, similar to the mass distribution of CO clumps) from 0.02 M⊙ to ~ 30 M⊙. This example is particularly useful as it allowed us to test the robustness of the conclusion that the observed prestellar CMF is significantly steeper than the mass distribution of CO clumps. The model cores had positions in a mass versus size diagram consistent with critical Bonnor-Ebert isothermal spheres at effective gas temperatures ~7–20 K. The dust continuum emission from the synthetic Bonnor-Ebert cores in all Herschel bands was simulated using an extensive grid of spherical dust radiative transfer models constructed by us with the MODUST code (e.g., Bouwman et al. 2000; Bouwman 2001). In particular, each of the synthetic prestellar cores was given a realistic dust temperature profile with a significant drop in dust temperature toward core center, as observed in the case of spatially-resolved starless cores (cf. Roy et al. 2014). The synthetic cores were spatially distributed randomly over the regions of the column density map where 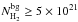 cm-2 (containing most, if not all, of the observed prestellar cores in the real data – see Sect. 5.2), with no particular mass segregation. Once satisfactory synthetic skies resembling the observed images had been generated, compact source extraction and core selection/classification were performed with getsources in the same way as for the real data (see Sects. 4.4 and 4.5).
cm-2 (containing most, if not all, of the observed prestellar cores in the real data – see Sect. 5.2), with no particular mass segregation. Once satisfactory synthetic skies resembling the observed images had been generated, compact source extraction and core selection/classification were performed with getsources in the same way as for the real data (see Sects. 4.4 and 4.5).
 |
Fig. B.1 Synthetic core mass function (CMF) derived from simulated source extractions (blue histogram) compared to the input mass function (dN/dlogM ∝ M-0.7) of a population of 5622 model cores (red curve) constructed as described in Appendix B.1. The estimated 90% completeness level (in observed core mass) is indicated by the vertical dashed line at 0.2 M⊙. The black solid line shows a power-law fit to the derived CMF above the 0.2 M⊙ completeness level; it is in excellent agreement with the input core mass function. The drop of the synthetic CMF below the input CMF at the high-mass end is due to the fact that the derived core masses tend to underestimate the true core masses by ~ 20% on average (see Fig. B.2a). |
As mentioned in Sect. 4.8 and shown in Fig. 8, the results of these Monte-Carlo simulations suggest that our Herschel census of prestellar cores in the Aquila cloud complex is ~ 90% complete down to ~ 0.3 M⊙ in true core mass. Figure B.1 further illustrates that the core mass function can be reliably determined down to the completeness mass limit. In this example, a Kolmogorov-Smirnov (K-S) test shows that the derived CMF is statistically indistinguishable (at the ~ 90% confidence level) from the input mass function above the completeness limit. In particular, the best-fit power-law function to the derived CMF (black solid line in Fig. B.1) is identical to the input dN/dlogM ∝ M-0.7 power law. This test therefore confirms that the best-fit power law to the observed CMF (dN/dlogM ∝ M− 1.33 ± 0.06 – see Sect. 5.5) is significantly steeper than the typical mass distribution of CO clumps/clouds (dN/dlogM ∝ M-0.7 – e.g. Blitz 1993; Kramer et al. 1998) and that this cannot be an artifact of the core extraction process.
The same Monte-Carlo simulations were also used to assess the accuracy of the main derived parameters (e.g. core mass, radius, and dust temperature) by comparing the estimated values after core extraction to the intrinsic input values of the model cores. Figure B.2a shows that the derived core masses tend to underestimate the true core masses by ~20–30% on average, and Fig. B.2b shows that the derived SED temperatures tend to overestimate the intrinsic mass-averaged dust temperatures of the cores by typically ~ 1 K. A similar plot for the core sizes (Fig. B.3) suggests that the derived core sizes (prior to deconvolution) are quite reliable and remain within ~ 5% of the true convolved core sizes on average. We interpret the mass effect (Fig. B.2a) as a direct consequence of the temperature effect (Fig. B.2b) since overestimating the dust temperatures leads to underestimating the core masses. The temperature effect arises from the fact that the dust temperature derived from a global fit to the SED of a starless core overestimates the mass-averaged dust temperature owing to a distribution of dust temperatures along the line of sight (see Roy et al. 2014, and Sect. 4.6).
Taking the ~20–30% mass effect into account, we conclude that the ~ 90% completeness limit at ~ 0.3 M⊙ in true core mass corresponds to ~ 0.2 M⊙ in observed core mass.
 |
Fig. B.2 a) Ratio of derived to intrinsic (or “true”) core mass as a function of derived core mass for the same set of simulated core extractions as used in Appendix B.1 and Fig. B.1. The error bars are ± 1σ where σ is the dispersion of the mass ratio in each mass bin. The median mass ratio is ~ 0.8 above 0.4 M⊙ (as indicated by the horizontal blue line) and ~ 0.7 close to the 90% completeness limit of 0.2 M⊙ in observed core mass. The horizontal dashed line marks the mass ratio of 1 expected in the case of perfect core extractions and mass estimates. b) Difference between derived SED temperature and intrinsic mass-averaged dust temperature as a function of derived core mass for the same set of simulated core extractions. The error bars are ± 1σ where σ is the dispersion of the temperature difference in each mass bin. The median temperature difference is about + 0.8 K above 0.4 M⊙ (as indicated by the horizontal blue line) and ~ 1 K close to a derived core mass of 0.2 M⊙ (completeness limit). The horizontal dashed line marks the zero difference expected in the case of perfect core extractions and temperature estimates. |
Appendix B.2: Model of the completeness problem
The Monte-Carlo simulations described above provide an estimate of the global completeness limit of the core survey. The completeness level of the core extractions is, however, expected to be background dependent. To assess the importance of this dependence, we constructed a simplified model of the core extraction process.
 |
Fig. B.3 Ratio of derived to true (convolved) core size as a function of derived core mass for the same set of simulated core extractions as in Fig. B.1 and Fig. B.2. The error bars are ± 1σ where σ is the dispersion of the size ratio in each mass bin. The horizontal dashed line marks the size ratio of 1 expected in the case of perfect core extractions and size estimates. Note how the median core size measured in each mass bin remains within 5% of the true core size above the ~ 90% completeness of ~ 0.2 M⊙ in derived core mass. |
Owing to the high sensitivity and quality of the Herschel images, the HGBS survey is not limited by instrumental noise but by confusion arising from small-scale cloud structure, an effect commonly referred to as “cirrus confusion noise” in the literature (e.g., see Gautier et al. 1992; Kiss et al. 2001; Roy et al. 2010). To estimate the level of such cirrus confusion noise from the Herschel data, we measured the rms level of background fluctuations in a sliding box 1′ × 1′ in size24 over the entire column density map of the Aquila complex after subtracting the sources identified by getsources. Correlating the resulting map of rms fluctuations with the input background column density map led to Fig. B.4, which clearly shows that the level of column density fluctuations increases with background column density approximately as a power law: 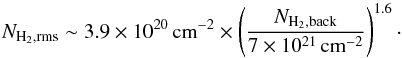 (B.1)The power-law index of 1.6 derived here from Herschel data is very similar to that reported in earlier papers discussing cirrus noise (e.g. Gautier et al. 1992; Kiss et al. 2001; Roy et al. 2010). Since the level of background fluctuations increases with column density, one expects core extraction to be increasingly more difficult and thus survey completeness to decrease significantly in higher column density areas within the field.
(B.1)The power-law index of 1.6 derived here from Herschel data is very similar to that reported in earlier papers discussing cirrus noise (e.g. Gautier et al. 1992; Kiss et al. 2001; Roy et al. 2010). Since the level of background fluctuations increases with column density, one expects core extraction to be increasingly more difficult and thus survey completeness to decrease significantly in higher column density areas within the field.
 |
Fig. B.4 Median root mean square (rms) level of background column density fluctuations as a function of background cloud column density as measured in a 1′ × 1′ sliding box over the clean background image of the Aquila complex produced by getsources from the high-resolution column density map. The error bars correspond to the interquartile range of background fluctuations about the median level in each column density bin. The straight line represents a weighted power-law fit to the data points above NH2 ~ 2 × 1021 cm-2. |
The model we used to estimate the magnitude of this effect and get around the problem of a background-dependent completeness level was based on the following assumptions:
-
•
A dense core is defined as the immediate vicinity of a column density peak departing significantly, i.e., by more than 5 × NH2,rms from the field of background cloud fluctuations.
A prestellar core, i.e., a self-gravitating starless core, can be approximately modeled as a critical Bonnor-Ebert spheroid of mass MBE and outer radius RBE, bounded by the gravitational pressure of the background cloud
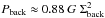 (McKee & Tan 2003), where Σback = μmH × NH2,back. The mean intrinsic column density contrast of such a model prestellar core is ΣBE/ Σback ~ 1.5, where
(McKee & Tan 2003), where Σback = μmH × NH2,back. The mean intrinsic column density contrast of such a model prestellar core is ΣBE/ Σback ~ 1.5, where 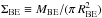 .
. The ability to detect a core in the Herschel data depends primarily on the apparent column density significance of the core defined as Σcore,obs/ Σrms, where Σcore,obs is the apparent (observed) column density of the core after convolution with the observing beam, i.e.,
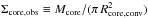 , and Σrms = μmH × NH2,rms. The Monte-Carlo simulations of Appendix B.1 are consistent with this assumption and suggest that the completeness level is ≳90% for cores with an apparent column density significance larger than 5 (see Fig. B.5).
, and Σrms = μmH × NH2,rms. The Monte-Carlo simulations of Appendix B.1 are consistent with this assumption and suggest that the completeness level is ≳90% for cores with an apparent column density significance larger than 5 (see Fig. B.5).
Two effects, beam dilution and temperature dilution, can make the apparent column density contrast ΣBE,obs/ Σback of a model core smaller than its intrinsic column density contrast of 1.5:
![$$\Sigma_{\rm BE, obs}/\Sigma_{\rm back} \sim 1.5 \times (R_{\rm BE}/R_{\rm BE, conv})^2 \times [B_{\nu_{\rm eff}}(T_{\rm core})/B_{\nu_{\rm eff}}(T_{\rm back})], $$](/articles/aa/full_html/2015/12/aa25861-15/aa25861-15-eq423.png) where νeff is a fiducial Herschel observing frequency which we take to correspond to λ ~ 350 μm. Taking advantage of the fact that the column density distribution of a Bonnor-Ebert core with outer radius RBE is well approximated by a Gaussian distribution of FWHM ~ RBE, the observed radius of the core is approximately
where νeff is a fiducial Herschel observing frequency which we take to correspond to λ ~ 350 μm. Taking advantage of the fact that the column density distribution of a Bonnor-Ebert core with outer radius RBE is well approximated by a Gaussian distribution of FWHM ~ RBE, the observed radius of the core is approximately 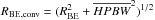 (where
(where  corresponds to the half-power beam width resolution of the column density map projected at the distance of the Aquila cloud), and the beam dilution factor can thus be expressed as
corresponds to the half-power beam width resolution of the column density map projected at the distance of the Aquila cloud), and the beam dilution factor can thus be expressed as ![\hbox{$ (R_{\rm BE}/R_{\rm BE, conv})^2 = 1/[1+(\overline{HPBW}/R_{\rm BE})^2] $}](/articles/aa/full_html/2015/12/aa25861-15/aa25861-15-eq428.png) .
. The apparent column density significance can be written as the product of the apparent column density contrast and a cirrus noise factor, ΣBE,obs/ Σrms = (ΣBE,obs/ Σback) × (Σback/ Σrms), where the cirrus noise factor is:
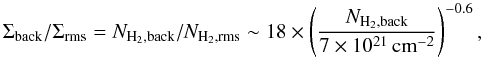 according to Eq. (B.1).
according to Eq. (B.1). -
Assuming that the fundamental completeness curve is the completeness function
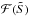 of apparent column density significance
of apparent column density significance 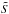 shown in Fig. B.5, completeness can be estimated as a function of core mass and background column density as
shown in Fig. B.5, completeness can be estimated as a function of core mass and background column density as ![\hbox{$ \mathcal{C}(M_{\rm BE},\Sigma_{\rm back}) = \mathcal{F}[\tilde{S}(M_{\rm BE},\Sigma_{\rm back})]$}](/articles/aa/full_html/2015/12/aa25861-15/aa25861-15-eq433.png) . The corresponding function of MBE is shown for five values of the background column density NH2,back in Fig. B.6. Figure B.6 shows how the completeness of prestellar core extractions is expected to decrease as background cloud column density and cirrus noise increase.
. The corresponding function of MBE is shown for five values of the background column density NH2,back in Fig. B.6. Figure B.6 shows how the completeness of prestellar core extractions is expected to decrease as background cloud column density and cirrus noise increase. 
Fig. B.5 Completeness curve as a function of apparent column density significance over local background cloud fluctuations derived from the Monte-Carlo simulations described in Appendix B.1.

Fig. B.6 Model completeness curves of Herschel prestellar core extractions in Aquila for five values of the background cloud column density expressed in units of visual extinction from AV,back = 5 to AV,back = 20.
To estimate a global completeness curve for our census of prestellar cores in the Aquila complex, we used the observed distribution of mass in the cloud as a function of background column density (cf. Figs. 5a,b) and took advantage of the existence of a column density “threshold” at AV,back ~ 5–7, above which the bulk of core and star formation is believed to occur (cf. Sect. 5.2 and Fig. 11) and the column density PDF is well fitted by a power-law distribution. We also assumed that the number of prestellar cores in the cloud scales linearly with cloud mass above the threshold. This assumption is consistent with recent infrared studies which find that the global star formation rate tends to be linearly proportional to the mass of dense gas above the threshold (e.g., Heiderman et al. 2010; Lada et al. 2010; Gao & Solomon 2004). It is also consistent with the roughly constant prestellar core formation efficiency found here above the threshold (see Fig. 12). The global completeness curve was thus computed as a weighted average of the individual completeness curves at fixed background column densities:
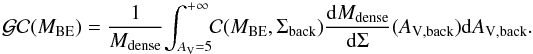
 |
Fig. B.7 Model global completeness curve of Herschel prestellar core extractions in the Aquila cloud complex (d = 260 pc) as a function of intrinsic model core mass. |
Appendix C: Effect of distance uncertainty
As mentioned in Sect. 2, there is some ambiguity concerning the distance to the Aquila molecular cloud complex. A number of arguments, presented by Bontemps et al. (2010) and
summarized in Sect. 2, suggest that the bulk of the region studied here and shown in Fig. 1 corresponds to a coherent cloud complex at d− = 260 pc (see also Gutermuth et al. 2008), which is the default distance adopted in the present paper. Other studies in the literature (see references in Sect. 2), however, place the complex at the larger distance, d+ = 415 pc, of the Serpens Main cloud (Dzib et al. 2010). It is thus worth discussing how our results would be affected if we had adopted the larger distance estimate, d+, instead of d−. The core mass estimates, which scale as Sνd2/ [ Bν(Td) κν ] where Sν is integrated flux density and Bν(Td) is the Planck function, would systematically increase by a factor of 2.5. This would shift the CMFs shown in Figs. 16 and 17 to the right and thus lower the efficiency ϵcore from 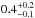 to 0.2 ± 0.1. In comparison, the core size estimates, which scale linearly with distance d, would increase by only 60%. The BE mass ratio αBE = MBE,crit/Mobs, listed in Col. 17 of Table A.2, scales as d-1 and would decrease by 60% for all cores. Accordingly, all cores would move upward as indicated by an arrow in the mass versus size diagram of Fig. 7, which would increase the fraction of prestellar cores among starless cores from 60% ± 10% to 70% ± 10%. More precisely, the number of candidate prestellar cores would increase from 446 to 565 and the number of robust prestellar cores would increase from 292 to 391, while the total number of starless cores (651) would remain the same. Accordingly, the estimated lifetime of candidate prestellar cores would also slightly increase from ~ 1.4 Myr to ~ 1.8 Myr, and that of robust prestellar cores from ~ 0.9 Myr to ~ 1.3 Myr (see Sect. 5.1), leading to tpre = 1.5 ± 0.3 Myr. The prestellar core formation efficiency (CFE) as a function of background column density (cf. Fig. 12), and in particular the roughly constant value CFEmax ≡ fpre ~ 15% at high column densities, would not change. Our corresponding estimate of the “efficiency” of the star formation process in dense gas (cf. Sect. 5.6), SFR /Mdense = fpre × ϵcore/tpre, would however decrease from 5 × 10-8 yr-1 to 2 × 10-8 yr-1, becoming closer to the efficiency value reported by Evans et al. (2014) and Gao & Solomon (2004) than to the value found by Lada et al. (2010). Finally, the column density maps shown in Figs. 1, 3, 4, 13, and 14, as well as the spatial correspondence between cores and filaments, would remain unchanged. The scaling of our column density maps in terms of mass per unit length along the filaments would however change by ~ 60% upward, since the characteristic physical width of the filaments would increase by ~ 60%. As a consequence, the white areas which highlight supercritical filaments in Figs. 3, 4, 13, and 14 would slightly expand, improving the correspondence between the spatial distribution of prestellar cores/protostars and that of supercritical filaments. To summarize, our main conclusions do not depend strongly on the adopted distance.
to 0.2 ± 0.1. In comparison, the core size estimates, which scale linearly with distance d, would increase by only 60%. The BE mass ratio αBE = MBE,crit/Mobs, listed in Col. 17 of Table A.2, scales as d-1 and would decrease by 60% for all cores. Accordingly, all cores would move upward as indicated by an arrow in the mass versus size diagram of Fig. 7, which would increase the fraction of prestellar cores among starless cores from 60% ± 10% to 70% ± 10%. More precisely, the number of candidate prestellar cores would increase from 446 to 565 and the number of robust prestellar cores would increase from 292 to 391, while the total number of starless cores (651) would remain the same. Accordingly, the estimated lifetime of candidate prestellar cores would also slightly increase from ~ 1.4 Myr to ~ 1.8 Myr, and that of robust prestellar cores from ~ 0.9 Myr to ~ 1.3 Myr (see Sect. 5.1), leading to tpre = 1.5 ± 0.3 Myr. The prestellar core formation efficiency (CFE) as a function of background column density (cf. Fig. 12), and in particular the roughly constant value CFEmax ≡ fpre ~ 15% at high column densities, would not change. Our corresponding estimate of the “efficiency” of the star formation process in dense gas (cf. Sect. 5.6), SFR /Mdense = fpre × ϵcore/tpre, would however decrease from 5 × 10-8 yr-1 to 2 × 10-8 yr-1, becoming closer to the efficiency value reported by Evans et al. (2014) and Gao & Solomon (2004) than to the value found by Lada et al. (2010). Finally, the column density maps shown in Figs. 1, 3, 4, 13, and 14, as well as the spatial correspondence between cores and filaments, would remain unchanged. The scaling of our column density maps in terms of mass per unit length along the filaments would however change by ~ 60% upward, since the characteristic physical width of the filaments would increase by ~ 60%. As a consequence, the white areas which highlight supercritical filaments in Figs. 3, 4, 13, and 14 would slightly expand, improving the correspondence between the spatial distribution of prestellar cores/protostars and that of supercritical filaments. To summarize, our main conclusions do not depend strongly on the adopted distance.
cf. http://gouldbelt-herschel.cea.fr/ for the list of all target regions.
The documentation and repository of the software can be found at: http://www2.iap.fr/users/roussel/herschel
http://gouldbelt-herschel.cea.fr/archives. The column density and temperature maps derived in Sect. 4.1 at 36.3″ resolution can also be retrieved from the same website.
Throughout this paper, by supercritical or subcritical filament, we mean a filament with a supercritical or subcritical mass per unit length (Mline>Mline,crit or Mline<Mline,crit – see Sect. 1), respectively. This notion should not be confused with the concept of a magnetically supercritical or subcritical cloud/core (e.g., Mouschovias 1991).
The HGBS first-generation catalog of cores presented in this paper (see Appendix A) was produced with the “November 2013” major release of getsources (v1.140127), which is publicly available from http://gouldbelt-herschel.cea.fr/getsources
In the presence of an anisotropic radiation field, due to a closeby HII region for instance, radiative transfer calculations show that the far-infrared emission expected from a starless core at, e.g., 160 μm is not centered on the column density peak but is shifted toward the source of illumination. Using a “temperature-corrected” 160 μm map instead of the original 160 μm map at the detection stage in getsources alleviates this problem and helps to better trace the intrinsic position of the underlying column density core.
The measurement S/N is estimated at the measurement step of the getsources extractions (see Sect. 4.4) and characterizes the flux measurement uncertainties. In crowded situations, the measurement S/N of a source with a high “detection significance” at the detection step can be low because of large deblending and background-subtraction uncertainties.
We use the term “Bonnor-Ebert-like” because the model cores were given the density structure of critical isothermal Bonnor-Ebert spheres, but their dust temperature distributions resulted from radiative transfer calculations and were thus not strictly isothermal, in agreement with detailed observational studies of individual cores (see, e.g., Roy et al. 2014, for the example of B68).
The lifetime estimate quoted for starless cores is given under the assumption that presently unbound starless cores are still growing in mass and will become gravitationally bound and prestellar in the future (cf. Simpson et al. 2011; Belloche et al. 2011; Kirk et al. 2013b).
In the initial, “single-freefall” model of Krumholz & McKee (2005), the relevant timescale is the free-fall time evaluated at the mean density of the cloud, tff(ρ0), and there is no density dependence at all. Hennebelle & Chabrier (2011) and Federrath & Klessen (2012) have shown that this model generally underestimates the SFRs determined by Heiderman et al. (2010) in nearby clouds.
Both ΔMcores(AV) and ΔMcloud(AV) represent observed masses directly estimated from the Herschel data using SED dust temperatures and the dust opacity of assumptions given in Sect. 4. ΔMcores(AV) was not corrected for the small ~25% effect due to the fact that the SED mass values tend to slightly underestimate the intrinsic core masses according to our simulations (see Sect. 4.6 and Appendix B.1).
In the case of a cloud with a spherical radial density distribution, ρ ∝ r− α, it is easy to show that both the column density PDF, dN/dlog NH2, and the surface area, S( >NH2), scale as 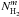 , where
, where 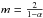 (see, e.g., Federrath & Klessen 2013).
(see, e.g., Federrath & Klessen 2013).
Strictly speaking, the formal agreement between 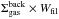 and Mline,crit is even better than 10%. For several reasons (e.g., factor of ~2 spread in filament width and distribution of filament inclination angles), however, the column density threshold is not a sharp boundary but a smooth transition (see discussion in Sect. 6.2 of André et al. 2014), as also observed in Fig. 11b.
and Mline,crit is even better than 10%. For several reasons (e.g., factor of ~2 spread in filament width and distribution of filament inclination angles), however, the column density threshold is not a sharp boundary but a smooth transition (see discussion in Sect. 6.2 of André et al. 2014), as also observed in Fig. 11b.
It is also worth noting that the potential timescale problem raised by Clark et al. (2007) is not a serious issue in the context of the gravo-turbulent theory of the CMF/IMF proposed by Hennebelle & Chabrier (2009), because the mass of cores corresponds to the turbulent Jeans mass in this theory and the free-fall time has only a very weak dependence on core mass.
As pointed out by a number of authors (e.g. Delgado-Donate et al. 2003; Goodwin et al. 2008; Hatchell & Fuller 2008), sub-fragmentation of prestellar cores into binary or multiple systems complicates the direct mapping of the prestellar CMF onto the IMF of individual stars. Lacking sufficient spatial resolution to probe core multiplicity with the present Herschel observations, we do not enter this debate here and concentrate on the relationship between the prestellar CMF and the system IMF.
Acknowledgments
SPIRE has been developed by a consortium of institutes led by Cardiff Univ. (UK) and including: Univ. Lethbridge (Canada); NAOC (China); CEA, LAM (France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, Univ. Sussex (UK); and Caltech, JPL, NHSC, Univ. Colorado (USA). This development has been supported by national funding agencies: CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC, UKSA (UK); and NASA (USA). PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KUL, CSL, IMEC (Belgium); CEA, OAMP (France); MPIA (Germany); IFSI, OAP/AOT, OAA/CAISMI, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI (Italy), and CICT/MCT (Spain). This work has received support from the European Research Council under the European Union’s Seventh Framework Programme (ERC Advanced Grant Agreements No. 291294 – “ORISTARS” – and No. 267934 – “MISTIC”) and from the French National Research Agency (Grant no. ANR–11–BS56–0010 – “STARFICH”). We are grateful to Neal Evans for providing us with an up-to-date list of YSOs from the combined c2d and Gould Belt Spitzer database. This research has made use of the SIMBAD database, operated at CDS, Strasbourg (France), and of the NASA/IPAC Extragalactic Database (NED), operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Alves, J. F., Lada, C. J., & Lada, E. A. 2001, Nature, 409, 159 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Alves, J., Lombardi, M., & Lada, C. J. 2007, A&A, 462, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alves de Oliveira, C., Schneider, N., Merín, B., et al. 2014, A&A, 568, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Ward-Thompson, D., & Barsony, M. 2000, Protostars and Planets IV, 59 [Google Scholar]
- André, P., Belloche, A., Motte, F., & Peretto, N. 2007, A&A, 472, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, Protostars and Planets VI, 27 [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Balog, Z., Müller, T., Nielbock, M., et al. 2014, Exp. Astron., 37, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beichman, C. A., Myers, P. C., Emerson, J. P., et al. 1986, ApJ, 307, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., Parise, B., Schuller, F., et al. 2011, A&A, 535, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bendo, G. J., Griffin, M. J., Bock, J. J., et al. 2013, MNRAS, 433, 3062 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard, J.-P., Paradis, D., Marshall, D. J., et al. 2010, A&A, 518, L88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertoldi, F., & McKee, C. F. 1992, ApJ, 395, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Klessen, R. S., Dullemond, C. P., & Henning, T. 2014, Protostars and Planets VI (Tucson: Univ. Arizona Press) [Google Scholar]
- Birkmann, S. M., Krause, O., & Lemke, D. 2006, ApJ, 637, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Blitz, L. 1993, in Protostars and Planets III, 125 [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnor, W. B. 1956, MNRAS, 116, 351 [CrossRef] [Google Scholar]
- Bontemps, S., André, P., Könyves, V., et al. 2010, A&A, 518, L85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwman, J. 2001, Ph.D. Thesis, University of Amsterdam [Google Scholar]
- Bouwman, J., de Koter, A., van den Ancker, M. E., & Waters, L. B. F. M. 2000, A&A, 360, 213 [NASA ADS] [Google Scholar]
- Burkert, A., & Hartmann, L. 2013, ApJ, 773, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Cambrésy, L. 1999, A&A, 345, 965 [NASA ADS] [Google Scholar]
- Chabrier, G. 2005, in The Initial Mass Function 50 Years Later, eds. E. Corbelli, F. Palla, & H. Zinnecker, Astrophys. Space Sci. Lib., 327, 41 [Google Scholar]
- Clark, P. C., Klessen, R. S., & Bonnell, I. A. 2007, MNRAS, 379, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., & Thaddeus, P. 1985, ApJ, 297, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., Ungerechts, H., Cohen, R. S., et al. 1987, ApJ, 322, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Delgado-Donate, E. J., Clarke, C. J., & Bate, M. R. 2003, MNRAS, 342, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Di Francesco, J., Evans, II, N. J., Caselli, P., et al. 2007, in Protostars and Planets V, 17 [Google Scholar]
- Dowell, C. D., Pohlen, M., Pearson, C., et al. 2010, in SPIE Conf. Ser., 7731, 36 [Google Scholar]
- Drew, J. E., Busfield, G., Hoare, M. G., et al. 1997, MNRAS, 286, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Crapsi, A., Evans, II, N. J., et al. 2008, ApJS, 179, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Arce, H. G., Allen, L. E., et al. 2013, AJ, 145, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Dzib, S., Loinard, L., Mioduszewski, A. J., et al. 2010, ApJ, 718, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., & Falgarone, E. 1996, ApJ, 471, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Evans, II, N. J., Sargent, A. I., et al. 2008, ApJ, 684, 1240 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, II, N. J., Rawlings, J. M. C., Shirley, Y. L., & Mundy, L. G. 2001, ApJ, 557, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, II, N. J., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, II, N. J., Heiderman, A., & Vutisalchavakul, N. 2014, ApJ, 782, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., & Klessen, R. S. 2012, ApJ, 761, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., & Klessen, R. S. 2013, ApJ, 763, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Fischera, J., & Martin, P. G. 2012, A&A, 542, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Friesen, R. K., Medeiros, L., Schnee, S., et al. 2013, MNRAS, 436, 1513 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, Y., & Solomon, P. M. 2004, ApJ, 606, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Gautier, III, T. N., Boulanger, F., Perault, M., & Puget, J. L. 1992, AJ, 103, 1313 [NASA ADS] [CrossRef] [Google Scholar]
- Goodwin, S. P., Nutter, D., Kroupa, P., Ward-Thompson, D., & Whitworth, A. P. 2008, A&A, 477, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Griffin, M. J., North, C. E., Schulz, B., et al. 2013, MNRAS, 434, 992 [NASA ADS] [CrossRef] [Google Scholar]
- Guillout, P. 2001, in From Darkness to Light: Origin and Evolution of Young Stellar Clusters, eds. T. Montmerle, & P. André, ASP Conf. Ser., 243, 677 [Google Scholar]
- Gutermuth, R. A., Bourke, T. L., Allen, L. E., et al. 2008, ApJ, 673, L151 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L. 2002, ApJ, 578, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Hatchell, J., & Fuller, G. A. 2008, A&A, 482, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatchell, J., Richer, J. S., Fuller, G. A., et al. 2005, A&A, 440, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiderman, A., Evans, II, N. J., Allen, L. E., et al. 2010, ApJ, 723, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Heithausen, A., Bertoldi, F., & Bensch, F. 2002, A&A, 383, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P. 2013, A&A, 556, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Chabrier, G. 2009, ApJ, 702, 1428 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Chabrier, G. 2011, ApJ, 743, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, T., Linz, H., Krause, O., et al. 2010, A&A, 518, L95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Hill, T., Motte, F., Didelon, P., et al. 2011, A&A, 533, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hill, T., André, P., Arzoumanian, D., et al. 2012, A&A, 548, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inutsuka, S.-I., & Miyama, S. M. 1997, ApJ, 480, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Jessop, N. E., & Ward-Thompson, D. 2000, MNRAS, 311, 63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnstone, D., Wilson, C. D., Moriarty-Schieven, G., et al. 2000, ApJ, 545, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Johnstone, D., Di Francesco, J., & Kirk, H. 2004, ApJ, 611, L45 [Google Scholar]
- Juvela, M., Ristorcelli, I., Pagani, L., et al. 2012, A&A, 541, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Henning, T., & Plume, R. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Banerjee, R., Federrath, C., & Henning, T. 2011, A&A, 530, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kauffmann, J., Bertoldi, F., Bourke, T. L., Evans, II, N. J., & Lee, C. W. 2008, A&A, 487, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kelly, B. C., Shetty, R., Stutz, A. M., et al. 2012, ApJ, 752, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, H., Johnstone, D., & Di Francesco, J. 2006, ApJ, 646, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, H., Myers, P. C., Bourke, T. L., et al. 2013a, ApJ, 766, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. M., Ward-Thompson, D., Palmeirim, P., et al. 2013b, MNRAS, 432, 1424 [NASA ADS] [CrossRef] [Google Scholar]
- Kiss, C., Ábrahám, P., Klaas, U., Juvela, M., & Lemke, D. 2001, A&A, 379, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Könyves, V., André, P., Men’shchikov, A., et al. 2010, A&A, 518, L106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramer, C., Stutzki, J., Rohrig, R., & Corneliussen, U. 1998, A&A, 329, 249 [NASA ADS] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & McKee, C. F. 2005, ApJ, 630, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Dekel, A., & McKee, C. F. 2012, ApJ, 745, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhn, M. A., Getman, K. V., Feigelson, E. D., et al. 2010, ApJ, 725, 2485 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., & Alves, J. F. 2010, ApJ, 724, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Forbrich, J., Lombardi, M., & Alves, J. F. 2012, ApJ, 745, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1985, MNRAS, 214, 379 [NASA ADS] [Google Scholar]
- Loinard, L. 2013, in IAU Symp., 289, ed. R. de Grijs, 36 [Google Scholar]
- Longmore, S. N., Bally, J., Testi, L., et al. 2013, MNRAS, 429, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Marsh, K. A., Griffin, M. J., Palmeirim, P., et al. 2014, MNRAS, 439, 3683 [NASA ADS] [CrossRef] [Google Scholar]
- Maury, A. J., André, P., Men’shchikov, A., Könyves, V., & Bontemps, S. 2011, A&A, 535, A77 [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Tan, J. C. 2003, ApJ, 585, 850 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Men’shchikov, A. 2013, A&A, 560, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Men’shchikov, A., André, P., Didelon, P., et al. 2010, A&A, 518, L103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Men’shchikov, A., André, P., Didelon, P., et al. 2012, A&A, 542, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miville-Deschênes, M.-A., Martin, P. G., Abergel, A., et al. 2010, A&A, 518, L104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., André, P., & Neri, R. 1998, A&A, 336, 150 [Google Scholar]
- Motte, F., Bontemps, S., Schilke, P., et al. 2007, A&A, 476, 1243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., Zavagno, A., Bontemps, S., et al. 2010, A&A, 518, L77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mouschovias, T. C. 1991, ApJ, 373, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C. 1983, ApJ, 270, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C. 1998, ApJ, 496, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C. 2009, ApJ, 700, 1609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakamura, F., Sugitani, K., Shimajiri, Y., et al. 2011, ApJ, 737, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Nielbock, M., Launhardt, R., Steinacker, J., et al. 2012, A&A, 547, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ntormousi, E., Hennebelle, P., André, P., & Masson, J. 2015, A&A, submitted [Google Scholar]
- Onishi, T., Mizuno, A., Kawamura, A., Ogawa, H., & Fukui, Y. 1998, ApJ, 502, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Ott, S. 2011, in Astronomical Data Analysis Software and Systems XX, eds. I. N. Evans, A. Accomazzi, D. J. Mink, & A. H. Rots, ASP Conf. Ser., 442, 347 [Google Scholar]
- Padoan, P., & Nordlund, Å. 2011, ApJ, 730, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Juvela, M., Goodman, A. A., & Nordlund, Å. 2001, ApJ, 553, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Federrath, C., Chabrier, G., et al. 2014, in Protostars and Planets VI, 77 [Google Scholar]
- Palmeirim, P., André, P., Kirk, J., et al. 2013, A&A, 550, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peretto, N., André, P., Könyves, V., et al. 2012, A&A, 541, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perrot, C. A., & Grenier, I. A. 2003, A&A, 404, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pezzuto, S., Elia, D., Schisano, E., et al. 2012, A&A, 547, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Pirogov, L., Ojha, D. K., Thomasson, M., Wu, Y.-F., & Zinchenko, I. 2013, MNRAS, 436, 3186 [NASA ADS] [CrossRef] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polychroni, D., Schisano, E., Elia, D., et al. 2013, ApJ, 777, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Prato, L., Rice, E. L., & Dame, T. M. 2008, in Handbook of Star Forming Regions, Vol. I, ed. B. Reipurth, 18 [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of scientific computing, 2nd edn. (Cambridge: University Press) [Google Scholar]
- Pudritz, R. E., & Kevlahan, N. K.-R. 2013, Roy. Soc. London Philosophical Trans. Ser. A, 371, 20248 [Google Scholar]
- Reid, M. A., & Wilson, C. D. 2006, ApJ, 650, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Roussel, H. 2013, PASP, 125, 1126 [Google Scholar]
- Roy, A., Ade, P. A. R., Bock, J. J., et al. 2010, ApJ, 708, 1611 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, A., André, P., Palmeirim, P., et al. 2014, A&A, 562, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schisano, E., Rygl, K. L. J., Molinari, S., et al. 2014, ApJ, 791, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, S., & Elmegreen, B. G. 1979, ApJS, 41, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Bontemps, S., Simon, R., et al. 2011, A&A, 529, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Csengeri, T., Hennemann, M., et al. 2012, A&A, 540, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., André, P., Könyves, V., et al. 2013, ApJ, 766, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, R. J., Johnstone, D., Nutter, D., Ward-Thompson, D., & Whitworth, A. P. 2011, MNRAS, 417, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J., Bentley, A., Castelaz, M., et al. 1985, ApJ, 291, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., Glover, S. C. O., & Klessen, R. S. 2014, MNRAS, 445, 2900 [NASA ADS] [CrossRef] [Google Scholar]
- Sousbie, T. 2011, MNRAS, 414, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Stamatellos, D., Whitworth, A. P., Bisbas, T., & Goodwin, S. 2007, A&A, 475, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stanke, T., Smith, M. D., Gredel, R., & Khanzadyan, T. 2006, A&A, 447, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starck, J. L., Donoho, D. L., & Candès, E. J. 2003, A&A, 398, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Straižys, V., Černis, K., & Bartašiūtė, S. 1996, Balt. Astron., 5, 125 [Google Scholar]
- Straižys, V., Černis, K., & Bartašiūtė, S. 2003, A&A, 405, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanaka, T., Nakamura, F., Awazu, Y., et al. 2013, ApJ, 778, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Teixeira, G. D. C., Kumar, M. S. N., Bachiller, R., & Grave, J. M. C. 2012, A&A, 543, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vallee, J. P. 1987, A&A, 178, 237 [NASA ADS] [Google Scholar]
- Vázquez-Semadeni, E., Kim, J., Shadmehri, M., & Ballesteros-Paredes, J. 2005, ApJ, 618, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Ward-Thompson, D., Scott, P. F., Hills, R. E., & André, P. 1994, MNRAS, 268, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Ward-Thompson, D., André, P., Crutcher, R., et al. 2007, in Protostars and Planets V, ed. B. Reipurth et al., 33 [Google Scholar]
- Ward-Thompson, D., Kirk, J. M., André, P., et al. 2010, A&A, 518, L92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ysard, N., Abergel, A., Ristorcelli, I., et al. 2013, A&A, 559, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Catalog of dense cores identified in the HGBS maps of the Aquila complex (the full catalog is at the CDS).
Derived properties of the dense cores identified in the HGBS maps of the Aquila region (the full table is at the CDS).
All Figures
 |
Fig. 1 a) H2 column density map of the Aquila region at 18.2″ angular resolution, as derived from HGBS data using the method described in Sect. 4.1. b) Same map as in the left panel with the positions of the 446 candidate prestellar cores and 58 protostellar cores identified in the Herschel images with getsources (see Sects. 4.4 and 4.5) shown as black and magenta triangles, respectively. Yellow triangles locate additional prestellar and protostellar cores which were excluded from the analysis and discussion of this paper, due to likely contamination by more distant objects belonging to background CO clouds at significantly higher LSR velocities than the bulk of the Aquila complex (cf. Sect. 4.3). The orientation of the galactic coordinate axes is indicated at the lower right of each panel. The lower left edge of the map is oriented almost parallel to the galactic longitude axis at Gb ~ 2° above the Galactic plane. (Color figure is available in the online version.) |
| In the text | |
 |
Fig. 2 Dust temperature map of the Aquila region at 36.3′′resolution, as derived from HGBS data (see Sect. 4.1). The white contour outlines the W40 HII region which has Td> 17 K. (Color figure is available in the online version.) |
| In the text | |
 |
Fig. 3 Left: network of filaments in the Aquila cloud complex as traced by the curvelet transform component (cf. Starck et al. 2003) of the Herschel high-resolution column density map shown in Fig. 1. Given the typical filament width Wfil ~ 0.1 pc (see Arzoumanian et al. 2011 and Fig. 18) and the relation Mline ≈ Σ0 × Wfil between the central gas surface density Σ0 of a filament, this curvelet column density map provides information on the mass per unit length along the filaments (cf. André et al. 2010), as indicated by the color bar on the right. The white areas highlight regions of the map where Σ × Wfil exceeds half the critical mass per unit length |
| In the text | |
 |
Fig. 4 Left: mask of the filamentary network traced by getfilaments (Men’shchikov 2013) in the Herschel high-resolution column density map of the Aquila cloud complex. For better visualization, only angular scales up to 320″ (i.e., ~0.4 pc at d = 260 pc) are shown. The color scale displayed within the filamentary mask corresponds to column density values in the column density map (Fig. 1). The crests of the filaments traced by DisPerSE (Sousbie 2011) are overlaid in blue (see Sect. 4.2 for details). Right: blow-up of the subfield marked by the white square in the left panel, using the same color scale. (Color figure is available in the online version.) |
| In the text | |
 |
Fig. 5 a) Probability density function of column density (N-PDF) in the Aquila cloud, derived from the 18.2′′-resolution column density image shown in Fig. 1. The left and right axes give the actual and normalized numbers of independent beams per logarithmic bin in the column density map, respectively. (The right axis thus provides an estimate of a proper N-PDF whose integral is 1.) A power-law fit to the high column density tail at AV> 7 gives dN/dlog |
| In the text | |
 |
Fig. 6 Distributions of beam-averaged column densities a) and beam-averaged volume densities b) at the resolution of the SPIRE 500 μm observations for the population of 446 candidate prestellar cores in Aquila (solid curves). In both panels, the dashed curves show the corresponding distributions for all 651 selected starless cores. (Color figure is available in the online version.) |
| In the text | |
 |
Fig. 7 Mass versus size diagram for the entire population of 651 starless cores identified with Herschel in the Aquila cloud. The core FWHM sizes were measured with getsources in the high-resolution column density map (Fig. 1) and deconvolved from an 18.2″ (HPBW) Gaussian beam; the vertical dashed line marks the corresponding physical |
| In the text | |
 |
Fig. 8 Completeness curve of our Herschel sample of candidate prestellar cores as a function of true core mass (solid line), as estimated from the Monte-Carlo simulations described in Sect. 4.8 and Appendix B.1. For comparison, the dashed line shows the global completeness curve predicted by the model discussed in Appendix B.2. (Color figure is available in the online version.) |
| In the text | |
 |
Fig. 9 Estimated lifetime against minimum average volume density (blue solid line and filled triangles) for the population of 446 candidate prestellar cores identified with Herschel in the Aquila cloud (blue triangles), similar to the “JWT” plot introduced by Jessop & Ward-Thompson (2000). The error bars only reflect |
| In the text | |
 |
Fig. 10 Average volume density versus observed core mass for the sample of 446 candidate prestellar cores. The blue solid triangles mark the median deconvolved volume density for each mass bin. (For comparison, the black open triangles show the median 36.3′′-beam-averaged densities for the upper three mass bins.) The error bars correspond to the interquartile range of densities in each mass bin. The data points become very uncertain at the high-mass end due to the small number of cores in the higher mass bins (see core mass function in Fig. 16 below). (No interquartile range can be plotted for the last bin which contains only two cores.) Note the weak, but significant, correlation between core density and core mass above ~2–3M⊙. The red curve represents a parabolic fit to the data points. (Color figure is available in the online version.) |
| In the text | |
 |
Fig. 11 a) Distribution of background cloud column densities for the population of 446 candidate prestellar cores identified with Herschel in the whole Aquila field. The vertical dashed line marks a fiducial threshold at an equivalent visual extinction level |
| In the text | |
 |
Fig. 12 Observed differential core formation efficiency (CFE) as a function of background column density expressed in AV units (blue histogram with error bars), obtained by dividing the mass in the form of prestellar cores in a given column density bin by the cloud mass observed in the same column density bin. The right axis gives the corresponding star formation rate per unit gas mass (in units of yr-1), estimated assuming a local star formation efficiency ϵcore = 0.4 at the core level and a prestellar core lifetime tpre = 1.2 Myr (see text). For comparison, the black curve shows the prediction of the multi-freefall version of the turbulence regulated model of the star formation rate initially proposed by Krumholz & McKee (2005) (see Hennebelle & Chabrier 2011). The vertical dashed line marks the same fiducial threshold at |
| In the text | |
 |
Fig. 13 Comparison of the spatial distribution of the prestellar core population identified in Sect. 4.7 using getsources (blue triangles) with the footprints of all the filaments traced with DisPerSE (red contours), both overlaid on the curvelet component of the high-resolution column density map (cf. Fig. 3). The gray scale corresponds to the color scale of Fig. 3. The red contours outline 0.1 pc–wide footprints around the crests of filaments. The green contours correspond to AV = 7 in the column density map smoothed to a resolution of 5′. (Color figure is available in the online version.) |
| In the text | |
 |
Fig. 14 Upper: curvelet component (cf. Starck et al. 2003) of a portion of the Herschel high-resolution column density map shown in Fig. 1. Given the typical filament width of ~0.1 pc (Arzoumanian et al. 2011), this map is equivalent to a map of the mass per unit length along the filaments (cf. André et al. 2010), as indicated by the color bar on the right. The white areas highlight regions of the map where the filaments have a mass per unit length larger than half the critical value |
| In the text | |
 |
Fig. 15 Comparison of the global column density PDF in the Aquila cloud (blue histogram with statistical error bars, identical to that shown in Fig. 5a) to the column density PDF measured after subtraction of dense cores (red solid line) and the PDF measured after subtraction of both dense cores and filaments (black solid line with statistical error bars). The vertical dashed line marks the same fiducial threshold at |
| In the text | |
 |
Fig. 16 Differential core mass function (dN/dlogM) of the 651 starless cores (dark green histogram), 446 candidate prestellar cores (upper blue histogram and open triangles), and 292 robust prestellar cores (lower blue histogram and filled triangles) identified with Herschel in the whole Aquila field. The error bars correspond to |
| In the text | |
 |
Fig. 17 Comparison of the CMF observed for the majority (~81%) of candidate prestellar cores lying within the 0.2 pc-wide footprints of the DisPerSE-detected filaments (light blue histogram) to that observed for the minority (~19%) of prestellar cores lying outside these filaments (magenta histogram). The upper dark blue histogram and the other lines are the same as in Fig. 16. (Color figure is available in the online version.) |
| In the text | |
 |
Fig. 18 Distribution of mean FWHM inner widths for the 90 filaments traced with DisPerSE in the Aquila entire field (see blue skeleton in Figs. 3 and 4 and Sect. 4.2). These widths result from a filament profile analysis similar to that described in Arzoumanian et al. (2011) and were deconvolved from the 18.2″ HPBW resolution of the high-resolution column density map used to construct the radial profiles of the filaments. The median filament width is 0.12 pc, as marked by the vertical dotted line, and the standard deviation of the distribution is 0.04 pc. |
| In the text | |
 |
Fig. A.1 Examples of Herschel spectral energy distributions (SEDs) for a prestellar core (left, see Fig. A.3 for the corresponding image cutouts) and a protostellar core (right, see Fig. A.4 for the corresponding image cutouts). These SEDs were constructed from the background-subtracted integrated flux densities (cross symbols) measured by getsources. A graybody fit to the SED observed longward of 160 μm is superimposed as a blue curve in both panels. Only upper limits are available at 70 μm and 160 μm for the prestellar core shown in the left panel. A single-temperature graybody rarely provides a good fit to the overall SED of a protostellar core but can nevertheless describe the SED longward of 160 μm reasonably well (cf. right panel). Similar SED plots are provided on http://gouldbelt-herschel.cea.fr/archives for all selected cores. |
| In the text | |
 |
Fig. A.2 Blow-up column density images of two Aquila subfields at 18.2″ resolution. Black and red ellipses mark the FWHM sizes of the starless cores and protostellar cores, respectively, selected from getsources extractions in these two subfields. Green ellipses show the FWHM sizes of the sources independently detected with CSAR (Kirk et al. 2013b) in the high-resolution column density image. |
| In the text | |
 |
Fig. A.3 Example blow-up Herschel images at 70/160/250/350/500 μm and high-resolution column density map for a (bound) prestellar core. Ellipses represent the estimated major and minor FWHM sizes of the core at each wavelength; they are shown as solid or dashed curves depending on whether the core is significantly detected or not, respectively, at a particular wavelength. See Table A.2 for the physical radius of the core and other derived properties. An angular scale of 30″ (i.e., ~ 0.038 pc at d = 260 pc) is shown at the bottom right. North is up, east is left. Similar image cutouts are provided on http://gouldbelt-herschel.cea.fr/archives for all selected starless cores. |
| In the text | |
 |
Fig. A.4 Same as Fig. A.3 for a protostellar core. Similar image cutouts are provided on http://gouldbelt-herschel.cea.fr/archives for all selected protostellar cores. |
| In the text | |
 |
Fig. B.1 Synthetic core mass function (CMF) derived from simulated source extractions (blue histogram) compared to the input mass function (dN/dlogM ∝ M-0.7) of a population of 5622 model cores (red curve) constructed as described in Appendix B.1. The estimated 90% completeness level (in observed core mass) is indicated by the vertical dashed line at 0.2 M⊙. The black solid line shows a power-law fit to the derived CMF above the 0.2 M⊙ completeness level; it is in excellent agreement with the input core mass function. The drop of the synthetic CMF below the input CMF at the high-mass end is due to the fact that the derived core masses tend to underestimate the true core masses by ~ 20% on average (see Fig. B.2a). |
| In the text | |
 |
Fig. B.2 a) Ratio of derived to intrinsic (or “true”) core mass as a function of derived core mass for the same set of simulated core extractions as used in Appendix B.1 and Fig. B.1. The error bars are ± 1σ where σ is the dispersion of the mass ratio in each mass bin. The median mass ratio is ~ 0.8 above 0.4 M⊙ (as indicated by the horizontal blue line) and ~ 0.7 close to the 90% completeness limit of 0.2 M⊙ in observed core mass. The horizontal dashed line marks the mass ratio of 1 expected in the case of perfect core extractions and mass estimates. b) Difference between derived SED temperature and intrinsic mass-averaged dust temperature as a function of derived core mass for the same set of simulated core extractions. The error bars are ± 1σ where σ is the dispersion of the temperature difference in each mass bin. The median temperature difference is about + 0.8 K above 0.4 M⊙ (as indicated by the horizontal blue line) and ~ 1 K close to a derived core mass of 0.2 M⊙ (completeness limit). The horizontal dashed line marks the zero difference expected in the case of perfect core extractions and temperature estimates. |
| In the text | |
 |
Fig. B.3 Ratio of derived to true (convolved) core size as a function of derived core mass for the same set of simulated core extractions as in Fig. B.1 and Fig. B.2. The error bars are ± 1σ where σ is the dispersion of the size ratio in each mass bin. The horizontal dashed line marks the size ratio of 1 expected in the case of perfect core extractions and size estimates. Note how the median core size measured in each mass bin remains within 5% of the true core size above the ~ 90% completeness of ~ 0.2 M⊙ in derived core mass. |
| In the text | |
 |
Fig. B.4 Median root mean square (rms) level of background column density fluctuations as a function of background cloud column density as measured in a 1′ × 1′ sliding box over the clean background image of the Aquila complex produced by getsources from the high-resolution column density map. The error bars correspond to the interquartile range of background fluctuations about the median level in each column density bin. The straight line represents a weighted power-law fit to the data points above NH2 ~ 2 × 1021 cm-2. |
| In the text | |
 |
Fig. B.5 Completeness curve as a function of apparent column density significance over local background cloud fluctuations derived from the Monte-Carlo simulations described in Appendix B.1. |
| In the text | |
 |
Fig. B.6 Model completeness curves of Herschel prestellar core extractions in Aquila for five values of the background cloud column density expressed in units of visual extinction from AV,back = 5 to AV,back = 20. |
| In the text | |
 |
Fig. B.7 Model global completeness curve of Herschel prestellar core extractions in the Aquila cloud complex (d = 260 pc) as a function of intrinsic model core mass. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.