| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A91 | |
| Number of page(s) | 33 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201525861 | |
| Published online | 26 November 2015 | |
Online material
Appendix A: A catalog of dense cores identified with Herschel in the Aquila cloud complex
Based on our Herschel SPIRE/PACS parallel-mode imaging survey of the Aquila cloud complex, we identified a total of 749 dense cores, including 685 starless cores and 64 protostellar cores. (Among these, 34 starless cores shown as yellow triangles in Fig. 1, as well as 6 protostellar cores, were excluded from the scientific discussion of Sect. 5 due to likely contamination by more distant, background objects – see Sect. 4.3.) The master
catalog listing the observed properties of all of these Herschel cores is available in Table A.1. A template of this online catalog is provided below to illustrate its form and content.
The derived properties (physical radius, mass, SED dust temperature, peak column density at the resolution of the 500 μm data, average column density, peak volume density, and average density) are given in Table A.2 for each core. A portion of this online table is also provided below. The derived properties of the Herschel-detected protostars and YSOs will be published in a forthcoming paper.
Catalog of dense cores identified in the HGBS maps of the Aquila complex (the full catalog is at the CDS).
Derived properties of the dense cores identified in the HGBS maps of the Aquila region (the full table is at the CDS).
|
Fig. A.1
Examples of Herschel spectral energy distributions (SEDs) for a prestellar core (left, see Fig. A.3 for the corresponding image cutouts) and a protostellar core (right, see Fig. A.4 for the corresponding image cutouts). These SEDs were constructed from the background-subtracted integrated flux densities (cross symbols) measured by getsources. A graybody fit to the SED observed longward of 160 μm is superimposed as a blue curve in both panels. Only upper limits are available at 70 μm and 160 μm for the prestellar core shown in the left panel. A single-temperature graybody rarely provides a good fit to the overall SED of a protostellar core but can nevertheless describe the SED longward of 160 μm reasonably well (cf. right panel). Similar SED plots are provided on http://gouldbelt-herschel.cea.fr/archives for all selected cores. |
|
| Open with DEXTER | |
|
Fig. A.2
Blow-up column density images of two Aquila subfields at 18.2″ resolution. Black and red ellipses mark the FWHM sizes of the starless cores and protostellar cores, respectively, selected from getsources extractions in these two subfields. Green ellipses show the FWHM sizes of the sources independently detected with CSAR (Kirk et al. 2013b) in the high-resolution column density image. |
|
| Open with DEXTER | |
 |
Fig. A.3
Example blow-up Herschel images at 70/160/250/350/500 μm and high-resolution column density map for a (bound) prestellar core. Ellipses represent the estimated major and minor FWHM sizes of the core at each wavelength; they are shown as solid or dashed curves depending on whether the core is significantly detected or not, respectively, at a particular wavelength. See Table A.2 for the physical radius of the core and other derived properties. An angular scale of 30″ (i.e., ~ 0.038 pc at d = 260 pc) is shown at the bottom right. North is up, east is left. Similar image cutouts are provided on http://gouldbelt-herschel.cea.fr/archives for all selected starless cores. |
| Open with DEXTER | |
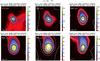 |
Fig. A.4
Same as Fig. A.3 for a protostellar core. Similar image cutouts are provided on http://gouldbelt-herschel.cea.fr/archives for all selected protostellar cores. |
| Open with DEXTER | |
Appendix B: Completeness of HGBS prestellar core extractions in Aquila
To estimate the completeness of our census of prestellar cores in Aquila, we used several sets of simulated data on the one hand (Appendix B.1), and a simple model of the core extraction process and completeness problem on the other (Appendix B.2).
Appendix B.1: Monte-Carlo simulations
To simulate real core extractions, we first constructed clean maps of the background emission at all Herschel wavelengths (including a column density plane), by subtracting the emission of the compact cores identified with getsources in the observed data (cf. Sects. 4.4 and 4.5). We then inserted several sets of model Bonnor-Ebert-like cores throughout the clean-background images in order to generate a full set of synthetic Herschel and column density images of the region. In the example illustrated in Figs. B.1 and B.2, for instance, we used a population of 5622 model starless cores with a flat input mass distribution (dN/dlog M ∝ M-0.7, similar to the mass distribution of CO clumps) from 0.02 M⊙ to ~ 30 M⊙. This example is particularly useful as it allowed us to test the robustness of the conclusion that the observed prestellar CMF is significantly steeper than the mass distribution of CO clumps. The model cores had positions in a mass versus size diagram consistent with critical Bonnor-Ebert isothermal spheres at effective gas temperatures ~7–20 K. The dust continuum emission from the synthetic Bonnor-Ebert cores in all Herschel bands was simulated using an extensive grid of spherical dust radiative transfer models constructed by us with the MODUST code (e.g., Bouwman et al. 2000; Bouwman 2001). In particular, each of the synthetic prestellar cores was given a realistic dust temperature profile with a significant drop in dust temperature toward core center, as observed in the case of spatially-resolved starless cores (cf. Roy et al. 2014). The synthetic cores were spatially distributed randomly over the regions of the column density map where ![]() cm-2 (containing most, if not all, of the observed prestellar cores in the real data – see Sect. 5.2), with no particular mass segregation. Once satisfactory synthetic skies resembling the observed images had been generated, compact source extraction and core selection/classification were performed with getsources in the same way as for the real data (see Sects. 4.4 and 4.5).
cm-2 (containing most, if not all, of the observed prestellar cores in the real data – see Sect. 5.2), with no particular mass segregation. Once satisfactory synthetic skies resembling the observed images had been generated, compact source extraction and core selection/classification were performed with getsources in the same way as for the real data (see Sects. 4.4 and 4.5).
 |
Fig. B.1
Synthetic core mass function (CMF) derived from simulated source extractions (blue histogram) compared to the input mass function (dN/dlogM ∝ M-0.7) of a population of 5622 model cores (red curve) constructed as described in Appendix B.1. The estimated 90% completeness level (in observed core mass) is indicated by the vertical dashed line at 0.2 M⊙. The black solid line shows a power-law fit to the derived CMF above the 0.2 M⊙ completeness level; it is in excellent agreement with the input core mass function. The drop of the synthetic CMF below the input CMF at the high-mass end is due to the fact that the derived core masses tend to underestimate the true core masses by ~ 20% on average (see Fig. B.2a). |
| Open with DEXTER | |
As mentioned in Sect. 4.8 and shown in Fig. 8, the results of these Monte-Carlo simulations suggest that our Herschel census of prestellar cores in the Aquila cloud complex is ~ 90% complete down to ~ 0.3 M⊙ in true core mass. Figure B.1 further illustrates that the core mass function can be reliably determined down to the completeness mass limit. In this example, a Kolmogorov-Smirnov (K-S) test shows that the derived CMF is statistically indistinguishable (at the ~ 90% confidence level) from the input mass function above the completeness limit. In particular, the best-fit power-law function to the derived CMF (black solid line in Fig. B.1) is identical to the input dN/dlogM ∝ M-0.7 power law. This test therefore confirms that the best-fit power law to the observed CMF (dN/dlogM ∝ M− 1.33 ± 0.06 – see Sect. 5.5) is significantly steeper than the typical mass distribution of CO clumps/clouds (dN/dlogM ∝ M-0.7 – e.g. Blitz 1993; Kramer et al. 1998) and that this cannot be an artifact of the core extraction process.
The same Monte-Carlo simulations were also used to assess the accuracy of the main derived parameters (e.g. core mass, radius, and dust temperature) by comparing the estimated values after core extraction to the intrinsic input values of the model cores. Figure B.2a shows that the derived core masses tend to underestimate the true core masses by ~20–30% on average, and Fig. B.2b shows that the derived SED temperatures tend to overestimate the intrinsic mass-averaged dust temperatures of the cores by typically ~ 1 K. A similar plot for the core sizes (Fig. B.3) suggests that the derived core sizes (prior to deconvolution) are quite reliable and remain within ~ 5% of the true convolved core sizes on average. We interpret the mass effect (Fig. B.2a) as a direct consequence of the temperature effect (Fig. B.2b) since overestimating the dust temperatures leads to underestimating the core masses. The temperature effect arises from the fact that the dust temperature derived from a global fit to the SED of a starless core overestimates the mass-averaged dust temperature owing to a distribution of dust temperatures along the line of sight (see Roy et al. 2014, and Sect. 4.6).
Taking the ~20–30% mass effect into account, we conclude that the ~ 90% completeness limit at ~ 0.3 M⊙ in true core mass corresponds to ~ 0.2 M⊙ in observed core mass.
|
Fig. B.2
a) Ratio of derived to intrinsic (or “true”) core mass as a function of derived core mass for the same set of simulated core extractions as used in Appendix B.1 and Fig. B.1. The error bars are ± 1σ where σ is the dispersion of the mass ratio in each mass bin. The median mass ratio is ~ 0.8 above 0.4 M⊙ (as indicated by the horizontal blue line) and ~ 0.7 close to the 90% completeness limit of 0.2 M⊙ in observed core mass. The horizontal dashed line marks the mass ratio of 1 expected in the case of perfect core extractions and mass estimates. b) Difference between derived SED temperature and intrinsic mass-averaged dust temperature as a function of derived core mass for the same set of simulated core extractions. The error bars are ± 1σ where σ is the dispersion of the temperature difference in each mass bin. The median temperature difference is about + 0.8 K above 0.4 M⊙ (as indicated by the horizontal blue line) and ~ 1 K close to a derived core mass of 0.2 M⊙ (completeness limit). The horizontal dashed line marks the zero difference expected in the case of perfect core extractions and temperature estimates. |
|
| Open with DEXTER | |
Appendix B.2: Model of the completeness problem
The Monte-Carlo simulations described above provide an estimate of the global completeness limit of the core survey. The completeness level of the core extractions is, however, expected to be background dependent. To assess the importance of this dependence, we constructed a simplified model of the core extraction process.
 |
Fig. B.3
Ratio of derived to true (convolved) core size as a function of derived core mass for the same set of simulated core extractions as in Fig. B.1 and Fig. B.2. The error bars are ± 1σ where σ is the dispersion of the size ratio in each mass bin. The horizontal dashed line marks the size ratio of 1 expected in the case of perfect core extractions and size estimates. Note how the median core size measured in each mass bin remains within 5% of the true core size above the ~ 90% completeness of ~ 0.2 M⊙ in derived core mass. |
| Open with DEXTER | |
Owing to the high sensitivity and quality of the Herschel images, the HGBS survey is not limited by instrumental noise but by confusion arising from small-scale cloud structure, an effect commonly referred to as “cirrus confusion noise” in the literature (e.g., see Gautier et al. 1992; Kiss et al. 2001; Roy et al. 2010). To estimate the level of such cirrus confusion noise from the Herschel data, we measured the rms level of background fluctuations in a sliding box 1′ × 1′ in size24 over the entire column density map of the Aquila complex after subtracting the sources identified by getsources. Correlating the resulting map of rms fluctuations with the input background column density map led to Fig. B.4, which clearly shows that the level of column density fluctuations increases with background column density approximately as a power law: 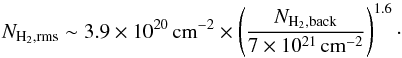 (B.1)The power-law index of 1.6 derived here from Herschel data is very similar to that reported in earlier papers discussing cirrus noise (e.g. Gautier et al. 1992; Kiss et al. 2001; Roy et al. 2010). Since the level of background fluctuations increases with column density, one expects core extraction to be increasingly more difficult and thus survey completeness to decrease significantly in higher column density areas within the field.
(B.1)The power-law index of 1.6 derived here from Herschel data is very similar to that reported in earlier papers discussing cirrus noise (e.g. Gautier et al. 1992; Kiss et al. 2001; Roy et al. 2010). Since the level of background fluctuations increases with column density, one expects core extraction to be increasingly more difficult and thus survey completeness to decrease significantly in higher column density areas within the field.
 |
Fig. B.4
Median root mean square (rms) level of background column density fluctuations as a function of background cloud column density as measured in a 1′ × 1′ sliding box over the clean background image of the Aquila complex produced by getsources from the high-resolution column density map. The error bars correspond to the interquartile range of background fluctuations about the median level in each column density bin. The straight line represents a weighted power-law fit to the data points above NH2 ~ 2 × 1021 cm-2. |
| Open with DEXTER | |
The model we used to estimate the magnitude of this effect and get around the problem of a background-dependent completeness level was based on the following assumptions:
-
•
A dense core is defined as the immediate vicinity of a column density peak departing significantly, i.e., by more than 5 × NH2,rms from the field of background cloud fluctuations.
A prestellar core, i.e., a self-gravitating starless core, can be approximately modeled as a critical Bonnor-Ebert spheroid of mass MBE and outer radius RBE, bounded by the gravitational pressure of the background cloud
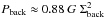 (McKee & Tan 2003), where Σback = μmH × NH2,back. The mean intrinsic column density contrast of such a model prestellar core is ΣBE/ Σback ~ 1.5, where
(McKee & Tan 2003), where Σback = μmH × NH2,back. The mean intrinsic column density contrast of such a model prestellar core is ΣBE/ Σback ~ 1.5, where 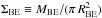 .
. The ability to detect a core in the Herschel data depends primarily on the apparent column density significance of the core defined as Σcore,obs/ Σrms, where Σcore,obs is the apparent (observed) column density of the core after convolution with the observing beam, i.e.,
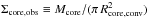 , and Σrms = μmH × NH2,rms. The Monte-Carlo simulations of Appendix B.1 are consistent with this assumption and suggest that the completeness level is ≳90% for cores with an apparent column density significance larger than 5 (see Fig. B.5).
, and Σrms = μmH × NH2,rms. The Monte-Carlo simulations of Appendix B.1 are consistent with this assumption and suggest that the completeness level is ≳90% for cores with an apparent column density significance larger than 5 (see Fig. B.5).
Two effects, beam dilution and temperature dilution, can make the apparent column density contrast ΣBE,obs/ Σback of a model core smaller than its intrinsic column density contrast of 1.5:
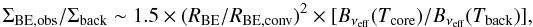 where νeff is a fiducial Herschel observing frequency which we take to correspond to λ ~ 350 μm. Taking advantage of the fact that the column density distribution of a Bonnor-Ebert core with outer radius RBE is well approximated by a Gaussian distribution of FWHM ~ RBE, the observed radius of the core is approximately
where νeff is a fiducial Herschel observing frequency which we take to correspond to λ ~ 350 μm. Taking advantage of the fact that the column density distribution of a Bonnor-Ebert core with outer radius RBE is well approximated by a Gaussian distribution of FWHM ~ RBE, the observed radius of the core is approximately 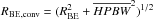 (where
(where 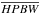 corresponds to the half-power beam width resolution of the column density map projected at the distance of the Aquila cloud), and the beam dilution factor can thus be expressed as
corresponds to the half-power beam width resolution of the column density map projected at the distance of the Aquila cloud), and the beam dilution factor can thus be expressed as 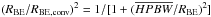 .
. The apparent column density significance can be written as the product of the apparent column density contrast and a cirrus noise factor, ΣBE,obs/ Σrms = (ΣBE,obs/ Σback) × (Σback/ Σrms), where the cirrus noise factor is:
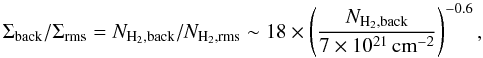 according to Eq. (B.1).
according to Eq. (B.1). -
Assuming that the fundamental completeness curve is the completeness function
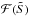 of apparent column density significance
of apparent column density significance 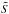 shown in Fig. B.5, completeness can be estimated as a function of core mass and background column density as
shown in Fig. B.5, completeness can be estimated as a function of core mass and background column density as 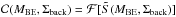 . The corresponding function of MBE is shown for five values of the background column density NH2,back in Fig. B.6. Figure B.6 shows how the completeness of prestellar core extractions is expected to decrease as background cloud column density and cirrus noise increase.
. The corresponding function of MBE is shown for five values of the background column density NH2,back in Fig. B.6. Figure B.6 shows how the completeness of prestellar core extractions is expected to decrease as background cloud column density and cirrus noise increase. 
Fig. B.5 Completeness curve as a function of apparent column density significance over local background cloud fluctuations derived from the Monte-Carlo simulations described in Appendix B.1.
Open with DEXTER 
Fig. B.6 Model completeness curves of Herschel prestellar core extractions in Aquila for five values of the background cloud column density expressed in units of visual extinction from AV,back = 5 to AV,back = 20.
Open with DEXTER To estimate a global completeness curve for our census of prestellar cores in the Aquila complex, we used the observed distribution of mass in the cloud as a function of background column density (cf. Figs. 5a,b) and took advantage of the existence of a column density “threshold” at AV,back ~ 5–7, above which the bulk of core and star formation is believed to occur (cf. Sect. 5.2 and Fig. 11) and the column density PDF is well fitted by a power-law distribution. We also assumed that the number of prestellar cores in the cloud scales linearly with cloud mass above the threshold. This assumption is consistent with recent infrared studies which find that the global star formation rate tends to be linearly proportional to the mass of dense gas above the threshold (e.g., Heiderman et al. 2010; Lada et al. 2010; Gao & Solomon 2004). It is also consistent with the roughly constant prestellar core formation efficiency found here above the threshold (see Fig. 12). The global completeness curve was thus computed as a weighted average of the individual completeness curves at fixed background column densities:
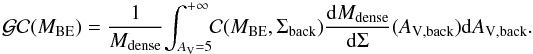
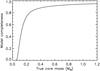 |
Fig. B.7
Model global completeness curve of Herschel prestellar core extractions in the Aquila cloud complex (d = 260 pc) as a function of intrinsic model core mass. |
| Open with DEXTER | |
Appendix C: Effect of distance uncertainty
As mentioned in Sect. 2, there is some ambiguity concerning the distance to the Aquila molecular cloud complex. A number of arguments, presented by Bontemps et al. (2010) and
summarized in Sect. 2, suggest that the bulk of the region studied here and shown in Fig. 1 corresponds to a coherent cloud complex at d− = 260 pc (see also Gutermuth et al. 2008), which is the default distance adopted in the present paper. Other studies in the literature (see references in Sect. 2), however, place the complex at the larger distance, d+ = 415 pc, of the Serpens Main cloud (Dzib et al. 2010). It is thus worth discussing how our results would be affected if we had adopted the larger distance estimate, d+, instead of d−. The core mass estimates, which scale as Sνd2/ [ Bν(Td) κν ] where Sν is integrated flux density and Bν(Td) is the Planck function, would systematically increase by a factor of 2.5. This would shift the CMFs shown in Figs. 16 and 17 to the right and thus lower the efficiency ϵcore from ![]() to 0.2 ± 0.1. In comparison, the core size estimates, which scale linearly with distance d, would increase by only 60%. The BE mass ratio αBE = MBE,crit/Mobs, listed in Col. 17 of Table A.2, scales as d-1 and would decrease by 60% for all cores. Accordingly, all cores would move upward as indicated by an arrow in the mass versus size diagram of Fig. 7, which would increase the fraction of prestellar cores among starless cores from 60% ± 10% to 70% ± 10%. More precisely, the number of candidate prestellar cores would increase from 446 to 565 and the number of robust prestellar cores would increase from 292 to 391, while the total number of starless cores (651) would remain the same. Accordingly, the estimated lifetime of candidate prestellar cores would also slightly increase from ~ 1.4 Myr to ~ 1.8 Myr, and that of robust prestellar cores from ~ 0.9 Myr to ~ 1.3 Myr (see Sect. 5.1), leading to tpre = 1.5 ± 0.3 Myr. The prestellar core formation efficiency (CFE) as a function of background column density (cf. Fig. 12), and in particular the roughly constant value CFEmax ≡ fpre ~ 15% at high column densities, would not change. Our corresponding estimate of the “efficiency” of the star formation process in dense gas (cf. Sect. 5.6), SFR /Mdense = fpre × ϵcore/tpre, would however decrease from 5 × 10-8 yr-1 to 2 × 10-8 yr-1, becoming closer to the efficiency value reported by Evans et al. (2014) and Gao & Solomon (2004) than to the value found by Lada et al. (2010). Finally, the column density maps shown in Figs. 1, 3, 4, 13, and 14, as well as the spatial correspondence between cores and filaments, would remain unchanged. The scaling of our column density maps in terms of mass per unit length along the filaments would however change by ~ 60% upward, since the characteristic physical width of the filaments would increase by ~ 60%. As a consequence, the white areas which highlight supercritical filaments in Figs. 3, 4, 13, and 14 would slightly expand, improving the correspondence between the spatial distribution of prestellar cores/protostars and that of supercritical filaments. To summarize, our main conclusions do not depend strongly on the adopted distance.
to 0.2 ± 0.1. In comparison, the core size estimates, which scale linearly with distance d, would increase by only 60%. The BE mass ratio αBE = MBE,crit/Mobs, listed in Col. 17 of Table A.2, scales as d-1 and would decrease by 60% for all cores. Accordingly, all cores would move upward as indicated by an arrow in the mass versus size diagram of Fig. 7, which would increase the fraction of prestellar cores among starless cores from 60% ± 10% to 70% ± 10%. More precisely, the number of candidate prestellar cores would increase from 446 to 565 and the number of robust prestellar cores would increase from 292 to 391, while the total number of starless cores (651) would remain the same. Accordingly, the estimated lifetime of candidate prestellar cores would also slightly increase from ~ 1.4 Myr to ~ 1.8 Myr, and that of robust prestellar cores from ~ 0.9 Myr to ~ 1.3 Myr (see Sect. 5.1), leading to tpre = 1.5 ± 0.3 Myr. The prestellar core formation efficiency (CFE) as a function of background column density (cf. Fig. 12), and in particular the roughly constant value CFEmax ≡ fpre ~ 15% at high column densities, would not change. Our corresponding estimate of the “efficiency” of the star formation process in dense gas (cf. Sect. 5.6), SFR /Mdense = fpre × ϵcore/tpre, would however decrease from 5 × 10-8 yr-1 to 2 × 10-8 yr-1, becoming closer to the efficiency value reported by Evans et al. (2014) and Gao & Solomon (2004) than to the value found by Lada et al. (2010). Finally, the column density maps shown in Figs. 1, 3, 4, 13, and 14, as well as the spatial correspondence between cores and filaments, would remain unchanged. The scaling of our column density maps in terms of mass per unit length along the filaments would however change by ~ 60% upward, since the characteristic physical width of the filaments would increase by ~ 60%. As a consequence, the white areas which highlight supercritical filaments in Figs. 3, 4, 13, and 14 would slightly expand, improving the correspondence between the spatial distribution of prestellar cores/protostars and that of supercritical filaments. To summarize, our main conclusions do not depend strongly on the adopted distance.
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


