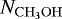| Issue |
A&A
Volume 658, February 2022
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 46 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202142023 | |
| Published online | 10 February 2022 | |
The evolution of temperature and density structures of OB cluster-forming molecular clumps
1
Max Planck Institute for Radio Astronomy,
Auf dem Hügel 69,
53121
Bonn,
Germany
e-mail: ylin@mpifr-bonn.mpg.de
2
Institute of Astronomy and Astrophysics, Academia Sinica,
11F of Astronomy-Mathematics Building, AS/NTU No.1, Sec. 4, Roosevelt Rd,
Taipei
10617,
Taiwan,
ROC
3
European Southern Observatory,
Karl-Schwarzschild-Str. 2,
85748
Garching bei München,
Germany
4
Leiden Observatory, Leiden University,
PO Box 9513,
2300 RA
Leiden,
The Netherlands
5
OASU/LAB-UMR5804, CNRS, Université Bordeaux, allée Geoffroy Saint-Hilaire,
33615
Pessac,
France
6
INAF – Osservatorio Astronomico di Cagliari,
Via della Scienza 5,
09047
Selargius (CA),
Italy
Received:
15
August
2021
Accepted:
2
December
2021
Context. OB star clusters originate from parsec-scale massive molecular clumps, while individual stars may form in ≲0.1 pc scale dense cores. The thermal properties of the clump gas are key factors governing the fragmentation process, and are closely affected by gas dynamics and feedback of forming stars.
Aims. We aim to understand the evolution of temperature and density structures on the intermediate-scale (≲0.1–1 pc) extended gas of massive clumps. This gas mass reservoir is critical for the formation of OB clusters, due to their extended inflow activities and intense thermal feedback during and after formation.
Methods. We performed ~0.1 pc resolution observations of multiple molecular line tracers (e.g., CH3CCH, H2CS, CH3CN, CH3OH) that cover a wide range of excitation conditions, toward a sample of eight massive clumps. The sample covers different stages of evolution, and includes infrared-weak clumps and sources that are already hosting an HII region, spanning a wide luminosity-to-mass ratio (L∕M) range from ~1 to ~100 (L⊙/M⊙). Based on various radiative transfer models, we constrain the gas temperature and density structures and establish an evolutionary picture, aided by a spatially dependent virial analysis and abundance ratios of multiple species.
Results. We determine temperature profiles varying in the range 30–200 K over a continuous scale, from the center of the clumps out to 0.3–0.4 pc radii. The clumps’ radial gas density profiles, described by radial power laws with slopes between −0.6 and ~−1.5, are steeper for more evolved sources, as suggested by results based on dust continuum, representing the bulk of the gas (~104 cm−3), and on CH3OH lines probing the dense gas (≳106–108 cm−3) regime. The density contrast between the dense gas and the bulk gas increases with evolution, and may be indicative of spatially and temporally varying star formation efficiencies. The radial profiles of the virial parameter show a global variation toward a sub-virial state as the clump evolves. The linewidths probed by multiple tracers decline with increasing radius around the central core region and increase in the outer envelope, with a slope shallower than the case of the supersonic turbulence (σv ∝ r0.5) and the subsonic Kolmogorov scaling (σv ∝ r0.33). In the context of evolutionary indicators for massive clumps, we also find that the abundance ratios of [CCH]/[CH3OH] and [CH3CN]/[CH3OH] show correlations with clump L∕M.
Key words: ISM: clouds / dust, extinction / ISM: structure / ISM: abundances / ISM: molecules / ISM: kinematics and dynamics
© Y. Lin et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1 Introduction
Massive star-forming clumps are progenitors of OB clusters (Williams et al. 2000; Motte et al. 2018). They typically have masses of ≳ 1000 M⊙ over a spatial scale of ~1 pc. Fragmentation and accretion processes of OB star clusters are strongly influenced by the evolution of the kinematics, density, and temperaturestructure of parsec-scale gas clumps (Girichidis et al. 2011; Lee & Hennebelle 2019; Padoan et al. 2020), and vice versa (Krumholz et al. 2012; Offner et al. 2009; Hennebelle et al. 2020). In particular, the stellar initial mass function (IMF) appears to be universal; it varies weakly from one environment to another in the Milky Way, indicating that the formation of the most massive stars is deterministic, favoring particular physical environments instead of randomly occurring in molecular clouds (Kroupa et al. 2013). This, together with dominant feedback caused by massive stars, may determine the evolutionary track of massive clumps. Accordingly, observational evidence can be collected by sampling a wide range of clumps at different evolutionary stages.
The process of gas collapse resulting in protostars has been studied for decades; among the first are the works by Larson (1969), Penston (1969), and Shu (1977). These are commonly referred to as “outside-in” and “inside-out” models, indicating the succession of the spherical collapse of isothermal clouds, which describe the gas flows immediately prior to and after development of a protostar singularity, respectively. The density profiles of Larson (1969) and Penston (1969) exhibit a r−2 relation, while the density profile of the inner free-falling and outer static envelopes of the Shu (1977) model follow r−1.5 and r−2, separately. On the other hand, when turbulent pressure is taken into account to explain the observed linewidth-size scaling relation, the logatropic (nonisothermal) gas follows a flatter profile proportional to r−1 (e.g., McLaughlin & Pudritz 1997) in the outer region. Recently, the process of spherically symmetric cloud collapse has been revisited extensively: Coughlin (2017) presents solutions for arbitrary initial density profiles, extending to non-self-similar regimes, and Murray & Chang (2015) and Murray et al. (2017) consider turbulent energy generated from gravitational collapse and a highly dynamic system (compared to hydrostatic equilibrium assumed by Shu 1977). Furthermore, due to significant heating sources and high opacities associated with massive star-forming clouds, the assumption of isothermality might break down and a polytropic equation of state (EOS) needs to be introduced which quantifies the balance of gas cooling and heating and can incorporate turbulent pressure (Curry & McKee 2000). The polytropic index γ (with T ∝ ργ−1) has been shown to have a decisive effect on the dynamical evolution of molecular clouds (Passot & Vázquez-Semadeni 1998; Spaans & Silk 2000) and eventually on the IMF (e.g., Klessen et al. 2007; Jappsen et al. 2005; Lee & Hennebelle 2018; Hennebelle et al. 2020). However, a simple analytical form of gas EOS may not fully capture the gas thermal properties when stellar radiation feedback sets in. The radiative feedback has been suggested to have an impact in determining the characteristics of the stellar spectrum (e.g. Bate 2009; Urban et al. 2010; Guszejnov et al. 2016, 2017). Such impact can be only moderate in setting the peak of the IMF in typical galactic environment (Hennebelle et al. 2020), but it may be critical for boosting the formation of the more massive stars (Krumholz et al. 2007; Hennebelle et al. 2020). Given these theoretical developments, the time is right to measure with observations the detailed gas temperature and density distribution inside massive clumps.
Understanding how the mass of massive clumps is distributed over different density regimes is fundamental to understanding the evolution of the star formation rate (SFR) and star formation efficiency (SFE) on larger physical scales (e.g., Lee et al. 2015; Parmentier 2019). On cloud scales (≳10 pc), the gas column density distribution follows a log-normal probability function (N-PDF) in a turbulent medium, while it develops a power-law tail as significant gravitational collapse commences in high-density regimes (e.g., Klessen 2000; Kritsuk et al. 2011). The relevant scales are readily resolved in nearby star-forming clouds and OB cluster-forming regions (e.g., Kainulainen et al. 2009; Lin et al. 2016, 2017). The power-law shape is thought to originate from power-law density profiles (Federrath & Klessen 2013, Myers 2015). Hence, measurements of clump density profiles can provide insights into how the dense gas of molecular clouds leads to the power-law excess of N-PDFs.
Most previous works on the density structure of massive clumps are based on single-dish observations of both continuum and molecular lines. Works discussing samples of sources include (but are not limited to) van der Tak et al. (2000), Mueller et al. (2002), Beuther et al. (2002), Hatchell & van der Tak 2003, Rolffs et al. (2011), Williams et al. (2005), and Palau et al. (2014). With the advent of wide-band receivers, especially those equipping interferometers, spatially resolved multi-line observations have become efficient (e.g., Beuther et al. 2007, Li et al. 2019, Gieser et al. 2021), and are indispensable to measure the broad density and temperature ranges associated with massive star formation.
We conducted a pilot survey of eight massive clumps with the Submillimeter Array (SMA) and the APEX telescope. For the target clump selection we followed the criterion elaborated in Sect. 2.1. The main molecular lines of interest are listed in Table 1, which include multiple efficient thermometers and densitometers for massive clumps, as suggested by single-dish observations toward a statistically large sample (Giannetti et al. 2017; Leurini et al. 2004, 2007). We use various modeling methods to quantify the clump density and temperature structure using these lines. Throughout the paper, We follow the existing nomenclature in the literature (e.g., Williams et al. 2000; Zhang et al. 2009; Liu et al. 2012; Motte et al. 2018). In this way, massive molecular clumps refer to structures with sizes of ~0.5–1 pc, massive molecular cores refer to the <0.1 pc size structures embedded within a clump, and condensations refer to the distinct molecular substructures within a core. In Fig. 1, we provide a schematic picture of different scales of a molecular cloud. The physical characteristics across the scales, as elaborated above, are indicated for individual structures. We are interested in understanding the physical structure of massive clumps, which have a vast range of gas densities and are the building blocks of the star-forming clouds; in particular, they compose the high-density tail of the cloud N-PDF.
The paper is organized as follows. In Sect. 2, we describe the observations and data reduction. In Sect. 3, we describe the radiative transfer modeling procedure and elaborate on the analysis of both line and continuum observations to derive the temperature, density, linewidth, and virial parameter profiles, and the abundances of multiple species. Section 3.1 gives a general outline of the radiative modeling methods and procedures we adopted. Section 3.3 provides an overview of the distribution of the molecular lines used as thermometers and densitometers in this paper. Sections 3.4 and 3.5, in addition to Appendices E and F, focus on the radiative transfer modeling procedures and results of continuum and molecular lines. In Sect. 3.2, the properties of the sources extracted from SMA 1.2 mm continuum are presented. An analysis of some complementary lines is presented in Appendix D. In Sect. 4, we discuss the outcome of the modeling results, with a comparison between target sources and the physical implications. Finally in Sect. 5, we conclude on our findings.
2 Observations and data reduction
2.1 Source selection
The target sources are selected from the APEX Telescope Large Survey of the Galaxy (ATLASGAL; Schuller et al. 2009), and are located at a distance of 4–6 kpc (Urquhart et al. 2018). They cover different evolutionary stages, suggested by different L∕M (Fig. 2) and different signposts of star formation activity (see further details in Appendix A). For comparison, in Fig. 2 we present the distribution of luminosity and mass for ATLASGAL sources that (1) are located at a distance within 4–8 kpc with a radius of <2 pc (Urquhart et al. 2018), and (2) have masses and peak fluxes higher than 300 M⊙ and peak flux ~2 Jy beam−1, respectively.The background contours illustrate the distribution of ATLASGAL sources in a distance range of 4–8 kpc, with masses over 300 M⊙ and peak flux ≳2 Jy beam−1 with a radius of less than 2 pc.
In Fig. 2, we also include several evolutionary tracks. The empirical evolutionary tracks for massive clumps with envelope masses of 80, 140, 350, 700, and 2000 M⊙ which will form a single protostar with varying accretion rates based on a turbulent core model (McKee & Tan 2003) are shown (gray lines), as derived in Molinari et al. (2008). Evolutionary tracks of massive clumps having constant accretion rates of 10−5 M⊙ yr−1 (dotted), 10−4 M⊙ yr−1 (dashed) and 10−3 M⊙ yr−1 (solid), for the most massive star in the cluster are also indicated (green lines). In these tracks, the other stellar members follow an equal accretion stopping probability, with an accretion rate ∝ M1.5. The orange pluses mark the time epoch of 2 × 104 yr for each accretion track. The SFE is assumed to be 30% and the underlying stellar population follows canonical IMF (Kroupa et al. 1993). Accretion luminosities are estimated by interpolating massive protostar models in Hosokawa & Omukai (2009).
The lower mass limit of 300 M⊙ corresponds to the mass of a massive clump in which at least one >8 M⊙ star will form according to the normal IMF with an assumed star formation efficiency (SFE) of 30% (Kroupa et al. 1993; Sanhueza et al. 2017). The peak flux density of 2 Jy beam−1 with beam full width at half maximum (FWHM) ~20″ at 870 μm from ATLASGAL, considering a distance of 6 kpc, implies a mass of >100 M⊙ concentrated in the clump central ~0.5 pc region, assuming a dust temperature of 50 K and dust opacity of 1.8 cm2 g−1 with a gas-to-dust ratio of 100. Thus, this selection criterion yields a sample of eight massive clumps (Table 2) with moderate to high central concentration. We note that our target sample is representative of more evolved sources with respect to those that fulfill these criteria. These sources can be easily detected with 1 mm lines given their favorable excitation conditions, and we further complement the sample with an infrared dark source, G18.
Molecular lines of interest covered by the SMA observations.
2.2 SMA observations
We performed SMA observations in the ~1 mm band toward seven clumps in the subcompact array configuration in June 2017, and in the compact array configuration in August 2017. The selected target sources are summarized in Table 2. Detailed information about each target source from previous studies is summarized in Appendix A. We used the dual receivers mode supported by the SMAWideband Astronomical ROACH2 Machine (SWARM) backend: The RxA receivers covered the frequency ranges of 188.4–196.7 GHz and 204.4–212.7 GHz in the lower and upper sidebands, respectively; the RxB receivers covered the frequency ranges of 238.5–246.8 GHz and 254.5–262.8 GHz, respectively. The intrinsic spectral channel width was 140 kHz. The molecular line transitions we covered are summarized in Table 1.
In addition, we retrieved archival SMA data toward the luminous ultra-compact HII region G10.624–0.38, which remains deeply embedded in a Mgas = 103–104 M⊙ molecular clump and harbors a cluster of OB stars. These observations covered the CH3OH J = 5–4 and J = 7–6 and the CH3CN J = 19–18 line multiplets. We refer to Liu et al. (2010, 2011, 2012) for details of these observations.
We followed the standard SMA data calibration strategy. The application of system temperature (Tsys) information and the absolute flux, passband, and gain calibrations were carried out using the MIR IDL software package (Qi 2003). The absolute flux scalings were derived by comparing the visibility amplitudes of the gain calibrators with those of the absolute flux standard sources of the SMA, which were Callisto and Neptune for the subcompact and compact array observations, respectively. After calibration, we performed zeroth-order fitting of continuum levels from line-free channels and the joint weighted imaging adopting robust weighting of all continuum data were performed using the MIRIAD software package (Sault et al. 1995). The resultant synthesized beam is typically 4.″ 5 at 241 GHz. The sensitivity (3σ) of continuum observation is ~0.04 Jy beam−1 and of lines ~0.5 K. For clump G18 we do not obtain robust detection of the thermometer lines of CH3CCH, H2CS, and CH3CN (Table 1) with this achieved line sensitivity. We used the previously published result from IRAM 30m telescope observations of 3 mm CH3CCH and CH3CN lines (Giannetti et al. 2017) instead.
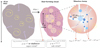 |
Fig. 1 Schematic picture of molecular cloud structure over spatial scales from >10 pc to ~0.1 pc: from cloud to core scale. A molecular cloud starts contraction from an initial stage that appears to be an infrared dark cloud (IRDC) and evolves into a star-forming one, embedding a number of molecular clumps. The massive clumps, ~1 pc in size, are generally composed of filamentary structures and cores at different evolutionary stages. In all figures, the yellow curved arrows represent turbulent motions and the purple arrows indicate gravitational contractionor gas inflows (along filaments). In the rightmost figure, the thick lines show filaments and the blue ovals indicate cores of different masses; the color gradient of the clump indicates a density gradient of the bulk gas. The characteristics of different structures are linked to textboxes by dotted arrows. |
 |
Fig. 2 Luminosity–mass diagram of target sources (three-branched triangles). The evolutionary tracks of massive clumps of different envelope masses that form a cluster of stars with different accretion rates are shown as dotted and solid green lines; the evolutionary tracks of clumps of different envelope masses that are assumed to form a single massive star are shown as dash-dotted gray lines with arrows (Molinari et al. 2008; for more details see Sect. 2.1). |
Target sources.
2.3 APEX observations
Single-dish observations at 1 mm toward our target sources were performed with the MPIfR principal investigator (PI) instrument PI230 on the Atacama Pathfinder Experiment 12-m submillimeter telescope (APEX, Güsten et al. 2006), between March and September 2017 and July 2018 (Project M-099.F-9513A-2017, PI: Yuxin Lin). The PI230 receiver is a dual polarization sideband separating heterodyne system with a total of 32 GHz bandwidth working at 230 GHz, and can cover the spectral range of 200–270 GHz. We conducted observations with two spectral setups, covering frequency ranges of 202.2–210.0 GHz, 218.0–225.8 GHz and 239.2–247.0 GHz, 255.0–262.8 GHz. For each target source, a region of 3′ × 3′ centered at the source position was mapped in the on-the-fly (OTF) mode with both setups.
During the observations, the typical precipitable water vapor (PWV) was ~1.5–2.5 mm. The pointing was determined by continuum observations on Saturn when available, or CO J = 2–1 observationson bright nearby evolved stars (e.g., RAFGL2135, R-Dor). The pointing accuracy was found to be within 3″. The focus was checked on Saturn every 2–4 h. The main beam efficiency (ηmb) for the PI230 instrument varied over the observing period, with a range of ~63–72%1. The calibration uncertainty was typically within 20%, estimated based on the flux measurement of the pointing sources.
Basic data reductions were done with the GILDAS software package2, including flagging of bad spectra, baseline subtraction, unit conversion (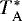 to Tmb), and building spectral cubes. Final spectral cubes were re-sampled to 0.5 km s−1 spectral resolution for all lines.
to Tmb), and building spectral cubes. Final spectral cubes were re-sampled to 0.5 km s−1 spectral resolution for all lines.
2.4 SMA-APEX combination and imaging
For our primary target lines covered by both SMA and APEX, which have extended emission, namely CH3CCH J = 12–11, CH3OH J = 5–4, C2H J = 3–2, H13CO+ J = 3–2, CS J = 5–4, C34S J = 5–4, and SO J = 45–34, we combined the two data sets in the Fourier domain (uv-domain) with MIRIAD. This combination is essentially imaging together the pseudo-visibilities generated from single-dish observations and interferometer measurements, so that the short-spacing information including zero baseline that is obtained with a single dish can be complemented by the interferometry data; the method is commonly referred to as the joint deconvolution or joint reconstruction method (Kurono et al. 2009; Koda et al. 2011).
In the combination procedure, we first deconvolved the APEX data from the single-dish Gaussian beam (FWHM ~ 30″) and then multiplied the resultant image with the primary beam of the SMA observations. The obtained image was then used to generate a single-dish uv model (i.e., the pseudo-visibilities) by randomly sampling a visibility distribution to match that of the single-dish beam pattern. The zero spacing visibility was also sampled and added to the produced pseudo-visibilities. Finally, the pseudo- and interferometric visibilities were imaged together to produce the combined image. In the final imaging step, we applied a Gaussian tapering function of FWHM ~ 2″ to increase the detectability of extended emission. In the end we adopted a final step to linearly combine the product of this standard joint deconvolution method with the single-dish image in the Fourier domain, using immerge in the MIRIAD package. This step was necessary and was found to preserve the single-dish overall fluxes better than using solely the joint deconvolution method, due to the fact that the deconvolution method is not flux conserving; a similar procedure is adopted in Monsch et al. (2018), among others. The combined images have comparable total fluxes to the APEX data, within a difference of 15%.
For details on the proper weighting scheme in the joint deconvolution method and the impact of sensitivities of single-dish and interferometry data, we refer to Kurono et al. (2009).
2.5 Ancillary data: mid- to far-infrared and submm continuum data from multiple single-dish telescopes
We used the single-dish mid- and far-infrared, and submillimeter (submm) continuum data to constrain the bulk gas structures and construct the SEDs (Fig. 3). In addition to the 870 μm data from ATLASGAL survey (Schuller et al. 2009; Csengeri et al. 2016) obtained by APEX-LABOCA (Siringo et al. 2009), we also adopted 350 μm data obtained by the CSO-SHARC2 or APEX-SABOCA instrument. The information of the observations and data reduction procedure are detailed in Lin et al. (2017) and Lin et al. (2019). For sources without available 350 μm from ground-based telescope (of 10″ angular resolution), we used the available observations from James Clerk Maxwell Telescope (JCMT)3 Submillimetre Common-User Bolometer Array 2 (SCUBA2; Dempsey et al. 2013; Chapin et al. 2013) at 450 μm from the online data archive.
We also retrieved the archival Herschel4 images at 70/160 μm and 250/350/500 μm from the Herschel Infrared Galactic Plane (Hi-GAL) survey (Molinari et al. 2010) taken by the PACS (Poglitsch et al. 2010) and SPIRE instruments (Griffin et al. 2010). For the mid-infrared data, we used the 24 μm images fromthe MIPS Galactic Plane Survey (MIPSGAL, Carey et al. 2009) taken by Spitzer telescope.
 |
Fig. 3 Overall work flow showing the radiative transfer modeling procedure followed in this work. |
3 Results and analysis
3.1 Outline of the modeling and analysis procedure
In this work, we aim to provide a description of the gas density and temperature of massive clumps by performing radiative transfer calculations of molecular lines and the multi-wavelength dust continuum. In this section, we introduce the workflow of the modeling, starting by basic definitions of molecular line excitation. The modeling steps (shown in Fig. 3) are explained in more detail in Sects. 3.4–3.6 and in Appendices E and F. The results of the radiative transfer models are discussed in Sect. 4.
Massive clumps have average molecular hydrogen densities of typically ~104 cm−3 (Csengeri et al. 2014; Urquhart et al. 2018); the collisional partner participating in the excitation and de-excitation of molecular lines considered in this paper is primarily hydrogen gas. The critical density (ncrit) (Table 3) defines the way in which a molecule in an excited state decays to ground state. When the main collisional partner is hydrogen, it stands for the critical hydrogen density at which timescales of radiative decay and collisional de-excitation are comparable; in other words, the net radiative decay rate from level J to a certain lower level equals the rate of collisional de-population out of the upper level J for a multi-level system (e.g., Wilson et al. 2013).
With gas densities close to and well above ncrit, the thermalization of energy levels is achieved, such that the excitation temperature (Tex) can approximate the gas kinetic temperature (Tkin), with the population of energy levels reaching Boltzmann prediction (local thermodynamic equilibrium, LTE). On the other hand, if gas densities are below ncrit (subthermal excitation), then the population of the upper energy level is sensitive to varying gas densities. Observations of multiple transitions with different ncrit can probe a range of gas densities by showing rather different ratios of line intensities. In particular, if the energy levels associated with these transitions are of similar energy, then the dependence of line ratios on temperature is minimized, and so does the degeneracy of the mutual effect of gas temperature and density in determining level populations. We take advantage of these radiative properties to use selected molecular transitions as densitometers of our target sources.
In a simple view, massive star-forming clumps may be thought of as multi-layered gas structures showing centrally peaked gas density profiles. This is a natural outcome under self-gravity. From the outermost layer to the innermost region, transitions of higher and higher ncrit are thermalized progressively. Using a combination of thermometers of different ncrit, based on LTE assumption, can constrain gas temperatures over continuous spatial scales (with respect to the clump center). Analogous to a densitometer, a thermometer is defined here as a set of molecular lines of a certain species whose level population is only (or dominantly) sensitive to gas temperature, which arise from energy levels spanning a wide energy range and are connected ideally only through collisions, provided for example by K-ladder lines of symmetric top molecules.
Considering the gas density regime of massive star-forming clumps, and based on previous single-dish experiments (Giannetti et al. 2017), we have identified CH3CCH, H2CS, and CH3CN lines at the 1 mmband (listed in Table 1) as ideal tracers for measuring temperature profiles of massive clumps. These tracers have ncrit of several 104, 105, and 106 cm−3, respectively (Table 3). On the other hand, the combination of distinct ncrit triggers a filtering effect, such that with each thermometer the region it probes is limited to the gas density regimes ranging around and above its ncrit. Contamination by foreground and background gas layers of lower density to the observed emission is therefore negligible. This means that the line-of-sight (averaging) effect is reduced to the gas component of a limited density range.
In addition, optical depths (τ) are low when typical abundances and excitation conditions are considered for these molecules, which implies that line ratios probe the gas kinetic temperature at the inner location of the gas layer. With these properties in mind, we derive the rotational temperature (Trot) maps under the LTE assumption using multiple thermometers in Sect. 3.4. Temperature measurements of the outer regions are obtained using the extended CH3CCH and H2CS emission, and combined with temperatures derived from CH3CN, which is confined to the central region of the clumps. This combination allows us to establish the full radial temperature profile of the clumps. We also use multi-wavelength single-dish dust emission (SD continuum, as in Fig. 3) to derive dust temperature maps by building spectral energy distributions (SEDs) assuming single-component modified blackbody emission (Lin et al. 2016, 2019). The dust temperatures at the outer layer of clumps, are used to complete the temperature profile at larger radii for the clumps. With the simple one-component LTE modeling and one-component dust SED construction, we derive the projected radial profile of the obtained multiple temperature maps as the radial profiles, denoted T(r). With this approximation, a natural difference caused by line-of-sight (LOS) projection effects may appear as a function of radius due to density-weighted emission. However, as previously mentioned, due to the density-filtering effect by combination of multiple thermometers, the difference between the two profiles is largely minimized. Moreover, the projected radial temperature profile used as radial temperature profile is further benchmarked and refined by SED construction from a full radiative transfer modeling of dust based on a density profile adopted for the clump (Sect. 3.6, Appendix E), and further shown to be able to produce the observed CH3CCH lines and their spatial variation by full line radiative transfer models (Appendix F).
To probe the gas density, we rely on the CH3OH line series in the 1 mm band as a densitometer. We adopt one-component non-LTE models to derive the hydrogen volume density (n(H2)) maps and benchmark the results using full non-LTE radiative transfer modeling (Sect. 3.6, Appendix F). The highest and lowest ncrit of the adopted line series are listed in Table 3. Moreover, with measured radial temperature profiles, the degeneracy of temperature and density can be further reduced by introducing Tkin (T(r)) in the non-LTE modeling, to constrain solely n(H2). We adopt this strategy in Sect. 3.5 (see also Appendix C). In Sect. 3.5, we use the one-component non-LTE model of CH3OH lines to constrain n(H2). As mentioned before, the excitation of molecular lines has a selective effect on gas densities. Since we are also interested in the bulk gas density structure of massive clumps, we complement the density distribution measure with single-dish multi-wavelength dust emission. We conduct full radiative transfer modeling of dust to fit these data (Appendix E), again incorporating the T(r) initially measured from thermometers. To benchmark the one-component non-LTE models, and to understand the difference of gas density results between modeling dust emission and simple non-LTE modeling of CH3OH, we utilize non-LTE full radiative transfer calculation of lines in Appendix F, for CH3OH and CH3CCH lines. This also helps us to examine the possibility of spatial abundance variations of these lines as an additional factor in affecting the distribution of line emission. In this effort, particularly, the full non-LTE modeling of CH3CCH provides a sanity check on the measured radial temperature profile T(r) from rotational temperature maps. The workflow of the whole procedure is graphically summarized in Fig. 3.
Critical density for transitions of interest.
 |
Fig. 4 Spitzer IRAC RGBs (R: 8.0 μm; G: 4.5 μm B: 3.6 μm) maps of the target sources. Yellow contours show the ATLASGAL 870 μm emission from 1 Jy beam−1 to the peak flux for each source, using seven levels with uniform spacing. White contours show SMA 1.2 mm emission from 3σ to the peak flux using five levels with uniform spacing. Negative flux levels of the 1.2 mm continuum are shown in contours of dotted lines, from − 1σ to the minimum negative flux with two levels. The beam of the SMA continuum is shown in the lower left corner of each plot. The beam size of the archival data for source G10 is much smaller than other sources (Sect. 2.2). The primary beam size is shown in each plot as a blue dashed circle. |
3.2 SMA 1.2 mm continuum
The SMA 1.2 mm dust continuum images resolved two compact sources (separated by ~7.″ 2, ~0.15 pc) in G18, and resolved isolated compact sources in the rest of the samples (Fig. 4). Hereafter we refer to these compact sources as core structures. Before any further analyses, we utilized the archival centimeter band data to subtract free-free contamination in G08b, G31, and G10, assuming optically thin emission (i.e., 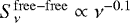 ; for details see Appendix B). Then the core radius is defined as the area above 5σ emission contours of the 1.2 mm images. The core effective radius, peak flux, and integrated flux are listed in Table 4.
; for details see Appendix B). Then the core radius is defined as the area above 5σ emission contours of the 1.2 mm images. The core effective radius, peak flux, and integrated flux are listed in Table 4.
We assumed that dust emission in all cores is optically thin at 1.2 mm. Based on the OH5 opacity model (i.e., κ1.2mm = 0.81 cm2 g−1; Ossenkopf & Henning 1994), we converted the continuum intensity detected at >5σ to dust mass surface density, which was subsequently converted to gas mass surface density by assuming that the gas-to-dust mass ratio is 100. In these mass estimates, we assumed that dust temperature is identical to the gas temperature T(r) which we derived (and refined, Eq. (3)) (see Sects. 3.4, 3.6, and Appendix E).
There is a subtlety in the way we applied T(r), which is related to the assumption of the thermal and density structures of the cores. We compared two ways of applying T(r). In the first, we defined a mean core gas temperature 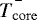 by making averages of T(r) within the core size. For each pixel, we then adopted a dust temperature which is equal to
by making averages of T(r) within the core size. For each pixel, we then adopted a dust temperature which is equal to 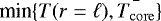 when deriving n(H2), where ℓ is the projected distance from the pixel to the 1.2 mm continuum peak (i.e., centers of the sources). This means that we use the lower value of the two temperatures (average core temperature and radial temperature) at each pixel position to estimate the gas mass probed by dust emission. This is a reasonable assumption since dust emission is sampling all the gas components along the LOS and the average mass temperature is likely dominated by the outer, colder gas component. Given that the projected radius ℓ is always smaller than the radius r, this approach still tends to overestimate the dust temperatures at small projected radii, although it is alleviated. This in turn results in an underestimate of n(H2).
when deriving n(H2), where ℓ is the projected distance from the pixel to the 1.2 mm continuum peak (i.e., centers of the sources). This means that we use the lower value of the two temperatures (average core temperature and radial temperature) at each pixel position to estimate the gas mass probed by dust emission. This is a reasonable assumption since dust emission is sampling all the gas components along the LOS and the average mass temperature is likely dominated by the outer, colder gas component. Given that the projected radius ℓ is always smaller than the radius r, this approach still tends to overestimate the dust temperatures at small projected radii, although it is alleviated. This in turn results in an underestimate of n(H2).
In a second approach, we assumed that the cores are spherically symmetric and optically thin. We used an Abel transform to convert the observed azimuthally averaged intensity profile of 1.2 mm emission to gas density ρ(r) (for more details, see Roy et al. 2014), as
![\begin{equation*} \rho(r) = -\frac{1}{\pi\kappa_{\nu}B_{\nu}[T(r)]}\int_{r}^{r_{\mathrm{eff}}} \frac{\mathrm{d} I_{\nu}}{\mathrm{d}b}\frac{\mathrm{d}b}{\sqrt{b^{2}-r^{2}}}, \end{equation*}](/articles/aa/full_html/2022/02/aa42023-21/aa42023-21-eq5.png) (1)
(1)
where reff is the core effective radius. We then integrated ρ(r) over the LOS to obtain another version of the n(H2) map. The two versions of the n(H2) maps agree within a factor of 1.5–2. The average dust temperature within the core, two sets of mass estimates Mcore and 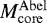 , and average core density are summarized in Table 4.
, and average core density are summarized in Table 4.
Source properties from 1.2 mm SMA continuum.
3.3 Distribution of emission from CH3CCH, H2CS, CH3CN, CH3OH lines and 1.2 mm continuum
Figure 4 shows the 1.2 mm dust continuum images taken with the SMA. We resolved two compact sources (separated by ~7.″ 2, ~0.15 pc) in G18, and resolvedisolated compact sources in the rest of the samples. Figures 5–6 show the integrated intensity maps of CH3CCH, H2CS, and CH3CN, which are overlaid on the integrated intensity maps of CH3OH. In general, the CH3OH lines and the lower K ladders of CH3CCH were resolved on 0.3–0.4 pc scales, while the CH3CN lines and higher K ladders of H2CS were resolved on 0.1–0.2 pc scales. The results of our quantitative analyses are presented in the following subsections.
3.4 Deriving pixel-based gas rotational temperature maps with LTE modeling for multiple thermometers
3.4.1 Thermometers
CH3CCH and CH3CN are symmetric top molecules. Their K-ladder populations at a certain J level are determined primarily through collisions. Therefore, they have been regarded as thermometers for molecular clouds (Kuiper et al. 1984; Bergin et al. 1994). Given their similar geometry and molecular weight, CH3CCH and CH3CN are often assumed to have the same collisional coefficients, while CH3CN has higher dipole moments than CH3CCH. This means that a molecular clump can exhibit brighter CH3CN line emission than CH3CCH even when the excitation of the CH3CN molecules is limited to small pockets of dense gas (e.g., confined to the hot core region).
The CH3CN lines have been very commonly observed (Cummins et al. 1983; Sutton et al. 1986; Fayolle et al. 2015). They have been regarded as good tracers of hot molecular cores owing to the fact that they were mainly detected around significantly heated regions. On the other hand, CH3CCH has been detected in spatially more extended, lower temperature regions (e.g., Bergin et al. 1994; Öberg et al. 2014) and is therefore particularly advantageous for probing sources in relatively early evolutionary stages (Molinari et al. 2016), prior to hot core formation. Giannetti et al. (2017) showed that among the various thermometers the kinetic temperature constrained by CH3CCH is representative of gas temperatures of massive clumps.
The H2CS molecule is a near-prolate rotor. Its transitions between levels at various K ladders are also excellent indicators of the gas kinetic temperature (Blake et al. 1994). As a sulfur-bearing species, the gas phase H2CS abundance can be enhanced either by direct evaporation or by outflow or shock sputtering (e.g., Bachiller & Gutiérrez 1997; Minh et al. 2011). Previous observations have also revealed that the H2CS emission originates from extended warm regions surrounding compact hot cores (e.g., Helmich & van Dishoeck 1997).
3.4.2 Modeling procedure
Using the XCLASS package (Möller et al. 2017), we established a pixel-by-pixel LTE model-fitting procedure for the observed CH3CCH, H2CS, CH3CN, and CH3OH νt = 1 lines (for G10), which returns the best fit of source size, rotational temperature (Trot), molecular column density (Nmol), linewidth (ΔV), and the source velocity (Vsource). In this specific implementation, we fixed the source size to the synthesized beam size (i.e., assuming beam filling factor of 1) and optimized the rest of the free parameters. The optimization procedure employed an initial global parameter search using the bees algorithm (Pham et al. 2006), which was followed by Levenberg–Marquardt iterations. This procedure helps avoid trapping in local minima. We fit the J = 15–14 and J = 14–13 ladders of CH3CCH together, and the J = 12–11 ladders separately, given that the former lines show less extended emission and appear to trace hotter gas. Examples of the fitted spectra are presented in Fig. 7. Examples of the obtained rotational temperaturemaps are shown in Fig. 8. When deriving these rotational temperature maps, we use pixels where the intensity of the third lowest energy transition in consideration is greater than our 3σ detection limit. For the hot molecular core G31, in addition to the few molecular species that we targeted, the fittings also considered several other species that can potentially make a prominent contribution in our spectra. They are shown in Fig. 7 for G31 in different colors. For clump G18 we do not have robust detection of these thermometer lines from our SMA observations, and we rely on previous IRAM 30 m telescope observations (Giannetti et al. 2017) to describe the temperature profile, with the same thermometers but their lower transitions. These pointed observations from the IRAM 30 m telescope did not give information on relevant physical scales; rather, based on a fixed temperature profile (T(r) ∝ R0.4L−0.25, Giannetti et al. 2017) the radius of a certain measured rotational temperature was deduced. Following the same workflow (Fig. 3), these measurements are combined with one-component dust temperatures (Lin et al. 2019) in the outer region of the clump, to compose an initial temperature profile T(r) to be refined later by SED comparison using RADMC-3D.
3.5 Deriving the pixel-based hydrogen volume density maps with non-LTE RADEX model
3.5.1 Methanol lines
Methanol (CH3OH) is a slightly asymmetric top molecule. It has three types of symmetry, which are denoted A, E1, and E2. The E1 and E2 states can be though of as doubly degenerate states of the E symmetry where the quantum number of the angular momentum along the symmetry axis of the CH3 group (k) can take either positive and negative values. The torsional ground state transitions E−CH3OH 5k,5 − 4k,4, K = 0, ±1, ±2, ±3, ±4 (vt = 0) were found to be a good densitometer for gas denser than 104 cm−3 (Leurini et al. 2004, 2007).
The excitation of these K ladders is usually observed to be subthermal. These K = 0 and K = ±1 ladders occupy a rather narrow range of upper level energies (Eup ~ 40–55 K). At the same time, they cover a wide range of critical densities (~105 to ≳107 cm−3) (Table 3), which implies that the line ratios of two K components can be good density probes. The higher K components (K ≥ 3, Eup > 80 K) are generally excited in hot regions where the gas volume densities are close to or higher than the critical densities. Hence, ratios of the K ≥ 3 components provide additional constraints on kinetic temperature. Apart from the high abundance of CH3OH, it is this property of the methanol energy system and the relatively low upper level energies of the K < 3 transitions that make this line series sensitive to gas density for a broad range of physical conditions in molecular clouds (Leurini et al. 2004).
As illustrated in Fig. 5, the CH3OH emission appears clumpy and exhibits elongated structures, extending for up to 0.5 pc with respect to the continuum peak. The K < 2 transitions of E−CH3OH (5–4) (νt = 0) are excited over an extended region, while the emission of the K > 2 lines are confined to the central region of the clumps.
 |
Fig. 5 Integrated intensity maps (gray contours) of CH3CCH, H2CS, and CH3CN toward sources G19, G08a, and G08b. Integrated intensity of CH3OH 50,5 –40,4 ([vlsr −3, vlsr + 3] km s−1) is shown in color scale. Gray contours show the intensity levels with uniform intervals from 5σ up to the peak flux, with the emission range (Jy beam−1 km s−1) indicated in the lower left corner of each panel. Colored contour in the left panel shows the location of 0.8 × peak emission of the 1.2 mm SMA continuum image. The green ellipses indicate beams of corresponding molecular lines (open) and CH3OH 50,5 –40,4 line (filled). |
3.5.2 Modeling procedure
We produced a series of large velocity gradient (LVG) RADEX models (van der Tak et al. 2007) to search for the best fits of n(H2), CH3OH column density, N(CH3OH-E)/N(CH3OH-A), and kinetic temperature (Tkin) to the observed CH3OH (J = 5–4, νt = 0) lines. We took the collisional rates from Rabli & Flower (2010), which were evaluated for temperatures from 10 to 200 K. We adopted a Markov chain Monte Carlo (MCMC) method to derive the parameters and estimate the associated uncertainties, taking into consideration the upper limits for weakly detected line components. The details of the modeling procedure are elaborated in Appendix C where the formulas used for the likelihood function are given. In the fitting, for each pixel we enforced the posterior distribution of Tkin to be a narrow Gaussian distribution centralized at T(r) (see Sect. 3.6), as measured in Sect. 3.4 from the multiple rotational temperature maps. Although the ratios between the lower K ladders of CH3OH lines depend only weakly on the kinetic temperature, having a fixed term helps avoid randomly converged parameters, which is useful to ensure that the resultant parameter maps are continuous. The obtained n(H2) maps are shown in Fig. 9. The CH3OH column density maps are shown in Fig. C.2.
3.6 Radial density and temperature profiles used in full radiative transfer models
We used the RADMC-3D code (Dullemond et al. 2012) in our full radiative transfer analyses (Fig. 3; Sect. 3.1) for the multi-wavelength dust continuum (Appendix E). We assumed that the gas density profile for the bulk gas (ρbulk(r)) is described by the functional form
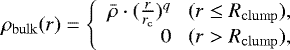 (2)
(2)
where 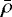 is the mean hydrogen gas number density, and rc is the radiuswhere
is the mean hydrogen gas number density, and rc is the radiuswhere 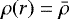 , Rclump is the assumed outer radii of the clumps that were fixed to the FHWM measured from the ATLASGAL 870 μm maps (see Contreras et al. 2013). When converting gas density to mass density, we assume that the mass per hydrogen molecule is 2.8 mH, where mH is the hydrogen atom mass. We assumed that the gas-to-dust mass ratio is 100.
, Rclump is the assumed outer radii of the clumps that were fixed to the FHWM measured from the ATLASGAL 870 μm maps (see Contreras et al. 2013). When converting gas density to mass density, we assume that the mass per hydrogen molecule is 2.8 mH, where mH is the hydrogen atom mass. We assumed that the gas-to-dust mass ratio is 100.
We parameterized the measured temperature profiles T(r) by
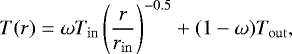 (3)
(3)
where  is an exponential tapering function characterized by outer radius rout, and Tin and Tout are the characteristic temperatures at the radius rin and at asymptotically large radii, respectively. In this equation, the first term describes radiative heating by the centrally embedded stars, while the second term can be attributed to the ambient radiation fields of the massive clumps (Liu et al. 2019). The multiplicative factors ω and (1 − ω) prescribe the transition from one heating regime to the other.
is an exponential tapering function characterized by outer radius rout, and Tin and Tout are the characteristic temperatures at the radius rin and at asymptotically large radii, respectively. In this equation, the first term describes radiative heating by the centrally embedded stars, while the second term can be attributed to the ambient radiation fields of the massive clumps (Liu et al. 2019). The multiplicative factors ω and (1 − ω) prescribe the transition from one heating regime to the other.
Based on the multiple rotational temperature maps, we derived the (projected) radially averaged temperature profile and obtained best-fit parameters Tin, Tout, and rout, while rin was initially kept as a fiducial value of 0.02 pc. Figures 10 and 11 show the comparison between these multi-wavelength radial intensity profiles and the SEDs evaluated from best-fit RADMC-3D (Dullemond et al. 2012) models. Based on this comparison, we re-adjusted the rin of Eq. (3) in the RADMC-3D modeling to obtain an SED profile consistent with the observed data points. The parameter T(r) was then updated by the refined temperatureprofile. The parameters Tin, Tout, rin, and rout that define T(r) are listed in Table 5. With T(r) defined, we fixed the dust temperature profile in the multi-wavelength continuum modeling for the bulk gas and obtain ρbulk(r). The best-fit parameters 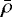 and q as in Eq. (2) are listed in Table 6.
and q as in Eq. (2) are listed in Table 6.
From RADEX modeling of CH3OH lines we constrained the radial density profiles for the dense gas, ρdense(r), from the obtained n(H2) maps. Similarly, when deriving the n(H2) maps (Fig. 9) we fixed the gas kinetic temperature in the modeling to T(r) for each pixel. We adopted a single power-law form as Eq. (2) to characterize the dense gas density profiles,
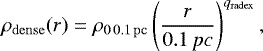 (4)
(4)
where ρ0 0.1 pc is the reference gas density at 0.1 pc. The description is valid up to a maximum scale of Rmax, which is determined from the largest radius where n(H2) can be robustly estimated. These parameters are also listed in Table 5. Figure 12 shows the comparison between the model fits and the observed radial profiles.
We then conducted full radiative transfer modeling with LIME (Brinch & Hogerheijde 2010) to benchmark and refine these results. In the LIME modeling of CH3OH and CH3CCH lines, we first adopted the bulk gas density profile ρbulk(r) constrained from single-dish dust continuum modeling, and T(r) with assumed abundance profiles to find the best-fit models. We parameterized the molecular abundance profiles (Xmol(r)) as
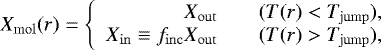 (5)
(5)
where Tjump is a threshold temperature chosen to be either 30 or 80 K, Xout is the abundance at the outer radii, and finc is an increment factor to characterize the abundance enhancement in the inner regions of higher temperature. This form is driven by previous chemical models of CH3OH and CH3CCH, in which prominent abundance enhancement is seen around the two Tjump temperatures (see Appendix F). The best-fit parameters Tjump, Xout, and finc for this model (hereafter model A) are listed in Table 7 (Col. A). For all sources we find that with the assumed density profile of ρbulk(r) the models cannot reproduce the observed high ratios between the higher and lower K components of CH3OH lines, as shown in Fig. 13 (presenting the comparisons between modeled results and observations toward clump G08a and G08b), which points to, as also indicated by the RADEX modeling results, a much higher gas density regime from which these CH3OH higher K components originate. Therefore, we complemented the LIME models with density profiles of the dense gas component ρdense(r) as in Eq. (4) (the RADEX results of gas density radial profiles):
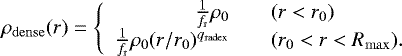 (6)
(6)
Here, r0 denotes the reference radius of 0.1 pc or 0.05 pc (for G13 and G31) and ρ0 is the reference density at r0. These values, together with Rmax, were derived by RADEX modeling. Here fr is a reduction factor applied to ρ0. This parameter is empirically added to the density profile so that the LIME models more closely match the observed data. In essence, it means that RADEX results of one-component non-LTE modeling tend to overestimate the projected radial density in a 3D structure clump. We manually adjusted fr and Xmol(r) to seek for better fits to the observational data. In what remains, we refer to qradex as qdense as this slope is fitted based on n(H2) maps of CH3OH RADEX modeling and is retained as the slope for the dense gas profile in full radiative transfer LIME models. The best-fit model parameters Tjump, Xout, finc, and fr for this model (hereafter model B) are summarized in Table 7 (Col. B). Figure 14 shows a comparison between the CH3OH line profiles reproduced from model B and the observations toward clump G08a and G08b. The comparisons between model A, model B, and the observations for other target sources are shown in Appendix G.
 |
Fig. 7 Example spectra of thermometer lines CH3CN J = 13-12, CH3CCH J = 14-13, H2CS J = 6-5, H2CS J = 7-6 at the continuum peak of the target source. The blue profiles show the XCLASS LTE fitting results. For source G31.412+0.307, which presents significant line blending from other species, the fittings also included those species and transitions that can potentially make prominent contributions to the spectrum. |
 |
Fig. 8 Rotational temperature maps of source G08b derived from multiple thermometer lines using the XCLASS package (Sect. 3.4). The green contours indicate SMA 1.2 mm continuum levels from 0.3 to 0.9 × peak flux (Table 4) in five steps of uniform interval. The beams of the continuum and the respective lines are shown in the lower left corner as green and hatched ellipses, respectively. |
 |
Fig. 9 CH3OH derived n(H2) maps from RADEX modeling of all target sources. The beam of the CH3OH 5−1 -4−1 E line is indicated in the bottom left corner. The gray contours indicate the SMA 1.2 mm continuum level from 0.1 to 0.9 × peak flux represented by five steps of uniform interval. |
3.7 Comparison of the samples: density and temperature structures
We make a comparison of the fitted and refined T(r) profiles (Eq. (3)) of all sources in Fig. 15 (left panel). We can see (for all the clumps) that at 0.1 pc the resolved gas temperatures are in the range 30–80 K, and at 1 pc around 20–30 K. Moreover, the gas temperature at a certain clump radius is not a monotonic function of the bolometric luminosity of the clump. Particularly, the hot massive core G31 and the source G13 display higher temperatures in the inner regions than their immediate more luminous sources in the sample. We discuss these temperature profiles in more detail in Sect. 4.1.
In Fig. 15 (right panel), we also compare the derived radial gas density profile of the dense gas from CH3OH modeling with RADEX/LIME. It can be seen that n(H2) is several ~105 to 107 cm−3 at ~0.2–0.3 pc (projected) radii. In the inner ~0.1 pc where the SMA identified continuum cores (Sect. 3.2), n(H2) ranges from several ~106 to 108 cm−3. There are exceptionally high n(H2) values at the center of G31. Although we have verified the high level of dense gas of this source compared with the rest of the sample by full radiative transfer modeling of CH3OH lines (Appendix F), we caution that in this density regime the CH3OH (5-4) lines become heavily optically thick and the critical density for the considered line transitions is reached (e.g., n >ncrit, Table 3), such that the relative differences between the level populations do not serve as ideal densitometers anymore. Nonetheless, we can safely argue that the hot massive core G31 has much higher gas densities in its inner region than other sources, which is also reflected by the very monolithic nature of its central core from higher angular resolution observations (~2000 au, see Beltrán et al. 2018). For source G10, there are prominently higher gas densities at extended radii of 0.1–0.4 pc than for other sources, which is related to the presence of a large disk-like flattened structure. We discuss further the density profiles among the sample in Sect. 4.2.
We compare the steepness of the radial gas density profiles (qbulk and qdense, for ρbulk and ρdense) as a function of source evolutionary stages, which is indicated by the clump bolometric luminosity-to-mass ratio L∕M (Fig. 16). Using the Spearman correlation measure, we find that there are positive correlations (correlation coefficient ρ = −0.95 and −0.61) between the density power-law slopes with L∕M for the dense gas component and for the bulk gas structures, although the significance of the correlation of the former is low (p-value = 0.15). The slopes range from –0.6 to –1.7 for the bulk gas, and –0.25 to –1.7 for the dense gas, for L∕M spanning from 10 to ~100 (L⊙ ∕M⊙) of all sources. The correlation between L∕M and the density slope representing the bulk gas distribution is clearly stronger. A similar evolutionary trend was reported by Beuther et al. (2002) based on the analyses of 1.2 mm dust continuum emission of a sample of massive clumps, in which the bulk gas density structure was probed. Comparably, other works on the density structures of massive clumps typically derived power-law slopes from −2.25 to −0.75 and peaking at −1.8 to −1.6 (Mueller et al. 2002; Beuther et al. 2002; van der Tak et al. 2000). In the early-stage sources (L∕M < 20), the slopes we derived are relatively shallow (>−1.0) for both the bulk gas and dense gas density structures. We note that the slope derived for the dense gas structure of the early-stage source G18 is valid for a confined region of ~0.1 pc (just above the beam size), which merely reflects a pocket of dense gas that is rather compact and remains unresolved. Yet, for other early-stage sources (G28 and G19), the statistics for determining the density slope are adequate, and these two sources exhibit shallow slopes of ~−0.6. We note that different analysis methods of density structure could result in systematic biases in the derived density slopes. In addition, the analyses of dust continuum that were based on the optically thin assumption, instead of relying on full radiative transfer models, suffer from the degeneracy of density and temperature profiles in determining the radial intensity profiles. Moreover, close to the source center, the optically thin assumption for dust emission may also break down. Although a qualitative comparison can be made, a careful gauge between the different analyses conducted are necessary for a stringent comparison between different works. In Sect. 4.5 we discuss the relation between density profiles of massive clumps and statistics on cloud structure in greater detail. We also elaborate on the physical implications by comparing ρbulk and ρdense from the sample.
 |
Fig. 10 Radial intensity profile comparisons between observations and best-fit RADMC-3D models. Gray horizontal dashed lines indicate the noise level (3σ). Gray vertical lines indicate the clump radius used in the modeling. The dotted line indicates beam shape in each plot. For source G18, G19, G08a, G13, and G31, the model fit after re-adjusting T(r) is shown. The gray vertical line indicates the clump radius Rclump. |
 |
Fig. 11 Comparison of SEDs of the best-fit RADMC-3D models with measured multi-wavelength fluxes (green dots with error bars indicating 0.8 and 1.2 times the flux level) for each source. The black line indicates the SED generated from assumed T(r) and the corresponding best density profile fits. The blue dashed line indicates the SED generated from refined T(r) and the re-iterated best density profile fits. The blue shaded regions indicate a 20% difference around the blue dashed SED profile. The red line shows the SED generated by self-consistently calculating the dust temperature adopting a central heating ZAMS star plus the re-iterated best density profile (for more details, see Appendix E). |
3.8 Molecular linewidths and virial parameter
To understand the dynamic states of the target clumps, we examined how the linewidths and virial parameters vary with clump radii. Part of these analyses were based on the thermometer lines, CH3CN, H2CS, and CH3CCH. They primarily trace the dense gas close to the centers (0.1–0.4 pc) of the clumps. In addition, we examined the CS and C34S (5-4) and H13CO+ (3-2) lines which can trace spatially more extended clump structures due to their lower excitation conditions. We performed single component Gaussian fits to the CS, C34S (5-4), and H13CO+ (3-2) line cubes in a pixel-by-pixel manner to obtain the linewidth maps. For the analysis, we trimmed the pixels that have fitting errors of linewidth larger than 2 times the velocity channel widths (ΔV < 2 km s−1).
The virial parameter αvir characterizes an important aspect of the physical states of the molecular clumps. The ordinary definition of αvir (i.e., ignoring magnetic field; see Bertoldi & McKee 1992) is
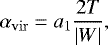 (7)
(7)
where 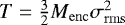 is the kinetic energy,
is the kinetic energy, 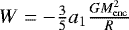 is the gravitational potential energy, Menc is the enclosed mass, and a1 is a geometric factor that accounts for the inhomogeneity of the density distribution (e.g., Bertoldi & McKee 1992; McKee & Holliman 1999). For a spherical clump that has a ∝ r−q radial gas density profile,
is the gravitational potential energy, Menc is the enclosed mass, and a1 is a geometric factor that accounts for the inhomogeneity of the density distribution (e.g., Bertoldi & McKee 1992; McKee & Holliman 1999). For a spherical clump that has a ∝ r−q radial gas density profile, 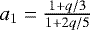 . With this definition, a source in energy equipartition (T ~ |W|) has a critical virial parameter of αcr = 2a1. In a virialized source (2T ~ |W|), it stands that αvir = a1 with αvir ∕αcr = 0.5. In the following we refer to the states of αvir∕αcr < 0.5, ~0.5–1, and >1 as sub-virial, virial, and super-virial, respectively.
. With this definition, a source in energy equipartition (T ~ |W|) has a critical virial parameter of αcr = 2a1. In a virialized source (2T ~ |W|), it stands that αvir = a1 with αvir ∕αcr = 0.5. In the following we refer to the states of αvir∕αcr < 0.5, ~0.5–1, and >1 as sub-virial, virial, and super-virial, respectively.
When deriving αvir, it is critical that the tracers observed for the measurement of Menc and σrms predominantly emanate from the same gas entity (Traficante et al. 2018). The mass tracer we adopted, which is the dust continuum emission, traces a broad range of gas volume density values distributed over a wide range of radius values. Our selected tracers to indicate linewidths, as the way the temperature profile is measured, show emission of progressively larger radii, which are complemented with the aforementioned three tracers of more extended emission. We can now examine the spatial variation of linewidths and αvir based on multiple tracers that cover distinct critical densities (Table 3), and hence different spatial scales. We evaluated how αvir∕αcr varies with radius using the best-fit density models from the RADMC-3D continuum modeling (Appendix E) to obtain Menc, a1 and the linewidth maps from the tracers. Compared with the SMA observations, we note that the RADMC-3D models constrained by the coarser resolution single-dish continuum data systematically underpredict the 1.2 mm fluxes in the inner radii. To avoid this bias, we adopted the Menc as 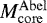 (Sect. 3.2) for the inner regions. We recall that
(Sect. 3.2) for the inner regions. We recall that 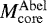 is calculated by applying the derived T(r) to SMA 1.2 mm continuum. We discuss the obtained radial profiles of linewidth and virial parameter in Sect. 4.3.
is calculated by applying the derived T(r) to SMA 1.2 mm continuum. We discuss the obtained radial profiles of linewidth and virial parameter in Sect. 4.3.
Parameters of CH3OH derived radialdensity ρdense(r) and multi-thermometer derived temperature profiles T(r).
Best-fit parameters from RADMC-3D modeling of the dust continuum in 350 or 450 μm, and 870 μm.
3.9 Molecular abundance and abundance ratios
To facilitate the analysis on clump evolutionary stages, we derived the LOS integrated abundance maps (Nmol/N(H2)) for some relevant molecular species for all sources. The bulk gas density profiles (ρbulk (r), Sect. 3.6, and Appendix E) were adopted and smoothed to the angular resolution of the specific line transition when deriving Nmol/N(H2). The calculation of Nmol for CH3CCH, CH3CN, H2CS, and CH3OH is introduced in Sects. 3.4 and 3.5. The calculations of the Nmol maps of the CS/C34S, SO, SO2, and CCH lines were based on LTE assumption and are detailed in Appendix D. We then derived the projected radial averaged abundance profiles for each molecule. Naturally, the projected radial averaging suppresses the contrast in the spatial variations of the abundance for the molecules that are enriched in the clump center or other localized regions (which reduces N(H2) to localized values rather than integration along the LOS extension). Nevertheless, this does not qualitatively change the overall radial trends as long as the abundance is increasing or decreasing with radius monotonically, with a steeper profile than that of the column density, while the latter is rather shallow, following Σ ∝ ρr ∝ ρ1+q < ρ−0.7. In Figs. 17 and 18, we show the relations between the clump bolometric luminosity and the radial abundance variations of the carbon-chain and sulfur-bearing molecules in consideration, respectively.
In Fig. 17, we note that the abundances of CH3OH, CH3CCH, and CH3CN show similar behaviors. They appear largest in the hot massive cores G31; in the rest of the sources, the abundances of CH3OH and CH3CCH are in the range of several 10−9–10−8, while the abundances of CH3CN are in the range of 10−10–10−9. These abundances are slightly positively correlated with the clump luminosity. The abundances of CH3CN and CH3OH appear more tightly correlated with the source temperatures in the inner ~0.1 pc regions (see the insets in Fig. 17). These trends are consistent with theoretical predictions that the de-sorption of these molecules from the grain surface becomes more efficient with increasing temperature. We note that these results cannot be obtained if the gas temperature distributions are derived based merely on the assumptions of bolometric luminosity scaling instead of being derived based on multi-transition rotational temperature maps, since we have previously seen that the gas temperatures at certain radii do not necessarily increase monotonically with clump luminosity (Fig. 15, left panel). This result demonstrates the importance of measuring detailed temperature profiles when studying chemical evolution.
We observed a weak correlation of abundance of CH3CCH and bulk gas temperature, which is reminiscent of the small variation of the CH3CCH abundance toward massive clumps of various evolutionary stages reported by Giannetti et al. (2017) (see also Öberg et al. 2014). Other higher angular resolution observations of this species indicated a mixed behavior of its spatial distribution, depending on whether the emission coincides with the localized hot cores or appears offset and/or shows more extended structures (Bøgelund et al. 2019, Öberg et al. 2014, Fayolle et al. 2015). Comparing rotational temperature maps of CH3CCH (12-11), the temperatures of G13 and G31 in the core region is 20–30 K higher than those of G19, G08a, and G08b. In addition, the higher J transitions CH3CCH (14-13), (15-14) trace systematically higher temperatures in the core region toward all sources. This evidence indicates that the emission of CH3CCH has a contribution from gas components residing inside or in the vicinity of hot cores. As for the result of CCH, except for the earliest-stage source G18, its abundance appears enhanced at outer radii. We can also see that the abundance of CCH measured in the inner ~0.1–0.2 pc region is anti-correlated with the clump luminosity. These results are consistent with previous observations that show shell-like CCH emission toward late-stage massive star-forming regions (Beuther et al. 2008; Jiang et al. 2015).
The abundance ratios of CCH, CH3CCH, and CH3CN with CH3OH in the clump center (0.1–0.15 pc) are shown in Fig. 19. Here, normalization with CH3OH allows exploring the chemicalevolution or initial condition by eliminating the effect of different desorption levels among the sample. There are substantial variations of [CCH]/[CH3OH] and [CH3CN/CH3OH] across L∕M, while variations of [CH3CCH/CH3OH] appear moderate.
The abundances of sulfur-bearing species in the central regions of the clumps also show correlation with temperatures (Fig. 18). Comparing the relative abundance of C34S and H2CS with respect to SO as a function of L∕M (Fig. 19, bottom panel), it seems there is a mixed behavior; except for source G13, the other sources show a weak increasing trend above L∕M ≳ 10. For X(SO2)/X(SO), there is a moderate increasing trend with source L∕M. We discuss the abundance variations further in Sect. 4.4 in a broader context, with comparisons with published results from chemical modeling.
 |
Fig. 12 Projected radial averaged n(H2) radial profiles derived from n(H2) maps shown in Fig. 9. The thick gray line indicates the best-fit single power-law model (beam convolution considered). The gray shadowed band indicates the 3σ confidence band of the best-fit model. The model parameters and 1σ errors are listed in Table 5. |
 |
Fig. 13 LIME modeling result (best-fit parameters listed in Table 7, Col. A) based on best-fit density model from RADMC-3D continuum modeling. From left to right: Annular beam-averaged spectra from the continuum center to the outer envelope. Considering the typical beam FWHM of our observations: the distance from the center of each annular region to the center of the source is indicated at the top of each spectra. The line components of A- and E-type CH3OH are indicated with short-dashed vertical lines in green and gray, respectively. |
4 Discussion
4.1 Temperature structure and heating mechanisms of massive star-forming clumps
The temperature measurement from multiple Trot maps and the fitted and refined temperature profile T(r) (Eq. (3)) are shown in Fig. 20. The d logT/d logR profiles are also summarized in the bottom right panel. Except for sources G13 and G31, the d logT/d logR profiles asymptotes from –0.5 to zero from inner to outer radii. The levelling-off of the temperature at the outer radius of the clump is expected since all these massive star-forming clumps are immersed in intense interstellar radiation fields. At gas densities >104.5–105 cm−3, thermal coupling between gas and dust can be quickly achieved due to collisions (Goldsmith 2001; Glover & Clark 2012). However, the 104.5 cm−3 density threshold is not met in the outer layers of the sources that have lower masses. As we explain below, the thermal decoupling between gas and dust is seen in some of these sources. The outer envelope dust temperature for all these sources flattens around 18–25 K. These values are consistent with an elevated infrared radiation field associated with these regions. Based on these temperatures, the scaling factors of the local ISRF (Mathis et al. 1983) to characterize the radiation field surrounding these clumps are roughly ≳102.5-104 (estimated in the optically thick limit, Krumholz 2014), which are typical values found in the vicinity of Galactic massive star-formingcomplexes (Binder & Povich 2018).
The T(r) and d logT/d logR in the inner regions can be approximated by the analytic temperature profile of thermally balanced dust grains distributed around a central heating point source (e.g., Adams 1991). With optically thin condition and a submillimeter dust opacity spectral index (β), the model of Adams (1991) predicted that the radial temperature profile for dust grains in thermal balance around a central heating point source is proportional to r−2∕(4+β). If β has no spatial variations, then d logT/d logR should be a constant of radius. In the diffuse interstellar medium β is around 1.8 (for a review, see Hildebrand 1983), which yields a temperature slope of ~ −0.35. In high-density regions, β may become lower due to dust growth (e.g., Ossenkopf & Henning 1994), resulting in a steeper temperature profile. Values of β lower than 1.8 have been have been reported by some previous observations toward Class 0-II young stellar objects (YSOs), and toward protostellar and prestellar cores (e.g., Beckwith & Sargent 1991; Jørgensen et al. 2007; Bracco et al. 2017, and references therein). This comes with the caveat that the previous (sub)millimeter observations of dust growth might have systematically underestimated β values owing to underestimating optical depths (e.g., Li et al. 2017), neglecting the effect of dust scattering opacity (e.g., Liu 2019), and the effects of temperature mixing when performing SED fittings (e.g., Juvela et al. 2018). From a modern point of view, on the spatial scales of molecular clumps, there might not yet be solid evidence for the presence of β <1 (i.e., a flattened SED curve at longer wavelengths). We note that observations revealing a prevalent excess of 3 mm emission compared to the generic modified blackbody model have been reported (e.g., Lowe et al. 2021); however, the origin of such a feature remains uncertain.
In Fig. 20, we also compare the observed temperature profiles with the centrally heated models evaluated for β = 1 (i.e., 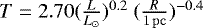 ), based on the assumption of a dust sublimation temperature of 1.1 × 103K in the derivation (Adams 1991, for more calculation details see the Appendix therein), and with the simple expectation based on the Stefan-Boltzmann law (i.e.,
), based on the assumption of a dust sublimation temperature of 1.1 × 103K in the derivation (Adams 1991, for more calculation details see the Appendix therein), and with the simple expectation based on the Stefan-Boltzmann law (i.e., 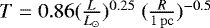 ). We found that these profiles qualitatively agree with the measurements of T(r) except for G13 and G31.
). We found that these profiles qualitatively agree with the measurements of T(r) except for G13 and G31.
In Fig. 20, it can be seen that the temperature profiles of G13 and G31 deviate from the form of a single power law. Specifically, they show abrupt changes as well as elevated temperatures in the ranges of 0.1–0.3 pc and 0.1–0.5 pc radii, respectively. After we adjusted T(r) (Appendix E) according to dust SED profiles, G13 shows a less prominent temperature enhancement in the center, while G31 still stands out. Beltrán et al. (2018) also noted the steep temperature profile of G31 within the central 0.1 pc. Their measurement consistently falls onto the functional form we fitted (i.e., the thick purple line in Fig. 20) which was based on our independent measurements of Trot on the larger spatial scales.
The rapid decrease in radial temperatures observed in G31 and G13 may be explained by their density profiles of the embedded dense gas structures (i.e., ρdense(r)). In Fig. 12, it can be seen that these two sources have the most steeply decreasing ρdense(r). In addition, their central ~0.1 pc regions show prominent high-densityplateaus. The optically thin assumption of Adams (1991) may break down in the central region of the G31 and G13. This higher concentration of dense gas may steepen the temperature distribution in the inner envelope according to 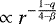 (e.g., Adams & Shu 1985; Rolffs et al. 2011), where q is the power-law index of radial density profile. This is close to the diffusion approximation, which effectively means that a higher optical depth gas would mimic the lower value of β in determining the temperature structure. The presence of flattened (protostellar) disks could also induce a steeper gradient (~–0.75) of temperature variations due to the gas heating by infall and accretion shocks (e.g., Lynden-Bell & Pringle 1974; Walch et al. 2009). Interestingly, hydrodynamic calculations of protostellar collapse demonstrate that a centrally flattened density profile results in a transitory phase of energetic accretion (Foster & Chevalier 1993, see also Henriksen et al. 1997), which may also be related to the elevated temperatures of G13 and G31.
(e.g., Adams & Shu 1985; Rolffs et al. 2011), where q is the power-law index of radial density profile. This is close to the diffusion approximation, which effectively means that a higher optical depth gas would mimic the lower value of β in determining the temperature structure. The presence of flattened (protostellar) disks could also induce a steeper gradient (~–0.75) of temperature variations due to the gas heating by infall and accretion shocks (e.g., Lynden-Bell & Pringle 1974; Walch et al. 2009). Interestingly, hydrodynamic calculations of protostellar collapse demonstrate that a centrally flattened density profile results in a transitory phase of energetic accretion (Foster & Chevalier 1993, see also Henriksen et al. 1997), which may also be related to the elevated temperatures of G13 and G31.
Observations toward dense massive cores and envelopes of YSOs and disks generally find temperature slopes in the range of ~[–0.35,–0.7] (e.g., Palau et al. 2014; Beuther et al. 2007; Persson et al. 2016; Jacobsen et al. 2018; van ’t Hoff et al. 2020; Gieser et al. 2021). However, the exceptionally steep temperature profile of slope steeper than –0.9 is seen at 1000–2000 au around the massive YSO W3IRS4 (Mottram et al. 2020), reminiscent of the result of G31 based on observations of similar spatial scales (Beltrán et al. 2018).
Strong radiative feedback has been invoked as a possible mechanism to prevent overfragmentation, which favors the formation of massive stars and such effect can be influential in ultra-dense environment (e.g., Krumholz et al. 2012). When observed with ~2000 au resolution, source G31 consists of two cores with one major core dominating the emission (~60 times flux difference at 1 mm continuum, Beltrán et al. 2018). The elevated temperature in the inner 0.1 pc might have suppressed the fragmentation of the envelope structure of the main core, leaving only one satellite core surrounding it. The highly concentrated dense gas structure of G13 traced by methanol lines (Fig. 9) that does not extend further beyond its continuum emission (except to the west) may also indicate a featureless fragmentation; high-resolution (1″) mid-IR imaging by Varricatt et al. (2018) reveals a binary system, although the mass contrast between the two YSOs embedded is not as drastic as that of G31.
 |
Fig. 14 LIME modeling result (best-fit parameters listed in Table 7, Col. B) after manually adjusting the density profile obtained from RADEX modeling (Eq. (4)), which is prescribed as a piecewise power law (Eq. (6)). From left to right: annular beam-averaged spectra from the continuum center to the outer envelope. Considering the typical beam FWHM of our observations: the distance from the center of each annular region to the center of the source is indicated at the top of each spectra. |
 |
Fig. 15 Radial temperature and density profiles of target clumps. Left panel: radial temperature profiles T(r) for all the target sources (Eq. (3), refined T(r) is used for the relevant source). The thickness of the lines increases with increasing luminosity. Right panel: radial (projected radial averaged) density profile of the dense gas (ρdense) of all the target sources, from n(H2) maps derived by RADEX modeling of CH3OH lines. The range of the y-axis is trimmed to increase contrast. For both panels the luminosity and clump mass are calculated from RADMC-3D best-fit model (Table 6), which takes into account all the gas components present in the clumps. |
 |
Fig. 16 Radial gas density slopes of all target clumps. Left panel: density power-law slope derived from continuum (q) based on RADMC-3D modeling detailed in Appendix E. The luminosity, clump mass, and enclosed mass within 0.5 pc are calculated from the RADMC-3D best-fit model, as listed in Table 6. Right panel: density power-law slope derived from n(H2) maps (qradex) from the CH3OH RADEX modeling detailed in Sect. 3.5. The yellow horizontal line in both plots shows a slope of –1.5, indicating the free-falling density profile of a singular isothermal sphere (with an initial density slope of –2) as in Shu 1977, and the attractor solution of the gravo-turbulent collapsing in Murray et al. (2017). |
 |
Fig. 17 Abundance profiles of molecules CH3OH, CH3CN, CCH, and CH3CCH toward target sources. The symbols are color-coded based on relative distance to the clump center (the 1.2 mm continuum peak). Stars represent abundances at the clump center, and hollow circles or triangles indicate abundances obtained from different radii: the larger and darker these symbols, the closer the distance to the continuum peak. For clump G28 the data points at outer radii are shown as triangles, whereas those for other clumps are shown as circles, to further avoid confusion. X(CCH) for source G10 is taken from Jiang et al. (2015). The inset plot for CH3CN shows the central abundance vs. gas temperature at 0.1 pc; the plot for CH3CCH shows the envelope abundance vs. gas temperature at 0.3 pc. |
4.2 Density structure evolution: comparison with theoretical predictions
Figure 9 shows the n(H2) maps that were derived based on the RADEX modeling for the CH3OH lines (Sect. 3.5). In general, n(H2) decreases radially with respect to the continuum center, although some sources appear notably asymmetric and present localized overdensities at large radii. We use single power-law forms (Eq. (4)) with the parameters listed in Table 5 to describe the radial change of n(H2) maps. Comparing the observed profile to the fitted single power-law form (Fig. 12), it can be seen that there are higher density plateaus at the centers of G13 and G31, such that these two sources are better described by piece-wise power law including a central density profile of slope ~0. Source G10 harbors even more dense gas at >0.1 pc radii compared to its best-fit single power-law model, which is due to the highly flattened dense gas geometry of an edge-on rotational disk, as revealed by gas kinematics (Liu 2017). For G10 the slope of the dense gas profile qdense is an average of two distributions: a geometrically flattened high-density pseudo-disk with a slope shallower than –0.5, and an envelope whose gas density decreases sharply (Fig. 9). Clumps G28, G19, and G08a may also harbor high-densityplateaus at the centers although they are not as significantly resolved as those in G10, G13, and G31.
We note that the two sets of power-law density slopes derived reflect clump gas in different density regimes: from the single-dish continuum the slope represents density distribution of averaged (mass-weighted) bulk gas ( ~ 104.5 cm3) where the spherical symmetry might be a good approximation of source geometry, while the slope deduced from the methanol emission reflects the truncated central dense gas portion (ρ ≳ 106.5 cm−3) with an extension of 0.1–0.5 pc. This dense gas structure is likely highly fragmented and of reduced dimension due to the dominant role of self-gravity at increasingly smaller scales and denser regimes.
~ 104.5 cm3) where the spherical symmetry might be a good approximation of source geometry, while the slope deduced from the methanol emission reflects the truncated central dense gas portion (ρ ≳ 106.5 cm−3) with an extension of 0.1–0.5 pc. This dense gas structure is likely highly fragmented and of reduced dimension due to the dominant role of self-gravity at increasingly smaller scales and denser regimes.
Figure 16 reveals the evolutionary trend of the radial density profiles of bulk gas and dense gas structures of the target massive clumps. Our results indicate that in the initial stage of massive clump evolution, gas may be less concentrated than the singular isothermal sphere (SIS, Shu 1977), and even the logatropic model (McLaughlin & Pudritz 1997). Observations toward low-mass cores at early stages have generally found density profiles with a central plateau (e.g., Ward-Thompson et al. 1999; Bacmann et al. 2002). This density structure implies low-pressure gradients at small radii, and hence in quasi-static models additional support of magnetic fields is required. The magnetic field and subsequent ambipolar diffusion may explain the existence and evolution of the shallower radial density profile of the gas, which is at an initial stage of equilibrium (e.g., Mouschovias & Morton 1991). Alternatively, in an isothermal state, the incoherently converging compression wave of shocks propagating outside-in can also disrupt the centrally peaked density profile (Whitworth et al. 1996). Finally, hydrostatic models of a self-gravitating gas externally heated (e.g., Falgarone & Puget 1985) can also result in a similar density configuration. On the other hand, we cannot rule out the possibility that the shallower density profiles reflect the underlying fragmentation that is distributed widely within the clump, and that the fragments do not show significant mass segregation (Sanhueza et al. 2019). Their imprints would result in a uniform density profile for the clumps.
Following the definitions in Sect. 3.6, we denote the power-law slopes for the radial gas density of bulk gas and dense gas as qbulk and qdense. In G18 and G28, both qbulk and qdense are shallower than −1 (Fig. 15). This may be due to a combination of the heated gas profiles and a higher level of turbulence, which effectively slow down gravitational collapse at early stages (Fig. 21; more in Sect. 4.3). Although these two sources have L∕M ≲ 10, and are classified to be younger than or just reaching the zero age main sequence (ZAMS) phase (Molinari et al. 2008; Giannetti et al. 2017), it is possible that the enhanced energy release of accretion associated with the massive star formation already introduces an observable temperature gradient (Fig. 20).
The more evolved source G08a has a slightly shallower overall distribution of gas (qbulk ~ –1.2) than its dense gas component (qdense ~ –1.3), although the difference is within the errors. Interestingly, source G19 displays an opposite relation between the two slopes (qbulk ~ –1.4, qdense ~ –0.6; Fig. 16). Comparing the virial state of these two sources (Fig. 21), it seems G19 is close to a global state of energy balance, while G08a has excessive kinetic energy in the central 0.2 pc, possibly caused by energy transfer and induced motions from gravitational collapse (see Sect. 4.3 for further details). If a steeper density profile corresponds to a more dominant role of gravitational collapse, then the kinematic differences inferred from linewidths are compatible with the relation between density slopes on local (dense gas regime) and global (bulk gas regime) scales for these two sources. We discuss this in more detail in Sect. 4.5.
The overall trend seen in the right panel of Fig. 15 can be qualitatively explained by the growing role of self-gravity in the evolution of gas dynamics in massive clumps (Lee et al. 2015; Gómez et al. 2021). This is illustrated in hydrodynamic simulations of star-forming clouds with continuously driven turbulence (Lee et al. 2015); the simulations show that self-gravity plays the dominant role for all changes that happen with density structures on scales up to >0.1 pc. Their results reveal that the power-law slopes around density peaks change from –1.3 to –1.55 before and after the onset of star formation, of 0.75 and 1.25 times global free-fall timescale (tff). By separating the scales based on the dominant mass contributor of gas or forming stars, Murray et al. (2017) demonstrate that close to the (proto)stars the gas density profile has a slope of –1.5 (an attractor solution, see also Coughlin 2017) and in the outer envelope the slope ranges from –1.6 to –1.8. These values are in quantitative agreement with the evolved sources in our sample. The three sources having bulk gas density slopes shallower than –1 (left panel of Fig. 16) may reflect an initial condition close to a constant-density core when gravitational collapse has not significantly altered the gas density profile, for both the bulk gas and dense gas structures (G18 and G28) or only the dense gas component (G19). The tendency of an initial flat inner density profile remaining flat over one tff determined by the gas central density is also discussed in Henriksen et al. (1997), which is attributed to the fact that the cloud center has the fastest growing velocity mode. The timescale is fleetingly short without further support of turbulence.
 |
Fig. 19 Comparisons of abundance ratios for relevant molecular species of target clumps. Top: abundance ratios of carbon-chain molecules; Bottom: abundance ratios of sulfur-bearing molecules at clump center (0.1–0.15 pc, beam averaged), shown against source L∕M ratios. |
 |
Fig. 20 Derived radial averaged temperature profiles of the target sources from multiple thermometers. The error bars show the standard deviations for each annular average. The dashed and dotted lines show a radial temperature profile that follows ∝ L0.25r−0.5 (β = 0) and L0.2r−0.4 (β = 1), respectively (for details, see Sect. 3.6). For G13 and G31 an additional radial temperature profile of ∝ L0.17r−0.34 (β = 1.8, Adams 1991) is shown (dash-dotted line). Whenever available, temperature measurements from higher angular resolution observations from previous works are included in the plots as gray crosses. The thick purple line indicates the fitted temperature profile T(r) described in Sect. 3.6. The blue thin line indicates the refined temperature profile by varying rin in T(r) (Eq. (3)) to fit with dust SED (refined T(r), Appendix E). The plots in the bottom right panel show the first derivative d log T/d logR (for all sources, top) calculated from the fitted profile T(r), and the refined T(r) (for five sources, bottom). |
 |
Fig. 21 Derived averaged radial linewidth and virial parameter profiles. The dash-dotted line in each upper panel indicates the power-law fit to the linewidths from the thermometer lines. In each upper panel the gray dotted line indicates the relation found by Caselli & Myers (1995) of Orion low-mass cores scaled up by a factor of 5, which roughly matches the observed linewidth in our case, of
|
4.3 Kinematic state of clumps: radial profiles of molecular linewidth and virial parameter
Based on the calculations in Sect. 3.8, Fig. 21 shows the radial profiles of the molecular linewidths (ΔV = 2.355σv) for individual species. We fitted a power law to the radial linewidth profiles traced by thermometer lines (i.e., excluding the data points from C34S and H13CO+). In G08a, G31, and G13, the linewidths traced by these lines decrease radially with power-law indices of –0.40, –0.31, –0.56, respectively. Except for the sources G18 and G19, the linewidths on the extended regions traced by C34S and H13CO+ are systematically larger than those traced by the thermometer lines. Again, for clump G18 we had to rely on pointed observations from the IRAM 30m telescope to tentatively determine the radii of the linewidths obtained from thermometer lines, based on a fixed temperature profile (Sect. 3.4). We therefore note that the analysis for this clump is not based on the same spatially resolved measurement as the other clumps.
In general, the variation in linewidths does not seem to follow a monotonic radial change, as opposed to the σv ∝ r1∕2 universal law observed in giant molecular clouds and low-mass cores (i.e., Larson’s first law; Larson 1981). This is in agreement with the results presented in Izquierdo et al. (2021, Fig. 7), where they show that the linewidth–size relationship is not uniform, but instead depends on the analyzed spatial scale and the physical processes taking place there (see also Hacar et al. 2016).
In high-mass star-forming regions, the observed linewidths are systematically larger, and σv may have a shallower power-law relation with scales (e.g., Plume et al. 1997; Caselli & Myers 1995). In addition, the virial equilibrium naturally infers that σv has a dependence on gas surface density, such that σv ∝  (Heyer et al. 2009).
(Heyer et al. 2009).
Moreover, recent 1D simulations incorporating gravitation-driven turbulence (i.e., adiabatic heating; see Robertson & Goldreich 2012) found distinct relations between σv and spatial scales for star-forming clumps, due to the change of the dominant turbulent driving mechanism from the inner to the outer regions (Murray & Chang 2015). It has been found that vT ∝ r−0.5 holds within the sphere enclosed by the stellar influence radius, which is defined as the radius where the enclosed gas mass is comparable (1–3 times) to the stellar mass (Murray & Chang 2015; Murray et al. 2017; see also Coughlin 2017; Xu & Lazarian 2020 for the analytic derivations).
As a rough estimate of the stellar influence radius, assuming the Lbol of each source is contributed solely by the luminosity of a single ZAMS star, adopting the stellar evolution model of Choi et al. (2016), the stellar mass M⋆ is estimated to be 12 M⊙ for G19, 15–16 M⊙ for G08a, G13 and G28, and 30 M⊙ for G08b. Grave & Kumar (2009) fit radiative transfer accretion models of YSOs to source G19 and G13 by building SEDs from the near-infrared to the submm, and their derived stellar masses are consistent with our rough estimates. For G10, previous observations suggest a stellar mass of ~200M⊙ (Liu et al. 2010). We note that inferring stellar mass from luminosity assuming the sole contribution from a single star leads to a lower limit, as these clumps are forming a cluster of stars following the IMF. With the same total bolometric luminosity, this corresponds to a higher total stellar mass. In comparison with the central core masses we derived from 1.2mm continuum (Table 4), it seems we marginally resolved the influence radius (about half beam FWHM) for sources G13, G08a, and G10, but a bit further in the case of G08b. This may partially explain why in the inner region of G08b the observed linewidths do not decrease rapidly with radius. In G10 the observed linewidths have shallower variations with radius. This may be due to the presence of the ~0.2 pc scale edge-on rotational disk (Liu 2017), toward which gas settles into coherent rather than random motions.
For the early-stage clumps G18, G19, and G28, the bolometric luminosity is likely dominated by accretion energy. This leads to an overestimation of the stellar mass, such that in reality there appears to be a more drastic difference between the embedded stellar mass and the gas mass at the scale probed, with respect to our rough estimates. Therefore, it is likely that we do not see the decreasing trend of linewidths with radius in their inner regions due to the too coarse resolution to resolve the stellar influence radius. In addition, assuming turbulent velocity scales as the local infall velocity, Coughlin (2017) demonstrates that there is temporal steepening of the radial profile of the rms velocities, due to gravitational field starting to dominate the dynamics of inflowing gas, which changes from vT ∝ r−0.2 to vT ∝ r−0.5. Hence, it may also be that early-stage clumps have a shallower inner slope that tend to flatten out, further smeared in coarser resolution measurements.
Exterior to the stellar influence radius, simulations found that vT ∝ r0.2 (see also Lee et al. 2015). Compared to classical subsonic turbulence following the Kolmogorov law (vT ∝ r1∕3) or supersonic turbulence (vT ∝ r1∕2), the shallower scaling relation between linewidth and spatial scale of the region beyond stellar influence radius could be due to additional energy converted partly from gravitational collapse (Ballesteros-Paredes et al. 2011; Xu & Lazarian 2020) and/or kinetic energy of the extended inflow gas transported by radial motions (Padoan et al. 2020). Klessen & Hennebelle (2010) demonstrate that the conversion efficiency to internal turbulence depends on the density contrast between the accreting entity and the inflowing gas. These may explain why in the outer regions of G08a, G08b, G13, and G10 the observed linewidths increase with radius, having a power-law slope of ≳0.2–0.3.
In light of the radial profiles of αvir, it appears that our target clumps can be classified into three types, based on their αvir∕αcr ratios: sources G08b, G31, and G10 are in an overall virial to sub-virial state; G18, G08a, and G13 show super-virial states in the center and sub-virial states in the outer envelope; G28 and G19 have uniform αvir fluctuating mostly above αcr (see the detailed description in Table 8). To explain the observed super-virial states in the central regions of some of these clumps, it is required to introduce other line-broadening mechanisms.
The three sources that have large virial parameters in the centers have the lowest central core masses and densities (Table 4). If central cores are treated as a decoupled structure from the clump envelope, the more massive and denser coresbeing more sub-virial is consistent with previous observations toward massive star-forming regions (e.g., Kauffmann et al. 2013; Liu et al. 2015; Traficante et al. 2018). However, due to the insufficient angular resolution, the estimate of αvir in the clump center may suffer from larger uncertainties, for example there is possibly higher level of clumpiness with complex velocity structures that confuse the linewidth measurement. In addition, the αvir in the centermost is derived from linewidth of CH3CN. CH3CN has been shown to trace the interface of convergent flows in high-mass clumps (Csengeri et al. 2011), which is also enhanced in shocks (Bell et al. 2014) and associated with hot accretion flows (Liu et al. 2015).
Camacho et al. (2016) and Ballesteros-Paredes et al. (2018) have shown that the observed high αvir may not be indicative of pressure confining or gas dispersal. Alternatively, for low column density clumps this picture might be due to highly dynamic externally driven gas accumulation. For high column density clumps it might be a result of neglecting the stellar mass or accreting materials outside the cores in contributing to the gravitational energy. The latter may qualitatively explain the super-virial state in the center of the three sources G18, G08a, and G13, which does not necessarily indicate a halt of collapse. On the other hand, the inclusion of infall velocities to the observed linewidth may also cause the source which is undergoing collapse to appear seemingly unbound (e.g., Smith et al. 2009). Infall motions of dense cores that have large αvir (~5–8) are revealed by Cesaroni et al. (2019), inside a massive cluster-forming clump.
Giannetti et al. (2017) suggest that CH3CCH is a reliable tracer for the kinematics of bulk gas structures in the massive clumps. From the αvir derived based on the CH3CCH lines, it appears that all clumps are in sub-virial or virial status, but at smaller scales in the central region of the clumps the gas can appear super-virial. In addition to the three clumps showing large αvir in the center, other clumps show an evolution of globally (for all radii) decreasing αvir with increasing L∕M. Ballesteros-Paredes et al. (2018) and Camacho et al. (2020) investigated the evolution of αvir in molecular clouds based on numerical simulations. They showed that the gas structures may be initially assembled due to the large-scale turbulence. Afterward, the assembled gas structures evolve from super-virial to sub-virial status, and finally approach energy equipartition, or further become super-virial after one tff due to gas expulsion. Our observations do not show such non-monotonic evolution of αvir with L∕M. This is likely because all target clumps remain in early to intermediate evolutionary stages, which are prior to or in the stage of active star formation when the gas mass dominates the mass budget, preceding the gas dispersal stage.
Properties related to radial linewidth and virial parameter profiles of the target clumps.
4.4 Comparison with chemical models: carbon-chain molecules and sulfur-bearing species
The formation pathways of molecules and chemical rates are strongly influenced by gas temperature and volume density. In Sect. 3.9, we used the molecular column densities of CH3CCH, H2CS, CH3CN, CH3OH, C34S, CCH, SO, and SO2 to derive the molecular abundance distributions and abundance ratios between relevant species. We discuss comparisons between these resultswith predictions from chemical models in this section.
4.4.1 CH3OH, CH3CCH, CH3CN, and CCH
CH3CCH is designated as a “cold molecule” (Bisschop et al. 2007) since it presents low excitation temperatures compared to other complex organic molecules (COMs) such as CH3CN and CH3OCH3. The formation pathways of CH3CCH include coldgas phase reactions and grain-surface chemistry (Calcutt et al. 2019). The reactions in gas phase involve thermal desorption which requires low temperatures. Calcutt et al. (2019) suggested that CH3CCH is a “gateway” molecule that traces the interface between hot cores–corinos and the colder envelope, and extends further out in the envelope. The inset in Fig. 17 shows measured CH3CCH abundances averaged from the outer region (≳0.1 pc) of the clumps with the gas temperature measured at 0.3 pc. These properties represent the bulk luke-warm gas. The small variation of CH3CCH abundance across our sample indicates that it is not a sensitive molecule to trace the ≳100 K thermal desorption of hot core regions. Its emission instead traces the more extended gas and is a good kinematic tracer for >0.1 pc gas structures within massive clumps (e.g., Giannetti et al. 2017). There is also no drastic radial change of the abundances of the other two COMs CH3OH and CH3CN for individual sources (Fig. 17). This is expected since our angular resolution is not sufficiently high to reveal the >100 K region (confined within 0.1 pc) where prominent abundance enhancement of COMs is expected (Garrod et al. 2017).
The abundance profiles of CCH exhibit an increase toward the outer clump envelope for most the sources in the sample (Fig. 17) and an overall decrease in abundance with clump luminosity. These results reflect that CCH is abundant at an early stage and then transformed to other molecules in the clump center (Beuther et al. 2002). The abundance of CCH in outer regions is maintained by reproduction of CO dissociated by an external UV field. Similarly, in early-stage low-mass cores, CCH is also tracing more quiescent gas, e.g., the outer part of a circumbinary envelope (van Dishoeck et al. 1995).
We compare the abundance ratios between CCH, CH3CN, and CH3CCH with CH3OH in Fig. 19. In low-mass star-forming cores, the ratio [CCH]/[CH3OH] is usually used to distinguish less evolved warm carbon-chain cores with hot corinos (e.g., Graninger et al. 2016). The strong anti-correlation of [CCH]/[CH3OH] with L∕M indicates that in the central region of massive clumps this ratio serves as an evolutionary indicator. The ratio [CH3CN]/[CH3OH] has a correlation with L∕M as well: except the hot massive core G31, the other sources show a clear monotonic increase in [CH3CN]/[CH3OH] with increasing L∕M. This is consistent with the formation timescale of the two species: CH3OH forms at early stages (10 K) on grain surfaces, primarily via successive hydrogenation of CO (e.g., Watanabe et al. 2003), while the formation of CH3CN appears late through radiative association between HCN and CH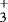 on the grain surface and between CH3 and CN in the gas phase (Nomura & Millar 2004).
on the grain surface and between CH3 and CN in the gas phase (Nomura & Millar 2004).
4.4.2 Sulfur-bearing molecules
Time-dependent theoretical chemical models of sulfur-bearing species find that the evaporation of H2S and subsequent chemical reactions in hot cores lead to an increasing abundance ratio of SO2/SO (Wakelam et al. 2011; Esplugues et al. 2014). At a late stage of hot core evolution, H2CS and CS are also drastically enhanced; together with SO2, they become the most abundant sulfur-bearing species. In shocked regions similar trends along evolution are predicted (Wakelam et al. 2005; Esplugues et al. 2014), but observations seem to suggest opposite variations of X(CS)/X(SO) with source evolutionary stages (Li et al. 2015; Gerner et al. 2014; Herpin et al. 2009). Assuming the same 34S/S isotopic ratio for our target clumps, we find a similar result, which is reflected by the feature in Fig. 19 (left panel, bottom row). Similar results of X(H2CS)/X(SO) and X(SO2)/X(SO) with clump L∕M are derived in Fig. 19 (middle and right panel, bottom row); there are no prominent correlations found. We note that the temporal evolution of abundance of sulfur-bearing species is highly dependent on the source physical structure (Wakelam et al. 2005; Wakelam et al. 2011), which require tailored chemical modeling for individual source to disentangle this impact and the evolutionary time.
4.5 Density structure: relation with cloud structure and implications for different dense gas conversions
In this section we discuss how the radial density profiles of massive clumps (see Sect. 4.2) may be linked to statistics of parental cloud structures on large scales (≳10 pc). We also elaborate on the physical implications of the radial density profiles comparisons between bulk gas and dense gas structures, ρbulk and ρdense.
Gravoturbulence simulations of molecular clouds (e.g., Kritsuk et al. 2011; Lee et al. 2015) showed that the cloud volume density probability distribution functions (ρ-PDF, ps) have lognormal and power-law forms in the low- and high-density regimes, respectively (Fig. 1). The lognormal form is attributed to the primordial and maintained supersonic turbulence, while the power-law tail is usually regarded as a sign of gravitational collapse. Thus, the study of PDF statistics is a useful method to understand the physical mechanisms at play in molecular clouds. Gravitational contraction converts a fraction of low-density gas to high-density structures over a timescale comparable to the free-fall timescale (tff) of the mean density. With this process, the slope of the power-law tail s changes from s ≈ −3 to s ≈ −1.5−1 (e.g., Girichidis et al. 2014; Guszejnov et al. 2018) in a mean free-fall time. When the power-law tail of the ρ-PDF is dominated by a single gravitationally bound massive clump with a ρ (r) ∝ rq density profile, there is a relation s = 3∕q (Federrath & Klessen 2013). In other words, q is expected to evolve from ≈−1 to −3 to −2 over a mean tff. Observational works usually constrain the column density probability distribution function (N-PDF, pη) rather than ρ-PDF. In this case the power-law slope of the N-PDF (sN) can be related to the radial density profile of the molecular clump by 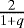 . Column density mapping toward Galactic massive star-forming complexes yield power-law slopes for N-PDF ranging between ~–4 to –2 (Lin et al. 2017). The evolutionary trend of steepening density profiles (the bulk gas density profile) of the massive clumps resolved in this work is in general consistent with the prediction from cloud-scale statistics.
. Column density mapping toward Galactic massive star-forming complexes yield power-law slopes for N-PDF ranging between ~–4 to –2 (Lin et al. 2017). The evolutionary trend of steepening density profiles (the bulk gas density profile) of the massive clumps resolved in this work is in general consistent with the prediction from cloud-scale statistics.
The cloud-scale (10 pc) dense gas fraction can be relatively well described by statistics of ρ/N-PDFs, which do not factor in features of spatial distribution. Within the ~1 pc scale clump structure, the spatial configuration of dense gas can be critical in determining the properties of final star clusters. We discussed the gas radial density profiles probed by the dust emission and dense gas tracer (CH3OH) separately in Sect. 4.2. Here we note again that dust emission traces averaged (mass-weighted) bulk gas structures (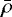 ~ 104.5 cm3), while CH3OH emission probes dense gas regimes (ρ ≳ 106.5 cm−3, up to several 108 cm−3) within the massive clumps. We note that the gas density difference seen by dust and higher angular resolution CH3OH emission can also be partially related to the coarser resolution of the single-dish continuum images, which tend to smear out the gas overdensities at smaller spatial scales. However, the major cause of the difference is that CH3OH transitions selectively trace the higher density gas component, while the dust emission does not critically depend on the volume density of the gas (in the regimes we are interested in), providing a measure of bulk gas properties. By relying on two density probes for different gas density regimes, we go beyond the self-similar solution of gravitational collapse by characterizing the density configuration of massive clumps with two layers, ρbulk and ρdense, each of which is described by a power-law form. The ρdense traced by CH3OH from RADEX modeling (Sect. 3.5) is verified by full radiative transfer non-LTE models described in Appendix F, by introducing a volume filling factor ffdens (Table 7) to spherical models. The low volume filling factor indicates that the dense gas is highly clumpy and may be organized into filament- or sheet-like structures, which is a natural outcome of supersonic turbulence and gravitational collapse (Smith et al. 2020). In general there seems to be a higher density contrast (decreasing ffdens) with increasing L∕M (listed sequentially in Table 7, last column). While ffdens provides an upper limit of the volume filling factor of high-density gas, we make some inferences here for the dense gas mass fraction based on intuitive assumptions and references to numerical simulations. The aim is to establish the ratio of the bulk gas to dense gas density profiles, ρbulk/ρdense, as a measure of the dense gas fraction, and the radial profile of this ratio as an indicator of different star formation modes (or temporal variations of the SFE) for the massive clumps.
~ 104.5 cm3), while CH3OH emission probes dense gas regimes (ρ ≳ 106.5 cm−3, up to several 108 cm−3) within the massive clumps. We note that the gas density difference seen by dust and higher angular resolution CH3OH emission can also be partially related to the coarser resolution of the single-dish continuum images, which tend to smear out the gas overdensities at smaller spatial scales. However, the major cause of the difference is that CH3OH transitions selectively trace the higher density gas component, while the dust emission does not critically depend on the volume density of the gas (in the regimes we are interested in), providing a measure of bulk gas properties. By relying on two density probes for different gas density regimes, we go beyond the self-similar solution of gravitational collapse by characterizing the density configuration of massive clumps with two layers, ρbulk and ρdense, each of which is described by a power-law form. The ρdense traced by CH3OH from RADEX modeling (Sect. 3.5) is verified by full radiative transfer non-LTE models described in Appendix F, by introducing a volume filling factor ffdens (Table 7) to spherical models. The low volume filling factor indicates that the dense gas is highly clumpy and may be organized into filament- or sheet-like structures, which is a natural outcome of supersonic turbulence and gravitational collapse (Smith et al. 2020). In general there seems to be a higher density contrast (decreasing ffdens) with increasing L∕M (listed sequentially in Table 7, last column). While ffdens provides an upper limit of the volume filling factor of high-density gas, we make some inferences here for the dense gas mass fraction based on intuitive assumptions and references to numerical simulations. The aim is to establish the ratio of the bulk gas to dense gas density profiles, ρbulk/ρdense, as a measure of the dense gas fraction, and the radial profile of this ratio as an indicator of different star formation modes (or temporal variations of the SFE) for the massive clumps.
It is a well-known fact that there is a strong correlation between SFR and dense gas. Based on a gravo-turbulent fragmentation scenario, Padoan et al. (2012, 2017) derived an empirical relation between SFR per free-fall time ϵff (the fraction of a cloud’s mass that is converted to stellar mass over a free-fall timescale, Krumholz & McKee 2005) and αvir,
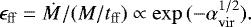 (8)
(8)
In a hierarchical description of cloud structure where gas density increases with decreasing scale, the conservation of Ṁ (or equivalently SFR) translates into
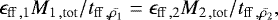 (9)
(9)
where the number indices of 1 and 2 denote two adjacent levels in a hierarchy. We assume ρbulk represents the gas density of a lower level structure in the hierarchy from which a higher level structure of gas density ρdense originates from. We further assume that only the dense gas ρdense participates in the star formation process. Then with a scale-invariant ϵff (or equivalently scale-invariant αvir) Eq. (9) translates to Mdense = Mtot(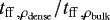 ). Substitutingthe free-fall timescale tff ∝ ρ−1∕2 into the equation, we obtain
). Substitutingthe free-fall timescale tff ∝ ρ−1∕2 into the equation, we obtain
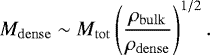 (10)
(10)
Naively, this relation means that at a certain scale, the closer the derived dense gas density is to the bulk gas density, the more mass fraction of the clump is occupied by the dense gas. We note that even without the assumption of scale-invariant ϵff, considering only that the two set of densities are each the mass-weighted value in their respective density regimes, the mass fraction of dense gas to total clump gas is also largely determined by ρbulk∕ρdense when the ratio between density of bulk gas andgas not seen by CH3OH is similar among sources and does not vary with scale.
Figure 22 shows the density profiles ρdense and ρbulk. This figure also shows the ratios between these two profiles, which provide a measure of dense gas mass fraction (DGMF): Mdense/Mtot. We found that the DGMF in G19, G08b, and G10 decreases with radius, while it increases with radius in G28, G08a, G13, and G31. For G31, the optical depths of the CH3OH lines are high such that the line ratios are less effective densitometers in the density regimes it associates with than the other sources. We thus omit discussion on this source, while noting that the clump indeed holds the highest density values for dense gas seen by CH3OH among all target sources. Of the other six sources, G19 shows a decreasing DGMF from 25% to 19%, G08b from 22% to 18%, and G10 from 24% to 15%. For G28, the DGMF increases from 15% to ~17% at 0.1–0.2 pc. In G08a and G13, the DGMF is ~19% at their centers and achieve ~22% at 0.2–0.3 pc radii.
Given these radial variations of DGMF, it might be indicative that of these six sources, G19 and G10 may be most efficiently converting gas into the dense gas regime, having a focused DGMF toward clump center. G08b exhibits a similarly high DGMF that changes slightly with scale, while early-phase clump G08a and the least massive G13 have DGMF peaking around the intermediate scales relative to the center. Another early-stage source, G28, has the smallest DGMF overall and also shows a relatively invariant DGMF over scales. This trend is only partially reflected in the density profile slope of ρbulk(r), which is generally regarded as a measure of dense gas concentration that directly inflates the SFR (e.g., Parmentier 2019). It is noteworthy that radial variations of the DGMF for individual sources are in general compatible with the radial dependence of the virial parameter shown in Sect. 4.3 (Fig. 21). These two measures are both indicative of the capability of the source in converting gas into the denser regime at different positions relative to the bottom of the clump’s gravitational potential. It is clear that the three classes of increasing, flattened, and decreasing DGMF as a function of radius, for a particular source, correspond respectively to a shallower, similar, and steeper dense gas profile (qdense) compared to that of its bulk gas (qbulk) on the basis of Eqs. (2), (4), and 10. In the non-homologous spherical collapse framework, the physical condition of an outer shell can be regarded as an earlier stage preceding the inner shell (e.g., Vázquez-Semadeni et al. 2019), then a radially decreasing (increasing) DGMF corresponds to an accelerating (retarding) dense gas conversion and temporal increase (decrease) of SFE for a particular source.
The localized behavior of dense gas conversion may be causing the chaotic and scattered SFR versus gas density relation, and this behavior goes beyond the self-similar solutions for collapsing clumps. The non-self-similar behavior is suggested to be relevant even for the spherical collapse, as shown theoretically by Coughlin (2017), dependent on the initial conditions. The spatial variations of the DGMF may also reflect two competing gravitational collapses within these massive clumps: collapse toward the global potential center and collapse of dense regions into ambient filaments surrounding the center. The latter process is mostly induced by turbulence (Girichidis et al. 2011). The dominance of one or another process maydepend on the initial density profile and turbulence driving modes (Girichidis et al. 2011; Lomax et al. 2015).
We can also establish ρbulk∕ρdense as a measure of DGMF from another perspective, with a weaker assumption. In the framework of turbulent convergent flows, the gas density enhancement after a compressive shock has an inverse length scale relation following
 (11)
(11)
where L0 and lpost denote the length scales of the preshock and postshock gas, and ρ0 and ρpost the gas densities, respectively; Ms denotes the sonic Mach number, 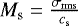 . This shock jump condition is at the origin of the lognormal distribution of PDF. As Eq. (11) links the gas length scale to density with an inverse relation, then the mass ratio of postshock dense gas versus the preshock gas may also be represented by a power-law form following (ρ0 /ρpost)−s with slope s dependent on the assumed geometry. With a cylindrical geometry describing infinite filaments, the gas mass is ∝ ρl2, where l denotes thickness (radius), with slope s = 1.
. This shock jump condition is at the origin of the lognormal distribution of PDF. As Eq. (11) links the gas length scale to density with an inverse relation, then the mass ratio of postshock dense gas versus the preshock gas may also be represented by a power-law form following (ρ0 /ρpost)−s with slope s dependent on the assumed geometry. With a cylindrical geometry describing infinite filaments, the gas mass is ∝ ρl2, where l denotes thickness (radius), with slope s = 1.
If the enhancement of gas density (ρdense) as traced by CH3OH is regarded as the result of compressive turbulence on the preshock gas that has a density represented by ρbulk, the ratio (ρ0 /ρpost) still holds as a DGMF measure. Compared to Eq. (10) (s = 1∕2), the different scaling of s = 1 does not change the general trend of the radial change of this measure, but only increases the contrast between the outer layer and inner region.
In any case, the dense gas probed by CH3OH does have contributions from shock entrainment, as suggested by locally increased Ms and the fact that CH3OH is likely enhanced in shocked regions. On the other hand, we have already seen in Sect. 4.3 that gravitational collapse has altered the general scaling relation of vT (hence 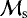 ), which makes the slope s vary. A more stringent comparison of radial change of dense gas mass fraction to indicate the dense gas conversion efficiency would benefit from properly separating the part of dense gas associated with transient gas substructures with virialized cores and coherent flows, which is achievable with finer resolution observations (both spectral and spatial).
), which makes the slope s vary. A more stringent comparison of radial change of dense gas mass fraction to indicate the dense gas conversion efficiency would benefit from properly separating the part of dense gas associated with transient gas substructures with virialized cores and coherent flows, which is achievable with finer resolution observations (both spectral and spatial).
 |
Fig. 22 Comparison between gas density profiles derived by modeling continuum and CH3OH line emission. The ratio of densities derived by CH3OH LIME modeling (ρdense) to continuum results (ρbulk) are shown aspluses (following right y-axis). The density estimated by SMA 1.2 mm continuum observations representing the central core average density is shown as a verticalorange line in each plot (Table 4). |
5 Conclusions
The gas thermal properties are critical to the star formation process. For massive star formation, the density structure of the nursery gas clumps may not be well predicted by previous hydrostatic equilibrium core models, which are generally representative of low-mass cores, due to a higher level of turbulence and gravitational collapse set at largerscales. We conducted a SMA and APEX line survey toward a sample of eight massive star-forming clumps in order to understand the evolution of temperature and density structures. The major findings are as follows:
- 1.
Transitions of multiple molecular species (CH3CN, CH3CCH, H2CS) of distinct critical densities, together with dust emission, provide a reasonably good sampling of different gas temperature regimes (≳200–20 K) over the full clump scale. There is not a single power-law relation dependent only on source luminosity that could describe all the radial temperature variations in our sample. The elevated temperature of a less luminous source may be related to the intermittency of accretion and shock-related activities.
- 2.
CH3OH line series are good density probes for massive clumps, selectively tracing density regimes of ≳106 cm−3. Systematic steepening of density profiles along clump evolution, indicated by L∕M, is revealed in the sample via continuum (bulk gas) and CH3OH line (dense gas) modeling. The density slopes change from > −1 to ~ −1.5. The dense gas component becomes denser with increasing L/M, and the volume filling factor of which decreases, corresponding to a higher density contrast along clump evolution.
- 3.
The radial linewidth profile traced by multiple lines displays a scale-dependent relation. Several sources, which have comparable stellar mass and gas content at the scale probed, have a central decreasing trend of vT ∝ r−0.4 and vT ∝ r0.2 in the outer envelope, which may be related to conversion of gravitational energy to turbulence. On larger scales (0.2–0.5 pc) all clumps are close to virial state (αvir∕αcri ~1), as indicated by CH3CCH, H13CO+ lines. Small scale (≲0.1 pc) virial parameters traced by CH3CN and H2CS can exceed equilibrium values for some of the sources, the origin of which is hindered by our limited resolution. Overall, we observe that the clump gas evolves from a super-virial to sub-virial state with increasing L∕M.
- 4.
The abundances of CH3OH, CH3CN, and H2CS show better correlation with source central temperature than with luminosity. Abundance ratios of [CCH]/[CH3OH] and [CH3CN]/[CH3OH] are in good correlation with clump L∕M, and can be used as indicators of evolutionary stages of massive star-forming clumps.
- 5.
The evolutionary trend of clump density profiles is compatible with cloud-scale diagnosis that frequently reveal the time-varying power-law tail of PDFs. In a hierarchical view, the radial variation in the dense gas mass fraction, which can be approximated by the density ratio representing the averaged bulk gas (dust continuum, no spatial filtering) to that probed by a high-density tracer (CH3OH), may be indicative of the efficiency of the source in dense gas conversion and dense gas focusing to the global gravitational center. The bulk gas density profile is a less distinct measure because self-similar approximation does not adequately describe the clumpy gas structures within massive clumps.
In this work, weattempted to understand the role of self-gravity in shaping the gas structure as massive clumps evolve over time. Our results are based on ≲0.1 pc observations, although a dense gas filling factor (probed by CH3OH) indicates, on smaller scales, a clumpy gas environment of higher density contrast along the evolutionary track. Detailed fragmentation properties, cores and filaments, and their kinematics remain unresolved. In any case, deduction of line-of-sight cloud geometry is difficult. With the unknown cloud thickness, the mass scale of the high-density gas regime remains highly uncertain.
Existing observations have broadly revealed transonic to subsonic linewidths associated with localized substructures in massive star-forming regions, the length scale of which is well above sonic scale, indicating an efficient turbulence dissipation process. More robust velocity linewidth profiles require better resolved observations to disentangle multiple velocity components, and confusion from stellar feedback (outflows). In addition, while the scale-dependent linewidth versus radius relation is indirect evidence (based on the assumption that it mirrors radial infall velocity) of the changing role of gravitational collapse in dominating gas dynamics, more direct evidence would be measurement of infall velocities, or accretion rates as a function of radius. The latter is indispensable to distinguish different collapse models (e.g., Padoan et al. 2020). This calls for observations of multiple “infall tracers” sensitive to different gas density regimes, along with a proper description of the physical structure.
Acknowledgements
We are thankful to the referee whose comments and suggestions helped us to greatly increase the clarity of the paper. This work was partly funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Collaborative Research Council 956, sub-project A6. Y.L. is a member of the International Max-Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne. H.B.L. is supported by the Ministry of Science and Technology (MoST) of Taiwan (Grant Nos. 108-2112-M-001-002-MY3 and 110-2112-M-001-069-). The Submillimeter Array is a joint project between the Smithsonian Astrophysical Observatory and the Academia Sinica Institute of Astronomy and Astrophysics and is funded by the Smithsonian Institution and the Academia Sinica.
Appendix A Target sources
A.1 G19.882-00.534
G19.882-00.534 (IRAS 18264–1152) is classified as an extended green object (EGO, Cyganowski et al. 2008), located at 3.7 kpc with luminosity of >104 L⊙. The most prominent features of this source are the high-velocity outflow (Qiu et al. 2007, Leurini et al. 2014)and the high level of maser activity (among a sample of 56 high-mass star-forming regions, Rodríguez-Garza et al. 2017). The outflow is oriented in an east–west direction, showing enhanced H2 near-infrared emission as well (Varricatt et al. 2010). Sensitive 7 mm and 1.3 cm observations resolved the source into a triple system, consisting of two optically thin HII or dust emitting sources, and a thermal jet or a partially optically thick HII region (Zapata et al. 2006).
A.2 G08.684-00.366 and G08.671-00.356
These two massive star-forming clumps are part of the IRAS 18032-2137 star-forming cloud located at 4.8 kpc (Purcell et al. 2006). Multiple water, methanol, and hydroxide masers are detected toward both sources (Hofner & Churchwell 1996, Caswell 1998, Gómez et al. 2010). G08.671-00.356 (~ 9000 L⊙) is a UCHII region (Wood & Churchwell 1989), while G08.684-00.366 (~ 3000 L⊙) is a less evolved relatively infrared weak source, lying 1′ offset in the northeastern direction. Strong SiO emission toward G08.684-00.366 indicates that star formation already takes place in this source (Harju et al. 1998). Previous SMA observations resolve the source into three dense cores accompanied by extended outflow components traced by CO (2-1) emission; the core masses are in the range of ~2-15 M⊙, a small fraction of the total clump mass (Longmore et al. 2011).
A.3 G10.624-00.380
G10.624-00.380 is an extremely luminous and massive (>105 L⊙, ~5000 M⊙) OB cluster-forming clump in the galaxy, located at 4.95 kpc (Sanna et al. 2014). Previous high angular resolution submm and centimeter observations revealed that the clump in the central 0.6 pc is a flattened rotating system (Keto et al. 1987, 1988) where multiple UCHII regions are deeply embedded (Ho & Haschick 1986, Sollins et al. 2005); the clump is fed by the converging flows from ambient filamentary clouds (Liu et al. 2011, 2012). Within the HII region, absorption lines indicate that gas accretion continues despite the ionizing and radiative pressure (Keto 1990). Overall, the clumps seems to be in a global collapsing state with a rotating Toomre-unstable disk-like structure in the center (Liu 2017).
A.4 G13.658-00.599
G13.658-00.599 (IRAS 18144-1723) is a molecular clump with a luminosity of >104 L⊙ at 3.7 kpc. It is associated with multiple water and methanol masers (Gómez-Ruiz et al. 2016). The H2 emission displays a bowshock feature 18″ offset in thewest from the center of the IRAS emission, which seems to originate from an extended K-band continuum source associated with the IRAS source (Varricatt et al. 2010). The bowshock feature is surrounded by multiple 44 GHz methanol masers (Gómez-Ruiz et al. 2016), indicating it is likely caused by outflow activity. Deep mid-infrared imaging reveals that the central source hosts two YSOs separated by ~ 10000 au, at different evolutionary stages; the outflow traced by the CO(3-2) line coincides closely with the H2 emission, and is likely caused by the younger source in formation (Varricatt et al. 2018).
A.5 G31.412+00.307
G31.412+00.307 is a well-known hot massive core that has been extensively studied by both single-dish and interferometry observations (e.g., Cesaroni et al. 1994, Beltrán et al. 2004, 2018, Rivilla et al. 2017), a source showing great chemical richness. It is located at a kinematic distance of 7.9 kpc (Churchwell et al. 1990), and has a luminosity of ≳105 L⊙. The central hot core structure is massive and compact (~500 M⊙ of ~8000 au in size, Cesaroni et al. 2011, Beltrán et al. 2004). There is an ultra-compact HII region 5″ away from the core (Churchwell et al. 1990). The kinematic features consistently support a rotating core experiencing infall motions (Cesaroni et al. 2011, Wyrowski et al. 2012). Recent ALMA observations of higher angular (~1700 au) resolution suggest that the rotation and infall velocities both increase toward the center, and that the core is composed of a main core of size ~5300 au and a satellite core of much smaller mass (Beltrán et al. 2018). The overall monolithic feature of source G31 makes it an ideal source for understanding the high-mass star formation scenario in light of gas mass origin and evolution.
A.6 G18.606-00.074
G18.606-00.074 is a massive infrared-dark clump located in a ~4 pc long filamentary cloud associated with IRAS18223 (Carey et al. 2000, Beuther et al. 2002, Sridharan et al. 2005). The parental molecular cloud is part of an even larger (>50 pc) molecular gas filament (e.g., Kainulainen et al. 2011, Ragan et al. 2014), which is undergoing star formation activity at various evolutionary stages (e.g., Beuther et al. 2002, 2007, 2010, Fallscheer et al. 2009, Ragan et al. 2012). G18.606-00.074 (also known as IRDC18223-3, or as core 11 in Beuther et al. 2015), compared to its ambient core and clump structures, appears to have a larger mass reservoir, showing larger linewidth of N2H+ (Beuther et al. 2015).
A.7 G28.397+00.080
G28.397+00.080 (known as P2 in Wang et al. 2008) is a molecular clump located in a massive (>104 M⊙) filamentary infrared dark cloud, G28.34+0.06 (Carey et al. 2000, Pillai et al. 2006, Lin et al. 2017). The central region of the clump is not associated with any near-infrared compact source counterpart, while it appears bright at 24 and 70 μm wavelength (Fig. 4, Wang et al. 2008). It also shows line emission of COMs such as CH3OCH3 and CH3CHO (Zhang et al. 2009, Vasyunina et al. 2014), likely hosting massive protostar(s) which heats the gas up to 45 K, as measured from NH3 observations(Zhang et al. 2009).
Appendix B Subtraction of free-free emission from SMA 1.2 mm continuum
We used centimeter radio continuum data collected from the NRAO data archive5 for Very Large Array (VLA) for sources G08b, G31 and G10 to estimate the free-free emission contribution to the 1.2 mm flux. Given the time variability of centimeter emission, we selected the most recent data products, whose basic information is listed in Table B.1.
Information of the centimeter continuum data collected from NRAO archive.
Assuming that the dust and free-free emission are both optically thin, and that the dust emission follows a spectral index β = 1.0, then the relationsSν ∝ ν2+β and Sν ∝ ν−0.1 describe the variation in the two emission components as a function of frequency. The free-free emission at 1.2 mm can then be solved using simultaneous equations of total flux, at two considered frequencies. The centimeter data was smoothed and regridded to match the 1.2 mm data and subtraction was done on a pixel-by-pixel basis. The total flux contributed from free-free emission to the 1.2 mm continuum is also listed in Table B.1.
Appendix C RADEX modeling of CH3OH lines and the MCMC procedure
For both E-type and A-type CH3OH, we generated RADEX model grids in the column density (N/Δv) range from 1012 to 1018 cm−2 (with 60 logarithmically spaced uniform intervals), in the density range from 104 to 109 cm−3 (with 100 logarithmically spaced uniform intervals), and in the kinetic temperature range from 10 to 200 K (with 80 uniform intervals). In the RADEX models the linewidth is taken as 1 km/s for all the grids of parameters, while the total column densities (shown in Fig. C.2) are obtained by multiplying the fitted N/Δv with the linewidth obtained from Gaussian fits (Sect. 3.5). The external radiation field was taken to be the cosmic background at 3 K. We used a linear interpolator to estimate the line intensities for parameters in the intervals to better constrain the parameters and to allow for a continuous examination of parameter space. Nevertheless, the accuracy of the best-fit parameters remains limited by the resolution of the grid.
 |
Fig. C.1 Posterior distribution of parameters from MCMC RADEX fitting of CH3OH (5-4) line series. The column densities of A∕E type are velocity averaged values (log cm−2/km s−1). The vertical dashed lines in the 1D histograms show the quantiles of 10%, 25%, 50%, 75%, and 90%. The contour levels in the 2D histograms indicate 0.5σ, 1σ, 1.5σ, and 2σ. The figure shows an example of the fitted parameters of observed lines in one pixel of clump G08b. |
 |
Fig. C.2 CH3OH column density maps ( |
We fitted the A- and E−CH3OH (5-4) (νt = 0) line profiles with Gaussian models pixel-by-pixel for all the sources. We assumed that the linewidth is identical for all the K components and for A and E types. We also took into consideration that the HNCO 110,11 − 100,10 line is blended with the CH3OH 5−1 − 4−1 E line (δV ~ 8.44 km s−1) and removed the contribution from this HNCO line by fitting an additional Gaussian component of which the linewidth and amplitude are free parameters.
We employ the Markov chain Monte Carlo (MCMC) method with an affine invariant sampling algorithm6 (emcee, Foreman-Mackey et al. 2013) to perform the pixel-by-pixel fitting. Our prior assumption for each pixel adopted the temperature Trot predicted from the temperature profiles in Section 3.4, which means that for Tkin we assumed a normal distribution centering at Trot and with a standard deviation of 5 K. For the other parameters, the priors were assumed to be uniform distributions. We used a likelihood distribution function which takes into account observational thresholds,
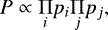 (C.1)
(C.1)
where pi stands for probabilities of the ith data that is a robust detection and pj the jth data that gives a constraint by an upper limit. We adopt the normal distribution as likelihood function,
![\begin{equation*} p_{i} \propto \mathrm{exp}\,[-\frac{1}{2}(\frac{f^{\mathrm{obs}}_{i}-f^{\mathrm{model}}_{i}}{\sigma^{\mathrm{obs}}_{i}})^{2}]\Delta f_{i} ,\end{equation*}](/articles/aa/full_html/2022/02/aa42023-21/aa42023-21-eq38.png) (C.2)
(C.2)
![\begin{equation*} p_{j} \propto \int _{-\infty}^{f^{\mathrm{obs}}_{lim,j}} \mathrm{exp}\,[-\frac{1}{2}(\frac{f_{j}-f^{\mathrm{model}}_{j}}{\sigma_{j}})^{2}]df_{j}, \end{equation*}](/articles/aa/full_html/2022/02/aa42023-21/aa42023-21-eq39.png) (C.3)
(C.3)
where 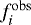 (or fj) stands for the observed intensity (or intensity upper limit) obtained from Gaussian fit;
(or fj) stands for the observed intensity (or intensity upper limit) obtained from Gaussian fit; 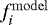 (or
(or 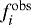 ) the model intensity;
) the model intensity; 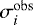 the standard error of the observed intensity, which was adopted as the fitted 1σ error of the Gaussian fit, Δfi being the data offset from the true value of fi; and dfj the integrated flux probability to the detection threshold
the standard error of the observed intensity, which was adopted as the fitted 1σ error of the Gaussian fit, Δfi being the data offset from the true value of fi; and dfj the integrated flux probability to the detection threshold 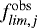 .
.
The starting points (initialization) for the chains were chosen to be the parameter set corresponding to a global χ2 minimum calculated between the grid models and the observed values. We also employed the burn-in phase in the MCMC chains and several resets of the starting-points to ensure the final chains are reasonably stable around the maximum of the probability density. An example posterior distribution of the fitted parameters is shown in Figure C.1. The obtained n(H2) maps and column density maps of CH3OH for all sources are shown in Figure 9 and Figure C.2, respectively.
After the first run of generating parameter maps, we find that the n(H2) of clump G31 are truncated to ~109 cm−3, the parameter boundary of our conducted RADEX models. Therefore we also ran a larger grid with n(H2) up to ~1011 cm−3 with the same range of Tkin and Nmol as the first grid, and re-derived the parameter maps for this clump.
Appendix D LTE analysis for other lines
D.1 CS/C34S (5-4)
CS transitions are commonly adopted tracers for dense gas. Our spectral setup covered the J=5-4 transition of CS and its rare isotopolog C34S for the seven sources. For G10 the data we utilized only covered the C34S (5-4) line. In the observed sources the CS line and the 1.2 mm continuum emission trace similar structures. Additionally, the CS line images revealed some spatially more extended structures.
Assuming that CS and C34S trace gas ofidentical temperature and linewidths, the optical depth of the C34S line can be estimated by
![\begin{equation*} \frac{W_{\mathrm{CS}}}{W_{\mathrm{C^{34}S}}} = \frac{[1-\mathrm{exp}\,(-R\tau_{\mathrm{C^{34}S}})]}{[1-\mathrm{exp}\,(-\tau_{\mathrm{C^{34}S}})]}, \end{equation*}](/articles/aa/full_html/2022/02/aa42023-21/aa42023-21-eq45.png) (D.1)
(D.1)
where WCS and 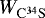 are the integrated line intensities, and we assumed a 32S/34S abundance ratio of R = 22.6, which is consistent with terrestrial value (e.g., Lodders 2003), although there are indications that the ratio varies as a function of galactocentric distance (e.g., Humire et al. 2020). The CS line, as expected, is broader than the C34S line, and shows self-absorption profiles in most of the cases. These are two effects that can mitigate each other in biasing the
are the integrated line intensities, and we assumed a 32S/34S abundance ratio of R = 22.6, which is consistent with terrestrial value (e.g., Lodders 2003), although there are indications that the ratio varies as a function of galactocentric distance (e.g., Humire et al. 2020). The CS line, as expected, is broader than the C34S line, and shows self-absorption profiles in most of the cases. These are two effects that can mitigate each other in biasing the 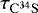 estimate as our derivation was based on the integrated intensity ratios. We found that
estimate as our derivation was based on the integrated intensity ratios. We found that 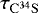 ranges from less than 0.1 to 0.25 in most of the sources, while it reaches 0.3-0.45 in G08b and values as high as 0.9 in G31.
ranges from less than 0.1 to 0.25 in most of the sources, while it reaches 0.3-0.45 in G08b and values as high as 0.9 in G31.
Assuming a beam filling factor f = 1, a lower limit of the excitation temperature (Tex) can be estimated from the brightness temperature of C34S,
![\begin{equation*} J(T_{\mathrm b}) = \left[J(T_{\mathrm{ex}}) - J(T_{\mathrm{bg}})\right]\left[1-\mathrm{exp}\,(-\tau_{\mathrm{C^{34}S}})\right]. \end{equation*}](/articles/aa/full_html/2022/02/aa42023-21/aa42023-21-eq49.png) (D.2)
(D.2)
Since the ncrit of CS is higher than the thermometers except CH3CN used in Sect. 3.4, and because there is more extended cold envelope gas contributing to the emission of CS line, as expected, the derived Tex is in general lower than the Trot profiles derived from the observations of multiple transitions of the other molecular thermometers (see Sect. 3.4). The derived Tex is <10 K in G18, in the range of 20-30 K in most of the other sources, and reaches ~45 K at the emission peak of G31.
Under an LTE assumption, the overall column densities of the C34S (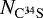 ) can then be estimated by evaluating the partition functions, adopting Tex, with
) can then be estimated by evaluating the partition functions, adopting Tex, with
![\begin{equation*} N_{\mathrm{tot}} = \frac{8\pi\nu^{3}}{c^{3}A_{\mathrm{ul}}}\frac{Q_{\mathrm{rot}}}{g_{u}}\mathrm{exp}(\frac{E_{\mathrm{up}}}{kT_{\mathrm{ex}}})[\mathrm{exp}(\frac{h\nu}{kT_{\mathrm{ex}}})-1]^{-1}\int\tau_{\mathrm{C^{34}}S}dv, \end{equation*}](/articles/aa/full_html/2022/02/aa42023-21/aa42023-21-eq51.png) (D.3)
(D.3)
where gu stands for the level degenaracy and Qrot the partition function at Tex. The derived C34S column densities are in the range of 4.4 × 1012 - 5.0 × 1014 cm−2.
In an alternative approach, we assumed that the Tex of C34S is the same with the Trot measured from the other molecular thermometers, and then directly solved for 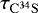 based on an LTE assumption. The
based on an LTE assumption. The 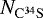 derived this way is 1.1–1.5 times larger for warmer sources except for G18. In G18 the
derived this way is 1.1–1.5 times larger for warmer sources except for G18. In G18 the 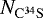 derived with this approach is ~10 times smaller than that derived based on the CS/C34S intensity ratio. This is due to the dependence between
derived with this approach is ~10 times smaller than that derived based on the CS/C34S intensity ratio. This is due to the dependence between 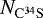 and Tex under LTE assumption:
and Tex under LTE assumption:  drops significantly below ~30 K and slowly increases for larger values of Tex.
drops significantly below ~30 K and slowly increases for larger values of Tex.
D.2 CCH (3-2)
The hyperfine line components of CCH resulting from electron-nucleus interactions allow for an direct measure of the CCH line optical depth. We followed a fitting procedure similar to that described in Estalella (2017), adopting relative line intensities from LTE predictions. From hyperfine line fitting we derived excitation temperature and optical depth on a pixel-by-pixel basis, and then used these values to estimate the CCH column densities. We found that the optical depth of the main line τm ~0.1 in extended regions, but can become optically thick at high column densities in localized regions. In most of the sources, τm reaches ~3, but in G18 τm reaches ~10 at the center, which is close to the upper limit in our fitting procedure. The column density of CCH ranges between 1.2 × 1014 and 6 × 1015 cm−2 across the emission region for all the sources. In general, the CCH column density distribution shows porosity over extended regions (~0.2-0.3 pc) except G18, and is systematically larger in the outer regions, resembling a ring-like structure, especially for clump G08b and G31. The central region of the hot massive core G31 is almost completely devoid of CCH emission. Jiang et al. (2015) presented high angular resolution CCH observations toward clump G10 together with three other more evolved high-mass clumps than those in our sample, which also exhibit ring-like distributions.
D.3 SO and SO2
Our spectral setup covered three SO lines (Table 3) which have similar upper level energies Eup. These three lines were detected in all clumps except G18. The resolved SO intensities were spatially compact and were confined to the area where 1.2 mm continuum emission was detected. The SO2 140,14-131,13 (Eup ~94 K) line was detected in the all clumps except G18 and G28; in G28 a lower excitation transition SO2 32,2-21,1 (Eup ~15 K) was marginally detected.
These SO and SO2 transitions are likely thermalized given that the emission closely follows the extension of the central core, and are of relatively high critical densities (Table 3). We cannot directly derive the excitation temperatures of the SO and SO2 molecules because they do not cover multiple transitions, or because the covered transitions have similar Eup. Therefore, we adopted the gas temperature derived from the thermometer lines (Section 3.4) when estimating their column densities, assuming LTE conditions.
Appendix E Radiative transfer modeling of multi-wavelength continuum
We divided the 870 μm (using APEX/LABOCA), 450 μm (using JCMT/SCUBA-2), or 350 μm (using CSO/SHARCII or APEX/SABOCA) images (whenever available) of each clump into annuli that have intervals equal to half of the beam FWHM, and then (projected) radially averaged the intensities in the annuli. When the intensity distribution is largely asymmetric with respect to the clump center (e.g., when there is a bright adjacent core or clump or a bright external gas filament), we trimmed the contribution from those asymmetric (sub)structures before making the averages. In practice, at each radius we first derived the mean and standard deviation (Istd) of the intensities and then masked the pixels at which the sum of the radial intensities deviates from the mean by more than 0.9 times the sum of radial Istd.
We used radiative transfer models to invert these derived radial intensity profiles to radial density profiles. We employed the publicly available Monte Carlo radiative transfer code RADMC-3D (Dullemond et al. 2012). To find the simulated intensity profiles that match the observed ones, our modeling ergodically visited the parameter spaces of the assumed functional form for density (Equation 2, Sect. 3.6). This means that the resultant models, when their number is sufficiently large (we adopt 10,000 models), can represent the average statistical properties of the models constructed from the full parameter space.
To benchmark and refine the radial temperature profile, we conducted aperture photometry with multi-wavelength dust continuum data. We used thetools in Python package photutils (Bradley et al. 2021). The total fluxes at each wavelength of 24, 70, 160, 250, 350, and 500 μm from Spitzer/MIPS (Carey et al. 2009), Herschel/PACS, and Herschel/SPIRE images are measured and they provide an observed SED profile. We then let RADMC-3D generate the SEDs ranging from mid-IR to millimeter wavelengths and ensure that the best-fit model can reproduce an SED profile which is broadly consistent with the observed SED.
We assumed that dust opacity does not have spatial variation and quoted the opacity model from Ossenkopf & Henning (1994). Specifically, we quoted the column evaluated for the thin ice mantle coated dust which was coagulated for 105 years in an environmentwith 106 cm−3 gas density (hereafter OH5 model). This model has been successfully applied in previous studies to explain the radial profiles of dust emission around high-mass embedded protostars (Mueller et al. 2002; Rolffs et al. 2011). The maximum grain size in the OH5 opacity model is under the Rayleigh limit, and thus the scattering opacity can be neglected in the modeling.
The hydrogen gas density profile (ρbulk(r)) is described by the functional form of Equation 2. Using a Monte Carlo radiative transfer to evaluate the temperature distributions (e.g., based on assumptions of heating sources and interstellar radiation field) is subject to a very large degree of freedom. Instead, we adopted the radial gas temperature profile probed by the thermometers in Section 3.4, following the form of Equation 3.
The overall mass of individual clumps derived by single-component SED fitting (Msed as in Table 2) is used as a prior for our subsequent modeling. Given that we only need to fit two free parameters (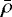 , q, cf. Equation 2), the MCMC method has no clear advantage. Instead, for each observed molecular clump, we drew 10,000 samplers from the parameter space of q = 0.0-2.5,
, q, cf. Equation 2), the MCMC method has no clear advantage. Instead, for each observed molecular clump, we drew 10,000 samplers from the parameter space of q = 0.0-2.5, 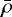 =103-106 cm−3 with a random process. The likelihood function of the clump total mass follows the truncated normal distribution (e.g., Lynch 2007):
=103-106 cm−3 with a random process. The likelihood function of the clump total mass follows the truncated normal distribution (e.g., Lynch 2007):
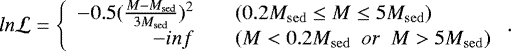 (E.1)
(E.1)
We then ran RADMC-3D for each sample and convolved the derived images with the corresponding Gaussian beams for comparison with the multi-wavelength observations. When summing the χ2, we assumed that the observational data can have nominal ~20% errors, and thus adopted one standard deviation in the radial profile calculation as the uncertainty of the observational data. The χ2 calculation follows
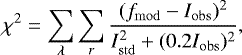 (E.2)
(E.2)
where 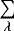 and
and 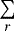 respectively denote summing over all wavelengths and sampled radii, and fmod stands for the model intensity at a certain radius.
respectively denote summing over all wavelengths and sampled radii, and fmod stands for the model intensity at a certain radius.
Figure 10 compares the observed radial intensity profiles with the best-fit models. The fitted values of q and 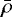 , the predetermined clump radius, overall clump mass, and the characteristic density determined from the best-fit model at 0.1 pc radius are summarized in Table 6. The posterior probability distributions of
, the predetermined clump radius, overall clump mass, and the characteristic density determined from the best-fit model at 0.1 pc radius are summarized in Table 6. The posterior probability distributions of 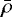 -q are shown in Figure E.1, with the best-fit parameter set indicated. In Figure 11 the observed multi-wavelength flux densities are compared with the SED generated from best-fit RADMC-3D models.
-q are shown in Figure E.1, with the best-fit parameter set indicated. In Figure 11 the observed multi-wavelength flux densities are compared with the SED generated from best-fit RADMC-3D models.
 |
Fig. E.1 χ2 converted probability distribution of the 10 000 parameter set of RADMC-3D models for all clumps. The orange point indicates the best-fit model. Blue crosses give the positions of the 30 best-fit models, so there could be overlaps between the different parameter sets due to the binning. For sources G31, G13, G08a, and G19 the results before re-adjusting T(r) based on SED are shown as light blue contours. |
It can be seen that the observed SEDs of sources G18, G19, G08a, G13, and G31 show large deviations from those of the best-fit models that were produced based on the assumed T(r) profiles. Forsources G18, G19, G08a, and G13 the deviations are partially expected as these three sources exhibit the lowest densities in the sample, from the clump center to the outer region. It is likely that Trot estimated from the aforementioned thermometers is biased to the small proportion of the dense gas at each radius (clumpiness), while the temperature for the bulk gas at each layer or the average gas temperature is lower. In addition, for the intermediate-scale gas having densities ≲105 cm−3, which are mostly probed by CH3CCH (12-11) and H2CS lines in terms of gas temperature, the higher gas temperature than dust temperature may also have an origin from turbulent heating, as under such gas densities thermal coupling between dust and gas is weaker (Pan & Padoan 2009). For G31, which is much denser in terms of bulk gas radially but shows the most prominent monolithic core in the center, the overestimation of temperature likely originates from the optical depth effect.
To refine T(r) as guided by the observed SED shape, we retain the parametric form (Equation 3) as elaborated in Section 3.6, and only adjust the parameter rin (Equation 3), scaled by a factor <1. Based on the adjustment, we regenerate SED profiles from RADMC modeling and find the best-fit rescaled rin, which is listed in Table 6 for the five sources. For these five sources we then iterate the fitting of radial density profiles from RADMC-3D calculations, based on the adjusted temperature profiles T(r). From Figure E.1, the best-fit parameter set before and after adjusting T(r) are shown together. Decreasing rin in the temperature form is equivalent to reducing the steepness and absolute value of temperature radial profile, which results in an increment of mean gas density and density profile slope in the radial intensity profile fits, as expected. As a further benchmark, we use RADMC-3D to self-consistently calculate the dust temperature. To convert the clump luminosity to a central stellar source, we use the stellar evolution models of solar metallicity from Choi et al. (2016), which give relations between luminosity, mass, radius, and temperature for ZAMS to estimate the stellar Teff. The re-iterated best-fit density model is used to describe the envelope structure. The resultant SED is also shown in Figure 11.
Appendix F Radiative transfer modeling of CH3OH and CH3CCH lines: Benchmarking the results from one-component non-LTE and LTE models
The RADEX analysis of CH3OH (5-4) lines in Section 3.5, with one-component non-LTE assumption, can be biased due to the mixed contribution along the LOS. On the other hand, the RADMC-3D modelings for dust continuum in Appendix E better represents the enclosed masses within certain radii by constraining ρbulk, while they cannot provide constraints on the higher volume density internal structures. To refine our estimates of the physical parameters, we built on these two efforts to conduct 3D radiation transfer forward modelings of CH3OH (5-4) and CH3CCH (12-11) lines. Specifically, we performed the non-LTE modeling for the excitation conditions using the LIME code (Brinch & Hogerheijde 2010) and then compared the synthetic spectra with the observed spectral cubes. The spatial distributions of CH3OH (5-4) and CH3CCH (12-11) line emission are rather extended such that they better characterize the majority of dense gas in the clumps. We focus on benchmarking the radial density profile of the dense gas (ρdense). We fixed the gas temperatureprofiles (T(r); Section 3.6) according to the profiles obtained in Section 3.4 (and refined in Appendix E), when constructing the input models. As T(r) has been verified by full radiative transfer of dust continuuum by building SEDs, the CH3CCH (12-11) modeling conducted here is further used as a sanity check that the assumed temperature profile can reproduce the line emission of this thermometer.
The gas density radial profiles were initially specified to be the best fits from the modeling continuum intensity profiles, ρbulk (Equation 2, see details in Appendix E). Based on this density model and temperature profile T(r), we then experimented with various assumptions of the abundance spatial variations of CH3OH and CH3CCH, motivated by the results of the chemical network from Belloche et al. (2017) and Calcutt et al. (2019).
Based on the chemical network of Belloche et al. (2017), Calcutt et al. (2019) calculated the variation in gas-phase abundance of CH3CCH as a function of warm-up time at different densities which range from 107 to 1010 cm−3. In these calculations, a two-stage physical evolution is assumed: a cold collapse stage is followed by a static warm-up stage that reaches a gas temperature of 400 K. The CH3CCH abundance is enhanced when the gas temperature reaches 30-40 K due to desorption of CH4 to form CH3CCH (i.e., dissociative recombination of larger hydrocarbons). The CH3CCH abundance is significantly enhanced again when the gas temperature reaches 80-100 K, due to the direct desorption of CH3CCH from grain surfaces. Finally, the models with higher final gas density present a systematically lower CH3CCH abundance since in these high-density models CH4 desorbs at slightly higher temperatures (lower panel of Figure F.1). Similarly, according to the chemical model of Garrod et al. (2017), the abundance of CH3OH experiences two significant enhancements at gas temperatures of 30-40 K and 80-100 K (upper panel of Figure F.1). The chemical modeling include three warm-up models, depending on the timescale for the system to increase from 10-200 K, over 5 × 104 (fast), 2 × 105 (medium), and 1 × 106(slow) yr (Garrod & Herbst 2006).
 |
Fig. F.1 Abundance variations of CH3OH and CH3CCH from chemical models (lines) and the explored parameter space (filled) for the LIME models based on ρbulk density model (column A of Table 7). The results from the chemical models are shown as lines (solid, dashed, and dotted): for CH3OH the abundance profiles for different warm-up timescales are shown (Garrod et al. 2017); for CH3CCH, abundance profiles of different final collapse densities are shown (Calcutt et al. 2019). The dark green filled region indicates the lower abundance range explored for Xout by the LIME models, and the light green filled region the upper range explored for Xin. The verticalgray lines indicate the jump in temperature of 30 and 80 K. |
To mimic the abundance enhancement in the warm or lukewarm regions described by these chemical models, we parameterized the CH3OH and CH3CCH abundance profiles as Equation 5. Again, we assumed that the A- and E-type CH3OH have the same abundance. The parameter ranges of Xin and Xout were chosen by referencing to Nmol for CH3CCH and CH3OH from the XCLASS/RADEX modeling results (Sections 3.4-3.5) and the aforementioned chemical models. Figure F.1 shows a comparison between the parameter space we explored and the chemical modeling results.
Currently, only the collisional coefficients of CH3OH with para-H2 are available, although it seems that only in hot shocked gas is there a significant difference between the thermal rate coefficients of collisions with ortho- and para-H2 (Flower et al. 2010). Our non-LTE models were not affected by the uncertain collisional coefficients because we assumed a low ortho- to para-H2 ratio (OPR), such that the collisions with ortho-H2 is negligible. Chemical models and observations toward early-stage dense cores indeed indicate an OPR value of ~10−3-10−2 (Flower et al. 2006, cf. Troscompt et al. 2009), which is well below the equilibrium value of 3. In the postshock gas, the OPR may remain low since the short timescale does not allow significant conversion from para-H2 to ortho-H2 (Leurini et al. 2016).
When performing non-LTE modeling of CH3CCH, the collisional rates of CH3CN (Green 1986) were substituted by those of CH3CCH. This is a common approach since CH3CCH and CH3CN have similar molecular weights and configuration, while collisional rates for CH3CCH have not yet been published. The collisional rates of CH3OH were quotedfrom Rabli & Flower (2010) (see Section 3.5).
To create the distributions of physical properties we adopted the sf3dmodels package (Izquierdo et al. 2018)to generate homogeneous grids in Cartesian coordinates, which were then interpolated onto the LIME input format of randomly generated set of points. We used the linear resolution of ~0.015-0.03 pc (depending on the source radius Rclump, Table 6) as the grid size that corresponds to better than one-fifth the beam size for each source. On each grid we specified a mean gas velocity using a random process to mimic the turbulent velocity field; the direction was uniformly sampled from the 4π solid angle, while the magnitude of the velocity was drawn from a Gaussian distribution with σ =3.5 km s−1. We additionally adopted a uniform Doppler broadening of 0.4 km s−1 (σturb = 0.4 km s−1) to accommodate the unresolved (micro-)turbulence velocity. Therefore the intrinsic linewidth for each model is σ1D = 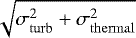 , where σthermal is determined by the assumed gas temperature. This yields linewidths comparable to the observed values (ΔV = 5.3 ± 2.0 km s−1).
, where σthermal is determined by the assumed gas temperature. This yields linewidths comparable to the observed values (ΔV = 5.3 ± 2.0 km s−1).
We postprocessed the output of LIME to match the angular and velocity resolutions of our observations, and then compared the annularly and beam averaged synthetic spectra with those from observed spectral cubes. For each observed clump, the best-fit model was taken as the one with the lowest χ2. The parameters of these best-fit chemical models are summarized in Table 7, column A.
We found that these initial models systematically underestimated the intensities of the higher K components of CH3OH lines in the inner regions for all sources (Figure 13). There are some sources in which the intensities of the higher K components were underestimated also at outer radii. This implies that, in general, the density profiles ρbulk derived from dust continuum modeling (Appendix E) were not high enough to collisionally excite the high K levels of CH3OH (e.g., gas may be concentrated in substructures of higher volume density). This was expected, as was revealed by the comparison to the ρdense derived by RADEX modeling: gas densities are 50-200 times higher than that of ρbulk derived by single-dish dust continuum. Therefore, we updated the radial density profile in the models according to the RADEX results ρdense (Section 3.5) following Equation 6. We manually adjusted the flexible parameters, which are the density scaling factor fn (Equation 6) and finc, to quantify the abundance profile of Xmol(r) in Equation 5, in a trial-and-error manner to seek for better fits to the observational data. Figure F.2 demonstrates how the line ratios of CH3OH K components vary with gas density and molecular abundance while keeping a fixed overall molecular column density, as an example using the density model of G08b.
 |
Fig. F.2 Line ratios of CH3OH (5-4) K components from LIME models based on density profile of G08b (ρ0 corresponds to the adjusted reference density at 0.1 pc for this source, as in Equation 6). The abundance value corresponds to the outer abundance (Xout), as in Table 7. The central symbol at the horizontal line of y = 1 corresponds to the best-fit model listed in Table. 7 (column B). The comparison of observations with model spectra is presented in Figure 14, top panel. |
Our best-fit model parameters for all the clumps are summarized in Table 7, column B. In these results fr ranges from1.5 to 5 in all the sources except G31, indicating RADEX results only moderately overestimated the gas densities. As mentioned in Section 3.7, the rather large fr in G31 is due to the very high optical depth of its lower CH3OH K components in the central region. In this case the CH3OH (5-4) lines do not provide meaningful constraints for the RADEX modeling which was based on the assumption of moderate optical depth.
When spatially integrating Equation 6 with a spherical symmetric assumption, the resulting overall molecular gas masses (Mmod) considerably exceed those derived based on modeling dust continuum emission, by integrating ρbulk (see Appendix E). This implies that the dense gas structures traced by CH3OH do not have spherically symmetric distributions. Instead, they are local gas concentrations that have small volume filling factors. To reconcile the mass difference, we defined ffdens ≡ Menc/Mmod, where Menc designates the enclosed molecular gas mass within 0.5 pc radius (a scale encompassing the CH3OH emission entirely for all sources) derived from the dust continuum models following ρbulk (Equation 2, Appendix E). ffdens can be regarded roughly as an upper limit of volume filling factor of the dense gas traced by CH3OH. From the radiative transfer modeling point of view, to fit the observed line profiles, in the optically thin limit, varying the dense gas volume does not affect line intensity ratios, while the values of Xmol(r) can be adjusted accordingly such that the overall molecular column densities are not altered. We discuss the implications from the inferred volume filling factor of dense gas, and the dense gas mass fraction based on comparing ρbulk and ρdense in Section 4.5.
Appendix G Comparison between observed spectra and modeling results: Other targets
 |
Fig. G.7 Example spectra (archival SMA data, Sect. 2) of thermometer lines and the XCLASS fits of G10. |
References
- Adams, F. C. 1991, ApJ, 382, 544 [Google Scholar]
- Adams, F. C., & Shu, F. H. 1985, ApJ, 296, 655 [Google Scholar]
- Bachiller, R., & Gutiérrez, M. P. 1997, ApJ, 487, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Bacmann, A., Lefloch, B., Ceccarelli, C., et al. 2002, A&A, 389, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballesteros-Paredes, J., Vázquez-Semadeni, E., Gazol, A., et al. 2011, MNRAS, 416, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Ballesteros-Paredes, J., Vázquez-Semadeni, E., Palau, A., & Klessen, R. S. 2018, MNRAS, 479, 2112 [NASA ADS] [Google Scholar]
- Bate, M. R. 2009, MNRAS, 392, 1363 [CrossRef] [Google Scholar]
- Beckwith, S. V. W., & Sargent, A. I. 1991, ApJ, 381, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, T. A., Cernicharo, J., Viti, S., et al. 2014, A&A, 564, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Meshcheryakov, A. A., Garrod, R. T., et al. 2017, A&A, 601, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beltrán, M. T., Cesaroni, R., Neri, R., et al. 2004, ApJ, 601, L187 [Google Scholar]
- Beltrán, M. T., Cesaroni, R., Rivilla, V. M., et al. 2018, A&A, 615, A141 [Google Scholar]
- Bergin, E. A., Goldsmith, P. F., Snell, R. L., & Ungerechts, H. 1994, ApJ, 431, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Bertoldi, F., & McKee, C. F. 1992, ApJ, 395, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Schilke, P., Menten, K. M., et al. 2002, ApJ, 566, 945 [Google Scholar]
- Beuther, H., Leurini, S., Schilke, P., et al. 2007, A&A, 466, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Semenov, D., Henning, T., & Linz, H. 2008, ApJ, 675, L33 [Google Scholar]
- Beuther, H., Henning, T., Linz, H., et al. 2010, A&A, 518, L78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Ragan, S. E., Johnston, K., et al. 2015, A&A, 584, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binder, B. A., & Povich, M. S. 2018, ApJ, 864, 136 [CrossRef] [Google Scholar]
- Bisschop, S. E., Jørgensen, J. K., van Dishoeck, E. F., & de Wachter, E. B. M. 2007, A&A, 465, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blake, G. A., van Dishoeck, E. F., Jansen, D. J., Groesbeck, T. D., & Mundy, L. G. 1994, ApJ, 428, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Bøgelund, E. G., Barr, A. G., Taquet, V., et al. 2019, A&A, 628, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bracco, A., Palmeirim, P., André, P., et al. 2017, A&A, 604, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradley, L., Sipöcz, B., Robitaille, T., et al. 2021, astropy/photutils: 1.2.0 [Google Scholar]
- Brinch, C., & Hogerheijde, M. R. 2010, A&A, 523, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calcutt, H., Willis, E. R., Jørgensen, J. K., et al. 2019, A&A, 631, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Camacho, V., Vázquez-Semadeni, E., Ballesteros-Paredes, J., et al. 2016, ApJ, 833, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Camacho, V., Vázquez-Semadeni, E., Palau, A., Busquet, G., & Zamora-Avilés, M. 2020, ApJ, 903, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Feldman, P. A., Redman, R. O., et al. 2000, ApJ, 543, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Noriega-Crespo, A., Mizuno, D. R., et al. 2009, PASP, 121, 76 [Google Scholar]
- Caselli, P., & Myers, P. C. 1995, ApJ, 446, 665 [Google Scholar]
- Caswell, J. L. 1998, MNRAS, 297, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Cesaroni, R., Olmi, L., Walmsley, C. M., Churchwell, E., & Hofner, P. 1994, ApJ, 435, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Cesaroni, R., Beltrán, M. T., Zhang, Q., Beuther, H., & Fallscheer, C. 2011, A&A, 533, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cesaroni, R., Beuther, H., Ahmadi, A., et al. 2019, A&A, 627, A68 [EDP Sciences] [Google Scholar]
- Chapin, E. L., Berry, D. S., Gibb, A. G., et al. 2013, MNRAS, 430, 2545 [Google Scholar]
- Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [Google Scholar]
- Churchwell, E., Walmsley, C. M., & Cesaroni, R. 1990, A&AS, 83, 119 [NASA ADS] [Google Scholar]
- Contreras, Y., Schuller, F., Urquhart, J. S., et al. 2013, A&A, 549, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coughlin, E. R. 2017, ApJ, 835, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Csengeri, T., Bontemps, S., Schneider, N., et al. 2011, ApJ, 740, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Csengeri, T., Urquhart, J. S., Schuller, F., et al. 2014, A&A, 565, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csengeri, T., Weiss, A., Wyrowski, F., et al. 2016, A&A, 585, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cummins, S. E., Green, S., Thaddeus, P., & Linke, R. A. 1983, ApJ, 266, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Curry, C. L., & McKee, C. F. 2000, ApJ, 528, 734 [CrossRef] [Google Scholar]
- Cyganowski, C. J., Whitney, B. A., Holden, E., et al. 2008, AJ, 136, 2391 [Google Scholar]
- Dempsey, J. T., Friberg, P., Jenness, T., et al. 2013, MNRAS, 430, 2534 [Google Scholar]
- Dullemond, C. P., Juhasz, A., Pohl, A., et al. 2012, Astrophysics Source Code Library [record ascl:1202.015] [Google Scholar]
- Esplugues, G. B., Viti, S., Goicoechea, J. R., & Cernicharo, J. 2014, A&A, 567, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Estalella, R. 2017, PASP, 129, 025003 [NASA ADS] [CrossRef] [Google Scholar]
- Falgarone, E., & Puget, J. L. 1985, A&A, 142, 157 [NASA ADS] [Google Scholar]
- Fallscheer, C., Beuther, H., Zhang, Q., Keto, E., & Sridharan, T. K. 2009, A&A, 504, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fayolle, E. C., Öberg, K. I., Garrod, R. T., van Dishoeck,E. F., & Bisschop, S. E. 2015, A&A, 576, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Federrath, C., & Klessen, R. S. 2013, ApJ, 763, 51 [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Walmsley, C. M. 2006, A&A, 449, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Rabli, D. 2010, MNRAS, 409, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Foster, P. N., & Chevalier, R. A. 1993, ApJ, 416, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T., Belloche, A., Müller, H. S. P., & Menten, K. M. 2017, A&A, 601, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerner, T., Beuther, H., Semenov, D., et al. 2014, A&A, 563, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giannetti, A., Leurini, S., Wyrowski, F., et al. 2017, A&A, 603, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gieser, C., Beuther, H., Semenov, D., et al. 2021, A&A, 648, A66 [EDP Sciences] [Google Scholar]
- Girichidis, P., Federrath, C., Banerjee, R., & Klessen, R. S. 2011, MNRAS, 413, 2741 [Google Scholar]
- Girichidis, P., Konstandin, L., Whitworth, A. P., & Klessen, R. S. 2014, ApJ, 781, 91 [CrossRef] [Google Scholar]
- Glover, S. C. O., & Clark, P. C. 2012, MNRAS, 421, 9 [NASA ADS] [Google Scholar]
- Goldsmith, P. F. 2001, ApJ, 557, 736 [Google Scholar]
- Gómez, L., Luis, L., Hernández-Curiel, I., et al. 2010, ApJS, 191, 207 [CrossRef] [Google Scholar]
- Gómez, G. C., Vázquez-Semadeni, E., & Palau, A. 2021, MNRAS, 502, 4963 [CrossRef] [Google Scholar]
- Gómez-Ruiz, A. I., Kurtz, S. E., Araya, E. D., Hofner, P., & Loinard, L. 2016, ApJS, 222, 18 [CrossRef] [Google Scholar]
- Graninger, D. M., Wilkins, O. H., & Öberg, K. I. 2016, ApJ, 819, 140 [Google Scholar]
- Grave, J. M. C., & Kumar, M. S. N. 2009, A&A, 498, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, S. 1986, ApJ, 309, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Green, J. A., & McClure-Griffiths, N. M. 2011, MNRAS, 417, 2500 [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [EDP Sciences] [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guszejnov, D., Krumholz, M. R., & Hopkins, P. F. 2016, MNRAS, 458, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Guszejnov, D., Hopkins, P. F., & Ma, X. 2017, MNRAS, 472, 2107 [NASA ADS] [CrossRef] [Google Scholar]
- Guszejnov, D., Hopkins, P. F., & Grudić, M. Y. 2018, MNRAS, 477, 5139 [NASA ADS] [CrossRef] [Google Scholar]
- Hacar, A., Kainulainen, J., Tafalla, M., Beuther, H., & Alves, J. 2016, A&A, 587, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harju, J., Lehtinen, K., Booth, R. S., & Zinchenko, I. 1998, A&AS, 132, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatchell, J., & van der Tak, F. F. S. 2003, A&A, 409, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helmich, F. P., & van Dishoeck, E. F. 1997, A&AS, 124, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., Commerçon, B., Lee, Y.-N., & Chabrier, G. 2020, ApJ, 904, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Henriksen, R., Andre, P., & Bontemps, S. 1997, A&A, 323, 549 [NASA ADS] [Google Scholar]
- Herpin, F., Marseille, M., Wakelam, V., Bontemps, S., & Lis, D. C. 2009, A&A, 504, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heyer, M., Krawczyk, C., Duval, J., & Jackson, J. M. 2009, ApJ, 699, 1092 [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Ho, P. T. P., & Haschick, A. D. 1986, ApJ, 304, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Hofner, P., & Churchwell, E. 1996, A&AS, 120, 283 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hosokawa, T., & Omukai, K. 2009, ApJ, 691, 823 [Google Scholar]
- Humire, P. K., Thiel, V., Henkel, C., et al. 2020, A&A, 642, A222 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izquierdo, A. F., Galván-Madrid, R., Maud, L. T., et al. 2018, MNRAS, 478, 2505 [NASA ADS] [CrossRef] [Google Scholar]
- Izquierdo, A. F., Smith, R. J., Glover, S. C. O., et al. 2021, MNRAS, 500, 5268 [Google Scholar]
- Jacobsen, S. K., Jørgensen, J. K., van der Wiel, M. H. D., et al. 2018, A&A, 612, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jappsen, A. K., Klessen, R. S., Larson, R. B., Li, Y., & Mac Low, M. M. 2005, A&A, 435, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiang, X.-J., Liu, H. B., Zhang, Q., et al. 2015, ApJ, 808, 114 [Google Scholar]
- Jørgensen, J. K., Bourke, T. L., Myers, P. C., et al. 2007, ApJ, 659, 479 [Google Scholar]
- Juvela, M., He, J., Pattle, K., et al. 2018, A&A, 612, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Henning, T., & Plume, R. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Banerjee, R., Federrath, C., & Henning, T. 2011, A&A, 530, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kauffmann, J., Pillai, T., & Goldsmith, P. F. 2013, ApJ, 779, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E. R. 1990, ApJ, 355, 190 [CrossRef] [Google Scholar]
- Keto, E. R., Ho, P. T. P., & Reid, M. J. 1987, ApJ, 323, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E. R., Ho, P. T. P., & Haschick, A. D. 1988, ApJ, 324, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S. 2000, ApJ, 535, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., & Hennebelle, P. 2010, A&A, 520, A17 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., Spaans, M., & Jappsen, A.-K. 2007, MNRAS, 374, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Koda, J., Sawada, T., Wright, M. C. H., et al. 2011, ApJS, 193, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Kritsuk, A. G., Norman, M. L., & Wagner, R. 2011, ApJ, 727, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Weidner, C., Pflamm-Altenburg, J., et al. 2013, The Stellar and Sub-Stellar Initial Mass Function of Simple and Composite Populations, eds. T. D. Oswalt & G. Gilmore, 5, 115 [NASA ADS] [Google Scholar]
- Krumholz, M. R. 2014, MNRAS, 437, 1662 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & McKee, C. F. 2005, ApJ, 630, 250 [Google Scholar]
- Krumholz, M. R., Klein, R. I. & McKee, C. F. 2007, ApJ, 656, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Klein, R. I., & McKee, C. F. 2012, ApJ, 754, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, T. B. H., Kuiper, E. N. R., Dickinson, D. F., Turner, B. E., & Zuckerman, B. 1984, ApJ, 276, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Kurono, Y., Morita, K.-I., & Kamazaki, T. 2009, PASJ, 61, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1969, MNRAS, 145, 271 [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [Google Scholar]
- Lee, Y.-N., & Hennebelle, P. 2018, A&A, 611, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, Y.-N., & Hennebelle, P. 2019, A&A, 622, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, E. J., Chang, P., & Murray, N. 2015, ApJ, 800, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Leurini, S., Schilke, P., Menten, K. M., et al. 2004, A&A, 422, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leurini, S., Schilke, P., Wyrowski, F., & Menten, K. M. 2007, A&A, 466, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leurini, S., Codella, C., López-Sepulcre, A., et al. 2014, A&A, 570, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leurini, S., Menten, K. M., & Walmsley, C. M. 2016, A&A, 592, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, J., Wang, J., Zhu, Q., Zhang, J., & Li, D. 2015, ApJ, 802, 40 [Google Scholar]
- Li, J. I.-H., Liu, H. B., Hasegawa, Y., & Hirano, N. 2017, ApJ, 840, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Li, S., Zhang, Q., Pillai, T., et al. 2019, ApJ, 886, 130 [Google Scholar]
- Lin, Y., Liu, H. B., Li, D., et al. 2016, ApJ, 828, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Liu, H. B., Dale, J. E., et al. 2017, ApJ, 840, 22 [CrossRef] [Google Scholar]
- Lin, Y., Csengeri, T., Wyrowski, F., et al. 2019, A&A, 631, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, H. B. 2017, A&A, 597, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, H. B. 2019, ApJ, 877, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H. B., Ho, P. T. P., Zhang, Q., et al. 2010, ApJ, 722, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H. B., Zhang, Q., & Ho, P. T. P. 2011, ApJ, 729, 100 [CrossRef] [Google Scholar]
- Liu, H. B., Quintana-Lacaci, G., Wang, K., et al. 2012, ApJ, 745, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H. B., Galván-Madrid, R., Jiménez-Serra, I., et al. 2015, ApJ, 804, 37 [Google Scholar]
- Liu, H. B., Chen, H.-R. V., Román-Zúñiga, C. G., et al. 2019, ApJ, 871, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [Google Scholar]
- Lomax, O., Whitworth, A. P., & Hubber, D. A. 2015, MNRAS, 449, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Longmore, S. N., Pillai, T., Keto, E., Zhang, Q., & Qiu, K. 2011, ApJ, 726, 97 [CrossRef] [Google Scholar]
- Lowe, I., Mason, B., Bhandarkar, T., et al. 2021, ArXiv e-prints, [arXiv:2105.13432] [Google Scholar]
- Lynch, S. M. 2007, Introduction to Applied Bayesian Statistics and Estimation for Social Scientists (New York, NY: Springer Science & Business Media, LLC.) [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 500, 259 [NASA ADS] [Google Scholar]
- McKee, C. F.,& Holliman, John H., I. 1999, ApJ, 522, 313 [CrossRef] [Google Scholar]
- McKee, C. F.,& Tan, J. C. 2003, ApJ, 585, 850 [Google Scholar]
- McLaughlin, D. E., & Pudritz, R. E. 1997, ApJ, 476, 750 [Google Scholar]
- Minh, Y. C., Liu, S. Y., Chen, H. R., & Su, Y. N. 2011, ApJ, 737, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Pezzuto, S., Cesaroni, R., et al. 2008, A&A, 481, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Merello, M., Elia, D., et al. 2016, ApJ, 826, L8 [Google Scholar]
- Möller, T., Endres, C., & Schilke, P. 2017, A&A, 598, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monsch, K., Pineda, J. E., Liu, H. B., et al. 2018, ApJ, 861, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Bontemps, S., & Louvet, F. 2018, ARA&A, 56, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Mottram, J. C., Beuther, H., Ahmadi, A., et al. 2020, A&A, 636, A118 [EDP Sciences] [Google Scholar]
- Mouschovias, T. C., & Morton, S. A. 1991, ApJ, 371, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [Google Scholar]
- Mueller, K. E., Shirley, Y. L., Evans, Neal J., I., & Jacobson, H. R. 2002, ApJS, 143, 469 [Google Scholar]
- Murray, N., & Chang, P. 2015, ApJ, 804, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, D. W., Chang, P., Murray, N. W., & Pittman, J. 2017, MNRAS, 465, 1316 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C. 2015, ApJ, 806, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Nomura, H., & Millar, T. J. 2004, A&A, 414, 409 [CrossRef] [EDP Sciences] [Google Scholar]
- Öberg, K. I., Fayolle, E. C., Reiter, J. B., & Cyganowski, C. 2014, Faraday Discuss., 168, 81 [CrossRef] [Google Scholar]
- Offner, S. S. R., Klein, R. I., McKee, C. F., & Krumholz, M. R. 2009, ApJ, 703, 131 [CrossRef] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Padoan, P., Haugbølle, T., & Nordlund, Å. 2012, ApJ, 759, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Haugbølle, T., Nordlund, Å., & Frimann, S. 2017, ApJ, 840, 48 [Google Scholar]
- Padoan, P., Pan, L., Juvela, M., Haugbølle, T., & Nordlund, Å. 2020, ApJ, 900, 82 [Google Scholar]
- Palau, A., Estalella, R., Girart, J. M., et al. 2014, ApJ, 785, 42 [Google Scholar]
- Pan, L., & Padoan, P. 2009, ApJ, 692, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Parmentier, G. 2019, ApJ, 887, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Passot, T., & Vázquez-Semadeni, E. 1998, Phys. Rev. E, 58, 4501 [Google Scholar]
- Penston, M. V. 1969, MNRAS, 144, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Persson, M. V., Harsono, D., Tobin, J. J., et al. 2016, A&A, 590, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pham, D. T., Ghanbarzadeh, A., Koç, E., et al. 2006, in The Bees Algorithm - A Novel Tool for Complex Optimisation Problems [Google Scholar]
- Pillai, T., Wyrowski, F., Carey, S. J., & Menten, K. M. 2006, A&A, 450, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plume, R., Jaffe, D. T., II, N. J. E., Martin-Pintado, J., & Gomez-Gonzalez, J. 1997, ApJ, 476, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Purcell, C. R., Balasubramanyam, R., Burton, M. G., et al. 2006, MNRAS, 367, 553 [Google Scholar]
- Qi, C. 2003, in SFChem 2002: Chemistry as a Diagnostic of Star Formation, eds. C. L. Curry, & M. Fich, 393 [Google Scholar]
- Qiu, K., Zhang, Q., Beuther, H., & Yang, J. 2007, ApJ, 654, 361 [CrossRef] [Google Scholar]
- Rabli, D., & Flower, D. R. 2010, MNRAS, 406, 95 [Google Scholar]
- Ragan, S., Henning, T., Krause, O., et al. 2012, A&A, 547, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ragan, S. E., Henning, T., Tackenberg, J., et al. 2014, A&A, 568, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rivilla, V. M., Beltrán, M. T., Cesaroni, R., et al. 2017, A&A, 598, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robertson, B.,& Goldreich, P. 2012, ApJ, 750, L31 [CrossRef] [Google Scholar]
- Rodríguez-Garza, C. B., Kurtz, S. E., Gómez-Ruiz, A. I., et al. 2017, ApJS, 233, 4 [CrossRef] [Google Scholar]
- Rolffs, R., Schilke, P., Wyrowski, F., et al. 2011, A&A, 527, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roy, A., André, P., Palmeirim, P., et al. 2014, A&A, 562, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanhueza, P., Jackson, J. M., Zhang, Q., et al. 2017, ApJ, 841, 97 [Google Scholar]
- Sanhueza, P., Contreras, Y., Wu, B., et al. 2019, ApJ, 886, 102 [Google Scholar]
- Sanna, A., Reid, M. J., Menten, K. M., et al. 2014, ApJ, 781, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, in ASP Conf. Ser., 77, Astronomical Data Analysis Software and Systems IV, eds. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, 433 [Google Scholar]
- Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shirley, Y. L. 2015, PASP, 127, 299 [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [Google Scholar]
- Siringo, G., Kreysa, E., Kovács, A., et al. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, R. J., Longmore, S., & Bonnell, I. 2009, MNRAS, 400, 1775 [Google Scholar]
- Smith, R. J., Treß, R. G., Sormani, M. C., et al. 2020, MNRAS, 492, 1594 [NASA ADS] [CrossRef] [Google Scholar]
- Sollins, P. K., Zhang, Q., Keto, E., & Ho, P. T. P. 2005, ApJ, 624, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Spaans, M., & Silk, J. 2000, ApJ, 538, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Sridharan, T. K., Beuther, H., Saito, M., Wyrowski, F., & Schilke, P. 2005, ApJ, 634, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Sutton, E. C., Blake, G. A., Genzel, R., Masson, C. R., & Phillips, T. G. 1986, ApJ, 311, 921 [NASA ADS] [CrossRef] [Google Scholar]
- Traficante, A., Lee, Y. N., Hennebelle, P., et al. 2018, A&A, 619, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Troscompt, N., Faure, A., Maret, S., et al. 2009, A&A, 506, 1243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urban, A., Martel, H., & Evans, N. J. II 2010, ApJ, 710, 1343 [NASA ADS] [CrossRef] [Google Scholar]
- Urquhart, J. S., König, C., Giannetti, A., et al. 2018, MNRAS, 473, 1059 [Google Scholar]
- van der Tak, F. F. S., van Dishoeck, E. F., Evans, Neal J., I., & Blake, G. A. 2000, ApJ, 537, 283 [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., Blake, G. A., Jansen, D. J., & Groesbeck, T. D. 1995, ApJ, 447, 760 [Google Scholar]
- van ’t Hoff, M. L. R., van Dishoeck, E. F., Jørgensen, J. K., & Calcutt, H. 2020, A&A, 633, A7 [Google Scholar]
- Varricatt, W. P., Davis, C. J., Ramsay, S., & Todd, S. P. 2010, MNRAS, 404, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Varricatt, W. P., Wouterloot, J. G. A., Ramsay, S. K., & Davis, C. J. 2018, MNRAS, 480, 4231 [NASA ADS] [CrossRef] [Google Scholar]
- Vasyunina, T., Vasyunin, A. I., Herbst, E., et al. 2014, ApJ, 780, 85 [Google Scholar]
- Vázquez-Semadeni, E., Palau, A., Ballesteros-Paredes, J., Gómez, G. C., & Zamora-Avilés, M. 2019, MNRAS, 490, 3061 [Google Scholar]
- Wakelam, V., Ceccarelli, C., Castets, A., et al. 2005, A&A, 437, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Hersant, F., & Herpin, F. 2011, A&A, 529, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walch, S., Burkert, A., Whitworth, A., Naab, T., & Gritschneder, M. 2009, MNRAS, 400, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y., Zhang, Q., Pillai, T., Wyrowski, F., & Wu, Y. 2008, ApJ, 672, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Ward-Thompson, D., Motte, F., & Andre, P. 1999, MNRAS, 305, 143 [Google Scholar]
- Watanabe, N., Shiraki, T., & Kouchi, A. 2003, ApJ, 588, L121 [Google Scholar]
- Whitworth, A. P., Bhattal, A. S., Francis, N., & Watkins, S. J. 1996, MNRAS, 283, 1061 [NASA ADS] [Google Scholar]
- Wienen, M., Wyrowski, F., Menten, K. M., et al. 2015, A&A, 579, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, J. P., Blitz, L., & McKee, C. F. 2000, in Protostars and Planets IV, eds. V. Mannings, A. P. Boss, & S. S. Russell, 97 [Google Scholar]
- Williams, S. J., Fuller, G. A., & Sridharan, T. K. 2005, A&A, 434, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, T. L., Rohlfs, K., & Hüttemeister, S. 2013, Tools of Radio Astronomy [Google Scholar]
- Wood, D. O. S., & Churchwell, E. 1989, ApJS, 69, 831 [Google Scholar]
- Wyrowski, F., Güsten, R., Menten, K. M., Wiesemeyer, H., & Klein, B. 2012, A&A, 542, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, S., & Lazarian, A. 2020, ApJ, 890, 157 [Google Scholar]
- Zapata, L. A., Rodríguez, L. F., Ho, P. T. P., Beuther, H., & Zhang, Q. 2006, AJ, 131, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q., Wang, Y., Pillai, T., & Rathborne, J. 2009, ApJ, 696, 268 [Google Scholar]
The James Clerk Maxwell Telescope is operated by the East Asian Observatory on behalf of The National Astronomical Observatory of Japan, Academia Sinica Institute of Astronomy and Astrophysics, the Korea Astronomy and Space Science Institute, the National Astronomical Observatories of China and the Chinese Academy of Sciences (Grant No. XDB09000000), with additional funding support from the Science and Technology Facilities Council of the United Kingdom and participating universities in the United Kingdom and Canada. The James Clerk Maxwell Telescope has historically been operated by the Joint Astronomy Centre on behalf of the Science and Technology Facilities Council of the United Kingdom, the National Research Council of Canada and the Netherlands Organization for Scientific Research. Additional funds for the construction of SCUBA-2 were provided by the Canada Foundation for Innovation.
All Tables
Parameters of CH3OH derived radialdensity ρdense(r) and multi-thermometer derived temperature profiles T(r).
Best-fit parameters from RADMC-3D modeling of the dust continuum in 350 or 450 μm, and 870 μm.
Properties related to radial linewidth and virial parameter profiles of the target clumps.
All Figures
 |
Fig. 1 Schematic picture of molecular cloud structure over spatial scales from >10 pc to ~0.1 pc: from cloud to core scale. A molecular cloud starts contraction from an initial stage that appears to be an infrared dark cloud (IRDC) and evolves into a star-forming one, embedding a number of molecular clumps. The massive clumps, ~1 pc in size, are generally composed of filamentary structures and cores at different evolutionary stages. In all figures, the yellow curved arrows represent turbulent motions and the purple arrows indicate gravitational contractionor gas inflows (along filaments). In the rightmost figure, the thick lines show filaments and the blue ovals indicate cores of different masses; the color gradient of the clump indicates a density gradient of the bulk gas. The characteristics of different structures are linked to textboxes by dotted arrows. |
| In the text | |
 |
Fig. 2 Luminosity–mass diagram of target sources (three-branched triangles). The evolutionary tracks of massive clumps of different envelope masses that form a cluster of stars with different accretion rates are shown as dotted and solid green lines; the evolutionary tracks of clumps of different envelope masses that are assumed to form a single massive star are shown as dash-dotted gray lines with arrows (Molinari et al. 2008; for more details see Sect. 2.1). |
| In the text | |
 |
Fig. 3 Overall work flow showing the radiative transfer modeling procedure followed in this work. |
| In the text | |
 |
Fig. 4 Spitzer IRAC RGBs (R: 8.0 μm; G: 4.5 μm B: 3.6 μm) maps of the target sources. Yellow contours show the ATLASGAL 870 μm emission from 1 Jy beam−1 to the peak flux for each source, using seven levels with uniform spacing. White contours show SMA 1.2 mm emission from 3σ to the peak flux using five levels with uniform spacing. Negative flux levels of the 1.2 mm continuum are shown in contours of dotted lines, from − 1σ to the minimum negative flux with two levels. The beam of the SMA continuum is shown in the lower left corner of each plot. The beam size of the archival data for source G10 is much smaller than other sources (Sect. 2.2). The primary beam size is shown in each plot as a blue dashed circle. |
| In the text | |
 |
Fig. 5 Integrated intensity maps (gray contours) of CH3CCH, H2CS, and CH3CN toward sources G19, G08a, and G08b. Integrated intensity of CH3OH 50,5 –40,4 ([vlsr −3, vlsr + 3] km s−1) is shown in color scale. Gray contours show the intensity levels with uniform intervals from 5σ up to the peak flux, with the emission range (Jy beam−1 km s−1) indicated in the lower left corner of each panel. Colored contour in the left panel shows the location of 0.8 × peak emission of the 1.2 mm SMA continuum image. The green ellipses indicate beams of corresponding molecular lines (open) and CH3OH 50,5 –40,4 line (filled). |
| In the text | |
 |
Fig. 6 Same as Fig. 5, but for target clumps G13, G28, and G31. |
| In the text | |
 |
Fig. 7 Example spectra of thermometer lines CH3CN J = 13-12, CH3CCH J = 14-13, H2CS J = 6-5, H2CS J = 7-6 at the continuum peak of the target source. The blue profiles show the XCLASS LTE fitting results. For source G31.412+0.307, which presents significant line blending from other species, the fittings also included those species and transitions that can potentially make prominent contributions to the spectrum. |
| In the text | |
 |
Fig. 8 Rotational temperature maps of source G08b derived from multiple thermometer lines using the XCLASS package (Sect. 3.4). The green contours indicate SMA 1.2 mm continuum levels from 0.3 to 0.9 × peak flux (Table 4) in five steps of uniform interval. The beams of the continuum and the respective lines are shown in the lower left corner as green and hatched ellipses, respectively. |
| In the text | |
 |
Fig. 9 CH3OH derived n(H2) maps from RADEX modeling of all target sources. The beam of the CH3OH 5−1 -4−1 E line is indicated in the bottom left corner. The gray contours indicate the SMA 1.2 mm continuum level from 0.1 to 0.9 × peak flux represented by five steps of uniform interval. |
| In the text | |
 |
Fig. 10 Radial intensity profile comparisons between observations and best-fit RADMC-3D models. Gray horizontal dashed lines indicate the noise level (3σ). Gray vertical lines indicate the clump radius used in the modeling. The dotted line indicates beam shape in each plot. For source G18, G19, G08a, G13, and G31, the model fit after re-adjusting T(r) is shown. The gray vertical line indicates the clump radius Rclump. |
| In the text | |
 |
Fig. 11 Comparison of SEDs of the best-fit RADMC-3D models with measured multi-wavelength fluxes (green dots with error bars indicating 0.8 and 1.2 times the flux level) for each source. The black line indicates the SED generated from assumed T(r) and the corresponding best density profile fits. The blue dashed line indicates the SED generated from refined T(r) and the re-iterated best density profile fits. The blue shaded regions indicate a 20% difference around the blue dashed SED profile. The red line shows the SED generated by self-consistently calculating the dust temperature adopting a central heating ZAMS star plus the re-iterated best density profile (for more details, see Appendix E). |
| In the text | |
 |
Fig. 12 Projected radial averaged n(H2) radial profiles derived from n(H2) maps shown in Fig. 9. The thick gray line indicates the best-fit single power-law model (beam convolution considered). The gray shadowed band indicates the 3σ confidence band of the best-fit model. The model parameters and 1σ errors are listed in Table 5. |
| In the text | |
 |
Fig. 13 LIME modeling result (best-fit parameters listed in Table 7, Col. A) based on best-fit density model from RADMC-3D continuum modeling. From left to right: Annular beam-averaged spectra from the continuum center to the outer envelope. Considering the typical beam FWHM of our observations: the distance from the center of each annular region to the center of the source is indicated at the top of each spectra. The line components of A- and E-type CH3OH are indicated with short-dashed vertical lines in green and gray, respectively. |
| In the text | |
 |
Fig. 14 LIME modeling result (best-fit parameters listed in Table 7, Col. B) after manually adjusting the density profile obtained from RADEX modeling (Eq. (4)), which is prescribed as a piecewise power law (Eq. (6)). From left to right: annular beam-averaged spectra from the continuum center to the outer envelope. Considering the typical beam FWHM of our observations: the distance from the center of each annular region to the center of the source is indicated at the top of each spectra. |
| In the text | |
 |
Fig. 15 Radial temperature and density profiles of target clumps. Left panel: radial temperature profiles T(r) for all the target sources (Eq. (3), refined T(r) is used for the relevant source). The thickness of the lines increases with increasing luminosity. Right panel: radial (projected radial averaged) density profile of the dense gas (ρdense) of all the target sources, from n(H2) maps derived by RADEX modeling of CH3OH lines. The range of the y-axis is trimmed to increase contrast. For both panels the luminosity and clump mass are calculated from RADMC-3D best-fit model (Table 6), which takes into account all the gas components present in the clumps. |
| In the text | |
 |
Fig. 16 Radial gas density slopes of all target clumps. Left panel: density power-law slope derived from continuum (q) based on RADMC-3D modeling detailed in Appendix E. The luminosity, clump mass, and enclosed mass within 0.5 pc are calculated from the RADMC-3D best-fit model, as listed in Table 6. Right panel: density power-law slope derived from n(H2) maps (qradex) from the CH3OH RADEX modeling detailed in Sect. 3.5. The yellow horizontal line in both plots shows a slope of –1.5, indicating the free-falling density profile of a singular isothermal sphere (with an initial density slope of –2) as in Shu 1977, and the attractor solution of the gravo-turbulent collapsing in Murray et al. (2017). |
| In the text | |
 |
Fig. 17 Abundance profiles of molecules CH3OH, CH3CN, CCH, and CH3CCH toward target sources. The symbols are color-coded based on relative distance to the clump center (the 1.2 mm continuum peak). Stars represent abundances at the clump center, and hollow circles or triangles indicate abundances obtained from different radii: the larger and darker these symbols, the closer the distance to the continuum peak. For clump G28 the data points at outer radii are shown as triangles, whereas those for other clumps are shown as circles, to further avoid confusion. X(CCH) for source G10 is taken from Jiang et al. (2015). The inset plot for CH3CN shows the central abundance vs. gas temperature at 0.1 pc; the plot for CH3CCH shows the envelope abundance vs. gas temperature at 0.3 pc. |
| In the text | |
 |
Fig. 18 Same as Fig. 17, but for H2CS, C34S, SO, and SO2. |
| In the text | |
 |
Fig. 19 Comparisons of abundance ratios for relevant molecular species of target clumps. Top: abundance ratios of carbon-chain molecules; Bottom: abundance ratios of sulfur-bearing molecules at clump center (0.1–0.15 pc, beam averaged), shown against source L∕M ratios. |
| In the text | |
 |
Fig. 20 Derived radial averaged temperature profiles of the target sources from multiple thermometers. The error bars show the standard deviations for each annular average. The dashed and dotted lines show a radial temperature profile that follows ∝ L0.25r−0.5 (β = 0) and L0.2r−0.4 (β = 1), respectively (for details, see Sect. 3.6). For G13 and G31 an additional radial temperature profile of ∝ L0.17r−0.34 (β = 1.8, Adams 1991) is shown (dash-dotted line). Whenever available, temperature measurements from higher angular resolution observations from previous works are included in the plots as gray crosses. The thick purple line indicates the fitted temperature profile T(r) described in Sect. 3.6. The blue thin line indicates the refined temperature profile by varying rin in T(r) (Eq. (3)) to fit with dust SED (refined T(r), Appendix E). The plots in the bottom right panel show the first derivative d log T/d logR (for all sources, top) calculated from the fitted profile T(r), and the refined T(r) (for five sources, bottom). |
| In the text | |
 |
Fig. 21 Derived averaged radial linewidth and virial parameter profiles. The dash-dotted line in each upper panel indicates the power-law fit to the linewidths from the thermometer lines. In each upper panel the gray dotted line indicates the relation found by Caselli & Myers (1995) of Orion low-mass cores scaled up by a factor of 5, which roughly matches the observed linewidth in our case, of
|
| In the text | |
 |
Fig. 22 Comparison between gas density profiles derived by modeling continuum and CH3OH line emission. The ratio of densities derived by CH3OH LIME modeling (ρdense) to continuum results (ρbulk) are shown aspluses (following right y-axis). The density estimated by SMA 1.2 mm continuum observations representing the central core average density is shown as a verticalorange line in each plot (Table 4). |
| In the text | |
 |
Fig. C.1 Posterior distribution of parameters from MCMC RADEX fitting of CH3OH (5-4) line series. The column densities of A∕E type are velocity averaged values (log cm−2/km s−1). The vertical dashed lines in the 1D histograms show the quantiles of 10%, 25%, 50%, 75%, and 90%. The contour levels in the 2D histograms indicate 0.5σ, 1σ, 1.5σ, and 2σ. The figure shows an example of the fitted parameters of observed lines in one pixel of clump G08b. |
| In the text | |
 |
Fig. C.2 CH3OH column density maps ( |
| In the text | |
 |
Fig. E.1 χ2 converted probability distribution of the 10 000 parameter set of RADMC-3D models for all clumps. The orange point indicates the best-fit model. Blue crosses give the positions of the 30 best-fit models, so there could be overlaps between the different parameter sets due to the binning. For sources G31, G13, G08a, and G19 the results before re-adjusting T(r) based on SED are shown as light blue contours. |
| In the text | |
 |
Fig. F.1 Abundance variations of CH3OH and CH3CCH from chemical models (lines) and the explored parameter space (filled) for the LIME models based on ρbulk density model (column A of Table 7). The results from the chemical models are shown as lines (solid, dashed, and dotted): for CH3OH the abundance profiles for different warm-up timescales are shown (Garrod et al. 2017); for CH3CCH, abundance profiles of different final collapse densities are shown (Calcutt et al. 2019). The dark green filled region indicates the lower abundance range explored for Xout by the LIME models, and the light green filled region the upper range explored for Xin. The verticalgray lines indicate the jump in temperature of 30 and 80 K. |
| In the text | |
 |
Fig. F.2 Line ratios of CH3OH (5-4) K components from LIME models based on density profile of G08b (ρ0 corresponds to the adjusted reference density at 0.1 pc for this source, as in Equation 6). The abundance value corresponds to the outer abundance (Xout), as in Table 7. The central symbol at the horizontal line of y = 1 corresponds to the best-fit model listed in Table. 7 (column B). The comparison of observations with model spectra is presented in Figure 14, top panel. |
| In the text | |
 |
Fig. G.1 Same as Figure 13, but for other target sources. |
| In the text | |
 |
Fig. G.2 Same as Figure 14, but for other target sources. |
| In the text | |
 |
Fig. G.3 Same as Figure 13, but for other target sources. |
| In the text | |
 |
Fig. G.4 Same as Figure 14, but for other target sources. |
| In the text | |
 |
Fig. G.5 Same as Figure 13, but for other target sources. |
| In the text | |
 |
Fig. G.6 Same as Figure 14, but for other target sources. |
| In the text | |
 |
Fig. G.7 Example spectra (archival SMA data, Sect. 2) of thermometer lines and the XCLASS fits of G10. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.