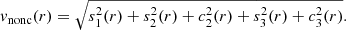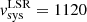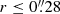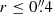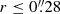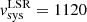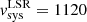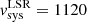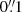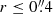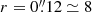| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 28 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201936606 | |
| Published online | 28 November 2019 | |
ALMA images the many faces of the NGC 1068 torus and its surroundings⋆
1
Observatorio Astronómico Nacional (OAN-IGN)-Observatorio de Madrid, Alfonso XII, 3, 28014 Madrid, Spain
e-mail: s.gburillo@oan.es
2
Observatoire de Paris, LERMA, CNRS, 61 Av. de l’Observatoire, 75014 Paris, France
3
Instituto de Astrofísica de Canarias, Calle Vía Láctea, s/n, 38205 La Laguna, Tenerife, Spain
4
Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain
5
Centro de Astrobiología (CSIC-INTA), ESAC Campus, 28692 Villanueva de la Cañada, Madrid, Spain
6
INAF-Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy
7
LESIA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ. Paris 06, Univ. Paris Diderot, Sorbonne Paris Cité, 5 Place Jules Janssen, 92195 Meudon, France
8
Department of Earth and Space Sciences, Chalmers University of Technology, Onsala Observatory, 439 94 Onsala, Sweden
9
European Southern Observatory (ESO), Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
10
Department of Physics and Astronomy, UCL, Gower Place, London WC1E 6BT, UK
11
Leiden Observatory, Leiden University, PO Box 9513, 2300 Leiden, The Netherlands
12
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
13
Astronomy Department, King Abdulazizi University, PO Box 80203, Jeddah 21589, Saudi Arabia
14
Joint ALMA Observatory, Alonso de Córdova, 3107, Vitacura, Santiago 763-0355, Chile
15
European Southern Observatory (ESO), Alonso de Córdova, 3107, Vitacura, Santiago 763-0355, Chile
16
Institut de Radio Astronomie Millimétrique (IRAM), 300 Rue de la Piscine, Domaine Universitaire de Grenoble, 38406 St. Martin d’Hères, France
17
Max-Planck-Institut für Extraterrestrische Physik, Postfach 1312, 85741 Garching, Germany
Received:
30
August
2019
Accepted:
13
October
2019
Aims. We investigate the fueling and the feedback of nuclear activity in the nearby (D = 14 Mpc) Seyfert 2 barred galaxy NGC 1068 by studying the distribution and kinematics of molecular gas in the torus and its connections to the host galaxy disk.
Methods. We used the Atacama Large Millimeter Array (ALMA ) to image the emission of a set of molecular gas tracers in the circumnuclear disk (CND) and the torus of the galaxy using the CO(2–1), CO(3–2), and HCO+(4–3) lines and their underlying continuum emission with high spatial resolutions (0.03″ − 0.09″ ≃ 2 − 6 pc). These transitions, which span a wide range of physical conditions of molecular gas (n(H2)⊂103 − 107 cm−3), are instrumental in revealing the density radial stratification and the complex kinematics of the gas in the torus and its surroundings.
Results. The ALMA images resolve the CND as an asymmetric ringed disk of D ≃ 400 pc in size and ≃1.4 × 108 M⊙ in mass. The CND shows a marked deficit of molecular gas in its central ≃130 pc region. The inner edge of the ring is associated with the presence of edge-brightened arcs of NIR polarized emission, which are identified with the current working surface of the ionized wind of the active galactic nucleus (AGN). ALMA proves the existence of an elongated molecular disk/torus in NGC 1068 of Mtorusgas ≃ 3 × 105 M⊙, which extends over a large range of spatial scales D ≃ 10 − 30 pc around the central engine. The new observations evidence the density radial stratification of the torus: the HCO+(4–3) torus, with a full size DHCO+(4 − 3) = 11 ± 0.6 pc, is a factor of between two and three smaller than its CO(2–1) and CO(3–2) counterparts, which have full sizes of DCO(3 − 2) = 26 ± 0.6 pc and DCO(2 − 1) = 28 ± 0.6 pc, respectively. This result brings into light the many faces of the molecular torus. The torus is connected to the CND through a network of molecular gas streamers detected inside the CND ring. The kinematics of molecular gas show strong departures from circular motions in the torus, the gas streamers, and the CND ring. These velocity field distortions are interconnected and are part of a 3D outflow that reflects the effects of AGN feedback on the kinematics of molecular gas across a wide range of spatial scales around the central engine. In particular, we estimate through modeling that a significant fraction of the gas inside the torus (≃ 0.4 − 0.6 × Mtorusgas) and a comparable amount of mass along the gas streamers are outflowing. However, the bulk of the mass, momentum, and energy of the molecular outflow of NGC 1068 is contained at larger radii in the CND region, where the AGN wind and the radio jet are currently pushing the gas assembled at the Inner Lindblad Resonance (ILR) ring of the nuclear stellar bar.
Conclusions. In our favored scenario a wide-angle AGN wind launched from the accretion disk of NGC1068 is currently impacting a sizable fraction of the gas inside the torus. However, a large gas reservoir (≃1.2 − 1.8 × 105 M⊙), which lies close to the equatorial plane of the torus, remains unaffected by the feedback of the AGN wind and can therefore continue fueling the AGN for at least ≃1 − 4 Myr. Nevertheless, AGN fueling currently seems thwarted on intermediate scales (15 pc ≤r ≤ 50 pc).
Key words: galaxies: individual: NGC 1068 / galaxies: ISM / galaxies: kinematics and dynamics / galaxies: nuclei / galaxies: Seyfert / radio lines: galaxies
Reduced datacubes and maps are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/632/A61
© ESO 2019
1. Introduction
The fueling of super-massive black holes (SMBHs) explains the onset of nuclear activity in galaxies. High-resolution observations of molecular gas have been instrumental to our understanding of how active galactic nuclei (AGNs) are fueled (e.g., García-Burillo et al. 2005; García-Burillo & Combes 2012; Combes et al. 2013, 2014; Storchi-Bergmann & Schnorr-Müller 2019). These observations have also started to reveal that the vast amounts of energy released during the feeding process can help regulate gas accretion through the launching of molecular outflows in different types of active galaxies (e.g., Feruglio et al. 2010; Sturm et al. 2011; Alatalo et al. 2011, 2014; Aalto et al. 2012, 2016; Combes et al. 2013; Morganti et al. 2013, 2015; Cicone et al. 2014; García-Burillo et al. 2014, 2015; Querejeta et al. 2016; Barcos-Muñoz et al. 2018; Alonso-Herrero et al. 2019). Molecular outflows are a manifestation of AGN feedback and constitute a key ingredient to understanding the co-evolution of galaxies and SMBHs, which is inferred from the observed scaling laws relating the mass of nuclear black holes (MBH) to the properties of the spheroidal components of galaxies, like the mass (Mbulge; e.g., Kormendy & Richstone 1995; Magorrian et al. 1998; Marconi & Hunt 2003) or the stellar velocity dispersion (σ; e.g., Gebhardt et al. 2000; Merritt & Ferrarese 2001; Ferrarese & Ford 2005; Gültekin et al. 2009).
Observational properties of AGNs are used to classify them into two categories: Type 1 AGNs show broad line regions (BLRs), while type 2 AGNs only show narrow line regions (NLRs). Lines are broadened in BLRs close to the central engine, while they are narrow farther out in the NLRs. The central engines of type 2 objects are thought to be hidden behind a screen of obscuring material located in a dusty torus of between a few and ten parsecs in size (Miller & Antonucci 1983; Antonucci & Miller 1985; Urry & Padovani 1995; Elitzur 2012; Netzer 2015; Ramos Almeida & Ricci 2017). Determining the physical parameters of the putative torus and its surroundings from observations has been challenging due to the foreseen small size of these structures. The list of key parameters to be determined includes the size, mass, and dynamical state of the gas in the torus (rotating, outflowing, and/or inflowing). Furthermore, we need a description of how the torus is connected to the host galaxy disk.
In the absence of observational constraints, the first estimates of the torus size came from theoretical models of the spectral energy distribution (SED). Pier & Krolik (1992) favored compact tori with an outer radius ≤5 − 10 pc. Later works extended these compact structures out to radii ≃30 − 100 pc (e.g., Pier & Krolik 1993; Granato & Danese 1994). A recent compilation of high-resolution observations in the near and mid-infrared (NIR and MIR) of 23 nearby Seyfert galaxies found relatively compact sizes for their AGN tori, yet with a remarkable range of wavelength-dependent values, from r ≃ 0.1 − 1 pc in the NIR, to r ≃ 1−a few pc in the MIR (e.g., Burtscher et al. 2013, and references therein). Furthermore, the observed nuclear NIR-to-MIR SED (including MIR spectroscopy) of Seyferts was reproduced with clumpy tori of sizes r ≃ 1 − 14 pc (Ramos Almeida et al. 2011; Alonso-Herrero et al. 2011; Ichikawa et al. 2015; García-Bernete et al. 2019).
The question of the dynamical status of the torus has also evolved from the first proposed scenario, depicting the torus as a geometrically thick rotating doughnut-like disk in hydrostatic equilibrium (Krolik & Begelman 1988), towards a more dynamical picture, describing the torus as an outflowing structure, where clouds are embedded in a hydro-magnetically or radiatively driven wind (Blandford & Payne 1982; Emmering et al. 1992; Bottorff et al. 1997; Kartje et al. 1999; Elitzur & Shlosman 2006; Wada 2012, 2015; Wada et al. 2016; Hönig & Kishimoto 2017; Chan & Krolik 2016, 2017; Williamson et al. 2019; Hönig 2019). This outflowing torus may be part of the obscuring structures that have been identified as polar-like dust components in a notable fraction of Seyferts observed with interferometers in the MIR (Tristram et al. 2009; Burtscher et al. 2013; Hönig et al. 2013; López-Gonzaga et al. 2014, 2016).
Due to their limited (u, v)-coverage, MIR interferometers have not yet been optimized to provide a direct image of the torus and its surroundings. This limitation can be overcome by millimeter(mm)/submillimeter(submm) interferometers like the Atacama Large Millimeter Array (ALMA). Building on an exquisite coverage of the (u, v)-plane, ALMA has begun imagining with high fidelity the distribution and kinematics of molecular gas in the tori of nearby Seyfert galaxies (D ≤ 10 − 30 Mpc), thanks to its ability to reach angular resolutions ≤0.05″ − 0.1″ (García-Burillo et al. 2016; Gallimore et al. 2016; Imanishi et al. 2016, 2018; Alonso-Herrero et al. 2018, 2019; Izumi et al. 2018; Combes et al. 2019; Impellizzeri et al. 2019; Audibert et al. 2019).
The nearby (D ∼ 14 Mpc; Bland-Hawthorn et al. 1997) Seyfert 2 galaxy NGC 1068 has been a testbed for unifying theories of AGNs after the discovery of polarized optical continuum and broad-line emission in this source (Miller & Antonucci 1983; Antonucci & Miller 1985). Single-dish observations in the NIR and MIR showed the existence of emission extending over a wide range of spatial scales (≃5–70 pc) around the AGN (Bock et al. 2000; Marco & Alloin 2000; Tomono et al. 2001; Rouan et al. 2004; Galliano et al. 2005; Gratadour et al. 2006, 2015; Lopez-Rodriguez et al. 2016). Interferometric observations in the NIR and MIR confirmed the existence of two components (Jaffe et al. 2004; Weigelt et al. 2004; Raban et al. 2009; Burtscher et al. 2013; López-Gonzaga et al. 2014): a compact 0.5–1.4 pc-sized disk centered at the AGN with a position angle PA ≃ 140°, and a 3–10 pc-sized elongated structure oriented along the north–south axis. The compact disk contains hot (≃800 K) dust co-spatial with the H2O megamaser disk (Greenhill et al. 1996; Greenhill & Gwinn 1997; Gallimore et al. 2001, 2004), while the elongated source contains warm (≃300 K) dust likely associated with the ionization cone.
García-Burillo et al. (2016) and Gallimore et al. (2016) used ALMA to map the emission of the CO(6–5) line and its underlying continuum in NGC 1068 with a spatial resolution of ∼4 pc. These observations imaged the dust and molecular line emission from the torus of NGC 1068. The ≃7 − 10 pc CO/dusty torus extends along PA ≃ 112 ± 20° over spatial scales a factor of four larger than the MIR sources detected at the AGN (Burtscher et al. 2013; López-Gonzaga et al. 2014). The CO torus shows a lopsided disk morphology, an orientation roughly perpendicular to the AGN wind/jet axis, and surprisingly perturbed kinematics, the origin of which remains a matter of debate. Firstly, García-Burillo et al. (2016) reported the apparent counter-rotation of the outer disk r ≃ 3.5 pc (imaged in CO(6–5)), relative to the inner r ≃ 1 pc (imaged in H2O maser emission). This apparent counter-rotation has also been evidenced by the recent HCN(3–2) and HCO+(3–2) ALMA maps of the torus (Imanishi et al. 2018; Impellizzeri et al. 2019). Secondly, the maps of García-Burillo et al. (2016) and Gallimore et al. (2016) show a velocity gradient along the morphological minor axis of the torus. This velocity gradient could be explained by gas being entrained in the outflow (García-Burillo et al. 2016; Gallimore et al. 2016; Impellizzeri et al. 2019). This interpretation is nevertheless challenged by the fact that the reported radial shift of velocities in the torus is reversed farther out (r ≥ 100 − 200 pc) at the circumnuclear disk (CND), where the CO outflow imaged by García-Burillo et al. (2014) follows the pattern of low-ionization lines (see discussion in García-Burillo et al. 2016). Alternatively, the disturbed kinematics of the torus could be the signature of the Papaloizou-Pringle instability (PPI) predicted to drive the dynamical evolution of AGN tori on scales of r ≤ 0.1 pc (Papaloizou & Pringle 1984). This instability has been studied both in isolated tori (Kiuchi et al. 2011; Korobkin et al. 2013) and also in tori perturbed due to the accretion of gas (Dönmez 2014; Donmez 2017). These simulations show the growth of a long-lasting non-axisymmetric m = 1 mode. The PPI is able to sustain a lopsided distribution and noncircular motions in the gas. However, whether this instability can propagate efficiently and in due time to the significantly larger radii of the CO torus is still an open question.
Furthermore, several groups found evidence of the existence of gas streamers connecting the torus with the CND out to r ≃ 30 pc. These gas streamers emit in the 2.12 μm H2 line, a tracer mostly sensitive to hot molecular gas (Tk ≥ 103 K). However, these works have led to contradicting conclusions regarding the interpretation of the kinematics of the gas in these structures, interpreted in terms of either inflow (Müller Sánchez et al. 2009) or outflow motions (Barbosa et al. 2014; May & Steiner 2017). García-Burillo et al. (2016) detected no clear CO(6–5) counterpart of the NIR streamers or tongues. The nature of the CND-torus connection and the question of what the fueling budget is in this Seyfert are therefore mostly unsettled.
The new ALMA observations presented in this paper image the emission of molecular gas in the CND and the torus of NGC 1068 using the CO(2–1), CO(3–2), and HCO+(4–3) lines, with a set of spatial resolutions of ≃0.03 − 0.09″ (2–6 pc) that improve by a significant factor ( ≥ 6 − 10) the best spatial resolutions achieved in these lines in the previous maps of Schinnerer et al. (2000) and García-Burillo et al. (2014). The use of these transitions, which purposely span a wide range of physical conditions of molecular gas (n(H2)⊂103 − 107 cm−3), is instrumental in revealing the density radial stratification of the gas in the torus. The non-detection by García-Burillo et al. (2016) of a CO(6–5) counterpart of the NIR streamers/tongues may be due to the fact that the gas in the connecting bridges has volume densities below the critical density of the CO(6–5) line (≥105 cm−3). In this context, the choice of the CO(2–1) line, which is sensitive to densities n(H2)≃103cm−3, is motivated by the need to trace the bulk of the H2 gas in the CND, the torus, and also in the structures connecting the CND with the torus. Furthermore, with the chosen requirement on what should be the minimum largest angular scale (LAS) recovered (≃1.3″ − 1.8″ = 90 − 130 pc), the spatial resolution goal in both ALMA Bands (# 6 and # 7) is still compatible with the ability to recover the emission in the CND and also in the CND-torus connections.
We describe in Sect. 2 the new ALMA observations used in this work. Section 3 presents the continuum maps derived at 229.7 GHz and 344.5 GHz. The distribution and kinematics of molecular gas derived from the CO and HCO+ line maps in the CND and the torus are discussed in Sects. 4 and 5 respectively. We describe in Sect. 6 the gas connections between the torus and the CND and attempt to find a global description for the kinematics of the gas in the torus and the large-scale molecular outflow in Sect. 7. The main conclusions of this work are summarized in Sect. 8.
2. Observations
We observed the emission of the CO(2–1), CO(3–2), and HCO+(4–3) lines and their underlying continuum emission in the CND of NGC 1068 with ALMA during Cycle 4 using Band 6 and Band 7 receivers (project-ID: #2016.1.0232.S; PI: S. García-Burillo). The phase tracking center was set to α2000 = 02h42m40.771s, δ2000 = −00° 00′47.84″, which is the center of the galaxy according to SIMBAD taken from the Two Micron All Sky Survey-2MASS survey (Skrutskie et al. 2006). The tracking center is offset by ≤1″ relative to the AGN position: α2000 = 02h42m40.71s, δ2000 = −00° 00′47.94″ (Gallimore et al. 1996, 2016, 2004; García-Burillo et al. 2014, 2016; Imanishi et al. 2016, 2018). The data in the two bands were calibrated using the ALMA reduction package CASA1. The calibrated uv-tables were exported to GILDAS2-readable format in order to perform the mapping and cleaning steps as detailed below. For both bands we estimate that the absolute flux accuracy is about 10%, which is in line with the goal of standard ALMA observations at these frequencies. Rest frequencies for all the lines used in this work were corrected for the recession velocity initially assumed to be vo(LSR) = 1129 km s−1 = vo(HEL) = 1140 km s−1. Systemic velocity is nevertheless re-determined in this work as vsys(LSR) = 1120 km s−1 = vsys(HEL) = 1131 km s−1. When appropriate, relative velocities throughout the paper refer to vsys. We also use the continuum map of NGC 1068 obtained with ALMA during Cycle 0 using Band 9 receivers (project-ID: #2011.0.00083.S; PI: S. García-Burillo) and published by García-Burillo et al. (2014) and Viti et al. (2014). Hereafter we assume a distance to NGC 1068 of D ≃ 14 Mpc (Bland-Hawthorn et al. 1997); the latter implies a spatial scale of ≃70 pc/″.
2.1. Band 7 data
We used a single pointing with a field of view (FoV) of 17″. In total two tracks were observed between October 2016 and September 2017 resulting in a total of 411 278 visibilities. We had 46 antennas available during the observations with projected baselines ranging from 18 m to 7.4 km. Four spectral windows were placed, two in the lower side band (LSB) and two in the upper sideband (USB). The four windows were centered on the following sky frequencies: 344.484 GHz and 345.681 GHz in the LSB and 355.380 GHz and 357.339 GHz in the USB. All the sub-bands have a spectral bandwidth of 1.875 GHz, except for the one centered around 345.681 GHz, which is a factor of two narrower. This setup allowed us to simultaneously observe CO(J = 3 − 2) (345.796 GHz at rest) and H13CO+(J = 4 − 3) (346.998 GHz at rest) in the LSB bands, and HCO+(J = 4 − 3) (356.734 GHz at rest) and the continuum emission in the USB bands. Images of the continuum emission were obtained by averaging those channels free of line emission in each of the three sub-bands centered around spectral lines. These maps were used to subtract, in the (u, v)-plane, the underlying continuum emission from the visibilities and subsequently obtain continuum-free spectral line images for all the lines. In this paper we present the CO(3–2) and HCO+(4–3) maps but omit any discussion on the H13CO+(4–3) data due to its low S/N.
Table 1 summarizes the main observational parameters. We obtain two sets of angular resolutions by changing the robust parameter (b) in the GILDAS task UV-MAP from 1 (in the moderate spatial resolution (MSR) data set) to 0.1 (in the high spatial resolution (HSR) data set). The range of angular resolutions obtained is 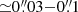 (2–7 pc) in the CO(3–2) line, and
(2–7 pc) in the CO(3–2) line, and 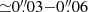 (2–4 pc) in the HCO+(4–3) line. The conversion factors between mJy beam−1 and K are 1.2 K mJy−1 beam (MSR) and 8.4 K mJy−1 beam (HSR) for the CO(3–2) line, and 2.6 K mJy−1 beam (MSR) and 8.5 K mJy−1 beam (HSR) for the HCO+(4–3) line. The line data cubes were binned to a common frequency resolution of 23.1 MHz (equivalent to ∼20 km s−1 in Band 7). The point source sensitivities in the line data cubes were derived selecting areas free from emission in all channels, resulting in a common value of 0.23 mJy beam−1 for the CO(3–2) line and 0.28 mJy beam−1 for the HCO+(4–3) line, in channels of 20 km s−1 width. The corresponding point source sensitivity for the continuum is 46 μJy beam−1.
(2–4 pc) in the HCO+(4–3) line. The conversion factors between mJy beam−1 and K are 1.2 K mJy−1 beam (MSR) and 8.4 K mJy−1 beam (HSR) for the CO(3–2) line, and 2.6 K mJy−1 beam (MSR) and 8.5 K mJy−1 beam (HSR) for the HCO+(4–3) line. The line data cubes were binned to a common frequency resolution of 23.1 MHz (equivalent to ∼20 km s−1 in Band 7). The point source sensitivities in the line data cubes were derived selecting areas free from emission in all channels, resulting in a common value of 0.23 mJy beam−1 for the CO(3–2) line and 0.28 mJy beam−1 for the HCO+(4–3) line, in channels of 20 km s−1 width. The corresponding point source sensitivity for the continuum is 46 μJy beam−1.
Observational parameters.
As our observations do not contain short-spacing correction, we expect that the flux will start to be filtered out on scales ≥1.8″ (130 pc). We nevertheless foresee that the highly clumpy distribution of the gas and the strong velocity gradients of the emission in the nuclear regions will help us recover the bulk of the flux on the spatial scales of the CND relevant to this paper. As a sanity check, we compared the total flux of the CO(3–2) line integrated over the CND region, shown in Fig. 3, with the corresponding value derived using the ALMA map of García-Burillo et al. (2014), which is expected to recover all the flux out to scales ≃6″ ≃ 420 pc, which are similar to the total size of the CND (≃300 − 400 pc). Within the calibration errors, we obtain virtually identical fluxes from the two data sets: 1500 Jy km s−1 (García-Burillo et al. 2014) and ≃1450 Jy km s−1 (this work), an indication that the emission stemming from spatial scales ≃130 − 420 pc in the new CND map is kept to a minimum. We can therefore conclude that the new CO(3–2) map contains the bulk of the flux for the whole range of spatial scales of the CND analyzed in this work. Furthermore, we can assume that a similar scenario is valid for the HCO+(4–3) line, considering that this transition is likely tracing comparatively denser and in all probability clumpier molecular gas complexes in the CND.
2.2. Band 6 data
Similarly to Band 7, we used a single pointing that translates at the lower frequencies of Band 6 into a FoV of 25″. We observed three tracks between October 2016 and September 2017 resulting in a total of 1 718 451 visibilities. We had 50 antennas available during the observations with projected baselines ranging from 18 m to 12 km. We placed five spectral windows, two in the LSB and three in the USB. The five windows were centered on the sky frequencies: 217.647 GHz and 216.281 GHz in the LSB and 229.663 GHz, 230.343 GHz, and 231.021 GHz in the USB. This setup allowed us to observe H2CO[3(2,2)–2(2,1)] (218.476 GHz at rest) and SiO(J = 5 − 4) (217.105. GHz at rest) in the LSB bands, and CO(J = 2 − 1) (230.538 GHz at rest), 13CS(J = 5 − 4) (231.221 GHz at rest), and H30α (231.901 GHz at rest) in the USB bands. Images of the continuum emission were obtained by averaging those channels free of line emission in all sub-bands. As for Band 7, these maps were used to obtain continuum-free spectral line images for all the lines. In this work we discuss the results obtained in the CO(2–1) line and leave out any discussion on the remaining lines, to be presented in a forthcoming paper.
The main observational parameters are listed in Table 1. Similarly to Band 7, we use two sets of angular resolutions for the CO(2–1) line that lie in the range 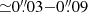 (2–6 pc). The conversion factors between mJy beam−1 and K are 3 K mJy−1 beam (MSR) and 18 K mJy−1 beam (HSR). For the sake of comparison with the Band 7 data, we binned the Band 6 data to a frequency resolution of 15.4 MHz (equivalent to ∼20 km s−1). The corresponding point source sensitivities in the line data cubes range from 0.11 mJy beam−1 (MSR) to 0.14 mJy beam−1 (HSR) in channels of 20 km s−1 width. The corresponding point source sensitivity for the continuum is 30 μJy beam−1.
(2–6 pc). The conversion factors between mJy beam−1 and K are 3 K mJy−1 beam (MSR) and 18 K mJy−1 beam (HSR). For the sake of comparison with the Band 7 data, we binned the Band 6 data to a frequency resolution of 15.4 MHz (equivalent to ∼20 km s−1). The corresponding point source sensitivities in the line data cubes range from 0.11 mJy beam−1 (MSR) to 0.14 mJy beam−1 (HSR) in channels of 20 km s−1 width. The corresponding point source sensitivity for the continuum is 30 μJy beam−1.
As for Band 7, we checked whether or not the lack of short spacing correction in the CO(2–1) map, which implies that the flux will start to be filtered out on scales ≥1.3″ (90 pc), can affect the results discussed in this work. To this aim, we compared the flux integrated over the CND region estimated from the IRAM Plateau de Bure interferometer (PdBI) array image of Krips et al. (2011), which recovers the flux out to scales3 ≃3″ ≃ 210 pc, with that derived from the new ALMA map of Fig. 3. This comparison yielded similar values for the flux recovered within the errors: 530 Jy km s−1 (Krips et al. 2011) ≃580 Jy km s−1 (this work). This suggests that the emission stemming from the missing spatial scales in the range ≃90 − 210 pc of the new CND map is negligible. In conclusion, our comparisons show that the new CO(2–1) map of the CND contains most if not all of the flux for the range of spatial scales that are relevant to this paper.
3. Continuum maps
Figure 1 shows the continuum maps derived at 229.7 GHz (1306 μm) and 344.5 GHz (871 μm) in the inner r ≤ 1″(70 pc) region of NGC 1068. We also show the continuum map obtained by García-Burillo et al. (2016) at 694 GHz (432 μm). At the three frequencies examined, the strongest emission corresponds to a point-like source. We used the GILDAS task UV-FIT to locate this source at α2000 = 02h42m40.709s, 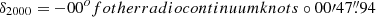 . This is in agreement with the position of the source S1, identified as the AGN core in the previous subarcsecond radio continuum maps of Gallimore et al. (1996, 2004). We also detect significant emission extending over ≃70 pc in a highly clumpy jet-like structure at the two lowest frequencies. As illustrated in Fig. 1, the millimeter continuum clumps at 229.7 GHz and 344.5 GHz show a good correspondence with sources S2, C, and NE, which form the inner section of the collimated jet emitting synchrotron emission (Gallimore et al. 1996, 2004). This correspondence is much weaker at 694 GHz. The jet is seen to be diverted at C due to a jet–ISM interaction (Bicknell et al. 1998; Gallimore et al. 1996, 2001). The C knot is also characterized by highly polarized MIR emission (Lopez-Rodriguez et al. 2016). Reflecting this interaction, the jet changes its orientation from PA ≃ 10° ±5° along its inner section defined by the C-S1-S2 clumps, towards PA ≃ 30° ±5°, as defined by the NE-C axis. The latter aligns with the general orientation of the AGN wind on larger scales (PAoutflow ≃ 30° ±5°; Macchetto et al. 1994; Arribas et al. 1996; Crenshaw & Kraemer 2000; Tecza et al. 2001; Cecil et al. 2002; Müller-Sánchez et al. 2011; Gratadour et al. 2015).
. This is in agreement with the position of the source S1, identified as the AGN core in the previous subarcsecond radio continuum maps of Gallimore et al. (1996, 2004). We also detect significant emission extending over ≃70 pc in a highly clumpy jet-like structure at the two lowest frequencies. As illustrated in Fig. 1, the millimeter continuum clumps at 229.7 GHz and 344.5 GHz show a good correspondence with sources S2, C, and NE, which form the inner section of the collimated jet emitting synchrotron emission (Gallimore et al. 1996, 2004). This correspondence is much weaker at 694 GHz. The jet is seen to be diverted at C due to a jet–ISM interaction (Bicknell et al. 1998; Gallimore et al. 1996, 2001). The C knot is also characterized by highly polarized MIR emission (Lopez-Rodriguez et al. 2016). Reflecting this interaction, the jet changes its orientation from PA ≃ 10° ±5° along its inner section defined by the C-S1-S2 clumps, towards PA ≃ 30° ±5°, as defined by the NE-C axis. The latter aligns with the general orientation of the AGN wind on larger scales (PAoutflow ≃ 30° ±5°; Macchetto et al. 1994; Arribas et al. 1996; Crenshaw & Kraemer 2000; Tecza et al. 2001; Cecil et al. 2002; Müller-Sánchez et al. 2011; Gratadour et al. 2015).
 |
Fig. 1. Left panel: continuum emission map of the central r ≤ 1″ (70 pc) region of NGC 1068 obtained with ALMA at 229.7 GHz (1306 μm). The map is shown in grayscale with contour levels -2σ (dashed contour), 2σ, 5σ, 10σ, 20σ, 50σ, 100σ, and 200σ, where 1σ = 30 μJy beam−1. Middle panel: same as left panel but showing the continuum emission at 344.5 GHz (871 μm). Contour spacing is as in left panel, but with 1σ = 50 μJy beam−1. Right panel: same as left panel but showing the continuum emission at 694 GHz (432 μm) published by García-Burillo et al. (2016). Contour levels are −2σ (dashed contour), 2σ, 5σ, 7σ, 9σ, 12σ, and 16σ, where 1σ = 0.5 mJy beam−1. The (red) filled ellipses at the bottom left corners of the panels represent the beam sizes of ALMA at 229.7 GHz ( |
Figure 2 shows the spectral index maps α (with Sν ∝ να) derived from the continuum emissions at ν = 344.5 GHz and 694 GHz (α1), and from ν = 229.7 GHz and 344.5 GHz (α2) derived for a common aperture size of 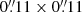 (8 pc × 8 pc). We also show in Fig. 2 the corresponding SED in the (sub)mm range at different regions of the CND. Large and positive values of the two spectral indexes α ≃ 3–4 can be attributed to the prevalence of dust emission in those regions of the CND that are located far from the radio jet trajectory (e.g., the E-knot) or at the edges of the jet trail itself. Spectral indexes are flat or marginally positive at the location of the torus and close to its southern polar elongation (knots S1 and S2, respectively). In contrast, spectral indexes become clearly negative (α ≤ −1) throughout the radio jet (e.g., the NE-C axis), as expected for synchrotron-like emission.
(8 pc × 8 pc). We also show in Fig. 2 the corresponding SED in the (sub)mm range at different regions of the CND. Large and positive values of the two spectral indexes α ≃ 3–4 can be attributed to the prevalence of dust emission in those regions of the CND that are located far from the radio jet trajectory (e.g., the E-knot) or at the edges of the jet trail itself. Spectral indexes are flat or marginally positive at the location of the torus and close to its southern polar elongation (knots S1 and S2, respectively). In contrast, spectral indexes become clearly negative (α ≤ −1) throughout the radio jet (e.g., the NE-C axis), as expected for synchrotron-like emission.
 |
Fig. 2. Spectral index maps (α, with Sν ∝ να) derived from the continuum emissions at ν = 344.5 GHz and 694 GHz (α1: left panel), and from ν = 229.7 GHz and 344.5 GHz (α2: middle panel). Contours span the range α = [ − 3, 3] in steps of 1. The common aperture adopted to derive the spectral index map is |
We used the spectral index values measured in the CND regions dominated by dust emission (α ≃ 3–4) to derive the fraction of emission at 871 μm that can be attributed to dust at the S1 knot and estimated this to be ≤10%, in close agreement with the estimate derived at lower spatial resolution (≃35 pc) by García-Burillo et al. (2014, 2016). This result warns against the use of submm continuum emission at ∼850 − 870 μm as a straightforward tracer of the dust content of AGN tori and/or of their immediate surroundings, in particular in active galaxies that are not radio-silent such as NGC 1068 (see also the recent discussion in Alonso-Herrero et al. 2019 and Pasetto et al. 2019).
4. Molecular line emission: the circumnuclear disk
4.1. The CO maps
Figure 3 shows the CO(2–1) and CO(3–2) velocity-integrated intensity maps of the CND. The line fluxes have been integrated to include any significant emission that arises over the full velocity span due to rotation and outflow motions in NGC 1068: ![$ v-v_{\mathrm{sys}}^{\mathrm{HEL}}\subset[ -350, 350] $](/articles/aa/full_html/2019/12/aa36606-19/aa36606-19-eq21.gif) km s−1 (García-Burillo et al. 2014, 2016; Gallimore et al. 2016). The maps have also been corrected for primary beam attenuation at the respective frequencies.
km s−1 (García-Burillo et al. 2014, 2016; Gallimore et al. 2016). The maps have also been corrected for primary beam attenuation at the respective frequencies.
 |
Fig. 3. Left panel: CO(2–1) integrated intensity map obtained with ALMA in the CND of NGC 1068 using the MSR data set as defined in Table 1. The map is shown in color scale spanning the range [3σ, 300σ] in logarithmic scale with contour levels −5σ (dashed contour), 5σ, 10σ, 20σ, 40σ, 60σ, 100σ–250σ in steps of 50σ where 1σ = 13 mJy km s−1 beam−1. Right panel: same as left panel but showing the CO(3–2) integrated intensity map. The color scale spans the range [3σ, 430σ] in logarithmic scale with contour levels −5σ (dashed contour), 5σ, 10σ, 20σ, 40σ, 60σ, 100σ–400σ in steps of 50σ where 1σ = 27 mJy km s−1 beam−1. The AGN locus lies at the intersection of the dashed lines in both panels. The (red) filled ellipses in the bottom left corners of both panels represent the beam sizes in CO(2–1) ( |
Based on the measured total flux of the 2–1 line (≃580 Jy km s−1), we used Eq. (3) of Bolatto et al. (2013) and estimated the molecular gas mass of the CND to be Mgas ≃ 1.4 × 108 M⊙, including the mass of helium. In our estimate we assumed an average 2–1/1–0 brightness temperature ratio ≃2.2, as measured by Viti et al. (2014) in the CND, and a galactic CO-to-H2 conversion factor (XCO = 2 × 1020 mol cm−2 (K km s−1)−1).
The high spatial resolution of the ALMA data fully resolves the CND, which displays in both lines of CO the shape of a highly structured asymmetric ringed disk. The CND has a total size 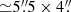 0 (400 pc × 300 pc) and shows an east–west orientation of its principal axes (PA ≃ 90°). If we de-project the CND size onto the plane of the galaxy, assuming PA = 286° ±5° and i = 41° ±2°(García-Burillo et al. 2014), we derive a nearly circular shape for the CND, which would have a diameter of ≃400 pc. The CND ring feature likely corresponds to the molecular gas assembly at the inner Lindblad resonance (ILR) region of the nuclear bar detected in the NIR (Scoville et al. 1988; Bland-Hawthorn et al. 1997; Schinnerer et al. 2000; Emsellem et al. 2006; García-Burillo et al. 2014). The center of the CND is noticeably shifted ≃70 pc southwest relative to the position of the central engine, an indication that the morphology of the ring may have been shaped to a large extent by the feedback of nuclear activity, as we discuss in Sect. 4.2.
0 (400 pc × 300 pc) and shows an east–west orientation of its principal axes (PA ≃ 90°). If we de-project the CND size onto the plane of the galaxy, assuming PA = 286° ±5° and i = 41° ±2°(García-Burillo et al. 2014), we derive a nearly circular shape for the CND, which would have a diameter of ≃400 pc. The CND ring feature likely corresponds to the molecular gas assembly at the inner Lindblad resonance (ILR) region of the nuclear bar detected in the NIR (Scoville et al. 1988; Bland-Hawthorn et al. 1997; Schinnerer et al. 2000; Emsellem et al. 2006; García-Burillo et al. 2014). The center of the CND is noticeably shifted ≃70 pc southwest relative to the position of the central engine, an indication that the morphology of the ring may have been shaped to a large extent by the feedback of nuclear activity, as we discuss in Sect. 4.2.
Although the two CO line maps show notable differences at small radii, r ≤ 50 pc, their overall morphology elsewhere at larger radii is remarkably similar down to spatial scales of a few parsecs. Molecular line emission is detected in both CO lines at and around the AGN locus stemming from a spatially resolved elongated disk, which has a diameter ≥20 pc. Hereafter we refer to this disk as the torus. The torus is partly connected to the CND through gas streamers that display different morphologies in the 2–1 and 3–2 lines of CO. The torus and its connections to the host are described in detail in Sects. 5 and 6, respectively.
4.2. The CND morphology: evidence of an outflowing ring ?
Leaving aside the gas concentration at the torus and its surroundings mentioned above, the CND shows a deficit of molecular gas in its central ≃130 pc region. This deficit leaves the imprint of a highly contrasted ring structure on the CND. The inner edge of the ring shows a steep radial profile that delimits a gas-deficient region of elliptical shape. The principal axes of the gas-deficient region (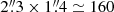 pc ×100 pc) are oriented roughly at right angles relative to the overall orientation of the CND. Compared to the 2–1 line, this hole in the 3–2 line seems to shrink in size closer to the central engine. The outer edge of the CND is connected on larger scales to the bar region through a network of spiral gas lanes from r ≥ 100 − 150 pc. These bar-CND connections were previously identified in the map of García-Burillo et al. (2014).
pc ×100 pc) are oriented roughly at right angles relative to the overall orientation of the CND. Compared to the 2–1 line, this hole in the 3–2 line seems to shrink in size closer to the central engine. The outer edge of the CND is connected on larger scales to the bar region through a network of spiral gas lanes from r ≥ 100 − 150 pc. These bar-CND connections were previously identified in the map of García-Burillo et al. (2014).
While the central ≃130 pc of the CND is deficient in molecular gas, this region is known to be pervaded by strong emission from a wide-angle bicone of ionized gas oriented along PA ≃ 30° (Macchetto et al. 1994; Arribas et al. 1996; Crenshaw & Kraemer 2000; Cecil et al. 2002; Das et al. 2006; Müller-Sánchez et al. 2011; Barbosa et al. 2014). The morphology and the kinematics of the gas in this component have been interpreted in terms of an outflowing AGN-driven wind. In particular, the presence of blueshifts and redshifts on either side of the AGN locus along the outflow axis is consistent with a model where the AGN wind axis is oriented close the plane of the galaxy disk (e.g., Cecil et al. 2002). This geometry would favor a strong coupling between the AGN wind and the molecular ISM in the disk. Based on the analysis of the distortions of the molecular gas velocity field, studied with ALMA at a spatial resolution of ≃35 pc, García-Burillo et al. (2014) concluded that the ionized outflow is responsible for launching a molecular outflow in the disk over a region extending from r ≃ 50 pc out to r ≃ 500 pc. The highly contrasted ring morphology of the CND imaged by the new ALMA data shown in Fig. 3, which reveals a remarkably steep radial profile on its inner edge, likely reflects the accumulation of molecular gas at the working surface of the AGN wind. The outflowing CND scenario of García-Burillo et al. (2014) is re-examined in Sects. 4.4 – 4.6, based on a first analysis of the gas kinematics derived from the new ALMA maps.
Further evidence showing the existence of a large-scale shock in the CND is provided by the comparison of the ALMA CO maps with the hourglass structure displayed by the NIR polarized emission imaged by Gratadour et al. (2015). This comparison, illustrated in Fig. 4, shows a fair correspondence between the inner edge of the CND and the edge-brightened arcs of NIR polarized emission, which are prominent at the northern and, most particularly, southern regions of the CND4. In the model proposed by Das et al. (2006), and more recently by Barbosa et al. (2014), the AGN wind occupies a hollow bicone that is oriented along PA ≃ 30° and is characterized by an opening angle, measured from the inner to the outer edge of the bicone, ranging from FWHMinner ≃ 40° to FWHMouter ≃ 80°. Based on this model the interaction of the AGN wind with the molecular ISM of the disk is expected to be at work mainly at the northern and the southern extremes of the CND. The increased degree of polarization shown by the dust-scattered NIR emission seems to be taking place at the working surface of the AGN wind as a result of a significant gas and dust pile-up. We also find an increased degree of polarization of NIR emission along the gas streamers connecting the torus with the CND (see discussion in Sect. 6).
 |
Fig. 4. Left panel: we overlay the CO(2–1) contour map (levels as in Fig. 3) on the image of linear polarization of dust emission obtained in the H band by Gratadour et al. (2015) (color logarithmic scale from 1.5% to 13%). Right panel: same as left panel but showing the comparison between the CO(3–2) map and the polarization degree. The magenta lines identify the region occupied by the AGN wind bicone modeled by Das et al. (2006): PAoutflow = 30°, FWHMouter = 80° (see also Barbosa et al. 2014). |
4.3. The HCO+ map
Figure 5 shows the HCO+(4–3) integrated intensity map of the CND. In stark contrast to the CO line maps shown in Fig. 3, the brightest emission of the HCO+(4–3) line in the CND corresponds to the molecular torus. The HCO+ torus is notably smaller in size (D < 10 pc) compared to the CO molecular tori (see discussion in Sect. 5). Significant HCO+ emission is also detected at the E-knot, a spatially resolved region located ≃70 pc east of the AGN, as well as in a number of isolated clumps throughout the CND. The different distributions of HCO+ and CO line emissions in the CND reflect the wide range of critical densities probed by these transitions, which span nearly four orders of magnitude: n(H2)⊂103 − 107 cm−3. The location of the brightest HCO+ emission in Fig. 5, namely the molecular torus and the E-knot, is a signpost of the location of the densest molecular gas: n(H2) ≃ a few 105–a few 106 cm−3, according to the analysis of the different line ratios studied by Viti et al. (2014) at the common ≃35 pc spatial resolution achieved in the maps of García-Burillo et al. (2014).
 |
Fig. 5. HCO+(4–3) integrated intensity map obtained with ALMA in the CND of NGC 1068 using the MSR data set as defined in Table 1. The map is shown in color scale spanning the range [3σ, 40σ] with contour levels −5σ (dashed contour), 5σ, 7σ, 12σ, 20σ, and 30σ where 1σ = 33 mJy km s−1 beam−1. Symbols and markers as in Fig. 3. The (red) filled ellipse at the bottom left corner represents the beam size in HCO+(4–3) ( |
4.4. Kinematics of the CND: mean-velocities
Figure 6 shows the mean-velocity fields derived from the CO(2–1) and CO(3–2) lines in the CND of NGC 1068. To maximize the reliability of the maps, isovelocities have been obtained by integrating the emission with a threshold of 4σ in the two lines.
 |
Fig. 6. Mean-velocity fields derived for the CO(2–1) (left panel) and CO(3–2) (right panel) lines in the CND of NGC 1068, as obtained from the MSR data set. Isovelocity contours and color scale span the range [−200 + vsys, 200 + vsys] km s−1, where |
The apparent kinematic major axis of the CND at small radii is roughly oriented along the north–south direction (PA ≃ 360°). However, the orientation of the major axis changes at the outer edge of the CND towards PA ≃ 290°, that is, it tends to align with the large-scale disk of the galaxy, defined by PA = 286° ±5° and i = 40° ±3°, where the southwest (northeast) side of the disk corresponds to the near (far) side (Bland-Hawthorn et al. 1997). García-Burillo et al. (2014) used the software package kinemetry (Krajnović et al. 2006) to account for a similar yet less extreme tilt of the major axis identified in previous ALMA observations of NGC 10685. García-Burillo et al. (2014) concluded that the distortions of the mean-velocity field of molecular gas in the CND could be reproduced by the inclusion of an outflowing radial component (see also Krips et al. 2011). In the following section we use the package kinemetry in an attempt to improve the fit of the mean-velocity field distortions derived from the new higher-resolution ALMA data presented in this work.
4.5. Modeling the mean-velocity field with kinemetry: a coplanar outflow?
The observed mean-velocity field of a galaxy disk, vmean(r, ψ), expressed as a function of the radius (r) and the phase angle (ψ, measured from the receding side of the line of nodes), can be divided into a number of elliptical ring profiles with a geometry defined by the position angle and inclination (PA, i). We can decompose vmean(r, ψ) as a Fourier series with harmonic coefficients cj(r) and sj(r), where
While c1 accounts for the contribution from circular rotation, the other terms of the series contain the contributions from noncircular motions, vnonc, which by construction has an axisymmetric dependence (Schoenmakers et al. 1997; Schoenmakers 1999). In particular, if we expand the series out to n = 3:
We used the software package kinemetry developed by Krajnović et al. (2006) to fit the CO(2–1) mean-velocity field of the CND of Fig. 6 purposely using a minimum number of free parameters. In particular, we first assumed that the dynamical center coincides with the AGN position derived in Sect. 3. Secondly, we adopt the solution found by kinemetry for the basic parameters of the large-scale r ≃ 1.5 kpc disk covered by the first ALMA observations of García-Burillo et al. (2014), defined by PA = 289 ± 5° and i = 41 ± 2°, and apply it to the relevant radii of the CND. These parameters were obtained to fit the mean-velocity field derived from the previous lower-resolution CO(3–2) ALMA map of the galaxy (see, for a detailed discussion, García-Burillo et al. 2014). This approach implicitly assumes that the molecular gas kinematics in the CND can be modeled by coplanar orbits in a thin disk6. From this first iteration we obtained the best fit for the systemic velocity: vsys(LSR) = 1120 ± 3 km s−1 = vsys(HEL) = 1131 ± 3 km s−1; this is compatible within the errors with the values reported in the literature inferred using different diagnostics (e.g., Greenhill & Gwinn 1997; García-Burillo et al. 2014). We then subtract vsys from vmean and re-derive the Fourier decomposition of Eq. (1) for a set of 20 radii sampling the CND from 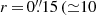 pc) to r = 3″ (≃210 pc).
pc) to r = 3″ (≃210 pc).
Figure 7a represents the radial profiles of the deprojected circular and noncircular components of the CO(2–1) velocity field obtained in the fit (vcirc = c1/sin(i) and vnonc/sin(i), respectively). The fit fails to converge to a physically sound solution for vcirc at small radii r < 40 pc, where kinemetry finds anomalous retrograde rotation and/or very high values of the vnonc/vcirc ratio. This reflects the random pattern of the observed vmean at these small radii (Fig. 6). As we shall argue in Sects. 4.6 and 6, vmean gives an incomplete representation of the complex kinematics of molecular gas in this region, which is characterized by different velocity components around vsys. Outside r ≃ 40 pc, the value of vnonc/vcirc stays within the range ∼0.6 − 1 over a sizable fraction of the CND (40 pc < r < 190 pc; Fig. 7b). As shown in Fig. 7c, the main contribution to vnonc comes from the s1 term. In particular, the sign (> 0) and normalized strength of s1 (s1/c1 ≃ 0.4 − 0.8) indicate significant outflow radial motions in the CND, which reach deprojected values, evaluated by the s1/sin(i) term, of up to ≃85 km s−1. This result is compatible with the average value reported by García-Burillo et al. (2014) for the CND, obtained using a much coarser radial sampling and a significantly lower spatial resolution. Furthermore, at the outer edge of the CND (r ≃ 190–210 pc), strong noncircular motions (vnonc/vcirc > 1) are also required to fit the complexity of the observed velocity field, which partly reflects the bar-driven gas inflow (s1/c1 ≃ −0.4). The gas inflow due to the bar extends farther out in the disk up to r ≃ 1.5 kpc, as discussed by García-Burillo et al. (2014).
 |
Fig. 7. Left panel: radial profile of the c1/sin(i) ratio, which represents the best fit obtained by kinemetry for the deprojected axisymmetric circular component of the velocity field (vcirc; black curve and filled symbols). We also plot the radial profile of the deprojected noncircular motions (vnonc/sin(i)) derived from the Fourier decomposition until third order (red curve and open symbols). Middle panel: variation of the absolute value of vnonc/vcirc ratio as function of radius (black curve and open symbols). Right panel: variation of the s1/c1 ratio as function of radius. The s1 coefficient represents the best fit of the (projected) axisymmetric radial component of the velocity field (black curve and open symbols). The hatched gray-filled rectangles in panels (b) and (c) identify the region where the solution found by kinemetry is judged less reliable. |
Figure 8 shows the residual mean-velocity field obtained after subtraction of the rotation component derived in the analysis above7. The residual velocity field of the CND shows the largest departures from rotation (locally up to ±200 km s−1) for the molecular gas located in the region being swept by the AGN wind bicone. The signs of the residuals, mostly redshifted (blueshifted) on the northern (southern) side of the CND across the AGN wind trail, indicate that the kinematics of the gas are shaped by outward radial motions, as captured by the axisymmetric fit of kinemetry. In conclusion, these results confirm that the imprint of the outflow on the mean-velocity field of the molecular gas can be accounted for to first order by a scenario where the gas is being pushed by the AGN wind inside the disk creating a radial expansion of the CND with velocities that are on average ≃85 km s−1 from r ≃ 50 pc out to r ≃ 200 pc, with maximum deprojected values that can reach ≃200 km s−1 locally. As expected, the residual velocity field of the CND shown in Fig. 8 exhibits significantly larger departures from circular rotation compared to the lower-resolution CO map of García-Burillo et al. (2014), as displayed in their Fig. 15.
 |
Fig. 8. Residual mean-velocity field of the CND obtained after subtraction of the best-fit rotation component from the CO(2–1) MSR data, as described in Sect. 4.5. The color scale spans the range [−200, 200] km s−1 relative to |
The mass of gas in the outflow was calculated from the CO(2–1) data cube after subtraction of the projected rotation curve derived by kinemetry, by integrating the emission of the line outside a velocity interval ⟨vres⟩=[vsys − 50, vsys + 50] km s−1 that encompasses by construction most of the expected virial range attributable to turbulence. We determine that ≃55% of the total CO(2–1) flux in the CND stems from the outflow component, which implies that around half of the mass of the CND participates in the outflow. A similar percentage (≃50%) was derived by García-Burillo et al. (2014).
4.6. Kinematics of the CND: line-widths
Figure 9 shows the line width maps (FWHM) of the CND derived for the 2–1 and 3–2 lines using a 4σ-clipping. The picture drawn from both lines is similar: line widths lie in the range ≤25 − 50 km s−1 only at the outer edge of the CND, while they increase up to significantly higher values ≥100 km s−1 at the smaller radii of the inner edge of the CND, coinciding with the region associated with the working surface of the AGN wind. Line widths can reach very high values (≃200 − 250 km s−1) at a fairly large number of positions located on the northern and southern extremes of the CND, that is, in the way of the jet and AGN wind trajectories. The extreme broadening of the spectra identified in these regions cannot be easily explained by the beam smearing of velocity gradients produced by a combination of rotation and noncircular motions in a coplanar geometry, considering firstly the high spatial resolution of the observations (≃2 − 7 pc) and secondly the moderate inclination of the galaxy disk (i = 41° ±2°; García-Burillo et al. 2014).
 |
Fig. 9. Velocity-width maps in units of FWHM derived for the CO(2–1) (left panel) and CO(3–2) (right panel) lines in the CND of NGC 1068, as obtained from the MSR data set. Contours and color scale span the range [20, 200] km s−1 in steps of 30 km s−1. Symbols and markers as in Figs. 3 and 4. |
Figure 10 shows the CO 2–1 and 3–2 spectra obtained at a representative offset where we have identified extreme line broadening ([Δα, Δδ] = [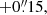 +0
+0 94], where offsets are measured relative to the AGN; see Sect. 2). At this position, the CO profiles show line splitting into two velocity components that are shifted by ≥250 km s−1 relative to each other. As illustrated by Fig. 10, this velocity span is mostly independent of the range of aperture sizes used to extract the spectra, which coincide with the spatial resolutions of the observations, namely ≃2 − 7 pc. This is an indication that the main contributor to the widening of the spectra must necessarily come from the projection of gas motions perpendicular to the plane of the galaxy.
94], where offsets are measured relative to the AGN; see Sect. 2). At this position, the CO profiles show line splitting into two velocity components that are shifted by ≥250 km s−1 relative to each other. As illustrated by Fig. 10, this velocity span is mostly independent of the range of aperture sizes used to extract the spectra, which coincide with the spatial resolutions of the observations, namely ≃2 − 7 pc. This is an indication that the main contributor to the widening of the spectra must necessarily come from the projection of gas motions perpendicular to the plane of the galaxy.
 |
Fig. 10. Spectra extracted at [Δα, Δδ] = [ |
As argued in Sect. 4.4 and 4.5, the coplanar outflow scenario is a first-order explanation for the overall redshift of the line emission at the northern region of the CND: Fig. 10 shows that the mean-velocity predicted by the best-fit model found by kinemetry (vkin) is shifted by ≃ + 100 km s−1 relative to the radial velocity attributable to circular motions (vcir). A similar blueshift of CO lines relative to the predicted motions due to circular rotation at the southern region CND is also explained. However, the observed line splitting and the implied extreme broadening of the spectra illustrated by Fig. 10 strongly suggest that the molecular gas in the CND has also been forced to leave the plane of the galaxy and has therefore adopted a 3D shell-like geometry. We defer to Sects. 6 and 7 for a more detailed discussion of the kinematics of the large-scale outflow and its relation to the dynamics of the molecular torus and its immediate surroundings.
5. Molecular line emission: the torus
5.1. Morphology, size, and orientation
Figure 11 shows a zoom on the inner r ≤ 20 pc region of the CO and HCO+ maps around the position of the AGN. The maps were obtained using the MSR data set, as defined in Table 1. We also show in Fig. 12 the maps obtained using the HSR data set (see Table 1).
 |
Fig. 11. Left panel: CO(2–1) map of the central |
The images shown in Figs. 11 and 12 prove the existence of a spatially resolved molecular disk or torus that extends over a significantly large range of spatial scales ≃10 − 30 pc around the central engine. This result adds supporting evidence for the existence of a spatially resolved molecular disk or torus in NGC 1068, which has been claimed based on previous high-resolution ALMA images of the galaxy obtained in a different set of molecular lines and dust continuum emission: CO(6–5) and dust emission (García-Burillo et al. 2016; Gallimore et al. 2016); HCN(3–2) and HCO+(3–2) (Imanishi et al. 2016, 2018; Impellizzeri et al. 2019).
 |
Fig. 12. Same as Fig. 11 but showing the maps obtained using the HSR data set, as defined in Table 1. The CO(2–1) contours are: −3σ (dashed), 3σ, 5σ, 7σ, 9σ, and 11σ, where 1σ = 22 mJy km s−1 beam−1. The CO(3–2) contours are −3σ (dashed), 3σ, 5σ, 7σ, 9σ, 12σ, 15σ, and 18σ, where 1σ = 35 mJy km s−1 beam−1. The HCO+(4–3) are −3σ (dashed), 3σ, 5σ, 7σ, 9σ, 12σ and 15σ, where 1σ = 34 mJy km s−1 beam−1. |
Table 2 lists the size, position, and orientation of the molecular disks identified in Fig. 11, derived using elliptical Gaussians to fit the images in the plane of the sky8. We also list the sizes and orientations derived after deconvolution by the corresponding beams at each frequency.
AGN position and fitted torus parameters.
The physical parameters listed in Table 2 differ notably depending on the line transition used to image the torus, a result that brings into light the many faces of the molecular torus in NGC 1068. As a common pattern, the torus is shifted overall ≃0.7 − 2 pc east relative to the AGN. However, the off-centering is a factor of ≃2 − 3 larger in the CO lines compared to that derived in HCO+(4–3). Furthermore, there is a clear trend showing comparatively larger sizes for the torus (Dmajor) imaged in the lower-density tracers. In particular, the deconvolved FWHM-sizes of the torus go from ≃15 ± 0.3 pc in CO(2–1) to ≃13 ± 0.3 pc in CO(3–2), and down to ≃6 ± 0.3 pc in HCO+(4–3). The equivalent full sizes of the tori, defined as the sizes of the disks measured at a ≃3σ intensity level of the Gaussian used in the fit, range from ≃28 ± 0.6 pc in CO(2–1), to ≃26 ± 0.6 pc in CO(3–2), and ≃11 ± 0.6 pc in HCO+(4–3).
The orientations of the molecular tori, measured anticlockwise from north, are found within the range PA ⊂ [112° −138° ] ± 5°. This range encompasses, within the errors, the values previously reported for the CO(6–5) and dust continuum tori (PACO(6 − 5) = 112° ±20°; PAdust = 143° ±23°; García-Burillo et al. 2016; Gallimore et al. 2016), as well as for the maser disk (PAmaser = 140° ±5°; Greenhill et al. 1996; Gallimore et al. 2001).
The orientation of the molecular torus, PA = 113°, derived from the average of the values listed in Table 2, is roughly perpendicular to the orientation of the jet and the ionized wind axes (PA ≃ 10 − 30° ±5°). Furthermore, the molecular torus is closely aligned with the ≃1–1.5 pc scale disk imaged in radio continuum by Gallimore et al. (2004). The described geometry adds supporting evidence that this is the orientation of the accretion disk in NGC 1068. In this context it is noteworthy that a recent high-resolution radio continuum imaging of four low-luminosity AGNs published by Kamali et al. (2019) has found that the orientations of the radio jets are misaligned with the normal to the known maser disks in these sources by less than 30°.
We measured aspect ratios for the tori within the range Dmajor/Dminor ≃ 2 − 3. The implied lower limit to the inclination of the disks is i ≥ 60 − 70°. This indicates that molecular gas is settling around the central engine of NGC 1068 on the observed spatial scales ≃10 − 30 pc on a highly inclined disk, which is significantly tilted relative to the large-scale disk of the galaxy (i ≃ 41° ±2°; Bland-Hawthorn et al. 1997; García-Burillo et al. 2014). The high inclination of the molecular torus of NGC 1068 is expected given the Type 2 classification for this Seyfert. Recent ALMA observations of a sample of nine nearby Seyferts published by Combes et al. (2019) and Alonso-Herrero et al. (2018, 2019), have confirmed that NGC 1068 is not an exception: the molecular tori identified in the targets observed by ALMA are generally not aligned with the main disks of the AGN hosts, but their measured orientation tends to be in agreement with their optical Type 1–2 classification. Most remarkably, this decoupling is seen to be taking place on spatial scales ≥10 − 30 pc, similar to those identified in NGC 1068.
5.2. Masses and column densities
We derived the mass of the molecular torus by integrating the CO(2–1) line emission inside the area defined by the full size of the best-fit Gaussian disk derived in Sect. 5.1 (≃1.43 Jy km s−1). Based on Eq. (3) of Bolatto et al. (2013), we estimated the molecular gas mass of the 2–1 torus to be 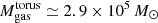 , including the mass of helium. In our estimate we assumed a 2–1/1–0 brightness temperature ratio ≃2.5, as measured by Viti et al. (2014) at the AGN knot, and a galactic CO-to-H2 conversion factor (XCO = 2 × 1020 mol cm−2 (K km s−1)−1). Similarly, the torus mass derived using the CO(3–2) flux integrated inside the region delimited by the red ellipse of the middle panel of Fig. 11 (≃3.54 Jy km s−1) is
, including the mass of helium. In our estimate we assumed a 2–1/1–0 brightness temperature ratio ≃2.5, as measured by Viti et al. (2014) at the AGN knot, and a galactic CO-to-H2 conversion factor (XCO = 2 × 1020 mol cm−2 (K km s−1)−1). Similarly, the torus mass derived using the CO(3–2) flux integrated inside the region delimited by the red ellipse of the middle panel of Fig. 11 (≃3.54 Jy km s−1) is 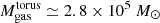 , assuming a 3–2/1–0 brightness temperature ratio ≃2.9 at the AGN knot (Viti et al. 2014). Overall, the 3–2 and 2–1 line-based estimates for
, assuming a 3–2/1–0 brightness temperature ratio ≃2.9 at the AGN knot (Viti et al. 2014). Overall, the 3–2 and 2–1 line-based estimates for 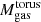 are both a factor of approximately three higher than the value obtained by García-Burillo et al. (2016) from the dust continuum emission measured at 694 GHz. This is not unexpected in view of the comparatively small size measured by García-Burillo et al. (2016) for the dusty torus/disk (diameter ≃7 pc).
are both a factor of approximately three higher than the value obtained by García-Burillo et al. (2016) from the dust continuum emission measured at 694 GHz. This is not unexpected in view of the comparatively small size measured by García-Burillo et al. (2016) for the dusty torus/disk (diameter ≃7 pc).
The H2 column densities measured towards the position of the AGN are N(H2) = (1.1–3.2) × 1023 mol cm−2 and N(H2) = (1.5–4.4) × 1023 mol cm−2 from the 2–1 and 3–2 intensities, respectively, measured at the corresponding apertures. In either case, the range of column densities encompasses the values derived from the moderate(≃6–7 pc)- and the high(≃2–3 pc)-spatial-resolution data sets. As expected, the higher column densities are obtained at the highest spatial resolution due to the lower beam dilution of the obscuring material. These values are still a factor of between two and three below the Compton-thick limit (N(H2) ≥ 1024 mol cm−2) required to explain the nature of the Type 2 nucleus of NGC 1068. This mismatch may be an indication that X-ray absorption by clouds which lie in the dust-free inner region of the torus would be responsible for most of the obscuration (see, e.g., discussion in Elitzur 2008). However, within the uncertainties associated to the values of XCO in a harsh AGN environment (of up to about an order of magnitude; see, e.g., Wada et al. 2018), the molecular torus detected by ALMA could nevertheless contribute significantly to the properties of obscuration of the central engine of NGC 1068 on the spatial scales of ≃2–3 pc. In this context it is noteworthy that the recent NuSTAR observations of NGC 1068, published by Marinucci et al. (2016), found evidence of a ∼40% decrease of the absorbing column density from N(H2) ∼ 5 × 1024 mol cm−2 to ∼3.3 × 1024 mol cm−2 on a timescale of 2 years (December 2012–February 2015). The change of column densities required to explain the X-ray variability of the AGN in NGC 1068 could be associated with the small-scale structure of the molecular torus imaged by ALMA.
The range of N(H2) reported above for the 2–1 line of CO at the AGN locus translates into a range of Av ≃ 120–350, derived using the ratio N(H2)/Av = 0.9 × 1021 mol cm−2 mag−1 of Bohlin et al. (1978). This range of Av is compatible within the errors with the value inferred by Grosset et al. (2018) from the 20 mag extinction in the Ks band that these authors used to explain their NIR polarization data, which would imply Av ≃ 180. Furthermore, our estimate is only a factor of two higher than the value used by Rouan et al. (2019) to explain the measured radial profile in the Ks band.
5.3. Previous evidence of a molecular torus
The use of different transitions, which purposely span a wide range of physical conditions of molecular gas (n(H2) ⊂ 103 − 107 cm−3), is instrumental in helping to reveal the density radial stratification of the gas in the torus. As expected for the contribution of a comparatively cooler gas component, the sizes reported for the molecular torus traced by the low-J CO lines are more than an order of magnitude greater compared with the sizes of the NIR and MIR sources of the hot dust (Jaffe et al. 2004; Weigelt et al. 2004; Raban et al. 2009; Burtscher et al. 2013; López-Gonzaga et al. 2014)
The parameters of the HCO+ torus listed in Table 2 are similar within the errors to those derived by García-Burillo et al. (2016), Gallimore et al. (2016), and Imanishi et al. (2018) for the molecular torus imaged in the CO(6–5), HCO+(3–2), and HCN(3–2) lines. Such an agreement is expected among these transitions as they probe a similar range of high densities for molecular gas (n(H2)⊂105 − 107 cm−3). In contrast, the lower densities to which the 2–1 and 3–2 transitions are sensitive (n(H2)⊂103 − 104 cm−3) seem to trace preferentially the outer region of the molecular torus of NGC 1068.
Previous evidence supporting the existence of a dusty disk that extends well beyond the canonical parsec-scale in NGC 1068 was discussed by Gratadour et al. (2015), based on NIR polarimetric imaging data. In particular, Gratadour et al. (2015) found that the inferred linear polarization vectors in the CND change their orientation from a centro-symmetric pattern, associated with the hourglass structure shown in Fig. 4, to an orientation perpendicular to the bicone axis, which is oriented along PA ≃ 30°. These observations show the existence of an extended patch of linear polarization arising from a spatially resolved elongated nuclear disk of dust of ≃50 − 60 pc in diameter and oriented along PA ≃ 120°. The change of orientation of the polarization vectors is interpreted by Gratadour et al. (2015) as the result of a double scattering of the radiation from the central engine by a dusty disk: photons in the ionization cone are scattered a first time on electrons or on dust grains towards the outskirts of the torus where they suffer a second scattering towards the observer (see, e.g., Murakawa 2010, for a general description of a similar phenomenology expected in the dusty disks around young stellar objects). Photons scattered towards the inner regions of the torus would not be able to escape because of extinction. This would explain why polarization traces preferentially the outer and less dense regions of the torus.
Figure 13 shows the overlay of the CO maps on the image showing the difference between the polarization angle derived from the H-band map of Gratadour et al. (2015) and a purely centro-symmetric pattern. The angle-difference map alone cannot be used as a direct tracer of the dust column densities in the disk. However, Fig. 13 shows a tantalizing agreement between the maximum extent and overall orientation of the putative dusty disk, identified by Gratadour et al. (2015), and those of the CO torus imaged by ALMA.
 |
Fig. 13. Left panel: we overlay the CO(2–1) contours of Fig. 11 on the difference between the polarization angle map and a purely centro-symmetric pattern derived from the H-band map of Gratadour et al. (2015) (in color scale in units of degrees) in the central |
5.4. Kinematics of the molecular torus
Figure 14 shows the mean-velocity fields derived from the CO(2–1), CO(3–2), and HCO+(4–3) lines in the central r ≤ 20 pc region around the central engine of NGC 1068. By contrast with the CND, the three lines show a surprising lack of a regular pattern and/or a defined velocity gradient in the torus. As argued below, the existence of different velocity components inside the torus, but also in the surrounding region that connects the torus to the host (see Sect. 6), adds to the extreme complexity of the velocity field, most particularly in the case of the CO(2–1) line.
 |
Fig. 14. Mean-velocity fields derived from the CO(2–1) (left panel), CO(3–2) (middle panel) and HCO+(4–3) (right panel) lines in the central |
Figure 15 shows the CO and HCO+ emission spectra extracted at the position of the AGN using the MSR and HSR data sets for a common aperture of ≃6–7 pc and ≃2–3 pc, respectively. Most of the emission for the three lines stems from a core component, which corresponds to gas at low velocities: |v − vsys|≤100 km s−1. Furthermore we detect significant emission at highly redshifted velocities in the 2–1 and 3–2 lines of CO up to v − vsys ≃ +450 km s−1. There is a remarkable absence of any significant blueshifted counterpart of the high-velocity gas in the CO lines. A similar yet less pronounced asymmetry in the emission of high-velocity gas was present in the AGN profile of the CO(6–5) line of Gallimore et al. (2016). By contrast, we detect both redshifted and blueshifted high-velocity gas emission in the HCO+(4–3) spectrum of the AGN, although with a maximum velocity span that is smaller compared to that reported for the CO lines: |v − vsys|≤300 − 350 km s−1. As argued below, this high-velocity regime corresponds to the range of velocities displayed by the H2O megamaser spots identified in the inner r ≤ 1 pc region (Greenhill et al. 1996; Gallimore et al. 2001). Unlike the emission at low velocities, the high-velocity gas component is mostly spatially unresolved, as expected if this emission comes from a region localized very close to the inner edge of the torus (r ≤ 1 pc; see Fig. 15).
 |
Fig. 15. Emission spectra extracted at the position of the AGN from the MSR data set for the J = 2 − 1 line of CO (left panel), the J = 3 − 2 line of CO (middle panel), and the J = 4 − 3 line of HCO+ (right panel) using a common aperture of ≃6–7 pc-size (yellow-filled histograms). We also show in blue-hatched histograms the corresponding spectra obtained from the HSR data set using a common aperture of ≃2–3 pc. The red line highlights the value of |
Assuming a geometry similar to that of the H2O megamaser spots, where redshifted velocities are located on the west side of the disk, the reported asymmetry of high-velocity CO emission would imply that the gas at the inner edge of the torus is lopsided to the west. However, the global off-centering described in Sect. 5.1 would imply that the overall gas lopsidedness of the torus changes side to the east. As the bulk of the gas in the torus emits at low velocities and at correspondingly large radii, this behavior is suggestive of the presence of a m = 1–spiral in the gas. This asymmetry is expected if the molecular torus reflects the propagation of the Papaloizou-Pringle instability (PPI; Papaloizou & Pringle 1984; Kiuchi et al. 2011; Korobkin et al. 2013; Dönmez 2014; Donmez 2017).
The kinematics of the molecular torus is further illustrated in Figs. 16 and 17, which show the position–velocity (p − v) diagrams obtained along the average fitted major axis of the nuclear disk or torus (PA = 113°: taken from the average of the values listed in Table 2). Figures 16 and 17 show that a significant fraction of the emission spreads over the bottom left and top right quadrants of the diagrams. Furthermore, the observed terminal velocities are fairly compatible with the predicted extrapolation of the sub-Keplerian (Keplerian) rotation curve vrot ∝ r−α of Greenhill et al. (1996) with α = 0.31 (0.50). Gallimore et al. (2016) also found evidence for Keplerian rotation which is relatively consistent with the compact maser disk based on their CO(6–5) ALMA data. However, we also find significant emission arising from the upper left and lower right quadrants of the p − v diagrams, especially in the 2–1 line of CO. Taken at face value, this anomalous component would indicate the existence of gas in apparent counter-rotation. The emission at velocities that are forbidden in the frame of a circular velocity model is also identified in the CO(3–2) line, although this component appears at comparatively lower velocities in the p − v diagram.
 |
Fig. 16. Position–velocity (p − v) diagrams obtained with the MSR data set along the major axis of the torus of NGC 1068 along PA = 113° in the J = 2 − 1 line of CO (left panel), the J = 3 − 2 line of CO (middle panel), and the J = 4 − 3 line of HCO+ (right panel). Gray-scale and contours are −2.5σ, 2.5σ, 4σ, 6σ to 18σ in steps of 3σ, with 1σ = 0.11 mJy beam−1 (left panel), −2.5σ, 2.5σ, 5σ, 8σ,12σ, 20σ, 35σ and 50σ, with 1σ = 0.23 mJy beam−1 (middle panel), and −2.5σ, 2.5σ, 4σ, 6σ, 9σ, 12σ, 15σ, and 19σ, with 1σ = 0.28 mJy beam−1 (right panel). Offsets along the x axis (Δx) are measured in arc seconds relative to the AGN locus (vertical dashed lines) with positive (negative) values corresponding to the SE (NW) side of the disk. Velocities are measured in LSR scale with |
 |
Fig. 17. Same as Fig. 16 but obtained with the HSR data set. Contours are −2.5σ, 2.5σ, 4σ, 6σ, and 9σ, with 1σ = 0.14 mJy beam−1 (left panel), −2.5σ, 2.5σ, 4σ, 6σ, 9σ, 12σ, and 16σ, with 1σ = 0.23 mJy beam−1 (middle panel), and −2.5σ, 2.5σ, 4σ, 6σ, 9σ, and 12σ, with 1σ = 0.28 mJy beam−1 (right panel). |
The configuration of two apparently counter-rotating disks described above would be nevertheless dynamically unstable: the dissipative nature of the gas would make the two disks collapse on the timescale of the orbital time. The implied fast evolution of the system would make observations of this configuration very unlikely. As we shall argue in Sect. 7, we favor an alternative scenario where the apparent counter-rotation signature in the major axis p − v diagram would rather reflect the presence of noncircular motions in the gas.
6. The torus-CND connections
6.1. The central r ≤ 30 pc region: the gas streamers
Figure 18 shows a zoomed-in view of the CO(2–1) channel map obtained in the central  pc × 60 pc region located around the AGN torus. The maps show that beyond the region identified in Sect. 5.1 as the torus (the blue empty ellipse in Fig. 18) there is significant emission that bridges the torus with the inner edge of the CND ring out to r = 0.4″ (≃30 pc). A sizable fraction of this component is detected inside or at the boundaries of the region in the disk that is suspected to be swept by the AGN wind (PAoutflow ± 40°, with PAoutflow ≃ 30°; e.g., Das et al. 2006; Barbosa et al. 2014) and the radio jet (PAjet ≃ 10°; e.g. Gallimore et al. 1996, 2004). The strongest emission of these features arises at velocities that are shifted by up to ≃ ± 140 km s−1 relative to vsys.
pc × 60 pc region located around the AGN torus. The maps show that beyond the region identified in Sect. 5.1 as the torus (the blue empty ellipse in Fig. 18) there is significant emission that bridges the torus with the inner edge of the CND ring out to r = 0.4″ (≃30 pc). A sizable fraction of this component is detected inside or at the boundaries of the region in the disk that is suspected to be swept by the AGN wind (PAoutflow ± 40°, with PAoutflow ≃ 30°; e.g., Das et al. 2006; Barbosa et al. 2014) and the radio jet (PAjet ≃ 10°; e.g. Gallimore et al. 1996, 2004). The strongest emission of these features arises at velocities that are shifted by up to ≃ ± 140 km s−1 relative to vsys.
 |
Fig. 18. CO(2–1) channel maps obtained in the central |
Figure 19 shows the CO(2–1) intensities integrated inside the two velocity ranges that encompass the bulk of the emission in the CND-torus connections (vblue = [vsys − 140, vsys] km s−1 and vred = [vsys, vsys + 140] km s−1) overlaid on the millimeter continuum image of Fig. 1. Inspection of Fig. 19 confirms that the brightest emission features come from two gas streamers that spring northward and southward respectively from the torus. The emission in the blueshifted channels is stronger than in its redshifted counterpart in the southern streamer, while blueshifted and redshifted emissions of comparable strength are present in the northern streamer. The uneven balance between blueshifted and redshifted emission explains the appearance of the mean-velocity field of Fig. 14, which shows blueshifted velocities in the southern streamer and a more chaotic pattern in the northern streamer. Further emission with a similar split into redshifted and blueshifted channels is detected in a gas lane connecting the torus with the CND eastward, as well as at a fairly large number of positions located inside the region occupied by the AGN bicone.
 |
Fig. 19. Left panel: central |
The northern and southern gas streamers are located close to the trajectory of the inner radio jet and the AGN wind. Overall, this association suggests that the interaction of the radio jet and the AGN wind with the molecular gas in the disk creates the observed line splitting reported above. In this scenario, besides a radial expansion in the disk (the coplanar outflow discussed in Sect. 4.5), the gas may have also been forced to leave the plane of the galaxy and adopt a 3D shell geometry (the vertical outflow) in the region connecting the torus with the CND.
Figure 20 shows the CO(2–1) and CO(3–2) position–velocity diagrams taken along PA = −10° (see the yellow line in the left panel of Fig. 19) as well as the corresponding profiles representative of the NW and SE sections of the strip. The chosen strip goes across the NW and SE boundaries of the AGN bicone and also across the peaks of the connecting structures detected in the 2–1 line. The CO(3–2) profiles along PA = −10° indicate that the emission of this line is spread over a narrower range of velocities compared to the 2–1 line. The 2–1 line profile shows several components that encompass those of the 3–2 line. In contrast to the CO(3–2) line, the CO(2–1) emission peaks at the most extreme velocities relative to the centroid dictated by circular rotation. Although the gas streamers are detected in both molecular lines, the described nested structure suggests that the lower density gas traced by the CO(2–1) line in the vertical outflow has been pushed to higher velocities compared to the denser gas traced by the CO(3–2) line. This may be the scenario resulting from the passage of C- and J-type shocks impacting on a stratified medium, whereby the CO (2–1) transition traces a lower-density gas compared to the CO (3–2) transition: the piston effect from the shock would then lead to the lower-density gas moving at higher velocities than the denser gas. We cannot exclude, however, an additional, evolutionary effect whereby depending on the flow time the transitions peak at different velocities with higher flow times corresponding to higher velocities, which means a more evolved shock. Time-dependent simulations of oblique C-type shocks in inhomogeneous media by Ashmore et al. (2010) show very complex density structures that vary with time. A similar nested structure is found on the larger scales of the outflow when we compare the CO lines with the ionized gas lines of the AGN wind, as shall be discussed in Sect. 6.2.
 |
Fig. 20. Left panel: CO position–velocity diagrams taken along the gas streamers that connect the torus with the CND at PA = –10°. The CO(2–1) line emission is shown in gray linear scale spanning the range [2σ, 18σ] with 1σ = 0.11 mJy beam−1. The CO(3–2) position–velocity diagram is shown in (blue) contours: −2σ (dashed), 2σ, 4σ, 6σ, 10σ to 40σ in steps of 10σ, with 1σ = 0.23 mJy beam−1. The (red) line and square markers show the mean velocities that can be attributed to circular rotation along PA = –10° (according to the fit of Sect. 7). The spatially integrated CO 2–1 and 3–2 line profiles averaged over the SE and NW segments of the connecting gas streamers (as defined in left panel) are shown, respectively, in the middle panel and in the right panel. |
6.1.1. Gas streamers seen at other wavelengths: evidence of outflow
As mentioned in Sect. 4.2, there is independent evidence of a significant pile-up of dusty material along the location of the northern and southern molecular streamers detected by ALMA. As illustrated in Fig. 4, both gas streamers are characterized by an increased degree of polarization of their dust-scattered NIR emission. There is observational evidence that the C knot of the northern streamer, located at 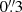 (≃20 pc) from the AGN core, is spatially co-incident with the interaction of the jet and the molecular ISM. Lopez-Rodriguez et al. (2016) argue that this interaction can explain the increase of the polarization degree of the MIR emission in this region. Furthermore, gas streamers connecting the CND and the torus with an extent and morphology similar to the ones imaged by ALMA were previously detected in the 2.12 μm H2 line, a tracer of hot (Tk ≥ 103 K) molecular gas (Müller Sánchez et al. 2009; Barbosa et al. 2014; May & Steiner 2017).
(≃20 pc) from the AGN core, is spatially co-incident with the interaction of the jet and the molecular ISM. Lopez-Rodriguez et al. (2016) argue that this interaction can explain the increase of the polarization degree of the MIR emission in this region. Furthermore, gas streamers connecting the CND and the torus with an extent and morphology similar to the ones imaged by ALMA were previously detected in the 2.12 μm H2 line, a tracer of hot (Tk ≥ 103 K) molecular gas (Müller Sánchez et al. 2009; Barbosa et al. 2014; May & Steiner 2017).
Our interpretation of the kinematics of the gas detected by ALMA in these structures favors the outflow scenario, which was also invoked by Barbosa et al. (2014) and May & Steiner (2017), rather than the inflow scenario first proposed by Müller Sánchez et al. (2009). We note that the inflow interpretation of Müller Sánchez et al. (2009) was based on an analysis of the mean-velocity field of the gas streamers. In our case, and due to the extreme complexity of the CO(2–1) line profiles in the streamers characterized by the existence of different velocity components of comparable strengths, the use of mean-velocity fields to diagnose the prevalence of inflow or outflow motions in these structures would be misleading. Similarly, the detection of multiple velocity components in the gas streamers traced by the 2.12 μm H2 line, put forward after a reanalysis of Müller Sánchez et al. (2009) data (Vives-Arias et al., in prep.), has confirmed the 3D geometry of the molecular outflow.
6.1.2. Molecular gas mass of the streamers
The spatially integrated flux of the torus-CND connections out to r ≃ 30 pc amounts to 820 mJy km s−1. This is equivalent to a molecular gas mass ≃1.7 × 105 M⊙9. Overall, the mass of the bridging gas streamers (Mstreamers) represents a sizable fraction of the mass of the molecular torus (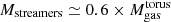 ), while it is only a tiny fraction of the mass of the outflowing CND (
), while it is only a tiny fraction of the mass of the outflowing CND (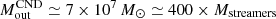 ; García-Burillo et al. 2014, and this work). The remarkably different masses but similar outflow velocities, estimated through modeling in Sect. 7 for the torus-CND connections and the CND, imply that the radial profile of the molecular outflow rate shows a sharp discontinuity beyond r ≃ 50 pc.
; García-Burillo et al. 2014, and this work). The remarkably different masses but similar outflow velocities, estimated through modeling in Sect. 7 for the torus-CND connections and the CND, imply that the radial profile of the molecular outflow rate shows a sharp discontinuity beyond r ≃ 50 pc.
6.2. Connection with the large-scale molecular outflow: the 30 pc ≤r≤200 pc region
The splitting of the line emission into two velocity ranges identified in the gas streamers (Sect. 6.1) is similar to the one observed at larger radial distances over the northern and southern extremes of the CND ring. As discussed in Sect. 4.6, these regions of the CND lie along the path of the jet and AGN wind trajectories. Zooming out on the torus and its surroundings allows us to obtain a wider view of the entire outflow region out to r ≤ 200 pc.
In an attempt to characterize the global kinematics of the outflow we constructed a representative p − v plot of the region, as follows. Firstly, we subtracted the contribution from circular motions derived from the rotation curve model of Sect. 4.5 from the CO data cubes on a pixel-by-pixel basis. Secondly, the re-shuffled version of the data cubes were used to average the emission along a range of strips derived for a set of PA and radial distances, which are designed to cover a large fraction of the outflow region under study, here defined by: r ⊂ [0, 200] pc and PA ⊂ [PAoutflow − 20° ,PAoutflow + 20° ], that is, covering the outflow section over its FWHMinner ≃ 40°. In this diagram obtained from the rotation-subtracted cube, the line emission outside a range generously defined as ≃vsys ± (25 − 50) km s−1, which can be attributed to turbulence, would be produced by the contribution of (unsubtracted) noncircular motions. The latter could result from streaming motions in the plane of the galaxy (coplanar radial inflow/outflow or tangential motions) or outside the plane of the galaxy (vertical inflow or outflow). As the range of PA values used in the averages are close to PAminor = 19°, we can foresee that the contribution from the tangential component of streaming motions will be negligible10. The result is shown in Fig. 21 for the CO(2–1) and CO(3–2) lines.
 |
Fig. 21. Comparison of the average position–velocity (p − v) plot obtained for the outflow region out to r = 3″ (≃210 pc) in CO(2-1): contours are −2.5σ [dashed], 2.5σ, 4σ, 6σ, 9σ, 12σ, 17σ, 25σ, 35σ, 50σ, 70σ to 160σ in steps of 30σ, with 1σ = 0.04 mJy beam−1 and CO(3–2). The color logarithmic scale is [2.5σ, 230σ] with 1σ = 0.08 mJy beam−1. The emission has been averaged using data cubes where the rotation curve model of Sect. 4.5 has been subtracted over a range of PA: [PAoutflow − 20°, PAoutflow + 20°], where PAoutflow = 30°. Offsets along the x-axis are measured in arc seconds relative to the AGN locus. |
An inspection of Fig. 21 shows that for a large range of radii a significant fraction of the CO emission stems from gas in noncircular motions. For the brightest features, which correspond to the crossings of the CND ring, the emission is on average redshifted by ≥50 km s−1 on the northern side of the CND (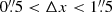 ), while it is blueshifted by ≥100 km s−1 on the southern side (
), while it is blueshifted by ≥100 km s−1 on the southern side (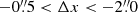 ). This reflects the sign and the right order of magnitude of the mean-velocity field deviations seen in the CO map of the CND (Fig. 8), which have been interpreted in terms of a coplanar outflow. However, the emission at the crossings of the CND ring spreads over a surprisingly large velocity range (up to ≃400 − 500 km s−1) around the reported red- and blueshifted values and it shows signs of multiple velocity components. In particular, a smaller but significant fraction of the emission is blueshifted (redshifted) on the northern (southern) side of the CND. In conclusion, although the coplanar outflow scenario can explain the bulk of the velocity distortions identified in the outflow region, the large linewidths and the reported line-splitting of the CO lines along the outflow axis require the inclusion of a vertical component.
). This reflects the sign and the right order of magnitude of the mean-velocity field deviations seen in the CO map of the CND (Fig. 8), which have been interpreted in terms of a coplanar outflow. However, the emission at the crossings of the CND ring spreads over a surprisingly large velocity range (up to ≃400 − 500 km s−1) around the reported red- and blueshifted values and it shows signs of multiple velocity components. In particular, a smaller but significant fraction of the emission is blueshifted (redshifted) on the northern (southern) side of the CND. In conclusion, although the coplanar outflow scenario can explain the bulk of the velocity distortions identified in the outflow region, the large linewidths and the reported line-splitting of the CO lines along the outflow axis require the inclusion of a vertical component.
The proposed geometry is illustrated in Fig. 22, which shows a scaled cross-cut view of the NLR of NGC 1068 along the projected direction of the outflow axis (PAoutflow ≃ 30° ±5°). This is a revised version of the scheme proposed in Fig. 17 of García-Burillo et al. (2014), where the authors first accounted for the molecular outflow detected by ALMA in the CND by including only a coplanar outflowing component. The existence of a vertical molecular outflow would explain the simultaneous detection of blueshifts and redshifts on either side of the AGN locus in the torus-CND connections and throughout the entire outflow region, as evidenced by the new ALMA data.
 |
Fig. 22. Revised scheme presenting a cross-cut view of the NLR of NGC 1068 along the projected direction of the ionized outflow axis (PA ∼ 30°; shown by the green line). The new ALMA data show that CO line emission is split into blueshifted and redshifted components (relative to vsys) along the outflow axis, from the torus out to the edge of the CND, here represented by Knot N and Knot S. We highlight the extent of the AGN-ionized wind (gray shade) and the assumed geometry defined by the inclination of the galaxy disk, i = 41°, the inclination of the outflow axis, ioutflow ≥ 80°, and the full opening angle of the outflow, FWHMouter ≃ 80°. |
Figure 23 compares the p − v diagrams of the outflow obtained in the CO(2–1) line and in the NIR line of [SiVI], a highly ionized species imaged with the SINFONI instrument of the VLT (Ric Davies, priv. comm.). Compared to the cold molecular gas traced by the CO lines, the emission of this tracer of highly ionized gas in the AGN wind is spread throughout the outflow region over a much wider velocity range: up to v − vsys ≃ ±900 − 1000 km s−1 (see Fig. 23). In the scheme depicted by Fig. 22, the ionized wind would encounter less molecular gas, and consequently less resistance against expansion, above (below) the midplane of the galaxy on the northern (southern) side of the disk. This would explain why the sign of the velocity shifts for the strongest emission components of the [SiVI] line is noticeably reversed with respect to CO along the outflow axis.
 |
Fig. 23. Same as Fig. 21 but showing the comparison between CO(2–1) (contours) and [SiVI] (color scale spanning the range [3σ, 1700σ]). For visualization purposes the v-scale has been highly compressed relative to that of Fig. 21 (identified by the magenta dashed lines). [SiVI] is a high-ionization line (≃205 eV) that traces the emission of high-velocity ionized gas in the outflow up to v − vsys ≃ ±800 km s−1 inside the CND region. |
7. Towards a global model for the outflow
7.1. 3DBarolo fit
As argued in Sects. 4–6, the kinematics of molecular gas show strong departures from circular motions in the torus, the torus–CND connections, and the CND ring. These velocity field distortions are interconnected and reflect the effects of feedback of the AGN on the kinematics of molecular gas on a wide range of spatial scales around the central engine. In the following we attempt to define the main features of a global model that best accounts for the complex kinematics of the molecular gas revealed by ALMA in NGC 1068.
To this aim we used the software 3DBarolo (3D-Based Analysis of Rotating Objects from Line Observations) developed by Di Teodoro & Fraternali (2015). 3DBarolo uses a set of tilted-ring models to fit the emission-line 3D data cubes, which have two spatial dimensions and one spectral dimension. Compared to the kinemetry software used in Sect. 4.5, which fits with tilted-ring models the 2D mean-velocity images, 3DBarolo provides a more complete exploration of the 3D geometrical and kinematic parameter space and also takes into account the effects of beam smearing in finding the best-fit model. Furthermore, when we ran the fit routine we adopted the pixel-based normalization option of the program to generate the modeled maps. This allows us to have a non-axisymmetric model in density, which is excluded from the fit, while the dependance of all the physical parameters found by 3DBarolo is by construction axisymmetric.
Among the set of output parameters that can be obtained for the optimum solution, 3DBarolo provides the profiles of the circular rotation as a function of radius (vrot, equivalent to the c1/sin(i) term of kinemetry), and the corresponding profiles of the radial motions (vrad, equivalent to the s1/sin(i) term of kinemetry). The list of parameters that can be fitted also includes the velocity dispersion (σgas), the position angle (PA), the inclination (i), and the Gaussian scale-height for the disk (H). In all the fit runs we used a set of 103 radii sampling the CND from 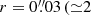 pc) to r = 3″ (≃210 pc), which is the same region used to fit the velocity field with kinemetry in Sect. 4.5.
pc) to r = 3″ (≃210 pc), which is the same region used to fit the velocity field with kinemetry in Sect. 4.5.
As a sanity check we first benchmarked the solutions found by 3DBarolo against the output of kinemetry, using a common set of fixed parameters as detailed in Appendix A. Notwithstanding the different approach used by 3DBarolo compared to kinemetry, the vrad and vrot profiles found are in relatively good agreement. In particular, similarly to kinemetry, 3DBarolo finds a vrad-profile indicative of radial outflow motions of ≃50 − 100 km s−1 in the plane of the galaxy in a range of radii r ≃ 50–210 pc (the coplanar outflow).
In a second 3DBarolo run, which is described in detail in Appendix A, we allowed for a more generous exploration of the parameter space by only fixing the AGN position and vsys and letting free vrot, vrad, vdisp, PA, i, and H. As an additional degree of freedom we also introduced a velocity field perpendicular to the plane of the galaxy at each radius, vvert, in an attempt to account for the 3D nature of the outflow suggested by observations, which call for the inclusion of a vertical outflow component. This second run was executed in two steps. We first derived a model by fitting all the parameters simultaneously, while in a second iteration we used values interpolated from the previous iteration for PA and i while the rest of parameters are let free. The radial profiles of the best-fit parameters in this two-step process are shown in Fig. A.2. We summarize below the main features describing the best-fit solution found as follows:
– The overall fit reflects the fact that the angular momentum axis of the gas in the molecular torus is tilted by α ≃ 60° relative to the angular momentum of the gas in the large-scale disk: α = 180° −(⟨idisk⟩−⟨itorus⟩) ≃ 60°, where ⟨idisk⟩≃41° and ⟨itorus⟩≃ − 80°.
– The vrad profile, which accounts for the coplanar outflow component, reflects a change of sign, similar to the one described in Appendix A for vrot, from the torus region, where vrad < 0, to the outer disk, where vrad > 0. In either case the sign and order of magnitude of the vrad solution imply the existence of a significant outward radial component of ≃50 − 100 km s−1 throughout the fitted region r ≤ 210 pc.
– The best-fit favors a value of vvert ≃ 100 km s−1 for the vertical outflow component up to at least r ≃ 150 pc. Combined with the vrad profile, the vvert value implies the existence of 3D outflow velocities ≃100–140 km s−1 up to r ≃ 150 pc.
We illustrate the goodness of the best-fit solution in Fig. 24, where we overlay the CO(2–1) emission contours observed by ALMA on the corresponding emission derived by 3DBarolo (color scale) in two p − v plots oriented along PA = 291° = 180° +111° and PA = 21°. The latter correspond, respectively, to the mean values describing the orientation of the major and minor axes, determined inside the region used in the fit (0 pc < r < 210 pc).
 |
Fig. 24. Overlay of CO(2–1) p − v plots (contours in Jy beam−1-units) along the average major axis (upper panel: PA = 291° = 180° +111°; where we adopt the orientation of the receding side of the major axis) and average minor axis (lower panel: PA = 21°) on the corresponding synthetic p − v plots (in logarithmic color scale) generated by 3DBarolo for the best-fit model described in Sect. 7. In our convention Δx-offsets are > 0 to the SE and Δy-offsets are > 0 to the NE. Contour levels in the upper panel are 1.3%, 3%, 5%, and then 10%–90% in steps of 10% of the peak value = 23.1 mJy beam−1. Contour levels in the lower panel are 2.7%, 5%, and then 10%–90% in steps of 10% of the peak value = 9.1 mJy beam−1. The regions identified as OUT-N and OUT-S in the lower panel correspond to the crossings of the AGN-wind working surface with the molecular gas at the N and S extremes of the CND. |
Overall, the parameter space occupied by the observations along the major and minor axis p − v plots is reasonably accounted for by the 3DBarolo solution. However, there are a number of noticeable disagreements between the observations and the model. These discrepancies are explained to some extent by the inability of the model to reproduce any substantial deviation from the axisymmetric dependence of the kinematic parameters inherent to 3DBarolo. Figure 24 shows that the combination of vrad and vvert in the model is able to significantly spread the emission over blueshifted and redshifted velocities relative to vsys through the inner section of the minor axis up to 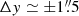 (±100 pc). However, the observations show a larger velocity spread (Δvtot ≃ 400 − 500 km s−1) of the emission at
(±100 pc). However, the observations show a larger velocity spread (Δvtot ≃ 400 − 500 km s−1) of the emission at 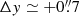 (+50 pc) and Δy ≃ −2″ (–150 pc). These regions, identified as (OUT-N) and (OUT-S) in Fig. 24, correspond to the suspected contact points of the working surface of the AGN wind with the molecular gas at the N and S crossings of the CND, respectively. Observations also show a significant yet comparatively less dramatic spread of the emission (Δvtot ≃ 200 km s−1) along the major axis up to Δx ≃ ±2″ (±150 pc). This observational feature, which is fairly well accounted for by the model, suggests that although the AGN feedback on the kinematics of molecular gas is admittedly more extreme at the regions that lie closer to the outflow axis, the kinematics of the CND seem to be globally affected.
(+50 pc) and Δy ≃ −2″ (–150 pc). These regions, identified as (OUT-N) and (OUT-S) in Fig. 24, correspond to the suspected contact points of the working surface of the AGN wind with the molecular gas at the N and S crossings of the CND, respectively. Observations also show a significant yet comparatively less dramatic spread of the emission (Δvtot ≃ 200 km s−1) along the major axis up to Δx ≃ ±2″ (±150 pc). This observational feature, which is fairly well accounted for by the model, suggests that although the AGN feedback on the kinematics of molecular gas is admittedly more extreme at the regions that lie closer to the outflow axis, the kinematics of the CND seem to be globally affected.
7.2. An outflowing torus?
The global 3DBarolo fit of the kinematics of the CO(2–1) emitting gas discussed in Sect. 7.1 favors a 3D-outflow solution that applies to a wide range of spatial scales from the ≃400 pc CND down to the ≃10 − 30 pc molecular torus. This scenario, which explains the distribution and kinematics of the gas in the torus and its connections, suggests that a significant fraction of the gas traced by the 2–1 line of CO inside the torus could be entrained by the AGN-driven wind.
The left panel of Fig. 25 compares the distribution of the HCO+(4–3) line emission with that of the CO(2–1) line in the molecular torus, as derived from the MSR data sets used in this work. This overlay underlines that the densest molecular gas probed by HCO+ is located in the inner region of the torus, as discussed in Sect. 5. Moreover, already at this spatial resolution the CO and the HCO+ images show a spatially resolved vertical structure of the torus. In particular, the HCO+ contours of the MSR image provide tantalizing evidence of a boxy structure, which is fully resolved in the image obtained from the HSR data set shown in the right panel of Fig. 25. This higher-resolution HCO+ image shows a network of gas protrusions that stem from the central r ≤ 2 pc region around the AGN. These gas protrusions extend over a wide range of angles measured from the kinematic major axis of the CO torus derived in Sect. 7.1. Taken at face value, these observations would lend support to a dynamical model where a substantial fraction of the dense gas inside the torus is being swept along the edges of an ionized wind bicone that emerges from the accretion disk, giving rise to a molecular and dusty wind or outflow. This outflow would adopt the geometry of a hollow cone, seen in projection as an X-shaped feature. The AGN wind could peel off the inner layers of the torus and push the gas outward. An X-shaped structure that extends on spatial scales similar to the ones reported above has recently been identified in the ALMA 256 GHz continuum image of the torus published by Impellizzeri et al. (2019).
 |
Fig. 25. Overlay of the HCO+(4–3) (blue) contours on the CO(2–1) grayscale image of the molecular torus of NGC 1068 derived from the MSR data set (left panel). We show a zoomed view of the inner |
In addition to the direct morphological evidence illustrated by Fig. 25, the kinematics of molecular gas inside the torus, discussed in Sect. 5.4, reveal the existence of strong noncircular motions: a sizable fraction of gas emission arises at velocities that are forbidden in the frame of a circular velocity model, that is, gas in apparent counter-rotation. These noncircular motions are to first order accounted for by the 3DBarolo fit of Sect. 7.1 in terms of a molecular outflow with a significant equatorial component, without directly invoking counter-rotating gas.
In an attempt to further constrain both the geometry and the mass of the molecular gas that may be entrained by the AGN wind through this type of mechanism, we built up a simple 3D morpho-kinematic model of the NGC 1068 torus. In this model the gas is assumed to be in a toroidal ringed disk geometry and to follow circular rotation. A fraction of the gas inside the torus, as determined by the intersection of the AGN wind bicone with the torus, is perturbed by the AGN wind creating a 3D radial outflow superposed to rotation. The latter is determined by the area of the circular section of the torus that intersects with the AGN wind bicone and is therefore a function of the half-opening angle of the wind (θ = FWHM/2) on the scale of the torus. The parameters assumed for the model are based on the geometry (size, orientation, and aspect ratio) and CO luminosities derived from the observations in Sects. 5.1 and 5.2, as well as on the kinematic parameters provided by the 3DBarolo fit of Sect. 7.1, that is, rotation (vrot) and outflow velocities (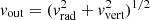 ). In particular, we assume a purposely fixed toroidal ringed disk geometry where the gas fills with constant density a volume generated by a disk of ≃4 − 5 pc in radius, which revolves about a vertical axis located at a radius of ≃5 − 6 pc. The full size of the modeled torus is therefore ≃20 − 22 pc. We adopt a PA = 113° and an i = −80°. The rotation curve for the gas is taken from the observed maser kinematics. We scale the data cube of the model (in Tmb-units) to the observed luminosity of the CO(2–1) line, convolve the gas distribution by a Gaussian beam that has a FWHM of 5 pc to mimic the effect of beam smearing, and regrid the output to the same pixel scale as the observations.
). In particular, we assume a purposely fixed toroidal ringed disk geometry where the gas fills with constant density a volume generated by a disk of ≃4 − 5 pc in radius, which revolves about a vertical axis located at a radius of ≃5 − 6 pc. The full size of the modeled torus is therefore ≃20 − 22 pc. We adopt a PA = 113° and an i = −80°. The rotation curve for the gas is taken from the observed maser kinematics. We scale the data cube of the model (in Tmb-units) to the observed luminosity of the CO(2–1) line, convolve the gas distribution by a Gaussian beam that has a FWHM of 5 pc to mimic the effect of beam smearing, and regrid the output to the same pixel scale as the observations.
Figure 26 illustrates the geometry and kinematics of the gas in the torus model projected along the line of sight for θ = 60° and vout = 150 km s−1. While we explore different values of the outflow radial velocities for the gas swept by the AGN wind from vout = 50 to 150 km s−1 based on the values of vrad and vvert found by 3DBarolo, the main free parameter of the model is the amount of mass actually entrained by the outflow, which is a function of θ. This angle is allowed to vary from θ = 0° (i.e., no outflow) to θ = 90° (i.e., the outflow affects the bulk of the gas in the torus). To choose among the range of values assumed for θ and vout, we minimize the standard goodness-of-fit parameter χ2 = ∑[D(i,j)−M(i,j)/σ]2 derived for the major and minor axes of the torus and subsequently normalized those by the number of pixels used in the fit. The sum extends over the common set of pixels of the model and the observations (M(i, j) and D(i, j), respectively) and σ stands for the observed rms derived from the 2–1 line data cube.
 |
Fig. 26. View of the kinematic model of the molecular torus described in Sect. 7 projected along the line of sight. The arrows represent the velocity field of the gas in the torus (with Keplerian rotation) and over the working surface of the AGN wind on the torus (with outflowing motions). The arrows are color-coded using red, yellow, and blue according to the absolute value and the sign of the radial velocities projected along the line-of-sight measured relative to vsys. The major axis of the modeled torus has the orientation of the observed torus (PA ≃ 113°). The adopted inclination (i ≃ −70°) is lower than the average value found by 3DBarolo (i ≃ −80°) for a better illustration of the different velocity components of the model. |
Figure 27 shows the p-v plots along the major and minor axes of the torus for the best solution found for θ ≃ 80° and vout ≃ 100 km s−1, hereafter referred to as the OUT-model. We also show in Fig. 27 the corresponding p − v plots generated by a reference model of the same toroidal disk, hereafter referred to as the CR-model, where we eliminate outflow motions but include counter-rotation of the gas at r > 1 pc. A counter-rotating torus scenario, which is the basis of the CR-model explored here, has been previously invoked by Imanishi et al. (2018) and Impellizzeri et al. (2019) to explain the complex kinematics of molecular gas in the torus. Not surprisingly, the goodness-of-fit parameters are admittedly large in either case (≥4) due to the number of inherent assumptions in both models, which include the axisymmetry and the smoothness of the gas distribution in the torus. However, the OUT-model qualifies as a more likely scenario compared to the CR-model, based not only on its χ211 that is lower by a factor ≃1.2 − 1.3, but mainly because it better explains the following key observational signatures:
 |
Fig. 27. Upper panels: overlay of CO(2–1) p − v plots (in contours) along the major and minor axis of the torus (upper left and upper right panels, respectively) on the corresponding synthetic p − v plots (in logarithmic color scale in K-units) generated by the best-fit model of the torus described in Sect. 7.2 (OUT-model). The CO(2–1) contour levels are as in Figs. 16 and 20. Lower panels: same as upper panels but for the CR-model described in Sect. 7.2. |
1. The gas emission detected in apparent counter-rotation in the major-axis p − v plot is to a large extent explained by the OUT-model as due to the projection of outflowing motions that are present at the torus AGN-wind working surface encapsulated in the beam, without having to resort to the addition of an unphysical true counter-rotating component.
2. The contribution of the outflow in the OUT-model also easily explains the presence of three distinct velocity components detected along the minor axis p − v plot. The central component around vsys would be explained by gas unaffected by the outflow close to the equatorial plane of the torus, while the ≃100 km s−1 redshifted (blueshifted) component would reflect the contribution from the outflowing gas below (above) the equatorial plane captured by the beam. This is not reproduced by the CR-model.
3. Overall, at this spatial resolution the superposition of circular and noncircular motions in the OUT-model significantly widens the spectra to the level required by observations, in contrast to the CR-model.
4. Figure 28 shows that an outflow model predicts that there should be a measurable yet shallow gradient of the mean-velocity centroid along the minor axis: from redshifted velocities S of the AGN to blueshifted velocities N of the AGN. This gradient is not detected in the CO(2–1) data, probably because at this spatial resolution the contribution from gas components located outside the torus in the gas streamers, which are not included in the model, wash out any potential trend inside the beam. However, the gradient is tentatively detected in the CO(6–5) minor axis p − v plot12, as illustrated in Fig. 28. By construction, the CR-model is unable to reproduce this gradient. The OUT-model easily explains why the velocity shift measured along the minor axis of the CO(6–5) torus, first reported by García-Burillo et al. (2016) and Gallimore et al. (2016), is reversed out at larger radii on the scales of the CND.
 |
Fig. 28. Comparison of the minor axis p − v plot predicted by the OUT-model of the torus described in Sect. 7.2 with the corresponding CO(6–5) minor axis p − v plot obtained from the combined data set of García-Burillo et al. (2016) and Gallimore et al. (2016). The square markers highlight in both panels the velocity centroid of the emission as a function of position along the minor axis. |
5. The marked asymmetry shown by the high-velocity emission in the CO(2–1) and CO(3–2) AGN spectra, which is not reproduced by HCO+(4–3), could be explained by an outflow model that includes radiative transfer effects in the torus. The different behavior displayed by CO and HCO+ may be due to a larger contribution of absorption of the pc-scale central continuum source by the comparatively lower-density gas traced by CO in the outflow. This asymmetry cannot be easily reproduced by a (counter)rotating disk without imposing a strong asymmetry in the gas distribution (see Sect. 5.4).
Numerical simulations have long predicted the existence of dusty winds coming out from AGN tori at highly variable geometries, which depend on the different treatment of radiation pressure driven by photons at different wavelengths (IR, X-ray, and UV), on the assumed degree of anisotropy of the AGN radiation, and on the details of the particular hydrodynamic code used in these simulations (e.g., Wada 2015; Wada et al. 2016; Chan & Krolik 2016, 2017; Namekata & Umemura 2016; Williamson et al. 2019). Furthermore, as recently argued by Giustini & Proga (2019), theoretical analyses predict that radiation-driven accretion disk winds in AGN can have a fairly large equatorial component in Seyfert galaxies that are characterized by Eddington ratios (Eddratio) and black hole masses (MBH) similar to those of NGC 1068 (Eddratio ≃ 0.5, log10(MBH/M⊙)≃7.2; Greenhill et al. 1996). The interaction of this class of AGN winds with the NGC 1068 torus could launch locally a molecular/dusty outflow with a significant equatorial component.
The value of θ ≃ 80° favored by the OUT-model described above implies that this class of wide-angle AGN wind is currently impacting a sizable fraction of the gas in the NGC 1068 torus. Based on the model, we estimate this fraction to be 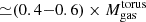 . The gas mass experiencing outflowing motions inside the torus is comparable to the molecular gas mass derived in Sect. 6.1 for the streamers, which connect the torus with the CND. Taken at face value, this coincidence highlights the continuity in the outflow mass radial profile out to r ≃ 30 pc, an indication that the two components are part of the same outflowing feature. However, the bulk of the mass, momentum, and energy of the molecular outflow of NGC 1068 is contained in the CND region, where the AGN wind and the radio jet are currently pushing ≃7 × 107 M⊙ of the gas that has been assembled at the ILR ring of the bar at r ≃ 50 − 200 pc.
. The gas mass experiencing outflowing motions inside the torus is comparable to the molecular gas mass derived in Sect. 6.1 for the streamers, which connect the torus with the CND. Taken at face value, this coincidence highlights the continuity in the outflow mass radial profile out to r ≃ 30 pc, an indication that the two components are part of the same outflowing feature. However, the bulk of the mass, momentum, and energy of the molecular outflow of NGC 1068 is contained in the CND region, where the AGN wind and the radio jet are currently pushing ≃7 × 107 M⊙ of the gas that has been assembled at the ILR ring of the bar at r ≃ 50 − 200 pc.
8. Summary and conclusions
We used ALMA to image the emission of molecular gas and dust in the CND and the torus of NGC 1068 using the CO(2–1), CO(3–2), and HCO+(4–3) lines and their underlying continuum emission with a set of spatial resolutions (0.03″ − 0.09″ ≃ 2 − 6 pc). The use of these transitions, which span a wide range of physical conditions of molecular gas (n(H2)⊂103 − 107 cm−3), is instrumental in revealing the density radial stratification and the complex kinematics of the gas in the torus and its connections to the host.
We detect continuum emission at 229.7 GHz and 344.5 GHz stemming from a highly clumpy ≃70 pc-size jet-like structure characterized by synchrotron-like emission. The spectral index of the continuum shows the prevalence of dust emission in the regions of the CND located far from the radio jet trajectory itself. In contrast, spectral indexes are flat or marginally positive at the location of the AGN core.
The ALMA images resolve the CND, which displays the shape of an asymmetric ringed disk with a de-projected diameter of ≃400 pc and mass of ≃1.4 × 108 M⊙. The CND shows a marked deficit of molecular gas in its central ≃130 pc region, which is to a large extent filled by the emission stemming from the AGN wind. This deficit leaves the imprint of a contrasted ring morphology on the CND. The inner edge of the ring is associated with the presence of edge-brightened arcs of NIR polarized emission, which are identified with the current working surface of the AGN wind.
The kinematics of the gas in the CND are shaped by an outflow that is captured by the fit of kinemetry. The gas is being pushed by the AGN wind inside the disk creating a radial expansion of the CND with average velocities ≃85 km s−1 from r ≃ 50 pc out to r ≃ 200 pc. Furthermore, the CO emission profiles show extreme line broadening and line splitting into two velocity components, which can be shifted by up to ≃250 km s−1 relative to each other, at a number of positions of the CND that are located in the path of the AGN wind trajectory. This result indicates that the molecular gas in the CND has been forced to leave the plane of the galaxy and has adopted a 3D outflow geometry. This scenario is confirmed by a global model of the outflow obtained with 3DBarolo.
The new data prove the existence of an elongated molecular disk or torus in NGC 1068 of 3 × 105 M⊙, which extends over a significantly large range of spatial scales D ≃ 10 − 30 pc around the central engine. These observations capture the density radial stratification of the torus: compared to the picture drawn from the HCO+(4–3) line, the molecular disk is bigger and more lopsided in the lower-J CO transitions, a result that brings into light the many faces of the molecular torus.
The H2 column densities measured towards the position of the AGN are up to N(H2) = 3–4 × 1023 mol cm−2. These values are a factor of between approximately two and three below the Compton-thick limit required to explain the nature of the Type 2 nucleus of NGC 1068. Furthermore, the change of column densities required to account for X-ray variability of the AGN could be explained by the small-scale structure of the molecular torus. This is an indication that the molecular torus detected by ALMA may contribute to the obscuration of the central engine of the galaxy on spatial scales of ≃2–3 pc. The torus is connected to the CND through a network of molecular gas streamers detected in the gas-deficient region. These connecting structures are associated with molecular gas that is being swept along the edges of the bicone structure of the AGN wind detected in ionized gas.
The kinematics of molecular gas show strong departures from circular motions in the torus, the gas streamers, and the CND ring. These velocity field distortions are interconnected and are part of a 3D outflow that reflects the effects of feedback of the AGN on the kinematics of molecular gas on a wide range of spatial scales around the central engine. In particular, we estimate through modeling that a significant fraction of the gas inside the torus (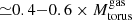 ) is outflowing.
) is outflowing.
NGC 1068 is not the only case of an outflowing torus reported in the literature. The presence of an equatorial outflow has also been proposed to account for the complex kinematics of molecular gas in the torus or disk of the Seyfert 2 galaxy NGC 5643 imaged by ALMA (Alonso-Herrero et al. 2018). These equatorial outflows detected close to the central engines of Seyfert galaxies would reflect the AGN feedback driven by the ionized wind on the molecular reservoir of the torus, playing the role of a self-regulation mechanism.
Although the total accretion timescales of SMBHs likely exceed 107 − 8 yr (e.g., Marconi et al. 2004), there is both observational and theoretical evidence that AGNs can have much shorter “flickering” timescales ranging from a few years up to ≃105 yr (Schawinski et al. 2015; King & Nixon 2015). Assuming that the AGN luminosity of NGC 1068 is 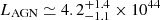 erg s−1 (García-Burillo et al. 2014), and for a canonical mass-to-luminosity accretion efficiency of ϵ ≃ 0.1, we can estimate an accretion rate for its SMBH of Ṁ = LAGN/(ϵ × c2) ≃ 0.05 − 0.1 M⊙ yr−1. Although the outflowing gas in the torus is a significant fraction of its total mass (
erg s−1 (García-Burillo et al. 2014), and for a canonical mass-to-luminosity accretion efficiency of ϵ ≃ 0.1, we can estimate an accretion rate for its SMBH of Ṁ = LAGN/(ϵ × c2) ≃ 0.05 − 0.1 M⊙ yr−1. Although the outflowing gas in the torus is a significant fraction of its total mass (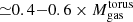 ), a large gas reservoir (≃1.2 − 1.8 × 105 M⊙) close to its equatorial plane remains mostly unaffected by the feedback of the AGN wind. The latter implies that the molecular torus can continue fueling the AGN for at least ≃1 − 4 Myr, which is a time span ≈10–40 times longer than the expected “flickering” timescale.
), a large gas reservoir (≃1.2 − 1.8 × 105 M⊙) close to its equatorial plane remains mostly unaffected by the feedback of the AGN wind. The latter implies that the molecular torus can continue fueling the AGN for at least ≃1 − 4 Myr, which is a time span ≈10–40 times longer than the expected “flickering” timescale.
We estimate that about half of the molecular gas in the CND is outflowing (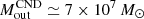 ; see also García-Burillo et al. 2014). This molecular outflow at r ≃ 50 − 200 pc is likely launched when the AGN wind and the radio jet impact the gas accumulated at the ILR ring. After accounting for this outflowing component, a large amount of molecular gas in the CND may still serve as a reservoir for future fueling episodes. However, AGN fueling seems to be currently thwarted on the intermediate scales corresponding to the torus-CND connections (15 pc ≤r ≤ 50 pc). We estimate that the outflow rate measured for the gas streamers at rstreamers ≃ 30 pc is Ṁstreamers ≃ Mstreamers × vout / rstreamers ≃ 0.6 M⊙ yr−1, which is still a factor ≥100 lower than the mass outflow rate measured at the CND scales.
; see also García-Burillo et al. 2014). This molecular outflow at r ≃ 50 − 200 pc is likely launched when the AGN wind and the radio jet impact the gas accumulated at the ILR ring. After accounting for this outflowing component, a large amount of molecular gas in the CND may still serve as a reservoir for future fueling episodes. However, AGN fueling seems to be currently thwarted on the intermediate scales corresponding to the torus-CND connections (15 pc ≤r ≤ 50 pc). We estimate that the outflow rate measured for the gas streamers at rstreamers ≃ 30 pc is Ṁstreamers ≃ Mstreamers × vout / rstreamers ≃ 0.6 M⊙ yr−1, which is still a factor ≥100 lower than the mass outflow rate measured at the CND scales.
Forthcoming ALMA observations of NGC 1068 will use a set of molecular tracers similar to those presented in this work but with a beam that is smaller by a factor of approximately six ( ), corresponding to an unprecedented spatial resolution of ≤1 pc. These new ALMA images of the torus will be used to better characterize the noncircular motions inside the torus. In particular, we aim to better resolve and disentangle the outflowing component from rotation and identify and model any inflowing component in the gas velocity field. Furthermore, the future ALMA images of the torus and its surroundings will be combined with planned interferometric observations with the MATISSE instrument at the VLT. The latter will probe the warm dust in the polar outflowing component and the hot dust in the inner walls of the torus with spatial resolutions down to
), corresponding to an unprecedented spatial resolution of ≤1 pc. These new ALMA images of the torus will be used to better characterize the noncircular motions inside the torus. In particular, we aim to better resolve and disentangle the outflowing component from rotation and identify and model any inflowing component in the gas velocity field. Furthermore, the future ALMA images of the torus and its surroundings will be combined with planned interferometric observations with the MATISSE instrument at the VLT. The latter will probe the warm dust in the polar outflowing component and the hot dust in the inner walls of the torus with spatial resolutions down to 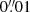 (0.07 pc) at 10 μm and
(0.07 pc) at 10 μm and 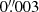 (0.02 pc) at 3.3 μm.
(0.02 pc) at 3.3 μm.
The southern arcs are brighter in NIR polarized emission due to the higher extinction of the optical emission coming from the southern lobe of the AGN wind, which is partly located below the plane of the galaxy (see Fig. 22).
Differences with respect to the magnitude of the distortions of the velocity field reported here can be attributed to the comparatively lower spatial resolution of the observations used by García-Burillo et al. (2014).
More realistic 3D scenarios are explored in Sect. 7.
For the inner 40-pc region where the kinemetry solution is judged doubtful we adopt the solution found by 3DBarolo instead, as discussed in Sect. 7.
We base our estimates on the same hypotheses used in Sect. 5.2.
The pattern of noncircular motions displayed in Fig. 21 is virtually the same as the one displayed in the minor-axis p − v plot where the projection of the tangential component of streaming motions is zero by construction; this confirms our working hypothesis.
Obtained from the combined data set of García-Burillo et al. (2016) and Gallimore et al. (2016).
Acknowledgments
We thank our referee, Prof. Masatoshi Imanishi, for his detailed referee report. We acknowledge the staff of ALMA in Chile and Edwige Chapillon from the ARC at IRAM-Grenoble in France for their invaluable help during the data reduction process. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2016.1.0232.S and #2011.0.00083.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. We used observations made with the NASA/ESA Hubble Space Telescope, and obtained from the Hubble Legacy Archive, which is a collaboration between the Space Telescope Science Institute (STScI/NASA), the Space Telescope European Coordinating Facility (ST-ECF/ESA), and the Canadian Astronomy Data center (CADC/NRC/CSA). SGB and AU acknowledge support from the Spanish MINECO and FEDER funding grants AYA2016-76682-C3-2-P, AYA2016-79006-P and ESP2015-68964-P. CRA acknowledges the Ramón y Cajal Program of the Spanish Ministry of Economy and Competitiveness through project RYC-2014-15779 and the Spanish Plan Nacional de Astronomía y Astrofísica under grant AYA2016-76682-C3-2-P. AAH acknowledges support from the Spanish MINECO and FEDER funding grant AYA2015-6346-C2-1-P. AAH, SGB. and AU acknowledge support through grant PGC2018-094671-B-I00 (MCIU/AEI/FEDER,UE). AAH’s work was done under project No. MDM-2017-0737 Unidad de Excelencia “María de Maeztu”- Centro de Astrobiología (INTA-CSIC). AF acknowledges support from the Spanish MINECO funding grant AYA2016-75066-C2-2.
References
- Alatalo, K., Blitz, L., Young, L. M., et al. 2011, ApJ, 735, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Aalto, S., Garcia-Burillo, S., Muller, S., et al. 2012, A&A, 537, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alatalo, K., Nyland, K., Graves, G., et al. 2014, ApJ, 780, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Aalto, S., Costagliola, F., Muller, S., et al. 2016, A&A, 590, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso-Herrero, A., Ramos Almeida, C., Mason, R., et al. 2011, ApJ, 736, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., Pereira-Santaella, M., García-Burillo, S., et al. 2018, ApJ, 859, 144 [Google Scholar]
- Alonso-Herrero, A., García-Burillo, S., Pereira-Santaella, M., et al. 2019, A&A, 628, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antonucci, R. R. J., & Miller, J. S. 1985, ApJ, 297, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Arribas, S., Mediavilla, E., & Garcia-Lorenzo, B. 1996, ApJ, 463, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Ashmore, I., van Loo, S., Caselli, P., Falle, S. A. E. G., & Hartquist, T. W. 2010, A&A, 511, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Audibert, A., Combes, F., García-Burillo, S., et al. 2019, A&A, in press, https://doi.org/10.1051/0004-6361/201935845 [Google Scholar]
- Barbosa, F. K. B., Storchi-Bergmann, T., McGregor, P., Vale, T. B., & Rogemar Riffel, A. 2014, MNRAS, 445, 2353 [NASA ADS] [CrossRef] [Google Scholar]
- Barcos-Muñoz, L., Aalto, S., Thompson, T. A., et al. 2018, ApJ, 853, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Bicknell, G. V., Dopita, M. A., Tsvetanov, Z. I., & Sutherland, R. S. 1998, ApJ, 495, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Bland-Hawthorn, J., Gallimore, J. F., Tacconi, L. J., et al. 1997, Ap&SS, 248, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Bock, J. J., Neugebauer, G., Matthews, K., et al. 2000, AJ, 120, 2904 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
- Bottorff, M., Korista, K. T., Shlosman, I., & Blandford, R. D. 1997, ApJ, 479, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Burtscher, L., Meisenheimer, K., Tristram, K. R. W., et al. 2013, A&A, 558, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cecil, G., Dopita, M. A., Groves, B., et al. 2002, ApJ, 568, 627 [Google Scholar]
- Chan, C.-H., & Krolik, J. H. 2016, ApJ, 825, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, C.-H., & Krolik, J. H. 2017, ApJ, 843, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Cicone, C., Maiolino, R., Sturm, E., et al. 2014, A&A, 562, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Combes, F., García-Burillo, S., Casasola, V., et al. 2013, A&A, 558, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Combes, F., García-Burillo, S., Casasola, V., et al. 2014, A&A, 565, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Combes, F., García-Burillo, S., Audibert, A., et al. 2019, A&A, 623, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crenshaw, D. M., & Kraemer, S. B. 2000, ApJ, 532, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Das, V., Crenshaw, D. M., Kraemer, S. B., & Deo, R. P. 2006, AJ, 132, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Di Teodoro, E. M., & Fraternali, F. 2015, MNRAS, 451, 3021 [NASA ADS] [CrossRef] [Google Scholar]
- Dönmez, O. 2014, MNRAS, 438, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Donmez, O. 2017, Mod. Phys. Lett. A, 32, 1750108 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M. 2008, New Astron. Rev., 52, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M. 2012, ApJ, 747, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M., & Shlosman, I. 2006, ApJ, 648, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Emmering, R. T., Blandford, R. D., & Shlosman, I. 1992, ApJ, 385, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Fathi, K., Wozniak, H., et al. 2006, MNRAS, 365, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., & Ford, H. 2005, Space Sci. Rev., 116, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Feruglio, C., Maiolino, R., Piconcelli, E., et al. 2010, A&A, 518, L155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galliano, E., Pantin, E., Alloin, D., & Lagage, P. O. 2005, MNRAS, 363, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Gallimore, J. F., Baum, S. A., O’Dea, C. P., & Pedlar, A. 1996, ApJ, 458, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Gallimore, J. F., Henkel, C., Baum, S. A., et al. 2001, ApJ, 556, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Gallimore, J. F., Baum, S. A., & O’Dea, C. P. 2004, ApJ, 613, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Gallimore, J. F., Elitzur, M., Maiolino, R., et al. 2016, ApJ, 829, L7 [NASA ADS] [CrossRef] [Google Scholar]
- García-Bernete, I., Ramos Almeida, C., Alonso-Herrero, A., et al. 2019, MNRAS, 486, 4917 [NASA ADS] [CrossRef] [Google Scholar]
- García-Burillo, S., & Combes, F. 2012, J. Phys. Conf. Ser., 372, 012050 [CrossRef] [Google Scholar]
- García-Burillo, S., Combes, F., Schinnerer, E., Boone, F., & Hunt, L. K. 2005, A&A, 441, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Combes, F., Usero, A., et al. 2014, A&A, 567, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Combes, F., Usero, A., et al. 2015, A&A, 580, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Combes, F., Ramos Almeida, C., et al. 2016, ApJ, 823, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Kormendy, J., Ho, L. C., et al. 2000, ApJ, 543, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Giustini, M., & Proga, D. 2019, A&A, 630, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Granato, G. L., & Danese, L. 1994, MNRAS, 268, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Gratadour, D., Rouan, D., Mugnier, L. M., et al. 2006, A&A, 446, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratadour, D., Rouan, D., Grosset, L., Boccaletti, A., & Clénet, Y. 2015, A&A, 581, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greenhill, L. J., & Gwinn, C. R. 1997, Ap&SS, 248, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Greenhill, L. J., Gwinn, C. R., Antonucci, R., & Barvainis, R. 1996, ApJ, 472, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Grosset, L., Rouan, D., Gratadour, D., et al. 2018, A&A, 612, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gültekin, K., Richstone, D. O., Gebhardt, K., et al. 2009, ApJ, 698, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Hönig, S. F. 2019, ApJ, 884, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Hönig, S. F., & Kishimoto, M. 2017, ApJ, 838, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Hönig, S. F., Kishimoto, M., Tristram, K. R. W., et al. 2013, ApJ, 771, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Ichikawa, K., Packham, C., Ramos Almeida, C., et al. 2015, ApJ, 803, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Imanishi, M., Nakanishi, K., & Izumi, T. 2016, ApJ, 822, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Imanishi, M., Nakanishi, K., Izumi, T., & Wada, K. 2018, ApJ, 853, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Impellizzeri, C. M. V., Gallimore, J. F., Baum, S. A., et al. 2019, ApJ, 884, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Izumi, T., Wada, K., Fukushige, R., Hamamura, S., & Kohno, K. 2018, ApJ, 867, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Jaffe, W., Meisenheimer, K., Röttgering, H. J. A., et al. 2004, Nature, 429, 47 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kamali, F., Henkel, C., Koyama, S., et al. 2019, A&A, 624, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kartje, J. F., Königl, A., & Elitzur, M. 1999, ApJ, 513, 180 [NASA ADS] [CrossRef] [Google Scholar]
- King, A., & Nixon, C. 2015, MNRAS, 453, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Kiuchi, K., Shibata, M., Montero, P. J., & Font, J. A. 2011, Phys. Rev. Lett., 106, 251102 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Richstone, D. 1995, ARA&A, 33, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Korobkin, O., Abdikamalov, E., Stergioulas, N., et al. 2013, MNRAS, 431, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Krajnović, D., Cappellari, M., de Zeeuw, P. T., & Copin, Y. 2006, MNRAS, 366, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Krips, M., Martín, S., Eckart, A., et al. 2011, ApJ, 736, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Krolik, J. H., & Begelman, M. C. 1988, ApJ, 329, 702 [NASA ADS] [CrossRef] [Google Scholar]
- López-Gonzaga, N., Jaffe, W., Burtscher, L., Tristram, K. R. W., & Meisenheimer, K. 2014, A&A, 565, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Gonzaga, N., Burtscher, L., Tristram, K. R. W., Meisenheimer, K., & Schartmann, M. 2016, A&A, 591, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lopez-Rodriguez, E., Packham, C., Roche, P. F., et al. 2016, MNRAS, 458, 3851 [NASA ADS] [CrossRef] [Google Scholar]
- Macchetto, F., Capetti, A., Sparks, W. B., Axon, D. J., & Boksenberg, A. 1994, ApJ, 435, L15 [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Marco, O., & Alloin, D. 2000, A&A, 353, 465 [NASA ADS] [Google Scholar]
- Marconi, A., & Hunt, L. K. 2003, ApJ, 589, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Marinucci, A., Bianchi, S., Matt, G., et al. 2016, MNRAS, 456, L94 [NASA ADS] [CrossRef] [Google Scholar]
- May, D., & Steiner, J. E. 2017, MNRAS, 469, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D., & Ferrarese, L. 2001, ApJ, 547, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. S., & Antonucci, R. R. J. 1983, ApJ, 271, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Morganti, R., Frieswijk, W., Oonk, R. J. B., Oosterloo, T., & Tadhunter, C. 2013, A&A, 552, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morganti, R., Oosterloo, T., Oonk, J. B. R., Frieswijk, W., & Tadhunter, C. 2015, A&A, 580, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller Sánchez, F., Davies, R. I., Genzel, R., et al. 2009, ApJ, 691, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Müller-Sánchez, F., Prieto, M. A., Hicks, E. K. S., et al. 2011, ApJ, 739, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Murakawa, K. 2010, A&A, 518, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Namekata, D., & Umemura, M. 2016, MNRAS, 460, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H. 2015, ARA&A, 53, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., & Pringle, J. E. 1984, MNRAS, 208, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Pasetto, A., González-Martín, O., Esparza-Arredondo, D., et al. 2019, ApJ, 872, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Pier, E. A., & Krolik, J. H. 1992, ApJ, 401, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Pier, E. A., & Krolik, J. H. 1993, ApJ, 418, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Querejeta, M., Schinnerer, E., García-Burillo, S., et al. 2016, A&A, 593, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raban, D., Jaffe, W., Röttgering, H., Meisenheimer, K., & Tristram, K. R. W. 2009, MNRAS, 394, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., Levenson, N. A., Alonso-Herrero, A., et al. 2011, ApJ, 731, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., & Ricci, C. 2017, Nat. Astron., 1, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Rouan, D., Lacombe, F., Gendron, E., et al. 2004, A&A, 417, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rouan, D., Grosset, L., & Gratadour, D. 2019, A&A, 625, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schawinski, K., Koss, M., Berney, S., & Sartori, L. F. 2015, MNRAS, 451, 2517 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E., Eckart, A., Tacconi, L. J., Genzel, R., & Downes, D. 2000, ApJ, 533, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Schoenmakers, R. H. M. 1999, PhD Thesis, University of Groningen [Google Scholar]
- Schoenmakers, R. H. M., Franx, M., & de Zeeuw, P. T. 1997, MNRAS, 292, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N. Z., Matthews, K., Carico, D. P., & Sanders, D. B. 1988, ApJ, 327, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Storchi-Bergmann, T., & Schnorr-Müller, A. 2019, Nat. Astron., 3, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Sturm, E., González-Alfonso, E., Veilleux, S., et al. 2011, ApJ, 733, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Tecza, M., Thatte, N., & Maiolino, R. 2001, in Galaxies and their Constituents at the Highest Angular Resolutions, ed. R. T. Schilizzi, IAU Symp., 205, 216 [NASA ADS] [Google Scholar]
- Tomono, D., Doi, Y., Usuda, T., & Nishimura, T. 2001, ApJ, 557, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Tristram, K. R. W., Raban, D., Meisenheimer, K., et al. 2009, A&A, 502, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Viti, S., García-Burillo, S., Fuente, A., et al. 2014, A&A, 570, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wada, K. 2012, ApJ, 758, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K. 2015, ApJ, 812, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Schartmann, M., & Meijerink, R. 2016, ApJ, 828, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Fukushige, R., Izumi, T., & Tomisaka, K. 2018, ApJ, 852, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Weigelt, G., Wittkowski, M., Balega, Y. Y., et al. 2004, A&A, 425, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williamson, D., Hönig, S., & Venanzi, M. 2019, ApJ, 876, 137 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: A 3DBarolo model of the NGC 1068 outflow
The velocity field of molecular gas reveals strong noncircular motions and a high degree of complexity on a wide range of spatial scales in the CND of NGC 1068. In the following we attempt to define the main features of a global model that best accounts for the main features of the gas kinematics derived from the CO(2–1) data using the 3DBarolo software.
We first benchmarked the solutions found by 3DBarolo against the output provided by kinemetry in Sect. 4.5. For this purpose we ran 3DBarolo assuming the common set of fixed parameters used in Sect. 4.5 for the AGN position, the disk geometry (PA, i), and the systemic velocity (vsys), but allowing vrot, vrad, and the velocity dispersion (σgas) to vary for a set of 103 radii sampling the CND from 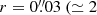 pc) to r = 3″ (≃210 pc). We also adopted a fixed Gaussian scale-height for the disk (H = 10 pc) to reproduce the 2D model of the kinemetry disk, which is by construction collapsed along its vertical axis.
pc) to r = 3″ (≃210 pc). We also adopted a fixed Gaussian scale-height for the disk (H = 10 pc) to reproduce the 2D model of the kinemetry disk, which is by construction collapsed along its vertical axis.
As shown in Fig. A.1, the vrad and vrot profiles found by 3DBarolo and kinemetry are roughly compatible within the errors. In particular, taking into account the known orientation of the large-scale disk of NGC 1068, i.e., the NE (SW) side of the disk corresponds the far (near) side, the positive sign and modulus of the vrad profile (vrad ≃ (0.4 − 0.8)×vrot for 30 pc < r < 210 pc) similarly found by 3DBarolo and kinemetry identify the presence of a coplanar outward radial component.
 |
Fig. A.1. Radial profiles of vrad (upper panel) and vrot (lower panel) found by 3DBarolo (blue histograms) and kinemetry (black line and markers) to fit the CO(2–1) data of the CND region out to r ≃ 210 pc. |
Based on the available observational constraints, for the second 3DBarolo run we imposed two restrictions on the starting range of the initial values for the two geometrical parameters: (1) PA = PAkinemetry ± 20° = 289 ± 20° and (2) i = ikinemetry ± 20° = 41 ± 20° at all radii. We relax this restriction in the torus region and its connections (r < 30 pc), where we gradually change from the known orientation of the highly inclined torus, by adopting −60° > i > −90° in the range r < 20 pc, towards the orientation of the disk of the galaxy at larger radii. We note that the negative sign of i in the inner region reflects here that the N(S) side of the tilted torus is the near (far) side, as dictated by the favored geometry of the NLR of the galaxy shown in Fig. 22.
In order to minimize the occurrence of discontinuities in the derived vrot and vrad profiles, which may appear when the geometrical parameters of the disk are simultaneously fit with the kinematic profiles, we adopted the parameter regularization approach described by Di Teodoro & Fraternali (2015). This requires execution of the second fitting routine using a two-step process. We first derived a model by fitting all the free parameters simultaneously (step-1), while in a second iteration we fixed the geometrical parameters to a Bezier function that interpolates the values found in the previous iteration for PA and i with the rest of parameters being let free (step-2). The resulting radial profiles of the best-fit parameters found after this second run are shown in Fig. A.2.
 |
Fig. A.2. Radial profiles of the best fit found by 3DBarolo for vrot, vrad, vdisp (σgas), PA (ϕ), and i. The position of the AGN (xo and yo in pixel units) and the systemic velocity (vsys) are fixed to the values previously found by kinemetry. The size of the vertical bars in the radial profile of integrated intensities (Σ) reflect the deviations from axisymmetry in the gas distribution. The gray and red markers represent the output values of the fitted parameters obtained after the first (step-1) and second (step-2) runs, respectively. |
We note that vrot and vrad are seen to change sign at r ≃ 20 pc: both parameters change from negative values inside this boundary to positive values at larger radii. This change of sign accounts for the change of orientation of the plane of the galaxy relative to the observer, described above. Furthermore, as the vvert parameter is not iteratively fitted by the version of 3DBarolo used in the fit, we chose to explore four different values of vvert (0, 25, 50, 100, and 150 km s−1) and constrained the range of the best-fit solutions to vvert ≃ 100 ± 50 km s−1. In this paper we show the output of the best-fit solution for vvert ≃ 100 km s−1. The H profile (not shown) shows values going from 7 to 10 pc in the torus region (r < 20 pc), to higher values ≃20 − 50 pc in the outer disk up to r ≃ 210 pc. The main characteristics of the best-fit solution encapsulated in the radial profiles shown in Fig. A.2 are described in Sect. 7.
All Tables
All Figures
 |
Fig. 1. Left panel: continuum emission map of the central r ≤ 1″ (70 pc) region of NGC 1068 obtained with ALMA at 229.7 GHz (1306 μm). The map is shown in grayscale with contour levels -2σ (dashed contour), 2σ, 5σ, 10σ, 20σ, 50σ, 100σ, and 200σ, where 1σ = 30 μJy beam−1. Middle panel: same as left panel but showing the continuum emission at 344.5 GHz (871 μm). Contour spacing is as in left panel, but with 1σ = 50 μJy beam−1. Right panel: same as left panel but showing the continuum emission at 694 GHz (432 μm) published by García-Burillo et al. (2016). Contour levels are −2σ (dashed contour), 2σ, 5σ, 7σ, 9σ, 12σ, and 16σ, where 1σ = 0.5 mJy beam−1. The (red) filled ellipses at the bottom left corners of the panels represent the beam sizes of ALMA at 229.7 GHz ( |
| In the text | |
 |
Fig. 2. Spectral index maps (α, with Sν ∝ να) derived from the continuum emissions at ν = 344.5 GHz and 694 GHz (α1: left panel), and from ν = 229.7 GHz and 344.5 GHz (α2: middle panel). Contours span the range α = [ − 3, 3] in steps of 1. The common aperture adopted to derive the spectral index map is |
| In the text | |
 |
Fig. 3. Left panel: CO(2–1) integrated intensity map obtained with ALMA in the CND of NGC 1068 using the MSR data set as defined in Table 1. The map is shown in color scale spanning the range [3σ, 300σ] in logarithmic scale with contour levels −5σ (dashed contour), 5σ, 10σ, 20σ, 40σ, 60σ, 100σ–250σ in steps of 50σ where 1σ = 13 mJy km s−1 beam−1. Right panel: same as left panel but showing the CO(3–2) integrated intensity map. The color scale spans the range [3σ, 430σ] in logarithmic scale with contour levels −5σ (dashed contour), 5σ, 10σ, 20σ, 40σ, 60σ, 100σ–400σ in steps of 50σ where 1σ = 27 mJy km s−1 beam−1. The AGN locus lies at the intersection of the dashed lines in both panels. The (red) filled ellipses in the bottom left corners of both panels represent the beam sizes in CO(2–1) ( |
| In the text | |
 |
Fig. 4. Left panel: we overlay the CO(2–1) contour map (levels as in Fig. 3) on the image of linear polarization of dust emission obtained in the H band by Gratadour et al. (2015) (color logarithmic scale from 1.5% to 13%). Right panel: same as left panel but showing the comparison between the CO(3–2) map and the polarization degree. The magenta lines identify the region occupied by the AGN wind bicone modeled by Das et al. (2006): PAoutflow = 30°, FWHMouter = 80° (see also Barbosa et al. 2014). |
| In the text | |
 |
Fig. 5. HCO+(4–3) integrated intensity map obtained with ALMA in the CND of NGC 1068 using the MSR data set as defined in Table 1. The map is shown in color scale spanning the range [3σ, 40σ] with contour levels −5σ (dashed contour), 5σ, 7σ, 12σ, 20σ, and 30σ where 1σ = 33 mJy km s−1 beam−1. Symbols and markers as in Fig. 3. The (red) filled ellipse at the bottom left corner represents the beam size in HCO+(4–3) ( |
| In the text | |
 |
Fig. 6. Mean-velocity fields derived for the CO(2–1) (left panel) and CO(3–2) (right panel) lines in the CND of NGC 1068, as obtained from the MSR data set. Isovelocity contours and color scale span the range [−200 + vsys, 200 + vsys] km s−1, where |
| In the text | |
 |
Fig. 7. Left panel: radial profile of the c1/sin(i) ratio, which represents the best fit obtained by kinemetry for the deprojected axisymmetric circular component of the velocity field (vcirc; black curve and filled symbols). We also plot the radial profile of the deprojected noncircular motions (vnonc/sin(i)) derived from the Fourier decomposition until third order (red curve and open symbols). Middle panel: variation of the absolute value of vnonc/vcirc ratio as function of radius (black curve and open symbols). Right panel: variation of the s1/c1 ratio as function of radius. The s1 coefficient represents the best fit of the (projected) axisymmetric radial component of the velocity field (black curve and open symbols). The hatched gray-filled rectangles in panels (b) and (c) identify the region where the solution found by kinemetry is judged less reliable. |
| In the text | |
 |
Fig. 8. Residual mean-velocity field of the CND obtained after subtraction of the best-fit rotation component from the CO(2–1) MSR data, as described in Sect. 4.5. The color scale spans the range [−200, 200] km s−1 relative to |
| In the text | |
 |
Fig. 9. Velocity-width maps in units of FWHM derived for the CO(2–1) (left panel) and CO(3–2) (right panel) lines in the CND of NGC 1068, as obtained from the MSR data set. Contours and color scale span the range [20, 200] km s−1 in steps of 30 km s−1. Symbols and markers as in Figs. 3 and 4. |
| In the text | |
 |
Fig. 10. Spectra extracted at [Δα, Δδ] = [ |
| In the text | |
 |
Fig. 11. Left panel: CO(2–1) map of the central |
| In the text | |
 |
Fig. 12. Same as Fig. 11 but showing the maps obtained using the HSR data set, as defined in Table 1. The CO(2–1) contours are: −3σ (dashed), 3σ, 5σ, 7σ, 9σ, and 11σ, where 1σ = 22 mJy km s−1 beam−1. The CO(3–2) contours are −3σ (dashed), 3σ, 5σ, 7σ, 9σ, 12σ, 15σ, and 18σ, where 1σ = 35 mJy km s−1 beam−1. The HCO+(4–3) are −3σ (dashed), 3σ, 5σ, 7σ, 9σ, 12σ and 15σ, where 1σ = 34 mJy km s−1 beam−1. |
| In the text | |
 |
Fig. 13. Left panel: we overlay the CO(2–1) contours of Fig. 11 on the difference between the polarization angle map and a purely centro-symmetric pattern derived from the H-band map of Gratadour et al. (2015) (in color scale in units of degrees) in the central |
| In the text | |
 |
Fig. 14. Mean-velocity fields derived from the CO(2–1) (left panel), CO(3–2) (middle panel) and HCO+(4–3) (right panel) lines in the central |
| In the text | |
 |
Fig. 15. Emission spectra extracted at the position of the AGN from the MSR data set for the J = 2 − 1 line of CO (left panel), the J = 3 − 2 line of CO (middle panel), and the J = 4 − 3 line of HCO+ (right panel) using a common aperture of ≃6–7 pc-size (yellow-filled histograms). We also show in blue-hatched histograms the corresponding spectra obtained from the HSR data set using a common aperture of ≃2–3 pc. The red line highlights the value of |
| In the text | |
 |
Fig. 16. Position–velocity (p − v) diagrams obtained with the MSR data set along the major axis of the torus of NGC 1068 along PA = 113° in the J = 2 − 1 line of CO (left panel), the J = 3 − 2 line of CO (middle panel), and the J = 4 − 3 line of HCO+ (right panel). Gray-scale and contours are −2.5σ, 2.5σ, 4σ, 6σ to 18σ in steps of 3σ, with 1σ = 0.11 mJy beam−1 (left panel), −2.5σ, 2.5σ, 5σ, 8σ,12σ, 20σ, 35σ and 50σ, with 1σ = 0.23 mJy beam−1 (middle panel), and −2.5σ, 2.5σ, 4σ, 6σ, 9σ, 12σ, 15σ, and 19σ, with 1σ = 0.28 mJy beam−1 (right panel). Offsets along the x axis (Δx) are measured in arc seconds relative to the AGN locus (vertical dashed lines) with positive (negative) values corresponding to the SE (NW) side of the disk. Velocities are measured in LSR scale with |
| In the text | |
 |
Fig. 17. Same as Fig. 16 but obtained with the HSR data set. Contours are −2.5σ, 2.5σ, 4σ, 6σ, and 9σ, with 1σ = 0.14 mJy beam−1 (left panel), −2.5σ, 2.5σ, 4σ, 6σ, 9σ, 12σ, and 16σ, with 1σ = 0.23 mJy beam−1 (middle panel), and −2.5σ, 2.5σ, 4σ, 6σ, 9σ, and 12σ, with 1σ = 0.28 mJy beam−1 (right panel). |
| In the text | |
 |
Fig. 18. CO(2–1) channel maps obtained in the central |
| In the text | |
 |
Fig. 19. Left panel: central |
| In the text | |
 |
Fig. 20. Left panel: CO position–velocity diagrams taken along the gas streamers that connect the torus with the CND at PA = –10°. The CO(2–1) line emission is shown in gray linear scale spanning the range [2σ, 18σ] with 1σ = 0.11 mJy beam−1. The CO(3–2) position–velocity diagram is shown in (blue) contours: −2σ (dashed), 2σ, 4σ, 6σ, 10σ to 40σ in steps of 10σ, with 1σ = 0.23 mJy beam−1. The (red) line and square markers show the mean velocities that can be attributed to circular rotation along PA = –10° (according to the fit of Sect. 7). The spatially integrated CO 2–1 and 3–2 line profiles averaged over the SE and NW segments of the connecting gas streamers (as defined in left panel) are shown, respectively, in the middle panel and in the right panel. |
| In the text | |
 |
Fig. 21. Comparison of the average position–velocity (p − v) plot obtained for the outflow region out to r = 3″ (≃210 pc) in CO(2-1): contours are −2.5σ [dashed], 2.5σ, 4σ, 6σ, 9σ, 12σ, 17σ, 25σ, 35σ, 50σ, 70σ to 160σ in steps of 30σ, with 1σ = 0.04 mJy beam−1 and CO(3–2). The color logarithmic scale is [2.5σ, 230σ] with 1σ = 0.08 mJy beam−1. The emission has been averaged using data cubes where the rotation curve model of Sect. 4.5 has been subtracted over a range of PA: [PAoutflow − 20°, PAoutflow + 20°], where PAoutflow = 30°. Offsets along the x-axis are measured in arc seconds relative to the AGN locus. |
| In the text | |
 |
Fig. 22. Revised scheme presenting a cross-cut view of the NLR of NGC 1068 along the projected direction of the ionized outflow axis (PA ∼ 30°; shown by the green line). The new ALMA data show that CO line emission is split into blueshifted and redshifted components (relative to vsys) along the outflow axis, from the torus out to the edge of the CND, here represented by Knot N and Knot S. We highlight the extent of the AGN-ionized wind (gray shade) and the assumed geometry defined by the inclination of the galaxy disk, i = 41°, the inclination of the outflow axis, ioutflow ≥ 80°, and the full opening angle of the outflow, FWHMouter ≃ 80°. |
| In the text | |
 |
Fig. 23. Same as Fig. 21 but showing the comparison between CO(2–1) (contours) and [SiVI] (color scale spanning the range [3σ, 1700σ]). For visualization purposes the v-scale has been highly compressed relative to that of Fig. 21 (identified by the magenta dashed lines). [SiVI] is a high-ionization line (≃205 eV) that traces the emission of high-velocity ionized gas in the outflow up to v − vsys ≃ ±800 km s−1 inside the CND region. |
| In the text | |
 |
Fig. 24. Overlay of CO(2–1) p − v plots (contours in Jy beam−1-units) along the average major axis (upper panel: PA = 291° = 180° +111°; where we adopt the orientation of the receding side of the major axis) and average minor axis (lower panel: PA = 21°) on the corresponding synthetic p − v plots (in logarithmic color scale) generated by 3DBarolo for the best-fit model described in Sect. 7. In our convention Δx-offsets are > 0 to the SE and Δy-offsets are > 0 to the NE. Contour levels in the upper panel are 1.3%, 3%, 5%, and then 10%–90% in steps of 10% of the peak value = 23.1 mJy beam−1. Contour levels in the lower panel are 2.7%, 5%, and then 10%–90% in steps of 10% of the peak value = 9.1 mJy beam−1. The regions identified as OUT-N and OUT-S in the lower panel correspond to the crossings of the AGN-wind working surface with the molecular gas at the N and S extremes of the CND. |
| In the text | |
 |
Fig. 25. Overlay of the HCO+(4–3) (blue) contours on the CO(2–1) grayscale image of the molecular torus of NGC 1068 derived from the MSR data set (left panel). We show a zoomed view of the inner |
| In the text | |
 |
Fig. 26. View of the kinematic model of the molecular torus described in Sect. 7 projected along the line of sight. The arrows represent the velocity field of the gas in the torus (with Keplerian rotation) and over the working surface of the AGN wind on the torus (with outflowing motions). The arrows are color-coded using red, yellow, and blue according to the absolute value and the sign of the radial velocities projected along the line-of-sight measured relative to vsys. The major axis of the modeled torus has the orientation of the observed torus (PA ≃ 113°). The adopted inclination (i ≃ −70°) is lower than the average value found by 3DBarolo (i ≃ −80°) for a better illustration of the different velocity components of the model. |
| In the text | |
 |
Fig. 27. Upper panels: overlay of CO(2–1) p − v plots (in contours) along the major and minor axis of the torus (upper left and upper right panels, respectively) on the corresponding synthetic p − v plots (in logarithmic color scale in K-units) generated by the best-fit model of the torus described in Sect. 7.2 (OUT-model). The CO(2–1) contour levels are as in Figs. 16 and 20. Lower panels: same as upper panels but for the CR-model described in Sect. 7.2. |
| In the text | |
 |
Fig. 28. Comparison of the minor axis p − v plot predicted by the OUT-model of the torus described in Sect. 7.2 with the corresponding CO(6–5) minor axis p − v plot obtained from the combined data set of García-Burillo et al. (2016) and Gallimore et al. (2016). The square markers highlight in both panels the velocity centroid of the emission as a function of position along the minor axis. |
| In the text | |
 |
Fig. A.1. Radial profiles of vrad (upper panel) and vrot (lower panel) found by 3DBarolo (blue histograms) and kinemetry (black line and markers) to fit the CO(2–1) data of the CND region out to r ≃ 210 pc. |
| In the text | |
 |
Fig. A.2. Radial profiles of the best fit found by 3DBarolo for vrot, vrad, vdisp (σgas), PA (ϕ), and i. The position of the AGN (xo and yo in pixel units) and the systemic velocity (vsys) are fixed to the values previously found by kinemetry. The size of the vertical bars in the radial profile of integrated intensities (Σ) reflect the deviations from axisymmetry in the gas distribution. The gray and red markers represent the output values of the fitted parameters obtained after the first (step-1) and second (step-2) runs, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



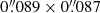
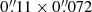
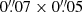
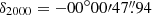
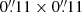
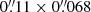
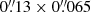
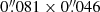
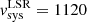
![$$ \begin{aligned} v_{\rm mean} (r, \psi )= c_0 + \sum _{j=1}^n [c_j(r) \cos (j\psi ) + s_j(r) \sin (j\psi )] . \end{aligned} $$](/articles/aa/full_html/2019/12/aa36606-19/aa36606-19-eq28.gif)