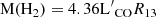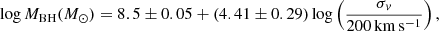| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201834560 | |
| Published online | 07 March 2019 | |
ALMA observations of molecular tori around massive black holes⋆
1
Observatoire de Paris, LERMA, CNRS, PSL Univ., Sorbonne University, UPMC, Paris, France
e-mail: francoise.combes@obspm.fr
2
College de France, 11 Pl. Marcelin Berthelot, 75231 Paris, France
3
Observatorio Astronómico Nacional (OAN)-Observatorio de Madrid, Alfonso XII, 3, 28014 Madrid, Spain
4
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi, 5, 50125 Firenze, Italy
5
I. Physikalisches Institut, Universität zu Köln, Zülpicher Str. 77, 50937 Köln, Germany
6
Dep. of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory, 43992 Onsala, Sweden
7
INAF – Istituto di Radioastronomia, Via Piero Gobetti 101, 40129 Bologna, Italy
8
CNRS, IRAP, 9 Av. colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
9
RAM, 300 rue de la Piscine, Domaine Universitaire, 38406 Saint Martin d’Hères, France
10
Dep. of Physics and Astronomy, UCL, Gower Place, London WC1E 6BT, UK
11
Academia Sinica, Institute of Astronomy and Astrophysics, Taiwan
12
Dep. of Astrophysics, Astronomy & Mechanics, Faculty of Physics, National and Kapodistrian University of Athens, Panepistimiopolis, Zografou 15784, Greece
13
National Observatory of Athens, Institute for Astronomy, Astrophysics, Space Applications and Remote Sensing, Penteli 15236 Athens, Greece
14
Leiden Observatory, Leiden Univ., PO Box 9513 2300 RA Leiden, The Netherlands
15
European Southern Observatory, Alonso de Córdova, 3107, Vitacura, Santiago 763-0355, Chile
16
Joint ALMA Observatory, Alonso de Córdova, 3107 Vitacura, Santiago 763-0355, Chile
Received:
2
November
2018
Accepted:
26
January
2019
We report Atacama Large Millimeter/submillimeter Array (ALMA) observations of CO(3-2) emission in a sample of seven Seyfert/LINER galaxies at the unprecedented spatial resolution of 0.″1 = 4−8 pc. Our aim is to explore the close environment of active galactic nuclei (AGN), and the dynamical structures leading to their fueling, through the morphology and kinematics of the gas inside the sphere of influence of the black hole. The selected galaxies host low-luminosity AGN and have a wide range of activity types (Seyferts 1 to 2, LINERs), and barred or ringed morphologies. The observed maps reveal the existence of circumnuclear disk structures, defined by their morphology and decoupled kinematics, in most of the sample. We call these structures molecular tori, even though they often appear as disks without holes in the center. They have varying orientations along the line of sight, unaligned with the host galaxy orientation. The radius of the tori ranges from 6 to 27 pc, and their mass from 0.7 × 107 to 3.9 × 107 M⊙. The most edge-on orientations of the torus correspond to obscured Seyferts. In only one case (NGC 1365), the AGN is centered on the central gas hole of the torus. On a larger scale, the gas is always piled up in a few resonant rings 100 pc in scale that play the role of a reservoir to fuel the nucleus. In some cases, a trailing spiral is observed inside the ring, providing evidence for feeding processes. More frequently, the torus and the AGN are slightly off-centered with respect to the bar-resonant ring position, implying that the black hole is wandering by a few 10 pc amplitude around the center of mass of the galaxy. Our spatial resolution allows us to measure gas velocities inside the sphere of influence of the central black holes. By fitting the observations with different simulated cubes, varying the torus inclination and the black hole mass, it is possible to estimate the mass of the central black hole, which is in general difficult for such late-type galaxies, with only a pseudo-bulge. In some cases, AGN feedback is revealed through a molecular outflow, which will be studied in detail in a subsequent article.
Key words: galaxies: active / galaxies: ISM / galaxies: kinematics and dynamics / galaxies: nuclei / galaxies: spiral
© F. Combes et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The growth of supermassive black holes in galaxies produces phenomenon of active galactic nuclei (AGN), one of the brightest and most energetic events in the Universe. In recent years, the subsequent appearance of AGN feedback has been widely established through the existence of fast outflows of ionized and atomic gas (e.g., Veilleux et al. 2005; Tombesi et al. 2010; Fiore et al. 2017). In parallel, observations of the molecular component of the circumnuclear environment have brought a great deal of progress in the question of how AGN are fueled in galaxies (e.g., García-Burillo et al. 2005; Combes et al. 2013, 2014), and how the energy generated by the AGN can in turn regulate its gas accretion through molecular outflows (e.g., Feruglio et al. 2010; Aalto et al. 2012; Cicone et al. 2014; García-Burillo et al. 2014). This has important implications for the co-evolution of galaxies and black holes which is observed through the now well-established MBH-σ relation (e.g., Gültekin et al. 2009).
Active galactic nuclei are observed in two categories, type 1 with broad-line regions (BLR) and type 2 with only narrow-line regions (NLR). Lines are broad only very close to the black hole, in the accretion disk, while they are narrow farther out in the NLR of ∼0.1–1 kpc size. The original unification paradigm proposes that the BLR in type 2 is obscured by a dusty molecular torus, along the line of sight of the observer (e.g., Antonucci & Miller 1985; Urry & Padovani 1995). However, since this early work many observations have shown that inclination and obscuration are not the only parameters distinguishing types 1 and 2; some of these types are intrinsically different and/or nuclear starbursts are confusing the picture (e.g., Imanishi & Wada 2004; Hatziminaoglou et al. 2009). A strong challenge of the unification paradigm also comes from AGN changing look from type 1 to type 2 and vice versa, without evidence of variable obscuration (e.g., LaMassa et al. 2015; McElroy et al. 2016).
The expected torus is so small (3–30 pc in size) that it was not possible to resolve it until recently, where CO(6-5) emission was detected for the first time with ALMA, as well as continuum and dense gas tracers, in a 10 pc-diameter torus in the Seyfert 2 NGC 1068 (García-Burillo et al. 2016; Gallimore et al. 2016; Imanishi et al. 2016, 2018). Dusty tori have also been seen in the near or mid-infrared (e.g., Asmus et al. 2011; Gratadour et al. 2015), although sometimes the dust emission is seen in the polar direction instead (Asmus et al. 2016).
García-Burillo et al. (2016) have obtained a high-resolution map in CO(6-5) with ALMA towards the center of NGC 1068: there is a circumnuclear disk (CND) ∼300 pc in size, which is also detected in dust continuum. The AGN is offset with respect to the center of this disk. Around the AGN, a peak of CO emission is detected. This is identified as the molecular torus surrounding the AGN. The dust emission coincides spatially with the molecular torus. Two components were revealed, a dust torus ∼7 pc in diameter, oriented along PA = 142°, aligned with the H2O maser disk (Greenhill et al. 1996) and some polar emission that extends 10 pc to the SW. The CO(6-5) torus is a bit larger in size (diameter ∼10 pc) than the dust torus, and it appears tilted, with a PA = 112° with respect to the dust torus and accretion disk. The extent of the torus depends slightly on its tracer; it is somewhat larger with low-J CO emission (García-Burillo et al., in prep.) or in dense gas tracers (Imanishi et al. 2018). There is no CO counterpart for the polar emission. The molecular torus reveals strong non-circular motions and a large degree of turbulence. It also appears more face-on at larger radii, being probably warped. The perturbations in the morphology and kinematics of the torus can be interpreted in terms of the Papaloizou & Pringle (1984) instability (PPI), predicted in particular for the dynamical evolution of AGN tori.
The discovery of such a perturbed and turbulent torus was a surprise. Is it due to continuous accretion from the CND onto the torus, triggering tilt, warp, and PPI instabilities, and finally leading to the AGN fueling? How does the molecular outflow detected farther away (García-Burillo et al. 2014) arise from the torus? Are perturbed and turbulent tori the norm in AGN-dominated galaxies?
In the present paper, we describe our effort to gather more information on possible molecular tori in nearby Seyfert galaxies. We have observed with high spatial resolution seven barred galaxies with active nuclei in order to explore both the AGN fueling and the feedback processes, and also to characterize the molecular content inside the central kpc at 4–9 pc resolution. In many cases the gas kinematics allows us to refine the determination of the central black hole mass. Section 2 presents the galaxy sample, and Sect. 3 the details of the ALMA observations. The results are then described in Sect. 4 with first a brief discussion of the main features discovered, whether there is a molecular torus, the determination of its properties, and then the estimation of black hole masses. Section 5 summarizes and discusses our findings.
2. The sample
In addition to NGC 1433 and 1566 (Combes et al. 2013, 2014), we selected the five nearby southern AGN galaxies for which we previously gathered CO(3-2) observations at 0.14″ resolution. They span more than a factor of 100 in AGN power (X-ray and radio luminosities), a factor of 10 in star formation rate (SFR), and a wide range of galaxy inner morphology (with or without double bars). This sample has been selected to provide a wide range of gas inflow rate, AGN feeding rate, and therefore test the various possible phases of evolution for the molecular tori. The galaxies were also selected to be sufficiently nearby to allow ALMA, with its exquisite spatial resolution, to resolve the torus if present. All galaxies have single-dish millimeter data with the SEST (see references in Table 1), and we have obtained ALMA cycle 0 or 3 intermediate resolution data, in addition to the present high-resolution ALMA cycle 3-4 CO maps. Some of the targets have also been observed by previous authors with ALMA at lower resolution of 50–100 pc (e.g., for NGC 613 and NGC 1808 Miyamoto et al. 2017; Salak et al. 2016, 2017). We used these observations in the archive when available. Our targets have high-resolution Hubble Space Telescope (HST) images, and are found in the IRAS Bright Galaxy Sample (Sanders et al. 2003). Most of these galaxies have been searched for H2O masers (tracing the accretion disk) with a 2/7 detection rate (Zhang et al. 2012; Surcis et al. 2009) and for star-forming (“active”) inner rings by Comerón (2013). In addition, we have proprietary SINFONI IFU observations of all galaxies, so that we can compare warm H2 morphology, ionized gas distributions, and kinematics with the cold molecular counterparts. We summarize the galaxy properties in Table 1, and the nuclear morphologies in Fig. 1.
Characteristics of the sample.
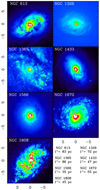 |
Fig. 1. Red HST images (F814W) for the seven sample galaxies in the same FOV = 18″ as obtained with ALMA in Band 7. The axis labels correspond to arcsec, with north up and east to the left. |
3. Observations
To explore and characterize molecular tori in nearby Seyferts, we targeted the CO(3-2) line. For this transition, the J is low enough that it is still a tracer of density and mass more than excitation; it also has a relatively high flux and affords a high spatial resolution. It appears as the best compromise between spatial resolution, sensitivity, and field of view. To estimate H2 column densities and masses, we use in Sect. 4.3 the usual ratios applicable to active galaxy centers. The detailed study by Papadopoulos et al. (2012) has shown that the excitation ratios begin to depart from common ones at J = 5 and beyond, and mainly for starbursts.
The observations were carried out with the ALMA telescope in cycles 3 and 4, with 36 to 40 antennas, during the years 2016 and 2017. The corresponding ALMA projects ID were #2015.1.00404.S and #2016.1.00296.S, both with PI F. Combes. In cycle 3, five galaxies (NGC 613, NGC 1326, NGC 1365, NGC 1672, and NGC 1808) were observed simultaneously in CO(3-2), HCO+(4-3), HCN(4-3), and continuum, with Band 7. The compact configuration (TC, baselines 15 to 630 m) and extended (TE, baselines 15 to 1400 m) combined to give a synthesized beam of 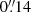 (∼15 pc), and an rms sensitivity of 1 mJy beam−1 in 10 km s−1 channels (80 μJy beam−1 in the continuum). The total integration time, including calibration and overheads, was 1 h per source. This choice of correlator configuration, selected to simultaneously observe three lines, provided a velocity range of 1600 km s−1 for each line. However, the various lines are not centered, and in particular a compromise had to be made for the CO(3-2) and HCN(4-3). These two lines are sampled with only 200 km s−1 on one side and 1400 km s−1 on the other. This is adequate for nearly face-on galaxies, but prevents seeing outflows on one side. The bandwidth was 1800 MHz for the continuum bands.
(∼15 pc), and an rms sensitivity of 1 mJy beam−1 in 10 km s−1 channels (80 μJy beam−1 in the continuum). The total integration time, including calibration and overheads, was 1 h per source. This choice of correlator configuration, selected to simultaneously observe three lines, provided a velocity range of 1600 km s−1 for each line. However, the various lines are not centered, and in particular a compromise had to be made for the CO(3-2) and HCN(4-3). These two lines are sampled with only 200 km s−1 on one side and 1400 km s−1 on the other. This is adequate for nearly face-on galaxies, but prevents seeing outflows on one side. The bandwidth was 1800 MHz for the continuum bands.
In cycle 4, the seven galaxies were observed at higher spatial resolution, 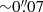 or 4 to 9 pc (depending on the various distances), to search for molecular tori. For the frequency tuning we chose to observe the CO(3-2) and the HCO+(4-3) lines, and the continuum in Band 7. The HCN(4-3) transition was not observed in order to avoid a restricted velocity range in the expected broader spectral lines towards the nuclei. The observations were done in several blocks, a compact configuration (TM2, baselines 19 to 500 m ) and extended (TM1, baselines 19 to 3100 m), with a total duration of two hours per galaxy. When combining two or more of these configurations, all calibrated observations with all baselines were included to obtain the UV-tables in CASA or GILDAS. The sensitivity reached was between 0.6 and 0.8 mJy in 10 km s−1 channels. A summary of all configurations observed is given in Table 2.
or 4 to 9 pc (depending on the various distances), to search for molecular tori. For the frequency tuning we chose to observe the CO(3-2) and the HCO+(4-3) lines, and the continuum in Band 7. The HCN(4-3) transition was not observed in order to avoid a restricted velocity range in the expected broader spectral lines towards the nuclei. The observations were done in several blocks, a compact configuration (TM2, baselines 19 to 500 m ) and extended (TM1, baselines 19 to 3100 m), with a total duration of two hours per galaxy. When combining two or more of these configurations, all calibrated observations with all baselines were included to obtain the UV-tables in CASA or GILDAS. The sensitivity reached was between 0.6 and 0.8 mJy in 10 km s−1 channels. A summary of all configurations observed is given in Table 2.
The observations were all centered on the nuclei, with a single pointing covering a field of view (FOV) of 18″. For NGC 1365, due to the large size of the galaxy and nuclear ring and the strength of CO emission, we performed a rectangular 13-point mosaic, ensuring a FOV of 45 × 36″, aligned on the major axis. The galaxies were observed in dual polarization mode with 1.875 GHz total bandwidth per baseband, and a channel spacing of 0.488 MHz corresponding to ∼0.8 km s−1, after Hanning smoothing. The spectra were then smoothed to 11.7 MHz (10.2 km s−1) to build channel maps.
The total integration time provided an rms of 30 μJy beam−1 in the continuum, and ∼0.6 mJy beam−1 in the line channel maps (corresponding to ∼1.2 K at the obtained spatial resolution). The flux calibration was done with nearby quasars, which are regularly monitored at ALMA, and resulted in 10% accuracy.
The data were calibrated, imaged, and cleaned with the CASA software (versions 4.5.3 to 4.7.2; McMullin et al. 2007) and the analysis was then finalized with the GILDAS software (Guilloteau & Lucas 2000). The final cubes at high resolution are at the maximum 1800 × 1800 pixels with 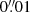 per pixel in the plane of the sky, and have 60 channels of 10 km s−1 width. The maps were made with Briggs weighting and a robustness parameter of 0.5, i.e., a trade-off between uniform and natural weighting. The data were cleaned using a mask made from the integrated CO(3-2) map. The continuum was subtracted from all line maps.
per pixel in the plane of the sky, and have 60 channels of 10 km s−1 width. The maps were made with Briggs weighting and a robustness parameter of 0.5, i.e., a trade-off between uniform and natural weighting. The data were cleaned using a mask made from the integrated CO(3-2) map. The continuum was subtracted from all line maps.
The final maps were corrected for primary beam attenuation. Very little CO(3-2) emission was detected outside the full width half power (FWHP) primary beam. Because of missing short spacings, the interferometer plays the role of a high-frequency filter, insensitive to smooth and extended emission; the scales that might be filtered out are those larger than ∼3″, in each channel map. Since the velocity gradients are high in galaxy nuclei, this does not affect the line measurements too much; indeed, the size in each velocity channel is not expected to be extended. However, the missing-flux problem might affect continuum maps. Low-level negative sidelobes adjacent to bright emission were observed.
The exact values of missing flux amount will be detailed in forthcoming papers. We estimated the total CO(3-2) line flux for the two galaxies previously observed in cycle 0 (with the most compact configuration) to give an order of magnitude (see Table 3). The difference between the cycle 0 observations with beams of 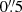 and the combination TM1+TM2 shows that we are missing ∼25% of the total flux, on large angular scales. This will affect only slightly the masses estimated for the tori since they are not extended, except for NGC 1566. In future papers, all configurations will be combined to minimize flux losses.
and the combination TM1+TM2 shows that we are missing ∼25% of the total flux, on large angular scales. This will affect only slightly the masses estimated for the tori since they are not extended, except for NGC 1566. In future papers, all configurations will be combined to minimize flux losses.
Estimation of the missing CO(3-2) flux in the FOV of 18″ for the two galaxies observed in cycle 0.
4. Results
Figures 2–5 display the CO(3-2) flux distribution (moment 0) together with the velocity field (moment 1) of the seven targets; they demonstrate the wide variety of morphologies encountered. There are both resonant rings and spiral arms, and six galaxies host a molecular torus, either nearly face-on or more edge-on. We define a torus by the smallest decoupled circumnuclear structure in the CO(3-2) line, and from its morphology and kinematics. The morphology decoupling means that a nuclear disk or ring is clearly detached from the outside spiral structure or outer rings, and the corresponding kinematic displays a strong velocity gradient compared to the outside structure. In some cases the kinematic major axis of the inner torus is not aligned with the kinematic major axis of the outside structure (e.g., NGC 613, NGC 1566, NGC 1672 and NGC 1808). The HCO+(4-3) line, when clearly detected, supports this definition (see Fig. 7). The dust continuum may also trace this circumnuclear structure, but it is weaker and tends to be less extended radially. Also, the central point source, coming in general from synchrotron AGN emission, perturbs its morphology. We emphasize that the radial extent of the torus may depend on the tracer considered, as already found in NGC 1068 (García-Burillo et al. 2016, and in prep.). Most of the time there are departures from symmetry, and the central torus is slightly offset from the barycenter of the 1 kpc-structure. In two cases (NGC 613 and NGC 1566) there is a clear trailing spiral inside the inner Lindblad resonance (ILR) ring, a “smoking gun” signature for ongoing fueling of the central black hole. The main morphological and kinematical features are described for each galaxy below.
 |
Fig. 2. Top panel: CO(3-2) moment 0 and 1 of galaxy NGC 613 (left and middle, TE+TM1). Right panel: zoom-in of the CO(3-2) contours (of the TM1 observations at high resolution) superposed on a color scale of the continuum emission in Band 7. The three panels have been centered on the central continuum source, and the labels are the offset in arcseconds from the phase center. For the two first panels the beam size is indicated at the bottom left. In the third panel is shown the ellipse (in red) used to define the molecular tori in Sect. 4.3. The contours are from 25σ to 1600σ, and follow each other by factor 2 multiplication. The scale bar in the right panel is 20 pc long. The color scale in the middle panel is in km s−1. Bottom panel: same, but for galaxy NGC 1326. The contours are from 3σ to 96σ, and follow each other by factor 2 multiplication. |
 |
Fig. 3. Top panel: same as Fig. 2 for NGC 1365 (from the center of the mosaic; the size of the beam has been multiplied by 1.5 to become visible in the first panel) – the contours are from 4σ to 256σ, and follow each other by factor 2 multiplication – and bottom panel: for NGC 1433 (in the latter case, TM2+TM1 in all 3 panels). The continuum emission (color plot in the right panel) maximizes at 0.2 mJy (i.e., only slightly above 3σ) and was not detected in the TM1 configuration alone (detection only when combining TM1+TM2). The CO(3-2) line contours are from 3σ to 192σ, and follow each other by factor 2 multiplication. |
 |
Fig. 4. Top panel: same as Fig. 2, but for NGC 1566 (in this case TM2+TM1 instead of TE+TM1 in the first two panels). The contours are from 5σ to 160σ, and follow each other by factor 2 multiplication. Bottom panel: same, but for NGC 1672. The contours are from 3σ to 192σ, and follow each other by factor 2 multiplication. |
 |
Fig. 5. Same as Fig. 2, but for NGC 1808. The contours are from 3σ to 384σ, and follow each other by factor 2 multiplication. The color scale in the middle panel is in km s−1. |
4.1. Continuum emission and AGN position
All galaxies were observed with their phase center coinciding with the position given in NED. However, we now have a high spatial resolution, and when the nucleus has a strong continuum point source, it is possible to refine the position of the central black hole, expected to be the source of strong radio emission. A central continuum point source has been detected in all galaxies, except in NGC 1433 where we had a tentative detection in our previous work (Combes et al. 2013), but were not able to subsequently confirm it. We adopt, however, the same previously determined position for the center, which corresponds to the center of the inner nuclear ring. For all others, the center position adopted is the pixel of maximum continuum emission, determined with an error equal to the TM1 beam indicated in Table 2, typically 0.1″. These positions are displayed in Table 1, and in the following are considered to coincide with the actual AGN nucleus. These positions are now better determined than the optical nuclei defined by the maximum brightness in the HST images of Fig. 1, which have an astrometry accurate to within ≤1″. Our adopted positions also coincide most of the time with the maximum velocity dispersion in the CO(3-2) line (except for NGC 1365 and NGC 1566).
There is also the possibility that some continuum emission from the unresolved central source is coming from the inner torus around the AGN. Most galaxies in the sample are low-luminosity AGN in which the dust emission close to the nucleus is expected to emerge between 10 and 300 μm (Casey 2012). We expect that the continuum point source at 0.8 mm is dominated by synchrotron emission (Prieto et al. 2010). Around the unresolved continuum sources, Figs. 2–5 show that we detect extended emission which might be dominated by dust emission from the inner tori; however, these tori are better traced by the CO line emission.
4.2. Molecular gas distribution and morphology
NGC 613. shows an incomplete ring with high-density contrast, as seen in our large-scale map of CO(3-2) (Fig. 2), and emission from a clear trailing two-arm spiral structure in the circumnuclear disk (CND). This galaxy has a typical ILR nuclear ring, of radius 3.5 arcsec (or 300 pc), just inside the two characteristic leading dust lanes of the bar, which are tangent to the ring. Inside the ring, there is a central molecular component, or CND of radius ∼1″ = 83 pc. Water masers have been detected in the nucleus (Kondratko et al. 2006). Miyamoto et al. (2017) have mapped the ring in CO(1-0) and CO(3-2) with ALMA at 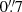 and
and 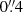 , respectively, and found a clumpy ring, globally regular, but with spots of active and efficient star formation. ALMA finds a continuum jet at 95 GHz with a PA = 20° (Miyamoto et al. 2017), which corresponds to the 4.9 GHz and 14.9 GHz jets (Hummel & Jorsater 1992), close to the minor axis of the ring. At 350 GHz, the central continuum source remains unresolved at our resolution of
, respectively, and found a clumpy ring, globally regular, but with spots of active and efficient star formation. ALMA finds a continuum jet at 95 GHz with a PA = 20° (Miyamoto et al. 2017), which corresponds to the 4.9 GHz and 14.9 GHz jets (Hummel & Jorsater 1992), close to the minor axis of the ring. At 350 GHz, the central continuum source remains unresolved at our resolution of 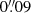 . The negative slope found for the flux over frequency α ∼ 0.6 is compatible with synchrotron emission, with a small fraction of free-free.
. The negative slope found for the flux over frequency α ∼ 0.6 is compatible with synchrotron emission, with a small fraction of free-free.
The ring reveals two breaks into two winding spiral arms to the north and south. The bar has a position angle PA = 130° and is delineated on its leading sides by two dust lanes: one runs from the SW of the nucleus to the east side of the bar (PA = 130°), and the other from the NE of the nucleus to the west side of the bar (PA = −50°) (see Fig. 1). The spiral arms are the beginning of these characteristic dust lanes along the bar: they are the contact points between the tangent lanes and the ring.
Dense gas (> 106 cm−3) is detected in various lines of HCN, HCO+, CS, and SiO at the edges of the jets (Miyamoto et al. 2017). We find that at high resolution with HCO+(4-3) (Fig. 7) the dense molecular gas is very concentrated towards the nucleus, with skewed kinematics, suggesting an outflow along the jets; this will be described in a future paper (Audibert et al., in prep.). A first look at it can be seen in Fig. 14, where both the velocity field and velocity dispersion are perturbed. The outflow has already been suggested by the high-velocity dispersion of the [FeII] line along the radio jet (Falcón-Barroso et al. 2014; Davies et al. 2017).
A coherent chronology of star formation possibly driven by the gas motions in the ring was sought by Böker et al. (2008) with SINFONI images in Brγ, HeI, and [FeII] (spectral resolution R = 2000, and without adaptive optics). They identified clumps along the ring, color-coded according to the different star formation phases. These authors searched for a coherent chronology of star formation, starting from the dust lanes, fueling gas into the ring. At least in the southern part of the ring the expected sequence of star formation was indeed observed: the hottest stars were found near the contact point (defined above between the dust lane and the ring), and then fewer hot stars were found along the ring. The star formation scenario is not the random one, where new stars light up like a popcorn model. If gas is inflowing from the bar dust lanes into the ring, as expected from gravity torques (García-Burillo et al. 2005), there must also be an inflow in the CND due to the nuclear trailing spiral, as already observed and interpreted for NGC 1566 (Combes et al. 2014). The detailed nature of the gas flows in NGC 613 will be studied in a future work. Inside the nuclear spiral structure, there is a very dense and compact (radius ∼14 pc) rotating component, which might be interpreted as the molecular torus. The torus is also distinguished by a kinematic decoupling, with a major axis PA = 0°, (better seen in HCO+(4-3)), while the outside axis is PA = 105°. The excitation of the ionized gas in the torus is dominated by shocks (Davies et al. 2017).
NGC 1326. is a lenticular barred galaxy with a contrasted ring at ILR, of radius 5.7″ = 410 pc. Garcia-Barreto et al. (1991) detected radio continuum in the ring at 20, 6, and 2 cm with the VLA at ∼3″ resolution, and also a molecular mass of 2.7 × 108 M⊙ from CO emission with the SEST-15m telescope. There is no evidence of a strong central continuum point source at centimeter wavelengths. At 350 GHz, we detect a weak continuum source, coinciding with the maximum of the CO(3-2) emission (Fig. 2). About 83% of the Hα emission of the galaxy is coming from this nuclear ring (Crocker et al. 1996). There are no conspicuous dust lanes along the bar, and the ring is not interrupted by spiral structure at their contact. The ring in CO and also in Hα is oriented at PA = 90° roughly perpendicular to the bar (PA = 20°), suggesting either that the gas is on x2 orbits, or that it forms a decoupled nuclear ring, with a pattern speed higher than that of the primary bar. In any case, this means that the primary bar pattern speed is slow enough to allow the presence of two ILRs. When the rotation curve of the galaxy (Garcia-Barreto et al. 1991; Storchi-Bergmann et al. 1996) is considered, the ring corresponds to the inner ILR.
The HST image in Hα (Buta et al. 2000) reveals a marked asymmetry of the ring, which we do not see in CO(3-2) with ALMA. While the 14″-diameter (1 kpc) ring overlaps very well in Hα and CO(3-2) emissions, it is depleted on its west side only in Hα. This must therefore be due to strong dust extinction in the west side. The ring is made of hundreds compact sources, which could be star clusters, and also some diffuse emission, tightly wrapped and spiral in character. This spiral structure is seen in our CO(3-2) high-resolution map as well. Stellar populations were studied from U,B,V, I colors and Hα-filter images by Buta et al. (2000). The age range of the stellar population in the ring is 10–200 Myr and the derived star formation rate is 1 M⊙/yr (Buta et al. 2000). Inside the nuclear ring, the CO emission reveals a central CND, of radius ∼0.3″ = 21 pc. This central structure appears slightly more inclined on the sky than the main galaxy, and is likely a tilted torus.
NGC 1365. is a strongly barred spiral galaxy with the characteristic dust lanes delineating the bar, which are particularly contrasted and curved. As an archetypal barred galaxy, it has been extensively observed (e.g., Lindblad 1999). While the Seyfert 1.8 nucleus is obvious in optical and X-rays (Nardini et al. 2015), it is hardly seen in radio. Stevens et al. (1999) discuss a marginal radio jet, the center of which corresponds to the central X-ray position.
The main part of the radio emission at centimeter wavelengths is the nuclear ring, with hot spots corresponding to star formation. Sakamoto et al. (2007) have mapped in CO(2-1) and isotopes a mosaic with SMA at 2″ resolution, that shows clearly a 2 kpc-extent oval ring, connected to the leading dust lanes, characteristics of the bar morphology. The AGN has only a small contribution (∼5%) to the central infrared emission, which is dominated by star formation (Alonso-Herrero et al. 2012).
At 350 GHz, we detect a central continuum point source, as can be seen in Fig. 3. Our large-scale CO(3-2) map reveals the contrasted nuclear ring of radius ∼9″ = 770 pc. Inside this ring, which corresponds to the ILR of the bar, we detect a more compact molecular component, a CND with a ring shape, of radius 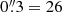 pc. This rotating ring just encircles the central continuum source, and might be interpreted as the molecular torus.
pc. This rotating ring just encircles the central continuum source, and might be interpreted as the molecular torus.
Lena et al. (2016) have recently presented optical integral field spectroscopy for the inner 6″. They find evidence for a fan-shaped blueshifted outflow in [NII] and Hα kinematics, corresponding to the outflow in a cone seen with the [OIII] emission lines, extending at more than 1 kpc from the center along the minor axis (Hjelm & Lindblad 1996; Venturi et al. 2017). From gravity torques, it was possible to show that the gas is inflowing to the center, driven by the bar, on a timescale of 300 Myr (Tabatabaei et al. 2013). We will discuss in a future paper the possibility of an outflow in the molecular component (Audibert et al., in prep.).
NGC 1433. is a strongly barred spiral galaxy, nicknamed the “Lord of Rings” because of the presence of clear nuclear, inner, and outer rings at the bar resonances (Buta & Combes 1996). Our previous cycle 0 ALMA observations in Band 7, with 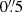 resolution, have revealed that inside the nuclear ring at ∼400 pc, there is also an inner nuclear ring at ∼200 pc, corresponding to the inner ILR (Combes et al. 2013). These observations revealed also a mild molecular outflow along the minor axis, of 7 M⊙/yr, the smallest molecular outflow ever observed in the Local Universe. It is possible that the outflow in a previous more powerful phase has destroyed a potential torus. The tentative continuum point source near the center is not confirmed, and there is no evidence of any molecular torus.
resolution, have revealed that inside the nuclear ring at ∼400 pc, there is also an inner nuclear ring at ∼200 pc, corresponding to the inner ILR (Combes et al. 2013). These observations revealed also a mild molecular outflow along the minor axis, of 7 M⊙/yr, the smallest molecular outflow ever observed in the Local Universe. It is possible that the outflow in a previous more powerful phase has destroyed a potential torus. The tentative continuum point source near the center is not confirmed, and there is no evidence of any molecular torus.
The only small velocity gradient in the center corresponds to the outflow along the minor axis. This is supported by the coincidence of the optical and near-infrared emission in the center, showing no extinction (Smajić et al. 2014). The CO(3-2) emission has a very filamentary structure at small scale, as can be seen in Fig. 3. The nuclear ring is the site of a starburst (Sánchez-Blázquez et al. 2011), and the gas is transiently stalled there though gravity torques (Smajić et al. 2014).
NGC 1566. is an intermediate barred spiral galaxy, possessing nuclear, inner and outer rings at resonances (Agüero et al. 2004). The broad lines detected in the nucleus, and the observed variability are typical of a Seyfert 1 (Alloin et al. 1985). It appears that this low-luminosity AGN appears has been increasing its activity over the last few hundred years; the line excitation is much higher in the BLR than along the NLR cone (Baribaud et al. 1992; Reunanen et al. 2002; Smajić et al. 2015).
Our previous cycle 0 ALMA observations have shown that the molecular gas followed a trailing spiral inside the nuclear ring, fueling the central black hole. The gravity torques due to the bar on the gas change sign at each resonance, and also change sign as the winding of spirals change from trailing to leading (Buta & Combes 1996). When the spiral is leading inside the ring located at the inner Lindblad resonance, the torques are positive and the gas inside the ring is driven back to the ring. Instead, when the spiral is trailing, the torques are negative, the gas loses angular momentum, and is driven towards the nucleus. The sense of winding of the spiral must be due to the gravitational influence of the black hole itself (Combes et al. 2014; Smajić et al. 2015). The image at high resolution confirms the trailing spiral structure in the nuclear disk (Fig. 4). The nucleus is also the site of young star formation, and of a consequent velocity dispersion drop, also called σ-drop (da Silva et al. 2017; Emsellem et al. 2001).
Inside the inner spiral fueling the nucleus, there is a ringed structure of 0.7″ = 24 pc radius, kinematically decoupled, which can be considered a molecular torus. As can be seen in Fig. 4, the torus kinematic major axis is vertical (PA = 0°), while the rest of the disk has a kinematic major axis PA = 60°.
NGC 1672. is a strongly barred Seyfert 2 galaxy, with a high star-forming activity in its center. The AGN activity is therefore hard to find through line diagnostics (Storchi-Bergmann et al. 1996; Kewley et al. 2000). Brandt et al. (1996) with ROSAT find a diffuse X-ray nuclear source, rather soft, compatible with a superbubble interpretation (i.e., thermal emission from star formation). The star formation rate implies enough supernovae over a 107 yr period to blow a superbubble, as computed by Mac Low & McCray (1988), although the X-ray gas pressure and density appear too high (Brandt et al. 1996). While finding two additional X-ray sources at the bar extremities, de Naray et al. (2000) conclude that the Seyfert 2 activity must be obscured by a Compton-thick nucleus with a column density of at least 1024 cm−2. The X-ray emission at the center appears diffuse and dominated by a starburst nucleus. Jenkins et al. (2011) with the high resolution of Chandra are the first to find a hard X-ray emission associated with the nucleus in addition to a ring. This confirms that the galaxy is actually a low-luminosity AGN, a Seyfert 2.
The circumnuclear ring, of 5″ = 275 pc radius, is conspicuous in the radio emission at 3 cm from the VLA, and also in the Spitzer 8 μm band, tracing essentially the PAH dust (Jenkins et al. 2011). Díaz et al. (1999) provide the Hα velocity field in the central 2kpc: it has a strong velocity gradient, with a mass of 9 × 108 M⊙ inside 125 pc. The ring is located at the inner ILR, and is also quite contrasted in the CO(3-2) emission (Fig. 4). Inside the ring, some thin filaments join towards a central concentration, which looks like a torus of radius 0.5″ = 27 pc seen more inclined than the large-scale disk. A kinematic decoupling helps to define the torus, with a kinematic major axis of the torus of PA = 90°, and an outside axis of PA = 135°. The continuum emission peaks just at the center.
NGC 1808. is a barred starburst containing a Seyfert 2 nucleus. Optically, it is possible to see the dust lanes expelled perpendicular to the major axis. There is evidence of large-scale (1 kpc) outflows, likely due to the starburst, and NGC 1808 has been classified as a superwind galaxy, similar to M 82 (Dahlem et al. 1990, 1994). The outflow is also seen in HI (Koribalski et al. 1993). Surprisingly, the outflow is not observed in the molecular component at the small scales sampled here (Audibert et al., in prep.). The outflow is thus apparently generated at a large distance from the nucleus (> 300 pc), favoring a starburst-driven flow over an AGN-driven one.
Star formation is very active through hot spots aligned on a ring of radius 10″ = 450 pc (Koribalski et al. 1996). Inside this ring, also contrasted in CO (Salak et al. 2016), there is a circumnuclear disk or ring of radius 200 pc. Within this circumnuclear disk it is possible to see a trailing spiral in the CO (Fig. 5), which is even more contrasted in the dense gas tracers: HCO+(4-3), CS. The continuum is a point source inside the nuclear spiral, and may also correspond to a torus of radius 0.13″ = 6 pc. The previous ALMA observations by Salak et al. (2017) have shown the nuclear ring, and from the two contact points of the characteristic dust-lanes, two starting spiral arms. With a beam of 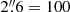 pc, Salak et al. (2017) had insufficient spatial resolution to see the trailing spiral inside the nuclear ring. They call the nuclear ring a torus even if this component does not obscure the AGN. In the following, we will define the torus as the smaller compact structure of radius 6 pc inside the nuclear spiral. The kinematic major axis of the torus is PA = 100°, misaligned with the outside axis of PA = 140°.
pc, Salak et al. (2017) had insufficient spatial resolution to see the trailing spiral inside the nuclear ring. They call the nuclear ring a torus even if this component does not obscure the AGN. In the following, we will define the torus as the smaller compact structure of radius 6 pc inside the nuclear spiral. The kinematic major axis of the torus is PA = 100°, misaligned with the outside axis of PA = 140°.
Busch et al. (2017) have published a near-infrared IFU spectroscopy of the inner 600 pc with SINFONI in seeing-limited mode and R = 1500−4000 spectral resolution. They determine an indicative black hole mass of 107 M⊙. The age of the stars on the ring is homogeneous and younger than 10 Myr. They find shocked H2 warm gas near the nucleus, with non-circular motions. Although there is much gas streaming inside a radius of 1″ = 45 pc, there is no strong sign of nuclear activity.
4.3. Masses of possible tori
In at least six of the seven galaxies, there is evidence of a compact central ring or disk in CO emission, which can be interpreted as a molecular torus. These structures can be seen in CO(3-2) contours overlaid over HST images in Fig. 6. Their kinematics are also displayed with models, starting from Fig. 11. For NGC 1433, there is no evidence of a nuclear disk rotating around the nucleus, although there is a piece of spiral arm superposed on it. The molecular nuclear disks or tori are clearly decoupled from the rest of the disks in the kinematics as well. This is seen in Figs. 2–5, and also particularly in the dense gas maps in HCO+(4-3) which will be discussed in future papers. The example of NGC 613 is displayed in Fig. 7. In all galaxies, except for NGC 613 and NGC 1808, the size of the torus is much larger than the beam size (8–26 times). For NGC 613 and NGC 1808, the torus is only 4 times the beam, and the size reported in Table 4 has been deconvolved from the beam.
 |
Fig. 6. Red HST images (F814W) for the seven sample galaxies, zoomed into the central field of 70 pc radius, with the CO(3-2) contours overlaid. The axis labels are in pc. |
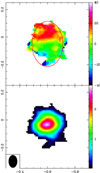 |
Fig. 7. First moments of the HCO+(4-3) map of NGC 613. The color scale of the intensity at the bottom is in Jy beam−1 × km s−1, and the velocity at the top is in km s−1. The red ellipse at the top indicates the definition of the molecular torus. The RA-Dec scale is in arcsec. |
Radii, masses, and inclinations of the molecular tori.
We have identified in the CO(3-2) data cube these components through ellipse-fitting with the adopted center as the continuum point source identified with the nucleus (at the coordinates given in Table 1). The sizes of the tori are illustrated by red ellipses in Fig. 2 and beyond. From the integrated flux S(CO) dV (Jy km s−1) found within the region, the derived molecular mass is obtained through the formula
where νrest = 345.796 GHz, and DL is the luminosity distance in Mpc (e.g., Solomon & Vanden Bout 2005). The molecular mass, including helium, is then derived from
assuming the standard CO-to-H2 conversion factor of XCO = 2 × 1020 cm−2 (K km s−1), applicable to Milky Way-like galaxies, and 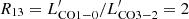 (e.g., Tacconi et al. 2013). Although this ratio was applied for high-z galaxies, it should also be appropriate to local galaxy nuclei, where the molecular gas is dense (e.g., Braine & Combes 1992; Dumke et al. 2001). The actual excitation of the molecular gas in the tori, close to the AGN, is yet not well known, and we refer to the above-mentioned papers, where our data on HCN, HCO+, and CS lines are discussed.
(e.g., Tacconi et al. 2013). Although this ratio was applied for high-z galaxies, it should also be appropriate to local galaxy nuclei, where the molecular gas is dense (e.g., Braine & Combes 1992; Dumke et al. 2001). The actual excitation of the molecular gas in the tori, close to the AGN, is yet not well known, and we refer to the above-mentioned papers, where our data on HCN, HCO+, and CS lines are discussed.
We display in Table 4 the size and molecular masses of the tori. They vary from 6 to 27 pc and 0.7 to 3.9 × 107 M⊙. In NGC 1326, 1672, and 1808, the torus is rather inclined on the sky plane, and could obscure the nucleus. This is well correlated with the Sy 2 type. The uncertainties on the torus size are determined from the extrema of the possible fits, taking into account both moments zero and one, and are never smaller than the beam size. The error bars on the integrated flux and other properties follow from these definitions, assuming a fixed excitation ratio and CO-to-H2conversion ratio.
To gain insight on the possible H2 column densities of the torus, we computed the average H2 surface densities over the central beam on the highest CO(3-2) resolution maps (TM1). The resulting H2 colum densities are displayed in Table 4 together with the size of the beam in parsec. These column densities are lower limits on the actual molecular surface densities, both because of possible dilution in the beam, and also possible missing flux. Conversely, they might be sometimes an overestimation, if the CO(3-2) line becomes partially optically thin, due to high gas temperature and large turbulent line-width. In either case, from these central column densities, we can derive the molecular mass enclosed in the central beam, Mcent, displayed in Table 4. For NGC 1365, the central beam is empty, and the column density was taken from the peak surface density of the torus. The value of Mcent is in general much lower than the expected central black hole mass, except in the case of NGC 613. This does not affect our BH mass estimation, since the gas mass is taken into account for the gravitational potential.
It is interesting to compare the H2 column densities inferred from our molecular measurements with the column densities derived from X-ray absorption. While our derived column density towards NGC 613 nucleus would suggest that it is Compton thick, Castangia et al. (2013) find NH values from X-ray spectral fitting that are lower, ∼4 × 1023 cm−2. This may be explained by a clumpy torus. Nardini et al. (2015) examine NGC 1365 during a Compton-thick state, but NGC 1365 is a well-known “changing-look” AGN (Matt et al. 2003). In NGC 1566, Kawamuro et al. (2013) find a NH column of ∼3 × 1022 cm−2 (with a 26% covering fraction). For NGC 1672, Jenkins et al. (2011) find inconclusive evidence for a Compton-thick X-ray source, although there is some evidence for NH ∼ 2 × 1024 cm−2 in agreement with our finding (de Naray et al. 2000). Jiménez-Bailón et al. (2005) find NH ∼ 3 × 1022 cm−2 for the hard nuclear source in NGC 1808. In summary, our very high-resolution data are not directly comparable to the X-ray measurements possible up to now. Our results are lower limits, allowing quite high column densities in some regions of the torus, but the latter can be quite clumpy. To be compatible with the X-ray estimations, the covering or surface filling factor has to be on the order of 0.01−0.1.
When there is a nuclear spiral structure, we have identified the torus as the nuclear component inside this structure (NGC 613, 1672, and 1808). It is likely that the torus is replenished in gas through this spiral structure. In that sense, the torus is the last axisymmetric structure before the nucleus. It is however difficult to define a typical torus in Seyfert galaxies: according to the larger scale dynamics (resonances, nuclear rings, or spirals), the size of the torus may vary widely. Other tori in the literature of even more varying sizes have been found: if the torus in NGC 1068 is comparable (4 pc radius, García-Burillo et al. 2016, or an extended one in the near-infrared of 27 pc radius Gratadour et al. 2015), others are larger, from 30–100 pc in the OH-megamasers of Mrk 231 (Klöckner et al. 2003), or smaller (1 pc for Circinus, Tristram et al. 2014, as well as Seyfert with H2O masers, with molecular transition at a fraction of a pc Madejski et al. 2000; Herrnstein et al. 2005). It is not yet clear whether the obscuring structure must be a thick doughnut-shaped torus, or could be a warped thin disk (e.g., Elitzur & Shlosman 2006). In NGC 3079, the torus has been identified with clumps elevated from the warped and flared disk, at 0.5 pc, forming a geometrically thick structure of a few 106 M⊙ (Kondratko et al. 2005).
4.4. Determination of the mass of the black hole
With the obtained ALMA spatial resolution, up to 2 pc for NGC 1566, we are now reaching the sphere of influence (SoI) of the black holes in our nearby Seyfert galaxies. The SoI is defined as the region inside which the gravity of the black hole of mass MBH dominates the gravitational potential of the host galaxy. There are two possible expressions for the SoI, one is from Merritt (2004), when the stellar mass inside the SoI1 M*(r < SoI1) is twice MBH, and the second involves the central velocity dispersion of the stars σv, i.e., SoI2 = 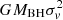 . We display both in Table 6. In the following, we also consider for the gravitational potential and the computation of the black hole mass; the example of NGC 1068 is presented here in comparison with the seven galaxies. Our previous high-resolution ALMA observations of its molecular torus have also reached the BH SoI (García-Burillo et al. 2016, and in prep.).
. We display both in Table 6. In the following, we also consider for the gravitational potential and the computation of the black hole mass; the example of NGC 1068 is presented here in comparison with the seven galaxies. Our previous high-resolution ALMA observations of its molecular torus have also reached the BH SoI (García-Burillo et al. 2016, and in prep.).
4.4.1. Model of the gravitational potential
To compute the stellar distribution of stars in each of our galaxies, we use the S4G 3.6 μm infrared images and their galfit decomposition in bulge and disk components from Salo et al. (2015). More precisely, there are in most cases three components, including an additional bar component. These components are determined by their Sersic index, their magnitude, their effective radius, and the axis ratio. In two galaxies only, there is also a point-source component corresponding to 7% and 4% of the total mass respectively for NGC 1365 and NGC 1566. In these cases, we represented this component by an exponential, with effective radius equal to the PSF of the 3.6 μm observations, which has a FWHM of 2.1″ (Salo et al. 2015). All disks are exponential. As for bars, the adopted distribution is the modified Ferrers ellipsoids (Ferrers 1877), with a surface density varying as ![$ \left[1-\left(\frac{r}{R_{\mathrm{bar}}}\right)^2\right]^2 $](/articles/aa/full_html/2019/03/aa34560-18/aa34560-18-eq17.gif) , where Rbar is its outer truncation radius. We adopt a mass-to-light ratio of M/L = 0.5 M⊙/L⊙ for this 3.6 μm band (e.g., Sani et al. 2011; McGaugh & Schombert 2014; Lelli et al. 2016). All the adopted mass components for our seven galaxies, with NGC 1068 added for comparison, are displayed in Table 5.
, where Rbar is its outer truncation radius. We adopt a mass-to-light ratio of M/L = 0.5 M⊙/L⊙ for this 3.6 μm band (e.g., Sani et al. 2011; McGaugh & Schombert 2014; Lelli et al. 2016). All the adopted mass components for our seven galaxies, with NGC 1068 added for comparison, are displayed in Table 5.
Stellar mass components from S4G 3.6 μm (Salo et al. 2015).
To have a first estimation of the black hole masses, it is interesting to exploit the well-known MBH-σ relation for classical bulges (e.g., Tremaine et al. 2002; Marconi & Hunt 2003; Gültekin et al. 2009). We use the hyperleda compilation (Makarov et al. 2014) for the central velocity dispersion, and also Garcia-Rissmann et al. (2005) when the data are not present in this data base. To derive the BH mass, we use the recent MBH-σ relation,
compiled by Kormendy & Ho (2013). The resulting masses are listed in Table 6, together with an indication of the bulge-to-black hole mass ratio (according to the S4G 3.6 μm bulge decomposition) and the derived estimation of the SoI radius. The derived mass models from Table 5, including the BH masses of Table 6 are displayed in Fig. 8. The individual components from the galfit 3.6 μm models are color-coded, and the vertical axis shows the SMBH versus galaxy mass ratios. From these values, it is clear that the ALMA observations can sample the dynamics inside the BH SoI in all galaxies. It can be seen in Fig. 8 that the enclosed stellar mass is not dominant in the regions sampled by the molecular tori, and the uncertainties on the determination of the stellar masses will not have a large influence on our modeling.
Central velocity dispersions and derived BH masses.
 |
Fig. 8. Representation of the enclosed mass as a function of radius, taking into account every component of the galfit 3.6 μm model (Table 5), with their respective geometry (spherical bulges, and flat disks and bars) for the eight galaxies. The vertical scale is normalized to their black hole mass, estimated from their central velocity dispersion (Table 6). The total mass is in black, the bulge in red, the disk in green, the bar in blue, and a possible nucleus in cyan. |
Many studies have shown that pseudo-bulges and/or barred galaxies may be offset from the main MBH-σ relation (Sani et al. 2011; Graham et al. 2011; Kormendy & Ho 2013; Ho & Kim 2014). Some of our galaxies may be in this category, and thus these first BH masses may be overestimated. It is therefore interesting to compare these values with several other BH mass estimations, such as the spiral pitch angle (Davis et al. 2014), or the Sersic index (Mutlu-Pakdil et al. 2016). These values are indicated in Table 7, and are indeed about 1–30 times (on average 4 times) below the previous ones.
BH masses from literature, and our derived ones.
From our ALMA data on the six galaxies with well-defined kinematic tori (the seven galaxies in Table 4, but without NGC 1433), we can try to derive the CO line kinematics inside the SoI. We use the position-velocity (PV) diagrams along the major axis, as employed by the WISDOM project (Onishi et al. 2017; Davis et al. 2017, 2018a) in deriving the supermassive black hole masses in three early-type galaxies from the molecular gas kinematics. We postpone to future work the modeling of the full velocity field of each galaxy because most objects are barred and subject to non-circular motions (S-shape), as seen in Figs. 2–5. As for the black-hole mass determination, we only focus on the central part of the PV diagram since the tori are frequently misaligned and tilted with respect to the main disk (Fischer et al. 2013). To determine the PA of the possibly decoupled tori, we plotted PV diagrams for a wide range of position angles (the first 36 separated by 10°, then with a separation of 5° around the most probable PA), and selected the largest velocity gradient. Only the cubes with the most extended ALMA configuration were considered for this analysis (TM1). The analysis of the PV diagram in NGC 1808 did not allow the construction of an unambiguous mass model; the dynamics in the center is highly chaotic, probably due to the starburst and associated feedback. We therefore analyzed only the five remaining galaxies (the seven from Table 4, but without NGC 1433 and NGC 1808), with the methodology described here.
4.4.2. Fitting the PV diagrams, and the moment maps
To be able to predict the gas dynamics in the inner nuclear disk with more flexibility, and with tilted decoupled dynamics, we performed numerical simulations of gas particles in a selected potential. We represent the gaseous disks by Miyamoto-Nagai disks of particles (Miyamoto & Nagai 1975), with radial scales and heights corresponding to the observed tori. We used typically one million particles to ensure sufficient statistics. We plunge the gas disks into a potential made of the stellar distribution determined by galfit to each galaxy, as described in the previous section. The potential of the dark matter halo is negligible inside radii of 100 pc. We take into account the gas mass to build the total gravitational potential. The gas particles are distributed in circular orbits, in equilibrium with the total potential, with a velocity distribution corresponding to a Toomre Q-parameter of 1. The ratio between tangential and radial velocity dispersion was taken from the epicyclic theory (e.g., Toomre 1964). It should be noted that we simulate only axisymmetric disks. Here we consider bar or spiral perturbations to be secondary, and will study their effects in future papers.
Figure 9 illustrates the small-scale rotation curves predicted by our mass models where the colors correspond to the same structural components as in Fig. 8. The quality of the potentials was checked by comparing at larger scales the modeled rotation curve with previous observations. These rotation curves come from Hα, HI, or low-resolution CO observations, and do not have enough spatial resolution to sample the curve below 100 pc, but give a calibration at 0.2–1 kpc. Within these radii, the dark matter contribution is negligible. The curves are generally good approximations to those on larger scales, with some scatter which could come from the effect of non-circular motions. As will be seen below, the influence of the large-scale rotation has limited impact inside the sphere of influence of the black hole.
 |
Fig. 9. Corresponding rotation curves for the eight galaxies, derived from the mass models in Fig. 8. The contribution of the three or four components is color-coded as in Fig. 8. The contribution of the black holes is included, with masses derived from the MBH-σ relation (Table 6). |
To compare the model to observations, we built data cubes by projecting the model on the sky, with the best fit large-scale inclinations and position angles (see above), and computing the line-of-sight velocity distribution. We select the same pixel size as the observed data cube (around 0.01 arsec according to each galaxy), and channels of 10 km s−1, and the data were smoothed to the observed beam (Table 1). The sizes in pixels of the cubes were between (180, 180, 60) and (360, 360, 60) to best sample the various tori studied. Because the gas distribution is not homogeneous, but asymmetric and patchy, and this impacts the mass-weighted velocity at each observed beam, we normalized the model cube to the zeroth moment map of the CO observations, pixel by pixel in this 2D projection. This plays the role of a multiplicative filter for our homogenous gas disks. This means that each CO spectrum at each position of the model is normalized to the observed integrated flux at this position.
We tested the methodology on the most regular PV diagram obtained, that of NGC 1672, as shown in Fig. 10. The three first moments of the model cube can be seen in Fig. 11. The first step is to run, as a comparison, a model with no black-hole, which is displayed in the left panel of Fig. 10. Then as a first estimate, the value derived from a standard MBH-σ relation, as given in Table 6. We explore around this by small increments in MBH, which will allow us to obtain the best fit, maximizing the overlap between the contours of the model and the observed map in the PV diagram, and also fitting the three first moments. Typically a dozen values are explored for each parameter, which yield the best fit with error bars displayed in Table 7.
 |
Fig. 10. Position-velocity diagram of the CO(3-2) line in NGC 1672, with a linear color scale (TM1 only). Superposed in red are the contours of the model without any black hole and torus inclination of 66° (left panel), with a black hole as derived from the MBH-σ relation (Table 6) of 2.5 × 107 M⊙ with i = 66° (middle panel), and the best fit: a black hole of 5.0 × 107 M⊙, with i = 66° (right panel). The mass model is that based on the galfit decomposition, and the predicted circular velocity is reproduced in blue lines (Fig. 9). |
 |
Fig. 11. Left panel: three first moments of the model cube for NGC 1672. The RA-Dec offsets are in parsec. The velocity color scales are in km s−1. The cube corresponds to the best PV fit, with a BH mass of 5.0 × 107 M⊙, and an inclination of 66°. Right panel: three moments for the observations (TM1 only). The RA-Dec offsets are in arcsec with respect to the phase center. |
Two parameters were varied: the inclination of the central molecular disk/torus, and the mass of the black hole. To quantify the goodness of fit, we computed the least-squares values summing the difference of all pixels between the observed and model maps, either at 2D on the PV diagram, or the moment maps, or at 3D on the cubes. We concentrate on the nuclear part, with 3 × 104 pixels in 2D or 2 × 106 pixels in 3D, corresponding to a region 120 pc in diameter, with a resolution of 0.66 pc and 10 km s−1. The model and observed maps are normalized to the same total flux over this region, and the squares difference is weighted by the observed flux in this pixel. The criterion is then to minimize the quantity: 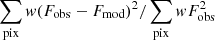 , with the weighting function w = Fobs > 0. The result for NGC 1672 is illustrated in Fig. 12 for the PV diagram and the total cube.
, with the weighting function w = Fobs > 0. The result for NGC 1672 is illustrated in Fig. 12 for the PV diagram and the total cube.
 |
Fig. 12. Least-squares fitting between the observed and modeled PV diagram (black curve) and 3D cube (red curve) as a function of inclination of the torus (left panel) and the black hole mass (right panel). The criterion is defined in Sect. 4.4.2. The curves have been slightly translated vertically for clarity. If there is a minimum for inclination, there is none for MBH, and larger masses are preferred, as for NGC 1672. |
The fit for the PV diagram and also for the 3D-cube tend to point towards large masses for the black hole. However, these high masses are not realistic, since they created a central velocity dispersion that is too large, as can be seen in Fig. 11. The best fit must therefore be a compromise between the PV diagram and the velocity dispersion map.
The same fitting procedure has been applied to NGC 613 (Figs. 13 and 14, showing in addition the perturbed velocity field and velocity dispersion due to the outflow), NGC 1326 (Figs. 15 and 16), NGC 1365, where the best compromise was obtained with the outer disk inclination (Figs. 17 and 18), and the same for NGC 1566 (Figs. 19 and 20). The morphology was too complex in NGC 1808 to obtain a satisfying fit, as mentioned in the previous section, perhaps because of supernovae feedback molecular flows there.
 |
Fig. 13. Same as Fig. 10 for NGC 613, without any black hole (left panel), with a black hole of 7.4 × 106 M⊙ (middle panel), and the best fit: 3.7 × 107 M⊙, as derived from the MBH-σ relation (Table 6) (right panel). The inclination of the torus is i = 46°. The mass model is that based on the galfit decomposition, and the predicted circular velocity is reproduced in blue lines (Fig. 9). |
 |
Fig. 14. Same as Fig. 11 for NGC 613 (left is the model, right the observations). The cube corresponds to the best PV fit, with a BH mass of 3.7 × 107 M⊙ and an inclination of 46°. |
 |
Fig. 15. Same as Fig. 10 for NGC 1326, without any black hole, i = 60° (left panel); with a black hole of 3 × 107 M⊙ from the MBH-σ relation, i = 60° (middle panel); and the best fit: 6.5 × 106 M⊙, with i = 60° (right panel). |
 |
Fig. 16. Same as Fig. 11 for NGC 1326 (left is the model, right the observations). The cube corresponds to the best PV fit, with a BH mass of 6.5 × 106 M⊙ and an inclination of 60°. |
 |
Fig. 17. Same as Fig. 10 for NGC 1365, without any black hole (left panel), with a black hole of 6.9 × 107 M⊙ from the MBH-σ relation (middle panel), and the best fit: 4 × 106 M⊙ (right panel). The adopted inclination i = 63° is from the galaxy to be conservative. Higher BH masss would be derived with the lower 27° inclination estimated for the torus. |
 |
Fig. 18. Same as Fig. 11 for NGC 1365 (left is the model, right the observations). The cube corresponds to the best PV fit, with a BH mass of 4 × 106 M⊙ and an inclination of 63°. |
 |
Fig. 19. Same as Fig. 10 for NGC 1566, without any black hole (left panel), with a black hole of 1.35 × 107 M⊙ from the MBH-σ relation (middle panel), and the best fit: 6.7 × 106 M⊙ (right panel). As for NGC 1365, the adopted inclination i = 48° is from the galaxy. |
 |
Fig. 20. Same as Fig. 11 for NGC 1566 (left is the model, right the observations). The cube corresponds to the best PV fit, with a BH mass of 6.7 × 106 M⊙ and an inclination of 48°. |
4.4.3. Summary of results on black hole masses
The black hole masses obtained are between 4 × 106 and 5 × 107 M⊙, in good agreement with the previous estimations of Tables 6 and 7: they have the tendency to follow the relation obtained for pseudo-bulge galaxies, determined by Ho & Kim (2014). It is now fairly well established that classical bulges and ellipticals follow a tighter and shallower MBH-σ relation than galaxies with pseudo-bulges (e.g., Graham et al. 2011, but see Bennert et al. 2015). The eight galaxies studied in this paper can all be considered pseudo-bulges: the Sersic index of their bulges are all close to 1, and always < 1.4 (Table 5). Also their bulge-to-disk ratios are all below 0.4, which is the location of pseudo-bulges (e.g., Fisher & Drory 2008; Gadotti 2009).
With the range of black hole masses found, the corresponding Eddington luminosities LEdd range from 1.3 × 1011 and 1.6 × 1012 L⊙, or log (LEdd) in erg s−1 between 44.7 and 45.8. From the X-ray luminosities listed in Table 1 and the bolometric corrections computed by Marconi et al. (2004), we estimated the AGN bolometric luminosities for all our galaxies, LAGN (see Table 7). The Eddington ratio LAGN/LEdd in our galaxies is therefore mostly < < 1, namely between ∼0.2 (NGC 1068) and 3 × 10−7 (NGC 1672).
The positions of the galaxies studied here in the M-σ diagram are displayed in Fig. 21, together with the compilation by van den Bosch (2016). The values measured recently with CO emission by the WISDOM collaboration are also plotted in blue: they apply to classical bulges with much higher black hole masses. Galaxies with pseudo-bulges and with lower masses are harder to determine, and their relation is affected by a larger scatter. In addition, barred galaxies appear in general below the standard MBH-σ relation (e.g., Graham et al. 2011), which contributes to the scatter. The scatter in barred galaxies may be due to a varying velocity dispersion, because the orientation of the bar is random with respect to the line of nodes. In barred galaxies, gas driven into the center by gravity torques may boost a nuclear starburst, which produces a σ-drop (Wozniak et al. 2003). Also, in pseudo-bulge galaxies, the classical bulge is in general too light, and the black hole mass might be better compared to the total baryonic mass (Davis et al. 2018b). All eight galaxies studied in this paper are barred, and their scatter (Fig. 21) is not unexpected. It is, however, crucial to obtain BH masses in this low-mass end region to better understand the different processes for black hole growth, either through mergers (classical bulges) or secular evolution (pseudo-bulges).
 |
Fig. 21. Location of our galaxies in the MBH-σ relation, compiled by van den Bosch (2016), represented by the gray points and the fitted line, of slope 5.35. Our galaxies are in red, while in blue are plotted other values recently obtained from the CO line: NGC 1097 (Onishi et al. 2015), NGC 1332 (Barth et al. 2016), NGC 3665 (Onishi et al. 2017), NGC 4429 (Davis et al. 2018a), NGC 4526 (Davis et al. 2013), NGC 4697 (Davis et al. 2017). Previous estimations of the BH masses of our sample galaxies are also plotted in green (Table 6), turquoise and pink (Cols. 2 and 3 in Table 7). |
It is interesting to compare the black hole masses derived in this paper with the previous estimations: in Fig. 21, the green points are the values derived from the MBH-σ relation of Kormendy & Ho (2013) and displayed in Table 6. These values are slightly above the MBH-σ relation compiled by van den Bosch (2016). The turquoise points are the values from Col. 2 in Table 7, estimated from the spiral pitch angle (Davis et al. 2014), and the pink points are the values from Col. 3 in Table 7 (various references). The red points appear less scattered.
5. Discussion and summary
We have presented our first ALMA results for a sample of 7 active galaxies, all low-luminosity AGN. The high spatial resolution allows to enter the sphere of influence of the central black holes, and to reveal the small-scale circumnuclear molecular structures that we associate with possible molecular tori. For 6 out of 7 galaxies, we indeed detect a nuclear disk, decoupled in morphology and dynamics from the main disk. Such a structure is also detected in an eighth galaxy studied by our group, NGC 1068 (García-Burillo et al. 2016, and in prep.).
5.1. Characteristics of the tori
The decoupled molecular tori (Table 4) may correspond to the required obscuration for type 2 AGN, even if they do not have the expected inclination for a type 2 classification. They sometimes show a gas hole or depletion in the center (NGC 1365, NGC 1566, NGC 1672) which make them approach a doughnut morphology. Their sizes extend over a wide range, from 6 to 27 pc, but their masses are less scattered from ∼1 to 4 × 107 M⊙. There is no relation to the total stellar masses of the galaxies, which vary from 1 to 9 × 1010 M⊙ (Table 5). The mass of the gas in the molecular tori appears slightly anticorrelated to the AGN strength, as traced by the X-ray luminosity (Table 1), although with large scatter. More galaxies are needed to build a relation.
5.1.1. Orientation of the tori
One of the striking results emerging of these ALMA observations is that the gas in the molecular tori is rarely aligned with the main disk, but present different inclination and position angles. This decoupling was already observed for instance in NGC 1068 (Gratadour et al. 2015; García-Burillo et al. 2016). Given the widely different scales, 3–30 pc for the nuclear disks and 1–10 kpc for the main disk, the dynamical timescales are largely different, from ∼1 to 300 Myr. It is then natural that these scales may decouple. It is sufficient that the central disk accretes some gas infalling with some angle to the plane for it to warp and change its orientation, averaging its old angular momentum vector with the tilted one from the newly accreted gas. The accretion could come either from the kpc scales or from stellar mass loss or feedback from its own star formation (e.g., Emsellem et al. 2015). Alternatively, the tori could be unstable to non-axisymmetric modes growing on a dynamical timescale (Papaloizou & Pringle 1984).
5.1.2. Asymmetries: offsets and lopsidedness
In addition, the molecular tori display asymmetries and off-centering. These circumnuclear disks are frequently located inside a star-forming ring, coincident with the ILR of the bar, but are not centered in the ring (for instance NGC 1326). The distance between the disk center (scale of a few hundred pc) and the AGN or torus center (which coincide) is displayed in Table 4. They are on the order of a few tens of pc, i.e., ∼10% of the scale of the ILR rings. This lopsidedness implies that the black hole is also wandering with a small amplitude around the center of mass of the galaxy. Several mechanisms for this off-centering and implied BH oscillations have been reviewed by Jog & Combes (2009). The off-centering and wandering, characteristic of a Keplerian potential, may be explained by the eccentric instability proposed by Shu et al. (1990), when the masses of the central object and the disk are comparable. This mechanism occurs with the exchange of angular momentum between the central mass and the disk (Woodward et al. 1994). It will be interesting to establish whether the stellar component also displays m = 1 instabilities, as the M 31 nucleus does, for example (e.g., Bender et al. 2005). These instabilities may help to fuel the AGN as predicted by Hopkins et al. (2012).
5.1.3. Cases of the nuclear spirals
In two cases, NGC 613 and NGC 1566, the CO emission has revealed a nuclear spiral, which has the distinction of being trailing, like the large-scale one. Inside the nuclear ring at the ILR of the bar, a leading spiral is usually expected to develop transiently and generate positive torques, which drive the inner gas onto the ring. However, when the gravitational impact of the black hole is significant, the spiral can then be trailing and the torques negative, to fuel the nucleus (e.g., Buta & Combes 1996). The special case of NGC 613 will be studied in a forthcoming paper (Audibert et al., in prep.).
5.2. Black hole masses
The estimation of the black hole masses from the gas kinematics suffers from specific uncertainties, discussed in detail by previous authors (Barth et al. 2016; Onishi et al. 2015, 2017; Davis et al. 2017, 2018a). They discuss in particular the problem of edge-on systems, which do not have enough resolution on the minor axis or spatial resolution, which is barely equal to the radius of the SoI of the black hole. Our galaxies do not suffer from either of these problems: the spatial resolution of our ALMA observations is sufficient to probe the SoI, and therefore the impact of the stellar potential, and the uncertainties on the stellar mass-to-light ratio are less important here. However, our BH mass estimates still have the uncertainties related to the distance scale, and the trade-off needed to accommodate both the PV diagram fits and the observed velocity dispersion maps as discussed below.
All our galaxies are barred, at various strength levels, and certainly some non-circular motions are present, and must be included in the uncertainties. A typical S-shaped velocity pattern is seen in the NGC 1672 circumnuclear region (Fig. 11). We postpone to further work the simulation of the non-circular motions in these barred galaxies, including both small and large scale.
Another caveat might come from the observed CO velocity dispersion: we tried to take into account this projected velocity dispersion when comparing the moment 2 of the data cubes with the moments of our models. However, the molecular gas is patchy, and especially inside 50 pc in radius it is likely that there is an insufficient number of molecular clouds to sample all the velocity gradients of the inner regions. In the model with one million particles, we sample almost continuously the velocity gradient, and this results in a large apparent dispersion along the line of sight towards the center in the case of a massive black hole. This apparent dispersion is only due to a beam-smearing of the velocity gradient along the line of sight. The intrinsic dispersion of the gas is negligible, between 2 and 10 km s−1. It is even more negligible when there is a massive central mass, since then the value of κ the epicyclic frequency is significantly elevated, and the critical velocity to stabilize the disk in the Toomre sense is very low. In some cases, even when the velocity gradient is high and can only be obtained with a massive central component, the observed dispersion is surprisingly low. There are cases where the molecular gas is depleted or absent in the center, which is also a factor that supresses the large dispersion. This has to be taken into account in the minimizing criteria.
Perhaps the most important uncertainty in the black hole mass determination of these low-mass late-type objects is the decoupling of the molecular torus. On the one hand, these nuclear disks are dense enough to give kinematical information and subsist in the SoI, but their true inclination and position angle might be quite different from those of the main disks. It thus requires more 3D data to be able to disentangle both the decoupled morphology and the actual motions around the black hole.
In summary, ALMA at high resolution brings a wealth of new information on the decoupled molecular tori near the black holes. In the present paper, we described the properties of the decoupled molecular tori and estimated the mass of the central black holes, when possible, as displayed in Fig. 21. In future work, we will address the fueling efficiency through torque computation, and the feedback efficiency by estimating the gas outflows and their energetics in these low-luminosity AGN.
Acknowledgments
We warmly thank the referee for the constructive comments and suggestions. The ALMA staff in Chile and ARC-people at IRAM are gratefully acknowledged for their help in the data reduction. We particularly thank Philippe Salomé for his useful advice. SGB is thankful for the support from Spanish grant AYA2016-76682-C3-2-P. LKH acknowledges funding from the INAF PRIN-SKA 2017 program 1.05.01.88.04. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2015.0.00404.S, and ADS/JAO.ALMA#2016.0.00296.S. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. We used observations made with the NASA/ESA Hubble Space Telescope, and obtained from the Hubble Legacy Archive, which is a collaboration between the Space Telescope Science Institute (STScI/NASA), the Space Telescope European Coordinating Facility (ST-ECF/ESA), and the Canadian Astronomy Data Centre (CADC/NRC/CSA). We made use of the NASA/IPAC Extragalactic Database (NED) and of the HyperLeda database. This work was supported by the Programme National Cosmology et Galaxies (PNCG) of CNRS/INSU with INP and IN2P3, co- funded by CEA and CNES.
References
- Aalto, S., Booth, R. S., Black, J. H., Koribalski, B., & Wielebinski, R. 1994, A&A, 286, 365 [Google Scholar]
- Aalto, S., Garcia-Burillo, S., Muller, S., et al. 2012, A&A, 537, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Agüero, E. L., Díaz, R. J., & Bajaja, E. 2004, A&A, 414, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alloin, D., Pelat, D., Phillips, M., & Whittle, M. 1985, ApJ, 288, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., Sánchez-Portal, M., Ramos Almeida, C., et al. 2012, MNRAS, 425, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, R. R. J., & Miller, J. S. 1985, ApJ, 297, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Asmus, D., Gandhi, P., Smette, A., Hönig, S. F., & Duschl, W. J. 2011, A&A, 536, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asmus, D., Hönig, S. F., & Gandhi, P. 2016, ApJ, 822, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Bajaja, E., Wielebinski, R., Reuter, H.-P., Harnett, J. I., & Hummel, E. 1995, A&AS, 114, 147 [Google Scholar]
- Baribaud, T., Alloin, D., Glass, I., & Pelat, D. 1992, A&A, 256, 375 [NASA ADS] [Google Scholar]
- Barth, A. J., Boizelle, B. D., Darling, J., et al. 2016, ApJ, 822, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Bender, R., Kormendy, J., Bower, G., et al. 2005, ApJ, 631, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Bennert, V. N., Treu, T., Auger, M. W., et al. 2015, ApJ, 809, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Böker, T., Falcón-Barroso, J., Schinnerer, E., Knapen, J. H., & Ryder, S. 2008, AJ, 135, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Braine, J., & Combes, F. 1992, A&A, 264, 433 [NASA ADS] [Google Scholar]
- Brandt, W. N., Halpern, J. P., & Iwasawa, K. 1996, MNRAS, 281, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Busch, G., Eckart, A., Valencia-S, M., et al. 2017, A&A, 598, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buta, R., & Combes, F. 1996, Fund. Cosmic Phys., 17, 95 [Google Scholar]
- Buta, R., Treuthardt, P. M., Byrd, G. G., & Crocker, D. A. 2000, AJ, 120, 1289 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M. 2012, MNRAS, 425, 3094 [Google Scholar]
- Castangia, P., Panessa, F., Henkel, C., Kadler, M., & Tarchi, A. 2013, MNRAS, 436, 3388 [NASA ADS] [CrossRef] [Google Scholar]
- Cicone, C., Maiolino, R., Sturm, E., et al. 2014, A&A, 562, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Combes, F., García-Burillo, S., Casasola, V., et al. 2013, A&A, 558, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Combes, F., García-Burillo, S., Casasola, V., et al. 2014, A&A, 565, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comerón, S. 2013, A&A, 555, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crocker, D. A., Baugus, P. D., & Buta, R. 1996, ApJS, 105, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlem, M., Aalto, S., Klein, U., et al. 1990, A&A, 240, 237 [NASA ADS] [Google Scholar]
- Dahlem, M., Hartner, G. D., & Junkes, N. 1994, ApJ, 432, 598 [NASA ADS] [CrossRef] [Google Scholar]
- da Silva, P., Steiner, J. E., & Menezes, R. B. 2017, MNRAS, 470, 3850 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. L., Groves, B., Kewley, L. J., et al. 2017, MNRAS, 470, 4974 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, T. A., Bureau, M., Cappellari, M., Sarzi, M., & Blitz, L. 2013, Nature, 494, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, B. L., Berrier, J. C., Johns, L., et al. 2014, ApJ, 789, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, T. A., Bureau, M., Onishi, K., et al. 2017, MNRAS, 468, 4675 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, T. A., Bureau, M., Onishi, K., et al. 2018a, MNRAS, 473, 3818 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, B. L., Graham, A. W., & Cameron, E. 2018b, ApJ, 869, 113 [NASA ADS] [CrossRef] [Google Scholar]
- de Naray, P. J., Brandt, W. N., Halpern, J. P., & Iwasawa, K. 2000, AJ, 119, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz, R., Carranza, G., Dottori, H., & Goldes, G. 1999, ApJ, 512, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Dumke, M., Nieten, C., Thuma, G., Wielebinski, R., & Walsh, W. 2001, A&A, 373, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elitzur, M., & Shlosman, I. 2006, ApJ, 648, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Greusard, D., Combes, F., et al. 2001, A&A, 368, 52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Emsellem, E., Renaud, F., Bournaud, F., et al. 2015, MNRAS, 446, 2468 [NASA ADS] [CrossRef] [Google Scholar]
- Falcón-Barroso, J., Ramos Almeida, C., Böker, T., et al. 2014, MNRAS, 438, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrers, N. M. 1877, Pure Appl. Math., 14, 1 [Google Scholar]
- Feruglio, C., Maiolino, R., Piconcelli, E., et al. 2010, A&A, 518, L155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fiore, F., Feruglio, C., Shankar, F., et al. 2017, A&A, 601, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fisher, D. B., & Drory, N. 2008, AJ, 136, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, T. C., Crenshaw, D. M., Kraemer, S. B., & Schmitt, H. R. 2013, ApJS, 209, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gadotti, D. A. 2009, MNRAS, 393, 1531 [NASA ADS] [CrossRef] [Google Scholar]
- Gallimore, J. F., Henkel, C., Baum, S. A., et al. 2001, ApJ, 556, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Gallimore, J. F., Elitzur, M., Maiolino, R., et al. 2016, ApJ, 829, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia-Barreto, J. A., Dettmar, R.-J., Combes, F., Gerin, M., & Koribalski, B. 1991, Rev. Mex. Astron. Astrofis., 22, 197 [Google Scholar]
- García-Burillo, S., Combes, F., Schinnerer, E., Boone, F., & Hunt, L. K. 2005, A&A, 441, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Combes, F., Usero, A., et al. 2014, A&A, 567, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Combes, F., Ramos Almeida, C., et al. 2016, ApJ, 823, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia-Rissmann, A., Vega, L. R., Asari, N. V., et al. 2005, MNRAS, 359, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W., Onken, C. A., Athanassoula, E., & Combes, F. 2011, MNRAS, 412, 2211 [NASA ADS] [CrossRef] [Google Scholar]
- Gratadour, D., Rouan, D., Grosset, L., Boccaletti, A., & Clénet, Y. 2015, A&A, 581, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greenhill, L. J., Gwinn, C. R., Antonucci, R., & Barvainis, R. 1996, ApJ, 472, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Guilloteau, S., & Lucas, R. 2000, ASP Conf. Ser., 217, 299 [Google Scholar]
- Gültekin, K., Richstone, D. O., Gebhardt, K., et al. 2009, ApJ, 698, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Hatziminaoglou, E., Fritz, J., & Jarrett, T. H. 2009, MNRAS, 399, 1206 [NASA ADS] [CrossRef] [Google Scholar]
- Herrnstein, J. R., Moran, J. M., Greenhill, L. J., & Trotter, A. S. 2005, ApJ, 629, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Hjelm, M., & Lindblad, P. O. 1996, A&A, 305, 727 [NASA ADS] [Google Scholar]
- Ho, L. C., & Kim, M. 2014, ApJ, 789, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hayward, C. C., Narayanan, D., & Hernquist, L. 2012, MNRAS, 420, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Hummel, E., & Jorsater, S. 1992, A&A, 261, 85 [NASA ADS] [Google Scholar]
- Imanishi, M., & Wada, K. 2004, ApJ, 617, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Imanishi, M., Nakanishi, K., & Izumi, T. 2016, ApJ, 822, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Imanishi, M., Nakanishi, K., Izumi, T., & Wada, K. 2018, ApJ, 853, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, L. P., Brandt, W. N., Colbert, E. J. M., et al. 2011, ApJ, 734, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Bailón, E., Santos-Lleó, M., Dahlem, M., et al. 2005, A&A, 442, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jog, C. J., & Combes, F. 2009, Phys. Rep., 471, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Jungwiert, B., Combes, F., & Axon, D. J. 1997, A&AS, 125, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kawamuro, T., Ueda, Y., Tazaki, F., & Terashima, Y. 2013, ApJ, 770, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Heisler, C. A., Dopita, M. A., et al. 2000, ApJ, 530, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Klöckner, H.-R., Baan, W. A., & Garrett, M. A. 2003, Nature, 421, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Kondratko, P. T., Greenhill, L. J., & Moran, J. M. 2005, ApJ, 618, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Kondratko, P. T., Greenhill, L. J., Moran, J. M., et al. 2006, ApJ, 638, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Koribalski, B., Dahlem, M., Mebold, U., & Brinks, E. 1993, A&A, 268, 14 [NASA ADS] [Google Scholar]
- Koribalski, B., Dettmar, R.-J., Mebold, U., & Wielebinski, R. 1996, A&A, 315, 71 [NASA ADS] [Google Scholar]
- Kormendy, J., & Ho, L. C. 2013, ARA&A, 51, 511 [Google Scholar]
- LaMassa, S. M., Cales, S., Moran, E. C., et al. 2015, ApJ, 800, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., McGaugh, S. S., & Schombert, J. M. 2016, AJ, 152, 157 [Google Scholar]
- Lena, D., Robinson, A., Storchi-Bergmann, T., et al. 2016, MNRAS, 459, 4485 [NASA ADS] [CrossRef] [Google Scholar]
- Lindblad, P. O. 1999, A&ARv, 9, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Lodato, G., & Bertin, G. 2003, A&A, 398, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mac Low, M.-M., & McCray, R. 1988, ApJ, 324, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Madejski, G., Życki, P., Done, C., et al. 2000, ApJ, 535, L87 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Makarov, D., Prugniel, P., Terekhova, N., Courtois, H., & Vauglin, I. 2014, A&A, 570, A13 [CrossRef] [EDP Sciences] [Google Scholar]
- Marconi, A., & Hunt, L. K. 2003, ApJ, 589, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, G., Guainazzi, M., & Maiolino, R. 2003, MNRAS, 342, 422 [NASA ADS] [CrossRef] [Google Scholar]
- McElroy, R. E., Husemann, B., Croom, S. M., et al. 2016, A&A, 593, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGaugh, S. S., & Schombert, J. M. 2014, AJ, 148, 77 [NASA ADS] [CrossRef] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, ASP Conf. Ser., 376, 127 [Google Scholar]
- Merritt, D. 2004, Coevol. Black Holes Galaxies, 263 [Google Scholar]
- Miyamoto, M., & Nagai, R. 1975, PASJ, 27, 533 [NASA ADS] [Google Scholar]
- Miyamoto, Y., Nakai, N., Seta, M., et al. 2017, PASJ, 69, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Mould, J., Reynolds, T., Readhead, T., et al. 2012, ApJS, 203, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Mutlu-Pakdil, B., Seigar, M. S., & Davis, B. L. 2016, ApJ, 830, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Nardini, E., Gofford, J., Reeves, J. N., et al. 2015, MNRAS, 453, 2558 [NASA ADS] [CrossRef] [Google Scholar]
- Onishi, K., Iguchi, S., Sheth, K., & Kohno, K. 2015, ApJ, 806, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Onishi, K., Iguchi, S., Davis, T. A., et al. 2017, MNRAS, 468, 4663 [NASA ADS] [CrossRef] [Google Scholar]
- Papadopoulos, P. P., van der Werf, P. P., Xilouris, E. M., et al. 2012, MNRAS, 426, 2601 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., & Pringle, J. E. 1984, MNRAS, 208, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Prieto, M. A., Reunanen, J., Tristram, K. R. W., et al. 2010, MNRAS, 402, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Reunanen, J., Kotilainen, J. K., & Prieto, M. A. 2002, MNRAS, 331, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., Miniutti, G., Elvis, M., et al. 2009, ApJ, 696, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, K., Ho, P. T. P., Mao, R.-Q., Matsushita, S., & Peck, A. B. 2007, ApJ, 654, 782 [NASA ADS] [CrossRef] [Google Scholar]
- Salak, D., Nakai, N., Hatakeyama, T., & Miyamoto, Y. 2016, ApJ, 823, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Salak, D., Tomiyasu, Y., Nakai, N., et al. 2017, ApJ, 849, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Salo, H., Laurikainen, E., Laine, J., et al. 2015, ApJS, 219, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Ocvirk, P., Gibson, B. K., Pérez, I., & Peletier, R. F. 2011, MNRAS, 415, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Mazzarella, J. M., Kim, D.-C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [Google Scholar]
- Sandqvist, A. 1999, A&A, 343, 367 [Google Scholar]
- Sani, E., Marconi, A., Hunt, L. K., & Risaliti, G. 2011, MNRAS, 413, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Tremaine, S., Adams, F. C., & Ruden, S. P. 1990, ApJ, 358, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Smajić, S., Moser, L., Eckart, A., et al. 2014, A&A, 567, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smajić, S., Moser, L., Eckart, A., et al. 2015, A&A, 583, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solomon, P. M., & Vanden Bout, P. A. 2005, ARA&A, 43, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Steer, I., Madore, B. F., Mazzarella, J. M., et al. 2017, AJ, 153, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Stevens, I. R., Forbes, D. A., & Norris, R. P. 1999, MNRAS, 306, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Storchi-Bergmann, T., Rodriguez-Ardila, A., Schmitt, H. R., Wilson, A. S., & Baldwin, J. A. 1996, ApJ, 472, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Surcis, G., Tarchi, A., Henkel, C., et al. 2009, A&A, 502, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabatabaei, F. S., Weiß, A., Combes, F., et al. 2013, A&A, 555, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tacconi, L. J., Neri, R., Genzel, R., et al. 2013, ApJ, 768, 74 [Google Scholar]
- Tombesi, F., Cappi, M., Reeves, J. N., et al. 2010, A&A, 521, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [Google Scholar]
- Tremaine, S., Gebhardt, K., Bender, R., et al. 2002, ApJ, 574, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Tristram, K. R. W., Burtscher, L., Jaffe, W., et al. 2014, A&A, 563, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, R. C. E. 2016, ApJ, 831, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Cecil, G., & Bland-Hawthorn, J. 2005, ARA&A, 43, 769 [Google Scholar]
- Venturi, G., Marconi, A., Mingozzi, M., et al. 2017, Front. Astron. Space Sci., 4, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Woodward, J. W., Tohline, J. E., & Hachisu, I. 1994, ApJ, 420, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Wozniak, H., Combes, F., Emsellem, E., & Friedli, D. 2003, A&A, 409, 469 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, J. S., Henkel, C., Guo, Q., & Wang, J. 2012, A&A, 538, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Estimation of the missing CO(3-2) flux in the FOV of 18″ for the two galaxies observed in cycle 0.
All Figures
 |
Fig. 1. Red HST images (F814W) for the seven sample galaxies in the same FOV = 18″ as obtained with ALMA in Band 7. The axis labels correspond to arcsec, with north up and east to the left. |
| In the text | |
 |
Fig. 2. Top panel: CO(3-2) moment 0 and 1 of galaxy NGC 613 (left and middle, TE+TM1). Right panel: zoom-in of the CO(3-2) contours (of the TM1 observations at high resolution) superposed on a color scale of the continuum emission in Band 7. The three panels have been centered on the central continuum source, and the labels are the offset in arcseconds from the phase center. For the two first panels the beam size is indicated at the bottom left. In the third panel is shown the ellipse (in red) used to define the molecular tori in Sect. 4.3. The contours are from 25σ to 1600σ, and follow each other by factor 2 multiplication. The scale bar in the right panel is 20 pc long. The color scale in the middle panel is in km s−1. Bottom panel: same, but for galaxy NGC 1326. The contours are from 3σ to 96σ, and follow each other by factor 2 multiplication. |
| In the text | |
 |
Fig. 3. Top panel: same as Fig. 2 for NGC 1365 (from the center of the mosaic; the size of the beam has been multiplied by 1.5 to become visible in the first panel) – the contours are from 4σ to 256σ, and follow each other by factor 2 multiplication – and bottom panel: for NGC 1433 (in the latter case, TM2+TM1 in all 3 panels). The continuum emission (color plot in the right panel) maximizes at 0.2 mJy (i.e., only slightly above 3σ) and was not detected in the TM1 configuration alone (detection only when combining TM1+TM2). The CO(3-2) line contours are from 3σ to 192σ, and follow each other by factor 2 multiplication. |
| In the text | |
 |
Fig. 4. Top panel: same as Fig. 2, but for NGC 1566 (in this case TM2+TM1 instead of TE+TM1 in the first two panels). The contours are from 5σ to 160σ, and follow each other by factor 2 multiplication. Bottom panel: same, but for NGC 1672. The contours are from 3σ to 192σ, and follow each other by factor 2 multiplication. |
| In the text | |
 |
Fig. 5. Same as Fig. 2, but for NGC 1808. The contours are from 3σ to 384σ, and follow each other by factor 2 multiplication. The color scale in the middle panel is in km s−1. |
| In the text | |
 |
Fig. 6. Red HST images (F814W) for the seven sample galaxies, zoomed into the central field of 70 pc radius, with the CO(3-2) contours overlaid. The axis labels are in pc. |
| In the text | |
 |
Fig. 7. First moments of the HCO+(4-3) map of NGC 613. The color scale of the intensity at the bottom is in Jy beam−1 × km s−1, and the velocity at the top is in km s−1. The red ellipse at the top indicates the definition of the molecular torus. The RA-Dec scale is in arcsec. |
| In the text | |
 |
Fig. 8. Representation of the enclosed mass as a function of radius, taking into account every component of the galfit 3.6 μm model (Table 5), with their respective geometry (spherical bulges, and flat disks and bars) for the eight galaxies. The vertical scale is normalized to their black hole mass, estimated from their central velocity dispersion (Table 6). The total mass is in black, the bulge in red, the disk in green, the bar in blue, and a possible nucleus in cyan. |
| In the text | |
 |
Fig. 9. Corresponding rotation curves for the eight galaxies, derived from the mass models in Fig. 8. The contribution of the three or four components is color-coded as in Fig. 8. The contribution of the black holes is included, with masses derived from the MBH-σ relation (Table 6). |
| In the text | |
 |
Fig. 10. Position-velocity diagram of the CO(3-2) line in NGC 1672, with a linear color scale (TM1 only). Superposed in red are the contours of the model without any black hole and torus inclination of 66° (left panel), with a black hole as derived from the MBH-σ relation (Table 6) of 2.5 × 107 M⊙ with i = 66° (middle panel), and the best fit: a black hole of 5.0 × 107 M⊙, with i = 66° (right panel). The mass model is that based on the galfit decomposition, and the predicted circular velocity is reproduced in blue lines (Fig. 9). |
| In the text | |
 |
Fig. 11. Left panel: three first moments of the model cube for NGC 1672. The RA-Dec offsets are in parsec. The velocity color scales are in km s−1. The cube corresponds to the best PV fit, with a BH mass of 5.0 × 107 M⊙, and an inclination of 66°. Right panel: three moments for the observations (TM1 only). The RA-Dec offsets are in arcsec with respect to the phase center. |
| In the text | |
 |
Fig. 12. Least-squares fitting between the observed and modeled PV diagram (black curve) and 3D cube (red curve) as a function of inclination of the torus (left panel) and the black hole mass (right panel). The criterion is defined in Sect. 4.4.2. The curves have been slightly translated vertically for clarity. If there is a minimum for inclination, there is none for MBH, and larger masses are preferred, as for NGC 1672. |
| In the text | |
 |
Fig. 13. Same as Fig. 10 for NGC 613, without any black hole (left panel), with a black hole of 7.4 × 106 M⊙ (middle panel), and the best fit: 3.7 × 107 M⊙, as derived from the MBH-σ relation (Table 6) (right panel). The inclination of the torus is i = 46°. The mass model is that based on the galfit decomposition, and the predicted circular velocity is reproduced in blue lines (Fig. 9). |
| In the text | |
 |
Fig. 14. Same as Fig. 11 for NGC 613 (left is the model, right the observations). The cube corresponds to the best PV fit, with a BH mass of 3.7 × 107 M⊙ and an inclination of 46°. |
| In the text | |
 |
Fig. 15. Same as Fig. 10 for NGC 1326, without any black hole, i = 60° (left panel); with a black hole of 3 × 107 M⊙ from the MBH-σ relation, i = 60° (middle panel); and the best fit: 6.5 × 106 M⊙, with i = 60° (right panel). |
| In the text | |
 |
Fig. 16. Same as Fig. 11 for NGC 1326 (left is the model, right the observations). The cube corresponds to the best PV fit, with a BH mass of 6.5 × 106 M⊙ and an inclination of 60°. |
| In the text | |
 |
Fig. 17. Same as Fig. 10 for NGC 1365, without any black hole (left panel), with a black hole of 6.9 × 107 M⊙ from the MBH-σ relation (middle panel), and the best fit: 4 × 106 M⊙ (right panel). The adopted inclination i = 63° is from the galaxy to be conservative. Higher BH masss would be derived with the lower 27° inclination estimated for the torus. |
| In the text | |
 |
Fig. 18. Same as Fig. 11 for NGC 1365 (left is the model, right the observations). The cube corresponds to the best PV fit, with a BH mass of 4 × 106 M⊙ and an inclination of 63°. |
| In the text | |
 |
Fig. 19. Same as Fig. 10 for NGC 1566, without any black hole (left panel), with a black hole of 1.35 × 107 M⊙ from the MBH-σ relation (middle panel), and the best fit: 6.7 × 106 M⊙ (right panel). As for NGC 1365, the adopted inclination i = 48° is from the galaxy. |
| In the text | |
 |
Fig. 20. Same as Fig. 11 for NGC 1566 (left is the model, right the observations). The cube corresponds to the best PV fit, with a BH mass of 6.7 × 106 M⊙ and an inclination of 48°. |
| In the text | |
 |
Fig. 21. Location of our galaxies in the MBH-σ relation, compiled by van den Bosch (2016), represented by the gray points and the fitted line, of slope 5.35. Our galaxies are in red, while in blue are plotted other values recently obtained from the CO line: NGC 1097 (Onishi et al. 2015), NGC 1332 (Barth et al. 2016), NGC 3665 (Onishi et al. 2017), NGC 4429 (Davis et al. 2018a), NGC 4526 (Davis et al. 2013), NGC 4697 (Davis et al. 2017). Previous estimations of the BH masses of our sample galaxies are also plotted in green (Table 6), turquoise and pink (Cols. 2 and 3 in Table 7). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.