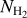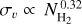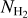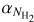| Issue |
A&A
Volume 660, April 2022
|
|
|---|---|---|
| Article Number | A56 | |
| Number of page(s) | 20 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202141699 | |
| Published online | 13 April 2022 | |
Velocity structure of the 50 pc long NGC 6334 filamentary cloud
Hints of multiple compressions and their impact on the cloud properties
1
Aix Marseille Univ., CNRS, CNES, LAM,
Marseille,
France
2
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP,
Rua das Estrelas,
4150–762
Porto,
Portugal
3
Division of Science, National Astronomical Observatory of Japan,
2-21-1 Osawa,
Mitaka,
Tokyo
181–8588,
Japan
e-mail: doris.arzoumanian@nao.ac.jp
4
Department for Physics, Engineering Physics and Astrophysics, Queen’s University,
Kingston,
ON,
K7L 3N6,
Canada
5
Laboratoire d’Astrophysique (AIM), CEA/DRF, CNRS, Université Paris-Saclay, Université Paris Diderot,
Sorbonne Paris Cité,
91191
Gif-sur-Yvette,
France
6
Department of Physics, Graduate School of Science, Nagoya University,
Furo-cho, Chikusa-ku, Nagoya,
Aichi
464–8602,
Japan
7
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77,
50937
Köln,
Germany
8
Astronomy Section, Nagoya City Science Museum,
2-17-1 Sakae, Naka-ku, Nagoya,
Aichi
460–0008,
Japan
Received:
2
July
2021
Accepted:
10
January
2022
Context. The interstellar medium is observed to be organized in filamentary structures, and in neutral (H I) and ionized (H II) bubbles. The expanding nature of these bubbles shapes the surrounding medium and possibly plays a role in the formation and evolution of the interstellar filaments. The impact of the expansion of these bubbles on the interstellar medium is not well understood.
Aims. Our aim is to describe the kinematics of a filamentary molecular cloud forming high-mass stars and hosting multiple H II regions in order to study the possible environmental impact on the properties of molecular filaments.
Methods. We present APEX 13CO and C18O(2–1) mapping observations of the 10 × 50 pc NGC 6334 molecular cloud complex. We investigated the gas velocity structure along and across the 50 pc long cloud and toward velocity-coherent filaments (VCFs).
Results. The NGC 6334 complex is observed to have a coherent velocity structure smoothly varying by ~5 km s−1 over its 50 pc elongation parallel to the Galactic plane. We identify a sample of 75 VCFs in the C18O(2–1) position-position-velocity cube and present the properties of 47 VCFs with a length ≳1 pc (five beams). We measure a large number of velocity gradients along the VCFs. The amplitudes of these velocity gradients and the velocity dispersion measured along the crests increase with the column density of the VCFs. We derive the column density and velocity power spectra of the VCFs. These power spectra are well represented with power laws showing similar slopes for the two quantities (with a mean of about −2), although some differ by up to a factor of 2. The position velocity diagrams perpendicular to three VCFs (selected from different physical environments) show the V-shaped velocity pattern corresponding to a bent structure in velocity space with the filament at the tip of the V surrounded by an extended structure connected to it with a velocity gradient. This velocity structure is qualitatively similar to that resulting from numerical simulations of filament formation from large-scale compression from propagating shock fronts. In addition, the radial profiles perpendicular to these VCFs hint to small-scale internal impacts from neighboring H II bubbles on two of them, while the third is mostly unaffected.
Conclusions. The observed opposite curvature in velocity space (V- and A-shaped) toward the VCFs points to various origins of large-scale external compressions from propagating H I bubbles. This suggests the plausible importance of multiple H I compressions, separated in space and time, in the formation and evolution of molecular clouds and their star formation history. These atomic compressions due to past and distant star formation events are complemented by the impact of H II bubbles from present time and local star formation activity.
Key words: stars: formation / ISM: clouds / ISM: kinematics and dynamics / ISM: structure / submillimeter: ISM
© D. Arzoumanian et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Observations of the interstellar medium (ISM), especially its molecular component, reveal the impressive organization of the dust and gas into complex networks of filaments (e.g., Schneider & Elmegreen 1979; Molinari et al. 2010; Men’shchikov et al. 2010; Umemoto et al. 2017; Mattern et al. 2018; Schisano et al. 2020). In molecular clouds, gravitationally unstable filaments are now identified as the main birthplaces of individual solar-type stars (e.g., André et al. 2010, 2014; Tafalla & Hacar 2015), while the hubs that formed at their intersections are associated with stellar clusters and high-mass stars (Myers 2009; Schneider et al. 2012; Peretto et al. 2014; Kumar et al. 2020, 2022). Filamentary structures and hubs are also observed in the ISM of external galaxies (e.g., the Magellanic clouds, Fukui et al. 2019). This extragalactic filamentary ISM, now revealed thanks to high angular resolution observations with the Atacama Large Millimeter Array (ALMA), seem to be associated with the star formation process similar to that in our Galaxy, suggesting that filaments are also important for star formation in galaxies in general. An important question, which is still highly debated, is to understand the formation and evolution of these filaments and to describe the physical processes leading to their fragmentation into star-forming cores.
The matter cycle in the ISM is regulated by heating and cooling processes, and the compression and expansion of this interstellar material. There are two broad types of compressions and expansions that affect both distant (~100 pc scale) and local (a few parsecs) environments: (1) large-scale (~100 pc) external, mostly neutral, compressions from expansion of H I shells or supershells (e.g., Dawson et al. 2011; Bracco et al. 2020) generated mainly by supernovae, and (2) small-scale (~1–5 pc) local and internal compressions, mostly ionized, due to present-time stellar feedback from mainly H II regions, stellar winds, and outflows (e.g., Russeil et al. 2016).
Recent theoretical models clearly demonstrate the role of expanding H I shells for the formation of molecular clouds (e.g., Hennebelle et al. 2008; Heitsch et al. 2009; Inoue & Inutsuka 2009). In particular, these models highlight the importance of multiple compressions for the formation of magnetized filamentary molecular clouds (e.g., Inutsuka et al. 2015; Iwasaki et al. 2019). The typical timescale of such compressions is estimated in the Galactic disk to be on average ~1 Myr (McKee & Ostriker 1977; Inutsuka et al. 2015). Thus, the formation of molecular clouds may last from a few million years to ~10 Myr or more (see, e.g., Kobayashi et al. 2017). These successive compressions may continuously alter the density, velocity, and magnetic field structures of the clouds, and also have a strong impact on the formation of new generations of filaments and consequently that of stars. While the first generation of stars form and impact their (local) surroundings (through outflow, jets, winds, and ionizing radiation), new cold matter is continuously assembled replenishing the sites of star formation (i.e., filaments and hubs). This matter replenishment may be channeled from within the cloud itself through molecular filaments toward dense ridge-like main filaments (Schneider et al. 2010; Palmeirim et al. 2013) or toward hubs (Myers 2009; Peretto et al. 2013, 2014; Treviño-Morales et al. 2019). Matter can also be brought into the system (the cloud) by a new event of external collision (e.g., Fukui et al. 2018b). Arzoumanian et al. (2018) identified, in position-velocity (PV) diagrams, extended structures with mean line-of-sight (LOS) velocities offset with respect to, and connected to the velocity of, a filament. They suggested a multi-interaction scenario where sheet-like extended structures interact, in space and time, with a star-forming filament, and are responsible for its compression or disruption. Arzoumanian et al. (2018) also identified a bent velocity structure in the PV space. They showed that such a V- or Λ-shaped velocity structure can result from the filament formation process by shock compression as proposed by the theoretical model of Inoue et al. (2018). In this model, a filament is formed due to convergence of a flow of matter generated by the bending of the ambient magnetic field structure induced by an interstellar shock compression (see also Inoue & Fukui 2013; Vaidya et al. 2013). This velocity structure has also been observed toward another filament, the Musca filament (Bonne et al. 2020). More recently, in a theoretical study, Abe et al. (2021) proposed a classification of filament formation mechanisms resulting from the variation in the relative importance between the shock velocity, the turbulence, and the magnetic field strength (see also the theoretical study by Chen et al. 2020a).
To make progress in our understanding of the impact of these two types of compressions, internal-ionized and external-neutral, on star-forming molecular clouds, in this paper we analyze the velocity structure of the NGC 6334 high-mass star-forming complex as a whole and on smaller scales toward dense filaments, both in the vicinity and away from local stellar feedback and H II regions. NGC 6334 is a well-studied molecular cloud complex (see Persi & Tapia 2008, for an extensive review) at a relatively nearby distance of 1.3 ± 0.3 kpc (Chibueze et al. 2014). NGC 6334 looks like a cat’s paw with a large number of H II regions (Persi & Tapia 2010; Russeil et al. 2016, and see Fig. 1) surrounding an elongated filamentary cloud that is very bright at (sub)millimeter wavelengths (Kraemer & Jackson 1999; Matthews et al. 2008; Russeil et al. 2013; Zernickel et al. 2013; Tigé et al. 2017) and actively forming high-mass stars (Sandell 2000; McCutcheon et al. 2000; Muñoz et al. 2007; Qiu et al. 2011). This filamentary cloud is dominated by a 10 pc long main filament with a line mass ranging from Mline ~ 500 M⊙/pc to ~2000 M⊙/pc over its crest (André et al. 2016) and it is fragmented into a series of cores with a mean mass ~10 M⊙ (e.g., Shimajiri et al. 2019). The filament inner width is observed to be on the order of 0.1 pc (André et al. 2016), compatible with the findings derived from the statistical analysis of dust continuum Her schel observations of nearby and less massive filaments (Arzoumanian et al. 2011, 2019; Koch & Rosolowsky 2015). This similarity suggests that the gravitational fragmentation of ~0.1 pc wide filaments may also be the main mode of intermediate-mass star formation (Shimajiri et al. 2019; André et al. 2019).
In this paper we study the velocity structure of the ~50pc long NGC 6334 high-mass star-forming region as traced by 12CO(2–1), 13CO(2–1), and C18O(2–1) molecular line emission. This paper is organized as follows. In Sect. 2, we describe the observational data used in the analysis. In Sect. 3, we present the velocity structure observed toward the 50 pc long NGC 6334 cloud. In Sects. 4, 5, and 6, we analyze in greater detail the velocity structure along and across a sample of velocity-coherent filaments identified toward the studied field. In Sect. 7, we discuss the possible physical origin of the observed velocity structures of the cloud and filaments, and suggest a scenario for the dynamical formation of this high-mass star-forming filamentary cloud. We give a summary of the analysis and results in Sect. 8.
2 Observations
2.1 13CO(2–1) and C18O(2–1) APEX data
The on-the-fly (OTF) mapping observations of the 13CO(2–1) and C18O(2–1) lines were conducted in the frame of the program 091.F-9512(A) with the Atacama Pathfinder Experiment (APEX) and the Swedish Heterodyne Facility Instrument (SHeFI) (Vassilev et al. 2008). The data reduction and the first analysis of these data were performed by Zernickel (2015). We summarize here the data characteristics. The spectral range is 216.8–220.8 GHz with a spectral resolution of 88.5 kHz (corresponding to a velocity resolution of 0.12 km s−1 at 220 GHz). The spectra were smoothed to a velocity resolution of 0.3 km s−1 to give a final average root mean square (rms) noise per 0.3 km s−1 channel of 0.44 K for 13CO and 0.55 K for C18O. The final angular resolution of both 13CO and C18O cubes is 30.″2 (0.19 pc at the 1.3 kpc distance of the cloud). Both cubes were reprojected on the same grid with a pixel size of 14.″3. The longitude range of the map is from 350.″4 to 352.″6 covering the well-known NGC 6334 main star-forming region, and also the GM 24 region to the west and the inter-filament region toward NGC 6357 to the east (see Fig. 1). Zernickel (2015) notes that due to the offset position contamination by foreground and background clouds, spectral absorption features at −141, −88, −33, −17, and +24 km s−1 are seen over the whole map (see Fig. 4. of Zernickel 2015). In the following we focus the analysis on the [−20, +10] km s−1 velocity range that covers the kinematics of the gas associated with NGC 6334.
 |
Fig. 1 Herschel maps toward the NGC 6334 cloud. Top: column density map of the NGC 6334 cloud derived from Herschel HOBYS data (Motte et al. 2010) (see explanation in Sect. 2.4). The map is at the resolution of 18.″2 and the contours are at column densities of 1.8 and 5 × 1022 cm-2. The coverage of the APEX observations is shown in magenta. The three identified subregions are indicated (in yellow) from east to west: the inter-filament system (IFS) for 352.″3 > l > 351.″8, the main filament system (MFS) for 351.″8 > l > 351″, and the GM 24 filament system (GM24FS) for 351° > l > 350.″4. Middle: dust temperature map at 36.″3 (see Sect. 2.4). The contours are the same as in the top panel. Bottom: color composite image of NGC 6334 derived from Herschel data, where the 70 µm, 160 µm, and 250 µm intensities are represented in blue, green, and red, respectively. This image is from Causi et al. (2016). The contours trace the column density as in the top panel. The red circles show the positions and sizes of the H II regions from Anderson et al. (2014) and Langston et al. (2000), and are the same as those plotted in Fig. 1 of Russeil et al. (2016). |
2.2 12CO(2–1) NANTEN2 data
We included in the analysis the 12CO(2 – 1) velocity cubes obtained with the 4 m millimeter/sub-millimeter radio telescope of Nagoya University (NANTEN2) and described in Fukui et al. (2018b). The final beam size of the data cube we used in this work is 90° (0.57 pc at the 1.3 kpc distance of the cloud), with a velocity resolution of 0.08 km s−1, and a typical rms noise level of 1.1 K ch−1.
2.3 H I data
We complemented the molecular line data with the atomic H I cube observed as part of the Southern Galactic Plane Survey1 and described in McClure-Griffiths et al. (2005) and Haverkorn et al. (2006). This data cube has angular and spectral resolutions of 117° (0.73 pc at the distance of the cloud) and 0.82 km s−1, respectively.
2.4 Herschel column density and dust temperature maps
In the analysis presented in this paper, we also make use of the column density (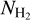 ) and dust temperature maps (Tdust) derived from Herschel imaging data taken as part of the HOBYS key program (Motte et al. 2010).
) and dust temperature maps (Tdust) derived from Herschel imaging data taken as part of the HOBYS key program (Motte et al. 2010).
The 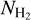 and Tdust maps were produced following the same procedure as described in some of the papers analyzing Herschel data, such as Könyves et al. (2015) and Schisano et al. (2020). These
and Tdust maps were produced following the same procedure as described in some of the papers analyzing Herschel data, such as Könyves et al. (2015) and Schisano et al. (2020). These 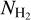 maps were calculated adopting a mean molecular weight per hydrogen molecule
maps were calculated adopting a mean molecular weight per hydrogen molecule 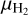 = 2.8 (e.g., Kauffmann et al. 2008) and have an estimated accuracy of better than ~50% (see Könyves et al. 2015; Roy et al. 2013, Roy et al. 2014). We derived both standard
= 2.8 (e.g., Kauffmann et al. 2008) and have an estimated accuracy of better than ~50% (see Könyves et al. 2015; Roy et al. 2013, Roy et al. 2014). We derived both standard 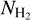 maps at the 36.″3 (half power beam width, HPBW) resolution of Herschel/SPIRE 500 µm data and high-resolution
maps at the 36.″3 (half power beam width, HPBW) resolution of Herschel/SPIRE 500 µm data and high-resolution 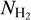 maps at the 18.″2 resolution of Herschel/SPIRE 250 µm data. The 18.″2 resolution corresponds to 0.11 pc at the 1.3 kpc distance of the cloud. The multi-scale decomposition method used to derive Herschel column density maps at 18.″2 resolution is described in detail in Appendix A of Palmeirim et al. (2013). We here used the module hires of the getsf extraction code (Men’shchikov 2021) to produce these
maps at the 18.″2 resolution of Herschel/SPIRE 250 µm data. The 18.″2 resolution corresponds to 0.11 pc at the 1.3 kpc distance of the cloud. The multi-scale decomposition method used to derive Herschel column density maps at 18.″2 resolution is described in detail in Appendix A of Palmeirim et al. (2013). We here used the module hires of the getsf extraction code (Men’shchikov 2021) to produce these 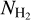 and Tdust maps. We also smoothed the 18.″2
and Tdust maps. We also smoothed the 18.″2 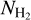 map to the resolution of the APEX CO maps at 30.″2. In this paper all the
map to the resolution of the APEX CO maps at 30.″2. In this paper all the 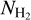 and Tdust values correspond to those derived from Herschel data. Figure 1 shows the gas column density and the dust temperature maps toward the NGC 6334 complex. The footprint of the APEX maps is also shown.
and Tdust values correspond to those derived from Herschel data. Figure 1 shows the gas column density and the dust temperature maps toward the NGC 6334 complex. The footprint of the APEX maps is also shown.
In the remainder of the paper, we refer to the entire region studied in this work as the NGC 6334 complex. We further identify three subregions as indicated in Fig. 1-top: the inter-filament system (IFS) for 352.″3 > l > 351.″8, the main filament system (MFS) for 351.″8 > l > 351″, and the GM 24 filament system (GM24FS) for 351° > l > 350.″4. The IFS refers to the filamentary region that connects the NGC 6334 main star-forming region to the NGC 6357 region at l ~ 353° (Russeil et al. 2010). The GM24FS corresponds to the filamentary structures observed in the west toward the GM 24 nebula (Fukui et al. 2018a).
 |
Fig. 2 Integrated intensity maps, in units of K kms-1, of the 12CO(2–1),13CO(2-1), and C18O(2–1) emission (from top to bottom). The 13CO(2–1) and C18O(2–1) maps have a spatial resolution of 30.′2 (corresponding to 0.19 pc at the 1.3 kpc distance of the cloud) and the emission is integrated over the LSR velocity range -12 to 4 kms-1. The 12CO(2–1) map has a spatial resolution of 90° and the emission is integrated over the LSR velocity range -25 to 12 kms-1. The blue contours trace column densities of 1.8 and 5.0 × 1022 cm-2 derived from Herschel data (at 36.″3) and are the same in all three panels. |
3 Velocity structure of the 50 pc long NGC 6334 cloud
3.1 Velocity integrated intensity maps
Figure 2 presents the velocity integrated intensity maps for the three lines observed toward the NGC 6334 molecular cloud complex. For the 13CO(2–1) and C18O(2–1) lines the emission is integrated for the local standard of rest (LSR) velocity range between –12 and 4 kms−1, which encompasses the bulk of the emission associated with the complex as can be seen on the spectra averaged across the field (Fig. 3-bottom). Gaussian fits to the average spectra of the 13CO(2–1) and C18O(2–1) lines yield a mean LSR velocity of the cloud of about −3.6 km s−1 and a FWHM velocity width of about 5 km s−1 (similar for the two lines). This indicates the coherence in velocity of the 50 pc long NGC 6334 complex analyzed here.
The C18O(2–1) integrated emission traces the elongated filamentary structures of the cloud with column densities 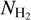 > 1.8 × 1022 cm−2 derived from Herschel data. The 13CO and 12CO integrated intensity maps show more extended structures toward the cloud.
> 1.8 × 1022 cm−2 derived from Herschel data. The 13CO and 12CO integrated intensity maps show more extended structures toward the cloud.
We derived the 13CO(2–1)/C18O(2–1) ratio maps from the peak intensity observed over the LSR velocity range −12 to 4 km s−1, and estimated the mean optical depth of the lines assuming a mean value of the abundance ratio [13CO]/[C18O] = 5.5 (Wilson & Rood 1994) in the local ISM (see details in Appendix A). As shown in Fig. A.1, the C18O(2–1) emission is optically thin all over the observed field. The 13CO(2–1) emission is mostly optically thin, but shows optical depth values up to ~4 in the densest regions. The 12CO(2–1) emission is optically thick.
This filamentary molecular cloud is associated with the atomic medium traced with the atomic H I 21 cm line. The mean H I spectrum (Fig. 3-top) shows a dip at velocities of about −3.6 km s−1 associated with the molecular gas of the NGC 6334 complex. The observed extended emission of the H I spectrum around the velocities of the molecular cloud suggests that this cloud is embedded in and probably formed from a large-scale atomic medium spanning a wider range in velocities.
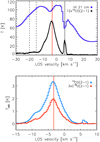 |
Fig. 3 Positionally averaged spectra for the observed molecular and atomic emission. The spectra are averaged across the same observed region defined by the footprint of the APEX maps (cf. Fig. 2). The red vertical line indicates the peak position of the 13CO(2–1) and C18O(2–1) emission at -3.3 kms-1. The solid black vertical line gives the position of the extended emission at 6 km s-1, observed in emission and absorption, in 12CO(2–1) and HI, respectively. The dashed black vertical lines indicate the extent of the cloud emission identified in the 12CO(2–1) V1 velocity range (see Sect. 3.2). |
3.2 Position velocity diagrams
Figure 4 shows position-velocity (PV) diagrams along the Galactic longitude and averaged in latitude. These PV diagrams trace a coherent velocity structure smoothly varying from ~0 km s−1 to ~ − 5, −10 km s−1 from east to west over the ~50 pc (~2.″2) long filamentary cloud, which is impressively coherent in velocity with an overall velocity range of only ~5 km s−1 (FWHM of the averaged 13CO and C18O spectra shown in Fig. 3). Such large-scale (≳10 pc) velocity coherent elongated collections of filamentary structures have also been identified recently in a number of observational studies, and are referred to as giant molecular filaments (e.g., Ragan et al. 2014; Kohno et al. 2022) or Galactic bones (e.g., Goodman et al. 2014; Zucker et al. 2015). Zernickel (2015) have investigated the possible link between the observed ~0.1 km s−1 pc−1 velocity gradient along the NGC 6334 complex and the velocity structure expected from the Galactic rotation, and concluded that this velocity gradient is larger than what would be expected from Galactic rotation models at the location of the NGC 6334 complex. Hence, this velocity gradient may not result from the Galactic rotation and may have a different origin.
Averaging the emission in latitude increases the signal-to-noise ratio (S/N), which makes it possible to detect the faint 12CO(2–1) emission at LRS velocities between −20 and −12 km s−1. This extended component spanning velocities from about −20 to −12 km s−1 where it connects to the velocity of the denser gas of the NGC 6334 cloud has been suggested by Fukui et al. (2018b) to trace an interaction event (started a few million years ago) between the cloud seen now at ~−20 km s−1 and the NGC 6334 complex at the mean velocity of ~− 3 km s−1 (velocity channel maps are shown in Fig. 5 and described in Sect. 3.3). Bridge features connecting two clouds in velocity space have been used in observations to trace physical interactions between clouds with distinct bulk velocities (e.g., Torii et al. 2011; Fukui et al. 2018b; Enokiya et al. 2021) and have been reproduced in numerical simulations of cloud-cloud collision (Takahira et al. 2014; Haworth et al. 2015a,b; Priestley & Whitworth 2021). We note, however, that velocity bridges are not unambiguous signatures of cloud-cloud collision. Additional evidence of physical connection (e.g., similar distance estimates and complementarity in spatial distribution of the velocity components of the two clouds) are also needed to further confirm the interaction (see, e.g., Fukui et al. 2018c).
The 12CO(2–1) PV map shows a narrow component at 6 km s−1, which is also detected in 13CO(2–1) at Galactic longitudes around l ~ 350.″7, 351.″7, and 352.″5. This narrow component in velocity space has been reported by Radhakrishnan et al. (1972) and Russeil et al. (2016), from the analysis of H I spectra, to be associated with a foreground extended cloudlayerclose to the Sun andnotassociated with the NGC 6334 complex.
3.3 Velocity channel maps
Figure 5 presents velocity channel maps derived from the 12CO(2–1) and 13CO(2–1) cubes. We do not show here the channel maps derived from the C18O(2–1) cubes, which are very similar to the 13CO channel maps.
The V1 channel map is derived from the integration of the intensity over the velocity range [−21, −12] km s−1 tracing the cloud with the blueshifted velocity suggested to be interacting with the NGC 6334 complex (see Sect. 3.2, and Fukui et al. 2018b). The V2 channel maps (V2a, V2b, and V2c) trace the main emission of NGC 6334 in the velocity range [−12, 0] km s−1, where the 50 pc filamentary structures are detected. The V3 channel map traces the main extension of the cloud toward the east and the bulk emission of the inter-region filaments connecting the NGC 6334 and NGC 6357 clouds (Russeil et al. 2010); hereafter we call this extension IFS (see Fig. 1, top). The NGC 6357 complex is located on the east around the 353° Galactic longitude and is observed to be connected in velocity to the NGC 6334 complex (Fukui et al. 2018b). The V4 channel map derived from the integration of the emission in the velocity range [5, 10] km s−1, traces extended structures at a mean velocity of ~6 km s−1 (see Fig. 5, top), thought to be a foreground gas structure close to the Sun (Radhakrishnan et al. 1972; Russeil et al. 2016).
 |
Fig. 4 Position–velocity (PV) diagrams in units of K(TMB) for the 12CO(2-1), 13CO(2-1), and C18O(2-1) emission (from top to bottom). The 13CO(2-1) and C18O(2-1) maps have a spatial resolution of 30.″2. The 12CO(2-1) map has a spatial resolution of 90″. These PV diagrams are averaged in latitude across the cloud for 0.″4 = b = 1″. The white contours indicate the C18O(2–1) intensity at 1 K and are the same for the three panels. In the top panel the thick white contour corresponds to the 12CO(2–1) intensity at 0.6 K. |
 |
Fig. 5 Velocity channel maps in units of K kms-1 for the 12CO(2–1) and 13CO(2–1) emission (left and right, respectively). The velocity ranges of the channel maps are indicated at the bottom left of each panel. The range of the color scale (indicated by the bar for each panel) is different for each plot. This scale was chosen to represent the dynamical range of the emission for each velocity channel map. |
4 Identification of velocity-coherent filaments (VCFs)
In the following we describe the multi-velocity-component Gaussian fitting of the observed lines. We then present the method used to trace elongated crests in three-dimensional (3D) position-position-velocity (PPV) space and identify velocity-coherent filaments (VCFs). For this analysis, we use the C18O(2–1) cube at the spatial resolution of 30.″2 (projected onto a grid with 14.″3 pixel size) and 0.3 km s−1 velocity resolution. We analyze the C18O(2–1) emission, which is optically thin over the cloud (see Appendix A).
4.1 Multi-component spectral fitting
We modeled the observed cube by least-squares fitting of the C18O(2–1) spectrum at each pixel position of the 2D positionposition (PP) space. We assume that the observed spectrum is the sum of several velocity components with line shapes close to Gaussian functions. We thus use a multi-Gaussian function with n velocity components. The model spectra, at each pixel of the (x, y) PP space, is thus the sum of n Gaussians
![$T_{{\rm{MB}}}^{{\rm{model}}}\left(\upsilon \right) = \sum\limits_i^n {T_i^{{\rm{peak}}}} \exp \left[{ - {{{{\left({\upsilon - {\upsilon _i}} \right)}^2}} \over {2\sigma _{{\upsilon _i}}^2}}} \right],$](/articles/aa/full_html/2022/04/aa41699-21/aa41699-21-eq11.png) (1)
(1)
where 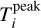 , υi, and
, υi, and 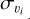 are the line peak temperature [K], the centroid velocity [km s−1], and the velocity dispersion [km s−1] of the ith velocity component. The first step is to identify the total number of velocity components n of each spectrum (see also Appendix B). This is done using the first and second derivatives of the spectrum with emission
are the line peak temperature [K], the centroid velocity [km s−1], and the velocity dispersion [km s−1] of the ith velocity component. The first step is to identify the total number of velocity components n of each spectrum (see also Appendix B). This is done using the first and second derivatives of the spectrum with emission 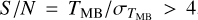 , where
, where 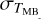 is the rms of the spectrum calculated from emission free velocities. The identified n-components are fitted using Eq. (1). Then the fitted velocity components with peak temperature
is the rms of the spectrum calculated from emission free velocities. The identified n-components are fitted using Eq. (1). Then the fitted velocity components with peak temperature 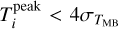 and the components υi with a minimal separation with its neighboring components υi+1 smaller than five times the velocity resolution of 0.3 km s−1 (i.e., |υi − υi+1| < 1.5 km s−1) are discarded. The algorithm continues iterating until the remaining fitted components satisfy the S/N and the velocity separation conditions (see Fig. B.1 for an example). We performed several tests comparing the observed and modeled spectra to find the parameters that most closely reproduce the observations, and set a S/N = 4 for the peak intensity and a minimum velocity separation of five times the velocity resolution of 0.3 km s−1. In Appendix B we show the velocity integrated intensity maps of the observed and modeled cubes, and the ratio map between the observed and model cubes R(x, y, υ) =
and the components υi with a minimal separation with its neighboring components υi+1 smaller than five times the velocity resolution of 0.3 km s−1 (i.e., |υi − υi+1| < 1.5 km s−1) are discarded. The algorithm continues iterating until the remaining fitted components satisfy the S/N and the velocity separation conditions (see Fig. B.1 for an example). We performed several tests comparing the observed and modeled spectra to find the parameters that most closely reproduce the observations, and set a S/N = 4 for the peak intensity and a minimum velocity separation of five times the velocity resolution of 0.3 km s−1. In Appendix B we show the velocity integrated intensity maps of the observed and modeled cubes, and the ratio map between the observed and model cubes R(x, y, υ) = 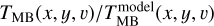 . The ratio map has a median, mean, and standard deviation of 1.02, 1.10, and 0.46, respectively, suggesting that the modeled cube represents the observations well. A total of 13283 spectra were fitted. As can be seen in Fig. B.3, more than 88% of the spectra are fitted with a single velocity component. Only ~10% and ~2% of the spectra required two or three velocity components to describe the observations, respectively.
. The ratio map has a median, mean, and standard deviation of 1.02, 1.10, and 0.46, respectively, suggesting that the modeled cube represents the observations well. A total of 13283 spectra were fitted. As can be seen in Fig. B.3, more than 88% of the spectra are fitted with a single velocity component. Only ~10% and ~2% of the spectra required two or three velocity components to describe the observations, respectively.
 |
Fig. 6 Integrated intensity map, in units of K km s-1, of the C18O(2–1) emission (same as Fig. 2). The colored curves show the crests of the velocity coherent filaments (VCFs) identified using CRISPy. The crests with total length (L) larger than 10 pixels are traced in cyan and numbered. VCFs 1, 32, and 47 are identified with red arrows. The dotted purple boxes indicate the regions from which the averaged radial profiles and the PV maps are derived (see Sects. 6.1 and 6.2). The white crosses indicate the seven infrared high-mass star-forming regions, which are usually referred to as sources I(N), E, I, II, III, IV, and V (from east to west) (Persi & Tapia 2008; Arzoumanian et al. 2021). Source I is indicated with the green arrow. |
4.2 VCF identification
We traced the crests of elongated filamentary structures running CRISPy on the modeled PPV cube. CRISPy (Chen et al. 2020b) is based on the Subspace Constrained Mean Shift Algorithm (developed by Chen et al. 2014, Chen et al. 2015).
We ran CRISPy setting a minimum intensity detection threshold of 2 K (S/N ~ 4) and a smoothing length of 2 pixels (~beam). We subsequently gridded the raw CRISPy result onto our modeled cube and pruned away extra branches in each ridge from its longest path using the algorithm and the methods by Chen et al. (2020b). This 3D graph-theory-based pruning method is based on the 2D software developed by Koch & Rosolowsky (2015), and the current implementation of this 3D version simply prunes all structures that are not part of the longest path without the need for user inputs. Further details on the pruning methods are detailed in those papers.
The pruned 3D skeleton is then referenced to sort the modeled velocity components into VCFs using the method described in Chen et al. (2020b), with a maximum velocity separation of 0.9 km s−1 (~3 times the velocity resolution). This analysis yields a total of 75 VCFs identified toward the whole studied region at the angular and spectral resolutions of 30.″2 and 0.3 km s−1, respectively. In the following we present the analysis of 47 VCFs out of the 75 VCFs, that have a length greater than ~5× beam (0.9 pc and 10 pixels). We selected this length to ensure the sampled VCFs have a minimum aspect ratio of 1:5 at our angular resolution, thus distinctively longer than what is considered a core. This selection also provides a minimum number of 10 pixels to measure statistical properties (e.g., mean, dispersion) along the crests of the VCFs.
5 Statistical properties of the identified 47 VCFs
Figure 6 shows the derived crests of the 75 VCFs overplotted on the C18O(2–1) velocity integrated intensity map. Table 1 summarizes the main properties of the 47 VCFs.
Properties of the 47 velocity-coherent filaments identified toward NGC 6334 in the 3D PPV C18O(2–1) cube at the spatial and velocity resolutions of 30.″2 and 0.3 km s−1, respectively.
 |
Fig. 7 Scatter plots of measured parameters for the 47 VCFs. The values are averaged along the crests of the VCFs. The data points in red, yellow, and blue indicate VCFs 1, 32, and 47, respectively. Left: velocity dispersion vs. column density. The horizontal and vertical bars indicate the 1s dispersions of |
5.1 Mean properties along the VCF crests
The mean length of the VCFs is ~2 pc with some of them as long as ~5 pc. They span a column density range of an order of magnitude about a mean value of ~4 × 1022 cm−2 (as derived from Herschel data). The LOS averaged dust temperature map as derived from Herschel data indicates a mean value of ~20 K, which is on average larger than the dust temperature observed toward low-mass star-forming regions of the Gould Belt (e.g., Arzoumanian et al. 2019), indicating the possible influence of young (massive) stars in heating the dense gas (at least the external layers of the filaments). This heating may originate from the surroundings of the filaments, from neighboring H II regions for example, or it may originate from inside the filaments, from young massive stars or star clusters forming along the filaments (see discussion in Sect. 6.1 below). These filaments are mostly thermally supercritical with line masses (Mline) greater than the critical equilibrium value for isothermal cylinders 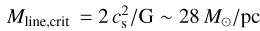 for a gas temperature of 20 K (e.g., Ostriker 1964; Inutsuka & Miyama 1997). The mass per unit length of the VCFs is calculated as
for a gas temperature of 20 K (e.g., Ostriker 1964; Inutsuka & Miyama 1997). The mass per unit length of the VCFs is calculated as 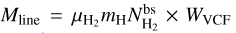 , where WVCF = 0.13 pc is the VCF width2,
, where WVCF = 0.13 pc is the VCF width2, 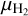 = 2.8 is the mean molecular weight per hydrogen molecule, mH is the mass of a hydrogen atom, and
= 2.8 is the mean molecular weight per hydrogen molecule, mH is the mass of a hydrogen atom, and 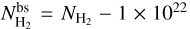 cm−2 is the background subtracted column density (derived from Herschel data) averaged along the VCF. The background value ~1 × 1022 cm−2 is the mean
cm−2 is the background subtracted column density (derived from Herschel data) averaged along the VCF. The background value ~1 × 1022 cm−2 is the mean 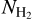 toward the regions of the molecular cloud not traced by C18O (see also the discussion of the similar background value estimated in this region by Arzoumanian et al. 2021).
toward the regions of the molecular cloud not traced by C18O (see also the discussion of the similar background value estimated in this region by Arzoumanian et al. 2021).
Figure 7, left shows the mean velocity dispersions of the VCFs as a function of their mean column density. The mean velocity dispersion corresponds to the mean value of the fitted velocity dispersions (i.e., line width) of the corresponding velocity component at each position along the VCF. The mean velocity dispersions of the VCFs show an increasing trend as a function of their mean column density with a best fit linear relation of 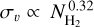 (Fig. 7, left). This relation is similar to what was derived for the sample of thermally supercritical filaments presented in Arzoumanian et al. (2013) and was interpreted as resulting from the evolution of the filaments by accretion of surrounding matter. We measure many velocity gradients along the VCF crests. We quantify the velocity gradients with linear 1D fits of the observed velocity along the crests (see Fig. 10, middle). We find a large scatter in the measured velocity gradients for filaments with
(Fig. 7, left). This relation is similar to what was derived for the sample of thermally supercritical filaments presented in Arzoumanian et al. (2013) and was interpreted as resulting from the evolution of the filaments by accretion of surrounding matter. We measure many velocity gradients along the VCF crests. We quantify the velocity gradients with linear 1D fits of the observed velocity along the crests (see Fig. 10, middle). We find a large scatter in the measured velocity gradients for filaments with 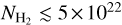 cm−2 and a tentative increasing trend for filaments with
cm−2 and a tentative increasing trend for filaments with 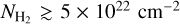 cm−2 (Fig. 7, middle). The filaments with larger velocity gradients tend to also show larger velocity dispersions. We note, however, that the observed velocities are LOS projected velocities and small velocity gradients may be due to the orientation of the filament close to the plane of the sky or to the variation in the sign of the gradient along the crest, as is the case for VCF 32 (see Fig. 7-middle and Sect. 6).
cm−2 (Fig. 7, middle). The filaments with larger velocity gradients tend to also show larger velocity dispersions. We note, however, that the observed velocities are LOS projected velocities and small velocity gradients may be due to the orientation of the filament close to the plane of the sky or to the variation in the sign of the gradient along the crest, as is the case for VCF 32 (see Fig. 7-middle and Sect. 6).
5.2 Column density and velocity power spectra of the VCFs
In order to quantify the observed column density and velocity fluctuations, in this section we present the analysis of the one-dimensional (1D) power spectrum along the crests of the identified VCFs. The power spectrum P(k) of Y(l) (one of the VCF properties) is proportional to the square of its Fourier transform, and can be expressed in 1D as
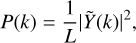 (2)
(2)
where 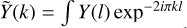 dl is the Fourier transform of Y(l), l is the spatial position along the crest, k is the angular frequency, and L = ∫ dl is the total VCF length. Figure 8 shows the power spectra of
dl is the Fourier transform of Y(l), l is the spatial position along the crest, k is the angular frequency, and L = ∫ dl is the total VCF length. Figure 8 shows the power spectra of 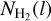 and v(l) of three VCF 1, 32, and 47 (see also Sect. 6 for the analysis of these three selected VCFs). No characteristic scales can be seen on the power spectra of both
and v(l) of three VCF 1, 32, and 47 (see also Sect. 6 for the analysis of these three selected VCFs). No characteristic scales can be seen on the power spectra of both 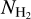 and υ, which are well represented by power laws down to the angular resolution of the data (30″2 or s ~ 1.2 arcmin−1). The observed power spectra are fitted with a power law function in log-log space where k = 1.2 arcmin−1 (the smallest resolved scale) is the highest frequency data point used for the fit. Figure 9-top shows the distribution of the
and υ, which are well represented by power laws down to the angular resolution of the data (30″2 or s ~ 1.2 arcmin−1). The observed power spectra are fitted with a power law function in log-log space where k = 1.2 arcmin−1 (the smallest resolved scale) is the highest frequency data point used for the fit. Figure 9-top shows the distribution of the 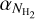 and αυ slopes of the
and αυ slopes of the 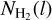 and υ(l) power spectra, with mean values of ~−1.9 ± 0.7 and ~−2.0 ± 0.9, respectively (see Table 1). Figure 9-bottom shows that the statistical difference between the
and υ(l) power spectra, with mean values of ~−1.9 ± 0.7 and ~−2.0 ± 0.9, respectively (see Table 1). Figure 9-bottom shows that the statistical difference between the 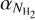 and αυ slope values for the same filaments are close to zero with a mean value of 0.15 ± 0.99. This difference is 0.07 ± 0.81 and closer to zero when only the VCFs with length L > 0 pixels are considered. A subselection of VCFs with L > 20 pixels (10 beams) ensures a statistically larger number of resolution elements to describe the fluctuations along the VCF crests.
and αυ slope values for the same filaments are close to zero with a mean value of 0.15 ± 0.99. This difference is 0.07 ± 0.81 and closer to zero when only the VCFs with length L > 0 pixels are considered. A subselection of VCFs with L > 20 pixels (10 beams) ensures a statistically larger number of resolution elements to describe the fluctuations along the VCF crests.
The best fit slope value of the 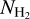 fluctuation along VCF 1 is also similar to the value found by Arzoumanian et al. (2021) for a longer section of the filament, namely the combined crests of VCFs 41 and 1, and at higher angular resolution (down to 14″). We discuss possible implications of this analysis in Sect. 7 below.
fluctuation along VCF 1 is also similar to the value found by Arzoumanian et al. (2021) for a longer section of the filament, namely the combined crests of VCFs 41 and 1, and at higher angular resolution (down to 14″). We discuss possible implications of this analysis in Sect. 7 below.
 |
Fig. 8 Power spectra of the column density (blue) and the velocity (purple) for the VCF crests 1 (left), 32 (middle), and 47 (right). The amplitudes of the power spectra are scaled so they can be plotted on the same panel. The red lines show the best linear fit to the power spectra and the values of the slopes are indicated in the corresponding panels. The vertical black solid lines indicate the 30.″2 angular resolution of the data equivalent to ~1.2 arcmin-1, which is the highest frequency data point used to fit the power spectra. |
 |
Fig. 9 Distributions of the power spectrum slopes. Top: distribution of the power spectrum slopes of the column density ( |
6 Properties along and across the crests of selected VCFs
Figure 10 shows the variation of the properties along the crests of three VCFs 1, 32, and 47, which are part of the subregions IFS and MFS, respectively (see Fig. 6). We select these VCFs because they are located in different environments, yet are part of the same molecular cloud and connected in velocity (see Fig. 5). We compare below their observed properties to study the environmental impact on the formation and evolution of filament systems.
6.1 Description and properties of selected VCFs
VCF 1. VCF 1 corresponds to a section of the well-studied star-forming NGC 6334 main filament (e.g., Russeil et al. 2013; André et al. 2016; Sadaghiani et al. 2020; Arzoumanian et al. 2021). This VCF has a length of ~3.7 pc, a mean column density of ~2 × 1023 cm−2, a column density contrast of ~30, and a mean LOS averaged dust temperature of ~24 K. This VCF corresponds to the MFS-warm region in Fig. 6. The PACS 70 µm emission along the crest shows values of ~50 MJy sr−1 over the southern ~ 1 pc tracing the heated dust from the surrounding H II regions and also a narrower 70 µm peak of ~ 100 MJy sr−1 toward its other end tracing the feedback from the young star cluster (identified as source I; see, e.g., Persi & Tapia 2008).
The radial profiles across the MFS-warm region, perpendicular to the VCF 1 crest, present the properties of its immediate environment (Fig. 11-right). The effect of compression is visible in the radial column density profile, which is sharper on the side (r > 0) associated with the stronger and extended PACS 70 µm emission and higher dust temperatures associated with the feedback from the H II regions.
In our observations we detected a single VCF, while two or three velocity components have been fitted toward localized spectra in this region (see Fig. B.3). However, the other velocity components were not identified as elongated and continuous velocity components in our analysis of the C18O(2–1) data given the conditions in terms of intensity threshold and minimum velocity separation (see Sect. 4.1). ALMA high angular resolution N2H+ observations, however, resolve at least two elongated velocity-coherent structures (Shimajiri et al. 2019).
A large-scale velocity gradient of a magnitude of ~2 km s−1 pc−1 is seen over its crest (Fig. 10). This large-scale velocity gradient was identified by Zernickel et al. (2013) using HCO+ APEX data and is thought to be tracing longitudinal infall motions along the filament. Another strong velocity gradient of ~8.5 km s−1 pc−1 across 0.7 pc toward the location of the source I is also detected (see red line in Fig. 10). This strong velocity gradient is associated with the loop-like structure in PP space joining the straight section of VCF 1 (e.g., the main filament or the ridge in André et al. 2016; Arzoumanian et al. 2021) to the star-cluster-forming infrared source I (see Fig. 6) and may be tracing the infall of matter onto the massive star cluster. Such velocity gradients around star-forming cores have been reported in a number of studies suggesting to be tracing gravitational infall (e.g., Hacar & Tafalla 2011; Liu et al. 2019; Henshaw et al. 2020). The mass accretion rate of 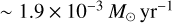 ~ 1.9 × 10−3 M⊙ yr−1 derived here toward source I is approximately the same as that reported earlier for high-mass protostellar cores (e.g., Schneider et al. 2010; Peretto et al. 2013). The mass accretion rate
~ 1.9 × 10−3 M⊙ yr−1 derived here toward source I is approximately the same as that reported earlier for high-mass protostellar cores (e.g., Schneider et al. 2010; Peretto et al. 2013). The mass accretion rate 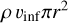 is estimated from the density
is estimated from the density 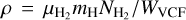 with
with 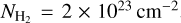 , the infall velocity υinf = GυL with the velocity gradient Gυ = 8.5 kms−1 pc−1 over the length L = 0.7 pc, and r = WVCF/2 = 0.13/2 = 0.065 pc (the cross-section radius of the filament).
, the infall velocity υinf = GυL with the velocity gradient Gυ = 8.5 kms−1 pc−1 over the length L = 0.7 pc, and r = WVCF/2 = 0.13/2 = 0.065 pc (the cross-section radius of the filament).
 |
Fig. 10 Properties along VCF crests 1, 32, and 47 (from left to right). The zero offsets correspond to the most southwestern end of the crests (as seen on Fig. 6). Rows from top to bottom: (1) column density derived from Herschel data. (2) LOS averaged dust temperature derived from Herschel data. The horizontal blue lines indicate the mean background temperature around the VFCs of ~17.9 ± 0.2 K. (3) PACS 70 µm flux. The horizontal blue line indicates the mean background emission of ~146 ± 23 MJy sr-1. (4) Velocity. The black vertical lines on each data point show the velocity dispersion (same as the values shown in row 5). The black lines show a linear fit to these data points. The velocity resolution of 0.3 km s-1 is indicated by the vertical blue lines. For VCF 1, a linear fit to the velocity >2.8 km s-1 over a length of 0.7 pc is indicated in red and corresponds to the crest crossing the young star cluster identified as source I (see, e.g., Persi & Tapia 2008). The position of source I is indicated with the vertical dashed green line (see also the green arrow in Fig. 6). (5) Velocity dispersion. The velocity resolution of 0.3km s-1 is indicated by the vertical blue lines. |
 |
Fig. 11 Radial profiles across the MFS-warm, MFS-cold, and IFS regions (from left to right; see boxes in Fig. 6). The column density, the PACS 70 µm emission, and the dust temperature are shown as solid black, blue dashed, and red dot-dashed lines, respectively. The scaling of the different curves is indicated in the caption of each panel. The r > 0 values correspond to the Galactic north. |
VCF 32
VCF 32 corresponds to the MFS-cold region in Fig. 6. It is located near VCF 1, but with slightly lower column density (~1 × 1023 cm−2) and dust temperature (~18 K) values. The PACS 70 µm emission along the crest shows values that increase toward the MFS-warm region and there is an excess of the emission (as in the case of MFS-warm) on its northern side (Fig. 11-middle) that may result from dust heating from the surrounding H II regions. This northern side also shows a sharper profile (r > 0) compared to the southern side that may be tracing the effect of compression from neighboring expanding H II regions. This VCF also shows an increase in the column density and the velocity dispersion toward VCF 1 or the MFS-warm region (the zero offset in Fig. 11-middle is the closest to VCF 1), where we also notice a change in the sign of the velocity gradient. This VCF is also thought to be undergoing merging with a neighboring filament and onto VCF 1 (Arzoumanian et al. 2021). Higher angular and spectral resolution observations are needed to further study the different components toward VFC 32 and its possible connection and/or interaction with VCF 1.
VCF 47
VCF 47 is identified in the east of the field (indicated as IFS in Figs. 1 and 6). VCF 47 and the associated filament system (IFS) is located between the two bright high-mass star-forming regions NGC 6334 and NGC 6357 and is not well studied (identified as the inter-region filaments in Russeil et al. 2010). The mean column density ~5 × 1022 cm−2, column density contrast of ~3, and mean dust temperature ~16 K makes it significantly less dense and colder than the MFS region. VCF 47 is surrounded by a cold medium not affected by nearby H II regions (Figs. 1 and 11-left). VCF 47 is star forming as can be traced with the PACS 70 µm localized peaks toward the young protostellar sources (Fig. 10-bottom). Localized strong velocity gradients are also observed toward the position of these pro-tostellar sources (with spatial offset between the velocity and column density fluctuations; see Hacar & Tafalla 2011) suggesting filament fragmentation and matter infall from the filament onto the compact sources (see also Chen et al. 2020b, showing localized velocity gradients, which do not appear to correspond to overdensities). In contrast to VCF 1, there is no large-scale velocity gradient along the ~3.5 pc crest of VCF 47. This difference in the large-scale velocity structure of these two VCFs may point to the absence of a single dominant potential well dragging the matter along the filament and to a less evolved stage of the star formation activity and matter accumulation in VCF 47.
6.2 Position velocity diagrams across selected VCFs
Here we study the velocity structure in the surroundings of the IFS and the MFS regions to investigate the influence of the environment on the filament properties. As presented above, these two regions are located in different environments, yet part of the same molecular cloud complex. In addition we divided the MFS region into a warm part and a cold part toward VCF 1 and VCF 32, respectively, as indicated in Fig. 6. For these three regions, we derived position-velocity (PV) diagrams perpendicular to the crests of the VCFs and averaged the emission along their crests. Figure 12 shows the PV diagrams of the C18O(2–1) and 13CO(2–1) emission, across the VCFs and up to a distance of ~6 pc on either side of their crests.
The PV diagrams of the three regions and for both C18O and 13CO lines show a Λ- or V-shaped velocity structure (Fig. 12). This velocity structure can be described as an extended structure bent in velocity space with the filament at the tip of the Λ or the V connected physically, and in velocity, through a velocity gradient, to the extended sheet-like structure. This velocity structure was first identified by Arzoumanian et al. (2018) toward a low column density filament in the Taurus molecular cloud, and is thought to trace the formation of a filament from the accumulation of matter flowing within a sheet-like structure compressed by a propagating shock front. This velocity structure is consistent with the filament formation scenario in compressed magnetized sheets proposed by Inoue et al. (2018) (see also Inoue & Fukui 2013; Vaidya et al. 2013; Abe et al. 2021). We note, however, that both the mass and the spatial scales of the analyzed filaments in Arzoumanian et al. (2018) and this work are different. In the latter the filament has Mline ~ 1 M⊙ pc−1 and the PV diagram shows the velocity structure across ~0.2 pc, while the filaments analyzed here have Mline > 100 M⊙ pc−1 and the scale of the PV diagram is ~10 pc. Hence, variations in the PV diagrams at these different scales are expected.
We also notice the difference in the velocity shape of the PV diagrams of the different regions, with a Λ-shape for the IFS and the MFS-warm and a V-shape for the MFS-cold (identified with the red arrows in Fig. 12). Since the IFS and the MFS regions are part of the same cloud, the opposite-sided compression scenario is the only logical explanation. For the IFS and the MFS-warm, the observed Λ-shaped structure suggests that the original velocity of the compressing structure should be blueshifted (in the LSR) with respect to the velocity of the VCF crest with a velocity gradient connecting both structures. For the MFS-cold, the observed V-shaped structure suggests that the original velocity of the compressing structure should be redshifted (in the LSR) with respect to the velocity of the VCF crest with a velocity gradient connecting the two structures (see Fig. 13 for a schematic representation). Longitudinal PV diagrams along the crest of the MFS-cold region all show V-shaped velocity structures although the structures vary in space from east to west (Fig. C.1).
An extended emission at about −16 and −20 km s−1 is seen on the 12CO(2–1) PV diagram in Fig. 4 (hereafter referred to as the −20 km s−1-cloud). Velocity bridge-like structures connecting the velocities of this cloud and the mean velocity of the MFS and IFS are also seen. These velocity bridges have already been reported by Fukui et al. (2018b) toward the NGC 6334 complex, and are thought to be tracing a physical connection and interactions between these clouds with different mean velocities (see also results from numerical simulations; e.g., Haworth et al. 2015a,b). This blueshifted −20 km s−1-cloud may be the cloud interacting with the NGC 6334 complex at a mean LSR velocity of −3 km s−1, and at the origin of the observed Λ-shaped velocity structure. The causal connection between the blueshifted cloud and the Λ-shaped velocity structure toward the analyzed filament system is, however, speculative at this stage.
The V-shaped velocity structure that we see now toward the MFS-cold could be the result of a different (redshifted) compression. There is atomic H I emission at velocities >0 km s−1 (Fig. 3); it is, however, not possible to identify the compressing redshifted cloud with these data alone.
 |
Fig. 12 Position-velocity (PV) diagrams perpendicular to and averaged along the main axes of the MFS-warm, MFS-cold, and IFS regions (from left to right, see boxes in Fig. 6). The PV maps are in units of K(TMB) and correspond to the 13CO(2–1) and C18O(2–1) emission at the top and bottom, respectively. The white contours indicate the C18O(2–1) intensity and are the same for the two panels of the same filament system. The magenta contours in the left panel correspond to the 13CO(2–1) intensity. The zero offset position (on the x-axes) corresponds to the Galactic south side of the filament systems. At the distance of this cloud 10’ corresponds to 3.8 pc. The position of the filaments are indicated with a dark blue circle and the velocity gradients induced by the compression are shown as converging red dashed arrows toward the filament. Longitudinal PV diagrams along the crest of VCF 32 of the MFS-cold region are shown in Fig. C.1. |
 |
Fig. 13 Schematic view of the suggested scenario where propagating extended gas structures interact with the NGC 6334 complex, resulting in the formation or altering the properties of the filament systems MFS-warm, MFS-cold, and IFS (from left to right). These sketches are in the PP space perpendicular to the filament along the axes. The velocities of the different structures are indicated in the LSR frame according to the PV diagrams (Fig. 12). The shock front is indicated in the post-shock configuration. The left and right arrows (<< and >>) indicate the more blueshifted and more redshifted velocities, respectively, with respect to the velocity of the extended sheet-like structures. The velocity of the sheet-like structure is connected to the filament velocity through a velocity gradient. The ambient 5-field (indicated by the black lines) is parallel to the shock front. |
7 Interpretation and discussion
The NGC 6334 complex is one of the most prominent Galactic high-mass star-forming regions at <2 kpc. It has an extent of ~50 pc parallel to the Galactic plane. The dense gas is observed to be filamentary. While new generations of stars are forming along these dense gravitationally unstable filaments, the surrounding warm and diffuse medium is shaped by expanding ionized (H II) regions (at scales of ~1–10 pc) generated by the feedback from more evolved massive stars (Russeil et al. 2016, and see Fig. 1). The asymmetry in the emission (an indication of the total present mass) on either side of the VCFs crest of the MFS-cold and -warm regions is likely due to the compression of the matter by expanding H II region(s) on the northern side of the MFS (Figs. 11 and 12, middle and left).
The 12CO(2–1) PV diagram shows the presence of an extended structure at velocities of about −20 km s−1 (Fig.4). The presence of this blueshifted −20 km s−1 -cloud with velocity bridges connecting the velocities of this cloud with the mean velocity of the NGC 6334 complex (see Sect. 3) has been interpreted as evidence for the impact of expanding neutral H I clouds and/or shells on ~100 pc scales corresponding to the extent of the NGC 6334 complex and its neighbor NGC 6357 star-forming region (Fukui et al. 2018b). The origin of this diffuse component around −20 km s−1 is not clear, however. It could probably originate from the Galactic plane, as suggested by Russeil et al. (2016). Such a large-scale compression may be at the origin of the coherence in velocity of the ~50 pc long molecular NGC 6334 complex.
We suggest that the observed large-scale smoothly varying velocity from ~0 km s−1 to ~−5, −10 km s−1 from east to west of the complex (Fig. 4) may be tracing a spatial and temporal variation of the collision. This would be expected, for example, when the plane of the propagating shock front is inclined with respect to the 50 pc extent of the NGC 6334 cloud (or over the 100 pc cloud if the NGC 6357 complex is also considered). The GM24FS region at l ~ 351″, with mean velocities closer to that of the diffuse blueshifted −20 km s−1 -cloud (see Fig. 4), may have experienced the interaction earlier, while the interaction from l ~ 351° to l ~ 352.″5 could be more recent and ongoing from west to east.
We compared the PV diagrams of the IFS and MFS regions, toward the middle and the eastern side of the field (see Fig. 1), respectively, and noticed a difference in the bending of the velocity structure with V- and Λ-shaped velocity structures in the PV space. As discussed in Sect. 6.2, it has been suggested that these velocity structures trace filament formation due to compression. Moreover, here, the different velocity structures of the gas in the surroundings of the IFS and MFS regions suggest that the propagating shock fronts compressing these regions may be propagating in different (possibly opposite) directions. We thus suggest that these regions were formed (or at least affected) by compressions, as hinted by the observed velocity pattern; however, these compressions may not be coeval or from the same origin (see Fig. 13). The 12CO(2–1) PV diagram shows velocity bridges between the cloud at −20 km s−1 and the systemic velocity of the NGC 6334 complex (Fig. 4), suggesting that the compression is currently ongoing and the Λ-shaped velocity structure observed toward the IFS and the MFS-warm may be a result of this compression. The PV diagram of the MFS-cold shows a V-shaped velocity structure suggesting that this part of the MFS probably formed or was impacted by another episode of compression from a propagating cloud with redshifted velocities (see Fig. 13).
The difference in the velocity structure (V- or Λ-shaped) toward these two regions of the same cloud points to different origins of the compressions (Fig. 13), which can be currently observed. These observational hints may indicate the importance of multiple compressions in the formation and evolution of molecular clouds as predicted by theory (e.g., Inutsuka et al. 2015; Iwasaki et al. 2019).
The PV diagrams in Fig. 12 also show stronger CO emission (a larger mass reservoir) in the surroundings of the MSF region suggesting more available matter to be accreted onto the star-forming filament compatible with the intense star-forming activity in this region. Matter accretion onto VCF 1 and the hubs of the region are also suggested by the velocity gradients (of about ~ 1–3 km s−1 pc1; see Table 1) identified along VCFs 11, 18, 24, 28, and 40 converging toward VCF 1. The increase in the velocity dispersion as a function of the column density of the VCFs may also trace this matter flow along the filaments and onto hubs. The magnetic field structure as derived from polarization observations is perpendicular to VCF 1 and along the filaments (i.e., VCFs 11, 18, 24, 28, and 40) connected to VCF 1 from the side (Arzoumanian et al. 2021), compatible with the filament formation scenario described in Sect. 6.2. The IFS, on the other hand, shows much less CO emission (smaller mass) in the surrounding of VCF 47, which has probably already accreted a large fraction of the matter present in the compressed sheet-like cloud. VCF 47 is undergoing star formation traced by the dense fragments and the presence of protostellar sources, but it is less active than its MSF neighbor.
We analyzed the velocity and column density power spectra along the crests of the VCFs, to compare with theoretical models. While velocity structure function analyses along filaments have been previously analyzed (Hacar et al. 2016), in this paper the slopes of the velocity power spectra along filaments are quantified for the first time observationally to be directly compared with theoretical models. Misugi et al. (2019) recently found that cylindrical filaments characterized by a 1D Kolmogorov velocity power spectrum slope of −5/3 will fragment into cores showing a distribution of angular momentum compatible with the observations. They demonstrated that this 1D Kolmogorov velocity fluctuations (with a slope of −5/3) along the cylindrical filaments may be inherited from the 3D Kolmogorov velocity fluctuations (with a slope of −11/3) of the surrounding cloud provided the mass in the filaments is a small fraction of the total mass of the cloud (compatible with the results of Arzoumanian et al. 2019). Inutsuka (2001) has also suggested that filaments with column density fluctuations with a power-law slope of −1.5 (close to −5/3) would fragment and form stars with a distribution of mass following the expected Salpeter (1955) power-law slope at the high-mass end. This theoretically suggested slope for column density fluctuations is compatible with the statistical results (−1.6 ± 0.3) found by Roy et al. (2015) from the 1D analysis of the column density (mass per unit length) along the crest of a sample of 80 filaments observed by Herschel in the Gould Belt.
The mean values of the slopes α of the 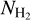 and the υ power spectra measured here toward the 47 VCFs are about −2, with a mean difference between the slopes of
and the υ power spectra measured here toward the 47 VCFs are about −2, with a mean difference between the slopes of 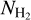 and v of 0.15 ± 0.99 for the VCFs with a length > 10 pixels and 0.07 ± 0.81 for the VCFs with a length >20 pixels. The similarity between the observed slopes of
and v of 0.15 ± 0.99 for the VCFs with a length > 10 pixels and 0.07 ± 0.81 for the VCFs with a length >20 pixels. The similarity between the observed slopes of 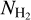 and υ power spectra suggested by theoretical models and measured here observationally indicates the dynamical coupling of the
and υ power spectra suggested by theoretical models and measured here observationally indicates the dynamical coupling of the 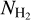 and the υ fluctuations along a filament. These fluctuations along the filaments may be inherited from the turbulent fluctuation of the surrounding ISM as a result of the filament formation process through compression. These density and velocity fluctuations may play an important role in the fragmentation of the filaments into star-forming cores. Consequently, some of the properties of these cores (e.g., mass, angular momentum) would be inherited from the properties of their host filaments (as suggested by Misugi et al. 2019). About 50% of the measured slopes are close to −5/3 (e.g., for VCF 1 in Fig. 9) and would be compatible with the theoretical prediction of Misugi et al. (2019) from the formation of cylindrical filaments out of a more massive cloud with 3D Kolmogorov velocity fluctuations. We plan future investigations, using higher angular and spectral resolution data and dedicated MHD numerical simulations to better understand the origin of the observed distributions of the power spectrum slopes.
and the υ fluctuations along a filament. These fluctuations along the filaments may be inherited from the turbulent fluctuation of the surrounding ISM as a result of the filament formation process through compression. These density and velocity fluctuations may play an important role in the fragmentation of the filaments into star-forming cores. Consequently, some of the properties of these cores (e.g., mass, angular momentum) would be inherited from the properties of their host filaments (as suggested by Misugi et al. 2019). About 50% of the measured slopes are close to −5/3 (e.g., for VCF 1 in Fig. 9) and would be compatible with the theoretical prediction of Misugi et al. (2019) from the formation of cylindrical filaments out of a more massive cloud with 3D Kolmogorov velocity fluctuations. We plan future investigations, using higher angular and spectral resolution data and dedicated MHD numerical simulations to better understand the origin of the observed distributions of the power spectrum slopes.
8 Summary and conclusions
In this paper we presented the velocity structure of the −50 pc long NGC 6334 high-mass star-forming region as traced by NANTEN2 12CO(2–1) and APEX 13CO(2–1) and C18O(2–1) molecular line emission. Our main results can be summarized as follows:
This cloud has a coherent velocity structure over its 10 × 50 pc extent with a smoothly varying velocity field from ~0 km s−1 to ~−5, −10 km s−1 from east to west (Fig.4). The C18O(2–1) emission traces the elongated filamentary structures of the cloud with column densities
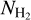 > 1.8 × 1022 cm−2 derived from Herschel data. The 13CO and 12CO emission show more extended structures toward the cloud (Fig. 2).
> 1.8 × 1022 cm−2 derived from Herschel data. The 13CO and 12CO emission show more extended structures toward the cloud (Fig. 2).We traced velocity-coherent-filaments (VCF) in the 3D PPV C18O(2 – 1) cubes. We identified a total of 75 VCFs in the fully studied field. Of these 75 VCFs, 47 have a length greater than 5 beams (0.9 pc). We analyzed the observed properties along these 47 VCFs (Table1).
The mean length of the VCFs is ~2 pc; some are as long as ~5 pc. They span a column density range (as derived from Herschel data) of an order of magnitude about a mean value of ~4 × 1022 cm−2. The LOS averaged dust temperature derived from Herschel data indicates a mean value of ~20 K. The mean velocity dispersion of the VCFs show an increasing trend as a function of their mean column density with a linear relation of
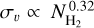 . Most of the identified VCFs show longitudinal velocity gradients along theircrests. The filaments with larger velocity gradients also tend to show larger velocity dispersions and mean column densities (Fig. 7).
. Most of the identified VCFs show longitudinal velocity gradients along theircrests. The filaments with larger velocity gradients also tend to show larger velocity dispersions and mean column densities (Fig. 7).We measured the column density (
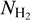 ) and velocity (υ) power spectra of the VCFs. We show that the power spectra of both
) and velocity (υ) power spectra of the VCFs. We show that the power spectra of both 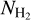 and υ can be well represented by a power-law function, and no characteristic scales are detected down to the resolution of the data. The slopes of both the
and υ can be well represented by a power-law function, and no characteristic scales are detected down to the resolution of the data. The slopes of both the 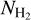 and υ power spectra for each VCFs are similar. The mean power spectra slope of the full sample is α ~ − 2. The mean and the standard deviation of the statistical difference between the two quantities are 0.15 and 0.99, respectively (see Table 1).
and υ power spectra for each VCFs are similar. The mean power spectra slope of the full sample is α ~ − 2. The mean and the standard deviation of the statistical difference between the two quantities are 0.15 and 0.99, respectively (see Table 1).We described in greater detail the properties of three VCFs (1, 32, and 47) and we compared their observed properties. VCF 1 corresponds to a section of the well-studied NGC 6334 main filament actively forming (high-mass) stars and affected by stellar feedback from young massive stars and stellar clusters. A large-scale velocity gradient of a magnitude of ~2 km s−1 pc−1 can be seen over its crest tracing matter flowing along the filament and infalling onto the massive star cluster (Fig. 10). Other identified VCFs connected to VCF 1 show velocity gradients indicating matter flow onto VCF 1 and hubs formed along its crest. VCF 32 also shows signatures of compressions, but is colder on average. VCF 47 seems to be colder, younger, and less impacted by surrounding stellar feedback.
We compared the PV diagrams of the three filament systems associated with VCF 1, 32, and 47 (IFS, MFS-cold, and MFS-warm, respectively; see Fig. 12). The three PV diagrams show V- and Λ-shaped velocity structures compatible with the filament formation by compression (Sect. 7 and Fig. 13). Moreover, we suggest that the presently observed difference in the curvature of the velocity structure (i.e., V- and Λ-shaped) toward these filament systems may result from different origins of the compressions. This may also indicate the importance of multiple compressions in the formation and evolution of filamentary molecular clouds.
The observational results presented in this paper suggest the formation and evolution of filamentary molecular clouds induced by multiple compressions from expanding shells. However, the origin of these shells is not well constrained. We anticipate future studies to better understand the origin and the impact of these propagating shells on the surrounding medium and on the star formation process. Quantitative comparisons with dedicated MHD numerical simulations will also be important to better understand the role of compressions from expanding shells in the formation and evolution of filamentary molecular clouds. High angular and spectral resolution observations toward this filamentary cloud would also be valuable to better constrain the origin and the variations of the velocity and density structures along and across these filaments.
Acknowledgements
We thank the anonymous referee for their detailed report, which helped improving the presentation of our results. DA thanks M.S.N. Kumar for motivating discussions on hub-filament systems. We thank Y. Fukui for sharing the NANTEN2 data and for insightful discussions on the velocity structure of the region. AZ thanks the support of the Institut Universitaire de France. We thank F. Wyrowski and the APEX staff for carrying out the observations and A. Zernickel for making the reduced data available. This research has made use of data from the Herschel HOBYS project (http://hobys-herschel.cea.fr). HOBYS is a Herschel Key Project jointly carried out by SPIRE Specialist Astronomy Group 3 (SAG3), scientists of the LAM laboratory in Marseille, and scientists of the Herschel Science Center (HSC). The present study has also made use of NANTEN2 data. NANTEN2 is an international collaboration of ten universities: Nagoya University, Osaka Prefecture University, University of Cologne, University of Bonn, Seoul National University, University of Chile, University of New South Wales, Macquarie University, University of Sydney, and Zurich Technical University. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
Appendix A Ratio maps and optical depth
Figure A.1-left shows the 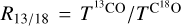 ratio map of the peak intensity observed over the LSR velocity range −12 to 4 kms−1, and the estimated mean optical depth values τ13 and τ18 of the 13CO and the C18O lines, respectively. The mean optical depth values of the lines are derived from the R13/18 ratio by solving the relation
ratio map of the peak intensity observed over the LSR velocity range −12 to 4 kms−1, and the estimated mean optical depth values τ13 and τ18 of the 13CO and the C18O lines, respectively. The mean optical depth values of the lines are derived from the R13/18 ratio by solving the relation
![${R_{13/18}} = {{T_{{\rm{ex}}}^{13}\left[{1 - \exp \left({ - {\tau ^{13}}} \right)} \right]} \over {T_{{\rm{ex}}}^{18}\left[{1 - \exp \left({ - {\tau ^{18}}} \right)} \right]}}$](/articles/aa/full_html/2022/04/aa41699-21/aa41699-21-eq61.png) (A.1)
(A.1)
on a pixel by pixel basis (see also, e.g., Arzoumanian et al. 2013; Zernickel 2015). In Eq. A.1 τ13 = Xτ18, with X = [13CO]/[C18O] = 5.5 (the mean value of the abundance ratio in the local ISM; e.g., Wilson & Rood 1994) and we assume a uniform excitation temperature (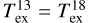 ) along the LOS for both isotopomers.
) along the LOS for both isotopomers.
As shown in Fig. A.1, the C18O(2–1) emission is optically thin all over the observed field. The 13CO(2–1) emission is mostly optically thin but shows optical depth values up to ~4 in the densest regions. The 12CO(2–1) emission is optically thick. We thus use the C18O(2–1) PPV cube to identify the velocity-coherent filaments.
 |
Fig. A.1 Intensity ratio and optical depth estimates. Top: Ratio map |
Appendix B Multi-velocity component fitting results
We use an automated procedure to identify multiple velocity peaks along each spectra to be fitted with a multi-Gaussian function as described in Sect. 4.1. We use the first and second derivatives to find the surroundings of the peaks to be fitted, where the absolute value of the first derivative reaches a maximum and the second derivative changes sign. Figure B.1 shows an example of a spectrum fitted with two velocity components.
Figure B.2 shows the velocity integrated intensity maps derived from the observed (TMB(x, y, υ)) and modeled (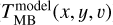 ) C18O(2 – 1) cubes toward the middle and west regions of the field (i.e., the MFS and GM24FS regions). The median, mean, and standard deviation values of the ratio map
) C18O(2 – 1) cubes toward the middle and west regions of the field (i.e., the MFS and GM24FS regions). The median, mean, and standard deviation values of the ratio map 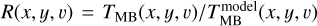 are 1.02, 1.10, and 0.46, respectively, for an intensity threshold of S/N = 4. We also derived modeled cubes for S/N = 3 and 5. The mean and standard deviation values of the ratio maps are 1.16 and 0.75 for the S/N = 3 run, and 1.08 and 0.37 for the S/N = 5 run, respectively. The standard deviation of the ratio map for the S/N = 3 run is larger than the runs with S/N = 4 and 5. The run with S/N = 5 has ~30% fewer fitted spectra compared to the run with S/N = 4. For the analysis presented in this paper we thus selected the modeled cube derived with S/N = 4.
are 1.02, 1.10, and 0.46, respectively, for an intensity threshold of S/N = 4. We also derived modeled cubes for S/N = 3 and 5. The mean and standard deviation values of the ratio maps are 1.16 and 0.75 for the S/N = 3 run, and 1.08 and 0.37 for the S/N = 5 run, respectively. The standard deviation of the ratio map for the S/N = 3 run is larger than the runs with S/N = 4 and 5. The run with S/N = 5 has ~30% fewer fitted spectra compared to the run with S/N = 4. For the analysis presented in this paper we thus selected the modeled cube derived with S/N = 4.
Figure B.2 also shows a map of the number of velocity components fitted for each pixel (toward each LOS). More than 88% of the spectra are fitted with a single velocity component and only ~12% of the spectra required two or three velocity components to describe the observations.
 |
Fig. B.1 Example of an observed spectrum and the different steps of the n-Gaussian fitting procedure. Top: Observed C18O(2–1) spectra toward a position in the center of the map (top). The blue and red curves show the five individual Gaussian functions and the sum of all the fitted Gaussians, respectively. The dotted line shows the intensity threshold corresponding to S/N = 4s. Here s = 0.6 K. The second derivative of the C18O(2–1) spectra shown in the top panel (bottom). The blue horizontal lines show the region where the first guess for each of the Gaussian fits is identified indicated by the red symbols defining the points surrounding a peak to be fitted. Middle: Second iteration of the Gaussian fits where the Gaussian component not following the given criterion on the velocity resolution (5 × 0.3 km s-1) are discarded. A new multi-component fit is done on the remaining positions. The result is a combined Gaussian with three components. Bottom: Third iteration of the Gaussian fits following the same procedure of the second iteration. The result is a combined Gaussian with two components. Both components follow the defined criteria and correspond to the final result of the n-Gaussian fit. |
 |
Fig. B.2 Examples of observed and modeled maps. Left: Observed and modeled moment zero map of the C18O(2–1) emission toward the MFS (top and bottom, respectively). The intensity is shown in K km s-1. The bottom map shows the ratio of the above two maps. The median, mean, and standard deviation values of this ratio map are 1.02, 1.10, and 0.46, resepctively. Right: Observed and modeled moment one map of the C18O(2–1) emission toward the GM24FS (top and bottom, respectively). The unit of the maps is km s-1. The bottom map shows the number of velocity components fitted for each pixel (toward each LOS). |
 |
Fig. B.3 Map showing the number of fitted velocity components for each C18O(2–1) spectra. The blue and red contours indicate velocity components = 2 and = 3, respectively. More than 88% of the spectra are fitted with a single velocity component and only ~12% of the spectra required two or three velocity components to fit the observed spectra. The cyan curves trace the crests of the identified velocity coherent filaments (same as in Fig. 6). The black arrow toward the MFS indicates the location of the spectrum shown in Fig. B.1. The red lines indicate the central positions of the slices used to derive the PV diagrams shown in Fig. C.1. |
Appendix C PV diagrams along the VCF crest
In this section we show longitudinal position–velocity (PV) diagrams along the crest of VCF 32 for the 13CO(2–1) and C18O(2–1) emission from east to west. The PV diagrams are perpendicular to the crest and averaged over 4 pixels (2×beams).
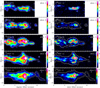 |
Fig. C.1 Longitudinal position–velocity (PV) diagrams along the crest of VCF 32 for the 13CO(2–1) and C18O(2–1) emission (left and right, respectively). The PV maps are in units of K(TMB). Each PV diagram is perpendicular to the crest and averaged over 4 pixels (2×beams). The slices from 1 to 5 correspond to positions along the crest from east to west. The central positions of the slices are indicated on Fig. B.3. The white contours indicate the 13CO(2–1) intensity of 1 K and 2 K and are the same for the two panels of the same slice. The zero offset position (on the x-axes) corresponds to the Galactic south side of the filament systems. At the distance of this cloud 10’ corresponds to 3.8 pc. The position of the filaments is between 9’ and 10’. |
References
- Abe, D., Inoue, T., Inutsuka, S.-I., & Matsumoto, T. 2021, ApJ, 916, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L. D., Bania, T. M., Balser, D. S., et al. 2014, ApJS, 212, 1 [Google Scholar]
- André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, Protostars and Planets VI, 27 [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, A102 [Google Scholar]
- André, P., Revéret, V., Könyves, V., et al. 2016, A&A, 592, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Arzoumanian, D., Könyves, V., Shimajiri, Y., & Palmeirim, P. 2019, A&A, 629, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, A6 [Google Scholar]
- Arzoumanian, D., André, P., Peretto, N., & Könyves, V. 2013, A&A, 553, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arzoumanian, D., Shimajiri, Y., Inutsuka, S.-I., Inoue, T., & Tachihara, K. 2018, PASJ, 70, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Arzoumanian, D., André, P., Könyves, V., et al. 2019, A&A, 621, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arzoumanian, D., Furuya, R. S., Hasegawa, T., et al. 2021, A&A, 647, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonne, L., Bontemps, S., Schneider, N., et al. 2020, A&A, 644, A27 [EDP Sciences] [Google Scholar]
- Bracco, A., Bresnahan, D., Palmeirim, P., et al. 2020, A&A, 644, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Causi, G. L., Schisano, E., Liu, S. J., Molinari, S., & Giorgio, A. D. 2016, in Space Telescopes and Instrumentation 2016: Optical, Infrared, and Millimeter Wave, eds. H. A. MacEwen, G. G. Fazio, M. Lystrup, et al. 9904, International Society for Optics and Photonics (SPIE), 1829 [Google Scholar]
- Chen, Y.-C., Genovese, C. R., & Wasserman, L. 2014, Generalized Mode and Ridge Estimation [Google Scholar]
- Chen, Y.-C., Ho, S., Tenneti, A., et al. 2015, MNRAS, 454, 3341 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C.-Y., Mundy, L. G., Ostriker, E. C., Storm, S., & Dhabal, A. 2020a, MNRAS, 494, 3675 [Google Scholar]
- Chen, M. C.-Y., Di Francesco, J., Rosolowsky, E., et al. 2020b, ApJ, 891, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Chibueze, J. O., Omodaka, T., Handa, T., et al. 2014, ApJ, 784, 114 [Google Scholar]
- Dawson, J. R., McClure-Griffiths, N. M., Kawamura, A., et al. 2011, ApJ, 728, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Enokiya, R., Ohama, A., Yamada, R., et al. 2021, PASJ, 73, S256 [Google Scholar]
- Fukui, Y., Kohno, M., Yokoyama, K., et al. 2018a, PASJ, 70, S44 [NASA ADS] [Google Scholar]
- Fukui, Y., Kohno, M., Yokoyama, K., et al. 2018b, PASJ, 70, S41 [NASA ADS] [Google Scholar]
- Fukui, Y., Torii, K., Hattori, Y., et al. 2018c, ApJ, 859, 166 [Google Scholar]
- Fukui, Y., Tokuda, K., Saigo, K., et al. 2019, ApJ, 886, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Alves, J., Beaumont, C. N., et al. 2014, ApJ, 797, 53 [CrossRef] [Google Scholar]
- Hacar, A., & Tafalla, M. 2011, A&A, 533, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., Kainulainen, J., Tafalla, M., Beuther, H., & Alves, J. 2016, A&A, 587, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haverkorn, M., Gaensler, B. M., McClure-Griffiths, N. M., Dickey, J. M., & Green, A. J. 2006, ApJS, 167, 230 [CrossRef] [Google Scholar]
- Haworth, T. J., Shima, K., Tasker, E. J., et al. 2015a, MNRAS, 454, 1634 [NASA ADS] [CrossRef] [Google Scholar]
- Haworth, T. J., Tasker, E. J., Fukui, Y., et al. 2015b, MNRAS, 450, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Heitsch, F., Stone, J. M., & Hartmann, L. W. 2009, ApJ, 695, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., Banerjee, R., Vázquez-Semadeni, E., Klessen, R. S., & Audit, E. 2008, A&A, 486, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henshaw, J. D., Kruijssen, J. M. D., Longmore, S. N., et al. 2020, Nat. Astron., 4, 1064 [CrossRef] [Google Scholar]
- Inoue, T., & Fukui, Y. 2013, ApJ, 774, L31 [Google Scholar]
- Inoue, T., & Inutsuka, S.-I. 2009, ApJ, 704, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, T., Hennebelle, P., Fukui, Y., et al. 2018, PASJ, 70, S53 [NASA ADS] [Google Scholar]
- Inutsuka, S.-I. 2001, ApJ, 559, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Inutsuka, S., & Miyama, S. M. 1997, ApJ, 480, 681 [Google Scholar]
- Inutsuka, S.-I., Inoue, T., Iwasaki, K., & Hosokawa, T. 2015, A&A, 580, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iwasaki, K., Tomida, K., Inoue, T., & Inutsuka, S.-I. 2019, ApJ, 873, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, J., Bertoldi, F., Bourke, T. L., Evans, N. J., & Lee, C. W. 2008, A&A, 487, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kobayashi, M. I. N., Inutsuka, S.-I., Kobayashi, H., & Hasegawa, K. 2017, ApJ, 836, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, E. W., & Rosolowsky, E. W. 2015, MNRAS, 452, 3435 [Google Scholar]
- Kohno, M., Nishimura, A., Fujita, S., et al. 2022, PASJ, 74, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Könyves, V., André, P., Men’shchikov, A., et al. 2015, A&A, 584, A91 [Google Scholar]
- Kraemer, K. E., & Jackson, J. M. 1999, ApJS, 124, 439 [Google Scholar]
- Kumar, M. S. N., Palmeirim, P., Arzoumanian, D., & Inutsuka, S. I. 2020, A&A, 642, A87 [EDP Sciences] [Google Scholar]
- Kumar, M. S. N., Arzoumanian, D., Men’shchikov, A., et al. 2022, A&A, 658, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Langston, G., Minter, A., D’Addario, L., et al. 2000, AJ, 119, 2801 [Google Scholar]
- Liu, H.-L., Stutz, A., & Yuan, J.-H. 2019, MNRAS, 487, 1259 [Google Scholar]
- Mattern, M., Kauffmann, J., Csengeri, T., et al. 2018, A&A, 619, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matthews, H. E., McCutcheon, W. H., Kirk, H., White, G. J., & Cohen, M. 2008, AJ, 136, 2083 [Google Scholar]
- McClure-Griffiths, N. M., Dickey, J. M., Gaensler, B. M., et al. 2005, ApJS, 158, 178 [NASA ADS] [CrossRef] [Google Scholar]
- McCutcheon, W. H., Sandell, G., Matthews, H. E., et al. 2000, MNRAS, 316, 152 [Google Scholar]
- McKee, C. F., & Ostriker, J. P. 1977, ApJ, 218, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Men’shchikov, A. 2021, A&A, 649, A89 [EDP Sciences] [Google Scholar]
- Men’shchikov, A., André, P., Didelon, P., et al. 2010, A&A, 518, L103 [Google Scholar]
- Misugi, Y., Inutsuka, S.-I., & Arzoumanian, D. 2019, ApJ, 881, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., Zavagno, A., Bontemps, S., et al. 2010, A&A, 518, L77 [CrossRef] [EDP Sciences] [Google Scholar]
- Muñoz, D. J., Mardones, D., Garay, G., et al. 2007, ApJ, 668, 906 [Google Scholar]
- Myers, P. C. 2009, ApJ, 700, 1609 [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [Google Scholar]
- Palmeirim, P., André, P., Kirk, J., et al. 2013, A&A, 550, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peretto, N., Fuller, G. A., Duarte-Cabral, A., et al. 2013, A&A, 555, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peretto, N., Fuller, G. A., André, P., et al. 2014, A&A, 561, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Persi, P., & Tapia, M. 2008, Star Formation in NGC 6334, ed. B. Reipurth, 5, 456 [Google Scholar]
- Persi, P., & Tapia, M. 2010, Mem. Soc. Astron. It., 81, 171 [NASA ADS] [Google Scholar]
- Priestley, F. D., & Whitworth, A. P. 2021, MNRAS, 506, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Qiu, K., Wyrowski, F., Menten, K. M., et al. 2011, ApJ, 743, L25 [Google Scholar]
- Radhakrishnan, V., Goss, W. M., Murray, J. D., & Brooks, J. W. 1972, ApJS, 24, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Ragan, S. E., Henning, T., Tackenberg, J., et al. 2014, A&A, 568, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roy, A., Martin, P. G., Polychroni, D., et al. 2013, ApJ, 763, 55 [Google Scholar]
- Roy, A., André, P., Palmeirim, P., et al. 2014, A&A, 562, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roy, A., André, P., Arzoumanian, D., et al. 2015, A&A, 584, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Russeil, D., Zavagno, A., Motte, F., et al. 2010, A&A, 515, A55 [CrossRef] [EDP Sciences] [Google Scholar]
- Russeil, D., Schneider, N., Anderson, L. D., et al. 2013, A&A, 554, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Russeil, D., Tigé, J., Adami, C., et al. 2016, A&A, 587, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sadaghiani, M., Sánchez-Monge, Á., Schilke, P., et al. 2020, A&A, 635, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sandell, G. 2000, A&A, 358, 242 [NASA ADS] [Google Scholar]
- Schisano, E., Molinari, S., Elia, D., et al. 2020, MNRAS, 492, 5420 [Google Scholar]
- Schneider, S., & Elmegreen, B. G. 1979, ApJS, 41, 87 [Google Scholar]
- Schneider, N., Csengeri, T., Bontemps, S., et al. 2010, A&A, 520, A49 [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Csengeri, T., Hennemann, M., et al. 2012, A&A, 540, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shimajiri, Y., André, P., Palmeirim, P., et al. 2019, A&A, 623, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tafalla, M., & Hacar, A. 2015, A&A, 574, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takahira, K., Tasker, E. J., & Habe, A. 2014, ApJ, 792, 63 [Google Scholar]
- Tigé, J., Motte, F., Russeil, D., et al. 2017, A&A, 602, A77 [Google Scholar]
- Torii, K., Enokiya, R., Sano, H., et al. 2011, ApJ, 738, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Treviño-Morales, S. P., Fuente, A., Sánchez-Monge, Á., et al. 2019, A&A, 629, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Umemoto, T., Minamidani, T., Kuno, N., et al. 2017, PASJ, 69, 78 [Google Scholar]
- Vaidya, B., Hartquist, T. W., & Falle, S. A. E. G. 2013, MNRAS, 433, 1258 [Google Scholar]
- Vassilev, V., Meledin, D., Lapkin, I., et al. 2008, A&A, 490, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [Google Scholar]
- Zernickel, A. 2015, PhD thesis, I. Physikalisches Institut der Universität zu Köln [Google Scholar]
- Zernickel, A., Schilke, P., & Smith, R. J. 2013, A&A, 554, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zucker, C., Battersby, C., & Goodman, A. 2015, ApJ, 815, 23 [NASA ADS] [CrossRef] [Google Scholar]
This 0.13 pc width value corresponds to an effective filament width of 1.3 × 0.1 pc measured by Arzoumanian et al. (2019) to enclose the mass of a 0.1 pc wide filament with non-Gaussian wings beyond the 0.1 pc inner width.
All Tables
Properties of the 47 velocity-coherent filaments identified toward NGC 6334 in the 3D PPV C18O(2–1) cube at the spatial and velocity resolutions of 30.″2 and 0.3 km s−1, respectively.
All Figures
 |
Fig. 1 Herschel maps toward the NGC 6334 cloud. Top: column density map of the NGC 6334 cloud derived from Herschel HOBYS data (Motte et al. 2010) (see explanation in Sect. 2.4). The map is at the resolution of 18.″2 and the contours are at column densities of 1.8 and 5 × 1022 cm-2. The coverage of the APEX observations is shown in magenta. The three identified subregions are indicated (in yellow) from east to west: the inter-filament system (IFS) for 352.″3 > l > 351.″8, the main filament system (MFS) for 351.″8 > l > 351″, and the GM 24 filament system (GM24FS) for 351° > l > 350.″4. Middle: dust temperature map at 36.″3 (see Sect. 2.4). The contours are the same as in the top panel. Bottom: color composite image of NGC 6334 derived from Herschel data, where the 70 µm, 160 µm, and 250 µm intensities are represented in blue, green, and red, respectively. This image is from Causi et al. (2016). The contours trace the column density as in the top panel. The red circles show the positions and sizes of the H II regions from Anderson et al. (2014) and Langston et al. (2000), and are the same as those plotted in Fig. 1 of Russeil et al. (2016). |
| In the text | |
 |
Fig. 2 Integrated intensity maps, in units of K kms-1, of the 12CO(2–1),13CO(2-1), and C18O(2–1) emission (from top to bottom). The 13CO(2–1) and C18O(2–1) maps have a spatial resolution of 30.′2 (corresponding to 0.19 pc at the 1.3 kpc distance of the cloud) and the emission is integrated over the LSR velocity range -12 to 4 kms-1. The 12CO(2–1) map has a spatial resolution of 90° and the emission is integrated over the LSR velocity range -25 to 12 kms-1. The blue contours trace column densities of 1.8 and 5.0 × 1022 cm-2 derived from Herschel data (at 36.″3) and are the same in all three panels. |
| In the text | |
 |
Fig. 3 Positionally averaged spectra for the observed molecular and atomic emission. The spectra are averaged across the same observed region defined by the footprint of the APEX maps (cf. Fig. 2). The red vertical line indicates the peak position of the 13CO(2–1) and C18O(2–1) emission at -3.3 kms-1. The solid black vertical line gives the position of the extended emission at 6 km s-1, observed in emission and absorption, in 12CO(2–1) and HI, respectively. The dashed black vertical lines indicate the extent of the cloud emission identified in the 12CO(2–1) V1 velocity range (see Sect. 3.2). |
| In the text | |
 |
Fig. 4 Position–velocity (PV) diagrams in units of K(TMB) for the 12CO(2-1), 13CO(2-1), and C18O(2-1) emission (from top to bottom). The 13CO(2-1) and C18O(2-1) maps have a spatial resolution of 30.″2. The 12CO(2-1) map has a spatial resolution of 90″. These PV diagrams are averaged in latitude across the cloud for 0.″4 = b = 1″. The white contours indicate the C18O(2–1) intensity at 1 K and are the same for the three panels. In the top panel the thick white contour corresponds to the 12CO(2–1) intensity at 0.6 K. |
| In the text | |
 |
Fig. 5 Velocity channel maps in units of K kms-1 for the 12CO(2–1) and 13CO(2–1) emission (left and right, respectively). The velocity ranges of the channel maps are indicated at the bottom left of each panel. The range of the color scale (indicated by the bar for each panel) is different for each plot. This scale was chosen to represent the dynamical range of the emission for each velocity channel map. |
| In the text | |
 |
Fig. 6 Integrated intensity map, in units of K km s-1, of the C18O(2–1) emission (same as Fig. 2). The colored curves show the crests of the velocity coherent filaments (VCFs) identified using CRISPy. The crests with total length (L) larger than 10 pixels are traced in cyan and numbered. VCFs 1, 32, and 47 are identified with red arrows. The dotted purple boxes indicate the regions from which the averaged radial profiles and the PV maps are derived (see Sects. 6.1 and 6.2). The white crosses indicate the seven infrared high-mass star-forming regions, which are usually referred to as sources I(N), E, I, II, III, IV, and V (from east to west) (Persi & Tapia 2008; Arzoumanian et al. 2021). Source I is indicated with the green arrow. |
| In the text | |
 |
Fig. 7 Scatter plots of measured parameters for the 47 VCFs. The values are averaged along the crests of the VCFs. The data points in red, yellow, and blue indicate VCFs 1, 32, and 47, respectively. Left: velocity dispersion vs. column density. The horizontal and vertical bars indicate the 1s dispersions of |
| In the text | |
 |
Fig. 8 Power spectra of the column density (blue) and the velocity (purple) for the VCF crests 1 (left), 32 (middle), and 47 (right). The amplitudes of the power spectra are scaled so they can be plotted on the same panel. The red lines show the best linear fit to the power spectra and the values of the slopes are indicated in the corresponding panels. The vertical black solid lines indicate the 30.″2 angular resolution of the data equivalent to ~1.2 arcmin-1, which is the highest frequency data point used to fit the power spectra. |
| In the text | |
 |
Fig. 9 Distributions of the power spectrum slopes. Top: distribution of the power spectrum slopes of the column density ( |
| In the text | |
 |
Fig. 10 Properties along VCF crests 1, 32, and 47 (from left to right). The zero offsets correspond to the most southwestern end of the crests (as seen on Fig. 6). Rows from top to bottom: (1) column density derived from Herschel data. (2) LOS averaged dust temperature derived from Herschel data. The horizontal blue lines indicate the mean background temperature around the VFCs of ~17.9 ± 0.2 K. (3) PACS 70 µm flux. The horizontal blue line indicates the mean background emission of ~146 ± 23 MJy sr-1. (4) Velocity. The black vertical lines on each data point show the velocity dispersion (same as the values shown in row 5). The black lines show a linear fit to these data points. The velocity resolution of 0.3 km s-1 is indicated by the vertical blue lines. For VCF 1, a linear fit to the velocity >2.8 km s-1 over a length of 0.7 pc is indicated in red and corresponds to the crest crossing the young star cluster identified as source I (see, e.g., Persi & Tapia 2008). The position of source I is indicated with the vertical dashed green line (see also the green arrow in Fig. 6). (5) Velocity dispersion. The velocity resolution of 0.3km s-1 is indicated by the vertical blue lines. |
| In the text | |
 |
Fig. 11 Radial profiles across the MFS-warm, MFS-cold, and IFS regions (from left to right; see boxes in Fig. 6). The column density, the PACS 70 µm emission, and the dust temperature are shown as solid black, blue dashed, and red dot-dashed lines, respectively. The scaling of the different curves is indicated in the caption of each panel. The r > 0 values correspond to the Galactic north. |
| In the text | |
 |
Fig. 12 Position-velocity (PV) diagrams perpendicular to and averaged along the main axes of the MFS-warm, MFS-cold, and IFS regions (from left to right, see boxes in Fig. 6). The PV maps are in units of K(TMB) and correspond to the 13CO(2–1) and C18O(2–1) emission at the top and bottom, respectively. The white contours indicate the C18O(2–1) intensity and are the same for the two panels of the same filament system. The magenta contours in the left panel correspond to the 13CO(2–1) intensity. The zero offset position (on the x-axes) corresponds to the Galactic south side of the filament systems. At the distance of this cloud 10’ corresponds to 3.8 pc. The position of the filaments are indicated with a dark blue circle and the velocity gradients induced by the compression are shown as converging red dashed arrows toward the filament. Longitudinal PV diagrams along the crest of VCF 32 of the MFS-cold region are shown in Fig. C.1. |
| In the text | |
 |
Fig. 13 Schematic view of the suggested scenario where propagating extended gas structures interact with the NGC 6334 complex, resulting in the formation or altering the properties of the filament systems MFS-warm, MFS-cold, and IFS (from left to right). These sketches are in the PP space perpendicular to the filament along the axes. The velocities of the different structures are indicated in the LSR frame according to the PV diagrams (Fig. 12). The shock front is indicated in the post-shock configuration. The left and right arrows (<< and >>) indicate the more blueshifted and more redshifted velocities, respectively, with respect to the velocity of the extended sheet-like structures. The velocity of the sheet-like structure is connected to the filament velocity through a velocity gradient. The ambient 5-field (indicated by the black lines) is parallel to the shock front. |
| In the text | |
 |
Fig. A.1 Intensity ratio and optical depth estimates. Top: Ratio map |
| In the text | |
 |
Fig. B.1 Example of an observed spectrum and the different steps of the n-Gaussian fitting procedure. Top: Observed C18O(2–1) spectra toward a position in the center of the map (top). The blue and red curves show the five individual Gaussian functions and the sum of all the fitted Gaussians, respectively. The dotted line shows the intensity threshold corresponding to S/N = 4s. Here s = 0.6 K. The second derivative of the C18O(2–1) spectra shown in the top panel (bottom). The blue horizontal lines show the region where the first guess for each of the Gaussian fits is identified indicated by the red symbols defining the points surrounding a peak to be fitted. Middle: Second iteration of the Gaussian fits where the Gaussian component not following the given criterion on the velocity resolution (5 × 0.3 km s-1) are discarded. A new multi-component fit is done on the remaining positions. The result is a combined Gaussian with three components. Bottom: Third iteration of the Gaussian fits following the same procedure of the second iteration. The result is a combined Gaussian with two components. Both components follow the defined criteria and correspond to the final result of the n-Gaussian fit. |
| In the text | |
 |
Fig. B.2 Examples of observed and modeled maps. Left: Observed and modeled moment zero map of the C18O(2–1) emission toward the MFS (top and bottom, respectively). The intensity is shown in K km s-1. The bottom map shows the ratio of the above two maps. The median, mean, and standard deviation values of this ratio map are 1.02, 1.10, and 0.46, resepctively. Right: Observed and modeled moment one map of the C18O(2–1) emission toward the GM24FS (top and bottom, respectively). The unit of the maps is km s-1. The bottom map shows the number of velocity components fitted for each pixel (toward each LOS). |
| In the text | |
 |
Fig. B.3 Map showing the number of fitted velocity components for each C18O(2–1) spectra. The blue and red contours indicate velocity components = 2 and = 3, respectively. More than 88% of the spectra are fitted with a single velocity component and only ~12% of the spectra required two or three velocity components to fit the observed spectra. The cyan curves trace the crests of the identified velocity coherent filaments (same as in Fig. 6). The black arrow toward the MFS indicates the location of the spectrum shown in Fig. B.1. The red lines indicate the central positions of the slices used to derive the PV diagrams shown in Fig. C.1. |
| In the text | |
 |
Fig. C.1 Longitudinal position–velocity (PV) diagrams along the crest of VCF 32 for the 13CO(2–1) and C18O(2–1) emission (left and right, respectively). The PV maps are in units of K(TMB). Each PV diagram is perpendicular to the crest and averaged over 4 pixels (2×beams). The slices from 1 to 5 correspond to positions along the crest from east to west. The central positions of the slices are indicated on Fig. B.3. The white contours indicate the 13CO(2–1) intensity of 1 K and 2 K and are the same for the two panels of the same slice. The zero offset position (on the x-axes) corresponds to the Galactic south side of the filament systems. At the distance of this cloud 10’ corresponds to 3.8 pc. The position of the filaments is between 9’ and 10’. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.