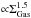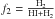| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A126 | |
| Number of page(s) | 26 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201424171 | |
| Published online | 18 August 2015 | |
Evolution of the Milky Way with radial motions of stars and gas
I. The solar neighbourhood and the thin and thick disks⋆
1
Institut d’Astrophysique de Paris, UMR 7095 CNRS,
Univ. P., & M. Curie, 98bis Bd.
Arago,
75104
Paris,
France
e-mail: kubryk@iap.fr; prantzos@iap.fr
2
Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique
de Marseille) UMR 7326, 13388
Marseille,
France
e-mail:
lia@lam.fr
Received: 9 May 2014
Accepted: 20 April 2015
Context. We study the role of radial migration of stars on the chemical evolution of the Milky Way disk.
Aims. We are interested in the impact of that process on the local properties of the disk (age-metallicity relation and its dispersion, metallicity distribution, evolution of abundance ratios) and on the morphological properties of the resulting thick and thin disks.
Methods. We use a model with several new or up-dated ingredients: atomic and molecular gas phases, star formation that depends on molecular gas, yields from a recent homogeneous grid and observationally inferred SNIa rates. We describe radial migration with parametrised time- and radius-dependent diffusion coefficients, based on the analysis of an N-body+SPH simulation. We also consider parametrised radial gas flows, induced by the action of the Galactic bar.
Results. Our model reproduces current values of most of the main global observables of the MW disk and bulge, and also the observed “stacked” evolution of MW-type galaxies. The azimuthally averaged radial velocity of gas inflow is constrained to less than a few tenths of km s-1. Radial migration is constrained by the observed dispersion in the age-metallicity relation. Assuming that the thick disk is the oldest (>9 Gyr) part of the disk, we find that the adopted radial migration scheme can quantitatively reproduce the main local properties of the thin and thick disk: metallicity distributions, “two-branch” behaviour in the O/Fe vs. Fe/H relation and the local surface densities of stars. The thick disk extends up to ~11 kpc and has a scale length of 1.8 kpc, which is considerably shorter than the thin disk, because of the inside-out formation scheme. We also show how, in this framework, current and forthcoming spectroscopic observations can constrain the nucleosynthesis yields of massive stars for the metallicity range of 0.1 Z⊙ to 2−3 Z⊙.
Key words: Galaxy: general / Galaxy: disk / Galaxy: evolution / Galaxy: abundances / solar neighborhood / Galaxy: structure
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The Milky Way (MW) offers the possibility of detailed observations of a large number of galactic properties, which are inaccessible in the case of other galaxies. Information on chemical composition and kinematics is now available for a few thousand stars of various ages, in the solar vicinity, across the MW disk and away from the Galactic plane. A large amount of information also exists for the gaseous content of the Galaxy (its molecular and atomic components and its chemical composition) as a function of galactocentric radius.
The chemical properties of the MW (local age-metallicity relation, local metallicity distribution, abundance ratios vs. metallicity, abundance profiles across the disk) have been extensively studied long before the era of large scale numerical simulations. Such studies were performed with simple numerical models, either for the solar neighbourhood or for the whole disk (with “independent ring” models) and revealed some key aspects of the chemical evolution of the Galaxy: the need for a supplementary source of Fe (beyond massive stars), namely SNIa, to reproduce the observed decline of O/Fe with metallicity; the need of a long-term early infall, to reproduce the early part of the G-dwarf metallicity distribution and the high present-day abundance of deuterium; the need for a radial variation in the efficiency of star formation (and/or the corresponding infall timescale) in order to obtain the observed gradients in the radial abundance profiles (e.g. Pagel 2009; Matteucci 2012). The aforementioned results are robust qualitatively but not quantitatively, because of large uncertainties in the observational data (e.g. dispersion in the age-metallicity relation, shape of the metallicity distribution) and also because of the poorly understood role of radial gaseous flows. Although they are justified on physical grounds (e.g. Lacey & Fall 1985 ) radial flows were never shown conclusively to play an important role in the chemical evolution of the Milky Way, because of the impossibility to observe or to infer from theory the corresponding radial velocity profiles in the Galaxy.
The action of the bar can mix radially not only gas but also stars, and the effects of stellar radial motions on the abundance profiles have been studied to some extent with N-body+SPH codes by Friedli & Benz (1993) and Friedli et al. (1994). Observations in the 90s revealed that the MW does have a bar (Blitz & Spergel 1991), but its origin, size and age are not well known yet; as a result, its impact on the evolution of the MW is difficult to evaluate quantitatively.
Independently of the role of the bar, Sellwood & Binney (2002) show that, in the presence of recurring transient spirals, stars in a galactic disk could undergo important radial displacements. Stars found at corotation with a spiral arm may be scattered to different galactocentric radii (inwards or outwards), a process that preserves overall angular momentum distribution and does not contribute to the radial heating of the stellar disk. Using a simple model, they showed how this process can increase the dispersion in the local metallicity vs. age relation, well above the amount due to the epicyclic motion. This development paved the way for a large number of theoretical studies on radial migration, both with N-body codes (e.g. Roškar et al. 2008; Sánchez-Blázquez et al. 2009; Martínez-Serrano et al. 2009; Sales et al. 2009; Roskar 2010; Minchev & Famaey 2010; Minchev et al. 2011, 2012b; Brunetti et al. 2011; Grand et al. 2012; Baba et al. 2013; Bird et al. 2013; Di Matteo et al. 2013; Kubryk et al. 2013; Grand et al. 2014) and with semi-analytical models (Lépine et al. 2003; Prantzos 2009; Schönrich & Binney 2009a; Minchev et al. 2013, 2014; Wang & Zhao 2013). Because of the difficulty in producing realistic MW-like disks, the former class of models focused mostly on generic properties of radial migration (origins of it and impact on some observables), while the latter focused exclusively on the properties of the MW.
Roškar et al. (2008) investigated the implications of radial migration for the chemical evolution of galactic disks with N-body+SPH simulations. The main effects they found and analysed are: the resulting dispersion in the age-metallicity relation, the broadening of the local metallicity distribution, the flattening of observed past abundance profiles and the flattening of the observed past star formation history.
Schönrich & Binney (2009a) introduced a parametrised prescription of radial migration (distinguishing epicyclic motions from migration due to transient spirals) in a semi-analytical chemical evolution code. They suggest that radial mixing could also explain the formation of the Galaxy’s thick disk, by bringing a kinematically “hot” stellar population from the inner disk to the solar neighbourhood. That possibility was subsequently investigated with N-body models, but controversial results have been obtained up to now. While Loebman et al. (2011) find that secular processes (i.e. radial migration) are sufficient to explain the kinematic properties of the local thick disk, Minchev et al. (2012a) find this mechanism insufficient and suggest that an external agent (e.g. early mergers) is required for that. This is still being debated, e.g. Sales et al. (2009), Wilson et al. (2011), Navarro et al. (2011), Bekki & Tsujimoto (2011), Brook et al. (2012), Forbes et al. (2012), Steinmetz (2012), Liu & van de Ven (2012), Bird et al. (2013), Kordopatis et al. (2013), Haywood et al. (2013), Roškar et al. (2013). On the other hand, using mono-abundance populations (i.e. defined in the plane of [O/Fe] vs. [Fe/H]), Bovy et al. (2012b) conclude that the thick disk is not really a distinct component of the Milky Way, as initially suggested in Schönrich & Binney (2009b; see also Rix & Bovy 2013, for a review).
Minchev & Famaey (2010) suggest a different mechanism for radial migration than transient recurring spirals, namely resonance overlap of the bar and spiral structure (Sygnet et al. 1988). This strongly nonlinear coupling leads to a more efficient redistribution of angular momentum in the disk and produces a stellar velocity dispersion that increases with time, in broad agreement with local observations. This bar-spiral coupling was studied in detail by Shevchenko (2011) and Brunetti et al. (2011). The latter study found that the extent of radial migration also depends on the kinematic state of the disk and is reduced in the case of kinematically hot disks. They also show that radial migration can be assimilated to a diffusion process, albeit with time- and position-dependent diffusion coefficients. That idea was confirmed by the analysis of N-body+SPH simulations of a disk galaxy by Kubryk et al. (2013): they extracted such coefficients from the simulation of an early-type barred disk and, applying them in a semi-analytical model of that same disk, they showed that all the main features of the N-body+SPH simulation can be reproduced to a good accuracy. They also showed that radial migration moves around not only “passive” tracers of chemical evolution (i.e. long-lived stars, keeping on the surfaces the chemical composition of the gas at the time and place of their birth), but also “active” agents of chemical evolution, i.e. long-lived nucleosynthesis sources (mainly SNIa producing Fe and ~1.5 M⊙ stars producing s-process elements).
In this work we present a model for the evolution of the MW disk that includes radial motions of gas and stars. Our treatment of radial migration of stars is a mixture of the techniques adopted in some pevious works in the field. As in Sellwood & Binney (2002) and Schönrich & Binney (2009a) – but unlike Minchev et al. (2013, 2014) or Kubryk et al. (2013) – we consider separately the epicyclic motion of stars (blurring) from the true variation in their guiding radius (churning). For the former, we adopt an analytic formalism based on the epicyclic approximation. For the latter, we are inspired by N-body+SPH simulations – as in Minchev et al. (2013) and Kubryk et al. (2013) – and we adopt a parametrised description, using time- and radius-dependent diffusion coefficients. In this way, we are able to quantitatively study the impact of epicyclic motion alone to the dispersion of the local age-metallicity relation and, of course, the collective impact of the two processes (blurring+churning).
The ingredients of our model are presented in Sect. 2 and some of them are described in more detail in Appendices B and C. Some of the observational constraints are presented in Sect. 2.5, while the adopted gas and star formation rate (SFR) profiles are discussed in detail in Appendices A and B. The global evolution of the Galaxy (i.e. various quantities as a function of time and radius) is presented in Sect. 3 and the results are compared to observations; in particular, in Sect. 3.2 we discuss the diffusion coefficients adopted in our model and the amount of the radial migration they produce along the disk. The results concerning the solar vicinity (age-metallicity relation and its dispersion, metallicity distribution, abundance ratios) are presented in Sects. 4.1 and 4.2. We then analyse the properties of the thick disk, which is assumed here to be just the old part of the disk (age >9 Gyr) and show that this assumption leads to results that are in fair agreement with most of the observed chemical and morphological properties of the thick disk (Sect. 4.3). A summary of the results is presented in Sect. 5.
2. The model
Our model is based on a considerably updated version of the “independent-ring” model for the MW presented in Prantzos & Aubert (1995), Prantzos et al. (1996), and Boissier & Prantzos (1999). The main differences include:
-
Star formation rate depending on molecular gas, instead of total gas (Appendix B);
-
A new routine for the SNIa rate, based on observations at various redshifts, instead of theoretical precriptions (Appendix C);
-
Stellar yields from Nomoto et al. (2013), extending to super-solar metallicities (Appendix C), instead to those of Woosley & Weaver (1995) which reach metallicities only up to solar;
-
A new numerical scheme to handle chemical evolution through single stellar populations (Appendix C), instead of adopting the classical formalism (with integration over mass);
to which one should add:
-
The introduction of radial gas flows (Sect. 2.3).
-
The treatment of radial migration through blurring (Sect. 2.2.1) and churning (Sect. 2.2.2).
2.1. Building the Galaxy: dark matter, baryonic infall and star formation
In our model, we construct the Galaxy “backwards”, i.e. we are guided in the selection of the model parameters by the present-day properties of the Milky Way (e.g. radial profiles of baryonic matter and rotational velocity, which also depend on the distribution of the dark matter halo). Some of those properties play an important role in determining the extent of radial displacement of stars; this is the role of the rotation curve for blurring, for example (Sect. 2.2.1). Unfortunately, determination of the structural parameters of the various components of the Galaxy still suffers from degeneracy problems; see e.g. the excellent summary of mass models of the Milky Way in Sect. 4 of Courteau et al. (2014).
For the purpose of this work, we describe the Milky Way as a superposition of three components: a DM halo, a bulge and a disk. We note, however, that the actual distribution of the baryonic material within the inner 2 kpc is much more complex than assumed here, because it can contain a number of components such as a boxy/peanut bulge, a disky bulge and a classical bulge as well as the inner extension of the Galactic disk. These have very different shapes, kinematics and formation histories. Our model, which is essentially 1D, cannot describe all this complexity. We thus do not extend our study to the region inwards of two kpc, which is designated as “ the bulge” here (we use the term “disk” for the region outside 2 kpc).
The current virial mass of the DM halo of the MW is typically estimated to MDH = 1012M⊙, although variations by a factor greater than two around that value are found in the literature, e.g. Rashkov et al. (2013) and references therein. For the evolution of the DM halo we used the simulations of Li et al. (2007), who calculated the growth of DM haloes in a ΛCDM model. We extracted about 200 DM haloes with final mass of 1012M⊙ from that simulation and took an average over all masses at each redshift. We adopted this smoothed evolution as a reasonable approximation for the evolution of the DM halo of the MW, at least for the past 8 Gyr, where no major merger is thought to have occurred. We do not account for any concentration effect due to the interaction of baryons with the DM halo, that is, we assume that the DM halo has, at all redshifts z, a Navarro-Frenk-White profile, with the central density varying with time or redshift as to have the mass mDM(z) enclosed within the virial radius.
We assume that the MW is built gradually from gas infalling in the potential well of the DM halo. with the radial profile for the infall rate a function of time. Once the time variation of infall in each zone r is assumed (in most cases an exponential decay law, with a characteristic time scale τ(r)), the gas infall rate per unit area of the disk Fgr,(t) (M⊙/pc2/yr) is constrained by the requirement that its integral over time equals the total baryonic (i.e. stars+gas) surface density ΣTot,Obs(r,T) at present time T: 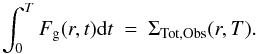 (1)In the case of independent-ring disk models, Eq. (1) is used to fix Fg(r,t) uniquely and accurately. When radial migration is taken into account, the final baryonic profile depends not only on the integral of Fg(r,t) over time, but also on the extent of migration. In those conditions, it becomes difficult to reproduce ΣTot,Obs(r,T) accurately in the end of the simulation. Here we adopt – after some iterations – a profile for
(1)In the case of independent-ring disk models, Eq. (1) is used to fix Fg(r,t) uniquely and accurately. When radial migration is taken into account, the final baryonic profile depends not only on the integral of Fg(r,t) over time, but also on the extent of migration. In those conditions, it becomes difficult to reproduce ΣTot,Obs(r,T) accurately in the end of the simulation. Here we adopt – after some iterations – a profile for 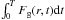 that depends on our migration coefficients: the combination of the adopted infall and star formation prescriptions and the adopted radial migration scheme produces a quasi-exponential stellar profile in the end of the simulation.
that depends on our migration coefficients: the combination of the adopted infall and star formation prescriptions and the adopted radial migration scheme produces a quasi-exponential stellar profile in the end of the simulation.
Concerning the infall timescales, we adopt τ = 2 Gyr for the bulge (hereafter taken as the region within r = 2 kpc) and a smoothly increasing function, reaching τ(20 kpc) = 8 Gyr for the disk (r> 2 kpc). The adopted profile of τ(r) can be seen in the bottom right panel of Fig. 4. The composition of the infall is equally important when it comes discussing the evolution of abundances and abundance ratios in the MW disk. Observations are of little help at present: although they generally find low metallicities for gas clouds presently falling to the MW disk (~0.1 Z⊙, e.g. Wakker et al. 1999), but they provide no information on the past metallicity of such clouds or on their abundance ratios. Here we adopt the simplest possible (but still arbitrary) assumption, namely that the infalling gas always has primordial composition, i.e. only for i = H, D, 3He, 4He and 7Li is the term Fg,i(r,t) = Fg(r,t)Xi(r,t) different from zero (where Xi(r,t) is the mass fraction of isotope i). This assumption hardly affects the results for the chemical evolution of the disk, but it allows for the existence of disk stars with metallicities lower than [ Fe / H ] =−1 (see Bensby 2014, and references therein).
Most of the SFR laws adopted in semi-analytical models of galactic evolution make use of the total gaseous profile of the disk. Based on detailed, sub-kpc scale, observations of a large sample of disk galaxies, Bigiel et al. (2008) have found that the SFR appears to follow the H2 surface density, rather than the HI or the total gas surface density. Based on an updated set of observational data, Krumholz (2014) concludes in his recent review that “the correlation between star formation and H2 is the fundamental one”.
Following these studies, we checked whether such a correspondence between the adopted SFR and molecular gas profiles also holds in the MW disk. The comparison, as discussed in Appendix B appears to favour that idea, as also noticed (albeit with older data sets) by Blitz & Rosolowsky (2006). In view of this observational support, both for the MW disk (this work) and for external galaxies (Bigiel et al. 2008; Leroy et al. 2008), we adopted a star formation law that depends on the H2 surface density. To calculate it in the model of chemical evolution, we adopted the semi-empirical method of Blitz & Rosolowsky (2006) to evalulate the ratio Rmol = H2/HI in a galactic disk (see Appendix A). We note that this method provides two more observational constraints to disk models, namely the present-day radial profiles of atomic and molecular gas, which are not usually considered (see, however, Ferrini et al. 1994; Mollá & Díaz 2005). We also notice that a SFR proportional to the surface density of molecular gas has recently been used in disk models by Kang et al. (2012), Lagos et al. (2011) and Fu et al. (2013).
2.2. Stellar migration
The orbit of a test particle (star) in the potential of a galactic disk is commonly described, to first order approximation, as the superposition of a main circular motion (defining the guiding radius), and harmonic oscillations called epicycles. Following Schönrich & Binney (2009a), we call “blurring” the radial oscillations around the guiding radius and “churning” the modifications of the guiding radius. Churning may occur through resonant interactions of the star with non-axisymmetric structures of the gravitational potential (spirals, bar), causing changes in the angular momentum of the stars. The process conserves the overall distribution of angular momentum and does not add random motion, that is, it does not “heat” the disk radially. In contrast, blurring conserves the angular momentum of individual stars but it heats the disk in the radial direction (the epicyclic radius increases with time).
In N-body schemes, the overall effects of both blurring and churning are naturally obtained. Semi-analytical models based on N-body simulations use the knowledge obtained from the N-body run to describe the extent of radial migration, without distinguishing beween the two effects, such as in Minchev et al. (2013, 2014), Kubryk et al. (2013). Here, we follow SB02 and Schönrich & Binney (2009a) and we parametrise blurring and churning separately.
2.2.1. Epicyclic motion (blurring)
Folowing Sellwood & Binney (2002), we adopt a global mixing scheme, where a star born at radius r′ at time t′ may be found at time t (i.e. after time τ = t − t′) in radius r with a probability P(r,r′,τ) given by a Gaussian function ![\begin{equation} P(r,r',\tau)\ =\ (2\pi\sigma_{\tau}^{2})^{-1/2}\exp\left[-\frac{(r-r')^{2}}{2\sigma_{\tau}^{2}}\right] \label{eq:prob} \end{equation}](/articles/aa/full_html/2015/08/aa24171-14/aa24171-14-eq42.png) (2)where στ is the 1σ dispersion in the radial displacement of the particles of age τ at radius r. SB02 adopted, for illustration purposes, a time-independent dispersion amplitude for blurring of σb = 0.16 R0 in the the solar neighbourhood (R0 = 8 kpc). We improve by adopting a time-dependent, better motivated and easy to implement description for the epicyclic motion based on the epicyclic approximation (Binney & Tremaine 2008), where the oscillations of stars around their guiding radius are described by the resulting dispersion in their radial position as
(2)where στ is the 1σ dispersion in the radial displacement of the particles of age τ at radius r. SB02 adopted, for illustration purposes, a time-independent dispersion amplitude for blurring of σb = 0.16 R0 in the the solar neighbourhood (R0 = 8 kpc). We improve by adopting a time-dependent, better motivated and easy to implement description for the epicyclic motion based on the epicyclic approximation (Binney & Tremaine 2008), where the oscillations of stars around their guiding radius are described by the resulting dispersion in their radial position as 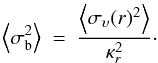 (3)The frequency κr of harmonic oscillations at radius r is given as a function of the rotational velocity VC(r) by
(3)The frequency κr of harmonic oscillations at radius r is given as a function of the rotational velocity VC(r) by 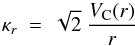 (4)in the case of VC(r) = const. For the radial velocity dispersion συ(r) we adopt the presently (time t = T) observed one in the Milky Way (Lewis & Freeman 1989), parametrised as
(4)in the case of VC(r) = const. For the radial velocity dispersion συ(r) we adopt the presently (time t = T) observed one in the Milky Way (Lewis & Freeman 1989), parametrised as 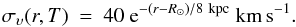 (5)For the time dependence of the radial velocity dispersion we adopt
(5)For the time dependence of the radial velocity dispersion we adopt 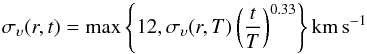 (6)which agrees with, for example, the evaluation of Holmberg et al. (2007) for local stars. The time dependence of the rotational velocity VC(r,t) is obtained self-consistently from our model. The probability distribution obtained by Eq. (2) is not symmetric with respect to the birth radius r′ of the stars, because the dispersion στ(r) depends on the final radius r through Eqs. (3)−(5).
(6)which agrees with, for example, the evaluation of Holmberg et al. (2007) for local stars. The time dependence of the rotational velocity VC(r,t) is obtained self-consistently from our model. The probability distribution obtained by Eq. (2) is not symmetric with respect to the birth radius r′ of the stars, because the dispersion στ(r) depends on the final radius r through Eqs. (3)−(5).
We notice that Schönrich & Binney (2009a) also treated blurring and churning separately. For the former, they adopted a more physical treatment than ours, starting from first principles. They used the distribution function of angular momentum of stars and made plausible assumptions on the radial and temporal dependence of the stellar radial velocity dispersion to describe its evolution. Our heuristic formulation of blurring approximates the results of Schönrich & Binney (2009a) rather well, as discussed in Sect. 3.2 and Fig. 7 (middle panel).
2.2.2. Radial migration (churning)
In this work, we adopt a probabilistic description of churning, à la SB02, where the amplitude of the radial mixing of stars of age τ found at radius r (Eq. (2)) is the sum of the blurring (σb) and churning (σc) terms: 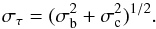 (7)As discussed in Sect. 1, that parametrization of churning as a diffusion processes appears to be supported by the analysis of numerical simulations by Brunetti et al. (2011) and Kubryk et al. (2013). The method is similar to the one adopted by Minchev et al. (2013), who sampled the stellar positions of an N-body simulation and applied the results in an independent semi-analytical model of the chemical evolution of the MW. These methods differ qualitatively from Schönrich & Binney (2009a), who adopted a local scheme (in which only stars from up to the second-nearest neighbouring zones can exchange places during a time step) with a probability adjusted to reproduce some observables in the solar neighbourhood, such as the metallicity distribution.
(7)As discussed in Sect. 1, that parametrization of churning as a diffusion processes appears to be supported by the analysis of numerical simulations by Brunetti et al. (2011) and Kubryk et al. (2013). The method is similar to the one adopted by Minchev et al. (2013), who sampled the stellar positions of an N-body simulation and applied the results in an independent semi-analytical model of the chemical evolution of the MW. These methods differ qualitatively from Schönrich & Binney (2009a), who adopted a local scheme (in which only stars from up to the second-nearest neighbouring zones can exchange places during a time step) with a probability adjusted to reproduce some observables in the solar neighbourhood, such as the metallicity distribution.
The coefficients describing the amplitude of radial migration are extracted from the N-body+SPH simulation analysed in Kubryk et al. (2013). We note that Kubryk et al. (2013) extracted total (i.e. churning+blurring) coefficients, while here we extract coefficients for churning only: we follow the variations of the angular momentum of stars, which correspond to variations in their guiding radius. We fit the corresponding radial distributions with Gaussian functions1 of 1σ width as a function of birth radius ri and time t since stellar birth : 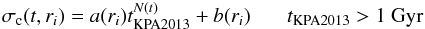 (8)and we find N ~ 0.5 for t> 1 Gyr. However, the disk galaxy analysed in Kubryk et al. (2013) has a strong and long bar, reaching a length of ~8 kpc in the end of the simulation at 10 Gyr. In contrast, the Milky Way has a small bar, not necessarily as old as 10 Gyr (see next section). Its effect on churning will then be smaller than in the aforementioned simulation. Indeed, if we adopt the coefficients of Kubryk et al. (2013) we obtain a large dispersion in the local age-metallicity relation in the framework of our model. We chose then to reduce these coefficients of Kubryk et al. (2013) while keeping their temporal and radial dependence, by applying the transformation
(8)and we find N ~ 0.5 for t> 1 Gyr. However, the disk galaxy analysed in Kubryk et al. (2013) has a strong and long bar, reaching a length of ~8 kpc in the end of the simulation at 10 Gyr. In contrast, the Milky Way has a small bar, not necessarily as old as 10 Gyr (see next section). Its effect on churning will then be smaller than in the aforementioned simulation. Indeed, if we adopt the coefficients of Kubryk et al. (2013) we obtain a large dispersion in the local age-metallicity relation in the framework of our model. We chose then to reduce these coefficients of Kubryk et al. (2013) while keeping their temporal and radial dependence, by applying the transformation 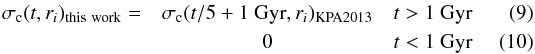 i.e. we assume that the evolution at, say, t ~ 10 Gyr in our model is similar to the one at t ~ 3 Gyr in the simulation of Kubryk et al. (2013). Physically, this corresponds to the epoch where the bar in the N-body simulation has similar size to the one of the current MW bar and other key properties of the disk (surface density profile, scalelength, presence of spiral arms) are similar to the ones of the present day MW (see Figs. 1 and 2 in Kubryk et al. 2013). As we shall see (Sect. 4), this transformation leads to acceptable results for the observed dispersion in the local age-metallicity relation. We checked that slightly different values of the churning coefficients, corresponding to the transformation t to t/ 6 and up to t to t/ 4, produce acceptable results for the dispersion in the age-metallicity relation. The churning coefficients of our model are presented, discussed and compared to those of Schönrich & Binney (2009a) in Sect. 3.2.
i.e. we assume that the evolution at, say, t ~ 10 Gyr in our model is similar to the one at t ~ 3 Gyr in the simulation of Kubryk et al. (2013). Physically, this corresponds to the epoch where the bar in the N-body simulation has similar size to the one of the current MW bar and other key properties of the disk (surface density profile, scalelength, presence of spiral arms) are similar to the ones of the present day MW (see Figs. 1 and 2 in Kubryk et al. 2013). As we shall see (Sect. 4), this transformation leads to acceptable results for the observed dispersion in the local age-metallicity relation. We checked that slightly different values of the churning coefficients, corresponding to the transformation t to t/ 6 and up to t to t/ 4, produce acceptable results for the dispersion in the age-metallicity relation. The churning coefficients of our model are presented, discussed and compared to those of Schönrich & Binney (2009a) in Sect. 3.2.
The two migration mechanisms are treated independently of each other in our model, meaning that we can consider the effects of blurring or churning alone. This allows us to evaluate the impact of each one of them on the radial mixing of the disk and on the resulting dispersion in the age-metallicity relation in the solar neighbourhood (see Sect. 4). Of course, both of them are considered in our baseline model.
The mechanism of radial migration discussed in this section, is not applied to the gas in our model. In contrast to the dissipationless stellar fluid, gas is dissipative and affected little by that mechanism. This can be seen e.g. by comparing Figs. 4 (stars) and 5 (gas) in Kubryk et al. (2013). The bar, however, drives gas inwards and we describe this radial inflow in the next section.
2.3. Radial gas flows
The pioneering works of Tinsley & Larson (1978) and Mayor & Vigroux (1981) emphasized the potential importance of radial gaseous flows for the chemical evolution of galactic disks. Lacey & Fall (1985) presented a systematic investigation of the causes of such flows: i) viscosity of the gaseous layer of the disk, ii) mismatch of angular momentum between the gas of the disk and the gas infalling on it, and iii) gravitational interactions between the gas and a bar or a spiral density wave in the disk. They found that in all cases it is difficult to predict the magnitude and the profile of the corresponding inflow velocity and explored the impact of such effects on the chemical evolution of the Galaxy with parametrized calculations.
Among the alleged causes of radial inflows, the impact of a galactic bar is well established both from simulations and from observations. Numerical simulations (Athanassoula 1992; Friedli & Benz 1993) showed that the presence of a non-axisymmetric potential from a bar can drive important amounts of gas inwards of corotation fuelling star formation in the galactic nucleus, while at the same time gas is pushed outwards outside corotation. In a disk galaxy, this radial flow mixes gas of metal-poor regions into metal-rich ones (and vice-versa). Bars were previously believed to flatten the disk chemical abundance profile because of the streaming motions they induce, as shown by Friedli et al. (1994), Zaritsky et al. (1994), Martin & Roy (1994), Dutil & Roy (1999). But recent studies with two-dimensional (2D) higher spectral and spatial resolution integral field units show that there are negligible differences in abundance gradients between barred and unbarred galaxies, e.g. Sánchez et al. (2012). In our recent study with a high-resolution N-body+SPH simulation of an isolated barred disk (Kubryk et al. 2013), we find that the bar indeed drives large amounts of gas from corotation inwards, but no significant gas displacement occurs outside corotation (see Fig. 5 in Kubryk et al. 2013). It seems now that bars may be changing the chemical abundance profile inside the corotation radius but they they only have a small impact outside the bar itself.
One of the (many) difficulties of introducing the effect of a bar on the radial gas flows of a galactic disk in semi-analytical models, is the uncertainty on its strength and length evolution. The length of the MW bar is estimated to 2.5−3 kpc (Babusiaux & Gilmore 2005; Bobylev et al. 2014), although higher values have also been reported (Cabrera-Lavers et al. 2007).
For the purpose of this work, we adopt a radial inflow velocity profile induced by a bar of current size RB = 3. kpc, having a corotation radius at RC = 1.2RB, which is a typical relation between bar length and corotation radius (e.g. Athanassoula 1992). The flow outside corotation is outwards and we assume it extends up to the outer Lindblad resonance (OLR), located at radius ROLR ~ 1.7 RC (e.g. Athanassoula et al. 1982), which corresponds to ~6.2 kpc today. Those values are somewhat less than those adopted in the recent work of Monari et al. (2013, 2014). The flow velocity profile υf(r) has azimuthally averaged absolute velocities of a few tenths of km s-1, similar to the one of Portinari & Chiosi (2000). The adopted gas velocity profile is displayed in Fig. 5.
Our treatment of infall and radial flow is not self-consistent: as Mayor & Vigroux (1981) and Lacey & Fall (1985) have pointed out, the two are coupled through conservation of angular momentum. However, a quantitative treatment of the effect implies that the angular momentum of the infalling gas is known, but this is not the case, since the rotational profile of the infalling gas is unknown. A parametrised exploration of that effect is performed in the recent work of Bilitewski & Schönrich (2012). Here, we simply ignore that effect, implicitly assuming that the infalling gas has the same angular momentum as the disk gas at the accretion radius.
2.4. Chemical evolution
Radial migration introduces important modifications to the treatment of chemical evolution in semi-analytical models. As already emphasized in Kubryk et al. (2013), long-lived stars have enough time to migrate away from their birth place before dying and releasing their gas there. This concerns not only the “passive” tracers of chemical evolution (low-mass stars carrying the chemical composition of their birth place on their surface), but also “active” agents of chemical evolution: interesting metal producers like SNIa (for Fe-peak nuclei) and stars of ~1.3−2 M⊙ (producers of s-nuclei); “sinks” of isotopes (i.e. long-lived stars ejecting material poor in a given isotope), which deplete deuterium and dilute the other metal abundances. This imposes a coupling of the various radial zones of the model, through the transfer probabilities described in Sect. 2.2. Furthermore, while in the independent-ring models for disk evolution, one may work with surface densities of all extensive properties as functions of galactocentric distance r, any coupling of the rings (through gaseous radial inflows or migration of stars) makes it necessary to work with properties integrated over the whole ring of radius r. In the following we shall consider the equations of chemical evolution by integrating all extensive quantities over the surface area of the ring centered at r![\begin{equation} A(r) \ = \ \pi \ [ (r+{\rm d}r/2)^2-(r-{\rm d}r/2)^2]. \end{equation}](/articles/aa/full_html/2015/08/aa24171-14/aa24171-14-eq76.png) (11)The mass of gas in the ring is, obviously, mg(r) = A(r)Σg(r), where Σg(r) is the gas surface density, and similar expressions hold for all other extensive quantities. The evolution of the mass (in M⊙) of a given isotope i with mass fraction Xi in the zone r is given by
(11)The mass of gas in the ring is, obviously, mg(r) = A(r)Σg(r), where Σg(r) is the gas surface density, and similar expressions hold for all other extensive quantities. The evolution of the mass (in M⊙) of a given isotope i with mass fraction Xi in the zone r is given by 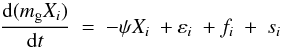 (12)where
(12)where
-
ψ(r,t)is the SFR in the whole ring;
-
εi(r,t)is the rate of isotopic mass release in r by stars produced in all previous epochs everywhere in the disk (including zone r) and are found in r at time t;
-
fi(r,t)is the net rate of isotope i entering zone r from outside the disk (i.e. any infalling minus outflowing material); and
-
si(r,t)is the net rate of isotope i brought in zone r (i.e. gas entering minus gas leaving that zone) because of radial flows from adjacent disk regions.
The first term of the right-hand member ψ(r,t) = A(r)Ψ(r,t) has already been discussed in Sect. 2.1: the SFR density Ψ(r,t) = αΣH2(r,t) is proportional to the surface density of the molecular gas (Appendix B).
Since we do not consider outflows from the disk in this work, the term fi(r,t) = A(r)Fg,i(r,t) simply represents the infalling material in the disk and it is always positive. The characteristic timescale τ(r) is displayed graphically in Fig. 4 (bottom right panel).
The term εi(r,t) is calculated as a sum over all zones Nr′ (including zone r) and all times t′ ≤ t of the ejection rate of isotope i, Ei(r′,t − t′) from a single stellar population (SSP) formed at time t − t′ in zone r′ and found in zone r at time t with a probability P: 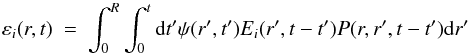 (13)where ψ(r′,t′)dt′ is the stellar mass created in the annulus r′ at time t′ during the timestep dt′ and Ei(r′,t − t′) is the ejection rate of isotope i at time t from a SSP of unit mass formed at time t′ with the metallicity Z(r′,t′) of the gas of zone r′ at that time. The latter quantity depends on the adopted stellar initial mass function (IMF) and the adopted stellar yields and is extensively discussed in Appendix C, where we provide information about the SNIa rates and yields. We consider 82 isotopes of all elements from H to Ge, summing their abundances at each timestep in order to calculate the abundances of the corresponding 32 elements. The term Ei(r′,t − t′) also includes the contribution from SNIa.
(13)where ψ(r′,t′)dt′ is the stellar mass created in the annulus r′ at time t′ during the timestep dt′ and Ei(r′,t − t′) is the ejection rate of isotope i at time t from a SSP of unit mass formed at time t′ with the metallicity Z(r′,t′) of the gas of zone r′ at that time. The latter quantity depends on the adopted stellar initial mass function (IMF) and the adopted stellar yields and is extensively discussed in Appendix C, where we provide information about the SNIa rates and yields. We consider 82 isotopes of all elements from H to Ge, summing their abundances at each timestep in order to calculate the abundances of the corresponding 32 elements. The term Ei(r′,t − t′) also includes the contribution from SNIa.
Radial migration is implemented by multiplying the mass of stars created in time t′ in zone r′ (Ms(t′,r′) = Ψ(t′,r′)dt) that are still alive after time τ = t − t′ with the probability P(r,r′,τ) in order to find the fraction of those stars that have migrated to zone r after τ. They carry the chemical composition Xi(r′,t′) but also release material corresponding to that composition and to the age t − t′. The probabilities P(r,r′,τ) are normalized to 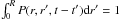 to insure mass conservation.
to insure mass conservation.
The use of the SSP formalism leads to the creation of “star particles” of variable mass dms(r,t) = ψ(r,t)dt endowed with the set of chemical abundances Xi(r,t) corresponding to the place and time of their formation. One may then use the same tools for the analysis of the results as in the case of the N-body simulations, and obtain a self-consistent comparison of results between semi-analytical models and N-body simulations, as in Kubryk et al. (2013).
Although we use two phases of the ISM, the ejecta of the stars are uniformly and “instantaneously” mixed locally in the total amount of gas. The reason is that the timestep in our model (~30 Myr) is longer than the timescales of the mixing of the ejecta (a few Myr, typically) or the timescales for the survival of molecular clouds. Thus, the ISM in each zone (HI and H2) is characterised by a unique composition at each timestep.
2.5. Observational constraints for the Milky Way
Global observational constraints for the MW.
A successful model of the chemical evolution of the Milky Way, especially one involving a large number of parameters (such as all semi-analytical models that feature radial motions of stars and gas), should satisfy a large number of observational constraints, both global (concerning the whole Galaxy) and local ones (concerning the solar neighbourhood). Unfortunately, the values of most of the observational constraints depend heavily on underlying model assumptions. Thus, the mass of the bulge is estimated to be as low as 9 × 109M⊙ (McMillan 2011) or as high as 2.4 × 1010M⊙ (Picaud & Robin 2004). Similar uncertainties affect the stellar disk, (Flynn et al. 2006; McMillan 2011), concerning its scalelength (from ~2 to more than 3 kpc) and total mass (from ~3 to more than 5 × 1010M⊙. For the purpose of this work, we adopted the results of the analysis of Flynn et al. (2006; their Fig. 15), showing that for a local stellar surface density of 39 M⊙/pc2 (35.5 M⊙/pc2 “counted”, plus an assumed 10% enhancement from azimuthal average of spiral arms) and for scalelengths in the range 2.2−3.5 kpc, the mass of the disk lies in the range 3−4 × 1010M⊙ and the one of the bulge in the range 1−2 × 1010M⊙. The total stellar mass (bulge+disk) is much better constrained, ~5 × 1010M⊙.
In Table 1 we present the basic observational facts concerning the current amounts of gas and stars in the bulge and the disk of the Milky Way. We also present adopted values and references for the rates of star formation, infall (fairly uncertain), core collapse supernovae (CCSN) and thermonuclear supernovae (SNIa). Radial profiles for all those quantities (except the uncertain profile of the infall rate and the unknown ones of supernovae rates) also constitute important constraints for the models and are discussed in Appendices A and B. We include the rotational velocity of the gas in the constraints, since radial migration changes the distribution of the baryonic component and thus affects the rotation curve. Radial abundance profiles of stars and gas constitute equally important constraints, but they also depend on adopted nucleosynthesis yields. Here we consider only the O and Fe profiles and leave a detailed discussion of all other elements for an accompanying paper.
Local observational constraints (surface densities of gas and stars – in M⊙/pc2 – at R0 = 8 kpc)
The observational constraints for the solar neighbourhood include the “classical” ones: local amounts of gas and stars (Table 2), age-metallicity relation, metallicity distribution, and abundance ratios vs. metallicity. The introduction of stellar radial migration makes it possible to use some new constraints: Schönrich & Binney (2009a) suggest that this ingredient may help explain quantitatively the observed “two-branch” behaviour of the [O/Fe] vs. [Fe/H] relation, namely the local thick vs. thin disk dichotomy. We confirm this here, using large data sets from recent surveys. We also use the observed (albeit yet uncertain) dispersion in the local age-metallicity relation as a supplementary constraint of our model. We refer to all those constraints in Sect. 4. We would like, however, to draw attention to the fact that comparing model results to observations is not a straightforward enterprise, because of various selection biases affecting the latter (magnitude-limited, kinematic etc.). In our case, all local observables of this model concern the so-called “solar cylinder”, which is all stars found in the end of the simulation in a cylinder of radius 0.25 kpc (half the size of our radial bin), perpendicular to the Galactic plane and centred on the solar position, at Galactocentric distance R0 = 8 kpc. In those conditions, a successful comparison to observations does not imply that the model is necessarily correct, only that it possesses potentially interesting features. The wealth of current and forthcoming data (with e.g. RAVE, LAMOST, Gaia etc.) will make it necessary to adopt in the models the same selection criteria as the observational surveys, to draw meaningful and quantitative conclusions.
Finally, we also compare our results to the “average histories” of mass building of Milky Way type galaxies (total stellar mass of 5 × 1010M⊙) from the recent analysis of HST+SDSS data from van Dokkum et al. (2013).
 |
Fig. 1 Evolution of various quantities in the baseline scenario. In all panels, solid bluecurves correspond to the evolution of the disk (r> 2 kpc) and dotted redones to that of the bulge (r< 2 kpc), respectively. Vertical bars at 12 Gyr represent observational constraints (see text and Table 1). |
 |
Fig. 2 Comparison of the model results to the observed “stacked” evolution of disk galaxies of stellar mass 5 × 1010M⊙ (dotted curves) from van Dokkum et al. (2013). Top: evolution of the total SFR (black solid curve), decomposed into bulge and disk contributions. Bottom: evolution of the stellar mass of the bulge (r< 2 kpc) and of the disk (r> 2 kpc) of the model (solid red and blue curves, respectively). |
 |
Fig. 3 Evolution of various quantities in the baseline scenario as a function of time, for five different radial zones, at 2 (red), 5 (green), 8 (thick blue), 11 (cyan) and 14 (magenta) kpc. Observational data for local surface densities of gas and stars (from Table 1) are indicated with filled circles at T = 12 Gyr. |
3. Global evolution
The results of our model for all the main outputs (total mass, mass of stars and gas, either atomic or molecular, rates of star formation, infall, CCSN and SNIa, as well as the scalelength of the stellar disk) as a function of time are displayed in Fig. 1.
The results reproduce the aforementioned present day observational constraints fairly well, with the exception of the gas amounts in the bulge, which our model overpredicts. We notice, however, that a significant fraction of the bulge gas is in the form of ionised gas (~3 × 107M⊙), Ferrière et al. 2007, increasing the total gas amount of the bulge by ~30%; if this is taken into account, the discrepancy with our model (which does not account for ionized gas) is reduced considerably.
Regarding the evolution of the gas, we find that its mass in the disk remains quasi-constant after the first ~2 Gyr, while it decreases by almost a factor of 30 in the bulge. It is interesting to note that the adopted prescriptions for the evaluation of the molecular fraction and the corresponding SFR (Sect. 3.1 and Appendix B) lead to a different evolution between the atomic and molecular contents of the bulge and the disk: the bulge is dominated today by H2, while the disk is dominated by HI, as observed. Also, the total disk SFR, ~2 M⊙/yr, corresponds fairly well to the observed one. This was not obvious a priori, because we assume that the SFR depends on the molecular gas, which is concentrated in the inner Galaxy (see discussion below).
Finally, the scalelength of the stellar disk increases steadily from ~1.5 kpc at 2 Gyr to 2.3 kpc at 12 Gyr. The latter value is in reasonable agreement with values in the literature: 2.1 ± 0.3 kpc from the TMGS survey (Porcel et al. 1998), 2.25 kpc from COBE/DIRBE data analysis (Drimmel & Spergel 2001), and 2.15 ± 0.14 kpc from the dynamical analysis of SEGUE G dwarfs (Bovy & Rix 2013). In Sect. 4.3 we shall discuss further the issues of thin and thick disk scalelengths.
The question of whether the Milky Way is a typical spiral galaxy or not is an open one, since it appears underluminous for its rotational velocity of 220 km s-1 (Flynn et al. 2006; Hammer et al. 2007). One may also ask whether the Milky Way evolved as an average disk galaxy of the same present-day mass of 5 × 1010M⊙. In a recent study van Dokkum et al. (2013) provide relevant data by studying progenitors galaxies of that mass out to redshift z = 2.5, using data from the 3D-HST and CANDELS Treasury surveys. They find that ~90% of the stellar mass of those galaxies was built since z = 2.5, with most of the star formation occurring before z = 1. Furthermore, the mass in the central 2 kpc of those galaxies increased by a factor of ~3 between z = 2.5 and z = 1, implying that bulges likely formed in lockstep with disks during that period. However, after z = 1 the growth in the central regions gradually stopped but the disk continued to be built up.
In Fig. 2 we compare our results to those of van Dokkum et al. (2013; their Fig. 4, where we converted redshifts in lookback time assuming a ΛCDM cosmology with parameters from the recent Planck analysis). It can be seen that our result for the total SFR (upper panel) lie slightly below the SFR of van Dokkum et al. (2013) (by ~20% at the peak of SFR, the difference gradually decreasing with time. At late times, there is a fairly good agreement between our model and the data. Concerning the stellar masses (lower panel), our results, both for the bulge (assumed to be the region of radius r< 2 kpc, as in van Dokkum et al. 2013) and the disk (r> 2 kpc) are in fairly good agreement with the observed “stacked” evolution of MW-type galaxies. Overall, we conclude that our results are compatible with the idea that the MW evolved as a typical disk galaxy of stellar mass ~5 × 1010M⊙ at the present epoch.
In Fig. 3 we present the evolution of several key observables for selected radial zones (2, 5, 8, 11, 14 kpc) of our model. The main common feature is the more rapid evolution of the inner disk, reflected in the earlier rise of the stellar surface density of the inner zones and in the more rapid decrease in the corresponding gas fractions. In the cases of the stellar and gaseous surface densities, the local observations at r = 8 kpc (Table 2) are nicely reproduced.
The net gas depletion timescale (i.e. taking both the SFR and the infall rates into account) is shorter in the inner Galaxy than in the outer one: the ratio of the infall rate to the SFR becomes smaller than unity within ~1 Gyr at r = 2 kpc but only after 10 Gyr at r = 14 kpc. This gives a measure of the radially varying star formation efficiency of the model, due to the adopted SFR dependence on the molecular gas.
Finally, the evolution of [Fe/H] in the local gas (bottom right panel of Fig. 3) never saturates, even in the inner zones: there is always a steady albeit small increase in metallicity, even at late times. This result agrees with the work of Minchev et al. (2013), but it contrasts with the results of Schönrich & Binney (2009a), who find little evolution in metallicity for all the zones of their model after the first couple of Gyr.
3.1. Gaseous profiles and the SFR
 |
Fig. 4 Model profiles (red solid curves) at 4, 8 Gyr (thin curves) and at 12 Gyr (thick curves) of various quantities and comparison of the latter with observational data concerning the present-day disk of the Milky Way. For all gaseous profiles (gas, HI, H2, gas fraction and molecular fraction), observational constraints are those discussed in Appendix A and presented in Fig. A.2. For stars, the shaded area is bounded by two exponential curves with scalelengths Rd = 2.1 and 2.7 kpc, respectively, which fix the range of plausible values for the stellar disk; they are normalised to a surface density of Σ∗(R = 8 kpc) = 38 ± 2 M⊙/pc2 in the solar neighbourhood. Data for the MW rotation curve are from Sofue (2012); the dashed curves represent the contributions of the bulge, disk and dark matter (blue, green and red, respectively ; see text for the bulge contribution). Data for the SFR profile are discussed in Appendix B and displayed in Fig. B.1. The observed present-day profile of infall rate (dotted curve) is based on estimates of Marasco et al. (2012) (see text). The bottom right panel displays the adopted timescales for exponential infall. Data for oxygen are from HI regions (Simpson et al. 1995; Afflerbach et al. 1997) and OB stars (Smartt & Rolleston 1997; Daflon & Cunha 2004) and for iron from Cepheids (Luck & Lambert 2011; Lemasle et al. 2013; Genovali et al. 2013). |
Figure 4 presents a synthetic view of the main results of our model, compared to observations. Except for the top right (velocity curve) and bottom (infall timescale) panels, all other panels display three profiles, at 4, 8 and 12 Gyr; the last (thick curve) is to be compared with observational data.
The infall timescale of the disk as a function of radius (bottom right panel) is tailored to smoothly match the bulge timescale of τ(r< 2 kpc) ~ 1.5 Gyr to the timescale of the outer disk while going through the value of τ(r = 8 kpc)~7−8 Gyr for the solar neighbourhood. The latter has been shown to provide a good fit to the local metallicity distribution in simple (independent-ring) models of the MW chemical evolution (e.g. Chiappini et al. 1997; Boissier & Prantzos 1999) and we show that this is also the case here (Sect. 4), although the adopted SNIa rate and the effects of radial migration also play a role. The resulting profiles of infall rate appear in the right panel just above the bottom. Because of the shorter infall timescales in the inner disk, the final infall profile peaks around 3 kpc.
In a recent work, Marasco et al. (2012) use a model of the Galactic fountain to simulate the neutral-hydrogen emission of the Milky Way. Their model was developed to account for external galaxies with sensitive HI data. For appropriate parameter values, their model reproduces the observed HI emission of the MW. They find a global current value of ~2 M⊙/yr for the MW, and they derive the infall profile displayed in the right panel above the bottom (dashed curve), which peaks at ~9 kpc. In our model we obtain a similar value for the total present-day infall rate (~1 M⊙/yr, see Fig. 2), but our infall profile peaks at ~3 kpc. We notice that the existence of a peak in the current infall profile appears naturally in our model, albeit not in the claimed position. Further studies and understanding of the properties of the gas accreted onto the MW, including its velocity profile, will provide much stronger constraints in evolution models of the Galaxy.
The radial profiles of gas (total, HI and H2) are in rather good agreement with observations, for the largest part of the disk. In the inner disk, the presence of the bar plays an important role, inducing radial flows of both gas (see below) and stars. Had the migrating long lived stars remained in place, they could return their H-rich ejecta in the local ISM at late times. The overall result of those motions is a total gas profile going through a broad maximum at ~7 kpc, still compatible with the observations. This is also true for the HI profile. In contrast, the “molecular ring” in the inner disk is not reproduced well; it is not clear whether this is due to the poor fit of the BR2006 prescription to MW data (see their Fig. 4) or to some combination of the various relevant ingredients adopted here (SFR, infall, radial inflow, evaluation of HI profile).
The model rotation curve at t = 12 Gyr compares fairly well to the data of Sofue (2013) (right, 1st row panel in Fig. 4). It peaks at ~212 km s-1 in the solar neighbourhood, where the contribution of the disk exceeds slightly the one of dark matter. This is slightly lower than the canonical IAU value of 220 km s-1 and clearly lower than some values recently proposed in the literature (see Bhattacharjee et al. 2014, and references therein). The rotation curve is used in all time-steps to evaluate the epicyclic motion and the extent of blurring in the disk (see Sect. 2.2.1).
 |
Fig. 5 Top: adopted velocity profile for radial inflow. Positive velocities indicate flow inwards (towards the Galactic centre) and negative ones an outward flow. The flow velocity is everywhere zero before the assumed appearance of the bar at t = 6.5 Gyr. Profiles are given at t = 6, 8, 10 and and 12 Gyr (cyan long-dashed, blue short-dashed, green dotted and red solid, respectively). As corotation moves outwards (see text), the flow pattern moves also. Middle: corresponding mass flow profiles through radial zones r. Bottom: corresponding mass infall profiles (rate of mass infalling over the ring of radius r and width Δr = 0.5 kpc, at t = 6, 8, 10 and and 12 Gyr. |
The gaseous profiles are affected by the radial inflow induced by the bar, which is modelled here as shown in Fig. 5. It is assumed that the bar radius increases from 2 kpc at 6 Gyr to 3 kpc at 12 Gyr and its corotation radius from 2.4 kpc initially to 3.6 kpc in the end. Simulations show indeed that in disks with large gas fractions, the appearance of a bar can be delayed for several Gyr (Athanassoula et al. 2013), compared to cases with no gas. It then grows with time while slowing down, pushing the corotation resonance outwards, as in our model. The velocity profile has positive values (towards the Galactic centre) inside corotation and negative ones (towards the anti-centre) outside corotation and up to the OLR. Maximum absolute values of the (azimuthally averaged) radial flow velocity are 0.5 km s-1. Higher values for the adopted duration of the bar would lead to substantial depletion of the gaseous layer in the inner disk, impossible to replenish by infall. Indeed, the middle and bottom panels of Fig. 5 display the net radial flow rate through the ring of radius r (middle) and the rate of infall onto that same ring (bottom). Around corotation, the former (calculated as fr = 2πrυr Σg(r)) is higher than the latter. Although our 1D prescription for radial inflow is inadequate for describing an intrinsically 2D effect and none of the adopted parameters can be observationally determined at present, the range of the velocity values we find is similar to the ones adopted in Portinari & Chiosi (2000) for the case of a simulated bar (their Fig. 13), i.e. υr< 0.5 km s-1.
The current profiles of gas and SFR reflect short-term features of the Milky Way and do not constitute strong constraints; indeed, on a timescale of 107 yr, comparable to the timestep of our model, they may change considerably. Constraints obtained through time-integrated profiles (with negligible late variations within short timescales) are more severe in that respect. The profiles of stars and metallicity belong to this class. As already discussed (see Sect. 2.3 and references therein) one of the main effects of the radial flow induced by a bar is to flatten the abundance gradients in the region around the corotation (the other one being to fuel star formation in the central regions). This is clearly seen in the final oxygen profile (bottom left panel of Fig. 4), which displays a flattening in the region 3−5 kpc. The iron profile (bottom middle panel of Fig. 4) is less affected, because the sources of Fe (mainly SNIa) are less affected by those of O (CCSN) in that region. The latter are distributed as the gas, which has a flat profile in that region, whereas the former – belonging to an older population – have a steeper distribution. The evolution of the metallicity profiles is similar to the one obtained in many other studies (e.g. Boissier & Prantzos 1999; Hou et al. 2000) and reflects the inside-out formation of the disk, with the profiles flattening with time. Those profiles are widely used in Sect. 4 to study the main observables in the solar neighbourhood. A detailed study of the evolution of the abundance profiles of all the elements of our model, both in the gas and in the stellar populations, is presented elsewhere (Kubryk et al. 2015).
 |
Fig. 6 SFR vs. gas surface density. Model results are displayed for three different epochs, after 4 Gyr (green curve), 8 Gyr (blue) and 12 Gyr (red). The last is compared to the observationally inferred SFR profile of the Milky Way (dotted magenta curve), obtained as discussed in Appendix B. The data points concern extragalactic measurements, compiled by Krumholz et al. (2012) (see also Fig. B.2). The dotted line is |
Figure 6 displays the star formation profiles of our models as a function of the local gas surface density for three different epochs: at t = 4, 8, and 12 Gyr. Comparison is made to the data compiled by Krumholz et al. (2012) for a large number of star-forming galaxies. It can be seen that our values lie in the low range of the observed SFR values for a given gas surface density. In particular, the rate at 12 Gyr presents the steep rise at ΣGas ~ 10M⊙/pc2 that is “observed” in the MW disk; however, it is slightly lower than “observed” in the inner disk and slightly higher than “observed” in the outer disk. These discrepancies are also displayed in the SFR profile presented in Figs. 4 (below the top right panel) and B.2. The key point here is the absence of a correlation between the SFR and the local gas surface density in both the data and the model. It implies that some other factor is in play, namely molecular gas, as discussed in Appendix B and in the recent review by Krumholz (2014).
3.2. Stellar profiles
The model stellar profiles result from the combined history of star formation and radial migration. The former is discussed in the previous section. Here we analyse the impact of stellar radial migration.
The adopted radial velocity dispersion profile σv,r appears in Fig. 7 (top panel) for two epochs, at t = 2 Gyr and 12 Gyr2. The corresponding local values (at r = 8 kpc) are 21 km s-1 and 40 km s-1, respectively. We then calculated the probabilities of radial displacement due to epicyclic motion. The results for the same two epochs and three different radial zones are displayed in the middle panel. The curves are asymmetric about the birth radius r′ despite the symmetry of the adopted Gaussian function for blurring (Eq. (2)), because the corresponding velocity dispersion σ is taken at the final radius r. The thick solid curves correspond to an age of 12 Gyr, i.e. to σv,r = 40 km s-1 for the stars in the solar neighbourhood, and it may be compared to the corresponding curve obtained by Schönrich & Binney (2009a) (dotted curve in middle panel). Our formulation of the epicyclic motion produces similar distributions to those of Schönrich & Binney (2009a) in the solar neighbourhood and beyond and somewhat narrower distributions in the innermost disk, but the overall agreement is quite good.
 |
Fig. 7 Top: model radial velocity dispersion at 2 Gyr (thin curve) and 12 Gyr (thick curve). Middle: probabilities of blurring. Bottom: probabilities of churning. In all panels our results (solid curves) are displayed for stars of home radius r = 5, 7.6 and 10 kpc, and for 2 Gyr (thin) and 12 Gyr (thick curves). The latter should be compared to the corresponding quantities reported in Schönrich & Binney (2009a) (dotted histograms). |
The corresponding probability functions for churning appear in the lower panel of Fig. 7. They are evaluated as discussed in Sect. 2.2.2 and are broader than those of blurring. In the inner disk, they are not very different for the ones adopted in Schönrich & Binney (2009a), but they are clearly narrower than the latter in the outer disk. There is clearly a difference in the amount of radial migration between the inner and outer disks, both in Schönrich & Binney (2009a) and in our case, but this difference is more important in our case than in theirs. We think that this can be attributed to the action of the bar, which plays an imortant role in the former simulation, while the latter only considered the effect of transient spirals, which are more uniformly distributed over the disk.
In the top panel of Fig. 8 we present the total probabilities (blurring + churning) of a stellar population born in a given radius (here: 4, 8 and 12 kpc) to be found in some other disk radius r after times 4, 8 and 12 Gyr. We recall that the radial bin in our simulation has a size Δr = 0.5 kpc. As discussed in Sect. 2.2 (see also Fig. 7) for the blurring and churning probabilities separately, the probability of finding a star from the inner disk to the outer one is greater than the inverse, because of the larger variations in the gravitational potential perturbations in the inner disk than in the outer disk.
 |
Fig. 8 Top: probabilities of stellar migration (blurring + churning) adopted in this work (see text); they are shown for three birth radii (4, 8 and 12 kpc) and for three snapshots (after 4, 8 and 12 Gyr). Middle: fractions of stars which are born in radii 4, 8 and 12 kpc and are found in galactocentric radius r in the end of the simulation, at T = 12 Gyr. Bottom: fractions of stars found at the end of the simulation in radii 4, 8 and 12 kpc according to their birth radius r. In all panels, radial bins are Δr = 0.5 kpc wide, as indicated by the bin width of the histograms and the size of the coloured boxes. |
The middle panel of that figure displays the fractions of stars born in those same radii, which are found at radius r at the end of the simulation; those fractions are the time-integrated probabilities of the upper panel, weighted by the corresponding SFR(r,t) history. This explains why the distribution of the outer region is more peaked and less wide than the inner one in the middle panel than in the top one: stars are formed in the inner disk earlier than in the outer one, on average, because of the inside-out formation scheme adopted here. As a result, inner disk stars have on average more time to migrate than those formed in the outer disk. Even if the probability distributions in the top panel were identical at all birth radii (assuming, for instance, the same potential inhomogeneities over the whole disk), those in the middle panel would still be wider in the inner disk, simply because of the inside-out star formation.
The bottom panel in Fig. 8 displays the fractions of stars found at the end of the simulation in final galactocentric radii rf = 4, 8 and 12 kpc, respectively, and born in other positions r in the disk. These fractions integrate not only the probability distributions (upper panel) and the SFR histories (as in the middle panel), but also the fact that there is more mass in the inner disk than in the outer one, because the surface density profile decreases exponentially outwards. For that reason, the resulting fractions are asymmetric in each radius, with more originating in the inner disk than in the outer one. Thus, from all the stars presently found in the bin at r = 8 ± 0.25 kpc, only ~10% are formed in that bin; if the “extended solar neighbourhood” (defined as r = 8 ± 1 kpc) is considered, the corresponding percentage rises to 38%. Only 7% of the remaining stars originate outside the extended solar neighbourhood (at radii r> 9. kpc), while 55% of the stars of that region are formed in r< 7 kpc and have migrated here: ~12% of its stars have migrated from r< 4 kpc. In contrast, a negligible amount of stars presently found in r = 13 kpc originates from r = 8 kpc.
 |
Fig. 9 Average radius of origin of stars (top), average stellar age (middle) and star surface density profile (bottom), as a function of galactocentric radius. In all panels, the continuous (red) curve corresponds to the results of the model with radial migration (churning+blurring), while the dotted (blue) curve shows the results with no radial migration. In the top and middle panels, the shaded area contains the ±1σ values – containing ±34% of the stars – around the average. In the bottom panel, a best fit exponential with scalelength rd = 2 of the exponentially decreasing outwards. 25 kpc in the 3 to 13 kpc region and with Σ(r = 8 kpc) = 38 M⊙/pc2 is also displayed (green dashed line). |
The impact of radial migration (blurring+churning) on some radial properties of the disk appears in Fig. 9. It can be seen that stars presently found in the region 5 <rf< 10 kpc, originate in regions located on average ~1.–2. kpc inwards. On the other hand, stars presently found in the bulge (here taken to be the region r< 2 kpc) have a significant fraction of them originating from the inner disk, from up to 3 kpc. Finally, stars beyond r = 13 kpc are affected very little by radial migration on average (at least with the adopted scheme for churning). We note that Minchev et al. (2013) find a bimodal distribution function for the average birth radius of stars presently in the solar neighbourhood (their Fig. 3, right): the maximum is located in the region ~5.6 kpc and a secondary maximum is found at ~7 kpc, compared to a single maximum at ~6.2 kpc in our model. It is difficult to compare the two models, since they are based on different N-body simulations and different descriptions of the radial migration.
The aforementioned results also explain the average age of stars in each galactocentric radius (middle panel in Fig. 9). The average age of stars formed in the bulge (r< 2 kpc) is ~9 Gyr, in the solar neighbourhood ~5 Gyr and beyond 12 kpc it is 4 Gyr. Stars presently found in the region 5 <rf< 11 kpc are, on average, 1−2 Gyr older than those formed in situ, because their population has been altered by the radial migration of stars from the inner disk. Again, beyond r = 13 kpc, the average stellar age is not affected. It should be noted that a uniform age dispersion of ~ ± 3 Gyr is found at all radii.
4. Local evolution
The results discussed in the previous section for the whole disk help for understanding the results obtained for the solar annulus, defined here as the radial bin at r = 8 ± 0.25 kpc. We stress – as already done in Sect. 2.5 – that this region is not neccessarily representative of the solar neighbourhood, and any strict comparison to observational results should take the corresponding observational biases into account.
Figure 10 displays the average birth radius of stars found in this zone at the end of the simulation, as a function of their age. In the absence of any radial migration, the birth radius would be the horizontal line at r = 8 kpc. As expected – in view of the discussion in Sect. 3.2 – the average birth radius when radial migration is considered, is close to 8 kpc for the youngest stars, but it decreases steadily for older stars. The reason for that decrease is twofold: first, the older stars have more time to migrate from other regions and, in particular, from the inner disk; second, the SFR at r = 8 kpc is low in the first few Gyr, while it is quite high in the inner disk during that same period (see top right panel in Fig. 3). Thus, the old stars migrating here from the inner disk overwhelm by number the few old stars formed locally. A local “average star” of age =4.5 Gyr originates at r ~7 kpc, whereas stars older than 8 Gyr were born inwards of 5.5 kpc, on average. Equally interesting is the spread in birth radii that increases as a function of age (the associated 1σ dispersion in the birth radius is indicated by the shaded area). Thus, about two thirds of the local stars of solar age have birth radii ranging between 5.5 and 8.5 kpc, while two thirds of those with an age of 8 Gyr were born between 2.5 and 8 kpc. Their birth place affects their chemical composition and the properties of the solar annulus. The same behaviour of birth radius vs. age, not only qualitatively but also quantitatively, is obtained in the N-body simulation of e.g. Loebman et al. (2011), Brook et al. (2012), which are not tuned to reproducing a Milky Way disk: the oldest stars of their simulation presently in the “solar cylinder” (between 7 and 9 kpc from the centre), have home radii as small as 2 kpc.
4.1. The local age-metallicity relation and its dispersion
 |
Fig. 10 Solar neighbourhood: average birth radius (top), average [Fe/H] (middle) and average [O/Fe] of stars (bottom) as function of their age. In all panels, the dotted (blue) curves display the results for stars formed in situ and the solid (red) curves the results for all stars found at T = 12 Gyr in radius r = 8 ± 0.25 kpc. The shaded areas in all panels enclose ±1σ values around the corresponding averages. Data points are from the survey of Bensby et al. (2014). The dotted vertical line at 9 Gyr separates the thin from thick disk stars, according to the assumption made here (see Sect. 4.1). The symbol ⊙ denotes the position of the Sun in the corresponding panel, as well as in Figs. 11−13. |
The impact of radial migration on the chemical evolution of the local disk appears in the middle and bottom panels of Fig. 10. The local average age-metallicity relation (middle panel, red solid curve ) is flatter than the one for the locally born stars; the latter represents the metallicity evolution of the local ISM. The flattening depends on both the adopted radial migration scheme (the churning coefficients) and the whole history of the disk (the inside-out formation and the resulting abundance profiles). Since the gas is well mixed locally today – and presumably at earlier times as well – the fact that the metallicity of the Sun 4.5 Gyr ago is larger than the corresponding gas value in our model, implies that the Sun was not born locally, but migrated from inner galactic regions as suggested in Wielen et al. (1996). Although it is rather early to draw definitive conclusions, it appears that the hypothesis that the Sun was formed inwards (by 1−2 kpc) of its present galactic position, is the most convenient one for explaining several observational facts (see Nieva & Przybilla 2012, for an updated discussion and references).
The bottom panel of Fig. 10 displays the O/Fe vs. age relation. It starts at values around [O/Fe] ~ 0.5 for the oldest stars – where only CCSN enrich the ISM – and then decreases smoothly to [O/Fe] ~ 0 for the youngest stars, because of the steady Fe input from SNIa. This distinctive behaviour in the decrease in [O/Fe] for old and young stars is also apparent in the work of Haywood et al. (2013) who reanalysed a sample of local stars with high quality abundance determinations (their Figs. 6 and 7). However, they interpret their data as two clearly differing regimes with different slopes of [α/Fe] vs. age, while we find just a gradual decline of the [α/Fe] ratio, albeit with a strong reduction of the corresponding slope with time. The dispersion in the [O/Fe] relation is quite small (~0.1 dex) at every age; the reason is the quasi-similar evolution of the SNIa/CCSN ratio in all radial zones of our model (right above-bottom panel of Fig. 3), except those of the bulge. This fact justifies the use of [O/Fe] as a proxy for age, as suggested e.g. in Bovy et al. (2012b).
The top panel of Fig. 11, displays the fraction of stars born in the solar annulus as a function of stellar age and the corresponding fraction of all stars currently present in the solar annulus (i.e. born anywhere but found in 8 ± 0.25 kpc at the end of the simulation). The fraction of stars born in-situ is a decreasing fraction of stellar age, because of the SFR rate history (see Fig. 3, top right panel). On the other hand, the fraction of all stars currently in the solar neighbourhood increases between 0 and 8 Gyr because large numbers of old stars have migrated to the solar neighbourhood, shifting the average age to higher values (see Fig. 9). In particular, almost all stars older than 10 Gyr have been formed inwards of r = 5 kpc, on average. (see also Roškar et al. 2008).
This result has some important implications: it implies that radial migration makes it impossible to try to infer the past local SFR through star counts as function of stellar age (e.g. Rocha-Pinto et al. 2000): most of the old stars presently found here were formed elsewhere, whereas the opposite holds for the younger stars. For that same reason, it becomes impossible to use the method of the luminosity function of white dwarfs to infer the star formation history of the solar neighbourhood, e.g. Isern et al. (2013) and references therein.
 |
Fig. 11 Solar annulus: top: fraction of all stars ever born in situ in the solar annnulus (blue dotted) and fraction of all stars found in the solar annulus at T = 12 Gyr (red solid) as a function of stellar age. Average [Fe/H] of stars (middle) and 1σ dispersion around the average (bottom) as function of stellar age, compared to observations. The solid (red) curve in the middle panel displays the results for all stars found at T = 12 Gyr in radius r = 8 ± 0.25 kpc. In both panels, the shaded (yellow) areas represent the ±1σ limits of the model; the brown (dotted) and green (dashed) curves represent the corresponding averages and ±1σ limits of the observations of Casagrande et al. (2011) and Bensby et al. (2014), respectively. The narrower blue shaded areain the bottom panel shows the results of a calculation with blurring alone. |
In the middle panel of Fig. 11 we compare the model [Fe/H] vs. age relation to data of two recent major surveys. We display observational data from a re-analysis of the Geneva-Copenhagen survey (Casagrande et al. 2011) and from the survey of Bensby et al. (2014). In both cases, we determine average values and ±1σ widths around those averages in the [Fe/H] vs. age relation, by using age bins of 1 Gyr and apply the same statistics to our model stars. To better compare the metallicity dispersion vs. age between observations and the model, we show in the bottom panel of Fig. 11 the 1σ dispersion around the average value. We display our results for blurring only and for blurring plus churning, and we compare with the corresponding dispersions of the data in Bensby et al. (2014) and Casagrande et al. (2011). We note some differences between the two data sets, the one of Bensby et al. (2014) having a slightly larger dispersion than the one of Casagrande et al. (2011). This may be due to kinematic biases and to magnitude selection effects.
The epicyclic motion, as calculated in our model, produces a uniform dispersion of ±0.1 dex for most stellar ages. Only the older ones – age >9 Gyr – have a slightly larger dispersion, up to ±0.2 dex. The epicyclic motion is not sufficient to explain the observed dispersion in the age-metallicity relation. When churning is also considered, dispersion increases steadily, up to ±0.3−0.4 dex. For thick disk stars (assumed here to be older than 9 Gyr), the model dispersion starts decreasing. The reason is that these old local stars are formed almost exclusively in the innermost disk regions, where the very rapid evolution produced a quasi-identical age-metallicity relation; as a result, these stars show smaller dispersion in their metallicities. Our analysis of the data of Casagrande et al. (2011) and Bensby et al. (2014) shows no such decrease for old stars. We notice however, that a re-analysis of the data of the GCS survey and of Adibekyan et al. (2011) by Haywood et al. (2013), leads to a decreasing dispersion in [Fe/H] for the older stars, in line with our model (at least qualitatively).
In summary, the dispersion in the age-metallicity relation stems from the extent of churning (which is related to the inhomogeneities of the gravitational potential) and the SFR history of the disk. Comparison of theoretical dispersions to observed ones constrains the combination of those processes, not the just churning (or churning+blurring). Comparison to other data, e.g. past and present metallicity gradients, will be necessary to disentangle the various effects.
4.2. The local metallicity distribution
 |
Fig. 12 Solar neighbourhood: average age of stars (top), average birth radius (middle) and number distribution of stars (metallicity distribution, bottom) as function of their metallicity. In all panels, the dotted (blue) curves display the results for stars formed in situ and the solid (red) curves the results for the average values of all stars found at T = 12 Gyr in radius r = 8 ± 0.250 kpc. The shaded areas in the top and middle panels enclose ±1σ values around the corresponding averages. The dashed histogram in the lower panel is calculated with the effect of epicycles only. |
In Fig. 12 we present our results for the local metallicity distribution (MD). The lower panel displays the MD of stars formed in situ (dotted histogram), which peaks at 0.08 dex and terminates abruptly at 0.1 dex. It also displays the MD obtained with only the epicyclic motion considered, which peaks at the same metallicity and is slightly broader, extending up to 0.15 dex. Finally, the total MD – including blurring and churning – is considerably broader than the previous two distributions and extends up to [Fe/H] = 0.4. It was already pointed out by Chiappini (2009) that the local evolution cannot produce stars as metal-rich as [Fe/H] = 0.4. Here we show that the conclusion holds even if epicyclic motion is considered. Only radial migration can account for such stars in the solar neighbourhood.
The upper panel of Fig. 12 shows the average age of the local stars (i) for those formed in situ and (ii) for all stars. The latter are always older than the former, by 1 Gyr for the less metallic ones and by 2.5 Gyr for those of [Fe/H] = 0. For higher metallicities, there are no stars formed in situ and the average age of those present in the solar neighbourhood – coming from inner regions – is around 3−4 Gyr. The middle panel of Fig. 12 shows the average birth radius of the local stars. The average birth radius of all local stars is at r ~ 6.5 kpc, as stated in Sect. 2.2. Star more metallic than the Sun have birth radii increasingly closer to the galactic centre, with those of [Fe/H] = 0.4 coming from the region around 2−3 kpc.
The results of the previous paragraph are presented in greater detail in Fig. 13. The upper panel displays the MDs of four age ranges, namely 0−3 Gyr, 3−6 Gyr, 6−9 Gyr and >9 Gyr. The younger the stars, the narrower their MD (because metallicity increases less rapidly at late times) and the more it peaks to higher [Fe/H] values. The lower panel displays the MDs of five radial ranges, namely <3 kpc, 3−5 kpc, 5−7 kpc, 7−9 kpc (=“extended solar annulus”) and 9−11 kpc. There are practically no stars entering the solar neighbourhood from beyond 11 kpc in our model. Most stars originate in the 7−9 kpc range and their MD peaks at [Fe/H] = 0. The smaller the average birth radius of stars (down to 3 kpc), the more they contribute to the most metallic stars at [Fe/H] = 0.4. Stars from the 9−11 kpc range do not contribute to metallicities higher than solar.
 |
Fig. 13 Solar annulus: top: metallicity distribution in the region of radius r = 8 ± 0.25 kpc, with the age ranges of the corresponding stellar populations. Bottom: metallicity distribution in the region of radius r = 8 ± 0.25 kpc, with the radial ranges of the birth radii of the corresponding stellar populations. |
4.3. Thin vs. thick disk: age, composition, structure
A large number of formation scenarios of the thick disk have been proposed up to now, involving either external influences or secular evolution through radial mixing, e.g. Sales et al. (2009), Minchev et al. (2013), Rix & Bovy (2013) and references therein. In particular, radial migration has been suggested as a potential thick disk formation mechanism by Schönrich & Binney (2009a), who developed a semi-analytical model (similar in some respects to the present one) and investigated the resulting chemical and kinematic properties extensively. They showed that for some values in the parameter space, their model can reproduce several key properties of the thick disk just by secular processes: morphology (i.e. the two-slope vertical star density profile in the solar neighbourhood), the vertical abundance gradient and the puzzling “two-branch” behaviour of O/Fe vs. Fe/H, with the thick disk displaying higher O/Fe values than the thin disk for the same range of metallicities. Some of those results were also found in N-body simulations, e.g. Loebman et al. (2011), but others, especially the claimed dynamical behaviour of thick disk stars, were not confimed and are still debated (see e.g. Minchev et al. 2013, and references therein).
In this work we do not consider any properties of the disk vertical to the plane (either chemical or kinematic) and we focus on its radial properties, in particular concerning the solar neighbourhood. In view of the uncertainties as to the best defining feature of the thick disk, we adopt the simplest possible criterion, namely age. Following Binney & Sanders (2014) and Haywood et al. (2013), we assume that the thick disk is simply the early period of the MW disk formation, lasting from −12 to −9 Gyr, whereas the thin disk corresponds to the subsequent 9 Gyr of evolution. There is no physical ingredient in our model that marks the transition between the two eras: star formation, infall and radial migration all over the disk are continuous functions of time and space. Still, the consequences of that simple assumption are quite important, as can be seen in Fig. 14, where various data are plotted as a function of [Fe/H] and compared to relevant observations.
 |
Fig. 14 Solar annulus: top: [α/Fe] (left) and [O/Fe] (right) vs. metallicity, for all stars present today (solid brown curve) and for all stars born in situ (dotted blue curve). Middle: [α]/Fe (left) and [O/Fe] (right) vs. metallicity, for stars of the thick disk (>9 Gyr, green curve) and for stars of the thin disk (<9 Gyr, red curve). They are compared to corresponding data from Adibekyan et al. (2011; left) and from Bensby et al. (2014; right). In the top and middle panels the shaded areas enclose the ±1σ values around the corresponding model averages. The MD data for the thick disk of Bensby et al. (2014) are arbitrarily reduced by a factor of 3 (see text). |
In the upper panels of Fig. 14 we display the evolution of [α/Fe] (left)3 and [O/Fe] (right) vs. [Fe/H] for all the stars currently present in the radial bin r = 8 ± 0.25 kpc and for those born in situ. As expected, the curve of the [α/Fe] evolution of the in situ stars lies lower than the one of all the stars present in the solar cylinder. The latter is affected by old stars migrated from inner regions, which have higher [α/Fe]for the same value of [Fe/H]. The same holds for [O/Fe].
In the middle panels of Fig. 14 we display separately the evolutions of the “old” stars (>9 Gyr, aka thick disk) and of the “young” stars (<9 Gyr, aka thin disk). As expected from the results already presented in Fig. 10, thick disk stars cover a wide range of metallicities extending to approximately solar, while thin disk stars appear around [Fe/H] ~ –0.8 and extend up to [Fe/H] ~ 0.4. Our average trends of [α/Fe] vs. [Fe/H] are in good agreement with the data of Adibekyan et al. (2013)4, both for the thick and the thin disk and we consider this to be a successful test of the idea that the thick disk can be identified with the component of the disk older than 9 Gyr. We note that the model 1σ dispersion of [α/Fe] of the thick disk is larger than the corresponding one of the thin disk.
In the case of the thin disk, the evolution of [α/Fe] corresponds practically to the one of the in situ formed stars (the dotted curve, same as in the upper panel), an important feature already identified in the work of Schönrich & Binney (2009a). However, this does not imply that thin disk stars are mostly formed in situ: a large fraction of thin disk stars are formed in other galactic regions and migrated in the solar neighbourhood, during the last 9 Gyr. But in the beginning of that period, the value of [α/Fe] all over the inner disk was already reduced to ~0.2 – because of the previous activity of SNIa – and it evolved very slowly afterwards (see Fig. 10, bottom panel).
Our results for [O/Fe] vs. [Fe/H] are displayed in the right top and middle panels of Fig. 14 and they are compared with the data of Bensby et al. (2014)5. The behaviour is qualitatively, but not quantitatively, similar to the one of [α/Fe]. Although oxygen is an α element, its evolution is slightly different from the one of [α/Fe] here, because we included Si in the definition of [α/Fe]. A non-negligible amount of Si is produced by SNIa, while this is not the case for oxygen. As a result, [O/Fe] varies more than [α/Fe] extending both to higher and lower values. However, despite the resulting large variation in [O/Fe], our results do not satisfactorily match the data of Bensby et al. (2014) which extend from [O/Fe] > 0.6 to values lower than –0.2. The decline of [O/Fe] in the data is much steeper than in our model. It is difficult to say whether this discrepancy is due to the model (inadequate yields or SNIa rates) or to the data (uncertainties in the oxygen abundances).
In the bottom panel of Fig. 14 we present the resulting metallicity distributions for the thin and thick disks, and we compare them to the data of Adibekyan et al. (2013) (left) and Bensby et al. (2014) (right). The metallicity distribution of the thick disk is already presented in Fig. 13 (top panel): it is the curve corresponding to stars old than 9 Gyr. It is quite broad, it extends up to [Fe/H] ~ 0 and it peaks at [Fe/H] ~ –0.6 to –0.5. the thin disk MD of the model is much narrower, it extends up to [Fe/H] ~ 0.45 and it peaks at [Fe/H] ~ 0.
The thin disk MD is in excellent agreement with the data of both Adibekyan et al. (2013) and Bensby et al. (2014). As for the thick disk MD, it extends only up to [Fe/H] = 0 and thus does not reach the metallicity range of high-alpha metal-rich stars (hamr) in the sample of Adibekyan et al. (2013), which appears to be bi-modal in that respect; this bi-modality, which still needs to be confirmed, cannot be explained in the framework of our model. The sample of Bensby et al. (2014) is biased in favour of thick disk stars (it contains 234 stars in a total of 629), so we reduced the proportion of its thick disk a factor of 3, to bring it in agreement with our results in Fig. 14.
The results of Fig. 14 confirm the suggestion of Schönrich & Binney (2009a) that radial migration can explain the two branches observed in the [O/Fe] vs. [Fe/H] relation. They also provide further support to the idea that the local thick disk was formed by that process, since they successfully reproduce the local distributions of both the thick and the thin disk. However, the absence of any features in our model (either morphological or kinematic) concerning the direction vertical to the Galactic plane, does not allow us to explore this issue further.
We now turn to the radial distribution of the thick and thin disks in our scenario. In Fig. 15 we show (upper panel) the radial surface density profiles of stars older and younger than 9 Gyr, respectively, after radial migration. The main results concerning local surface densities and scalelengths ar displayed in Table 3.
 |
Fig. 15 Thin vs. thick disk: left: stars plus stellar remnants; right: luminous stars only. Top: present-day stellar profiles: magenta: total; green: (thick disk); red: thin disk. In all curves, there is an attached best-fit exponential (dashed line of same colour) in the 5−11 kpc range, with scalelengths and column densities at R0 = 8 kpc as reported in Table 3. Bottom: cumulative fraction of the thin and thick disk masses with respect to the corresponding total disk mass Mdisk: Mthin( <r) /Mdisk (red curve) and Mthick( <r) /Mdisk (green curve) as a function of radius r. |
The recent work of Bovy & Rix (2013) who analysed the dynamics of 16 269 G-type dwarfs from SEGUE (sampling the radial range 5 kpc <r< 12 kpc) leads to a dynamically determined surface density of stars+remnants Σ∗ = 38 ± 4M⊙/pc2 at r = 8 kpc. In our case, stellar remnants contribute 5 M⊙/pc2, and stars still shining 33 M⊙/pc2 (our IMF extending from 0.1 M⊙ to 100 M⊙, we included no brown dwarfs). We note that in their analysis of the local surface density contributed by mono-abundance populations, Bovy et al. (2012a) find a total surface density contributed by stars of Σ∗ = 30 ± 1M⊙/pc2, which depends slightly on the adopted IMF: for a Kroupa (2001) IMF, they obtain Σ∗ = 32M⊙/pc2, in excellent agreement with our results. Our total baryonic surface density in the solar neighbourhood, is 51.2 M⊙/pc2, including 13.2 M⊙/pc2 for the total gas. This is in agreement with the local baryonic contribution of Σgas + Σ∗ = 55 ± 5M⊙/pc2 estimated in Zhang et al. (2013) or Σgas + Σ∗ = 51 ± 4M⊙/pc2 estimated in Bovy & Rix (2013).
Properties of the Galactic disks (r> 2 kpc).
The scalelength of the total (stars plus stellar remnants) disk of our model (2.25 kpc) is in excellent agreement with the recent dynamical estimate of Bovy & Rix (2013) for the Milky Way: 2.15 ± 0.14 kpc. We note that their analysis of the combination of constraints from rotation-curve shape and surface-density measurements leads to a local value for the rotational velocity of Vc = 218 ± 10 km s-1, which is not very different from the value of 212 km s-1 of our model (see Fig. 4). The total stellar mass of our disk is lower than the value of 4.6 × 1010M⊙ obtained by Bovy & Rix (2013), because they obviously include the region inside 2 kpc in their calculation of the disk mass, while we do not include it. For those reasons, our estimate of the total stellar disk mass of 3.4 × 1010M⊙ (end point of our calculations in Fig. 1) corresponds to the total stellar mass outside r = 2 kpc. If we add the final stellar mass 1.3 × 1010M⊙ that we find inside 2 kpc, we obtain a total stellar mass of 4.7 × 1010M⊙, again in agreement with the estimates of Bovy & Rix (2013).
We systematically find that the thick disk is more centrally condensed than the thin disk, i.e. with a scalelength shorter by ~1 kpc. The reason is the inside-out star formation of the Galaxy: the old stellar population is more centrally condensed than the young one and radial migration does not change that feature (although it certainly attenuates it).
The scalelength of the stellar thick disk in our model (1.8 kpc) is in fair agreement with recent estimates, e.g. Bensby et al. (2011), Cheng et al. (2012), Bovy et al. (2012b) who find 2., 1.8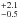 and 2.01 ± 0.05 kpc, respectively. However, the scalelength of our thin disk (2.35 kpc) is substantially shorter than those obtained in these studies (respectively, 3.8, 3.4, and 3.6 ± 0.2 kpc).
and 2.01 ± 0.05 kpc, respectively. However, the scalelength of our thin disk (2.35 kpc) is substantially shorter than those obtained in these studies (respectively, 3.8, 3.4, and 3.6 ± 0.2 kpc).
As already discussed extensively in the literature (e.g. Rix & Bovy 2013, and references therein) the radial extension of the thin and thick disks can be used to constrain various scenarios for thick disk formation. In particular, the lack of high-α stars at r> 10 kpc and large distances from the plane, constrains the strength of migration due to transient spiral structure: it cannot be very efficient beyond that distance. In our case, the thick disk has a short scalelength and the efficiency of radial migration is indeed small beyond r = 11−12 kpc, as seen in the profiles in the top and middle panels of Fig. 9. However, the thin disk appears to be shorter than in the observations.
The lower panels of Fig. 15 display the corresponding cumulative fractions of the thin and thick disks as a function of distance r. As already stated in Sect. 3 and Fig. 3, we define here the disk as the region of radius r> 2 kpc, the region inside belonging to the bulge. The resulting fractions differ very little in the two cases (stars + remnants and stars only): the thick disk contributes almost as much as the thin disk in the inner Galaxy (where a large fraction of the stars was formed in the first 3 Gyr) and its contribution gradually lags behind the one of the thin disk with radius. In total, the thick disk weighs about half the mass of the thin disk, i.e. their stellar masses are 1.2 × 1010M⊙ and 2.2 × 1010M⊙, respectively.
The derived mass ratio of the thick and thin disks of the MW Mthick/Mthin ~ 1 / 2 is substantially higher than expected from observations of external disk galaxies by Yoachim & Dalcanton (2006). They find that Mthick, ∗/Mthin, ∗ is a decreasing function of the rotational velocity of disks, ranging from 1−2 at VC ~ 70 km s-1 to 0.2 at VC ~ 200 km s-1; the ratio we find is almost 3 times larger than the latter value. On the other hand, based on Spitzer observations of a sample of ~30 galaxies, Comerón et al. (2011) find that thick and thin disks have, typically, similar masses. Our value of 0.5 lies between those two results.
 |
Fig. 16 Average composition of 4.5 Gyr old stars in the solar neighbourhood, elemental (top) and isotopic (bottom) compared to the observed solar composition. Most elements and isotopes are co-produced within a factor of two of their solar value. The corresponding values for the local ISM 4.5 Gyr ago are ~0.1−0.15 dex lower for all elements but H and He. No normalisation of the results is made here. |
4.4. Abundances in local thin and thick disks
Up to now, we used only two elements, namely O and Fe, to study the chemical evolution of the MW disks. These are key elements in galactic chemical evolution studies, because they are abundant and easy to measure. However, the evaluation of oxygen abundances in stars is not straightforward (see e.g. the monography by Stasinska 2012, and references therein), while the evolution of Fe is affected by uncertainties on its massive star yields and on the rate of SNIa.
 |
Fig. 17 [X/Fe] vs. [Fe/H] for various intermediate mass elements in the solar neighbourhood: comparison of the average stellar abundances of the model to data of Adibekyan et al. (2013). The data are split into thick disk (green) and thin disk (red) according to the prescription of Adibekyan et al. (2013), in the middle panel of their Fig. 2. The model results are normalised such as the average abundance over all stars of age = 4.5 Gyr that are present today in the solar neighbourhood is solar (see text). |
 |
Fig. 18 [X/Fe] vs. [Fe/H] for various intermediate mass elements in the solar neighbourhood: comparison of model to data of Bensby et al. (2014). The data are split into thick disk (green, P> 2) and thin disk (red, P< 0.5) according to the probabilities P given in Bensby et al. (2014). The model results are normalized so that the average abundance over all stars of age =4.5 Gyr that are present today in the solar neighbourhood is solar. |
A wealth of data from recent and forthcoming surveys will allow one to explore the diagnostic potential of many more elements – produced mainly in massive stars – thereby complementing the information obtained from O and Fe. Such observations will also help to constrain the stellar yields, which suffer still from large uncertainties in some cases (see Romano et al. 2010, for a recent study of the impact of stellar yields on the chemical evolution of the MW).
Figure 16 presents our results for the average composition of local stars of 4.5 Gyr. As discussed in previous sections, the O and Fe abundances are very close to solar, making the analysis of Sect. 4 possible. For other elements, however, the situation is less satisfactory: this is the case for all elements between (and including) P and Ti and most of their isotopes, which are severely underproduced. Obviously, if the yields of Nomoto et al. (2013) were taken at face value, the observed evolution of those elemental ratios vs. Fe/H would not be reproduced.
We assume here that the isotopic yields of Nomoto et al. (2013) differ from the “real life” yields by various factors (of the order of unity), but their metallicity dependence is correct. We correct for those factors by normalising the average composition of local stars 4.5 Gyr old to be exactly solar and we apply the derived correction factor for each isotope to its evolution at all places. In that way, we force all isotopic abundances and ratios to be exactly solar for an average local star of age 4.5 Gyr, because we assume that the Sun is such an average star. We proceed then with the analysis of the thin vs. thick disks as in the previous section for O vs. Fe.
We display our results in Fig. 17, and compare them with data from the survey of Adibekyan et al. (2013) for the local thin and thick disks. It can be seen that the observations of the α elements are nicely reproduced in the framework of our model: the model accounts quantitatively for the evolution of Mg, Si, Ca and Cr in both the thin and thick disks. A qualitative agreement is also obtained for the cases of Na and Al, while Co and Ni reproduce the data for the thin disk alone. In contrast, the model fails to reproduce Ti (which behaves observationally as an α element), V, Mn and Co. The failure of the adopted yields to reproduce these observations does not necessarily imply that there is something wrong with the yields, at least not in all cases. After all, the solar abundances of a large number of elements still suffer from systematic uncertainties and are subject to revision (see e.g. Scott et al. 2015 for the Fe group elements). Cross-checks with respect to other observational data (concerning e.g. the halo stars) should be made and the role of the IMF investigated before concluding. We note here that there is certainly a problem with the Nomoto et al. (2013) yields for the cases of Ti and V, as can be seen from Fig. 10 in that work, where comparison is made of a simple GCE evolution model with halo and local disk data: it is obvious that, even after normalisation to solar values, the observed evolution of Ti and V cannot be reproduced.
In a similar vein, we compare our results to the data of the Bensby et al. (2014) survey in Fig. 18. The agreement of the model to observations of α-elements Mg, Si and Ca is excellent, as in Fig. 17; in contrast, the evolution of oxygen is poorly reproduced, as discussed in Sect. 4.3. The agreement with Al and Na is qualitatively, but not quantitatively, good and the failure in the case of Ti as bad as before.
We note that the separation into thin and thick disks is made on the basis of different criteria in Adibekyan et al. (2013) and Bensby et al. (2014): chemical vs. kinematic, respectively. Despite that, there is rather good agreement between the two data sets, making a comparison of model to the data meaningful. Here we attempted such a comparison for the first time, showing the strong potential of such detailed observations to constrain both stellar yields and evolutionary models for the MW disk.
5. Summary
In this work we presented a model for the evolution of the MW disk, involving radial motions of gas and stars. We considered the epicyclic motion of stars (blurring) separately from the true variation in their guiding radius (churning). Our parametrisation of radial migration corresponds to a barred disk galaxy, like the MW, in contrast to the work of Sellwood & Binney (2002) or Schönrich & Binney (2009a). We compared our results to an extended set of recent observational data, concerning the global evolution of the MW, the present-day radial profiles of various quantities and the solar cylinder.
Our model reproduces the present-day values of all the main “global” observables of the MW disk and bulge (here taken to correspond to regions outside and inside r = 2 kpc, respectively): stellar, atomic and molecular gas masses, rates of infall, SFR, CCSN and SNIa (Fig. 1). We obtain a very good agreement between the model evolution of the bulge and disk stellar mass and the corresponding observations of the “stacked evolution” of MW-type disks of van Dokkum et al. (2013) (Fig. 2) and in the light of these data, the MW appears as a fairly average disk galaxy. The present-day profiles of stars, gas (HI and H2), SFR, and rotational velocity are also reproduced well by the model (Fig. 4).
The main focus of this study was the impact of stellar radial migration on the properties of the Galactic disk. We find that, with the adopted scheme for radial migration (blurring+churning), the regions mostly affected are those in the range 4−12 kpc and in particular the zone between 5 and 9 kpc. Stars in those regions are formed on average ~1−2 kpc inwards of their current position and are, on average, ~1−2 Gyr older than locally formed stars (Fig. 9). This implies, in particular, that the Sun was probably formed ~1.2 kpc inwards of its present position of R0 = 8 kpc from the Galactic centre.
As already shown in previous studies, we find that radial migration brings mostly old and metal-poor stars into the solar neighbourhood, thus flattening the age-metallicity relation. It also considerably increases the dispersion in metallicity at every age, making it larger with age, as found in Sellwood & Binney (2002).
We emphasize that the local observables of our model concern the so-called “solar cylinder”, that is all stars found in the end of the simulation in a cylinder of radius 0.25 kpc (half the size of our radial bin), perpendicular to the Galactic plane and centered on the solar position, at Galactocentric distance R0 = 8 kpc. We do not apply any selection biases on those results in order to compare with specific observations. For that reason, a successful comparison to observations does not imply that the model is necessarily correct, only that it possesses potentially interesting features.
We show quantitatively that – at least in the framework of this model and with the caveat of the previous paragraph – epicyclic motions cannot produce the observed metallicity dispersion; in contrast, our adopted radial migration scheme reproduces available observations of dispersion in the age-metallicity relation (Fig. 11). We argue that this observable provides one of the most powerful probes of the extent of radial migration in the MW and that it should be scrutinized in future observational and theoretical studies. On the other hand, the local [O/Fe] abundance ratio is found to have very little dispersion with age, making it a much better proxy for age than [Fe/H] and this is true for other [α/Fe] ratios.
We analyse the origin of the stellar populations presently found in the solar annulus as a function of their metallicity (Fig. 12). We find that, at all metallicities, stars are ~1 Gyr older, on average, than locally formed stars of the same metallicity; they also display an age dispersion of ~1−3 Gyr around the average age. Cleary, radial migration affects the relation between age and metallicity dramatically, allowing for young stars of low metallicity to co-exist with old stars of high metallicity. In our model, the less metallic local stars are ~11 Gyr old, and they originate, on average, in the region at r ~ 5−6 kpc, while stars of solar metallicity are ~4.5 Gyr old and originate at r ~ 7 kpc. The most metallic local stars ([Fe/H] ~ 0.3−0.4 Z⊙) are 3−4 Gyr old and originate in the inner Galaxy, at r ~ 2−3 kpc. We find that stars of different ages and different birth radii contribute to some extent to all metallicity bins (Fig. 13).
To handle the issue of the thin vs. thick disks we adopt a simple criterion that has already been suggested in the literature, namely age (another reason for that choice being the absence of the z-direction in our model, making it impossible to use kinematic or spatial quantities in that direction). We assume that stars older than 9 Gyr belong to the thick disk and younger ones to the thin disk. That simple criterion allows us to reproduce fairly well the observed [α/Fe] vs. Fe/H behaviour of stars classified as belonging to the thin and thick disks on the basis of different criteria (chemical or kinematic). At the same time, we reproduce the corresponding metallicity distributions, very well for the thin disk and satisfactorily for the thick disk (Fig. 14). Both results provide strong support to the idea that the thick disk is simply the early part of the MW disk (corresponding to the first few Gyr of its formation) and that the local thick disk results largely from the radial migration of stars from the inner disk.
We evaluate quantitatively the radial structure of the thin and thick disks in our model. We find that, because of the inside-out formation adopted, the thick disk has a considerably shorter scalelength than the thin disk (Fig. 15), even though it has undergone a much more important radial migration than the latter. The local surface densities of both disks are in excellent agreement with recent evaluations, and this is also true for the scalelength of the thick disk; however, we obtain a thin disk with a scalelength shorter by ~1 kpc than the one observationally determined. Overall, the thick disk accounts for one-third of the total stellar disk and for one-fourth of the local stellar disk surface density.
Finally, we investigate the evolution of several elemental abundances in the local thin and thick disk and we compare our results to the large data sets obtained from recent surveys. We argue that such a study requires fine and homogeneous grids of stellar yields (such as the one provided by Nomoto et al. (2013), adopted here). We find that several observed features, i.e. the behaviour of [α/Fe] vs. Fe/H, can be reproduced fairly well for both the thick and thin disks, but the situation is much less satisfactory for other elements. Current and forthcoming data in this field will provide powerful constraints on stellar nucleosynthesis and the overall evolution of the MW disk, especially when combined with kinematic and spatial information.
Online material
Appendix A: Gas in the MW disk
 |
Fig. A.1 Surface density profiles of atomic hydrogen HI (top), molecular hydrogen H2 (middle) and total gas ΣG = 1.4 (HI+H2) (bottom). Disk data (beyond 2 kpc) are from: Dame (1993), solid; Olling & Merrifield (2001), dotted ; and Nakanishi & Sofue (2003, 2006), dashed. The dot-dashed curve in the HI panel corresponds to data from Kalberla & Dedes (2008) and in the H2 panel to data from Pohl et al. (2008). Bulge data (inner 2 kpc) in all panels are from Ferrière (2001). |
 |
Fig. A.2 Average profiles of the previous figure. Top: atomic and molecular hydrogen; middle: total gas ; bottom: fractions of gas (solid) and molecular gas (dashed). For the latter panel, an exponential stellar density profile with a scale-length of 2.3 kpc normalised to Σ∗(R = 8 kpc) = 38 M⊙/pc2 is adopted, while the molecular fraction is evaluated with the formalism of Appendix B. |
In Fig. A.1 we present the data adopted for the gas profiles of the MW. Atomic hydrogen (HI) is displayed in the upper panel and molecular hydrogen (H2) in the middle panel. In both cases, data are from Dame (1993), Olling & Merrifield (2001) and Nakanishi & Sofue (2003). The data have been rescaled to a distance of R0 = 8 kpc of the Sun from the Galactic centre. The bottom panel shows the total gas surface density ΣG = 1.4(HI+H2), where the factor 1.4 accounts for the presence of ~28% of He. In all panels, the data for the inner Galaxy (R< 2 kpc) are from Ferrière et al. (2007) and they are provided for completeness, since the evolution of the bulge is not studied here.
Despite systematic differences in the data, the gas profiles in the three panels of Fig. A.1 have some common features:
-
The HI profile is essentially flat in the 4−12 kpc region.
-
The H2 profile displays the well known “molecular ring” in the 4−5 kpc region and declines rapidly outwards.
-
The total gas profile is approximately constant (or slowly declining outwards) in the 4−12 kpc region; it declines more rapidly inside the molecular ring, as well as outside 13 kpc, where it has a scalelength of 3.75 kpc (Kalberla & Dedes 2008).
To minimize systematic uncertainties in the following, we adopt the averages of the aforementioned observed profiles as a function of galactocentric radius as the “reference gaseous profiles” for the MW disk. They appear in Fig. A.2, top panel for HI and H2 and middle panel for the total gas. As a typical uncertainty in each radius, we adopt either 50% of the average value (typical statistical uncertainty in e.g. Nakanishi & Sofue 2006) or half the difference between the minimum and maximum values in each radial bin (whichever is larger). The resulting values for the total galactic content of HI, H2 and gas appear in Table A.1. The derived masses appear lower than the ones obtained with the mass model of the ISM in the Milky Way of Misiriotis et al. (2006), who find total masses of MH2 = 1.3 × 109M⊙ and MHI = 8.2 × 109, but they match the FIR emission of the whole Galaxy, whereas we quote here results for the 2−19 kpc range. There are considerable amounts of HI in the outer disk, as discussed in e.g. Kalberla & Dedes (2008).
Gas in the MW disk (2−19 kpc) in 109M⊙.
We find then that the Galactic disk has a total gaseous content of ~ 8.2 ± 3.5 × 109M⊙ in the 2−19 kpc range. Assuming an exponential stellar profile with a scalelength Rd = 2.3 kpc for the MW disk, normalised to a local (R0 = 8 kpc) surface density Σ∗ ,0 = 38M⊙/pc2 (Flynn et al. 2006), we find a total stellar mass of 3.2 × 1010M⊙ and obtain the radial profile of the gas fraction 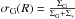 . It is displayed in the bottom panel of Fig. A.2 and it is a monotonically increasing function of radius. Integrating as before the gaseous and stellar profiles over the disk region between 2 and 19 kpc we find an average gas fraction of σG = 0.20 ± 0.05 for the disk. If the bulge (of stellar mass ~1.5 × 1010M⊙ and negligible gas) is also included, the gas fraction of the MW is found to be ~14%.
. It is displayed in the bottom panel of Fig. A.2 and it is a monotonically increasing function of radius. Integrating as before the gaseous and stellar profiles over the disk region between 2 and 19 kpc we find an average gas fraction of σG = 0.20 ± 0.05 for the disk. If the bulge (of stellar mass ~1.5 × 1010M⊙ and negligible gas) is also included, the gas fraction of the MW is found to be ~14%.
In that same panel we display the molecular fraction 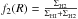 , which shows a plateau of f2 ~ 0.65 in the region of the molecular ring (3−6 kpc) and decreases strongly outwards, down to a few per cent (although with large uncertainties).
, which shows a plateau of f2 ~ 0.65 in the region of the molecular ring (3−6 kpc) and decreases strongly outwards, down to a few per cent (although with large uncertainties).
Appendix B: Star formation in the MW disk
Star formation in the MW is discussed in the recent review of Kennicutt & Evans (2012). They discuss only “traditional” tracers of star formation, also used in extragalactic studies, like FIR emission. In their Fig. 7, they display a radial distribution of the SFR, claimed to be based on data from Misiriotis et al. (2006), who made a full 3D model of the Galactic FIR and NIR emission observed with COBE. Misiriotis et al. (2006) found that their modelling of the IR emission corresponds to a 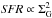 and they compared their findings to a compilation of old star formation tracers for the MW provided in Boissier & Prantzos (1999), who considered HII regions, but also pulsars and supernova remnants. Here we consider such tracers related to massive, short-lived, stars and their residues: pulsars, supernova remnants (SNR), and OB associations. Those objects have ages up to a few My for SNR and up to a few tens of My for OB associations and isolated radio pulsars, so they can probe recent star formation.
and they compared their findings to a compilation of old star formation tracers for the MW provided in Boissier & Prantzos (1999), who considered HII regions, but also pulsars and supernova remnants. Here we consider such tracers related to massive, short-lived, stars and their residues: pulsars, supernova remnants (SNR), and OB associations. Those objects have ages up to a few My for SNR and up to a few tens of My for OB associations and isolated radio pulsars, so they can probe recent star formation.
Galactic radial distributions of luminous massive stars, pulsars, SNR and OB associations appear in Fig. B.1.The distribution of luminous massive stars is from Urquhart et al. (2014); the one displayed on Fig. B.1 is the average between the southern and northern hemispheres and is considered to be complete for luminisities above 2 × 104L⊙. The pulsar distribution (Lorimer 2004; Lorimer et al. 2006) contains more than 1000 pulsars. All distributions have a broad peak in the region of the molecular ring and their radial variation agrees well with the much sparser data of Williams & McKee (1997) on OB associations. Lorimer et al. (2006) proposed an analytical fit to the pulsar distribution, which is in perfect agreement with the one proposed for the distribution of Galactic SNR in the recent compilation of Green (2014), who used 56 bright SNR (to avoid selection effects). The latter distribution (thick dotted curve, corresponding to model C of that work) is also displayed in the upper panel of Fig. B.1 and is given by ![\appendix \setcounter{section}{2} \begin{equation} \Psi(R) \ = \ A \ \left(\frac{R}{R_0}\right)^B \ \exp\left[-C\left(\frac{R-R_0}{R_0}\right)\right] \label{Eq:SFR} \end{equation}](/articles/aa/full_html/2015/08/aa24171-14/aa24171-14-eq221.png) (B.1)where R0 = 8 kpc and parameters B = 2. and C = 5.1 (Lorimer et al. 2006, give B = 1.9 and C = 5.).
(B.1)where R0 = 8 kpc and parameters B = 2. and C = 5.1 (Lorimer et al. 2006, give B = 1.9 and C = 5.).
 |
Fig. B.1 Top: observed surface density profiles of various SFR tracers (see text); the dotted curve – with no error bars – is the analytical form suggested by Green (2013) and it is here adopted as representative of the MW SFR profile. Middle: theoretical or empirical SF rates compared to the adopted profile of SFR tracers (the dotted curve from the upper panel); all profiles are normalised to the same value in R0 = 8 kpc. Bottom: ratio of the theoretical or empirical profiles to the adopted observed one. |
 |
Fig. B.2 Top: SFR surface density vs. total gas surface density (left) and vs. H2 (right) for the MW disk, in the region between 2 and 13 kpc. In both panels, curves represent the same quantities as in Fig. B.1; the long dashed curve (SFR ∝ Σ(H2)) corresponds quantitatively to the fit of Bigiel et al. (2008) to extragalactic data and fits the adopted “observed” SFR profile in the MW disk quite well. Bottom: the “observed” SFR vs. gas relation in the MW is compared to a compilation of extragalactic data from Krumholz et al. (2012). |
There is reasonably good agreement between all the SFR tracers of Fig. B.1, with the exception of the one for luminous massive stars of the RMS survey (Urquhart et al. 2014), which differs considerably from the others inside 4 kpc (where selection biases are expected to be more important, even for such luminous stars) and displays an unexpected enhancement in the region around 9 kpc. Baring those differences, we adopt Eq. (B.1) as the expression for the radial dependence of the SFR in the MW disk, after normalising it (by putting A = 3.5M⊙/kpc2/y) to the total SFR rate of the Milky Way ΨMW = 2M⊙/y (Chomiuk & Povich 2011): 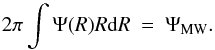 (B.2)In the middle panel of Fig. B.1, we compare the “observed” SFR profile with various theoretical or empirical profiles in the literature, which make use of the corresponding profiles of total or molecular gas discussed in this section. All of them are normalised to the adopted observed value of the SFR in the solar neighbourhood.
(B.2)In the middle panel of Fig. B.1, we compare the “observed” SFR profile with various theoretical or empirical profiles in the literature, which make use of the corresponding profiles of total or molecular gas discussed in this section. All of them are normalised to the adopted observed value of the SFR in the solar neighbourhood.
The most widely used SFR prescription is the so-called “Schmidt-Kennicut” law, based on observations of quiescent and active disk galaxies: 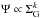 , where the gas surface density ΣG runs over three orders of magnitude and the data suggest k = 1.5. It turns out that this form of the SFR, with k = 1.5 is too flat to fit the MW data: Misiriotis et al. (2006) find k = 2 from their modelling of the IR emission of the MW. Also, it is well known that a steeper function is required in galactic chemical evolution models to explain the observed abundance gradients in the MW disk.
, where the gas surface density ΣG runs over three orders of magnitude and the data suggest k = 1.5. It turns out that this form of the SFR, with k = 1.5 is too flat to fit the MW data: Misiriotis et al. (2006) find k = 2 from their modelling of the IR emission of the MW. Also, it is well known that a steeper function is required in galactic chemical evolution models to explain the observed abundance gradients in the MW disk.
 |
Fig. B.3 Top: observed molecular fraction |
Boissier & Prantzos (1999) adopted a law of the form 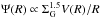 ; the factor V(R) /R is ∝ 1 /R for a flat curve of the rotational velocity V(R) and is attributed to spiral waves inducing star formation with that frequency (Wyse 1986; Wyse & Silk 1989). On the other hand, models by Chiappini (2001) adopt
; the factor V(R) /R is ∝ 1 /R for a flat curve of the rotational velocity V(R) and is attributed to spiral waves inducing star formation with that frequency (Wyse 1986; Wyse & Silk 1989). On the other hand, models by Chiappini (2001) adopt 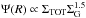 , where ΣTOT is the total disk surface density (dominated in the inner Galaxy by the rapidly increasing stellar profile), and they introduced a cut-off in the SFR efficiency, below 2 M⊙/pc2. Both SFR laws also appear in the middle and lower panels of Fig. B.1: they fit relatively well the “observed” SFR profile and it turns out that the corresponding models reproduce several key properties of the MW disk relatively well.
, where ΣTOT is the total disk surface density (dominated in the inner Galaxy by the rapidly increasing stellar profile), and they introduced a cut-off in the SFR efficiency, below 2 M⊙/pc2. Both SFR laws also appear in the middle and lower panels of Fig. B.1: they fit relatively well the “observed” SFR profile and it turns out that the corresponding models reproduce several key properties of the MW disk relatively well.
The aforementioned laws make use of the total gaseous profile of the disk. Based on a detailed, sub-kpc scale, observations of a large sample of disk galaxies, Bigiel et al. (2008) have found that the SFR appears to follow the H2 surface density, rather than the HI or the total gas surface density. In a companion paper, Leroy et al. (2008) argue that the observed radial decline in star formation efficiency is too steep to be reproduced only by increases in the free-fall time or orbital time and they find no clear indications of a cut-off in the SFR.
Following these studies, we checked whether such a correspondence between the adopted SFR and molecular gas profiles also holds in the MW disk. The comparison, presented in the middle and lower panels of Fig. B.1, is favourable to that idea: the SFR follows the H2 profile to better than 30% in the 3−13 kpc range.
Figure B.2 displays the data in a different way, with SFR surface density vs. gas (total or molecular) surface densities. In the top left panel, it appears that the “observed” SFR varies too steeply with the total gas density and it cannot be fit with a simple Schmidt-Kennicutt" law 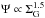 ; a strong radial dependence of the SF efficiency, such as the aforementioned ones, is required to improve the situation. In the top right panel it is seen that the “observed” SFR increases almost linearly with H2, and that the SFR proposed by Bigiel et al. (2008), Ψ = 0.009ΣH2/(10 M⊙/pc2), reproduces the data quite well. The measurement of Bigiel et al. (2008) concern H2 surface densities above 3 M⊙/pc2, i.e. they correspond to the upper half of the figure. It appears that, at least in the case of the MW, that dependence is prolonged to even smaller surface densities. In the bottom panel of Fig. B.2 the “observed” SFR vs. gas relation in the MW disk is compared to data of a sample of disk galaxies from Krumholz et al. (2012). It is clearly seen that the MW disk SFR corresponds to a narrow range of gas surface densities, so the extragalactic data of SFR vs. gas cannot be used as guide to the MW SFR; in contrast, data on MW SFR vs. H2 cover a wider dynamical range of H2 and offer convincing evidence of a linear relationship between the two quantities.
; a strong radial dependence of the SF efficiency, such as the aforementioned ones, is required to improve the situation. In the top right panel it is seen that the “observed” SFR increases almost linearly with H2, and that the SFR proposed by Bigiel et al. (2008), Ψ = 0.009ΣH2/(10 M⊙/pc2), reproduces the data quite well. The measurement of Bigiel et al. (2008) concern H2 surface densities above 3 M⊙/pc2, i.e. they correspond to the upper half of the figure. It appears that, at least in the case of the MW, that dependence is prolonged to even smaller surface densities. In the bottom panel of Fig. B.2 the “observed” SFR vs. gas relation in the MW disk is compared to data of a sample of disk galaxies from Krumholz et al. (2012). It is clearly seen that the MW disk SFR corresponds to a narrow range of gas surface densities, so the extragalactic data of SFR vs. gas cannot be used as guide to the MW SFR; in contrast, data on MW SFR vs. H2 cover a wider dynamical range of H2 and offer convincing evidence of a linear relationship between the two quantities.
In view of this observational support, both for the MW disk (this work) and for external galaxies (Bigiel et al. 2008; Leroy et al. 2008), we adopt here a star formation law depending on the H2 surface density. In order to calculate it in the model of chemical evolution we adopt the semi-emi-empirical prescription of Blitz & Rosolowsky (2006) for the ratio Rmol = H2/HI and we find rather good agreement between the observed and theoretically calculated molecular fractions in the MW disk 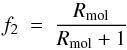 (B.3)as seen in the top panel of Fig. B.3. The resulting radial profiles H2(R) = f2(R) ΣG(R) and HI(R) = [ 1−f2(R) ] ΣG(R) also compare favourably to the observed ones (middle panel). Finally, the corresponding SFR (Eq. (3) in Bigiel et al. 2008, but with a coefficient 0.0016 instead of 0.008)
(B.3)as seen in the top panel of Fig. B.3. The resulting radial profiles H2(R) = f2(R) ΣG(R) and HI(R) = [ 1−f2(R) ] ΣG(R) also compare favourably to the observed ones (middle panel). Finally, the corresponding SFR (Eq. (3) in Bigiel et al. 2008, but with a coefficient 0.0016 instead of 0.008) 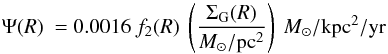 (B.4)reproduces well the “observed” SFR profile of the MW disk in the 4−12 kpc region, and somewhat less successfully outside that region (bottom panel). This agreement has already found in Blitz & Rosolowsky (2006), but with older data for the gas and SFR profiles of the MW.
(B.4)reproduces well the “observed” SFR profile of the MW disk in the 4−12 kpc region, and somewhat less successfully outside that region (bottom panel). This agreement has already found in Blitz & Rosolowsky (2006), but with older data for the gas and SFR profiles of the MW.
Appendix C: Chemical evolution
In studies of galactic chemical evolution, the changes in the chemical composition of the system are described by a system of integro-differential equations. The mass of element/isotope i in the gas is mi = mGXi, (where mG is the mass of the gas and Xi is the mass fraction of i) and its evolution is given by: 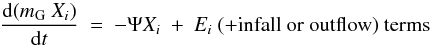 (C.1)i.e. star formation at a rate Ψ removes element i from the ISM at a rate ΨXi, while at the same time stars inject in the ISM that element at a rate Ei(t). The rate of ejection of element i by stars is given by:
(C.1)i.e. star formation at a rate Ψ removes element i from the ISM at a rate ΨXi, while at the same time stars inject in the ISM that element at a rate Ei(t). The rate of ejection of element i by stars is given by: 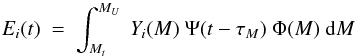 (C.2)where the star of mass M, created at the time t − τM, dies at time t (if its lifetime τM is lower than t) and releases a mass Yi(M) in the form of element/isotope i (stellar yield of i from mass M). Here, Φ(M) = dN/ dM is the IMF, assumed to be independent of time t, Mt is the mass of the smallest star that has lifetime τM = t and MU is the most massive star of the IMF.
(C.2)where the star of mass M, created at the time t − τM, dies at time t (if its lifetime τM is lower than t) and releases a mass Yi(M) in the form of element/isotope i (stellar yield of i from mass M). Here, Φ(M) = dN/ dM is the IMF, assumed to be independent of time t, Mt is the mass of the smallest star that has lifetime τM = t and MU is the most massive star of the IMF.
 |
Fig. C.1 Top: stellar mass vs. lifetime. Middle: stellar death rate after an initial “burst” forming 1 M⊙ of stars: dN/ dt = dN/ dM × dM/ dt, where dN/ dM is the stellar IMF and dM/ dt the derivative of the curve in the top panel. The thick portion of the curve (up to ~35 My, corresponding to a star of 8 M⊙) is the rate of CCSN. The bottom right part of the middle panel displays the corresponding SNIa rate (the time delay distribution or TDD) adopted in this work (thick curve); it is a mixture of the Greggio (2005) formulation for the SD scenario up to 4.5 Gyr and an extrapolation ∝ t-1 after that time, in order to fit the data points from Maoz et al. (2012; filled circles) and from Maoz et al. (2010; squares). Bottom: time-integrated numbers of CCSN (thick portion of upper curve), single stars of mass M< 8M⊙ (thin portion of upper curve) and SNIa (lower curve), as a function of time, for an initial “burst” of 1 M⊙. |
Because of the presence of the term Ψ(t − τM), Eqs. (C.1) and (C.2) have to be solved numerically (except if specific assumptions, like the instantaneous recycling approximation – IRA – are made). The integral (C.2) is evaluated over the stellar masses, properly weighted by the term Ψ(t − τM) corresponding in each mass M. It is explicitly assumed in that case that all the stellar masses created in a given place, release their ejecta in that same place.
This assumption does not hold anymore if stars are allowed to travel away from their birth places before dying. In that case, the mass Ei(t) released in a given place of spatial coordinate R and at time t is the sum of the ejecta of stars born in various places R′ and times t − t′, with different SFRs Ψ(t′,R′) for all stellar masses M with lifetimes τM<t − t′ Instead of Eq. (C.2), the isochrone formalism, concerning instantaneous “bursts” of star formation or single stellar populations (SSP), has to be used then Eq. (C.2) is rewritten as 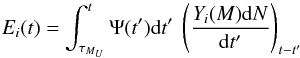 (C.3)where dN = Φ(M)dM is the number of stars between M and M + dM and Ψ(t′)dt′ is the mass of stars (in M⊙) created in time interval dt′ at time t′. The term (dN/ dt′)t − t′ represents the stellar death rate (by number) at time t of a unit mass of stars born in an instantaneous burst at time t − t′. The term Yi(M)dN/ dt represents the corresponding rate of release of element i in M⊙/yr.
(C.3)where dN = Φ(M)dM is the number of stars between M and M + dM and Ψ(t′)dt′ is the mass of stars (in M⊙) created in time interval dt′ at time t′. The term (dN/ dt′)t − t′ represents the stellar death rate (by number) at time t of a unit mass of stars born in an instantaneous burst at time t − t′. The term Yi(M)dN/ dt represents the corresponding rate of release of element i in M⊙/yr.
Expression (C.3) is equivalent to expression (C.2) and it is used in N-body+SPH simulations (see Lia et al. 2002 or Wiersma et al. 2009), since it allows one to account for the ejecta released in a given place by “star particles” produced with different SFRs in other places (see main text). It naturally incorporates the metallicity dependence of the stellar yields and of the stellar lifetimes, both found in the term Yi(M,Z)(dN/ dt)(Z).
 |
Fig. C.2 Ejection rates of hydrogen, carbon, oxygen and Fe from a stellar population of 1 M⊙ as a function of time. Yields are from Nomoto et al. (2013).The curves represent different metallicities, as indicated in the top panel. The dotted curves show the contribution of SNIa (resulting from a SSP of 1 M⊙) to the production of those elements. |
As in Boissier & Prantzos (1999), we use here the stellar lifetimes τ(M,Z) of Schaller et al. (1992) for stars in the mass range 0.1−120 M⊙ and for two metallicities Z⊙ and 0.05 Z⊙ (covering the metallicity of the MW disk during its whole evolution except, perhaps, its earliest phases).
We adopt the stellar IMF of Kroupa (2002) in the mass range 0.1−100 M⊙, but with a slope x = −2.7 in the range 1−100 M⊙ (the “Scalo slope”), since the “Salpeter slope” of −2.35 overproduces metals in the evolution of the solar neighbourhood. Moreover, the “Scalo” slope is similar to the one of the integrated galactic IMF (IGIMF) suggested in e.g. Kroupa (2008), which is appropriate for galactic evolution studies.
We adopt the yields provided by Nomoto et al. (2013)6. They concern both low and intermediate mass stars in the mass range 0.9 to 3.5 M⊙ (calculations from Karakas 2010)
and for massive stars in the range 11−40 M⊙. They are particularly adapted to the study of the galactic disk, because they cover a uniform grid of 6 initial metallicities (Z = 0, 0.001, 0.002, 0.004, 0.008, 0.02 and 0.05, i.e. from 0 to about 3 times solar), allowing for a detailed study of both the inner and the outer MW regions. This constitutes a clear advantage over other sets of widely used yields (e.g. Woosley & Weaver 1995). The massive star models of Nomoto et al. (2013) have mass loss but no rotation; yields of hypernovae (very energetic explosions) are also provided but we do not use them here. We include all 82 stable isotopic species from H to Ge. We calculate their evolution and we sum up at each time step to obtain the corresponding evolution of their elemental abundances. We note that the use of the yields in chemical evolution calculations requires some interpolation in the mass range of the super-AGB stars (6 or 8 to 11 M⊙).
We force the sum of the ejected masses of all isotopes of a star to be equal to the original stellar mass minus the one of the compact residue (white dwarf, neutron star or black hole). This is important in order to ensure mass conservation in the system during the evolution. We interpolate logarithmically the yields in metallicity and in the mass range between 3.5 and 11 M⊙, and we include a detailed treatment for the production of the light nuclides Li, Be and B by cosmic rays (Prantzos 2012).
For the rate of SNIa we adopt a semi-empirical approach: the observational data of recent surveys are described well by a power-law in time, of the form ∝ t-1, e.g. Maoz & Mannucci (2012) and references therein. At the earliest times, the DTD is unknown/uncertain, but a cut-off must certainly exist before the formation of the first white dwarfs (~35−40 Myr after the birth of the SSP). We adopt then the formulation of Greggio (2005) for the single-degenerate (SD) scenario of SNIa. That formulation reproduces, in fact, the observations up to ~4−5 Gyr (see Fig. C.1, middle panel) quite well. For longer timescales, where the SD scenario fails, we simply adopt the t-1 power law. The corresponding SNIa rate at time t from all previous SSP is obtained as 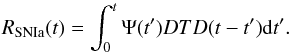 (C.4)As in GP2000 we adopt the SNIa yields of Iwamoto et al. (1999) for Z = 0 and Z = Z⊙, interpolating logarithmically in metallicity between those values.
(C.4)As in GP2000 we adopt the SNIa yields of Iwamoto et al. (1999) for Z = 0 and Z = Z⊙, interpolating logarithmically in metallicity between those values.
In Fig. C.1 we show the results for a SSP concerning the stellar death rates, including the CCSN rate, the SNIa rate (middle panel) and the corresponding time-integrated rates. With the adopted IMF, there are about 4.5 × 10-3 CCSN and 1.2 × 10-3 SNIa for every M⊙ of stars formed.
In Fig. C.2 we present the ejection rates for H, C, O and Fe as a function of time, for single stars (3 initial metallicities) and for SNIa. SNIa produce more than half of solar Fe and they make minor contributions to the production of “light” metals like C or O (but substantial ones to the production of Si or Ca).
We made extensive tests of the implemented SSP formalism (Eq. (C.3)) against the “classical” one (Eq. (C.1)) and found excellent agreement in all cases.
We assume that [α/Fe] = ([Mg/Fe] + [Si/Fe])/2, although Adibekyan et al. (2011) assume that [α/Fe] = ([Mg/Fe] + [Si/Fe] + [Ti/Fe])/3; however, the adopted massive star yields of Nomoto et al. (2013) – but also other yields, e.g. Woosley & Weaver (1995) – fail to reproduce the observed behaviour of Ti as an α element in the halo of the MW. For that reason, we adopt two α elements with well behaved yields.
We classify stars in the sample of Adibekyan et al. (2011) into thin and thick disks by applying the criterion (dividing line in the [O/Fe] vs. [Fe/H] plane) suggested in Adibekyan et al. (2013).
We use the criterion suggested by Bensby et al. (2014) for the classification into thin and thick disk, namely probabilities higher than 2 for the former and smaller than 0.5 for the latter.
Particular care is required from users of those yields. The ones for low mass stars are “net yields” for all metallicities except Z = 0. The ones of massive stars are “total yields” coming out through the final explosion. One has then to include the composition of the envelope (calculated as the mass of the star minus the mass of the remnant minus the sum of the explosion ejecta), assumed to have the initial composition.
Acknowledgments
We are grateful to T. Bensby for providing data before their publication and advice on their use. E.A. acknowledges financial support to the DAGAL network from the People Programme (Marie Curie Actions) of the European Union’s Seventh Framework Programme FP7/2007–2013/ under REA grant agreement number PITN-GA-2011-289313 and from the CNES (Centre National d’Études Spatiales – France). We also acknowledge partial support from the PNCG (Programme National Cosmologie et Galaxies – France) and from the European Science Foundation (ESF) project EuroGENESIS/MASCHE. The simulation used for the modelling in this paper was run using the HPC resources from GENCI – TGCC/CINES (Grants x2013047098 and x2014047098).
References
- Adibekyan, V. Z., Santos, N. C., Sousa, S. G., & Israelian, G. 2011, A&A, 535, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Figueira, P., Santos, N. C., et al. 2013, A&A, 554, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Afflerbach, A., Churchwell, E., & Werner, M. W. 1997, ApJ, 478, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E. 1992, MNRAS, 259, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E., Bosma, A., Creze, M., & Schwarz, M. P. 1982, A&A, 107, 101 [NASA ADS] [Google Scholar]
- Athanassoula, E., Machado, R. E. G., & Rodionov, S. A. 2013, MNRAS, 429, 1949 [NASA ADS] [CrossRef] [Google Scholar]
- Baba, J., Saitoh, T. R., & Wada, K. 2013, ApJ, 763, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Babusiaux, C., & Gilmore, G. 2005, MNRAS, 358, 1309 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K., & Tsujimoto, T. 2011, ApJ, 738, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T. 2014, IAU Symp., 298, 17 [NASA ADS] [Google Scholar]
- Bensby, T., Alves-Brito, A., Oey, M. S., Yong, D., & Meléndez, J. 2011, ApJ, 735, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., & Oey, M. S. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhattacharjee, P., Chaudhury, S., & Kundu, S. 2014, ApJ, 785, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Bilitewski, T., & Schönrich, R. 2012, MNRAS, 426, 2266 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Sanders, J. L. 2014, in IAU Symp. 298, eds. S. Feltzing, G. Zhao, N. A. Walton, & P. Whitelock, 117 [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics, Second Edition (Princeton University Press) [Google Scholar]
- Bird, J. C., Kazantzidis, S., Weinberg, D. H., et al. 2013, ApJ, 773, 43 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Blitz, L., & Rosolowsky, E. 2006, ApJ, 650, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Blitz, L., & Spergel, D. N. 1991, ApJ, 379, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Bobylev, V. V., Mosenkov, A. V., Bajkova, A. T., & Gontcharov, G. A. 2014, Astron. Lett., 40, 86 [Google Scholar]
- Boissier, S., & Prantzos, N. 1999, MNRAS, 307, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., & Rix, H.-W. 2013, ApJ, 779, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Rix, H.-W., & Hogg, D. W. 2012a, ApJ, 751, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Rix, H.-W., Liu, C., et al. 2012b, ApJ, 753, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, C. B., Stinson, G. S., Gibson, B. K., et al. 2012, MNRAS, 426, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, M., Chiappini, C., & Pfenniger, D. 2011, A&A, 534, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabrera-Lavers, A., Hammersley, P. L., González-Fernández, C., et al. 2007, A&A, 465, 825 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cheng, J. Y., Rockosi, C. M., Morrison, H. L., et al. 2012, ApJ, 752, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C. 2009, in IAU Symp. 254, eds. J. Andersen, B. M, Nordströara, & J. Bland-Hawthorn, 191 [Google Scholar]
- Chiappini, C., Matteucci, F., & Gratton, R. 1997, ApJ, 477, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Chomiuk, L., & Povich, M. S. 2011, AJ, 142, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Comerón, S., Elmegreen, B. G., Knapen, J. H., et al. 2011, ApJ, 741, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Courteau, S., Cappellari, M., de Jong, R. S., et al. 2014, Rev. Mod. Phys., 86, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Daflon, S., & Cunha, K. 2004, ApJ, 617, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M. 1993, in Back to the Galaxy, eds. S. S. Holt, & F. Verter, AIP Conf. Ser., 278, 267 [Google Scholar]
- Di Matteo, P., Haywood, M., Combes, F., Semelin, B., & Snaith, O. N. 2013, A&A, 553, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drimmel, R., & Spergel, D. N. 2001, ApJ, 556, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Dutil, Y., & Roy, J.-R. 1999, ApJ, 516, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrière, K., Gillard, W., & Jean, P. 2007, A&A, 467, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrini, F., Molla, M., Pardi, M. C., & Diaz, A. I. 1994, ApJ, 427, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Flynn, C., Holmberg, J., Portinari, L., Fuchs, B., & Jahreiß, H. 2006, MNRAS, 372, 1149 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Forbes, J., Krumholz, M., & Burkert, A. 2012, ApJ, 754, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Friedli, D., & Benz, W. 1993, A&A, 268, 65 [NASA ADS] [Google Scholar]
- Friedli, D., Benz, W., & Kennicutt, R. 1994, ApJ, 430, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, J., Kauffmann, G., Huang, M.-L., et al. 2013, MNRAS, 434, 1531 [NASA ADS] [CrossRef] [Google Scholar]
- Genovali, K., Lemasle, B., Bono, G., et al. 2013, A&A, 554, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grand, R. J. J., Kawata, D., & Cropper, M. 2012, MNRAS, 421, 1529 [CrossRef] [Google Scholar]
- Grand, R. J. J., Kawata, D., & Cropper, M. 2014, MNRAS, 439, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Green, D. A. 2014, in IAU Symp. 296, eds. A. Ray & R. A. McCray, 188 [Google Scholar]
- Greggio, L. 2005, A&A, 441, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hammer, F., Puech, M., Chemin, L., Flores, H., & Lehnert, M. D. 2007, ApJ, 662, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., Katz, D., & Gómez, A. 2013, A&A, 560, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Hou, J. L., Prantzos, N., & Boissier, S. 2000, A&A, 362, 921 [NASA ADS] [Google Scholar]
- Isern, J., Artigas, A., & García-Berro, E. 2013, in Eur. Phys. J. Web Conf., 43, 5002 [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kalberla, P. M. W., & Dedes, L. 2008, A&A, 487, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kang, X., Chang, R., Yin, J., et al. 2012, MNRAS, 426, 1455 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I. 2010, MNRAS, 403, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kordopatis, G., Gilmore, G., Wyse, R. F. G., et al. 2013, MNRAS, 436, 3231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kroupa, P. 2008, in Pathways Through an Eclectic Universe, eds. J. H. Knapen, T. J. Mahoney, & A. Vazdekis, ASP Conf. Ser., 390, 3 [Google Scholar]
- Krumholz, M. R. 2014, Phys. Rep., 539, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Dekel, A., & McKee, C. F. 2012, ApJ, 745, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Kubryk, M., Prantzos, N., & Athanassoula, E. 2013, MNRAS, 436, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Kubryk, M., Prantzos, N., & Athanassoula, E. 2015, A&A, 580, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacey, C. G., & Fall, S. M. 1985, ApJ, 290, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Lagos, C. D. P., Baugh, C. M., Lacey, C. G., et al. 2011, MNRAS, 418, 1649 [NASA ADS] [CrossRef] [Google Scholar]
- Lehner, N., & Howk, J. C. 2011, Science, 334, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Lemasle, B., François, P., Genovali, K., et al. 2013, A&A, 558, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lépine, J. R. D., Acharova, I. A., & Mishurov, Y. N. 2003, ApJ, 589, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, J. R., & Freeman, K. C. 1989, AJ, 97, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y., Mo, H. J., van den Bosch, F. C., & Lin, W. P. 2007, MNRAS, 379, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Lia, C., Portinari, L., & Carraro, G. 2002, MNRAS, 330, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, C., & van de Ven, G. 2012, MNRAS, 425, 2144 [NASA ADS] [CrossRef] [Google Scholar]
- Loebman, S. R., Roškar, R., Debattista, V. P., et al. 2011, ApJ, 737, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lorimer, D. R. 2004, in Young Neutron Stars and Their Environments, eds. F. Camilo & B. M. Gaensler, IAU Symp., 218, 105 [Google Scholar]
- Lorimer, D. R., Faulkner, A. J., Lyne, A. G., et al. 2006, MNRAS, 372, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., & Lambert, D. L. 2011, AJ, 142, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., & Mannucci, F. 2012, PASA, 29, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Sharon, K., & Gal-Yam, A. 2010, ApJ, 722, 1879 [Google Scholar]
- Maoz, D., Mannucci, F., & Brandt, T. D. 2012, MNRAS, 426, 3282 [NASA ADS] [CrossRef] [Google Scholar]
- Marasco, A., Fraternali, F., & Binney, J. J. 2012, MNRAS, 419, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, P., & Roy, J.-R. 1994, ApJ, 424, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Serrano, F. J., Serna, A., Doménech-Moral, M., & Domínguez-Tenreiro, R. 2009, ApJ, 705, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F. 2012, Chemical Evolution of Galaxies (Springer Verlag) [Google Scholar]
- Mayor, M., & Vigroux, L. 1981, A&A, 98, 1 [NASA ADS] [Google Scholar]
- McMillan, P. J. 2011, MNRAS, 414, 2446 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., & Famaey, B. 2010, ApJ, 722, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Famaey, B., Combes, F., et al. 2011, A&A, 527, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Famaey, B., Quillen, A. C., et al. 2012a, A&A, 548, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Famaey, B., Quillen, A. C., et al. 2012b, A&A, 548, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2013, A&A, 558, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2014, A&A, 572, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Misiriotis, A., Xilouris, E. M., Papamastorakis, J., Boumis, P., & Goudis, C. D. 2006, A&A, 459, 113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mollá, M., & Díaz, A. I. 2005, MNRAS, 358, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Monari, G., Antoja, T., & Helmi, A. 2013, ArXiv e-prints [arXiv:1306.2632] [Google Scholar]
- Monari, G., Helmi, A., Antoja, T., & Steinmetz, M. 2014, A&A, 569, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakanishi, H., & Sofue, Y. 2003, PASJ, 55, 191 [Google Scholar]
- Nakanishi, H., & Sofue, Y. 2006, PASJ, 58, 847 [NASA ADS] [Google Scholar]
- Navarro, J. F., Abadi, M. G., Venn, K. A., Freeman, K. C., & Anguiano, B. 2011, MNRAS, 412, 1203 [NASA ADS] [Google Scholar]
- Nieva, M.-F., & Przybilla, N. 2012, A&A, 539, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nomoto, K., Kobayashi, C., & Tominaga, N. 2013, ARA&A, 51, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Olling, R. P., & Merrifield, M. R. 2001, MNRAS, 326, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel, B. E. J. 2009, Nucleosynthesis and Chemical Evolution of Galaxies (Cambridge University Press) [Google Scholar]
- Picaud, S., & Robin, A. C. 2004, A&A, 428, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pohl, M., Englmaier, P., & Bissantz, N. 2008, ApJ, 677, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Porcel, C., Garzon, F., Jimenez-Vicente, J., & Battaner, E. 1998, A&A, 330, 136 [NASA ADS] [Google Scholar]
- Portinari, L., & Chiosi, C. 2000, A&A, 355, 929 [NASA ADS] [Google Scholar]
- Prantzos, N. 2009, in IAU Symp. 254, eds. J. Andersen, B. Nordström, & J. Bland-Hawthorn, 381 [Google Scholar]
- Prantzos, N. 2012, A&A, 542, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prantzos, N., & Aubert, O. 1995, A&A, 302, 69 [NASA ADS] [Google Scholar]
- Prantzos, N., Aubert, O., & Audouze, J. 1996, A&A, 309, 760 [NASA ADS] [Google Scholar]
- Prantzos, N., Boehm, C., Bykov, A. M., et al. 2011, Rev. Mod. Phys., 83, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Rashkov, V., Pillepich, A., Deason, A. J., et al. 2013, ApJ, 773, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Rix, H.-W., & Bovy, J. 2013, A&ARv, 21, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T. P., & Whitney, B. A. 2010, ApJ, 710, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Rocha-Pinto, H. J., Scalo, J., Maciel, W. J., & Flynn, C. 2000, A&A, 358, 869 [NASA ADS] [Google Scholar]
- Romano, D., Karakas, A. I., Tosi, M., & Matteucci, F. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roskar, R. 2010, Ph.D. Thesis, University of Washington [Google Scholar]
- Roškar, R., Debattista, V. P., Quinn, T. R., Stinson, G. S., & Wadsley, J. 2008, ApJ, 684, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Roškar, R., Debattista, V. P., & Loebman, S. R. 2013, MNRAS, 433, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Sales, L. V., Helmi, A., Abadi, M. G., et al. 2009, MNRAS, 400, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Marino, R. A., et al. 2012, A&A, 546, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Blázquez, P., Courty, S., Gibson, B. K., & Brook, C. B. 2009, MNRAS, 398, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [Google Scholar]
- Schönrich, R., & Binney, J. 2009a, MNRAS, 396, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., & Binney, J. 2009b, MNRAS, 399, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, P., Asplund, M., Grevesse, N., Bergemann, M., & Sauval, A. J. 2015, A&A, 573, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sellwood, J., & Binney, J. 2002, MNRAS, 336, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Shevchenko, I. I. 2011, ApJ, 733, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, J. P., Colgan, S. W. J., Rubin, R. H., Erickson, E. F., & Haas, M. R. 1995, ApJ, 444, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J., & Rolleston, W. R. J. 1997, ApJ, 481, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Sofue, Y. 2012, PASJ, 64, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Sofue, Y. 2013, PASJ, 65, 118 [NASA ADS] [Google Scholar]
- Steinmetz, M. 2012, Astron. Nachr., 333, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Sygnet, J. F., Tagger, M., Athanassoula, E., & Pellat, R. 1988, MNRAS, 232, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Tinsley, B. M., & Larson, R. B. 1978, ApJ, 221, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Urquhart, J. S., Figura, C. C., Moore, T. J. T., et al. 2014, MNRAS, 437, 1791 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Leja, J., Nelson, E. J., et al. 2013, ApJ, 771, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Wakker, B. P., Howk, J. C., Savage, B. D., et al. 1999, Nature, 402, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wang, Y., & Zhao, G. 2013, ApJ, 769, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Wielen, R., Fuchs, B., & Dettbarn, C. 1996, A&A, 314, 438 [NASA ADS] [Google Scholar]
- Wiersma, R. P. C., Schaye, J., Theuns, T., Dal la Vecchia, C., & Tornatore, L. 2009, MNRAS, 399, 574 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., & McKee, C. F. 1997, ApJ, 476, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, M. L., Helmi, A., Morrison, H. L., et al. 2011, MNRAS, 413, 2235 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Wyse, R. F. G. 1986, ApJ, 311, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Wyse, R. F. G., & Silk, J. 1989, ApJ, 339, 700 [NASA ADS] [CrossRef] [Google Scholar]
- Yoachim, P., & Dalcanton, J. J. 2006, AJ, 131, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Kennicutt, Jr., R. C., & Huchra, J. P. 1994, ApJ, 420, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, L., Rix, H.-W., van de Ven, G., et al. 2013, ApJ, 772, 108 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Local observational constraints (surface densities of gas and stars – in M⊙/pc2 – at R0 = 8 kpc)
All Figures
 |
Fig. 1 Evolution of various quantities in the baseline scenario. In all panels, solid bluecurves correspond to the evolution of the disk (r> 2 kpc) and dotted redones to that of the bulge (r< 2 kpc), respectively. Vertical bars at 12 Gyr represent observational constraints (see text and Table 1). |
| In the text | |
 |
Fig. 2 Comparison of the model results to the observed “stacked” evolution of disk galaxies of stellar mass 5 × 1010M⊙ (dotted curves) from van Dokkum et al. (2013). Top: evolution of the total SFR (black solid curve), decomposed into bulge and disk contributions. Bottom: evolution of the stellar mass of the bulge (r< 2 kpc) and of the disk (r> 2 kpc) of the model (solid red and blue curves, respectively). |
| In the text | |
 |
Fig. 3 Evolution of various quantities in the baseline scenario as a function of time, for five different radial zones, at 2 (red), 5 (green), 8 (thick blue), 11 (cyan) and 14 (magenta) kpc. Observational data for local surface densities of gas and stars (from Table 1) are indicated with filled circles at T = 12 Gyr. |
| In the text | |
 |
Fig. 4 Model profiles (red solid curves) at 4, 8 Gyr (thin curves) and at 12 Gyr (thick curves) of various quantities and comparison of the latter with observational data concerning the present-day disk of the Milky Way. For all gaseous profiles (gas, HI, H2, gas fraction and molecular fraction), observational constraints are those discussed in Appendix A and presented in Fig. A.2. For stars, the shaded area is bounded by two exponential curves with scalelengths Rd = 2.1 and 2.7 kpc, respectively, which fix the range of plausible values for the stellar disk; they are normalised to a surface density of Σ∗(R = 8 kpc) = 38 ± 2 M⊙/pc2 in the solar neighbourhood. Data for the MW rotation curve are from Sofue (2012); the dashed curves represent the contributions of the bulge, disk and dark matter (blue, green and red, respectively ; see text for the bulge contribution). Data for the SFR profile are discussed in Appendix B and displayed in Fig. B.1. The observed present-day profile of infall rate (dotted curve) is based on estimates of Marasco et al. (2012) (see text). The bottom right panel displays the adopted timescales for exponential infall. Data for oxygen are from HI regions (Simpson et al. 1995; Afflerbach et al. 1997) and OB stars (Smartt & Rolleston 1997; Daflon & Cunha 2004) and for iron from Cepheids (Luck & Lambert 2011; Lemasle et al. 2013; Genovali et al. 2013). |
| In the text | |
 |
Fig. 5 Top: adopted velocity profile for radial inflow. Positive velocities indicate flow inwards (towards the Galactic centre) and negative ones an outward flow. The flow velocity is everywhere zero before the assumed appearance of the bar at t = 6.5 Gyr. Profiles are given at t = 6, 8, 10 and and 12 Gyr (cyan long-dashed, blue short-dashed, green dotted and red solid, respectively). As corotation moves outwards (see text), the flow pattern moves also. Middle: corresponding mass flow profiles through radial zones r. Bottom: corresponding mass infall profiles (rate of mass infalling over the ring of radius r and width Δr = 0.5 kpc, at t = 6, 8, 10 and and 12 Gyr. |
| In the text | |
 |
Fig. 6 SFR vs. gas surface density. Model results are displayed for three different epochs, after 4 Gyr (green curve), 8 Gyr (blue) and 12 Gyr (red). The last is compared to the observationally inferred SFR profile of the Milky Way (dotted magenta curve), obtained as discussed in Appendix B. The data points concern extragalactic measurements, compiled by Krumholz et al. (2012) (see also Fig. B.2). The dotted line is |
| In the text | |
 |
Fig. 7 Top: model radial velocity dispersion at 2 Gyr (thin curve) and 12 Gyr (thick curve). Middle: probabilities of blurring. Bottom: probabilities of churning. In all panels our results (solid curves) are displayed for stars of home radius r = 5, 7.6 and 10 kpc, and for 2 Gyr (thin) and 12 Gyr (thick curves). The latter should be compared to the corresponding quantities reported in Schönrich & Binney (2009a) (dotted histograms). |
| In the text | |
 |
Fig. 8 Top: probabilities of stellar migration (blurring + churning) adopted in this work (see text); they are shown for three birth radii (4, 8 and 12 kpc) and for three snapshots (after 4, 8 and 12 Gyr). Middle: fractions of stars which are born in radii 4, 8 and 12 kpc and are found in galactocentric radius r in the end of the simulation, at T = 12 Gyr. Bottom: fractions of stars found at the end of the simulation in radii 4, 8 and 12 kpc according to their birth radius r. In all panels, radial bins are Δr = 0.5 kpc wide, as indicated by the bin width of the histograms and the size of the coloured boxes. |
| In the text | |
 |
Fig. 9 Average radius of origin of stars (top), average stellar age (middle) and star surface density profile (bottom), as a function of galactocentric radius. In all panels, the continuous (red) curve corresponds to the results of the model with radial migration (churning+blurring), while the dotted (blue) curve shows the results with no radial migration. In the top and middle panels, the shaded area contains the ±1σ values – containing ±34% of the stars – around the average. In the bottom panel, a best fit exponential with scalelength rd = 2 of the exponentially decreasing outwards. 25 kpc in the 3 to 13 kpc region and with Σ(r = 8 kpc) = 38 M⊙/pc2 is also displayed (green dashed line). |
| In the text | |
 |
Fig. 10 Solar neighbourhood: average birth radius (top), average [Fe/H] (middle) and average [O/Fe] of stars (bottom) as function of their age. In all panels, the dotted (blue) curves display the results for stars formed in situ and the solid (red) curves the results for all stars found at T = 12 Gyr in radius r = 8 ± 0.25 kpc. The shaded areas in all panels enclose ±1σ values around the corresponding averages. Data points are from the survey of Bensby et al. (2014). The dotted vertical line at 9 Gyr separates the thin from thick disk stars, according to the assumption made here (see Sect. 4.1). The symbol ⊙ denotes the position of the Sun in the corresponding panel, as well as in Figs. 11−13. |
| In the text | |
 |
Fig. 11 Solar annulus: top: fraction of all stars ever born in situ in the solar annnulus (blue dotted) and fraction of all stars found in the solar annulus at T = 12 Gyr (red solid) as a function of stellar age. Average [Fe/H] of stars (middle) and 1σ dispersion around the average (bottom) as function of stellar age, compared to observations. The solid (red) curve in the middle panel displays the results for all stars found at T = 12 Gyr in radius r = 8 ± 0.25 kpc. In both panels, the shaded (yellow) areas represent the ±1σ limits of the model; the brown (dotted) and green (dashed) curves represent the corresponding averages and ±1σ limits of the observations of Casagrande et al. (2011) and Bensby et al. (2014), respectively. The narrower blue shaded areain the bottom panel shows the results of a calculation with blurring alone. |
| In the text | |
 |
Fig. 12 Solar neighbourhood: average age of stars (top), average birth radius (middle) and number distribution of stars (metallicity distribution, bottom) as function of their metallicity. In all panels, the dotted (blue) curves display the results for stars formed in situ and the solid (red) curves the results for the average values of all stars found at T = 12 Gyr in radius r = 8 ± 0.250 kpc. The shaded areas in the top and middle panels enclose ±1σ values around the corresponding averages. The dashed histogram in the lower panel is calculated with the effect of epicycles only. |
| In the text | |
 |
Fig. 13 Solar annulus: top: metallicity distribution in the region of radius r = 8 ± 0.25 kpc, with the age ranges of the corresponding stellar populations. Bottom: metallicity distribution in the region of radius r = 8 ± 0.25 kpc, with the radial ranges of the birth radii of the corresponding stellar populations. |
| In the text | |
 |
Fig. 14 Solar annulus: top: [α/Fe] (left) and [O/Fe] (right) vs. metallicity, for all stars present today (solid brown curve) and for all stars born in situ (dotted blue curve). Middle: [α]/Fe (left) and [O/Fe] (right) vs. metallicity, for stars of the thick disk (>9 Gyr, green curve) and for stars of the thin disk (<9 Gyr, red curve). They are compared to corresponding data from Adibekyan et al. (2011; left) and from Bensby et al. (2014; right). In the top and middle panels the shaded areas enclose the ±1σ values around the corresponding model averages. The MD data for the thick disk of Bensby et al. (2014) are arbitrarily reduced by a factor of 3 (see text). |
| In the text | |
 |
Fig. 15 Thin vs. thick disk: left: stars plus stellar remnants; right: luminous stars only. Top: present-day stellar profiles: magenta: total; green: (thick disk); red: thin disk. In all curves, there is an attached best-fit exponential (dashed line of same colour) in the 5−11 kpc range, with scalelengths and column densities at R0 = 8 kpc as reported in Table 3. Bottom: cumulative fraction of the thin and thick disk masses with respect to the corresponding total disk mass Mdisk: Mthin( <r) /Mdisk (red curve) and Mthick( <r) /Mdisk (green curve) as a function of radius r. |
| In the text | |
 |
Fig. 16 Average composition of 4.5 Gyr old stars in the solar neighbourhood, elemental (top) and isotopic (bottom) compared to the observed solar composition. Most elements and isotopes are co-produced within a factor of two of their solar value. The corresponding values for the local ISM 4.5 Gyr ago are ~0.1−0.15 dex lower for all elements but H and He. No normalisation of the results is made here. |
| In the text | |
 |
Fig. 17 [X/Fe] vs. [Fe/H] for various intermediate mass elements in the solar neighbourhood: comparison of the average stellar abundances of the model to data of Adibekyan et al. (2013). The data are split into thick disk (green) and thin disk (red) according to the prescription of Adibekyan et al. (2013), in the middle panel of their Fig. 2. The model results are normalised such as the average abundance over all stars of age = 4.5 Gyr that are present today in the solar neighbourhood is solar (see text). |
| In the text | |
 |
Fig. 18 [X/Fe] vs. [Fe/H] for various intermediate mass elements in the solar neighbourhood: comparison of model to data of Bensby et al. (2014). The data are split into thick disk (green, P> 2) and thin disk (red, P< 0.5) according to the probabilities P given in Bensby et al. (2014). The model results are normalized so that the average abundance over all stars of age =4.5 Gyr that are present today in the solar neighbourhood is solar. |
| In the text | |
 |
Fig. A.1 Surface density profiles of atomic hydrogen HI (top), molecular hydrogen H2 (middle) and total gas ΣG = 1.4 (HI+H2) (bottom). Disk data (beyond 2 kpc) are from: Dame (1993), solid; Olling & Merrifield (2001), dotted ; and Nakanishi & Sofue (2003, 2006), dashed. The dot-dashed curve in the HI panel corresponds to data from Kalberla & Dedes (2008) and in the H2 panel to data from Pohl et al. (2008). Bulge data (inner 2 kpc) in all panels are from Ferrière (2001). |
| In the text | |
 |
Fig. A.2 Average profiles of the previous figure. Top: atomic and molecular hydrogen; middle: total gas ; bottom: fractions of gas (solid) and molecular gas (dashed). For the latter panel, an exponential stellar density profile with a scale-length of 2.3 kpc normalised to Σ∗(R = 8 kpc) = 38 M⊙/pc2 is adopted, while the molecular fraction is evaluated with the formalism of Appendix B. |
| In the text | |
 |
Fig. B.1 Top: observed surface density profiles of various SFR tracers (see text); the dotted curve – with no error bars – is the analytical form suggested by Green (2013) and it is here adopted as representative of the MW SFR profile. Middle: theoretical or empirical SF rates compared to the adopted profile of SFR tracers (the dotted curve from the upper panel); all profiles are normalised to the same value in R0 = 8 kpc. Bottom: ratio of the theoretical or empirical profiles to the adopted observed one. |
| In the text | |
 |
Fig. B.2 Top: SFR surface density vs. total gas surface density (left) and vs. H2 (right) for the MW disk, in the region between 2 and 13 kpc. In both panels, curves represent the same quantities as in Fig. B.1; the long dashed curve (SFR ∝ Σ(H2)) corresponds quantitatively to the fit of Bigiel et al. (2008) to extragalactic data and fits the adopted “observed” SFR profile in the MW disk quite well. Bottom: the “observed” SFR vs. gas relation in the MW is compared to a compilation of extragalactic data from Krumholz et al. (2012). |
| In the text | |
 |
Fig. B.3 Top: observed molecular fraction |
| In the text | |
 |
Fig. C.1 Top: stellar mass vs. lifetime. Middle: stellar death rate after an initial “burst” forming 1 M⊙ of stars: dN/ dt = dN/ dM × dM/ dt, where dN/ dM is the stellar IMF and dM/ dt the derivative of the curve in the top panel. The thick portion of the curve (up to ~35 My, corresponding to a star of 8 M⊙) is the rate of CCSN. The bottom right part of the middle panel displays the corresponding SNIa rate (the time delay distribution or TDD) adopted in this work (thick curve); it is a mixture of the Greggio (2005) formulation for the SD scenario up to 4.5 Gyr and an extrapolation ∝ t-1 after that time, in order to fit the data points from Maoz et al. (2012; filled circles) and from Maoz et al. (2010; squares). Bottom: time-integrated numbers of CCSN (thick portion of upper curve), single stars of mass M< 8M⊙ (thin portion of upper curve) and SNIa (lower curve), as a function of time, for an initial “burst” of 1 M⊙. |
| In the text | |
 |
Fig. C.2 Ejection rates of hydrogen, carbon, oxygen and Fe from a stellar population of 1 M⊙ as a function of time. Yields are from Nomoto et al. (2013).The curves represent different metallicities, as indicated in the top panel. The dotted curves show the contribution of SNIa (resulting from a SSP of 1 M⊙) to the production of those elements. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.