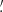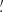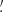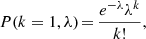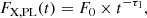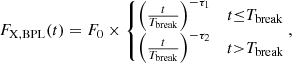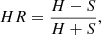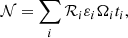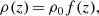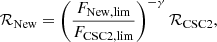| Issue |
A&A
Volume 663, July 2022
|
|
|---|---|---|
| Article Number | A168 | |
| Number of page(s) | 43 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202243047 | |
| Published online | 29 July 2022 | |
Extragalactic fast X-ray transient candidates discovered by Chandra (2000–2014)
1
Instituto de Astrofísica, Pontificia Universidad Católica de Chile, Casilla 306, Santiago 22, Chile
e-mail: jquirola@astro.puc.cl
2
Millennium Institute of Astrophysics (MAS), Nuncio Monseñor Sótero Sanz 100, Providencia, Santiago, Chile
3
Department of Astrophysics/IMAPP, Radboud University, PO Box 9010 6500 GL Nijmegen, The Netherlands
4
Space Science Institute, 4750 Walnut Street, Suite 205, Boulder, Colorado 80301, USA
5
SRON Netherlands Institute for Space Research, Niels Bohrweg 4, 2333 CA Leiden, The Netherlands
6
Department of Astronomy & Astrophysics, 525 Davey Laboratory, The Pennsylvania State University, University Park, PA 16802, USA
7
Institute for Gravitation and the Cosmos, The Pennsylvania State University, University Park, PA 16802, USA
8
Department of Physics, 104 Davey Laboratory, The Pennsylvania State University, University Park, PA 16802, USA
9
Texas A&M University, Physics and Astronomy, 4242 TAMU, College Station, TX 77843-4242, USA
10
George P. and Cynthia Woods Mitchell Institute for Fundamental Physics and Astronomy, Texas A&M University, College Station, TX 77843-4242, USA
11
Department of Physics, University of Warwick, Coventry CV4 7AL, UK
12
CAS Key Laboratory for Research in Galaxies and Cosmology, Department of Astronomy, University of Science and Technology of China, Hefei 230026, PR China
13
School of Astronomy and Space Science, University of Science and Technology of China, Hefei 230026, PR China
14
Leiden Observatory, Leiden University, PO Box 9513 2300 RA Leiden, The Netherlands
15
School of Astronomy and Space Science, Nanjing University, Nanjing, PR China
16
Key Laboratory of Modern Astronomy and Astrophysics (Nanjing University), Ministry of Education, Nanjing 210093, PR China
Received:
5
January
2022
Accepted:
11
April
2022
Context. Extragalactic fast X-ray transients (FXRTs) are short flashes of X-ray photons of unknown origin that last a few seconds to hours.
Aims. Our ignorance about their physical mechanisms and progenitor systems is due in part to the lack of clear multiwavelength counterparts in most cases, because FXRTs have only been identified serendipitously.
Methods. We develop a systematic search for FXRTs in the Chandra Source Catalog (Data Release 2.0; 169.6 Ms over 592.4 deg2, using only observations with |b|> 10° and before 2015), using a straightforward X-ray flare search algorithm and incorporating various multiwavelength constraints to rule out Galactic contamination and characterize the candidates.
Results. We report the detection of 14 FXRT candidates from a parent sample of 214 701 sources. Candidates have peak 0.5–7 keV fluxes between 1 × 10−13 and 2 × 10−10 erg cm−2 s−1 and T90 values from 4 to 48 ks. The sample can be subdivided into two groups: six “nearby” FXRTs that occurred within d ≲ 100 Mpc and eight “distant” FXRTs with likely redshifts ≳0.1. Three distant FXRT candidates exhibit light curves with a plateau (≈1–3 ks duration) followed by a power-law decay and X-ray spectral softening, similar to what was observed for the previously reported FXRT CDF-S XT2, a proposed magnetar-powered binary neutron star merger event. After applying completeness corrections, we calculate event rates for the nearby and distant samples of 53.7−15.1+22.6 and 28.2−6.9+9.8 deg−2 yr−1, respectively.
Conclusions. This novel sample of Chandra-detected extragalactic FXRT candidates, although modest in size, breaks new ground in terms of characterizing the diverse properties, nature, and possible progenitors of these enigmatic events.
Key words: X-rays: general / X-rays: bursts
© J. Quirola-Vásquez et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
The Chandra, Swift, and X-ray Multi-mirror Mission Newton (XMM-Newton) observatories have accumulated sensitive 0.5–7 keV imaging observations over the past two decades that cover a sizeable fraction of the sky despite their relatively narrow fields of view. This has enabled the serendipitous discovery and characterization of several novel faint extragalactic transients (e.g., Soderberg et al. 2008; Jonker et al. 2013; Glennie et al. 2015; Irwin et al. 2016; Bauer et al. 2017; Lin et al. 2018, 2019, 2020, 2021, 2022; Xue et al. 2019; Alp & Larsson 2020; Novara et al. 2020; Ide et al. 2020; Pastor-Marazuela et al. 2020; Sazonov et al. 2021). The high angular resolution afforded by these space observatories has been critical for associating counterparts1 (or lack thereof) and host galaxies with these transients, and hence elucidating their astrophysical nature.
In general, fast X-ray transients (FXRTs) produce short flashes of X-ray emission with durations from a few minutes to hours. Among the few extragalactic FXRTs that have been identified to date (mainly from systematic searches of serendipitous detections), in only one case, X-ray transient (XRT) 080109/SN 2008D (Mazzali et al. 2008; Soderberg et al. 2008; Modjaz et al. 2009)2, has it been possible to identify a multiwavelength counterpart after the initial detection. The most stringent limits come from deep optical Very Large Telescope imaging serendipitously acquired 80 min after the onset of XRT 141001 (mR > 25.7 AB mag; Bauer et al. 2017). Moreover, only a few FXRTs have had clear host-galaxy associations, and even fewer have firm distance constraints (e.g., Soderberg et al. 2008; Irwin et al. 2016; Bauer et al. 2017; Xue et al. 2019). Hence, it is not trivial to discern their energetics and distance scale or, by extension, their physical origin.
Several scenarios could explain the X-ray flares of extragalactic FXRTs, including the following four. First, in nearby galaxies, X-ray binaries (XRBs) – which includes ultra-luminous X-ray sources (ULXs) and quasi-periodic oscillations – soft gamma repeaters (SGRs), quasi-periodic eruptions, and anomalous X-ray pulsars (AXPs) are possible explanations of FXRTs with LX, peak ≲ 1042 erg s−1 (Colbert & Mushotzky 1999; Kaaret et al. 2006; Woods & Thompson 2006; Miniutti et al. 2019; and references therein).
A second scenario involves shock breakouts (SBOs; LX, peak ≈ 1042–1047 erg s−1) from a core-collapse supernova (CC-SN), whereby the X-ray emission is generated from the breakout of the supernova explosion shock once it crosses the surface of an evolved star (e.g., Soderberg et al. 2008; Nakar & Sari 2010; Waxman et al. 2017; Novara et al. 2020; Alp & Larsson 2020). Third are tidal disruption events (TDEs; LX, peak ≈ 1042–1050 erg s−1 considering jetted emission) that involve a white dwarf (WD) and an intermediate-mass black hole (IMBH), whereby X-rays are produced by the tidal disruption and subsequent accretion of the compact WD in the gravitational field of the IMBH (e.g., Jonker et al. 2013; Glennie et al. 2015). The fourth is mergers of binary neutron stars (BNSs; LX, peak ≈ 1047–1051 erg s−1 considering jetted emission; e.g., Dai et al. 2018; Jonker et al. 2013; Fong et al. 2015; Bauer et al. 2017; Xue et al. 2019), whereby the X-rays are created by the accretion of fallback material onto the remnant magnetar or black hole (BH).
It has been argued that some of these FXRTs can be related to either long or short gamma-ray bursts (LGRBs or SGRBs, respectively) observed off-axis (e.g., Jonker et al. 2013; Bauer et al. 2017; Xue et al. 2019; Alp & Larsson 2020). Zhang (2013) proposed a type of XRT associated with the merger product of a BNS, a rapidly spinning magnetar, where our line of sight is offset from the jet of an SGRB. Soon thereafter, Luo et al. (2014) and Zheng et al. (2017) identified two new unusual FXRTs in the 7 Ms Chandra Deep Field-South (CDF-S) data set, XRT 141001 and XRT 150321, denoted “CDF-S XT1” and “CDF-S XT2”. These two FXRTs were studied later in detail by Bauer et al. (2017) and Xue et al. (2019), respectively. In the case of CDF-S XT2, its multiwavelength constraints and host galaxy properties are consistent with the expected features of off-axis SGRBs (Xue et al. 2019), although other possibilities cannot be completely ruled out (e.g., a TDE origin; Peng et al. 2019). CDF-S XT2 is particularly intriguing because it exhibits a flat, extended X-ray light curve that suggests a magnetar wind origin (Sun et al. 2019; Xiao et al. 2019; Lü et al. 2019), similar to GRB 160821B (Troja et al. 2019) and others and in line with the aforementioned predictions of Zhang (2013). The X-ray afterglows of gamma-ray bursts (GRBs) also show similar plateaus in their light curves (e.g., Lyons et al. 2010; Rowlinson et al. 2013; Yi et al. 2014), suggestive of a central engine related to a magnetar wind or an accreting BH (Troja et al. 2007; Li et al. 2018).
On the other hand, CDF-S XT1 could be associated with a few possible scenarios: (i) an “orphan” X-ray afterglow from an off-axis SGRB with weak optical emission (Bauer et al. 2017; Sarin et al. 2021), (ii) a low-luminosity GRB at high redshift with no prompt gamma-ray emission below ∼20 keV rest frame (Bauer et al. 2017), or (iii) a highly beamed IMBH–WD TDE (Bauer et al. 2017; Peng et al. 2019). More recently, Sun et al. (2019) proposed a possible origin as a magnetar remnant of a neutron star merger, viewed at a larger off-axis angle than CDF-S XT2 and strongly obscured by ejecta material at early times. While none of these scenarios completely explain all observed properties, the large redshift uncertainty makes it difficult to discard them outright. Notably, the event rate of CDF-S XT1-like events is comparable to those of orphan and low-luminosity GRBs, as well as TDEs, implying an untapped regime for a known transient class or a new type of variable phenomenon (Bauer et al. 2017).
In order to understand if, and if so how, FXRTs, GRBs, and gravitational wave (GW) events (such as GW 170817; Abbott et al. 2017a; Nakar 2020; Margutti & Chornock 2021; Hajela et al. 2022) are related, we need to enlarge the sample of FXRTs. To this end, Yang et al. (2019) conducted a systematic search for CDF-S XT1- and CDF-S XT2-like objects in ∼19 Ms of Chandra blank-field survey data with good ancillary imaging. They constrained the event rate systematically but unfortunately found no new FXRTs. The discovery, confirmation, and characterization of more FXRTs and stricter limits on their number density can place valuable constraints on the unknown electromagnetic (EM) properties of several families of astronomical transients.
In this paper we extend the efforts of Yang et al. (2019) with a search of the entire Chandra Source Catalog 2.0 (CSC2; Evans et al. 2010), identifying 14 extragalactic FXRTs, of which at least three share similar properties to CDF-S XT2 and may be related with off-axis GRBs. We recover five events previously identified and classified as FXRTs by Jonker et al. (2013), Glennie et al. (2015), Bauer et al. (2017), and Lin et al. (2019, 2022).
This manuscript is organized as follows. We explain the methodology and selection criteria in Sect. 2. We present the results of the search and the cross-match with other catalogs in Sect. 2.6, a spectral and timing analysis of our final candidates in Sect. 3, and the properties of the identified potential host galaxies in Sect. 4. In Sect. 5 we discuss possible interpretations of some FXRTs and provide a comparison with other transients. We derive local and volumetric rates for the FXRTs in Sect. 6 and the expected number in current and future X-ray missions. Finally, we present final comments and conclusions in Sect. 7.
Throughout the paper, a concordance cosmology with parameters H0 = 70 km s−1 Mpc−1, ΩM = 0.30, and ΩΛ = 0.70 is adopted. All magnitudes are quoted in the AB system.
2. Methodology and sample selection
We describe below our search algorithm for FXRT candidates in individual Chandra exposures (Sect. 2.1), CSC2 data selection criteria (Sect. 2.2), light curve extraction methodology (Sect. 2.3), initial candidate results (Sect. 2.4) and additional criteria to filter non-transient and Galactic-stellar events to clean our sample (Sect. 2.5), respectively. Finally, we explore tentative related EM sources using different catalogs (Sect. 2.6).
2.1. Algorithm for transient-candidate selection
We adopt the algorithm presented in Yang et al. (2019, see their Sect. 2.1 for more details), with some modifications to extend it to larger instrumental off-axis angles (as related to the position of the detector aimpoint) and/or higher background levels, which we discuss below. This method depends on the total (Ntot) and background (Nbkg) counts of the event, working on an unbinned Chandra light curve (this is advantageous because it does not depend on how the light curve is built). Based on simulations, Yang et al. (2019) adopt an identification efficiency requirement [≳ 90% for events with log(Fpeak) > −12.6] located at < 8 0. They enforce this instrumental off-axis angle limit because Chandra’s detection sensitivity (as measured by, e.g., effective area and point-spread-function size) drops significantly beyond this limit (Vito et al. 2016; Yang et al. 2016).
0. They enforce this instrumental off-axis angle limit because Chandra’s detection sensitivity (as measured by, e.g., effective area and point-spread-function size) drops significantly beyond this limit (Vito et al. 2016; Yang et al. 2016).
The algorithm is split into two passes of the same light curve. Pass 1 calculates the total number of counts N1 and N2 in the two halves of the light curve at t = (ts, tm) and t = (tm, te) respectively, where ts and te are the start and end times of the Chandra exposure, respectively, while tm = (ts + te)/2 is the midpoint of the observation. The method selects a source in an observation as a transient candidate if it satisfies all of the following criteria: (i) Ntot is larger than the 5σ Poisson upper limit of Nbkg; (ii) N1 and N2 are statistically different at a > 4σ significance level; and (iii) N1 > 5 × N2 or N2 > 5 × N1.
Criterion (i) rules out faint sources with low signal-to-noise (S/N) and helps to avoid false detections caused by rare background flares. Criterion (ii) selects sources that have significantly different counts between the first-half and second-half exposures. This comparison is made via an E-test (Krishnamoorthy & Thomson 2004), which assesses whether N1 and N2 are drawn from the same Poisson distribution, factoring in statistical fluctuations. Both criteria (i) and (ii) are based on statistical significance, and they chose high S/N sources with significant variability. On the other hand, criterion (iii) permits events to be discarded, such as active galactic nuclei (AGNs) with a strong stochastic variability, requiring that the flux-variation amplitude be large.
The above sequence (Pass 1), however, will not efficiently select transients that occur around t ≈ tm, because N1 and N2 may have a similar number of counts. Thus, a second sequence (Pass 2) is used to account for transient events that occur near tm, whereby the number of counts 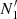 and
and 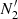 within windows around the edges and middle of the light curve are computed, respectively. Pass 2 identifies transient candidates in observations that satisfy all of the following criteria: (i) Ntot is larger than the 5σ Poisson upper limit of Nbkg; (ii)
within windows around the edges and middle of the light curve are computed, respectively. Pass 2 identifies transient candidates in observations that satisfy all of the following criteria: (i) Ntot is larger than the 5σ Poisson upper limit of Nbkg; (ii) 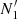 and
and 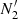 are statistically different at a > 4σ significance level; and (iii)
are statistically different at a > 4σ significance level; and (iii) 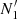 > 5×
> 5×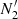 or
or 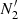 > 5×
> 5×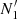 .
.
This algorithm depends strongly on the background event rate and the degradation of the Chandra point spread function (PSF) at high instrumental off-axis angles. To analyze the performance of the method, we simulate the detection probability (Pdet) of CDF-S XT1 and CDF-S XT2-like events at energies 0.5–7.0 keV as a function of the Chandra exposure time (Texp). We consider the following conditions with instrumental off-axis angles of 5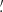 0/8
0/8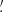 0/11
0/11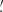 0: a fiducial light-curve model similar to CDF-S XT1 and CDF-S XT2 (identical to that used by Yang et al. 2019, see their Sect. 2.2.1), taking into account their timing and spectral properties (power-law with photon index of Γ = 1.7), a conversion between Fpeak and total net counts of Nnet ≈ 1.6 × 1014Fpeak cts, aperture background count rates of 5.6 × 10−5, 2.5 × 10−4, and 7.0 × 10−4 cts s−1 for 5
0: a fiducial light-curve model similar to CDF-S XT1 and CDF-S XT2 (identical to that used by Yang et al. 2019, see their Sect. 2.2.1), taking into account their timing and spectral properties (power-law with photon index of Γ = 1.7), a conversion between Fpeak and total net counts of Nnet ≈ 1.6 × 1014Fpeak cts, aperture background count rates of 5.6 × 10−5, 2.5 × 10−4, and 7.0 × 10−4 cts s−1 for 5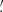 0, 8
0, 8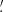 0 and 11
0 and 11 0, respectively, and log(Fpeak) from −13.0 to −12.6. The ratio of aperture background count rates at 5
0, respectively, and log(Fpeak) from −13.0 to −12.6. The ratio of aperture background count rates at 5 0, 8
0, 8 0 and 11
0 and 11 0 instrumental off-axis angles are ≈9.5, 42, and 119 times larger than at 0
0 instrumental off-axis angles are ≈9.5, 42, and 119 times larger than at 0 5, respectively, highlighting the importance of defining the algorithm’s effectiveness at different locations across Chandra’s field-of-view (FoV). For all simulations, we adopt as the background count rate the median value from the Chandra Deep Field North/South surveys (Xue et al. 2016; Luo et al. 2017; Yang et al. 2019).
5, respectively, highlighting the importance of defining the algorithm’s effectiveness at different locations across Chandra’s field-of-view (FoV). For all simulations, we adopt as the background count rate the median value from the Chandra Deep Field North/South surveys (Xue et al. 2016; Luo et al. 2017; Yang et al. 2019).
Figure 1, left panel, shows the detection probability Pdet as a function of Texp, assuming instrumental off-axis angles of 5 0 (solid lines, representative of ∼20th–30th percentile), 8
0 (solid lines, representative of ∼20th–30th percentile), 8 0 (dashed lines, representative of ∼50th-70th percentile), or 11
0 (dashed lines, representative of ∼50th-70th percentile), or 11 0 (dotted lines, representative of worst case ∼100th percentile). It is clear that Pdet decreases substantially for events at 8
0 (dotted lines, representative of worst case ∼100th percentile). It is clear that Pdet decreases substantially for events at 8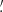 0 (by 20–50%) and 11
0 (by 20–50%) and 11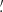 0 (by 50–100%) at log(Fpeak) ≲ − 12.7 (for reference log(Fpeak) ≲ − 12.7 equates to ≲ 32 counts for a CDF-S XT1-like event), especially at Texp ≳ 30 ks. Thus, candidates with large instrumental off-axis angles, which incur higher background levels, subsequently have worse flux sensitivity limits using this algorithm.
0 (by 50–100%) at log(Fpeak) ≲ − 12.7 (for reference log(Fpeak) ≲ − 12.7 equates to ≲ 32 counts for a CDF-S XT1-like event), especially at Texp ≳ 30 ks. Thus, candidates with large instrumental off-axis angles, which incur higher background levels, subsequently have worse flux sensitivity limits using this algorithm.
 |
Fig. 1. Detection probability (Pdet) as a function of the Chandra exposure time (Texp) for typical instrumental off-axis angles of 5 |
To mitigate this problem, we chop each light curve into segments of 20 ks (Twindow = 20 ks), and carry out Passes 1 and 2 separately on each window. This reduces the integrated number of background counts and thus enables identification of fainter events at larger instrumental off-axis angles. To maintain efficient selection of transients across the gaps between windows, we sequence through the entire light curve in three iterations: a forward division into 20 ks windows plus a remainder window, a backward division into 20 ks windows plus a remainder, and finally a forward division after a 10 ks shift into 20 ks windows plus a remainder window and the initial 10 ks window. As an example, for a 45 ks exposure, we divide it as follows: one iteration with windows of Texp = 20, 20, and 5 ks; another iteration with windows of Texp = 5, 20, and 20 ks, and a final iteration with windows of Texp = 10, 20, 15 ks. Then for each separate window of 0–20 ks duration, we apply Passes 1 and 2. This window time is well matched to the expected durations for CDF-S XT1 and CDF-S XT2, which have T90 of 5.0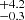 and 11.1
and 11.1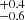 ks, respectively; here, T90 measures the time over which the event emits the central 90% (i.e., from 5% to 95%) of the total measured number of counts (Bauer et al. 2017; Xue et al. 2019). We explored how Pdet changes considering two other window sizes, Twindow = 10 and 25 ks. In the case of Texp = 10 ks, Pdet decreases by ≈30% at Texp = 10 ks, since the window size starts to become comparable to or smaller than the T90 values of the simulated light curves. For Twindow = 25 ks, Pdet does not change dramatically.
ks, respectively; here, T90 measures the time over which the event emits the central 90% (i.e., from 5% to 95%) of the total measured number of counts (Bauer et al. 2017; Xue et al. 2019). We explored how Pdet changes considering two other window sizes, Twindow = 10 and 25 ks. In the case of Texp = 10 ks, Pdet decreases by ≈30% at Texp = 10 ks, since the window size starts to become comparable to or smaller than the T90 values of the simulated light curves. For Twindow = 25 ks, Pdet does not change dramatically.
This additional modification to the algorithm of Yang et al. (2019, they only chopped observations with exposures longer than 50 ks) is crucial because it allows instrumental off-axis FXRTs to be detected to fainter flux limits and across Chandra’s entire FoV. Indeed, FXRTs previously published by Jonker et al. (2013) and Glennie et al. (2015) were identified at large instrumental off-axis angles (13 0). Figure 1, right panel, shows the detection probability Pdet considering Twindow = 20 ks (but otherwise the same conditions as in the previous simulations). The Pdet clearly improves by up to several tens of percent, especially for events fainter than log(Fpeak)≲ − 12.7 and Texp ≳ 20–30 ks. We note that Yang et al. (2019) adopted limits of log(Fpeak) ≳ − 12.6, instrumental off-axis angles ≲8
0). Figure 1, right panel, shows the detection probability Pdet considering Twindow = 20 ks (but otherwise the same conditions as in the previous simulations). The Pdet clearly improves by up to several tens of percent, especially for events fainter than log(Fpeak)≲ − 12.7 and Texp ≳ 20–30 ks. We note that Yang et al. (2019) adopted limits of log(Fpeak) ≳ − 12.6, instrumental off-axis angles ≲8 0, and Twindow ≤ 50 ks. With the above modification, we increase the chance to recover new FXRTs even at large instrumental off-axis (or high background levels), albeit at lower sensitivity and completeness thresholds.
0, and Twindow ≤ 50 ks. With the above modification, we increase the chance to recover new FXRTs even at large instrumental off-axis (or high background levels), albeit at lower sensitivity and completeness thresholds.
We confirmed that our algorithm detects FXRTs with different light-curve shapes such as XRT 110103 (where the flux-to-counts conversion factor for this transient is Nnet ≈ 3.2 × 1012Fpeak cts; Yang et al. 2019). For instance, those of CDF-S XT1 and CDF-S XT2, with main peak durations of ≈5–11 ks, are quite distinct from the events found by Jonker et al. (2013) and Glennie et al. (2015) with peak emission durations of only ≈0.1–0.2 ks. Importantly, our algorithm successfully recovered all these events, and thus is flexible enough to recognize FXRTs with different light-curve shapes. We stress that this is a key advantage compared to matched filter techniques that assume an underlying model profile.
In this work, the false rate of spurious detections is inherited from the CSC2, which serves as our input catalog. The CSC2 includes real X-ray sources detected with flux estimates that are at least 3 times their estimated 1σ uncertainties in at least one energy band (between 0.2–7.0 keV), while maintaining the number of spurious sources at a level of ≲1 false source per field for a 100 ks observation (Evans et al. 2010, 2019, 2020a). Although this number seems small, spurious events could be an important source of contamination, especially for events without a clear optical or near-infrared (NIR) association. To avoid this problem, we adopt a more restrictive 5σ cut, which should serve to remove all truly spurious sources (see above). Moreover, we make a final visual inspection to reject potential spurious FXRTs that appear “constant” and associated with known diffuse/extended sources, or vary in the same way that the background varies with time (see Sect. 2.5.5). To summarize, our strict cuts and visual review should produce a final sample that is largely free from spurious contamination.
2.2. Data selection
To extend previous efforts to search for FXRTs, we conducted a search through the CSC23 which provides uniformly extracted properties for 317 167 unique compact and extended X-ray sources (928 280 individual observation detections) identified in 10 382 Chandra Advanced CCD Imaging Spectrometer (ACIS) and High Resolution Camera (HRC-I) imaging observations released publicly through the end of 2014. The sensitivity limit for compact sources in CSC2 is ∼5 net counts (a factor of ≥2 better than the previous catalog release). For uniformity, we consider only ACIS observations in the energy range 0.5–7.0 keV, noting that HRC-I observations comprise only a few percent of the overall observations and have a poorer and softer response and limited energy resolution compared with the ACIS detectors.
The CSC2 database includes a wide variety of astrophysical objects, from galaxy clusters to stellar objects, although the CSC2 does not provide detailed source classifications. To this end, we apply the criteria explained in Sect. 2.1 to select FXRT candidates, while the criteria explained below (Sect. 2.5) are chosen in order to discard objects that are considered contamination to our search. Given the extragalactic nature of the FXRTs CDF-S XT1 and CDF-S XT2 and the high contamination rate from flaring stars (e.g., Yang et al. 2019 recovered CDF-S XT1/XT2 but otherwise only found stellar flares in 19 Ms of data), we limit our initial light-curve search to CSC2 sources with Galactic latitudes |b|> 10 deg. A secondary benefit of considering objects with |b|> 10 deg is that it helps to minimize the effects of Galactic extinction in characterizing the spectral properties of our candidates. From the previous search developed by Yang et al. (2019), the probability of detecting FXRTs such as CDF-S XT1 or CDF-S XT2 decreases dramatically in observations with exposure times < 8 ks (similar to our case, where Pdet ≲ 0.9 for events log(Fpeak)≲ − 12.7; see Fig. 1). Therefore, we exclude such short observations from further study in order to limit uncertainties associated with large completeness corrections when estimating the event rate (see Sect. 6). The above two criteria yield a sample of 214 701 X-ray sources detected within 5303 Chandra observations, equating to ≈169.6 Ms of exposure over ≈592.4 deg2; this is roughly nine times more than explored in Yang et al. (2019).
To facilitate our search, we use the full-field per-observation event files available from the CSC2 data products4 along with the detection properties provided in the CSC2 catalog (Evans et al. 2010). Figure 2 shows the cumulative and histogram distributions of the Chandra observations used in this work as a function of exposure time.
 |
Fig. 2. Histogram (red; left Y axis) and cumulative (black; right Y axis) distributions of the exposure time of the 5303 Chandra observations used in this work. The inset provides a zoomed-in view to show the high-exposure-time tail of the distribution. The vertical dashed blue line indicates the median exposure time (=32 ks) of the total sample. We adopt an exposure time of 8 ks as a lower bound due to the strongly decreasing probability of distinguishing FXRTs in short exposures. |
2.3. Generation of light curves
We began by downloading the Chandra full-field per-observation data products from the CSC2 for all CSC2-detected sources with |b|> 10 deg. These products are preprocessed following the standard methods developed by the CSC2 (Evans et al. 2010, 2019, 2020a). We use the astropy.io (Astropy Collaboration 2013, 2018) package to extract the photon information.
The event file of full-field observations contains photon event data stored as a table, with information such as photon arrival time, energy, position on the detector, sky coordinates, and observing conditions. One advantage of using Chandra over all other X-ray satellites currently in operation is the low average number of background counts, which enables a robust detection of transient candidates with as few as ≳10 total counts (at ≳99% confidence; e.g., Kraft et al. 1991), allowing searches for faint FXRTs potentially in the CSC2 catalog. To construct light curves, we extract the photon arrival times in the 0.5–7.0 keV range from each event file using an aperture of 1.5 × R90 (following the same process developed by Yang et al. 2019), where R90 is the radius encircling 90% of the X-ray counts, which is a function of instrumental off-axis (and depends on the photon energy; for more details, see Vito et al. 2016; Hickox & Markevitch 2006). We consider this aperture (1.5 × R90) because, based on simulations by Yang et al. (2019), it encircles ≳98% of X-ray counts regardless of instrumental off-axis angle. Meanwhile, we calculate Nbkg using an annulus with inner and outer aperture radii of 1.5 × R90 and 1.5 × R90+20 pixels, respectively. If the background region overlaps another nearby X-ray source, we mask the nearby source (with radius of 1.5 × R90), and do not include the masked area when estimating the background. To correct the source light curve for the effect that background photons would have, we weight Nbkg by the source-to-background area ratio.
The typical counts of our candidates imply that we are in the Poissonian statistical regime, and therefore we adopt the distribution proposed by Kraft et al. (1991) to compute the confidence intervals of the background subtracted light curves (we use the package astropy.stats from Astropy Collaboration 2018). Figure 3 shows example light curves (black circles) detected by our method, as well as light curves for CDF-S XT1 and CDF-S XT2 (red circles) following our extraction methodology.
 |
Fig. 3. X-ray light curves extracted as described in Sect. 2.3 and identified via our algorithm described in Sect. 2.1. The four light curves in black denote randomly selected sources from initial FXRTs found in the CSC2. For comparison, we show in red the FXRT sources CDF-S XT1 and CDF-S XT2. For visualization purposes, background-subtracted light curves are presented with either 1 ks or 2 ks bins with 1σ errors. In all cases, the vertical dashed gray line represents the end of the observation. |
2.4. Initial candidate results
To summarize, we apply the FXRT detection algorithm to the 0.5–7.0 keV light curves of 214,701 CSC2 sources outside of the Galactic plane (|b|> 10 deg, splitting up long exposures into sub-20 ks segments), resulting in 728 FXRT candidates. This sample has total net counts, instrumental off-axis angles and time-averaged fluxes spanning ≈6.5–42720 (mean value of 754), ≈0.3–20.5 (mean value of 4.4) arcmin, and FX ≈ 2.6 × 10−16–7.1 × 10−12 (mean value of 1.2 × 10−13) erg cm−2 s−1, respectively. As expected, our method selects FXRTs with a diverse range of light curve properties.
2.5. Initial purity criteria
It should be stressed that our search method does not guarantee a high-purity sample of real extragalactic FXRTs. Thus, we adopt some additional criteria based on archival X-ray data (prior and posterior X-ray detections of candidate FXRTs) and multiwavelength counterparts (e.g., bright stars) to help differentiate real extragalactic FXRTs from Galactic transients and variables among the 728 unique FXRT candidates. We explain and describe these additional criteria below. Table 1 summarizes the number and percentage, relative to the total, of events that pass criteria (column 5), as well as ignoring all previous steps (column 4). Figure 4 shows the steps to select/reject FXRTs taking into account our algorithm described in Sect. 2.1 and the additional criteria that we explain below Sects. 2.5.1–2.5.5. We discuss the completeness of our search and selection criteria in Sect. 2.5.6.
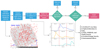 |
Fig. 4. Methodology flowchart considered in this work to find FXRT candidates. |
2.5.1. Criterion 1: Archival X-ray data
One important criterion to confirm the transient nature of the FXRT candidates is non-detection in prior and subsequent X-ray observations. We consider separately detections from: Chandra, based on other observations in the CSC2; XMM-Newton, based on individual observations of sources in the Serendipitous Source (4XMM-DR9; Rosen et al. 2016; Traulsen et al. 2019; Webb et al. 2020) and Slew Survey Source Catalogues (XMMSL2; Saxton et al. 2008); and Swift-XRT based on individual observations in the Swift-XRT Point Source (2SXPS) catalog (Evans et al. 2014). In all cases, we require that the FXRT candidate remain undetected (consistent with zero counts) at 3σ confidence in all observations outside of the one in which the FXRT candidate is found; we convert any detection or limit from the broadest original band to an equivalent 0.5–7.0 keV flux (using PIMMS) assuming a power-law (PL) with slope Γ = 2. This requirement helps to exclude a large number of Galactic flaring sources, but may exclude FXRTs that occur in AGNs or strongly star-forming galaxies. For instance, CDF-S XT1 has 105 additional Chandra observations from the 7 Ms CDF-S survey, and its detection is > 5σ higher than the limits from other observations and conforms with our adopted constraints.
The CSC2 provides uniform source extractions for all Chandra observations associated with each candidate, at least up to 2014. For 33 candidates, more recent archival observations also exist. We downloaded and manually extracted photometry for these cases, adopting consistent source and background regions and aperture corrections compared to those used for the CSC2. In total, 580 FXRT candidates were observed in multiple Chandra observation IDs, while 148 candidates have only a single Chandra visit (available in CSC2).
To recover possible XMM-Newton and Swift-XRT detections, we match to the 4XMM-DR9, XMMSL2 and 2SXPS catalogs, adopting a search radius equivalent to the 3σ combined positional errors of the Chandra detection and tentative XMM-Newton or Swift-XRT match.
We additionally search the X-ray upper limit servers FLIX5, 2SXPS6, and ULS7. The latter provides upper limits for many X-ray observatory archives (including XMM-Newton pointed observations and slew surveys; Swift pointed observations; Röntgen Satellite (ROSAT) pointed observations and all-sky survey; Einstein pointed observations), but does not necessarily use the same versions of the reduction pipeline as the first two and has somewhat different area coverage limits for the same observations. Based on visual inspections, we found that the reported detections are not always reliable, and hence we require detections to be ≥5σ. We found that: 397 candidates are observed with XMM-Newton 4XMM-DR9, with 206 candidates detected; 590 candidates are observed with XMM-Newton XMMSL2, with 6 candidates detected; 351 candidates are observed with Swift-XRT 2SXPS, with 31 candidates detected; 355 candidates are observed with ROSAT pointed observations, with zero candidates detected; 443 candidates are observed with Einstein pointed observations, with 1 candidate detected; finally all candidates are observed with the ROSAT All-Sky Survey, with 30 candidates detected. The upper limits from Chandra and XMM-Newton pointed observations are all comparable to or lower than our FXRT candidate peak fluxes, such that further similar transient behavior would have been detectable in such observations if present. The Swift-XRT, XMM-Newton-Slew, ROSAT, and Einstein limits are not nearly as constraining.
In total, 645 candidates have multiple hard (meaning Chandra, XMM-Newton, or Swift-XRT pointed observations) X-ray constraints, of which 580 candidates have been visited more than once by Chandra. This implies re-detected fractions of at least ≈80% among the candidate sample. On the other hand, 513 candidates have multiple soft (meaning ROSAT or Einstein pointed observations) X-ray constraints, of which 31 candidates have been detected more than once. The implied re-detection fractions are much lower, ≈4%, among the candidate sample, presumably due to the much shallower sensitivities of these past observatories. The high X-ray re-detection fraction indicates that this is a very effective criterion if additional Chandra, XMM-Newton or Swift observations are available. For the remaining 215 candidates that show no additional X-ray detections, we note that, in general, their X-ray constraints are much shallower than the detected sources, and thus we might expect a significant fraction to be persistent/recurrent if observed again for similar exposure times with Chandra or XMM-Newton.
Finally, 170 candidates pass this criterion (see Table 1). Also, it is important to mention that 72 candidates are discarded by this criterion but not by the others. The left panels of Fig. 5 show the net-count and flux distributions for the 170 events that pass this criterion. To conclude, this criterion appears to be an extremely effective means to identify persistent or repeat transients, when data are available.
 |
Fig. 5. Comparison of 0.5–7.0 keV net-count (top panels) and flux (bottom panels; 0.5–7.0 keV) distributions for the initial (filled blue histograms) and final (filled black histograms) samples, as well as subsets covered by various purity criteria (colored, unfilled histograms) for the sample. Net counts and fluxes are provided by the CSC2. |
2.5.2. Criterion 2: Optical detections in Gaia
As discussed in Yang et al. (2019), a large fraction of FXRT candidates are Galactic in origin, associated with relatively bright stellar sources. To identify these, we cross-match with the Gaia Early Data Release 3 (Gaia EDR3; Gaia Collaboration 2021) catalog, which contains relatively uniform photometric and astrometric constraints for more than 1.8 billion sources in the magnitude range G = 3–21 mag across the entire sky, based on observations collected during the first 34 months of its operational phase; these include parameters such as position, parallax, and proper motion in the Milky Way and throughout the Local Group (Lindegren et al. 2018; Gaia Collaboration 2018).
We employ the VizieR package (EDR3 catalog), adopting the CSC2 3σ positional uncertainty associated with each source as our search radius. In general, this search radius is sufficiently small to find a unique counterpart, given Chandra’s high spatial resolution and demonstrated astrometric precision (≈0 5; Rots & Budavári 2011); 26 candidates show multiple Gaia sources in their cone search area, for which we adopt the nearest Gaia source.
5; Rots & Budavári 2011); 26 candidates show multiple Gaia sources in their cone search area, for which we adopt the nearest Gaia source.
In total, 521 candidates have cross-matched sources in Gaia EDR3. However, we only reject candidates matched to stellar Gaia EDR3 optical detections (i.e., those with significant nonzero proper motion and/or parallax detected at > 3σ significance), which amounts to 454 candidates from the initial sample. These stellar counterparts span a wide range in magnitude G = 10–20.8 mag (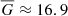 mag) and proper motion μ = [0.05 − 186] mas yr−1 (
mag) and proper motion μ = [0.05 − 186] mas yr−1 (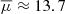 mas yr−1). To characterize better the X-ray sources classified as stars according to Criterion 2, we construct a color-magnitude diagram of their Panoramic Survey Telescope and Rapid Response System (Pan-STARRS) archive and Dark Energy Camera (DECam) counterparts (see Fig. B.1) and compare to theoretical isochrones taken from the MESA Isochrones & Stellar Tracks (MIST) package (Dotter 2016; Choi et al. 2016) with different metallicities (from [Fe/H] = −3.0 to +0.5), ages (log(Age/yr) = 7.0, 9.0, 10.0, and 10.3) and attenuation (AV = 0.0 and 5.0). The sample of X-ray sources classified as stars covers a wide range in the parameter space (see Fig. B.1), as expected for such an inhomogeneous sample of stars.
mas yr−1). To characterize better the X-ray sources classified as stars according to Criterion 2, we construct a color-magnitude diagram of their Panoramic Survey Telescope and Rapid Response System (Pan-STARRS) archive and Dark Energy Camera (DECam) counterparts (see Fig. B.1) and compare to theoretical isochrones taken from the MESA Isochrones & Stellar Tracks (MIST) package (Dotter 2016; Choi et al. 2016) with different metallicities (from [Fe/H] = −3.0 to +0.5), ages (log(Age/yr) = 7.0, 9.0, 10.0, and 10.3) and attenuation (AV = 0.0 and 5.0). The sample of X-ray sources classified as stars covers a wide range in the parameter space (see Fig. B.1), as expected for such an inhomogeneous sample of stars.
The central panels of Fig. 5 show the net-count and flux distributions of the 274 events that pass this criterion. Among the total sample, ≈65% are associated with bright stars, highlighting the importance of this cross-match. Moreover, this criterion discards 56 sources that the other criteria do not. Nevertheless, due to the relatively bright magnitude limit and optical window of the Gaia EDR3 objects with proper motion and parallax constraints, this criterion may not identify all persistent or recurring transient Galactic objects, as we discuss in the next subsection. As a running total, only 63 candidates successfully pass both this and the previous criterion (see Table 1).
2.5.3. Criterion 3: NED, SIMBAD, and VizieR Search
To identify further known Galactic and Local Group objects, we search for associated objects (counterparts or host galaxies) in several large databases using the astroquery package: the NASA/IPAC Extragalactic Database (NED; Helou et al. 1991), the Set of Identifications, Measurements, and Bibliography for Astronomical Data (SIMBAD; Wenger et al. 2000), and VizieR (which provides the most complete library of published astronomical catalogs; Ochsenbein et al. 2000). There is non-negligible redundancy here compared to the previous two searches, as these databases have ingested previous versions of X-ray serendipitous catalogs and Gaia EDR3 in the case of VizieR. To begin, we performed a cone search per candidate considering a radius equivalent to the 3σ positional error to find associated sources. These databases integrate many catalogs across the EM spectrum, helping rule out objects of our sample that were classified previously as stars, young stellar objects (YSOs), or objects associated with globular clusters, nebulae, or high-mass X-ray binaries (HMXBs) in either our Galaxy or the Local Group. However, we should stress that these catalogs are highly heterogeneous, and we must take care to not misinterpret candidate matches. Around 212 candidates have one or more entries in the various databases when cross-correlating to a region encompassing the 3σ uncertainty of the FXRT positions. In all the cases, the multiple entries had the same source classification. We uniquely identify 31 objects in this way, either as YSOs embedded in nebulae or stars identified by other catalogs, for instance, the VISTA Hemisphere Survey (VHS), the United Kingdom InfraRed Telescope (UKIRT) Infrared Deep Sky Survey, the Sloan Digital Sky Survey (SDSS), or the catalog sources from combined the Wide-field Infrared Survey Explorer (WISE) and the near-Earth objects WISE (NEOWISE) all-sky survey data at 3.4 and 4.6 μm (CatWISE) (McMahon et al. 2013; Dye et al. 2018; Marocco et al. 2021). This step is also critical because ≈78% of the initial sample show associated sources in these databases. The right panels of Fig. 5 show the net-count and flux distribution for the 203 events that pass this criterion. Applying all criteria thus far, the sample is reduced to 29 candidates.
2.5.4. Archival image search
In order to rule out fainter stellar counterparts, we carried out a search of ultraviolet (UV), optical, NIR, and mid-infrared (MIR) image archives; We perform a cone search within a radius equal to the 3σ uncertainty on the Chandra error position of the respective FXRTs (see Table 2) in the following archives: the Hubble Legacy Archive8; the Pan-STARRS archive (Flewelling et al. 2020)9; the National Science Foundation’s National Optical-Infrared Astronomy Research (NOIR) Astro Data Lab archive10, which includes images from the Dark Energy Survey (DES; Dark Energy Survey Collaboration 2016) and the Legacy Survey (DR8); the Gemini Observatory Archive11; the National Optical Astronomy Observatory (NOAO) science archive; the ESO archive science portal12 the VISTA Science Archive13 the Spitzer Enhanced Imaging Products archive (Teplitz et al. 2010)14; the UKIRT/Wide Field Camera (WFCAM) Science Archive15 and the WISE archive (Wright et al. 2010).
Properties of the extragalactic FXRT candidates detected and/or discussed in this work, ordered by subsample and date.
For images obtained under good seeing (< 1″) conditions, we visually search for counterparts or host galaxies in the 3σ uncertainty on the X-ray location of the FXRT (ensuring that the optical images are co-aligned to Gaia EDR3). We only undertake this step for the candidates that remain after the selection applied in Sect. 2.5.3. If a source is found, we quantify its significance and assess its extent and radial profile visually. We identify sources as stellar if they are consistent with the spatial resolution of the imaging. We reject nine candidates in this way: five sources are embedded in obvious Galactic nebulae with point-like NIR counterparts, and four candidates are identified as stars in Hubble Space Telescope (HST) images. The latter have no clear nearby galaxy associations, suggesting that they are likely field stars, perhaps the fainter tail of the population probed by Gaia DR3. This reduces the number of candidates to 20.
2.5.5. Instrumental effects
As a final step, we perform additional manual and visual cross-checks to rule out false positive candidates that might arise from background flares, bad pixels or columns, or cosmic-ray afterglows. Again, we only undertake this step for the remaining candidates after Sect. 2.5.4. To rule out events that occur during strong background flaring episodes (≳3σ mean value) in the energy range 0.5–7 keV, we employ the dmextract script (excluding counts associated with X-ray sources identified by CSC2 in the Chandra FoV) to investigate the evolution of the background count rate during the observations. Using the deflare script, we identify and reject six candidate FXRTs found in a circular region with radius 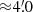 around the planetary nebula (PN) NGC 246 in the Chandra observation ID 2565 that are affected by background flares, reducing the number of candidates to 14. We confirm that none of the remaining 14 sources is caused by detector artifacts (bad columns or hot pixels) or are associated with bad quality flags (confused source and background regions or saturation) in the CSC2 catalog entries. Furthermore, we confirm that the counts from all sources are detected in (many) dozens to hundreds of individual pixels tracing out portions of Chandra’s Lissajous dither pattern (appearing as a sinusoidal-like evolution of x and y detector coordinates as a function of time; see Fig. A.2) over their duration, which reinforces that they are real astrophysical sources. Therefore, we have a final sample of 14 FXRTs.
around the planetary nebula (PN) NGC 246 in the Chandra observation ID 2565 that are affected by background flares, reducing the number of candidates to 14. We confirm that none of the remaining 14 sources is caused by detector artifacts (bad columns or hot pixels) or are associated with bad quality flags (confused source and background regions or saturation) in the CSC2 catalog entries. Furthermore, we confirm that the counts from all sources are detected in (many) dozens to hundreds of individual pixels tracing out portions of Chandra’s Lissajous dither pattern (appearing as a sinusoidal-like evolution of x and y detector coordinates as a function of time; see Fig. A.2) over their duration, which reinforces that they are real astrophysical sources. Therefore, we have a final sample of 14 FXRTs.
2.5.6. Completeness
Below, we explore the probability that real FXRTs might have been discarded erroneously. To estimate this, we determine the likelihood that the position of a candidate FXRT overlaps, by chance, that of another X-ray source and/or star. The probability (assuming Poisson statistics; P(k, λ)) of one source (k = 1) being found by chance inside the 3σ localization uncertainty region of another is
where λ is the source density of X-ray sources and/or stars on the sky multiplied by the 3σChandra localization uncertainty area. To measure the X-ray or optical source density, we consider X-ray detections from the CSC2, 4XMM-DR9 and 2SXPS catalogs (Evans et al. 2010, 2014; Webb et al. 2020), and the Gaia EDR3 catalog for stars (Gaia Collaboration 2021), respectively. This probability is 0.0091 and 0.0071 for X-ray and optical sources, respectively. Taking the 72 and 56 X-ray sources that are discarded solely on the basis of Criteria 1 or 2 (see Table 1), respectively, we expect ≪1 of these to be discarded erroneously. If we consider the 665 X-ray sources discarded by both Criteria 1 and 2, the combined probability is 6.5 × 10−5, and thus the expected number of erroneously dismissed sources is also ≪1. The contribution of Criterion 3 to the completeness is not easy to assess, given the highly distributed nature of the databases. Based on the high fraction of discarded sources that overlap with the other criteria, we assume that the databases used in Criterion 3 are accurate and this criteria does not disproportionately discard real FXRTs (i.e., also ≪1). To summarize, our rejection of contaminating sources does not appear to impact the completeness of our FXRT candidate sample.
2.5.7. Summary
We discover 14 FXRT candidates in the CSC2, five of which had been discovered previously as FXRTs while an additional six had been detected in published works but not properly characterized (see Sect. 2.6 for more details).
Table 2 provides the coordinates, instrumental off-axis angle, flux, positional uncertainty, hardness ratio (HR; computed following Park et al. 2006), and S/N. Figure 6 shows the background-subtracted 0.5–7.0 keV light curves of our final sample of FXRT candidates: short-term, in units of counts (first column) and count rates (second column); long-term in units of counts for Chandra only (third column) and flux to compare uniformly Chandra, XMM-Newton and Swift-XRT data (fourth column). We highlight that the three criteria (X-ray archival data, Gaia detection cross-match, and NED/SIMBAD/VizieR catalogs, respectively) contribute in complementary ways to clean the sample. We stress that the sample may still contain contamination from faint and/or extremely red Galactic objects, which we address below.
 |
Fig. 6. 0.5–7 keV light curves for each FXRT candidate: full exposure, in units of counts (first column 1); zoomed-in view, from the detection of the first photon to the end of the exposure, in units of count rate (cts s−1), with log-log scaling and five counts per bin (second column); long-term light curve, with each point representing individual Chandra exposures (cyan circles with 1σ error bars) to highlight the significance of detections and non-detections, in units of counts (third column); long-term light curve, with each point representing individual Chandra (cyan), XMM-Newton (red), and Swift-XRT (green) exposures in units of flux (erg s−1 cm−2) (fourth column). For the long-term light curves, the observation that includes the transient is denoted by a large blue star (1σ error bars), while triangles denote observations with (3σ) upper limits. All the fluxes are reported in the 0.5–7 keV band in the observer’s frame. In the case of FXRT 4 in Col. 4, additional data points are partially blocked by the blue star. |
 |
Fig. 6. continued. |
We designate each candidate by “XRT” followed by the date (the first two numbers correspond to the year, the second two numbers to the month, and the last two numbers to the day; see Table 2, second column). However, to identify each event quickly throughout this manuscript we also denominate them by “FXRT”+# (ordered by subsample and date; see Table 2, first column). Furthermore, from the final 14 events, 3 of them (FXRT 2, FXRT 4, and FXRT 5) were classified previously as HMXBs in galaxies at ≳4 Mpc. Nevertheless, we keep them to be consistent with the selection criteria of this work (see Sect. 2.6.1 for more details).
We note that FXRTs CDF-S XT2 (XRT 150321; Xue et al. 2019), XRT 170831 (Lin et al. 2019, 2022), and XRT 210423 (Lin et al. 2021) are not part of this work because CSC2 only includes data released publicly up to the end of 2014.
2.6. Fainter electromagnetic detections
Having ruled out obvious Galactic and spurious transients, we now focus on a detailed multiwavelength assessment of each remaining candidate using a variety of archival multiwavelength data, in order to try to understand their origin. In Sects. 2.6.1–2.6.3, we describe a search counterparts or host galaxies, from radio to gamma rays, of our final sample. To confirm that the final FXRT sample is consistent with real transient objects, in the next section we explain a cross-match with other catalogs.
2.6.1. Ultraviolet, optical, and near-infrared sources
To search for possible UV, optical, NIR and MIR detections of a counterpart or host of each of the FXRTs, we perform a cone search within a radius equivalent to the 3σChandra error position (see Table 2) in the following catalogs: GALEX Data Release 5 (GR5; Bianchi et al. 2011), Pan-STARRS Data Release 2 (Pan-STARRS–DR2; Flewelling 2018), the DES Data Release 2 (DES–DR2; Abbott et al. 2021a), the SDSS Data Release 16 (SDSS–DR16; Ahumada et al. 2020), the NOAO Source Catalog Data Release 2 (NSC–DR2; Nidever et al. 2021), the Hubble Source Catalog version 3 (HSCv3; Whitmore et al. 2016), the UKIRT InfraRed Deep Sky Survey Data Release 11+(UKIDSS–DR11+; Warren et al. 2007), the UKIRT Hemisphere Survey Data Release 1 (UHS–DR1; Dye et al. 2018), the Two Micron All Sky Survey (2MASS; Skrutskie et al. 2006), the VHS band-merged multi-waveband catalogs Data Release 5 (DR5; McMahon et al. 2013), the Spitzer Enhanced Imaging Products Source List (Teplitz et al. 2010), and the unWide-field Infrared Survey Explorer catalog (unWISE; Schlafly et al. 2019), as well as the ESO Catalogue Facility and the NED (Helou et al. 1991), SIMBAD (Wenger et al. 2000), and VizieR (Ochsenbein et al. 2000) databases. We supplement this with any large extended sources found during our archival image analysis in Sect. 2.5.4. We assume that uncertainties in the UV through MIR positions contribute negligibly to the overall error budget. Figure 7 shows images of the FXRTs (one per row) from Pan-STARRS, DECam, or HST in the optical (1st–4th columns, using g, r, i and z or the corresponding HST filters), VISTA, UKIRT or 2MASS in the NIR (5th and 6th columns, using J, H or K filters), unWISE in the MIR (7th column, in the 3.6μm) band, and the Chandra-ACIS image (8th column, in the 0.5–7.0 keV band).
 |
Fig. 7. Archival optical, NIR, MIR, and X-ray images of extragalactic FXRT candidates; the telescope or instrument plus filter and FXRT ID name are shown in the upper-left and upper-right corners, respectively. Each cutout is centered on the X-ray position, and red circles denote 3σChandra errors in the source localization. Columns 1–4: optical band (DECam, Pan-STARRS, and HST) images. Columns 5 and 6: NIR J or H and K (UKIRT or VISTA) images. Column 7: 3.4μm (unWISE) images. Column 8: X-ray Chandra (ACIS) 0.5–7 keV images. |
 |
Fig. 7. continued. |
We find clear optical/NIR/MIR extended sources in the above catalogs for two FXRT candidates: FXRT 8 and FXRT 9. In the case of FXRT 13 there is a faint point source inside the 2σ localization uncertainty, but only in the i band (see Fig. 7). A further six FXRT candidates lie in the immediate vicinity of large, nearby galaxies: FXRT 1, FXRT 2, FXRT 3, FXRT 4, FXRT 5, and FXRT 6. For FXRT 2, FXRT 3, FXRT 4, and FXRT 5, it was possible to identify potential counterparts. This leaves four FXRT candidates (FXRT 7, FXRT 10, FXRT 11, and FXRT 12) where we could only derive upper limits to the presence of a host or counterpart in moderate-depth imaging; typical limits we derive are mr > 23.7 and mz > 22.4 AB mag. We note that the fields of FXRT 1 and FXRT 14 have been observed by Jonker et al. (2013) and Bauer et al. (2017), respectively. In Table 3 we list the position, angular offset, and magnitudes of the candidate optical/NIR counterparts or host galaxies when available, and upper limits when not. We briefly describe the counterpart or host galaxy constraints for each FXRT below.
Host and/or counterpart’s photometric data or upper limits of FXRT candidates.
FXRT 1/XRT 000519 (identified previously by Jonker et al. 2013) is located in the outskirts of the galaxy M86 (mR = 8.6 AB mag; ≈17 Mpc) in the Virgo cluster, at an angular (projected) distance of 12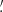 2 (≈60 kpc). This association is still under debate; the Poisson probability of a chance alignment is 3.6 × 10−4 based on its angular offset and the space density of mR < 9 mag galaxies (using the GLADE catalog; Dálya et al. 2018), implying a possible association; however, the binomial probability that this FXRT is a background source is ≈0.3, indicating that the association with M86 is weak (see Sect. 3.5 for more details). The transient was previously reported by Jonker et al. (2013) to have two tentative counterparts with mi = 24.3 AB mag (with an offset of 0
2 (≈60 kpc). This association is still under debate; the Poisson probability of a chance alignment is 3.6 × 10−4 based on its angular offset and the space density of mR < 9 mag galaxies (using the GLADE catalog; Dálya et al. 2018), implying a possible association; however, the binomial probability that this FXRT is a background source is ≈0.3, indicating that the association with M86 is weak (see Sect. 3.5 for more details). The transient was previously reported by Jonker et al. (2013) to have two tentative counterparts with mi = 24.3 AB mag (with an offset of 0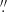 8) and mg = 26.8 AB mag (with an offset of 1
8) and mg = 26.8 AB mag (with an offset of 1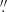 2) in deeper images taken by the Isaac Newton Telescope (INT) and the Canada France Hawaii Telescope (CFHT), respectively (Jonker et al. 2013).
2) in deeper images taken by the Isaac Newton Telescope (INT) and the Canada France Hawaii Telescope (CFHT), respectively (Jonker et al. 2013).
FXRT 2/XRT 010908 (cataloged as an X-ray source by Wang et al. 2016; Liu 2011; and Mineo et al. 2012, although never classified as an FXRT), a local FXRT, is located in the disk of the edge-on SB(s)cd galaxy M108 (also known as NGC 3556; mR≈ 9.2 AB mag and ≈ 9.0 Mpc; Dálya et al. 2018; Tully et al. 2013), at an angular (projected) distance of 0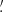 4 (≈1.1 kpc). The probability of a chance alignment is 3.2 × 10−6 based on its angular offset and the space density of mR < 9.2 AB mag galaxies (using the GLADE catalog; Dálya et al. 2018), thus implying a highly probable association; the binomial probability that this FXRT is a background source is ≈8.4 × 10−7, reinforcing an association with M108 (see Sect. 3.5 for more details). FXRT 2 appears to lie at the edge and intersection of two extended star-forming regions (see Fig. 7, sources #1 and #2 in the northeast and southwest directions, respectively), with several potential, unresolved, optical/NIR candidate counterparts in the HST F606W image inside the Chandra 3σ error circle. The estimated magnitudes of sources #1 and #2 are mF606W = 18.4 and 18.2 AB mag (i.e., MF606W ≳ −11.4 and −11.6 AB mag), respectively (taken from the HSCv3; Whitmore et al. 2016). As such, FXRT 2 is likely associated with a region of enhanced high-mass star formation.
4 (≈1.1 kpc). The probability of a chance alignment is 3.2 × 10−6 based on its angular offset and the space density of mR < 9.2 AB mag galaxies (using the GLADE catalog; Dálya et al. 2018), thus implying a highly probable association; the binomial probability that this FXRT is a background source is ≈8.4 × 10−7, reinforcing an association with M108 (see Sect. 3.5 for more details). FXRT 2 appears to lie at the edge and intersection of two extended star-forming regions (see Fig. 7, sources #1 and #2 in the northeast and southwest directions, respectively), with several potential, unresolved, optical/NIR candidate counterparts in the HST F606W image inside the Chandra 3σ error circle. The estimated magnitudes of sources #1 and #2 are mF606W = 18.4 and 18.2 AB mag (i.e., MF606W ≳ −11.4 and −11.6 AB mag), respectively (taken from the HSCv3; Whitmore et al. 2016). As such, FXRT 2 is likely associated with a region of enhanced high-mass star formation.
FXRT 3/XRT 070530 (cataloged as an X-ray source by Liu 2011 and Wang et al. 2016, although never classified as an FXRT) is located in the S0 peculiar galaxy NGC 5128 (Cen A; mR ≈ 6.3 AB mag; ≈3.1 Mpc), at an angular (projected) distance of 5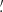 5 (≈5.0 kpc). The probability of this association occurring by chance is 1.3 × 10−5 based on the FXRT–galaxy offset and the space density of mR < 12 AB mag galaxies, thus implying a highly probable association; the binomial probability that this FXRT is a background source is ≈1.7 × 10−2, reinforcing an association with NGC 5128 (see Sect. 3.5 for more details). There are several dozen possible faint counterpart candidates within the 3σ X-ray error region in the HST F606W and F814W images (typically mF606W and mF814W ≳ 25 AB mag; see Fig. 7), of which one very red object stands out near the center (source #1 in Fig. 7) with mF606W = 25.4 and mF814W = 22.1 AB mag (MF606W = −2.1 and MF814W = −5.4 AB mag, respectively; taken from the HSCv3; Whitmore et al. 2016) or from DECam mz = 22.3 and my = 21.7 AB mag (Mz = −5.2 and My = −5.7 AB mag), which might be typical of either a small globular cluster or a red supergiant star. Based on the lack of young stars in the local host environment, we associate FXRT 3 with the former.
5 (≈5.0 kpc). The probability of this association occurring by chance is 1.3 × 10−5 based on the FXRT–galaxy offset and the space density of mR < 12 AB mag galaxies, thus implying a highly probable association; the binomial probability that this FXRT is a background source is ≈1.7 × 10−2, reinforcing an association with NGC 5128 (see Sect. 3.5 for more details). There are several dozen possible faint counterpart candidates within the 3σ X-ray error region in the HST F606W and F814W images (typically mF606W and mF814W ≳ 25 AB mag; see Fig. 7), of which one very red object stands out near the center (source #1 in Fig. 7) with mF606W = 25.4 and mF814W = 22.1 AB mag (MF606W = −2.1 and MF814W = −5.4 AB mag, respectively; taken from the HSCv3; Whitmore et al. 2016) or from DECam mz = 22.3 and my = 21.7 AB mag (Mz = −5.2 and My = −5.7 AB mag), which might be typical of either a small globular cluster or a red supergiant star. Based on the lack of young stars in the local host environment, we associate FXRT 3 with the former.
FXRT 4/XRT 071203 (cataloged as an X-ray source by Mineo et al. 2012 and Wang et al. 2016, although never classified as an FXRT) is located in the SA(s)cd peculiar dwarf galaxy NGC 5474 (mR = 10.8 AB mag; ≈5.9 Mpc), at an angular (projected) distance of 0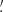 4 (≈0.7 kpc). NGC 5474 is a highly asymmetric late-type peculiar dwarf galaxy in the M101 group, thought to be interacting with M101. The probability of this occurring by chance is 1.9 × 10−6 based on its angular offset and the space density of mR < 10.8 AB mag galaxies, thus implying a highly probable association; the binomial probability that this FXRT is a background source is ≈9.9 × 10−4, reinforcing an association with NGC 5474 (see Sect. 3.5 for more details). The FXRT candidate appears to lie at the center of a resolved blue star cluster with a spatial extent of ≈40 pc, with ≈10 candidate unresolved optical/NIR counterparts in HST imaging inside the Chandra 3σ error circle (Fig. 7 shows the four most obvious optical and NIR counterparts). The majority of the candidate counterparts have blue colors, with brightness peaking in F275W and F606W with mF275W ≈ 21.6–23.0 and mF606W ≈ 22.2–22.9 AB mag (MF275W ≈ −5.9/−7.3 and MF606W ≈ −6.0/−6.7 AB mag, and hence consistent with O stars), while source #3 is redder, peaking between F814W and F160W, with mF606W ≈ 22.3 and mF814W ≈ 22.1 AB mag (MF606W ≈ −6.5 and MF814W ≈ −6.7 AB mag, respectively, typical of a massive red supergiant star). The photometric data are taken from the HSCv3 (Whitmore et al. 2016). As such, FXRT 4 is likely associated with a region of enhanced high-mass star formation.
4 (≈0.7 kpc). NGC 5474 is a highly asymmetric late-type peculiar dwarf galaxy in the M101 group, thought to be interacting with M101. The probability of this occurring by chance is 1.9 × 10−6 based on its angular offset and the space density of mR < 10.8 AB mag galaxies, thus implying a highly probable association; the binomial probability that this FXRT is a background source is ≈9.9 × 10−4, reinforcing an association with NGC 5474 (see Sect. 3.5 for more details). The FXRT candidate appears to lie at the center of a resolved blue star cluster with a spatial extent of ≈40 pc, with ≈10 candidate unresolved optical/NIR counterparts in HST imaging inside the Chandra 3σ error circle (Fig. 7 shows the four most obvious optical and NIR counterparts). The majority of the candidate counterparts have blue colors, with brightness peaking in F275W and F606W with mF275W ≈ 21.6–23.0 and mF606W ≈ 22.2–22.9 AB mag (MF275W ≈ −5.9/−7.3 and MF606W ≈ −6.0/−6.7 AB mag, and hence consistent with O stars), while source #3 is redder, peaking between F814W and F160W, with mF606W ≈ 22.3 and mF814W ≈ 22.1 AB mag (MF606W ≈ −6.5 and MF814W ≈ −6.7 AB mag, respectively, typical of a massive red supergiant star). The photometric data are taken from the HSCv3 (Whitmore et al. 2016). As such, FXRT 4 is likely associated with a region of enhanced high-mass star formation.
FXRT 5/XRT 080331 (cataloged as an X-ray source by Wang et al. 2016 and Sazonov & Khabibullin 2017, although never classified as an FXRT) is located in the disk of the SAB(s)b galaxy M66 (mr = 9.6 AB mag, ≈11 Mpc), at an angular (projected) distance of 1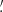 3 (≈4.3 kpc). M66 is a barred spiral galaxy in the Leo group. The probability of this occurring by chance is 2.8 × 10−6 based on its angular offset and the space density of mR < 9.6 AB mag galaxies, implying a highly probable association; the binomial probability that this FXRT is a background source is ≈3.9 × 10−3, reinforcing an association with M66 (see Sect. 3.5 for more details). The FXRT candidate error region is located in a high extinction region of the disk, at the edge of the bar, with very few optical counterpart candidates (≲10 sources). However, the X-ray centroid is notably well aligned with two knots of strong Hα emission (sources 1 and 2 in the HST/ACS-F658N image of Fig. 7) with m658N ≈ 21.0 AB mag (or M658N ≈ −9.2 AB mag). This suggests a link with a high-mass star formation region, while the 3σ error circle encompasses at least ten fainter, unresolved candidate counterparts in the F110W and F160W images (m160W ≳ 22.5 or M160W ≳ −7.7 AB mag).
3 (≈4.3 kpc). M66 is a barred spiral galaxy in the Leo group. The probability of this occurring by chance is 2.8 × 10−6 based on its angular offset and the space density of mR < 9.6 AB mag galaxies, implying a highly probable association; the binomial probability that this FXRT is a background source is ≈3.9 × 10−3, reinforcing an association with M66 (see Sect. 3.5 for more details). The FXRT candidate error region is located in a high extinction region of the disk, at the edge of the bar, with very few optical counterpart candidates (≲10 sources). However, the X-ray centroid is notably well aligned with two knots of strong Hα emission (sources 1 and 2 in the HST/ACS-F658N image of Fig. 7) with m658N ≈ 21.0 AB mag (or M658N ≈ −9.2 AB mag). This suggests a link with a high-mass star formation region, while the 3σ error circle encompasses at least ten fainter, unresolved candidate counterparts in the F110W and F160W images (m160W ≳ 22.5 or M160W ≳ −7.7 AB mag).
FXRT 6/XRT 130822 (cataloged as an X-ray source by Wang et al. 2016, although never classified as an FXRT) is situated in the outskirts of the galaxy NGC 7465 (mR = 12.0 AB mag; ≈27 Mpc), which is part of the merging NGC 7448 group, at an angular (projected) distance of 1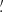 2 (9.4 kpc). The probability of this occurring by chance is 1.5 × 10−4 based on its offset and the space density of mR < 12 AB mag galaxies, thus implying a probable association; the binomial probability that this FXRT is a background source is ≈1.5 × 10−2, reinforcing an association with NGC 7465 (see Sect. 3.5 for more details). The FXRT position overlaps with a blue spiral arm and lies in between two diffuse blue candidate sources in DECam images (see Fig. 7, sources #1 and #2 in g- and r-band images). These have offsets of ≈1
2 (9.4 kpc). The probability of this occurring by chance is 1.5 × 10−4 based on its offset and the space density of mR < 12 AB mag galaxies, thus implying a probable association; the binomial probability that this FXRT is a background source is ≈1.5 × 10−2, reinforcing an association with NGC 7465 (see Sect. 3.5 for more details). The FXRT position overlaps with a blue spiral arm and lies in between two diffuse blue candidate sources in DECam images (see Fig. 7, sources #1 and #2 in g- and r-band images). These have offsets of ≈1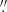 3 to the northwest and 1
3 to the northwest and 1 5 to the northeast, respectively, which lie just slightly outside of the 3σ X-ray error region, but their proximity suggests that FXRT 6 is likely associated with a region of high-mass star formation.
5 to the northeast, respectively, which lie just slightly outside of the 3σ X-ray error region, but their proximity suggests that FXRT 6 is likely associated with a region of high-mass star formation.
For FXRT 7/XRT 030511 (identified previously by Lin et al. 2019, 2022), no optical and NIR sources are detected within the 3σ X-ray error region of this event in the DECam, VISTA, or unWISE images (see Fig. 7). Upper limits are given in Table 3.
FXRT 8/XRT 041230 lies close to a mr ≈ 23.1 AB mag source, at an angular distance of 0 7, detected in DECam and VISTA images (see Fig. 7, source #1). The probability of a false match (adopting the formalism developed by Bloom et al. 2002) is P < 0.003 for such offsets from similar or brighter objects. We analyze the properties of this extended optical/NIR source in detail in Sect. 4.
7, detected in DECam and VISTA images (see Fig. 7, source #1). The probability of a false match (adopting the formalism developed by Bloom et al. 2002) is P < 0.003 for such offsets from similar or brighter objects. We analyze the properties of this extended optical/NIR source in detail in Sect. 4.
FXRT 9/XRT 080819 lies close to a mr ≈ 21.1 AB mag source, at an angular distance of 0 5, detected in DECam, VISTA, and unWISE images (see Fig. 7, source #1). The probability of a false match is P < 0.0004 for such offsets from similar or brighter objects. We analyze the properties of this extended optical/NIR source in detail in Sect. 4.
5, detected in DECam, VISTA, and unWISE images (see Fig. 7, source #1). The probability of a false match is P < 0.0004 for such offsets from similar or brighter objects. We analyze the properties of this extended optical/NIR source in detail in Sect. 4.
Regarding FXRT 10/XRT 100831, no optical/NIR sources are detected within the 3σ X-ray error region of this event in the DECam or 2MASS images; upper limits are given in Table 3. There is a moderately bright, marginal DECam object, at an angular distance of 2 6, just outside the 3σ error region to the northeast (see Fig. 7, source #1 in the i-band DECam image).
6, just outside the 3σ error region to the northeast (see Fig. 7, source #1 in the i-band DECam image).
Regarding FXRT 11/XRT 110103 (identified previously by Glennie et al. 2015), no optical/NIR sources are detected within the 3σ X-ray error region of this event in the DECam, Pan-STARRS, or VISTA imaging (see Fig. 7); upper limits are given in Table 3. This FXRT was discovered in an observation of the galaxy cluster Abell 3581 (at a distance of ≈94.9 Mpc; Johnstone et al. 2005; Glennie et al. 2015), where the nearest known member of the cluster, LEDA 760651 (mJ ≈ 16.7 AB mag), is 2 7 (≈71.4 kpc) from the Chandra transient position (Glennie et al. 2015). The probability of this occurring by chance is 0.15 based on its offset and the space density of mJ < 16.7 AB mag galaxies, thus implying a low probability of association; the binomial probability that this FXRT is a background source is ≈7.8 × 10−2, reinforcing an unlikely association with LEDA 760651 (see Sect. 3.5 for more details).
7 (≈71.4 kpc) from the Chandra transient position (Glennie et al. 2015). The probability of this occurring by chance is 0.15 based on its offset and the space density of mJ < 16.7 AB mag galaxies, thus implying a low probability of association; the binomial probability that this FXRT is a background source is ≈7.8 × 10−2, reinforcing an unlikely association with LEDA 760651 (see Sect. 3.5 for more details).
Regarding FXRT 12/XRT 110919 (identified previously by Lin et al. 2019, 2022), no significant optical and NIR sources are detected within the 3σ X-ray error region of this event in the DECam, VISTA or unWISE imaging (see Fig. 7) and catalogs, although we note that a marginal source (≲2σ) appears in red filters (DECam z-band and VISTA K-band); upper limits are given in Table 3.
FXRT 13/XRT 140327 lies close to a faint, mi ≈ 24.7 AB mag source (see Fig. 7, source #1), at an angular distance of 1 5, detected in DECam i-band and marginally visible in r-band imaging. The probability of a false match is P < 0.004 for such offsets from similar or brighter objects.
5, detected in DECam i-band and marginally visible in r-band imaging. The probability of a false match is P < 0.004 for such offsets from similar or brighter objects.
Finally, FXRT 14/XRT 141001/CDF-S XT1 (identified previously by Bauer et al. 2017) lies close to a faint (mR = 27.2 and mJ = 27.1 AB mag or MR ≈ − 19.0 and MJ ≈ −19.1 AB mag, respectively, assuming zpho = 2.23), extended (rKron = 0 56) optical and NIR source in HST imaging (see Fig. 7), with an angular offset of 0
56) optical and NIR source in HST imaging (see Fig. 7), with an angular offset of 0 13.
13.
Overall, we find that six of the 14 FXRT candidates (FXRT 1–6) have high probabilities of being associated with nearby galaxies (< 30 Mpc: FXRTs 2–5 show clear potential counterparts and FXRT 6 lies on top of faint optical emission, while FXRT 1 is still under consideration to be a distant event; Eappachen et al. 2022)16 Among the other eight candidates, three (FXRTs 8, 9, and 13) are coincident with moderately bright extended sources within the 3σ position error, FXRT 14/CDF-S XT1 is coincident with a faint extended source, and for three (FXRTs 7, 10, and 12) no optical or IR emission is detected to moderate-depth limits (mr ≲ 24.5 AB mag). In the case of FXRT 11, we do not discard its association with nearby galaxies completely (≈94.9 Mpc); however, a relation with a background source could be more likely. Finally, based on arguments given in Sect. 3.4, FXRTs 7, 10, 11, and 12 are highly likely to be extragalactic and have relatively distant and faint optical or NIR hosts similar to or fainter than CDF-S XT1.
2.6.2. Higher energy counterparts
To investigate if the sky locations of the FXRTs are covered by hard X-ray and γ-ray observations, we performed a cone search in the Swift-Burst Alert Telescope (Swift-BAT; Sakamoto et al. 2008), INTErnational Gamma-Ray Astrophysics Laboratory (INTEGRAL; Rau et al. 2005), High Energy Transient Explorer 2 (HETE-2; Hurley et al. 2011), InterPlanetary Network (Ajello et al. 2019), and Fermi (von Kienlin et al. 2014; Narayana Bhat et al. 2016) archives. We adopt a 10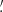 0 search radius for the INTEGRAL, Swift-BAT, HETE-2 and Interplanetary Network Gamma-Ray Bursts catalogs, while for the Gamma-ray Burst Monitor (GBM) and the Large Area Telescope (LAT) Fermi Burst catalogs we take a search radius of 4 deg (which represents typical source positional uncertainties at the ≈68% confidence level for those detectors; Connaughton et al. 2015). We find no hard X-ray or γ-ray counterparts associated with INTEGRAL, Swift-BAT, HETE-2, and Interplanetary Network catalogs. Some of the nearby (FXRTs 3, 4, and 6) and distant (FXRTs 7, 8, and 9) candidates have a potential gamma ray association in the GBM Fermi Burst catalog; however, we rule out their association for FXRTs 3, 4, 6, 7, and 8 because of a large difference in time between the FXRT and gamma-ray detection (≳4 years).
0 search radius for the INTEGRAL, Swift-BAT, HETE-2 and Interplanetary Network Gamma-Ray Bursts catalogs, while for the Gamma-ray Burst Monitor (GBM) and the Large Area Telescope (LAT) Fermi Burst catalogs we take a search radius of 4 deg (which represents typical source positional uncertainties at the ≈68% confidence level for those detectors; Connaughton et al. 2015). We find no hard X-ray or γ-ray counterparts associated with INTEGRAL, Swift-BAT, HETE-2, and Interplanetary Network catalogs. Some of the nearby (FXRTs 3, 4, and 6) and distant (FXRTs 7, 8, and 9) candidates have a potential gamma ray association in the GBM Fermi Burst catalog; however, we rule out their association for FXRTs 3, 4, 6, 7, and 8 because of a large difference in time between the FXRT and gamma-ray detection (≳4 years).
In the case of FXRT 9, it has a GBM Fermi GRB detection (called GRB 080812 at α = 11h46m48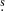 00, δ = −33°12′) seven days before the Chandra trigger, with an offset of ≈1.9 deg, positional uncertainty of 4.1 deg, and T90 ≈ 15 s (Narayana Bhat et al. 2016). In an on-axis scenario, the beamed X-ray emission should be detected effectively concurrently with the GRB; this is inconsistent with the observed light curve shown in Fig. 6. For an off-axis scenario, a delay between the gamma-ray trigger and its peak X-ray afterglow depends on both intrinsic (e.g., the off-axis angle and the deceleration timescale of the outflow) and extrinsic (e.g., the low densities density of the BNS environment and the observer location) properties (e.g., Granot et al. 2002, 2018a,b; Troja et al. 2020; Lamb et al. 2021), effectively spanning all timescales. Strong X-ray flares have been known to occur on top of X-ray afterglow emission, but these typically occur during the early phase of the afterglow (≲103–104 s; e.g., Yi et al. 2016). As such, an association between GRB 080812 and FXRT 9 seems unlikely.
00, δ = −33°12′) seven days before the Chandra trigger, with an offset of ≈1.9 deg, positional uncertainty of 4.1 deg, and T90 ≈ 15 s (Narayana Bhat et al. 2016). In an on-axis scenario, the beamed X-ray emission should be detected effectively concurrently with the GRB; this is inconsistent with the observed light curve shown in Fig. 6. For an off-axis scenario, a delay between the gamma-ray trigger and its peak X-ray afterglow depends on both intrinsic (e.g., the off-axis angle and the deceleration timescale of the outflow) and extrinsic (e.g., the low densities density of the BNS environment and the observer location) properties (e.g., Granot et al. 2002, 2018a,b; Troja et al. 2020; Lamb et al. 2021), effectively spanning all timescales. Strong X-ray flares have been known to occur on top of X-ray afterglow emission, but these typically occur during the early phase of the afterglow (≲103–104 s; e.g., Yi et al. 2016). As such, an association between GRB 080812 and FXRT 9 seems unlikely.
In summary, none of our FXRT candidates has an associated detection at hard X-ray or gamma-ray wavelengths.
2.6.3. Radio counterparts
To search for possible radio counterparts to our FXRT candidates, we utilize the RADIO–Master Radio Catalog, which is a periodically revised master catalog that contains selected parameters from a number of the HEASARC database tables that hold information on radio sources from 34 MHz to 857 GHz. This catalog contains inputs from several telescopes and surveys such as the Australia Telescope Compact Array, the Very Large Array, the Very Long Baseline Array, and the Wilkinson Microwave Anisotropy Probe. Given the relatively poor angular resolution of some of these radio telescopes, we perform an initial cone search for radio sources within 60″. Only FXRTs 2, 4, and 5, all of which are associated with hosts at ≲10 Mpc, have radio sources within 60″. Following this initial 60″ cut, we refine our search using limiting radii consistent with the combined radio + X-ray 3σ positional errors, which yields no matches. Due to their mutual association with nearby galaxies, we cannot rule out a chance association, as the radio emission could easily arise from other mechanisms within the host galaxies. Therefore, we conclude that none of the FXRTs is unambiguously detected at radio wavelengths.
3. Spatial, temporal, and X-ray spectral properties
We investigate the spatial distribution of the final sample of FXRT candidates in Sect. 3.1. Furthermore, the X-ray temporal and spectral properties can provide essential information about the origin and physical processes behind the FXRT candidates, and thus we describe these in Sects. 3.2 and 3.3, respectively. With these in hand, we revisit whether any of the remaining FXRT candidates could be Galactic stellar flares in Sect. 3.4. Finally, we explore the robustness of the existence of two populations of FXRTs in Sect. 3.5.
3.1. Spatial properties
If the FXRT candidates are extragalactic, and given the isotropy of the universe on large scales, we expect the FXRT spatial distribution to be randomly distributed on the sky (see Fig. 8). First, we investigate the sky distribution of all the Chandra observations considered in this work using the nonparametric Kolmogorov–Smirnov (K–S) test (Kolmogorov 1933; Massey 1951; Ishak 2017). We generate 5303 points (equal to the total number of observations in the CSC2 at |b|> 10 deg) randomly distributed (in Galactic coordinates), and we compare the generated random distributions and the real Chandra observations using a 2D K–S test following Peacock (1983) and Fasano & Franceschini (1987). We performed this process 10 000 times. As a result, we found that the null hypothesis 𝒩ℋ that the random sample and the real data come from the same distribution is rejected in ≈20% of the draws (rejection of 𝒩ℋ occurs when P < 0.05). This is not surprising, since the Chandra pointings are not completely random and some sky regions are observed much more often than others (e.g., Magellanic clouds, Chandra Deep Field South/North; Tananbaum et al. 2014; Wilkes & Tucker 2019).
 |
Fig. 8. Positions on the sky, in Galactic coordinates, of FXRT candidates. The initial 728 candidates are represented by blue triangles. The final sample of 14 extragalactic FXRT candidates from this work are denoted by large red stars. The 5303 Chandra observations used in this work are also shown (cyan squares). |
Next, we investigate whether the spatial distribution of the sample of FXRTs is random. Here we simulate 10 000 samples of 214 701 random sources (i.e., the number of X-ray sources analyzed in this work) distributed over the sky, taking as a prior distribution the CSC2 sky positions (which are functions of the pointings and exposures). Out of these 214 701 source we randomly select 14 sources, which we compare to the spatial distribution of the 14 FXRT candidates. We can reject the null hypothesis that these sources are drawn from the same (random) distribution only in ≈0.25% of the draws. Therefore, we conclude that the sample of 14 FXRT candidates are randomly distributed over the Chandra CSC2 observations of the sky.
3.2. Temporal properties
We characterize the X-ray light curves of the candidate FXRTs using single PL and broken power-law (BPL) models, and measure the break times and light-curve slopes. Both models describe the majority of the X-ray light curves well, although FXRTs 1, 4, 5, and 11 have more complex light curves and are not well described by these simple models. Nevertheless, in what follows we describe the most important results of these fits. The PL model is given by
where τ1 and F0 are the PL index and normalization, respectively. Moreover, the BPL model takes the form
where Tbreak, τ1, τ2, and F0 are the break time, the PL slope before and after the break, and normalization, respectively. The best-fit model parameters and statistics are given in Table 4, while the light curves (in flux units; light curves have five counts per bin, except FXRT 1, which has ten counts per bin) and best-fit models are shown in Fig. 9. We used the Bayesian information criterion (BIC)17 to determine which of the two models describes the data best.
 |
Fig. 9. Light curves, the evolution of the HR over time, and the best fitting models of the FXRT sample. Top panels: observed 0.5–7.0 keV X-ray light curves in cgs units (blue points), starting at T = 20 s. For FXRTs 1 and 11, we only show the main event. For ten FXRT candidates, we also plot the best-fit BPL or simple PL model (red solid lines), while for the remaining four FXRT candidates we do not because they are not well described by either model. The light curves contain five counts per bin (except that of FXRT 1, which has 20 counts per bin). Bottom panels: HR evolution (the soft and hard energy bands are 0.5–2.0 keV and 2.0–7.0 keV, respectively), following the Bayesian method of Park et al. (2006). The dashed red line denotes an HR equal to zero. For XRT 000519/FXRT 1 and XRT 110103/FXRT 11, we show close-ups of the main flare to highlight in more detail their spectral behavior. Here, T0 = 0 s is defined as the time when the count rate is 3σ higher than the Poisson background level. |
Best-fit parameters obtained using a broken power-law (BPL) and a power-law (PL) model fit to the X-ray light curves.
For events where the adopted model does not provide a statistically good fit (because of the complex light curve shape), we only explain their main characteristics. We define the light curve zero point (T = 0 s) as the time when the count rate is 3σ higher than the Poisson background level18. The light curves and the fits (where applicable) are shown in Fig. 9, while the model fit results are given in Table 4 for all the FXRTs. We briefly describe the timing properties for each candidate.
The light curve of FXRT 1/XRT 000519 exhibits a strong flare at ≈9.6 ks into the observation. It has some faint precursor emission (not shown in Fig. 9) during the ∼4 ks prior to the flare at flux levels of ≈2–5 × 10−13 erg cm−2 s−1, followed by a sudden increase (in ≈20 s) reaching a peak flux of ≈1.0 × 10−10 erg cm−2 s−1. Using a bin-width of 10 s, the main flare is resolved into two peaks, as was also reported by Jonker et al. (2013). From there, the flux decreases rapidly for ≈100 s, followed by a slow decline around ≲1–2 × 10−12 erg cm−2 s−1 for the next ≈15 ks (with an index of −0.3 ± 0.1; Jonker et al. 2013) until the end of the observation.
Based on the BIC, the light curve of FXRT 2/XRT 010908 is described better by a BPL model than by a PL model. The plateau phase has a duration and flux of Tbreak ≈ 6.0 ks and ≈5 × 10−14 erg cm−2 s−1, respectively, followed by a PL decay with an index of ≈ − 1.7.
The light curve of FXRT 3/XRT 070530 is well described by a BPL model, although the ΔBIC is only −2.3 with respect to the PL fit. Initially, the light curve increases slightly with an index of ≈0.1 until Tbreak ≈ 1.5 ks, reaching a flux of ≈2 × 10−14 erg cm−2 s−1. After Tbreak, the light curve decays slowly with a slope of ≈0.8.
The light curve of candidate FXRT 4/XRT 071203 shows three counts during the first ≈9–10 ks (equivalent to a flux of ≲2 × 10−15 erg cm−2 s−1), before its flux increases to ≈4 × 10−14 erg cm−2 s−1 around ≈20–24 ks, for a duration of ≈12–14 ks.
The light curve of FXRT 5/XRT 080331 shows multiple peaks. In the first ≈20 ks prior to the bright flares, the flux is around ≳2 × 10−15 erg cm−2 s−1. However, the main flares appear at ≈20 and 40 ks after the start of the Chandra observation, reaching fluxes of ≈(1–2) × 10−13 erg cm−2 s−1. Between both flares, there is a quiescent epoch where the flux diminishes by a factor of ≈7, with large errors, with respect to the main flares.
The light curve of FXRT 6/XRT 130822 is well described by a PL model with an index of ≈0.3, although at ≈10 ks into the event, a slight enhancement in flux beyond that expected for a PL decay occurs.
The light curve of FXRT 7/XRT 030511 is described well by a BPL model (ΔBIC = − 208.3). The flux duration of the plateau phase until the break is Tbreak ≈ 1.1 ks with a rough flux of ≈1 × 10−12 erg cm−2 s−1, followed by a PL decay with an index of ≈1.6.
The light curve of FXRT 8/XRT 041230 is described slightly better by a BPL than by a PL model (although ΔBIC = 2.2). The source flux is consistent with being constant at a value of ≈2 × 10−15 erg cm−2 s−1 for about ≈10 ks, then it rises.
The light curve of FXRT 9/XRT 080819 is relatively symmetric in time, and hence not perfectly described by a BPL model (ΔBIC = − 1.6), with a flux rising from ≲5 × 10−14 to ≈1 × 10−13 erg cm−2 s−1. After 10 ks into the observation, the flux decreases to ≈1 × 10−14 erg cm−2 s−1 with a PL index of ≈2.8 for ≈5 ks.
The light curve of FXRT 10/XRT 100831 is well fitted by a BPL model (ΔBIC = − 8.3), with a clear plateau and a subsequent PL decay. The plateau duration is Tbreak ≈ 2.7 ks, with a flux of ≈2 × 10−14 erg cm−2 s−1. The decay has an index of ≈1.9.
The light curve of FXRT 11/XRT 110103 is similar to that of FXRT 1/XRT 000519. The flux is ≲1 × 10−13 erg cm−2 s−1 until a sudden increase to a flux of ≈1–2 × 10−10 erg cm−2 s−1. The main burst lasts just a few hundred seconds (but without a double-peak structure as in FXRT 1/XRT 000519) followed by a slow PL decay over the remainder of the observation (Glennie et al. 2015).
The light curve of FXRT 12/XRT 110919 is well fitted by a BPL model, with a plateau phase duration of Tbreak ≈ 1.8 ks and flux of ≈2 × 10−13 erg cm−2 s−1. The decays follows a PL index of ≈1.9.
The light curve of FXRT 13/XRT 140327 is similar to that of FXRT 6/XRT 130822 (i.e., a PL describes the data well). The decay index is ≈0.2.
The light curve of FXRT 14/XRT 141001/CDF-S XT1 is well described by a BPL model, although there is no plateau phase. The flux rises rapidly until Tbreak ≈ 100–200 s., reaching a flux of ≈3 × 10−12 erg cm−2 s−1. The flux subsequently decreases following a PL slope of index ≈1.6 until T ≈ 20 ks, after which no counts are detected. These values agree at the 1σ confidence level with the values reported by Bauer et al. (2017).
In summary, the lights curves of two nearby (FXRTs 2 and 3) and four distant (FXRTs 7, 10, 12, 14/CDF-S XT1) extragalactic FXRTs are well described by BPL models, with mean PL indexes of 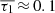 and
and 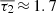 before and after the break, respectively. Among these, all except FXRT 14/CDF-S XT1 show a few ks plateau phase. On the other hand, FXRTs 8 and 9 are not well described by BPL (see Table 4). Meanwhile, the light curves of FXRTs 6 and 13 follow pure PL decays, with mean PL indexes of
before and after the break, respectively. Among these, all except FXRT 14/CDF-S XT1 show a few ks plateau phase. On the other hand, FXRTs 8 and 9 are not well described by BPL (see Table 4). Meanwhile, the light curves of FXRTs 6 and 13 follow pure PL decays, with mean PL indexes of 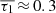 . The slow decay until the end of the Chandra observation after the main flare for FXRTs 1 and 11 (previously reported by Jonker et al. 2013 and Glennie et al. 2015, respectively) is not seen in any of the other candidate FXRTs. Finally, the light curve of FXRT 5 shows clear multiple flares, while weaker events like FXRTs 4 and 6 show marginal hints of multiple-flare structure.
. The slow decay until the end of the Chandra observation after the main flare for FXRTs 1 and 11 (previously reported by Jonker et al. 2013 and Glennie et al. 2015, respectively) is not seen in any of the other candidate FXRTs. Finally, the light curve of FXRT 5 shows clear multiple flares, while weaker events like FXRTs 4 and 6 show marginal hints of multiple-flare structure.
3.3. Spectral properties
In this section we describe the spectral properties of the sample of FXRT candidates using some basic models, as well as their HR and photon index evolution with time.
3.3.1. Spectral parameters
We generate X-ray spectra and response matrices following standard procedures for point-like sources using CIAO with the specextract script. The source and background regions are the same as those for generating the light curves (see Sect. 2.3). Due to the low number of counts per bin, we adopt maximum likelihood statistics for a Poisson distribution, the so-called Cash-statistics (C-stat, with C = − 2lnLPoisson + const; Cash 1979) to find the best-fit model. Although C-stat is not distributed like χ2, meaning that the standard goodness-of-fit is not applicable (Buchner et al. 2014; Kaastra 2017). Thus, to evaluate if there are differences in the goodness-of-fit between models, we use the Bayesian X-ray Astronomy (BXA) package (Buchner et al. 2014), which joins the Monte Carlo nested sampling algorithm MultiNest (Feroz et al. 2009) with the fitting environment of XSPEC (Arnaud 1996). BXA computes the integrals over parameter space, called the evidence (𝒵), which is maximized for the best-fit model. For BXA, we assume uniform model priors.
We consider three simple continuum models: (i) an absorbed PL model (phabs*zphabs*po, hereafter the PO model); (ii) an absorbed thermal Bremsstrahlung model (phabs*zphabs*bremss, hereafter the BR model); and (iii) an absorbed black-body model (phabs*zphabs*bb, hereafter the BB model). The PO model is typically thought to be produced by a nonthermal electron distribution, while the other two models have a thermal origin. We chose these models because we do not know the origin and the processes behind the spectral properties of FXRTs, while the limited numbers of counts do not warrant more complex models. The spectral components phabs and zphabs represent the Galactic and intrinsic contribution to the total absorption, respectively. The Galactic absorption (NH, Gal) was fixed at the values of Kalberla et al. (2005) and Kalberla & Haud (2015) during the fit, while for the intrinsic redshifted absorption, we adopt z = 0, which provides a strict lower bound.
The best fitting spectral models (and residuals) and their parameters are provided in Fig. 10 and Table 5, respectively, while Fig. 11 shows the histograms of the best-fit intrinsic neutral hydrogen column densities in addition to the Galactic value (NH; top panels) and photon index (Γ; bottom panels) for nearby (left panels) and distant (right panels) extragalactic FXRTs candidates. The NH covers ranges for nearby (distant) candidates of NH, PO = 0.3–8.1(1.1–9.4), NH, BR = 0.1–3.5(0.5–3.9), and NH, BB = 0.1–2.7(0.2–3.7) × 1021 cm−2, and mean values of 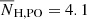 (4.2),
(4.2), 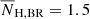 (1.4), and
(1.4), and 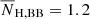 (1.2) × 1021 cm−2, respectively. Furthermore, we compare the best-fit NH, PO with the HI constraints from Kalberla et al. (2005) and Kalberla & Haud (2015) and note that in all cases aside from FXRT 1 and FXRT 3, the bulk of the measured NH, PO are higher than NH, Gal (a factor of ≈2–15 higher).
(1.2) × 1021 cm−2, respectively. Furthermore, we compare the best-fit NH, PO with the HI constraints from Kalberla et al. (2005) and Kalberla & Haud (2015) and note that in all cases aside from FXRT 1 and FXRT 3, the bulk of the measured NH, PO are higher than NH, Gal (a factor of ≈2–15 higher).
 |
Fig. 10. Observed time-integrated spectra fitted with different spectral models. Top panels: X-ray spectra (black dots; the data were grouped to at least one count per bin), in units of counts (cts s−1 keV−1). We also plot the best-fit PO (blue lines), BR (orange lines), and BB (green lines) spectral models; see Table 5 for the corresponding best fitting parameters. Bottom panels: residuals (defined as data-model normalized by the uncertainty; (D − M)/σ) of each spectral model. |
 |
Fig. 11. Distribution of best-fit X-ray parameters for nearby (left panels) and distant (right panels) FXRT candidates. Top panels: histogram of neutral hydrogen column densities, in units of cm−2, obtained using the PL, BR, and BB models. Bottom panels: histogram of the photon indices obtained using a PL model. |
Results of the 0.5–7 keV X-ray spectral fits for the CSC2 FXRT candidates.
The best-fit PL photon index ranges between Γ = 2.1–5.9 (1.9–3.7) for the nearby (distant) candidate FXRTs, with mean values of 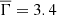 (2.7). According to Lin et al. (2012) (which classified sources detected by XMM-Newton), the photon index covers a wide range for different types of sources such as stars, AGNs or compact objects; however, only stars and compact objects have photon indices as high as Γ ∼ 6. For BR models, the best-fit temperatures range from kTBR = 1.1–36.2(4.1–39.0) keV for nearby (distant) candidates, while BB temperatures span kTBB = 0.2–0.8 (0.4–53.2) keV for nearby (distant) candidate FXRTs. The events with BR temperatures kTBR ≳ 10 keV are FXRTs 2, 4, 8, 9, 10, 13, and 14, while with BB temperatures kTBB ≳ 5 keV are FXRTs 8, and 10. Both temperatures (especially kTBB) are important to eventually analyze a possible association with SBOs (kTSBOs ≈ 0.03–3.0 keV, based on the progenitor star; Matzner & McKee 1999; Nakar & Sari 2010; Sapir et al. 2013).
(2.7). According to Lin et al. (2012) (which classified sources detected by XMM-Newton), the photon index covers a wide range for different types of sources such as stars, AGNs or compact objects; however, only stars and compact objects have photon indices as high as Γ ∼ 6. For BR models, the best-fit temperatures range from kTBR = 1.1–36.2(4.1–39.0) keV for nearby (distant) candidates, while BB temperatures span kTBB = 0.2–0.8 (0.4–53.2) keV for nearby (distant) candidate FXRTs. The events with BR temperatures kTBR ≳ 10 keV are FXRTs 2, 4, 8, 9, 10, 13, and 14, while with BB temperatures kTBB ≳ 5 keV are FXRTs 8, and 10. Both temperatures (especially kTBB) are important to eventually analyze a possible association with SBOs (kTSBOs ≈ 0.03–3.0 keV, based on the progenitor star; Matzner & McKee 1999; Nakar & Sari 2010; Sapir et al. 2013).
3.3.2. Hardness ratio and photon index evolution
The HR can be used to classify X-ray sources and study their spectral evolution, particularly when low number statistics prevail (e.g., Lin et al. 2012; Peretz & Behar 2018). Below, we investigate the HR for the population of FXRTs, compare these to candidates previously classified as “stars”, and look at the evolution of the HR and photon indices over the duration of the flare. The HR is defined as
where H and S are the number of X-ray photons in the soft and hard energy bands, defined as the 0.5–2.0 and 2.0–7.0 keV bands, respectively. For each candidate, we calculate the HR using the Bayesian code BEHR (Park et al. 2006), which we list in Table 2, column 13, and plot in Fig. 12 (top panel).
 |
Fig. 12. Photon index and HR distribution of our selected transient candidates. Top panel: HR of each FXRT candidate (using the Bayesian BEHR code; Park et al. 2006). Middle panel: HR distributions of our final samples of nearby (hashed black histogram) and distant (hashed orange histogram) FXRTs, compared to the XRTs classified as “stars” according to Criterion 2 using Gaia (filled cyan histogram). Bottom panel: photon indices for FXRT candidates where the light curve was best fit by a BPL model, before (filled circles) and after (open squares) the break time (Tbreak) taken from Table 4. In all cases, errors bars are at the 90% confidence level. |
Notably, Yang et al. (2019) found differences between stellar objects and the FXRT CDF-S XT1/XT2 (see their Fig. 5), where the latter has an average HR ≳ − 0.16. Taking into account the 472 objects identified as stars according to Criterion 2 in Sect. 2.5.2, we compare the HRs of these objects (see Fig. 12, middle panel, cyan histogram) to the final sample of nearby and distant FXRTs (black and orange histograms). Stars typically have very soft X-ray spectra (Güdel & Nazé 2009), with some notable exceptions like Be stars (e.g., Be star HD 110432 has an HR ≳ 0.0; Lopes de Oliveira et al. 2007). We find that the HR distribution of “star” candidates also strongly skews toward softer HRs, but demonstrates that stars associated with X-ray flares cover essentially all HRs, ranging from −0.99 to +0.97 (see Fig. 12, middle panel). Importantly, there is a smooth, non-negligible tail to harder values, with ≈20% of stars having HR ≳ 0.0 (possibly related to magnetic cataclysmic variables). Given this, we conclude that the X-ray HR is not a useful discriminator on its own.
Next, we analyze if, and if so how, the HR and PL index of the X-ray spectrum evolve with time. To start, we compute the HR for each bin of the light curves using the BEHR code of Park et al. (2006), which we show in the lower panels of Fig. 9. For light curves that are well fit by a BPL model, we additionally split the event files at Tbreak and extract “before” and “after” spectra to compute the spectral slopes (Γbefore and Γafter, respectively; see Table 6) using the best-fit PO model (see Table 5). We fit both intervals together assuming fixed constant NH, Gal and NH (taken from Table 5).
Spectral slope computed “before” and “after” the Tbreak.
The resulting evolution of the HRs and the PL spectral indices are shown in Figs. 9 and 12 (bottom panel), respectively. FXRTs 1 and 11 show significant early softening in their HR evolution (Figs. 9) during the ∼50 s following their main peaks (consistent with Glennie et al. 2015), while FXRTs 2, 7, and 12 show marginal (∼90% confidence) spectral softening after the plateau stage, like CDF-S XT2 trends, and FXRT 8 appears to soften marginally (∼90% confidence) throughout its light curve. None of the other FXRTs show any evidence of spectral evolution.
3.4. Galactic origin
FXRTs 2, 3, 4, 5, 6, 8, 9, and 14 can be associated with extended host galaxies, proving and/or strengthening their extragalactic origin (see Sect. 2.6 for more details). FXRTs 1 and 11 are located near the outskirts of M86 and Abell 3581 (Jonker et al. 2013; Glennie et al. 2015), respectively, which, while suggestive of an extragalactic nature, is not definitive. Below, we investigate whether some FXRTs could still be associated with Galactic M- or brown-dwarf flares.
Magnetically active dwarfs (which comprise around 30% of M dwarfs and 5% of brown dwarfs) are known to exhibit flares on timescales of minutes to hours, with flux increases (not only in X-ray) by one or two orders of magnitude (Schmitt & Liefke 2004; Mitra-Kraev et al. 2005; Berger 2006; Welsh et al. 2007). The coldest object observed to flare in X-rays is an L1 dwarf (De Luca et al. 2020). Flares can be classified in two groups according to a time–luminosity relation (following previous efforts by Bauer et al. 2017): (i) short “compact” flares (L ≲ 1030 erg s−1 and Δt ≲ 1 h), and (ii) “long” flares (L ≲ 1032 erg s−1 and Δt ≳ 1 h). The flaring episodes often occur recurrently on timescales from hours to years. The flares typically have thermal spectra with temperatures of kT = 0.5–1 keV. M-dwarf stars have optical and NIR absolute magnitudes in the range of Mz ∼ 8–13 mag (Hawley et al. 2002) and MKs ∼ 3–10 mag (Avenhaus et al. 2012), respectively, while brown dwarfs have Mz ∼ 13–18 mag (Hawley et al. 2002) and MJ ∼ 15–25 mag (Tinney et al. 2014), respectively. In the case of X-ray emission, M dwarfs show flares in the range of 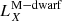 ≈ 1028–1032 erg s−1 (Pallavicini et al. 1990; Pandey & Singh 2008; Pye et al. 2015), while brown dwarf flares span
≈ 1028–1032 erg s−1 (Pallavicini et al. 1990; Pandey & Singh 2008; Pye et al. 2015), while brown dwarf flares span 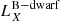 ≈ 1027–1030 erg s−1 (Berger 2006; Robrade et al. 2010). Furthermore, cold M dwarfs and L dwarfs typically exhibit ratios no larger than log(LX/Lbol) ≲ 0.0 and ≲ − 3.0 (the dwarf star flare saturation limit), respectively, where LX and Lbol are the X-ray flare and average (non-flare) bolometric luminosities, respectively (e.g., García-Alvarez et al. 2008; De Luca et al. 2020).
≈ 1027–1030 erg s−1 (Berger 2006; Robrade et al. 2010). Furthermore, cold M dwarfs and L dwarfs typically exhibit ratios no larger than log(LX/Lbol) ≲ 0.0 and ≲ − 3.0 (the dwarf star flare saturation limit), respectively, where LX and Lbol are the X-ray flare and average (non-flare) bolometric luminosities, respectively (e.g., García-Alvarez et al. 2008; De Luca et al. 2020).
Thus, it is possible to discard a stellar flare explanation for FXRTs using their optical and NIR detections and/or upper limits compared to the expected absolute magnitudes in these bands (see above), as well as the ratio log(LX/Lbol) = log(FX/Fbol) ≲ − 3.0 (García-Alvarez et al. 2008)19.
We derive a lower limit to the distance for each source using the expected z-band absolute magnitude ranges for M-dwarf and brown dwarf stellar flares listed above. We subsequently convert the X-ray flux to a lower limit on the luminosity using these distance limits. If this lower limit is above the maximum luminosity observed for M-dwarf and brown dwarf stellar flares, we rule out this explanation for the FXRT. In this way, we explore the possible Galactic origin of each FXRT without a clear extragalactic host.
For FXRT 1/XRT 000519, the deep detections mg = 26.8 and mi = 24.3 imply limits to the distance of putative M- and brown dwarfs responsible for the X-ray flares of 0.6–6.5 kpc and 0.06–0.7 kpc, respectively. The corresponding X-ray flare luminosities are 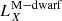 ∼ (8.7–880) × 1033 and
∼ (8.7–880) × 1033 and 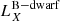 ∼ (8.8–876) × 1031 erg s−1, respectively, at least 1.5 dex higher than the known range. Furthermore, the ratio log(FX/Fbol) ≈ 2.7–3.2 is well above the known range. Thus, FXRT 1 is unlikely to be a stellar flare, consistent with the conclusions drawn in Jonker et al. (2013).
∼ (8.8–876) × 1031 erg s−1, respectively, at least 1.5 dex higher than the known range. Furthermore, the ratio log(FX/Fbol) ≈ 2.7–3.2 is well above the known range. Thus, FXRT 1 is unlikely to be a stellar flare, consistent with the conclusions drawn in Jonker et al. (2013).
For FXRT 7/XRT 030511, the limit of my > 23.7 implies distance lower limits of > 1.7–17 kpc and > 0.2–1.7 kpc for M- and brown-dwarfs, respectively, and corresponding X-ray flare luminosities are 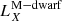 ≳ (8.3–800) × 1032 and
≳ (8.3–800) × 1032 and 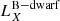 ≳ (8.3–831) × 1030 erg s−1, respectively, at least 0.9 dex higher than the known range. The ratio log(FX/Fbol) ≳ 1.6–2.1 is also well above the known range, ruling out a stellar flare origin.
≳ (8.3–831) × 1030 erg s−1, respectively, at least 0.9 dex higher than the known range. The ratio log(FX/Fbol) ≳ 1.6–2.1 is also well above the known range, ruling out a stellar flare origin.
For FXRT 10/XRT 100831, the limit of mg> 24.5 yields distance lower limits of > 0.2–2300 and > 0.02–0.2 kpc for M- and brown-dwarfs, respectively, and corresponding X-ray flare luminosities are 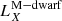 ≳ (2.9–300) × 1030 and
≳ (2.9–300) × 1030 and 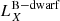 ≳ (2.9–290) × 1028 erg s−1, respectively. The lower bound of the g-band estimate remains consistent with the known range. The ratio log(FX/Fbol) ≳ − 0.8 to −0.3 also remains mildly consistent with for example, the extreme spectral type L1 J0331-27 star (De Luca et al. 2020), implying that we cannot completely rule out an extreme stellar flare origin for FXRT 10.
≳ (2.9–290) × 1028 erg s−1, respectively. The lower bound of the g-band estimate remains consistent with the known range. The ratio log(FX/Fbol) ≳ − 0.8 to −0.3 also remains mildly consistent with for example, the extreme spectral type L1 J0331-27 star (De Luca et al. 2020), implying that we cannot completely rule out an extreme stellar flare origin for FXRT 10.
For FXRT 11/XRT 110103, the limit of mg> 23.2 implies distance lower limits of > 0.1–1.3 and > 0.01–0.1 kpc for M- and brown dwarfs, respectively, and corresponding X-ray flare luminosities are 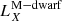 ≳ (4.8–480) × 1032 and
≳ (4.8–480) × 1032 and 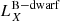 ≳ (4.8–500) × 1030 erg s−1, respectively, at least 0.7 dex higher than the known range. The ratio log(FX/Fbol) ≳ 1.4–1.9 also implies that FXRT 11 is not caused by a stellar flare, consistent with the conclusions drawn in Glennie et al. (2015).
≳ (4.8–500) × 1030 erg s−1, respectively, at least 0.7 dex higher than the known range. The ratio log(FX/Fbol) ≳ 1.4–1.9 also implies that FXRT 11 is not caused by a stellar flare, consistent with the conclusions drawn in Glennie et al. (2015).
For FXRT 12/XRT 110919, the limit of mz> 24.8 leads to distance lower limits of > 0.3–2.6 and > 0.02–0.3 kpc, respectively, and corresponding X-ray flare luminosities are 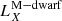 ≳ (2.4–240) × 1030 and
≳ (2.4–240) × 1030 and 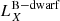 ≳ (2.4–242) × 1028 erg s−1, respectively. The lower bound of the g-band estimate is marginally overlaps at the known range of luminosities. The ratio log(FX/Fbol) ≳ − 0.9 to −0.4 also remains mildly consistent with for instance, the extreme type L1 J0331-27 star (De Luca et al. 2020), implying that we cannot completely rule out an extreme stellar flare origin for FXRT 12.
≳ (2.4–242) × 1028 erg s−1, respectively. The lower bound of the g-band estimate is marginally overlaps at the known range of luminosities. The ratio log(FX/Fbol) ≳ − 0.9 to −0.4 also remains mildly consistent with for instance, the extreme type L1 J0331-27 star (De Luca et al. 2020), implying that we cannot completely rule out an extreme stellar flare origin for FXRT 12.
For FXRT 13/XRT 140327, the detection at mi = 24.7 implies a distance range of ≈1.2–12 000 and ∼0.1–1.2 kpc, respectively, and corresponding X-ray flare luminosities of 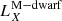 ∼ (2.1–200) × 1031 and
∼ (2.1–200) × 1031 and 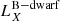 ∼ (2.1–208) × 1029 erg s−1, respectively. This is not enough to discard a Galactic stellar flare nature. However, we find a ratio log(FX/Fbol) ≈ 0.0–0.6, implying that FXRT 13 is not caused by a stellar flare.
∼ (2.1–208) × 1029 erg s−1, respectively. This is not enough to discard a Galactic stellar flare nature. However, we find a ratio log(FX/Fbol) ≈ 0.0–0.6, implying that FXRT 13 is not caused by a stellar flare.
As a summary, the multiwavelength photometry for four FXRTs appears inconsistent with expectations for flares from Galactic M dwarfs and brown dwarfs, while deeper limits are still required to completely rule out this out for FXRTs 10 and 12.
3.5. One or two populations of FXRTs?
A key question is how robust individual FXRT associations with local or distant populations are. In particular, there remains some probability that FXRTs associated with the local sample are in fact background distant FXRTs that simply lie in projection with nearby large-scale structures. A first consideration here is to identify and isolate the fraction of Chandra observations that actively target nearby galaxies. While distant FXRTs can be detected in any Chandra observation (i.e., in the background of nearby galaxy observations), nearby FXRTs can only be detected if nearby galaxies lie within the Chandra FoV. To this end, the fraction of useful20Chandra observations that target nearby galaxies at ≤100 Mpc is ≈20% of the total sample or ≈36.7 Ms (based on a match with the GLADE catalog; Dálya et al. 2018), while 80% is spent observing distant extragalactic sky, respectively. In these fractions, we find 6 and 8 FXRTs, respectively.
Extrapolating from 8 FXRTs in 80% of the observations, we can expect ≈2 distant FXRTs should occur in the 20% fraction dedicated to nearby objects, and thus the true number of nearby FXRTs would be 6 − 2 ≈ 4. However, given that we are in the Poisson regime, we need to know whether this excess is significant. If we assume a null hypothesis, 𝒩ℋ, whereby the sample consists of just one population of FXRTs, such that there are 14 distant FXRTs detected in 100% of our data, then we expect 2.8 sources in the 20% of the extragalactic fields that overlap with local galaxies, and yet we observe 6. This corresponds to an excess at 90% confidence level (i.e., detecting 6 is inconsistent with 2.8 at 90% confidence), which is likely related with an additional nearby population of FXRTs. So there is tentative (at 90% confidence level) evidence for two different population of FXRTs.
More systematically, we explore the likelihood of whether each individual local FXRT could in fact be a distant FXRT in projection with a nearby galaxy. Adopting Poisson statistics, following a similar approach to Sect. 2.5.6, and taking the density of distant FXRTs as = 6.5 × 10−6 arcmin−2 (i.e., considering the number of secure distant FXRTs found among all nonlocal Chandra observations), we compute the probability of finding by chance a distant FXRT within the specific angular offset (Pdist.FXRT; see Table 7 column 4) of each local FXRT to its associated host galaxy (see Table 7 column 2). Additionally, we calculated the Binomial probability [P(k; N; Pdis.FXRT); see Table 7 column 6], where the number of detections is taken to be the number of local FXRTs detected in a galaxy at least as bright as the specific associated local FXRT host at a distance less than or equal to the offset distance of each the specific local FXRT, and the number of trials is taken to be the number of Chandra observations of local galaxies at least as bright as the specific associated local FXRT host (see Table 7 column 5). Table 7 shows that only FXRT 1 has a significant probability (≈0.3) to be related with the distant sample; in the case of FXRT 11, it also shows a nonzero probability of being related with the distant sample (≈8.0 × 10−2), reinforcing the idea that this source is not likely associated with nearby galaxies. Thus, there remains some uncertainty as to which population FXRTs 1 and 11 belong. For the moment, we have tentatively assigned FXRT 1 to the local sample (due to the similarity of its associated host with others in that category) and FXRT 11 to the distant sample. However, we interpret them throughout leaving both possibilities open (see Sect. 5).
Probabilities related to the local sample.
In summary, our results here reinforce the existence of two different populations of FXRTs and rules out a possible relation of FXRTs 2–6 with the distant sample.
4. Host galaxy features
The host galaxy or host environment of an FXRT can provide important information on its nature. Five nearby FXRTs (2, 3, 4, 5 and 6) and three distant FXRTs (8, 9, and 14/CDF-S XT1) have very probable associated optical/NIR host galaxy detections. It remains less certain whether FXRT 1 is associated with M86.
4.1. Nearby extragalactic FXRT sample
The nearby events (FXRTs 1, 2, 3, 4, 5, and 6) are located in well-studied local galaxies, although the association of FXRT 1 with M86 is less clear. We collect information from the literature in Table 8, although we caution that this is a heterogeneous data set, and deriving consistent global parameters is beyond the scope of this work.
Parameters obtained from the literature and by our SED fitting to archival photometric data using the BAGPIPES package (Carnall et al. 2018).
Figure 13 compares the host galaxy star-formation rate (SFR) versus stellar mass (M*) values of our sample to hosts of other transients (LGRBs, low-luminosity LGRBs, SGRBs, CC-SNe, thermonuclear SNe, SN 2020bvc, and GW 170817/GRB 170817A). It is clear that the different classes of transients fall in specific regions of the SFR-M* plane. For instance, thermonuclear type Ia supernovae lie preferentially below the galaxy main sequence (dashed cyan line; Peng et al. 2010), that is to say, they are related with older (redder or recently quenched) stellar populations within galaxies; meanwhile, CC-SNe (type Ib, Ic, and II; Tsvetkov & Bartunov 1993; Galbany et al. 2014) fall closer the galaxy main sequence, highlighting their relation with ongoing star-formation in galaxies. LGRBs (Li et al. 2016), which are related to massive progenitor stars, lie above the galaxy main sequence (where so-called high-SFR starburst galaxies lie). In contrast, the location of SGRBs (Li et al. 2016) shows a large spread in this figure (i.e., SGRBs occur in a mixed population of early-type and star-forming galaxies). GW 170817/GRB 170817A (Im et al. 2017) is singled out among SGRBs, due to the unusually low SFR (≈0.001–0.01 M⊙ yr−1) of its host galaxy NGC 4993. We also single out the off-axis LGRB candidate SN 2020bvc (Chang et al. 2015; Izzo et al. 2020; Ho et al. 2020), the host galaxy UGC 9379 of which has a low SFR (≈0.08 M⊙ yr−1) but a stellar mass M* ≈ 1.9 × 1010 M⊙ similar to the Milky Way and other large spirals (Hjorth & Bloom 2012; Taggart & Perley 2021; Ho et al. 2020).
 |
Fig. 13. Comparison of the stellar mass (M*) and SFR of host galaxies of different types of transients: nearby (colored hexagons) and distant (colored stars) FXRT candidates, LGRBs and SGRBs (Li et al. 2016), low-luminosity LGRBs (LL-LGRBs; GRB 980425, GRB 020903, GRB 030329, GRB 031203, GRB 050826, GRB 060218, and GRB 171205A; Christensen et al. 2008; Michałowski et al. 2014; Levesque 2014; Krühler et al. 2017; Wiersema et al. 2007; Wang et al. 2018; Arabsalmani et al. 2019), GW 170817 (Im et al. 2017), SN 2020bvc (Chang et al. 2015; Izzo et al. 2020; Ho et al. 2020), FXRT 14/CDF-S XT1 (Bauer et al. 2017) and CDF-S XT2 (Xue et al. 2019), and supernovae events (Types Ia, Ib, Ic, and II; Tsvetkov & Bartunov 1993; Galbany et al. 2014). The solid cyan line shows the best-fit local galaxy main sequence relation from Peng et al. (2010). The gray background contours are the galaxy distribution from the SDSS (data taken from Brinchmann et al. 2004). The dashed colored lines are the boundaries separating the star-forming and quiescent galaxies and its evolution with redshift (at z = 0.0, 0.1, 0.2, 0.3, and 0.4, from bottom to top; Moustakas et al. 2013). |
Among the nearby sample, the hosts of FXRTs 2, 3, 4, 5, and 6 fall just below (within a factor of two) of the local galaxy main sequence, implying they are probably related to active star formation processes or young stellar populations. In the cases of FXRTs 2, 3, 4, and 5, there are clear spatial associations with compact HII regions or young stellar clusters, strengthening the link to young, presumably massive stars. FXRT 1/XRT 000519 is probably related with M86, which has a low SFR (≈0.01 M⊙ yr−1), as expected for elliptical galaxies.
4.2. Distant extragalactic FXRT sample
The optical/NIR hosts of the distant events FXRTs 8 and 9 are classified as extended sources (galaxies) by the VHS catalog (McMahon et al. 2013), but their properties have not been analyzed previously. We used photometric data of their putative host galaxies to constrain the host properties through spectral energy distribution (SED) model fitting.
We initially explored the spectral nature of FXRTs 8, 9, and 14 based on their i − Ks versus g − i colors in Fig. 14. FXRTs 8, 9, and 14 were compared to the counterparts of the X-ray sources classified as stars according to Criterion 2 (gray points; see Sect. 2.5.2) and the expected parameter space for stars (orange region) with different ages (log(Age/yr) = 7.0–10.3), metallicities (from [Fe/H] = − 3.0–0.5), and attenuations (AV = 0.0–5.0 mag) from theoretical stellar isochrones (MIST; Dotter 2016; Choi et al. 2016). The bulk of the stellar X-ray variables form a much tighter sequence than what is conceivably allowed by the full range of isochrones. The stellar X-ray sources that appear as outliers are identified as PNe, YSOs (e.g., eruptive variable stars, T Tauri stars), or emission-line stars. The FXRTs generally lie outside of or at the edge of the stellar region, away from the tight stellar locus, although the large error bars or limits in the NIR photometry preclude any definitive statements here. We conclude that the SED by itself is not a clear-cut discriminator and thus the spatially resolved nature of the counterparts remains vital to their confirmation.
 |
Fig. 14. Color-color diagram of FXRTs 8, 9, and 14 and X-ray sources classified as stars according to Criterion 2 (see Sect. 2.5.2) with Pan-STARRS, DECam, and 2MASS counterparts (gray filled circles). The expected parameter space of stars with different ages (log(Age) = 7.0–10.3), metallicities (from [Fe/H] = − 3.0–0.5), and attenuations (AV = 0.0–5.0) taken from the MIST package (Dotter 2016; Choi et al. 2016) is overplotted as an orange region. |
Next, we employ the code BAGPIPES (Bayesian Analysis of Galaxies for Physical Inference and Parameter EStimation; Carnall et al. 2018), which fits stellar-population models taking star-formation history and the transmission function of neutral/ionized ISM into account to broadband photometry and spectra using the MultiNest nested sampling algorithm (Feroz & Hobson 2008; Feroz et al. 2009), to derive constraints on the host-galaxy properties. BAGPIPES gives the posterior distributions for the host-galaxy redshift (z), age, extinction by dust (AV), SFR, metallicity (Z), stellar mass (M*), specific star formation rate. To account for dust attenuation in the SEDs, we use the parametrization developed by Calzetti et al. (2000), where AV is a free parameter within the range 0.0 to 3.0 mag.
We assume an exponentially declining star formation history function parametrized by the star formation timescale (free parameter). Table 8 provides the best-fit parameters obtained with BAGPIPES for the hosts of FXRTs 8 and 9, while Fig. 15 shows the 16th to 84th percentile range for the posterior spectrum and photometry. The posterior distribution for the fitted parameters is shown in the bottom panels. We have confirmed the obtained photometric redshifts of 0.61 and 0.7
and 0.7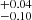 for FXRTs 8 and 9 with our 2D spectra taken by X-Shooter (PIs: Quirola and Bauer, program ID: 105.20HY.001). A detailed analysis of the spectral data will be presented in future work.
for FXRTs 8 and 9 with our 2D spectra taken by X-Shooter (PIs: Quirola and Bauer, program ID: 105.20HY.001). A detailed analysis of the spectral data will be presented in future work.
 |
Fig. 15. Best fitting SED models obtained using the BAGPIPES package (Carnall et al. 2018) for FXRTs 8 (left panels) and 9 (right panels). Top panels: 16th to 84th percentile range for the posterior spectrum and photometry (shaded orange). The used photometric data and their uncertainties are given by the blue markers. Bottom panels: posterior distribution for the five fitted parameters (SFR, age, galaxy stellar mass, metallicity, and redshift). The 16th, 50th, and 84th percentile posterior values are indicated by the vertical dashed black lines. |
FXRT 13 only has a single i-band DECam source associated with it. The non-detections in other bands may suggest that the i-band DECam image (≈6948–8645 Å) includes a dominant flux contributions from a high equivalent width emission line. Considering the most important emission lines of galaxies (such as Hα, Hβ, [OIII]λλ4959, 5007 Å), the expected redshift range of FXRT 13 is z ≈ 0.2–1.1.
Finally, Bauer et al. (2017) associated FXRT 14 (CDF-S XT1) with an extremely faint, small zphoto ∼ 2.23 host galaxy with a relatively flat SED (see Tables 3 and 8).
Among the FXRTs identified as distant candidates, FXRTs 8 and 14 are located above the galaxy main sequence, while FXRT 9 lies significantly below it. We also show the host of CDF-S XT2, which also lies just above the galaxy main sequence. Thus, a sizable fraction of distant FXRTs appear to be associated with vigorous star formation; we should stress here, however, that the statistics are poor and the uncertainties from the SED model fits remain large (see Table 8).
5. Possible interpretations
To understand the origin of our sample of FXRTs, we compare them with other well-known transients. We split our discussion here into nearby (Sect. 5.1) and distant (Sect. 5.2) samples. The former have well-established distances, and therefore we can compare their light curves in luminosity units. As we do not know the redshift of several distant FXRTs, we compare their X-ray light curves in luminosity units assuming nominal distances. Given the uncertainty in the associations for FXRTs 1 and 11, we discuss them under both the nearby and distant extragalactic scenarios.
First, from the best-fit PL spectral model, we compute the X-ray peak flux (corrected for Galactic and intrinsic absorption; Fpeak)21, the associated intrinsic X-ray peak luminosity (LX, peak), and the Eddington mass (defined as MEdd = 7.7 × 10−39LX, peak in solar mass units). We report these values in Table 9 in the energy range 0.3–10.0 keV.
Energetics of the FXRT sample (fluxes are corrected for Galactic and intrinsic absorption, and calculated over the energy range 0.3–10 keV).
5.1. Nearby extragalactic FXRT sample
The nearby FXRTs 2, 3, 4, 5, and 6 have peak isotropic X-ray luminosities in the range of LX, peak ≈ 1038–1040 erg s−1 (see Table 9). This appears inconsistent with origins as SBOs (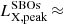 1042–1047 erg s−1; Ensman & Burrows 1992; Soderberg et al. 2008; Modjaz et al. 2009; Waxman et al. 2017; Alp & Larsson 2020), TDEs (
1042–1047 erg s−1; Ensman & Burrows 1992; Soderberg et al. 2008; Modjaz et al. 2009; Waxman et al. 2017; Alp & Larsson 2020), TDEs (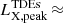 1042–1050 erg s−1; Rees 1988; MacLeod et al. 2014; Maguire et al. 2020; Saxton et al. 2021, considering a jetted emission), or on-axis GRBs (
1042–1050 erg s−1; Rees 1988; MacLeod et al. 2014; Maguire et al. 2020; Saxton et al. 2021, considering a jetted emission), or on-axis GRBs (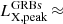 1047–1051 erg s−1; Berger 2014; Bauer et al. 2017, considering a jetted emission).
1047–1051 erg s−1; Berger 2014; Bauer et al. 2017, considering a jetted emission).
These lower luminosities fall into the realm of ULXs (extragalactic X-ray emitters located off-center of their host galaxy and with luminosities in excess of 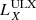 ≈ 1039 erg s−1, if the emission is isotropic, well above the Eddington limit for neutron stars; Bachetti et al. 2014; Kaaret et al. 2017) and Galactic XRBs (X-ray emitters where a compact object accretes mass from a companion star with
≈ 1039 erg s−1, if the emission is isotropic, well above the Eddington limit for neutron stars; Bachetti et al. 2014; Kaaret et al. 2017) and Galactic XRBs (X-ray emitters where a compact object accretes mass from a companion star with 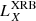 ≲ 1039 erg s−1; Remillard & McClintock 2006; van den Eijnden et al. 2018). Most ULXs are semi-persistent X-ray emitters for years to decades (Kaaret et al. 2017), and in extreme cases can reach high luminosities such as NGC 5907 ULX1 (≈5 × 1040 erg s−1; Walton et al. 2016). The much shorter and stronger variability of our FXRTs compared to ULXs implies that they are caused by a different phenomenon.
≲ 1039 erg s−1; Remillard & McClintock 2006; van den Eijnden et al. 2018). Most ULXs are semi-persistent X-ray emitters for years to decades (Kaaret et al. 2017), and in extreme cases can reach high luminosities such as NGC 5907 ULX1 (≈5 × 1040 erg s−1; Walton et al. 2016). The much shorter and stronger variability of our FXRTs compared to ULXs implies that they are caused by a different phenomenon.
Another alternative could be XRBs. Figure 16 shows the X-ray light curves of FXRTs 1, 2, 3, 4, 5, 6, and 11 one per panel, compared to several well-known XRB flaring episodes. XRBs in the Milky Way exhibit pronounced variability whereby the X-ray flux changes from quiescent to flare states on timescales of weeks to months (Remillard & McClintock 2006). Particularly, FXRTs 2 and 4 reach peak luminosities (LX, peak ≈ 1038–1039 erg s−1) similar to some XRBs’ flares (e.g., the flare luminosity of GX339-4 of ≈4 × 1038 erg s−1), which suggests that these FXRTs could be related with the tip of longer flares. Nevertheless, they are not in agreement with the duration (in the order of weeks) and timescale evolution (following a slow PL decay FX ∝ t−0.3) of XRBs flares. Thus, FXRTs 2, 3, 4 are unlikely to be related with XRBs. Meanwhile, FXRTs 1, 3, 5, 6, and 11 are not related with XRBs because of their high luminosity (LX, peak ≳ 1039 erg s−1).
 |
Fig. 16. 0.3–10 keV light curves of the five local CSC2 FXRTs, plus FXRTs 1 and 11, in luminosity units. The 0.3–10 keV light curves are obtained by multiplying the 0.3–7 keV light curves by the factor derived from extrapolating the best-fit PO model flux to the 0.5–7.0 keV spectrum to the 0.3–10 keV band and correcting it for the effects of Galactic plus intrinsic absorption. For comparison, we overplot flaring episodes for several individual well-known Galactic XRBs: GX339-4 (9 kpc, green line; Heida et al. 2017), Swift J1357.2−0933 (8 kpc, magenta line; Mata Sánchez et al. 2015), MAXI J1543−564 (5 kpc, gray line; Stiele et al. 2012), and MAXI J1659−152 (6 kpc, blue line; Jonker et al. 2012b). The light curves of the comparison sources are taken from the 2SXPS catalog (Evans et al. 2020b). |
Next, we compare the FXRTs to SGRs and AXPs, which are both believed to be related to young, highly magnetic neutron stars (Woods & Thompson 2006). Soft gamma repeaters and AXPs are very faint in quiescence but can flare by factors of hundreds to thousands on timescales of tens of ms to seconds (Göğüş et al. 1999; Aptekar et al. 2001) and on very rare occasions can generate giant flares by factors of 105 over several-minute timescales (e.g., SGR 1806-20, SGR 1900+14; Hurley et al. 1999; Terasawa et al. 2005; Woods & Thompson 2006). On such occasions they can reach X-ray luminosities as high as 1040–1041 ergs s−1, although SGR 1900+14 experienced a giant flare with a peak luminosity of > 1044 erg s−1 (at hard X-rays 40–700 keV; Mazets et al. 1999; Feroci et al. 2001), and generate bolometric outputs up to ∼1046 erg in total (Palmer et al. 2005; Terasawa et al. 2005; Strohmayer & Watts 2005; Israel et al. 2005). The weaker flares generally have a soft spectrum, while the giant flares are quite hard, and the flare durations follow a log-normal distribution (Göğüş et al. 1999). At the distances of our nearby FXRTs, we would presumably only see the most luminous portions of these rare giant bursts (a few seconds at most) and not be sensitive to the fainter bursts or quiescent emission. They should be quite spectrally hard (e.g., SGR 1900+14 has a photon index range Γ ≈ 1.0–2.0; Tamba et al. 2019) and given the relation to young, highly magnetic neutron stars, seen to be originating from young star clusters and HII regions (Woods & Thompson 2006). In this sense, FXRTs 2, 4, 5, and 6 share some similarities with the SGR and AXP phenomena. For instance, they seem related to star-formation galaxies (see Fig. 13), although their spectra remain relatively soft and their light curve lengths last thousands of seconds. In the case of FXRT 5, we see multiple flares over ≈35 ks. On the other hand, FXRTs 1, 3, and 11 are not associated with young star clusters, and thus seem far less likely to be explained by an SGR/AXP origin.
A final point of comparison is with the FXRTs discovered in NGC 4636 and NGC 5128 (Cen A) by Irwin et al. (2016) and NGC 4627 by Sivakoff et al. (2005). All exhibit rapid (∼50–100 s) flares with peak luminosities of ∼1039–1041 erg s−1, but remain detectable by Chandra in quiescence. In two cases, multiple flares are observed across multiple observations, while two transients are spatially associated with globular clusters in their host galaxies (similar to FXRT 3, which intriguingly is also associated with NGC 5128). Overall, while the luminosities are comparable, the faster timescales, multiple outbursts, and quiescent detections are unlike the behavior seen among the nearby sample of FXRTs, although it could be the case that (some) FXRTs have quiescent fluxes well below the sensitivity of Chandra and XMM-Newton and/or have not been observed frequently enough to see multiple outbursts (e.g., FXRT 6 has not been observed again by Chandra or XMM-Newton; see Fig. 6).
In the case of FXRTs 1 and 11, their origin remains unclear. For FXRT 1, assuming the association with M86 (≈16.4 Mpc; Jonker et al. 2013), it is characterized by a peak luminosity of ≈6 × 1042 erg s−1 (see Table 9). According Jonker et al. (2013), this X-ray flash (XRF) could have been caused by the disruption of a compact WD by a 4.9 × 104 M⊙ BH. Nevertheless, other scenarios such as a highly off-axis GRB (Dado & Dar 2019) cannot be discarded because of distance uncertainties. For FXRT 11, assuming the association with the galaxy cluster Abell 3581 (≈94.9 Mpc; Glennie et al. 2015; Johnstone et al. 2005), its peak luminosity and Eddington mass are ≈2 × 1044 erg s−1 and ≈1.9 × 106 M⊙ (see Table 9). Glennie et al. (2015) suggest that FXRT 11 could be consistent with the early X-ray emission typically seen in GRB light curves; however, its similarities with FXRT 1 also suggest that both events share the same origin.
Overall, the behavior of the nearby FXRTs appears to represent a genuinely new phase space of transient phenomena. The wide variety of observed properties strongly suggests that multiple physical origins may be at work.
5.2. Distant extragalactic FXRT sample
For the moment, we split the discussion of FXRTs into those with fairly secure hosts and reasonable distance estimates (see Sect. 5.2.1) versus those with less certain or no clear hosts (see Sect. 5.2.2). Here we analyze the scenario where the FXRTs 1 and 11 are related to distant extragalactic objects (see Sect. 5.2.2).
5.2.1. FXRTs with known distances
Using the photometric host redshifts calculated in Sect. 4, FXRTs 8 and 9 reach peak X-ray luminosities of LX, peak ≈ 1.5 × 1044 and 1.3 × 1045 erg s−1, respectively (see Table 9 and Fig. 17 for a light curve comparison). The FXRTs have an isotropic fluence of EX ≈ 2.2 × 1047 and 3.9 × 1047 erg, respectively.
 |
Fig. 17. 0.3–10 keV light curves of the nine CSC2 FXRTs in luminosity units (as in Fig. 16, 0.3–10 keV light curves were converted from 0.5–7 keV ones). The X-ray afterglow light curves of 64 LGRBs plus 32 SGRBs (taken from Bernardini et al. 2012; Lü et al. 2015) are shown as a 2D histogram, as are the X-ray afterglows of GRB 170817A (off-axis SGRB, solid dark green line; Nynka et al. 2018; D’Avanzo et al. 2018; Troja et al. 2020, 2022), SN 2020bvc (the first off-axis LGRB candidate, solid light green line; Izzo et al. 2020), and the ultra-long duration GRB 111209A (solid magenta line, z = 0.677; Levan et al. 2014). Additionally, several individual transients are overplotted: the low-luminosity supernova SBO XRF 080109/SN 2008D (solid cyan lines, 27 Mpc;), XRF 060218/SN 2006aj (solid blue lines, 145 Mpc;), XRF 100316D/SN 2010bh (solid orange lines, 263 Mpc; Barniol Duran et al. 2015; Starling et al. 2011; Modjaz et al. 2009; Evans et al. 2007, 2009; Soderberg et al. 2008; Campana et al. 2006), the relativistically beamed TDE Swift J1644+57 (solid black lines, z = 0.3543; Bloom et al. 2011; Levan et al. 2011), the non-beamed TDE J2150-05 (solid pink line, z = 0.055; Lin et al. 2018), and CDF-S XT2 (solid indigo lines; Xue et al. 2019). For FXRTs 1, 7, 10, 11, 12, and 13 (open symbols), we assume z = 1.0, we adopt zphoto = 2.23 for FXRT 14 from Bauer et al. (2017), and for FXRTs 8 and 9 we consider the values from Table 8. |
Such luminosities fall with the ranges predicted or detected for SBOs (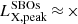 1042–1047 erg s−1; Soderberg et al. 2008; Modjaz et al. 2009; Waxman et al. 2017; Alp & Larsson 2020), although both FXRTs exhibit energy released that are at least one to two orders of magnitude higher than the energy predicted by SBO models (e.g., Waxman et al. 2017) or detected from the enigmatic SBO XRT 080109/SN 2008D (EX ≈ 2×1046 erg; Soderberg et al. 2008). As such, we rule out an SBO interpretation for FXRTs 8 and 9.
1042–1047 erg s−1; Soderberg et al. 2008; Modjaz et al. 2009; Waxman et al. 2017; Alp & Larsson 2020), although both FXRTs exhibit energy released that are at least one to two orders of magnitude higher than the energy predicted by SBO models (e.g., Waxman et al. 2017) or detected from the enigmatic SBO XRT 080109/SN 2008D (EX ≈ 2×1046 erg; Soderberg et al. 2008). As such, we rule out an SBO interpretation for FXRTs 8 and 9.
Considering an on-axis GRB origin, we note that no gamma-ray signals detected near the time of discovery were associated with FXRTs 8 or 9, and neither exhibits a characteristic PL decay phase (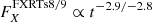 associated with GRB afterglows
associated with GRB afterglows 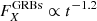 ; Evans et al. 2009; Racusin et al. 2009), although some GRBs show strong X-ray flaring in the tail of the X-ray afterglow distribution that could mimic the observed temporal behavior (Barthelmy et al. 2005; Campana et al. 2006; Chincarini et al. 2010; Margutti et al. 2011). Critically, Fig. 17 demonstrates that the X-ray light curves of both FXRTs are fainter than almost any known on-axis GRB X-ray afterglow over the same timescale, with (prompt) initial luminosities > 3–4 dex below the luminosity ranges observed for GRBs (
; Evans et al. 2009; Racusin et al. 2009), although some GRBs show strong X-ray flaring in the tail of the X-ray afterglow distribution that could mimic the observed temporal behavior (Barthelmy et al. 2005; Campana et al. 2006; Chincarini et al. 2010; Margutti et al. 2011). Critically, Fig. 17 demonstrates that the X-ray light curves of both FXRTs are fainter than almost any known on-axis GRB X-ray afterglow over the same timescale, with (prompt) initial luminosities > 3–4 dex below the luminosity ranges observed for GRBs (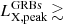 1047 erg s−1). Based on their best-fit X-ray spectral slopes of ΓFXRTs 8/9 ≈ 2.7/3.0, they formally lie at the edge of the standard afterglow distribution (ΓGRBs = 1.5–3.0; Berger 2014; Wang et al. 2015; Bauer et al. 2017) overlapping at the 1σ confidence level. In terms of their host-galaxy properties (see Fig 13 and Table 8), FXRT 8’s host has a low-SFR (≈0.5 M⊙ yr−1) and old stellar population (≳1 Gyr). It is classified as a quiescent galaxy according to the criteria from Moustakas et al. (2013), and is thus a potential host for an SGRB. Nevertheless, an association with low-luminosity LGRBs (LL-LGRBs) could be discarded due to the high stellar mass of its host galaxy.
1047 erg s−1). Based on their best-fit X-ray spectral slopes of ΓFXRTs 8/9 ≈ 2.7/3.0, they formally lie at the edge of the standard afterglow distribution (ΓGRBs = 1.5–3.0; Berger 2014; Wang et al. 2015; Bauer et al. 2017) overlapping at the 1σ confidence level. In terms of their host-galaxy properties (see Fig 13 and Table 8), FXRT 8’s host has a low-SFR (≈0.5 M⊙ yr−1) and old stellar population (≳1 Gyr). It is classified as a quiescent galaxy according to the criteria from Moustakas et al. (2013), and is thus a potential host for an SGRB. Nevertheless, an association with low-luminosity LGRBs (LL-LGRBs) could be discarded due to the high stellar mass of its host galaxy.
FXRT 9’s galaxy is a massive blue starburst galaxy (≈120 M⊙ yr−1) with a young stellar population (≈0.15 Gyr). Hence, FXRT 9 might be related to an LGRB origin, although an association with SGRBs cannot be discarded. On the other hand, an association with LL-LGRBs could be ruled out because of the high stellar mass of its host galaxy relative to LL-LGRBs’ hosts (higher than one order of magnitude; see Fig 13). Unfortunately, the low angular resolution of the current archival images does not permit us to compute the offset from the host center.
Alternatively, these FXRTs could be related to ultra-long duration GRBs. Several ultra-long GRBs (longer than thousands of seconds) have been detected (Thöne et al. 2011; Campana et al. 2011; Gendre et al. 2013; Virgili et al. 2013; Stratta et al. 2013). Their nature still unclear. Gendre et al. (2013) and Levan et al. (2014) argued that ultra-long duration GRBs form another distinct group of GRBs; for example, Levan et al. (2014) argue that the long duration of this population of GRBs may be explained by engine driven explosions of stars of much larger radii than typical LGRB progenitors (which are thought to have compact Wolf-Rayet progenitor stars). Figure 17 shows a comparison of both FXRTs and the ultra-long GRB 111209A. At early times their luminosities are ≈6–7 dex lower than that of GRB 111209A. Nevertheless, we cannot discard an association with this population of GRBs because of the uncertainty in the zero point of our FXRTs, which when changed could match well with the temporal decay (FX ∝ t−1.4/−5.3) and spectral trend (Γ ≈ 2.4 at t> 40 ks) of this GRB.
The possibility of an off-axis orphan GRB origin still remains plausible, given the lack of an initial gamma-ray detection and lower luminosity. Here we compare to the light curves of XRF 060218/SN 2006aj (Campana et al. 2006), XRF 100316D/SN 2010bh (Starling et al. 2011), and SN 2020bvc (Izzo et al. 2020), which have all been argued to be potential off-axis LGRBs, as well as GRB 170817A (Nynka et al. 2018; D’Avanzo et al. 2018; Troja et al. 2020) and CDF-S XT2 (Xue et al. 2019), and thus possible off-axis SGRBs (see Fig. 17). We note in particular that the plateau phases of FXRTs 8 and 9 are ≈1–3 dex lower than those of XRF 060218, XRF 100316D, and CDF-S XT2, although the break and late-time light curves (to the extent that they can be quantified) appear to match reasonably well. By extension, SN 2020bvc and GRB 170817A appear to be even weaker, and join with the faint declining tails of the XRFs at very late times. We speculate that perhaps FXRTs 8 and 9 could be weaker or higher inclination versions of off-axis SGRB and LGRBs (e.g., Granot et al. 2002), respectively, somewhere intermediate between the XRFs and SN 2020bvc/GRB 170817A along the possible viewable parameter space of such events. Unfortunately, the poor count statistics (to constrain any spectral evolution) and the lack of additional EM counterparts do not permit us to analyze this picture in detail.
Finally, in the TDE scenario, if we interpret the peak luminosities as the Eddington luminosity, we derive masses of ≳1.2 × 106 and 1.0 × 107 M⊙ for FXRT 8 and FXRT 9, respectively. These masses fall in the supermassive black hole (SMBH) range (Barack et al. 2019), and assuming that a large fraction of the total stellar mass of the host galaxies as derived in Sect. 4.2 is associated with a spheroid component, could be approximately consistent with the stellar velocity dispersion (σ) of a galaxy bulge and the mass of the SMBH (MBH) at its center (MBH − σ relation; e.g., Ferrarese & Merritt 2000). These luminosities are in rough agreement with the recent sample of TDEs published by Sazonov et al. (2021).
Alternatively, these FXRTs could be related with an IMBH–WD or IMBH–MS TDEs (which could occur in dwarf galaxies and stellar systems such as globular clusters; Jonker et al. 2012a; Reines et al. 2013), assuming the observed luminosities are super-Eddington or due to relativistic beaming. The FXRTs are offset from the nuclei of their associated optical and NIR sources by only 0 5 and 0
5 and 0 7 (or projected physical distances of 3 and 3.5 kpc), respectively, and hence remain consistent with both on-axis and off-axis scenarios within the positional uncertainties (see Fig. 7).
7 (or projected physical distances of 3 and 3.5 kpc), respectively, and hence remain consistent with both on-axis and off-axis scenarios within the positional uncertainties (see Fig. 7).
Saxton et al. (2021) review the observed and theoretical X-ray properties of TDE candidates. Among confirmed SMBH–MS TDEs detected to date, several exhibit peak luminosities similar to those of FXRTs 8 and 9. However, the X-ray spectra of SMBH–MS TDEs are generally softer and none exhibit short-term X-ray variability comparable to what see from the FXRTs, but instead show much slower declines over timescales of months to years. For this reason, we disfavor such an explanation, but cannot completely rule out a possible detection bias here, given the limited sensitivity of current all-sky instruments. One intriguing possibility for generating higher luminosities, faster variability, and harder spectra is relativistic beaming from jetted TDEs such as Swift J1644+57 (Bloom et al. 2011; Levan et al. 2011). This could also significantly relax the mass and/or accretion rate limits quoted above. In the case of Swift J1644+57, shown in Fig. 17, it has a peak luminosity of ≈1048 erg s−1 and time-averaged photon index of Γ = 1.6–1.8 (Levan et al. 2011), although the photon index increases and softens with decreasing flux (Bloom et al. 2011). Clearly FXRTs 8 and 9 remain ∼3 dex fainter, but otherwise have potentially consistent spectral and temporal properties. As neither has multiple X-ray observations, we cannot say anything about their long-term evolution. We can also compare the timing and spectral properties of the off-nuclear ultrasoft hyper-luminous 3XMM J215022.4-055108, an IMBH TDE candidate (hereafter TDE J2150-05; Lin et al. 2018, 2020). TDE J2150-05 shows a peak luminosity of ≈1 × 1043 erg s−1, a light curve PL decay of FX ∝ t−5/3 during ≳14 yr (see Fig.17), and ultrasoft X-ray spectra with kT ≲ 0.25 keV, which soften with time (Lin et al. 2018, 2020). This lies in stark contrast with FXRTs 8 and 9, which show a short and fast timescale variability, and somewhat hotter/harder X-ray spectra. In summary, FXRTs 8 and 9 do not conform to the “traditional” expectations of TDEs, in terms of slow temporal evolution or ultrasoft X-ray spectra, but relativistically beamed emission from an IMBH-TDE scenario cannot be discarded.
Unlike the other events, FXRT 14 has been constrained by multiwavelength counterparts (Bauer et al. 2017). The available data are consistent with expectations for off-axis SGRBs, although other possibilities might not be ruled out. For instance, Peng et al. (2019) argue for an IMBH–WD TDE, Sun et al. (2019) explain the X-ray emission considering a magnetar remnant after a BNS merger observer at an off-axis viewing angle, while Sarin et al. (2021) discuss an association with an off-axis afterglow of a BNS merger, without discarding that its X-ray properties could be related to compact object such as an asteroid hitting an isolated foreground neutron star (Colgate & Petschek 1981; van Buren 1981; Campana et al. 2011). It is important to mention that FXRT 14/CDF-S XT1 and XT2 seem to fall in the same host’s properties parameter space as the LL-LGRBs and SGRBs at lower stellar masses (≲109 M⊙; see Fig. 13). This reinforces the likely association with SGRBs.
5.2.2. FXRTs with unknown distances
FXRTs 7, 10, 12, and 13 do not have clear host associations as yet, and hence have wildly uncertain distances. Based on their typical optical and NIR upper limits (e.g., mr ≳ 23.3 and mz ≳ 22 AB mag), and considering distances of other FXRT host galaxies such as FXRTs 8 and 9 (zphoto/spec ∼ 0.7), FXRT 14 (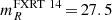 AB mag and
AB mag and 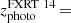 0.39–3.21; Bauer et al. 2017), and CDF-S XT2 (
0.39–3.21; Bauer et al. 2017), and CDF-S XT2 (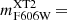 25.35 AB mag and
25.35 AB mag and 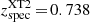 ; Xue et al. 2019), we adopt a nominal redshift of z = 1 for these sources. Figure 17 (open markers) compares FXRTs 7, 10, 12 and 13 (at z = 1.0) to several classes of transients.
; Xue et al. 2019), we adopt a nominal redshift of z = 1 for these sources. Figure 17 (open markers) compares FXRTs 7, 10, 12 and 13 (at z = 1.0) to several classes of transients.
We note that FXRTs 7, 10, and 12 have light curves that exhibit plateau phases of ≈1–3 ks, followed by PL decays (FX ∝ t−2.4/−1.6) that are accompanied by possible softening of the spectra for FXRTs 7 and 12 (see Table 6). Spectral softening has been seen previously in SBOs (e.g., XRF 080109/SN 2008D), GRBs afterglows, TDEs (e.g., MacLeod et al. 2014; Malyali et al. 2019), and CDF-S XT2 (Xue et al. 2019). FXRTs 7, 10 and 12 have photon indices (see Table 5) similar to the SBO XRF 080109/SN 2008D (Γ ≈ 2.3; Soderberg et al. 2008) and GRB afterglows (Γ ≈ 1.5–3.0; Berger 2014; Wang et al. 2015) at a 1σ confidence level. If these events lie at z ≳ 0.5, we can discard the SBO scenario, however, due to their high X-ray luminosities (LX, peak ≳ 1044 erg s−1); an SBO association would only be expected at low redshift (z ≲ 0.5). The light curves (at z = 1.0) also appear inconsistent with on-axis GRBs. Although they share similar luminosities and PL decays beyond ∼103 s, the early plateau phases of FXRTs are inconsistent with the typical PL or BPL decays of on-axis GRBs and afterglows. A subset of SGRBs exhibit plateau phases (Rowlinson et al. 2010, 2013), although these generally have plateau luminosities ≳1046 erg s−1 (although if no redshift is known the mean SGRB redshift is assumed, z ∼ 0.72; energy band 0.3–10 keV), which are inconsistent with FXRTs 10 and 12 lying at z ≲ 2.1. An off-axis GRB afterglow scenario seems unlikely. To observe luminosities similar to SN 2020bvc (LX, max ≈ 1.8 × 1041 erg s−1) and GRB 170817 (LX, max ≈ 4 × 1039 erg s−1), our sources must be at low redshifts, z ≲ 0.1, which could be discarded by the non-detection of hosts. Furthermore, Fig. 17 shows a comparison of these FXRTs with the ultra-long GRB 111209A. Assuming z = 1.0, at early times their luminosities are orders of magnitude lower than GRB 111209A.
On the other hand, the luminosities and light curve shapes of FXRTs 7, 10, and 12 share remarkable similarities to X-ray flashes XRF 060218/SN 2006aj and XRF 100316D/SN 2010bh (which may be related to shock breakout from choked GRB jets; Campana et al. 2006; Bromberg et al. 2012; Nakar & Sari 2012), as well as CDF-S XT2 (which is consistent with being powered by a millisecond magnetar; Xue et al. 2019; Sun et al. 2019). The light curves of FXRTs 7, 10, and 12 follow the expected shape for IMBH–WD TDEs (e.g., see MacLeod et al. 2014; Malyali et al. 2019). For instance, the photon index and flux PL decay of these FXRTs are similar to the IMBH TDE candidate TDE J2150-05 (Γ ≲ 4.8 and FX ∝ t−5/3; Lin et al. 2018). Assuming z = 1, only FXRT 7 reaches a luminosity close to the beamed TDE Swift J1644+57 (LX, peak ≈ 1046–1047 erg s−1; see Fig. 17; Bloom et al. 2011; Levan et al. 2011), but without flaring episodes. Again, the poor count statistics (to constrain any spectral evolution) and the lack of host or additional EM counterparts do not permit us to analyze this picture in detail.
FXRT 13 exhibits a single PL light curve with a slow decay (FX ∝ t−0.2). This seems to exclude a SBO nature for this FXRT. There is a faint optical source likely associated with this FXRT, only visible in i-band DECam images (mi ≈ 24.7 AB mag), which does not constrain its origin significantly.
Finally, assuming FXRTs 1 and 11 are actually background objects that randomly overlap with nearby sources, we find that their light curves remain unique. Given the uncertainties in their distances, we adopt nominal redshifts of z = 1 as above (see Fig. 17). Their X-ray luminosities of reach values LX, peak ≈ 1047 and 5 × 1047 erg s−1, respectively, ruling out an association with SBOs but falling in the range of XRFs (e.g., XRF 060218/SN 2006aj and XRF 100316D/SN 2010bh; Campana et al. 2006; Bromberg et al. 2012; Nakar & Sari 2012) and beamed TDEs (e.g., TDE J1644+57; see Fig. 17). The duration and shapes do not appear consistent with XRFs, but do resemble individual flares seen from TDE J1644+57.
Unfortunately, the unknown distances of these FXRTs do not permit better constraints on their origin.
6. Rates
We computed the event rates of FXRTs and compared them with those for other transients to explore possible associations and interpretations. We derived the event rates (deg−2 yr−1; Sect. 6.1), the volumetric rate for nearby and distant samples (yr−1 Gpc−3; Sect. 6.2), the local density rate (Sect. 6.3), and the expected number of events for current and future X-ray missions (Sect. 6.4).
6.1. Event-rate estimation
We found 14 FXRTs (including XRT 000519, XRT 110103 and CDF-S XT1; Jonker et al. 2013; Glennie et al. 2015; Bauer et al. 2017) within 160.96 Ms of CSC2 data. For a set of Chandra observations, the number of transients can be written as
where ℛi is the event rate, Ωi and ti are the FoV and exposure time, respectively, and εi is an area correction factor, with the subscript i denoting each Chandra observation.
The area correction factor, εi, is important for the faintest FXRTs and captures the changes in sensitivity over the Chandra detector. εi is defined as the area within which we expect successful FXRT detections (S/N ≳ 3.0) normalized by the total detection area. To determine εi, we simulate 1,000 fake instances of each FXRT, randomly distributed in position (using MARX and simulate_psf scripts taking into account the particular features per Chandra observation) within Chandra’s FoV for each individual observation. We compute the S/N for fake FXRTs in the energy range of 0.3–10 keV. Thus, εi falls in the range εi ∈ [0.0, 1.0]. For the brightest FXRTs, εi ≈ 1.0, meaning that they are detectable across the entire detector FoV, while for fainter FXRTs, εi ≲ 1.0, such that only a portion of the detector is sensitive to them.
We assume that ℛi is constant (such that ℛi = ℛ), because the universe is isotropic on large scales and we are focusing on extragalactic sources (Yang et al. 2019). Ωi depends on which chips of the detector are turned on; due to the degradation of the PSF at higher instrumental off-axis angles, we consider only chips I0–I3 for ACIS-I and chips S1–S4 for ACIS-S, respectively. Therefore, the expected number of events depends on Ωi, ti, and εi per observation as
such that the event rate, ℛ, is
We derive the rate of our sample considering two cases: (i) five nearby events (seven if we include FXRT 1/XRT 000519 and FXRT 11/XRT 110103, which have unclear associations with M86 and the galaxy cluster Abell 3581, respectively; called Case I), and (ii) seven distant events (nine if we include FXRT 1/XRT 000519 and FXRT 11/XRT 110103; called Case II). Because our algorithm does not have good efficiency in detecting objects in observations with exposure times < 8 ks (in fact, we do not detect any candidates for such exposures), we do not consider such observations to derive the rates. Another consideration when estimating the event rates for both FXRT samples is to identify and isolate the fraction of observations that target nearby galaxies. While distant FXRTs can be detected in any Chandra observation (i.e., in the background of nearby galaxy observations), nearby FXRTs can only be detected if nearby galaxies lie within the Chandra FoV. Thus for Case II, we consider just Chandra observations that target non-nearby galaxies, while for Case I, we only consider the fraction of Chandra observations that target nearby galaxies at < 100 Mpc (≈21% of the total sample; see Sect. 3.5).
Therefore, we estimate the event-rates (fully accounting for the ambiguity of FXRTs 1 and 11 in the errors) of nearby FXRTs to be ℛCase I = 53.7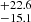 deg−2 yr−1; while for distant FXRTs it is ℛCase II = 28.2
deg−2 yr−1; while for distant FXRTs it is ℛCase II = 28.2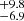 deg−2 yr−1 (for FX, peak ≳ 1 × 10−13 erg cm−2 s−1). The distant rate is consistent with the rate of ℛYang + 19 ≈ 59
deg−2 yr−1 (for FX, peak ≳ 1 × 10−13 erg cm−2 s−1). The distant rate is consistent with the rate of ℛYang + 19 ≈ 59 deg−2 yr−1 at the Poisson 1σ confidence level, as derived by Yang et al. (2019), but is ≈0.9 dex higher than the rate of ≈3.4 deg−2 yr−1 derived by Glennie et al. (2015). The latter discrepancy is not surprising, however, since Glennie et al. (2015) calculated the rate for a much higher peak flux of FX, peak ≳ 10−10 erg cm−2 s−1.
deg−2 yr−1 at the Poisson 1σ confidence level, as derived by Yang et al. (2019), but is ≈0.9 dex higher than the rate of ≈3.4 deg−2 yr−1 derived by Glennie et al. (2015). The latter discrepancy is not surprising, however, since Glennie et al. (2015) calculated the rate for a much higher peak flux of FX, peak ≳ 10−10 erg cm−2 s−1.
It is essential to mention again that FXRTs previously discovered as CDF-S XT2 (XRT 150321; Xue et al. 2019), XRT 170831 (Lin et al. 2019) and XRT 210423 (Lin et al. 2021) are not part of this work because of the date cut-off of CSC2. As we showed in Sect. 2.5.6, the number of FXRTs that is removed from our sample by our selection criteria erroneously is probably less than 1. Therefore, the estimated event rates are robust results for FXRT candidates brighter than log(Fpeak) ≳ − 12.6 for Chandra observations with Texp> 8 ks.
The event rate (event rate per dex of flux) behaves as a PL function as  , where γ is a positive value. In Fig. 18, we plot the observed cumulative log 𝒩–log S distribution for our entire sample, which appears to follow γ ≈ 0.5 (red line). We also plot the extrapolation of the best-fit slope, γ = 1.0, based on the estimates of FXRTs at bright fluxes (≳10−10 erg cm−2 s−1) from Arefiev et al. (2003). We caution that Arefiev et al. (2003) do not specify an exact energy band and make no distinction between various potential Galactic and extragalactic classes, although it is noteworthy that the sky distribution at these bright fluxes is also isotropic. We see that the brightest sources in our CSC2 sample are consistent with this extrapolation, while the fainter sources fall well below it by ∼1 dex, implying a potential break around a fluence of 3 × 10−8 erg cm−2 to our best-fit slope.
, where γ is a positive value. In Fig. 18, we plot the observed cumulative log 𝒩–log S distribution for our entire sample, which appears to follow γ ≈ 0.5 (red line). We also plot the extrapolation of the best-fit slope, γ = 1.0, based on the estimates of FXRTs at bright fluxes (≳10−10 erg cm−2 s−1) from Arefiev et al. (2003). We caution that Arefiev et al. (2003) do not specify an exact energy band and make no distinction between various potential Galactic and extragalactic classes, although it is noteworthy that the sky distribution at these bright fluxes is also isotropic. We see that the brightest sources in our CSC2 sample are consistent with this extrapolation, while the fainter sources fall well below it by ∼1 dex, implying a potential break around a fluence of 3 × 10−8 erg cm−2 to our best-fit slope.
 |
Fig. 18. Observed cumulative log 𝒩–log S distribution of our sample of FXRTs as a function of fluence (in units of Crab† × second). Also shown are two PL models, N(> S)∝S−γ, with slopes γ = 0.5 (red line) and 1.0 (blue line). The γ = 0.5 line denotes the best fit to the CSC2 sample. The γ = 1 line represents the best fit and 1σ error of Arefiev et al. (2003) based on bright FXRTs. The brightest sources in our sample appear to be consistent with this bright-end extrapolation, although our fainter sources fall ∼1 dex below, implying a break. For comparison with Arefiev et al. (2003), we convert the fluence to 2–10 keV. †A Crab is a standard astrophotometric unit for measurement of the intensity of celestial X-ray sources. |
For comparison, a spatially homogenous distribution of identical (standard candle) sources would yield a Euclidean slope of 1.5. Based on this, we adopt γ = 1.0 when extrapolating to brighter fluxes, and γ = 0.5 to fainter fluxes.
6.2. Volumetric rate estimate
In addition to the event rate on the sky (deg−2), we compute the volumetric density rate ρ(z), in units of yr−1 Gpc−3, to compare with other known transient classes (GRBs, SBOs, or TDEs). Following Zhang (2018), the number of FXRTs, 𝒩, identified per unit (observing) time, dt, per unit redshift bin, dz, can be written as
where dV(z)/dz is the derivative of the volume with regards to z. Integrating the previous equation by dt and dz, we can estimate the density rate at a particular redshift z as
where Vc, max is the maximum co-moving volume (at the maximum co-moving distance Dc, max), while Ω and T are the FoV and the exposure time used in this work (corrected by εi; see Sect. 6.1), respectively.
For Case I (between five and seven local FXRTs), the density rate at ≲100 Mpc is ρCase I = (5.9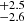 ) × 10−2 yr−1 Mpc−3, at a 1σ confidence level. Due to the small distance of these FXRTs, we can approximate this result at z ≈ 0, also called the local density rate (denoting as ρ0), that is, ρCase I ≈ ρ0,Case I. This value is consistent with previously derived rates for ULXs, taking ULX M82 as an example (1.75 × 10−2 yr−1 Mpc−3; Kaaret et al. 2006; Swartz et al. 2011; Pradhan et al. 2020).
) × 10−2 yr−1 Mpc−3, at a 1σ confidence level. Due to the small distance of these FXRTs, we can approximate this result at z ≈ 0, also called the local density rate (denoting as ρ0), that is, ρCase I ≈ ρ0,Case I. This value is consistent with previously derived rates for ULXs, taking ULX M82 as an example (1.75 × 10−2 yr−1 Mpc−3; Kaaret et al. 2006; Swartz et al. 2011; Pradhan et al. 2020).
For Case II (distant FXRTs), redshift and cosmological effects become important. Currently, we only have photometric redshifts for FXRT 8 and FXRT 9 (zphot ≈ 0.7), and suspect that FXRT 13 must have a broadly similar redshift range (z ≈ 0.2–1.1 and 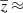 0.7; see Sect. 4). Thus we only compute the cosmological rate for these FXRTs. Using Eq. (9) and assuming that FXRTs 8, 9, and 13 occurred at z ≈ 0.7, the density rate of these three FXRTs is ρFXRTs 8/9/13 = (4.8
0.7; see Sect. 4). Thus we only compute the cosmological rate for these FXRTs. Using Eq. (9) and assuming that FXRTs 8, 9, and 13 occurred at z ≈ 0.7, the density rate of these three FXRTs is ρFXRTs 8/9/13 = (4.8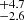 ) × 103 yr−1 Gpc−3 at a maximum redshift of zmax ≈ 2.1 (assuming a mean value of
) × 103 yr−1 Gpc−3 at a maximum redshift of zmax ≈ 2.1 (assuming a mean value of 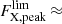 1 × 10−13 erg cm−2 s−1 as the threshold limit detection and an isotropic luminosity
1 × 10−13 erg cm−2 s−1 as the threshold limit detection and an isotropic luminosity 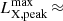 3 × 1045 erg s−1). In a similar way, we compute the density rate for CDF-S XT1 at zmax ≈ 3 of ρCDF − S XT1 = (4.8
3 × 1045 erg s−1). In a similar way, we compute the density rate for CDF-S XT1 at zmax ≈ 3 of ρCDF − S XT1 = (4.8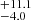 ) × 102 yr−1 Gpc−3. In Fig. 19, left panel, we compare the density rates for FXRTs 8/9/13 (cyan star) and CDF-S XT1 (red square) to other transient classes. We note that these rate could increase by a factor of up to ≈2, considering that we do not have firm redshifts for ∼50% of the FXRT candidates.
) × 102 yr−1 Gpc−3. In Fig. 19, left panel, we compare the density rates for FXRTs 8/9/13 (cyan star) and CDF-S XT1 (red square) to other transient classes. We note that these rate could increase by a factor of up to ≈2, considering that we do not have firm redshifts for ∼50% of the FXRT candidates.
 |
Fig. 19. Density rate as a function of redshift for several known transient classes compared to our sample. Left panel: density rate as a function of redshift for FXRT 8/9/13 (cyan star) and CDF-S XT1/FXRT 14 (red square), and upper limits (black triangle) for FXRTs without measured redshifts. We also show the density rate of CDF-S XT2 (purple square; Xue et al. 2019), CC-SNe (dotted orange line; Madau & Dickinson 2014), the redshift-dependent intrinsic event rate densities of LGRBs (blue-filled region; taken from Sun et al. 2015 and Wanderman & Piran 2010, normalized to the local universe value and corrected for jet-aperture as ρ0, LGRBs ∼ 250–500 yr−1 Gpc−3), LL-LGRBs (green-filled region; taken from Zhang 2018, normalized to the local universe value and corrected for jet-aperture as ρ0, LGRBs ∼ 100–200 yr−1 Gpc−3), SGRBs considering a merger delay Gaussian model (red-filled region; taken from Sun et al. 2015 and Wanderman & Piran 2015, normalized to the local universe value and corrected for jet-aperture as ρ0, SGRBs ∼ 13–75 yr−1 Gpc−3), and TDEs (gray-filled region, taken from Sun et al. 2015, normalized to the local universe as ρ0, TDEs ∼ 104–105 yr−1 Gpc−3 at luminosities ∼1042–1044 erg s−1). Right panel: local density rate for FXRT 8/9/13 considering they are related to GRBs (cyan star), TDEs (blue star), or FXRT 14/CDF-S XT1 (red square) (see Sect. 6.3). As a comparison, we also plot the local event rate of CDF-S XT2-like events (purple square; Xue et al. 2019), GW 170817 (green square; Abbott et al. 2017b), and GRB 170817A (magenta square; Zhang et al. 2018), as well other kinds of transients, such as the new SBO candidate in XMM-Newton data (yellow square and circle; Xu et al. 2008; Novara et al. 2020), the TDE rate of SMBH–MS TDEs (black triangle; Sun et al. 2015) and the IMBH–WD TDE rate (orange triangle and circle; Malyali et al. 2019; Tanikawa et al. 2021), the CC-SN rate (magenta triangle), the merger rate of BNS systems (light green circle; Abbott et al. 2021c), and the merger rate of neutron star and BH systems (gray circles; Abbott et al. 2021b). The local event rate of LGRBs, LL-LGRBs, and SGRBs are plotted (blue, green, and red horizontal shaded regions, corrected for the jet aperture factor; Zhang 2018). |
Considering first the density rate for FXRT 8/9/13, we find that ρFXRT 8/9/13 is comparable to the rate of events like CDF-S XT2, (ρXT2(zmax = 1.9) = (1.3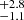 ) × 104 yr−1 Gpc−3; purple square, Fig. 19 left panel; Xue et al. 2019), at a similar redshift. Excluding FXRT 13 due to its uncertain redshift and computing the density rate only for FXRTs 8 and 9, the density rate drops by a factor of ∼1.6. ρFXRT 8/9/13 remains a factor ≳100 lower than the expected rate of CC-SNe (dotted orange line; Madau & Dickinson 2014), but is in good agreement with the density rate expected at z ∼ 2.0 for LGRBs [blue-filled region; assuming ρ0, LGRBs = 250–500 yr−1 Gpc−3 from Wanderman & Piran (2010) and Zhang (2018), and the normalized rate redshift evolution from Sun et al. (2015)] and TDEs [gray-filled region; assuming ρ0, TDEs = 104–105 yr−1 Gpc−3 from Sun et al. (2015) and luminosities L ≈ 1042–1044 erg s−1] reinforcing a possible association with these kinds of events. For LGRBs, we adopted a jet correction factor of ≈500 (Frail et al. 2001; Zhang 2018); however, other works argue for lower corrections of ≈50–100 (Piran 2004; Guetta et al. 2005). The ρFXRT 8/9/13 also overlaps with the expected density rate of LL-LGRBs (green-filled region; with Lmin = 5 × 1046 erg s−1, ρ0, LL − LGRBs = 100–200 yr−1 Gpc−3 and the normalized rate redshift evolution from Sun et al. 2015), adopting a beaming correction of ≈1 since observations of LL-LGRBs do not show strong evidence of collimation, suggesting wider jet opening angles (Virgili et al. 2009; Pescalli et al. 2015).
) × 104 yr−1 Gpc−3; purple square, Fig. 19 left panel; Xue et al. 2019), at a similar redshift. Excluding FXRT 13 due to its uncertain redshift and computing the density rate only for FXRTs 8 and 9, the density rate drops by a factor of ∼1.6. ρFXRT 8/9/13 remains a factor ≳100 lower than the expected rate of CC-SNe (dotted orange line; Madau & Dickinson 2014), but is in good agreement with the density rate expected at z ∼ 2.0 for LGRBs [blue-filled region; assuming ρ0, LGRBs = 250–500 yr−1 Gpc−3 from Wanderman & Piran (2010) and Zhang (2018), and the normalized rate redshift evolution from Sun et al. (2015)] and TDEs [gray-filled region; assuming ρ0, TDEs = 104–105 yr−1 Gpc−3 from Sun et al. (2015) and luminosities L ≈ 1042–1044 erg s−1] reinforcing a possible association with these kinds of events. For LGRBs, we adopted a jet correction factor of ≈500 (Frail et al. 2001; Zhang 2018); however, other works argue for lower corrections of ≈50–100 (Piran 2004; Guetta et al. 2005). The ρFXRT 8/9/13 also overlaps with the expected density rate of LL-LGRBs (green-filled region; with Lmin = 5 × 1046 erg s−1, ρ0, LL − LGRBs = 100–200 yr−1 Gpc−3 and the normalized rate redshift evolution from Sun et al. 2015), adopting a beaming correction of ≈1 since observations of LL-LGRBs do not show strong evidence of collimation, suggesting wider jet opening angles (Virgili et al. 2009; Pescalli et al. 2015).
On the other hand, ρFXRT 8/9/13 is a factor of ≈1.5 higher than the estimated SGRB rate (red-filled regions; assuming ρ0, SGRBs = 13–75 yr−1 Gpc−3 from Wanderman & Piran 2015; Zhang 2018, a merger delay Gaussian model (Virgili et al. 2011; Wanderman & Piran 2015), and the normalized rate redshift evolution from Sun et al. 2015). However, some SGRBs are collimated (Burrows et al. 2006; De Pasquale et al. 2010), with typical jet aperture correction factors of ≈25 (Fong et al. 2015), although other authors claim a wider range of ≈70 ± 40 (Berger 2014). Given the large uncertainties, the rates of ρFXRT 8/9/13 and SGRBs might remain compatible.
We now consider the density rate for CDF-S XT1/FXRT 14 (ρCDF − S XT1 = (4.8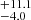 ) × 102 yr−1 Gpc−3). It remains consistent with TDEs, falls on the high side of SGRBs at z ≈ 3, and is a factor of ≈2–5 lower than LGRBs, and falls on the low side of the LL-LGRBs. Keeping in mind the uncertainty in the jet aperture correction, it is impossible to discard the association with LGRBs. On the other hand, the rates are ≈2 order of magnitude lower than those of CC-SNe.
) × 102 yr−1 Gpc−3). It remains consistent with TDEs, falls on the high side of SGRBs at z ≈ 3, and is a factor of ≈2–5 lower than LGRBs, and falls on the low side of the LL-LGRBs. Keeping in mind the uncertainty in the jet aperture correction, it is impossible to discard the association with LGRBs. On the other hand, the rates are ≈2 order of magnitude lower than those of CC-SNe.
Finally, five potential distant FXRTs (FXRTs 1, 7, 10, 11, and 12) lack redshift constraints of any kind. To constrain their contribution to the density rate, we compute upper limits assuming that they all lie in a single redshift bin of Δz ≈ 0.5. Figure 19, left panel, shows the resulting upper limits (black triangles) on the rate of these FXRTs. These limits are consistent with the density rate computed for FXRTs 8, 9, and 13, CDF-S XT1, and CDF-S XT2 (Xue et al. 2019), but are inconsistent with CC-SNe beyond z ≳ 0.5. Clearly, with firmer distance constraints on these objects, we will be able to pin down the density rates with higher precision.
6.3. Local density rate
Additionally, we extrapolate the density rates of FXRTs 8, 9, and 13 and CDF-S XT1 to the local universe (i.e., z ≈ 0) and compare them to other transients. The density rate of any transient evolves through redshift following Sun et al. (2015),
where f(z) is a function that describes the density rate evolution (normalized to z = 0) and ρ0 is the density rate at z = 0. Therefore, it is possible to determine the local density rate if f(z) is known.
We adopted ρFXRT 8/9/13 = (4.8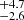 ) × 103 yr−1 Gpc−3 at zmax = 2.1, and use the average f(z) between LGRBs and SGRBs (considering the Gaussian merger delay model because of the slight overlap with our result) taken from Sun et al. (2015); there is not much difference between the relative evolutions of LGRBs and SGRBs. This yields a local density rate for FXRTs 8, 9, and 13 of
) × 103 yr−1 Gpc−3 at zmax = 2.1, and use the average f(z) between LGRBs and SGRBs (considering the Gaussian merger delay model because of the slight overlap with our result) taken from Sun et al. (2015); there is not much difference between the relative evolutions of LGRBs and SGRBs. This yields a local density rate for FXRTs 8, 9, and 13 of 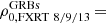 (5.8
(5.8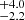 ) × 102 yr−1 Gpc−3. Meanwhile, for CDF-S XT1, we find
) × 102 yr−1 Gpc−3. Meanwhile, for CDF-S XT1, we find 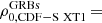 (5.4
(5.4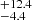 ) × 102 yr−1 Gpc−3. The range of ρFXRT 8/9/13 is also consistent with that of TDEs (see Fig. 19, left panel), and based on the density rate evolution of TDEs from Sun et al. (2015), this yields a local density rate for FXRTs 8/9/13 of
) × 102 yr−1 Gpc−3. The range of ρFXRT 8/9/13 is also consistent with that of TDEs (see Fig. 19, left panel), and based on the density rate evolution of TDEs from Sun et al. (2015), this yields a local density rate for FXRTs 8/9/13 of 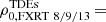 (5.9
(5.9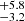 ) × 104 yr−1 Gpc−3. This value is ≈2 order of magnitude higher than the recent extended ROentgen Survey with an Imaging Telescope Array (eROSITA) average TDE volumetric rate reported by Sazonov et al. (2021) of ≈210 yr−1 Gpc−3 (at z = 0.0–0.6).
) × 104 yr−1 Gpc−3. This value is ≈2 order of magnitude higher than the recent extended ROentgen Survey with an Imaging Telescope Array (eROSITA) average TDE volumetric rate reported by Sazonov et al. (2021) of ≈210 yr−1 Gpc−3 (at z = 0.0–0.6).
The right panel in Fig. 19 shows the local density rate of FXRTs 8/9/13 assuming evolution as GRBs (cyan star), TDEs (blue star) and CDF-S XT1-like events (red square), as well as a comparison with CDF-S XT2-like events (purple square; Xue et al. 2019) and other transients. The GRB local density rates of FXRTs 8, 9, and 13 (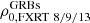 ), CDF-S XT1, and CDF-S XT2-like events remain consistent with the values observed for most flavors of GRBs (given the large uncertainties), as well as GRB 170817A and GW 170817 (green and magenta squares, respectively; Abbott et al. 2017b), BNSs (light green circle; Abbott et al. 2021c), and neutron star and BH mergers (NS–BH) (gray circle; Abbott et al. 2021b). These rates are, however, 1–3 dex below those expected for SBOs (yellow circle and square; Madau & Dickinson 2014; Novara et al. 2020), CC-SNe (magenta triangle; Madau & Dickinson 2014), and SMBH-MS TDEs (Sun et al. 2015). The difference with SMBH-MS TDEs may simply be a consequence of the f(z) assumption. Moreover, the TDE local density rate of FXRTs 8, 9, and 13 (
), CDF-S XT1, and CDF-S XT2-like events remain consistent with the values observed for most flavors of GRBs (given the large uncertainties), as well as GRB 170817A and GW 170817 (green and magenta squares, respectively; Abbott et al. 2017b), BNSs (light green circle; Abbott et al. 2021c), and neutron star and BH mergers (NS–BH) (gray circle; Abbott et al. 2021b). These rates are, however, 1–3 dex below those expected for SBOs (yellow circle and square; Madau & Dickinson 2014; Novara et al. 2020), CC-SNe (magenta triangle; Madau & Dickinson 2014), and SMBH-MS TDEs (Sun et al. 2015). The difference with SMBH-MS TDEs may simply be a consequence of the f(z) assumption. Moreover, the TDE local density rate of FXRTs 8, 9, and 13 (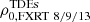 ) remains consistent with SMBH-MS TDE rates (Sun et al. 2015) but not with IMBH-WD TDEs (Tanikawa et al. 2021), likely due to the different progenitor system.
) remains consistent with SMBH-MS TDE rates (Sun et al. 2015) but not with IMBH-WD TDEs (Tanikawa et al. 2021), likely due to the different progenitor system.
6.4. Expected events in current and future missions
Taking the computed rates from Sect. 6.1, we examine the prospects for detecting FXRTs in other ongoing and future X-ray missions. The expected event rate of a new mission (called ℛNew) regarding our results using CSC2 is
where ℛNew and FNew, lim are the event rate and X-ray flux limit of the new mission, respectively. Then, the expected total number of events must be
where ΩNew and TNew are the FoV and the operational time of a new mission, respectively. It is important to realize that Eq. (12) takes into account the ratio between the new mission (FNew, lim) and Chandra (the limit imposed by our method FCSC2, lim = 1.5 × 10−13 erg cm−2 s−1) X-ray flux limits, respectively, which is a correction factor between both instruments. Given the low-count statistics, we quote estimates incorporating the Poisson 1σ errors.
Current operating observatories such as XMM-Newton, Swift–XRT, and eROSITA have sufficient sensitivity and/or history in orbit to detect similar FXRTs to those found here.
The European Photon Imaging Camera (EPIC; pn plus Metal Oxide Semi-conductor CCD arrays) on board the XMM-Newton telescope have an instantaneous FoV ≈ 0.25 deg2, flux sensitivity of ≈10−14 erg cm−2 s−1 in the energy range of 0.15–12 keV, and have an archive of roughly ≈476 Ms total exposure time during ∼20 years in orbit (mean value between pn and MOS cameras; Ehle et al. 2003). Adopting a spectral slope of Γ = 1.7, typical of FXRTs (e.g., CDF-S XT1), a correction factor to account for the contribution of background flares (assuming that 30–40% of exposure time is affected by them) and a flux cutoff of FXMM, lim ∼ 10−13 erg cm−2 s−1 (to avoid effects from Poisson noise), we predict up to ≈68–135 Case I and ≈37–68 Case II FXRTs, respectively.
Similarly, Swift–XRT has a FoV ≈ 0.15 deg2, a flux sensitivity of ≈8 × 10−14 erg cm−2 s−1 in the energy band of 0.2–10 keV, and has accumulated ≈ 315.4 Ms of archival data over ∼14 years operational time (Hill et al. 2000; Burrows et al. 2003). Adopting a flux limit of FXRT, lim ∼ 8 × 10−13 erg cm−2 s−1 (again, to avoid Poisson noise effects), the expected number of FXRTs are ≈27–55 Case I and ≈15–27 Case II events.
The above implies that there should be a substantial number of FXRTs hidden within the XMM-Newton and Swift–XRT archives and catalogs. The X-ray transient and variable sky (EXTraS) project (De Luca et al. 2021) and systematic searches such as Alp & Larsson (2020) have reported 136 and a dozen candidates to date, respectively, which presents a lower bound to the total numbers estimated above. Also, in the systematic search developed by the EPIC-pn XMM-Newton Outburst Detector (EXOD) search project (Pastor-Marazuela et al. 2020), 2536 potential XRTs have been identified, but this large number is dominated by stellar flares, cataclysmic variables, type I X-ray bursts, supergiant FXRTs, SBOs, AGNs, and more.
Finally, the Spectrum-Roentgen-Gamma (SRG)–eROSITA mission, launched in July 2019, is scanning the entire sky in the X-ray band (0.2–10 keV) with a FoV ≈ 0.833 deg2 during SRG–eROSITA’s official 4-year survey phase. This should provide roughly equivalent coverage in sky area per time to the current XMM-Newton archive. The SRG–eROSITA all sky survey is expected to yield flux limits of ≈10−14 and ≈10−13 erg cm−2 s−1 in the 0.5–2 and 2–10 keV energy bands, respectively. Avoiding Poisson noise effects as above, we adopt an SRG–eROSITA 0.5–2 keV flux limit for FXRTs of FeROSITA, lim ≈ 10−13 erg cm−2 s−1. Thus, during the 4-year survey, the expected number of FXRTs detected by SRG–eROSITA (in the 0.5–2 keV band) should be ≈50–100 and 27–50 events for Case I and Case II, respectively.
Concerning future missions, the Advanced Telescope for High ENergy Astrophysics (Athena) has been selected by European Space Agency to characterize the hot and energetic universe, with an anticipated launch in the mid 2030s. It is projected to have an effective area of 0.25–2.0 m2, energy range of 0.3–12 keV, and a nominal lifetime of five years, although consumables (such as fuel) have been rated for 10 years in the case of a mission extension (Nandra et al. 2013; Barret et al. 2013). The Wide Field Imager (WFI) is one of two detectors on board Athena, with a spectral resolution of ΔE < 170 eV at 7 keV, spatial resolution of ≤10 arcsec PSF on-axis), and FoV of 0.44 deg2 (Rau et al. 2016). To estimate the number of extragalactic FXRTs, we conservatively assume a flux threshold 10 times higher than the nominal 60 ks (longer than the expected duration of the FXRTs) flux limit due to Poisson fluctuations of FWFI, lim ≈ 10−15 erg cm−2 s−1 (where the point source detection limit is ≈10−16 erg cm−2 s−1 for the WFI deep fields). This flux limit is a factor of 100 deeper than the SRG–eROSITA sky survey flux limit. Thus, during a ≈4 year mission, adopting γ = 0.5 for the faint-end slope extrapolation the expected number of FXRTs detected by Athena will ≈130–270 and 72–130 events for Case I and Case II, respectively. This sample size of bright and fainter events can be used to probe the multiwavelength properties with coordinated campaigns. Assuming that the WFI observations will be spread evenly during the mission and that those observations will also be performed during the Athena ground contact, approximately one-sixth of the events (≈9 and 16) could have Athena alerts with latencies < 4 h.
We also consider the Einstein Probe (EP), which aims to monitor high-energy transient and variable phenomena in 0.5–4.0 keV band (Yuan et al. 2015, 2017). The EP is scheduled for launch by the end of 2023, with a 3-year operational lifetime and 5-year goal (Yuan et al. 2017). EP will carry two scientific instruments, the Wide-field X-ray Telescope (WXT) with a large instantaneous FoV of 3600 deg2 and a narrow-field Follow-up X-ray Telescope, as well as a fast alert downlink system (Yuan et al. 2015). To estimate the expected number of FXRTs, we consider just the WXT instrument, which has a threshold sensitivity of FWXT ≈ 5 × 10−11 erg cm−2 s−1 at 1 ks, that is, ≈500 times higher than our flux limit and γ ≈ 1.0.
Thus, during the ≈3 year mission, the expected number of FXRTs detected by EP should be ≈69–138 and 38–69 events for Case I and Case II, respectively.
7. Conclusions and future work
In this work we search for extragalactic FXRTs hidden in CSC2. We have applied a modified version of the algorithm developed by Yang et al. (2019) to 214,701 X-ray sources identified in the CSC2 with |b|> 10 deg (i.e., 5303 Chandra observations, totaling ≈169.6 Ms and 592 deg2). Considering additional criteria (analyzing further X-ray observations taken by Chandra, XMM-Newton, Swift–XRT, Einstein, and ROSAT) and other astronomical catalogs (Gaia, NED, SIMBAD, VHS, DES, Pan-STARRS, and others), we identify 14 FXRTs that remain consistent with an extragalactic origin. We rediscover all (five) previously reported Chandra events covered by CSC2: XRT 000519 (previously identified by Jonker et al. 2013), XRT 110103 (previously identified by Glennie et al. 2015), XRT 030511 and XRT 110919 (previously identified by Lin et al. 2019, 2022), and XRT 141001/CDF-S XT1 (previously identified by Bauer et al. 2017).
Candidates have peak 0.5–7 keV fluxes between ≈1.0 × 10−13 and 2 × 10−10 erg cm−2 s−1 and T90 values from ≈4 to 40 ks. None of the FXRTs are detected in gamma rays near the time of the detection of the transient X-ray light. Based on multiwavelength constraints, we rule out a Galactic origin (e.g., as Galactic M or brown-dwarf stellar flares) in all but two cases (for these, existing data cannot yet rule out extreme stellar X-ray flares). The origin of the extragalactic FXRT sample appears to be diverse: five events are robustly associated with local galaxies (≲100 Mpc; called the local sample); seven are likely distant events (≳100 Mpc; called the distant sample); and two events, XRT 000519 and XRT 110103, have nearby associations that remain somewhat ambiguous. Among the distant FXRTs, we identify hosts for four FXRTs, which span a wide range of magnitudes (mi ≈ 20.6–27.0 AB mag), while we can only place upper limits on five FXRTs.
We have studied the spectral and timing properties of the FXRTs. The X-ray spectra can be well fitted by PLs with a median slope of Γ = 2.5 and an overall range Γ ≈ 1.7–4.0. Furthermore, we observe potential spectral softening for six FXRTs with time (for XRT 000519 and XRT 110103, the softening is highly significant and occurs during the main flare; Glennie et al. 2015. In the case of timing properties, five FXRTs show plateaus in their X-ray light curves, similar to CDF-S XT2 (Xue et al. 2019), with durations of ∼2–10 ks followed by PL decays with slopes ranging from ∼1.2 to 2.6. For three FXRTs we see, simultaneously with the plateau and decay, possible spectral softening (at 90% confidence), similar to CDF-S XT2 (Xue et al. 2019).
The five local FXRTs have projected physical offsets between ≈0.7 and 9.4 kpc, with four being co-spatial with apparent star-forming regions or young star clusters. Adopting their host distances, these local events have peak isotropic X-ray luminosities of LX, peak ≈ 1038–1040 erg s−1, well below expectations for GRBs, TDEs, XRFs, and supernova SBOs. Such luminosities are comparable to those of ULXs and Galactic XRBs, although the durations and time variability properties of the local FXRTs are quite distinct. As such, we speculate that several may represent a new type of X-ray phenomenon related to massive stars.
Among the distant FXRT sample, two are associated with relatively bright optical and NIR extended sources, allowing us to derive galaxy properties using photometric archival data. The other two host associations are very faint extended sources; one is detected only in a single band, and hence lacks physical constraints, while the other is fortuitously observed by the HST but has only weak constraints on its properties. Both bright hosts have similar redshifts (zphot ≈ 0.5–0.7) and stellar masses (M* ≈ 3 × 1010 M⊙), but starkly different SFRs (SFR ≈ 0.5 vs. ≈125 M⊙ yr−1), and the faint HST host has an uncertain redshift (zphot ≈ 0.4–3.2) and associated host properties (Bauer et al. 2017). Adopting  0.7 for all four events, the peak luminosities, energetics, and spectro-temporal properties robustly rule out an SBO origin but potentially remain consistent with origins as on-axis GRBs, and even off-axis GRBs in the tail of the X-ray afterglow, or TDEs involving an IMBH and a WD.
0.7 for all four events, the peak luminosities, energetics, and spectro-temporal properties robustly rule out an SBO origin but potentially remain consistent with origins as on-axis GRBs, and even off-axis GRBs in the tail of the X-ray afterglow, or TDEs involving an IMBH and a WD.
For the three FXRTs that lack optical and NIR host detections, interpretations are broader. An association with SBOs remains possible at low redshifts (z ≲ 0.5), as long as potential hosts are low-mass, low-SFR dwarf galaxies. An on-axis GRB scenario remains possible for z ≳ 1.0 and naturally explains the non-detection of faint host galaxies by existing optical and NIR facilities. An off-axis GRB afterglow scenario is also viable, except perhaps for very low redshifts (z ≲ 0.1), where the lack of any association with a host becomes problematic. Finally, a TDE scenario remains possible across a broad redshift range, although the lack of a detectable host requires strong beaming, for instance, similar to Swift J1644+57.
Finally, we compute the event rates of local (Case I) and distant (Case II) FXRTs of ℛCase I = 53.7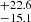 and ℛCase II = 28.2
and ℛCase II = 28.2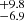 deg−2 yr−1, respectively. Additionally, for three distant FXRTs (assuming
deg−2 yr−1, respectively. Additionally, for three distant FXRTs (assuming 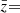 0.7), we derive a volumetric rate (in units of yr−1 Gpc−3) of ρFXRT 8/9/13 = (4.8
0.7), we derive a volumetric rate (in units of yr−1 Gpc−3) of ρFXRT 8/9/13 = (4.8 ) × 103 yr−1 Gpc−3 at zmax = 2.1. This value is in good agreement with the value derived by Xue et al. (2019) at a similar redshift (zmax = 1.9), as well as with other transient classes such as LGRBs, SGRBs, and TDEs. Nevertheless, this rate is ≈2 order of magnitude lower than that of CC-SNe.
) × 103 yr−1 Gpc−3 at zmax = 2.1. This value is in good agreement with the value derived by Xue et al. (2019) at a similar redshift (zmax = 1.9), as well as with other transient classes such as LGRBs, SGRBs, and TDEs. Nevertheless, this rate is ≈2 order of magnitude lower than that of CC-SNe.
Our investigation of 14 Chandra-detected extragalactic FXRT candidates breaks new ground in terms of characterizing their diverse properties and nature, although the lack of firm distances and host properties for the distant subset clearly leaves much to speculation. The Chandra sample provides the most accurate positions among existing X-ray missions, which is critical for pinpointing potential host galaxies and potential physical offsets. Given the low numbers of distant FXRTs (both found here and predicted in other archives) and the diverse range of host redshifts and properties, it will be critical to identify and follow up their associated host galaxies with dedicated spectroscopy and/or deep multiwavelength imaging in order to place extragalactic FXRTs in a proper physical and cosmological context. The contemporaneous multiwavelength nature of FXRTs remains completely unknown. Given the short duration of these events, progress here will crucially hinge upon the ability of current and future X-ray observatories to carry out efficient strategies for (onboard) detection and alert generation to trigger follow-up campaigns while the FXRTs are still active in X-rays and, presumably, at other wavelengths. The launch of narrow- and wide-field observatories such as Athena and EP should provide a watershed moment for expanding samples.
As future work, we plan to characterize this new sample of FXRTs using recent optical and NIR observations to catch their host galaxies and thus constraint their energetics. Also, we plan to extend our search to Chandra data not considered in the CSC2 to identify new FXRTs and thus better understand their elusive nature.
The most favored model for XRT 080109/SN 2008D is a breakout from a wind (regarding the breakout from the stellar surface), which changes the expected X-ray luminosity (e.g., Balberg & Loeb 2011).
BIC = − 2lnℒ + klnN, where ℒ is the maximum value of the data likelihood, k is the number of model parameters, and N is the number of data points (Ivezić et al. 2014).
It is important to note that the light curve parameters (slopes and break time) can change considering different zero points, especially for FXRTs with high background levels and/or high offset angles. For instance, in Bauer et al. (2017) and Xue et al. (2019), the zero point is arbitrarily set to be 10 seconds before the arrival of the first photon. This is consistent with our method and does not change interpretations because of the low background level of both observations.
To compute the ratio log(LX/Lbol), we normalize stellar synthetic models of dwarf stars (taken from Phillips et al. 2020, 1000 ≲ Teff ≲ 3000 K and 2.5 ≲ log g ≲ 5.5) to the deepest photometric upper limits and/or detections (as listed in Table 3), and compute bolometric fluxes by integrating the normalized models at optical/NIR wavelengths.
Due to the lack of a standardized method to estimate the Fpeak, we consider the following. First, we find the shortest time interval during which 25% of the counts are detected, and we compute a count rate during this shortest interval. Next, to convert the peak-count rates to fluxes, we multiply the flux from the time-averaged Spectral fits by the ratio between the peak and the time-averaged count rates (i.e., we assume no spectral evolution).
Acknowledgments
We acknowledge support from: ANID grants Programa de Capital Humano Avanzado folio #21180886 (J.Q–V), CATA-Basal AFB-170002 (J.Q–V, F.E.B.), FONDECYT Regular 1190818 (J.Q–V, F.E.B.), 1200495 (J.Q–V, F.E.B.) and Millennium Science Initiative ICN12_009 (J.Q–V, F.E.B.); NSF grant AST-2106990 and Chandra X-ray Center grant GO0-21080X (W.N.B.); the National Natural Science Foundation of China grant 11991053 (B.L.); support from NSFC grants 12025303 and 11890693 (Y.Q.X.); support from the George P. and Cynthia Woods Mitchell Institute for Fundamental Physics and Astronomy at Texas A&M University, from the National Science Foundation through grants AST-1614668 and AST-2009442, and from the NASA/ESA/CSA James Webb Space Telescope through the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-03127 (G.Y.). The scientific results reported in this article are based on observations made by the Chandra X-ray Observatory. This research has made use of software provided by the Chandra X-ray Center (CXC). This research uses services or data provided by the Astro Data Lab at NSF’s National Optical-Infrared Astronomy Research Laboratory. NOIRLab is operated by the Association of Universities for Research in Astronomy (AURA), Inc. under a cooperative agreement with the National Science Foundation.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017a, ApJ, 848, L12 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017b, ApJ, 848, L13 [CrossRef] [Google Scholar]
- Abbott, T. M. C., Adamów, M., Aguena, M., et al. 2021a, ApJS, 255, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, R., Abbott, T. D., Abraham, S., et al. 2021b, ApJ, 915, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, R., Abbott, T. D., Abraham, S., et al. 2021c, Phys. Rev. X, 11 [Google Scholar]
- Ahumada, R., Prieto, C. A., Almeida, A., et al. 2020, ApJS, 249, 3 [Google Scholar]
- Ajello, M., Arimoto, M., Axelsson, M., et al. 2019, ApJ, 878, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Alp, D., & Larsson, J. 2020, ApJ, 896, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Aptekar, R., Frederiks, D., Golenetskii, S., et al. 2001, ApJS, 137, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Arabsalmani, M., Roychowdhury, S., Starkenburg, T. K., et al. 2019, MNRAS, 485, 5411 [NASA ADS] [CrossRef] [Google Scholar]
- Arefiev, V. A., Priedhorsky, W. C., & Borozdin, K. N. 2003, ApJ, 586, 1238 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, in XSPEC: The First Ten Years, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Avenhaus, H., Schmid, H. M., & Meyer, M. R. 2012, A&A, 548, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bachetti, M., Harrison, F. A., Walton, D. J., et al. 2014, Nature, 514, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Balberg, S., & Loeb, A. 2011, MNRAS, 414, 1715 [NASA ADS] [CrossRef] [Google Scholar]
- Barack, L., Cardoso, V., Nissanke, S., et al. 2019, Classical Quantum Gravity, 36, 143001 [NASA ADS] [CrossRef] [Google Scholar]
- Barniol Duran, R., Nakar, E., Piran, T., & Sari, R. 2015, MNRAS, 448, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Barret, D., Nandra, K., Barcons, X., et al. 2013, in SF2A-2013: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. L. Cambresy, F. Martins, E. Nuss, & A. Palacios, 447 [Google Scholar]
- Barthelmy, S. D., Chincarini, G., Burrows, D. N., et al. 2005, Nature, 438, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Bauer, F. E., Treister, E., Schawinski, K., et al. 2017, MNRAS, 467, 4841 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E. 2006, ApJ, 648, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E. 2014, ARA&A, 52, 43 [CrossRef] [Google Scholar]
- Bernardini, M. G., Margutti, R., Mao, J., Zaninoni, E., & Chincarini, G. 2012, A&A, 539, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Meidt, S., Schinnerer, E., Paladino, R., & Leroy, A. 2017, A&A, 597, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, L., Herald, J., Efremova, B., et al. 2011, Ap&SS, 335, 161 [Google Scholar]
- Bloom, J. S., Kulkarni, S. R., & Djorgovski, S. G. 2002, AJ, 123, 1111 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, J. S., Giannios, D., Metzger, B. D., et al. 2011, Science, 333, 203 [CrossRef] [PubMed] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [Google Scholar]
- Bromberg, O., Nakar, E., Piran, T., & Sari, R. 2012, ApJ, 749, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A&A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2003, AIP Conf. Proc., 662, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, D. N., Grupe, D., Capalbi, M., et al. 2006, ApJ, 653, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Buta, R. J., Sheth, K., Athanassoula, E., et al. 2015, ApJS, 217, 32 [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Mangano, V., Blustin, A. J., et al. 2006, Nature, 442, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Lodato, G., D’Avanzo, P., et al. 2011, Nature, 480, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Emsellem, E., Krajnović, D., et al. 2011, MNRAS, 413, 813 [Google Scholar]
- Carnall, A. C., McLure, R. J., Dunlop, J. S., & Davé, R. 2018, MNRAS, 480, 4379 [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [Google Scholar]
- Chang, Y.-Y., van der Wel, A., da Cunha, E., & Rix, H.-W. 2015, ApJS, 219, 8 [Google Scholar]
- Chincarini, G., Mao, J., Margutti, R., et al. 2010, MNRAS, 406, 2113 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [Google Scholar]
- Christensen, L., Vreeswijk, P. M., Sollerman, J., et al. 2008, A&A, 490, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colbert, E. J. M., & Mushotzky, R. F. 1999, ApJ, 519, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Colgate, S. A., & Petschek, A. G. 1981, ApJ, 248, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Connaughton, V., Briggs, M. S., Goldstein, A., et al. 2015, ApJS, 216, 32 [Google Scholar]
- Crnojević, D., Sand, D. J., Spekkens, K., et al. 2016, ApJ, 823, 19 [Google Scholar]
- Dado, S., & Dar, A. 2019, ApJ, 884, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, L., McKinney, J. C., Roth, N., Ramirez-Ruiz, E., & Miller, M. C. 2018, ApJ, 859, L20 [Google Scholar]
- Dálya, G., Galgóczi, G., Dobos, L., et al. 2018, MNRAS, 479, 2374 [Google Scholar]
- Dark Energy Survey Collaboration (Abbott, T., et al.) 2016, MNRAS, 460, 1270 [Google Scholar]
- D’Avanzo, P., Campana, S., Salafia, O. S., et al. 2018, A&A, 613, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davis, T. A., Young, L. M., Crocker, A. F., et al. 2014, MNRAS, 444, 3427 [NASA ADS] [CrossRef] [Google Scholar]
- De Luca, A., Stelzer, B., Burgasser, A. J., et al. 2020, A&A, 634, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Luca, A., Salvaterra, R., Belfiore, A., et al. 2021, A&A, 650, A167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Pasquale, M., Schady, P., Kuin, N. P. M., et al. 2010, ApJ, 709, L146 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A. 2016, ApJS, 222, 8 [Google Scholar]
- Drozdovsky, I. O., & Karachentsev, I. D. 2000, A&AS, 142, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dye, S., Lawrence, A., Read, M. A., et al. 2018, MNRAS, 473, 5113 [Google Scholar]
- Eappachen, D., Jonker, P. G., Fraser, M., et al. 2022, MNRAS, 514, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Ehle, M., Breitfellner, M., Dahlem, M., et al. 2003, XMM-Newton Users Handbook, 2, 2003 [Google Scholar]
- Ensman, L., & Burrows, A. 1992, ApJ, 393, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Espada, D., Verley, S., Miura, R. E., et al. 2019, ApJ, 887, 88 [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2007, A&A, 469, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [Google Scholar]
- Evans, I. N., Primini, F. A., Glotfelty, K. J., et al. 2010, ApJS, 189, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Osborne, J. P., Beardmore, A. P., et al. 2014, ApJS, 210, 8 [Google Scholar]
- Evans, I. N., Allen, C., Anderson, C. S., et al. 2019, AAS/High Energy Astrophys. Div., 17, 114.01 [Google Scholar]
- Evans, I. N., Primini, F. A., Miller, J. B., et al. 2020a, Am. Astron. Soc. Meeting Abstracts, 235, 154.05. [NASA ADS] [Google Scholar]
- Evans, P. A., Page, K. L., Osborne, J. P., et al. 2020b, ApJS, 247, 54 [Google Scholar]
- Fasano, G., & Franceschini, A. 1987, MNRAS, 225, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Feroci, M., Hurley, K., Duncan, R. C., & Thompson, C. 2001, ApJ, 549, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., & Hobson, M. P. 2008, MNRAS, 384, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [Google Scholar]
- Flewelling, H. 2018, Am. Astron. Soc. Meeting Abstracts, 231, 436.01 [NASA ADS] [Google Scholar]
- Flewelling, H. A., Magnier, E. A., Chambers, K. C., et al. 2020, ApJS, 251, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Fong, W., Berger, E., Margutti, R., & Zauderer, B. A. 2015, ApJ, 815, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Frail, D. A., Kulkarni, S. R., Sari, R., et al. 2001, ApJ, 562, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galbany, L., Stanishev, V., Mourão, A. M., et al. 2014, A&A, 572, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Alvarez, D., Drake, J. J., Kashyap, V. L., Lin, L., & Ball, B. 2008, ApJ, 679, 1509 [CrossRef] [Google Scholar]
- Gendre, B., Stratta, G., Atteia, J. L., et al. 2013, ApJ, 766, 30 [Google Scholar]
- Glennie, A., Jonker, P. G., Fender, R. P., Nagayama, T., & Pretorius, M. L. 2015, MNRAS, 450, 3765 [NASA ADS] [CrossRef] [Google Scholar]
- Göğüş, E., Woods, P. M., Kouveliotou, C., et al. 1999, ApJ, 526, L93 [CrossRef] [Google Scholar]
- González-Fernández, C., Hodgkin, S. T., Irwin, M. J., et al. 2018, MNRAS, 474, 5459 [Google Scholar]
- Granot, J., Panaitescu, A., Kumar, P., & Woosley, S. E. 2002, ApJ, 570, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J., De Colle, F., & Ramirez-Ruiz, E. 2018a, MNRAS, 481, 2711 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J., Gill, R., Guetta, D., & De Colle, F. 2018b, MNRAS, 481, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Güdel, M., & Nazé, Y. 2009, A&A Rv., 17, 309 [Google Scholar]
- Guetta, D., Piran, T., & Waxman, E. 2005, ApJ, 619, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Ferguson, H. C., Giavalisco, M., et al. 2013, ApJS, 207, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Hajela, A., Margutti, R., Bright, J. S., et al. 2022, ApJ, 927, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, S. L., Covey, K. R., Knapp, G. R., et al. 2002, AJ, 123, 3409 [NASA ADS] [CrossRef] [Google Scholar]
- Heida, M., Jonker, P. G., Torres, M. A. P., & Chiavassa, A. 2017, ApJ, 846, 132 [Google Scholar]
- Helou, G., Madore, B. F., Schmitz, M., et al. 1991, in The NASA/IPAC Extragalactic Database, eds. M. A. Albrecht, & D. Egret, Astrophys. Space Sci. Library, 171, 89 [NASA ADS] [Google Scholar]
- Hewett, P. C., Warren, S. J., Leggett, S. K., & Hodgkin, S. T. 2006, MNRAS, 367, 454 [Google Scholar]
- Hickox, R. C., & Markevitch, M. 2006, ApJ, 645, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, J. E., Zugger, M. E., Shoemaker, J., et al. 2000, in X-Ray and Gamma-Ray Instrumentation for Astronomy XI, Int. Soc. Opt. Photonics, 4140, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Hjorth, J., & Bloom, J. S. 2012, The Gamma-Ray Burst - Supernova Connection, 169 [CrossRef] [Google Scholar]
- Ho, A. Y. Q., Kulkarni, S. R., Perley, D. A., et al. 2020, ApJ, 902, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, K., Atteia, J. L., Barraud, C., et al. 2011, ApJS, 197, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, K., Cline, T., Mazets, E., et al. 1999, Nature, 397, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Ide, S., Hayashida, K., Noda, H., et al. 2020, PASJ, 72, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Im, M., Yoon, Y., Lee, S.-K. J., et al. 2017, ApJ, 849, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J. A., Maksym, W. P., Sivakoff, G. R., et al. 2016, Nature, 538, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Ishak, B. 2017, Contemp. Phys., 58, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, G. L., Belloni, T., Stella, L., et al. 2005, ApJ, 628, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Connolly, A. J., VanderPlas, J. T., & Gray, A. 2014, in Statistics, DataMining, and Machine Learning in Astronomy (Princeton University Press) [CrossRef] [Google Scholar]
- Izzo, L., Auchettl, K., Hjorth, J., et al. 2020, A&A, 639, L11 [EDP Sciences] [Google Scholar]
- Johnstone, R. M., Fabian, A. C., Morris, R. G., & Taylor, G. B. 2005, MNRAS, 356, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Jonker, P. G., Heida, M., Torres, M. A. P., et al. 2012a, ApJ, 758, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Jonker, P. G., Miller-Jones, J. C. A., Homan, J., et al. 2012b, MNRAS, 423, 3308 [NASA ADS] [CrossRef] [Google Scholar]
- Jonker, P. G., Glennie, A., Heida, M., et al. 2013, ApJ, 779, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaret, P., Simet, M. G., & Lang, C. C. 2006, ApJ, 646, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaret, P., Feng, H., & Roberts, T. P. 2017, ARA&A, 55, 303 [Google Scholar]
- Kaastra, J. S. 2017, A&A, 605, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., & Haud, U. 2015, A&A, 578, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kolmogorov, A. 1933, in Inst. Ital. Attuari Giorn., 4, 83 [Google Scholar]
- Kraft, R. P., Burrows, D. N., & Nousek, J. A. 1991, ApJ, 374, 344 [Google Scholar]
- Krishnamoorthy, K., & Thomson, J. 2004, J. Stat. Planning Inference, 119, 23 [CrossRef] [Google Scholar]
- Krühler, T., Kuncarayakti, H., Schady, P., et al. 2017, A&A, 602, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamb, G. P., Fernández, J. J., Hayes, F., et al. 2021, Universe, 7, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Lanz, L., Zezas, A., Brassington, N., et al. 2013, ApJ, 768, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Levan, A. J., Tanvir, N. R., Cenko, S. B., et al. 2011, Science, 333, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Levan, A. J., Tanvir, N. R., Starling, R. L. C., et al. 2014, ApJ, 781, 13 [Google Scholar]
- Levesque, E. M. 2014, PASP, 126, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y., Zhang, B., & Lü, H.-J. 2016, ApJS, 227, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L., Wu, X.-F., Lei, W.-H., et al. 2018, ApJS, 236, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D., Webb, N. A., & Barret, D. 2012, ApJ, 756, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D., Strader, J., Carrasco, E. R., et al. 2018, Nat. Astron., 2, 656 [Google Scholar]
- Lin, D., Irwin, J., & Berger, E. 2019, ATel., 13171, 1 [NASA ADS] [Google Scholar]
- Lin, D., Strader, J., Romanowsky, A. J., et al. 2020, ApJ, 892, L25 [Google Scholar]
- Lin, D., Irwin, J. A., & Berger, E. 2021, ATel., 14599, 1 [NASA ADS] [Google Scholar]
- Lin, D., Irwin, J. A., Berger, E., & Nguyen, R. 2022, ApJ, 927, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, J. 2011, ApJS, 192, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Lopes de Oliveira, R., Motch, C., Smith, M. A., Negueruela, I., & Torrejón, J. M. 2007, A&A, 474, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lü, H.-J., Zhang, B., Lei, W.-H., Li, Y., & Lasky, P. D. 2015, ApJ, 805, 89 [CrossRef] [Google Scholar]
- Lü, H. J., Yuan, Y., Lan, L., et al. 2019, Res. Astron. Astrophys., accepted [arXiv:1904.06664] [Google Scholar]
- Luo, B., Brandt, N., & Bauer, F. 2014, ATel., 6541, 1 [NASA ADS] [Google Scholar]
- Luo, B., Brandt, W. N., Xue, Y. Q., et al. 2017, ApJS, 228, 2 [Google Scholar]
- Lyons, N., O’Brien, P. T., Zhang, B., et al. 2010, MNRAS, 402, 705 [NASA ADS] [CrossRef] [Google Scholar]
- MacLeod, M., Goldstein, J., Ramirez-Ruiz, E., Guillochon, J., & Samsing, J. 2014, ApJ, 794, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [Google Scholar]
- Maguire, K., Eracleous, M., Jonker, P. G., MacLeod, M., & Rosswog, S. 2020, Space Sci. Rev., 216, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Malyali, A., Rau, A., & Nandra, K. 2019, MNRAS, 489, 5413 [NASA ADS] [CrossRef] [Google Scholar]
- Margutti, R., & Chornock, R. 2021, ARA&A, 59, 43 [Google Scholar]
- Margutti, R., Bernardini, G., Barniol Duran, R., et al. 2011, MNRAS, 410, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Marocco, F., Eisenhardt, P. R. M., Fowler, J. W., et al. 2021, ApJS, 253, 8 [Google Scholar]
- Massey, F. J., Jr 1951, J. Am. stat. Assoc., 46, 68 [CrossRef] [Google Scholar]
- Mata Sánchez, D., Muñoz-Darias, T., Casares, J., Corral-Santana, J. M., & Shahbaz, T. 2015, MNRAS, 454, 2199 [CrossRef] [Google Scholar]
- Matzner, C. D., & McKee, C. F. 1999, ApJ, 510, 379 [Google Scholar]
- Mazets, E. P., Cline, T. L., Aptekar’, R. L., et al. 1999, Astron. Lett., 25, 635 [Google Scholar]
- Mazzali, P. A., Valenti, S., Della Valle, M., et al. 2008, Science, 321, 1185 [NASA ADS] [CrossRef] [Google Scholar]
- McMahon, R. G., Banerji, M., Gonzalez, E., et al. 2013, The Messenger, 154, 35 [NASA ADS] [Google Scholar]
- Michałowski, M. J., Hunt, L. K., Palazzi, E., et al. 2014, A&A, 562, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mineo, S., Gilfanov, M., & Sunyaev, R. 2012, MNRAS, 419, 2095 [Google Scholar]
- Miniutti, G., Saxton, R. D., Giustini, M., et al. 2019, Nature, 573, 381 [Google Scholar]
- Mitra-Kraev, U., Harra, L. K., Güdel, M., et al. 2005, A&A, 431, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Modjaz, M., Li, W., Butler, N., et al. 2009, ApJ, 702, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., Coil, A. L., Aird, J., et al. 2013, ApJ, 767, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Nakar, E. 2020, Phys. Rep., 886, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Nakar, E., & Sari, R. 2010, ApJ, 725, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Nakar, E., & Sari, R. 2012, ApJ, 747, 88 [CrossRef] [Google Scholar]
- Nandra, K., Barret, D., & Barcons, X. 2013, ArXiv e-prints [arXiv:1306.2307] [Google Scholar]
- Narayana Bhat, P., Meegan, C. A., von Kienlin, A., et al. 2016, ApJS, 223, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Nidever, D. L., Dey, A., Fasbender, K., et al. 2021, AJ, 161, 192 [Google Scholar]
- Novara, G., Esposito, P., Tiengo, A., et al. 2020, ApJ, 898, 37 [Google Scholar]
- Nynka, M., Ruan, J. J., Haggard, D., & Evans, P. A. 2018, ApJ, 862, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Ochsenbein, F., Bauer, P., & Marcout, J. 2000, A&AS, 143, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pallavicini, R., Tagliaferri, G., & Stella, L. 1990, A&A, 228, 403 [NASA ADS] [Google Scholar]
- Palmer, D. M., Barthelmy, S., Gehrels, N., et al. 2005, Nature, 434, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Pandey, J. C., & Singh, K. P. 2008, MNRAS, 387, 1627 [NASA ADS] [CrossRef] [Google Scholar]
- Park, T., Kashyap, V. L., Siemiginowska, A., et al. 2006, ApJ, 652, 610 [Google Scholar]
- Pastor-Marazuela, I., Webb, N. A., Wojtowicz, D. T., & van Leeuwen, J. 2020, A&A, 640, A124 [EDP Sciences] [Google Scholar]
- Peacock, J. A. 1983, MNRAS, 202, 615 [NASA ADS] [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [Google Scholar]
- Peng, Z.-K., Yang, Y.-S., Shen, R.-F., et al. 2019, ApJ, 884, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Peretz, U., & Behar, E. 2018, MNRAS, 481, 3563 [NASA ADS] [CrossRef] [Google Scholar]
- Pescalli, A., Ghirlanda, G., Salafia, O. S., et al. 2015, MNRAS, 447, 1911 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. W., Tremblin, P., Baraffe, I., et al. 2020, A&A, 637, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piran, T. 2004, Rev. Mod. Phys., 76, 1143 [Google Scholar]
- Pradhan, P., Falcone, A. D., Kennea, J. A., & Burrows, D. N. 2020, J. Astron. Telescopes Instruments Syst., 6, 038002 [NASA ADS] [Google Scholar]
- Pye, J. P., Rosen, S., Fyfe, D., & Schröder, A. C. 2015, A&A, 581, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Racusin, J. L., Liang, E. W., Burrows, D. N., et al. 2009, ApJ, 698, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Rau, A., Kienlin, A. V., Hurley, K., & Lichti, G. G. 2005, A&A, 438, 1175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rau, A., Nandra, K., Aird, J., et al. 2016, in Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray, eds. J. W. A. den Herder, T. Takahashi, & M. Bautz, SPIE Conf. Ser., 9905, 99052B [Google Scholar]
- Rees, M. J. 1988, Nature, 333, 523 [Google Scholar]
- Reines, A. E., Greene, J. E., & Geha, M. 2013, ApJ, 775, 116 [Google Scholar]
- Rejkuba, M., Harris, W. E., Greggio, L., & Harris, G. L. H. 2011, A&A, 526, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [Google Scholar]
- Rhode, K. L., Zepf, S. E., Kundu, A., & Larner, A. N. 2007, AJ, 134, 1403 [NASA ADS] [CrossRef] [Google Scholar]
- Robrade, J., Poppenhaeger, K., & Schmitt, J. H. M. M. 2010, A&A, 513, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosen, S. R., Webb, N. A., Watson, M. G., et al. 2016, A&A, 590, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rots, A. H., & Budavári, T. 2011, ApJS, 192, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Rowlinson, A., O’Brien, P. T., Metzger, B. D., Tanvir, N. R., & Levan, A. J. 2013, MNRAS, 430, 1061 [NASA ADS] [CrossRef] [Google Scholar]
- Rowlinson, A., O’Brien, P. T., Tanvir, N. R., et al. 2010, MNRAS, 409, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, T., Barthelmy, S. D., Barbier, L., et al. 2008, ApJS, 175, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Sapir, N., Katz, B., & Waxman, E. 2013, ApJ, 774, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Sarin, N., Ashton, G., Lasky, P. D., et al. 2021, ApjL, submitted [arXiv:2105.10108] [Google Scholar]
- Saxton, R. D., Read, A. M., Esquej, P., et al. 2008, A&A, 480, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saxton, R., Komossa, S., Auchettl, K., & Jonker, P. G. 2021, Space Sci. Rev., 217, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Sazonov, S., & Khabibullin, I. 2017, MNRAS, 466, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Sazonov, S., Gilfanov, M., Medvedev, P., et al. 2021, MNRAS, 508, 3820 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Schlafly, E. F., Meisner, A. M., & Green, G. M. 2019, ApJS, 240, 30 [Google Scholar]
- Schmitt, J. H. M. M., & Liefke, C. 2004, A&A, 417, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sivakoff, G. R., Sarazin, C. L., & Jordán, A. 2005, ApJ, 624, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Soderberg, A. M., Berger, E., Page, K. L., et al. 2008, Nature, 454, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Sorce, J. G., Tully, R. B., Courtois, H. M., et al. 2014, MNRAS, 444, 527 [Google Scholar]
- Starling, R. L. C., Wiersema, K., Levan, A. J., et al. 2011, MNRAS, 411, 2792 [NASA ADS] [CrossRef] [Google Scholar]
- Stiele, H., Muñoz-Darias, T., Motta, S., & Belloni, T. M. 2012, MNRAS, 422, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Stratta, G., Gendre, B., Atteia, J. L., et al. 2013, ApJ, 779, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T. E., & Watts, A. L. 2005, ApJ, 632, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, H., Zhang, B., & Li, Z. 2015, ApJ, 812, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, H., Li, Y., Zhang, B.-B., et al. 2019, ApJ, 886, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Swartz, D. A., Soria, R., Tennant, A. F., & Yukita, M. 2011, ApJ, 741, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Taggart, K., & Perley, D. A. 2021, MNRAS, 503, 3931 [NASA ADS] [CrossRef] [Google Scholar]
- Tamba, T., Bamba, A., Odaka, H., & Enoto, T. 2019, PASJ, 71, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Tananbaum, H., Weisskopf, M., Tucker, W., Wilkes, B., & Edmonds, P. 2014, Rep. Prog. Phys., 77, 066902 [NASA ADS] [CrossRef] [Google Scholar]
- Tanikawa, A., Giersz, M., & Arca Sedda, M. 2021, MNRAS, submitted [arXiv:2103.14185] [Google Scholar]
- Teplitz, H. I., Capak, P., & Brooke, T. 2010, in The Spitzer Source List, eds. Y. Mizumoto, K. I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 437 [NASA ADS] [Google Scholar]
- Terasawa, T., Tanaka, Y. T., Takei, Y., et al. 2005, Nature, 434, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Thöne, C. C., de Ugarte Postigo, A., Fryer, C. L., et al. 2011, Nature, 480, 72 [CrossRef] [Google Scholar]
- Tinney, C. G., Faherty, J. K., Kirkpatrick, J. D., et al. 2014, ApJ, 796, 39 [Google Scholar]
- Traulsen, I., Schwope, A. D., Lamer, G., et al. 2019, A&A, 624, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Troja, E., Cusumano, G., O’Brien, P. T., et al. 2007, ApJ, 665, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Troja, E., Castro-Tirado, A. J., Becerra González, J., et al. 2019, MNRAS, 489, 2104 [Google Scholar]
- Troja, E., van Eerten, H., Zhang, B., et al. 2020, MNRAS, 498, 5643 [NASA ADS] [CrossRef] [Google Scholar]
- Troja, E., O’Connor, B., Ryan, G., et al. 2022, MNRAS, 510, 1902 [Google Scholar]
- Tsvetkov, D. Y., & Bartunov, O. S. 1993, Bull. Inf. Centre Donnees Stellaires, 42, 17 [NASA ADS] [Google Scholar]
- Tully, R. B., Courtois, H. M., Dolphin, A. E., et al. 2013, AJ, 146, 86 [NASA ADS] [CrossRef] [Google Scholar]
- van Buren, D. 1981, ApJ, 249, 297 [NASA ADS] [CrossRef] [Google Scholar]
- van den Eijnden, J., Degenaar, N., Russell, T. D., et al. 2018, Nature, 562, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Virgili, F. J., Liang, E.-W., & Zhang, B. 2009, MNRAS, 392, 91 [Google Scholar]
- Virgili, F. J., Zhang, B., O’Brien, P., & Troja, E. 2011, ApJ, 727, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Virgili, F. J., Mundell, C. G., Pal’shin, V., et al. 2013, ApJ, 778, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Vito, F., Gilli, R., Vignali, C., et al. 2016, MNRAS, 463, 348 [NASA ADS] [CrossRef] [Google Scholar]
- von Kienlin, A., Meegan, C. A., Paciesas, W. S., et al. 2014, ApJS, 211, 13 [Google Scholar]
- Walton, D. J., Fürst, F., Bachetti, M., et al. 2016, ApJ, 827, L13 [Google Scholar]
- Wanderman, D., & Piran, T. 2010, MNRAS, 406, 1944 [NASA ADS] [Google Scholar]
- Wanderman, D., & Piran, T. 2015, MNRAS, 448, 3026 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X.-G., Zhang, B., Liang, E.-W., et al. 2015, ApJS, 219, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S., Liu, J., Qiu, Y., et al. 2016, ApJS, 224, 40 [Google Scholar]
- Wang, J., Zhu, Z. P., Xu, D., et al. 2018, ApJ, 867, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, S. J., Cross, N. J. G., Dye, S., et al. 2007, ArXiv e-prints [arXiv:astro-ph/0703037] [Google Scholar]
- Waxman, E., & Katz, B. 2017, in Shock Breakout Theory, eds. A. W. Alsabti, & P. Murdin, 967 [Google Scholar]
- Webb, N. A., Coriat, M., Traulsen, I., et al. 2020, A&A, 641, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Welsh, B. Y., Wheatley, J. M., Seibert, M., et al. 2007, ApJS, 173, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitmore, B. C., Allam, S. S., Budavári, T., et al. 2016, AJ, 151, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegert, T., Irwin, J., Miskolczi, A., et al. 2015, AJ, 150, 81 [Google Scholar]
- Wiersema, K., Savaglio, S., Vreeswijk, P. M., et al. 2007, A&A, 464, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilkes, B., & Tucker, W. 2019, The Chandra X-ray Observatory (IOP Publishing), 2514 [Google Scholar]
- Woods, P. M., & Thompson, C. 2006, in Soft Gamma Repeaters and Anomalous X-ray Pulsars: Magnetar Candidates, 39, 547 [NASA ADS] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, ApJ, 140, 1868 [Google Scholar]
- Xiao, D., Zhang, B.-B., & Dai, Z.-G. 2019, ApJ, 879, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, D., Watson, D., Fynbo, J., et al. 2008, in 37th COSPAR Scientific Assembly, 37, 3512 [NASA ADS] [Google Scholar]
- Xue, Y. Q., Luo, B., Brandt, W. N., et al. 2016, ApJS, 224, 15 [Google Scholar]
- Xue, Y. Q., Zheng, X. C., Li, Y., et al. 2019, Nature, 568, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, G., Brandt, W. N., Luo, B., et al. 2016, ApJ, 831, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, G., Brandt, W. N., Zhu, S. F., et al. 2019, MNRAS, 487, 4721 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, S. X., Dai, Z. G., Wu, X. F., & Wang, F. Y. 2014, ApjL, submitted [arXiv:1401.1601] [Google Scholar]
- Yi, S.-X., Xi, S.-Q., Yu, H., et al. 2016, ApJS, 224, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, W., Zhang, C., Feng, H., et al. 2015, PoS, SWIFT 10, 006 [Google Scholar]
- Yuan, W., Zhang, C., Ling, Z., et al. 2017, in The X-ray Universe, eds. J.-U. Ness, & S. Migliari, 240 [Google Scholar]
- Zhang, B. 2013, ApJ, 763, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B. 2018, The Physics of Gamma-Ray Bursts (Cambridge University Press) [Google Scholar]
- Zheng, X. C., Xue, Y. Q., Brandt, W. N., et al. 2017, ApJ, 849, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B. B., Zhang, B., Sun, H., et al. 2018, Nat. Commun., 9, 447 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Spatial location and duration of X-ray events
To estimate the duration of the final sample of FXRTs, we computed the T90 duration parameter. T90 measures the time over which the event emits from 5% to 95% of its total measured counts (in the 0.5–7.0 keV band in our case). Figure A.1 shows the T90 duration (orange region) for each event, as well as their light curves (with a bin time of 1 ks) in unit of counts.
 |
Fig. A.1. Light curves for each FXRT candidate in units of counts and the region covering the T90 (which measures the time over which the event emits from 5% to 95% of its total measured counts; orange region) The light curves have a bin width of 1 ks. |
Furthermore, Fig. A.2 confirms that the final sample of FXRT candidates are real celestial sources in the sky rather than detector artifacts. Due to Chandra’s Lissajous dither pattern, executed during observation, the X-ray photons of the FXRTs are distributed over dozens to hundreds of individual pixels on the detector. The first column of the figure shows the light curves, color-coded by the phase in the light curve evolution. The second column shows the spatial location in x and y chip detector coordinates, also color-coded by time, tracing out a sinusoidal-like evolution in x and y coordinates over time. The third and fourth columns show the x and y position changes (in blue and purple, respectively, over time, with the light curve superimposed in dark gray.
 |
Fig. A.2. Lissajous dither pattern in detector coordinates. First column: FXRT 0.5–7.0 keV light curves in count units, color-coded as a function of time. Second column:Chandra 0.5–7.0 keV images in detector coordinates, with the same color-coding as a function of time, demonstrating the temporal movement of the source on the detector in response to the Lissajous dither pattern. A flaring pixel would appear as a point on these plots. Third and fourth columns: x (blue) and y (purple) detector coordinates, respectively, of the detected X-ray photons from the FXRTs as a function of time, with the candidate light curves superimposed as solid dark gray lines. |
 |
Fig. A.2. (continued) |
Appendix B: Color-magnitude diagram of stellar matches
To further demonstrate the stellar-like nature of the star candidates (beyond identification by Gaia), we show an example Mg versus g − i color-magnitude diagram (see Fig. B.1) considering all Pan-STARRS and DECam counterparts of X-ray sources classified as stars according to Criterion 2 (see Sect. 2.5.2). Isochrones with different ages (from log(Age) = 7.0 − 10.0) taken from the MIST package (Dotter 2016; Choi et al. 2016) are overplotted, with each panel representing different metallicities (from [Fe/H] = − 3.0 to +0.5). Solid and dashed lines denote isochrones with attenuations of AV = 0.0 and 5.0, respectively. The vast majority of the stars fall on these tracks. According to SIMBAD, the outliers are identified as PNe, YSOs, or emission-line stars. We additionally stress that the Pan-STARRS and DECam colors are not necessarily taken in a purely simultaneous manner; in the case of Pan-STARRS, they are averaged over the duration of the survey, while for DECam they come from only a few disjoint epochs.
 |
Fig. B.1. Color-magnitude diagrams, considering only Pan-STARRS and DECam counterparts (gray background points) of X-ray sources classified as stars according to Criterion 2 (see Sect. 2.5.2). As a comparison, we overplot isochrones with different ages (from log(Age) = 7.0 − 10.0) taken from the MIST package (Dotter 2016; Choi et al. 2016). Each panel represents different metallicities (from [Fe/H] = − 3.0 to +0.5), while solid and dashed lines are isochrones with attenuations of AV = 0.0 and 5.0, respectively. |
All Tables
Properties of the extragalactic FXRT candidates detected and/or discussed in this work, ordered by subsample and date.
Best-fit parameters obtained using a broken power-law (BPL) and a power-law (PL) model fit to the X-ray light curves.
Parameters obtained from the literature and by our SED fitting to archival photometric data using the BAGPIPES package (Carnall et al. 2018).
Energetics of the FXRT sample (fluxes are corrected for Galactic and intrinsic absorption, and calculated over the energy range 0.3–10 keV).
All Figures
 |
Fig. 1. Detection probability (Pdet) as a function of the Chandra exposure time (Texp) for typical instrumental off-axis angles of 5 |
| In the text | |
 |
Fig. 2. Histogram (red; left Y axis) and cumulative (black; right Y axis) distributions of the exposure time of the 5303 Chandra observations used in this work. The inset provides a zoomed-in view to show the high-exposure-time tail of the distribution. The vertical dashed blue line indicates the median exposure time (=32 ks) of the total sample. We adopt an exposure time of 8 ks as a lower bound due to the strongly decreasing probability of distinguishing FXRTs in short exposures. |
| In the text | |
 |
Fig. 3. X-ray light curves extracted as described in Sect. 2.3 and identified via our algorithm described in Sect. 2.1. The four light curves in black denote randomly selected sources from initial FXRTs found in the CSC2. For comparison, we show in red the FXRT sources CDF-S XT1 and CDF-S XT2. For visualization purposes, background-subtracted light curves are presented with either 1 ks or 2 ks bins with 1σ errors. In all cases, the vertical dashed gray line represents the end of the observation. |
| In the text | |
 |
Fig. 4. Methodology flowchart considered in this work to find FXRT candidates. |
| In the text | |
 |
Fig. 5. Comparison of 0.5–7.0 keV net-count (top panels) and flux (bottom panels; 0.5–7.0 keV) distributions for the initial (filled blue histograms) and final (filled black histograms) samples, as well as subsets covered by various purity criteria (colored, unfilled histograms) for the sample. Net counts and fluxes are provided by the CSC2. |
| In the text | |
 |
Fig. 6. 0.5–7 keV light curves for each FXRT candidate: full exposure, in units of counts (first column 1); zoomed-in view, from the detection of the first photon to the end of the exposure, in units of count rate (cts s−1), with log-log scaling and five counts per bin (second column); long-term light curve, with each point representing individual Chandra exposures (cyan circles with 1σ error bars) to highlight the significance of detections and non-detections, in units of counts (third column); long-term light curve, with each point representing individual Chandra (cyan), XMM-Newton (red), and Swift-XRT (green) exposures in units of flux (erg s−1 cm−2) (fourth column). For the long-term light curves, the observation that includes the transient is denoted by a large blue star (1σ error bars), while triangles denote observations with (3σ) upper limits. All the fluxes are reported in the 0.5–7 keV band in the observer’s frame. In the case of FXRT 4 in Col. 4, additional data points are partially blocked by the blue star. |
| In the text | |
 |
Fig. 6. continued. |
| In the text | |
 |
Fig. 7. Archival optical, NIR, MIR, and X-ray images of extragalactic FXRT candidates; the telescope or instrument plus filter and FXRT ID name are shown in the upper-left and upper-right corners, respectively. Each cutout is centered on the X-ray position, and red circles denote 3σChandra errors in the source localization. Columns 1–4: optical band (DECam, Pan-STARRS, and HST) images. Columns 5 and 6: NIR J or H and K (UKIRT or VISTA) images. Column 7: 3.4μm (unWISE) images. Column 8: X-ray Chandra (ACIS) 0.5–7 keV images. |
| In the text | |
 |
Fig. 7. continued. |
| In the text | |
 |
Fig. 8. Positions on the sky, in Galactic coordinates, of FXRT candidates. The initial 728 candidates are represented by blue triangles. The final sample of 14 extragalactic FXRT candidates from this work are denoted by large red stars. The 5303 Chandra observations used in this work are also shown (cyan squares). |
| In the text | |
 |
Fig. 9. Light curves, the evolution of the HR over time, and the best fitting models of the FXRT sample. Top panels: observed 0.5–7.0 keV X-ray light curves in cgs units (blue points), starting at T = 20 s. For FXRTs 1 and 11, we only show the main event. For ten FXRT candidates, we also plot the best-fit BPL or simple PL model (red solid lines), while for the remaining four FXRT candidates we do not because they are not well described by either model. The light curves contain five counts per bin (except that of FXRT 1, which has 20 counts per bin). Bottom panels: HR evolution (the soft and hard energy bands are 0.5–2.0 keV and 2.0–7.0 keV, respectively), following the Bayesian method of Park et al. (2006). The dashed red line denotes an HR equal to zero. For XRT 000519/FXRT 1 and XRT 110103/FXRT 11, we show close-ups of the main flare to highlight in more detail their spectral behavior. Here, T0 = 0 s is defined as the time when the count rate is 3σ higher than the Poisson background level. |
| In the text | |
 |
Fig. 10. Observed time-integrated spectra fitted with different spectral models. Top panels: X-ray spectra (black dots; the data were grouped to at least one count per bin), in units of counts (cts s−1 keV−1). We also plot the best-fit PO (blue lines), BR (orange lines), and BB (green lines) spectral models; see Table 5 for the corresponding best fitting parameters. Bottom panels: residuals (defined as data-model normalized by the uncertainty; (D − M)/σ) of each spectral model. |
| In the text | |
 |
Fig. 11. Distribution of best-fit X-ray parameters for nearby (left panels) and distant (right panels) FXRT candidates. Top panels: histogram of neutral hydrogen column densities, in units of cm−2, obtained using the PL, BR, and BB models. Bottom panels: histogram of the photon indices obtained using a PL model. |
| In the text | |
 |
Fig. 12. Photon index and HR distribution of our selected transient candidates. Top panel: HR of each FXRT candidate (using the Bayesian BEHR code; Park et al. 2006). Middle panel: HR distributions of our final samples of nearby (hashed black histogram) and distant (hashed orange histogram) FXRTs, compared to the XRTs classified as “stars” according to Criterion 2 using Gaia (filled cyan histogram). Bottom panel: photon indices for FXRT candidates where the light curve was best fit by a BPL model, before (filled circles) and after (open squares) the break time (Tbreak) taken from Table 4. In all cases, errors bars are at the 90% confidence level. |
| In the text | |
 |
Fig. 13. Comparison of the stellar mass (M*) and SFR of host galaxies of different types of transients: nearby (colored hexagons) and distant (colored stars) FXRT candidates, LGRBs and SGRBs (Li et al. 2016), low-luminosity LGRBs (LL-LGRBs; GRB 980425, GRB 020903, GRB 030329, GRB 031203, GRB 050826, GRB 060218, and GRB 171205A; Christensen et al. 2008; Michałowski et al. 2014; Levesque 2014; Krühler et al. 2017; Wiersema et al. 2007; Wang et al. 2018; Arabsalmani et al. 2019), GW 170817 (Im et al. 2017), SN 2020bvc (Chang et al. 2015; Izzo et al. 2020; Ho et al. 2020), FXRT 14/CDF-S XT1 (Bauer et al. 2017) and CDF-S XT2 (Xue et al. 2019), and supernovae events (Types Ia, Ib, Ic, and II; Tsvetkov & Bartunov 1993; Galbany et al. 2014). The solid cyan line shows the best-fit local galaxy main sequence relation from Peng et al. (2010). The gray background contours are the galaxy distribution from the SDSS (data taken from Brinchmann et al. 2004). The dashed colored lines are the boundaries separating the star-forming and quiescent galaxies and its evolution with redshift (at z = 0.0, 0.1, 0.2, 0.3, and 0.4, from bottom to top; Moustakas et al. 2013). |
| In the text | |
 |
Fig. 14. Color-color diagram of FXRTs 8, 9, and 14 and X-ray sources classified as stars according to Criterion 2 (see Sect. 2.5.2) with Pan-STARRS, DECam, and 2MASS counterparts (gray filled circles). The expected parameter space of stars with different ages (log(Age) = 7.0–10.3), metallicities (from [Fe/H] = − 3.0–0.5), and attenuations (AV = 0.0–5.0) taken from the MIST package (Dotter 2016; Choi et al. 2016) is overplotted as an orange region. |
| In the text | |
 |
Fig. 15. Best fitting SED models obtained using the BAGPIPES package (Carnall et al. 2018) for FXRTs 8 (left panels) and 9 (right panels). Top panels: 16th to 84th percentile range for the posterior spectrum and photometry (shaded orange). The used photometric data and their uncertainties are given by the blue markers. Bottom panels: posterior distribution for the five fitted parameters (SFR, age, galaxy stellar mass, metallicity, and redshift). The 16th, 50th, and 84th percentile posterior values are indicated by the vertical dashed black lines. |
| In the text | |
 |
Fig. 16. 0.3–10 keV light curves of the five local CSC2 FXRTs, plus FXRTs 1 and 11, in luminosity units. The 0.3–10 keV light curves are obtained by multiplying the 0.3–7 keV light curves by the factor derived from extrapolating the best-fit PO model flux to the 0.5–7.0 keV spectrum to the 0.3–10 keV band and correcting it for the effects of Galactic plus intrinsic absorption. For comparison, we overplot flaring episodes for several individual well-known Galactic XRBs: GX339-4 (9 kpc, green line; Heida et al. 2017), Swift J1357.2−0933 (8 kpc, magenta line; Mata Sánchez et al. 2015), MAXI J1543−564 (5 kpc, gray line; Stiele et al. 2012), and MAXI J1659−152 (6 kpc, blue line; Jonker et al. 2012b). The light curves of the comparison sources are taken from the 2SXPS catalog (Evans et al. 2020b). |
| In the text | |
 |
Fig. 17. 0.3–10 keV light curves of the nine CSC2 FXRTs in luminosity units (as in Fig. 16, 0.3–10 keV light curves were converted from 0.5–7 keV ones). The X-ray afterglow light curves of 64 LGRBs plus 32 SGRBs (taken from Bernardini et al. 2012; Lü et al. 2015) are shown as a 2D histogram, as are the X-ray afterglows of GRB 170817A (off-axis SGRB, solid dark green line; Nynka et al. 2018; D’Avanzo et al. 2018; Troja et al. 2020, 2022), SN 2020bvc (the first off-axis LGRB candidate, solid light green line; Izzo et al. 2020), and the ultra-long duration GRB 111209A (solid magenta line, z = 0.677; Levan et al. 2014). Additionally, several individual transients are overplotted: the low-luminosity supernova SBO XRF 080109/SN 2008D (solid cyan lines, 27 Mpc;), XRF 060218/SN 2006aj (solid blue lines, 145 Mpc;), XRF 100316D/SN 2010bh (solid orange lines, 263 Mpc; Barniol Duran et al. 2015; Starling et al. 2011; Modjaz et al. 2009; Evans et al. 2007, 2009; Soderberg et al. 2008; Campana et al. 2006), the relativistically beamed TDE Swift J1644+57 (solid black lines, z = 0.3543; Bloom et al. 2011; Levan et al. 2011), the non-beamed TDE J2150-05 (solid pink line, z = 0.055; Lin et al. 2018), and CDF-S XT2 (solid indigo lines; Xue et al. 2019). For FXRTs 1, 7, 10, 11, 12, and 13 (open symbols), we assume z = 1.0, we adopt zphoto = 2.23 for FXRT 14 from Bauer et al. (2017), and for FXRTs 8 and 9 we consider the values from Table 8. |
| In the text | |
 |
Fig. 18. Observed cumulative log 𝒩–log S distribution of our sample of FXRTs as a function of fluence (in units of Crab† × second). Also shown are two PL models, N(> S)∝S−γ, with slopes γ = 0.5 (red line) and 1.0 (blue line). The γ = 0.5 line denotes the best fit to the CSC2 sample. The γ = 1 line represents the best fit and 1σ error of Arefiev et al. (2003) based on bright FXRTs. The brightest sources in our sample appear to be consistent with this bright-end extrapolation, although our fainter sources fall ∼1 dex below, implying a break. For comparison with Arefiev et al. (2003), we convert the fluence to 2–10 keV. †A Crab is a standard astrophotometric unit for measurement of the intensity of celestial X-ray sources. |
| In the text | |
 |
Fig. 19. Density rate as a function of redshift for several known transient classes compared to our sample. Left panel: density rate as a function of redshift for FXRT 8/9/13 (cyan star) and CDF-S XT1/FXRT 14 (red square), and upper limits (black triangle) for FXRTs without measured redshifts. We also show the density rate of CDF-S XT2 (purple square; Xue et al. 2019), CC-SNe (dotted orange line; Madau & Dickinson 2014), the redshift-dependent intrinsic event rate densities of LGRBs (blue-filled region; taken from Sun et al. 2015 and Wanderman & Piran 2010, normalized to the local universe value and corrected for jet-aperture as ρ0, LGRBs ∼ 250–500 yr−1 Gpc−3), LL-LGRBs (green-filled region; taken from Zhang 2018, normalized to the local universe value and corrected for jet-aperture as ρ0, LGRBs ∼ 100–200 yr−1 Gpc−3), SGRBs considering a merger delay Gaussian model (red-filled region; taken from Sun et al. 2015 and Wanderman & Piran 2015, normalized to the local universe value and corrected for jet-aperture as ρ0, SGRBs ∼ 13–75 yr−1 Gpc−3), and TDEs (gray-filled region, taken from Sun et al. 2015, normalized to the local universe as ρ0, TDEs ∼ 104–105 yr−1 Gpc−3 at luminosities ∼1042–1044 erg s−1). Right panel: local density rate for FXRT 8/9/13 considering they are related to GRBs (cyan star), TDEs (blue star), or FXRT 14/CDF-S XT1 (red square) (see Sect. 6.3). As a comparison, we also plot the local event rate of CDF-S XT2-like events (purple square; Xue et al. 2019), GW 170817 (green square; Abbott et al. 2017b), and GRB 170817A (magenta square; Zhang et al. 2018), as well other kinds of transients, such as the new SBO candidate in XMM-Newton data (yellow square and circle; Xu et al. 2008; Novara et al. 2020), the TDE rate of SMBH–MS TDEs (black triangle; Sun et al. 2015) and the IMBH–WD TDE rate (orange triangle and circle; Malyali et al. 2019; Tanikawa et al. 2021), the CC-SN rate (magenta triangle), the merger rate of BNS systems (light green circle; Abbott et al. 2021c), and the merger rate of neutron star and BH systems (gray circles; Abbott et al. 2021b). The local event rate of LGRBs, LL-LGRBs, and SGRBs are plotted (blue, green, and red horizontal shaded regions, corrected for the jet aperture factor; Zhang 2018). |
| In the text | |
 |
Fig. A.1. Light curves for each FXRT candidate in units of counts and the region covering the T90 (which measures the time over which the event emits from 5% to 95% of its total measured counts; orange region) The light curves have a bin width of 1 ks. |
| In the text | |
 |
Fig. A.2. Lissajous dither pattern in detector coordinates. First column: FXRT 0.5–7.0 keV light curves in count units, color-coded as a function of time. Second column:Chandra 0.5–7.0 keV images in detector coordinates, with the same color-coding as a function of time, demonstrating the temporal movement of the source on the detector in response to the Lissajous dither pattern. A flaring pixel would appear as a point on these plots. Third and fourth columns: x (blue) and y (purple) detector coordinates, respectively, of the detected X-ray photons from the FXRTs as a function of time, with the candidate light curves superimposed as solid dark gray lines. |
| In the text | |
 |
Fig. A.2. (continued) |
| In the text | |
 |
Fig. B.1. Color-magnitude diagrams, considering only Pan-STARRS and DECam counterparts (gray background points) of X-ray sources classified as stars according to Criterion 2 (see Sect. 2.5.2). As a comparison, we overplot isochrones with different ages (from log(Age) = 7.0 − 10.0) taken from the MIST package (Dotter 2016; Choi et al. 2016). Each panel represents different metallicities (from [Fe/H] = − 3.0 to +0.5), while solid and dashed lines are isochrones with attenuations of AV = 0.0 and 5.0, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.