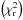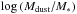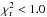© ESO, 2017

1. Introduction

Star formation occurs within dense (n(H₂) ~ 10²−10⁵ cm^-3), massive (10⁴−10⁶M_⊙), and cold (T_gas ~ 10–50 K) giant (10 ~ 100 pc) molecular clouds (GMC; Kennicutt & Evans 2012), where atomic gas, mainly atomic Hydrogen (HI), is transformed into molecular gas (mainly H₂) on dust grain surfaces (e.g., Scoville 2013). Dust grains are formed within the cool, extended atmospheres of low-mass (1–4 M_⊙) asymptotic giant branch (AGB) stars and are dispersed into the ISM via the strong AGB star winds (Gehrz 1989). In other words, the dust content is related to the star formation history of the galaxy. Since much of our current knowledge of galaxy properties and evolution comes from studies of high-temperature (T > 10³ K) regions, a global understanding of star formation requires a better knowledge of the role of cold gas and dust in the star formation process.

Dust grains emit mainly in the far infrared (FIR; 40 <λ< 300 μm) and sub-millimeter (sub-mm; 300 <λ< 1000 μm). Early studies of dust content and emission have been done both from space (IRAS, see Neugebauer et al. 1984 and ISO; see Kessler et al. 1996) and from the ground (SCUBA, see Holland et al. 1999, at the James Clerk Maxwell Telescope and MAMBO at the IRAM 30 m telescope). More recent missions – in the mid-infrared (e.g., WISE; Spitzer), far-infrared (e.g., AKARI; Herschel), and sub-mm (e.g., Planck) – have revolutionized the field (e.g., Lutz 2014).

The IR to sub-mm emission of dust has been characterized in many samples (e.g., SLUGs by Dunne et al. 2000; HRS by Boselli et al. 2010; KINGFISH/SINGS by Kennicutt et al. 2003; Dale et al. 2005; SDSS-IRAS by da Cunha et al. 2010; ATLAS 3D by Cappellari et al. 2011; ERCSC by Negrello et al. 2013) and at high-z (e.g., GOODS-Herschel by Magnelli et al. 2010; H-ATLAS by Eales et al. 2010). Early studies modeled the dust grain emission using gray-body emission from one or two dust-temperature components (e.g., Dunne et al. 2000; Dunne & Eales 2001). More complex and sophisticated dust-emission models available today include the MAGPHYS (da Cunha et al. 2010) code, which contains empirically-derived spectral energy density (SED) libraries from the ultraviolet (UV) to infrared (IR), and the model developed by Draine & Li (2007, DL07 hereafter), which provides a more extensive SED library covering the IR to sub-mm. The DL07 model has been successfully applied to the Spitzer Nearby Galaxy Survey (SINGS) galaxies (Draine et al. 2007), and these authors note that the presence of sub-mm photometry is crucial to constrain the mass of the cold dust component.

The results on dust properties coming from many of the studies mentioned above are limited by poor statistics as a consequence of small samples and/or the limited sampling of the SED (especially at sub-mm wavelengths), which decreases the reliability of the SED modeling. Since dust properties are increasingly used at all redshifts to determine the evolutionary state of a galaxy, and in general for galaxy evolution studies, it is crucial to fully characterize these properties and their relationships and degeneracies in large samples of galaxies. Of specific interest is the degeneracy between dust temperatures and dust emissivity index, the inter-relationships between dust mass, temperature, and luminosity, and the relationships between these dust properties and other properties of the galaxy (e.g., stellar and gas masses, SFR, specific star formation rate; sSFR = SFR/M_∗[yr^-1]).

The recent availability of Planck sub-mm (350 μm to 850 μm) fluxes for thousands of nearby galaxies which are well studied in the optical to IR, allows, for the first time, comprehensive and accurate dust model fits to these. With a comprehensively modeled large sample of nearby galaxies in hand, one can test and refine the many scaling relations and estimators now being used at all redshifts, for example, estimating gas mass from a single flux measurement at 850 μm (Scoville 2013), or estimating dust masses (Dunne et al. 2000; Dunne & Eales 2001) and/or luminosities (e.g., Sanders & Mirabel 1996; Elbaz et al. 2010) from a few IR flux measurements.

The “starburstiness” of a galaxy is normally obtained from the ratio of the SFR and the stellar mass (M_∗). The SFR –M_∗ plane shows that while most “normal” star forming galaxies follow a “main sequence” (MS) of secular star formation (Elbaz et al. 2007), a small fraction of galaxies show excessive SFR for a given M_∗ : these galaxies are referred to as starburst (SB). The MS of galaxies is observed over the redshift range z ~ 0–4 (e.g., Elbaz et al. 2007; Magdis et al. 2010; Rodighiero et al. 2011; Elbaz et al. 2011; Pannella et al. 2015; Schreiber et al. 2015) and changes smoothly with redshift (Elbaz et al. 2011). In this work we use the MS proposed by Elbaz et al. (2011), at z = 0: $\mathit{SFR}\mathrm{=}\frac{{\mathit{M}}_{\mathrm{\ast }}}{\mathrm{4.0}\mathrm{\times }{\mathrm{10}}^{\mathrm{9}}}\left[\frac{{\mathit{M}}_{\mathrm{\odot }}}{\mathrm{yr}}\right]\mathrm{·}$(1)This equation defines the specific star formation rate ${\mathrm{(}}^{}\mathit{sSFR}\mathrm{\left[}\mathrm{y}{\mathrm{r}}^{-1}\mathrm{\right]}\mathrm{=}\mathit{SFR}\mathit{/}{{\mathit{M}}_{\mathrm{\ast }}}^{\mathrm{)}}$ expected for MS galaxies (MS; − 0.5 < sSFR [yr^-1] < 0.5). We define SB galaxies as those having sSFR [yr^-1] > 0.8, and passive (PAS) galaxies as those at sSFR [yr^-1] < −0.8. The two “transition” zones between the above three classifications, that is, 0.5 ≤ SFR [M_⊙ yr^-1] < 0.8 dex with regards to the MS locus (an intermediate SB zone) and; − 0.8 ≤ SFR [M_⊙ yr^-1] < −0.5 dex with regards to the MS locus (an intermediate passive zone) are excluded in order to avoid contamination.

In this paper, we capitalize on the recent availability of sub-mm (Planck) fluxes (for better dust model fits) and WISE fluxes (for stellar mass determinations) to fit DL07 dust models to all nearby bright galaxies for which sufficient (for a reasonable fit to DL07 models) multi-wavelength uniform data are available from WISE, IRAS, Planck, and/or SCUBA. The resulting model fits are used to explore the relationship between dust properties (mass, luminosity, temperature) and their relationship with other galaxy-wide properties (e.g., stellar and gas masses, sSFR). The comprehensive dust modeling also allows us to refine estimations of total IR luminosity from one to a few IR to sub-mm fluxes, the dust mass from a single sub-mm flux, and sSFR from IR to sub-mm colors.

Throughout this paper we adopt a flat cosmology with Ω_m = 0.3 and H₀ = 72 km s^-1 Mpc^-1.

2. Samples and data

We use two samples of nearby galaxies: (a) the sample of nearby galaxies with detections in Planck High Frequency Instruments (HFI) Second Data Release catalog and global CO J:1-0 observations (Nagar et al., in prep.); and (b) all galaxies from the 2MASS Redshift Survey (2MRS; Huchra et al. 2012), which are listed as detections in the second Planck Catalog of Compact Sources at 350 μm, 550 μm, and 850 μm (PCCS2; Planck Collaboration XXVII 2016).

The Nagar et al. (in prep.) sample is a compilation of approximately 600 nearby galaxies (⟨ z ⟩ = 0.06) with global CO J:1-0 observations, and sub-mm fluxes from Planck catalogs at 350 μm, 550 μm, and 850 μm or SCUBA 850 μm observations. The names of the catalogs with the respective references are summarized in Table 1.

The sample spans a range of morphological types – including spiral, elliptical and interacting galaxies – and luminosities from normal to Ultra-Luminous Infrared Galaxies (ULIRGs).

The 2MRS sample consists of 44,599 nearby (⟨ z ⟩ = 0.03) 2MASS (Shectman et al. 1996) galaxies with K_s ≥ 11.75 mag and Galactic latitude | b | ≥ 5 for which spectroscopic redshifts have been obtained to 97.6% completeness (Huchra et al. 2012). We matched the 2MRS sample with the (PCCS2), using a maximum matching radius of 1 arcmin. The PCCS2 catalog contains only galaxies with high reliabilities (>80%; signal to noise >5 in DETFLUX). Sources with lower or unknown reliabilities are listed in the equivalent excluded catalog (PCCS2E), which we have not used.

The Planck satellite has a beam resolution of the order of 1 arcmin (e.g., 4.22 arcmin at 350 μm, Planck Collaboration XXVII 2016), and the reliability catalog contains approximately 1000 sources (e.g., 4891 galaxies at 350 μm, Planck Collaboration XXVII 2016), with a density <1 sources/deg² (e.g., 0.26 sources/deg² at 350 μm, Planck Collaboration XXVII 2016). This means that the resolutions of WISE and 2MASS (~1 arcsec) do not represent a problem for the match with the Planck source catalog, as we adopt a search radius of 1.0 arcmin. In order to remove any multiple matches, we performed a visual inspection of all the matched objects. In some cases, we selected all the galaxies that have companions in the WISE, 2MASS, and SDSS images and classified them as interacting systems. Furthermore, multiple detections in one Planck beam do not represent a problem either because the galaxies in our sample have a median diameter (parametrized as the D25 reported in HyperLeda¹) of 1.5 arcmin, with only 291 having D25 < 1.0 arcmin (~18% of the final sample).

2.1. Flux densities and derived stellar mass

The Planck collaboration (Planck Collaboration XXVII 2016) showed that, at 350 μm, for sources with APERFLUX > 1.0 Jy, the APERFLUXes reported in the Planck catalog are in agreement with those in the Herschel Reference Survey.

Nagar et al. (in prep.) compare the Planck observations at 850 μm with SCUBA data (at 850 μm) in nearby galaxies, revealing that the APERFLUX and the DETFLUX from Planck show the existence of some systematic difference. However, Nagar et al. (in prep.) also show that simple corrections can solve this problem. They find that the observation of fluxes smaller than twice the 90% completeness limit (304 mJy at 850 μm) needs smaller corrections if the DETFLUX is used (the correction is f_{Planck 850 μm} = f_{SCUBA 850 μm}+70), and for greater fluxes (greater than twice the 90% completeness limit) the fluxes are more consistent with the APERFLUX (using the correction: f_{Planck 850 μm} = f_{SCUBA 850 μm}+139). Assuming a gray-body with a temperature of T = 25 K and β = 1.8, Nagar et al. (in prep.) obtain similar corrections for Planck observations at 350 and 550 μm. For each wavelength, Nagar et al. (in prep.) obtain three corrections: one with free slope and intercept, a second with intercept zero and free slope, and a third with with free intercept and fixed slope. We use the last kind of correction in our work. Additionally, to correct for the typical spectral shape of dust gray-body emission, we used correction factors of 0.976, 0.903, and 0.887 at 350 μm, 550 μm and 850 μm, respectively Negrello et al. (2013). Following Nagar et al. (in prep.), we assumed a 3% contamination from the CO emission line at Planck 850 μm and negligible CO emission line contamination at Planck 350 and 550 μm. After these flux density corrections are applied, the limits obtained for the Planck-derived flux densities in our sample are 500 mJy, 315 mJy, and 175 mJy, at 350 μm, 550 μm, and 850 μm, respectively.

Mid-infrared (MIR) fluxes are obtained from the AllWISE Source Catalog “g” magnitudes². These “g” magnitudes are calculated over apertures defined using 2MASS images, with additional corrections as described in Jarrett et al. (2013). The WISE (W1-W4) filters have a limiting sensitivity of 0.08, 0.11, 1, and 6 mJy, respectively. We select only sources with signal to noise (S/N) ≥ 5, except for W4, where we consider a S/N ≥ 3. We calculate the galaxy stellar mass (M_∗) using the WISE W1 filter (3.4 μm) and the W1-W2 (4.6 μm) color following the Cluver et al. (2014) calibration. The stellar mass ranges between 10⁹ and 10¹¹M_⊙ for our sample. To test the consistency of our WISE-estimated stellar masses, we compare our stellar masses to those in three other catalogs based on SDSS-derived quantities (i.e., NASA-Sloan Atlas, Chang et al. 2015, and MPA-JHU catalogs, see Appendix C). We obtained a good agreement with the M_∗ obtained in the NASA-Sloan Atlas (see Appendix C for more details).

The infrared (IR) data comes from the Infrared Astronomical Satellite (IRAS) at 12, 25, 60 and 100 μm, obtained from the Galaxies and Quasars catalog (Fullmer & Lonsdale 1989). We consider only sources with moderate- or high- quality fluxes (no upper limits), with signal to noise ≥ 3.

Figure 1 shows the filter band-passes of all filters for which we compiled flux densities which were then used to constrain the DL07 dust model fits: WISE W3 (12 μm) and W4 (22 μm); IRAS 12, 25, 60 and 100 μm; Planck 350, 550 and 850 μm and SCUBA 850 μm. When multiple flux density measurements at the same wavelength are available, we use WISE W3 and W4 in preference to IRAS 12 and 25 μm, and Planck 850 μm in preference to SCUBA 850 μm.

2.2. Gas masses and distances

For the comparison between the dust masses and the ISM content, we require HI data for our galaxies. The integrated flux of HI is obtained from different surveys, detailed in Table 2.

The molecular gas mass (M_mol) is calculated from global (non-interferometric) observations of the CO(J: 1-0) line (expressed in terms of the velocity-integrated flux or 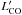${\mathit{L}}_{\mathrm{CO}}^{\mathrm{\prime }}$ [K km s^-1 pc²] Solomon et al. 1997 ) and the conversion factor α_CO (Solomon & Vanden Bout 2005; Bolatto et al. 2013). The correlation between the galaxy metallicity and the α_CO value (Leroy et al. 2011; Sandstrom et al. 2013) shows that the α_CO takes values ~ 2 to ~ 20 times the Galactic value for sources with metallicities (12+log(O/H)) smaller than 8.2. In our sample, the stellar mass ranges between 10⁹ and 10¹¹M_⊙. Over this stellar mass range, metallicities are expected to be between 8.4 and 9.1 (Tremonti et al. 2004). Over this limited metallicity range, it is valid to use a constant value of α_CO (Leroy et al. 2011). In our study, we use α_CO = 4.3 [M_⊙ (K km s^-1 pc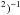${}^{\mathrm{2}}\mathrm{)}^{-1}$] which includes a correction for heavy elements of 36% (Bolatto et al. 2013).

Galaxy distances are derived from the redshift listed in 2MRS or the NASA/IPAC Extragalactic Database (NED)³ except for very nearby galaxies (z< 0.045; D_L< 20 Mpc) for which we use distances from the Extragalactic Distance Database (EDD)⁴.

2.3. AGN contamination

Since our study is focused on dust emission, it is crucial to discard galaxies in which the IR and sub-mm fluxes are highly contaminated by AGN emission. We use the Véron-Cetty & Véron (2010) catalog to identify and discard sources with AGN. This catalog contains 168 941 objects at redshifts between 0 and 6.43 (from which 5569 are at z< 0.1). We discarded all (345) sources in our sample which fall within 30′′ of any source in the Véron-Cetty & Véron (2010) catalog. Additionally, using the AGN selection criteria showed by Cluver et al. (2014) based on WISE colors (using filters W1,W2 and W3), we rejected 43 galaxies. Finally, we excluded all (73) sources with Rayleigh-Jeans (RJ; λ> 300 μm) spectral slope significantly lower than that expected from a gray-body with β = 1.3 and T = 15 K, since for these sources the emission in the RJ regime is likely contaminated by synchrotron emission. In other words, these β and T values imply the exclusion of all sources with colors: f₃₅₀/f₅₅₀< 2.3, f₃₅₀/f₈₅₀< 6.6 and f₅₅₀/f₈₅₀< 2.9 where f₃₅₀, f₅₅₀ and f₈₅₀ are the Planck fluxes at 350, 550 and 850 μm, respectively.

2.4. Final sample

Since our analysis requires accurate fitting of dust model SEDs from IR to sub-mm data, we restrict the two samples above to only those galaxies for which meaningful spectral fits are found (see Sect. 4.1). The final sample – with dust SED fits – comprises 1630 galaxies, which all have reliable M_∗ estimations. Of these galaxies, 136 are CO-detected and 1230 have HI masses. From visual inspection of the SDSS and 2MASS images we classified 87 galaxies as interacting in the sample.

The redshift distribution of the final sample is shown in the left panel of Fig. 2. The median redshift is ⟨ z ⟩ = 0.015 for the entire sample, with a mean of 0.012 and sigma = 0.011. For the subsample of galaxies with CO measurements, the median value is ⟨ z ⟩ = 0.0066. with mean of 0.0032 and sigma of 0.0042. The distribution of the number of photometric data points (between 12 μm and 850 μm) per galaxy is shown in the right panel of Fig. 2: 21% of the sample have more than six photometric points, 67% have five, and only 12% have four photometric points. The subsample of galaxies with CO observations has a median of six photometric points per galaxy; 59% of these galaxies have ≥six photometric data points and only 6% have four photometric data points. In all cases we cover both sides of the emission peak at ~100 μm; for the few galaxies with only 5 photometric data points, these are distributed as 2 or 3 points at λ< 100 μm and 1 or 2 at λ> 100 μm.

3. Modeling dust emission

The DL07 model describes the total galaxy spectrum by a linear combination of one stellar component, approximated by a black body with a specific color temperature T_∗, and two dust components. One component with dust fraction = (1−γ) is located in the diffuse interstellar medium (ISM) and heated by a radiation field with constant intensity U = U_min; the other component with dust fraction = γ is exposed to a radiation field generated by photo-dissociation regions (PDRs) parametrized by a power-law U^α, over a range of intensities U_min<U<U_max, with U_max ≫ U_min.

Thus, the canonical model emission spectrum of a ga- laxy is: ${\mathit{f}}_{\mathit{\nu }}^{\mathrm{model}}\mathrm{=}{\mathrm{\Omega }}_{\mathrm{\ast }}{\mathit{B}}_{\mathit{\nu }}\mathrm{\left(}{\mathit{T}}_{\mathrm{\ast }}\mathrm{\right)}\mathrm{+}\frac{{\mathit{M}}_{\mathrm{dust}}}{\mathrm{4}\mathit{\pi }{\mathit{D}}_{\mathrm{L}}^{\mathrm{2}}}\mathrm{[}\left(\mathrm{1}\mathrm{-}\mathit{\gamma }\right){\mathit{p}}_{\mathit{\nu }}^{\mathrm{\left(}\mathrm{0}\mathrm{\right)}}\mathrm{+}\mathit{\gamma }{\mathit{p}}_{\mathit{\nu }}\mathrm{]}\mathit{,}$(2)where Ω_∗ is the solid angle subtended by stellar photospheres, M_dust is the dust mass, D_L is the luminosity distance, and ${\mathit{p}}_{\mathit{\nu }}^{\mathrm{\left(}\mathrm{0}\mathrm{\right)}}\left({\mathit{q}}_{\mathrm{PAH}}\mathit{,}{\mathit{U}}_{\min }\right)$ 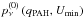is the emitted power per unit frequency per unit dust mass from dust heated by a single starlight intensity U_min. The dust is a mixture of carbonaceous and amorphous silicate grains characterized by the polycyclic aromatic hydrocarbon (PAH) index, q_PAH, defined as the percentage of the total grain mass contributed by PAHs with less than 10³ carbon atoms. Finally, p_ν(q_PAH,U_min,U_max,α) is similar to the previous term but for dust heated by a power law distribution of starlight intensities dM/ dU ∝ U^{− α} extending from U_min to U_max. For a known galaxy distance, the canonical dust model is thus characterized by eight free parameters: Ω_∗,T_∗,q_PAH,U_min,U_max,α,γ and M_dust .

The use of all eight free parameters in the DL07 model requires extensive observational datasets and it is computationally demanding. For the former reason, we limit the number and range of the free parameters as follows: (a) we use the Draine & Lee model library (available on the web⁵). That library uses a limited parameter range for 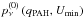${\mathit{p}}_{\mathit{\nu }}^{\mathrm{\left(}\mathrm{0}\mathrm{\right)}}\left({\mathit{q}}_{\mathrm{PAH}}\mathit{,}{\mathit{U}}_{\min }\right)$ and p_ν(q_PAH,U_min,U_max,α) in Eq. (2); in which q_PAH takes 11 values between 0.01 and 4.58, U_min takes 22 values between 0.10 to 25.0 and U_max takes 5 values between 10³ to 10⁷ (as a reference, U = 1 corresponds to the starlight intensity estimate for the local ISM) and fixed the value α = 2; (b) we follow Draine et al. (2007), who show that the dust emission of the galaxies of the KINGFISH sample can be well fitted using DL07 models with fixed value of U_max = 10⁶; (c) the stellar component, the first term in Eq. (2), is significant only at λ ≲ 10 μm. Given that we use photometric data at 12 μm ≤ λ ≤ 1000 μm, then we do not require to use this stellar component. To test the influence of the stellar component in fluxes at 12 and 22 μm, we extrapolate the power law obtained from fluxes at 3.4 and 4.6 μm (W1 and W2, respectively), deriving an influence of 4% and 1% at 12 and 22 μm, respectively. This means that the stellar component does not affect our dust emission results. In summary: two parameters (Ω_∗ and T_∗) are not used since we do not model the stellar component, two parameters (U_max and α) are fixed to a single value, two parameters (q_PAH and U_min) are limited in their range, and only M_dust and γ are allowed to vary freely (the M_dust is fixed after the minimization described below in Eq. (4) and γ runs between 0.0 and 100 in steps of 0.1). With these restrictions, we generate 24 200 template SEDs with luminosities per dust mass (νL_ν/M_dust) in [L_⊙/M_⊙] and wavelengths (λ) in [μm]. Each observed galaxy SED is fitted to each of the 24 200 SED templates solely by varying M_dust . The best fit value of M_dust is calculated by the minimization of χ², where 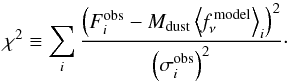${\mathit{\chi }}^{\mathrm{2}}\mathrm{\equiv }\sum _{\mathit{i}}\frac{{\left({\mathit{F}}_{\mathit{i}}^{\mathrm{obs}}\mathrm{-}{\mathit{M}}_{\mathrm{dust}}{\mathrm{⟨}{{\mathit{f}}_{\mathit{\nu }}^{\mathrm{model}}}^{\mathrm{⟩}}}_{\mathit{i}}\right)}^{\mathrm{2}}}{{\mathrm{(}{{\mathit{\sigma }}_{\mathit{i}}^{\mathrm{obs}}}^{\mathrm{)}}}^{\mathrm{2}}}\mathrm{·}$(3)Here 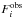${\mathit{F}}_{\mathit{i}}^{\mathrm{obs}}$ is the observed flux at the ith band in Jy with an error 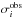${\mathit{\sigma }}_{\mathit{i}}^{\mathrm{obs}}$ , and $\mathrm{⟨}{\mathit{f}}_{\mathit{\nu }}^{\mathrm{model}}{\mathrm{⟩}}_{\mathit{i}}$ 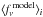is the DL07 template flux per unit dust mass in units of (Jy /M_⊙), convolved with the response function for the ith band.

The minimization of the Eq. (3) gives:${\mathit{M}}_{\mathrm{dust}}\left[{\mathit{M}}_{\mathrm{\odot }}\right]\mathrm{=}\sum _{\mathit{i}\mathrm{=}\mathrm{0}}^{\mathit{N}}\frac{{\mathit{F}}_{\mathit{i}}^{\mathrm{obs}}{\mathrm{⟨}{{\mathit{f}}_{\mathit{\nu }}^{\mathrm{model}}}^{\mathrm{⟩}}}_{\mathit{i}}}{{\mathrm{(}{{\mathit{\sigma }}_{\mathit{i}}^{\mathrm{obs}}}^{\mathrm{)}}}^{\mathrm{2}}}{\left(\sum _{\mathit{i}\mathrm{=}\mathrm{0}}^{\mathit{N}}\frac{{\mathrm{⟨}{{\mathit{f}}_{\mathit{\nu }}^{\mathrm{model}}}^{\mathrm{⟩}}}_{\mathit{i}}^{\mathrm{2}}}{{\mathrm{(}{{\mathit{\sigma }}_{\mathit{i}}^{\mathrm{obs}}}^{\mathrm{)}}}^{\mathrm{2}}}\right)}^{-1}\mathrm{·}$(4)The accuracy of the fit is parametrized by the reduced χ²$\mathrm{(}{\mathit{\chi }}_{\mathit{r}}^{\mathrm{2}}\mathrm{\equiv }{\mathit{\chi }}^{\mathrm{2}}$/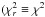d.o.f.; d.o.f. = degrees of freedom) value.

For this best fit value of M_dust (and for each of the 24 200 SED templates) we calculate the template spectrum from Eq. (2) and obtain the total infrared [8 to 1000 μm] luminosity (L_IR) following: $\mathit{L}\mathrm{=}{\mathrm{\int }}_{{\mathit{\lambda }}_{\min }}^{{\mathit{\lambda }}_{\max }}{\mathit{L}}_{\mathit{\nu }}\mathrm{(}{\mathit{\lambda }}^{\mathrm{)}}\mathrm{\times }\frac{\mathit{c}}{{\mathit{\lambda }}^{\mathrm{2}}}\left[{\mathit{L}}_{\mathrm{\odot }}\right]\mathrm{d}\mathit{\lambda }\mathit{.}$(5)Instead of using only the final best fit template for a given galaxy, it is more robust to use a final template fit (FTF) which is the weighted mean of all templates for which ${\mathit{\chi }}_{\mathit{r}}^{\mathrm{2}}\mathrm{\le }\min {}^{\mathrm{\right(}}{\mathit{\chi }}_{\mathit{r}}^{\mathrm{2}}^{\mathrm{\left)}}\mathrm{+}\mathrm{1}$. 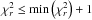Thus, the values of M_dust and L_IR are calculated as the geometric mean, weighted by the individual 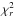${\mathit{\chi }}_{\mathit{r}}^{\mathrm{2}}$, of all templates which satisfy our 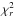${\mathit{\chi }}_{\mathit{r}}^{\mathrm{2}}$ criteria.

Given that the dust in the DL07 models is distributed in two components (diffuse and PDR, each with a different radiation field intensity) a large range of dust temperatures is present. For several reasons – especially to search for systematic changes with other parameters – it is useful to characterize the dust as having a single, or at most two, temperature(s). We use two methods to characterize the effective temperature(s) of the FTF. We calculate the luminosity weighted temperature (T_weight) of the FTF, defined as: ${\mathit{T}}_{\mathrm{weight}}\mathrm{\left[}\mathrm{K}\mathrm{\right]}\mathrm{=}\sum _{\mathit{i}\mathrm{=}\mathrm{0}}^{\mathit{N}}\frac{\mathit{b}}{{\mathit{\lambda }}_{\mathit{i}}}{\mathit{L}}_{\mathit{\lambda ,i}}{\left(\sum _{\mathit{i}\mathrm{=}\mathrm{0}}^{\mathit{N}}{\mathit{L}}_{\mathit{\lambda ,i}}\right)}^{-1}\mathit{,}$(6)where b is the Wien’s displacement constant (~2897 [μm K]), and L_λ,i is the monochromatic luminosity at wavelength λ_i. We also fit a two-temperature dust model to the FTF of the galaxy, using a cold dust component 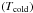${}^{\mathrm{(}}\mathit{T}_{\mathrm{cold}}{\mathrm{)}}^{}$ and a warm dust component 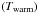${}^{\mathrm{(}}\mathit{T}_{\mathrm{warm}}{\mathrm{)}}^{}$, each described by a gray-body spectrum: 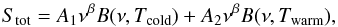${\mathit{S}}_{\mathrm{tot}}\mathrm{=}{\mathit{A}}_{\mathrm{1}}{\mathit{\nu }}^{\mathit{\beta }}\mathit{B}\mathrm{\left(}\mathit{\nu ,}{\mathit{T}}_{\mathrm{cold}}\mathrm{\right)}\mathrm{+}{\mathit{A}}_{\mathrm{2}}{\mathit{\nu }}^{\mathit{\beta }}\mathit{B}\mathrm{\left(}\mathit{\nu ,}{\mathit{T}}_{\mathrm{warm}}\mathrm{\right)}\mathit{,}$(7)where ν is the frequency, A₁ and A₂ are normalization factors for each gray-body, β is the dust emissivity index (assumed to be the same for both components)⁶, and B(ν,T_cold) and (B(ν,T_warm) are the Planck functions for the cold and warm dust components, respectively. The fit was performed using the MPFIT code⁷, which uses a robust minimization routine to obtain the best fit. The two-temperature dust model fits were performed over the wavelength range 22–1000 μm; wavelengths shorter than 22 μm were not used to avoid the complexity of the PAH emission features.

In this work we use dust mass (M_dust) obtained from the DL07 fits, that is, from the FTF. However, for comparison, we also calculate the dust mass implied by the two temperature dust model fit (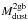${\mathit{M}}_{\mathrm{dust}}^{\mathrm{2}\mathrm{gb}}$). The total dust mass of the two temperature dust model fit is calculated as follows: (see Dunne & Eales 2001): ${\mathit{M}}_{\mathrm{dust}}^{\mathrm{2}\mathrm{gb}}\mathrm{=}\frac{{\mathit{S}}_{\mathrm{850}}{\mathit{D}}_{\mathrm{L}}^{\mathrm{2}}}{{\mathit{\kappa }}_{\mathrm{850}}}\mathrm{\times }\left[\frac{{\mathit{N}}_{\mathrm{cold}}}{\mathit{B}\mathrm{\left(}\mathrm{850}\mathit{,}{\mathit{T}}_{\mathrm{cold}}\mathrm{\right)}}\mathrm{+}\frac{{\mathit{N}}_{\mathrm{warm}}}{\mathit{B}\mathrm{\left(}\mathrm{850}\mathit{,}{\mathit{T}}_{\mathrm{warm}}\mathrm{\right)}}\right]\mathit{,}$(8)where S₈₅₀, κ₈₅₀, and B(850,T) are the observed flux, the dust emissivity and the black body emission at 850 μm, respectively, T_cold and T_warm are the dust temperatures of the cold and warm components, and N_cold and N_w are the relative masses of the cold and warm dust components. Using the SLUGs sample, Dunne et al. (2000) obtained a dust emissivity value of κ₈₅₀ = 0.077 m² kg^-1. However, more recent works support lower emissivity values at 850 μm: κ₈₅₀ = 0.0383 m² kg^-1 (Draine 2003), that is, higher dust masses for a given observed flux. In our study, we use the latter value to calculate the dust mass using the two dust components.

4. Results

4.1. Spectral fits

Using the procedure outlined in the previous Section, we were able to obtain a FTF for 1630 galaxies. The distribution of the 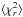$\mathrm{⟨}{\mathit{\chi }}_{\mathit{r}}^{\mathrm{2}}\mathrm{⟩}$ obtained for these fits is shown in Fig. 3: the median value is 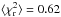$\mathrm{⟨}{\mathit{\chi }}_{\mathrm{r}}^{\mathrm{2}}\mathrm{⟩}\mathrm{=}\mathrm{0.62}$ and 92% of the spectral fits satisfy ${\mathit{\chi }}_{\mathit{r}}^{\mathrm{2}}\mathit{<}\mathrm{2.0}$.

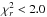For our sample, the DL07 dust model fits result in the following parameter ranges. γ ranges between 0.0 and 0.02 with a median value equal to 0.01; 75% of the sample have U_min in the range between 0.2 to 3.0, with a typical value equal to 1.5; q_PAH shows a typical value 3.19, and 91% of the sample are best fit with templates based on Milky Way models (see Appendix A for more details).

Figure 4 shows eight example SED fits – both DL07 model fits and two temperature component fits – to galaxies in our sample. Clearly, when observed fluxes at ≤25 μm are absent, a large number of DL07 templates can be fitted: these templates show large differences at λ< 60 μm, but are similar at wavelengths in the Rayleigh-Jeans tail (λ> 300 μm). However, as shown by the robustness test (Sect. 4.2 and Appendix B) for a two-temperature component fit, the warm dust component (blue spectrum) is not affected by the absence of an observed flux at ≤25 μm if we follow our fitting criteria (see Sect. 3 and Appendix B). In a similar way, the cold dust component (red spectrum) does not vary significantly between different templates, as long as the galaxy has at least one measurement in the Rayleigh-Jeans tail. The figure also illustrates that the two temperature component model (green spectrum) reproduces well both the best fit SED (yellow spectrum) and the final template fit used by us (FTF; black spectrum).

To obtain the typical SEDs of galaxies with normal (MS) and high (SB) sSFR, we use the geometric mean (weighted by χ²) of all MS and SB galaxies. The left panel of Fig. 5 shows the composite SED of all 875 MS galaxies (red spectrum) and all 26 SB galaxies (blue spectrum), where the SB galaxies have sSFR> 0.8 [yr^-1]. We also show the composite SEDs of two “cleaner” sub-samples: those closest to the MS (0.8 <sSFR [yr^-1] < 1.2, orange spectrum) and those with the highest SFR in our sample (sSFR> 1.6 [yr^-1], purple spectrum).

For each individual composite (MS and SB, Fig. 5 – middle panel) SED, the dispersions are small in the RJ tail: they are thus easily distinguishable from one another at wavelengths longer than λ> 200 μm, as long as a good short-wavelength (~25 μm) point is available for relative normalization. The largest differences between the two template spectra are seen near the FIR peak: high sSFR (SB) galaxies have a more dominant warm dust component: thus their emission peak is shifted to smaller wavelengths and the width of the peak is larger.

To compare our composite SEDs to those of galaxies with well characterized SEDs, we use the spectra available in the SWIRE template library (Polletta et al. 2007)⁸. The SWIRE templates, which are based on the GRASIL code (Silva et al. 1998), contain SEDs for ellipticals, spirals, and starburst galaxies.

The composite SED of our galaxies closest to the MS is compared to templates of Sa (black line) and Sc (green line) spiral galaxies (the Sb template is not shown as it is very similar to that of Sa galaxies) in the middle panel of Fig. 5. Clearly, there is a good agreement – within the 3σ dispersion – for λ> 10 μm; at shorter wavelengths the stellar component, present in the Sa and Sc templates but not in our MS composite, is the main reason for the observed differences. The composite SED of our highest sSFR subsample is compared to the spectrum of Arp 220 (gray), IRAS 22491–1808 (green) and IRAS 19254–7245 South (black) in the right panel of Fig. 5. The latter three spectra show a shift of the emission peak to shorter wavelengths compared to our SB composite SED, and IRAS 22491–1808 and IRAS 19254–7245 South show large absorption features at λ< 25μm which are not seen in our composite SED or indeed in any individual DL07 template.

4.2. Robustness of the SED fitting

To test the robustness of our SED fitting, we examine 24 galaxies of our sample with 7 photometric observations. Then, we explore how the M_dust , L_IR , dust temperatures (cold and warm), quantity of SEDs, χ² and reduced χ² vary with the amount of points and the rejection of specific points (e.g., how it is affected by the rejection of the flux at 12 and 22 μm or at 350 μm). The result of this test reveals that our results are very robust, with the parameters showing factors of difference smaller than 0.1 (for M_dust , L_IR , and dust temperatures). This means that the final results and relations obtained in our work, are robust and not affected by the amount of points or the distribution in wavelengths of them (following our SED fitting criteria, see Sect. 3). For more details, we refer to Appendix B.

4.3. Star formation mode

The SFR is often estimated from the IR (integrated between 8 to 1000 μm) and ultraviolet (λ = 2700 Å) luminosities (e.g., Murphy et al. 2011; Santini et al. 2014). Santini et al. (2014) suggest that both luminosities together provide the best estimate of SFR, but if only one is available, then L_IR , rather than UV luminosity, is the more reliable. We estimate the SFR for our sample galaxies using L_IR derived from our DL07 model fits and the relationship in Kennicutt (1998, assumes a Salpeter initial mass function) which assumes a $\mathit{SFR}\left[\frac{{\mathit{M}}_{\mathrm{\odot }}}{\mathrm{yr}}\right]\mathrm{=}\mathrm{1.78}\mathrm{\times }{\mathrm{10}}^{-10}{\mathit{L}}_{\mathrm{IR}}\left[{\mathit{L}}_{\mathrm{\odot }}\right]\mathit{.}$(9)The top panels of Fig. 6 show the L_IR distribution (black histogram) for our full sample. Infrared luminosities are 3.9 × 10⁶ to 7.0 × 10¹¹L_⊙ with a typical error of 13% and median value of 2.2 × 10¹⁰L_⊙. Comparing the L_IR measured for the KINGFISH galaxies and our final sample with good SED fitting, we obtain a median ratio of 1.4. The bottom panel in Fig. 6 shows the distribution of the stellar mass (M_∗), which ranges between 3.5 × 10⁸ and 7.9 × 10¹¹M_⊙ with a median value of 3.6 × 10¹⁰M_⊙ and typical error of 20%.

Figure 7 shows all our sample galaxies in the SFR-M_∗ plane. The sample covers roughly three orders of magnitude in both SFR and stellar mass, and are distributed on both sides of the locus of the Elbaz et al. (2011) MS line. Given the cutoffs in sSFR we use for SB, MS, and passive galaxies (see Sect. 1), the percentages of these sub-groups in our sample are 2.0%, 58.9%, and 15.%, respectively. In an equivalent manner, the Elbaz et al. (2007) MS (dotted red line in Fig. 7) is used and the same sSFR displacements from the MS are used to define MS, SB, and PAS galaxies. We see no great changes in the number of MS galaxies. However, the number of SBs increases (factor 1.8) and PAS galaxies decrease (factor 4.6).

4.4. Dust masses, temperatures, and emissivity index (β)

The presence of multiple dust temperatures in the DL07 models (see Sect. 3) precludes the direct application of Wien’s law to the model template (and thus our FTF) in order to obtain a dust temperature. For this reason we use two temperature component model fits to the FTF to parameterize the dust temperature (see Sect. 3). Figure 8 shows the distributions of the gray-body emissivity index (β), the temperatures of the cold (T_cold) and warm (T_warm) dust components in the two temperature component fits, (Eq. (7)), and the luminosity weighted dust temperature (T_weight, Eq. (6)). In agreement with previous results (e.g., Dunne & Eales 2001; Clements et al. 2010; Clemens et al. 2013) for nearby galaxies, our fitted values of β are distributed over 1.3–1.9, with a median of ~1.7 (Fig. 8). The β distributions for the sSFR-classified sub-samples are significantly different: PAS galaxies show the lowest values (median β ~ 1.4), MS galaxies typically show values in the range β = 1.3–1.9 with ⟨ β ⟩ ~ 1.7, and SB galaxies typically show values of β = 1.7 to 1.9 with ⟨ β ⟩ ~ 1.9. Similar differences are seen in the distributions of, and median, temperatures of the cold dust component: the median temperature of the cold dust component is 21.4 K for PAS galaxies, 23.6 K for MS galaxies, and 27.1 K for SB galaxies.

For the full sample, the warm dust component (from the two component fit; Fig. 8) shows a median value of T_warm = 57 K. Unexpectedly, the PAS galaxies show the hottest warm components, though the relative luminosity of this warm component is neglible with regards to the luminosity of the cold component. MS galaxies have warm component temperatures distributed relatively tightly around T_warm = 57 K while SB galaxies show a more uniform spread in the distribution of T_warm . In relative luminosity, however, the SBs are more dominated by the warm dust component: SB and MS galaxies show a median warm component luminosity to total luminosity (cold plus warm component) ratio of 0.01 and 0.14, respectively. If, instead, the FTF is characterized by the weighted dust temperature, the full sample shows a median weighted temperature of 24.1 K. PAS, MS and SB galaxies are clearly separated in T_weight, with median values of 21.0, 25.2 and 31.1 K, respectively.

Figure 9 shows the distribution of the dust masses, as derived from the DL07 model fits (see Sect. 3), for the entire sample (black), and for the different sSFR sub-samples (SB in blue, MS in red and PAS in green). In the full sample, dust masses range between 6.2 × 10⁵M_⊙ and 8.6 × 10⁸M_⊙, with a median value of 7.5 × 10⁷M_⊙ and an estimated typical error of 20%. This median value is similar (considering our errors) to that obtained by Clemens et al. (2013; 7.8 × 10⁷M_⊙), who used MAGPHYS modeling. Note that they corrected their model results to an emissivity value of κ₈₅₀ = 0.0383 m² kg^-1, the same value assumed in our dust mass estimations from two dust components and in agreement with the results obtained with the DL07 templates (see below). Passive galaxies tend to have lower dust masses than MS and SB galaxies. The median dust mass for PAS, MS, and SB galaxies are 6.2 × 10⁷, 7.6 × 10⁷, and 1.7 × 10⁸M_⊙, respectively. For the two temperature component models, the cold dust component dominates the total dust mass: the median contribution of warm dust to the total (warm plus cold) dust mass (M_w/M_tot) is 0.2%, with 97% of the sample at M_w/M_tot< 1%. The highest values of M_w/M_tot (up to 4%) are seen in SB galaxies.

A comparison of the dust masses derived using DL07 models to the dust masses derived from our two component 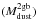$\mathrm{\left(}{\mathit{M}}_{\mathrm{dust}}^{\mathrm{2}\mathrm{gb}}\mathrm{\right)}$; Eq. (8) fits is shown in Fig. 10. Clearly there is a systematic difference in the two values. Recall that the two component model was obtained via fits to the DL07 FTF fit rather than a fit to the individual photometric data points. The dust mass ratios 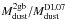${\mathit{M}}_{\mathrm{dust}}^{\mathrm{2}\mathrm{gb}}\mathit{/}{\mathit{M}}_{\mathrm{dust}}^{\mathrm{DL}\mathrm{07}}$ show a median of 0.91, and the best fit relating the two dust masses (see Fig. 10) is: $\frac{{\mathit{M}}_{\mathrm{dust}}^{\mathrm{2}\mathrm{gb}}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}\mathrm{=}{\mathrm{10}}^{\mathrm{-}\mathrm{0.34}\mathrm{\pm }\mathrm{0.06}}{\left(\frac{{\mathit{M}}_{\mathrm{dust}}^{\mathrm{DL}\mathrm{07}}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}\right)}^{\mathrm{1.04}\mathrm{\pm }\mathrm{0.01}}\mathit{.}$(10)The symbol colors (by IR luminosity) clearly reveal that the inconsistency in the DL07 and two-component derived dust masses is correlated to the IR luminosity: sources with lower L_IR show relatively higher DL07 model dust masses, while sources with higher L_IR have relatively higher two gray-body-fit dust masses. Alternatively, the difference in the two masses is related to the dust temperature of the cold component, showing an increment from the bottom left corner to the right top corner for the points in the figure. The difference in masses is likely a result of the DL07 models using a more complex calculation of dust mass for a given dust luminosity, that is, different grain types and sizes related to the parameter q_PAH (see details in Draine et al. 2007), while the dust mass of the two temperature component fit is derived via a single emissivity index. In any case, the difference in dust masses is less than 0.2 dex (factor of 1.58), so these differences are relatively unimportant in the correlations presented in the following sections (which use the DL07-derived dust masses).

4.5. L_IR, M_dust and t_dust plane

The relationship between dust mass, dust temperature, and dust luminosity (L_IR) is in general well understood (e.g., Draine & Li 2007; Scoville 2013): when dust grains absorb UV photons from young OB stars, they are heated and re-emit their energy at IR wavelengths. Clemens et al. (2013) have shown a strong correlation between the SFR/M_dust ratio and the dust temperature of the cold dust component, especially for sources with T_dust,cold> 18 K. Our sample shows a similar correlation, and our larger sample size allows us to clearly demonstrate that all galaxies lie in a single plane, which we refer to as the dust plane, in the L_IR (thus SFR), M_dust and T_dust phase space (similar to the relation shown by Genzel et al. 2015).

Figure 11 shows a projection of this dust plane in our sample: in this case we plot L_IR against M_dust and color the symbols by the (cold component) dust temperature. The dashed black lines delineate the L_IR –M_dust relationships for different cold component dust temperature bins, and the purple line shows the relation between L_IR and M_dust obtained by da Cunha et al. (2010). Here the dust temperature used is that of the cold component of the two component fit; this is the dominant component, in mass and luminosity, for all galaxies in the sample. The best fit to this dust plane is: $\log \left(\frac{{\mathit{L}}_{\mathrm{IR}}}{\mathrm{\left[}{\mathit{L}}_{\mathrm{\odot }}\mathrm{\right]}}\right)\mathrm{-}\mathrm{1.07}\log \left(\frac{{\mathit{M}}_{\mathrm{dust}}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}\right)\mathrm{-}\mathrm{0.19}\left(\frac{{\mathit{T}}_{\mathrm{cold}}}{\mathrm{\left[}\mathrm{K}\mathrm{\right]}}\right)\mathrm{+}\mathrm{2.53}\mathrm{=}\mathrm{0.}$(11)Clearly, the placement of a galaxy in the dust plane is most sensitive to the temperature of the cold component, rather than the values of M_dust and L_IR . For example, if the dust temperature is constant and we change M_dust by a factor of 10, the L_IR is required to change by a factor of 12. However, increasing T_cold by 10 K, with constant M_dust , requires L_IR to increase by a factor 80. An increase in L_IR is more easily achieved by increasing the dust temperature rather than the dust mass. The data of Clemens et al. (2013) are consistent with a plane similar to that defined by Eq. (11). However, their data suggest higher values of both L_IR and M_dust for a given value of T_cold .

If the luminosity weighted dust temperature (T_weight) is used instead of T_cold , the sample galaxies still fall on a single dust plane, though there is a larger scatter. In this case, the dust plane is parametrized by: $\log \left(\frac{{\mathit{L}}_{\mathrm{IR}}}{\mathrm{\left[}{\mathit{L}}_{\mathrm{\odot }}\mathrm{\right]}}\right)\mathrm{-}\mathrm{1.02}\log \left(\frac{{\mathit{M}}_{\mathrm{dust}}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}\right)\mathrm{-}\mathrm{0.10}\left(\frac{{\mathit{T}}_{\mathrm{weight}}}{\mathrm{\left[}\mathrm{K}\mathrm{\right]}}\right)\mathrm{+}\mathrm{0.30}\mathrm{=}\mathrm{0.}$(12)If the temperature of the warm component (from the two components fit) of the dust is used instead of the temperature of the cold component, the sample galaxies no longer fall on a single dust plane.

The correspondence between interacting galaxies and SB galaxies is one-to-one only for extreme starbursts: of all interacting galaxies in the sample, only those with high cold-dust component temperature (T_cold> 27 K) and high SFR (log (L_IR/L_⊙) > 11, that is, LIRGs) are classified as SBs.

While the dust plane provides a powerful tool to relate the dust mass, total IR luminosity and dust temperature of the cold component, or derive any one parameter from the other two, the comprehensive dataset available for our large local sample is difficult to obtain for other samples, especially those at high redshift. We thus provide several scaling relationships which can be used to estimate the location of a galaxy in the dust plane in the presence of limited data or, alternatively, to derive one or all parameters of the dust plane phase space.

Since the dust plane is most sensitive to changes in T_cold , we present several relations to estimate its value using sub-mm to IR colors. Previous works, for example, Soifer et al. (1987), Chanial et al. (2007), Hwang et al. (2010), have typically derived dust temperatures from IRAS colors: IRAS 60/IRAS 100. Here we present that based on the 100 μm and 350 μm color; we refer to Appendix D for the equivalent results from other IR to sub-mm colors. The relationship between the cold component dust temperature and the 100 μm to 350 μm flux ratio is shown in the right panel of Fig. 12. The best fit to this relationship is: $\frac{{\mathit{T}}_{\mathrm{cold}}}{\mathrm{\left[}\mathrm{K}\mathrm{\right]}}\mathrm{=}{\mathrm{10}}^{\mathrm{(}\mathrm{1.280}\mathrm{\pm }\mathrm{0.001}\mathrm{)}}{\left(\frac{{\mathit{f}}_{\mathrm{100}}}{{\mathit{f}}_{\mathrm{350}}}\right)}^{\mathrm{(}\mathrm{0.160}\mathrm{\pm }\mathrm{0.001}\mathrm{)}}\mathit{.}$(13)To obtain a cleaner relation, large crosses in Fig. 12 show the mean value of T_cold in bins of 0.5 mag in the color f₁₀₀/f₃₅₀. Interestingly, the coefficients of the best fit (red dashed line) show that the values are consistent within the errors with the coefficients obtained for the complete sample.

Both the dust mass and the total IR luminosity can be estimated from a single monochromatic luminosity in the RJ tail of the dust emission. The dependence of M_dust and L_IR on the 350 μm luminosity is shown in the left and middle panels of Fig. 12, respectively. At first glance, these relationships appear to have a large scatter. However, it is clear that this scatter can be fully explained (and removed) by the use of the temperature of the cold dust component. Thus the estimation of M_dust and/or L_IR can be made very accurately in the presence of an estimate of the cold dust temperature (see previous paragraph) or at least roughly in the absence of a cold dust temperature. We will address both scenarios below for the case of using the 350 μm luminosity for the RJ tail luminosity (see Appendices E and F for the results of using other sub-mm frequencies).

Using the monochromatic luminosity at 350 μm in the presence of a value for T_cold , we obtain two planes to determinate L_IR or M_dust : $\begin{array}{ccc}\log \left(\frac{{\mathit{L}}_{\mathrm{IR}}}{\mathrm{\left[}{\mathit{L}}_{\mathrm{\odot }}\mathrm{\right]}}\right)& \mathrm{-}& \mathrm{1.017}\log \left(\frac{{\mathit{L}}_{\mathrm{350}}}{\mathrm{[}\mathrm{W}\mathrm{H}{\mathrm{z}}^{-1}\mathrm{]}}\right)\\ & \mathrm{-}& \mathrm{0.118}\left(\frac{{\mathit{T}}_{\mathrm{cold}\mathit{,}\mathrm{dust}}}{\mathrm{\left[}\mathrm{K}\mathrm{\right]}}\right)\mathrm{+}\mathrm{16.45}\mathrm{=}\mathrm{0}\\ \log \left(\frac{{\mathit{M}}_{\mathrm{dust}}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}\right)& \mathrm{-}& \mathrm{0.940}\log \left(\frac{{\mathit{L}}_{\mathrm{350}}}{\mathrm{[}\mathrm{W}\mathrm{H}{\mathrm{z}}^{-1}\mathrm{]}}\right)\\ & \mathrm{+}& \end{array}$(14)In the absence of a T_cold estimation, one has to accept the full scatter seen in the left and middle panels of Fig. 12, that is, a dispersion of 0.5 dex and 1 dex in the estimation of M_dust and L_IR from a single 350 μm luminosity. The best fit to the data points (blue lines in Fig. 12, right and middle panels) is: $\begin{array}{ccc}\frac{{\mathit{L}}_{\mathrm{IR}}}{\mathrm{\left[}{\mathit{L}}_{\mathrm{\odot }}\mathrm{\right]}}& \mathrm{=}& {\mathrm{10}}^{\mathrm{-}\mathrm{14.388}\mathrm{\pm }\mathrm{0.002}}{\left(\frac{{\mathit{L}}_{\mathrm{350}}}{\mathrm{[}\mathrm{W}\mathrm{H}{\mathrm{z}}^{-1}\mathrm{]}}\right)}^{\mathrm{1.046}\mathrm{\pm }\mathrm{0.005}}\\ \frac{{\mathit{M}}_{\mathrm{dust}}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}& \mathrm{=}& \end{array}$(15)Estimations of the dust mass and IR luminosity from other monochromatic IR or sub-mm fluxes, and estimates of the temperature of the cold dust component from other IR and sub-mm colors can be found in Appendices D, E, and F.

4.6. Dust to stellar mass ratio

The typical M_dust/M_∗ ratios are 0.21% and 0.25% for our entire sample and for all star forming (non-passive) galaxies, respectively. These ratios are smaller than those obtained by Clemens et al. (2013; median M_dust/M_∗ = 0.46% in a well defined sample of 234 nearby galaxies detected by Planck) and Clark et al. (2015; median M_dust/M_∗ = 0.44% in the HAPLESS sample, a blind sample of 42 nearby galaxies detected by Herschel). Another three works, using the MAGPHYS code, show similar values for the dust to stellar mass ratio. da Cunha et al. (2010) shows a value between 0.23% and 0.14% depending on the stellar mass bin used in a sample of 1658 galaxies at z< 0.1; Smith et al. (2012) obtain a dust to stellar mass of 0.22% from a sample of 184 galaxies at z< 0.1; while Pappalardo et al. (2016) show a value of 0.18% in their main sample.

An anticorrelation between the M_dust /M_∗ and M_∗ has been shown by Cortese et al. (2012, in Virgo cluster galaxies), Clemens et al. (2013) and Clark et al. (2015).

We see the same anticorrelation in our sample (Fig. 13), with the points showing a large dispersion. The fits to our full sample (FS; purple line) and to all our star forming (SF) galaxies (non-passive galaxies; black line), are: $\begin{array}{ccc}\frac{{\mathit{M}}_{\mathrm{dust}}}{{\mathit{M}}_{\mathrm{\ast }}}& \mathrm{=}& {\mathrm{10}}^{\mathrm{-}\mathrm{0.4}\mathrm{\pm }\mathrm{0.2}}{\left(\frac{{\mathit{M}}_{\mathrm{\ast }}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}\right)}^{\mathrm{-}\mathrm{0.28}\mathrm{\pm }\mathrm{0.02}}\mathrm{FS}\\ \frac{{\mathit{M}}_{\mathrm{dust}}}{{\mathit{M}}_{\mathrm{\ast }}}& \mathrm{=}& {\mathrm{10}}^{\mathrm{-}\mathrm{1.3}\mathrm{\pm }\mathrm{0.2}}{\left(\frac{{\mathit{M}}_{\mathrm{\ast }}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}\right)}^{\mathrm{-}\mathrm{0.12}\mathrm{\pm }\mathrm{0.02}}\mathrm{SF}\mathit{.}\end{array}$(16)When we separate the galaxies by star-forming mode (bottom panels of Fig. 13), we find two interesting results: (a) SB galaxies show a much steeper anticorrelation than the other sub-samples, and (b) the source of the scatter in the anticorrelation can be traced by the temperature of the cold dust component, T_cold (or the weighted dust temperature T_weight). The anticorrelations obtained individually for each subsample are: $\begin{array}{ccc}\frac{{\mathit{M}}_{\mathrm{dust}}}{{\mathit{M}}_{\mathrm{\ast }}}& \mathrm{=}& {\mathrm{10}}^{\mathrm{7.4}\mathrm{\pm }\mathrm{0.8}}{\left(\frac{{\mathit{M}}_{\mathrm{\ast }}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}\right)}^{\mathrm{-}\mathrm{0.92}\mathrm{\pm }\mathrm{0.08}}\mathrm{SB}\\ \frac{{\mathit{M}}_{\mathrm{dust}}}{{\mathit{M}}_{\mathrm{\ast }}}& \mathrm{=}& {\mathrm{10}}^{\mathrm{-}\mathrm{2.1}\mathrm{\pm }\mathrm{0.2}}{\left(\frac{{\mathit{M}}_{\mathrm{\ast }}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}\right)}^{\mathrm{-}\mathrm{0.09}\mathrm{\pm }\mathrm{0.01}}\mathrm{MS}\\ \frac{{\mathit{M}}_{\mathrm{dust}}}{{\mathit{M}}_{\mathrm{\ast }}}& \mathrm{=}& {\mathrm{10}}^{\mathrm{-}\mathrm{1.2}\mathrm{\pm }\mathrm{0.4}}{\left(\frac{{\mathit{M}}_{\mathrm{\ast }}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}\right)}^{\mathrm{-}\mathrm{0.17}\mathrm{\pm }\mathrm{0.04}}\mathrm{PAS}\mathit{.}\end{array}$(17)Essentially, the dust to stellar mass ratio in SB galaxies (typically 1.3%) is higher than that in MS galaxies (typically 0.24%), though the difference is smaller for galaxies at the highest stellar masses. Passive galaxies show a very low dust to stellar mass ratio, with a typical value of M_dust/M_∗ = 0.1%. Additionally, for all sSFR groups, at a given stellar mass, the galaxies with the highest T_cold (T_weight) have the smaller dust to stellar mass ratios.

4.7. Dust to gas mass ratio

To more easily study the relation between dust and gas masses, we separate the total gas mass (hereafter referred to as interstellar medium mass or M_ISM ) into two components: the molecular gas mass (M_mol), and the atomic (hydrogen) gas mass (M_HI): M_ISM = M_mol + M_HI. Figure 14 shows the relation between the dust mass and the atomic (left panel), molecular (middle panel) and total (right panel) gas masses.

The median gas fraction (M_ISM/ (M_∗ + M_ISM)) for the full sample is 33 ± 11%. The medians for MS, PAS, and SB galaxies are 32 ± 8%, 5.0 ± 0.8% and 68 ± 25%, respectively. For all sources with HI and CO measurements, the molecular to atomic gas mass ratios (M_mol/M_HI) show a median value of 0.8 ± 0.2. Even for MS and PAS galaxies, the same value is observed, however SB galaxies show a huge value (4 ± 1; see Table 3).

The median values of M_dust/M_HI are 1.6% and 1.3% for the galaxies with both M_HI and M_mol and for those with only M_HI measurements, respectively (see Tables 3 and 4). These values are smaller than those obtained by Clements et al. (2010,2.2%) and Clark et al. (2015,3.9%). PAS galaxies show the highest dust to atomic mass ratios, followed by SB and finally MS galaxies. The median dust to molecular gas mass ratio is 2.1% for all galaxies with both M_HI and M_mol, and 2.0% for all galaxies with only M_mol. Passive galaxies show the largest dust to molecular gas mass ratios followed by MS galaxies, with SB galaxies showing the lowest values. The median dust to ISM mass ratios are similar for the full sample, MS, and SB galaxies (0.8%, 0.7%, and 0.6%, respectively), while PAS galaxies show larger values (1.4%).

Figure 14 shows a clear correlation between dust mass and molecular and atomic gas mass, individually. But the correlation between dust and M_ISM shows the smallest dispersion, with the best fit: $\frac{{\mathit{M}}_{\mathrm{ISM}}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}\mathrm{=}\mathrm{6.03}{\left(\frac{{\mathit{M}}_{\mathrm{dust}}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}\right)}^{\mathrm{0.7}}\mathrm{·}$(18)This correlation between ISM and dust mass has been noted previously by Leroy et al. (2011, in five Local Group galaxies) and Corbelli et al. (2012, in 35 metal-rich Virgo spirals).

The dust to gas ratio (δ_DGR = M_dust/M_ISM) does not systematically vary with the stellar mass for our sample galaxies (Fig. 15), despite the expected metallicity range (between 8.4 and 9.1) for this stellar mass range (10⁹ < M_∗ [M_⊙] < 10¹¹) (Tremonti et al. 2004). Our full sample shows a large scatter in δ_DGR (±0.5 dex), but the scatter significantly decreases when considering SB, MS, and PAS galaxies separately. MS and PAS galaxies show a dispersion in δ_DGR of ±0.3 dex, and SBs show a dispersion of only ±0.2 dex. The median values of δ_DGR for MS and SB galaxies (red and blue lines in Fig. 15, respectively) are very similar to the median value of the full sample; however, PAS galaxies show a higher median δ_DGR (green line in Fig. 15). Additionally, the symbol colors show that the galaxies with higher gas fractions have lower values of δ_DGR, especially MS and PAS galaxies.

5. Discussion

We have modeled the dust emission using detailed DL07 dust models in an unprecedentedly large sample of 1630 nearby (z< 0.1, ⟨ z ⟩ = 0.015) galaxies with uniform photometric data from WISE (3.4 to 22 μm), IRAS (12 to 100 μm), Planck (350 to 850 μm) and/or SCUBA (850 μm). This sample covers a significant parameter space in stellar mass and SFR, and thus sSFR, going from starburst (SB; LIRGs; L_IR> 10¹¹L_⊙) to passive (PAS; L_IR ~ 10^8.3L_⊙) galaxies.

In comparison, previous studies that present detailed dust models to galaxies with sub-mm data include the KINGFISH/SINGS sample (Dale et al. 2012) of 65 nearby, normal (L_IR< 10¹¹L_⊙) spiral galaxies with photometry from IRAS, Spitzer, Herschel, and SCUBA, and the ERCSC sample Negrello et al. (2013), Clemens et al. (2013) of 234 local (z< 0.1) galaxies with photometry from IRAS, WISE, Spitzer, Herschel and Planck. The ERCSC sample was created by matching four Herschel samples, HRS, HeViCS, KINGFISH and H-ATLAS, to the Planck Early Release Compact Source Catalogue.

Note that the other large nearby sample of galaxies with dust modeling results, the sample of 1658 galaxies in da Cunha et al. (2010), used MAGPHYS modeling applied to UV, optical, and limited IR data (2MRS, IRAS); the lack of sub-mm data is expected to lead to less reliable dust mass estimates (e.g., Draine et al. 2007).

The advantages of our sample over the ERCSC sample include: a) a sample size approximately seven times larger with equivalent and consistent data observations; b) the use of the Second Planck catalog of Compact Sources, which contains only reliable detections (in this release the Planck collaboration separated the less reliable detections into a separate “excluded” catalog which we do not use); c) the fact that the catalogs of the Planck second release are deeper than those of the Early Release; d) the use of flux corrections to the Planck catalog fluxes (Nagar et al., in prep.) to ensure consistency with the SCUBA flux scale.

We remind the reader that all galaxies fitted with dust models had between four and seven photometric points distributed between 12 μm and 850 μm. In all cases these points populated both sides of the SED peak with ≥2 photometric points shortward of λ ≤ 100 μm and ≥ one photometric point at λ ≥ 350 μm. A further indication that the available number of photometric points sufficiently constrained the fitted SED is that all templates matched to the photometry with 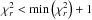${\mathit{\chi }}_{\mathit{r}}^{\mathrm{2}}\mathit{<}\min {}^{\mathrm{\right(}}{\mathit{\chi }}_{\mathit{r}}^{\mathrm{2}}^{\mathrm{\left)}}\mathrm{+}\mathrm{1}$ have similar spectral shapes and parameters (such as M_dust or L_IR ), despite the extremely large number of templates (24 200) in our work.

The differences in the dust masses obtained by us and those obtained by Draine et al. (2007, who used similar modeling but more extensive photometric data at λ ≤ 100 μm in 17 KINGFISH/SINGS galaxies, ranges between −0.3 dex and 0.4 dex, with a median of −0.07 dex. The equivalent differences in the IR luminosities obtained by us and those obtained by Draine et al. (2007) range between −0.017 dex and 0.5 dex with a median of 0.14 dex. The largest discrepancies are seen in galaxies (e.g., NGC 6946) for which Draine et al. (2007) did not use sub-mm data. Dale et al. (2012) explore the dust modeling in a larger KINGFISH/SINGS sample, which contains 64 galaxies with sub-mm fluxes. However, the dust masses and IR luminosities obtained from the model fits were not explicitly listed, thus we can not compare our results. Additionally, the values of L_IR and L_FIR calculated from the dust model fits are in overall agreement with those estimated from IRAS fluxes using the Sanders et al. (1991) equations. In fact, we use our SED-derived L_IR and L_FIR values to recalibrate the equations to estimate these values from only IRAS photometry (Appendix E).

The advantage of our sample compared to previous works listed in Table 1 is that, for the first time, we have a large amount of nearby galaxies (more than ten times larger than previous studies) with one or more sub-mm measurements. Additionally, as a consequence of the all-sky observation by Planck, our sample reduces its selection effects only to the cutoffs of Planck (its reliable zones), without selection effects for a specific type of galaxy (for example, the KINGFISH/SINGS sample, which contains only star forming galaxies).

5.1. Interpreting the dust temperature

We can interpret the dust temperature of the cold component (T_cold) as the equilibrium temperature of the diffuse ISM. This interpretation is supported by the strong correlation between T_cold and the starlight intensity parameter of the diffuse ISM (U_min) in DL07. This correlation has been demonstrated by Aniano et al. (2012, in a sample of two resolved galaxies) and used by Ciesla et al. (2014, in the HRS sample) to compare their SED fitting results with the results of other works. The problem with this interpretation is that the temperature of the diffuse ISM (thus T_cold ) is not expected to correlate with the SFR (produced in PDRs rather than the diffuse ISM). However, the dust plane shown here implies a close connection between L_IR , M_dust , and T_cold (see Sect. 4.5). Furthermore, the SFR – M_∗ relation also shows a dependence on T_cold ; T_cold increases as one moves from sources with higher M_∗ and lower SFR to sources with lower M_∗ and higher SFR. To solve this contradiction, Clemens et al. (2013) propose that the lower dust masses in star-forming regions allow the escape of UV photons thus increasing the starlight intensity impinging on the diffuse ISM, which in turn would increase its temperature.

In agreement with the Clemens et al. (2013) results, we find that L_IR , M_dust , and other parameters do not correlate with the warm dust component temperature (T_warm). The parameters U_min and γ (the percentage of dust mass PDRs) show only a weak correlation with T_warm . Nevertheless, the importance of using a warm component is that when it is used, the cold component temperature (T_cold; rather than the temperature obtained from a single component fit) shows much cleaner correlations with L_IR , M_dust , and the dust plane, and also better explains the systematics in, for example, the M_dust /M_∗ versus M_∗ anticorrelation. Further, T_cold , rather than, for example, T_weight, is more cleanly correlated with the IR to sub-mm colors.

It is useful to compare the luminosity weighted dust temperature (T_weight) with the temperatures obtained from the two component fits, since T_weight is independent of our assumptions made in the two-component fits. Figure 16 shows the relationship between T_weight and the T_cold ; the scatter in the data points is primarily correlated with T_warm . The tightest correlation is found for MS and PAS galaxies with T_warm≤ 58 K. SBs and Intermediate SB galaxies (typically at T_warm≥ 58 K) show a larger scatter. A cleaner correlation is observed if we compare T_weight with a temperature obtained from a weighted addition of T_cold and T_warm , where the weights are the respective flux fractions (e.g., S_c/ (S_w + S_c)). That is, the increase in the scatter seen in Fig. 16 for T_warm≥ 58 K is a consequence of the increment in the fractional flux of the warm component. The use of T_weight instead of T_cold in all the relevant relations presented in Sect. 4 produces similar results but with a larger scatter. Furthermore, IR and sub-mm colors (see Appendix D) can be used to estimate T_cold with a smaller scatter than T_weight.

We obtain a better estimation of the dust temperature of the cold component using a color. This color is based on a IR flux (λ< 100 μm) and a sub-mm (λ> 350 μm) flux. These estimates show a stronger relation than compared to using only two IR fluxes or only two sub-mm fluxes (e.g., the color 60 to 100 μm). The lowest end of our wavelength range (12 and 22 μm) shows the least reliable estimates of T_cold using an IR and sub-mm color. This is a consequence of the warm component influence within these fluxes. However, the T_weight shows a tight correlation with the color obtained using the flux at 22 μm and one sub-mm flux, but not with the color at 12 μm. This is a consequence of its proximity to the PAHs emission.

5.2. Dust mass as a tracer of total gas mass

Figure 17 shows the relationships between the atomic gas mass to stellar mass ratio, the ${\mathit{L}}_{\mathrm{CO}}^{\mathrm{\prime }}$ to stellar mass ratio and the dust to stellar mass ratio, with the distance of the galaxy from the MS (log (sSFR/sSFR_MS)). These plots reveal that log (sSFR/ sSFR_MS) is weakly correlated with M_HI and ${\mathit{L}}_{\mathrm{CO}}^{\mathrm{\prime }}$, but tightly correlated with the dust to stellar mass ratio.

The evolution of the dust to stellar mass ratio as tracer of star-formation mode (sSFR classification) was previously studied in galaxies within the redshift range 0 <z< 4 by Tan et al. (2014), who use different dust to stellar mass ratios for normal star forming galaxies and extreme SB galaxies (ULIRGs) over the redshift range 0 to 2. The largest difference was found at z ~ 0 where for normal galaxies they used the averaged value of the normal galaxies in the da Cunha et al. (2010) sample. In comparison, the normal galaxies in our sample show a large scatter (~1.3 dex) in their dust to stellar mass ratios (see right panel of Fig. 17), so that they overlap with the median dust to stellar mass ratio of extreme starbursts. This scatter is related to the gas fraction of these galaxies, where gas-rich galaxies show higher dust to stellar mass ratios. Our sample does show that SB and InSB galaxies have higher dust to stellar mass ratios than MS and PAS galaxies; in fact their dust to stellar mass ratios are higher than the data point of extreme SBs at z ~ 0 in Tan et al. (2014) even though our SBs and InSB samples are made up of LIRGs instead of ULIRGs. Thus overall, we observe median dust to stellar mass ratios higher than those used by Tan et al. (2014), and an overlap in the dust to stellar mass distributions of normal and SB galaxies.

Garn & Best (2010) have showed that galaxies with higher dust masses have higher stellar masses. However, in our work we reveal a more complex picture, in which the dust-to-stellar-mass ratio anticorrelates with the stellar mass, and the strength of the anticorrelation changes in sub-samples of galaxies separated by their star-forming mode (i.e., by sSFR; see Sect. 4.6). Thus, low-stellar-mass SB galaxies are dustier than massive PAS galaxies. This result is in agreement with the discussion in Clemens et al. (2013), where they conclude that despite (δ_DGR) and M_∗ being directly proportional to metallicity (Z), galaxies with smaller M_∗ show higher M_ISM/M_∗ and this effect prevails over the tendency of galaxies with smaller M_∗ to have smaller Z.

Passive galaxies of course show the lowest sSFR, dust to ISM mass ratios, and ISM to stellar mass ratios (Fig. 17). But Fig. 15 shows that even though PAS galaxies have smaller gas fractions, they have larger δ_DGR in comparison with MS and SB galaxies. That is, at low SFRs, decreasing SFR results in the ISM mass decreasing faster than the dust mass.

5.3. Estimating ISM mass from a single sub-mm measurement

The technique of using a single rest-frame monochromatic luminosity at 850 μm to obtain a reasonably accurate ISM mass, developed by Scoville (2013), Scoville et al. (2014, 2016), is based on two primary assumptions: (1) a constant δ_DGR for galaxies with M_∗ between 10⁹ and 10¹¹M_⊙, and (2) the assumption of a uniform dust temperature for all galaxies, justified because a change by factor ~ 2 in the dust temperature will introduce an error of only factor ~ 2 (0.3 dex) in the ISM mass. With these assumptions, α₈₅₀ (=L₈₅₀/M_ISM) can be used to convert a sub-mm luminosity to an ISM mass. In our sample, the median value of α₈₅₀ is 12.56, with a rms of ~ 0.3 dex (Fig. 18). This value is 0.44 dex (factor 2.8) lower than that obtained by Scoville et al. (2014) and 0.15 dex (factor 1.4) lower than that obtained by Hughes et al. (2017) using the VALES sample that contains 67 MS galaxies at 0.02 <z< 0.35. The scatter, and its systematics, could be explained by the two steps required to calculate α₈₅₀. First, the conversion of L_submm to M_dust (e.g., Figs. 12 and F.1) is relatively straightforward: the two quantities are highly proportional and almost all the scatter (factor 1.33 or 0.12 dex; take rms from the Fig. 12) seen in this relationship is a consequence of the variation of cold dust temperature. The conversion of dust mass to ISM mass, however, is subject to a larger (and dominant) scatter (rms = 0.25 dex; Fig. 14). We note that we found no dependence of α₈₅₀ on either the IR luminosity or the galaxy stellar mass. The L_IR values (colored bar in Fig. 18) reveal that the Scoville (2013), Scoville et al. (2014, 2016) sample (large triangles) contains LIRGs galaxies, ULIRGs and galaxies with log L_IR< 11 and do not show any correlation with the constant α₈₅₀ and the luminosity at 850 μm. However, our galaxies (circles) show weak correlation between the α₈₅₀ and the L_IR , where galaxies with smaller L_IR show smaller values of α₈₅₀. A brief analysis of the images and SEDs on the Scoville (2013), Scoville et al. (2014, 2016) sample, with data taken from NED, reveals that the SED in all the galaxies of that sample show prominent synchrotron emission and an infrared peak emission at wavelength smaller than 100 μm, which is consistent with a cold dust component with high temperature. Additionally, the images of the sample show that all the galaxies have irregular and/or disturbing morphologies consistent with ongoing galaxy interactions. This suggests that the Scoville (2013), Scoville et al. (2014, 2016) sample could have a possible bias caused by selection effects, which allows the tight and constant value for α₈₅₀. On the other hand, the VALES sample excludes the interacting galaxies, and its median α₈₅₀ is closer to our value.

6. Conclusions

Here we present reliable and accurate dust mass properties obtained by fitting DL07 dust models to a large (1630) sample of nearby galaxies. The principal results from our analysis are the following:

• The dust temperature of the cold dust component (T_cold) and theweighted dust temperature of the fitted SED model are closelycorrelated to both L_IR and M_dust , forming a plane which werefer to as the dust plane.

• The dust mass (and infrared luminosity) can be estimated from a single monochromatic luminosity within the Rayleigh Jeans tail of the dust emission. The error in this estimation is 0.12 (0.20) dex. This error can be significantly reduced by using an estimate of the dust temperature of the cold component: errors in the estimation now reduce to 0.05 (0.10) dex.

• The dust mass is better correlated with the total ISM mass (M_ISM∝M_dust^0.7) than with the molecular or atomic gas mass separately.

• The conversion factor between the single monochromatic luminosity at 850 μm and the total ISM mass (α_{850 μm}) shows a large scatter (rms = 0.29 dex) for our sample galaxies and a weak correlation with the L_IR .

• The star-formation mode of a galaxy (based on its sSFR) is correlated with both the gas and dust masses: the dustiest (high M_dust /M_∗) galaxies are gas rich and have high SFRs.

• the detailed DL07 model fits, and their resulting parameters, have been used to determine accurate estimators of L_IR , L_FIR , M_dust , and dust temperature from limited photometric data, as detailed in the paper and the appendices.

• The results of fitting a large number of passive, MS, and SB galaxies with DL07 templates have allowed us to determine typical ranges of value for the DL07 input parameters for galaxies with different star-forming modes, potentially easing model fitting (i.e., reducing the number of input templates) to galaxies with limited photometry.

Determinations of the true dust temperatures and gas masses of galaxies require detailed studies of the star-formation regions and the conversion factor α_CO in a statistically relevant sample of galaxies with different star-forming modes. Such studies are extremely expensive and almost impossible to perform at present. Thus, the empirical scaling relations presented in this work are very useful for studying the global gas and dust properties of galaxies, and constraining their evolutionary stage.

---

Acknowledgments

We would like to thank the referee all for his/her very useful comments and suggestions. This work was supported by the European Commission through the FP7 SPACE project ASTRODEEP (Ref. No: 312725) and Programa Financiamiento Basal PFB-06 ETAPA II. G.O. acknowledges the support provided by CONICYT(Chile) through Programa Nacional de Becas de Doctorado 2012 (21120496), and FONDECYT postdoctoral research grant No. 3170942. P.C.-C. acknowledges the support provided by CONICYT(Chile) through Programa Nacional de Becas de Doctorado 2014 (21140882) P.C. acknowledges the support provided by FONDECYT postdoctoral research grant No. 3160375. R.L. acknowledges support from Comité Mixto ESO-GOBIERNO DE CHILE, GEMINI-CONICYT FUND 32130024, and FONDECYT Grant 3130558. We acknowledge the usage of the following databases and codes: HyperLeda (http://leda.univ-lyon1.fr), NED (https://ned.ipac.caltech.edu), IRSA (http://irsa.ipac.caltech.edu), EDD (http://edd.ifa.hawaii.edu/), SDSS (www.sdss3.org), NASA-Sloan Atlas (http://www.nsatlas.org/) and MPFIT (http://www.physics.wisc.edu/~craigm/idl/idl.html).

References

Appendix A: Distribution of DL07 model parameters

The Draine & Li models (DL07) need a large number of parameters (six parameters in total) to characterize the emission from the IR to the sub-mm wavelengths. Despite some restrictions in DL07 libraries and Draine et al. (2007), the amount of avoided SED templates is large (in our case 24 200 templates).

In this work, we summarize the use of three DL07 parameters (U_min, γ and q_PAH). Additionally, the MS classification allows a reduction of the number of SED templates for samples with less available data.

Figure A.1 shows the distribution of the parameter γ (top panel), U_min (middle) and q_pah (bottom panel), using the values restricted by the available libraries for our complete sample (black histogram). The range of values for γ is between 0.0 and 0.24. Moreover, 91% of the selected values are between 0.0 and 0.02, and just two sources show γ> 0.1. For U_min, the range expands between 0.2 and 15, but 75% of the subsample show values between 1.0 and 3.0. The q_pah parameter shows a total range between 0.047 and 0.01, where values between 0.47 to 4.58 come from models based on the Milky Way (MW), between 0.75 to 2.37 are based on the Large Magellanic Cloud (LMC) and the value 0.01 is a model based on the Small Magellanic Cloud (SMC). Figure A.1 shows this groups of values separated by the purple solid and black dashed lines: values based on MW models are on the left side of the solid line, based on LMC are between purple solid and black dashed lines and based on SMC are on the right side of the black dashed line⁹. The q_PAH parameter ranges between 1.77 and 3.90 including 74% of the sample, all of them belong to models based on the MW. The q_PAHs based on MW model are the most relevant values since they cover 91% of the complete sample.

Following the sSFR classification, it is possible to select more specific values for these parameters. See Tables A.1–A.3 for more details.

Appendix B: Robustness test

As we mention in Sect. 4.2, we prepare a robustness test using 24 galaxies with 7 photometric observations and good SED fits. In this test, we explore the robustness of our SED fitting considering our SED fitting criteria: a) observations at 60 and 100 μm; b) observations at 12 and 22 μm or 22 μm; c) minimum of 4 points with two possible distributions, 3 at λ ≤ 100 μm and 1 at λ ≥ 350 μm or 2 at λ ≤ 100 μm and 2 at λ ≥ 350 μm. This criterion plus the technique of weighted geometric mean to obtain the final value of the parameters (described in Sect. 3), proves to be very robust. In our test, we systematically discard different amounts of points at different wavelength; this technique evaluates the reduction of the measurements and the influence of the position of this measurement in the SED fitting. Table B.1 shows the rejected points (e.g., f₃₅₀ is the flux at 350 μm) and the number of points in each SED fitting test. To characterize the change of the parameter values for each restriction, we study the distribution of the value for the parameter normalized with the value of them, using the fitting with seven points. Columns 1 to 7 show the mean value of each normalized distribution; the quoted error is the standard deviation. The normalized number of templates (Col. 1) shows a great increment (~10 times) of accepted templates in the SED fitting, in absence of the wavelengths at 12 and 22 μm. However, in absence of the sub-mm data, the amount of accepted templates is only reduced by a factor of 0.1 to 0.3. The value of the χ² and the reduced χ² show a direct dependence on the amount of points used and a weak dependence on the wavelength of the rejected points. On the other hand, the dust mass, IR luminosity and the temperature of the cold and warm dust components show, in general, factors of difference smaller than 0.1 with a standard deviation smaller than 0.1 (the dust mass shows greater factors of difference and greater standard deviation when the sub-mm data are rejected, as is expected Draine & Li 2007).

Appendix C: Stellar mass comparison

A frequently used parameter to characterize galaxies and their evolution is the stellar mass (M_∗). Different methods are used in order to obtain the M_∗ from different data and models. For our study, we use the relations obtained by Cluver et al. (2014), who uses W1 and W2 (at 3.4 and 4.6 μm, respectively) from WISE observations. The advantage is that no correction by opacity is needed, in contrast to other methods using optical photometry. To compare our results, we use three other samples: (1) The Nasa Sloan Atlas (NSA)¹⁰ based on all sources from the Sloan Digital Sky Survey (SDSS) data release 8 (DR8) at redshifts z < 0.005 with observations from the Galaxy Evolution Explorer (GALEX). (2) the Chang catalog (Chang et al. 2015), which is a compilation of catalogs based on SDSS and WISE photometry for sources with z < 0.6. (3) the MPA-JHU database with redshift z < 0.1, which is based on the SDSS data release 8 (DR8).

The Nasa Sloan Atlas derives its M_∗ from SDSS ugriz photometry, assigning a mass to light ratio according to the galaxy broad-band colors and a Salpeter IMF (Bell et al. 2003).

Chang et al. (2015) obtain its M_∗ from SDSS ugriz photometry and WISE W1-W2 photometry using the MAGPHYS code (da Cunha et al. 2008), which contains a large library of SED templates covering the UV to IR range.

The MPA-JHU’s M_∗ is estimated using a Bayesian methodology from SDSS spectroscopy and ugriz galaxy photometry with a correction for nebular emission (Kauffmann et al. 2003).

The stellar mass from NSA (Fig. C.1 top panel) shows a tight correlation with our stellar mass, the mass ratio (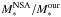${\mathit{M}}_{\mathrm{\ast }}^{\mathrm{NSA}}\mathit{/}{\mathit{M}}_{\mathrm{\ast }}^{\mathrm{our}}$) shows at 1σ dispersion of 0.25 dex (factor 1.8) and a 3σ dispersion of 0.7 dex (factor 5.0). However, NSA stellar masses are systematically larger than our stellar masses for interacting galaxies (crosses), while some other non-interacting galaxies with apparent diameter > 1.2′ show smaller stellar masses than our estimations.

The stellar mass from the Chang et al. (2015) sample (Fig. C.1 middle panel) shows a good correlation with our stellar masses, where 1σ dispersion between the stellar masses is 0.5 dex (factor of 3.2). Interacting galaxies show greater stellar masses in the Chang et al. (2015) estimations, but many non-interacting galaxies with apparent diameter >1.0′ show greater values in our stellar mass estimation.

The stellar mass from the SDSS MPA-JHU sample (Fig. C.1 bottom panel) shows no consistency with our stellar masses, since the 1σ dispersion is 0.8 dex (factor 6.3). The MPA-JHU estimation seems to overestimate the stellar mass of the majority of our sources with M_∗ < 10^9.5M_⊙ and to underestimate the stellar mass of half of the sample by M_∗> 10¹⁰M_⊙.

Comparing the SDSS photometry, the NSA has the strongest data because its standard pipeline to calibrate SDSS images oversubtract the sky in large sources. To do this, the NSA SDSS photometry uses the technique developed by Blanton et al. (2011) and the pipeline developed by Lupton et al. (2001). Additionally, its flux measurements use the SDSS petrosian magnitude and azimuthally-averaged profiles optimizing extended sources. On the other hand, the SDSS MPA-JHU estimates stellar masses from SDSS spectroscopy measurements with a fiber aperture of 3′′. This technique is optimized for sources with sizes less than 0.5′.

Chang et al. (2015) sample uses WISE “pro” magnitude, which is optimized for point-sources and underestimates the magnitude from extended sources.

Appendix D: Estimating dust temperature from IR and sub-mm data

The dust temperature of the cold component is an important parameter as dust mass M_dust and the total IR luminosity L_IR correlate with it (see Sect. 4.5).

Figure D.1 shows the correlation between the dust temperature of the cold component with different colors at IR and sub-mm wavelengths. The best fit of each panel is given by the equation $\frac{{\mathit{T}}_{\mathrm{cold}}}{\mathrm{\left[}\mathrm{K}\mathrm{\right]}}\mathrm{=}{\mathrm{10}}^{\mathit{a}\mathrm{\pm }\mathrm{\Delta }\mathit{a}}{\left(\frac{{\mathit{f}}_{{\mathit{\lambda }}_{\mathrm{1}}}}{{\mathit{f}}_{{\mathit{\lambda }}_{\mathrm{2}}}}\right)}^{\mathit{b}\mathrm{\pm }\mathrm{\Delta }\mathit{b}}\mathit{,}$(D.1)where the values of the parameters (a, Δa,b,Δb) are shown in Table D.1.

The dust temperature of the cold component shows greater point dispersions for colors based on fluxes at 22 and 12 μm. The light-weighted dust temperature shows tight correlations with the colors based on the flux at 22 μm and at 12 μm, due the relevance of the warm component at this wavelength. Figure D.2 shows a tight correlation between the color based at 22 μm (12 μm) and the light-weighted dust temperature, where the best fits are: $\frac{{\mathit{T}}_{\mathrm{weight}}}{\mathrm{\left[}\mathrm{K}\mathrm{\right]}}\mathrm{=}{\mathrm{10}}^{\mathit{c}\mathrm{\pm }\mathrm{\Delta }\mathit{c}}{\left(\frac{{\mathit{f}}_{{\mathit{\lambda }}_{\mathrm{1}}}}{{\mathit{f}}_{{\mathit{\lambda }}_{\mathrm{2}}}}\right)}^{\mathit{d}\mathrm{\pm }\mathrm{\Delta }\mathit{d}}\mathit{,}$(D.2)where the factors (c, Δc,d, Δd) are shown in Table D.2. Other colors (based on 60 or 100 μm) correlate with the light-weighted dust temperature in a similar way to that in which they correlate with T_cold , although with larger point dispersions.

The large red crosses in Figs. D.1 and D.2 show the mean values of T_cold different bins, to obtain a cleaner correlation. The best fit coefficients of the crosses (red dashed line) have values that are consistent within the errors with the best fit coefficients for all points.

Appendix E: Estimating L_IR and L_FIR from IR and sub-mm data

To study the SFR of a galaxy, either the estimation of the total infrared luminosity (L_IR) or the far infrared luminosity (L_FIR) is fundamental. The absence of photometric measurements at IR and sub-mm wavelengths obstructs the use of good SED fittings to estimate any of these parameters. Thus it is crucial to establish a scaling relation between a few measurements and the IR luminosity.

The total L_IR is defined between λ = 8 and 1000 μm, and the L_FIR , between 40 and 500 μm. In our sample, the direct integration of the SED fitting shows a L_IR ranging from 3.9 × 10⁶L_⊙ to 7.0 × 10¹¹L_⊙, with a typical error of 9%, and median value of 2.2 × 10¹⁰L_⊙. L_FIR ranges between 3.3 × 10⁶L_⊙ and 5.1 × 10¹¹L_⊙, with a typical error of 12%, and median value of 1.8 × 10¹⁰L_⊙.

Galaxies show a linear relation between the SED integrated quantities L_IR and L_FIR (Fig. E.1), with a median value of 1.20 and rms of 0.08 for L_IR /L_FIR. These values can be contrasted to those obtained by Graciá-Carpio et al. (2008, median L_IR /L_FIR~ in a sample of 17 local (z ≤ 0.7) LIRGs and ULIRGs, and da Cunha et al. (2010, median L_IR /L_FIR in a sample of ~3000 nearby (z ≤ 0.1) SDSS galaxies.

Sanders & Mirabel (1996; hereafter SM96) show the most often used relation to obtain L_FIR and L_IR as a linear combination of fluxes at 12, 25, 60 and 100 μm (observed frame).

They have used the following equations: $\begin{array}{ccc}& & {\mathit{F}}_{\mathrm{IR}}\mathrm{=}\mathrm{1.8}\mathrm{\times }{\mathrm{10}}^{-14}\left(\mathrm{13.48}{\mathit{f}}_{\mathrm{12}}\mathrm{+}\mathrm{5.16}{\mathit{f}}_{\mathrm{25}}\mathrm{+}\mathrm{2.58}{\mathit{f}}_{\mathrm{60}}\mathrm{+}{\mathit{f}}_{\mathrm{100}}\right)\mathrm{[}{\mathrm{W}{\mathrm{m}}^{-2}}^{\mathrm{]}}\\ & & {\mathit{L}}_{\mathrm{IR}}\mathrm{(}\mathrm{8}\mathrm{-}\mathrm{1000}\mathit{\mu }\mathrm{m}\mathrm{)}\mathrm{=}\mathrm{4}\mathit{\pi }{\mathit{D}}_{\mathrm{L}}^{\mathrm{2}}{\mathit{F}}_{\mathrm{IR}}\left[{\mathit{L}}_{\mathrm{\odot }}\right]\\ & & {\mathit{F}}_{\mathrm{FIR}}\mathrm{=}\mathrm{1.26}\mathrm{\times }{\mathrm{10}}^{-14}\left(\mathrm{2.58}{\mathit{f}}_{\mathrm{60}}\mathrm{+}{\mathit{f}}_{\mathrm{100}}\right)\mathrm{[}{\mathrm{W}{\mathrm{m}}^{-2}}^{\mathrm{]}}\\ & & {\mathit{L}}_{\mathrm{FIR}}\mathrm{(}\mathrm{40}\mathrm{-}\mathrm{500}\mathit{\mu }\mathrm{m}\mathrm{)}\mathrm{=}\mathrm{4}\mathit{\pi }{\mathit{D}}_{\mathrm{L}}^{\mathrm{2}}\mathit{C}{\mathit{F}}_{\mathrm{FIR}}\left[{\mathit{L}}_{\mathrm{\odot }}\right]\mathit{,}\end{array}$(E.1)where f_x is the respective IRAS flux expressed in Jy, D_L is the source luminosity distance in Mpc, and C is the color correction constant normally related to the f₁₀₀/f₆₀ color, which is related to the IR peak emission.

Figure E.2 top panel shows the relation between the ratio of L_FIR from SM96 (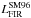${\mathit{L}}_{\mathrm{FIR}}^{\mathrm{SM}\mathrm{96}}$) and our L_FIR values obtained from direct integration of the final SED fits. Considering a constant value of C = 1.4 (Sanders & Mirabel 1996) in SM96’s equation for L_FIR , we observe an underestimation of the L_FIR compared with our results. The median value of the 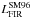${\mathit{L}}_{\mathrm{FIR}}^{\mathrm{SM}\mathrm{96}}$/L_FIR ratio is 0.8. Also, the luminosities ratio shows a dispersion strongly related to the dust temperature of the cold component. The 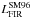${\mathit{L}}_{\mathrm{FIR}}^{\mathrm{SM}\mathrm{96}}$/L_FIR ratio is equal to 1 only for sources with T_cold between 24 and 26 K.

The bottom panel of Fig. E.2 shows the same comparison as the top panel but for L_IR . The ratio between the result obtained from SM96 equation (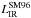${\mathit{L}}_{\mathrm{IR}}^{\mathrm{SM}\mathrm{96}}$) and our L_IR has a median value of median 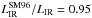${\mathit{L}}_{\mathrm{IR}}^{\mathrm{SM}\mathrm{96}}\mathit{/}{\mathit{L}}_{\mathrm{IR}}\mathrm{=}\mathrm{0.95}$ with a small dispersion (σ = 0.005). However, since the SM96’s equation to obtain the total L_IR needs four data points (fluxes at 12, 25, 60 and 100 μm), the number of sources is very limited (e.g., only 72 sources have L_IR but 1599 have L_FIR , as the SM96’s equations need only two fluxes in order to estimate L_FIR .)

The SM96 calibration is based on the use of only IRAS fluxes (mainly at 60 and 100 μm), and a modified gray-body with β between 1 and 2. The problem is that this calibration uses the simplest dust emission model with no information at wavelengths greater than 100 μm. Thus this model has the problem that the peak emission near 100 μm is not well defined and, therefore, it is not possible to identify the position of the peak of the IR emission. Additionally, it is expected that the flux between 50 to 1000 μm contributes ~65% of L_IR , implying that it is important to have information from the sub-mm. However, in general terms, the calibration showed by SM96 is an excellent first approximation of L_IR (λ = 8–1000 μm) and for the far-infrared luminosity (λ = 40–500 μm). However, now we have access to a greater range of photometric measurements (with more points within this range) and the access to more detailed dust emission models, with deeper physical constrains (e.g., the DL07 models). With this idea in mind, we re-calibrate the SM96 equations and furthermore, we propose an easier and simpler linear combination of the IRAS filters in order to estimate the L_IR and L_FIR using only two filters (at 60 μm and 100 μm).

Our calibration is expressed by the following equations:

For FIR luminosity (40–500 μm) $\begin{array}{ccc}\frac{{\mathit{F}}_{\mathrm{FIR}}}{\left[\mathrm{W}{\mathrm{m}}^{-2}\right]}& \mathrm{=}& \mathrm{1.26}\mathrm{\times }{\mathrm{10}}^{-14}\left(\mathrm{0.752}\frac{{\mathit{f}}_{\mathrm{60}}}{\left[\mathrm{Jy}\right]}\mathrm{+}\mathrm{3.236}\frac{{\mathit{f}}_{\mathrm{100}}}{\left[\mathrm{Jy}\right]}\right)\end{array}$(E.2)For total IR luminosity (8–1000 μm) $\begin{array}{ccc}\frac{{\mathit{F}}_{\mathrm{IR}}}{\left[\mathrm{W}{\mathrm{m}}^{-2}\right]}& \mathrm{=}& \mathrm{1.8}\mathrm{\times }{\mathrm{10}}^{-14}\left(\mathrm{1.439}\frac{{\mathit{f}}_{\mathrm{60}}}{\left[\mathrm{Jy}\right]}\mathrm{+}\mathrm{2.450}\frac{{\mathit{f}}_{\mathrm{100}}}{\left[\mathrm{Jy}\right]}\right)\end{array}$(E.3)where the luminosity is obtained from the conventional equation: $\frac{\mathit{L}}{\left[{\mathit{L}}_{\mathrm{\odot }}\right]}\mathrm{=}\mathrm{3.13}\mathrm{\times }{\mathrm{10}}^{\mathrm{19}}{\left(\frac{{\mathit{D}}_{\mathrm{L}}}{\left[\mathrm{Mpc}\right]}\right)}^{\mathrm{2}}\frac{\mathit{F}}{\left[\mathrm{W}{\mathrm{m}}^{-2}\right]}\mathrm{·}$(E.4)Figure E.3 top (bottom) panel shows the ratio between the L_FIR (L_IR) obtained with our calibration using the values derived the direct integration of the SED templates, as a function of the L_FIR (L_IR) also obtained for the integration of the SED templates.

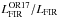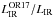We use 1599 sources and find that the median value of the ${\mathit{L}}_{\mathrm{FIR}}^{\mathrm{OR}\mathrm{17}}\mathit{/}{\mathit{L}}_{\mathrm{FIR}}$ and ${\mathit{L}}_{\mathrm{IR}}^{\mathrm{OR}\mathrm{17}}\mathit{/}{\mathit{L}}_{\mathrm{IR}}$ ratios ~1.001 with standard deviation ~0.13.

One other advantage of our calibration is that these is no correlation between the dispersion and the T_cold . Furthermore, our equations do not need a temperature correction (as shown the SM96 with the C factor) to compensate for over- or underestimations.

Another interesting way to obtain the total L_IR from a single measurement comes from the use of the luminosity at 22 μm (WISE W4 filter). Using a sub-sample of 924 galaxies with at least five photometric points for a SED fitting with 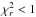${\mathit{\chi }}_{\mathit{r}}^{\mathrm{2}}\mathit{<}\mathrm{1}$, we obtain that the best fit equation is expressed by: $\frac{{\mathit{L}}_{\mathrm{IR}}}{\mathrm{\left[}{\mathit{L}}_{\mathrm{\odot }}\mathrm{\right]}}\mathrm{=}{\mathrm{10}}^{\mathrm{-}\mathrm{10.60}\mathrm{\pm }\mathrm{0.17}}{\left(\frac{{\mathit{L}}_{\mathrm{22}\mathit{\mu }\mathrm{m}}}{\mathrm{[}\mathrm{W}\mathrm{H}{\mathrm{z}}^{-1}\mathrm{]}}\right)}^{\mathrm{0.926}\mathrm{\pm }\mathrm{0.008}}\mathit{,}$(E.5)with rms = 0.096. The best-fit line for our data is plotted in Fig. E.4 as a red solid line. Similar relations are shown in different works, where the SFR of the galaxy is derived from the flux at 24 μm. In particular, Fig. E.4 reports two examples, one from Jarrett et al. (2013; green line) and the other from Rieke et al. (2009; blue line). The point dispersion in our calibration does not show correlations with T_cold , M_∗ , or M_dust .

Finally, we find a correlation between the sub-mm fluxes (at 350 μm, 550 μm, 850 μm) and the total L_IR . We present these correlations in Sect. 4.5 for the flux at 350 μm.

Figure E.5 shows the correlation between the L_IR and the luminosity at 550 μm (top panel) and 850 μm (bottom panel), where the best fits (blue lines) are determined by the following equations, respectively: $\begin{array}{ccc}\frac{{\mathit{L}}_{\mathrm{IR}}}{\mathrm{\left[}{\mathit{L}}_{\mathrm{\odot }}\mathrm{\right]}}& \mathrm{=}{\mathrm{10}}^{\mathrm{-}\mathrm{14.588}\mathrm{\pm }\mathrm{0.002}}{\left(\frac{{\mathit{L}}_{\mathrm{550}}}{\mathrm{[}\mathrm{W}\mathrm{H}{\mathrm{z}}^{-1}\mathrm{]}}\right)}^{\mathrm{1.074}\mathrm{\pm }\mathrm{0.005}}& \\ \frac{{\mathit{L}}_{\mathrm{IR}}}{\mathrm{\left[}{\mathit{L}}_{\mathrm{\odot }}\mathrm{\right]}}& \mathrm{=}{\mathrm{10}}^{\mathrm{-}\mathrm{17.135}\mathrm{\pm }\mathrm{0.002}}{\left(\frac{{\mathit{L}}_{\mathrm{850}}}{\mathrm{[}\mathrm{W}\mathrm{H}{\mathrm{z}}^{-1}\mathrm{]}}\right)}^{\mathrm{1.221}\mathrm{\pm }\mathrm{0.0051}}\mathrm{·}& \end{array}$(E.6)These relations show that the dispersion is related to the dust temperature of the cold component. Following the same idea of the dust plane shown in Sect. 4.5, we define a plane using the total IR luminosity, the luminosity at 550 μm (at 850 μm ), and the dust temperature of the cold component. The best fits are described as follow: $\begin{array}{ccc}\log \left(\frac{{\mathit{L}}_{\mathrm{IR}}}{\mathrm{\left[}{\mathit{L}}_{\mathrm{\odot }}\mathrm{\right]}}\right)& \mathrm{-}& \mathrm{1.00}\mathrm{\times }\log \left(\frac{{\mathit{L}}_{\mathrm{550}}}{\mathrm{[}\mathrm{W}\mathrm{H}{\mathrm{z}}^{-1}\mathrm{]}}\right)\\ & \mathrm{-}& \mathrm{0.13}\mathrm{\times }\left(\frac{{\mathit{T}}_{\mathrm{cold}}}{\mathrm{\left[}\mathrm{K}\mathrm{\right]}}\right)\mathrm{+}\mathrm{16.03}\mathrm{=}\mathrm{0}\\ \log \left(\frac{{\mathit{L}}_{\mathrm{IR}}}{\mathrm{\left[}{\mathit{L}}_{\mathrm{\odot }}\mathrm{\right]}}\right)& \mathrm{-}& \mathrm{1.01}\mathrm{\times }\log \left(\frac{{\mathit{L}}_{\mathrm{850}}}{\mathrm{[}\mathrm{W}\mathrm{H}{\mathrm{z}}^{-1}\mathrm{]}}\right)\\ & \mathrm{-}& \mathrm{0.15}\mathrm{\times }\left(\frac{{\mathit{T}}_{\mathrm{cold}}}{\mathrm{\left[}\mathrm{K}\mathrm{\right]}}\right)\mathrm{+}\mathrm{15.93}\mathrm{=}\mathrm{0.}\end{array}$(E.7)A similar dust plane is defined for the luminosity at 350 μm, see Sect. 4.5 for more details.

Appendix F: Estimating dust masses from limited sub-mm data

The most common approach to estimate the dust mass in a galaxy from a single measurement is using the flux at 850 μm (e.g., Dunne et al. 2000; Dunne & Eales 2001). This is because the most common approach would be to have a set of measurements, and then perform a fit according to a physical dust model. The aforementioned results were limited by the data, since at that time there were not deep measurements between 100–500 μm. In Sect. 4.5 we show a correlation between the dust mass and the luminosity at 350 μm. Now we extend this correlation to the luminosities at 550 μm and 850 μm.

Figure F.1 shows the correlations between the M_dust and the sub-mm luminosities at 550 μm (top panel) and 850 μm (bottom panel), where the color-scale shows the dust temperature of the cold component. The best fit (blue lines) equations are represented by: $\begin{array}{ccc}\frac{{\mathit{M}}_{\mathrm{dust}}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}& \mathrm{=}& {\mathrm{10}}^{\mathrm{-}\mathrm{13.606}\mathrm{\pm }\mathrm{0.002}}{\left(\frac{{\mathit{L}}_{\mathrm{550}}}{\mathrm{[}\mathrm{W}\mathrm{H}{\mathrm{z}}^{-1}\mathrm{]}}\right)}^{\mathrm{0.927}\mathrm{\pm }\mathrm{0.05}}\\ \frac{{\mathit{M}}_{\mathrm{dust}}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}& \mathrm{=}& {\mathrm{10}}^{\mathrm{-}\mathrm{12.84}\mathrm{\pm }\mathrm{0.002}}{\left(\frac{{\mathit{L}}_{\mathrm{850}}}{\mathrm{[}\mathrm{W}\mathrm{H}{\mathrm{z}}^{-1}\mathrm{]}}\right)}^{\mathrm{0.920}\mathrm{\pm }\mathrm{0.005}}\mathrm{·}\end{array}$(F.1)Analogously to the dust plane (Sect. 4.5), we define a plane among the luminosities in the sub-mm,the dust mass and the dust temperature of the cold component. The equations for the best fits are: $\begin{array}{ccc}\log \left(\frac{{\mathit{M}}_{\mathrm{dust}}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}\right)& \mathrm{-}& \mathrm{0.961}\mathrm{\times }\log \left(\frac{{\mathit{L}}_{\mathrm{550}}}{\mathrm{[}\mathrm{W}\mathrm{H}{\mathrm{z}}^{-1}\mathrm{]}}\right)\\ & \mathrm{+}& \mathrm{0.064}\mathrm{\times }\left(\frac{{\mathit{T}}_{\mathrm{cold}}}{\mathrm{\left[}\mathrm{K}\mathrm{\right]}}\right)\mathrm{+}\mathrm{12.933}\mathrm{=}\mathrm{0}\\ \log \left(\frac{{\mathit{M}}_{\mathrm{dust}}}{\mathrm{\left[}{\mathit{M}}_{\mathrm{\odot }}\mathrm{\right]}}\right)& \mathrm{-}& \mathrm{0.993}\mathrm{\times }\log \left(\frac{{\mathrm{L}}_{\mathrm{850}}}{\mathrm{[}\mathrm{W}\mathrm{H}{\mathrm{z}}^{-1}\mathrm{]}}\right)\\ & \mathrm{+}& \mathrm{0.054}\mathrm{\times }\left(\frac{{\mathit{T}}_{\mathrm{cold}}}{\mathrm{\left[}\mathrm{K}\mathrm{\right]}}\right)\mathrm{+}\mathrm{13.310}\mathrm{=}\mathrm{0.}\end{array}$(F.2)These relations are independent to the sSFR classification.

All Tables

All Figures