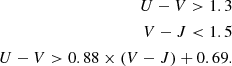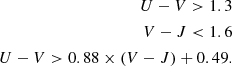| Issue |
A&A
Volume 678, October 2023
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 23 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202346066 | |
| Published online | 29 September 2023 | |
In pursuit of giants
II. Evolution of dusty quiescent galaxies over the last six billion years from the hCOSMOS survey
1
National Centre for Nuclear Research, Pasteura 7, 02-093 Warsaw, Poland
e-mail: darko.donevski@ncbj.gov.pl
2
SISSA, Via Bonomea 265, 34136 Trieste, Italy
3
IFPU – Institute for fundamental physics of the Universe, Via Beirut 2, 34014 Trieste, Italy
4
Department of Astronomy and Physics, Saint Mary’s University, 923 Robie Street, Halifax, NS B3H 3C3, Canada
5
Canada Research Chair in Astronomy and Astrophysics, Tier II, Canada
6
Department of Physics & Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, BC V6T 1Z1, Canada
7
INAF – Osservatorio di Astrofisica e Scienza dello Spazio, Via Gobetti 93/3, 40129 Bologna, Italy
8
INAF – OAPD, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
9
Department of Astronomy, University of Florida, 211 Bryant Space Sciences Center, Gainesville, FL, USA
10
Cosmic Dawn Center (DAWN), Rådmandsgade 64, 2200 Copenhagen, Denmark
11
Institute for Astronomy, Royal Observatory, University of Edinburgh, Edinburgh EH9 3HJ, UK
12
Department of Physics & Astronomy, University of the Western Cape, Robert Sobukwe Rd, Bellville 7535, South Africa
13
Steward Observatory, University of Arizona, 933 North Cherry Avenue, Tucson, AZ 85721, USA
14
Astronomy Program, Department of Physics and Astronomy, Seoul National University, 1 Gwanak-ro, Gwanak-gu, Seoul 08826, Republic of Korea
15
Smithsonian Astrophysical Observatory, 60 Garden Street, Cambridge, MA 02138, USA
16
CEA, CNRS, Université Paris-Saclay, 91191 Gif-sur-Yvette, France
17
Max-Planck-Institute für Astrophysik, Karl-Schwarzschild-Strasse 1, 85740 Garching, Germany
Received:
2
February
2023
Accepted:
10
July
2023
The physical mechanisms that link the termination of star formation in quiescent galaxies and the evolution of their baryonic components, stars, and the interstellar medium (ISM; dust, gas, and metals) are poorly constrained beyond the local Universe. In this work, we characterise the evolution of the dust content in 545 quiescent galaxies observed at 0.1 < z < 0.6 as part of the hCOSMOS spectroscopic redshift survey. This is, to date, the largest sample of quiescent galaxies at intermediate redshifts for which the dust, stellar, and metal abundances are consistently estimated. We analyse how the crucial markers of a galaxy dust life cycle, such as specific dust mass (Mdust/M⋆), evolve with different physical parameters, namely gas-phase metallicity (Zgas), time since quenching (tquench), stellar mass (M⋆), and stellar population age. We find morphology to be an important factor in the large scatter in Mdust/M⋆ (∼2 orders of magnitude). Quiescent spirals exhibit strong evolutionary trends of specific dust mass with M⋆, stellar age, and galaxy size, in contrast to the little to no evolution experienced by ellipticals. When transitioning from solar to super-solar metallicities (8.7 ≲ 12 + log(O/H)≲9.1), quiescent spirals undergo a reversal in Mdust/M⋆, indicative of a change in dust production efficiency. By modelling the star formation histories of our objects, we unveil a broad dynamical range of post-quenching timescales (60 Myr < tquench < 3.2 Gyr). We show that Mdust/M⋆ is highest in recently quenched systems (tquench < 500 Myr), but its further evolution is non-monotonic, as a consequence of different pathways for dust formation, growth, or removal on various timescales. Our data are best described by simulations that include dust growth in the ISM. While this process is prevalent in the majority of galaxies, for ∼15% of objects we find evidence of additional dust content acquired externally, most likely via minor mergers. Altogether, our results strongly suggest that prolonged dust production on a timescale of 0.5 − 1 Gyr since quenching may be common in dusty quiescent galaxies at intermediate redshifts, even if their gas reservoirs are heavily exhausted (i.e. cold gas fraction < 1 − 5%).
Key words: galaxies: evolution / galaxies: formation / galaxies: ISM
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The general population of passively evolved galaxies, the so-called quiescent galaxies (QGs), are known to have no or little ongoing star formation activity, which usually places them below the star-forming main sequence (MS; e.g. Daddi et al. 2005; Toft et al. 2007; van Dokkum et al. 2010; Schreiber et al. 2015). Whatever physical mechanism is in place, one of the important outcomes of quenching star formation is the evolution of its agents – gas and dust in the cold interstellar medium (ISM).
The abundance of dust in the ISM is regulated by a complex network of dust formation and destruction channels (see e.g. Zhukovska et al. 2016, and references therein). Even though many details of the involved physical and chemical processes are not fully understood, the study of dust in galaxies is essential to understanding their evolution for a number of reasons. On one hand, dust is critical in the thermal balance of gas and in shielding the dense clouds from ultraviolet (UV) radiation, which supports star formation (Cuppen et al. 2017). Dust further affects the spectral energy distributions (SEDs) of massive galaxies to the extent that, at shorter wavelengths, stellar light is absorbed by dust and re-emitted in the far-infrared (FIR). On the other hand, the interplay of dust with metals and gas in the ISM constitutes a vital component of the baryon cycle. Metals in the gas phase are proposed to play a role in the growth of dust particles (Asano et al. 2013; Slavin et al. 2015; Zhukovska et al. 2016; Hirashita & Nozawa 2017; Popping et al. 2017; Pantoni et al. 2019), and dust itself is an important constituent of the cold ISM, often considered its reliable tracer not only in star-forming galaxies (e.g. Scoville et al. 2016) but also in QGs (Magdis et al. 2021).
The recent advent of IR/sub-millimetre instruments such as Herschel, NOEMA, and ALMA have allowed us to identify QGs with substantial masses of dust and molecular gas (Mdust > 107 M⊙, Mgas > 109 M⊙; Smith et al. 2014; Gobat et al. 2018; Belli et al. 2021). These findings have challenged the historical picture of QGs: that they contain very little ISM material in proportion to their stellar mass. The vast majority of known studies have focused on the dust and gas in the QGs in the local Universe (z ∼ 0), through galaxy FIR continuum emission (e.g. Smith et al. 2014; Rowlands et al. 2014; Michałowski et al. 2019) and/or low transition CO lines (e.g. Davis et al. 2013; De Vis et al. 2017; Li et al. 2019a; Sansom et al. 2019). Moreover, several recent works used extensive ALMA and NOEMA follow-ups to identify a small number of dusty QGs in the distant Universe (z > 1 − 3; Williams et al. 2021; Whitaker et al. 2021a). Nevertheless, there is no consensus on whether the observed dust in QGs is solely of internal origin (due to past star formation) or whether external contributions (i.e. from mergers) are influential as well. It is also debatable how long the dust and gas in the ISM will survive after the quenching. Some studies report significant dust and gas content and prolonged timescales for ISM removal (≳1 Gyr; Rowlands et al. 2014; Rudnick et al. 2017; Gobat et al. 2018; Michałowski et al. 2019; Woodrum et al. 2022), whereas others report a rapid depletion of dust and gas (≲100 − 500 Myr; Sargent et al. 2015; Williams et al. 2021; Whitaker et al. 2021a).
Quantifying changes in dust abundance as galaxies evolve is of particular interest when studying dusty QGs. To that end, specific dust masses (Mdust/M⋆) have been proposed as a useful marker of the dust life cycle against multiple destruction processes (Calura et al. 2017; Donevski et al. 2020). Michałowski et al. (2019) used the anti-correlation of Mdust/M⋆ with stellar age to derive the time for dust removal in QGs and to understand its connection with the cessation of star formation. When Mgas is unavailable, the Mdust/M⋆ is often used as an observational proxy for the molecular gas fraction (Rémy-Ruyer et al. 2014; Magdis et al. 2021). Furthermore, as dust depletes metals from the gas-phase ISM, adding the information of gas metallicity (Zgas) to the relation between Mdust and M⋆ allows us to better constrain the dominant dust formation mechanisms (Feldmann 2015; De Vis et al. 2017). Beyond the local Universe, such a connection has only been studied in the dusty star-forming galaxies (DSFGs) observed with ALMA at z ∼ 2.3 (Shivaei et al. 2022). Despite its importance, the evolution of specific dust masses as a function of both redshift and physical quantities (in particular, Zgas, stellar age, and time since quenching) has not yet been constrained for a statistical sample of QGs at intermediate redshifts. The task has multiple challenges: (1) To properly determine dust quantities – namely dust luminosity (LIR) and Mdust – well-sampled IR SEDs towards the Rayleigh-Jeans tail are required. (2) QGs have considerably fainter IR continuum emission than DSFGs, and a careful de-blending of fluxes obtained with single-dish instruments is required to model the IR SEDs (e.g. Man et al. 2016; Galliano et al. 2021). (3) Finally, it has been demonstrated that obtaining direct gas-metallicity measurements for QGs is a demanding task (Leethochawalit et al. 2019; Kumari et al. 2021). To partially overcome these issues, Magdis et al. (2021) applied multi-wavelength stacking analysis to massive QGs (log(M⋆/M⊙) > 10.8) from the COSMOS field up to z ∼ 1.5. They report a sharp decline in Mdust/M⋆ from z ∼ 1 to z = 0, interpreting it as a consequence of a rapid exhaustion of molecular gas. However, stacking does not allow the investigation of the physical markers of dust evolution in individual sources. This prevents us from answering important questions, such as which processes of dust production and/or removal are dominant in QGs during their evolution.
From a theoretical standpoint, there is a growing number of studies that have modelled the dust evolution in different classes of cosmological simulations (McKinnon et al. 2017; Davé et al. 2019; Hou et al. 2019; Graziani et al. 2020; Aoyama et al. 2020), semi-analytic models (Lacey et al. 2016; Popping et al. 2017; Cousin et al. 2019; Vijayan et al. 2019; Lagos et al. 2019; Pantoni et al. 2019), and chemical evolution models (Asano et al. 2013; Nanni et al. 2020). While some of them show success in reproducing dust-related properties of star-forming galaxies, observational constraints from statistical samples of QGs at z > 0 are lacking. On top of this, there is an active debate regarding the dominant dust producers in massive galaxies. One group of models advocates for a major contribution from stellar sources – either from asymptotic giant branch (AGB) stars (e.g. Clemens et al. 2010; Valiante et al. 2011) or supernovae (SNe; Gall & Hjorth 2018) – while others predict a prevalence of dust grain growth in the ISM (e.g. Asano et al. 2013; Hirashita et al. 2015). The latter channel is thought to be important at late cosmic epochs (z < 2), but it is strongly dependent on a ‘critical’ gas-metallicity, beyond which it takes over stellar production (Triani et al. 2020). Thus, the observed co-evolution between the Mdust, M⋆, and Zgas in QGs is crucial to challenging (and eventually ruling out) some of the prescriptions related to the growth and destruction of dust.
The present paper addresses these challenges. The first major question we aim to address is how a specific dust mass evolves after quenching in individually detected QGs. We assembled a statistical dataset of spectroscopically selected dusty QGs at 0.1 < z < 0.6 to achieve this goal. We complement a deep multi-wavelength catalogue with the IR fluxes of the carefully de-blended sources and apply physically motivated SED modelling to self-consistently derive sources’ physical properties. By considering independent spectroscopic information such as Zgas and the stellar age index (Dn4000), we study how the Mdust/M⋆ changes with metallicity, stellar mass, and time since quenching. We then address the second big question, namely, how the observed evolution of dust properties in QGs can be understood within the framework of galaxy formation and evolution.
The paper is organised as follows. In Sect. 2 we describe the data analysed in this work. In Sect. 3 we explain the SED fitting methodology and provide statistical properties for our sample. In Sect. 4 we present how the Mdust/M⋆ in the general population of dusty QGs scales with the galaxy redshift and specific star formation rate (sSFR). In Sect. 5 we investigate the morphological impact on the evolution of the Mdust/M⋆ with physical parameters such as Zgas and M⋆. The interpretation of results with state-of-the-art simulations is presented in Sect. 6, and our main conclusions are outlined in Sect. 7. Throughout the paper, we assume a Planck Collaboration XIII (2016) cosmology and the Chabrier initial mass function (IMF; Chabrier 2003).
2. Data and sample selection
The starting point of our sample is the hCOSMOS spectroscopic survey catalogue (for comprehensive description of the survey, target selection and observational design, see Damjanov et al. (2018). Briefly, the hCOSMOS is a dense spectroscopic survey, designed for providing spectra of galaxies from the COSMOS UltraVISTA catalogue (Muzzin et al. 2013). The hCOSMOS survey is the magnitude limited survey with no colour selection, and targets UltraVISTA galaxies that have r-band magnitude within the range of 17.8 < r < 21.3. The bright limit of r = 17.8 is set to match the limiting magnitude of the Sloan Digital Sky Survey (SDSS) main galaxy sample. The hCOSMOS survey was done with the multi-fibre-fed spectrograph Hectospec, mounted on the 6.5 m MMT (Fabricant et al. 2005). Hectospec is a 300-fibre optical spectrograph with an ∼1 deg2 field of view (FoV) and a fibre diameter of 1.5″. In total, hCOSMOS survey observed ∼1.5 deg2 covering the wavelength range between 370 nm and 910 nm at a resolution of R ∼ 1500. The hCOSMOS catalogue includes 4362 galaxies with a science quality spectra. The galaxies are identified across the redshift range of 0.01 < z < 0.7.
We supplemented each source from the hCOSMOS sample with rich panchromatic photometry from publicly available photometric catalogues. Namely, for SED modelling of the data, we adopted homogeneously calibrated multi-wavelength catalogues released by the Herschel Extragalactic Legacy Project (Małek et al. 2018; Shirley et al. 2019). The catalogue was created with the use of a state-of-the-art de-blending method and cross-matching procedure of individual galaxies across broad wavelengths. In particular, the de-blending of confusion limited PACS (100 and 160 μm), and SPIRE (250, 350, and 500 μm) maps was performed with the probabilistic de-blending code XID+ (Hurley et al. 2017). The code exploits prior information on the redshift and source position available from the higher-resolution maps observed at 3.6 μm, and extracts PACS and SPIRE fluxes beyond the conventional Herschel confusion limit, achieving a 1σ cut depth of ∼1 mJy at 250 μm. The detailed de-blending procedure is explained in Pearson et al. (2018) and Shirley et al. (2019), who demonstrate that such an approach takes the big advantage of fluctuations within the confused maps and place strong constraints on the peak of sources’ FIR SEDs even in IR-faint galaxies. All hCOSMOS sources have wealthy multi-wavelength coverage that consists of at least 15 photometric bands: along with their information in the IR part of the spectra, the optical to mid-infrared (MIR) data come from Subaru Suprime-Cam (six broadband filters, V, g, r, i, z and Y), VISTA (J, H, Ks bands), Spitzer IRAC (four bands), and Spitzer MIPS.
We defined the sample of QGs on the basis of a spectral indicator Dn4000, which is a ratio of flux in the 4000−4100 Å and 3850−3950 Å bands. The Dn4000 measures the strength of the 4000 Å break produced by a large number of absorption lines where ionised metals are the main contributors to the opacity. Because the strength of the 4000 Å break increases with the population age, it is often used as an indicator of a quiescence. It is worth noting that Dn4000 is a strong evolutionary marker because it is insensitive to reddening and does not require a K-correction, opposite to galaxy colours. From the full hCOSMOS catalogue of 4362 sources, we select QGs as those with Dn4000 > 1.5 (1737 sources in total). This criterion is commonly used for selecting QGs. The choice of using Dn4000 > 1.5 to select QGs is motivated by findings from large spectroscopic surveys demonstrating that Dn4000 is strongly bimodal, and offers a robust division between emission line star-forming galaxies and QGs at Dn4000 ∼ 1.5 (e.g. Zahid et al. 2016; Haines et al. 2017; Damjanov et al. 2018; Wu et al. 2018, 2021; Utsumi et al. 2020). Additionally, it has been shown that selections based on broadband colours alone are sometimes inefficient in identifying the recently quenched galaxies (Vergani et al. 2018; Wu et al. 2020). The selection based on Dn4000 is also proven to be very robust and effective when combined with the equivalent width Hδ absorption line (EW(Hδ)). On average, the S/N of individual hCOSMOS spectra is not high enough for measuring EW(Hδ) for the full parent mass-complete sample, but we note that recent deep spectroscopy studies of QGs at z ∼ 0.8 from the LEGA-C survey unveil the tight relation between EW(Hδ) and Dn4000 at Dn4000 ≳ 1.5 (Wu et al. 2018; Zhang et al. 2023). Nevertheless, all QG selection criteria produce samples with some levels of contamination from star-forming outliers. For the full hCOSMOS catalogue, Damjanov et al. (2018) compared the identification of QGs and star-forming galaxies on the basis of their rest-frame UVJ colours with the identification based on Dn4000, and found only ∼13% of contaminants (galaxies that have Dn4000 > 1.5, but their UVJ colours are consistent with being star-forming). Interestingly, the reported fraction is lower than for any of the colour-based classifiers tested in Moresco et al. (2013), who applied a variety of methods to select QGs up to z ∼ 0.5.
Finally, from all selected QGs, we built a sample of ‘dusty QGs’ suitable for our analysis, by imposing source detections in the IR with S/N ≥ 3 in at least four photometric bands in the MIR-to-FIR range (8 μm < λ < 500 μm)1. These requirements are important for achieving the robustness to dust-related physical parameters estimated from SED fitting, in particular Mdust (see e.g. Berta et al. 2016). From the parent sample of 1737 QGs, we find detectable dust in 618 galaxies (35% of total). Because our goal is to explore the interplay between the stars, dust and metals in individually detected objects, we further chose the sources with reliable measurements of gas-phase metallicity (Zgas, expressed as 12 + log(O/H)). Gas phase metallicities of hCOSMOS galaxies are derived by following the method described in Zahid et al. (2013) and Sohn et al. (2019). The main details of the procedure are introduced in Appendix A. In this way, we slightly narrowed the list to 603 dusty QGs for the further SED analysis. We thus leave the analysis of unselected sources for our ongoing work (Lorenzon et al., in prep.). All 603 galaxies selected for our SED analysis have available spectroscopic redshifts (zspec), distributed over a wide range (0.1 < z < 0.6).
Additionally, we checked whether the results presented in the rest of the text hold if alternative selection criteria for QGs are applied (see Appendix C). Namely, on the fiducial sample of QGs mentioned above, we applied additional QG selections based on UVJ rest-frame colours (e.g. Muzzin et al. 2013; Schreiber et al. 2015), but we also probe more conservative spectroscopic cut (Dn4000 > 1.6). We find that 83% (94%) of our parent sample satisfies the UVJ selection suggested by Muzzin et al. (2013) and Schreiber et al. (2015), respectively. We additionally demonstrate that, while the fraction of galaxies considered ‘QGs’ may vary depending on criteria, alternative selections produce results that are consistent with those from our parent sample. We thus conclude that imposing additional criteria for quiescence has little to no impact on the findings presented in the next sections.
3. Panchromatic SED modelling of the data
3.1. Tools: CIGALE
We applied full SED (UV+IR) modelling to our QG using the newest release of Code Investigating GALaxy Emission (CIGALE; Noll et al. 2009; Boquien et al. 20192), a state-of-the-art SED modelling and fitting code that combines UV-optical stellar SED with an IR component. For each parameter, CIGALE conducts a probability distribution function analysis, providing the output value as the likelihood-weighted mean of the probability distribution function (with corresponding error as a likelihood-weighted standard deviation). In the following, we briefly summarise the choice of modules and parameters presented in Table 1.
Parameters used for modelling the SEDs with CIGALE.
3.1.1. Stellar component
We constructed the stellar component of our SED model adopting the Bruzual & Charlot stellar population synthesis model (BC03; Bruzual & Charlot 2003) with a (Chabrier 2003) IMF. We used a range of three stellar metallicities closest to that inferred from the mass-metallicity relation for each object.
Because our primary goal is to infer physical characteristics of QGs, we adopted the flexible star formation history (SFH), which is composed of a delayed component with an additional flexible time at which the star formation is instantaneously affected. Our choice was motivated by recent studies demonstrating that the addition of an extra flexibility in the recent SFH is needed to better recover physical properties (in particular the star formation rate) in a broad range of QGs (e.g. Ciesla et al. 2016, 2021; Hunt et al. 2019; Suess et al. 2022). The SFH is parametrised as
where τmain represents the e-folding time of the main stellar population, while ttrunc represents the time at which star formation is instantaneously affected (quenched). The parameter r is the ratio between the star formation rates (SFRs) after quenching and at the moment of quenching.
3.1.2. Dust attenuation
We adopted the Charlot & Fall (2000) double power-law attenuation (CF00), which assumes that birth clouds (BCs) and the ISM each attenuate light according to fixed power-law attenuation curves. The formalism is based on age-dependent differential attenuations between young (age < 107 yr) and old (age > 107 yr) stars. In this way, the attenuation law intrinsically takes into account variations in the attenuation curves with time. Both attenuations are modelled by a power-law function, providing the amount of attenuation in the V band defined as 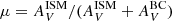 . Following Battisti et al. (2020) and Ciesla et al. (2021) we chose to keep both power-law slopes (BC and ISM) of the attenuation fixed at −0.7, and the parameter μ fixed to 0.3. Because stars older than < 107 yr are only attenuated by AISM, we keep parameter AISM varying between 0.3 and 3, which is demonstrated a good choice for the fitting of quenched objects with detectable dust emission, as recently pointed out by Ciesla et al. (2021).
. Following Battisti et al. (2020) and Ciesla et al. (2021) we chose to keep both power-law slopes (BC and ISM) of the attenuation fixed at −0.7, and the parameter μ fixed to 0.3. Because stars older than < 107 yr are only attenuated by AISM, we keep parameter AISM varying between 0.3 and 3, which is demonstrated a good choice for the fitting of quenched objects with detectable dust emission, as recently pointed out by Ciesla et al. (2021).
3.1.3. Dust emission
For modelling the galaxies’ IR SEDs we adopted the physically motivated dust library of Draine & Li (2007, hereafter DL07). In DL07, IR SEDs are calculated for dust grains heated by starlight for various distributions of intensities. The majority of the dust is heated by a radiation field with constant intensity from the diffuse ISM, while a much smaller fraction of dust (γ) is exposed to starlight with interstellar radiation field (ISRF) intensity in a range between Umin to Umax following a power-law distribution. We fixed the maximum radiation field intensity to Umax = 106 and sample different Umin, keeping the emission slope fixed at β = 2. The fraction of the Mdust in the form of polycyclic aromatic hydrocarbon (PAH) grains (qPAH) was sampled within the range (0.47 < qPAH < 4.6). We log-sample illumination fractions (γ) between 0.001 and 0.1 with the step of 0.01. As showed in Berta et al. (2016), sampling towards larger γ may increase the chance of overestimating Mdust. In our modelling, LIR is an integral of a SED over the rest-frame wavelength range of λ = 8 − 1000 μm, while Mdust is derived by fitting and normalising the IR photometry to the DL07 library.
We also chose to derive the fractional contribution of the active galactic nucleus (AGN), defined as the relative impact of the dusty torus of the AGN to the LIR (‘AGN fraction’). We adopted AGN templates presented in Fritz et al. (2006; see also Feltre et al. 2012). The parameters in the AGN model were matched to those from Donevski et al. (2020). Due to computational reasons we somewhat reduce the number of input options, and model the two extreme values for inclination angle (0° and 90°).
3.1.4. Constraints on the parameters
We fit the full datasets with the models defined in previous section. To do so, we performed the full SED (UV-to-FIR) modelling but chose the option in CIGALE to predict Dn4000. We did several runs of fits until we obtain a good match between the modelled and the observed Dn4000. This procedure is important and ensures that our choice of modelling parameters with the inclusion of dust correctly matches the galaxy ages and SFH, which is important to overcome possible degeneracies. Before using our SED-derived quantities for the science analysis, we confirm that all fitted SEDs are of a good quality, indicated with a small average χ2 (median is find to be χ2 = 1.12 ± 0.33). We also assign the modelling option available within CIGALE to produce mock catalogues, then following the approach implemented by Małek et al. (2018) and Donevski et al. (2020) to verify that our SED fitting procedure does not introduce significant systematics to our dust-related measurements, in particular Mdust (see Appendix B).
3.2. Statistical properties of our sample
From the further analysis we exclude AGN-powered objects based on their SED output (58/603 sources with fAGN > 0.25, or 9% of the total sample)3. After this step, the remaining 545 sources are used for our final analysis4. We stress here that none of QGs from our final sample is classified as ‘star-forming’ based on BPT diagnostics, while a very minor number of objects (18 out of 545) are classified as ‘composite’5. In Fig. 1, we show the distribution of SED derived properties. We infer the median redshift of z = 0.37 with the corresponding 16th–84th percentile range (z = 0.26 − 0.48). As expected for evolved objects, QGs from our hCOSMOS sample are very massive systems (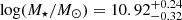 ), The median spectral age indicator is Dn4000 = 1.73, while the median and interquartile range of IR luminosity is
), The median spectral age indicator is Dn4000 = 1.73, while the median and interquartile range of IR luminosity is 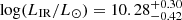 , which is two orders of magnitude lower than in DSFGs at a given redshift and stellar mass range. We applied the functional form of the MS defined by Speagle et al. (2014, their ‘best fit’, provided via Eq. (28)) to check the position of our QGs with respect to the MS. With this check we unveil that 88% of dusty QGs from our sample reside well bellow the MS, with the linear offset to the SFR expected for MS objects being log(ΔMS)≤ − 0.6. Remaining ∼12% of sources can be considered dusty QGs hidden within the ‘green valley’ or ‘MS’ (see Sect. 6.5 for a brief description of potential caveats).
, which is two orders of magnitude lower than in DSFGs at a given redshift and stellar mass range. We applied the functional form of the MS defined by Speagle et al. (2014, their ‘best fit’, provided via Eq. (28)) to check the position of our QGs with respect to the MS. With this check we unveil that 88% of dusty QGs from our sample reside well bellow the MS, with the linear offset to the SFR expected for MS objects being log(ΔMS)≤ − 0.6. Remaining ∼12% of sources can be considered dusty QGs hidden within the ‘green valley’ or ‘MS’ (see Sect. 6.5 for a brief description of potential caveats).
 |
Fig. 1. Distributions of the physical properties estimated for our candidate QGs from the SED fitting with CIGALE. Clockwise, from the top left to the bottom right: goodness of fit expressed as reduced χ2; galaxy redshift; stellar mass; SFR; dust mass; and the linear offset of the galaxy’s observed SFR from the SFR expected from the modelled MS (ΔMS in log scale) as a function of redshift. To guide the eye, we also plot a dashed red line that marks the value that is four times lower than the MS. |
4. ISM diagnostics of the general population of QGs from hCOSMOS
4.1. Evolution of Mdust/M⋆ with redshift
In order to gain insight into evolution of galaxy dust content in our QG, we applied Mdust/M⋆ as a tool to assess the efficiency of the specific dust production and destruction mechanisms. From our multi-band SED fitting, we find the median of 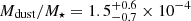 . This is more than an order of magnitude lower than what has been estimated for MS DSFGs within the same redshift and stellar mass range (e.g. da Cunha et al. 2010; Driver et al. 2018), and is two orders of magnitude lower than in dusty starbursts (da Cunha et al. 2015; Donevski et al. 2020; Pantoni et al. 2021). As seen in Fig. 2, where we show the redshift evolution of the Mdust/M⋆ for the full sample, some of our dusty QGs are approaching the MS relation modelled for ALMA identified dusty galaxies at z < 1 (see Sect. 4.4 in Donevski et al. 2020 for details). That said, a handful of QGs in our sample have Mdust/M⋆ comparable to those of MS DSFGs despite having lower LIR values on average. The median values of our QGs agrees reasonably well with the modelled cosmic evolution of Mdust/M⋆ in QGs at 0 < z < 1, obtained from stacking IR-to-radio maps of colour-selected, massive (M⋆ > 1010 M⊙) galaxies in the COSMOS field (Magdis et al. 2021). The average Mdust/M⋆ from Magdis et al. (2021) are 0.2−0.5 dex bellow the medians from this work, which is expected due to the stacking technique they used to reach fainter Ldust. Nevertheless, our data agree within 1σ but suggest a slightly milder decline with z. As radio-mode AGN feedback is expected to dominate the faster decline of Mgas (and supposedly Mdust; Feldmann 2015; Wu et al. 2018), the exclusion of candidate AGNs from our final sample likely contribute to the shallower evolutionary trend with respect to those inferred by Magdis et al. (2021). This implies a less dramatic cosmic evolution of the ISM in dusty QGs in comparison to the general population of QGs.
. This is more than an order of magnitude lower than what has been estimated for MS DSFGs within the same redshift and stellar mass range (e.g. da Cunha et al. 2010; Driver et al. 2018), and is two orders of magnitude lower than in dusty starbursts (da Cunha et al. 2015; Donevski et al. 2020; Pantoni et al. 2021). As seen in Fig. 2, where we show the redshift evolution of the Mdust/M⋆ for the full sample, some of our dusty QGs are approaching the MS relation modelled for ALMA identified dusty galaxies at z < 1 (see Sect. 4.4 in Donevski et al. 2020 for details). That said, a handful of QGs in our sample have Mdust/M⋆ comparable to those of MS DSFGs despite having lower LIR values on average. The median values of our QGs agrees reasonably well with the modelled cosmic evolution of Mdust/M⋆ in QGs at 0 < z < 1, obtained from stacking IR-to-radio maps of colour-selected, massive (M⋆ > 1010 M⊙) galaxies in the COSMOS field (Magdis et al. 2021). The average Mdust/M⋆ from Magdis et al. (2021) are 0.2−0.5 dex bellow the medians from this work, which is expected due to the stacking technique they used to reach fainter Ldust. Nevertheless, our data agree within 1σ but suggest a slightly milder decline with z. As radio-mode AGN feedback is expected to dominate the faster decline of Mgas (and supposedly Mdust; Feldmann 2015; Wu et al. 2018), the exclusion of candidate AGNs from our final sample likely contribute to the shallower evolutionary trend with respect to those inferred by Magdis et al. (2021). This implies a less dramatic cosmic evolution of the ISM in dusty QGs in comparison to the general population of QGs.
 |
Fig. 2. Observed redshift evolution of Mdust/M⋆ in dusty QGs from this work. Individual values are displayed with circles, coloured according to the corresponding Dn4000. Binned medians and associated uncertainties (16th–84th percentile range) are shown with sandy brown circles and lines, respectively. For comparison, with the dashed red line we show the best fit from the stacking analysis of Magdis et al. (2021). The dark grey line and shaded area describe the modelled evolution of ALMA-detected MS galaxies with a functional form of Mdust/M⋆ ∝ k × (1 + z)2.5 (Donevski et al. 2020), while the dashed dark grey line shows the shift of 1 dex of this MS scaling relation. |
In Fig. 2 we see that galaxies with higher Dn4000 generally attain lower specific dust masses than those with smaller Dn4000. Because Dn4000 is a proxy for stellar population age, more evolved systems with older stellar populations are naturally expected to have lower Mdust/M⋆ (e.g. Hjorth et al. 2014; Pantoni et al. 2019; Michałowski et al. 2019). However, Fig. 2 reveals that even for objects observed at the same redshift, there is a significant spread in Mdust/M⋆ that does not always coincide with Dn4000. This could imply a range of ISM conditions in our QGs, (i.e. large variability of molecular gas fractions, recent merger activities etc.), which may result in different dust production and/or destruction timescales. This slightly challenges the interpretation by Magdis et al. (2021), who argue that prompt decline of Mdust/M⋆ must be due to quick gas removal with no further replenishment (i.e. due to minor mergers or accretion from the cosmic web).
4.2. Evolution of Mdust/M⋆ with sSFR
In star-forming galaxies, dust mass is expected to be a good tracer of the Mgas (da Cunha et al. 2010; Santini et al. 2014; Rowlands et al. 2014; Scoville et al. 2017; Kirkpatrick et al. 2017; Aoyama et al. 2020), while Mgas and SFR are linked through the known Kennicutt–Schmidt relation (Schmidt 1959; Kennicutt 1998; Sargent et al. 2014). It is thus important to unveil how Mdust, M⋆, and SFR are related in dusty QGs at intermediate redshifts.
In Fig. 3, we show two ISM diagnostics as a function of the sSFR: Mdust/M⋆ (left panel), and Mdust/SFR (right panel). Both relations extend over two orders of magnitude, with standard deviations of ∼0.4 − 0.5 dex in each sSFR bin. This hints at the complexity of ISM conditions in dusty QGs, similar to those seen in high-z DSFGs (e.g. da Cunha et al. 2015; Calura et al. 2017; Strandet et al. 2017; Dudzevičiūtė et al. 2020; Donevski et al. 2020). Such a significant spread in Mdust/M⋆ and Mdust/SFR is interesting to understand, as QGs are expected to share similar, redshift-independent SEDs, consequence of their almost constant dust temperature (Tdust ∼ 20 K) and less turbulent ISM as compared to DSFGs (Andreani et al. 2018; Magdis et al. 2021). If we adopt our SED derived ⟨U⟩min and convert it to Tdust via calibration given by Schreiber et al. (2018), we obtain values ranging from 17 K to 33 K, with the median and corresponding absolute median deviation of 24 ± 2.3 K. This Tdust is ∼4 K warmer than the average value found by Magdis et al. (2021). Variations in Tdust are seen in each sSFR bin, in agreement with Martis et al. (2019) and Nersesian et al. (2019) who reveal the similarly wide range of values among the dusty galaxies with low sSFRs. Differences in Tdust can be due to the dust grains being exposed to different ISRFs (Nersesian et al. 2019) but can also be related to the intrinsic properties of dust, such that galaxies with a higher fraction of larger (smaller) grains produce cooler (warmer) SEDs (Relaño et al. 2022; Nishida et al. 2022). This, again, refers to diverse channels for the ISM evolution in observed QGs.
 |
Fig. 3. Evolution with sSFR for Mdust/M⋆ (left) and Mdust/SFR (right). Left panel: binned medians and corresponding 16th–84th percentiles of this sample shown as the black circles and the dark grey shaded area, respectively. Open crosses indicate the subsample of quiescent objects drawn from the Dustpedia archive (Galliano et al. 2021). Filled crosses show the compilation of dusty QGs and post-SB galaxies at z < 0.1 detected in H-ATLAS (Dariush et al. 2016). Displayed with salmon-coloured symbols are estimates for the stacked and individual QGs at higher-z’s: stacks are represented with diamonds and pentagons (Gobat et al. 2018; Magdis et al. 2021), while the individual detections are annotated with triangles (Whitaker et al. 2021b). In both panels, the cyan-shaded region illustrates the parameter space where the majority of dusty post-SB galaxies detected with ALMA reside (Li et al. 2019a). Right panel: symbols have the same meaning as in the left panel. Dashed lines roughly track the position of sources within different Tdust, calculated by scaling the strength of the ISRF intensity as derived from CIGALE. |
The relations shown in Fig. 3 can provide insight into the evolutionary stages of our dusty QGs. For example, the trend of Mdust/M⋆ with sSFR can be partially interpreted as an age-evolutionary sequence (Calura et al. 2017), meaning QGs from the upper-right side of the diagram could be dominated by objects that have younger stellar ages and higher gas fractions (fgas = Mgas/(M⋆ + Mgas)). The subsequent decrease in the sSFR is then mostly due to exhaustion of their gas reservoirs, reflecting the efficiency of ISM removal (Gobat et al. 2020). The anti-correlation of Mdust/SFR and sSFR is often viewed either as a proxy for the metallicity-dependent gas depletion timescale (Mdust/SFR ∝ τdep(Z/Z⊙); e.g. Béthermin et al. 2015; Magdis et al. 2021) or as the inverse of the mean radiation field (⟨Umean⟩; e.g. Hunt et al. 2014; Martis et al. 2019). The former implies that galaxies with smaller Mdust/SFRs and high sSFRs can be compatible with shorter gas depletion timescales (i.e. τdep ∼ 500 Myr −1 Gyr), indicative of MS DSFGs (Béthermin et al. 2015; Scoville et al. 2016; Liu et al. 2019). Consequently, objects that populate the upper left part of the Mdust/SFR–sSFR plane are expected to have a longer depletion, order of a few gigayears.
Interestingly, the literature lacks systematically selected statistical datasets of dusty QGs that would be fully suitable for comparison with our sample. Therefore, we chose to compare our data to the widely used benchmark samples of dusty galaxies in the nearby Universe, such as the H-ATLAS sample of optically red, dusty galaxies (Dariush et al. 2016, hereafter D16), and the Dustpedia archive (Galliano et al. 2021, hereafter G21; see also Lianou et al. 2019; Nersesian et al. 2019). The D16 sample comprises 78 galaxies at z < 0.1 that are selected based on > 5σ Herschel detection at 250 μm, and for which SDSS counterparts have red colours based on N U V − r diagnostics. The sample from G21 consists of ∼770 very local galaxies with angular sizes of D25 > 1′ and similarly significant Herschel detections. The majority of Dustpedia sources are star-forming galaxies, and for comparison we only chose those sources (180 in total) within the same range of sSFRs and M⋆ as our QGs (log(sSFR/yr−1) < − 10 and M⋆ > 1010 M⊙). However, this only allows for a very rough comparison because Dustpedia galaxies are not specifically selected as quiescent (i.e. the selection is not based on their Dn4000). On top of this, the median stellar mass of G21 sample is log(M⋆/M⊙) = 10.4, which is ∼0.5 dex below the median of our QGs. Therefore, we stress that any conclusion resulting from comparisons with these two samples should be taken with caution.
Nevertheless, as can be derived from both panels of Fig. 3, our estimates follow the similar evolutionary shape with the sSFR as galaxies from G21 and D16, while the derived dust-related properties differ among the samples. The points from G21 depart from our median Mdust/M⋆ and Mdust/SFR at higher sSFRs, while those from D16 lie systematically above our QGs over the entire sSFR range.
In G21, CIGALE was used to obtain M⋆, while Mdust was inferred by the code HerBIE (Galliano et al. 2018), which adopts the framework of THEMIS dust model (Jones et al. 2017). The properties of D16 are derived by MAGPHYS (da Cunha et al. 2008). We homogenise the reported stellar masses to the ones corresponding to Chabrier IMF, and corrected Mdust of Dustpedia galaxies by applying a factor of 0.7 (as suggested by Galliano et al. 2021), to ensure a fair comparison with the DL07 model. We did not attempt to correct Mdust of D16 objects as (Hunt et al. 2019) showed there exists a good agreements between the two codes. Therefore, although all three works applied different fitting methods and model assumptions. It is more likely that diversity in values is due to physics and selection bias. The Tdust derived in G21 has a median of ∼19 K, which is ∼5 K colder than average Tdust of our sample. Therefore, the difference with G21 seen towards higher sSFRs likely arises due to G21 galaxies being less massive and colder than our QGs. The average M⋆ of D16 galaxies, on the other hand, is similar to ours (log(M⋆/M⊙) = 10.8), but their Mdust are systematically higher. This can be a consequence of selection bias and noise effects. The H-ATLAS survey covers an area that is ∼100 times larger but ∼5 times shallower than the COSMOS field. Hence, > 5σ selection would return the most extreme objects that are much brighter and ‘dustier’ than our QGs. In addition, noise effects can impact Mdust estimation (e.g. Berta et al. 2016). As a consequence, most objects from D16 enter the region of ALMA-observed post-starburst galaxies (Li et al. 2019a, marked as the cyan shaded area in Fig. 3).
The median trend of our specific dust masses agree within 1σ with those derived for QGs at higher-z (0.5 < z < 2; Gobat et al. 2018; Magdis et al. 2021; Whitaker et al. 2021b). These studies reach somewhat contrasting conclusions regarding the physical properties of detected objects. Magdis et al. (2021) argue of long τdep (> 1 Gyr) and roughly constant Tdust ∼ 20 K, whereas the two QGs from Whitaker et al. (2021b) are characterised by shorter depletion timescales (τdep ∼ 100 Myr), and very different Tdust (14 K and 34 K, respectively), and fgas (4.6 ± 0.5% and 0.6 ± 0.1%, respectively). The dusty QG identified by Gobat et al. (2018) is found to host a larger cold gas fraction (5 − 10%) under dust temperature of Tdust = 20 K. Whitaker et al. (2021b) suggested that a large range in specific dust masses hints to diverse evolutionary routes to quiescence. Therefore, it is of vital importance to investigate what causes the large dispersion in Mdust/M⋆ seen in QGs. We thoroughly explore this question in the next section.
5. Morphological impact on the evolution of dust abundance in QGs
Galaxy morphology is often directly linked to some of the dust-related properties of galaxies (e.g. Smith et al. 2014; Nersesian et al. 2019; Casasola et al. 2020). Our goal in this section is to explore if the observed evolution of specific dust mass at intermediate redshifts is driven by the morphological type of our galaxies. For this reason we adopted the morphological classification by Tasca et al. (2009). They infer morphological types of galaxies in COSMOS by applying the automated method on parameters such as the concentration (Cn), Gini index (G), asymmetry, and M20 moment, calculated from the Hubble Space Telescope (HST) F814W imaging (Cassata et al. 2007). With this we split the full sample of our QGs into two sub-classes: elliptical quiescent galaxies (eQGs; 382 objects out of 545; 70%) and spiral quiescent galaxies (sQGs; 163 objects out of 545; 30%)6. The distributions of their main structural and physical properties are presented in Fig. 4. Through the rest of the paper, we extensively investigate evolution of specific dust mass with different parameters in these two morphological groups.
 |
Fig. 4. Structural and SED-derived physical properties of QGs from hCOSMOS. Normalised distributions of values for various physical quantities are displayed for two morphological categories: quiescent spirals and ellipticals (sQGs and eQGs; yellow and dark cyan colours, respectively). The first row delineates properties obtained from the Hectospec spectroscopy. The redshift, Dn4000, and gas metallicity (i.e. oxygen abundance) are expressed as 12 + log(O/H). The second row displays some of the main structural properties derived from HST images observed via the F814W filter (Gini index, concentration, and effective radius in kiloparsecs) from the catalogue of Cassata et al. (2007). The third and fourth rows show various physical properties estimated from multi-wavelength SED modelling of our QGs with the code CIGALE. These are, from the upper left to lower right: log(M⋆/M⊙), log(Age/yr), log(tquench/Myr), log(Mdust/M⊙), Tdust, and log(Ldust/L⊙). |
5.1. The relationship between Mdust/M⋆ and gas-phase metallicity
Gas-phase metallicity is considered one of the crucial parameters influencing the dust life cycle in galaxies (e.g. Asano et al. 2013; Pantoni et al. 2019; Hou et al. 2019; Triani et al. 2020). The unique aspect of our hCOSMOS dataset is a combination of self-consistently SED-derived Mdust and M⋆, and independent measurements of Zgas. This enables us to investigate, for the first time, how the Mdust/M⋆ evolves as a function of Zgas in two different morphological categories of QGs beyond the local Universe. The majority of our objects (76%) have ‘super-solar’ Zgas with the median that reaches twice the solar value (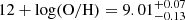 ). Both distributions and medians of Zgas are similar between the two morphological groups (see Fig. 4). In Fig. 5. we showcase the relation of Mdust/M⋆ with Zgas for two stellar mass bins, colour-coding their stellar mass surface densities (defined as
). Both distributions and medians of Zgas are similar between the two morphological groups (see Fig. 4). In Fig. 5. we showcase the relation of Mdust/M⋆ with Zgas for two stellar mass bins, colour-coding their stellar mass surface densities (defined as 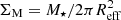 , where Reff is effective radius in kpc based on the measurements from Cassata et al. 2007).
, where Reff is effective radius in kpc based on the measurements from Cassata et al. 2007).
 |
Fig. 5. Evolution of Mdust/M⋆ as a function of gas-phase metallicities in QGs from this work. The circles are colour-coded by the stellar mass surface densities (expressed on a logarithmic scale). Galaxies are divided into two mass bins: log(M⋆/M⊙) < 11 (left) and log(M⋆/M⊙) > 11 (right). Brown markers and shaded regions represent the binned medians and 16th–84th percentile range of the resulting distribution for morphologically classified sub-samples of dusty QGs: those classified as eQGs (squares) and sQGs (circles). The typical errors in gas-metallicity estimates for solar and super-solar values are displayed with horizontal lines. |
The Fig. 5 reveals several interesting features: (1) At fixed Zgas the observed Mdust/M⋆ varies amongst morphological types. The specific dust mass is systematically higher in sQGs than in eQGs, and it evolves in a more complex way. When transiting from (sub-)solar to the super-solar gas metallicities, sQGs undergo turnover of the relation between Mdust/M⋆ and Zgas. Such behaviour is visible in both mass bins, being more prominent for 10 < log(M⋆/M⊙) < 11. We note that the trend observed in sQGs should be consider rather tentative, as typical uncertainties in Zgas measurements are quite large (∼0.4) for 12 + log(O/H)≤8.8. Irrespective of this, eQGs maintain remarkably flat Mdust/M⋆ over range of metallicities. To our knowledge, this is the first time that the morphological dependence in Mdust/M⋆ with Zgas has been observed in QGs at intermediate redshifts. This result strongly indicates that morphology-type impact on the dust content extends at least to z ∼ 0.6, complementing the conclusions from known studies of QGs at z ∼ 0 (Smith et al. 2014; Beeston et al. 2018; Nersesian et al. 2019; Casasola et al. 2022); (2) For 12 + log(O/H)∼9 there is a range of specific dust masses that extends over ∼2 orders of magnitude and exceeds the median deviation in both morphological types. This implies that our QGs are subject to complex interplay of processes contributing to the dust life cycle.
In the first place, dust particles can be internally produced via core-collapse supernovae (CC SNe) and in outflows of AGB stars, and can further grow via collisions and accretion of free metals in the ISM. The absence of a clear trend in Fig. 5 suggests that the balance between the formation and destruction of dust grains is altered at super-solar Zgas. Specific dust masses in eQGs saturates around Mdust/M⋆ ∼ 10−4 over range of metallicities. Interpreting such behaviour is not trivial. For evolved galaxies, the Mdust/M⋆ is expected to arise from the ‘competition’ between the dust-to-gas ratio (δDGR) increasing and fgas decreasing (e.g. Asano et al. 2013; Béthermin et al. 2015). By using resolved observations of M 101 galaxy, Vílchez et al. (2019) find constant Mdust/M⋆ with Zgas in the outer part characterised by sub-solar Zgas. They interpret such a flat trend as a consequence of a constant yield ratio dominated by stellar sources under a constant gas fraction (fgas ∼ 0.1). Nevertheless, such a scenario seems unlikely for our sample, as it is favoured for sub-solar environments, but not for the metal-rich ISM. Furthermore, cold gas fraction in our QGs is expected to vary, consequence of the cosmic evolution. If the dust yield is solely by stellar sources and subsequently removed by efficient outflows, one would expect strong anti-correlation between Mdust/M⋆ and Zgas, as known in most of local, DSFGs (e.g. Casasola et al. 2022). This contradicts our data and suggests that prolonged dust productions of varying efficiencies may be required to balance destructive processes responsible for gas (and subsequently, dust) decline.
In this regard, growing number of theoretical studies propose the grain growth of dust in ISM to play important role in metal-rich galaxies (e.g. Asano et al. 2013; Rémy-Ruyer et al. 2014; Hirashita et al. 2015; Zhukovska et al. 2016; De Vis et al. 2019; Aoyama et al. 2020). In such a scenario, if Zgas in a galaxy exceeds a certain critical value that strongly depends on the galaxy SFH, the grain growth becomes active and the Mdust rapidly increases until metals are depleted from the ISM. The evolution of specific dust mass in our sQGs qualitatively agrees with the predictions from the grain growth scenario. Mdust/M⋆ first rises up to certain Zgas, and levels off when most of the available metals are depleted onto the dust grains. At the same time, global dust destruction should decrease available cold gas, reducing the material for the further dust production. This interpretation was proposed in Casasola et al. (2020) who explore the morphological impact on the scatter in dust scaling relations with Zgas in Dustpedia galaxies. They invoke the effect of grain growth to explain the observed specific dust masses (Mdust/M⋆ > 0.0001) and high average dust-to-gas ratio (δDGR ≳ 1/100) in objects with super-solar Zgas. In principle, expected accretion time for grain growth scales to the inverse of the cold gas fraction, being very rapid (∼107 − 108 yr) in QGs with fgas > 0.1 (Hirashita et al. 2015; Hirashita & Nozawa 2017). With this production channel being dominant, the observed scatter in Mdust/M⋆ at a given Zgas may reflect the variation of growth efficiencies. The significance of such a process can be traced via dust depletion to metals (quantified as the ‘dust-to-metal ratio’, δDTM; De Vis et al. 2019), which we explicitly investigate with models in Sect. 6.4.
Our QGs span a wide range of optical sizes, with stellar mass surface densities (defined as 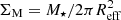 ) extending over ≳2 orders of magnitude. From Fig. 5 we see that over range of metallicities, dusty QGs with lower surface densities tend to have larger Mdust/M⋆. This may suggests that processes driving the size growth in the QGs may leave observational imprints on their relative dust abundance. Because the presence of a companion galaxy can affect the dust scaling relations, several works argue that the extended sizes of dusty QGs support the idea that some fraction of dust and metals is acquired via external sources, most likely via mergers with dust-rich satellites (Rowlands et al. 2012; Martini et al. 2013; Lianou et al. 2016; Dariush et al. 2016; Kokusho et al. 2019). We return to the connection with surface densities in the sections where we examine implications related to the channels of dust production and dust removal, and their link with post-quenching timescales (Sects. 5.4 and 5.5). The comprehensive theoretical interpretation based on the models will be presented in Sect. 6.
) extending over ≳2 orders of magnitude. From Fig. 5 we see that over range of metallicities, dusty QGs with lower surface densities tend to have larger Mdust/M⋆. This may suggests that processes driving the size growth in the QGs may leave observational imprints on their relative dust abundance. Because the presence of a companion galaxy can affect the dust scaling relations, several works argue that the extended sizes of dusty QGs support the idea that some fraction of dust and metals is acquired via external sources, most likely via mergers with dust-rich satellites (Rowlands et al. 2012; Martini et al. 2013; Lianou et al. 2016; Dariush et al. 2016; Kokusho et al. 2019). We return to the connection with surface densities in the sections where we examine implications related to the channels of dust production and dust removal, and their link with post-quenching timescales (Sects. 5.4 and 5.5). The comprehensive theoretical interpretation based on the models will be presented in Sect. 6.
5.2. Dissecting the age-dependent evolution of Mdust/M⋆
We now focus on analysing the Mdust/M⋆ under the age-evolutionary framework. To achieve this goal, we adopted the mass-weighted stellar ages (t⋆), derived from our self-consistent SED fitting. In Fig. 6 we show the trends of Mdust/M⋆ with the mass-weighted stellar ages (t⋆) for two morphological sub-groups. From Fig. 6 we see that Mdust/M⋆ in sQGs has the overall decreasing trend with increasing stellar age, contrary to eQGs, which maintain a very shallow evolution. The median stellar age of sQGs is, on average, ∼1 Gyr younger than in eQGs (log(Age/yr) = 9.65 and log(Age/yr) = 9.79, respectively). The large scatter is especially pronounced at older ages (e.g. t⋆ > 5 Gyr), while the difference between the two sub-groups almost vanishes towards the largest stellar ages.
 |
Fig. 6. Evolution of Mdust/M⋆ as a function of mass-weighted stellar age, colour-coded by the stellar-mass surface density. Brown symbols have the same meaning as in Fig. 5. The dotted line is the best fit (exponentially declining function) to the sQGs. |
Inferred mass-weighted stellar ages inform that the majority of stellar content was produced in early times in both morphological groups. There is a tail towards younger ages visible for the sQGs, while the same in not observed for the eQGs. The large spread in t⋆ as seen for our sQGs is in agreement with Tojeiro et al. (2013) and Zhou et al. (2021), who found that some fraction of sQGs at low-z have exceptionally younger ages (< 0.5 Gyr) than the general population of eQGs and sQGs. By investigating the mass-size growth in the full sample of hCOSMOS QGs, Damjanov et al. (2022) show that the non-negligible number of extended QGs with younger stellar populations (as seen in our dustiest sQGs) are recently quenched galaxies. Interestingly, they found the evolution of the mass-size relation for those recently quenched QGs to be mostly a consequence of progenitor bias rather than of minor mergers.
Negative correlation between Mdust/M⋆ and stellar age (as seen in our sQGs) can be interpreted as age-evolutionary sequence (Michałowski et al. 2019; Burgarella et al. 2020). Within this framework, the level of specific dust decline with t⋆ can be used for quantifying the removal time for dust. For the smaller sample of H-ATLAS red spirals and ellipticals at z ∼ 0.1, Michałowski et al. (2019) found the exponentially declining function to the Mdust/M⋆ with age, inferring long dust removal timescales (∼2.25 Gyr). If we apply the same method to our sQGs, we would obtain τd = 2.75 ± 0.5 Gyr, which agrees within 1σ with estimates from Michałowski et al. (2019) despite some noticeable differences between the two samples7. Contrary to sQGs, the evolution of Mdust/M⋆ in eQGs is almost independent of stellar age, indicative of very slow dust removal, which likely be prolonged over several gigayears. A weak evolution of Mdust/M⋆ at high stellar ages, and especially in eQGs, can strengthen the idea presented in previous section that dust abundance in our QGs could be of mixed origin. For example, flattening of specific dust mass with age is expected if dust is continuously produced by AGB stars or is supported externally via mergers (see e.g. Smith et al. 2014; Richtler et al. 2018; Kokusho et al. 2019). An additional clue on this can be gained from mass surface densities. Many older QGs are generally expected to have undergone the size growth via minor mergers, which would increase the M⋆, but decrease the surface density. This would introduce the scatter in ΣM per given age, in line to what is seen at Fig. 6. Optical studies of QGs at low and intermediate redshifts (e.g. Beverage et al. 2021; Barone et al. 2022) pointed out that the scatter in surface densities per given age reflects the diverse conditions of the Universe when a galaxy becomes quiescent.
5.3. The evolution of Mdust/M⋆ with M⋆
Our data indicate a general anti-correlation between the Mdust/M⋆ with M⋆. As is evident from Fig. 7, for given M⋆, there is a distinction between the sQGs and eQGs at log(M⋆/M⊙)≲10.75, with very little overlap between the two. Strong difference vanishes above this stellar mass with many sQGs entering the region populated by eQGs (Mdust/M⋆ < 10−4). The anti-correlation with M⋆ in sQG and eQGs can be best described with following fitting functions:
 |
Fig. 7. Evolution of Mdust/M⋆ with M⋆ in observed dusty QGs. Upper panel: evolution of Mdust/M⋆ with M⋆, colour-coded as a function of galaxy size (represented with effective radius, Reff, in kpc). Median values in different stellar mass bins are displayed with brown circles and squares for sQGs and eQGs, respectively. The typical errors are shown as brown crosses. The straight lines are the best linear fits that describe the data for sQGs and eQGs. Line symbols and fitting functions are indicated in the legend, and the shaded regions represent 95% confidence intervals of the fit. Lower panel: evolution of Mdust/M⋆ with M⋆ in sQGs (left) and eQGs (right) as a function of time after quenching (tquench). Coloured lines show the evolution of the specific dust mass (as median values in three stellar mass bins) for different post-quenching intervals. The meaning of the coloured lines is indicated in the legend. |
for sQGs and
for eQGs. The Spearman rank coefficient is find to be −0.62 for sQGs, and −0.32 for eQGs, while for both morphological groups we obtain a small probability (corresponding to the high significance of ∼5.5σ and 4.2σ, respectively) that there is no correlation. Recent works on local dusty galaxies reported morphological impact on the relation between Mdust/M⋆ with M⋆ (Nersesian et al. 2019; Casasola et al. 2020). Interestingly, the evolutionary slope we infer for our eQGs is identical to the one found in studies of nearby star-forming galaxies (Casasola et al. 2020), and in ALMA-detected MS DSFGs at z ∼ 1 (Donevski et al. 2020). This suggests that DSFGs and eQGs likely share some common processes in their dust evolution, namely removal and/or quenching (Lapi et al. 2018).
Negative correlation of Mdust/M⋆ with M⋆ observed in our QGs is in agreement with known observational studies of dusty galaxies in different environments (e.g. Bourne et al. 2012; Casasola et al. 2020; Donevski et al. 2020). It is usually interpreted as a natural reflection of the dust life cycle: M⋆ grows with time as galaxy evolve, while dust grains decrease from the budget being incorporated into the stellar mass. By applying the chemical galaxy model to proto-spheroidal galaxies, Calura et al. (2017) find that Mdust/M⋆ is larger in galaxies with 10 < log(M⋆/M⊙) < 11 because these are characterised both by a lower specific destruction rate and by a larger growth rate than in more massive galaxies. This may explain why our QGs with relatively high specific dust mass (log(Mdust/M⋆) > − 3) are identified exclusively at log(M⋆/M⊙) < 11). Casasola et al. (2022) recently analysed the spatially resolved Dustpedia galaxies and show that variations in Mdust/M⋆ exist even for galaxies within the same morphological group, attributing it to the variations in dust growth efficiencies.
There is another important aspect of the analysis presented in Fig. 7. Namely, the uppermost part of the plane at log(M⋆/M⊙)≲11 is dominated by sQGs that are characterised by larger sizes and stellar populations younger than in eQGs with the same M⋆. A further increase in optical sizes towards log(M⋆/M⊙)≳11 is followed by reduced difference between the specific dust masses of eQGs and sQGs. That said, the growth in galaxy size with M⋆ (as confirmed by many works on the mass-size relation) does not correspond to the similar increase in Mdust. Damjanov et al. (2022) demonstrate that sizes of QGs from this work increase as log(Reff/kpc)∼0.75 × log(M⋆/M⊙). While this evolution is find to be almost redshift independent, it emerges from different processes, both internal and external. Such a dichotomy can modulate gas fraction and quenching efficiency, which in turn would impact the evolution of the dust content in galaxies.
5.4. How dust evolution and post-quenching timescales are connected
One of the main questions that arises from the presented results regards how we can use the observed evolution of dust content to learn about the evolution of QGs following their quenching. To answer this question, from the SFHs modelled in CIGALE, we adopted post-quenching time (tquench), which is the time passed since the star formation is quenched, and is defined as the age of the galaxy minus ttrunc from Eq. (1). Our modelling procedure reveals a wide distribution of tquench, from 60 Myr to 3.2 Gyr, which ensures that QGs from this work probe broad dynamical ranges in terms of quenching age. The median tquench is found to be 436 ± 215 Myr for sQGs, and 704 ± 282 Myr for eQGs. Lower panel in Fig. 7 shows that QGs generally experience trend of Mdust/M⋆ declining with post-quenching time increasing, which applies for both morphological groups. Morphology impact on Mdust/M⋆ is evident by comparing the two sub-populations within the same range of M⋆ and tquench. The difference in Mdust/M⋆ between the sQGs and eQGs is the largest in ‘recently quenched’ QGs (tquench < 500 Myr), and smallest for ‘early quenched’ galaxies (tquench > 1 Gyr). Nevertheless, the average vertical drop in specific dust mass per given M⋆ is relatively small within the morphological groups: it is ∼0.5 dex for sQGs and even lower (∼0.25 dex) for eQGs. Therefore, the observed trend of Mdust/M⋆ with M⋆ is mainly driven by an increase in M⋆ with tquench, while Mdust exhibits remarkably shallow decline within the first ∼1 Gyr following quenching.
Considering above, we can draw several conclusions: (1) Our data provide strong evidence that there is a link between the morphology and observed Mdust/M⋆. Under the assumption that the level of SFR cessation correlates with tquench, we can deduce that for the majority of our QGs the removal of cold gas and dust are interlinked. However, our data strongly suggest the link is non-monotonic, which is manifested as flattening of a trend between Mdust/M⋆ and M⋆ within certain tquench; (2) Such a shallow evolution in Mdust/M⋆ with increasing M⋆ cannot be explained with age-evolutionary scenario, and is rather indicative of ‘dust abundance recovery’ counterbalancing the drop of star formation over different timescales. The dust abundance recovery in sQGs happens on timescales shorter than in eQGs (tquench < 500 Myr vs tquench > 500 Myr, respectively). The difference may be caused by the initial cold gas available after quenching, which would affect the accretion timescales (see Sect. 5.5). Evidence of flattening can be seen even in the most massive QGs that quenched > 1 Gyr ago, but these objects have lower than average Mdust/M⋆, which is likely a consequence of ISM removal mechanisms (e.g. gas heating, Smercina et al. 2018) starting to be visible against the prolonged dust production.
Dusty QGs from this work can serve as a benchmark for better understanding the connection between their structural properties and the ISM evolution. For instance, if Mdust/M⋆ mirrors the change of molecular gas fraction (e.g. Imara et al. 2018; Whitaker et al. 2021b; Magdis et al. 2021), results from Fig. 7 implies that fgas is the highest soon after the quenching episode, and that sQGs have on average a higher cold gas content than eQGs. Within both morphological categories, more extended galaxies have a larger specific dust mass. Chen et al. (2020) and Barone et al. (2022) argue that extended QGs with smaller surface densities undergo less extreme kinetic mode feedback (and consequently slower quenching), than similarly massive compact sources, which would leave them with more residual molecular gas.
Furthermore, the effective presence of dust in our QGs along with inferred tquench may provide important clues on quenching mechanisms. As evolution in Mdust/M⋆ changes its pace (Fig. 7 reveals phases that are both accelerated and slowed down within the same range of tquench), it is likely no one mechanism is responsible for quenching star formation in our QGs. This is consistent with observational studies of passive spirals (Fraser-McKelvie et al. 2018) and passive ellipticals (Zhou et al. 2021). It is also consistent with the TNG-50 simulation study, which reported a variety of quenching timescales and time since quiescence, ranging from 1−4 Gyr in eQGs and sQGs (Park et al. 2022). Similarly, Mahajan et al. (2020) found that local dusty QGs from GAMA survey are primarily affected by quenching acting on longer timescales (order of several Gyr) due to a lack of morphological transformation associated with the transition in optical colour. Ciesla et al. (2021) demonstrate how variations in dust properties (i.e. Ldust) per given tquench resemble the ‘strength’ of quenching processes in a small sample of local dusty QGs from the Herschel Reference Survey (HRS). They proposed how the dust abundance observed in objects that quenched ∼1 Gyr ago can be explained if quenching is caused by ram-pressure stripping, which is known for affecting mostly gas, but not stars and dust in the central regions. The same mechanism is recently found to be responsible for galaxy size increase (Grishin et al. 2021) and some of our most extended sQGs with the highest specific dust masses appear to be compatible with this scenario. Interestingly, the average Mdust/M⋆ as well as the large spread with stellar age, are comparable to those of dusty post-starbursts for which (Li et al. 2019a) reported offset of several hundred Myr between the SFR quenching and decline in gas-fraction and dust mass.
5.5. Implications for the production of dust in QGs
Results presented throughout Sect. 5 impose important constraints on the timelines and mechanisms of dust production and dust removal in QGs. Below, we summarise possible scenarios, and continue with analysis with models in Sect. 6.
Implications for internal dust growth. In galaxies dominated by older stellar populations, there will be time for AGB stars to contribute significantly to the dust mass budget. The total mass of dust formed by AGB intermediate mass stars (1 M⊙ ≲ M⋆ < 8 M⊙) depends on the initial mass of the star, with the maximal yield proposed to lay within ∼4 × 10−4 and ∼3 × 10−3 M⊙ for the case of solar and super-solar metallicities, respectively (Zhukovska et al. 2008; Ventura et al. 2020). By imposing maximal production in ∼1010 AGB stars, we would obtain Mdust between 4 × 106 M⊙ and 3 × 107 M⊙. However, the average production efficiency by the AGB stars is at least 10−20 times (depending on the stellar model) lower than the maximal one (Schneider et al. 2014), resulting in dust masses ≲3 × 106 M⊙. This is still below the average value of eQGs, suggesting insufficient dust yield solely produced by AGB stars to fully match our data8. On the other hand, average value in sQGs is even higher (Mdust > 2.6 × 107 M⊙), difficult to explain even with maximally efficient SNe dust production in the early stages of galaxy history, as demonstrated by several works (e.g. Michałowski et al. 2019). Instead, our data favour dust grain growth as a relatively fast production mechanism to overcome the dust loss. As mentioned in Sect. 5.1, in metal-rich galaxies this process can increase Mdust until metals are depleted from the ISM. Timescales for dust growth in QGs are proposed to be relatively rapid, up to ∼50 − 250 Myr, if the lifetime of the cold gas is long enough (∼107 yr, Hirashita et al. 2015). If we stay conservative and account for the factor of ∼3 uncertainty due to expected variations in the fgas of our QGs, accretion timescales would remain shorter than tquench for most of our galaxies. This may explain why the dust emission in our QGs is detectable in timescales longer than those expected for dust destruction due to gas heating (∼108 yr).
Implications for external sources of dust. The most massive of our eQGs lack the clear evolution of Mdust/M⋆ with stellar ages, metallicity and stellar mass. This qualitatively agrees with scenarios proposing external contribution to Mdust from minor mergers (Kartaltepe et al. 2010; Rowlands et al. 2012; Martini et al. 2013; Lianou et al. 2016; Richtler et al. 2018; Kokusho et al. 2019). Our sample contains only 17 QGs (4%) with ‘disturbance’ signatures (extended objects with morphologies that are on the edge between discs and irregulars). However, this should be considered a lower limit since there is a possibility that mergers occur long time ago enough to erase the clear disturbance signature. We thus follow the approach by Nevin et al. (2019) who investigate simulated mergers (both gas-poor and gas-rich) within a wide range of mass ratios. They leverage the strength of concentration coefficient and Gini index as the most sensitive predictors for minor mergers in their later stages, since these parameters generally enhance as the merger progresses. If we adopted the same criteria proposed by Nevin et al. (2019, their Fig. 5), we would end up with 86 merger candidates or 16% of our sample. Such criteria correspond to galaxies in their final, post-coalescence stage, t > 3.5 Gyr since the merging started. Interestingly, the same authors find that the difference in fgas between gas-poor and gas-rich mergers does not produce a significant distinction in the concentration of the remnant. Thus, we caution that candidate merging QGs in our sample can be a mix of both, gas-rich and gas-poor. In principle, galaxies that show strong positive excess in their Mdust/M⋆ are likely to be compatible with the gas-rich scenario. The majority of our minor merger candidates (75/86) are eQGs of older ages (> 7 − 10 Gyr) and higher stellar masses (log(M⋆/M⊙) > 10.9). Only 11/86 candidates are sQGs. As a result, we anticipate that internal mechanisms will dominate dust content in QGs, with minor mergers contributing more to eQGs (75/386, or ∼19%) than sQGs (11/162, or 6%) We checked the catalogue of merging Spitzer galaxies in the COSMOS field (Kartaltepe et al. 2010) and find 14 objects from our sample that are present in this catalogue, and are classified as minor mergers. These QGs have Mdust/M⋆ fluctuating within ±0.3 dex of the median of our full sample. In addition, there is tentative evidence in our data that candidate mergers have Zgas ∼ 0.1 dex below the median, consistent with suggestions from the literature of mergers causing the scatter in mass-metallicity relation (Bustamante et al. 2018; Griffith et al. 2019). This all support the idea that merging environment can have visible impact on the evolution of Mdust/M⋆ with M⋆, Zgas and stellar age in QGs. Recent observational tests conducted with ALMA support such a possibility by identifying ISM complexity in a small sample of the brightest dusty eQGs at z ∼ 0.05 (Sansom et al. 2019). This study reveals examples of massive molecular gas discs, but also objects with dusty companions contributing to > 50% of the FIR emission.
5.6. Implications for the survival of dust in massive QGs
The lack of evolution in specific dust mass of eQGs with Zgas, age and M⋆ is compatible with very slow dust removal. This can be a result of weak outflows, long destruction timescales due to SN shocks and inefficient thermal sputtering. Below we briefly examine some of the possibilities.
Thermal sputtering. Galaxies in massive halos and clusters are expected to undergo significant thermal destruction of their grains. As presented in Donevski et al. (in prep), ∼15% of QGs from this work reside in galaxy clusters. The observed Mdust/M⋆ in these sources would be difficult to interpret if the sputtering timescale due to the exposition of dust grains to a hot ISM is extremely short. Timescales within which dust grains are efficiently destroyed in QGs are given as 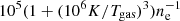 yr for typical 0.1 μm-sized grains (Hirashita & Nozawa 2017). While the typical values are quite short (1−10 Myr, Vogelsberger et al. 2019), it would be possible to obtain longer destruction timescales (tsput > 1 Gyr) if grains are larger and/or gas is of lower density (Smercina et al. 2018). Such longer sputtering timescales of tquench > 0.5 − 1 Gyr are another indication of a prolonged dust growth as they support the production of large grains, which are expected to be reduced relatively slowly in hot halos (Relaño et al. 2022; Priestley et al. 2022). Another interesting possibility would be that the dust removal in 15% of our cluster QGs is driven by ram-stripping, rather than thermal sputtering (e.g. Cortese et al. 2016). However, future multi-phase (atomic and molecular) ISM characterisations are needed to confirm or rule out this possibility. On top of this, along with the sputtering in hot halos, dust cooling may be operating through the emission of IR radiation, as proposed by recent hydrodynamical simulations (Vogelsberger et al. 2019). However, this solution would likely produce excess in the sub-millimetre wavelengths, which we did not observe in existing SCUBA-2 data.
yr for typical 0.1 μm-sized grains (Hirashita & Nozawa 2017). While the typical values are quite short (1−10 Myr, Vogelsberger et al. 2019), it would be possible to obtain longer destruction timescales (tsput > 1 Gyr) if grains are larger and/or gas is of lower density (Smercina et al. 2018). Such longer sputtering timescales of tquench > 0.5 − 1 Gyr are another indication of a prolonged dust growth as they support the production of large grains, which are expected to be reduced relatively slowly in hot halos (Relaño et al. 2022; Priestley et al. 2022). Another interesting possibility would be that the dust removal in 15% of our cluster QGs is driven by ram-stripping, rather than thermal sputtering (e.g. Cortese et al. 2016). However, future multi-phase (atomic and molecular) ISM characterisations are needed to confirm or rule out this possibility. On top of this, along with the sputtering in hot halos, dust cooling may be operating through the emission of IR radiation, as proposed by recent hydrodynamical simulations (Vogelsberger et al. 2019). However, this solution would likely produce excess in the sub-millimetre wavelengths, which we did not observe in existing SCUBA-2 data.
Destruction due to SN shocks. The total rate of dust mass destruction due to SN shocks is given by Ṁdest ∝ Mdust/τdestr, where dust destruction timescale is usually approximated as (Slavin et al. 2015)
Here ΣMgas is the surface density of molecular gas mass, fISM is the value that accounts for the effects of correlated SNe, RSN is the SNe rate, τSN is the mean interval between SNe in the Galaxy (the inverse of the rate) and Mcl is the total ISM mass swept-up by a SN event. Here is important to note that Mcl varies with the ambient gas density and metallicity, and as metals being efficient cooling channel in the ISM, higher Zgas would result in smaller swept mass (see Asano et al. 2013; Hou et al. 2019). We can roughly approximate range of destruction timescales by using estimated Zgas, and applying conservative approach for converting Mdust to Mgas through metallicity-dependent δDGR (Rémy-Ruyer et al. 2014). Following Eq. (4), we infer range of τdestr from 0.11 Gyr to 9.5 Gyr, with the median of 1.28 Gyr for sQGs, and 1.75 Gyr for eQGs. This informs that destruction due to SNe shocks in not expected to be crucial in our sample.
Overall, the brief analysis from this section hints at an expected small influence of dust destruction due to SNe shocks, while effect of thermal sputtering can be significantly prolonged if grains are growing inside QGs. On top of this, effect of outflows (e.g. due to stellar and X-ray feedback) is expected to be more important (e.g. De Looze et al. 2016). To investigate this, in the next section we analyse outputs from different simulations of dust formation that have these effects included.
6. Interpretation of results with models
To evaluate our results within the framework of dusty galaxy formation, in this section we inspect analytic models and the state-of-the-art cosmological simulations that track the dust life cycle in a self-consistent way.
6.1. Models
We analysed the predictions from the (1) cosmological galaxy formation simulation with self-consistent dust growth and feedback (SIMBA; Davé et al. 2019); and (2) the chemical model of Nanni et al. (2020).
6.1.1. SIMBA cosmological simulation
The cosmological galaxy formation simulation, SIMBA, utilises mesh-free finite mass hydrodynamics, and is successor of MUFASA simulation (Davé et al. 2016) with improvements to the sub-grid prescriptions for star formation, AGN feedback and X-ray feedback, as well as implementation of dust physics. We refer the reader to Davé et al. (2019) for extensive description of the simulation. Self-consistent dust framework that models the production, growth and destruction of dust grains in SIMBA is introduced in Li et al. (2019b). Overall, SIMBA accounts for dust grains produced from stellar populations (SNe and AGB stars), which can further grow via accreting gas-phase metals. Dust can be destroyed via different processes such as thermal sputtering, SNe shocks and astration (consumption by star formation). Dust can instantaneously be destroyed in gas impacted by jet-mode AGN feedback, while outflow processes such as radiative-mode Eddington AGN feedback and stellar feedback can heat up and transport dust out of the galaxy.
The net rate of dust production/destruction in SIMBA can be generalised as
The first term on the right side of Eq. (5) describes the dust produced by condensation of a fraction of metals from the ejecta of SNe and AGB stars; the second term describes the dust by accretion in the ISM; the third term describes the dust destructed by SNe shock waves and thermal sputtering; the fourth term is the consumption of dust due to astration; the fifth term is an additional dust production by gas infall; the sixth term describes the dust mass that is ejected out of the ISM due to feedback processes. The last two mechanisms are responsible for heating up and removal of gas into the dark matter halo, or even further out. The dust model within SIMBA does not include a contribution from Ia SNe, which is opposite to models that propose that Type Ia SNe and Type II SNe have the same condensation efficiency (Dwek 1998; McKinnon et al. 2017; Popping et al. 2017). The condensation efficiencies for AGB stars and and CC:SNe are updated based on the theoretical models of Ferrarotti & Gail (2006) and Bianchi & Schneider (2007). The evolution of dust grains in ISM is simulated with single-sized dust model where the grains are assumed to all have the same initial radius and density (a = 0.1 μm and σ = 2.4 g cm−3, respectively). SIMBA was run on a number of volumes with different resolutions. Here we use the largest one, which has 10243 dark matter particles and 10243 gas elements in a cube of 140 Mpc h−1 per side. This simulation run includes the full feedback and dust physics, which is ideal for our goal of studying the statistical sample of dusty QGs. We note that this SIMBA run results in dust mass functions and dust-to-metal ratios in a good agreement with observations at z < 1 (Li et al. 2019b), and is able to explain the observed sub-millimetre number counts up to z ∼ 2 (Lovell et al. 2021) and the dust content of QGs observed at z ∼ 1 − 2 (Williams et al. 2021).
6.1.2. The Nanni et al. (2020) model
The chemical model of Nanni et al. (2020, hereafter N20) introduces a new set of analytical solutions for the dust evolution in galaxies. The model assumes that dust formed in SN remnants, around evolved AGB stars and in the ISM is composed predominantly by silicates (olivine and pyroxene), amorphous carbon dust and metallic iron. Similar to SIMBA, Type Ia SNe are not considered important contributors to the dust enrichment. In N20 different physical processes are considered for affecting the time evolution of Mdust: astration of gas and metals due to formation of stars; dust destruction by SN shock waves that propagate in the ISM, and dust removal by galactic outflows. The model does not include thermal sputtering of dust in hot halos. The following theoretical yields are adopted: Kobayashi et al. (2006) for AGB stars, Cristallo et al. (2015) for Type II SNe, and Iwamoto et al. (1999) for Type Ia SNe Consistently with the calculations of gas and metal evolution, N20 accounts for the inflow material being composed of pristine gas that does not change the total content of dust. At each time-step the galactic outflow is considered to be regulated through the ‘mass-loading’ (ML) factor and assumes the outflow to be due to the stellar feedback in the ISM. The ML parameter is quantitatively defined as the ratio of outflow rate to the SFR (ML = Ṁout/SFR) and is related to the initial baryon mass in the galaxy, which is fully composed of gas at the beginning of simulation and converted to stars afterwards. In N20 model, Mgas is set as a multiple of M⋆ normalised to 1 M⊙ at 13 Gyr. While the fiducial N20 model excludes explicit growth of dust particles in ISM, here we test the importance of this mechanism by switching it on and off in different simulation runs. It is worth noting that N20 model showed success in reproducing total dust mass and SFR in nearby galaxies and their Lyman-break galaxy analogues at high-z (Burgarella et al. 2020).
6.2. Comparison between models and data
We now confront our observational findings to the models described above. To ensure consistency between observed and simulated data, we impose the same range of modelled M⋆, Mdust and sSFRs as in our observations (log(M⋆/M⊙) > 10, log(Mdust/M⊙) > 6 and log(sSFR/yr−1) < − 10). In addition, we follow Damjanov et al. (2018) and infer the 90% stellar-mass completeness limit of our hCOSMOS data by fitting the function M⋆ = 10.6 − log(0.4/z)−0.2. We find that 46 dusty QGs reside below the completeness limit defined in this way. Furthermore, only sources identified within the 90% completeness limit are taken into account when comparing to models. We note that same IMF (Chabrier 2003) is adopted both in simulations, and for the SED fitting of observed data.
In Fig. 8 we show how the Mdust/M⋆ in models evolves as a function of the sSFR and Zgas. Predictions from SIMBA match our data very well as the simulation shows a great potential of simultaneously reproducing observed trends of Mdust/M⋆ with sSFR and Zgas.
 |
Fig. 8. Evolution of Mdust/M⋆ as a function of sSFR (left) and Zgas (right) modelled with the state-of-the-art cosmological simulation SIMBA (Davé et al. 2019, blue lines) and the chemical evolution model of Nanni et al. (2020, light and dark violet lines). In the panels, darker (lighter) curves related to the N20 model are simulations that include (exclude) dust grain growth in the ISM. These simulation runs include different values of ML factors and grain condensation efficiencies, as indicated in the legend. The solid blue line shows the SIMBA model prediction that is the result of the flagship run (100 Mpc h−1 box), which includes ISM dust growth on metals and all feedback variants. In the right panel, along with the median trend for all selected dusty QGs in SIMBA, we also display average tracks for QGs with different δDGR (dashed blue line for δDGR < 1/100 and dotted-dashed blue line for 1/100 < δDGR < 1/2000). Data from this work (contributing to the ∼90% completeness) are displayed as binned 2D histograms, with the colour bar showing the number of observed QGs in each cell. |
For the N20 model we showcase predictions of different simulation runs. These account for different outflow rates (ML = 0.5 × Mgas, 0.5 × Mgas and 0.6 × Mgas) and different dust condensation fractions by Type II SNe (namely, low fraction of 25%, and high fraction of 50%). The total ISM mass swept in each SNe event is adopted to be Msw = 6800 M⊙, which is a standard value proposed in the literature (Dwek et al. 2014). We also explore cases where we switch on/off modelled dust growth in ISM. We find that the evolution of Mdust/M⋆ with the sSFR in N20 is well reproduced when the dust grain growth in the ISM is included, and is accompanied with the moderate outflow and higher dust condensation fraction (∼50%). By performing controlled simulation experiments with N20 we find the evolution of specific dust mass is extremely sensitive to the changes of ML factor. Namely, the higher outflow rates (ML > 0.6) would rapidly reduce Mdust/M⋆ to the values lower than 10−5 in older stellar populations (> 5 − 10 Gyr). This would produce swift decline of specific dust mass with the sSFR. In addition, for weaker outflows Mdust/M⋆ remains too flat for decreasing values of the sSFR, indicating that dust astration and destruction from SNe are not sufficient to explain the anti-correlation of Mdust/M⋆ with the sSFR, even if we impose maximum efficiency of dust destruction. While the best-matching model of N20 reproduces observed trend of Mdust/M⋆ with the sSFR, at the same time it falls relatively short to reproduce the relation with Zgas. As seen from Fig. 8, Mdust/M⋆ are 4−5 times too low for the values we infer in super-solar Zgas, while decline in dust abundance is slightly steeper as compared to SIMBA. At (sub-)solar Zgas both models predict higher Mdust/M⋆ than inferred by our data. As we note in Sect. 5.1, the difference may be just an artefact due to large uncertainties on estimated Zgas. Otherwise, lower Mdust/M⋆ than seen in models for (sub-)solar Zgas may indicate interesting cases of objects missed by simulations, for example galaxies that accrete gaseous material from the cosmic web but still did not have enough time to significantly increase their dust abundance.
6.3. Sources of dust in QGs at intermediate redshifts: Insights from models
Confronting the different theoretical models and simulations allows us to better understand the contributors for dust abundance in QGs. Results from both observations and models presented throughout this paper strongly support the scenario where dust growth due to grain collisions in the metal-rich ISM may play a vital role in dusty QGs. This conclusion is in general agreement with other observational studies exploring dust content in QGs (Michałowski et al. 2019; Richtler et al. 2018), and with recent theoretical predictions (Hirashita et al. 2015; Hirashita & Nozawa 2017; Vijayan et al. 2019; Triani et al. 2021). Indeed, it has been demonstrated that excluding ISM grain growth in SIMBA yields Mdust that are ∼0.5 dex lower than in QGs for which ISM dust growth is included (e.g. Whitaker et al. 2021a). Similarly, by turning off the effect of ISM grain growth in N20, simulated Mdust/M⋆ are lower by ≳0.4 dex as compared to cases when dust growth is included9. We note that the shortfall of data in N20 cannot be cured by imposing lower ML factors, which would result in an overall flat trend with the sSFR, inconsistent with our data (left panel of Fig. 8). Interestingly, Nanni et al. (2020) found that dust growth has irrelevant role in the dust content in Lyman-break galaxies and local dwarf galaxies. This clearly demonstrates that different mechanisms for the dust build-up are in place in later phases of massive galaxy evolution.
Since the timescale for dust growth in the ISM changes as a function of gas surface density for given Zgas, good agreement of our results with SIMBA implies that dusty QGs in hCOSMOS have enough available cold gas to support dust growth over quite short timescales (∼100 − 250 Myr). SIMBA predicts median gas masses of Mgas ∼ 2 × 109 M⊙, but higher fgas in sQGs than in eQGs (fgas = 0.11 ± 0.04 vs fgas = 0.06 ± 0.03, respectively). In addition, while checking simulation results, we also notice that sQGs in SIMBA tend to have more extended distributions of cold gas mass as compared to the stellar mass, which is not the case in eQGs. This can be explained either with higher ratios of accreting gas from the outskirts after minor mergers or if the gas is mostly distributed in the disc regions and the stellar component is very compact. Such a difference in fgas supports our earlier qualitative conclusion from Sects. 5.4 and 5.5, and may be the at the heart of why the observed Mdust/M⋆ is larger in sQGs than in eQGs.
Quenching timescales in SIMBA are strongly bimodal, with the rapid ones (< 250 − 500 Myr) being overly effective within very specific mass range (10 < log(M⋆/M⊙) < 10.5) due to black hole feedback mechanism (Rodríguez Montero et al. 2019; Zheng et al. 2022). The vast majority of dusty QGs that quench at higher stellar masses (log(M⋆/M⊙) > 10.5) are expected to be preferentially influenced by the ‘slow quenching’ mode (order of ≳0.5 − 2 Gyr). This mass range corresponds to the ∼75% of our sources. Observed shallower decline and large spread of Mdust/M⋆ towards older ages and higher M⋆ are consistent with this scenario. While black hole feedback in SIMBA is responsible for heating halo gas, it explicitly does not affect most of the cold gas in the ISM since it is hydrodynamically decoupled. In other words, even if there is no star formation, there still would be a material to support the dust growth within ∼107 − 108 yr after the quenching. Consequently, prolonged growth of dust would not be possible in the case of X-ray feedback as it has been showed that in SIMBA it efficiently pushes central gas outwards over very short timescales (Appleby et al. 2020).
The requirement that ISM growth is needed for simultaneously explaining the evolution of specific dust mass with the sSFR and Zgas also supports the predictions of the semi-analytical model from Triani et al. (2021). They show that lack of strong SNe destruction events in dust-rich quenched galaxies supports the super-solar Zgas and prolonged build-up of dust. While abundance of metals in the ISM provides material for galaxies to accumulate dust mass, stating that grain growth is the only process responsible for observed Mdust in QGs can be misleading. In the previous section we offer different lines of evidence that ∼15% of our QGs obey signs of (past) merging activities. Accretion of a gas-rich satellite would sustain prolonged dust grain growth in the accreted cold ISM if Zgas is above certain threshold10. We however expect that minor mergers play secondary role in the dust build up in dusty QGs in SIMBA. Rodríguez Montero et al. (2019) show that there is a small fraction (< 10%) of low-level rejuvenation events mostly related to minor mergers with gas-rich satellites at z < 1. These processes contribute to the young discs and more cold gas in the outskirts, and are followed by fast (∼100 Myr) quenching events.
Aside from the two favourable mechanisms outlined above, there are other factors that might be responsible for the dust content observed in our QGs. Nanni et al. (2020) predicts an increase in dust yields by a factor of 3 to 4 if a non-standard ‘top-heavy’ IMF is applied (but also see the discussion in McKinnon et al. 2017). At the same time, we expect a non-trivial connection between dusty QGs and their large-scale environments. A detailed analysis of this interplay is beyond the scope of this paper but will be addressed in future work (Donevski et al., in prep.).
6.4. The extent that the specific dust mass mirrors the molecular gas fraction in QGs
Finally, relying on a good agreement with SIMBA, we linked our observed and simulated data to inform future observations on the expected interplay between the dust, gas, and metals in QGs. In previous sections we show that observed Mdust/M⋆ can be resulting from a dust growth, for which timescales may be offsetting from those attributed to the decline of star formation and gas exhaustion. We can ask to what extent the observed evolution of Mdust/M⋆ mirrors the evolution of molecular gas. To give a sense of how the evolution of Mdust/M⋆ with Zgas can be used to deduce the cold gas-mass properties, we follow Tan et al. (2014) and rewrite the Mdust/M⋆ as
where Mgas/M⋆ is molecular gas ratio, and δDTM is dust-to-metal ratio.
There are two possible approaches to solving this equation. One is to follow the method applied by Magdis et al. (2021), who assumed constant, metallicity-dependent δDGR for all QGs (they adopt δDGR = 1/92(1/35)) for solar and super-solar Zgas, respectively). However, this solution implies a constant dust-to-metal ratio, in which case the evolution of Mdust/M⋆ entirely mirrors the evolution of molecular gas fraction. While this offers an appealing empirical explanation for the observed evolution of the ISM properties of QGs, it does not account for the possible variations in dust-to-metal ratio. Indeed, δDTM would remain constant if dust and metals are created from stars at same rates throughout galaxy evolution. Otherwise, with metals supporting the dust grain growth, δDTM would change and becomes important marker of the growth efficiency (e.g. Feldmann 2015; De Vis et al. 2019).
We thus applied another approach that benefits from the good agreement with SIMBA. We explored what lies behind the scatter in Mgas/M⋆ at a given Zgas in simulations. To illustrate how fgas and δDTM relate to Mdust/M⋆, in Fig. 9 we display simulated QGs that have δDGR within the restricted range of values that are usually adopted in observations to convert observed Mdust to Mgas (1/20 < δDGR < 1/100; e.g. Leroy et al. 2011; Schreiber et al. 2018; Dudzevičiūtė et al. 2020; Whitaker et al. 2021b; Magdis et al. 2021). From the upper panel of Fig. 9 we see that even for such a relatively small difference in δDGR, specific dust masses display wider spread in values (∼8 × 10−5 < Mdust/M⋆ < 3 × 10−3).
 |
Fig. 9. Different diagnostics of the evolution of specific dust masses in QGs, as simulated with the SIMBA full-volume simulation run. Upper panel: modelled Mdust/M⋆ as a function of Zgas in SIMBA. Circles represent the modelled QGs within the restricted range of dust-to-gas mass ratios (1/20 < δDGR < 1/100). Grey contours show the distribution of all QGs selected in the simulations with the criteria described in Sect. 6.1. The points are colour-coded by δDTM, with circle sizes scaling to fgas. The inset sketch qualitatively describes the behaviour of Mdust/M⋆: up to a certain Zgas it mostly resembles the change in the molecular gas fraction, while at 12 + log(O/H)≳8.9 it reflects the level of dust growth through the gradual increase in δDTM. Lower panel: evolution of Mdust/M⋆ with fgas for the same simulated sources plotted in the upper panel. The dashed blue and orange lines show median trends for two regimes of Zgas, as indicated in the legend. The effect of an increased dust growth in QGs is most pronounced in sources with heavily exhausted gas reservoirs, as indicated by the lower molecular gas fractions (fgas < 1 − 5%). To highlight this effect through the rise in δDTM, we sketch the shaded area between the two tracks and colour-code it to roughly match the colour bar convention from the upper panel. |
Most importantly, Fig. 9 reveals that the gas fraction is not the faithful tracer of Mdust/M⋆ over the entire range of Zgas. SIMBA predicts that up to 12 + log(O/H)≲8.85 − 8.9, observed Mdust/M⋆ mainly traces fgas, but this correlation is weaker for 12 + log(O/H)≳8.85 − 8.9, when increase in δDTM becomes more important. In other words, it is a gradual evolution of δDTM, rather than of gas the fraction, that is responsible for the spread in observed specific dust mass in super-solar dusty QGs. Therefore, some of very metal-rich QGs with δDTM > 0.5 may still have relatively high specific dust masses (10−3 < Mdust/M⋆ < 10−4) despite heavily exhausted gas reservoirs (fgas < 1 − 5%). This important theoretical prediction is illustrated in the lower panel of Fig. 9. The effect of prolonged dust growth on metals causes different pathways (slower and faster) for the decline in Mdust/M⋆. The corresponding offset in Mdust/M⋆ starts to increase below certain fgas. In galaxies that show positive excess, thermal sputtering acts on longer timescales (> 1 Gyr) due to inefficiency in swiftly destroying larger grains produced via grain growth. If this is not the case, QGs would end up with extremely low δDGR as reported in some dusty QGs observed in the local Universe (e.g. Lianou et al. 2016; Casasola et al. 2020). For that reason, any use of Mdust/M⋆ to convert to fgas and ultimately to Mgas must be carefully treated when QGs have super-solar Zgas. This is particularly important for planning the observations (i.e. with ALMA) to detect the molecular gas via CO[2−1]. At a given Mdust/M⋆, galaxies with the highest Zgas would require significantly longer integration times than those with Zgas ∼ Z⊙ due to their higher δDGR and subsequently lower Mgas. This suggests that care should be taken when interpreting the nature of dust evolution in metal-rich QGs.
6.5. Caveats
Here we outline some important considerations to bear in mind when analysing results of this study. Firstly, our analysis relies on a single spectroscopic criteria for quiescence. Under the assumption that such a method may introduce some fraction of outliers (i.e. star-forming interlopers), one can consider imposing an additional cut on the parent spectroscopic selection in order to increase the purity of the final sample. As noted in Sect. 2, the detailed analysis related to this task (Appendix C), which includes rest-frame UVJ selection and more conservative spectroscopy cut, ensures that conclusions in this paper are marginally affected by the definition of quiescence. We thus prefer not to introduce additional selection bias by mixing the spectroscopic criterion with other definitions of quiescence (i.e. with those based on rest-frame colours).
Our sample of 545 QGs also contains 52 QGs for which the negative offset from the MS is less than −0.6 dex (i.e. points above the dashed red line in the last panel of Fig. 1). Due to their spectroscopic properties and red optical colours, we consider these objects ‘dusty QGs hidden within the MS’ rather than ‘star-forming interlopers’. After removing those 52 QGs from the final sample, we recover the same evolutionary trend for the specific dust mass as for the parent sample that we show in Fig. 2. Although the median values at a given redshift become slightly lower by ∼0.2 dex, they remain consistent (within 1σ) with those from our fiducial selection.
Secondly, our conclusions are valid only for QGs with measurable dust emission. The dust masses that result from our procedure are fairly robust and show that DL07 models can well describe the dust emission even in QGs. However, information of the cold dust emission is based on low-resolution measurements, and although we did a careful treatment of resolution effects, future sub-millimetre observations of representative samples are needed to fully confirm our findings, in particular the fraction of dusty satellites. In this regard, a future inclusion of James Webb Space Telescope (JWST) data is particularly relevant for those DL07 parameters that require richer sampling in the MIR for the refined determination (in particular γ and qPAH).
7. Conclusions
We have presented the first statistical study of the evolution of dust-related properties in QGs observed at intermediate redshifts (0.1 < z < 0.6) as part of the hCOSMOS spectroscopic survey. We analysed 545 massive QGs (M⋆ > 1010 M⊙) that were systematically selected based on their spectral age indices (Dn4000 > 1.5). We combined spectroscopic information with a self-consistent, multi-band SED fitting method to explore trends in Mdust/M⋆ as a function of various physical parameters, including independently measured gas-phase metallicities. This is the largest sample of QGs for which the evolution of the dust, metal, and stellar contents has been estimated to date. We fully verified our findings with state-of-the-art simulations of dusty galaxy formation. Our main results are summarised as follows:
-
Dusty QGs at intermediate redshifts experience the cosmic evolution in Mdust/M⋆, but we find it to be shallower than in known studies on stacked samples. A large spread in Mdust/M⋆ (> 2 orders of magnitude) suggests non-uniform ISM conditions in these massive galaxies.
-
Morphological and structural parameters are important factors in the scatter in specific dust masses. The Mdust/M⋆ in sQGs is ≳4 times greater than in eQGs of a similar M⋆. At M⋆ < 1011 M⊙, higher specific dust masses are associated with lower stellar mass surface densities and younger stellar population ages, whereas the same relationship is less obvious at M⋆ > 1011 M⊙.
-
The sQGs exhibit evolutionary trends of Mdust/M⋆ with M⋆, stellar age, and galaxy size, in contrast to the little to no evolution seen for eQGs.
-
Although both sQGs and eQGs have median super-solar Zgas (12 + log(O/H)∼9), sQGs have a reversal in Mdust/M⋆ towards the highest Zgas, whereas eQGs have a flat trend. We interpret this as a change in the efficiency of dust production and removal since quenching.
-
We derive a broad dynamical range of post-quenching timescales in QGs (60 Myr < tquench < 3.2 Gyr). In general, Mdust/M⋆ is highest in recently quenched systems (tquench < 500 Myr), but its further evolution is non-monotonic, which is strong evidence for different pathways for prolonged dust growth, or removal on various timescales. The moderately shallow evolution of Mdust/M⋆ implies that quenching mechanisms usually attributed to a quick removal of gas and dust (i.e. powerful outflows and X-ray feedback) are not overly influential within our sample.
-
The state-of-the art cosmological simulation SIMBA and the chemical model from Nanni et al. (2020) are both capable of producing the dustiest QGs observed in this work (Mdust/M⋆ ≳ 10−3), with the difference that chemical models fall short of fully explaining the observed specific dust masses at super-solar Zgas. The prolonged grain growth on ISM metals is required in simulations to account for the observed dust content in QGs. Without this assumption, the models have a larger discrepancy with the data, even when adopting substantial stellar yields with high condensation efficiencies and moderate outflows.
-
Our results strongly suggest that the observed Mdust/M⋆ in dusty QGs is due to two factors: (1) The dominant channel is prolonged dust growth in metal-rich ISM. Such a process is viable in the first 1 Gyr after quenching, and it helps dusty QGs significantly prolong the destruction timescales expected for gas heating. (2) For ∼15% of our sources we find evidence that the dust content is supported or acquired externally, most likely via minor mergers.
-
The cosmological simulation SIMBA predicts that the enhancement in Mdust/M⋆, as observed in many QGs with super-solar Zgas, mirrors the enhancement in the dust-to-metal ratio rather than the rise in the molecular gas fraction. This prediction has an important observational consequence in that QGs can still be observed as dust-rich (Mdust/M⋆ ≃ 10−3) even if their gas reservoirs are heavily exhausted (with the gas fraction < 1 − 5%).
The complexity of galaxies’ dust life cycles revealed by our study motivates future observational investigations of dusty QGs. The model predictions described in Sect. 6 (in particular the diversity in δDTM) are rooted in the mechanisms dominating dust production and removal. Many observational tests of these predictions are now directly accessible via JWST instruments. The JWST MIRI, in particular, can be used to probe the warm dust and molecular gas through MIR diagnostics in individual dusty QGs at various cosmic epochs up to z ∼ 2 − 3. Along with independent metallicity measurements, the JWST MIRI can be used to place strong constraints on the fractions and sizes of PAH grains through multiple PAH features with a large wavelength separation. At the same time, it can help in unveiling the impact of dust-hidden AGN activity that would influence dust removal. Furthermore, silicate strengths and a rising MIR emission longwards of ≥10 μm would offer insights into dust grain growth. There are numerous synergistic opportunities with high-resolution sub-millimetre observations (e.g. with ALMA and NOEMA) that would provide information on the cold dust and gas in QGs. Finally, in our ongoing works, we examine how large-scale environments influence the interplay of dust and metals in QGs (Donevski et al., in prep.) and present the key differences in SEDs of dusty versus non-dusty QGs (Lorenzon et al., in prep.).
When available, for the purpose of our SED fitting we also included upper limits based on 850 μm non-detections from the SCUBA-2 Cosmology Legacy Survey (S2CLS; Geach et al. 2017).
We also double-check for additional X-ray-bright AGNs in the COSMOS (Civano et al. 2016) and find that ∼30% of AGNs we identify via SED modelling also have excess X/radio emission.
Associated data can be retrieved at https://zenodo.org/record/8231067
We note that morphological classification remains almost unchanged when using other methods, i.e. the Zurich estimator of structural types (ZEST) from Scarlata et al. (2007).
The sample from Michałowski et al. (2019) is composed of H-ATLAS objects that are described to have very bright SPIRE fluxes. In addition, their sample also contains ‘bluer’ objects with Dn4000 smaller than the cut we applied to systematically select our QGs (Dn4000 > 1.5).
Various combinations of galactic outflows and condensation efficiencies nay introduce some degeneracies in the models, making the predictions strongly dependent on how one regulates the outflow (see Nanni et al. 2020 for a discussion).
The exact value of Zgas where dust growth becomes dominant over stellar production is proposed to vary. For example, recent analytic models suggest 12 + log(O/H) > 8.5 for Mgas > 109 M⊙; e.g. Triani et al. (2020).
Acknowledgments
We are thankful to the anonymous referee for very constructive comments which improved the initial version of the paper. We would like to acknowledge Anna Feltre, Kasia Malek, Marcella Massardi, Lorenzo Zanisi, Katarina Kraljic and Alessandro Bressan for useful discussions and comments D.D. acknowledges support from the National Science Center (NCN) grant SONATA (UMO-2020/39/D/ST9/00720). I.D. acknowledges the support of the Canada Research Chair Program and the Natural Sciences and Engineering Research Council of Canada (NSERC; funding reference No. RGPIN-2018-05425). A.M. acknowledges the support of the Natural Sciences and Engineering Research Council of Canada (NSERC) through grant reference number RGPIN-2021-03046. M.R. and A.N. acknowledge support from the Narodowe Centrum Nauki (UMO-2020/38/E/ST9/00077). D.N. acknowledges support from the NSF via AST-1909153.
References
- Andreani, P., Boselli, A., Ciesla, L., et al. 2018, A&A, 617, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aoyama, S., Hirashita, H., & Nagamine, K. 2020, MNRAS, 491, 3844 [NASA ADS] [Google Scholar]
- Appleby, S., Davé, R., Kraljic, K., Anglés-Alcázar, D., & Narayanan, D. 2020, MNRAS, 494, 6053 [NASA ADS] [CrossRef] [Google Scholar]
- Asano, R. S., Takeuchi, T. T., Hirashita, H., & Inoue, A. K. 2013, Earth Planets Space, 65, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Barone, T. M., D’Eugenio, F., Scott, N., et al. 2022, MNRAS, 512, 3828 [NASA ADS] [CrossRef] [Google Scholar]
- Battisti, A. J., Cunha, E. D., Shivaei, I., & Calzetti, D. 2020, ApJ, 888, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Beeston, R. A., Wright, A. H., Maddox, S., et al. 2018, MNRAS, 479, 1077 [NASA ADS] [Google Scholar]
- Belli, S., Contursi, A., Genzel, R., et al. 2021, ApJ, 909, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, S., Lutz, D., Genzel, R., Förster-Schreiber, N. M., & Tacconi, L. J. 2016, A&A, 587, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Daddi, E., Magdis, G., et al. 2015, A&A, 573, A113 [Google Scholar]
- Beverage, A. G., Kriek, M., Conroy, C., et al. 2021, ApJ, 917, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S., & Schneider, R. 2007, MNRAS, 378, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Bisigello, L., Kuchner, U., Conselice, C. J., et al. 2020, MNRAS, 494, 2337 [NASA ADS] [CrossRef] [Google Scholar]
- Blánquez-Sesé, D., Gómez-Guijarro, C., Magdis, G. E., et al. 2023, A&A, 674, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourne, N., Maddox, S. J., Dunne, L., et al. 2012, MNRAS, 421, 3027 [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Burgarella, D., Nanni, A., Hirashita, H., et al. 2020, A&A, 637, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bustamante, S., Sparre, M., Springel, V., & Grand, R. J. J. 2018, MNRAS, 479, 3381 [Google Scholar]
- Calura, F., Pozzi, F., Cresci, G., et al. 2017, MNRAS, 465, 54 [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Casasola, V., Bianchi, S., De Vis, P., et al. 2020, A&A, 633, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casasola, V., Bianchi, S., Magrini, L., et al. 2022, A&A, 668, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassata, P., Guzzo, L., Franceschini, A., et al. 2007, ApJS, 172, 270 [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Charlot, S., & Fall, S. M. 2000, ApJ, 539, 718 [Google Scholar]
- Chen, Z., Faber, S. M., Koo, D. C., et al. 2020, ApJ, 897, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Ciesla, L., Boselli, A., Elbaz, D., et al. 2016, A&A, 585, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ciesla, L., Buat, V., Boquien, M., et al. 2021, A&A, 653, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Civano, F., Marchesi, S., Comastri, A., et al. 2016, ApJ, 819, 62 [Google Scholar]
- Clemens, M. S., Jones, A. P., Bressan, A., et al. 2010, A&A, 518, L50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortese, L., Bekki, K., Boselli, A., et al. 2016, MNRAS, 459, 3574 [Google Scholar]
- Cousin, M., Buat, V., Lagache, G., & Bethermin, M. 2019, A&A, 627, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cristallo, S., Straniero, O., Piersanti, L., & Gobrecht, D. 2015, ApJS, 219, 40 [Google Scholar]
- Cuppen, H. M., Walsh, C., Lamberts, T., et al. 2017, Space Sci. Rev., 212, 1 [Google Scholar]
- da Cunha, E., Charlot, S., & Elbaz, D. 2008, MNRAS, 388, 1595 [Google Scholar]
- da Cunha, E., Eminian, C., Charlot, S., & Blaizot, J. 2010, MNRAS, 403, 1894 [Google Scholar]
- da Cunha, E., Walter, F., Smail, I. R., et al. 2015, ApJ, 806, 110 [Google Scholar]
- Daddi, E., Renzini, A., Pirzkal, N., et al. 2005, ApJ, 626, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Damjanov, I., Zahid, H. J., Geller, M. J., Fabricant, D. G., & Hwang, H. S. 2018, ApJS, 234, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Damjanov, I., Sohn, J., Utsumi, Y., Geller, M. J., & Dell’Antonio, I. 2022, ApJ, 929, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Dariush, A., Dib, S., Hony, S., et al. 2016, MNRAS, 456, 2221 [NASA ADS] [CrossRef] [Google Scholar]
- Davé, R., Thompson, R., & Hopkins, P. F. 2016, MNRAS, 462, 3265 [Google Scholar]
- Davé, R., Anglés-Alcázar, D., Narayanan, D., et al. 2019, MNRAS, 486, 2827 [Google Scholar]
- Davis, T. A., Alatalo, K., Bureau, M., et al. 2013, MNRAS, 429, 534 [Google Scholar]
- De Looze, I., Baes, M., Bendo, G. J., et al. 2016, MNRAS, 459, 3900 [CrossRef] [Google Scholar]
- De Vis, P., Gomez, H. L., Schofield, S. P., et al. 2017, MNRAS, 471, 1743 [Google Scholar]
- De Vis, P., Jones, A., Viaene, S., et al. 2019, A&A, 623, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donevski, D., Lapi, A., Małek, K., et al. 2020, A&A, 644, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [CrossRef] [Google Scholar]
- Driver, S. P., Andrews, S. K., da Cunha, E., et al. 2018, MNRAS, 475, 2891 [Google Scholar]
- Dudzevičiūtė, U., Smail, I., Swinbank, A. M., et al. 2020, MNRAS, 494, 3828 [Google Scholar]
- Dwek, E. 1998, ApJ, 501, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., Staguhn, J., Arendt, R. G., et al. 2014, ApJ, 788, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Fabricant, D., Fata, R., Roll, J., et al. 2005, PASP, 117, 1411 [NASA ADS] [CrossRef] [Google Scholar]
- Feldmann, R. 2015, MNRAS, 449, 3274 [NASA ADS] [CrossRef] [Google Scholar]
- Feltre, A., Hatziminaoglou, E., Fritz, J., & Franceschini, A. 2012, MNRAS, 426, 120 [Google Scholar]
- Ferrarotti, A. S., & Gail, H. P. 2006, A&A, 447, 553 [CrossRef] [EDP Sciences] [Google Scholar]
- Fraser-McKelvie, A., Brown, M. J. I., Pimbblet, K., Dolley, T., & Bonne, N. J. 2018, MNRAS, 474, 1909 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, J., Franceschini, A., & Hatziminaoglou, E. 2006, MNRAS, 366, 767 [Google Scholar]
- Gall, C., & Hjorth, J. 2018, ApJ, 868, 62 [CrossRef] [Google Scholar]
- Gallazzi, A., Charlot, S., Brinchmann, J., White, S. D. M., & Tremonti, C. A. 2005, MNRAS, 362, 41 [Google Scholar]
- Galliano, F., Galametz, M., & Jones, A. P. 2018, ARA&A, 56, 673 [Google Scholar]
- Galliano, F., Nersesian, A., Bianchi, S., et al. 2021, A&A, 649, A18 [EDP Sciences] [Google Scholar]
- Geach, J. E., Dunlop, J. S., Halpern, M., et al. 2017, MNRAS, 465, 1789 [Google Scholar]
- Gobat, R., Daddi, E., Magdis, G., et al. 2018, Nat. Astron., 2, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Gobat, R., Magdis, G., D’Eugenio, C., & Valentino, F. 2020, A&A, 644, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graziani, L., Schneider, R., Ginolfi, M., et al. 2020, MNRAS, 494, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Griffith, E., Martini, P., & Conroy, C. 2019, MNRAS, 484, 562 [CrossRef] [Google Scholar]
- Grishin, K. A., Chilingarian, I. V., Afanasiev, A. V., et al. 2021, Nat. Astron., 5, 1308 [NASA ADS] [CrossRef] [Google Scholar]
- Haines, C. P., Iovino, A., Krywult, J., et al. 2017, A&A, 605, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirashita, H., & Nozawa, T. 2017, Planet. Space Sci., 149, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Hirashita, H., Nozawa, T., Villaume, A., & Srinivasan, S. 2015, MNRAS, 454, 1620 [NASA ADS] [CrossRef] [Google Scholar]
- Hjorth, J., Gall, C., & Michałowski, M. J. 2014, ApJ, 782, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Hou, K.-C., Aoyama, S., Hirashita, H., Nagamine, K., & Shimizu, I. 2019, MNRAS, 485, 1727 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., Palazzi, E., Michałowski, M. J., et al. 2014, A&A, 565, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., De Looze, I., Boquien, M., et al. 2019, A&A, 621, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurley, P. D., Oliver, S., Betancourt, M., et al. 2017, MNRAS, 464, 885 [Google Scholar]
- Imara, N., Loeb, A., Johnson, B. D., Conroy, C., & Behroozi, P. 2018, ApJ, 854, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., Köhler, M., Ysard, N., Bocchio, M., & Verstraete, L. 2017, A&A, 602, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kartaltepe, J. S., Sanders, D. B., Le Floc’h, E., et al. 2010, ApJ, 721, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr. 1998, ARA&A, 36, 189 [Google Scholar]
- Kirkpatrick, A., Pope, A., Sajina, A., et al. 2017, ApJ, 843, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, C., Umeda, H., Nomoto, K., Tominaga, N., & Ohkubo, T. 2006, ApJ, 653, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., & Kewley, L. J. 2004, ApJ, 617, 240 [CrossRef] [Google Scholar]
- Kokusho, T., Kaneda, H., Bureau, M., et al. 2019, A&A, 622, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kumari, N., Maiolino, R., Trussler, J., et al. 2021, A&A, 656, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacey, C. G., Baugh, C. M., Frenk, C. S., et al. 2016, MNRAS, 462, 3854 [Google Scholar]
- Lagos, C. D. P., Robotham, A. S. G., Trayford, J. W., et al. 2019, MNRAS, 489, 4196 [NASA ADS] [CrossRef] [Google Scholar]
- Lapi, A., Pantoni, L., Zanisi, L., et al. 2018, ApJ, 857, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Leethochawalit, N., Kirby, E. N., Ellis, R. S., Moran, S. M., & Treu, T. 2019, ApJ, 885, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Leja, J., Tacchella, S., & Conroy, C. 2019, ApJ, 880, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Bolatto, A., Gordon, K., et al. 2011, ApJ, 737, 12 [Google Scholar]
- Li, Z., French, K. D., Zabludoff, A. I., & Ho, L. C. 2019a, ApJ, 879, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Q., Narayanan, D., & Davé, R. 2019b, MNRAS, 490, 1425 [CrossRef] [Google Scholar]
- Lianou, S., Xilouris, E., Madden, S. C., & Barmby, P. 2016, MNRAS, 461, 2856 [NASA ADS] [CrossRef] [Google Scholar]
- Lianou, S., Barmby, P., Mosenkov, A. A., Lehnert, M., & Karczewski, O. 2019, A&A, 631, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, D., Schinnerer, E., Groves, B., et al. 2019, ApJ, 887, 235 [Google Scholar]
- Lovell, C. C., Geach, J. E., Davé, R., Narayanan, D., & Li, Q. 2021, MNRAS, 502, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Magdis, G. E., Gobat, R., Valentino, F., et al. 2021, A&A, 647, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mahajan, S., Gupta, K. K., Rana, R., et al. 2020, MNRAS, 491, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Małek, K., Buat, V., Roehlly, Y., et al. 2018, A&A, 620, A50 [Google Scholar]
- Man, A. W. S., Greve, T. R., Toft, S., et al. 2016, ApJ, 820, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Martini, P., Dicken, D., & Storchi-Bergmann, T. 2013, ApJ, 766, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Martis, N. S., Marchesini, D. M., Muzzin, A., et al. 2019, ApJ, 882, 65 [NASA ADS] [CrossRef] [Google Scholar]
- McKinnon, R., Torrey, P., Vogelsberger, M., Hayward, C. C., & Marinacci, F. 2017, MNRAS, 468, 1505 [NASA ADS] [CrossRef] [Google Scholar]
- Michałowski, M. J., Hjorth, J., Gall, C., et al. 2019, A&A, 632, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moresco, M., Pozzetti, L., Cimatti, A., et al. 2013, A&A, 558, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muzzin, A., Marchesini, D., Stefanon, M., et al. 2013, ApJ, 777, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Nanni, A., Burgarella, D., Theulé, P., Côté, B., & Hirashita, H. 2020, A&A, 641, A168 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nersesian, A., Xilouris, E. M., Bianchi, S., et al. 2019, A&A, 624, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nevin, R., Blecha, L., Comerford, J., & Greene, J. 2019, ApJ, 872, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Nishida, K. Y., Takeuchi, T. T., Nagata, T., & Asano, R. S. 2022, MNRAS, 514, 2098 [NASA ADS] [CrossRef] [Google Scholar]
- Noll, S., Burgarella, D., Giovannoli, E., et al. 2009, A&A, 507, 1793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Sausalito: University Science Books) [Google Scholar]
- Pantoni, L., Lapi, A., Massardi, M., Goswami, S., & Danese, L. 2019, ApJ, 880, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Pantoni, L., Lapi, A., Massardi, M., et al. 2021, MNRAS, 504, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Park, M., Tacchella, S., Nelson, E. J., et al. 2022, MNRAS, 515, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, W. J., Wang, L., Hurley, P. D., et al. 2018, A&A, 615, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popping, G., Somerville, R. S., & Galametz, M. 2017, MNRAS, 471, 3152 [NASA ADS] [CrossRef] [Google Scholar]
- Priestley, F. D., Chawner, H., Barlow, M. J., et al. 2022, MNRAS, 516, 2314 [NASA ADS] [CrossRef] [Google Scholar]
- Relaño, M., De Looze, I., Saintonge, A., et al. 2022, MNRAS, 515, 5306 [CrossRef] [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2014, A&A, 563, A31 [Google Scholar]
- Richtler, T., Hilker, M., Voggel, K., et al. 2018, A&A, 620, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez Montero, F., Davé, R., Wild, V., Anglés-Alcázar, D., & Narayanan, D. 2019, MNRAS, 490, 2139 [CrossRef] [Google Scholar]
- Rowlands, K., Dunne, L., Maddox, S., et al. 2012, MNRAS, 419, 2545 [NASA ADS] [CrossRef] [Google Scholar]
- Rowlands, K., Dunne, L., Dye, S., et al. 2014, MNRAS, 441, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Rudnick, G., Hodge, J., Walter, F., et al. 2017, ApJ, 849, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Sansom, A. E., Glass, D. H. W., Bendo, G. J., et al. 2019, MNRAS, 482, 4617 [NASA ADS] [CrossRef] [Google Scholar]
- Santini, P., Maiolino, R., Magnelli, B., et al. 2014, A&A, 562, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sargent, M. T., Daddi, E., Béthermin, M., et al. 2014, ApJ, 793, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, M. T., Daddi, E., Bournaud, F., et al. 2015, ApJ, 806, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Scarlata, C., Carollo, C. M., Lilly, S., et al. 2007, ApJS, 172, 406 [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, R., Valiante, R., Ventura, P., et al. 2014, MNRAS, 442, 1440 [NASA ADS] [CrossRef] [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, C., Elbaz, D., Pannella, M., et al. 2018, A&A, 609, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N., Sheth, K., Aussel, H., et al. 2016, ApJ, 820, 83 [Google Scholar]
- Scoville, N., Lee, N., Vanden Bout, P., et al. 2017, ApJ, 837, 150 [Google Scholar]
- Shirley, R., Roehlly, Y., Hurley, P. D., et al. 2019, MNRAS, 490, 634 [Google Scholar]
- Shivaei, I., Popping, G., Rieke, G., et al. 2022, ApJ, 928, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Siudek, M., Małek, K., Pollo, A., et al. 2018, A&A, 617, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Slavin, J. D., Dwek, E., & Jones, A. P. 2015, ApJ, 803, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Smercina, A., Smith, J. D. T., Dale, D. A., et al. 2018, ApJ, 855, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. J. B., Jarvis, M. J., Hardcastle, M. J., et al. 2014, MNRAS, 445, 2232 [Google Scholar]
- Sohn, J., Geller, M. J., Zahid, H. J., & Fabricant, D. G. 2019, ApJ, 872, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [Google Scholar]
- Strandet, M. L., Weiss, A., De Breuck, C., et al. 2017, ApJ, 842, L15 [Google Scholar]
- Suess, K. A., Leja, J., Johnson, B. D., et al. 2022, ApJ, 935, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, Q., Daddi, E., Magdis, G., et al. 2014, A&A, 569, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tasca, L. A. M., Kneib, J. P., Iovino, A., et al. 2009, A&A, 503, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toft, S., van Dokkum, P., Franx, M., et al. 2007, ApJ, 671, 285 [CrossRef] [Google Scholar]
- Tojeiro, R., Masters, K. L., Richards, J., et al. 2013, MNRAS, 432, 359 [Google Scholar]
- Triani, D. P., Sinha, M., Croton, D. J., Pacifici, C., & Dwek, E. 2020, MNRAS, 493, 2490 [NASA ADS] [CrossRef] [Google Scholar]
- Triani, D. P., Sinha, M., Croton, D. J., Dwek, E., & Pacifici, C. 2021, MNRAS, 503, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Utsumi, Y., Geller, M. J., Zahid, H. J., et al. 2020, ApJ, 900, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Valiante, R., Schneider, R., Salvadori, S., & Bianchi, S. 2011, MNRAS, 416, 1916 [Google Scholar]
- van Dokkum, P. G., Whitaker, K. E., Brammer, G., et al. 2010, ApJ, 709, 1018 [Google Scholar]
- Ventura, P., Dell’Agli, F., Lugaro, M., et al. 2020, A&A, 641, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vergani, D., Garilli, B., Polletta, M., et al. 2018, A&A, 620, A193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vijayan, A. P., Clay, S. J., Thomas, P. A., et al. 2019, MNRAS, 489, 4072 [NASA ADS] [CrossRef] [Google Scholar]
- Vílchez, J. M., Relaño, M., Kennicutt, R., et al. 2019, MNRAS, 483, 4968 [CrossRef] [Google Scholar]
- Vogelsberger, M., McKinnon, R., O’Neil, S., et al. 2019, MNRAS, 487, 4870 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Williams, C. C., Mowla, L., et al. 2021a, Nature, 597, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Narayanan, D., Williams, C. C., et al. 2021b, ApJ, 922, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, C. C., Spilker, J. S., Whitaker, K. E., et al. 2021, ApJ, 908, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Woodrum, C., Williams, C. C., Rieke, M., et al. 2022, ApJ, 940, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, P.-F., van der Wel, A., Bezanson, R., et al. 2018, ApJ, 868, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, P.-F., van der Wel, A., Bezanson, R., et al. 2020, ApJ, 888, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, P.-F., Nelson, D., van der Wel, A., et al. 2021, AJ, 162, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Zahid, H. J., Geller, M. J., Kewley, L. J., et al. 2013, ApJ, 771, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Zahid, H. J., Baeza Hochmuth, N., Geller, M. J., et al. 2016, ApJ, 831, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J., Li, Y., Leja, J., et al. 2023, ApJ, 952, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, Y., Dave, R., Wild, V., & Montero, F. R. 2022, MNRAS, 513, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, S., Li, C., Hao, C.-N., et al. 2021, ApJ, 916, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Zhukovska, S., Gail, H. P., & Trieloff, M. 2008, A&A, 479, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhukovska, S., Dobbs, C., Jenkins, E. B., & Klessen, R. S. 2016, ApJ, 831, 147 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Gas-phase metallicities
We derive the gas phase metallicity of hCOSMOS galaxies following the method described in Zahid et al. (2013) and Sohn et al. (2019), which is based on measuring the emission line strengths. We first derive the model continuum of each galaxy based on the stellar population synthesis model by Bruzual & Charlot (2003). Then, we fit each emission line with a Gaussian from the continuum subtracted spectrum. The uncertainties in the line flux measurements were also computed using standard error propagation from the uncertainties in the spectrum. We then applied a dust extinction correction based on the Cardelli et al. (1989) extinction curve. We applied the Kobulnicky & Kewley (2004) technique, which determines the gas metallicities (i.e. 12 + log (O/H)) of galaxies. This technique uses R23 and O32 indices that are defined as
and
Here, we use the line fluxes of each emission line. We note that [OII]λ3727 indicates the sum [OII]λ3726 + λ3729 doublet, which is hardly resolved in Hectospec spectra. We also use 1.33 times [OIII]λ5007 as the sum of [OIII] line flux based on the assumption that the flux ratio [OIII]λ4959/[OIII]λ5007 is equal to 3 (Osterbrock & Ferland 2006). We finally determine the metallicity based on the relative positions of R23 and O23 indices with respect to model grids with an intrinsic measurement uncertainty of ∼0.1 dex (Kobulnicky & Kewley 2004). All of our sources lack Hα while vast majority of sources (> 85%) have Hβ emission strength of ∼0.2 − 0.3 dex lower than the median of star-forming hCOSMOS galaxies, confirming their quiescent nature.
Appendix B: SED fitting systematics
In order to evaluate our SED modelling method and explore the eventual biases, we produce the simulated dataset and fit it using the exact same method that we applied to our observed galaxies. The purpose of using simulations is to analyse eventual observational effects on our SED fitting results. To achieve this goal, we use the functionality available in CIGALE to create mock catalogue of objects for each galaxy for which the physical parameters are known. We build the simulated sample by adopting the best-fit SED model for each fitted QG from our sample. As a result, the procedure gives one artificial model per galaxy. The best SED model per object (with known parameters) is then integrated through the same set of filters as in our observational sample. We then perturb the input fluxes from the best SEDs by adding a randomised noise, following a Gaussian distribution with σ corresponding to the observed uncertainty per each photometric band. The SED fitting of galaxies from the mock catalogue is further performed with the exact same choice of physical models and their input parameters as for our real data. This procedure allows the results of the Bayesian analysis provided by CIGALE on the mock ‘true’ catalogue to be compared to the input parameters used to build it.
As can be seen in Fig. B.1, our procedure shows a good agreement between the input and output values, which ensures a good constrain on the critical parameters such as the stellar population age and tquench. In both cases the overall trend follows the one-to-one relation, with r2 (a measure of how close the data points are to the fitted true line) being 0.87 and 0.93, respectively. As expected, slightly larger dispersion is observed for the galaxies with lowest stellar ages and tquench. We further conduct the similar test to check if there is any significant trend against the Dn4000. The difference (on a log-scale) between the input physical properties and the best output parameters of the simulated catalogue is further shown in Fig. B.2. All values presented on y-axes are plotted as a function of input Dn4000, as we want to ensure that our fitting methods does not produce significant systematics as a function of independently measured strength of the 4000 Å break. We consider that a strong constraint on a given parameter is obtained if difference between the input and output approaches zero, followed by the small average dispersion. We find that for the main physical quantities analysed in this work, the dispersion of recovered values (input-output) follows the normal distribution, with more than 80% of sources lying within the mean offset of ±0.25. As expected, slightly dispersed distribution is observed for tquench. Nevertheless, despite the known difficulty in fully constraining this parameter (see e.g. Ciesla et al. 2021), the overall trend with Dn4000 is flat, which assures that our choice of SFH is well suited for most of our QGs. Therefore, we conclude that our SED fitting procedure properly recovers the true physical properties of our objects and does not introduce any significant systematics.
 |
Fig. B.1. Results of the Bayesian-like mock analysis with CIGALE. The ‘true’ values (labelled ‘IN’) were used to build the mock catalogue and are shown on the x-axes, while the SED fitting outputs (labelled ‘OUT’) are shown on the y-axes. The one-to-one relation is indicated as a solid red line. This exercise ensures that the stellar ages and times since quenching obtained from our SED fitting method are well constrained with the data at hand. |
 |
Fig. B.2. Results of our mock analysis where we quantify the difference between the input parameters used to build the simulated catalogue in CIGALE and results of the SED fitting of this mock catalogue. The offset between the simulated and ‘observed’ physical parameters with CIGALE is expressed on the y-axis in log scale. From top to bottom: Stellar mass, dust mass, and time since quenching modelled with use of a flexible SFH. The offset between the ‘true’ and ‘recovered’ values is evaluated as a function of input Dn4000 from simulated catalogues. We consider that a good constraint on a given parameter is obtained if the difference between the input and output approaches zero, which is indicated by the solid blue lines. The trends following the binned means are displayed with red circles with corresponding 1σ errors, while dotted red lines represent a 0.25 dex offset from zero. Our analysis shows a good overall agreement between the input and output values, even in simulated galaxies with higher Dn4000. |
Appendix C: Testing the different selections of QGs
As demonstrated by many studies investigating QGs, all samples that meet the certain QG criteria produce some level of contamination from star-forming interlopers (see e.g. Moresco et al. 2013; Siudek et al. 2018; Leja et al. 2019; Bisigello et al. 2020; Zhang et al. 2023). Here we test up to which level our results may depend on the method used for selecting the dusty QGs. To accomplish this, we applied some additional, commonly used definitions of quiescence to the main sample of 545 QGs analysed in this work. Namely, we consider QG selection based on UVJ rest-frame colours (e.g. Muzzin et al. 2013; Schreiber et al. 2015), and selection based on more conservative spectroscopic criteria (Dn4000 > 1.6; e.g. Brinchmann et al. 2004; Gallazzi et al. 2005). In this way, we quantify the level of potential contaminants, assuming that our alternative selection criteria is providing a ‘clean’ sample of QGs. Normally, this is a very conservative assumption, as it is known that no selection can return a pure sample of QGs. For example, for the full hCOSMOS catalogue, Damjanov et al. (2018) used the selection proposed by Muzzin et al. (2013) to separate star-forming galaxies from QGs. They found ∼10% of objects with Dn4000 < 1.5 that would be considered QGs based on UVJ selection. In contrast, for the colour-selected star-forming galaxies, they discover 13% of objects that would be considered QG based on spectroscopic criteria (Dn4000 > 1.5).
Here we perform the similar comparison with the goal to check if selection of dusty QGs introduces significantly larger number of contaminants. For the main UVJ colour selection, we consider Muzzin et al. 2013, who proposed the following criteria to separate star-forming and passively evolving galaxies at 0 < z < 0.6:
We also checked another popular, redshift invariant UVJ selection proposed in Schreiber et al. (2015). It is defined as
In this analysis, we stayed conservative and considered any outlier at the intersection of our main selection (Dn4000 > 1.5) and the alternative one to be a ‘contaminant’. We then compared the resulting distributions of some key physical parameters (specific dust masses, stellar ages, and the offset from the MS) for such selected QG samples to the distributions from our parent sample presented in the main text. Results of this analysis are shown in Table C.1 and Fig. C.1.
 |
Fig. C.1. Comparisons between the different criteria for selecting QGs. Upper panel: Distributions of Mdust/M⋆, ΔMS and stellar age for our parent sample (solid black line) against the samples satisfying additional criteria of quiescence: UVJ selection proposed in Muzzin et al. (2013) (dark red line) and Dn4000 > 1.6 (orange line). Lower panel (left:) Positions of 545 dusty QGs from this work in the UVJ rest-frame colour plane. Regions defined with solid and dashed lines correspond to the criteria indicated in the legend. Coloured circles represent QGs with 1.5 < Dn4000 < 1.6 and can be considered potential contaminants; (right:) Evolution of specific dust mass as a function of M⋆. The meanings of the symbols are the same as in the left panel. Best linear fits are shown for eQGs and sQGs for two different cases: the main selection that includes 545 QGs (dark grey lines) and the selection that fulfils the stricter spectroscopic criterion Dn4000 > 1.6 (salmon coloured lines). |
Cross-section between the parent sample of 545 QGs with other selection criteria of QGs.
Regardless of the criteria, it is evident that the vast majority of our 545 dusty QGs reside in the quiescent population region defined by galaxy rest-frame UVJ colours. The fraction of our dusty QGs that satisfy these additional criteria is 83% for the UVJ selection of Muzzin et al. (2013), and 94% in the case of the UVJ selection proposed by Schreiber et al. (2015). Furthermore, if we imposed a stricter spectroscopic criterion (Dn4000 > 1.6), we would narrow down our parent sample to 420 objects, or 77% of the initial sample. Therefore, the sample ‘purity’ in all three cases is very high, ranging from 77% to 94% (as the fraction of contaminants varies between 6 − 23%; see Table C.1). We thus ensure that the selection of IR-detectable dusty QGs does not produce a significant impact on the sample purity compared to the samples that have no IR-detection. It is worth noting that the selection by UVJ criteria proposed in Schreiber et al. (2015) has recently been applied for sampling the dusty QGs at z ∼ 1.5 in the GOODS-S field (Blánquez-Sesé et al. 2023). Therefore, our parent sample, which almost entirely satisfies that selection, can be used as a benchmark for probing the dust evolution against the stacking samples analysed at higher-z’s.
The upper panel of Fig. C.1 shows that, irrespective of applied definitions of quiescence, specific dust masses, stellar ages, and ΔMS follow the same distribution as our main sample of QGs selected as Dn4000 > 1.5. Strong agreements in dust-related properties among samples selected in different ways ensure that the selection of IR-detectable dusty QGs does not have a significant impact on the sample purity. As expected, removal of these outliers produces a relative decrease in the number of recently quenched objects from the tail the specific dust mass distribution. However, we checked and found that ‘outliers’ have all the characteristics of QGs, no detection of Hα emission lines, and very prominent negative offset from the MS (median of log(ΔMS) = − 0.82). As illustrated in the lower right panel of Fig. C.1, our conclusions regarding morphological impact on the evolution of dust-related parameters are entirely preserved even if we change the selection criteria. Therefore, we conclude that the findings and conclusions in this paper are marginally affected by the definition of quiescence.
All Tables
Cross-section between the parent sample of 545 QGs with other selection criteria of QGs.
All Figures
 |
Fig. 1. Distributions of the physical properties estimated for our candidate QGs from the SED fitting with CIGALE. Clockwise, from the top left to the bottom right: goodness of fit expressed as reduced χ2; galaxy redshift; stellar mass; SFR; dust mass; and the linear offset of the galaxy’s observed SFR from the SFR expected from the modelled MS (ΔMS in log scale) as a function of redshift. To guide the eye, we also plot a dashed red line that marks the value that is four times lower than the MS. |
| In the text | |
 |
Fig. 2. Observed redshift evolution of Mdust/M⋆ in dusty QGs from this work. Individual values are displayed with circles, coloured according to the corresponding Dn4000. Binned medians and associated uncertainties (16th–84th percentile range) are shown with sandy brown circles and lines, respectively. For comparison, with the dashed red line we show the best fit from the stacking analysis of Magdis et al. (2021). The dark grey line and shaded area describe the modelled evolution of ALMA-detected MS galaxies with a functional form of Mdust/M⋆ ∝ k × (1 + z)2.5 (Donevski et al. 2020), while the dashed dark grey line shows the shift of 1 dex of this MS scaling relation. |
| In the text | |
 |
Fig. 3. Evolution with sSFR for Mdust/M⋆ (left) and Mdust/SFR (right). Left panel: binned medians and corresponding 16th–84th percentiles of this sample shown as the black circles and the dark grey shaded area, respectively. Open crosses indicate the subsample of quiescent objects drawn from the Dustpedia archive (Galliano et al. 2021). Filled crosses show the compilation of dusty QGs and post-SB galaxies at z < 0.1 detected in H-ATLAS (Dariush et al. 2016). Displayed with salmon-coloured symbols are estimates for the stacked and individual QGs at higher-z’s: stacks are represented with diamonds and pentagons (Gobat et al. 2018; Magdis et al. 2021), while the individual detections are annotated with triangles (Whitaker et al. 2021b). In both panels, the cyan-shaded region illustrates the parameter space where the majority of dusty post-SB galaxies detected with ALMA reside (Li et al. 2019a). Right panel: symbols have the same meaning as in the left panel. Dashed lines roughly track the position of sources within different Tdust, calculated by scaling the strength of the ISRF intensity as derived from CIGALE. |
| In the text | |
 |
Fig. 4. Structural and SED-derived physical properties of QGs from hCOSMOS. Normalised distributions of values for various physical quantities are displayed for two morphological categories: quiescent spirals and ellipticals (sQGs and eQGs; yellow and dark cyan colours, respectively). The first row delineates properties obtained from the Hectospec spectroscopy. The redshift, Dn4000, and gas metallicity (i.e. oxygen abundance) are expressed as 12 + log(O/H). The second row displays some of the main structural properties derived from HST images observed via the F814W filter (Gini index, concentration, and effective radius in kiloparsecs) from the catalogue of Cassata et al. (2007). The third and fourth rows show various physical properties estimated from multi-wavelength SED modelling of our QGs with the code CIGALE. These are, from the upper left to lower right: log(M⋆/M⊙), log(Age/yr), log(tquench/Myr), log(Mdust/M⊙), Tdust, and log(Ldust/L⊙). |
| In the text | |
 |
Fig. 5. Evolution of Mdust/M⋆ as a function of gas-phase metallicities in QGs from this work. The circles are colour-coded by the stellar mass surface densities (expressed on a logarithmic scale). Galaxies are divided into two mass bins: log(M⋆/M⊙) < 11 (left) and log(M⋆/M⊙) > 11 (right). Brown markers and shaded regions represent the binned medians and 16th–84th percentile range of the resulting distribution for morphologically classified sub-samples of dusty QGs: those classified as eQGs (squares) and sQGs (circles). The typical errors in gas-metallicity estimates for solar and super-solar values are displayed with horizontal lines. |
| In the text | |
 |
Fig. 6. Evolution of Mdust/M⋆ as a function of mass-weighted stellar age, colour-coded by the stellar-mass surface density. Brown symbols have the same meaning as in Fig. 5. The dotted line is the best fit (exponentially declining function) to the sQGs. |
| In the text | |
 |
Fig. 7. Evolution of Mdust/M⋆ with M⋆ in observed dusty QGs. Upper panel: evolution of Mdust/M⋆ with M⋆, colour-coded as a function of galaxy size (represented with effective radius, Reff, in kpc). Median values in different stellar mass bins are displayed with brown circles and squares for sQGs and eQGs, respectively. The typical errors are shown as brown crosses. The straight lines are the best linear fits that describe the data for sQGs and eQGs. Line symbols and fitting functions are indicated in the legend, and the shaded regions represent 95% confidence intervals of the fit. Lower panel: evolution of Mdust/M⋆ with M⋆ in sQGs (left) and eQGs (right) as a function of time after quenching (tquench). Coloured lines show the evolution of the specific dust mass (as median values in three stellar mass bins) for different post-quenching intervals. The meaning of the coloured lines is indicated in the legend. |
| In the text | |
 |
Fig. 8. Evolution of Mdust/M⋆ as a function of sSFR (left) and Zgas (right) modelled with the state-of-the-art cosmological simulation SIMBA (Davé et al. 2019, blue lines) and the chemical evolution model of Nanni et al. (2020, light and dark violet lines). In the panels, darker (lighter) curves related to the N20 model are simulations that include (exclude) dust grain growth in the ISM. These simulation runs include different values of ML factors and grain condensation efficiencies, as indicated in the legend. The solid blue line shows the SIMBA model prediction that is the result of the flagship run (100 Mpc h−1 box), which includes ISM dust growth on metals and all feedback variants. In the right panel, along with the median trend for all selected dusty QGs in SIMBA, we also display average tracks for QGs with different δDGR (dashed blue line for δDGR < 1/100 and dotted-dashed blue line for 1/100 < δDGR < 1/2000). Data from this work (contributing to the ∼90% completeness) are displayed as binned 2D histograms, with the colour bar showing the number of observed QGs in each cell. |
| In the text | |
 |
Fig. 9. Different diagnostics of the evolution of specific dust masses in QGs, as simulated with the SIMBA full-volume simulation run. Upper panel: modelled Mdust/M⋆ as a function of Zgas in SIMBA. Circles represent the modelled QGs within the restricted range of dust-to-gas mass ratios (1/20 < δDGR < 1/100). Grey contours show the distribution of all QGs selected in the simulations with the criteria described in Sect. 6.1. The points are colour-coded by δDTM, with circle sizes scaling to fgas. The inset sketch qualitatively describes the behaviour of Mdust/M⋆: up to a certain Zgas it mostly resembles the change in the molecular gas fraction, while at 12 + log(O/H)≳8.9 it reflects the level of dust growth through the gradual increase in δDTM. Lower panel: evolution of Mdust/M⋆ with fgas for the same simulated sources plotted in the upper panel. The dashed blue and orange lines show median trends for two regimes of Zgas, as indicated in the legend. The effect of an increased dust growth in QGs is most pronounced in sources with heavily exhausted gas reservoirs, as indicated by the lower molecular gas fractions (fgas < 1 − 5%). To highlight this effect through the rise in δDTM, we sketch the shaded area between the two tracks and colour-code it to roughly match the colour bar convention from the upper panel. |
| In the text | |
 |
Fig. B.1. Results of the Bayesian-like mock analysis with CIGALE. The ‘true’ values (labelled ‘IN’) were used to build the mock catalogue and are shown on the x-axes, while the SED fitting outputs (labelled ‘OUT’) are shown on the y-axes. The one-to-one relation is indicated as a solid red line. This exercise ensures that the stellar ages and times since quenching obtained from our SED fitting method are well constrained with the data at hand. |
| In the text | |
 |
Fig. B.2. Results of our mock analysis where we quantify the difference between the input parameters used to build the simulated catalogue in CIGALE and results of the SED fitting of this mock catalogue. The offset between the simulated and ‘observed’ physical parameters with CIGALE is expressed on the y-axis in log scale. From top to bottom: Stellar mass, dust mass, and time since quenching modelled with use of a flexible SFH. The offset between the ‘true’ and ‘recovered’ values is evaluated as a function of input Dn4000 from simulated catalogues. We consider that a good constraint on a given parameter is obtained if the difference between the input and output approaches zero, which is indicated by the solid blue lines. The trends following the binned means are displayed with red circles with corresponding 1σ errors, while dotted red lines represent a 0.25 dex offset from zero. Our analysis shows a good overall agreement between the input and output values, even in simulated galaxies with higher Dn4000. |
| In the text | |
 |
Fig. C.1. Comparisons between the different criteria for selecting QGs. Upper panel: Distributions of Mdust/M⋆, ΔMS and stellar age for our parent sample (solid black line) against the samples satisfying additional criteria of quiescence: UVJ selection proposed in Muzzin et al. (2013) (dark red line) and Dn4000 > 1.6 (orange line). Lower panel (left:) Positions of 545 dusty QGs from this work in the UVJ rest-frame colour plane. Regions defined with solid and dashed lines correspond to the criteria indicated in the legend. Coloured circles represent QGs with 1.5 < Dn4000 < 1.6 and can be considered potential contaminants; (right:) Evolution of specific dust mass as a function of M⋆. The meanings of the symbols are the same as in the left panel. Best linear fits are shown for eQGs and sQGs for two different cases: the main selection that includes 545 QGs (dark grey lines) and the selection that fulfils the stricter spectroscopic criterion Dn4000 > 1.6 (salmon coloured lines). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



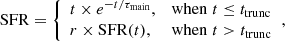
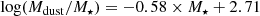
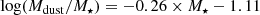
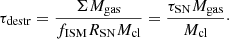
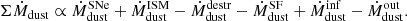
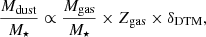
![$$ \begin{aligned} R_{23} = \frac{[\mathrm{OII}]\lambda 3727 + [\mathrm{OIII}]\lambda 4959 + [\mathrm{OIII}]\lambda 5007}{H\beta } \end{aligned} $$](/articles/aa/full_html/2023/10/aa46066-23/aa46066-23-eq16.gif)
![$$ \begin{aligned} O_{32} = \frac{[\mathrm{OIII}]\lambda 4959 + [\mathrm{OIII}]\lambda 5007}{[\mathrm{OII}]\lambda 3727}\cdot \end{aligned} $$](/articles/aa/full_html/2023/10/aa46066-23/aa46066-23-eq17.gif)