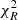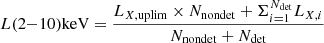| Issue |
A&A
Volume 653, September 2021
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 26 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202040067 | |
| Published online | 03 September 2021 | |
HST grism spectroscopy of z ∼ 3 massive quiescent galaxies
Approaching the metamorphosis
1
CEA, Irfu, DAp, AIM, Université Paris-Saclay, Université de Paris, CNRS, 91191 Gif-sur-Yvette, France
e-mail: chiara.deugenio@cea.fr
2
Instituto de Física, Pontificia Universidad Católica de Valparaíso, Casilla, 4059 Valparaíso, Chile
3
Faculty of Physics, Ludwig-Maximilians-Universität, Scheinerstr. 1, 81679 Munich, Germany
4
University of Trieste, Piazzale Europa, 1, 34127 Trieste, TS, Italy
5
INAF – Osservatorio Astronomico di Brera, Via Brera 28, 20121 Milano, Via Bianchi 46, 23807 Merate, Italy
6
INAF – Osservatorio Astronomico di Trieste, Via Tiepolo 11, 34131 Trieste, Italy
7
Instituto de Astrofísica de Canarias (IAC), 38205 La Laguna, Tenerife, Spain
8
Universidad de La Laguna, Dpto. Astrofísica, 38206 La Laguna, Tenerife, Spain
9
Università di Bologna, Dipartimento di Fisica e Astronomia, Via Gobetti 93/2, 40129 Bologna, Italy
10
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
11
Subaru Telescope, National Astronomical Observatory of Japan, National Institutes of Natural Sciences, 650 North A’ohoku Place, Hilo, HI 96720, USA
12
Department of Astronomical Science, SOKENDAI (The Graduate University for Advanced Studies), 650 North A’ohoku Place, Hilo, HI 96720, USA
Received:
4
December
2020
Accepted:
26
May
2021
Tracing the emergence of the massive quiescent galaxy (QG) population requires the build-up of reliable quenched samples by distinguishing these systems from red, dusty star-forming sources. We present Hubble Space Telescope WFC3/G141 grism spectra of ten quiescent galaxy candidates selected at 2.5 < z < 3.5 in the COSMOS field. Spectroscopic confirmation for the whole sample is obtained within one to three orbits through the detection of strong spectral breaks and Balmer absorption lines. When their spectra are combined with optical to near-infrared photometry, star-forming solutions are formally rejected for the entire sample. Broad spectral indices are consistent with the presence of young A-type stars, which indicates that the last major episode of star formation has taken place no earlier than ∼300–800 Myr prior to observation. This confirms clues from their post-starburst UVJ colors. Marginalising over three different slopes of the dust attenuation curve, we obtain young mass-weighted ages and an average peak star formation rate (SFR) of ∼103 M⊙ yr−1 at zformation ∼ 3.5. Although mid- and far-IR data are too shallow to determine the obscured SFR on a galaxy-by-galaxy basis, the mean stacked emission from 3 GHz data constrains the level of residual-obscured SFR to be globally below 50 M⊙ yr−1, three times below the scatter of the coeval main sequence. Alternatively, the very same radio detection suggests a widespread radio-mode feedback by active galactic nuclei (AGN) four times stronger than in z ∼ 1.8 massive QGs. This is accompanied by a 30% fraction of X-ray luminous AGN with a black hole accretion rate per unit SFR enhanced by a factor of ∼30 with respect to similarly massive QGs at lower redshift. The average compact, high Sérsic index morphologies of the galaxies in this sample, coupled with their young mass-weighted ages, suggest that the mechanisms responsible for the development of a spheroidal component might be concomitant with (or preceding) those causing their quenching.
Key words: galaxies: elliptical and lenticular, cD / galaxies: formation / galaxies: evolution / galaxies: high-redshift / galaxies: stellar content / techniques: spectroscopic
© C. D’Eugenio et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The formation channels that lead to the build-up of the red sequence of massive, quiescent galaxies (QGs) are still to be fully understood. In the present-day Universe, 75% of the total stellar mass budget is locked into spheroids, either elliptical galaxies or bulges in spirals. These are several Gyr old, pressure-supported stellar systems that are unable to host a significant amount of star formation (Renzini 2006). The majority of massive galaxies (log(M⋆/M⊙) > 10.5) in the local Universe appears to be quenched, with QGs outnumbering star-forming galaxies by a factor of 10 at log(M⋆/M⊙) > 11.5 (Baldry et al. 2004). Fossil record studies have established that the most massive galaxies are those in which the oldest stellar populations are found, implying an anti-correlation between their stellar mass and the duration of their main star formation episode (Gallazzi et al. 2005; Thomas et al. 2005; Citro et al. 2016). These results have been reinforced by the first identifications of QGs at increasing redshifts (Dunlop et al. 1996; Franx et al. 2003; Cimatti et al. 2004; Daddi et al. 2005) allowed by near-infrared (NIR) sensitive detectors that sample the rest-frame optical at z ≥ 1.5. These advances were essential to show that the assembly and quenching of massive systems took place at z > 1−1.5, with little evolution thereafter of the high-mass end of their stellar mass function, especially compared to the progressive rise of the low-mass end (Fontana et al. 2004; Cimatti et al. 2006; Arnouts et al. 2007; Drory et al. 2009; Pozzetti et al. 2010; van Dokkum et al. 2014; Gargiulo et al. 2016; Davidzon et al. 2017; Kawinwanichakij et al. 2020). The growth of the lower-mass end of the red sequence can be thought of as the result of the generalised progressive decline in global star formation rate (SFR) density through gas consumption, cluster-related processes, and cosmic starvation affecting the star-forming population mostly at z < 1.5 (e.g., Emsellem et al. 2011; Saracco et al. 2011; Carollo et al. 2013; Madau & Dickinson 2014; Sargent et al. 2014; Schreiber et al. 2015; Wild et al. 2016; Maltby et al. 2018; Matharu et al. 2019; Kawinwanichakij et al. 2020). On the other hand, understanding how massive galaxies quenched in an epoch in which galaxies were generally gas rich and prodigiously star-forming (2 < z < 4, Daddi et al. 2010; Tacconi et al. 2010; Genzel et al. 2010; Madau & Dickinson 2014) is in itself non-trivial.
Historically, the progressive discovery of populations of massive QGs already in place at high-z (Dunlop et al. 1996; Franx et al. 2003; Cimatti et al. 2004; Daddi et al. 2005; Kriek et al. 2009; Gobat et al. 2012; Glazebrook et al. 2017) posed challenges to hierarchical models of structure formation (e.g., Cimatti et al. 2006; Steinhardt et al. 2016). Hydrodynamical simulations and semi-analytical models have struggled to reproduce the comoving number densities of massive, passively evolving galaxies at z > 2–3, falling short by roughly an order of magnitude (Wellons et al. 2015; Nelson et al. 2015; Steinhardt et al. 2016; Davé et al. 2016; Cecchi et al. 2019; Schreiber et al. 2018). In recent years, however, confirmations of quiescent galaxies extended up to z ∼ 4 (Glazebrook et al. 2017; Schreiber et al. 2018; Valentino et al. 2020; Forrest et al. 2020a,b) while cosmological simulations progressively increased in volume, spatial and mass resolution, as well as in improvements of feedback schemes and subgrid physics regulating star formation (Illustris: Vogelsberger et al. 2014a,b; Genel et al. 2014; Nelson et al. 2015; Illustris TNG: Pillepich et al. 2018; Nelson et al. 2019; EAGLE: Schaye et al. 2015; SIMBA: Davé et al. 2019). The most recent estimates of the number density of QGs, either from observational samples or from state-of-the-art cosmological simulations, appear to broadly agree on the number density of quiescent galaxies up to z ∼ 3, but it is unclear whether this holds at z ∼ 4 and if a population of passive objects exists as early as z ∼ 5 in significant numbers. Additionally, the degree to which this agreement is robust against systematics, such as the exact details of sample selection, is not firmly established (Merlin et al. 2019; Valentino et al. 2020).
Despite the major progress accomplished so far in this field, it remains unclear whether there is a dominant process that causes quenching (Man & Belli 2018). The extreme stellar densities of compact quiescent systems at z ∼ 2 (Franx et al. 2003; Daddi et al. 2005; van Dokkum et al. 2008; Newman et al. 2012) suggest that they are remnants of an intense burst of star formation triggered by the rapid collapse of a large amount of gas that occurred at z > 4. This could be resulting, for instance, from starbursts plunging down into quiescence after dissipative gas-rich mergers (Cimatti et al. 2008; Elbaz et al. 2018; Gómez-Guijarro et al. 2018, 2019; Puglisi et al. 2019) or from a more “secular-like” evolution of high-redshift dusty star-forming galaxies that quickly accrete and consume gas through disk instabilities, leaving compact passive remnants (e.g., Dekel et al. 2009; Barro et al. 2013; Toft et al. 2014; Zolotov et al. 2015). Increased consensus among semi-analytic models and hydrodynamical simulations has been reached on ascribing the shut-down of star formation in massive galaxies to active galactic nucleus (AGN) feedback (De Lucia & Blaizot 2007; Henriques et al. 2017; Girelli et al. 2020). Major mergers or violent disk instabilities can compress the gas into massive compact cores and trigger starburst events that rapidly consume the gas of the system (Dekel & Silk 1986; Murray et al. 2005). Quasar activity is ignited by these processes, launching powerful outflows into the circumgalactic medium and depleting the host galaxy from its reservoirs (Sanders et al. 1988; Di Matteo et al. 2005; Hopkins et al. 2006). However, AGN feedback is not the only process that can halt or reduce star formation in high-z galaxies. Cosmological starvation (Feldmann & Mayer 2015) and the development of a stable virial shock in sufficiently massive haloes (Dekel & Birnboim 2006; Cattaneo et al. 2006) could play a role, followed by maintenance processes such as radio-mode feedback from radiatively inefficient accretion onto a supermassive black hole (SMBH; Best et al. 2005; Croton et al. 2006), gravitational heating of the diffuse medium from infalling satellites (Dekel & Birnboim 2006; Khochfar & Ostriker 2008; Johansson et al. 2009, 2012) or morphological quenching (Martig et al. 2009). The detailed study of large, statistically relevant samples of massive quiescent galaxies is crucial to distinguish among these mechanisms. Robust samples of quiescent galaxies are challenging to build up, however: the spectra necessary to reject low-redshift interlopers or star-forming contaminants become increasingly more difficult to obtain at z > 1.4 because it requires either long integrations in 8–10 m class ground-based telescopes or space-based observations. Moreover, the rapid drop in number density of massive quenched objects at z > 1.5 requires large areas covered by deep observations. On a positive note, on the other hand, the boundedness of the age of the Universe can be used to investigate the demographics of the quiescent population across cosmic time as it keeps emerging. As the population becomes younger and younger at increasing redshift, the discerning power of rest-frame optical spectra at mapping the early star formation of massive QGs surpasses the one at low redshift. This is because around z ≳ 2, the Universe starts to be young enough to make stellar age differences of ∼1 Gyr, down to few hundreds Myr, visible through the rapid appearance of Balmer absorption lines in stellar populations of ages < 1 Gyr, when A-type stars enter the turn-off, increasingly dominating the integrated stellar spectra. Relatively large samples of QGs have been assembled up to z ∼ 2.5 in COSMOS and the CANDELS fields exploiting large telescopes (e.g., Bezanson et al. 2013; Belli et al. 2015, 2019; Onodera et al. 2015; Kriek et al. 2016; Stockmann et al. 2020) or the Hubble Space Telescope (HST) in combination with strong lensing (Whitaker et al. 2012, 2013; Newman et al. 2018a). These studies have been tracing the progressive decrease in stellar age of log(M⋆/M⊙) > 11 QGs with look-back time, revealing an increasing spread in stellar age and dust extinction with bulk values of about 1–2 Gyr and AV = 0–1.0 mag at z ∼ 2, respectively. This is apparently happening while keeping high metallicities and with velocity dispersions up to a factor of two higher than local scaling relations (Toft et al. 2012; Onodera et al. 2012; van de Sande et al. 2013; Belli et al. 2015; Kriek et al. 2016; Belli et al. 2017; Estrada-Carpenter et al. 2019, 2020; Stockmann et al. 2020; Tanaka et al. 2019). The progressive appearance of the quenched population can therefore be quantified through the relative fraction of young versus old systems once an age threshold is defined (e.g., age > 1 Gyr, Whitaker et al. 2013). At even higher redshifts, the colour selections generally applied to photometric samples already indicate a substantial migration of QGs towards bluer colours (Whitaker et al. 2011; Muzzin et al. 2013), accompanied by the drop by roughly one order of magnitude of their number densities (Straatman et al. 2014; Davidzon et al. 2017). Spectroscopic follow-ups have the advantage of refining this picture by testing the colours of selected galaxies against photometric errors, star-forming interlopers, or AGN interfering with their spectral energy distribution (SED). Moreover, detailed spectra allow us to potentially break or at least reduce the degeneracy between age, dust extinction, and metallicity if the signal-to-noise ratio and spectral coverage are high enough. Here we present one of the largest samples of spectroscopically confirmed QGs at 2.4 < z < 3.3 obtained with HST dedicated observations. In Sect. 2 we describe the sample selection. In Sect. 3 we give details on the observational strategy and data reduction. In Sect. 4 we present the spectral analysis and the spectroscopic confirmation of our targets. Section 5 presents their formal classification, the effect of adding COSMOS2015 photometry with or without calibration of zero-points, as well as the use of marginalising over multiple attenuation laws. In Sect. 7 we constrain their recent star formation history (SFH) by comparing the relative strength of the Balmer and 4000 Å breaks. In Sect. 8 we investigate the incidence of AGN in our sample. In Sect. 9 we discuss our results in the context of the current literature. Finally, in Sect. 10, we summarise our results and conclusions. We assume a ΛCDM cosmology with H0 = 70 km s−1 Mpc−1, ΩM = 0.27, ΩΛ = 0.73, and a Salpeter (1955) initial mass function (IMF), unless otherwise specified. Magnitudes are given in the AB photometric system.
2. Sample selection
Since the expected number density of high-z massive quiescent galaxies is low, large fields with deep photometric coverage are required to identify these systems and reliably assess their SEDs. For this reason, we exploited the 2 deg2 COSMOS field. Sources with Ktot < 22.5 were extracted from the catalogue of McCracken et al. (2010), limiting the selection to those satisfying the observed-frame BzK colour criterion for passive systems (Daddi et al. 2004). Targets formally classified as star-forming BzK (sBzK) with a signal-to-noise ratio S/N < 5 in the B and z bands were retained since these photometric candidates are degenerate with quiescent galaxies becoming fainter in these bands with increasing redshift and decreasing mass. Photometric redshifts specifically calibrated for high-z QGs were derived with EAZY (Brammer et al. 2008) as in Onodera et al. (2012) and Strazzullo et al. (2015). This calibration was based on the sample of 34 spectroscopically confirmed passive galaxies at 1.3 < zspec < 2.1 observed with VLT/VIMOS that later appeared in Gobat et al. (2017) and the sample of 18 passive galaxies at 1.4 < zspec < 1.9 of Onodera et al. (2012) observed with Subaru/MOIRCS. The calibrated zphot were used to select galaxies within 2.5 ≤ zphot ≤ 3.5 and to remove objects with UVJ rest-frame colours inconsistent with passive evolution (Pozzetti & Mannucci 2000; Labbé et al. 2005; Williams et al. 2009). SED fitting was performed using FAST (Kriek et al. 2009), allowing for constant and delayed exponentially declining SFHs. Optical dust attenuation was left free to vary up to AV = 5 mag assuming a Calzetti et al. (2000) attenuation law. Fits were repeated by adopting purely quiescent templates only. All passive UVJ candidates whose SED fits to optical-NIR photometry could not reject dusty star-forming solutions at high confidence were further discarded. Contamination from dusty star-forming galaxies was further minimised by removing objects with Spitzer/MIPS 24 μm S/N ≥ 4 detections in the Le Floc’h et al. (2009) catalogue, except for galaxies with high-confidence passive SEDs, which are indicative of mid-infrared (MIR) emission caused by a central dusty AGN torus. This selection provided a total of 174 passive candidates with UVJ-quiescent colours (47 of which were pBzK in the original selection, plus 67 and 60 uncertain sBzK with and without significant MIPS detections, respectively). The maximum required magnitude to obtain HST/G141 spectra with sufficient S/N in order to secure spectroscopic confirmation within one to two orbits was assessed by simulating their grism spectra based on their best-fitting SED templates. This yielded a magnitude cut of HAB < 22, which narrowed the sample down to 23 objects. A total of 10 galaxies were targeted for HST WFC3/IR G141 near-IR observations: 9 randomly drawn galaxies with HAB < 22 (M⋆ > 1.1 × 1011 M⊙) plus 1 robust candidate with HAB = 22.9 (M⋆ = 8 × 1010 M⊙) selected to be the highest-z candidate based on its high-confidence passive SED. More details about the selection are available in Lustig et al. (2021).
3. HST WFC3 F160W imaging and G141 grism spectroscopy
Ground-based observations have already confirmed the existence of quiescent galaxies at z ∼ 4 (Schreiber et al. 2018; Valentino et al. 2020; Forrest et al. 2020a,b). However, in the framework of high-z galaxy evolution, their statistical power is mostly modulated by the time-expensiveness of these campaigns. Moreover, OH sky emission lines and related background notoriously affect the quality of the spectra, sometimes effectively cutting them in correspondence to spectral regions that are crucial to estimate stellar ages. Space-based observations, on the other hand, ensure extended and continuous spectral coverage. The HST WFC3 G141 slitless spectrograph has a spectral coverage from 1.1 to 1.7 μm, reaching maximum transmission at 1.45 μm. This allows access to the rest-frame near-UV/optical and specifically to the Balmer/4000 Å break region up to z ∼ 3.2. The G141 dispersion in the first spectral order is 46.5 Å pixel−1 and R ∼ 130 for unresolved sources and compact objects such as those considered in this paper. For resolved sources, the spectral resolution is determined by their morphology, namely their size along the dispersion axis. For these reasons, HST WFC3 observations of the selected sources include F160W imaging exposures. As this paper focuses mostly on the spectroscopic analysis, we refer to Lustig et al. (2021) for a thorough analysis of their morphology.
3.1. Observing strategy
Observations for program GO 15229 took place from January 11, 2018, to December 2, 2018. Each pointing was observed from one to three orbits according to each target HAB magnitude for a total of 17 orbits (see Table 1). For each target the first orbit was split into a direct F160W exposure (for a total of 984 s) and a grism G141 exposure (for a total of 1498 s) adopting the WFC3-IR-DITHER-LINE-3PT dither pattern. For targets with two orbits, the second orbit was also split in two, with a total exposure of 73 s in F160W and 2496 s in G141, adopting the WFC3-IR-DITHER-BLOB dither pattern. The third orbit for ID 4 was a repetition of the second orbit. The ORIENT was carefully chosen for each target in order to avoid any contamination from neighbouring sources.
Coordinates and orbit details for the targeted galaxies.
3.2. Data reduction
The data reduction of direct F160W and grism G141 exposures was performed by adopting the pipeline grizli, version number 0.7.0-34-g91c94121. After relative alignment of each direct and grism exposures, absolute astrometric registration was performed, providing the pipeline with COSMOS ACS I-band reference catalogues of RA-Dec positions of sources brighter than IAB < 27 mag within a radius of 5′ from each target. Grism sky background subtraction was performed by grizli by means of the Master sky images from Brammer et al. (2015), applying a grey correction using the F160W flat field for the G141 grism. The residuals of the background subtraction are generally of the order of 0.5–1% of the overall background level and are further subtracted, removing a column-average of the sky pixels in the grism exposures. During this phase, the pipeline also runs Astrodrizzle to reject cosmic rays, persistence, and other artifacts. The final drizzling parameters were kept as default. A segmentation map is produced out of the drizzled and combined direct exposure. This is later used to identify and model the spectral trace of each object in each of the grism exposures and to generate model contaminants to be subtracted from the target cutout. The reduced and decontaminated 2D spectra of our targets are presented in Fig. 1 together with their relative F160W cutouts. At this stage, the detector’s FOV is parsed and modelled assuming simple linear continua for all objects in the field (brighter than 25 mag).
 |
Fig. 1. F160W imaging cutouts (left) and 2D G141 spectra (right) at the native WFC3 pixel scale. Redshift increases from top to bottom. The colour scale is in linear scale. |
Grizli then refines the modelling of the brightest objects ([16, 24] mag) with a second-order polynomial fit, fitting spectra directly after subtracting the model for contaminants. At this stage, the background was further fitted for in each of the target beams to account for further residuals. The coefficients of this fit were used to optimally extract any residual background level, which was subtracted from the optimally extracted 1D spectrum of the target. The final scale of the extracted 1D spectra is 0.8 in units of the native dispersion of the G141 spectrograph. Sources brighter than HAB < 22 provide a mean S/N ∼ 15 over 100 Å at 1.6 μm within a relatively low number of one to two orbits per target.
In the following sections we give a detailed description of the method we used to measure the redshifts, as well as the criteria we adopted to establish the nature of our sources. In brief, we first fitted the spectra alone to extract zspec and check the quality of the zphot calibration (Sect. 4). Secondly, we added COSMOS2015 photometry from Laigle et al. (2016) adopting the newly derived zspec for SED fitting. We tested the performance of the combined fits when the zero-point (ZP) corrections were dropped as proposed in Laigle et al. (2016) (Sect. 5.1) and when different dust attenuation laws were used (Sect. 5.2). After the best configuration was identified, we tested the quiescence of individual targets on the basis of their rest-frame UV-to-NIR emission as well as judging from the constraints from the MIR, far-infrared (FIR), and radio emission on dust-obscured star formation (Sect. 6). Lastly, using the combined information from both spectroscopy and photometry, we characterised our targets in terms of mass-weighted age and dust extinction (Sect. 7). We also attempted a direct estimation of the relative light-weighted strength of the Balmer and 4000 Å breaks to determine the post-starburst (PSB) nature of individual sources suggested by their UVJ colours.
4. Spectroscopic confirmation
In this section we describe the procedure we adopted to obtain our grism redshifts. We also compare our results with the calibrated zphot used for the sample selection as well as with zphot available in Muzzin et al. (2013).
4.1. Fitting setup
The optimally extracted spectra were fitted with a custom IDL routine that compares the 1D spectra with composite stellar population templates by χ2-minimisation. These templates were generated on the fly by combining a grid of Bruzual & Charlot (2003, hereafter BC03) simple stellar population (SSP) models with a set of parametric SFHs: a constant, an exponentially declining, a delayed exponentially declining, and a truncated SFH. In the latter, the initial SFR drops to zero after a cutoff time τtr from the onset of star formation. In standard τ-models, however, τ is the e-folding timescale of the SFH. The ratios of t/τ and t/τtr, when above unity, approximate the description of an SSP. Due to an apparent systematic excessive broadening when the imaging cutouts are used to estimate the line spread function, the adopted templates were smoothed to the G141 resolution adopting a FWHM computed by fitting the stacked absorption lines of each galaxy with the IRAF task splot, resulting in relatively good agreement after visual inspection. The variety in SFHs was chosen in order to allow for both passive and dusty star-forming solutions. The routine fits the observed spectra simultaneously with a set of emission lines complexes using standard line ratios (Anders & Fritze-v. Alvensleben 2003) and the SFR–Hα calibration of Kennicutt (1998), where the SFR is taken from the model grid (see Gobat et al. 2012 for further details). In Table 2 we list the grid of parameters we used for the fit. To identify the redshift, the Calzetti et al. (2000) attenuation law was adopted, and the stellar metallicity was left free to vary from 0.4 Z⊙ to 2.5 Z⊙. The age of templates was constrained to be younger than the age of the Universe at a limiting redshift as described in the following: in order to reduce the computational cost, we fitted the observed spectra through a first pass from z = 0.01 to z = 5.0 with a low-resolution redshift grid (dz = 0.01). The probability of a given redshift was computed by comparing the χ2 difference between the best-fitting solution and all other solutions following Avni (1976) to determine the 1σ confidence range. After the most probable peaks were identified, we narrowed down the redshift grid around the 1σ peaks, allowing for an interval of Δz ∼ 0.2 with a step of dz = 0.001. This time, we limited the template library to the age of the Universe corresponding to the lowest redshift among the identified 1σ peaks. This approach led to the redshift probability distributions shown in the upper panels of Fig. 2.
 |
Fig. 2. Upper panels: redshift probability distribution for each target. Solid lines from light to dark red mark 1, 2, and 3σ confidence levels. Green points for ID 7 mark the redshift solutions obtained by combining spectroscopy and photometry as described in Sect. 4.2. Middle panels: optimally extracted 1D grism spectra (black) and best-fitting solutions (red) of our targets. The noise vector is shown in grey in each panel. Bottom panels: corresponding 2D G141 spectra. The colour scale is in linear scale. Galaxies are shown in order of increasing redshift. |
 |
Fig. 2. continued. |
Grid of parameters for the spectral fit and the optical-to-NIR SED modelling.
4.2. Redshift identification
Seven of our sources showed unambiguous redshift solutions at a 3σ confidence already during the low-resolution pass (dz = 0.01). Two show a secondary peak within the same confidence level, and one (ID 7) lacks a marked spectral break. Nine galaxies out of ten are consistent with single solutions at 1σ. Despite the low resolution of the G141 spectrograph, a redshift identification is made possible based on prominent spectral breaks and strong absorption lines for most of the targets (see Fig. 2). For the highest-redshift sources, namely ID 3, 4 and 8, MgI and MgII 2640 – 2850 Å absorption lines also enter the spectrograph, but with a relatively low S/N. Notably, ID 7 lacks absorption features that are as strong as for the remaining sample. This makes the spectrum formally consistent with multiple redshift solutions (0.4 < z < 3.5) within 1σ confidence. We verified the consistency of the lowest redshift solutions with the available COSMOS2015 photometry, placing z > 1.5 as a lower-limit, confirmed by its SED, which rises in flux from J to H band. The final spectroscopic confirmation of this source was obtained by performing the combined fit of its photometry and grism spectrum across the 1 < z < 3.5 redshift range at high resolution (dz = 0.001). This test confirmed the previously derived best-fit solution and reduced the error bars on zspec at all confidence levels. At 1σ, it yields 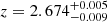 , whereas at 3σ, it yields
, whereas at 3σ, it yields 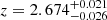 , showing the stability of the best-fit solution compared to the information derived from spectroscopy alone (see Fig. 2). In the remaining analysis, we refer to the former confidence level, as done for the remaining sources.
, showing the stability of the best-fit solution compared to the information derived from spectroscopy alone (see Fig. 2). In the remaining analysis, we refer to the former confidence level, as done for the remaining sources.
ID 10 shows excess flux at 11 870 Å. The secondary peak in the redshift probability distribution is placed at z = 2.3, where the fitting routine attempts to reproduce the two most prominent absorption lines with Hδ and Hγ instead of Hϵ and Hδ that are favoured by the best-fitting template. This redshift is not low enough to explain the excess flux with a [OII]λ3727 emission line. This line would have to be placed at z = 2.18, but it would not match any of the absorption features present in the spectrum. We therefore interpret it as a spurious noise-driven feature.
4.3. Performance of photometric redshifts
We compared the resulting zspec with the calibrated photometric redshifts used for the sample selection to assess the quality of the latter (Fig. 3). The quoted normalised median absolute deviation of the adopted photo-zs2 was σNMAD = 0.025, estimated on the spectroscopically confirmed sample at z ∼ 1.5. This decreased to 0.018 after galaxies with less reliable zspec were excluded. As clarified in Strazzullo et al. (2015), the accuracy is maximum for bright objects (such as those used for spectroscopic confirmation) and decreases for fainter ones (either less massive sources or at higher z). In order to take this into account, in Fig. 3 we show the error bars computed using the zphot accuracy estimated by the authors for faint objects, as a function of the K-band magnitude in McCracken et al. (2010). For objects between K = [20.8, 22], such as in our case, the expected uncertainty is ∼0.040(1 + z). The zphot used for the selection of our sample largely agree with the zspec derived here, with a small systematic underestimation of 0.04%. We included the performance of photometric redshifts from Muzzin et al. (2013) as well. ID 1 and ID 2 are outside the UltraVISTA area and therefore are absent in this latter catalogue. The nominal σNMAD we derived here by comparison with our spectroscopic sample are 0.057 and 0.033 for the two catalogues. We ascribe this difference in redshift accuracy to the different depths and number of photometric bands of the two catalogues. As noted in Strazzullo et al. (2015), already at z ∼ 1.5, the same photo-z calibration method yielded an accuracy similar to that independently provided by Muzzin et al. (2013) (Δz/(1 + z) = 0.015) when the photometry of Muzzin et al. (2013) was used instead of that of McCracken et al. (2010).
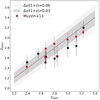 |
Fig. 3. Comparison of calibrated zphots and spectroscopic redshifts. Black squares mark the original calibrated zphots used for the selection. Red squares mark zphots from Muzzin et al. (2013). The solid black line and relative shaded area mark the 1:1 relation and the nominal dispersions between the original calibrated zphots and the newly derived zspec (see text). Redshifts from Muzzin et al. (2013) are shifted horizontally by −0.005 for clarity. |
5. Combining spectroscopy and NUV-NIR photometry
In order to characterise the physical properties of the targets, the HST grism spectroscopy was combined with COSMOS2015 broad-band photometry from CFHT/u* to IRAC/5.8 μm3 (Laigle et al. 2016). A lower limit of 0.05 mag was used for the photometric errors in all the bands. The two data sets were fit separately and were later combined by adding the χ2 matrices of the two fits. This procedure allows determining the solution that best fits both data sets, minimising the effect of residual mismatches in normalisation between the spectrum and the photometric SED. The same range of model parameters as was used for the spectral fitting is used in Fig. 4 except for the redshift grid, which was fixed to the 1σ range around the best-fitting zspec. At this stage, the metallicity was fixed to the solar value according to the normalisation and scatter of the local ETG mass-metallicity relation (Thomas et al. 2010). Recent clues from HST/G102 grism spectra of 1 < z < 1.8 QGs as part of the CLEAR survey seem to support the idea that massive quenched galaxies were enriched to approximately solar metallicity already at z ∼ 3 (Estrada-Carpenter et al. 2019). As we describe in Sect. 6.1, the results we obtained were tested against the choice of template metallicities.
 |
Fig. 4. Photometry from the Laigle et al. (2016) catalogue (black dots). Grey curves show the best-fitting templates smoothed to the G141 resolution. The observed-frame grism spectra are superimposed, rebinned for clarity. |
5.1. Photometric zero-point calibrations
When the mass-weighted ages and dust extinction values obtained from the modelling of the grism data alone are compared with the grism data combined with broad-band photometry (see Sect. 5), we find them to be inconsistent at more than 3σ in most cases. Our SED fits to total fluxes resulted in relatively high reduced χ2 (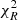 ), as shown in Fig. 5. Specifically, the probability associated with the total χ2 is ∼0.5%, given the total degrees of freedom of the photometric fit of the whole sample. Changing the IMF or leaving the metallicity of templates free did not improve the
), as shown in Fig. 5. Specifically, the probability associated with the total χ2 is ∼0.5%, given the total degrees of freedom of the photometric fit of the whole sample. Changing the IMF or leaving the metallicity of templates free did not improve the 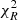 distribution.
distribution.
 |
Fig. 5. Distributions of photometric reduced χ2 before (red dots) and after removing the ZPs re-calibration (black dots). Median values are marked with solid red and black lines. |
As shown in Fig. 6, the means of the distributions of the normalised residuals in each band appear to show systematic shifts, namely B, V, i+, z++ (marginally), J, H, IRAC/3.6 μm, and IRAC/4.5 μm. As noted in Capozzi et al. (2016), the procedure of recalibrating photometric zero-points (ZPs) to optimise photometric redshift retrieval (commonly performed when building photometric catalogues) can affect the results of SED fitting. These tweaks can introduce systematics in several bands because the recalibrations are often based on specific samples at a specific redshift. In the case of COSMOS2015 these were tailored on various samples of spectroscopically confirmed QGs at z < 2.5 (Onodera et al. 2012; Krogager et al. 2014; Stockmann et al. 2020), among a much larger number of star-forming galaxies. In addition to this, the templates used to derive these adjustments can also have a role in introducing systematics. In particular, those used in COSMOS2015 are two BC03 templates with an exponentially declining SFH with a timescale τ = 0.3 Gyr and extinction-free templates as in Ilbert et al. (2013), a set of 31 templates including spiral and elliptical galaxies from Polletta et al. (2007), and 12 BC03 templates of young blue star-forming galaxies.
 |
Fig. 6. Normalised residual distribution of target galaxies in each photometric band. Red and black histograms show residuals adopting recalibrated and original photometric zero-points, respectively. Solid red and black curves show Gaussian fits to these distributions. Their means, standard mean errors, and standard deviations are listed in each panel. |
The offsets that we find in our data suggest that model fluxes tend to overestimate observed fluxes when COSMOS2015 ZP corrections subtract flux from the observed signal and vice versa (see Fig. 7). Dropping ZP corrections reduces most of the wavelength-dependent systematics, producing a better agreement between models and the originally observed fluxes. Figures 6 and 5 show that dropping ZP offsets has the largest effect compared to changing grid parameters at reducing the median of the 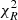 distribution. With this choice, the probability associated with the resulting total χ2 is 9%. A high
distribution. With this choice, the probability associated with the resulting total χ2 is 9%. A high 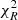 might also indicate systematically low photometric errors. A common practice in this case is to rescale photometric errors to reach a
might also indicate systematically low photometric errors. A common practice in this case is to rescale photometric errors to reach a 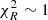 . However, given the behaviour highlighted in Figs. 6 and 5, a rescaling like this appears to be unnecessary. When the rescaled ZP offsets are not used, the median
. However, given the behaviour highlighted in Figs. 6 and 5, a rescaling like this appears to be unnecessary. When the rescaled ZP offsets are not used, the median 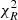 is very close to 1.
is very close to 1.
 |
Fig. 7. Mean residuals of photometric bands as a function of the systematic offset to be applied to correct photometric ZPs. Error bars mark the standard error on the mean shown in Fig. 6. |
Lastly, a high 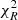 could be caused by broad residual distributions produced, for example, by some outliers in the sample. Visual inspections of imaging cutouts relative to each object in each band did not reveal peculiarities. We therefore conclude that use of the ZP recalibrations derived in Laigle et al. (2016) increase the inconsistencies between our spectroscopic and photometric data. For these reasons, the remaining analysis was performed on the original COSMOS2015 photometry, that is, without making use of any ZP correction.
could be caused by broad residual distributions produced, for example, by some outliers in the sample. Visual inspections of imaging cutouts relative to each object in each band did not reveal peculiarities. We therefore conclude that use of the ZP recalibrations derived in Laigle et al. (2016) increase the inconsistencies between our spectroscopic and photometric data. For these reasons, the remaining analysis was performed on the original COSMOS2015 photometry, that is, without making use of any ZP correction.
5.2. Dust attenuation laws
After the effect of photometric recalibrations was reduced, we explored whether any inconsistency in terms of Δχ2 between the best-fit spectroscopic solution and the combined solution could be ascribed, for example, to an unsuitable attenuation law or to an SFH that was too smooth to simultaneously reproduce the NUV emission from young stellar populations and the NIR emission arising from the bulk of the stellar mass. The use of attenuation laws steeper than Calzetti has been suggested to depend on the SSFRs of galaxies (Kriek & Conroy 2013; Salim et al. 2018). The slope of the curve is generally dependent on the grain size distribution and geometry, with steeper curves associated with differential attenuation according to the age of stellar populations. To test the role of dust attenuation recipes, we included in the fitting library alternative attenuation curves in addition to Calzetti et al. (2000). We adopted the method proposed in Salim et al. (2018), following from Noll et al. (2009), in which the Calzetti curve is multiplied by a power-law term with an exponent δ that sets the slope of the curve itself. Negative δ values imply a steeper slope in Aλ/AV than in the Calzetti law at rest frame λ < 5500 Å. In this formalism, the Calzetti law has δ = 0 by definition, whereas δ = −0.4 is similar to the SMC curve. The curve is further modified by introducing the UV bump (Fitzpatrick & Massa 1986), modelled as a Drude profile Dλ, with fixed central wavelength λ0 = 2187 Å, FWHM = 274 Å from the best-fit results in Noll et al. (2009) in GMASS galaxies at 1.5 < z < 2.5, for which the bump was clearly spectroscopically detected. The amplitude of the bump was linked to δ according to the linear relation found by Kriek & Conroy (2013, see their Eqs. (4) and (5) solving for WHα). Hence the law was constrained mainly by one parameter, its slope, which we let free to vary between 0, −0.4 and −0.7. This latter value was introduced to test the expected behaviour of local quiescent galaxies as shown in Salim et al. (2018). In Fig. 8 we show the distribution of the 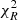 of spectroscopic, photometric, and combined fits (upper panels), as well as the χ2 difference between their respective best-fit solutions obtained with δ = 0 and the best-fit solutions using δ = −0.4 and −0.7 (e.g.,
of spectroscopic, photometric, and combined fits (upper panels), as well as the χ2 difference between their respective best-fit solutions obtained with δ = 0 and the best-fit solutions using δ = −0.4 and −0.7 (e.g., 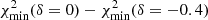 , lower panels). The curve with δ = −0.4 appears to reduce the dispersion of the
, lower panels). The curve with δ = −0.4 appears to reduce the dispersion of the 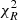 distribution for the combined fits and also shows systematically a smaller χ2 with respect to δ = 0. When we tested the overall goodness of fit in terms of the slope, δ = −0.4 was the best-fit solution preferred by the majority of the targets in Fig. 8. Five galaxies out of nine tend to reject δ = −0.7 at a 5% level (but not at 1%). However, given the overall similar
distribution for the combined fits and also shows systematically a smaller χ2 with respect to δ = 0. When we tested the overall goodness of fit in terms of the slope, δ = −0.4 was the best-fit solution preferred by the majority of the targets in Fig. 8. Five galaxies out of nine tend to reject δ = −0.7 at a 5% level (but not at 1%). However, given the overall similar 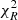 distributions of the combined fits, it was not possible to reject any of the adopted curves consistently for the entire sample. The probabilities associated with the median combined
distributions of the combined fits, it was not possible to reject any of the adopted curves consistently for the entire sample. The probabilities associated with the median combined 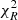 are 89, 76, and 67% for δ = 0, δ = −0.4, and δ = −0.7, respectively. For the remaining analysis, we therefore let δ to vary, marginalising over it when we derived physical parameters.
are 89, 76, and 67% for δ = 0, δ = −0.4, and δ = −0.7, respectively. For the remaining analysis, we therefore let δ to vary, marginalising over it when we derived physical parameters.
 |
Fig. 8. Top: reduced χ2 distributions of the fits to the spectroscopy (left), photometry (middle), and the combined data sets (right panel) as a function of the extinction law. Vertical lines mark the medians of the distributions. Bottom: χ2 difference of the best-fitting solutions obtained using δ = −0.4 and δ = −0.7 with respect to δ = 0. Grey dashed lines mark the levels of ±Δχ2 = 2.3. |
6. Quiescence of individual targets
We tested the quiescence of our galaxies based on the emission from their stellar component. First we tested the information that can be extracted solely from the grism spectra, then we compared with the results obtained by adding the available broad-band NUV-NIR photometry. We further extended the test to longer wavelengths to probe possible obscured star formation.
6.1. Results from the stellar component
We tested the quiescent versus dusty star-forming nature of each galaxy by comparing the goodness-of-fit of the best-fitting constant star-forming (CSF) template with a free dust extinction parameter with that of a solution defined as passive by constraining the best-fitting SFH as follows: t50 ≥ 0.3 Gyr, AV < 0.8 mag, and t/τ ≥ 3, where t50 is the lookback time at which the galaxy formed half of its stellar mass (our mass-weighted ages), t is the lookback time at the onset of star formation, and τ is the timescale of the SFH. This ratio corresponds to a drop in SFR of about a factor of 20 with respect to the initial value for an exponentially declining SFH. To classify a galaxy as quiescent, the probability of a CSF solution relative to the passive solution has to show a probability of < 0.01, as inferred from their χ2 difference. This simple parametrisation is able to discern to a zero-order level the consistency of both the spectrum and the photometry with a heavily dust-attenuated star-forming component, whether it fits better than the passive solution and the confidence level of its consistency. The test was performed fixing the redshift to zspec. We first tested the spectra alone and then combined the photometric information by summing the χ2 matrices of the two fits. In Fig. 9 we show the results of the test. We verified that letting zspec vary within its 1σ confidence range does not affect the probabilities significantly. Letting the metallicity of the templates vary (adopting 0.4, 1, and 2.5 Z⊙) has a similarly negligible effect. When the redshift of the target can be constrained to a sufficient accuracy, the addition of the photometry, with its wide wavelength coverage and overall quality, can help rejecting an SFH when spectroscopy alone is not able to robustly distinguish between the two.
 |
Fig. 9. Probability of constant star-forming solutions relative to that of passive solutions. Blue bars mark the results from spectroscopy alone. Red bars show the probabilities from the combined fit. Bars with relative probabilities lower than 10−6 are not shown. |
The test on ID 7 was performed letting zspec vary within its 3σ confidence level of the combined fit used for its spectroscopic confirmation (see Sect. 4.2). Because prominent (emission or absorption) lines are lacking, the spectrum alone is not able to reject star-forming solutions. The combined fit, however, rejects these solutions (P = 0, Δχ2 = 183, 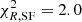 , and
, and 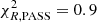 ), even when tighter constraints on the passive solution are adopted (e.g., t/τ > 10 and t > 0.5). The second object showing the highest consistency with a star-forming template is ID 10. Despite the addition of photometry rejecting star-forming solutions, it should be noted that this object lies in a region of the UVJ diagram in which contamination is expected to be more frequent (see Lustig et al. 2021). Moreover, its best-fitting combined mass-weighted age and Av still indicate a very young and dust-reddened stellar content (
), even when tighter constraints on the passive solution are adopted (e.g., t/τ > 10 and t > 0.5). The second object showing the highest consistency with a star-forming template is ID 10. Despite the addition of photometry rejecting star-forming solutions, it should be noted that this object lies in a region of the UVJ diagram in which contamination is expected to be more frequent (see Lustig et al. 2021). Moreover, its best-fitting combined mass-weighted age and Av still indicate a very young and dust-reddened stellar content (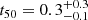 and
and 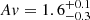 ). We discuss very young sources with MIPS and Chandra detections in the following sections. We anticipate here that we consider ID 10 in particular an AGN host and likely an object close to its quenching phase. Based on the arguments presented above, we conclude with reasonable confidence that all of our galaxies can be classified as passive on the basis of their UV-to-NIR emission.
). We discuss very young sources with MIPS and Chandra detections in the following sections. We anticipate here that we consider ID 10 in particular an AGN host and likely an object close to its quenching phase. Based on the arguments presented above, we conclude with reasonable confidence that all of our galaxies can be classified as passive on the basis of their UV-to-NIR emission.
6.2. SFR constraints from multi-wavelength data sets
The stellar component of our galaxies suggests that they are inconsistent with being highly attenuated star-forming galaxies. SFRs estimates based on near-UV/optical tracers can nonetheless be underestimated in the presence of complex dust geometries (Poggianti & Wu 2000). This is particularly compelling in our case because our galaxies appear to be very recently quenched. We explore here the realistic constraints on the possible presence of obscured star formation or AGN activity by taking advantage of the recently released IR to (sub)millimetre Super-deblended catalogue of Jin et al. (2018, hereafter J18) and of the Chandra COSMOS-Legacy Survey catalogue of Civano et al. (2016). First, we convert the flux densities of our 24 μm detections into the SFRs expected from z ∼ 3 similarly massive MS galaxies and compare them to the available FIR constraints. Afterwards, we convert the very same flux densities into hard X-ray luminosities to determine whether they are consistent with being powered by AGN. Finally, we derive individual 3σ upper limits on the obscured SFR from VLA 3GHz flux densities.
The prior-extraction method used in J18 fits the PSF of MIPS 24 μm, VLA 1.4, and 3 GHz images (Smolčić et al. 2017) at the positions of known KS-selected (plus radio 3 GHz-selected) sources. This procedure improves faint-source identification with respect to blindly extracted catalogues such as in Le Floc’h et al. (2009) by significantly reducing flux errors (by roughly a factor of two) while also improving source deblending. This allows us to investigate in more detail individual mid- or FIR detections that could have been missed by previous catalogues or judged to be of low significance. In particular, we recall here that our sample selection allowed for objects with Spitzer/MIPS 24 μm detections (S/N ≥ 4) from the Le Floc’h et al. (2009) catalogue, or of higher S/N in case of SEDs with no acceptable star-forming solutions suggestive of an AGN-driven MIR flux. We refer to Appendix A, where we report the multi-wavelength cutouts as well as the available reliable detections and upper limits for our sources. SED fitting attempts were performed only for galaxies for which priors were available for source deblending. We caution that the best-fitting AGN components are only intended to display the maximum AGN contribution allowed by the 24 μm detections.
6.2.1. IR
The super-deblended catalogue marks five of our galaxies as detections in the MIPS 24 μm band (ID 1, 5, 6, 7, and 10, see Table 3). None of them is significantly detected in the FIR. Specifically, all of them have an S/NFIR + mm < 5, where S/NFIR + mm is the square root of the quadratic sum of the S/N computed in each band from 100 μm to 1.2 mm. ID 1 formally counts multiple detections in Spitzer/MIPS and Herschel/PACS bands, but it is flagged as unreliable because it lies in a region of COSMOS that is affected by incomplete prior coverage and underestimated flux uncertainties. Visual inspection of its MIR and FIR cutouts did not reveal any detection at the source position (see Appendix A). We thus consider the IR detections of ID 1 as unreliable and exclude it from the following test.
Best fit values and their 1σ uncertainties.
At the mean redshift of this sample, observed-frame 24 μm emission corresponds approximately to 6 μm rest frame. Emission at these wavelengths can arise from a range of processes: star formation (policyclic aromatic hydrocarbons (PAH) emission lines and/or warm dust continuum), a dusty torus obscuring a central AGN, and warm diffuse cirrus clouds heated by old stellar populations or circumstellar dust around asymptotic giant branch (AGB) stars (Draine & Li 2007; Béthermin et al. 2015; Fumagalli et al. 2014). The ∼6″ FWHM of Spitzer/MIPS PSF is larger than the typical optical projected size of our galaxies (< 1″ at 5000 Å rest frame) and prevents us from determining whether the emission is extended or centrally concentrated.
We computed the individual SFRs expected from the remaining four 24 μm detections under the hypothesis that their emission is powered by star formation at the MS level emitting at the observed flux density. We corrected the flux densities by a factor of 1.7, as recommended in J18, and adopted conversions from Magdis et al. (2012). These conversions were driven from template SEDs of MS galaxies whose variation as a function of redshift is mainly driven by the strength of the mean radiation field ⟨U⟩, which maps the sSFR evolution. These templates assume a fraction of dust mass into PAH of qPAH = 2.5% for z > 1.5 MS galaxies.
The results can be found in Table 3, where we also report individual 3σ upper limits for undetected sources. The 24 μm derived SFRs range between ≈300 and 900 M⊙ yr−1. This is the same order of magnitude as for z ∼ 3 log(M⋆/M⊙) ∼ 11 MS galaxies, but somewhat higher and inconsistent with FIR non-detections. These MS galaxies typically show FIR Herschel flux densities of about a few to 10 mJy (Schreiber et al. 2015; Liu et al. 2018; Jin et al. 2018), which would be detected in Herschel/SPIRE. ID 10, 6, and 5 appear to tentatively show SPIRE/250- and 350 μm signal at the source position, as revealed by visual inspection. For the latter two, the contamination by nearby projected FIR-bright sources due to poor spatial resolution is evident. For ID 10, the J18 catalogue formally provides non-detections at 100 and 160 μm and no deblending at longer wavelengths. In postage stamps, the SPIRE/250 μm signal appears to show emission centred on the source position in the middle between two other 24 μm bright sources. J18 attributed the 250- and 350 μm signal to the severe blending of these two sources within the SPIRE large PSF, larger than the distance of these sources from our target (≈10″). For the sources that remain individually undetected at 24 μm, the 3σ upper limits are too shallow to reject milder (but substantial) SFRs. Stacking the remaining sample at 24 μm results in 0.036 ± 0.018 mJy, which translates into a shallow upper limit of < 200 M⊙ yr−1. We caution that the available 3σ depth of the super-deblended data from Spitzer/MIPS, Herschel/SPIRE, and Herschel/PACS in COSMOS is not sufficient to securely reject sub-MS levels of obscured star formation on a galaxy-by-galaxy basis.
6.2.2. X-rays
ID 10, ID 6, and ID 7 have counterparts in the hard X-ray domain with rest-frame luminosities of the order of log(LX, 2−10 keV[erg s−1]) ∼ 43.7, 44.3, and 44.3 respectively, assuming a photon index Γ = 1.4 (e.g., Gilli et al. 2007). We tested whether their 24 μm emission is consistent with being powered by an accreting black hole by converting the observed-frame 24 μm flux densities into unobscured rest-frame X-ray (2–10 keV) luminosities, adopting the relation of Fiore et al. (2009, see their Eq. (1)). This relation assumes that the 2–10 keV luminosity, computed directly from the observed fluxes without any correction for intervening absorption, can be considered representative of the intrinsic X-ray luminosity. The relation has a scatter of 0.2 dex and outliers in the case of significant X-ray absorption. The expected L(2−10 keV)24 μm of these three sources agree with the observed ones within the uncertainties (see Table 3). Although we cannot reject the scenario in which some level of star formation would contribute to the rest-frame 6 μm emission, we therefore conclude that our data are fully explained by an AGN that is obscured by a dusty absorber.
Lastly, ID 5 shows a 0.1 mJy 24 μm detection at 10σ significance that is not matched by an X-ray detection. Its spectrum and photometry both indicate a passive nature, therefore we tend to favour the hypothesis according to which strong obscuration might be playing a role in hiding X-ray photons from the central engine.
6.2.3. Radio
We derived individual 3σ upper limits on the obscured SFR from the super-deblended VLA 3 GHz flux densities using the FIR-radio correlation of Delvecchio et al. (2021), assuming that radio emission is given by star formation alone. One galaxy is detected at 3GHz at 19σ (ID 1). The unphysically high SFR estimated for it (∼104 M⊙ yr−1, see Table 3) implies that the origin of its radio emission is to be ascribed to AGN radio jets. Otherwise, the inferred upper limits result in < 120–190 M⊙ yr−1, which does not conclusively rule out sub-MS levels of star formation on a galaxy-by-galaxy basis. Finally, as derived in D’Eugenio et al. (2020), the peak flux density of S3 GHz = 2.72 ± 0.93 μJy obtained by mean-stacking 3 GHz-undetected sources translates into an upper limit on the global obscured SFR of ∼50–60 M⊙ yr−1. This level of star formation is a factor of 5–6 lower than the coeval MS.
In summary, the average obscured SFR of our sample has been constrained to be below ∼50–60 M⊙ yr−1 by a mean-stack detection at 3 GHz. However, individual 3 GHz radio upper limits to the obscured SFR are < 120–190 M⊙ yr−1, which is not sufficient to reject, on a galaxy-by-galaxy basis, star formation at 1σ below the estimated value for the MS at z ∼ 2.8 corresponding to our stellar masses. Our sample contains four secure MIPS 24 μm detections (f24 μm ∼ 0.1–0.2 mJy) with no FIR counterparts, also considering the shallow upper limits at these redshifts. Three of these detections are consistent with being AGN-powered judging from their luminous X-ray counterparts. The combined passive stellar emission for the remaining MIPS source suggests that a galaxy like this is a likely obscured AGN host. The lack of individual strong constraints on the residual obscured SFR at these redshifts, combined with very young mass-weighted ages and high dust extinction values for some of our targets, renders the classification on a galaxy-by-galaxy basis somewhat ambiguous. We argue that extended spectral coverage (e.g., covering Hα and [NII]) could be of help on this matter and that conclusive evidence on the nature of these high-z QGs can only be obtained with targeted deep millimetre observations.
7. Age determination
7.1. Spectral fit
Recent works suggest that to estimate age and optical dust extinction, relatively simple parametrisations of the SFH perform similarly as more flexible ones and, all in all, behave in a relatively stable way at high redshift (Belli et al. 2019; Valentino et al. 2020). We conservatively marginalised over the different SFHs adopted here to render the best-fitting values and their uncertainties more robust. Figure 10 shows the resulting t50 and AV extracted from the grism spectra (blue points) compared to those derived including COSMOS2015 photometry (red points). Light to dark shading marks 3, 2, and 1σ level confidence values, obtained following Avni (1976) with two interesting parameters. The degeneracy between t50 and AV appears to be strongly mitigated by the addition of the photometry when the redshift is constrained with sufficient accuracy to the spectroscopic value. The bulk of our targets is consistent with having formed half of their stellar mass relatively recently, systematically having t50 below 1 Gyr. In some cases, such as ID 6 and 10, the best-fitting combination suggests dust enshrouded young stellar populations. Intriguingly, these two galaxies are also detected in X-rays and 24 μm, as discussed in Sects. 6.1 and 6.2, and might be galaxies that just entered into their quiescent phase or have residual star formation below the levels probed our FIR data.
 |
Fig. 10. Mass-weighted ages and dust extinction values for our targets. Blue squares mark the confidence regions (3 to 1 σ going from light to dark points) extracted from the spectra alone. Red points show the solutions of the combined fit. Blue and red stars in each panel mark the best-fit solution from the spectroscopic fit and the combined fit, respectively. The relative probabilities of the extinction laws are shown for each galaxy. As a reference, we report the best-fitting combined solution at fixed extinction law as black and grey dots. Their colour-coding follows that of the aforementioned relative probabilities. |
7.2. Relative strength of spectral breaks
The choice of SFH to infer evolutionary parameters intrinsically carries a degeneracy with the adopted functional form. A more direct approach is to quantify the light-weighted contribution of recent star formation by measuring the relative contribution to the integrated stellar spectrum of short-lived massive stars with respect to long-lived lower-mass stars. Balmer absorption lines reach their maximum strength in A-type stars with a spectral break at 3646 Å. Stars of lower mass and lower effective temperature produce metal absorption lines (CaII H & K, Fe, and Mg) which result in a sharp spectral break at 4000 Å. Moreover, the underlying continuum changes shape with time, progressively losing emission in the NUV-blue spectral range while flattening in the NIR. The different evolutionary rates of the stars producing the lines and their fractional contribution to the optical light at fixed mass enable tracing the evolutionary stage of a galaxy. In Fig. 11 (upper panels) we show the evolution of the spectral break measured through the DB definition (Kriek et al. 2006) and the Dn4000 definition (Balogh et al. 1999), as well as the relative strength (the ratio) between the two (lower left panel). Lighter shaded curves show the variation with increasing duration of star formation. The ratio is shown as a function of age of composite templates built with a short truncated SFH. The ratio is only mildly dependent on dust reddening because the two indices share a similar wavelength range. Moreover, the two indices are fairly robust against low resolution. The ratio varies strongly during the first 1 Gyr or so, reaching its maximum around 0.3–0.5 Gyr. Eventually, it drops below 1 when the light-weighted contribution from A-type stars fades away. Constant star formation instead results in a ratio of ∼1.1 that is rather constant with time. Varying the metallicity of the input templates has the effect of anticipating the transition to DB/Dn4000 > 1. This effect is strongest when supersolar metallicity (2.5Z⊙) is adopted in which case the transition is reached at 0.9 Gyr. We suggest that this ratio could be used to spot PSB galaxies with high dust attenuation along and across the UVJ diagram when high-resolution spectra are unavailable.
 |
Fig. 11. Spectral indices and evolutionary properties derived for our galaxies. Upper left: variation in Balmer and 4000 Å breaks for CSPs as a function of their age using BC03 templates at solar metallicity. Lighter curves mark the evolution for a truncated SFH with increasing duration of star formation. The effect of adopting templates of different metallicity is displayed for the values that produce the largest variation, i.e., 2.5Z⊙ (triangles). Dotted and solid grey curves show the behaviour of a constant SFH for the two breaks, respectively. Upper right: individual values of DB and Dn4000 for our targets. The red track shows their evolution with age and is attenuated by 1 mag. The dashed grey line marks the 1:1 relation. Lower left: variation of the index ratio as a function of age for an SSP-like template. The effect of smoothing templates to the HST resolution is shown by the dashed black curve. The effect of a AV = 1 mag attenuation is instead shown by the red curve. The full transition between a Balmer-dominated and a 4000 Å -dominated spectrum is flagged when DB/Dn4000 = 1 (dashed grey line), which occurs around 1.3 Gyr of passive evolution. Dark grey triangles mark the evolution for 2.5Z⊙ templates. Lower right: best-fit values for the dust attenuation and mass-weighted age from the combined fit. Chandra X-ray, VLA 3GHz, and Spitzer/MIPS 24 μm detections are marked by black crosses and yellow and black hexagons, respectively. |
In Fig. 11 (upper right) we show the two indices computed on our targets. The dashed grey line highlights the transition where the PSB ratio equals 1. The mean error in each side band was divided by the square root of the number of pixels within it. For ID 4, whose rest-frame spectrum does not cover the entire wavelength range required to compute the Dn4000 red sideband, the average flux density was taken as the mean of the best-fitting template in the same range. The error was computed as the mean of the noise spectrum taken on the last ten spectral bins. We flagged this galaxy with a red diamond. The red star marks the values obtained on the average spectrum in D’Eugenio et al. (2020). Despite the large uncertainties driven by the S/N of our spectra, the indices all lie well above the 1:1 relation, thus marking the presence of young stellar populations in all of our targets. This supports the results of the spectral modelling, highlighting that some of the most massive high-z QGs appear to be only recently quenched (Stockmann et al. 2020; Valentino et al. 2020; Forrest et al. 2020b). An overview of the physical parameters derived for our target galaxies can be found in Table 3.
8. Tracing AGN activity
We investigated the incidence and strength of BH activity on newly quiescent galaxies in the framework of SMBH-galaxy coevolution. In particular, we assessed the level of mechanical feedback on our galaxies by studying the rest-frame 1.4 GHz luminosity averaged over the entire sample and the incidence of radiatively efficient accretion by constraining the fraction of X-ray detected galaxies and their rest-frame hard X-ray luminosity.
8.1. Radio
As mentioned, one galaxy (ID 1) is securely detected at 3 GHz. Because of the unphysically high SFR estimated for it (∼104 M⊙ yr−1), we ascribe the origin of its radio emission to AGN radio jets. Stacking the radio-undetected sources, D’Eugenio et al. (2020) obtained a peak flux density of S3 GHz = 2.72 ± 0.93 μJy. This translates into a K-corrected rest-frame luminosity of L(1.4 GHz) = (2.0 ± 0.7)×1023 W Hz−1, which we interpret in this section as arising from low-luminosity AGN activity. Figure 12 shows the observed 3 GHz flux density of our targets, compared to the observed stacked SED of z ∼ 1.8 analogues presented in Gobat et al. (2018, hereafter G18). Under the assumption that z ∼ 2.8 quiescent galaxies share this FIR-to-radio SED similar to that of z ∼ 1.8 analogues, our observed flux density appears to be a factor of 2.7 higher than the best-fit model in G18 rescaled to our redshift and average SFR. The 1.4 GHz luminosity expected from residual star formation according to the FIR-radio correlation is Lmod = 1.64 × 1022 W Hz−1. Our observed L(1.4 GHz) is 12 times higher than Lmod, implying an excess of 1.9 × 1023 W Hz−1. This excess, in turn, is a factor of 3.8 higher than the excess found in z ∼ 1.8 similarly massive QGs (5 × 1022 W Hz−1, G18).
 |
Fig. 12. Radio excess observed in our galaxies compared to the average FIR-to-radio SED of similarly massive QGs at intermediate redshift. Top: observed 3 GHz flux for our sample (red dot) compared to the observed FIR-to-radio SED for ⟨M⋆⟩∼1.1 × 1011 M⊙ galaxies at z ∼ 1.8 in Gobat et al. (2018) (black dots). The best-fitting template of Gobat et al. (2018) is shown as a black curve. The same template, but rescaled to our redshift and average SFR (D’Eugenio et al. 2020), is shown as a red curve. Bottom: observed flux normalised to the respective model at the corresponding wavelength. |
The low statistics implied by our sample size prevents us from making meaningful considerations on the overall duty cycle of AGN activity. It is worth mentioning, however, that the 0.66 duty cycle estimated in G18 from z = 1.4 to z = 2.5 implied a burst duration of 1.2 Gyr, which is 1.6 times longer than our observational window (the cosmic time spanned by our sample is 0.72 Gyr). Together with the ensemble radio detection, this might imply that we are sampling an epoch when low-level AGN activity is almost always on in newly quiescent galaxies, with a stronger radio AGN activity with respect to what is inferred for lower-z massive analogues.
8.2. X-ray
LX can be viewed as a tracer of the typical rate of black hole growth in a given galaxy sample. A recent stacked analysis of quiescent galaxies in COSMOS has constrained the average level of rest-frame hard X-ray emission to be LX = 2 × 1043 erg s−1 (Carraro et al. 2020, hereafter C20)4. While our non-detections are consistent with C20, our mean rest-frame L(2−10)keV obtained as
is higher by a factor of 2–3 at face value (see Fig. 13). The error bar on the average is computed as the error on the weighted mean.
 |
Fig. 13. X-ray luminosity in the 2–10 keV band as a function of stellar mass for quiescent (red squares), star-forming (cyan diamonds), and starburst galaxies (violet circles) at 2.25 < z < 3.50. Adapted from Carraro et al. (2020). |
Assuming the Lusso et al. (2012) bolometric corrections and a MBH = M⋆/500 conversion as in Häring & Rix (2004), we computed Eddington ratios for each target, defined as the bolometric X-ray luminosity (or its 3σ upper limit) divided by the Eddington luminosity expected at the stellar mass of the galaxy. We obtain Eddington ratios of λEDD ∼ 2−11% for detected sources and 3σ upper limits lower than 1% for all the undetected ones. When we repeated the test using 24 μm derived L(2−10)keV, we obtained λEDD that were a factor of 2 higher on average.
This λEDD translate into black hole accretion rates (BHAR)5 that largely agree with C20 at z ∼ 3. Dividing the mean ⟨BHAR⟩ by the average ⟨SFR[OII]⟩ estimated from the 5σ [OII] detection from the average spectrum of nine of our targets (see D’Eugenio et al. 2020), we obtain an increase by a factor of ∼30 with respect to 1.3 < z < 2.25 QGs at the same mass (see Fig. 14), consistent with the lower limit for massive 2.3 < z < 3.5 QGs inferred from the same paper. Our mean LX is marginally consistent with that star-forming galaxies in the same mass and redshift range, whereas the [OII]-derived dereddened SFR lies around ∼60 times below the MS. This translates into ⟨BHAR⟩/⟨SFR⟩ being a factor of ∼60 higher than the high-mass end of the MS at z ∼ 3. We recall that this ratio would be even higher if even part of the oxygen ionisation were powered by AGN activity rather than actual star formation. This supports the idea that while the stellar mass growth of the host galaxy has already ceased, the BH mass growth in high-z QGs takes longer to fade away, as already pointed out in C20, and might have had a role in quenching.
 |
Fig. 14. BHAR (top) and BHAR per unit SFR (bottom) as a function of stellar mass for quiescent galaxies (greyscale points) in COSMOS. Different symbols mark different redshift bins. Main-sequence galaxies in the same redshift range as studied in this work are added in the bottom panel as cyan stars. Error bars on the average BHAR reflect the dispersion of the weighted mean on the rest frame L(2–10 keV) of the sample. The average SFR[OII] was converted into a Chabrier IMF. Adapted from Carraro et al. (2020). |
The stochastic nature of detectable AGN activity implies that it is usually only observed in a small fraction of galaxies at a given time. Aird et al. (2019) reported that high-z massive QGs exhibit enhanced AGN fractions compared to low-z SF galaxies hosting an equivalent SFR, suggesting that AGN activity in QGs might be fuelled and sustained by stellar mass loss rather than the availability of cold gas. Their fraction of highly accreting quiescent galaxies (λsBHAR > 0.1, i.e., at more than 10% the Eddington limit) reaches 2–3% around z ∼ 3. The fraction of normally accreting AGN (λsBHAR > 0.01) reaches 20–30% in the quiescent population with SFRs of about 0.5–1 M⊙ yr−1.
Schreiber et al. (2018) reported 18% of X-ray detections in 3.2 < z < 3.7 massive UVJ-quiescent galaxies, plus an additional 30% in the young-quiescent (lower left) region of the UVJ diagram. Several of their young-quiescent SEDs show similarities with our ID 5 and 6 in terms of SED shape and possibly young age. Olsen et al. (2013) reported a 19%±9% luminous AGN fraction in a mass-complete sample of massive UVJ-selected quiescent galaxies at 1.5 < z < 2.5, with a total low-luminosity AGN fraction up to 70%–100%, which argues in favour of the scenario in which episodic AGN activity maintains a low SFRs in quiescent galaxies. Including a possibly Compton thick source, our sample likely contains a fraction of 40% of luminous AGN. We currently do not know in which direction the incompleteness due to the sample selection will affect the AGN fraction because we focus on high-mass quiescent galaxies while excluding the strongest 24 μm detections. As noted in Aird et al. (2019), stellar mass-loss and AGN feedback tend to be disfavoured mechanisms for causing relatively high accretion rates and high AGN fractions in sub-MS and quiescent galaxies. The former could sustain the accretion onto the central BH by providing a relatively stable supply of low-angular momentum gas, but is expected to result in relatively low accretion rates. Moreover, stellar mass loss is most efficient soon after star formation (2–5 Myr) and declines exponentially afterwards, meaning that its contribution is likely not sufficient to explain the highest λEDD measured for some of our objects (unless non-negligible SF occurs). Instead, AGN feedback assumes that the gas supply, once used by the galaxy to sustain SF, is accreted by the central SMBH. However, even the youngest ages shown by our stellar populations would imply a stability of the radiatively efficient AGN feedback of several hundred Myr, whereas radiatively efficient accretion is expected to be stable on timescales of 0.1 Myr. One other mechanism proposed by Aird et al. (2019) could be the build-up of a compact bulge, which would increase the stellar density of the host galaxy, hence increasing the rate at which the AGN is triggered by infalling gas, as also supported by observations (Barro et al. 2013). Figure 15 shows that our likely AGN hosts are among the most compact ones in the sample, but they also show the lowest Sérsic indices (n = 1.2–2.6), implying that no clear-cut connection between radiative AGN feedback and central stellar density can be established with the present sample. Globally, the 30–40% fraction of AGN that are tentatively associated with young objects (seen also as young quiescent galaxies in Schreiber et al. 2018) might suggest that episodic AGN feedback might be triggered before a completely passive stellar core is settled.
 |
Fig. 15. Comparison of our mass-weighted ages and the morphological parameters derived in Lustig et al. (2021), namely Sérsic index n and effective radius Re at 5000 Å rest frame. |
9. Discussion
We have characterised one of the largest representative samples of ten high-z massive QGs in terms of spectroscopic confirmation and age estimation. We showed that HST observations are able to probe the (H-band) brightest end of the massive QG population providing access to clear spectral breaks in the majority of the objects. These breaks can be used to quantitatively compare the amplitude of the Balmer absorption lines with metal lines, hence quantifying the light-weighted contribution of young versus old stars at fixed stellar mass in early QGs. In other words, with relatively few HST orbits, it is possible to both perform spectroscopic confirmation of QGs up to z ∼ 3.2 and start quantifying the incidence of newly quenched objects within the population.
The particular configuration of spectral breaks characterising our sample (strong DB and weak Dn4000) is due to the presence of luminous A-type stars. These often indicate a relatively recent shutdown of star formation, but they have been also linked to galaxies hosting substantial amounts of obscured star formation that contaminates the rest-frame colours that are commonly used when high-z quiescent galaxies are selected (Poggianti & Wu 2000; Lemaux et al. 2017). The quiescence of our targets was first tested and confirmed through their combined spectral (rest-frame NUV/optical) and photometric (rest-frame UV-to-NIR) emission, rejecting the presence of catastrophic photometric errors or prominent emission lines. They are consistent with very young mass-weighted ages, however, which makes their final interpretation less clear.
Because the upper limits on the obscured SFR placed by the current Spitzer/MIPS and Herschel/PACS and SPIRE data are shallow, we relied on the mean-stacked shallow detection at 3 GHz to constrain the potential obscured SFR to be on average below 50–60 M⊙ yr−1 (D’Eugenio et al. 2020), which is five to six times lower than the coeval MS at most. The individual 24 μm flux densities of three 5–10σ detections in the J18 super-deblended catalogue were converted into hard X-ray luminosities, compared to Chandra COSMOS Legacy X-ray detections, and judged to be consistent with being powered by AGN. A conversion of individual 3 GHz 3σ upper limits into SFRs results in < 120–190 M⊙ yr−1, which is not conclusive to exclude substantial obscured star formation on a galaxy-by-galaxy basis. We also note that the origin of the MIR emission is in principle unclear because it can arise from multiple phenomena such as a dusty AGN torus, star formation, hot circumstellar dust around AGB stars, and/or the presence of diffuse cirrus clouds heated by hot stellar populations (Fumagalli et al. 2014) or a combination thereof. From the broad agreement between the prominent Balmer breaks and the mass-weighted ages of our galaxies, we conclude that they have quenched relatively recently prior to observation. However, dedicated millimetre observations are required for 40% of our objects to conclusively assess the level of residual star formation. These objects might represent examples of rapidly transitioning galaxies that underwent a sharp truncation of their star formation, possibly through AGN feedback.
9.1. Emergence of massive quiescent galaxies at high-z
Despite the overall stability of the spectral fitting mentioned above, we recall that age estimates still rely upon the spectral fitting scheme adopted, on the assumptions made in the choice of template libraries, and ultimately, on the shape of the SFH used. Keeping these caveats in mind, we can start making meaningful statements on the ages of our QGs through relative comparisons of the mass-weighted ages within our sample. The bulk of our targets is consistent with having suppressed their star formation very recently, between 300–800 Myr prior to observation. The median value is 0.5 Gyr with a dispersion of 0.2 Gyr. Two outliers are present, ID 6 and ID 10, showing younger ages than the bulk of the sample, 0.1 and 0.25 Gyr, respectively. Although for ID 10 the DB/Dn4000 ratio appears to be strongest (hence suggesting the highest contribution of A-type stars with respect to the underlying stellar population), the S/N of our spectra prevents us from identifying significant differences among our galaxies. Moreover, the downward trend of the DB/Dn4000 ratio at t50 ≤ 0.1 Gyr precludes the possibility of testing the age inferred from the spectral fit, such as for ID 6. Assuming an exponentially declining SFH and our best-fit t50, our galaxies are consistent with having formed half of their stellar mass around zform ∼ 3.5 at an SFR ∼ 1800–3000 M⊙ yr−1, similarly to what was reported in Valentino et al. (2020), but shifted at a later epoch. We caution, however, that these simple representations of SFHs are unlikely to be representative of the peak SFR if the true SFH were more complex, as in the case of multiple phases in the SFR (Barro et al. 2016) or mergers (which imply a degeneracy with mass assembly, hence in lower SFRs split between the progenitors). Interestingly, the common selection of high-z QGs preferentially selects bright blue UVJ quiescent objects where “dust-poor” PSBs often lie. In some cases, it extends to a bluer region outside the standard quiescent boundaries (either in the UVJ or in the NUVrJ selection) where compact transitioning galaxies are thought to lie along their fast drop in SFR (Belli et al. 2019; Schreiber et al. 2018; Valentino et al. 2020; Forrest et al. 2020a). This implies that high-z quiescent galaxies are selected more or less in the same evolutionary phase, namely after O and B stars exited the turn-off and before the same happens for A-type stars. This appears to be manifesting through similar distributions of (mass-weighted) ages in the highest-z samples (perhaps unsurprisingly, see Fig. 16). This also means that the magnitude cut necessary for spectral acquisition biases the selection of high-z QGs against dusty PSBs or galaxies that transition more slowly into quiescence (Belli et al. 2019). Moreover, considering the cosmic time between z = 2.8 and z = 1.8, the mass-weighted ages inferred for our targets appear to be broadly consistent with passive evolution into old QGs at intermediate redshifts (Whitaker et al. 2013). This is not the case for higher-z massive QGs, confirming that the high-z selection directly probes the continuous injection of new compact quiescent galaxies into the passive population. The enhanced fraction of PSBs (60%–70%, D’Eugenio et al. 2020; Lustig et al. 2021) among photometrically selected log(M⋆/M⊙) ≥ 11 QGs at z ∼ 3 is linked to the progressive migration of the red sequence towards bluer colours with increasing redshift. PSBs represent a increasing fraction of the whole QGs population with redshift (Wild et al. 2016). In particular, because the transition from Balmer to CaII absorption lines is fast compared to the overall lifetime of a galaxy at low redshift (at the epochs spanned in this work, this phase instead naturally represents a much larger fraction of a galaxy lifetime). When the growth of the red sequence is considered, the observed fraction of PSBs in massive QGs remains low < 1–3% from z = 0 to z ∼ 0.5 (Tran et al. 2003) and increases between z ∼ 1−2 to ∼20%–50%, with percentage variations mirroring different selection criteria (Le Borgne et al. 2006; Whitaker et al. 2013; Wild et al. 2016). The mounting fraction of massive QGs with evidence of recent quenching already accounts for half of the population at z ∼ 2, when their number densities start to match (Whitaker et al. 2012). This is further supported by the growth rate of log(M⋆/M⊙) ≥ 10.8 PSBs of less than 1 Gyr at z ∼ 2, which accounts for half that of the whole quiescent population (Belli et al. 2019). The decrease in cosmic time allows us to study the width of the distribution in quenching times of QGs: in the emerging picture, a continuous injection of objects into the quenched population manifests in the fast increase in the number density of young quiescent galaxies starting at z ∼ 1.5−2 (Whitaker et al. 2011, 2013) with a reversal of their relative contribution to the red sequence with respect to old galaxies by z ∼ 3. This trend appears to continue towards higher redshifts, at which relatively old quiescent galaxies appear to be still unobserved (Forrest et al. 2020b; Marsan et al. 2020). The latest spectroscopic constraints at z ∼ 3.5 appear to find quasars or star-forming redshift interlopers among the reddest objects in the passive UVJ region, but the long integrations required limit the number and quality of these spectra (Forrest et al. 2020b). The question of whether PSBs scatter also into the reddest area of the passive UVJ region6 due to photometric errors or intrinsic properties such as dust or metallicity (which can also be read to mean whether the z ∼ 3 population is missing the descendants of any z ∼ 4−5 massive quiescent galaxies) can currently only be addressed with very expensive targeted observations. The enhanced sensitivity of the JWST will enable mapping the full distribution of PSBs in the UVJ diagram to the highest redshifts. Establishing a detailed demographics of z ∼ 3 (or higher) QGs to the faintest magnitudes will help clarify the distribution of dust attenuation in spectroscopically confirmed extremely red objects and in turn provide insights into the global star formation history of high-z QGs.
 |
Fig. 16. Stellar ages as a function of observed redshift of log(M⋆/M⊙) > 10.5 quiescent galaxies. Adapted from Onodera et al. (2015). Here mass-weighted ages from the literature differ from t50 in that they do not specifically refer to the lookback time at which 50% of M⋆ is formed. The four targets selected from Schreiber et al. (2018) correspond to those recently followed up by Esdaile et al. (2021). Solid grey lines show, from thin to thick, the age of simple stellar populations made at a zform from 1.5 to 5. The dotted red line marks the age of the Universe as a function of redshift. |
9.2. Morphology of quiescent galaxies at z ∼ 3
We here use the results obtained by Lustig et al. (2021) on the H-band imaging of our targets to interpret their plausible evolutionary stage considered their ages and morphology. When we exclude our only object with a Sérsic index n = 1.2 (ID5), nine (eight) of our galaxies have n > 2 (2.5), even those objects with an axis ratio of about 0.5–0.6. This indicates that a centrally peaked, bulge-like stellar component is already established in these recently quenched galaxies. Similarly, Almaini et al. (2017) showed that photometrically selected log(M⋆/M⊙) > 10.5 PSBs at 1 < z < 2 consist of compact proto-spheroids, with Sérsic indices consistent with the established passive galaxy population at the same epoch and significantly larger than those of star-forming galaxies. They reported evidence that PSBs are more compact on average than fully passive galaxies at the same epoch. Based on these elements, they argued that for z > 1 PSBs structural transformation preceded (or accompanied) the quenching event, leaving a compact remnant that later grew in size. Although the small number statistics prevents us from finding any significant correlation between morphology (either Re or n) and t50 on a galaxy-by-galaxy basis, the data at our disposal show that our galaxies have median Sérsic indices and axis ratios of 4.5 and 0.73
and 0.73 , respectively. The spectra, on the other hand, are consistent with our sample being very recently quenched. Additionally, as noted in Lustig et al. (2021, see their Fig. 6 and 8), our galaxies have significantly higher Sérsic indices on average with respect to the coeval star-forming population, and Re is about a factor of 3 smaller. Under the assumption that our mass-weighted ages are not significantly underestimated and that PSB features are not driven by minor rejuvenation effects leading to small variations in stellar mass, the young ages retrieved for our galaxies suggest that their average formation epoch is around zformation ∼ 3.5. Under the assumption that typical star-forming galaxies at our zformation ∼ 3.5 follow the extrapolation of the size evolution in van der Wel et al. (2014) and rescaling at half of our stellar mass, our galaxies would still be more compact by a factor of 2. Although the intrinsic scatter of the mass-size relation for late-type galaxies would make the two populations marginally consistent, the evolution of Sérsic indices with redshift for star-forming galaxies indicates the prevalence of exponential profiles (n ∼ 1–1.5) at least in the rest-frame UV (Shibuya et al. 2015). These aspects support the idea that the development of a compact bulge-dominated structure is involved in creating quiescent systems and that this process precedes or at least accompanies SFR suppression. The large uncertainties on our median axis ratio make our sample consistent with both quiescent galaxies at lower redshift and star-forming samples at 2 < z < 3. Photometric samples at lower redshift indicate a general flattening of the massive QG population approaching z ∼ 2 or higher, judging from their rest-frame optical projected axis ratio distributions (e.g., van der Wel et al. 2011). This flattening has been interpreted as an increasing fraction of disk-dominated QGs as opposed to classical triaxial spheroids (60% at z ∼ 2 at log(M⋆/M⊙) ≳ 11.1 Chang et al. 2013a,b). We note, however, that the distinction between bulge-dominated and disk-dominated systems is not clear cut and it is often dependent on the tracer used. Axis ratios, for example, do not fully take a bulge component into account. The Sérsic indices in these works are mostly n > 2–2.5 in the rest-frame optical, which indicates that at least a spheroidal stellar component is already present in massive quiescent galaxies at z ∼ 2. Evidence in this regard is also presented in Belli et al. (2017), Almaini et al. (2017), Stockmann et al. (2020) at z ∼ 2. Despite the small number statistics that affects our sample, our data are inconsistent with the majority of massive quiescent galaxies being ‘pure disks’ at z ∼ 3: the probability associated with finding only one object with n ∼ 1 (ID 5) in a sample of ten galaxies is 1% assuming a 50% fraction of pure disks and assuming that these morphologies are evenly distributed in the passive UVJ diagram. Along the same line, the fraction of pure disks that is consistent at 1σ with our data is lower than 30%. Interestingly, spectroscopically confirmed QGs z ∼ 3–3.5 for which detailed morphology is available mostly show n = 3−4 and with varying q (see Esdaile et al. 2021; Marsan et al. 2015; Saracco et al. 2020), with the exception of Gobat et al. (2012). One possibility could be that the magnitude cut imposed for the spectroscopic confirmation biases spectroscopic samples towards objects with a high Sérsic index. This would reinforce the idea that recently quenched systems generally undergo fast quenching, leaving a bulge-dominated remnant, likely without much dust reddening, in most cases. Another possibility could be that the rest-frame near-UV/optical sampled by HST/F160W at z ∼ 3–3.5 is more centrally peaked than the rest-frame 5000 Å sampled at z ∼ 2. High-resolution NIR imaging at longer wavelengths than those sampled by the present work will help clarify this point. Lastly, for ID 8, Lustig et al. (2021) measured
, respectively. The spectra, on the other hand, are consistent with our sample being very recently quenched. Additionally, as noted in Lustig et al. (2021, see their Fig. 6 and 8), our galaxies have significantly higher Sérsic indices on average with respect to the coeval star-forming population, and Re is about a factor of 3 smaller. Under the assumption that our mass-weighted ages are not significantly underestimated and that PSB features are not driven by minor rejuvenation effects leading to small variations in stellar mass, the young ages retrieved for our galaxies suggest that their average formation epoch is around zformation ∼ 3.5. Under the assumption that typical star-forming galaxies at our zformation ∼ 3.5 follow the extrapolation of the size evolution in van der Wel et al. (2014) and rescaling at half of our stellar mass, our galaxies would still be more compact by a factor of 2. Although the intrinsic scatter of the mass-size relation for late-type galaxies would make the two populations marginally consistent, the evolution of Sérsic indices with redshift for star-forming galaxies indicates the prevalence of exponential profiles (n ∼ 1–1.5) at least in the rest-frame UV (Shibuya et al. 2015). These aspects support the idea that the development of a compact bulge-dominated structure is involved in creating quiescent systems and that this process precedes or at least accompanies SFR suppression. The large uncertainties on our median axis ratio make our sample consistent with both quiescent galaxies at lower redshift and star-forming samples at 2 < z < 3. Photometric samples at lower redshift indicate a general flattening of the massive QG population approaching z ∼ 2 or higher, judging from their rest-frame optical projected axis ratio distributions (e.g., van der Wel et al. 2011). This flattening has been interpreted as an increasing fraction of disk-dominated QGs as opposed to classical triaxial spheroids (60% at z ∼ 2 at log(M⋆/M⊙) ≳ 11.1 Chang et al. 2013a,b). We note, however, that the distinction between bulge-dominated and disk-dominated systems is not clear cut and it is often dependent on the tracer used. Axis ratios, for example, do not fully take a bulge component into account. The Sérsic indices in these works are mostly n > 2–2.5 in the rest-frame optical, which indicates that at least a spheroidal stellar component is already present in massive quiescent galaxies at z ∼ 2. Evidence in this regard is also presented in Belli et al. (2017), Almaini et al. (2017), Stockmann et al. (2020) at z ∼ 2. Despite the small number statistics that affects our sample, our data are inconsistent with the majority of massive quiescent galaxies being ‘pure disks’ at z ∼ 3: the probability associated with finding only one object with n ∼ 1 (ID 5) in a sample of ten galaxies is 1% assuming a 50% fraction of pure disks and assuming that these morphologies are evenly distributed in the passive UVJ diagram. Along the same line, the fraction of pure disks that is consistent at 1σ with our data is lower than 30%. Interestingly, spectroscopically confirmed QGs z ∼ 3–3.5 for which detailed morphology is available mostly show n = 3−4 and with varying q (see Esdaile et al. 2021; Marsan et al. 2015; Saracco et al. 2020), with the exception of Gobat et al. (2012). One possibility could be that the magnitude cut imposed for the spectroscopic confirmation biases spectroscopic samples towards objects with a high Sérsic index. This would reinforce the idea that recently quenched systems generally undergo fast quenching, leaving a bulge-dominated remnant, likely without much dust reddening, in most cases. Another possibility could be that the rest-frame near-UV/optical sampled by HST/F160W at z ∼ 3–3.5 is more centrally peaked than the rest-frame 5000 Å sampled at z ∼ 2. High-resolution NIR imaging at longer wavelengths than those sampled by the present work will help clarify this point. Lastly, for ID 8, Lustig et al. (2021) measured  and
and 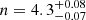 . These values could be interpreted as due to a strong bar in a fast-rotating compact S0 galaxy lacking an extended and bright outer disk, or alternatively, due to a compact spheroid surrounded by a lower-mass edge-on disk. On a more general note, the question of whether recently quenched galaxies at high-z are compact, bulge-dominated objects with residual rotational support is very interesting (Belli et al. 2017; Newman et al. 2018b). It appears unlikely that high-z quiescent galaxies closely resemble low-z slow rotators because the cosmic time interval for minor mergers to fully cancel any rotational component is shorter. However, the assessment of any rotational support is currently not feasible with the data at our disposal.
. These values could be interpreted as due to a strong bar in a fast-rotating compact S0 galaxy lacking an extended and bright outer disk, or alternatively, due to a compact spheroid surrounded by a lower-mass edge-on disk. On a more general note, the question of whether recently quenched galaxies at high-z are compact, bulge-dominated objects with residual rotational support is very interesting (Belli et al. 2017; Newman et al. 2018b). It appears unlikely that high-z quiescent galaxies closely resemble low-z slow rotators because the cosmic time interval for minor mergers to fully cancel any rotational component is shorter. However, the assessment of any rotational support is currently not feasible with the data at our disposal.
10. Summary and conclusions
We have obtained HST WFC3/G141 grism spectra for one of the first representative samples of ten log(M⋆/M⊙) > 10.8 quiescent galaxies at high redshift (2.4 < z < 3.2). HST observations efficiently provided us with the largest sample of QGs with a full continuous coverage in the Balmer/4000 Å spectral region at these redshifts. This allowed us to perform spectroscopic confirmation of QGs up to z ∼ 3.2, and based on widespread prominent Balmer breaks, we were able to start quantifying the incidence of newly quenched objects within the massive quenched population against contamination by lower-redshift interlopers. The quiescence of our targets was tested by means of the combined information of our newly acquired rest-frame NUV/optical spectra and COSMOS2015 UV-to-NIR photometry. In addition, we also considered MIR, FIR, and radio detections from recently released super-deblended photometry (Jin et al. 2018). Our main conclusions are summarised below.
-
Successful spectroscopic confirmation was achieved for the full sample, confirming the quality of the original photometric selection.
-
The joint analysis of our newly acquired rest-frame NUV/optical spectra and COSMOS2015 broad-band UV-to-NIR photometry confirms the quiescent nature of all our targets.
-
Although IR-based constraints on the obscured SFRs of our individual targets are weak with the available data (< 120–190 M⊙ yr−1), the quiescent nature inferred from grism spectra and optical/NIR SEDs is globally supported from the 3GHz stack of the sample, yielding an obscured SFR < 50 M⊙ yr−1 (D’Eugenio et al. 2020).
-
Photometric zero-point recalibrations proposed in Laigle et al. (2016) appear to be disfavoured by our data. These corrections were derived on a set of spectroscopically confirmed quiescent among a much larger number of star-forming galaxies at intermediate redshifts and might not be necessary to extract the SEDs of QGs at high-z.
-
An attenuation curve with slope δ = −0.4, which is steeper than in Calzetti, tends to reduce the median and the dispersion of the
 distribution for the photometric fits. It also shows lower χ2 in general. Nonetheless, our data do not allow us to securely distinguish among the different slopes that were adopted.
distribution for the photometric fits. It also shows lower χ2 in general. Nonetheless, our data do not allow us to securely distinguish among the different slopes that were adopted. -
Marginalising the spectrophotometric fit over different attenuation curves and SFHs, we inferred the typical mass-weighted ages our objects. They range from 300–800 Myr, which indicates a recent rapid suppression of their SFR. Their global strength was quantified and compared to that of the 4000 Å break by means of the DB/Dn4000 ratio, which is systematically higher than 1. This spectroscopically confirms on a galaxy-by-galaxy basis the PSB nature of massive bright QGs, which was pointed out before by means of stacking (D’Eugenio et al. 2020) and by individual high-resolution spectra (Forrest et al. 2020b). More observational efforts are required to explore to which extent strong Balmer absorption lines are spread among objects with a lower mass-to-light ratio.
-
When we interpret our MIR and X-ray individual detections and the radio-stack shallow detection as a signature of AGN activity, our results are consistent with a widespread radio AGN activity that is a factor of 4 stronger than in similarly massive QGs at intermediate redshifts, and a 30–40% incidence of luminous AGN in which the BH mass growth is substantially enhanced with respect to z ∼ 2 quiescent analogues (×30) and to coeval star-forming galaxies at the same stellar mass (×60). This agrees with the recent results of Carraro et al. (2020) for the stacked emission of photometrically selected populations of QGs at 2.25 < z < 3.50.
-
Our galaxies are globally characterised by a bulge-dominated, compact morphology (Lustig et al. 2021). Although we found no clear trend between mass-weighted ages and Re or Sérsic indices in the sample, the young ages yielded by their grism spectra and broad-band photometry suggest that structural transformation may precede or be concomitant with quenching in similarly selected high-z galaxies.
The fast evolutionary phase probed by the magnitude-limited colour selection seems the one in which the majority of z > 2.5 QGs are caught, systematically selecting newly quenched (quenching) objects that enter the quiescent population. We expect the number density of spectroscopically confirmed PSBs (which already matched that of old systems at z ∼ 2 based on photometric selections (Whitaker et al. 2013)) to fully dominate the QGs mass-function at z ∼ 3. The JWST and ALMA will be crucial to trace the full demographics the quiescent population in an effort to map the distribution in quenching times, dust, and molecular gas content to obtain further insights into the global SFH of the emerging massive quenched systems.
σNMAD = 1.48 ⋅ median(|zphot − zspec|/(1 + zspec)), Hoaglin et al. (1983).
Acknowledgments
We wish to thank the anonymous referee for their constructive and helpful comments. We are grateful to G. Brammer for assistance with the data reduction, to C. Vignali for providing X-ray spectra and M. Salvato for additional redshift constraints and helpful discussions. C.D. is grateful to C. Gomez-Guijarro, F. Valentino and F. Rizzo for helpful discussions. V.S. acknowledges support from the ERC-StG ClustersXCosmo grant agreement 716762. I.D. acknowledges the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 788679. A.C. acknowledges the support from the grants PRIN-MIUR 2017and ASI n.2018-23-HH.0. Based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under ESO programme ID 179.A-2005 and on data products produced by TERAPIX and the Cambridge Astronomy Survey Unit on behalf of the UltraVISTA consortium (Laigle cat.). This paper made use of Astropy (http://www.astropy.org), a community-developed core Python package for Astronomy (Astropy Collaboration 2013), Matplotlib (Hunter 2007) and Numpy (Harris et al. 2020).
References
- Aird, J., Coil, A. L., & Georgakakis, A. 2019, MNRAS, 484, 4360 [NASA ADS] [CrossRef] [Google Scholar]
- Almaini, O., Wild, V., Maltby, D. T., et al. 2017, MNRAS, 472, 1401 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, P., & Fritze-v Alvensleben, U. 2003, A&A, 401, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnouts, S., Walcher, C. J., Le Fèvre, O., et al. 2007, A&A, 476, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Avni, Y. 1976, ApJ, 210, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Baldry, I. K., Glazebrook, K., Brinkmann, J., et al. 2004, ApJ, 600, 681 [Google Scholar]
- Balogh, M. L., Morris, S. L., Yee, H. K. C., Carlberg, R. G., & Ellingson, E. 1999, ApJ, 527, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Barro, G., Faber, S. M., Pérez-González, P. G., et al. 2013, ApJ, 765, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Barro, G., Faber, S. M., Dekel, A., et al. 2016, ApJ, 820, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Belli, S., Newman, A. B., & Ellis, R. S. 2015, ApJ, 799, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Belli, S., Newman, A. B., & Ellis, R. S. 2017, ApJ, 834, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Belli, S., Newman, A. B., & Ellis, R. S. 2019, ApJ, 874, 17 [CrossRef] [Google Scholar]
- Best, P. N., Kauffmann, G., Heckman, T. M., et al. 2005, MNRAS, 362, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Béthermin, M., Daddi, E., Magdis, G., et al. 2015, A&A, 573, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bezanson, R., van Dokkum, P., van de Sande, J., Franx, M., & Kriek, M. 2013, ApJ, 764, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., & Coppi, P. 2008, ApJ, 686, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G., Ryan, R., & Pirzkal, N. 2015, Source-dependent master sky images for the WFC3/IR grisms, Space Telescope WFC Instrument Science Report [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Capozzi, D., Maraston, C., Daddi, E., et al. 2016, MNRAS, 456, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Carollo, C. M., Bschorr, T. J., Renzini, A., et al. 2013, ApJ, 773, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Carraro, R., Rodighiero, G., Cassata, P., et al. 2020, A&A, 642, A65 [EDP Sciences] [Google Scholar]
- Cattaneo, A., Dekel, A., Devriendt, J., Guiderdoni, B., & Blaizot, J. 2006, MNRAS, 370, 1651 [NASA ADS] [CrossRef] [Google Scholar]
- Cecchi, R., Bolzonella, M., Cimatti, A., & Girelli, G. 2019, ApJ, 880, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, Y.-Y., van der Wel, A., Rix, H.-W., et al. 2013a, ApJ, 773, 149 [CrossRef] [Google Scholar]
- Chang, Y.-Y., van der Wel, A., Rix, H.-W., et al. 2013b, ApJ, 762, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Cimatti, A., Daddi, E., Renzini, A., et al. 2004, Nature, 430, 184 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cimatti, A., Daddi, E., & Renzini, A. 2006, A&A, 453, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cimatti, A., Cassata, P., Pozzetti, L., et al. 2008, A&A, 482, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Citro, A., Pozzetti, L., Moresco, M., & Cimatti, A. 2016, A&A, 592, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Civano, F., Marchesi, S., Comastri, A., et al. 2016, ApJ, 819, 62 [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Cimatti, A., Renzini, A., et al. 2004, ApJ, 617, 746 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Renzini, A., Pirzkal, N., et al. 2005, ApJ, 626, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Bournaud, F., Walter, F., et al. 2010, ApJ, 713, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Davé, R., Thompson, R., & Hopkins, P. F. 2016, MNRAS, 462, 3265 [NASA ADS] [CrossRef] [Google Scholar]
- Davé, R., Anglés-Alcázar, D., Narayanan, D., et al. 2019, MNRAS, 486, 2827 [NASA ADS] [CrossRef] [Google Scholar]
- Davidzon, I., Ilbert, O., Laigle, C., et al. 2017, A&A, 605, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dekel, A., & Birnboim, Y. 2006, MNRAS, 368, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Silk, J. 1986, ApJ, 303, 39 [Google Scholar]
- Dekel, A., Sari, R., & Ceverino, D. 2009, ApJ, 703, 785 [Google Scholar]
- De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Delvecchio, I., Daddi, E., Sargent, M. T., et al. 2021, A&A, 647, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Eugenio, C., Daddi, E., Gobat, R., et al. 2020, ApJ, 892, L2 [CrossRef] [Google Scholar]
- Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Drory, N., Bundy, K., Leauthaud, A., et al. 2009, ApJ, 707, 1595 [NASA ADS] [CrossRef] [Google Scholar]
- Dunlop, J., Peacock, J., Spinrad, H., et al. 1996, Nature, 381, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Leiton, R., Nagar, N., et al. 2018, A&A, 616, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Emsellem, E., Cappellari, M., Krajnović, D., et al. 2011, MNRAS, 414, 888 [Google Scholar]
- Esdaile, J., Glazebrook, K., Labbé, I., et al. 2021, ApJ, 908, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Estrada-Carpenter, V., Papovich, C., Momcheva, I., et al. 2019, ApJ, 870, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Estrada-Carpenter, V., Papovich, C., Momcheva, I., et al. 2020, ApJ, 898, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Feldmann, R., & Mayer, L. 2015, MNRAS, 446, 1939 [NASA ADS] [CrossRef] [Google Scholar]
- Fiore, F., Puccetti, S., Brusa, M., et al. 2009, ApJ, 693, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 1986, ApJ, 307, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Fontana, A., Pozzetti, L., Donnarumma, I., et al. 2004, A&A, 424, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Forrest, B., Annunziatella, M., Wilson, G., et al. 2020a, ApJ, 890, L1 [CrossRef] [Google Scholar]
- Forrest, B., Marsan, Z. C., Annunziatella, M., et al. 2020b, ApJ, 903, 47 [CrossRef] [Google Scholar]
- Franx, M., Labbé, I., Rudnick, G., et al. 2003, ApJ, 587, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Fumagalli, M., Labbé, I., Patel, S. G., et al. 2014, ApJ, 796, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Charlot, S., Brinchmann, J., White, S. D. M., & Tremonti, C. A. 2005, MNRAS, 362, 41 [Google Scholar]
- Gargiulo, A., Saracco, P., Tamburri, S., Lonoce, I., & Ciocca, F. 2016, A&A, 592, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genel, S., Vogelsberger, M., Springel, V., et al. 2014, MNRAS, 445, 175 [Google Scholar]
- Genzel, R., Tacconi, L. J., Gracia-Carpio, J., et al. 2010, MNRAS, 407, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Gilli, R., Comastri, A., & Hasinger, G. 2007, A&A, 463, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girelli, G., Pozzetti, L., Bolzonella, M., et al. 2020, A&A, 634, A135 [CrossRef] [EDP Sciences] [Google Scholar]
- Glazebrook, K., Schreiber, C., Labbé, I., et al. 2017, Nature, 544, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Gobat, R., Strazzullo, V., Daddi, E., et al. 2012, ApJ, 759, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Gobat, R., Daddi, E., Strazzullo, V., et al. 2017, A&A, 599, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gobat, R., Daddi, E., Magdis, G., et al. 2018, Nat. Astron., 2, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez-Guijarro, C., Toft, S., Karim, A., et al. 2018, ApJ, 856, 121 [Google Scholar]
- Gómez-Guijarro, C., Magdis, G. E., Valentino, F., et al. 2019, ApJ, 886, 88 [Google Scholar]
- Häring, N., & Rix, H.-W. 2004, ApJ, 604, L89 [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [CrossRef] [PubMed] [Google Scholar]
- Henriques, B. M. B., White, S. D. M., Thomas, P. A., et al. 2017, MNRAS, 469, 2626 [Google Scholar]
- Hoaglin, D. C., Mosteller, F., & Tukey, J. W. 1983, Wiley Series in Probability and Mathematical Statistics (New York: Wiley) [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2006, ApJS, 163, 1 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jin, S., Daddi, E., Liu, D., et al. 2018, ApJ, 864, 56 [Google Scholar]
- Johansson, P. H., Naab, T., & Ostriker, J. P. 2009, ApJ, 697, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Johansson, P. H., Naab, T., & Ostriker, J. P. 2012, ApJ, 754, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Kawinwanichakij, L., Papovich, C., Ciardullo, R., et al. 2020, ApJ, 892, 7 [Google Scholar]
- Kennicutt, R. C., Jr 1998, ARA&A, 36, 189 [Google Scholar]
- Khochfar, S., & Ostriker, J. P. 2008, ApJ, 680, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Kriek, M., & Conroy, C. 2013, ApJ, 775, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Kriek, M., van Dokkum, P. G., Franx, M., et al. 2006, ApJ, 645, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Kriek, M., van Dokkum, P. G., Labbé, I., et al. 2009, ApJ, 700, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Kriek, M., Conroy, C., van Dokkum, P. G., et al. 2016, Nature, 540, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Krogager, J. K., Zirm, A. W., Toft, S., Man, A., & Brammer, G. 2014, ApJ, 797, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Labbé, I., Huang, J., Franx, M., et al. 2005, ApJ, 624, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Le Borgne, D., Abraham, R., Daniel, K., et al. 2006, ApJ, 642, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Le Floc’h, E., Aussel, H., Ilbert, O., et al. 2009, ApJ, 703, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Lemaux, B. C., Le Floc’h, E., Le Fèvre, O., et al. 2017, A&A, 597, C1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, D., Daddi, E., Dickinson, M., et al. 2018, ApJ, 853, 172 [Google Scholar]
- Lusso, E., Comastri, A., Simmons, B. D., et al. 2012, MNRAS, 425, 623 [Google Scholar]
- Lustig, P., Strazzullo, V., D’Eugenio, C., et al. 2021, MNRAS, 501, 2659 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Magdis, G. E., Daddi, E., Béthermin, M., et al. 2012, ApJ, 760, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Maltby, D. T., Almaini, O., Wild, V., et al. 2018, MNRAS, 480, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Man, A., & Belli, S. 2018, Nat. Astron., 2, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Marsan, Z. C., Marchesini, D., Brammer, G. B., et al. 2015, ApJ, 801, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Marsan, Z. C., Muzzin, A., Marchesini, D., et al. 2020, ApJ, submitted [arXiv:2010.04725] [Google Scholar]
- Martig, M., Bournaud, F., Teyssier, R., & Dekel, A. 2009, ApJ, 707, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Matharu, J., Muzzin, A., Brammer, G. B., et al. 2019, MNRAS, 484, 595 [CrossRef] [Google Scholar]
- McCracken, H. J., Capak, P., Salvato, M., et al. 2010, ApJ, 708, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Merlin, E., Fortuni, F., Torelli, M., et al. 2019, MNRAS, 490, 3309 [NASA ADS] [CrossRef] [Google Scholar]
- Mullaney, J. R., Alexander, D. M., Goulding, A. D., & Hickox, R. C. 2011, MNRAS, 414, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, N., Quataert, E., & Thompson, T. A. 2005, ApJ, 618, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Muzzin, A., Marchesini, D., Stefanon, M., et al. 2013, ApJ, 777, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, D., Genel, S., Vogelsberger, M., et al. 2015, MNRAS, 448, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, D., Springel, V., Pillepich, A., et al. 2019, Comput. Astrophys. Cosmol., 6, 2 [Google Scholar]
- Newman, A. B., Ellis, R. S., Bundy, K., & Treu, T. 2012, ApJ, 746, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Belli, S., Ellis, R. S., & Patel, S. G. 2018a, ApJ, 862, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Belli, S., Ellis, R. S., & Patel, S. G. 2018b, ApJ, 862, 126 [CrossRef] [Google Scholar]
- Noll, S., Pierini, D., Cimatti, A., et al. 2009, A&A, 499, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olsen, K. P., Rasmussen, J., Toft, S., & Zirm, A. W. 2013, ApJ, 764, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Onodera, M., Renzini, A., Carollo, M., et al. 2012, ApJ, 755, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Onodera, M., Carollo, C. M., Renzini, A., et al. 2015, ApJ, 808, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Pillepich, A., Springel, V., Nelson, D., et al. 2018, MNRAS, 473, 4077 [Google Scholar]
- Polletta, M., Tajer, M., Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., & Wu, H. 2000, ApJ, 529, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzetti, L., & Mannucci, F. 2000, MNRAS, 317, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzetti, L., Bolzonella, M., Zucca, E., et al. 2010, A&A, 523, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puglisi, A., Daddi, E., Liu, D., et al. 2019, ApJ, 877, L23 [Google Scholar]
- Renzini, A. 2006, ARA&A, 44, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Boquien, M., & Lee, J. C. 2018, ApJ, 859, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sanders, D. B., Soifer, B. T., Elias, J. H., et al. 1988, ApJ, 325, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Saracco, P., Longhetti, M., & Gargiulo, A. 2011, MNRAS, 412, 2707 [NASA ADS] [CrossRef] [Google Scholar]
- Saracco, P., Marchesini, D., La Barbera, F., et al. 2020, ApJ, 905, 40 [CrossRef] [Google Scholar]
- Sargent, M. T., Daddi, E., Béthermin, M., et al. 2014, ApJ, 793, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Schaye, J., Crain, R. A., Bower, R. G., et al. 2015, MNRAS, 446, 521 [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, C., Glazebrook, K., Nanayakkara, T., et al. 2018, A&A, 618, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shibuya, T., Ouchi, M., & Harikane, Y. 2015, ApJS, 219, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Smolčić, V., Novak, M., Bondi, M., et al. 2017, A&A, 602, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinhardt, C. L., Capak, P., Masters, D., & Speagle, J. S. 2016, ApJ, 824, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Stockmann, M., Toft, S., Gallazzi, A., et al. 2020, ApJ, 888, 4 [CrossRef] [Google Scholar]
- Straatman, C. M. S., Labbé, I., Spitler, L. R., et al. 2014, ApJ, 783, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Strazzullo, V., Daddi, E., Gobat, R., et al. 2015, A&A, 576, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tacconi, L. J., Genzel, R., Neri, R., et al. 2010, Nature, 463, 781 [Google Scholar]
- Tanaka, M., Valentino, F., Toft, S., et al. 2019, ApJ, 885, L34 [Google Scholar]
- Thomas, D., Maraston, C., Bender, R., & Mendes de Oliveira, C. 2005, ApJ, 621, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., Schawinski, K., Sarzi, M., & Silk, J. 2010, MNRAS, 404, 1775 [NASA ADS] [Google Scholar]
- Toft, S., Gallazzi, A., Zirm, A., et al. 2012, ApJ, 754, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Toft, S., Smolčić, V., Magnelli, B., et al. 2014, ApJ, 782, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Tran, K.-V. H., Franx, M., Illingworth, G., Kelson, D. D., & van Dokkum, P. 2003, ApJ, 599, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Valentino, F., Tanaka, M., Davidzon, I., et al. 2020, ApJ, 889, 93 [Google Scholar]
- van der Wel, A., Rix, H.-W., Wuyts, S., et al. 2011, ApJ, 730, 38 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Franx, M., van Dokkum, P. G., et al. 2014, ApJ, 788, 28 [NASA ADS] [CrossRef] [Google Scholar]
- van de Sande, J., Kriek, M., Franx, M., et al. 2013, ApJ, 771, 85 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Bezanson, R., van der Wel, A., et al. 2014, ApJ, 791, 45 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Franx, M., Kriek, M., et al. 2008, ApJ, 677, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Vogelsberger, M., Genel, S., Springel, V., et al. 2014a, Nature, 509, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Vogelsberger, M., Genel, S., Springel, V., et al. 2014b, MNRAS, 444, 1518 [NASA ADS] [CrossRef] [Google Scholar]
- Wellons, S., Torrey, P., Ma, C.-P., et al. 2015, MNRAS, 449, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Labbé, I., van Dokkum, P. G., et al. 2011, ApJ, 735, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Kriek, M., van Dokkum, P. G., et al. 2012, ApJ, 745, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., van Dokkum, P. G., Brammer, G., et al. 2013, ApJ, 770, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Wild, V., Almaini, O., Dunlop, J., et al. 2016, MNRAS, 463, 832 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, R. J., Quadri, R. F., Franx, M., van Dokkum, P., & Labbé, I. 2009, ApJ, 691, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Zolotov, A., Dekel, A., Mandelker, N., et al. 2015, MNRAS, 450, 2327 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional plots
We here add the multi-wavelength cutouts (from Ks band to 20 cm) of our sources together with their SED fits when available. SEDs for IDs 1 and 2 are not present because ID1 lies in a region that is subject to unreliable IR fluxes and uncertainties, while ID 2 is absent from the J18 catalogue due to lack of UltraVISTA Ks and VLA 3 GHz radio priors. We recall that the plots on the right are only intended to display the available data and to show the maximum AGN component allowed by our 24 μm detections.
For completeness we recall that the SED fitting was carried out by fixing the redshift to the best-fitting grism value of each galaxy and includes two components: a stellar component from BC03 templates (black curve), and a MIR AGN torus from Mullaney et al. (2011) (red curve). The downward arrows show the 2σ upper limit at a given wavelength.
 |
Fig. A.1. NIR-to-radio photometry available for our sample. Left panel: multi-band cutouts of our targets. The green text marks the instrument, the observed wavelength in units of μm, and the size of the field of view. Right panel: fits to the SEDs of our galaxies. We do not report the SED of ID1 because it lies in an area of UltraVista that is affected by unreliable flux uncertainties. ID2 is absent from the catalogue of Jin et al. (2018) due to the lack of Ks and VLA 3 GHz priors. The SEDs are fitted with a stellar component (blue curve; Bruzual & Charlot 2003) and an AGN torus component (red curve; Mullaney et al. 2011). The fits where fixed to the grism redshifts derived as in the main text. Upper limits are at 2σ. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
All Tables
All Figures
 |
Fig. 1. F160W imaging cutouts (left) and 2D G141 spectra (right) at the native WFC3 pixel scale. Redshift increases from top to bottom. The colour scale is in linear scale. |
| In the text | |
 |
Fig. 2. Upper panels: redshift probability distribution for each target. Solid lines from light to dark red mark 1, 2, and 3σ confidence levels. Green points for ID 7 mark the redshift solutions obtained by combining spectroscopy and photometry as described in Sect. 4.2. Middle panels: optimally extracted 1D grism spectra (black) and best-fitting solutions (red) of our targets. The noise vector is shown in grey in each panel. Bottom panels: corresponding 2D G141 spectra. The colour scale is in linear scale. Galaxies are shown in order of increasing redshift. |
| In the text | |
 |
Fig. 2. continued. |
| In the text | |
 |
Fig. 3. Comparison of calibrated zphots and spectroscopic redshifts. Black squares mark the original calibrated zphots used for the selection. Red squares mark zphots from Muzzin et al. (2013). The solid black line and relative shaded area mark the 1:1 relation and the nominal dispersions between the original calibrated zphots and the newly derived zspec (see text). Redshifts from Muzzin et al. (2013) are shifted horizontally by −0.005 for clarity. |
| In the text | |
 |
Fig. 4. Photometry from the Laigle et al. (2016) catalogue (black dots). Grey curves show the best-fitting templates smoothed to the G141 resolution. The observed-frame grism spectra are superimposed, rebinned for clarity. |
| In the text | |
 |
Fig. 5. Distributions of photometric reduced χ2 before (red dots) and after removing the ZPs re-calibration (black dots). Median values are marked with solid red and black lines. |
| In the text | |
 |
Fig. 6. Normalised residual distribution of target galaxies in each photometric band. Red and black histograms show residuals adopting recalibrated and original photometric zero-points, respectively. Solid red and black curves show Gaussian fits to these distributions. Their means, standard mean errors, and standard deviations are listed in each panel. |
| In the text | |
 |
Fig. 7. Mean residuals of photometric bands as a function of the systematic offset to be applied to correct photometric ZPs. Error bars mark the standard error on the mean shown in Fig. 6. |
| In the text | |
 |
Fig. 8. Top: reduced χ2 distributions of the fits to the spectroscopy (left), photometry (middle), and the combined data sets (right panel) as a function of the extinction law. Vertical lines mark the medians of the distributions. Bottom: χ2 difference of the best-fitting solutions obtained using δ = −0.4 and δ = −0.7 with respect to δ = 0. Grey dashed lines mark the levels of ±Δχ2 = 2.3. |
| In the text | |
 |
Fig. 9. Probability of constant star-forming solutions relative to that of passive solutions. Blue bars mark the results from spectroscopy alone. Red bars show the probabilities from the combined fit. Bars with relative probabilities lower than 10−6 are not shown. |
| In the text | |
 |
Fig. 10. Mass-weighted ages and dust extinction values for our targets. Blue squares mark the confidence regions (3 to 1 σ going from light to dark points) extracted from the spectra alone. Red points show the solutions of the combined fit. Blue and red stars in each panel mark the best-fit solution from the spectroscopic fit and the combined fit, respectively. The relative probabilities of the extinction laws are shown for each galaxy. As a reference, we report the best-fitting combined solution at fixed extinction law as black and grey dots. Their colour-coding follows that of the aforementioned relative probabilities. |
| In the text | |
 |
Fig. 11. Spectral indices and evolutionary properties derived for our galaxies. Upper left: variation in Balmer and 4000 Å breaks for CSPs as a function of their age using BC03 templates at solar metallicity. Lighter curves mark the evolution for a truncated SFH with increasing duration of star formation. The effect of adopting templates of different metallicity is displayed for the values that produce the largest variation, i.e., 2.5Z⊙ (triangles). Dotted and solid grey curves show the behaviour of a constant SFH for the two breaks, respectively. Upper right: individual values of DB and Dn4000 for our targets. The red track shows their evolution with age and is attenuated by 1 mag. The dashed grey line marks the 1:1 relation. Lower left: variation of the index ratio as a function of age for an SSP-like template. The effect of smoothing templates to the HST resolution is shown by the dashed black curve. The effect of a AV = 1 mag attenuation is instead shown by the red curve. The full transition between a Balmer-dominated and a 4000 Å -dominated spectrum is flagged when DB/Dn4000 = 1 (dashed grey line), which occurs around 1.3 Gyr of passive evolution. Dark grey triangles mark the evolution for 2.5Z⊙ templates. Lower right: best-fit values for the dust attenuation and mass-weighted age from the combined fit. Chandra X-ray, VLA 3GHz, and Spitzer/MIPS 24 μm detections are marked by black crosses and yellow and black hexagons, respectively. |
| In the text | |
 |
Fig. 12. Radio excess observed in our galaxies compared to the average FIR-to-radio SED of similarly massive QGs at intermediate redshift. Top: observed 3 GHz flux for our sample (red dot) compared to the observed FIR-to-radio SED for ⟨M⋆⟩∼1.1 × 1011 M⊙ galaxies at z ∼ 1.8 in Gobat et al. (2018) (black dots). The best-fitting template of Gobat et al. (2018) is shown as a black curve. The same template, but rescaled to our redshift and average SFR (D’Eugenio et al. 2020), is shown as a red curve. Bottom: observed flux normalised to the respective model at the corresponding wavelength. |
| In the text | |
 |
Fig. 13. X-ray luminosity in the 2–10 keV band as a function of stellar mass for quiescent (red squares), star-forming (cyan diamonds), and starburst galaxies (violet circles) at 2.25 < z < 3.50. Adapted from Carraro et al. (2020). |
| In the text | |
 |
Fig. 14. BHAR (top) and BHAR per unit SFR (bottom) as a function of stellar mass for quiescent galaxies (greyscale points) in COSMOS. Different symbols mark different redshift bins. Main-sequence galaxies in the same redshift range as studied in this work are added in the bottom panel as cyan stars. Error bars on the average BHAR reflect the dispersion of the weighted mean on the rest frame L(2–10 keV) of the sample. The average SFR[OII] was converted into a Chabrier IMF. Adapted from Carraro et al. (2020). |
| In the text | |
 |
Fig. 15. Comparison of our mass-weighted ages and the morphological parameters derived in Lustig et al. (2021), namely Sérsic index n and effective radius Re at 5000 Å rest frame. |
| In the text | |
 |
Fig. 16. Stellar ages as a function of observed redshift of log(M⋆/M⊙) > 10.5 quiescent galaxies. Adapted from Onodera et al. (2015). Here mass-weighted ages from the literature differ from t50 in that they do not specifically refer to the lookback time at which 50% of M⋆ is formed. The four targets selected from Schreiber et al. (2018) correspond to those recently followed up by Esdaile et al. (2021). Solid grey lines show, from thin to thick, the age of simple stellar populations made at a zform from 1.5 to 5. The dotted red line marks the age of the Universe as a function of redshift. |
| In the text | |
 |
Fig. A.1. NIR-to-radio photometry available for our sample. Left panel: multi-band cutouts of our targets. The green text marks the instrument, the observed wavelength in units of μm, and the size of the field of view. Right panel: fits to the SEDs of our galaxies. We do not report the SED of ID1 because it lies in an area of UltraVista that is affected by unreliable flux uncertainties. ID2 is absent from the catalogue of Jin et al. (2018) due to the lack of Ks and VLA 3 GHz priors. The SEDs are fitted with a stellar component (blue curve; Bruzual & Charlot 2003) and an AGN torus component (red curve; Mullaney et al. 2011). The fits where fixed to the grism redshifts derived as in the main text. Upper limits are at 2σ. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.