EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 688 (August 2024) A&A, 688 (2024) A210 Full HTML
Open Access
Issue
A&A
Volume 688, August 2024
Article Number A210
Number of page(s) 35
Section Catalogs and data
DOI https://doi.org/10.1051/0004-6361/202349031
Published online 28 August 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model.

Open Access funding provided by Max Planck Society.

1 Introduction

In the last decades, two outstanding cosmological questions have been raised. What is the nature of dark matter? What drives the accelerated expansion in the late-time Universe? These puzzles can be addressed using observations of the large-scale structure (LSS). There exist two sets of LSS-based cosmological observables (e.g., see the reviews from Weinberg et al. 2013; Will 2014; Ishak 2019). The first set is connected to the homogeneous cosmological background. These probes use standard rulers such as baryon acoustic oscillations and are sensitive to the geometry and the expansion history of the Universe. The second and complementary set of observables relates to the inhomogeneous universe and how the large-scale structure has grown with time: cluster counts, redshift-space distortions in galaxy clustering, and cosmic shear. The growth of the structures in the cosmic web is mainly related to the cosmological model through the n-point statistical functions of the dark matter halos (halo mass function, power spectrum, bi-spectrum, etc.). Provided that the cluster scaling relation or the galaxy bias function is under control, one can constrain a set of cosmological parameters from the cluster number counts or the galaxy clustering. Currently, the largest samples of intra-cluster medium (ICM) selected clusters of galaxies considered in cosmological analysis are in the regime of few hundreds (Vikhlinin et al. 2009a,b; Pacaud et al. 2016, 2018; Planck Collaboration XXVII 2016; Zubeldia & Challinor 2019; de Haan et al. 2016; Bocquet et al. 2019). Their constraint on the cosmological model alone is not stringent and depends strongly on the calibration of the mass-observable relation.

eROSITA, on board the Spektrum Roentgen Gamma (SRG) orbital observatory launched in 2019, is a sensitive, wide-field X-ray telescope which has performed an all-sky survey of unprecedented depth (Merloni et al. 2012; Predehl et al. 2021). The sensitivity of eROSITA extends to 10 keV on the high end, but is at its highest in the soft X-ray band, specifically in the 0.2-2.3 keV range, which makes it particularly suitable for detecting and studying emission from the hot gas in galaxy clusters. eROSITA is now delivering an outstanding sample of all the most massive clusters up to redshift z = 1.32 (Bulbul et al. 2024, and this analysis) to constrain cosmological parameters with percent-level precision (Ghirardini et al. 2024) using a mass observable relation calibrated using weak gravitational lensing (Grandis et al. 2024; Kleinebreil et al. 2024; Pacaud et al., in prep.).

To make the most of the unprecedentedly large X-ray-selected galaxy cluster sample provided by eROSITA, it is vital to measure accurately the redshifts of the galaxy clusters. Measuring redshifts based on X-ray data is only possible from the emission lines found in the X-ray spectra of the ICM (e.g., Hashimoto et al. 2004; Lamer et al. 2008; Lloyd-Davies et al. 2011; Yu et al. 2011). For eROSITA, this venue is available only for a small subset of the clusters and at a relatively low precision (~10%) (Borm et al. 2014). Indeed, since the redshift precision depends strongly on the ICM gas temperature and signal-to-noise ratio of the X-ray spectra, precise measurements are only feasible for very bright clusters observed with long exposure times (e.g., at the ecliptic poles of the eRASS1).

Galaxy clusters contain over-densities of early-type galaxies relative to the field (Dressler 1980). Up to date, the most accurate and precise cluster redshifts are obtained from an ensemble of galaxy redshifts (e.g., Beers et al. 1990; Böhringer et al. 2004; Clerc et al. 2016; Ider Chitham et al. 2020) measured via optical spectroscopy (e.g., Szokoly et al. 2004; Koulouridis et al. 2016; Clerc et al. 2020). Dedicated spectroscopic observations of the galaxies in eROSITA clusters are ongoing with the SDSS-V (Kollmeier et al. 2017) and soon to be started with 4MOST (Finoguenov et al. 2019), so that by 2029 (planned end of 4MOST) essentially all eROSITA clusters will have measured spectroscopic redshifts. Until then, we estimate photometric redshifts using multi-band photometric data to sample the spectral energy distribution of the sources of interest (e.g., review from Salvato et al. 2009). The performance of photometric redshift techniques depends on the quality of the photometry, how well the desired spectral features are sampled by the subset of the spectrum encompassed by the photometric filters, the robustness of the calibration methods, and how representative the spectroscopic training datasets are. Estimating the cluster photometric redshift consists of two steps: identifying cluster-bound galaxies in the optical and infrared data and estimating their redshift via ensemble averaging. Optical cluster finding algorithms are classified by their methodology: matched-filter based algorithms (e.g., Postman et al. 1996; Olsen et al. 2007; Szabo et al. 2011), Voronoi tessellation methods (e.g., Ramella et al. 2001; Soares-Santos et al. 2011; Murphy et al. 2012), friends-of-friends (e.g., Wen et al. 2012) and percolation algorithms (e.g., Dalton et al. 1997; Rykoff et al. 2014). Photometric redshift estimation methods are classified by the information they use: red sequence (e.g., Gladders & Yee 2000; Gladders et al. 2007; Oguri 2014), color overdensities (e.g., Miller et al. 2005), brightest cluster galaxies (BCG) (e.g., Koester et al. 2007; Hao et al. 2010), photometric redshifts of all galaxies (e.g., Wen et al. 2012; Tempel et al. 2018; Bellagamba et al. 2018; Aguena et al. 2021), or spectroscopic galaxy surveys (e.g., Duarte & Mamon 2015; Old et al. 2015).

In this analysis, we consider a sample of candidate clusters detected as extended X-ray sources in the first eROSITA all-sky survey (eRASS1, Merloni et al. 2024; Bulbul et al. 2024). We measure each cluster’s photometric redshift and optical richness following the method of Rykoff et al. (2014). The basis for these measurements is the optical and near-infrared inference models of the extragalactic sky published in the 9th and 10th data releases of the DESI Legacy Imaging Surveys (Dey et al. 2019)1. It covers almost all the extragalactic sky with a footprint extending over 24069 deg2. In the event of sufficient coverage with galaxy spectra, we measure the cluster spectroscopic redshift and cluster line-of-sight-velocity dispersion using the method from Clerc et al. (2020) and Kirkpatrick et al. (2021).

The article is organized as follows. In Sec. 2, we introduce the optical and X-ray data. Section 3 describes the optical cluster finding method and defines how the different redshift types are measured. Our main result, the eRASS1 identified cluster and group catalog, is presented in Sec. 4. We evaluate its properties in the following sections. With the help of consistently reanalyzed catalogs of known clusters, we estimate the optical completeness of the eRASS1 catalog in Sec. 5. In Sec. 6, we compute cluster number densities and examine their dependence on the optical survey depth. We discuss the purity and the properties of the remaining contaminants in the eRASS1 catalog in Sec. 7. The accuracy and precision of the photometric redshifts are quantified in Sec. 8. Finally, in Sect. 9, we combine all cluster catalogs to tightly constrain the richness-velocity dispersion relation and measure its intrinsic scatter. Our results are summarized in Sect. 10.

Throughout the paper, we assume a flat cosmology with H0 = 70 km s−1 Mpc−1, Ωm = 0.3, and σ8 = 0.8. Redshifts are given in the heliocentric reference frame. No corrections for Virgo infall or the CMB dipole moment have been applied.

2 X-ray, optical, and near-infrared data

In this section, we introduce the data considered in the X-ray wavelength domain (Sec. 2.1) and in the optical and near-infrared range (Sec. 2.2). The observed X-ray radiation of galaxy clusters stems from thermal bremsstrahlung and line emission by the hot Intra-Cluster Medium (ICM). In the optical and near-infrared, old stellar populations emit most of the received light. The different wavelengths thus trace distinct parts of the galaxy clusters.

2.1 The X-ray eRASS1 cluster catalog

Galaxy cluster candidates are selected from the first eROSITA All-Sky Survey catalog (eRASS1, Merloni et al. 2024). It consists of X-ray sources in half of the sky at Galactic longitude 179.9442° < l < 359.9442°. Galaxy clusters emit X-ray radiation from their diffuse hot gas. They appear as extended sources in the eROSITA observations as opposed to point sources such as Active Galactic Nuclei (AGNs) or stars, although there can be misclassifications. Therefore, we consider extended eRASS1 sources as galaxy cluster candidates. This sample is described in detail in Bulbul et al. (2024) and forms the basis for the eRASS1 cluster candidate catalog.

The survey area of eROSITA used here is that to which the German consortium holds data rights and covers half the sky: 20626 deg2 (see Fig. 1). The joint coverage of this with the DESI Legacy Imaging Surveys (LS, Dey et al. 2019) (see Sec. 2.2) is 13 178 deg2, primarily because the LS avoids the area around the Galactic plane and the Magellanic clouds. As described in Bulbul et al. (2024), we further masked regions of known non-cluster extended X-ray sources (using the flag IN_XGOOD=False), in total 62 deg2. This reduces the eRASS1 cluster candidate catalog area to 13 116 deg2.

A fraction of the extended sources are cataloged multiple times. Most of these split sources were removed by applying the SPLIT_CLEANED flag (Bulbul et al. 2024). In total, the eRASS1 cluster candidate catalog contains 14 818 cleaned sources in the common region between the German part of the eROSITA survey and the LS. Figure 1 shows the sky density of cleaned galaxy cluster candidates. The deeper exposures towards the ecliptic poles cause the gradient of source density. This is the main cluster catalog analyzed in the article. Other cluster catalogs analyzed are presented in Sec. 5.

thumbnail Fig. 1

Pixelized number density of 22718 cleaned eRASS1 extended sources, that is, cluster candidates in the German part of the eROSITA survey. The HEALPix map has a resolution of NSIDE = 16 =^$\[\hat{=}\]$ 13.4 deg2. The highest number density occurs near the southern ecliptic pole around RA = 90° and Dec ≈ −67° where the exposure time is largest. Another overdensity of extended sources near the Galactic plane around RA ≈ 135° and Dec ≈ −45° is associated with the Vela supernova remnant. It lies outside the common footprint with the Legacy Surveys (see Fig. 2).

2.2 DESI Legacy Imaging Surveys, 9th and 10th releases

We combined the optical and near-infrared inference model data from the 9th and 10th release of the DESI Legacy Imaging Surveys (LS, Dey et al. 2019) to obtain the largest coverage of the extragalactic sky (Galactic latitude |b| ≳ 20°). The Galactic plane was not covered by the observations and was thereby excluded from our analysis. Observations at optical wavelengths were carried out with three different telescopes as described in Sects. 2.2.1 and 2.2.2. Consequently, the survey area was split at a declination of ≈32.375°. We refer to the southern part as LS DR10 South and the northern part as LS DR9 North.

To increase the wavelength coverage, the LS utilized 7 yr (LS DR10) or 6 yr (LS DR9) of infrared imaging data from the Near-Earth Object Wide-field Infrared Survey Explorer (NEOWISE, Lang 2014; Mainzer et al. 2014; Meisner et al. 2017a,b). The limitation of blended sources due to the much lower spatial resolution in the NEOWISE data (≈6″) compared to the LS data (≲1″) was partly overcome by applying forced photometry on the “un”-blurred WISE maps (unWISE, Lang 2014) at the locations of the sources that were detected in the LS. Including the 3.4 μm W1 band in our analysis allowed us to extend the galaxy cluster samples to higher redshift (z ≳ 0.8).

Photometry was measured consistently for all surveys using The Tractor algorithm (Lang et al. 2016) based on seeing-convolved PSF, de Vaucouleurs, exponential disk, or composite de Vaucouleurs + exponential disk models. All magnitudes are given in the AB system. We applied the correction for Galactic extinction provided in the LS catalogs. Those corrections were derived using the maps from Schlegel et al. (1998) with updated extinction coefficients for the DECam.

thumbnail Fig. 2

Maps of the limiting magnitude in the z band for sources detected with 10σ significance. The footprint maps show the coverage for the Legacy Surveys DR10 south (top panel) and DR9 north (bottom panel). Only regions with data in all the g-, r-, and z-bands were considered. The half sky that is covered by eRASS1 corresponds to the region below the red line. The limiting magnitudes in the z band directly translate to the limiting redshift zvlim (see Appendix B for details).

2.2.1 LS DR10 south

The catalogs were obtained by processing CTIO/DECam observations (Flaugher et al. 2015) from the DECam Legacy Survey (DECaLS, Dey et al. 2019), the Dark Energy Survey (DES, The Dark Energy Survey Collaboration 2005; Dark Energy Survey Collaboration 2016), and publicly released DECam imaging (NOIRLab Archive) from other projects, including the DECam eROSITA survey (DeROSITAs; PI: A. Zenteno). In the DES area (~ 5000 deg2), the depth reached is higher than elsewhere in the footprint, see Fig. 2.

The LS DR10 south covers 19 342 deg2 in the g, r, and z-bands (see also Fig. 3). When the i-band is included, the survey area is 15 326 deg2. The overlap with eRASS1 is 12791 (12205) deg2 when the i-band is excluded (included). We describe the calculation of the survey area in Appendix B.

thumbnail Fig. 3

Effective survey area for the Legacy Surveys DR10 south and DR9 north depending on redshift. At the limiting redshift zvlim, the faintest considered cluster member galaxy was observed with 10σ confidence in the z band. Details are given in Appendix B. The luminosity of that galaxy is L = 0.2 L* for the eROMaPPer (eROSITA Matched-filter Probabilistic Percolation cluster finder) runs which used the grz and griz filter bands and L = 0.4L* for the runs that also included the w1 band. The dashed lines correspond to the full LS footprint while the continuous lines show the area that is reduced to the overlapping region with eRASS1 (see Fig. 2).

2.2.2 LS DR9 north

In the north (Decl. > 32.375°), LS uses the Beijing-Arizona Sky Survey (BASS, Zou et al. 2017) for g- and r-band coverage, and The Mayall z-band Legacy Survey (MzLS, Silva et al. 2016) for the z-band coverage. Since no additional observations were obtained between DR9 and DR10, the inference catalogs for this part of the sky are that of DR9. It covers 5068 deg2 (see Fig. 2). The overlap with eRASS1 is 462 deg2.

2.2.3 Processing of released catalogues

We processed the LS DR10 south and LS DR9 north data independently because the filter responses of the DECam differ from those of the cameras used by the MzLS and BASS. Fortunately, there is a common area of 341 deg2 between the two survey parts, which we used to perform consistency checks (see Sect. 4.1.2).

Each source in the LS has MASKBITS and FITBITS flags. They encode possible issues encountered in the data (mask) or during the catalog inference process (fit)2. We discarded sources that have set any of the MASKBITS=[0,1,4,7,10,11,12,13] when FITBITS!=9. This mainly affects regions around bright and medium bright stars, around bright galaxies in the Siena Galaxy Atlas (Moustakas et al. 2023), and around globular clusters. The bright galaxies in the Siena Galaxy Atlas were kept even when the listed MASKBITS had been set.

2.3 Spectroscopic galaxy redshift compilation

We have compiled 4 882 137 spectroscopic galaxy redshifts from the literature. This compilation serves two goals: calibrating the red-sequence models (Appendix C; ~90000 redshifts) and calculating spectroscopic cluster redshifts and velocity dispersions. The references considered to create the compilation are listed in Appendix D. There, we list the selection criteria applied to the published catalogs to retrieve high-quality redshifts and to avoid stars or quasi-stellar objects. Dedicated spectroscopic follow-up programs are being undertaken for eRASS1 clusters. We included 154 unpublished galaxy redshifts from Balzer et al. (in prep), who utilize the VIRUS instrument (Hill et al. 2021) on the Hobby-Eberly Telescope (Ramsey et al. 1998; Hill et al. 2021).

All galaxies in the spectroscopic compilation were matched to sources in the LS catalogs using a search radius of 1″. If multiple redshifts were available for a source, we chose the redshift from the closest match.

3 Measurement of cluster candidate counterparts in the optical and near-infrared

Star formation in galaxies is quickly quenched after the galaxy reaches the first peri-center on its orbit in the cluster (e.g., Oman & Hudson 2016; Lotz et al. 2019). Optical and near-infrared colors of quenched galaxies are relatively insensitive to stellar ages older than a few Gyrs (e.g., Bruzual & Charlot 2003). Hence, cluster members can be identified by relatively uniform optical and near-infrared colors. These colors strongly depend on redshift, enabling the measurement of photometric cluster redshifts. We identify an X-ray extended source (cluster candidate) as a genuine galaxy cluster by associating it with a coincident overdensity of red-sequence galaxies. The reliability of the identification depends on several factors that we investigate and quantify in the following sections.

We introduce the cluster finder redMaPPer in Sec. 3.1 and our enhancements to it in the following subsections. We refer to the enhanced redMaPPer package as eROMaPPer (eROSITA Matched-filter Probabilistic Percolation cluster finder).

3.1 redMaPPer

We applied the well-tested and publicly available red-sequence Matched-filter Probabilistic Percolation cluster finder (redMaPPer3, Rykoff et al. 2012, 2014, 2016). Its usage is flexible and multi-purpose (e.g., Rykoff et al. 2012; Rozo & Rykoff 2014; Rykoff et al. 2016; Bleem et al. 2020; Finoguenov et al. 2020). The redMaPPer algorithm applies three filters in luminosity, color, and sky position. It finds clusters and creates samples thereof. Spectroscopic verification demonstrates the high purity of the cluster samples obtained: ≳ 90% of the redMaPPer-identified systems are condensations in redshift space, even at the lowest values of optical richness in the HectoMAP redshift survey down to r = 21.3 (Sohn et al. 2018b, 2021). Further tests by reshuffling members of true clusters and re-detecting those clusters confirm a high purity of ≳95% in the SDSS when z ∈ [0.1,0.6) (Rykoff et al. 2014), meaning these clusters are not significantly affected by projection effects. In this paper, we define purity as the probability that an extended eRASS1 X-ray source that was optically identified using eROMaPPer is neither an X-ray background fluctuation nor an AGN. The completeness of the returned samples has been estimated for a similar red-sequence-based cluster finder (RedGOLD, Licitra et al. 2016a,b) to be ~100% (~70%) at z < 0.6 (z < 1.0) for galaxy clusters with M > 1014 M⊙ (Euclid Collaboration 2019). The decreasing completeness at high redshift relative to results from other cluster finders like AMICO (Bellagamba et al. 2018) is likely attributed to the increasing fraction of blue star-forming galaxies (Nishizawa et al. 2018) to which redMaPPer is insensitive.

Many spectroscopic observing campaigns use a target selection based on redMaPPer catalogs (e.g., Clerc et al. 2016; Rykoff et al. 2016; Rines et al. 2018; Sohn et al. 2018b; Clerc et al. 2020; Kirkpatrick et al. 2021). It has also been used for numerous cosmological experiments (e.g., Costanzi et al. 2019b; Kirby et al. 2019; Ider Chitham et al. 2020; Costanzi et al. 2021), as well as mass calibration analyses (e.g., Saro et al. 2015; Baxter et al. 2016; Farahi et al. 2016; Melchior et al. 2017; Jimeno et al. 2018; Murata et al. 2018; Capasso et al. 2019; McClintock et al. 2019; Palmese et al. 2020; Raghunathan et al. 2019). The impact of projection effects (e.g., Costanzi et al. 2019a; Myles et al. 2021), centering (e.g., Rozo & Rykoff 2014; Hoshino et al. 2015; Hikage et al. 2018; Hollowood et al. 2019; Zhang et al. 2019) and intrinsic alignment (Huang et al. 2018) have also been studied in detail.

redMaPPer can be configured in several different modes, two of which are used in this paper. When configured in blind (cluster-finding) mode, only the optical and near-infrared galaxy catalogs from the LS are used to identify clusters. When configured in scanning mode, redMaPPer also considers a positional prior from an input cluster catalog. The search radius for cluster members around the fixed input coordinates is equivalent to the cluster radius Rλ (see Eq. (4) in Rykoff et al. 2014) Rλ=1.0h−1Mpc⁡(λ/100)0.2.$\[R_\lambda=1.0 h^{-1} \operatorname{Mpc}(\lambda / 100)^{0.2}.\]$(1)

To identify a cluster at a fixed location, redMaPPer evaluates a likelihood function L$\[\mathcal{L}\]$λ on a redshift grid (see Eq. (76) in Rykoff et al. 2014): ln⁡Lλ=−λS−∑iln⁡(1−pmem,i),$\[\ln \mathcal{L}_\lambda=-\frac{\lambda}{S}-\sum_i \ln \left(1-p_{\mathrm{mem}, i}\right),\]$(2)

where λ denotes the optical richness (see Eq. (3)). The likelihood depends only on the membership probabilities pmem, which in turn depend on the color distance from the red-sequence model in all considered filter bands, galaxy luminosity, galaxy spatial distribution, and global background galaxy density (Rykoff et al. 2014, 2016). The richness λ is defined as the sum of the membership probabilities multiplied by a scaling factor S, which depends amongst other properties on the masked fraction (Rykoff et al. 2014, see also Sect. 11): λ=S⋅∑ipmem,i.$\[\lambda=S \cdot \sum_i p_{\mathrm{mem}, i}.\]$(3)

The masked fraction of a cluster is calculated from the number of sources inside Rλ with nonzero MASKBITS and FITBITS (see Sec. 2.2) over the total number of sources within Rλ. Using simulations, it was estimated that the richness errors quoted in the redMaPPer catalogs underestimate the observational uncertainties by ~40-70% due to observational noise in the membership probabilities (Costanzi et al. 2019a). A cluster with richness λ = 20 has a typical signal-to-noise ratio of 3.

In the case of a free cluster center (redMaPPer blind mode), a centering likelihood is logarithmically added to ln L$\[\mathcal{L}\]$λ(z). The maximum ln L$\[\mathcal{L}\]$max of the resulting likelihood ln L$\[\mathcal{L}\]$(z) is determined, and the corresponding redshift is taken as the photometric cluster redshift zλ. All other optical cluster properties are evaluated at this redshift. A minimum of two initial member galaxies is required to start the algorithm. A richness cut of λ > 3 was applied at a later stage.

Enhancements to redMaPPer

First, we promoted redMaPPer to a strongly parallel application using the pyspark4 programming interface. This makes it feasible to run in blind mode on the full LS DR9 and DR10 galaxy catalogs (almost all of the extragalactic sky) within a few days. Second, we adopted the spectroscopic post-processing from SPIDERS (Clerc et al. 2020; Kirkpatrick et al. 2021); see Sec. 3.3. Finally, we wrote a module to select and rank targets for dedicated spectroscopic follow-up programs from SDSS-V (BHM-clusters) and 4MOST (S5). In the following sections, the package encapsulating these features will be referred to as eROMaPPer.

3.2 Cluster counterpart association, photometric redshift, and richness measurements

The optical cluster-finding process and the determination of the cluster optical properties (photometric redshift, richness, etc.) are simultaneous and interdependent. This can result in three distinct outcomes.

3.2.1 Cases with a single optical cluster counterpart

We determined the photometric cluster redshift, denoted zλ, by the maximum value of a parabola that is fitted to the L$\[\mathcal{L}\]$λ(z) curve. It is close to the highest peak of the blue curve in the example in Fig. 4, bottom-right panel. The likelihood includes via the membership probabilities the color distance to our red-sequence model, which is described in Appendix C. We analyze the accuracy and precision of the photometric redshifts in Sec. 8.

3.2.2 Ambiguous cases with multiple optical clusters along the line of sight

We identified ambiguous cases with multiple distinct peaks in ln L$\[\mathcal{L}\]$(z). These correspond to multiple red-sequence overdensities that overlap along the line of sight without necessarily being physically connected. We define the two Gaussians as distinct if their peaks are farther apart than |zλ,1 − zλ,2| > 0.05, the logarithmic peak ratio is at least ln L$\[\mathcal{L}\]$(zλ,2/ ln L$\[\mathcal{L}\]$(zλ,1) > 0.2, and both cluster likelihoods are above ln L$\[\mathcal{L}\]$(zλ,i) > 10 (which roughly corresponds to a richness λ > 14). In this consideration, zλ,1 is the redshift for the peak of the Gaussian that is closest to the photometric cluster redshift zλ, and zλ,2 is the redshift for the peak of the secondary Gaussian.

3.2.3 Cases with no optical cluster counterpart

Cluster candidates (extended X-ray sources) are considered unidentified by eROMaPPer if 1) it is unable to identify at least two red-sequence galaxies at any redshift, 2) the richness of the cluster is λ < 3, or 3) the cluster candidate is sufficiently far outside of the LS footprint. Clusters near the edge of the footprint can still be detected when the circle with radius Rλ partly overlaps with the footprint. More information for these cases is given in Appendix A.4.

thumbnail Fig. 4

Illustrative example 1eRASS J041610.4-240351 from the eRASS1 cluster catalog. The panels in the top row show an LS grz image of the full cluster overlaid with eRASS1 X-ray contours (left) and cluster members detected in this work (circles, right). Spectroscopic information is available for all cluster members marked by dashed circles. The bottom-left panel shows a zoom-in. The red circle marks the BCG, which agrees with the optical cluster center (green cross). The orange circle is located at the position of the central galaxy, which is the one closest to the X-ray center (yellow cross). North is up; east is left. In the bottom-right panel, upper subpanel, the cluster likelihood ln L$\[\mathcal{L}\]$(z) shows one peak at z = 0.385 which is close to the cluster photometric redshift zλ, = 0.3910 ± 0.0082. The bottom-right panel, lower subpanel, demonstrates the measurements of the spectroscopic redshift and the velocity dispersion for the shown cluster. The cluster has a richness of λ = 128.7 ± 8.5. The 127 photometric members are marked by circles. Of those, 121 have spectroscopic redshifts and are marked by dashed circles. The black histogram in the bottom panel shows the spectroscopic redshifts of the photometric members. Ten outlier galaxies with z ≶ zspec ± 3σ (blue dashed lines) are discarded, leaving Nmembers = 111 spectroscopic members. The cluster velocity dispersion is σ = 1034 ± 67 km s−1 (light blue line). The photometric cluster redshift (light red shades) agrees with the spectroscopic cluster redshift zspec = 0.39936 ± 0.00039 (darker blue line). The redshift of the galaxy at the optical center is zspec,cg = 0.3967 ± 0.0004 (green line). The literature redshift zlit = 0.38989 (purple line) is a photometric redshift from MARDY3 (Klein et al. 2019).

3.3 Spectroscopic cluster redshifts

Spectroscopic cluster redshifts zspec provide ~10 times more accurate estimates of the true cluster redshifts compared to our photometric redshifts (zλ; see Sec. 8). They are on the other hand more expensive to obtain in terms of telescope time and, therefore, are currently only available for a subset of the clusters. Moreover, they provide a means to estimate the bias and uncertainties of the photometric redshifts (see Sec. 8) and allow us to calculate cluster velocity dispersions σ.

The automated algorithm to obtain the spectroscopic cluster redshifts has been adopted from the work of Clerc et al. (2016) and Ferragamo et al. (2020) and is the basis of the automatic spectroscopic redshift pipeline used within the SPIDERS cluster program (Ider Chitham et al. 2020; Clerc et al. 2020; Kirkpatrick et al. 2021). The algorithm is iterative, with the subscript k referring to the kth iteration of the procedure.

First, we matched the cluster members selected by eROMaPPer to our spectroscopic galaxy compilation (see Sec. 2.3). The number of matches is Nspec,0. Fig. 4, bottom panel, shows the member redshift distribution for the example cluster 1eRASS J085401.2+290316 by the gray bars. The initial spectroscopic cluster redshift was estimated by the bi-weight location estimate (Beers et al. 1990) zbwt=z^+∑|uj|<1(zj−z^)[1−uj2(z,zj,6)]2∑|uj|<1[1−uj2(z,zj,6)]2,$\[z_{\mathrm{bwt}}=\hat{z}+\frac{\sum_{\left|u_j\right|<1}\left(z_j-\hat{z}\right)\left[1-u_j^2\left(z, z_j, 6\right)\right]^2}{\sum_{\left|u_j\right|<1}\left[1-u_j^2\left(z, z_j, 6\right)\right]^2},\]$(4)

where z is a vector of galaxy redshifts, z^$\[\hat{z}\]$ is the sample median, j is the index of the spectroscopic member galaxy and uj is given by uj(z,zj,a)=(zj−z^)a×MAD⁡(z).$\[u_j\left(z, z_j, a\right)=\frac{\left(z_j-\hat{z}\right)}{a \times \operatorname{MAD}(z)}.\]$(5)

Here, a = 6 is the tuning constant that regulates the weighting and corresponds to the clipping threshold in units of the median absolute deviation MAD(z) of the member galaxy redshifts.

The proper line-of-sight velocity offset (Danese et al. 1980) of all member galaxies was then computed relative to the estimate of the cluster redshift; vjc=zj−zbwt1+zbwt.$\[\frac{v_j}{c}=\frac{z_j-z_{\mathrm{bwt}}}{1+z_{\mathrm{bwt}}}.\]$(6)

Figure 4, bottom panel, illustrates for the example cluster 1eRASS J041610.3-240351 the necessity to clip outliers. While the bulk of member redshifts is concentrated around z = 0.40, ten photometrically selected member galaxies have significantly lower or higher redshifts. Therefore, we performed an initial velocity clipping of members with |vj| > 5000 km s−1 to reject them from the spectroscopic sample of member galaxies. This results in Nspec,1 spectroscopic members for the first iteration (k = 1), which are used to recompute the bi-weight cluster redshift using Eq. (4). This procedure is iterated until Nspec,k converges or a maximum of k = 20 iterations is reached. In each iteration k > 1, the clipping velocity is recalculated as vj > 3σk, where σk is the cluster velocity dispersion for the k-th iteration (see Sec. 3.6). There are several possible outcomes of the clipping procedure:

  • 1)

    Nspec,1 = 0: the initial 5000 km s−1 clipping rejected all members: the procedure cannot proceed and a flag is issued to indicate that convergence failed. This can occur for true systems when several distinct structures along the line of sight are far apart in redshift space.

  • 2)

    0 < Nspec,k < 3: There is an insufficient number of spectroscopic members left after k steps: it is not possible to estimate the bi-weight redshift estimate (Eq. (4)) or the velocity dispersion (Eq. (8)) and a flag is issued accordingly.

  • 3)

    Nspec,k ≥ 3: the process successfully converged, and the cluster redshift and velocity dispersion are estimated.

In the last case, the remaining objects are called spectroscopic members. Even when the iterative procedure converges, it is essential to check the final clipping velocity. If it is larger than the initial 5000 km s−1, there is likely a substructure that biases the spectroscopic cluster redshift. A flag was assigned in this case. The spectroscopic cluster redshift zspec was calculated by taking the mean of all zbwt values, calculated after bootstrapping the clipped spectroscopic member redshifts 64 times. The standard deviation of these zbwt values was adopted as the spectroscopic cluster redshift uncertainty δzspec.

In cases 1) and 2), it can still be possible to assign a spectroscopic redshift to a cluster. If there was a spectroscopic redshift available for the identified central galaxy (CG), it was taken as the cluster redshift zspec,cg. The uncertainty of the CG redshift was used as the cluster redshift uncertainty. This underestimates the cluster redshift uncertainty because the central galaxy can have a non-negligible line-of-sight velocity with respect to the cluster as a whole (Lauer et al. 2014). We quantify this effect for the eRASS1 clusters in Sect. 4.2.2. For an example cluster in Fig. 4, we mark zspec,cg by the green line. The darker blue line shows the confidence interval δzspec of the more robust zspec.

Table 1

Literature catalogs matched to the eRASS1 extended X-ray sources.

3.4 Literature cluster redshifts

We matched all X-ray cluster candidates (including those outside the LS footprint) with the public catalogs listed in Table 1. The matching radius was 2′! and if multiple matches were found, we selected the cluster nearest to the X-ray centroid. This enabled us to assign redshifts to eRASS1 clusters that were not found by eROMaPPer or even choose the literature redshift zlit as our best redshift zbest if an incorrect optical counterpart was selected (see Sect. 4.2.2). The literature redshift can either be photometric or spectroscopic. We did not distinguish these two cases.

3.5 Assigning the best redshift type

We selected the best redshift zbest from the available spectroscopic zspec or zspec,cg, photometric zλ, and literature redshifts zlit by assigning priorities to them in the following order:

  1. zspec if the cluster has at least three spectroscopic members and the final velocity clipping converged,

  2. zspec,cg if there is a spectroscopic redshift for the galaxy at the optical center,

  3. zλ if a photometric redshift is available and it is within the calibrated redshift range (see below),

  4. zlit otherwise.

The spectroscopic redshift zspec received the highest priority because it has a low uncertainty and is unbiased. The zspec,cg is also unbiased. Still, it has a larger uncertainty because the central galaxy can have a non-zero line-of-sight velocity relative to the cluster (see example in Fig. 4). We perform a detailed analysis of the photometric redshift accuracy in Sec. 8.

The photometric redshifts were calibrated in a limited red-shift range 0.05 < zλ < 0.9 (for the grz & griz runs), or 0.05 < zλ < 1.2 (for the grzw1 & grizw1 runs). Details are given in Appendix C. Only photometric redshifts inside that range are reliable. If a cluster photometric redshift is outside these limits and no spectroscopic redshift is available, we adopted the literature redshift as the best redshift if it was available.

3.6 Velocity dispersion from spectroscopic member redshifts

Simultaneously with the spectroscopic cluster redshifts (see Sec. 3.3), the velocity dispersion (Beers et al. 1990) was calculated using the biweight scale estimator (Eq. (7), if Nspec,k ≥ 15) or the gapper estimator (Eq. (8), if 3 ≤ Nspec,k < 15).

The biweight scale estimator (Tukey 1958) is defined5 as σbwt(Nspec)=Nspec∑|uj|<1(vi−v^)2(1−uj2)4|(∑|uj|<1(1−uj2)(1−5uj2))|,$\[\sigma_{\mathrm{bwt}}\left(N_{\mathrm{spec}}\right)=\sqrt{N_{\mathrm{spec}}} \frac{\sqrt{\sum_{\left|u_j\right|<1}\left(v_i-\hat{v}\right)^2\left(1-u_j^2\right)^4}}{\left|\left(\sum_{\left|u_j\right|<1}\left(1-u_j^2\right)\left(1-5 u_j^2\right)\right)\right|},\]$(7)

where uj = uj(v, vj, 9) (see Eq. (5)). The gapper estimator (Wainer & Thissen 1976) is based on the gaps of an ordered statistic, xj, xi+1,..., xn. It is defined as a weighted average of gaps: σgap(Nspec)=πNspec(Nspec−1)∑j=1Nspec −1wjgj,$\[\sigma_{\mathrm{gap}}\left(N_{\mathrm{spec}}\right)=\frac{\sqrt{\pi}}{N_{\mathrm{spec}}\left(N_{\mathrm{spec}}-1\right)} \sum_{j=1}^{N_{\text {spec }}-1} w_j g_j,\]$(8)

where weights and gaps are given by wj and gj respectively wj=j(Nspec −1),$\[w_j=j\left(N_{\text {spec }}-1\right),\]$(9) gj=xj+1−xj.$\[g_j=x_{j+1}-x_j.\]$(10)

Spectroscopic galaxies with vj > 3σ were rejected as outliers during a further σ clipping process. This procedure was iterated until no outlier galaxies remained or up to a maximum of 20 iterations (k ≤ 20).

Analogous to the spectroscopic cluster redshift, the velocity dispersion was calculated 64 times after bootstrapping member galaxies. The mean of these results was adopted as the final value for the velocity dispersion, and the standard deviation was adopted as the uncertainty. The ratio of the numbers of flagged converged bootstrapping results to all converged bootstrapping results was stored as the velocity dispersion flag. The closer it is to 1, the less robust the velocity dispersion is.

4 The eRASS1 identified cluster and group catalog

The main outcome of this work is the optical properties (redshifts, richnesses, etc.; see Appendix E) of the galaxy clusters and groups detected in eRASS1. Most extended X-ray sources are genuine galaxy clusters. However, AGN (or other point sources), as well as random background fluctuations and supernova remnants may have been detected as extended sources, inducing contamination among the cluster candidates. The contamination rate is anti-correlated with the brightness of the source and its likelihood to be extended L$\[\mathcal{L}\]$ext. Using simulations, Seppi et al. (2022) predicted that the purity is ~97% (~50%) when considering a sample with L$\[\mathcal{L}\]$ext > 3 and above an average flux limit of 8.0 (0.4) ×10−13 ergs s−1 cm−2. The eRASS1 cluster candidate catalog is not strictly flux-limited because of the spatially varying exposure time. The precise limits are described by the selection function (Clerc et al. 2024, in particular their Fig. E.1). However, an approximate flux limit in an aperture enclosing 500 times the critical density of the Universe at the cluster’s redshift is F500 ≈ 0.4 × 10−13 ergs s−1 cm−2 (Bulbul et al. 2024). Depending on the science case, more or less pure and complete samples can be selected by applying cuts in F500 or L$\[\mathcal{L}\]$ext.

For the same flux thresholds, the completeness is expected to be ~90% (~11.3%). Selecting cluster candidates with a higher threshold in L$\[\mathcal{L}\]$ext yields higher purity but at the cost of lower completeness for the same flux limit (see also Bulbul et al. 2024). The threshold of L$\[\mathcal{L}\]$ext > 3 was applied in this work to prefer high completeness. The low purity for the low flux threshold was increased significantly in this work by requiring cluster candidates to be identified using optical and near-infrared imaging data.

In that process, we cleaned the eRASS1 cluster candidate catalog of 2497 extended X-ray source detections for which we found no counterpart in the optical data, and of 458 detections which we classified visually as contamination. These results were achieved by running eROMaPPer in scan mode on the positions of all candidate galaxy clusters and groups in eRASS1. We detail the procedure for constructing the catalog in Sec. 4.1 and describe its contents in Sec. 4.2.

4.1 Constructing the catalog

In scan mode, we fixed the cluster coordinates to the cataloged X-ray coordinates (RA, Dec). The member search radius is given in Eq. (1). The eROMaPPer runs were done with different combinations of the g,r,i,z, and w1 filters. The optimal filter band combination changes with redshift. We find in Sects. 8.1 and 8.2 that grz performed well at low and intermediate redshifts zλ ≤ 0.8 while grizw1 was best suited for high redshifts zλ > 0.8. For the catalogs obtained in eROMaPPer scan mode, we merged the different runs afterward using a priority scheme.

The richness λ measurement varied from run to run. That is because membership probabilities change when more filter bands are included and different galaxy luminosity cuts are applied. We calculate a normalized richness λnorm where these systematic effects are corrected in Sect. 4.1.2.

4.1.1 Catalog merging

Six different eROMaPPer runs were done on the eRASS1 cluster candidate catalog: four of them for the southern LS in the filter band combinations grz, griz, grizw1, and grzw1, and two of them for the northern LS in the filter band combinations grz and grzw1. No i-band data are available for the northern surveys. The resulting catalogs were merged using the following priority scheme:

1. LS DR10 south grz if zλ ≤ 0.8 (10,823),
2. LS DR10 south griz if zλ ≤ 0.8 (314),
3. LS DR9 north grz if zλ ≤ 0.8 (202),
4. LS DR10 south grizw1 if zλ > 0.8 (485),
5. LS DR10 south grzw1 if zλ > 0.8 (113),
6. LS DR9 north grzw1 if zλ > 0.8 (7),
7. other (303),
————
(12,247).

Most clusters were identified in more than one run. The priority scheme avoids multiple entries in the merged catalog for the same cluster by selecting the result only from the run with the highest priority. In parenthesis is the number of clusters for each category that went into the merged eRASS1 identified catalog. For example, in run 1, we found 10823 clusters, while adding the i band (run 2) complemented the catalog by an additional 314 clusters6. In the category “other” fall clusters that are either at z > 0.8 and only detected in the grz or griz runs (114), or at z ≤ 0.8 and only detected in the grizw1 or grzw1 runs (35). If they were detected in more than one run and were always outside the constrained redshift range (7), we still followed the priority scheme but neglected the redshift constraint. Moreover, we included clusters with no counterpart in the LS but are matched with a cluster from the literature (147). The result is a robustly constructed catalog of the optical properties for 12 247 identified eRASS1 galaxy clusters and groups.

4.1.2 Richness normalization

The cluster richness λ is the scaled sum of the membership probabilities pmem,i (see Eq. (3)). Calculating the scaling factor (“SCALEVAL” in the catalog or S in Eq. (3)) is part of the redMaPPer algorithm (Rykoff et al. 2014) and includes corrections for the masked area and the limited depth in the optical images (see Appendix B). In this section, we homogenize the richness measurements depending on the filter band combination and the minimum galaxy luminosity. For the grz and griz runs, we selected only galaxies with a minimum luminosity of L > 0.2 L*, where L* is the break of the Schechter luminosity function (Schechter 1976). This luminosity cut minimizes the scatter of the X-ray luminosity at fixed richness (Rykoff et al. 2012). Where the LS is sufficiently deep to reliably (with 10σ significance) measure galaxy luminosities down to the minimum member galaxy luminosity (i.e., zλ < zvlim), the luminosity cut ensures consistent richness measurements across redshift because L* is an intrinsic property of the galaxy populations. For the grzw1 and grizw1 runs, we applied a higher minimum luminosity of L > 0.4 L* to obtain (noisier but) unbiased richnesses at higher redshift z > 0.8 (see Appendix B). When the luminosity threshold increases, the richness is systematically smaller because fewer galaxies are selected. To correct for this effect, we define a normalized richness; λnorm =S normλ$\[\lambda_{\text {norm }}=S_{~\text {norm}} \lambda\]$(11)

and its uncertainty δλnorm =S normδλ$\[\delta \lambda_{\text {norm }}=S_{~\text {norm}} \delta \lambda\]$(12)

It was determined by comparing the richness of the same clusters measured in different runs. The relations were fit by minimizing the uncertainty-weighted squared orthogonal distances to the best-fit line (Boggs et al. 1989). We also applied an orthogonal cut at low richness to not bias the slope. The resulting scaling factors are given in Table 2.

Table 2

Richness scaling factors.

4.1.3 Assigning the BCG

Near the center of a galaxy cluster often resides a disproportionately bright and extended early-type galaxy called the Brightest Cluster Galaxy (BCG). These galaxies are distinct from normal massive early-type galaxies due to their embedding in the faint Intracluster Light (ICL, see recent reviews by Contini 2021; Arnaboldi & Gerhard 2022; Montes 2022).

The choice of the BCG can be ambiguous in ~20% of the cases (Kluge et al. 2020). For simplicity, we defined the BCG as the brightest member galaxy in the z band. We explore the justification for this definition in Sec. 5.5.

4.2 Properties of the eRASS1 catalog of identified clusters and groups

In this section, we detail the overall statistics of the results obtained with the eROMaPPer runs on the eRASS1 cluster candidate catalog.

4.2.1 Cluster identification statistics

The eRASS1 source catalog covers half of the sky. It contains 26 682 extended sources (Merloni et al. 2024). After cleaning split sources and masking regions of known non-cluster extended X-ray sources (see Sec. 2.1 and Bulbul et al. 2024), we obtain a sample of 22718 cluster candidates with extent likelihood L$\[\mathcal{L}\]$ext > 3. We ran eROMaPPer in scan mode on this sample and obtained optical properties (redshifts, richnesses, optical centers, and BCG positions) for 12 705 clusters.

Most of the rejected candidates (7516) are outside of the LS footprint (see Fig. 2 and Appendix A.4) and have no match to known clusters in the literature (see Sec. 3.4). A further 2497 rejected candidates have LS coverage, but no optical red sequence counterpart has been found with eROMaPPer. These X-ray sources are most likely AGN or random background fluctuations misidentified as extended sources (Bulbul et al. 2022). We discuss the properties of these contaminating sources in Sec. 7. It is also possible that some real clusters were not optically identified because their redshift is higher than the limiting redshift of the LS z ≫ zvlim. Finally, we performed a visual cleaning procedure as described in Sect. 4.2.2. This further reduced the sample to a final size of 12247 eRASS1 clusters in a sky area of 13 116 deg2, so an average density of about one cluster per square degree.

The association of the X-ray signal with the optical cluster was straightforward in 97% of the cases. For the remaining 332 eRASS1 clusters (3%) with zλ < zvlim, we found overlapping structures in projection. A secondary photometric redshift zλ,2 is provided in these cases. It is mentioned in Bulbul et al. (2024) that one eFEDS cluster (eFEDSJ091509.5+051521, Klein et al. 2022; Liu et al. 2022) has inconsistent redshift (z = 0.249) to its counterpart 1eRASS J091510.8+051440 (zspec = 0.136). We find that it agrees with zλ,2 = 0.269.

Close but separate X-ray sources can have a large number of common members identified when their separation is smaller than the optical cluster radius Rλ. This leads to a small number of 413 (3%) eRASS1 clusters that share >70% of their members with another cluster that has a higher likelihood L$\[\mathcal{L}\]$max. We marked the cluster with lower L$\[\mathcal{L}\]$max in the eRASS1 catalog by flagging it as SHARED_MEMBERS.

4.2.2 Cluster redshifts

Each of the 12 247 eRASS1 clusters has at least one redshift assigned. In 5428 cases where multiple redshifts are available, we followed a priority scheme to assign the best redshift zbest from up to four available redshift types (see Sec. 3.5). Table 3 summarizes the results for the eRASS1 identified catalog. Most values of zbest are photometric (72%). We perform a detailed analysis of the accuracy of the photometric redshifts in Sec. 8. Higher-quality spectroscopic redshifts are available for a significant fraction (26%). Literature redshifts were adopted only in rare cases (2%). Figure 5 shows the number of clusters per redshift bin with associated redshifts. At low redshifts z < 0.15, more than half of the eRASS1 clusters have a reliable spectroscopic redshift. This number falls below 10% above z > 0.6.

The spectroscopic redshifts are calculated using the robust bootstrapped bi-weight method (15%; see Sec. 3.3) or adopted from the spectroscopic redshift of the central galaxy (12%). We note that the formal uncertainties for the latter method underestimate the real cluster redshift uncertainties because individual cluster member galaxies can have a non-negligible line-of-sight velocity with respect to the cluster rest frame (see Sec. 3.3 and Fig. 4). For the eRASS1 clusters, the mean offset velocity is 80% of the cluster velocity dispersion. This corresponds to a mean uncertainty of δz = 0.0013.

Literature redshifts, when available, were adopted for clusters (a) outside of the LS footprint (126 cases), (b) within the LS footprint but without an optical detection (21 cases), (c) where we decided after visual inspection that the optical detection is in projection to the X-ray source (95 cases), or (d) at low or high redshifts where zλ is outside of the calibration range for the red sequence (z < 0.05 and z > 1.2, see Appendix C) and no spectroscopic redshift was available (5 cases). In total, 247 eRASS1 clusters have zbest = zlit. The 21 matched clusters within the LS footprint but without optical detection by us, are (a) at very low redshift zlit < 0.05 (14 cases), (b) at higher redshift than the limiting redshift of the LS (2 cases), (c) a very poor group (1eRASS J022946.2-293740), (d) consist only of late-type galaxies (1eRASS J091433.5+063417), or not detected for unknown reasons (1eRASS J050808.8-525124, 1eRASS J055136.2-532733, 1eRASS J102144.9+235552).

Furthermore, there are cases in which more than one cluster is projected near the X-ray emission. In these cases, eROMaPPer chooses the cluster with the highest likelihood ln L$\[\mathcal{L}\]$max, which correlates with the richness by definition. This is generally a good strategy when the galaxy sample is complete. However, we show in Sec. 5.3 that the optical completeness drops below z ≲ 0.05 because we discarded galaxies near bright and extended galaxies. Consequently, if the cluster is at low redshift, eROMaPPer often chooses a background cluster. We identified these cases by

  • matching all clusters with the NGC catalog (Dreyer 1888) using a 30″ search radius,

  • looking for a secondary low-zλ,2 peak in the ln L$\[\mathcal{L}\]$(z) distributions (see Sec. 3.2),

  • selecting clusters with low zlit,

  • searching for close pairs in the X-ray images

and inspecting their X-ray images, optical images, and member galaxy distributions visually. For the cases that we judged to be misidentified, we set zbest = zlit if a literature redshift was available (87 cases). If no zlit was available or we judged that the X-ray signal is not spatially associated with the cluster’s ICM emission, we discarded that cluster (458 cases). This includes 31 cases where the X-ray signal is associated with the central emission of a nearby late-type or strongly distorted galaxy at zlit < 0.01.

Table 3

Redshift types and occurrences in the eRASS1 catalog.

thumbnail Fig. 5

Number (top panel) and relative fraction (bottom panel) of eRASS1 clusters per redshift bin depending on their best redshift type. The total numbers are 8790 photometric redshifts (zλ, Sec. 3.2), 1759 spectroscopic redshifts determined using the bootstrap method (zspec, Sec. 3.3), 1451 spectroscopic redshifts of the galaxy at the optical center (zspec,cg, Sec. 3.3), and 247 literature redshifts (zlit, Sec. 3.4). Clusters with unflagged velocity dispersion information (Sec. 3.6) have the same distribution as the zspec sample.
thumbnail Fig. 6

Slice of the cosmic volume with eRASS1 clusters with available spectroscopic redshifts zspec overplotted onto our spectroscopic galaxy compilation (gray points). The slice has a thickness of ±2° around Decl. = 0°. Red points mark the positions of eRASS1 clusters when spectroscopic redshifts were used. They trace the nodes of the cosmic web. Green points mark the same clusters, but this time, we used the photometric redshifts. They scatter around the nodes of the cosmic web because of the higher redshift uncertainty.

4.2.3 eRASS1 clusters in the large-scale structure

Massive galaxy clusters are located at the nodes of the cosmic web. Galaxies trace this web and can be visualized by selecting a thin slice limited in declination around ±2°. Figure 6 shows a zoom-in on the redshift range 0 ≤ z ≤ 0.2. We also restricted the range in right ascension (125° < RA < 223°) to the overlapping area in the western Galactic hemisphere that is well covered by eROSITA (see Fig. 2). Gray data points correspond to the redshifts of the galaxies in our spectroscopic compilation (see Sec. 2.3 and Appendix D). Three slices in RA have a high galaxy density. They correspond to the GAMA fields G09, G12, and G15 (Driver et al. 2022). Overplotted in green are the positions of the eRASS1 clusters when using their photometric redshifts. We show in Sec. 8.2 that these redshifts have an uncertainty of δZ ≈ 0.005-0.015. This is sufficiently large to cause an apparent displacement of the eRASS1 clusters from their true position in the cosmic web. The red points correspond to the same clusters but are located at their spectroscopic redshifts, with a ~10 times higher precision (see Sec. 8). In these cases, the eRASS1 clusters trace the cosmic web well, as can be seen for example around z ≈ 0.08 and RA ≈ 200°.

thumbnail Fig. 7

Fraction of eRASS1 clusters with consistent best redshift zbest and literature redshift zlit depending on richness λnorm. Four different redshift tolerances are applied.

4.2.4 Consistency with known clusters

We matched all eRASS1 cluster candidates with the public catalogs in Table 1 as described in Sec. 3.4 and found 3886 pairs. The consistency of zbest with the matched zlit is shown in Fig. 7. We only considered clusters where the best redshift type is not the literature redshift and the masking fraction is below < 10%. The four colored lines refer to different allowed redshift deviations. Above a richness of λnorm = 20, 94% of the matched clusters have consistent redshifts within |zbest − zlit|/(1 + zlit) < 0.02. The fraction increases to > 98% with larger allowed redshift deviations |zbest − zlit|/(1 + zlit) < 0.10. The remaining inconsistencies are explained by ambiguous cluster choices in the presence of multiple structures along the line of sight (see Sect. 3.2.2). At low richness (λnorm < 20), these ambiguous choices become more frequent because the purity decreases as we show in Sec. 7. Here, about 80% (92%) of the matched clusters have consistent redshifts within |zbest − zlit|/(1 + zlit) < 0.02 (< 0.10).

Surprisingly, two matched clusters with large richnesses λnorm > 100 are inconsistent with the literature redshift. The first outlier, 1eRASS J094813.0+290709, is a rich cluster with λ = 133 ± 7 at high redshift zλ = 0.766 ± 0.013. The eRASS1 X-ray signal is well centered on that cluster. Its matched counterpart in the CODEX catalog has a significantly lower redshift zlit = 0.253 and lower richness λlit = 19 ± 2. We identify another cluster in close proximity (2.4′ east) in our blind-mode eROMaPPer catalog, which we describe in Sec. 6.1. Its redshift zspec = 0.254 is consistent with the CODEX redshift. One likely reason for the different choices is the limited depth. CODEX was limited to a lower redshift range z ≲ 0.6 because it relied on shallower SDSS data where the high-z cluster is not visible. Another possibility is miscentering. CODEX relied on ROSAT data with a much larger PSF. This could have played a role in determining the cluster center in the CODEX catalog.

The second outlier, 1eRASS J020628.4-145358 (Abell 305), has a robust redshift of zλ = 0.298 ± 0.006. Its matched counterpart MCXC J0206.4-1453 is at zlit = 0.153. The literature redshift was measured using spectroscopic redshifts of two galaxies (Romer 1994). We identified one late-type galaxy LEDA 918533 close (≈20″) to the eRASS1 X-ray emission peak, which could be a foreground galaxy that was misclassified as a cluster member by Romer (1994).

thumbnail Fig. 8

Number of clusters per redshift interval Δzλ = 0.05. For catalogs created in this work (blue), we used the best redshift zbest, and for literature catalogs, we used the published redshift zlit. Each panel refers to a different cluster selection method. The smoothed histograms were obtained by summing over the redshift posteriors of all clusters. For better visibility, the distributions were additionally smoothed with a Gaussian kernel with a standard deviation Δzλ = 0.04. For the eRASS1 catalog, the upper border of the filled region refers to all 12 247 clusters, and the lower border refers to the subset of 10 959 clusters with zλ < zvlim. A richness cut λnorm > 16 and a limiting redshift cut zλ < zvlim were only applied to the optically selected combined LS DR10 south and LS DR9 north catalogs (LS N+S). That makes them comparable to the DES year 1 catalog, which has a consistent richness cut of λ > 20 applied (see Sec. 5.4).

4.2.5 Cluster velocity dispersions

For all eRASS1 clusters with at least three spectroscopic member galaxies, we calculated the cluster velocity dispersion σ as the line-of-sight velocity dispersion of those galaxies. The total number of eRASS1 clusters with an estimated velocity dispersion is identical to the number of 1906 clusters with available spectroscopic redshift zspec (see Table 3). However, the flagging is stricter. For zspec, we required the velocity clipping of the full sample of spectroscopic members to converge. For σ, we required the velocity clipping for all bootstrapped realizations to converge. This gave more robust results by reducing the number of clusters with substructure. Of the 1906 spectroscopic clusters, 1499 were not flagged and, hence, have robust σ estimates.

The clusters with robust σ estimates against redshift are similar to the distribution shown for zspec in Fig. 5 by the orange line. We do not show the histogram for σ explicitly.

Of those 1499 clusters, 358 have high-quality velocity dispersion values calculated with the bi-weight scale estimator (see Sec. 3.6). As we required a large number of Nmembers ≥ 15 spectroscopic members for this method, these values have a low relative uncertainty: δσ/σ ~ 20%. The remaining 1141 velocity dispersions were calculated with the gapper estimator. The relative uncertainties are on the order of δσ/σ ~ 40%. In total, 6.5% of the photometric members with spectroscopic redshift information were discarded by the velocity clipping procedure.

5 Quality assessments of the eRASS1 catalog

In addition to the eRASS1 catalog, we ran eROMaPPer in scan mode on various catalogs of candidate clusters from the literature, selected using different methodologies. By doing so, we can compare our results to the redshifts and richnesses measured in previous works. In addition to this, we ran eROMaPPer in blind mode on the full LS DR10 south and LS DR9 north. This enabled the analysis of selection effects that arose purely from processing the optical and near-infrared data. These effects can manifest as a depth-dependent contamination rate and possible deviations of the cluster number density from a theoretical halo-mass function.

The input catalogs used are listed in Table 4. These include clusters that are selected using their X-ray signal: CODEX (Finoguenov et al. 2020), MCXC (Piffaretti et al. 2011), NORAS (Böhringer et al. 2017), XXL (Adami et al. 2018), XCLASS (Koulouridis et al. 2021), using the Sunyaev Zeldovich (SZ) effect: ACT (Hilton et al. 2021), SPT (Bleem et al. 2015), Planck (Planck Collaboration XXVII 2016), or via optical overdensities of galaxies: ACO (Abell et al. 1989), DES (Abbott et al. 2020). The number of clusters contained in these catalogs against redshift is shown in Fig. 8. Approximate footprints are shown in Fig. 9. Black heal pixels, each covering an area of 13.4 deg2, are within the footprint of the LS, and gray heal pixels are outside of them. Patchy maps indicate a low number density of clusters.

5.1 Comparison to other X-ray-selected catalogs

We show the number of eRASS1 clusters against redshift zbest as the blue line in Fig. 8, left panel. The median redshift of the eRASS1 sample is zbest = 0.31, and the highest is zbest = 1.32 (1eRASS J020547.4-582902). The line width increases toward higher redshift. Its upper border corresponds to the full sample of 12 247 clusters. The lower border corresponds to the subsample of 10959 clusters with zλ < zvlim; that is, the photometric redshift must be below the local limiting redshift of the LS (see Appendix B). We explore the increasing contamination associated with exceeding the limiting redshift in Sec. 6.6.

The eRASS1 cluster catalog contains the largest number of identified clusters of all considered literature catalogs (see Table 4). Compared to other X-ray-selected catalogs, the advantage is the larger survey area than XMM-Newton (green lines in Fig. 8, see also Fig. 9 and Table 4) and the better sensitivity and smaller PSF than ROSAT (orange lines in Fig. 8).

For CODEX, the source detection on RASS data had been improved, reaching a similar depth to eRASS1. The contamination in the cluster candidate sample is high but the published catalog had already been cleaned by identifying the candidates using redMaPPer and SDSS data. A great advantage of eROSITA over ROSAT is that the sharper PSF is better suited to filter sources at high redshift by their extent, leading to purer cluster samples. Moreover, the CODEX sample was limited in redshift to z ≲ 0.6 by the usage of shallower SDSS imaging data.

thumbnail Fig. 9

Footprint maps for the cluster catalogs used in this work. The HEALPix resolution is NSIDE = 16 =^$\[\hat{=}\]$ 13.4 deg2. Black regions overlap with the LS footprint and gray regions are outside of it. White holes within the footprint indicate that the local cluster number density in a catalog is less than 1 per heal pixel.

5.2 High-z optical completeness

We estimated the high-z completeness of the eRASS1 identified catalog using SZ-selected catalogs. The SZ signal is independent of redshift7, which has been exploited to produce highly complete catalogs with 90% completeness for M500c > 3.8 × 1014 M⊙ at (ACT, Hilton et al. 2021) or nearly 100% completeness for M500c>7×1014h70−1 M⊙$\[M_{500 \mathrm{c}}>7 \times 10^{14} h_{70}^{-1} ~M_{\odot}\]$ at z > 0.25 (SPT, Bleem et al. 2015). Figure 8, middle panel, confirms that the number of clusters remains large at high literature redshift in the ACT, SPT, and Planck catalogs. Hence, they are well suited for testing the optical completeness of high-z clusters in the eRASS1 catalog. For this, we ran eROMaPPer in scan mode on the locations of the literature clusters. We define the optical completeness C as the number of eROMaPPer-identified clusters Nlit&ero to the total number of clusters Nlit in the SZ-selected literature catalogs C(z)=Nlit&ero(z)Nlit(z).$\[C(z)=\frac{N_{\text {lit&ero}}(z)}{N_{\text {lit}}(z)}.\]$(13)

Thereby, we only considered clusters that lie within the LS footprint. Furthermore, the literature redshift must be lower than the limiting redshift of the LS zlit < zvlim. To avoid mismatches in the cases of overlapping clusters, we required |zbest − zlit| < 0.1 for a cluster to be considered a match. Figure 10, right panel, confirms a high optical completeness C > 0.95 for zλ < 1.1. We emphasize that the optical completeness does not take the completeness of the X-ray source catalog into account (see Sec. 4). It is solely sensitive to the processing of the optical and near-infrared data.

The median richness is λnorm = 50 for the ACT and SPT catalogs. For Planck, it is λnorm = 70, which explains the lower number of clusters even though it is an all-sky survey. In the eRASS1 catalog, the median richness is lower with λnorm = 25 because eROSITA is more sensitive to galaxy groups, especially at low redshift (Bahar et al. 2024).

5.3 Low-z optical completeness

We estimated the low-z completeness of the eRASS1 identified catalog with the help of the optically selected ACO catalog (Abell et al. 1989). The ACO catalog had been compiled by visually inspecting photographic plates. It is more sensitive to lower redshifts. For the following investigation, we selected 577 ACO clusters with a cataloged redshift zACO < 0.14 that lie within the LS footprint. Additionally, we included 16 ACO clusters that are formally outside the footprint. However, they were only classified as such because the clean region around the BCG was masked due to the assigned MASKBITS (see Sects. 2.2.3 and 3.1).

Figure 10, left panel, shows the ratio of ACO clusters confirmed after running eROMaPPer in scan mode on the ACO coordinates over total ACO clusters. The redshift zACO was taken from the ACO catalog. The yellow curve demonstrates a high optical completeness of C ≈ 95% beyond zaco > 0.05. Below zaco < 0.05, the optical completeness drops steeply: of 185 ACO clusters, we confirmed 132 (C = 71%). The optical limitation stemmed from the LS photometry around bright extended galaxies. While we kept galaxies cataloged in the Siena Galaxy Atlas, we excluded those that overlap with them. These optical detections are often spurious. The consequence of the removal is that a background cluster was frequently preferred over a low-z cluster.

Table 4

Overview of the catalogs analyzed with eROMaPPer in this work.

thumbnail Fig. 10

Optical completeness defined as the ratio of clusters confirmed after running eROMaPPer in scan mode on the cluster coordinates in various catalogs from the literature. At low redshifts, we used the ACO catalog and quantified the completeness for four different redshift tolerances. At high redshifts, we used the SPT, ACT, and Planck catalogs and considered clusters as confirmed when the redshifts agreed within |zbest − zlit|/(1 + zlit) < 0.1. We restricted the samples to clusters where the LS are sufficiently deep, that is, zbest < zvlim. A minimum of five clusters was required per redshift bin.

5.4 Richness comparison

The DES year 1 catalog was created using the cluster finder redMaPPer, similar to this work (Abbott et al. 2020). This allowed a direct comparison of the measured richnesses. The catalog was obtained in redMaPPer blind mode, that is, without positional priors. The redshift range was limited to 0.2 < zλ < 0.65. Figure 11 compares the richnesses computed in this work λnorm against the published richnesses λDESY1 (Abbott et al. 2020). We used 4716 clusters with good redshift agreement Δz/(1 + zλ) < 0.01, a low masking fraction (<10%), and which were identified in the LS DR10 south using the grz filter band combination, for which λ = λnorm (see Sect. 4.1.2 and Table 2).

To compute the systematic scaling factor, we fitted a linear relation to the data points by minimizing the orthogonal residuals. To avoid biases due to the sharp richness cut at λDESY1 = 20, we made an additional orthogonal cut below the line defined by λnorm < −1/α · λDESY1 + 50, where α = 0.79 is the best-fit slope. This procedure rejected 365 additional data points. We obtained the best-fit relation; λnorm =0.79⋅λDESY1.$\[\lambda_{\text {norm }}=0.79 \cdot \lambda_{\text {DESY1}}.\]$(14)

The richnesses measured in this work are, on average, 21% lower for identical DES year 1 clusters. A possible explanation is the different handling of galaxy outliers with respect to the red-sequence model in earlier versions of redMaPPer. We did not correct for this effect. Moreover, the data points in Fig. 11 were color-coded by the cluster redshift zλ. We did not see any obvious dependency of the scaling factor on redshift.

thumbnail Fig. 11

Comparison between the richnesses λ measured using eROMaPPer and the published richnesses for the same DES year 1 clusters color-coded by their photometric redshift in the eROMaPPer catalog. The 1:1 relation is shown in gray and the red line is the best-fit linear relation with a slope of α = 0.79.

5.5 BCG selection

A BCG is, by definition, the brightest member galaxy. Ambiguity arises from using BCGs as proxies for the cluster center and the association with the intracluster light that surrounds BCGs. The three commonly used selection criteria (being the brightest, most extended, and most central member) resemble the historical definition of a cD galaxy (Matthews et al. 1964; Morgan & Lesh 1965; Morgan et al. 1975; Albert et al. 1977). These qualities can conflict in up to 20% of the cases, especially when shallow photometry underestimates the faint light in the outskirts. (Von Der Linden et al. 2007; Kluge et al. 2020). Moreover, merging or unrelaxed clusters can have a significantly miscentered BCG or two similarly bright BCGs (in 7% of the cases in the total sample from Kluge et al. 2020). Therefore, we explore three options for selecting the BCG:

  1. located at the X-ray center,

  2. located at the optical cluster center,

  3. being the brightest member.

Figure 4 shows an illustrative example. The zoomed image in the bottom-left panel is centered on the galaxy, which visually fulfills best all commonly used selection criteria for BCGs. That galaxy is one of the most luminous and extended cluster members, and it is well-centered within the X-ray contours (white). The location of the initial X-ray detection in the catalog (before refined modeling, Bulbul et al. 2024) is shown by the yellow cross. The nearest galaxy is marked by an orange circle. Due to its compactness, it is clearly not a good choice for the BCG. The BCG chosen by eROMaPPer (the brightest member galaxy) is marked by the red circle. In this example and in 70% of the eRASS1 clusters, it coincides with the optical cluster center (green cross). However, selecting it as the BCG is inconsistent with our visual preference in this example.

The optical center is often, but not always well-centered on the X-ray peak. Seppi et al. (2023) found in 31% of their analyzed clusters good agreement with only very small offsets of ΔX-O < 0.05 × R500c, where R500c is the radius enclosing 500 times the critical density of the Universe. Visual inspection suggested no general preference for either choice. Either the optical center or the brightest member galaxy agreed with our visual preference in ~85% of the cases. Hence, we decided to follow the simplest approach and define the BCG in this work as the brightest member galaxy within Rλ (see Eq. (1)).

To further evaluate the automatic BCG choice at low redshift z < 0.1, we ran eROMaPPer on the cluster catalog of Kluge et al. (2020). This catalog is mostly a subset of the ACO catalog with each cluster carefully centered on the BCG. The BCG was chosen as the largest and most central galaxy based on visual inspection of deep images that revealed visual features on levels 27–28 g′ mag arcsec−2. Of the 154 cataloged clusters that are within the LS footprint, we identified 130 cases with consistent redshift (|zbest − zlit| < 0.01). The lost fraction is attributed to the growing incompleteness at low redshifts (see Sec. 5.3). The median redshift of the sample from Kluge et al. (2020) is z = 0.06. Of the 130 clusters, our automatic BCG selection is in 85 cases consistent with the choice made by Kluge et al. In 23 cases, the BCG is not a member galaxy according to eROMaPPer, even though its redshift is consistent with the cluster redshift. These BCGs are typically marginal outliers in color space. By only considering the remaining 107 clusters, the agreement with the BCG choice by Kluge et al. (2020) is 80%, precisely what we expected (see beginning of this section). Larger color uncertainties at intermediate or higher redshift likely keep the BCG colors consistent with the red-sequence colors. Therefore, we expect for the full eRASS1 and reanalyzed literature samples that the selected BCG is a good choice in ~80% of the clusters.

6 Number densities and mass limits

The eRASS1 cluster catalog’s lower mass limit increases with redshift due to a combination of the lower total flux received and the effect of cosmic dimming of the X-ray surface brightness in more distant clusters. Only the most luminous clusters can be detected at high redshifts. This behavior is quantified in our X-ray selection function (Clerc et al. 2024).

An additional inhomogeneous optical selection function can alter the cluster catalog further. We examined its effect using the catalogs created with eROMaPPer in blind mode. This mode does not use positional priors. Hence, the obtained catalogs allow us to investigate purely optical selection effects. Our analysis utilized the full LS DR9 north and LS DR10 south surveys, making the blind-mode cluster catalog the most extensive to date (see Fig. 8 and Table 4). The crucial disadvantage is, however, that the selection function is not well known. This knowledge is imperative to perform precise cosmological studies, for which eROSITA was designed.

Number densities are computed by dividing the number of clusters per redshift bin by the survey area or comoving volume. The usable survey area depends on redshift because of the non-uniform depth of the LS. Therefore, we used the dashed curves in Fig. 3 to calculate the redshift-dependent survey area and comoving volume for the eROMaPPer blind-mode catalogs.

thumbnail Fig. 12

Cluster number density per sky area (left) and comoving volume (right) against redshift. Red and purple lines refer to clusters detected using the eROMaPPer blind mode on the LS DR10 south and LS DR9 north, respectively, in the grz filter band combination. We restricted the samples to a reliable redshift range zλ < zvlim. The orange line refers to the eRASS1 clusters. A discontinuity at zλ = 0.8 arises from the merging of the low-z-optimized and high-z-optimized eROMaPPer runs (see Sect. 4.1.1). A richness cut of λnorm > 16 was applied only to the LS DR9 north and LS DR10 south catalogs. Volume densities for the SDSS DR8 and DES SVA catalogs were adopted from Rykoff et al. (2016) and for DES year 1, calculated assuming a survey area of 1437 deg2 with uniform depth (see Table 4). The curves were normalized for a bin size of Δz = 0.05 and smoothed using a Gaussian kernel with a standard deviation of Δz = 0.02. The width of the lines corresponds to the Poissonian error for the same bin size, consistently as in Rykoff et al. (2016).

6.1 Construction of blind-mode catalogs

As described in Sect. 4.1.1, we ran eROMaPPer in blind mode on six independent filter band and survey combinations. We did not merge the resulting catalogs because the clusters were not detected at the exact same locations in the different runs. Table 4 lists the total number of detected clusters for each run. We restricted the blind-mode samples to a reliable redshift range zλ < zvlim. Moreover, we removed galaxy groups to increase the purity. Therefore, we were restricting the richness to λnorm > 16, which corresponds to a halo mass restriction of M200m ≳ 1014 M⊙ according to the best-fit scaling relation for DES year 1 data (McClintock et al. 2019, see also Sect. 4.1.2).

The resulting blind-mode catalog for the grz filter bands contains 140 125 sources, 112 609 + 27 516 from the LS DR10 south and LS DR9 north, respectively. Another blind-mode catalog optimized for high redshifts using the grzw1 filter bands contains 366 377 sources (273 150 + 93 227). More details are given in Table 4.

6.2 Resulting catalogs

The number of blind-mode clusters against redshift is shown by the blue lines in Fig. 8, right panel. The continuous (dashed) line corresponds to the grz (grzw1) catalog for the combined LS DR9 and LS DR10 survey areas. For the grzw1 runs, we only considered brighter galaxies L > 0.4 L* (compared to L > 0.2 L* for the grz runs), which increases the usable survey volume (see Appendix B). Below zbest < 0.4, the grz and grzw1 runs have the same effective survey area (see Fig. 3). If there was no contamination and perfect completeness, the continuous and dashed lines should agree. The fact that they disagree indicates a higher level of contamination in the grzw1 run compared to the grz run. This is expected because the higher galaxy luminosity threshold allows for less secure cluster detections. At high redshift (zbest > 0.6), the lines begin to deviate much more from each other. The reason is the larger effective survey area for the grzw1 runs (see Fig. 3). Number densities per area (nA, left panel) and volume (nv, right panel) are shown in Fig. 12. The red (purple) curve corresponds to the LS DR10 south (DR9 north) grz catalog. We find that the number density profiles for the clusters detected in the LS DR9 north and LS DR10 south are consistent within the amplitude of the systematic oscillations. The oscillations are larger than the statistical uncertainties and arise from the redshift-dependent redshift bias. We perform a detailed analysis in Sect. 8.1.

6.3 Comparison to literature

Table 4 lists the total number of clusters for various catalogs used in this work. The sample size of the eROMaPPer blind-mode catalogs surpasses the DES year 1 sample size by a factor of 10 in the overlapping redshift range 0.2 < zbest < 0.65 (see Fig. 8). The main reason for this improvement is the ~10 times larger survey area of the LS compared to the DES year 1 area as listed in Table 4 and shown in the last two panels in Fig. 9.

We compare our obtained volume number densities with results for the DES SVA (dark gray, zλ > 0.2) and SDSS DR8 (light gray, 0.08 < zλ < 0.33) by adopting the volume number densities from Rykoff et al. (2016). Additionally, we calculated the number densities for the public DES year 1 cluster catalog (black, 0.2 < zλ < 0.65) assuming a redshift-independent survey area of 1437 deg2 (see Table 4). All curves are consistent with each other within the amplitude of the systematic oscillations.

thumbnail Fig. 13

Dependency of the cluster number density on survey depth. The cluster number density per sky area nA was calculated for the clusters detected using the eROMaPPer blind mode in the LS DR10 south using the grz filter bands. The data was split into five bins in photometric cluster redshift zλ. For each redshift bin, the densities were calculated for bins in limiting redshift zvlim and richness λnorm. We consider the cluster properties reliable when local survey depth is sufficiently deep, that is, zλ < zvlim (see Appendix B for details). Those clusters are located to the right of the red line where the number density does not depend on zvlim. The number density left of the red line increases, which indicates a growing number of false-positive detections.

6.4 Comparison to theoretical halo masses

For the LS cluster catalogs obtained in eROMaPPer blind mode, we applied a richness cut. As richness correlates with halo mass, we compared the number densities with halo model predictions. We computed theoretical number densities by integrating the halo mass function (Tinker et al. 2008; Diemer 2018) above five different mass limits.

The results are overlaid on Fig. 12 with black lines. The mass limit M500c ≳ 1014 M⊙ (densely dash-dotted line) corresponds to our richness cut of λnorm > 16 that is applied to the blindmode catalogs (red and purple lines). The curves agree with the amplitude of the systematic oscillations. We conclude from the comparison that the impact of the optical selection function is small above M500c ≳ 1014 M⊙ because the observed number densities are consistent with the prediction.

We note that the predicted and observed number densities depend on cosmology. Applying the eRASS1 cosmology (H0 = 67.77 km s−1 Mpc−1, Ωm = 0.29, and σ8 = 0.88, Ghirardini et al. 2024) shifts the predicted curves slightly upward.

6.5 Conclusions for eRASS1

We overplotted the number densities for the eRASS1 clusters in Fig. 12 in orange. They agree with the blind-mode sample below zλ ≲ 0.1 and the predictions for a mass limit M500c ≲ 1014 M⊙ at zλ < 0.1. Beyond that, the number densities of the eRASS1 sample are lower, as expected. The sensitivity of eROSITA decreases for groups at higher redshift because of their low X-ray flux. The eRASS1 mass limit corresponds to M500c ≳ 2 × 1014 M⊙ at zλ = 0.2 and M500c ≳ 3 × 1014 M⊙ at zλ = 0.8.

The intercepts between the eRASS1 number densities and the model predictions roughly agree with the redshift-dependent mass limits of the eRASS1 sample, obtained from the scaling relation between X-ray count rate and weak lensing shear (Ghirardini et al. 2024). The detection likelihood decreases toward higher redshifts and lower masses. This behavior is accounted for in the X-ray-selection function (Clerc et al. 2024). At zλ = 0.8, we notice a discontinuity in the eRASS1 cluster number surface density. It arises from merging the catalogs obtained for different filter band combinations (see Sect. 4.1.1).

6.6 Dependency on LS survey depth – richness bias

We utilized the blind-mode catalog obtained in the LS DR10 south (grz) further to demonstrate that the survey depth has no significant effect on the cluster number densities as long as only clusters with zλ < zvlim are selected, where zvlim is the spatially dependent limiting redshift of the LS. Figure 13 shows the blind-mode cluster numbers per sky area binned in intervals of limiting redshift zvlim and richness λnorm for five cluster redshift bins. The measured cluster number density increases where the LS is too shallow for the considered redshift (see Appendix B). This effect must arise from measurement errors because the intrinsic cluster number density should not directly depend on the survey properties. A plausible explanation is an increasing number of false-positive member galaxies in shallower survey areas. This can occur due to the negative low-mass slope of the galaxy luminosity function (e.g., Blanton et al. 2005), which can lead to an increasing Eddington bias. Moreover, higher uncertainties in color can lead to an increased misidentification of interloping galaxies, or even stars, as cluster members. This can statistically inflate cluster richnesses, consequently increasing the observed cluster number densities. The affected clusters can be avoided by selecting only systems with photometric redshift lower than the local limiting redshift zλ < zvlim. The red line in Fig. 13 marks the required minimum depth for each cluster redshift bin. The red arrow indicates the direction to where the reliable clusters are located.

7 Purity of the eRASS1 cluster catalog

The eRASS1 catalog was optimized for high completeness by selecting cluster candidates above a low extent likelihood threshold L$\[\mathcal{L}\]$ext > 3. The trade-off is high contamination. Using this selection, we expect from simulations (Seppi et al. 2022) that only ~50% of the extended sources are genuine galaxy clusters above the approximate eRASS1 flux limit of F500 ≈ 4 × 10−14 ergs s−1 cm−2 (Bulbul et al. 2024). Most other sources are misclassified point sources, such as AGNs (and stars). A smaller contribution comes from random background fluctuations (Seppi et al. 2022).

During the optical identification of these contaminants, it can either happen that no overdensity of red-sequence galaxies is found and the cluster candidate is discarded (2497 eRASS1 extended sources in the LS footprint, see Sect. 4.2.1)8, or the contaminant can be associated with an overdensity of red galaxies. In the latter case, these are either (a) line-of-sight projections of galaxies that are not bound to one cluster or (b) real overdensities of red galaxies around AGN as galaxies tend to cluster. We considered these sources as contaminants because the X-ray signal is not associated with the ICM.

To quantify the remaining contamination in the eRASS1 cluster catalog after our optical identification procedure, we introduce a mixture model in Ghirardini et al. (2024) (see also Bulbul et al. 2024). It compares the properties of contaminants to those of clusters and attributes a probability 0 ≤ Pcont ≤ 1, quantifying how likely each individual cluster is to be a contaminant. A detailed mathematical description of this mixture model can be found in Ghirardini et al. (2024). In this work, we provide details on the optical properties of the contaminating sources and how they were used to estimate the contamination probability of the eRASS1 clusters.

To estimate the contribution of both types of contaminants, we ran eROMaPPer on 1250 795 eRASS1 point sources (Merloni et al. 2024) and 1 000 000 random positions in the sky. Overdensities of red-sequence galaxies were identified for ~850000 and ~490 000 sources, respectively. The exact numbers depend on the filter band combination. Random points were positioned at least five cluster radii Rλ away from extended eRASS1 sources. We analyzed the distribution of the randoms and eRASS1 point sources in redshift and richness space (see Fig. 14, first two panels). The majority of the contaminants lie at low richnesses, as expected. We identified two peaks around zbest ≈ 0.2 and zbest ≈ 0.5. They are similarly pronounced for the point sources, while for the randoms, the second peak is slightly more dominant. The second peak is also apparent in the cluster sample (third panel). It indicates that there is indeed contamination left in the eRASS1 cluster catalog after the optical cleaning was performed in this work.

The global amplitudes of the kernel density estimates for both types of contaminants were fitted in the mixture model (Ghirardini et al. 2024). For the primary eRASS1 cluster sample with L$\[\mathcal{L}\]$ext > 3, we obtained a three times higher amplitude for the point sources fAGN = 0.0768 than for the randoms frand = 0.0246. This aligns with the expectation that most of the contamination in the eRASS1 cluster candidate catalog arises from X-ray point sources (Seppi et al. 2022).

Even though the distributions for the point sources and random points are similar in zbest−λnorm space, we can disentangle their contributions using the X-ray count rate CR,X. Figure 15 shows three projections of the 3-D distribution of the eRASS1 clusters in zbest−λnorm−CR,X space. The contamination probability Pcont is color-coded. AGNs typically have a higher X-ray flux than random background fluctuations. We modeled the λnorm−CR,X distribution empirically using a redshift-dependent Schechter function (Schechter 1976). Thereby, we assumed the power-law component to be the relation for clusters because both properties depend on the halo mass. Given this assumption, the exponential drop-off is due to the contamination. These objects are prominent in the right panel of Fig. 15 as red points at low richnesses and high X-ray flux. It shows a selected redshift slice between 0.4 < zbest < 0.5. By averaging the Pcont values of all N = 12 247 eRASS1 clusters, we calculated the residual contamination of the eRASS1 catalog to be ∑iPcont,i/N=14%.$\[\sum_i P_{\text {cont,} \mathrm{i}} / N=14 \%.\]$(15)

Using this result, we also computed the purity of the eRASS1 cluster candidate catalog (before optical identification). There are 16 336 cluster candidates in the LS footprint and N · ∑i (1 − Pcont,i) ≈ 10 581 sources were optically identified after statistically removing the remaining contamination. The ratio of the two numbers gives a purity of 65%, which is slightly higher than the predicted purity of 50% (Seppi et al. 2022).

The advantage of our contamination estimator compared to traditional richness and redshift cuts (Klein et al. 2022, 2023), is that we keep lower-richness groups in our sample (Bahar et al. 2024). We discuss the limitations of our contamination estimator, in particular for low-redshift groups, in Appendix A.2.

thumbnail Fig. 14

Kernel density estimates of AGNs, random points, and clusters in redshift (zbest)–richness (λnorm) space (first three panels). The right panel shows the individual cluster data points color-coded by their probability of being a contaminant.

8 Photometric redshift accuracy

In this section, we quantify the accuracy of the photometric redshifts derived from eROMaPPer. We characterize this to first order by bias and uncertainty. The bias Δzλ is the systematic offset from the true redshift z and is the floor reached when averaging many photometric redshifts. It arises primarily from red-sequence calibration errors (see Appendix C). The uncertainty δzλ is the statistical 1σ error that arises from effects such as galaxy color measurement errors and interloping galaxies (e.g., see Fig. 4, bottom panel). The uncertainty decreases with increasing richness, thanks to ensemble averaging.

Both bias and uncertainty depend on the true redshift z: Δzλ(z) and δzλ(z). We assumed negligible spectroscopic redshift uncertainties δzspec ≪ δzλ and zero spectroscopic bias Δzspec = 0, that is, we used zspec as a proxy for the true redshift. The spectroscopic cluster redshifts have, on average, 1~7 (5~15) times lower uncertainties than the photometric cluster redshifts when less than 5 (more than 20) spectroscopic members are known.

We estimated the bias and uncertainty by comparing the photometric redshifts zλ to the high-quality spectroscopic redshifts zspec. By high quality, we mean a minimum number of spectroscopic members to Nmembers ≥ 10 for zspec < 0.3, Nmembers ≥ 7 for 0.3 < zspec < 0.6, and Nmembers ≥ 3 for zspec > 0.6 To have a sufficient sample size at high redshift, we ran eROMaPPer on a large set of test clusters compiled from the works listed in Table 1 and Böhringer et al. (2000); Clerc et al. (2012); Balogh et al. (2014); Paterno-Mahler et al. (2017); Streblyanska et al. (2019); Huang et al. (2020a,b). The test cluster compilation comprises 151 781 clusters distributed across the entire LS area. For a subset of 22 450 clusters, we measured spectroscopic redshifts. We obtained 9522 clusters with high-quality spectroscopic red-shifts to compare with the photometric redshifts (see black dots in Fig. 16).

We mention as a caveat to these bias and uncertainty estimates that the high-quality spectroscopic sample does not fairly sample the parent cluster sample. There could remain subtle biases that we can only uncover with more spectroscopy or narrow-band photometry. This task can be reassessed once the dataseis from SDSS-V (10000 clusters), 4MOST (40000 clusters), DESI (DESI Collaboration 2024), and Euclid (Laureijs et al. 2011) become available.

The cosmological analysis in a companion paper (Ghirardini et al. 2024) includes the empirical redshift uncertainties derived in this paper. The bias, however, was not included because it has negligible impact on the inferred cosmological parameters (Ghirardini et al. 2024). The redshift uncertainties were also accounted for in the study of superclusters and large-scale structures presented in another paper (Liu et al. 2024), which is sensitive to distance measurements.

thumbnail Fig. 15

Distribution of clusters in redshift (zbest)-richness (λnorm)–X-ray count rate (CR,X) space. The left panel shows the full distribution, and the right panel shows a slice in redshift 0.4 < zbest < 0.5 to enhance the dependence on the λnorm−CR,X relation. The data points are projected on each side of the canvas. The probability of being a contaminant Pcont is color-coded. The top-right projection is equivalent to Fig. 14, right panel.
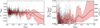thumbnail Fig. 16

Bias and uncertainty of the photometric cluster redshifts zλ estimated by comparing to high-quality spectroscopic cluster redshifts zspec. Black points refer to 9522 clusters with high-quality spectroscopic redshifts (see Sect. 8). The catalogs were merged as described in Sect. 4.1.1. The red line is the running median, and the red shaded regions give the uncertainty δzλ taken as the 16th and 84th percentiles of the distribution. In the left panel, the continuous red line is the redshift bias Δzλ, and the dashed lines give the redshift uncertainty δzλ. The right panel shows the absolute errors normalized by 1 + zspec, which is proportional to the line-of-sight velocity v (Eq. (6)).

8.1 Redshift bias

We estimated the redshift bias by applying a running median filter to the points shown in Fig. 16: Δzλ(z)= zspec ∈[zmin,zmax)median(zλ−zspec ),$\[\Delta z_\lambda(z)=~_{z_{\text {spec }} \in\left[z_{\min }, z_{\max }\right)}^{\operatorname{\quad{median}}}\left(z_\lambda-z_{\text {spec }}\right),\]$(16)

where the window interval [zmin, zmax) was adjusted such that it had a minimum width of Δz = 0.02 and encompassed a minimum of 100 clusters. Each result Δzλ was assigned to a redshift z at the median zspec in each interval. For the next step, we moved the window by Δz = 0.01 from the previous initial redshift z. Finally, the data points Δzλ(z) were linearly interpolated. The result is shown by the continuous red line in Fig. 16. It scatters around zero for 0.05 < zspec < 0.4 and becomes slightly negative beyond that. Δzλ                 (zspec <0.05)=+0.0040±0.0056,Δzλ      (0.05<zspec <0.4)=+0.0004±0.0016,Δzλ         (0.4<zspec <0.8)=−0.0041±0.0026,Δzλ(0.8<zspec )=−0.0178±0.0242.$\[\begin{array}{lcl}\Delta z_\lambda & ~~~~~~~~~~~~~~~~~\left(z_{\text {spec }}<0.05\right) & =+0.0040 \pm 0.0056, \\\Delta z_\lambda & ~~~~~~\left(0.05<z_{\text {spec }}<0.4\right) & =+0.0004 \pm 0.0016, \\\Delta z_\lambda & ~~~~~~~~~\left(0.4<z_{\text {spec }}<0.8\right) & =-0.0041 \pm 0.0026, \\\Delta z_\lambda & \left(0.8<z_{\text {spec }}\right) & =-0.0178 \pm 0.0242.\end{array}\]$(17)

We notice stronger deviations around zspec = 0.4 (see also Rykoff et al. 2014). Here, the 4000 Å break gets redshifted to the filter transition between the g and r bands. Consequently, neither the g − r nor the r − z color is sensitive to this redshift (see Appendix C). A positive bias just before zspec < 0.4 and a negative bias just after zspec > 0.4 creates an artificial clumping of clusters in redshift space at this location (see Fig. 12). A similar feature is visible at zspec = 0.7. Here, the 4000 Å break gets redshifted to the wavelength region between the r and z filters. Nevertheless, the bias remains below |zλ − zspec| < 0.01 for intermediate redshifts 0.6 < zspec < 0.9. Beyond zspec > 0.9, the bias increases to |zλ − zspec| > 0.02. Here, we reach the limiting redshift of the LS (see Fig. 3). The colors become less sensitive to redshift (see Appendix C), even though we included the i- and w1-band magnitudes for the red sequence colors beyond zλ > 0.8. At very low redshifts zspec < 0.05, the bias increases steeply because the red-sequence model was not calibrated (see Appendix C).

The right panel of Fig. 16 shows the absolute deviations |zλ − zspec| normalized by 1 + zspec. We find |zλ−zspec|1+zspec ≲0.005 for zspec ≲0.9. $\[\begin{aligned}&\frac{\left|z_\lambda-z_{\text {spec}}\right|}{1+z_{\text {spec }}} \lesssim 0.005&\qquad\qquad\text { for } z_{\text {spec }} \lesssim 0.9 \text {. }\end{aligned}\]$(18)

The running median is below or around 0.5% for zspec ≲ 0.9. The previously discussed bias peaks around zspec = 0.4 and zspec = 0.7 are apparent here, too.

8.1.1 Small-scale patterns in Δzλ

There are small-scale oscillations in photometric redshift bias with an amplitude of zλ − zspec ≈ 0.003 and a period of Δzspec ≈ 0.05-0.10. This is visible as the systematic variations of the red line in Fig. 16, left panel. The effect is especially prominent around zspec ≈ 0.4, where neither the g − r nor the r − z colors are very sensitive to redshift (see Appendix C). The origin of these residuals can be traced back to the red-sequence model calibration. Our tests showed that the amplitude of these oscillations increased when we included the i-band in the z < 0.8 eROMaPPer runs. Even though the statistical uncertainties decreased mildly because more information was being used, the systematic uncertainties increased because of color variations on small scales in redshift space. For this reason, we gave higher priority to the grz and grzw1 eROMaPPer runs over the runs that include the i band (see Sect. 4.1.1). In the future, we plan to improve this using finer-spaced spline fitting of the red sequence colors that include the i band.

8.1.2 Average bias correction

The photometric redshifts can be corrected for the bias. To do so, we calculated Δz(zλ) instead of Δz(zspec) because zλ is known for every cluster and zspec is only available for a subset. The procedure is equivalent to Eq. (16). We computed Δz(zλ) for the subset of clusters with known zspec and subtracted it from zλ to obtain a bias-corrected photometric redshift zλ,corr: zλ,corr=zλ−Δzλ(zλ).$\[z_{\lambda, \text {corr}}=z_\lambda-\Delta z_\lambda\left(z_\lambda\right).\]$(19)

The corrected redshifts zλ,corr are provided in the catalog, although all optical cluster properties were calculated at the uncorrected redshifts. As stated in Sec. 8, the redshift bias has a negligible impact on the inferred cosmological parameters in Ghirardini et al. (2024).

8.2 Redshift uncertainties

The formal redshift uncertainty δzλfml$\[\delta z_\lambda^{\mathrm{fml}}\]$ was calculated by eROMaPPer for each cluster using the standard deviation of the redshift posterior P(z) (see Sect. 3.2.1). We compared it to an empirical uncertainty δzλemp$\[\delta z_\lambda^{\mathrm{emp}}\]$ derived from the comparison to spectroscopic cluster redshifts. The empirical uncertainties were calculated as the running 16th and 84th percentiles of the zspec − zλ distribution. It is analogous to the procedure described in Sec. 8.1, but we replaced the median with the percentiles and subtracted the redshift bias to isolate the contribution from the statistical uncertainties. The results for the upper and lower values of δzλemp$\[\delta z_\lambda^{\mathrm{emp}}\]$ are δzλemp                     (zspec <0.05)=+0.0093,−0.0078,δzλemp       (0.05<zspec <0.4)=+0.0062,−0.0061,δzλemp          (0.4<zspec <0.8)=+0.0095,−0.0110,δzλemp (0.8<zspec )=+0.0153,−0.0242.$\[\begin{array}{lcc}\delta z_\lambda^{\text {emp }} & ~~~~~~~~~~~~~~~~~~~~\left(z_{\text {spec }}<0.05\right) & =+0.0093,-0.0078, \\\delta z_\lambda^{\text {emp }} & ~~~~~~\left(0.05<z_{\text {spec }}<0.4\right) & =+0.0062,-0.0061, \\\delta z_\lambda^{\text {emp }} & ~~~~~~~~~\left(0.4<z_{\text {spec }}<0.8\right) & =+0.0095,-0.0110, \\\delta z_\lambda^{\text {emp }} & \left(0.8<z_{\text {spec }}\right) & =+0.0153,-0.0242.\end{array}\]$(20)

These uncertainties are relatively small and almost symmetric at low to intermediate redshifts 0.05 < zspec < 0.4. Below zspec = 0.05, the 4000 Å break reaches the blue limit of the g band filter transmission curve, making the g − r color less sensitive to redshift (see Appendix C). In the future, u-band data from LSST (Ivezić et al. 2019) will solve this issue. Above zspec > 0.6, the uncertainties increase because of higher photometric uncertainties for the fainter sources.

The running upper and lower percentiles are also shown in Fig. 16, left panel, by the dashed red lines. They confirm the mostly symmetric shape and the increase of δzλemp$\[\delta z_\lambda^{\mathrm{emp}}\]$ around zspec ≈ 0.7. That increase happens because the 4000 Å break is redshifted between the g and r filters.

We compare both types of uncertainties in Fig. 17. The black points show δzλfml$\[\delta z_\lambda^{\mathrm{fml}}\]$ for the individual clusters, and the red dashed line is the average of the upper and lower percentiles for δzλemp(zλ)$\[\delta z_\lambda^{\mathrm{emp}}\left(z_\lambda\right)\]$. In the range 0.1 < zλ < 0.8, the empirical uncertainties are consistent with the lower boundary of the formal uncertainties, but individual values for δzλfml$\[\delta z_\lambda^{\mathrm{fml}}\]$ scatter upward. The redshift uncertainty is anti-correlated with richness, so as expected, the upscattering happens for poorer clusters with λ ≲ 10. Around zλ ≈ 0.4 and zλ ≈ 0.7, both uncertainties increase due to filter transitions. Above z > 0.8, the formal uncertainties underestimate the empirical uncertainties by a factor of ≈2.

The continuous red line in Fig. 17 is the absolute value of the redshift bias evaluated on a grid for zλ. It is lower than the uncertainties. That is, for an individual cluster, the statistical uncertainty dominates the error budget over the systematic error. We adopted the formal uncertainties, which were calculated by eROMaPPer as the standard deviation of the redshift posterior P(z), as the final photometric redshift uncertainties zλ,err=δzλfml$\[z_{\lambda, \mathrm{err}}=\delta z_\lambda^{\mathrm{fml}}\]$ because they also capture the richness dependence. Hence, they are a better estimate of an individual cluster’s redshift uncertainty than the averaged empirical uncertainty for the ensemble.

thumbnail Fig. 17

Uncertainties of the eRASS1 photometric cluster redshifts. The black dots are the formal uncertainties δzλfml$\[\delta z_\lambda^{\mathrm{fml}}\]$ calculated by eROMaPPer as the standard deviation of the redshift posterior P(z). We adopted them as the final redshift uncertainties zλ,err. The dashed red line is the mean of the upper and lower empirical uncertainties δzλspec $\[\delta z_\lambda^{\text {spec }}\]$ derived from the comparison to the spectroscopic cluster redshifts. The continuous red line is the absolute redshift bias |Δzλ|.

9 The richness – velocity dispersion scaling relation

We investigate the scaling relation between two cluster properties that correlate with cluster mass. The line-of-sight velocity dispersion σ traces the dynamical mass Mdyn of a cluster Mdyn(<r)=cσ2rG,$\[M_{\mathrm{dyn}}(<r)=c \frac{\sigma^2 r}{G},\]$(21)

where G is the gravitational constant, r is the cluster radius, and c corrects effects from 2D projection and orbit anisotropy (Binney & Tremaine 2008). The richness λnorm also correlates with total cluster mass (e.g., McClintock et al. 2019) because deeper gravitational potential wells attract more baryonic matter.

To correct for redshift evolution, we multiplied λnorm with E(z)=Ωm(1+z)3+Ωλ$\[E(z)=\sqrt{\Omega_{\mathrm{m}}(1+z)^3+\Omega_\lambda}\]$ (Damsted et al. 2023), although the effect is small. Most spectroscopic clusters are at low redshift (see Fig. 5). We explore the σ − λnorm relation for the eRASS1 sample augmented by the literature samples. The scaling relation between X-ray, weak lensing, and optical observables are detailed in companion papers (Ghirardini et al. 2024; Grandis et al. 2024; Pacaud et al., in prep.).

9.1 Cluster selection

For the analysis, we considered only clusters with high-quality (unflagged) velocity dispersions determined using the bi-weight scale estimator (see Sec. 3.6). As we required a large number of ≥15 spectroscopic members for this method, these clusters also have a high richness and a low relative uncertainty: δσ/σ ~ 20%. We show how these clusters populate the σ − λnorm plane in Fig. 18. The figure contains data for 1699 clusters with a low masking fraction of <20%. Of them, 309 are eRASS1 clusters.

We assumed that sample selection effects are unimportant for this analysis. For eRASS1, the X-ray count rate is the primary selection variable. For a thin redshift slice, the velocity dispersion and the richness correlate with the X-ray count rate. Hence, the net selection effect is along the relation and, therefore, unimportant when applying orthogonal distance regression.

9.2 Relation fitting

We fitted a linear relation with free parameters α and β to the logarithm of both variables; log⁡(λnorm )=α×log⁡(σ[kms−1])+β.$\[\log \left(\lambda_{\text {norm }}\right)=\alpha \times \log \left(\sigma\left[\mathrm{km} \mathrm{s}^{-1}\right]\right)+\beta.\]$(22)

Our preferred fitting method (ODR, Boggs et al. 1989) minimizes the orthogonal residuals from the relation. Additionally, we weighed the individual data points by their measurement uncertainties in both variables and included the non-negligible intrinsic scatter. The method is described in detail in Kluge & Bender (2023). An advantage is that the method is insensitive to switching variables.

The best-fit values are α=2.401±0.055,$\[\alpha=2.401 \pm 0.055,\]$(23) β=−5.074±0.156,$\[\beta=-5.074 \pm 0.156,\]$(24)

with a covariance of COV(log λnorm, log σ) = −8.6 × 10−3. Our best-fit slope agrees within 1.5σ confidence with α=1/(0.323 ±0.057)=3.10−0.46+0.66$\[\alpha=1 /(0.323 ~\pm0.057)=3.10_{-0.46}^{+0.66}\]$ obtained by Kirkpatrick et al. (2021). The agreement improves to 0.8σ (α = 2.734 ± 0.082) confidence when we use the same fitting method (BCES, Akritas & Bershady 1996; Nemmen et al. 2012).

Moreover, our best-fit slope also agrees within 1.6σ confidence with α=1/(0.365±0.029)=2.74−0.20+0.23$\[\alpha=1 /(0.365 \pm 0.029)=2.74_{-0.20}^{+0.23}\]$ obtained by Damsted et al. (2023). However, their applied fitting method linmix (Kelly 2007) is sensitive to switching variables. Using that method, we got consistent results only for (σ|λnorm): 1/α = 0.392 ± 0.010. For (λnorm|σ), we got α = 1.753 ± 0.045, a 9σ deviation.

The statistical uncertainties of the best-fit slopes improved by a factor of 4–10 compared to previous works. This is attributed to the large gain in sample size of clusters with Nmembers ≥ 15 spectroscopic members. Our sample includes 1699 clusters compared to 530 clusters (Damsted et al. 2023). The sample of (Kirkpatrick et al. 2021) includes 2740 clusters but with a lower median of 10 spectroscopic members.

thumbnail Fig. 18

Relation for cluster line-of-sight velocity dispersion σ and richness λnorm. The black data points are for all clusters in our analyzed catalogs (see Table 4) apart from the blind-mode runs. In total, 1699 clusters with Nmembers ≥ 15 spectroscopic members were selected. The red line is the best fit to the data, and the light red shades show the uncertainty of the relation. The observed scatter δobs,orth (orange) was measured orthogonal to the best-fit relation in 9 bins. The median orthogonal component of the measurement uncertainties δm,orth is shown for each bin in blue. By subtracting δm,orth from δobs,orth in quadrature, we estimated the intrinsic scatter δin for each bin. It is shown in green.

9.3 Intrinsic scatter

We estimated the intrinsic scatter following the procedure in Kluge & Bender (2023). First, we calculated the observed orthogonal scatter δobs,orth and the median orthogonal component of the measurement uncertainties δm,orth. Then, the intrinsic scatter δin was estimated by δin =δobs,orth2−δm,orth2.$\[\delta_{\text {in }}=\sqrt{\delta_{\mathrm{obs}, \mathrm{orth}}^2-\delta_{\mathrm{m}, \mathrm{orth}}^2}.\]$(25)

To capture a possible variation with σ or λnorm, we split the sample into 9 equal-sized bins perpendicular to the best-fit line. In each bin, we calculated δobs,orth, δobs,orth, and δin, and show results in Fig. 18 by the orange, blue, and green shades, respectively. Notably, not only do the measurement uncertainties increase for the lower σ or λnorm, as expected, but also the intrinsic scatter increases.

We report the obtained values for two larger bins, split at σ = 620 km s−2 and λnorm = 43. For the subsample at high σ and λnorm, we obtained (δobs,orth = 0.100 dex, δm,orth = 0.039 ± 0.026 dex, and δin = 0.092 ± 0.008 dex. For the subsample at low σ and λnorm, we obtained (δobs,orth = 0.118 dex, δm,orth = 0.058 ± 0.029 dex, and δin = 0.102 ± 0.012 dex. This is slightly lower than δin = 0.138 ± 0.017 obtained by Damsted et al. (2023), possibly because we applied different fitting and scatter-estimation methods. We conclude that the σ − λnorm relation obtained in this work is dominated by intrinsic scatter and not by measurement uncertainties.

10 Summary

The first eROSITA All-Sky Survey (eRASS1) provides the largest sample of ICM-selected galaxy clusters and groups in the western Galactic hemisphere to date. In this work, we identify 12 247 candidates by associating them with a coincident overdensity of red-sequence galaxies or, in 247 cases, by matching them with known clusters from the literature. We ran the red-sequence-based cluster finder eROMaPPer on optical and near-infrared data from DESI Legacy Imaging Surveys DR9 (at Decl. > 32.375°) and DR10 (at Decl. < 32.375°) on 13 116 deg2 of the sky. The eRASS1 sample of cluster and group candidates is designed to be as complete as possible. After discarding candidates without optical identification, we estimated the purity using a mixture model to be 86%.

We provide optical (redshifts, richnesses, optical centers, BCG position) and spectroscopic (redshifts and velocity dispersions) properties. The photometric redshifts have an excellent accuracy of Δz/(1 + z) ≲ 0.005 for 0.05 < z < 0.9. For individual clusters, the accuracy is dominated by statistical uncertainties.

Spectroscopic redshifts were calculated for a subsample of 3210 eRASS1 clusters and groups. Of those, 1759 have at least three spectroscopic members. The spectroscopic galaxy redshifts were compiled from public catalogs from the literature and dedicated follow-up programs and matched to the photometrically selected member galaxies. The spectroscopic cluster redshifts are, on average, 1~7 (5~15) times more accurate than the photometric cluster redshifts when less than 5 (more than 20) spectroscopic members are known. This improvement in accuracy makes the eRASS1 clusters align well with the large-scale structure as traced by individual spectroscopic galaxy redshifts. Velocity dispersions were measured for 1906 clusters, of which 1499 are robust, and 358 have high quality with relative uncertainty δσ/σ ≈ 20%.

In addition to the eRASS1 catalog, we consistently remeasured the redshifts on known clusters from the literature. We recovered consistent redshifts in the range 0.05 ≲ z ≲ 1.1 for > 95% of the clusters detected with the high-z-sensitive Sunyaev-Zeldovich effect or low-z-sensitive optical selection. The outliers are explained by multiple structures coinciding along the line of sight.

Moreover, we detected galaxy clusters without positional priors in the full footprint of the Legacy Surveys (24 069 deg2). The number density of the found clusters is independent of the optical survey depth below the local limiting redshift zvlim. The depth of the LS limits the high-quality subsample at around zvlim ≈ 0.7 for a minimum galaxy luminosity of 0.2 L*. By increasing the luminosity threshold to L > 0.4 L* and including the i and w1 filter bands, we increased the limiting depth to zvlim ≈ 1.0 and even higher locally.

Combining all analyzed cluster catalogs, we obtained a sample of 1699 clusters with high-quality velocity dispersion measurements. We correlated it with the richness and found a best-fit relation log(λnorm) = 2.401(±0.055) × log(σ[km s−1]) −5.074(±0.156), which agrees with previous results from other studies. The scatter in the relation is dominated by an intrinsic scatter δin for the full range 300 ≲ σ ≲ 1000 km s−1 and 10 ≲ λ ≲ 200. It increases only slightly from δin = 0.092 ± 0.008 dex to δin = 0.102 ± 0.012 dex toward lower σ and λ.

In the future, the next-generation eROSITA cluster catalogs will be supported by a wealth of spectroscopic input from SDSS-V (10000 clusters), 4MOST (40000 clusters), LSST, and Euclid. These data will expand bias-free redshift measurements to higher redshifts. A complete sampling of the nodes of the cosmic web will yield exquisite constraints on cosmological models and primordial non-Gaussianity (Stopyra et al. 2021).

Data availability

We make available the optical properties of the eRASS1 galaxy clusters and groups as a catalog in electronic form. It can be accessed at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/688/A210. Alternatively, the catalog is available via the following webpage: https://erosita.mpe.mpg.de/dr1/AllSkySurveyData_dr1/Catalogues_dr1/. Moreover, the measured optical properties of the clusters from literature catalogs and eROMaPPer runs without positional priors are made available, too. They can be accessed and explored using a visual inspection tool on the following webpage: https://erass-cluster-inspector.com. Reasonable requests for the member galaxy catalogs can be made to the corresponding author.

Acknowledgements

The authors thank the referee for helpful and constructive comments on the draft. This work is based on data from eROSITA, the soft X-ray instrument aboard SRG, a joint Russian-German science mission supported by the Russian Space Agency (Roskosmos), in the interests of the Russian Academy of Sciences represented by its Space Research Institute (IKI), and the Deutsches Zentrum für Luft und Raumfahrt (DLR). The SRG spacecraft was built by Lavochkin Association (NPOL) and its subcontractors and is operated by NPOL with support from the Max Planck Institute for Extraterrestrial Physics (MPE). The development and construction of the eROSITA X-ray instrument was led by MPE, with contributions from the Dr. Karl Remeis Observatory Bamberg & ECAP (FAU Erlangen-Nuernberg), the University of Hamburg Observatory, the Leibniz Institute for Astrophysics Potsdam (AIP), and the Institute for Astronomy and Astrophysics of the University of Tübingen, with the support of DLR and the Max Planck Society. The Argelander Institute for Astronomy of the University of Bonn and the Ludwig Maximilians Universität Munich also participated in the science preparation for eROSITA. The eROSITA data shown here were processed using the eSASS software system developed by the German eROSITA consortium. V. Ghirardini, E. Bulbul, A. Liu, C. Garrel, E. Artis, M. Kluge, and X. Zhang acknowledge financial support from the European Research Council (ERC) Consolidator Grant under the European Union’s Horizon 2020 research and innovation program (grant agreement CoG DarkQuest No 101002585). N. Clerc was financially supported by CNES. T. Schrabback and F. Kleinebreil acknowledge support from the German Federal Ministry for Economic Affairs and Energy (BMWi) provided through DLR under projects 50OR2002, 50OR2106, and 50OR2302, as well as the support provided by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under grant 415537506. The Legacy Surveys consist of three individual and complementary projects: the Dark Energy Camera Legacy Survey (DECaLS; Proposal ID #2014B-0404; PIs: David Schlegel and Arjun Dey), the Beijing-Arizona Sky Survey (BASS; NOAO Prop. ID #2015A-0801; PIs: Zhou Xu and Xiaohui Fan), and the Mayall z-band Legacy Survey (MzLS; Prop. ID #2016A-0453; PI: Arjun Dey). DECaLS, BASS and MzLS together include data obtained, respectively, at the Blanco telescope, Cerro Tololo Inter-American Observatory, NSF’s NOIR-Lab; the Bok telescope, Steward Observatory, University of Arizona; and the Mayall telescope, Kitt Peak National Observatory, NOIRLab. Pipeline processing and analyses of the data were supported by NOIRLab and the Lawrence Berkeley National Laboratory (LBNL). The Legacy Surveys project is honored to be permitted to conduct astronomical research on Iolkam Du’ag (Kitt Peak), a mountain with particular significance to the Tohono O’odham Nation. NOIR-Lab is operated by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation. LBNL is managed by the Regents of the University of California under contract to the U.S. Department of Energy. This project used data obtained with the Dark Energy Camera (DECam), which was constructed by the Dark Energy Survey (DES) collaboration. Funding for the DES Projects has been provided by the U.S. Department of Energy, the U.S. National Science Foundation, the Ministry of Science and Education of Spain, the Science and Technology Facilities Council of the United Kingdom, the Higher Education Funding Council for England, the National Center for Supercomputing Applications at the University of Illinois at Urbana-Champaign, the Kavli Institute of Cosmological Physics at the University of Chicago, Center for Cosmology and Astro-Particle Physics at the Ohio State University, the Mitchell Institute for Fundamental Physics and Astronomy at Texas A&M University, Financiadora de Estudos e Projetos, Fundacao Carlos Chagas Filho de Amparo, Financiadora de Estudos e Projetos, Fundacao Carlos Chagas Filho de Amparo a Pesquisa do Estado do Rio de Janeiro, Conselho Nacional de Desenvolvimento Científico e Tecnologico and the Ministerio da Ciencia, Tecnologia e Inovacao, the Deutsche Forschungsgemeinschaft and the Collaborating Institutions in the Dark Energy Survey. The Collaborating Institutions are Argonne National Laboratory, the University of California at Santa Cruz, the University of Cambridge, Centro de Investigaciones Energeticas, Medioambientales y Tecnologicas-Madrid, the University of Chicago, University College London, the DES-Brazil Consortium, the University of Edinburgh, the Eidgenossische Technische Hochschule (ETH) Zurich, Fermi National Accelerator Laboratory, the University of Illinois at Urbana-Champaign, the Institut de Ciencies de l’Espai (IEEC/CSIC), the Institut de Fisica d’Altes Energies, Lawrence Berkeley National Laboratory, the Ludwig Maximilians Universitat Munchen and the associated Excellence Cluster Universe, the University of Michigan, NSF’s NOIRLab, the University of Nottingham, the Ohio State University, the University of Pennsylvania, the University of Portsmouth, SLAC National Accelerator Laboratory, Stanford University, the University of Sussex, and Texas A&M University. BASS is a key project of the Telescope Access Program (TAP), which has been funded by the National Astronomical Observatories of China, the Chinese Academy of Sciences (the Strategic Priority Research Program “The Emergence of Cosmological Structures” Grant # XDB09000000), and the Special Fund for Astronomy from the Ministry of Finance. The BASS is also supported by the External Cooperation Program of Chinese Academy of Sciences (Grant # 114A11KYSB20160057), and Chinese National Natural Science Foundation (Grant # 12120101003, # 11433005). The Legacy Survey team makes use of data products from the Near-Earth Object Wide-field Infrared Survey Explorer (NEOWISE), which is a project of the Jet Propulsion Laboratory/California Institute of Technology. NEOWISE is funded by the National Aeronautics and Space Administration. The Legacy Surveys imaging of the DESI footprint is supported by the Director, Office of Science, Office of High Energy Physics of the U.S. Department of Energy under Contract No. DE-AC02-05CH1123, by the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility under the same contract; and by the U.S. National Science Foundation, Division of Astronomical Sciences under Contract No. AST-0950945 to NOAO. The Hobby-Eberly Telescope (HET) is a joint project of the University of Texas at Austin, the Pennsylvania State University, Ludwig-Maximillians-Universität München, and Georg-August Universität Göttingen. The HET is named in honor of its principal benefactors, William P. Hobby and Robert E. Eberly. VIRUS is a joint project of the University of Texas at Austin, Leibniz-Institut für Astrophysik Potsdam (AIP), Texas A&M University (TAMU), Max-Planck-Institut für Extraterrestrische Physik (MPE), Ludwig-Maximilians-Universität Muenchen, Pennsylvania State University, Institut für Astrophysik Göttingen, University of Oxford, and the Max-Planck-Institut für Astrophysik (MPA). In addition to Institutional support, VIRUS was partially funded by the National Science Foundation, the State of Texas, and generous support from private individuals and foundations.

Appendix A Limitations & caveats

This section gives a concise overview of the limitations of the eRASS1 cluster and group catalog.

A.1 Completeness

The optical completeness decreases at low redshift z < 0.05 because we discarded galaxies that overlap with large galaxies (see Sections 2.2.3 and 5.3). This affects especially clusters or groups that host a cD galaxy. At high redshifts, the catalog is almost complete for high cluster masses and is mostly limited by the depth of the LS. It is quantified by the parameter zvlim (see Appendix B). If a cluster was found at a higher redshift zλ > zvlim, the probability increases that the detection is a contaminant (see Figure 13). Avoiding these clusters using the boolean catalog parameter IN_ZVLIM is advisable for selecting a clean sample.

Our cluster finder is based on the colors of galaxies, which follow the red sequence. Hence, star-forming late-type galaxies cannot be part of our member galaxy sample. To confirm this, we ran eROMaPPer on the Hickson compact group catalog (Hickson 1982), which consists mostly of low-z late-type galaxies. We recovered 17/100 groups that consist of mostly early-type galaxies at zλ < 0.1. The remaining 83/100 groups were not detected by eROMaPPer, as expected.

The intrinsic proportion of blue star-forming galaxies increases not only for lower masses but also for higher redshifts, known as the Butcher–Oemler effect (Butcher & Oemler 1978). In the densest clusters, the fraction of quiescent galaxies over all galaxies decreases from 75% at z = 0 to 45% at z = 0.7 (Hahn et al. 2015). Assessing the precise impact on the optical completeness of the eRASS1 catalog would require running eROMaPPer on simulated galaxy catalogs (e.g., To et al. 2024). No such dedicated analysis exists to our knowledge, yet. Nevertheless, we can infer a plausible range for the optical completeness based on existing comparisons for different types of cluster finders. A red-sequence-based cluster finder similar to eROMaPPer yields a relative optical completeness of ~100% (~70%) at z < 0.6 (z < 1.0) compared to a redshift-based cluster finder that is more sensitive to blue star-forming galaxies (see Section 3 for more details). However, the cluster masses of M > 1014 M⊙ in that analysis are lower than the mass limit of the eRASS1 catalog at z > 0.6 with M ≈ 3 × 1014 M⊙ (see Figure 12). Given the observed decrease in the proportion of blue, star-forming galaxies with increasing cluster mass (Hahn et al. 2015), we can regard the 70% optical completeness as a lower limit. Moreover, the eRASS1 mass limit at z > 0.6 is comparable to the mass limit in the ACT survey with which we estimated a high optical completeness for the eRASS1 identified catalog of > 95% (see Section 5.2). Finally, the good agreement of the cluster number densities obtained with the eROMaPPer run in blind mode with the theoretical prediction for the halo mass function (see Figure 12) underlines that the optical completeness remains high out to high redshift.

A.2 Contamination estimates for galaxy groups

Our contamination estimator (see Section 7) performs well at assigning a high contamination probability Pcont to possible AGN for high X-ray count rates and low richnesses (see Figure 15, right panel, top left projection). However, sources with low X-ray count rates always received Pcont ≈ 0. These count rates occurred during the multi-component fitting using MBproj2D (see Bulbul et al. 2024). They are not part of the expected count rates forr andom sky points. Hence, the kernel density estimate for this region in parameter space is almost zero for the contaminants. Consequently, our contamination estimator underestimated the true contamination on the galaxy group scale.

In contrast, visual inspection of real groups (λnorm ≲ 10) at low redshift (zbest ≲ 0.1) revealed that many of them received a high Pcont value. In principle, lowering the member luminosity threshold below L < 0.2 L* can help distinguish them better from AGN. This would increase the measured richnesses of real groups while we expect the richnesses of AGN to remain low.

A.3 Cluster properties

The cluster parameters were always calculated at the photometric redshift zλ. This concerns the galaxy memberships, richnesses λ and λnorm, optical centers, and velocity dispersions σ. In cases where the best redshift type was changed to a literature redshift, the cluster parameters are not reliable because they refer to a foreground or background cluster.

A.4 Masked clusters

Few clusters had a large mask applied, which covered roughly one-half of their extent. One example is 1eRASS J022553.0-415457 with a masking fraction of 40%. We noticed that we detected member galaxies only on the other side of this cluster when we ran eROMaPPer on a location within the initial mask. That means, the mask was not created based on flagged photometry in the LS. We suspect that this effect occurs when a cluster is located near the edge of a heal pixel. Nevertheless, the richnesses were corrected for the masking fraction (see Section 3), and, hence, they are noisier but unbiased. Also, we have no reason to assume that the photometric redshifts would be biased in the described cases. Moreover, only a small fraction of the eRASS1 clusters is affected. Four percent of them have a masking fraction of > 40% and for most of them, a saturated nearby star is the reason for the large mask.

A.5 Velocity dispersion

We provide cluster velocity dispersions even when the velocity clipping diverged in some of the bootstrapped samples (see Section 3.6). This affects 407 out of 1906 cases that can be identified by the flag VDISP_FLAG_BOOT>0. Two examples with unrealistically high velocity dispersions σ > 10000 km s−1 are 1eRASS J104344.4+240537 and 1eRASS J025101.7-353415. In both cases, the velocity dispersion is high because one wrongly measured redshift around zspec = 0 was not clipped. This error is taken into consideration in the uncertainty δσ > 10000 km s−1, which is almost equal to σ itself. The spectroscopic redshifts are less affected by these outliers because the biweight location for the spectroscopic cluster redshifts happens to be more robust than the gapper estimator for the velocity dispersion.

A.6 Bias-corrected photometric redshifts

Red-sequence model calibration errors (see Section C) propagate to biases in the photometric cluster redshifts (see Section 8.1). We have measured this bias and provide corrected photometric redshifts zλ,corr (see Eq. (19)) and corresponding uncertainties. These corrections are small at low redshifts but become increasingly important at z ≳ 0.8. In particular, the formal uncertainties underestimate the real uncertainties significantly at z ≳ 0.8.

Appendix B Limiting depth and limiting redshift

To minimize the number of spurious sources, it is necessary to know whether the local survey depth is sufficiently deep. This information is stored in depth maps. The sky position-dependent depth was estimated via a parametric model (Rykoff et al. 2015) that uses the galaxy magnitudes and uncertainties in the LS. The limiting magnitude is defined by that of a galaxy with a detection confidence of 10σ, that is, its measured flux has a signal-to-noise ratio of 10. These limits vary across the sky and for different filter bands. Depth maps store this information in the HEALPix format (Górski et al. 2005). We used a spatial resolution of NSIDE=4096, which corresponds to an area of ~ 1′ × 1′ per pixel. If a heal pixel contained an insufficient number of galaxies for the model to converge, the depth was approximated by recursively expanding out to the next largest pixel in the nested scheme until it did.

One depth map was created for each filter band and for each of the LS DR10 south and LS DR9 north survey parts (see Figure B.1). The spatial coverage for the different filter bands is similar but not identical. Therefore, we set all heal pixels to empty which were also empty in at least one of the depth maps used in each eROMaPPer run. The resulting z-band depth map for the grz filter band combination is shown in Figure 2. The top panel refers to the LS DR10 south and the bottom panel refers to the LS DR9 north.

thumbnail Fig. B.1

Depth maps showing the limiting magnitude for the Legacy Surveys DR10 south (top panels) and DR9 north (lower panels) in different filter bands. The maps present the full coverage in each band independently rather than combining the footprints as in Figure 2. The limiting magnitude is defined as the brightness of a galaxy whose flux has a signal-to-noise ratio of 10.

Saturated sources leave small holes in the depth maps. If a cluster center is located within such a hole, we describe it as formally outside the footprint and flagged it in the catalog as IN_FOOTPRINT=False. Part of the cluster can still be detected when the cluster radius Rλ is larger than the size of the masked region. This affects 363 eRASS1 clusters. We show one example in Figure B.2. A bright foreground star overlaps with a cluster in the background. The galaxies in projected proximity have flagged photometry in the LS. They were rejected by eROMaPPer (see Section 3). However, cluster members in the outskirts of the cluster were still detected and marked by the circles. As expected, the masking fraction is high with MASKFRAC=0.51, and therefore, the richness λ was upscaled by a factor of SCALEVAL=2.03. We consider the photometric redshift zλ = 0.400 ± 0.012 reliable because 45 member galaxies were detected despite the high masking fraction. For this reason, we kept these clusters in our sample.

thumbnail Fig. B.2

Example of a cluster 1eRASS J010123.5-764801 located in a masked area of the footprint map. The saturated foreground star near the X-ray detection (yellow cross) was responsible for the mask. Cluster member galaxies are marked by circles (see Figure 4 for further descriptions of the labels). Only the members in the outskirts of the cluster were identified. North is up, east is left.

The limiting magnitude in our reference band, the z band, can be converted to a limiting redshift zvlim for non-empty heal pixels. It is defined as the redshift, at which a member galaxy at the low-luminosity limit Lthresh can still be detected with a 10σ significance. To calculate this limit, we predicted the brightness in the DECam z band of a galaxy with luminosity Lthresh for all redshifts 0.01 < z < 1.45 using the tool EzGal (Mancone et al. 2013). Thereby, we assumed that it behaves according to the prediction for a passively evolving single stellar population (Bruzual & Charlot 2003). We set the low-luminosity limit to Lthresh. = 0.2 L* for the eROMaPPer runs using the grz and griz filter bands, and Lthresh = 0.4 L* for the runs that include the w1 band (see Section 4.1.1 and Figure B.3). Hereby, L* is the luminosity at the break of the Schechter function (Schechter 1976). The magnitude of an L* galaxy was normalized to 17.85 i mag in the Sloan photometric system at redshift z = 0.2, consistently to Rykoff et al. (2016).

thumbnail Fig. B.3

Conversion from limiting z-band magnitude to limiting redshift zvlim for galaxies with a luminosity L = 0.2 L* (orange) and L = 0.4 L* (blue). Restricting the sample to brighter members allows for probing higher redshifts. For reference, the green histogram shows the distribution of limiting magnitudes in the z band for the combined full LS DR10 south and LS DR9 north areas.

Our choice to base the largest reliable redshift purely on the z band deviates from Rykoff et al. (2016) who used a combination of the limiting magnitudes in every filter band to calculate a maximum redshift zmax. We have shown that the cluster number density remains unbiased for clusters zλ < zvlim (see Figure 13). As zmax < zvlim, this allowed us to probe even higher redshifts. We emphasize that we did not discard clusters with higher than the limiting redshift zλ > zvlim. They were kept in the catalogs with a flag IN_ZVLIM=False.

Appendix C Red sequence models

Photometric redshifts were calculated by comparing the galaxy colors to a spline-based red-sequence model (Rykoff et al. 2014). The color–redshift relations for the red-sequence model must be calibrated with the colors of red galaxies with known spectroscopic redshifts. For this, we utilized our spectroscopic galaxy redshift compilation (see Section 2.3 and Appendix D). As explained in Section 4.1.1, we ran eROMaPPer six times using different filter band combinations. The red-sequence model was calibrated for each run independently, corresponding to the six rows in Figure C.1.

We began the model fitting procedure by assuming an initial red-sequence model derived from the predictions of a passively evolving single stellar population (Bruzual & Charlot 2003). We then selected red galaxies whose colors are consistent with the initial model. Figure C.1 shows the color-coded point density of the final sample for each photometric color.

The spline nodes of the red-sequence model (red points) were then fitted to the colors in redshift bins. Outliers were iteratively clipped. We chose a small node spacing of Δzspec = 0.05 for the grz and griz filter band combinations to capture high-frequency color variations. If not fitted well, systematic residuals lead to a higher local redshift bias (see Section 8.1), which in turn leads to local clumping of the cluster number densities (see Figure 12). A larger node spacing of Δzspec = 0.10 was applied for the grizw1 and grzw1 filter band combinations. This was better suited for the red-sequence model calibration for the high-redshift (zλ > 0.8) eROMaPPer runs because the number of training galaxies became low.

The minimum redshift of the model is zspec = 0.05. The maximum redshift is zspec = 0.9 for the grz and griz filter band combinations and zspec = 1.2 for the grzw1 and grizw1 combinations. Including the near-infrared w1 band helps to constrain better cluster redshifts at z > 0.8 because the z − w1 colors have a non-negligible slope. However, it does not necessarily help for low–z cluster redshifts because of the relatively large scatter of the z − w1 colors. For this reason and the more uncertain photometry in the w1 band (see Section 2.2), we did exclude it for the low-z eROMaPPer runs.

As mentioned previously, photometric redshifts were calculated by comparing the galaxy colors to the red-sequence model. Thereby, all filter bands were taken into account at all redshifts. Figure C.1 confirms that different filter bands are suited better or worse to constrain specific redshift intervals. The higher the slope of the color–redshift relation, the better the color constrains the redshift. Hence, each color was weighted by the local slope of its color–redshift relation.

thumbnail Fig. C.1

Red-sequence models for the six different calibrations (rows). Each filter band combination and LS parts are labeled in the titles of the subpanels. The combination of n filter bands results in red-sequence models for n − 1 colors (columns). The red-sequence models are shown by the red splines and red points mark the spline nodes. The training galaxies are color-coded according to their point density. Their total numbers are, after clipping, ~93 000 for LS DR10 (grz and grzw1), ~72000 for LS DR10 (griz and grizw1), and ~36000 for LS DR9 north (grz and grzw1).

Appendix D Details about the spectroscopic galaxy redshift compilation

The spectroscopic galaxy compilation is used to calibrate the red-sequence models and to calculate spectroscopic cluster redshifts and velocity dispersions. Figure D.1 shows the distribution of all redshifts. Table D.1 lists the individual references in column (1), the number of unique galaxy redshifts in column (2), and the applied selection criteria in column (3). Please note that the Zou et al. (2019) source is a compilation of several spectroscopic surveys: 2dFGRS (Colless et al. 2001), 2SLAQ (Cannon et al. 2006), 6dFGS (Jones et al. 2004, 2009), CFRS (Lilly et al. 1995), CNOC2 (Yee et al. 2000), DEEP2 (Davis et al. 2003; Newman et al. 2013), SDSS DR14 (Abolfathi et al. 2018), VIPERS (Garilli et al. 2014; Guzzo et al. 2014), VVDS (Le Fèvre et al. 2005; Garilli et al. 2008), WiggleZ (Drinkwater et al. 2010; Parkinson et al. 2012), and zCOSMOS (Lilly et al. 2007).

thumbnail Fig. D.1

Redshift distribution of the spectroscopic galaxy redshift compilation.
Table D.1

Spectroscopic galaxy compilation.

Appendix E Catalog column descriptions

Table E.1 gives an overview of the column names, data types, and descriptions of the columns in the eRASS1 identified cluster catalog. The data are available in electronic form at the CDS. More X-ray properties of the clusters can be found in Bulbul et al. (2024).

Table E.1

Column names, data types, and descriptions of the eRASS1 identified cluster catalog.

References

  1. Abbott, T. M. C., Aguena, M., Alarcon, A., et al. 2020, Phys. Rev. D, 102, 023509 [Google Scholar]
  2. Abdullah, M. H., Klypin, A., & Wilson, G. 2020, ApJ, 901, 90 [NASA ADS] [CrossRef] [Google Scholar]
  3. Abell, G. O., Corwin, Harold G., J., & Olowin, R. P. 1989, ApJS, 70, 1 [NASA ADS] [CrossRef] [Google Scholar]
  4. Abolfathi, B., Aguado, D. S., Aguilar, G., et al. 2018, ApJS, 235, 42 [NASA ADS] [CrossRef] [Google Scholar]
  5. Adami, C., Giles, P., Koulouridis, E., et al. 2018, A&A, 620, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Aguado-Barahona, A., Barrena, R., Streblyanska, A., et al. 2019, A&A, 631, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Aguena, M., Benoist, C., da Costa, L. N., et al. 2021, MNRAS, 502, 4435 [NASA ADS] [CrossRef] [Google Scholar]
  8. Agulli, I., Aguerri, J. A. L., Sánchez-Janssen, R., et al. 2016, MNRAS, 458, 1590 [NASA ADS] [CrossRef] [Google Scholar]
  9. Ahumada, R., Allende Prieto, C., Almeida, A., et al. 2020, ApJS, 249, 3 [NASA ADS] [CrossRef] [Google Scholar]
  10. Akritas, M. G., & Bershady, M. A. 1996, ApJ, 470, 706 [Google Scholar]
  11. Alam, S., Albareti, F. D., Allende Prieto, C., et al. 2015, ApJS, 219, 12 [Google Scholar]
  12. Albert, C. E., White, R. A., & Morgan, W. W. 1977, ApJ, 211, 309 [NASA ADS] [CrossRef] [Google Scholar]
  13. Almeida, A., Anderson, S. F., Argudo-Fernández, M., et al. 2023, ApJS, 267, 44 [NASA ADS] [CrossRef] [Google Scholar]
  14. Amodeo, S., Mei, S., Stanford, S. A., et al. 2018, ApJ, 853, 36 [NASA ADS] [CrossRef] [Google Scholar]
  15. Andernach, H. 1991, in ASP Conf. Ser., 15, Large-scale Structures and Peculiar Motions in the Universe, eds. D. W. Latham & L. A. N. da Costa, 279 [Google Scholar]
  16. Arnaboldi, M., & Gerhard, O. 2022, Front. Astron. Space Sci., 9, 872283 [NASA ADS] [CrossRef] [Google Scholar]
  17. Bacon, R., Brinchmann, J., Conseil, S., et al. 2023, A&A, 670, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Bahar, Y. E., Bulbul, E., Ghirardini, V., et al. 2024, A&A, submitted [arXiv:2401.17276] [Google Scholar]
  19. Balogh, M. L., McGee, S. L., Mok, A., et al. 2014, MNRAS, 443, 2679 [NASA ADS] [CrossRef] [Google Scholar]
  20. Balogh, M. L., van der Burg, R. F. J., Muzzin, A., et al. 2021, MNRAS, 500, 358 [Google Scholar]
  21. Baxter, E. J., Rozo, E., Jain, B., Rykoff, E., & Wechsler, R. H. 2016, MNRAS, 463, 205 [NASA ADS] [CrossRef] [Google Scholar]
  22. Bayliss, M. B., Hennawi, J. F., Gladders, M. D., et al. 2011, ApJS, 193, 8 [Google Scholar]
  23. Bayliss, M. B., Ruel, J., Stubbs, C. W., et al. 2016, ApJS, 227, 3 [NASA ADS] [CrossRef] [Google Scholar]
  24. Bayliss, M. B., Zengo, K., Ruel, J., et al. 2017, ApJ, 837, 88 [NASA ADS] [CrossRef] [Google Scholar]
  25. Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [Google Scholar]
  26. Bellagamba, F., Roncarelli, M., Maturi, M., & Moscardini, L. 2018, MNRAS, 473, 5221 [NASA ADS] [CrossRef] [Google Scholar]
  27. Bezanson, R., van der Wel, A., Pacifici, C., et al. 2018, ApJ, 858, 60 [NASA ADS] [CrossRef] [Google Scholar]
  28. Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton: Princeton Univ. Press) [Google Scholar]
  29. Blake, C., Amon, A., Childress, M., et al. 2016, MNRAS, 462, 4240 [NASA ADS] [CrossRef] [Google Scholar]
  30. Blanton, M. R., Lupton, R. H., Schlegel, D. J., et al. 2005, ApJ, 631, 208 [Google Scholar]
  31. Bleem, L. E., Stalder, B., de Haan, T., et al. 2015, ApJS, 216, 27 [Google Scholar]
  32. Bleem, L. E., Bocquet, S., Stalder, B., et al. 2020, ApJS, 247, 25 [Google Scholar]
  33. Bocquet, S., Dietrich, J. P., Schrabback, T., et al. 2019, ApJ, 878, 55 [Google Scholar]
  34. Boggs, P. T., Donaldson, J. R., Byrd, R. h., & Schnabel, R. B. 1989, ACM Trans. Math. Softw., 15, 348 [Google Scholar]
  35. Böhringer, H., Voges, W., Huchra, J. P., et al. 2000, ApJS, 129, 435 [Google Scholar]
  36. Böhringer, H., Schuecker, P., Guzzo, L., et al. 2004, A&A, 425, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Böhringer, H., Chon, G., Retzlaff, J., et al. 2017, AJ, 153, 220 [Google Scholar]
  38. Borm, K., Reiprich, T. H., Mohammed, I., & Lovisari, L. 2014, A&A, 567, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Bradshaw, E. J., Almaini, O., Hartley, W. G., et al. 2013, MNRAS, 433, 194 [NASA ADS] [CrossRef] [Google Scholar]
  40. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  41. Bulbul, E., Liu, A., Pasini, T., et al. 2022, A&A, 661, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Bulbul, E., Liu, A., Kluge, M., et al. 2024, A&A, 685, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Butcher, H., & Oemler, A. J., 1978, ApJ, 219, 18 [NASA ADS] [CrossRef] [Google Scholar]
  44. Caminha, G. B., Grillo, C., Rosati, P., et al. 2017, A&A, 600, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Caminha, G. B., Rosati, P., Grillo, C., et al. 2019, A&A, 632, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Cannon, R., Drinkwater, M., Edge, A., et al. 2006, MNRAS, 372, 425 [NASA ADS] [CrossRef] [Google Scholar]
  47. Capasso, R., Mohr, J. J., Saro, A., et al. 2019, MNRAS, 486, 1594 [NASA ADS] [CrossRef] [Google Scholar]
  48. Carrasco, M., Barrientos, L. F., Anguita, T., et al. 2017, ApJ, 834, 210 [CrossRef] [Google Scholar]
  49. Castagné, D., Soucail, G., Pointecouteau, E., et al. 2012, A&A, 548, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Castignani, G., Pandey-Pommier, M., Hamer, S. L., et al. 2020, A&A, 640, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Cava, A., Bettoni, D., Poggianti, B. M., et al. 2009, A&A, 495, 707 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Childress, M. J., Lidman, C., Davis, T. M., et al. 2017, MNRAS, 472, 273 [Google Scholar]
  53. Clerc, N., Sadibekova, T., Pierre, M., et al. 2012, MNRAS, 423, 3561 [NASA ADS] [CrossRef] [Google Scholar]
  54. Clerc, N., Merloni, A., Zhang, Y.-Y., et al. 2016, MNRAS, 463, 4490 [Google Scholar]
  55. Clerc, N., Kirkpatrick, C. C., Finoguenov, A., et al. 2020, MNRAS, 497, 3976 [NASA ADS] [CrossRef] [Google Scholar]
  56. Clerc, N., Comparat, J., Seppi, R., et al. 2024, A&A, 687, A238 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Coe, D., Umetsu, K., Zitrin, A., et al. 2012, ApJ, 757, 22 [NASA ADS] [CrossRef] [Google Scholar]
  58. Coil, A. L., Blanton, M. R., Burles, S. M., et al. 2011, ApJ, 741, 8 [Google Scholar]
  59. Colless, M., Dalton, G., Maddox, S., et al. 2001, MNRAS, 328, 1039 [Google Scholar]
  60. Connelly, J. L., Wilman, D. J., Finoguenov, A., et al. 2012, ApJ, 756, 139 [NASA ADS] [CrossRef] [Google Scholar]
  61. Connor, T., Kelson, D. D., Blanc, G. A., & Boutsia, K. 2019, ApJ, 878, 66 [NASA ADS] [CrossRef] [Google Scholar]
  62. Contini, E. 2021, Galaxies, 9, 60 [NASA ADS] [CrossRef] [Google Scholar]
  63. Cool, R. J., Moustakas, J., Blanton, M. R., et al. 2013, ApJ, 767, 118 [NASA ADS] [CrossRef] [Google Scholar]
  64. Cooper, M. C., Yan, R., Dickinson, M., et al. 2012, MNRAS, 425, 2116 [NASA ADS] [CrossRef] [Google Scholar]
  65. Costanzi, M., Rozo, E., Rykoff, E. S., et al. 2019a, MNRAS, 482, 490 [CrossRef] [Google Scholar]
  66. Costanzi, M., Rozo, E., Simet, M., et al. 2019b, MNRAS, 488, 4779 [NASA ADS] [CrossRef] [Google Scholar]
  67. Costanzi, M., Saro, A., Bocquet, S., et al. 2021, Phys. Rev. D, 103, 043522 [Google Scholar]
  68. Crawford, S. M., Wirth, G. D., Bershady, M. A., & Hon, K. 2011, ApJ, 741, 98 [NASA ADS] [CrossRef] [Google Scholar]
  69. Czoske, O., Kneib, J. P., Soucail, G., et al. 2001, A&A, 372, 391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Dalton, G. B., Maddox, S. J., Sutherland, W. J., & Efstathiou, G. 1997, MNRAS, 289, 263 [CrossRef] [Google Scholar]
  71. Damsted, S., Finoguenov, A., Clerc, N., et al. 2023, A&A, 676, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Danese, L., de Zotti, G., & di Tullio, G. 1980, A&A, 82, 322 [NASA ADS] [Google Scholar]
  73. Dark Energy Survey Collaboration (Abbott, T., et al.) 2016, MNRAS, 460, 1270 [Google Scholar]
  74. Davis, M., Faber, S. M., Newman, J., et al. 2003, SPIE Conf. Ser., 4834, 161 [NASA ADS] [Google Scholar]
  75. Davis, M., Guhathakurta, P., Konidaris, N. P., et al. 2007, ApJ, 660, L1 [NASA ADS] [CrossRef] [Google Scholar]
  76. Dawson, W. A. 2013, ApJ, 772, 131 [NASA ADS] [CrossRef] [Google Scholar]
  77. Deger, S., Rudnick, G., Kelkar, K., et al. 2018, ApJ, 869, 6 [Google Scholar]
  78. de Haan, T., Benson, B. A., Bleem, L. E., et al. 2016, ApJ, 832, 95 [NASA ADS] [CrossRef] [Google Scholar]
  79. Demarco, R., Rosati, P., Lidman, C., et al. 2005, A&A, 432, 381 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Demarco, R., Rosati, P., Lidman, C., et al. 2007, ApJ, 663, 164 [NASA ADS] [CrossRef] [Google Scholar]
  81. Demarco, R., Wilson, G., Muzzin, A., et al. 2010, ApJ, 711, 1185 [CrossRef] [Google Scholar]
  82. Deshev, B., Finoguenov, A., Verdugo, M., et al. 2017, A&A, 607, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. DESI Collaboration (Adame, A. G., et al.) 2024, AJ, 168, 58 [NASA ADS] [CrossRef] [Google Scholar]
  84. Dey, A., Schlegel, D. J., Lang, D., et al. 2019, AJ, 157, 168 [Google Scholar]
  85. Diemer, B. 2018, ApJS, 239, 35 [NASA ADS] [CrossRef] [Google Scholar]
  86. Dressler, A. 1980, ApJ, 236, 351 [Google Scholar]
  87. Dressler, A., Smail, I., Poggianti, B. M., et al. 1999, ApJS, 122, 51 [NASA ADS] [CrossRef] [Google Scholar]
  88. Dreyer, J. L. E. 1888, MmRAS, 49, 1 [Google Scholar]
  89. Drinkwater, M. J., Jurek, R. J., Blake, C., et al. 2010, MNRAS, 401, 1429 [CrossRef] [Google Scholar]
  90. Driver, S. P., Hill, D. T., Kelvin, L. S., et al. 2011, MNRAS, 413, 971 [Google Scholar]
  91. Driver, S. P., Bellstedt, S., Robotham, A. S. G., et al. 2022, MNRAS, 513, 439 [NASA ADS] [CrossRef] [Google Scholar]
  92. Duarte, M., & Mamon, G. A. 2015, MNRAS, 453, 3848 [Google Scholar]
  93. Ebeling, H., Ma, C.-J., & Barrett, E. 2014, ApJS, 211, 21 [NASA ADS] [CrossRef] [Google Scholar]
  94. Ebeling, H., Qi, J., & Richard, J. 2017, MNRAS, 471, 3305 [NASA ADS] [CrossRef] [Google Scholar]
  95. Eisenhardt, P. R. M., Brodwin, M., Gonzalez, A. H., et al. 2008, ApJ, 684, 905 [Google Scholar]
  96. Euclid Collaboration (Adam, R., et al.) 2019, A&A, 627, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  97. Farahi, A., Evrard, A. E., Rozo, E., Rykoff, E. S., & Wechsler, R. H. 2016, MNRAS, 460, 3900 [NASA ADS] [CrossRef] [Google Scholar]
  98. Ferragamo, A., Rubiño-Martín, J. A., Betancort-Rijo, J., et al. 2020, A&A, 641, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Ferrari, C., Maurogordato, S., Cappi, A., & Benoist, C. 2003, A&A, 399, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  100. Finoguenov, A., Merloni, A., Comparat, J., et al. 2019, The Messenger, 175, 39 [NASA ADS] [Google Scholar]
  101. Finoguenov, A., Rykoff, E., Clerc, N., et al. 2020, A&A, 638, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  102. Flaugher, B., Diehl, H. T., Honscheid, K., et al. 2015, AJ, 150, 150 [Google Scholar]
  103. Foëx, G., Chon, G., & Böhringer, H. 2017, A&A, 601, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Foley, R. J., Andersson, K., Bazin, G., et al. 2011, ApJ, 731, 86 [NASA ADS] [CrossRef] [Google Scholar]
  105. Fossati, M., Fumagalli, M., Lofthouse, E. K., et al. 2019, MNRAS, 490, 1451 [NASA ADS] [CrossRef] [Google Scholar]
  106. Garilli, B., Le Fèvre, O., Guzzo, L., et al. 2008, A&A, 486, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  107. Garilli, B., Guzzo, L., Scodeggio, M., et al. 2014, A&A, 562, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  108. Garilli, B., McLure, R., Pentericci, L., et al. 2021, A&A, 647, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Geha, M., Wechsler, R. H., Mao, Y.-Y., et al. 2017, ApJ, 847, 4 [NASA ADS] [CrossRef] [Google Scholar]
  110. George, M. R., Leauthaud, A., Bundy, K., et al. 2011, ApJ, 742, 125 [Google Scholar]
  111. Ghirardini, V., Bulbul, E., Artis, E., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202348852 [Google Scholar]
  112. Girardi, M., Boschin, W., & Barrena, R. 2010, A&A, 517, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  113. Gladders, M. D., & Yee, H. K. C. 2000, AJ, 120, 2148 [NASA ADS] [CrossRef] [Google Scholar]
  114. Gladders, M. D., Yee, H. K. C., Majumdar, S., et al. 2007, ApJ, 655, 128 [CrossRef] [Google Scholar]
  115. Golovich, N., Dawson, W. A., Wittman, D. M., et al. 2019, ApJ, 882, 69 [NASA ADS] [CrossRef] [Google Scholar]
  116. Gómez, P. L., Valkonen, L. E., Romer, A. K., et al. 2012, AJ, 144, 79 [CrossRef] [Google Scholar]
  117. Gonzalez, A. H., Gettings, D. P., Brodwin, M., et al. 2019, ApJS, 240, 33 [NASA ADS] [CrossRef] [Google Scholar]
  118. Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [Google Scholar]
  119. Grandis, S., Ghirardini, V., Bocquet, S., et al. 2024, A&A, 687, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  120. Gschwend, J., Rossel, A. C., Ogando, R. L. C., et al. 2018, Astron. Comput., 25, 58 [NASA ADS] [CrossRef] [Google Scholar]
  121. Guennou, L., Biviano, A., Adami, C., et al. 2014, A&A, 566, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  122. Guglielmo, V., Poggianti, B. M., Vulcani, B., et al. 2018, A&A, 620, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  123. Guzzo, L., Scodeggio, M., Garilli, B., et al. 2014, A&A, 566, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  124. Hahn, C., Blanton, M. R., Moustakas, J., et al. 2015, ApJ, 806, 162 [NASA ADS] [CrossRef] [Google Scholar]
  125. Haines, C. 2021, in Extragalactic Spectroscopic Surveys: Past, Present and Future of Galaxy Evolution (GALSPEC2021), 51 [Google Scholar]
  126. Halliday, C., Milvang-Jensen, B., Poirier, S., et al. 2004, A&A, 427, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. Hansen, L., Olsen, L. F., & Jørgensen, H. E. 2002, A&A, 388, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  128. Hao, J., McKay, T. A., Koester, B. P., et al. 2010, ApJS, 191, 254 [Google Scholar]
  129. Hashimoto, Y., Barcons, X., Böhringer, H., et al. 2004, A&A, 417, 819 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  130. Hickson, P. 1982, ApJ, 255, 382 [NASA ADS] [CrossRef] [Google Scholar]
  131. Hikage, C., Mandelbaum, R., Leauthaud, A., Rozo, E., & Rykoff, E. S. 2018, MNRAS, 480, 2689 [CrossRef] [Google Scholar]
  132. Hill, G. J., Lee, H., MacQueen, P. J., et al. 2021, AJ, 162, 298 [NASA ADS] [CrossRef] [Google Scholar]
  133. Hilton, M., Sifón, C., Naess, S., et al. 2021, ApJS, 253, 3 [Google Scholar]
  134. Hollowood, D. L., Jeltema, T., Chen, X., et al. 2019, ApJS, 244, 22 [CrossRef] [Google Scholar]
  135. Hoshino, H., Leauthaud, A., Lackner, C., et al. 2015, MNRAS, 452, 998 [NASA ADS] [CrossRef] [Google Scholar]
  136. Huang, S., Leauthaud, A., Murata, R., et al. 2018, PASJ, 70, S6 [CrossRef] [Google Scholar]
  137. Huang, N., Bleem, L. E., Stalder, B., et al. 2020a, AJ, 159, 110 [Google Scholar]
  138. Huang, X., Storfer, C., Ravi, V., et al. 2020b, ApJ, 894, 78 [NASA ADS] [CrossRef] [Google Scholar]
  139. Huang, X., Storfer, C., Gu, A., et al. 2021, ApJ, 909, 27 [NASA ADS] [CrossRef] [Google Scholar]
  140. Huchra, J. P., Macri, L. M., Masters, K. L., et al. 2012, ApJS, 199, 26 [Google Scholar]
  141. Hwang, H. S., Geller, M. J., Diaferio, A., Rines, K. J., & Zahid, H. J. 2014, ApJ, 797, 106 [NASA ADS] [CrossRef] [Google Scholar]
  142. Ider Chitham, J., Comparat, J., Finoguenov, A., et al. 2020, MNRAS, 499, 4768 [NASA ADS] [CrossRef] [Google Scholar]
  143. Inami, H., Bacon, R., Brinchmann, J., et al. 2017, A&A, 608, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  144. Ishak, M. 2019, Liv. Rev. Rel., 22, 1 [NASA ADS] [CrossRef] [Google Scholar]
  145. Ivezić, Ž., Kahn, S. M., Tyson, J. A., et al. 2019, ApJ, 873, 111 [Google Scholar]
  146. Jimeno, P., Diego, J. M., Broadhurst, T., De Martino, I., & Lazkoz, R. 2018, MNRAS, 478, 638 [NASA ADS] [CrossRef] [Google Scholar]
  147. Jones, D. H., Saunders, W., Colless, M., et al. 2004, MNRAS, 355, 747 [NASA ADS] [CrossRef] [Google Scholar]
  148. Jones, D. H., Read, M. A., Saunders, W., et al. 2009, MNRAS, 399, 683 [Google Scholar]
  149. Jørgensen, I., Chiboucas, K., Toft, S., et al. 2014, AJ, 148, 117 [CrossRef] [Google Scholar]
  150. Jørgensen, I., Chiboucas, K., Berkson, E., et al. 2017, AJ, 154, 251 [CrossRef] [Google Scholar]
  151. Kaiser, N., Burgett, W., Chambers, K., et al. 2010, SPIE Conf. Ser., 7733, 77330E [Google Scholar]
  152. Karman, W., Caputi, K. I., Grillo, C., et al. 2015, A&A, 574, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  153. Kelly, B. C. 2007, ApJ, 665, 1489 [Google Scholar]
  154. Khabibullina, M. L., & Verkhodanov, O. V. 2009, Astrophys. Bull., 64, 340 [NASA ADS] [CrossRef] [Google Scholar]
  155. Khullar, G., Bleem, L., Bayliss, M., Gladders, M., & South Pole Telescope (SPT) Collaboration 2018, in Am. Astron. Soc. Meeting Abstracts, 232, 324.05 [NASA ADS] [Google Scholar]
  156. Kim, J., Jee, M. J., Hughes, J. P., et al. 2021, ApJ, 923, 101 [NASA ADS] [CrossRef] [Google Scholar]
  157. Kirby, M., Rozo, E., Morris, R. G., et al. 2019, arXiv e-prints [arXiv:1910.13548] [Google Scholar]
  158. Kirk, B., Hilton, M., Cress, C., et al. 2015, MNRAS, 449, 4010 [NASA ADS] [CrossRef] [Google Scholar]
  159. Kirkpatrick, C. C., Clerc, N., Finoguenov, A., et al. 2021, MNRAS, 503, 5763 [NASA ADS] [CrossRef] [Google Scholar]
  160. Klein, M., Grandis, S., Mohr, J. J., et al. 2019, MNRAS, 488, 739 [Google Scholar]
  161. Klein, M., Oguri, M., Mohr, J. J., et al. 2022, A&A, 661, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  162. Klein, M., Hernández-Lang, D., Mohr, J. J., Bocquet, S., & Singh, A. 2023, MNRAS, 526, 3757 [NASA ADS] [CrossRef] [Google Scholar]
  163. Kleinebreil, F., Grandis, S., Schrabback, T., et al. 2024, A&A, submitted [arXiv:2402.08456] [Google Scholar]
  164. Kluge, M., & Bender, R. 2023, ApJS, 267, 41 [NASA ADS] [CrossRef] [Google Scholar]
  165. Kluge, M., Neureiter, B., Riffeser, A., et al. 2020, ApJS, 247, 43 [Google Scholar]
  166. Koester, B. P., McKay, T. A., Annis, J., et al. 2007, ApJ, 660, 221 [NASA ADS] [CrossRef] [Google Scholar]
  167. Kollmeier, J. A., Zasowski, G., Rix, H.-W., et al. 2017, arXiv e-prints [arXiv:1711.03234] [Google Scholar]
  168. Koranyi, D. M., & Geller, M. J. 2002, AJ, 123, 100 [CrossRef] [Google Scholar]
  169. Koulouridis, E., Poggianti, B., Altieri, B., et al. 2016, A&A, 592, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  170. Koulouridis, E., Clerc, N., Sadibekova, T., et al. 2021, A&A, 652, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  171. Kovlakas, K., Zezas, A., Andrews, J. J., et al. 2021, MNRAS, 506, 1896 [NASA ADS] [CrossRef] [Google Scholar]
  172. Lamer, G., Hoeft, M., Kohnert, J., Schwope, A., & Storm, J. 2008, A&A, 487, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  173. Lang, D. 2014, AJ, 147, 108 [Google Scholar]
  174. Lang, D., Hogg, D. W., & Mykytyn, D. 2016, The Tractor: Probabilistic astronomical source detection and measurement, Astrophysics Source Code Library, [record ascl:1604.008] [Google Scholar]
  175. Lauer, T. R., Postman, M., Strauss, M. A., Graves, G. J., & Chisari, N. E. 2014, ApJ, 797, 82 [Google Scholar]
  176. Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, arXiv e-prints [arXiv:1110.3193] [Google Scholar]
  177. Lee, S.-K., Im, M., Hyun, M., et al. 2019, MNRAS, 490, 135 [NASA ADS] [CrossRef] [Google Scholar]
  178. Le Fèvre, O., Vettolani, G., Paltani, S., et al. 2004, A&A, 428, 1043 [CrossRef] [EDP Sciences] [Google Scholar]
  179. Le Fèvre, O., Vettolani, G., Garilli, B., et al. 2005, A&A, 439, 845 [Google Scholar]
  180. Le Fèvre, O., Cassata, P., Cucciati, O., et al. 2013, A&A, 559, A14 [Google Scholar]
  181. Lemze, D., Postman, M., Genel, S., et al. 2013, ApJ, 776, 91 [CrossRef] [Google Scholar]
  182. Licitra, R., Mei, S., Raichoor, A., Erben, T., & Hildebrandt, H. 2016a, MNRAS, 455, 3020 [NASA ADS] [CrossRef] [Google Scholar]
  183. Licitra, R., Mei, S., Raichoor, A., et al. 2016b, ApJ, 829, 44 [CrossRef] [Google Scholar]
  184. Lidman, C., Ardila, F., Owers, M., et al. 2016, PASA, 33, e001 [NASA ADS] [CrossRef] [Google Scholar]
  185. Lidman, C., Tucker, B. E., Davis, T. M., et al. 2020, MNRAS, 496, 19 [NASA ADS] [CrossRef] [Google Scholar]
  186. Lilly, S. J., Le Fevre, O., Crampton, D., Hammer, F., & Tresse, L. 1995, ApJ, 455, 50 [NASA ADS] [CrossRef] [Google Scholar]
  187. Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [Google Scholar]
  188. Lilly, S. J., Le Brun, V., Maier, C., et al. 2009, ApJS, 184, 218 [Google Scholar]
  189. Liske, J., Baldry, I. K., Driver, S. P., et al. 2015, MNRAS, 452, 2087 [Google Scholar]
  190. Liu, A., Yu, H., Diaferio, A., et al. 2018, ApJ, 863, 102 [NASA ADS] [CrossRef] [Google Scholar]
  191. Liu, F. S., Mao, S., & Meng, X. M. 2012, MNRAS, 423, 422 [NASA ADS] [CrossRef] [Google Scholar]
  192. Liu, A., Bulbul, E., Ghirardini, V., et al. 2022, A&A, 661, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  193. Liu, A., Bulbul, E., Kluge, M., et al. 2024, A&A, 683, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  194. Lloyd-Davies, E. J., Romer, A. K., Mehrtens, N., et al. 2011, MNRAS, 418, 14 [NASA ADS] [CrossRef] [Google Scholar]
  195. Lotz, M., Remus, R.-S., Dolag, K., Biviano, A., & Burkert, A. 2019, MNRAS, 488, 5370 [NASA ADS] [CrossRef] [Google Scholar]
  196. Mainzer, A., Bauer, J., Cutri, R. M., et al. 2014, ApJ, 792, 30 [Google Scholar]
  197. Mancone, C. L., Gonzalez, A. H., Moustakas, L. A., & Price, A. 2013, PASP, 125, 1514 [NASA ADS] [CrossRef] [Google Scholar]
  198. Mao, M. Y., Sharp, R., Norris, R. P., et al. 2012, MNRAS, 426, 3334 [NASA ADS] [CrossRef] [Google Scholar]
  199. Masters, D. C., Stern, D. K., Cohen, J. G., et al. 2017, ApJ, 841, 111 [Google Scholar]
  200. Masters, D. C., Stern, D. K., Cohen, J. G., et al. 2019, ApJ, 877, 81 [Google Scholar]
  201. Matthews, T. A., Morgan, W. W., & Schmidt, M. 1964, ApJ, 140, 35 [NASA ADS] [CrossRef] [Google Scholar]
  202. Maturi, M., Bellagamba, F., Radovich, M., et al. 2019, MNRAS, 485, 498 [Google Scholar]
  203. McClintock, T., Varga, T. N., Gruen, D., et al. 2019, MNRAS, 482, 1352 [Google Scholar]
  204. McDonald, M., Stalder, B., Bayliss, M., et al. 2016, ApJ, 817, 86 [Google Scholar]
  205. McLure, R. J., Pearce, H. J., Dunlop, J. S., et al. 2013, MNRAS, 428, 1088 [NASA ADS] [CrossRef] [Google Scholar]
  206. McLure, R., Pentericci, L., & VANDELS Team. 2017, The Messenger, 167, 31 [NASA ADS] [Google Scholar]
  207. Mehrtens, N., Romer, A. K., Hilton, M., et al. 2012, MNRAS, 423, 1024 [NASA ADS] [CrossRef] [Google Scholar]
  208. Meisner, A. M., Lang, D., & Schlegel, D. J. 2017a, AJ, 154, 161 [NASA ADS] [CrossRef] [Google Scholar]
  209. Meisner, A. M., Lang, D., & Schlegel, D. J. 2017b, AJ, 153, 38 [Google Scholar]
  210. Melchior, P., Gruen, D., McClintock, T., et al. 2017, MNRAS, 469, 4899 [CrossRef] [Google Scholar]
  211. Merloni, A., Predehl, P., Becker, W., et al. 2012, arXiv e-prints [arXiv:1209.3114] [Google Scholar]
  212. Merloni, A., Lamer, G., Liu, T., et al. 2024, A&A, 682, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  213. Miller, C. J., Nichol, R. C., Reichart, D., et al. 2005, AJ, 130, 968 [Google Scholar]
  214. Mirkazemi, M., Finoguenov, A., Pereira, M. J., et al. 2015, ApJ, 799, 60 [NASA ADS] [CrossRef] [Google Scholar]
  215. Momcheva, I. G., Brammer, G. B., van Dokkum, P. G., et al. 2016, ApJS, 225, 27 [Google Scholar]
  216. Montes, M. 2022, Nat. Astron., 6, 308 [NASA ADS] [CrossRef] [Google Scholar]
  217. Moran, S. M., Ellis, R. S., Treu, T., et al. 2005, ApJ, 634, 977 [NASA ADS] [CrossRef] [Google Scholar]
  218. Moretti, A., Gullieuszik, M., Poggianti, B., et al. 2017, A&A, 599, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  219. Morgan, W. W., & Lesh, J. R. 1965, ApJ, 142, 1364 [NASA ADS] [CrossRef] [Google Scholar]
  220. Morgan, W. W., Kayser, S., & White, R. A. 1975, ApJ, 199, 545 [CrossRef] [Google Scholar]
  221. Morris, R. A. H., Phillipps, S., Jones, J. B., et al. 2007, A&A, 476, 59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  222. Moustakas, J., Lang, D., Dey, A., et al. 2023, ApJS, 269, 3 [NASA ADS] [CrossRef] [Google Scholar]
  223. Murata, R., Nishimichi, T., Takada, M., et al. 2018, ApJ, 854, 120 [NASA ADS] [CrossRef] [Google Scholar]
  224. Murphy, D. N. A., Geach, J. E., & Bower, R. G. 2012, MNRAS, 420, 1861 [Google Scholar]
  225. Muzzin, A., Wilson, G., Yee, H. K. C., et al. 2009, ApJ, 698, 1934 [Google Scholar]
  226. Muzzin, A., Wilson, G., Yee, H. K. C., et al. 2012, ApJ, 746, 188 [Google Scholar]
  227. Myles, J., Gruen, D., Mantz, A. B., et al. 2021, MNRAS, 505, 33 [NASA ADS] [CrossRef] [Google Scholar]
  228. Nanayakkara, T., Glazebrook, K., Kacprzak, G. G., et al. 2016, ApJ, 828, 21 [NASA ADS] [CrossRef] [Google Scholar]
  229. Nastasi, A., Böhringer, H., Fassbender, R., et al. 2014, A&A, 564, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  230. Nemmen, R. S., Georganopoulos, M., Guiriec, S., et al. 2012, Science, 338, 1445 [NASA ADS] [CrossRef] [Google Scholar]
  231. Newman, J. A., Cooper, M. C., Davis, M., et al. 2013, ApJS, 208, 5 [Google Scholar]
  232. Nilo Castellón, J. L., Alonso, M. V., García Lambas, D., et al. 2014, MNRAS, 437, 2607 [CrossRef] [Google Scholar]
  233. Nishizawa, A. J., Oguri, M., Oogi, T., et al. 2018, PASJ, 70, S24 [CrossRef] [Google Scholar]
  234. Oguri, M. 2014, MNRAS, 444, 147 [NASA ADS] [CrossRef] [Google Scholar]
  235. Oguri, M., Lin, Y.-T., Lin, S.-C., et al. 2018, PASJ, 70, S20 [NASA ADS] [Google Scholar]
  236. Old, L., Wojtak, R., Mamon, G. A., et al. 2015, MNRAS, 449, 1897 [Google Scholar]
  237. Olsen, L. F., Hansen, L., Jørgensen, H. E., et al. 2003, A&A, 409, 439 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  238. Olsen, L. F., Benoist, C., da Costa, L., Hansen, L., & Jørgensen, H. E. 2005, A&A, 435, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  239. Olsen, L. F., Benoist, C., Cappi, A., et al. 2007, A&A, 461, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  240. Oman, K. A., & Hudson, M. J. 2016, MNRAS, 463, 3083 [Google Scholar]
  241. Owen, F. N., Ledlow, M. J., & Keel, W. C. 1995, AJ, 109, 14 [NASA ADS] [CrossRef] [Google Scholar]
  242. Owers, M. S., Nulsen, P. E. J., & Couch, W. J. 2011, ApJ, 741, 122 [Google Scholar]
  243. Pacaud, F., Clerc, N., Giles, P. A., et al. 2016, A&A, 592, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  244. Pacaud, F., Pierre, M., Melin, J. B., et al. 2018, A&A, 620, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  245. Palmese, A., Annis, J., Burgad, J., et al. 2020, MNRAS, 493, 4591 [Google Scholar]
  246. Parkinson, D., Riemer-Sørensen, S., Blake, C., et al. 2012, Phys. Rev. D, 86, 103518 [NASA ADS] [CrossRef] [Google Scholar]
  247. Paterno-Mahler, R., Blanton, E. L., Brodwin, M., et al. 2017, ApJ, 844, 78 [NASA ADS] [CrossRef] [Google Scholar]
  248. Pierre, M., Oukbir, J., Dubreuil, D., et al. 1997, A&AS, 124, 283 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  249. Pierre, M., Pacaud, F., Adami, C., et al. 2016, A&A, 592, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  250. Piffaretti, R., Arnaud, M., Pratt, G. W., Pointecouteau, E., & Melin, J. B. 2011, A&A, 534, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  251. Pimbblet, K. A., Smail, I., Edge, A. C., et al. 2006, MNRAS, 366, 645 [NASA ADS] [CrossRef] [Google Scholar]
  252. Planck Collaboration XXXII. 2015, A&A, 581, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  253. Planck Collaboration XXVII. 2016, A&A, 594, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  254. Postman, M., Lubin, L. M., Gunn, J. E., et al. 1996, AJ, 111, 615 [NASA ADS] [CrossRef] [Google Scholar]
  255. Postman, M., Lubin, L. M., & Oke, J. B. 2001, AJ, 122, 1125 [Google Scholar]
  256. Pranger, F., Böhm, A., Ferrari, C., et al. 2014, A&A, 570, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  257. Predehl, P., Andritschke, R., Arefiev, V., et al. 2021, A&A, 647, A1 [EDP Sciences] [Google Scholar]
  258. Psychogyios, A., Vika, M., Charmandaris, V., et al. 2020, A&A, 633, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  259. Raghunathan, S., Patil, S., Baxter, E., et al. 2019, ApJ, 872, 170 [NASA ADS] [CrossRef] [Google Scholar]
  260. Ramella, M., Boschin, W., Fadda, D., & Nonino, M. 2001, A&A, 368, 776 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  261. Ramsey, L. W., Adams, M. T., Barnes, T. G., et al. 1998, SPIE Conf. Ser., 3352, 34 [Google Scholar]
  262. Rescigno, U., Grillo, C., Lombardi, M., et al. 2020, A&A, 635, A98 [EDP Sciences] [Google Scholar]
  263. Rest, A., Scolnic, D., Foley, R. J., et al. 2014, ApJ, 795, 44 [Google Scholar]
  264. Ricci, M., Benoist, C., Maurogordato, S., et al. 2018, A&A, 620, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  265. Richard, J., Claeyssens, A., Lagattuta, D., et al. 2021, A&A, 646, A83 [EDP Sciences] [Google Scholar]
  266. Rines, K., Geller, M. J., Diaferio, A., Mohr, J. J., & Wegner, G. A. 2000, AJ, 120, 2338 [NASA ADS] [CrossRef] [Google Scholar]
  267. Rines, K. J., Geller, M. J., Diaferio, A., & Hwang, H. S. 2016, ApJ, 819, 63 [NASA ADS] [CrossRef] [Google Scholar]
  268. Rines, K. J., Geller, M. J., Diaferio, A., Hwang, H. S., & Sohn, J. 2018, ApJ, 862, 172 [NASA ADS] [CrossRef] [Google Scholar]
  269. Robotham, A. S. G., Norberg, P., Driver, S. P., et al. 2011, MNRAS, 416, 2640 [NASA ADS] [CrossRef] [Google Scholar]
  270. Romer, A. K. 1994, PhD thesis, Univ. Edinburgh, UK [Google Scholar]
  271. Rozo, E., & Rykoff, E. S. 2014, ApJ, 783, 80 [NASA ADS] [CrossRef] [Google Scholar]
  272. Rudnick, G., Jablonka, P., Moustakas, J., et al. 2017, ApJ, 850, 181 [Google Scholar]
  273. Ruel, J., Bazin, G., Bayliss, M., et al. 2014, ApJ, 792, 45 [NASA ADS] [CrossRef] [Google Scholar]
  274. Runge, J., & Yan, H. 2018, ApJ, 853, 47 [NASA ADS] [CrossRef] [Google Scholar]
  275. Rykoff, E. S., Koester, B. P., Rozo, E., et al. 2012, ApJ, 746, 178 [NASA ADS] [CrossRef] [Google Scholar]
  276. Rykoff, E. S., Rozo, E., Busha, M. T., et al. 2014, ApJ, 785, 104 [Google Scholar]
  277. Rykoff, E. S., Rozo, E., & Keisler, R. 2015, arXiv e-prints [arXiv:1509.00870] [Google Scholar]
  278. Rykoff, E. S., Rozo, E., Hollowood, D., et al. 2016, ApJS, 224, 1 [NASA ADS] [CrossRef] [Google Scholar]
  279. Salvato, M., Hasinger, G., Ilbert, O., et al. 2009, ApJ, 690, 1250 [CrossRef] [Google Scholar]
  280. Saro, A., Bocquet, S., Rozo, E., et al. 2015, MNRAS, 454, 2305 [Google Scholar]
  281. Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
  282. Schirmer, M., Hildebrandt, H., Kuijken, K., & Erben, T. 2011, A&A, 532, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  283. Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [Google Scholar]
  284. Scolnic, D., Rest, A., Riess, A., et al. 2014, ApJ, 795, 45 [Google Scholar]
  285. Seppi, R., Comparat, J., Bulbul, E., et al. 2022, A&A, 665, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  286. Seppi, R., Comparat, J., Nandra, K., et al. 2023, A&A, 671, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  287. Shectman, S. A., Landy, S. D., Oemler, A., et al. 1996, ApJ, 470, 172 [NASA ADS] [CrossRef] [Google Scholar]
  288. Sifón, C., Menanteau, F., Hasselfield, M., et al. 2013, ApJ, 772, 25 [CrossRef] [Google Scholar]
  289. Silva, D. R., Blum, R. D., Allen, L., et al. 2016, in Am. Astron. Soc. Meeting Abstracts, 228, 317.02 [NASA ADS] [Google Scholar]
  290. Silverman, J. D., Kashino, D., Sanders, D., et al. 2015, ApJS, 220, 12 [NASA ADS] [CrossRef] [Google Scholar]
  291. Skelton, R. E., Whitaker, K. E., Momcheva, I. G., et al. 2014, ApJS, 214, 24 [Google Scholar]
  292. Sluse, D., Rusu, C. E., Fassnacht, C. D., et al. 2019, MNRAS, 490, 613 [NASA ADS] [CrossRef] [Google Scholar]
  293. Smith, R. J., Lucey, J. R., Hudson, M. J., Schlegel, D. J., & Davies, R. L. 2000, MNRAS, 313, 469 [NASA ADS] [CrossRef] [Google Scholar]
  294. Soares-Santos, M., de Carvalho, R. R., Annis, J., et al. 2011, ApJ, 727, 45 [NASA ADS] [CrossRef] [Google Scholar]
  295. Sohn, J., Chon, G., Böhringer, H., et al. 2018a, ApJ, 855, 100 [NASA ADS] [CrossRef] [Google Scholar]
  296. Sohn, J., Geller, M. J., Rines, K. J., et al. 2018b, ApJ, 856, 172 [NASA ADS] [CrossRef] [Google Scholar]
  297. Sohn, J., Geller, M. J., & Zahid, H. J. 2019a, ApJ, 880, 142 [NASA ADS] [CrossRef] [Google Scholar]
  298. Sohn, J., Geller, M. J., Zahid, H. J., & Fabricant, D. G. 2019b, ApJ, 872, 192 [NASA ADS] [CrossRef] [Google Scholar]
  299. Sohn, J., Geller, M. J., Diaferio, A., & Rines, K. J. 2020, ApJ, 891, 129 [NASA ADS] [CrossRef] [Google Scholar]
  300. Sohn, J., Geller, M. J., Hwang, H. S., et al. 2021, ApJ, 909, 129 [NASA ADS] [CrossRef] [Google Scholar]
  301. Song, H., Hwang, H. S., Park, C., & Tamura, T. 2017, ApJ, 842, 88 [NASA ADS] [CrossRef] [Google Scholar]
  302. Stanford, S. A., Gonzalez, A. H., Brodwin, M., et al. 2014, ApJS, 213, 25 [CrossRef] [Google Scholar]
  303. Stanford, S. A., Masters, D., Darvish, B., et al. 2021, ApJS, 256, 9 [NASA ADS] [CrossRef] [Google Scholar]
  304. Stopyra, S., Pontzen, A., Peiris, H., Roth, N., & Rey, M. P. 2021, ApJS, 252, 28 [CrossRef] [Google Scholar]
  305. Stott, J. P., Edge, A. C., Smith, G. P., Swinbank, A. M., & Ebeling, H. 2008, MNRAS, 384, 1502 [NASA ADS] [CrossRef] [Google Scholar]
  306. Straatman, C. M. S., van der Wel, A., Bezanson, R., et al. 2018, ApJS, 239, 27 [NASA ADS] [CrossRef] [Google Scholar]
  307. Strait, V., Bradač, M., Hoag, A., et al. 2018, ApJ, 868, 129 [NASA ADS] [CrossRef] [Google Scholar]
  308. Streblyanska, A., Aguado-Barahona, A., Ferragamo, A., et al. 2019, A&A, 628, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  309. Sullivan, M., Guy, J., Conley, A., et al. 2011, ApJ, 737, 102 [NASA ADS] [CrossRef] [Google Scholar]
  310. Szabo, T., Pierpaoli, E., Dong, F., Pipino, A., & Gunn, J. 2011, ApJ, 736, 21 [NASA ADS] [CrossRef] [Google Scholar]
  311. Szokoly, G. P., Bergeron, J., Hasinger, G., et al. 2004, ApJS, 155, 271 [NASA ADS] [CrossRef] [Google Scholar]
  312. Tanaka, M., Lidman, C., Bower, R. G., et al. 2009, A&A, 507, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  313. Tasca, L. A. M., Le Fèvre, O., Ribeiro, B., et al. 2017, A&A, 600, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  314. Tempel, E., Kruuse, M., Kipper, R., et al. 2018, A&A, 618, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  315. The Dark Energy Survey Collaboration 2005, arXiv e-prints [arXiv:astro-ph/0510346] [Google Scholar]
  316. Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [Google Scholar]
  317. To, C.-H., DeRose, J., Wechsler, R. H., et al. 2024, ApJ, 961, 59 [NASA ADS] [CrossRef] [Google Scholar]
  318. Tran, K.-V. H., Franx, M., Illingworth, G. D., et al. 2007, ApJ, 661, 750 [NASA ADS] [CrossRef] [Google Scholar]
  319. Treu, T., Schmidt, K. B., Brammer, G. B., et al. 2015, ApJ, 812, 114 [Google Scholar]
  320. Tukey, J. W. 1958, Ann. Math. Statist., 29, 581 [CrossRef] [Google Scholar]
  321. Verdugo, M., Ziegler, B. L., & Gerken, B. 2008, A&A, 486, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  322. Vikhlinin, A., Burenin, R. A., Ebeling, H., et al. 2009a, ApJ, 692, 1033 [Google Scholar]
  323. Vikhlinin, A., Kravtsov, A. V., Burenin, R. A., et al. 2009b, ApJ, 692, 1060 [Google Scholar]
  324. Von Der Linden, A., Best, P. N., Kauffmann, G., & White, S. D. M. 2007, MNRAS, 379, 867 [Google Scholar]
  325. Wainer, H., & Thissen, D. 1976, Psychometrika, 41, 9 [CrossRef] [Google Scholar]
  326. Weinberg, D. H., Mortonson, M. J., Eisenstein, D. J., et al. 2013, Phys. Rep., 530, 87 [Google Scholar]
  327. Wen, Z. L., & Han, J. L. 2018, MNRAS, 481, 4158 [CrossRef] [Google Scholar]
  328. Wen, Z. L., Han, J. L., & Liu, F. S. 2012, ApJS, 199, 34 [Google Scholar]
  329. Will, C. M. 2014, Liv. Rev. Rel., 17, 4 [Google Scholar]
  330. Willis, J. P., Clerc, N., Bremer, M. N., et al. 2013, MNRAS, 430, 134 [NASA ADS] [CrossRef] [Google Scholar]
  331. Wilson, M. L., Zabludoff, A. I., Ammons, S. M., et al. 2016, ApJ, 833, 194 [CrossRef] [Google Scholar]
  332. Xu, W., Ramos-Ceja, M. E., Pacaud, F., Reiprich, T. H., & Erben, T. 2022, A&A, 658, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  333. Yang, M., Wu, H., Yang, F., et al. 2018, ApJS, 234, 5 [NASA ADS] [CrossRef] [Google Scholar]
  334. Yee, H. K. C., Morris, S. L., Lin, H., et al. 2000, ApJS, 129, 475 [NASA ADS] [CrossRef] [Google Scholar]
  335. Yu, H., Tozzi, P., Borgani, S., Rosati, P., & Zhu, Z. H. 2011, A&A, 529, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  336. Zaznobin, I. A., Burenin, R. A., Bikmaev, I. F., et al. 2020, Astron. Lett., 46, 79 [NASA ADS] [CrossRef] [Google Scholar]
  337. Zeimann, G. R., Stanford, S. A., Brodwin, M., et al. 2013, ApJ, 779, 137 [Google Scholar]
  338. Zhang, Y., Jeltema, T., Hollowood, D. L., et al. 2019, MNRAS, 487, 2578 [NASA ADS] [CrossRef] [Google Scholar]
  339. Zou, H., Zhou, X., Fan, X., et al. 2017, PASP, 129, 064101 [CrossRef] [Google Scholar]
  340. Zou, H., Gao, J., Zhou, X., & Kong, X. 2019, ApJS, 242, 8 [Google Scholar]
  341. Zubeldia, Í., & Challinor, A. 2019, MNRAS, 489, 401 [NASA ADS] [CrossRef] [Google Scholar]
5

Strictly the prefix is (Nspec2Nspec−1)$\[\sqrt{\left(\frac{N_{\mathrm{spec}}^2}{N_{\mathrm{spec}}-1}\right)}\]$ although Nspec $\[\sqrt{N_{\text {spec }}}\]$ is an adequate approximation for large Nspec.

6

Vice versa, there were 446 out of 10 320 clusters identified in the LS DR10 south grz run that also have i-band coverage but were rejected when the i band was included in the eROMaPPer run. The mean probability of being a contaminant is high for those clusters: Pcont = 49% (see Sec. 7). Most of them (95%) have low richnesses λ < 16, for which the i-band might help to identify random line-of-sight projections.

7

While the SZ signal is theoretically independent of redshift, in practice, the detection efficiency, particularly for observations made by the Planck satellite, was affected by the angular resolution of the instrument’s beam. This can result in a slightly higher detectability of the SZ effect for galaxy clusters at lower redshifts.

8

There is also the possibility that the X-ray signal originates from a real cluster whose redshift is much higher than the local limiting redshift of the LS.

All Tables

Table 1

Literature catalogs matched to the eRASS1 extended X-ray sources.

In the text
Table 2

Richness scaling factors.

In the text
Table 3

Redshift types and occurrences in the eRASS1 catalog.

In the text
Table 4

Overview of the catalogs analyzed with eROMaPPer in this work.

In the text
Table D.1

Spectroscopic galaxy compilation.

In the text
Table E.1

Column names, data types, and descriptions of the eRASS1 identified cluster catalog.

In the text

All Figures

thumbnail Fig. 1

Pixelized number density of 22718 cleaned eRASS1 extended sources, that is, cluster candidates in the German part of the eROSITA survey. The HEALPix map has a resolution of NSIDE = 16 =^$\[\hat{=}\]$ 13.4 deg2. The highest number density occurs near the southern ecliptic pole around RA = 90° and Dec ≈ −67° where the exposure time is largest. Another overdensity of extended sources near the Galactic plane around RA ≈ 135° and Dec ≈ −45° is associated with the Vela supernova remnant. It lies outside the common footprint with the Legacy Surveys (see Fig. 2).
In the text
thumbnail Fig. 2

Maps of the limiting magnitude in the z band for sources detected with 10σ significance. The footprint maps show the coverage for the Legacy Surveys DR10 south (top panel) and DR9 north (bottom panel). Only regions with data in all the g-, r-, and z-bands were considered. The half sky that is covered by eRASS1 corresponds to the region below the red line. The limiting magnitudes in the z band directly translate to the limiting redshift zvlim (see Appendix B for details).
In the text
thumbnail Fig. 3

Effective survey area for the Legacy Surveys DR10 south and DR9 north depending on redshift. At the limiting redshift zvlim, the faintest considered cluster member galaxy was observed with 10σ confidence in the z band. Details are given in Appendix B. The luminosity of that galaxy is L = 0.2 L* for the eROMaPPer (eROSITA Matched-filter Probabilistic Percolation cluster finder) runs which used the grz and griz filter bands and L = 0.4L* for the runs that also included the w1 band. The dashed lines correspond to the full LS footprint while the continuous lines show the area that is reduced to the overlapping region with eRASS1 (see Fig. 2).
In the text
thumbnail Fig. 4

Illustrative example 1eRASS J041610.4-240351 from the eRASS1 cluster catalog. The panels in the top row show an LS grz image of the full cluster overlaid with eRASS1 X-ray contours (left) and cluster members detected in this work (circles, right). Spectroscopic information is available for all cluster members marked by dashed circles. The bottom-left panel shows a zoom-in. The red circle marks the BCG, which agrees with the optical cluster center (green cross). The orange circle is located at the position of the central galaxy, which is the one closest to the X-ray center (yellow cross). North is up; east is left. In the bottom-right panel, upper subpanel, the cluster likelihood ln L$\[\mathcal{L}\]$(z) shows one peak at z = 0.385 which is close to the cluster photometric redshift zλ, = 0.3910 ± 0.0082. The bottom-right panel, lower subpanel, demonstrates the measurements of the spectroscopic redshift and the velocity dispersion for the shown cluster. The cluster has a richness of λ = 128.7 ± 8.5. The 127 photometric members are marked by circles. Of those, 121 have spectroscopic redshifts and are marked by dashed circles. The black histogram in the bottom panel shows the spectroscopic redshifts of the photometric members. Ten outlier galaxies with z ≶ zspec ± 3σ (blue dashed lines) are discarded, leaving Nmembers = 111 spectroscopic members. The cluster velocity dispersion is σ = 1034 ± 67 km s−1 (light blue line). The photometric cluster redshift (light red shades) agrees with the spectroscopic cluster redshift zspec = 0.39936 ± 0.00039 (darker blue line). The redshift of the galaxy at the optical center is zspec,cg = 0.3967 ± 0.0004 (green line). The literature redshift zlit = 0.38989 (purple line) is a photometric redshift from MARDY3 (Klein et al. 2019).
In the text
thumbnail Fig. 5

Number (top panel) and relative fraction (bottom panel) of eRASS1 clusters per redshift bin depending on their best redshift type. The total numbers are 8790 photometric redshifts (zλ, Sec. 3.2), 1759 spectroscopic redshifts determined using the bootstrap method (zspec, Sec. 3.3), 1451 spectroscopic redshifts of the galaxy at the optical center (zspec,cg, Sec. 3.3), and 247 literature redshifts (zlit, Sec. 3.4). Clusters with unflagged velocity dispersion information (Sec. 3.6) have the same distribution as the zspec sample.
In the text
thumbnail Fig. 6

Slice of the cosmic volume with eRASS1 clusters with available spectroscopic redshifts zspec overplotted onto our spectroscopic galaxy compilation (gray points). The slice has a thickness of ±2° around Decl. = 0°. Red points mark the positions of eRASS1 clusters when spectroscopic redshifts were used. They trace the nodes of the cosmic web. Green points mark the same clusters, but this time, we used the photometric redshifts. They scatter around the nodes of the cosmic web because of the higher redshift uncertainty.
In the text
thumbnail Fig. 7

Fraction of eRASS1 clusters with consistent best redshift zbest and literature redshift zlit depending on richness λnorm. Four different redshift tolerances are applied.
In the text
thumbnail Fig. 8

Number of clusters per redshift interval Δzλ = 0.05. For catalogs created in this work (blue), we used the best redshift zbest, and for literature catalogs, we used the published redshift zlit. Each panel refers to a different cluster selection method. The smoothed histograms were obtained by summing over the redshift posteriors of all clusters. For better visibility, the distributions were additionally smoothed with a Gaussian kernel with a standard deviation Δzλ = 0.04. For the eRASS1 catalog, the upper border of the filled region refers to all 12 247 clusters, and the lower border refers to the subset of 10 959 clusters with zλ < zvlim. A richness cut λnorm > 16 and a limiting redshift cut zλ < zvlim were only applied to the optically selected combined LS DR10 south and LS DR9 north catalogs (LS N+S). That makes them comparable to the DES year 1 catalog, which has a consistent richness cut of λ > 20 applied (see Sec. 5.4).
In the text
thumbnail Fig. 9

Footprint maps for the cluster catalogs used in this work. The HEALPix resolution is NSIDE = 16 =^$\[\hat{=}\]$ 13.4 deg2. Black regions overlap with the LS footprint and gray regions are outside of it. White holes within the footprint indicate that the local cluster number density in a catalog is less than 1 per heal pixel.
In the text
thumbnail Fig. 10

Optical completeness defined as the ratio of clusters confirmed after running eROMaPPer in scan mode on the cluster coordinates in various catalogs from the literature. At low redshifts, we used the ACO catalog and quantified the completeness for four different redshift tolerances. At high redshifts, we used the SPT, ACT, and Planck catalogs and considered clusters as confirmed when the redshifts agreed within |zbest − zlit|/(1 + zlit) < 0.1. We restricted the samples to clusters where the LS are sufficiently deep, that is, zbest < zvlim. A minimum of five clusters was required per redshift bin.
In the text
thumbnail Fig. 11

Comparison between the richnesses λ measured using eROMaPPer and the published richnesses for the same DES year 1 clusters color-coded by their photometric redshift in the eROMaPPer catalog. The 1:1 relation is shown in gray and the red line is the best-fit linear relation with a slope of α = 0.79.
In the text
thumbnail Fig. 12

Cluster number density per sky area (left) and comoving volume (right) against redshift. Red and purple lines refer to clusters detected using the eROMaPPer blind mode on the LS DR10 south and LS DR9 north, respectively, in the grz filter band combination. We restricted the samples to a reliable redshift range zλ < zvlim. The orange line refers to the eRASS1 clusters. A discontinuity at zλ = 0.8 arises from the merging of the low-z-optimized and high-z-optimized eROMaPPer runs (see Sect. 4.1.1). A richness cut of λnorm > 16 was applied only to the LS DR9 north and LS DR10 south catalogs. Volume densities for the SDSS DR8 and DES SVA catalogs were adopted from Rykoff et al. (2016) and for DES year 1, calculated assuming a survey area of 1437 deg2 with uniform depth (see Table 4). The curves were normalized for a bin size of Δz = 0.05 and smoothed using a Gaussian kernel with a standard deviation of Δz = 0.02. The width of the lines corresponds to the Poissonian error for the same bin size, consistently as in Rykoff et al. (2016).
In the text
thumbnail Fig. 13

Dependency of the cluster number density on survey depth. The cluster number density per sky area nA was calculated for the clusters detected using the eROMaPPer blind mode in the LS DR10 south using the grz filter bands. The data was split into five bins in photometric cluster redshift zλ. For each redshift bin, the densities were calculated for bins in limiting redshift zvlim and richness λnorm. We consider the cluster properties reliable when local survey depth is sufficiently deep, that is, zλ < zvlim (see Appendix B for details). Those clusters are located to the right of the red line where the number density does not depend on zvlim. The number density left of the red line increases, which indicates a growing number of false-positive detections.
In the text
thumbnail Fig. 14

Kernel density estimates of AGNs, random points, and clusters in redshift (zbest)–richness (λnorm) space (first three panels). The right panel shows the individual cluster data points color-coded by their probability of being a contaminant.
In the text
thumbnail Fig. 15

Distribution of clusters in redshift (zbest)-richness (λnorm)–X-ray count rate (CR,X) space. The left panel shows the full distribution, and the right panel shows a slice in redshift 0.4 < zbest < 0.5 to enhance the dependence on the λnorm−CR,X relation. The data points are projected on each side of the canvas. The probability of being a contaminant Pcont is color-coded. The top-right projection is equivalent to Fig. 14, right panel.
In the text
thumbnail Fig. 16

Bias and uncertainty of the photometric cluster redshifts zλ estimated by comparing to high-quality spectroscopic cluster redshifts zspec. Black points refer to 9522 clusters with high-quality spectroscopic redshifts (see Sect. 8). The catalogs were merged as described in Sect. 4.1.1. The red line is the running median, and the red shaded regions give the uncertainty δzλ taken as the 16th and 84th percentiles of the distribution. In the left panel, the continuous red line is the redshift bias Δzλ, and the dashed lines give the redshift uncertainty δzλ. The right panel shows the absolute errors normalized by 1 + zspec, which is proportional to the line-of-sight velocity v (Eq. (6)).
In the text
thumbnail Fig. 17

Uncertainties of the eRASS1 photometric cluster redshifts. The black dots are the formal uncertainties δzλfml$\[\delta z_\lambda^{\mathrm{fml}}\]$ calculated by eROMaPPer as the standard deviation of the redshift posterior P(z). We adopted them as the final redshift uncertainties zλ,err. The dashed red line is the mean of the upper and lower empirical uncertainties δzλspec $\[\delta z_\lambda^{\text {spec }}\]$ derived from the comparison to the spectroscopic cluster redshifts. The continuous red line is the absolute redshift bias |Δzλ|.
In the text
thumbnail Fig. 18

Relation for cluster line-of-sight velocity dispersion σ and richness λnorm. The black data points are for all clusters in our analyzed catalogs (see Table 4) apart from the blind-mode runs. In total, 1699 clusters with Nmembers ≥ 15 spectroscopic members were selected. The red line is the best fit to the data, and the light red shades show the uncertainty of the relation. The observed scatter δobs,orth (orange) was measured orthogonal to the best-fit relation in 9 bins. The median orthogonal component of the measurement uncertainties δm,orth is shown for each bin in blue. By subtracting δm,orth from δobs,orth in quadrature, we estimated the intrinsic scatter δin for each bin. It is shown in green.
In the text
thumbnail Fig. B.1

Depth maps showing the limiting magnitude for the Legacy Surveys DR10 south (top panels) and DR9 north (lower panels) in different filter bands. The maps present the full coverage in each band independently rather than combining the footprints as in Figure 2. The limiting magnitude is defined as the brightness of a galaxy whose flux has a signal-to-noise ratio of 10.
In the text
thumbnail Fig. B.2

Example of a cluster 1eRASS J010123.5-764801 located in a masked area of the footprint map. The saturated foreground star near the X-ray detection (yellow cross) was responsible for the mask. Cluster member galaxies are marked by circles (see Figure 4 for further descriptions of the labels). Only the members in the outskirts of the cluster were identified. North is up, east is left.
In the text
thumbnail Fig. B.3

Conversion from limiting z-band magnitude to limiting redshift zvlim for galaxies with a luminosity L = 0.2 L* (orange) and L = 0.4 L* (blue). Restricting the sample to brighter members allows for probing higher redshifts. For reference, the green histogram shows the distribution of limiting magnitudes in the z band for the combined full LS DR10 south and LS DR9 north areas.
In the text
thumbnail Fig. C.1

Red-sequence models for the six different calibrations (rows). Each filter band combination and LS parts are labeled in the titles of the subpanels. The combination of n filter bands results in red-sequence models for n − 1 colors (columns). The red-sequence models are shown by the red splines and red points mark the spline nodes. The training galaxies are color-coded according to their point density. Their total numbers are, after clipping, ~93 000 for LS DR10 (grz and grzw1), ~72000 for LS DR10 (griz and grizw1), and ~36000 for LS DR9 north (grz and grzw1).
In the text
thumbnail Fig. D.1

Redshift distribution of the spectroscopic galaxy redshift compilation.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.