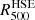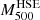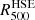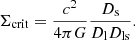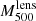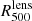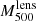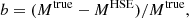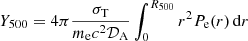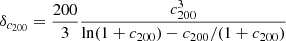| Issue |
A&A
Volume 671, March 2023
|
|
|---|---|---|
| Article Number | A28 | |
| Number of page(s) | 22 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202244981 | |
| Published online | 01 March 2023 | |
Multi-probe analysis of the galaxy cluster CL J1226.9+3332
Hydrostatic mass and hydrostatic-to-lensing bias
1
Univ. Grenoble Alpes, CNRS, LPSC-IN2P3, 53 avenue des Martyrs, 38000 Grenoble, France
e-mail: miren.munoz@lpsc.in2p3.fr
2
Université Paris-Saclay, Université Paris-Cité, CEA, CNRS, AIM, 91191 Gif-sur-Yvette, France
3
LLR (Laboratoire Leprince-Ringuet), CNRS, École Polytechnique, Institut Polytechnique de Paris, Av. Chasles, 91120 Palaiseau, France
4
School of Physics and Astronomy, Cardiff University, Queen’s Buildings, The Parade, Cardiff CF24 3AA, UK
5
INAF, IASF-Milano, Via A. Corti 12, 20133 Milano, Italy
6
Aix-Marseille Univ., CNRS, CNES, LAM (Laboratoire d’Astrophysique de Marseille), 38 rue Frédéric Joliot Curie, 13013 Marseille, France
7
Institut Néel, CNRS, Université Grenoble Alpes, 25 Av. des Martyrs, 38042 Grenoble, France
8
Institut de RadioAstronomie Millimétrique (IRAM), 300 rue de la Piscine, 38400 Saint-Martin-d’Hères, France
9
Dipartimento di Fisica, Sapienza Università di Roma, Piazzale Aldo Moro 5, 00185 Roma, Italy
10
Univ. Grenoble Alpes, CNRS, IPAG, 414 rue de la Piscine, 38400 Saint-Martin-d’Hères, France
11
Centro de Astrobiología (CSIC-INTA), Torrejón de Ardoz, 28850 Madrid, Spain
12
High Energy Physics Division, Argonne National Laboratory, 9700 South Cass Avenue, Lemont, IL 60439, USA
13
Instituto de Radioastronomía Milimétrica (IRAM), Av. Divina Pastora, 7, 18012 Granada, Spain
14
LERMA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Université, UPMC, 75014 Paris, France
15
School of Earth and Space Exploration and Department of Physics, Arizona State University, Tempe, AZ 85287, USA
16
IRFU, CEA, Université Paris-Saclay, 91191 Gif-sur-Yvette, France
17
Univ. de Toulouse, UPS-OMP, CNRS, IRAP, 31028 Toulouse, France
18
Laboratoire de Physique de l’École Normale Supérieure, ENS, PSL Research University, CNRS, Sorbonne Université, Université de Paris, 75005 Paris, France
19
INAF-Osservatorio Astronomico di Cagliari, Via della Scienza 5, 09047 Selargius, Italy
20
Department of Physics and Astronomy, University of Pennsylvania, 209 South 33rd Street, Philadelphia, PA 19104, USA
21
Institut d’Astrophysique de Paris, CNRS (UMR7095), 98 bis boulevard Arago, 75014 Paris, France
22
Univ. Lyon, Univ. Claude Bernard Lyon 1, CNRS/IN2P3, IP2I Lyon, 69622 Villeurbanne, France
23
Caltech, 1200 E California Blvd, Pasadena, CA 91125, USA
24
Departamento de Física Teórica and CIAFF, Facultad de Ciencias, Modulo 8, Universidad Autánoma de Madrid, 28049 Madrid, Spain
Received:
15
September
2022
Accepted:
18
December
2022
The precise estimation of the mass of galaxy clusters is a major issue for cosmology. Large galaxy cluster surveys rely on scaling laws that relate cluster observables to their masses. From the high-resolution observations of ∼45 galaxy clusters with the NIKA2 and XMM-Newton instruments, the NIKA2 Sunyaev-Zel’dovich Large Program should provide an accurate scaling relation between the thermal Sunyaev-Zel’dovich effect and the hydrostatic mass. In this paper we present an exhaustive analysis of the hydrostatic mass of the well-known galaxy cluster CL J1226.9+3332, the highest-redshift cluster in the NIKA2 Sunyaev-Zel’dovich Large Program at z = 0.89. We combined the NIKA2 observations with thermal Sunyaev-Zel’dovich data from the NIKA, Bolocam, and MUSTANG instruments and XMM-Newton X-ray observations, and tested the impact of the systematic effects on the mass reconstruction. We conclude that slight differences in the shape of the mass profile can be crucial when defining the integrated mass at R500, which demonstrates the importance of the modelling in the mass determination. We prove the robustness of our hydrostatic mass estimates by showing the agreement with all the results found in the literature. Another key factor for cosmology is the bias of the masses estimated assuming the hydrostatic equilibrium hypothesis. Based on the lensing convergence maps from the Cluster Lensing And Supernova survey with Hubble (CLASH) data, we obtain the lensing mass estimate for CL J1226.9+3332. From this we are able to measure the hydrostatic-to-lensing mass bias for this cluster, which spans from 1 − bHSE/lens ∼ 0.7 to 1, presenting the impact of data sets and mass reconstruction models on the bias.
Key words: galaxies: clusters: intracluster medium / galaxies: clusters: individual: CL J1226.9+3332 / techniques: high angular resolution / cosmology: observations
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Galaxy clusters are formed by gravitational collapse at the last step of the hierarchical structure formation process (Kravtsov & Borgani 2012). Thus, they are tracers of the large-scale structure formation physics. Their abundance in mass and redshift is sensitive to the initial conditions in the primordial Universe and its expansion history and matter content (Huterer et al. 2015). Therefore, galaxy clusters are probes of the underlying cosmology (Allen et al. 2011).
Large catalogues of clusters (e.g., Planck Collaboration XVIII 2015; Rykoff et al. 2016; Adami et al. 2018; Bleem et al. 2020) have allowed us, in the past few years, to constrain cosmological parameters. Nevertheless, these results show some tension with respect to the cosmology obtained from the cosmic microwave background (CMB) power spectrum analysis (Planck Collaboration XXI 2013; Planck Collaboration XXIV 2015; Salvati et al. 2018), in line with a more general problem, in that early and late Universe probes are giving different results (Verde et al. 2019). Cluster-based cosmological analyses rely on their distribution in mass and one source of the discrepancy may be the inaccuracy of those mass estimates (e.g., Pratt et al. 2019; Salvati et al. 2020).
About 85% of the total mass of clusters of galaxies is composed of dark matter. The remaining 15% corresponds to the hot intracluster medium (ICM) and the galaxies in the cluster. For this reason, most of the mass content of the clusters is not directly observable and it needs to be estimated either from the gravitational potential reconstruction or via scaling relations that link cluster observables to their masses (Pratt et al. 2019). The gravitational potential of clusters can be inferred from their gravitational lensing effect on background sources (Bartelmann 2010), from the dynamics of member galaxies (Biviano & Girardi 2003; Aguado-Barahona et al. 2022), or from the combination of the thermodynamical properties of the gas in the ICM under the hydrostatic equilibrium (HSE) hypothesis. Scaling relations that allow us to recover the mass have been measured and calibrated for various cluster observables at different wavelengths: in the optical and infrared domains the galaxy member richness (Andreon & Hurn 2010), in X-ray the emitted luminosity of the hot gaseous ICM (Pratt et al. 2009), and at millimetre wavelengths the amplitude of the Sunyaev-Zel’dovich (SZ) effect (Sunyaev & Zeldovich 1972; Planck Collaboration XI 2011) proportional to the thermal energy in the ICM.
The thermal SZ (tSZ) effect (Sunyaev & Zeldovich 1972), corresponding to the spectral distortion of the CMB photons due to the inverse-Compton scattering on the hot thermal electrons of the ICM, is an excellent way of detecting clusters as its amplitude is not affected by cosmological dimming. Large surveys, in particular the Planck satellite observations (Planck Collaboration XVIII 2015) and the ground-based Atacama Cosmology Telescope (ACT, Hilton et al. 2018, 2021) and South Pole Telescopes (SPT, Bleem et al. 2020), have obtained large SZ-detected galaxy cluster catalogues. However, they need to rely on the SZ-mass scaling relation in order to carry out cosmological analyses. To date, most of the SZ-mass scaling relations have been mainly determined from low-redshift (z < 0.5) cluster samples with masses obtained from X-ray observations (Arnaud et al. 2010; Planck Collaboration XI 2011). Other scaling relations, with optical data for example (Saro et al. 2017), are also used.
In any case, it is essential to study the redshift evolution of these scaling relations as they have an impact the cosmological results (Salvati et al. 2020). When building scaling relations, another key aspect is the impact of the assumptions on which the mass computations rely, such as the HSE hypothesis. High spatial resolution cluster observations help us to assess these assumptions as we study the impact of the dynamical states of clusters on the mass-observable scaling relations.
The NIKA2 SZ Large Program (Mayet et al. 2020; Perotto et al. 2022) described in Sect. 3.1.1 seeks to address the above-mentioned issues. The work presented in this paper constitutes the third analysis of a cluster in the NIKA2 SZ Large Program. The first analysis on PSZ2 G144.83+25.11 comprised a science verification study, as well as the proof of the impact of substructures in the reconstruction of the physical cluster properties (Ruppin et al. 2018). The second, the worst-case scenario for the NIKA2 SZ Large Program, analysed the ACT-CL J0215.4+0030 galaxy cluster, proving the quality of NIKA2 camera (Adam et al. 2018a; Bourrion et al. 2016; Calvo et al. 2016; Perotto et al. 2020) in the most challenging case of a high-redshift and low-mass cluster (Kéruzoré et al. 2020). In this work we present a study on the HSE mass of the CL J1226.9+3332 galaxy cluster and the impact of different systematic effects on the recovered mass, and make a thorough comparison to previous works. Moreover, we re-estimate its lensing mass and compare it to the mass obtained under the hydrostatic assumption, which allows us to compute the hydrostatic-to-lensing mass bias.
This paper is organised as follows. In Sect. 2 we present a summary of the results in the literature for CL J1226.9+3332. In Sect. 3 we describe the observations of the ICM with NIKA2 and XMM-Newton instruments. The reconstruction of the thermodynamical properties of the ICM is presented in Sect. 4. We detail the pressure profile reconstruction from NIKA2 maps, accounting for systematic effects due to the data reduction process and point source contamination. We compare these profiles to previous results and to the X-ray pressure profile. In Sect. 5 we describe the HSE mass estimates from the combination of SZ and X-ray data and test the robustness of the results against data processing and modelling effects. In Sect. 6 we present the lensing masses that we estimate for CL J1226.9+3332. All the results are discussed together in Sect. 7, where we compute the hydrostatic-to-lensing mass bias for this cluster. The conclusions are given in Sect. 8.
Throughout this paper we assume a flat ΛCDM cosmology with H0 = 70 km s−1 Mpc−1 and Ωm, 0 = 0.3. With this assumption, 1 arcmin corresponds to a distance of 466 kpc at the cluster redshift z = 0.89.
2. The CL J1226.9+3332 galaxy cluster
This paper focuses on the CL J1226.9+3332 galaxy cluster, also known as PSZ2-G160.83+81.66. Discovered by the Wide Angle ROSAT Pointed Survey (WARPS, Ebeling et al. 2001), it has already been studied at different wavelengths: X-ray (Maughan et al. 2004; Bonamente et al. 2006), visible (Jee & Tyson 2009), and millimetre (Bonamente et al. 2006; Mroczkowski et al. 2009; Korngut et al. 2011; Adam et al. 2015) wavelengths. Located at redshift 0.89 (Planck Collaboration XVIII 2015; Aguado-Barahona et al. 2022), it is the highest-redshift cluster of the NIKA2 SZ Large Program sample, with the X-ray peak at (RA, Dec)J2000 = (12h26m58.37s, +33d32m47.4s) according to Cavagnolo et al. (2009). Less than 2 arcsecond away from this peak, its brightest cluster galaxy (BCG) is located at (RA, Dec)J2000 = (12h26m58.25s, +33d32m48.57s) according to Holden et al. (2009).
2.1. Previous observations
Since the first SZ observations with BIMA (Joy et al. 2001), the projected morphology of CL J1226.9+3332 appeared to have a quite circular symmetry. Nevertheless, the combination of XMM-Newton and Chandra X-ray data (Maughan et al. 2007) showed a region, at ∼40″ to the south-west of the X-ray peak with much higher temperature than the average in the ICM. This substructure was also confirmed by posterior SZ analyses with MUSTANG (Korngut et al. 2011) and NIKA (Monfardini et al. 2011; Adam et al. 2015, 2018b). Romero et al. (2018; hereafter R18) performed a study combining SZ data from the NIKA, MUSTANG, and Bolocam instruments. Their different capabilities allowed us to probe different angular scales in the reconstruction of ICM properties and agreed with a non-relaxed cluster core description for CL J1226.9+3332. In this work we make use of the pressure profiles obtained from the NIKA, MUSTANG, and Bolocam data summarised in Table 2 in Romero et al. (2018).
Lensing data from the Cluster Lensing And Supernova survey with Hubble (CLASH, Zitrin et al. 2015), as well as the galaxy distribution in the cluster (Jee & Tyson 2009), agree on the existence of a main clump centred on the BCG and a secondary clump to the south-west. However, this second region does not appear as a structure in X-ray surface brightness (Maughan et al. 2007). One hypothesis presented in Jee & Tyson (2009) suggests that the mass of the southwestern galaxy group is not big enough to be observed as an X-ray overdensity. Motivated by the slight elongation of the X-ray peak towards the south-west, Jee & Tyson (2009) also hypothesise that the two-halo system is being observed after the less massive cluster has passed through the central one. A previous study (Maughan et al. 2004) also showed a region of cooler emission on the west side of the BCG, that is, in the north of the mentioned hot region. This was seen using Chandra data, and it was explained as a possible infall of some cooler body. Additionally, from the diffuse radio emission analysis with LOFAR data, Di Gennaro et al. (2020) showed that CL J1226.9+3332 hosts the most distant radio halo discovered to date: a radio emission with a size of 0.7 Mpc that follows the thermal gas distribution. In brief, CL J1226.9+3332 shows evidence of disturbance in the core, but a relaxed morphology at large scales.
2.2. The mass of CL J1226.9+3332
Regarding the mass of CL J1226.9+3332, which constitutes the main topic in this study, we present here the results obtained in previous works (summarised in Table A.1). These masses have not been homogenised or scaled to the same cosmology, and are the values extracted directly from different analyses. We define MΔ as the mass of the cluster inside a sphere of radius RΔ; RΔ is the radius at which the mean mass density of the cluster is Δ times the critical density of the Universe at its redshift ρc = 3H(z)2/(8πG), where H(z) is the Hubble function.
The first SZ mass analysis of this cluster was done in Joy et al. (2001) and they estimated 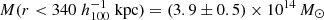 . Using Chandra X-ray data from Cagnoni et al. (2001) and assuming an isothermal β-model, Jee & Tyson (2009) obtained the hydrostatic projected mass
. Using Chandra X-ray data from Cagnoni et al. (2001) and assuming an isothermal β-model, Jee & Tyson (2009) obtained the hydrostatic projected mass 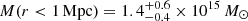 . Also assuming an isothermal β-model and hydrostatic equilibrium, Maughan et al. (2004) obtained
. Also assuming an isothermal β-model and hydrostatic equilibrium, Maughan et al. (2004) obtained 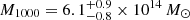 and M200 = (1.4 ± 0.5) × 1015 M⊙ with XMM-Newton data. The subsequent analysis of three-dimensional hydrodynamical properties with Chandra and XMM-Newton by Maughan et al. (2007), again under the assumptions of spherical symmetry and hydrostatic equilibrium, concluded that
and M200 = (1.4 ± 0.5) × 1015 M⊙ with XMM-Newton data. The subsequent analysis of three-dimensional hydrodynamical properties with Chandra and XMM-Newton by Maughan et al. (2007), again under the assumptions of spherical symmetry and hydrostatic equilibrium, concluded that 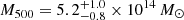 . According to the X-ray analysis in Mantz et al. (2010), M500 = (7.8 ± 1.1) × 1014 M⊙.
. According to the X-ray analysis in Mantz et al. (2010), M500 = (7.8 ± 1.1) × 1014 M⊙.
From the combination of Sunyaev-Zel’dovich Array (SZA, Muchovej et al. 2007) interferometric data and the Chandra X-ray observations, under the hydrostatic equilibrium hypothesis, Mroczkowski et al. (2009) obtained 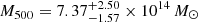 and
and 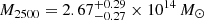 . This was compared to the results using only the X-ray data and assuming an isothermal β-model:
. This was compared to the results using only the X-ray data and assuming an isothermal β-model: 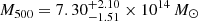 ,
, 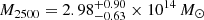 . Using a new approach that instead relies on the virial relation and the Navarro-Frenk-White (NFW, Navarro et al. 1996) density profile, Mroczkowski (2011, 2012) estimated the mass for CL J1226.9+3332 using only SZ data from SZA:
. Using a new approach that instead relies on the virial relation and the Navarro-Frenk-White (NFW, Navarro et al. 1996) density profile, Mroczkowski (2011, 2012) estimated the mass for CL J1226.9+3332 using only SZ data from SZA: 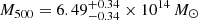 and
and 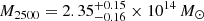 assuming a pressure described by a generalised Navarro-Frenk-White (gNFW, Nagai et al. 2007) profile with (a, b, c) = (0.9, 5.0, 0.4) parameters and
assuming a pressure described by a generalised Navarro-Frenk-White (gNFW, Nagai et al. 2007) profile with (a, b, c) = (0.9, 5.0, 0.4) parameters and 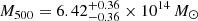 and
and 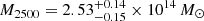 with (a, b, c) = (1.0510, 5.4905, 0.3081) as in Arnaud et al. (2010). Some years before, Muchovej et al. (2007) fitted the temperature decrement due to the cluster’s SZ effect to the SZA data and assuming hydrostatic equilibrium and isothermality estimated
with (a, b, c) = (1.0510, 5.4905, 0.3081) as in Arnaud et al. (2010). Some years before, Muchovej et al. (2007) fitted the temperature decrement due to the cluster’s SZ effect to the SZA data and assuming hydrostatic equilibrium and isothermality estimated 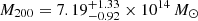 and
and 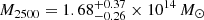 .
.
Another approach was considered in Bulbul et al. (2010) to compute the hydrostatic mass, with the polytropic equation of state and using only Chandra X-ray observations, 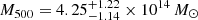 and
and 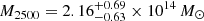 . According to the Planck Collaboration XVIII (2015) results, the hydrostatic mass of the cluster is
. According to the Planck Collaboration XVIII (2015) results, the hydrostatic mass of the cluster is 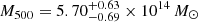 . This mass was obtained using the SZ-mass scaling relation given in Eq. (7) of Planck Collaboration XX (2013).
. This mass was obtained using the SZ-mass scaling relation given in Eq. (7) of Planck Collaboration XX (2013).
In addition, combining SZ data from NIKA and Planck with the X-ray electron density from the Chandra ACCEPT data (Cavagnolo et al. 2009), Adam et al. (2015) obtained three hydrostatic mass estimates for different parameters in their gNFW pressure profile modelling: 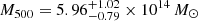 using (a, b, c) = (1.33, 4.13, 0.014),
using (a, b, c) = (1.33, 4.13, 0.014), 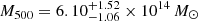 with (b, c) = (4.13, 0.014) and
with (b, c) = (4.13, 0.014) and 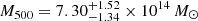 with (a, b, c) = (0.9, 5.0, 0.4). Also combining NIKA and Chandra data, Castagna & Andreon (2020) reconstructed
with (a, b, c) = (0.9, 5.0, 0.4). Also combining NIKA and Chandra data, Castagna & Andreon (2020) reconstructed 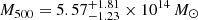 .
.
The weak-lensing analysis in Jee & Tyson (2009) realised by fitting a NFW density profile found that M200 = (1.38 ± 0.20) × 1015 M⊙. Similarly, they computed the weak-lensing mass estimate at R500 from Maughan et al. (2007): M(r < (0.88 ± 0.05) Mpc) = (7.34 ± 0.71) × 1014 M⊙, and found a 30% higher mass than the X-ray estimate in Maughan et al. (2007). This discrepancy was explained in Jee & Tyson (2009) as a sign of an ongoing merger in the cluster that would create an underestimation of the hydrostatic mass with X-rays without altering the lensing estimate. Jee & Tyson (2009) also estimated the projected mass in each of the two big substructures within r < 20″; for the most massive and central clump they found M(r < 20″) = (1.3 ± 0.1) × 1014 M⊙, and for the structure at ∼40″ to the south-west of the BCG M(r < 20″) = (8.5 ± 0.6) × 1013 M⊙. Merten et al. (2015) performed a lensing analysis and obtained M200 = (2.23 ± 0.14) × 1015 M⊙, M500 = (1.54 ± 0.12) × 1015 M⊙, and M2500 = (0.61 ± 0.10) × 1015 M⊙ by fitting a NFW density profile to the CLASH data. In addition, based on the weak and strong lensing analysis from Sereno & Covone (2013), Sereno (2015) followed the same procedure as for all clusters in the CoMaLit1 sample and obtained M500 = (7.96 ± 1.44) × 1014 M⊙.
Moreover, a recent study based on the velocity dispersion of galaxy members in Aguado-Barahona et al. (2022) obtained two dynamical mass estimates for CL J1226.9+3332: M500 = (4.7 ± 1.0) × 1014 M⊙ and M500 = (4.8 ± 1.0) × 1014 M⊙ from the velocities of 52 and 49 member galaxies, respectively.
We display in Fig. 1 the different M500 estimates found in the literature. Grey diamonds with error bars correspond to the HSE mass estimates. We distinguish the HSE masses obtained from the combination of SZ and X-ray data (filled diamonds) and the X-ray-only results (empty diamonds). The mass given by Planck Collaboration XVIII (2015) is considered here to be an SZ+X result, but it is important to keep in mind that this mass was obtained applying a scaling relation (derived from X-ray data) to the Planck SZ signal. The empty pink squares show the M500 assuming the virial relation and using only SZ data (Mroczkowski 2011, 2012). The purple circles are the dynamical masses from Aguado-Barahona et al. (2022) and the brown stars the lensing estimates from Merten et al. (2015) and Sereno (2015). We decided not to present in the same figure the projected masses, as it would be misleading to compare them to the masses integrated in a sphere. The figure shows that both HSE and lensing masses among them vary more than 40% from one analysis to another.
 |
Fig. 1. M500 estimates for CL J1226.9+3332 in the literature. Filled grey diamonds represent HSE masses from the combination of SZ and X-ray data and empty ones correspond to X-ray-only results. Pink squares show the SZ-only mass assuming virial relation, purple circles are dynamical mass estimates, and brown stars correspond to lensing M500. |
All these mass estimates for CL J1226.9+3332 are hindered by systematic effects, which are difficult to deal with. Properly comparing masses obtained from different observables, methods, or modelling approaches is crucial, but very challenging. Moreover, as the shape of the HSE mass profile varies depending on the data and the analysis procedure that is considered, the value of R500 is not the same for all estimates presented in Fig. 1. Comparisons are thus delicate due to the correlation between the mass and the radius at which it is estimated. As mentioned, an accurate knowledge of the mass of galaxy clusters is essential for cosmological purposes (Pratt et al. 2019). This motivates the study in this paper, which follows the previous work of Ferragamo et al. (2022).
3. ICM observations
3.1. NIKA2
3.1.1. NIKA2 and the SZ Large Program
The NIKA2 camera (Adam et al. 2018a; Bourrion et al. 2016; Calvo et al. 2016) is a millimetre camera operating at the IRAM 30-meter telescope on Pico Veleta (Sierra Nevada, Spain). It observes simultaneously in two bands centred at 150 and 260 GHz with three arrays of kinetic inductance detectors (KIDs, Day et al. 2003; Shu et al. 2018), two operating at 260 GHz and one at 150 GHz. These frequency bands are adapted to detect the characteristic distortion of the tSZ effect, which shows a decrement in the CMB brightness at frequencies lower than ∼217 GHz and an increment at higher frequencies. As described in the instrument performance analysis review (Perotto et al. 2020), NIKA2 maps the sky with a 6.5′ field of view (FoV) and high angular resolution, 17.6′ and 11.1′ full width at half maximum at 150 and 260 GHz, respectively. These capabilities, combined with its high sensitivity (9 mJy s1/2 at 150 GHz and 30 mJy s1/2 at 260 GHz), enable us to study the ICM of galaxy clusters in detail, as has been proved in previous works (Ruppin et al. 2018; Kéruzoré et al. 2020). Substructures in clusters and contaminant sources can also be identified.
Part of the NIKA2 guaranteed time was allocated to the NIKA2 SZ Large Program. This programme is a high angular resolution follow-up of ∼45 galaxy clusters detected with Planck and ACT (Planck Collaboration XVIII 2015; Hasselfield et al. 2013). These clusters were chosen at intermediate to high redshift ranges (0.5 ≤ z ≤ 0.9) and covering a wide range of masses (3 ≤ M500/1014 M⊙ ≤ 10) estimated according to their tSZ signal and mass-observable scaling relations. The improvement in resolution with respect to the previous instruments, going below the arcminute scale, allows us to resolve distant clusters for which the apparent angular sizes are small. The SZ Large Program also benefits from the X-ray observations obtained with the XMM-Newton satellite. From the combination of tSZ and X-ray data, the NIKA2 SZ Large Program will be able to re-estimate precise HSE masses of the galaxy clusters in the sample and improve the current SZ-mass scaling relations. A more detailed explanation of the NIKA2 SZ Large Program is given in Mayet et al. (2020) and Perotto et al. (2022).
3.1.2. NIKA2 observations and maps of CL J1226.9+3332
CL J1226.9+3332 was observed for 3.6 h during the 15th NIKA2 science-purpose observation campaign (13–20 February 2018) as part of the NIKA2 Guaranteed Time (under project number 199-16) at the IRAM 30m telescope. The data consists of 36 raster scans of 8 × 4 arcmin in series of four scans with angles of 0, 45, 90, and 135 degrees with respect to the right ascension axis. The scans were centred at the XMM-Newton X-ray peak, (RA, Dec)J2000 = (12h26m58.08s, +33d32m46.6s). The mean elevation of the scans is 58.51°. Data at 150 and 260 GHz were acquired simultaneously.
The raw data were calibrated and reduced following the baseline method developed for the performance assessment of NIKA2 (Perotto et al. 2020) and extended to diffuse emission, as in Kéruzoré et al. (2020) and Rigby et al. (2021). The data for the two frequency bands are processed independently. Common modes of the most-correlated detectors are estimated for data outside a circular mask covering the cluster. These modes are subtracted from the raw data, and a new mask is defined at the positions where the significance of the signal is above a threshold, S/N > 3 in this case. At the next iteration the common modes are estimated outside the new mask and we repeat the procedure until convergence. We chose a 2 arcmin diameter disk centred at the centre of the scans as an initial mask.
We present in Fig. 2 the resulting NIKA2 surface brightness maps at 150 and 260 GHz for CL J1226.9+3332. Black contours indicate significance levels starting from 3σ with a 3σ spacing. The map at 150 GHz (left panel) shows the cluster as a negative decrement with respect to the background. This is the characteristic signature of the tSZ effect at frequencies lower than 217 GHz. In this map we also identify positive sources that can compensate the negative tSZ signal of the cluster, which is the case for the central south-eastern source. Moreover, in the 150 GHz map we observe an elongation of the tSZ peak towards the south-west. Similar structures were found by Maughan et al. (2007), Korngut et al. (2011), Adam et al. (2015), Zitrin et al. (2015), and Jee & Tyson (2009), as mentioned in Sect. 2. The 260 GHz map (right panel) is dominated by the signal of the point sources and can be used to identify them. Nonetheless, a tSZ signal of the cluster is not detected at this frequency. This is expected since the integrated tSZ signal is about three times weaker in the NIKA2 band centred at 260 GHz than at 150 GHz.
 |
Fig. 2. NIKA2 maps of CL J1226.9+3332 at 150 GHz (left) and 260 GHz (right) in Jy beam−1 units. Contours show S/N levels in multiples of ±3σ. Both maps have been smoothed with a 10′ FWHM Gaussian kernel. The position of the X-ray centre is shown as a magenta cross in the 150 GHz map and the elongation of the tSZ signal towards the south-west is indicated by the white arrow. White and red circles in the 260 GHz map show the submillimetre and radio point sources, respectively. |
3.1.3. Estimation of noise residuals in the NIKA2 maps
The residual noise in the final 150 GHz NIKA2 map of CL J1226.9+3332 needs to be quantified for the reconstruction of the pressure profile of the cluster. It is usually estimated on null maps, also known as jackknives (JKs), by computing half-differences of two statistically equivalent sets of scans in order to eliminate the astrophysical signal and recover the residuals. We developed two different noise estimates to evaluate possible systematic bias and uncertainties. The angle order (AO) noise map is computed from the half-differences of scans observed with the same angle with respect to the right ascension axis. This ensures that signal residuals from differential filtering along the scan direction are minimised in the null maps. Alternatively, the time order (TO) noise map is calculated from the half-differences of consecutive scans. This minimises the time-dependent effects that may be induced by atmospheric residual fluctuations. We present in Fig. 3 the power spectra of the AO and TO null maps at 150 GHz for CL J1226.9+3332, respectively. The AO null map has a flatter power spectrum for small wave numbers, meaning that it contains less large-scale correlated noise than the TO null map. This suggests that the TO null map might be affected by signal or atmospheric residuals differently filtered for each scanning angle. The power spectra shown in Fig. 3 were used to compute 1000 Monte Carlo noise realisations to estimate the pixel-pixel noise covariance matrices used in Sect. 4.1.1 (following the method developed in Adam et al. 2016).
 |
Fig. 3. Power spectra of noise map estimates for NIKA2 150 GHz data. The spectra for the JK maps estimated with angle ordered and time ordered scans are in pink and black, respectively. The power spectra of the different residual maps for the best-fit models shown in Fig. 5 are in blue and green. The grey regions represent the NIKA2 instrumental limits given by the field of view (for small angular frequencies) and the beam FWHM (for large angular frequencies). |
3.1.4. Pipeline transfer function estimation
The filtering induced by the observations and the data reduction process on the cluster signal needs to be evaluated to be accounted for when estimating the pressure profile of the cluster. The transfer function (TF) is calculated by repeating the data processing steps discussed above on a simulation of the cluster signal. It is computed in Fourier space as the ratio of the power spectrum of the simulation filtered by the processing and that of the input simulation. To simulate the cluster tSZ signal we used the universal pressure profile described in Arnaud et al. (2010) with the integrated tSZ signal2 and redshift of CL J1226.9+3332 given in the Planck Collaboration XVIII (2015) catalogue, 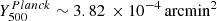 and z = 0.89. We added to the simulated cluster a Gaussian signal with flat spectrum (i.e. random white noise) to explore angular scales at which the cluster signal is negligible. Up to now the NIKA2 SZ Large Program and NIKA analyses (Adam et al. 2015; Ruppin et al. 2018; Kéruzoré et al. 2020) considered one-dimensional transfer functions (1D TF). In these cases, circular symmetry is assumed and the 1D TF is obtained by averaging the power spectra ratio in Fourier-domain annuli at a fixed angular scale. Nevertheless, it is expected that the filtering is not isotropic in the map as it might depend on the scanning direction. This motivates the use of the two-dimensional transfer function (2D TF). In the right panel of Fig. 4 we present the 2D TF describing the filtering in the NIKA2 150 GHz map of Fig. 2. The black line in the left panel of the figure shows the 1D TF, whereas the coloured lines correspond to the one-dimensional cuts of the 2D TF for the different directions represented in the right plot.
and z = 0.89. We added to the simulated cluster a Gaussian signal with flat spectrum (i.e. random white noise) to explore angular scales at which the cluster signal is negligible. Up to now the NIKA2 SZ Large Program and NIKA analyses (Adam et al. 2015; Ruppin et al. 2018; Kéruzoré et al. 2020) considered one-dimensional transfer functions (1D TF). In these cases, circular symmetry is assumed and the 1D TF is obtained by averaging the power spectra ratio in Fourier-domain annuli at a fixed angular scale. Nevertheless, it is expected that the filtering is not isotropic in the map as it might depend on the scanning direction. This motivates the use of the two-dimensional transfer function (2D TF). In the right panel of Fig. 4 we present the 2D TF describing the filtering in the NIKA2 150 GHz map of Fig. 2. The black line in the left panel of the figure shows the 1D TF, whereas the coloured lines correspond to the one-dimensional cuts of the 2D TF for the different directions represented in the right plot.
 |
Fig. 4. Transfer functions, 1D (left) and 2D (right), describing the filtering induced by data processing for the 150 GHz map in Fig. 2. The coloured lines in the left panel represent the values of the 2D transfer function for the directions shown with the same colours in the right panel. Grey-shaded areas correspond to the NIKA2 field of view (for small angular frequencies) and beam FWHM (for large angular frequencies) instrumental limits. |
Except for the scanning directions, the 2D TF is compatible with the 1D TF, and is greater than 0.8 at large angular scales, meaning that the signal is well preserved. On the contrary, filtering is significant for angular frequencies below ∼0.5 arcmin−1. At 0.4 arcmin−1 ≲ k ≲ 0.8 arcmin−1 the transfer function is larger than unity, meaning that the signal has been slightly enhanced by the data analysis process at these scales. In order to evaluate the impact of considering the anisotropy of the filtering, the analyses presented in the following sections will be carried out with both the 1D and 2D transfer functions (see Sect. 4.1.1).
3.1.5. Point source contamination
Point sources in the 150 GHz map contaminate the tSZ signal and also need to be considered. We start by identifying submillimetre sources by blindly searching for point sources in the NIKA2 260 GHz map of CL J1226.9+3332. By cross-checking the detections with a S/N greater than 3 with Herschel SPIRE and PACS catalogues, seven submillimetre sources were identified in the region covered by the NIKA2 maps. The position and fluxes from the above-mentioned catalogues for each submillimetre point source (PS1 to PS5, PS7, and PS8) are summarised in Table 1, and the corresponding Herschel names are given in Table 2.
Submillimetre point source coordinates and fluxes identified within a radius of 2′ around the centre of CL J1226.9+3332.
Submillimetre point sources fluxes and their corresponding names in Herschel SPIRE or PACS catalogue.
For each of these sources, a modified black-body spectrum model is adjusted to the fluxes in Table 1 together with the measurement of the flux at 260 GHz from the NIKA2 map. The spectra are then extrapolated to 150 GHz to obtain an estimate of the flux of each source at 150 GHz. In Table 2 we summarise the fluxes at 260 GHz obtained from the NIKA2 map and the extrapolated values at 150 GHz. The contribution of the noise and the filtering in the 260 GHz map are considered when measuring the fluxes. The estimates obtained with the AO and TO noise approaches give compatible results for all point sources. A more detailed explanation of the method used to deal with submillimetre point sources is given in Kéruzoré et al. (2020). The obtained probability distributions of the fluxes at 150 GHz are used as priors for the joint fit of the cluster pressure profile and the point sources fluxes described in Sect. 4.1.1.
Comparing results in Table 2, we find very large uncertainties for the extrapolated flux of PS1 at 150 GHz when estimated with the TO noise map, but this will not substantially affect the following results for the simultaneous fit of the PS1 flux (see Table B.1) when estimating the cluster pressure profile. Moreover, we can compare its flux at 260 GHz to the measurement in Adam et al. (2015), where the source is called PS260. Using NIKA data, they obtain F260 GHz = 6.8 ± 0.7 (stat.) ±1.0 (cal.) mJy, which is consistent with our estimates.
Source PS6 does not have a counterpart in the Herschel SPIRE and PACS catalogues, but it appears as a weak signal in the Herschel maps and as a 3σ detection in the 260 GHz NIKA2 map; moreover, it compensates the extended tSZ signal at 150 GHz (also clearly observed in Adam et al. 2015). For this source the modified black body is used to obtain prior knowledge of the flux at 150 GHz for the assumed prior distributions of the spectral index and temperature (Kéruzoré et al. 2020). Another tricky point source is PS7. The extrapolated 150 GHz values shown in Table 2 clearly overestimate the flux of the source. This is understandable since we do not have enough constraints for the low-frequency slope of the spectral energy distribution. We choose to use the obtained values as upper limits of a flat prior for the flux of PS7 in the estimation of the cluster pressure profile.
In addition to submillimetre sources, according to the VLA FIRST Survey catalogue (White et al. 1997), a radio source of 3.60 ± 0.13 mJy at 1.4 GHz is present in (RA, Dec)J2000 = (12h26m58.19s, +33d32m48.61s), hereafter PS9. This galaxy corresponds to the BCG identified in Holden et al. (2009) and the compact radio source detected with LOFAR in Di Gennaro et al. (2020). We know beforehand that the contribution of this radio source at 150 GHz is small, but given its central position, it is important to consider it. Assuming a synchrotron spectrum F(ν) = F0(ν/ν0)α with α = −0.7 ± 0.2, which describes the spectral energy distribution for an average radio source (Condon 1984), at 150 GHz we obtain 0.1 ± 0.2 mJy. The obtained probability distribution of the flux at 150 GHz is also used as a prior for the fit in Sect. 4.1.1. The extrapolation of fluxes from radio to millimetre wavelengths can be dangerous and lead to biasing the electron pressure reconstruction. However, this is not the case for our analyses (see results in Sect. 4.1.1 and Table B.2).
3.2. XMM-Newton
Regarding the X-ray data, CL J1226.9+3332 was observed by XMM-Newton (Obs ID 0200340101) for a total observation time of 90/74 ks (MOS/pn), reducing to 63/47 ks after cleaning. The data were reduced following the standard procedures described in Bartalucci et al. (2017). The raw data were processed using the XMM-Newton standard pipeline Science Analysis System (SAS version 16). Only standard events from the EMOS1, 2, and EPN detectors with PATTERN < 4 and < 13, respectively, were kept. The data were further filtered for badtime events and solar flares. Vignetting was accounted for following the weighting scheme described in Arnaud et al. (2001). Point sources were detected on the basis of wavelet-filtered images in low-energy ([0.3–2] keV) and high-energy ([2–5] keV) bands, then subsequently masked from the events list. This process was controlled by a visual check, allowing us to further extract obvious (sub-)structures present in the field. The instrumental background was modelled through the use of stacked filter-wheel closed observations, whilst the astrophysical contamination due to the Galaxy and the cosmic X-ray background were accounted for as a constant background in the 1D surface brightness analysis. This component was modelled in the spectral analysis following the method outlined in Pratt et al. (2010), using an annulus external to the target of radii 300″ < θ < 480″.
4. ICM thermodynamical profiles
4.1. Electron pressure reconstruction from tSZ
The spectral distortion of the CMB caused by the thermal energy in the cluster (i.e. the tSZ effect) is characterised by its amplitude or Compton parameter, y (Sunyaev & Zeldovich 1972). This is directly proportional to the thermal pressure of the electrons in the ICM, Pe, integrated along the line of sight,
where σT, me, and c are the Thomson cross-section, the electron rest mass, and the speed of light, respectively. Hence, the tSZ surface brightness is proportional to the Compton parameter integrated over the tSZ spectrum convolved by the NIKA2 bandpass, and therefore proportional to the integrated thermal pressure of the ICM in the cluster.
4.1.1. Pressure profile reconstruction with NIKA2
4.1.2. Reconstruction procedure
To reconstruct the electron pressure in the ICM of CL J1226.9+3332 we fit a model map of the surface brightness of the cluster to the NIKA2 150 GHz map.
The model map is obtained from the pressure profile of the galaxy cluster integrated along the line of sight in Compton parameter (y) units, following Eq. (1). We describe the pressure of the galaxy cluster with a radially binned spherical model (also called the non-parametric model in Ruppin et al. 2017; Romero et al. 2018),
where Pi and αi are the values of the pressure and the slope at the radial bin ri. The slope is directly calculated as
We initialise the pressure bin values by taking random values from a normal distribution centred at the corresponding pressure from the universal profile of Arnaud et al. (2010) at each radial bin. The radial bins are chosen to cover mainly the range between the NIKA2 resolution and field of view capabilities. We centre the pressure profile at the coordinates of the X-ray peak, as determined from XMM-Newton data analysis (Sects. 3.1.2 and 3.2). The derived y-map is convolved with the NIKA2 beam, which is approximated by a two-dimensional Gaussian with FWHM = 17.6″ (Perotto et al. 2020). In order to account for the attenuation or filtering effects due to data processing in the NIKA2 150 GHz map, the model map is also convolved with the transfer function (Sect. 3.1.4). We repeat this procedure for the 1D and 2D transfer functions. Finally, the y-map is converted into surface brightness units with a conversion coefficient, accounting for the tSZ spectra shape convolved by the NIKA2 bandpass, which is also left as a parameter of the fit (as done in Kéruzoré et al. 2020).
Furthermore, for the comparison with the 150 GHz NIKA2 map, we added the contribution of point sources to the model map. Point sources are modelled as two-dimensional Gaussian functions, and we repeat the procedure detailed in Kéruzoré et al. (2020) to fit the flux of each source at 150 GHz. Priors on the flux of the sources at 150 GHz are obtained from the results of the spectral fits presented in Sect. 3.1.5. The last component in the model map is a constant zero-level that we also adjust as a nuisance parameter.
The parameters (ϑ) of our fit are the pressure bins describing the ICM of the cluster, the fluxes of the contaminant point sources, the conversion factor from Compton to surface brightness units, and the zero-level. The likelihood that we use to compare our model ℳ pixel by pixel to the data 𝒟 is given by
Here Cpix − pix is the pixel-pixel noise covariance matrix accounting for the residual noise in the NIKA2 150 GHz map (Sect. 3.1.3). We repeat the fit with the covariance matrices from both AO and TO noise estimates.
We also compute the Y500 integrated Compton parameter and compare it in the likelihood to the integrated Compton parameter measured by Planck Collaboration XVIII (2015), 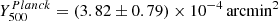 within an aperture of θ500 = 1.907 arcmin. We do not compare the integrated Compton parameter at 5θ500 as measured by Planck because it would require extrapolating the pressure profile far beyond the NIKA2 data.
within an aperture of θ500 = 1.907 arcmin. We do not compare the integrated Compton parameter at 5θ500 as measured by Planck because it would require extrapolating the pressure profile far beyond the NIKA2 data.
For the map fit we use the PANCO2 pipeline (Kéruzoré et al. 2022) and follow the procedure described in Adam et al. (2015), Ruppin et al. (2018), and Kéruzoré et al. (2020). This pipeline performs a Markov chain Monte Carlo (MCMC) fit using the emcee Python package (Foreman-Mackey et al. 2019; Goodman & Weare 2010). The sampling is performed using 40 walkers and 105 steps, with a burn-in of 103 samples, and convergence is monitored following the 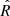 test of Gelman & Rubin (1992) and chains autocorrelation. The PANCO2 code has been successfully tested on simulations.
test of Gelman & Rubin (1992) and chains autocorrelation. The PANCO2 code has been successfully tested on simulations.
4.1.3. NIKA2 pressure radial profile
In order to estimate the robustness of the results of the above procedure, we performed the fit to the NIKA2 data in four different cases with respect to the choice of noise residuals and transfer function estimates. Thus, we consider AO1D (TO1D) and AO2D (TO2D) using the AO (TO) noise residual map and the 1D and 2D transfer functions, respectively. In Fig. 5 we compare the NIKA2 150 GHz map of CL J1226.9+3332 to the obtained best-fit models and their residuals for these four analyses. Comparing the power spectra of the residual maps to the power spectra of the noise estimate maps, we see in Fig. 3 that for the TO case the fit residuals and the noise estimates power spectra are consistent. However, for the AO cases there is an excess of power in the fit residuals, which could be interpreted as coming from the signal due to the differential filtering effects that are not captured in the AO noise, as discussed in Sect. 3.1.3. Regarding point sources, the reconstructed fluxes are consistent for the four analyses (see Tables B.1 and B.2).
 |
Fig. 5. 150 GHz maps of CL J1226.9+3332. Left: NIKA2 150 GHz surface brightness map of CL J1226.9+3332. Top: best-fit models of the tSZ signal and point sources. Bottom: residual maps, difference between the data map and each best-fit model. Results obtained with different transfer function and noise estimates (from left to right): AO1D, AO2D, TO1D, and TO2D. All maps have been smoothed with a 10′ Gaussian kernel for display purposes and are shown in units of Jy beam−1. |
We present in Fig. 6 the radially binned best-fit pressure profiles obtained for the four tested cases. The blue and cyan (dark and light green) dots correspond to the AO (TO) 1D and 2D transfer function estimates, respectively. The plotted uncertainties correspond to 1σ of the posterior distributions derived from the MCMC chains. Overall, the four NIKA2 analyses give consistent results, especially in the radial ranges where we expect the NIKA2 results to be reliable (i.e. between the beam and the FoV scales, both represented with dashed vertical lines in the figure). We give the HWHM of the NIKA2 beam (17.6″/2) and half the diameter of the FoV (6.5′/2) in the physical distances corresponding to the redshift of the cluster.
 |
Fig. 6. Pressure profile of the ICM of CL J1226.9+3332. Blue and green symbols correspond to the results obtained in this work from the NIKA2 150 GHz map. The error bar edges represent the 1σ uncertainties. Pink, yellow, and black stars show the reconstructed profiles in R18 for NIKA, MUSTANG, and Bolocam data, respectively. Empty symbols correspond to the pressure profile obtained from the combination of XMM-Newton electron density and temperature profiles. Vertical dashed lines indicate the instrumental limits of NIKA2 as radius of the beam and FoV. |
In terms of noise estimates we observe that the uncertainties on the pressure bin estimates are slightly larger for the time-ordered case, as expected. However, we note no significant bias between the time and angle ordered results. The effect of the transfer function is hard to evaluate: even if the 2D TF is a more precise description of the filtering in the map, when fitting a spherical cluster model the use of the 1D TF gives consistent results. In the following we use the results for the four analyses to evaluate possible systematic uncertainties induced by the NIKA2 processing.
4.1.4. Comparison to previous results
In Fig. 6 we compare our results to the profiles obtained in R18 with tSZ data from NIKA (pink), Bolocam (black), and MUSTANG (yellow). MUSTANG’s high angular resolution (9″ FWHM at 90 GHz) enables us to map the core of the cluster, whereas Bolocam’s large field of view (8′ at 140 GHz) allows us to recover the large angular scales. NIKA and the improved NIKA2 camera are able to cover all the intermediate radii. The consistency of the different pressure bins in the radial range from the NIKA2 beam to the FoV proves the reliability of the reconstruction with NIKA2 data.
Before going further, we have to consider again the effect of the filtering on the NIKA2 data. The filtering due to the data processing affects mainly small angular frequencies, i.e. small k numbers (Sect. 3.1.4), which is translated into large angular scales in real space. In this case it means that the region at ∼1000 kpc from the centre of the cluster is strongly filtered. For this reason, we cast doubt on the results of our fits for the last NIKA2 bin in pressure.
4.2. Thermodynamical profiles from X-rays
The electron density and temperature profiles were extracted following the methodology described by Pratt et al. (2010) and Bartalucci et al. (2017). In short, the vignetted-corrected and background-subtracted surface brightness profile obtained in concentric annuli from the X-ray peak is deconvolved from the point spread function (PSF) and geometrically deprojected assuming spherical symmetry using the regularisation technique described in Croston et al. (2006).
The temperature profile is derived in bins defined from the previously derived binned surface brightness profile through a spectral analysis modelling the ICM emission via an absorbed MEKAL model under XSPEC3 and accounting for both the instrumental and astrophysical backgrounds. The derived 2D temperature profile is then PSF-corrected and deprojected following the ‘non-parametric-like’ method presented in Bartalucci et al. (2018).
The gas pressure, P, and entropy, K, profiles were then derived from the deprojected density, ne, and temperature, T, profiles assuming P = ne × T and 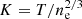 , respectively. In this paper we focus on the gas pressure profile, which is shown in Fig. 6 with open black circles. The electron density and temperature profiles are shown in Fig. 7.
, respectively. In this paper we focus on the gas pressure profile, which is shown in Fig. 6 with open black circles. The electron density and temperature profiles are shown in Fig. 7.
 |
Fig. 7. Electron density (left) and temperature (right) profiles reconstructed from XMM-Newton observations, with 1σ error bars. The profiles are centred at the X-ray peak (RA, Dec.)J2000 = (12h26m58.08s, +33d32m46.6s). |
5. Hydrostatic mass
5.1. Hydrostatic equilibrium
Under the hydrostatic equilibrium (HSE) hypothesis, for a spherical cluster we can compute the total cluster mass enclosed within the radius r as
where μ, mp, and G are the mean molecular weight of the ICM gas, the proton mass and the gravitational constant, respectively. We assume μ ≈ 0.6 (Pessah & Chakraborty 2013; Ettori et al. 2019) for the gas. Combining the pressure profiles obtained from the thermal SZ or X-ray data with the electron density from the X-ray, we can reconstruct the mass of the galaxy cluster as in Adam et al. (2015), Ruppin et al. (2018), and Kéruzoré et al. (2020).
5.2. Pressure profile modelling for mass estimation
Deriving the mass directly from the radially binned profiles presented above (see Fig. 6) leads to non-physical results (i.e. negative mass contributions) as no condition was imposed regarding the slope of the profile in the pressure reconstruction. This was done to prevent extra constraints on the pressure profile induced by assumptions on the model. To overcome this issue, we fit here pressure models ensuring physical mass profiles to the radially binned tSZ results from Sect. 4.1.1. We consider two different approaches: 1) a direct fit of a generalised Navarro-Frenk-White (gNFW) profile to the radially binned pressure, and 2) an indirect fit of a Navarro-Frenk-White (NFW) mass density model under the HSE assumption. Aiming for a precise reconstruction of the HSE mass, which requires having accurately constrained slopes for the pressure profile, in both cases we combine the NIKA2 pressure bins with the results obtained in R184.
5.2.1. gNFW pressure model
The first approach, which was used in previous NIKA2 studies (Ruppin et al. 2018; Kéruzoré et al. 2020; Ferragamo et al. 2022), consists in fitting the widely used gNFW pressure profile model (Nagai et al. 2007) to the tSZ data,
where P0 is the normalisation constant, b and c respectively the external and internal slopes, rp the characteristic radius of slope change, and a the parameter describing the steepness of the slope’s transition.
We perform a MCMC fit using emcee package. The likelihood function is given by
where PN2 and C represent the NIKA2 radially binned pressure profile bins and associated covariance matrix, 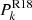 and
and 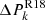 are the R18 pressure profile data and uncertainties, and PgNFW(ϑ) are the gNFW pressure profile values for a set of parameters ϑ = [P0, rp, a, b, c]. As we do not rely on the value of the last NIKA2 pressure bin, we chose to modify the NIKA2 inverse covariance matrix C−1 by setting the last diagonal term to [C−1]6, 6 = 0, so that the correlation of the last bin with the others is taken into account, but not its value. We also set a constraint on the integrated Compton parameter of the model
are the R18 pressure profile data and uncertainties, and PgNFW(ϑ) are the gNFW pressure profile values for a set of parameters ϑ = [P0, rp, a, b, c]. As we do not rely on the value of the last NIKA2 pressure bin, we chose to modify the NIKA2 inverse covariance matrix C−1 by setting the last diagonal term to [C−1]6, 6 = 0, so that the correlation of the last bin with the others is taken into account, but not its value. We also set a constraint on the integrated Compton parameter of the model 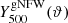 , again using the Planck satellite PSZ2 catalogue results,
, again using the Planck satellite PSZ2 catalogue results, 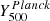 (Planck Collaboration XVIII 2015). However, we find that the impact of this constraint is completely negligible for this cluster. Furthermore, we added an extra condition to the fit to ensure increasing HSE mass profiles with radius:
(Planck Collaboration XVIII 2015). However, we find that the impact of this constraint is completely negligible for this cluster. Furthermore, we added an extra condition to the fit to ensure increasing HSE mass profiles with radius: 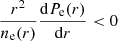 .
.
The best-fit gNFW pressure profiles (solid lines) and uncertainties (shaded area) are presented in the left panel of Fig. 8 for the four sets of NIKA2 data discussed in Sect. 4.1.1. We observe that the best-fit models are a good representation of the data over the full range in radius, as demonstrated by the corresponding reduced χ2, which are close to 1 for all the cases (see solid lines in Fig. C.2). The posterior distributions of the ϑgNFW parameters can be found in Appendix C.
 |
Fig. 8. Pressure profile and best fit for the gNFW (left) and NFW (right) models. The data points correspond to the NIKA2 radially binned results for the four data sets discussed above, and to the NIKA, MUSTANG, and Bolocam bins from R18. Blue and green solid lines represent the best-fit values for the four NIKA2 pressure estimates considered. The shaded regions show the 2.5th, 16th, 84th, and 97.5th percentiles. |
In addition, it is interesting to compare our results to those from Planck for which a similar modelling was used. In Fig. 9 we present the 2D posterior distributions of the integrated Compton parameter at 5R500 (with R500 calculated independently in each case) with respect to the Θs parameter of the gNFW model, at a confidence level (C.L.) of 68%, 95%, and 99%. The parameters Θs and rp are related via the angular diameter distance at the cluster redshift: tan(Θs) = rp/𝒟A. We compare the results obtained in Planck Collaboration XVIII (2015; with the MMF3 matched multi-filter, available in the Planck Legacy Archive5) to the constraints from the gNFW profiles obtained in this work with the NIKA2, R18, and XMM-Newton data. Our contours were obtained varying all the parameters in the gNFW model fit, while for Plancka, b, and c the parameters were fixed. For simplicity, we only show the contours for the NIKA2 AO1D case. This figure illustrates the important gain in precision due to high-resolution observations: resolving the galaxy cluster allows us to determine, even at such high redshift, the Θs characteristic radius. The contours are marginally in agreement.
 |
Fig. 9. Distribution of Y5R500 with respect to Θs for the gNFW pressure model fits to Planck data (grey) in Planck Collaboration XVIII (2015) and to the NIKA2 + R18 + XMM-Newton data (blue) in this work. Different contours show the 68%, 95%, and 99% confidence intervals. The black star corresponds to the intersection between the Planck Collaboration XVIII (2015) distribution and the X-ray scaling law shown in Fig. 16 in Planck Collaboration XVIII (2015). |
5.2.2. NFW density model
We present here a different approach for the modelling of the pressure profile in the scope of estimating the HSE mass. The estimation of the pressure derivative (Eq. (5)) can be very problematic, first because it is very sensitive to local variations in the slope of the pressure profile and because it requires, as discussed above, additional constraints to ensure recovering physical masses. To overcome these issues we model the pressure profile starting from a mass density model and assuming HSE. An equivalent idea is the ‘backward process’ of fitting X-ray temperatures described in Ettori et al. (2013) and references therein. This method was used for the mass reconstruction in Ettori et al. (2019) and in Eckert et al. (2022). From the HSE defined in Eq. (5), we can write
Moreover, we can relate a radial mass density profile ρ(R) to the mass by
which allows us to relate the pressure directly to a mass density profile. We use here the NFW model, which is a good description of dark matter halos (Navarro et al. 1996) and has been widely used in the literature (e.g., Ettori et al. 2019),
where ρc is the critical density of the Universe at the cluster redshift and δc2006 is a function that depends only on c200, the concentration parameter. Here we switch from an overdensity of 500 to 200 in order to conform to most of previous works. Finally, rs represents a characteristic radius and it is also a free parameter of the model. Using this definition, we obtain
where rzero is the radius at which we are dominated by a zero-level component.
We perform a MCMC analysis similar to the one described above for the gNFW pressure profile model. In this case the free parameters of the model are ϑ = [c200, rs, Pzero]. At each step of the MCMC we compute the integral in Eq. (11) to evaluate P(ϑ) as needed for the likelihood function in Eq. (7). Calculating the integral can be computationally very expensive. As the result of this integral depends only on rs and ra, we create a grid of the integrals for a range of rs values (from 100 to 2000 kpc) and ra the radial bins of interest. We use this grid to interpolate the values of the integrals at each step. Flat priors are given for the concentration and the characteristic radius, 0 < c200 < 8 and 100 kpc < rs < 2000 kpc. The values of the electron density at different radii are obtained by logarithmic interpolation. We also make use of the Python NFW package7.
The best-fit pressure profiles and uncertainties are presented in the right panel of Fig. 8 for the four NIKA2 radially binned data sets discussed above. The posterior probability distributions of the free parameters of the models are shown in Appendix C. The posterior distributions of the c200 and rs parameters can be compared to the results for the analysis of clusters in X-rays in Pointecouteau et al. (2005), Ettori et al. (2019), and Eckert et al. (2022). In these studies, c200 spans from 1 to 6 and rs from 200 kpc to 1200 kpc, which is compatible with our results. We find that the NFW model is overall a good fit to the data as shown by the reduced χ2 ∼ 1 (see Fig. C.2 for the distributions). However, we observe that the uncertainties increase significantly in the outskirts of the cluster with respect to the gNFW pressure profile model discussed in the previous section. This can probably be explained by the flexibility of the NFW-based approach, which is high enough to show that the last point in the profile is not well constrained by the data.
5.3. HSE mass estimates
We present in Fig. 10 the HSE mass profiles inferred from the gNFW best-fit pressure profile, in combination with the XMM-Newton electron density, and from the NFW density best-fit model. Uncertainties (shaded areas) are obtained directly from the MCMC chains by computing the HSE mass profile for each sample from the model parameters. For the sake of clarity, we only present the masses obtained with NIKA2 AO1D estimates, but we changed the colour-coding for the gNFW profile so that we can differentiate between the two results.
 |
Fig. 10. HSE mass profile estimates for CL J1226.9+3332 obtained with NIKA2 (angle order 1D) and R18 tSZ data combined with the XMM-Newton electron density profile. The solid magenta and dashed blue lines correspond to the gNFW and NFW methods, respectively. The shaded areas show the 2.5th, 16th, 84th, and 97.5th percentiles. Empty dots correspond to the HSE mass profile obtained from XMM-Newton-only data. Vertical dashed lines show the |
The capability of the pressure model to describe the shape of the profile slopes is the key element for a good mass reconstruction. From the above results it seems that the NFW approach does not have enough degrees of freedom to fully describe slope variations in the reconstructed pressure profile. Nevertheless, the resulting HSE mass profiles for the two models are compatible within 2σ. The vertical dashed lines in the figure represent the 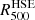 for each mass profile. Slight differences in the shape of the pressure profile at these radial ranges are critical for defining
for each mass profile. Slight differences in the shape of the pressure profile at these radial ranges are critical for defining 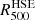 .
.
These mass profiles, obtained from the combination of tSZ and X-ray data, are also compared to the X-ray-only HSE mass estimate in Fig. 10. Assuming spherical symmetry, the X-ray mass profile was derived, following the Monte Carlo procedure detailed in Démoclès et al. (2010) and Bartalucci et al. (2017) with the XMM-Newton electron density and temperature profiles presented in Sect. 4.2.
Despite the different behaviour of the X-ray-only profile in the cluster core, it is consistent with the tSZ+X estimates at around 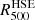 . We note that the difference must come from the estimate of the derivative of the pressure, which for X-analyses is computed using the density and temperature profiles. The temperature profile from the X-rays is not used to compute the HSE mass in the tSZ+X analyses.
. We note that the difference must come from the estimate of the derivative of the pressure, which for X-analyses is computed using the density and temperature profiles. The temperature profile from the X-rays is not used to compute the HSE mass in the tSZ+X analyses.
From the reconstructed HSE mass profiles we can obtain 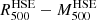 probability distributions for each of the considered cases. We present in the left and central panel of Fig. 11 the
probability distributions for each of the considered cases. We present in the left and central panel of Fig. 11 the 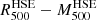 distributions for the gNFW and NFW models. They were obtained from the MCMC chains in the same way the uncertainties in Fig. 10 were computed. The results also account for the additional ∼20% uncertainty introduced by the electron density profile to M500. These uncertainties were computed by combining the best-fit NFW and gNFW profiles with random realisations of the electron density profile following a Gaussian distribution centred in the central values of ne and with the error bars as standard deviation. The width of the ellipses is an artefact from the display procedure, and each value of
distributions for the gNFW and NFW models. They were obtained from the MCMC chains in the same way the uncertainties in Fig. 10 were computed. The results also account for the additional ∼20% uncertainty introduced by the electron density profile to M500. These uncertainties were computed by combining the best-fit NFW and gNFW profiles with random realisations of the electron density profile following a Gaussian distribution centred in the central values of ne and with the error bars as standard deviation. The width of the ellipses is an artefact from the display procedure, and each value of 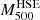 is associated with a single value of
is associated with a single value of 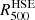 .
.
 |
Fig. 11. Probability distributions (1D and 2D) for |
We present here the results for the four NIKA2 analyses (AO1D/2D and TO1D/2D). The results are consistent, with little dependence on the chosen TF estimate. From the comparison of the left and central panels in Fig. 11 we verify that the largest uncertainty in the HSE mass estimates comes from the modelling of the pressure profile. In spite of this effect, the reconstructed HSE mass profiles are compatible within 1σ. The right panel of Fig. 11 shows the 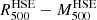 probability distribution obtained with XMM-Newton-only data. Even if it is compatible with the gNFW and NFW results, the X-ray-only results favour lower HSE masses. A similar effect was observed for the ACT-CL J0215.4+0030 cluster (Kéruzoré et al. 2020), but not for PSZ2 G144.83+25.11 (Ruppin et al. 2018). We summarise in Table 3 the marginalised
probability distribution obtained with XMM-Newton-only data. Even if it is compatible with the gNFW and NFW results, the X-ray-only results favour lower HSE masses. A similar effect was observed for the ACT-CL J0215.4+0030 cluster (Kéruzoré et al. 2020), but not for PSZ2 G144.83+25.11 (Ruppin et al. 2018). We summarise in Table 3 the marginalised 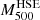 masses obtained in this work. We give the mean value and the 84th and 16th percentiles. For gNFW and NFW we combine the probability distributions obtained for the four NIKA2 results so that the results account for the systematic effects from the NIKA2 data processing. The error bars also account for the uncertainties related to the electron density.
masses obtained in this work. We give the mean value and the 84th and 16th percentiles. For gNFW and NFW we combine the probability distributions obtained for the four NIKA2 results so that the results account for the systematic effects from the NIKA2 data processing. The error bars also account for the uncertainties related to the electron density.
HSE masses for different estimates at 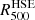 .
.
6. Lensing mass
Lensing masses, in contrast to HSE ones, probe the total mass without assumptions on the dynamical state of the cluster. For this reason it is of great interest to compare the HSE masses to lensing estimates. In this section we present the lensing mass estimate for CL J1226.9+3332.
6.1. Lensing data
We use the CLASH convergence maps (hereafter κ-maps) obtained from the weak and strong lensing analysis by Zitrin et al. (2015). In the analysis the authors reconstructed the κ-maps for the 25 massive CLASH clusters (Postman et al. 2012) using two different lensing models: 1) Light Traces Mass (LTM) and 2) Pseudo Isothermal Elliptical Mass Distribution plus an elliptical NFW dark matter halo (PIEMD+eNFW). These models have been detailed in previous studies (Zitrin et al. 2009, 2013a,b, 2015). In this work we compute the mass estimate for both κ-maps in order to account for differences in the convergence map modelling.
6.2. Lensing mass density profile
For the lensing mass profile reconstruction we followed a similar approach to the one described in Ferragamo et al. (2022). The convergence maps describe the projected mass density of the cluster, Σ, in critical density units, κ = Σ/Σcrit, with
Here Ds, Dl, and Dls correspond to the angular diameter distance between the observer and the source, between the observer and the lens (the cluster), and between the source and the lens, respectively. The publicly available CLASH κ-maps (Zitrin et al. 2015) have been normalised to Ds/Dls = 1.
To estimate the lensing mass profile of CL J1226.9+3332, we fit a mass density model to the Σ-map. We assume spherical symmetry and a NFW density profile. We choose to directly fit the analytical projected NFW density profile (Eq. (5) in Ferragamo et al. 2022, derived from Navarro et al. 1996; Bartelmann 1996) to the radially averaged projected profiles of the Σ-maps. We consider as free parameters rs and c200 (see Eq. (10)). The fit is performed via a MCMC analysis using the emcee software and the NFW Python package. We centre the projected mass profiles at the same position as for the pressure and electron density profiles in Sects. 4.1 and 4.2, the X-ray centre. The covariance matrix of the radial profile bins is built accounting for the 100 realisations provided for each model8 and the uncertainties from the dispersion in each radial bin.
We show in Fig. 12 the radial profiles of the projected mass density for CL 1226.9+3332 obtained from the CLASH LTM (left) and PIEMD+eNFW (right) convergence maps. We present for both profiles the projected best-fit NFW density model and percentiles (shaded area). We observe that for the LTM convergence map the best-fit NFW model underestimates the data except for cluster core and that the uncertainties in the model do not fully account for this. By contrast, the fit for the PIEMD+eNFW succeeds in representing the data.
 |
Fig. 12. Projected mass density profiles obtained from CLASH convergence maps for the LTM (left) and PIEMD+eNFW (right) models. We also show the best-fit NFW model (orange and red lines) and the 2.5th, 16th, 84th and 97.5th percentiles (shaded area). |
From these results we conclude that the main uncertainties in the reconstruction of the lensing density profile come from the reconstruction of the convergence map. Thus, in the following we account for those.
6.3. Lensing mass estimates
From the obtained NFW density profiles we can reconstruct the lensing mass profiles (Eq. (9)) and subsequently the 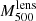 and
and 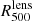 probability distributions. We present in Fig. 13 the main results of this analysis for both convergence map models: LTM and PIEMD+eNFW. We obtain consistent results, and accounting for their combined posterior distributions we measure
probability distributions. We present in Fig. 13 the main results of this analysis for both convergence map models: LTM and PIEMD+eNFW. We obtain consistent results, and accounting for their combined posterior distributions we measure 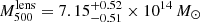 mean value and the 84th and 16th percentiles.
mean value and the 84th and 16th percentiles.
 |
Fig. 13. Probabiliy distribution for |
The Jee & Tyson (2009) weak-lensing analysis did not provide the direct 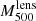 , but evaluated the lensing mass at the R500 from Maughan et al. (2007). This result, shown in purple in Fig. 13, is consistent within 1σ with our PIEMD+eNFW analysis when evaluating the lensing mass at the same radius (see red error bars in the figure) and less than 2σ away from LTM (orange error bars). Merten et al. (2015) performed an independent analysis of the CLASH data, reconstructing their own convergence map. The projected mass density profile presented in Fig. 16 in Merten et al. (2015) shows a denser cluster than the profiles from the convergence maps used in this work (Fig. 12). For this reason, Merten et al. (2015) obtained, also with a NFW density fit, 35% higher masses than Jee & Tyson (2009). The corresponding
, but evaluated the lensing mass at the R500 from Maughan et al. (2007). This result, shown in purple in Fig. 13, is consistent within 1σ with our PIEMD+eNFW analysis when evaluating the lensing mass at the same radius (see red error bars in the figure) and less than 2σ away from LTM (orange error bars). Merten et al. (2015) performed an independent analysis of the CLASH data, reconstructing their own convergence map. The projected mass density profile presented in Fig. 16 in Merten et al. (2015) shows a denser cluster than the profiles from the convergence maps used in this work (Fig. 12). For this reason, Merten et al. (2015) obtained, also with a NFW density fit, 35% higher masses than Jee & Tyson (2009). The corresponding 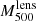 is shown as a filled brown star in Fig. 13. The disturbed state of CL J1226.9+3332 could be the reason, according to Merten et al. (2015), for the different lensing mass estimates. Moreover, the high redshift of the cluster makes the precise reconstruction of the convergence map more difficult. The empty brown star in Fig. 13 corresponds to the lensing mass from CoMaLit (Sereno 2015) obtained from the analysis in Sereno & Covone (2013). In this case, the result is compatible with our mass estimates.
is shown as a filled brown star in Fig. 13. The disturbed state of CL J1226.9+3332 could be the reason, according to Merten et al. (2015), for the different lensing mass estimates. Moreover, the high redshift of the cluster makes the precise reconstruction of the convergence map more difficult. The empty brown star in Fig. 13 corresponds to the lensing mass from CoMaLit (Sereno 2015) obtained from the analysis in Sereno & Covone (2013). In this case, the result is compatible with our mass estimates.
7. Comparison of mass estimates
7.1. CL J1226.9+3332 mass at R500
The comparison of different mass estimates is difficult and can lead to incorrect physical conclusions. In particular, when comparing integrated masses the radius at which the mass is computed has a significant impact: R500 and M500 being constrained at the same time, our data are affected by a degeneracy. For this reason, in Fig. 14 we show, in the R500 − M500 plane, the results from the literature compared with those obtained in this work.
 |
Fig. 14. R − M(< R) plane summarising the R500 − M500 results for CL J1226.9+3332. In the case of the HSE mass estimates the blue and green 1σ contours show the results obtained in this work combining tSZ and X-ray data for the four NIKA2 analyses. The solid and dashed lines are for the gNFW pressure and the NFW density models, respectively. The grey contour corresponds to the HSE mass estimate for the XMM-Newton-only data. In the case of literature data the filled (empty) grey diamonds represent HSE masses from the combination of tSZ and X-ray data (X-ray-only results). The red and orange contours correspond to the lensing mass estimates obtained from the CLASH LTM and PIEMD+eNFW convergence maps in this work, respectively. Pink squares show the tSZ-only mass assuming virial relation, purple circles are dynamical mass estimates, and brown stars the lensing estimates. Grey and brown crosses show HSE and lensing masses from the literature close to M500. The diagonal bright grey line defines the R500 − M500 relation. Slight deviations from this line are due to differences in the cosmological model used in each work. |
The green and blue contours show the 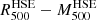 results obtained in this work for the gNFW (solid lines) and NFW (dashed lines) tSZ and X-ray data combined analyses. For comparison the filled grey diamonds correspond to the results from the literature presented in Fig. 1, also for combined tSZ and X-ray data. We observe that the results in this paper are compatible with previous analyses within 1σ, centred around ∼ 7 × 1014 M⊙.
results obtained in this work for the gNFW (solid lines) and NFW (dashed lines) tSZ and X-ray data combined analyses. For comparison the filled grey diamonds correspond to the results from the literature presented in Fig. 1, also for combined tSZ and X-ray data. We observe that the results in this paper are compatible with previous analyses within 1σ, centred around ∼ 7 × 1014 M⊙.
Regarding X-ray-only results, the HSE mass estimates obtained in this work with XMM-Newton data (grey contours) suggest mass values centred at ∼ 5 × 1014 M⊙. This is in agreement with the lowest estimates from the literature (empty grey diamonds) presented in Bulbul et al. (2010) and Maughan et al. (2007). On the contrary, the results from Mantz et al. (2010) and Mroczkowski et al. (2009) show higher masses. However, the 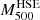 in Mantz et al. (2010) is not a direct measurement, but an extrapolation from a gas mass measured at R2500 converted into total mass, making this result less reliable. Overall, for CL J1226.9+3332 the HSE masses obtained only from X-ray data tend to lower values than those from the combination of tSZ and X-rays.
in Mantz et al. (2010) is not a direct measurement, but an extrapolation from a gas mass measured at R2500 converted into total mass, making this result less reliable. Overall, for CL J1226.9+3332 the HSE masses obtained only from X-ray data tend to lower values than those from the combination of tSZ and X-rays.
The result from Planck Collaboration XVIII (2015) is also a special case, as it is not a direct mass measurement, but a mass obtained from the X-ray-derived scaling relation (Eq. (7) in Planck Collaboration XX 2013) applied to the SZ measurement. This may explain why it lies at the border between the X-ray-only data and the tSZ+X combined results. The differences observed between X-ray-only and the combined tSZ+X results could have a physical and observational origin. For such a high-redshift cluster X-ray observations become challenging. If the south-western sub-clump in the cluster is really a hot but not dense structure (as suggested by Jee & Tyson 2009), the electron density measurements from X-ray observations might be difficult to perform.
We also show in Fig. 14 the lensing, dynamical and virial mass estimates. The lensing mass estimates from this work for the CLASH LTM and PIEMD+eNFW convergence maps are presented as dark orange and red contours, respectively. We observe that they are consistent with the lensing mass from Sereno (2015) and Sereno & Covone (2013) and with HSE mass estimates, but very different from the Merten et al. (2015) lensing estimate for the reasons explained in Sect. 6. The virial masses estimated in Mroczkowski (2011, 2012) without X-ray data are shown as pink squares. They rely on the virial relation and on given pressure and density profile models to relate directly the integrated tSZ flux to the mass (Eq. (15) in Mroczkowski 2011). This kind of analysis seems a good alternative to the HSE mass for clusters without X-ray data. The dynamical mass estimates (purple circles), which we would expect to be larger than the HSE estimate, appear particularly low for CL J1226.9+3332 (Aguado-Barahona et al. 2022). According to the 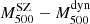 scaling relation obtained from the analysis of 297 Planck galaxy clusters in Aguado-Barahona et al. (2022, Eq. (8) and Table 2) and considering
scaling relation obtained from the analysis of 297 Planck galaxy clusters in Aguado-Barahona et al. (2022, Eq. (8) and Table 2) and considering 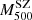 the value in Planck Collaboration XVIII (2015), the dynamical mass corresponding to CL J1226.9+3332 should be in the range 6 − 7.5 × 1014 M⊙, thus more in agreement with our lensing mass estimates. Similar problems are reported in Ettori et al. (2019) and Logan et al. (2022), the latter showing that a large number of galaxies with spectroscopic redshift measurements (> 200) are needed. The orientation of the merger could also be an explanation for the underestimation: if the merger is happening in the plane of the sky, the dispersion, and thus the mass, is lower. Finally, the brown and grey crosses show that the lensing and HSE mass estimates from the literature summarised in Table A.1 are close to M500, but have not been evaluated at R500 − M500: the M1000 from Maughan et al. (2004), the M200 from Muchovej et al. (2007), the mass at 880 kpc from Jee & Tyson (2009), and the mass at 1000 kpc from Sereno & Covone (2013) and Sereno (2015).
the value in Planck Collaboration XVIII (2015), the dynamical mass corresponding to CL J1226.9+3332 should be in the range 6 − 7.5 × 1014 M⊙, thus more in agreement with our lensing mass estimates. Similar problems are reported in Ettori et al. (2019) and Logan et al. (2022), the latter showing that a large number of galaxies with spectroscopic redshift measurements (> 200) are needed. The orientation of the merger could also be an explanation for the underestimation: if the merger is happening in the plane of the sky, the dispersion, and thus the mass, is lower. Finally, the brown and grey crosses show that the lensing and HSE mass estimates from the literature summarised in Table A.1 are close to M500, but have not been evaluated at R500 − M500: the M1000 from Maughan et al. (2004), the M200 from Muchovej et al. (2007), the mass at 880 kpc from Jee & Tyson (2009), and the mass at 1000 kpc from Sereno & Covone (2013) and Sereno (2015).
7.2. Hydrostatic-to-lensing mass bias
7.2.1. Hydrostatic mass bias problem
We do not expect the HSE to be fulfilled by all galaxy clusters in the Universe. We define the hydrostatic mass bias as
where Mtrue is the total true mass of the cluster.
From the observational point of view there are hints of a non-null hydrostatic bias. As mentioned in Sect. 1, one example is the tension observed between the cosmological parameters derived from Planck cluster number counts and those from the CMB analyses (Planck Collaboration XXI 2013). A possible explanation for this tension is that cluster masses are underestimated.
According to Planck Collaboration XXIV (2015) the bias needed to reconcile the cosmological constraints obtained from the CMB power spectra to the cluster counts is 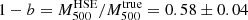 . A compatible value was obtained from the updated analysis in Salvati et al. (2019):
. A compatible value was obtained from the updated analysis in Salvati et al. (2019): 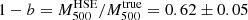 .
.
The hydrostatic bias has also been the topic of a large number of studies on numerical simulations (see Ansarifard et al. 2020; Gianfagna et al. 2021, and references therein). However, simulation-based analyses agree on values in the range of 0.75–0.9 for 1 − b, and thus not able to reconcile the mentioned tension.
In a hierarchical formation scenario one would expect clusters at higher redshift to be more disturbed, and therefore the hydrostatic equilibrium hypothesis to be less valid (Neto et al. 2007; Angelinelli et al. 2020). Thus, this possible redshift evolution has been studied in the literature; for example, Salvati et al. (2019) find a modest hint of redshift dependence for the bias. However, other works based on cluster observations (McDonald et al. 2017) do not find traces of evolution of the morphological state with redshift. To date, the possible bias dependence with redshift has not been confirmed in simulations (see Gianfagna et al. 2021, and references therein).
7.2.2. Hydrostatic-to-lensing mass bias estimates
From the observational point of view, the real HSE bias is unachievable as one cannot determine the true mass of a cluster. However, it can be approximated using mass estimates that do not rely on the HSE hypothesis and trace the total mass of the cluster, for instance the lensing mass. In this work we compute the hydrostatic-to-lensing mass bias using the results obtained in Sects. 5.3 and 6 (see Sereno & Ettori 2015, for an analysis of the CoMaLit samples). For the lensing mass 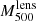 we combine the probability distributions of both lensing models in Fig. 13. On the contrary, we consider the different HSE mass estimates independently. Assuming that HSE and lensing masses are uncorrelated estimates, we combined their probability distributions and computed the ratio
we combine the probability distributions of both lensing models in Fig. 13. On the contrary, we consider the different HSE mass estimates independently. Assuming that HSE and lensing masses are uncorrelated estimates, we combined their probability distributions and computed the ratio 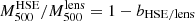 .
.
We present in Fig. 15 the hydrostatic-to-lensing mass ratio at R500. The same colour-coding as in previous figures is used to distinguish the HSE estimates that were obtained with each of the NIKA2 noise and filtering estimators. We draw with solid lines the results obtained modelling the pressure profile with the gNFW model and with dashed lines the results from the NFW fit. All of them are inferred from the NIKA2, R18, and XMM-Newton data. The grey contours show the bias using the X-ray-only HSE mass results. We present in Table 4 the marginalised hydrostatic-to-lensing mass ratio and uncertainties for the different cases considered. The results for the gNFW and NFW cases correspond to a combination of the four NIKA2 analyses. As concluded in Ferragamo et al. (2022), we observe that the value of the bias is sensitive to the considered data sets and modelling choices.
 |
Fig. 15. HSE mass estimates with respect to lensing estimates at R500. Blue and green solid lines correspond to the HSE masses obtained from the gNFW pressure model fit and dashed lines to the NFW method. The grey line corresponds to the HSE mass obtained with XMM-Newton-only data. We present the 1σ and 2σ contours. The lensing mass distribution is the combination of the results for the PIEMD+eNFW and LTM analyses. |
Hydrostatic-to-lensing mass ratio for different HSE mass estimates.
8. Summary and conclusions
The precise estimation of the mass of single clusters appears extremely complicated and affected by multiple systematic effects (Pratt et al. 2019), but it is the key to building accurate scaling relations for cosmology. The NIKA2 SZ Large Program provides an SZ-mass scaling relation from the combination of NIKA2 and XMM-Newton data. Within this programme, we presented a thorough study on the mass of the CL J1226.9+3332 galaxy cluster.
We obtained NIKA2 150 and 260 GHz maps, which allowed us to reconstruct the radially binned pressure profile for the ICM from the tSZ data. To characterise the impact of the data processing, we repeated the whole analysis for two pipeline-filtering transfer functions and noise estimates for the 150 GHz map. We accounted for the presence of point sources that contaminate the negative tSZ signal at 150 GHz. The reconstructed NIKA2 pressure bins are compatible, within the angular scales accessible to NIKA2, with the profiles obtained from three independent instruments in R18. This validates the pressure reconstruction procedure that will be used for the whole sample analysis in the NIKA2 SZ Large Program.
We compared two approaches to estimate the HSE mass from the combination of tSZ-obtained pressure and X-ray electron density profiles. We considered either a gNFW pressure model (traditionally used for this kind of analysis) or an integrated NFW density model. The second seems a promising approach to ensure radially increasing HSE mass estimates. However, other density models should be tested in order to describe more satisfactorily the shape of the pressure profile. Both methods give completely compatible HSE mass profiles and integrated 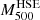 . From the comparison of the different mass estimates, we also conclude that for the moment, when estimating the HSE mass of the CL J1226.9+3332 galaxy cluster in the NIKA2 SZ Large Program, the error budget is dominated by model dependence rather than by the instrumental and data processing systematic effects that we investigated. In addition, these results are in agreement with the X-ray-only HSE mass estimate obtained in this paper from the XMM-Newton electron density and temperature profiles. Nevertheless, the X-ray-only estimate favours lower mass values than the combined tSZ+X-ray results.
. From the comparison of the different mass estimates, we also conclude that for the moment, when estimating the HSE mass of the CL J1226.9+3332 galaxy cluster in the NIKA2 SZ Large Program, the error budget is dominated by model dependence rather than by the instrumental and data processing systematic effects that we investigated. In addition, these results are in agreement with the X-ray-only HSE mass estimate obtained in this paper from the XMM-Newton electron density and temperature profiles. Nevertheless, the X-ray-only estimate favours lower mass values than the combined tSZ+X-ray results.
We also showed that our results are compatible with all the HSE mass estimates found in the literature within uncertainties, which are large. We think that the only way to reduce the current uncertainties is to precisely constrain the slope of the mass profile at ∼R500 (as already done in Ettori et al. 2019) since we have proved that very similar mass profiles overall can result in significant differences at M500.
From two differently modelled CLASH convergence maps, we reconstructed the lensing mass profile of CL J1226.9+3332 and measured the hydrostatic-to-lensing mass bias. We find that for CL J1226.9+3332 the bias is bHSE/lens ∼ 0.1 for tSZ+X-ray combined HSE masses and ∼0.4 for X-ray-only estimates, with ∼0.1 uncertainties depending on the models. Despite the large uncertainties, we have the sensitivity to measure the bias of a single cluster, even for the highest-redshift cluster of the NIKA2 SZ Large Program. This is the second cluster in the NIKA2 SZ Large Program with such a measurement (the first was studied in Ferragamo et al. 2022) and the analysis of the HSE-to-lensing bias for a larger sample will be the topic of a forthcoming work (as done in Bartalucci et al. 2018 with X-ray data). Measuring the hydrostatic-to-lensing mass bias associated with LPSZ clusters will bring a new perspective to the bias from the tSZ side for spatially resolved clusters at intermediate and high redshifts.
Comparing masses in the literature. Cluster lensing mass catalogue available at http://pico.oabo.inaf.it/~sereno/CoMaLit/
The binned profiles in R18 and those in this work are centred on positions at 3 arcsec of distance, which is the typical rms pointing error for NIKA2 (Perotto et al. 2020), so we consider that combining them is a valid approach.
Jörg Dietrich, 2013–2017, https://doi.org/10.5281/zenodo.50664
Acknowledgments
We would like to thank the referee for the careful reading and the constructive comments that helped improve the paper. We would like to thank the IRAM staff for their support during the campaigns. The NIKA2 dilution cryostat has been designed and built at the Institut Néel. In particular, we acknowledge the crucial contribution of the Cryogenics Group, and in particular Gregory Garde, Henri Rodenas, Jean-Paul Leggeri, Philippe Camus. This work has been partially funded by the Foundation Nanoscience Grenoble and the LabEx FOCUS ANR-11-LABX-0013. This work is supported by the French National Research Agency under the contracts “MKIDS”, “NIKA” and ANR-15-CE31-0017 and in the framework of the “Investissements d’avenir” program (ANR-15-IDEX-02). This work has benefited from the support of the European Research Council Advanced Grant ORISTARS under the European Union’s Seventh Framework Programme (Grant Agreement no. 291294). This work is based on observations carried out under project number 199-16 with the IRAM 30m telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain). E. A. acknowledges funding from the French Programme d’investissements d’avenir through the Enigmass Labex. A.R. acknowledges financial support from the Italian Ministry of University and Research – Project Proposal CIR01_00010. M. D. P. acknowledges support from Sapienza Università di Roma thanks to Progetti di Ricerca Medi 2021, RM12117A51D5269B. G.Y. would like to thank the Ministerio de Ciencia e Innovación (Spain) for financial support under research grant PID2021-122603NB-C21. This project was carried out using the Python libraries matplotlib (Hunter 2007), numpy (Harris et al. 2020) and astropy (Astropy Collaboration 2013, 2018).
References
- Adam, R., Comis, B., Macías-Pérez, J.-F., et al. 2015, A&A, 576, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adam, R., Comis, B., Bartalucci, I., et al. 2016, A&A, 586, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adam, R., Adane, A., Ade, P. A. R., et al. 2018a, A&A, 609, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adam, R., Hahn, O., Ruppin, F., et al. 2018b, A&A, 614, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adami, C., Giles, P., Koulouridis, E., et al. 2018, A&A, 620, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aguado-Barahona, A., Rubiño-Martín, J. A., Ferragamo, A., et al. 2022, A&A, 659, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, S. W., Evrard, A. E., & Mantz, A. B. 2011, ARA&A, 49, 409 [Google Scholar]
- Andreon, S., & Hurn, M. A. 2010, MNRAS, 404, 1922 [NASA ADS] [Google Scholar]
- Angelinelli, M., Vazza, F., Giocoli, C., et al. 2020, MNRAS, 495, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Ansarifard, S., Rasia, E., Biffi, V., et al. 2020, A&A, 634, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., Neumann, D. M., Aghanim, N., et al. 2001, A&A, 365, L80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bartalucci, I., Arnaud, M., Pratt, G. W., et al. 2017, A&A, 598, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bartalucci, I., Arnaud, M., Pratt, G. W., & Le Brun, A. M. C. 2018, A&A, 617, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bartelmann, M. 1996, A&A, 313, 697 [NASA ADS] [Google Scholar]
- Bartelmann, M. 2010, CQG, 27, 233001 [NASA ADS] [CrossRef] [Google Scholar]
- Biviano, A., & Girardi, M. 2003, ApJ, 585, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Bleem, L. E., Bocquet, S., Stalder, B., et al. 2020, ApJS, 247, 25 [Google Scholar]
- Bonamente, M., Joy, M. K., LaRoque, S. J., et al. 2006, ApJ, 647, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Bourrion, O., Benoit, A., Bouly, J., et al. 2016, J. Instrum., 11, P11001 [NASA ADS] [CrossRef] [Google Scholar]
- Bulbul, G. E., Hasler, N., Bonamente, M., & Joy, M. 2010, ApJ, 720, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Cagnoni, I., Elvis, M., Kim, D.-W., et al. 2001, ApJ, 560, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Calvo, M., Benoît, A., Catalano, A., et al. 2016, J. Low Temp. Phys., 184, 816 [CrossRef] [Google Scholar]
- Castagna, F., & Andreon, S. 2020, A&A, 639, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cavagnolo, K. W., Donahue, M., Voit, G. M., & Sun, M. 2009, ApJS, 182, 12 [Google Scholar]
- Condon, J. J. 1984, ApJ, 287, 461 [Google Scholar]
- Croston, J. H., Arnaud, M., Pointecouteau, E., & Pratt, G. W. 2006, A&A, 459, 1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Day, P. K., LeDuc, H. G., Mazin, B. A., Vayonakis, A., & Zmuidzinas, J. 2003, Nature, 425, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Démoclès, J., Pratt, G. W., Pierini, D., et al. 2010, A&A, 517, A52 [CrossRef] [EDP Sciences] [Google Scholar]
- Di Gennaro, G., van Weeren, R. J., Brunetti, G., et al. 2020, Nat. Astr., 5, 268 [CrossRef] [Google Scholar]
- Ebeling, H., Jones, L. R., Fairley, B. W., et al. 2001, ApJ, 548, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Eckert, D., Ettori, S., Pointecouteau, E., van der Burg, R. F. J., & Loubser, S. I. 2022, A&A, 662, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ettori, S., Donnarumma, A., Pointecouteau, E., et al. 2013, Space Sci. Rev., 177, 119 [Google Scholar]
- Ettori, S., Ghirardini, V., Eckert, D., et al. 2019, A&A, 621, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferragamo, A., Macías-Pérez, J. F., Pelgrims, V., et al. 2022, A&A, 661, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foreman-Mackey, D., Farr, W., Sinha, M., et al. 2019, J. Open Source Software, 4, 1864 [CrossRef] [Google Scholar]
- Gelman, A., & Rubin, D. B. 1992, Stat. Sci., 7, 457 [Google Scholar]
- Gianfagna, G., De Petris, M., Yepes, G., et al. 2021, MNRAS, 502, 5115 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hasselfield, M., Hilton, M., Marriage, T. A., et al. 2013, JCAP, 2013, 008 [Google Scholar]
- Hilton, M., Hasselfield, M., Sifón, C., et al. 2018, ApJS, 235, 20 [Google Scholar]
- Hilton, M., Sifón, C., Naess, S., et al. 2021, ApJS, 253, 3 [Google Scholar]
- Holden, B. P., Franx, M., Illingworth, G. D., et al. 2009, ApJ, 693, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Huterer, D., Kirkby, D., Bean, R., et al. 2015, Astropart. Phys., 63, 23 [Google Scholar]
- Jee, M. J., & Tyson, J. A. 2009, ApJ, 691, 1337 [NASA ADS] [CrossRef] [Google Scholar]
- Jee, M. J., Dawson, K. S., Hoekstra, H., et al. 2011, ApJ, 737, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Joy, M., LaRoque, S., Gregoet, L., et al. 2001, ApJ, 551, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Kéruzoré, F., Mayet, F., Pratt, G. W., et al. 2020, A&A, 644, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kéruzoré, F., Artis, E., Macías-Pérez, J.-F., et al. 2022, EPJ Web Conf., 257, 00024 [CrossRef] [EDP Sciences] [Google Scholar]
- Korngut, P. M., Dicker, S. R., Reese, E. D., et al. 2011, ApJ, 734, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., & Borgani, S. 2012, ARA&A, 50, 353 [Google Scholar]
- Logan, C. H. A., Maughan, B. J., Diaferio, A., et al. 2022, A&A, 665, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mantz, A., Allen, S. W., Ebeling, H., Rapetti, D., & Drlica-Wagner, A. 2010, MNRAS, 406, 1773 [NASA ADS] [Google Scholar]
- Maughan, B. J., Jones, L. R., Ebeling, H., & Scharf, C. 2004, MNRAS, 351, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Maughan, B. J., Jones, C., Jones, L. R., & Van Speybroeck, L. 2007, ApJ, 659, 1125 [Google Scholar]
- Mayet, F., Adam, R., Ade, P., et al. 2020, EPJ Web Conf., 228, 00017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McDonald, M., Allen, S. W., Bayliss, M., et al. 2017, ApJ, 843, 28 [Google Scholar]
- Merten, J., Meneghetti, M., Postman, M., et al. 2015, ApJ, 806, 4 [Google Scholar]
- Monfardini, A., Benoit, A., Bideaud, A., et al. 2011, ApJS, 194, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Mroczkowski, T. 2011, ApJ, 728, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Mroczkowski, T. 2012, ApJ, 746, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Mroczkowski, T., Bonamente, M., Carlstrom, J. E., et al. 2009, ApJ, 694, 1034 [Google Scholar]
- Muchovej, S., Mroczkowski, T., Carlstrom, J. E., et al. 2007, ApJ, 663, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D., Kravtsov, A. V., & Vikhlinin, A. 2007, ApJ, 668, 1 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [Google Scholar]
- Neto, A. F., Gao, L., Bett, P., et al. 2007, MNRAS, 381, 1450 [NASA ADS] [CrossRef] [Google Scholar]
- Perotto, L., Ponthieu, N., Macías-Pérez, J. F., et al. 2020, A&A, 637, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perotto, L., Adam, R., Ade, P., et al. 2022, EPJ Web Conf., 257, 00038 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pessah, M. E., & Chakraborty, S. 2013, ApJ, 764, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XI. 2011, A&A, 536, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2013, A&A, 571, A20 [Google Scholar]
- Planck Collaboration XXI. 2013, A&A, 571, A21 [Google Scholar]
- Planck Collaboration XVIII. 2015, A&A, 594, A27 [Google Scholar]
- Planck Collaboration XXIV. 2015, A&A, 594, A24 [Google Scholar]
- Pointecouteau, E., Arnaud, M., & Pratt, G. W. 2005, A&A, 435, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Postman, M., Coe, D., Benítez, N., et al. 2012, ApJS, 199, 25 [Google Scholar]
- Pratt, G. W., Croston, J. H., Arnaud, M., & Böhringer, H. 2009, A&A, 498, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Arnaud, M., Piffaretti, R., et al. 2010, A&A, 511, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Arnaud, M., Biviano, A., et al. 2019, Space Sci. Rev., 215, 25 [Google Scholar]
- Rigby, A. J., Peretto, N., Adam, R., et al. 2021, MNRAS, 502, 4576 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, C., McWilliam, M., Macías-Pérez, J.-F., et al. 2018, A&A, 612, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruppin, F., Adam, R., Comis, B., et al. 2017, A&A, 597, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruppin, F., Mayet, F., Pratt, G. W., et al. 2018, A&A, 615, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rykoff, E. S., Rozo, E., Hollowood, D., et al. 2016, ApJS, 224, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Salvati, L., Douspis, M., & Aghanim, N. 2018, A&A, 614, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salvati, L., Douspis, M., Ritz, A., Aghanim, N., & Babul, A. 2019, A&A, 626, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salvati, L., Douspis, Marian, & Aghanim, Nabila 2020, A&A, 643, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saro, A., Bocquet, S., Mohr, J., et al. 2017, MNRAS, 468, 3347 [CrossRef] [Google Scholar]
- Sereno, M. 2015, MNRAS, 450, 3665 [Google Scholar]
- Sereno, M., & Covone, G. 2013, MNRAS, 434, 878 [Google Scholar]
- Sereno, M., & Ettori, S. 2015, MNRAS, 450, 3633 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, S., Calvo, M., Goupy, J., et al. 2018, IEEE Trans. Terahertz Sci. Technol., 8, 605 [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comm. Astro. Space Phys., 4, 173 [Google Scholar]
- Verde, L., Treu, T., & Riess, A. G. 2019, Nat. Astron., 3, 891 [Google Scholar]
- White, R. L., Becker, R. H., Helfand, D. J., & Gregg, M. D. 1997, ApJ, 475, 479 [Google Scholar]
- Zitrin, A., Broadhurst, T., Umetsu, K., et al. 2009, MNRAS, 396, 1985 [NASA ADS] [CrossRef] [Google Scholar]
- Zitrin, A., Menanteau, F., Hughes, J. P., et al. 2013a, ApJ, 770, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Zitrin, A., Meneghetti, M., Umetsu, K., et al. 2013b, ApJ, 762, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Zitrin, A., Fabris, A., Merten, J., et al. 2015, ApJ, 801, 44 [Google Scholar]
Appendix A: Masses from the literature
We present in Table A.1 all the mass estimates found in the literature for CL J1226.9+3332 described in Sect. 2.2. We differentiate the masses reconstructed from ICM observables from the lensing effect on background sources and from the study of the dynamics of member galaxies.
Mass estimates found in the literature for CL J1226.9+3332.
Most of the masses were computed from spherical models, and we give the radius at which each mass is evaluated when available. When the mass has been evaluated at a given R = RΔ we also present the value of the density contrast Δ.
Appendix B: Pressure bins and point source fluxes at 150 GHz from joint fit
We present in Tables B.1 and B.2 the obtained point source fluxes at 150 GHz from the joint fit of the point sources with the pressure profile of the cluster in Sect. 4.1.1. We show the results for the nine sources (PS1 to PS9), and each column corresponds to the value obtained for each of the four analyses. The reconstructed fluxes are consistent within all the considered cases.
Submillimetre point sources fluxes. Fluxes at 150 GHz obtained from the joint point sources and pressure profile fits in Sect. 4.1.1.
Radio point source identified in the centre of the cluster. Fluxes obtained from the joint fits with the pressure profile of the cluster.
The binned pressure reconstructions are also listed in Table B.3 and the bin correlation matrices are shown in Fig. B.1.
 |
Fig. B.1. Correlation matrices of radially binned electron pressure bins. Results obtained with different transfer function and noise estimates (from left to right): AO1D, TO1D, AO2D, and TO2D. |
Radially binned pressure profile fits. Mean values and the 1σ uncertainties. The last bin results are trimmed.
Appendix C: Pressure profile fits
We show in figures C.1 and C.3 the posterior distributions of the parameters obtained from the fit of the pressure bins in Sect. 5.2.1 and 5.2.2. The reduced χ2 distributions corresponding to these fits are shown in Fig. C.2.
 |
Fig. C.1. Posterior distributions of the parameters obtained in the fit of the NIKA2 and R18 pressure bins for the gNFW pressure model. |
 |
Fig. C.2. Reduced χ2 of the gNFW (solid) and NFW (dashed) model fits to the NIKA2 and R18 pressure bins. The different colours show the NIKA2 bins used. |
 |
Fig. C.3. Posterior distributions of the parameters obtained in the fit of the NIKA2 and R18 pressure bins, combined with the XMM-Newton electron density, for the NFW density model fitted to the pressure. |
In Fig. C.4 we present the HSE mass profiles resulting from each of the fits.
 |
Fig. C.4. HSE mass profiles obtained with the gNFW (left) and NFW (right) fit methods. Each colour represents the profile obtained using the corresponding NIKA2 pressure bins. |
All Tables
Submillimetre point source coordinates and fluxes identified within a radius of 2′ around the centre of CL J1226.9+3332.
Submillimetre point sources fluxes and their corresponding names in Herschel SPIRE or PACS catalogue.
Submillimetre point sources fluxes. Fluxes at 150 GHz obtained from the joint point sources and pressure profile fits in Sect. 4.1.1.
Radio point source identified in the centre of the cluster. Fluxes obtained from the joint fits with the pressure profile of the cluster.
Radially binned pressure profile fits. Mean values and the 1σ uncertainties. The last bin results are trimmed.
All Figures
 |
Fig. 1. M500 estimates for CL J1226.9+3332 in the literature. Filled grey diamonds represent HSE masses from the combination of SZ and X-ray data and empty ones correspond to X-ray-only results. Pink squares show the SZ-only mass assuming virial relation, purple circles are dynamical mass estimates, and brown stars correspond to lensing M500. |
| In the text | |
 |
Fig. 2. NIKA2 maps of CL J1226.9+3332 at 150 GHz (left) and 260 GHz (right) in Jy beam−1 units. Contours show S/N levels in multiples of ±3σ. Both maps have been smoothed with a 10′ FWHM Gaussian kernel. The position of the X-ray centre is shown as a magenta cross in the 150 GHz map and the elongation of the tSZ signal towards the south-west is indicated by the white arrow. White and red circles in the 260 GHz map show the submillimetre and radio point sources, respectively. |
| In the text | |
 |
Fig. 3. Power spectra of noise map estimates for NIKA2 150 GHz data. The spectra for the JK maps estimated with angle ordered and time ordered scans are in pink and black, respectively. The power spectra of the different residual maps for the best-fit models shown in Fig. 5 are in blue and green. The grey regions represent the NIKA2 instrumental limits given by the field of view (for small angular frequencies) and the beam FWHM (for large angular frequencies). |
| In the text | |
 |
Fig. 4. Transfer functions, 1D (left) and 2D (right), describing the filtering induced by data processing for the 150 GHz map in Fig. 2. The coloured lines in the left panel represent the values of the 2D transfer function for the directions shown with the same colours in the right panel. Grey-shaded areas correspond to the NIKA2 field of view (for small angular frequencies) and beam FWHM (for large angular frequencies) instrumental limits. |
| In the text | |
 |
Fig. 5. 150 GHz maps of CL J1226.9+3332. Left: NIKA2 150 GHz surface brightness map of CL J1226.9+3332. Top: best-fit models of the tSZ signal and point sources. Bottom: residual maps, difference between the data map and each best-fit model. Results obtained with different transfer function and noise estimates (from left to right): AO1D, AO2D, TO1D, and TO2D. All maps have been smoothed with a 10′ Gaussian kernel for display purposes and are shown in units of Jy beam−1. |
| In the text | |
 |
Fig. 6. Pressure profile of the ICM of CL J1226.9+3332. Blue and green symbols correspond to the results obtained in this work from the NIKA2 150 GHz map. The error bar edges represent the 1σ uncertainties. Pink, yellow, and black stars show the reconstructed profiles in R18 for NIKA, MUSTANG, and Bolocam data, respectively. Empty symbols correspond to the pressure profile obtained from the combination of XMM-Newton electron density and temperature profiles. Vertical dashed lines indicate the instrumental limits of NIKA2 as radius of the beam and FoV. |
| In the text | |
 |
Fig. 7. Electron density (left) and temperature (right) profiles reconstructed from XMM-Newton observations, with 1σ error bars. The profiles are centred at the X-ray peak (RA, Dec.)J2000 = (12h26m58.08s, +33d32m46.6s). |
| In the text | |
 |
Fig. 8. Pressure profile and best fit for the gNFW (left) and NFW (right) models. The data points correspond to the NIKA2 radially binned results for the four data sets discussed above, and to the NIKA, MUSTANG, and Bolocam bins from R18. Blue and green solid lines represent the best-fit values for the four NIKA2 pressure estimates considered. The shaded regions show the 2.5th, 16th, 84th, and 97.5th percentiles. |
| In the text | |
 |
Fig. 9. Distribution of Y5R500 with respect to Θs for the gNFW pressure model fits to Planck data (grey) in Planck Collaboration XVIII (2015) and to the NIKA2 + R18 + XMM-Newton data (blue) in this work. Different contours show the 68%, 95%, and 99% confidence intervals. The black star corresponds to the intersection between the Planck Collaboration XVIII (2015) distribution and the X-ray scaling law shown in Fig. 16 in Planck Collaboration XVIII (2015). |
| In the text | |
 |
Fig. 10. HSE mass profile estimates for CL J1226.9+3332 obtained with NIKA2 (angle order 1D) and R18 tSZ data combined with the XMM-Newton electron density profile. The solid magenta and dashed blue lines correspond to the gNFW and NFW methods, respectively. The shaded areas show the 2.5th, 16th, 84th, and 97.5th percentiles. Empty dots correspond to the HSE mass profile obtained from XMM-Newton-only data. Vertical dashed lines show the |
| In the text | |
 |
Fig. 11. Probability distributions (1D and 2D) for |
| In the text | |
 |
Fig. 12. Projected mass density profiles obtained from CLASH convergence maps for the LTM (left) and PIEMD+eNFW (right) models. We also show the best-fit NFW model (orange and red lines) and the 2.5th, 16th, 84th and 97.5th percentiles (shaded area). |
| In the text | |
 |
Fig. 13. Probabiliy distribution for |
| In the text | |
 |
Fig. 14. R − M(< R) plane summarising the R500 − M500 results for CL J1226.9+3332. In the case of the HSE mass estimates the blue and green 1σ contours show the results obtained in this work combining tSZ and X-ray data for the four NIKA2 analyses. The solid and dashed lines are for the gNFW pressure and the NFW density models, respectively. The grey contour corresponds to the HSE mass estimate for the XMM-Newton-only data. In the case of literature data the filled (empty) grey diamonds represent HSE masses from the combination of tSZ and X-ray data (X-ray-only results). The red and orange contours correspond to the lensing mass estimates obtained from the CLASH LTM and PIEMD+eNFW convergence maps in this work, respectively. Pink squares show the tSZ-only mass assuming virial relation, purple circles are dynamical mass estimates, and brown stars the lensing estimates. Grey and brown crosses show HSE and lensing masses from the literature close to M500. The diagonal bright grey line defines the R500 − M500 relation. Slight deviations from this line are due to differences in the cosmological model used in each work. |
| In the text | |
 |
Fig. 15. HSE mass estimates with respect to lensing estimates at R500. Blue and green solid lines correspond to the HSE masses obtained from the gNFW pressure model fit and dashed lines to the NFW method. The grey line corresponds to the HSE mass obtained with XMM-Newton-only data. We present the 1σ and 2σ contours. The lensing mass distribution is the combination of the results for the PIEMD+eNFW and LTM analyses. |
| In the text | |
 |
Fig. B.1. Correlation matrices of radially binned electron pressure bins. Results obtained with different transfer function and noise estimates (from left to right): AO1D, TO1D, AO2D, and TO2D. |
| In the text | |
 |
Fig. C.1. Posterior distributions of the parameters obtained in the fit of the NIKA2 and R18 pressure bins for the gNFW pressure model. |
| In the text | |
 |
Fig. C.2. Reduced χ2 of the gNFW (solid) and NFW (dashed) model fits to the NIKA2 and R18 pressure bins. The different colours show the NIKA2 bins used. |
| In the text | |
 |
Fig. C.3. Posterior distributions of the parameters obtained in the fit of the NIKA2 and R18 pressure bins, combined with the XMM-Newton electron density, for the NFW density model fitted to the pressure. |
| In the text | |
 |
Fig. C.4. HSE mass profiles obtained with the gNFW (left) and NFW (right) fit methods. Each colour represents the profile obtained using the corresponding NIKA2 pressure bins. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



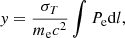
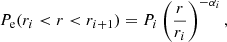
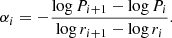
![$$ \begin{aligned}&\mathrm{log } \,\mathcal{L} (\vartheta ) = - \frac{1}{2} \sum _{i=1}^{n_{\mathrm{pixels} }} \left[ \left( \mathcal{M} (\vartheta ) - \mathcal{D} \right)^{T} C_{\mathrm{pix-pix} }^{-1} \left( \mathcal{M} (\vartheta ) - \mathcal{D} \right) \right] _{i}\nonumber \\&\qquad \qquad \,\,\, - \frac{1}{2}\left(\frac{ Y_{500}(\vartheta )-Y_{500}^{Planck}}{\Delta Y_{500}^{Planck}}\right)^{2}. \end{aligned} $$](/articles/aa/full_html/2023/03/aa44981-22/aa44981-22-eq26.gif)
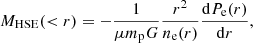
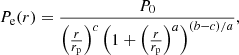
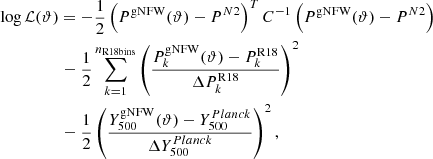
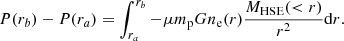
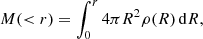
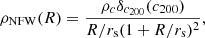
![$$ \begin{aligned}&P_{\rm zero} - P(r_{a}) = -\mu m_{\rm p}G 4 \pi \rho _{c} \delta _{c_{200}}(c_{200}) r_{\rm s}^3 \nonumber \\&\qquad \qquad \qquad \int _{r_a}^{r_{\rm zero}} \frac{ n_{\rm e}(r)}{r^2} \left[ \frac{1}{1+r/r_{\rm s}} + \ln (1+r/r_{\rm s}) -1 \right] \mathrm{d} r , \end{aligned} $$](/articles/aa/full_html/2023/03/aa44981-22/aa44981-22-eq41.gif)