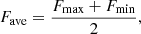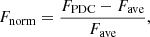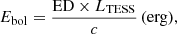| Issue |
A&A
Volume 686, June 2024
|
|
|---|---|---|
| Article Number | A164 | |
| Number of page(s) | 20 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202348342 | |
| Published online | 07 June 2024 | |
Magnetic activity of radio stars based on TESS and LAMOST surveys⋆
1
College of Physics, Guizhou University, 550025 Guiyang, PR China
e-mail: liy_zhang@hotmail.com
2
Dept. of Physics and Astronomy and SARA, Butler University, Indianapolis, IN 46208, USA
3
Department of Physics & Astronomy Howard University, Washington, DC 20059, USA
Received:
21
October
2023
Accepted:
4
March
2024
Aims. Stellar flares serve as crucial indicators stellar magnetic activity. Radio emissions were detectable across all stages of stellar evolution. We define radio stars in our paper as stars with radio continuum emission in the frequency region of about 1.4–375 GHz from the catalog published by Wendker (1995, A&AS, 109, 177; 2015, VizieR Online Data Catalog, VIII/99). We also include detected radio stars from the LOFAR Two-metre Sky Survey (LoTSS) and the Australian Square Kilometre Array Pathfinder (ASKAP), and VLA Sky Survey (VLASS) surveys, and present comparative discussions. We used the light curves from the Transiting Exoplanet Survey Satellite (TESS) survey coupled with low- and medium-resolution spectra from the Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST) survey to investigate the magnetic activity and statistical properties of radio stars.
Methods. We cross-matched the radio stars from the radio star catalog and the LoTSS, ASKAP, and VLASS surveys with the TESS survey. For the stars from the radio star catalog, we obtained a matched sample of 1537 stars (hereafter Sample 1) and downloaded their TESS light curves, which include 4001 light curves at a 120s cadence. For the stars from the LoTSS, ASKAP, and VLASS surveys, we obtain a matched sample of 98 stars (hereafter Sample 2) and downloaded their 120s TESS light curves, totaling 260. Subsequently, we employed repeated fitting techniques to distinguish stellar background light curves from flare events. For Sample 1, we successfully identify 12 155 flare events occurring on 856 stars. For Sample 2, we identify a total of 3992 flare events on 86 stars. Furthermore, by cross-referencing our samples with the Gaia survey, the TESS Input Catalog, and the LAMOST survey, we obtain additional stellar parameters, facilitating the determination of relationships between stellar and flare parameters.
Results. For stars in Sample 1, within the 12 155 flare events observed on the 856 flare-active radio stars, a majority of more than 97% have durations of less than 2 h, while for stars in Sample 2, all 3992 flare events have a duration of less than 2 hours. We calculated the flare occurrence percentage for each flare-active radio star, observing a decrease as effective temperature increased for both Sample 1 and Sample 2. We derived values of the power-law index (for Sample 1, the α value is approximately 1.50 ± 0.11 for single stars and 1.38 ± 0.09 for binary stars, for Sample 2, the α value is about 1.47 ± 0.11 for single stars and 1.42 ± 0.09 for binary stars) for the cumulative flare frequency distribution. In both Sample 1 and Sample 2, stars with lower effective temperatures tend to exhibit increased activity. Using LAMOST spectra and the Gaia DR3 chromospheric activity index, we note that the Hα equivalent width and Gaia Ca II IRT activity index of flare-active radio stars is significantly larger than that of nonflaring stars. An intriguing finding is our potential identification of a coronal rain candidate through asymmetry observed in the Hα line.
Key words: stars: activity / stars: flare / stars: statistics
Full Tables 1 and 2 are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/686/A164
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Flares, which are sudden and intense bursts of energy, are common phenomena observed on the Sun and other stars (Schaefer et al. 2000). Coronal mass ejections (CMEs) are also one of the spectacular eruptive phenomena occurring on stellar surfaces and usually result in material being unbound from the star (Forbes 2000). Superflares are often accompanied by CMEs, but the two events can also appear independently (Günther et al. 2020). The occurrence of flares and CMEs on stars hosting exoplanets can significantly impact planetary evolution and habitability, potentially leading to the destruction of planetary surface atmospheres or triggering the production of surface biosignatures (e.g., Lingam & Loeb 2017; Tu et al. 2020; Su et al. 2022). Flares have been observed on the Sun and other stars in a wide range of wavelengths from radio to gamma-rays (Haisch et al. 1991; Yang et al. 2017; Walkowicz et al. 2011; Lawson et al. 2019). With the increase in photometric surveys conducted by space telescopes, astronomers are detecting an increasing number of flare events and are determining their parameters.
Notably, the Sun and planets within our Solar System emit radio radiation (Pawsey et al. 1946; Kaiser & Desch 1984), further emphasizing the prevalence of stellar radio emissions. Stellar radio radiation has been observed across the entire Hertzsprung-Russell diagram (Gibson 1985; Güdel 2002). Furthermore, simultaneous optical, X-ray, or radio flares have been observed in stars such as EV Lac, YZ CMI, AD Leo, Proxima Centauri, and Wolf 424 AB (Webber et al. 1973; Spangler & Moffett 1976; Haisch et al. 1981; Doyle et al. 1988; Zic et al. 2020), revealing correlations between radio, X-ray, and optical emissions from flaring stars (Bastian 1990). Wendker (1995) published a catalog of radio stars or systems with information including names, positions, magnitudes, and spectroscopic types containing 3699 radio stars (Wendker 2015). Radio emission can be either thermal or nonthermal, and can be the result of various mechanisms, such as bremsstrahlung, gyromagnetic radiation, and the electron cyclotron maser mechanism (Güdel 2002; Matthews 2019). Recently, Matthews (2019) provided a review of radio emissions detected from a wide range of celestial objects, including hot and cool stars, ultracool dwarfs, stars exhibiting stellar activity, winds, and mass loss, and cataclysmic variables. Pope et al. (2021) used TESS data to study GJ 1151 and 14 M dwarfs detected by LOFAR, revealing the flare frequency of 12 M dwarfs. With advancements in multiwavelength astronomy, radio stars have become the subject of intense research.
Understanding the chromospheric activity behavior of radio stars in optical wavelengths is a fundamental aspect of stellar research. Chromospheric activity can be observed through emissions such as Hα and He D3, as well as core emissions in the Ca II H & K and IRT lines, as demonstrated in stars like AD Leo (Pettersen & Coleman 1981). Notably, evident Hα emissions and variations were observed in the M-type eclipsing binary YY Gem, particularly in conjunction with flare events and radio radiation (Butler et al. 2015).
The LAMOST survey has significantly contributed to our understanding of the spectroscopic properties of radio stars. Zhang et al. (2017) analyzed 783 high-signal-to-noise-ratio(S/N) stellar spectra of 659 radio stars obtained by cross-matching LAMOST DR2 with the radio star catalog provided by Wendker (1995) and The Faint Images of the Radio Sky at Twenty centimeters (FIRST) survey (Helfand et al. 1999), calculating their chromospheric activity indicator intensities. Further research by Zhang et al. (2022) used the LAMOST DR7 low-resolution spectral survey to obtain 449 stellar spectra of 258 radio stars (from the radio catalog provided by Wendker 1995). The authors noted that 63 radio stars exhibited Hα variations over an extended timescale of several months. However, there has been no comprehensive analysis combining flare events and chromospheric activity for hundreds of radio stars by integrating large datasets from both photometric and spectroscopic surveys.
In the present work, we used the TESS light curves and both low- and medium-resolution DR10 spectra of radio stars, as updated by Wendker (1995), to comprehensively study their magnetic activity. We introduce the photometric and spectroscopic data in Sect. 2. In Sect. 3, we present the methods used to identify flare events. In Sect. 4, we discuss the statistical analysis of flare parameters and explore the relationship between flares and stellar parameters. Additionally, we examine the relationships between magnetic activity intensity and stellar parameters. We also discuss the properties of magnetic activity indicators derived from the LAMOST Hα line. In Sect. 5, we provide a comprehensive summary of our findings.
2. Data
Wendker assembled a catalog of radio stars, consolidating information such as name, coordinates, and flux at radio frequencies provided by previous studies. The latest version of this catalog, comprising 3699 radio stars, was published in 1995, while two prior versions were published in 1978 and 1987 (Wendker 1995). Together with the radio stars catalog, there is also a radio data catalog (including observation frequency and radio intensity), with the latest update being in 2015 (Wendker 2015). For the present study, we used the most recent version of this latter catalog, which includes the aforementioned 3699 radio stars and the latest radio data. Previously, observations of radio stars largely focused on targeted studies of anomalously active stars (Callingham et al. 2021). Therefore, we supplemented our sample with 146 nontargeted radio stars obtained from the LoTSS, ASKAP, and VLASS surveys provided by the works of Callingham et al. (2023), Yiu et al. (2024), and Pritchard et al. (2024).
2.1. TESS data
The Transiting Exoplanet Survey Satellite (TESS), a NASA space telescope launched in April 2018, is primarily dedicated to the search for exoplanets orbiting bright and nearby stars (Ricker et al. 2015). TESS operates in the frequency range of 600–1000 nm, spanning from blue to near-infrared wavelengths. Its main targets for planet searches encompass approximately 200 000 stars across the entire sky. To facilitate our study, we cross-matched the TESS 120s cadence data, ensuring a matching tolerance of less than 2 arcsec. We acquired 1537 TESS stars (distributed across 1–59 sectors) after matching with 3699 stars in the radio stars catalog. In this paper, we refer to the sample consisting of 1537 TESS stars as Sample 1. After matching with the 146 nontargeted radio stars mentioned above, we acquired 98 TESS stars. In this paper, we refer to the sample consisting of 98 TESS stars as Sample 2. Leveraging the Python package lightkurve1, we efficiently downloaded the light curves for these stars. Ultimately, for Sample 1, we obtained 4001 light curves with 120s cadence data spanning the years 2018–2022. For Sample 2, we downloaded the 120s cadence data for a total of 260 light curves.
Because stellar radio emissions originating from different radiation mechanisms are detectable at almost every stage of stellar evolution, we divided the TESS sample into two categories, namely single stars and binary stars. We identified (1) binary stars that have already been identified in the radio stars catalog; (2) binary systems listed in the SIMBAD database; (3) binaries from the updated TESS eclipsing binary (EB) catalog from the Villanova EB Web site2 (Prša et al. 2022); (4) binaries with Gaia binarity indicators – classprobdsc_combmod_binarystar and classprob_dsc_specmod_binarystar – both larger than 0.8; and (5) binary systems as defined by the spectral types in the International Variable Star Index, which is provided by the American Association of Variable Star Observers (AAVSO;3Watson et al. 2006). If a star was not included in any of the above-mentioned binary datasets, we considered it as a single star. Finally, we identified 852 binary systems and 685 single stars in Sample 1 and 62 binary systems and 36 single stars in Sample 2. Referring to the 177 911 stars from the Kepler field provided by Berger et al. (2018) and supergiants from works of Bowman et al. (2019) and Spetsieri et al. (2019), we determined the evolutionary stages of the stars in our sample according to their effective temperature and log g. In Fig. 1, we plot the Gaia bp_rp versus absolute magnitude using data from Gaia DR3 (Gaia Collaboration 2023). In the upper right legends of all four panels, we show the colour coding of the reference background stars corresponding to main sequence stars, subgiants, red giants, and supergiants from the works of Berger et al. (2018), Bowman et al. (2019), and Spetsieri et al. (2019), respectively. From the left two panels, it can be seen that single stars and binary stars in Sample 1 are widely distributed across various evolutionary stages. In Sample 1, above and parallel to the main sequence, there exists a single star sequence predominantly composed of BY Draconis types and young stars (TTau* and YSO type in SIMBAD). Comparing the two panels on the right, although the distribution of supergiants is not observed, which may be due to the smaller sample size of Sample 2, stars are distributed across the main sequence, subgiant, and red giant stages, with single stars mainly distributed in the low-temperature main sequence stage.
 |
Fig. 1. Distribution of our radio star samples with the reference background. In the upper right legends of all four panels, we show the reference background of main sequence stars, subgiants, red giants, and supergiants from the works of Berger et al. (2018), Bowman et al. (2019), and Spetsieri et al. (2019), respectively. In the bottom-left corner, we provide the corresponding subclassification legend for this study (i.e., single stars, binary stars, and different evolutionary stages in both samples). The stars in both samples are distributed across various evolutionary stages, and for Sample 2, the radio-bright stars are predominantly located in the low-temperature main sequence. |
2.2. LAMOST data
The Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST), also known as the Guoshoujing Telescope, is an advanced four-meter reflective Schmidt telescope equipped with 4000 optical fibers (Cui et al. 2012; Luo et al. 2015). LAMOST operates in two primary observational modes. The first is the low-resolution mode, covering a wavelength range of 3000–9000 Å with a resolution of about 1800. The second is the medium-resolution mode, which comprises blue and red arms with a resolution of about 7500. These arms cover the wavelength ranges of 4900–5400 Å and 6300–6800 Å, respectively (Wang et al. 2020; Liu et al. 2020). Notably, the LAMOST medium-resolution spectroscopic survey incorporates a time-domain survey model, involving multiple (3–8) observations of the same target, each exposure lasting 1200 s (Lu et al. 2022). The capability to study chromospheric variations using LAMOST spectra at different times was demonstrated by Zhang et al. (2020).
In the present study, we conducted cross-matching between radio stars (both flaring and nonflaring) identified in the TESS survey and LAMOST DR10 data, employing a matching criterion of 2 arcseconds. Through this process, we successfully acquired 938 low-resolution spectra and 1145 medium-resolution spectra of Sample 1 for further analysis. For Sample 2, there are only 28 low-resolution and 8 medium-resolution spectra acquired.
3. Methods and results
3.1. Flare detection method
A flare is a sudden and intense burst of energy with a rapid rise and a slower decay. Various methods have been employed to detect flare events (Walkowicz et al. 2011; Wu et al. 2015; Feinstein et al. 2020b; Yang et al. 2023; Meng et al. 2023). One common approach involves initially subtracting the background light curve from the original stellar light curve. Another method employs convolutional neural networks (CNNs) or other machine learning algorithms for detection.
In the present study, we employed a method similar to that described in Yang et al. (2023) and Meng et al. (2023) for identifying flare events. We used the following formula to obtain a normalized flux from the Pre-search Data Conditioning Simple Aperture Photometry (PDCSAP) fluxes:
where Fmax is the maximum value, Fmin is the minimum value, Fave is the average PDCSAP flux value of each data set, FPDC is the PDCSAP flux, and Fnorm is the normalized PDCSAP flux.
After obtaining the normalized result, we removed the background light curve, detrended it, and employed polynomial functions to fit the background light curve. Next, we identified flare event candidates using points beyond three times the standard deviation 3σ. Finally, we manually verified these candidates. This approach aligns with methodologies used in previous works, with additional details provided in prior papers (Su et al. 2022; Meng et al. 2023; Yang et al. 2023).
3.2. Results
Through our automated program, we were able to successfully identify flare events by their typical profiles. However, it is important to note that the program occasionally flagged nonflare events as potential flares. To ensure precision, we conducted a manual review of each flagged candidate to accurately differentiate between flare and nonflare events.
During the program’s execution, we generated plots of all detected flare events alongside the stellar background for each light curve, enabling a visual inspection to validate the accuracy of our results. In this paper, we present three illustrative examples in Fig. 2. Additionally, Fig. 3 displays examples that were deemed nonflare events following manual review.
 |
Fig. 2. Three example light curves with flare events. Black dots represent stellar background light curves and red dots are the flare events. At the top of the panels, we list the corresponding TESS source id and sector number. The horizontal axis represents BJD time in days, and the vertical axis represents normalized flux. |
 |
Fig. 3. Three examples of flare candidates identified by the program and removed during the manual inspection process. If there were fewer than three points above the background light curve (left panel), or variations in the stellar background light curve were mistakenly identified as flare events (middle panel), or the profile of the candidate did not match the normal shape of flares (right panel), we removed these flare candidates to make our results more accurate. |
Ultimately, our manual assessment led to the precise identification of 12 155 flare events on 856 stars of Sample 1 and 3992 flare events on 86 stars of Sample 2 from the TESS light curves derived from 120s cadence data.
4. Discussion
To augment our understanding for the magnetic activity of radio stars, we cross-matched our TESS sample of radio stars with essential databases; namely the Gaia Data Release 2 (Gaia-DR2) (Gaia Collaboration 2018), the TESS Input Catalog (Stassun et al. 2019), and the LAMOST survey. This cross-matching enabled us to obtain additional stellar parameters, including effective temperature, mass, and radius. We employed TOPCAT, a desktop application known for interactive analysis of tabular data, especially catalogs (Taylor 2020), to facilitate this integration of information. In Table 1, we present the stellar parameters of radio stars in Sample 1 and Sample 2, encompassing crucial details such as stellar temperature, radius, and mass. Additionally, we compiled the specific flare parameters of the flaring radio stars in Table 2 (including flare events in both Sample 1 and Sample 2). These parameters encompass vital information such as the time of occurrence, duration, amplitude, and energy associated with each flare event.
Radio star parameters of TESS objects in Samples 1 and 2.
Parameters of flare events from radio stars (both Sample 1 and Sample 2 data).
4.1. Statistical properties of flare parameters
4.1.1. Duration and amplitude
Flare duration and amplitude are critical parameters characterizing a flare event. We calculated the flare percentage by dividing the number of flares in each subcategory by the total number of flares in the corresponding sample. In Fig. 4, we depict the distribution of flare duration in the top panels and amplitude in the bottom panels. For the three upper panels, the left panel shows the distribution of flare durations for all flaring stars in Sample 1 and Sample 2, as well as under the classifications of single and binary stars. For all stars in Sample 1, over 97% of the flares exhibit a duration of less than 2 h, with approximately 86% occurring within 1 h. For the stars of Sample 2, all flares have durations of less than 2 h. Comparing the distribution of flare durations between single and binary stars in the two samples, it can be observed that in Sample 2, the proportion of binary stars with flare durations of less than 0.4 h is significantly higher than that in Sample 1. This suggests that flares in Sample 2 are generally of a shorter durations. This difference could be attributed to Sample 1 being a curated set of known magnetically active stars, indicating stronger flare activity. In the middle and right panels, we plot the different evolutionary stages (i.e., main sequence, subgiant, red giant, and supergiant) for both Sample 1 and Sample 2. It can be observed that the duration of the majority of flares for different classifications is still within 1 h and flares are primarily contributed by stars in the main sequence stage. Yang et al. (2023) conducted a statistical analysis of TESS survey data from July 2018 to October 2020, revealing that more than 90% of the flares have a duration of less than 2 h. This aligns with our findings regarding radio stars, which shows a concentration of flares within the 2 h duration, with most having a duration of within 1 h.
 |
Fig. 4. Distribution of the percentage of flares in different intervals of the duration and amplitude, respectively. For each panel, we use different colors coupled with different markers to represent different classifications and provide explanations in the legend. The durations of most flares is less than 1 h in Sample 1, while for Sample 2, the duration of most flares is less than 0.5 hour. The amplitude of most flares is less than 0.05 for both samples. For Samples 1 and 2, the distribution of flares in different duration or amplitude ranges is dominated by main sequence stars. |
Amplitude, another crucial parameter, was determined by measuring the deviation of the flare peak from the corresponding points of the fitted background function. In the bottom three panels of Fig. 4, for all flare amplitudes in Sample 1 (all stars in left panel), over 88% of the amplitudes are less than 0.2, with a significant concentration (67.4%) falling below 0.05. Notably, amplitudes exceeding 0.5 constitute only about 3.4% of the distribution. For Sample 2, more than 96.5% of all flare amplitudes are less than 0.2. The proportion of flares with amplitudes less than 0.1 in Sample 2 of binary star flares is significantly higher than that in Sample 1, which is consistent with the above-mentioned finding of a higher proportion of short-duration flares in Sample 2. These statistical values corroborate the common occurrence of small flare amplitudes, typically falling within the range of 0.001–0.1, as reported in earlier studies (Walkowicz et al. 2011; Balona 2015; Tu et al. 2021; Yang et al. 2023). For both Sample 1 and Sample 2, by comparing the flare numbers for single and binary stars, or for different evolutionary stages across the different amplitude ranges, the majority of flares have amplitudes within the range of less than 0.05 and the flares in Sample 2 are more concentrated towards small amplitudes compared to those in Sample 1. The trend of the distribution changes of flares in different amplitude ranges under different subclassification types is basically consistent, namely, flares are more concentrated in the small amplitude range. The durations and amplitudes of flares are inherently tied to the exposure time and photometric precision of the space telescope (Howard & MacGregor 2022).
4.1.2. Trise and Tdecay
Flare events are characterized by their rapid rise (Trise) and subsequent exponential decay (Tdecay). Calculating Trise and Tdecay within the flare duration provides a deeper understanding of flare dynamics. In this work, we computed Trise and Tdecay for the flare events and present their distributions in Fig. 5.
 |
Fig. 5. Distribution of the flare percentage in different intervals of the flare rise and decay times, respectively. For each panel, we used different colors coupled with different markers to represent different classifications and provide explanations in the legend. The left panel is the distribution of the flare percentage versus the different rise and decay time ranges for all flares, single stars, and binary stars. The middle and right panels show the distribution of the different evolutionary stages for Samples 1 and 2. The rise time of flares in Sample 1 is mostly less than 20 min, while in Sample 2, the majority of flares have rise times of less than 10 min. The flare decay times in Sample 1 are mostly less than 40 min, while in Sample 2, they are mostly less than 20 min. |
The top three panels of Fig. 5 show the distribution of Trise for flares in both samples across various time intervals. From the left panel it can be observed that for Sample 1, the majority of flares have Trise of less than 20 min, while for Sample 2, most flares have a Trise of less than 10 min; indeed in Sample 2, the proportion of flares with relatively small Trise is higher than in Sample 1. In the middle and right panels, it can be seen that flares in different evolutionary stages in both Sample 1 and Sample 2 are predominantly characterized by short durations. Particularly for Sample 2, flares are mainly associated with main sequence stars, and flares with Trise of less than 5 min constitute the majority. In the bottom three panels of Fig. 5, for both samples, the decay times are concentrated between 5 and 25 min. However, the distribution of Tdecay in Sample 2 is more concentrated around values of less than 20 min. This is because the Tdecay of both single and binary star flares in Sample 2 is more concentrated within 20 min compared to flares in Sample 1. The middle and right panels display the distribution of Tdecay for flares from stars in different evolutionary stages. The distribution of Tdecay is mainly dominated by flares from the main sequence stage (i.e., Tdecay within 25 min in Sample 1 and within 20 min in Sample 2). For Sample 1, the median times for Trise and Tdecay are 8 and 16 min, respectively, while the mean times are 12.42 and 23.87 min, respectively. For Sample 2, the median times for Trise and Tdecay are 4 and 10 min, respectively, while the mean times are 3.6 and 10.9 min, respectively. This is consistent with the information conveyed by the flare duration in Fig. 4, indicating that flares in Sample 2 are more often of a shorter duration compared to those in Sample 1.
In comparison, for solar-like stars (Yan et al. 2021), the median times of Trise and Tdecay are 5.9 and 22.6 min, respectively, and the mean times are 8.8 and 33.7 min, respectively. Likewise, considering all stars in TESS sectors 1–30, the median times for Trise and Tdecay are 5 and 22 min, respectively, with mean times of 14.17 and 35.62 min, respectively (Yang et al. 2023). Notably, the mean Tdecay of radio stars in both samples is less than those reported in both solar-like stars (Yan et al. 2021) and the broader TESS dataset (Yang et al. 2023). This discrepancy may be attributed to the smaller sizes of flares observed in radio stars. In Sample 1, approximately 86% of flare events have a duration of no more than 1 h and for Sample 2, this proportion exceeds 99%. In contrast, a similar sample in the study by Yang et al. (2023) showed that only 71% of flares had a duration less than or equal to 1 h.
4.2. Flare occurrence percentage
To elucidate the flare activity within our sample, we conducted a cross-match between the radio star sample and both the TESS and Gaia surveys (Gaia Collaboration 2018; Stassun et al. 2019), allowing us to derive crucial stellar parameters such as effective temperature (Teff), mass, and rotation and/or orbital period. The dominant period could from various factors such as the rotational period of single stars, the orbital period for binaries induced by orbital modulation, or an asteroseismic period for a red giant.
The relationship between rotation or orbital period and flares has been studied extensively. Numerous previous works indicate that flare frequency decreases with an increase in rotation period for single stars. Many active binaries follow the activity–rotation relation established for single stars (Schrijver & Zwaan 2000). We used two methods to determine the rotation periods of the radio stars in our samples. The first method involves cross-matching radio stars with the International Variable Star Index (Watson et al. 2006) provided by AAVSO4. The second method uses the measuring rotation periods technique provided by stella5 (Feinstein et al. 2020a).
We computed the flare occurrence percentage for each radio star, representing the fraction of time spent in the flaring state (flare duty cycle) (Lin et al. 2019). The flare occurrence percentage can be calculated using the following equation (Walkowicz et al. 2011):
where ∑tflare is the summation of the flare duration for each star, and ∑tstar is the total observation time for each star. Figure 6 illustrates the distribution of flare occurrence percentage with respect to effective temperature for both samples. Here, we plot effective temperature versus flare occurrence percentage and overlay box-and-whisker plots to show relative trends. Due to limitations in the subdivided sample sizes, we only plot graphs for all stars, single stars, binary stars, and main sequence stars in the two samples. For Sample 1, as seen in the left four panels, overall the flare occurrence percentage decreases with increasing effective temperature. In the panels on the right regarding Sample 2 –except for single stars, where this trend was not observed due to sample size limitations–, Sample 2 overall, and in particular its binary stars and main sequence stars, exhibit the same trend as Sample 1, that is, flare occurrence percentage decreases with increasing effective temperature. Stars with relatively slow rotation rates exhibit a lower flare frequency (Notsu et al. 2013; Candelaresi et al. 2014; Feinstein et al. 2020b; Yang et al. 2023). For the relationship between rotation and/or orbital period and flare occurrence percentage of our radio star samples, we also overlaid violin plots with box-whisker plots to observe the changing trends in Fig. 7. In the left four panels of Sample 1, we do not observe a correlation between flare occurrence percentage and rotation or orbital periods. However, in the right panels of Sample 2, both all stars and binary stars show a trend where the flare occurrence percentage decreases with increasing rotation or orbital period. As Sample 2 is dominated by binary stars, the trend in the “all stars” panel is driven by the trend in binary stars. For single stars and main sequence stars in Sample 2, although they exhibit a similar trend to binary stars when the rotation or orbital period is less than 1.6 days, further verification is required because of the small sample size. In Fig. 8, we plot the distribution of flaring stars in the two dimensions of effective temperature and rotation or orbital period. The size of the red points reflects the value of flare occurrence percentage of the flaring stars. For both samples, we also confirm that the majority of flaring stars are concentrated in the lower effective temperature range. Additionally, the flare occurrence percentage is correspondingly higher in these regions, which indicates that a lower effective temperature might be an important factor.
 |
Fig. 6. Distribution of flare occurrence percentages with effective temperature in Sample 1 and Sample 2. In each panel, blue dots represent the effective temperature and flare occurrence percentage for each star. We overlaid box-and-whiskers plots on each scatter plot to reflect the trend of the scatter plot. In the left four panels corresponding to Sample 1 classifications, the flare occurrence percentage decreases with increasing effective temperature. Similarly, in the right four panels corresponding to Sample 2, except for the single star classification, where the trend observed in Sample 1 is not evident due to a smaller sample size, the other classifications exhibit the same pattern: the flare occurrence percentage decreases with increasing effective temperature. |
 |
Fig. 7. Distribution of flare occurrence percentages with rotation or orbital period in Samples 1 and 2. In each panel, blue dots represent the rotation or orbital periods and flare occurrence percentage for each star. We overlaid violin plots with box-and-whiskers plots on each scatter plot to reflect the trend of the scatter plot. For Sample 1, there no obvious correlation observed while for Sample 2 both all stars and binary stars show a trend where the flare occurrence percentage decreases with increasing rotation or orbital period. |
 |
Fig. 8. Flare occurrence percentages of all radio stars (left), single stars (middle), and binary stars (right) in the two dimensions of effective temperature and period (rotation or orbital) for both samples, where the size of the red circles represents the value of the flare occurrence percentage. The majority of flaring stars with higher flare occurrence percentage are distributed within smaller ranges of effective temperature. |
4.3. Relationships between flare energies and other parameters
Flare energy is a crucial metric for measuring the magnetic activity of stars. In this study, we calculated the bolometric energy of flare events using the following equation (more details can be seen in previous works of Petrucci et al. (2024) for stars in the TESS field and Hawley et al. (2014) for stars in the Kepler field):
where Ebol is the bolometric energy of flares, ED is the equivalent duration, which is the area under the flare light curve, and LTESS is the quiescent luminosity considering the TESS CCD response. The constant “c” with a value of 0.19 is the correction factor for the TESS CCD response representing the energy fraction released in the TESS band (Petrucci et al. 2024; Howard & MacGregor 2022). In this work, we calculated the bolometric energy for each flare event. As can be seen from the left two panels of Fig. 9, the range of flare energies in both samples is 1032–1039 erg. For Sample 1, the majority concentrate within 1033–1036 erg, while for Sample 2, the majority concentrate within 1034–1037 erg. The difference may be attributed to the higher proportion of binary stars in Sample 2 compared to Sample 1. In Sample 1, the proportion of binary stars is 55.4%, while in Sample 2, the proportion of binary stars is 63.2%. For flare energies exceeding 1035 erg, the proportion of superflares in binary systems is higher than that in single stars, which might be caused by stellar interactions. For flares with energy exceeding 1036 erg, as stars evolve from the main sequence to subgiants and then to red giants, the corresponding proportion of superflares shows a slight increase. Certainly, this could also be due to selection effects. For example, the giants in Sample 1 are relatively bright sources observed by TESS. In theory, we could still observe small flares on less luminous giants. More data are needed to confirm this trend given the limited sample sizes of the subcategories in Sample 1. In Sample 2, the proportion of binary-star flares is much higher than that of single-star flares. The middle and right panels of Fig. 9 illustrate the relationship between flare energy and flare occurrence percentage of the single stars and binaries, respectively. We used the linear function to fit them using the Markov chain Monte Carlo (MCMC) process provided by Python package pymc6 with ten chains. We have overlaid a range of posterior predictive samples to illustrate the trends, which are shown as gray lines in the figures. Finally, we plot the mean trend with a red line and determine the mean fitted slope along with its uncertainty. For both single and binary stars in Sample 1 and Sample 2, flare energies decrease as the flare occurrence percentage increases. The trend lines are consistent with each other.
 |
Fig. 9. Bolometric flare energy distribution and relationship between bolometric flare energy and flare occurrence percentage. The left panels illustrate the percentage of bolometric flare energy in different energy ranges, where different colors represent the distribution of different types of stars in the small panel. The middle and right panels show the relationship between flare energy and flare occurrence percentage for single and binary stars, respectively. For both samples, all the mean linear slopes are less than zero, which indicates that flare energy decreases as flare occurrence rates increase for both single and binary stars. |
The occurrence rate of superflares, characterized by the flare frequency distribution (FFD), often follows a power law, namely dN/dE ∝ E−α. Many studies based on TESS or Kepler data have obtained power-index values α of between 1.1 and 2.2, and find a dependency on stellar spectral type (Shibayama et al. 2013; Yang & Liu 2019; Tu et al. 2020, 2021; Yang et al. 2023). Based on the 120s cadence data, for Sample 1, over 30% of the total number of flare events fall within the energy range of 1035–1039 erg, while for Sample 2, this ratio exceeds 70%. We selected flare energies greater than or equal to 1 × 1035 erg as superflares to fit them and determined the alpha values for different classifications of the radio stars. The results are plotted in Fig. 10. For all stars in Sample 1 and Sample 2, α is about 1.46 and 1.42, respectively. In comparison to the range of α values obtained in previous studies, our values for the radio stars are also in the region of 1.1 and 2.2. When comparing the alpha values between single stars (α is about 1.50 in Sample 1 and 1.47 in Sample 2) and binary stars (α is about 1.38 in Sample 1 and 1.42 in Sample 2), we find that binary systems have a greater tendency to produce superflares. Similarly, when comparing the α values of Sample 1 in different evolutionary stages, higher energy superflares are less often produced in the main sequence stage than in the giant stages. This is consistent with the flare energy distribution of different evolutionary stages shown in the top left panel of Fig. 9. The different evolutionary stages of the stars of Sample 2 show the same behavior: by comparing their respective alpha values, we see that giant stars produce more higher energy superflares.
 |
Fig. 10. Flare frequency distribution for all stars, single stars, binary stars, and stars in different evolutionary stages for both samples. Here, the power index value of alpha was obtained by fitting the energy greater than or equal to 1 × 1035 (represented by red vertical dashed lines) erg using the MCMC method and the green error bars represent the statistical error obtained by taking the square root of the total number of flares in the corresponding energy range. |
4.4. Relationship between radio emission and bolometric flare energy
Radio stars display a wide range of evolutionary states (Matthews 2019). The top panel of Fig. 11 illustrates the distribution of flaring and nonflaring stars in both Sample 1 and Sample 2; the main sequence, subgiants, red giants, supergiants shown in the background are the same as in Fig. 1. From the distribution of flaring and nonflaring stars in both samples, it can be observed that both types of stars are widely distributed across various evolutionary stages. However, for Sample 2, stars with lower effective temperatures (higher Gaia bp_rp magnitude) are more likely to produce flares. Different physical mechanisms lead to radio emission of varying intensity (Matthews 2019). In order to investigate whether there is a correlation between radio intensity and flare energy, we also downloaded a catalog7 of radio data that includes information on radio intensity at different frequencies. To reduce the effects caused by interactions in binary star systems, we only selected flaring single stars in Sample 1. We selected radio data at three frequencies, namely 4885 MHz, 8440 MHz, and 230 000 MHz for they corresponding to the highest number of single stars (39, 80, and 49) respectively. In the bottom three panels of Fig. 11, we plot the relationship between flare energy and radio intensity. We performed linear fits to the MCMC method. We find no clear relationship between flare energy and radio intensity at the frequencies explored.
 |
Fig. 11. Flare and non-flare stars distribution in Gaia bp_rp vs. absolute magnitude plot and the relationship between bolometric flare energy and maximum radio flux intensity. The top panel is the distribution comparison between flare and nonflaring stars in both samples, and the upper-right legend is similar to that in Fig. 1. In the bottom-left legend, we show the symbols representing flare and nonflaring stars in both samples. It can be observed that both flare and nonflaring stars are widely distributed across various evolutionary stages. For the bottom panels, we illustrate the distribution of flare energy and the corresponding maximum radio flux intensity for single stars of Sample 1 at different radio frequencies (4885, 8440, and 230 000 MHz). Here, the red lines are the average linear fit, and the slopes are marked in small boxes. There is no clear relationship observed. |
4.5. LAMOST Hα activity indicator
LAMOST offers a wealth of optical spectra, including the Hα line, the Ca II H and K lines, and the Mg I triplet lines. Given the limited number of LAMOST spectra matched for Sample 2 (28 low-resolution and 8 medium-resolution spectra, all corresponding to flaring stars), we do not include the processing results of LAMOST spectra for Sample 2 here. For Sample 1, among the 938 low-resolution spectra, 755 belong to 406 flaring radio stars, and 183 spectra pertain to 104 nonflaring radio stars. In the case of 1145 medium-resolution spectra, 943 belong to 354 flaring radio stars, and 202 are associated with 88 nonflaring stars. Figure 12 displays two examples of LAMOST low- and medium-resolution spectra along with the Hα line. The medium-resolution spectrum showcases multiple time-domain spectra from different observations of the same target.
 |
Fig. 12. Two examples of low-resolution and medium-resolution spectra from LAMOST. The top two panels present the whole spectrum and their Hα lines are given in the bottom two panels, respectively. Please note that only the red arm of the medium-resolution spectra is shown. |
Spectroscopic observations provide a means to record changes induced by stellar magnetic field activity. The Hα line is particularly useful for studying stellar magnetic activity. We computed the Hα equivalent width (EW) for both flaring and nonflaring stars and show them in the left and middle panels of Fig. 13. The Hα EW of flaring stars is notably higher than that of nonflaring stars. Furthermore, we overlay box-and-whisker plots on the scatter plot to show the changing trend, revealing that as the effective temperature increases, the Hα EW of flaring stars decreases. This trend is consistent in both low- and medium-resolution data. This finding aligns with previous conclusions drawn from studies of Pleiades objects (Fang et al. 2016), flaring stars from the Tsinghua University-Ma Huateng Telescopes for Survey (Liu et al. 2023), and objects observed in the LAMOST and TESS fields (Zhang et al. 2023).
 |
Fig. 13. Comparision of flare and non-flare stars in indicators of Hα EW and/or Gaia activity index. The left panel displays Hα EW from low-resolution spectra of LAMOST for both flare and nonflare radio stars. The middle panel is the same as the left but for medium-resolution spectra. The right panel displays the distribution of the Gaia DR3 activity index matched with Sample 1. The red dots represent flaring stars, while the black dots represent nonflaring stars. The Gaia Ca II IRT line activity indicator and the LAMOST Hα activity indicator of flaring stars are significantly larger than those of nonflaring stars. |
4.6. Gaia DR3 chromospheric activity indicator
Lanzafame et al. (2023) published the Gaia DR3 catalog, including stellar activity index from the Ca II IRT lines (activityindex_espcs in nm unit). We cross-matched Sample 1 radio stars with the Gaia DR3 chromospheric activity index data to obtain their activity. There are 144 flaring stars and 134 nonflaring stars matched with Gaia chromospheric activity. We plot the relationship between the Gaia DR3 chromospheric activity indicator and effective temperature in the right panel of Fig. 13. Similar to the previous analysis with LAMOST activity indicators, we mark the flaring stars with red dots and nonflaring stars with black dots and overlay box-and-whisker plots on the scatter plot to show the changing trend. Although the data are limited, it is clear that the Gaia DR3 chromospheric activity indicator values for flaring stars are higher than those for nonflaring stars. Additionally, as effective temperature increases, the chromospheric activity index gradually decreases. The trends of Gaia activity indicator and LAMOST Hα intensity versus stellar effective temperature are consistent with each other.
4.7. Hα asymmetry
Stellar flares and stellar coronal mass ejections can impact a star’s atmosphere and even the habitability of exoplanets (Fuhrmeister et al. 2018; Koller et al. 2021; Wang et al. 2021). Lu et al. (2022) identified three stellar CME candidates by examining the blue shift and asymmetry of the Hα lines. Stellar type-II radio bursts have been observed in the Solar System, and may have been generated by energetic CMEs. Given that stars in our sample were detected with radio emission, and that some experienced flares, we sought to detect possible Hα asymmetry from the LAMOST medium-resolution spectra and to analyze the causes by looking at the behavior of Ha emission.
To this end, we initially normalized the medium-resolution spectrum. Using the average flux of the spectrum as a reference (i.e., baseline in Fig. 14), we determined the peak position of the Hα line. Subsequently, we calculated the red and blue widths on both sides of the peak flux position through integration regions. By computing the difference between the left and right sides, we ascertained the symmetry of the Hα profile. To determine whether the Hα emission underwent a red or blue shift, we plotted multiple spectra of the Hα line from the medium-resolution spectrum in a single graph. Using the method outlined above, we recorded positions on both sides of the Hα line where the flux ratios were 0.2, 0.4, 0.6, and 0.8 of the peak flux (after subtracting the maximum baseline). Employing these four positions, we calculated the line distribution of multiple spectra on both sides of the Hα lines. The difference in distribution density between the left and right lines helps us to determine whether the Hα line exhibits a blueshift or a redshift. If the absolute value of the mean difference between the two sides is greater than 0.56 Å (considering an error of 0.14 Å at each of the four ratio positions), we deem that a blueshift or redshift has occurred. After examining all the spectra and cross-referencing with the SIMBAD database (Wenger et al. 2000) to remove eclipsing binaries, all T Tauri stars, and the pulsating variables that significantly affect the Hα line, we identify 266 medium-resolution spectra with Hα emission potentially accompanied by a blueshift or a redshift. We plotted the Hα profiles of all these medium-resolution spectra and conducted a manual examination, ultimately identifying two objects with Hα asymmetry.
 |
Fig. 14. Two examples to show Hα profile asymmetries. The left panel corresponds to “LAMOST J043439.28+250101.0”, which has a LAMOST obsid = 634715116. The right panel corresponds to “LAMOST J043033.97+144452.7”, which has a LAMOST obsid = 763510066. The red and green dashed line represents the integration boundary, the pink and blue dashed lines represent the theoretical and actual peak positions of the Hα profile, respectively, and the bright blue and yellow line represents the integration area. The yellow dashed line is a double-Gaussian fitting result as a reference. |
The first asymmetric Hα line is observed on the flaring star TIC 268510346, identified as a RS CVn variable system in the SIMBAD database (Wenger et al. 2000). In Fig. 15, the top three panels display the Hα line spectra for TIC 268510346. The first two spectra (blue and red lines) show symmetric and almost unchanged intensities, suggesting relative stellar system quiescence. However, the third spectrum exhibits a significant enhancement of the red wing. The right panel illustrates a double-Gaussian fitting result for the contrast profile, which was derived using a similar method to that used by Lu et al. (2022). The vacuum wavelength of the Ha line is obtained from van Hoof (2018). The blue dashed line represents a slightly blueshifted component, which is likely caused by a flare during the rise phase. In contrast, the green dashed line exhibits a pronounced redshift.
 |
Fig. 15. Photometric and spectroscopic images for TIC 268510346. The top two (left and right) panels are normalized and smoothed Hα profiles, respectively. The red dashed line represents the peak position of the first spectrum. The LMJD, S/R, and Hα peak are shown in the legend. The top right panel is the double-Gaussian fitting result for the Hα contrast profile of the third active spectrum. The solid yellow line is the Hα contrast profile, and the solid red line is the double Gaussian fitting result. The dashed blue and green lines represent the two Gaussian components. The vertical dotted red and black lines indicate the wavelength of the Hα line at 6562.85 Å and the vacuum wavelength (6564.61 Å). The middle two panels show the TESS light curve of TIC 268510346 of SECTORs 44 and 43, and the bottom panel is the magnification of the blue area in SECTOR 43 light curve. |
By examining TESS light curves, we discovered that this star is highly active, experiencing several superflares during sectors 43 and 44. The red wing enhancement observed in the Ha line is a common phenomenon in solar or stellar observations, and is often attributed to chromospheric downward condensations or coronal rain (Canfield et al. 1990; Lu et al. 2022; Cao et al. 2023). The more plausible explanation is coronal rain, which is supported by a potential mutual interaction between adjacent flares observed in sector 43. The coronal rain generated by a previous flare influences the spectral properties of subsequent smaller flares. Using the first two spectra as references and applying the Doppler effect, we calculated a radial velocity of approximately 41.939 km s−1 for the third spectrum, which is consistent with typical coronal rain speeds (i.e., 30–150 km s−1) (Oliver et al. 2016; Lu et al. 2022). The light curves for sectors 43 and 44 are presented in Fig. 15 to support this, along with a magnified view of the blue region in the sector 43 light curve.
The second slightly blueshifted Hα line was observed on the flaring star TIC 245820477, which is classified as a high proper-motion star in the SIMBAD database (Wenger et al. 2000). In Fig. 16, the top two Hα line images show a slight blueshift in the spectral line for this star. The emission intensity increases and then decreases in the five observed spectra, indicating a flare. This is likely a microflare, characterized by a relatively short total duration of Trise and Tdecay. Microflares often induce such blueshifts (Testa & Reale 2020). Validating this hypothesis, the bottom image in Fig. 16 shows a zoom onto the blue region of the light curve, revealing numerous microflares occurring during a relatively quiet period.
 |
Fig. 16. Photometric and spectroscopic images for TIC 245820477. The top two panels have similar contents to the top two panels (left and middle) of Fig. 15. The middle and bottom panels are the light curve of TIC 245820477 SECTOR 44 and the magnification of the blue area. From the magnified section of the light curve, several minor flares can be seen, which may be the cause of the slight blue shift in the Hα lines. |
5. Summary
We conducted a study of stellar magnetic activity using TESS light curves and LAMOST spectra for both a manually curated radio star catalog (Wendker 1995) and radio star samples released from LoTSS, ASKAP, and VLASS surveys (Callingham et al. 2023; Yiu et al. 2024; Pritchard et al. 2024), particularly focusing on flare events and Hα lines. Our key findings are as follows:
1. For Sample 1, we identify a total of 12 155 flare events on 856 radio stars from TESS 120s cadence light curves. More than 57% of the radio stars that can be matched with TESS exhibit flare events. The majority of these flare events (over 97%) have durations of less than 2 h.
2. For Sample 2, we identify a total of 3992 flare events on 86 radio stars from TESS 120s cadence light curves. Compared to Sample 1, the proportion of binary stars in Sample 2 is significantly higher. Additionally, flares in Sample 2 tend to be of shorter duration, with all flares having durations of less than 2 h. This may indicate that smaller flares dominate coronal heating.
3. We find that the occurrence percentage of flares decreases with increasing stellar effective temperature. The cumulative flare frequency distribution follows a power-law index (α value) of approximately 1.50 ± 0.11 for single stars and 1.38 ± 0.09 for binary stars in Sample 1, and 1.47 ± 0.11 for single stars and 1.42 ± 0.09 for binary stars in Sample 2.
4. Our analysis of the LAMOST Hα EW Gaia Ca II IRT line activity indicator reveals that flaring radio stars exhibit significantly greater activity compared to nonflaring stars. Additionally, we identify a possible coronal rain candidate based on the asymmetry of the Hα emission line.
Overall, this study compares a manually collected sample of radio stars with a sample of nontargeted survey radio stars, and provides valuable insights into the magnetic activity of radio stars and their associated flare events, shedding light on the relationships between various stellar parameters and their impact on magnetic activity.
Acknowledgments
We would like to thank the anonymous referee for improving the work. Our research is supported by the Joint Fund of Astronomy of the NSFC and CAS Grant Nos. 11963002, and 12373032. We also thank the fostering project of GuiZhou University with No. 201911, and the CSST project on stellar activity and late evolutionary stage. We also acknowledge the science research grants from the China Manned Space Project with No. CMS-CSST-2021-B07 and the SIMBAD database.
References
- Balona, L. A. 2015, MNRAS, 447, 2714 [Google Scholar]
- Bastian, T. S. 1990, Sol. Phys., 130, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, T. A., Huber, D., Gaidos, E., et al. 2018, ApJ, 866, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, C. J., Erkan, N., Budding, E., et al. 2015, MNRAS, 446, 4205 [NASA ADS] [CrossRef] [Google Scholar]
- Bowman, D. M., Burssens, S., Pedersen, M. G., et al. 2019, Nat. Astron., 3, 760 [Google Scholar]
- Candelaresi, S., Hillier, A., Maehara, H., et al. 2014, ApJ, 792, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Canfield, R. C., Penn, M. J., Wulser, J.-P., et al. 1990, ApJ, 363, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Callingham, J. R., Vedantham, H. K., Shimwell, T. W., et al. 2021, Nat. Astron., 5, 1233 [NASA ADS] [CrossRef] [Google Scholar]
- Callingham, J. R., Shimwell, T. W., Vedantham, H. K., et al. 2023, A&A, 670, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cao, D., Gu, S., Wolter, U., et al. 2023, MNRAS, 523, 4146 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, X.-Q., Zhao, Y.-H., Chu, Y.-Q., et al. 2012, Res. Astron. Astrophys., 12, 1197 [Google Scholar]
- Doyle, J. G., Butler, C. J., Bryne, P. B., et al. 1988, A&A, 193, 229 [NASA ADS] [Google Scholar]
- Fang, X.-S., Zhao, G., Zhao, J.-K., et al. 2016, MNRAS, 463, 2494 [NASA ADS] [CrossRef] [Google Scholar]
- Feinstein, A., Montet, B., & Ansdell, M. 2020a, J. Open Source Software, 5, 2347 [NASA ADS] [CrossRef] [Google Scholar]
- Feinstein, A. D., Montet, B. T., Ansdell, M., et al. 2020b, AJ, 160, 219 [Google Scholar]
- Forbes, T. G. 2000, J. Geophys. Res., 105, 23153 [Google Scholar]
- Fuhrmeister, B., Czesla, S., Schmitt, J. H. M. M., et al. 2018, A&A, 615, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güdel, M. 2002, ARA&A, 40, 217 [Google Scholar]
- Günther, M. N., Zhan, Z., Seager, S., et al. 2020, AJ, 159, 60 [Google Scholar]
- Gibson, D. M. 1985, Radio Stars, 116, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Babusiaux, C., et al.) 2018, A&A, 616, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haisch, B. M., Slee, O. B., Siegman, B. C., et al. 1981, ApJ, 245, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Haisch, B., Strong, K. T., & Rodono, M. 1991, ARA&A, 29, 275 [Google Scholar]
- Hawley, S. L., Davenport, J. R. A., Kowalski, A. F., et al. 2014, ApJ, 797, 121 [Google Scholar]
- Helfand, D. J., Schnee, S., Becker, R. H., et al. 1999, AJ, 117, 1568 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, W. S., & MacGregor, M. A. 2022, ApJ, 926, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, M. L., & Desch, M. D. 1984, Rev. Geophys. Space Phys., 22, 373 [CrossRef] [Google Scholar]
- Koller, F., Leitzinger, M., Temmer, M., et al. 2021, A&A, 646, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanzafame, A. C., Brugaletta, E., Frémat, Y., et al. 2023, A&A, 674, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lawson, K. D., Wisniewski, J. P., Bellm, E. C., et al. 2019, AJ, 158, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, C.-L., Ip, W.-H., Hou, W.-C., et al. 2019, ApJ, 873, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Lingam, M., & Loeb, A. 2017, ApJ, 848, 41 [Google Scholar]
- Liu, C., Fu, J., Shi, J., et al. 2020, arXiv e-prints [arXiv:2005.07210] [Google Scholar]
- Liu, Q., Lin, J., Wang, X., et al. 2023, MNRAS, 523, 2193 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, H.-P., Tian, H., Zhang, L.-Y., et al. 2022, A&A, 663, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luo, A.-L., Zhao, Y.-H., Zhao, G., et al. 2015, Res. Astron. Astrophys., 15, 1095 [Google Scholar]
- Matthews, L. D. 2019, PASP, 131, 016001 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, G., Zhang, L.-Y., Su, T., et al. 2023, Res. Astron. Astrophys., 23, 055001 [CrossRef] [Google Scholar]
- Notsu, Y., Shibayama, T., Maehara, H., et al. 2013, ApJ, 771, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, R., Soler, R., Terradas, J., & Zaqarashvili, T. V. 2016, ApJ, 818, 128 [Google Scholar]
- Pawsey, J. L., Payne-Scott, R., & McCready, L. L. 1946, Nature, 157, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Pettersen, B. R., & Coleman, L. A. 1981, ApJ, 251, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Petrucci, R. P., Gómez Maqueo Chew, Y., Jofré, E., Segura, A., & Ferrero, L. V. 2024, MNRAS, 527, 8290 [Google Scholar]
- Pope, B. J. S., Callingham, J. R., Feinstein, A. D., et al. 2021, ApJ, 919, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Pritchard, J., Murphy, T., Heald, G., et al. 2024, MNRAS, 529, 1258 [CrossRef] [Google Scholar]
- Prša, A., Kochoska, A., Conroy, K. E., et al. 2022, ApJS, 258, 16 [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Schaefer, B. E., King, J. R., & Deliyannis, C. P. 2000, ApJ, 529, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., & Zwaan, C. 2000, in Solar and Stellar Magnetic Activity, (New York: Cambridge University Press), Camb. Astrophys. Ser., 34 [CrossRef] [Google Scholar]
- Shibayama, T., Maehara, H., Notsu, S., et al. 2013, ApJS, 209, 5 [Google Scholar]
- Spangler, S. R., & Moffett, T. J. 1976, ApJ, 203, 497 [CrossRef] [Google Scholar]
- Spetsieri, Z. T., Bonanos, A. Z., Yang, M., Kourniotis, M., & Hatzidimitriou, D. 2019, A&A, 629, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, AJ, 158, 138 [Google Scholar]
- Su, T., Zhang, L. Y., Long, L., et al. 2022, ApJS, 261, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2020, Astronomical Data Analysis Software and Systems XXVII, 522, 67 [Google Scholar]
- Testa, P., & Reale, F. 2020, ApJ, 902, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Tu, Z.-L., Yang, M., Zhang, Z. J., et al. 2020, ApJ, 890, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Tu, Z.-L., Yang, M., Wang, H.-F., et al. 2021, ApJS, 253, 35 [NASA ADS] [CrossRef] [Google Scholar]
- van Hoof, P. A. M. 2018, Galaxies, 6, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Walkowicz, L. M., Basri, G., Batalha, N., et al. 2011, AJ, 141, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, R., Luo, A.-L., Chen, J.-J., et al. 2020, ApJ, 891, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., Xin, L. P., Li, H. L., et al. 2021, ApJ, 916, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, C. L., Henden, A. A., & Price, A. 2006, Soc. Astron. Sci. Ann. Symp., 25, 47 [NASA ADS] [Google Scholar]
- Webber, J. C., Yoss, K. M., Deming, D., et al. 1973, PASP, 85, 739 [CrossRef] [Google Scholar]
- Wendker, H. J. 1995, A&AS, 109, 177 [NASA ADS] [Google Scholar]
- Wendker, H. J. 2015, VizieR Online Data Catalog: VIII/99 [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wu, C.-J., Ip, W.-H., & Huang, L.-C. 2015, ApJ, 798, 92 [Google Scholar]
- Yan, Y., He, H., Li, C., et al. 2021, MNRAS, 505, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H., & Liu, J. 2019, ApJS, 241, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H., Liu, J., Gao, Q., et al. 2017, ApJ, 849, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Z., Zhang, L., Meng, G., et al. 2023, A&A, 669, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yiu, T. W. H., Vedantham, H. K., Callingham, J. R., & Günther, M. N. 2024, A&A, 684, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, J., Dere, K. P., Howard, R. A., et al. 2001, ApJ, 559, 452 [Google Scholar]
- Zhang, L.-Y., Yue, Q., Lu, H.-P., et al. 2017, Res. Astron. Astrophys., 17, 105 [CrossRef] [Google Scholar]
- Zhang, L.-Y., Long, L., Shi, J., et al. 2020, MNRAS, 495, 1252 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, L., Cheng, Y., Han, X. L., et al. 2022, Universe, 8, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, L. Y., Su, T., Misra, P., et al. 2023, ApJS, 264, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Zic, A., Murphy, T., Lynch, C., et al. 2020, ApJ, 905, 23 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Distribution of our radio star samples with the reference background. In the upper right legends of all four panels, we show the reference background of main sequence stars, subgiants, red giants, and supergiants from the works of Berger et al. (2018), Bowman et al. (2019), and Spetsieri et al. (2019), respectively. In the bottom-left corner, we provide the corresponding subclassification legend for this study (i.e., single stars, binary stars, and different evolutionary stages in both samples). The stars in both samples are distributed across various evolutionary stages, and for Sample 2, the radio-bright stars are predominantly located in the low-temperature main sequence. |
| In the text | |
 |
Fig. 2. Three example light curves with flare events. Black dots represent stellar background light curves and red dots are the flare events. At the top of the panels, we list the corresponding TESS source id and sector number. The horizontal axis represents BJD time in days, and the vertical axis represents normalized flux. |
| In the text | |
 |
Fig. 3. Three examples of flare candidates identified by the program and removed during the manual inspection process. If there were fewer than three points above the background light curve (left panel), or variations in the stellar background light curve were mistakenly identified as flare events (middle panel), or the profile of the candidate did not match the normal shape of flares (right panel), we removed these flare candidates to make our results more accurate. |
| In the text | |
 |
Fig. 4. Distribution of the percentage of flares in different intervals of the duration and amplitude, respectively. For each panel, we use different colors coupled with different markers to represent different classifications and provide explanations in the legend. The durations of most flares is less than 1 h in Sample 1, while for Sample 2, the duration of most flares is less than 0.5 hour. The amplitude of most flares is less than 0.05 for both samples. For Samples 1 and 2, the distribution of flares in different duration or amplitude ranges is dominated by main sequence stars. |
| In the text | |
 |
Fig. 5. Distribution of the flare percentage in different intervals of the flare rise and decay times, respectively. For each panel, we used different colors coupled with different markers to represent different classifications and provide explanations in the legend. The left panel is the distribution of the flare percentage versus the different rise and decay time ranges for all flares, single stars, and binary stars. The middle and right panels show the distribution of the different evolutionary stages for Samples 1 and 2. The rise time of flares in Sample 1 is mostly less than 20 min, while in Sample 2, the majority of flares have rise times of less than 10 min. The flare decay times in Sample 1 are mostly less than 40 min, while in Sample 2, they are mostly less than 20 min. |
| In the text | |
 |
Fig. 6. Distribution of flare occurrence percentages with effective temperature in Sample 1 and Sample 2. In each panel, blue dots represent the effective temperature and flare occurrence percentage for each star. We overlaid box-and-whiskers plots on each scatter plot to reflect the trend of the scatter plot. In the left four panels corresponding to Sample 1 classifications, the flare occurrence percentage decreases with increasing effective temperature. Similarly, in the right four panels corresponding to Sample 2, except for the single star classification, where the trend observed in Sample 1 is not evident due to a smaller sample size, the other classifications exhibit the same pattern: the flare occurrence percentage decreases with increasing effective temperature. |
| In the text | |
 |
Fig. 7. Distribution of flare occurrence percentages with rotation or orbital period in Samples 1 and 2. In each panel, blue dots represent the rotation or orbital periods and flare occurrence percentage for each star. We overlaid violin plots with box-and-whiskers plots on each scatter plot to reflect the trend of the scatter plot. For Sample 1, there no obvious correlation observed while for Sample 2 both all stars and binary stars show a trend where the flare occurrence percentage decreases with increasing rotation or orbital period. |
| In the text | |
 |
Fig. 8. Flare occurrence percentages of all radio stars (left), single stars (middle), and binary stars (right) in the two dimensions of effective temperature and period (rotation or orbital) for both samples, where the size of the red circles represents the value of the flare occurrence percentage. The majority of flaring stars with higher flare occurrence percentage are distributed within smaller ranges of effective temperature. |
| In the text | |
 |
Fig. 9. Bolometric flare energy distribution and relationship between bolometric flare energy and flare occurrence percentage. The left panels illustrate the percentage of bolometric flare energy in different energy ranges, where different colors represent the distribution of different types of stars in the small panel. The middle and right panels show the relationship between flare energy and flare occurrence percentage for single and binary stars, respectively. For both samples, all the mean linear slopes are less than zero, which indicates that flare energy decreases as flare occurrence rates increase for both single and binary stars. |
| In the text | |
 |
Fig. 10. Flare frequency distribution for all stars, single stars, binary stars, and stars in different evolutionary stages for both samples. Here, the power index value of alpha was obtained by fitting the energy greater than or equal to 1 × 1035 (represented by red vertical dashed lines) erg using the MCMC method and the green error bars represent the statistical error obtained by taking the square root of the total number of flares in the corresponding energy range. |
| In the text | |
 |
Fig. 11. Flare and non-flare stars distribution in Gaia bp_rp vs. absolute magnitude plot and the relationship between bolometric flare energy and maximum radio flux intensity. The top panel is the distribution comparison between flare and nonflaring stars in both samples, and the upper-right legend is similar to that in Fig. 1. In the bottom-left legend, we show the symbols representing flare and nonflaring stars in both samples. It can be observed that both flare and nonflaring stars are widely distributed across various evolutionary stages. For the bottom panels, we illustrate the distribution of flare energy and the corresponding maximum radio flux intensity for single stars of Sample 1 at different radio frequencies (4885, 8440, and 230 000 MHz). Here, the red lines are the average linear fit, and the slopes are marked in small boxes. There is no clear relationship observed. |
| In the text | |
 |
Fig. 12. Two examples of low-resolution and medium-resolution spectra from LAMOST. The top two panels present the whole spectrum and their Hα lines are given in the bottom two panels, respectively. Please note that only the red arm of the medium-resolution spectra is shown. |
| In the text | |
 |
Fig. 13. Comparision of flare and non-flare stars in indicators of Hα EW and/or Gaia activity index. The left panel displays Hα EW from low-resolution spectra of LAMOST for both flare and nonflare radio stars. The middle panel is the same as the left but for medium-resolution spectra. The right panel displays the distribution of the Gaia DR3 activity index matched with Sample 1. The red dots represent flaring stars, while the black dots represent nonflaring stars. The Gaia Ca II IRT line activity indicator and the LAMOST Hα activity indicator of flaring stars are significantly larger than those of nonflaring stars. |
| In the text | |
 |
Fig. 14. Two examples to show Hα profile asymmetries. The left panel corresponds to “LAMOST J043439.28+250101.0”, which has a LAMOST obsid = 634715116. The right panel corresponds to “LAMOST J043033.97+144452.7”, which has a LAMOST obsid = 763510066. The red and green dashed line represents the integration boundary, the pink and blue dashed lines represent the theoretical and actual peak positions of the Hα profile, respectively, and the bright blue and yellow line represents the integration area. The yellow dashed line is a double-Gaussian fitting result as a reference. |
| In the text | |
 |
Fig. 15. Photometric and spectroscopic images for TIC 268510346. The top two (left and right) panels are normalized and smoothed Hα profiles, respectively. The red dashed line represents the peak position of the first spectrum. The LMJD, S/R, and Hα peak are shown in the legend. The top right panel is the double-Gaussian fitting result for the Hα contrast profile of the third active spectrum. The solid yellow line is the Hα contrast profile, and the solid red line is the double Gaussian fitting result. The dashed blue and green lines represent the two Gaussian components. The vertical dotted red and black lines indicate the wavelength of the Hα line at 6562.85 Å and the vacuum wavelength (6564.61 Å). The middle two panels show the TESS light curve of TIC 268510346 of SECTORs 44 and 43, and the bottom panel is the magnification of the blue area in SECTOR 43 light curve. |
| In the text | |
 |
Fig. 16. Photometric and spectroscopic images for TIC 245820477. The top two panels have similar contents to the top two panels (left and middle) of Fig. 15. The middle and bottom panels are the light curve of TIC 245820477 SECTOR 44 and the magnification of the blue area. From the magnified section of the light curve, several minor flares can be seen, which may be the cause of the slight blue shift in the Hα lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.