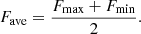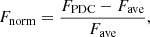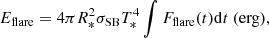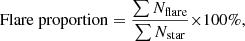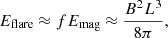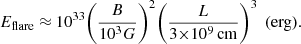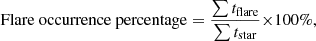| Issue |
A&A
Volume 669, January 2023
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 20 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202142710 | |
| Published online | 21 December 2022 | |
Properties of flare events based on light curves from the TESS survey⋆
1
College of Physics, Guizhou University, Huaxi Street 2708, 550025 Guiyang, PR China
e-mail: liy_zhang@hotmail.com
2
Dept. of Physics and Astronomy and SARA, Butler University, Indianapolis, IN 46208, USA
3
Department of Physics & Astronomy Howard University, Washington, DC 20059, USA
4
Kechuang Industrial Development Company Limited and Gui’an Supercomputing Center, Guiyang, PR China
5
College of medicine, Guizhou university of traditional Chinese medicine, Guiyang 550025, PR China
Received:
21
November
2021
Accepted:
29
September
2022
Aims. A stellar flare is a strong energy burst event. Understanding stellar flares is important for determining the properties of stellar magnetic activities. We aim to perform detailed statistical analyses on stellar flare characteristics in terms of the different stellar parameters using the light curves of the Transiting Exoplanet Survey Satellite (TESS) survey from July 2018 to October 2020.
Methods. By using repeated fitting to differentiate stellar background light curves from flare events, we precisely detected 60 810 flare events on 13 478 stars from sectors 1–30 of the TESS data and determined the flare parameters. After cross-matching our samples with the Gaia survey, we obtained more stellar parameters to determine the relationship between flare parameters and stellar parameters.
Results. The fraction of flaring stars decreases as stellar temperatures increase in the region of 2500–6500 K and stellar mass increases from 0.08 to 1.4 M⊙. The flare energies increase as the stellar temperature and the stellar mass decrease. There is a weak relationship between flare amplitude and Ro. We also confirm that M-type stars produce flares more frequently than F-, G-, and K-type stars. We find that the proportion of flaring stars increases from M0 to M5, and decreases from M5 to M7. We obtain a power-law index of 1.83 ± 0.15 for the cumulative flare frequency distribution. The index shows a decreasing trend from F- to K-type stars, and M-type stars rise for dwarf samples. The fraction of flaring stars decreases as the vertical absolute height increases in the range 0–200 pc but this fraction is stable in the range 200–800 pc. We find that eclipsing binary stars show more frequent flares than single stars.
Key words: stars: activity / stars: flare / stars: statistics
Full Tables 1 and 2 are only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/669/A15
© The Authors 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Solar activity is connected with lives of human beings. Solar flares can cause extensive electrical and communications disruptions (Choi et al. 2011). They represent a radiation hazard to instruments on Earth and reduce the lifetime of low-orbit spacecraft. An X-ray flare on 10 March 1989 created a geomagnetic storm two days later that destroyed the Quebec hydroelectric power system. Transformer failures, hundreds of relay and protection system failures, voltage aging, and power fluctuations were widespread in North America (Haisch et al. 1991). The frequent generation of large spots and flares during the lifetime of a star is important for planets around low-mass stars. The generation of spots and flares may have a great impact on planetary, atmospheric, and biological processes, affecting the habitability of planets (West et al. 2008). A flare is a short but intense energy release due to the reconnection of magnetic field rings in the photosphere of active stars in stellar photospheres that release energy in the X-ray, UV, optical, IR, and radio wavelengths on timescales of seconds to days (Yang et al. 2017; Walkowicz et al. 2011; Lawson et al. 2019; Jackman et al. 2021b). Flares are common phenomena for active stars and their statistical properties are important aspects for studying stellar activity.
In recent years, many astronomers have used the photometric light curve from space surveys (such as Kepler mission and K2 mission of the Kepler Space Telescope (Kepler and K2), the Transiting Exoplanet Survey Satellite (TESS), and so on) to study flare events. Maehara et al. (2012) used high-precision photometry from the Kepler survey and found many superflares, which are between 10 and 104 times more energetic than the largest solar flare. Hawley et al. (2014) focused on active star GJ 1243, and analyzed its classical and complex (multi-peak) flares, finding strong correlations between the flare energy, amplitude, duration, and decay time. Stelzer et al. (2016) discovered the connection between stellar magnetic activity and rotation by studying 134 bright and nearby M dwarfs based on K2 data. Doyle et al. (2019) found 1834 flares on 167 low-mass stars and calculated their energies, finding these to range from 6.0×1029 to 2.4×1035 erg. Using light curves from the K2 mission, Raetz et al. (2020) studied the relation between stellar rotation and magnetic activity with particular attention to stellar flares. Feinstein et al. (2020) used a convolutional neural network to search for flares and determined the flaring rates of young stars of a range of ages and spectral types using two-minute light curves from the TESS survey. Okamoto et al. (2021) found 2341 superflares on 265 solar-type stars and 26 superflares on 15 Sun-like stars using all Kepler Primary Mission Data. Jackman et al. (2021b) calculated flare parameters using data of 13s cadence from the Next Generation Transit Survey. The large time-resolved sky surveys with repeat observations of millions of stars on timescales of seconds to days ensure complete samples of flares on observed stars and can be used to derive their statistical properties (Kowalski et al. 2009; Silverberg et al. 2016).
Stellar flares have long been known to differ from standard solar models. The released energies of other solar-type stars exceed 1000 times that of the Sun (Haisch et al. 1991; Hawley & Pettersen 1991; Kowalski et al. 2013). Meanwhile, Walkowicz & Basri (2011) found M dwarfs tend to flare more frequently than K dwarfs. Shibayama et al. (2013) found that the occurrence rate of flares investigated in G-type stars satisfies a power-law relation, dN/dE ∝ E−α, with α ∼ 2 based on Kepler data. Hawley et al. (2014) obtained a similar index based on data for five M dwarfs. Yang et al. (2017) discovered 540 M dwarfs with flare events using the Kepler survey. Recently, many astronomers have focused on the K and M dwarfs. During the flare events in these studies, the total energy could be more than 1034 erg (Walkowicz et al. 2011; Hawley et al. 2014; Chang et al. 2017). Günther et al. (2020) searched the flares from 24 809 stars with a two-minute cadence in the first two sectors of the TESS mission and detected 8695 flares on 1228 flaring stars. These authors found that flares occur on 30% of middle and later M dwarfs, 5% of early M Dwarfs, and less than 1% of stars with F, G, and K spectral types. Günther et al. (2020) also solidified previous conclusions that fast-rotating M dwarfs are the most likely to flare and that the flare amplitudes are independent of stellar rotation periods. Tu et al. (2020) found 1216 superflares of 400 solar-type stars using TESS data, and determined a power-law index of the frequency distribution of about 2.16 (±0.10). Later, the same authors also revised the index of 1.76 (±0.11) between the flare frequency and energy (Tu et al. 2021). Feinstein et al. (2020) studied star clusters with ages of about 1–800 Myr in the first 20 sectors of the TESS mission, and found a sample of 3193 stars in the observation targets. For low-mass stars with temperatures of less than 4000 K, these latter authors found higher flare rates and flare energies than for hotter stars in all age groups. They also found that the hotter stars show higher flare rates and larger flare amplitudes when they are young (less than 50 Myr), with these becoming slower and weaker with age, respectively. Furthering our understanding of flares by studying their various characteristics is therefore important for elucidating stellar magnetic field properties.
At present, astronomy is entering an era of long-timescale photometric monitoring and therefore big data. On the basis of photometry data, a large number of studies have discovered relationships between flare parameters (flare frequency, energy, amplitude, and duration) and stellar parameters (rotation period, spectral type, age, etc.). However, most astronomers only study the flare properties of different types of stars, such as solar-type stars (G-type stars with effective temperatures in the range of 5100–6000 K), M dwarfs, cold main sequence stars, young stars, and so on. Some studies also focus on superflares that release energy of more than 1033 erg. Günther et al. (2020) expect that the analysis of flares can be extended to almost all bright small stars in the upcoming TESS data, which will provide a large sample and therefore reliable statistics for the physical properties of stellar flares. In our work, we use the two-minute-cadence light-curve data from sectors 1 to 30 of the TESS survey, as these allow us to detect more flares of shorter duration. The observation time is from July 25, 2018 to October 21, 2020, and the observation range covers the northern and southern hemispheres. We use all the light curves obtained by TESS, and our initial sample contains all the objects of the TESS survey. We then use a broader sample to determine their physical parameters and more reliably analyze their statistical properties.
2. Data
TESS is a space telescope of the NASA Explorer program, which is an all-sky transit survey and part of the Explorer program (Ricker et al. 2015). The combined view of the four TESS cameras is 24° ×96°, which divides the sky into two hemispheres, each divided into 13 blocks. The size of a block is the range of TESS view and the observation time of each block is about 27 days. After observing the first block, TESS moves to the second block, then the third block, and so on, until the whole sky is divided into 26 blocks. TESS will spend a year observing the northern hemisphere and another year observing the southern hemisphere, and its wide-field camera allows it to observe 85% of the sky in two years. TESS has a bandpass of 600–1000 nm and is centered on 786.5 nm, which is slightly redder than the Kepler survey (Gargaud et al 2015). TESS did not detect flare events with low energy owing to their emission at redder wavelengths (Doyle et al. 2019). Based on past findings, we cannot obtain short-duration, low-amplitude flares (Ramsay et al. 2020; Doyle et al. 2020). Tu et al. (2020) listed several advantages to studying stellar flares while detecting superflares based on TESS data. TESS can observe sufficiently bright stars with a high signal-to-noise ratio (S/N), and its two-minute cadence provides the possibility to study more attributes of the flare events.
Statistical studies of stellar flares require the observation of a large number of individual objects, and many researchers believe flares lack sufficient cadence and wavelength coverage or duration of observations to constrain the detailed behaviors of rise and decay times (Kowalski et al. 2009; Walkowicz et al. 2011; Stelzer et al. 2016; Yang et al. 2017). If most targets are observed in long cadence, namely of about 30 min, a large number of shorter flares will be ignored. The long-cadence light curve provides a complete sample for the study of high-energy events such as superflares, while the short-cadence data are important for the detection of shorter timescale flare events and for obtaining more information on their properties (Davenport 2016). We downloaded all TESS light curve files from the official TESS website. Finally, we obtained 587 760 light-curve files for 264 037 targets. In order to identify individual events, we looked at right ascension and declination; if the difference is less than 2 arcsec between these, we take this to be repeated data for the same target.
3. Flare detection
3.1. Flare-detection procedure
Flares are strong energy burst events on the stellar surface. They give rise to an obvious light curve variation with a rapid rise and a relatively slow decay. In recent years, there have been many works published on flare events. There are two kinds of methods used to identify flare events. One is to detect stellar flares by first subtracting the background light curve from the original light curve and then detecting the flare on the detrended data. The other kind is based on the convolutional neural network (CNN) or similar machine learning algorithms (Feinstein et al. 2020). Most works adopt the former with different methods and criteria for fitting the background light curve (Walkowicz et al. 2011; Davenport et al. 2014; Wu et al. 2015; Davenport 2016; Gao et al. 2016; Van Doorsselaere et al. 2017; Lu et al. 2019; Huang et al. 2020; Günther et al. 2020). In this work, we also eliminate the background light curve first, and make some improvements over previous methods.
First, we downloaded 587 760 optical curve files for 264 037 targets from the TESS mission. Simple aperture photometry (SAP) fluxes were extracted from the aperture, selected by a target after optimizing the S/N, and corrected according to the background. For our analysis, we used pre-search data conditioning SAP (PDCSAP) flux, which has had systematic errors removed – namely those caused by the satellite rolling – by co-trending basis vectors. Fmax is used to represent the maximum flux value of each data set, and Fmin represents the minimum value. We then get the average PDCSAP flux of each data set and, expressed in Fave:
We used the following formula to normalize the photometric data (PDCSAP flux):
where FPDC is the PDCSAP flux, and Fnorm is the normalized result. With the normalized flux, we were able to begin detecting flare events. We divided these data into two parts according to the period of the light curves. To ensure the polynomial functions can obtain the best possible results, we divided each light curve into several short parts in terms of time periods. For the TESS data, each of these parts represents one day, and we subtract the average time of data points in each part respectively, so that the overall data are distributed near the zero point of the coordinate.
To find flares more accurately from the light curve, we must first remove the background light curve and detrend it. We chose the polynomial functions to fit the background light curve. For each different light curve, we used a polynomial of different order to ensure that we obtained optimal results. In order to determine whether or not the best polynomial degree has been chosen, we calculate the difference between the standard deviation σ of the light curve and the fit curve, denoted by λ. When the polynomial order is changed, and the λ no longer decreases significantly, we take this to mean that the most appropriate fitting order has been chosen and the most effective fitting has been achieved. To avoid the possibility that fitting points belong to the flare procedure, we remove points with values of three times λ above the fitting curve, and in this process we of course use the polynomial of best order to fit it. We then use the same polynomial order to fit the remaining points again to get a new fitting function and λ. After ten repetitions, we regard the fitting curve we obtained as the final fitting function of the background light curve. The problem with this approach is that short periods of light curves can be mistaken for flare points and removed, particularly as periods are similar in duration to flare events. After subtracting the background light from the original light curve, we regard the points beyond the quadruple standard deviation 4σ as flare candidates, and make a final judgment on the candidates. If there are four or more points for a candidate flare event and the fitting results meet the characteristics of a flare, that is, a rapid rise and slow fall, then we determine this candidate to be a flare event. Otherwise we classify these points as noise. The amplitude of a flare event is determined from the point of flare peak minus the fitting function of the background light curve at the corresponding time.
Figure 1 depicts the process we use to search for flares events. Figure 2 shows two false flares that were directly excluded by the program. Although panels a and b show that the light curve shows the trend of the rapid rise and slow decline, and no less than four points (green line), there are still many data points below the base line, which we judge to be noise. Finally, we plot four detailed examples of flare events in Fig. 3. To ensure optimum accuracy, we visually inspected the detection results. After visual screening, we removed about 20% of the candidates that were mistaken for flare events, such as pulsating stars and nonflare outbursts. As shown in Fig. 4, the three examples meet the program screening conditions, but we found them not to be flare events during visual inspection and removed them.
 |
Fig. 1. Methods of searching for flare event. Top panel is the observational data, where green points are possible flare events. The middle panel is the observational and theoretical light curves, where blue points are the original data and the red line represents the tenth polynomial function and theoretical lines. The bottom panel shows the difference between the original data and theoretical light curve, where the red points are the flare event. |
 |
Fig. 2. Three flares removed by the program by default, although their light curves meet the characteristics of rapid rise and slow decline. |
 |
Fig. 3. Four examples of flares from the TESS survey in detail. |
 |
Fig. 4. Three examples that were judged as flare events by the program but were manually removed. |
3.2. Flare results
Using the above method, we obtained 60 810 flare events from the first 30 sectors of the TESS mission over two years of observation time. That is, a total of 60 810 flares occurred on 13 478 stars of the 264 037 observed targets. We list the parameters of these 60 810 flare events in Table 1. We also calculated the flare energy using the following equation:
Parameters of 60 810 flare events from TESS survey.
where Eflare is the flare energy, Fflare is the normalized PDCSAP flux, and σSB is the Stefan–Boltzmann constant. The stellar radius R* and the effective temperature T* were obtained from TESS published files, which can be supplemented by other space surveys (Kepler and Gaia) and the Sloan Digital Sky Survey (SDSS) projects (Alam et al. 2015; Huber et al. 2014; Bailer-Jones et al. 2018). The calculation of flare energies is described in previous works in detail (Lu et al. 2019; Zhang et al. 2020). All the stellar parameters of the flare stars are listed in Table 2, which includes the coordinates, the effective temperature, stellar radius, and SDSS magnitudes. There are many targets without an effective temperature or stellar radius. We cross-matched the TESS coordinates with Gaia data release 2 (DR2) as well as the catalogs of other missions. We finally obtained 57 961 flare events for which flare energies are available and 2849 flares for which such energies have not been calculated due to a lack of stellar parameters. We also list the corresponding effective temperature, stellar radius, and flare energy in Table 1, and the number of flares for each target in Table 2 (Col. 19).
Stellar parameters of TESS objects (including flare stars).
Our calculations of the energy released by the flare can be affected by several uncertainties. The first is the error of the effective temperature of the stellar surface and the stellar radius. The second is the determination error of the start and end points of the flare event and static level, which will also affect the integral term in Eq. (3). In addition, the effective temperature of the flare will change during the flaring process. Some studies assume that the spectrum of a flare can be described by black-body radiation with an effective temperature of 10 000 K (or 9000±500 K). However, Namekata et al. (2017) show that for solar white-light flares, when the effective temperature changes from 10 000 to 6000 K (or 7000 K), the estimated energy changes by 0.49 times. Shibayama et al. (2013) also mentioned that, assuming an effective temperature of 9000 K, the estimated energy is 66% of the actual value. Nevertheless, stars are not black-body radiators, and so this estimation is inaccurate, and there may errors of tens of percent. Therefore, we do not consider the temperature change during the flare process, which means that our calculation of energy is affected by an approximately 60% error. As the error is less than one order of magnitude, the impact on our final overall statistical discussion can be ignored.
4. Discussions
Among the 587 760 light curve files for 264 037 stars in the first 30 sectors of the TESS mission, we found 60 810 flare events on 13 478 stars. We cross-matched our catalog flaring stars with Gaia DR2 in order to obtain more stellar parameters, namely stellar radius and effective temperature, giving us as much information as possible on calculating the energies of the flares. Prša et al. (2022) published a catalog of 4584 eclipsing binaries during the first two years of TESS observations. We cross-matched our result with the catalog of 4584 eclipsing binaries published by Prša et al. (2022) and the maximum living catalog of variable stars (including eclipsing binaries) obtained by Watson et al. (2006). After cross-checking with the TESS light variation curve, we found that there are 838 eclipsing binary stars in the 13 478 flaring stars that we found in our initial search.
We used the standard mentioned by Yang & Liu (2019) to obtain the spectral type of each flaring star. Berger et al. (2018) provided the evolution of all Kepler stars, revealing that main sequence stars, subgiants, and red giants have obvious boundaries. As in Notsu et al. (2019), we used the samples given by Berger et al. (2018) as the background to decipher the evolutionary stages of the stars of our sample, which we show in Fig. 5. We then divided our sample into three stages, namely main sequence stars, subgiants, and red giants, based on the values of effective temperature and radius of each flaring star. It can be seen that most of our sample is made up of main sequence stars, and the eclipsing binary samples are also dominated by main sequence stars. We analyzed the statistical properties of all the flaring stars detected in this section as well as their flare events.
 |
Fig. 5. All the Kepler stars reported in Berger et al. (2018) used as the background for our reference sample. We use this to judge the evolutionary stages of the stars (main sequence, subgiants, and red giants). Most flaring stars are in the main sequence in the left panel. A similar distribution is seen for eclipsing binaries in the right panel. |
4.1. Flare duration and amplitude
Figure 6 shows the distribution of flare-event duration. More than 90% of the flares have a duration of less than 2 h, while events of no more than 1 h account for about 71% of the total. Furthermore, flare duration is concentrated around approximately 1 h. Walkowicz et al. (2011) found 373 stellar flares lasting about 3–5 h using Kepler survey data. According to Kepler data, Lin et al. (2019) found that the durations of flares are 1.5–5.5 h on low-mass stars from G to M type. Tu et al. (2021) found that, according to the data from the TESS mission, flare duration on solar-type stars is between 1 and 167 min. Moreover, we also plotted the flare amplitude distribution of all flare events in Fig. 7. The amplitude of most flare events is low. This result also confirms the advantage of using TESS data to find smaller flares (Günther et al. 2020). Our results are consistent with those of previous studies in that the amplitudes of flares are usually found to be small, in the range of 0.001–0.1, and most are found to be in the range of 0.01–0.1 (Walkowicz et al. 2011; Balona 2015; Tu et al. 2021). In summary, we confirm that TESS data can be used to find flare events of short duration, that is, of about 1 h, and with amplitudes in the range of 0.01–0.1. The durations and amplitudes of flares are related to the exposure time and photometric precision of the space telescope used for observations.
 |
Fig. 6. Number (left) and percentage (right) distributions of flare durations. |
 |
Fig. 7. Number (left) and percentage (right) distributions of flare amplitudes. |
4.2. Flare proportion
We obtained the stellar effective temperatures and masses of our objects by cross-matching with the data releases of other missions. Figure 8 shows the distribution of the number of flare events in different effective temperature and mass ranges. Flare events mainly occur on stars with an effective temperature of 2500–6500 K. About 62% of the flare events we identified happened on stars with an effective temperature in the range of 3000–4000 K. As can be seen from the diagram of the distribution of different mass ranges, the flare events mainly occurred on stars with a mass of less than 1.2 M⊙. Among them, about 70% took place on stars with a mass in the range of 0.2–0.8 M⊙.
 |
Fig. 8. Distributions of number (upper panel) and flaring star proportion (lower panel). Panels a and b are distributions in different effective temperature Teff ranges, and panels c and d are in different mass ranges. Panels e and f are a new division of the abscissa of panels a and b by spectral type. |
We calculated the ratio of the number of flaring stars to the total number of stars in each range of effective temperature or mass using the following formula:
where Nflare is the number of stars with flare events, and the Nstar is the total number of stars in the corresponding ranges. Figure 8 also shows the distributions of the proportions of flaring stars in the specific Teff and mass range. Nearly 24% of the stars with Teff in the range of 2500–3000 K show a flaring event. About 50% of the flare events were detected on stars with a mass of less than 0.6 M⊙.
Walkowicz et al. (2011) present the results of 373 flaring stars from 23000 cool dwarfs in the Kepler Quarter 1 long-cadence data, and their temperatures are in the range of 3600–4400 K. Lin et al. (2019) analyzed flare events on M and K dwarfs using the K2 observations, and found that the lower mass or cooler stars tend to have higher flare occurrence probabilities. These latter authors also found that a plateau appears in the temperature range of 2500–4000 K with stars in the range of about 2300–2500 K being the most likely to show a flaring event. Stars in the mass range of 0.1–0.3 M⊙ show the highest probabilities of flaring, with a particular peak around 0.08–0.1 M⊙. Günther et al. (2020) found that the falres are mainly detected in stars in the effective temperature range of 3000–4000 K. Jackman et al. (2021a) also found that the temperatures of stars with flare events were concentrated in range from 2500 to 4000 K. The temperature ranges we find in this respect are consistent with these previous works. We find that the fraction of flaring stars decreases as the stellar temperature increases in the range of 2500–6500 K and stellar mass increases in the region of 0.08–1.4 M⊙. Our results are not statistically significant for other ranges of stellar temperature and mass due to a lack of data for those ranges. In general, our results confirm those of previous studies for the temperature ranges where we do have statistically significant sample size (Lin et al. 2019).
We divide the abscissa by spectral type in panels e and f of Fig. 8. Günther et al. (2020) mentioned that the purpose of the TESS mission is to investigate bright dwarfs. We used a larger data sample and found the fraction flaring stars decreases from M- to F-type stars. This trend confirms the conclusions of Günther et al. (2020), who used data from the first two sectors of the TESS mission. The flares of M-type stars are more frequent and intense than those of F-, G-, and K-type stars, making their detection relatively straightforward. We also plot the number of flaring stars versus total stellar observations of TESS in different temperature ranges, and the fraction of flaring stars in more detailed divisions in Fig. 9. According to the standard given by Pecaut & Mamajek (2013), the spectral types of stars are divided into smaller, more specific groups. The left panel of Fig. 9 shows that with decreasing temperature, the fraction of flaring stars increases. As in the conclusion of Günther et al. (2020), M-type stars account for a larger fraction of flaring stars, and produce flares more frequently than F-, G-, and K-type stars. In order to discuss the fractions of flaring stars in the different M subtypes, we plot them in the right panel of Fig. 9. We find the fraction of flaring stars increases from M0 to M5 and decreases from M5 to M7. Günther et al. (2020) show that the fraction of flaring stars increases from M0 to M6 in general, and decreases from M0 to M1. However, we note that there are fewer M0, M1, and M6 stars in the samples used by these latter authors, and their sample contains no M7 stars. We therefore confirm the upward trend in flaring from M0 to M5 type stars. We detect a downward trend from M5 to M7 using more samples of M6 and new M7 samples.
 |
Fig. 9. Distributions of observation samples, flare star samples, and their flare proportion. Left: histogram showing the distribution of the number (upper panel) and proportion (lower panel) of flaring stars (orange part) and the total objects observed by TESS (gray part) in different effective temperature ranges, while the top axis indicates stellar type. Right: refinement of the M-type stars in the left figure into M0–M7. There are 143 and 2238 stars without effective temperatures in the flaring star samples and all the TESS objects. We calculated the upper and lower limits of the error bar and plotted them in different temperature ranges or spectral types. |
In order to discuss the effect of eclipsing binaries on magnetic activity, we plot the distributions of flaring and nonflaring eclipsing binaries by spectral type and effective temperature in the left panel of Fig. 10. We separated the eclipsing binaries and single stars in our sample and calculated the fraction of flaring stars; see the middle panel of Fig. 10. Flaring proportion increases in eclipsing binaries as the temperature decreases from 9000 to 3750 K. The proportion of single stars showing a flare event is relatively stable over this range but increases as the temperature decreases from 3250 to 2750 K. Eclipsing binaries on the other hand show a downward trend in flaring as effective temperature decreases in this temperature range. However, as can be seen in the left panel of Fig. 10, our sample size significantly decreases below 3000 K. There are only 21 single stars and 10 eclipsing binaries in our sample with temperatures of less than 3000 K. The different trends in flaring fraction may be due to our limited sample size in particularly parts of the temperature range. More data are required to cofirm these phenomena. Eclipsing binary stars are more likely to flare than single stars, especially when these are colder stars. This also confirms the conclusion of Huang et al. (2020), namely that the flare activity of eclipsing binaries is usually much higher than that of a single M dwarf, which may be due to the magnetic interaction between the two components in a binary system. Using a sample of 238 M dwarfs, West et al. (2015) concluded that the fraction of chromospheric active M dwarfs increased from M0 to M5, while for limited samples with spectral types later than M6, the active fraction changes very gently from M6 to M8. In the right panel of Fig. 10, we divided the stars with temperatures lower than 4000 K into M0–M7 spectral types (right panel). It can be seen that the proportion of flaring stars increases from M0 to M5, and decreases from M5 to M7. This trend is consistent in single stars and eclipsing binaries alike. Our findings for the stars of spectral types M1–M5 confirm the conclusions of West et al. (2015). At the same time, the M5–M7 stars from our sample show a downward trend in flaring activity. Due to our small sample size for M7–M9 dwarfs, we cannot come to any firm conclusions regarding their flaring activity.
 |
Fig. 10. Distributions of the counts and flare proportions of eclipsing binaries and single stars. Left: counts of all eclipsing binary stars (yellow) and flaring eclipsing binary stars (orange) in different spectral types (upper panel) and temperature ranges (lower panel). Middle: distributions of flare proportion in different spectral types (upper panel) and temperature ranges (lower panel) for eclipsing binary stars (yellow) and single stars (orange). Right: flaring proportion of the M dwarf sample (including the eclipsing binary and single stars) in different M subtypes. |
4.3. Flare energy
4.3.1. Distribution of flare parameters
We plot the distributions of flare energy in Fig. 11. The flare energies are found to be in the range 1 × 1030–1040 erg, and especially concentrated in the range of 1 × 1032–1036 erg. Now we discuss the relationships between flare energy and the effective temperature (Teff) and mass of flaring stars. Panels a and b of Fig. 12 provide a summary of the correlations between flare energy and stellar temperature and mass, respectively. We find power-law expressions for all the points of 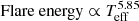 and Flare energy ∝ Mass2.25, while for G-, K-, and M-type stars these are
and Flare energy ∝ Mass2.25, while for G-, K-, and M-type stars these are 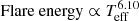 and Flare energy ∝ Mass2.16. These relationships are consistent with each other and show a positive correlation. However, the correlations between the amplitude of flare peak and the stellar parameters are negative; these comparisons are shown in panels c and d. The power-law expressions for all the points are
and Flare energy ∝ Mass2.16. These relationships are consistent with each other and show a positive correlation. However, the correlations between the amplitude of flare peak and the stellar parameters are negative; these comparisons are shown in panels c and d. The power-law expressions for all the points are 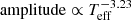 and amplitude ∝ Mass−1.43, while for the G-, K-, and M-type stars these are
and amplitude ∝ Mass−1.43, while for the G-, K-, and M-type stars these are 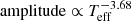 and amplitude ∝ Mass−1.39. Lin et al. (2019) used the K2 data and obtained the following expressions:
and amplitude ∝ Mass−1.39. Lin et al. (2019) used the K2 data and obtained the following expressions: 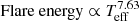 , Flare energy ∝ Mass2.43,
, Flare energy ∝ Mass2.43, 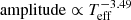 , and amplitude ∝ Mass−1.18. Comparing the black and red lines in Fig. 12 for G-, K-, and M-type stars, we see that we obtain similar results to those published using K2 data (Lin et al. 2019). When we extend the G, K, and M spectral types to A and F spectral types, the fitting results are similar. Therefore, we believe that these correlations are common for all spectral types. However, we require more data for A- and F-type stars to confirm these findings. The physical meaning of these positive and negative correlations is that the flare amplitude decreases with increasing stellar mass and effective temperature, and the flare energy increases with decreasing stellar mass and effective temperature. This result is consistent with the conclusions of Lin et al. (2019) based on 548 M dwarfs and 343 K flare dwarfs from the K2 observations. The total energy of the flare depends on stellar luminosity and flare duration and amplitude. The details of the flare energy estimates were described by Shibayama et al. (2013) and Lin et al. (2019). There are some data points with lower or higher energy and smaller or larger amplitude in our sample compared with the overall data, which may be due to the accuracy of the telescope observations of the TESS survey. In order to reduce the influence of this factor on the power-law relationship, we selected the amplitude region of 0.01–0.1 and energy region of 1 × 1033–1036 erg, respectively. The fitting results are shown by the pink and blue lines in Fig. 12. For all spectral types, we obtained
, and amplitude ∝ Mass−1.18. Comparing the black and red lines in Fig. 12 for G-, K-, and M-type stars, we see that we obtain similar results to those published using K2 data (Lin et al. 2019). When we extend the G, K, and M spectral types to A and F spectral types, the fitting results are similar. Therefore, we believe that these correlations are common for all spectral types. However, we require more data for A- and F-type stars to confirm these findings. The physical meaning of these positive and negative correlations is that the flare amplitude decreases with increasing stellar mass and effective temperature, and the flare energy increases with decreasing stellar mass and effective temperature. This result is consistent with the conclusions of Lin et al. (2019) based on 548 M dwarfs and 343 K flare dwarfs from the K2 observations. The total energy of the flare depends on stellar luminosity and flare duration and amplitude. The details of the flare energy estimates were described by Shibayama et al. (2013) and Lin et al. (2019). There are some data points with lower or higher energy and smaller or larger amplitude in our sample compared with the overall data, which may be due to the accuracy of the telescope observations of the TESS survey. In order to reduce the influence of this factor on the power-law relationship, we selected the amplitude region of 0.01–0.1 and energy region of 1 × 1033–1036 erg, respectively. The fitting results are shown by the pink and blue lines in Fig. 12. For all spectral types, we obtained 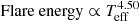 and Flare energy ∝ Mass1.820, and
and Flare energy ∝ Mass1.820, and 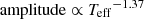 and amplitude ∝ Mass−0.556. For G-, K-, and M-type stars, these relationships are expressed as
and amplitude ∝ Mass−0.556. For G-, K-, and M-type stars, these relationships are expressed as 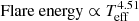 and Flare energy ∝ Mass1.821, and
and Flare energy ∝ Mass1.821, and 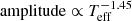 and amplitude ∝ Mass−0.552. After limiting the range of energy and amplitude, we can still see that the correlations between flare energy and the stellar parameters are positive, and that those between flare amplitude and stellar parameters are negative. However, the correlations are weaker than those described above.
and amplitude ∝ Mass−0.552. After limiting the range of energy and amplitude, we can still see that the correlations between flare energy and the stellar parameters are positive, and that those between flare amplitude and stellar parameters are negative. However, the correlations are weaker than those described above.
 |
Fig. 11. Distribution of flare energy. |
 |
Fig. 12. Relationships between the parameters of the flares and the physical properties of the flaring stars. Panels a and b show the positive relationship between flare energy and stellar parameters (temperature in panel a and mass in panel b). The negative relationship between the amplitude and the same stellar parameters shown in panels c and d. Orange dots are A-type stars, green dots are F-type stars, purple dots are G-type stars, yellow dots are K-type stars, and blue dots are M-type stars, while pink dots are stars with unknown spectral type. The black line is the fitting of all points in the figure, and the red line is the fitting of all the G-, K-, and M-type stars. The pink line is the fitting of all points with amplitude in the range of 0.01–0.1 and with energy in the range of 1 × 1033–1036 erg, and the blue line is all the G-, K-, and M-type stars with the same range of amplitude and energy. |
In previous studies of flares based on Kepler data, the flare energy was found to range between roughly 1 × 1033 and 1 × 1036 erg. However, there still exits an upper limit at about 1 × 1038 erg, while a small number of stars exhibit up to 1036 erg events (Shibayama et al. 2013; Wu et al. 2015; Davenport 2016; Lin et al. 2019; Zhang et al. 2020). In recent years, a number of studies focusing on flare events have based their analyses on data provided by the TESS mission. Doyle et al. (2019) found 1834 flares from the 167 low-mass stars with energies from 6 × 1029 to 2.4 × 1035 erg. Günther et al. (2020) gave a flare energy range between 1 × 1031 and 1036.9 erg, while other authors found flare energies to range between 1 × 1033 and 1038 erg (Tu et al. 2020, 2021). We plot the relationships between flare energy, duration, and amplitude in Fig. 13, where the red lines represent the linear fits. There is a positive relationship between flare energy and duration. The longer the flare event lasts, the more energy is released and the greater the probability of generating higher energies.
 |
Fig. 13. Relationships between flare energy and duration (left) or amplitude (right). In the left panel, we distinguish the duration of flare events with different colors at intervals of 0.5 h in the range of 0–7 h. |
4.3.2. Relations between flare energy, flare duration, and spectral type
Statistically, stellar and solar flares may have similar physical mechanisms, and the close correlation between flare energy and duration appears to support this conclusion (Tu et al. 2021). In Fig. 14a, we show the power-law correlation, T ∝ Eγ, with γ = 0.22 ± 0.002 for all samples, which is smaller than other values in the literature. Maehara et al. (2015) deduced that the theoretical value of γ is about 1/3 on the basis of magnetic reconnection theory, and obtained γ = 0.39 ± 0.03 from solar-type flares. For solar flares, Tu & Wang (2018) obtained γ = 0.33 ± 001. Subsequently, we divided the data into spectral type in Fig. 14, and obtain γ for A-, F-, G-, K-, and M-type stars as 0.27 ± 0.031, 0.38 ± 0.013, 0.37 ± 0.006, 0.35 ± 0.006, and 0.304 ± 0.003, respectively, according to the black fitting lines. When studying solar-type stars, we usually select stars with spectral type G. We obtain γ = 0.37 ± 0.006 for our G-type star sample, which is close to the previous conclusion. The results for other spectral samples are also around one-third.
 |
Fig. 14. Relationships between flare energy and duration in stars of different spectral type. Panel (a) shows the whole of our sample; (b) A-type stars; (c) F-type stars; (d) G-type stars; (e) K-type stars; (f) M-type stars; (g) all main sequence stars; and (h) all giants (subgiants and red giants). Values in parentheses are the corresponding number of flare events. |
We mentioned the lower limit of energy released by a flare event above. Now we pay attention to the upper limit of the flare energy. As can be seen from panel a of Figs. 12 and 14, there are some flare events with an energy of above 1036 erg. As we know that the energy released by the flare event will not exceed the magnetic energy stored in starspots, and using the equation for calculating the upper limit of fare energy given by Shibata et al. (2013) and Okamoto et al. (2021):
we can deduce the size of the starspots generated on the flaring stars, which must be smaller than or equal to the surface area of the star. Shibata & Magara (2011) manipulated Eq. (5) and obtained:
We used the stars with masses in the range of 0.08 M⊙ to 0.81 M⊙ as dwarfs according to Lin et al. (2019). We obtained a maximum flare energy for dwarfs of 3.7 × 1036 erg. We then found that there is a clear boundary at about 1036 erg. The flare energies of our dwarf stars are less than 1036 erg. For the higher energy samples above 1036 erg, we carefully checked and found that they are all giant stars with larger radius (subgiants or red giants). We also used a late-type giant example with a temperature of 4722 K, radius of 13.1 R⊙, and mass of 1.7 M⊙ (Kővári et al. 2020) to estimate the magnetic energy of superflares. We obtained a flare energy of 3.5 × 1039 erg using Eq. (6) if we assume B is 3000 G. In order to determine whether or not the flare energies in our sample of higher than 1036 erg are reasonable, we used the same method to estimate the maximum flare energy that can be released on these giant stars, and finally we found that the flare energies we obtained are within their theoretical energy range.
It is interesting to discuss the relationship between flare duration and energy for different stellar masses. For the dwarf star sample obtained by our mass limitation, we plotted the relationship between flare duration and energy in Fig. 14, and used the linear function to fit them (shown by the red line, dotted or dashed). Although there are a few dwarfs with spectral type A, F, and G, we also used the linear function to fit them (shown with dotted lines). The data are scattered and we need more data to confirm any possible relationships. In panels e and f of Fig. 14, we can see that the relationships between energy and duration of K and M dwarfs shown by γ are 0.420 ± 0.008 and 0.32 ± 0.003, respectively, while the γ of all samples of K- and M-type stars are 0.350 ± 0.006 and 0.304 ± 0.003. From panel g, the value of γ for the main sequence dwarf stars, namely γ = 0.30 ± 0.002, is larger than the value 0.230 ± 0.001 for the whole main sequence. Panel h shows that giant stars have γ = 0.290 ± 0.009, which is different from the value for subgiants γ = 0.370 ± 0.011 and red giants γ = 0.170 ± 0.017. We also consider the influence of single and eclipsing binary stars on the relationship T ∝ Eγ. In panels a–g of Fig. 14, we also use the linear function to fit the relationship of the samples without eclipsing binaries, which is marked by the green dot-dashed line. If there is no green line in the figure, this means that it is hidden by the black lines for the fitting result of all samples. After removing eclipsing binaries, the value of γ changes slightly, but it is still similar to the result of all star sample drawn by the black line in each panel. This lack of obvious difference may be due to the small proportion of eclipsing binaries in our sample. For the same reason, more data are needed to determine the influence of eclipsing binaries on the relationship between energy and duration for different spectral types of our sample. Although there are some differences between the different types of stars (dwarfs, main sequence, giant stars, and eclipsing binaries), most of the values of γ are in the region of 0.2–0.4. The difference might be explained by the fact that flare duration is also relative to the coronal magnetic field strength and flare length scale (Namekata et al. 2017; Kővári et al. 2020; Tu et al. 2021). In general, our results are similar to previous findings of 0.39 (0.03) for the superflares on solar-type stars (Maehara et al. 2015) and 0.38 (0.06) for the solar white-light flares (Namekata et al. 2017) and about 0.42 (0.01) for solar-type stars using TESS data (Tu et al. 2020, 2021). These similar power indexes of about one-third suggest that most stellar flares result from a similar mechanism to that of solar flares, which have been explained by magnetic reconnection theory (Maehara et al. 2015; Namekata et al. 2017).
4.4. Flare occurrence rate and flare duration
Figure 15 shows the distribution of stellar flare occurrence percentage, which reflects the proportion of the observed lifetime of a star spent flaring (Lin et al. 2019). The flare percentage can be derived from the equation (Walkowicz et al. 2011):
 |
Fig. 15. Distributions of occurrence percentage for each flaring star. Left panel: the yellow part is the distribution of occurrence percentage of all flare events, and the green part is of eclipsing binaries. The number above the bar graph represents the percentage of the eclipsing binaries and all samples in the corresponding X-axis interval. Right panel: the abscissa in the right panel is still the occurrence percentage of each flaring star, and the yellow part is the ratio of flaring single stars to all single stars within the abscissa range. The green part is the same but for eclipsing binaries. The number above the bar chart is the proportion of stars in this abscissa range in all our samples. |
where ∑tflare is the total flaring duration of each star, and ∑tstar is the total amount of time that star has been under observation. We find that the flare percentages are mainly concentrated in the range of 0–2.25% (see left panel of Fig. 15), with a maximum of 7.35%. Among the 13 478 stars with flare events, the flare percentages of 12 763 stars are between 0% and 1%. Our results are similar to those of Lin et al. (2019). It can be seen from Fig. 15 that the distribution of binary stars (green part) is relatively consistent with the distribution of all samples (yellow part). Huang et al. (2020) obtained that the flare frequency of eclipsing binaries is generally higher than that of single M dwarfs by a factor of about 10. We also plotted the flare occurrence percentage in the right panel of Fig. 15, where the yellow part is the ratio of flaring single stars to all single stars within the abscissa range, and the green part is the same ratio but for the eclipsing binaries. It can be seen that eclipsing binaries are more likely to flare frequently. Similarly, we present the flare occurrence percentage of each spectral type in Fig. 16. The higher the effective temperature of the star, the less likely it is to flare. This is consistent with the findings of Lin et al. (2019), namely that late-type stars tend to have higher flare percentages. We also plot the distribution of flare occurrence percentage in different effective temperature and mass ranges in Fig. 17. We calculated the mean value of the flare occurrence percentage in each step of the stellar effective temperature and mass range, which are marked by black squares in Fig. 17. We find that the black squares in the two panels show a trend of rising first and then falling. The flare occurrence trends are very similar for stellar temperature and mass. Also, stellar temperature and mass for the objects showing the highest flare occurrence percentage are about 4000 K and 0.7 M⊙, respectively.
 |
Fig. 16. Distributions of occurrence percentage of each flaring star for different spectral type. |
 |
Fig. 17. Distribution of the flare occurrence percentage in different effective temperature (left) and mass (right) ranges. |
4.5. Flare frequency distribution
The close correlations between their energies and durations, as well as the similarity between their frequency distributions, suggest that solar flares and superflares may be the result of similar mechanisms. In general, the flare frequency distribution (FFD) obeys a power law, namely dN/dE ∝ E−α with α ∼ 2. Figure 18 shows the FFD of all TESS flare events. The α for all of our data is about 1.83 ± 0.15, and the range of energy for it is from 1035 to 1038 erg. Crosby et al. (1993) indicated that the FFD with α varied between 1.44 and 2.0 based on data provided by the hard-X-Ray burst spectrometer. For superflares of solar-type stars, Tu et al. (2020) obtained an FFD with α ∼ 2.16 ± 0.10 for solar-type stars using the first year TESS data and Tu et al. (2021) revised α ∼ 1.76 ± 0.11 using TESS data in the second year. For different energy ranges, there was a small difference in α. Maehara et al. (2015) found a power-law distribution of superflares on solar-type stars with α ∼ 1.5 for flare energy in the range of 1033–1036 erg. Karoff et al. (2016) concluded that the index α of FFD is roughly 1.8 for Sun-like stars with energies ranging between 1024 and 1035 erg. Maehara et al. (2021) gave the index, α ∼ 1.75 ± 0.04, for flare events on M-type stars with energies ranging from 1032 to 1034 erg. Our results are similar to these results.
 |
Fig. 18. Cumulative FFD of all flare events for dwarfs and all stars. |
Lin et al. (2019) found the α of G-, K-, and M-type stars are 2.01 ± 0.03, 1.86 ± 0.02, and 1.82 ± 0.02, respectively, while Yang & Liu (2019) gave the power-law indices of the A-, F-, G-, K-, and M-type stars as 1.12 ± 0.08, 2.11 ± 0.09, 1.96 ± 0.04, 1.78 ± 0.02, and 2.13 ± 0.05. In order to investigate this topic, we divided the flare events into five parts according to the spectral types of the flaring stars and obtained their power-law index α; see Fig. 19. We found that for A-type, α ∽ 1.76 ± 0.19; for F-type, α ∽ 2.20 ± 0.24; for G-type, α ∽ 1.94 ± 0.30; for K-type, α ∽ 1.87 ± 0.25; for M-type, α ∽ 1.85 ± 0.13; and for giants, α ∽ 1.80 ± 0.11. All the values of power-law index α are listed in Table 3. Audard et al. (2000) obtained the α index for the EUV flares of ten stars from type F to M. These latter authors found that the α index were 2.28 for F- and G-type stars, 1.87 for K-type stars, and 1.84 for M-type stars. And therefore they believe that α may depend on stellar spectral type, and that FFD becomes flat in later spectral types. For the result of Yang & Liu (2019), there is a slow trend from F- to K-type stars, and it becomes steeper from K-type to M-type stars. Lin et al. (2019) found that the values of M- and K-type stars are almost similar, which is inconsistent with (Yang & Liu 2019). For our results, the FFD values show a decreasing trend from F- to K-type stars, and M- and K-type stars are almost similar, which verifies the conclusion obtained by Lin et al. (2019).
 |
Fig. 19. FFDs grouped by different spectral type and giants. In the panel of each spectral type (panels a–e), the counts of the corresponding samples are given in parentheses, and the numbers of flaring stars and flare events are connected by the short line. We drew the relationships of the sample that have removed eclipsing binary stars by blue lines, and shifted them upward by two orders of magnitude. For the results of K- and M-type stars (panels d and e), we also plot the corresponding dwarf samples with orange lines, which are shifted downward by two orders of magnitude. Panel f shows giants; we put the counts of flaring stars in brackets. The results of subgiants and red giants were shifted up and down by two orders of magnitude, respectively. |
Power-law index of flare frequency distributions for the different star types.
We plot the cumulative FFD of all flare events for the five spectral types stars in the left panel of Fig. 20. As can be seen from the figure, there are different energy ranges for the five spectral types. However, in general, they show a similar trend in the energy range of 1036–1038 erg. The energies released by flares based on data from the TESS mission are higher overall, compared to that derived from Kepler data. The high-energy flares observed during the TESS survey are probably due to the redder filter being more sensitive to the large flares (Tu et al. 2021). Meanwhile, Doyle et al. (2019) also concluded that TESS cannot detect the flare events with low energy due to the redder wavelengths. The α index is affected by the energy range used for fitting, the number of stars, and even the observation time, but it is generally around 2 (Yang & Liu 2019). From all the figures of cumulative FFD, it can be found that the trend of the line, in the low energy range, is close to the level, but then shows a significant downward trend with increasing energy. Therefore, when calculating the power-law relationship, we chose the medium range of the flare energy with a stable trend according to previous papers (Yang & Liu 2019; Tu et al. 2021), which allows us to avoid the influence of the approximate horizontal trend at the low energy range on the fitting results. We used larger data samples to verify the previous results, especially for K- and M-type stars, but did not find a steep jump from their value of α. Our results for α are still all around 2, from F-type stars to M-type stars, that is, as the temperature decreases, the value of α gradually decreases and finally remains stable. We obtained α ∽ 1.76 ± 0.19 for A-type stars using more samples, which is higher than the 1.12 ± 0.08 given by Yang & Liu (2019), but within the error range of 1.26 ± 0.56 given by Bai & Esamdin (2020). More data are needed to confirm this finding.
 |
Fig. 20. Comparison between FFDs of different spectral types. Left panel is the cumulative FFD of all flare events, where different types and color lines represent the different spectral types. Meanwhile we shifted the original graphs in the vertical direction to make graphs more clear and easier to be compared. The right panel is the corresponding cumulative FFD of flare events for all dwarf samples. |
Comparisons of dwarf stars of different spectral type are very helpful for understanding flare activities in the main sequence phase, which are important for understanding the effects of flare on surrounding planets. Therefore, we defined the dwarf stars in our samples according to the mass criterion (Lin et al. 2019) and plotted them in the right panel of Fig. 20. The fitting value (α ∽ 1.88 ± 0.31) of K-type dwarfs is similar to the value (1.87 ± 0.25) of all samples in Table 3. Our result is similar to the value of 1.78 ± 0.02 found by Yang & Liu (2019). The α of M-type dwarfs is 2.03 ± 0.26, which is also similar to 1.85 ± 0.13 of all the M-type samples within the error range. The α of M-type stars are also similar to the value of 2.13 ± 0.05 provided by Yang & Liu (2019). As the number of dwarf stars with spectral types of A, F, and G in our sample is limited, we only used the dotted lines to show them and did not fit them to calculate the value of α. For each spectral type, we also removed the eclipsing binary stars and fitted them again. The values of α for the G-, K-, and M-type stars are 1.94 ± 0.30, 1.87 ± 0.25, and 1.85 ± 0.13, respectively. While α for the G-, K-, and M-type stars without eclipsing binaries are 1.77 ± 0.40, 1.81 ± 0.17, and 1.86 ± 0.16. The difference in α with and without eclipsing binaries is within their errors. Therefore, the eclipsing binary stars have little influence on the power-law results. This might be due to the fact that the proportion of eclipsing binary stars in our sample is only 6.22%. We need more data to discuss these objects in the future.
4.6. Relationship between the rise and decay times
We performed a statistical analysis on the two important flare duration parameters Trise and Tdecay for the 60 810 flare events of our sample. Also, we calculated general statistical quantities of the two durations in Table 4, including median, mean, first quartile (Q1), third quartile (Q3), minimum (Min), maximum (Max), and their standard deviations (Std). The minimum value of Trise is about 1.00 min and the median value is 5.00 min. We find that 25% of the Trise values (Q1) are within 3.00 min and 75% of the Trise values (Q3) are within 11.50 min. The range of Tdecay is 3.00–477.01 min and its median value is 22.00 min. Our median value of the decay time is very close to the median values of 22.6 min derived by Yan et al. (2021). We also find that 25% of the Tdecay values (Q1) are no more than 10.50 min and 75% of the Tdecay values (Q3) are less than or equal to 47.00 min. The ratio of Trise and Tdecay for mean, median, Q1, and Q3 are about 0.398, 0.227, 0.286, and 0.245, respectively. The values of mean, median, Q1, and Q3 of Trise are shorter than the corresponding values of Tdecay. These values are typical of flaring events. We calculated the log-normal values of Trise and Tdecay and plotted them in Fig. 21. Both the rise and decay times of the TESS flares also follow a log normal distribution. Our results are similar to previous results obtained by Yan et al. (2021) for the flare events from the Kepler one-minute interval light curve survey. In Fig. 21, we can see there are some differences on the histogram distribution of rise and decay time compared with that of Yan et al. (2021). This may be because our samples are relatively more complex. Also, the exposure time is 2 min for TESS and 1 min for the Kepler survey. Furthermore, whereas we included flare events on many different types of stars in our statistical analysis, Yan et al. (2021) only included stellar flares on Sun-like stars.
 |
Fig. 21. Distributions of the rise (top) and decay (bottom) time of flare events. All samples are represented by a blank bar box, and the shaded area is the main sequence stars. The X-axes of the left panels are real values, and the vertical dashed and dotted lines indicate the statistical mean and median values of all samples, respectively, as listed in Table 4. The right axis of the right panel shows log-normal values, and the vertical dashed and dotted lines indicate the statistical mean and median values, respectively, of the lnTrise and lnTdecay values for the whole sample. The brown line is the normal distribution fitting of the bar graph of all samples, while the blue line is the same but for the main sequence stars. |
Statistical results of the rise time and decay time for 60 810 flare events.
4.7. The fraction of flare star distribution in the Milky Way
In order to investigate the distribution of the flaring stars among the TESS objects in the Milky Way, we obtained their Gaia distances (Bailer-Jones et al. 2018) and calculated their spatial positions in Galactocentric cylindrical coordinates. We plot these positions in the left panel of Fig. 22. To determine the spatial distribution of the flaring star fraction, we separated flaring stars into different bins with sizes of about 50 pc. We plot a 2D diagram of the proportion of flaring stars of the total number of stars in each bin in the middle panel, where the color represents the fraction of flaring stars. The flare star fraction decreases as the color changes from red to blue. For a quantitative analysis of the flaring star fraction, we also plot the flare star fraction versus the vertical height above the Galactic plane in the right panel. The flaring star fraction decreases as a function of absolute height from 0 to 200 pc above the Galactic plane and is stable from 200 to 800 pc. Pineda et al. (2013) and Zhang et al. (2021) found that the chromospheric activity fraction of M-type stars decreases with increasing vertical height above the middle disk plane of the Milky Way, and our results for the flaring star fraction are consistent with this.
 |
Fig. 22. Relationship between the flare events and the position of flaring stars in the Milky Way. The left panel shows the positions of flaring stars. The middle panel shows the 2D distribution the flaring star fraction in Galactocentric cylindrical coordinates. The right panel is the relationship between flaring star fraction and vertical height above the Galactic plane. |
More than 30 years ago, Wilson & Woolley (1970) obtained that the magnetic activity of stars is directly related to their age. Hawley et al. (2000) and Gizis et al. (2002) found that older stars are more likely to be found further away from the Galactic plane where they were born. The age–activity relationship is further supported by the conclusion that the proportion of active M-type stars decreases with vertical distance from the Galactic plane according to SDSS spectra (West et al. 2008). Therefore, we plot the relationship between the distance of our samples above the Galactic plane and the flare occurrence percentage in the left panel of Fig. 22. We conclude that stars close to the Galactic plane are more likely to produce flares. That is, the younger stars are more active.
4.8. The rotation period with flare events
The rotation period is also considered to be one of the parameters affecting flare events. The average flare frequency is lower for more slowly rotating stars (Noyes et al. 1984; Wright et al. 2011; Notsu et al. 2013; Candelaresi et al. 2014). In this study, we calculated the rotation period using the Lomb-Scargle method, and obtained rotation periods for 7082 stars (Lomb 1976; Scargle 1982). The relationship between activity and rotation is usually parameterized by the Rossby number (Ro). The Ro is defined as Ro = Prot/τ, where τ is the convective turnover timescale derived by Wright et al. (2011) using the stellar mass. Finally, we obtained the Ro values for 6145 stars. The right panel of Fig. 23 shows the relationship between stellar rotation period and flare occurrence percentage. It can be seen that the faster rotating stars show a higher incidence of flaring activity. We plotted the relationship between the maximum amplitude and the rotation period for different types of stars in Fig. 24. The amplitude increases with decreasing rotation period. The level of flaring activity drops sharply for those stars with rotation periods longer than 10 days (Lin et al. 2019; Yang & Liu 2019). The 28-day observation span with TESS is not sufficient to obtain values for the stars with slow rotation and a period of more than 10 days. Therefore, we cannot see an obvious turning point in the figure. We defined the flare activity as ΔFlare/L*, where L* is the stellar luminosity (Yang et al. 2017). We find that with increasing Ro, the maximum amplitude of flaring stars and their flaring activity decrease gradually; see the left panel of Fig. 25. Wright et al. (2011) found that the activity–rotation relations had a significant deflection at Ro = 0.13 ± 0.02 from the sample with X-ray luminosity. Yang & Liu (2019) showed a downward trend of the correlation between the flare activity and Ro when Ro > 0.1 for K- and M-type stars. Then we take Ro = 0.1 as the dividing line for both parts. It is found that there is an obvious downward trend for all samples and M-type star samples, which is marked with yellow and pink lines in Fig. 25.
 |
Fig. 23. Relationships between the flare occurrence percentage and flaring stars’ position and rotation period. Left panel: relationship between the height above the Galactic plane and its flare occurrence percentage. Right panel: relationship between the flare occurrence percentage and rotation period in steps of about 0.2 days. |
 |
Fig. 24. Relationship between the maximum amplitude of each flaring star and its rotation period. |
 |
Fig. 25. Correlations between the parameters of flare event and Ro. Left panel: ratio of the maximum flare amplitude versus Ro for 6142 flaring stars. Right panel: relationship between flare activity and Ro. The blue line is at Ro = 0.1. The red line is the fitting line of all samples. If the distribution trend of data points changes significantly near Ro = 0.1, fit the samples on both sides with yellow and pink lines respectively. The fitting range is not completely divided according to Ro = 0.1, but the properly adjusted boundary remains within Ro = 0.1–0.13. |
5. Summary
In this work, we used TESS light curves with two-minute exposure time in the first 30 sectors of the TESS data from July 2018 to October 2020. We obtained 587 760 light curves for 264 037 targets. We found 60 810 flare events on 13 478 stars. Meanwhile, we calculated flare parameters, such as start time, peak time, duration, amplitude, energy, and so on. We cross-matched our flare catalog with other surveys, namely Gaia and SDSS.
We performed a statistical analysis of the amplitude, duration, and energy of the flare events. We find that data obtained from TESS are beneficial to finding flare events of short duration and low amplitude. We obtained the distributions of the flare parameters. The energy we calculated for the flare events ranges from 1030 to 1040 erg, mainly in the range of 1032–1036 erg. The flare energies increase as the duration increases. We performed a statistical analysis of the two flare times trise and tdecay for the 60 810 flare events. We calculated the mean, median, Q1, and Q3 of trise to tdecay, and their corresponding ratios are 0.398, 0.227, 0.286 and 0.245, respectively. For the energies in the range of 1032–1038 erg, the flare events are of higher amplitude. The correlation between energy and amplitude is not obvious, but the amplitude shows an obvious correlation with the temperature and mass of flaring stars. There is a positive relationship between flare energy and duration. We can still see that the correlations between flare energy and stellar parameters (mass and effective temperature) are positive, while those between flare amplitude and stellar parameters are negative.
In our samples, flare events mostly occurred on the stars with effective temperatures of 2500–6500 K and masses of less than 1.4 M⊙. The fraction of flaring stars decreases as stellar temperature increases in the region of 2500–6500 K and stellar mass increases in the region of 0.08–1.4 M⊙. There is a trend from rise to decline for the relationship between flaring rate and temperature or mass, where the peak flaring rate values are at about 3500 K for effective temperature and 0.5 M⊙ for stellar mass. The flare energies increase as the stellar temperature and mass decrease. The power-law index α value is about 1.83 ± 0.15 for the cumulative flare frequency distribution. The flare frequency distributions of F- to K-type stars also show a decreasing trend. On the other hand, for the dwarf sample, the α value of M-type stars rises. Also, the α value for A-type stars is also quite different from the common value. Eclipsing binary stars are more likely to flare than single stars, especially for colder stars, with this likelihood being about ten times higher. Eclipsing binaries are also more likely to flare frequently. The flaring star fraction decreases as a function of vertical absolute height in the region of 0–200 pc above the Galactic plane and is stable from 200 to 800 pc. We also find that stars close to the Galactic plane are more likely to produce flares. This means that younger stars are more active. Furthermore, the faster the star rotates, the higher its incidence of flaring. Lastly, we find that flare amplitude decreases with increasing Ro.
Acknowledgments
Our research is supported by the Joint Fund of Astronomy of the NSFC and CAS Grant Nos.11963002, U1631236 and U1431114. We also thank the fostering project of GuiZhou University with No. 201911. We also acknowledge the science research grants from the China Manned Space Project with No. CMS-CSST-2021-B07.
References
- Alam, S., Albareti, F. D., Allende Prieto, C., et al. 2015, ApJS, 219, 12 [Google Scholar]
- Audard, M., Güdel, M., Drake, J. J., et al. 2000, ApJ, 541, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, J.-Y., & Esamdin, A. 2020, ApJ, 905, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., et al. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Balona, L. A. 2015, MNRAS, 447, 2714 [Google Scholar]
- Berger, T. A., Huber, D., Gaidos, E., et al. 2018, ApJ, 866, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Candelaresi, S., Hillier, A., Maehara, H., et al. 2014, ApJ, 792, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, H.-Y., Song, Y.-H., Luo, A.-L., et al. 2017, ApJ, 834, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, H.-S., Lee, J., Cho, K.-S., et al. 2011, Space Weather, 9, 06001 [Google Scholar]
- Crosby, N. B., Aschwanden, M. J., & Dennis, B. R. 1993, Sol. Phys., 143, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Davenport, J. R. A. 2016, ApJ, 829, 23 [Google Scholar]
- Davenport, J. R. A., Hawley, S. L., Hebb, L., et al. 2014, ApJ, 797, 122 [Google Scholar]
- Doyle, L., Ramsay, G., Doyle, J. G., et al. 2019, MNRAS, 489, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Doyle, L., Ramsay, G., & Doyle, J. G. 2020, MNRAS, 494, 3596 [NASA ADS] [CrossRef] [Google Scholar]
- Feinstein, A. D., Montet, B. T., Ansdell, M., et al. 2020, AJ, 160, 219 [Google Scholar]
- Gargaud, M., Irvine, W. M., Amils, R., et al. 2015, Encycl. Astrobiol., 2869 [Google Scholar]
- Gao, Q., Xin, Y., Liu, J.-F., et al. 2016, ApJS, 224, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Gizis, J. E., Reid, I. N., & Hawley, S. L. 2002, AJ, 123, 3356 [Google Scholar]
- Günther, M. N., Zhan, Z., Seager, S., et al. 2020, AJ, 159, 60 [Google Scholar]
- Haisch, B., Strong, K. T., & Rodono, M. 1991, ARA&A, 29, 275 [Google Scholar]
- Hawley, S. L., & Pettersen, B. R. 1991, ApJ, 378, 725 [Google Scholar]
- Hawley, S. L., Reid, I. N., & Tourtellot, J. G. 2000, Very Low-Mass Stars and Brown Dwarfs, (Cambridge University Press) 109 [CrossRef] [Google Scholar]
- Hawley, S. L., Davenport, J. R. A., Kowalski, A. F., et al. 2014, ApJ, 797, 121 [Google Scholar]
- Huang, L.-C., Ip, W.-H., Lin, C.-L., et al. 2020, ApJ, 892, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Silva Aguirre, V., Matthews, J. M., et al. 2014, ApJS, 211, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Jackman, J. A. G., Wheatley, P. J., Acton, J. S., et al. 2021a, MNRAS, 504, 3246 [NASA ADS] [CrossRef] [Google Scholar]
- Jackman, J. A. G., Shkolnik, E., & Loyd, R. O. P. 2021b, MNRAS, 502, 2033 [NASA ADS] [CrossRef] [Google Scholar]
- Karoff, C., Knudsen, M. F., De Cat, P., et al. 2016, Nat. Commun., 7, 11058 [NASA ADS] [CrossRef] [Google Scholar]
- Kővári, Z., Oláh, K., Günther, M. N., et al. 2020, A&A, 641, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kowalski, A. F., Hawley, S. L., Hilton, E. J., et al. 2009, AJ, 138, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Kowalski, A. F., Hawley, S. L., Wisniewski, J. P., et al. 2013, ApJS, 207, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Lawson, K. D., Wisniewski, J. P., Bellm, E. C., et al. 2019, AJ, 158, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, C.-L., Ip, W.-H., Hou, W.-C., et al. 2019, ApJ, 873, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
- Lu, H.-P., Zhang, L.-Y., Shi, J., et al. 2019, ApJS, 243, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Maehara, H., Shibayama, T., Notsu, S., et al. 2012, Nature, 485, 478 [NASA ADS] [Google Scholar]
- Maehara, H., Shibayama, T., Notsu, Y., et al. 2015, Earth Planets Space, 67, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Maehara, H., Notsu, Y., Namekata, K., et al. 2021, PASJ, 73, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Namekata, K., Sakaue, T., Watanabe, K., et al. 2017, ApJ, 851, 91 [Google Scholar]
- Notsu, Y., Shibayama, T., Maehara, H., et al. 2013, ApJ, 771, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Notsu, Y., Maehara, H., Honda, S., et al. 2019, ApJ, 876, 58 [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., et al. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Okamoto, S., Notsu, Y., Maehara, H., et al. 2021, ApJ, 906, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [Google Scholar]
- Pineda, J. S., West, A. A., Bochanski, J. J., et al. 2013, AJ, 146, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Prša, A., Kochoska, A., Conroy, K. E., et al. 2022, ApJS, 258, 16 [CrossRef] [Google Scholar]
- Raetz, S., Stelzer, B., Damasso, M., et al. 2020, A&A, 637, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramsay, G., Doyle, J. G., & Doyle, L. 2020, MNRAS, 497, 2320 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
- Shibata, K., & Magara, T. 2011, Liv. Rev. Sol. Phys., 8, 6 [Google Scholar]
- Shibata, K., Isobe, H., Hillier, A., et al. 2013, PASJ, 65, 49 [NASA ADS] [Google Scholar]
- Shibayama, T., Maehara, H., Notsu, S., et al. 2013, ApJS, 209, 5 [Google Scholar]
- Silverberg, S. M., Kowalski, A. F., Davenport, J. R. A., et al. 2016, ApJ, 829, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Stelzer, B., Damasso, M., Scholz, A., et al. 2016, MNRAS, 463, 1844 [NASA ADS] [CrossRef] [Google Scholar]
- Tu, Z. L., & Wang, F. Y. 2018, ApJ, 869, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Tu, Z.-L., Yang, M., Zhang, Z. J., et al. 2020, ApJ, 890, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Tu, Z.-L., Yang, M., Wang, H.-F., et al. 2021, ApJS, 253, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Van Doorsselaere, T., Shariati, H., & Debosscher, J. 2017, ApJS, 232, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Walkowicz, L. M., & Basri, G. S. 2011, 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun (Astronomical Society of the Pacific), 448, 177 [Google Scholar]
- Walkowicz, L. M., Basri, G., Batalha, N., et al. 2011, AJ, 141, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, C. L., Henden, A. A., & Price, A. 2006, Soc. Astron. Sci. Ann. Symp., 25, 47 [NASA ADS] [Google Scholar]
- West, A. A., Hawley, S. L., Bochanski, J. J., et al. 2008, AJ, 135, 785 [Google Scholar]
- West, A. A., Weisenburger, K. L., Irwin, J., et al. 2015, ApJ, 812, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, O., & Woolley, R. 1970, MNRAS, 148, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, N. J., Drake, J. J., Mamajek, E. E., et al. 2011, ApJ, 743, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, C.-J., Ip, W.-H., & Huang, L.-C. 2015, ApJ, 798, 92 [Google Scholar]
- Yan, Y., He, H., Li, C., et al. 2021, MNRAS, 505, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H., & Liu, J. 2019, ApJS, 241, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H., Liu, J., Gao, Q., et al. 2017, ApJ, 849, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, L.-Y., Long, L., Shi, J., et al. 2020, MNRAS, 495, 1252 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, L.-Y., Meng, G., Long, L., et al. 2021, ApJS, 253, 19 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Methods of searching for flare event. Top panel is the observational data, where green points are possible flare events. The middle panel is the observational and theoretical light curves, where blue points are the original data and the red line represents the tenth polynomial function and theoretical lines. The bottom panel shows the difference between the original data and theoretical light curve, where the red points are the flare event. |
| In the text | |
 |
Fig. 2. Three flares removed by the program by default, although their light curves meet the characteristics of rapid rise and slow decline. |
| In the text | |
 |
Fig. 3. Four examples of flares from the TESS survey in detail. |
| In the text | |
 |
Fig. 4. Three examples that were judged as flare events by the program but were manually removed. |
| In the text | |
 |
Fig. 5. All the Kepler stars reported in Berger et al. (2018) used as the background for our reference sample. We use this to judge the evolutionary stages of the stars (main sequence, subgiants, and red giants). Most flaring stars are in the main sequence in the left panel. A similar distribution is seen for eclipsing binaries in the right panel. |
| In the text | |
 |
Fig. 6. Number (left) and percentage (right) distributions of flare durations. |
| In the text | |
 |
Fig. 7. Number (left) and percentage (right) distributions of flare amplitudes. |
| In the text | |
 |
Fig. 8. Distributions of number (upper panel) and flaring star proportion (lower panel). Panels a and b are distributions in different effective temperature Teff ranges, and panels c and d are in different mass ranges. Panels e and f are a new division of the abscissa of panels a and b by spectral type. |
| In the text | |
 |
Fig. 9. Distributions of observation samples, flare star samples, and their flare proportion. Left: histogram showing the distribution of the number (upper panel) and proportion (lower panel) of flaring stars (orange part) and the total objects observed by TESS (gray part) in different effective temperature ranges, while the top axis indicates stellar type. Right: refinement of the M-type stars in the left figure into M0–M7. There are 143 and 2238 stars without effective temperatures in the flaring star samples and all the TESS objects. We calculated the upper and lower limits of the error bar and plotted them in different temperature ranges or spectral types. |
| In the text | |
 |
Fig. 10. Distributions of the counts and flare proportions of eclipsing binaries and single stars. Left: counts of all eclipsing binary stars (yellow) and flaring eclipsing binary stars (orange) in different spectral types (upper panel) and temperature ranges (lower panel). Middle: distributions of flare proportion in different spectral types (upper panel) and temperature ranges (lower panel) for eclipsing binary stars (yellow) and single stars (orange). Right: flaring proportion of the M dwarf sample (including the eclipsing binary and single stars) in different M subtypes. |
| In the text | |
 |
Fig. 11. Distribution of flare energy. |
| In the text | |
 |
Fig. 12. Relationships between the parameters of the flares and the physical properties of the flaring stars. Panels a and b show the positive relationship between flare energy and stellar parameters (temperature in panel a and mass in panel b). The negative relationship between the amplitude and the same stellar parameters shown in panels c and d. Orange dots are A-type stars, green dots are F-type stars, purple dots are G-type stars, yellow dots are K-type stars, and blue dots are M-type stars, while pink dots are stars with unknown spectral type. The black line is the fitting of all points in the figure, and the red line is the fitting of all the G-, K-, and M-type stars. The pink line is the fitting of all points with amplitude in the range of 0.01–0.1 and with energy in the range of 1 × 1033–1036 erg, and the blue line is all the G-, K-, and M-type stars with the same range of amplitude and energy. |
| In the text | |
 |
Fig. 13. Relationships between flare energy and duration (left) or amplitude (right). In the left panel, we distinguish the duration of flare events with different colors at intervals of 0.5 h in the range of 0–7 h. |
| In the text | |
 |
Fig. 14. Relationships between flare energy and duration in stars of different spectral type. Panel (a) shows the whole of our sample; (b) A-type stars; (c) F-type stars; (d) G-type stars; (e) K-type stars; (f) M-type stars; (g) all main sequence stars; and (h) all giants (subgiants and red giants). Values in parentheses are the corresponding number of flare events. |
| In the text | |
 |
Fig. 15. Distributions of occurrence percentage for each flaring star. Left panel: the yellow part is the distribution of occurrence percentage of all flare events, and the green part is of eclipsing binaries. The number above the bar graph represents the percentage of the eclipsing binaries and all samples in the corresponding X-axis interval. Right panel: the abscissa in the right panel is still the occurrence percentage of each flaring star, and the yellow part is the ratio of flaring single stars to all single stars within the abscissa range. The green part is the same but for eclipsing binaries. The number above the bar chart is the proportion of stars in this abscissa range in all our samples. |
| In the text | |
 |
Fig. 16. Distributions of occurrence percentage of each flaring star for different spectral type. |
| In the text | |
 |
Fig. 17. Distribution of the flare occurrence percentage in different effective temperature (left) and mass (right) ranges. |
| In the text | |
 |
Fig. 18. Cumulative FFD of all flare events for dwarfs and all stars. |
| In the text | |
 |
Fig. 19. FFDs grouped by different spectral type and giants. In the panel of each spectral type (panels a–e), the counts of the corresponding samples are given in parentheses, and the numbers of flaring stars and flare events are connected by the short line. We drew the relationships of the sample that have removed eclipsing binary stars by blue lines, and shifted them upward by two orders of magnitude. For the results of K- and M-type stars (panels d and e), we also plot the corresponding dwarf samples with orange lines, which are shifted downward by two orders of magnitude. Panel f shows giants; we put the counts of flaring stars in brackets. The results of subgiants and red giants were shifted up and down by two orders of magnitude, respectively. |
| In the text | |
 |
Fig. 20. Comparison between FFDs of different spectral types. Left panel is the cumulative FFD of all flare events, where different types and color lines represent the different spectral types. Meanwhile we shifted the original graphs in the vertical direction to make graphs more clear and easier to be compared. The right panel is the corresponding cumulative FFD of flare events for all dwarf samples. |
| In the text | |
 |
Fig. 21. Distributions of the rise (top) and decay (bottom) time of flare events. All samples are represented by a blank bar box, and the shaded area is the main sequence stars. The X-axes of the left panels are real values, and the vertical dashed and dotted lines indicate the statistical mean and median values of all samples, respectively, as listed in Table 4. The right axis of the right panel shows log-normal values, and the vertical dashed and dotted lines indicate the statistical mean and median values, respectively, of the lnTrise and lnTdecay values for the whole sample. The brown line is the normal distribution fitting of the bar graph of all samples, while the blue line is the same but for the main sequence stars. |
| In the text | |
 |
Fig. 22. Relationship between the flare events and the position of flaring stars in the Milky Way. The left panel shows the positions of flaring stars. The middle panel shows the 2D distribution the flaring star fraction in Galactocentric cylindrical coordinates. The right panel is the relationship between flaring star fraction and vertical height above the Galactic plane. |
| In the text | |
 |
Fig. 23. Relationships between the flare occurrence percentage and flaring stars’ position and rotation period. Left panel: relationship between the height above the Galactic plane and its flare occurrence percentage. Right panel: relationship between the flare occurrence percentage and rotation period in steps of about 0.2 days. |
| In the text | |
 |
Fig. 24. Relationship between the maximum amplitude of each flaring star and its rotation period. |
| In the text | |
 |
Fig. 25. Correlations between the parameters of flare event and Ro. Left panel: ratio of the maximum flare amplitude versus Ro for 6142 flaring stars. Right panel: relationship between flare activity and Ro. The blue line is at Ro = 0.1. The red line is the fitting line of all samples. If the distribution trend of data points changes significantly near Ro = 0.1, fit the samples on both sides with yellow and pink lines respectively. The fitting range is not completely divided according to Ro = 0.1, but the properly adjusted boundary remains within Ro = 0.1–0.13. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.