| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 35 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202348270 | |
| Published online | 05 April 2024 | |
Asymmetry in the atmosphere of the ultra-hot Jupiter WASP-76 b★,★★
1
Instituto de Astrofisica e Ciencias do Espaco, Universidade do Porto, CAUP,
Rua das Estrelas,
4150-762
Porto, Portugal
e-mail: olivier.demangeon@astro.up.pt
2
Departamento de Fisica e Astronomia, Faculdade de Ciencias, Universidade do Porto,
Rua do Campo Alegre,
4169-007
Porto, Portugal
3
INAF, Osservatorio Astrofisico di Torino,
Via Osservatorio, 20,
10025
Pino Torinese To, Italy
4
Space Research Institute, Austrian Academy of Sciences,
Schmiedlstrasse 6,
8042
Graz, Austria
5
INAF, Osservatorio Astrofisico di Catania,
Via S. Sofia 78,
95123
Catania, Italy
6
Department of Physics, University of Warwick,
Gibbet Hill Road,
Coventry
CV4 7AL, UK
7
Observatoire astronomique de l’Université de Genève,
Chemin Pegasi 51,
1290
Versoix, Switzerland
8
Centre Vie dans l’Univers, Faculté des sciences, Université de Genève,
Quai Ernest-Ansermet 30,
1211
Genève 4, Switzerland
9
Astrophysics Group, Lennard Jones Building, Keele University,
Staffordshire
ST5 5BG, UK
10
Center for Space and Habitability, University of Bern,
Gesellschaftsstrasse 6,
3012
Bern, Switzerland
11
Weltraumforschung und Planetologie, Physikalisches Institut, University of Bern,
Gesellschaftsstrasse 6,
3012
Bern, Switzerland
12
Dipartimento di Fisica e Astronomia “Galileo Galilei”, Universita degli Studi di Padova,
Vicolo dell’Osservatorio 3,
35122
Padova, Italy
13
INAF, Osservatorio Astronomico di Padova,
Vicolo dell’Osservatorio 5,
35122
Padova, Italy
14
Department of Astronomy, Stockholm University, AlbaNova University Center,
10691
Stockholm, Sweden
15
Instituto de Astrofisica de Canarias,
Via Lactea s/n,
38200
La Laguna, Tenerife, Spain
16
Departamento de Astrofisica, Universidad de La Laguna,
Astrofísico Francisco Sanchez s/n,
38206
La Laguna, Tenerife, Spain
17
European Space Agency (ESA), European Space Research and Technology Centre (ESTEC),
Keplerlaan 1,
2201 AZ
Noordwijk, The Netherlands
18
Admatis,
5. Kandó Kálmán Street,
3534
Miskolc, Hungary
19
Depto. de Astrofisica, Centro de Astrobiologia (CSIC-INTA),
ESAC campus,
28692
Villanueva de la Cañada (Madrid), Spain
20
Institute of Optical Sensor Systems, German Aerospace Center (DLR),
Rutherfordstrasse 2,
12489
Berlin, Germany
21
Centre for Exoplanet Science, SUPA School of Physics and Astronomy, University of St Andrews,
North Haugh,
St Andrews
KY16 9SS, UK
22
Institute of Planetary Research, German Aerospace Center (DLR),
Rutherfordstrasse 2,
12489
Berlin, Germany
23
Centre for Mathematical Sciences, Lund University,
Box 118,
221 00
Lund, Sweden
24
Aix Marseille Univ, CNRS, CNES, LAM,
38 rue Frédéric Joliot-Curie,
13388
Marseille, France
25
Astrobiology Research Unit, Université de Liège,
Allée du 6 Août 19C,
4000
Liège, Belgium
26
Space sciences, Technologies and Astrophysics Research (STAR) Institute, Université de Liège,
Allée du 6 Août 19C,
4000
Liège, Belgium
27
Leiden Observatory, University of Leiden,
PO Box 9513,
2300 RA
Leiden, The Netherlands
28
Department of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory,
439 92
Onsala, Sweden
29
Dipartimento di Fisica, Università degli Studi di Torino,
via Pietro Giuria 1,
10125,
Torino, Italy
30
Department of Astrophysics, University of Vienna,
Türkenschanzstrasse 17,
1180
Vienna, Austria
31
Institute for Theoretical Physics and Computational Physics, Graz University of Technology,
Petersgasse 16,
8010
Graz, Austria
32
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences,
1121
Budapest,
Konkoly Thege Miklós út 15–17, Hungary
33
ELTE Eötvös Loránd University, Institute of Physics,
Pázmány Péter sétány 1/A,
1117
Budapest, Hungary
34
IMCCE, UMR8028 CNRS, Observatoire de Paris, PSL Univ., Sorbonne Univ.,
77 av. Denfert-Rochereau,
75014
Paris, France
35
Institut d’astrophysique de Paris, UMR7095 CNRS, Université Pierre & Marie Curie,
98bis blvd. Arago,
75014
Paris, France
36
Dipartimento di Fisica e Astronomia “Galileo Galilei”, Università degli Studi di Padova,
Vicolo dell’Osservatorio 3,
35122
Padova, Italy
37
ETH Zurich, Department of Physics,
Wolfgang-Pauli-Strasse 2,
8093
Zurich, Switzerland
38
Cavendish Laboratory,
JJ Thomson Avenue,
Cambridge
CB3 0HE, UK
39
Zentrum für Astronomie und Astrophysik, Technische Universität Berlin,
Hardenbergstr. 36,
10623
Berlin, Germany
40
Institut fuer Geologische Wissenschaften, Freie Universitaet Berlin,
Maltheserstrasse 74-100,
12249
Berlin, Germany
41
Institut de Ciencies de l’Espai (ICE, CSIC),
Campus UAB, Can Magrans s/n,
08193
Bellaterra, Spain
42
Institut d’Estudis Espacials de Catalunya (IEEC),
Gran Capità 2-4,
08034
Barcelona, Spain
43
Weltraumforschung und Planetologie, Physikalisches Institut, University of Bern,
Sidlerstrasse 5,
3012
Bern, Switzerland
44
ELTE Eötvös Loránd University, Gothard Astrophysical Observatory,
9700
Szombathely,
Szent Imre h. u. 112, Hungary
45
HUN-REN–ELTE Exoplanet Research Group,
Szent Imre h. u. 112.,
Szombathely,
9700, Hungary
46
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA, UK
47
Max Planck Institute for Extraterrestrial Physics,
Gießenbachstraße,
85748
Garching, Germany
Received:
13
October
2023
Accepted:
16
January
2024
Context. WASP-76 b has been a recurrent subject of study since the detection of a signature in high-resolution transit spectroscopy data indicating an asymmetry between the two limbs of the planet. The existence of this asymmetric signature has been confirmed by multiple studies, but its physical origin is still under debate. In addition, it contrasts with the absence of asymmetry reported in the infrared (IR) phase curve.
Aims. We provide a more comprehensive dataset of WASP-76 b with the goal of drawing a complete view of the physical processes at work in this atmosphere. In particular, we attempt to reconcile visible high-resolution transit spectroscopy data and IR broadband phase curves.
Methods. We gathered 3 phase curves, 20 occultations, and 6 transits for WASP-76 b in the visible with the CHEOPS space telescope. We also report the analysis of three unpublished sectors observed by the TESS space telescope (also in the visible), which represents 34 phase curves.
Results. WASP-76 b displays an occultation of 260 ± 11 and 152 ± 10 ppm in TESS and CHEOPS bandpasses respectively. Depending on the composition assumed for the atmosphere and the data reduction used for the IR data, we derived geometric albedo estimates that range from 0.05 ± 0.023 to 0.146 ± 0.013 and from <0.13 to 0.189 ± 0.017 in the CHEOPS and TESS bandpasses, respectively. As expected from the IR phase curves, a low-order model of the phase curves does not yield any detectable asymmetry in the visible either. However, an empirical model allowing for sharper phase curve variations offers a hint of a flux excess before the occultation, with an amplitude of ~40 ppm, an orbital offset of ~ −30°, and a width of ~20º. We also constrained the orbital eccentricity of WASP-76 b to a value lower than 0.0067, with a 99.7% confidence level. This result contradicts earlier proposed scenarios aimed at explaining the asymmetry observed in high-resolution transit spectroscopy.
Conclusions. In light of these findings, we hypothesise that WASP-76 b could have night-side clouds that extend predominantly towards its eastern limb. At this limb, the clouds would be associated with spherical droplets or spherically shaped aerosols of an unknown species, which would be responsible for a glory effect in the visible phase curves.
Key words: techniques: photometric / planets and satellites: atmospheres / planets and satellites: composition
The CHEOPS raw and detrended photometric time-series data used in this paper are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/684/A27
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Whether they are viewed as stepping stones towards the study of the atmosphere of Earth-like planets or as ideal laboratories to unravel the composition and physical processes at work in extreme and fascinating worlds, ultra-hot Jupiters (UHJs) have been the subject of many observations and studies over the past years (e.g. Parmentier et al. 2018; Kreidberg et al. 2018; Hoeijmakers et al. 2019). Due to their high equilibrium temperature and the low mean molecular weight of their atmosphere, they possess the largest atmospheric pressure scale heights (e.g. Seager 2010, pp. 185–186). Cooler hot Jupiters (HJs) commonly harbour clouds and hazes which hide the signatures of their atmospheric constituent (Sing et al. 2016). On the contrary, UHJs tend to be cloud-free, at least on their day-sides (e.g. Parmentier et al. 2018; Kitzmann et al. 2018). Thanks to the combination of these two elements, UHJs are ideal targets for ground and space-based observatories. Their atmospheres can be probed with most of the available observational techniques, which provide a more extensive view than any other class of exoplanets.
Dozens of atomic and molecular species, some ionised, have already been detected in the atmosphere of UHJs (e.g. Azevedo Silva et al. 2022; Borsa et al. 2021). We have also seen a tremendous effort from the community to more closely model the physical processes driving these atmospheres in an attempt to explain the wealth of observational constraints (e.g. the identification of hydrogen dissociation as a dominant heat transport mechanism for UHJs; Bell & Cowan 2018; Tan & Komacek 2019; Mansfield et al. 2020). One-dimensional (1D) radiative transfer models embedded in Bayesian inference tools have successfully modelled low-resolution and high-resolution transmission spectroscopic observations. They have allowed us to infer the presence of many species and retrieve abundance ratios (e.g. Kitzmann et al. 2023; Pluriel et al. 2020; Gibson et al. 2020; Brogi & Line 2019). Three-dimensional (3D) global circulation models coupled with radiative transfer models and other types of models capable of accounting for the spatial inho-mogeneity of these atmospheres enabled the interpretation of orbital phase curves (PCs) and minute line-shape deformations (e.g. Kreidberg et al. 2018; Tan & Komacek 2019; Helling et al. 2021; Changeat et al. 2022; Jones et al. 2022; Seidel et al. 2023; Pelletier et al. 2023).
WASP-76 b is (arguably) considered an archetypal UHJ (West et al. 2016). From the ground, multiple studies have reported the detection of close to 20 different species (primarily atoms and ions), along with many more upper limits using high-resolution spectroscopic observation in the visible and the near infrared (NIR) obtained during transit (Tsiaras et al. 2018; Seidel et al. 2019, 2021; Ehrenreich et al. 2020; Azevedo Silva et al. 2022; Pelletier et al. 2023; Kesseli et al. 2020, 2022; Sánchez-López et al. 2022; Gandhi et al. 2022; Kawauchi et al. 2022; Kesseli & Snellen 2021; Casasayas-Barris et al. 2021; Landman et al. 2021; Deibert et al. 2021; Tabernero et al. 2021; Edwards et al. 2020). High-resolution observations in the NIR taken close to occultation have shown the presence of CO and hints of H2O emission lines indicative of the presence of a thermal inversion in the planet’s upper atmosphere (Yan et al. 2023). Space-based observatories not only provided low-resolution transit and emission spectroscopy, but also full PC in the NIR and mid-IR (May et al. 2021; Fu et al. 2021; Garhart et al. 2020; Tsiaras et al. 2018). This plethora of observations provides a unique opportunity to piece together one of the most comprehensive views of an exoplanet’s atmosphere.
The scientific interest in UHJs and, in particular, WASP-76 b has increased drastically after the detection and later confirmation of the asymmetric signature coming from the two limbs of WASP-76 b in transmission detected at ultra-high spectral resolution (Ehrenreich et al. 2020; Kesseli & Snellen 2021; Pelletier et al. 2023). Based on a toy model, Ehrenreich et al. (2020) interpreted these observations as an asymmetry in the iron composition: the upper atmosphere of the morning limb (also called leading limb or western limb) of WASP-76 b would be depleted in gaseous iron compared to its evening limb (also called trailing or eastern limb) due to the condensation of iron over the night-side. Naturally, Savel et al. (2022), Wardenier et al. (2021) and May et al. (2021) attempted to confront these observations with global circulation models (GCMs). All three studies have agreed that standard GCM models cannot reproduce the asymmetry detected by Ehrenreich et al. (2020). Savel et al. (2022) and Wardenier et al. (2021) both argued that an asymmetry in the composition of the limbs is not the only way to explain the observations. Savel et al. (2022) invoked the presence of clouds and a slight eccentricity of the planet’s orbit, while Wardenier et al. (2021) highlighted the importance of temperatures and wind dynamics. Both studies have argued that a weak drag, or long drag timescale (from 105 to 107 s), would be necessary to explain the asymmetry. May et al. (2021) took a slightly different approach to the problem, as they also presented the IR phase curves of WASP-76 b. The phase curves show little to no asymmetry which indicates a strong drag, or short drag time-scale (≤l04 s), in contrast with the results of high-resolution transmission spectroscopy.
In this paper, we provide new observational constraints on the puzzling atmosphere of WASP-76 b with phase curve, transit, and eclipse observations in the visible with the CHEOPS and TESS instruments (Sects. 2 and 4). We refine the properties of WASP-76 a and its stellar companion WASP-76 b (Sect. 3). We revisit the emission spectra of this planet (Sect. 5.1) and derive its geometric albedo (Ag). We discuss the available phase curves at visible and IR wavelengths (Sects. 5.2 and 5.2.2). Finally, we argue that the visible phase curves of WASP-76 b hold crucial elements to reach a comprehensive view of its atmosphere (Sect. 6).
2 Datasets
2.1 CHEOPS
We observed WASP-76 b with CHEOPS during 29 separate visits spread over 3 consecutive observability periods of WASP-76 as part of the CHEOPS Guaranteed Time Observations. We first observed 2 full PC, 15 occultations, and 2 transits between 2020-09-09 and 2020-12-16. One year later, we observed 1 additional PC, 5 more occultations and 3 transits from 2021-09-05 to 2021-12-07. Finally, a year later, on 2022-09-18, we observed 1 additional transit. The transits, occultations, and PCs were observed as part of programs PR100009, PR100016, and PR100036 respectively. The details of these observations are provided in Appendix A and Table A.1.
The light curves were extracted using the CHEOPS data reduction pipeline (DRP, Hoyer et al. 2020) version 13.1.0 which relies on aperture photometry. As described in Benz et al. (2021), CHEOPS data are affected by various instrumental trends. These instrumental trends need to be addressed for an accurate interpretation, especially when looking for astrophysical signals of a few hundreds ppm, like planetary occultations and PCs. CHEOPS is in a low-Earth Sun-synchronous orbit and also spins around its line of sight. The orbital and roll motions are synchronised, which allows the radiator to always point away from Earth. Both motions introduce instrumental trends in the CHEOPS data. The roll motion causes the field of view to rotate around the line of sight. This introduces trends in the photometry which typically correlate with the roll angle of the spacecraft. Due to its orbital motion, CHEOPS orbits above different regions of Earth with varying insolation and cloud coverage. This will produce trends that correlate with the roll angle but also with the background measured on the images. The pixel response non-uniformity (PRNU) triggers another common source of instrumental trends. Due to pointing jitter, the point spread function (PSF) of the target star slightly moves on the charge coupled device (CCD) from exposure to exposure and inaccuracies in the PRNU calibration produce trends in the photometry, which is correlated with the X and Y centroid positions of the target PSF on the CCD. The last typical source of instrumental trend is called the thermal ramp. CHEOPS is a mono-target instrument and it changes pointing for each target. This pointing change implies a change of solar illumination of the telescope tube and mechanical structure, which produces a temperature change and, in turn, the shape of the PSF changes. These changes lead to photometric trends that are usually correlated with the temperature measured by a sensor located on the telescope tube (thermFront_2, e.g. Morris et al. 2021).
We mitigated these instrumental trends using cubic spline decorrelations against the following decorrelation variables: the roll angle of the spacecraft, X and Y centroid positions of the target’s PSF on the CCD, background measured on the images, and the temperature of the telescope tube. The spline decorrelation is performed simultaneously with the fit of the astrophysical model (see Sect. 4.1). It consists of fitting a cubic spline model to the residuals of the astrophysical model versus the decorrelation variable. In order to decorrelate against multiple variables, we performed multiple spline fits sequentially. We started by performing the spline decorrelation against the roll angle using the same roll angle model for all visits. The residuals of this fit were then used for another fit of X and Y centroid positions using a 2D spline model. Over the course of the three seasons of observations, the location of the target stars on the CHEOPS were purposefully changed to occupy the region of the CCD that was the least affected by bad pixels at the time. Thus, we used three different models for the different locations on the CHEOPS CCD. This process was repeated two more times to perform the spline decorrelation against the telescope tube’s temperature and, finally, the measured background. In both of these cases, each visit was modelled independently of the others. The spline fits are implemented with the UnivariateSpline and the SmoothBivariateSpline python classes of the scipy.interpolate package for the 1D and 2D spline fits, respectively (Virtanen et al. 2020). When performing the fit, these two classes automatically selected the position of the knots. The user can influence the number of knots with the smoothing factor that we leave to None, which implies that this smoothing factor is set according to the number of data points.
2.2 TESS
TESS (Ricker et al. 2015) observed WASP-76 during sector 30 from 2020-09-22 to 2020-10-21 and one year later during sectors 42 and 43 from 2021-08-20 to 2021-10-12 and we retrieved the data through the MAST archive.
The data were extracted using the PDC-SAP photometry and PSF-SCALPELS aperture photometry. In Appendix B.2, we show a summary of our comparison of the two methods and justify our choice to use the PSF-SCALPELS photometry for the rest of this paper. For the PSF-SCALPELS photometry, we compute the shape change components of the TESS PSF following the procedure outlined in Wilson et al. (2022) that has been successfully shown to remove roll angle, contamination, and background effects in CHEOPS data (Hawthorn et al. 2023; Hoyer et al. 2022; Parviainen et al. 2022). In brief, for each sector, we conducted a principal component analysis (PCA) decomposition of the auto-correlation of the calibrated target pixel file frames to obtain a series of vectors that explain any variations in the PSF. We selected the most significant components for inclusion in the global analysis via a leave-one-out-cross-validation method. For all sectors, we re-extracted the TESS photometry, using a noise-optimised aperture photometry method (Wilson, in prep.).
These were background-corrected using custom sky-level masks, scattered-light-corrected using a PCA on background pixels, and jitter-corrected by detrending against co-trending basis vectors (CBVs) and two-second cadence engineering quaternion measurements following the approach in Delrez et al. (2021). We then mitigate the potential residual trends by performing a spline decorrelation simultaneously with the fit of the astrophysical model. The procedure is similar to the one used for the spline decorrelation of the CHEOPS data (see Sect. 2.1). For TESS, instead of using a roll angle, X and Y centroid position, temperature, and background, we have used the vectors resulting from the PCA decomposition of the auto-correlation of the calibrated images.
2.3 HST
HST observed WASP-76 b during four transits and one occultation. The first transit visit was obtained on 2015-11-26 using the WFC3 instrument with the G141 grism as part of program ID 14260 (PI: Deming). The remaining three transit visits were observed with the STIS instrument as part of program ID 14767 (PI: López-Morales & Sing): 2016-11-16 and 2017-01-17 with the G430L grism and 2017-02-19 with the G750L grism. The only occultation visit was obtained with the G141 grism of the WFC3 instrument on 2016-11-03 as part of program ID 14767. These data were already analysed and published in three papers. von Essen et al. (2020) analysed the STIS transit data only. Edwards et al. (2020, hereafter E20) analysed the WFC3 data only. Finally, Fu et al. (2021, hereafter F21) combined all HST (STIS and WFC3) data and the Spitzer transits and occultations (see Sect. 2.4).
We decided not to re-reduce the data and to rely on the published analyses of this dataset. Our focus was set in the occultation visits in order to model the thermal SED of WASP-76 b’s day-side (see Sects. 5.1.2 and 6.1). Therefore, we mostly set aside the STIS data and concentrated on the WFC3 data. The two reductions provided by F21 and E20 are not compatible and, as such, we compared the impact of the two data reductions on our analysis (see Sects. 5.1.2 and 6.1). We provide more details on the different reductions of the HST data in Appendix B.3.
2.4 Spitzer
Spitzer observed WASP-76 b during two occultations and three phase curves with the InfraRed Array Camera (IRAC, Fazio et al. 2004). The two occultations were acquired as part of the program 12085 (PI: Drake Deming). One was observed in the 3.6 µm channel (CH1 or IRAC1) on 2016-03-22, and the other in the 4.5 µm channel (CH2 or IRAC2) on 2016-04-01. The three phase curves were acquired as part of program 13038 (PI: Kevin Stevenson). The first one was observed in the 4.5 µm channel on 2017-04-17 and the two others were observed in the 3.6 µm channel on 2017-05-03 and 2018-04-23. These data have already been published by Garhart et al. (2020), F21 and May et al. (2021). However, due to the particularities of the data reduction of the Spitzer data, we chose to re-reduce and re-analyse them. These data were downloaded from the Spitzer Heritage Archive1.
The reduction and analysis processes applied to these datasets are similar to the approach in Demory et al. (2016b), where we modelled the IRAC intra-pixel sensitivity (Ingalls et al. 2016) using a modified implementation of the BLISS (BiLinearly-Interpolated Sub-pixel Sensitivity) mapping algorithm (Stevenson et al. 2012). In addition to the BLISS mapping (BM), our initial baseline model included a quadratic function of the PRF’s full width at half maximum (FWHM) along the x and y axes, which significantly reduces the level of correlated noise as shown in previous studies (e.g. Lanotte et al. 2014; Demory et al. 2016a,b; Gillon et al. 2017; Mendonça et al. 2018; Barros et al. 2022; Jones et al. 2022). We further found that including the background in the baseline model improved the fit slightly (ABIC=3). This baseline model (BM + PRF FWHM2 + BKG) does not include time-dependent parameters. We implemented this instrumental model in a Markov chain Monte Carlo (MCMC) framework already presented in the literature (Gillon et al. 2012). We included all data described in the paragraph above in the same fit. We ran two chains of 200 000 steps each to determine the corrected light curves at 3.6 and 4.5 µm that we later used in our study.
As already pointed out by May et al. (2021), we found that the 3.6 µm phase-curve parameters were very sensible to the choice of the instrument baseline model. We identified differences in excess of 2σ, in particular when increasing the order of the polynomial function of the FWHM along the Y axis from 1 to 3, which exhibits large variations in both of the 3.6 µm visits. The observed FWHM variations have timescales similar to the planetary phase-curve signal, which complicates a robust identification of the latter from instrumental correlated noise.
Equally concerning is the impact of data trimming at the beginning of the longer astronomical observation requests (AORs) on the phase-curve parameters, where differences between 0-min and 30-min trimming are beyond 1σ (see also May et al. 2021). For these reasons, we elect to retain only the 3.6 µm transit and occultations for the subsequent analysis.
A closer examination of the 4.5 µm data revealed that while the inclusion of the background in our baseline model only slightly improved the BIC (ΔBIC=3), it significantly impacted the phase curve amplitude which varied by more than 1σ. We found that the background as well as the PRF FWHM along the x-axis are both correlated with the flux, on timescales that are degenerate with the planetary phase-curve modulation signal. Using a quadratic function of the PRF FWHM and/or including the background in the instrumental model thus impacts the phase curve parameters. Finally, we implemented a baseline model using the noise pixel parameter (Mighell 2005; Lewis et al. 2013), which yielded phase-curve amplitude and offset in agreement with our adopted model described above (BM + PRF FWHM2 + BKG). This result speaks to the reliability of our approach for this channel. However, it doesn’t remove the degeneracies and probably explains the diversity of the results obtained from the analysis of this dataset (see Sects. 4.3, 5.1.2, and 5.2.1, and Tables 1–3).
Main parameters inferred from the Spitzer, TESS, and CHEOPS light curves
Day-side and night-side temperatures.
3 Stars: WASP-76 a and b
We determined the radius of WASP-76 a by using a modified MCMC IR flux method (MCMC IRFM; Blackwell & Shallis 1977; Schanche et al. 2020) that computes the apparent bolometric flux via a comparison of observed and synthetic broadband photometry that is converted to the stellar effective temperature and angular diameter. This yields the radius when combined with the parallax. For the WASP-76 system, we computed the synthetic broadband photometry by building a spectral energy distribution (SED) with the ATLAS Catalogues (Castelli & Kurucz 2003) of atmospheric models and two stellar components; the primary using the spectral parameters derived from ESPRESSO spectra by Ehrenreich et al. (2020) and the companion with parameters taken from the literature (Ngo et al. 2016; Bohn et al. 2020; Southworth et al. 2020; May et al. 2021) and empirical relations (Baraffe et al. 2015). By fitting the combined models to observed data taken from the most recent data releases for the following bandpasses; Gaia G, GBP, and GRP, 2MASS J, H, and K, and WISE W1 and W2 (Skrutskie et al. 2006; Wright et al. 2010; Gaia Collaboration 2023), and using the offset corrected Gaia DR3 parallax (Lindegren et al. 2021), we obtained a stellar radius of R⋆ = 1.764 ± 0.036R⊙. By fitting both stellar components of the SED to observed data, this approach also allows us to compute the contamination factor of the companion in our photometric light curve data, which is the percentage of the light collected in the photometric aperture that corresponds to the companion. Assuming that the light of both WASP-76 a and b are entirely captured by the photometric aperture, we found contamination factors in the TESS, CHEOPS, and IRAC 1 and 2 bandpasses of 0.037±0.002, 0.028±0.001, 0.095±0.005, and 0.090±0.004, respectively. We also derived the contamination factor coefficients for the HST-WFC3 bandpasses used by E20 that are provided in Table B.1.
Taking Teff, [Fe/H], and R⋆ (along with their uncertainties) as the input parameters, we finally determined the isochronal mass M⋆ and age t⋆ by using two different stellar evolutionary models. In detail, we retrieved a first pair of mass and age estimates thanks to the isochrone placement algorithm (Bonfanti et al. 2015,2016), which interpolates the input parameters within pre-computed grids of PARSEC2 v1.2S (Marigo et al. 2017) tracks and isochrones. A second pair of estimates, instead, is computed ‘on-the-fly’ by the CLES (Code Liégeois d’Évolution Stellaire; Scuflaire et al. 2008) code, which generates the best-fit evolutionary track accounting for the input constraints through the Levenberg-Marquardt minimisation scheme (Salmon et al. 2021). Once the two pairs of mass and age estimates were available, we checked their mutual consistency via the χ2 -based criterion as detailed in Bonfanti et al. (2021) and we finally merged the results, which yielded the following robust estimates: 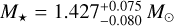 and
and 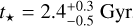 .
.
4 Light-curve fitting
4.1 Transit, occultation, and phase-curve and instrumental models
Our dataset includes planetary transits, PCs, and occultations. For the transits and occultation models, we use the model provided by the batman Python package (Kreidberg 2015). The transit model takes as its input the planetary orbital parameters, the planet over star radius ratio (Rp/R*) and the four coefficients of the non-linear limb-darkening model (u1, u2, u3, u4). Additionally, the occultation model implemented in batman also requires the planet over star flux ratio (Fp/F*) that drives the amplitude of the occultation. However, when the occultation is observed as part of, or in combination with a PC, we fix the flux ratio and the out-of-occultation flux to 1 and the occultation model is multiplied by the PC model. The occultation depth is thus defined by the PC’s amplitude at superior conjunction. The parametrisation that we used for the orbital parameters includes the stellar density (ρ*), the planetary orbital period (P), the time of inferior conjunction (tic), the products of the planetary orbital eccentricity by the cosine and sine of the argument of periastron passage of the planet’s orbit (e cos ω, e sin ω), and the cosine of the planetary orbital inclination (cos i).
We used five different models for the PC. The first model, FCos, is an empirical model which models the phase curve variations with a cosine function and is described by
![${F_{{\rm{Cos}}}} = {F_{\rm{n}}} + {{{A_0}} \over 2} \cdot \cos \,\,\left[ {{{2\pi } \over P}\left( {t - {t_{{\rm{ic}}}}} \right) - {\phi _0} + \pi } \right].$](/articles/aa/full_html/2024/04/aa48270-23/aa48270-23-eq18.png) (1)
(1)
The first term, Fn, quantifies the ratio of the planetary night-side flux over the stellar flux while the second term describes the phase variations with a cosine function of amplitude A0 and phase offset ϕ0.
The second model, FCos+Gauss, is another empirical model which adds a Gaussian to the cosine phase curve model to capture sharp features that the cosine function cannot (see Sect. 4.3). The expression for this model is
![${F_{{\rm{Cos + Gauss}}}} = {F_{{\rm{Cos}}}} + {A_1} \cdot \exp \,\left[ {{{{{\left( {\phi - {\phi _1}} \right)}^2}} \over {2 * \sigma _1^2}}} \right],$](/articles/aa/full_html/2024/04/aa48270-23/aa48270-23-eq19.png) (2)
(2)
where A1 is the amplitude of the Gaussian component, ϕ1 is the planetary orbital phase around which this component is centred and σ1 is the standard deviation, quantifying the width of the Gaussian component. The orbital phase ϕ is defined as 2π[(t – tic)%P – 0.5], where % is the modulo operator meaning that ϕ is ± π at mid-transit and equal to zero at half a period after mid-transit (at mid-eclipse for circular orbits).
We also used a third model, FGauss+Gauss, in an attempt to better capture the shape of the CHEOPS phase curve: a shape which seems to be composed of a broad feature which is a bit sharper than a cosine function and a second even sharper feature. More details are provided in Appendix B.1. The expression for this model is
![${F_{{\rm{Gauss}} + {\rm{Gauss}}}} = {F_{\rm{n}}} + {A_0} \cdot \exp \,\,\left[ {{{{{\left( {\phi - {\phi _0}} \right)}^2}} \over {2 * \sigma _0^2}}} \right] + {A_1} \cdot \exp \,\,\left[ {{{{{\left( {\phi - {\phi _1}} \right)}^2}} \over {2 * \sigma _1^2}}} \right].$](/articles/aa/full_html/2024/04/aa48270-23/aa48270-23-eq20.png) (3)
(3)
The fourth and fifth models are physically driven and aim at confronting physical hypothesis against the observed data. The fourth model, Kelp,therm, is designed to represent the thermal PC and uses the implementation provided by the kelp Python package (Morris et al. 2022). It describes the two-dimensional thermal brightness map of the exoplanet using parabolic cylinder basis functions which are a generalisation of the spherical harmonics. This set of functions has been shown by Heng & Workman (2014) to be adequate solutions to the equations describing the thermal behaviour of hot gas giants. Morris et al. (2022) have also shown that they can reproduce the outputs of general circulation models with enough precision for most current applications. Following the recommendations of Morris et al. (2022), we use only the basis function (Cl,m) of degree l = 1 and order m = 1. We also fixed the dimensionless fluid number (α) to 0.6, the dimensionless drag frequency (ωdrag) to 4.5 and the input bond albedo (A′B) to 0. We refer the reader to Morris et al. (2022) and reference therein, Heng & Workman (2014) in particular, for a more detailed explanation of these quantities. Besides the occultation model’s parameter and the fixed parameters that we just mentioned, this model depends on a few additional parameters: the greenhouse factor (f′), the planetary orbital phase offset (ϕKelp) and the amplitude of the basis function of degree and order 1 (C1,1). We note that ϕKelp is not exactly equivalent to the traditional hotspot offset as represented by ϕ0 in the cosine model. However, for values of ωdrag ≳ 3, we fixed it to 4.5 and found that the difference between the two is negligible (Morris et al. 2022). Finally, Kelp,therm requires us to specify the stellar spectrum and spectral transmission of the observations. For the stellar spectrum, we use a synthetic spectrum generated with the PHOENIX-ACES-AGSS-COND code by Husser et al. (2013) with an effective temperature (Teff) of 6300 K and a log g of 4.5 (see Sect. 3).
The fifth model, Kelp,refl, is designed to represent the reflected light PC produced by a planet with inhomogeneous reflective properties. It uses the implementation provided by the same kelp Python package, but described in Heng et al. (2021). The planetary day-side is decomposed into two regions that reflect light according to the Henyey-Greenstein law. One region has a low or baseline reflectivity characterised by a single scattering albedo ω0 and spans between the two longitudes x1 and x2. The other region, which occupies the rest of the day-side, has an increased reflectivity described by a single scattering albedo equals to ω0 + ω′ where ω′ is a positive number. This model also use Ag as parameter. From Ag, ω0, ω′, x1, x2, we can compute the scattering asymmetry (g) which is assumed to be identical in both regions. A value of g of −1, 0 and 1 corresponds to purely reverse, isotropic and forward scattering respectively (Heng et al. 2021).
Regarding the impact of the instruments on the data, we divided the model into two components, one that is specific to each instrument and which was described in the sections specific to each instrument (Sects. 2.1, 2.2, 2.4) and the other which is identical for each instrument. For all instruments, we need to account for the contamination of the light curve, also called 3rd light, coming from other stars than the target. This contamination can be considered as an instrumental effect as it can heavily depend on the angular resolution of the instrument. As such, we introduce a contamination factor parameter (c) for each instrument. The astrophysical models of the light curve described in the previous paragraphs are multiplied by (1 – c) to account for the effect of contamination. In our case and for all instruments, the contamination of the light curve is completely dominated by the contamination due to WASP-76 b that we estimated in Sect. 3. Another aspect common to all instruments is the photometric offset. All the astrophysical models mentioned before assume that the light curve is normalised. In the absence of stellar activity, this means that the stellar flux is equal to 1 in relative flux. The normalisation of the light curves performed prior to their modelling is rarely accurate enough. To mitigate that, for each instrument, we introduce a photometric offset parameter ((ΔF/F)*) that is added to the light curve model (including the contamination and the rest of the astrophysical model) to account for an imperfect normalisation.
WASP-76 b’s Ag estimates.
4.2 Fitting procedure
In order to fit the models to the data, we maximised the posterior probability of the model parameters. The likelihood involved in the posterior computation is a Gaussian likelihood with a jitter parameter (σinst) that is added in quadrature to the data’s error bars (Baluev 2009). We used one jitter parameter per instrument. The priors on the parameters were chosen to reflect physical boundaries or prior knowledge of the system from datasets independent of the ones used in this paper. The priors are described in more detail in Appendix D. In order to efficiently explore the parameter space and find and explore the vicinity of the global maximum of the posterior, we used the Python software emcee, which implements the affine invariant Markov chain Monte Carlo (MCMC) Ensemble sampler (Goodman & Weare 2010; Foreman-Mackey et al. 2013). We checked the convergence of the exploration using a modified version of the Geweke convergence criterion adapted to the multiple MCMC chains that emcee provides (Geweke 1992). We only conserved the iterations obtained after convergence. The best value of each parameter is defined as the 50th percentile of the converged iterations. As a consequence, we defined our best model as the model for which the value of each parameter is set to the best value. For the 68 % confidence interval, we use the 16th and 84th percentiles.
 |
Fig. 1 Reduced and phase-folded light-curves in CHEOPS, TESS, Spitzer-IRAC1 and Spitzer-IRAC2 bandpasses: The light-curves are corrected from the contamination and from modelled instrumental systematic. The zero flux level is set as the stellar flux, except for the Spitzer-IRAC1 data where, in the absence of a reliable PC, we set the out-of-transit and the out-of-eclipse flux level to zero. Here, we only show the data acquired around occultations. The grey points are the individual measurements. The red ones are their mean values within orbital phase bins regularly distributed. The solid red line represents the best model (see Sect. 4.2) using the cosine phase-curve model (described in Sect. 4.1). The solid blue and orange lines represent the two GCM models with low and high friction (see Sect. 5.2.2). Top: light curves displayed focusing on the transit. Bottom: focus on the PCs. |
4.3 Results
We first fit separately all the data obtained by each instrument using the cosine model for the PC. The instrumental models are described in Sect. 2 and the astrophysical models in Sect. 4.1. Figure 1 presents the reduced and phase-folded data of CHEOPS, TESS, Spitzer-IRAC1, and IRAC2 channels with the best models. Table 1 summarises the main results. The full table with all inferred parameters is provided in Appendix D.
We then fit the Spitzer-IRAC1 and Spitzer IRAC2 data with the Kelp,therm PC model (see Sect. 4.1) to provide a more physically motivated fit of the Spitzer PCs which will help the physical interpretation of the phase curves in terms of day and night-side temperature, Bond albedo, and redistribution factor that will be discussed in Sect. 5.2.1. Table 1 provides the main quantities obtained from the fit and the full table with all inferred parameters is provided in Appendix D.
The TESS and CHEOPS phase curves both display a flux excess before the eclipse (see Fig. 1). The width of this flux excess appears too small to be properly captured by the Cos or Kelp therm models. As such, we perform an additional fit of these data using the Cos+Gauss model for TESS and Gauss+Gauss model for CHEOPS, see Appendix B.1 for more details on the choice of models. Figure 2 presents the phase-folded light curves resulting from these fits. Table 1 presents the main quantities obtained from this fit that correspond to the first and widest component of both models. The quantities specific to the second narrowest component of the model are presented in Table 4. These results are discussed in Sect. 6.2 and the full table of inferred parameters is provided in Appendix D.
We also attempt to fit a more physically motivated model to the TESS and CHEOPS phase curves using a combination of the cosine model for the thermal contribution and a Kelp,refl model for the reflected light component. Figure 3 presents the phase-folded light curves resulting from these fits. Table 1 presents the main quantities obtained from this fit that correspond to the cosine components and the quantities specific to the Kelp,refl component of the model are presented in Table 5. These results are discussed in Sect. 6.2 and the full table of inferred parameters is provided in Appendix D.
Finally, in order to derive the most precise constraints on the orbits of WASP-76 b, we perform a fit of all the datasets together (CHEOPS, TESS, IRAC1 and IRAC2). We adopt the Cos phase curve model as it is the one with the lowest number of parameters and which is the least costly computationally. The full table of retrieved parameters is provided in Appendix D.
 |
Fig. 2 Reduced and phase-folded light-curves in CHEOPS and TESS bandpasses using the Cos+Gauss and Gauss+Gauss phase curve models: light-curves are corrected from the contamination and from modelled instrumental systematic. The zero flux level is set as the stellar flux. The grey points are the individual measurements. The red ones are their mean values within orbital phase bins regularly distributed. The solid black line represents the best model (see Sect. 4.2) using the Gauss+Gauss phase-curve model for CHEOPS and the Cos+Gauss model for TESS (both described in Sect. 4.1). The top two panels present the reduced phase-folded light curve of and residuals of the CHEOPS data and the bottom two panels are for the reduced phase-folded light curve of and residuals of the TESS data. |
Parameters of the second component of the Cos+Gauss and Gauss+Gauss PC models inferred from the TESS and CHEOPS light curves.
5 1D and 3D atmospheric models
5.1 1D emission spectra modelling
5.1.1 Modelling framework
We characterised the atmospheric properties of WASP-76 b by applying a suite of atmospheric retrievals constrained by the observed occultation spectra of the planet. To this end, we employed the open-source PYRAT BAY modelling framework (Cubillos & Blecic 2021), which enables atmospheric modelling, spectral synthesis, and atmospheric Bayesian retrievals. The atmospheric model consists of 1D parametric profiles of the temperature, volume mixing ratios (VMR), and altitude as a function of pressure. Our atmospheric model for WASP-76 b extends from 10−9 to 100 bar. For the temperature profile model, we adopted the prescription of Guillot et al. (1996). We modelled the composition under thermochemical equilibrium according to the temperature, pressure, and elemental composition at each layer. We adopted a network of 45 neutral and ionic species that are the main bearers of H, He, C, N, O, Na, Si, S, K, Ti, V, and Fe. We parameterised the chemical model by the elemental abundance of carbon, oxygen, and all other metals with respect to solar values (labelled [C/H], [O/H], [M/H], respectively). Finally, we computed the altitude of each layer assuming hydrostatic equilibrium.
For each atmospheric model, PYRAT BAY then computes the emission spectrum considering opacities from alkali lines (Burrows et al. 2000), Rayleigh scattering (Kurucz 1970), collision-induced absorption (Borysow et al. 1988, 1989, 2001; Borysow & Frommhold 1989; Borysow 2002; Jørgensen et al. 2000), H− bound-free and free-free opacity (John 1988), exo-mol molecular line lists for H2O, NH3, HCN, TiO, and VO (Tennyson et al. 2016), and HITEMP molecular line lists for CO, CO2, and CH4 (Rothman et al. 2010). To process the large molecular line-list opacity files, we applied the REPACK package (Cubillos 2017) to extract the dominant line transitions. To manage the atmospheric retrieval exploration PYRAT BAY uses the MC3 package (Cubillos et al. 2017), in this case using the Nested-sampling algorithm implemented via PyMultiNest (Feroz et al. 2009; Buchner et al. 2014).
The main goal of these retrieval analyses is to disentangle the thermal emission from the reflected light component of the occultation depths, with which we can later infer the Ag of WASP-76 b (see Sect. 6.1). Since our retrieval framework does not account for reflected light, we conducted the retrieval analyses only using the IR (longer wavelength) HST WFC3 and Spitzer occultation measurements, where the emission spectrum is dominated by thermal emission. Then as a post-process step, we derived from the retrieval posterior distributions the model-expected thermal emission at the CHEOPS and TESS bands. The residuals between the observed and thermal-modeled depths are then the planetary reflected light, which constrains the Ag (see Sect. 6.1).
Given the significant differences between the occultation depths derived from the HST and Spitzer observations (Appendix B.3 and Sect. 2.4), we opted to run retrieval analyses for three data sets: Dataset 1 (D1) includes only the HST WFC3 depths from E20. Dataset 2 (D2) includes the HST WFC3 depths from E20 and our Spitzer depths. Lastly, dataset 3 (D3) includes the HST WFC3 and Spitzer depths from Fu et al. (2021). This enabled us to perform a comprehensive exploration of the plausible physical scenarios for WASP-76 b, as well as compare our results to those of the literature.
Finally, we considered different scenarios for the presence of TiO and VO in the atmosphere. These molecules are strong absorbers in the optical and can significantly alter the emission spectrum (Fortney et al. 2008); however, an unambiguous detection of these species has remained largely elusive, even for some of the most highly irradiated planets (Hoeijmakers et al. 2022). It is possible that these heavy molecules condense out of the observable atmosphere in what is called a cold trap (Lodders 2002; Spiegel et al. 2009). Therefore, we ran retrieval analyses considering three scenarios: with TiO and VO, with VO only (motivated by Pelletier et al. 2023), and without TiO and VO.
5.1.2 Retrieval results
Figure 4 shows the retrieved spectra and temperature profiles for the retrievals including TiO and VO opacity. Each one of the three datasets leads to different spectra and thermal structures. To interpret these results we need to understand how the absorbers impact the thermal emission spectrum. The WFC3 wavelength range is dominated by a strong H2O opacity band at λ > 1.32 µm. A thermal inversion would then lead to a higher brightness temperature at these longer wavelengths since the stronger H2O opacity makes the atmosphere opaque at higher altitudes (i.e. the H2O features show as emission bands). In contrast, without a thermal inversion, the H2O bands show as absorption bands, and the emission at longer wavelengths will have a brightness temperature lower than that at the shorter wavelengths.
The retrieval of the D1 dataset, which considers only the HST/WFC3 occultation depths from E20, produce a thermal inversion since the depths over the H2O band have brightness temperatures slightly larger than those at the shorter wavelengths (see Fig. 5). Consequently, the contribution functions show that the WFC3 bands probe the pressures where the temperature inversion occurs (~ 10−2 bar).
When adding the Spitzer occultations from this work to the retrieval constraints (D2 dataset), we obtained a non-inverted thermal profile. This occurs because the Spitzer depths (in particular at 3.6 µm) have noticeably lower brightness temperatures than the WFC3 depths, requiring absorption bands from carbon-based species (mainly CO and CH4). This is shown by the Spitzer depths sitting below the blackbody model at T = 2630 K (dashed grey curve) consistent with the E20 depths. In this case, the WFC3 depths probe pressures where the atmosphere is nearly isothermal. Considering the noticeable scatter in the E20 depths and their relatively weak statistical evidence for a thermal inversion (not a strong variation in brightness temperatures) it is not unexpected for the retrieval to prefer the non-inverted solution.
This suggests that the Spitzer and HST data are incompatible to some degree.
Finally, when retrieving the F21 dataset (D3), we find the opposite scenario as for D2. Now the Spitzer depths have larger brightness temperatures than the WFC3 depths, leading the retrieval toward thermal inversion profile, while also remaining largely isothermal over the pressures probed by WFC3. Although this result appears more consistent with the D1 analysis, both showing a thermal inversion, the behaviour at short wavelengths is notoriously different, allowing for signs of TiO features for the D1 analysis. This stands in contrast to the lack of signs of TiO for the D3 analysis.
For each of the retrieval runs we computed the emission spectra from the posterior distributions, including at the short wavelengths covering the CHEOPS and TESS bands to estimate their thermal emission flux (Fig. 4, inset). Overall, given the retrieved thermal profiles, neither the D2 nor D3 datasets show any evidence for TiO or VO features at any wavelength. Only the D1 retrievals show TiO absorption at λ < 1.0 µm, thus affecting the estimated thermal emission over the CHEOPS and TESS bands (though it does not significantly impact the IR spectra). Therefore, the choice of dataset has the largest impact on the expected thermal emission at the CHEOPS and TESS bands. We found no indications of VO having an impact on the retrieved spectra.
When comparing our retrievals to their respective equivalents in the literature (D1 to E20 and D3 to F21) we obtained qualitatively consistent results. The composition posterior distribution parameters are generally broad or unconstrained (Fig. C.2), therefore, we should not read too much into their specific values, particularly considering that these results are based on multi-epoch observations with sparse spectral coverage. However, their rough distribution and correlations reveal the general properties of the spectra. The D1 retrievals support sub-solar C/O ratios, allowing for the presence of oxygen-bearing species like H2O, TiO, and VO. In contrast, the D2 and D3 retrievals support supersolar C/O ratios, favouring carbon-bearing species like CO and CH4 (Fig. C.3). In the D2 and D3 runs, TiO and VO are severely depleted, with volume mixing ratios remaining below the 10−10 level at the pressures probed by the observations. This is well consistent with the retrieved spectra shown in Fig. 4. Lastly, as a result of this dichotomy between oxygen-and carbon-dominated outcomes, for the D1 retrievals, we found that the expected pressures probed by the CHEOPS and TESS bands are at lower pressures than those of HST and Spitzer (due to the larger opacity from the oxygen-bearing species TiO and VO). For the D3 retrievals the CHEOPS and TESS bands probe similar pressures than HST (this time Spitzer probes lower pressures due to the carbon-bearing species CO and CH4). Appendix C presents the parameter posterior distribution for all of our retrieval runs.
 |
Fig. 3 Reduced and phase-folded light-curves in CHEOPS and TESS bandpasses using the Cos+Kelp,Refl phase curve models. As in Fig. 2, the light-curves are corrected from the contamination and from modelled instrumental systematic. The zero flux level is set as the stellar flux. The grey points are the individual measurements. The red ones are their mean values within orbital phase bins regularly distributed. The solid black line represents the best model (see Sect. 4.2) using the Cos+Kelp,refl phase-curve model for CHEOPS and TESS (described in Sect. 4.1). The top two panels present the reduced phase-folded light curve of and residuals of the CHEOPS data and the bottom two panels are for the reduced phase-folded light curve of and residuals of the TESS data. |
Parameters of the Kelp,refl component of the Cos+Kelp,refl model inferred from the TESS and CHEOPS light curves.
 |
Fig. 4 WASP-76 b occultation atmospheric retrievals. Left: light blue, dark blue, and orange curves and their associated shaded areas show the retrieved spectrum and 68% credible intervals when fitting the D1, D2, and D3 occultation observations, respectively (see legends). These retrievals include both TiO and VO opacities. The blue, red, and purple markers with error bars show the occultation depths from E20, F21, and this work, respectively. The grey markers show the CHEOPS and TESS occultation measurements, although the fits are not constrained by these observations. The dashed grey curves show spectra for two blackbody planetary models at 2480 and 2630 K (matching the HST observations). The grey curves at the bottom show the throughputs for the photometric bands. Inset: zoom on the CHEOPS and TESS wavelengths. The coloured square markers show the respective models integrated over these bands. Right: retrieved temperature profiles for each retrieval run (median and 68% credible interval). The curves at the left edge show the contribution functions, indicating the pressures probed by the observations. The colour code is the same as for the retrieved spectra (see legends). |
 |
Fig. 5 WASP-76 b occultation atmospheric retrievals zoomed over the HST-WFC3 bandpass. Models and data are the same as in Fig. 4. |
5.2 PC modelling
Phase curves are complex, but extremely informative observational diagnostics. They are currently one of the very few observational constraints that allow us to study the spatial inhomogeneities of exoplanets’ atmosphere (examples of other methods can be found in Ehrenreich et al. 2020; Gandhi et al. 2023; Falco et al. 2022; Pluriel et al. 2022; Zingales et al. 2022). In the Spitzer IRAC 1 and IRAC 2 bandpasses, where we expect the reflected light to be negligible, phase curves are a measure of the longitudinal temperature map (e.g. Cowan & Agol 2008; Knutson et al. 2007). At visible wavelengths and in the context of UHJs, phase surves can still probe the longitudinal temperature map (but not necessarily at the same pressure level as in the IR) and may also describe the longitudinal distribution of reflected light (clouds, hazes, e.g. Morris et al. 2022; Parmentier et al. 2016).
5.2.1 Day- and night-side temperatures, Bond albedo, and redistribution factor
In Table 2, we computed the day- and night-side brightness temperatures of WASP-76 b in the Spitzer IRAC2, IRAC1, TESS, and CHEOPS bandpasses using two different methods. The first one relies on the fit of the phase curve obtained with the cosine model (see Sect. 4.1). We used the transit depth, the eclipse depth, the night side flux measurements (see Table 1) and Eq. (6) from Cowan & Agol (2011) to compute the day- and night-side brightness temperatures. The second method relies on the fit of the phase curve obtained with the Kelp,therm thermal phase curve model (see Sect. 4.1). The Kelp,therm model allows us to directly fit a temperature map which can then be integrated to compute the day and night-side temperatures and uses PHOENIX stellar models from Husser et al. (2013) to compute the stellar flux in each bandpass which provides an arguably more reliable measurement (Morris et al. 2022). We note that the two measurements agree within 100 K and are compatible within 3σ. In Table 2, we also provide brightness temperature measurements in Spitzer IRAC 1 and 2 bandpasses extracted from the literature by Garhart et al. (2020) and May et al. (2021). Both Garhart et al. (2020) and May et al. (2021) derived the day-side and night-side brightness temperatures following a methodology close to our first method, based on Cowan & Agol (2011). Our day-side temperature estimates are in agreement with the literature values (compatible within 2σ). However, our night-side temperature in the IRAC2 bandpass is significantly hotter (by ~450 K) than the one derived by May et al. (2021). This discrepancy is not related to the interpretation of the light curve and resides in the difference in the data reduction of the Spitzer data (see Sect. 2.4). It is a representative example of the challenges that can still exist in the reduction of Spitzer planetary phase curve observations.
From the phase curves in the IR, if we assume that these observations allow a correct estimation of the bolometric flux emitted by the planet, we can infer the Bond albedo and energy redistribution factors of the planet (e.g. Cowan & Agol 2011). We derived these quantities from our Spitzer IRAC2 phase curve using two different methods. The first method uses Eqs. (4) and (5) of Cowan & Agol (2011) and the day- and night-side temperatures that we derived using Eq. (6) from the same authors. This methodology delivers a Bond albedo AB = −0.152 ± 0.036 and a redistribution factor ϵ = 0.319 ± 0.016. The nonphysical negative Bond Albedo indicates that some of the assumptions that we made to compute the day and night side temperature or the Bond albedo are not correct. Morris et al. (2022, Sect. 3.3) explain how the uniform day-side and night-side approach can lead to negative Bond albedo measurements and propose an alternative approach relying on the 2D temperature map that one can derive from phase curves. Using the 2D temperature map derived with our Kelp, therm phase curve model (see Sect. 4.1), we thus derive an improved estimate for the Bond albedo and the redistribution factor: AB = −0.072 ± 0.034 and ϵ = 0.289 ± 0.010. Despite the refined approach, the inferred Bond albedo is still negative but is now compatible with 0 at 2σ. The negative value still indicates a flaw in the approach. As mentioned by Morris et al. (2022), one possible explanation is that the inferred temperature map is not representative of the bolometric flux emitted by the planet. This can occur if the spectral energy distribution of the planet diverges from the one of a black body due to atomic or molecular absorption or emission (see Sect. 5.1) or because of the vertical (third) dimension ignored by the 2D thermal map.
5.2.2 GCM modelling
To assess the 3D climate of the planet, we used the 3D climate model experRT/MITgcm (Carone et al. 2020; Schneider et al. 2022), testing two scenarios with and without magnetic field interactions. The expeRT/MITgcm uses a pre-calculated grid of correlated-k opacities, where we use the S1 spectral resolution as described in Schneider et al. (2022). The selected opacity sources are Na, K, CH4, H2O, CO2, CO, H2S, HCN, SiO, PH3, FeH, Ti and VO with collision-induced absorption from H2, He and H− as well as Rayleigh scattering of H2 and He.
For the case with magnetic field interaction, we used a magnetic drag model and impose a uniform drag of timescale τdrag = 104 s to the whole modelling domain. Without magnetic drag, the simulation yields the canonical super-rotating equatorial zonal jet of a few km/s, with a small hot spot shift. Magnetic drag imposed by the interaction between the partially ionised flow at the day-side and the planetary magnetic field is expected to diminish the super-rotating jet and associated hot spot shift (e.g. Beltz et al. 2022; Komacek et al. 2017).
The choice of τdrag for WASP-76 b specifically is motivated by the work of Wardenier et al. (2021), where it was shown that such strong magnetic drag will suppress entirely the super-rotating equatorial jet and instead impose on the day-side a direct flow from the substellar point towards the night side. We selected this extreme scenario in addition to the ‘no drag’ model to compare two entirely different climate regimes – one with and one without super-rotation – thereby allowing us to explore the effects of these climates on the observations. In Fig. 1, we display the phase curves produced by these two scenarios in the Spitzer IRAC2, TESS, and CHEOPS bandpasses. This allows us to compare them with the observations. Comparing the low and high friction case, it is evident, that the magnetic drag (only present in the high friction case) reduces the hot spot shift and leads to greater day-side emission as a consequence of diminishing heat re-circulation. We can see that the high friction case (with magnetic drag) better reproduces the low bright spot offset observed at all wavelengths. On the contrary, the peak brightness tends to be better reproduced by the low friction case, except for the CHEOPS bandpass. Both models under-predict the night side flux in the IRAC2 channel. This can be due to two factors. First, the GCM that we used is cloud-free. Clouds tend to prevent efficient heat radiation to space and thus keep the night side warmer compared to a cloud-free model (Parmentier et al. 2021). Second, it does not account for the heat of dissociation of hydrogen molecules nor does it account for heating effects due to recombination which are known to increase heat transport for UHJs (Bell & Cowan 2018; Tan & Komacek 2019).
6 Discussion and conclusions
6.1 Challenge of deriving accurate Ag
By extending the retrieved emission spectra (see Sect. 5.1.2) over the CHEOPS and TESS bands, we can estimate how significant the thermal emission is at these wavelengths, and thus estimate the fraction of reflected light required to explain these observations and infer Ag. Table 3 provides the Ag estimates obtained from the different emission retrievals described in Sect. 5.1.2. The inferred Ag significantly depends on the dataset used to constrain the emission model. In all cases when the HST-WFC3 eclipses extracted by E20, whether it is in combination with our reduction of the Spitzer data or not (datasets D1 or D2), the albedo in the TESS and CHEOPS bandpasses are compatible.
Without TiO, Ag is around 0.11 in both bandpasses, whereas with TiO it is around 0.073 in CHEOPS and below 0.13 in TESS. When we use the WFC3 and Spitzer eclipses extracted by F21, the TESS and CHEOPS Ag are no longer compatible. The TESS Ag being ~30% higher than the CHEOPS one.
Table 3 illustrates the complexity of deriving accurate Ag for the ultra-hot of hot Jupiter population. For this class of planet, the contribution of thermal light to the visible measurements cannot be neglected. Neither HST nor Spitzer were designed for exoplanet sciences and their datasets present multiple data reduction and analysis challenges. Despite the tremendous improvements made over the year, there are still cases like WASP-76 b for which the data reduction remains a challenge (see Sects. 2.3 and 2.4). In these cases, the uncertainty associated with the reduction of the IR is the dominant factor that limits our precision on the determination of Ag in the optical. This emphasises the importance of IR space observatories whose design accounts for the specificities of exoplanetary science like JWST and Ariel for the full exploitation of CHEOPS and TESS in this particular context.
Nevertheless, we can attempt to put these results in context. Table 6 gathers the estimates of Ag at visible wavelength that we found in the literature. It shows that, as far as we can tell given the precision of our estimates, WASP-76 b is not standing out. It fits into the majority of UHJ’s that have a relatively low reflectivity (Ag ~ 0.1) as also noticed from a smaller and less precise sample by Mallonn et al. (2019). However, a few outliers seem to emerge on both sides of the distribution. KELT-1 b in the CHEOPS bandpass and WASP-18b in the TESS band-pass appears singularly black (Ag < 0.04, see Parviainen et al. 2022; Wong et al. 2021). Contrary to KELT-1 b and Kepler-13 b in the TESS bandpass which appears unusually reflective (Ag ~ 0.40, see Parviainen et al. 2022; Wong et al. 2021). KELT-1b and WASP-18b, two of the three outliers, are massive planets with higher gravity than most others in the sample. Zhang et al. (2018) reported a negative correlation between mass and Ag. As proposed by Heng & Demory (2013, Eq. (10)), a high gravity could promote rapid settling of cloud particles and explain the low albedo of WASP-18b in the TESS bandpass and KELT-1 b in the CHEOPS bandpass. However, It’s necessary here to remark that, in the case of KELT-1 b, Parviainen (2023) identified variability as a potential explanation for the behaviour of KELT-1 b in CHEOPS and TESS. A more systematic and homogeneous analysis of the available data might help to identify trends and variability in this population. Finally, Table 6 highlights the tremendous impact that CHEOPS and TESS already had on tackling this isssue over the last three years.
6.2 Phase-curve asymmetry
One specificity of WASP-76 b is the contrast between the asymmetry between the two limbs of the planet observed via high-resolution transit spectroscopy in the visible by Ehrenreich et al. (2020), Kesseli et al. (2020) and Pelletier et al. (2023) and the absence of asymmetry in the IR phase curve observed by May et al. (2021) and confirmed by our re-analysis of the Spitzer data (see Sect. 2.4, Fig. 1 and Table 1). All GCMs that attempted to replicate the high-resolution transit spectroscopy results invoke a weak drag scenario which implies a significant hotspot offset in IR phase curves (Savel et al. 2022; Wardenier et al. 2021).
May et al. (2021) proposed that the IR and the visible observations could probe two different layers of the atmosphere with two different wind patterns. The CHEOPS and TESS phase curves presented in Sects. 2.1 and 2.2, and Fig. 1 are thus particularly relevant to draw a more complete picture of WASP-76 b and attempt to reconcile high spectral resolution and broadband photometric data. As described in Sects. 2.1, 2.2, and 4, we paid great care to address as accurately as possible the shape and potential asymmetry in these two phase curves using different models and simultaneous detrending of instrumental variations. Table 1 shows that using a cosine phase curve model to fit the visible light curves does not yield a more significant asymmetry than the one obtained with the Spitzer light curves. However, as already mentioned in Sect. 4.3, looking carefully at Fig. 1, we can see that both CHEOPS and TESS phase curves display a slight increase of the flux before the eclipse. We can also notice that in the CHEOPS bandpass the width of the cosine function is superior to the width of the measured phase-curve. Thus, we used slightly more complex models with two components to capture these features: a cosine and Gaussian function for the TESS data and two Gaussian functions for the CHEOPS data (see Sect. 4 for more details). Figure 2, along with Tables 1 and 4 show that these new models are able to capture these excesses of flux. Given the precision of the estimates, the parameters of the Gaussian functions which capture the narrow flux excess are compatible in both bandpasses. The amplitudes and width are well consistent within 1 σ with amplitudes around 43 ppm, mean orbital phase offset around −33°. The standard deviations, which quantify the width, are slightly less consistent but still compatible at 1 σ and around 21°.
While additional observations are required to increase the significance of the detection of this flux excess. This observation indicates new avenues towards a better understanding of the atmosphere of WASP-76 b. The first avenue, already evoked by May et al. (2021) is the possibility that the dynamic of the atmospheric layers probed at visible and IR wavelengths are different. The tentative asymmetry of the phase curve at visible wavelength would indicate an asymmetric wind pattern from the west to the east in the layers probed by the visible band-passes while it remains symmetric in the layers probed by the IR. Seidel et al. (2021) also reported observations indicative of a change in the wind pattern with altitude. From a detailed analysis of the shape of the Na doublet observed at high spectral resolution with HARPS and ESPRESSO during transit, they inferred a uniform day-to-night wind of ~5 km s−1 in the lower atmosphere and a vertical wind of ~23 km s−1 higher up in the atmosphere connecting the interior to the evaporating exosphere. While both our and Seidel et al. (2021) interpretations invoke a change of the wind pattern with altitude, the patterns appear different.
The second avenue to explain a flux excess before eclipse is scattering. The flux excess observed in our visible phase curves is narrower than what is expected from thermal phase curves (Cowan & Agol 2008). This is confirmed by the fact that both our cosine and Kelp,therm models failed to properly capture these narrow flux excess. Thermal phase curves are the convolution of the longitudinal temperature map with the visible hemisphere of the planet. As such even if present, any odd mode of the temperature map is invisible in the thermal phase curve and the amplitudes of high-order modes are strongly attenuated. Reflected light phase curves are the convolution of the longitudinal reflective properties including the scattering phase function, the visible hemisphere and the illuminated hemisphere of the planet. Reflected light phase functions can thus produce narrower features in the phase curve. Therefore we attempted to reproduce the data with a model composed of a cosine function, to represent the thermal component of the phase curve, and, for the reflected light component, a model which represents the day-side of the planet with two regions that behave as Henyey-Greenstein reflector with different single scattering albedo (see Sect. 4). As shown in Table 5, the fits in both bandpasses point towards reverse scattering (g ~ −0.45), a western hemisphere with low reflectivity and a more reflective region on the second half of the Eastern hemisphere, close to the terminator (x2 ~ 40°). Sophisticated cloud scattering models such as Chubb et al. (2024) could, for example, use this kind of information to yield constraints on cloud particle composition, complementary to JWST observations. However, the current uncertainties do not allow for a deeper interpretation. The fit of the reflected light component is mostly unconstrained by the TESS data. While it is better constrained by the CHEOPS data, Fig. 3 displays a visually poorer fit than the one obtained with the empirical Cos+Gauss and Gauss+Gauss models (Fig. 2). It appears that the reflected light model that we used does not aptly reproduce the narrow flux excess observed before eclipse.
A narrow increase of the reflected light before eclipse has already been observed in the reflected light phase curve of Venus. García Muñoz et al. (2014) attributed this feature to glory (Adam 2002; van de Hulst 1981). Glories are commonly observed on Earth and are due to the backscattering of light by spherical droplets often found above liquid clouds. In the case of WASP-76 b, the flux increase is only observed on one side of the eclipse. Explaining the observation with the glory effect would require spherical droplets or highly reflective spherically shaped aerosols and clouds on the planet’s eastern hemisphere and not on the western hemisphere or with different properties that would not produce such a strong effect.
This hypothesis resonates with two previously proposed scenarios to explain the asymmetry observed in high spectral resolution transit spectroscopy. In the original paper reporting these observations, Ehrenreich et al. (2020) proposed that iron could condensate after the eastern terminator of WASP-76 b and effectively deplete the upper layers of the western terminator of iron. Condensation of iron or any other species could explain the presence of spherical droplets necessary to the glory effect on one side of the planet and not on the other.
Following this discovery, Savel et al. (2022) attempted to reproduce the observations using GCMs. They were unable to reproduce the observations with iron condensation alone in their self-consistent GCM modelling approach. They obtained better agreement when they added in post-processing an asymmetric cloud coverage that is thicker in the eastern part of the night hemisphere and a slight eccentricity to the planet’s orbit. Their finding is again in broad qualitative agreement with the glory hypothesis. Savel et al. (2022) do not propose a scenario for the formation of these clouds and mention that the exact composition of these clouds doesn’t affect the quality of the fit. However, we note that our joint analysis of the CHEOPS, TESS and Spitzer dataset, doesn’t confirm the hypothesis of a small orbital eccentricity. Savel et al. (2022) proposed an eccentricity of around 0.017. We find a 3 σ (99.7% confidence) upper limit of 0.0067.
More recently, Pelletier et al. (2023) reported new high spectral resolution transit spectroscopy observations of WASP-76 b. They confirmed the asymmetry observed by Ehrenreich et al. (2020) with iron, but also announced similar asymmetric signatures for multiple species with different condensation temperatures indicating that condensation of iron might not be the phenomenon responsible for these signatures. However, the presence of droplets due to the condensation of another species would explain the glory effect and the associated clouds would explain the high-resolution transit spectroscopy observations.
Helling et al. (2021, 2023); Baeyens et al. (2022) have shown that cloud and chemistry asymmetries between the morning and evening terminator can be expected on an ultra-hot Jupiter like WASP-76 b. But theoretical considerations, support a more complex scenario as opposed to simple liquid iron condensation. Helling et al. (2023, Fig. 10) have shown that clouds at the eastern terminator of such ultra-hot Jupiters should exhibit a mixture of particle sizes and material, mainly high-temperature conden-sates3: TiO2[s], Fe[s], A12O3[s], CaTiO3[s], and FeS[s]. Thus, it is still very much under discussion how signs of terminator differences can be interpreted.
A few elements challenge our hypothesis of a glory effect and associated clouds. The first element is their location on the Eastern hemisphere of the planet. Most observational constraints and global circulation models discussing clouds on the day-side of hot giant exoplanets favour the presence of clouds in the Western hemisphere (e.g. Hu et al. 2015; Parmentier et al. 2016; Lee et al. 2016; Helling et al. 2019). Clouds form on the cool night-side and are advected towards the day-side via equatorial west to east super-rotational jets. However, in the case of WASP-76 b, we do not observe a clear hot-spot offset in the Spitzer phase curve which puts into question the existence of west-east super-rotational jets for this planet (see Sect. 4.3 and also Wardenier et al. 2021). Without the west-east jets to advect the clouds from the night-side, they are not more likely to be present in one hemisphere compared to the other. However, the challenge becomes to form them on the day-side. The second element that challenges our hypothesis is the poor illumination near the terminator. Quantitative modelling is required to understand if even a strong increase in the reflectivity localised around this region can explain the observation.
The confirmation of the scenarios responsible for the observed phase curve asymmetry would thus require a quantitative assessment and additional observations to confirm the properties of the flux excess reported in this paper. Both aspects are out of the scope of this paper. However, it does represent an engaging avenue for pursuing a comprehensive view of WASP-76 b’s atmosphere.
UHJ Ag measurements.
Acknowledgements
We acknowledge the careful review and comments from the referee Nick Cowan. CHEOPS is an ESA mission in partnership with Switzerland with important contributions to the payload and the ground segment from Austria, Belgium, France, Germany, Hungary, Italy, Portugal, Spain, Sweden, and the UK. The CHEOPS Consortium would like to gratefully acknowledge the support received by all the agencies, offices, universities, and industries involved. Their flexibility and willingness to explore new approaches were essential to the success of this mission. CHEOPS data analysed in this article will be made available in the CHEOPS mission archive (https://cheops.unige.ch/archive_browser/). This work was supported by FCT – Fundação para a Ciência e a Tecnología through national funds and by FEDER through COMPETE2020 through the research grants UIDB/04434/2020, UIDP/04434/2020, 2022.06962.PTDC. O.D.S.D. is supported in the form of work contract (DL 57/2016/CP1364/CT0004) funded by national funds through FCT. P.E.C. is funded by the Austrian Science Fund (FWF) Erwin Schroedinger Fellowship, program J4595-N. V.Si., T.Zi., L.Bo., V.Na., I.Pa., G.Pi., R.Ra., and G.Sc. acknowledge support from CHEOPS ASI-INAF agreement no. 2019-29-HH.0. T.Wi. acknowledges support from the UKSA and the University of Warwick. L.Ca. and C.He. acknowledge support from the European Union H2020-MSCA-ITN-2019 under Grant Agreement no. 860470 (CHAMELEON). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (project FOUR ACES. grant agreement No 724427). It has also been carried out in the frame of the National Centre for Competence in Research PlanetS supported by the Swiss National Science Foundation (SNSF). D.E. acknowledges financial support from the Swiss National Science Foundation for project 200021_200726. PM acknowledges support from STFC research grant number ST/M001040/1. B.-O.D. acknowledges support from the Swiss State Secretariat for Education, Research and Innovation (SERI) under contract number MB22.00046. M.L. acknowledges support of the Swiss National Science Foundation under grant number PCEFP2_194576. S.G.S. acknowledge support from FCT through FCT contract nr. CEECIND/00826/2018 and POPH/FSE (EC). A.Br. was supported by the SNSA. Y.Al. acknowledges support from the Swiss National Science Foundation (SNSF) under grant 200020_192038. R.Al., D.Ba., E.Pa., and I.Ri. acknowledge financial support from the Agencia Estatal de Investigación of the Ministerio de Ciencia e Innovación MCIN/AEI/10.13039/501100011033 and the ERDF “A way of making Europe” through projects PID2019-107061GB-C61, PID2019-107061GB-C66, PID2021-125627OB-C31, and PID2021-125627OB-C32, from the Centre of Excellence “Severo Ochoa” award to the Instituto de Astrofísica de Canarias (CEX2019-000920-S), from the Centre of Excellence “María de Maeztu” award to the Institut de Ciències de l’Espai (CEX2020-001058-M), and from the Generalitat de Catalunya/CERCA programme. S.C.C.B. acknowledges support from FCT through FCT contracts nr. IF/01312/2014/CP1215/CT0004. C.Br. and A.Si. acknowledge support from the Swiss Space Office through the ESA PRODEX program. A.C.C. acknowledges support from STFC consolidated grant numbers ST/R000824/1 and ST/V000861/1, and UKSA grant number ST/R003203/1. This project was supported by the CNES. The Belgian participation to CHEOPS has been supported by the Belgian Federal Science Policy Office (BELSPO) in the framework of the PRODEX Program, and by the University of Liège through an ARC grant for Concerted Research Actions financed by the Wallonia-Brussels Federation. L.D. is an F.R.S.-FNRS Postdoctoral Researcher. M.F. and C.M.P. gratefully acknowledge the support of the Swedish National Space Agency (DNR 65/19, 174/18). D.G. gratefully acknowledges financial support from the CRT foundation under Grant No. 2018.2323 “Gaseousor rocky? Unveiling the nature of small worlds”. M.G. is an F.R.S.-FNRS Senior Research Associate. M.N.G. is the ESA CHEOPS Project Scientist and Mission Representative, and as such also responsible for the Guest Observers (GO) Programme. M.N.G. does not relay proprietary information between the GO and Guaranteed Time Observation (GTO) Programmes, and does not decide on the definition and target selection of the GTO Programme. S.H. gratefully acknowledges CNES funding through the grant 837319. K.W.F.L. was supported by Deutsche Forschungsgemeinschaft grants RA714/14-1 within the DFG Schwerpunkt SPP 1992, Exploring the Diversity of Extrasolar Planets. This work was granted access to the HPC resources of MesoPSL financed by the Région Île de France and the project Equip@Meso (reference ANR-10-EQPX-29-01) of the programme Investissements d’Avenir supervised by the Agence Nationale pour la Recherche. This work was also partially supported by a grant from the Simons Foundation (PI Queloz, grant number 327127). N.C.Sa. acknowledges funding by the European Union (ERC, FIERCE, 101052347). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. Gy.M.Sz. acknowledges the support of the Hungarian National Research, Development and Innovation Office (NKFIH) grant K-125015, a PRODEX Experiment Agreement No. 4000137122, the Lendület LP2018-7/2021 grant of the Hungarian Academy of Science and the support of the city of Szombathely. V.V.G. is an F.R.S-FNRS Research Associate. N.A.W. acknowledges UKSA grant ST/R004838/1. We acknowledge the use of the ExoAtmospheres database (http://research.iac.es/proyecto/exoatmospheres/) during the preparation of this work.
Appendix A Description of the CHEOPS observations
The detailed description of the CHEOPS observations is provided in Table A.1.
Description of the CHEOPS observations
Appendix B Comparison of different data reduction and analysis approaches
B.1 Modelling of the CHEOPS phase curve
As mentioned in Sections 4.1 and 4.3, we complicated the simple cosine phase curve model to better capture the flux excess seen before the occultation in CHEOPS and TESS phase curves (Fig. 1). We first simply added a narrow Gaussian component to the cosine (Cos+Gauss model, see details in 4.1), which appeared to convincingly model the TESS phase curve (see Fig. 2). However, for the CHEOPS phase curve we observed a strong degeneracy between the parameters of the cosine and Gaussian components. As can be seen in (Fig. 1), besides showing a flux excess before occultation, the whole CHEOPS phase curve appears narrower than the cosine function used in the model. Due to this, during the fit, the width of the Gaussian component is pulled towards high values and the amplitude of the cosine function is pulled towards lower values to better reduce the global width of the phase curve. The presence of the flux excess before occultation pulls the fit in the other direction which results in the observed degeneracy. When the number of iterations of the fitting procedure is sufficiently long, we can observe two main and distinct modes in the joint posterior distribution, see Fig. B.1 (we can actually also see a smaller third mode). For the first mode, the Gaussian component of the model has a comparatively high width (limited by the upper border of our prior) and a high amplitude, but also a small phase offset and is associated with a cosine component with a small amplitude. In this mode, the model better reproduces the width of wide phase curve variations but doesn’t reproduce the flux excess before occultation. For the second mode, the Gaussian component has a comparatively smaller width and amplitude but a stronger mean phase offset and the amplitude of the cosine function is larger. In this second mode, the model fails to reproduce the width of the wide phase curve variations but captures the flux excess before occultation.
For this reason, we decided to design another phase curve model composed of two Gaussian components: One with a large width (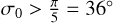 ) aimed at reproducing the wide phase curve variations and the other with a small width (
) aimed at reproducing the wide phase curve variations and the other with a small width (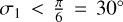 ) aimed at reproducing the sharp flux excess before occultation.
) aimed at reproducing the sharp flux excess before occultation.
 |
Fig. B.1 2D joint posterior probabilities of the fit of the CHEOPS data using the Cos+Gauss model: The full model is described in Section 4.1. For clarity, we only display a subset of the parameters of the model: A0 and A1 are the amplitudes of the cosine and Gaussian components of the model respectively. ϕ1 is the average phase offset of the Gaussian component and σ1 it’s standard deviation, both expressed in radians. |
While a correlation persists between the parameters of the two Gaussian components the posterior distribution becomes uni-modal (see Fig. B.2). As expected, we can see that the second mode of the joint posterior distribution of the Cos+Gauss model has similar characteristics (location, width) to the ones found in the mode of the Gauss+Gauss posterior distribution. However, due to the small correlation between the parameters of the two components in the Gauss+Gauss model compared to the Cos+Gauss model, even if were to isolate the second mode with the Cos+Gauss model, the uncertainties would be larger than when we use the Gauss+Gauss model. This added to a better agreement with the observed width of the wide phase curve variation led us to choose the Gauss+Gauss model for the CHEOPS phase curve.
B.2 Comparison of the TESS photometries
As mentioned in Section 2.2, we compared two different methods to obtain the photometry from WASP-76 b from the TESS data: One based on the PDC-SAP light curve and another based on the PSF-SCALPELS methodology. We have already described our PSF-SCALPELS methodology in Section 2.2. For the approach based on the PDC-SAP light curve, we cut the light curve into chunks at the time of each spacecraft momentum dump. This allowed us to more easily address the jump in the photometry that the momentum dumps can introduce. We then performed a detrending of each chunk of the light curve by fitting a cubic spline model with knots separated by three times the orbital period of WASP-76 b and we divided the light curve of each chunk by the result of their cubic spline fit. Once this detrending is done we perform the fit of the astrophysical models (see Section 4.1).
To compare the PDC-SAP and the PSF-SCALPELS methodology, we performed the fit of the data from each TESS sector separately with the cosine phase-curve model and using the two approaches. Fig. B.3 shows the posterior probability density function retrieved for a few key parameters of the models. From this figure, we note that the PDC-SAP and the PSF-SCALPELS methodology provide results which can differ by more than 1 σ. In particular the radius ratio in sectors 30 and 43, the phase curve phase offset in sectors 30 and 42 and the phase curve amplitude in sector 43. One of our objectives is to assess the amplitude and asymmetry of the phase curve in the TESS band-pass and these parameters are key in our interpretation. Contrary to our PDC-SAP methodology, our PSF-SCALPELS methodology offers a simultaneous modelling of the astrophysical model and the instrumental trends which should provide a more accurate determination of the astrophysical model parameters. For this reason, we choose to use the PSF-SCALPELS methodology for the rest of this paper. Finally, as already indicated by other studies like Wong et al. (2020, 2021), the results of this study reinforce the need to pay particular attention to the detrending of the remaining instrumental systematics of the TESS data for phase-curve studies, but also for radius determination.
 |
Fig. B.2 2D joint posterior probabilities of the fit of the CHEOPS data using the Gauss+Gauss model: The full model is described in Section 4.1. For clarity, we only display a subset of the parameters of the model: A0 and A1 are the amplitudes of the broad and narrow Gaussian components of the model respectively. ϕ1 is the average phase offset of the narrow Gaussian component and σ1 is its standard deviation, both expressed in radians. |
B.3 Comparison of the HST photometries
As mentioned in Section 2.3, HST observed two transit with the STIS instrument analysed and published in von Essen et al. (2020) and Fu et al. (2021), one transit with the WFC3 instrument analysed and published in Edwards et al. (2020) and Fu et al. (2021) and one eclipse with the WFC3 instrument analysed and published in Edwards et al. (2020) and Fu et al. (2021).
von Essen et al. (2020) and Fu et al. (2021) obtained transit depth of similar uncertainty, but von Essen et al. (2020) data show a more significant decrease of the transit depth towards the red than Fu et al. (2021). Edwards et al. (2020) and Fu et al. (2021) measure transit and eclipse depths with similar spectral variations. However, these measurements differ significantly in terms of average value and uncertainties. The transit depths measured by Fu et al. (2021) in the WFC3 bandpass are on average 490 ppm deeper than those measured by Edwards et al. (2020), which correspond to a 4% relative increase and 4.5 times the average uncertainty reported by Fu et al. (2021). Theis average uncertainty is 63 ppm higher than Edwards et al. (2020) which corresponds to a 136% increase. As far as the eclipse depths are concerned, Fu et al. (2021) measure this time depths that are on average 166 ppm smaller than Edwards et al. (2020), which correspond to a decrease of 23% and 3.3 times the average uncertainty reported by Fu et al. (2021). The uncertainties of the eclipse measurement reported by Fu et al. (2021) and Edwards et al. (2020) are very similar. Fu et al. (2021) commented on the differences with Edwards et al. (2020) and von Essen et al. (2020). They attributed these differences to a combination of the treatment of the contamination of the light curve by WASP-76 B and the contamination of several frames acquired during the transit observed with WFC3 by the passages of satellites in the field of view.
Regarding the comparison between the depth measurements of von Essen et al. (2020) and Fu et al. (2021), as the STIS visits were not affected by satellite crossing, the only possible culprit provided by Fu et al. (2021) is the contamination by WASP-76 B. Fu et al. (2021) used a similar approach to the one used in this paper (see Section 3). They fitted the SED of WASP-76 B and WASP-76 A on the available broadband photometry of the system in addition to a few flux ratios measured from high angular resolution images to estimate the radius and effective temperature of WASP-76 B. They then infer the flux of both WASP-76 A and B and the associated dilution factor in the different band-passes assuming that the photometric aperture encompasses the same fraction of the stellar flux for both stars. They use boot-strapping to estimate the uncertainties and use these estimates to correct the depth inferred from the light curve fits. As WASP-76 A and B are spatially resolved in the STIS data (see e.g. Fig. 1 of Fu et al. 2021), they purposefully extend the photometric apertures to encompass both stars. von Essen et al. (2020) use the fact the stars are spatially resolved and fit two Gaussian functions to disentangle the flux from the two stars. The approach used by von Essen et al. (2020) seems to make better use of the capacities of the STIS instrument and could be more reliable. The use of a larger aperture implies an increase in the noise and potential biases associated with bias, flat field or background corrections.
 |
Fig. B.3 Violin plot of the posterior probability density function of the parameters retrieved from the PDC-SAP and PSF-SCALPELS TESS light curves: The x-axis corresponds to the average time of each TESS sectors data from which the posteriors have been retrieved, sectors 30, 42 and 43 from left to right. The white circle in the middle of each violin plot corresponds to the median value of the distribution and the thick black line to the 68% confidence interval delimited by the 16th and 84th percentiles. We displayed only the key parameters for the planetary transit and its phase curve, from top to bottom: the radius ratio inferred from the transit, the amplitude of the phase curve, the night-side flux and the phase offset. The phase curve model used is the Cos model. More details on this model and its parameters are provided in Section 4.1. |
Regarding the comparison between the depth measurements of Edwards et al. (2020) and Fu et al. (2021), the two effects mentioned by Fu et al. (2021) are potential culprits. Fu et al. (2021) explains that there are two satellite crossing events affecting the WFC3 transit observations. While the second one has a negligible effect, the first one has a significant impact on data. They explain that while the actual crossing of the satellite happens during a single exposure, it has a lingering effect. Consequently, they discard 6 exposures after the event, while Edwards et al. (2020) discarded only two exposures due to their negative impact on the quality of the fit. Fu et al. (2021) note that removing two exposures would only result in a smaller transit depth, as obtained by Edwards et al. (2020). To treat the contamination of the light curves, Edwards et al. (2020) used the WFC3 simulator Wayne (Varley et al. 2017) to simulate images of both WASP-76 A and B separately and use them to infer the dilution factor that affects each bandpass. To simulate WASP-76 B, they used the stellar parameters inferred by Bohn et al. (2020). Bohn et al. (2020) spatially resolved WASP-76 A and B with the IDRIS-SPHERE instrument and measured the contrast between the two stars and thus the magnitude of WASP-76 B in the Ks band. From this measurement, they inferred the effective temperature and mass of WASP-76 B by comparing the observed magnitude to the one predicted by stellar models given the GAIA DR2 parallax measurement. The use, by Fu et al. (2021), of a two-component fit of the photometric SED in addition to the constraints from the high-resolution imaging should provide a more reliable estimate of WASP-76 B parameters and associated uncertainties than the one used by Edwards et al. (2020). However, the use of simulations to estimate the contribution of each star to the aperture could provide a more accurate determination of the dilution factors.
Contamination of the light curves in the HST-WFC3 bandpasses
In order to compare our estimates of the light curve contamination (see Section 3) with the one of Edwards et al. (2020) and Fu et al. (2021). We use our approach (described in Section 3) to compute the contamination and dilution factors in the WFC3 bandpasses used by Edwards et al. (2020). These values are provided in Table B.1 and Fig. B.4 shows the dilution factors estimated by the different analyses. The average dilution factor estimated by Edwards et al. (2020) is 2% higher than the one computed in this work and 4% higher than the one estimated by Fu et al. (2021). If the measured light curves by Edwards et al. (2020) and Fu et al. (2021) were the same, this would imply that Edwards et al. (2020) should obtain eclipse and transit depths that are 4% higher than Fu et al. (2021). Edwards et al. (2020) actually measure eclipse depths that are 23% higher than Fu et al. (2021) and transit depths that are 4% lower than. Consequently, the differences in the approach used by Edwards et al. (2020) and Fu et al. (2021) to estimate the contamination of the light curves by WASP-76 B cannot explain the difference in the depths that they measured. The difference between transit depths could still be explained by the treatment of the satellite crossings, but as the occultation observations were not affected by satellite crossing events, the reason for the difference in the measured occultation depths is unknown.
 |
Fig. B.4 Comparison of the dilution factors computed by different authors: E20 and F21 indicate that the blue and green dilution factors have been computed by Edwards et al. (2020) and Fu et al. (2021), respectively. |
Appendix C Occultation spectral retrievals
Table C.1 shows the retrieval model parameters, their priors, and values for all of our retrieval runs. Figure C.1 shows the retrieved spectrum and thermal profile for the runs without TiO opacity and without TiO or VO opacity. Figure C.2 shows the posterior distribution for the abundance parameters for all of our retrieval runs. Fig. C.3 shows the corresponding volume-mixing-ratio profiles for the runs including TiO and VO opacity. The other runs are qualitatively consistent.
Occultation spectral retrieval parameters and results
 |
Fig. C.1 WASP-76 b retrieved spectra and temperature profiles. Same as Figure 4 but for the runs without TiO opacity (top panels) and without TiO nor VO opacity (bottom panels). The spectra and thermal profiles show the same behaviour as the runs including TiO and VO opacity, with the only significant difference that the D1 model does not show the TiO emission over the CHEOPS and TESS bands, therefore predicting much lower thermal emission (insets). |
 |
Fig. C.2 WASP-76 b abundance parameter posterior distributions. The dashed diagonal lines in the pair-wise panels mark boundary when both variables have the same metallicity enhancement (with respect to solar values). The values at the top of each histogram panel report the median and boundaries of the central 68% credible interval for each marginal posterior. The shaded area in the histogram panels denote the span of these credible intervals. The black curves at the left edges show the contribution functions over the CHEOPS, TESS, HST, and Spitzer bands. |
 |
Fig. C.3 WASP-76 b retrieved volume mixing ratios: Volume mixing ratios derived from the posterior distributions for the case including TiO and VO opacity. The shaded areas (see legend) denote the span of the 68% credible interval for each species (only the most spectroscopically active species are shown). |
Appendix D Choice of priors and full set of retrieved parameters
In Section 4, we described the models and procedures used in this paper to fit the different light curves available. We are using a Bayesian approach and thus rely on priors to incorporate the knowledge of past observations and physical constraints into our fits. The priors used in all the light curve fits and their justifications are provided in Table D.1. Section 4 also provides a subset of the parameter estimates based on the posterior probabilities obtained in Tables 1 and 4. In Tables D.2, D.4 and D.5, we provide the full set of retrieved parameters from the joint fit of all datasets, from the fit of the CHEOPS and TESS datasets and from the fit of the Spitzer datasets, respectively.
Priors of the light curve fits
Posterior of the light curve fits of all the datasets
Posterior of the light curve fits of CHEOPS and TESS with the Cos+Kelp,refl model
Posterior of the light curve fits for TESS and CHEOPS with Cos, Cos+Gauss and Gauss+Gauss models
Posterior of the light curve fits for Spitzer
References
- Adam, J. A. 2002, Phys. Rep., 356, 229 [CrossRef] [Google Scholar]
- Akinsanmi, B. 2024, A&A, submitted [Google Scholar]
- Azevedo Silva, T., Demangeon, O. D. S., Santos, N. C., et al. 2022, A&A, 666, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baeyens, R., Konings, T., Venot, O., Carone, L., & Decin, L. 2022, MNRAS, 512, 4877 [NASA ADS] [CrossRef] [Google Scholar]
- Baluev, R. V. 2009, MNRAS, 393, 969 [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barros, S. C. C., Akinsanmi, B., Boué, G., et al. 2022, A&A, 657, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beatty, T. G., Wong, I., Fetherolf, T., et al. 2020, AJ, 160, 211 [Google Scholar]
- Bell, T. J., & Cowan, N. B. 2018, ApJ, 857, L20 [Google Scholar]
- Bell, T. J., Nikolov, N., Cowan, N. B., et al. 2017, ApJ, 847, L2 [Google Scholar]
- Beltz, H., Rauscher, E., Kempton, E. M. R., et al. 2022, AJ, 164, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W., Broeg, C., Fortier, A., et al. 2021, Exp. Astron., 51, 109 [Google Scholar]
- Blackwell, D. E., & Shallis, M. J. 1977, MNRAS, 180, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Blazek, M., Kabáth, P., Piette, A. A. A., et al. 2022, MNRAS, 513, 3444 [CrossRef] [Google Scholar]
- Bohn, A. J., Southworth, J., Ginski, C., et al. 2020, A&A, 635, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfanti, A., Ortolani, S., Piotto, G., & Nascimbeni, V. 2015, A&A, 575, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfanti, A., Ortolani, S., & Nascimbeni, V. 2016, A&A, 585, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfanti, A., Delrez, L., Hooton, M. J., et al. 2021, A&A, 646, A157 [EDP Sciences] [Google Scholar]
- Borsa, F., Allart, R., Casasayas-Barris, N., et al. 2021, A&A, 645, A24 [EDP Sciences] [Google Scholar]
- Borysow, A. 2002, A&A, 390, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borysow, A., & Frommhold, L. 1989, ApJ, 341, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, J., Frommhold, L., & Birnbaum, G. 1988, ApJ, 326, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, A., Frommhold, L., & Moraldi, M. 1989, ApJ, 336, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, A., Jorgensen, U. G., & Fu, Y. 2001, JQSRT, 68, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Brogi, M., & Line, M. R. 2019, AJ, 157, 114 [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A&A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burrows, A., Marley, M. S., & Sharp, C. M. 2000, ApJ, 531, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Carone, L., Baeyens, R., Mollière, P., et al. 2020, MNRAS, 496, 3582 [NASA ADS] [CrossRef] [Google Scholar]
- Casasayas-Barris, N., Orell-Miquel, J., Stangret, M., et al. 2021, A&A, 654, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, Proceedings of the 210th Symposium of the International Astronomical Union, IAU of ASP, 210, A20 [NASA ADS] [Google Scholar]
- Changeat, Q., Edwards, B., Al-Refaie, A. F., et al. 2022, ApJS, 260, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Chubb, K. L., Stam, D. M., Helling, C., Samra, D., & Carone, L. 2024, MNRAS, 527, 4955 [Google Scholar]
- Cowan, N. B., & Agol, E. 2008, ApJ, 678, L129 [Google Scholar]
- Cowan, N. B., & Agol, E. 2011, ApJ, 729, 54 [Google Scholar]
- Cubillos, P. E. 2017, ApJ, 850, 32 [CrossRef] [Google Scholar]
- Cubillos, P. E., & Blecic, J. 2021, MNRAS, 505, 2675 [NASA ADS] [CrossRef] [Google Scholar]
- Cubillos, P., Harrington, J., Loredo, T. J., et al. 2017, AJ, 153, 3 [Google Scholar]
- Deibert, E. K., de Mooij, E. J. W., Jayawardhana, R., et al. 2021, ApJ, 919, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Deline, A., Hooton, M. J., Lendl, M., et al. 2022, A&A, 659, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delrez, L., Ehrenreich, D., Alibert, Y., et al. 2021, Nat. Astron., 5, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B.-O., Gillon, M., de Wit, J., et al. 2016a, Nature, 532, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B.-O., Gillon, M., Madhusudhan, N., & Queloz, D. 2016b, MNRAS, 455, 2018 [NASA ADS] [CrossRef] [Google Scholar]
- Edwards, B., Changeat, Q., Baeyens, R., et al. 2020, AJ, 160, 8 [Google Scholar]
- Eftekhar, M., & Adibi, P. 2022, Planet. Sci. J., 3, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenreich, D., Lovis, C., Allart, R., et al. 2020, Nature, 580, 597 [Google Scholar]
- Falco, A., Zingales, T., Pluriel, W., & Leconte, J. 2022, A&A, 658, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [Google Scholar]
- Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Fortney, J. J., Lodders, K., Marley, M. S., & Freedman, R. S. 2008, ApJ, 678, 1419 [CrossRef] [Google Scholar]
- Fu, G., Deming, D., Lothringer, J., et al. 2021, AJ, 162, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gandhi, S., Kesseli, A., Snellen, I., et al. 2022, MNRAS, 515, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Gandhi, S., Kesseli, A., Zhang, Y., et al. 2023, AJ, 165, 242 [NASA ADS] [CrossRef] [Google Scholar]
- García Muñoz, A., Pérez-Hoyos, S., & Sánchez-Lavega, A. 2014, A&A, 566, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garhart, E., Deming, D., Mandell, A., et al. 2020, AJ, 159, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Geweke, J. 1992, Bayesian Stat., 4, 641 [Google Scholar]
- Gibson, N. P., Merritt, S., Nugroho, S. K., et al. 2020, MNRAS, 493, 2215 [Google Scholar]
- Gillon, M., Triaud, A. H. M. J., Fortney, J. J., et al. 2012, A&A, 542, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Demory, B. O., Lovis, C., et al. 2017, A&A, 601, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
- Guillot, T., Burrows, A., Hubbard, W. B., Lunine, J. I., & Saumon, D. 1996, ApJ, 459, L35 [Google Scholar]
- Hawthorn, F., Bayliss, D., Wilson, T. G., et al. 2023, MNRAS, 520, 3649 [NASA ADS] [CrossRef] [Google Scholar]
- Helling, Ch., Iro, N., Corrales, L., et al. 2019, A&A, 631, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helling, Ch., Lewis, D., Samra, D., et al. 2021, A&A, 649, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helling, C., Samra, D., Lewis, D., et al. 2023, A&A, 671, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heng, K., & Demory, B.-O. 2013, ApJ, 777, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Heng, K., & Workman, J. 2014, ApJS, 213, 27 [CrossRef] [Google Scholar]
- Heng, K., Morris, B. M., & Kitzmann, D. 2021, Nat. Astron., 5, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeijmakers, H. J., Ehrenreich, D., Kitzmann, D., et al. 2019, A&A, 627, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoeijmakers, H. J., Kitzmann, D., Morris, B. M., et al. 2022, A&A, submitted [arXiv:2218.12847] [Google Scholar]
- Hooton, M. J., Hoyer, S., Kitzmann, D., et al. 2022, A&A, 658, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoyer, S., Guterman, P., Demangeon, O., et al. 2020, A&A, 635, A24, 14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoyer, S., Bonfanti, A., Leleu, A., et al. 2022, A&A, 668, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hu, R., Demory, B.-O., Seager, S., Lewis, N., & Showman, A. P. 2015, ApJ, 802, 51 [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ingalls, J. G., Krick, J. E., Carey, S. J., et al. 2016, AJ, 152, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, T., & Kipping, D. 2020, MNRAS, 494, 4077 [Google Scholar]
- John, T. L. 1988, A&A, 193, 189 [NASA ADS] [Google Scholar]
- Jones, K., Morris, B. M., Demory, B. O., et al. 2022, A&A, 666, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jørgensen, U. G., Hammer, D., Borysow, A., & Falkesgaard, J. 2000, A&A, 361, 283 [Google Scholar]
- Kawauchi, K., Narita, N., Sato, B., & Kawashima, Y. 2022, PASJ, 74, 225 [CrossRef] [Google Scholar]
- Kesseli, A. Y., & Snellen, I. A. G. 2021, ApJ, 908, L17 [Google Scholar]
- Kesseli, A. Y., Snellen, I. A. G., Alonso-Floriano, F. J., Mollière, P., & Serindag, D. B. 2020, ApJ, 160, 228 [CrossRef] [Google Scholar]
- Kesseli, A. Y., Snellen, I. A. G., Casasayas-Barris, N., Mollière, P., & Sánchez-López, A. 2022, ApJ, 163, 107 [CrossRef] [Google Scholar]
- Kitzmann, D., Heng, K., Rimmer, P. B., et al. 2018, ApJ, 863, 183 [Google Scholar]
- Kitzmann, D., Hoeijmakers, H. J., Grimm, S. L., et al. 2023, A&A, 669, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Allen, L. E., et al. 2007, Nature, 447, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Komacek, T. D., Showman, A. P., & Tan, X. 2017, ApJ, 835, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Kreidberg, L. 2015, PASP, 127, 1161 [Google Scholar]
- Kreidberg, L., Line, M. R., Parmentier, V., et al. 2018, AJ, 156, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1970, SAO Special Report, 309 [Google Scholar]
- Landman, R., Sánchez-López, A., Mollière, P., et al. 2021, A&A, 656, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanotte, A. A., Gillon, M., Demory, B. O., et al. 2014, A&A, 572, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, E., Dobbs-Dixon, I., Helling, Ch., Bognar, K., & Woitke, P. 2016, A&A, 594, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lendl, M., Csizmadia, Sz., Deline, A., et al. 2020, A&A, 643, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lewis, N. K., Knutson, H. A., Showman, A. P., et al. 2013, ApJ, 766, 95 [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021, A&A, 649, A4 [EDP Sciences] [Google Scholar]
- Lodders, K. 2002, ApJ, 577, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Mallonn, M., Köhler, J., Alexoudi, X., et al. 2019, A&A, 624, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mallonn, M., Herrero, E., & von Essen, C. 2022, RNAAS, 6, 182 [NASA ADS] [Google Scholar]
- Mansfield, M., Bean, J. L., Stevenson, K. B., et al. 2020, ApJ, 888, L15 [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2017, ApJ, 835, 77 [Google Scholar]
- May, E. M., Komacek, T. D., Stevenson, K. B., et al. 2021, AJ, 162, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Mendonça, J. M., Malik, M., Demory, B.-O., & Heng, K. 2018, AJ, 155, 150 [Google Scholar]
- Mighell, K. J. 2005, MNRAS, 361, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, B. M., Delrez, L., Brandeker, A., et al. 2021, A&A, 653, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morris, B. M., Heng, K., Jones, K., et al. 2022, A&A, 660, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ngo, H., Knutson, H. A., Hinkley, S., et al. 2016, ApJ, 827, 8 [Google Scholar]
- Pagano, I., Scandariato, G., Singh, V., et al. 2024, A&A, 682, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parmentier, V., Fortney, J. J., Showman, A. P., Morley, C., & Marley, M. S. 2016, ApJ, 828, 22 [Google Scholar]
- Parmentier, V., Line, M. R., Bean, J. L., et al. 2018, A&A, 617, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parmentier, V., Showman, A. P., & Fortney, J. J. 2021, MNRAS, 501, 78 [Google Scholar]
- Parviainen, H. 2023, A&A, 671, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parviainen, H., & Aigrain, S. 2015, MNRAS, 453, 3821 [Google Scholar]
- Parviainen, H., Wilson, T. G., Lendl, M., et al. 2022, A&A, 668, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pelletier, S., Benneke, B., Ali-Dib, M., et al. 2023, Nature, 619, 7970 [Google Scholar]
- Pluriel, W., Whiteford, N., Edwards, B., et al. 2020, AJ, 160, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Pluriel, W., Leconte, J., Parmentier, V., et al. 2022, A&A, 658, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telescopes Instrum. Syst., 1, 014003 [Google Scholar]
- Rothman, L. S., Gordon, I. E., Barber, R. J., et al. 2010, JQSRT, 111, 2139 [NASA ADS] [CrossRef] [Google Scholar]
- Salmon, S. J. A. J., Van Grootel, V., Buldgen, G., Dupret, M. A., & Eggenberger, P. 2021, A&A, 646, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-López, A., Landman, R., Mollière, P., et al. 2022, A&A, 661, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savel, A. B., Kempton, E. M. R., Malik, M., et al. 2022, ApJ, 926, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Schanche, N., Hébrard, G., Collier Cameron, A., et al. 2020, MNRAS, 499, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, A. D., Carone, L., Decin, L., et al. 2022, A&A, 664, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scuflaire, R., Théado, S., Montalbán, J., et al. 2008, Astrophys. Space Sci., 316, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S. 2010, Exoplanet Atmospheres: Physical Processes [Google Scholar]
- Seidel, J. V., Ehrenreich, D., Wyttenbach, A., et al. 2019, A&A, 623, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seidel, J. V., Ehrenreich, D., Allart, R., et al. 2021, A&A, 653, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seidel, J. V., Borsa, F., Pino, L., et al. 2023, A&A, 673, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shporer, A., Wong, I., Huang, C. X., et al. 2019, AJ, 157, 178 [Google Scholar]
- Sing, D. K., Fortney, J. J., Nikolov, N., et al. 2016, Nature, 529, 59 [Google Scholar]
- Singh, V., Scandariato, G., Smith, A. M. S., et al. 2024, A&A, 683, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Bohn, A. J., Kenworthy, M. A., Ginski, C., & Mancini, L. 2020, A&A, 635, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spiegel, D. S., Silverio, K., & Burrows, A. 2009, ApJ, 699, 1487 [Google Scholar]
- Stevenson, K. B., Harrington, J., Fortney, J. J., et al. 2012, ApJ, 754, 136 [Google Scholar]
- Tabernero, H. M., Zapatero Osorio, M. R., Allart, R., et al. 2021, A&A, 646, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tan, X., & Komacek, T. D. 2019, ApJ, 886, 26 [Google Scholar]
- Tennyson, J., Yurchenko, S. N., Al-Refaie, A. F., et al. 2016, J. Mol. Spectrosc., 327, 73 [Google Scholar]
- Tsiaras, A., Waldmann, I. P., Zingales, T., et al. 2018, AJ, 155, 156 [NASA ADS] [CrossRef] [Google Scholar]
- van de Hulst, H. C. 1981, Light Scattering by Small Particles (New York: Dover) [Google Scholar]
- Varley, R., Tsiaras, A., & Karpouzas, K. 2017, ApJS, 231, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Burovski, E., et al. 2020, https://doi.org/18.5281/zenodo.3958354 [Google Scholar]
- von Essen, C., Mallonn, M., Hermansen, S., et al. 2020, A&A, 637, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wardenier, J. P., Parmentier, V., Lee, E. K. H., Line, M. R., & Gharib-Nezhad, E. 2021, MNRAS, 506, 1258 [NASA ADS] [CrossRef] [Google Scholar]
- West, R. G., Hellier, C., Almenara, J.-M., et al. 2016, A&A, 585, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, T. G., Goffo, E., Alibert, Y., et al. 2022, MNRAS, 511, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, I., Shporer, A., Daylan, T., et al. 2020, AJ, 160, 155 [Google Scholar]
- Wong, I., Kitzmann, D., Shporer, A., et al. 2021, AJ, 162, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
- Yan, F., Nortmann, L., Reiners, A., et al. 2023, A&A, 672, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, M., Knutson, H. A., Kataria, T., et al. 2018, AJ, 155, 83 [Google Scholar]
- Zingales, T., Falco, A., Pluriel, W., & Leconte, J. 2022, A&A, 667, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
PAdova and TRieste Stellar Evolutionary Code: http://stev.oapd.inaf.it/cgi-bin/cmd
All Tables
Parameters of the second component of the Cos+Gauss and Gauss+Gauss PC models inferred from the TESS and CHEOPS light curves.
Parameters of the Kelp,refl component of the Cos+Kelp,refl model inferred from the TESS and CHEOPS light curves.
Posterior of the light curve fits of CHEOPS and TESS with the Cos+Kelp,refl model
Posterior of the light curve fits for TESS and CHEOPS with Cos, Cos+Gauss and Gauss+Gauss models
All Figures
 |
Fig. 1 Reduced and phase-folded light-curves in CHEOPS, TESS, Spitzer-IRAC1 and Spitzer-IRAC2 bandpasses: The light-curves are corrected from the contamination and from modelled instrumental systematic. The zero flux level is set as the stellar flux, except for the Spitzer-IRAC1 data where, in the absence of a reliable PC, we set the out-of-transit and the out-of-eclipse flux level to zero. Here, we only show the data acquired around occultations. The grey points are the individual measurements. The red ones are their mean values within orbital phase bins regularly distributed. The solid red line represents the best model (see Sect. 4.2) using the cosine phase-curve model (described in Sect. 4.1). The solid blue and orange lines represent the two GCM models with low and high friction (see Sect. 5.2.2). Top: light curves displayed focusing on the transit. Bottom: focus on the PCs. |
| In the text | |
 |
Fig. 2 Reduced and phase-folded light-curves in CHEOPS and TESS bandpasses using the Cos+Gauss and Gauss+Gauss phase curve models: light-curves are corrected from the contamination and from modelled instrumental systematic. The zero flux level is set as the stellar flux. The grey points are the individual measurements. The red ones are their mean values within orbital phase bins regularly distributed. The solid black line represents the best model (see Sect. 4.2) using the Gauss+Gauss phase-curve model for CHEOPS and the Cos+Gauss model for TESS (both described in Sect. 4.1). The top two panels present the reduced phase-folded light curve of and residuals of the CHEOPS data and the bottom two panels are for the reduced phase-folded light curve of and residuals of the TESS data. |
| In the text | |
 |
Fig. 3 Reduced and phase-folded light-curves in CHEOPS and TESS bandpasses using the Cos+Kelp,Refl phase curve models. As in Fig. 2, the light-curves are corrected from the contamination and from modelled instrumental systematic. The zero flux level is set as the stellar flux. The grey points are the individual measurements. The red ones are their mean values within orbital phase bins regularly distributed. The solid black line represents the best model (see Sect. 4.2) using the Cos+Kelp,refl phase-curve model for CHEOPS and TESS (described in Sect. 4.1). The top two panels present the reduced phase-folded light curve of and residuals of the CHEOPS data and the bottom two panels are for the reduced phase-folded light curve of and residuals of the TESS data. |
| In the text | |
 |
Fig. 4 WASP-76 b occultation atmospheric retrievals. Left: light blue, dark blue, and orange curves and their associated shaded areas show the retrieved spectrum and 68% credible intervals when fitting the D1, D2, and D3 occultation observations, respectively (see legends). These retrievals include both TiO and VO opacities. The blue, red, and purple markers with error bars show the occultation depths from E20, F21, and this work, respectively. The grey markers show the CHEOPS and TESS occultation measurements, although the fits are not constrained by these observations. The dashed grey curves show spectra for two blackbody planetary models at 2480 and 2630 K (matching the HST observations). The grey curves at the bottom show the throughputs for the photometric bands. Inset: zoom on the CHEOPS and TESS wavelengths. The coloured square markers show the respective models integrated over these bands. Right: retrieved temperature profiles for each retrieval run (median and 68% credible interval). The curves at the left edge show the contribution functions, indicating the pressures probed by the observations. The colour code is the same as for the retrieved spectra (see legends). |
| In the text | |
 |
Fig. 5 WASP-76 b occultation atmospheric retrievals zoomed over the HST-WFC3 bandpass. Models and data are the same as in Fig. 4. |
| In the text | |
 |
Fig. B.1 2D joint posterior probabilities of the fit of the CHEOPS data using the Cos+Gauss model: The full model is described in Section 4.1. For clarity, we only display a subset of the parameters of the model: A0 and A1 are the amplitudes of the cosine and Gaussian components of the model respectively. ϕ1 is the average phase offset of the Gaussian component and σ1 it’s standard deviation, both expressed in radians. |
| In the text | |
 |
Fig. B.2 2D joint posterior probabilities of the fit of the CHEOPS data using the Gauss+Gauss model: The full model is described in Section 4.1. For clarity, we only display a subset of the parameters of the model: A0 and A1 are the amplitudes of the broad and narrow Gaussian components of the model respectively. ϕ1 is the average phase offset of the narrow Gaussian component and σ1 is its standard deviation, both expressed in radians. |
| In the text | |
 |
Fig. B.3 Violin plot of the posterior probability density function of the parameters retrieved from the PDC-SAP and PSF-SCALPELS TESS light curves: The x-axis corresponds to the average time of each TESS sectors data from which the posteriors have been retrieved, sectors 30, 42 and 43 from left to right. The white circle in the middle of each violin plot corresponds to the median value of the distribution and the thick black line to the 68% confidence interval delimited by the 16th and 84th percentiles. We displayed only the key parameters for the planetary transit and its phase curve, from top to bottom: the radius ratio inferred from the transit, the amplitude of the phase curve, the night-side flux and the phase offset. The phase curve model used is the Cos model. More details on this model and its parameters are provided in Section 4.1. |
| In the text | |
 |
Fig. B.4 Comparison of the dilution factors computed by different authors: E20 and F21 indicate that the blue and green dilution factors have been computed by Edwards et al. (2020) and Fu et al. (2021), respectively. |
| In the text | |
 |
Fig. C.1 WASP-76 b retrieved spectra and temperature profiles. Same as Figure 4 but for the runs without TiO opacity (top panels) and without TiO nor VO opacity (bottom panels). The spectra and thermal profiles show the same behaviour as the runs including TiO and VO opacity, with the only significant difference that the D1 model does not show the TiO emission over the CHEOPS and TESS bands, therefore predicting much lower thermal emission (insets). |
| In the text | |
 |
Fig. C.2 WASP-76 b abundance parameter posterior distributions. The dashed diagonal lines in the pair-wise panels mark boundary when both variables have the same metallicity enhancement (with respect to solar values). The values at the top of each histogram panel report the median and boundaries of the central 68% credible interval for each marginal posterior. The shaded area in the histogram panels denote the span of these credible intervals. The black curves at the left edges show the contribution functions over the CHEOPS, TESS, HST, and Spitzer bands. |
| In the text | |
 |
Fig. C.3 WASP-76 b retrieved volume mixing ratios: Volume mixing ratios derived from the posterior distributions for the case including TiO and VO opacity. The shaded areas (see legend) denote the span of the 68% credible interval for each species (only the most spectroscopically active species are shown). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


