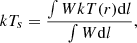| Issue |
A&A
Volume 672, April 2023
|
|
|---|---|---|
| Article Number | A156 | |
| Number of page(s) | 21 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202245012 | |
| Published online | 14 April 2023 | |
CHEX-MATE: Pressure profiles of six galaxy clusters as seen by SPT and Planck
1
Università degli studi di Roma ‘Tor Vergata’, Via della ricerca scientifica 1, 00133 Roma, Italy
e-mail: filippo.oppizzi@gmail.com
2
INFN, Sezione di Roma ‘Tor Vergata’, Via della Ricerca Scientifica 1, 00133 Roma, Italy
3
INAF, Osservatorio di Astrofisica e Scienza dello Spazio, Via Piero Gobetti 93/3, 40129 Bologna, Italy
4
INFN, Sezione di Bologna, Viale Berti Pichat 6/2, 40127 Bologna, Italy
5
INAF – Istituto di Astrofisica Spaziale e Fisica Cosmica di Milano, Via A. Corti 12, 20133 Milano, Italy
6
Jodrell Bank Centre for Astrophysics, Department of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester M13 9PL, UK
7
Center for Astrophysics, Harvard & Smithsonian, 60 Garden Street, Cambridge, MA 02138, USA
8
HH Wills Physics Laboratory, University of Bristol, Tyndall Ave, Bristol BS8 1TL, UK
9
IRAP, Université de Toulouse, CNRS, CNES, UPS, 9 av du colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
10
Université Paris-Saclay, Université Paris-Cité, CEA, CNRS, AIM, 91191 Gif-sur-Yvette, France
11
California Institute of Technology, 1200 East California Boulevard, Pasadena, California 91125, USA
Received:
19
September
2022
Accepted:
16
January
2023
Context. Pressure profiles are sensitive probes of the thermodynamic conditions and the internal structure of galaxy clusters. The intra-cluster gas resides in hydrostatic equilibrium within the dark-matter gravitational potential. However, this equilibrium may be perturbed; for example, as a consequence of thermal energy losses, feedback, and non-thermal pressure supports. Accurate measures of the gas pressure over cosmic time are crucial for constraining cluster evolution as well as the contributions from astrophysical processes.
Aims. In this work we present a novel algorithm for deriving the pressure profiles of galaxy clusters from the Sunyaev-Zeldovich (SZ) signal measured on a combination of Planck and South Pole Telescope (SPT) observations. The synergy of the two instruments makes it possible to track the profiles on a wide range of spatial scales. We exploited the sensitivity of the Planck High-Frequency Instrument to the larger scales in order to observe the faint peripheries, and took advantage of the higher spatial resolution of SPT to solve the innermost regions.
Methods. We developed a two-step pipeline to take advantage of the specifications of each instrument. We first performed a component separation on the two data sets separately in order to remove the background (CMB) and foreground (Galactic emission) contaminants. We then jointly fitted a parametric pressure profile model on a combination of Planck and SPT data.
Results. We validated our technique on a sample of six CHEX-MATE clusters detected by SPT. We compare the results of the SZ analysis with profiles derived from X-ray observations with XMM-Newton. We find excellent agreement between these two independent probes of the gas pressure structure.
Key words: cosmology: observations / cosmic background radiation / galaxies: clusters: intracluster medium / X-rays: galaxies: clusters / techniques: image processing / methods: statistical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Galaxy clusters are the most massive virialized objects in the Universe. They evolve from the largest gravitational overdensities in the primordial field, and probe the evolution of the Universe at the largest scales (Kravtsov & Borgani 2012; Voit 2005). Deep into the cluster potential well, a large amount of baryonic matter lies in the form of hot, ionised gas. In the standard picture, the gas pressure balances the gravitational potential driven by the dark matter (DM) halo. Gas pressure acts as the connection between the large-scale evolution that drives the growth of DM halos and the baryonic processes active within.
The tight correlation with the background density field links the clusters thermodynamic properties to the underlying cosmology, making them a powerful probe of the structure and evolution of the Universe. The hydrostatic equilibrium links the intra-cluster gas pressure to the total mass in a predictable way; if this condition holds, the simplest model of spherical collapse of scale-invariant perturbations predicts that the pressure profiles are self-similar (Kaiser et al. 1995; Bertschinger 1998; Kravtsov et al. 2006). This motivates the use of scaling relations linking the gas pressure with the cluster mass.
The self-similar behaviour is well respected at intermediate radii r ∼ r5001 (Arnaud et al. 2010; Planck Collaboration Int. V 2013; McDonald et al. 2014; Bourdin et al. 2017), while significant deviations are expected in the innermost regions and the outskirts. The former derive from the energetic non-gravitational processes taking place in the core; for example active galactic nuclei (AGN) feedback and cooling processes. In the peripheries instead, the infall of material into the virialized region induces the breakdown of the perfect hydrostatic equilibrium condition (Lau et al. 2009). Different processes related to the mass-accretion rates are responsible for these deviations reflecting non-thermal pressure support; for example inhomogeneities and anisotropies in the gas motion and the matter distribution surrounding the cluster, as well as turbulence and shocks (Lau et al. 2015; Nelson et al. 2014). Numerical simulations suggest that clusters experiencing higher mass accretion present steeper profiles at large radii (Battaglia et al. 2012; McCarthy et al. 2014). Furthermore, the complex physics of virialization is expected to affect the collisional baryons and the collisionless DM in different ways, leading to further deviations from the self-similarity in the outskirts (Lau et al. 2015). Thus, this effect may depend on redshift, following the mass-accretion history, as some measurements suggest (McDonald et al. 2014).
The Sunyaev-Zeldovich effect (SZ) in the cosmic microwave background (CMB) is a direct, weakly biased tracer of the gas pressure (Sunyaev & Zeldovich 1972; Birkinshaw 1999). Free electrons interact with the background radiation via inverse Compton scattering, leaving a characteristic imprint in the CMB spectrum. SZ depends only on the pressure integrated along the line of sight. The intensity of the SZ signal above the primordial microwave background, that is, the Compton y parameter, does not depend on the redshift. At the same time, the gas emits intense X-ray bremsstrahlung radiation, providing a second independent probe of the thermodynamic conditions of the gas. X-ray emission depends quadratically on the gas density, while the SZ dependence is linear. These properties together mean that X-ray and SZ are complementary when used to probe cluster structure at different density regimes.
In this work, we present a pipeline to extract pressure profiles of clusters from a combination of Planck and South Pole Telescope (SPT) data. Currently, these two instruments represent the state of the art of cosmological surveys at millimetre and submillimetre wavelengths. The Planck satellite, launched by the European Space Agency in 2009, delivered maps of the full sky at frequencies from 30 to 857 GHz with subJansky sensitivity and a maximum resolution of ∼5 arcmin (see Planck Collaboration I 2020) for a review of the main results of the Planck team). SPT is a 10 m telescope located at the Amundsen-Scott station at the South Pole (Carlstrom et al. 2011). Having a resolution < 1.7 arcmin, it can solve the inner regions of distant galaxy clusters inaccessible to space observations (Bleem et al. 2015). The high sensitivity of Planck and the high resolution of the SPT make the two instruments complementary in constraining the structure of clusters, from the core to the faint peripheries.
Thanks to the wide sky coverage and the independence on redshift, millimetric surveys are precious tools for studying cluster cosmology. The improvement in resolution and sensitivity of ground-based observations allows us to refine the results from Planck alone (Planck Collaboration Int. V 2013; Planck Collaboration XXVII 2016). Works exist in the literature that build cluster catalogues from the combination of Planck and SPT data (Melin et al. 2021; Salvati et al. 2022). Other works (Aghanim et al. 2019; Pointecouteau et al. 2021) show how to combine Planck observations with data from the Atacama Cosmology Telescope and measure the pressure profile on a sample of clusters. Here, we present for the first time pressure profiles of individual clusters observed with the SPT and Planck.
We compare the results of our pipeline and the profiles derived from X-ray data. We analyse six SPT clusters selected from the sample of the “Cluster HEritage project with XMM-Newton-Mass Assembly and Thermodynamics at the Endpoint of structure formation” (CHEX-MATE; The CHEX-MATE Collaboration 2021). X-ray data represent a powerful benchmark for our technique. We not only compare the profiles derived from two completely independent analyses, but thanks to the higher resolution of XMM-Newton data, we can also investigate the impact of substructures on the relation between the two.
The paper is organised as follows: in Sect. 2 we describe the data sets and the cluster sample selected for the analysis; in Sect. 3 we outline the data-reduction pipelines for the three data sets; in Sect. 4 we present our results; and in Sect. 5 we outline our conclusions.
In our analysis, we assume a ΛCDM cosmology with H0 = 70 Kms−1 Mpc−1, ΩM = 0.3, and ΩΛ = 0.7.
2. Data sets and cluster sample
2.1. The CHEX-MATE sample
We study a sample of six galaxy clusters common to the SPT-SZ catalogue (Bleem et al. 2015) and the CHEX-MATE cluster sample. The CHEX-MATE project is an X-ray follow up of 118 clusters detected by Planck and present in the PSZ2 catalogue with the ESA satellite XMM-Newton. The CHEX-MATE sample is designed to be minimally biased and has a limited signal-to-noise ratio (S/N > 6.5). In addition to millimetric and X-ray data sets, multi-wavelength observations in optical and radio are available for most targets. The purpose of CHEX-MATE is to study the most massive objects that have formed and statistically characterise the local cluster population. For this reason, the CHEX-MATE sample is further divided into two subsets: the Tier-1, collecting the most recently formed objects, with 0.05 < z < 0.2 and 2 × 1014 M⊙ < M500 < 9 × 1014 M⊙), and the Tier-2, assembling some of the most massive clusters in the Universe with z < 0.6 and M500 > 7.25 × 1014 M⊙. In particular, the six clusters studied in this paper are a subset of the Tier-2 subsample. We refer the reader to the introductory study (The CHEX-MATE Collaboration 2021) for a more detailed description of the cluster selection, the observational strategy, and the future outcomes of the collaboration.
This selection provides us with reliable X-ray counterparts as a benchmark for the pressure profiles derived with our technique from SPT and Planck. Our sample spans a redshift range from z = 0.16 to z = 0.60, and angular dimensions from r500 = 2.8 arcmin to r500 = 7.9 arcmin. The main properties of the clusters are summarised in Table 1. We report the SPT and the PSZ2 identifiers, the coordinates of the X-ray peak in right ascension (RA) and declination (Dec), the redshifts, the M500, and the angular dimensions r500. The redshifts and the masses come from the PSZ2 union catalogue (Planck Collaboration XXVII 2016), where the masses are computed assuming the best-fit Y-M scaling relation of Arnaud et al. (2010) as a prior. We derive r500 as a function of z and M500 for the given cosmology.
Main properties of the galaxy clusters sample.
2.2. Planck data
We use the data from the second public data release (PR2) of the Planck High-Frequency Instrument (HFI), from the full 30 month mission (Planck Collaboration VIII 2016). The data set comprises six full-sky maps in HEALPix format with Nside = 2048, (i.e. with pixel angular size of 1.72 arcmin) with nominal frequencies of 100, 143, 217, 353, 545, and 857 GHz, and resolution of 9.66, 7.22, 4.90, 4.92, 4.67, and 4.22 arcmin full width half maximum (FWHM) Gaussian, respectively. The Planck team detected more than 1000 galaxy clusters with an identified counterpart through the SZ effect (Planck Collaboration XXVII 2016).
2.3. SPT data
The SPT observes the microwave sky in three frequency bands centred at 95, 150, and 220 GHz with 1.7, 1.2, and 1.0 arcmin resolution, respectively. The SPT-SZ survey consists of three maps derived from the data collected from 2008 (2009 for the 150 GHz channel) to 2011 over an area of 2540 deg2 located in the southern hemisphere, from 20h to 7h in RA and from 65° to 40° in Dec (Chown et al. 2018).
In this area, the SPT team identified 677 clusters candidates, of which 516 have an optical and/or infrared counterpart (Bleem et al. 2015). The full sample spans a redshift range from z = 0.047 to z = 1.7; the sample is nearly mass limited independently of redshift, with a median mass of 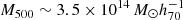 .
.
In this work, we use the public SPT data2, which are convolved with a common Gaussian beam with 1.75 arcmin FWHM. The SPT collaboration releases the data in HEALPix format with resolution parameter Nside = 8192 corresponding to a pixel angular size of 0.43 arcmin. We note that, despite the fact that the SPT team also provides combined Planck and SPT maps, in this work we use the ‘SPT Only’ products and process the two data sets independently.
2.4. X-ray data
The X-ray study of our galaxy cluster sample is based on a joint analysis of the observations performed with the three cameras, MOS1, MOS2, and PN, of the European Photon Imaging Camera (EPIC) of the XMM-Newton space telescope. In particular, all the public data available on the XMM-Newton Science Archive3 are collected and prepared for the analysis detailed in Sect. 3.2. In Table 2, we list all the XMM-Newton pointings we use for our sample, with the ObsID that identifies the observations in the XMM-Newton Science Archive.
XMM-Newton observations for the galaxy clusters of this work.
3. Methods
3.1. Millimetric data
Our pipeline consists of two steps. First, we perform a component separation to remove the background and foreground contaminants on the SPT and Planck observations separately. We then combine the two data sets in a joint fit to derive the pressure profiles.
3.1.1. Data processing of Planck observations
To obtain images of each cluster, we project the full sky Planck maps on smaller tiles of 512 × 512 pixels into the tangential plane, with a resolution of 1 arcmin/pixel (corresponding to ∼8.5° ×8.5°) around the XMM-Newton cluster centre. Each image is then processed with the technique developed in Bourdin et al. (2017) to isolate the cluster signal from the background and foreground components, namely the CMB and the dust emission from our Galaxy and the cluster itself. In the following, we summarise the data-reduction pipeline and refer to Bourdin et al. (2017) for additional details.
We first perform a high-pass filter convolving the maps with a third-order B-spline kernel (as defined by Curry & Schoenberg 1966) to remove large-scale fluctuations. The largest scales are more contaminated by CMB anisotropies and Galactic thermal dust (GTD). At the same time, we do not expect to find a significant contribution from the cluster at those scales.
We then build the spatial templates of the GTD with a wavelet reconstruction of the 857 GHz channel. As this frequency is strongly dust dominated, we do not expect to find any contribution from the other sky components in the 857 GHz maps. We expand the map with an isotropic undecimated wavelet transform and apply a thresholding on the coefficients with a 3σ threshold to clean the template from the noise. We model the dust spectral energy distribution (SED) as a two-temperature grey body as proposed in Meisner & Finkbeiner (2015), with the frequency scaling:
where Bν is the Planck function, T1 and T2 are the ‘cold’ and ‘hot’ component temperatures, βd, 1 and βd, 2 the respective power-law indices, f1 the cold component fraction, and q1 and q2 are the ratios of far-infrared emission to optical absorption. In our fit, we leave the overall amplitude, the cold component fraction f1, and spectral index βd, 1 free to vary, while the other parameters remain fixed to their all-sky values: q1/q2 = 8.22, βd, 2 = 2.82, T2 is derived from Planck and IRAS all-sky maps, and T1 = f(T2, q1/q2, βd, 1, βd, 2) (Meisner & Finkbeiner 2015; Finkbeiner et al. 1999; Planck Collaboration I 2014; Planck Collaboration XI 2014; Planck Collaboration Int. XXIX 2016).
We construct the CMB template as the difference between the 217 GHz map and the GTD template, denoised with the same wavelet procedure used on the 857 GHz map to obtain the dust template. These templates are then rescaled – with a convolution with the proper beam – to match the resolution of each channel.
To obtain the cluster templates, we work under the assumption that the pressure follows the spherically symmetric profile proposed in Nagai et al. (2007):
where x = c500r/r500, r500 is the radius where the density is 500 times the critical density, c500 is the concentration parameter, and α, β, and γ are the slopes at r ∼ r500/c500, r ≫ r500/c500, and r ≪ r500/c500, respectively. Following the self-similar model, P500 is given by:
where 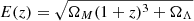 is the normalised expansion rate and the numerical coefficient is set as in Arnaud et al. (2010). To obtain the SZ signal, we first project the 3D profile in Eq. (2) integrating along the line of sight and then we convert this into SZ brightness ISZ, c for each frequency channel c:
is the normalised expansion rate and the numerical coefficient is set as in Arnaud et al. (2010). To obtain the SZ signal, we first project the 3D profile in Eq. (2) integrating along the line of sight and then we convert this into SZ brightness ISZ, c for each frequency channel c:
where σT is the Thomson scattering cross-section, me is the electron mass, and c is the speed of light. The sSZ, c coefficients define the frequency scaling and are derived from the non-relativistic Kompaneets equation adjusted for the channel spectral response Rc(ν):
where x(ν) = hν/kT, Rc(ν) is given by the HFI model (Planck Collaboration VII 2016).
Furthermore, we add a correction term to take into account contamination by the thermal dust emission from the cluster (CTD), which has been observed in Planck data (Planck Collaboration XXIII 2016; Planck Collaboration Int. XLIII 2016). The SED of this component sCTD(ν) is modelled as a grey body with spectral index βd, CTD = 1.5 and temperature T = 19.2/(1 + z)K, as in Planck Collaboration Int. XLIII (2016). We compute the spatial template as the projection along the line of sight of a Navarro-Frenk-White profile (Navarro et al. 1997) with concentration parameter c500 = 1. These cluster templates, SZ, and dust contributions are further convolved with the HFI beam and the same high-pass filter applied to the Planck maps.
The whole model, that is, GTD, CMB, CTD, and cluster SZ signal, is then fitted to the frequency maps to obtain the channel-by-channel amplitudes of the templates of the contaminant components marginalised over the cluster signal. The differences between the background and foreground templates are the cleaned cluster maps; we use these in the joint fit with SPT data processed as described in the following section.
3.1.2. Data processing of SPT observations
We preliminarily select patches of 1024 × 1024 pixels around the XMM-Newton cluster centre. We set the resolution of these maps to 0.5 arcmin/pixel. Each tile covers a region of ∼8.6° ×8.6°.
These data differ from the Planck data in frequency and the spatial scales covered. For this reason, we cannot process them with the component-separation technique described in the previous section. This latter technique exploits the Planck data structure and thus is not adapted to SPT observations. In particular, SPT lacks the high-frequency channels from which we could derive the dust templates required for the multi-component fit described in the previous section; furthermore, the 220 GHz channel of SPT is too noisy to recover the CMB templates at the required precision. Without the templates to fit, we resort to a different solution. In light of these limitations, we developed a method tailored to the SPT data structure, including information from Planck to improve the reconstruction on the larger spatial scales.
We recover the CMB signal from a linear combination (LC) of the three SPT channels and the 217 GHz channel of Planck. Similar methodologies are widely used in CMB analysis, and various implementations have been applied to many millimetre data sets released in recent decades (Bennett et al. 2003; Tegmark et al. 2003; Eriksen et al. 2004; Delabrouille et al. 2009; Remazeilles et al. 2011; Hurier et al. 2013; Oppizzi et al. 2020). To include the Planck 217 GHz channel in the analysis, we re-project it on a smaller region centred on the clusters with the same characteristics as the SPT ones (resolution: 0.5 arcmin/pixel, area: 8.6° ×8.6°).
The LC weights are computed to minimise the variance with respect to a signal constant in frequency (i.e. the CMB) and simultaneously to null the non-relativistic SZ component. Assuming that the data can be represented as the linear combination of different components (the so-called linear mixture model), the aforementioned conditions lead to the solution:
in this notation, the elements of the vector w correspond to the weights assigned to each frequency, C is the data covariance matrix between the Nchan channels, e is a vector of ones (i.e. e=(1,...,1)) of length Nchan, and A is a Nchan × 2 matrix accounting for the emission of the CMB and the SZ signal at the various frequencies. As our data are normalised to the CMB emission, the first column of A is constant and equal to one, while the second column contains the frequency scaling of the SZ signal:
where the sSZ, c coefficients are derived as in Eq. (5) with the channel spectral response of SPT Rc(ν) given in Chown et al. (2018).
The SPT window function changes with the channels. To combine them, we first equalise the frequency maps, including the Planck one, to the 150 GHz spatial response. As the window function also depends on the sky coordinates, we compute it independently for each cluster. The two instruments have different resolutions; to combine them, we follow a multi-scale approach. We split each SPT map into a low-pass-filtered map matching the Planck 217 GHz channel resolution, and a high-pass-filtered map containing the residual small-scale features. This operation corresponds to a convolution with a Gaussian beam of 5 arcmin to obtain the low-pass-filtered map, while the residual of this map with the original one corresponds to the high-pass-filtered map.
We then perform the LC separately on the low-passed maps and high-passed maps, including the Planck map in the combination of the large scales. We compute the LC weights on a subregion of 1.5 × 1.5 degrees around the cluster centre. This operation gives us two separate estimates of the large-scale and small-scale CMB fluctuations, which we re-combine into a single map. Finally, we rescale the template to the three SPT channel window functions to obtain the final templates. We finally subtract these templates from the SPT maps to obtain the background-cleaned maps. Schematically, our pipeline can be summarised as follows:
-
Equalise the maps at the 150 GHz window function.
-
Split the maps into low-pass- and high-pass-filtered maps.
-
Compute the LC of the low and high spatial frequency maps separately.
-
Recombine the two scales into a single template.
-
Re-convolve the map with the corresponding PSF to obtain the CMB template for each channel.
-
Subtract the templates from the SPT maps to remove the CMB background.
As mentioned above, we do not consider dust contamination in these data. Different considerations justify this choice. First, the dust emission is expected to be very low at the SPT frequencies where we plan to perform the fit of the SZ profile, namely 95 and 150 GHz. In addition, these clusters are located relatively far from the Galactic plane, where the GTD contamination is especially significant. Furthermore, due to the filter window function, SPT is blind to multipoles under ℓ = 300, corresponding to an angular separation ≳1°; as a consequence, any source of diffuse emission is highly suppressed in SPT data. This feature has noticeable implications on the contamination from Galactic thermal dust; as it comes in large part as diffuse emission, after the SPT spatial filtering, its residual contribution in the data is negligible.
As an example, we plot the results of the background removal for one cluster, PSZ2 G271.18-30.95, in Fig. 1 for Planck and in Fig. 2 for SPT. For Planck, we show the frequency channels used in the fit (100 GHz, 143 GHz, and 353 GHz (see the next Sect. 3.1.3 for details), and the 217 GHz channel used to check for background residuals. In the lower rows, we show the background (CMB) and foreground (Galactic dust) templates. All maps have side lengths of ∼12 × r500 = 42 arcmin. In the upper panels, we show the high-pass-filtered maps, which is why the very large spatial scales are suppressed. Despite the filtering, by the diffuse contaminant signal of the CMB and, at high frequencies, the Galactic dust dominates the data. We note that the latter (lower panels) is negligible at the low frequencies where SPT also observes, confirming our expectation. From an inspection of the 217 GHz cleaned maps, where both CMB and dust have noticeable amplitudes while the SZ signal is null, we do not find any evidence of residual contamination: the residual signal is consistent with random noise.
 |
Fig. 1. Planck maps and background templates of PSZ2 G271.18-30.9 from the 100 GHz (first column), 143 GHz (second column), 217 GHz (third column), and 353 GHz (fourth column) channels. The first and second rows show the raw and the cleaned maps, respectively. The third row shows the CMB templates, the fourth row the Galactic dust templates. Red circles mark r500 and the black circles represent the beam FWHM of each channel. The map size is 12r500 × 12r500 and the axes show the distance from the cluster centre in arcmin. The pixel size is 1 arcmin. |
Figure 2 represents the raw and cleaned maps (upper and middle row, respectively) of the three SPT channels, and the reconstruction of the CMB signal into SPT data in the lower panels, for the same cluster as Fig. 1. The side length of the maps is ∼12 × r500 = 22 arcmin. The most noticeable issue is the large residual in the 220 GHz cleaned map. To exclude the astrophysical origin of these residuals, we check for correlation with the other channels and with Planck. We do not find any evidence of correlation with the other frequencies, and we conclude that they are due to the very high noise of this channel. On the other hand, the 95 GHz and the 150 GHz cluster signal appear consistently separated from the CMB background. We only show the CMB templates for the 150 GHz channel. The differences between channels due to the different window functions are negligible and cannot be seen in these images. We therefore prefer to plot the full template together with the large (centre) and small (right) spatial scale reconstruction. As described in the previous paragraphs, we recover the larger scales from a linear combination including the 217 GHz channel of Planck, while the small scales are obtained only from SPT data. As a consequence, small-scale noise residuals could arise in the CMB template due to the high 220 GHz noise. We performed several tests to address the issue. We tried alternative techniques to exclude this channel from the background reconstruction. We also tried to denoise the CMB templates by applying a wavelet thresholding algorithm. Unfortunately, we find that, without the information from the 220 GHz channel, the risk of partially mixing a fraction of the cluster signal into the background template is very high. On the other hand, while thresholding the templates efficiently suppresses the noise, it also removes small-scale fluctuations from the CMB reconstruction. The denoised templates are too smoothed, and significant contamination from the CMB remains in the cleaned maps. In conclusion, we address this issue by considering this additional noise contribution in the covariances, as described in the following section.
 |
Fig. 2. SPT maps and background templates of PSZ2 G271.18-30.9. The upper and medium panels show the raw maps and the cleaned maps, respectively, of the 95 GHz (left), 150 GHz (centre), and 220 GHz (right) channels. In the lower panels, we show the CMB reconstruction: the full template (left), the lower spatial frequency reconstruction (centre), and the high spatial frequency reconstruction (right). The red circles mark r500 and the black circles represent the SPT beam FWHM. The map size is 6r500 × 6r500 and the axes show the distance from the cluster centre in arcmin. The pixel size is 0.5 arcmin. |
3.1.3. Joint fit of Planck and SPT data
Once we estimate the cluster signal from our component-separation pipelines, we combine the SPT and Planck data in a joint fit of the cluster thermal SZ template. The fitting functions are radially averaged SZ profiles 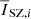 of the two-dimensional templates derived from Eq. (4); we fit them to the profiles computed on the yc maps obtained using the methods described in Sects. 3.1.1 and 3.1.2, which we denote
of the two-dimensional templates derived from Eq. (4); we fit them to the profiles computed on the yc maps obtained using the methods described in Sects. 3.1.1 and 3.1.2, which we denote 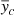 . We compute the profile value in a given radial bin defined as the average over the pixels whose centre falls inside an annulus delimited by the bin edges. We choose a linear binning scheme with circular bins of width 0.2r500 for SPT, and of 2 arcmin for Planck. The fit is performed up to 3r500. We include in the fit the 95 and 150 GHz channels of SPT, and the 100, 143, and 353 GHz channels of Planck. The other channels, namely SPT 220 GHz and Planck 217, 545, and 857 GHz, are used in the component separation but not included in the fit. We expect the cluster S/N to be low at these frequencies. By excluding them, we improve the computational time with a minimal loss of information. At the same time, we also minimise the risk of residual contamination from the dust emission that dominates these channels.
. We compute the profile value in a given radial bin defined as the average over the pixels whose centre falls inside an annulus delimited by the bin edges. We choose a linear binning scheme with circular bins of width 0.2r500 for SPT, and of 2 arcmin for Planck. The fit is performed up to 3r500. We include in the fit the 95 and 150 GHz channels of SPT, and the 100, 143, and 353 GHz channels of Planck. The other channels, namely SPT 220 GHz and Planck 217, 545, and 857 GHz, are used in the component separation but not included in the fit. We expect the cluster S/N to be low at these frequencies. By excluding them, we improve the computational time with a minimal loss of information. At the same time, we also minimise the risk of residual contamination from the dust emission that dominates these channels.
Likelihood. We start from a Gaussian likelihood for the profile parameters θ = [P0,c500,α,β,γ]:
where, for each instrument i, Ci is the covariance matrix, 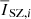 and
and 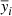 are the model and data vectors, respectively. For each instrument we take into account the correlation between all frequencies, while we consider the SPT and Planck channels to be uncorrelated with one another; we describe this process in more detail below.
are the model and data vectors, respectively. For each instrument we take into account the correlation between all frequencies, while we consider the SPT and Planck channels to be uncorrelated with one another; we describe this process in more detail below.
Covariance. We compute the covariances in order to take into account the residuals of the component-separation step. The use of common templates to clean different frequency channels increases the risk of introducing correlated residuals into the cleaned maps due to the propagation of errors on the reconstruction of the sky components. In particular, as we obtain the SPT CMB templates from a linear combination of different channels, the noise from one particularly noisy map could leak into the others through the background-subtraction step. As mentioned in the previous section, the CMB templates could present small-scale residuals due to the high noise of the 220 GHz channel. We address this issue by estimating the covariances directly from the cleaned maps, taking into account the possible correlation between channels. To this end, we first compute 100 profiles centred outside the cluster, in regions treated with the same foreground-cleaning technique but where we do not expect to find any signal of interest. We mask the point sources and exclude the gaps in the map in the computation of the profiles. We then concatenate the profiles of the various frequencies in a vector defined as in Eq. (8) and then compute the sample covariance between these profiles. We repeat the process for both instruments, which we consider to be uncorrelated as we use different component-separation techniques. The covariances obtained with this method account for both the instrumental noise and the correlation between channels.
Monte-Carlo sampling. With the y maps and the likelihood in hand, we perform the fit with the Cobaya MCMC sampler (Torrado & Lewis 2021). We try different combinations of parameters to optimise the convergence of our chains. To efficiently constrain all five parameters of the gNFW profile, we need information on a wide range of spatial scales. Our data sets are very sensitive to the faint outskirts of the cluster but lack the resolution to fully characterise the inner core. Therefore, while it is straightforward to leave the amplitude P0 and the outer slope β free to vary, the choice among the remaining parameters is not trivial. In case of limited resolution, strong degeneracies arise, meaning that the cases of c500 and α are particularly critical. The concentration c500 fixes the position of the transition region between the r−γ and the r−β regimes. As the range of physically significant values is of the same order of magnitude as the width of our bins and is much smaller than the SPT beam, we decided to keep it fixed. The other critical parameter is α, which indeed governs the slope around r500/c500, but it is better understood as the inverse of the logarithmic width of the transition region between the r−γ and the r−β regimes, which is proportional to α−1. Furthermore, α is strongly and nonlinearly correlated with P0 for values α < 1, and with both the other slopes. The correlation with γ is particularly problematic due to the limited resolution, as enlarging the transition width can restrict the effects of varying the inner slope to unresolved regions. These issues can be mitigated by changing the parameterization of Eq. (2), substituting α with α′ = 1/α and fitting for the logarithm of the amplitude log P0 to make the correlation linear. However, even with these precautions, the chains remain stuck in meaningless regions of the parameter space unless we put strict priors on α. Given these considerations and the results of our tests, we decided to leave the amplitude P0 and the inner and outer slopes γ and β free to vary and to keep the concentration parameter and the intermediate slope fixed to their universal values identified by Arnaud et al. (2010), of namely c500 = 1.177 and α = 1.0510.
3.2. X-ray analysis
We analyse the X-ray data following the scheme used in Bourdin et al. (2017) and De Luca et al. (in prep.), which consists of the three steps detailed below. We note that this pipeline differs from the standard analysis used by the CHEX-MATE collaboration to study the statistical properties of the cluster population (Bartalucci et al., in prep., Rossetti et al., in prep.). One of the differences between the two techniques concerns the normalisation of the background components, as detailed in Sect. 3.2.2. The products of the two X-ray pipelines are compared in a companion paper (De Luca et al., in prep.) to assess any differences in the results and any systematic uncertainties for a larger (and representative) sample of CHEX-MATE clusters. We find that the two pipelines return compatible spectroscopic temperature profiles.
3.2.1. Data preparation
The Observation Data Files (ODFs) from the XMM-Newton Science Archive are initially pre-processed to generate calibrated event files for the data reduction with the EMCHAIN and EPCHAIN tools of SAS, version 18.0.0. To clear flares or high-background periods, we follow Bourdin & Mazzotta (2008) and Bourdin et al. (2013), removing all the events that deviate by more than 3σ from the light-curve profile. MOS1 or MOS2 CCDs with anomalous count rates (e.g., see Kuntz & Snowden 2008) are also removed from the analysis. Point sources in the field of view are identified and masked using SEXTRACTOR (Bertin & Arnouts 1996).
3.2.2. Diffuse background and foreground emission
The remaining X-ray foreground and background4 are dominated by the quiescent particle background (QPB), the cosmic X-ray background (CXB), and the thermal emission associated with our Galaxy. We fit the normalisations of these components in a region where the cluster emission is negligible and with the spectral and spatial features described in Bourdin et al. (2013). In particular, we exclude all the data within 1.5R500 from the X-ray cluster peak. We identify the X-ray peak as the coordinates of the maximum of a sparse wavelet-denoised (Starck et al. 2002, 2009) surface brightness map in the soft ([0.5, 2.5] keV) X-ray band. We set this position as the cluster centre to compute the radial profiles for the X-ray and SZ analysis. The normalisation of the QPB spectrum (Katayama et al. 2004; Kuntz & Snowden 2008; Marelli et al. 2021) is estimated considering the energy band where this emission is dominant: [10 − 12] keV for MOS and [12 − 14] keV for PN cameras of the XMM-Newton telescope. As pointed out by many authors in the literature (see e.g., De Luca & Molendi 2004; Kuntz & Snowden 2008; Snowden et al. 2008; Leccardi & Molendi 2008; Bourdin et al. 2013; Lovisari & Reiprich 2019), a residual focused component, originally attributed to soft protons (SP) but whose origin is still debated (e.g., Fioretti et al. 2016; Salvetti et al. 2017; Gastaldello et al. 2022), can affect the X-ray observations even after the light-curve filtering. To account for this additional component, we model it as a power law with a fixed index (−0.6) and ratio (0.3) between MOS and PN. We estimate the normalisation of this component by performing a joint fit with the cluster spectrum (with the cluster metal abundance fixed to Z = 0.3 and with temperature and normalisation as free parameters), considering an annulus centred on the X-ray peak with radii [0.8 − 1]r500. In the ‘standard’ CHEX-MATE pipeline, a prior on the SP normalisation derives from the differences between count rates registered inside and outside the regions subtended by the field of view (FOV) for the EPIC cameras, which is similar to the method of De Luca & Molendi (2004), Leccardi & Molendi (2008) and Ghirardini et al. (2018). On the other hand, in the present work, the SP normalisation is inferred from a joint fit with the intra-cluster medium (ICM) emission measure in the outermost bin of the cluster temperature profile, which corresponds to the radius range [0.8–1.] r500. The two approaches provide very similar surface brightness and projected temperature profiles, as detailed in De Luca et al. (in prep.).
3.2.3. Galaxy cluster spectral model
The cluster emission from the hot plasma present in the ICM is modelled by combining the bremmsstrahlung continuum and the metal emission lines with the APEC5 spectral library and the absorption due to the Galactic medium. For the latter, we consider the photoelectric cross-sections from the work of Verner & Ferland (1996), the abundance table of Asplund et al. (2009), and the total hydrogen column density defined as: NH, tot = NHI + 2NH2. For the atomic hydrogen HI, we use the public data from the full-sky HI survey by the HI4PI Collaboration (2016). For the molecular (NH2) contribution, we use the results of Bourdin et al. (in prep.), who estimated the fraction of this component around the CHEX-MATE from the thermal dust emission excesses observed with the (sub)millimetre sky survey of the Planck-HFI in the combination with the HI4PI NHI maps.
The only exception for this procedure is the cluster PSZ2 G263.68-22.55. As we discuss more extensively in Appendix A, the molecular and the HI hydrogen column density towards this specific cluster do not accurately describe the X-ray absorption in the soft band. In particular, if we assume the NH, tot value, we observe an overestimate of the Galactic absorption for the cluster spectrum. Alternatively, using the atomic value in our modelling seems to overestimate the cluster spectrum in the soft band. Furthermore, if we consider the relation between NHI and NH, tot for our sample, this cluster has a molecular fraction that is an outlier in the relation of Bourdin et al. (in prep.), with an increment in the hydrogen column density of ΔNH/NHI = 70%. Therefore, we decided to estimate NH, tot directly from the X-ray data for a more accurate treatment of the X-ray spectrum of this cluster. In particular, we consider the cluster spectrum excluding the central region (where the higher metallicity could bias the fit) and the outskirts of the galaxy cluster, considering a circular annulus with radii [0.15, 0.6]R500. We leave NH, the cluster metallicity, temperature, and the spectrum normalisation free to vary in the fit. The χ2 minimisation of our background (see Sect. 3.2.2) plus cluster emission models in the energy range [0.3, 12.1]eV returns a value of 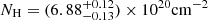 , with a reduced
, with a reduced 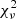 equal to 1.09 (or 356/328, for 328 degrees of freedom), which is significantly better than the molecular (χ2/d.o.f. = 485/328) and the only atomic (χ2/d.o.f. = 388/328) cases. We refer the reader to Appendix A for further details regarding the density content of the hydrogen column density towards this cluster of galaxies.
equal to 1.09 (or 356/328, for 328 degrees of freedom), which is significantly better than the molecular (χ2/d.o.f. = 485/328) and the only atomic (χ2/d.o.f. = 388/328) cases. We refer the reader to Appendix A for further details regarding the density content of the hydrogen column density towards this cluster of galaxies.
3.2.4. Surface brightness and temperature maps
The reconstruction of the clusters signal is shown in Fig. 3, where the contour plots of the soft X-ray surface brightness are superimposed on normalised temperature maps. The surface brightness contours are derived from wavelet analyses of photon images that we corrected for spatial variations of the effective area and background model.
 |
Fig. 3. Normalised cluster temperature maps overlaid on the point-source-removed X-ray surface brightness isocontours, as obtained from XMM-Newton data. The size of the maps is 2r500 × 2r500 centred on the X-ray peak. Contour levels are equally spaced by |
The photon images are denoised via the 4-σ soft-thresholding of variance-stabilised wavelet transforms (Zhang et al. 2008; Starck et al. 2009), which are especially suited to processing low photon counts. The uncertainty of the temperature maps depends on the photon counts (i.e. the surface brightness), and increases from the cluster centre to the outskirts. Thus, our maps have a variable relative uncertainty that spans from 4.2% to 50%, considering a 1σ uncertainty level estimated with bootstrapping methods. Image analyses include the inpainting of detected point sources and the spatial adaptation of wavelet coefficient thresholds to the spatial variations of the effective area.
The temperature maps are computed using a spectral-imaging algorithm that combines spatially weighted likelihood estimates of the projected intra-cluster medium temperature with a curvelet analysis. This algorithm can be seen as an adaptation of the spectral-imaging algorithm presented in Bourdin et al. (2015) to the X-ray data. Briefly, temperature log-likelihoods are first computed from spectral analysis in each pixel of the maps, and are then spatially weighted with kernels that correspond to the negative and positive parts of B3-spline wavelets functions. We use this method to derive wavelet coefficients of the temperature features and their expected fluctuation from spatially weighted Fisher information. We use such coefficients to derive wavelet and curvelet transforms that typically estimate features of apparent size in the range of [3.5, 60] arcsec. We finally reconstruct temperature maps from denoised curvelet transforms that we inferred from a 4-σ soft thresholding of the curvelet coefficients. The temperature maps in Fig. 3 are expressed in terms of the mean spectral temperatures estimated inside [0.15, 0.75]r500 and are generally used for YX = Mgas, 500TYX, the X-ray counterpart of the SZ Y parameter (Kravtsov et al. 2006). In particular, YX is estimated iteratively together with Mgas, 500, TYX, and an X-ray estimate of r500 obtained from the Arnaud et al. (2010) scaling relation. An exception to this procedure for the brightness and temperature maps (but also for the thermodynamical profiles) is adopted for PSZ2G339.63-69 – also known as the Phoenix cluster – because of the presence of strong AGN emission in the X-ray data. In Sect. 3.2.6, we discuss the alternative strategy adopted for this cluster in more detail. As can be seen from Fig. 3, this overlap of the SPT and CHEX-MATE samples collects clusters with a variety of cluster morphology and temperature features.
Regarding the cluster morphology, only two clusters (PSZ2G271.18-30.95, PSZ2G339.63-69) present regular and concentric X-ray isophotes and a cool core structure. PSZ2G259.98-63.43 and PSZ2G263.68-22.55 also show a temperature decrement towards the cluster centre, but exhibit local compressions of the X-ray isophotes that likely indicate cold fronts. For the last two clusters, PSZ2G262.73-40.92 and PSZ2G277.76-51.74, we do not observe any relevant temperature drop towards the centre, with the latter cluster also presenting a more complex and disturbed morphology. This qualitative visual inspection of the cluster appearance is corroborated by a morphological analysis of the overall CHEX-MATE sample carried out by Campitiello et al. (2022), who analysed each cluster in terms of several morphological parameters. In light of the results of these latter authors, we consider two members of our sample to be relaxed (PSZ2G271.18-30.95, PSZ2G339.63-69) galaxy clusters, one to be disturbed (PSZ2G277.76-51.74), and the remaining three to have an intermediate, ‘mixed’, morphology.
3.2.5. Radial profiles of thermodynamical quantities
Considering the background model described in Sect. 3.2.2, we estimate the thermodynamical X-ray profiles as done in Bourdin et al. (2017). We parameterise the emission measure [npne](r) and temperature T(r) profiles using the analytical expressions of Vikhlinin et al. (2006). These templates are integrated along the line of sight and fitted to the background-subtracted X-ray observable profiles: the projected temperature (estimated considering the energy band [0.3, 12.1] keV) and the soft ([0.5, 2.5] keV) X-ray surface brightness ΣX:
where z is the redshift of the cluster, Λ(T, Z) the cooling function of the cluster emission, T the temperature, Z the element abundances, and ΣX is in detector units (photons counts cm−2 arcmin−2 s−1).
The functional form suggested by Vikhlinin et al. (2006) for the emission measure can be written as
where we fix γ to γ = 3 and leave the other parameters free to vary in the fit. We parameterise the behaviour of the temperature profiles as in Vikhlinin et al. (2006), leaving all eight parameters free to vary:
with 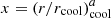 . For the temperature projection, we consider the spectroscopic-like temperature Ts weighting scheme of Mazzotta et al. (2004):
. For the temperature projection, we consider the spectroscopic-like temperature Ts weighting scheme of Mazzotta et al. (2004):
where k is the Boltzmann constant and the X-ray emissivity is used as a weight to better reproduce the effect of a single temperature fit in the spectroscopic analysis: 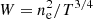 . This weighting scheme has been proven to be accurate in the temperature regime of the clusters in our sample (> 3 keV).
. This weighting scheme has been proven to be accurate in the temperature regime of the clusters in our sample (> 3 keV).
All the fits are conducted with a least-squares minimisation following the Levenberg?Marquardt algorithm. For uncertainty envelopes of the best-fit profiles, we perform 500 parametric bootstrap realisations of the observed profiles, which are estimated considering 12 radial bins inside R500 (and logarithmically spaced between [0.15, 0.8]R500) for the spectroscopic temperature, and 50 logarithmic radial bins for the surface brightness inside R500. We build the templates considering the XMM mirror PSF and the effect of the Galactic absorption described in Sect. 3.2.3. The projection also considers a metal abundance constant normalisation (Z = 0.3) for the cluster and the Planck (Eq. (80b), Planck Collaboration VI 2020) primordial helium abundance 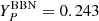 . As a consequence of these choices, the electron density can be estimated from Eq. (10) with a particle mean weight of μ = 0.592 and a proton-to-electron ratio of np/ne = 0.859. We report the 3D temperature and density profiles for all clusters in our sample in Appendix B.
. As a consequence of these choices, the electron density can be estimated from Eq. (10) with a particle mean weight of μ = 0.592 and a proton-to-electron ratio of np/ne = 0.859. We report the 3D temperature and density profiles for all clusters in our sample in Appendix B.
3.2.6. The Phoenix cluster PSZ2G339.63-69
The Phoenix cluster is a known astronomical object in X-ray, optical, and radio astronomy. McDonald et al. (2019) show with their work based on the Karl Jansky Very Large Array, Hubble, and Chandra space telescopes that the central temperature and entropy profiles are consistent with a pure cooling model. Kitayama et al. (2020) also measure a similar decrement towards the cluster centre by combining the SZ signal from ALMA and Chandra X-ray information. This efficient cooling in the centre of the cluster is highly related to the activity of the central galaxy, which hosts a powerful and obscured AGN (McDonald et al. 2012, 2013, 2019; Tozzi et al. 2015) that, with its feedback, supports the formation of a multi-phase condensation in the ICM.
At millimetric wavelengths, the AGN signal (1.8 mJy at 92 GHz measured with ALMA; Kitayama et al. 2020) is below the SPT noise (∼2 mJy at 95 GHz; Mocanu et al. 2013). Therefore, we do not include it in the modelling. In X-ray, instead, the AGN contaminates the XMM-Newton observations up to the cluster periphery due to the larger point spread function of XMM (half-energy width at aimpoint: 15″) compared to the Chandra telescope and the cluster apparent size (z = 0.596, R500 = 2.85 arcmin). As pointed out by Tozzi et al. (2015) and McDonald et al. (2019), the AGN is moderately obscured, with its emission that dominates the spectrum in the hard X-ray band above 2 keV. The AGN signal therefore makes it more difficult to reconstruct the cluster spectrum for XMM-Newton EPIC cameras without proper modelling of the AGN emission over the entire spectral band of interest ([0.3 − 12.1] keV). To reduce the impact of the AGN in the X-ray cluster modelling for the brightness and temperature maps or the thermodynamical profiles, we restrict the analysis to where the cluster dominates over the AGN signal, thus removing all the photons with E > 2 keV.
4. Results
In this section, we discuss the pressure profiles obtained with our SZ pipeline and compare them to the profiles derived from X-ray analysis.
4.1. Millimetric fit
We fit the profile on the 95 and 150 GHz channels of SPT, and 100, 143, 353 channels of Planck. We exclude the 220 GHz and 217 GHz channels of SPT and Planck, respectively. These channels do not carry relevant information about the cluster because the SZ signal is expected to be null around their frequencies. We also exclude the high-frequency channel of Planck, namely the 545 GHz and 857 GHz, because these are dominated by dust emission and the contribution of the cluster signal to the fit is marginal. We show the comparison between the best joint-fit cluster profiles and the SPT and Planck data in Figs. 4–9, from which we removed background and foreground signals. We also show the profiles of the background and foreground components. We note that none of the contaminant components is intrinsically positive or negative. Due to the high pass filter, we are looking at the fluctuations with respect to the underlying large-scale signal. Therefore, even if the total GTD emission is always positive, its small-scale fluctuations are not. Furthermore, we remember that the CTD component is not the cluster dust emission but a correction term to the total dust template accounting for the different SEDs of the two dust components. Thus, its sign varies depending on the specific features on each map.
 |
Fig. 4. Radial profile around PSZ2G259.98-63.43 for the three SPT channels (95-150-220, upper panels) and four Planck channels (100-143-217-353, lower panels). The black dots represent the radial average on the SZ maps, the red line is the best fit of the cluster profile, and the blue line is the radial mean of the total background signal. For Planck data, we also show the individual components of the background model: the dotted cyan line is the CMB, the dashed red line is the GTD, and the dash-dotted orange line is the cluster dust component. |
Our sky model, including the cluster contribution and the cosmological and Galactic contamination, provides an excellent reconstruction of both SPT and Planck data. Furthermore, we verify that the two data sets are highly consistent with one another. We note that we do not show the ‘raw’ data in the plots, but instead we include the foreground-cleaned data. The raw signal corresponds to the sum of the black dots and the contaminant components.
The above plots highlight the peculiarities of the two data sets that led us to implement specific component-separation pipelines for each instrument. As is evident, because of the difference in resolution and spectral response, Planck raw data are more contaminated by large-scale background and foreground signals than those of SPT. As mentioned above, SPT cannot detect these signals because of its intrinsic high-pass filter.
We recall that the 220 GHz SPT channel and the 217 GHz Planck channel are not included in the fit of the cluster profile, because we expect the SZ amplitude to be lower than the noise at those frequencies; however, they are more sensitive than the lower frequency channels to possible dust foreground residuals and therefore provide a good benchmark for the component-separation algorithms. It is especially relevant for SPT because the 220 GHz is the highest frequency channel, where the dust signal should be brighter. In this regard, we do not find any evidence of dust contamination in SPT data above the noise level, as is evident from the top-right panels of Figs. 4–9. Inspection of Planck data instead shows some level of dust contamination at high frequency in almost all the clusters. However, the amplitude at the lower frequencies common to SPT is not relevant compared to both the cluster signal and the noise. The explanation of the relatively low level of dust contamination also in Planck data comes from the position on the sky of SPT clusters, which is far from the Galactic plane, as well as from the high-pass filter that we applied to the data (described in Sect. 3.1.1). Only in the case of PSZ2G271.18-30.95 (see Fig. 7) is the dust emission particularly evident at the lower frequencies common to SPT. On the other hand, we do not find evidence of this emission in SPT data; however, a possible hint comes from a systematic negative excess at 220 GHz. However, this deviation seems too faint with respect to the noise level to be relevant. As this signal comes in the form of diffuse emission, the SPT window function high-pass filters a large part of it. These results support the choice – discussed in Sect. 3.1.2 – to neglect the dust contribution in the SPT data-reduction pipeline.
We conclude this section with a comment on the CMB reconstruction in SPT, which appears systematically different from and lower than that in the Planck data. The explanation comes again from the different spatial filtering of the two instruments combined with the shape of the CMB power spectrum. As the amplitude of CMB fluctuations decreases with the scale, the CMB signal is lower in SPT data where the larger scales are suppressed. Furthermore, as mentioned in Sect. 3.1.2, the small scales of the CMB estimate derived for SPT are dominated by the 220 GHz noise.
4.2. Comparison with X-ray profiles
X-ray data provide an independent benchmark for our pipeline. We compare the pressure profiles derived from the SZ maps with the expectations from X-ray observations. X-ray and SZ data are significantly different in sensitivity and resolution and they probe the cluster structure at different regimes. Therefore, we limit our comparison to the overlapping region between the two; that is, inside r500. The XMM-Newton sensitivity sets the upper limit: the X-ray cluster emission rapidly declines with the radius given its quadratic dependence on the density, and falls below the XMM-Newton background for r > r500.
We show a comparison of the two fits in Fig. 10. We find a perfect match between the two profiles outside the SPT FWHM (marked with a vertical dashed line). Remarkably, we also find good consistency for smaller radii for five out of six clusters. The credibility intervals overlap along the whole radius range tested. The agreement between SZ and X-ray profiles is good regardless of the angular size of the cluster. As the X-ray analysis highlights, our sample contains clusters with various morphological features. This comparison shows that our method provides consistent results regardless of the morphology. In only one case, namely the Phoenix cluster PSZ2 G339.63-69.34, do the results not match perfectly; we discuss this case in detail below. These results confirm that our method correctly recovers the profile up to the scale of the FWHM of the SPT beam. Some degree of divergence can be observed in the very inner regions, but this is not statistically relevant. These small deviations are no cause for concern because, in light of their limited resolution, SPT and Planck are not expected to be sensitive to these small scales, which are instead captured by XMM-Newton. Furthermore, the gNFW model fitted to the SZ data cannot reproduce small-scale features such as the changes of slope inside r500 present in some clusters (in particular in PSZ2 G339.63-69.34, but also noticeable e.g. in PSZ2 G263.68-22.55 and PSZ2 G259.98-63.43). We reiterate that the SZ fit is performed over radial bins of size 0.2r500, which are marked by the ticks on the horizontal axis in Fig. 10.
 |
Fig. 10. Comparison between pressure profiles from XMM-Newton data (dash dotted red lines) and from the SPT-Planck joint fit (blue lines). The shaded regions correspond to the 68% credible intervals. The light blue dashed section of the SPT-Planck line marks the region inside the innermost SPT data point. The dotted black lines show the universal profile from Arnaud et al. (2010) for comparison. The vertical dashed lines indicate the FWHM of the SPT beam. The lower panels represent the relative deviation with respect to the SZ results. The ticks on the horizontal axis correspond to the edges of the bins of SPT data. |
The Phoenix cluster, PSZ2G339.63-69.34, represents the only case where the two data sets appear slightly but systematically shifted. It is the cluster with the smallest angular diameter in the sample (see Table 1), and the one with the lowest S/N. As mentioned in Sect. 3.2, the strong emission of the AGN contaminates the X-ray signal and makes the XMM-Newton analysis challenging. Furthermore, the profile obtained from X ray data is relatively irregular, showing a number sharp changes of slope at small radii. As mentioned above, the resolution of the millimetric data is too low to detect this behaviour, and the model cannot account for it. In light of these limitations, we conclude that, despite the small deviations, the agreement between the two profiles is very good, suggesting that our method performs well, even in poor conditions.
For comparison, in Fig. 10 we also show the ‘universal’ profile of Arnaud et al. (2010). We observe a scatter around the profile but the sample is too small to draw any conclusion in this respect. We will investigate this topic further in future works on larger samples.
We report the best-fit value for the parameters in Table 3, with the universal profile parameters as a reference. The credibility intervals for each parameter are obtained by excluding the tails of the marginalised posterior symmetrically so that they contain 68% of the parameter space.
Best-fit parameters for the gNFW fit.
4.3. Joint fit versus SPT
In this section, we highlight the advantages of combining different probes. In Fig. 11, we compare the results of the SPT-Planck joint fit with the profiles obtained with SPT alone. We do not compare the fit on Planck data alone, as it does not converge with our choice of free parameters because of the limited resolution. A different combination of free parameters (e.g., to fix the central slope γ) would make the comparison unfair. We not that, unlike in Fig. 10, here we show all the scales considered in the fit, meaning that the plot extends up to 3r500. We mark the SPT and Planck beam FWHM with vertical dashed and dash-dotted lines, respectively. For Planck, we report the FWHM of the beam of the channels with the best resolution, corresponding to 5 arcmin. These plots showcase the fact that the Planck contribution significantly improves the fit on the outer regions. The uncertainties on the profiles become significantly narrower when we include the Planck channels. The inner parts of the profiles instead coincide for the two fits. This shows that the small scales are dominated by the information from SPT, as expected.
 |
Fig. 11. Comparison between pressure profiles from SPT data (dash dotted green lines) and from the joint fit on the two data sets (blue line). The vertical dashed lines indicate the FWHM of the SPT beam and the dash-dotted line the lower Planck beam FWHM (5 arcmin). The lower panels represent the relative deviation with respect to the joint fit. |
5. Conclusions
In this paper, we present a technique to measure the pressure profile of galaxy clusters in millimetric and submillimetric observations from SPT and Planck. To fully exploit the potential of the two data sets, we developed two independent component-separation pipelines specifically tailored to the characteristics of each instrument. For Planck, we took advantage of the high number of frequency channels to build a complete analytical model of the Galactic foreground and the cosmological background. For SPT, we adopt a linear combination to reconstruct the CMB signal and verified that the intrinsic spatial filtering minimises the dust foreground. We use a parametric model of the profiles to efficiently deconvolve the instrumental response to the cluster signal, taking into account the angular resolution of each channel.
We applied our algorithm to a sample of six galaxy clusters representing the intersection between the SPT and CHEX-MATE catalogues. We compared the profiles derived from the SPT-Planck joint fit to the ones obtained from XMM-Newton data. We find excellent agreement between the SZ and X-ray pressure profiles for all the clusters in the sample. The results are stable over a variety of angular sizes and for clusters of different morphology.
This consistency provides us with evidence of the robustness of our method. We probe the potential of large sky millimetric surveys to constrain the profiles of galaxy clusters. We show that combining the data from Planck and SPT greatly improves the constraints compared to the fit on a single instrument. Thanks to its high resolution, SPT can track the pressure profile up to the inner region of the cluster (∼0.1r500. Planck provides a robust anchor at large scales and a reliable absolute measurement. We obtain results consistent and comparable with X-ray analyses tracking the pressure of the cluster from the outskirts up to intermediate radii (∼10−1r500). The results of this comparison motivate us to extend our analysis to derive the SZ pressure profiles of all the clusters detected by both Planck and SPT in order to investigate the structure and evolution of the profiles through cosmic time.
For a summary of all the main background components that can afflict XMM-Newton observations, see: https://www.cosmos.esa.int/web/xmm-newton/epic-background-components
Acknowledgments
Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA, and with Planck (http://www.esa.int/Planck), an ESA science mission with instruments and contributions directly funded by ESA Member States, NASA, and Canada. F.O., F.D., H.B. P.M., S.E., L.L, M.S., M.R. and F.G. acknowledge financial contribution from the contracts ASI-INAF Athena 2019- 27-HH.0, “Attività di Studio per la comunità scientifica di Astrofisica delle Alte Energie e Fisica Astroparticellare” (Accordo Attuativo ASI-INAF n. 2017-14- H.0), from the European Union’s Horizon 2020 Programme under the AHEAD2020 project (grant agreement n. 871158). F.O., F.D., H.B. P.M., S.E., L.L and M.S. acknowledge support from INFN through the InDark initiative. J.S. acknowledges the NASA/ADAP Grant Number 80NSSC21K1571. B.J.M. acknowledges support from STFC grant ST/V000454/1. M.S. acknowledges financial contribution from contracts ASI-INAF n.2017-14-H.0 and INAF mainstream project 1.05.01.86.10. G.W.P. acknowledges funding from CNES, the French space agency.
References
- Aghanim, N., Douspis, M., Hurier, G., et al. 2019, A&A, 632, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Battaglia, N., Bond, J. R., Pfrommer, C., & Sievers, J. L. 2012, ApJ, 758, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Hill, R. S., Hinshaw, G., et al. 2003, ApJS, 148, 97 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertschinger, E. 1998, ARA&A, 36, 599 [Google Scholar]
- Birkinshaw, M. 1999, Phys. Rep., 310, 97 [Google Scholar]
- Bleem, L. E., Stalder, B., de Haan, T., et al. 2015, ApJS, 216, 27 [Google Scholar]
- Bourdin, H., & Mazzotta, P. 2008, A&A, 479, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourdin, H., Mazzotta, P., Markevitch, M., Giacintucci, S., & Brunetti, G. 2013, ApJ, 764, 82 [Google Scholar]
- Bourdin, H., Mazzotta, P., & Rasia, E. 2015, ApJ, 815, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Bourdin, H., Mazzotta, P., Kozmanyan, A., Jones, C., & Vikhlinin, A. 2017, ApJ, 843, 72 [Google Scholar]
- Campitiello, M. G., Ettori, S., Lovisari, L., et al. 2022, A&A, 665, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlstrom, J. E., Ade, P. A. R., Aird, K. A., et al. 2011, PASP, 123, 568 [CrossRef] [Google Scholar]
- Chown, R., Omori, Y., Aylor, K., et al. 2018, ApJS, 239, 10 [Google Scholar]
- Curry, H. B., & Schoenberg, I. J. 1966, Journal d’Analyse Mathématique, 17, 347 [Google Scholar]
- Delabrouille, J., Cardoso, J. F., Le Jeune, M., et al. 2009, A&A, 493, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Luca, A., & Molendi, S. 2004, A&A, 419, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eriksen, H. K., Banday, A. J., Górski, K. M., & Lilje, P. B. 2004, ApJ, 612, 633 [Google Scholar]
- Finkbeiner, D. P., Davis, M., & Schlegel, D. J. 1999, ApJ, 524, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Fioretti, V., Bulgarelli, A., Malaguti, G., Spiga, D., & Tiengo, A. 2016, Proc. SPIE, 9905, 99056W [NASA ADS] [CrossRef] [Google Scholar]
- Gastaldello, F., Marelli, M., Molendi, S., et al. 2022, ApJ, 928, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirardini, V., Ettori, S., Eckert, D., et al. 2018, A&A, 614, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurier, G., Macías-Pérez, J. F., & Hildebrandt, S. 2013, A&A, 558, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaiser, N., Squires, G., & Broadhurst, T. 1995, ApJ, 449, 460 [Google Scholar]
- Katayama, H., Takahashi, I., Ikebe, Y., Matsushita, K., & Freyberg, M. J. 2004, A&A, 414, 767 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kitayama, T., Ueda, S., Akahori, T., et al. 2020, PASJ, 72, 33 [Google Scholar]
- Kravtsov, A. V., & Borgani, S. 2012, ARA&A, 50, 353 [Google Scholar]
- Kravtsov, A. V., Vikhlinin, A., & Nagai, D. 2006, ApJ, 650, 128 [Google Scholar]
- Kuntz, K. D., & Snowden, S. L. 2008, A&A, 478, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lau, E. T., Kravtsov, A. V., & Nagai, D. 2009, ApJ, 705, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Lau, E. T., Nagai, D., Avestruz, C., Nelson, K., & Vikhlinin, A. 2015, ApJ, 806, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Leccardi, A., & Molendi, S. 2008, A&A, 486, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovisari, L., & Reiprich, T. H. 2019, MNRAS, 483, 540 [Google Scholar]
- Marelli, M., Molendi, S., Rossetti, M., et al. 2021, ApJ, 908, 37 [CrossRef] [Google Scholar]
- Mazzotta, P., Rasia, E., Moscardini, L., & Tormen, G. 2004, MNRAS, 354, 10 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, I. G., Le Brun, A. M. C., Schaye, J., & Holder, G. P. 2014, MNRAS, 440, 3645 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, M., Bayliss, M., Benson, B. A., et al. 2012, Nature, 488, 349 [Google Scholar]
- McDonald, M., Benson, B., Veilleux, S., Bautz, M. W., & Reichardt, C. L. 2013, ApJ, 765, L37 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, M., Benson, B. A., Vikhlinin, A., et al. 2014, ApJ, 794, 67 [Google Scholar]
- McDonald, M., McNamara, B. R., Voit, G. M., et al. 2019, ApJ, 885, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Meisner, A. M., & Finkbeiner, D. P. 2015, ApJ, 798, 88 [Google Scholar]
- Melin, J. B., Bartlett, J. G., Tarrío, P., & Pratt, G. W. 2021, A&A, 647, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mocanu, L. M., Crawford, T. M., Vieira, J. D., et al. 2013, ApJ, 779, 61 [Google Scholar]
- Nagai, D., Kravtsov, A. V., & Vikhlinin, A. 2007, ApJ, 668, 1 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [Google Scholar]
- Nelson, K., Lau, E. T., & Nagai, D. 2014, ApJ, 792, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Oppizzi, F., Renzi, A., Liguori, M., et al. 2020, JCAP, 2020, 054 [CrossRef] [Google Scholar]
- Planck Collaboration I. 2014, A&A, 571, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2020, A&A, 641, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VII. 2016, A&A, 594, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VIII. 2016, A&A, 594, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIII. 2016, A&A, 594, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVII. 2016, A&A, 594, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. V. 2013, A&A, 550, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXIX. 2016, A&A, 586, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLIII. 2016, A&A, 596, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pointecouteau, E., Santiago-Bautista, I., Douspis, M., et al. 2021, A&A, 651, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Remazeilles, M., Delabrouille, J., & Cardoso, J.-F. 2011, MNRAS, 418, 467 [Google Scholar]
- Salvati, L., Saro, A., Bocquet, S., et al. 2022, ApJ, 934, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Salvetti, D., Marelli, M., Gastaldello, F., et al. 2017, Exp. Astron., 44, 309 [Google Scholar]
- Snowden, S. L., Mushotzky, R. F., Kuntz, K. D., & Davis, D. S. 2008, A&A, 478, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starck, J. L., Pantin, E., & Murtagh, F. 2002, PASP, 114, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Starck, J. L., Fadili, J. M., Digel, S., Zhang, B., & Chiang, J. 2009, A&A, 504, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comm. Astrophys. Space Phys., 4, 173 [Google Scholar]
- Tegmark, M., de Oliveira-Costa, A., & Hamilton, A. J. 2003, Phys. Rev. D, 68, 123523 [Google Scholar]
- The CHEX-MATE Collaboration (Arnaud, M., et al.) 2021, A&A, 650, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torrado, J., & Lewis, A. 2021, JCAP, 2021, 057 [Google Scholar]
- Tozzi, P., Gastaldello, F., Molendi, S., et al. 2015, A&A, 580, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verner, D. A., & Ferland, G. J. 1996, ApJS, 103, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [Google Scholar]
- Zhang, B., Fadili, J. M., & Starck, J.-L. 2008, IEEE Trans. Image Process., 17, 1093 [CrossRef] [Google Scholar]
Appendix A: X-ray absorption towards the CHEX-MATE+SPT cluster sample
X-ray absorption and its relationship with the total (atomic+molecular) Galactic hydrogen density column towards CHEX-MATE galaxy clusters have been investigated in a companion analysis (Bourdin et al. in prep.). Briefly, a joint-analysis of Planck and HI4PI data allowed us to estimate the mass fraction of molecular gas across the lines of sight toward CHEX-MATE galaxy clusters, f = 2NH2/NH, by looking for thermal dust emission excesses with respect to the neutral atomic hydrogen density column, NHI. We found that the CHEX-MATE cluster catalogue can be divided into three categories: 40% are clusters located behind low NHI regions (NHI < 2 × 1020 cm−2) where the molecular mass fraction is negligible, 40% are clusters located behind intermediate NHI regions (2 × 1020cm−2 < NH < 5 × 1020cm−2) where the molecular gas fraction is ∼10% on average, and the remaining 20% of the cluster sample are located behind high NHI regions where higher molecular gas fractions could locally affect the analyses of a few observations. A comparison of NH estimates obtained from X-ray spectroscopy (XMM-Newton) and dust emission excesses (Planck+HI4PI) with respect to HI is shown in Fig. A.1. Given the scatter of 25% that separates these NH estimates, the regression line shows that both of them are compatible with one another. The present work focuses on a subsample of the CHEX-MATE cluster catalogue made of six clusters, listed in Table 1 and depicted using blue points in Fig. A.1. Among these CHEX-MATE+SPT clusters, four clusters belong to the low NHI category, a regime in which molecular gas fractions do not significantly affect temperature measurements. The remaining two clusters are PSZ2G271.18-30.95 and PSZ2G263.68-22.55, which belong to the intermediate and high NHI categories, respectively. For each CHEX-MATE+SPT cluster, except PSZ2G63.68-22.55, the relative difference between XMM and Planck+HI4PI inferences of the NH values is lower than the characteristic dispersion of 25% measured for the overall CHEX-MATE sample. XMM and Planck+HI4PI inferences of the NH values differ instead by a relative amount as high as dNH/NH = 70% in the case of PSZ2G63.68-22.55, which makes this cluster an outlier of the relationship observed between XMM and Planck+HI4PI inferences for the complete CHEX-MATE sample. Furthermore, the observed spectrum in the soft X-ray band of this galaxy cluster shows an overestimation of the Galactic absorption when the molecular fraction is considered. These characteristics of the CHEX-MATE+SPT subsample led us to adopt the Planck+HI4PI inferences of the NH values for all clusters except PSZ2G63.68-22.55. In the case of PSZ2G63.68-22.55, the NH value has been inferred from X-ray spectroscopy as a result of a joint fit with projected temperature and metallicities of the ICM in annular regions delimited by a cluster-centric radii range of [0.15, 0.6]R500. The resulting value of 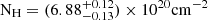 (χ2/d.o.f. = 356/328) yields a molecular gas fraction of f = 0.21, which is significantly positive but is two times lower than expected from Planck+HI4PI data.
(χ2/d.o.f. = 356/328) yields a molecular gas fraction of f = 0.21, which is significantly positive but is two times lower than expected from Planck+HI4PI data.
 |
Fig. A.1. Estimates of the hydrogen column density derived from X-ray spectroscopy and considering the dust emission excess from Planck+HI4PI (Bourdin et al. in prep.) towards the CHEX-MATE galaxy clusters. The six clusters analysed in this work are depicted as blue points in the figure. |
We show the effects of the different NH values in the X-ray cluster spectrum in Fig. A.2. The black curve in each panel of Fig. A.2 represents the observed spectrum, as seen from the three cameras (MOS1, MOS2, EPN) of the XMM-Newton telescope, while the light and dark blue curves are the fitted cluster spectrum and the background plus foreground model in the energy range ([0.3, 12.1] keV) in interest, respectively. In the two panels of Fig. A.2, we show the residuals of the fits for the two values of the NH examined in this work. In particular, we show the spectrum with the Planck+HI4PI NH hydrogen column density (χ2/d.o.f. = 485/328), and the results from the X-ray spectroscopy in the left and right panels, respectively. When the molecular contribution is considered in the fit, we observe an overestimate of the Galactic absorption (below 0.6 keV), while the observed spectrum of the cluster is more accurately modelled fitting the hydrogen column density (χ2/d.o.f. = 356/328). We also test the case where no molecular contribution is assumed in the X-ray spectral modelling, for which we observe a systematic underestimation of the Galactic absorption in the soft X-ray band, with a reduced χ2 of χ2/d.o.f. = 388/328.
 |
Fig. A.2. Fit and residuals of the X-ray spectrum of PSZ2G263.68-22.55 when we assume the molecular hydrogen column density from Bourdin et al. (in prep.) (left panel) or when NH is free to vary in the fit (right). For the three cameras (EPN, MOS1, and MOS2) of the XMM-Newton telescope, the light blue curve is the fitted model of the cluster spectrum, the dark blue line represents the total contribution from the background or foreground components (CXB plus QPB, SP, and the Galactic emission, see Sect. 3.2.2), the red curve is the sum of these two components, and the black curve is the observed spectrum. |
Appendix B: Temperature and density profiles
X-ray observables do not directly depend on the pressure, but on density and temperature. We derive the X-ray pressure profiles shown in Fig. 10 from the deprojected (3D) density and temperature profiles. In this Appendix, we show in the left and right panels of figures B.1 and B.2 the temperature and density profiles (with their corresponding 68% uncertainty envelope) for our galaxy cluster sample. The details of the joint fit with the Vikhlinin et al. (2006) analytical templates to the XMM-Newton observations are explained in section 3.2.5.
 |
Fig. B.1. Temperature (left panels, red lines) and density (right panels, green lines) profiles. The shaded regions correspond to the 68% credible intervals. |
All Tables
All Figures
 |
Fig. 1. Planck maps and background templates of PSZ2 G271.18-30.9 from the 100 GHz (first column), 143 GHz (second column), 217 GHz (third column), and 353 GHz (fourth column) channels. The first and second rows show the raw and the cleaned maps, respectively. The third row shows the CMB templates, the fourth row the Galactic dust templates. Red circles mark r500 and the black circles represent the beam FWHM of each channel. The map size is 12r500 × 12r500 and the axes show the distance from the cluster centre in arcmin. The pixel size is 1 arcmin. |
| In the text | |
 |
Fig. 2. SPT maps and background templates of PSZ2 G271.18-30.9. The upper and medium panels show the raw maps and the cleaned maps, respectively, of the 95 GHz (left), 150 GHz (centre), and 220 GHz (right) channels. In the lower panels, we show the CMB reconstruction: the full template (left), the lower spatial frequency reconstruction (centre), and the high spatial frequency reconstruction (right). The red circles mark r500 and the black circles represent the SPT beam FWHM. The map size is 6r500 × 6r500 and the axes show the distance from the cluster centre in arcmin. The pixel size is 0.5 arcmin. |
| In the text | |
 |
Fig. 3. Normalised cluster temperature maps overlaid on the point-source-removed X-ray surface brightness isocontours, as obtained from XMM-Newton data. The size of the maps is 2r500 × 2r500 centred on the X-ray peak. Contour levels are equally spaced by |
| In the text | |
 |
Fig. 4. Radial profile around PSZ2G259.98-63.43 for the three SPT channels (95-150-220, upper panels) and four Planck channels (100-143-217-353, lower panels). The black dots represent the radial average on the SZ maps, the red line is the best fit of the cluster profile, and the blue line is the radial mean of the total background signal. For Planck data, we also show the individual components of the background model: the dotted cyan line is the CMB, the dashed red line is the GTD, and the dash-dotted orange line is the cluster dust component. |
| In the text | |
 |
Fig. 5. As Fig. 4 but for PSZ2 G262.73-40.92. |
| In the text | |
 |
Fig. 6. As Fig. 4 but for PSZ2 G263.68-22.55. |
| In the text | |
 |
Fig. 7. As Fig. 4 but for PSZ2 G271.18-30.95. |
| In the text | |
 |
Fig. 8. As Fig. 4 but for PSZ2 G277.76-51.74. |
| In the text | |
 |
Fig. 9. As in Fig. 4 but for PSZ2 G339.63-69.34. |
| In the text | |
 |
Fig. 10. Comparison between pressure profiles from XMM-Newton data (dash dotted red lines) and from the SPT-Planck joint fit (blue lines). The shaded regions correspond to the 68% credible intervals. The light blue dashed section of the SPT-Planck line marks the region inside the innermost SPT data point. The dotted black lines show the universal profile from Arnaud et al. (2010) for comparison. The vertical dashed lines indicate the FWHM of the SPT beam. The lower panels represent the relative deviation with respect to the SZ results. The ticks on the horizontal axis correspond to the edges of the bins of SPT data. |
| In the text | |
 |
Fig. 11. Comparison between pressure profiles from SPT data (dash dotted green lines) and from the joint fit on the two data sets (blue line). The vertical dashed lines indicate the FWHM of the SPT beam and the dash-dotted line the lower Planck beam FWHM (5 arcmin). The lower panels represent the relative deviation with respect to the joint fit. |
| In the text | |
 |
Fig. A.1. Estimates of the hydrogen column density derived from X-ray spectroscopy and considering the dust emission excess from Planck+HI4PI (Bourdin et al. in prep.) towards the CHEX-MATE galaxy clusters. The six clusters analysed in this work are depicted as blue points in the figure. |
| In the text | |
 |
Fig. A.2. Fit and residuals of the X-ray spectrum of PSZ2G263.68-22.55 when we assume the molecular hydrogen column density from Bourdin et al. (in prep.) (left panel) or when NH is free to vary in the fit (right). For the three cameras (EPN, MOS1, and MOS2) of the XMM-Newton telescope, the light blue curve is the fitted model of the cluster spectrum, the dark blue line represents the total contribution from the background or foreground components (CXB plus QPB, SP, and the Galactic emission, see Sect. 3.2.2), the red curve is the sum of these two components, and the black curve is the observed spectrum. |
| In the text | |
 |
Fig. B.1. Temperature (left panels, red lines) and density (right panels, green lines) profiles. The shaded regions correspond to the 68% credible intervals. |
| In the text | |
 |
Fig. B.2. As in Fig. B.1 but for the other clusters our sample. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} s_{\rm GTD}(\nu )=\left[ \frac{f_1q_1}{q_2}\left(\frac{\nu }{\nu _0}\right)^{\beta _{d,1}}B_\nu (T_1)+(1-f_1)\left(\frac{\nu }{\nu _0}\right)^{\beta _{d,2}}B_\nu (T_2)\right], \end{aligned} $$](/articles/aa/full_html/2023/04/aa45012-22/aa45012-22-eq2.gif)
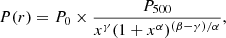
![$$ \begin{aligned} {P_{500}}=1.65\times 10^{-3}E(z)^\frac{8}{3}\times \left[ \frac{{M_{500}}}{3\times 10^{14}{M_{\odot }}}\right]^\frac{2}{3}h_{70}^2\frac{\mathrm{keV}}{\mathrm{cm}^{3}}, \end{aligned} $$](/articles/aa/full_html/2023/04/aa45012-22/aa45012-22-eq4.gif)
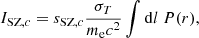
![$$ \begin{aligned} s_{\mathrm{SZ},c}=\int \mathrm{d} \nu \ R_c(\nu ) x(\nu )\left[ \frac{e^{x(\nu )}+1}{e^{x(\nu )}-1}-4\right] ,\end{aligned} $$](/articles/aa/full_html/2023/04/aa45012-22/aa45012-22-eq7.gif)
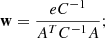
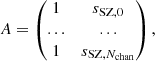
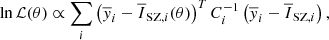
\Lambda (T,Z)\mathrm{d}l, \end{aligned} $$](/articles/aa/full_html/2023/04/aa45012-22/aa45012-22-eq18.gif)
![$$ \begin{aligned}&n_{\rm p} n_{\rm e} (r)= \frac{n_0^2(r/r_c)^{-\alpha }}{\left[1+(r/r_s)^\gamma \right]^{\epsilon /\gamma } \left[1+(r/r_{c})^2\right]^{3\beta _1-\alpha /2}} + \nonumber \\&\qquad \qquad + \frac{n_{0,2}^2}{\left[1+(r/r_{c,2})^2\right]^{3\beta _2}}, \end{aligned} $$](/articles/aa/full_html/2023/04/aa45012-22/aa45012-22-eq19.gif)
![$$ \begin{aligned} T(r)= T_0 \frac{x+T_{\min }/T_0}{x+1} \frac{(r/r_t)^{-a}}{\left[1+(r/r_t)^b\right]^{c/b}}, \end{aligned} $$](/articles/aa/full_html/2023/04/aa45012-22/aa45012-22-eq20.gif)