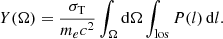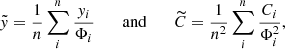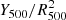| Issue |
A&A
Volume 651, July 2021
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202040213 | |
| Published online | 16 July 2021 | |
PACT
II. Pressure profiles of galaxy clusters using Planck and ACT
1
IRAP, Université de Toulouse, CNRS, CNES, UPS, Toulouse, France
e-mail: etienne.pointecouteau@irap.omp.eu
2
Departamento de Astronomía, DCNE, Universidad de Guanajuato, 36023 Guanajuato, Gto., Mexico
3
Université Paris-Saclay, CNRS, Institut d’astrophysique spatiale, Bâtiment 121, 91405 Orsay, France
4
Institute for Particle Physics and Astrophysics, Eidgenössische Technische Hochschule Zürich, Wolfgang-Pauli-Str. 27 8093 Zürich, Switzerland
5
Instituto de Física de Cantabria (CSIC-UC), Avda. Los Castros s/n, 39005 Santander, Spain
6
Centro de Estudios de Física del Cosmos de Aragñn (CEFCA), Plaza de San Juan, 1, Planta 2, 44001 Teruel, Spain
7
LPSC, Université Joseph Fourier Grenoble 1, CNRS/IN2P3, Institut National Polytechnique de Grenoble, 53 Av. des Martyrs, 38026 Grenoble, France
8
Dept. of Physics and Astronomy, Johns Hopkins University, 3400 N. Charles St., Baltimore, MD 21218, USA
9
Jodrell Bank Centre for Astrophysics, School of Physics and Astronomy, The University of Manchester, Manchester M13 9PL, UK
Received:
22
December
2020
Accepted:
10
May
2021
The pressure of hot gas in groups and clusters of galaxies is a key physical quantity, which is directly linked to the total mass of the halo and several other thermodynamical properties. In the wake of previous observational works on the hot gas pressure distribution in massive halos, we have investigated a sample of 31 clusters detected in both the Planck and Atacama Cosmology Telescope (ACT), MBAC surveys. We made use of an optimised Sunyaev-Zeldovich (SZ) map reconstructed from the two data sets and tailored for the detection of the SZ effect, taking advantage of both Planck coverage of large scales and the ACT higher spatial resolution. Our average pressure profile covers a radial range going from 0.04 × R500 in the central parts to 2.5 × R500 in the outskirts. In this way, it improves upon previous pressure-profile reconstruction based on SZ measurements. It is compatible, as well as competitive, with constraints derived from joint X-ray and SZ analysis. This work demonstrates the possibilities offered by large sky surveys of the SZ effect with multiple experiments with different spatial resolutions and spectral coverages, such as ACT and Planck.
Key words: galaxies: clusters: intracluster medium / large-scale structure of Universe / X-rays: galaxies: clusters
© E. Pointecouteau et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The thermal pressure from the hot gas in massive dark matter halos is the main force preventing the gravitational collapse of the gas towards their centre. Thermal pressure is fuelled by the infall of baryonic matter into the potential wells of groups and clusters of galaxies, inducing gravitational heating of the gas to temperatures of ∼107 − 108 K, that is ∼1−10 keV. The gas pressure is a key quantity for the physical characterisation of these systems and can be investigated either from the plasma X-ray emission (Sarazin 1988) or from its interaction with the cosmic microwave background (CMB), that is from the Sunyaev-Zeldovich effect (SZ effect Sunyaev & Zeldovich 1972). The former provides an indirect reconstruction of the pressure via the measurement of the gas density, ne, and temperature, T, from the X-ray surface brightness, 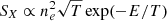 , where E is the energy. The gas pressure is derived as P = ne × T. Conversely, the SZ effect is a direct probe of the gas pressure, since the integrated SZ flux (quantified hereafter by the integrated Comptonisation parameter, Y) over the clusters directly links to the pressure as Y ∝ ∫VPdV.
, where E is the energy. The gas pressure is derived as P = ne × T. Conversely, the SZ effect is a direct probe of the gas pressure, since the integrated SZ flux (quantified hereafter by the integrated Comptonisation parameter, Y) over the clusters directly links to the pressure as Y ∝ ∫VPdV.
As expected from the simplest spherical collapse scenario, the population of groups and clusters of galaxies manifest several properties of similarity (Kaiser et al. 1995; Bertschinger 1998). This behaviour is observed via their global thermodynamical properties (e.g., Giodini et al. 2013) as well as for their internal distribution (e.g., Pratt et al. 2019). The gas thermal pressure is a remarkable example of this self-similar behaviour. The integrated pressure over the volume of the cluster, that is the SZ flux, has been shown to be an excellent proxy of the total gas content, thus of the total mass of the halo. Indeed the thermal pressure is mildly affected by non-gravitational physics (AGN feedback, radiation cooling, etc.) relative to other proxies (e.g., X-ray total luminosity, see Pratt et al. 2019; Mroczkowski et al. 2019, for recent reviews).
The advances made by SZ observations in the last two decades have allowed a precise measurement of the integrated pressure over statistically significant samples (Planck Collaboration X 2011; Planck Collaboration Int. III 2013; Czakon et al. 2015; Bender et al. 2016; Dietrich et al. 2019), demonstrating the coherent view of the gas content of galaxy clusters between X-ray and millimetre measurements. Increases in the spectral coverage, spatial resolution, and sensitivity of SZ observations have also improved constraints on the pressure distribution over the whole volume of clusters (Plagge et al. 2010; Planck Collaboration Int. V 2013; Sayers et al. 2013; Eckert et al. 2013). Both theory and numerical simulations of structure formation have provided a successful description of the gas behaviour under the influence of the key physical processes governing the intra-cluster medium (ICM, Nagai et al. 2007; Battaglia et al. 2010). One outcome of these simulations is the generalisation of the Navarro et al. (1996) profile (gNFW) for the distribution of dark matter derived from early numerical simulations, to the one for the gas pressure by Nagai et al. (2007):
where x = r/rs and rs = r500/c500. The quantities r500 and c500 are the characteristic radius and the concentration corresponding to a density contrast of 500 times the critical density of the Universe at the cluster redshift. The exponents γ, β, and α are the inner, external, and transition slopes (at rs) of the profile, respectively. The gNFW profile thus provides a simple parametric description, which can be tested against observational constraints (e.g., Arnaud et al. 2010; Planck Collaboration Int. V 2013; Eckert et al. 2013; Adam et al. 2015, 2016; Sayers et al. 2016; Romero et al. 2017; Bourdin et al. 2017; Ruppin et al. 2018). The afore-cited works have found a very good agreement between the gNFW model and the observed pressure distribution in X-ray or SZ, at least within the central part of the galaxy clusters. Beyond R500, the observational constraints mainly come from SZ observations and show an average agreement with the gNFW profile, although with some scatter (e.g., Sayers et al. 2016; Ghirardini et al. 2018). These variations are potentially linked to disparate samples providing a non-homogeneous sampling of the cluster population. They might also be the imprint of intrinsic variations in the outskirts across the population of massive halos due to the complex physics governing the virialisation of the gas (e.g., shocks, turbulent and bulk motions of the gas, and complex accretion from the larger surroundings leading, for instance, to inhomogeneities and substructures Simionescu et al. 2019; Walker et al. 2019).
In this paper, we pursue this observational investigation of the pressure distribution in clusters on the basis of the combination of the Planck and ACT maps by Aghanim et al. (2019) (see also the work by Madhavacheril et al. 2020). The resulting reconstructed SZ map is optimised for the detection of the SZ signal with its ∼1.5 arcmin spatial resolution and a tightly controlled noise. From the footprints of the two ACT-MBAC survey strips (Dünner et al. 2013), we have assembled a sample of massive clusters of galaxies detected by both Planck and ACT in order to investigate their thermal pressure distribution on the basis of the SZ observations only. This study is thus a test and pathfinder case for future work on larger survey areas, for example, the 18 000 sq. deg jointly covered by ACT and Planck (Aiola et al. 2020).
In the following section we briefly describe the PACT SZ map and the cluster sample defined for this work. In Sect. 3, we recall some basics on the SZ effect and the methodology adopted to reconstruct the pressure distribution in our clusters. Section 4 presents the validation procedure based on the comparison to the Planck data, and the related results of the various validation steps. The y- and pressure profiles are given in Sect. 5, before discussing the outcome of our work in Sect. 6
Throughout this paper, we assume a ΛCDM cosmology with H0 = 70 km s−1 Mpc−1, ΩM = 0.3, and ΩΛ = 0.7.
2. The Planck and ACT sample and SZ data
2.1. The joint SZ map
To extract the SZ signal for each individual cluster of our sample, we employed the joint Planck and ACT SZ map (hereafter called the PACT map, Aghanim et al. 2019), that is a y-map reconstructed from the linear combination of the Planck (Planck Collaboration VIII 2016) and ACT frequency maps (Dünner et al. 2013). While Planck is an all-sky survey, the ACT map is constituted of two strip maps, an equatorial and a southern one. This reconstruction is performed making use of an internal linear combination (ILC) method, MILCA (Modified Internal Linear Combination Algorithm Hurier et al. 2013). Such methods perform an optimal combination of frequency maps (from a single instrument or several instruments) for the reconstruction of a targeted frequency-dependent signal, that is the SZ effect in our case. They account for the intrinsic resolution and noise (instrumental and astrophysical) of each frequency map included in the combination.
As originally shown in Remazeilles et al. (2013), this combination takes advantage of the Planck frequency coverage and ACT spatial resolution. Also, Planck has the unique ability to provide the large spatial scales, which are excluded from the ACT signal after spatial filtering needed to reduce the impact of atmospheric brightness fluctuations. Hence the final PACT y-map inherits the spatial resolution of the ACT survey, which can be well approximated by a 1.4 arcmin full width at half maximum (FWHM) Gaussian, out to the outskirts of low-z systems provided by Planck. We refer to the first PACT paper, Sect. 3.2 for a detailed description of the y-map reconstruction and its characterisation (Aghanim et al. 2019). The MILCA y-map and its associated noise map are provided in units of the dimensionless Comptonisation parameter. Integrated measured SZ fluxes are expressed in units of arcmin2 and the SZ luminosities in Mpc2. We also made use, for validation purposes (see Sect. 4), of the Planck all-sky y-map. We used the public MILCA y-map (Planck Collaboration XXII 2016) which has an angular resolution of 10 arcmin FWHM. We also used a second (non-public) version of the MILCA y-map reconstructed at 7 arcmin FWHM. This map has been used for the extraction of the Planck SZ signal by the X-COP collaboration (Tchernin et al. 2016; Eckert et al. 2017; Ghirardini et al. 2018).
2.2. The cluster samples
We have defined our samples from SZ catalogues of galaxy clusters obtained from the Planck (Planck Collaboration VIII 2011; Planck Collaboration XXIX 2014; Planck Collaboration XXVII 2016, ESZ, PSZ1, PSZ2, respectively) and ACT (Hasselfield et al. 2013; Hilton et al. 2018) surveys. A total of 119 clusters are detected within the ACT footprint by either instrument. Here we focus on the 34 joint detections. We exclude three sources partially covered at the edges of ACT footprint or falling into the mask of Planck point sources (used to construct the PACT y-map). Our final sample is thus comprised of 31 clusters of galaxies, hereafter referred as PACT31, with 18 sources distributed in the equatorial strip and 13 in the southern one. By construction our sample is neither representative nor complete. The clusters range between 0.16 and 0.70 in redshift and from 3.7 × 1014 to 1.3 × 1015 M⊙ in M500, where M500 is the total mass contained within R500. The mean signal-to-noise ratio (S/N) of the sample is 6.0 in the Planck catalogues and 6.3 in ACT’s. The range of angular size over the sky is 2.5 < θ500 < 7.9 arcmin, with a mean value of 4.2 ± 1.1 arcmin.
We also consider the sample of 62 massive local clusters used in Planck Collaboration Int. V (2013, P13 hereafter) to derive the pressure profile of the hot intra-cluster gas from the first Planck all-sky survey. Here the Planck maps used to derive the y-map (see above) are those from the all-sky survey (i.e., 2015 data release Planck Collaboration VIII 2016). We therefore use this sample, hereafter PLCK62, in order to compare to the profiles derived from our PACT map (see Sect. 4). From the second Planck catalogue, PSZ2, the redshift of the PLCK62 sample ranges between 0.04 to 0.44 and the S/N from 7 to 49. The covered mass interval is 2.4 × 1014 < M500 < 2.0 × 1015 M⊙, for an angular size one of 3.7 < θ500 < 22.8 arcmin with a mean value of 9.8 ± 5.4 arcmin.
Masses for the PLCK62 sample are M500 hydrostatic masses from P13, derived from the XMM-Newton observations. For the PACT31 sample, we make use of the M500 values provided in the PSZ2 catalogue. The latest are derived from an Y500 − M500 relation calibrated with Planck SZ integrated fluxes and XMM-Newton hydrostatic masses (Planck Collaboration XX 2014; Planck Collaboration XXIV 2016). We checked the consistency between the P13 hydrostatic mass and the PSZ2 masses for the PLCK62 sample, finding a mean ratio of 0.98 ± 0.11. We provide, in Fig. 1, the distribution of the two samples in the M500 − z, M500 − θ500 and θ500 − z plans.
 |
Fig. 1. Distribution of the PACT31 (red dots) and PLCK62 (blue dots) in the M500 − z(left), M500 − θ500(middle) and θ500 − z(right). Crosses picture the median value and associated maximum absolute deviation over each sample. Values for the redshift, masses and angular radii are taken from the PSZ2 catalogue (Planck Collaboration XXVII 2016). |
3. Computation of the y and pressure profile
To recover the pressure profiles from the SZ y-map, we strictly followed the method described and used by P13. The SZ flux is the product of the SZ spectrum integrated over a frequency band and the integrated Compton parameter, Y, within a given solid angle, Ω. The latter is proportional to the thermal pressure of the ICM gas integrated over the line of sight:
The effect of the weakly relativistic velocities of the electrons as a function of the gas temperature on the SZ spectrum shape (e.g., Pointecouteau et al. 1998) are neglected in the y-map reconstruction as accounting for these effects would require a priori knowledge on the gas temperature distribution across the cluster.
From the y-map and error map, we extracted patches from the 20 × θ500 side centred on the ACT cluster position. We chose a pixel size defined in constant units of θ500, which is thus common to all clusters in our sample (i.e., all 31 patches have different angular pixel sizes). The pixel size also implies a sampling of the PACT PSF and therefore a possible oversampling of the y-map pixel (Sect. 4). We take into account and propagate the correlations induced by this oversampling factor.
We compute an azimuthal y-profile from the map. The value in each radial bin is obtained from the mean of the pixel values it encompasses. A background offset is estimated from radii greater than 5 × R500 and is subtracted. We masked point sources in a two step process: (i) obvious positive or negative1 sources are masked manually, and (ii) a pixel clipping is applied on the map with a 2.5σ criterium with respect to the mean map flux outside a radius of 5 × R500. To account for the correlation introduced by the aforementioned sampling and intrinsic correlated noise of the PACT y-map, we computed the covariance matrix associated to the y-profile. To do so, we estimated the power spectrum of the noise (astrophysics, instrument, systematics) in the region surrounding the cluster (θ > 5 × R500). We drew a thousand realisations of the noise patch, applied the same profile extraction as for the y-patches, and derived the covariance matrix as 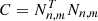 (where Nn, m is a matrix of n points per profiles ×m simulated noise profiles).
(where Nn, m is a matrix of n points per profiles ×m simulated noise profiles).
The 2D y-profiles are binned to maximise S/N out to the largest possible radius. To derive the 3D pressure profiles, we assumed spherical symmetry of our clusters and applied a regularised PSF deconvolution and geometrical deprojection algorithm, adapting the method described in Croston et al. (2006) for X-ray surface brightness profiles. Errors encoded in the 2D y-profile covariance matrix were propagated to the 3D pressure profile on the basis of the matrix’s Choleski decomposition (assuming correlated Gaussian noise), from which 10 000 random realisations of the y-profile are drawn. Each of these realisations is deconvolved from the PSF and deprojected individually. In the process, the dispersion in flux in each radial bin, derived from y-map, is used as a weight for each point of the y-profile. The covariance matrix of the pressure profile, CP, is derived from the combination of l = 10 000 realisations of the pressure profile, 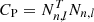 (where Nn, l is a matrix of n points per profiles ×m simulated noise profiles). Both profile and covariance matrix are then scaled in physical units.
(where Nn, l is a matrix of n points per profiles ×m simulated noise profiles). Both profile and covariance matrix are then scaled in physical units.
We followed the stacking procedure described in Sect. 4.3.2, Eq. (14) of P13 to stack the y-profiles. We recall here that the output stacked profile and associated covariance matrix are:
with 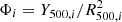 for the ith cluster, n the number of clusters in the sample and yi and Ci the y-profile and associated covariance matrix for the ith cluster. The staked pressure profile and its covariance matrix are derived in a similar way, with Φi = P500, i × f(Mi) for the ith cluster. P500 is the pressure integrated within R500 and
for the ith cluster, n the number of clusters in the sample and yi and Ci the y-profile and associated covariance matrix for the ith cluster. The staked pressure profile and its covariance matrix are derived in a similar way, with Φi = P500, i × f(Mi) for the ith cluster. P500 is the pressure integrated within R500 and 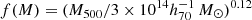 .
.
4. Validation of the PACT profiles
To fully assess our y and pressure profiles derived from the PACT maps, we proceeded through the following validation procedure which relies on two quantities: the SZ y-profiles and the SZ flux Y500 (integrated within the radius R500 as projected on the sky). Radial profiles, y(θ), are derived from the y-map together with their correlation matrix as described in the previous section. Each integrated SZ flux is derived from the corresponding y-profile, assuming a universal pressure profile (Arnaud et al. 2010, A10 hereafter), which is projected and convolved by the PACT PSF into a y-profile model, M. Folding in the covariance matrix, C, of the y-profile, the SZ flux, Y500, is obtained from the optimal solution minimising the chi-square : 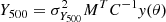 , with
, with 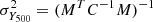 .
.
4.1. Working method and setup
We computed y(θ) and Y500 over the public and non-public Planck MILCA y-maps, with 10 and 7 arcmin FWHM, respectively, for the PLCK62 sample (i.e., named configurations D10 and D7, respectively), and over the latter only for the PACT31 sample (i.e., configuration P7120).
We first used the same setup adopted by P13 for the radial sampling, with δr = Δθ/θ500 = Δr/R500 = 0.25. We also later on used a value of δr = 0.08, a higher resolution sampling more appropriate for the PACT PSF. This value is derived in order to properly sample the PACT PSF accounting for the angular extension of our clusters (see Table 1). The PSF sampling imposed the need for δr < PSF/2 = 0.7 arcmin. As we extracted our profiles over a regular grid in units of R500 out to a value of 10, the number of radial bins is fixed by the cluster in our sample with the largest angular extension, that is C20 with θ500 = 7.9 arcmin. This led to a minimum of 112 bins with 10 × θ500, which we rounded up to 120 points. The PSF sampling thus complies with the Nyquist-Shannon criteria for all our objects, with the PSF oversampling rate increasing for clusters with smaller angular extent, and ranging from 2.1 to 6.6 pixel per PSF, with an average value of 4.2. The ensuing correlation between the successive radial bins in a given profile is encoded in the correlation matrix. The 120 points sampling applies to the setups D7120, P7120, and P7. (All the configurations defined above are summarised in Table 2.)
Properties of the PACT31 sample.
Definition of setups for the validation procedure.
We have compared the individual integrated SZ fluxes one-to-one and the stacked y profiles over the two samples for the various setups summarised in Table 2. We chose as reference fluxes the estimation of Y500 as derived from the matched multi-filter (MMF) procedure described and used in our first PACT paper (Aghanim et al. 2019). These fluxes were extracted with the MMF positioned at the ACT cluster coordinates and with a filter size fixed to θ500 for each source. For the profile comparison, we have cross-checked the stacked profile over the whole two samples, adopting as reference the y stacked profiles (and its dispersion envelop) derived for the PLCK62 sample by P13.
4.2. Validation on the Planck y-map
We first compared the integrated SZ fluxes and profiles derived from the first single all-sky Planck survey (P13) on PLCK62 (PIPV) with those derived for the second Planck public release. The latter accounts for more than five co-added all sky surveys (hereafter DR2015). Profiles and fluxes were derived for both all sky y-map reconstructed with a 10 arcmin (D10) and 7 arcmin (D7) resolution FWHM, respectively. The comparisons of fluxes and profiles are shown in Fig. 2, left-column. All three flux estimations are consistent with each other and with the PACT MMF one. The average ratios to the PACT MMF fluxes over the sample are 1.09 ± 0.13, 1.10 ± 0.07 and 1.07 ± 0.07 for PIPV, D10 and D7, respectively. The profiles for the three cases are also fully consistent in shape (the D7 profiles being more peaked is a simple consequence of the smaller PSF which convolves the actual y profile). This agreement demonstrates that, for profiles computed with a radial sampling of Δr/R500 = 0.25, there is no bias between the first all-sky survey and the full DR2015 Planck survey, and nor between the flux estimations from the 10 arcmin to 7 arcmin FWHM reconstructed MILCA y-map. We thereby adopted the D7 setup for further comparisons.
 |
Fig. 2. Top-row: one-to-one comparison of the integrated SZ flux, Y500, using as reference x-axis values fluxes computed from the PACT maps as presented in Aghanim et al. (2019). Bottom-row: average stacked y profiles in units of R500 and |
We recomputed over the 7 arcmin FWHM y-map, the profiles with a sampling of Δr/R500 = 0.08 and calculated the subsequently associated fluxes (i.e., D7120 setup). They are compared in Fig. 2, middle-column. The profiles are perfectly consistent and so are the fluxes with average ratios to the MMF fluxes of 1.06 ± 0.07 D7120, showing that no bias is introduced by further oversampling the PSF with the corresponding increased bin-to-bin correlation being properly encoded in the correlation matrix.
4.3. Validation on the PACT y-map
We switched to PACT31 and computed profiles and fluxes over the Planck 7 arcmin FWHM DR2015 map with a sampling factor of Δr/R500 = 0.08, that is P7120 setup, and over the PACT maps with the same sampling factor, that is the P7 setup. The latest is the nominal setup for the results on the PACT map and sample presented in this paper. The comparison of fluxes and profiles (see Fig 2, right-column) allows us to assess that no bias is introduced due to the difference in sample. The differences between the D7120 and P7120 stacked profiles reflects the intrinsic difference between the PACT31 and PLCK62 samples. As shown in Fig. 1, they are populating different regions of the mass and redshift plane. The two samples fully overlap in terms of the mass range (with PLCK62 covering a slightly broader range). The main difference lies in their respective redshift coverage. As a consequence the angular sizes of the PACT31 clusters are smaller, hence the increase dilution in the Planck beam explaining the flatter y profile for the P7120 setup. As a further consequence, the profile convolution by the beam redistributes power towards larger scales, and explains the slightly shallower shape at larger radii. Unsurprisingly, when switching to the P7 setup, the stacked y-profiles for the PACT31 sample as measured from the PACT map is more peaked at r < R500 than the one obtained from the Planck data only. This is the direct illustration of the differences in smoothing by a PSF of 1.4 arcmin with respect to 10 arcmin (public releases) for PACT and Planck, respectively. However the match in fluxes demonstrates that no bias is introduced in the integrated SZ flux, Y500, when switching to the PACT maps. The average ratios to the reference MMF values are 1.24 ± 0.27 and 0.95 ± 0.12 for P7120 and P7 respectively. The results on the PACT map and PACT31 sample are further discussed in the next section.
5. PACT profiles
Following the validation procedure presented in the previous section, we consider hereafter the PACT results only, thus we adopted the P7 configuration as defined in Table 2 for the rest of our study.
5.1. y profiles
We present in the left panel of Fig. 3, the individual y-profiles for the whole PACT31 sample, together with the stacked average and median profiles. The two stacked profiles present no significant differences, hence following (P13) we adopted the average over the median. The right panel shows the colour coded individual and associated stacked profiles for both equatorial and southern strip sub-samples, composed by 18 and 13 clusters, respectively. Within the limits of our sub-sample sizes, we did not find any significant differences between the two, and thereafter consider the PACT31 sample as a whole.
 |
Fig. 3. y profiles for the PACT31 sample. Left panel: stacked average (red) and median (blue) profiles. Right panel: average stacked profiles for the clusters in the equatorial (green) and southern (yellow) strips. The reported errors are correlated and correspond to the square root of the diagonal values of the covariance matrix for the y profile. Individual profiles are shown as solid lines. |
To give further support to our result, we followed the procedure described by P13, and we stacked the individual y maps across the sample. Each individual map, mi, was rescaled by the factor Φi (see Sect. 3) and randomly rotated by 0, 90, 180 or 270° before averaging. The stacked map was finally converted in units of Comptonisation parameter by ⟨Φi⟩. A null test map is built from ∑(−1)imi. The rms values of this null test map and of the stacked SZ map, outside 5 × R500, are 8.9 × 10−6 and 4.7 × 10−6, respectively. These two rms values are of the same order of magnitude. They are also compatible with the average value of the stacked error y map, 8.8 × 10−6. The stacked y-map is shown in Fig. 4. It displays a clear SZ signal out to ∼2 × R500. From our stacked average y-profile in Fig. 3, we detect the SZ signal out to a radius of ∼2.5 × R500. This is slightly less extended than for the Planck sample of P13. This is due to the difference in sample construction, where ours is made of more distant and compact clusters, as illustrated by their respective distribution in the θ500 − z in Fig. 1.
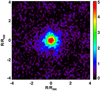 |
Fig. 4. Stacked scaled y map over the PACT31 sample (size is 8 × R500 on a side, displayed in units of 10−5 × y). Individual maps are rescaled by Φi (see Sect. 3) before averaging, and then multiplied by ⟨Φi⟩. |
5.2. Pressure profile
From the individual y profiles, we followed the methodology presented in P13 to reconstruct the 3D pressure profiles of each of our clusters. We then stacked them into a normalised average profile and also computed the associated stacked covariance matrix (details of the formalism are provided in Sect. 3, see Eq. (3)).
The derived stacked pressure profile for our sample is shown in Fig. 5 (right panel) and compared to previous results from different samples (left panel). Altogether, it is in perfect agreement with the profile derived from the PLCK62 sample by P13 within the dispersion of both samples. We recall that the PACT31 and PLCK62 samples contain 31 and 62 clusters, respectively. The outer slopes for both samples are in good agreement, whereas the inner part (i.e., r < R500) differs slightly, our PACT profile more shallower than the PLCK62 non-cool core sub-sample.
 |
Fig. 5. Stacked average pressure profiles over the PACT31 sample (red points). The reported errors bars on the data points are correlated and correspond to the square root of the diagonal valued of the covariance matrix for the pressure profile Left: comparison to published profiles over different samples by (A10; P13; Sayers et al. 2013, 2016) are overlaid as green, purple, yellow and blue lines and labelled as A10, P13, S13 and S16, respectively. The brown doted-dashed line, labelled N07, shows the original parametrisation from Nagai et al. (2007). For the P13 profiles, the solid and dashed lines correspond to the best fit to the whole PLCK62 sample and the non cool-core sub-sample, respectively. The purple shaded area picture the dispersion of the stacked Planck profiles for the PLCK62 sample (as published by P13, their Fig. 4). Right: best fit of our data to a gNFW pressure distribution (solid black line – see Table 3 and Sect. 5.2). The red shaded area shows the dispersion of the stacked profiles for the PACT31 sample. The dashed purple solid line is identical to the left panel. |
We fitted our stacked mean pressure profile to a gNFW model (Nagai et al. 2007) with a Monte Carlo Markov chain, making use of an implementation based on the Metropolis-Hastings algorithm (Hurtt & Armstrong 1996; Braswell et al. 2005; Zobitz et al. 2011). We accounted in the fit for the correlation between our points through the covariance matrix of the pressure profile, and of the dispersion on the mean across our sample. The latter is quadratically added to the diagonal elements of the profile covariance matrix. Following P13 and from the previous consideration we performed two fits with four and three free parameters, respectively. In both cases, since we lack the spatial resolution to resolve the inner profile, we fixed the slope to γ = 0.31, the best fit value from A10. We note that the joint MUSTANG-1 and Bolocam study by Romero et al. (2017) also converge towards this value. The four parameter fit let P0, c500, α, and β be free with uniform prior intervals of [0.5,20], Adam et al. (2016), Aghanim et al. (2019), [0.1,4], and Bender et al. (2016), respectively. The three parameter fit uses the same configuration, but the concentration parameter is fixed to the best fit value of A10, that is c500 = 1.18. Each MCMC fit was run with a 100 chains ending up with a number of iterations of ∼30000 each in the converged final chain. The fit processed is assessed on the basis of the likelihood logarithm, that is −χ2/2 and χ2 = (P − M)TC−1(P − M), where P, M and C are the observed profile, the model profile and the profile covariance matrix, respectively. The fit with four free parameters leads to a solution where c500 hits the lower boundary of the its prior interval. Letting this parameter run towards smaller value leads to a catastrophic degeneracy with the outer slope β. The scale radius rs = R500/c500 becomes very large, inducing a similarly large value for the external slope β, hence to a quite unphysical solution. We have thus preferred the fit with three free parameters, where the scale parameter is fixed. The results of the three-parameter fit are gathered in Table 3 together with the same from previous works, and displayed in Fig. 5. The heat map for each pair of free parameters and the associated posterior probabilities for P0, α, and β are shown on Fig. 6. The 68% confidence-level errors associated with the parameters are derived from the posterior probabilities and reported in Table 3. For our best fit with three free parameters, we find a χ2 = 2.19. We attribute the relatively low value of the χ2 to the fact of considering for the uncertainties of the stacked profile both the statistical uncertainties (propagated from the individual profiles) and the dispersion across the sample as discussed above. This might overestimate the actual uncertainties and as so artificially reduce the χ2. Conversely, the purely statistical error conveyed by the covariance matrix lead to a χ2 of 43.5 for our 18 data points profile. In this case the error is likely underestimated possibly due to some non-Gaussian correlated noise component in the y-map. In order to further assess the quality of our derived best parametrisation, we computed the associated F-test to our best fit against our pressure profile data points, and derived a significance of 0.49 denoting the goodness of our fit.
 |
Fig. 6. Posterior probability distributions and heat maps corresponding to our MCMC fit to a gGNFW pressure profile (see Sect. 5.2). The blue crosses in the 2D heat maps show the optimal solution reported in Table 3. The colour filled area show the locus of the 68, 95 and 99.7% confidence levels, respectively. |
Best fit parameter for the gNFW pressure profile.
6. Discussion and conclusion
From our Fig. 5, it is clear that the derived average stacked pressure profile for our PACT31 sample is consistent at large scales in external slope and normalisation with previous published works from distinct samples (i.e., A10; P13; Sayers et al. 2013, 2016). Within ∼0.5 × R500 our profile is slightly flatter, although the differences remain within the dispersions of these respective samples.
As emphasised by Mroczkowski et al. (2019), the point of a universal pressure profile is in its shape more than in the intrinsic values of its parameters. In our case, we note the very consistent shape of the outer parts of our profile with that derived from v. We are more marginally compatible with the S13 and S16, which are bracketing our dispersion. Within this dispersion, we are also compatible at large radii with the A10 profile, hence with the theoretical predictions from numerical simulations by Borgani et al. (2004), Nagai et al. (2007), Piffaretti & Valdarnini (2008), against which it is constrained beyond R500. The outer profile is also consistent (similar to P13) with the predictions from (Battaglia et al. 2012; Gupta et al. 2017). This result denotes that for both P13 and our profile, the large scales are constrained by the Planck measurements, with no obvious signature due to the differences in sample composition. The radial range [0.1,1] R500 presents the most differences with previously published profiles. As the P13 profile is derived from a joint Planck and XMM-Newton analysis, the inner parts are strongly constrained by the X-ray data (see their Fig 4, left panel). A fit performed on the Planck profile only, may have lead to a shallower profile. At the same time we are mainly consistent within this radial range and the respective dispersions with the S16 profile. Conversely, as shown on the left panel of Fig. 5, the comparison to the original parametrisation ![$ [P_0 h_{70}^{2/3},c_{500},\alpha,\beta,\gamma] = [3.3, 1.8,1.3,4.3,0.7] $](/articles/aa/full_html/2021/07/aa40213-20/aa40213-20-eq15.gif) published by (Nagai et al. 2007) normalised against Chandra observations of relaxed clusters (Vikhlinin et al. 2006) is mostly consistent with our profile within this inner radial range. The same stands for an update of this parametrisation, [α, β, γ] = [0.9, 5.0, 0.4] presented in Mroczkowski et al. (2009). The shallower shape of our profile in the central parts is likely due to the fainter and more compact nature of our clusters relative to those of P13 and S16.
published by (Nagai et al. 2007) normalised against Chandra observations of relaxed clusters (Vikhlinin et al. 2006) is mostly consistent with our profile within this inner radial range. The same stands for an update of this parametrisation, [α, β, γ] = [0.9, 5.0, 0.4] presented in Mroczkowski et al. (2009). The shallower shape of our profile in the central parts is likely due to the fainter and more compact nature of our clusters relative to those of P13 and S16.
Sayers et al. (2016) noted that the differences found in pressure profile analyses originate from various possible factors: the sample definition and selection, the biases intrinsic to instruments, and methods for data analysis. The comparison to the PLCK62 sample minimises the possible sources of these differences as we adopted the same data analysis methodology. While the instrumental setups differ, the approach for the reconstruction of the PACT y-map is similar to that of the Planck survey. We refer here to Aghanim et al. (2019) for the extensive validation of this dataset with respect to both ACT and Planck. For these two samples we attribute the differences in the mean pressure profile to the difference in composition of the PACT31 and PLCK62 samples. As shown in Fig. 1, the PACT31 and PLCK62 selections do sample two different regions of the M − z plane (and subsequently the M − θ and θ − z planes). Their direct comparison is not straightforward. Their respective selection function is different, and in both cases, neither quantified nor easy to apprehend. The PLCK62 sample is composed of 62 clusters with S/N > 6 from the first Planck all-sky survey. Our PACT31 sample, though of reasonable statistically size, is two times smaller with 31 clusters based on the union of the full Planck survey (i.e., more than 5 all-sky passes) and the ACT-MBAC survey with S/N going down to 4 in the Planck PSZ2 catalogue (see Table 1). As a simple verification, if we only consider clusters in the common box interval of 0.15 < z < 0.45 and 5 × 1014 < M500 < 1 × 1015 M⊙ between the PLCK62 and PACT31 samples, we obtained averaged values for the SZ flux (i.e., PSZ2 integrated Comptonisation parameter Y500), of 2.4 × 10−3 and 1.3 × 10−3 arcmin2, from 25 and 20 clusters, respectively. The latter is on average fainter by a factor of ∼2. This discrepancy is increased to a factor of ∼8 when Y500 are compared in units of Mpc2. This renders the detection of the SZ signal more difficult in the case of our PACT31 sample. As they are also more compact on average, the reconstruction of their 3D pressure profile is more prone to effects such as smoothing at large scales by the Planck beam, and thus potential biases from the regularised deconvolution and deprojection process.
Our PACT31 sample, as with all the samples used in previous published works on pressure profiles from SZ observations, has been assembled on a best-effort basis given specific observational constraints and working contexts. For instance, the PLCK62 sample is SZ selected, but is constrained by the XMM-Newton available archive data at the time of P13’s publication. Our PACT31 sample is fully SZ selected but constrained on the basis of the PACT construction and coverage. The Bolocam sample used in S13 and S16 was assembled on the basis of X-ray coverage by Chandra from the CLASH (Postman et al. 2012) and MACS samples (Ebeling et al. 2007). Thought, not actually SZ selected the SPT sample, followed-up through a very large Chandra programme, has led to several key results (e.g., McDonald et al. 2013, 2016). None of these is representative of the cluster population in its sampling of the mass and redshift space. The only representative sample to which we compare to is the REXCESS sample (Böhringer et al. 2007) from which the A10 universal pressure profile is parametrised. However this is an X-ray selected sample. Quantifying their differences and trying to promote one as a reference versus the others is therefore a complex and risky task. This limitation makes any extensive discussion on the physical meaning of the differences in the central parts of our mean pressure profile to others quite speculative at this stage. For instance, if we consider the evolution with redshift of the intrinsic SZ flux, Y500, at a given mass, the self-similar evolution is expected to be proportional to E(z)2/3 = [(1 + z)3 × Ωm + ΩΛ]1/3. At the average redshift value of the PACT31 and PLCK62 samples, that is 0.33 ± 0.11 versus 0.17 ± 0.11, respectively, we expect an average evolution of ∼6%. Accounting for the dispersion in redshift over the two samples, this expectation is uncertain by ∼12%. The likely differences in population sampling for the two samples, the associated dispersion of each sample in the M − z plane, and their proximity in redshift convolved by their underlying selection function prevent us from drawing any serious constraints on the evolution of the pressure profile.
The advantage provided by the combination of the Planck and ACT data lies on the combination of the ACT higher spatial resolution and the Planck large-scale coverage. It provides a more accurate description of the SZ signal from the central parts to the outskirts of individual clusters. Towards the cluster centre our constraints stretch down to r = 0.04 × R500 (see Fig. 5). This can be compared to the SZ-only reach of the P13 pressure profiles for the PLCK62 sample, which is 0.125 × R500 (see the red envelop in Fig. 5). With our adopted parametrisation (see Table 2) this is only illustrated by an extra central point in the reconstructed 3D pressure profile with respect to P13. This is however an improvement by more than a factor 3 in the central radial reach (obtained with a sample two times smaller). Our radial coverage towards the centre falls short of the P13 joint XMM-Newton X-ray and Planck SZ profile, which goes down in radius by an extra factor of 2, to 0.02 × R500. Such a resolution is achievable in SZ alone, making use of high resolution facilities such as MUSTANG-2 and NIKA-2 (e.g., Ruppin et al. 2018; Romero et al. 2020), though assembling data for a sample as large or larger than our PACT31 sample with these two facilities would require a very large amount of time (e.g., the NIKA-2 SZ guaranteed-time programme of 300 hours for 45 clusters, Mayet et al. 2020).
In conclusion, we have demonstrated the self consistency of two sets of SZ data by combining Planck and ACT data to reconstruct the ICM gas pressure distribution. We note that, as for previous works, the non-representative nature of our sample limits its broader applicability, beyond the basic comparisons given here. An unbiased sample at low-to-intermediate redshifts is needed to serve as a reference for the community. Such a sample will have to be a carefully selected sample, based on large SZ catalogues of clusters (e.g., Planck Collaboration XXIX 2014; Planck Collaboration XXVII 2016; Bleem et al. 2020; Hilton et al. 2021). The CHEX-MATE sample from the XMM-Newton heritage class programme ‘Witnessing the culmination of structure formation in the Universe’ fulfils this requirement by construction. (CHEX-MATE Collaboration et al. 2021). SZ selected from the Planck survey, it gathers 118 clusters with S/NPSZ2 > 6 and shall be fully covered by deep XMM-Newton observations. The combination of the XMM-Newton and Planck data following the work from P13 will provide a precise joint X-ray and SZ view of the ICM properties over this sample. This will provide a solid base to investigate changes in the pressure distribution with mass and redshift. Indeed, such variations impact the detection of clusters and the modelling of the SZ spectrum, as both rely on knowing the spatial distribution for the thermal pressure. Furthermore, as demonstrated in the present work, the combination with higher resolution SZ data constitutes a key improvement for its physical characterisation. Pointed observations with facilities such as MUSTANG-2 and NIKA-2 will be an asset, though the largest coverage of the aforementioned sample shall be achieved by the AdvACT survey, for which frequency maps over ∼18 000 sq. deg of the sky were recently publicly released (Naess et al. 2020).
Acknowledgments
This research was performed in the context of the ISSI international team project ‘SZ clusters in the Planck era’ (P.I. N. Aghanim & M. Douspis). We thank the anonymous referee. We thank Matthew Hasselfield for his participation to the early phase of this work. The authors acknowledge partial funding from the DIM-ACAV, the Agence Nationale de la Recherche under grant ANR-11-BS56-015, and PNCG/INSU/CNRS. The research leading to these results has received funding from the European Research Council under the H2020 Programme ERC grant agreement no 695561. JMD acknowledges the support of project PGC2018-101814-B-100 (MCIU/AEI/MINECO/FEDER, UE) Ministerio de Ciencia, Investigación y Universidades. This project was funded by the Agencia Estatal de Investigación, Unidad de Excelencia María de Maeztu, ref. MDM-2017-0765 DC acknowledges support from the South African Radio Astronomy Observatory, which is a facility of the National Research Foundation, an agency of the Department of Science and Technology. The development of Planck has been supported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN, JA and RES (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and PRACE (EU). This research has made use of the following databases: the NED and IRSA databases, operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the NASA; SIMBAD, operated at CDS, Strasbourg, France; SZ cluster database (szcluster-db.ias.u-psud.fr) operated by Integrated Data and Operation Centre (IDOC) operated by IAS under contract with CNES and CNRS. This research made use of Astropy, the community-developed core Python package.
References
- Adam, R., Comis, B., Macías-Pérez, J. F., et al. 2015, A&A, 576, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adam, R., Comis, B., Bartalucci, I., et al. 2016, A&A, 586, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aghanim, N., Douspis, M., Hurier, G., et al. 2019, A&A, 632, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aiola, S., Calabrese, E., Maurin, L., et al. 2020, J. Cosmol. Astropart. Phys., 2020, 047 [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, N., Bond, J. R., Pfrommer, C., Sievers, J. L., & Sijacki, D. 2010, ApJ, 725, 91 [Google Scholar]
- Battaglia, N., Bond, J. R., Pfrommer, C., & Sievers, J. L. 2012, ApJ, 758, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Bender, A. N., Kennedy, J., Ade, P. A. R., et al. 2016, MNRAS, 460, 3432 [Google Scholar]
- Bertschinger, E. 1998, ARA&A, 36, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Bleem, L. E., Bocquet, S., Stalder, B., et al. 2020, ApJS, 247, 25 [CrossRef] [Google Scholar]
- Böhringer, H., Schuecker, P., Pratt, G. W., et al. 2007, A&A, 469, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borgani, S., Murante, G., Springel, V., et al. 2004, MNRAS, 348, 1078 [Google Scholar]
- Bourdin, H., Mazzotta, P., Kozmanyan, A., Jones, C., & Vikhlinin, A. 2017, ApJ, 843, 72 [Google Scholar]
- Braswell, B. H., Sacks, W. J., Linder, E., & Schimel, D. S. 2005, Global Change Biol., 11, 335 [Google Scholar]
- CHEX-MATE Collaboration (Arnaud, M., et al.) 2021, A&A, 650, A104 [CrossRef] [EDP Sciences] [Google Scholar]
- Croston, J. H., Arnaud, M., Pointecouteau, E., & Pratt, G. W. 2006, A&A, 459, 1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Czakon, N. G., Sayers, J., Mantz, A., et al. 2015, ApJ, 806, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, J. P., Bocquet, S., Schrabback, T., et al. 2019, MNRAS, 483, 2871 [NASA ADS] [CrossRef] [Google Scholar]
- Dünner, R., Hasselfield, M., Marriage, T. A., et al. 2013, ApJ, 762, 10 [Google Scholar]
- Ebeling, H., Barrett, E., Donovan, D., et al. 2007, ApJ, 661, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Eckert, D., Molendi, S., Vazza, F., Ettori, S., & Paltani, S. 2013, A&A, 551, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eckert, D., Ettori, S., Pointecouteau, E., et al. 2017, Astron. Nachr., 338, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirardini, V., Ettori, S., Eckert, D., et al. 2018, A&A, 614, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giodini, S., Lovisari, L., Pointecouteau, E., et al. 2013, Space Sci. Rev., 177, 247 [Google Scholar]
- Gupta, N., Saro, A., Mohr, J. J., Dolag, K., & Liu, J. 2017, MNRAS, 469, 3069 [Google Scholar]
- Hasselfield, M., Hilton, M., Marriage, T. A., et al. 2013, J. Cosmol. Astropart. Phys., 7, 008 [Google Scholar]
- Hilton, M., Hasselfield, M., Sifón, C., et al. 2018, ApJS, 235, 20 [Google Scholar]
- Hilton, M., Sifón, C., Naess, S., et al. 2021, ApJS, 253, 3 [Google Scholar]
- Hurier, G., Macías-Pérez, J. F., & Hildebrandt, S. 2013, A&A, 558, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurtt, G. C., & Armstrong, R. A. 1996, Deep Sea Research Part II: Topical Studies in Oceanography, 43, 653 [Google Scholar]
- Kaiser, N., Squires, G., & Broadhurst, T. 1995, ApJ, 449, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Madhavacheril, M. S., Hill, J. C., Næss, S., et al. 2020, Phy. Rev. D, 102 [Google Scholar]
- Mayet, F., Adam, R., Ade, P., et al. 2020, Eur. Phys. J. Web Conf., 228, 00017 [Google Scholar]
- McDonald, M., Benson, B. A., Vikhlinin, A., et al. 2013, ApJ, 774, 23 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, M., Bulbul, E., de Haan, T., et al. 2016, ApJ, 826, 124 [Google Scholar]
- Mroczkowski, T., Bonamente, M., Carlstrom, J. E., et al. 2009, ApJ, 694, 1034 [Google Scholar]
- Mroczkowski, T., Nagai, D., Basu, K., et al. 2019, Space Sci. Rev., 215, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Naess, S., Aiola, S., Austermann, J. E., et al. 2020, J. Cosmol. Astropart. Phys., 2020, 046 [Google Scholar]
- Nagai, D., Vikhlinin, A., & Kravtsov, A. V. 2007, ApJ, 655, 98 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [Google Scholar]
- Piffaretti, R., & Valdarnini, R. 2008, A&A, 491, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plagge, T., Benson, B. A., Ade, P. A. R., et al. 2010, ApJ, 716, 1118 [Google Scholar]
- Planck Collaboration VIII. 2011, A&A, 536, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration X. 2011, A&A, 536, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2014, A&A, 571, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, 571, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VIII. 2016, A&A, 594, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXII. 2016, A&A, 594, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIV. 2016, A&A, 594, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVII. 2016, A&A, 594, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. III. 2013, A&A. 550, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. V. 2013, A&A, 550, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pointecouteau, E., Giard, M., & Barret, D. 1998, A&A, 336, 44 [NASA ADS] [Google Scholar]
- Postman, M., Coe, D., Benítez, N., et al. 2012, ApJS, 199, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Pratt, G. W., Arnaud, M., Biviano, A., et al. 2019, Space Sci. Rev., 215, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Remazeilles, M., Aghanim, N., & Douspis, M. 2013, MNRAS, 430, 370 [Google Scholar]
- Romero, C. E., Mason, B. S., Sayers, J., et al. 2017, ApJ, 838, 86 [Google Scholar]
- Romero, C. E., Sievers, J., Ghirardini, V., et al. 2020, ApJ, 891, 90 [CrossRef] [Google Scholar]
- Ruppin, F., Mayet, F., Pratt, G. W., et al. 2018, A&A, 615, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sarazin, C. L. 1988, S&T, 76, 639 [NASA ADS] [Google Scholar]
- Sayers, J., Mroczkowski, T., Zemcov, M., et al. 2013, ApJ, 778, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Sayers, J., Golwala, S. R., Mantz, A. B., et al. 2016, ApJ, 832, 26 [Google Scholar]
- Simionescu, A., ZuHone, J., Zhuravleva, I., et al. 2019, Space Sci. Rev., 215, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comments Astrophys. Space Phys., 4, 173 [NASA ADS] [EDP Sciences] [Google Scholar]
- Tchernin, C., Eckert, D., Ettori, S., et al. 2016, A&A, 595, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, S., Simionescu, A., Nagai, D., et al. 2019, Space Sci. Rev., 215, 7 [Google Scholar]
- Zobitz, J. M., Desai, A. R., Moore, D. J. P., & Chadwick, M. A. 2011, Oecologia, 167, 599 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Distribution of the PACT31 (red dots) and PLCK62 (blue dots) in the M500 − z(left), M500 − θ500(middle) and θ500 − z(right). Crosses picture the median value and associated maximum absolute deviation over each sample. Values for the redshift, masses and angular radii are taken from the PSZ2 catalogue (Planck Collaboration XXVII 2016). |
| In the text | |
 |
Fig. 2. Top-row: one-to-one comparison of the integrated SZ flux, Y500, using as reference x-axis values fluxes computed from the PACT maps as presented in Aghanim et al. (2019). Bottom-row: average stacked y profiles in units of R500 and |
| In the text | |
 |
Fig. 3. y profiles for the PACT31 sample. Left panel: stacked average (red) and median (blue) profiles. Right panel: average stacked profiles for the clusters in the equatorial (green) and southern (yellow) strips. The reported errors are correlated and correspond to the square root of the diagonal values of the covariance matrix for the y profile. Individual profiles are shown as solid lines. |
| In the text | |
 |
Fig. 4. Stacked scaled y map over the PACT31 sample (size is 8 × R500 on a side, displayed in units of 10−5 × y). Individual maps are rescaled by Φi (see Sect. 3) before averaging, and then multiplied by ⟨Φi⟩. |
| In the text | |
 |
Fig. 5. Stacked average pressure profiles over the PACT31 sample (red points). The reported errors bars on the data points are correlated and correspond to the square root of the diagonal valued of the covariance matrix for the pressure profile Left: comparison to published profiles over different samples by (A10; P13; Sayers et al. 2013, 2016) are overlaid as green, purple, yellow and blue lines and labelled as A10, P13, S13 and S16, respectively. The brown doted-dashed line, labelled N07, shows the original parametrisation from Nagai et al. (2007). For the P13 profiles, the solid and dashed lines correspond to the best fit to the whole PLCK62 sample and the non cool-core sub-sample, respectively. The purple shaded area picture the dispersion of the stacked Planck profiles for the PLCK62 sample (as published by P13, their Fig. 4). Right: best fit of our data to a gNFW pressure distribution (solid black line – see Table 3 and Sect. 5.2). The red shaded area shows the dispersion of the stacked profiles for the PACT31 sample. The dashed purple solid line is identical to the left panel. |
| In the text | |
 |
Fig. 6. Posterior probability distributions and heat maps corresponding to our MCMC fit to a gGNFW pressure profile (see Sect. 5.2). The blue crosses in the 2D heat maps show the optimal solution reported in Table 3. The colour filled area show the locus of the 68, 95 and 99.7% confidence levels, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \mathbb{P} (x) = \frac{P_0}{(c_{500}\, x)^\gamma [1+(c_{500}\, x)^\alpha ]^{(\beta -\gamma )/\alpha }} \end{aligned} $$](/articles/aa/full_html/2021/07/aa40213-20/aa40213-20-eq2.gif)