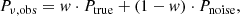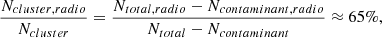| Issue |
A&A
Volume 653, September 2021
|
|
|---|---|---|
| Article Number | A135 | |
| Number of page(s) | 24 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202141200 | |
| Published online | 23 September 2021 | |
Atacama Cosmology Telescope measurements of a large sample of candidates from the Massive and Distant Clusters of WISE Survey
Sunyaev-Zeldovich effect confirmation of MaDCoWS candidates using ACT
1
Department of Physics and Astronomy, University of Pennsylvania, 209 South 33rd Street, Philadelphia, PA 19104, USA
2
Max-Planck-Institut für Astrophysik (MPA), Karl-Schwarzschild-Strasse 1, Garching 85741, Germany
3
Astronomy Unit, Department of Physics, University of Trieste, via Tiepolo 11, Trieste 34131, Italy
4
INAF – Osservatorio Astronomico di Trieste, via Tiepolo 11, Trieste 34131, Italy
5
IFPU – Institute for Fundamental Physics of the Universe, Via Beirut 2, 34014 Trieste, Italy
6
European Southern Observatory (ESO), Karl-Schwarzschild-Strasse 2, Garching 85748, Germany
e-mail: amroczko@eso.org
7
Department of Astronomy, Cornell University, Ithaca, NY 14853, USA
8
Department of Physics and Astronomy, University of Missouri, Kansas City, MO 64110, USA
9
Department of Physics, Cornell University, Ithaca, NY 14853, USA
10
Department of Astrophysical Sciences, Peyton Hall, Princeton University, Princeton, NJ 08544, USA
11
Joseph Henry Laboratories of Physics, Jadwin Hall, Princeton University, Princeton, NJ 08544, USA
12
Department of Astronomy, University of Florida, Gainesville, FL 32611, USA
13
Physics and Astronomy Department, Stony Brook University, Stony Brook, NY 11794, USA
14
Astrophysics Research Centre, University of KwaZulu-Natal, Westville Campus, Durban 4041, South Africa
15
School of Mathematics, Statistics & Computer Science, University of KwaZulu-Natal, Westville Campus, Durban 4041, South Africa
16
Department of Physics, Florida State University, Tallahassee, FL 32306, USA
17
Department of Physics and Astronomy, Rutgers, the State University of New Jersey, Piscataway, NJ 08854, USA
18
Centre for Radio Astronomy Techniques and Technologies, Department of Physics and Electronics, Rhodes University, Drosty Rd, Grahamstown 6139, South Africa
19
Department of Physics, Yale University, New Haven, CT 06520, USA
20
Department of Physics, University of Milano-Bicocca, Piazza della Scienza 3, 20126 Milano (MI), Italy
21
Kavli Institute at Cornell for Nanoscale Science, Cornell University, Ithaca, NY 14853, USA
22
Department of Physics and Astronomy, Haverford College, 370 Lancaster Ave, Haverford, PA 19041, USA
23
Department of Physics, Stanford University, Stanford, 94305 CA, USA
24
Kavli Institute for Particle Astrophysics and Cosmology, Stanford, CA 94305, USA
25
Department of Physics, California Institute of Technology, Pasadena, CA 91125, USA
26
Instituto de Física, Pontificia Universidad Católica de Valparaíso, Casilla, 4059 Valparaíso, Chile
27
Department of Physics and Astronomy, University of California, Davis, CA 95616, USA
28
Department of Physics, West Chester University of Pennsylvania, West Chester, PA 19383, USA
29
NASA Goddard Space Flight Center, 8800 Greenbelt Road, Greenbelt, MD 20771, USA
30
MIT Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
Received:
28
April
2021
Accepted:
21
June
2021
Context. Galaxy clusters are an important tool for cosmology, and their detection and characterization are key goals for current and future surveys. Using data from the Wide-field Infrared Survey Explorer (WISE), the Massive and Distant Clusters of WISE Survey (MaDCoWS) located 2839 significant galaxy overdensities at redshifts 0.7 ≲ z ≲ 1.5, which included extensive follow-up imaging from the Spitzer Space Telescope to determine cluster richnesses. Concurrently, the Atacama Cosmology Telescope (ACT) has produced large area millimeter-wave maps in three frequency bands along with a large catalog of Sunyaev-Zeldovich (SZ)-selected clusters as part of its Data Release 5 (DR5).
Aims. We aim to verify and characterize MaDCoWS clusters using measurements of, or limits on, their thermal SZ effect signatures. We also use these detections to establish the scaling relation between SZ mass and the MaDCoWS-defined richness.
Methods. Using the maps and cluster catalog from DR5, we explore the scaling between SZ mass and cluster richness. We do this by comparing cataloged detections and extracting individual and stacked SZ signals from the MaDCoWS cluster locations. We use complementary radio survey data from the Very Large Array, submillimeter data from Herschel, and ACT 224 GHz data to assess the impact of contaminating sources on the SZ signals from both ACT and MaDCoWS clusters. We use a hierarchical Bayesian model to fit the mass-richness scaling relation, allowing for clusters to be drawn from two populations: one, a Gaussian centered on the mass-richness relation, and the other, a Gaussian centered on zero SZ signal.
Results. We find that MaDCoWS clusters have submillimeter contamination that is consistent with a gray-body spectrum, while the ACT clusters are consistent with no submillimeter emission on average. Additionally, the intrinsic radio intensities of ACT clusters are lower than those of MaDCoWS clusters, even when the ACT clusters are restricted to the same redshift range as the MaDCoWS clusters. We find the best-fit ACT SZ mass versus MaDCoWS richness scaling relation has a slope of p1 = 1.84−0.14+0.15, where the slope is defined as M λ ∝15p1 and λ15 is the richness. We also find that the ACT SZ signals for a significant fraction (∼57%) of the MaDCoWS sample can statistically be described as being drawn from a noise-like distribution, indicating that the candidates are possibly dominated by low-mass and unvirialized systems that are below the mass limit of the ACT sample. Further, we note that a large portion of the optically confirmed ACT clusters located in the same volume of the sky as MaDCoWS are not selected by MaDCoWS, indicating that the MaDCoWS sample is not complete with respect to SZ selection. Finally, we find that the radio loud fraction of MaDCoWS clusters increases with richness, while we find no evidence that the submillimeter emission of the MaDCoWS clusters evolves with richness.
Conclusions. We conclude that the original MaDCoWS selection function is not well defined and, as such, reiterate the MaDCoWS collaboration’s recommendation that the sample is suited for probing cluster and galaxy evolution, but not cosmological analyses. We find a best-fit mass-richness relation slope that agrees with the published MaDCoWS preliminary results. Additionally, we find that while the approximate level of infill of the ACT and MaDCoWS cluster SZ signals (1–2%) is subdominant to other sources of uncertainty for current generation experiments, characterizing and removing this bias will be critical for next-generation experiments hoping to constrain cluster masses at the sub-percent level.
Key words: large-scale structure of Universe / cosmic background radiation / submillimeter: galaxies / radio continuum: galaxies / galaxies: clusters: general / galaxies: clusters: intracluster medium
© ESO 2021
1. Introduction
Astronomers have long sought an efficient and effective way to identify galaxy clusters as well as a convenient observational proxy for their mass (Abell 1958; Rykoff et al. 2012; Andreon 2015; Saro et al. 2015; Geach & Peacock 2017; Simet et al. 2017; Rettura et al. 2018; Gonzalez et al. 2019a; Chiu et al. 2020), particularly at high redshift, where their formation and distribution are sensitive probes of cosmology.
Recently, the Sunyaev-Zeldovich (SZ) effect (see Sunyaev & Zeldovich 1970, 1972 as well as Birkinshaw 1999; Carlstrom et al. 2002; Mroczkowski et al. 2019 for reviews) has been used to uncover large populations of distant clusters. In particular, the thermal SZ (tSZ) effect allows redshift-independent detections of clusters due to inverse-Compton scattering of photons from the Cosmic Microwave Background (CMB) as they pass through hot gas in the clusters1. Cluster masses can then be estimated from the amplitude of the SZ signals under the assumption of a universal pressure profile (e.g., Arnaud et al. 2010); we refer to such estimates as “SZ masses”. The Planck satellite, which provides the only all-sky SZ survey to date, has been limited by both sensitivity and angular resolution (10′ at 100 GHz) and has identified clusters with z < 1 (Planck Collaboration XXVII 2016). Ground-based surveys, such as the Atacama Cosmology Telescope (ACT; Fowler et al. 2007; Swetz et al. 2011; Thornton et al. 2016) and the South Pole Telescope (SPT; Carlstrom et al. 2011; Benson et al. 2014), have achieved 1–2′ resolution and are sensitive to high-redshift clusters but until recently only surveyed a small fraction of the sky. These surveys are also now more sensitive than Planck over large portions of the sky (see, e.g., Naess et al. 2020).
Meanwhile, surveys from optical through infrared (IR) wavelengths as well as analysis methods have progressed, offering new data, new selection techniques (e.g., weak lensing shear), and more advanced richness selection criteria. One such survey, the Massive and Distant Clusters of WISE Survey (MaDCoWS; Gonzalez et al. 2019a), relies on data from the Wide-field Infrared Survey Explorer (WISE). MaDCoWS provides an IR-selected sample of candidate clusters at redshifts 0.7 < z < 1.5. The MaDCoWS sample aims to extend richness selection to a higher average redshift than previous surveys.
ACT observed roughly 40% of the sky as of the fifth data release (hereafter referred to as DR5)2, which includes cluster data taken through the 2018 observing season (Hilton et al. 2021). This data release enables large, statistical comparisons between cluster richness, as measured by optical or IR surveys and their SZ mass. DR5 provides SZ measurements for a large fraction of the MaDCoWS candidates, well beyond the handful of systems targeted for individual SZ follow-up in Gonzalez et al. (2019a), Dicker et al. (2020), Di Mascolo et al. (2020), and Ruppin et al. (2020), for example.
In this work we use data from ACT DR5 to establish how SZ mass scales with the MaDCoWS definition of richness for a large sample of MaDCoWS cluster candidates. The work presented here complements the recent work by Madhavacheril et al. (2020), who report the mean mass, determined through stacked CMB lensing, of the MaDCoWS candidates located within the ACT survey region and above a richness of 20 (Sect. 2.1). Additionally, this work probes the mass-richness scaling relation, and hence cluster abundance, at a higher redshift than previous studies (e.g., Sehgal et al. 2013).
The paper is structured as follows. An overview of the ACT DR5 and MaDCoWS samples, as well as the ancillary data we use to test for radio and submillimeter source infill, is provided in Sect. 2. In Sect. 3 we detail the process used to identify clusters detected in both ACT and MaDCoWS samples and from this estimate the completeness of the MaDCoWS sample. In Sect. 4 we describe the forced photometry process used to obtain masses for the MaDCoWS clusters from the ACT maps. In Sect. 5 we review the corrections performed on the forced photometry mass estimates, including contamination by active galactic nuclei (AGN) and dusty submillimeter galaxies via ancillary radio and submillimeter data. In Sect. 6 we describe the process used to infer the mass-richness scaling relation. In Sect. 7 we discuss the inferred scaling relations and completeness of the MaDCoWS catalog, as well as the impact of contamination by IR and submillimeter sources on the SZ mass. In Sect. 8 we provide conclusions and give an outlook for further extensions to this work.
Throughout this work, we assume a flat Λ cold dark matter cosmology with ΩM = 0.307, ΩΛ = 0.693, and H0 = 67.7 km s−1 Mpc−1 from Planck Collaboration XIII (2016).
2. Data
In this work we primarily use the MaDCoWS cluster catalog (Gonzalez et al. 2019b) and the catalog and maps from ACT (Hilton et al. 2021). Additionally, we use data from the Herschel Space Observatory (Valiante et al. 2016; Smith et al. 2017) and the Very Large Array (VLA) (Condon et al. 1998; Lacy et al. 2020) to constrain dust and radio infill of the SZ signal, respectively. We also use the ACT 224 GHz maps to assess and constrain the impact of dust in-fill.
2.1. MaDCoWS
The MaDCoWS galaxy cluster catalog comprises 2839 cluster candidates spanning redshifts 0.7 ≲ z ≲ 1.5, selected using WISE (Wright et al. 2010) all-sky survey data (Gonzalez et al. 2019a)3. To reduce contamination by lower-redshift galaxies, MaDCoWS uses optical data from the Panoramic Survey Telescope and Rapid Response System (Pan-STARRS; Chambers & Pan-STARRS Team 2018) at declination δ > −30°, and SuperCOSMOS (Hambly et al. 2001a,b,c) at δ < −30° to reject low-redshift interlopers. MaDCoWS also uses data from the Sloan Digital Sky Survey (York et al. 2000, SDSS) for the same purpose over sections of the SDSS footprint. In total, 2433 cluster candidates were identified by the WISE–Pan-STARRS search, and 250 by the WISE–SuperCOSMOS search. The MaDCoWS catalog includes photometric redshifts for 1869 of its candidates, derived from Spitzer imaging. Spectroscopic measurements of a limited subsample of the MaDCoWS cluster candidates indicate that the photometric uncertainty is σz/(1 + z) ≈ 0.036. In addition to photometric redshifts, the Spitzer follow-up also enabled an estimate of cluster richness (λ15; see Sect. 6.3 of Gonzalez et al. 2019a). Briefly, the MaDCoWS richness parameter λ15 is the number of galaxies within a comoving 1 Mpc radius aperture for the candidate’s redshift having a flux density > 15 μJy after applying the color selection criteria described in Wylezalek et al. (2013) and subtracting the expected number of field galaxies. The color selection was designed to select only high-redshift clusters. Within the MaDCoWS catalog, 1869 of the 2839 cluster candidates have both richness and redshift estimates. For the purposes of determining a mass-richness scaling relationship, this subset was further restricted to those MaDCoWS cluster candidates lying in the ACT footprint, which totaled 1035. Additionally, 70 clusters lie in regions that are masked due to point source contamination: this leaves 965 MaDCoWS cluster candidates that were used in the analysis. To determine the radio and submillimeter properties of both the ACT and MaDCoWS clusters, we consider the full ACT and MaDCoWS cluster catalogs, necessarily restricted to those clusters for which we have radio and submillimeter data. Finally, in Sect. 4, we stacked on the MaDCoWS cluster locations to verify that the MaDCoWS cluster candidates did, on average, produce an SZ signal. In order to ensure that known ACT clusters did not dominate this stacked signal, we excluded MaDCoWS clusters that were also detected in ACT from the stacking analysis. We did however include clusters without a redshift measurement, resulting in the stacking analysis using a slightly different number of clusters (948) from the mass-richness fit.
2.2. ACT
ACT is a 6-meter, off-axis Gregorian telescope located in the Atacama Desert in Chile that has been operating since 2007 (Fowler et al. 2007). The Advanced ACTPol (AdvACT) receiver, which was deployed in 2016, is its latest camera (Henderson et al. 2016; Thornton et al. 2016). It performs polarization sensitive observations centered at 98, 150, and 224 GHz, corresponding to a diffraction-limited resolution of 2.2′, 1.4′, and 1.0′, respectively. Throughout, we use f090, f150, and f220 to refer to the maps made at those frequencies and 98, 150, and 224 GHz when referring specifically to the frequencies. ACT has undertaken a number of large area, unbiased cluster surveys using the SZ effect (Menanteau et al. 2010, 2013; Marriage et al. 2011; Sehgal et al. 2011; Hasselfield et al. 2013; Hilton et al. 2018, 2021). In this work, we use the DR5 cluster catalog (Hilton et al. 2021), which we refer to as the ACT cluster catalog, and whose members we call ACT clusters, as well as maps of the central Comptonization parameter (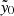 , often referred to as “SZ maps” in this work; see Sect. 2.3 of Hilton et al. 2021). To construct these SZ maps, we use the ACT maps filtered at the reference 2.4′ scale to perform forced photometry at the locations of clusters reported in the MaDCoWS catalog. This matched filtering essentially reduces the SZ detection of given cluster candidate to a single quantity,
, often referred to as “SZ maps” in this work; see Sect. 2.3 of Hilton et al. 2021). To construct these SZ maps, we use the ACT maps filtered at the reference 2.4′ scale to perform forced photometry at the locations of clusters reported in the MaDCoWS catalog. This matched filtering essentially reduces the SZ detection of given cluster candidate to a single quantity, 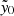 . The SZ map is constructed such that each pixel records the
. The SZ map is constructed such that each pixel records the 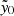 value that a cluster would have if it were detected at a given location in the map. Therefore, we simply extract
value that a cluster would have if it were detected at a given location in the map. Therefore, we simply extract 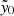 and S/N2.4 (the signal-to-noise measured in this 2.4′ scale map) values at the coordinates of each MaDCoWS cluster to produce a forced photometry catalog. Sub-pixel interpolation is performed using a bivariate third-order spline method. We warn that following Sect. 4.2 of Hilton et al. (2021), the SZ masses estimated here from these maps may be underestimated by ∼5–10%, and as such caution should be exercised when comparing the reported masses here to other cluster catalogs. Additionally, it is known that SZ measured masses are biased low by about 30% as compared to weak-lensing calibration (Miyatake et al. 2019). There are currently efforts underway to measure ACT cluster masses via weak-lensing: When available they will represent the most accurate, least biased cluster masses available.
and S/N2.4 (the signal-to-noise measured in this 2.4′ scale map) values at the coordinates of each MaDCoWS cluster to produce a forced photometry catalog. Sub-pixel interpolation is performed using a bivariate third-order spline method. We warn that following Sect. 4.2 of Hilton et al. (2021), the SZ masses estimated here from these maps may be underestimated by ∼5–10%, and as such caution should be exercised when comparing the reported masses here to other cluster catalogs. Additionally, it is known that SZ measured masses are biased low by about 30% as compared to weak-lensing calibration (Miyatake et al. 2019). There are currently efforts underway to measure ACT cluster masses via weak-lensing: When available they will represent the most accurate, least biased cluster masses available.
The DR5 catalog contains 4195 SZ-selected, optically confirmed clusters with signal-to-noise > 4 and with redshifts in the range 0.04 < z < 1.91 over 13,211 deg2 of the sky. The catalog has a 90% completeness mass limit of 3.8 × 1014 M⊙ at z = 0.5.
While the ACT cluster search was conducted using matched filters with a number of different scales, a fixed reference scale with θ500c = R500c/DA = 2.4′ was used for characterizing the SZ signal and its relation to mass. This scale is equivalent to a cluster with M500c = 2 × 1014 M⊙ at z = 0.4, assuming the Arnaud et al. (2010) pressure profile and associated scaling relation. In this work, we use the map of the central Comptonization parameter 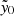 at this reference scale and the associated signal-to-noise map to estimate the masses of MaDCoWS clusters using forced photometry (see Sect. 4).
at this reference scale and the associated signal-to-noise map to estimate the masses of MaDCoWS clusters using forced photometry (see Sect. 4).
In addition to the 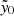 maps, we also used the individual frequency maps, f090 and f150, as well as
maps, we also used the individual frequency maps, f090 and f150, as well as  maps made with each frequency (98 and 150 GHz) individually. We also used the f220 maps constructed from observations at 224 GHz. While the f220 maps are noisier (50–60 μK arcmin) than the f090 and f150 data (≲30 μK arcmin typical; see Naess et al. 2020), the band is centered near the null in the SZ effect, providing a clean band for quantifying the dust emission in the ACT and MaDCoWS clusters, as is discussed in Sect. 5.2. For all these maps, the pixel size is 0.5′.
maps made with each frequency (98 and 150 GHz) individually. We also used the f220 maps constructed from observations at 224 GHz. While the f220 maps are noisier (50–60 μK arcmin) than the f090 and f150 data (≲30 μK arcmin typical; see Naess et al. 2020), the band is centered near the null in the SZ effect, providing a clean band for quantifying the dust emission in the ACT and MaDCoWS clusters, as is discussed in Sect. 5.2. For all these maps, the pixel size is 0.5′.
2.3. Herschel
We used the Herschel Astrophysical Terahertz Large Area Survey (H-ATLAS) DR1 (Valiante et al. 2016) and DR2 (Smith et al. 2017) to measure the thermal emission from dust in the ACT and MaDCoWS clusters within the H-ATLAS footprint. H-ATLAS covers 660 deg2 at 100, 160, 250, 350, and 500 μm using the PACS and SPIRE cameras. We used only the 250, 350, and 500 μm bands, all from the SPIRE camera. The SPIRE resolution is 18.2″, 25.2″, and 36.3″ at 250, 350, and 500 μm, respectively, with pixel size equal to the resolution. Due to the relatively small size of the H-ATLAS field, only 34 ACT and 66 MaDCoWS clusters have Herschel coverage.
2.4. Very Large Array
In order to determine if radio source in-fill impacts the SZ signals from MaDCoWS candidates, we examine data from the National Radio Astronomy Observatory (NRAO) VLA Sky Survey (NVSS; Condon et al. 1998) and the Very Large Array Sky Survey (VLASS; Lacy et al. 2020).
NVSS is a 1.4 GHz survey with 45″ FWHM angular resolution (15″ pixels) that covers approximately 82% of the sky at declinations δ ≥ −40°. The NVSS catalog includes a set of 2326 continuum images made with a large restoring beam to provide the sensitivity needed for completeness.
VLASS is an on-going 3 GHz radio survey producing Stokes I, Q, and U maps with an angular resolution ≈2.5″ (1″ pixel size). Like NVSS before it, the survey covers the entire sky visible to the VLA, a ∼34 000 deg2 (δ > −40°) area. The survey’s first observations began in September 2017. VLASS is expected to detect, by the project’s completion in 2024, ∼5 000 000 sources and record data with a continuum image RMS of 70 μJy beam−1 combined and 120 μJy beam−1 per-epoch. The first epoch survey of the entire VLASS footprint has been completed, and data products are available4. “Quicklook” 2D Stokes I images covering the entire survey were used to conduct our investigations into MaDCoWS radio source in-fill.
3. Co-detections in the MaDCoWS and ACT catalogs
In order to understand the completeness of MaDCoWS, we identify ACT-selected clusters that we consider to be matches with MaDCoWS candidates, which we refer to as co-detections. We consider a MaDCoWS candidate and an ACT cluster to be a co-detection (i.e., the same cluster) if the positional difference between the ACT entry and MaDCoWS entry was less than or equal to 2.5′. The criterion of a 2.5′ matching scale was chosen as it is approximately the resolution limit given the ACT catalog filter reference scale (2.4′). It should be noted that Hilton et al. (2021) find that 99.7% of the ACT cluster centers are within 1.9′ of the optical centers. Using this criterion, we identified 96 co-detections. We report these 96 cluster co-detections in Appendix C.1. Restricting our search to only include matches to MaDCoWS clusters in the Pan-STARRS footprint, that number is reduced to 80.
We explored co-detections with larger positional difference values as well, increasing the accepted positional difference from 2.5′ to 5′. However, doing so only resulted in an additional 7 co-detection candidates, which we deemed to be only chance superpositions. In Fig. 1, we show the typical offsets between the co-detections, indicating the match is generally within 0.7′.
 |
Fig. 1. Offsets in the right ascension and declination of ACT clusters (Hilton et al. 2021) and their co-detected MaDCoWS counterparts (Gonzalez et al. 2019b). The color bar indicates the redshift of the co-detection as recorded by ACT in the DR5 cluster catalog. The black-dotted circle is the radius (1.2′) that includes 89 (95%) of the co-detections. |
As discussed in Sect. 2.1, after restricting the MaDCoWS cluster catalog to the ACT footprint, masking point sources, and removing clusters without measured richnesses or redshifts, a total of 965 MaDCoWS clusters remain, which are used for the mass richness scaling relation. We note that discrepancies in the redshift determinations existed for several of the co-detections. Wherever these occurred, we used the redshift reported in Hilton et al. (2021) since these generally included newer and more complete data, and correspondingly smaller uncertainties.
To estimate what the background rate of line-of-sight coincidences between ACT and MaDCoWS clusters is, we simulated 100 000 surveys with the same angular density of ACT and MaDCoWS clusters as our paper (0.32 and 0.074 clusters per square degree, respectively), spread randomly over 13 211 deg2. We then simply counted the number of ACT and MaDCoWS clusters lying within 2.5′ of each other. We found that there was a chance coincidence of at least one cluster 87 ± 11% of the time, and that on average there were 2 ± 2 chance coincidences per survey. For each of our actual co-detections, we computed the difference in the measured ACT and MaDCoWS z divided by the quadrature sum of the z uncertainties:
We found that two co-detections (ACT-CL J0002.3+0131 and ACT-CL J0009.8−0205) are significantly discrepant (σz = 7.0 and 7.1, respectively), and could be line-of-sight coincidences. Additionally, ACT-CL J0009.1−4147 is marginal at σz = 3.1, given the sample size. The rest were σz ≲ 2, with most around 1. In principle spectroscopic follow-up would be able to disentangle line-of-sight coincidences.
Given the ACT cluster catalog, the number of co-detections sets an upper limit on the completeness with respect to the ACT catalog of the MaDCoWS cluster catalog and informs our understanding as to what extent these two surveys probe the same population of clusters. We first consider whether MaDCoWS detected all ACT clusters. Restricting the ACT catalog to match the MaDCoWS catalog in redshift (0.7 < z < 1.5) and footprint (δ > −30°, corresponding to the Pan-STARRS follow-up region) yields 712 ACT clusters compared to 80 co-detections restricted to the Pan-STARRS region. Relaxing the footprint constraint to include areas of SuperCOSMOS follow-up yields 1102 ACT clusters, compared to 96 co-detections. While this does not put a hard constraint on the completeness of MaDCoWS, it does suggest that it is ≲10%. A primary reason for this low completeness is expected to be the large non-Gaussian scatter between the mass and detection significance in the MaDCoWS search.MaDCoWS clusters were detected as galaxy excesses traced by the bright tip of the luminosity function, with the strength of the signal significantly affected by both Poisson statistics and blending of galaxies at the resolution of WISE. In other words, the selection function is not dominated by the richness of the clusters, but rather by other factors. This in turn means that the selection function is only weakly dependent on mass, so that it is not necessarily the case that all high-mass (i.e., ACT) clusters will be detected by MaDCoWS.
Qualitatively, we measure an intrinsic scatter (σlnλ|S/N = 0.26 ± 0.01) of the same order as the intrinsic scatter on the mass-richness scaling relation (σln(M)|λ = 0.22 ± 0.10; see Sect. 6.3). As such, the relationship between mass and S/N is quite scattered. Furthermore, given that S/N is a detection limited quantity (i.e., we only consider clusters with S/N > 5 when fitting for the richness-S/N relation), then the measured intrinsic scatter of this richness-S/N relation is going to be biased low, as we have excluded clusters with low S/N for their richness. All together, the effect is that the MaDCoWS selection function does not track mass particularly closely, and as such the number of ACT clusters co-detected by MaDCoWS is lower than one would expect.
We highlight in Fig. 2 a few prominent co-detections. Additionally, we compare the SZ masses for a number of ACT clusters to those from the literature in Appendix B. Overall, the masses inferred from these targeted observations agree within 1σ with the ACT-inferred mass estimates. One noteworthy exception is that of MOO J1142+1527, where the mass estimates using Combined Array for Research in Millimeter-wave Astronomy (CARMA) (Gonzalez et al. 2019a), New IRAM Kids Arrays (NIKA2)+CARMA (Ruppin et al. 2020), ACT, and MUSTANG2 (Dicker et al. 2020) differ at approximately the 2σ level. We note that Moravec et al. (2020) report this cluster as an ongoing merger and that it may require multiple SZ components to describe. In Fig. 3, we show the data used to infer scaling relations using CARMA and MUSTANG2 (Gonzalez et al. 2019a; Dicker et al. 2020, respectively). Additionally, there is some evidence in this figure that, for the ACT co-detections as well as the clusters from the previous SZ follow-up campaigns, there appears to be a bimodal split in the SZ mass of the high λ15 systems, which is more evident when plotted in log-space (see Fig. 12 below, left panel). The effect may be in part due to merging and pre-merger systems, which can have low SZ signals for their richness (Dicker et al. 2020). The suggestion of bimodal behavior in Fig. 3 becomes more evident in Fig. 4, in which the SZ signals of the entire MaDCoWS catalog as measured with ACT are plotted. The masses of the high-richness (λ15 ≳ 55) systems cluster into two branches, one higher  and higher slope, and one lower
and higher slope, and one lower  and lower slope. On the other hand, this bimodality may simply be scatter in the relatively low number of candidates at high richness. High resolution follow-up observations of these clusters could provide insight into whether the apparent bimodality is in fact due to merger history.
and lower slope. On the other hand, this bimodality may simply be scatter in the relatively low number of candidates at high richness. High resolution follow-up observations of these clusters could provide insight into whether the apparent bimodality is in fact due to merger history.
 |
Fig. 2. ACT S/N maps of the dozen highest-significance co-detections, where the S/N is with respect to |
 |
Fig. 3. Mass vs. richness relation for a selection of MaDCoWS clusters with SZ mass estimates. The purple circles correspond to the CARMA MaDCoWS cluster sample from Gonzalez et al. (2019a). The VACA LoCA points from Di Mascolo et al. (2020) are shown in red, and the MUSTANG2 measurements from Dicker et al. (2020) are shown in orange. The black data points are Chandra observations of MaDCoWS clusters. Points that are open are known active mergers, and points that are represented with triangles are consistent with no signal. We note that Fig. 12 provides a similar comparison for the complete sample of MaDCoWS candidates in the ACT survey footprint. |
 |
Fig. 4.
|
 |
Fig. 5. Stacks on MaDCoWS cluster positions in bins of richness on the ACT |
4. Forced photometry at MaDCoWS cluster candidate locations
As discussed in Sect. 2.2, to form the forced photometry catalog we simply record the  value in the SZ map at a MaDCoWS candidate location. The resulting distribution of
value in the SZ map at a MaDCoWS candidate location. The resulting distribution of 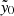 versus λ15, for the 965 candidates that have reported richness values, is shown in Fig. 4. The forced photometry catalog has no S/N limit, that is, it includes all 965 MaDCoWS cluster candidates that fall within the ACT survey footprint, excluding those that fall within masked regions (e.g., due to the dust mask or point sources; see Hilton et al. 2021). This means that the catalog is free from SZ-selection bias, and by fitting the
versus λ15, for the 965 candidates that have reported richness values, is shown in Fig. 4. The forced photometry catalog has no S/N limit, that is, it includes all 965 MaDCoWS cluster candidates that fall within the ACT survey footprint, excluding those that fall within masked regions (e.g., due to the dust mask or point sources; see Hilton et al. 2021). This means that the catalog is free from SZ-selection bias, and by fitting the 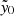 values at the MaDCoWS cluster locations through a Bayesian approach, we are able to infer the mass-richness relation (see Sect. 6) while addressing sample impurity and sources of contamination. Due to noise in the map, as well as radio or dusty sources in or near clusters, the MaDCoWS clusters may have negative
values at the MaDCoWS cluster locations through a Bayesian approach, we are able to infer the mass-richness relation (see Sect. 6) while addressing sample impurity and sources of contamination. Due to noise in the map, as well as radio or dusty sources in or near clusters, the MaDCoWS clusters may have negative 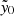 values; we account for this in Sects. 5.2, 5.3, and 6.1.
values; we account for this in Sects. 5.2, 5.3, and 6.1.
Conversion from 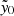 to mass was done following Hilton et al. (2021). We note that there is a small calibration difference between our masses and those of Gonzalez et al. (2019a); they used the Andersson et al. (2011) scaling relation, while our work uses the Arnaud et al. (2010) scaling relation. The difference between these two should be ≲5% (Andersson et al. 2011), which is subdominant to other sources of uncertainty in our main results (Sect. 6.3).
to mass was done following Hilton et al. (2021). We note that there is a small calibration difference between our masses and those of Gonzalez et al. (2019a); they used the Andersson et al. (2011) scaling relation, while our work uses the Arnaud et al. (2010) scaling relation. The difference between these two should be ≲5% (Andersson et al. 2011), which is subdominant to other sources of uncertainty in our main results (Sect. 6.3).
We verified the presence of SZ signal, on average, by stacking the ACT SZ maps on the MaDCoWS candidate locations. For this, we used the Pixell software suite5. We removed candidates outside the ACT footprint or lacking a richness estimate, as well as co-detections to ensure that the signal would not be dominated by known ACT clusters, after which 984 clusters remained for stacking. We divided these clusters into richness bins as shown in Fig. 5, starting at a richness of λ15 > 10. There are only 28 clusters in the remaining 984 with λ15 ≤ 10, and the signal in this stack is consistent with 0 to within 1σ. In each bin, we then stacked 20′×20′ cutout maps, centered on the MaDCoWS cluster positions. The results are shown in Fig. 5. We computed the average 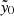 over the central 1.2′ radius in the stacks in each richness bin; uncertainties on this figure were evaluated via bootstrapping (see Appendix A). The lowest-richness bin (10 < λ ≤ 20) contains 191 cluster candidates; the stack on this bin is consistent with zero signal. In each of the remaining bins there is a clear detection at ≥3σ (see Table 1 for the exact
over the central 1.2′ radius in the stacks in each richness bin; uncertainties on this figure were evaluated via bootstrapping (see Appendix A). The lowest-richness bin (10 < λ ≤ 20) contains 191 cluster candidates; the stack on this bin is consistent with zero signal. In each of the remaining bins there is a clear detection at ≥3σ (see Table 1 for the exact 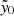 signals).
signals).
Stacks of 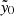 values for the MaDCoWS cluster candidates.
values for the MaDCoWS cluster candidates.
5. Mass estimate biases and corrections
The targeted SZ follow-up in Gonzalez et al. (2019a), Di Mascolo et al. (2020) and Dicker et al. (2020) mainly probes the high-richness tail in the distribution, and hence may present both Malmquist and Eddington biases (see e.g., Malmquist 1922; Kelly 2007) in the richness selection. Moreover, the CARMA sample exhibits a Malmquist bias in its SZ flux measurements; as noted in Gonzalez et al. (2019a), the CARMA sample was constructed by performing shallower observations of the higher-richness objects, based on the expectation that the integration times should be shorter, and only reported the results for robust detections. Correcting for these biases was one of the prime motivations of this paper. Since the MaDCoWS clusters were not SZ selected, it is unnecessary to de-boost our 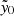 or mass estimates. However, three primary effects still need to be corrected in the forced photometry mass estimates:
or mass estimates. However, three primary effects still need to be corrected in the forced photometry mass estimates:
Firstly, the cluster locations that MaDCoWS reports are the peaks of a smoothed galaxy density map; the identified cluster location can be offset from the center of the cluster mass, and hence the center of the SZ signal (George et al. 2012; Sehgal et al. 2013; Viola et al. 2015), which leads to a suppression of the SZ signal. This scatter can be due to measurement uncertainty of the cluster’s MaDCoWS centroid (∼15″ in each of RA and Dec, Gonzalez et al. 2019a, Sect. 5.3) or SZ peak (1.5′ total Hilton et al. 2021), or it can be due to astrophysical reasons; in other words, the hot, virialized gas that is responsible for the SZ signal may not have the same spatial distribution as the galaxy number density used to determine the MaDCoWS centroid (George et al. 2012; Sehgal et al. 2013; Viola et al. 2015). Either way, the result is that for a set of clusters, stacking on the optical centroids produces a signal that is suppressed as compared to stacking on their SZ peak locations, which Ge et al. (2019) have found to be around the ≈10% level. This agrees with the typical suppression that we find in Sect. 5.1.
Secondly, the matched filter used in the forced photometry method as described in Sect. 4 cannot account for compact sources at cluster locations. If emission from compact sources, such as radio sources or dust, reduces the 98 and/or the 150 GHz emission, the effect will be to bias the  estimate low; the emission “infills” the SZ decrement causing the mass estimate from forced photometry to be biased low. The significantly negative
estimate low; the emission “infills” the SZ decrement causing the mass estimate from forced photometry to be biased low. The significantly negative  clusters (see Fig. 4) suggest that this might be occurring. Further, stacking the f220 maps on the MaDCoWS candidate locations produces a significant positive signal that is not present when stacking on the ACT cluster locations. We ascribe this excess to dusty submillimeter emission spatially correlated with the MaDCoWS cluster locations. Stacks on ACT and MaDCoWS cluster locations at radio frequencies show that the ACT clusters have higher observed radio flux density on average (Sect. 5.3). As such, the source of the excess MaDCoWS 224 GHz emission is likely not radio. From the f220 stacks and similar stacks on the H-ATLAS maps, we find that the MaDCoWS candidates have more significant infill at submillimeter wavelengths than the general population of ACT clusters. Further, we find that the spectral form of the submillimeter emission in the MaDCoWS cluster stacks is well described by a gray body (Eq. (6)). Such infill is typically due to dusty submillimeter galaxies (e.g., Casey et al. 2014). We combined the stacks on the f220 and H-ATLAS data set to estimate this contamination and remove it from the mass-richness scaling relation (see Sect. 5.2).
clusters (see Fig. 4) suggest that this might be occurring. Further, stacking the f220 maps on the MaDCoWS candidate locations produces a significant positive signal that is not present when stacking on the ACT cluster locations. We ascribe this excess to dusty submillimeter emission spatially correlated with the MaDCoWS cluster locations. Stacks on ACT and MaDCoWS cluster locations at radio frequencies show that the ACT clusters have higher observed radio flux density on average (Sect. 5.3). As such, the source of the excess MaDCoWS 224 GHz emission is likely not radio. From the f220 stacks and similar stacks on the H-ATLAS maps, we find that the MaDCoWS candidates have more significant infill at submillimeter wavelengths than the general population of ACT clusters. Further, we find that the spectral form of the submillimeter emission in the MaDCoWS cluster stacks is well described by a gray body (Eq. (6)). Such infill is typically due to dusty submillimeter galaxies (e.g., Casey et al. 2014). We combined the stacks on the f220 and H-ATLAS data set to estimate this contamination and remove it from the mass-richness scaling relation (see Sect. 5.2).
Thirdly and finally, in Sect. 5.3 we consider the effect of contamination at radio wavelengths on the MaDCoWS cluster candidates. Bright radio contamination, while declining at millimeter wavelengths, could potentially remain relatively significant at 98 and 150 GHz, once again in-filling the measured  toward lower values. We describe our correction for this effect in Sect. 5.3.
toward lower values. We describe our correction for this effect in Sect. 5.3.
5.1. Centroid offset
To correct for suppression of the SZ signals due to positional offsets in MaDCoWS-determined cluster centroids as compared to the ACT-determined centroids, we stacked the  maps on the 96 ACT/MaDCoWS co-detections twice, once on the ACT identified cluster locations and once on the MaDCoWS identified location. At each cluster location, we created a 20′ square sub-map of the
maps on the 96 ACT/MaDCoWS co-detections twice, once on the ACT identified cluster locations and once on the MaDCoWS identified location. At each cluster location, we created a 20′ square sub-map of the 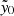 map centered on the cluster location. We normalized each sub-map to have unity amplitude, so that the suppression was not dominated by the particular scatter of the brightest clusters. We performed this stacking analysis on clusters with measured richness greater than 20, divided into 5 bins of even richness range. This left only about 15 clusters in each bin, leading to relatively large uncertainties as shown in Fig. 6.
map centered on the cluster location. We normalized each sub-map to have unity amplitude, so that the suppression was not dominated by the particular scatter of the brightest clusters. We performed this stacking analysis on clusters with measured richness greater than 20, divided into 5 bins of even richness range. This left only about 15 clusters in each bin, leading to relatively large uncertainties as shown in Fig. 6.
 |
Fig. 6. MaDCoWS to ACT |
To compute the suppression, for each of the stacks above we computed the aperture δTCMB within a 1.2′ radius of the stack center. For a given richness bin, the ratio of this statistic for the MaDCoWS centered stacks to the ACT centered ones sets the suppression. We computed the variance via bootstrapping. We then fit the richness-suppression relation to a sigmoid model of the form 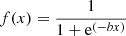 by maximizing the likelihood function:
by maximizing the likelihood function:
where yn is the ratio of the ACT to MaDCoWS signal in the nth richness bin and σn is the uncertainty in the nth that data point. The results are shown in Fig. 6. In our mass-richness fitting routine, we include a parameter to account for this suppression effect. We do not directly adjust the measured fluxes using this model; rather the model developed above enters into the fit as a richness-dependent prior on that suppression parameter (Sect. 6.2).
5.2. Submillimeter emission
Since the SZ effect at the frequencies of interest (98 and 150 GHz) manifests as a decrement of the CMB temperature, there is the potential that dusty, submillimeter sources could fill in or partially suppress the SZ signal. It is also known that dusty submillimeter galaxies (e.g., Erler et al. 2018), as well as radio AGN (considered in the next section), frequently reside within the centers of clusters, where feedback processes are strongest (see e.g., Coble et al. 2007; Sayers et al. 2013; Gralla et al. 2014, 2020; Zakamska et al. 2019).
To determine if the SZ signals of the MaDCoWS candidates are suppressed by a dusty contribution, we stacked the f220 maps on the MaDCoWS centers. The f220 map was matched filtered in the same way as the 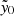 map to remove point sources, maintaining consistency. We then stacked the f220 maps on both the ACT (all 4195) and MaDCoWS (all 1572 in the ACT footprint) cluster positions and computed the aperture flux density in units of δTCMB within the 1.2′ radius of the stack center, corresponding to the ACT cluster finder reference filter scale of 2.4′.
map to remove point sources, maintaining consistency. We then stacked the f220 maps on both the ACT (all 4195) and MaDCoWS (all 1572 in the ACT footprint) cluster positions and computed the aperture flux density in units of δTCMB within the 1.2′ radius of the stack center, corresponding to the ACT cluster finder reference filter scale of 2.4′.
We used bootstrapping to estimate the uncertainty in this measure. We found that for the MaDCoWS clusters, the signal was 8.9 ± 1.2 μK, while for the stack on ACT clusters, the signal was −2.3 ± 0.6 μK, where the units are δTCMB. Additionally, we binned both the MaDCoWS and ACT data into 6 bins. For the MaDCoWS clusters, we binned them in richness, while for the ACT, we binned them in cluster mass. We then repeated the analysis using these bins. The results are shown in Fig. 7. For both the MaDCoWS and ACT clusters, there is no obvious trend in 224 GHz flux density with richness or mass, respectively. The excess emission in the MaDCoWS clusters we attribute to dust emission. The decrement in 224 GHz emission from the ACT clusters may be due to a small bias in the cluster finder algorithm; since the CMB serves as a source of noise when searching for the SZ signal, the algorithm preferentially finds clusters in regions of lower primary CMB signal (i.e., “cold spots”). Therefore, when stacking on the f220 maps, the result is a preferential stack on regions of low 224 GHz emission, leading to a decrement.
 |
Fig. 7. Average 224 GHz emission for MaDCoWS (blue) and ACT (orange) clusters. MaDCoWS clusters were binned in richness, while the ACT clusters were binned in mass. Richness is plotted on the lower x axis while mass is plotted on the upper; the two scales are not equivalent, and are simply co-plotted for convenience. Error bars were estimated via bootstrapping. The MaDCoWS clusters show a statistically significant excess emission at 224 GHz on the whole, while the ACT clusters show a small decrement. In neither the ACT nor the MaDCoWS clusters is there a trend with mass or richness. The dashed lines indicate the average 224 GHz emission across all MaDCoWS (blue) and ACT (orange) clusters. We attribute the signal from the MaDCoWS cluster candidates at 224 GHz to IR emission and follow up with Herschel data (Sect. 5.2). |
To quantify the dust emission, we stacked on the MaDCoWS cluster locations in the H-ATLAS maps (Valiante et al. 2016; Smith et al. 2017). For comparison, we also stacked the maps on ACT cluster locations and a sample of random locations generated by offsetting each MaDCoWS cluster location by 5′ in a random direction. Due to the small size of the H-ATLAS survey, we were only able to perform this analysis for 34 ACT clusters and 66 MaDCoWS cluster candidates, limiting our ability to determine if the in-fill has a richness or mass dependence. In order to compare with the emission at 224 GHz, we first converted each of the 250, 350, and 500 μm maps to MJy/pixel and then smoothed to 1.0′ (i.e., the ACT 220 GHz resolution) using a Gaussian kernel with the integral normalized to unity. We then stacked these maps on the MaDCoWS and ACT cluster locations using inverse-noise weighting and calculated the aperture flux density within 1.2′ of the stack center (i.e., in the central 2.4′ diameter corresponding to the reference filter scale used in Hilton et al. 2021). We computed the uncertainty in each stack via bootstrapping. For the ACT and randoms stack, the signal was consistent with zero; for the MaDCoWS there was a statistically significant excess (see Fig. 8). We converted the average fluctuation of δTCMB in the 224 GHz stack described above to emission (in MJy sr−1) using the derivative of the blackbody function (see, e.g., Mroczkowski et al. 2019):
 |
Fig. 8. Histograms of average surface brightness in Herschel submillimeter observations corresponding to a 1.2′ radius aperture flux, centered on ACT, MaDCoWS, and random cluster locations. The dashed lines show the average brightness for a given frequency and catalog. At 250 μm, the average surface brightness is 0.10 ± 0.08, 0.15 ± 0.10, and 0.22 ± 0.11 MJy sr−1 for the random, ACT, and MaDCoWS samples, respectively. At 350 μm, those surface brightnesses are respectively 0.05 ± 0.05, 0.08 ± 0.08, and 0.16 ± 0.09 MJy sr−1 for the random, ACT, and MaDCoWS samples. Finally, at 500 μm they are 0.01 ± 0.04, 0.03 ± 0.07, and 0.09 ± 0.06 MJy sr−1 for the random, ACT, and MaDCoWS. The statistically higher MaDCoWS emission at each Herschel frequency, along with the higher emission in the ACT 224 GHz channel (Fig. 7), indicates that the MaDCoWS clusters may be contaminated by dusty sources. |
where TCMB = 2.7255 K is the monopole temperature of the primary CMB, ΔI is the change in intensity above background, ΔTCMB is the fluctuation in temperature about the CMB monopole, and x = (hν)/(kBTCMB) ≈ ν/(56.8 GHz) is the dimensionless frequency. The normalization factor of the primary CMB spectrum is
The ΔI can then be converted to surface brightness ΔSν[Jy bm−1] via
For all three stacks, we estimated uncertainties via bootstrapping. Given the excess submillimeter emission detected in the MaDCoWS clusters, we then performed a maximum likelihood fit to the resulting surface brightnesses of the MaDCoWS stacks to a gray-body model of the form
where A is an amplitude normalization, ν0 = 3000 GHz is a reference frequency (Draine 2006), β is the dust emissivity spectral index, T is the dust temperature, and Bν(T) is the Planck blackbody function. To account for the effect of redshift, we fit using the rest frame frequencies, we converted from the observed frequencies by multiplying by (1 + ⟨z⟩) = 2.08, with ⟨z⟩ the average z for the subsample of MaDCoWS clusters in the H-ATLAS region for which there are photometric redshifts. We assumed a Gaussian function for the likelihood and estimated the uncertainties in our fit parameters using a Markov chain Monte Carlo (MCMC) method, implemented in the emcee (Foreman-Mackey et al. 2013) package. We placed flat, uninformative priors on T, A, and β, enforcing 0 K ≤ T < 200 K, −1 < A < 1, and −5 < β < 10. Results of the fit are presented in Fig. 9. Figure 9a shows the data with error bars in black, the best fit in blue, and the 68 and 95% confidence limits. In Fig. 9b we show constraints on the fit parameters Trest, β, and A.
 |
Fig. 9. Gray-body fit constraints. (a) Maximum likelihood best fit of the form Eq. (6) to the mean emission from stacks on the MaDCoWS clusters at 224 (ACT), 600, 857, and 1200 GHz (Herschel). The total number of clusters in the stack is the 66 clusters in the H-ATLAS footprint for the three Herschel bands and 1572 for the ACT 224 GHz band. The dashed blue line is the best fit, and the light and dark blue bands represent the 68 and 95% confidence limit, respectively. The y axis is the surface brightness averaged over a 1.2′ radius aperture at the center of the stack. Error bars were estimated via bootstrapping. (b) Constraints on the dust temperature, |
We find that for the MaDCoWS clusters in the H-ATLAS footprint, the best-fit temperature is 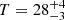 K. This is in good agreement with other measurements of the dust properties of IR and optically selected clusters (see, e.g., Smith et al. 2013; Erler et al. 2018; Amodeo et al. 2021; Fuzia et al. 2021; Vavagiakis et al. 2021). Our constraint on the dust emission spectral index,
K. This is in good agreement with other measurements of the dust properties of IR and optically selected clusters (see, e.g., Smith et al. 2013; Erler et al. 2018; Amodeo et al. 2021; Fuzia et al. 2021; Vavagiakis et al. 2021). Our constraint on the dust emission spectral index, 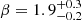 is somewhat higher than other measurements, but does agree within uncertainties (see, e.g., Magnelli et al. 2012; Smith et al. 2013; Sayers et al. 2019).
is somewhat higher than other measurements, but does agree within uncertainties (see, e.g., Magnelli et al. 2012; Smith et al. 2013; Sayers et al. 2019).
When performing the mass-richness scaling relation fit, we repeated the analysis above by including the dust model in the full joint probability distribution. This allowed for accounting of degeneracies between the dust model parameters and other parameters (see Sect. 6.1).
To get an estimate of the level of bias due to dusty emission in-filling the SZ signal in MaDCoWS cluster candidates, we converted the modeled emission at 98 GHz (77 ± 3 μJy) and 150 GHz (370 ± 50 μJy) to Compton y via
We then weighted the computed  at 98 and 150 GHz by their average relative contributions to
at 98 and 150 GHz by their average relative contributions to  (≈66 and 33%, respectively) and compared that weighted average to the
(≈66 and 33%, respectively) and compared that weighted average to the  signal for a 2 × 1014 M⊙ cluster at redshift of 1, following Hilton et al. (2021). We find that the in-fill is 1.5 ± 0.5% for the average MaDCoWS cluster candidate. The above computation ignores the effects of the matched filter, which will in general suppress the in-fill for a source not centered on the cluster, and should be considered an approximation only.
signal for a 2 × 1014 M⊙ cluster at redshift of 1, following Hilton et al. (2021). We find that the in-fill is 1.5 ± 0.5% for the average MaDCoWS cluster candidate. The above computation ignores the effects of the matched filter, which will in general suppress the in-fill for a source not centered on the cluster, and should be considered an approximation only.
5.3. Radio emission
In order to assess and quantify low frequency radio source in-fill strong enough to impact our 98 and 150 GHz measurements of the SZ signal, we require constraints on the radio flux density and spectral indices of the source population. Using both NVSS (1.4 GHz) and VLASS (nominally 3 GHz) allows us to estimate both. From these surveys (Sect. 2.4), we evaluate the distribution of radio in-fill associated with members of the ACT and MaDCoWS samples. For each cluster there are two statistics with which we are concerned: (1) the intrinsic luminosity of sources within the cluster in its frame of reference, and (2) the observed flux density in our frame of reference. We are concerned with the intrinsic radio luminosities as they tell us whether the ACT and MaDCoWS clusters were drawn from populations with the same intrinsic radio properties. We must also consider the observed fluxes, as they set the level of radio in-fill in the cluster. For clarity, whenever we refer to fluxes or surface brightness or use units of flux density or surface brightness ([Jy] or [Jy sr−1]), we are referring to the observed flux density or surface brightness in our frame of reference. Whenever we refer to radio luminosities or use units of luminosity ([W Hz−1)]), we are referring to the intrinsic radio luminosity. Our process is to first compute the observed flux density for each cluster, and then convert that into intrinsic radio luminosity.
To compute the radio flux, for each cluster we produced a cutout image (postage stamp) of the NVSS map centered at the cluster position and smoothed it to 1′ to match the ACT 224 GHz beam scale, in order to account for the effect of smoothing by the ACT beam on the f220 maps. We then calculate the aperture flux density in the central 1.2′ radius of the smoothed stamps. Additionally, for each stamp we estimate the local background flux density by computing the 1.2′ radius aperture flux density at 20 random locations in the stamp lying outside the central aperture and taking the median. We then subtracted the background flux density from the central flux density to form an estimate of the radio flux density for that cluster (see Fig. 10 for histograms of the ACT and MaDCoWS radio fluxes in NVSS). For ACT, we found a median flux density at 1.4 GHz of 6.1 ± 0.4 mJy for the 3341 clusters in the NVSS footprint. For MaDCoWS, we found a median flux density of 3.9 ± 0.4 mJy for the 1780 clusters in the NVSS footprint, where the uncertainties were estimated via bootstrapping the stack.
 |
Fig. 10. Histograms of the 1.4 GHz aperture flux density of the ACT (a) and MaDCoWS (b) cluster catalogs. Panel c: normalized cumulative histogram of the same data, cut at the aperture noise of 0.3 mJy, to better illustrate the difference in infill between the two samples. The fluxes shown are all for a 1.2′ radius aperture, while the percentage infill is the approximate infill of the SZ signal as described in Sect. 7.1.2. We note that due to differences in average redshift and spectral index of the ACT and MaDCoWS clusters, the same measured flux density at 1.4 GHz does not correspond to the same percentage infill. The ACT clusters show on average significantly more radio infill at 1.4 GHz than their MaDCoWS analogs. |
We used an identical method to measure the background subtracted fluxes for the clusters in the VLASS data. For each cluster with background subtracted flux density greater than the NVSS confusion limit of 2.5 mJy in both data sets, we proceeded to compute a spectral index α. However, in order to compute α, one requires more precise knowledge of the flux-weighted band center νVLASS for the wide bandwidth (2–4 GHz) VLASS data. For example, if the measured flux density in VLASS is lower than the flux density one would find by assuming a fiducial spectral index, the resulting α is steeper, and νVLASS will shift lower than that initially assumed; if the flux density is higher, α is flatter, and νVLASS shifts higher. This leads us to rely on a recursive or iterative approach when estimating νVLASS and the resulting α. Assuming a flat instrument passband from 2-4 GHz and emission of the form Sν = C0να for C0 the amplitude and α the spectral index, we compute the flux-weighted band average as:
We note that we assume the passband to be flat for simplicity. For a given cluster with a measured radio flux density in both the NVSS and VLASS surveys, we first computed the spectral index using the nominal VLASS band center of 3 GHz6. Using that spectral index and Eq. (8), we computed a new VLASS band center. We then calculated a new spectral index using this band center, and repeated the process until the difference between consecutive spectral indices was > 0.1%. The uncertainty on the spectral index was computed from the fluxes (S) and uncertainties (σ) following, for example, Zajaček et al. (2019), as
The population of spectral indices and fluxes that was generated in this manner was then used to correct the mass-richness scaling relation as described in Sect. 6.2. For both the ACT and MaDCoWS clusters, we find a fairly broad distribution of spectral indices computed between 1.4 and 3 GHz, with mean for the MaDCoWS candidates of ⟨αMaDCoWS⟩= − 0.9 and standard deviation σα = 0.7, and mean for the ACT clusters of ⟨αACT⟩= − 1.2 and standard deviation σα = 0.8. These mean spectral indices are broadly consistent with values typically found for radio AGN (Coble et al. 2007; Sayers et al. 2013), though we note our spectral index is also consistent with that found for star-forming regions (typically α < −0.6; see Calistro Rivera et al. 2017), so we cannot conclude whether AGN or star formation dominates the observed radio spectra.
Similarly to Sect. 5.2, we computed the bias in the measured SZ signal due to radio in-fill of the ACT and MaDCoWS clusters. We computed the in-fill percentage twice, once assuming our measured average spectral index of αMEAS = −0.91 and the other assuming a typical radio spectra of αTYP = −0.7. We refer to the in-fill percentages assuming their respective spectral indices as SMEAS and STYP, respectively. The high uncertainty on this number and strong dependence of the 98 and 150 GHz flux density on α mean that the bias for a specific cluster can vary quite a bit depending on its spectral index. For example, a 100 mJy source at 1.4 GHz with a spectral index of −0.91 produces a decrement of about 10%, while one with a spectral index of −1.2 produces only about 3%, and one with a spectral index of −0.7 produces a 26% in-fill, assuming M = 2 × 1014 M⊙, z = 1. For the MaDCoWS clusters, we continue to use the reference cluster with M = 2 × 1014 M⊙, z = 1 to compute the in-fill. For the ACT clusters, we use their individual measured masses and redshifts. Extrapolating flux density using spectral indices derived at 1.4 and 3.0 GHz out to 98 and 150 GHz can be risky not only due to the uncertainty in the spectral index but also because it is not assured that the index is consistent between those two frequency ranges. Sayers et al. (2013) found that spectral indices for radio galaxies in large clusters were generally consistent when computed between 1.4 and 30 GHz and 30 and 140 GHz, so that as an estimate it is justified to use the measured spectral indices to extrapolate our flux densities from 1.4 to 98 and 150 GHz. For precise determination of the radio infill, multifrequency observations near 98 and 150 GHz will be required to determine the effective spectral index of sources near the SZ frequencies.
The average in-fill for an ACT cluster is SMEAS = 0.8 ± 0.03% and STYP = 2.0 ± 0.1%, while for the MaDCoWS cluster candidates the average in-fill is SMEAS = 0.45 ± 0.05% and STYP = 0.83 ± 0.05%. However, while the average bias is quite low, for an appreciable number of the clusters the bias is non-negligible. For the 95th percentile of ACT clusters, SMEAS = 7.0 ± 0.5% and STYP = 18 ± 1%. We note that of the nine MaDCoWS clusters with 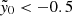 , 5 had significant radio in-fill (flux density ≳20 mJy at 1.4 GHz), including five of the top six with most negative
, 5 had significant radio in-fill (flux density ≳20 mJy at 1.4 GHz), including five of the top six with most negative 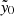 , suggesting that the significantly negative
, suggesting that the significantly negative 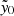 measurements could be due to radio in-fill. For example, one such cluster with very negative
measurements could be due to radio in-fill. For example, one such cluster with very negative 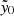 , MOO J2247+0507, has a flux density at 1.4 GHz of 160 ± 1 mJy and α = −0.61 ± 0.8 (its measured α) and z = 1.02; assuming it has a mass of 2 × 1014 M⊙, the bias at 98 GHz is SJ 2247 = 70 ± 17%, where the uncertainties have been propagated from the flux density uncertainty only.
, MOO J2247+0507, has a flux density at 1.4 GHz of 160 ± 1 mJy and α = −0.61 ± 0.8 (its measured α) and z = 1.02; assuming it has a mass of 2 × 1014 M⊙, the bias at 98 GHz is SJ 2247 = 70 ± 17%, where the uncertainties have been propagated from the flux density uncertainty only.
We emphasize that we have not included the effect of the matched filter, so the numbers presented above represent only an approximation of the effect of the infill. Further, since our radio fluxes were computed using aperture photometry, the measured fluxes and spectral indices are averages for all compact sources in the cluster. High resolution, multifrequency follow-up of cluster candidates would be required to precisely remove this infill.
Consistent with the above, we computed the intrinsic radio luminosities. To do so, we assumed a simple power law of the form Sν = C0να. This then leads to the usual K-correction; K(z) = (1 + z)−(1 + α) for redshift z. The intrinsic luminosity at frequency ν1 can then be computed from the observed flux density Sν2 at frequency ν2 using the luminosity distance DL(z):
For convenience we select ν1 to be 1.4 GHz. For each cluster then we calculated its intrinsic luminosity using the NVSS measured flux, its measured redshift, and the spectral index for that cluster as computed above. All the ACT clusters have measured redshifts; for the MaDCoWS candidates that do not have redshifts, we used the mean of the sample, ⟨z⟩ = 1.01. For clusters that did not have measured spectral indices, we used the average spectral index of that cluster’s catalog, either ACT (⟨αACT⟩= − 1.21) or MaDCoWS (⟨αMADCOWS⟩ = −0.91). The results are shown in Fig. 11. The average luminosity for ACT clusters is 5.4 ± 0.3 × 1024 W Hz−1, while for the MaDCoWS clusters it is 9.1 ± 1.0 × 1024 W Hz−1, where the statistical uncertainties have been computed via bootstrapping. Restricting the ACT clusters to the same redshift range as the MaDCoWS (0.7 ≤ z ≤ 1.5) raises the average luminosity of ACT clusters to 6.5 ± 0.7 × 1024 W Hz−1, suggesting that, even accounting for redshift, the MaDCoWS clusters are on average more radio loud than their ACT counterparts, although the average redshift of the ACT clusters after this restriction (⟨z⟩ = 0.89) is still lower than that of the MaDCoWS sample (⟨z⟩ = 1.01).
 |
Fig. 11. Intrinsic radio luminosities at 1.4 GHz for ACT (blue, 3341 clusters) and MaDCoWS (orange, 1780 clusters). The red line shows a 0.3 mJy flux density at 1.4 GHz in the observed frame of reference converted to 1.4 GHz in the emitted frame of reference for the given z according to Eq. (10), and assuming a spectral index of −0.91. The choice of 0.3 mJy corresponds to the variance of the background aperture flux density in the NVSS maps for a 1.2′ radius aperture, and thus roughly corresponds to the noise floor for our background subtracted fluxes. Therefore, the red line should guide the eye as to which radio luminosities are above the noise. We note that many clusters are not shown as they have very low or negative values for their radio fluxes due to subtraction of the background. |
6. The SZ mass-richness scaling
Given the results above, we attempt to investigate the MaDCoWS mass-richness scaling relation. In doing so, we hope to understand if richness provides a good proxy for mass in the MaDCoWS cluster catalog. Additionally, we address whether the preliminary mass-richness scaling relation found in Gonzalez et al. (2019a) is consistent with the scaling relation of the entire MaDCoWS catalog, and whether the full scaling relation follows self-similarity.
6.1. Regression technique
We adopt a hierarchical Bayesian approach that builds upon the work of Kelly (2007) and Sereno (2016), to which we refer for a thorough discussion of the fitting technique. Here we provide a summary of key details central to our analysis.
At each step of the modeling process and for each of the clusters within the considered sample, we consider an independent variable ξ drawn from a mixture of Gaussian probability distributions (Kelly 2007). This corresponds to the true value of the logarithm of the cluster richness, lnλ. We therefore fit richness as lnλ, which is related to the observed richness λobs through a Poisson probability distribution, P(λobs|ξ) = 𝒫(eξ).
In a similar manner to richness, we fit the mass as lnM. We define the dependent quantity η as the true value of the logarithm of the cluster mass, lnM, which we assume to be connected to the independent variable ξ through a normal probability distribution P(η|ξ) with mean
and variance corresponding to the intrinsic scatter of the true quantities about the mean scaling relation. Given the definition of the variables ξ and η, our choice of probability distribution is equivalent to using a log-normal model for describing the relation between the true mass and richness for a given cluster. Following, for example, Evrard et al. (2014) and Simet et al. (2017), it is hence possible to express the variance due to intrinsic scatter as
Here, the first term on the right-hand side accounts for the contribution to the total scatter due to Poisson noise on richness, while the second term describes the scatter inherent to the independent variable η = lnM. This is introduced to account for any additional deviation from the reconstructed scaling that is not accounted for in the observational uncertainties or intrinsic variable properties (e.g., due to unknown biases in the considered observables).
In principle, it should be possible to define a relation between the measured masses and the dependent variable η through a normal distribution centered on eη and with variance 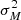 equal to the square of the observational uncertainties on the measured mass Mobs,
equal to the square of the observational uncertainties on the measured mass Mobs,
However, Fig. 12 shows that multiple data points from the compiled forced photometry catalog manifest negative values for the central Compton 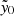 , corresponding to an unphysical negative cluster mass. In the case of low-mass clusters, with SZ signal below the sensitivity threshold of the ACT maps, noise fluctuations can cause this negative
, corresponding to an unphysical negative cluster mass. In the case of low-mass clusters, with SZ signal below the sensitivity threshold of the ACT maps, noise fluctuations can cause this negative 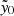 . However, as discussed in previous sections, radio sources as well as dust are found to contaminate the SZ signal of the clusters, leading to clusters with significantly negative
. However, as discussed in previous sections, radio sources as well as dust are found to contaminate the SZ signal of the clusters, leading to clusters with significantly negative 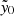 . Further, in Sect. 5.1 we show that miscentering effects may provide a significant suppression of the measured central Compton
. Further, in Sect. 5.1 we show that miscentering effects may provide a significant suppression of the measured central Compton 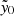 with respect to the true value. In order to properly account for such contributions, we compare the true scattered quantities η to the central Compton parameter
with respect to the true value. In order to properly account for such contributions, we compare the true scattered quantities η to the central Compton parameter 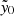 computed separately from the f090 and f150 maps. In particular, we assume the joint probability distribution to be described by a bivariate normal distribution,
computed separately from the f090 and f150 maps. In particular, we assume the joint probability distribution to be described by a bivariate normal distribution,
 |
Fig. 12. Mass-richness diagram displayed three ways. The left and center panels are respectively log-log and linear plots of |
where yf090 and yf150 are 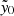 derived exclusively from the f090 and f150 maps, respectively. Here, the covariance matrix Σ is expressed as
derived exclusively from the f090 and f150 maps, respectively. Here, the covariance matrix Σ is expressed as
with σf090 and σf150 equal to the uncertainties on the 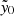 measured from the f090 and f150 maps, while ρ = 0.21 is the Pearson product-moment correlation coefficient for the two flattened frequency maps after filtering. The mean term is given by
measured from the f090 and f150 maps, while ρ = 0.21 is the Pearson product-moment correlation coefficient for the two flattened frequency maps after filtering. The mean term is given by
The first term on the right hand side is the product of the miscentering suppression factor c(ξ) (Sect. 5.1) and the mass-to-Compton y conversion mν(η) in Eq. (5) of Hilton et al. (2021). All the factors entering Eq. (16) (i.e., the relativistic SZ correction and the filter mismatch factor) are computed from the specific sets of cluster masses at each step of the modeling process. The terms in parentheses, dν(θdust = {A, β, Trest}) and rν(θradio = {C0, α}), provide the estimates of the level of dust and radio infill at the considered frequency, based on the respective spectral properties discussed in Sects. 5.2 and 5.3. The function gν is the nonrelativistic spectral dependence of the SZ effect (Sunyaev & Zeldovich 1970; Mroczkowski et al. 2019), which we adopt to convert the radio and dust surface brightness values to units of Compton y. We note that, in order to compute the infill components as in Eq. (16) shown above, we are assuming the radio and dust sources to be described by point-like signals centered on the cluster centroids.
Finally, we account for possible elements of the MaDCoWS cluster sample that are not well described by a mass-richness scaling relation (i.e., for which richness is not a good proxy for mass) by integrating the probability term described in Eq. (14) into a mixture model aimed at evaluating how likely well each point is to be drawn from a Gaussian centered on the mass-richness scaling relation versus a Gaussian centered on zero. For each given point, the total posterior probability distribution can then be written as
where the weight, w, is the probability that a data point is drawn by the mass-richness scaling relation versus the noise-like population, and Ptrue = P(yf090, yf150|ξ, η, θradio, θdust) is the joint probability distribution introduced in Eq. (15) for a data point that follows the mass-richness scaling relation. We instead assume the noise-like measurements to be drawn from Pnoise, for which we assume a normal distribution centered around zero and with standard deviation equal to the observational uncertainty associated with the 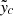 value of the considered measurement.
value of the considered measurement.
6.2. Parameter priors
Overall, our model comprises 965+12+3+3 free parameters, specifically corresponding to: the weight for each of the 965 data points entering the mixed probability distribution of Eq. (17); 12 parameters associated with three Gaussian kernels used for building the probability mixture discussed at the beginning of Sect. 6.1 (see Kelly 2007 and Sereno 2016 for details); the slope, intercept, and intrinsic scatter of the mass-richness scaling relation; and the parameters of the gray-body spectrum discussed in Sect. 5.2.
In addition, for every data point we marginalize over a set of four additional parameters, governing the effects due to miscentering (see Sect. 5.1) and radio and dust contamination. The regression is performed by means of the Hamiltonian Monte Carlo algorithm provided in the NumPyro (Bingham et al. 2019; Phan et al. 2019) Python package. The implementation of the Gaussian mixture model follows the same prescriptions adopted in Kelly (2007). We use uninformative uniform priors on all the parameters of the scaling relation except for the slope p1, for which we consider a Student’s t-distribution with one degree of freedom following Andreon & Hurn (2010) and Sereno (2016), as it does not bias the slope to high values. We then assume the probability weight w to be distributed uniformly in the range Abazajian et al. (2019).
The suppression factor due to miscentering for each of the considered clusters is modeled as a truncated normal distribution, bound between 0 and 1, with mode equal to 1 and standard deviation 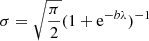 . The coefficient b corresponds to the best-fit parameter derived in Sect. 5.1, while the pre-factor
. The coefficient b corresponds to the best-fit parameter derived in Sect. 5.1, while the pre-factor 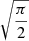 is introduced so that the mean of the prior distribution equals the average suppression (1 + e−bλ)−1 for a given true richness λ = eξ.
is introduced so that the mean of the prior distribution equals the average suppression (1 + e−bλ)−1 for a given true richness λ = eξ.
For the clusters with a clear identification of radio sources in the NVSS and VLASS fields, we employ normal priors on the estimated normalization C0 and spectral index α parameters, with mean and standard deviation set to the values derived for the specific cluster. Otherwise, we draw for each cluster a realization of C0 from an exponential distribution with mean equal to the average flux density measured from all the sources in the NVSS catalog. An analogous approach is considered for α, but used a normal prior with mean and standard deviations measured from the distribution of spectral indices estimated in Sect. 5.3.
Instead of introducing priors on the single parameters of the dust spectrum (Sect. 5.2), which would have neglected information on their degeneracy, we reanalyze the ACT 224 GHz and Herschel stacked measurements jointly with the mass and richness data. For full consistency, we consider exactly the same priors employed in Sect. 5.2.
6.3. Scaling relation results
In Fig. 12 we show the mass-richness scaling relation reconstructed from the ACT+MaDCoWS sample. As the selection of the clusters is unbiased with respect to the Eddington bias, we consider here the cluster masses without any correction for the steepness of the halo mass function. We note that, in this case, the reported masses represent an upper limit for the actual distribution, as the correction would de-boost the high-mass end of the sample.
For the model including the weight parameter from Eq. (17), we find that the best-fit slope to be 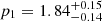 , where
, where 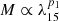 . This slope is consistent with Gonzalez et al. (2019a), although with an overall offset toward lower masses. Setting all the weights to unity (that is, assuming all clusters are drawn from the mass-richness scaling relation) leads to a slightly higher slope estimate (
. This slope is consistent with Gonzalez et al. (2019a), although with an overall offset toward lower masses. Setting all the weights to unity (that is, assuming all clusters are drawn from the mass-richness scaling relation) leads to a slightly higher slope estimate (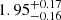 ), as well as a greater overall offset as compared to Gonzalez et al. (2019a).
), as well as a greater overall offset as compared to Gonzalez et al. (2019a).
Regarding the intrinsic scatter of the forced photometry data points (see Eq. (12) and related description), we estimate 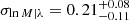 when including the weight parameter of Eq. (17) to account for sample contamination. Although already evident from the distribution of the ACT data points in the mass-richness distribution in relation to the scaling relation by Gonzalez et al. (2019a), such a large scatter provides a quantitative view of the limited capabilities of the MaDCoWS richness to provide a robust proxy for cluster masses. A similar scatter of
when including the weight parameter of Eq. (17) to account for sample contamination. Although already evident from the distribution of the ACT data points in the mass-richness distribution in relation to the scaling relation by Gonzalez et al. (2019a), such a large scatter provides a quantitative view of the limited capabilities of the MaDCoWS richness to provide a robust proxy for cluster masses. A similar scatter of 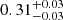 is found even when removing the negative Compton
is found even when removing the negative Compton  measurements from the fit.
measurements from the fit.
6.4. Cluster weights
From the results of the mass-richness fit including the probability term, it is clear that an appreciable fraction of the MaDCoWS candidates are not well described by the mass-richness scaling relation (Fig. 13); in other words, for a large subset of the MaDCoWS catalog, richness is not a good proxy for mass. Of the 965 candidates used in the fitting, only 419 had a weight greater than 50%; only 131 have a weight greater than 65%. The mean weight is 50.2%. Since we do not have an estimate of the uncertainties on individual weights, we do not place an uncertainty on these statistics. Moreover, while the mean does not fully encapsulate the bimodal distribution of the cluster probabilities, it does indicate that the MaDCoWS sample is likely composed largely of cluster candidates that are well below the SZ detection limit of the ACT survey. Examining the distribution of the probabilities, we see a clearly bimodal distribution (Fig. 13). One population, containing the majority of the clusters, is roughly normally distributed, centered on a probability of ≈50%. The other is centered at a higher probability of ≈70% with a much narrower distribution. In general, clusters with high-significance  [] and richness are given higher probabilities, while those with lower
[] and richness are given higher probabilities, while those with lower  , and specifically high richness and low
, and specifically high richness and low  , are given lower probabilities. Further examining Fig. 13, it is evident that the MaDCoWS sample is well described by a mass-richness scaling relation above λ15 ≳ 55, with 50% of such clusters having a weight w > 0.7, and an average weight for clusters above that richness of 0.63%. Additionally, all the high weight (w > 70%) clusters have λ15 > 27. Interestingly, examining the probabilities of individual cluster candidates reveals that the fitter identifies a number of the very negative
, are given lower probabilities. Further examining Fig. 13, it is evident that the MaDCoWS sample is well described by a mass-richness scaling relation above λ15 ≳ 55, with 50% of such clusters having a weight w > 0.7, and an average weight for clusters above that richness of 0.63%. Additionally, all the high weight (w > 70%) clusters have λ15 > 27. Interestingly, examining the probabilities of individual cluster candidates reveals that the fitter identifies a number of the very negative 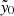 clusters, seen in the right hand panel of Fig. 12, as having high weight: these clusters have significant (⪆25 mJy) flux density at 1.4 or 3.0 GHz.
clusters, seen in the right hand panel of Fig. 12, as having high weight: these clusters have significant (⪆25 mJy) flux density at 1.4 or 3.0 GHz.
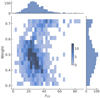 |
Fig. 13. 2D histogram of weight and richness (λ15). The weight is the probability that a MaDCoWS cluster data point is well described by a mass-richness scaling relation, as opposed to being drawn from the noise. Higher probabilities mean they are more likely to be real. The bimodal distribution is clear, with a large population of low probability clusters centered around 50% and a population of high probability clusters at ≈70%. |
7. Discussion
7.1. Population differences
The MaDCoWS sample comprises 2839 candidate high-z clusters, while the ACT DR5 sample comprises a nearly mass-limited, optically confirmed sample of 4195 clusters from across all redshifts. As noted in Sect. 3, our cross-matching criteria leads to a catalog of 96 co-detected clusters at the intersection of the ACT and MaDCoWS samples, reported in Table C.1.
We compared both richness and M500 measurements at different redshift ranges between the ACT and MaDCoWS populations. In Fig. 14, we plot the distribution of co-detections and MaDCoWS across four redshift ranges. We can see that there is no preferred redshift for the co-detected clusters with high richness. Figure 15 shows that ACT clusters are mostly found at z < 0.9, regardless of mass. We also see that MaDCoWS clusters as a whole tend to be lower in richness (and hence mass) than co-detected clusters, but are found more frequently at higher redshifts than ACT clusters. This is not unexpected, as the lower average mass of clusters at higher redshifts means that they are detected relatively less frequently. The MaDCoWS masses are from forced photometry, and we have cut off clusters with 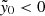 .
.
 |
Fig. 14. Comparisons of richness populations for the co-detected MaDCoWS and the remaining MaDCoWS in four redshift bins. At higher richness (λ15 > 60), there is no preferred redshift for the co-detections. This indicates that the disparity between the number of MaDCoWS in the ACT region and the number of co-detections is not a product of survey biases. |
 |
Fig. 15. M500 of ACT clusters vs. MaDCoWS in the same redshift ranges. These distributions suggest that ACT clusters are skewed toward lower redshifts, while the MaDCoWS distribution is even across higher redshifts. In addition, MaDCoWS clusters tend to be less massive than ACT clusters at a given redshift. |
The low rate by ACT of co-detections of MaDCoWS cluster candidates is due to the low SZ signal of many of those candidates, which is reflected in their correspondingly low weight. We discuss possible sources of this low weight in Sect. 7.4. As for the low rate by MaDCoWS of co-detections of ACT clusters, it is likely that the MaDCoWS catalog is missing them simply due to the MaDCoWS selection function. By construction, the MaDCoWS selection function does not precisely trace the Spitzer measured richness; the MaDCoWS cluster candidates are first selected from smoothed galaxy density maps created using WISE data, and then their MaDCoWS richnesses are measured using Spitzer follow-up. As such, the catalog is not richness limited, meaning that even under the assumption of some relation between mass and richness, the MaDCoWS cluster catalog cannot strictly be mass-limited. In any case, the MaDCoWS cluster catalog, while astrophysically interesting, should be approached with caution for computing cosmological parameters.
7.1.1. IR and dusty emission
The Herschel data, in combination with the ACT 224 GHz data, suggest that the ACT and MaDCoWS cluster catalogs comprise clusters with different properties and are potentially drawn from different populations; one, dustier population is preferentially sampled by MaDCoWS, and the other, more virialized, is preferentially sampled by ACT as described below. As was discussed in Sect. 5.2, the stacked H-ATLAS data on MaDCoWS clusters show a clear signal in each frequency band, whereas there is no obvious signal when stacking on the ACT clusters (see Fig. 16). In addition to the stacked emission, we also considered the emission for individual clusters. For each cluster in the H-ATLAS footprint in each of the ACT (34 clusters in the H-ATLAS footprint), MaDCoWS (66 clusters), and randoms (66 clusters) catalog (see Sect. 5.2), we calculated emission within 1.2′ radius of the cluster location at each of 250, 350, and 500 μm. A histogram of those values is shown in Fig. 8.
 |
Fig. 16. Stacks at 250, 350, and 500 μm (from left to right) on MaDCoWS (a, b, c) and ACT cluster locations (d, e, f), as well as a set of random locations (g, h, i) in the H-ATLAS data set. See Sect. 5.2 for details. The x axis of each plot is aligned with RA, while the y axis is aligned with declination; both are in units of arcmin. The color bars are in units of MJy sr−1. The red circles are 1.2′ in radius, the scale inside which we assigned excess flux density as being due to the cluster stack. |
A two-sample Kolmogorov–Smirnov (KS) test was applied to determine whether the central emission of ACT and MaDCoWS data sets was consistent with the central emission at random points and with each other. At all Herschel frequencies the distribution of MaDCoWS cluster central emissions is statistically inconsistent with that of the randomly offset central emissions and with that of the ACT clusters. The distribution of ACT cluster central emissions is statistically consistent with the randomly offset central emissions at 500 μm, while it is inconsistent at a p-value of 0.018 and 0.016 at 250 and 350 μm, respectively. The average central emission of the MaDCoWS cluster samples is more than one standard deviation higher than the average central emission of the randomly offset clusters at all frequencies. For the ACT clusters, at all wavelengths the central emission is statistically consistent with the randomly offset clusters. As evidenced by the goodness-of-fit of the gray-body model as shown in Sect. 5.2, we attribute this emission to the MaDCoWS clusters being dustier on average than the ACT clusters, and identify three causes for this effect. Firstly, in general clusters at high redshift have a greater proportion of blue galaxies in their cores than those at low redshift (Butcher & Oemler 1978; Dressler 1980; Brodwin et al. 2013). As blue galaxies tend to be dustier (Casey et al. 2014), and the mean redshift of the ACT clusters is lower than that of the MaDCoWS (∼0.5 vs. ∼1.01), the MaDCoWS clusters should be dustier on average. Secondly, at a given redshift, ACT preferentially finds clusters that contain more virialized gas, as virialized gas contributes most strongly to the integrated SZ effect signal (Motl et al. 2005; Poole et al. 2006, 2007; Wik et al. 2008; Krause et al. 2012). Finally, since dusty contamination contributes to the SZ infill of clusters, and hence biases SZ surveys like ACT against detecting them, ACT will preferentially select against cluster that contain significant dusty IR emission.
7.1.2. Radio emission
The radio data provides additional evidence that the ACT and MaDCoWS cluster catalogs preferentially sample from two different populations. As discussed in Sect. 5.3, the MaDCoWS clusters have higher intrinsic radio luminosity at 1.4 GHz as compared to the ACT clusters, even when the ACT clusters are restricted to the same redshift range as the MaDCoWS candidates. Moreover, performing a two-sample KS test on the ACT and MaDCoWS radio fluxes at 1.4 GHz confirms that they are drawn from different populations. To compare the populations, we first cut the ACT catalog to the same redshift range as the MaDCoWS catalog: 0.7 < z < 1.5. We then restricted both cluster catalogs to an intrinsic luminosity corresponding to the standard deviation of the background aperture fluxes, 0.3 mJy using Eq. (10), which roughly represents the noise floor for our background subtracted fluxes. Since the fluxes for both catalogs are taken from the same survey, they should have on average the same noise properties, so that if the non detections are not removed, they will bias the KS test toward high p-values, that is, toward determining that the two samples were drawn from the same underlying population. When we perform the two-sample KS test on the ACT and MaDCoWS catalogs with the flux density cut, we obtain p-value of 0.025, which suggests that the MaDCoWS and ACT clusters with radio sources represent different underlying populations. The above analysis ignores what proportion of clusters host radio sources. We also consider the intrinsic luminosities of the ACT and MaDCoWS clusters: We simply consider the percentage of clusters (still restricted to 0.7 < z < 1.5) that have intrinsic luminosities greater than the reference aperture flux density 0.3 mJy converted to luminosity as described above. We used bootstrapping to estimate the uncertainties on this number, which is 67.2 ± 1.7% for the ACT catalog and 58.6 ± 1.0% for the MaDCoWS catalog.
In summary, this analysis suggests that, restricting the ACT catalog optical photo-redshifts to match those of the MaDCoWS clusters, the ACT clusters host radio sources slightly more frequently than the MaDCoWS clusters, while the radio sources hosted by the MaDCoWS clusters are stronger by a factor of ≈2. We again note that the mean redshift of the ACT clusters is still somewhat lower than that of the MaDCoWS (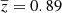 vs.
vs. 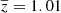 ).
).
Further, any contamination of the MaDCoWS catalog (Sect. 6.4) would in principle bias both the number density of radio sources and, accordingly, also the average inferred intrinsic luminosity, to lower values as radio sources are preferentially found in clusters as opposed to the field (Coble et al. 2007). Assuming an unrealistically high contamination of 10%, to set an upper bound on the percentage of clusters with contamination, and that contaminating candidates have radio sources at the rate of the field, which we take to be 10% the rate of the true candidates, we calculate the corrected percentage of MaDCoWS clusters with aperture flux density > 0.3 mJy as
which is not significantly different from the percentage found for ACT.
Finally, we briefly consider the richness evolution of radio luminosity fraction. Following Mo et al. (2020), we define a cluster to be radio loud if the intrinsic luminosity associated with the cluster is L1.4 GHz ≥ 1025W Hz−1, and the radio loud fraction (RLF) as the fraction of total clusters that are radio loud. For simplicity we continue to use our 1.2′ radial aperture, which corresponds to about 530–625 kpc, compared to 500 kpc used in Mo et al. (2020). The effect of this will generally be to raise the RLF as field radio sources are associated with clusters when they lie along the line-of-sight of that cluster, which will in turn flatten the richness-RLF relation. We binned the cluster radio luminosities into 8 bins of richness, and calculated the RLF in those bins, with the uncertainties calculated via bootstrapping. We fit the resulting data to a linear model using a maximum likelihood method, with the uncertainties in the parameters estimated via an MCMC method implemented in emcee (Foreman-Mackey et al. 2013). The results of that fit are shown in Fig. 17. We find the best-fit slope to be 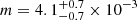 and the best-fit intercept to be
and the best-fit intercept to be 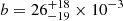 , and the reduced chi-squared of the fit χr = 0.45. The best-fit slope is somewhat higher than Mo et al. (2020), although only inconsistent at 1.2σ. We are inconsistent with the null hypothesis of no slope at 5.9σ.
, and the reduced chi-squared of the fit χr = 0.45. The best-fit slope is somewhat higher than Mo et al. (2020), although only inconsistent at 1.2σ. We are inconsistent with the null hypothesis of no slope at 5.9σ.
 |
Fig. 17. Best fit of a linear model to the RLF of the MaDCoWS clusters determined using NVSS 1.4 GHz fluxes (Sect. 5.3) vs. richness. The best fit is inconsistent with the null hypothesis of no evolution of the RLF with richness at 5.9σ. In comparison to Mo et al. (2020), we favor a higher slope for the relation at 1.2σ, although see the discussion in Sect. 7.1.2. |
7.2. Infill
While the average bias from radio emission detected in the ACT (SMEAS = 0.8 ± 0.03% and STYP = 2.0 ± 0.1%) and MaDCoWS cluster candidates (SMEAS = 0.45 ± 0.05% and STYP = 0.83 ± 0.05%) is at a low level, in both cases the samples include high infill tails. For example, 94 ACT clusters show radio emission consistent with a greater than 5% bias. Interestingly, that number of clusters (∼2.8% of the 3335 ACT clusters with NVSS fluxes) is consistent with the best-fit differential source counts near clusters found in Coble et al. (2007) (∼2.5%). Of course, the level of infill of the ACT-identified clusters is a biased measure of the true infill, as clusters with less infill are more likely to meet the ACT detection threshold for a given intrinsic mass ( ). For example, Gupta et al. (2017) estimated that 0.5% and 1.4% of clusters with mass 3 × 1014 M⊙ at redshift of 0.25 had their SZ signal completely suppressed by infill at 150 and 98 GHz, respectively. Moreover, accurately computing the infill correction is difficult; propagating the flux density from lower frequencies means accepting the uncertainty of extrapolating the spectral index across wide frequency ranges, while CMB measurements at 90 and 150 GHz frequently lack the spacial resolution to distinguish point sources in clusters from the SZ signal of that cluster. High resolution measurements of the point source flux densities at or near 90 and 150 GHz offer the best path forward. Dicker et al. (in prep.) undertook such a measurement using the MUSTANG2 instrument (Dicker et al. 2014) on the 100-meter Green Bank Telescope to perform 9″ resolution imaging of the SZ effect for a sample of galaxy clusters. This high resolution also allowed them to identify compact sources in the clusters, which would not be resolved by ACT, and to measure their flux density contributions at 90 GHz in order to assess the impact on SZ measurements. They found a similar distribution of infill, with 85% of clusters showing a change in the integrated SZ flux less than 5%, but 10% of the sample had very high (> 10%) infill. Further, the level of dust infill of the MaDCoWS cluster candidates may be biasing their measured SZ signal. From the model we developed in Sect. 5.2, we predict that the average dust infill of the SZ signal is 1.5 ± 0.5%. This result is limited by the limited IR follow-up available for the MaDCoWS cluster candidates, with Herschel data for only 66 candidates. While the distribution of the 66 candidates appears normal, we do not have enough data to rule out deviations from that distribution (e.g., a high flux density tail). While the effect is subdominant to other sources of uncertainty in this work, future large optical and IR surveys (e.g., the Vera C. Rubin observatory (Ivezić et al. 2019) and the Euclid telescope (Euclid Collaboration 2020)), as well as next-generation CMB experiments, which aim to place sub-percent constraints on cosmology from cluster abundance counts, will need to use methods that either address or are insensitive to this infill. In the near term, higher resolution measurements, both of the point source flux densities and of their spectral indices in the frequency ranges of interest, using, for example, MUSTANG-2, NIKA2, TolTEC, and Atacama Large Millimeter Array (ALMA), would enable improved constraints on the infill of the SZ signal by submillimeter and radio sources.
). For example, Gupta et al. (2017) estimated that 0.5% and 1.4% of clusters with mass 3 × 1014 M⊙ at redshift of 0.25 had their SZ signal completely suppressed by infill at 150 and 98 GHz, respectively. Moreover, accurately computing the infill correction is difficult; propagating the flux density from lower frequencies means accepting the uncertainty of extrapolating the spectral index across wide frequency ranges, while CMB measurements at 90 and 150 GHz frequently lack the spacial resolution to distinguish point sources in clusters from the SZ signal of that cluster. High resolution measurements of the point source flux densities at or near 90 and 150 GHz offer the best path forward. Dicker et al. (in prep.) undertook such a measurement using the MUSTANG2 instrument (Dicker et al. 2014) on the 100-meter Green Bank Telescope to perform 9″ resolution imaging of the SZ effect for a sample of galaxy clusters. This high resolution also allowed them to identify compact sources in the clusters, which would not be resolved by ACT, and to measure their flux density contributions at 90 GHz in order to assess the impact on SZ measurements. They found a similar distribution of infill, with 85% of clusters showing a change in the integrated SZ flux less than 5%, but 10% of the sample had very high (> 10%) infill. Further, the level of dust infill of the MaDCoWS cluster candidates may be biasing their measured SZ signal. From the model we developed in Sect. 5.2, we predict that the average dust infill of the SZ signal is 1.5 ± 0.5%. This result is limited by the limited IR follow-up available for the MaDCoWS cluster candidates, with Herschel data for only 66 candidates. While the distribution of the 66 candidates appears normal, we do not have enough data to rule out deviations from that distribution (e.g., a high flux density tail). While the effect is subdominant to other sources of uncertainty in this work, future large optical and IR surveys (e.g., the Vera C. Rubin observatory (Ivezić et al. 2019) and the Euclid telescope (Euclid Collaboration 2020)), as well as next-generation CMB experiments, which aim to place sub-percent constraints on cosmology from cluster abundance counts, will need to use methods that either address or are insensitive to this infill. In the near term, higher resolution measurements, both of the point source flux densities and of their spectral indices in the frequency ranges of interest, using, for example, MUSTANG-2, NIKA2, TolTEC, and Atacama Large Millimeter Array (ALMA), would enable improved constraints on the infill of the SZ signal by submillimeter and radio sources.
7.3. Mass-richness scaling
As noted in Sect. 6.3, our mass-richness scaling relation differs significantly from self-similarity, for which one would expect p1 ≈ 1 (Capasso et al. 2019; McClintock et al. 2019; Bleem et al. 2020; Grandis et al. 2021), although it is consistent with the previous measurement from Gonzalez et al. (2019a). We identify several issues that may bias the mass-richness scaling relation to higher slopes. Firstly, at low richness a portion of the MaDCoWS sample is not well described by a mass-richness scaling relation. If some number of low-richness candidates are either unvirialized systems with low SZ signal or line-of-sight chance superpositions with no intrinsic SZ signal, then the effect would be to bias the mass-richness relation to higher slopes, as these candidates would tilt the lower end of the relation downward (see Sect. 6.3). In a similar vein, if the richness measure is systematically biased to higher values due to line-of-sight interlopers, then the effect would also be to steepen the mass-richness relation. This effect would be especially apparent as a constant bias in richness is a larger relative effect at lower values for the richness, again having the effect of tilting the scaling relation slope to steeper values. Line-of-sight contaminants are known to bias optically selected clusters (Costanzi et al. 2019; Grandis et al. 2021), and correspondingly their mass-richness scaling relation. We would require a larger contamination fraction than either of those two studies to explain the low average weight we observe; however, the MaDCoWS cluster sample is very high redshift, and projection effects are stronger at high redshift (Yee et al. 2002; Costanzi et al. 2019). Moreover, it is unclear how often line-of-sight contaminated clusters pass the MaDCoWS selection function as compared to uncontaminated clusters. and it is further unclear how sensitive the MaDCoWS richness measurement is to line-of-sight interlopers. These effects together could cause projection effects to be more severe for the MaDCoWS cluster sample than other samples.
We also assessed the impact of infill from submillimeter and radio sources on the mass-richness scaling relation. As discussed in Sect. 5.2, we did not have enough Herschel submillimeter data to infer if infill scales with richness or mass. Therefore, it is possible that the proportionate infill of the SZ signal is higher at low richness than at high richness. We do, however, have 224 GHz data of many MaDCoWS clusters, which was used to quantify the submillimeter and millimeter source infill. We binned the MaDCoWS clusters in richness and stacked the f220 maps in these bins. There was no trend with richness in the 224 GHz emission, which suggests that the level of submillimeter and millimeter source infill is not strongly correlated with richness.
Finally, the higher IR emission of the MaDCoWS cluster candidates is consistent with a gray-body, dusty emission profile, and in general correlates with higher star formation rates (SFRs) (see e.g., Devlin et al. 2009). These high SFR clusters may deviate from self-similarity, and as such we would not a priori expect the slope of the mass-richness scaling relation to be unity.
7.4. Weights
As discussed in Sect. 6.4, the weights for the MaDCoWS candidates are split into two populations with a few high weight clusters (73 with weight > 0.7) and a large number (544) of candidates with low weights (< 0.5). The high weight clusters are well characterized by a mass-richness scaling relation; the low weight clusters are not. At very low richness (λ15 < 20) some of these candidates may be structures smaller than clusters, such as groups or line-of-sight superpositions.
Additionally, at higher richness, low weight candidates may be mergers or pre-mergers, or otherwise unvirialized but massive systems. Unvirialized gas in these mergers has been shown to suppress the SZ signal from these clusters both in simulations (e.g., Wik et al. 2008; Battaglia et al. 2012; Nelson et al. 2014) and observations (e.g., Hilton et al. 2018). While the merger can briefly enhance the SZ signal, the period during which it suppresses it is in general longer than that in which it enhances it. During the merger process, the SZ signal in a merging system can be suppressed ≈40% (Dicker et al. 2020) compared to a virialized cluster of the same total mass. This has the effect of making the observed SZ mass of the candidate less consistent with the mass-richness scaling relation and more consistent with noise (i.e., the effect is to reduce the weight of the cluster). In Dicker et al. (2020), which reports on SZ follow-up of high-richness MaDCoWS candidates, ≈25% of the MaDCoWS clusters observed were determined to be mergers. This ratio is significantly affected by Malmquist bias, however, as non-mergers have higher SZ brightness than merging systems. Further, Dicker et al. (2020) clusters are generally higher-richness systems (λ15 ≈ 50) and it is not clear how the fraction of systems that are undergoing a merger or are pre-merger changes with richness. Targeted follow-up is warranted to investigate further. Additionally, stacked measurements of the weak lensing of the CMB, in the vein of Madhavacheril et al. (2020), are indifferent to clusters that are undergoing mergers. As such, comparing the lensing inferred masses of low and high weight clusters would allow one to put constraints on the fraction of low weight clusters that are undergoing mergers. Similarly, the agreement between the average mass of the MaDCoWS cluster sample above richness of 20 as determined using the mass-richness scaling relation derived in this paper and in Madhavacheril et al. (2020) suggests that mergers and pre-mergers do not dominate the MaDCoWS cluster sample.
Finally, at low richness chance superpositions of galaxies may be causing spurious detections. Such spurious objects are hard to differentiate from low-mass groups in this analysis. In any case, caution must be exercised when using the low weight clusters for cosmology. Inaccurate cluster masses from both spurious clusters and clusters with low SZ signal for their mass (due to merger history, low gas fraction, or unvirialized components along the line-of-sight) will bias cosmological parameters.
8. Conclusions
In this work we identified co-detections of the ACT and MaDCoWS cluster catalogs. We note the very low rate of co-detections with respect to the size of both the ACT and the MaDCoWS cluster catalogs. We used forced photometry to evaluate the mass-richness scaling relation of the MaDCoWS cluster catalog. We quantified the infill of the sample by radio and submillimeter emission. We find that the best-fit scaling relation has a slope of 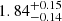 , higher than the unitary value one would expect for self-similar clusters (Andreon & Hurn 2010) but comparable to the preliminary work of Gonzalez et al. (2019a). We offer some possible reasons for this deviation in Sect. 7.3. These include, potentially, a bias in the richness measure and some amount of sample impurity with respect to mass. Instead of mass, the MaDCoWS selection function may preferentially include star-forming systems, leading to deviations from self-similarity. As part of the mass-richness scaling relation, we fit a weight to each cluster, which describes the relative probability that the SZ measurement associated with that cluster was drawn from a normal distribution centered on the mass-richness scaling relation versus a normal distribution centered on zero. We found that a large fraction of the MaDCoWS cluster candidates had weights lower than 50%. We ascribe the low weight of these clusters, and correspondingly their non-detection in the ACT cluster catalog, to a variety of factors, including suppression of the SZ signal by merger history and other unvirialized components along the line-of-sight, as well as to the MaDCoWS catalog containing very small clusters with SZ signals too low to detect. As for the MaDCoWS non-detections of ACT clusters, we conclude that the MaDCoWS selection function is not mass limited, and thus the overlap of the MaDCoWS catalog with a catalog such as ACT can be very incomplete.
, higher than the unitary value one would expect for self-similar clusters (Andreon & Hurn 2010) but comparable to the preliminary work of Gonzalez et al. (2019a). We offer some possible reasons for this deviation in Sect. 7.3. These include, potentially, a bias in the richness measure and some amount of sample impurity with respect to mass. Instead of mass, the MaDCoWS selection function may preferentially include star-forming systems, leading to deviations from self-similarity. As part of the mass-richness scaling relation, we fit a weight to each cluster, which describes the relative probability that the SZ measurement associated with that cluster was drawn from a normal distribution centered on the mass-richness scaling relation versus a normal distribution centered on zero. We found that a large fraction of the MaDCoWS cluster candidates had weights lower than 50%. We ascribe the low weight of these clusters, and correspondingly their non-detection in the ACT cluster catalog, to a variety of factors, including suppression of the SZ signal by merger history and other unvirialized components along the line-of-sight, as well as to the MaDCoWS catalog containing very small clusters with SZ signals too low to detect. As for the MaDCoWS non-detections of ACT clusters, we conclude that the MaDCoWS selection function is not mass limited, and thus the overlap of the MaDCoWS catalog with a catalog such as ACT can be very incomplete.
Additionally, by investigating their submillimeter and radio properties, we find evidence that the MaDCoWS candidates have a higher average submillimeter flux density and a higher average intrinsic radio luminosity than their ACT counterparts, even when the ACT clusters are restricted to the same redshift range as the MaDCoWS cluster candidates; however, the MaDCoWS clusters do have a lower average radio flux density in the observed frame of reference, such that the ACT clusters have high radio infill on average. We interpret this as the systems selected by MaDCoWS being on average dustier, while ACT clusters are less dusty and radio loud. We find no evidence that the submillimeter flux density of MaDCoWS clusters evolves with richness, although due to the paucity of Herschel data this is only based on 220 GHz stacks. We find that the RLF of the MaDCoWS clusters does increase with increasing richness, and we find that the relation agrees with prior studies (Mo et al. 2020).
Looking to the future, the next generation of MaDCoWS (MaDCoWS2) will use the deeper CatWISE2020 (Eisenhardt et al. 2020) WISE photometry in combination with deeper optical imaging. MaDCoWS2 is designed to extend from z ∼ 0.5 − 2 with an improved selection function at all redshifts. More in-depth studies of the radio and submillimeter properties of the MaDCoWS clusters in the short term will allow us to better understand the population differences between IR- and SZ-selected clusters and will allow us to better correct the mass-richness scaling relations. Continuing ACT operations and further data releases will increase the depth of SZ observations, allowing the survey to probe to lower masses and over larger regions.
Looking further, in the first half of the decade, data from Simons Observatory (SO; Zhu et al. 2021; The Simons Observatory Collaboration 2019; Ade et al. 2019), the CMB-S4 experiment (Abitbol et al. 2017; Abazajian et al. 2016, 2019), and the Cerro Chajnantor Atacama Telescope-prime (CCAT-prime; Vavagiakis et al. 2018; Aravena et al. 2019; Choi et al. 2020) will provide deeper and higher resolution SZ and submillimeter maps over a larger portion of the sky. Additionally, the Vera C. Rubin Observatory (Ivezić et al. 2019), Spectro-Photometer for the History of the Universe, Epoch of Reionization, and Ices Explorer (SPHEREx) (Bock 2018; Cooray 2018; Crill et al. 2020), and Euclid telescopes (Euclid Collaboration 2019) will provide larger and more accurate IR and optically selected cluster catalogs.
In the 2030s, the next-generation CMB-S4 experiment (Abazajian et al. 2016; Abitbol et al. 2017), CMB-HD experiment (Sehgal et al. 2019, 2020), and the Atacama Large Aperture Submillimeter Telescope (AtLAST; Klaassen et al. 2020) will potentially provide orders of magnitude increases in SZ map depth over significant fractions of the extragalactic sky, with the latter two providing a transformative leap in subarcminute resolution SZ and submillimeter studies at a significantly lower confusion limit.
The MaDCoWS catalog is available as a supplement on Vizier (Gonzalez et al. 2019b).
The VLASS data are available on the Canadian Astronomy Data Centre site, http://www.cadc-ccda.hia-iha.nrc-cnrc.gc.ca/en/search/?collection=VLASS&noexec=true#resultTableTab.
Acknowledgments
We thank the referee for the useful and constructive comments that helped improve this work. This work was supported by the US National Science Foundation through awards AST-1440226, AST0965625 and AST-0408698 for the ACT project, as well as awards PHY-1214379 and PHY-0855887. Funding was also provided by Princeton University, the University of Pennsylvania, and a Canada Foundation for Innovation (CFI) award to UBC. ACT operates in the Parque Astronómico Atacama in northern Chile under the auspices of the Comisión Nacional de Investigación Científica y Tecnológica de Chile (CONICYT), now La Agencia Nacional de Investigación y Desarrollo (ANID). Computations were performed on the GPC and Niagara supercomputers at the SciNet HPC Consortium. SciNet is funded by the CFI under the auspices of Compute Canada, the Government of Ontario, the Ontario Research Fund – Research Excellence; and the University of Toronto. The development of multichroic detectors and lenses was supported by NASA grants NNX13AE56G and NNX14AB58G. Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA. Colleagues at AstroNorte and RadioSky provide logistical support and keep operations in Chile running smoothly. We also thank the Mishrahi Fund and the Wilkinson Fund for their generous support of the project. Zhilei Xu is supported by the Gordon and Betty Moore Foundation. Kavilan Moodley acknowledges support from the National Research Foundation of South Africa. John P. Hughes acknowledges funding for SZ cluster studies from NSF grant number AST-1615657. Dongwon Han, Amanda MacInnis, and Neelima Sehgal acknowledge support from NSF grant number AST-1907657. Cristóbal Sifón acknowledges support from the ANID under FONDECYT grant no. 11191125. Luca Di Mascolo is supported by the ERC-StG ‘ClustersXCosmo’ grant agreement 716762.
References
- Abazajian, K. N., Adshead, P., Ahmed, Z., et al. 2016, ArXiv e-prints [arXiv:1610.02743] [Google Scholar]
- Abazajian, K., Addison, G., Adshead, P., et al. 2019, ArXiv e-prints [arXiv:1907.04473] [Google Scholar]
- Abell, G. O. 1958, ApJS, 3, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Abitbol, M. H., Ahmed, Z., Barron, D., et al. 2017, CMB-S4 Technology Book. First Edition [Google Scholar]
- Ade, P., Aguirre, J., Ahmed, Z., et al. 2019, JCAP, 2019, 056 [CrossRef] [Google Scholar]
- Amodeo, S., Battaglia, N., Schaan, E., et al. 2021, Am. Astron. Soc. Meeting Abstr., 53, 411.04 [NASA ADS] [Google Scholar]
- Andersson, K., Benson, B. A., Ade, P. A. R., et al. 2011, ApJ, 738, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S. 2015, A&A, 582, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S., & Hurn, M. A. 2010, MNRAS, 404, 1922 [NASA ADS] [Google Scholar]
- Aravena, M., Austermann, J., Basu, K., et al. 2019, The CCAT-Prime Submillimeter Observatory [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, N., Bond, J. R., Pfrommer, C., & Sievers, J. L. 2012, ApJ, 758, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, B. A., Ade, P. A. R., Ahmed, Z., et al. 2014, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VII, eds. W. S. Holland, J. Zmuidzinas, SPIE Conf. Ser., 9153, 91531P [CrossRef] [Google Scholar]
- Bingham, E., Chen, J. P., Jankowiak, M., et al. 2019, J. Mach. Learn. Res., 20, 1 [Google Scholar]
- Birkinshaw, M. 1999, Phys. Rep., 310, 97 [Google Scholar]
- Bleem, L. E., Bocquet, S., Stalder, B., et al. 2020, ApJS, 247, 25 [CrossRef] [Google Scholar]
- Bock, J., & SPHEREx Science Team 2018, Am. Astron. Soc. Meeting Abstr., 231, 354.21 [NASA ADS] [Google Scholar]
- Brodwin, M., Stanford, S. A., Gonzalez, A. H., et al. 2013, ApJ, 779, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Butcher, H., & Oemler, A. 1978, ApJ, 219, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Calistro Rivera, G., Williams, W. L., Hardcastle, M. J., et al. 2017, MNRAS, 469, 3468 [NASA ADS] [CrossRef] [Google Scholar]
- Capasso, R., Mohr, J. J., Saro, A., et al. 2019, MNRAS, 486, 1594 [CrossRef] [Google Scholar]
- Carlstrom, J. E., Holder, G. P., & Reese, E. D. 2002, ARA&A, 40, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Carlstrom, J. E., Ade, P. A. R., Aird, K. A., et al. 2011, PASP, 123, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M., Scoville, N. Z., Sanders, D. B., et al. 2014, ApJ, 796, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, K., & Pan-STARRS Team 2018, Am. Astron. Soc. Meeting Abstr., 231, 102.01 [NASA ADS] [Google Scholar]
- Chiu, I. N., Okumura, T., Oguri, M., et al. 2020, MNRAS, 498, 2030 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, S. K., Austermann, J., Basu, K., et al. 2020, J. Low Temp. Phys., 199, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Coble, K., Bonamente, M., Carlstrom, J. E., et al. 2007, AJ, 134, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Cooray, A., & SPHEREx Science Team 2018, Am. Astron. Soc. Meeting Abstr., 231, 354.27 [NASA ADS] [Google Scholar]
- Costanzi, M., Rozo, E., Rykoff, E. S., et al. 2019, MNRAS, 482, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Crill, B. P., Werner, M., Akeson, R., et al. 2020, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, SPIE Conf. Ser., 11443, 114430I [NASA ADS] [Google Scholar]
- Devlin, M. J., Ade, P. A. R., Aretxaga, I., et al. 2009, Nature, 458, 737 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dicker, S. R., Ade, P. A. R., Aguirre, J., et al. 2014, J. Low Temp. Phys., 176, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Dicker, S. R., Romero, C. E., Di Mascolo, L., et al. 2020, ApJ, 902, 144 [CrossRef] [Google Scholar]
- Di Mascolo, L., Mroczkowski, T., Churazov, E., et al. 2020, A&A, 638, A70 [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 2006, ApJ, 636, 1114 [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenhardt, P. R. M., Marocco, F., Fowler, J. W., et al. 2020, ApJS, 247, 69 [Google Scholar]
- Erler, J., Basu, K., Chluba, J., & Bertoldi, F. 2018, MNRAS, 476, 3360 [NASA ADS] [CrossRef] [Google Scholar]
- Euclid Collaboration (Adam, R., et al.) 2019, A&A, 627, A23 [CrossRef] [EDP Sciences] [Google Scholar]
- Euclid Collaboration (Blanchard, A., et al.) 2020, A&A, 642, A191 [CrossRef] [EDP Sciences] [Google Scholar]
- Evrard, A. E., Arnault, P., Huterer, D., & Farahi, A. 2014, MNRAS, 441, 3562 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Fowler, J. W., Niemack, M. D., Dicker, S. R., et al. 2007, Appl. Opt., 46, 3444 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fuzia, B. J., Kawinwanichakij, L., Mehrtens, N., et al. 2021, MNRAS, 502, 4026 [NASA ADS] [CrossRef] [Google Scholar]
- Ge, C., Sun, M., Rozo, E., et al. 2019, MNRAS, 484, 1946 [NASA ADS] [Google Scholar]
- Geach, J. E., & Peacock, J. A. 2017, Nat. Astron., 1, 795 [NASA ADS] [CrossRef] [Google Scholar]
- George, M. R., Leauthaud, A., Bundy, K., et al. 2012, ApJ, 757, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, A. H., Gettings, D. P., Brodwin, M., et al. 2019a, ApJS, 240, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, A. H., Gettings, D. P., Brodwin, M., et al. 2019b, VizieR Online Data Catalog: J/ApJS/240/33 [Google Scholar]
- Gralla, M. B., Crichton, D., Marriage, T. A., et al. 2014, MNRAS, 445, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Gralla, M. B., Marriage, T. A., Addison, G., et al. 2020, ApJ, 893, 104 [CrossRef] [Google Scholar]
- Grandis, S., Mohr, J. J., Costanzi, M., et al. 2021, MNRAS, 504, 1253 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, N., Saro, A., Mohr, J. J., et al. 2017, MNRAS, 467, 3737 [NASA ADS] [Google Scholar]
- Hambly, N., Davenhall, A., Irwin, M., & MacGillivray, H. 2001a, MNRAS, 326, 1315 [NASA ADS] [CrossRef] [Google Scholar]
- Hambly, N., Irwin, M., & MacGillivray, H. 2001b, MNRAS, 326, 1295 [NASA ADS] [CrossRef] [Google Scholar]
- Hambly, N., MacGillivray, H., Read, M., et al. 2001c, MNRAS, 326, 1279 [Google Scholar]
- Hasselfield, M., Hilton, M., Marriage, T. A., et al. 2013, JCAP, 2013, 008 [Google Scholar]
- Henderson, S. W., Allison, R., Austermann, J., et al. 2016, J. Low Temp. Phys., 184, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Hilton, M., Hasselfield, M., Sifón, C., et al. 2018, ApJS, 235, 20 [Google Scholar]
- Hilton, M., Sifón, C., Naess, S., et al. 2021, ApJS, 253, 3 [Google Scholar]
- Ivezić, Ž., Kahn, S. M., Tyson, J. A., et al. 2019, ApJ, 873, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, B. C. 2007, ApJ, 665, 1489 [Google Scholar]
- Klaassen, P. D., Mroczkowski, T. K., Cicone, C., et al. 2020, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, SPIE Conf. Ser., 11445, 114452F [Google Scholar]
- Krause, E., Pierpaoli, E., Dolag, K., & Borgani, S. 2012, MNRAS, 419, 1766 [NASA ADS] [CrossRef] [Google Scholar]
- Lacy, M., Baum, S. A., Chandler, C. J., et al. 2020, PASP, 132 [Google Scholar]
- Madhavacheril, M. S., Sifón, C., Battaglia, N., et al. 2020, ApJ, 903, L13 [Google Scholar]
- Magnelli, B., Lutz, D., Santini, P., et al. 2012, A&A, 539, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malmquist, K. G. 1922, Meddelanden fran Lunds Astronomiska Observatorium Serie I, 100, 1 [Google Scholar]
- Marriage, T. A., Acquaviva, V., Ade, P. A. R., et al. 2011, ApJ, 737, 61 [NASA ADS] [CrossRef] [Google Scholar]
- McClintock, T., Varga, T. N., Gruen, D., et al. 2019, MNRAS, 482, 1352 [NASA ADS] [CrossRef] [Google Scholar]
- Menanteau, F., González, J., Juin, J.-B., et al. 2010, ApJ, 723, 1523 [NASA ADS] [CrossRef] [Google Scholar]
- Menanteau, F., Sifón, C., Barrientos, L. F., et al. 2013, ApJ, 765, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Miyatake, H., Battaglia, N., Hilton, M., et al. 2019, ApJ, 875, 63 [CrossRef] [Google Scholar]
- Mo, W., Gonzalez, A., Brodwin, M., et al. 2020, ApJ, 901, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Moravec, E., Gonzalez, A. H., Stern, D., et al. 2020, ApJ, 888, 74 [Google Scholar]
- Motl, P. M., Hallman, E. J., Burns, J. O., & Norman, M. L. 2005, ApJ, 623, L63 [Google Scholar]
- Mroczkowski, T., Nagai, D., Basu, K., et al. 2019, Space Sci. Rev., 215, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Naess, S., Aiola, S., Austermann, J. E., et al. 2020, JCAP, 2020, 046 [Google Scholar]
- Nelson, K., Lau, E. T., Nagai, D., Rudd, D. H., & Yu, L. 2014, ApJ, 782, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Phan, D., Pradhan, N., & Jankowiak, M. 2019, ArXiv e-prints [arXiv:1912.11554] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVII. 2016, A&A, 594, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poole, G. B., Fardal, M. A., Babul, A., et al. 2006, MNRAS, 373, 881 [Google Scholar]
- Poole, G. B., Babul, A., McCarthy, I. G., et al. 2007, MNRAS, 380, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Rettura, A., Chary, R., Krick, J., & Ettori, S. 2018, ApJ, 867, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Ruppin, F., McDonald, M., Brodwin, M., et al. 2020, ApJ, 893, 74 [CrossRef] [Google Scholar]
- Rykoff, E. S., Koester, B. P., Rozo, E., et al. 2012, ApJ, 746, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Saro, A., Bocquet, S., Rozo, E., et al. 2015, MNRAS, 454, 2305 [NASA ADS] [CrossRef] [Google Scholar]
- Sayers, J., Mroczkowski, T., Czakon, N. G., et al. 2013, ApJ, 764, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Sayers, J., Montaña, A., Mroczkowski, T., et al. 2019, ApJ, 880, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Sehgal, N., Trac, H., Acquaviva, V., et al. 2011, ApJ, 732, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Sehgal, N., Addison, G., Battaglia, N., et al. 2013, ApJ, 767, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Sehgal, N., Aiola, S., Akrami, Y., et al. 2019, BAAS, 51, 6 [NASA ADS] [Google Scholar]
- Sehgal, N., Aiola, S., Akrami, Y., et al. 2020, ArXiv e-prints [arXiv:2002.12714] [Google Scholar]
- Sereno, M. 2016, MNRAS, 455, 2149 [Google Scholar]
- Simet, M., McClintock, T., Mandelbaum, R., et al. 2017, MNRAS, 466, 3103 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. J. B., Hardcastle, M. J., Jarvis, M. J., et al. 2013, MNRAS, 436, 2435 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. W. L., Ibar, E., Maddox, S. J., et al. 2017, ApJS, 233, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1970, Comm. Astrophys. Space Phys., 2, 66 [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comm. Astrophys. Space Phys., 4, 173 [Google Scholar]
- Swetz, D. S., Ade, P. A. R., Amiri, M., et al. 2011, ApJS, 194, 41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- The Simons Observatory Collaboration (Lee, A., et al.) 2019, BAAS, 51, 147 [NASA ADS] [Google Scholar]
- Thornton, R. J., Ade, P. A. R., Aiola, S., et al. 2016, ApJS, 227, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Valiante, E., Smith, M. W. L., Eales, S., et al. 2016, MNRAS, 462, 3146 [NASA ADS] [CrossRef] [Google Scholar]
- Vavagiakis, E., Ahmed, Z., Ali, A., et al. 2018, Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy IX [Google Scholar]
- Vavagiakis, E. M., Gallardo, P. A., Calafut, V., et al. 2021, Phys. Rev. D, 104, 043503 [NASA ADS] [CrossRef] [Google Scholar]
- Viola, M., Cacciato, M., Brouwer, M., et al. 2015, MNRAS, 452, 3529 [CrossRef] [Google Scholar]
- Wik, D. R., Sarazin, C. L., Ricker, P. M., & Randall, S. W. 2008, ApJ, 680, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
- Wylezalek, D., Galametz, A., Stern, D., et al. 2013, ApJ, 769, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Yee, H. K. C., & Gladders, M. D. 2002, in AMiBA 2001: High-Z Clusters, Missing Baryons, and CMB Polarization, eds. L. W. Chen, C. P. Ma, K. W. Ng, & U. L. Pen, ASP Conf. Ser., 257, 109 [NASA ADS] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., Jr, et al. 2000, ApJ, 120, 1579 [Google Scholar]
- Zajaček, M., Busch, G., Valencia-S., M., et al. 2019, A&A, 630, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zakamska, N. L., Sun, A.-L., Strauss, M. A., et al. 2019, MNRAS, 489, 497 [Google Scholar]
- Zhu, N., Bhandarkar, T., Coppi, G., et al. 2021, ArXiv e-prints [arXiv:2103.02747] [Google Scholar]
Appendix A: Bootstrapping
Throughout the paper, we are presented with a situation in which we have a data set, d, which we are interested in computing some statistic on, and for which we would like to estimate the uncertainty in that statistic. We use the bootstrapping method to do so: given d, we resample from that data set with replacement k times, resulting in a superset of data sets, {d1,…di,…dk} where the di are the resampled data sets. For each di, we compute a statistic on di, which we call μi, generally the mean, or in the case where the data are maps, the central emission. We then have a set of statistics, μ = {μ1,…μi,…μk}. We then take the average and standard deviation of μ as the average and standard deviation of that statistic on d.
Appendix B: ACT SZ masses versus CARMA, ACA, MUSTANG2, and NIKA2
Comparison of the masses inferred using ACT data to those from SZ observations with CARMA (Gonzalez et al. 2019a), ACA (Di Mascolo et al. 2020), MUSTANG2 (Dicker et al. 2020), and NIKA2 (Ruppin et al. 2020).
Appendix C: MaDCoWS/ACT co-detections
ACT/MaDCoWS Co-detections.
All Tables
Comparison of the masses inferred using ACT data to those from SZ observations with CARMA (Gonzalez et al. 2019a), ACA (Di Mascolo et al. 2020), MUSTANG2 (Dicker et al. 2020), and NIKA2 (Ruppin et al. 2020).
All Figures
 |
Fig. 1. Offsets in the right ascension and declination of ACT clusters (Hilton et al. 2021) and their co-detected MaDCoWS counterparts (Gonzalez et al. 2019b). The color bar indicates the redshift of the co-detection as recorded by ACT in the DR5 cluster catalog. The black-dotted circle is the radius (1.2′) that includes 89 (95%) of the co-detections. |
| In the text | |
 |
Fig. 2. ACT S/N maps of the dozen highest-significance co-detections, where the S/N is with respect to |
| In the text | |
 |
Fig. 3. Mass vs. richness relation for a selection of MaDCoWS clusters with SZ mass estimates. The purple circles correspond to the CARMA MaDCoWS cluster sample from Gonzalez et al. (2019a). The VACA LoCA points from Di Mascolo et al. (2020) are shown in red, and the MUSTANG2 measurements from Dicker et al. (2020) are shown in orange. The black data points are Chandra observations of MaDCoWS clusters. Points that are open are known active mergers, and points that are represented with triangles are consistent with no signal. We note that Fig. 12 provides a similar comparison for the complete sample of MaDCoWS candidates in the ACT survey footprint. |
| In the text | |
 |
Fig. 4.
|
| In the text | |
 |
Fig. 5. Stacks on MaDCoWS cluster positions in bins of richness on the ACT |
| In the text | |
 |
Fig. 6. MaDCoWS to ACT |
| In the text | |
 |
Fig. 7. Average 224 GHz emission for MaDCoWS (blue) and ACT (orange) clusters. MaDCoWS clusters were binned in richness, while the ACT clusters were binned in mass. Richness is plotted on the lower x axis while mass is plotted on the upper; the two scales are not equivalent, and are simply co-plotted for convenience. Error bars were estimated via bootstrapping. The MaDCoWS clusters show a statistically significant excess emission at 224 GHz on the whole, while the ACT clusters show a small decrement. In neither the ACT nor the MaDCoWS clusters is there a trend with mass or richness. The dashed lines indicate the average 224 GHz emission across all MaDCoWS (blue) and ACT (orange) clusters. We attribute the signal from the MaDCoWS cluster candidates at 224 GHz to IR emission and follow up with Herschel data (Sect. 5.2). |
| In the text | |
 |
Fig. 8. Histograms of average surface brightness in Herschel submillimeter observations corresponding to a 1.2′ radius aperture flux, centered on ACT, MaDCoWS, and random cluster locations. The dashed lines show the average brightness for a given frequency and catalog. At 250 μm, the average surface brightness is 0.10 ± 0.08, 0.15 ± 0.10, and 0.22 ± 0.11 MJy sr−1 for the random, ACT, and MaDCoWS samples, respectively. At 350 μm, those surface brightnesses are respectively 0.05 ± 0.05, 0.08 ± 0.08, and 0.16 ± 0.09 MJy sr−1 for the random, ACT, and MaDCoWS samples. Finally, at 500 μm they are 0.01 ± 0.04, 0.03 ± 0.07, and 0.09 ± 0.06 MJy sr−1 for the random, ACT, and MaDCoWS. The statistically higher MaDCoWS emission at each Herschel frequency, along with the higher emission in the ACT 224 GHz channel (Fig. 7), indicates that the MaDCoWS clusters may be contaminated by dusty sources. |
| In the text | |
 |
Fig. 9. Gray-body fit constraints. (a) Maximum likelihood best fit of the form Eq. (6) to the mean emission from stacks on the MaDCoWS clusters at 224 (ACT), 600, 857, and 1200 GHz (Herschel). The total number of clusters in the stack is the 66 clusters in the H-ATLAS footprint for the three Herschel bands and 1572 for the ACT 224 GHz band. The dashed blue line is the best fit, and the light and dark blue bands represent the 68 and 95% confidence limit, respectively. The y axis is the surface brightness averaged over a 1.2′ radius aperture at the center of the stack. Error bars were estimated via bootstrapping. (b) Constraints on the dust temperature, |
| In the text | |
 |
Fig. 10. Histograms of the 1.4 GHz aperture flux density of the ACT (a) and MaDCoWS (b) cluster catalogs. Panel c: normalized cumulative histogram of the same data, cut at the aperture noise of 0.3 mJy, to better illustrate the difference in infill between the two samples. The fluxes shown are all for a 1.2′ radius aperture, while the percentage infill is the approximate infill of the SZ signal as described in Sect. 7.1.2. We note that due to differences in average redshift and spectral index of the ACT and MaDCoWS clusters, the same measured flux density at 1.4 GHz does not correspond to the same percentage infill. The ACT clusters show on average significantly more radio infill at 1.4 GHz than their MaDCoWS analogs. |
| In the text | |
 |
Fig. 11. Intrinsic radio luminosities at 1.4 GHz for ACT (blue, 3341 clusters) and MaDCoWS (orange, 1780 clusters). The red line shows a 0.3 mJy flux density at 1.4 GHz in the observed frame of reference converted to 1.4 GHz in the emitted frame of reference for the given z according to Eq. (10), and assuming a spectral index of −0.91. The choice of 0.3 mJy corresponds to the variance of the background aperture flux density in the NVSS maps for a 1.2′ radius aperture, and thus roughly corresponds to the noise floor for our background subtracted fluxes. Therefore, the red line should guide the eye as to which radio luminosities are above the noise. We note that many clusters are not shown as they have very low or negative values for their radio fluxes due to subtraction of the background. |
| In the text | |
 |
Fig. 12. Mass-richness diagram displayed three ways. The left and center panels are respectively log-log and linear plots of |
| In the text | |
 |
Fig. 13. 2D histogram of weight and richness (λ15). The weight is the probability that a MaDCoWS cluster data point is well described by a mass-richness scaling relation, as opposed to being drawn from the noise. Higher probabilities mean they are more likely to be real. The bimodal distribution is clear, with a large population of low probability clusters centered around 50% and a population of high probability clusters at ≈70%. |
| In the text | |
 |
Fig. 14. Comparisons of richness populations for the co-detected MaDCoWS and the remaining MaDCoWS in four redshift bins. At higher richness (λ15 > 60), there is no preferred redshift for the co-detections. This indicates that the disparity between the number of MaDCoWS in the ACT region and the number of co-detections is not a product of survey biases. |
| In the text | |
 |
Fig. 15. M500 of ACT clusters vs. MaDCoWS in the same redshift ranges. These distributions suggest that ACT clusters are skewed toward lower redshifts, while the MaDCoWS distribution is even across higher redshifts. In addition, MaDCoWS clusters tend to be less massive than ACT clusters at a given redshift. |
| In the text | |
 |
Fig. 16. Stacks at 250, 350, and 500 μm (from left to right) on MaDCoWS (a, b, c) and ACT cluster locations (d, e, f), as well as a set of random locations (g, h, i) in the H-ATLAS data set. See Sect. 5.2 for details. The x axis of each plot is aligned with RA, while the y axis is aligned with declination; both are in units of arcmin. The color bars are in units of MJy sr−1. The red circles are 1.2′ in radius, the scale inside which we assigned excess flux density as being due to the cluster stack. |
| In the text | |
 |
Fig. 17. Best fit of a linear model to the RLF of the MaDCoWS clusters determined using NVSS 1.4 GHz fluxes (Sect. 5.3) vs. richness. The best fit is inconsistent with the null hypothesis of no evolution of the RLF with richness at 5.9σ. In comparison to Mo et al. (2020), we favor a higher slope for the relation at 1.2σ, although see the discussion in Sect. 7.1.2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



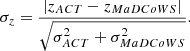
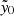
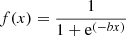
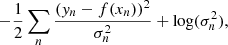
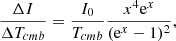
![$$ \begin{aligned} I_0 = \frac{2(k_{\rm B} T_{cmb })^3}{(hc)^2} \approx 270.33 \left[ \frac{T_{cmb }}{2.7255~\text{ K}}\right]^3\,\mathrm{MJy}\,\mathrm{sr}^{-1}. \end{aligned} $$](/articles/aa/full_html/2021/09/aa41200-21/aa41200-21-eq43.gif)
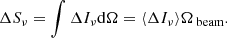
![$$ \begin{aligned} \Delta S(\nu ) = A \, B_{\nu }(T) \, \left[ 1 - \mathrm{e}^{-(\nu / \nu _0)^{\beta }} \right], \end{aligned} $$](/articles/aa/full_html/2021/09/aa41200-21/aa41200-21-eq45.gif)
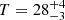
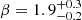
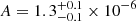
![$$ \begin{aligned} y\approx \Delta I_{\nu }\times \left[I_0\left(\frac{x}{\tanh {(0.5x)}}-4\right)\left(\frac{x^4 \mathrm{e}^x}{(\mathrm{e}^x-1)^2}\right) \right]^{-1}. \end{aligned} $$](/articles/aa/full_html/2021/09/aa41200-21/aa41200-21-eq51.gif)
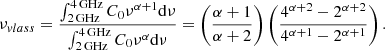
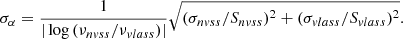
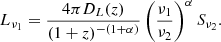
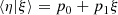
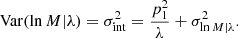
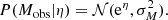
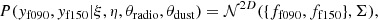
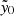
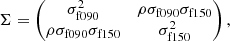
![$$ \begin{aligned}&f_{\nu } = f_{\nu }(\xi ,\eta ,\theta _{\mathrm{radio} },\theta _{\mathrm{dust} }) \nonumber \\&\ \ \ = c(\xi )\cdot m_{\nu }(\eta )+{ g}_{\nu }\left[d_{\nu }(\theta _{\mathrm{dust} })+ r_{\nu }(\theta _{\mathrm{radio} })\right]. \end{aligned} $$](/articles/aa/full_html/2021/09/aa41200-21/aa41200-21-eq80.gif)