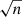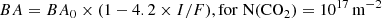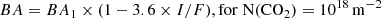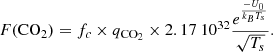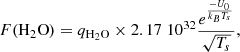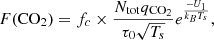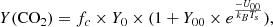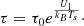| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | L11 | |
| Number of page(s) | 21 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202451599 | |
| Published online | 17 October 2024 | |
Letter to the Editor
A patchy CO2 exosphere on Ganymede revealed by the James Webb Space Telescope
1
LESIA, Observatoire de Paris, Université PSL, Sorbonne Université, Université Paris Cité, CNRS, 92195 Meudon, France
2
Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
3
LATMOS/CNRS, Sorbonne Université, UVSQ, Paris, France
4
Department of Astronomy, University of California, 22 Berkeley, CA 94720, USA
5
Department of Earth and Planetary Science, University of California, 22 Berkeley, CA 94720, USA
6
Space and Plasma Physics, KTH Royal Institute of Technology, Stockholm, Sweden
7
Institute of Geophysics and Meteorology, University of Cologne, Albertus Magnus Platz, 50923 Cologne, Germany
8
University of Wisconsin, Madison, WI 53706, USA
9
Department of Astronomy & Astrophysics, University of California, San Diego, La Jolla, CA 92093, USA
10
Division of Geological and Planetary Sciences, Caltech, Pasadena, CA 91125, USA
11
Johns Hopkins University Applied Physics Laboratory, 11001 Johns Hopkins Rd, Laurel, MD 20723, USA
12
Faculty of Aerospace Engineering, Delft University of Technology, Delft, The Netherlands
13
School of Physics and Astronomy, University of Leicester, University Road, Leicester LE1 7RH, UK
14
Istituto Nazionale di AstroFisica – Istituto di Astrofisica e Planetologia Spaziali (INAF-IAPS), 00133 Rome, Italy
15
Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA
Received:
22
July
2024
Accepted:
19
September
2024
Jupiter’s icy moon Ganymede has a tenuous exosphere produced by sputtering and possibly sublimation of water ice. To date, only atomic hydrogen and oxygen have been directly detected in this exosphere. Here, we present observations of Ganymede’s CO2 exosphere obtained with the James Webb Space Telescope. CO2 gas is observed over different terrain types, mainly over those exposed to intense Jovian plasma irradiation, as well as over some bright or dark terrains. Despite warm surface temperatures, the CO2 abundance over equatorial subsolar regions is low. CO2 vapor has the highest abundance over the north polar cap of the leading hemisphere, reaching a surface pressure of 1 pbar. From modeling we show that the local enhancement observed near 12 h local time in this region can be explained by the presence of cold traps enabling CO2 adsorption. However, whether the release mechanism in this high-latitude region is sputtering or sublimation remains unclear. The north polar cap of the leading hemisphere also has unique surface-ice properties, probably linked to the presence of the large atmospheric CO2 excess over this region. These CO2 molecules might have been initially released in the atmosphere after the radiolysis of CO2 precursors, or from the sputtering of CO2 embedded in the H2O ice bedrock. Dark terrains (regiones), more widespread on the north versus south polar regions, possibly harbor CO2 precursors. CO2 molecules would then be redistributed via cold trapping on ice-rich terrains of the polar cap and be diurnally released and redeposited on these terrains. Ganymede’s CO2 exosphere highlights the complexity of surface-atmosphere interactions on Jupiter’s icy Galilean moons.
Key words: planets and satellites: atmospheres / planets and satellites: composition / planets and satellites: individual: Ganymede
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Jupiter’s icy satellites, Europa, Ganymede and Callisto, are known to have rarefied atmospheres. The surface composition of these moons is dominated by H2O ice and non-ice components (possibly salts, hydrated minerals and organics) that host volatiles such as CO2 (Carlson et al. 1996; McCord et al. 1998; Tosi et al. 2024). Sublimation and weathering processes, such as sputtering by charged particles from Jupiter’s magnetosphere and micro-meteoroid bombardment, lead to the formation of weakly bound atmospheres composed primarily of H2O, O2, OH, H, O, and CO2 species. Because of strong telluric absorption by Earth’s atmosphere, detection of atomic and molecular emissions from icy moon exospheres is difficult from ground-based facilities. Most of our knowledge comes from the detection of auroral O and H emission lines in the atmospheres of the three icy moons (Hall et al. 1998; Cunningham et al. 2015; Barth et al. 1997; Roth et al. 2017a,b; de Kleer et al. 2023), with some constraints obtained on H2O vapor content for Ganymede (Roth et al. 2021). To date, atmospheric CO2 has only been detected in the atmosphere of Callisto (Carlson 1999; Cartwright et al. 2024). The maximum CO2 column densities do not coincide with the subsolar region, nor the regions with the greatest solid-state CO2 abundance on Callisto’s surface, suggesting that CO2 gas may be partly sourced by outgassing from its crust (Cartwright et al. 2024). Characterizing how icy moon exospheres are formed and sustained is pivotal for understanding surface-atmosphere interactions, geomorphological and chemical changes driven by erosion.
Ganymede is the only known moon with an intrinsic magnetic field, which results in a complex space plasma environment that has been explored by the in situ flybys of the Galileo and Juno spacecraft (e.g., Kivelson et al. 1996; Allegrini et al. 2022; Ebert et al. 2022; Clark et al. 2022). The intrinsic magnetic field directs most of the external Jovian magnetospheric plasma in a way that it primarily interacts with the moon’s surface where Ganymede’s mini-magnetosphere has open field lines (i.e., around the polar regions) (Poppe et al. 2018; Liuzzo et al. 2020; Greathouse et al. 2022). This results in specific surface properties with respect to shielded equatorial latitudes, such as the formation of H2O ice-rich patches at the polar caps (Khurana et al. 2007; Ligier et al. 2019; Stephan et al. 2020; King & Fletcher 2022) with higher amounts of amorphous H2O ice (Ligier et al. 2019; Bockelée-Morvan et al. 2024), radiolytically produced H2O2 (Trumbo et al. 2023), and CO2 possibly trapped in amorphous H2O ice (Bockelée-Morvan et al. 2024). In addition, asymmetries between the north and south polar caps, and leading and trailing hemispheres are observed (Ligier et al. 2019; de Kleer et al. 2021; Trumbo et al. 2023; Bockelée-Morvan et al. 2024). Here we present the first detection of CO2 in the exosphere of Ganymede, achieved using the James Webb Space Telescope (JWST), and we link the observed highly hetereogeneous CO2 exosphere to surface properties and processes. This Letter follows the investigation of Ganymede’s surface properties from the same JWST data set (Bockelée-Morvan et al. 2024, hereafter Paper I).
2. JWST observations of Ganymede’s exosphere
Observations undertaken with the Near-Infrared Spectrograph integral field unit (NIRSpec/IFU) provided spatially resolved spectra (0.1″ pixel size, with ∼190 pixels across Ganymede’s disk) of the leading and trailing sides of Ganymede in the 2.9−5.2 μm range at high spectral resolution (R ∼ 3000) (Paper I and Appendix A). Ro-vibrational emission lines of the CO2ν3 band at 4.26 μm were detected within the broad solid-state CO2 absorption band (Figs. 1, B.1). We used several data processing techniques to extract the CO2 gas signal and best evaluate the confidence level of the detection for weak signals (Appendices B, C). CO2 column densities were inferred using a nonlocal thermal equilibrium (non-LTE) excitation model (Appendices D, E). The distributions of column densities for the two hemispheres are shown in Fig. 1. Figure 2 presents the dependence on latitude, from the analysis of spectra after averaging pixels over ranges of latitude.
 |
Fig. 1. CO2 in Ganymede’s exosphere. The top and bottom rows are for the leading and trailing sides, respectively. The left column shows Bond albedo maps derived by de Kleer et al. (2021) from Voyager-Galileo mosaic. The middle column shows line-of-sight CO2 column density maps inferred from spectral modeling (Appendices B–D). The trailing data were smoothed using a 3 × 3 boxcar filter. The color scales for the leading and trailing sides differ, and are indicated above the plots. The pixel sizes are 0.1 × 0.1″ and the PSF is ∼0.19″ (FWHM). The CO2 maximal emission in the leading hemisphere (based on central contour) is at 81°W, 51°N (∼12 h local time); correcting for the line of sight, the maximum vertical column density is at 72°W, 45°N (12.6 h local time, see Figs. 4A, O.2). The third column shows CO2 gaseous emission spectra obtained after removing the continuum emission from Ganymede’s surface, averaged over latitudes 45−90°N for leading (top), and 30−60°S for trailing (bottom). The best fit synthetic spectra are shown in cyan, with a fitted rotational temperature of 108 ± 8 K for the leading side, and a fixed rotational temperature of 105 K for the trailing side. The y scale is μJy per pixel. The green lines on the maps show the OCFBs at the time of the JWST observations (Appendix J, Duling et al. 2022). The subsolar point is shown by a red star in the Bond albedo maps. |
The distribution of CO2 gas shows strong regional variations (Fig. 1) and is at odds with expectations that the peak surface location of the exosphere would be at the dawn terminator due to condensation on the surface at night and early morning re-evaporation (Steckloff et al. 2022). The CO2 exosphere is most prominent over the north polar regions of the leading hemisphere, peaking at 81°W, 51°N (12 h local time), with a column density along the line of sight of (1.5 ± 0.11) × 1018 m−2 corresponding to a pressure at the surface of 1 pbar. The rotational temperature of CO2 measured in this region (107 ± 5 K, Fig. H.1) constrains the gas kinetic temperature in Ganymede’s exosphere (Appendix H). A point-spread function (PSF) correction to the CO2 column density map suggests that the decrease poleward of 50°N is real (Appendix M). At southern latitudes of the leading hemisphere, and on the trailing hemisphere, the CO2 exosphere is on average at least five times less dense (Fig. 2). Low column densities are measured at or near equatorial latitudes for both hemispheres. The trailing hemisphere displays a north–south asymmetry, with the exosphere extending over a broader range of latitudes in the southern hemisphere. Noticeable in Fig. 1 (see also Fig. O.1) is a CO2 gas enhancement in a large region around (30°W, 25°N), encompassing the Tros crater (27°W, 11°N). CO2 excess is also present at around 30°S on the leading side, which corresponds to the position of the expected southern open-closed field-line boundary (OCFB, Appendix J).
 |
Fig. 2. Variation of CO2 gas line-of-sight column density with latitude. The blue and red symbols refer to the leading and trailing sides, respectively. The column densities were derived from spectra that were averaged in latitude bins of 7.5° (leading, Fig. B.2) and 15° (trailing). The blue (resp. pink) vertical domains show the latitude range of the OCFBs for the leading and trailing sides, respectively, restricted to longitudes of 10−130°W (leading) and 210−330°W (trailing). |
Exospheric H2O was unsuccessfully searched for in 5.5−7.1 μm spectro-imaging data acquired with the JWST Mid-Infrared Instrument (MIRI) Medium Resolution Spectroscopy (MRS) mode (see Appendix I). Our 3σ upper limit on the H2O column density for the subsolar region of the leading side (6.8 × 1019 m−2, Table I.1) is about an order of magnitude higher than the minimum of 6 × 1018 m−2 required to explain UV Hubble Space Telescope (HST) data of atomic oxygen emission lines (Roth et al. 2021). On the other hand, for the trailing side, our derived upper limit for a 105 K atmosphere (3.1 × 1019 m−2) is slightly below the lower limit from HST (3.6 × 1019 m−2, Roth et al. 2021). Since HST constrains the H2O/O2 ratio and not directly the H2O abundance, this could imply that the atmosphere is overall more dilute and that the H2O and O2 densities are both lower than assumed in Roth et al. (2021). This would contradict recent results that suggested a denser global atmosphere based on plasma measurements (Carnielli et al. 2020a; Waite et al. 2024). Alternatively, a higher atmospheric temperature (e.g., 130 K, Table I.1), as might be expected above subsolar regions, increases the JWST upper limit to values consistent with the HST lower limits.
3. Processes releasing CO2 in Ganymede’s exosphere
Possible processes that release CO2 into Ganymede’s exosphere include surface ice sublimation and sputtering by energetic particles. We investigated whether these mechanisms, acting either on H2O ice containing CO2 molecules or on pure CO2 ice, could be distinguished from the observed properties of Ganymede’s exosphere. For this purpose, we used the Exospheric Global Model (EGM, Leblanc et al. 2017), a multi-species 3D Monte Carlo model that considers sources and sinks (photodestruction, surface sticking, gravitational escape) of such exospheres (Appendix K). The simulations (Appendix L) were designed to explain to first order the CO2 column density peak observed in the northern latitudes of the leading hemisphere, and the dichotomy between the trailing and leading hemispheres.
A key question to address is the localized character of the atmosphere. Mean surface temperatures, even in the polar regions (100−110 K, Fig. K.1), are much warmer than the expected condensation temperature of pure CO2 (73 K at 1 pbar pressure). Hence, the CO2 atmosphere might have been expected to be more widespread, as shown by EGM calculations considering mean surface temperatures (Appendix L.1). This indicates that CO2 interacts with the surface material much more strongly than expected in such a simplistic view. Similar conclusions were reached for O2 gas at Ganymede (Waite et al. 2024), but also at Dione and Rhea (Teolis & Waite 2016), based on inconsistencies on O2 column densities between exospheric models and measurements. In those moons of Saturn, the O2 source rates implied by the observations are 50 (Dione) to 300 (Rhea) times less than expected from the known O2 radiolysis yields from ion-irradiated pure water ice measured in the laboratory, and surface interactions (adsorption or diffusion) appear to control the exospheric structure, density, and seasonal variability. We note that for CO2 at Ganymede, the prime evidence for strong surface-atmosphere interactions comes from the nonglobal character of the atmosphere rather than the absolute CO2 column densities (which remain difficult to explain, see below).
To explain the atmospheric patchiness, Ganymede’s surface may have properties that increase the effective binding and desorption energies of O2 and CO2. In addition to surface roughness producing cold traps, surface irradiation (creating defects) and microstructure (enabling diffusion, and re-adsorption on adjacent grains) could increase the effective binding and desorption energies of adsorbates (Yakshinskiy & Madey 2000; Cassidy et al. 2015; Sarantos & Tsavachidis 2020). These hypotheses were drawn to explain the distribution of alkali gases surrounding Mercury and the Moon. In the EGM simulations, the surface temperature model considers surface roughness, as constrained from JWST/MIRI brightness temperature maps (Paper I), and simulates the presence of local cold spots through a temperature distribution (Appendix K). As shown in Appendix L.1, CO2 diffusion is, to a large extent, controlled by the ability of molecules to condense on cold traps, thereby explaining localized enhancements of the CO2 exosphere at high latitudes.
Figure 3 shows simulations of Ganymede’s CO2 exosphere above the leading hemisphere, assuming that the release of CO2 is induced by the sublimation (left panel) or the sputtering (right panel) of H2O ice containing CO2 molecules. Sublimation of CO2 ice was also investigated (Figs. L.2c, d). In all three cases the CO2 column density peaks at the correct latitude, as long as the source region covers the north polar cap (latitude > 40−50°N, longitude range 0−180°), and follows a diurnal-longitudinal trend with a maximum at ∼13.1 to 13.4 h, slightly shifted from the maximum surface temperature (12.5 h, Fig. K.1) and observed CO2 peak (12 h). Sputtering explains the smooth diurnal variation of the CO2 column density better than sublimation (Fig. L.2f).
 |
Fig. 3. Calculated line-of-sight column-density maps of the CO2 exosphere of Ganymede above the leading side from the EGM model (in units of 1018 m−2). Left: CO2 release associated with H2O sublimation with a CO2/H2O relative abundance of 5 for an H2O areal ice fraction of 50% at latitudes > 50°N. Right: Sputtering of H2O ice with CO2/H2O = 0.01 at latitudes > 40°N; the result was multiplied by 382 to match the observations (Appendices K, L). The green lines display the OCFBs. The subsolar point is at 2.6°N, 82°W. |
In our models where CO2 is released through sputtering of H2O ice with 1% CO2 molecules, we had to multiply the sputtered flux from Leblanc et al. (2017) by a factor of ∼380 to match the observed peak column density. The need to increase the sputtered flux significantly might be related to the approach used by Leblanc et al. (2017) to calculate this flux (see Appendix K), which consisted in using the yield definition of Cassidy et al. (2013) and a precipitating Jovian ion flux of 106 particles/cm2/s, ignoring any sputtered component from electron impact. Carnielli et al. (2020a) modeled the ion population in the ionosphere and concluded, based on electron measurements from the Galileo spacecraft, that ionospheric ions could be a significant source of ion precipitation, especially on the leading hemisphere (Carnielli et al. 2020b). Using measurements from the Juno spacecraft, Waite et al. (2024) and Vorburger et al. (2024) concluded that low-energy electrons are an important sputtering agent. Another source of uncertainty is sputtering yields for production of CO2 by ion and electron impacts, which are unconstrained because the relevant experiments are sparse. Simulations investigating sputtering on the entire surface of Ganymede (Appendix L.4) show that it might be possible to explain the overall distribution of CO2 exosphere by considering strong regional variations of surface properties.
A consequence of the factor of 380 enhancement of the sputtered flux from Leblanc et al. (2017) is that to first order the O2 column density in our model is multiplied by the same factor, bringing it to values ∼1.5 × 1017 O2/cm2, at odds with results from Leblanc et al. (2023) and Roth et al. (2021), based on the atomic O line intensities in the UV. This result goes in the same direction as the ionospheric calculations of Carnielli et al. (2020b) and the post-Juno analyses of Vorburger et al. (2024) and Waite et al. (2024), who advocated for O2 columns that are ∼20 times enhanced compared to previous estimates, but the discrepancy is much larger here, which at face value could be taken as an argument against sputtering being at the origin of the CO2 atmosphere.
In our sublimation models where CO2 gas is released in proportion to the H2O sublimation flux, reproducing the peak column density requires an unrealistic CO2 abundance relative to water, three orders of magnitude higher than estimated for the surface (∼1% in mass, Paper I). Hence, this scenario cannot explain the CO2 exospheric excess on the northern polar cap of the leading side. On the other hand, direct sublimation of CO2 ice is a possible mechanism as only a very small amount of surface coverage (3 × 10−14, Table L.1) is required to explain the peak column density, albeit with an expected diurnal variation more extreme than observed (Fig. L.2d). Regarding the subsolar regions and considering H2O ice sublimation with an areal H2O abundance of 20% appropriate for the leading side (Ligier et al. 2019), our model predicts a H2O column density of 4.1 × 1019 m−2, consistent with the JWST upper limit for Ganymede’s leading hemisphere (Table I.1), but a factor of 7 above the minimum value derived from HST data for this hemisphere (6 × 1018 m−2, Roth et al. 2021).
In summary, the processes that release CO2 in Ganymede’s exosphere are not well understood. The smooth diurnal variation of the CO2 column density favors sputtering, but explaining the measured column densities with this process requires further model developments that take advantage of the most recent magnetospheric data acquired by the Juno mission. We can anticipate that the interpretation of Callisto’s CO2 exosphere (Cartwright et al. 2024), which is one order of magnitude denser than Ganymede’s CO2 exosphere, will be similarly challenging.
4. Linking Ganymede’s CO2 exosphere to surface properties
The 4.26 μm absorption band of surface CO2 is ubiquitous on Ganymede, and is caused by CO2 under different physical states. However, the CO2 gas column density does not correlate with the CO2 surface distribution globally (Figs. 4A, B; see Appendix N and Figs. N.1A, C, D, F). Rather, the prominence of the CO2 exosphere on the northern polar cap is associated with other surface properties.
 |
Fig. 4. Comparing CO2 exosphere to surface properties on Ganymede’s leading hemisphere. (A) Vertical CO2 gas column density (in units of 1018 m−2, this work, see also Fig. O.2); (B) Depth of CO2-solid absorption band (Paper I); (C) Central wavelength of CO2-solid absorption band (Paper I); (D) Reflectance at 3.65 μm (Paper I); (E) Central wavelength of H2O Fresnel peak (Paper I); (F) Relative amplitude of the maximum reflectance between 3.5 and 4 μm (H2O interband amplitude, Paper I). The north pole of the leading hemisphere possesses the most redshifted absorption band center of solid CO2, consistent with CO2 trapped in amorphous H2O ice (Paper I). It also has the highest reflectance at 3.65 μm and H2O interband amplitude, indicative of a higher density of facets in H2O ice for the photons (i.e., smaller grains and/or more internal defects and/or higher micro-roughness or porosity), and the most blueshifted central wavelength of the H2O Fresnel peak due to a higher proportion of amorphous water ice (Mastrapa et al. 2009). |
According to Galileo high-resolution images, Ganymede’s polar caps are actually made of discrete patches of optically thick ice, preferentially located on pole-facing slopes (Khurana et al. 2007), likely formed by H2O ice sputtering and subsequent re-deposition on these coldest locations (Khurana et al. 2007). On both hemispheres, Ganymede’s north polar regions show spectral properties indicative of H2O ice particles having a higher density of facets for the photons (i.e., smaller grains and/or more internal defects and/or higher micro-roughness/porosity) causing multiple scattering and a higher proportion of amorphous ice than the south polar regions (Denk et al. 2009; Ligier et al. 2019, Paper I) (Figs. 4D, E, F).
Remarkably, these north-south polar asymmetries in spectral properties are most pronounced on the leading hemisphere. As shown in Fig. 4, the fact that the peak column density of CO2 gas is found over regions where water ice has the highest density of facets, the largest amorphous fraction, and the most redshifted absorption band center of solid CO2 (indicative of CO2 trapped in amorphous H2O ice) suggests that all these properties are probably linked. They are co-located poleward of 40°N, so they are probably specific to the ice-rich patches constituting the polar cap. The CO2 exosphere is maximum over the polar cap, but it extends over all of the northern open field-lines area.
During the JWST observation of the leading side, the southern hemisphere of Ganymede was facing toward the center of the plasma sheet, where the column density of plasma along Jupiter’s magnetospheric field lines is higher than on the northern side of the plasma sheet. On the plasma sheet facing hemisphere, the auroral band of Ganymede is brighter than on the other hemisphere (Saur et al. 2022; Greathouse et al. 2022; Milby et al. 2024). The reason for the auroral asymmetry is not fully understood. It could be due to the greater plasma momentum and resultant greater magnetic stresses on hemispheres facing the plasma sheet center and/or asymmetric reconnection processes (e.g., Saur et al. 2022; Milby et al. 2024). The higher auroral brightness requires higher auroral electron fluxes of which the largest fraction will collide with the surface. Additionally, the hemisphere facing the center of the plasma sheet is facing higher fluxes of energetic ions and electrons. Integrating these electron and ion fluxes over a full Jovian synodic rotation period should however lead to similar fluxes on the northern and southern polar regions (Poppe et al. 2018; Liuzzo et al. 2020). The observations of higher density of CO2 gas and of enhanced/specific surface properties on the northern hemisphere of the leading side are thus not consistent with what would be expected from either instantaneous or time-averaged plasma effects. Therefore, the specifics of the north polar regions of the leading hemisphere are likely an inherent property of Ganymede’s surface.
The north and south polar caps mainly differ in the nature of their underlying terrains. Galileo Regio, the largest patch of the darker and more cratered terrains on Ganymede, encompasses much of the leading north polar latitudes, while the leading south polar latitudes have fewer of these dark cratered terrains (Fig. O.3 from Patterson et al. 2010). The low-albedo material, concentrated in topographic lows by sublimation and mass wasting (Prockter et al. 1998), may be a remnant of Ganymede’s formation building blocks and/or may have been deposited by comet-like bodies (Zahnle et al. 1998; Bottke et al. 2013), so it could contain CO2 precursors (organic and inorganic carbon-bearing components), whose radiolysis and/or disaggregation by energetic particles may produce and/or release CO2. As shown by laboratory experiments, the radiolysis of complex organic matter (Gomis & Strazzulla 2005; Raut et al. 2012) or carbonates (Costagliola et al. 2017) in the presence of H2O forms CO2. In addition, the disaggregation of carbonaceous chondrite-like material (Yuen et al. 1984) or the radiolysis of some of their inorganic carbon-bearing components (carbonates and other minerals, Nakamura et al. 2023) could also release or produce CO2. This CO2 production may be specifically enhanced in the northern open field-lines area of the leading hemisphere because they host the largest extent of dark cratered terrains than the southern ones (Fig. O.3).
However, the peak in CO2 column density is not only over the fraction of Galileo Regio poleward of the OCFB, but over the water ice polar cap (Figs. 4A, D, F; Fig. N.1B), covering diverse terrain types (Fig. 1). Moreover, the peak of the CO2 vertical column density is at 72°W, 45°N (12.6 h local time), on the boundary between Galileo Regio and the bright terrain Xibalba Sulcus (Figs. 1, O.3). Therefore, if the CO2 is initially produced on the dark terrains, it should migrate and accumulate over the polar cap on the long term, before being diurnally released and redeposited over the polar cap as is possibly observed. This redistribution might also occur if the CO2 is initially produced from other sources, for example by a relatively recent resurfacing event (impact, mass movement) that would have exposed to the surface CO2 or CO2 precursors originating from the sub-surface and/or from the impactor. Notably, several impact craters with bright ejecta are present over the part of Xibalba Sulcus showing maximum CO2 column density (Collins et al. 2014), and the ice bedrock of this relatively recent region is thought to contain significant CO2 based on its geomorphology (Moore et al. 1999). If this CO2 exosphere is permanent, geological mass-wasting events (Moore et al. 1999; Pappalardo et al. 2004) and possibly micrometeoritic gardening, may regularly expose new CO2 or CO2 precursors to the surface, maintaining the CO2 exosphere over the long-term. The release of CO2 gas from ongoing volcanic activity seems unlikely given the surface age (0.5−1 Ga with large uncertainties, Zahnle et al. 1998; Showman et al. 2004), but gravity anomalies were identified around this region (Gomez Casajus et al. 2022).
The produced CO2 may then preferentially co-deposit with H2O and accumulate on high-latitude cold traps, which potentially explains the redshift of the CO2 absorption band with latitude (Fig. 4C). The maximum CO2 column densities and the H2O ice having the highest density of facets both peak around a longitude at the maximum solar illumination and maximum surface temperature at this latitude (Paper I), suggesting a diurnal process that releases CO2 from the ice in the atmosphere (Figs. 4A, D, F). According to our analyses, sputtering appears to have a temperature dependence that is the most consistent with the observation (Fig. L.2). At mid-day, the maximum temperature of the ice enhances sputtering and thermal stress that may generate more ice facets, resulting in surface micro-roughness or internal cracks, which could further enhance CO2 release (Baragiola 2003, and references therein). Later in the day and night, re-deposition and/or molecular movements induced by energetic ions might fill in these pores or cracks, decreasing the density of facets and trapping the CO2 again.
5. Summary
In summary, the north-south polar asymmetry in the distribution of CO2 gas of the leading hemisphere could be explained by the larger extent of dark terrains over the northern polar region, providing a larger initial source of CO2 produced by radiolysis of organic or inorganic precursors. The existence of other initial sources specific to this region (impact, mass movement, cryo-volcanism) cannot be excluded, but there is a lack of compelling evidence. After its initial production, CO2 may migrate and accumulate on cold traps of the polar cap and be diurnally released and redeposited, explaining the co-location of the northern polar atmosphere with the H2O and CO2 surface properties. Whether the release mechanism in this high-latitude region is sputtering or sublimation remains unclear. Outside of the open field-line areas, CO2 gas is located above various terrain types, including the dark terrain Melotte and some other terrains having more (or smaller) grains of H2O ice or H2O-bearing minerals and/or salts (Figs. N.1B, E). This spatial distribution suggests the existence of several mechanisms producing and releasing CO2. Future investigations of Ganymede from JWST and space missions, together with further models and experiments dedicated to sputtering processes, are needed to unravel the origin of Ganymede’s patchy CO2 exosphere.
Acknowledgments
This work is based on observations made with the NASA/ESA/CSA James Webb Space Telescope. The data were obtained from the Mikulski Archive for Space Telescopes at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-03127 for JWST. These observations are associated with program 1373, which is led by co-PIs Imke de Pater and Thierry Fouchet and has a zero-exclusive-access period. D.B.-M., E.Q., E.L., T.F., and O.P. acknowledge support from the French Agence Nationale de la Recherche (program PRESSE, ANR-21-CE49-0020-01). I.dP. and M.H.W. were in part supported by the Space Telescope Science Institute grant nr. JWST-ERS-01373. L.F. was supported by STFC Consolidated Grant reference ST/W00089X/1; for the purpose of open access, the author has applied a Creative Commons Attribution (CC BY) licence to the Author Accepted Manuscript version arising from this submission. Some of this research was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration (80NM0018D0004).
References
- Allegrini, F., Bagenal, F., Ebert, R. W., et al. 2022, Geophys. Res. Lett., 49, e2022GL098682 [NASA ADS] [CrossRef] [Google Scholar]
- Baragiola, R. A. 2003, Planet. Space Sci., 51, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Barth, C. A., Hord, C. W., Stewart, A. I. F., et al. 1997, Geophys. Res. Lett., 24, 2147 [NASA ADS] [CrossRef] [Google Scholar]
- Blauer, J., & Nickerson, G. 1973, GA Survey of Vibrational Relaxation Rate Data for Processes Important to CO2–N2–H2O Infrared Plume Radiation, U.S. Geological Survey [Google Scholar]
- Bockelée-Morvan, D., Lellouch, E., Poch, O., et al. 2024, A&A, 681, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bottke, W. F., Vokrouhlický, D., Nesvorný, D., & Moore, J. M. 2013, Icarus, 223, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Carlson, R. W. 1999, Science, 283, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Carlson, R., Smythe, W., Baines, K., et al. 1996, Science, 274, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Carnielli, G., Galand, M., Leblanc, F., et al. 2020a, Icarus, 343, 113691 [CrossRef] [Google Scholar]
- Carnielli, G., Galand, M., Leblanc, F., et al. 2020b, Icarus, 351, 113918 [NASA ADS] [CrossRef] [Google Scholar]
- Cartwright, R. J., Villanueva, G. L., Holler, B. J., et al. 2024, Planet. Sci. J., 5, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Cassidy, T. A., Paranicas, C. P., Shirley, J. H., et al. 2013, Planet. Space Sci., 77, 64 [Google Scholar]
- Cassidy, T. A., Merkel, A. W., Burger, M. H., et al. 2015, Icarus, 248, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, G., Kollmann, P., Mauk, B. H., et al. 2022, Geophys. Res. Lett., 49, e2022GL098572 [NASA ADS] [CrossRef] [Google Scholar]
- Collins, G. C., Patterson, G. W., Head, J. W., et al. 2014, Global Geologic Map of Ganymede, Tech. Rep. 3237, U.S. Geological Survey [Google Scholar]
- Costagliola, A., Vandenborre, J., Blain, G., et al. 2017, J. Phys. Chem. C, 121, 24548 [CrossRef] [Google Scholar]
- Crovisier, J. 1987, A&AS, 68, 223 [NASA ADS] [Google Scholar]
- Cunningham, N. J., Spencer, J. R., Feldman, P. D., et al. 2015, Icarus, 254, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Davidsson, B. J. R., & Hosseini, S. 2021, MNRAS, 506, 3421 [CrossRef] [Google Scholar]
- de Kleer, K., Butler, B., de Pater, I., et al. 2021, Planet. Sci. J., 2, 5 [NASA ADS] [CrossRef] [Google Scholar]
- de Kleer, K., Milby, Z., Schmidt, C., Camarca, M., & Brown, M. E. 2023, Planet. Sci. J., 4, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Denk, T., Neukum, G., Khurana, K. K., & Pappalardo, R. T. 2009, European Planetary Science Congress 2009, held 14–18 September in Potsdam, Germany, 572 [Google Scholar]
- Duling, S., Saur, J., Clark, G., et al. 2022, Geophys. Res. Lett., 49, e2022GL101688 [NASA ADS] [CrossRef] [Google Scholar]
- Ebert, R. W., Fuselier, S. A., Allegrini, F., et al. 2022, Geophys. Res. Lett., 49, e2022GL099775 [NASA ADS] [CrossRef] [Google Scholar]
- Famá, M., Shi, J., & Baragiola, R. A. 2008, Surf. Sci., 602, 156 [CrossRef] [Google Scholar]
- Fray, N., & Schmitt, B. 2009, Planet. Space Sci., 57, 2053 [Google Scholar]
- Gomez Casajus, L., Ermakov, A. I., Zannoni, M., et al. 2022, Geophys. Res. Lett., 49, e2022GL099475 [NASA ADS] [CrossRef] [Google Scholar]
- Gomis, O., & Strazzulla, G. 2005, Icarus, 177, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, I. E., Rothman, L. S., Hargreaves, R. J., et al. 2022, J. Quant. Spectr. Rad. Transf., 277, 107949 [NASA ADS] [CrossRef] [Google Scholar]
- Greathouse, T. K., Gladstone, G. R., Molyneux, P. M., et al. 2022, Geophys. Res. Lett., 49, e2022GL099794 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, D. T., Feldman, P. D., McGrath, M. A., & Strobel, D. F. 1998, ApJ, 499, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 1984, Icarus, 59, 41 [Google Scholar]
- Hase, F., Wallace, L., McLeod, S. D., Harrison, J. J., & Bernath, P. F. 2010, J. Quant. Spectr. Rad. Transf., 111, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Hayne, P. O., Aharonson, O., & Schörghofer, N. 2021, Nat. Astron., 5, 169 [Google Scholar]
- Hibbitts, C. A., McCord, T. B., & Hansen, G. B. 2000, J. Geophys. Res.: Planets, 105, 22541 [NASA ADS] [CrossRef] [Google Scholar]
- Hibbitts, C. A., Pappalardo, R. T., Hansen, G. B., & McCord, T. B. 2003, J. Geophys. Res.: Planets, 108, 5036 [CrossRef] [Google Scholar]
- Hom, E. F. Y., Marchis, F., Lee, T. K., et al. 2007, J. Opt. Soc. Am. A, 24, 1580 [NASA ADS] [CrossRef] [Google Scholar]
- Itikawa, Y. 2002, J. Phys. Chem. Ref. Data, 31, 749 [Google Scholar]
- Khurana, K. K., Pappalardo, R. T., Murphy, N., & Denk, T. 2007, Icarus, 191, 193 [NASA ADS] [CrossRef] [Google Scholar]
- King, O., & Fletcher, L. N. 2022, J. Geophys. Res.: Planets, 127, e2022JE007323 [NASA ADS] [CrossRef] [Google Scholar]
- Kivelson, M. G., Khurana, K. K., Russell, C. T., et al. 1996, Nature, 384, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Leblanc, F., Oza, A. V., Leclercq, L., et al. 2017, Icarus, 293, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Leblanc, F., Roth, L., Chaufray, J. Y., et al. 2023, Icarus, 399, 115557 [NASA ADS] [CrossRef] [Google Scholar]
- Ligier, N., Paranicas, C., Carter, J., et al. 2019, Icarus, 333, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Liuzzo, L., Poppe, A. R., Paranicas, C., et al. 2020, J. Geophys. Res.: Space Phys., 125, e2020JA028347 [CrossRef] [Google Scholar]
- Mâlin, M., Boccaletti, A., Charnay, B., Kiefer, F., & Bézard, B. 2023, A&A, 671, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mastrapa, R. M., Sandford, S. A., Roush, T. L., Cruikshank, D. P., & Dalle Ore, C. M. 2009, ApJ, 701, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- McCord, T. B., Hansen, G. B., Clark, R. N., et al. 1998, J. Geophys. Res.: Planets, 103, 8603 [NASA ADS] [CrossRef] [Google Scholar]
- Milby, Z., de Kleer, K., Schmidt, C., & Leblanc, F. 2024, Planet. Sci. J., 5, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, J. M., Asphaug, E., Morrison, D., et al. 1999, Icarus, 140, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, T., Matsumoto, M., Amano, K., et al. 2023, Science, 379, abn8671 [NASA ADS] [CrossRef] [Google Scholar]
- Pappalardo, R. T., Collins, G. C., Head, J. W., et al. 2004, Jupiter. The Planet, Satellites and Magnetosphere (Cambridge: Cambridge University Press) [Google Scholar]
- Patterson, G. W., Collins, G. C., Head, J. W., et al. 2010, Icarus, 207, 845 [NASA ADS] [CrossRef] [Google Scholar]
- Poppe, A. R., Fatemi, S., & Khurana, K. K. 2018, J. Geophys. Res.: Space Phys., 123, 4614 [NASA ADS] [CrossRef] [Google Scholar]
- Prockter, L. M., Head, J. W., Pappalardo, R. T., et al. 1998, Icarus, 135, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Raut, U., Fulvio, D., Loeffler, M. J., & Baragiola, R. A. 2012, ApJ, 752, 159 [CrossRef] [Google Scholar]
- Roth, L., Alday, J., Becker, T. M., Ivchenko, N., & Retherford, K. D. 2017a, J. Geophys. Res.: Planets, 122, 1046 [CrossRef] [Google Scholar]
- Roth, L., Retherford, K. D., Ivchenko, N., et al. 2017b, AJ, 153, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Roth, L., Ivchenko, N., Gladstone, G. R., et al. 2021, Nat. Astron., 5, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Sandford, S., & Allamandola, L. 1990, ApJ, 355, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Sarantos, M., & Tsavachidis, S. 2020, Geophys. Res. Lett., 47, e88930 [NASA ADS] [CrossRef] [Google Scholar]
- Saur, J., Duling, S., Roth, L., et al. 2015, J. Geophys. Res.: Space Phys., 120, 1715 [NASA ADS] [CrossRef] [Google Scholar]
- Saur, J., Duling, S., Wennmacher, A., et al. 2022, Geophys. Res. Lett., 49, e2022GL098600 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., Mosqueira, I., & Head, J. W. 2004, Icarus, 172, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A. G., de Kok, R. J., de Mooij, E. J. W., & Albrecht, S. 2010, Nature, 465, 1049 [Google Scholar]
- Steckloff, J. K., Goldstein, D., Trafton, L., Varghese, P., & Prem, P. 2022, Icarus, 384, 115092 [NASA ADS] [CrossRef] [Google Scholar]
- Stephan, K., Hibbitts, C. A., & Jaumann, R. 2020, Icarus, 337, 113440 [NASA ADS] [CrossRef] [Google Scholar]
- Teolis, B. D., & Waite, J. H. 2016, Icarus, 272, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Teolis, B. D., Plainaki, C., Cassidy, T. A., & Raut, U. 2017, J. Geophys. Res.: Planets, 122, 1996 [NASA ADS] [CrossRef] [Google Scholar]
- Tosi, F., Mura, A., Cofano, A., et al. 2024, Nat. Astron., 8, 82 [Google Scholar]
- Trumbo, S. K., Brown, M. E., Bockelée-Morvan, D., et al. 2023, Sci. Adv., 9, eadg3724 [NASA ADS] [CrossRef] [Google Scholar]
- Villanueva, G. L., Smith, M. D., Protopapa, S., Faggi, S., & Mandell, A. M. 2018, J. Quant. Spectr. Rad. Transf., 217, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Vorburger, A., Fatemi, S., Carberry Mogan, S. R., et al. 2024, Icarus, 409, 115847 [NASA ADS] [CrossRef] [Google Scholar]
- Waite, J. H., Greathouse, T. K., Carberry Mogan, S. R., et al. 2024, J. Geophys. Res.: Planets, 129, e2023JE007859 [NASA ADS] [CrossRef] [Google Scholar]
- Yakshinskiy, B. V., & Madey, T. E. 2000, Surf. Sci., 451, 160 [CrossRef] [Google Scholar]
- Yuen, G., Blair, N., Marais, D. J. D., & Chang, S. 1984, Nature, 307, 252 [CrossRef] [Google Scholar]
- Zahnle, K., Dones, L., & Levison, H. F. 1998, Icarus, 136, 202 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: JWST observations and data reduction
NIRSpec/IFU observations of the leading and trailing sides of Ganymede were obtained as part of the Early Release Science (ERS) program #1373 (PIs I. de Pater, T. Fouchet). These observations, acquired with the G395H/F290LP grating/filter pair, provided spatially resolved imaging spectroscopy in the range 2.86–5.28 μm over a 3”×3” field of view with 0.1”×0.1” spatial elements (310 × 310 km at Ganymede), and a nominal spectral resolution of R ∼ 2700. The estimated full width at half maximum of the point spread function (PSF) is ∼0.19” (Appendix M). Detailed information on these observations is provided in Trumbo et al. (2023) and Paper I, focused on the analysis of solid state spectral features from CO2, H2O, and H2O2. For the data reduction we followed the procedure adopted in Bockelée-Morvan et al. (2024) (Paper I). The updated JWST pipeline version 1.12.5 and context file version jwst_1148.pmap were used. Correction for the 1/f noise was done as explained in Trumbo et al. (2023) and Paper I.
ERS #1373 comprised also observations of the leading and trailing sides of Ganymede using the Mid-Infrared Instrument/medium resolution spectroscopy (MIRI/MRS), which are described in Paper I. These observations, made with the four IFU channels, provided spatially-resolved unsaturated spectra in the 4.9–11.7 μm range. Channel 1 (4.9–7.65 μm) covers the ν2 vibrational band (and weaker ν2+ν3-ν3 and ν2+ν1-ν1 hot-bands) of H2O in vapor phase from which the H2O content in Ganymede’s exosphere can be studied. For Channel 1, the spaxel (aka pixel in main text) size is 0.13” and the spectral resolution is ∼3700. The data were re-reduced using most recent JWST pipeline version 1.11.3, and context file jwst_1119.pmap, and processed as in Paper I.
Ganymede spectra are crowded with solar lines. For the study of solid-state features in NIRSpec spectra, the output of the JWST pipeline, calibrated in radiance units (MJy/sr), were divided by the solar spectrum (Hase et al. 2010) at the spectral resolution of NIRSpec, giving data in units of radiance factor I/F (Paper I). To obtain spectra in radiance units and corrected from solar lines, the data in I/F units were multiplied by the solar continuum. In the spectral 4.2–4.3 μm region where strong ro-vibrational lines of the CO2ν3 band are present, solar lines are not numerous and much fainter than in nearby spectral regions. Nevertheless, we payed special attention to solar-line removal as gaseous emission lines from Ganymede are faint. We determined that solar lines present in the 4.4–4.6 μm range are best removed when applying a correction factor of ∼0.87 to the nominal spectral dispersion provided by JWST documentation (i.e., increasing the wavelength-dependent spectral resolution by 1.15). We used this factor (giving R = 3365 at 4.2–4.3 μm) in subsequent analyses, including for producing synthetic line profiles.
In MIRI spectra, the most intense ro-vibrational lines from the H2O ν2 band are expected between 5.6 and 7.4 μm (Fig. I.1). In this spectral region, both reflected light and thermal emission from Ganymede’s surface contribute to the continuum, especially at the lowest wavelengths where the two components have similar intensities (Paper I). Therefore, spectra were corrected from solar lines by isolating the reflected-light component, and applying the method used for NIRSpec data.
Appendix B: Extraction of CO2 gaseous lines
The ν3 bands of CO2 in gaseous form and in solid state lie at the same wavelengths. The solid-state absorption band of CO2 shows strong variations in shape and intensity on the surface of Ganymede (Paper I). Hence, to isolate the weak ro-vibrational emission lines from CO2 gas from the broad absorption band, we developed specific tools, which were tested on synthetic spectra. We restricted the analysis to the 4.220–4.295 μm range where the strongest CO2 gaseous lines and only weak solar lines are present.
In a first step, the solid-state contribution was estimated by applying low-pass filtering with a Butterworth filter. The optimum cutoff frequency that preserves best the gaseous signatures was determined by applying the method to synthetic spectra combining the Ganymede CO2-solid absorption band and CO2-gas fluorescence emission. In a second step, the residual CO2 gas signature (called DIFF) was obtained by subtracting this estimated solid-state signal from the observed spectra. Two examples of residual DIFF spectra are shown in Figs B.1C, F. This method does not allow retrieval of the correct shape of the CO2 gaseous band. We show in Figs B.1B, E (and Fig. 1) CO2 gas spectra from Ganymede displaying the expected ro-vibrational structure of the CO2ν3 band for fluorescence emission. They were obtained through several iterations, by computing the envelope of the residual DIFF signal and adding the bottom part of the envelope to the solid-state signal extracted from low-pass filtering. From synthetic spectra processed in the same manner, we found that this third step produced an overestimation of the strength of the CO2 gas signature, especially for faint signals at the limit of noise. Hence, analyses were made on DIFF spectra.
 |
Fig. B.1. CO2ν3 band gas spectra from Ganymede’s exosphere. Left (A–C): North polar cap of the leading side of Ganymede (averaged spectra for latitudes > 45° N); Right (D–F): Southern hemisphere of the trailing side (latitudes 30–60° S). A, D) Observed spectra showing both the CO2ν3 absorption band from CO2 in solid state, and ro-vibrational emission lines of gaseous CO2; B, E) CO2 gaseous emission spectra obtained after removing the continuum emission shown in red in panels A and D (Appendix B). C, F) Residual CO2-gas DIFF spectra obtained by removing the continuum obtained from low-pass filtering (Appendix B). Best fit synthetic spectra are shown in blue, with a fitted rotational temperature of 108±8 K for the leading side, and a fixed rotational temperature of 105 K for the trailing side. In all plots, vertical-axis unit is μJy per pixel (1 pixel = 0.1”× 0.1”). |
In order to evaluate the significance of detection of gas emissions, we computed the Pearson correlation coefficient Cp between the DIFF spectra and a forward model. The forward model consists in a DIFF spectrum computed by applying the same treatment as for the data to a synthetic spectrum obtained by combining the Ganymede average CO2 absorption band observed on the leading side (obtained from low-pass filtering) and a CO2 fluorescence spectrum at 105 K convolved to the instrumental spectral resolution R = 3365. The Pearson correlation coefficient Cp was computed for each individual spaxel on the leading side. Due to the faintness of the CO2 gas emission lines on the trailing side, the trailing data were smoothed using a 3×3 boxcar filter. Cp ranges from −0.22 to 0.87 on the leading side, and from −0.11 to 0.50 on the trailing side (left panels of Fig. O.1). Except for the northern regions of the leading Ganymede disk, Cp values do not exceed 0.5. Hence the confidence level of the detection of the CO2 exosphere is rather low for several regions, calling for the use of other detection criteria (cross-correlation technique).
 |
Fig. B.2. DIFF spectra on the leading hemisphere as a function of latitude. Data were averaged over latitude bins of 7.5° and treated as explained in Appendix B. Fitted fluorescence DIFF spectra are shown in black. The Pearson correlation coefficient for each spectrum is given in the legend. Vertical-axis unit is the flux density per pixel. |
Appendix C: Cross-correlation technique
We used the cross-correlation technique to obtain additional criteria for confirming weak CO2 detections. This method is widely used, for example to search for molecular signatures in exoplanet spectra (Snellen et al. 2010; Mâlin et al. 2023). We computed the cross-correlation function (CCF) between the Ganymede DIFF spectra and the forward model over a velocity range (-3000, 3000) km/s (in total 127 spectral resolution elements, aka spectels) using velocity steps δv spaced by 10 km/s (0.21 spectels). Cross-correlating the forward model with itself, the maximum of the autocorrelation function is obviously at δv = 0. Because of the periodicity in frequency of the CO2 ro-vibrational lines, which are equally spaced every 0.003 μm (∼4 spectels), the autocorrelation function and CCFs present strong secondary peaks (reaching 80% of the maximum for the closest secondary peaks) spaced by the corresponding value in velocity units (Fig. C.1). The criterion used for confident CO2 exosphere detection is that the maximum of the CCF stands close to δv = 0, namely is shifted by at most one spectel element.
 |
Fig. C.1. Cross-correlation functions (CCFs). Top: from averaged data at latitudes > 45°N on the leading hemisphere. Bottom: from averaged data at latitudes 30–60°S on the trailing hemisphere. The forward model for computing the cross-correlation is a fluorescence CO2 spectrum. In both cases the CCF peaks at δv = 0, indicating CO2 exosphere detection. The maximum of the CCF is lower for the trailing side due to a fainter CO2 signal. |
 |
Fig. C.2. Study of 4.22–4.295 μm spectra averaged over latitude bins. A) Pearson correlation coefficient between residual CO2 DIFF spectra and a synthetic DIFF spectrum which uses a CO2 fluorescence synthetic spectrum at T = 105 K as input. B) CO2 line-of-sight column density retrieved from the fit of CO2 DIFF spectra. C) shift, in fraction of spectel, of the maximum of the cross-correlation function (CCF) between CO2 DIFF spectra and the synthetic DIFF spectrum; secure detection is indicated when the shift is close to zero. D) S/N of the cross-correlation function at shift = 0. The S/N is obtained by computing the CCFnoise obtained by using as input a simulated noisy spectrum, with the r.m.s deduced from the ERR entry in the Level 3 data cube, and scaled in |
We estimated the signal-to-noise ratio (S/NCCF) of the CCF at δv = 0 to quantitatively measure the confidence level of the detections. For that purpose, we generated synthetic spectra adding random Gaussian noise to the Ganymede average CO2 absorption band observed on the leading side obtained from low-pass filtering. As there is no possibility of estimating the noise level from the acquired spectra themselves (noise-like features are dominated by residuals in solar lines subtraction), we used the error cube given in the Level 3 hyperspectral data cubes to set the r.m.s., and assumed that it scales as σ/ , when n spaxels are averaged. The generated synthetic spectra were then processed as for the Ganymede data, and the resulting DIFF spectra were cross-correlated with the forward model to obtain a cross correlation function CCFnoise for a spectrum containing only noise. We then measured the standard deviation of the CCFnoise curve. Eighty random-noise synthetic spectra were processed in this way, to derive a representative standard deviation σCCFnoise from the median of the values obtained for each shot. For processed Ganymede spectra, S/NCCF is obtained by dividing the CCF at δv = 0 by σCCFnoise.
, when n spaxels are averaged. The generated synthetic spectra were then processed as for the Ganymede data, and the resulting DIFF spectra were cross-correlated with the forward model to obtain a cross correlation function CCFnoise for a spectrum containing only noise. We then measured the standard deviation of the CCFnoise curve. Eighty random-noise synthetic spectra were processed in this way, to derive a representative standard deviation σCCFnoise from the median of the values obtained for each shot. For processed Ganymede spectra, S/NCCF is obtained by dividing the CCF at δv = 0 by σCCFnoise.
The cross-correlation technique was applied on data averaged over latitude bins (Figs. 2, C.1, C.2). Spectra with a Pearson correlation coefficient Cp > 0.3 all display a CCF with S/NCCF > 5, and a maximum shifted by less than 1 spectel element. From those criteria, the CO2 exosphere is detected with good confidence both in the northern and southern hemispheres of the leading and trailing sides of Ganymede. On the other hand, the S/N (and inferred CO2-gas signal) is low near the equator for both hemispheres, indicating a more tenuous CO2 exosphere in these regions. The decrease of the CO2 signal observed at the most polar latitudes could be related to PSF blurring since spaxels probing extreme polar latitudes are near the limb of Ganymede disk. However, this decrease is still observed after deconvolution with modeled NIRSpec PSFs (Fig. M.1).
Appendix D: SMART-EVE excitation-radiative transfer model
A non-LTE Stochastic Modeling of Atmospheric Radiative Transfer-Exospheric Vibrational Excitation (SMART-EVE) has been developed to calculate the ro-vibrational populations of the (1) H2O ν2 mode (010) at 6.25 μm, and (2) CO2ν3 mode (001) at 4.25 μm. SMART-EVE solves the locally defined statistical equilibrium equations (SEEs) for all the energy levels considered and the radiative transfer equations (RTEs) for all the bands connecting these levels. Due to nonlinearities arising from radiative transfer and/or collisional coupling, the resulting equation system is solved iteratively using the Accelerated Lambda iteration approach which alternates SEE calculations involving all the energy levels with RTE calculations involving all atmospheric layers.
The 1D model of the atmosphere is described by the kinetic gas temperature, assumed vertically uniform, and the gas density which follows hydrostatic equation. The model assumes that the atmosphere is illuminated by the Sun from the top, and by the surface thermal emission and the reflected solar and atmospheric radiance from below. The model parameters are: the column density and kinetic temperature Tkin of the atmosphere, the surface temperature Ts and reflectance factor Ref, and the heliocentric distance. Electron-impact excitation of CO2 is not considered, as most likely insignificant (Supplementary Information).
The radiative processes considered are spontaneous and stimulated emissions, absorption of the upward thermal flux, incident solar, and reflected solar and atmospheric irradiance from the surface, as well as exchanges between layers. A single collisional process is considered for the vibrational state, its vibration-to-translation (V–T) relaxation/excitation in intermolecular collisions. However, vibrational de-excitation by collisions is insignificant in Ganymede’s exosphere (see Appendix G). It is assumed that rotational levels are at LTE at all altitudes with a rotational temperature Trot = Tkin.
The model is run from the surface up to 100 km, with 1-km thick layers. The spectral data are taken from the HITRAN database (Gordon et al. 2022). We considered only (010)–(000) (H2O) and (001-000) (CO2) vibrational transitions, with a total number of lines of 1017 for H2O and 129 for CO2. The solar spectrum was taken from Paper I.
 |
Fig. D.1. CO2 simulated nadir spectra. Input model parameters are: CO2 column density N(CO2) = 1018 m−2, surface temperature Ts = 145 K, gas rotational temperature Trot = 105 K, for I/F values of 0.04 (red) and 0.12 (green). The fluorescence spectrum (black) corresponds to I/F = 0 and Ts = 0 K. Ganymede’s exosphere is described by hydrostatic equilibrium. |
Appendix E: Determination of CO2 column density
CO2 line-of-sight column densities were derived using a two-step approach. First, column densities were derived under the assumption of fluorescence equilibrium and optically thin lines. In the second step, a correction factor was applied, using prescriptions obtained from the SMART-EVE model described above.
For CPU-time considerations, we used the Planetary Spectrum Generator (PSG) (Villanueva et al. 2018) for the first step. Optically thin CO2ν3 band fluorescence spectra at high spectral resolution (0.1 cm−1) were generated (outputs for cometary atmospheres) and downloaded for a range of rotational temperatures in steps of 1 K (and fixed column density). As done for the forward model described above, they were combined with Ganymedes’s solid-state CO2 band and synthetic DIFF spectra were computed. This bank of synthetic spectra was utilized to fit the Ganymede DIFF spectra using the Levenberg-Marquardt algorithm (we used the limfit Python package), with a normalizing factor as free parameter. The rotational temperature was set as a free parameter for the analysis of the high S/N spectra of the north hemisphere of the leading side (Fig. H.1), and fixed to 105 K elsewere (i.e., equal to the inferred value in leading north hemisphere, Appendix H). The CO2 column density was derived from the inferred normalizing factor. For the uncertainty in the CO2 column density, we used that provided by the limfit package and derived from the covariance matrix.
Model simulations for the CO2ν3 band (Fig. D.1) show that spectral profiles from Ganymede’s exosphere are expected to be less intense than in the assumption of cometary-like fluorescence emission (case Ref = 0, Ts = 0), which neglects absorption of surface reflected solar radiation by CO2 gas, reflection of CO2 gas emission on the surface, and surface thermal radiation. While this latter process is not significant at 4.25 μm, the other two processes affect the total band intensity of the ν3 band BA according to:
where I/F is the radiance factor on the surface, and BA0, BA1, BA2 are equal to 4.10×10−8, 4.27×10−7, and 3.84×10−6 W m−2 sr−1, respectively. BA0 is consistent with the value of 4.06×10−8 W m−2 sr−1 retrieved from PSG (Villanueva et al. 2018) for optically thin cometary-like fluorescence emission at 4.95 au from the Sun with N(CO2) = 1017 m−2. Eqs E.1–E.3 were obtained from multiple simulations fixing Ts = 145 K and Trot = 105 K, and varying I/F.
We applied a correction factor intermediate between Eqs E.1 and E.2 (i.e., slope of −4.0 for the dependence with I/F) on the CO2 column density inferred assuming fluorescence equilibrium, using radiance factors I/F at ∼4.25 μm measured from JWST (Paper I).
Appendix F: Electron impact excitation of CO2
We made estimations for electron-impact excitation of the CO2ν3 band using cross-sections from Itikawa (2002). Electron populations were assumed to follow a Maxwellian distribution around a mean temperature. For the total electron density and the temperature, values that explain the highest UV brightnesses (OI 1356 Å) of 1000 R (Waite et al. 2024) measured for Ganymede were used. Specifically, we assumed an electron temperature of 20 eV and a high number density of 2500 cm−3. CO2 emission from this process is found to be more than two orders of magnitude lower than fluorescence emission. The CO2ν3 band could be excited by much cooler electrons, well below 10 eV. However, information on these cold electrons is missing. Cross-sections for electron-impact excitation of the CO2ν3 band increase with decreasing electron energy (Itikawa 2002). Using an electron temperature of 1 eV and the same number density, CO2 emission from electron impact excitation is only two times higher than for 20 eV electrons.
Appendix G: CO2ν3-band collisional relaxation
We have evaluated the role of de-excitation of the CO2ν3 band by collisions with H2O, O2, and CO2 versus spontaneous emission. The result is that these processes are not significant in Ganymede’s exosphere. The rate for collisional de-excitation of the CO2ν3 band via CO2-H2O collisions is 1.2×10−13 cm3/s at 120 K (Blauer & Nickerson 1973). The H2O number density is at most 1.4×1010 cm−3 at the surface, derived from hydrostatic equilibrium for a water column density of 5×1020 m−2 (Roth et al. 2021). This gives a collision rate of at most 1.7×10−3 s−1, which is much lower than the spontaneous emission rate of the ro-vibrational levels (on the order of 400 s−1). So the quenching is negligible.
The rates for de-excitation of CO2ν3 band via collisions with O2 and CO2 are much lower than for CO2-H2O collisions. So these collisional processes are still less significant.
Appendix H: Rotational temperature of CO2
For fluorescence emission, the relative intensities of the ro-vibrational lines of the CO2ν3 band are set by the population distribution in the ground vibrational state, described by a Boltzmann distribution at the rotational temperature Trot. Rotational temperatures of CO2 derived on the northern latitudes (> 30° N) of the leading hemisphere are shown in Fig. H.1 and are on the order of 105–110 K (see Appendix B for details on how Trot was derived). This is slightly lower than the surface temperature of Ganymede at these latitudes (from 120 to 140 K, Fig. K.1). This rotational temperature possibly reflects the kinetic temperature of the exosphere at low altitudes where collisions with the major gas (H2O or CO2) are still efficient enough to thermalize CO2 molecules. Alternatively, it might reflect the rotational energy of the CO2 molecules when they left the surface, and be representative of the temperature of the surface where CO2 molecules were released. The CO2 molecule has no dipole moment, so radiative rotational decay within the ground vibrational state does not take place. The rotation temperature is expected to increase with residence time in the atmosphere due to radiative decay from the excited vibrational states. However, one should mention that during their residence time in the exosphere (at most 18 h, which is the CO2 lifetime set by electron-impact ionization), CO2 molecules undergo at most 7 fluorescence cycles. Based on fluorescence calculations for cometary atmospheres, CO2 molecules reach a warm fluorescence equilibrium only after about 3500 fluorescence cycles at 5 au from the Sun Crovisier (1987). In summary, the measured Trot should reflect the thermal environment where last thermalizing collisions occurred, or the excitation state of the molecules when they left the surface.
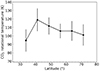 |
Fig. H.1. CO2 rotation temperature in the north hemisphere of the leading hemisphere. Spaxels within latitude bins of width 7.5° were averaged. Values were derived from the fitting of DIFF spectra using as model fluorescence emission with Trot as a free parameter (Appendix B). The weighted mean value is Trot = 107±5 K. |
Appendix I: H2O analysis
We analysed MIRI/MRS Channel-1 spectra obtained by either 1) averaging spaxels around the subsolar point, namely eight spaxels for which the solar zenith angle (SZA) is less than 15° at the center of the spaxel; 2) averaging seven spaxels covering the region of the leading hemisphere where the CO2 exosphere is prominent. Neither one shows any hint of the presence of water lines (Fig. I.1) and the nondetection of H2O was further confirmed by applying the cross-correlating technique using a forward model of a synthetic spectrum of H2O computed with the SMART-EVE code.
 |
Fig. I.1. Continuum-divided spectra of Ganymede observed with MIRI and synthetic H2O spectra. Spectra for the leading and trailing sides are shown in red and blue, respectively, with the spectrum of the trailing side shifted vertically. Spaxels for which the solar zenith angle is less than 15° at the center of the spaxel have been averaged. Synthetic spectra are superimposed, with input parameters indicated in the legend (Appendix I) and N(H2O) = 1020 m−2. The Ganymede spectra do not show any hint of H2O lines. |
In the exosphere of Ganymede, the thermal radiation from the surface competes with the Sun’s direct radiation for the excitation of the H2O ν2 band at 6.2 μm (Paper I). In addition, in nadir viewing, absorption of the radiation from Ganymede’s surface by the H2O exosphere might compete with ν2 fluorescence emission, so that the band might be in absorption under certain conditions and a simple fluorescence model would not apply. Therefore, we used the SMART-EVE model described above to derive upper limits on the H2O column density (N(H2O)).
Radiance factor values of 0.04 and 0.08 were assumed for the leading and trailing hemispheres, respectively (see Fig. 26 of Paper I). The surface temperature was chosen such that the brightness temperature in the synthetic spectra matches the TBB value at 6.2 μm measured on the MIRI spectrum. For the "subsolar" spectra (SZA < 15°), Ts (and TBB) are closed to 155 K (leading) and 160 K (trailing). For the spectrum extracted at the position of the CO2 northern source, Ts is about 140 K. Synthetic spectra for the subsolar region are shown in Fig. I.1. Ro-vibrational lines at λ < 6.2 μm are expected in absorption whereas emission lines are expected at λ > 6.2 μm. As a matter of fact, the vibrational temperature of the ν2 band (mainly controlled by solar IR pumping) is ∼158–159 K, i.e. very close to the brightness temperature near 6.4 μm. The change from absorption to emission regimes is related to the fact that the vibrational temperature is close to the wavelength-dependent brightness temperatures near 6.2 μm.
Table I.1 presents measured 1-σ uncertainties for the H2O band area in the 5.7–6.2 and 6.2–7.1 μm spectral ranges, considering the 10–15 expected strongest lines (with intensities > 0.2 the intensity of the strongest line). From the measured band areas in each wavelength window, we derived a 3σ upper limit for line-of-sight N(H2O), using SMART-EVE model with appropriate parameters. The results were then combined. The final results are given in Table I.1 for two values (105 and 130 K) of the H2O rotational temperature.
H2O and CO2 line-of-sight column densities in selected Ganymede’s areas.
Appendix J: Open-closed field-line boundary
The OCFB location is determined through magnetohydrodynamic modeling of Ganymede’s magnetosphere similar to the method described in Duling et al. (2022). Due to the variation of the upstream magnetic field and plasma density at Ganymede’s position relative to the Jovian current sheet, the OCFB location can oscillate with an amplitude ranging between 2 to 6 degree latitude during Jupiters’s approximative 10-h rotation period (Saur et al. 2015). We modeled the OCFB analogous (Duling et al. 2022) by adapting the upstream conditions to estimates for the times of the JWST observations. During the observation of the leading side, Ganymede was above the center of the current sheet and we used 61 amu/cm3 and (−11, −66, −79)nT for the upstream plasma mass density and magnetic field respectively. During the trailing side observation Ganymede was at the center of the current sheet and we used 100 amu/cm3 and (−18, −6, −79)nT.
Appendix K: CO2, H2O Ganymede exospheric model
We simulated the CO2 exosphere using the Exospheric Global Model (EGM), a multi-species Monte Carlo model describing the fate of test particles in a gravitational field, interacting with a surface or an atmosphere and subject to sources of ionization and dissociation. EGM has been extensively used to model the exospheres of H2O and related species (e.g., O2, H) in various objects, in particular Ganymede (Leblanc et al. 2017, 2023). We considered two possible mechanisms of ejection of the CO2 molecules from the surface: i) sputtering, i.e. ejection following bombardment of H2O ice containing CO2 molecules by the incident Jovian energetic ions and electrons; and ii) sublimation of the CO2 molecules from Ganymede surface. We considered the release of CO2 either from the sublimation of pure CO2 ice or from the sublimation of H2O ice containing CO2 molecules. We took into account that CO2 molecules re-impacting cold areas of the surface eventually recondense. The H2O exosphere is also computed. The calculated images from the simulations (e.g., Fig. 3) consider the orbital position of Ganymede around Jupiter at the time of the JWST observations and the viewing geometry of JWST observations (for the observations of the leading hemisphere, sub-observer coordinates were 2°N, 72°W). Convolution with a FWHM = 0.185” PSF is applied (Appendix M). Line-of-sight CO2 column densities averaged over latitude bins of 7.5° or 15° were computed for comparison with the data shown in Fig. 2. For the study of the CO2 exosphere above the north polar cap of the leading hemisphere, we extracted the longitudinal variation of the CO2 column density for latitudes in the range 42–62° N.
 |
Fig. K.1. Ganymede’s surface temperature used in EGM model, representative of the leading hemisphere. Left panel: facet temperature distribution (cumulative probability) of the surface temperatures at 12 h local time for various latitudes indicated in the plot. Right panel: latitude/longitude map of the average surface temperature with the subsolar point being at a latitude of 2°N (as for JWST observations, Paper I) and longitude of 180°. |
Sublimation: For a CO2 release associated with the sublimation of water ice, the release rate is in proportion with the H2O sublimation rate (cm−2 s−1):
where U0/kB = 5950 K, and qH2O is the areal surface fraction of H2O. The relative abundance of CO2 in the sublimated gases (in number) is qCO2/qH2O. The description of F(H2O) follows Leblanc et al. (2023). Ts is the surface temperature. fc is a factor introduced to reproduce the CO2 JWST data.
For the sublimation of CO2 ice, the sublimation rate (cm−2 s−1) is given by:
where Ntot = 1018 cm−2 s K0.5 is determined from a fit of the polynomial relation of CO2-ice vapor pressure with temperature (Fray & Schmitt 2009) and using U1/kB = 2860 K (surface binding energy for CO2 on H2O ice, (Sandford & Allamandola 1990)) and τ0 = 3.45 10−13 s (Sandford & Allamandola 1990). fc is a factor introduced to reproduce the JWST data.
Sputtering: The ejection of CO2 molecules by sputtering is described by the efficiency by which CO2 molecules are emitted from a surface when an incident ion or electron impacts the surface with a given energy. We hypothesized that CO2 molecules are trapped in/on H2O ice, so we assumed that the sputtering yield follows the same temperature dependence as for H2O, and used the same definition as for H2O (Cassidy et al. 2013; Leblanc et al. 2023):
with Y0 = 1200. We made the assumption that CO2 molecules are released into the exosphere along with H2, O2, H2O2 and H2O molecules ejected when pure H2O ice is bombarded, therefore U00 and Y00 are set to be the same as for the bombardment of pure H2O ice (Famá et al. 2008): U00 = 0.06 eV (700 K), Y00 = 220. As for the energy and angular distributions of the CO2 molecules when ejected from the surface, we followed the approach used for sputtered O2 in Leblanc et al. (2017) and assumed a Maxwell-Boltzmann energy distribution at the local surface temperature. Regarding the intensity and spatial distribution of the Jovian ions impacting the surface, we assumed a given ion flux of 106 particles/cm2/s derived from Cassidy et al. (2013) as in Leblanc et al. (2017), impacting Ganymede’s surface only in the open-field-line regions. Electron impacts are not considered. The flux of the CO2 molecules released at a given position on Ganymede’s surface is therefore the product of Y(CO2) (Eq. K.4) times qCO2 times the flux of impacting particles. The flux of H2O follows the same equation, using qH2O instead. A multiplying factor fc is introduced in Eq. K.4 with respect to Cassidy et al. (2013) and Leblanc et al. (2023) that is adjusted to reproduce the CO2 column density measured by JWST. This factor is also applied to the flux of H2O sputtered molecules. In our model, sputtering of water ice is assumed to release mainly H2O molecules with a ratio H2O/O2 = 20 (Leblanc et al. 2017; Cassidy et al. 2013).
Surface adsorption: To determine the fate of a CO2 molecule re-impacting the surface, we define the CO2 residence time at the surface as:
where U1/kB = 2860 K is the binding energy for CO2 adsorbed on H2O ice, and τ0 = 3.45 10−13 s (Sandford & Allamandola 1990). We considered that when the CO2 residence time is longer than the model time step (0.25 s), any particle hitting the surface gets trapped in the surface. We then calculated at each step and for each trapped particle a probability to be re-ejected as being equal to the ratio between the time step of the simulation and the residence time calculated from the surface temperature at the position of the particle. This probability is then compared to a random number between 0 and 1 and if higher than this random number, the particle is re-emitted into the exosphere. We checked that the results are not sensitive to the model time step.
Surface temperature: In Leblanc et al. (2017) and Leblanc et al. (2023), the Ganymede’s surface temperature was calculated using a 1-D heat conduction model. Such description had some limitations, in particular it ignored surface roughness that leads to a distribution of facet temperatures (instead of a single temperature) at a given latitude, longitude and local time. Bockelée-Morvan et al. (2024) (Paper I) showed that matching the JWST/MIRI brightness temperature maps, in particular the low to high latitude and the noon to dawn or dusk temperature contrasts, requires considering surface roughness effects. In the framework of a model for the distribution of slopes inherited from Hapke (1984), they found that the data could be fit by invoking mean slope angles s = 15°–20° on the trailing side and 20°–25° on the leading side, with some variations depending on the adopted surface albedo model. Here we adopted the following parameters, relevant to the leading side: s = 25°, Bond albedo = 0.30, thermophysical parameter Θ = 0.3 (i.e. thermal inertia Γ = 22.5 SI units). We used a spatially constant Bond albedo to keep the number of free parameters tractable. Such rough temperature distributions were calculated on a 37 × 48 latitude × local time (or longitude) grid, i.e. with a 5° latitude and 0.5 h local time step. Figure K.1 (left) shows examples of cumulative facet temperature distributions at noon local time and various latitudes, while the right panel shows the facet-averaged temperature map, where the maximum temperature is at 12.5 h local time. The multiplicity of temperatures at a given latitude/local time enables condensation in regions where it would not be expected without surface roughness. At the equator, the probability to find a surface element at a temperature smaller than 73 K (the theoretical condensation temperature of CO2 at Ganymede atmospheric pressure of 1 pbar) is zero, even in presence of surface roughness. However, the probability of encountering temperatures lower than 73 K increases with latitude, to 1% at +30°, 12% at +60° and 30% at +90°.
For describing the temperature of the surface of the trailing side (used for the calculations shown in Appendix L.4), we adopted the following parameters, which fit at best the JWST/MIRI brightness temperature map of this hemisphere: s = 20°, Bond albedo = 0.20, thermophysical parameter Θ = 0.3.
We stress that, as indicated in Paper 1, our thermal model describes roughness purely as a slope effect, and does not account for other more complex effects associated with topography, such as shadowing and self-heating due to scattering and reabsorption of solar and thermal radiation within craters, as done for investigating cold traps for water ice on the Moon (Hayne et al. 2021; Davidsson & Hosseini 2021). Applying such more advanced thermophysical models is left to future investigations.
Appendix L: Simulated exospheres from EGM simulations
L.1. CO2 gas spreading
 |
Fig. L.1. Vertical CO2 column density using a distribution of temperature at each location (rough surface, left panel) or the mean temperature (right panel). The simulations consider the sublimation of CO2 ice from a 300×300 km region at 52°N, with qCO2 × fc = 3 ×10−14. |
A question to address is the localized character of Ganymede’s CO2 exosphere. Indeed, CO2 does not condense efficiently at the typical Ganymede’s surface temperatures, even in the polar regions (100-110 K), and therefore could spread out over the whole illuminated disk, possibly condensing only in the non-illuminated areas. To study the spreading of CO2 molecules, we performed EGM simulations (Appendix K) assuming that CO2 is released by the sublimation of CO2 ice from a small surface area (300×300 km) at 52°N. The calculations were performed using a distribution of facet temperatures for each location, as computed with our thermal model with surface roughness (Appendix K), and, for comparison, using instead the facet-average temperature map (Fig. K.1, right). Figure L.1 shows the vertical CO2 column density in the two cases. It shows that the resulting atmospheric distribution is quite different for the rough surface. The migration distance is much smaller in this case, showing that the diffusion of CO2 molecules is substantially controlled by the ability to condense on cold traps. These cold traps are probably the discrete patches of optically thick ice, preferentially located on pole-facing slopes, that constitute the polar cap (Khurana et al. 2007). The limited horizontal spreading of CO2 gas indicates that local column-density maxima are associated with local sources.
Line-of-sight column densities from EGM simulations.
L.2. CO2 exosphere: Leading CO2 source only
The most significant feature of Ganymede’s CO2 exosphere being the large excess in the northern hemisphere of leading side, our simulations (see Appendix K for model description) were designed to reproduce this feature. Specifically, we calculated line-of-sight column density maps N(CO2), and extracted latitudinal and longitudinal profiles of N(CO2) for comparison with observations. Model simulations were performed assuming qCO2 = 1% in a northern cap extending from latc to 90° in latitude and ranging from 0 to 180°W in longitude. Elsewhere, qCO2 was set to 0. The input value qCO2 = 1% was set as it is consistent within a factor of a few with the rough estimation of the CO2 abundance at the surface based on the depth of the CO2-solid 4.3 μm band (CO2/H2O ∼ 1% in mass, Paper I). The limiting latitude latc and the correction factor fc to the CO2 flux were adjusted to best reproduce the position in latitude and value of the column-density peak in the latitudinal profile of N(CO2) shown in Fig. 2.
 |
Fig. L.2. CO2 gas line-of-sight column density as a function of latitude (left) and longitude (right) for the leading side. Light blue symbols show model results from EGM and dark blue symbols refer to JWST observations. Top panels (a, b): CO2 release associated to H2O sublimation with surface flux fc × qCO2 = 2.6 at latitudes > 50°N and qCO2 = 0 elsewhere. Middle panels (c, d): CO2 release associated to CO2 ice sublimation with surface flux fc × qCO2 = 3.× 10−14 at latitudes > 50°N and qCO2 = 0 elsewhere. Bottom panels (e, f): sputtering only with surface abundance qCO2 = 1% at latitudes > 40°N, and qCO2 = 0 elsewhere, and a multiplying factor to surface CO2 flux fc = 382. In the left panels (a, c, e) column densities are averages in latitude bins of 7.5°. Longitudinal variations shown in right panels (b, d, f) consider latitudes in the range 42–62°N (i.e., encompassing the northern region of the leading hemisphere with CO2 gas enhancement). Calculated CO2 column density maps for all three cases are shown in the left panels. |
Column density maps obtained for sputtering, CO2 release associated with H2O sublimation and sublimation of CO2 ice (Appendix K) are shown in Fig. L.2 (and in the main text Fig. 3 for the first two production mechanisms). EGM latitudinal profiles of line-of-sight column densities are compared to observations in the left panels of Fig. L.2. Longitudinal variations for latitudes in the range 42–62° N (i.e., encompassing the northern region of the leading hemisphere with CO2 gas enhancement) are compared in the right-hand panels of Fig. L.2. Table L.1 lists model input parameters, and average column densities in the subsolar region and so-called "Leading CO2 source" defined in Table I.1. For CO2 release associated with H2O sublimation (top panels), the latitudinal profile is reproduced for latc = 50°N and multiplying the flux of CO2 molecules by fc = 260 (as fc × qCO2 = 260×0.01 = 2.6, this corresponds to a CO2/H2O relative abundance of 5 for an H2O areal ice fraction of 50%). Since the H2O sublimation flux is highly dependent of the surface temperature (Eq. K.2) and is therefore strongly favored at low latitudes, latc must be close to the latitude at which the peak of the CO2 column density is observed (Fig. 1). For the CO2-ice sublimation case (middle panels), latc is also close to 50°N, and fc = 3×10−12. For the sputtering scenario (bottom panels), a limiting latitude latc = 40°N best reproduces the latitudinal trend of the column density (a too narrow distribution in latitude is obtained for latc = 50°N), and the flux of the sputtered CO2 molecules had to be multiplied by fc = 382.
As shown in Fig. L.2, the sputtering only scenario (panels e and f) provides a better fit of the spatial distribution of CO2 exosphere than sublimation. Especially, for the sublimation scenarios, a strong variation with longitude (i.e., local time) is obtained whereas the diurnal variation is flatter and almost consistent with the observations for sputtering. This is essentially due to the difference in the temperature dependence of these mechanisms (Eqs K.1, K.3, K.4). However, the peak of the CO2 line-of-sight column-density distribution for sputtering is more shifted toward the afternoon (∼13.4 h) than in the sublimation cases (∼13.1 h) and for the observed peak (∼12 h).
 |
Fig. L.3. Calculated line-of-sight column-density maps of the H2O exosphere of Ganymede (in 1018 m−2). The green lines display the boundary between open and closed field lines (OCFBs). Left panel: sublimation only source. Right panel: sputtering only source with fc = 382. The H2O areal surface fraction is set to qH2O = 20%. The subsolar point is at 2.6°N, 82°W. |
 |
Fig. L.4. Simulation of the entire CO2 exosphere formed by sputtering only. No sputtering is simulated inside the closed-field-line region. Input parameters are given in the text. Panel a: 2D line-of-sight column density map of CO2 (in 1018 CO2/m2), Ganymede-leading side. Panel b: same as panel a but for the Ganymede-trailing side. Panel c: latitudinal variation of the longitudinal average column density for the Ganymede-leading side (for bins of 7.5° in latitude). Panel d: same as for panel c but for the Ganymede-trailing side and bins in latitude of 15°. Dark blue symbols: JWST observations. Light blue symbols: EGM simulation. Red symbols: JWST observations. Orange symbols: EGM simulation. |
L.3. H2O exosphere
EGM simulations of Ganymede’s H2O exosphere were already performed by Leblanc et al. (2017, 2023), but the used surface temperature model did not consider surface roughness, unlike the present calculations. Figure L.3 displays the H2O column density as seen from JWST for the sublimation (left panel) and sputtering (right panel) cases. The H2O ice areal surface fraction qH2O is set to 20% all over the surface, a value which is consistent with measured water ice abundances on the leading side for latitudes ≤30–40° Ligier et al. (2019). For latitudes of 40–50°N, values of 40–50% would be more appropriate Ligier et al. (2019). As expected the sublimation of H2O follows the surface temperature distribution. A North/South asymmetry can be clearly seen which is driven by the small asymmetry in surface temperature associated with the positive subsolar latitude (see Fig. K.1). A dawn to dusk asymmetry with higher H2O column densities toward the dusk is also present. A similar dawn-dusk asymmetry, related to surface thermal inertia, is present for the CO2 simulated exosphere (Fig. 3, left panel).
The calculated line-of-sight H2O column densities in the leading subsolar region (solar zenith angle SZA < 15°) and so called "Leading CO2 source" are given in Table L.1. They are below the upper limits set by JWST (7–17×1019 m−2 for subsolar, 2×1019 m−2 for CO2 source region, Table I.1), summing the contributions from sputtering and sublimation. When considering a more appropriate value of qH2O = 40–50% for the northern region of the leading hemisphere, the modeled column density for this region is of the order of the JWST upper limit. The value obtained for the subsolar region (4.1 1019 m−2) is a factor of 7 above the minimum value derived from HST OI data for the leading hemisphere (6×1018 m−2, Roth et al. 2021).
We stress that calculated H2O sputtered fluxes are under the hypothesis that H2O is the major species released by sputtering of H2O ice Cassidy et al. (2013). However, the major mass loss from water ice by particle bombardment might not be H2O, as assumed here, but rather via the ejection of O2 and H2 (or at least in significant proportion) according to laboratory experiments Teolis et al. (2017). Hence, H2O sputtered fluxes given in Table L.1 can be considered as upper limits. This reinforces our conclusion that JWST H2O upper limits measured in the north polar cap of the leading hemisphere are fully consistent with expectations.
L.4. Simulation of CO2 sputtering on entire Ganymede’s surface
We also investigated CO2 sputtering over the southern open-field-line region of the leading hemisphere and over the southern and northern open-field-line regions of the trailing hemisphere. This approach allowed us to illustrate how the sputtering ejection rate would need to be changed from a region to another to explain the JWST observations. The surface temperature of the trailing side was calculated using the same approach as for leading side (see parameters of the thermal model in Appendix K). Figure L.4 provides one example of results obtained by using the same qCO2 and fc values for the two hemispheres, the only difference being the location of the OCFBs. The distribution of sputtered CO2 over the whole surface is described according to:
-
a region (1) of sputtering above a latitude of 50°N, with a flux of sputtered CO2 molecules determined as described in section I, with fc= 640 and qCO2 = 1%,
-
a region (2) in the northern hemisphere open field-lines region with fc= 80 and qCO2 = 1% (e.g., describing regions between northern OCFB and > 50°N polar cap on the leading hemisphere),
-
a region (3) in the southern hemisphere open field-lines region with fc= 60 and qCO2 = 1%,
-
a region (4) in close field-lines region with fc= 0.
Assuming the same fc = 640 value for all regions, would be equivalent to adopting qCO2 = 1%, 0.13%, 0.09 %, and 0% for regions (1), (2), (3), (4) respectively. With these assumptions, the shape of the latitudinal distribution observed on the leading side is reproduced but not that of the trailing side (Fig. L.4). Reproducing at least approximately Ganymede’s CO2 exosphere with the sputtering mechanism might be possible by adjusting fc or qCO2 parameters geographically over the surface. However, this model cannot explain the exospheric excess observed at equatorial to mid latitudes in the southern regions of the trailing hemisphere (Fig. 1) taking into account that, at the time of the trailing-side observation, Ganymede was inside the plasma sheet of Jupiter’s magnetosphere, so southern polar regions were not over-exposed to plasma bombardment with respect to northern regions (Appendix J).
Appendix M: PSF deconvolution of CO2 gas map
In order to analyze the spatial distribution of the CO2 exosphere on Ganymede’s leading side in more detail, we applied a deconvolution procedure. The deconvolution process was done using the AIDA algorithm in classical mode (Hom et al. 2007) that requires science and PSF data files. Reported Full Width at Half Maximum (FWHM) measured at 4.25 μm from JWST point-source observations range from 0.14 to 0.17” ()Deugenio2023 and are expected to vary with the observational mode (e.g., number of dithers). Unfortunately, no reference star was observed during the observations of Ganymede, so we used the WebbPSF software (https://www.stsci.edu/jwst/science-planning/proposal-planning-toolbox/psf-simulation-tool) which can calculate monochromatic PSFs for NIRSPec in spectroscopic mode. PSFs were generated at various wavelengths to explore how deconvolved images vary with the PSF FWHM.
 |
Fig. M.1. PSF deconvolution. Top: deconvolved CO2-gas maps (leading hemisphere) obtained with the AIDA algorithm using NIRSpec PSFs calculated with WebbPSF at 3.5 μm (FWHM = 0.165”), 4.2 μm (FWHM = 0.185”) and 5 μm (FWHM = 0.205”). Bottom: residuals of the deconvolution for each calculated PSF; plotted are (O − C)2, where O is the original CO2 column-density map (leading hemisphere, top-right plot), and C is the convolution of the deconvolved O map. Color bars are in unit of 1018 m−2. |
We show in Fig. M.1 the deconvolution of the CO2 gas map above the leading hemisphere for PSFs with FWHMs of 0.165, 0.185 and 0.205” corresponding to WebbPSF outputs at 3.5, 4.2 and 5 microns, respectively. For this purpose, we used the CO2 column density map derived for the full 37× 43 spaxels IFU frame (i.e., including results outside Ganymede disk). The deconvolved maps were then reconvolved with the PSFs used for the deconvolution. Residuals with respect to the original data are shown in Fig. M.1 (bottom row) for the three assumed PSFs, and do not differ much. The deconvolved CO2 gas distribution confirms that the northern CO2 excess is confined in longitude and latitude, and that the decrease of the column density above latitudes of 60°N is real. The deconvolved map also clearly shows the excess nearby the southern OCFB.
Appendix N: Spatial variations of surface CO2 band depth
The CO2 absorption band around 4.26 μm is widespread over the surface of Ganymede. Globally, the CO2 band depth appears anti-correlated with bond albedo and water ice absorption band depths, with the maximum CO2 band depth on the equatorial regions but much lower values on regions poleward of 30°N (Fig. N.1, Hibbitts et al. 2003, Paper I). The CO2 band center (Fig. 4C) and shape show stronger relationship with surface brightness for both hemispheres, redshifting and getting narrower/asymmetric as we reach polar latitudes, respectively. As discussed in Paper I these changes of band position and shape may be due to contributions of CO2 under varying physical states/matrices depending on the latitude: adsorbed on minerals or salts at the equatorial latitudes, and possibly mixed in amorphous water ice at the poles (Fig. 4C). But why is the CO2 band depth weaker at the polar regions, where CO2 gas appears to be released from the surface? Actually, the poles of Callisto also have weaker CO2 band depths and finer-grained water ice than the equatorial regions, just like Ganymede. From Galileo/NIMS data, this was interpreted as fine-grained ice physically covering and spectrally masking the CO2, although such a masking effect was not demonstrated numerically or experimentally (McCord et al. 1998; Hibbitts et al. 2000, 2003). JWST/NIRSpec data of Ganymede also show some anti-correlation between the spatial distribution of the CO2 band depth and that of the H2O 4.5-μm band depth (Fig. N.1). However, the lower CO2 band depth at the polar regions may not be (only) due to a putative spectral-masking effect, but to other factors. Maybe the surface areal abundance of CO2 is lower within the open-field-line areas because the irradiation releases it more efficiently from its mineral association. As a result, CO2 may be less concentrated over non-ice mineral-rich terrains and only present on bright ice-rich patches (the coldest surfaces), reducing its geographically averaged band depth and making its band shape and position more compatible to CO2 mixed in water ice. Another explanation might also be that the absorption coefficient of CO2 decreases at the poles because CO2 is in a different state/matrix and/or at a different temperatures than at equatorial regions.
 |
Fig. N.1. Comparing CO2 exosphere to H2O and CO2 distribution on Ganymede’s surface. Top and bottom rows are for the leading and trailing hemispheres, respectively. A, D: CO2 gas column density maps at a 3×3 smoothed resolution (this work); B, E: H2O band depth at 4.5 μm (Paper I); C, F: CO2-solid 4.3-μm band depth (Paper I). In these plots, unlike in Figs 1 and O.1, the same color scales and boxcar smoothing are used for leading and trailing. |
Despite the lack of correlation between the global distribution of CO2 gas column density and solid CO2 band depth, there are some local areas where both are minimum (in the south polar regions and in an area at about 260-300°W and 30°S-50°N, Fig. N.1), and some spaxels at the extreme north of the leading hemisphere show an enhanced CO2 band depth (Fig. 4).
Appendix O: Additional figures
 |
Fig. O.1. CO2 gas distribution above Ganymede surface. First and second rows are for the leading side, at the original and 3×3 boxcar smoothed (for higher S/N) resolutions, respectively. Bottom row is for the trailing side at 3×3 smoothed resolution. Plots on the first column show the Pearson correlation coefficient between continuum-filtered residual CO2 gas emission and a forward CO2 fluorescence model at 105 K (Fig. H.1). Plots on the second and third column show the line-of-sight CO2 column density and S/N inferred by fitting synthetic CO2 fluorescence spectra (Appendix B). The color scales for the leading and trailing sides are different, and indicated above the plots. Pixel sizes are 0.1×0.1”. The green lines show the open-closed field-line boundary Duling et al. (2022) |
 |
Fig. O.2. CO2 vertical column density maps of the leading (left) and trailing (right) hemispheres. They were deduced from the line-of-sight column density maps, by multiplying them by the cosine of the angle between local zenith and line of sight directions. For the leading hemisphere, the central contour for the north excess is at about 72°W (12.6 h local time), 45°N. Trailing data were smoothed using a 3×3 boxcar filter. |
 |
Fig. O.3. Geological map of Ganymede (Plate 2 of Patterson et al. (2010)). The green lines show the open-closed field-line boundary at the time of the JWST observations Duling et al. (2022). |
All Tables
All Figures
 |
Fig. 1. CO2 in Ganymede’s exosphere. The top and bottom rows are for the leading and trailing sides, respectively. The left column shows Bond albedo maps derived by de Kleer et al. (2021) from Voyager-Galileo mosaic. The middle column shows line-of-sight CO2 column density maps inferred from spectral modeling (Appendices B–D). The trailing data were smoothed using a 3 × 3 boxcar filter. The color scales for the leading and trailing sides differ, and are indicated above the plots. The pixel sizes are 0.1 × 0.1″ and the PSF is ∼0.19″ (FWHM). The CO2 maximal emission in the leading hemisphere (based on central contour) is at 81°W, 51°N (∼12 h local time); correcting for the line of sight, the maximum vertical column density is at 72°W, 45°N (12.6 h local time, see Figs. 4A, O.2). The third column shows CO2 gaseous emission spectra obtained after removing the continuum emission from Ganymede’s surface, averaged over latitudes 45−90°N for leading (top), and 30−60°S for trailing (bottom). The best fit synthetic spectra are shown in cyan, with a fitted rotational temperature of 108 ± 8 K for the leading side, and a fixed rotational temperature of 105 K for the trailing side. The y scale is μJy per pixel. The green lines on the maps show the OCFBs at the time of the JWST observations (Appendix J, Duling et al. 2022). The subsolar point is shown by a red star in the Bond albedo maps. |
| In the text | |
 |
Fig. 2. Variation of CO2 gas line-of-sight column density with latitude. The blue and red symbols refer to the leading and trailing sides, respectively. The column densities were derived from spectra that were averaged in latitude bins of 7.5° (leading, Fig. B.2) and 15° (trailing). The blue (resp. pink) vertical domains show the latitude range of the OCFBs for the leading and trailing sides, respectively, restricted to longitudes of 10−130°W (leading) and 210−330°W (trailing). |
| In the text | |
 |
Fig. 3. Calculated line-of-sight column-density maps of the CO2 exosphere of Ganymede above the leading side from the EGM model (in units of 1018 m−2). Left: CO2 release associated with H2O sublimation with a CO2/H2O relative abundance of 5 for an H2O areal ice fraction of 50% at latitudes > 50°N. Right: Sputtering of H2O ice with CO2/H2O = 0.01 at latitudes > 40°N; the result was multiplied by 382 to match the observations (Appendices K, L). The green lines display the OCFBs. The subsolar point is at 2.6°N, 82°W. |
| In the text | |
 |
Fig. 4. Comparing CO2 exosphere to surface properties on Ganymede’s leading hemisphere. (A) Vertical CO2 gas column density (in units of 1018 m−2, this work, see also Fig. O.2); (B) Depth of CO2-solid absorption band (Paper I); (C) Central wavelength of CO2-solid absorption band (Paper I); (D) Reflectance at 3.65 μm (Paper I); (E) Central wavelength of H2O Fresnel peak (Paper I); (F) Relative amplitude of the maximum reflectance between 3.5 and 4 μm (H2O interband amplitude, Paper I). The north pole of the leading hemisphere possesses the most redshifted absorption band center of solid CO2, consistent with CO2 trapped in amorphous H2O ice (Paper I). It also has the highest reflectance at 3.65 μm and H2O interband amplitude, indicative of a higher density of facets in H2O ice for the photons (i.e., smaller grains and/or more internal defects and/or higher micro-roughness or porosity), and the most blueshifted central wavelength of the H2O Fresnel peak due to a higher proportion of amorphous water ice (Mastrapa et al. 2009). |
| In the text | |
 |
Fig. B.1. CO2ν3 band gas spectra from Ganymede’s exosphere. Left (A–C): North polar cap of the leading side of Ganymede (averaged spectra for latitudes > 45° N); Right (D–F): Southern hemisphere of the trailing side (latitudes 30–60° S). A, D) Observed spectra showing both the CO2ν3 absorption band from CO2 in solid state, and ro-vibrational emission lines of gaseous CO2; B, E) CO2 gaseous emission spectra obtained after removing the continuum emission shown in red in panels A and D (Appendix B). C, F) Residual CO2-gas DIFF spectra obtained by removing the continuum obtained from low-pass filtering (Appendix B). Best fit synthetic spectra are shown in blue, with a fitted rotational temperature of 108±8 K for the leading side, and a fixed rotational temperature of 105 K for the trailing side. In all plots, vertical-axis unit is μJy per pixel (1 pixel = 0.1”× 0.1”). |
| In the text | |
 |
Fig. B.2. DIFF spectra on the leading hemisphere as a function of latitude. Data were averaged over latitude bins of 7.5° and treated as explained in Appendix B. Fitted fluorescence DIFF spectra are shown in black. The Pearson correlation coefficient for each spectrum is given in the legend. Vertical-axis unit is the flux density per pixel. |
| In the text | |
 |
Fig. C.1. Cross-correlation functions (CCFs). Top: from averaged data at latitudes > 45°N on the leading hemisphere. Bottom: from averaged data at latitudes 30–60°S on the trailing hemisphere. The forward model for computing the cross-correlation is a fluorescence CO2 spectrum. In both cases the CCF peaks at δv = 0, indicating CO2 exosphere detection. The maximum of the CCF is lower for the trailing side due to a fainter CO2 signal. |
| In the text | |
 |
Fig. C.2. Study of 4.22–4.295 μm spectra averaged over latitude bins. A) Pearson correlation coefficient between residual CO2 DIFF spectra and a synthetic DIFF spectrum which uses a CO2 fluorescence synthetic spectrum at T = 105 K as input. B) CO2 line-of-sight column density retrieved from the fit of CO2 DIFF spectra. C) shift, in fraction of spectel, of the maximum of the cross-correlation function (CCF) between CO2 DIFF spectra and the synthetic DIFF spectrum; secure detection is indicated when the shift is close to zero. D) S/N of the cross-correlation function at shift = 0. The S/N is obtained by computing the CCFnoise obtained by using as input a simulated noisy spectrum, with the r.m.s deduced from the ERR entry in the Level 3 data cube, and scaled in |
| In the text | |
 |
Fig. D.1. CO2 simulated nadir spectra. Input model parameters are: CO2 column density N(CO2) = 1018 m−2, surface temperature Ts = 145 K, gas rotational temperature Trot = 105 K, for I/F values of 0.04 (red) and 0.12 (green). The fluorescence spectrum (black) corresponds to I/F = 0 and Ts = 0 K. Ganymede’s exosphere is described by hydrostatic equilibrium. |
| In the text | |
 |
Fig. H.1. CO2 rotation temperature in the north hemisphere of the leading hemisphere. Spaxels within latitude bins of width 7.5° were averaged. Values were derived from the fitting of DIFF spectra using as model fluorescence emission with Trot as a free parameter (Appendix B). The weighted mean value is Trot = 107±5 K. |
| In the text | |
 |
Fig. I.1. Continuum-divided spectra of Ganymede observed with MIRI and synthetic H2O spectra. Spectra for the leading and trailing sides are shown in red and blue, respectively, with the spectrum of the trailing side shifted vertically. Spaxels for which the solar zenith angle is less than 15° at the center of the spaxel have been averaged. Synthetic spectra are superimposed, with input parameters indicated in the legend (Appendix I) and N(H2O) = 1020 m−2. The Ganymede spectra do not show any hint of H2O lines. |
| In the text | |
 |
Fig. K.1. Ganymede’s surface temperature used in EGM model, representative of the leading hemisphere. Left panel: facet temperature distribution (cumulative probability) of the surface temperatures at 12 h local time for various latitudes indicated in the plot. Right panel: latitude/longitude map of the average surface temperature with the subsolar point being at a latitude of 2°N (as for JWST observations, Paper I) and longitude of 180°. |
| In the text | |
 |
Fig. L.1. Vertical CO2 column density using a distribution of temperature at each location (rough surface, left panel) or the mean temperature (right panel). The simulations consider the sublimation of CO2 ice from a 300×300 km region at 52°N, with qCO2 × fc = 3 ×10−14. |
| In the text | |
 |
Fig. L.2. CO2 gas line-of-sight column density as a function of latitude (left) and longitude (right) for the leading side. Light blue symbols show model results from EGM and dark blue symbols refer to JWST observations. Top panels (a, b): CO2 release associated to H2O sublimation with surface flux fc × qCO2 = 2.6 at latitudes > 50°N and qCO2 = 0 elsewhere. Middle panels (c, d): CO2 release associated to CO2 ice sublimation with surface flux fc × qCO2 = 3.× 10−14 at latitudes > 50°N and qCO2 = 0 elsewhere. Bottom panels (e, f): sputtering only with surface abundance qCO2 = 1% at latitudes > 40°N, and qCO2 = 0 elsewhere, and a multiplying factor to surface CO2 flux fc = 382. In the left panels (a, c, e) column densities are averages in latitude bins of 7.5°. Longitudinal variations shown in right panels (b, d, f) consider latitudes in the range 42–62°N (i.e., encompassing the northern region of the leading hemisphere with CO2 gas enhancement). Calculated CO2 column density maps for all three cases are shown in the left panels. |
| In the text | |
 |
Fig. L.3. Calculated line-of-sight column-density maps of the H2O exosphere of Ganymede (in 1018 m−2). The green lines display the boundary between open and closed field lines (OCFBs). Left panel: sublimation only source. Right panel: sputtering only source with fc = 382. The H2O areal surface fraction is set to qH2O = 20%. The subsolar point is at 2.6°N, 82°W. |
| In the text | |
 |
Fig. L.4. Simulation of the entire CO2 exosphere formed by sputtering only. No sputtering is simulated inside the closed-field-line region. Input parameters are given in the text. Panel a: 2D line-of-sight column density map of CO2 (in 1018 CO2/m2), Ganymede-leading side. Panel b: same as panel a but for the Ganymede-trailing side. Panel c: latitudinal variation of the longitudinal average column density for the Ganymede-leading side (for bins of 7.5° in latitude). Panel d: same as for panel c but for the Ganymede-trailing side and bins in latitude of 15°. Dark blue symbols: JWST observations. Light blue symbols: EGM simulation. Red symbols: JWST observations. Orange symbols: EGM simulation. |
| In the text | |
 |
Fig. M.1. PSF deconvolution. Top: deconvolved CO2-gas maps (leading hemisphere) obtained with the AIDA algorithm using NIRSpec PSFs calculated with WebbPSF at 3.5 μm (FWHM = 0.165”), 4.2 μm (FWHM = 0.185”) and 5 μm (FWHM = 0.205”). Bottom: residuals of the deconvolution for each calculated PSF; plotted are (O − C)2, where O is the original CO2 column-density map (leading hemisphere, top-right plot), and C is the convolution of the deconvolved O map. Color bars are in unit of 1018 m−2. |
| In the text | |
 |
Fig. N.1. Comparing CO2 exosphere to H2O and CO2 distribution on Ganymede’s surface. Top and bottom rows are for the leading and trailing hemispheres, respectively. A, D: CO2 gas column density maps at a 3×3 smoothed resolution (this work); B, E: H2O band depth at 4.5 μm (Paper I); C, F: CO2-solid 4.3-μm band depth (Paper I). In these plots, unlike in Figs 1 and O.1, the same color scales and boxcar smoothing are used for leading and trailing. |
| In the text | |
 |
Fig. O.1. CO2 gas distribution above Ganymede surface. First and second rows are for the leading side, at the original and 3×3 boxcar smoothed (for higher S/N) resolutions, respectively. Bottom row is for the trailing side at 3×3 smoothed resolution. Plots on the first column show the Pearson correlation coefficient between continuum-filtered residual CO2 gas emission and a forward CO2 fluorescence model at 105 K (Fig. H.1). Plots on the second and third column show the line-of-sight CO2 column density and S/N inferred by fitting synthetic CO2 fluorescence spectra (Appendix B). The color scales for the leading and trailing sides are different, and indicated above the plots. Pixel sizes are 0.1×0.1”. The green lines show the open-closed field-line boundary Duling et al. (2022) |
| In the text | |
 |
Fig. O.2. CO2 vertical column density maps of the leading (left) and trailing (right) hemispheres. They were deduced from the line-of-sight column density maps, by multiplying them by the cosine of the angle between local zenith and line of sight directions. For the leading hemisphere, the central contour for the north excess is at about 72°W (12.6 h local time), 45°N. Trailing data were smoothed using a 3×3 boxcar filter. |
| In the text | |
 |
Fig. O.3. Geological map of Ganymede (Plate 2 of Patterson et al. (2010)). The green lines show the open-closed field-line boundary at the time of the JWST observations Duling et al. (2022). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.