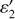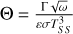| Issue |
A&A
Volume 681, January 2024
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 34 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202347326 | |
| Published online | 03 January 2024 | |
Composition and thermal properties of Ganymede’s surface from JWST/NIRSpec and MIRI observations
1
LESIA, Observatoire de Paris, Université PSL, Sorbonne Universite, Université Paris Cité, CNRS,
92195
Meudon,
France
e-mail: dominique.bockelee@obspm.fr
2
Univ. Grenoble Alpes, CNRS, IPAG,
38000
Grenoble,
France
3
Faculty of Aerospace Engineering, Delft University of Technology,
Delft,
The Netherlands
4
Leiden Observatory, Leiden University,
PO Box 9513,
2300 RA
Leiden,
The Netherlands
5
Department of Astronomy, University of California,
22 Berkeley,
CA
94720,
USA
6
Department of Earth and Planetary Science, University of California,
22 Berkeley,
CA
94720,
USA
7
University of Wisconsin,
Madison,
WI
53706,
USA
8
Istituto Nazionale di AstroFisica – Istituto di Astrofisica e Planetologia Spaziali (INAF-IAPS),
00133
Rome,
Italy
9
Division of Geological and Planetary Sciences,
Caltech,
Pasadena,
CA
91125,
USA
10
School of Physics and Astronomy, University of Leicester,
University Road,
Leicester
LE1 7RH,
UK
11
Space and Plasma Physics, KTH Royal Institute of Technology,
Stockholm,
Sweden
12
Institute of Geophysics and Meteorology, University of Cologne,
Albertus Magnus Platz,
50923
Cologne,
Germany
13
Cornell Center for Astrophysics and Planetary Science, Cornell University,
Ithaca,
NY
14853,
USA
14
Department of Solar System Science, JAXA Institute of Space and Astronautical Science,
Japan
15
Jet Propulsion Laboratory, California Institute of Technology,
Pasadena,
California
91109,
USA
16
SETI Institute,
Mountain View,
CA
94043,
USA
Received:
30
June
2023
Accepted:
20
October
2023
Context. We present the first spectroscopic observations of Ganymede by the James Webb Space Telescope undertaken in August 2022 as part of the proposal “ERS observations of the Jovian system as a demonstration of JWST’s capabilities for Solar System science”.
Aims. We aimed to investigate the composition and thermal properties of the surface, and to study the relationships of ice and non-water-ice materials and their distribution.
Methods. NIRSpec IFU (2.9–5.3 μm) and MIRI MRS (4.9–28.5 μm) observations were performed on both the leading and trailing hemispheres of Ganymede, with a spectral resolution of ~2700 and a spatial sampling of 0.1 to 0.17″ (while the Ganymede size was ~1.68″). We characterized the spectral signatures and their spatial distribution on the surface. The distribution of brightness temperatures was analyzed with standard thermophysical modeling including surface roughness.
Results. Reflectance spectra show signatures of water ice, CO2, and H2O2. An absorption feature at 5.9 μm, with a shoulder at 6.5 μm, is revealed, and is tentatively assigned to sulfuric acid hydrates. The CO2 4.26-μm band shows latitudinal and longitudinal variations in depth, shape, and position over the two hemispheres, unveiling different CO2 physical states. In the ice-rich polar regions, which are the most exposed to Jupiter’s plasma irradiation, the CO2 band is redshifted with respect to other terrains. In the boreal region of the leading hemisphere, the CO2 band is dominated by a high wavelength component at ~4.27 μm, consistent with CO2 trapped in amorphous water ice. At equatorial latitudes (and especially on dark terrains), the observed band is broader and shifted toward the blue, suggesting CO2 adsorbed on non-icy materials, such as minerals or salts. Maps of the H2O Fresnel peak area correlate with Bond albedo maps and follow the distribution of water ice inferred from H2O absorption bands. Amorphous ice is detected in the ice-rich polar regions, and is especially abundant on the northern polar cap of the leading hemisphere. Leading and trailing polar regions exhibit different H2O, CO2, and H2O2 spectral properties. However, in both hemispheres the north polar cap ice appears to be more processed than the south polar cap. A longitudinal modification of the H2O ice molecular structure and/or nanometer- and micrometer-scale texture, of diurnal or geographic origin, is observed in both hemispheres. Ice frost is tentatively observed on the morning limb of the trailing hemisphere, which possibly formed during the night from the recondensation of water subliming from the warmer subsurface. Reflectance spectra of the dark terrains are compatible with the presence of Na- and Mg-sulfate salts, sulfuric acid hydrates, and possibly phyllosilicates mixed with fine-grained opaque minerals, with a highly porous texture. Latitude and local time variations of the brightness temperatures indicate a rough surface with mean slope angles of 15°–25° and a low thermal inertia Γ = 20 − 40 J m−2 s−0.5 K−1, consistent with a porous surface, with no obvious difference between the leading and trailing sides.
Key words: planets and satellites: composition / planets and satellites: individual: Ganymede / infrared: planetary systems
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Ganymede is the largest Galilean satellite and the largest natural satellite in our Solar System. Ganymede’s internal structure reveals a differentiated body with a molten core producing an intrinsic magnetic field, a silicate mantle, and a complex icy crust that hides a deep ocean, making it an archetype of water worlds. Ganymede also possesses a thin oxygen atmosphere (Hall et al. 1998) and two auroral ovals (Feldman et al. 2000).
Ganymede’s main provinces are the dark Regiones and bright, ice-rich, grooved terrains. Based on photo-interpretation and crater counting, the Regiones are older than the bright terrains, holding clues about Ganymede’s geologic evolution. Similar to other Galilean moons immersed in Jupiter’s magnetosphere, the icy surface of Ganymede undergoes space weathering processes due to the impact of energetic particles, solar (UV) flux, thermal cycling, and bombardment by micro-meteoroids. Optical images returned by previous space missions revealed that Ganymede’s polar caps are brighter than the equatorial region, and that the trailing hemisphere is darker than the leading hemisphere in the equatorial region (e.g., Khurana et al. 2007). Ganymede’s magnetosphere is thought to play an important role in shielding the equatorial region at latitudes below 40° from the incident plasma, while the radiolytic flux is much higher at polar latitudes (e.g., Fatemi et al. 2016; Poppe et al. 2018; Liuzzo et al. 2020; Plainaki et al. 2020).
Current knowledge of Ganymede’s surface composition comes from close exploration carried out by the NASA Galileo and Juno spacecrafts, and ground-based telescopic observations. Near-infrared reflectance spectra of Ganymede, returned by the Near Infrared Mapping Spectrometer (NIMS) on board Galileo (Carlson et al. 1992) revealed the presence of amorphous ice, especially in the polar regions, which probably formed by the more intense energetic bombardment in these regions (Hansen & McCord 2004). They also revealed spectral features at 3.4, 3.88, 4.05, 4.25, and 4.57 µm – weaker than those on Callisto – which are attributable to sulfur dioxide (SO2), carbon dioxide (CO2), and organic compounds (McCord et al. 1997, 1998, 2001). Observations at shorter wavelengths returned by the Very Large Telescope (VLT) in recent years suggested the contributions of chlorinated and sulfate salts as well as sulfuric acid hydrates (Ligier et al. 2019; King & Fletcher 2022).
The most abundant non-ice compound, CO2, does not display any clear leading or trailing asymmetry on large regional scales, whereas such asymmetry was observed on Callisto (Hibbitts et al. 2002, 2003). Also, unlike Callisto, there are no systematic correlations at the local scale (e.g., CO2-enriched impact craters, Hibbitts et al. 2003), even though some CO2-rich impact craters may not be ruled out (Tosi et al. 2023). CO2 appears to be mostly correlated with moderately hydrated non-ice material primarily associated with the dark Regiones (Hibbitts et al. 2009). Observations of Ganymede by Juno/Jovian Infrared Auroral Mapper (JIRAM; Adriani et al. 2017) revealed a latitudinal trend in the strength of the CO2 feature, with a band depth slightly higher at low latitudes (Mura et al. 2020), consistent with previous NIMS results (Hibbitts et al. 2003). While in the 3–5 µm range, the strongest signature of free CO2 ice is centered at 4.27 µm, on Ganymede this signature is slightly shifted to shorter wavelengths at 4.25–4.26 µm, on average, similar to what is observed on Saturn’s icy satellites. This reveals that the CO2 molecule must be trapped in another host material rather than present as pure ice (Chaban et al. 2007; Cruikshank et al. 2010).
Radiolytic H2O2 has a diagnostic, weak absorption at 3.5 µm and was first observed on Europa by NIMS (Carlson et al. 1999a), providing the rationale for investigating the presence of this compound also on Ganymede. Newly detected and mapped on Ganymede with the James Webb Space Telescope (JWST), this species exists primarily at the polar caps, consistent with the production by radiolysis driven by particles directed by Ganymede’s magnetic field (Trumbo et al. 2023). Ganymede’s intrinsic magnetic field and its effects on the charged particle precipitation are also relevant for the generation of the sputtered atmosphere. The global O2 atmosphere is thought to be sourced by ice radiolysis from sputtering in the polar regions (Marconi 2007). Around the subsolar point, H2O from surface sublimation (not affected by the magnetic field) is suggested to be more abundant than O2 (Roth et al. 2021; Leblanc et al. 2023).
Following previous observations, there remain several open questions on the nature, origin, and processes making up Ganymede’s current surface composition. Here, we discuss the first spectroscopic observations of Ganymede by JWST as part of the proposal “ERS observations of the Jovian system as a demonstration of JWST’s capabilities for Solar System science”, submitted in response to the ERS call and selected in November 2017 (de Pater et al. 2022). The program’s objectives on Ganymede were the investigation of both the surface and the exosphere. JWST observations of Ganymede were performed in August 2022 using the Mid-Infrared Instrument/medium resolution spectroscopy (MIRI/MRS, 4.9–28.5 µm), and the Near Infrared Spectrograph/integral field unit (NIRSpec/IFU, 2.9–5.3 µm, grating G395H). This paper focuses on the main results obtained on the surface, with an emphasis on: i) the mapping of the CO2 molecule to derive constraints on the properties of the material in which it is trapped; ii) the distribution and properties of water ice mainly from the Fresnel reflection peaks; iii) the origin of a newly detected 5.9-µm absorption band; and iv) the physical properties of the surface as derived from its thermal emission.
2 Observations
2.1 NIRSpec observations and data reduction
Ganymede Trailing and Leading hemispheres were observed with NIRSpec/IFU on board JWST on 3 August (Obs. 28) and 7 August 2022 (Obs. 19), respectively. NIRSpec IFU observations provide spatially resolved imaging spectroscopy over a 3″ × 3″ field-of-view with 0.1″ × 0.1″(310 × 310 km at Ganymede) spatial elements (spaxels). They were taken with the G395H/F290LP grating/filter pair, and cover the spectral range 2.86–5.28 µm (with gaps) with an average spectral resolution of ~2700. In this high-spectral resolution configuration, the dispersion direction in the focal plane is covered by two NIR-Spec detector arrays (NRS1 and NRS2) separated by a physical gap which is responsible for missing wavelengths in the ~4.0–4.1 µm range. The observations were taken with a four-point dither (offset of about 0.4″ between dithers), with 4 integrations constituted of 10 groups (i.e., single exposures) per dither position. The data were acquired with the NRSRAPID readout pattern appropriate for bright sources. Details concerning the dates, geometries, and exposure times are given in Table 1.
The data reduction was performed with the JWST pipeline version 1.9.0., using the context file version jwst_1039.pmap. The individual raw images were first processed for detector-level corrections using the Detector1Pipeline module of the pipeline (Stage 1). The resulting count-rate images were corrected from the 1/ƒ noise introduced during the detector readout using the method described by Trumbo et al. (2023). The cleaned countrate images were then calibrated using the Calwebb_spec2 module (Stage 2). At this stage, WCS-correction, flat-fielding, and flux calibrations were applied to convert the data from units of count rate to flux density. The individual Stage 2 dither images were then resampled and combined onto a final data cube through the Calwebb_spec3 processing (Stage 3). In this processing stage, the outlier_detection step was ultimately not applied, as it rejected pixels on the Ganymede disk. The cube_build step, which produces the final Level-3 3-D spectral cubes, was run with the drizzle-weighting and ifualign-geometry options. In this geometry, the IFU cube is aligned with the instrument IFU plane, so that north is not along the y axis, contrary to the default skyalign option. The ifualign option is recommended to minimize artifacts in the cube-build step.
The observations were affected by some pointing issues that were taken into account to compute the geographical coordinates of each spaxel, and recenter the images. The central position of the NRS1 and NRS2 images were calculated as the (signal-unweighted) mean RA, Dec value of all spaxels where the measured radiance (at 2.89 µm for NRS1 and 4.20 µm for NRS2) is above some threshold (ensuring that the spaxel sees signal from the target; a threshold of 5% of the maximum signal was found optimal). The measured offsets with respect to the position given by the header are in the range ~0.43–0.46″ in RA and less than 0.04″ in Dec.
Essentially all the detected signal from Ganymede with NIR-Spec/IFU is reflected sunlight. Indeed, the relative contribution of thermal emission is typically 12% at the longest wavelengths (5.2 µm), but less than 5% in average at wavelengths shorter than 4.9 µm based on MIRI data and associated thermal modeling (Sect. 4). The measured radiances were therefore converted into the radiance factor I/F (i.e., uncorrected from solar incidence and emission angles), where F = I⊙/π, and I⊙ is the solar radiance at the heliocentric distance of Ganymede. At the spectral resolution of these observations (spectral resolution element size of 1.49 nm), the detailed spectrum of the Sun is critical for properly calibrating the data in I/F and correcting for the solar lines. We used the ACE-FTS atlas of Hase et al. (2010), which provides the depth of the infrared solar lines from 2.6 to 5.4 µm with a step of 0.005 cm−1, and the infrared solar continuum from R.L. Kurucz1. The solar spectrum was convolved to the NIRSpec G395H spectral resolution, and resampled at the wavelengths of the spectral elements in the Ganymede velocity rest frame, taking into account the heliocentric velocity of Ganymede and Ganymede’s velocity with respect to JWST. It was found that solar lines are best removed by slightly shifting the wavelength of the spectel elements2 by a fraction of the dispersion element (of 0.66 nm). Applying these shifts, solar lines residuals are however observed in the I/F spectra at the 0.5% level. Spikes present in the I/F spectra were flagged using sigma-clipping (which identifies spectels that are above a specified number of standard deviations; we set a 3-σ threshold), and replaced by the mean I/F of the ten nearest spectels. Inspecting the spectrum associated with each spaxel, those at the limb present mid-frequency wave-like structures, and so may be less reliable.
JWST observations of Ganymede.
2.2 MIRI observations and data reduction
MIRI/MRS observations of Ganymede were taken on Aug. 3, 2022 (trailing side, Obs. 28) and Aug. 7, 2022 (leading side, Obs. 17). The instrument has 4 separate IFUs (channels 1 through 4), each covering a separate wavelength range between 4.9 and 27.9 µm. All four channels are observed simultaneously, but covering the entire spectral range requires the use of three grating settings: SHORT (A), MEDIUM (B), and LONG (C). Combining the four channels and three grating settings, this yields 12 different bands increasing in wavelength from 1A to 4C. Observations were acquired in the form of a four-point dither optimized for extended targets. We used the FASTR1 readout mode, with five groups (Ngroups = 5) per integration to optimize the slope-fitting algorithm. For each dither and grating position, 44 integrations were acquired, for a total 8758 sec exposure time for each visit. Given the way observations were conducted (grating A, dither positions 1–4; then grating B, 1–4; then grating C, 1–4), and the 7.15455-day rotation period of Ganymede, spectra in gratings A, B, C do not exactly correspond to the same geographical locations on Ganymede, with a shift of 4° longitude between grating A and grating C; this small effect was ignored upon spectra reconstruction3. Table 1 summarizes the observational and some relevant ephemeris parameters. The distance of Ganymede from Jupiter center was 340±1″ for Obs. 27 and 331±5″ for Obs. 18.
Background observations were also acquired. The goal of these observations was both to evaluate the straylight from Jupiterat Ganymede’s distance and to mitigate the effects of bad pixels in the Ganymede data. These observations were obtained on July 26 (Obs. 29), Aug. 4 (Obs. 30), and Aug. 6 (Obs. 22), but it turned out that the specified background position (20″ north of Ganymede) was too close to Ganymede. As a consequence, the background data actually show scattered light from Ganymede itself. Therefore, these data were not used.
Observations were initially reduced using the standard JWST pipeline (version 1.9.2, context file jwst_1041.pmap), with the skyalign option. MIRI observations are known to be affected by fringing issues, caused by interferences between the reflective layers of the detectors. Those were handled at the data reduction level, using the alternative “residual fringe correction step” patch while running the Stage 3 processing in the pipeline. As expected, the use of Ngroups = 5 in data acquisition led to partial or total saturation of the signals at least over some parts of the Ganymede disk, especially near disk center, longward of 8.5 µm (from bands 2B to 4C). Therefore, data were also reduced restricting the ramps to Ngroups = 2 and Ngroups = 1. For Ngroups = 1, the calibration was performed by applying a band-dependent correction factor to the uncalibrated UNCAL data. The factor was determined by comparing, on non-saturated spaxels, the Level-2 calibrated radiances obtained when restricting the ramp to a single group to those obtained using the full ramp (Ngroups = 5). The correction factor ranges from 1.02 to 1.14 depending on the band. Doing so considerably alleviates saturation issues, but at the expense of signal-to-noise ratio S/N. With an appropriate choice of Ngroups for each band, we could recover unsaturated and high S/N data at all wavelengths from 4.9 to 11.7 µm (bands 1A to 2C). The pipeline output consists of 3D cubes (2D spaxels × 1D spectels) in fits format, calibrated in radiance (MJy/sr), with spaxel (x,y) coordinates aligned with sky RA, Dec.
Starting from the fits files, we applied the following steps to construct cubes usable for scientific analysis. All of steps (1–6) described below were applied independently to data corresponding to the different dither positions.
Bad pixel correction. Spectra at one given spatial position appear affected by spikes, presumably due to bad pixels and cosmic rays. These were removed spectrum-by-spectrum and band-by-band using sigma-clipping at 5-σ threshold and subsequent reinterpolation.
Resampling of the cubes to a common RA, Dec grid. The 2D spaxel grid delivered by the pipeline has a NX × NY size that depends on band (e.g., 37 × 37 for band 1A, 35 × 33 for band 2C, etc.) and the size of the spaxels is also band-dependent (0.13″, 0.17″, 0.20″, and 0.35″ in channels 1, 2, 3, 4). All cubes were resampled from interpolation to a common RA, Dec grid (that of band 1A).
Merging of data with different Ngroups. By combining data with different values of Ngroups, we optimized both S/N and usable spectral coverage. Specifically, for trailing side (Obs. 27) data, we kept Ngroups = 5 for bands 1A to 1C, Ngroups = 2 for band 2A and Ngroups = 1 for band 2B, 2C. (A single Ngroup value, independent of spaxel and spectel, was adopted for a given band.) For the leading side (Obs. 18) where signals are slightly lower due to lower surface temperatures (see below), we could use Ngroups = 2 for band 2B. Data in channels 3 and 4 remained unusable in all cases, being saturated even at Ngroups = 1.
Cube recentering. As for NIRSpec, spectral images are not centered, that is, Ganymede is shifted, typically by 0.05″–0.25”, with respect to the sky position indicated by the MT-RA, MT-Dec header keywords. For each spectel of each band, we computed the central position of the image using the method adopted for NIRSpec data, taking a threshold value of 10% of the maximum signal over the image, found to be optimum (see Sect. 2.1). For each band, we then adopted the median of the values determined from each spectel. If the approach was perfect, the so-determined central position should be exactly the same for the different bands associated with the same grating position (i.e., 1A and 2A, 1B and 2B, 1C and 2C), given that the 4 channels are observed simultaneously. In reality, residual differences (mostly in Dec) between channels at the 0.03–0.05″ level occurred, indicating that the recentering method is accurate to only ~1/3 of a spaxel. The cubes were then spatially shifted according to the determined central position, and resampled to a common RA, Dec grid (that of band 1A).
Calibration adjustment. Spectra extracted at a variety of positions on the common RA, Dec grid show slight flux discontinuities at band edges (typically a few percent within the disk, and somewhat more near the limb, a likely result of the pointing corrections being imperfect). To minimize flux discontinuities, we proceeded as follows. For each pair of adjacent bands (e.g., 1C/2A), the longer-wavelength channel was scaled in flux to match the shorter-wavelength channel in the overlapping region. In doing so, the flux scale in band 1A was taken (arbitrarily) as the reference. Although there is some arbitrariness in selecting this particular band, the calibration of bands 1A to 1C may be somewhat more trustworthy due to the larger number of retained groups. This led to correction factors usually of 0.97–1.03, occasionally reaching 1.08. Absolute flux uncertainties of ~5% are inconsequential for the analysis.
Wavelength calibration. Similarly to NIRSpec, we used the solar line spectrum from Hase et al. (2010) to calibrate the wavelength scale in bands 1A and 1B. At longer wavelengths, where solar lines are more rare and weak and where the spectrum becomes progressively dominated by thermal emission, this approach could not be applied, so the default wavelengths from the pipeline were adopted.
Finally, for most of the scientific analyses, we co-added the recentered and recalibrated data from the different dither positions to enhance signal-to-noise. In doing so, we admittedly lose one of the features enabled by dithering, that is, a better sampling of the spatial point spread function. Nonetheless, this possibility is anyways compromised by the pointing inaccuracies described above.
The possible contribution of straylight from Jupiter was found to be negligible. On the example of the leading side (Obs. 18) data, Fig. 1 shows the variation of mean radiance in each band (normalized to its maximum value) as a function of distance to Ganymede center. This radial distribution indicates a smooth decrease with distance, with no sign of plateauing at large distances that could indicate a “background” due to Jupiter straylight, except may be in band 2C at the ~0.01 level. In Band 2C, band-averaged equivalent brightness temperatures for Obs. 18 (resp. 27) are 145 K (resp. 153 K) at disk center and ~132 K (resp. 136 K) at a distance of 0.65” (5 spaxels) from disk center (see Fig. 14). At this mean wavelength (11 µm), a “contamination” level corresponding to 1% of the maximum flux is equivalent to a 0.2 K offset in the TB at disk center, and 0.35 K at 0.65″, and can be safely ignored in the analysis.
3 NIRSpec data analysis and results
3.1 NIRSpec reflectance spectra and maps
Figure 2 shows maps of the radiance at selected wavelengths of 3.6 µm (NRS 1) and 4.4 µm (NRS2; 3rd and 4th row). In the first row of this figure are shown Bond albedo (AB) maps at 1° resolution derived by de Kleer et al. (2021) from the Voyager-Galileo mosaic4. For each NIRSpec spaxel, we averaged the AB values of these maps projecting on that spaxel. The resulting “projected maps” of the Bond albedo are shown in the second row of Fig. 2, and will be used to study correlations of derived parameters with AB.
In Fig. 2 and some following figures, we show the open-closed-field-line boundary (OCFB). This is the boundary between Ganymede’s closed field line region, that is, where both ends of field lines from Ganymede intersect with Ganymede’s surface, and open field lines, that is, where one end of the field line intersects with Ganymede’s surface and the other end reaches Jupiter. The open-field-line region, which covers a relative large area over the poles, is populated with energetic ions and electrons of Jupiter’s magnetosphere and thus the surface is much more exposed to plasma irradiation than on the closed field line regions. The location of the OCFB is in the range 20–30° and 40–50° latitude N/S for the leading and trailing sides, respectively. It oscillates and additionally shifts latitudinally by up to 10° on the downstream side of Jupiter’s magnetospheric plasma flow (i.e., leading side) as a function of Ganymede’s position in Jupiter’s magnetosphere, that is, primarily with a period of about 10 hours (Saur et al. 2015). On the upstream (i.e., trailing) side, the variability might be larger, but a dedicated study has not been made. The OCFB shown on the figures is that calculated for the Juno PJ34 flyby of Ganymede, when the moon was near the center of the plasma sheet, that is, exposed to comparably large plasma ram pressure (Duling et al. 2022).
Maps of the reflectance are given in Fig. 3. The reflectance at each spaxel was determined from the I/F value, applying the photometric model of Oren & Nayar (1994). Indeed, it has been shown that the Lambert model is not appropriate for Ganymede at UV wavelengths (Alday et al. 2017), as well as in the near-IR (Ligier et al. 2019; King & Fletcher 2022), and we found that this turns out to be also the case for the NIRSpec data. The Oren-Nayar model is a widely used reflectivity model for rough diffuse surfaces, where the roughness is defined by a Gaussian distribution of facet slopes, with variance σ2. The Oren-Nayar model simplifies to the Lambert model (radiance ∝ cos(θi), where θi is the solar incidence angle) for σ = 0. Following Ligier et al. (2019), we adopted a value of σ = 20°. Varying σ by ± 5° (Ligier et al. 2019 derived values from 16±6° to 21±6°), the reflectance maps look similar. We did not correct for PSF filling effects which are significant for the spaxels near the limb. Therefore reflectance values are inaccurate for those spaxels.
Reflectance spectra from 2.86 to 5.28 µm across Ganymede’s leading and trailing hemispheres are shown as average spectra over latitude bins in Fig. 4. On average in this wavelength range, the trailing hemisphere is brighter than the leading hemisphere. This is due to a higher abundance of non-ice materials at the surface of the trailing hemisphere, contaminating the water ice. Some of these non-ice materials (such as opaque minerals) are darker than water ice in the visible and near infrared, but brighter than water ice in the mid-infrared (Hibbitts et al. 2003; Pappalardo et al. 2004; Calvin & Clark 1991; Sultana et al. 2023). The Bond albedo and 4.4-µm reflectance maps are indeed anti-correlated on both hemispheres (Figs. 2 and 3). Ganymede’s spectral reflectance variations are dominated by the relative surface abundance of water ice and non-ice materials.
The spectra averaged over latitude bins shown in Fig. 4 highlight several spectral features, with the highest signal-to-noise and spectral resolution available to date: 1) Strong spectral features due to water ice (absorption bands around 3.1, 4.5 µm; inter-bands at 3.65, 5 µm; Fresnel peaks at 2.95, 3.1, 3.2 µm); 2) CO2 absorption band at 4.26 µm together with an absorption band at 4.38 µm, which coincides in wavelength with 13CO2, but whose attribution is uncertain (see below); 3) the H2O2 absorption band at 3.505 µm analyzed by Trumbo et al. (2023); and 4) weak signatures at 3.426 µm and 3.51 µm, best seen at low latitudes on spectra of the trailing hemisphere.
The strongest spectral features are caused by water ice. Water ice absorption bands are centered at 2.94 and 3.1 µm for the fundamental symmetric (v1) and asymmetric stretching modes (v3), at 3.18 µm for the overtone of the bending mode (2v2), and at 4.48 µm for the combination of fundamental bending and libration modes (v2 + vL; Ockman 1958; Mastrapa et al. 2009). The narrow local maxima at 2.95 (weak), 3.1 and 3.2 µm are the Fresnel reflection peaks due to the strong increase of water ice refractive index near these maxima of absorption, which are characteristic of the presence of surficial water ice. The broad local maxima at 3.65 and 5 µm are due to light scattering by the water ice grains between absorption bands centered at 3.1, 4.48 and 6–6.2 µm. The intensity and position of the maximum around 3.65 µm is known to depend on the ice grain size (Hansen & McCord 2004) and temperature (Filacchione et al. 2016), and is also affected by the presence of non-ice materials. In the following paragraphs, this spectral feature will be called the “inter-band” (see Sect. 5.1).
Spectra of the dark (i.e., low albedo) terrains – in the trailing and at low latitudes of the leading hemisphere – present a reduction of the amplitude of the water ice spectral features whose positions are shifted to higher wavelengths (e.g., the position of the inter-band is shifted from 3.65 to 3.9 µm, Fig. 4). Maps in Fig. 3 show that the reflectance at 3.6 µm is the highest on the darkest terrains of the trailing hemisphere, whereas on the leading hemisphere, it is maximum at the poles, due to the higher abundance and possibly smaller grain size of water ice, causing an increased reflectance at the inter-band (see Sect. 5.1).
The absorption band at 4.26 µm can be firmly attributed to the asymmetric stretching mode of C=O in CO2 in solid phase. However, pure CO2 ice is not expected to be thermodynamically stable under Ganymede’s surface temperature and pressure conditions, so the CO2 molecule is trapped in a host material, or is interacting with other materials (see Sect. 5.2). Figure 4 shows that, the darker the terrains are (trailing versus leading hemispheres, and equatorial versus polar regions), the more the inter-band shifts to longer wavelengths. The CO2 band is also deeper on the equatorial regions than at the poles.
The faint (2% depth, Sect. 3.2.4) band at 4.38 µm coincides in wavelength with the corresponding stretching mode of13 CO2. However, the NIRSpec IFU flux calibration is not yet definitive, especially for the G395H grating, so definitive conclusions about the reality of individual features at the level of 1 or 2% cannot be drawn (Charles R. Proffitt, NIRSpec Team, priv. comm.). Another faint feature is observed at 4.995 µm, which is not observed in the MIRI spectra of Ganymede. This feature is an artifact seen in several NIRSpec modes that has been confirmed to us by the NIRSpec Team.
Spectra of Ganymede acquired with NIMS/Galileo and JIRAM/Juno instruments suggest the presence of several faint additional absorption features (e.g., at 3.4, 3.88, and 4.57 µm, McCord et al. 1998, at 3.01, 3.30, 3.38 and 3.42 µm, Mura et al. 2020). But it must be noted that these features from Juno/JIRAM are very shallow, and not visible in all spectra acquired by Juno. With the exception of the 3.01-µm water ice signature, which appears as a distortion in the blue wing of the Fresnel peak observed on the leading hemisphere (Fig. 4), none of them are firmly identified in JWST spectra. Two faint and narrow absorption bands at 3.426 and 3.51 µm (i.e., nearby the H2O2 band), that may be attributable to organic C–H stretch signatures, are present in the NIRSpec spectra. Their depths (about 1% for both features and for both hemispheres) do not show measurable trends with latitude. Their confirmation is pending a more robust calibration. The 3.88-µm band detected with a depth of 2–3% in NIMS/Galileo spectra (a possible signature of H2CO3, see discussion in Sect. 5.3) is not seen. A marginal signal at the 0.3–0.6% level is not excluded, but again a more robust calibration is needed.
 |
Fig. 1 Radial dependence of band-averaged radiances for Obs. 18. We note that because the RA, Dec grid extends up to ±2.34″, distances beyond this distance are only partially sampled. |
 |
Fig. 2 Ganymede Bond albedo and 3.6-µm, 4.4-µm radiance maps. From top to bottom: context Bond albedo maps derived by de Kleer et al. (2021) from Voyager-Galileo mosaic with the dashed green lines showing the open-closed-field line-boundary (Duling et al. 2022), resulting Bond albedo maps after projection in the NIRSpec IFU spaxels (see text), NIRSpec radiance images at 3.6 (NRS1) and 4.4 (NRS2) µm. In the context maps, dark Regiones are indicated by their names in yellow, and the blue circle shows the position of the Tros crater. Iso-latitude and longitude lines are drawn by increments of 30°. The color scale is different for each map, except for the Bond albedo maps. Left side: leading hemisphere. Right side: trailing hemisphere. |
 |
Fig. 3 Ganymede 3.6-µm and 4.4-µm reflectance maps. From top to bottom: reflectance images at 3.6 (NRS1) and 4.4 µm (NRS2) for Leading (left) and Trailing (right) hemispheres. Iso-latitude and longitude lines are drawn by increments of 30°. The color scale is different for each map. The reflectance at the spaxels near the limb is somewhat inaccurate, as no PSF correction was applied. |
 |
Fig. 4 NIRSpec reflectance spectra of Ganymede surface. Left: leading hemisphere. Right: trailing hemisphere. Averages over bins of latitudes are plotted, as labeled in the upper left panels. Thermal emission was not subtracted, so reflectance values are significantly overestimated at λ > 4.9 µm (dashed lines, see text). The absolute scale is also inaccurate for the highest latitudes due to PSF filling effects (see text). Spectral identifications of the three H2O Fresnel peaks (2.95, 3.1 and 3.2 µm), absorption bands of H2O2 (3.5 µm) and CO2 (4.26 µm) are indicated. The absorption signatures at the position of the 13CO2 band (4.38 µm), and those at 3.426 and 3.51 µm indicated by question marks, are most likely spurious (see text). The feature seen in absorption at 4.995 µm at the 2% level is not of Ganymede origin as it is not observed in MIRI spectra. The spectral continuum is dominated by water ice for the mid and high latitudes of the leading hemisphere, with local maxima at 3.65 and 5 µm (H2O inter-bands) and a minimum at 4.45 µm (H2O absorption band). In other regions, the higher concentration of non-ice materials (minerals, etc.) induces the increase of the reflectance with wavelength, the reduction of the amplitude of the water ice spectral features, and the shift of the water inter-band to 3.9 µm. |
3.2 Spectral analysis of NIRSpec data
The relative strength, position and shapes of the above mentioned spectral features are diagnostic of the physical and compositional properties of the surface which vary across the disk (e.g., Ligier et al. 2019; King & Fletcher 2022). Noticeable in Fig. 4 is the variation of the CO2 band shape and position with latitude, shifting to higher wavelengths at the poles, thereby confirming Juno/JIRAM results (Mura et al. 2020). In this section, we describe how we characterized each band to study their spectral and spatial variations.
3.2.1 Fresnel reflection peaks and H2O 4.5-µm water band
We characterized the Fresnel reflection peak by measuring the central wavelengths of the two components at 3.1 and 3.2 µm (referred to as as peak 1 and peak 2, respectively) and the equivalent width of the whole reflection peak. Formally, the equivalent width is defined as:
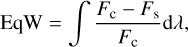 (1)
(1)
where Fs is the intensity (here I/F) of the spectrum, and Fc is the continuum beneath the reflectivity peaks. In other words, the equivalent width is the peak area normalized by the underlying continuum. In the following, the equivalent width (in µm) will be referred to as the peak area.
To determine the central wavelengths of the Fresnel peaks, we modeled the I/F emission in the 3.0–3.4 µm range by the sum of two Gaussians and a 4th-order polynomial. The Fresnel-peak area was computed from 3.0 to 3.27 µm, taking as underlying continuum a straight line passing through the mean of the intensity in the 2.97–3.0 µm and 3.27–3.30 µm adjacent ranges. This was done for each spaxel. The resulting distributions are shown in Fig. 5.
Similar JWST/NIRSpec maps of the Fresnel-peak area were previously presented in Trumbo et al. (2023). The Fresnel-peak area is lower on the trailing hemisphere (between 0.0032–0.04 µm) than on the leading hemisphere (between 0.03 to 0.12 µm). Both hemispheres present strong latitudinal, as well as longitudinal, variations that correlate with the Bond albedo (Fig. 6C). The Fresnel peak area is maximum in the polar regions of the leading hemisphere. Noticeable is the local maximum on the Tros crater (27°W, 11°N). The Fresnel peak area is small on the Galileo, Perrine, and Nicholson dark regiones, comparing to their surroundings. Interestingly, the distribution of the Fresnel peak area, which is probing ice at the very top surface, closely matches the water ice distribution inferred from the depth of the H2O 1.65 µm and 2.02 µm bands (Ligier et al. 2019; King & Fletcher 2022), which are probing ice below the surface. It is also in good agreement with the distribution of the 4.5-µm band-depth proxy shown in Fig. 7 (see definition in the caption), characterizing shallower sub-surface layers than the 1.65 µm and 2.02 µm bands. Therefore, the maps shown here (Fig. 5) are indicative of the presence of water ice not only at the top surface but also at shallow depth. However, one should keep in mind that the ice band depths and Fresnel peak area strongly depend on the way ice is mixed with other components (Ciarniello et al. 2021), and also on the crystallinity of the ice (Mastrapa et al. 2009). Therefore, their variations over the disk cannot be uniquely interpreted in terms of variations of areal abundance of water ice, and the potential influences of the ice crystallinity and of the mixing mode with non-ice materials should be kept in mind.
The distribution of the Fresnel peak area on the trailing side shows a “bull’s-eye” pattern (Fig. A.1) with the minimum centered near the equator (261°W, 7°N, 13.21 h local time) and inside the dark Melotte Regio (245°W, 12°S). The same pattern is observed on near-IR H2O-ice data of Ganymede (Ligier et al. 2019) and is also observed for Europa, with the difference that for Europa the pattern is centered on the apex of the trailing hemisphere (270° W). For Europa, which does not possess an intrinsic magnetic field, this distribution might be related to the electron precipitation pattern on the surface (Liuzzo et al. 2020), or to the implantation of iogenic sulfur ions (Cassidy et al. 2013).
The Fresnel peak area and the Bond albedo correlate well, but with a linear correlation which is different for the two hemispheres (Fig. 6C). One can notice high peak area values near the morning limb of the trailing hemisphere (longitudes 310–330° W), which are in the range of those measured in the leading side in regions with similar Bond albedo (Fig. 6C). This ice excess is not observed on the H2O 4.5-µm map (Fig. 7).
The central wavelength of the Fresnel peak 1 shows striking regional variations (Fig. 5). The mean value is 3232.3 cm−1 (3.0938 µm) for both hemispheres. It is significantly blueshifted (by 2 cm−1, i.e., 0.0019 µm, with respect to the mean) at the north polar cap of the leading hemisphere. This trend is not seen at the south polar cap of the leading hemisphere nor for the trailing hemisphere. In addition a trend for redshifted central wavelengths for earlier local times is observed on both hemispheres. The central wavelength of Fresnel peak 2 (not shown in Fig. 5) presents similar regional variations on the leading side (no conclusions can be drawn for the trailing side due to the low S/N) and is on average 3124.7/3125.7 cm−1 (3.2003/3.1993 µm) for leading/trailing hemispheres.
 |
Fig. 5 Spatial variations of the Fresnel reflection-peak properties. From top to bottom: context Bond albedo maps, maps of the area of Fresnel reflection peak and central wavelength of Fresnel peak 1 from NIRSpec (NRS1) data. Maps of the leading and trailing hemispheres are shown on the left and right, respectively. |
 |
Fig. 6 Correlations with Bond albedo. From top to bottom: A) CO2 band area, B) CO2 band center, and C) Fresnel-peak area (i.e., EqW). Data for the leading and trailing hemispheres are shown with blue and red symbols, respectively. Filled and open dots are for latitudes lower and higher than 40° N/S, respectively. Data in the morning limb of the Trailing hemisphere (namely longitudes > 320°) are shown with the star symbol. |
 |
Fig. 7 Spatial variations of the H2O 4.5-µm band-depth indicator. This band depth BD is calculated with respect to the reflectance value at 4.205 µm (BD = (1−R4.48 µm/R4.205 µm)× 100, where R4.48 µm and R4.205 µm are the reflectance values at 4.48 and 4.205 µm, respectively). Negative values indicate a significant contribution of non-ice material in the continuum. |
3.2.2 Inter-band
The wavelength of the continuum reflectance peak (referred to as the inter-band) longward of 3.6 µm was determined by fitting the 3.3–4.0 µm I/F spectra by a 6th-order polynomial, and finding the position of the maximum of the fitted curve. The inferred distributions are plotted in Fig. 8 (bottom maps). On the leading hemisphere, the distribution of the inter-band wavelength position shows a strong contrast between high and mid or equatorial latitudes and overall follows the distribution of the Fresnel-peak area (Fig. 5), with a minimum value of 3.65 µm at the highest latitudes (>60° N/S), and a mean value of 3.93 µm at equatorial latitudes. The bright (icy) Tros crater also stands out. Latitudinal variations are also observed for the trailing hemisphere, with a mean value of 3.95 µm in the equatorial regions, and in the range 3.81–3.92 µm poleward of 40° N/S, consistent with the ice excess observed in polar regions.
Figure 8 (top) also shows maps of the amplitude of the reflectance peak at the position of the inter-band, measured in % with respect to the reflectance at 3.28 µm:
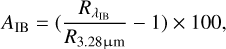 (2)
(2)
where 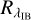 and R3.28μm are the reflectance values at the wave length of the inter-band and at 3.28 µm, respectively. For both hemispheres the inter-band is more intense in the north polar caps compared to the south polar caps.
and R3.28μm are the reflectance values at the wave length of the inter-band and at 3.28 µm, respectively. For both hemispheres the inter-band is more intense in the north polar caps compared to the south polar caps.
 |
Fig. 8 Spatial variations of 3.6–3.9 µm inter-band properties. Inter-band amplitude AIB (top) and wavelength position (bottom) for the leading (left) and trailing (right) hemispheres. |
3.2.3 CO2 band
The shape of the CO2 band at ~4.26 µm is asymmetric. Therefore, to best measure the position, shape, and width of the band, the band was fitted by an asymmetric Gaussian, composed of two adjacent half Gaussians of the same peak intensity, and peak wavelength, but of different width. This method allows us also to measure the asymmetry of the band through the asymmetry parameter asp, defined as the ratio between the width of the half-Gaussian in the red side to that in the blue side (see example in Fig. 9). We considered the spectral region from 4.2 to 4.5 µm (excluding the 4.335–4.40 µm range where the 4.38-µm feature is present) for each spaxel on Ganymede, and fitted the combination of a 4th-order polynomial and an asymmetric Gaussian through curve fitting. The CO2 band depth is measured with respect to the local continuum in %.
Figure 10 shows averages of CO2 spectra over latitude bins, normalized to the underlying continuum. The results of the asymmetric Gaussian fit are given in Table 2. For these averages, the CO2 band depth varies from 9 to 18% on the trailing side, and from 13 to 19% on the leading side, increasing with decreasing latitudes, except for the leading side where a deep CO2 band is observed poleward of 60° N. The band center is at smaller wavelengths in the trailing side (varying in the range 4.2571–4.2640 µm) than in the leading side (4.2600–4.2695 µm) especially at low to mid latitudes (<35°S/N), and shifts toward larger wavelengths as the latitude increases. The band shape also changes with latitude, getting narrower and more asymmetric as we reach polar latitudes.
Figure 11 shows maps of CO2 band depth, band center position and band width across the two hemispheres. The CO2 band depth ranges from 11 to 21%, with a median at 16% for the leading hemisphere, and from 8 to 22% with a median at 15% for the trailing hemisphere. These values are overall consistent with the NIMS/Galileo measurements (values of 5 to 20%) which probed primarily the anti-Jovian hemisphere but acquired a few dataset on the leading and trailing side (Hibbitts et al. 2003). Therefore, JWST data confirm that there is no large leading/trailing side difference in the depth of the CO2 band, nor is there a difference with the anti-Jovian hemisphere. However, the NIRSpec data show that regions poleward of 30°N/S on the trailing side present lower CO2 band depths, comparatively to the leading side. This is clearly shown in the scatter plot of Fig. 12, where the CO2 band depth is plotted as a function of latitude. Poleward of 30° N/S, the band depth slowly varies with latitude on the leading side, in contrast to the trailing side which shows a steep drop with increasing latitude. In addition, the CO2 band depth exhibits striking longitudinal variations on the trailing side, causing a large scatter at mid and equatorial latitudes in Fig. 12.
In the anti-Jovian hemisphere from NIMS/Galileo data, the largest band depths of CO2 were found to be generally associated with the less icy regions (?). This trend is observed for the trailing hemisphere (see CO2 maps in Fig. 11 compared to the Bond albedo context map in Fig. 2). The scatter plot in Fig. 6A shows a moderate anticorrelation between CO2 band area (i.e., equivalent width) and Bond albedo for the trailing hemisphere (Spearman rank correlation r =−0.56 with 8.2 σ significance), whereas this trend is less obvious for the leading hemisphere (r = −0.26 with 3.9 σ significance). However, when considering only equatorial regions (<40°N/S) or within the open-closed-field line-boundary, the relationship between the two quantities is weak to absent for both hemispheres (2–4 σ significance). A similar result is obtained when looking how the CO2 band area correlates with surface ice abundance (Fig. E.1A), using the Fresnel peak area as a proxy (see Sect. 3.2.1). In summary, latitudinal and regional trends are observed for the CO2 band area, but the link with ice abundance is not observed.
The trends between band depth, width and position observed in the latitudinal averages are seen at the pixel scale in the maps. This is conspicuous for the trailing hemisphere which presents large CO2 band depth variations at latitudes <30° that are associated with variations in band center, band width (Fig. 11) and band asymmetry parameter asp (not plotted in Fig. 11). The anticorrelations between asp and the band center position (when expressed in wavelength), and between the band width and the band center position are shown as scatter plots in Fig. 13. It is striking to see how the data points at the poles (especially for the leading north pole) are detached from the rest of the data, indicative of the peculiar physical state of CO2 in this region. At the poles, the band asymmetry parameter asp reaches values below 0.4, and the band width is up to 40% lower than in equatorial regions.
Both hemispheres show a striking trend between CO2 band center position and Bond albedo (r = 0.62 and 0.66 with a significance of 9.1 σ and 9.3 σ, for leading and trailing, respectively), with the CO2 band center shifting toward longer wavelengths as the surface brightness increases (Fig. 6B). Unlike the CO2 band area, the trend is also present when considering only the equatorial regions (r = 0.47 and 0.43 with a significance of 6.1 σ and 5.5 σ, for leading and trailing, respectively). Since the surface brightness is correlated with water ice abundance (Fig. 6C) a similar correlation is expected between the CO2 band center and the ice abundance (i.e., Fresnel peak area). This is indeed observed (at 6−7 σ) for the leading hemisphere even when considering only equatorial latitudes (Fig. E.1B). However, the equatorial latitudes (<40°N/S) of the trailing hemisphere do not show a significant trend between CO2 band center and ice abundance (r = 0.20, 2.4 σ), although the ice-rich polar regions do present peculiar CO2 spectra, as discussed in the previous paragraph. So, in summary, the CO2 band center and shape show a strong relationship with surface brightness for both hemispheres. Their correlation with the ice abundance is only seen on the leading hemisphere, and at the poles of the trailing hemisphere.
 |
Fig. 9 Illustration of asymmetric Gaussian fitting of the CO2 band. In black, a latitude average NIRSpec spectrum (30–45°S, leading, in Fig. 10). In blue and red dotted lines, the two fitted half-Gaussians, with their width (HWHPblue and HWHPred, respectively) indicated. The vertical line shows the central position of the fitted asymmetric Gaussian. |
CO2 band parameters for average spectra over bins of latitudes.
 |
Fig. 10 CO2 4.26-µm band spectra as a function of latitude. CO2 band normalized to the underlying continuum, from averages over latitude bins of I/F spectra. Latitude bins are given in the right panels, with spectra from southern latitudes drawn in dashed lines and northern latitudes in solid lines. The vertical lines show the central positions (given in Table 2) of the fitted asymmetric Gaussians with the same color code as for the spectra. |
 |
Fig. 11 Spatial variations of CO2 4.26-µm band properties. Maps of CO2 band depth (top), band center (middle), and band width (bottom) from NIRSpec NRS2 data. Maps of the leading and trailing hemispheres are shown on the left and right, respectively. |
 |
Fig. 12 Dependence of CO2 band depth with latitude. Blue dots and red dots are used for the leading and trailing hemispheres, respectively. Each data point corresponds to a spaxel in Fig. 11. Empty symbols correspond to spaxels which are not entirely on Ganymede disk and can be less reliable. |
3.2.4 The 4.38-µm band
A faint signature is observed at the wavelength of the 4.38-µm 13CO2 band. We characterized the depth (in %) and position of this band fitting the 4.29–4.50 µm region in the I/F spectra by the combination of a Gaussian and a third-order polynomial. The mean central wavelength of the band over the disk is 4.3779 µm (leading) and 4.3766 µm (trailing) with a standard deviation of 0.0025 µm, so in average at 4.377 µm. The depth does not show significant spaxel-to-spaxel variations over the two hemispheres, and has a mean value of 1.67+0.39% and 1.53+0.35% on the leading and trailing sides, respectively. In addition to the uncertain reality of features at 1-2% level in NIRSPec spectra discussed in Sect. 3.1, this faint feature cannot be firmly attributed to 13CO2 as spatial variations following those observed for the CO2 band (Sect. 3.2.3) are not observed. In addition, this band is not present when using the data reduction procedure of Trumbo et al. (2023), where Ganymede spectra are divided (for flux calibration and solar-line removal) by those acquired on a solar-type G0V star also observed with JWST/NIRSpec and calibrated using the same JWST pipeline as for Ganymede. It is also worth noting that this feature at 4.380 was also only visible in one Juno/JIRAM spectrum out of seven in Mura et al. (2020), so it was not firmly ascribed to13 CO2.
 |
Fig. 13 Correlations between CO2 band width and band center, and between asymmetry parameter asp and band center. Each data point corresponds to one NIRSpec spaxel on the Ganymede disk. The different symbols and colors indicate the latitude range as given in the inset. Upper plots: leading hemisphere; bottom plots: trailing hemisphere. |
4 MIRI data analysis and modeling
4.1 Qualitative analysis of spectra
The 4.9–11.7 µm range corresponds to the overlap of the solar reflected and thermal components. We show sample spectra at two spatial positions and for both visits in Fig. 14. Spectra are calibrated either in brightness temperature (left panels) or radiance factor (I/F, right panels). Radiance factors are typically 5–10% in band 1A (and larger on trailing side than leading, unlike the behavior in the visible), and the fact that they sharply increase above unity beyond ~7 µm demonstrates the dominance of the thermal component there. Beyond this expected behavior, a remarkable feature is the monotonic (and quasi-linear) decrease of the brightness temperatures with increasing wavelength (λ), by more than 10 K from 7 µm to 11 µm at disk center. Qualitatively, this can result from at least three effects, which may well be at play simultaneously, and stem from the non-linear character of the Planck function5.
A spectrally constant but less than unity spectral emissivity.
A decrease of the spectral emissivity with increasing wavelength.
Planck-weighted mixing of a variety of surface temperatures within the PSF. This effect may be amplified by the fact that the PSF width increases with λ, causing long wavelengths to “see” more near-limb (i.e., colder) terrains than short-wavelengths for points within the disk.
The other feature obvious in Fig. 14 is the presence of an absorption band near 5.9 µm, which shows up as an inflexion in the brightness temperatures or radiance factors there. A first assessment of the band parameters is shown in Fig. 15. For this, for the two disk center spectra, we fit the observed radiances by the sum of the two components, where the thermal one is modeled phenomenologically by a single surface temperature Tsurf and spectral emissivity s (case 1 above), and the solar component is characterized by a single free parameter, the I/F radiance factor (Rad f). Tsurf, s, and Rad f are found from Levenberg-Marquardt minimization. This approach, whose physical meaning is admittedly limited – given the unrealistically large (resp. low) values of Tsurf (resp. s) – confirms a large band depth and width (~20% and ~1 µm in these examples) and permits the assessment of the relative contribution of the thermal and solar reflected components, which show crossover near 5.5 µm.
 |
Fig. 14 MIRI sample spectra at 4.9–11.7 µm. Shown are spectra from Obs. 18 (leading hemisphere, solid line) and 27 (trailing hemisphere, dashed line), at reconstructed disk center (spaxel 18, 18, top) and at off-sets RA = 0.65″, Dec = 0″ from this position (spaxel 24, 18, bottom). Spectra are calibrated either in brightness temperature (TB, left panels) with different colors illustrating different bands from 1A to 2C, or radiance factor (I/F, right panels). They are not corrected for any account of “filling factor” associated with the fact that for positions close to limb, the PSF partly samples empty space. |
 |
Fig. 15 Example of spectral fits to MIRI data. Left panels: fit of disk-center spectra (spaxel 18, 18) in Obs. 18 (leading, top) and 27 (trailing, bottom) in radiance units with the sum of thermal and solar reflected components. Black: data. Red: thermal component. Green: solar reflected component. Blue: total model. Right panels: ratios between observations and models. |
 |
Fig. 16 Brightness temperature and Bond albedo maps. Maps of the 8.25-µm (top) and 11.25-µm (middle) brightness temperature, and spaxel-averaged Bond albedo maps (bottom) from de Kleer et al. (2021; see text). Left: leading side (Obs. 18). Right: trailing side (Obs. 27). |
4.2 Thermal maps and models
We now analyze the thermal emission continuum, focusing on the long-wavelength part (>8 µm) unaffected by the 5.9-µm band. To describe the TB decrease with λ we consider two representative intervals, 8.0–8.5 µm and 11.0–11.5 µm and averaged the TB in those, yielding the so-called TB,8,25 and TB,11.25 brightness temperatures. Figure 16 shows maps of TB,8.25 and TB,11.25 for the two datasets, along with “projected maps” of the Bond albedos (AB). To obtain the latter we used the 1° resolution Bond albedo map from de Kleer et al. (2021); for each observed spaxel, we averaged (in a (1-AB)0.25 sense) the AB values of the map elements projecting into that spaxel. As indicated above, the four dithers were averaged at this step and in future analyses. Rms differences in TB,8,25 and TB,11.25 between data from individual dithers and their average are typically 0.4 – 0.7 K, that is, comparable and somewhat smaller than the best fits we achieve (see below).
Brightness temperatures are consistently higher on the trailing vs leading side, as may be expected from the somewhat darker albedos there. However, correlations between TB’s and Bond’s albedos, while present, are not very pronounced (Spearman correlation coefficient r = −0.50 and 5.7 σ significance on the trailing side, r = −0.23 and 2.7 σ on the leading), being presumably erased by PSF smoothing and dwarfed by other effects (latitude and local time variability).
Focusing on the TB,8.25 maps, we performed standard thermophysical modeling, separately for the two observations. The main model parameters are (i) the thermal inertia (Γ, assumed constant over one side, parameterized by the thermophysical parameter Θ (Spencer et al. 1989)6; for Ganymede at 4.96 au, Θ =1 typically corresponds to Γ = 75 SI units (J m−2 K−1 s−0.5) and (ii) the Bond albedo; we either let it be a free parameter (constant for a given side) or use the projected Bond albedo maps from Fig. 16, as such or with an adjustable scaling factor. A Bond emissivity (and a spectrally constant emissivity) ɛ = 0.90 as adopted, that is, we purposedly do not include spectral emissivity effects. As detailed below, we also introduced surface roughness in the model using a description of slopes. For each model, local fluxes were calculated on the 0.13″ spaxel grid and then convolved by the beam, for which we used FWHM (arcsec) = 0.0328 × λ (µm) and a simplified description of the secondary Airy pattern, and finally converted in a 8.25 µm brightness temperature. Model parameters were determined by Levenberg-Marquardt fit.
Data (in the form of TB,8.25 vs local time and TB vs latitude) are displayed in the first column of Fig. F.1 and in the first and second columns of Fig. 17. They clearly show that peak TB,8.25 occur near the equator and near 12:30 pm local time, suggestive of low thermal inertia effects. Results for the best-fit models without roughness are shown in Cols. 2–4 of Fig. F.1, for the three descriptions of the Bond albedo respectively. A common feature of these models is that they overestimate the diurnal variation of TB,8.25, overpredicting the temperatures near noon and underpredicting the dawn and dusk temperatures, leading to relatively large model-observation residuals (2–3.5 K rms). Temperatures at high latitudes (~50°) are also underpredicted. Increasing the thermal inertia could improve the diurnal contrast, but would unacceptably shift the maximum temperatures toward afternoon hours and further lower the model high-latitude temperatures. We also note that models using the fixed Bond albedo map from de Kleer et al. (2021) result in a zero thermal inertia and provide a relatively bad fit. They can be improved by scaling the AB by factors of 0.60 (trailing) − 0.80 (leading) but the problem of the too large diurnal contrast remains.
Including surface roughness is a possible solution to improve fits. The effect of a distribution of local surface slopes at any scale within each spaxel is to decrease temperatures and emission near disk center (i.e, subsolar point) and increase them near the limb (due to facets preferentially oriented toward the Sun). We followed the description of Hapke (1984) for macroscopic roughness, in which facets (with dimensions much larger than particle size) are randomly tilted from the local smooth surface normal, with a uniform distribution in azimuth and a Gaussian distribution in zenith angles. The distribution of slopes is characterized by a mean slope angle s (noted  and defined by Eqs. (5) and (44) of Hapke 1984). At a given position on Ganymede, a facet with a given orientation owns an “effective” latitude and longitude, which determines its diurnal insolation pattern and local time. In practice, we generated 10 000 facets with random orientation on a sphere and calculated their temperature according to their effective coordinates. Then at each spaxel position, Planck emissions from these 10 000 facets were combined, with a weighting defined by the angle between the facet normal and the local smooth surface normal (i.e., Eq. (44) from Hapke 1984). This approach thus adds one free parameter, s. As shown in Cols. 5–7 of Fig. F.1 and in Cols. 3-4 of Fig. 17, substantially improved fits are achieved, with rms residuals below 1 K in the best cases, and subdued systematic trends in the residuals. Mean slopes s = 15–20° on the trailing side and s = 20–25° on the leading are found, somewhat lower but reasonably consistent with the surface roughness estimates from optical photometry using the same Hapke definition of slopes (s = 35° and 28°, respectively, Domingue & Verbiscer 1997). Although in the model, slopes may occur at any scale smaller than the spaxel (450 km across), the relatively large values of s probably result from roughness at the scale of tens of meters at most, as for example stereo and photoclinometric analysis of Galileo and Voyager images of Ganymede indicate mean slopes of 3.5–8° only at 630 m scale (Berquin et al. 2013). Presumably, the roughness measured here pertains to scales of 0.1 mm–10 cm, as indicated by roughness statistics of the lunar surface (Helfenstein & Shepard 1999).
and defined by Eqs. (5) and (44) of Hapke 1984). At a given position on Ganymede, a facet with a given orientation owns an “effective” latitude and longitude, which determines its diurnal insolation pattern and local time. In practice, we generated 10 000 facets with random orientation on a sphere and calculated their temperature according to their effective coordinates. Then at each spaxel position, Planck emissions from these 10 000 facets were combined, with a weighting defined by the angle between the facet normal and the local smooth surface normal (i.e., Eq. (44) from Hapke 1984). This approach thus adds one free parameter, s. As shown in Cols. 5–7 of Fig. F.1 and in Cols. 3-4 of Fig. 17, substantially improved fits are achieved, with rms residuals below 1 K in the best cases, and subdued systematic trends in the residuals. Mean slopes s = 15–20° on the trailing side and s = 20–25° on the leading are found, somewhat lower but reasonably consistent with the surface roughness estimates from optical photometry using the same Hapke definition of slopes (s = 35° and 28°, respectively, Domingue & Verbiscer 1997). Although in the model, slopes may occur at any scale smaller than the spaxel (450 km across), the relatively large values of s probably result from roughness at the scale of tens of meters at most, as for example stereo and photoclinometric analysis of Galileo and Voyager images of Ganymede indicate mean slopes of 3.5–8° only at 630 m scale (Berquin et al. 2013). Presumably, the roughness measured here pertains to scales of 0.1 mm–10 cm, as indicated by roughness statistics of the lunar surface (Helfenstein & Shepard 1999).
Once again, we find that the fixed Bond albedo map, being “too bright”, gives worse results and drives zero thermal inertia, and recovering good fits requires multiplying the AB map by factors of 0.60–0.75. The best fits in this case are shown in Fig.17. We do not have a simple interpretation for this, since the de Kleer et al. (2021) map is based on well-documented maps of normal albedos and phase integrals from Voyager measurements. A possible explanation is that our thermal models describe roughness purely as a slope effect, and do not account for other more complex effects associated with topography, such as shadowing and self-heating due to scattering and reabsorption of solar and thermal radiation within craters (see e.g., Rozitis & Green 2011). Applying such more advanced thermophysical models is left to future investigations.
For now, restricting ourselves to the two best classes of models (Cols. 5 and 7 in Fig. F.1) and Col. 3 in Fig. 17, the suite of solutions indicates thermal inertia parameters Θ = 0.3–0.5, that is, thermal inertias in the range Γ = 20−40 SI, with no obvious difference between leading and trailing side. These values are slightly below the “canonical” value Γ = 70 derived from Voyager/IRIS spectra over 7−50 µm (Spencer 1987; Spencer et al. 1989), but further analyses including Galileo/PPR data have indicated that two-component models provided better fits, with end member thermal inertias values between 16 (associated with dust) and 1000 (ice), with dark and grooved terrains covering the Γ = 70−150 range (Pappalardo et al. 2004; see also de Kleer et al. 2021). Given that PPR covered the 17-110µm range and that radiation at the shorter wavelengths is progressively dominated by warmer (i.e., lower thermal inertia, for dayside measurements) areas, it is probably not surprising that the Γ values we derive at 8.25 µm are in the lower range of the PPR results. Similarly, de Kleer et al. (2021) determined Γ = 400−800 from ALMA data at 0.9−3 mm; such wavelengths sample all temperatures equally and (unlike the mid-IR emission which originates from the topmost surface layers) probe the subsurface, where material compaction may account for the higher thermal inertias. Low thermal inertias at the surface are probably indicative of material porosity.
We searched for thermal anomalies, by examining the difference between observed and modeled TB,8.25 for one of the best models. The top two panels of Fig. 18 do not indicate clear outliers in the difference, although there is a suggestion that the model overestimates the observed TB,8.25 in the high northern and southern latitudes, by 2–3 K. If real, these residuals may be due to locally higher than assumed albedos, larger thermal inertia, or higher Bond emissivity, all of which leading to lower TB.
However, the main drawback of the models tailored to the 8.25-µm emission is that as such they do not match the 11.25 µm fluxes. This is visualized in the bottom two rows of Fig. 18 where the observed and modeled TB,8.25 – TB,11,25 are compared for the rough model using the rescaled Bond albedos. As anticipated qualitatively in Sec. 4.1, the mixing of temperatures does produce a decrease of TB with increasing λ, but our calculated temperatures differences are too small (2–5 K vs 6–8 K observed) and strikingly do not show the observed dependence with incidence angles. In the model, maximum TB,8.25 – TB,11.25 occur near the terminators (where temperature gradients are larger), but this behavior (also obtained for the non-rough models) is not seen in the data, which rather show a mild decrease of TB,8.25 – TB,11.25 from the subsolar region to the terminators. We note that based on Voyager-IRIS data, Spencer (1987) also found that “the Ganymede spectrum slopes7 cannot be due primarily to topographic temperature contrasts. The main effect of topography on the thermal emission spectrum is to increase the spectrum slope with increasing solar incidence angle, a trend not observed on Ganymede”. The similarity of the second row of Fig. 18 with Fig. 19 of Spencer (1987) is noteworthy. As shown in the third row of Fig. 18, the observed TB,8.5 – TB,11.25 decreases from dawn to dusk, again a behavior not reproduced in our model. We speculate that the TB negative gradient with λ is dominated by (e.g., angle-dependent) spectral emissivity effects, which, for a reason that remains unclear at this point, mask the expected behavior from thermophysical model. Based on Fig. 18, these emissivity effects deplete the TB,11.25 by ~5 K, which for TB,11.25 ~ 145 K, corresponds to a spectral emissivity of ~0.75. More elaborate thermophysical models than presented here are probably needed to address this question with more realism.
 |
Fig. 17 Observed and modeled 8.25-µm brightness temperature (TB). 8.25-µm TB for Obs. 18 (leading side, first row) and Obs. 27 (trailing side, second row), plotted as a function of local time (first column) or latitude (second column). The data are color-coded according to latitude (i.e., to equal values of the latitude difference from the sub-observer point) in the TB vs local time plots, and according to local time in the TB vs latitude plots. In the third and fourth columns, the data are compared to one of the best models, that includes both a rescaling of the Bond albedo map and surface roughess (see text). In these panels, data are in black, models in red, and the data minus model difference in blue, with the 0 value indicated by the dashed line. Parameter values and rms of fit are indicated in each panel. |
 |
Fig. 18 Difference plots. Top: difference between observed and modeled TB,8.25, for the rough, Bond albedo-rescaled, model (last column of Fig. F.1). Middle: TB,8.25 – TB,11.25 brightness temperature difference as a function of incidence angle. Bottom: TB,8.25 – TB,11.25 brightness temperature difference as a function of local time. Black: data. Red: model. Left: leading side (Obs. 18). Right: trailing side (Obs. 27). |
4.3 5-µm reflectance and 5.9-µm band maps
The blue part of the MIRI spectra shows the onset of solar reflected radiation and evidence for a 5.9-µm absorption band (Fig. 15). Given the difficulties, outlined above, to fit simultaneously the spatial distribution of TB’s and their spectral dependence, we now restrict the modeling to the 4.9–8.5 µm and fit the spectra on a spaxel-by-spaxel basis, using the three types of continuum models envisaged above, with the following free parameters:
Model 1 (lower than unit emissivity): surface temperature (T1), spectrally constant emissivity (ɛ1), spectrally constant I/F reflectivity (Radf1).
Model 2 (wavelength-dependent emissivity): surface temperature (T2), spectral emissivity gradient (
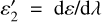 , in µm−1), spectrally constant I/F reflectivity (Radf2). In this case, the emissivity is taken as 1.0 at 4.9 µm and
, in µm−1), spectrally constant I/F reflectivity (Radf2). In this case, the emissivity is taken as 1.0 at 4.9 µm and 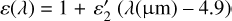 .
.Model 3 (distribution of temperatures): central surface temperature (T3) and temperature range (±∆T), and spectrally constant I/F reflectivity (Radf3). In this case, we consider a distribution of surface temperatures T over T3±3∆T, assigning a Gaussian weight to each contribution according to
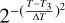 .
.
The three models are meant to represent end-member solutions for the spectral slope over 4.9–8.5 µm, providing robustness on the 5.9-µm band characterization. Unlike the I/F reflectivities which have a clear physical meaning, the other parameters are more phenomenological; in particular ɛ1, 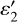 , and ∆T are proxies for the amount of deviation of the thermal part of the spectrum from a blackbody; for example, ɛ1 ~1 (resp. << 1),
, and ∆T are proxies for the amount of deviation of the thermal part of the spectrum from a blackbody; for example, ɛ1 ~1 (resp. << 1), 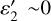 (resp. << 0), and small (resp. large) ∆T are associated with a weak (resp. large) departure from Planck emission. For each of the three models, Fig. F.2 shows maps of three model fit parameters, and of the rms residuals between observation and models, expressed in brightness temperature units. Such residuals are on the order of 0.3–0.7 K at most spaxels. As visible in the first column of Fig. F.2, T1, T2, and T3 are correlated to the surface temperature, with T2 being the closest representation of TB,8.25 (see Fig. 16). Given also that model 2 yields the best rms fit (see Fig. F.2) it is adopted as the nominal one. Median values of
(resp. << 0), and small (resp. large) ∆T are associated with a weak (resp. large) departure from Planck emission. For each of the three models, Fig. F.2 shows maps of three model fit parameters, and of the rms residuals between observation and models, expressed in brightness temperature units. Such residuals are on the order of 0.3–0.7 K at most spaxels. As visible in the first column of Fig. F.2, T1, T2, and T3 are correlated to the surface temperature, with T2 being the closest representation of TB,8.25 (see Fig. 16). Given also that model 2 yields the best rms fit (see Fig. F.2) it is adopted as the nominal one. Median values of 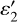 are –0.061 and –0.058 µm−1 for Obs. 18 and 27, respectively, indicative of a decrease of the spectral emis-sivity from 1 at 4.9 µm to ~0.81 at 8 µm. The sign of
are –0.061 and –0.058 µm−1 for Obs. 18 and 27, respectively, indicative of a decrease of the spectral emis-sivity from 1 at 4.9 µm to ~0.81 at 8 µm. The sign of 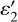 is negative as expected, and its magnitude is large but reasonable given the end-member character of the model. The last column of Fig. F.2 shows the reflectance. To convert I/F to reflectance, we followed Ligier et al. (2019) and King & Fletcher (2022) in adopting the Oren & Nayar (1994) model which generalizes the Lambert model for rough surfaces. Specifically, we used the small phase angle limit of the model and adopted a surface roughness s = 20°, which (perhaps coincidentally given that the definitions of roughness are not exactly the same) matches both our above estimate of the slopes based on the thermophysical model and the near-IR results of Ligier et al. (2019). The resulting reflectances appear anticorrelated with the Bond albedo (see Fig. 16), with a Spearman correlation coefficient of r = –0.62 (trailing) to –0.56 (leading) and a significance level of 6–7 σ. The trailing side also appears to be ~1.5 times more 5-µm reflective than the leading (median reflectances of 0.092 and 0.061, respectively), while being ~7 K warmer. Both aspects argue for 5-µm bright material being optically dark, which is consistent with NIRSpec observations (see Sect. 5.1.5).
is negative as expected, and its magnitude is large but reasonable given the end-member character of the model. The last column of Fig. F.2 shows the reflectance. To convert I/F to reflectance, we followed Ligier et al. (2019) and King & Fletcher (2022) in adopting the Oren & Nayar (1994) model which generalizes the Lambert model for rough surfaces. Specifically, we used the small phase angle limit of the model and adopted a surface roughness s = 20°, which (perhaps coincidentally given that the definitions of roughness are not exactly the same) matches both our above estimate of the slopes based on the thermophysical model and the near-IR results of Ligier et al. (2019). The resulting reflectances appear anticorrelated with the Bond albedo (see Fig. 16), with a Spearman correlation coefficient of r = –0.62 (trailing) to –0.56 (leading) and a significance level of 6–7 σ. The trailing side also appears to be ~1.5 times more 5-µm reflective than the leading (median reflectances of 0.092 and 0.061, respectively), while being ~7 K warmer. Both aspects argue for 5-µm bright material being optically dark, which is consistent with NIRSpec observations (see Sect. 5.1.5).
The 5.9-µm band properties were then determined from Gaussian fitting of the Obs./Model ratios. Results (see Fig. 19 for the preferred Model 2 and the comparison to models 1 and 3 in Fig. F.3) are reassuringly consistent for each of the three continuum models. The inferred band depths vary over 12–30%, with the shallowest bands occurring near disk center, and minimum absorptions on the trailing side. Band depths are correlated with local time and latitude, but the clearest aspect is a strongly negative (r ~ −0.9,10 σ significance) correlation between band depth and surface temperature (TB,8.25 proxy). Since the 5.9-µm band occurs near the cross-over of the thermal (TH) and solar reflected (SR) components, the most likely explanation is that apparent band depth variations reflect relative variations of the two components. The second column of Figs. 19 and F.3 shows band depths corrected for the thermal contribution, that is, rescaled by 1. + TH/SR at band center. This correction, meant to yield the band contrast in the solar reflected component, removes most of the correlation between band depth and surface temperature (red points in fifth column in Figs. 19 and F.3). Spatial variations of this corrected band contrast are still present, with values ranging typically over 35–54% (resp. 30–52%) on the leading (trailing) side, but with no clear geographical trend, so we regard them with caution. We also note that this correction assumes that the band does not show up as an emissivity feature in the thermal component; therefore, the presented corrected band depths may in fact be lower limits to the actual depths in the reflected component.
Band central wavelengths determined from Gaussian fits have mean values of 5.92+0.04 µm (leading) and 5.87+0.05 µm (trailing), where the error bar reflects the 1-σ dispersion over the disk. On both hemispheres, the band seems blueshifted in high-latitude regions (third column of Fig. F.3). However, this conclusion must be taken with caution. Indeed, Fig. 20, in which the band aspect (with respect to Model 2) is shown in seven latitude bins, illustrates that the “–70°” and “70°” ratio spectra (which correspond to the [−90°,−50°] and [+50°,90°] bins) are of relatively low quality, being especially affected by significant flux discontinuities at MIRI channel edges near 5.7 µm (1A/1B) and 6.6 µm (1B/1C); the severity of the problem is presumably related to the low number of spectra in these latitude bins and their near-limb position, making fluxes more sensitive to residual pointing reconstruction errors. Another interesting aspect is that the variation in band position on the leading side (third column in Figs. 19 and F.3) seems correlated to that seen for the H2O 3.1-µm Fresnel peak area and inter-band position (see Sects. 3.2.1, 3.2.2 and Trumbo et al. 2023).
Finally, to further explore the band shape, we created large spectral averages, separately for leading and trailing sides, by coadding all spectra within the disk. Figure 21 shows such spectra and their fits with model 2. In addition to the 5.9-µm minimum, the resulting ratio spectrum shows hints for a secondary absorption near 6.5 µm in the wing of the main feature, especially on the leading side. We also attempted determining the mean band profile in the solar reflected component, by subtracting the (model) thermal component from both the observed and modeled radiances before ratioing them (red lines in Fig. 21). This approach yields reasonable results up to ~6.7 µm but as expected fails beyond that due to the huge dominance of the subtracted term. The 6.5 µm secondary absorption and its prevalence on the leading side are confirmed. The relative depth of the 6.5 µm band with respect to the main 5.9-µm band is typically ~15–25% (trailing/leading) in the total spectrum, and ~30–50% after thermal correction. The possible carriers of these bands are discussed in Sect. 5.3.
 |
Fig. 19 Fitted characteristics of the 5.9-µm band. Shown are results for Obs. 18 (leading side, first row) and Obs. 27 (trailing side, second row), using model 2 described in the text: observed band depth relative to total continuum, band depth corrected for thermal contribution (i.e., relative to model solar reflected component), band position (offset from 5.90 µm), and band FWHM width. The last column shows the correlation between the observed (black) and corrected (red) band depths with the observed 8.25 µm TB. Spearman correlation coefficients and number of standard deviations significance are indicated as insets. Similar figures for models 1 and 3 can be found in Fig. F.3. |
 |
Fig. 20 Spectra of the 5.9 µm band (Observation/Model 2). Shown are averages in 7 latitude bins ([−90°,−50°], [−50°,−30°], [−30°,−10°], [−10°,10°], [10°,30°], [30°,50°] and [−50°,−90°]. Left: leading side (Obs. 18). Right: trailing side (Obs. 27). The band appears blueshifted in the high-latitude bins, but spectra are of more modest quality there. |
5 Discussion: Interpretation of the results
In this section we discuss the properties and distribution of H2O, CO2 and non-ice components as derived from the NIRSpec data, and the possible carriers of the 5.9-µm band detected with MIRI. Part of the discussion is based on ratios of spectra of different terrains: moderately bright vs bright on high-latitude regions (Fig. 22), at polar vs equatorial regions (Fig. 23). These spectral ratios reveal differences of abundance and/or mixture modality of species (geographical or intimate mixtures, deposits etc.) and/or differences of the chemical and/or physical properties (nature, grain size, solid phase, temperature, etc.) between terrain types and/or hemispheres. In turn, these differences can be due to processes affecting each hemisphere differently (energetic particle bombardment, meteoroid gardening). The spectral ratios leading/trailing and between terrains of different Bond albedo show variations of the H2O, H2O2 and CO2 spectral features (other minor spectral features at 3.43, 3.51, 3.88, and 4.38 µm, do not show up in these ratios, indicating that they do not vary over the surface or may be spurious, as discussed in Sect. 3). For this discussion, we also produced merged NIRSPec and MIRI spectra corrected from the contribution of thermal emission (Figs. 24–26), as described in Appendix C.
 |
Fig. 21 Disk-average spectra at 4.9–7.5 µm. Top panels: data (solid line) and continuum fit with model 2 (dashed line). Bottom panel: observation/model ratios. Black: ratio in the total spectrum. Red: ratio in the solar component (see text for details). Left: leading side (Obs. 18). Right: trailing side (Obs. 27). |
 |
Fig. 22 Comparison of bright and moderately bright terrains in Ganymede’s leading and trailing hemispheres, through spectral ratios. Moderately bright and bright terrains are defined by a Bond albedo AB = 0.35 − 0.4, AB = 0.4 − 0.6, respectively. For the leading hemisphere, only the northern regions at latitudes >35°N are considered, whereas for the trailing hemisphere, we consider both northern and southern high-latitude regions (>35°N/S). The spectrum shown in green dashed line is a spectrum of amorphous water ice obtained using Fresnel’s formulae (applicable for flat surfaces; Born & Wolf 1999) and the optical constants at 120 K of Mastrapa et al. (2009). The vertical dashed lines are at the wavelengths of the two main H2O Fresnel peaks (3.09 and 3.20 µm), H2O2 (3.505 µm) and CO2 (4.26 µm) absorption bands. The vertical dashed-dotted line at 3.6 µm is roughly at the H2O inter-band position. |
 |
Fig. 23 Comparison of the CO2 band in polar (>45 °N/S) and equatorial (<30 °N/S) regions through spectral ratios. (A) Spectral ratios Leading/Trailing for polar regions; (B) spectral ratios Polar/Equatorial for leading (red) and trailing (blue) hemispheres. The vertical dashed line is at 4.27 µm (2341.9 cm−1). |
 |
Fig. 24 Laboratory reflectance spectra of several hydrated salts and sulfuric acic hydrates. They are possibly present on Ganymede according to previous near-infrared observations (Ligier et al. 2019; King & Fletcher 2022). The spectrum of Magnesium chloride (~250 µm, JB-JLB-G32-A) is from the NASA Reflectance Experiment LABoratory (RELAB) spectral database. Spectrum of Epsomite (GDS149) is from the USGS Spectral Library (Kokaly et al. 2017). Spectra of Bloedite (〜250 µm, Jim Crowley, USGS) and Hexahydrate (<45 µm, SPT143) are from the database of the Centre For Terrestrial and Planetary Exploration (C-TAPE) of University Winnipeg. The spectrum of sulfuric acid tetrahydrate at 160 K is from Loeffler et al. (2011). We note that this is a transmittance spectrum. A reflectance spectrum of Ganymede’s trailing side equatorial region (<30° latitude N/S, see Fig. 26) is scaled for comparison (black line). The vertical dotted lines indicate H2O inter-band positions in NIRSpec spectrum, and the vertical dashed lines indicate the band positions in MIRI spectrum. |
5.1 H2O ice and non-ice materials
The variations of the H2O Fresnel peaks and inter-bands obtained by NIRSpec over the disk of Ganymede provide insights on the properties of the water ice (grain size, temperature, crystallinity, etc.) and on the presence of non-ice materials, complementing previous observations of water ice spectral features at shorter wavelengths (Ligier et al. 2019; King & Fletcher 2022) or at lower spectral resolution (Hansen & McCord 2004).
5.1.1 Known properties of H2O ice spectral features
The Fresnel peaks are produced after the first reflection on a facet of water ice, so they are indicative of the properties of the very first interface of Ganymede’s surface. Crystalline water ice is characterized by three well-defined peaks (at 2.95, 3.1, 3.2 µm) whereas amorphous water ice has a broad and featureless 3-µm reflection peak shifted to shorter wavelengths (Hansen & McCord 2004; Mastrapa et al. 2009). The intensity of the Fresnel peaks tends to increase with increasing ice grain size (when larger than several micrometers), but decreases with increasing ice temperature (Stephan et al. 2021). Any non-H2O contaminant covering the ice surface decreases the amplitude of the peaks (Ciarniello et al. 2021). Finally, the peak position has been observed to slightly shift to longer wavelengths with decreasing temperature (Stephan et al. 2021; Mastrapa et al. 2009). Concerning the H2O inter-band around 3.6 µm, its amplitude AIB with respect to the local minimum at 〜3.3 µm (Eq. (2)) increases with decreasing grain size and decreasing temperature (Poch et al. 2016; Stephan et al. 2019). The inter-band wavelength position depends on the temperature (Clark et al. 2012; Filacchione et al. 2016) and also on the amount of amorphous vs. crystalline water ice (Mastrapa et al. 2009). The increase of inter-band amplitude with decreasing grain size is due to the increased density of facets with which photons interact, reducing their mean free path and inducing multiple scattering, increasing the reflectance at wavelengths in between absorption bands. Therefore, any reduction of mean free path in H2O ice (due to e.g., grain size, defects, porosity etc.) would increase the inter-band amplitude. Contaminants can increase or decrease the amplitude of the inter-band and may shift its position depending on their spectra. Given the high number of parameters controlling these spectral features, the variations observed on Ganymede are equivocal. Therefore, here we propose a preliminary interpretation of the observed NIRSpec spectra of Ganymede, based on this current knowledge. Additional radiative transfer modeling and experimental measurements would be needed to provide a more detailed interpretation.
 |
Fig. 25 Influence of porosity on spectra of phyllosilicates. (a) Laboratory reflectance spectra of Aguas Zarcas CM2 meteorite powder and several phyllosilicate powders and (b) influence of the porosity on the reflectance spectrum of Aguas Zarcas sub-µm powder. Spectra of Aguas Zarcas were measured at IPAG (Institut de Planétologie et d’Astrophysique de Grenoble, see Appendix B). Ganymede’s trailing side equatorial region (<30° latitude N/S) reflectance spectrum (see caption of Fig. 26) is plotted at the same reflectance scale in plot (b) (black line), with the gray dashed-dotted line in plot indicating the potential continuum obtained by drawing a line between the points at 3.9 and 5.1 µm (inter-bands). This continuum has a positive (red) spectral slope, possibly due to a relatively high surface porosity of dark terrains. Spectra of Cronsdetite (M3542) is from the USGS Spectral Library (Kokaly et al. 2017). Spectra of Saponite (<45 µm, SA-EAC-059) and Beidellite (<12 µm, JB-JLB-919-A) are from the NASA Reflectance Experiment LABoratory (RELAB) spectral database. The vertical dotted lines indicate H2O inter-band positions in NIRSpec spectrum, and the vertical dashed lines indicate the band positions in MIRI spectrum. |
5.1.2 Global distribution of H2O ice
Maps of the H2O Fresnel peak area (Fig. 5) are consistent with the distribution of water ice inferred from H2O bands at 4.5-µm (Fig. 7) and in the near-infrared (Ligier et al. 2019; Stephan et al. 2020; Mura et al. 2020; King & Fletcher 2022), and from the visible albedo maps (Fig. 2), as discussed in Sect. 3.2.1. Ganymede is globally covered by H2O ice (Fig. 4), and all spectral ratios of Fig. 22 have an inter-band centered at 3.55–3.65 µm, indicating that variations of H2O ice surface abundance and/or properties are the main sources of differences between terrains and hemispheres. In particular, Ganymede’s H2O surface ice is more or less contaminated by non-ice materials in proportions that vary regionally. The strong contrast of the H2O Fresnel peak area, 10 to 40 times higher on the leading hemisphere than on trailing hemisphere (Fig. 6C), can be attributed to a higher abundance of non-ice materials covering the ice on the trailing hemisphere, whereas more ice is directly exposed to the surface of the leading hemisphere. As discussed in Ligier et al. (2019) and King & Fletcher (2022), compared to the trailing hemisphere, the leading hemisphere may receive (1) a higher flux of (and/or more energetic) ions and electrons causing surface sputtering and deposition of fresh ice (Plainaki et al. 2022; Liuzzo et al. 2020; Poppe et al. 2018), and (2) a higher flux of micro-meteoroids (Bottke et al. 2013) excavating the ice and also exposing fresh ice at the surface, whereas most of the ice on the trailing side remains below a low-albedo lag deposit of non-ice materials.
5.1.3 Properties of H2O ice in polar regions
The maximum of H2O Fresnel peak area and intensity is reached in the polar regions of the leading side, which appear to have more water ice directly exposed at the surface than other terrains on Ganymede. This is confirmed by the inter-band position, transitioning abruptly from 3.9 to 3.66 µm poleward of 30° latitude (Fig. 8). These polar regions are where the highest flux of energetic ions is expected to irradiate the surface (Fatemi et al. 2016; Poppe et al. 2018; Liuzzo et al. 2020; Plainaki et al. 2022). It is striking to see how close the inter-band transition follows Ganymede’s open-closed field line boundary (Fig. 8). The purity of the ice exposed at the surface of the leading polar regions may thus be explained by the combination of micrometeoroid gardening, excavating the ice, and ion irradiation, sputtering the excavated ice followed by local re-accretion of water vapor forming purer water ice on top of the non-ice materials (Johnson & Jesser 1997; Khurana et al. 2007). Moreover, the leading north polar region spectrum has the highest interband amplitude (Figs 4, 8), indicating that this region is covered by water ice particles offering the smallest mean free path to photons on Ganymede, which should be smaller than 70 µm (Stephan et al. 2021), in agreement with the conclusions of previous studies (≤50 µm according to Hibbitts et al. 2003; Ligier et al. 2019; King & Fletcher 2022; Stephan et al. 2020). Physically, this smallest mean free path may be due to the presence of (1) the smallest ice grains and/or (2) more internal defects (crystal defects, voids, bubbles, etc.) in large ice grains (Johnson & Jesser 1997) and/or (3) a higher micro-roughness (porosity) of the ice grains, increasing the scattering of the light similar to smaller grains. All could result from the processes triggered by energetic particles irradiations (Johnson & Jesser 1997; Johnson & Quickenden 1997; Khurana et al. 2007). Dedicated numerical and/or experimental models of NIRSpec spectra could be used to discriminate these possibilities, and improve our knowledge of the ice texture.
On the trailing side, no such abrupt transition at 30° latitude is observed, but a progressive shift of the inter-band position toward lower values at the poles (Fig. 8), indicative of a higher proportion of ice and/or smaller optical mean free path in ice as the latitude increases. The polar regions of the trailing side have much less ice and/or larger optical mean free path in ice (so larger grains and/or less internal defects and/or lower microroughness and porosity) than the polar regions of the leading side (Fig. 4).
Figure 22 shows the ratio between the spectra of the brightest northern polar regions of the leading hemisphere, with spectra of the surrounding darker terrains. The ratios between these spectra indicate the variations of H2O ice surface abundance and/or properties. This ratio has a Fresnel peak shifted to 3.0583 µm, indicative of the predominance of amorphous water ice in the north polar cap of the leading hemisphere (see Fig. 22, and Mastrapa et al. 2009), possibly as a deposit on top of the surface. The predominance of amorphous ice in the polar regions is consistent with previous analyses of the shape of the Fresnel reflectance peak from NIMS data (Hansen & McCord 2004) and with analyses of the H2O near-infrared bands observed with the VLT (Ligier et al. 2019).
Amorphous ice can form (1) via the direct irradiation of crystalline ice by magnetospheric energetic ions and electrons (Famá et al. 2010), (2) via the recondensation of water vapor produced after a micro-meteoroid impact, and/or (3) via the recondensation after sputtering by energetic particles. In addition, for amorphous ice to be observed, its recrystallization timescale must be longer than its formation timescale (Faure et al. 2015; Mitchell et al. 2017). This seems only possible in Ganymede’s polar regions because they experience the lowest temperatures (i.e., longest recrystallization timescales) and receive the highest flux of energetic ions forming amorphous ice. Amorphous water ice is expected to be present as a layer at the surface of icy crystalline grains. The thickness of this amorphous layer is however unknown, due to the extent of resurfacing processes that controls the actual sputtering rate, and therefore both the kinetics of amorphization and recrystallization (see Johnson et al. 2004 for extensive details).
The wavelength shift of the Fresnel peak is slightly more pronounced on the leading north polar cap than the south polar cap (Fig. 5). This is possibly due to a slightly higher abundance of amorphous ice in the north polar cap. According to the thermal maps and models presented in Sect. 4 (Fig. F.2) the poles have similar temperatures, so a temperature difference cannot explain this shift. This asymmetry is intriguing, as it suggests there are differences in the processes transforming the ice in the north and south polar caps.
Contrary to the leading hemisphere, on the trailing hemisphere the Fresnel peak is redshifted in the polar caps compared to the surrounding regions (Fig. 5). As seen in Fig. 22, the spectral ratio between the polar and surrounding regions is extremely different between hemispheres, suggesting that the polar ices have different origins and/or undergo different transformations depending on the hemisphere. However, both hemispheres have their north polar caps with a Fresnel peak blueshifted and a 3.6-µm inter-band more intense compared to their south polar caps (Figs. 5 and 8). A possible explanation is that the processes forming amorphous ice also decrease the optical mean free path in ice (forming smaller grains and/or more internal defects and/or higher micro-roughness/porosity). These processes appear to be enhanced on the north polar cap.
The temperature of the surfaces of Saturn’s icy satellites has been derived from the spectral position of the 3.6 µm inter-band, using laboratory reflectance spectra of crystalline water ice at different temperatures (Filacchione et al. 2016; Clark et al. 2012). Applying the same approach, and assuming fine-grained crystalline water ice (measurements by Clark et al. 2012), we derive a temperature of 155 K for the polar caps of Ganymede’s leading hemisphere (inter-band at 3.66 µm; see Fig. D.1). However, as previously discussed, water ice is partially in amorphous form at the poles of the leading hemisphere. For amorphous ice, the position of the inter-band exhibits no trend with temperature, and lies at lower wavelengths than for crystalline ice (see Appendix D). This implies that the temperature derived by comparing the position of the inter-band to spectra of crystalline ice only, is an upper limit. Moreover, the presence of larger ice grains and/or of non-ice materials would also decrease the temperature derived via this method. This upper limit of 155 K is consistent with a surface temperature of 135 K poleward of 60° latitude obtained with the thermal model with surface roughness that most closely reproduces the MIRI data.
NIRSpec observations discussed above, and especially the presence of amorphous ice, tend to favor ion sputtering as the mechanism forming Ganymede’s polar caps. Other past studies have also explained their formation by the migration of water ice, sublimating in the equatorial regions and recondensing at higher/colder latitudes (Purves & Pilcher 1980), a mechanism which may not be excluded.
 |
Fig. 26 Simulated spectrum compared with merged NIRSpec/MIRI I/F spectra of the leading and trailing hemispheres. The model parameters are: grain sizes DCO2 = 0.05 µm, DH2O = 10 µm, Ddark = 1 µm; mass ratio relative to water mCO2 = 1%; relative areas of the ice:dark terrains = 10:90. Averages NIRSpec/MIRI merged spectra covering the full disk, low and high latitudes regions are shown, as indicated in the inset. NIRSpec and MIRI spectra are corrected from the contribution of thermal emission (see Appendix C). The simulated spectrum cannot explain the 5.9-µm feature. |
5.1.4 Longitudinal and diurnal variations of H2O ice at low latitudes
Some spectral variations of the Fresnel peaks over Ganymede’s longitudes, shown in Fig. 5, are uncorrelated with Bond albedo variations. They may indicate diurnal processes and/or exogenous processes specific to some longitudes, affecting the surficial water ice.
First, on the trailing hemisphere, the Fresnel peak area is maximum at low latitudes of the morning limb (Fig. 5). The terrains of this morning limb have a Bond albedo (Fig. 2) and a 3.6-µm band position (Fig. 8) similar to the surroundings, and the lowest 4.5-µm H2O band depth on the trailing disk (Fig. 7), suggesting that the ice responsible for this peculiar morning limb behavior is thin and may be transient, specific to the local hour. These ice crystals could have formed by the condensation of water vapor present in the exosphere, but this cannot explain an excess of ice only seen on the morning limb. In addition, even a H2O column density of 1016 cm−2 – which is probably an upper limit given observational (Hartogh et al. 2013; Roth et al. 2021) and model (e.g., Leblanc et al. 2017, 2023) results – corresponds to a mere 0.003 µm ice layer. Another mechanism is the direct condensation of water vapor sublimating from the subsurface during the night. Transient (e.g., early morning) frost was observed at the surface of comet 67P/Churyumov-Gerasimenko, and explained by the low thermal inertia of the highly porous 67P’s nucleus causing a temperature inversion at the beginning of the night with surface layers getting colder than the interior layers (De Sanctis et al. 2015). This mechanism might be at work on Ganymede since the upper layer of the surface has the lowest thermal inertia, as derived from MIRI (Sect. 4.2) and Galileo data (de Kleer et al. 2021), whereas layers few centimeters deeper have higher thermal inertia (de Kleer et al. 2021). Such process should occur globally on all terrains having a low-enough thermal inertia at the top surface, so frost would also be observed on the morning limb of the leading hemisphere. In reality, Fig. 5 does not show a maximum of Fresnel peak area on the leading morning limb. However, the albedo and Fresnel peak area of the morning limb of the trailing side are similar to those of terrains of the leading side (Fig. 6C). Therefore, the formation of such morning frost might be more difficult to detect on the surface of the leading side, because it is covered by more permanent water ice than the trailing side, whose Fresnel peak could mask that of the morning frost. Alternatively, this scenario of diurnal frost may be wrong or incomplete, and these terrains may be peculiar because of endogenous processes similar to those affecting the leading side. In particular, the “morning” limb of the trailing side observed here probes Ganymede’s sub-Jovian (toward Jupiter) hemisphere, which may be affected by different energetic particles bombardments than the trailing apex, altering the surficial ice differently (Liuzzo et al. 2020; Plainaki et al. 2022).
Another unexpected result is the variation of the central wavelength of the Fresnel peak with longitude (Fig. 5), observed at low latitudes (typically ≤40°) for both hemispheres. The central wavelength has a similar value at the west limb of the two hemispheres (corresponding to the earliest local times). But as the longitude changes from the west to the east, the Fresnel peak position becomes more and more blueshifted, reaching the maximum blueshift at the east limb (latest local times), with a bluer wavelength on the trailing hemisphere. Remarkably, neither the H2O Fresnel peak area nor the H2O inter-band position exhibit such longitudinal variation, and one should note that this shift is extremely small (0.004 µm, Fig. 5). Therefore, the modification of the H2O ice inducing this shift may be limited to the first nanometers and micrometers of ice grains and/or to very minor geographical extents (much smaller than NIRSpec spatial resolution of about 300 km per spaxel on Ganymede). This longitudinal variation may be geographic and possibly linked to regional differences of magnetospheric energetic particles bombardment, or it may be diurnal and linked to solar radiations. Such as small shift of the H2O Fresnel peak position toward smaller wavelengths can have various physical origins. It could be due to a modification of the surface ice molecular structure, changing its optical index: either an increased fraction of amorphous ice, or a higher ice temperature, or another change of the ice molecular structure (other phase change, chemical change etc.). But it could also be due to a modification of the nanometer or micrometer-scale texture of the ice surface, changing the relative contribution of absorption versus reflection of the light within the first nanometers and/or micrometers of the ice surface: for example an increased surface roughness induced by sublimation and/or recondensation and/or photodesorption of H2O ice. If this shift was caused by solar heating of the ice, we would expect the Fresnel peak position to be the bluest at the center of the disk (around noon, where the temperature is maximum as seen in Fig. 16), and not at the longitude corresponding to the evening. More likely, this pattern might be explained by a progressive and cumulative modification of the H2O ice molecular structure and/or nano/micrometer-scale texture, induced by the accumulation of solar radiation from the morning to the evening. Solar radiation not only regulates Ganymede’s surface heat, inducing sublimation or recondensation of H2O ice, but it also induces photochemical processes (including photodissociation of H2O followed by further chemistry, H2O photodesorption, and H2O ice amorphization), and radiolytic processes due to solar energetic particles. The spectral ratio between more blueshifted and less blueshifted low latitudes (not shown) is inconsistent with the spectrum of pure amorphous ice. Moreover, as discussed in Sect. 5.1.3, amorphous ice should not be thermodynamically stable at these latitudes, although a detailed investigation of the dynamic of recrystallization and amorphization under Ganymede’s surface conditions may still be needed to conclude. Moreover, this modification of the surface ice is reversible so that during the night the Fresnel peak position is shifted back to its original position on the morning, possibly via a mechanism of relaxation of the ice (recondensation, metamorphization, phase change, chemical change, etc.). Constraining the mechanism at the origin of this shift requires dedicating modeling and/or laboratory investigations of these various processes, which are out of the scope of this paper. The leading-trailing differences in the Fresnel peak shift indicates that the mechanism is enhanced during the day on the trailing side, possibly because of its higher surface temperature. Maybe this phenomenon could have a link with the maximum sublimation rate of water at the subsolar point, previously modeled (Leblanc et al. 2023) and observed (Roth et al. 2021).
5.1.5 Non-ice materials composition and texture
Spectra of the dark terrains (see those at mid latitudes 0– 30° in Fig. 4) all have a maximum H2O inter-band at 3.9 µm (3.935 µm for leading, and 3.950 µm for trailing) and a continuum with a positive (red) spectral slope from 3.9 to 7 µm (i.e., the reflectance at the inter-bands − 3.9, 5.1, 7 µm – increases with the wavelength, see Fig. 24). Both of these spectral characteristics are incompatible with water ice (water ice inter-band maximum cannot be at more than 3.7 µm; Clark et al. 2012; Filacchione et al. 2016) so they are due to the presence of non-ice materials. Several H2O-bearing minerals, such as phyllosilicates, sulfates and chlorides, exhibit a H2O inter-band around 3.9 µm, as shown in Figs. 24 and 25a. Figure 24 shows infrared reflectance spectra of some sulfate and chloride salts and a sulfuric acid hydrate expected to be present on Ganymede’s surface based on the shape of the water absorption bands in the near-infrared (Ligier et al. 2019; King & Fletcher 2022). Among these species, bloedite (Na2Mg(SO4)2(H2O)4) and hexahydrate (MgSO4(H2O)6) spectra best match Ganymede’s dark terrain spectrum from 3.3 to 4 µm (general shape and position of the H2O inter-band maximum). However, none of the salt spectra match Ganymede’s dark terrain spectrum from 4 to 7 µm. Ganymede’s dark terrain spectrum exhibits a 4.5-µm H2O absorption band attributed mainly to water ice. Several salts spectra also exhibit a H2O band centered around 4.5 µm, but bloedite and hexahydrate spectra show an abrupt increase of reflectance from 4.8 to 4.9 µm which is absent on Ganymede’s dark terrain spectrum. Sulfuric acid tetrahydrate (H2SO4(H2O)4) spectrum exhibits smoother spectral variations than the salts, although not identical to Ganymede’s dark terrain spectrum. Notably, the shape of the absorption band of sulfuric acid tetrahydrate centered at 5.8-µm is similar to the one observed by MIRI on Ganymede, although its position is different (Fig. 24). The attribution of the 5.9-µm band observed on Ganymede will be discussed in Sect. 5.3. Finally, Ganymede’s dark terrain continuum has a positive (red) spectral slope from 3.9 to 7 µm, unlike reflectance spectra of salts. Therefore this spectral feature is probably caused by other components of the dark terrains.
Previous studies have noted similarities between the 3-µm absorption band of Ganymede, Callisto and Amalthea’s dark terrains, with that of phyllosilicates present in carbonaceous chondrites (Calvin & Clark 1991; Schenk & McKinnon 1991; Takato et al. 2004). Phyllosilicates are hydrated minerals known to be formed by aqueous alteration of silicates. Serpentine and smectite phyllosilicates are among the main constituents of the matrix of carbonaceous chondrites (especially CI and CM groups), which are dark meteorites from undifferentiated bodies (C-type asteroids). If present on Ganymede, such phyllosilicates may have endogenous and/or exogenous origins, formed by aqueous alteration in its subsurface, or brought by impacting bodies. Figure 25a shows reflectance spectra of some of these phyllosilicates, together with the spectrum of a CM chondrite (Aguas Zarcas) in powder form. Cronsdetite is a Fe-rich serpentine, beidellite and saponite are smectites. Beidellite and saponite, as well as Aguas Zarcas, exhibit a 3.9-µm H2O interband having a maximum at similar wavelength than Ganymede’s dark terrains (Fig. 4), but with a much larger width (Fig. 25a). Moreover, these phyllosilicates have a negative spectral slope from 4 to 6 µm, unlike Ganymede’s dark terrain continuum with a positive spectral slope from 3.9 to 7 µm.
In summary, Ganymede’s dark terrain 3.9-µm and 5.1-µm H2O inter-bands correspond better to Na- and Mg-sulfates or sulfuric acid hydrates than phyllosilicates, but none of these compounds explain Ganymede’s dark terrain red spectral continuum between 3.9 to 7 µm (Figs. 24 and 25a). In fact, this latter part of the spectrum may be dominated not by absorption but by scattering effects induced by the peculiar surface texture of Ganymede’s dark terrains (85% porosity, de Kleer et al. 2021). Figure 25b shows that sub-micrometer-sized carbonaceous chondrite powder with porosity >80% exhibits a strong red (positive) spectral slope reminiscent of the one observed on Ganymede’s dark terrains continuum from 4.6 to 7 µm (see Appendix B for details on the preparation of this sample). The radiative transfer mechanism explaining how an increase of porosity induces a spectral reddening is not yet established (it will be the subject of an upcoming study), but it appears to require the presence of sub-µm opaque grains such as iron sulfides or magnetite found in carbonaceous chondrites. We note that opaque minerals have already been suggested as constituents of the dark terrains of Callisto (Calvin & Clark 1991) and they could also be the spectrally flat darkening agent necessary to fit Ganymede’s nearinfrared spectral properties (Ligier et al. 2019; King & Fletcher 2022). When mixed with other components, even at few percent levels, fine-grained opaque minerals dominate the light scattering and control the reflectance level, masking absorption bands of the other components (Sultana et al. 2023). At visible and near-infrared wavelengths, the salt and hydrate candidates discussed above have relatively high reflectances (Carlson et al. 1999b). Therefore, the low reflectance of Ganymede’s dark terrains could be explained by a mixture of salts and/or hydrates with opaque minerals and/or by radiation-induced color changes of salts (Hibbitts et al. 2019).
In conclusion, JWST spectra of Ganymede’s dark terrains seem compatible with the presence of H2O-bearing non-ice compounds such as Na- and Mg-sulfate salts, sulfuric acid hydrates, and possibly phyllosilicates, mixed with fine-grained opaque minerals, having an highly porous surficial texture. However, neither previous NIR spectra (NIMS/Galileo and VLT) nor these NIRSpec spectra show diagnostic absorption bands that would enable firm identifications of Ganymede’s dark terrain constituents. The 5.9-µm band observed by MIRI is present all over Ganymede’s surface, in dark and bright terrains, so it is due to constituent(s) present on both terrain types, possibly sulfuric acid hydrates as discussed in Sect. 5.3.
5.2 CO2
The band at ~4.26 µm in Ganymede observations is assigned to the asymmetric stretching mode v3 of CO2. The analysis of NIRSpec spectra presented before has led to the following conclusions:
The band is asymmetric (Fig. 10).
The band center shifts toward higher wavelengths with increasing latitude (Figs. 10, 11, Table 2), and with increasing Bond albedo (Fig. 6) and Fresnel peak area (Fig. E.1). The CO2 band center ranges from 4.257 to 4.260 µm (2349− 2347 cm−1) on equatorial regions, is at 4.264 µm (2345.3 cm−1) on trailing north and south poles and leading south pole, and at 4.270 µm (2342 cm−1) on the north polar cap of the leading hemisphere.
The band depth decreases with increasing latitude, for both the leading and trailing hemispheres (Fig. 12, Table 2).
A rough estimate of the CO2 concentration can be estimated through Hapke modeling (Hapke 1993). We considered two terrains geographically separated: (1) a granular intimate mixture with grains made of pure crystalline water ice and pure carbon dioxide (optical constants from Mastrapa et al. 2009, and Trotta & Schmitt 1996); (2) a dark terrain, simulated by a mature coal, which intends to mimic opaque ultramafic assemblages as observed in primitive carbonaceous chondrites and cometary grains (Quirico et al. 2016). The optical constants n and k of this dark material are equal to 1.9 and 2.9 over the whole spectral range, respectively, and are averages of values taken from Foster & Howarth (1968).
As mentioned above, pure CO2 ice is not expected at Ganymede’s surface due to its high volatility in the temperature range 90–160 K (Fray & Schmitt 2009). Therefore, optical constants of pure CO2 ice are used here to estimate the CO2 abundance in water ice, that is, to reproduce the CO2 band area but not its shape, width and band center (Fig. 26). Our simulations show that no set of parameters is able to accurately match the reflectance level, nor the shape of the continuum at low latitudes (in particular the position of the inter-band region at 3.9 µm). The misfit of the inter-band region could be due to the absence of salts in the surface model, which are likely present (see Sect. 5.1), but unfortunately, no optical constants are available (Ligier et al. 2019). The global reflectance misfit cannot be fully resolved by tuning the relative area of the dark terrain, because at some point the continuum amplitude gets too weak compared to that in observations. In addition, the reflectance of the sole dark terrain does not reach values below 0.06. A more sophisticated model is definitely needed, but despite its limitations, the abundance of CO2 trapped in water ice can be estimated to 〜1% (in mass). This crude estimate is used below to discuss the relevance of laboratory experiments to interpret the physical state of CO2.
5.2.1 CO2 in water ice
The latitudinal variations of the CO2 band and its asymmetric band shape support the view that different CO2 physical states are involved. At high latitudes, the band is dominated by a long wavelength (low wavenumber) component. At lower latitudes (and especially on dark terrains) the band broadens and shifts toward the blue, thus showing that other components of CO2 dominate (Figs. 10, 6B, and 13). As pointed out above, pure CO2 is not stable at the surface of Ganymede, but CO2 trapped in water ice can be stabilized in the range of temperature 90–160 K.
The position of the v3 CO2 band diluted at ppm levels in crystalline water ice, that is, isolated in the lattice, lies at 2340.7 cm−1 at 20 K (4.2722 µm; unpublished data from IPAG). Similarly, we made a compilation of the position of the v3 CO2 band trapped as an impurity in several ices: Ar, N2, N2:O2, CH4, C2H4, C2H6, NO and SO2 (Schmitt et al. 1998; Quirico & Schmitt 1997; unpublished data from Institut de Planétologie et d’Astrophysique de Grenoble (IPAG)). The peak position varies between 2333.5 and 2348.5 cm−1 (4.2854 and 4.2580 µm), which does not encompass the full spectral range of the CO2 band in Ganymede spectra.
Infrared spectra of CO2 clathrate hydrate (135 K) show two components at 2338 and 2347 cm−1 (4.277 and 4.261 µm; Fleyfel & Devlin 1991). However, the position of the most intense component lies at the edge of the CO2 band in Ganymede spectra (Fig. 27), which shows that clathrates contribution is, at best, weak.
Spectra of a H2O:CO2=10:1 ice mixture collected from 10 to 170 K (Ehrenfreund et al. 1999) show that (1) carbon dioxide can be stabilized in the solid state when mixed with amorphous and crystalline water ice, over the whole range of temperature at Ganymede’s surface; (2) the band is shifted toward high wavelengths (resp. low wavenumbers) when CO2 is mixed with crystalline water ice; (3) even at 10% concentration, CO2 molecules do not form crystallites of pure CO2, but are more likely distributed in the lattice as multimers. In spectra of H2O:CO2 = 10:1 mixtures collected at 170 K, the CO2 peak is located at 2337.2 cm−1 (4.2786 µm), at the edge of the Ganymede CO2 band. For amorphous water ice at 80 K, as shown in Fig. 28, the band is located at 2340.6 cm−1 (4.2724 µm), closer to the Ganymede CO2 band at high latitudes. High latitudes of the leading hemisphere are precisely where amorphous water ice is detected by NIRSpec (Fig. 22), as discussed in Sect. 5.1.3.
In the study of He et al. (2018), a H2O:CO2= 50:100 mixture was deposited at 10 K, and subsequently warmed up. The CO2 band lies between 2345 and 2350 cm−1 (4.264 and 4.255 µm) in the range 90−138 K (Fig. 28 for 138 K), highlighting CO2 segregated in the water matrix. But in this experiment, pure crystalline CO2 ice is present in the sample (no pure CO2 ice is observed for samples with a CO2 concentration <23%). In all these experiments, the wavenumber of the CO2 band remains lower or equal to ~2350 cm−1 (λ ≥ 4.255 μm).
The theoretical calculations of Chaban et al. (2007) show that the position of the CO2 band for CO2-H2O complexes becomes blueshifted by 8 to 46 cm−1, with respect to isolated CO2, and reach values well beyond 2350 cm−1 (4.255 μm). They have been used to suggest that CO2 could be present in the form of complexes at the surface of icy bodies such as Iapetus, Hyperion, and Dione (Cruikshank et al. 2010). However, the position of isolated CO2 is predicted at 2361 and 2384 cm−1 (4.236 and 4.195 μm), depending on the base used in DFT calculations. In addition, these positions are far from the position of CO2 in the gas phase, 2349 cm−1 (4.257 μm), which shows that these predictions of the positions of the CO2-H2O complexes are not reliable. Last, Jones et al. (2014) report an experimental study of CO2 produced from the radiolysis of almost pure H2CO3. They observe a feature as broad as the CO2 band in Ganymede’s spectra (Fig. 28, shown as CO2 complexed), which is inconsistent with the observed presence of several spectral components.
To sum up, the main conclusion of this section is that CO2 trapped in water ice cannot account for the whole CO2 band observed in Ganymede spectra. Therefore, a contribution from non-ice materials must be examined.
 |
Fig. 27 Comparison with laboratory data. CO2 band in Ganymede spectra at the pole (60–75°N; dotted light gray lines) and the equator (0–15°N; dot-dashed gray lines) of the leading hemisphere compared with transmission spectra from Berlanga et al. (2016; carboneous chondrites), Bekhti et al. (2021; zeolites), Ehrenfreund et al. (1999; CO2 ice and CO2-H2O ice mixture) and Fleyfel & Devlin (1991; CO2 clathrates). Some spectra are vertically shifted for the sake of clarity. |
 |
Fig. 28 Comparison with laboratory data. CO2 band in Ganymede spectra at the pole (60–75°N; dotted gray line) and the equator (0–15°N; dot-dashed gray line) of the leading hemisphere compared to several experimental measurements of CO2 mixed with water ice at 170 K (Ehrenfreund et al. 1999; blue line), CO2 segregated in water ice at 138 K (He et al. 2018; yellow line) and CO2 complexed Jones et al. (2014; green line). |
5.2.2 CO2 in non-ice materials
The position of the v3 band of CO2 mixed in water ice is at wavenumbers less than 2350 cm−1, therefore other spectral components are required to explain the whole CO2 band. We discuss here the issue of CO2 adsorbed or trapped inside microporosity of non-ice materials (McCord et al. 1998; Hibbitts & Szanyi 2007). Linearly adsorbed CO2 preserves its linear geometry (D∞h symmetry) and leads to a v3 CO2 band around 4.26 μm, with position and width controlled by the nature of the surrounding cations and the local crystalline structure. In the case of zeolites doped with a variety of cations, linearly adsorbed CO2 displays peak positions at around 2349 cm−1 (K+), 2354 cm−1 (Na+), 2367 cm−1 (Ca2+) and 2372 cm−1 (K+) (resp. 4.257, 4.248, 4.225 and 4.216 μm; estimated from data of Forster & Schumann 1989; Bonelli et al. 2000; Martra et al. 2002; Bekhti et al. 2021; Taifan et al. 2016, see Fig. 27). These values account well for the high wavenumbers region of the CO2 band in Ganymede spectra. We have satisfactorily fitted the CO2 band in Ganymede spectra using a model based on three Lorentzian components, with peak positions covering the ranges 2340–2345, 2348–2351 and 2352–2367 cm−1 (resp. 4.274– 4.264, 4.259−4.254 and 4.252−4.225 μm). However, zeolites are Al-rich tectosilicates and are expected to be scarce on the surface of Ganymede. Therefore, the question arises whether other minerals would display similar infrared features to zeolites. Unfortunately, far fewer studies have been devoted to mafic minerals, oxides, sulfides and salts, which could be present on the surface of Ganymede (Taifan et al. 2016). The study of Berlanga et al. (2016) reports adsorption measurements on a series of 13 carbonaceous chondrites, spanning a diversity of chemical groups, mineralogical compositions and post-accretional histories. The highest abundance of adsorbed CO2 at 150 K was, unsurprisingly, observed with Ivuna (CI), the most finely grained, porous and brittle object, mostly devoid of metals and sulfides. For other chondrites, the abundance of adsorbed CO2 is lower by a factor of 7. The range of variations of the band position over the full range of chondrites is 2337.5–2345.2 cm−1 (4.278–4.264 μm) and no correlation with the mineralogical composition nor organic matter abundance was found. Carbonaceous chondrites are therefore not good candidates for accounting for the long wavelength components of the CO2 band. Another plausible candidate is cometary dust (Poppe 2016), which is essentially made of organic polyaromatic matter (Bardyn et al. 2017), mafic silicates as Mg-rich olivine and pyroxenes, sulfides, metals and possibly glasses (Dobricǎ et al. 2009). However, we lack data about the adsorption properties of these assemblages. Last, one needs to keep in mind that non-ice materials have been continuously irradiated by magnetospheric electrons and ions (H, O and S), leading to modifications of their topography and porosity, and possibly their adsorption properties. To our knowledge, no relevant data are yet available in the literature.
5.2.3 Consistency with observations
The correlations between the band center and the asymmetry parameter of the CO2 band on one hand, and with the bandwidth on the other hand, support the presence of several components (Fig. 13). The CO2 band in the bright northern polar cap of the leading hemisphere is very redshifted and narrower compared to other terrains. The spectral ratios shown in Fig. 23 suggest a component at 2340 cm−1 (4.274 μm) which is very narrow and essentially present on the leading hemisphere, mostly in the polar regions. This narrow band at 2340 cm−1 is very similar to the band of CO2 mixed with amorphous water ice (Fig. 28). The association of the CO2 responsible for this narrow band with amorphous water ice is further confirmed because the exact same area of the leading north pole has the most redshifted CO2 band and the most blueshifted H2O Fresnel peak position (Figs. 11, 5 and 13), due to a higher abundance of amorphous H2O ice (see Sect. 5.1.3, Fig. 22). Therefore, the CO2 responsible for the red-shifted component of the band is probably mixed with H2O ice, and particularly with amorphous H2O ice at the leading pole. Figure 23 also suggests that the other components of the band are broader and that residual CO2 is associated with non-ice material(s) in the polar regions.
At lower latitudes, we observe a fairly linear correlation between the CO2 band center (expressed in wavelength) and the Bond albedo, and, for the leading side, a correlation with the area of the Fresnel peak area (Figs. 6B, and E.1B). The contribution of CO2 associated with dark materials blueshifts the band, and also broadens it, as observed from the correlation between width and band center (Fig. 13).
In contrast, excluding the polar regions, the variations of the CO2 abundance (i.e., CO2 band area; Fig. 12) do not display significant correlations with the Bond albedo, nor with the area of the Fresnel peaks (Sect. 3.2.3). The CO2 abundance is possibly controlled by sputtering due to surface irradiation. The sputtering yield of CO2 is higher than that of water ice, at least in the case of electronic interactions, which holds for electrons and protons (Brown et al. 1984; Dartois et al. 2015; Seperuelo Duarte et al. 2009). It means that, when CO2 is trapped within water ice, CO2 is preferentially sputtered, resulting in the decrease of its abundance. In the case of CO2 adsorbed on dark material, we expect as well a higher sputtering yield of CO2 compared to atoms or molecular groups forming the dark materials. The flux density of ions and electrons is weaker in the equatorial regions, and, in this respect, we expect a lower sputtering efficiency at low latitudes. This is consistent with the latitudinal variations of the CO2 band depth (Fig. 12). Note that this mechanism also requires a regolith turnover that brings unirradiated grains to the top of the surface, where sputtering happens.
5.3 Origin of the 5.9-μm band
The MIRI spectra show an absorption feature at 5.9 μm (centered between 5.80 and 5.94 μm – respectively 1724 cm−1 and 1683 cm−1 – taking into account uncertainties), with a shoulder at 6.5 μm (1538 cm−1; Sect. 4.3).
The band at 5.9 μm cannot be attributed to water ice. Indeed, the v2 water absorption band is located at slightly longer wavelengths (~6.2 μm, 1613 cm−1) and this water band is expected to be broader (Mastrapa et al. 2009) than the band reported in our observations (0.8 μm-width). This is illustrated in Fig. 26 where merged I/F NIRSpec/MIRI spectra of the leading and trailing hemispheres for several latitude bins are plotted together with the simulated spectrum of CO2/H2O mixture (Appendix C explains how these merged spectra corrected for thermal radiation, including in the NIRSPec wavelength range, were obtained). In addition, the band depth of the 5.9-μm band corrected for thermal emission shows some variations but without a clear geographical trend (Fig. F.3), while the Fresnel peaks and Bond albedo, which are indicative of the abundance and properties of water ice, vary with latitude, type of terrains, and hemisphere. Still, water ice is present all over the surface, so it influences the MIRI spectrum to some extent. Notably, the derived reflectance at 5 μm, which is the location of a H2O ice inter-band, shows a marked anticorrelation with the Bond albedo (Fig. F.2, Sect. 4.3). Moreover, the 5.9-μm band is also present all over Ganymede’s surface and is slightly enhanced on the leading hemisphere, following an overall trend similar to that of water ice. Interestingly, the spectra of the polar regions of leading and trailing hemispheres exhibit marked differences in their water ice spectral features and in the shape of the 5.9-μm band as well (Fig. 26). In addition, on the leading hemisphere the 5.9 μm band position (Figs. 19 and F.3) seems correlated with H2O ice Fresnel peak area and inter-band position (Figs. 5 and 8). Therefore, although the 5.9-μm band is not attributed to water ice, it may be influenced by the presence of water ice, and it might be possible that the component responsible for it is associated to H2O ice.
The 5.9-μm band falls in the 1750–1650 cm−1 (5.714–6.061 μm) region where the carbonyl C=O stretching mode has a strong absorption band. Other double bonds such as C=C and C=N have absorptions in lower frequency regions of about 1500–1650 cm−1 (6.667–6.061 μm). The assignment of the 5.9-μm band to such compounds is challenging as no other unattributed functional groups (e.g., C–H or N–H stretching modes) are seen in NIRSpec spectra.
Organic materials in carbonaceous chondrites and cometary dust, in particular the insoluble fraction, display a C=O band around 1710 cm−1 (5.8480 μm), along with features in the range 2800–3000 cm−1 (3.571–3.333 μm; CH2 and CH3 stretching modes), at 1600 cm−1 (6.250 μm; aromatic C=C), 1450 cm−1 (6.897 μm; CH2 deformation), 1380 cm−1 (7.246 μm; CH3 deformation) and a broad congested feature centered at ~1200 cm−1 (8.333 μm). Carbonaceous chondrites that have experienced short-duration thermal metamorphism, presumably controlled by hypervelocity impacts, have a much lower aliphatic abundance resulting in a weak 2800–3000 cm−1 band (Flynn et al. 2003; Kebukawa et al. 2011; Orthous-Daunay et al. 2013; Quirico et al. 2018). However, they also often display a C=O band of lower intensity, and, in addition, the width of the C=O band is significantly lower than that of the 5.9-μm band. It is then unlikely that this feature is due to chondritic or cometary insoluble organic matter.
We also investigated whether these features could be attributed to carbonic acid (H2CO3), which has been predicted to be present on icy moons for decades (Carlson et al. 2005; Johnson et al. 2004; Peeters et al. 2010; Ioppolo et al. 2021), since it is an irradiation product of CO2 and water ice mixtures (Moore & Khanna 1991; Zheng & Kaiser 2007; Jones et al. 2014; Brucato et al. 1997; Gerakines et al. 2000). H2CO3 has an absorption band assigned to the C=O stretch at 1719 cm−1 (5.817 μm) and the C–OH asymmetric stretch at 1508 cm−1 (6.631 μm; Gerakines et al. 2000), that is, nearby the wavelength of the observed features. However, it presents a strong absorption band around 2600 cm−1 (3.846 μm), which is not observed in NIRSpec spectra. In addition, the band strengths of the above mentioned mid-IR bands have been reported to be of 11 ± 1 and 6.5 ± 0.6 × 10−17 cm molecule−1, respectively (Gerakines et al. 2000). These band strengths are strong and on the order of the band strength of pure CO2 at 2342 cm−1 (4.2699 μm) of 7.6 × 10−17 cm molecule−1 (Gerakines et al. 1995) and of 7.6× 10−17 − 1.1 × 10−16 in other studies (Bouilloud et al. 2015). The area of the 5.9-μm band is tens to hundred times larger than the area of the CO2 band. Since the band strengths are of the same order for CO2 and H2CO3, this would imply that H2CO3 would be a dominating species on the entire surface of Ganymede, and that CO2 would be only a small fraction of H2CO3. H2CO3 is very unstable to radiation (Gerakines et al. 2000; Jones et al. 2014), which makes this hypothesis unlikely.
Another possible carrier of the 5.9-μm bands is non-linearly physisorbed CO2. In that case, the v3 band shifts toward low wavenumbers, covering a broad range of values (1780– 1340 cm−1, resp. 5.618–7.463 μm) depending on the type of binding arrangement and the nature of the cations. The amplitude of the shift correlates with the number of metal cations to which the molecule is bonded (Taifan et al. 2016). As the CO2 molecule is bent, its symmetry changes from D∞h to C2υ and the v1 symmetric stretching mode becomes infrared active, with a range of values of 1340–980 cm−1 (7.463–10.204 μm). Complicating this picture, CO2 can also be chemically adsorbed into carbonates, through a variety of binding configurations (free symmetrical, monodentate, bidentate, polydentate). Those different speciations lead to strong spectral shifts and splitting depending both on the nature of cations and binding arrangements, compared to the positions of the v2, v3 and v4 vibration modes of isolated carbonates (Farmer 1974). Therefore, interestingly, the bands observed in MIRI spectra at ~ 5.9 and 6.5 μm could be controlled by non-linearly adsorbed or chemically adsorbed CO2. As discussed before, it is not possible to assign them univocally to specific cations and binding arrangements, and dedicated experiments are required. Additional bands due to physisorbed or chemisorbed CO2 are not expected in the MIRI and NIRSPec spectral ranges.
H2SO4.8H2O has been proposed to be present at the surface of Ganymede, as this compound leads to a better fit of the water bands in the near-infrared region (Shirley et al. 2010; Ligier et al. 2019; King & Fletcher 2022). The H2SO4/H2O phase diagram displays several sulfuric acid hydrates, depending on H2SO4 concentration: monohydrate, dihydrate, trihydrate, tetrahydrate, heptahydrate and octahydrate (Kinnibrugh & Fister 2022). The spectra of monohydrate, tetrahydrate and octahydrate have been determined experimentally (Nash et al. 2001; Beyer et al. 2003). The spectra show a group of bands between 800 and 1350 cm−1 (12.50–7.41 μm), associated with S–O bonds; a band in the range 1698–1720 cm−1 (5.889–5.814 μm) assigned to a deformation mode of H3O+ or 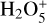 ; and bands in the range 2800–2900 cm−1 (3.571–3.448 μm), due stretching modes of H3O+,
; and bands in the range 2800–2900 cm−1 (3.571–3.448 μm), due stretching modes of H3O+, 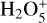 or OH. Except at boundaries between different stability fields of those hydrates, a H2SO4-H2O mixture is made of two different hydrates (except at the edges of the phase diagram, where one hydrate is mixed with either H2O ice or solid H2SO4). That said, the position of the 5.9-μm band in Ganymede (in the range 1678–1718 cm−1 (5.96–5.82 μm), considering uncertainties and both hemispheres, Sect. 4.3) is consistent with the band positions at 1698, 1715 and 1720 cm−1 (5.889, 5.831 and 5.814 μm) for octa (SAO), tetra (SAT) and monohydrates (SAM), respectively. In addition, its width is quite similar to those in experimental spectra (around 170 cm−1). However, according to Nash et al. (2001), features are present between 2800 and 2900 cm−1 (resp. 3.571 and 3.448 μm) due to stretching modes in H3O+,
or OH. Except at boundaries between different stability fields of those hydrates, a H2SO4-H2O mixture is made of two different hydrates (except at the edges of the phase diagram, where one hydrate is mixed with either H2O ice or solid H2SO4). That said, the position of the 5.9-μm band in Ganymede (in the range 1678–1718 cm−1 (5.96–5.82 μm), considering uncertainties and both hemispheres, Sect. 4.3) is consistent with the band positions at 1698, 1715 and 1720 cm−1 (5.889, 5.831 and 5.814 μm) for octa (SAO), tetra (SAT) and monohydrates (SAM), respectively. In addition, its width is quite similar to those in experimental spectra (around 170 cm−1). However, according to Nash et al. (2001), features are present between 2800 and 2900 cm−1 (resp. 3.571 and 3.448 μm) due to stretching modes in H3O+, 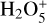 and OH bonded to the S–O core. In fact, these assignments are unclear. We have reanalyzed the spectra of SAM, SAT and SAO from Nash et al. (2001) and Beyer et al. (2003), and found several arguable interpretations. The spectrum of SAM displays a broad feature centered at 2881 cm−1, however, it does not fit with the spectrum of the H3O+ -rich HCl ice, which peaks at 3250 cm−1. The spectra of SAO and SAT display a broad feature centered at 3250 cm−1, but this feature looks more similar to water ice. All in all, we get to the conclusion that (i) the assignment of these broad structures is unclear, (ii) but they are broad and likely share similarities with water ice in terms of position (3250 cm−1, i.e., 3.076 μm) and broadness. As a consequence, we expect them to essentially contribute to the continuum along with water ice. Last, as discussed at the beginning of this section, the component responsible for the 5.9-μm band might be associated with H2O ice, favoring hydrates, and possibly H2SO4 hydrate(s), over other non-ice candidates.
and OH bonded to the S–O core. In fact, these assignments are unclear. We have reanalyzed the spectra of SAM, SAT and SAO from Nash et al. (2001) and Beyer et al. (2003), and found several arguable interpretations. The spectrum of SAM displays a broad feature centered at 2881 cm−1, however, it does not fit with the spectrum of the H3O+ -rich HCl ice, which peaks at 3250 cm−1. The spectra of SAO and SAT display a broad feature centered at 3250 cm−1, but this feature looks more similar to water ice. All in all, we get to the conclusion that (i) the assignment of these broad structures is unclear, (ii) but they are broad and likely share similarities with water ice in terms of position (3250 cm−1, i.e., 3.076 μm) and broadness. As a consequence, we expect them to essentially contribute to the continuum along with water ice. Last, as discussed at the beginning of this section, the component responsible for the 5.9-μm band might be associated with H2O ice, favoring hydrates, and possibly H2SO4 hydrate(s), over other non-ice candidates.
In conclusion, the 5.9-μm band in Ganymede spectra can be tentatively assigned to a sulfuric acid hydrate. A firmer assignment would require more robust experimental data.
5.4 H2O2
H2O2 is present all over Ganymede’s surface, with a higher abundance in the polar regions (Trumbo et al. 2023), which are the regions where the water ice is the most abundant and/or have the smallest optical mean free path (Sect. 5.1.3, Fig. 8). These observations are consistent with H2O2 being a product of water ice radiolysis, enhanced in the open field line regions (Trumbo et al. 2023). However, the H2O2 and CO2 maps are not well correlated (see CO2 map in Fig. 11 and H2O2 map in Trumbo et al. 2023), making CO2 abundance unlikely to influence H2O2 production. Moreover, although the CO2 responsible for the red-shifted component of the band, interpreted as CO2 associated with water ice, is enhanced on the polar regions of the leading, similar to H2O2, there is no exact pixel-to-pixel match between the locations of both species. In addition, on the trailing hemisphere, the redshifted CO2 component is enhanced on the polar regions, whereas the H2O2 is not.
As described in Trumbo et al. (2023), the distribution of H2O2 on Ganymede (H2O2 abundance enhanced on the most ice-rich and coldest regions) is at odds with that observed on Europa (H2O2 abundance enhanced on the most ice-poor and warmest regions; Spencer et al. 1999; Rathbun et al. 2010; Trumbo et al. 2018, 2019). The enhanced abundance of H2O2 on Europa’s chaos terrains has been hypothesized to be related to the presence of CO2 or possibly other electron-accepting ice contaminants, which may scavenge destructive electrons created during the irradiation of the ice, thereby slowing down the destruction of H2O2 (Trumbo et al. 2019, 2023). Ganymede’s NIRSpec observations do not support CO2 to be an electron scavenger enhancing H2O2. However, the production and destruction pathways of H2O2 may be different on Europa and Ganymede, and/or other species might play the role of electron scavengers.
6 Summary
Ganymede leading and trailing hemispheres were observed with the NIRSpec/IFU (2.9–5.3 μm) and MIRI/MRS (unsaturated data from 4.9–11.7 μm) instruments of JWST, as part of the ERS program 1373 “ERS observations of the Jovian system as a demonstration of JWST’s capabilities for Solar System science”. The aim was to investigate the composition and thermal properties of the surface, as well as its exosphere. These observations led to the first detection of H2O2, published by Trumbo et al. (2023). Results on the exosphere will be reported elsewhere. Although the S/N was the highest ever obtained in the near-IR for Ganymede, minor signatures observed with Galileo/NIMS and Juno/JIRAM at 3.3, 3.4, 3.88, 4.38, and 4.57 μm were not confirmed. In this paper, we focused on the distribution and spectral properties of CO2 and water ice signatures observed with NIR-Spec, and on the analysis of the MIRI data. The main results are:
Maps of the H2O Fresnel peak area at ~3.1 μm are consistent with the distribution of water ice inferred from H2O bands at 4.5 μm and in the near-IR (Ligier et al. 2019; King & Fletcher 2022), and they correlate with Bond albedo maps. Water ice is the most abundant on the polar regions of the leading hemisphere. On the trailing side, the Fresnel peak area shows a minimum slightly eastward (by 9°) from the central longitude (270°), increasing around this minimum with a bull’s-eye distribution, with some excess at the poles. An excess of ice is also observed on the trailing morning limb, which may trace the formation of ice crystals during the night, from the recondensation of water subliming from the warmer subsurface;
At low to mid latitudes, the central wavelength of the H2O Fresnel peaks shifts with longitude, and this is observed for both the leading and trailing sides. This shift seems to indicate a progressive and cumulative modification of the H2O ice molecular structure (possibly via amorphization, other phase changes, or chemical changes) and/or a nanometer- or micrometer-scale texture (potentially via sublimation, recondensation, or photodesorption), induced by the accumulation of solar radiation from the morning to the evening, and which is reversible during the night. Dedicated studies are needed to constrain the origin of this longitudinal modification of the surface ice;
Amorphous water ice, probably formed by irradiation from Jupiter’s magnetospheric energetic particles, is detected in the polar regions, where temperature conditions block the kinetics of water ice recrystallization. The polar regions of the leading side contain more amorphous ice than those of the trailing side, and the boreal region of the leading hemisphere is the richest;
As expected, maps of the wavelength position of the H2O inter-band (in the range 3.65–3.95 μm) correlate with the distribution and abundance of water ice inferred from the band at 4.5 μm and the Fresnel peak area. The wavelength position of the inter-band in dark terrains seems to be compatible with the presence of Na- and Mg- sulfate salts, sulfuric acid hydrates, and possibly phyllosilicates. The positive (red) spectral slope of Ganymede’s dark and equatorial terrain spectrum continuum from 3.9 to 7 μm is consistent with the mixing of such compounds with fine-grained opaque minerals with a highly porous surficial micro-texture. However, no absorption bands that would enable firm identification of compounds specific to Ganymede’s dark terrain are observed;
The CO2 4.26 μm band displays latitudinal and regional variations in the band center and band shape over the two hemispheres, which indicate that CO2 is present in different physical states on the surface. The band center and shape are correlated with the Bond albedo and H2O ice abundance;
The CO2 band depth shows a latitudinal gradient, from 8 to 22% on the trailing side, and from 11 to 21% on the leading side with the lower values in polar regions. The CO2 band depth does not show a significant correlation with Bond albedo and ice content in the equatorial regions;
In the ice-rich polar regions, which are the most exposed to Jupiter’s plasma irradiation, the CO2 band is redshifted with respect to other terrains. In the boreal region of the leading hemisphere, the CO2 band is dominated by a high wavelength component at ~4.27 μm, consistent with CO2 trapped in amorphous water ice. In the same region, amorphous water ice is observed. Therefore, the formation and/or trapping of this CO2 may be linked to the formation and/or structure of the amorphous water ice;
At equatorial latitudes (and especially on dark terrains), the observed band broadening and blueshift suggest CO2 was adsorbed or trapped on non-icy materials, such as minerals or salts;
From Hapke modeling, the abundance of CO2 trapped in water ice is roughly 1% in mass;
Clathrate hydrates cannot explain the characteristics of the CO2 band, and are a minor contributor at best;
The brightness temperature from 7 to 11 μm exhibits a monotonic (and quasi-linear) decrease with increasing wavelength, by over 10 K at disk center, which may be due to a spectral emissivity < 1, and/or an emissivity that decreases with increasing wavelength, and/or a Planck-weighted mixing of a variety of surface temperatures within the PSF;
From thermophysical modeling, the distribution of the brightness temperatures at 8.25 μm indicates a rough surface at scales of 0.1 mm–10 cm, with mean slope angles of 15°–25° and thermal inertias in the range Γ = 20–40 SI, with no obvious difference between leading and trailing sides;
The MIRI spectra show an absorption feature at 5.9 μm, which is present all over Ganymede’s surface, with a depth in the reflected sunlight component, typically ranging over 35–54% on the leading side, and 30–52% on the trailing side, and a width of ~0.8 μm, with evidence for an absorption shoulder at 6.5 μm (more pronounced on the leading side). The 5.9 μm band cannot be attributed to the v2 band of water ice, which is expected to be broader and at a slightly higher wavelength. The features cannot be assigned to carbonic acid H2CO3, which has been predicted to be present on icy moons for decades. These bands could be controlled by nonlinearly physisorbed or chemically adsorbed CO2. Sulfuric acid hydrates H2SO4.nH2O appear to be good candidates to explain the 5.9-μm band;
H2O2 is enhanced in Ganymede’s polar regions, where it is probably produced by water ice radiolysis. These observations do not support CO2 to be an electron scavenger enhancing H2O2 on Ganymede, contrary to what was hypothesized on Europa.
The spectral properties of the polar regions are very different for leading versus trailing sides. The leading polar caps have less exposed non-ice materials, a smaller optical mean free path in water ice (indicative of a larger external or internal surface such as cracks or pores), more amorphous water ice, as well as deeper CO2 (more redshifted) and H2O2 absorption bands than trailing poles. The origins of these differences remain to be investigated, in particular considering leading and trailing asymmetries in Jovian plasma precipitation and micro-meteoroid gardening, and how these processes influence the icy surface physico-chemical transformations.
Radiative transfer modeling and experimental measurements are needed to provide deeper data interpretations. From an observational perspective, this JWST investigation has shown that observations designed to investigate diurnal variations of Ganymede’s surface properties may unravel unexpected processes. Altogether the results obtained in this study will certainly help in optimizing the observation strategies of the Moons And Jupiter Imaging Spectrometer (MAJIS) on board the ESA/JUICE mission which will explore Ganymede further.
Acknowledgements
This work is based on observations made with the NASA/ESA/CSA James Webb Space Telescope. The data were obtained from the Mikulski Archive for Space Telescopes at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-03127 for JWST. These observations are associated with program 1373, which is led by co-PIs Imke de Pater and Thierry Fouchet and has a zero-exclusive-access period. I.d.P., M.H.W., P.M.F., M.R.S. are in part supported by the Space Telescope Science Institute grant nr. JWST-ERS-01373. The work of O.P., E.Q. and B.S. was in part supported by the CNES. D.B.-M, E.Q., E.L., T.F., and O.P. acknowledge support from the French Agence Nationale de la Recherche (program PRESSE, ANR-21-CE49-0020-01). L.N.F. was supported by a European Research Council Consolidator Grant (under the European Union’s Horizon 2020 research and innovation programme, grant agreement No 723890) at the University of Leicester. G.S.O. was supported at the Jet Propulsion Laboratory under contract with the National Aeronautics and Space Administration (80NM0018D004). J.S. received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 884711).
Appendix A Bull’s eye structure of Fresnel peak area distribution on the trailing hemisphere
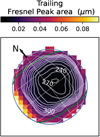 |
Fig. A.1 Distribution of the Fresnel peak area on the trailing hemisphere. Iso-contours (levels spaced by 0.0025 μm with the central level at 0.0035 μm) are overplotted. |
Appendix B Preparation of Aguas Zarcas hyperfine and hyperporous sample
Mid-infrared reflectance spectra are extremely dependent on the surface texture (grain size, porosity; Salisbury & Wald 1992), and we know from recent observations the extreme surface porosity of some Ganymede’s dark terrains (85%, de Kleer et al. 2021).
Therefore, we have tested how such extreme porosity influences the reflectance spectrum of a dark material of composition potentially analog to Ganymede’s dark terrains. We chose the Aguas Zarcas (CM) meteorite, which is a recent fall (2019). It is mainly made of phyllosilicates constituting a fine-grained matrix, hosting anhydrous silicates, calcite, opaque minerals (iron sulfides, magnetite etc.), and salts among other constituents (Garvie 2021). The fine-grained opaque minerals appear to be responsible for the low albedo of the meteorite, and possibly of many primitive bodies such as comets or P-/D-type asteroids (Quirico et al. 2016). Moreover, we know that the degree of dispersion/agglomeration of sub-micrometer-sized grains of opaques and silicates (hydrated or not) controls their spectroscopic properties from visible to mid-infrared wavelengths (Sultana et al. 2023). Therefore, we have produced a hyperfine powder (i.e., made of sub-micrometer-sized grains) of the Aguas Zarcas meteorite, and we have made a hyperporous (>80%) sample of this powder to measure its mid-infrared reflectance spectrum.
The detailed experimental protocol for the production of the hyperfine and hyperporous sample is given in Sultana et al. (2021). Aguas Zarcas was grounded in sub-micrometer-sized grains using a planetary ball mill and following a series of grinding and sieving steps. This hyperfine powder was then mixed in liquid water and produced frozen droplets of this mixture, which were put in a thermal-vacuum chamber for the water to sublimate. After complete sublimation of the water, a hyperporous (>80%) sublimation lag deposit was formed, made of the Aguas Zarcas sub-μm grains arranged in a highly porous structure. The spectrum of this lag deposit shown in Fig. 25b exhibits a strong positive (red) spectral slope reminiscent of the spectral slope of the continuum of Ganymede’s dark terrains from 3.9 to 7 μm (dashed-dotted gray line in Fig. 25b). The radiative transfer mechanism explaining how an increase of porosity induces a spectral reddening is not yet established (it will be the subject of an upcoming study), but it requires the presence of sub-μm opaque grains such as sulfides.
Aguas Zarcas spectrum exhibits absorption bands centered at 2.8-2.9 μm due to OH/H2O in phyllosilicates, at 6.09 μm due to adsorbed H2O and at 6.89 μm due to carbonates.
Appendix C Merged NIRSpec/MIRI spectra
Thermal emission affects to some extent the continuum emission in the long wavelength part of NIRSpec NRS2 spectra. We used the models developed for analysing the MIRI observations to estimate the thermal contribution at the longest NIRSpec wavelengths. For that, we extrapolated the calculations of the thermal and reflected components down to 4 μm, yielding the thermal to solar reflected (T H/S R) ratio as a function of wavelength and I/F. In doing so, we used Model 2 of Sect. 4.3, and assumed unit spectral emissivity shortward of 4.9 μm. This estimate was done for spectra averaged over the whole disk, equatorial and polar latitudes (Fig. 26). For these various spectra shown in Fig. 26 (and also in Figs 24 and 25), the TH/SR varies from 0.12–0.25 at 5.3 μm, and depending on the spectra, falls below 0.01 at 4.4–4.65 μm. This ratio was then used to iteratively correct the NIRSPec spectra for thermal radiation. A correcting factor from 0.95 to 1.14 was then applied to the MIRI spectra to produce the merged NIRSPec/MIRI spectra shown in Fig. 26.
Appendix D Estimation of polar H2O ice temperature from 3.6-μm inter-band position
The correlation between the temperature of pure H2O ice and the wavelength at which the reflectance bump of the 3.6-μm H2O ice inter-band is maximum is represented in Fig. D.1. For crystalline ice, laboratory reflectance from Clark et al. (2012) and Stephan et al. (2021) are reported. For amorphous H2O ice, the reflectance spectra for ice ranging between 15 K and 120 K are represented. To do so, we used the optical constants of amorphous H2O ice (Mastrapa et al. 2009) to predict the inter-band spectra in reflectance (Hapke 1993), and applied a shift similar than the shift observed for crystalline H2O ice between calculated reflectance (with optical constants from Mastrapa et al. 2009) and laboratory spectra (Clark et al. 2012). By considering that this shift (of 0.1 μm) is similar for amorphous and crystalline ice, the reflectance peaks simulated for amorphous ice are presented. As shown in the figure, these maxima are mostly located at lower temperatures than for crystalline ice. We here therefore assume that the inter-band maxima for amorphous ice are located at lower wavelengths than those for crystalline ice.
 |
Fig. D.1 Correlation between the temperature of pure H2O ice and the wavelength at which the reflectance bump of the 3.6-μm H2O ice inter-band is maximum. For pure crystalline H2O ice, the laboratory reflectance spectra are from Clark et al. (2012) and Stephan et al. (2021). For amorphous ice, points have been estimated by reflectance spectra with Mastrapa et al. (2009) optical constants, and applying a shift of 0.1 μm. |
Appendix E Correlations between CO2 band parameters and Fresnel peak area
 |
Fig. E.1 Correlations between CO2 band characteristics and water ice. CO2 band area (A) and band center (B) as a function of Fresnel-peak area (i.e., EqW). Data for the leading and trailing hemispheres are shown with blue and red symbols, respectively. Filled and open dots are for latitudes lower and higher than 40° N/S, respectively. The data in the morning limb of the trailing hemisphere (namely longitudes > 320°) are shown with the star symbol. The positive correlation between CO2 band center (in wavelength) and Fresnel peak area has a Spearman’s rank coefficient r = 0.62 and 0.52 with a significance of 6.6σ and 6.9σ for leading and trailing hemispheres, respectively. A weak negative correlation between CO2 band area and Fresnel peak area is present when considering all data (r = −0.31 (4.5σ) and r = −0.53 (6.6 σ) for leading/trailing hemispheres respectively), but not when considering only equatorial (< 40°) latitudes (r ~ 0 (0σ) and r = −0.15 (1.8 σ), for leading/trailing hemispheres, respectively). These calculations of correlation coefficients exclude data on the morning limb of the trailing hemisphere. |
Appendix F Additional figures describing MIRI data fits
 |
Fig. F.1 Observed and modeled 8.25-μm brightness temperature (TB). 8.25 μm TB for Obs. 18 (first two rows) and Obs. 27 (last two rows), plotted as a function of local time (first and third rows) or latitude (second and fourth rows). In each row, observational data (first column) are compared to a series of models. In the first column, the data are color-coded according to latitude (i.e., to equal values of the latitude difference from the sub-observer point) in the TB vs local time plots, and according to local time in the TB vs latitude plots. The following six column describe the six considered models, with the three options for the Bond albedos and inclusion or not of surface slopes (see text for details). In those panels, data are in black, models in red, and the data minus model difference in blue, with the 0 value indicated by the dashed line. Parameter values and rms of fit are indicated in each panel. |
 |
Fig. F.2 MIRI thermal-modeling outputs. Fitted model parameters for Obs. 18 (Leading, first three rows) and Obs. 27 (Trailing, last three rows), for the three models described in Sect. 4.3: temperature (T1, T2, or T3), second fit parameter (ɛ1, |
 |
Fig. F.3 5.9-μm band properties. Fitted characteristics of the 5.9-μm band in Obs. 18 (leading side, first three rows) and Obs. 27 (trailing side, last three rows), for the three models described in the text: observed band depth relative to total continuum, band depth corrected for thermal contribution (i.e., relative to model solar reflected component), band position (offset from 5.90 μm), and band FWHM width. The last column shows the correlation between the observed (black) and corrected (red) band depths with the observed 8.25 μm TB. Spearman correlation coefficients and number of standard deviations significance are indicated as insets. |
References
- Adriani, A., Filacchione, G., Di Iorio, T., et al. 2017, Space Sci. Rev., 213, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Alday, J., Roth, L., Ivchenko, N., et al. 2017, Planet. Space Sci., 148, 35 [Google Scholar]
- Bardyn, A., Baklouti, D., Cottin, H., et al. 2017, MNRAS, 469, S712 [NASA ADS] [CrossRef] [Google Scholar]
- Bekhti, H., Boucheffa, Y., Blal, A. A., & Travert, A. 2021, Vibrat. Spectrosc., 117, 103313 [CrossRef] [Google Scholar]
- Berlanga, G., Hibbitts, C. A., Takir, D., Dyar, M. D., & Sklute, E. 2016, Icarus, 280, 366 [NASA ADS] [CrossRef] [Google Scholar]
- Berquin, Y., Kofman, W., Herique, A., Alberti, G., & Beck, P. 2013, Planet. Space Sci., 77, 40 [Google Scholar]
- Beyer, K. D., Hansen, A. R., & Poston, M. 2003, J. Phys. Chem. A, 107, 2025 [NASA ADS] [CrossRef] [Google Scholar]
- Bonelli, B., Civalleri, B., Fubini, B., et al. 2000, J. Phys. Chem. B, 104, 10978 [CrossRef] [Google Scholar]
- Born, M., & Wolf, E. 1999, Principle of OPTICS (Pergamon, Oxford) [CrossRef] [Google Scholar]
- Bottke, W. F., Vokrouhlický, D., Nesvorný, D., & Moore, J. M. 2013, Icarus, 223, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Bouilloud, M., Fray, N., Bénilan, Y., et al. 2015, MNRAS, 451, 2145 [Google Scholar]
- Brown, W., Augustyniak, W., Marcantonio, K., et al. 1984, Nucl. Instrum. Methods Phys. Res. Sect. B , 1, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Brucato, J. R., Palumbo, M. E., & Strazzulla, G. 1997, Icarus, 125, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Calvin, W. M., & Clark, R. N. 1991, Icarus, 89, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Carlson, R. W., Weissman, P. R., Smythe, W. D., Mahoney, J. C., & The NIMS Science and Engineering Teams 1992, Space Sci. Rev., 60, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Carlson, R. W., Anderson, M. S., Johnson, R. E., et al. 1999a, Science, 283, 2062 [NASA ADS] [CrossRef] [Google Scholar]
- Carlson, R. W., Johnson, R. E., & Anderson, M. S. 1999b, Science, 286, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Carlson, R. W., Hand, K. P., Gerakines, P. A., Moore, M. H., & Hudson, R. L. 2005, in AAS/Division for Planetary Sciences Meet. Abstr., 37, 58.05 [NASA ADS] [Google Scholar]
- Cassidy, T. A., Paranicas, C. P., Shirley, J. H., et al. 2013, Planet. Space Sci., 77, 64 [Google Scholar]
- Chaban, G. M., Bernstein, M., & Cruikshank, D. P. 2007, Icarus, 187, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Ciarniello, M., Moroz, L. V., Poch, O., et al. 2021, Minerals, 11, 1222 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, R. N., Cruikshank, D. P., Jaumann, R., et al. 2012, Icarus, 218, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Cruikshank, D. P., Meyer, A. W., Brown, R. H., et al. 2010, Icarus, 206, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Dartois, E., Augé, B., Boduch, P., et al. 2015, A&A, 576, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Kleer, K., Butler, B., de Pater, I., et al. 2021, PSJ, 2, 5 [NASA ADS] [Google Scholar]
- de Pater, I., Fletcher, L. N., Reach, W. T., et al. 2021, PSJ, 2, 226 [NASA ADS] [CrossRef] [Google Scholar]
- de Pater, I., Fouchet, T., Wong, M., et al. 2022, in AAS/Division for Planetary Sciences Meet. Abstr., 54, 306.07 [NASA ADS] [Google Scholar]
- De Sanctis, M. C., Capaccioni, F., Ciarniello, M., et al. 2015, Nature, 525, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Dobricǎ, E., Engrand, C., Duprat, J., et al. 2009, Meteor. Planet. Sci., 44, 1643 [CrossRef] [Google Scholar]
- Domingue, D., & Verbiscer, A. 1997, Icarus, 128, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Duling, S., Saur, J., Clark, G., et al. 2022, Geophys. Res. Lett., 49, e2022GL101688 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenfreund, P., Kerkhof, O., Schutte, W. A., et al. 1999, A&A, 350, 240 [NASA ADS] [Google Scholar]
- Famá, M., Loeffler, M., Raut, U., & Baragiola, R. 2010, Icarus, 207, 314 [CrossRef] [Google Scholar]
- Farmer, V. C., ed. 1974, The Infrared Spectra of Minerals (Mineralogical Society of Great Britain and Ireland) [CrossRef] [Google Scholar]
- Fatemi, S., Poppe, A. R., Khurana, K. K., Holmström, M., & Delory, G. T. 2016, Geophys. Res. Lett., 43, 4745 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, M., Quirico, E., Faure, A., et al. 2015, Icarus, 261, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, P. D., McGrath, M. A., Strobel, D. F., et al. 2000, ApJ, 535, 1085 [NASA ADS] [CrossRef] [Google Scholar]
- Filacchione, G., D’Aversa, E., Capaccioni, F., et al. 2016, Icarus, 271, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Fleyfel, F., & Devlin, J. P. 1991, J. Phys. Conf. Ser., 95, 3811 [NASA ADS] [Google Scholar]
- Flynn, G. J., Keller, L. P., Feser, M., Wirick, S., & Jacobsen, C. 2003, Geochim. Cosmochim. Acta, 67, 4791 [CrossRef] [Google Scholar]
- Förster, H., & Schumann, M. 1989, J. Chem. Soc. Faraday Trans. 1, 85, 1149 [CrossRef] [Google Scholar]
- Foster, P., & Howarth, C. 1968, Carbon, 6, 719 [CrossRef] [Google Scholar]
- Fray, N., & Schmitt, B. 2009, Planet. Space Sci., 57, 2053 [Google Scholar]
- Garvie, L. A. 2021, Am. Mineralogist, 106, 1900 [NASA ADS] [CrossRef] [Google Scholar]
- Gerakines, P. A., Schutte, W. A., Greenberg, J. M., & van Dishoeck, E. F. 1995, A&A, 296, 810 [NASA ADS] [Google Scholar]
- Gerakines, P. A., Moore, M. H., & Hudson, R. L. 2000, A&A, 357, 793 [NASA ADS] [Google Scholar]
- Hall, D. T., Feldman, P. D., McGrath, M. A., & Strobel, D. F. 1998, ApJ, 499, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, G. B., & McCord, T. B. 2004, J. Geophys. Res. Planets, 109, E01012 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 1984, Icarus, 59, 41 [Google Scholar]
- Hapke, B. 1993, Theory of Reflectance and Emittance Spectroscopy (Cambridge University Press) [Google Scholar]
- Hartogh, P., Bockelée-Morvan, D., Rezac, L., et al. 2013, in #42, The Universe Explored by Herschel, 61.03 [Google Scholar]
- Hase, F., Wallace, L., McLeod, S. D., Harrison, J. J., & Bernath, P. F. 2010, J. Quant. Spec. Radiat. Transf., 111, 521 [NASA ADS] [CrossRef] [Google Scholar]
- He, J., Emtiaz, S., Boogert, A., & Vidali, G. 2018, ApJ, 869, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Helfenstein, P., & Shepard, M. K. 1999, Icarus, 141, 107 [Google Scholar]
- Hibbitts, C. A. & Szanyi, J. 2007, Icarus, 191, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Hibbitts, C. A., Klemaszewski, J. E., McCord, T. B., Hansen, G. B., & Greeley, R. 2002, J. Geophys. Res., 107 [Google Scholar]
- Hibbitts, C. A., Pappalardo, R. T., Hansen, G. B., & McCord, T. B. 2003, J. Geophys. Res. Planets, 108, 5036 [NASA ADS] [CrossRef] [Google Scholar]
- Hibbitts, C. A., Stephan, K., Collins, G., & Hansen, G. B. 2009, in EPSC Abstracts, 4, 632 [Google Scholar]
- Hibbitts, C., Stockstill-Cahill, K., Wing, B., & Paranicas, C. 2019, Icarus, 326, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Ioppolo, S., Kanuchová, Z., James, R. L., et al. 2021, A&A, 646, A172 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, R. E., & Jesser, W. A. 1997, ApJ, 480, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, R. E., & Quickenden, T. I. 1997, J. Geophys. Res. Planets, 102, 10985 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, R. E., Carlson, R. W., Cooper, J. F., et al. 2004, in Jupiter. The Planet, Satellites and Magnetosphere, eds. F. Bagenal, T. E. Dowling, & W. B. McKinnon (Cambridge University Press), 1, 485 [NASA ADS] [Google Scholar]
- Jones, B. M., Kaiser, R. I., & Strazzulla, G. 2014, ApJ, 788, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Kebukawa, Y., Alexander, C. M. O. D., & Cody, G. D. 2011, Geochim. Cos-mochim. Acta, 75, 3530 [NASA ADS] [CrossRef] [Google Scholar]
- Khurana, K., Pappalardo, R., Murphy, N., & Denk, T. 2007, Icarus, 191, 193 [NASA ADS] [CrossRef] [Google Scholar]
- King, O., & Fletcher, L. N. 2022, J. Geophys. Res. Planets, 127, e2022JE007323 [NASA ADS] [CrossRef] [Google Scholar]
- Kinnibrugh, T. & Fister, T. 2022, J. Phys. Chem. B, 126, 3099 [NASA ADS] [CrossRef] [Google Scholar]
- Kokaly, R. F., Clark, R. N., Swayze, G. A., et al. 2017, United States Geological Survey (USGS): Reston, VA, USA, 61 [Google Scholar]
- Leblanc, F., Oza, A. V., Leclercq, L., et al. 2017, Icarus, 293, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Leblanc, F., Roth, L., Chaufray, J. Y., et al. 2023, Icarus, 399, 115557 [NASA ADS] [CrossRef] [Google Scholar]
- Ligier, N., Paranicas, C., Carter, J., et al. 2019, Icarus, 333, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Liuzzo, L., Poppe, A. R., Paranicas, C., et al. 2020, J. Geophys. Res. Space Phys., 125, e28347 [NASA ADS] [CrossRef] [Google Scholar]
- Loeffler, M. J., Hudson, R. L., Moore, M. H., & Carlson, R. W. 2011, Icarus, 215, 370 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, M. L. 2007, Icarus, 190, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Martra, G., Ocule, R., Marchese, L., Centi, G., & Coluccia, S. 2002, Catal. Today, 73, 83 [CrossRef] [Google Scholar]
- Mastrapa, R. M., Sandford, S. A., Roush, T. L., Cruikshank, D. P., & Dalle Ore, C. M. 2009, ApJ, 701, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- McCord, T. B., Carlson, R. W., Smythe, W. D., et al. 1997, Science, 278, 271 [NASA ADS] [CrossRef] [Google Scholar]
- McCord, T. B., Hansen, G. B., Clark, R. N., et al. 1998, J. Geophys. Res., 103, 8603 [NASA ADS] [CrossRef] [Google Scholar]
- McCord, T. B., Hansen, G. B., & Hibbitts, C. A. 2001, Science, 292, 1523 [NASA ADS] [CrossRef] [Google Scholar]
- Mitchell, E. H., Raut, U., Teolis, B. D., & Baragiola, R. A. 2017, Icarus, 285, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, M. H., & Khanna, R. K. 1991, Spectrochim. Acta Part A: Mol. Spectrosc., 47, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Mura, A., Adriani, A., Sordini, R., et al. 2020, J. Geophys. Res. Planets, 125, e06508 [NASA ADS] [CrossRef] [Google Scholar]
- Nash, K. L., Sully, K. J., & Horn, A. B. 2001, J. Phys. Chem. A, 105, 9422 [NASA ADS] [CrossRef] [Google Scholar]
- Ockman, N. 1958, Adv. Phys., 7, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Oren, A., & Nayar, S. 1994, SIGGRAPH 94 (ACM Press), 239 [CrossRef] [Google Scholar]
- Orthous-Daunay, F. R., Quirico, E., Beck, P., et al. 2013, Icarus, 223, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Pappalardo, R. T., Collins, G. C., Head, James W., I., et al. 2004, in Jupiter. The Planet, Satellites and Magnetosphere, eds. F. Bagenal, T. E. Dowling, & W. B. McKinnon (Cambridge University Press), 1, 363 [NASA ADS] [Google Scholar]
- Peeters, Z., Hudson, R. L., Moore, M. H., & Lewis, A. 2010, Icarus, 210, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Plainaki, C., Massetti, S., Jia, X., et al. 2020, ApJ, 900, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Plainaki, C., Massetti, S., Jia, X., et al. 2022, ApJ, 940, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Poch, O., Yoldi, Z., & Jost, B. 2016, Vis-NIR bidirectional reflection spectra of spherical water ice particles for different sizes (2–100 µm), temperatures (173 and 223 K) and temporal evolutions, “SSHADE/BYPASS+CSS (OSUG Data Center). Dataset/Spectral Data.” [Google Scholar]
- Poppe, A. R. 2016, Icarus, 264, 369 [Google Scholar]
- Poppe, A. R., Fatemi, S., & Khurana, K. K. 2018, J. Geophys. Res. Space Phys., 123, 4614 [NASA ADS] [CrossRef] [Google Scholar]
- Purves, N. G., & Pilcher, C. B. 1980, Icarus, 43, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Quirico, E., & Schmitt, B. 1997, Icarus, 127, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Quirico, E., Moroz, L. V., Schmitt, B., et al. 2016, Icarus, 272, 32 [CrossRef] [Google Scholar]
- Quirico, E., Bonal, L., Beck, P., et al. 2018, Geochim. Cosmochim. Acta, 241, 17 [CrossRef] [Google Scholar]
- Rathbun, J. A., Rodriguez, N. J., & Spencer, J. R. 2010, Icarus, 210, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Roth, L., Ivchenko, N., Gladstone, G. R., et al. 2021, Nat. Astron., 5, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Rozitis, B., & Green, S. F. 2011, MNRAS, 415, 2042 [NASA ADS] [CrossRef] [Google Scholar]
- Salisbury, J. W., & Wald, A. 1992, Icarus, 96, 121 [Google Scholar]
- Saur, J., Duling, S., Roth, L., et al. 2015, J. Geophys. Res. Space Phys., 120, 1715 [NASA ADS] [CrossRef] [Google Scholar]
- Schenk, P. M., & McKinnon, W. B. 1991, Icarus, 89, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, B., Quirico, E., Trotta, F., & Grundy, W. M. 1998, Astrophys. Space Sci. Lib., 227, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Seperuelo Duarte, E., Boduch, P., Rothard, H., et al. 2009, A&A, 502, 599 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shirley, J. H., Dalton, J. B., Prockter, L. M., & Kamp, L. W. 2010, Icarus, 210, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Spencer, J. R. 1987, PhD thesis, University of Arizona, USA [Google Scholar]
- Spencer, J. R., Lebofsky, L. A., & Sykes, M. V. 1989, Icarus, 78, 337 [Google Scholar]
- Spencer, J. R., Tamppari, L. K., Martin, T. Z., & Travis, L. D. 1999, Science, 284, 1514 [NASA ADS] [CrossRef] [Google Scholar]
- Stephan, K., Ciarniello, M., Poch, O., Haack, D., & Raponi, A. 2019, Vis-NIR reflectance spectra of H2O ice with varying grain sizes (70–1060 µm), shapes (spherical or irregular) and three mixtures, from 70 to 220 K, “SSHADE/CSS (OSUG Data Center). Dataset/Spectral Data.” [Google Scholar]
- Stephan, K., Hibbitts, C. A., & Jaumann, R. 2020, Icarus, 337, 113440 [NASA ADS] [CrossRef] [Google Scholar]
- Stephan, K., Ciarniello, M., Poch, O., et al. 2021, Minerals, 11, 1328 [NASA ADS] [CrossRef] [Google Scholar]
- Sultana, R., Poch, O., Beck, P., Schmitt, B., & Quirico, E. 2021, Icarus, 357, 114141 [CrossRef] [Google Scholar]
- Sultana, R., Poch, O., Beck, P., et al. 2023, Icarus, 395, 115492 [NASA ADS] [CrossRef] [Google Scholar]
- Taifan, W., Boily, J.-F., & Baltrusaitis, J. 2016, Surf. Sci. Rep., 71, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Takato, N., Bus, S. J., Terada, H., Pyo, T.-S., & Kobayashi, N. 2004, Science, 306, 2224 [NASA ADS] [CrossRef] [Google Scholar]
- Tosi, F., Galluzzi, V., Lucchetti, A., et al. 2023, J. Geophys. Res. Planets, 128, e2023JE007836 [NASA ADS] [CrossRef] [Google Scholar]
- Trotta, F., & Schmitt, B. 1996, Mid-IR and Far-IR optical constants of crystalline CO2 ice at 15 K, “SSHADE/GhoSST OSUG (Data Center)” [Google Scholar]
- Trumbo, S. K., Brown, M. E., & Butler, B. J. 2018, AJ, 156, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Trumbo, S. K., Brown, M. E., & Hand, K. P. 2019, AJ, 158, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Trumbo, S. K., Brown, M. E., Bockelée-Morvan, D., et al. 2023, Sci. Adv., 9, eadg3724 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, W., & Kaiser, R. I. 2007, Chem. Phys. Lett., 450, 55 [NASA ADS] [CrossRef] [Google Scholar]
Combining SOFIA data over 8–37 µm with radio data, de Pater et al. (2021) find that such a trend persists up to the mm-cm range, where the very low TB (~60–70 K) results from a dramatic collapse of the spectral emissivity with wavelength.
defined in his case as the TB difference between 20 and 40 µm. Spencer (1987) is available online at https://www.boulder.swri.edu/~spencer/dissn/
All Tables
All Figures
 |
Fig. 1 Radial dependence of band-averaged radiances for Obs. 18. We note that because the RA, Dec grid extends up to ±2.34″, distances beyond this distance are only partially sampled. |
| In the text | |
 |
Fig. 2 Ganymede Bond albedo and 3.6-µm, 4.4-µm radiance maps. From top to bottom: context Bond albedo maps derived by de Kleer et al. (2021) from Voyager-Galileo mosaic with the dashed green lines showing the open-closed-field line-boundary (Duling et al. 2022), resulting Bond albedo maps after projection in the NIRSpec IFU spaxels (see text), NIRSpec radiance images at 3.6 (NRS1) and 4.4 (NRS2) µm. In the context maps, dark Regiones are indicated by their names in yellow, and the blue circle shows the position of the Tros crater. Iso-latitude and longitude lines are drawn by increments of 30°. The color scale is different for each map, except for the Bond albedo maps. Left side: leading hemisphere. Right side: trailing hemisphere. |
| In the text | |
 |
Fig. 3 Ganymede 3.6-µm and 4.4-µm reflectance maps. From top to bottom: reflectance images at 3.6 (NRS1) and 4.4 µm (NRS2) for Leading (left) and Trailing (right) hemispheres. Iso-latitude and longitude lines are drawn by increments of 30°. The color scale is different for each map. The reflectance at the spaxels near the limb is somewhat inaccurate, as no PSF correction was applied. |
| In the text | |
 |
Fig. 4 NIRSpec reflectance spectra of Ganymede surface. Left: leading hemisphere. Right: trailing hemisphere. Averages over bins of latitudes are plotted, as labeled in the upper left panels. Thermal emission was not subtracted, so reflectance values are significantly overestimated at λ > 4.9 µm (dashed lines, see text). The absolute scale is also inaccurate for the highest latitudes due to PSF filling effects (see text). Spectral identifications of the three H2O Fresnel peaks (2.95, 3.1 and 3.2 µm), absorption bands of H2O2 (3.5 µm) and CO2 (4.26 µm) are indicated. The absorption signatures at the position of the 13CO2 band (4.38 µm), and those at 3.426 and 3.51 µm indicated by question marks, are most likely spurious (see text). The feature seen in absorption at 4.995 µm at the 2% level is not of Ganymede origin as it is not observed in MIRI spectra. The spectral continuum is dominated by water ice for the mid and high latitudes of the leading hemisphere, with local maxima at 3.65 and 5 µm (H2O inter-bands) and a minimum at 4.45 µm (H2O absorption band). In other regions, the higher concentration of non-ice materials (minerals, etc.) induces the increase of the reflectance with wavelength, the reduction of the amplitude of the water ice spectral features, and the shift of the water inter-band to 3.9 µm. |
| In the text | |
 |
Fig. 5 Spatial variations of the Fresnel reflection-peak properties. From top to bottom: context Bond albedo maps, maps of the area of Fresnel reflection peak and central wavelength of Fresnel peak 1 from NIRSpec (NRS1) data. Maps of the leading and trailing hemispheres are shown on the left and right, respectively. |
| In the text | |
 |
Fig. 6 Correlations with Bond albedo. From top to bottom: A) CO2 band area, B) CO2 band center, and C) Fresnel-peak area (i.e., EqW). Data for the leading and trailing hemispheres are shown with blue and red symbols, respectively. Filled and open dots are for latitudes lower and higher than 40° N/S, respectively. Data in the morning limb of the Trailing hemisphere (namely longitudes > 320°) are shown with the star symbol. |
| In the text | |
 |
Fig. 7 Spatial variations of the H2O 4.5-µm band-depth indicator. This band depth BD is calculated with respect to the reflectance value at 4.205 µm (BD = (1−R4.48 µm/R4.205 µm)× 100, where R4.48 µm and R4.205 µm are the reflectance values at 4.48 and 4.205 µm, respectively). Negative values indicate a significant contribution of non-ice material in the continuum. |
| In the text | |
 |
Fig. 8 Spatial variations of 3.6–3.9 µm inter-band properties. Inter-band amplitude AIB (top) and wavelength position (bottom) for the leading (left) and trailing (right) hemispheres. |
| In the text | |
 |
Fig. 9 Illustration of asymmetric Gaussian fitting of the CO2 band. In black, a latitude average NIRSpec spectrum (30–45°S, leading, in Fig. 10). In blue and red dotted lines, the two fitted half-Gaussians, with their width (HWHPblue and HWHPred, respectively) indicated. The vertical line shows the central position of the fitted asymmetric Gaussian. |
| In the text | |
 |
Fig. 10 CO2 4.26-µm band spectra as a function of latitude. CO2 band normalized to the underlying continuum, from averages over latitude bins of I/F spectra. Latitude bins are given in the right panels, with spectra from southern latitudes drawn in dashed lines and northern latitudes in solid lines. The vertical lines show the central positions (given in Table 2) of the fitted asymmetric Gaussians with the same color code as for the spectra. |
| In the text | |
 |
Fig. 11 Spatial variations of CO2 4.26-µm band properties. Maps of CO2 band depth (top), band center (middle), and band width (bottom) from NIRSpec NRS2 data. Maps of the leading and trailing hemispheres are shown on the left and right, respectively. |
| In the text | |
 |
Fig. 12 Dependence of CO2 band depth with latitude. Blue dots and red dots are used for the leading and trailing hemispheres, respectively. Each data point corresponds to a spaxel in Fig. 11. Empty symbols correspond to spaxels which are not entirely on Ganymede disk and can be less reliable. |
| In the text | |
 |
Fig. 13 Correlations between CO2 band width and band center, and between asymmetry parameter asp and band center. Each data point corresponds to one NIRSpec spaxel on the Ganymede disk. The different symbols and colors indicate the latitude range as given in the inset. Upper plots: leading hemisphere; bottom plots: trailing hemisphere. |
| In the text | |
 |
Fig. 14 MIRI sample spectra at 4.9–11.7 µm. Shown are spectra from Obs. 18 (leading hemisphere, solid line) and 27 (trailing hemisphere, dashed line), at reconstructed disk center (spaxel 18, 18, top) and at off-sets RA = 0.65″, Dec = 0″ from this position (spaxel 24, 18, bottom). Spectra are calibrated either in brightness temperature (TB, left panels) with different colors illustrating different bands from 1A to 2C, or radiance factor (I/F, right panels). They are not corrected for any account of “filling factor” associated with the fact that for positions close to limb, the PSF partly samples empty space. |
| In the text | |
 |
Fig. 15 Example of spectral fits to MIRI data. Left panels: fit of disk-center spectra (spaxel 18, 18) in Obs. 18 (leading, top) and 27 (trailing, bottom) in radiance units with the sum of thermal and solar reflected components. Black: data. Red: thermal component. Green: solar reflected component. Blue: total model. Right panels: ratios between observations and models. |
| In the text | |
 |
Fig. 16 Brightness temperature and Bond albedo maps. Maps of the 8.25-µm (top) and 11.25-µm (middle) brightness temperature, and spaxel-averaged Bond albedo maps (bottom) from de Kleer et al. (2021; see text). Left: leading side (Obs. 18). Right: trailing side (Obs. 27). |
| In the text | |
 |
Fig. 17 Observed and modeled 8.25-µm brightness temperature (TB). 8.25-µm TB for Obs. 18 (leading side, first row) and Obs. 27 (trailing side, second row), plotted as a function of local time (first column) or latitude (second column). The data are color-coded according to latitude (i.e., to equal values of the latitude difference from the sub-observer point) in the TB vs local time plots, and according to local time in the TB vs latitude plots. In the third and fourth columns, the data are compared to one of the best models, that includes both a rescaling of the Bond albedo map and surface roughess (see text). In these panels, data are in black, models in red, and the data minus model difference in blue, with the 0 value indicated by the dashed line. Parameter values and rms of fit are indicated in each panel. |
| In the text | |
 |
Fig. 18 Difference plots. Top: difference between observed and modeled TB,8.25, for the rough, Bond albedo-rescaled, model (last column of Fig. F.1). Middle: TB,8.25 – TB,11.25 brightness temperature difference as a function of incidence angle. Bottom: TB,8.25 – TB,11.25 brightness temperature difference as a function of local time. Black: data. Red: model. Left: leading side (Obs. 18). Right: trailing side (Obs. 27). |
| In the text | |
 |
Fig. 19 Fitted characteristics of the 5.9-µm band. Shown are results for Obs. 18 (leading side, first row) and Obs. 27 (trailing side, second row), using model 2 described in the text: observed band depth relative to total continuum, band depth corrected for thermal contribution (i.e., relative to model solar reflected component), band position (offset from 5.90 µm), and band FWHM width. The last column shows the correlation between the observed (black) and corrected (red) band depths with the observed 8.25 µm TB. Spearman correlation coefficients and number of standard deviations significance are indicated as insets. Similar figures for models 1 and 3 can be found in Fig. F.3. |
| In the text | |
 |
Fig. 20 Spectra of the 5.9 µm band (Observation/Model 2). Shown are averages in 7 latitude bins ([−90°,−50°], [−50°,−30°], [−30°,−10°], [−10°,10°], [10°,30°], [30°,50°] and [−50°,−90°]. Left: leading side (Obs. 18). Right: trailing side (Obs. 27). The band appears blueshifted in the high-latitude bins, but spectra are of more modest quality there. |
| In the text | |
 |
Fig. 21 Disk-average spectra at 4.9–7.5 µm. Top panels: data (solid line) and continuum fit with model 2 (dashed line). Bottom panel: observation/model ratios. Black: ratio in the total spectrum. Red: ratio in the solar component (see text for details). Left: leading side (Obs. 18). Right: trailing side (Obs. 27). |
| In the text | |
 |
Fig. 22 Comparison of bright and moderately bright terrains in Ganymede’s leading and trailing hemispheres, through spectral ratios. Moderately bright and bright terrains are defined by a Bond albedo AB = 0.35 − 0.4, AB = 0.4 − 0.6, respectively. For the leading hemisphere, only the northern regions at latitudes >35°N are considered, whereas for the trailing hemisphere, we consider both northern and southern high-latitude regions (>35°N/S). The spectrum shown in green dashed line is a spectrum of amorphous water ice obtained using Fresnel’s formulae (applicable for flat surfaces; Born & Wolf 1999) and the optical constants at 120 K of Mastrapa et al. (2009). The vertical dashed lines are at the wavelengths of the two main H2O Fresnel peaks (3.09 and 3.20 µm), H2O2 (3.505 µm) and CO2 (4.26 µm) absorption bands. The vertical dashed-dotted line at 3.6 µm is roughly at the H2O inter-band position. |
| In the text | |
 |
Fig. 23 Comparison of the CO2 band in polar (>45 °N/S) and equatorial (<30 °N/S) regions through spectral ratios. (A) Spectral ratios Leading/Trailing for polar regions; (B) spectral ratios Polar/Equatorial for leading (red) and trailing (blue) hemispheres. The vertical dashed line is at 4.27 µm (2341.9 cm−1). |
| In the text | |
 |
Fig. 24 Laboratory reflectance spectra of several hydrated salts and sulfuric acic hydrates. They are possibly present on Ganymede according to previous near-infrared observations (Ligier et al. 2019; King & Fletcher 2022). The spectrum of Magnesium chloride (~250 µm, JB-JLB-G32-A) is from the NASA Reflectance Experiment LABoratory (RELAB) spectral database. Spectrum of Epsomite (GDS149) is from the USGS Spectral Library (Kokaly et al. 2017). Spectra of Bloedite (〜250 µm, Jim Crowley, USGS) and Hexahydrate (<45 µm, SPT143) are from the database of the Centre For Terrestrial and Planetary Exploration (C-TAPE) of University Winnipeg. The spectrum of sulfuric acid tetrahydrate at 160 K is from Loeffler et al. (2011). We note that this is a transmittance spectrum. A reflectance spectrum of Ganymede’s trailing side equatorial region (<30° latitude N/S, see Fig. 26) is scaled for comparison (black line). The vertical dotted lines indicate H2O inter-band positions in NIRSpec spectrum, and the vertical dashed lines indicate the band positions in MIRI spectrum. |
| In the text | |
 |
Fig. 25 Influence of porosity on spectra of phyllosilicates. (a) Laboratory reflectance spectra of Aguas Zarcas CM2 meteorite powder and several phyllosilicate powders and (b) influence of the porosity on the reflectance spectrum of Aguas Zarcas sub-µm powder. Spectra of Aguas Zarcas were measured at IPAG (Institut de Planétologie et d’Astrophysique de Grenoble, see Appendix B). Ganymede’s trailing side equatorial region (<30° latitude N/S) reflectance spectrum (see caption of Fig. 26) is plotted at the same reflectance scale in plot (b) (black line), with the gray dashed-dotted line in plot indicating the potential continuum obtained by drawing a line between the points at 3.9 and 5.1 µm (inter-bands). This continuum has a positive (red) spectral slope, possibly due to a relatively high surface porosity of dark terrains. Spectra of Cronsdetite (M3542) is from the USGS Spectral Library (Kokaly et al. 2017). Spectra of Saponite (<45 µm, SA-EAC-059) and Beidellite (<12 µm, JB-JLB-919-A) are from the NASA Reflectance Experiment LABoratory (RELAB) spectral database. The vertical dotted lines indicate H2O inter-band positions in NIRSpec spectrum, and the vertical dashed lines indicate the band positions in MIRI spectrum. |
| In the text | |
 |
Fig. 26 Simulated spectrum compared with merged NIRSpec/MIRI I/F spectra of the leading and trailing hemispheres. The model parameters are: grain sizes DCO2 = 0.05 µm, DH2O = 10 µm, Ddark = 1 µm; mass ratio relative to water mCO2 = 1%; relative areas of the ice:dark terrains = 10:90. Averages NIRSpec/MIRI merged spectra covering the full disk, low and high latitudes regions are shown, as indicated in the inset. NIRSpec and MIRI spectra are corrected from the contribution of thermal emission (see Appendix C). The simulated spectrum cannot explain the 5.9-µm feature. |
| In the text | |
 |
Fig. 27 Comparison with laboratory data. CO2 band in Ganymede spectra at the pole (60–75°N; dotted light gray lines) and the equator (0–15°N; dot-dashed gray lines) of the leading hemisphere compared with transmission spectra from Berlanga et al. (2016; carboneous chondrites), Bekhti et al. (2021; zeolites), Ehrenfreund et al. (1999; CO2 ice and CO2-H2O ice mixture) and Fleyfel & Devlin (1991; CO2 clathrates). Some spectra are vertically shifted for the sake of clarity. |
| In the text | |
 |
Fig. 28 Comparison with laboratory data. CO2 band in Ganymede spectra at the pole (60–75°N; dotted gray line) and the equator (0–15°N; dot-dashed gray line) of the leading hemisphere compared to several experimental measurements of CO2 mixed with water ice at 170 K (Ehrenfreund et al. 1999; blue line), CO2 segregated in water ice at 138 K (He et al. 2018; yellow line) and CO2 complexed Jones et al. (2014; green line). |
| In the text | |
 |
Fig. A.1 Distribution of the Fresnel peak area on the trailing hemisphere. Iso-contours (levels spaced by 0.0025 μm with the central level at 0.0035 μm) are overplotted. |
| In the text | |
 |
Fig. D.1 Correlation between the temperature of pure H2O ice and the wavelength at which the reflectance bump of the 3.6-μm H2O ice inter-band is maximum. For pure crystalline H2O ice, the laboratory reflectance spectra are from Clark et al. (2012) and Stephan et al. (2021). For amorphous ice, points have been estimated by reflectance spectra with Mastrapa et al. (2009) optical constants, and applying a shift of 0.1 μm. |
| In the text | |
 |
Fig. E.1 Correlations between CO2 band characteristics and water ice. CO2 band area (A) and band center (B) as a function of Fresnel-peak area (i.e., EqW). Data for the leading and trailing hemispheres are shown with blue and red symbols, respectively. Filled and open dots are for latitudes lower and higher than 40° N/S, respectively. The data in the morning limb of the trailing hemisphere (namely longitudes > 320°) are shown with the star symbol. The positive correlation between CO2 band center (in wavelength) and Fresnel peak area has a Spearman’s rank coefficient r = 0.62 and 0.52 with a significance of 6.6σ and 6.9σ for leading and trailing hemispheres, respectively. A weak negative correlation between CO2 band area and Fresnel peak area is present when considering all data (r = −0.31 (4.5σ) and r = −0.53 (6.6 σ) for leading/trailing hemispheres respectively), but not when considering only equatorial (< 40°) latitudes (r ~ 0 (0σ) and r = −0.15 (1.8 σ), for leading/trailing hemispheres, respectively). These calculations of correlation coefficients exclude data on the morning limb of the trailing hemisphere. |
| In the text | |
 |
Fig. F.1 Observed and modeled 8.25-μm brightness temperature (TB). 8.25 μm TB for Obs. 18 (first two rows) and Obs. 27 (last two rows), plotted as a function of local time (first and third rows) or latitude (second and fourth rows). In each row, observational data (first column) are compared to a series of models. In the first column, the data are color-coded according to latitude (i.e., to equal values of the latitude difference from the sub-observer point) in the TB vs local time plots, and according to local time in the TB vs latitude plots. The following six column describe the six considered models, with the three options for the Bond albedos and inclusion or not of surface slopes (see text for details). In those panels, data are in black, models in red, and the data minus model difference in blue, with the 0 value indicated by the dashed line. Parameter values and rms of fit are indicated in each panel. |
| In the text | |
 |
Fig. F.2 MIRI thermal-modeling outputs. Fitted model parameters for Obs. 18 (Leading, first three rows) and Obs. 27 (Trailing, last three rows), for the three models described in Sect. 4.3: temperature (T1, T2, or T3), second fit parameter (ɛ1, |
| In the text | |
 |
Fig. F.3 5.9-μm band properties. Fitted characteristics of the 5.9-μm band in Obs. 18 (leading side, first three rows) and Obs. 27 (trailing side, last three rows), for the three models described in the text: observed band depth relative to total continuum, band depth corrected for thermal contribution (i.e., relative to model solar reflected component), band position (offset from 5.90 μm), and band FWHM width. The last column shows the correlation between the observed (black) and corrected (red) band depths with the observed 8.25 μm TB. Spearman correlation coefficients and number of standard deviations significance are indicated as insets. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.