EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 682 (February 2024) A&A, 682 (2024) A78 Full HTML
Open Access
Issue
A&A
Volume 682, February 2024
Article Number A78
Number of page(s) 19
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202348118
Published online 06 February 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

The embedded protostellar phase of star formation is very rich in terms of chemistry. The James Webb Space Telescope (JWST) provides unique new opportunities for probing these deeply embedded protostellar sources (Yang et al. 2022; Harsono et al. 2023; van Dishoeck et al. 2023; Beuther et al. 2023; Gieser et al. 2023). An interesting element to study is sulfur, as the total volatile sulfur budget in protostars appears to be depleted by more than two orders of magnitude with respect to the diffuse clouds (Ruffle et al. 1999). The sulfur likely resides in unobservable refractory reservoirs, sulfur allotropes, or FeS inclusions (Woods et al. 2015; Kama et al. 2019). Even among the volatile species, the sulfur budget remains poorly constrained (e.g., Drozdovskaya et al. 2018; Navarro-Almaida et al. 2020; Kushwahaa et al. 2023). It is therefore important to constrain the physical conditions in which the volatile sulfur-bearing species reside in order to understand their chemistry and constrain the main sulfur reservoirs. JWST has proven that it can detect sulfurbearing species both in interstellar ices (e.g., SO2 and OCS; Yang et al. 2022; McClure et al. 2023; Rocha et al. 2024) and in exoplanetary atmospheres (e.g., SO2; Tsai et al. 2023). Here, we present one of the first detected medium-resolution mid-infrared (MIR) spectra of a low-mass Class 0 protostellar system, NGC 1333 IRAS 2A, containing the first detection of gaseous SO2 in emission at MIR wavelengths.

One of the most frequently detected sulfur-bearing species toward low-mass protostellar systems in millimeter observations is SO2 (e.g., Artur de la Villarmois et al. 2023). It is a shock tracer that is often present in outflow and jet shocks (e.g., Blake et al. 1987; Codella et al. 2014; Taquet et al. 2020; Tychoniec et al. 2021), where it is either sputtered from icy dust grains or formed through gas-phase chemistry (e.g., Pineau des Forêts et al. 1993). SO2 is also often observed on smaller scales in accretion shocks at the disk–envelope boundary (e.g., Sakai et al. 2014; Oya et al. 2019; Artur de la Villarmois et al. 2019, 2022; Garufi et al. 2022), where it is either formed through gas-phase chemistry or thermally sublimated from the ices (Miura et al. 2017; van Gelder et al. 2021). Furthermore, it is also a good tracer of disk winds (Tabone et al. 2017) and hot core regions, where the bulk of the ices are sublimating (e.g., Drozdovskaya et al. 2018; Codella et al. 2021). Most of these studies are based on submillimeter observations with interferometers such as the Atacama Large Millimeter/submillimeter Array (ALMA) or the NOrthern Extended Millimeter Array (NOEMA), which can trace the pure rotational transitions of the vibrational ground state of SO2 but are not able to detect ro-vibrational transitions.

These ro-vibrational lines are best traced at MIR wavelengths (i.e.,∼ 5–30 µm). SO2 has three fundamental vibrational modes: the v1 symmetrical stretching mode around 8.5–9 µm, the v2 bending mode around 18–20 µm, and the v3 asymmetrical stretching mode around 7.2–7.4 µm (Briggs 1970). At MIR wavelengths, gaseous SO2 has thus far only been observed in absorption toward high-mass protostellar systems (Keane et al. 2001; Dungee et al. 2018; Nickerson et al. 2023). These studies have shown that the SO2 in these high-mass systems resides at typical temperatures of ∼100–300 K, although higher temperatures of up to 700 K have also been reported (Keane et al. 2001). The average abundances with respect to H2 are >10−7, which is consistent with the SO2 abundance of interstellar ices (Boogert et al. 1997, 2015; Zasowski et al. 2009; McClure et al. 2023; Rocha et al. 2024) and cometary ices (Altwegg et al. 2019; Rubin et al. 2019), suggesting that gaseous SO2 may originate from ice sublimation in the inner hot cores of these high-mass protostellar systems. A MIR detection of gaseous SO2, either in absorption or emission, toward low-mass protostellar systems is, to the best of our knowledge, still lacking.

Most studies at submillimeter wavelengths assume local thermodynamic equilibrium (LTE) when deriving the physical conditions of SO2 (i.e., column density and excitation temperature), which is a good approximation given that most pure rotational levels can be collisionally populated at typical inner envelope densities (106−108 cm−3) and can therefore be characterized by a single excitation temperature. However, when studying ro-vibrational lines at MIR wavelengths, it is important to be aware of non-LTE effects. The critical densities of these ro-vibrational transitions are typically >1010 cm−3 (e.g., for HCN and CO2; Bruderer et al. 2015; Bosman et al. 2017), meaning that vibrationally excited levels are only collisionally populated in the inner ≲1 au around low-mass protostars. Furthermore, molecules can be pumped into a vibrationally excited state by a strong infrared radiation field which boosts the line fluxes of MIR transitions far above what is expected from collisional excitation (e.g., Boonman et al. 2003; Sonnentrucker et al. 2007). For SO2, no collisional rate coefficients are available for its ro-vibrational transitions in the MIR, therefore preventing a full non-LTE analysis, but its MIR transitions likely have high critical densities similar to those of HCN and CO2. However, the importance of non-LTE effects can still be constrained through the comparison of ro-vibrational transitions detected at MIR wavelengths to pure rotational transitions in the vibrational ground state measured at submillimeter wavelengths.

In this paper we present JWST/Mid-InfraRed Instrument (MIRI; Rieke et al. 2015; Wright et al. 2015, 2023) observations from the JWST Observations of Young protoStars (JOYS+) program, providing the first MIR detection of SO2 in emission toward the low-mass protostellar system NGC 1333 IRAS 2A (hereafter IRAS 2A), and we compare it to the results of high-angular-resolution ALMA data of the same region. IRAS 2A is a binary Class 0 system with a separation between IRAS 2A1 (VLA1) and IRAS 2A2 (VLA2) of ∼0.6″ (i.e., ~180 au; Tobin et al. 2015, 2016; Jørgensen et al. 2022) located in the Perseus star-forming region at a distance of about 293 pc (Ortiz-León et al. 2018). It hosts one of the most famous hot corinos (e.g., Jørgensen et al. 2005; Bottinelli et al. 2007; Maury et al. 2014; Taquet et al. 2015) and drives two powerful almost perpendicular large-scale outflows (e.g., Arce et al. 2010; Tobin et al. 2015; Taquet et al. 2020). Recently, Jørgensen et al. (2022) showed that the binary interaction results in a misalignment in the outflow and infalling streamers around IRAS 2A1. Furthermore, IRAS 2A was part of the Spiter Cores to Disks (c2d) survey, which revealed the main components of the ices (Boogert et al. 2008; Öberg et al. 2011), but the Infrared Spectrograph (IRS) of Spiter only had a spectral resolving power of R = 60–120 at the critical wavelength range of 5–10 µm and a large aperture (>5″). Here, we present MIRI observations taken with the Medium Resolution Spectrometer (MRS; Wells et al. 2015; Labiano et al. 2021; Argyriou et al. 2023; Jones et al. 2023) with a spectral resolving power of R ~ 3500 at 5–10 µm and subarcsecond resolution (~0.2–0.4″). This is one of the first JWST/MIRI-MRS spectra of a low-mass Class 0 protostellar system to be detected (see also, e.g., IRAS 15398-3359; Yang et al. 2022).

This paper is structured as follows. In Sect. 2 the JWST/MIRI and ALMA observations are described together with the method of fitting the SO2 emission. The results are presented in Sect. 3 and discussed in Sect. 4. Our main conclusions are summarized in Sect. 5.

2 Observations and analysis

2.1 Observations

2.1.1 MIRI-MRS

The MIRI-MRS observations were carried out as part of the Cycle 1 guaranteed time observations (GTO) program 1236 (PI: M. E. Ressler) on January 9, 2023, with a two-point dither pattern optimized for extended sources. A dedicated background observation was also taken with two-point dither pattern to allow for a proper subtraction of the telescope background and detector artifacts. In both cases, the FASTR1 readout mode was used with all three gratings (A, B, and C) in all four channels, providing the full wavelength coverage of MIRI-MRS (4.9–28.6 µm). The integration time in each grating was 111 s, resulting in a total integration time of 333 s. All observations included simultaneous off-source imaging using the F1500W filter.

The observations were processed through all three stages of the JWST calibration pipeline version 1.11.0 (Bushouse et al. 2023) using the reference context jwst_1097.pmap of the JWST Calibration Reference Data System (CRDS; Greenfield & Miller 2016). The raw data were first processed through the DetectorlPipeline using the default settings. Following this, the Spec2Pipeline was performed, including the correction for fringes with the fringe flat for extended sources (Mueller et al., in prep.) and applying the detector level residual fringe correction (Kavanagh et al., in prep.). Furthermore, the background was also subtracted at this step using the rate files of the dedicated background. A bad-pixel routine was applied to the Spec2Pipeline products outside of the default MIRI-MRS pipeline using the Vortex Image Processing (VIP) package (Christiaens et al. 2023). The data were further processed using the Spec3Pipeline with both the master background and outlier rejection routines switched off. The background was already subtracted in the Spec2Pipeline and the outlier rejection routine was skipped because it did not significantly improve the quality of the data. Moreover, the data cubes created with the Spec3Pipeline were created for each band of each channel separately.

The main component of the binary, IRAS 2A1 (VLA1; Tobin et al. 2015), is clearly detected across all wavelengths whereas the companion protostar, IRAS 2A2 (VLA2), is not detected (see Fig. 1). The reason for the non-detection could be because it is about an order of magnitude less massive and less luminous than IRAS 2A1 (Tobin et al. 2016, 2018), or because it is more embedded. Therefore, only one spectrum was manually extracted from the peak of the MIR continuum (RA (J200) 03h28m55.57s, Dec (J2000) 31d 14m36.76s) at 5.5 µm (channel 1A; see Fig. 1) and is assumed to only contain emission related to IRAS 2A1 (hereafter IRAS 2A). The diameter of the aperture was set to 4 × FWHMPSF , with FWHMPSF the empirically derived full width at half maximum of the MIRI-MRS point spread function (FWHMPSF = 0.033(λ/µm) + 0.106″, i.e., 0.35″ at 7.35 µm; Law et al. 2023), in order to capture as much emission as possible without adding too much noise. An additional spectrum level residual fringe correction was applied primarily to remove the high-frequency dichroic fringes in channel 3 and 4 (Kavanagh et al., in prep.). No additional spectral stitching was applied between the bands.

thumbnail Fig. 1

Spectrum (top panel) and continuum images at various wavelengths (bottom row) of IRAS 2A. In the top panel, four insets are presented: around the SO2 v3 asymmetric stretching mode (~7.35 µm), SO2 v1 symmetric stretching mode (~8.7 µm), SO2 v2 bending mode (~19 µm), and CO2 v2 bending mode (~15 µm). In the latter, the emission originates mostly from the outflow (see Fig. B.1). The 12 sub-bands of the MIRI-MRS spectrum are not stitched and show minor offsets in overlapping wavelengths (see, e.g., the inset on the SO2 v1 symmetric stretching mode). The bottom row shows, from left to right, the dust continuum around 5.3 µm, 8.1 µm, 12.5 µm, and 19.3 µm; a sqrt stretch has been used to enhance fainter features without over-saturating bright emission. The open white circle indicates the size of the aperture from which the spectrum was extracted (i.e, 1.1″, 1.5″, 2.1″, and 3.0" in diameter at 5.3 µm, 8.1 µm, 12.5 µm, and 19.3 µm, respectively), which increases as a function of wavelength with the increase in the size of the PSF. A scale bar is displayed in the bottom left of each panel, and the size of the PSF is presented as the filled white circle in the bottom right.

2.1.2 ALMA data

The ALMA data analyzed in this paper are taken from program 2021.1.01578.S (PI: B. Tabone), which targeted several Class 0 protostars in Perseus in Band 7, covering several transitions of SO2 and34 SO2. These data were taken in an extended configuration (C-6, θbeam = 0.12″ × 0.09″) and in a more compact configuration (C-3, θbeam = 0.58″ × 0.34″) to include larger-scale emission. All spectral windows have a velocity resolution of 0.22 km s−1 except for two windows that have a resolution of 0.44 km s−1 and one continuum window at 0.87 km s−1. The data were pipeline calibrated and imaged with the Common Astronomy Software Applications1 (CASA; McMullin et al. 2007) version 6.4.1.12. The continuum was subtracted with the uvcontsub task using carefully selected line-free channels. Following this, the two configurations were combined using the tclean task for a Briggs weighting of 0.5 with a circular mask with a radius of 2" centered on the main continuum peak. The synthesized beam of the final data cubes is θbeam = 0.13″ × 0.10″. In order for direct comparison to the MIRI data, spectra were extracted from a 1.4″ diameter aperture centered on the continuum position of IRAS 2A1. The noise level of the extracted spectrum is 0.015 Jy, and a flux calibration uncertainty of 5% was assumed.

thumbnail Fig. 2

Subtracting the local continuum around the SO2 v3 band. Top: spectrum of IRAS 2A around 7.35 µm showing the gas-phase SO2 emission superimposed at various ice absorption bands. The red line shows the estimated local continuum based on a fourth-order polynomial fit through the red dots. Middle: spectrum of IRAS 2A with the local continuum subtracted. The 7.25 µm complex organics ice absorption feature is clearly present. A simple Gaussian fit to this ice absorption feature based on fitting the spectrum in the shaded region is shown in green. Bottom: final continuum- and ice-feature-subtracted spectrum.

2.2 Continuum subtraction around the SO2 v3 band

SO2 is an asymmetric rotor and has three fundamental vibrational modes: a symmetrical stretching mode (v1 = 1151 cm−1, λ ~ 8.5–9.0 µm), a bending mode around (v2 = 518 cm−1, λ ~ 18–20 µm), and an asymmetrical stretching mode (v3 = 1362 cm−1, λ ~ 7.2–7.4 µm; Briggs 1970; Person & Zerbi 1982). Around 7.35 µm, clear molecular emission originating from the v3 band is present (see the inset in Fig. 1), but both the v1 and v2 bands are not detected. The analysis of the MIRI-MRS data will therefore be focused on the v3 band and the absence of the v1 and v2 bands will be further discussed in Sect. 4.1.1.

In order to fit the SO2 emission in the v3 band, the local continuum had to be subtracted. However, the spectral region surrounding the emission features is dominated by absorption of ices such as the 7.25 and 7.4 µm ice bands that are typically ascribed to complex organics including ethanol (CH3CH2OH) and acetaldehyde (CH3CHO) or the formate ion (HCOO−; e.g., Schutte et al. 1999; Öberg et al. 2011; Boogert et al. 2015; Terwisscha van Scheltinga et al. 2018; Rocha et al. 2024). A fourth-order polynomial was fitted through obvious linefree channels (i.e., 7.015, 7.113, 7.162, 7.442, 7.489, 7.545, and 7.635 µm; see the top panel of Fig. 2) selected outside of the SO2 emission range and the 7.25 and 7.4 µm ice bands to estimate the local continuum. Following the subtraction of this local continuum, a clear ice absorption feature remains around 7.25 µm. The generally equally strong 7.4 µm ice feature appears to be absent, but this likely originates from the superposition with the P-branch of the SO2 emission (see Sect. 3). To estimate the strength of the 7.25 µm ice absorption band, a simple Gaussian model was fitted to the part of the spectrum where no clear molecular emission features are present (7.1–7.26 µm; green shaded area in Fig. 2). Using this Gaussian fit, the contribution of the 7.25 µm ice feature was subtracted, providing a spectrum with only the contribution of the molecular emission (Fig. 2 bottom).

2.3 LTE slab model fitting

The molecular emission features in the continuum-subtracted spectra were fitted with simple slab models assuming LTE. This is a similar approach to what is applied to other low- and high-mass sources (Carr & Najita 2008; Salyk et al. 2011; Tabone et al. 2023; Grant et al. 2023; Perotti et al. 2023; Francis et al. 2024). It is important to note here that the assumption of LTE is likely not valid for the MIR ro-vibrational transitions of SO2 detected in IRAS 2A. Nevertheless, LTE models can still constrain physical quantities such as the rotational temperature within a vibra-tionally excited state. The implications of the assumption of LTE will be further discussed in Sect. 4.1.

In the slab models, the emission is assumed to arise from a slab of gas with an excitation temperature Tex (which in the case of LTE is approximately equal to the kinetic temperature), a column density N, and an emitting area equal to πR2. The latter was parameterized as a circular emitting area with a radius R, but could in reality originate from any shaped region with an area equal to πR2. The intrinsic velocity broadening ∆V was fixed to 3.5 km s−1 based on ALMA data covering SO2 (see Sect. 3.2). It is important to note that in case of optically thin emission, the derived column densities are independent of ∆V, whereas in case of optically thick emission the column density scales with 1/∆V (Tabone et al. 2023). Given that SO2 has many ro-vibrational lines close to each other in wavelength in the MIR, it was important to take line overlap into account in order to derive an accurate column density and excitation temperature. Moreover, the spectral resolving power of MIRI-MRS around 7.35 µm is about λ/∆λ ~ 3500 (Labiano et al. 2021; Jones et al. 2023), corresponding to a velocity resolution of ~ 85 km s−1, which means that the lines are not spectrally resolved and could be blended with other lines (of, e.g., SO2 itself, H2O) in the MIRI data.

The spectroscopic information (i.e., line wavelengths, Einstein Ajj, upper energy level Eup, degeneracy gup) of the MIR ro-vibrational transitions of SO2 was taken from the HITRAN database2 (Gordon et al. 2022) and converted to the Leiden Atomic and Molecular Database (LAMDA) format (van der Tak et al. 2020) in order to make it compatible with the slab model code. The partition function of SO2 was calculated with the TIPS_2021_PYTHON code provided by the HITRAN database.

The best-fitting N and Tex were computed by creating a large grid covering 1014–1019 cm−2 in steps of 0.05 in log10 and 50–250 K in steps of 1 K, respectively. Any higher column densities or temperatures were excluded by visual inspection of the spectrum. For each grid point, the LTE spectrum of SO2 was calculated at a spectral resolving power of R = 3500 and the best-fitting emitting area was computed by minimizing the χ2 (see Appendix C of Grant et al. 2023, for more details). Only selected channels (i.e.,7.23–7.255, 7.258–7.268, and 7.2755–7.3535 µm) that do not include obvious emission or absorption features related to other molecules (i.e., H2O) or artifacts are taken into account. Specifically, all wavelengths longer than >7.3535 µm were excluded because of the contribution of the 7.4 µm ice feature to the flux. Similarly, the noise level was estimated from line-free channels (7.06–7.13, 7.195–7.225, 7.477.50 µm) to be about 0.59 mJy, and a flux calibration uncertainty of 5% was assumed (Argyriou et al. 2023). The LTE models were corrected for an absolute extinction of AV = 55 mag; using the modified version of the extinction law of McClure (2009) introduced in Appendix C. The effect of differential extinction caused by the 7.25 µm and 7.4 µm ice absorption on the molecular emission is assumed to be negligible. The best-fit parameters (N, Tex, and R) and their uncertainties were derived from the grid by minimizing the χ2

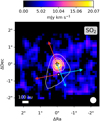thumbnail Fig. 3

Integrated intensity map of SO2 observed with MIRI-MRS in color. The image is integrated over the Q-branch of the v3 band: [7.34,7.35] µm and shown using a sqrt stretch to enhance fainter emission. The continuum around 7.35 µm is overlaid in white contours and peaks on the primary component, IRAS 2A1, extending somewhat toward the south in the direction of the scattered light. The positions of IRAS 2A1 and IRAS 2A2 are depicted with the white stars. A white scale bar is displayed in the bottom left, and the size of the PSF is presented as the filled white circle in the bottom right. The directions of the two outflows originating from IRAS 2A1 and IRAS 2A2 are indicated with the colored arrows (Tobin et al. 2015).

3 Results

3.1 MIRI-MRS

The full spectrum of IRAS 2A is presented in the top panel of Fig. 1. In the bottom panels of Fig. 1, the continuum maps are presented at four increasing wavelengths, each obtained at a different MIRI-MRS channel. At the shortest wavelengths (~5.3 µm; left panel), the continuum clearly shows scattered light from the blue-shifted outflow cavity extending toward the south. This scattered light is visible up to wavelengths of ~8 µm (middle-left panel), but is no longer present at longer wavelengths (>8.5 µm; two panels on the right). Only the main component of the binary, IRAS 2A1 (VLA1; Tobin et al. 2015), is detected whereas the companion protostar, IRAS 2A2 (VLA2), is not detected. The non-detection of IRAS 2A could originate from it being an order of magnitude less massive and luminous (Tobin et al. 2016, 2018), or because it is more embedded.

The integrated intensity map over the SO2 v3 Q-branch in the (continuum-subtracted) MIRI-MRS data is presented in Fig. 3.

The SO2 emission is mostly located around the continuum peak of IRAS 2A1. After deconvolution with the size of the PSF (Law et al. 2023), the extent of SO2 emission is 0.5″ × 0.3″ in diameter (i.e., ~150 × 90 au). This very similar to the extent of H2O emission lines that are likely tracing the inner hot corino (see Fig. B.l). Some very weak extended SO2 emission (on ~500 au scales) is also present in the direction of the blue-shifted lobe of the north-south outflow (Tobin et al. 2015; Jørgensen et al. 2022). However, the extended SO2 emission could also be related to IRAS 2A2, which is located about ~0.6″ (i.e., ~180 au) from IRAS 2A1 to the southwest (Tobin et al. 2015, 2016, 2018; Jørgensen et al. 2022).

The SO2 emission is clearly tracing a more compact component than the CO2 emission around 15 µm, which peaks more toward the blue-shifted part of the north-south outflow than toward the central protostellar component (see Fig. B.l). Similarly, the lower S-branch lines of H2 (e.g., S(l)) are also peaking in the blue-shifted outflow, but higher S-branch lines (e.g., S(7)) originating from higher Eup levels are mostly peaking on the continuum position (see Fig. B.l). Furthermore, several ice absorption features, including those of SO2 ice, are detected toward the bright continuum source and have been analyzed by Rocha et al. (2024). Any gas emission and absorption features other than SO2 in this source, including the CO2 emission in the outflow, will also be presented in future papers.

The best-fit LTE slab model to the v3 band is presented in Fig. 4 overlaid on the continuum-subtracted spectrum. The fit slightly overestimates the Q-branch around 7.35 µm but provides a very reasonable fit to the P-branch around 7.3 µm. The P-branch lines around 7.4 µm were not included in the fit because the contribution of the 7.4 µm ice feature, which decreases the measured fluxes of the P-branch lines, could not be disentangled from the gas-phase emission of SO2 a priori. Armed with a good model for the Q- and P-branches, Fig. B.2 clearly shows that the local continuum was estimated too high in the 7.4 µm region, proving that in fact the 7.4 µm ice absorption feature is present. The emission of the SO2 P-branch is almost equally strong as the absorption caused by the ices.

The χ2 map is shown in Fig. 5. Based on the χ2 map, the best-fitting excitation temperature can be accurately constrained (with a 1er error) at Tex = 92 ± 8 K. Any lower excitation temperature results in a too strong and too narrow Q-branch compared to the P-branch, whereas higher excitation temperatures result in a too broad Q-branch and also start overshooting the P-branch. Furthermore, the SO2 emission is optically thin since optically thick emission would give a lower ratio between the measured P- and Q-branch fluxes. The column density and emitting area are therefore completely degenerate with each other (i.e., the vertical profile of the contours in Fig. 5). Optically thick emission would appear as a more banana-shaped profile in Fig. 5 and allow both the column density and emitting area to be constrained (see, e.g., Pontoppidan et al. 2002; Salyk et al. 2011; Grant et al. 2023; Tabone et al. 2023). Given the degeneracy, no accurate column density of SO2 can be derived, but the total number of molecules, g = NπR2, can be determined: g = 4.5 + 4.0 × 1051 molecules.

However, the data can only be accurately fitted for a very large emitting area of ≳ 5000 au, which is in strong contrast with the extent of the emission in Fig. 3 (<150 au).

This is a clear indication that the assumption of LTE is not valid and thus that derived physical quantities, most notably the number of molecules, should be analyzed in more detail. Since the rotational distribution within the v3 band is well-fitted by a single temperature, this temperature accurately describes the rotational temperature within this vibrationally excited state, but it does not necessarily represent the kinetic temperature. On the other hand, the values derived for the total number of molecules and the size of the emitting area are not valid, both because of the conflict with the measured size of the emitting area as well as the large discrepancy with the values derived for the vibrational ground state in the ALMA data (see Sect. 3.2). This will be further discussed in Sect. 4.1.

thumbnail Fig. 4

Continuum-subtracted spectrum (blue) overlaid with the best-fit SO2 model (orange). The orange bars in the bottom indicate the wavelength ranges that were included in the fit, and the black bars show the wavelength ranges over which σ is calculated. The P-branch lines around 7.4 µm appear to be overfitted since the 7.4 µm ice absorption could not be disentangled from the gas-phase emission.
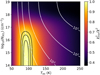thumbnail Fig. 5

χ2 map of the LTE slab model fit of SO2. The χ2 values are inversely normalized by the minimum χ2 and shown in color. The 1, 2, and 3σ confidence intervals are presented as the black contours. The best-fitting emitting radius, R (in au), is represented by the white contours and is calculated for each grid point by minimizing the χ2 assuming a circular emitting area of πR2. The χ2 map clearly reveals that the SO2 emission is optically thin with an excitation temperature of 92 ± 8 K.
thumbnail Fig. 6

Integrated intensity maps of the SO2 82,6−71,7 (left, Eup = 43 K), SO2 164,12−163,13 (middle, Eup = 164 K), and 34SO2 174,14−173,15 (right, Eup = 178 K) transitions in color. The images are integrated over [−2,2] km s−1 with respect to the Visr of 6.7 km s−1. The white vertical bar in the colorbar on top of each image indicates the 3σ threshold. The 0.875 mm continuum is overlaid as black contours. The main continuum peak is associated with IRAS 2A1 and the secondary peak toward the south with IRAS 2A2. The directions of the two outflows originating from IRAS 2A1 and IRAS 2A2 are indicated with the colored arrows in the middle panel (Tobin et al. 2015). The size of the beam is shown in the bottom right, and in the bottom left a scale bar is displayed.

3.2 Comparison to ALMA data

Integrated intensity maps of the SO2 82,6−71,7 (Eup = 43 K), SO2 164,12−163,13 (Eup = 164 K), and 34SO2 174,14−173,15 (Eup = 178 K) pure rotational transitions in their vibrational ground states (i.e., v = 0) are presented in Fig. 6. The emission is spatially resolved and is extended in the northwest to southeast direction, following the direction of the outflow of IRAS 2A1 (e.g., Tobin et al. 2015; Jørgensen et al. 2022). However, most of the emission is concentrated in the inner ~1″, similar to what is seen in the MIRI-MRS data (Fig. 3). After deconvolution with the beam, the size of the emission originating from the SO2 164,12−163,13 transition is ~0.5″ × 0.3″ in diameter, corresponding to ~150 × 90 au. The SO2 82,6−71,7 transition has a slightly larger deconvolved emitting size of ~0.6″ × 0.4″ (~180 × 120 au) likely because its lower Eup makes it more sensitive to colder and more extended material in the envelope and outflow. The size of the 34SO2 emission is slightly smaller with a deconvolved size of ~0.4″ × 0.2″ (~120 × 60 au), but this likely originates from the lower signal-to-noise of this transition. These emitting areas are consistent with that of HDO 33,1−42,2 (Eup = 335 K) and complex organics such as methanol (CH3OH) and methyl formate (CH3OCHO; see Fig. A.3) and with the compact emission in the MIRI-MRS data (i.e., 0.5″ × 0.3″ in diameter; see Fig. 3).

The pure rotational lines of SO2 and 34SO2 detected by ALMA were fitted using the same LTE slab model fitting procedure as for the MIRI-MRS data (Sect. 2.3). The submillimeter line lists of both SO2 and 34SO2 were taken from the Cologne Database for Molecular Spectroscopy3 (CDMS; Müller et al. 2001, 2005; Endres et al. 2016), where the entry of SO2 was mostly taken from Müller & Brünken (2005) and the entry of 34SO2 is based on several spectroscopic works (e.g., Lovas 1985; Belov et al. 1998, for transitions at ALMA Band 7 frequencies). The ALMA data cover in total five pure rotational (i.e., v = 0) transitions of SO2 and also five transitions of the 34SO2 isotopologue (see Table A.1). However, several of these transitions are blended with strong emission of complex organics such as CH3OCHO and CH3 CHO. Fortunately, two transitions of SO2 and one transition of 34SO2 are (relatively) unblended. This is important to determine the column density and excitation temperature. All lines of SO2 and 34SO2 are spectrally resolved with a FWHM of 3.5 km s−1, which is similar to the FWHM of the lines of HDO 33,1 − 42,2 and the complex organics. No vibrational correction is necessary for the column densities derived from the pure rotational lines since the first excited vibrational states are included in the partition function.

Interestingly, the excitation temperature Tex (i.e., rotational temperature Trot since it is derived from pure rotational lines) derived for SO2 from the ALMA data is very similar to that derived for MIRI: 104 ± 5 K (see Figs. A.1 and A.2). This suggests that ALMA is probing the same gas as that being probed with MIRI with the temperature reflecting the distribution of rotational levels within the v = 0 state. The column density can be accurately constrained at 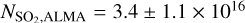NSO2,ALMA=3.4±1.1×1016${N_{{\rm{S}}{{\rm{O}}_2},{\rm{ALMA}}}} = 3.4 \pm 1.1 \times {10^{16}}$ cm−2 for an emitting area with a radius of R = 85 au. In contrast to MIRI, the column density and emitting area can be fairly accurately constrained since the lines are marginally optically thick (τ ~ 0.1). Moreover, the derived column density does not suffer severely from optical depth effects given that the column density derived from the optically thin 34SO2 isotopologue is 2.7 ± 0.5 × 1015 cm−2, giving a 32SO2/34SO2 ratio of 13 ± 5, which is within a factor of 2 of the average32 S/34 S derived for the local ISM (32S/34S = 22; Wilson 1999). However, the total number of SO2 molecules measured by ALMA is g = 1.6 ± 0.2 × 1047 molecules, which is ~4 orders of magnitude lower than what is detected by MIRI. This discrepancy cannot be explained by a difference in dust opacity since such an effect would only worsen the discrepancy in the detected number of molecules between ALMA and MIRI. The most logical explanation is the importance of non-LTE effects for the ro-vibrational transitions detected by MIRI.

4 Discussion

4.1 Importance of non-LTE effects

4.1.1 Absence of the v1 and v2 bands

If the emission originating from the v3 asymmetric stretching mode were in LTE, both the v1 symmetric stretching mode (λ ~ 8.5–9 µm) and v2 bending mode (λ ~ 18–20 µm) should also have been detected. However, no SO2 emission is detected in the v1 and v2 bands (see Fig. 1). The v2 bending mode in particular has a significantly lower vibrational energy (518 cm−1, 745 K) than the v3 asymmetrical stretching mode (1362 cm−1, 1960 K; Briggs 1970; Person & Zerbi 1982) and is therefore more easily collisionally excited. The expected SO2 flux in the 18–20 µm region by employing the best-fit LTE models of the v3 band around 7.35 µm (Sect. 3.1) and the vibrational ground state (i.e., (v1; v2, v3) = (0, 0, 0), denoted as v = 0) in the ALMA data (Sect. 3.2) are presented in Fig. B.3. Similar to the analysis of the v3 band, both models are corrected for an extinction of AV = 55 mag (Rocha et al. 2024) using a modified version of the McClure (2009) extinction law (see Appendix C). No obvious SO2 emission features are present in the data whereas the best-fit v3 LTE model clearly predicts that we should have seen the SO2 at these wavelengths. On the other hand, the LTE model derived from the pure rotational lines in the ALMA data agrees with the non-detection of the v2 band, predominantly due to the larger extinction at MIR wavelengths compared to millimeter wavelengths (e.g., McClure 2009; Chapman et al. 2009).

One solution for the lack of emission in the v2 band could be that the line-to-continuum ratio is too low in this region, since the continuum flux level is on the order of ~1 Jy at 18–20 µm compared to ~20 mJy around 7.35 µm. The predicted line emission peaks at ~1 Jy for the strongest peaks of the v3 model, corresponding to a line-to-continuum ratio of 1 . This suggests that this cannot explain the absence of the v2 band since a line-to-continuum ratio down to 0.01 should still be detectable on a strong continuum. Moreover, this would also not explain the discrepancy between the number of molecules needed in the LTE slab models to explain the emission in v = 0 state with ALMA and the v3 band with MIRI. Scattered continuum radiation is present out to ~8 µm but not to longer wavelengths (see Fig. 1), suggesting that the v3 band could be infrared-pumped on ~100 au scales whereas this does not occur for the v2 band at 19 µm. The infrared radiation around 19 µm originates from thermal dust emission that is not extended (see Fig. 1).

Similarly to the v2 bending mode, the v1 symmetrical stretching mode between 8.5 and 9 µm is overproduced by the best-fit v3 model (see Fig. B.4). The absence of the emission from the v1 band can be simply explained by the large extinction due to strong silicate absorption feature around these wavelengths

4.1.2 Infrared pumping

The critical densities of ro-vibrational transitions are typically > 1010 cm−3 (e.g., for HCN and CO2; Bruderer et al. 2015; Bosman et al. 2017, for SO2 no collisional rates are available for the MIR transitions but they are expected to be similar), suggesting that LTE conditions are only valid for ro-vibrational transitions in the inner <1 au. However, SO2 is present in IRAS 2A on ~100 au scales (see Figs. 3 and 6) where the densities are typically 106−108 cm−3 (e.g., Jørgensen et al. 2004, 2022; Kristensen et al. 2012), far below the critical densities of the MIR transitions, further suggesting that the vibrational level populations are not collisionally excited. The critical densities for the v = 0 transitions probed by ALMA are much lower, on the order of ~106−107 cm−3, meaning that the LTE assumption is valid for these pure rotational lines.

Despite the fact that the assumption of LTE is not valid for the MIR transitions, physical information can still be derived. The rotational temperature derived from the LTE models of the MIR v3 transitions is well constrained given the accuracy of the fit to the R- and Q-branches. It is very similar to the rotational temperature derived for the v = 0 state, for which the LTE assumption is valid. Combined with the similar extent of the emission in the MIRI and ALMA images (Figs. 3 and 6, respectively), this strongly suggests that they are probing SO2 gas on similar scales (i.e., 50–100 au). Because the rotational levels within the v = 0 state can be characterized by a single temperature, the column density of SO2 derived from the ALMA data is also robust. However, the total number of SO2 molecules derived from the v3 MIR transitions is found to be > 4 orders of magnitude higher than what is measured for the v = 0 state. This suggests that the v3 vibrational state is more highly populated than just through collisional excitation by itself.

A likely explanation for populating the v3 vibrational level could be infrared pumping. Vibrational levels can become more highly populated due to the absorption of infrared photons in the presence of a strong infrared radiation field, boosting the line fluxes far above that expected from collisional excitation alone (e.g., Bruderer et al. 2015; Bosman et al. 2017). During the infrared radiative pumping process, the distribution of rotational levels within the vibrational states is largely maintained since only ∆J = 0, ±1 transitions are allowed. Infrared pumping thus leads to a more highly populated vibrational level without significantly changing the rotational distribution (i.e., rotational temperature), supporting the similarity in rotational temperatures measured in the v3 = 1 and v = 0 states.

The importance of infrared pumping can be further quantified by comparing the results of the LTE models to the v3 band and the v = 0 state. Assuming the v3 = 1 vibrational level is radiatively pumped from the v = 0 state, the vibrational level population is set following the Boltzmann distribution by a vibrational temperature Tvjb that is different from the rotational temperature, Tvib ≠ Trot. The difference between the total number of molecules predicted in LTE models of the MIRI and ALMA data can then be approximated as 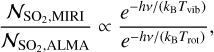NSO2,MIRINSO2, ALMA ∝e−hv/(kBTvib)e−hv/(kBTrot ),${{{{\cal N}_{{\rm{S}}{{\rm{O}}_2},{\rm{MIRI}}}}} \over {{{\cal N}_{{\rm{S}}{{\rm{O}}_2},{\rm{ALMA}}}}}} \propto {{{e^{ - hv/\left( {{k_{\rm{B}}}{T_{{\rm{vib}}}}} \right)}}} \over {{e^{ - hv/\left( {{k_{\rm{B}}}{T_{{\rm{rot}}}}} \right)}}}},$(1)

where gALMA and gMIRI are the total number of molecules needed in the LTE models of the ALMA and MIRI data, respectively, Trot the derived rotational temperature in the v = 0 state with ALMA (i.e., 104 ± 5 K; Sect. 3.2), Tvib the vibrational temperature, v the frequency of the MIR transitions, and h and kB Planck’s and Boltzmann’s constants, respectively. In Eq. (1), g factors have been neglected for simplicity. In the case where both v3 = 1 and v = 0 are collisionally excited, Tvib = Trot and the number of SO2 molecules predicted by the LTE models of the MIRI and ALMA data should have been equal, gALMA = gMIRI. However, for the derived 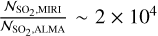NSO2,MIRINSO2,ALMA~2×104${{{{\cal N}_{{\rm{S}}{{\rm{O}}_2},{\rm{MIRI}}}}} \over {{{\cal N}_{{\rm{S}}{{\rm{O}}_2},{\rm{ALMA}}}}}}\~2 \times {10^4}$ and Trot = 104 K, Eq. (1) results in Tvib ~ 200 K at a wavelength of 7.35 µm (i.e., v = 40.79 THz), which is ~80 K higher than the derived Trot of the vibrational ground state. We estimate an uncertainty on Tvib of 50 K based on the assumption of similar rotational temperatures in the v3 = 1 and v = 0 states and ignoring g factors in Eq. (1).

If infrared pumping is indeed the cause for the elevated vibrational temperature, the brightness temperature of the infrared radiation around 7.35 µm, TIR, has to be similar to Tvib, 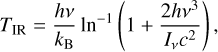TIR=hvkBln−1(1+2hv3Ivc2),${T_{{\rm{IR}}}} = {{hv} \over {{k_{\rm{B}}}}}{\ln ^{ - 1}}\left( {1 + {{2h{v^3}} \over {{I_v}{c^2}}}} \right),$(2)

where Iv is the observed intensity (in Jy sr−1) of the continuum at a frequency v and c is the speed of light. Given that Iv ~ 6 × 104 MJy sr−1 (i.e., 1.4 Jy arcsec−2) around 7.35 µm (i.e., 40.79 THz) and assuming an extinction of AV = 55 mag (Rocha et al. 2024), this results in TIR ~ 180 K. This is in very good agreement with Tvib ~ 200 K and therefore strongly suggests that the vibrational temperature of the v3 band of SO2 is indeed set by the infrared radiation field of the protostar rather than by collisions.

In turn, this means that both MIRI and ALMA are in fact tracing the same molecular gas with the same rotational temperature, but that the transitions in the v3 band are just pumped by the strong infrared radiation field of the central star and originate from a region much smaller than 5000 au. ALMA thus measures the true number of SO2 molecules (1.8 ± 0.2 × 1047), and in order to directly derive the physical properties (i.e., excitation temperature, column density, emitting area) from the ro-vibrational transition of SO2 at MIR wavelengths it is important to take into account non-LTE processes such as infrared radiative pumping.

4.2 Physical origin of the SO2

The SO2 emission detected with both ALMA and MIRI is clearly tracing warm inner regions of the protostellar system on disk scales of ≲ 100 au in radius. This implies that the emission either originates from the central hot core where many complex organics are detected (e.g., Jørgensen et al. 2005; Bottinelli et al. 2007; Maury et al. 2014; Taquet et al. 2015), or that the emission originates from an accretion shock at the disk-envelope interface (e.g., Artur de la Villarmois et al. 2019, 2022; van Gelder et al. 2021). Alternatively, the SO2 could be located in a jet or outflow close to the source (e.g., Codella et al. 2014; Taquet et al. 2020; Tychoniec et al. 2021), or even in a disk wind (e.g., Tabone et al. 2017). However, since the emission in the MIRI data is clearly centrally peaked with only little extended emission (≲ 100 au in radius; see Fig. 3) and the line widths of the pure rotational lines detected by ALMA are ~3.5 km s−1 (compared to >10 km s−1 typically observed in outflows; e.g., Taquet et al. 2020; Tychoniec et al. 2019,2021), an extended outflow origin is less likely. On the contrary, CO2 is clearly detected in the outflow and not on the continuum peak (see Fig. B.1), which will be further discussed in a separate paper.

One way to investigate further the possible origin of the SO2 emission is to estimate its abundance with respect to H2. The most direct way to determine the number of H2 molecules is using the detected H2 MIR lines (see Appendix D). However, H2 does not only trace the warm inner regions but is also present in outflows and disk winds (Tychoniec et al., in prep.). Indeed, in IRAS 2A H2 is mostly located in the outflow toward the southwest (see Fig. B.1). Moreover, the rotational temperature of the warm component is >300 K (see Fig. D.2), which further suggests that H2 may not be tracing the same gas as SO2 (Trot = 104 ± 5 K).

Another method for determining the amount of ~100 K H2 gas is to use the ALMA Band 7 continuum. The total gas mass, Mgas, can be determined using the equation from Hildebrand (1983), 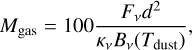Mgas =100Fvd2κvBv(Tdust ),${M_{{\rm{gas}}}} = 100{{{F_v}{d^2}} \over {{\kappa _v}{B_v}\left( {{T_{{\rm{dust}}}}} \right)}},$(3)

where Fv is the continuum flux density at a frequency v, d the distance (293 pc; Ortiz-León et al. 2018), κv the dust opacity, Bv (Tdust) the Planck function evaluated at a dust temperature Tdust, and the factor 100 the assumed gas-to-dust mass ratio. Here, Tdust is assumed to be 30 K, which is a typical dust temperature for protostellar envelopes at ~100 au scales (Whitney et al. 2003). For a measured Fv = 0.396 ± 0.079 Jy in a 1.4″ diameter aperture (i.e., the same as was used in the spectral extraction) and a dust opacity of κv = 1.84 cm−2 g−1 at a frequency of 340 GHz (Ossenkopf & Henning 1994), a gas mass of Mgas = 0.11 ± 0.02 M⊙ is derived. The derived gas mass is consistent within a factor of 2 with other recent measurements (e.g., Tobin et al. 2018; Tychoniec et al. 2020). Assuming that this gas mass is predominantly in H2 (i.e., taking a mean molecular weight 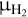μH2${{\rm{\mu }}_{{{\rm{H}}_{\rm{2}}}}}$ per hydrogen atom for gas composed of 71% hydrogen; Kauffmann et al. 2008), this results in 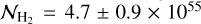NH2=4.7±0.9×1055 ${{\cal N}_{{{\rm{H}}_2}}} = 4.7 \pm 0.9 \times {10^{55}}{\rm{ }}$ molecules. This is in good agreement with 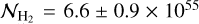NH2=6.6±0.9×1055${{\cal N}_{{{\rm{H}}_2}}} = 6.6 \pm 0.9 \times {10^{55}}$ molecules derived for IRAS 2A from C18O lines up to J = 9−8 with Herschel-HIFI (assuming a CO/H2 ratio of 10−4 and rotational temperature of ~40 K; Yıldız et al. 2013). However, the derived radius of the SO2 emitting area (~100 au) is smaller than the physical radius of the aperture (205 au for 1.4″ diameter aperture) used for computing 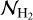NH2${{\cal N}_{{{\rm{H}}_2}}}$. The derived 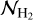NH2${{\cal N}_{{{\rm{H}}_2}}}$ can be scaled to the derived emitting area of SO2 assuming that the density scales as nH ∝ R−p, 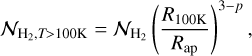NH2,T>100 K=NH2(R100 KRap )3−p,${{\cal N}_{{{\rm{H}}_2},T > 100{\rm{K}}}} = {{\cal N}_{{{\rm{H}}_2}}}{\left( {{{{R_{100{\rm{K}}}}} \over {{R_{{\rm{ap}}}}}}} \right)^{3 - p}},$(4)

where R100K is the derived size emitting area of SO2 from the ALMA and MIRI-MRS maps (~100 au; see Sect. 3) and Rap is physical radius of the aperture (205 au for 1.4″ diameter aperture). Taking a density power-law index of 1.7 for IRAS 2A1 (Kristensen et al. 2012), this results in 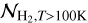NH2,T>100 K${{\cal N}_{{{\rm{H}}_2},T > 100{\rm{K}}}}$ = 1.8 ± 0.4 × 1055 molecules. This is almost equal to what is derived directly from the H2 lines (1.7 ± 0.9 × 1055 molecules; Appendix D), which suggests that the H2 0-0 lines themselves are likely sensitive to most of the T > 100 K gas despite the high rotational temperature (Trot = 356 ± 41 K).

The total number of SO2 molecules derived from the emission of the vibrational ground state in the ALMA data can be directly compared to H2. This results in an SO2 abundance on the order of 1.0 ± 0.3 × 10−8 with respect to H2, which is in agreement with other recent SO2 abundance measurements in low-mass Class 0 systems (>6.6 × 10−10; Artur de la Villarmois et al. 2023). The abundance of ~10−8 implies that the SO2 gas is not the dominant sulfur carrier in IRAS 2A since the cosmic [S/H] abundance is about ~10−5 (Savage & Sembach 1996; Goicoechea et al. 2006). It is also means that SO2 does not contain a significant amount of the total volatile sulfur budget in dense clouds (volatile [S/H] ~ 10−7, i.e., the amount of sulfur that is not locked up in refractory formats; Woods et al. 2015; Kama et al. 2019). Furthermore, the derived SO2 abundance is on the lower side compared with estimates of the SO2 abundances in interstellar ices (10−8−10−7; Boogert et al. 1997, 2015; Zasowski et al. 2009) and cometary ices (~10−7; Altwegg et al. 2019; Rubin et al. 2019). In particular, SO2 ice was also recently detected in absorption toward IRAS 2A itself with a very similar abundance with respect to H2 as other low-mass protostars (~10−7;Rocha et al. 2024).

Although the gaseous SO2 abundance is on the lower side compared to the ices, it suggests that the observed gaseous SO2 could be sublimated from the ices in the central hot core since the sublimation temperature of SO2 (~60 K, Ebin = 3010 K; Penteado et al. 2017) is similar to H2O and many complex organics. It also naturally explains the compactness of the SO2 emission in both the MIRI data and the ALMA data (see Figs. 3 and 6) with an extent very similar to that of H2O, HDO, and complex organics (see Figs. B.1 and A.3). In fact, the emitting areas derived from the MIRI-MRS and ALMA integrated intensity maps (~100 au in radius) agree well with that of a hot core based on the luminosity (i.e., R100K = 147 au, where 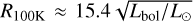R100 K≈15.4Lbol/L⊙${R_{100{\rm{K}}}} \approx 15.4\sqrt {{L_{{\rm{bol}}}}/{L_ \odot }} $; Bisschop et al. 2007; van’t Hoff et al. 2022). The hot core origin is further supported by the line width in the ALMA data (~3.5 km s−1), which is similar to that of lines from HDO and complex organics.

Another possibility for the SO2 emission could be weak shocks on ≲ 100 au scales such as accretion shocks at the disk–envelope boundary (e.g., Sakai et al. 2014; Oya et al. 2019; Artur de la Villarmois et al. 2019, 2022). Recent shock models have suggested that SO2 could be a good tracer of such accretion shocks (Miura et al. 2017; van Gelder et al. 2021). Abundances up to 10−8−10−7 with respect to H2 are easily reached in low-velocity accretion shocks, as long as a significant ultraviolet (UV) radiation field is present (i.e., stronger than the interstellar radiation field; van Gelder et al. 2021). Given the luminosity of IRAS 2A (~60–90 L⊙; Murillo et al. 2016; Karska et al. 2018), having a considerable UV field in the inner envelope out to 100 au scales is likely (see e.g., van Kempen et al. 2009; Yıldız et al. 2012, 2015). The emission morphology seen in the ALMA data (Fig. 6) shows that the emission is extended more in the direction of the outflow than along the disk. Furthermore, the line width of ~3.5 km s−1 is consistent with those of the complex organics whereas accretion shocks are expected to show broader emission lines (~10 km s−1; Oya et al. 2019; Artur de la Villarmois et al. 2019, 2022). A hot core origin is therefore a more likely explanation for the gaseous SO2.

The SO2 emission in IRAS 2A could be tracing similar components as the MIR SO2 absorption that was detected toward multiple high-mass protostellar sources (e.g, Keane et al. 2001; Dungee et al. 2018; Nickerson et al. 2023). Typical temperatures of this SO2 absorption are ~100–300 K (e.g., Dungee et al. 2018; Nickerson et al. 2023), which is very similar to the rotational temperature derived for IRAS 2A (~100 K), though temperatures up to ~700 K have also been reported (Keane et al. 2001). The most common origin of the SO2 absorption toward these high-mass sources is also suggested to be a hot core rather than a shock, similar to what SO2 is tracing in IRAS 2A, with the main difference that it is in absorption against the bright infrared continuum of the central high-mass protostar. The typical SO2 abundances derived for these high-mass protostars are ≳10−7 with respect to H2 (Keane et al. 2001; Dungee et al. 2018; Nickerson et al. 2023), which is an order of magnitude higher than what is derived for IRAS 2A.

It remains unknown whether the presence of ro-vibrational lines of SO2 in IRAS 2A is unique or whether it is more common among low-mass protostars. One other low-mass protostar in the JOYS+ sample, NGC 1333 IRAS1A, shows emission of the SO2 v3 Q-branch (R- and P-branches are not detected) and similarly does not show any emission from the v1 and v2 bands, suggesting that infrared radiative pumping may also be responsible for the emission in the v3 band of this source. IRAS 2A has a high luminosity (~60–90 L⊙; Murillo et al. 2016; Karska et al. 2018) and is suggested to currently be in a burst phase (e.g., Hsieh et al. 2019; van’t Hoff et al. 2022), whereas IRAS 1A has a lower luminosity (~10 L⊙; Tobin et al. 2016). On the other hand, the low-mass Class 0 protostar IRAS 15398-3359 does not show gaseous SO2 and has a lower luminosity of ~1.5 L⊙ (Yang et al. 2018, 2022). Given the importance of infrared pumping in detecting the SO2 lines, a high luminosity could be important. However, a larger sample of JWST/MIRI-MRS spectra of low-mass and high-mass embedded protostellar systems is needed to further investigate the importance of luminosity (and other source properties) on the presence of MIR SO2 emission. Future MIRI-MRS observations from the JOYS+ program will cover a few other luminous low-mass protostellar systems (e.g., Serpens SMM1, Lbol ~ 100 L⊙; Karska et al. 2018), as well as several high-mass protostellar systems (e.g., IRAS 18089-1732, Lbol ~ 104 L⊙; Urquhart et al. 2018).

5 Conclusions

This paper presents one of the first medium-resolution MIR spectra and images taken with JWST/MIRI-MRS of a Class 0 protostellar source, NGC 1333 IRAS 2A, and presents the first detection of gas-phase SO2 emission at MIR wavelengths. We analyzed the spectral lines of the v3 asymmetric stretching mode of SO2 using LTE slab models and find a rotational temperature of 92 ± 8 K. This is very similar to the rotational temperature of 104 ± 5 K derived from the pure rotational lines in the high-resolution ALMA data. Since the SO2 emission in the MIRI-MRS data is optically thin, the column density could not be constrained accurately due to the degeneracy with the emitting area. However, the total number of molecules can be constrained and is predicted by LTE models of the MIRI-MRS data to be a factor of ~2 × 104 higher than that derived from the ALMA data. Based on these results, our main conclusions are as follows:

  • The v3 asymmetric stretching mode of SO2 detected around 7.35 µm with MIRI is not in LTE but rather radiatively pumped by a strong infrared radiation field scattered out to ~100 au distances. The discrepancy between the best-fit LTE models of the MIRI-MRS and ALMA data can be explained by a vibrational temperature (~200 K) that is higher than the rotational temperature derived within the vibrational ground state (104 ± 5 K). The vibrational temperature is consistent with the brightness temperature of the continuum around 7.35 µm (~180 K). The similarity in rotational temperatures suggests that MIRI-MRS and ALMA are in fact still tracing the same molecular gas.

  • Assuming that ALMA is probing the total amount of SO2, the abundance of gaseous SO2 is estimated to be 1.0 ± 0.3 × 10-8 with respect to H2, which is consistent with both a hot core and accretion shock origin. Based on the size of the emitting area (~ 100 au in radius) and the small line width of the SO2 lines (~3.5 km s−1) in the ALMA data, a hot core origin is suggested to be the most likely.

Our results show the importance of taking non-LTE effects into account when analyzing ro-vibrational lines at MIR wavelengths. The synergy between JWST probing the hot spots and the spatial and spectral resolution of ALMA proves to be crucial in determining the physical origin of molecules in embedded protostellar systems. Future astrochemical modeling with non-LTE effects included will be valuable for inferring the physics and the chemistry of SO2 in the earliest phases of star formation and their connection to the sulfur depletion problem.

Acknowledgements

We would like to thank the anonymous referee for their constructive comments on the manuscript, and Valentin Christiaens, Matthias Samland, and Danny Gasman for valuable support with the MIRI-MRS data reduction. This work is based on observations made with the NASA/ESA/CSA James Webb Space Telescope. The data were obtained from the Mikulski Archive for Space Telescopes at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-03127 for JWST. These observations are associated with program #1236. The following National and International Funding Agencies funded and supported the MIRI development: NASA; ESA; Belgian Science Policy Office (BELSPO); Centre Nationale d’Études Spatiales (CNES); Danish National Space Centre; Deutsches Zentrum fur Luftund Raumfahrt (DLR); Enterprise Ireland; Ministerio De Economiá y Competividad; The Netherlands Research School for Astronomy (NOVA); The Netherlands Organisation for Scientific Research (NWO); Science and Technology Facilities Council; Swiss Space Office; Swedish National Space Agency; and UK Space Agency. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2021.1.01578.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. The PI acknowledges assistance from Aida Ahmadi from Allegro, the European ALMA Regional Center node in the Netherlands. M.v.G., E.v.D., L.F., H.L., K.S., and W.R. acknowledge support from ERC Advanced grant 101019751 MOLDISK, TOP-1 grant 614.001.751 from the Dutch Research Council (NWO), The Netherlands Research School for Astronomy (NOVA), the Danish National Research Foundation through the Center of Excellence "InterCat" (DNRF150), and DFG-grant 325594231, FOR 2634/2. The work of M.E.R. was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. P.J.K. acknowledges support from the Science Foundation Ireland/Irish Research Council Pathway programme under Grant Number 21/PATH-S/9360. L.M. acknowledges the financial support of DAE and DST-SERB research grants (SRG/2021/002116 and MTR/2021/000864) from the Government of India.

Appendix A Additional ALMA figures and table

Table A.1

Transitions of SO2 and 34SO2 covered in the 2021.1.01578.S ALMA program.

thumbnail Fig. A.1

Continuum-subtracted ALMA spectra (blue) for the SO2 82,6 − 71,7 (left, Eup = 43 K), SO2 164,12 − 163,13 (middle, Eup = 164 K), and 34SO2 174,14 − 173,15 (right, Eup = 178 K) transitions. The best-fit LTE slab models are overlaid in orange. All other transitions (see Table A.1) of SO2 and 34SO2 are either blended with other molecular species or not detected.
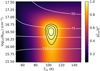thumbnail Fig. A.2

χ2 map for SO2 derived from pure rotational lines in the ALMA data. The χ2 values are inversely normalized by the minimum χ2 and shown in color. The 1, 2, and 3σ confidence intervals are presented as the black contours. The best-fitting emitting radius, R (in au), is represented by the white contours and is calculated for each grid point by minimizing the χ2 assuming a circular emitting area of πR2. The χ2 map indicates that the SO2 emission has an excitation temperature of 104 ± 5 K and is marginally optically thick (τ ~ 0.1) with an emitting area of ~ 85 au in radius.
thumbnail Fig. A.3

Integrated intensity maps of the HDO 33,1 – 42,2 (Eup = 335 K), CH3OH 161,15 − 152,14 (middle, Eup = 331 K), and CH3OCHO 2710,17 − 2610,16 (right, Eup = 190 K) transitions in color. The images are integrated over [-2,2] km s−1 with respect to the V1sr of 6.7 km s−1. The white vertical bar in the colorbar on top of each image indicates the 3σ threshold. The 0.875 mm continuum is overlaid as black contours. The main continuum peak is associated with IRAS2A1 and the secondary peak toward the south with IRAS2A2. The directions of the two outflows originating from IRAS2A1 and IRAS2A2 are indicated with the colored arrows in the middle panel (Tobin et al. 2015). The size of the beam is shown in the bottom right, and in the bottom left a scale bar is displayed.

Appendix B Additional MIRI-MRS figures

thumbnail Fig. B.1

Integrated intensity map of the CO2 v2 = 1 – 0 Q-branch (top left), H2O v2 = 1 – 0 42,3 – 53,2 (top right), H2 0-0 S(1) (bottom left), and H2 0-0 S(7) (bottom right) observed with MIRI-MRS in color. The images are integrated over [14.9,15.0] µm for CO2, [7.145-7.15] µm for H2O, and [−0.01,0.01] µm with respect to the transitions of H2. The extent of the continuum around the respective wavelengths is overlaid as white contours. A white scale bar is displayed in the bottom left of each panel, and the size of the PSF is presented as the filled white circle in the bottom right. The directions of the two outflows originating from IRAS2A1 and IRAS2A2 are indicated with the colored arrows in the top-left panel (Tobin et al. 2015). The H2O emission is peaking on-source on the same scales as SO2, whereas the CO2 and H2 0-0 S(1) emissions are clearly peaking in the outflow toward the southwest. The H2 0-0 S(7) line peaks mostly on-source but also has a component in the southwestern outflow.
thumbnail Fig. B.2

Spectrum of IRAS2A in blue centered around the v3 band of SO2 as observed by JWST/MIRI-MRS. The local continuum fit is shown in red and the best-fit LTE slab model in orange at a +5 mJy offset. In green, the SO2-subtracted data are presented, revealing the 7.4 µm ice absorption feature that was hidden by the P-branch of the SO2 v3 band. The Q-branch is slightly overfitted, resulting in a subtraction residual. The ice absorption bands are further analyzed by Rocha et al. (2024).
thumbnail Fig. B.3

JWST/MIRI-MRS continuum-subtracted spectrum (blue) centered on the v2 band of SO2 around 19 µm. No clear emission or absorption features of SO2 are detected. Overlaid are LTE slab models obtained using the best-fit parameters derived from the v3 band around 7.35 µm (red) and the pure rotational lines in the ALMA data (green). The MIRI slab model is scaled down by a factor of 10−3 for clarity. Both models are offset with respect to the data and are corrected for an extinction of AV = 55 mag (Rocha et al. 2024) using a modified version of the McClure (2009) extinction law (see Appendix C).
thumbnail Fig. B.4

JWST/MIRI-MRS continuum-subtracted spectrum (blue) centered on the v1 band of SO2 around 8.5 µm. The two overlapping MIRI-MRS sub-bands (channel 2A and 2B) have been stitched for clarity. No clear emission or absorption features of SO2 are detected. Overlaid are slab models obtained using the best-fit parameters derived from the v3 band around 7.35 µm (red) and the pure rotational lines in the ALMA data (green). Both models are offset with respect to the data and are corrected for an extinction of AV = 55 mag (Rocha et al. 2024) using a modified version of the McClure (2009) extinction law (see Appendix C).

Appendix C Extinction correction

A modified version of the extinction law of McClure (2009) was created for the extinction correction because the depths of the dominant absorption features (e.g., H2O, CO2, and silicates) did not match with those measured toward IRAS2A. The total extinction (in units of optical depth) toward IRAS2A (τtot(λ) = Aλ/1.086) was therefore decomposed into two components, 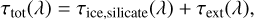τtot (λ)=τice, silicate (λ)+τext (λ),${\tau _{{\rm{tot}}}}(\lambda ) = {\tau _{{\rm{ice,silicate}}}}(\lambda ) + {\tau _{{\rm{ext}}}}(\lambda ),$(C.1)

where τice,silicate(λ) is the differential extinction caused by the ice and silicate absorption features and τext(λ) is the absolute extinction.

The differential extinction τice,silicate(λ) was obtained in a similar matter to what is used for typical ice analysis studies. The optical depth was computed with respect to a third-order polynomial fitted through obvious absorption-free wavelengths (i.e., 5.1, 5.3, 7.6, 22, and 24 µm; see the top panel of our Fig C.1; Rocha et al. 2024). The optical depth could then be calculated via 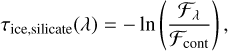τice,silicate (λ)=−ln(ℱλℱcont ),${\tau _{{\rm{ice,silicate}}}}(\lambda ) = - \ln \left( {{{{{\cal F}_\lambda }} \over {{{\cal F}_{{\rm{cont}}}}}}} \right),$(C.2)

where tλ is the measured flux with MIRI-MRS and tcont the continuum flux. The differential extinction in units of optical depth is presented in the bottom panel of Fig C.1.

The absolute extinction τext was computed by fitting a power-law model to the extinction law of McClure (2009) for an extinction of AK > 1. Only the wavelengths outside of the major absorption features were taken into account (i.e., 4.9-5.4, 7.2-7.3, and 28-29 µm). In this case, the power of the power law was also fitted. The extinction law was fitted for the case of AV = 1 mag (assuming AK = AV/7.75 mag; McClure 2009) in units of optical depth (τext(λ) = Aλ/1.086). The fit to the extinction law is presented in Fig. C.2. Using this fit, the absolute extinction was derived to be 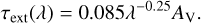τext(λ)=0.085λ−0.25AV.${\tau _{{\rm{ext}}}}(\lambda ) = 0.085{\lambda ^{ - 0.25}}{A_{\rm{V}}}.$(C.3)

Here, AV = 55 was adopted based in the depth of the silicate absorption (Rocha et al. 2024), leading to τext ~ 3 around 5 µm and τext ~ 2 around 25 µm (see bottom panel of Fig C.1). The total extinction toward IRAS2A in units of optical depth is presented in the bottom panel of Fig. C.1.

thumbnail Fig. C.1

Determining the extinction due to ice and silicate absorption. Top: Observed MIRI-MRS spectrum of IRAS2A (blue) with the global continuum estimate (red) overplotted. The continuum is based on a third-order polynomial fit to emission- and absorption-free wavelength ranges. The positions of the H2 v = 0 rotational transitions are indicated with the vertical dashed gray lines. Bottom: Differential extinction in units of optical depth (blue) of the absorption features as a function of wavelength derived from the global continuum estimate (Eq. (C.2)). Overplotted is the absolute extinction (orange) computed using Eq. (C.3); see the main text for more details. The total extinction (green) is computed from the sum of the two (Eq. (C.1)).
thumbnail Fig. C.2

McClure (2009) extinction law for AV = 1 mag (assuming AK = AV/7.75 mag) in blue with the best-fit power-law model to the absorption-free regions (dots) overplotted in red. Both the extinction law and the best-fit model are plotted in units of optical depth for AV = 1 mag but are directly proportional to AV.

Appendix D H2 analysis

D.1 Fitting of the H2 lines

The MIRI range covers the v = 0 pure rotational lines of H2 from the S(0) line at 28.22 µm till the S(8) line at 5.05 µm. However, the S(0) line lies at the very edge of channel 4C (λ > 14 µm) where the sensitivity drops significantly and the flux calibration is very poor. Some weak line emission appears to be present (see Fig. D.1, bottom-middle panel) but since the peak intensity is equally strong as that of residual fringes present surrounding the line, it was excluded form the rotational diagram analysis. All other H2 v = 0 transitions are detected except for the S(8) transition. The detected transitions were fitted with a simple Gaussian emission profile (see Fig. D.1). A flux calibration uncertainty of 5% was assumed. The H2 line fluxes were corrected for total extinction based on a modified version of the extinction law of McClure (2009) introduced in Appendix C The integrated line fluxes are reported in Table D.1.

D.2 Fitting the rotational diagram

A rotational diagram was created following the formalism of Goldsmith & Langer (1999) and presented in Fig. D.2. The rotational diagram can be best fitted using a two-component model: a warm component with a rotational temperature of Twarm = 356 ± 41 K and a column density of Nwarm = 5.6 ± 1.9 × 1013 cm−1 and a hot component with Thot = 901 ± 158 K and a column density of Nhot = 4.4 ± 5.1 × 1011 cm−1. The total number of molecules can be constrained to 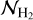NH2${{\cal N}_{{{\rm{H}}_2}}}$ molecules. An emitting area with a diameter of 1.4″ is used (i.e., Rsource = 105 au at a distance of 193 pc), equal to the size of the aperture at 7.35 µm. However, since the H2 emission is assumed to be optically thin, the value of gtot does not depend on the assumed emitting area.

Table D.1

Integrated line fluxes of H2 transitions.

thumbnail Fig. D.1

Observed MIRI-MRS spectrum (blue) centered around H2 v = 0 pure rotational lines from the S(7) line in the top-left panel to the S(0) line in the bottom-middle panel. The best-fit Gaussian model is presented in orange in each panel. All presented lines are considered detected except for the S(0) line since the flux is similar to that of several strong residual fringes located in the vicinity of the S(0) line.
thumbnail Fig. D.2

Rotational diagram of H2 derived from the MIRI-MRS data. The black data points indicate the measured fluxes that are corrected for extinction (see Table. D.l). The best-fit two-component model is presented as the solid green line, and the two individual components are shown as the dashed blue (warm) and orange (hot) lines. The best-fit parameters are displayed in the top right.

References

  1. Altwegg, K., Balsiger, H., & Fuselier, S. A. 2019, ARA&A, 57, 113 [NASA ADS] [CrossRef] [Google Scholar]
  2. Arce, H. G., Borkin, M. A., Goodman, A. A., Pineda, J. E., & Halle, M. W. 2010, ApJ, 715, 1170 [NASA ADS] [CrossRef] [Google Scholar]
  3. Argyriou, I., Glasse, A., Law, D. R., et al. 2023, A&A, 675, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Artur de la Villarmois, E., Jørgensen, J. K., Kristensen, L. E., et al. 2019, A&A, 626, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Artur de la Villarmois, E., Guzmán, V. V., Jørgensen, J. K., et al. 2022, A&A, 667, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Artur de la Villarmois, E., Guzmán, V. V., Yang, Y. L., Zhang, Y., & Sakai, N. 2023, A&A, 678, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Belov, S. P., Tretyakov, M. Y., Kozin, I. N., et al. 1998, J. Mol. Spectrosc., 191, 17 [NASA ADS] [CrossRef] [Google Scholar]
  8. Beuther, H., van Dishoeck, E. F., Tychoniec, L., et al. 2023, A&A, 673, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bisschop, S. E., Jørgensen, J. K., van Dishoeck, E. F., & de Wachter, E. B. M. 2007, A&A, 465, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Blake, G. A., Sutton, E. C., Masson, C. R., & Phillips, T. G. 1987, ApJ, 315, 621 [Google Scholar]
  11. Boogert, A. C. A., Schutte, W. A., Helmich, F. P., Tielens, A. G. G. M., & Wooden, D. H. 1997, A&A, 317, 929 [NASA ADS] [Google Scholar]
  12. Boogert, A. C. A., Pontoppidan, K. M., Knez, C., et al. 2008, ApJ, 678, 985 [Google Scholar]
  13. Boogert, A. C. A., Gerakines, P. A., & Whittet, D. C. B. 2015, ARA&A, 53, 541 [Google Scholar]
  14. Boonman, A. M. S., van Dishoeck, E. F., Lahuis, F., et al. 2003, A&A, 399, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Bosman, A. D., Bruderer, S., & van Dishoeck, E. F. 2017, A&A, 601, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Bottinelli, S., Ceccarelli, C., Williams, J. P., & Lefloch, B. 2007, A&A, 463, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Briggs, A. G. 1970, J. Chem. Education, 47, 391 [NASA ADS] [CrossRef] [Google Scholar]
  18. Bruderer, S., Harsono, D., & van Dishoeck, E. F. 2015, A&A, 575, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Bushouse, H., Eisenhamer, J., Dencheva, N., et al. 2023, ASP Conf. Ser., 527, 583 [NASA ADS] [Google Scholar]
  20. Carr, J. S., & Najita, J. R. 2008, Science, 319, 1504 [Google Scholar]
  21. Chapman, N. L., Mundy, L. G., Lai, S.-P., & Evans, Neal J., I. 2009, ApJ, 690, 496 [NASA ADS] [CrossRef] [Google Scholar]
  22. Christiaens, V., Gonzalez, C., Farkas, R., et al. 2023, J. Open Source Softw., 8, 4774 [NASA ADS] [CrossRef] [Google Scholar]
  23. Codella, C., Maury, A. J., Gueth, F., et al. 2014, A&A, 563, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Codella, C., Bianchi, E., Podio, L., et al. 2021, A&A, 654, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Drozdovskaya, M. N., van Dishoeck, E. F., Jørgensen, J. K., et al. 2018, MNRAS, 476, 4949 [Google Scholar]
  26. Dungee, R., Boogert, A., DeWitt, C. N., et al. 2018, ApJ, 868, L10 [NASA ADS] [CrossRef] [Google Scholar]
  27. Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Müller, H. S. P. 2016, J. Mol. Spectrosc., 327, 95 [NASA ADS] [CrossRef] [Google Scholar]
  28. Francis, L., van Gelder, M. L., van Dishoeck, E. F., et al. 2024, A&A, in press https://doi.org/10.1051/0004-6361/202348105 [Google Scholar]
  29. Garufi, A., Podio, L., Codella, C., et al. 2022, A&A, 658, A104 [CrossRef] [EDP Sciences] [Google Scholar]
  30. Gieser, C., Beuther, H., van Dishoeck, E. F., et al. 2023, A&A, 679, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Goicoechea, J. R., Pety, J., Gerin, M., et al. 2006, A&A, 456, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [Google Scholar]
  33. Gordon, I. E., Rothman, L. S., Hargreaves, R. J., et al. 2022, J. Quant. Spec. Radiat. Transf., 277, 107949 [NASA ADS] [CrossRef] [Google Scholar]
  34. Grant, S. L., van Dishoeck, E. F., Tabone, B., et al. 2023, ApJ, 947, L6 [NASA ADS] [CrossRef] [Google Scholar]
  35. Greenfield, P., & Miller, T. 2016, Astron. Comput., 16, 41 [NASA ADS] [Google Scholar]
  36. Harsono, D., Bjerkeli, P., Ramsey, J. P., et al. 2023, ApJ, 951, L32 [NASA ADS] [CrossRef] [Google Scholar]
  37. Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
  38. Hsieh, T.-H., Murillo, N. M., Belloche, A., et al. 2019, ApJ, 884, 149 [Google Scholar]
  39. Jones, O. C., Álvarez-Márquez, J., Sloan, G. C., et al. 2023, MNRAS, 523, 2519 [Google Scholar]
  40. Jørgensen, J. K., Bourke, T. L., Myers, P. C., et al. 2005, ApJ, 632, 973 [Google Scholar]
  41. Jørgensen, J. K., Kuruwita, R. L., Harsono, D., et al. 2022, Nature, 606, 272 [CrossRef] [Google Scholar]
  42. Jørgensen, J. K., Schöier, F. L., & van Dishoeck, E. F. 2004, A&A, 416, 603 [Google Scholar]
  43. Kama, M., Shorttle, O., Jermyn, A. S., et al. 2019, ApJ, 885, 114 [Google Scholar]
  44. Karska, A., Kaufman, M. J., Kristensen, L. E., et al. 2018, ApJS, 235, 30 [NASA ADS] [CrossRef] [Google Scholar]
  45. Kauffmann, J., Bertoldi, F., Bourke, T. L., Evans, N. J., I., & Lee, C. W. 2008, A&A, 487, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Keane, J. V., Boonman, A. M. S., Tielens, A. G. G. M., & van Dishoeck, E. F. 2001, A&A, 376, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Kristensen, L. E., van Dishoeck, E. F., Bergin, E. A., et al. 2012, A&A, 542, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Kushwahaa, T., Drozdovskaya, M. N., Tychoniec, L., & Tabone, B. 2023, A&A, 672, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Labiano, A., Argyriou, I., Álvarez-Márquez, J., et al. 2021, A&A, 656, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Law, D. D., Morrison, J. E., Argyriou, I., et al. 2023, AJ, 166, 45 [NASA ADS] [CrossRef] [Google Scholar]
  51. Lovas, F. J. 1985, J. Phys. Chem. Ref. Data, 14, 395 [NASA ADS] [CrossRef] [Google Scholar]
  52. Maury, A. J., Belloche, A., André, P., et al. 2014, A&A, 563, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. McClure, M. 2009, ApJ, 693, L81 [NASA ADS] [CrossRef] [Google Scholar]
  54. McClure, M. K., Rocha, W. R. M., Pontoppidan, K. M., et al. 2023, Nat. Astron., 7, 431 [NASA ADS] [CrossRef] [Google Scholar]
  55. McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, ASP Conf. Ser., 376, 127 [Google Scholar]
  56. Miura, H., Yamamoto, T., Nomura, H., et al. 2017, ApJ, 839, 47 [NASA ADS] [CrossRef] [Google Scholar]
  57. Müller, H. S. P., & Brünken, S. 2005, J. Mol. Spectr., 232, 213 [CrossRef] [Google Scholar]
  58. Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [Google Scholar]
  59. Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [Google Scholar]
  60. Murillo, N. M., van Dishoeck, E. F., Tobin, J. J., & Fedele, D. 2016, A&A, 592, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Navarro-Almaida, D., Le Gal, R., Fuente, A., et al. 2020, A&A, 637, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Nickerson, S., Rangwala, N., Colgan, S. W. J., et al. 2023, ApJ, 945, 26 [NASA ADS] [CrossRef] [Google Scholar]
  63. Öberg, K. I., Boogert, A. C. A., Pontoppidan, K. M., et al. 2011, ApJ, 740, 109 [Google Scholar]
  64. Ortiz-León, G. N., Loinard, L., Dzib, S. A., et al. 2018, ApJ, 865, 73 [Google Scholar]
  65. Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
  66. Oya, Y., López-Sepulcre, A., Sakai, N., et al. 2019, ApJ, 881, 112 [Google Scholar]
  67. Penteado, E. M., Walsh, C., & Cuppen, H. M. 2017, ApJ, 844, 71 [Google Scholar]
  68. Perotti, G., Christiaens, V., Henning, T., et al. 2023, Nature, 620, 516 [NASA ADS] [CrossRef] [Google Scholar]
  69. Person, W. B., & Zerbi, G. 1982, Vibrational Intensities in Infrared and Raman Spectroscopy, Studies in Physical and Theoretical Chemistry (Amsterdam: Elsevier Scientific Publishing Company) [Google Scholar]
  70. Pineau des Forêts, G., Roueff, E., Schilke, P., & Flower, D. R. 1993, MNRAS, 262, 915 [CrossRef] [Google Scholar]
  71. Pontoppidan, K. M., Schöier, F. L., van Dishoeck, E. F., & Dartois, E. 2002, A&A, 393, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Rieke, G. H., Wright, G. S., Böker, T., et al. 2015, PASP, 127, 584 [NASA ADS] [CrossRef] [Google Scholar]
  73. Rocha, W. R. M., van Dishoeck, E. F., Ressler, M. E., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202348427 [Google Scholar]
  74. Rubin, M., Altwegg, K., Balsiger, H., et al. 2019, MNRAS, 489, 594 [Google Scholar]
  75. Ruffle, D. P., Hartquist, T. W., Caselli, P., & Williams, D. A. 1999, MNRAS, 306, 691 [Google Scholar]
  76. Sakai, N., Sakai, T., Hirota, T., et al. 2014, Nature, 507, 78 [Google Scholar]
  77. Salyk, C., Pontoppidan, K. M., Blake, G. A., Najita, J. R., & Carr, J. S. 2011, ApJ, 731, 130 [Google Scholar]
  78. Savage, B. D., & Sembach, K. R. 1996, ARA&A, 34, 279 [Google Scholar]
  79. Schutte, W. A., Boogert, A. C. A., Tielens, A. G. G. M., et al. 1999, A&A, 343, 966 [NASA ADS] [Google Scholar]
  80. Sonnentrucker, P., González-Alfonso, E., & Neufeld, D. A. 2007, ApJ, 671, L37 [NASA ADS] [CrossRef] [Google Scholar]
  81. Tabone, B., Cabrit, S., Bianchi, E., et al. 2017, A&A, 607, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Tabone, B., Bettoni, G., van Dishoeck, E. F., et al. 2023, Nat. Astron., 7, 805 [NASA ADS] [CrossRef] [Google Scholar]
  83. Taquet, V., López-Sepulcre, A., Ceccarelli, C., et al. 2015, ApJ, 804, 81 [Google Scholar]
  84. Taquet, V., Codella, C., De Simone, M., et al. 2020, A&A, 637, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Terwisscha van Scheltinga, J., Ligterink, N. F. W., Boogert, A. C. A., van Dishoeck, E. F., & Linnartz, H. 2018, A&A, 611, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Tobin, J. J., Dunham, M. M., Looney, L. W., et al. 2015, ApJ, 798, 61 [Google Scholar]
  87. Tobin, J. J., Looney, L. W., Li, Z.-Y., et al. 2016, ApJ, 818, 73 [CrossRef] [Google Scholar]
  88. Tobin, J. J., Looney, L. W., Li, Z.-Y., et al. 2018, ApJ, 867, 43 [CrossRef] [Google Scholar]
  89. Tsai, S.-M., Lee, E. K. H., Powell, D., et al. 2023, Nature, 617, 483 [CrossRef] [Google Scholar]
  90. Tychoniec, Ł., Hull, C. L. H., Kristensen, L. E., et al. 2019, A&A, 632, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Tychoniec, Ł., Manara, C. F., Rosotti, G. P., et al. 2020, A&A, 640, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Tychoniec, Ł., van Dishoeck, E. F., van’t Hoff, M. L. R., et al. 2021, A&A, 655, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Urquhart, J. S., König, C., Giannetti, A., et al. 2018, MNRAS, 473, 1059 [Google Scholar]
  94. van der Tak, F. F. S., Lique, F., Faure, A., Black, J. H., & van Dishoeck, E. F. 2020, Atoms, 8, 15 [Google Scholar]
  95. van Dishoeck, E. F., Grant, S., Tabone, B., et al. 2023, Faraday Discuss., 245, 52 [NASA ADS] [CrossRef] [Google Scholar]
  96. van Gelder, M. L., Tabone, B., van Dishoeck, E. F., & Godard, B. 2021, A&A, 653, A159 [CrossRef] [EDP Sciences] [Google Scholar]
  97. van Kempen, T. A., van Dishoeck, E. F., Güsten, R., et al. 2009, A&A, 501, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. van’t Hoff, M. L. R., Harsono, D., van Gelder, M. L., et al. 2022, ApJ, 924, 5 [CrossRef] [Google Scholar]
  99. Wells, M., Pel, J. W., Glasse, A., et al. 2015, PASP, 127, 646 [NASA ADS] [CrossRef] [Google Scholar]
  100. Whitney, B. A., Wood, K., Bjorkman, J. E., & Cohen, M. 2003, ApJ, 598, 1079 [CrossRef] [Google Scholar]
  101. Wilson, T. L. 1999, Rep. Prog. Phys., 62, 143 [Google Scholar]
  102. Woods, P. M., Occhiogrosso, A., Viti, S., et al. 2015, MNRAS, 450, 1256 [Google Scholar]
  103. Wright, G. S., Wright, D., Goodson, G. B., et al. 2015, PASP, 127, 595 [NASA ADS] [CrossRef] [Google Scholar]
  104. Wright, G. S., Rieke, G. H., Glasse, A., et al. 2023, PASP, 135, 048003 [NASA ADS] [CrossRef] [Google Scholar]
  105. Yang, Y.-L., Green, J. D., Evans, Neal J., I., et al. 2018, ApJ, 860, 174 [NASA ADS] [CrossRef] [Google Scholar]
  106. Yang, Y.-L., Green, J. D., Pontoppidan, K. M., et al. 2022, ApJ, 941, L13 [NASA ADS] [CrossRef] [Google Scholar]
  107. Yıldız, U. A., Kristensen, L. E., van Dishoeck, E. F., et al. 2012, A&A, 542, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  108. Yıldız, U. A., Kristensen, L. E., van Dishoeck, E. F., et al. 2013, A&A, 556, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Yıldız, U. A., Kristensen, L. E., van Dishoeck, E. F., et al. 2015, A&A, 576, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  110. Zasowski, G., Kemper, F., Watson, D. M., et al. 2009, ApJ, 694, 459 [CrossRef] [Google Scholar]

All Tables

Table A.1

Transitions of SO2 and 34SO2 covered in the 2021.1.01578.S ALMA program.

In the text
Table D.1

Integrated line fluxes of H2 transitions.

In the text

All Figures

thumbnail Fig. 1

Spectrum (top panel) and continuum images at various wavelengths (bottom row) of IRAS 2A. In the top panel, four insets are presented: around the SO2 v3 asymmetric stretching mode (~7.35 µm), SO2 v1 symmetric stretching mode (~8.7 µm), SO2 v2 bending mode (~19 µm), and CO2 v2 bending mode (~15 µm). In the latter, the emission originates mostly from the outflow (see Fig. B.1). The 12 sub-bands of the MIRI-MRS spectrum are not stitched and show minor offsets in overlapping wavelengths (see, e.g., the inset on the SO2 v1 symmetric stretching mode). The bottom row shows, from left to right, the dust continuum around 5.3 µm, 8.1 µm, 12.5 µm, and 19.3 µm; a sqrt stretch has been used to enhance fainter features without over-saturating bright emission. The open white circle indicates the size of the aperture from which the spectrum was extracted (i.e, 1.1″, 1.5″, 2.1″, and 3.0" in diameter at 5.3 µm, 8.1 µm, 12.5 µm, and 19.3 µm, respectively), which increases as a function of wavelength with the increase in the size of the PSF. A scale bar is displayed in the bottom left of each panel, and the size of the PSF is presented as the filled white circle in the bottom right.
In the text
thumbnail Fig. 2

Subtracting the local continuum around the SO2 v3 band. Top: spectrum of IRAS 2A around 7.35 µm showing the gas-phase SO2 emission superimposed at various ice absorption bands. The red line shows the estimated local continuum based on a fourth-order polynomial fit through the red dots. Middle: spectrum of IRAS 2A with the local continuum subtracted. The 7.25 µm complex organics ice absorption feature is clearly present. A simple Gaussian fit to this ice absorption feature based on fitting the spectrum in the shaded region is shown in green. Bottom: final continuum- and ice-feature-subtracted spectrum.
In the text
thumbnail Fig. 3

Integrated intensity map of SO2 observed with MIRI-MRS in color. The image is integrated over the Q-branch of the v3 band: [7.34,7.35] µm and shown using a sqrt stretch to enhance fainter emission. The continuum around 7.35 µm is overlaid in white contours and peaks on the primary component, IRAS 2A1, extending somewhat toward the south in the direction of the scattered light. The positions of IRAS 2A1 and IRAS 2A2 are depicted with the white stars. A white scale bar is displayed in the bottom left, and the size of the PSF is presented as the filled white circle in the bottom right. The directions of the two outflows originating from IRAS 2A1 and IRAS 2A2 are indicated with the colored arrows (Tobin et al. 2015).
In the text
thumbnail Fig. 4

Continuum-subtracted spectrum (blue) overlaid with the best-fit SO2 model (orange). The orange bars in the bottom indicate the wavelength ranges that were included in the fit, and the black bars show the wavelength ranges over which σ is calculated. The P-branch lines around 7.4 µm appear to be overfitted since the 7.4 µm ice absorption could not be disentangled from the gas-phase emission.
In the text
thumbnail Fig. 5

χ2 map of the LTE slab model fit of SO2. The χ2 values are inversely normalized by the minimum χ2 and shown in color. The 1, 2, and 3σ confidence intervals are presented as the black contours. The best-fitting emitting radius, R (in au), is represented by the white contours and is calculated for each grid point by minimizing the χ2 assuming a circular emitting area of πR2. The χ2 map clearly reveals that the SO2 emission is optically thin with an excitation temperature of 92 ± 8 K.
In the text
thumbnail Fig. 6

Integrated intensity maps of the SO2 82,6−71,7 (left, Eup = 43 K), SO2 164,12−163,13 (middle, Eup = 164 K), and 34SO2 174,14−173,15 (right, Eup = 178 K) transitions in color. The images are integrated over [−2,2] km s−1 with respect to the Visr of 6.7 km s−1. The white vertical bar in the colorbar on top of each image indicates the 3σ threshold. The 0.875 mm continuum is overlaid as black contours. The main continuum peak is associated with IRAS 2A1 and the secondary peak toward the south with IRAS 2A2. The directions of the two outflows originating from IRAS 2A1 and IRAS 2A2 are indicated with the colored arrows in the middle panel (Tobin et al. 2015). The size of the beam is shown in the bottom right, and in the bottom left a scale bar is displayed.
In the text
thumbnail Fig. A.1

Continuum-subtracted ALMA spectra (blue) for the SO2 82,6 − 71,7 (left, Eup = 43 K), SO2 164,12 − 163,13 (middle, Eup = 164 K), and 34SO2 174,14 − 173,15 (right, Eup = 178 K) transitions. The best-fit LTE slab models are overlaid in orange. All other transitions (see Table A.1) of SO2 and 34SO2 are either blended with other molecular species or not detected.
In the text
thumbnail Fig. A.2

χ2 map for SO2 derived from pure rotational lines in the ALMA data. The χ2 values are inversely normalized by the minimum χ2 and shown in color. The 1, 2, and 3σ confidence intervals are presented as the black contours. The best-fitting emitting radius, R (in au), is represented by the white contours and is calculated for each grid point by minimizing the χ2 assuming a circular emitting area of πR2. The χ2 map indicates that the SO2 emission has an excitation temperature of 104 ± 5 K and is marginally optically thick (τ ~ 0.1) with an emitting area of ~ 85 au in radius.
In the text
thumbnail Fig. A.3

Integrated intensity maps of the HDO 33,1 – 42,2 (Eup = 335 K), CH3OH 161,15 − 152,14 (middle, Eup = 331 K), and CH3OCHO 2710,17 − 2610,16 (right, Eup = 190 K) transitions in color. The images are integrated over [-2,2] km s−1 with respect to the V1sr of 6.7 km s−1. The white vertical bar in the colorbar on top of each image indicates the 3σ threshold. The 0.875 mm continuum is overlaid as black contours. The main continuum peak is associated with IRAS2A1 and the secondary peak toward the south with IRAS2A2. The directions of the two outflows originating from IRAS2A1 and IRAS2A2 are indicated with the colored arrows in the middle panel (Tobin et al. 2015). The size of the beam is shown in the bottom right, and in the bottom left a scale bar is displayed.
In the text
thumbnail Fig. B.1

Integrated intensity map of the CO2 v2 = 1 – 0 Q-branch (top left), H2O v2 = 1 – 0 42,3 – 53,2 (top right), H2 0-0 S(1) (bottom left), and H2 0-0 S(7) (bottom right) observed with MIRI-MRS in color. The images are integrated over [14.9,15.0] µm for CO2, [7.145-7.15] µm for H2O, and [−0.01,0.01] µm with respect to the transitions of H2. The extent of the continuum around the respective wavelengths is overlaid as white contours. A white scale bar is displayed in the bottom left of each panel, and the size of the PSF is presented as the filled white circle in the bottom right. The directions of the two outflows originating from IRAS2A1 and IRAS2A2 are indicated with the colored arrows in the top-left panel (Tobin et al. 2015). The H2O emission is peaking on-source on the same scales as SO2, whereas the CO2 and H2 0-0 S(1) emissions are clearly peaking in the outflow toward the southwest. The H2 0-0 S(7) line peaks mostly on-source but also has a component in the southwestern outflow.
In the text
thumbnail Fig. B.2

Spectrum of IRAS2A in blue centered around the v3 band of SO2 as observed by JWST/MIRI-MRS. The local continuum fit is shown in red and the best-fit LTE slab model in orange at a +5 mJy offset. In green, the SO2-subtracted data are presented, revealing the 7.4 µm ice absorption feature that was hidden by the P-branch of the SO2 v3 band. The Q-branch is slightly overfitted, resulting in a subtraction residual. The ice absorption bands are further analyzed by Rocha et al. (2024).
In the text
thumbnail Fig. B.3

JWST/MIRI-MRS continuum-subtracted spectrum (blue) centered on the v2 band of SO2 around 19 µm. No clear emission or absorption features of SO2 are detected. Overlaid are LTE slab models obtained using the best-fit parameters derived from the v3 band around 7.35 µm (red) and the pure rotational lines in the ALMA data (green). The MIRI slab model is scaled down by a factor of 10−3 for clarity. Both models are offset with respect to the data and are corrected for an extinction of AV = 55 mag (Rocha et al. 2024) using a modified version of the McClure (2009) extinction law (see Appendix C).
In the text
thumbnail Fig. B.4

JWST/MIRI-MRS continuum-subtracted spectrum (blue) centered on the v1 band of SO2 around 8.5 µm. The two overlapping MIRI-MRS sub-bands (channel 2A and 2B) have been stitched for clarity. No clear emission or absorption features of SO2 are detected. Overlaid are slab models obtained using the best-fit parameters derived from the v3 band around 7.35 µm (red) and the pure rotational lines in the ALMA data (green). Both models are offset with respect to the data and are corrected for an extinction of AV = 55 mag (Rocha et al. 2024) using a modified version of the McClure (2009) extinction law (see Appendix C).
In the text
thumbnail Fig. C.1

Determining the extinction due to ice and silicate absorption. Top: Observed MIRI-MRS spectrum of IRAS2A (blue) with the global continuum estimate (red) overplotted. The continuum is based on a third-order polynomial fit to emission- and absorption-free wavelength ranges. The positions of the H2 v = 0 rotational transitions are indicated with the vertical dashed gray lines. Bottom: Differential extinction in units of optical depth (blue) of the absorption features as a function of wavelength derived from the global continuum estimate (Eq. (C.2)). Overplotted is the absolute extinction (orange) computed using Eq. (C.3); see the main text for more details. The total extinction (green) is computed from the sum of the two (Eq. (C.1)).
In the text
thumbnail Fig. C.2

McClure (2009) extinction law for AV = 1 mag (assuming AK = AV/7.75 mag) in blue with the best-fit power-law model to the absorption-free regions (dots) overplotted in red. Both the extinction law and the best-fit model are plotted in units of optical depth for AV = 1 mag but are directly proportional to AV.
In the text
thumbnail Fig. D.1

Observed MIRI-MRS spectrum (blue) centered around H2 v = 0 pure rotational lines from the S(7) line in the top-left panel to the S(0) line in the bottom-middle panel. The best-fit Gaussian model is presented in orange in each panel. All presented lines are considered detected except for the S(0) line since the flux is similar to that of several strong residual fringes located in the vicinity of the S(0) line.
In the text
thumbnail Fig. D.2

Rotational diagram of H2 derived from the MIRI-MRS data. The black data points indicate the measured fluxes that are corrected for extinction (see Table. D.l). The best-fit two-component model is presented as the solid green line, and the two individual components are shown as the dashed blue (warm) and orange (hot) lines. The best-fit parameters are displayed in the top right.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.