| Issue |
A&A
Volume 676, August 2023
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 26 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202345858 | |
| Published online | 08 August 2023 | |
The role of grain size in active galactic nuclei torus dust models
1
Instituto de Radioastronomía y Astrofísica (IRyA), Universidad Nacional Autónoma de México, Antigua Carretera a Pátzcuaro #8701, Ex-Hda. San José de la Huerta, 58431 Morelia, Michoacán, Mexico
e-mail: o.gonzalez@irya.unam.mx
2
Instituto de Astrofísica de Canarias, Calle Vía Láctea, s/n, 38205 La Laguna, Tenerife, Spain
3
Departamento de Astrofísica, Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
4
Centro de Astrobiología (CAB), CSIC-INTA, Camino Bajo del Castillo s/n, 28692 Villanueva de la Cañada, Madrid, Spain
5
School of Physics & Astronomy, University of Southampton, Southampton SO17 1BJ, UK
6
Astrophysics, University of Oxford, DWB, Keble Road, Oxford OX1 3RH, UK
7
Observatorio de Madrid, OAN-IGN, Alfonso XII, 3, 28014 Madrid, Spain
8
Astronomical Observatory, Volgina 7, 11060 Belgrade, Serbia
9
Sterrenkundig Observatorium, Universiteit Gent, Krijgslaan 281-S9, Gent 9000, Belgium
Received:
5
January
2023
Accepted:
8
May
2023
Context. Active galactic nuclei (AGN) are surrounded by dust within the central parsecs. The dusty circumnuclear structures, referred to as the torus, are mainly heated by radiation from the AGN and emitted at infrared wavelengths, producing the emergent dust continuum and silicate features. Fits to the infrared spectra from the nuclear regions of AGN can place constraints on the dust properties, distribution, and geometry by comparison with models. However, none of the currently available models fully describe the observations of AGN currently available.
Aims. Among the aspects least explored, here we focus on the role of dust grain size. We offer the community a new spectral energy distribution (SED) library which is based on the two-phase torus model developed before with the inclusion of the grain size as a model parameter, parameterized by the maximum grain size Psize or equivalently the mass-weighted average grain size ⟨P⟩.
Methods. We created 691 200 SEDs using the SKIRT code, where the maximum grain size can vary within the range Psize = 0.01 − 10.0 μm (⟨P⟩ = 0.007 − 3.41 μm). We fit this new library and several existing libraries to a sample of 68 nearby and luminous AGN with Spitzer/IRS spectra dominated by AGN-heated dust.
Results. We find that the GoMar23 model can adequately reproduce up to ∼85–88% of the spectra. The dust grain size parameter significantly improves the final fit in up to 90% of these spectra. Statistical tests indicate that the grain size is the third most important parameter in the fitting procedure (after the size and half opening angle of the torus). The requirement of a foreground extinction by our model is lower compared to purely clumpy models. We find that ∼41% of our sample requires that the maximum dust grain size is as large as Psize ∼ 10 μm (⟨P⟩∼3.41 μm). Nonetheless, we also remark that disk+wind and clumpy torus models are still required to reproduce the spectra of a nonnegligible fraction of objects, suggesting the need for several dust geometries to explain the infrared continuum of AGN.
Conclusions. This work provides tentative evidence for dust grain growth in the proximity of the AGN.
Key words: galaxies: active / galaxies: nuclei / galaxies: Seyfert / infrared: galaxies
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Active galactic nuclei (AGN) are powered by supermassive black holes (SMBHs) at the center of galaxies with accretion disks emitting ∼1040 − 47 erg s−1 from a region as small as the Solar System. AGN were originally classified based on their spectroscopic signatures, ranging from type-1 AGN, showing both broad and narrow emission lines, to type-2 AGN, showing only narrow lines. Antonucci & Miller (1985) suggested that the continuum and broad-line emission regions are located inside an optically and geometrically thick “disk”, which was later on referred as the torus (Krolik & Begelman 1986). Continuum and broad-line photons are scattered into the line of sight by free electrons above and below the torus. This orientation bias is what makes the AGN depend so strongly on the orientation that our current classification schemes are dominated by random pointing directions instead of more interesting physical properties (Urry & Padovani 1995).
However, the torus does not only act as a bridge for unifying the AGN phenomenon, but it is also expected to explain the majority of the infrared dust emission of AGN (Ramos Almeida & Ricci 2017). Indeed, a significant proportion of the optical/UV photons produced by the AGN accretion disk are reprocessed by dust located beyond the sublimation radius and reemitted in the infrared. However, one of the challenges faced by such unified theories is to match the observed infrared emission of AGN to that predicted for such a dust structure (Pier & Krolik 1992; Granato & Danese 1994; Efstathiou & Rowan-Robinson 1995).
Until the arrival of extremely large single-aperture telescopes (e.g., the Extreme Large Telescope), the dust emission morphology will not be unambiguously resolved in the near- or mid-infrared to be compared with models (Nikutta et al. 2021a,b), except for the brightest AGN with interferometric observations with VLTI/MIDI (Hönig et al. 2012; Tristram et al. 2014; López-Gonzaga et al. 2016; Hönig & Kishimoto 2017; Leftley et al. 2018) and MATISSE (Isbell et al. 2022; Gámez Rosas et al. 2022). Although unresolved point-like (< 1–2 pc) emission at 800 μm imaged by ALMA in AGN can be contaminated by a contribution from synchrotron or free-free emission (Pasetto et al. 2019), we rely on dust continuum-dominated submillimeter images for constraining the torus properties (García-Burillo et al. 2021). However, submillimeter observations are more sensitive to colder dust, which is located further away from the accretion disk, as compared to mid-infrared ones. This explains the large and geometrically thin disks with radial sizes up to 50 pc found with ALMA (García-Burillo et al. 2021), while the majority of the mid-infrared emission remains confined to the central parsecs (Alonso-Herrero et al. 2021, and references therein) except for a few cases (Bock et al. 2000; Radomski et al. 2003; Packham et al. 2005; Asmus et al. 2016; Asmus 2019).
In this work, we fit the infrared spectral energy distribution (SED) of AGN to constrain the parameters of the torus models. For this purpose, we use the so-called geometrical-phenomenological models (Ramos Almeida & Ricci 2017, for a review). According to Efstathiou & Rowan-Robinson (1995), a successful AGN torus model must fulfill the following three minimum requirements, dictated by the shape of the infrared dust continuum (see also the updated description of this shape given by Hao et al. 2005): (1) the predicted spectrum should be quite broad in terms of wavelength range, at least for face-on views, and peak in the mid infrared; and (2) the model should also predict (moderate) absorption features at 10 μm for edge-on views, and very weak (or featureless) spectra for face-on views. Indeed, early observations showed that silicate emission features were weak in AGN, which was unexpected if the dust is heated by the central AGN (Roche et al. 1991; Laor & Draine 1993). Furthermore, for those objects in which the silicate dust is seen in emission, it often shows an anomalous spectral profile where the peak is shifted to longer wavelengths (Sturm et al. 2005; Mason et al. 2013) and with a broad profile (Li et al. 2008; Smith et al. 2010); and (3) the infrared SEDs of some type-1 Seyferts and quasars (QSOs) show a ∼3 μm bump (Edelson & Malkan 1986) that cannot be easily reproduced (Mor et al. 2009; García-Bernete et al. 2017). We now know that this feature can be seen up to 7 − 8 μm for most QSOs and bright AGN (García-Bernete et al. 2019; Martínez-Paredes et al. 2020, 2021).
Several radiative transfer models in the past couple of decades have focused on the study of infrared emission and absorption from this putative dusty torus at several viewing angles, including pioneering works such as those by Pier & Krolik (1992) and Rowan-Robinson (1995). Initially, the debate was focused on the distribution of the dust. Torus models with a homogeneous dust distribution (smooth torus), predicted strong 9.7 μm silicate features, both in absorption and in emission. However, this does not match the weak absorption features generally observed for type-2 AGN or the almost absent features for type-1 AGN (Roche et al. 1991; Laor & Draine 1993; Nenkova et al. 2002; Nikutta et al. 2009). The clumpy torus model can naturally explain the weakness of the silicate feature but cannot produce sufficient near-infrared emission from hot dust to explain the near-infrared excess of some AGN (Mor et al. 2009; Ramos Almeida et al. 2009; García-Bernete et al. 2019, 2022b). This near-infrared excess might be accounted for when including a two-phase dust distribution (i.e., smooth+clumpy, Stalevski et al. 2012, 2016). However, this two-phase model has only moderate success at explaining the overall observed infrared spectral shape of AGN (failing at describing the silicate features and the mid-infrared slopes of bright AGN, González-Martín et al. 2019b).
Geometry is indeed key in these models. The near-infrared excess could also be reproduced with a disk (i.e., torus-disk equatorial dust component) and a wind (conical-polar dust component) that produces the majority of the mid-infrared emission (Hönig & Kishimoto 2017); although, other aspects such as chemistry might play a significant role (García-Bernete et al. 2022b). The AGN in the Circinus galaxy is a clear example of polar-wind dust component present from scales going from the central parsecs up to hundreds of parsecs (Tristram et al. 2014; Packham et al. 2005; Roche et al. 2006; Stalevski et al. 2017, 2019; Isbell et al. 2022). However, although successful at explaining the brightest AGN (Martínez-Paredes et al. 2021), the disk+wind model has only moderate success at describing low- and intermediate-luminosity (type-2) AGN (González-Martín et al. 2019b; García-Bernete et al. 2022b) which show striking differences in the mid-infrared spectral shape compared to luminous AGN (González-Martín et al. 2015, 2017). The reason is that this wind model fails to reproduce moderately deep absorption silicate features observed in some type-2 and low-luminosity AGN due to the enhancement of graphite grains for the wind.
One of the least explored aspects of these torus models is the grain size distribution. Grain size should have a strong impact on the resulting infrared spectral shape. In particular, the size of graphite grains could contribute to the enhancement of the near-infrared continuum because grain temperature increases with decreasing dust grain size. In particular, graphite grains with sizes of 0.005 μm have their emission peak at around 1 μm, while grain sizes of 0.25 μm more efficiently contribute to the 3–5 μm flux (see Fig. 9 by Laor & Draine 1993). At the same time, small grains are preferentially destroyed by the AGN radiation and shocks, while large grains are more resilient (Schartmann et al. 2008; Almeyda et al. 2017). Moreover, the silicate feature is broader with a lower strength if the grain size is micron-sized, up to its disappearance when the grain size exceeds 10 μm (Laor & Draine 1993). Indeed, micron-sized grains have also been suggested to explain the anomalous silicate feature observed in the low-luminosity AGN in M81 (Smith et al. 2010). Lyu et al. (2014) also suggested that the low AV/τ9.7μm ratio found in their analysis could be due to the predominance of large grains in the AGN torus (see also Shao et al. 2017), while Xie et al. (2017) found that micron-sized particles can help to reproduce up to 90% of the type-1 AGN explored in their analysis (see also Smith et al. 2010); although, other aspects such as geometry (e.g., wind, disk, or torus) were not included in their analysis. Near-infrared interferometry suggests, throughout the normalization of the relation between inner radius and luminosity, an emission region that is more compact than expected, which might be explained by the presence of large graphite dust grains (Kishimoto et al. 2007, 2011; GRAVITY Collaboration 2020). Lyu & Rieke (2021) also found that the hot dust reverberation signals for NGC 4151 come from two distinct dust populations at separate radii, consistent with the expected properties of sublimating graphite and silicate dust grains.
Most of the current geometrical models assume the distribution of dust grains reported for the interstellar medium (ISM) in our Galaxy (Mathis et al. 1977; Laor & Draine 1993; Weingartner & Draine 2001; Li & Draine 2001). The clumpy (Nenkova et al. 2008b; Hönig & Kishimoto 2010), smooth (Fritz et al. 2006), and two-phase (Stalevski et al. 2016) torus models assume a maximum grain size of 0.25 μm, while the minimum grain size is in the range between 0.005–0.025 μm. Hönig & Kishimoto (2010) investigated an alternative grain size distribution called “ISM large grains” containing grains between 0.1–1 μm. In the ISM large grain configuration, the disk-torus area of hot dust is smaller than in the standard ISM dust grain distribution (due to a steeper temperature profile), resulting in a shift of the mid-infrared emission peak toward longer wavelengths (see Fig. 5 in Hönig & Kishimoto 2010). For the disk+wind geometry, the hot dust is assumed to be primarily composed by large graphite grains, which is theoretically and observationally motivated (Kishimoto et al. 2007; Hönig & Kishimoto 2017; Hönig 2019) where these grains produce the near-infrared excess due to the high temperatures they can survive (García-González et al. 2017). Indeed, this model is better at reproducing spectra below ∼7 μm when compared with observations (see also González-Martín et al. 2019b; Martínez-Paredes et al. 2021; García-Bernete et al. 2022b).
Although some works have investigated the role of grain size for a given geometrical model (e.g., Hönig & Kishimoto 2010) or it has been used to explain a particular spectrum (e.g., N- and Q-band spectra of NGC 1068, Victoria-Ceballos et al. 2022), maximum grain size has not been included as a free parameter of the model. This manuscript presents a new SED library that includes variations of the maximum grain size into a geometrical model. This paper subsequently shows that the inclusion of this parameter significantly improves the adequacy of the model to AGN mid-infrared spectra observed with Spitzer. The paper is organized as follows: Sect. 2 shows the AGN sample and data used to confront currently available models (described in Sect. 3) and our new model (described in Sect. 4) with mid-infrared spectra. The methodology applied to the data includes an analysis of the spectral shape compared with models and spectral fits (see Sect. 5). Results are included in Sect. 6 and discussed in Sect. 7. Finally, a summary of our main findings is included in Sect. 8.
2. Sample and data
We compile a sample of AGN with Spitzer/IRS spectra representative of a variety of silicate features and continuum shapes. Our parent AGN samples are: (1) 53 local AGN with available NuSTAR spectra reported by Esparza-Arredondo et al. (2020), (2) 110 nearby AGN drawn from the 105-months Swift/BAT survey (Oh et al. 2018) reported by González-Martín et al. (2019b), and (3) the 19 QSOs (one is excluded due to the lack of Spitzer spectrum) reported by Martínez-Paredes et al. (2017). All of them have been chosen due to the availability of Spitzer/IRS spectra needed for this analysis. We note that the first two parent samples are restricted to the nearby Universe to mitigate the low spatial resolution of Spitzer/IRS spectra. The sample reported by Martínez-Paredes et al. (2017) is not restricted to the nearby universe but they ensure the AGN dominates the mid-infrared Spitzer/IRS spectrum from the comparison with ground-based N-band spectra. We downloaded all the spectra from Combined Atlas of Sources with Spitzer IRS Spectra CASSIS1. Only objects with full coverage 5–35 μm spectra and good signal-to-noise ratio (S/N) > 20) were selected.
To ensure that the mid-infrared spectrum is dominated by AGN-heated dust, we impose the following criteria. We first exclude Spitzer spectra marked as extended by CASSIS because these sources are expected to have a significant contribution from circumnuclear emission. We then remove objects with strong PAH features (i.e., EW(PAH) > 0.233 μm) and very steep slopes above 20 μm (i.e., slopes between 20 and 30 μm such that log(νLν(20 μm)/νLν(30 μm)) > −0.24), which excludes sources containing significant circumnuclear starbursts (González-Martín et al. 2015). Finally, we also impose that the AGN dust component accounts at least for 80% of the flux in the 5–30 μm wavelength range inferred from spectral decomposition. Note that spectral decomposition was already done for the two nearby AGN parent samples reported above, that is fitting mid-infrared spectra with ISM, stellar, and AGN-heated dust templates (see González-Martín et al. 2019b, and references there in). However, we repeat the analysis here for homogeneity. In the QSO sample, the spectra are AGN dominated because they show the same flux level and spectral shape as ground-based spectra (see Martínez-Paredes et al. 2017).
With all these restrictions we selected 68 AGN with available Spitzer/IRS spectra, good S/N and dominated by the AGN-heated dust within the Spitzer/IRS aperture (3.6–7 arcsec). Table C.1 includes the redshift, AGN classification, X-ray 2–10 keV intrinsic luminosity, and black-hole masses for our sample. Figure 1 shows the mid-infrared spectra (type-1 and type-2 AGN in black and gray, respectively). A residual contamination of the spectra from star-forming processes is still visible, although the impact in the resulting spectral fit should be negligible (see González-Martín et al. 2019a). Among them, 43 are type-1 and 25 are type-2 AGN according to the NASA extragalactic database (NED). The sample includes low- (e.g., M 106), intermediate- (e.g., IC 5063), and high-luminosity AGN (e.g., PG 0804+761). We also show in Fig. 1 X-ray luminosities versus redshifts in our sample. No particular bias is observed when type-1 and type-2 AGN are compared. However, it is obviously biased toward high-luminosity sources and type-1 AGN because these are the objects less affected by circumnuclear star formation within the Spitzer/IRS aperture. In this sense, our results are more representative of relatively luminous nearby AGN rather than low-luminosity AGN. Indeed, only two objects show X-ray luminosities below LX < 1042 erg s−1. JWST observations with higher angular resolution would be required to explore AGN with lower luminosities.
 |
Fig. 1. Spectra of our sample of 68 AGN normalized to the flux at 14 μm. Type-1 and type-2 AGN are shown in black and gray, respectively. Vertical dot-dashed lines indicate the locus of the wavelengths chosen to compute the spectral slopes (see text). The bottom-right inset shows the distribution of X-ray luminosities versus redshift in our sample. |
3. Previous SED models
We aim to provide a new SED library of models that better reproduce the mid-infrared continuum emission of AGN. Thus a proper comparison with the results presented with previous SED libraries is mandatory. In the following, we provide a brief description of each model with particular emphasis on the dust grain size used for each model. Full description of the models can be found in the references below and in several recent works using these models (González-Martín et al. 2019b; Martínez-Paredes et al. 2021; García-Bernete et al. 2022b).
– Smooth torus model by Fritz et al. (2006, hereinafter smooth Fritz06 torus models): They use a simple toroidal geometry, consisting of a flared disk with the inner radius corresponding to the sublimation distance. The silicate and graphite grains have radii in the range of 0.025–0.25 and 0.005–0.25 μm, respectively.
– Clumpy torus model by Nenkova et al. (2008a,b, hereinafter clumpy Nenkova08 torus models): They used a formalism that accounts for the concentration of dust in clouds, forming a torus-like structure. The silicate and graphite grains have both radii in the range of 0.005–0.25 μm.
– Clumpy torus model by Hönig & Kishimoto (2010; see also Hönig et al. 2006, 2010, hereinafter clumpy Hoenig10 torus models): Radiative transfer model of three-dimensional clumpy dust tori using optically thick dust clouds and a low torus volume filling factor. The size of silicate and graphite grain is in the range of 0.025–0.25 μm.
– Two-phase torus model by Stalevski et al. (2016, hereinafter two-phase Stalev16 torus models): They model the dust in a torus geometry with a two-phase medium, consisting of high-density clumps embedded in a smooth dusty component of low density. The silicate and graphite grains have both radii in the range of 0.005–0.25 μm.
– Clumpy disk and outflow model by Hönig & Kishimoto (2017, hereinafter clumpy disk+wind Hoenig17 models): The model consists of a clumpy disk plus a polar outflow. This model uses a sublimation model that accounts for different sublimation conditions, with grain sizes of 0.025–0.25 μm for silicate, and 0.075–1.0 μm for graphite.
Note that we also explore the clumpy disk model by Hönig & Kishimoto (2017; i.e., removing the wind component in the disk+wind model), the anisotropically illuminated version of the clumpy torus model presented by García-González et al. (2017), and the two-phase torus model presented by Siebenmorgen et al. (2015). However, after performing spectral fitting to our sample, these models were not able to fully describe any of our objects (and provide acceptable fits for less than 10% of the sample). Thus, we exclude them from our analysis for simplicity.
4. New SED model GoMar23
We use the radiative transfer code SKIRT2 (Baes et al. 2003; Baes & Camps 2015; Camps & Baes 2015, 2020) in its version 9 to produce synthetic spectra with different dust and geometrical properties. We divide this section into the details of the overall setup of the simulations in common with the two-phase model created in Stalevski et al. (2016; Sect. 4.1), the particularities of the grain size distribution (Sect. 4.2), and a summary of the grid of parameter values for GoMar23 model.
4.1. Setup of the simulations
SKIRT has already been used by Stalevski et al. (2016) to produce a two-phase torus model (Stalev16, see Sect. 3). We set our initial geometry and parameter space to that of Stalev16 model (see Fig. 1 by Stalevski et al. 2012). This allows us to set a benchmark for the model because at least we should be able to provide good fits for the same objects that are already reproduced by the Stalev16 model. Furthermore, the two-phase medium (clumps within a smooth distribution) seems to be the most plausible scenario for the dust within the torus (Wada 2015). Stalev16 model parameters are the viewing angle toward the observer, i, the ratio between the outer and the inner radius of the torus, Y = Rout/Rdust (with the inner radius anchored to the dust sublimation radius Rdust), the half opening angle of the torus, σ, the indices that set dust density gradient with the radial, p, and polar, q, distribution of dust, and the 9.7 μm average edge-on optical depth, τ9.7 μm. Figure 2 shows a schematic view of the model.
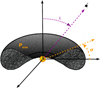 |
Fig. 2. Schematic view of GoMar23 model (see text). |
The geometry of the model consists of a flared disk (TORUSGEOMETRY within SKIRT). The inner radius is fixed to the dust sublimation radius Rdust = 0.14 pc, which is obtained from Barvainis (1987):
for an AGN with a bolometric luminosity of Lbol = 1011 L⊙ and a sublimation temperature Tsub to 1250 K. Note that, unlike Stalevski et al. (2016) we assume that the accretion disk emits isotropically.
To fully define the torus geometry, two parameters are required: the half-opening angle, σ, and the outer radius of the torus, Rout. Following several previous prescriptions (e.g., Fritz et al. 2006; Nenkova et al. 2008b; Stalevski et al. 2016), we report the values of the outer radius of the torus as a multiplier of the inner radius, that is Y = Rout/Rin. In the Stalev16 model, this parameter takes only three values at Y = [10, 20, 30]. However, we find significant improvements by evaluating this parameter in a wider range and with a slightly finer step. In fact, this is the parameter with the lower number of values in Stalev16 model. In particular, we choose the following set of values: Y = [2, 5, 10, 15, 20, 25, 30, 35, 40]. For the half opening angle, we use the same values as in Stalev16 model, that is σ = 10 − 80° with Δσ = 10°.
The model is indeed two-phase (i.e., smooth+clumpy) thanks to the “decorator” module CLUMPYGEOME TRYDECORATOR within SKIRT that creates a clumpy-distributed medium from a continuously distributed one. The geometry used is called flared disk, which consists of a sphere where two cones are removed from the polar direction. Therefore, the width of the torus grows with the radius, keeping the angular width constant. Following the parameters used by Stalevski et al. (2016), the percentage of the mass locked up in clumps is set to 25%, the radius of each cloud is linked to the outer radius of the system as Rcl = Rout/12.5, and the total number of clumps is set to 3000. Within the flared disk geometry, the dust is distributed following a variable radial power law and polar exponential density distribution of dust:
where r and θ are the coordinates in polar coordinate system. The parameters associated with the radial and polar dust-density gradients are called p and q, respectively. Following the work by Stalevski et al. (2016), we use the same range for both p and q parameters including 0–1.5 (four values with Δp = Δq = 0.5). The model also requires the edge-on optical depth at 9.7 μm, defined at the equator of the system, τ9.7. The range explored by Stalevski et al. (2016) for this parameter is τ9.7 = 3 − 11 with Δτ9.7 = 2. We set our model to the same range but extend the grid to τ9.7 = 13. Note that in our library of models, τ9.7 is defined along the x-axis of the system.
4.2. Grain size distribution
Particles are assumed to obey a power-law distribution of sizes of the form (Mathis et al. 1977):
where P is the dust particle size, “a” is the slope of the particle dust distribution (assumed to be a = 3.5), nH is the number density of H nuclei, and the constant A gives the normalization with respect to hydrogen abundance for each dust component (in units of particles per H atom per micron). These constants would only affect the normalization with respect to the hydrogen abundance, and not the SED scaling/normalization (which is dominated by the mass of dust). We use the normalization factors assumed in the two-phase torus model presented by Stalevski et al. (2016) is log(A) = − 24.82 for silicate grains. Also following the prescription given by Stalevski et al. (2016), we choose a percentage of 51% for silicate grains and 49% for graphite grains. Note that we also ran some tests using a percentage of silicate grains in the range used in other works (i.e., 47–53%, see Mathis et al. 1977; Draine & Lee 1984; Weingartner & Draine 2001), finding no significant impact on the resulting SEDs.
This new SED library explores the role of dust grain size. The grain size distribution (see Eq. (3)) also requires the minimum and maximum grain size for each population. Note that the effect of grain size can be investigated in various ways: changing the maximum/minimum of the grain size distribution, the slope of the grain size distribution, or combining these possibilities. Victoria-Ceballos et al. (2022) recently explored the effect of both the minimum and maximum grain sizes in the shape of the mid-infrared spectra of NGC 1068, finding no significant impact on the resulting SED for the minimum grain size, while changing the maximum grain size turned out to strongly affect the SEDs. Furthermore, the fluctuations induced by absorption of a single X-ray photon eliminate grains with sizes Psize < 0.005 μm up to large distances from the center (within tens of parsecs Laor & Draine 1993). Voit (1991) showed that grains with sizes below 0.001 μm are easily destroyed by the radiation field of the AGN while grains with sizes in the range of 0.001 − 0.005 μm have little effect on the total grain emission. Thus, we decided to focus on the maximum grain size, hereinafter Psize, while the minimum grain size is fixed to 0.005 μm, consistent with the model presented by Stalevski et al. (2016). For that purpose, we explore SEDs with maximum dust grain sizes in the range Psize = 0.01 − 10 μm with Δlog(Psize)≃0.3 (i.e., ten values). We set the maximum grain size to 10 μm because silicate features completely disappear when the grain size exceeds that value (Laor & Draine 1993). Finally, we remark that we choose to focus on the maximum grain size, but keep in mind that flatter grain size distributions compared to the usual a = 3.5 have the same impact, that is to say it changes the small to large grain abundance (Maiolino et al. 2001).
Another way to report the grain size is throughout the weighted average grain size ⟨P⟩ (Mishra & Li 2017):
where w(P) is the weight, which takes the form of Pβ with β = 3 for the mass-weighted average. This equation is integrated between the minimum grain size Pmin = 0.005 μm and the maximum grain size in the range Psize = 0.01 − 10 μm. This results in a mass-weighted average grain size in the range ⟨P⟩ = 0.007 − 3.41 μm. We use both definitions of Psize and ⟨P⟩ throughout the text.
4.3. Overall grid
Each SKIRT simulation can provide as many SEDs with different viewing angles as requested. Given the symmetry of the system, we requested viewing angles in the range i = 0 − 90° with Δi = 10°, where the viewing angle is measured from the pole toward the equator of the system (see Fig. 2). The final model has seven parameters (eight when including the flux-normalization of the final fit). A summary of the parameters involved in the model is included in Table 1. For comparison purposes, we also include the original parameter space of Stalev16 model.
Parameter space for the new GoMar23 model.
Each simulation was computed using 106 photon packages (consistent with other torus simulations, see Stalevski et al. 2017) and a spatial hierarchical octree grid with a variable size of the cell named TREESPATIALGRID. We initially set the number of random density samples for determining spatial cell mass to 100. The cells are then recursively partitioned into subcells until the optical depth for each of them is lower than one or the simulation reaches the maximum number of cell subdivisions, 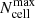 , that we set to
, that we set to 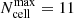 . Note that this maximum number, when reached, already requires at least 30GB of RAM, depending on the geometrical configuration of the simulation. Thus, further subdivisions are not allowed in order to limit computational times due to the maximum RAM available for these simulations. However, we run a test to quantify if the resulting SEDs depend on this maximum number of subdivisions. In particular, we simulated 7290 SEDs using the minimum, medium, and maximum values for each parameter with
. Note that this maximum number, when reached, already requires at least 30GB of RAM, depending on the geometrical configuration of the simulation. Thus, further subdivisions are not allowed in order to limit computational times due to the maximum RAM available for these simulations. However, we run a test to quantify if the resulting SEDs depend on this maximum number of subdivisions. In particular, we simulated 7290 SEDs using the minimum, medium, and maximum values for each parameter with 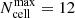 . The difference between these SEDs and those using
. The difference between these SEDs and those using 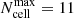 is always lower than 5%. This ensures that
is always lower than 5%. This ensures that 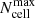 does not have a strong impact on the resulting SEDs because the cells are optically thin for all of our simulations.
does not have a strong impact on the resulting SEDs because the cells are optically thin for all of our simulations.
All together we produce 691 200 SEDs in the range of 0.001–5000 μm with all the parameters evaluated at least at four grid points. We use a nested logarithmic wavelength grid, with 81 steps in the range 0.001–5000 μm and 101 additional steps in the range 1–100 μm. This SED library has among the largest number of SEDs performed; below the ∼1.2 million SEDs produced for the clumpy torus model by Nenkova et al. (2008b) but well above the ∼130 thousand SEDs produced for the disk+wind model by Hönig & Kishimoto (2017), which is the second largest library. The computing time for this grid was around 200 days on a cluster3 able to produce 16-20 SEDs per hour thanks to the parallel processing capabilities. Following our own nomenclature in previous works (González-Martín et al. 2019a,b; Martínez-Paredes et al. 2021; García-Bernete et al. 2022b), we name this model according to the initials of the first author of this manuscript as GoMar23 model.
5. Methodology
5.1. Spectral shape characterization
The continuum shape of the mid-infrared spectra of many AGN is distinctive with a monotonic increase in flux density with wavelength and reaching a maximum at ∼18 − 20 μm (see spectral slopes reported by García-González et al. 2017) and a flattening at longer wavelengths González-Martín et al. (2019b; see Fig. 1). Furthermore, silicate features have been reported in absorption as well as in emission (e.g., Roche et al. 1991; Shi et al. 2006; Alonso-Herrero et al. 2016). Two silicate features can be seen in the Spitzer/IRS spectral window around 10 and 18 μm. The 10 μm feature is easier to characterize because it is more prominent than the 18 μm feature in our sample. Although the vast majority of type-2 (type-1) AGN show silicate features in absorption (emission), the opposite behavior is not uncommon (see Fig. 1 and also Feltre et al. 2012).
On top of the AGN dust continuum, observed AGN spectra also show emission lines associated with the ionization gas in the nuclei (e.g., [OIV]) or to some level of circumnuclear star formation (e.g., [NeII]). These lines must be carefully removed to properly measure the AGN infrared continuum. We fit each spectrum to a 6th-order polynomial and then smooth it to remove the effect of emission lines in the fitted continuum. We then divided the original spectrum by this fitted continuum to produce a clean spectrum of emission lines. Where prominent lines are detected in the latter, we replace the spectral window with the smooth polynomial fit to the continuum.
In order to characterize the spectral shape of the objects in our sample, we define three spectral slopes (denoted with α) within the Spitzer/IRS wavelength range. These slopes are computed as:
where λ1 and λ2 are the two wavelengths where the slope is computed and λ1 < λ2. Negative (positive) values are found when the flux increases (decreases) with wavelength. These three slopes are called α5.5 − 7.5 μm, α7.5 − 14 μm, and α25 − 30 μm and correspond to [λ1, λ2] equal to [5.5, 7.5], [7.5, 14], and [25, 30] μm, respectively. These slopes are selected as in González-Martín et al. (2019a).
Following the analysis done by Kemper et al. (2004), we characterize the optical depth at 10 μm as:
where Fcont is the underlying continuum, and it is obtained by fitting the continuum to a 6th order polynomial excluding the silicate feature. For the observed AGN spectra, the two spectral windows are at ∼7–8.5 μm (blueward of the silicate feature) and at ∼12–14.5 μm (redward of the silicate feature). However, note that this is particularized for each object to optimize the process. For SED models we fit the 7–32 μm spectral window, excluding both the 10 μm (8–13 μm) and the 18 μm (15.5–24 μm) silicate features.
We define two quantities to quantify the 10 μm silicate emission/absorption features: (1) the silicate feature central peak wavelength (denoted as C10 μm); and (2) the silicate feature strength (denoted as S10 μm). These two quantities are widely used in the literature to study the shape of the silicate feature (see for instance Fig. 16 in Nenkova et al. 2008b). Note that we use this sign convention so absorption (emission) features show positive (negative) values for S10 μm. The central peak wavelength and the silicate strength were obtained by fitting the core4 of the emission/absorption feature to a Gaussian profile to determine the locus of the minimum/maximum. In order to obtain the errors of the fits for the AGN spectra in our sample, we perform 100 Monte Carlo simulations including the error bars of the spectra.
We construct diagrams combining the three slopes, and the silicate strength, and the central wavelength to compare the spectral shape of the AGN sample with models. Results are shown in Sect. 6.
5.2. Spectral fitting method
We used the software XSPEC (Arnaud 1996) to perform the spectral fitting of the Spitzer/IRS spectra to the models. This is a command-driven, interactive, spectral-fitting program within the HEASOFT5 package. XSPEC provides a wide range of tools to perform spectral fittings to the data, being able to work in parallel processes in order to speed them up. Thus, it is ideal for our spectral fitting requirements.
We converted the Spitzer/IRS spectra into XSPEC format using the FLX2XSP task within HEASOFT. These files are easily read by XSPEC to perform statistical tests when fitting to models. In González-Martín et al. (2019a), we already reported the conversion of several AGN dust models into XSPEC format. We also convert our new GoMar23 model in the same way. Very briefly, we first created an additive one-parameter table (in fits format) associated with all the SEDs using the FLX2TAB task within HEASOFT. We then used a Python routine used by González-Martín et al. (2019a) to change the headers associating each SED with a set of parameters. This model has seven free parameters, plus redshift (which is usually fixed to the known value) and normalization (linked to the luminosity of the system). Note that XSPEC internally interpolates among the given values of the model. However, this could lead to local rather than global solutions if the parameter space is not well sampled. This is the reason why we decided to improve the coverage of some parameters with respect to Stalev16 model (e.g., Y which was only evaluated at three values by Stalev16 model, see Sect. 4).
We also added foreground extinction by dust grains to the dusty models using the ZDUST component (Pei 1992), already included as a multiplicative component within XSPEC. Among the options of ZDUST, we use the standard Galactic extinction curve. However, using the extinction curves of the Magellanic clouds does not change the main results of this paper. The main impact on the resulting spectrum of this extinction model is the attenuation of the near-infrared emission and the inclusion of silicate absorption features. The free parameter is the color excess E(B − V). Note that we test the importance of foreground extinction by comparing the final fit when including and excluding this component, and the results are presented in the following section. We use two definitions of χ2 to get insights on the best model; 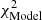 compares the residuals with the model and
compares the residuals with the model and 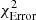 compares the residuals with the errors associated with the data. Furthermore, we use the f-test and AIC to compare spectral fits. Appendix A gives further details on the statistical tools used for this analysis.
compares the residuals with the errors associated with the data. Furthermore, we use the f-test and AIC to compare spectral fits. Appendix A gives further details on the statistical tools used for this analysis.
6. Results
6.1. Spectral shape
Table C.1 reports the silicate central peak wavelength, silicate strength, and three continuum slopes measured from the Spitzer/IRS spectra of the AGN sample used here. Figure 3 (top-left panel) shows the resulting optical depths for the type-1 and type-2 AGN. We have produced four diagrams comparing these five parameters (Fig. 3). In general type-1 AGN show silicate emission features (black lines) and type-2 AGN show silicate absorption features (gray lines). However, two type-1 AGN show weak absorption features, and eight type-2 AGN show emission features (top-left panel of Fig. 3 and Table C.1). This behavior is already reported in the literature (Hönig et al. 2010; González-Martín et al. 2013), and it is easily explained by the stochastic nature of the clumpiness of the system and its combination of viewing angle, density profile, and optical depths. The range of optical depths at 10 μm is τ10 μm ∼ [ − 1, 1] and absorption features are usually narrower than emission features, and the latter show a central plateau. The central wavelength of the feature is different when it is in absorption (around 9.7 μm) compared to when it is in emission. In the case of the emission features, they are usually shifted to 10.5 μm except in a few objects. The continuum slopes are correlated, as expected, being mostly negative for α5.5 − 7.5 μm and α7.5 − 14 μm (both in the range [−3.5, 0.5]) while α25 − 30 μm show both negative and positive values in the range [−2.5, 1.5]. Moreover, Type-1 AGN have flatter slopes than type-2 AGN.
 |
Fig. 3. Shape of the 9.7 μm silicate feature in optical depth units for our AGN sample (see text, top-left). Black and gray lines show type-1 and type-2 AGN, respectively. Observational diagrams for the AGN sample: 7.5–14 μm versus 5.5–7.5 μm slopes (top-middle); 25–30 μm versus 7.5–14 μm slopes (top-right); S10 μm versus C10 μm (bottom-left), and S10 μm versus 5.5–7.5 μm slope (bottom-right). Black squares and gray diamonds show the measurements in the Spitzer spectra for type-1 and type-2 AGN, respectively. |
All these spectral shape properties should be reproduced by any SED library. To explore this, Fig. 4 shows these four diagrams for all the studied models, including our new GoMar23 model (top panel in purple). Most models reproduce the spectral shape measurement of our AGN sample. The exception is the α5.5 − 7.5 μm and/or α7.5 − 14 μm for the Hoenig10 model (fourth row from top to bottom). The Hoenig17 model reproduces α7.5 − 14 μm versus α5.5 − 7.5 μm (sixth row, left panel) but fails to reproduce α25 − 30 μm versus α7.5 − 14 μm, with a clear shift toward higher values of α25 − 30 μm (fifth row, second panel from left to right). Interestingly, Hoenig10 and Hoenig17 models show the narrowest range for the silicate strengths and match well the observed range for emission features. Except for the Stalev16 model, the shapes found in each SED library include a wider range of values compared to the observed AGN properties. In particular, the Nenkova08 model shows quite prominent 10 μm silicate emission features (S10 μm < −2) which are not needed by our AGN sample. It also includes slopes α < −3 that are never observed (this is also the case for Hoenig10 and Hoenig17 models). On the other hand, Fritz06 model shows large silicate absorption strengths that do not have an observational counterpart.
 |
Fig. 4. Comparison between the spectral shapes of our AGN sample (black squares for type-1 AGN and gray diamonds for type-2 AGN) and the spectral shapes of the SED libraries. From left to right we show mid-infrared versus near-infrared slopes, far-infrared versus mid-infrared slopes, the 10 μm feature silicate strength versus its center, and the 10 μm feature silicate strength versus the near-infrared slope. From top to bottom we show the results for GoMar23 (purple), Fritz06 (blue), Nenkova08 (green), Hoenig10 (red), Stalev16 (magenta), and Hoenig17 (orange) models. Note that the tabulated values of the center of the silicate emission feature C10 μm in some of the models (e.g., Fritz06 or GoMar23 models) are an artifact of the spectral resolution used for to generate each SED library. |
Our new GoMar23 model is also able to reproduce all these spectral characteristics (top row in Fig. 4) but it also shows a wider range of spectral shape measurements, compared with observations. In particular, it includes steeper slopes (α < −3) and deeper silicate absorption features than observed. This might indicate that the complexity of the model (i.e., number of parameters or parameter space) might not be needed by the data or that a particular range of configurations is required. In order to explore this, we study how these diagrams are populated depending on the parameter space. Figure 5 shows the impact of the maximum grain size Psize when fixed to 0.01, 0.25, 1.0 and 10 μm (corresponding to a mass-weighted average of ⟨P⟩ 0.007, 0.097, 0.36, and 3.41 μm) and Fig. 6 shows the results for each of the other parameters of GoMar23 model. For each of them, we show the results for the minimum, maximum, and intermediate values using a different color. Note that we exclude the S10 μm versus C10 μm diagram because all these plots are similar irrespective of the parameter space, except when τ9.7 μm is large, which naturally produces large values of S10 μm. We also exclude the polar slopes of the density distribution, q parameter, because it shows a negligible impact on the diagrams. The main findings are:
 |
Fig. 5. Resulting diagrams for the GoMar23 model when the maximum grain size of the dust particles is explored (colored area) compared with the overall space parameter (empty area). From left to right the areas show the locus of SEDs for Psize = 0.01μm (⟨P⟩ = 0.007 μm, blue), Psize = 0.25 μm (⟨P⟩ = 0.097 μm, purple), Psize = 1.0 μm (⟨P⟩ = 0.36 μm, pink), and Psize = 10.0 μm (⟨P⟩ = 3.41 μm, violet). From top to bottom: α5.5 − 7.5 μm versus α7.5 − 14 μm, α25 − 30 μm versus α7.5 − 14 μm, and S10 μm versus α5.5 − 7.5 μm. Black squares and gray diamonds show the locus for type-1 AGN and type-2 AGN, respectively. |
 |
Fig. 6. Resulting diagrams for the GoMar23 model when the following parameters vary (from left to right): the viewing angle, the half opening angle, the ratio between the outer and the inner radius, the optical extinction at the equator, and the radial distribution of the dust. From top to bottom: α5.5 − 7.5 μm versus α7.5 − 14 μm, α25 − 30 μm versus α7.5 − 14 μm, and S10 μm versus α5.5 − 7.5 μm. The gray contour shows the result for the entire SED library. The blue, purple, and pink areas show the locus of SEDs for the minimum, medium, and maximum values of the parameter, respectively (see legend in the top panels). The results for the maximum grain size are shown in Fig. 5. We skip the results for the polar density distribution of the dust since no differences are found. |
-
We find that the area occupied in these diagrams is similar when the viewing angle is set to the outer wall of the torus (i.e., i = σ) than when a theoretical type-1 view (i.e., i < σ) is set. Type-2 views (i.e., i > σ) can explain most of the AGN while type-1 views fail to reproduce some type-2 AGN because of the lack of the low values of the spectral slopes. Type-1 views also fail at reproducing the deepest silicate absorption features. Notice that type-2 (type-1) views can also produce silicate emission (absorption) features, as found in our AGN sample.
-
Intermediate to high values of the half opening angle of the torus, σ, seem to better match observations (in particular the trend of α25 − 30 μm versus α7.5 − 14 μm), although low values are also required for some objects.
-
Relatively small values of the ratio between the outer and the inner radius, Y, could explain the lack of deep absorption features.
-
Low and intermediate values of the equatorial optical depth at 9.7 μm, τ9.7 μm, are able to explain most of the type-1 AGN spectra in our sample but the locus in α7.5 − 14 μm versus α5.5 − 7.5 μm and α25 − 30 μm versus α7.5 − 14 μm diagrams for some type-2 AGN are better explained with large values of τ9.7 μm.
-
The maximum size of the dust particles, Psize, plays a crucial role on the resulting diagrams. Particles in the range 0.25 < Psize < 10 μm (i.e., ⟨P⟩=[0.097 − 3.41] μm) better matches the S10 μm versus α5.5 − 7.5 μm diagram. In particular, Psize = 1 μm (i.e., ⟨P⟩ = 0.36 μm) nicely matches the observed spectral shapes in this diagram (pink shaded area, the third column in Fig. 5). Although not shown here, we would like to emphasize that the grain size has not a preferential role on the center of the silicate feature at 9.7 μm (C10 μm).
Numerical works in the literature, yielding theoretical SEDs for AGN emission, usually provide thousands or more, and one quick way to check their reliability is through diagrams such as those presented in this section (e.g., García-González et al. 2017; González-Martín et al. 2019b). Nevertheless, these diagrams are only partially informative of the ability of a model to represent the emission of real objects. What they can highlight, is the inability of a model to reproduce a given set of observational features. But a successful model should be able to properly reproduce all the spectral features with one single parameter set, something that these kinds of diagrams are unable to capture. An appropriate SED should hence at least show the same range of slope and silicate strength as observed, and to approach the problem we calculate the number of SEDs able to reproduce the observed spectral features for each object. Among the 68 objects in our sample, 25, 34, 6, 20, 9, and 59 objects can be reproduced (i.e., their spectral shape measurements are compatible with those of the SEDs, within errors) with at least one SED within Fritz06, Nenkova08, Hoenig10, Stalev16, Hoenig17, and GoMar23 models, respectively. Therefore, although the available models include SEDs with the appropriate range for each of these spectral characteristics, they lack the right combination to reproduce all the spectral shape features simultaneously. It is worth noticing that the model able to reproduce all the spectral characteristics for the largest number of objects is GoMar23 model. However, this is just a crude analysis since the spectral fitting is required to interpolate among the SED libraries and add foreground extinction when appropriate. This is the main subject of the following section.
6.2. Spectral fits
We fit the spectra of our AGN sample using the five models reported before and the new GoMar23 model presented in this paper. We use χ2(error) to minimize the errors and therefore obtain the best set of parameters among the SED libraries. As an example of a typical type-1 AGN, Fig. 7 shows the resulting best fits for IZw1 using each of the tested models. Note that we performed the fits with (red) and without (green) foreground extinction to show its impact on the final fit. In the case of IZw1, it is clear that Nenkova08, Hoenig10, and Hoenig17 models cannot reproduce the observations. Significantly better fits (χ2/d.o.f. < 2) are obtained by Fritz06, Stalev16, and GoMar23 models, the last model being statistically preferred. The same conclusion is drawn from this object if no foreground extinction is included. Interestingly, Fritz06, Stalev16, and GoMar23 models converge to a thin torus with σ ∼ 10 − 30°. In this case the maximum dust grain size is Psize ∼ 10 μm (⟨P⟩∼3.41 μm), well above the canonical 0.25 μm (⟨P⟩∼0.097 μm) assumed in previous models.
 |
Fig. 7. Spectral fits obtained for the type-1 AGN IZw1. The black line and gray shaded areas show the Spitzer spectrum and its error bars, respectively. The red and green lines show the best SED for each model with and without foreground extinction, respectively (see text). The top panel shows the spectral fit and the bottom panel shows the residuals. The inset within the top panel shows zoom-in to the 7–14 μm wavelength range associated with the 9.7 μm silicate feature. Reduced χ2 is given at the bottom-right corner of the top panel (error/model), including the degree of freedom within brackets (red and green for the SED with and without foreground extinction). Above each panel, we show the resulting parameters for each model when foreground extinction is included. |
We consider good fits those with 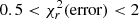 . Values of
. Values of 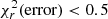 indicate that the model is too complex for the data and values of
indicate that the model is too complex for the data and values of 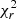 (error) > 2 are found when the model is too simplistic for the data. However, as explained in Appendix A,
(error) > 2 are found when the model is too simplistic for the data. However, as explained in Appendix A, 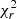 (error) might also show low values due to the overestimation of the error bars while large
(error) might also show low values due to the overestimation of the error bars while large 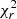 (error) might indicate an underestimation. For this reason, we explore the evaluation of the goodness of the fit using both χ2(error) and χ2(model) (see Eqs. (A.1)–(A.2)). Figure 8 shows the comparison between these two χ2 for each of the models. Objects below χ2(error) = 0.5 and χ2(model) = 1.5 × 10−3 (dashed area) are over-fitted by the model. This is particularly relevant for Hoenig17 model (with eight objects in the dashed area) which indeed is the model with the highest number of free parameters. GoMar23, Fritz06, Nenkova08 and Hoenig10 have 4, 1, 1, and 1 objects in the dashed area of Fig. 8, respectively.
(error) might indicate an underestimation. For this reason, we explore the evaluation of the goodness of the fit using both χ2(error) and χ2(model) (see Eqs. (A.1)–(A.2)). Figure 8 shows the comparison between these two χ2 for each of the models. Objects below χ2(error) = 0.5 and χ2(model) = 1.5 × 10−3 (dashed area) are over-fitted by the model. This is particularly relevant for Hoenig17 model (with eight objects in the dashed area) which indeed is the model with the highest number of free parameters. GoMar23, Fritz06, Nenkova08 and Hoenig10 have 4, 1, 1, and 1 objects in the dashed area of Fig. 8, respectively. 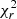 (model)∼5.5 × 10−3 is equivalent to
(model)∼5.5 × 10−3 is equivalent to 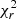 (error)∼2 and
(error)∼2 and 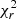 (model)∼1.5 × 10−3 is equivalent to
(model)∼1.5 × 10−3 is equivalent to 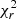 (error)∼0.5, with both quantities correlated. Figure 8 guarantee that the use of
(error)∼0.5, with both quantities correlated. Figure 8 guarantee that the use of 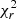 (error) is equivalent to
(error) is equivalent to 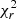 (model). We therefore use
(model). We therefore use 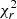 (error) in the subsequent analysis.
(error) in the subsequent analysis.
 |
Fig. 8. Reduced χ2 using the errors in the χ2 definition (χ2(error)/d.o.f., see Eq. (A.1)), versus that using the model in the χ2 definition (χ2(model)/d.o.f., see Eq. (A.2)). Filled and empty symbols show the values when foreground extinction is included and neglected in the spectral fitting procedure, respectively. The dot-dashed line shows the locus expected if both measurements agree with each other. The continuous lines show a factor of five of agreement between both χ2 definitions. An object located in the blank area shows complexity not well fitted by the model. The dashed area shows the locus when the model is too complex for the data (χ2/d.o.f. < 0.5). The dark-gray shaded area shows the locus where both reduced χ2 indicate that the model provides a statistically acceptable fit (i.e., χ2/d.o.f.(error) < 2 and χ2/d.o.f.(model) < 1.5 × 10−3). The light-gray shaded area shows the region where the object is expected to locate if the error bars of the spectra are overestimated and underestimated although the spectral fit is good. Each panel shows the results for one of the models. We show the percentage of good spectral fits per model, considering those objects in the gray areas (the result without foreground extinction is shown next to it). The percentage of objects statistically requesting foreground extinction (FG extinct.) is shown in the top-left corner of each figure. |
Before attempting to obtain the final statistics of good fits, we explore the role of foreground extinction. Figure 8 shows the results when foreground extinction is excluded (empty symbols) and included (filled symbols) into the spectral fit. The percentage of objects well fitted with each model is included on top of each panel (the percentage within brackets shows the results without foreground extinction). Furthermore, we also quantify the number of objects requesting foreground extinction by comparing the χ2 statistics with and without foreground extinction using the f-statistic test (f-value < 10−4 implies statistically need for foreground extinction). Nenkova08, Hoenig10, and Hoenig17 models require foreground extinction for ∼90% of the sample (i.e., the spectral fit is statistically better compared with the result when E(B − V) = 0) while Fritz06, Stalev16, and GoMar23 keep this percentage at ∼15 − 35%, with the lowest percentage obtained by the Fritz06 model (∼15%). Indeed, the use of foreground extinction strongly affects the percentage of objects well-fitted by the models. The most extreme example is Nenkova08 model, which goes from ∼50% of successful fits up to above 80% when foreground extinction is included. Hoenig10 and Hoenig17 also show an increment of ∼15% on the number of objects well fitted. In the opposite scenario, the percentage of good fits is not affected at all for Fritz06 model, while a minor effect (below 5%) is seen for Stalev16 and GoMar23 models. Therefore, we find that a smooth distribution of dust helps to mitigate the need for foreground extinction, as expected since smooth distribution produces deeper silicate absorption features. The role of foreground extinction is further explored in Appendix B.
We also studied which is the best model for each object. Table C.2 shows the best model among the already available SED libraries in Col. 2 and the corresponding χ2/d.o.f. in Col. 3. We mark with a dot when χ2/d.o.f. > 2. We then report in Col. 4 the χ2/d.o.f. obtained for the GoMar23 model and the final best-fit model in Col. 5. Figure 9a,b summarize these results. The results strongly depend on the inclusion of foreground extinction (inner square-filled and outer circle-filled pie-charts when foreground extinction is excluded and included, respectively). If no foreground extinction is included for the spectral fitting procedure and before the use of GoMar23 model, Fritz06, Nenkova08, and Hoenig17 models equally fit ∼20% of the sample and Stalev16 model describes ∼12% of the sample, respectively. Hoenig10 model fails to describe most of the objects, being the best fit only in 3% of the sample. The inclusion of foreground extinction significantly helps to improve Nenkova08, Hoenig10, and Hoenig17 models, with a percentage of best fits of ∼34%, ∼10%, and ∼34%, respectively (outer circle-filled pie-chart of Fig. 9a).
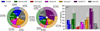 |
Fig. 9. Panels a and b show the percentage of object best fitted with each of the models tested before (panel a) and after (panel b) the inclusion of GoMar23 model. The inner (squared-filled) and outer (circle-filled) pie charts show the results without and with foreground extinction in the spectral fits, respectively. Panel c shows the final percentage of objects best fitted to each model when including statistically similar fits using AIC probability (see text). The square-filled and circle-filled areas show the results without and with foreground extinction in the spectral fits, respectively. |
When we include into the analysis GoMar23 model (Fig. 9b), it is the best model for ∼35% of the sample before the inclusion of foreground extinction (inner pie-chart). Among the others, the most relevant are Nenkova08 and Hoenig17 model, which is the best fit for ∼15% of the sample. However, when foreground extinction is included in the fit, there are three models describing ∼25 − 28% of the sample: Nenkova08 (∼25%), Hoenig17 (∼28%) and GoMar23 (∼28%) (outer circle-filled pie-chart of Fig. 9b).
The above results refer to the best fit (i.e., minimum 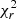 ). However, several models might give a statistically similar result. Figure 10 shows the comparison of
). However, several models might give a statistically similar result. Figure 10 shows the comparison of 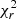 obtained with GoMar23 model and those models previously reported in the literature. The top (bottom) row shows the results before (after) the inclusion of foreground extinction. Empty hexagons show statistically similar results according to the AIC probability (i.e., less than 200 times as probable as the GoMar23 model, see Appendix A). Purple-filled hexagons are marked when GoMar23 model is preferred over the other model and hexagons with other colors (color code given in Fig. 9) are those objects that statistically prefer the other model instead of GoMar23 model. The range given in the subsequent text refers to the inclusion or exclusion of the foreground extinction. As expected, Stalev16 model is preferred over GoMar23 model only in 1-2 objects because GoMar23 model contains all the SEDs included by Stalev16 model. This small percentage preferring Stalev16 model might be the result of the stochastic nature of radiative transfer simulations or the inclusion of an anisotropic accretion disk. Furthermore, roughly ∼65–71% of the sample show statistically better results when using GoMar23 instead of Stalev16 model. As explained before, this is due to the better sampling of the parameter space (e.g., lower half opening angles) and/or the inclusion of the dust grain size into the model. The best-fit
obtained with GoMar23 model and those models previously reported in the literature. The top (bottom) row shows the results before (after) the inclusion of foreground extinction. Empty hexagons show statistically similar results according to the AIC probability (i.e., less than 200 times as probable as the GoMar23 model, see Appendix A). Purple-filled hexagons are marked when GoMar23 model is preferred over the other model and hexagons with other colors (color code given in Fig. 9) are those objects that statistically prefer the other model instead of GoMar23 model. The range given in the subsequent text refers to the inclusion or exclusion of the foreground extinction. As expected, Stalev16 model is preferred over GoMar23 model only in 1-2 objects because GoMar23 model contains all the SEDs included by Stalev16 model. This small percentage preferring Stalev16 model might be the result of the stochastic nature of radiative transfer simulations or the inclusion of an anisotropic accretion disk. Furthermore, roughly ∼65–71% of the sample show statistically better results when using GoMar23 instead of Stalev16 model. As explained before, this is due to the better sampling of the parameter space (e.g., lower half opening angles) and/or the inclusion of the dust grain size into the model. The best-fit 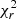 for Fritz06 model is correlated with that of GoMar23 model, although in 54–66% of the sample, the latter is statistically preferred. This is probably due to the fact that Fritz06 model is geometrically similar to Stalev16 and GoMar23 models so somehow included with GoMar23 model as well. Nenkova08 and Hoenig17 are preferred in 6–19% and 22–26% of the sample over the GoMar23 model, respectively. Meanwhile, GoMar23 model is preferred in 50–78% and 34–50% of the sample over Nenkova08 and Hoenig17 models, respectively.
for Fritz06 model is correlated with that of GoMar23 model, although in 54–66% of the sample, the latter is statistically preferred. This is probably due to the fact that Fritz06 model is geometrically similar to Stalev16 and GoMar23 models so somehow included with GoMar23 model as well. Nenkova08 and Hoenig17 are preferred in 6–19% and 22–26% of the sample over the GoMar23 model, respectively. Meanwhile, GoMar23 model is preferred in 50–78% and 34–50% of the sample over Nenkova08 and Hoenig17 models, respectively.
 |
Fig. 10. Comparison of |
We repeat this analysis for all the model combinations, adding the AIC probability into the analysis to quantify how many models can describe each object. The last column of Table C.2 includes all the statistically similar best-fit models (other than the one providing the best fit, which is given in the previous column). The final percentage of objects (equally) best fitted with each model is shown in Fig. 9c. This panel shows the results without (with) foreground extinction using squared-filled (circle-filled) bars. Note that the sum of the percentages is higher than 100% because several models can equally fit a single object. Only in five objects (namely Mrk 3, Mrk 110, MCG-03-34-064, IC 4518W, and Fairall 51), none of the models produce a statistically good fit.
In 24 objects (∼35%) a single model is preferred. Among them, nine prefer Nenkova08 model, six Hoenig17 model, six GoMar23 model, and three of them prefers Hoenig10 model. Among those objects only fitted with GoMar23 model, we have the one with the highest silicate absorption feature, indicating that this model might be particularly useful for buried AGN. Five out of these six objects that are well-fitted only to GoMar23 and Hoenig17 models are type-1 AGN (the exceptions are 2MASSXJ 10594361+6504063 and Mrk 417, respectively). Without the inclusion of foreground extinction, except for Hoenig10 model, most of the already available models are good at describing ∼20 − 30% of the sample. Our new GoMar23 model stands out as the best of them, giving the best fits for 71% of the sample. Once foreground extinction is included, Nenkova08 and Hoenig17 models increase their percentages up to 54% and 41%, respectively, while Fritz06 and Stalev16 models decrease to 18 and 16%, respectively. Although slightly decreasing after the inclusion of foreground extinction, GoMar23 model still shows the largest percentage with 60% of the sample. No relation between the model selection and the AGN luminosity is found for our sample. However, note that this AGN sample shows a relatively narrow luminosity range (⟨log(LX) = 43.5 ± 0.6⟩). A broader range of AGN luminosities is needed to explore the impact of AGN luminosity on the model selection.
6.3. GoMar23 model parameters
Beyond the model selection, the infrared spectral fitting technique is commonly used to infer the parameters of these models with the aim of constraining the geometry and distribution of the dust (e.g., Ramos Almeida et al. 2009, 2011; Alonso-Herrero et al. 2011; García-Bernete et al. 2019, 2022b; González-Martín et al. 2019b; Martínez-Paredes et al. 2021; Esparza-Arredondo et al. 2021). The resulting best-fit parameters and their associated errors through the χ2 statistics for GoMar23 model are reported in Table C.3. The XSPEC software also gives the opportunity to study the convergence of the parameter by computing how χ2 changes across the parameter space. Figure 11 shows the posterior distribution of each parameter for GoMar23 model for the object IZw1 as an example. The squares (linked with continuous lines) show the locus of the χ2 for each point of the model grid. The dotted-green line shows the interpolation given by the XSPEC software, which in general agrees well with the continuous line. In general, all the parameters show monotonous behavior along the parameter space. Only viewing angle (i), half opening angle (σ), the radial slope of the dust distribution (p), and the ratio between the outer and inner radius (Y) are restricted (at 3-σ level) with a clear minimum along the parameter space.
 |
Fig. 11. Convergence of χ2 for each parameter of GoMar23 model for IZw1. Squares show the value of χ2 at the given values of the parameters sampled in GoMar23 grid (continuous line linearly links these black squares). Dashed lines show the internal interpolation performed by XSPEC. Green and red squares and lines report the results before and after the foreground extinction is included in the spectral fit procedure. The best value for each parameter is shown above the upper-left corner of each panel (when including foreground extinction). The top-left panel shows the resulting χ2/d.o.f.(sigma) in the upper-left corner. The percentage of variation of χ2 compared to the minimum value is shown above the upper-right corner of each panel. The horizontal blue dot-dashed line in the third-column lower panel shows the χ2 computed when the grain size is fixed to 0.25 μm. Note in this panel for Psize we also include the f-test probability that the grain size is consistent with 0.25 μm (see text). This panel also shows the x-axis expressed in terms of the average grain size in light-gray colors. |
Figure 11 also shows that not all the parameters equally contribute to obtaining a minimal χ2. It is clear that variation on the slopes (p and q) and the optical depth at 9.7 μm (τ9.7) of the density distribution contribute much less to the final fit compared to variations on the half opening angle, σ, for instance. In order to quantify this, we compute the percentage of χ2 variations compared to the parameter giving the maximal variation, denoted as Δχ2:
where par denote the parameter evaluated and pref is the GoMar23 model parameter giving the maximal χ2 variation. This number is given in the upper-right corner of each panel of Fig. 11. In IZw1 the maximal χ2 variation is obtained with the ratio between the outer and the inner radius of the torus (Y). The half opening angle (σ), the maximum dust grain size (Psize), the viewing angle (i), and significantly contribute to the minimization process with Δχ2 of 85 %, 78%, and 71%, respectively. On the other hand, the optical depth at 9.7 μm (τ9.7) contributes 44% while 18% is found for the slopes of the density distribution (p). Thus, for this particular object, the maximum dust grain size, Psize (or equivalently the weighted-average grain size ⟨P⟩), is the third most relevant parameter (below Y and σ). In order to further explore the need for this parameter in the final fit, we performed the same fit but kept the maximum dust grain size fixed to the canonical value of Psize = 0.25 μm (⟨P⟩ = 0.097 μm). The resulting minimum χ2 for this fit is shown as the dot-dashed blue line in the panel associated with Psize/∠P⟩ of Fig. 11. We then run the f-statistic test to compute the probability that allowing the maximum dust grain size to vary significantly improves the final fit (this number is quoted within the same panel). Indeed, the maximum dust grain size is requested by the data to significantly improve the fit for IZw1.
We then perform the above analysis for the full AGN sample. Rows 1 and 3 (from top to bottom) in Fig. 12 show the resulting distribution for each parameter for the AGN sample, and rows 2 and 4 show the distribution of Δχ2 as computed above. Note that the bins of the parameter-space histograms are set to match the grid points. At first look, most of the parameters require the full range explored by the grid (i.e., no bins with zero objects are found). The parameters on the polar and radial density distribution of dust (p and q) cluster to flat distributions of dust (i.e., p = q = 0). In 28 out of the 68 objects (41% of the sample) prefer very large particles with Psize ∼ 10 μm (⟨P⟩∼3.41 μm). Only 6 out of the 68 objects (9% of the sample) fall in the bin with the canonical value of Psize ∼ 0.25 μm (⟨P⟩∼0.097 μm). After comparing the resulting best fit when fixing Psize = 0.25 μm (⟨P⟩∼0.097 μm) to those in which the grain size is allowed to vary, we find that, according to f-test, 90% of the objects in our sample statistically prefer.
 |
Fig. 12. Rows 1 and 3 show in purple the histograms of the resulting parameters for the AGN sample when using GoMar23 model. We use the same bins as those used for the SED grid. Rows 2 and 4 show the histogram of the relative importance of each parameter in the convergence of the fit. It is obtained as the maximal variation of χ2 for each parameter range compared to the parameter giving the maximum variation, denoted as Δχ2 (see Fig. 11). Each panel also shows the percentage of objects with Δχ2 above 5 and 95%. |
Inside panels in rows 2 and 4, the percentage of objects giving Δχ2 above 5 and 95% of the variations is included. Δχ2 > 95% shows the percentage of objects where the considered parameter is the most fundamental one to obtain the fit, while above Δχ2 > 5% shows the percentage of objects where the considered parameter significantly improves the fit compared to the most important parameter. The parameter that systematically gave the maximal variation on the Δχ2 (i.e., Δχ2 > 95%) for 62% of the sample is the half opening angle, σ. Attending to Δχ2 > 5% (i.e., the significant improvement of the fit) the parameters can be sorted out from the most relevant to the less relevant as: σ => Y => Psize / ⟨P⟩ => i => τ9.7 => p => q (ranging from 100 down to 18% of the sample). Therefore, variations in the maximum dust grain size, Psize (or equivalently the mass-weighted average grain size ⟨P⟩), produces Δχ2 > 5% for 65% of the sample, which makes it the third most relevant parameter for improving the fits.
Finally, although the study of the parameters is out of the scope of this paper, we warn the reader that the spectral coverage and/or sensitivity of the Spitzer/IRS spectra might not be enough to recover all the parameters at the same time. In particular, we find a clear degeneracy between the viewing angle and the half-opening angle of the torus (r = 0.9), which is also found for Stalev16 model. We plan a future investigation on model constrain using JWST near and mid-infrared observations.
7. Discussion
7.1. Adequacy of GoMar23 model to the AGN dust continuum
The thermal infrared SED emission from the central region of an AGN depends on the geometry, distribution, and composition of the dust. Although quite challenging from the observational point of view, it is key to study AGN nuclear dust to explain the AGN classes and possible interplay between the AGN and its host, acting as the outer layer of the nurturing/feedback mechanism (see the most recent reviews Ramos Almeida & Ricci 2017; Hönig 2019). The infrared observations of nearby AGN show a broad continuum that could be interpreted as the sum of two different components: one of them producing a ∼3 μm bump, which corresponds to dust close to the sublimation temperature, and another component that peaks at wavelengths longer than 10 − 20 μm. These components were interpreted by Mor & Netzer (2012) respectively as the hot pure graphite dust outside the BLR (García-Bernete et al. 2022b), and the clumpy torus, which resides on larger scales and produces the mid-infrared emission. Furthermore, the mid-infrared spectra show moderate silicate absorption features for most of the type-2 AGN, and weak silicate emission features for most of the type-1 AGN (Hönig et al. 2010; González-Martín et al. 2013; Alonso-Herrero et al. 2016; García-Bernete et al. 2019, see also Fig. 3), although exceptions to this are also found (Mason et al. 2012; Martínez-Paredes et al. 2020).
From the theoretical point of view, reproducing the infrared SED of AGN has turned to be challenging, particularly the silicate features and the overall infrared continuum slopes (González-Martín et al. 2019b; Martínez-Paredes et al. 2021; García-Bernete et al. 2022b, and references therein). We show that the currently available models are good at providing the range of infrared slopes and silicate strengths (see Fig. 4) but they fail at reproducing the whole mid-infrared spectrum of a given AGN with a single SED. Between 25–50% of our sample cannot be well matched to the available SED libraries, unless foreground extinction is included (Fig. 8).
7.1.1. Smooth versus clumpy models
If we focus on the differences found between smooth and clumpy models in our analysis, the main one is associated with the need for foreground extinction applied to the data (Fig. 8). Foreground extinction has little impact on the models including a smooth dust distribution provided by Fritz et al. (2006, Fritz06) and Stalevski et al. (2016, Stalev16), with less than ∼30% of the sample requiring this component. On the other hand, the purely clumpy models by Nenkova et al. (2008b, Nenkova08), Hönig & Kishimoto (2010, Hoenig10), and Hönig & Kishimoto (2017, Hoenig17) require foreground extinction for ∼90% of the sample analysed in this work. The most extreme result is obtained for the clumpy torus model by Nenkova et al. (2008b) which is able to provide good fits for 50% of the sample without the inclusion of foreground extinction while this percentage increases up to 84% otherwise. Therefore, we conclude that purely clumpy models may have insufficient self-absorption to reproduce the observed shallow silicate absorption features and steeper near-infrared slopes. Although the nature of the foreground extinction is out of the scope of this analysis, it is worth mentioning that the E(B–V) values listed in this analysis are well above the expected values for the ISM of the Milky Way, when using the NH hydrogen column densities derived from the full sky HI survey by the HI4PI Collaboration (HI4PI Collaboration 2016) and the standard gas-to-dust ratio of NH/AV = 1.8 × 1021 atoms cm−2 mag−1. Instead, they are roughly consistent with the E(B–V) of the host galaxies as derived from the Hα/Hβ Balmer decrement (we compiled Balmer decrements for 62 out of the 68 AGN, mostly from the measurement of the BASS survey, Koss et al. 2022; Oh et al. 2022). A detailed analysis of the foreground extinction and its role in the SED fitting technique is planned for a future investigation.
Perhaps, the two-phase dust distribution models (e.g., smooth+clumpy torus model developed by Stalevski et al. 2016) are preferred since they might provide a more realistic treatment of the distribution of dust from the stability point of view because a smooth distribution of dust alone could suffer from the self-destruction of the dust due to its temperature. However, some fine-tuning is still needed because Stalev16 models have moderate success explaining the overall observed mid-infrared spectra, accounting only for 25–40% of the sample (Fig. 9, see also González-Martín et al. 2019b, although it might be due to the somewhat limited number of SEDs computed). A smooth distribution for the disk/torus and a clumpy distribution for the wind might also be a good representation according to MHD simulations (Wada 2015; Williamson et al. 2020).
The new SED library presented by this work is based on the two-phase clumpy torus model described by Stalevski et al. (2016, Stalev16) with the inclusion of the maximum grain size as a free parameter. This new SED library provides good fits for 85–88% of the sample, irrespective of the inclusion of foreground extinction, and provides the best model for 60–70% of the sample (being the best among the models, see Figs. 8 and 9). Indeed, foreground extinction is required only for 34% of the sample, consistent with the other models including a smooth distribution of dust. GoMar23 model gives a statistically better fit than Stalev16 model in 65–70% of the sample (see Fig. 10) with only 1–3% preferring the Stalev16 model. This is mostly due to the fact that Stalev16 model is nested within GoMar23 model, while this small percentage prefers Stalev16 model might be the result of the stochastic nature of radiative transfer simulations or the inclusion of anisotropy for the accretion disk emission in Stalev16 model.
7.1.2. Torus versus wind models
The most recent torus SED library was produced in an attempt to study the impact of a different geometry of the dust, which is assumed to be a combination of a (relatively) thin disk plus a hollow cone-like structure (Hönig & Kishimoto 2017). In fact, it is important to bear in mind that, besides the dust torus explored here, molecular lines show the presence of large and massive disks of cold gas (García-Burillo et al. 2016, 2021; Alonso-Herrero et al. 2018; Combes et al. 2019) and infrared observations reveal polar component at least for some objects (interpreted as a dusty wind, see Hönig 2019; Alonso-Herrero et al. 2021). When we compare the spectral fits of our new SED library (GoMar23) with the disk+wind clumpy model provided by Hönig & Kishimoto (2017, Hoenig17), we find that GoMar23 model is statistically preferred in 34–50% of the sample while Hoenig17 model is statistically better in 22–26% (see Fig. 10). Thus, this disk+wind geometry might be key to explain at a nonnegligible fraction of nearby AGN. According to the recent work by Alonso-Herrero et al. (2021), the presence of polar dust in the mid-infrared might depend on the column density and Eddington ratio (see also Venanzi et al. 2020; García-Bernete et al. 2022b). Evidence for a diffuse mid-infrared emitting polar component has been found in six AGN, including both type-1 and type-2 sources using interferometric observations (Circinus Galaxy, NGC 424, NGC 1068, NGC 3783, ESO 323-G77, and NGC 5506, see López-Gonzaga et al. 2016; Leftley et al. 2018; Hönig 2019, and references therein). Only NGC 3783 is included in our sample. Indeed this object favors the disk+wind Hoenig17 model, which is preferred given the spatially resolved data, although our torus-like GoMar23 model also provides an equally acceptable fit according to the AIC statistics.
We want to stress that these two models (torus- versus wind-like configurations) are not competing scenarios but probably two simplifications of a more dynamical scenario. Wada (2015) proposed that the nuclear dust in AGN is not static, but rather a dynamic moving failed dusty outflow or “fountain” that produces the geometrically thick polar-elongated structure. Indeed, Williamson et al. (2020) showed that a radiation-driven polar wind is almost inevitable for luminous AGN. The fountain is supported by the radiation pressure from the geometrically thin gas/dust disk. Baskin & Laor (2018) also explored the idea that the BLR is also part of this failed dust wind conformed by large-size (> 0.3 μm) graphite grains (see also Czerny & Hryniewicz 2011). The radiation pressure from the AGN naturally produces an inflated torus-like structure, with a predicted peak height at the outer radius of the BLR. Sarangi et al. (2019) present detailed calculations of the chemistry of silicate dust formation in (magnetohydrodynamic) winds launched by AGN accretion disk. They show that the resultant distribution of the dense dusty gas resembles a failed wind (which could mimic a toroidal shape), with high column density and optical depths along the equatorial viewing angles, in agreement with the AGN unification picture. This explains why both torus-like and wind-like geometries are able to fit some of the AGN (even for the same object), as found for several authors already (González-Martín et al. 2019b; Martínez-Paredes et al. 2021; García-Bernete et al. 2022b). The goal we must pursue is to establish under which conditions each geometry dominates because it will shed light on the evolutionary stages of this failed wind and the role of dust in this cycle.
7.2. The role of the grain size
As discussed in the introduction, many of the previous AGN dust models used the dust grain size distribution of the Galactic diffuse interstellar medium. However, the assumption that the properties of dust in the extreme conditions of the circumnuclear region of AGN are similar to those of the Galactic diffuse ISM is somewhat naive, given that even in dense clouds of our Galaxy the extinction curve already differs from that of the ISM, suggesting that a universal grain size distribution is not feasible (Mathis 1990). The improvement of the GoMar23 model presented here, compared to similar models, resides in the addition of the grain size (tabulated as the maximum or the mass-weighted average) as a parameter of the model.
In this work, we showed that the grain size, as a parameter properly included in the SED library, is required to significantly improve the final spectral fit in ∼90% of the sample. Furthermore, among the seven parameters considered in our model, the grain size is the third most important parameter to achieve the best fit (see Fig. 12), only after the half opening angle and the ratio between the outer and the inner radius of the torus. However, note that the lower relevance of the viewing angle might be related to its degeneracy with the half-opening angle of the torus which is most probably associated with the narrow wavelength range or low sensitivity of Spitzer spectra. The grain size helps to reproduce the central wavelength of the silicate feature at 9.7 μm, which is shifted to longer wavelengths for emission features in AGN. It also helps to reproduce the excess toward near-infrared wavelengths, called the near-infrared bump (see below).
Previous studies already showed that the removal of small grains and/or the prevalence of large grains makes the silicate feature less prominent (Laor & Draine 1993). We show that variations in the grain size help the silicate strength and infrared slopes to be better reproduced at the same time in our sample (see Fig. 5). In order to further explore the effect of the grain size on the spectral shape, we compare in Fig. 13 the best spectral fit with those obtained using the maximum grain size of Psize = 0.01 μm (⟨P⟩ = 0.007 μm, green), Psize = 0.25 μm (⟨P⟩ = 0.097 μm, blue), and Psize = 10 μm (⟨P⟩ = 3.41 μm, red) for IZw1. IZw1 requires a maximum grain size of Psize ∼ 10 μm (⟨P⟩ = 3.41 μm). Note that all the parameters except for the grain size are fixed to those found for the best-fitted model (black line) so that the effect of the grain size can be isolated and better highlighted in the fits. It is clear that the role of grain size is significant. Smaller grains produce deeper silicate absorption features and a steeper slope at longer wavelengths.
 |
Fig. 13. Effect of the maximum grain size on the spectral fit. We use as examples the type-1 AGN IZw1. The first row shows the best spectral fit using GoMar23 model (black continuous line). We also show the fit to three fixed maximum grain size Psize of 0.01 μm (⟨P⟩ = 0.007 μm, green), 0.25 μm (⟨P⟩ = 0.097 μm, blue), and 10 μm (⟨P⟩ = 3.41 μm, red), while other parameters are kept as those obtained from the best fit. The two insets in these top panels show the set of SEDs with the same parameters and varying the maximum grain size Psize from 0.01 μm (⟨P⟩ = 0.007 μm, green) to 10 μm (⟨P⟩ = 3.41 μm, red). Note that in these insets the SEDs are normalized at 15 μm. Bottom panels show the residuals of the best fit (black) and those using dust maximum grain size Psize of 0.01 μm (⟨P⟩ = 0.007 μm, green), 0.25 μm (⟨P⟩ = 0.097 μm, blue), and 10 μm (⟨P⟩ = 3.41 μm, red). |
The net effect on the spectral shape can be further explored in Fig. 14, where we show the locus of the SEDs with different dust grain sizes in the spectral shape diagrams for PKS 2356-61. In these plots, green/small dots are the results for small particles (i.e., from Psize = 0.01 μm or ⟨P⟩ = 0.007 μm) while red/large dots show the effect of increasing the grain size explored in this analysis (i.e., up to Psize = 10 μm or ⟨P⟩ = 3.41 μm, ). Note that the locus of the observational values for PKS 2356-61 is shown as a gray diamond. The spectral shapes of this object are well reproduced after including the grain size as a free parameter, where the best fit (yellow star) is close to the observed value. Indeed, the canonical maximum grain size of Psize = 0.25 μm (⟨P⟩ = 0.097 μm, blue dot) is far from the best value. Note that in most of the objects, the effect on the spectral shape is similar. As long as the grain size increases up to Psize = 1 μm (⟨P⟩ = 0.36 μm) the α5.5 − 7.5 μm and α7.5 − 14 μm become steeper, while the α25 − 30 μm and the silicate strength remains the same. This is easily explained by the size of graphite grains since they contribute to the enhancement of the near-infrared continuum compared to small grains as the central source efficiency to heat the grains increases when the grain size decreases. However, when we use particle distributions with maximum sizes above 1 μm (⟨P⟩ = 0.36 μm) the silicate strength decreases. This combined effect is crucial in the model to explain the weaker silicate absorption features together with the spectral slopes.
 |
Fig. 14. Effect of the maximum grain size on the diagrams of spectral shapes for the type-2 AGN PKS 2356-61. It shows the locus of the SEDs computed using the best-fit parameters and varying the maximum grain size Psize from 0.01 to 10 μm (i.e., ⟨P⟩ from 0.007 to 3.41 μm). The spectral shape diagrams are Silicate depth versus α5.5 − 7.5 μm (left panels), α7.5 − 14 μm versus α5.5 − 7.5 μm slopes (middle panels), and α25 − 30 μm versus α7.5 − 14 μm (right panels). The empty-filled distribution is that from the entire SED library for GoMar23 model. Green small dots correspond to smaller grain sizes and redder and larger dots correspond to larger grain sizes (linked with lines). We mark as a blue dot the locus of the resulting values for the SEDs with Psize = 0.25 μm (⟨P⟩ = 0.097 μm) and as a yellow star the locus of the resulting values for the best fitted SED. The type-1 AGN are marked as black squares and type-2 AGN as gray diamonds. |
It is important to remark that our GoMar23 SED libraries are created by varying the maximum size of both graphite and silicate grains at the same time. However, the dust sublimation radius depends on the dust composition and the grain size (Baskin & Laor 2018, and references therein). Therefore, silicate grain size distribution might differ from that of graphite grains. This was already shown by García-González et al. (2017) for the clumpy torus model by Hönig et al. (2010), which indeed is one of the key improvements of the disk+wind model by Hönig & Kishimoto (2017). Although out of the scope of this work, this improvement in the model might further help to better reproduce the infrared slopes (mostly affected by graphite grains) and the silicate strengths (associated with the silicate grains).
7.3. The role of large grains
Depletion of small grains or excess of large grains in a sizable fraction of the AGN is well established in our sample (41% is clustered at Psize = 10 μm (⟨P⟩ = 3.41 μm) according to the results shown in Fig. 12). Gaskell et al. (2004) provided evidence for flat extinction curves in AGN, indicative of a larger fraction of larger dust grains in the dusty population. Lyu et al. (2014) also suggested that the low AV/τ9.7 μm ratio found in their analysis could be due to the predominance of large grains in the AGN torus. Xie et al. (2017) already suggested that μm-sized particles can help to reproduce up to 90% of the type-1 AGN explored in their analysis (see also Smith et al. 2010), although other aspects as geometry were not considered. Moreover, Maiolino et al. (2001) already suggested that the dust composition in the circumnuclear region of AGN could be dominated by large grains (Psize ∼ 1 μm or equivalently ⟨P⟩ = 0.36 μm), making the extinction curve flatter and featureless to explain the reduction of the E(B − V)/NH and AV/NH ratios compared to the ISM value (see also Shao et al. 2017). The decrement of E(B − V)/NH was recently confirmed by Esparza-Arredondo et al. (2021) from a detailed analysis of the SEDs considering the opacity of the torus.
Large grains (Psize = 0.1 − 1 μm or equivalently ⟨P⟩ = 0.042 − 0.36 μm) were preferred for the polar component found for Circinus galaxy (Stalevski et al. 2017, 2019). Within the disk+wind geometry proposed by Hönig & Kishimoto (2017), the hot dust is assumed to be primarily comprised of larger grains in the range 0.075–1 μm (or equivalently ⟨P⟩ = 0.033 − 0.36 μm), because they are located in inner radii where large grains better survive. The near-infrared excess is explained under the assumption that it might trace dust at temperatures that can only be survived by the largest graphite grains (García-González et al. 2017). Indeed, this model is better at reproducing spectra shortward ∼7 μm when compared with observations (see also González-Martín et al. 2019b; Martínez-Paredes et al. 2021; García-Bernete et al. 2022b). Recently, García-Bernete et al. (2022b) studied the available SED dust libraries in a volume-limited sample of well-isolated and nearby AGN, finding that type-1/bright AGN are best fitted to the disk+wind Hoenig17 model due to a better performance in reproducing the near-infrared bump. They argue that it is likely due to the combination of removing most silicate and small graphite grains due to sublimation and self-absorption effects due to the wind at intermediate and high inclinations (see also Martínez-Paredes et al. 2021). Thus, large grains are again a required element in these models.
Even for the ISM, micron-sized graphite grains account for 2.5% of the total IR emission (Wang et al. 2015), which helped to unify distance estimates derived from spectroscopy and parallax by considering extinction by large grains (Siebenmorgen 2023). However, the origin of such an enhancement of large particles is still unclear. Several effects could explain a preponderance of large grains in the dusty structure near the AGN. We gather them into two classes: grain destruction and grain growth. An obvious form of dust destruction in AGN is due to its radiation field. This trend has also been found for PAH emission of AGN (García-Bernete et al. 2022a). At the outer envelope of the sublimation radius of silicates (which sublimate at lower temperatures than graphite grains), we expect that the grain size distribution might be biased to large grains since they better resist the radiation field of the AGN. Thus, grains size distributions skewed to large grains might be due to the preferential destruction of small grains in the AGN radiation field (Draine & Salpeter 1979).
If not destroyed, AGN radiation pressure combined with radiation pressure on dust can sweep out the particles away from the nucleus with an increasing speed that is inverse proportional to grain size, as long as grains are larger than ∼0.1 μm (so the radiation pressure efficiency can be approximated to one, see Tazaki & Ichikawa 2020). Therefore, small grains require less time to reach the terminal velocity. After reaching a terminal velocity, the destruction of dust grains occurs due to sputtering by shock-heated gas (Draine & Salpeter 1979). This sputtering makes the grain lifetime proportional to the grain size (i.e., sputtering destroys small grains faster than the large ones Tazaki & Ichikawa 2020), producing a preponderance of large grains in the wind where this destruction process of small grains enhances the shift of the distribution toward larger sizes. Larger grains may also form either by accretion from the gas phase or by grain coagulation (Li & Draine 2001). Sarangi et al. (2019), from their calculations of the chemistry of silicate dust in AGN winds, reported that these winds have physical conditions suitable to form significant amounts of dust, especially for objects with an accretion rate close to their Eddington limit, making luminous AGN a source of dust in the universe. Since the grain coagulation rate increases with density (proportional to the square root of the density Draine & Lee 1984), the effect is expected to be dramatic in the circumnuclear clouds of AGN (Maiolino et al. 2001). Maiolino et al. (2001) showed that dust grains have time to coagulate before being replaced by gas coming from the outer regions.
Therefore, a dust distribution biased in favor of large grains, probably as a consequence of a trade-off between coagulation and accretion processes, is also naturally expected in the extreme physical conditions of the gas in the circumnuclear region of AGN. Furthermore, a significant variation of the maximum grain size for each object is expected depending on the evolutionary stage of the AGN (including wind phase) and its local conditions (Sarangi et al. 2019), which is also consistent with our results.
8. Summary
The role of grain size in geometrical models of AGN dust continuum is poorly explored in the literature. In order to fill this gap, we created a new SED library (including over 700 000 SEDs) based on the two-phase (smooth+clumpy) torus model described by Stalevski et al. (2016), including the grain size (denoted by the maximum grain size Psize or equivalently by the mass-weighted average grain size ⟨P⟩) as a model parameter. We then compared our new and previous models with a sample of nearby AGN (mainly Seyfert galaxies with intermediate luminosities) observed with Spitzer/IRS (carefully selected to provide spectra dominated by the AGN component). The explored models are: the smooth torus model by Fritz et al. (2006), the clumpy torus models by Nenkova et al. (2008b) and by Hönig & Kishimoto (2010), the two-phase torus model by Stalevski et al. (2016), and the clumpy disk+wind model by Hönig & Kishimoto (2017). We named our new model GoMar23, following the last name of the first author of the paper and the year of its submission (as we did for the other models). The main results are summarized as:
-
Although the range of spectral shapes of the objects in our sample is recovered with most of the models, a unique SED capable of reproducing the whole mid-infrared spectra of AGN is not found for a nonnegligible fraction of objects (at least 15%) with the already available models. The GoMar23 model represents a significant improvement of this, providing good fits for 85% of the sample.
-
We demonstrate (with statistical tests) that allowing the maximum dust grain size up to sizes of 10 μm (or the mass-weighted average grain size of 3.41 μm) is required to successfully reproduce the SEDs of 90% of the sample. The canonical value of Psize ∼ 0.25 μm (⟨P⟩∼0.097 μm) is preferred for ∼9% of the sample; very large particles with Psize ∼ 10 μm (⟨P⟩∼3.41 μm) are preferred for 41% of the sample.
-
The dust grain size is the third parameter in the order of its importance to obtain a good spectral fit. Only the half-opening angle and the ratio between the outer and inner radius of the dusty structure are above the dust grain size in this prioritized list of parameters.
-
The inclusion of foreground extinction for the smooth or two-phase models (i.e., the Fritz06, GoMar23, and Hoenig17 models) is irrelevant in 70–90% of the objects, while it is required in ∼90% of the objects when a purely clumpy distribution is used (i.e., the Nenkova08, Hoenig10, and Hoenig17 models). Therefore, the incorporation of a smooth dust distribution (smooth or smooth+clumpy) helps to reproduce the spectra without the need for additional foreground extinction for most of the objects.
As a concluding remark, these geometrical models gain in importance with the upcoming new data from JWST. Its superior sensitivity will allow us to obtain near- and mid-infrared spectra of fainter and/or more distant AGN that could be compared with these models to infer the properties of AGN nuclear dust. The GoMar23 SED library is the first step to providing an improved geometrical model including the maximum grain size into the parameter space. However, there are several aspects that need to be further explored, including the geometry of the components (e.g., the polar-wind dusty component), dust composition (e.g., the fraction of graphite versus silicate grains), grain shape, or the slope of the grain size distribution. These aspects should be the focus of future investigations.
Acknowledgments
We thank the anonymous referee for his/her useful comments. We thank Dr. Peter Camps for his useful suggestions on the SKIRT’s convergency tests. This research is mainly funded by the UNAM PAPIIT project IN105720 and CONACyT “Frontera de la Ciencia” project CF-2023-G-100 (PI OG-M). This research has made use of dedicated servers (IRyAGN2, Galaxias and Arambolas servers, and Calzonzin and Mouruka clusters) maintained by Daniel Díaz- González, Miguel Espejel, Alfonso Ginori González, and Gilberto Zavala at IRyA-UNAM. All of them are gratefully acknowledged. C.R.A. acknowledges financial support from the project “Feeding and feedback in active galaxies”, with reference PID2019-106027GB-C42, funded by MICINN-AEI/10.13039/501100011033. A.A.H. acknowledges support from grant PID2021-124665NB-I00 Êfunded by the Spanish Ministry of Science and Innovation and the State Agency of Research MCIN/AEI/10.13039/501100011033. D.E.-A. acknowledges support from the Spanish Ministry of Science, Innovation, and Universities (MCIU), Agencia Estatal de Investigación (AEI), and the Fondo Europeo de Desarrollo Regional (EU-FEDER) under projects with references AYA2015-68217-P and PID2019- 107010GB-100. I.G.B. acknowledges support from STFC through grant ST/S000488/1. N.O.C. acknowledges support from CONACYT scholarship 897887. M.S. acknowledges support by the Science Fund of the Republic of Serbia, PROMIS 6060916, BOWIE, and by the Ministry of Education, Science and Technological Development of the Republic of Serbia through the contract No. 451-03-9/2022-14/200002. C.V.-C. acknowledges support from a CONACyT scholarship.
References
- Almeyda, T., Robinson, A., Richmond, M., et al. 2017, ApJ, 843, 3 [Google Scholar]
- Alonso-Herrero, A., Ramos Almeida, C., Mason, R., et al. 2011, ApJ, 736, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., Esquej, P., Roche, P. F., et al. 2016, MNRAS, 455, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., Pereira-Santaella, M., García-Burillo, S., et al. 2018, ApJ, 859, 144 [Google Scholar]
- Alonso-Herrero, A., García-Burillo, S., Hönig, S. F., et al. 2021, A&A, 652, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antonucci, R. R. J., & Miller, J. S. 1985, ApJ, 297, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, Astron. Data Anal. Software Syst. V, 101, 17 [NASA ADS] [Google Scholar]
- Asmus, D. 2019, MNRAS, 489, 2177 [NASA ADS] [CrossRef] [Google Scholar]
- Asmus, D., Hönig, S. F., & Gandhi, P. 2016, ApJ, 822, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Baes, M., & Camps, P. 2015, Astron. Comput., 12, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Baes, M., Davies, J. I., Dejonghe, H., et al. 2003, MNRAS, 343, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Barlow, R. J. 1989, Statistics: A Guide to the Use of Statistical Methods in the Physical Sciences (New York: Wiley-Interscience) [Google Scholar]
- Barvainis, R. 1987, ApJ, 320, 537 [Google Scholar]
- Baskin, A., & Laor, A. 2018, MNRAS, 474, 1970 [Google Scholar]
- Bock, J. J., Neugebauer, G., Matthews, K., et al. 2000, AJ, 120, 2904 [NASA ADS] [CrossRef] [Google Scholar]
- Camps, P., & Baes, M. 2015, Astron. Comput., 9, 20 [Google Scholar]
- Camps, P., & Baes, M. 2020, Astron. Comput., 31, 100381a [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F., García-Burillo, S., Audibert, A., et al. 2019, A&A, 623, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Czerny, B., & Hryniewicz, K. 2011, A&A, 525, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [CrossRef] [Google Scholar]
- Draine, B. T., & Salpeter, E. E. 1979, ApJ, 231, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R. A., & Malkan, M. A. 1986, ApJ, 308, 59 [CrossRef] [Google Scholar]
- Efstathiou, A., & Rowan-Robinson, M. 1995, MNRAS, 273, 649 [Google Scholar]
- Emmanoulopoulos, D., Papadakis, I. E., Epitropakis, A., et al. 2016, MNRAS, 461, 1642 [NASA ADS] [CrossRef] [Google Scholar]
- Esparza-Arredondo, D., Osorio-Clavijo, N., González-Martín, O., et al. 2020, ApJ, 905, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Esparza-Arredondo, D., Gonzalez-Martín, O., Dultzin, D., et al. 2021, A&A, 651, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feltre, A., Hatziminaoglou, E., Fritz, J., et al. 2012, MNRAS, 426, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, J., Franceschini, A., & Hatziminaoglou, E. 2006, MNRAS, 366, 767 [Google Scholar]
- Gámez Rosas, V., Isbell, J. W., Jaffe, W., et al. 2022, Nature, 602, 403 [CrossRef] [Google Scholar]
- García-Bernete, I., Ramos Almeida, C., Landt, H., et al. 2017, MNRAS, 469, 110 [CrossRef] [Google Scholar]
- García-Bernete, I., Ramos Almeida, C., Alonso-Herrero, A., et al. 2019, MNRAS, 486, 4917 [Google Scholar]
- García-Bernete, I., González-Martín, O., Ramos Almeida, C., et al. 2022a, A&A, 667, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Bernete, I., Rigopoulou, D., Alonso-Herrero, A., et al. 2022b, MNRAS, 509, 4256 [Google Scholar]
- García-Burillo, S., Combes, F., Ramos Almeida, C., et al. 2016, ApJ, 823, L12 [Google Scholar]
- García-Burillo, S., Alonso-Herrero, A., Ramos Almeida, C., et al. 2021, A&A, 652, A98 [NASA ADS] [CrossRef] [Google Scholar]
- García-González, J., Alonso-Herrero, A., Hönig, S. F., et al. 2017, MNRAS, 470, 2578 [CrossRef] [Google Scholar]
- Gaskell, C. M., Goosmann, R. W., Antonucci, R. R. J., et al. 2004, ApJ, 616, 147 [NASA ADS] [CrossRef] [Google Scholar]
- González-Martín, O., Rodríguez-Espinosa, J. M., Díaz-Santos, T., et al. 2013, A&A, 553, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Martín, O., Masegosa, J., Márquez, I., et al. 2015, A&A, 578, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Martín, O., Masegosa, J., Hernán-Caballero, A., et al. 2017, ApJ, 841, 37 [Google Scholar]
- González-Martín, O., Masegosa, J., García-Bernete, I., et al. 2019a, ApJ, 884, 11 [Google Scholar]
- González-Martín, O., Masegosa, J., García-Bernete, I., et al. 2019b, ApJ, 884, 10 [Google Scholar]
- Granato, G. L., & Danese, L. 1994, MNRAS, 268, 235 [Google Scholar]
- GRAVITY Collaboration (Dexter, J., et al.) 2020, A&A, 635, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hao, L., Spoon, H. W. W., Sloan, G. C., et al. 2005, ApJ, 625, L75 [NASA ADS] [CrossRef] [Google Scholar]
- HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hönig, S. F. 2019, ApJ, 884, 171 [Google Scholar]
- Hönig, S. F., & Kishimoto, M. 2010, A&A, 523, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hönig, S. F., & Kishimoto, M. 2017, ApJ, 838, L20 [Google Scholar]
- Hönig, S. F., Beckert, T., Ohnaka, K., et al. 2006, A&A, 452, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hönig, S. F., Kishimoto, M., Gandhi, P., et al. 2010, A&A, 515, A23 [CrossRef] [EDP Sciences] [Google Scholar]
- Hönig, S. F., Kishimoto, M., Antonucci, R., et al. 2012, ApJ, 755, 149 [CrossRef] [Google Scholar]
- Isbell, J. W., Meisenheimer, K., Pott, J.-U., et al. 2022, A&A, 663, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kemper, F., Vriend, W. J., & Tielens, A. G. G. M. 2004, ApJ, 609, 826 [Google Scholar]
- Kishimoto, M., Hönig, S. F., Beckert, T., et al. 2007, A&A, 476, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kishimoto, M., Hönig, S. F., Antonucci, R., et al. 2011, A&A, 536, A78 [CrossRef] [EDP Sciences] [Google Scholar]
- Koss, M. J., Trakhtenbrot, B., Ricci, C., et al. 2022, ApJS, 261, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Krolik, J. H., & Begelman, M. C. 1986, ApJ, 308, L55 [CrossRef] [Google Scholar]
- Laor, A., & Draine, B. T. 1993, ApJ, 402, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Leftley, J. H., Tristram, K. R. W., Hönig, S. F., et al. 2018, ApJ, 862, 17 [Google Scholar]
- Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
- Li, M. P., Shi, Q. J., & Li, A. 2008, MNRAS, 391, L49 [Google Scholar]
- Lira, P., Videla, L., Wu, Y., et al. 2013, ApJ, 764, 159 [Google Scholar]
- López-Gonzaga, N., Burtscher, L., Tristram, K. R. W., et al. 2016, A&A, 591, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyu, J., & Rieke, G. H. 2021, ApJ, 912, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Lyu, J., Hao, L., & Li, A. 2014, ApJ, 792, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Marconi, A., & Oliva, E. 2001, A&A, 365, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manske, V., Henning, T., & Men’shchikov, A. B. 1998, A&A, 331, 52 [NASA ADS] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [Google Scholar]
- Martínez-Paredes, M., Aretxaga, I., Alonso-Herrero, A., et al. 2017, MNRAS, 468, 2 [Google Scholar]
- Martínez-Paredes, M., González-Martín, O., Esparza-Arredondo, D., et al. 2020, ApJ, 890, 152 [Google Scholar]
- Martínez-Paredes, M., González-Martín, O., HyeongHan, K., et al. 2021, ApJ, 922, 157 [CrossRef] [Google Scholar]
- Mason, R. E., Lopez-Rodriguez, E., Packham, C., et al. 2012, AJ, 144, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, R. E., Ramos Almeida, C., Levenson, N. A., et al. 2013, ApJ, 777, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S. 1990, ARA&A, 28, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Mishra, A., & Li, A. 2017, ApJ, 850, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Mor, R., & Netzer, H. 2012, MNRAS, 420, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Mor, R., Netzer, H., & Elitzur, M. 2009, ApJ, 705, 298 [Google Scholar]
- Nenkova, M., Ivezić, Ž., & Elitzur, M. 2002, ApJ, 570, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Nenkova, M., Sirocky, M. M., Ivezić, Ž., et al. 2008a, ApJ, 685, 147 [Google Scholar]
- Nenkova, M., Sirocky, M. M., Nikutta, R., et al. 2008b, ApJ, 685, 160 [Google Scholar]
- Nikutta, R., Elitzur, M., & Lacy, M. 2009, ApJ, 707, 1550 [Google Scholar]
- Nikutta, R., Lopez-Rodriguez, E., Ichikawa, K., et al. 2021a, ApJ, 923, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Nikutta, R., Lopez-Rodriguez, E., Ichikawa, K., et al. 2021b, ApJ, 919, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Oh, K., Koss, M., Markwardt, C. B., et al. 2018, ApJS, 235, 4 [Google Scholar]
- Oh, K., Koss, M. J., Ueda, Y., et al. 2022, ApJS, 261, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Orlandini, M., Frontera, F., Masetti, N., et al. 2012, ApJ, 748, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Osorio-Clavijo, N., González-Martín, O., Papadakis, I. E., et al. 2020, MNRAS, 491, 29 [Google Scholar]
- Packham, C., Radomski, J. T., Roche, P. F., et al. 2005, ApJ, 618, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Pasetto, A., González-Martín, O., Esparza-Arredondo, D., et al. 2019, ApJ, 872, 69 [Google Scholar]
- Pei, Y. C. 1992, ApJ, 395, 130 [Google Scholar]
- Pier, E. A., & Krolik, J. H. 1992, ApJ, 401, 99 [Google Scholar]
- Protassov, R., van Dyk, D. A., Connors, A., et al. 2002, ApJ, 571, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Radomski, J. T., Piña, R. K., Packham, C., et al. 2003, ApJ, 587, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., & Ricci, C. 2017, Nat. Astron., 1, 679 [Google Scholar]
- Ramos Almeida, C., Levenson, N. A., Rodríguez Espinosa, J. M., et al. 2009, ApJ, 702, 1127 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., Levenson, N. A., Alonso-Herrero, A., et al. 2011, ApJ, 731, 92 [Google Scholar]
- Ramos Almeida, C., Alonso-Herrero, A., Levenson, N. A., et al. 2014, MNRAS, 439, 3847 [Google Scholar]
- Roche, P. F., Aitken, D. K., Smith, C. H., et al. 1991, MNRAS, 248, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Roche, P. F., Packham, C., Telesco, C. M., et al. 2006, MNRAS, 367, 1689 [NASA ADS] [CrossRef] [Google Scholar]
- Rowan-Robinson, M. 1995, MNRAS, 272, 737 [NASA ADS] [Google Scholar]
- Sarangi, A., Dwek, E., & Kazanas, D. 2019, ApJ, 885, 126 [Google Scholar]
- Schartmann, M., Meisenheimer, K., Camenzind, M., et al. 2008, A&A, 482, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shao, Z., Jiang, B. W., & Li, A. 2017, ApJ, 840, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, Y., Rieke, G. H., Hines, D. C., et al. 2006, ApJ, 653, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Siebenmorgen, R. 2023, A&A, 670, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siebenmorgen, R., Heymann, F., & Efstathiou, A. 2015, A&A, 583, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, H. A., Li, A., Li, M. P., et al. 2010, ApJ, 716, 490 [Google Scholar]
- Srinivasan, S., Kemper, F., Zhou, Y., et al. 2017, Planet Space Sci., 149, 56 [CrossRef] [Google Scholar]
- Stalevski, M., Fritz, J., Baes, M., et al. 2012, MNRAS, 420, 2756 [NASA ADS] [CrossRef] [Google Scholar]
- Stalevski, M., Ricci, C., Ueda, Y., et al. 2016, MNRAS, 458, 2288 [Google Scholar]
- Stalevski, M., Asmus, D., & Tristram, K. R. W. 2017, MNRAS, 472, 3854 [NASA ADS] [CrossRef] [Google Scholar]
- Stalevski, M., Tristram, K. R. W., & Asmus, D. 2019, MNRAS, 484, 3334 [NASA ADS] [CrossRef] [Google Scholar]
- Sturm, E., Schweitzer, M., Lutz, D., et al. 2005, ApJ, 629, L21 [Google Scholar]
- Tazaki, R., & Ichikawa, K. 2020, ApJ, 892, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Tristram, K. R. W., Burtscher, L., Jaffe, W., et al. 2014, A&A, 563, A82 [CrossRef] [EDP Sciences] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Venanzi, M., Hönig, S., & Williamson, D. 2020, ApJ, 900, 174 [Google Scholar]
- Victoria-Ceballos, C., González-Martín, O., Fritz, J., et al. 2022, ApJ, 926, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, G. M. 1991, ApJ, 379, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K. 2015, ApJ, 812, 82 [Google Scholar]
- Wang, S., Li, A., & Jiang, B. W. 2015, ApJ, 811, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [Google Scholar]
- Williamson, D., Hönig, S., & Venanzi, M. 2020, ApJ, 897, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Xie, Y., Li, A., & Hao, L. 2017, ApJS, 228, 6 [Google Scholar]
Appendix A: Spectral fitting evaluation procedure
We use the χ2 statistics as the main mathematical support to infer if a model is able to reproduce an observed SED and to find the best-fit solution minimizing this statistic. The χ2 is formally written as:
where errori is the error bar associated with each spectral bin on the data. Note that this definition of χ2 is called 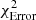 (since it uses the error on the spectrum) in order to distinguish it from the definition below where the errors are not involved. Under this definition, the best result should have an associated χ2 close to the degree of freedom (hereinafter dof). Thus, the reduced χ2 (
(since it uses the error on the spectrum) in order to distinguish it from the definition below where the errors are not involved. Under this definition, the best result should have an associated χ2 close to the degree of freedom (hereinafter dof). Thus, the reduced χ2 (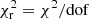 ) should be close to unity. Lower values of
) should be close to unity. Lower values of  might indicate that the model has too many free parameters (i.e., the model shows a complexity that is not required by the data) or that the errors are overestimated. Large values could also indicate that the errors are underestimated or that the data show a complexity that cannot be recovered by the model. Indeed, Spitzer spectra might show issues on the error bars due to a poor understanding of the uncertainties. To mitigate this issue, we also explore the following χ2 definition:
might indicate that the model has too many free parameters (i.e., the model shows a complexity that is not required by the data) or that the errors are overestimated. Large values could also indicate that the errors are underestimated or that the data show a complexity that cannot be recovered by the model. Indeed, Spitzer spectra might show issues on the error bars due to a poor understanding of the uncertainties. To mitigate this issue, we also explore the following χ2 definition:
which has no dependence on the error bars of the data. In contrast with the previous definition of χ2, 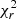 should approach zero to consider it as a good fit. We also use the Akaike information criterion (AIC) to compare the goodness of the fit of different models for a single AGN spectrum. This is a common method applied when different models (i.e., not nested) are compared (e.g., Emmanoulopoulos et al. 2016; Osorio-Clavijo et al. 2020; Esparza-Arredondo et al. 2021; Martínez-Paredes et al. 2021; García-Bernete et al. 2022b). This method allows an evaluation of the best fit by comparing the minimum
should approach zero to consider it as a good fit. We also use the Akaike information criterion (AIC) to compare the goodness of the fit of different models for a single AGN spectrum. This is a common method applied when different models (i.e., not nested) are compared (e.g., Emmanoulopoulos et al. 2016; Osorio-Clavijo et al. 2020; Esparza-Arredondo et al. 2021; Martínez-Paredes et al. 2021; García-Bernete et al. 2022b). This method allows an evaluation of the best fit by comparing the minimum 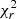 with any other model providing a statistically good fit to the data. In particular, we calculate the Bayes factor through the Akaike information criterion, AICc. To this end, we use the eq. 5 in Emmanoulopoulos et al. (2016):
with any other model providing a statistically good fit to the data. In particular, we calculate the Bayes factor through the Akaike information criterion, AICc. To this end, we use the eq. 5 in Emmanoulopoulos et al. (2016):
where CL is the constant likelihood of the true hypothetical model, k is number of model parameters, and N is the number of data points (where dof = N − k − 1). We then calculate the difference between two different models, Δ[AICc]
where model 1 is the model providing the best statistic (i.e., the minimum χ2). Finally, we estimate the evidence ratio, ϵ
The evidence ratio or Bayes factor is a measure of the relative likelihood of the best model versus another model. When the Bayes factor is ≤0.01, the best model is more likely to be the "correct" one because it is at least 100 times better than the second model. If > 0.01 we consider the second model as good as the first one.
In order to study if the fit improved by allowing one of the parameters to vary, we used the f-statistic test (f-test Barlow 1989). Particularly, we use this test to explore if the dust grain size parameter provides a statistically better fit to the data compared to the model without this parameter. The likelihood ratio test (LRT) statistic or the related F-statistic is designed to choose between two models, where one model (the null model) is a simple or more parsimonious version of the other model (Protassov et al. 2002). The F-statistic is computed as:
where dof2 < dof1 because the number of free parameters k1 is larger than k2 (with the same number of data points). We then compute the p-value associated with the F-statistic which is a measure of the probability that an observed difference could have occurred just by random chance. We consider that model 2 is needed when the p-value is p < 0.0001. Note that this method cannot be applied to multiplicative models (e.g., in our analysis of the need for foreground extinction Protassov et al. 2002) or for the inclusion of components affecting only a narrow range of the spectrum (e.g., the need of emission lines Orlandini et al. 2012). However, it is useful to test if allowing one parameter of the model to be varied is needed by the data, which is the main purpose in our analysis.
Appendix B: The role of foreground extinction into the final fits
As discussed in Section 6, the inclusion of foreground extinction has a strong impact on the results for some of the available models. Here we further explore this by comparing the obtained foreground extinction and the spectral shape properties in our sample (see Fig. B.1). This plot clearly shows that Nenkova08, Hoenig10, and Hoenig17 models statistically require the inclusion of the foreground in a large percentage of objects and it is less required by Fritz06, Stalev16, and GoMar23 (already quantified in Section 6). This is probably due to the inclusion of a smooth dust distribution for these latter models. When E(B-V) is constrained, the silicate strength is significantly correlated with E(B-V). Indeed, high absorption features require E(B-V)∼1, irrespective of the model used. This correlation is statistically significant (r > 0.5 and f-valuer < 10−4) for all but Fritz06 and Stalev16 models (probably due to the low number of objects with constrained E(B-V)). Therefore, foreground extinction is required to reproduce deep silicate absorption features. Interestingly, among the infrared slopes used in this paper, we also found a significant anticorrelation between the far-infrared slope and E(B-V) for Hoenig17 model (r = 0.6 and f−value = 2 × 106). Therefore, the inclusion of relatively large E(B-V) helps to reproduce steep (i.e., negative) FIR slopes with Hoenig17 model, which indeed is one of the main issues of this model when compared with data (see Fig. 4).
 |
Fig. B.1. Strength of the 9.7μm silicate feature (positive and negative values for emission and absorption features, respectively), α5.5 − 7.5μm, α7.5 − 14μm, and α25 − 30μm versus E(B-V) foreground extinction for model fitting. The gray arrow indicates E(B-V) upper limits and empty symbols are objects where foreground extinction is constrained but its inclusion is not statistically needed by the data. |
Although E(B-V) roughly shows the same range of values irrespective of the model used, we also find significant differences when we compare the resulting E(B-V) found when used in combination with the tested models. GoMar23 and Stalev16 models show fully consistent E(B-V) values. This is expected since Stalev16 is nested within GoMar23 model. Fritz06 model shows a factor of two lower values compared with GoMar23 model while Nenkova08, Hoenig10, and Hoenig17 systematically show at least a factor of two higher E(B-V) compared with GoMar23 model and the disagreement is larger for lower E(B-V) values.
Appendix C: Additional tables
Observational details of the sample of AGN observed by Spitzer, including spectral shape measurements (see text).
Best fit model and statistic before (Col. 2 & 3) and after (Col. 4 & 5) our new GoMar23 model is included into the analysis.
Resulting parameters when fitting the spectra of each object in the sample to GoMar23.
All Tables
Observational details of the sample of AGN observed by Spitzer, including spectral shape measurements (see text).
Best fit model and statistic before (Col. 2 & 3) and after (Col. 4 & 5) our new GoMar23 model is included into the analysis.
Resulting parameters when fitting the spectra of each object in the sample to GoMar23.
All Figures
 |
Fig. 1. Spectra of our sample of 68 AGN normalized to the flux at 14 μm. Type-1 and type-2 AGN are shown in black and gray, respectively. Vertical dot-dashed lines indicate the locus of the wavelengths chosen to compute the spectral slopes (see text). The bottom-right inset shows the distribution of X-ray luminosities versus redshift in our sample. |
| In the text | |
 |
Fig. 2. Schematic view of GoMar23 model (see text). |
| In the text | |
 |
Fig. 3. Shape of the 9.7 μm silicate feature in optical depth units for our AGN sample (see text, top-left). Black and gray lines show type-1 and type-2 AGN, respectively. Observational diagrams for the AGN sample: 7.5–14 μm versus 5.5–7.5 μm slopes (top-middle); 25–30 μm versus 7.5–14 μm slopes (top-right); S10 μm versus C10 μm (bottom-left), and S10 μm versus 5.5–7.5 μm slope (bottom-right). Black squares and gray diamonds show the measurements in the Spitzer spectra for type-1 and type-2 AGN, respectively. |
| In the text | |
 |
Fig. 4. Comparison between the spectral shapes of our AGN sample (black squares for type-1 AGN and gray diamonds for type-2 AGN) and the spectral shapes of the SED libraries. From left to right we show mid-infrared versus near-infrared slopes, far-infrared versus mid-infrared slopes, the 10 μm feature silicate strength versus its center, and the 10 μm feature silicate strength versus the near-infrared slope. From top to bottom we show the results for GoMar23 (purple), Fritz06 (blue), Nenkova08 (green), Hoenig10 (red), Stalev16 (magenta), and Hoenig17 (orange) models. Note that the tabulated values of the center of the silicate emission feature C10 μm in some of the models (e.g., Fritz06 or GoMar23 models) are an artifact of the spectral resolution used for to generate each SED library. |
| In the text | |
 |
Fig. 5. Resulting diagrams for the GoMar23 model when the maximum grain size of the dust particles is explored (colored area) compared with the overall space parameter (empty area). From left to right the areas show the locus of SEDs for Psize = 0.01μm (⟨P⟩ = 0.007 μm, blue), Psize = 0.25 μm (⟨P⟩ = 0.097 μm, purple), Psize = 1.0 μm (⟨P⟩ = 0.36 μm, pink), and Psize = 10.0 μm (⟨P⟩ = 3.41 μm, violet). From top to bottom: α5.5 − 7.5 μm versus α7.5 − 14 μm, α25 − 30 μm versus α7.5 − 14 μm, and S10 μm versus α5.5 − 7.5 μm. Black squares and gray diamonds show the locus for type-1 AGN and type-2 AGN, respectively. |
| In the text | |
 |
Fig. 6. Resulting diagrams for the GoMar23 model when the following parameters vary (from left to right): the viewing angle, the half opening angle, the ratio between the outer and the inner radius, the optical extinction at the equator, and the radial distribution of the dust. From top to bottom: α5.5 − 7.5 μm versus α7.5 − 14 μm, α25 − 30 μm versus α7.5 − 14 μm, and S10 μm versus α5.5 − 7.5 μm. The gray contour shows the result for the entire SED library. The blue, purple, and pink areas show the locus of SEDs for the minimum, medium, and maximum values of the parameter, respectively (see legend in the top panels). The results for the maximum grain size are shown in Fig. 5. We skip the results for the polar density distribution of the dust since no differences are found. |
| In the text | |
 |
Fig. 7. Spectral fits obtained for the type-1 AGN IZw1. The black line and gray shaded areas show the Spitzer spectrum and its error bars, respectively. The red and green lines show the best SED for each model with and without foreground extinction, respectively (see text). The top panel shows the spectral fit and the bottom panel shows the residuals. The inset within the top panel shows zoom-in to the 7–14 μm wavelength range associated with the 9.7 μm silicate feature. Reduced χ2 is given at the bottom-right corner of the top panel (error/model), including the degree of freedom within brackets (red and green for the SED with and without foreground extinction). Above each panel, we show the resulting parameters for each model when foreground extinction is included. |
| In the text | |
 |
Fig. 8. Reduced χ2 using the errors in the χ2 definition (χ2(error)/d.o.f., see Eq. (A.1)), versus that using the model in the χ2 definition (χ2(model)/d.o.f., see Eq. (A.2)). Filled and empty symbols show the values when foreground extinction is included and neglected in the spectral fitting procedure, respectively. The dot-dashed line shows the locus expected if both measurements agree with each other. The continuous lines show a factor of five of agreement between both χ2 definitions. An object located in the blank area shows complexity not well fitted by the model. The dashed area shows the locus when the model is too complex for the data (χ2/d.o.f. < 0.5). The dark-gray shaded area shows the locus where both reduced χ2 indicate that the model provides a statistically acceptable fit (i.e., χ2/d.o.f.(error) < 2 and χ2/d.o.f.(model) < 1.5 × 10−3). The light-gray shaded area shows the region where the object is expected to locate if the error bars of the spectra are overestimated and underestimated although the spectral fit is good. Each panel shows the results for one of the models. We show the percentage of good spectral fits per model, considering those objects in the gray areas (the result without foreground extinction is shown next to it). The percentage of objects statistically requesting foreground extinction (FG extinct.) is shown in the top-left corner of each figure. |
| In the text | |
 |
Fig. 9. Panels a and b show the percentage of object best fitted with each of the models tested before (panel a) and after (panel b) the inclusion of GoMar23 model. The inner (squared-filled) and outer (circle-filled) pie charts show the results without and with foreground extinction in the spectral fits, respectively. Panel c shows the final percentage of objects best fitted to each model when including statistically similar fits using AIC probability (see text). The square-filled and circle-filled areas show the results without and with foreground extinction in the spectral fits, respectively. |
| In the text | |
 |
Fig. 10. Comparison of |
| In the text | |
 |
Fig. 11. Convergence of χ2 for each parameter of GoMar23 model for IZw1. Squares show the value of χ2 at the given values of the parameters sampled in GoMar23 grid (continuous line linearly links these black squares). Dashed lines show the internal interpolation performed by XSPEC. Green and red squares and lines report the results before and after the foreground extinction is included in the spectral fit procedure. The best value for each parameter is shown above the upper-left corner of each panel (when including foreground extinction). The top-left panel shows the resulting χ2/d.o.f.(sigma) in the upper-left corner. The percentage of variation of χ2 compared to the minimum value is shown above the upper-right corner of each panel. The horizontal blue dot-dashed line in the third-column lower panel shows the χ2 computed when the grain size is fixed to 0.25 μm. Note in this panel for Psize we also include the f-test probability that the grain size is consistent with 0.25 μm (see text). This panel also shows the x-axis expressed in terms of the average grain size in light-gray colors. |
| In the text | |
 |
Fig. 12. Rows 1 and 3 show in purple the histograms of the resulting parameters for the AGN sample when using GoMar23 model. We use the same bins as those used for the SED grid. Rows 2 and 4 show the histogram of the relative importance of each parameter in the convergence of the fit. It is obtained as the maximal variation of χ2 for each parameter range compared to the parameter giving the maximum variation, denoted as Δχ2 (see Fig. 11). Each panel also shows the percentage of objects with Δχ2 above 5 and 95%. |
| In the text | |
 |
Fig. 13. Effect of the maximum grain size on the spectral fit. We use as examples the type-1 AGN IZw1. The first row shows the best spectral fit using GoMar23 model (black continuous line). We also show the fit to three fixed maximum grain size Psize of 0.01 μm (⟨P⟩ = 0.007 μm, green), 0.25 μm (⟨P⟩ = 0.097 μm, blue), and 10 μm (⟨P⟩ = 3.41 μm, red), while other parameters are kept as those obtained from the best fit. The two insets in these top panels show the set of SEDs with the same parameters and varying the maximum grain size Psize from 0.01 μm (⟨P⟩ = 0.007 μm, green) to 10 μm (⟨P⟩ = 3.41 μm, red). Note that in these insets the SEDs are normalized at 15 μm. Bottom panels show the residuals of the best fit (black) and those using dust maximum grain size Psize of 0.01 μm (⟨P⟩ = 0.007 μm, green), 0.25 μm (⟨P⟩ = 0.097 μm, blue), and 10 μm (⟨P⟩ = 3.41 μm, red). |
| In the text | |
 |
Fig. 14. Effect of the maximum grain size on the diagrams of spectral shapes for the type-2 AGN PKS 2356-61. It shows the locus of the SEDs computed using the best-fit parameters and varying the maximum grain size Psize from 0.01 to 10 μm (i.e., ⟨P⟩ from 0.007 to 3.41 μm). The spectral shape diagrams are Silicate depth versus α5.5 − 7.5 μm (left panels), α7.5 − 14 μm versus α5.5 − 7.5 μm slopes (middle panels), and α25 − 30 μm versus α7.5 − 14 μm (right panels). The empty-filled distribution is that from the entire SED library for GoMar23 model. Green small dots correspond to smaller grain sizes and redder and larger dots correspond to larger grain sizes (linked with lines). We mark as a blue dot the locus of the resulting values for the SEDs with Psize = 0.25 μm (⟨P⟩ = 0.097 μm) and as a yellow star the locus of the resulting values for the best fitted SED. The type-1 AGN are marked as black squares and type-2 AGN as gray diamonds. |
| In the text | |
 |
Fig. B.1. Strength of the 9.7μm silicate feature (positive and negative values for emission and absorption features, respectively), α5.5 − 7.5μm, α7.5 − 14μm, and α25 − 30μm versus E(B-V) foreground extinction for model fitting. The gray arrow indicates E(B-V) upper limits and empty symbols are objects where foreground extinction is constrained but its inclusion is not statistically needed by the data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



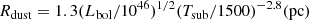
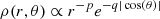
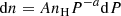
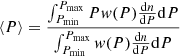
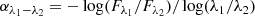
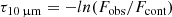
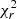
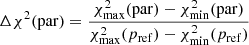
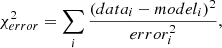
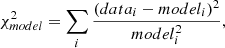
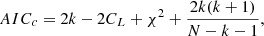
![$$ \begin{aligned} \Delta [AIC_{c}] = AIC_{c,2} - AIC_{c,1} ,\end{aligned} $$](/articles/aa/full_html/2023/08/aa45858-23/aa45858-23-eq39.gif)
![$$ \begin{aligned} \epsilon = e^-\frac{\Delta [AIC_{c}]}{2} .\end{aligned} $$](/articles/aa/full_html/2023/08/aa45858-23/aa45858-23-eq40.gif)