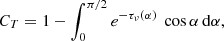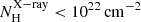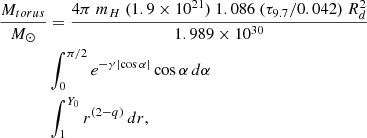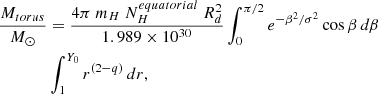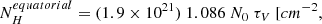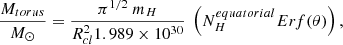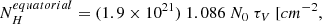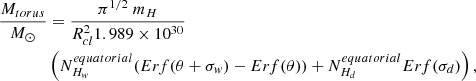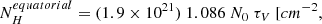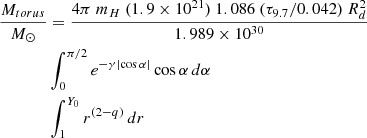| Issue |
A&A
Volume 667, November 2022
|
|
|---|---|---|
| Article Number | A140 | |
| Number of page(s) | 43 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202244230 | |
| Published online | 18 November 2022 | |
Torus and polar dust dependence on active galactic nucleus properties
1
Department of Physics, University of Oxford, Keble Road, Oxford OX1 3RH, UK
e-mail: igbernete@gmail.com
2
Instituto de Radioastronomía and Astrofśica (IRyA-UNAM), 3-72 (Xangari), 8701 Morelia, Mexico
3
Instituto de Astrofísica de Canarias, Calle Vía Láctea, s/n, 38205 La Laguna, Tenerife, Spain
4
Departamento de Astrofśica, Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
5
Centro de Astrobiología (CAB), CSIC-INTA, Camino Bajo del Castillo s/n, 28692 Villanueva de la Cañada, Madrid, Spain
6
Korea Astronomy and Space Science Institute 776, Daedeokdae-ro, Yuseong-gu, Daejeon 34055, Republic of Korea
7
Centre for Extragalactic Astronomy, Durham University, South Road, Durham DH1 3LE, UK
8
Kavli Institute for Particle Astrophysics and Cosmology (KIPAC), Stanford University, Stanford, CA 94305, USA
Received:
9
June
2022
Accepted:
5
October
2022
We present a statistical analysis of the properties of the obscuring material around active galactic nuclei (AGN). This study represents the first of its kind for an ultra-hard X-ray (14–195 keV; Swift/BAT), volume-limited (DL < 40 Mpc) sample of 24 Seyfert (Sy) galaxies (BCS40 sample) using high angular resolution infrared data and various torus models: smooth, clumpy, and two-phase torus models and clumpy disc+wind models. We find that torus models (i.e. without including the polar dusty wind component) and disc+wind models provide the best fits for a comparable number of galaxies, 8 out of 24 (33.3%) and 9 out of 24 (37.5%), respectively. We find that the best-fit models depend on the hydrogen column density (NHX−ray), which is related to the X-ray (unobscured or obscured) and optical (Sy1/Sy2) classification. In particular, smooth, clumpy, and two-phase torus models are best at reproducing the infrared (IR) emission of AGN with relatively high hydrogen column density (median value of log (NHX−ray cm−2) = 23.5 ± 0.8; i.e. Sy2). However, clumpy disc+wind models provide the best fits to the nuclear IR spectral energy distributions (SEDs) of Sy1/1.8/1.9 (median value of log (NHX−ray cm−2) = 21.0 ± 1.0) – specifically, in the near-infrared (NIR) range. The success of the disc+wind models in fitting the NIR emission of Sy1 galaxies is due to the combination of adding large graphite grains to the dust composition and self-obscuration effects caused by the wind at intermediate inclinations. In general, we find that the Seyfert galaxies having unfavourable (favourable) conditions, namely, nuclear hydrogen column density and Eddington ratio, for launching IR dusty polar outflows are best-fitted with smooth, clumpy, and two-phase torus (disc+wind) models, confirming the predictions from simulations. Therefore, our results indicate that the nature of the inner dusty structure in AGN depends on the intrinsic AGN properties.
Key words: galaxies: active / galaxies: Seyfert / techniques: high angular resolution / infrared: galaxies
© I. García-Bernete et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Active galactic nuclei (AGN) are powered by accretion of material onto supermassive black holes (SMBHs), which releases energy in the form of radiation and mechanical outflows to the interstellar medium (ISM) of the host galaxy. The impact of the energy released by AGN in its surrounding environment has been proposed as a key mechanism responsible for regulating star formation in galaxies (Hopkins & Quataert 2010). Although they comprise a relatively small fraction of the galaxies in the local universe (∼10%), AGN are now considered to be a short phase (< 100 Myr; e.g., Hopkins et al. 2005) that might take place throughout all galaxies (e.g., Hickox et al. 2014).
Nearby Seyfert (Sy) galaxies are intermediate luminosity AGN which are close enough (∼tens of Mpc) to study their nuclear emission and characterize the properties of the nuclear obscurer on ∼100 pc scales (at the average angular resolution of 8-10 m-class ground-based telescopes ∼0.3″ at 10 μm). The dusty torus1 (disc) is the key piece of the AGN unified model (Antonucci 1993). Depending on its orientation, it obscures the central engines of type 2 AGN and provides a direct view of the central engine in the case of type 1 AGN. This nuclear dust absorbs a significant part of the AGN radiation and then reprocesses it to emerge in the infrared (IR; e.g., Pier & Krolik 1992).
Early works using direct imaging and interferometric data have found a relatively compact torus (∼0.1–10 pc) in the mid-IR (MIR; ∼5–30 μm; e.g., Jaffe et al. 2004; Packham et al. 2005; Tristram et al. 2007, 2009, 2014; Radomski et al. 2008; Burtscher et al. 2009, 2013; Raban et al. 2009; López-Gonzaga et al. 2016; Leftley et al. 2018). Recently, Atacama Large Millimeter/submillimeter Array (ALMA) observations of the cold dust in Seyfert galaxies have spatially resolved the submillimetre counterpart of the torus (e.g., Gallimore et al. 2016; García-Burillo et al. 2016, 2021; Imanishi et al. 2018; Impellizzeri et al. 2019). García-Burillo et al. (2021) found that the bulk of the nuclear cold dust emission in Sy galaxies is equatorial, with a median diameter of ∼42 pc. These dusty molecular tori have been also detected in molecular gas observations of Seyfert galaxies and low-luminosity AGN (e.g., Alonso-Herrero et al. 2018, 2019, 2021; Combes et al. 2019; García-Burillo et al. 2021). These results suggest a multi-phase nature for the torus structure.
Due to the small angular size of the dusty and molecular tori, specially in the IR, 8–10 m-class ground-based telescopes cannot resolve it. Thus, comparing torus models to the observed nuclear IR spectral energy distributions (SEDs) is a powerful tool for constraining the properties of the nuclear dusty structure. Torus models can be broadly grouped in two categories: dynamical (i.e. radiation hydrodynamical and magneto-hydrodynamical simulations; e.g., Wada & Norman 2002; Schartmann et al. 2008; Wada 2012; Dorodnitsyn & Kallman 2017; Kudoh et al. 2020; Takasao et al. 2022) and static (i.e. radiative transfer models; e.g., Pier & Krolik 1992; Efstathiou & Rowan-Robinson 1995; Fritz et al. 2006; Nenkova et al. 2008a,b; Hönig & Kishimoto 2010, 2017; Stalevski et al. 2012, 2016; Siebenmorgen et al. 2015). The dynamical models include processes such as supernova and AGN feedback. However, they require large computational times and thus it is more difficult to compare them with observations. On the other hand, static torus models can be easily compared with the observations, assuming various geometries and compositions of the dust (see Ramos & Ricci 2017; Hönig 2019 for reviews).
For the sake of simplicity, the first geometrical torus models assumed a uniform distribution of the dust (e.g., Pier & Krolik 1992; Fritz et al. 2006). However, pioneering works have shown that a clumpy distribution of the dust is necessary to prevent the destruction of grains (Krolik & Begelman 1988). Therefore, a clumpy formalism has been employed in the majority of torus models (e.g., Nenkova et al. 2008a,b; Hönig & Kishimoto 2010, 2017). Moreover, several hydrodynamical simulations predict that the torus is a multiphase structure (e.g., Wada & Norman 2002; Schartmann et al. 2014), with a combination of smooth and clumpy dust distributions (i.e. two-phase torus models; e.g., Stalevski et al. 2012, 2016; Siebenmorgen et al. 2015).
Since the first torus models were developed, our view of the dusty torus has changed considerably. For instance, recent observations using IR interferometry have motivated the search for a more complex scenario to explain the IR nuclear emission of Seyfert galaxies. Hönig et al. (2013) suggested that a significant fraction of the MIR emission is produced by dust located in the polar direction, whereas the near-infrared (NIR) flux is produced by a clumpy and compact disc (i.e. the dusty torus). Thus, some of the geometrical torus models also include a polar dust component (e.g., Hönig & Kishimoto 2017; hereafter, clumpy disc+wind models). This polar emission has been detected on a small scale (i.e. a few pc) so far in 6 sources of the 23 observed using IR interferometry (López-Gonzaga et al. 2016; Leftley et al. 2018; Gámez et al. 2022; Isbell et al. 2022). In addition, previous works also showed a large scale polar dust component (up to few hundred parsec; e.g., Bock et al. 2000; Radomski et al. 2003; Packham et al. 2005; Asmus et al. 2014; Asmus 2019; Alonso-Herrero et al. 2021).
Although the nuclear dust properties of nearby Seyfert galaxies have been extensively studied in the literature, only a few works have compared SED fits with different torus models to investigate which of them better reproduces the SED of Seyfert galaxies (e.g., González-Martín et al. 2019a,b; hereafter, GM19A,19B; Esparza-Arredondo et al. 2019, 2021) and type-1 QSOs (Martínez-Paredes et al. 2021). Given the different assumptions used to build the various available torus models, it is crucial to compare how they fit the observational data. Using Spitzer/IRS spectra (∼5–35 μm), GM19B found that the clumpy disc+wind models (Hönig & Kishimoto 2017) reproduce well the MIR emission of Sy1, whereas Sy2 are almost equally fitted by clumpy torus models (Nenkova et al. 2008a,b; ∼43% of the Sy2s) or clumpy disc+wind models (∼40% of the Sy2s). However, this study was limited by the spatial resolution (∼4″) and spectral coverage (5–30 μm) of Spitzer/IRS. Furthermore, Ramos Almeida et al. (2014) reported that the minimum combination of subarcsecond angular resolution data needed to constrain torus model parameters is N-band spectroscopy (8–13 μm) and NIR photometry (at least two data-points) when using the clumpy torus models by Nenkova et al. (2008a,b). However, there is a lack of detailed studies comparing different torus models to high angular resolution NIR-to-MIR data of Sy galaxies.
In this work, we investigate, for the first time, how various geometrical torus models (i.e. smooth, clumpy, two-phase) and disc+wind models fit the nuclear IR (∼1–30 μm) SED of the ultra-hard X-ray volume-limited sample of Sy galaxies (BCS40 sample) presented in García-Bernete et al. (2016). This approach allows us to improve our understanding of the geometry, chemical composition, and grain sizes and distribution of the nuclear dust. In addition, this will help in testing the validity of the various torus models.
The paper is organized as follows. Section 2 describes the sample selection. Section 3 gives a summary of the models used throughout this paper. The nuclear IR SED modelling is presented in Sect. 4. The main results are included in Sect. 5 and discussed in Sect. 6. Finally, in Sect. 7, we summarize the main conclusions of this work.
2. Sample selection
Our sample consists of 24 Seyfert galaxies selected from the nine-month catalogue (Tueller et al. 2008) observed with Swift/BAT. This sample was previously presented in García-Bernete et al. (2016) (hereafter, BAT Complete Seyfert sample at DL < 40 Mpc, BCS40 sample). The ultra-hard 14–195 keV band used to select the parent sample is far less sensitive to the effects of obscuration than optical or softer X-ray wavelengths, making this AGN selection one of the least biased for NH < 1024 cm−2 to date (see e.g., Winter et al. 2009, 2010; Weaver et al. 2010; Ichikawa et al. 2012; Ricci et al. 2015; Ueda et al. 2015). We selected all the Seyfert galaxies in the nine-month catalogue with luminosity distances DL < 40 Mpc. We used this distance limit to ensure a resolution element of ≤50 pc in the MIR, considering the average angular resolution of 8–10 m class ground-based telescopes (∼0.3″ at 10 μm). The sample contains eight Sy1 (Sy1, Sy1.2 and Sy1.5), six Sy1.8/1.9, and ten Sy2 galaxies. This sample covers an AGN luminosity range log(Lbol erg s−1) ∼ 41.75–44.752 and X-ray hydrogen column densities of 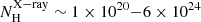 cm−2. We note that we used bolometric luminosities derived by using the commonly employed bolometric correction of 20 (Lbol = 20 × L2 − 10 keV; e.g., Vasudevan & Fabian 2009) at the 2–10 keV luminosities listed in Table 1. The main properties of the BCS40 sample are shown in Table 1.
cm−2. We note that we used bolometric luminosities derived by using the commonly employed bolometric correction of 20 (Lbol = 20 × L2 − 10 keV; e.g., Vasudevan & Fabian 2009) at the 2–10 keV luminosities listed in Table 1. The main properties of the BCS40 sample are shown in Table 1.
Main properties of the BCS40 sample.
3. Torus models
We chose six models comprising different dust compositions, distributions and geometries (see also González-Martín et al. 2019a and references therein). In Fig. 1, we summarize the dust geometries and compositions, sublimation temperatures, and main parameters of each model used in this work. We also present a brief description of the models below.
 |
Fig. 1. Scheme showing the different dust geometries and compositions of the various torus models used in this work. See Appendix A for further details on the individual model parameters. Note that the clumpy disc H17D models are not represented in this figure. However, the latter models consist of clumpy disc component of the clumpy disc+wind H17 models. (a) Smooth F06 torus models, (b) Clumpy N08 torus models, (c) Clumpy H10 torus models, (d) Two-phase S16 torus models, (e) Clumpy disk+wind H17 models. |
3.1. Smooth F06 torus models
The smooth torus models by Fritz et al. (2006, hereafter, smooth F06 torus models) used a simple toroidal geometry, consisting of a flared disc represented as two concentric spheres having the polar cones removed. These two spheres delimit the inner and the outer torus radius, respectively. For the composition of dust the model considered a standard Galactic mix of 53% silicates and 47% graphite. The silicate and graphite grains have radii of ag = 0.025–0.25 and ag = 0.005–0.25 μm, respectively. The parameters of the model are the viewing angle toward the torus, i, the half opening angle of the torus, σ, the exponent of the logarithmic azimuthal and radial density distribution, γ and β, respectively, the ratio between external and internal radii, Y = Ro/Rd, and the edge-on optical depth at 9.7 μm, τ9.7,μm (see Table A.1).
3.2. Clumpy N08 torus models
The clumpy torus models by Nenkova et al. (2008a,b, hereafter, clumpy N08 torus models) used a formalism that accounts for the concentration of dust in clouds, forming a torus-like structure. They assumed spherical dust grains and a standard Galactic mix of 53% silicates and 47% graphite. The parameters of the model are: the view angle toward the torus, i, the number of clouds, N0, the half opening angle of the torus, σ, the ratio between external and internal radii, Y = Ro/Rd, the slope of the radial density distribution, q, and the optical depth of the individual clouds, τν (see Table A.2).
3.3. Clumpy H10 torus models
The clumpy toroidal models by Hönig & Kishimoto (2010; see also Hönig et al. 2006, 2010, hereafter, clumpy H10 torus models) are radiative transfer models of three-dimensional clumpy dust tori using optically thick dust clouds and a low torus volume filling factor. The majority of the models use a standard ISM dust mixture of graphite (47%) and silicate (53%) dust grains with a classical MRN size distribution (Mathis et al. 1977) and a maximum size of 0.25 μm. By contrast, clumpy H10 torus models also include ISM-like large grains with sizes between 0.1 and 1.0 μm (i.e. using the same graphite/silicate mixture) and a population of graphite dominated grains (high refractory material), with 70% fraction of graphites (30% silicates) and maximum sizes of 0.25 μm. The parameters of this library of SEDs are: the viewing angle i, the number of clouds along an equatorial line-of-sight, N0, the half-opening angle of the distribution of clouds, θ, the radial dust-cloud distribution power law index a, and the opacity of the clouds, τcl. The outer torus radius, Ro, is fixed to the inner radius as Ro = 150 Rd (see Table A.3).
3.4. Two-phase S16 torus models
The two-phase torus models by Stalevski et al. (2016, hereafter, two-phase S16 torus models) used a torus geometry with a two-phase dusty medium, consisting of high-density clumps embedded in a smooth dusty component of low density. The dust chemical composition is set to a mixture of silicate and graphite grains. Model parameters are: the viewing angle toward the observer, i, the ratio between the outer and the inner radius of the torus, Y = Ro/Rd, the half opening angle of the torus, σ, the indices that set dust density gradient with the radial p and polar q distribution of dust, and the 9.7 μm average edge-on optical depth, τ9.7μm (see Table A.4).
3.5. Clumpy disc+wind H17 models
The clumpy disc and outflow models by Hönig & Kishimoto (2017, hereafter, clumpy disc+wind H17 models) consist of a clumpy disc plus a polar outflow. The authors used the same dust composition as in the clumpy H10 torus models, but they also included a second population of large pure-graphite grains (0.75–1.0 μm) which are more resilient than small silicates in hard environments (see e.g., Waxman & Draine 2000; Perna et al. 2003; Schartmann et al. 2008; Lu et al. 2016; Almeyda et al. 2017; García-González et al. 2017; Hönig & Kishimoto 2017). The parameters for this model are the viewing angle, i, and the number of clouds in the equatorial plane, N0, the exponent of the radial distribution of clouds in the disc, a, the optical depth of individual clouds in the disc, τcl (fixed to 50), the index of the dust cloud distribution power-law along the wind, aw, the half-opening angle of the wind, θ, the angular width of the hollow wind cone, σ, and the wind-to-disc ratio, fwd (defines the ratio between the number of clouds along the cone and N0; see Table A.5). We note that this model assumes a fixed cloud radius (Rcl = 0.035 × rsub).
3.6. Clumpy disc H17D models
The clumpy disc models by Hönig & Kishimoto (2017, hereafter, clumpy disc H17D models) consist of clumpy disc component of the previously described clumpy disc+wind H17 models (i.e. removing the wind component). Thus, the authors used the same dust grain composition and dust sublimation formalism as in the clumpy disc+wind H17 models (see text above and Table A.5). Note that we include this model to further investigate the impact of the pure-graphite polar dust component on the fits (see Sect. 6.3).
It is worth noting that the main differences between the various models employed in this study are: a) nuclear dust geometry (i.e. torus, disc+wind), b) dust distribution (i.e. smooth, clumpy or two-phase), and c) dust composition and the treatment of the sublimation temperature of the dust grains. In particular, clumpy disc+wind H17 models are significantly different from the other torus models described above, both in the dust geometry and composition (see Sect. 3). Hönig & Kishimoto (2017) proposed that a polar dusty outflow is launched near the dust sublimation zone and thus the polar dust composition should be similar to the dust in the inner regions of the disc (see Hönig & Kishimoto 2017; Isbell et al. 2021). Therefore, they only included a population of large pure-graphite grains in the polar dust component assuming that it is swept-up dust from the inner wall of the torus (disc) where silicate grains are destroyed by the intense emission from the AGN. In contrast, they included both silicate and graphite grains in the torus (disc) component. To account for the different dust compositions, Hönig & Kishimoto (2017) used a physically motivated dust sublimation model considering that larger grains are heated less efficiently than smaller grains. This leads to various grain radial layers (species and sizes), where large graphite grains are hotter and closer to the AGN (e.g., Schartmann et al. 2008). We note that this sublimation temperature treatment is not taken into account in the other torus models considered here (e.g., Nenkova et al. 2008a,b; Hönig & Kishimoto 2010; Stalevski et al. 2016), although the smooth F06 torus models use different sublimation temperatures (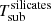 = 1000 K and
= 1000 K and 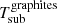 = 1500 K). We note that for simplicity throughout this work we will use the term ’torus models’ to refer to the smooth, clumpy and two-phase torus models (i.e. those models that do not include the dusty polar component).
= 1500 K). We note that for simplicity throughout this work we will use the term ’torus models’ to refer to the smooth, clumpy and two-phase torus models (i.e. those models that do not include the dusty polar component).
4. SED fitting with torus models
4.1. Accretion disc contribution
The subarcsecond resolution NIR fluxes of type 2 AGN are dominated by emission from hot AGN-heated dust with very little or no contribution from the accretion disc. However, another contribution to the NIR emission can be stellar emission from the host galaxy. To separate (as much as possible) the nuclear NIR emission from the stellar emission the highest possible spatial resolution is required (see e.g., Alonso-Herrero et al. 1998, 2003). Then, we assume that the flux contained in the scaled PSF (i.e. scaled PSF-star to the peak of the galaxy emission at different percentages; e.g., García-Bernete et al. 2015, 2016, 2019, and references therein) corresponds to the unresolved component and it is practically uncontaminated by star formation.
In the case of type 1 AGN, the NIR emission is mainly produced by very hot dust and the direct emission from the accretion disc of the AGN (see e.g., Hernán-Caballero et al. 2016, García-Bernete et al. 2019; hereafter GB19, Landt et al. 2019 and references therein). To quantify the contribution from the accretion disc to the nuclear NIR emission, we followed the same procedure described in Hernán-Caballero et al. (2016) using a semi-empirical model consisting of a template for the accretion disc and two blackbodies to fit the optical and NIR emission of each galaxy individually (see GB19). In GB19 we found that the accretion disc contribution to the nuclear IR SEDs (∼0.4 arcsec) of Sy1s was, on average, 46 ± 28, 23 ± 13, and 11 ± 5% in the J, H, and K bands, respectively. Therefore, we subtracted the accretion disc component in the NIR range of each source prior to fitting the nuclear IR SEDs with the various torus models (see GB19 for further details).
4.2. SED fitting procedure
Using the torus models described in Sect. 3 and XSPEC (Arnaud 1996), which is a command-driven and interactive spectral-fitting program within the HEASOFT3 software, we fit all the nuclear NIR-to-MIR SEDs of our sample of Seyfert galaxies. This tool provides an easy way to incorporate new models using additive tables4 together with a wide range of tools to perform spectral fittings to the data.
To construct high angular resolution NIR-to-MIR SEDs for the whole sample, we compiled the highest angular resolution IR (∼1–30 μm) nuclear fluxes available from the literature. The published MIR photometry and N-band spectroscopy (7.5–13 μm) used in this work was obtained with 8–10 m-class ground-based telescopes and different instruments (e.g., Gran Telescopio CANARIAS/CanariCam, Very Large Telescope/VISIR, Gemini/T-ReCS and MICHELLE). The nuclear NIR fluxes are from both ground- and space-based (i.e. Hubble Space Telescope) data (see Table 2 of GB19). In this work, we used the nuclear IR SEDs as in GB19 (see e.g., Fig. 2 and Appendix A). We converted the N-band spectra and IR photometric data into XSPEC format using the FLX2XSP task within HEASOFT.
 |
Fig. 2. Example of the nuclear IR SED of NGC 3227 fitted with the clumpy disc+wind H17 models (top panel) and its residuals (bottom panel). The grey diamonds correspond to the high angular resolution photometric points. The black arrows represent low angular resolution data, which are treated as upper limits. Black crosses correspond to the high angular resolution N-band spectrum. The solid blue line is the best-fitted model. |
We masked those regions containing narrow spectral features, the 11.3 μm feature attributed to polycyclic aromatic hydrocarbon molecules (PAHs), and [S IV]λ10.5 μm and [Ne II]λ12.8 μm emission lines, to reveal the IR continuum. Note that other weak emission lines are not masked, since they do not affect the fit and that the other PAH emission bands are relatively weak in this sample. Previous studies also showed the importance of including an IR extinction law for fitting the IR SED of Sy galaxies (e.g., Ramos Almeida et al. 2011, hereafter RA11; Alonso-Herrero et al. 2011, hereafter AH11; Ramos Almeida et al. 2014; GB19). This is especially important for sources with very deep silicate features which generally show prominent dust lanes or are hosted in highly inclined galaxies (e.g., AH11; González-Martín et al. 2013). To do so, we use the IR extinction curve of Pei (1992), which is already included as a multiplicative component within XSPEC.
High spatial resolution N-band spectroscopy provides information on the silicate feature around 9.7 μm which is important for the restriction of the model parameters (see e.g., Martínez-Paredes et al. 2020). However, including spectral and photometric data in the fit is not a straightforward task from the statistical point of view. The χ2 statistic method takes every point into account equally so the best fit would tend to match the N-band spectral region over the photometric points. To avoid this, we performed the spectral fitting in two steps. We first fit the photometric data and low spectral resolution N-band spectrum (LR fit). The LR spectra were computed to match the average bandpass of the photometric data. Then, we computed the 3σ errors for each parameter, which we used as priors for the SED fitting using the full resolution N-band spectra (HR fit). We note that the same methodology was used in Martínez-Paredes et al. (2021) for a sample of QSOs.
We compute the χ2 statistics for both the LR and HR fits. We consider the fit to be acceptable if the reduced χ2 (for both HR and LR; see e.g., GM19A,GM19B) is 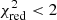 . Among the fits, the best one provides a minimum
. Among the fits, the best one provides a minimum 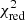 and we consider two fits equally good if
and we consider two fits equally good if 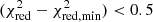 . In Appendix A, we present the results of the nuclear IR SED fitting process with the various torus models (see Sect. 3). Tables A.6–A.8 show the results for Sy1, Sy1.8/1.9, and Sy2 galaxies.
. In Appendix A, we present the results of the nuclear IR SED fitting process with the various torus models (see Sect. 3). Tables A.6–A.8 show the results for Sy1, Sy1.8/1.9, and Sy2 galaxies.
To further evaluate the goodness of the fits, we used two methods. First, we used a qualitative method for performing a visual inspection of the residuals. To do so, we constructed the average residuals using the entire N-band spectra and IR photometry, but excluding the upper limits (i.e. lower angular resolution data). For consistency, we used the same wavelength grid for all photometry (1.6, 2.2, 5.5, 18.0, 25.0, and 30 μm) employing a quadratic interpolation of nearby values for each galaxy. Secondly, we used the Akaike information criterion (AIC). This method allows for an evaluation of the best fit by comparing the minimum 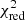 with comparably good fits, such that (
with comparably good fits, such that (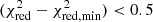 ). To determine the best fit to the data, we compared the Akaike weights (Emmanoulopoulos et al. 2016) of the models providing acceptable fits (ϵ = Wmodel1/Wmodel2). We assume that we have found the best fit when ϵ < 0.01, which means that a given fit is (at least) ten times better than other good fits (see e.g., Martínez-Paredes et al. 2021). Finally, to investigate whether the goodness of the fit depends on the Seyfert type and other AGN properties, we used Fisher’s exact test5 that is commonly employed for testing for the independence (see Sect. 5.1). In Table 2, we present the best (and comparably good) fits to the LR and HR SEDs, which are practically the same. Therefore in the following, we only discuss the HR results.
). To determine the best fit to the data, we compared the Akaike weights (Emmanoulopoulos et al. 2016) of the models providing acceptable fits (ϵ = Wmodel1/Wmodel2). We assume that we have found the best fit when ϵ < 0.01, which means that a given fit is (at least) ten times better than other good fits (see e.g., Martínez-Paredes et al. 2021). Finally, to investigate whether the goodness of the fit depends on the Seyfert type and other AGN properties, we used Fisher’s exact test5 that is commonly employed for testing for the independence (see Sect. 5.1). In Table 2, we present the best (and comparably good) fits to the LR and HR SEDs, which are practically the same. Therefore in the following, we only discuss the HR results.
Summary of models producing the best fit for each galaxy.
5. Comparison of the various torus models
5.1. Best model fits
5.1.1. Average fitting residuals
To determine which are the best suited models for reproducing the entire nuclear NIR-to-MIR SED of the various Sy groups, we first use a qualitative analysis of the average residuals of the spectral fitting. Figure 3 presents these average residuals of our sample for each of the models considered in this work (see Sect. 3). The average residuals are computed by grouping the various Seyfert types: from left to right panels of Fig. 3 are Sy1, Sy1.8/1.9, Sy2, and the full sample. From a visual inspection of Fig. 3, the average residuals of Sy1/1.8/1.9 indicate a clear excess at NIR emission for smooth, clumpy, and two-phase torus models (i.e. torus models). This NIR excess was first reported by Neugebauer et al. (1979) using a sample of quasars and confirmed by Edelson & Malkan (1986) in Seyfert galaxies. The clumpy disc H17D models generally produce slightly smaller residuals in the IR emission of Sy1 galaxies than other torus models used in this work. However, the models including the polar dust component produce the flattest residuals in the NIR for the entire sample (see Fig. 3).
 |
Fig. 3. Average residuals (units as in Fig. 2) of the spectral fitting for each torus model used in this work. Blue, green, red, and black stars (and solid lines) correspond to Sy1, Sy1.8/1.9, Sy2, and the full sample, respectively. The regions masked in the fitting process are highlighted in beige vertical lines. |
The N-band spectra are equally well-fitted with most of the models, except for the clumpy N08 torus models and two-phase S16 torus models in the 8–10 μm range. However, this can be in part due to contamination from the 7.7 μm PAH band. On the other hand, the clumpy H10 torus models, clumpy disc+wind H17 models and clumpy disc H17D models show flatter average fitting residuals for the N-band spectra than the other models. Furthermore, the 18–30 μm range is generally well reproduced by the various torus models, with the only exception of the smooth F06 torus models, which slightly over-predicts the emission above 20 μm. Therefore, the clumpy disc+wind H17 models produce the best fits in the entire NIR-to-MIR range of the Sy1 galaxies in our sample.
5.1.2. Quantitative methods
In general, all models provide acceptable fits (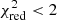 ) to the majority (19 out of 24) of the nuclear IR SEDs (see Appendix A). Using the AIC method (see Sect. 4.2), we find that the fraction of best fits provided by clumpy disc+wind and torus models is similar, 37.5 and 33.3% (i.e. 9 out of 24 and 8 out of 24 sources), respectively. Furthermore, 2 out of 24 galaxies (8.3%) are equally fitted by clumpy disc+wind or torus models and 5 out of 24 are not well fitted by any of the models used in this work (see Table 2). According to the best fits, the IR SEDs of Sy1 (and Sy1.8 and 1.9) galaxies are best reproduced by clumpy disc+wind H17 models, whereas torus models are best suited to Sy2 galaxies (see Table 3). Using Fisher’s exact test we find that these differences are statistically significant.
) to the majority (19 out of 24) of the nuclear IR SEDs (see Appendix A). Using the AIC method (see Sect. 4.2), we find that the fraction of best fits provided by clumpy disc+wind and torus models is similar, 37.5 and 33.3% (i.e. 9 out of 24 and 8 out of 24 sources), respectively. Furthermore, 2 out of 24 galaxies (8.3%) are equally fitted by clumpy disc+wind or torus models and 5 out of 24 are not well fitted by any of the models used in this work (see Table 2). According to the best fits, the IR SEDs of Sy1 (and Sy1.8 and 1.9) galaxies are best reproduced by clumpy disc+wind H17 models, whereas torus models are best suited to Sy2 galaxies (see Table 3). Using Fisher’s exact test we find that these differences are statistically significant.
Summary of the Fisher’s exact test results.
The difference in the results for Sy1 and Sy2 galaxies confirms the trend first reported by GM19B using lower spatial resolution Spitzer/IRS MIR spectra of a sample of AGN. However, in this work we confirm them using, for the first time, an ultra-hard X-ray selected sample of Seyferts and high-spatial resolution NIR-to-MIR data that allow us to better isolate the nuclear emission. Moreover, we do not find a clear trend between the models producing the best fits and AGN luminosity or Eddington ratio (see left and central panels of Fig. 4). However, the right panel of Fig. 4 shows that it depends on the line-of-sight hydrogen column density.
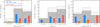 |
Fig. 4. Best fit distributions of the BCS40 sample per bolometric luminosity (left panel), Eddington ratio (central panel), and hydrogen column density (right panel) bin. The grey hatched and filled histograms are the distribution of unfitted and fitted sources. The blue and red filled histograms correspond to sources best fitted by clumpy disc+wind H17 models and torus models, respectively. The orange filled histograms are sources that have been equally fitted by clumpy disc+wind H17 models and torus models. |
In particular, clumpy disc+wind H17 models better reproduce the IR emission of AGN with relatively low hydrogen column densities (median value of log (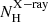 cm−2) = 21.0 ± 1.0; i.e. Sy1 and Sy1.8/1.9 galaxies) than torus models. On the other hand, torus models better reproduce the SEDs of AGN with high X-ray hydrogen column densities (median value of log (
cm−2) = 21.0 ± 1.0; i.e. Sy1 and Sy1.8/1.9 galaxies) than torus models. On the other hand, torus models better reproduce the SEDs of AGN with high X-ray hydrogen column densities (median value of log (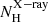 cm−2) = 23.5 ± 0.8; i.e. Sy2s). This is in good agreement with theoretical predictions reported by Venanzi et al. (2020), where the authors found that for nuclear column densities of log(NH cm−2) < 23 the IR radiation pressure becomes effective and polar outflows start to emerge (see also AH21).
cm−2) = 23.5 ± 0.8; i.e. Sy2s). This is in good agreement with theoretical predictions reported by Venanzi et al. (2020), where the authors found that for nuclear column densities of log(NH cm−2) < 23 the IR radiation pressure becomes effective and polar outflows start to emerge (see also AH21).
5.2. Torus model parameters
In this section, we investigate the main differences between the derived torus model parameters for the BCS 40 sample using, for the first time, high angular resolution data and various models (see Sect. 3). We note that we find similar fits using clumpy disc H17D and clumpy H10 torus models. Therefore, in the following, we do not discuss the individual parameters of clumpy disc H17D models.
A general trend is seen indicating that even for acceptable fits (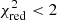 ), the model parameters are not well constrained (see Tables A.6, A.7, and A.8). This result is independent of the torus model, Seyfert type, X-ray absorption along the line of sight or AGN luminosity. Nevertheless, rather than looking at the individual fits (see Appendix A), we focus on the global statistics of the torus model parameters. For this purpose, we derived the combined probability distributions by concatenating together the individual arrays of the parameter probability distributions for all objects in each subgroup (see e.g., GB19). To quantify the differences between the combined probability distributions, we use the Kullback-Leibler divergence (KLD; Kullback & Leibler 1951). This approach takes into account the overall shape of the combined distribution which always has a positive value. The larger the value the greater the difference of the distribution. This value is equal to zero for the case of two identical distributions. RA11 suggested that for values larger than 1 (boldface in Tables B.1–B.5), two combined distributions may be considered to be significantly different.
), the model parameters are not well constrained (see Tables A.6, A.7, and A.8). This result is independent of the torus model, Seyfert type, X-ray absorption along the line of sight or AGN luminosity. Nevertheless, rather than looking at the individual fits (see Appendix A), we focus on the global statistics of the torus model parameters. For this purpose, we derived the combined probability distributions by concatenating together the individual arrays of the parameter probability distributions for all objects in each subgroup (see e.g., GB19). To quantify the differences between the combined probability distributions, we use the Kullback-Leibler divergence (KLD; Kullback & Leibler 1951). This approach takes into account the overall shape of the combined distribution which always has a positive value. The larger the value the greater the difference of the distribution. This value is equal to zero for the case of two identical distributions. RA11 suggested that for values larger than 1 (boldface in Tables B.1–B.5), two combined distributions may be considered to be significantly different.
Only a few model parameters can be directly compared between the various torus models, for example, the torus (disc) inclination angle and its width. According to the KLD test, the differences in the torus (disc) inclination angle between Sy subgroups are significant for the smooth F06 torus models, the clumpy H10 torus models and the clumpy disc+wind H17 models (see Fig. 5). In general, more edge-on values of the torus (disc) inclination are needed for Sy2s than Sy1s. In particular, clumpy disc+wind H17 model results show the following trend for the disc inclination: iSy1 < iSy1.8/1.9 < iSy2. The differences in the angular width of the torus (disc) between Sy subgroups are also significant for the various models (see Fig. 6 and Appendix B). In general, the angular widths of the torus of Sy2 galaxies are larger than those of Sy1s (see Fig. 6). The only exception is found for the two-phase S16 torus models, which require a larger angular width of the torus for Sy1/1.8/1.9 than for Sy2 galaxies. In addition, for the clumpy disc+wind H17 models, there are no statistically significant differences between the angular width of Sy1 and Sy2 discs. This is likely related with the fact that clumpy disc+wind H17 models have relatively “thin” discs and, thus, it would be difficult to find differences between Sy1 and Sy2 discs. Summarizing, our results indicate that generally Sy1 galaxies have tori with smaller angular width and more face-on values of the torus inclination than those of type 2 Seyferts.
 |
Fig. 5. Comparison between the torus (disc) inclination combined probability distributions for different models considered here. Blue dotted, green dashed, red solid, and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. We note that 90-iF06 = iN08 = iH10 = iS16 = iH17. |
 |
Fig. 6. Comparison between the torus (disc) angular width combined probability distributions for different models considered here. Blue dotted, green dashed, red solid, and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. We note that σH10 = 90-θH10. In the case of the clumpy disc+wind H17 models, the h parameter is the scale height of the dusty disc. |
5.3. Derived torus covering factor, size, and mass
5.3.1. Covering factor of the nuclear obscuring material
The nuclear obscuration is strongly dependent on the covering factor (CT) which is defined as the fraction of sky covered by the obscuring material. The covering factor is one of the main elements regulating the intensity of the reprocessed AGN radiation (e.g., RA11, Ramos & Ricci 2017).
For the various models, CT can be calculated as:
where τν(α) is the line-of-sight optical depth, which depends on the azimuthal angle (α). The line-of-sight optical depth is computed from the distribution of clouds for clumpy torus models and from the equatorial opacity, and from the density distribution for smooth torus models (see GM19B and references therein).
Since the covering factor is defined as the fraction of the sky at the AGN centre covered by obscuring material, it strongly depends on the torus dust distribution and geometry assumed by the model (see Fig. 7; also GM19B). To further investigate the differences between the various models, we produced the CT combined probability distributions of the models sampling the entire space of parameters of each model. For example, the clumpy+wind H17 model consists of a clumpy dusty disc plus a hollow dusty cone which will naturally produce lower values of the covering factor (CT < 0.6; see yellow distribution in left panel of Fig. 7) than a dusty torus with a large range of angular sizes. On the other hand, the two-phase S16 torus models provide large values of the covering factor (CT > 0.6; see red dot distribution in the left panel of Fig. 7). Therefore, caution must be taken when comparing covering factors between various torus models due to the different ranges of parameter space.
 |
Fig. 7. Comparison between the covering factor parameter space. Left panel: combined probability distributions for all the models used in this work. Right panel: combined probability distributions derived for the entire Sy sample using each model. |
In order to compare the CT probability distributions of the models with those of the observations, we also derived the CT combined probability distributions (for each model) by concatenating the individual CT probability distributions of the various galaxies. Indeed, we find that the CT combined probability distributions of the models and those derived for the entire sample are similar (Fig. 7). For instance, small values of the CT are derived for the fitted data when using clumpy+wind H17 models whereas clumpy H10, clumpy N08 and two-phase S16 models require larger CT. However, the CT distributions derived for clumpy+wind H17 models tend to have smaller values than the parent distribution. The same applies for the smooth F06 models, whereas the derived CT distributions for clumpy N08 models favour intermediates CT values compared with those of the models which peak at larger values. Considering the different CT ranges covered by the various models, in the following, we have consistently used the same models when comparing covering factors of the Sy groups.
Figure 8 shows that generally Sy1 have smaller median values of the covering factor than Sy2. According to the KLD test, there are statistically significant differences in the covering factor of Sy1 and Sy2 for the smooth F06 torus models and the clumpy H17 disc+wind models (see Appendix B). There is a similar trend, but with less significant (using the KLD test), for the clumpy N08 torus models (see e.g., RA11, AH11, Ichikawa et al. 2015 and GB19). Earlier works using clumpy N08 torus models also showed statistically significant differences between the covering factor of Sy1 and Sy2 galaxies (e.g., RA11, AH11, Ichikawa et al. 2015 and GB19). The lower significance found here might be due to the fact that we are not using priors for the angular width of the torus (based on [O III] data), unlike previous works.
 |
Fig. 8. Comparison between the covering factor combined probability distributions for different models considered here. Blue dotted, green dashed, red solid, and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. |
Finally, we find that the covering factor remains broadly constant within the errors for the majority of the models throughout the luminosity range: log(Lbol erg s−1) ∼ 41.8–45.9. The same applies when using Eddington ratios (λEdd: −3.40 to −0.26) instead of the bolometric luminosity.
5.3.2. Torus (disc) size and mass
Using the radial extent of the torus (disc), Y = Ro/Rd, and the dust sublimation radius, Rd, we can derive the physical radius of the torus (disc), Ro. The dust sublimation radius also depends on the dust sublimation temperature and the bolometric luminosity. We note that the clumpy H10 torus models and clumpy+disc H17 models fixed the Y parameter to a large value for all the SEDs (Y = 150 and Y = 500, respectively).
The radius distributions of Sy2 for the smooth F06 torus models and the two-phase S16 models show a tail towards larger tori in comparison with those of Sy1 (see Fig. 9). In particular, in the case of the smooth F06 torus models, we derived median values of the torus size for Sy2 galaxies larger (∼3–5 times) than those of Sy1 and Sy1.8/1.9. We note that using the smooth F06 torus models the radius probability distribution for Sy2 galaxies reaches maximum values of ∼30 pc. However, the clumpy N08 torus models do not show statistically significant differences between Sy1 and Sy2 radii. In general, we find relatively compact (1–15 pc) torus radii for all the Seyfert galaxies in our sample (see Fig. 9). We note that we use the term compact torus for those with sizes below the largest resolution element in the MIR for our sample (i.e. < 50 pc).
 |
Fig. 9. Comparison between the torus size (Rout) combined probability distributions for different models considered here. Blue dotted, green dashed, red solid, and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. |
Using the Galactic dust-to-gas ratio (Bohlin et al. 1978), we can also estimate the torus gas mass associated with the fitted nuclear dusty structure by integrating the density distribution function for each model (see Appendix C, see also GM19B and references therein). We computed the torus mass within the fitted dusty structure volume, thus, it may not be representative of the whole torus gas mass distribution which is traced by the cold gas (see e.g., Hönig 2019 and Sect. 6.2 for further discussion). We find slightly larger values of the torus (disc) gas mass for Sy2 than for Sy1 galaxies, but their differences are generally within the errors (see Fig. 10). The total gas masses of the tori are in the range log(Mtorus) ∼ 2–6 M⊙ and the majority of the models used in this work provide similar values of the total gas mass within the errors (median values of log(Mtorus) ∼ 4 M⊙). The exceptions are the smooth F06 torus (log(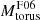 ) = 5.6 ± 1.9 M⊙) and disc+wind H17 models (log(
) = 5.6 ± 1.9 M⊙) and disc+wind H17 models (log(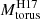 ) = 2.6 ± 0.8 M⊙), for which we find larger gas masses and smaller masses respectively than for the other torus models.
) = 2.6 ± 0.8 M⊙), for which we find larger gas masses and smaller masses respectively than for the other torus models.
 |
Fig. 10. Comparison between the torus gas mass combined probability distributions for different models considered here. Blue dotted, green dashed, red solid, and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. |
The derived dusty torus (disc) sizes (∼1–15 pc) are similar to those found using MIR imaging and interferometric data (r < 10 pc; see Sect. 6.2 for further discussion). However, they are generally smaller than those observed in cold dust by ALMA (∼42 pc; García-Burillo et al. 2021), indicating that larger values of the of the radial extent of the torus (disc), Y, than those covered by the models are needed to match the torus sizes measured in ALMA submillimetre observations at Sy-like luminosities. Indeed, we found larger torus sizes (∼1–34 pc) for the clumpy+disc H17 models that use a large value of the radial extent (fixed value of Y = 500)6. Thus, we compare the fitted values of Y with the range covered by the models. The left panel of Fig. 11 shows that the three models compared here do not favour the largest values of Y.
 |
Fig. 11. Luminosity dependence of the radial extent of the torus/disc (Y = Ro/Rd; left panels) and of the torus (disc) radius (right panels). From top to bottom panels the result for the various models with free Y parameter used in this work (see text for details). The first three bins correspond to the Sy galaxies of BCS40 sample. We note that we also include two additional bins of a sample of QSOs with higher bolometric luminosities from Martínez-Paredes et al. (2021). |
Finally, we also investigate the relation between the bolometric luminosity and the torus (disc) size dividing our sample into several luminosity bins (see Fig. 11). In the first bin, we included the three sources with log(Lbol erg s−1) < 42.75, while the rest of the sample was divided into two bins of equal logarithmic width (1 dex). We note that we also include data from QSOs (i.e. two additional bins from Martínez-Paredes et al. 2021) to expand the range of luminosities beyond our original Sy sample. These authors used the same methodology as here to fit the high angular resolution NIR-to-MIR SEDs of a sample of type 1 QSOs with log(Lbol erg s−1) ∼ 44.2–45.9. Therefore, these two bins do not include type 2 AGN. All these models show the same trend throughout the entire luminosity range (log(Lbol erg s−1) ∼ 41.8–45.9): the higher the luminosity the larger the size (see right panel of Fig. 11). The same applies when using the BH mass instead of the bolometric luminosity. However, we do not find a clear dependence of Y for higher luminosities (see left panel of Fig. 11).
On the other hand, the torus (disc) size depends on the Y parameter and dust sublimation radius (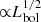 ). Therefore, to further investigate the relationship of the torus size with the luminosity, we compare our results with the expected torus sizes at a given bolometric luminosity and Y parameter (dashed grey lines in right panel of Fig. 11). Considering the almost constant Y values (within the errors) for each luminosity bin and model in the left panel of Fig. 11, the torus size–luminosity correlations might be caused (at least in part) by the sublimation radius dependence with the bolometric luminosity. Futhermore, we find that the derived torus (disc) masses also depend on the bolometric luminosities, as expected, given the relation between the torus size and luminosity.
). Therefore, to further investigate the relationship of the torus size with the luminosity, we compare our results with the expected torus sizes at a given bolometric luminosity and Y parameter (dashed grey lines in right panel of Fig. 11). Considering the almost constant Y values (within the errors) for each luminosity bin and model in the left panel of Fig. 11, the torus size–luminosity correlations might be caused (at least in part) by the sublimation radius dependence with the bolometric luminosity. Futhermore, we find that the derived torus (disc) masses also depend on the bolometric luminosities, as expected, given the relation between the torus size and luminosity.
6. Discussion
6.1. The covering factor
It has been suggested that the bolometric luminosity (e.g., Lawrence 1991; Simpson 2005) and Eddington ratio (e.g., Buchner & Bauer 2017; Ricci et al. 2017a) may be the key parameters determining the covering factor. However, according to our results, we do not find a clear dependence of the torus model covering factor with the bolometric luminosity (or the Eddington ratio; see also GB19), although the ranges probed by our sample are relatively reduced (log(Lbol erg s−1) ∼4 1.8–45.9; λEdd: −3.40 to −0.26). This lack of dependence was also reported by Mateos et al. (2016, 2017), Netzer et al. (2016), Stalevski et al. (2016), Lani et al. (2017), Ichikawa et al. (2019); GM19B and GB19. Regarding the covering factor, we find that Sy2 galaxies generally have larger values of the covering factor (and angular width of the torus) than Sy1s, for the majority of the models used. This was first reported by RA11 (see also e.g., AH11, Ichikawa et al. 2015 and GB19) but using clumpy N08 torus models only.
Using high-spatial resolution NIR-to-MIR data of an ultra-hard X-ray selected sample of Seyferts, this work confirms that the covering factor of Sy1 and Sy2 galaxies are different. Therefore, our findings indicate that the Seyfert type classification depends not only on the dusty structure inclination but also on the intrinsic differences (e.g., covering factor) of type-1 and type-2 AGN.
6.2. Mid-IR versus submillimetre torus observations
As shown in Sect. 5.3.2, we find differences on the outer radius of the torus with the AGN type and luminosity, although they depend on the torus models used. In this section, we further explore these parameters by comparing the torus (disc) size and mass derived from the fitted nuclear IR SED with those measured from IR and submillimetre data (i.e. VLT/SINFONI, NOEMA, and ALMA). For all the models, we derive relatively compact dusty torus (disc) sizes (∼1–15 pc). This is in agreement with the torus sizes reported in previous works using the clumpy N08 torus models (see e.g., Ramos Almeida et al. 2009; RA11; AH11; Lira et al. 2013; Ichikawa et al. 2015; Fuller et al. 2016; GB19). The derived torus sizes in this work are of the same order of magnitude as those upper-limit sizes derived from MIR observations. For example, using MIR direct imaging, Packham et al. (2005) and Radomski et al. (2008) found that the MIR size of the torus is less than ∼4 pc (diameter) for Circinus and Centaurus A. Furthermore, modelled MIR interferometric data (e.g., Jaffe et al. 2004; Tristram et al. 2007, 2009; Burtscher et al. 2009, 2013; Raban et al. 2009; López-Gonzaga et al. 2016) also show a relatively compact torus of r < 10 pc. However, recent works using ALMA submillimetre observations of low-luminosity AGN and Seyfert galaxies measure large molecular discs with physical scales (diameters) ranging from 10 to 130 pc, with a typical value of 42 pc (e.g., Alonso-Herrero et al. 2018, 2019, 2021; Combes et al. 2019; García-Burillo et al. 2021). The larger sizes measured in the submillimetre compared to those inferred from IR observations are expected since submillimetre sizes correspond to the colder and, thus, more external material within the torus (e.g., Lopez-Rodriguez et al. 2018; Hönig 2019; Alonso-Herrero et al. 2021; Nikutta et al. 2021a,b).
ALMA observations made possible to estimate the molecular gas masses of nearby Seyferts (including a large fraction of the galaxies in this work) and low-luminosity AGN, in the range 105–107 M⊙ (see e.g., Alonso-Herrero et al. 2018, 2020; Combes et al. 2019; García-Burillo et al. 2021). Using the H2 1-0S(1) emission line at 2.12 μm of a sample of Sy galaxies, Hicks et al. (2009) derived the torus (disc) gas masses within the inner 30 pc (radius): 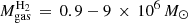 . As expected, the torus masses derived from the fitted nuclear IR SED are relatively lower (∼102–106 M⊙) than those derived from high angular resolution submillimetre data due to the different inferred IR sizes of the torus and those measured in the submillimetre. Therefore, our result is consistent with a temperature-driven stratified disc (torus), where the inner radius is dominated by the hot and warm dust emitting at NIR and MIR wavelengths – while the submillimetre observations trace a more extended (and more massive) colder component (see also García-Burillo et al. 2021).
. As expected, the torus masses derived from the fitted nuclear IR SED are relatively lower (∼102–106 M⊙) than those derived from high angular resolution submillimetre data due to the different inferred IR sizes of the torus and those measured in the submillimetre. Therefore, our result is consistent with a temperature-driven stratified disc (torus), where the inner radius is dominated by the hot and warm dust emitting at NIR and MIR wavelengths – while the submillimetre observations trace a more extended (and more massive) colder component (see also García-Burillo et al. 2021).
6.3. Torus dust composition and geometry
Our findings indicate that torus models are better at reproducing the NIR-to-MIR emission of AGN with relatively high hydrogen column density (i.e. Sy2s), whereas those of Sy1/Sy1.8/1.9 (with low hydrogen column density) are best fitted by the disc+wind H17 model (see Sect. 4). We also showed that the disc+wind dust models improve the spectral fit toward the NIR emission for Sy1/1.8/1.9 galaxies (see also García-González et al. 2017; González-Martín et al. 2019b; Isbell et al. 2021; Martínez-Paredes et al. 2021).
The origin of the NIR bump in the SED remains unclear. Direct emission from the accretion disc of the AGN might be an important contribution of the NIR emission for Sy1 galaxies (e.g., Hernán-Caballero et al. 2016, GB19, Landt et al. 2019 and references therein), but in this work we have remove it from their SEDs. An alternative explanation for the observed NIR excess in Sy1s is an extra contribution of a hot pure-graphite component (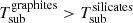 ) heated by the AGN and located in the inner regions of torus (Mor et al. 2009). García-Bernete et al. (2017) found a tight correlation between the hard X-ray fluxes (Nuclear Spectroscopic Telescope Array; NuSTAR) and the NIR emission of a sample of 24 unobscured type 1 AGN, suggesting that the observed NIR bump is produced by AGN-heated hot dust (
) heated by the AGN and located in the inner regions of torus (Mor et al. 2009). García-Bernete et al. (2017) found a tight correlation between the hard X-ray fluxes (Nuclear Spectroscopic Telescope Array; NuSTAR) and the NIR emission of a sample of 24 unobscured type 1 AGN, suggesting that the observed NIR bump is produced by AGN-heated hot dust (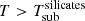 ).
).
Clumpy disc+wind H17 models predict that the included polar dust (ranging from few pc to tens of pc) mainly contributes to the MIR and submillimetre emission. However, the clumpy disc+wind H17 models also include very hot dusty clouds close to the AGN that can reach T ∼ 1900 K (pure-graphite dust; i.e. 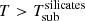 ) whose emission peaks at NIR wavelengths. Thus, in Sect. 4 we tested if the NIR bump can be explained by including graphite grains. To do so, we repeated the fitting process using only the SEDs of the clumpy disc component of these models (clumpy H17D disc models). The fits have slightly smaller residuals in the NIR range of Sy1 galaxies than other torus models (see Fig. 3). This might be related, at least in part, to the addition of large graphite grains in the dust composition of the disc.
) whose emission peaks at NIR wavelengths. Thus, in Sect. 4 we tested if the NIR bump can be explained by including graphite grains. To do so, we repeated the fitting process using only the SEDs of the clumpy disc component of these models (clumpy H17D disc models). The fits have slightly smaller residuals in the NIR range of Sy1 galaxies than other torus models (see Fig. 3). This might be related, at least in part, to the addition of large graphite grains in the dust composition of the disc.
Therefore, it is important to include large pure-graphite grains that are able to survive at high temperatures, along with physically motivated dust sublimation models for reproducing, at least in part, the nuclear IR emission of Sy1s. However, the clumpy flared disc from H17D models still produce larger NIR residuals than those of the models including the polar dust component (i.e. clumpy disc+wind H17 models). We also note that torus models (i.e. without including the polar dusty wind component) can produce NIR and MIR model images with emission strongly elongated in the polar directions for certain torus parameters (e.g., Lopez-Rodriguez et al. 2018; Nikutta et al. 2021a,b, and references therein). However, Nikutta et al. (2021a,b) found that the observed elongations in IR interferometric data of Seyfert galaxies are difficult to reproduce with a single component torus model (see also Stalevski et al. 2017).
6.4. A clumpy disc+wind versus clumpy disc IR emission
To further investigate how including the polar dust component modifies the predicted IR emission, we compared the SEDs of the clumpy disc+wind H17 models with those of the clumpy disc H17D models. We defined two representative set of parameters for Sy1 and Sy2 based on the average values found for each subgroup (see Appendix B). Using the combined probability distributions of the clumpy disc+wind H17 models, we find centrally peaked wind components (i.e. 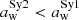 ) for Sy2 and less extended disc components (i.e. aSy1 < aSy2) for Sy1 galaxies (see Fig. 12 and Appendix B). Therefore, we selected representative SEDs for Sy1 and Sy2 galaxies using different cloud radial distributions for the disc and the wind, but keeping the other parameters to the same values (N = 7, h = 0.20, fwd = 0.6, θ = 45° and σ = 10°; see Table A.5 and corresponding Appendix A for a description of the model parameters). In particular, we used two configurations of the radial distributions of the clouds: a) Sy1 configuration with a centrally peaked disc (a = −2.5) and an extended wind (aw = −1.0); and b) Sy2 configuration with a relatively extended disc (a = −1.0) and a centrally peaked wind (aw = −2.0).
) for Sy2 and less extended disc components (i.e. aSy1 < aSy2) for Sy1 galaxies (see Fig. 12 and Appendix B). Therefore, we selected representative SEDs for Sy1 and Sy2 galaxies using different cloud radial distributions for the disc and the wind, but keeping the other parameters to the same values (N = 7, h = 0.20, fwd = 0.6, θ = 45° and σ = 10°; see Table A.5 and corresponding Appendix A for a description of the model parameters). In particular, we used two configurations of the radial distributions of the clouds: a) Sy1 configuration with a centrally peaked disc (a = −2.5) and an extended wind (aw = −1.0); and b) Sy2 configuration with a relatively extended disc (a = −1.0) and a centrally peaked wind (aw = −2.0).
 |
Fig. 12. Comparison between the clumpy disc+wind H17 model parameters combined probability distributions for the optical classification: for the radial dust-cloud distribution power law index (a) shown in the left panel and for the dust-cloud distribution power law along the wind (aw) in the right panel. Blue dot-dashed, green dashed, and red solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, and Sy2 galaxies, respectively. |
Fig. 13 shows the clumpy disc+wind H17 model SEDs (blue solid lines) of the Sy1 and Sy2 configurations for inclinations of 0, 45 and 90° (i.e. face-on, intermediate inclination and edge-on), and the clumpy disc H17D model SEDs (orange dashed lines) using the same parameters7. The SEDs for the Sy2 configuration are practically identical regardless of the addition of the polar dust component (see right panels of Fig. 13), except at intermediate inclinations (i.e. 45°) in the NIR and MIR where the self-obscuration of the inner wall of the dusty structure produced by the cone walls is expected to be relevant (see some of the MIR model images presented by Alonso-Herrero et al. 2021). The SEDs of disc+wind H17 models are significantly different from those of the clumpy disc H17D models for the Sy1 configuration (see left panels of Fig. 13). The far-IR and submillimetre emission of the Sy1 configuration is strongly enhanced by the extra polar dust component. In addition, the torus angular width can play an important role on the self-obscuration of the inner walls. Furthermore, extra self-obscuration takes place by including a dusty wind component. We find that the strong impact of the self-obscuration from the dusty cone takes place in the NIR and MIR range, especially at intermediate inclinations. The polar dust cone walls can produce moderate self-obscuration up to ∼10 μm at all inclinations (see left panels of Fig. 13; see also Alonso-Herrero et al. 2021). However, the polar dust does not produce strong self-obscuration effects at long wavelengths (> 20 μm). Thus, the polar-dust component has a negligible impact in the spectral fit for Sy2 nuclei whereas it produces an enhancement of emission at far-IR and submillimetre wavelengths and an extra self-obscuration at NIR and MIR wavelengths for Sy1 nuclei. This is key to explain the better performance of the disc+wind model for Sy1 nuclei.
 |
Fig. 13. Clumpy disc+wind H17 (blue solid lines) and clumpy disc H17 (orange dashed lines) model SEDs (normalized at 20 μm). Left panel: Sy1 configuration, which consists of a concentrated disc (a = −2.5) and an extended wind (aw = −1.0). Right panel: Sy2 configuration, which consists of a relatively extended disc (a = −1.0) and a concentrated wind (aw = −2.0). From top to bottom panels: Face-on, intermediate (45°), and edge-on values of the inclination angle for the clumpy disc and disc+wind dusty structure. We note that all the models use N = 7, and the clumpy disc+wind H17 models use fwd = 0.6, θ = 45° and σ = 10° (see main text for further details on the parameters of the models). |
6.5. Dependence of the best–fitted model with the AGN properties
Recently, Venanzi et al. (2020) presented a semi-analytical model to investigate the simulation of radiatively accelerated dusty winds launched by the AGN. In this model, the primary mass reservoir for the outflow is the material within the dusty disc. Their simulations show that the wind and its orientation (polar vs. equatorial) depend on the Eddington ratio, AGN luminosity, and nuclear column density. At relatively high column densities (NH > 1023 cm−2), the gravity strongly dominates and all the orbits are confined in a compact thick toroidal structure (i.e. the uplift of dusty material is suppressed) for representative values of Sy-like Eddington ratios. At lower values of the column density (NH < 1023 cm−2), their model predicted that IR dusty outflows can take place above a certain Eddington ratio. From the observational point of view, Alonso-Herrero et al. (2021) found that 7 out of 12 Sy galaxies showed Eddington ratios and nuclear 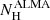 favourable for the launching of the dusty winds, unlike the remaining five galaxies.
favourable for the launching of the dusty winds, unlike the remaining five galaxies.
Figure 14 shows the line-of-sight (LOS) hydrogen column density measured at X-rays (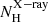 ) versus the Eddington ratios for our sample. The black dashed line represents the blowout limit predicted by Fabian et al. (2008). The orange solid line is the limit for producing IR dusty outflows derived by Venanzi et al. (2020) (assuming LAGN = 2.2 × 1043 erg s−1). We note that we used
) versus the Eddington ratios for our sample. The black dashed line represents the blowout limit predicted by Fabian et al. (2008). The orange solid line is the limit for producing IR dusty outflows derived by Venanzi et al. (2020) (assuming LAGN = 2.2 × 1043 erg s−1). We note that we used 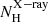 measurements which are representative of all the material along a pencil-beam line-of-sight to the accretion disc and, thus, it depends on the viewing direction. Alonso-Herrero et al. (2021) show a similar plot but but using NH derived from ALMA observations. García-Burillo et al. (2021) compared the hydrogen column densities derived by X-rays and the nuclear integrated values from ALMA for the GATOS8 sample and found a good agreement between these NH estimates for obscured Sys (i.e.
measurements which are representative of all the material along a pencil-beam line-of-sight to the accretion disc and, thus, it depends on the viewing direction. Alonso-Herrero et al. (2021) show a similar plot but but using NH derived from ALMA observations. García-Burillo et al. (2021) compared the hydrogen column densities derived by X-rays and the nuclear integrated values from ALMA for the GATOS8 sample and found a good agreement between these NH estimates for obscured Sys (i.e. 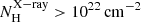 ), whereas the molecular gas column density of the torus probed by ALMA is systematically larger than the
), whereas the molecular gas column density of the torus probed by ALMA is systematically larger than the 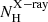 for unobscured Sy galaxies (i.e.
for unobscured Sy galaxies (i.e. 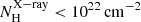 ). In particular, all Sy1 galaxies in García-Burillo et al. (2021) have
). In particular, all Sy1 galaxies in García-Burillo et al. (2021) have 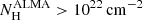 . This could be explained as the X-ray absorption in Sys is related with a smaller pc-scale dust-free gas component compared with the scales probed by ALMA (∼10 pc; see e.g., García-Burillo et al. 2021). Therefore, the
. This could be explained as the X-ray absorption in Sys is related with a smaller pc-scale dust-free gas component compared with the scales probed by ALMA (∼10 pc; see e.g., García-Burillo et al. 2021). Therefore, the 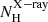 value of Sy1 and Sy1.8/1.9 galaxies might be underestimating the molecular gas column density of the torus. To interpret this plot, we add a yellow shaded region highlighting the region where the X-ray column density might be not representative of the torus structure.
value of Sy1 and Sy1.8/1.9 galaxies might be underestimating the molecular gas column density of the torus. To interpret this plot, we add a yellow shaded region highlighting the region where the X-ray column density might be not representative of the torus structure.
 |
Fig. 14. Relation between the X-ray hydrogen column density and the Eddington ratio for the BCS40 sample. Blue, green, and red symbols represent Sy1, Sy1.8/1.9 and Sy2, respectively. The yellow shaded region corresponds to the region where X-ray column density might not be representative of the molecular gas column density of the torus (i.e. |
We plot in Fig. 14 galaxies with best fits provided by torus models (i.e. smooth, clumpy, and two-phase torus models) and by disc+wind H17 models (see Sect. 4), using different symbols as shown in the legend. Galaxies with 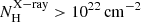 are located in a region not conducive to launching IR dusty polar outflows,which is in good agreement with our result that their SEDs are best fitted with torus models. On the other hand, relatively close to the favourable region in the diagram to launching dusty winds, we find a larger number Sys whose SEDs are better fitted with the clumpy disc+wind H17 models. Finally, the majority of Sy1 and Sy1.8/1.9 galaxies are located in the blowout limit region. This might be related, at least in part, to the
are located in a region not conducive to launching IR dusty polar outflows,which is in good agreement with our result that their SEDs are best fitted with torus models. On the other hand, relatively close to the favourable region in the diagram to launching dusty winds, we find a larger number Sys whose SEDs are better fitted with the clumpy disc+wind H17 models. Finally, the majority of Sy1 and Sy1.8/1.9 galaxies are located in the blowout limit region. This might be related, at least in part, to the 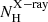 measurements. Therefore, this dynamical model is able to broadly explain our main result on the dust configurations and it shows the complexity of the AGN torus.
measurements. Therefore, this dynamical model is able to broadly explain our main result on the dust configurations and it shows the complexity of the AGN torus.
7. Conclusions
We present a detailed comparison of the nuclear dust emission of an ultra-hard X-ray (14–195 keV) volume-limited (DL < 40 Mpc) sample of 24 Seyfert galaxies to a set of torus models comprising different dust compositions, distributions, and geometries. This sample covers AGN luminosity log(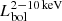 ) ∼ 41.75–44.75 erg s−1) and Eddington ratio (λEdd: −3.40 to −0.26) ranges. We include data from QSOs to expand the range of luminosities (log(
) ∼ 41.75–44.75 erg s−1) and Eddington ratio (λEdd: −3.40 to −0.26) ranges. We include data from QSOs to expand the range of luminosities (log(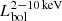 erg s−1) ∼ 44.2–45.9) beyond our original Sy sample. We fit, for the first time, the nuclear IR SEDs (∼1–30 μm) obtained with high angular resolution data with six different torus models to find the model that most closely reproduces the nuclear IR SEDs of type 1 and 2 Seyfert galaxies. Finally, we investigated the relation of the bolometric luminosity, hydrogen column density, and Eddington ratio with different torus parameters. The main results are as follows.
erg s−1) ∼ 44.2–45.9) beyond our original Sy sample. We fit, for the first time, the nuclear IR SEDs (∼1–30 μm) obtained with high angular resolution data with six different torus models to find the model that most closely reproduces the nuclear IR SEDs of type 1 and 2 Seyfert galaxies. Finally, we investigated the relation of the bolometric luminosity, hydrogen column density, and Eddington ratio with different torus parameters. The main results are as follows.
-
The various torus models used in this work provide acceptable fits (
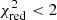 ) to the majority (19/24) of the nuclear IR SEDs. The fraction of best fits provided by smooth, clumpy, and two-phase torus models (i.e. those models that do not include the dusty polar component) and disc+wind models is practically the same, 33.3 and 37.5% (i.e. 8/24 and 9/24 sources), respectively.
) to the majority (19/24) of the nuclear IR SEDs. The fraction of best fits provided by smooth, clumpy, and two-phase torus models (i.e. those models that do not include the dusty polar component) and disc+wind models is practically the same, 33.3 and 37.5% (i.e. 8/24 and 9/24 sources), respectively. -
The disc+wind models reproduce better the NIR-to-MIR emission of AGN with relatively low X-ray hydrogen column density (median value of log (
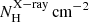 ) = 21.0 ± 1.0; i.e. Sy1/Sy1.8/1.9), whereas the nuclear IR SED of Sy2 (median value of log (
) = 21.0 ± 1.0; i.e. Sy1/Sy1.8/1.9), whereas the nuclear IR SED of Sy2 (median value of log (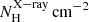 ) = 23.5 ± 0.8) are best fitted by smooth, clumpy and two-phase torus models without including the polar dusty wind component.
) = 23.5 ± 0.8) are best fitted by smooth, clumpy and two-phase torus models without including the polar dusty wind component. -
The inclusion of large graphite grains with Tsub ∼ 1900 K, in addition to the self-obscuration produced by the polar component at intermediate inclinations (or a thick torus) are crucial to reproduce reproduce the observed nuclear NIR and MIR SED of Sy1/1.8/1.9s.
-
In general, we find that the Seyfert galaxies having unfavourable (favourable) conditions, namely, the nuclear hydrogen column density and Eddington ratio, for launching IR dusty polar outflows are best-fitted with smooth, clumpy and two-phase torus (disc+wind) models confirming the predictions from simulations.
Our results indicate that there is a relationship between the choice of model and the hydrogen column density and, thus, the X-ray (unobscured or obscured) and optical (Sy1/Sy2) classification. These findings suggest that the torus dusty geometry and grain composition might depend on the amount of nuclear material (NH) and AGN properties. This work demonstrates the power of the spectral fitting technique to infer the properties of the inner dusty structure in AGN. In the future, the unprecedented combination of high sensitivity and spatial resolution provided by the James Webb Space Telescope (JWST) will be crucial for attaining a better understanding of the nuclear dusty region of AGN using this technique.
González-Martín et al. (2019a) showed how to create an XSPEC additive table for each of the models employed.
Acknowledgments
I.G.B. and D.R. acknowledge support from STFC through grant ST/S000488/1. O.G.M. acknowledges support from the UNAM PAPIIT project IN105720. C.R.A. acknowledges financial support from the European Union’s Horizon 2020 research and innovation programme under Marie Skłodowska-Curie grant agreement No. 860744 (BiD4BESt) and from the project “Feeding and feedback in active galaxies”, with reference PID2019-106027GB-C42, funded by MICINN-AEI/10.13039/501100011033. AAH acknowledges support from grant PGC2018-094671-B-I00 funded by MCIN/AEI/10.13039/501100011033 and by ERDF A way of making Europe. EAD acknowledges support from the Agencia Estatal de Investigación del Ministerio de Ciencia e Innovación (AEI-MCINN) under project with reference PID2019-107010GB100. Finally, we thank the anonymous referee for their useful comments.
References
- Almeyda, T., Robinson, A., Richmond, M., Vazquez, B., & Nikutta, R. 2017, ApJ, 843, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., Simpson, C., Ward, M. J., & Wilson, A. S. 1998, ApJ, 495, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., Quillen, A. C., Rieke, G. H., Ivanov, V. D., & Efstathiou, A. 2003, AJ, 126, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., Ramos Almeida, C., Mason, R., et al. 2011, ApJ, 736, 82 425, 311 [NASA ADS] [Google Scholar]
- Alonso-Herrero, A., Pereira-Santaella, M., García-Burillo, S., et al. 2018, ApJ, 859, 144 [Google Scholar]
- Alonso-Herrero, A., García-Burillo, S., Pereira-Santaella, M., et al. 2019, A&A, 628, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso-Herrero, A., Pereira-Santaella, M., Rigopoulou, D., et al. 2020, A&A, 639, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso-Herrero, A., García-Burillo, S., Hönig, S. F., et al. 2021, A&A, 652, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Arnaud, K. A. 1996, Astronomical Data Analysis Software and Systems V, 101, 17 [Google Scholar]
- Asmus, D. 2019, MNRAS, 489, 2177 [NASA ADS] [CrossRef] [Google Scholar]
- Asmus, D., Hönig, S. F., Gandhi, P., Smette, A., & Duschl, W. J. 2014, MNRAS, 439, 1648 [NASA ADS] [CrossRef] [Google Scholar]
- Binggeli, B., Sandage, A., & Tammann, G. A. 1985, AJ, 90, 1681 [Google Scholar]
- Bock, J. J., Neugebauer, G., Matthews, K., et al. 2000, AJ, 120, 2904 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [Google Scholar]
- Buchner, J., & Bauer, F. E. 2017, MNRAS, 465, 434 [Google Scholar]
- Burtscher, L., Jaffe, W., Raban, D., et al. 2009, ApJ, 705, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Burtscher, L., Meisenheimer, K., Tristram, K. R. W., et al. 2013, A&A, 558, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Combes, F., García-Burillo, S., Audibert, A., et al. 2019, A&A, 623, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorodnitsyn, A., & Kallman, T. 2017, ApJ, 842, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R. A., & Malkan, M. A. 1986, ApJ, 308, 59 [CrossRef] [Google Scholar]
- Efstathiou, A., & Rowan-Robinson, M. 1995, MNRAS, 273, 649 [Google Scholar]
- Emmanoulopoulos, D., Papadakis, I. E., Epitropakis, A., et al. 2016, MNRAS, 461, 1642 [NASA ADS] [CrossRef] [Google Scholar]
- Esparza-Arredondo, D., González-Martín, O., Dultzin, D., et al. 2019, ApJ, 886, 125 [Google Scholar]
- Esparza-Arredondo, D., Gonzalez-Martín, O., Dultzin, D., et al. 2021, A&A, 651, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C., Vasudevan, R. V., & Gandhi, P. 2008, MNRAS, 385, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, J., Franceschini, A., & Hatziminaoglou, E. 2006, MNRAS, 366, 767 [Google Scholar]
- Fuller, L., Lopez-Rodriguez, E., Packham, C., et al. 2016, MNRAS, 462, 2618 [NASA ADS] [CrossRef] [Google Scholar]
- Gallimore, J. F., Elitzur, M., Maiolino, R., et al. 2016, ApJ, 829, L7 [Google Scholar]
- Gámez, Rosas V., Isbell, J. W., Jaffe, W., et al. 2022, Nature, 602, 403 [CrossRef] [Google Scholar]
- García-Bernete, I., Ramos, Almeida C., Acosta-Pulido, J. A., et al. 2015, MNRAS, 449, 1309 [CrossRef] [Google Scholar]
- García-Bernete, I., Ramos Almeida, C., Alonso-Herrero, A., et al. 2016, MNRAS, 463, 3531 [CrossRef] [Google Scholar]
- García-Bernete, I., Ramos, Almeida C., Landt, H., et al. 2017, MNRAS, 469, 110 [CrossRef] [Google Scholar]
- García-Bernete, I., Ramos Almeida, C., Alonso-Herrero, A., et al. 2019, MNRAS, 486, 4917 [Google Scholar]
- García-Burillo, S., Ramos, Almeida C., Acosta-Pulido, J. A., et al. 2016, ApJ, 823, L12 [CrossRef] [Google Scholar]
- García-Burillo, S., Alonso-Herrero, A., Ramos, Almeida C., et al. 2021, A&A, 652, A98 [NASA ADS] [CrossRef] [Google Scholar]
- García-González, J., Alonso-Herrero, A., Hönig, S. F., et al. 2017, MNRAS, 470, 2578 [CrossRef] [Google Scholar]
- González-Martín, O., Rodríguez-Espinosa, J. M., Díaz-Santos, T., et al. 2013, A&A, 553, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Martín, O., Masegosa, J., García-Bernete, I., et al. 2019a, ApJ, 884, 10 [Google Scholar]
- González-Martín, O., Masegosa, J., García-Bernete, I., et al. 2019b, ApJ, 884, 11 [Google Scholar]
- Hernán-Caballero, A., Hatziminaoglou, E., Alonso-Herrero, A., & Mateos, S. 2016, MNRAS, 463, 2064 [Google Scholar]
- Hicks, E. K. S., Davies, R. I., Malkan, M. A., et al. 2009, ApJ, 696, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Hickox, R. C., Mullaney, J. R., Alexander, D. M., et al. 2014, ApJ, 782, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Hönig, S. F. 2019, ApJ, 884, 171 [Google Scholar]
- Hönig, S. F., & Kishimoto, M. 2010, A&A, 523, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hönig, S. F., & Kishimoto, M. 2017, ApJ, 838, L20 [Google Scholar]
- Hönig, S. F., Beckert, T., Ohnaka, K., & Weigelt, G. 2006, A&A, 452, 459 [Google Scholar]
- Hönig, S. F., Kishimoto, M., Gandhi, P., et al. 2010, A&A, 515, A23 [CrossRef] [EDP Sciences] [Google Scholar]
- Hönig, S. F., Kishimoto, M., Tristram, K. R. W., et al. 2013, ApJ, 771, 87 [Google Scholar]
- Hopkins, P. F., & Quataert, E. 2010, MNRAS, 407, 1529 [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., Di Matteo, T., et al. 2005, ApJ, 630, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Ichikawa, K., Ueda, Y., Terashima, Y., et al. 2012, ApJ, 754, 45 [Google Scholar]
- Ichikawa, K., Packham, C., Ramos Almeida, C., et al. 2015, ApJ, 803, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Ichikawa, K., Ricci, C., Ueda, Y., et al. 2019, ApJ, 870, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Imanishi, M., Nakanishi, K., Izumi, T., & Wada, K. 2018, ApJ, 853, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Impellizzeri, C. M. V., Gallimore, J. F., Baum, S. A., et al. 2019, ApJ, 884, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Isbell, J. W., Burtcher, L., Asmus, D., et al. 2021, ApJ, 910, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Isbell, J. W., Meisenheimer, K., Pott, J.-U., et al. 2022, A&A, 663, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jaffe, W., Meisenheimer, K., Röttgering, H. J. A., et al. 2004, Nature, 429, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Koss, M., Trakhtenbrot, B., Ricci, C., et al. 2017, ApJ, 850, 74 [Google Scholar]
- Krolik, J. H., & Begelman, M. C. 1988, ApJ, 329, 702 [Google Scholar]
- Kudoh, Y., Wada, K., & Norman, C. 2020, ApJ, 904, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Kullback, S., & Leibler, A. 1951, Ann. Math. Stat, 22, 79 [CrossRef] [Google Scholar]
- Landt, H., Ward, M. J., Kynoch, D., et al. 2019, MNRAS, 489, 1572 [NASA ADS] [CrossRef] [Google Scholar]
- Lani, C., Netzer, H., & Lutz, D. 2017, MNRAS, 471, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Lawrence, A. 1991, MNRAS, 252, 586 [NASA ADS] [Google Scholar]
- Leftley, J. H., Tristram, K. R. W., Hönig, S. F., et al. 2018, ApJ, 862, 17 [Google Scholar]
- Lira, P., Videla, L., Wu, Y., et al. 2013, ApJ, 764, 159 [Google Scholar]
- López-Gonzaga, N., Burtscher, L., Tristram, K. R. W., Meisenheimer, K., & Schartmann, M. 2016, A&A, 591, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lopez-Rodriguez, E., Fuller, L., Alonso-Herrero, A., et al. 2018, ApJ, 859, 99 [Google Scholar]
- Lu, W., Kumar, P., & Evans, N. J. 2016, MNRAS, 458, 575 [Google Scholar]
- Martínez-Paredes, M., González-Martín, O., Esparza-Arredondo, D., et al. 2020, ApJ, 890, 152 [Google Scholar]
- Martínez-Paredes, M., González-Martín, O., HyeongHan, K., et al. 2021, ApJ, 922, 157 [CrossRef] [Google Scholar]
- Mateos, S., Carrera, F. J., Alonso-Herrero, A., et al. 2016, ApJ, 819, 166 [Google Scholar]
- Mateos, S., Carrera, F. J., Barcons, X., et al. 2017, ApJ, 841, L18 [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [Google Scholar]
- Mor, R., Netzer, H., & Elitzur, M. 2009, ApJ, 705, 298 [Google Scholar]
- Mould, J. R., Jeremy, R., Huchra, J. P., et al. 2000, ApJ, 529, 786 [NASA ADS] [CrossRef] [Google Scholar]
- Nenkova, M., Sirocky, M. M., Ivezić, Ž., & Elitzur, M. 2008a, ApJ, 685, 147 [Google Scholar]
- Nenkova, M., Sirocky, M. M., Nikutta, R., Ivezić, Ž., & Elitzur, M. 2008b, ApJ, 685, 160 [Google Scholar]
- Netzer, H., Lani, C., Nordon, R., et al. 2016, ApJ, 819, 123 [Google Scholar]
- Neugebauer, G., Oke, J. B., Becklin, E. E., & Matthews, K. 1979, ApJ, 230, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Nikutta, R., Lopez-Rodriguez, E., Ichikawa, K., et al. 2021a, ApJ, 919, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Nikutta, R., Lopez-Rodriguez, E., Ichikawa, K., et al. 2021b, ApJ, 923, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Packham, C., Radomski, J. T., Roche, P. F., et al. 2005, ApJ, 618, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Pei, Y. C. 1992, ApJ, 395, 130 [Google Scholar]
- Perna, R., Lazzati, D., & Fiore, F. 2003, ApJ, 585, 775 [Google Scholar]
- Pier, E. A., & Krolik, J. H. 1992, ApJ, 401, 99 [Google Scholar]
- Raban, D., Jaffe, W., Röttgering, H., Meisenheimer, K., & Tristram, K. R. W. 2009, MNRAS, 394, 1325 [Google Scholar]
- Radomski, J. T., Piña, R. K., Packham, C., et al. 2003, ApJ, 587, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Radomski, J. T., Christopher, P., Levenson, N. A., et al. 2008, ApJ, 681, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos, Almeida C., & Ricci, C. 2017, NatAs, 1, 679 [NASA ADS] [Google Scholar]
- Ramos Almeida, C., Levenson, N. A., Rodríguez Espinosa, J. M., et al. 2009, ApJ, 702, 1127 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., Levenson, N. A., Alonso-Herrero, A., et al. 2011, ApJ, 731, 92 [Google Scholar]
- Ramos Almeida, C., Alonso-Herrero, A., Esquej, P., et al. 2014, MNRAS, 445, 1130 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, C., Ueda, Y., Koss, M. J., et al. 2015, ApJ, 815, L13 [Google Scholar]
- Ricci, C., Trakhtenbrot, B., Koss, M. J., et al. 2017a, Nature, 549, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, C., Trakhtenbrot, B., Koss, M. J., et al. 2017b, ApJS, 233, 17 [Google Scholar]
- Schartmann, M., Meisenheimer, K., Camenzind, M., et al. 2008, A&A, 482, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schartmann, M., Wada, K., Prieto, M. A., Burkert, A., & Tristram, K. R. W. 2014, MNRAS, 445, 3878 [NASA ADS] [CrossRef] [Google Scholar]
- Siebenmorgen, R., Heymann, F., & Efstathiou, A. 2015, A&A, 583, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simpson, C. 2005, MNRAS, 360, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Stalevski, M., Fritz, J., Baes, M., Nakos, T., & Popović, L. Č. 2012, MNRAS, 420, 2756 [Google Scholar]
- Stalevski, M., Ricci, C., Ueda, Y., et al. 2016, MNRAS, 458, 2288 [Google Scholar]
- Stalevski, M., Asmus, D., & Tristram, K. R. W. 2017, MNRAS, 472, 3854 [NASA ADS] [CrossRef] [Google Scholar]
- Takasao, S., Shuto, Y., & Wada, K. 2022, ApJ, 926, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Tristram, K. R. W., Meisenheimer, K., Jaffe, W., et al. 2007, A&A, 474, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tristram, K. R. W., Meisenheimer, K., Jaffe, W., et al. 2009, A&A, 502, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tristram, K. R. W., Burtscher, L., Jaffe, W., et al. 2014, A&A, 563, A82 [CrossRef] [EDP Sciences] [Google Scholar]
- Tueller, J., Mushotzky, R. F., Barthelmy, S., et al. 2008, ApJ, 681, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Ueda, Y., Hashimoto, Y., Ichikawa, K., et al. 2015, ApJ, 815, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., & Fabian, A. C. 2009, MNRAS, 392, 1124 [CrossRef] [Google Scholar]
- Vasudevan, R. V., Fabian, A. C., Gandhi, P., Winter, L. M., & Mushotzky, R. F. 2010, MNRAS, 402, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Venanzi, M., Hönig, S., & Williamson, D. 2020, ApJ, 900, 174 [Google Scholar]
- Wada, K. 2012, ApJ, 758, 66 [Google Scholar]
- Wada, K., & Norman, C. A. 2002, ApJ, 566, L21 [CrossRef] [Google Scholar]
- Waxman, E., & Draine, B. T. 2000, ApJ, 537, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, K. A., Meléndez, M., Mushotzky, R. F., et al. 2010, ApJ, 716, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Winter, L. M., Mushotzky, R. F., Reynolds, C. S., & Tueller, J. 2009, ApJ, 690, 1322 [NASA ADS] [CrossRef] [Google Scholar]
- Winter, L. M., Lewis, K. T., Koss, M., et al. 2010, ApJ, 710, 503 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Torus model parameters and nuclear IR SED fits
Using the various torus models, we fit all the nuclear NIR-to-MIR SEDs in our sample (See Section 4). In Tables A.1-A.5 we present the different torus model parameters. The values of the model parameters fitted to the individual nuclear IR SEDs are reported in Tables A.6, A.7 and A.8. In addition, the individual fits are shown in Figures (A1-A24).
Smooth F06 torus model parameters.
Clumpy N08 torus model parameters.
Clumpy H10 torus model parameters.
Two-phase S16 torus model parameters.
Clumpy disc+wind H17 torus model parameters.
Spectral fit results for Type-1 Seyferts.
Spectral fit results for Type 1.8/1.9 Seyferts.
Spectral fit results for Type-2 Seyferts.
 |
Fig. A.1. Nuclear IR SED of ESO005-G004. Solid blue line correspond to the best fit per torus model. Grey diamond and black crosses are the photometric data points and N-band spectrum, respectively. The black arrows represent low angular resolution data, which are treated as upper limits. |
 |
Fig. A.10. Nuclear IR SED of NGC4051. Symbols and lines same as in Fig. A.1. |
 |
Fig. A.11. Nuclear IR SED of NGC4138. Symbols and lines same as in Fig. A.1. |
 |
Fig. A.12. Nuclear IR SED of NGC4151. Symbols and lines same as in Fig. A.1. |
 |
Fig. A.13. Nuclear IR SED of NGC4388. Symbols and lines same as in Fig. A.1. |
 |
Fig. A.14. Nuclear IR SED of NGC4395. Symbols and lines same as in Fig. A.1. |
 |
Fig. A.15. Nuclear IR SED of NGC4945. Symbols and lines same as in Fig. A.1. |
 |
Fig. A.16. Nuclear IR SED of NGC5128. Symbols and lines same as in Fig. A.1. |
 |
Fig. A.17. Nuclear IR SED of NGC5506. Symbols and lines same as in Fig. A.1. |
 |
Fig. A.18. Nuclear IR SED of NGC6300. Symbols and lines same as in Fig. A.1. |
 |
Fig. A.19. Nuclear IR SED of NGC6814. Symbols and lines same as in Fig. A.1. |
 |
Fig. A.20. Nuclear IR SED of NGC7172. Symbols and lines same as in Fig. A.1. |
 |
Fig. A.21. Nuclear IR SED of NGC7213. Symbols and lines same as in Fig. A.1. |
 |
Fig. A.22. Nuclear IR SED of NGC7314. Symbols and lines same as in Fig. A.1. |
 |
Fig. A.23. Nuclear IR SED of NGC7582. Symbols and lines same as in Fig. A.1. |
 |
Fig. A.24. Nuclear IR SED of UGC6728. Symbols and lines same as in Fig. A.1. |
Appendix B: Combined probability distributions
In general, the various torus models provide acceptable fits (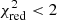 ) to the majority (19/24) of the nuclear IR SEDs (see Appendix A). However, it is difficult to see trend using the individual fit parameters, which can be not well constrained. Therefore, we obtain a global statistical analysis of the torus model parameters of the various Seyfert galaxy types, rather than focusing on the individual fits. Figs. B.1, B.2, B.3, B.4m and B.5 show the combined probability distribution of the different torus model parameters for all the objects in each Sy subgroup. Finally, in Tables B.1, B.2, B.3, B.4, and B.5 we present the KLD results for each torus parameter and Sy subgroup.
) to the majority (19/24) of the nuclear IR SEDs (see Appendix A). However, it is difficult to see trend using the individual fit parameters, which can be not well constrained. Therefore, we obtain a global statistical analysis of the torus model parameters of the various Seyfert galaxy types, rather than focusing on the individual fits. Figs. B.1, B.2, B.3, B.4m and B.5 show the combined probability distribution of the different torus model parameters for all the objects in each Sy subgroup. Finally, in Tables B.1, B.2, B.3, B.4, and B.5 we present the KLD results for each torus parameter and Sy subgroup.
 |
Fig. B.1. Comparison between the smooth F06 torus model parameter combined probability distributions. Blue dotted, green dashed, red solid and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. |
KLD results for the smooth F06 torus models.
 |
Fig. B.2. Comparison between the clumpy NO8 torus model parameter combined probability distributions. Blue dotted, green dashed, red solid and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. |
KLD results for the clumpy N08 torus models.
 |
Fig. B.3. Comparison between the clumpy H10 torus model parameter combined probability distributions. Blue dotted, green dashed, red solid and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. |
KLD results for the clumpy H10 torus models.
 |
Fig. B.4. Comparison between the clumpy disc+wind H17 model parameter combined probability distributions. Blue dotted, green dashed, red solid and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. |
KLD results for the clumpy disc+wind H17 models.
 |
Fig. B.5. Comparison between the two-phase S16 torus model parameter combined probability distributions. Blue dotted, green dashed, red solid and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. |
KLD results for the two-phase S16 torus models.
Appendix C: Derived torus (disc) sizes and masses
For each torus model, we can derive the physical radius of the dusty torus (Ro) by using the radial extent of the torus (Y=Ro/Rd), the bolometric luminosity, and the dust sublimation radius (Rd) definition (see e.g. RA11, AH11, Ichikawa et al. 2015, Esparza-Arredondo et al. 2019, GB19, GM19B, Martínez-Paredes et al. 2021). Finally, the torus gas mass for each model can be calculated as follows:
C.1. Smooth F06 torus models
The torus gas mass associated with the fitted nuclear dusty structure can be calculated as:
where the 1.9 × 1021 value is the Galactic dust-to-gas ratio from Bohlin et al. (1978).
C.2. Clumpy N08 torus models
The torus gas mass associated with the fitted nuclear dusty structure can be calculated as:
where 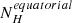 is:
is:
where the 1.9 × 1021 value is the Galactic dust-to-gas ratio from Bohlin et al. (1978).
C.3. Clumpy H10 torus models
The torus gas mass associated with the fitted nuclear dusty structure can be calculated as (assuming b=1; see H10):
where 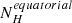 is:
is:
where the 1.9 × 1021 value is the Galactic dust-to-gas ratio from Bohlin et al. (1978).
C.4. Clumpy disc+wind H17 models
The disc+wind gas mass associated with the fitted nuclear dusty structure can be calculated as (assuming b=1; see H10):
where 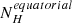 is:
is:
where the 1.9 × 1021 value is the Galactic dust-to-gas ratio from Bohlin et al. (1978).
C.5. Two-phase S16 torus models
The torus gas mass associated with the fitted nuclear dusty structure can be calculated as:
where the 1.9 × 1021 value is the Galactic dust-to-gas ratio from Bohlin et al. (1978).
All Tables
All Figures
 |
Fig. 1. Scheme showing the different dust geometries and compositions of the various torus models used in this work. See Appendix A for further details on the individual model parameters. Note that the clumpy disc H17D models are not represented in this figure. However, the latter models consist of clumpy disc component of the clumpy disc+wind H17 models. (a) Smooth F06 torus models, (b) Clumpy N08 torus models, (c) Clumpy H10 torus models, (d) Two-phase S16 torus models, (e) Clumpy disk+wind H17 models. |
| In the text | |
 |
Fig. 2. Example of the nuclear IR SED of NGC 3227 fitted with the clumpy disc+wind H17 models (top panel) and its residuals (bottom panel). The grey diamonds correspond to the high angular resolution photometric points. The black arrows represent low angular resolution data, which are treated as upper limits. Black crosses correspond to the high angular resolution N-band spectrum. The solid blue line is the best-fitted model. |
| In the text | |
 |
Fig. 3. Average residuals (units as in Fig. 2) of the spectral fitting for each torus model used in this work. Blue, green, red, and black stars (and solid lines) correspond to Sy1, Sy1.8/1.9, Sy2, and the full sample, respectively. The regions masked in the fitting process are highlighted in beige vertical lines. |
| In the text | |
 |
Fig. 4. Best fit distributions of the BCS40 sample per bolometric luminosity (left panel), Eddington ratio (central panel), and hydrogen column density (right panel) bin. The grey hatched and filled histograms are the distribution of unfitted and fitted sources. The blue and red filled histograms correspond to sources best fitted by clumpy disc+wind H17 models and torus models, respectively. The orange filled histograms are sources that have been equally fitted by clumpy disc+wind H17 models and torus models. |
| In the text | |
 |
Fig. 5. Comparison between the torus (disc) inclination combined probability distributions for different models considered here. Blue dotted, green dashed, red solid, and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. We note that 90-iF06 = iN08 = iH10 = iS16 = iH17. |
| In the text | |
 |
Fig. 6. Comparison between the torus (disc) angular width combined probability distributions for different models considered here. Blue dotted, green dashed, red solid, and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. We note that σH10 = 90-θH10. In the case of the clumpy disc+wind H17 models, the h parameter is the scale height of the dusty disc. |
| In the text | |
 |
Fig. 7. Comparison between the covering factor parameter space. Left panel: combined probability distributions for all the models used in this work. Right panel: combined probability distributions derived for the entire Sy sample using each model. |
| In the text | |
 |
Fig. 8. Comparison between the covering factor combined probability distributions for different models considered here. Blue dotted, green dashed, red solid, and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. |
| In the text | |
 |
Fig. 9. Comparison between the torus size (Rout) combined probability distributions for different models considered here. Blue dotted, green dashed, red solid, and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. |
| In the text | |
 |
Fig. 10. Comparison between the torus gas mass combined probability distributions for different models considered here. Blue dotted, green dashed, red solid, and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. |
| In the text | |
 |
Fig. 11. Luminosity dependence of the radial extent of the torus/disc (Y = Ro/Rd; left panels) and of the torus (disc) radius (right panels). From top to bottom panels the result for the various models with free Y parameter used in this work (see text for details). The first three bins correspond to the Sy galaxies of BCS40 sample. We note that we also include two additional bins of a sample of QSOs with higher bolometric luminosities from Martínez-Paredes et al. (2021). |
| In the text | |
 |
Fig. 12. Comparison between the clumpy disc+wind H17 model parameters combined probability distributions for the optical classification: for the radial dust-cloud distribution power law index (a) shown in the left panel and for the dust-cloud distribution power law along the wind (aw) in the right panel. Blue dot-dashed, green dashed, and red solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, and Sy2 galaxies, respectively. |
| In the text | |
 |
Fig. 13. Clumpy disc+wind H17 (blue solid lines) and clumpy disc H17 (orange dashed lines) model SEDs (normalized at 20 μm). Left panel: Sy1 configuration, which consists of a concentrated disc (a = −2.5) and an extended wind (aw = −1.0). Right panel: Sy2 configuration, which consists of a relatively extended disc (a = −1.0) and a concentrated wind (aw = −2.0). From top to bottom panels: Face-on, intermediate (45°), and edge-on values of the inclination angle for the clumpy disc and disc+wind dusty structure. We note that all the models use N = 7, and the clumpy disc+wind H17 models use fwd = 0.6, θ = 45° and σ = 10° (see main text for further details on the parameters of the models). |
| In the text | |
 |
Fig. 14. Relation between the X-ray hydrogen column density and the Eddington ratio for the BCS40 sample. Blue, green, and red symbols represent Sy1, Sy1.8/1.9 and Sy2, respectively. The yellow shaded region corresponds to the region where X-ray column density might not be representative of the molecular gas column density of the torus (i.e. |
| In the text | |
 |
Fig. A.1. Nuclear IR SED of ESO005-G004. Solid blue line correspond to the best fit per torus model. Grey diamond and black crosses are the photometric data points and N-band spectrum, respectively. The black arrows represent low angular resolution data, which are treated as upper limits. |
| In the text | |
 |
Fig. A.2. Nuclear IR SED of MCG-05-23-016. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.3. Nuclear IR SED of MCG-06-30-015. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.4. Nuclear IR SED of NGC1365. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.5. Nuclear IR SED of NGC2110. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.6. Nuclear IR SED of NGC2992. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.7. Nuclear IR SED of NGC3081. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.8. Nuclear IR SED of NGC3227. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.9. Nuclear IR SED of NGC3783. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.10. Nuclear IR SED of NGC4051. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.11. Nuclear IR SED of NGC4138. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.12. Nuclear IR SED of NGC4151. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.13. Nuclear IR SED of NGC4388. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.14. Nuclear IR SED of NGC4395. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.15. Nuclear IR SED of NGC4945. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.16. Nuclear IR SED of NGC5128. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.17. Nuclear IR SED of NGC5506. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.18. Nuclear IR SED of NGC6300. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.19. Nuclear IR SED of NGC6814. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.20. Nuclear IR SED of NGC7172. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.21. Nuclear IR SED of NGC7213. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.22. Nuclear IR SED of NGC7314. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.23. Nuclear IR SED of NGC7582. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. A.24. Nuclear IR SED of UGC6728. Symbols and lines same as in Fig. A.1. |
| In the text | |
 |
Fig. B.1. Comparison between the smooth F06 torus model parameter combined probability distributions. Blue dotted, green dashed, red solid and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. |
| In the text | |
 |
Fig. B.2. Comparison between the clumpy NO8 torus model parameter combined probability distributions. Blue dotted, green dashed, red solid and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. |
| In the text | |
 |
Fig. B.3. Comparison between the clumpy H10 torus model parameter combined probability distributions. Blue dotted, green dashed, red solid and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. |
| In the text | |
 |
Fig. B.4. Comparison between the clumpy disc+wind H17 model parameter combined probability distributions. Blue dotted, green dashed, red solid and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. |
| In the text | |
 |
Fig. B.5. Comparison between the two-phase S16 torus model parameter combined probability distributions. Blue dotted, green dashed, red solid and black solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, Sy2, and the entire sample, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.