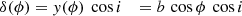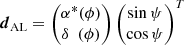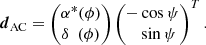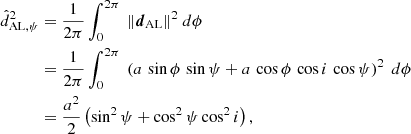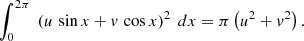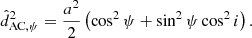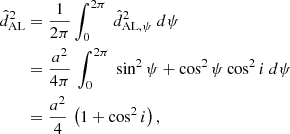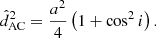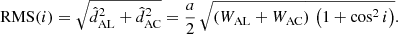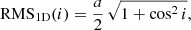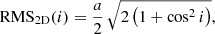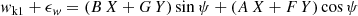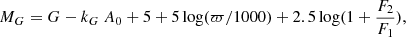| Issue |
A&A
Volume 674, June 2023
Gaia Data Release 3
|
|
|---|---|---|
| Article Number | A34 | |
| Number of page(s) | 58 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202243782 | |
| Published online | 16 June 2023 | |
Gaia Data Release 3
Stellar multiplicity, a teaser for the hidden treasure
1
GEPI, Observatoire de Paris, Université PSL, CNRS, 5 place Jules Janssen, 92190 Meudon, France
2
Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
3
School of Physics and Astronomy/Space Park Leicester, University of Leicester, University Road, Leicester LE1 7RH, UK
4
School of Physics and Astronomy, Tel Aviv University, Tel Aviv 6997801, Israel
5
Institut d’Astronomie et d’Astrophysique, Université Libre de Bruxelles CP 226, Boulevard du Triomphe, 1050 Brussels, Belgium
6
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris, 5 Place Jules Janssen, 92190 Meudon, France
7
Department of Astronomy, University of Geneva, Chemin Pegasi 51, 1290 Versoix, Switzerland
8
RHEA for European Space Agency (ESA), Camino Bajo del Castillo, s/n, Urbanizacion Villafranca del Castillo, Villanueva de la Cañada 28692 Madrid, Spain
9
Department of Particle Physics and Astrophysics, Weizmann Institute of Science, Rehovot 7610001, Israel
10
INAF – Osservatorio Astrofisico di Torino, Via Osservatorio 20, 10025 Pino Torinese, TO, Italy
11
Institut d’Astrophysique et de Géophysique, Université de Liège, 19c Allée du 6 Août, 4000 Liège, Belgium
12
CRAAG – Centre de Recherche en Astronomie, Astrophysique et Géophysique, Route de l’Observatoire Bp 63 Bouzareah, 16340 Algiers, Algeria
13
F.R.S.-FNRS, Rue d’Egmont 5, 1000 Brussels, Belgium
14
Université de Strasbourg, CNRS, Observatoire Astronomique de Strasbourg, UMR 7550, 11 rue de l’Université, 67000 Strasbourg, France
15
Department of Astronomy, University of Geneva, Chemin d’Ecogia 16, 1290 Versoix, Switzerland
16
University of Turin, Department of Physics, Via Pietro Giuria 1, 10125 Torino, Italy
17
Telespazio UK S.L. for European Space Agency (ESA), Camino Bajo del Castillo, s/n, Urbanizacion Villafranca del Castillo, Villanueva de la Cañada 28692 Madrid, Spain
18
Faculty of Mathematics and Physics, University of Ljubljana, Jadranska ulica 19, 1000 Ljubljana, Slovenia
19
Leiden Observatory, Leiden University, Niels Bohrweg 2, 2333 CA Leiden, The Netherlands
20
INAF – Osservatorio astronomico di Padova, Vicolo Osservatorio 5, 35122 Padova, Italy
21
European Space Agency (ESA), European Space Research and Technology Centre (ESTEC), Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
22
Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität Heidelberg, Mönchhofstr. 12-14, 69120 Heidelberg, Germany
23
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, Bd de l’Observatoire, CS 34229, 06304 Nice Cedex 4, France
24
Laboratoire d’Astrophysique de Bordeaux, Univ. Bordeaux, CNRS, B18N, Allée Geoffroy Saint-Hilaire, 33615 Pessac, France
25
Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
26
European Space Agency (ESA), European Space Astronomy Centre (ESAC), Camino Bajo del Castillo, s/n, Urbanizacion Villafranca del Castillo, Villanueva de la Cañada 28692 Madrid, Spain
27
Aurora Technology for European Space Agency (ESA), Camino Bajo del Castillo, s/n, Urbanizacion Villafranca del Castillo, Villanueva de la Cañada 28692 Madrid, Spain
28
Institut de Ciències del Cosmos (ICCUB), Universitat de Barcelona (IEEC-UB), Martí i Franquès 1, 08028 Barcelona, Spain
29
Lohrmann Observatory, Technische Universität Dresden, Mommsenstraße 13, 01062 Dresden, Germany
30
Lund Observatory, Department of Astronomy and Theoretical Physics, Lund University, Box 43, 22100 Lund, Sweden
31
CNES Centre Spatial de Toulouse, 18 Avenue Edouard Belin, 31401 Toulouse Cedex 9, France
32
INAF – Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy
33
Max Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
34
European Space Agency, Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
35
INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Piero Gobetti 93/3, 40129 Bologna, Italy
36
DAPCOM for Institut de Ciències del Cosmos (ICCUB), Universitat de Barcelona (IEEC-UB), Martí i Franquès 1, 08028 Barcelona, Spain
37
Royal Observatory of Belgium, Ringlaan 3, 1180 Brussels, Belgium
38
Observational Astrophysics, Division of Astronomy and Space Physics, Department of Physics and Astronomy, Uppsala University, Box 516, 751 20 Uppsala, Sweden
39
ALTEC S.p.a, Corso Marche, 79, 10146 Torino, Italy
40
Sednai Sàrl, Geneva, Switzerland
41
Mullard Space Science Laboratory, University College London, Holmbury St Mary, Dorking, Surrey RH5 6NT, UK
42
Gaia DPAC Project Office, ESAC, Camino Bajo del Castillo, s/n, Urbanizacion Villafranca del Castillo, Villanueva de la Cañada 28692 Madrid, Spain
43
SYRTE, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, LNE, 61 Avenue de l’Observatoire, 75014 Paris, France
44
National Observatory of Athens, I. Metaxa and Vas. Pavlou, Palaia Penteli 15236 Athens, Greece
45
IMCCE, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Univ. Lille, 77 Av. Denfert-Rochereau, 75014 Paris, France
46
Serco Gestión de Negocios for European Space Agency (ESA), Camino Bajo del Castillo, s/n, Urbanizacion Villafranca del Castillo, Villanueva de la Cañada 28692 Madrid, Spain
47
Institute for Astronomy, University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, UK
48
ATG Europe for European Space Agency (ESA), Camino Bajo del Castillo, s/n, Urbanizacion Villafranca del Castillo, Villanueva de la Cañada 28692 Madrid, Spain
49
CIGUS CITIC – Department of Computer Science and Information Technologies, University of A Coruña, Campus de Elviña s/n, A Coruña 15071, Spain
50
Kavli Institute for Cosmology Cambridge, Institute of Astronomy, Madingley Road, Cambridge CB3 0HA, UK
51
Leibniz Institute for Astrophysics Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
52
CENTRA, Faculdade de Ciências, Universidade de Lisboa, Edif. C8, Campo Grande, 1749-016 Lisboa, Portugal
53
Department of Informatics, Donald Bren School of Information and Computer Sciences, University of California, Irvine, 5226 Donald Bren Hall, 92697-3440 CA, Irvine, USA
54
INAF – Osservatorio Astrofisico di Catania, Via S. Sofia 78, 95123 Catania, Italy
55
Dipartimento di Fisica e Astronomia “Ettore Majorana”, Università di Catania, Via S. Sofia 64, 95123 Catania, Italy
56
INAF – Osservatorio Astronomico di Roma, Via Frascati 33, 00078 Monte Porzio Catone, Roma, Italy
57
Space Science Data Center – ASI, Via del Politecnico SNC, 00133 Roma, Italy
58
Department of Physics, University of Helsinki, PO Box 64 00014 Helsinki, Finland
59
Finnish Geospatial Research Institute FGI, Geodeetinrinne 2, 02430 Masala, Finland
60
Institut UTINAM CNRS UMR6213, Université Bourgogne Franche-Comté, OSU THETA Franche-Comté Bourgogne, Observatoire de Besançon, BP1615, 25010 Besançon Cedex, France
61
HE Space Operations BV for European Space Agency (ESA), Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
62
Dpto. de Inteligencia Artificial, UNED, c/ Juan del Rosal 16, 28040 Madrid, Spain
63
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences, Eötvös Loránd Research Network (ELKH), MTA Centre of Excellence, Konkoly Thege Miklós út 15-17, 1121 Budapest, Hungary
64
ELTE Etvs Loránd University, Institute of Physics, Pázmány Péter sétány 1A, 1117 Budapest, Hungary
65
Instituut voor Sterrenkunde, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
66
Department of Astrophysics/IMAPP, Radboud University, PO Box 9010 6500 GL Nijmegen, The Netherlands
67
University of Vienna, Department of Astrophysics, Türkenschanzstraße 17, 1180 Vienna, Austria
68
Institute of Physics, Laboratory of Astrophysics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
69
Kapteyn Astronomical Institute, University of Groningen, Landleven 12, 9747 AD Groningen, The Netherlands
70
Thales Services for CNES Centre Spatial de Toulouse, 18 Avenue Edouard Belin, 31401 Toulouse Cedex 9, France
71
Depto. Estadística e Investigación Operativa. Universidad de Cádiz, Avda. República Saharaui s/n, 11510 Puerto Real, Cádiz, Spain
72
Center for Research and Exploration in Space Science and Technology, University of Maryland Baltimore County, 1000 Hilltop Circle, Baltimore, MD, USA
73
GSFC – Goddard Space Flight Center, Code 698, 8800 Greenbelt Rd, 20771 MD, Greenbelt, USA
74
EURIX S.r.l., Corso Vittorio Emanuele II 61, 10128 Torino, Italy
75
Porter School of the Environment and Earth Sciences, Tel Aviv University, Tel Aviv 6997801, Israel
76
Harvard-Smithsonian Center for Astrophysics, 60 Garden St., MS 15, Cambridge, MA 02138, USA
77
ATOS for CNES Centre Spatial de Toulouse, 18 Avenue Edouard Belin, 31401 Toulouse Cedex 9, France
78
HE Space Operations BV for European Space Agency (ESA), Camino bajo del Castillo, s/n, Urbanizacion Villafranca del Castillo, Villanueva de la Cañada 28692 Madrid, Spain
79
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762 Porto, Portugal
80
LFCA/DAS, Universidad de Chile, CNRS, Casilla 36-D, Santiago, Chile
81
SISSA – Scuola Internazionale Superiore di Studi Avanzati, Via Bonomea 265, 34136 Trieste, Italy
82
Telespazio for CNES Centre Spatial de Toulouse, 18 avenue Edouard Belin, 31401 Toulouse Cedex 9, France
83
University of Turin, Department of Computer Sciences, Corso Svizzera 185, 10149 Torino, Italy
84
Dpto. de Matemática Aplicada y Ciencias de la Computación, Univ. de Cantabria, ETS Ingenieros de Caminos, Canales y Puertos, Avda. de los Castros s/n, 39005 Santander, Spain
85
Centro de Astronomía – CITEVA, Universidad de Antofagasta, Avenida Angamos 601, Antofagasta 1270300, Chile
86
DLR Gesellschaft für Raumfahrtanwendungen (GfR), mbH Münchener Straße 20, 82234 Weßling, Germany
87
Centre for Astrophysics Research, University of Hertfordshire, College Lane AL10 9AB Hatfield, UK
88
University of Turin, Mathematical Department “G. Peano”, Via Carlo Alberto 10, 10123 Torino, Italy
89
INAF – Osservatorio Astronomico d’Abruzzo, Via Mentore Maggini, 64100 Teramo, Italy
90
Instituto de Astronomia, Geofìsica e Ciências Atmosféricas, Universidade de São Paulo, Rua do Matão, 1226, Cidade Universitaria, 05508-900 São Paulo, SP, Brazil
91
APAVE SUDEUROPE SAS for CNES Centre Spatial de Toulouse, 18 avenue Edouard Belin, 31401 Toulouse Cedex 9, France
92
Mésocentre de calcul de Franche-Comté, Université de Franche-Comté, 16 route de Gray, 25030 Besançon Cedex, France
93
Astrophysics Research Centre, School of Mathematics and Physics, Queen’s University Belfast, Belfast BT7 1NN, UK
94
Centre de Données Astronomique de Strasbourg, Strasbourg, France
95
Institute for Computational Cosmology, Department of Physics, Durham University, Durham DH1 3LE, UK
96
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
97
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Straße 1, 85748 Garching, Germany
98
Data Science and Big Data Lab., Pablo de Olavide University, 41013 Seville, Spain
99
Barcelona Supercomputing Center (BSC), Plaça Eusebi Güell 1-3, 08034 Barcelona, Spain
100
ETSE Telecomunicación, Universidade de Vigo, Campus Lagoas-Marcosende, 36310 Vigo, Galicia, Spain
101
Asteroid Engineering Laboratory, Space Systems, Luleå University of Technology, Box 848, 981 28 Kiruna, Sweden
102
Vera C Rubin Observatory, 950 N. Cherry Avenue, Tucson, AZ 85719, USA
103
Department of Astrophysics, Astronomy and Mechanics, National and Kapodistrian University of Athens, Panepistimiopolis, Zografos 15783 Athens, Greece
104
TRUMPF Photonic Components GmbH, Lise-Meitner-Straße 13, 89081 Ulm, Germany
105
IAC – Instituto de Astrofisica de Canarias, Via Láctea s/n, 38200 La Laguna S.C., Tenerife, Spain
106
Department of Astrophysics, University of La Laguna, Via Láctea s/n, 38200 La Laguna S.C., Tenerife, Spain
107
Faculty of Aerospace Engineering, Delft University of Technology, Kluyverweg 1, 2629 HS Delft, The Netherlands
108
Radagast Solutions, Simon Vestdijkpad 24, 2321 WD Leiden, The Netherlands
109
Laboratoire Univers et Particules de Montpellier, CNRS Université Montpellier, Place Eugène Bataillon, CC72, 34095 Montpellier Cedex 05, France
110
Université de Caen Normandie, Côte de Nacre Boulevard Maréchal Juin, 14032 Caen, France
111
SRON Netherlands Institute for Space Research, Niels Bohrweg 4, 2333 CA Leiden, The Netherlands
112
Astronomical Observatory, University of Warsaw, Al. Ujazdowskie 4, 00-478 Warszawa, Poland
113
Scalian for CNES Centre Spatial de Toulouse, 18 Avenue Edouard Belin, 31401 Toulouse Cedex 9, France
114
Université Rennes, CNRS, IPR (Institut de Physique de Rennes), UMR 6251, 35000 Rennes, France
115
INAF – Osservatorio Astronomico di Capodimonte, Via Moiariello 16, 80131 Napoli, Italy
116
Shanghai Astronomical Observatory, Chinese Academy of Sciences, 80 Nandan Road, Shanghai 200030, PR China
117
University of Chinese Academy of Sciences, No. 19(A) Yuquan Road, Shijingshan District, Beijing 100049, PR China
118
Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen Ø, Denmark
119
DXC Technology, Retortvej 8, 2500 Valby, Denmark
120
Las Cumbres Observatory, 6740 Cortona Drive Suite 102, Goleta, CA 93117, USA
121
CIGUS CITIC, Department of Nautical Sciences and Marine Engineering, University of A Coruña, Paseo de Ronda 51, 15071 A Coruña, Spain
122
Astrophysics Research Institute, Liverpool John Moores University, 146 Brownlow Hill, Liverpool L3 5RF, UK
123
IPAC, Mail Code 100-22, California Institute of Technology, 1200 E. California Blvd., Pasadena, CA 91125, USA
124
IRAP, Université de Toulouse, CNRS, UPS, CNES, 9 Av. colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
125
MTA CSFK Lendület Near-Field Cosmology Research Group, Konkoly Observatory, MTA Research Centre for Astronomy and Earth Sciences, Konkoly Thege Miklós út 15-17, 1121 Budapest, Hungary
126
Departmento de Física de la Tierra y Astrofísica, Universidad Complutense de Madrid, 28040 Madrid, Spain
127
Ruđer Bošković Institute, Bijenička cesta 54, 10000 Zagreb, Croatia
128
Villanova University, Department of Astrophysics and Planetary Science, 800 E Lancaster Avenue, Villanova, PA 19085, USA
129
INAF – Osservatorio Astronomico di Brera, Via E. Bianchi, 46, 23807 Merate, LC, Italy
130
STFC, Rutherford Appleton Laboratory, Harwell, Didcot OX11 0QX, UK
131
Charles University, Faculty of Mathematics and Physics, Astronomical Institute of Charles University, V Holesovickach 2, 18000 Prague, Czech Republic
132
Department of Astrophysical Sciences, 4 Ivy Lane, Princeton University, Princeton, NJ 08544, USA
133
Departamento de Astrofísica, Centro de Astrobiología (CSIC-INTA), ESA-ESAC, Camino Bajo del Castillo s/n, 28692 Villanueva de la Cañada, Madrid, Spain
134
naXys, University of Namur, Rempart de la Vierge, 5000 Namur, Belgium
135
CGI Deutschland B.V. & Co. KG, Mornewegstr. 30, 64293 Darmstadt, Germany
136
Institute of Global Health, University of Geneva, Geneva, Switzerland
137
Astronomical Observatory Institute, Faculty of Physics, Adam Mickiewicz University, Poznań, Poland
138
H H Wills Physics Laboratory, University of Bristol, Tyndall Avenue, Bristol BS8 1TL, UK
139
Department of Physics and Astronomy G. Galilei, University of Padova, Vicolo dell’Osservatorio 3, 35122 Padova, Italy
140
CERN, Esplanade des Particules 1, PO Box 1211, Geneva, Switzerland
141
Applied Physics Department, Universidade de Vigo, 36310 Vigo, Spain
142
Association of Universities for Research in Astronomy, 1331 Pennsylvania Ave. NW, Washington, DC 20004, USA
143
European Southern Observatory, Alonso de Córdova, 3107 Casilla 19, Santiago, Chile
144
Sorbonne Université, CNRS, UMR7095, Institut d’Astrophysique de Paris, 98bis Bd. Arago, 75014 Paris, France
Received:
13
April
2022
Accepted:
9
June
2022
Context. The Gaia DR3 catalogue contains, for the first time, about 800 000 solutions with either orbital elements or trend parameters for astrometric, spectroscopic, and eclipsing binaries, and combinations of these three.
Aims. With this paper, we aim to illustrate the huge potential of this large non-single-star catalogue.
Methods. Using the orbital solutions and models of the binaries, we have built a catalogue of tens of thousands of stellar masses or lower limits thereof, some with consistent flux ratios. Properties concerning the completeness of the binary catalogues are discussed, statistical features of the orbital elements are explained, and a comparison with other catalogues is performed.
Results. Illustrative applications are proposed for binaries across the Hertzsprung-Russell Diagram (HRD). Binarity is studied in the giant branch and a search for genuine spectroscopic binaries among long-period variables is performed. The discovery of new EL CVn systems illustrates the potential of combining variability and binarity catalogues. Potential compact object companions are presented, mainly white dwarf companions or double degenerates, but one candidate neutron star is also found. Towards the bottom of the main sequence, the orbits of previously suspected binary ultracool dwarfs are determined and new candidate binaries are discovered. The long awaited contribution of Gaia to the analysis of the substellar regime shows the brown dwarf desert around solar-type stars using true rather than minimum masses, and provides new important constraints on the occurrence rates of substellar companions to M dwarfs. Several dozen new exoplanets are proposed, including two with validated orbital solutions and one super-Jupiter orbiting a white dwarf, all being candidates requiring confirmation. Besides binarity, higher order multiple systems are also found.
Conclusions. By increasing the number of known binary orbits by more than one order of magnitude, Gaia DR3 will provide a rich reservoir of dynamical masses and an important contribution to the analysis of stellar multiplicity.
Key words: binaries: general / astrometry / planetary systems / stars: fundamental parameters / catalogs / white dwarfs
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The success of Gaia (Gaia Collaboration 2016b), with parallaxes for around 1.5 billion sources, could overshadow the difficulties faced in measuring the first stellar distances. The two millennia during which this research was unsuccessfully carried out were littered with unrelated but equally fundamental discoveries. In particular, Herschel, following the suggestion by Ramponi to Galileo in 1611 (Siebert 2005), observed pairs of stars in order to measure their differential parallaxes, but did not succeed. Instead, what he demonstrated for the first time, in 1802, was the existence of orbits for these stars, changing their nature from unrelated double stars to binaries, proving that the law of gravitation was universal.
After Bessel obtained the first convincing parallax measurement in 1838, he also deduced in 1844, from the non-linear proper motion of Sirius and Procyon, that there could exist not only visual binaries but also invisible binaries, nowadays referred to as astrometric binaries. Astrometry and binarity have therefore been intimately linked from the start. Indeed, it was not until much later, by observing the periodic Doppler shift of Algol’s lines, that Vogel correctly deduced in 1889 that this latter was due to its orbital motion, making Algol the first spectroscopic binary. Furthermore, the periodic eclipse of Algol was hypothesised by John Goodricke in 1782, making this star also the first eclipsing binary (Leverington 1995).
Since then, binary stars have been found to be important for deriving the physical properties of stars but also for their fundamental role in stellar evolution; understanding the statistical properties of binary and multiple stars is therefore of utmost importance for developing our knowledge of the Galaxy. The properties of companions down to the substellar regime are also important for understanding stellar formation. Unfortunately, until now, small sample sizes, selection effects, and the absence of the required astrometric precision have complicated the analysis of the various existing ground-based data.
As a large survey, Gaia should be in an ideal place to bring a new and much broader perspective to these fundamental topics. What makes Gaia so unique is its ability to find, and above all, to parameterise most types of binaries simultaneously, whether they be visual, astrometric, spectroscopic, or eclipsing, and even through stellar parametrisation, with a remarkable homogeneity of epoch, level of calibration accuracy, data reduction, and process organisation.
The Gaia precursor, HIPPARCOS, had already discovered and measured double stars (Lindegren 1997), mostly resolved ones but also several categories of unresolved astrometric binaries, which allowed stellar masses to be determined (Söderhjelm et al. 1997; Martin et al. 1997) albeit for only a small number of sources.
With the successive Gaia DR1 (Gaia Collaboration 2016a), DR2 (Gaia Collaboration 2018b), and then EDR3 (Gaia Collaboration 2021a), multiple stars were still not handled, with analysing single stars already posing a significant challenge, and these successive releases represent the improvement of calibrations and source analysis. This does not mean that non-single stars were absent. Whether double or binaries, they are indeed present and processing them as single stars seriously degrades their results. Nevertheless, several flags in the Gaia catalogue inform us about the potential duplicity, and the combination of these first Gaia releases with HIPPARCOS data already allowed the community to detect long-period binaries (Kervella et al. 2019a, 2022; Brandt 2021).
The advent of Gaia DR3 (Gaia Collaboration 2023b) now presents impressive new data products among which, to quote only a few, variability (Eyer et al. 2023), radial velocities (RV, Katz et al. 2023), and astrophysical parameters (Creevey et al. 2023) determined using either high-resolution (RVS) or low-resolution data (BP − RP photometers, De Angeli et al. 2023) for a very large fraction of the catalogue. Gaia DR3 also contains the first analysis of the unresolved binary star contents, covering the typical binary classes (astrometric, spectroscopic, photometric) and presented in several tables: two-body orbits, astrometric or spectroscopic accelerations, and variable binaries. These tables contain the orbital or trend parameters of the binaries that have been discovered. Above all, this offers the prospect of deriving the physical properties of the individual components. This should also improve the measurements of these systems in the main catalogue, with better astrometric parameters or systemic radial velocity.
Although the maturity of the analysis of Gaia data now makes it possible to obtain, for the first time, a multi-type catalogue of binaries that is much larger than has been compiled – with difficulty – over the previous centuries, it must be stressed that only a small fraction of the binary content of the main catalogue has been analysed for DR3. This data analysis is described in the documentation (Pourbaix et al. 2022)1 and the articles accompanying this data release, namely Halbwachs et al. (2023), Holl et al. (2023b), Gosset et al. (in prep.), Mowlavi et al. (2023) and Siopis (in prep.).
The purposes of this publication are manifold. It is first intended to describe the possible use cases of the catalogue, illustrating in particular the potential complementarity of the different data processing chains. This is essentially an appetiser that shows the quality of the data, highlighting the basic results that can be readily obtained, in particular estimating masses which were not part of the non-single star tables. In addition, this performance verification paper acts as a final validation step before releasing the data. It is beyond the scope of this publication to explore the data in detail, and we do not intend to compare them with models or to confirm candidates of various kinds, as these will be the goals of scientific exploitation by the community, but we wish to facilitate this exploitation by describing what has been learnt from our analysis of the data so far.
We start by describing the data content. Useful statistical properties are then clarified together with what is known about the selection function. We then focus on orbits, and not on acceleration solutions (for astrometry) or trend solutions (for spectroscopic binaries), and instead propose a catalogue of masses for these orbital solutions. From this, we present an impressionistic panorama of the potential of this catalogue concerning basic statistical properties and candidate sources of various types; for example EL CVn, compact companions, white dwarfs and high-mass dwarfs, and then ultracool dwarfs and substellar companions. Finally, multiple systems are discussed.
2. Data description
2.1. Table contents
The non-single star (NSS) tables are presented by type of solution or period range rather than according to binary type. The first of the four tables, nss_two_body_orbit, contains the orbital parameters for all three categories, that is, astrometric, spectroscopic, and eclipsing binary, all being unresolved. The table nss_acceleration_astro contains accelerations or derivative of this parameter for sources that have an astrometric motion better described using a quadratic or cubic rather than a linear proper motion. Similarly, the nss_non_linearspectro are trend (long-period) solutions of spectroscopic binaries. The solutions in the nss_vim_fl table are different in that the photocentre displacement due to the photometric variability of one component of fixed binaries required the correction of the astrometric parameters (variable-induced movers fixed, VIMF). A summary of the solutions is given in Table 1.
Content of the four non-single star tables.
The astrometric orbits in the nss_two_body_orbit table have a nss_solution_type name starting with Orbital* and the orbital parameters are described in Appendix B.1. The spectroscopic binaries with either one component being parametrised (SB1) or both (SB2) have their parameters described in Appendix B.2 and short periods may have a circular solution (nss_solution_type = SB1C). As a source may simultaneously be, for example, an astrometric binary and a spectroscopic binary, combined solutions have been computed in some cases (nss_solution_type = AstroSpectroSB1). For the same reason, the EclipsingSpectro solutions are combinations of eclipsing and spectroscopic solutions. However, when no combination has been performed, then two solutions for the same source may be present in the nss_two_body_orbit table; that is, a query by source_id may return several solutions. These multiple solutions may indicate either triple systems, or some inconsistency that users may wish to sort out, and then possibly combine these solutions offline.
For the same reason, some sources may also have solutions in several tables simultaneously. To take an example, there are 160 eclipsing binaries that also have a VIMF solution. As the VIMF model should have improved their astrometric solution, and the distance of eclipsing binaries is of interest, this solution should in principle be preferred over the one given in the gaia_source table. This potential multiplicity of solutions for a given source explains why the total number of unique NSS sources is 813 687 while the total number of NSS solutions is larger, 839 098.
The distributions of the various orbital solutions with magnitude are shown Fig. 1. As expected, the brightest are the SB1 and SB2, and consequently also their intersection with astrometric binaries, AstroSpectroSB1, and with eclipsing binaries, EclipsingSpectro. The orbital astrometric binaries (brighter than G < 19) peak at G ≈ 14 while the OrbitalTargetedSearch span the entire magnitude range as the sources were given as input list. The eclipsing binaries are the faintest. We note that the NSS eclipsing binaries are a small subset of the ones detected by photometry (Mowlavi et al. 2023), for which an orbital solution has been computed (Siopis, in prep.); we refer to the much more complete vari_eclipsing_binary table for comparison.
 |
Fig. 1. Magnitude distribution for each solution type in the nss_two_body_orbit table. |
The distribution of periods, by construction restricted to the nss_two_body_orbit table, is depicted in Fig. 2. The short-period eclipsing and long-period astrometric binaries are nicely bridged by the SBs. Within a few years, Gaia has covered the impressive 0.28 − 1500-day period range (99% CI) for thousands of sources, which should prove very valuable for the statistics of binary properties. The coverage in the joint distribution of period and magnitude is qualitatively illustrated in Fig. 3.
 |
Fig. 2. Number of solutions for each solution type in the nss_two_body_orbit table as a function of period. |
 |
Fig. 3. G apparent magnitude vs. period in the nss_two_body_orbit table. |
The Hertzsprung-Russell diagrams (HRDs) for the various categories are represented Fig. 4 for sources with a parallax signal-to-noise ratio (S/N) > 5. We note that the used parallax is that from the NSS solution for what concerns the putative astrometric binaries, while we use the one from the main catalogue for spectroscopic and eclipsing binaries.
 |
Fig. 4. Gaia HRD, uncorrected for extinction, for all NSS solutions with a relative parallax error of better than 20%. No selection is done on the photometric quality. The colour scale represents the square root of the relative density of stars. Top: astrometric binaries, (a): allOrbital*solutions plusAstroSpectroSB1, (b): Acceleration solutions, (c): VIMF; bottom: Spectroscopic binaries with (d): SB* orbits and (e): NonLinearSpectro, (f): eclipsing binaries. |
2.2. Table construction
Although we refer to the online documentation and the articles accompanying this data release for a detailed understanding of the data processing, it is of interest to describe how the NSS data were obtained, starting with their input data selection, as this is one first key to understanding the NSS selection function.
The basic NSS processing procedure selected its input sources from those that had a poor goodness of fit (GoF) in the upstream results, either in the astrometric or in the spectroscopic processing, or from those that were detected as eclipsing variables; the only exception is the OrbitalTargetedSearch (see Sect. 2.2.2), where a predefined source list was given as input to the astrometric orbital fit, irrespective of their actual GoF in the single star solution.
2.2.1. Astrometric binaries: main processing
As Gaia DR3 is the first publication of NSS solutions, we decided to limit the content to the most significant ones, this criterion being relaxed for further releases, and the motivation for this is explained below. The definition of the input source list started after Gaia DR2, where it was assumed that the sources with ruwe > 1.4 represented a reasonable threshold for sources with problematic astrometric solutions2. A more recent analysis (e.g. Penoyre et al. 2022) appears to suggest that a lower threshold could have been chosen, but this value also has the advantage that it decreases the processing requirements.
To this ruwe > 1.4 criterion, G < 19 was added in order to keep the best S/N. The sample defined in this way contains many contaminants, partially resolved rather than unresolved sources. In particular, for a double star with a projected separation between components of between ≈9 mas and ≈0.27″ (Lindegren 2022), depending on the magnitude difference, the epoch position is not exactly on the photocentre3, meaning that the astrometry of such sources is perturbed and the source is likely to have been selected.
Consequently, the criterion ipd_frac_multi_peak ≤ 2 was added to avoid double stars with a large separation and ipd_gof_harmonic_amplitude < 0.1 was also added to reject pairs with smaller separations. The visibility_periods_used > 11 criterion was also added (> 12 for orbital solutions) in order to avoid spurious solutions4.
However, the sample was still polluted, and so another criterion was added, this time based on photometry, as an attempt to avoid sources with light being contaminated by a neighbour. For this purpose, we made use of the corrected BP and RP flux excess factor C* associated to its uncertainty σC*(G) as defined by Riello et al. (2021, Eqs. (6) and (18)), selecting sources with |C*|< 1.645σC* only.
2.2.2. Astrometric binaries: alternative processing
As described by Holl et al. (2023b), alternative orbit determination algorithms have been run on two different input lists. The first one is based on astrometric binaries that could not be successfully modelled by any model in the main processing pipeline, for which a more complex handling was attempted, nss_solution_type = OrbitalAlternative*. These sources originate from the same list as described in Sect. 2.2.1. The second one is a sample of sources with detected companions published in the literature, nss_solution_type = OrbitalTargetedSearch*, where all sources have been kept for processing.
2.2.3. Spectroscopic binaries
The selection of the sources that had to be treated by the spectroscopic binary pipeline was based on sources with enough measurements, and a large enough dispersion of these measurements, rejecting stars not having rv_renormalised_gof > 4, rv_nb_transits ≥ 10, and 3875 K < rv_template_teff < 8125 K, or detected as SB2. One may notice that there are more than 6000 sources with a SB solution that have no average radial velocity in the gaia_source main catalogue. In that case (as in the other cases where a SB solution is given), the center_of_mass_velocity gives the systemic velocity. The absence of a mean RV for what concerns SB2s is normal, as the main spectroscopic processing did not compute this value. For SB1s, it may be useful to note that the computation had not been performed for the sources that were considered either peculiar, potentially SB2, too hot, or with emission lines. Consequently, when some SB results appear doubtful, it may then be useful to check whether gaia_source.radial_velocity is NULL for these sources. More details are given in Gosset et al. (in prep.).
2.2.4. Eclipsing binaries
The input list for candidate eclipsing binaries contained about 2.1 million sources that can be found in the vari_eclipsing_binaryGaia DR3 table. Their selection is described by Mowlavi et al. (2023); see also the online documentation. The selection of the subset therein for which an orbital solution has been computed is described by Siopis (in prep.).
2.3. Output filtering
Once the first processing results were analysed, it appeared that the cleaning of the input list had still left a very large fraction of spurious solutions. This is why it was decided to keep the most significant solutions for Gaia DR3: a general filter was applied to keep those with goodness of fit smaller than 50 and significance > 5 (> 2 for OrbitalTargetedSearch*). The significance is computed as the S/N of the semi-major axis for astrometric orbits, (a0/σa0), as the S/N of the acceleration module for acceleration solutions, and as the S/N of the semi-amplitude for spectroscopic binaries, (K1/σK1). Supplementary filtering was applied during the processing or at post-processing level as described for the various models below.
Astrometric binaries: acceleration solutions. One could naively hope that the estimated accelerations would allow us to detect binaries of intermediate period and provide some useful information about the binary, such as the minimum mass producing the given acceleration on the primary. However, the situation appears more complex. The acceleration values themselves are not discussed, and it can be seen that these solutions improve the baseline solution; for example, the giant branch appears slightly thinner for an HRD produced using the parallaxes from the acceleration solution compared to those from the main catalogue.
However, two effects conspire to make the interpretation of the acceleration term unclear. The first one originates from the organisation of the NSS processing: acceleration solutions were attempted before any other solutions, and kept if found to be sufficiently significant with a reasonable GoF. The (unwanted) effect is that some solutions that could have received a full orbit parametrisation were not attempted and appear in the NSS catalogue with an acceleration solution instead. The second effect is that an acceleration term can be significant even for short periods or very long periods. This is demonstrated by the analysis by Lindegren (2022).
The following filtering has been applied (see documentation and Halbwachs et al. 2023, for details): the sources which have been kept are those with significance s > 20 and ϖ/σϖ > 1.2 s1.05 and GoF < 22 for Acceleration7 and ϖ/σϖ > 2.1 s1.05 and GoF < 25 for Acceleration9. Despite this, it is known that a large fraction of the acceleration solutions are not intermediate-period binaries as one would expect, but are rather short- or long-period binaries instead.
Astrometric binaries: Orbital solutions. The processing of orbital solutions starts by a period search. Unfortunately, this may lead to the detection of periods related to the scan law, rather than due to some true periodic motion: partially resolved objects with fixed position may give a signal depending on the scanning angle with respect to the orientation of the pair. This problem is fully analysed by Holl et al. (2023a). Consequently, most detected periods below ≈100 days were erroneous, leading to solutions with huge and incorrect mass functions.
To circumvent this problem, the following filtering was adopted (Halbwachs et al. 2023): parallax S/N > 20 000/ period, significances = a0/σa0 > 5, and s > 158/  , eccentricity_error < 0.182 * log10(period) −0.244.
, eccentricity_error < 0.182 * log10(period) −0.244.
Astrometric binaries: alternative processing. Aggressive post-processing filtering approaches for both samples produced subsets of solutions that were assigned OrbitalAlternative* and OrbitalTargetedSearch* solution types, respectively, in the Gaia DR3 archive. For both cases, subsamples of sources that passed a variety of validation procedures were further assigned OrbitalAlternativeValidated and OrbitalTargetedSearchValidated solution types (see Holl et al. 2023b, for details).
Inspection of the OrbitalAlternative solutions reveals that the caveat of unrealistically large inferred companion masses at short orbital periods is not entirely removed. A few percent of spurious solutions still likely contaminates this sample.
Spectroscopic binaries. Only the sources with GoF < 3, |center_of_mass_velocity|< 1000 km s−1, K1 < 250 km s−1, and efficiency > 0.1 were kept, where efficiency is a measure of the correlation between parameters. One of the most important problems found after processing was the presence of many spurious SB detections with short periods. For this reason, the lower confidence threshold on the period was adapted depending on the period itself: it was set to 0.995 for P < 1 d, 0.95 for P > 10 d, and −0.045 log P + 0.995 in between. For details on this and other filtering during the spectroscopic processing, see Gosset et al. (in prep.).
Despite all this, the comparison of NSS results with catalogues of known binaries shows that for a few percent of the SB1 solutions, the period may still be incorrect, mainly because of the sparse time sampling. When these sources have both an SB1 and Orbital solution, such cases may be spotted by comparing the respective semi-amplitudes. Short periods with large ruwe (e.g. > 1.4) are frequently suspect; some may be the inner system of a triple system, but most may instead be some kind of aliases of a longer period.
Inspecting the SB1 solutions, an overdensity of solutions with periods around the precession period (62.97 days) can be noted, in particular by selecting sources with large astrometric excess noise (see Fig. 5). These solutions are spurious and due to some offset in the astrometric coordinates, which generates in turn a spurious variation of the computed epoch radial velocities; as this offset depends on the scanning angle, it occurs with a periodicity linked to the precession of the satellite. The inaccuracy of the astrometric coordinates is most probably due to the fact that they are partially resolved binaries or double stars, which is confirmed by the fact that we also see this overdensity when selecting sources with ipd_frac_multi_peak > 20. Holl et al. (2023a) describe the effect of the scanning law on the NSS solutions in more detail.
 |
Fig. 5. K1 semi-amplitude vs. period diagram of SB1 solutions, colour coded according to their astrometric_excess_noise. The diagram shows the presence of an overdensity of solutions at periods near the precession period (marked with a vertical line) with large astrometric excess noise. The histogram at the top shows the density of solutions with astrometric excess noise larger than 1 mas (blue line) and of those with ipd_frac_multi_peak > 20 (orange line). |
Spurious SB1 solutions can also be generated by pulsation of the source, as in RR Lyrae and Cepheids. In many cases, the SB1 solution will have the same period as the pulsation, but in other cases, due to the sparse sampling, the pipeline can find a Keplerian fitting solution at a different, typically shorter period. During the release validation, SB1 solutions of sources identified by Gaia as RR Lyrae or Cepheids were removed from the release.
Another source of spurious SB1 solutions is contamination from a nearby, brighter star. As explained by Seabroke et al. (2021), and noted by Boubert et al. (2019), the RVS spectrum of sources extracted at a given transit can be contaminated by a nearby source, producing spurious values of the radial velocity. In Gaia DR3, the RVS pipeline includes a deblending algorithm, which is nevertheless limited to spectra with overlapping windows (see Seabroke et al. 2021, for details).
Eclipsing binaries. At post-processing, only the sources with 0.2 < efficiency ≤ 1 and g_rank ≥ 0.6 were kept, where the rank is a measure of the quality of the fit. See the online documentation (Pourbaix et al. 2022, Sect. 7.6) for details.
3. Completeness
The resulting NSS dataset is the result of a selection process in three successive steps: (a) the selection of the input list, discussed Sect. 2.2; (b) the sources for which the orbital motion can be preferentially detected by the processing; (c) the filtering done at post processing, indicated Sect. 2.3.
In this section, we give some indications concerning the second step. One main reason for the expected non-uniformity of orbit detections is the number of observations and their temporal distribution. As this is governed by the scanning law of the Gaia satellite (see e.g. Fig. 7), this should appear clearly on a sky plot, and this is discussed in Sect. 3.1.
However, even with a given set of observations, all orbits are not perfectly equivalent. First, the period distribution of astrometric orbits shows a prominent lack of solutions around one year, which was obviously expected due to the difficulty in decoupling the orbital from the parallactic effect. There are other more subtle biases depending on the orbit itself; these are discussed Sect. 3.2. The distribution of solutions is finally discussed within the 100 pc horizon at Sect. 3.3 and the completeness is also studied for HIPPARCOS stars Sect. 4.2.2.
3.1. Sky distribution
Over the sky, the distribution of the various solution types shows the expected higher density along the Galactic plane together with a larger excess at high ecliptic latitudes around l ± 100°. The latter is due to a larger number of observations, and therefore to a larger probability of detecting periodically variable motions.
However, this tells us little about whether or not the (in)completeness is uniform over the sky. Although we may have for example more eclipsing binaries among young stars, let us assume for a moment that F, the true (unknown) fraction of binaries, is uniform over the sky, and that our NSS samples are roughly complete up to some given magnitude Gmax.
Dividing up the sky in healpix (Górski et al. 2005) level 4 equal-area pixels, we note Nj the number of sources up to G < Gmax in the full Gaia catalogue in a given healpix cell j, and nj the corresponding number of NSS of a given type up to G < Gmax. With f = med(nj/Nj), the empirical median of the ratio over the sky as estimate of F, we call ‘sky density factor’ 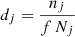 . This factor gives the up or down factor of the average NSS fraction and should be a noisy value around 1 if F is approximately constant over the sky.
. This factor gives the up or down factor of the average NSS fraction and should be a noisy value around 1 if F is approximately constant over the sky.
Figure 6 shows the sky density factor for several solution types truncated up to a reasonable Gmax value in healpix level 4 pixels. As this density factor may be attributed to the number of observations available, Fig. 7 presents the ratio of useful observations over the sky for photometry and astrometry, with the same scale for comparison purposes.
 |
Fig. 6. Sky density factor (Galactic coordinates, healpix level 4, log scale, see text) illustrating the excess or deficit factors of NSS sources compared to their sky average value. Panel a: SB*, panel b: Acceleration, panel c: EclipsingBinary, panel d: Orbital*. |
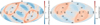 |
Fig. 7. Ratio of the number of photometric observations over their median values for G < 18 (left) and the ratio of the number of visibility periods used in astrometry over their median values for G < 15 (right), with the same colour scale (from |
For all types of binaries, the expected deficit of sources near the Galactic centre can be seen because of both high density and poor coverage. The distribution of spectroscopic binaries (GRVS − max = 12, Fig. 6a) is also as expected with a smooth pattern of regions with higher numbers of field-of-view transits. The non-uniformity is less expected for eclipsing binaries (Gmax = 18, Fig. 6c) with a slight excess at the anticentre and an excess – larger than expected from the number of transits – around l ± 100° towards high ecliptic latitudes. For acceleration solutions (Gmax = 15, Fig. 6b), there is a deficit in the Galactic plane and an excess at high ecliptic latitudes. This is worse for Orbital solutions (Gmax = 15, Fig. 6d), which may be due to the fact that orbital solutions require a greater number of observations than acceleration solutions as there are a greater number of parameters to determine. Again, the sky density factor is relative to the average over the sky, meaning that an excess in some regions may rather indicate a deficit in the rest of the sky. Some or part of the above features of the astrometric solutions likely originate from the input source selection, where sources suspected to be resolved doubles were excluded, which is more frequent in the Galactic plane.
3.2. Astrometric orbit detection sensitivity as a function of orbital inclination
Gaia is observing sources with a cadence and scan angle ψ determined by its scanning law. Depending on whether a binary system is seen face-on (inclination i = 0° or i = 180°) or edge-on (i = 90°), the detection probability of the astrometric orbit varies. An edge-on orbit that is oriented north-south and is being observed only with 1D astrometry along the east-west axis is undetectable. This extreme example does not occur for Gaia, but it illustrates that we can expect continuous variation as a function of inclination angle, with edge-on orbits having the lowest detection probability.
To obtain an empirical estimate of the expected dependency, we simulated 50 000 circular orbits (e = 0, ω = 0) with the following fixed parameters: distance 20 pc; period of 500 days; primary mass 1 ℳ⊙; companion mass of 1 ℳJup, and hence a semi-major axis of a0 = 0.059 mas for the orbit of the host. The ascending node Ω was uniformly distributed. We simulated inclinations such that cos i is uniformly distributed, as expected for isotropic orbit orientation in space.
To each orbit we assigned a realistic Gaia DR3 time sampling with associated scan angles randomly retrieved from approximately 1000 real sources distributed over the entire sky with the aim of averaging scan-law-dependent effects. We then computed the rms dispersion of the AL signal wk1, Eq. (B.6), caused by the astrometric orbit only, that is, neglecting proper and parallactic motion. This dispersion shows a clear dependence on inclination angle (see Fig. 8), with the expected minimum for edge-on orbits. The vertical scatter is caused by the variation in the number of assigned Gaia observations and their scan-angle distribution for a particular time-series realisation. The dependence on ascending node (Fig. 8, bottom) is much weaker but noticeable. Because we limited our simulation to circular orbits, there is no dependence on the argument of periastron.
 |
Fig. 8. Density histograms of simulated orbit signal dispersion as a function of cos i (top) and Ω (bottom). The black solid curve shows the running median value. Top panel: the empirical and analytic models are shown as dashed grey and black lines, respectively. Edge-on orbits have cos i = 0 and face-on configurations have |cos i |=1. |
In Appendix C we analytically derive the following expression, Eq. (C.10), for the rms of wk1 as a function of cos i, which is valid for one-dimensional (1D) along-scan (AL) observations as used for DR3 (Lindegren et al. 2021) under the assumption of circular orbits and random scan angles:
This dependency is shown as ‘Analytic model’ in Fig. 8. A fit with a quadratic polynomial is also shown as ‘Empirical model’. The analytic model reproduces the data very well, both in absolute amplitude and shape, except for a small amplitude offset which probably reflects the fact that the Gaia scan angles are not random and are sometimes restricted in range.
Because the amplitude of the orbit signal is the principal factor in deciding whether an orbit can be detected5, there is no need to simulate the complete processing chain (Halbwachs et al. 2023; Holl et al. 2023b). Our simulations demonstrate that the signal of a face-on orbit is 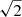 larger than that of an edge-on orbit, which means that the former is more likely to be detected.
larger than that of an edge-on orbit, which means that the former is more likely to be detected.
3.3. The Gaia catalogue of nearby stars
A clean catalogue of 331 312 sources within 100 pc of the Sun (Gaia Collaboration 2021b, GCNS) was published together with Gaia EDR3. This catalogue would represent a useful subset for the completeness analysis.
As the NSS parallaxes of Orbital or acceleration solutions may supersede the EDR3 ones, it is of interest to first analyse their potential impact on the GCNS content. One finds 116 orbital sources that would now enter GCNS using the following query: Using a similar query, 89 sources with an acceleration solution would enter GCNS, giving a total of 205 sources. These numbers would change by 13% only if we were to take a 1σ margin, and so the random errors have a weak influence on this.
SELECT NSS.source_id, GS.phot_g_mean_mag, NSS.parallax, NSS.parallax_error, GS.parallax as gs_parallax, GS.parallax_error as gs_parallax_error FROM user_dr3int6.nss_two_body_orbit NSS, user_dr3int6.gaia_source GS LEFT JOIN external.gaiaedr3_gcns_main_1 GCNS ON NSS.source_id = GCNS.source_id WHERE GCNS.source_id IS NULL AND NSS.source_id = GS.source_id AND NSS.parallax > 10
Conversely, one may count sources that should no longer belong to GCNS according to their new parallax: amounting to 415 sources for orbital solutions plus 413 sources for acceleration solutions, giving a total of 828 sources.
SELECT NSS.source_id, GS.phot_g_mean_mag, NSS.parallax, NSS.parallax_error, GS.parallax as gs_parallax, GS.parallax_error as gs_parallax_error FROM user_dr3int6.nss_two_body_orbit NSS, user_dr3int6.gaia_source gs, external.gaiaedr3_gcns_main_1 GCNS WHERE NSS.source_id = GS.source_id AND NSS.source_id = GCNS.source_id AND NSS.parallax < 10,
Having 4723+4523 = 9246 astrometric NSS sources which are in the GCNS, these 828 sources represent 9% of the orbital plus acceleration solutions which may no longer be in the GCNS while 2% may now enter. This means that any study of the NSS completeness within the GCNS should use the NSS parallax rather than the one from the main catalogue.
One may also note that the balance between the number of NSSs that would be rejected from GCNS and the number that would enter illustrates one long-since recognised adverse effect of the random errors (Eddington 1913; Trumpler & Weaver 1953). The parallaxes of NSS sources managed as single stars in DR3 have a significant error, which should now be much reduced in the NSS tables; this, added to the asymmetric distribution of the parallaxes, means that binary sources preferentially entered GCNS that should not belong to it. As the DR3 NSS catalogue contains only a small fraction of the actual unresolved astrometric binaries, using the GCNS to compute a binarity fraction may produce a small positive bias.
As a clarification of the GCNS content using the NSS parallax is outside the scope of this article, we keep the GCNS for reference in what follows. We show the fraction of NSS sources among G < 19 GCNS sources as a function of parallax for all solution types (see right panel of Fig. 9). In these figures and the following, we add the AstroSpectroSB1 counts both to orbital solution counts and SB counts, in addition to counting them independently and, for the comparison to be fair, we restricted the ratios to the typical magnitude ranges used respectively for astrometric, spectroscopic, and eclipsing binaries.
 |
Fig. 9. Fraction of NSS solutions among EDR3 sources vs. parallax (left) and fraction of NSS sources in GCNS (right). In both figures, we added AstroSpectroSB1 counts to Orbital counts and to SB*=SB1+SB2 counts in addition to counting them individually, and we restrict the ratios to GRVS < 12 sources only for SB* and NonLinearSpectro, to G < 19 for Orbital and Acceleration solutions, and to G < 20 for eclipsing binaries. |
What first appears is the conspicuous increase in the fraction of SBs up to 100 pc. One reason for this may be the transition from the GRVS < 12 population of dwarfs to giants, as can be seen in Fig. 4d, with the latter having a better intrinsic RV precision at a given apparent magnitude (Katz et al. 2023), and thus a larger binary detection probability; however, a difference in the binary fraction between dwarfs and giants cannot be excluded. Second, contrary to what might have been expected, the total fraction of orbital and acceleration solutions, about 3%, appears roughly constant with distance in the GCNS, despite all the complex filtering that has been applied. For comparison, the fraction of NSSs among DR3 sources (left panel of Fig. 9) shows a drop in astrometric solutions with distance beyond 100 pc, while the fraction of spectroscopic binaries (SB+nss_non_linearspectro) does not vary as sharply. From this comparison, we retain the fact that even if the absolute value of the astrometric binary fraction is difficult to extrapolate after all the filtering done, the fact that it appears roughly uniform with distance in a first approximation in the GCNS sample means that this sample could be useful for studying the properties of the astrometric binaries.
Consequently, the fraction of NSSs among GCNS may provide useful insights, and Fig. 10 represents this ratio versus G apparent and absolute magnitude of the pair, respectively. The absolute magnitude mg_gspphot originates from the General Stellar Parametrizer from Photometry (GSP-Phot), which computed the astrophysical parameters of stars from the low-resolution BP/RP spectra and is available in the astrophysical_parameters table.
 |
Fig. 10. Fraction of NSS solutions among GCNS sources vs. G apparent magnitude (left) and vs. G GSP-Phot absolute magnitude (right). The same constraints as mentioned in Fig. 9 have been applied. |
4. Caveats
Many validations have been performed and described in the catalogue documentation (Pourbaix et al. 2022), accompanying papers (Halbwachs et al. 2023; Holl et al. 2023b; Gosset et al., in prep.; Siopis, in prep.), and the independent validation of all catalogues (Babusiaux et al. 2023). Elsewhere in this article, we also check the distribution tails of some parameters which allowed us to discover undesired aspects and we indicate ways to circumvent them. Here, we describe two supplementary tests that draw attention to some properties of the catalogue, the first analysing the distribution of orbital parameters, the second comparing the results to binaries detected externally.
4.1. Distributions and biases of astrometric orbit parameters
Under the assumption that the orbits of binary systems are randomly oriented, we can infer the expected distributions in the geometric elements of the corresponding astrometric orbits, that is, the inclination i, the argument of periastron ω, and the longitude of the ascending node Ω6. In an ideal experiment, we expect to recover uniform distributions in cos i, Ω, and ω. Here, we inspect the observed distributions of these parameters in DR3.
4.1.1. Observed distributions of geometric elements in DR3 solutions
Figure 11 shows the distributions of cos i, Ω, and ω for the solution types Orbital and AstroSpectroSB1. To mitigate effects related to incomplete orbit coverage, we selected solutions with orbital periods shorter than 1000 days, which roughly corresponds to the DR3 time span.
 |
Fig. 11. Normalised distributions of cos i (left), Ω (middle), and ω (right) parameters. Orbital (solid lines, 122 989 entries) and AstroSpectroSB1 (dashed lines, 29 770 entries) solutions with P < 1000 d are shown. The orb6 solutions from the literature (3405 entries, without filter on period) are shown in grey. Left panel: the dotted line shows the empirical model defined in Sect. 3.2, which was re-scaled on the five central histogram bins. Right panel: we have suppressed the circular solutions with ω = 0. |
For Orbital solutions, there is a strong modulation in cos i. Although the expected suppression of edge-on orbits is present, the observed distribution deviates significantly from the empirical model defined in Sect. 3.2. For progressively face-on configurations with increasing |cos i | there is an excess of solutions compared to the model. Beyond the modes |cos i |≳0.85, the number of detected almost-face-on orbits drops sharply and far below the expected level. We also observe a smooth modulation of the Ω distribution7 with a single minimum at Ω = 90° and a bimodal modulation of the ω distribution with minima at ω = 90° and 270°.
For AstroSpectroSB1 solutions resulting from the combined analysis of Gaia astrometry and RVs, the cos i distribution shows good agreement with the empirical model for edge-on and intermediate configurations without regions of excess detections. However, there is also a clear lack of face-on orbits compared to the empirical expectation. This is influenced by the decreasing orbital RV signature towards face-on orbits. As AstroSpectroSB1 solutions require independent detections in both astrometry and RV, the lack of face-on orbits can be expected. The modulation in Ω is similar to Orbital solutions but weaker8 and there is no apparent modulation in the ω distribution.
Figure 12 shows the cos i distributions for systems within 200 pc, where the S/N is on average higher and the astrometric-orbit detection can be expected to be more complete. This is confirmed by the Orbital solutions that follow the empirical model nicely across most of the inclination range. This validates our model for the inclination-dependent detection efficiency of astrometric surveys (Sect. 3.2). The Ω and ω distributions for this subset of solutions are approximately uniform. We inspected other astrometric solution types but do not discuss these here because they have fewer (< 1000) entries and are therefore less suitable for distribution analyses.
 |
Fig. 12. Normalised distributions of cos i within 200 pc for Orbital (solid line, 9106 entries) and AstroSpectroSB1 (grey-filled, 5735 entries) solutions with P < 1000 d and ϖ > 5 mas. The dashed line shows the empirical model defined in Sect. 3.2. |
4.1.2. Origins of the geometric element biases
Concentrating on the Orbital solutions, we identify three main deviations from the expected uniform distributions in the low-S/N regime, which comprise most solutions and therefore dominate the overall distributions in Fig. 11: (a) a pronounced suppression of face-on orbits; (b) a smooth modulation of the Ω distribution with a single minimum; and (c) a bimodal modulation of the ω distribution.
In Appendix D.1 we identify the origin of features (a) and (b) in the linear fit of the Thiele-Innes coefficients to noisy data and reproduce these biases qualitatively in simulations. The noise bias in the recovered inclination shifts solutions away from face-on configurations leading to the observed excess at intermediate inclinations9. A modulation akin to feature (c) can also be caused by noise biases, albeit with a 90° phase shift. In Appendix D.2, we show that feature (c) is instead explained by the application of a semi-major axis significance threshold when selecting the solutions to be published.
4.1.3. Geometric elements from Monte Carlo resampled Thiele-Innes coefficients
Instead of using the linearised formulae (e.g. Halbwachs et al. 2023) for converting A, B, F, and G values and uncertainties to a0, i, Ω, and ω, one can use Monte Carlo resampling which accounts more accurately for the parameter correlations (Appendix D.3). As an example of the potential effects that this may have, we computed an alternative estimate of the orbital inclination for individual solutions as the median of the resampled Monte Carlo distribution. The difference between linearised and Monte Carlo estimates on the inclination distribution is shown in Fig. 13, where we see that the apparent depletion of face-on orbits is more pronounced when applying the resampling. We note that the resampled distributions of a0, i, Ω, and ω are seldom Gaussian and the median value is not always a good representation. Whether it is advisable to use the linearised estimate or Monte Carlo resampling depends on the particular problem and individual orbital solution.
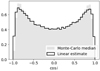 |
Fig. 13. Normalised distributions of cos i for non-circular Orbital solutions with P < 1000 d (121 207 entries). The linearised and Monte Carlo estimates are shown as a solid line and a filled grey area, respectively. |
4.1.4. Comparison with known astrometric orbits
Figure 11 also shows the distributions of geometric elements compiled in the “Sixth Catalog of Orbits of Visual Binary Stars” (orb6, Hartkopf et al. 2001)10. The orb6 inclination distribution is bimodal with modes at |cos i|≃0.5, which could be interpreted as the same signature of lacking face-on orbits as for GaiaOrbital but setting in earlier. The comparison with the simulated inclination biases in Fig. would then lead to the interpretation that the average S/N is higher for the Gaia orbits than for the orb6 solutions. However, we caution that the orb6 dataset is of heterogeneous nature and such comparisons have to be made more carefully by accounting for differences in period range, significance, and other factors.
The orb6 Ω distribution does not seem to exhibit the minimum at Ω = 90° seen for GaiaOrbital. In contrast, the orb6 ω distribution shows clear modes at ω = 90° and 270°, that is, shifted by 90° relative to GaiaOrbital. Our simulations in Fig. reproduce the peak location for orb6 orbits but not for Orbital solutions.
It is clear that the increase in astrometric orbit solutions by a factor of more than 40 delivered by Gaia DR3 compared to orb6 will facilitate a multitude of population-level studies and push forward our understanding of stellar binary systems.
4.1.5. Recommendations
The observed features in the distributions of i, ω, and Ω are the result of variations in the detection sensitivity of the survey, of selection effects, and of biases that are introduced in the astrometric non-single star processing. Their presence is not specific to Gaia and astrometric orbits in the literature show similar features. The geometric elements of DR3 orbits are encoded in the Thiele-Innes coefficients and different conversion methods can be applied depending on the use case and individual solution. Both the distribution features and the conversion aspects have to be considered in scientific analyses of Gaia DR3 orbital parameters and their distributions.
4.2. Proper motion anomaly of HIPPARCOS stars of the NSS sample
4.2.1. Comparison sample
In this section, we compare the properties of the HIPPARCOS stars based on the proper-motion anomaly (PMa) approach (Kervella et al. 2022; see also Brandt 2021) and the NSS analysis. The PMa approach is described in detail by Kervella et al. (2019a). The general principle is to look for a difference in proper motion (PM) between the long-term PM computed from the HIPPARCOS (epoch 1991.25; van Leeuwen 2007a, see also ESA 1997) and Gaia DR3 (2016.0; Gaia Collaboration 2021a) astrometric (α, δ) positions on the one hand and the individual short-term PM vector from the Gaia DR3 catalogue on the other. For a single star, the long-term PM is identical to the short-term PM measured by Gaia, as its space velocity is constant with time. For a binary star, the short-term PM includes in addition the tangential component of the orbital velocity of its photocentre. As the latter is changing with time over the orbital period of the system, a deviation appears between the short-term and long-term PMs of the star which is due to the curvature of its sky trajectory. The PMa, namely, the difference between the short-term and long-term PM, is therefore an efficient and sensitive indicator of non-single stars.
In order to compare the NSS catalogue with the PMa approach, we cross-matched the NSS catalogue with the PMa catalogue11 of Kervella et al. (2022), which covers 116 343 HIPPARCOS stars. This resulted in a list of 2767 common targets with astrometric NSS Acceleration7 or Acceleration9 solutions and 5416 stars with Orbital, AstroSpectroSB1, or OrbitalTargetedSearch* orbital solutions. In addition, 4385 HIPPARCOS targets are listed in the NSS tables with EclipsingBinary (photometric), SB1 or SB2 (radial velocity) solutions. Overall, 12 568 HIPPARCOS/PMa stars have an entry in the NSS catalogue, that is, 10.8% of the HIPPARCOS/PMa catalogue.
4.2.2. Completeness of the NSS sample for HIPPARCOS stars
The Gaia stars that are present in the NSS catalogue were selected based on criteria on parameters from their single-star solutions tailored to identify the most probable binaries. For the astrometric solutions based on astrometry, this includes the presence of a ruwe higher than 1.4 in their single-star solution. As pointed out by Belokurov et al. (2020) and Stassun & Torres (2021), this criterion is efficient at identifying the stars that host partially resolved companions. Furthermore, based on the PMa analysis, the binary fraction was found to remain high for ruwe values lower than 1.4 by Kervella et al. (2022) with for example 30% of the stars with ruwe ≈ 1.2 exhibiting a PMa S/N > 3 (their Fig. 11). As a consequence, the degree of completeness of the star sample present in the NSS is likely relatively low because of its selection threshold on the ruwe value. To estimate the completeness of the NSS for the HIPPARCOS stars, we first applied to the PMa catalogue the same selection criteria as the NSS input sources (Sect. 2.2.1) – except the condition ruwe > 1.4 – resulting in a subsample of 92 240 stars (79.3%). Within this subsample, 28 111 stars are high-probability astrometric binaries as their PMa S/N > 3. Restricting the count to the NSS stars that have an astrometric solution (Acceleration7, Acceleration9, Orbital, AstroSpectroSB1 or OrbitalTargetedSearch*), we obtain a completeness level of the NSS catalogue relative to the PMa catalogue of 8183/28 111 = 29.1%.
However, this high-level estimate based on global target numbers does not directly reflect the actual efficiency of the NSS reduction in detecting that a star is a binary or not compared to the PMa technique. To estimate this efficiency, we consider the same initial sample – following the NSS selection criteria including ruwe > 1.4 – and we derive the fraction of stars with an NSS solution within this common sample. The results are listed in Table 2. Overall, the astrometric solutions provided in the NSS catalogue represent 41% of the potential binaries present in the NSS reference sample, compared to 92% for the PMa catalogue.
Comparison of the PMa and NSS astrometric detection rate on the common HIPPARCOS star sample.
In summary, because of the stringent selection of the solutions for the NSS, the catalogue comprises approximately 40% of the binaries from the HIPPARCOS–Gaia PMa catalogue that were potentially detectable from Gaia astrometry alone.
4.2.3. Statistics of the proper motion anomaly of NSS targets
The PMa is an efficient tracer of the presence of a massive orbiting companion, but its sensitivity is limited by two factors. Firstly, the time baseline between HIPPARCOS and Gaia (24.75 years), although long, significantly reduces the PMa signature of companions with orbital periods longer than approximately three times the HIPPARCOS–Gaia time, that is, 75 yr. Secondly, the fact that the Gaia DR3 proper motions are the result of an averaging over a time window of 34 months strongly smears out the signature of companions with orbital periods shorter than approximately 4 yr. In summary, the PMa technique is most sensitive for companions with orbital periods of between ≈4 and 75 yr. On the other hand, the capacity to determine orbital solutions directly from Gaia astrometry (or radial velocity) time series is significantly higher for binaries with periods of shorter than the Gaia DR3 measurement window. The longer periods remain detectable, mostly up to about twice the measurement window. However, the astrometric displacement of long-period binaries is generally detected only as an acceleration, that is, without a period determination.
Figure 14 shows the histograms of the number of NSSs with different kinds of solutions as a function of their PMa S/N. The five histograms that are colour coded in blue correspond to NSS solutions that include the Gaia DR3 astrometry either exclusively (Acceleration7, Acceleration9, Orbital) or in conjunction with spectroscopic radial velocities (AstroSpectroSB1) or previously known substellar orbital parameters (OrbitalTargetedSearch*). The eclipsing binary stars (EclipsingBinary; green colour) are characterised from the Gaia photometric data, and the spectroscopic binaries (SB1, SB2; yellow colour) rely on the spectroscopic radial velocities measured by the Gaia RVS (Cropper et al. 2018; Katz et al. 2019).
 |
Fig. 14. Histogram of the number of NSS stars with different solution types that are present in the HIPPARCOS catalogue, as a function of the S/N of their Gaia DR3 proper motion anomaly from Kervella et al. (2022). The total number of targets N and the fraction of stars with a PMa S/N larger than 3 is displayed in each panel. |
4.2.4. Orbital periods and sensitivity
Almost all the HIPPARCOS targets with an Acceleration7 or Acceleration9 solution show a significant PMa signal. This behaviour is expected for two reasons: (1) The NSS astrometric solutions were selected among the Gaia sources with a ruwe larger than 1.4. This favours partially resolved binary stars, which often have orbital periods within the sensitivity range of the PMa technique. (2) For orbital periods longer than the Gaia measurement window, the PMa and the acceleration are physically similar quantities, both related to the curvature of the sky trajectory of the star.
The NSS catalogue stars with Orbital or AstroSpectroSB1 solutions generally have shorter orbital periods than the Gaia DR3 time window. Because of the time smearing of the Gaia EDR3 proper motions, this usually prevents the production of a clear signature in PMa. Nevertheless, approximately two-thirds of the stars of these NSS classes exhibit a significant PMa signal with S/N > 3 (Fig. 14). As shown in Fig. 15, the longer Gaia EDR3 time window compared to the DR2 results in a decrease of the PMa S/N for the binaries whose orbital period is shorter than ≈1000 days. This is caused by the stronger time smearing of the astrometric signal by the integration window in the Gaia DR3 compared to that of the DR2, which is not compensated by the increase in measurement accuracy in the Gaia DR3. The systems with shorter orbital periods than the Gaia integration window exhibit a median PMa S/N ≈ 3. This indicates that despite the smearing, statistically, the mean Gaia PM vector still contains a significant signature of the binarity. The vast majority of Gaia NSS targets with orbital periods longer than the Gaia time window (both for the DR2 and EDR3) exhibit a significant PMa S/N > 3.
 |
Fig. 15. Proper motion anomaly S/N as a function of the NSS catalogue orbital period for the DR2 PMa (top panel) from Kervella et al. (2019a); and the EDR3 PMa (bottom panel) from Kervella et al. (2022). The horizontal dashed line indicates the PMa S/N = 3 significance limit. |
4.2.5. Long-term HIPPARCOS–Gaia proper motion
Here we compare the long-term proper motion deduced from the difference in position between the HIPPARCOS (1991.25) and Gaia DR3 (2016.0) epochs by Kervella et al. (2022; hereafter μHG) with the short-term proper motion as determined in the NSS catalogue (μNSS). Figure 16 shows the observed differences Δμ = μNSS − μHG between these two quantities for the HIPPARCOS catalogue stars with either accelerations (Acceleration7, Acceleration9) or orbital (Orbital, AstroSpectroSB1) solutions in the NSS. There is a significantly larger divergence of the long-term proper motions between the stars with NSS accelerations only for which σ(Δμ)≈2.6 mas a−1 than for the stars with an orbital solution for which σ(Δμ)≈0.1 mas a−1. The relatively poor agreement for the NSS acceleration stars may be explained by the fact that the measurement of the curvature of the sky trajectory is significantly easier with the longer HIPPARCOS–Gaia temporal baseline. For the full NSS orbital solutions, the agreement between the HIPPARCOS–Gaia PM and the NSS PM is remarkably good, demonstrating that the orbital fit procedure does not introduce systematic biases on the estimation of the mean PM value.
 |
Fig. 16. Comparison of the long-term proper motions determined from the HIPPARCOS and Gaia DR3 positions μHG with the Gaia DR3 proper motions μNSS for NSS stars with acceleration solutions (left panel) and orbital solutions (right panel). We highlight the different scales. |
5. Catalogue of masses
As the nss_two_body_orbit table only gives access to the orbital parameters, it was found desirable to provide an estimate of the masses, the flux ratio, or the lower and upper limits of these, wherever possible. Here, we describe the construction and content of the table binary_masses which is made available in the Gaia archive.
5.1. Computation of the masses
The astrometric binaries give access to an astrometric mass function which depends on the flux ratio (F2/F1) of the components:
while the spectroscopic binaries provide a spectroscopic mass function which also depends on the inclination:
with P the period in days and K1 the semi-amplitude of the primary in km s−1. For AstroSpectroSB1, we have access to the Thiele Innes coefficients instead of K1 which leads to the equivalent formula:
The inclination can be provided by an astrometric solution or an eclipsing one. Without the inclination, Eq. (3) only leads to minimum mass function information. When a SB2 solution is provided, we have access to the mass ratio ℳ2/ℳ1 = K1/K2. When a system has a SB2 solution and either an astrometric solution or an eclipsing one, the primary mass can be derived directly from the binary orbital parameters.
Two estimates of ℳ1 are provided in the Gaia DR3 by the FLAME module (Creevey et al. 2023): mass_flame, based on GSP-Phot parameters and available in the astrophysical_parameters table, and mass_flame_spec, based on GSP-Spec parameters and available in the astrophysical_parameters_supp table. However the FLAME masses have three main limitations for our NSS sample: they are based on the parallax from the main catalogue while we now have a more accurate estimate for all astrometric solutions; these also assume a null flux ratio, which we know is not appropriate for a significant fraction of the NSS solutions, in particular the SB2 ones; these are not available for stars with masses smaller than 0.5 ℳ⊙. We therefore implemented a specific code to derive the mass of the primary that allows us to manipulate the luminosity ratio and is described in detail in Appendix E. These masses are only derived for stars on the main sequence – as estimations for evolved stars are degenerate (e.g. Creevey et al. 2023) – and are referred to hereafter as ‘IsocLum’ masses. For white dwarfs, we simply assumed a fixed mass of 0.65 ± 0.16 ℳ⊙ (Giammichele et al. 2012).
The uncertainties on the masses and flux ratios obtained are derived using a Monte Carlo simulation of 1000 points. We take into account the covariance matrix of the orbital parameters. For a0 as well as for the AstroSpectroSB1 spectroscopic part 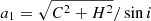 , we use a Gaussian distribution with a local linearisation error estimation as Monte Carlo techniques are not adapted to the Thiele Innes coefficients (see Babusiaux et al. 2023). Only sources with a significance > 5 are present in NSS solutions, meaning that a Gaussian distribution of the semi-major axis errors is a reasonable assumption. The uncertainties for the SB2 and eclipsing solutions have been re-scaled according to their goodness-of-fit. For the IsocLum masses, we use the full mass distribution function as we have it available. We then compute the 16th and 84th quantiles (corresponding to ±1σ) of the derived parameter distributions to estimate the lower and upper values, respectively. The direct values are provided whenever applicable for m1, m2, and fluxratio.
, we use a Gaussian distribution with a local linearisation error estimation as Monte Carlo techniques are not adapted to the Thiele Innes coefficients (see Babusiaux et al. 2023). Only sources with a significance > 5 are present in NSS solutions, meaning that a Gaussian distribution of the semi-major axis errors is a reasonable assumption. The uncertainties for the SB2 and eclipsing solutions have been re-scaled according to their goodness-of-fit. For the IsocLum masses, we use the full mass distribution function as we have it available. We then compute the 16th and 84th quantiles (corresponding to ±1σ) of the derived parameter distributions to estimate the lower and upper values, respectively. The direct values are provided whenever applicable for m1, m2, and fluxratio.
When combining two NSS solutions, we only use those with periods and eccentricities compatible within 5σ, assuming an uncertainty of 0.1 on the eccentricity for sources with a fixed eccentricity. A weighted mean of the periods and eccentricities of both solutions is then used in Eqs. (2) and (3). For the combination of astrometric and spectroscopic solutions, the primary mass is tested for different flux ratios in steps of 0.01; for each of these, the secondary mass is then derived from Eq. (3) and the flux ratio from Eq. (2), and only solutions that are consistent with the tested flux ratio are kept. When no solution is consistent, the closest one is used.
For Orbital solutions, only upper and lower values can be derived as the flux ratio is not known. Different flux ratios are tested in steps of 0.01. The lower (respectively upper) secondary mass value is computed from the mass distribution obtained with the lower flux ratio (respectively upper). The solution with fluxratio = 0 is always kept, as soon as the primary star magnitude is compatible with the isochrones. For the other flux ratios tested, the secondary mass derived is accepted if consistent with a secondary star on the main sequence. In practice, the Monte Carlo masses of the secondary lead to a range of possible absolute magnitudes from the isochrones, which, for the flux ratio tested, are converted into an absolute magnitude of the system which is accepted when it is at less than 3 sigma from the absolute magnitude of the system measured by Gaia. In some cases, this means that no flux ratio is kept. These can be either pre-main sequence stars, in which case our masses are invalid, or triple systems with a primary, which needs a flux ratio, but a secondary mass not consistent with it. To handle this second option, the minimum flux ratio compatible with a primary on the main sequence is used to derive the primary mass but the secondary mass is derived with F2/F1 = 0. These cases can be isolated with a ‘fluxratio_upper is NULL’ query. No limit is tested on the maximum flux ratio for white dwarfs. For SB1 solutions, the lowest valid flux ratio is used to derive the primary mass and the lower secondary mass value is derived on the distribution assuming sin i = 1. For eclipsing binaries, the flux ratio is fixed by g_luminosity_ratio.
The catalogue of masses we derive is available in the Gaia Archive table binary_masses. A summary of the number of dynamical masses and flux ratio is presented in Table 3. We selected only sources with a S/N higher than 5 on the astrometric semi-major axis and on the spectroscopic primary semi-amplitude, as well as a S/N of higher than 2 for the eclipsing binary and astrometric sin i and the spectroscopic secondary semi-amplitude. For AstroSpectroSB1 solutions, we verify that both the S/N for the spectroscopic part, computed as 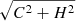 , and for a1 are higher than 5. If not, the AstroSpectroSB1 is treated as an Orbital solution only. OrbitalAlternative solutions with log10(parallax/parallax_error) < 3.7−1.1 log10(period) have been excluded. There are 76 sources duplicated, having both an astrometric solution and either an eclipsing binary (6) or a SB2 solution (70), with the astrometric solution period being larger than the other one by more than 10 sigma. For sources with both an SB1 and an Orbital solution, only the Orbital solution has been kept.
, and for a1 are higher than 5. If not, the AstroSpectroSB1 is treated as an Orbital solution only. OrbitalAlternative solutions with log10(parallax/parallax_error) < 3.7−1.1 log10(period) have been excluded. There are 76 sources duplicated, having both an astrometric solution and either an eclipsing binary (6) or a SB2 solution (70), with the astrometric solution period being larger than the other one by more than 10 sigma. For sources with both an SB1 and an Orbital solution, only the Orbital solution has been kept.
Content summary of the catalogue of masses.
A particularly interesting subset of this table are the astrometric solutions with fluxratio_upper = 0. There is only one star (Gaia DR3 4288765058313593856) for which the secondary mass is sufficiently small (0.57 ℳ⊙) compared to the primary (1.26 ℳ⊙), meaning that fluxratio_upper = 0 is compatible with the secondary star being on the main sequence. The others are systems for which the secondary mass solutions for flux ratio > 0 did not have a mass compatible with any of the flux ratios tested. The secondary mass distribution of these is presented in Fig. 17. There are 12 stars with a secondary mass smaller than the minimum mass handled by the isochrones of 0.1 ℳ⊙ and a low mass for the primary as well. Three other stars with low-mass secondaries could be either triple or pre-main sequence stars for which the primary mass is not correct. The most predominant peak is that of the white dwarfs at ℳ2 = 0.61 ℳ⊙ which has a standard deviation of 0.07 ℳ⊙. We note that some white dwarf companions should actually have a flux ratio > 0, such as Gaia DR3 6416572288572864512 which is an AstroSpectroSB1 with a significant flux ratio; the primary mass has been estimated as that of a metal-poor star because of its location on the left of the main sequence; if it had been solved as an astrometric solution only, it would have had fluxratio_upper = 0 and an underestimated secondary mass. A long tail of high-mass secondaries is also present. These could be compact objects, but also triple stars for which the single primary star hypothesis was not valid (see Sect. 7.1), primary stars that started to evolve, or metal-poor giants for which the primary mass is not correct.
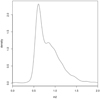 |
Fig. 17. Distribution of the secondary mass of astrometric solutions with fluxratio_upper = 0 in Table 3. |
5.2. Masses using external data
In this section, we illustrate how other mass estimates can be obtained thanks to various kinds of combinations with external data.
5.2.1. External SB2
Combining astrometric orbits with spectroscopic ones from large surveys is not a recently developed procedure, and was done for example with HIPPARCOS (Arenou et al. 2000). Once the inclination is known from the astrometric orbit, the semi-amplitudes from the spectroscopic orbit allow the masses and luminosities of the two components to be determined simultaneously. Recently, APOGEE DR17 data were used to detect 8105 SB2 or higher order systems (Kounkel et al. 2021). Once the required number of epochs become available, individual masses and magnitude differences will be obtained for the sources with an NSS Orbital* solution. Here, we simply take the example of Gaia DR3 702393458327135360, with K1 = 19.53 ± 0.95 km s−1 and K2 = 21 ± 1.1 km s−1. The masses are found to be ℳ1 = 1.14 ± 0.38 ℳ⊙ and ℳ2 = 1.06 ± 0.35 ℳ⊙ with a 0.567 ± 0.071 flux ratio.
5.2.2. Occultations
Occultations represent a method to constrain the sum of masses of binaries thanks to the measurement of their separation at a given epoch. We illustrate this with Gaia DR3 3162827836766605440 (HIP 36189) which is a V ≈ 6.5m K giant that was discovered to be double thanks to an occultation by (704) Interamnia on 23 March 2003. Its acceleration had been detected in Kervella et al. (2019a); Kervella et al. (2022), and Brandt (2021). Satō et al. (2014) indicate a ρ = 12 ± 3 mas separation while a more precise indication is given by Herald et al. (2020): ρ = 13.0 ± 0.7 mas with position angle θ = 231.9 ± 4.0°. Satō et al. (2014) evaluate the magnitude difference between components to about 1.5, to which we attribute a 0.2 mag uncertainty, accounting in particular for the observation in a band different from the G band. This source received an Orbital solution with a 2.6 yr period. From the combined information, the masses of the components are found to be ℳ1 = 3.9 ± 2.2 ℳ⊙ and ℳ2 = 3.5 ± 1.6 ℳ⊙.
5.2.3. One SB1 Cepheid
Although it is known that many Cepheids are in binary systems (e.g. Kervella et al. 2019b), not many orbits are present in the NSS catalogue. On the spectroscopic orbit side, the Gaia DR3 data processing does not yet include the simultaneous handling of orbit and Cepheid pulsations, meaning that it is only the latter that were detected. Consequently, these solutions were filtered out from the catalogue to avoid any confusion. On the astrometric orbit side, one Cepheid received an Orbital solution.
Gaia DR3 470361114339849472 = RX Cam is known to be a G2Ib+A0V spectroscopic binary from Imbert (1996). The Gaia solution has a period of 999 ± 104 d and an eccentricity of 0.514 ± 0.049, consistent at 1σ with respectively 1113.8 ± 0.5 d and 0.459 ± 0.007 from Groenewegen (2013). The inclination is 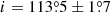 . We may safely assume that there is no flux contribution (in the G band) from the companion, as confirmed by the difference between the semi-major axis of the primary and that of the photocentre a1 − a0 = 0.04 ± 0.12 au. Using the semi-amplitude K1 = 14.27 ± 0.11 km s−1 from Groenewegen (2013) and the estimation of the primary mass from Kervella et al. (2019b), ℳ1 = 5.40 ± 0.81 ℳ⊙, we obtain ℳ2 = 2.87 ± 0.34 ℳ⊙.
. We may safely assume that there is no flux contribution (in the G band) from the companion, as confirmed by the difference between the semi-major axis of the primary and that of the photocentre a1 − a0 = 0.04 ± 0.12 au. Using the semi-amplitude K1 = 14.27 ± 0.11 km s−1 from Groenewegen (2013) and the estimation of the primary mass from Kervella et al. (2019b), ℳ1 = 5.40 ± 0.81 ℳ⊙, we obtain ℳ2 = 2.87 ± 0.34 ℳ⊙.
6. Special binaries in the HRD
In this section, we select several illustrative cases where the NSS catalogue can provide useful insights into populations of the HRD. For further reference, Fig. 18 presents the period–eccentricity diagram for the NSS solutions with orbits.
 |
Fig. 18. Eccentricity vs. period for most solutions with orbits. |
6.1. Spectroscopic binaries along the main sequence
In this section, we present and briefly discuss the eccentricity–period (hereafter e − P) diagrams of SB1s along the main sequence, defined as −7.5 + 10 (GBP, 0 − GRP, 0) < MG, 0 (Fig. 19), with the photometry being de-reddened in the same way as for the mass derivation (see Appendix E). Stars along the main sequence are divided according to (GBP, 0 − GRP, 0) bins, as indicated in Fig. 19.
 |
Fig. 19. Location in the dereddened HRD of the (GBP, 0 − GRP, 0) bins used in Fig. 20. Small blue dots correspond to the SB1s not selected by our selection criteria. The radius is the FLAME estimate. |
The e − P diagrams along the main sequence are displayed in Fig. 20. Because of the aliasing problems faced by the SB1 processing (see Sect. 2.3), these diagrams are shown for different filtering based on the significance of the RV semi-amplitude, namely K1/σK1 larger than 10, 20, or 40 (from left to right). This filtering removes both high-eccentricity short-period orbits and long-period orbits. The former filtering is designed to remove possibly spurious solutions, while the disappearance of the long-period solutions is a side effect due to the fact that long periods have on average smaller K1 and thus smaller significances as well. Nevertheless, this filtering has the consequence of revealing the shape expected for any e − P diagram, namely short-period orbits being almost exclusively circular below a given ‘transition’ period (see e.g. Mazeh 2008, for a detailed discussion).
 |
Fig. 20. The e − P diagram for SB1s along the main sequence, filtered according to significance factors larger than 10, 20, or 40 (from left to right), and for different (GBP, 0 − GRP, 0) spans (top to bottom). Filtering on the significance removes potentially spurious high-eccentricity solutions at small periods with the side effect of removing long period solutions. The drop in the number of systems at P = 0.5 yr due to insufficient sampling at this specific period. The color codes for the FLAME radius estimate. |
The e − P diagrams along the main sequence, when ordered according to bins of increasing GBP, 0 − GRP, 0 and properly filtered on a significance larger than 40 (right panels of Fig. 20), reveal that this transition period does not vary strongly between the various GBP, 0 − GRP, 0 bins, which is contrary to the situation prevailing along the giant branch, as discussed below (Sect. 6.2). Mazeh (2008) reviewed the processes shaping e − P diagrams, and concluded that the constancy of the transition period along the main sequence would naturally result if the circularisation occurred during the pre-main sequence phase when the stars were large, following a suggestion by Zahn & Bouchet (1989) for F, G, and K stars from 0.25 to 1.25 ℳ⊙. The transition period of these stars indeed remains constant along the main sequence at about 8 d as, although the transition period observed in Fig. 20 appears slightly shorter.
Mazeh (2008) also argues that short-period binaries (i.e. below the transition period) with non-circular orbits could result from a third distant companion pumping eccentricity into the binary orbit. However, at present, because of the confusion caused by possible period aliasing among short-period SB1 systems, this possibility cannot be tested with confidence.
6.2. Binaries along the RGB and AGB
The goal of this section is to show that the transition period between circular and non-circular orbits increases with radius and luminosity along the red giant branch (RGB) and asymptotic giant branch (AGB). To select stars on these branches, it is more efficient to use the 2MASS colour–magnitude diagram (J − K, MK) rather than the usual Gaia colour–magnitude diagram. We used the 2MASS cross-match with EDR3 available within the data archive12 and used the following criteria to select giants:
as illustrated below.
6.2.1. Period–radius diagram
The existence of a circularisation threshold period in the e − P diagram was demonstrated by Pourbaix et al. (2004) in their Fig. 4 (see also Zahn & Bouchet 1989; Verbunt & Phinney 1995; Mazeh 2008; Jorissen et al. 2009; Escorza et al. 2019). Its analytic form in a period–radius diagram may be easily obtained from the simple expression of the Roche radius RR around the star of mass ℳ1 with a companion of mass ℳ2 (Paczyński 1971):
Substituting Kepler’s third law, and assuming that the period threshold (expressed in days) corresponds to the situation where the star radius is equal to the Roche radius, one finds after some algebra:
where c1 only depends on the masses. These thresholds are represented in Fig. 21 as dashed lines (corresponding to different choices for the pair ℳ1, ℳ2). Figure 21 presents all SB1 solutions falling along the RGB and AGB as defined above based on the (J − K, MK) colour–magnitude diagram; however, it reveals that there are many SB1 solutions involving giant stars that do not fulfill the condition P ≥ Pthresh expressed by Eqs. (7) and (8), especially when the significance K1/σK1 is smaller than 40.
 |
Fig. 21. Period–radius diagram for all SB1 solutions falling along the RGB and AGB according to criterion (5), and with a radius available from radius_flame. The dashed lines correspond to the threshold periods expressed by Eq. (7) for ℳ1 = 1.3 ℳ⊙ and ℳ2 = 1.0 ℳ⊙ (red dashed line) and ℳ1 = 1.3 ℳ⊙ and ℳ2 = 0.2 ℳ⊙ (cyan dashed line). Left (a): unfiltered, 44 706 SB1 solutions (among which 3056 unphysical, that is, below the cyan dashed line). Middle (b): filtered by significance K1/σK1 > 20, 27 404 solutions are rejected and 17 302 are kept (among which 214 unphysical). Right (c): filtered by significance > 40, 37 850 solutions are rejected and 6856 are kept (among which 21 unphysical). |
6.2.2. e–P, P–f(ℳ) diagrams
Figure 22 presents the e − P diagram for the same set of SB1 solutions (left panel) as shown in Fig. 21a, as compared to astrometric binaries along the RGB and AGB (right panel). The difference between the period range covered by SB1 and astrometric solutions is striking. As most astrometric orbits have periods longer than about 200 d, they clearly satisfy the criterion expressed by the dashed line in Fig. 21 and do not overfill their Roche lobe, contrary to the short-period SB1 solutions.
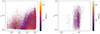 |
Fig. 22. e − P diagrams for all SB1 (left panel: unfiltered; adequately filtered e − P diagrams for SB1 with an RGB and AGB primary are presented in Fig. 24) and astrometric (right panel) solutions falling along the RGB and AGB according to criterion (5), and with a radius available from radius_flame. We highlight the restricted period scale of the astrometric binaries as compared to the SB1, and the lack of binaries with periods close to 1 yr among astrometric binaries. |
Figure 23a is similar to Fig. 22 but replacing eccentricities by mass functions, and revealing again two populations of SB1 solutions, the short-period ones being characterised by very small mass functions f(ℳ). The origin of this population of short-period SB1 solutions among RGB and AGB stars clearly requires clarification. In the following, we show that they are associated with poorly defined solutions. It appears indeed that almost all unphysical SB1 solutions may be eliminated by using the same purely observational criterion as used in Sect. 6.1, and based on the value of the significance of the SB1 solution (available in Table nss_two_body_orbit from the Gaia archive), that is, K1/σK1, K1 being the semi-amplitude of the first component.
 |
Fig. 23. P − f(ℳ) diagrams for SB1 along the RGB/AGB. Left (a): unfiltered. The yellow tail extending down to f(ℳ) ∼ 10−5 ℳ⊙ at periods in the range 300−800 d corresponds to pseudo-orbits associated to long-period pulsators (see Sect. 6.2.3). Middle (b): filtered by significance > 20 and > 40 (right (c)). |
Almost no outlier remains in the P − R (Fig. 21c) and P − f(ℳ) (Fig. 23c) diagrams when that significance exceeds 40; a few outliers remain when it exceeds 20 but many more solutions are kept, as may be seen from Table 4. This latter table shows that the gradual disappearance of unphysical SB1 solutions as the significance increases corresponds to a real filtering out of unphysical solutions, because the fraction of remaining unphysical solutions truly diminishes as the significance increases (passing from 6.8% in the absence of any filtering to 0.3% when the significance threshold is set at 40; see Table 4). However, the drawback of a filtering on significance is that it tends to also filter out solutions with long orbital periods, as those have on average smaller K1 values (this was also very clear from Fig. 20). Alternatively, if one does not want to loose the long-period orbits as a result of filtering on significance, filtering is also possible with the physical condition P ≥ Pthresh – Eq. (7) – with appropriate mass values; however Fig. 21 reveals that for systems with periods above 10 d, the boundary between physical and unphysical systems does not depend sensitively on the choice of ℳ1, ℳ2.
Sizes of the SB1 sample involving RGB and AGB primaries for different filtering on the significance threshold.
Now that the sample of RGB and AGB stars has been adequately cleaned of its unphysical orbits, it is possible to investigate the properties of the e − P diagram for giant stars. Figure 24 presents those for bins of increasing radius (as taken from the corresponding radius_flame field), as indicated in the figure labels. As expected from the dashed lines in Fig. 21, the minimum period increases with increasing radius. In the following discussion, we adopt ℳ1 = 1.3 ℳ⊙ and ℳ2 = 1.0 ℳ⊙ (corresponding to the red dashed line in Fig. 21, and c1 = −0.274 in Eq. (8)), as these values nicely match the observed trend. The above value for c1 combined with the upper bound of the radius range adopted in each panel of Fig. 24 defines the lower bound on the orbital period Pmin for e = 0. It appears that the upper envelope of the data cloud observed in each panel of Fig. 24 is well fitted by the empirical relation P = Pmin(1 − e)3 represented by the solid black lines in Fig. 24, as already found by Pourbaix et al. (2004) in their analysis of the Ninth Catalogue of Spectroscopic Binary Orbits (their Fig. 5). Despite the fact that this curve matches the uppermost data points in almost all panels rather well, it must be stressed that there seems to be no physical justification for this specific analytical form. However, a closer look at each of these panels reveals an interesting substructure. At the shortest periods, each panel is dominated by a large number of (nearly) circular orbits caused by circularisation operating in those systems where the giant stars with their convective envelope are close to filling their Roche lobe. As shown above, Pmin in each panel actually refers to systems where the giants with the shortest radius in the considered range fill their Roche lobe (see e.g. Verbunt & Phinney 1995; Mazeh 2008, for details).
 |
Fig. 24. e − P diagram for SB1 systems along the giant branch, filtered according to significance factors larger than 40, for various radius spans. Top panel: is the full sample. The solid black lines correspond to the loci where P(1 − e)3 is constant (see text). The sample sizes are, from top to bottom, 1960, 2358, 1643, 737, and 40. The location in the HRD of the SB1 systems with 0.7 < log(R/R⊙)≤1.0 (second panel from top), 1.3 < log(R/R⊙)≤1.6 (fourth panel from top) and 1.9 < log(R/R⊙) (bottom panel) is shown in Fig. 25. |
6.2.3. A search for genuine SB1s among giants
The identification of SB1 among highly evolved giants and long-period variables (LPVs) is made difficult by the envelope pulsation (Alvarez et al. 2001; Hinkle et al. 2002; Jorissen 2004; Jorissen et al. 2019). Other methods have therefore previously been used (Jorissen & Frankowski 2008; Sahai et al. 2008; Decin et al. 2020; Ortiz & Guerrero 2021) to identify true binaries. Gaia on the other hand, with its survey combining radial velocity and photometry data, offers exquisite prospects to disentangle pulsational from orbital RV variations. In that respect, the bottom panel of Fig. 24 offers an interesting benchmark sample of giant stars with R > 80 R⊙ with a SB1-like signature in their RVs. There are 40 such giants if the significance threshold is set at 4013. No Orbital or AstroSpectroSB1 solutions are present in Gaia DR3 among those giants with large radii (compare with Fig. 22). Table 5 lists their main properties, while their location in the HRD is shown as the yellow crosses in Fig. 25.
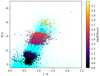 |
Fig. 25. Location in the HRD of three among the samples displayed in Fig. 24, namely 0.7 < log(R/R⊙)≤1.0 (dots), 1.3 < log(R/R⊙)≤1.6 (plus symbols), and 1.9 < log(R/R⊙) (crosses). Small cyan dots correspond to the SB1 not selected by our selection criteria. See Table 5 for a full discussion of the properties of the yellow crosses. |
As mentioned above, as there is the risk that some of these SB1 solutions may be caused by envelope pulsation mistaken as SB1s, a proxy for the amplitude of the photometric variation in the G band has been listed as well, namely phot_g_mean_mag_error from the gaia_source table. We also performed a cross-match with table vari_long_period_variable and the photometric period, whenever available, has been listed in the column Plpv. It appears that only one LPV is present in this list (a carbon star also known as V688 Cas), as confirmed by its largest ΔG value in Table 5. As Plpv = Pnss for this star, the RV variations are not due to orbital motion but to envelope pulsations. Many other such cases will be discussed below (Table 6). There are only four other stars appearing in the vari_long_period_variable table in common with Table 5, and these four have the unexpected property that Plpv = 0.5 Pnss, with a moderate ΔG value (on the order of 0.001−0.003 mag). We argue below, in relation to Table 6, that these are ellipsoidal variables and therefore true binaries, where the giant primary is close to filling its Roche lobe. Based on the fact that these ellipsoidal variables identified in table vari_long_period_variable have small eccentricities (e < 0.1), we suspect that Table 5 contains many more such ellipsoidal variables, namely those with e < 0.1 and ΔG > 0.001 mag, flagged as ‘Ell. var.?’ in the last column of Table 5.
A few illustrative examples of ellipsoidal variables (Plpv/Pnss = 0.5) mistaken as LPVs in the vari_long_period_variable table, LPVs with a pseudo SB1 orbit (Plpv/Pnss = 1, ΔG > 0.1 mag, Plpv > 180 d) in the nss_two_body_orbit table and short-period (Plpv < 100 d) ‘LPVs’ with Plpv/Pnss = 1.
The longest period found in Table 5 is 1261 d, a value that is nicely in line with the Gaia DR3 time span, but short with respect to the periods expected among evolved giants (consider for instance the 17 yr period found by Jorissen et al. 2019 for the carbon Mira V Hya). Such long periods are not detectable at the current stage of the Gaia mission, either as SB1 or as astrometric binaries. Nevertheless, one may look for acceleration solutions (there is only one solution from table nss_acceleration_astro matching the giant criteria defining Table 5; regarding acceleration solutions, we refer to Sect. 4.2.3 and Wielen et al. 1999; Makarov & Kaplan 2005; Frankowski et al. 2007; Kervella et al. 2019a, 2022; Brandt 2021) or for solutions with a trend in the RVs (121 solutions for giants found in nss_non_linearspectro, not listed here).
6.2.4. Combining photometry and spectroscopy to diagnose RV variations in giants: pulsation, ellipsoidal variables, and rotational modulation
With the initial aim being to further investigate how many LPVs may be mistaken as SB1, we searched for targets in common between SB1 from the NSS nss_two_body_orbit table and LPVs as provided by the variability study in the vari_long_period_variable table. However, this cross-match revealed some surprises. The following query yields 1869 entries, as shown in Fig. 26:
SELECT * from gaiadr3.nss_two_body_orbit TBO, gaiadr3.vari_long_period_variable LPV where LPV.source_id = TBO.source_id and LPV.frequency is not null
 |
Fig. 26. Orbital period from the nss_two_body_orbit table vs. photometric period from the vari_long_period_variable table. Top, middle, and bottom panels: correspond to different filtering based on the SB1 significance (respectively, larger than 5, 20, and 40). The two sequences observed in all panels correspond to Plpv/Pnss = 0.5 (ellipsoidal variables; upper sequence) and Plpv/Pnss = 1 (LPVs or rotational modulation in a synchronised system; lower sequence). Top panel: crosses denote NSS solutions for which the Roche-lobe filling factor is above unity, and therefore unphysical. The filtering with significance larger than 40 makes these latter disappear almost entirely. |
The three panels differ in terms of the level of filtering applied on the SB1 significance parameter, as defined above: > 5 (default, top panel), > 20 (middle panel), and > 40 (bottom panel). Striking are the two straight sequences observed in all three panels. The upper sequence corresponds to Plpv/Pnss = 0.5 (as expected for ellipsoidal variables), whereas the lower sequence corresponds to Plpv/Pnss = 1 (as expected for pulsating stars or rotational modulation in a synchronised system). The lower sequence is further made of two distinct clumps, one at short periods (Plpv ≲ 100 d; which could be due to starspot modulation on a spin–orbit synchronised star) and the other at long periods (200 ≲ Plpv ≲ 1000 d; LPVs). These are discussed in turn below.
6.3. Ellipsoidal variables
Besides the obvious property of their light-to-RV period ratio equal to 0.5, the ellipsoidal–variable sequence is further confirmed from its following properties: (i) small eccentricities (e ≲ 0.1), (ii) large filling factors (R1/RR, 1 ≳ 0.65 from Eq. (6), adopting radii from FLAME and the same typical masses as above – ℳ1 = 1.3 ℳ⊙, ℳ2 = 1.0 ℳ⊙) whenever available, and (iii) small G amplitudes (0.01 ≤ ΔG ≤ 0.1 mag; see Table 6). We confirmed the ellipsoidal nature of these stars by a comparison between the light and RV curves. As expected, the maximum light indeed occurs at the quadratures, when the RV is maximum or minimum. In Fig. 24, at any given radius range, these ellipsoidal variables are located in the nearly circular tail of each panel. The full list of ellipsoidal variables is not provided here as the reader may easily obtain it from the ADQL query mentioned at the beginning of this section and filtering on Plpv/Pnss around 0.5 (370 stars in the inclusive range 0.45−0.55, most of them having significances in excess of 20). The first part of Table 6 nevertheless lists a few randomly selected examples. Figure 27 shows the position in the 2MASS infrared colour–magnitude diagram (MK, J − K) of the 370 stars with 0.45 ≤ Plpv/Pnss ≤ 0.55 (dots). These ellipsoidal variables are located from the tip of the RGB14 to 3 mag below. We note that some among these stars might be young pre-main sequence stars. Gaia DR3 2162167694508896128 = V1540 Cyg listed in Table 6 is one such case (on Fig. 27, it is located at MK = −6.2 and J − K = 1.41).
 |
Fig. 27. Location in the infrared colour–magnitude diagram of the stars with 0.45 ≤ Plpv/Pnss ≤ 0.55 (ellipsoidal variables) from Table 6 (dots). Stars with 0.95 ≤ Plpv/Pnss ≤ 1.05 are represented by crosses; they appear in two different locations, among LPVs with low orbital significance on one hand, and among less luminous giants with much larger orbital significance on the other, perhaps suggesting starspot modulation or short-period pulsators. The dots (Plpv/Pnss ∼ 0.5) fall in between these two groups, as they are located just below the tip of the RGB. |
6.4. Long-period variables
The transition between dots and crosses in Fig. 27 corresponds to the transition across the RGB tip. Above the RGB tip, most stars from the vari_long_period_variable table belong to the sequence Plpv/Pnss around unity. They correspond to LPVs with a RV variation caused by the envelope pulsation. Although displayed in Fig. 27, the full source list is not given here as they are easily obtained in a way similar to that discussed above for ellipsoidal variables. Table 6 nevertheless lists a few randomly selected examples.
These LPVs are easily identified by their velocity semi-amplitudes, which are smaller than 10 km s−1 (in that sense, they differ markedly from the ellipsoidal variables which generally have much larger K1 values) and periods in excess of 180 d, as expected for Mira pulsations (Alvarez et al. 2001; Hinkle et al. 2002). Therefore, given these relatively small values of K1, the significance of the SB1-like solution (namely K1/σK1) may in several cases be smaller than 20, but the identity of the NSS and LPV periods is in itself an indication of the reliability of the RV model. We note that the filling factor has no meaning in this stellar category, because there is no true orbit associated. Mira variables are recognised as well by their large amplitude in G (> 0.1 mag). The pseudo-eccentricities found by Hinkle et al. (2002) for Miras and semi-regular variables were clustered around 0.35, with a few cases below 0.1 as well. Here, the pseudo eccentricities range all the way from 0.09 to 0.48 (Table 6). Furthermore, it has been checked that the maximum RV is reached at phase 0.8 while maximum light is reached at phase 1.0, a phase lag that is expected for Mira pulsators. Furthermore, as for these stars, K1 is relatively small and P is long, the pseudo mass functions are consequently smaller than 10−3 ℳ⊙, with some values as small as 10−5 ℳ⊙, in agreement with the findings of Hinkle et al. (2002; their Table 2) for Mira and semi-regular variables. LPVs with low values of f(ℳ) are most clearly seen in Fig. 23a as the yellow tail extending down to f(ℳ) ∼ 10−5 ℳ⊙ for periods between 300 d and 1000 d. On that same figure, many more stars with large radii (R > 100 R⊙) are found at shorter periods, but those are spurious ‘SB1-like’ solutions because their periods do not even match the LPV one, and when available, their filling factors are above unity, which is non-physical. Furthermore, their mass functions are quite small (down to 10−8 ℳ⊙). Therefore, these targets cannot be genuine binaries.
6.5. Genuine binaries
Genuine binaries among Miras are expected to have much longer orbital periods than currently detectable by Gaia DR3 (as is the case for instance for the carbon Mira V Hya quoted above). Intriguingly, several genuine SB1s have nevertheless been found among stars with Plpv > 150 d, a property generally associated to LPVs. In the fourth part of Table 6 are listed 14 SB1s selected among the 1189 SB1 solutions in common with the vari_long_period_variable table. These SB1s have a significance of greater than 20, the 1σ confidence range of Plpv/Pnss falling outside the ranges 0.45−0.55 and 0.9−1.1 (to avoid SB1-like variations caused by pulsations), Pnss > 20 d and Plpv > 150 d. Their RV curves were checked visually and showed no peculiarity that would make the solution dubious. This visual inspection nevertheless revealed that some kind of aliasing problems remain with the NSS SB1 periods. The star Gaia DR3 1989628623330891904 was originally considered as a possible genuine binary among LPVs because Plpv = 419 d as compared to Pnss = 25 d. However, the visual inspection of the RV curve revealed that the LPV period of 419 d is clearly present in the RV curve, although it was not selected by the period-selection algorithm, which gave no warning about a possible problem with that solution (significance = 21, period confidence = 1.000, ruwe = 1.09) except for the goodness-of-fit of 2.5. Therefore, that star has been added to the ‘Large-amplitude LPVs’ section.
6.6. Rotational modulation on a spin–orbit synchronised star
The final category of interest in Table 6 contains targets with short periods (i.e. P ≲ 100 d) on the Plpv/Pnss = 1 sequence. These are listed in the fourth part of Table 6 and identified in the HRD of Fig. 27 as the crosses at the bottom of the giant branch. Contrary to the situation prevailing for ellipsoidal variables and long-period variables discussed above, the phase lag between velocity and light curves now appears to be anything between 0 and π. For this reason, their light variation could be due to starspot modulation on a spin–orbit synchronised primary star (e.g. Mazeh 2008). A less likely possibility is that they could be small-amplitude pulsating stars.
6.7. Identifying EL CVn systems in Gaia data
EL CVn systems are short-period eclipsing binaries (EBs) consisting of an A/F-type main sequence (MS) primary and a low-mass pre-helium white dwarf (pre-He-WD) secondary. These systems are a result of mass transfer from the evolved pre-He-WD progenitor to the currently observed primary star (e.g. van Kerkwijk et al. 2010; Maxted et al. 2011; Rappaport et al. 2015). EL CVn systems are at a rare stage of binary evolution in which the young pre-He-WD is bloated, with a radius of up to ∼0.5 R⊙, and hotter than the more luminous A/F-type primary. As a result, such systems, harbouring a low-mass WD precursor, are detectable even in ground-based photometric surveys. EL CVns with smaller and cooler He-WD secondaries can be detected in space photometry (Faigler et al. 2015). Consequently, 10, 18, and 36 such systems were discovered in the Kepler (van Kerkwijk et al. 2010; Carter et al. 2011; Breton et al. 2012; Rappaport et al. 2015; Faigler et al. 2015), WASP (Maxted et al. 2011, 2014), and PTF (van Roestel et al. 2018) photometric surveys, respectively.
The detection of these systems in photometric surveys is based on identifying an eclipsing-binary folded light curve with a ‘boxy’ deeper eclipse (steep ingress and egress and a flat bottom) and a shallower eclipse with a limb-darkening curved bottom. In an EL CVn, the deeper boxy eclipse is actually the secondary eclipse (total eclipse of the pre-He-WD secondary by the MS primary), while the shallower eclipse is the primary eclipse (pre-He-WD transit of the primary star). This is because the pre-He-WD secondary is hotter than the primary. Such photometric detections usually require confirmation through follow-up spectroscopic RV observations, which enable the light-curve primary and secondary eclipses to be identified from the RV-curve phase.
However, the Gaia data enable direct detection of EL CVn systems by combining the Gaia photometry and RV data. Figure 28 shows the folded Gaia G, GBP, and GRP photometry and RV data, for a known EL CVn-type system (HD 23692, Maxted et al. 2014), together with the Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015) binned data. Detrending of the TESS data was done using cosine detrending following Faigler et al. (2015). The Gaia EB-model period and deeper-eclipse epoch were used as the folding period and phase zero, respectively. The RV plot enables us to identify the phase-zero eclipse as the secondary eclipse, and the 0.5-phase eclipse as the primary eclipse. The figure shows that for this system, indeed the secondary eclipse is box-shaped and deeper than the primary one, the main signatures of an EL CVn system. In addition, we see that the GBP secondary eclipse is much deeper than the GRP one, an additional indication for the high temperature of the secondary.
 |
Fig. 28. Folded Gaia G, GBP, and GRP photometry and RV data of HD 23692, together with TESS binned data. Top panel: Gaia RV data, while the second panel presents the Gaia G data. Third panel: Gaia GBP and GRP data, with medians shifted to the Gaia G median for clarity, and the bottom panel presents the TESS data binned to 200 phase bins. All plots were folded using the Gaia EB-model period and deeper-eclipse epoch as the folding period and phase zero, respectively. We note that the primary eclipse is at phase 0.5, while the secondary eclipse is at phase zero. Observed TESS-eclipse phase drift is due to the more than 1300 day delay from the last Gaia point to the first TESS point. For clarity, the three bottom panels use the same y-axis scale. |
6.7.1. Sorting through the Gaia data
To build the initial sample, from which we can identify EL CVn systems, we selected from the Gaia DR3 data systems with (a) an eclipsing-binary solution from Gaia photometry, (b) a SB solution (SB1, SB1C, SB2 or SB2C) derived from the Gaia RV data, (c) an orbital-frequency difference between the EB and SB solutions of smaller than 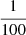 d−1, and (d) an orbital period of shorter than 2 d. The maximum orbital-frequency difference was selected as significantly larger than the inverse of the data time span (∼1000 d), a rough estimate for the orbital-frequency uncertainty lower limit. Limiting the orbital-frequency difference to
d−1, and (d) an orbital period of shorter than 2 d. The maximum orbital-frequency difference was selected as significantly larger than the inverse of the data time span (∼1000 d), a rough estimate for the orbital-frequency uncertainty lower limit. Limiting the orbital-frequency difference to 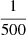 d−1 yielded the same sample. An orbital-period limit of 2 days was chosen because most discovered EL CVn systems are below it (see Fig. 5 of van Roestel et al. 2018). These criteria resulted in an initial sample of 1174 systems.
d−1 yielded the same sample. An orbital-period limit of 2 days was chosen because most discovered EL CVn systems are below it (see Fig. 5 of van Roestel et al. 2018). These criteria resulted in an initial sample of 1174 systems.
Next, we calculated the phase difference between the SB-model primary eclipse and the EB-model deeper eclipse for all stars in our sample. For a common binary, for example one consisting of two MS stars, we expect this phase difference to be zero. However, for an EL CVn, in which the secondary is hotter and therefore the secondary eclipse is deeper, we expect the phase difference to be ∼0.5, assuming a small eccentricity. Figure 29 shows the phase-difference histogram of our initial sample, with a main peak at phase zero, and a much smaller peak at phase 0.5, as expected.
 |
Fig. 29. Histogram of phase difference between SB-model primary eclipse and EB-model deeper eclipse, for 1174 stars in our sample. |
Based on this, we selected an initial list of EL CVn candidates with: (a) an eclipse phase difference in the 0.4 − 0.6 range, (b) an eccentricity smaller than 0.3, and (c) an EB-model eclipse-depth difference with a S/N of higher than 5. The eclipse-depth difference S/N was required because our method relies on reliably identifying a secondary eclipse that is significantly deeper than the primary one. These criteria yielded 16 systems. Finally, we visually inspected the Gaia photometry and RV data and models of the 16 systems in our initial list, and identified five systems as the most promising EL CVn candidates.
6.7.2. Five EL CVn-type candidates
After identifying the five EL CVn candidates, we realised that all have a GaiaSB1 model, and one of them is actually a known EL CVn-type system (Gaia DR3 5087757377681887232 (G5087); TIC-ID 121078334; HD 23692; Maxted et al. 2014), which is shown in Fig. 28. This system serves as an initial validation for our discovery method and the rest of the candidates. Figure 30 shows the Gaia and TESS data (except for Gaia DR3 2048990809445098112 (G2048), for which we could not find TESS photometry) for the four new candidates presented as in Fig. 28. A selected set of Gaia parameters of the five candidates is listed in Table 7.
 |
Fig. 30. Gaia and TESS data of four new EL CVn candidates presented as in Fig. 28. We could not find TESS photometry for Gaia DR3 2048990809445098112, so its TESS panel was left empty. |
Parameters of five EL CVn candidate systems.
In principle, one can use the rich Gaia photometry, RV, and derived properties, together with the TESS data, to fit an astrophysical model and estimate the pre-He-WD mass, radius, effective temperature, and other properties. Such an analysis was performed by Maxted et al. (2014), Faigler et al. (2015), and van Roestel et al. (2018) for multiple EL CVn systems they identified. However, this analysis is beyond the scope of this ‘teaser’ paper.
6.8. Ultracool dwarf binaries
Multiplicity studies of ultracool dwarfs (UCDs, which comprise both very low-mass stars and brown dwarfs) at separations ≲1 au have long since been hampered by the relative faintness of those objects and the associated observational limitations. The separation and mass (or magnitude) ratio distribution of known UCD binaries therefore carries a significant observational bias, which is also affecting the estimated UCD binary fraction of 10%−30% (e.g. Burgasser et al. 2007). Surveys of small samples indicate that the occurrence of compact UCD binaries is significant (Blake et al. 2010; Bardalez Gagliuffi et al. 2014; Sahlmann et al. 2014a) and that many of those systems have photocentre orbit amplitudes measurable in milliarcseconds. It has therefore been predicted that Gaia astrometry will eventually enable the characterisation of hundreds of UCD binary orbits (Sahlmann et al. 2014b) and significantly improve our knowledge of the occurrence and properties of compact UCD binaries.
Here we have a first look at the UCD orbits in Gaia DR3. Figure 31 shows the Gaia colour–magnitude diagram of all sources with nss_solution_type = OrbitalTargetedSearch*. Large grey circles indicate the known UCD sources from the Gaia ultra-cool dwarf (GUCD, Smart et al. 2019) sample, where we used the gaiaedr3.dr2_neighbourhood table to match a source_id from Gaia DR2 to Gaia DR3.
 |
Fig. 31. Colour–magnitude diagram of 533 sources with OrbitalTargetedSearch* solutions (black circles). The larger grey circles indicate sources that are listed in the GUCD sample (Smart et al. 2019), the grey squares indicate red sources discussed in the text, and the diamond indicates the WD discussed in Sect. 8.8. |
The only non-single star solutions for GUCD sources are found in the nss_two_body_orbit table with solution type OrbitalTargetedSearch*. No GUCD could be matched with an Orbital solution or an acceleration solution. This is mainly because a large fraction (∼75%) of GUCDs are fainter than the G < 19 cut-off for processing with the nominal NSS pipelines (Sect. 2.2.1). As described in Holl et al. (2023b), the full GUCD sample was nevertheless included in the targeted search for orbital signals.
Thirteen sources with DR3 orbits are part of the GUCD catalogue, and only five of those are brighter than G = 19. Table 8 lists the GUCD sources with DR3 orbital solutions.
Identifiers and basic properties of 13 UCD binaries in DR3.
There are three binaries with previously published astrometric orbit solutions. These are J0805+4812 (Sahlmann et al. 2020), J0823−4912 (Sahlmann et al. 2013, 2015), and J1610−0040 (Dahn et al. 2008; Koren et al. 2016). Generally, the DR3 orbit parameters agree with these published solutions.
The J0320−0446 binary has a published RV orbit and both the Gaia period and eccentricity agree well. The Gaia solution indicates an almost edge-on configuration, in agreement with the expectations from the RV modelling by Blake et al. (2008). The Thiele-Innes coefficients for this low-eccentricity solution are highly correlated, which leads to correlated and skewed distributions when resampling the geometric parameters. This has to be accounted for when using the Gaia solution parameters for estimating the companion mass in particular.
Two sources in this list have only been identified as spectrum binaries, that is, typically L+T-dwarf systems in which the spectrum of the companion is discernible in the combined-light near-infrared spectrum. In principle, the Gaia orbital solutions will make it possible to constrain the masses of the binary components. The orbital parameters refer to the system photocentre, but the applicable constraints depend on the brightness- and mass-ratio of the system, which are not usually determined by Gaia. Therefore, external information and assumptions have to be incorporated. As an example, we explore the orbit of J2026−2943, which has previously been identified as a spectrum binary with components of spectral types L1+T6 (Bardalez Gagliuffi et al. 2014; Gelino & Burgasser 2010). If we assume a field-age mass of 0.080 ± 0.005 ℳ⊙ for the L1 primary and that the light contribution of the T6 companion is negligible in the G band, then the Gaia orbit solution implies a companion mass of 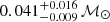 , where we account for all parameter covariances using Monte Carlo resampling. This mass estimate is compatible with expectations for a T6 brown dwarf and adds a valuable entry in the list of low-mass systems with dynamically determined masses (Dupuy et al. 2019; Sahlmann et al. 2020). Examples of combining astrometric orbit solutions with RVs, spectrum-binary indicators, and spatially resolved observations to investigate the physics of UCDs can be found in the literature (e.g. Garcia et al. 2017; Sahlmann et al. 2021, 2020; Brandt et al. 2020).
, where we account for all parameter covariances using Monte Carlo resampling. This mass estimate is compatible with expectations for a T6 brown dwarf and adds a valuable entry in the list of low-mass systems with dynamically determined masses (Dupuy et al. 2019; Sahlmann et al. 2020). Examples of combining astrometric orbit solutions with RVs, spectrum-binary indicators, and spatially resolved observations to investigate the physics of UCDs can be found in the literature (e.g. Garcia et al. 2017; Sahlmann et al. 2021, 2020; Brandt et al. 2020).
For the remaining seven sources, we find no previously identified multiplicity indicators in the literature. These are therefore potentially new UCD binary discoveries made in Gaia DR3. These could be confirmed by independent observations of their spectroscopic properties or with RV monitoring. Because of its long period and proximity, the J0031−3840 system has an estimated relative semi-major axis of ∼60 mas and could possibly be spatially resolved with specialised instruments, which can give access to model-independent mass determinations.
As expected, the UCD binaries discussed above are compact systems with estimated relative separations ≲1.5 au because a large fraction of their orbit is covered by the DR3 data. Their period–eccentricity distribution is mostly unaffected by the complications in terms of mass determination discussed above and can be used to investigate UCD formation mechanisms or dynamical histories (e.g. Dupuy & Liu 2011). Figure 32 shows these parameters in comparison with the Orbital solutions. The high eccentricity of the long-period solution for J0031−3840 may be affected by the incomplete orbit coverage with Gaia data, which tends to push eccentricity up as also shown by the Orbital solutions.
 |
Fig. 32. Orbital eccentricity as a function of period for the UCD systems listed in Table 8 (black symbols). The parameters of Orbital solutions within 200 pc are shown in grey. |
Comparison with Fig. 18 of Dupuy & Liu (2017, which includes a few sources in common) shows that these generally intermediate eccentricities are in agreement. Importantly, Gaia is filling in the period range of ∼0.5 − 5 yr which until now has been sparsely populated because of the resolution limit of direct-imaging instruments. This will help to build statistically robust samples of UCD binaries that can be used for comparison with stellar binaries. Finally, we inspected the orbits of the three reddest objects; these are not in the GUCD catalogue, and are highlighted with squares in Fig. 31:
J0219–3925. This is 2MASS J02192210−3925225, which was characterised as a young late-M dwarf with a wide (4″) substellar companion by Artigau et al. (2015). The Gaia astrometric orbit corresponds to an inner companion to the M-dwarf, which (if dark) could have a mass as low as 11.2 ± 0.9 ℳJup for the primary mass of 113 ± 12 ℳJup (Artigau et al. 2015). Another possible explanation is a more massive companion, whose light contribution dilutes the photocentre orbit. Auxiliary data or observations have to be considered to better characterise the inner companion.
LHS1610. This mid-M dwarf was identified as an RV binary by Winters et al. (2018) and the Gaia astrometry independently confirms the eccentric 10.6-day orbit. The Gaia solution indicates a close-to edge-on configuration and a companion-mass estimate of 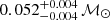 when assuming a primary mass of 0.17 ± 0.02 ℳ⊙, i.e. it establishes the substellar nature of the companion.
when assuming a primary mass of 0.17 ± 0.02 ℳ⊙, i.e. it establishes the substellar nature of the companion.
L 601−78 A. This is the primary component of the wide binary L 601−78. It was identified as a lens candidate for mass determination using astrometric microlensing by Gaia (Klüter et al. 2020).
7. Compact-object companions
In what follows, we point out a few methods for identifying binary candidates in our tables that might harbour compact-object companions. The discussion is meant to provide ideas for further studies that are needed to confirm the nature of these binaries. We first underline the method used for astrometric orbits, and then discuss white dwarf secondaries, and then larger masses, including those found using SB1 orbits.
7.1. Astrometric binaries with compact-object companions using the triage algorithm
To identify unresolved astrometric binaries that are likely to host a compact object as their faint binary companion, we use the triage classification of Shahaf et al. (2019). The algorithm divides the astrometric binaries into three classes: (a) class-I binaries, where the companion is most likely a single MS star (but can also be a close binary or a compact object), (b) class-II binaries, where the companion cannot be a single MS star; therefore, it is most likely a close MS binary (but can also be a compact object), and (c) class-III binaries, where the companion cannot be a single MS star or a close MS binary; therefore, these systems most likely host a compact object as secondary.
The distinction between the three classes depends on the value of the newly defined astrometric mass ratio function (AMRF), 𝒜, given by
where a0 is the derived angular semi-major axis of the photocentric orbit, ϖ is the parallax, ℳ1 is the mass of the primary star, and P is the orbital period of the binary.
The AMRF can be written as a function of the mass ratio q = ℳ2/ℳ1 and the luminosity ratio of the two components of the astrometric binary 𝒮 = F2/F1 as
(see details in Shahaf et al. 2019). The luminosity ratio modelling is based on the Pecaut & Mamajek (2013) MS colour and effective temperature tables, assuming no extinction. As emphasised by Shahaf et al. (2019), there are two limiting AMRF values: the maximal value for a single MS companion (class I sources), and the maximal value assuming a close binary of two identical MS stars as the secondary companion (class II sources).
Figure 33 presents the derived AMRF values for the Gaia unresolved astrometric binaries presented in this work, with primaries in the range of 0.2 − 2.0 ℳ⊙ and significance larger than 20, using the primary mass values reported in Table 3. Systems with AMRF values that exceed the maximal possible value for triple stars by more than 4σ, where the uncertainty σ was calculated by propagating the uncertainties of the quantities in Eq. (9). These are presented in Fig. 33 as bold black points and are likely to host a compact-object companion. As the light contribution of the companions of these systems is negligible, namely 𝒮 ≃ 0, we can derive the mass ratio and then the mass of the secondary of these systems. Their mass values are presented in the right hand panel of the figure.
 |
Fig. 33. Triage of the Gaia astrometric binaries, with classes I to III from bottom to top delineated by dotted and dashed lines respectively. Left: AMRF vs. mass of the primary for the astrometric solutions of this paper. The systems with a probable compact-object companion (class III) are presented as bold black points (see text). For reference, the rest of the sample is plotted as fine black points. Right: masses of the compact companions derived from the AMRF as a function of their primary mass. The remaining systems do not appear in this panel. The yellow star is the neutron star candidate Gaia DR3 5136025521527939072 discussed in Sect. 7.3. |
We compare the obtained masses with the conservative lower limit estimate of the companion mass (Sect. 5.1) in the left panel of Fig. 34. Additionally, because the photocentre coincides with the position of the primary star for faint companions, we expect the semi-major axes derived from the astrometry and the RV spectroscopy to be similar, as demonstrated in the right panel of Fig. 34 for the AstroSpectroSB1 cases. The CMD of these class III systems is shown Fig. 35.
 |
Fig. 34. Left: comparison between the minimum companion mass derived in Sect. 5.1, and the AMRF-derived masses for the compact-object candidates. The sources where the AMRF mass is smaller than the minimum mass are AstroSpectroSB1, which have a non-negligeable flux ratio. Right: comparison between semi-major axes derived for the AstroSpectroSB1 systems using the astrometric parameters (horizontal axis) and the spectroscopic parameters (vertical axis). The yellow star is Gaia DR3 5136025521527939072. |
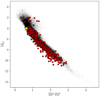 |
Fig. 35. Class-III CMD. Black points show Orbital and AstroSpectro objects for reference. Red points are AMRF class-III. The yellow star is Gaia DR3 5136025521527939072. |
Figure 36 presents a mass histogram of the secondaries of the astrometric binaries assumed to have a compact companion of up to 2.1 ℳ⊙. It seems as though most of the companions are white dwarfs, with a clear narrow peak at ∼0.6 ℳ⊙, as is the case for field white dwarfs. Obviously, the secondary mass population is heavily biased by the way it was derived, and so any astrophysical interpretation should be made carefully. In any case, the circularisation at large periods is striking (see Fig. 37).
 |
Fig. 36. A histogram of the companion masses for compact object candidates up to a mass of 2.1 ℳ⊙. |
 |
Fig. 37. e − P diagram. Black points are Orbital and AstroSpectro objects for reference. Red points are AMRF class-III. The yellow star is Gaia DR3 5136025521527939072. |
The histogram of secondary masses in Fig. 36 has been limited to 2 ℳ⊙. There are four sources with a larger mass (identified as AMRFClassIII in the table binary_masses), but we find indications that they may be artefacts.
7.2. A closer look at the astrometric binaries with white-dwarf companions
White dwarfs are often present in binary systems. The co-eval context with their companion star makes such systems important benchmarks for understanding stellar evolution. WDs in wide systems can be detected relatively easily through searches for common proper motion objects (e.g. El-Badry & Rix 2018). However, in closer systems, the WD can be very difficult to detect because of the overwhelming brightness of the companion, particularly for early spectral types. In that case, the WD may be hidden until revealed by astrometric motion, spectroscopic variability, or a photometric excess. A classic example is the discovery of Sirius B (Bessel 1844), which is both an astrometric and spectroscopic binary (e.g. Barstow et al. 2005; Bond et al. 2017). Sirius represents a class of binary systems, the Sirius-type binaries, consisting of a primary star of spectral type earlier than late-K and a WD. Examples of such systems have often been identified by flux excesses at wavelengths shorter than those spanned by the primary, in the UV, Extreme UV (EUV), or X-ray (see e.g. Barstow et al. 1994). A fraction have subsequently been resolved by space-based observations (e.g. Barstow et al. 2001).
The number of known Sirius-type binaries lies in the tens of objects, with selection effects playing a strong role in identification of an individual system. For example, unless resolved, the flux of any cool WD will always be buried in the light of the primary companion. Whether or not a system can be resolved depends on the separation and distance of the components. Binary systems comprising two WDs (double degenerates) or a WD with an M dwarf companion are easier to find as they will sit closer to the main WD cooling tracks in the HRD. Even so, the nature of any double degenerates might not be apparent if the stars have similar or featureless spectra. The SPY survey sought to identify double degenerates from radial velocity variations, finding 39 double degenerate systems and 46 WDs with cool companions from a sample of 643 stars (Napiwotzki et al. 2020).
The Gaia stellar catalogue is an enormous resource that will potentially increase the number of known binary systems with WD components by at least an order of magnitude. In Gaia DR2 and Gaia EDR3, the number of known WDs expanded by such a factor (Gentile Fusillo et al. 2019, 2021). While many WD+M systems can by identified by their location in the HRD, double degenerates will typically show significant overlap with the isolated WD cooling tracks and Sirius-like systems largely overlap with the main sequence. The release of eclipse, astrometry, and spectroscopy data related to the identification of NSSs in Gaia DR3 is an important step forward. In principle, these new resources can be used to search for the presence of WDs in a variety of binary systems.
7.2.1. Selection of candidate binary systems with WD components
The wavelength coverage of the Gaia RVS is not optimised for the study of WDs, which typically have broad absorption lines in their photospheres, when present. Therefore, we would expect only the primary stars in Sirius-like binaries to be detected as radial velocity variables. These will therefore most likely be found in the sample of SB1 systems. If the secondary is a WD, it will not contribute significantly to the brightness of the system in the Gaia bands. However, if hot enough, there may be a measurable excess at shorter wavelengths. In addition, the secondary mass will lie between ≈0.4 and 1.4 ℳ⊙, where the Chandrasekhar limit defines the upper bound.
Binaries with WD components might also be detected astrometrically or as eclipsing binaries. Therefore, we assembled an initial list of potential candidate binary systems with WD components from the NSSs selected for all these possibilities using the following nss_solution_type keywords: AstroSpectroSB1, SB1C, SB1, Orbital, OrbitalAlternative, Eclipsing*, and OrbitalTargetedSearch. We did not apply any quality selection criteria except to reject any objects with G greater than 20. This selection yielded a total of 355 524 NSSs for further analysis. The AMRF sample, which is based on AstroSpectroSB1 and Orbital solutions alone, is a subset of these candidates for which we have good estimates of the component masses.
In the search for WD companions, we use the AMRF data to restrict the mass range of compact objects to lie below the 1.4 ℳ⊙ Chandrasekhar limit. Applying this criterion yields 676 objects, which are shown in green in Fig. 38 and compared to the locus of the GCNS (grey data points). The secondary mass alone cannot be used to definitively determine whether or not these are WD components, as F, G, K and the earliest M main sequence stars also occupy this mass range. However, several factors indicate that these objects are highly likely to be Sirius-type binaries. Any unresolved main sequence binaries should appear to be over-luminous. Evolution on the main sequence and the range of possible luminosity combinations may prevent a clear separation of binaries and isolated stars, but unresolved main sequence binaries should appear as SB2 systems in the NSS Gaia catalogue. Finally, as noted above, the mass distribution for the secondaries in these unresolved astrometric binaries has a strong peak at 0.55 − 0.6 ℳ⊙ corresponding to the known peak of the mass distribution of field WDs (Fig. 36). This is in contrast to the smooth mass distribution expected for MS stars.
 |
Fig. 38. HRD of the candidate NSSs with WD components with a secondary mass solution below the Chandrasekhar limit (< 1.4 ℳ⊙, green data points). These are compared with the locus of stars in the GCNS (grey data points). |
While the vast majority of selected objects lie on the MS, as shown in Fig. 38, there are 39 objects that match WD colours and magnitudes, indicating a WD primary; these are shown in Fig. 39. The majority of these objects lie above the main concentration of the isolated white dwarfs, and therefore these systems are highly likely to be double degenerates, where the brightness of two unresolved objects combines to yield an apparent excess in luminosity.
 |
Fig. 39. WD with orbital solutions (green points, corrected from extinction) overplotted on the Gaia DR3 low-extinction HRD. Most of the points lie above the hydrogen sequence. The red dots and WD 0141–675 (orange square) are discussed in Sect. 8.8. |
As discussed above, when we know the secondary mass and the binary is not revealed as an SB2 system, we can be very confident that the secondary is a WD and therefore that the binary is a Sirius-type system. However, it is likely that there are many more Sirius-type systems in the non-SB2 sample. An unresolved binary system can be revealed by a flux excess in a waveband where the contribution from the primary star is expected to be weak. A number of Sirius-type binary discoveries have been made by detecting the WD in the EUV and UV wavebands. The GALEX mission surveyed most of the sky in two broad far-UV (FUV) and near-UV (NUV) bands. Cross-correlating the GALEX database with the Gaia DR3 non-SB2 binaries will potentially reveal the Sirius-type systems with a hot WD component. This is illustrated by applying this to the astrometric binaries in the sample. Figures 40 and 41 show the G vs. GBP − GRP HRD for the cross-match of the GALEX GR6+7 AIS catalogue with this sample for NUV and FUV bands, respectively. The small grey data points are the GCNS stars in each figure while the coloured symbols are the NUV (Fig. 40) and FUV detections (Fig. 41) colour-coded according to the absolute NUV or FUV magnitude, as indicated in the side bar. These magnitude ranges can be compared to the typical values for white dwarfs in the optical colour–absolute magnitude diagram, as indicated in Fig. 39. The absolute NUV magnitude correlates well with the GBP − GRP colour, an indicator of the temperature of the primary star. However, a few systems show a strong NUV excess for the systems with cooler main sequence primaries, indicated by red to yellow colours compared to green to blue in that region of the diagram. Hence, the integrated NUV flux is not generally a good indicator of the presence of the white dwarf. In contrast, there is little if any correlation between the absolute FUV magnitude and GBP − GRP colour, indicating that the FUV is a better discriminator than the NUV, the measured magnitudes potentially providing an estimate of the WD temperature. However, this can only be applied to the relatively few stars that are sufficiently hot to have a measurable FUV flux. We note that the FUV magnitude is not a completely unique indicator of the presence of a WD, as MS stars with an active corona can also generate an enhancement in the total FUV flux through the strong C IV (154.8 nm & 155.0 nm) and He II (164 nm) emission lines.
 |
Fig. 40. G vs. GBP − GRP HRD showing the cross-match between the GALEX GR6+7 AIS catalogue with the GCNS (small symbols) and the candidate list of binaries with WD components with computed secondary star masses below the Chandrasekhar limit (< 1.4 ℳ⊙). The symbols are colour coded with the absolute NUV magnitude. |
 |
Fig. 41. G vs. GBP − GRP HRD showing the cross-match between the GALEX GR6+7 AIS catalogue with the GCNS (small symbols) and the candidate list of binaries with WD components with computed secondary star masses below the Chandrasekhar limit (< 1.4 ℳ⊙). The symbols are colour coded with the absolute FUV magnitude. |
We also cross-matched the full Gaia DR3 non-SB2 binaries with the GALEX GR6+7 AIS catalogue. The results are shown in Fig. 42, with 29 000 stars of the list of 355 000 objects having a GALEX FUV counterpart. The FUV detections in the WD region of the HRD provide an indication of the range of FUV absolute magnitudes – namely between about 8 and 20 – that correspond to WDs. Many of the FUV counterparts in Fig. 42 have similar magnitudes, but without further information it is not possible to categorically identify these as WDs and rule out alternative explanations for the FUV flux.
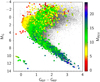 |
Fig. 42. G vs. GBP − GRP HRD showing the cross-match between the GALEX GR6+7 AIS catalogue and the full list of non-SB2 binaries selected here (large symbols). The symbols are colour coded according to absolute FUV magnitude as indicated by the side-bar. The small grey data points are the full list of non-SB2 binaries. |
A more detailed modelling of the predicted primary and WD fluxes across the expected range of temperatures should be able to refine the discriminatory power of this approach to selecting Sirius-type systems, but this is beyond the scope of this Gaia DR3 companion paper.
7.3. A possible binary with a dormant neutron star with an AstroSpectroSB1 orbit
Only a few tens of dynamically confirmed Galactic stellar black holes (BHs) and neutron stars (NSs) are known to reside in binary systems. These are discovered either by their X-ray emission, fueled by mass transfer from their non-compact stellar companions (e.g. Fabian et al. 1989; Remillard & McClintock 2006; Orosz et al. 2007; Ziolkowski 2014), or, in the case of active pulsars, by their radio pulsed emission.
Obviously, most BH in binaries have not yet been detected, because their optical counterparts are well within their Roche lobes, and so mass is not transferred and X-rays are not generated, making these systems dormant (see discussion on the frequency of such systems and the prospect of their detection with Gaia astrometry by Breivik et al. 2017; Mashian & Loeb 2017; Shao & Li 2019; Wiktorowicz et al. 2019). Similar arguments apply to dormant NSs – the pulsation phase lasts for only 10 to 100 million years when the pulsar is young (Faucher-Giguère & Kaspi 2006; Bransgrove et al. 2018) – and to binaries with WD companions (see discussion above). Such dormant binaries can be found by the orbital motion of the primary, detected either by astrometry or RVs. In all three classes of dormant companions, the challenge is to identify the binaries, estimate the mass of the unseen companion, and rule out a faint MS companion.
One of the systems identified by the triage algorithm as having a compact companion, Gaia DR3 5136025521527939072, is in fact an AstroSpectroSB1 binary, with a primary mass of 1.2 ℳ⊙ and a secondary mass of 1.5 ℳ⊙, consistent with a binary having a dormant NS with a period of 536 days. Its location is marked in the pertinent figures of the triage analysis above.
The astrometric orbit and the phase-folded radial velocity of this source are shown in Fig. 4315. In order to validate the orbit, we requested observing time on the SOPHIE spectrograph mounted at the 1.93 m telescope of the Observatoire de Haute-Provence (France). The SOPHIE pipeline (Bouchy et al. 2009) together with a G2 mask was used and we obtained a RV = 40.603 ± 0.023 km s−1 with a FWHM = 9.274 km s−1 on BJD 2459541.389492. The consistency of this RV obtained about 4.5 years after the end of the Gaia data segment used for Gaia DR3 confirms the quality of the predicted orbit.
 |
Fig. 43. Top panel: phase-folded radial velocity data of Gaia DR3 5136025521527939072, together with the orbits using the astrometric (red dot-dashed line) and spectroscopic (blue solid line) orbital elements separately; the OHP/Sophie external measurement (green squared point) was not part of the fit. Bottom panel: along-scan residuals of the mean epoch astrometric measurements (black symbols) relative to the model positions (grey circles) and the astrometric orbit (red solid line) of the same source. The red cross marks the focus of the orbit and the grey square is the periastron location. |
7.4. Compact objects in SB1 solutions
While the search for compact object companions above was carried out using the astrometric orbits, we complete the search using the SB1 solution. A search for SB1 sources with large mass functions has long since been proposed as a way to identify candidates with a BH or NS companion (Trimble & Thorne 1969; Guseinov & Zel’dovich 1966). Among the SB1 sources, 94 have significance larger than 20 and f(ℳ) > 1.4 ℳ⊙, and 20 among them f(ℳ) > 3 ℳ⊙. The SB1 solution of Gaia DR3 2006840790676091776 shall be dismissed because of contamination by a nearby bright source. Inspection of RVS spectra of Gaia DR3 5259215388421037696 shows that the source is probably an SB2 and the radial velocities, computed with an incorrect template, are most probably incorrect, and so the SB1 solution of this star will be discarded. Gaia DR3 878555832642451968 has a RV measurement in the LAMOST (Luo et al. 2015) survey (−100.86 km s−1 at BJD 2458068.5) which does not agree with the SB1 solution. A reanalysis of the RVS epoch RV shows that an alternative solution with a period of 8.438 days is also possible and in better agreement with LAMOST data. The SB1 solution in the Gaia archive should therefore be considered as dubious. In Fig. 44 we show the position of the sources with f(ℳ) > 1.4 ℳ⊙ in the colour–magnitude diagram. The relevant data of the sources with f(ℳ) > 3 ℳ⊙ are reported in Table 9.
 |
Fig. 44. HRD of SB1 solutions with f(ℳ) > 1.4 ℳ⊙ and significance > 20. Squared symbols are for sources with 1.4 ℳ⊙ < f(ℳ)≤3 ℳ⊙, star symbols for sources with f(ℳ) > 3 ℳ⊙. The background grey scale shows the density distribution of all SB1 solutions. |
SB1 solutions with f(ℳ) > 3 ℳ⊙.
From Fig. 44, we can see that the vast majority of the selected sources are not main sequence stars. It is therefore challenging to determine the real nature of these systems, because if the primary is a giant star, it can easily outshine a companion on the main sequence. In some cases, the secondary, although on the main sequence, can be more massive than the primary because of mass transfer, as in Algol-type systems (see El-Badry et al. 2022, for recent examples of BH candidates dismissed as main sequence companions of stripped stars). We recall that such systems are much more common objects than dormant BH. Another possible explanation for such large mass-function values is that the unseen companion is itself a binary composed of two main sequence stars. The understanding of the nature of the other systems would require a deeper analysis using external data and follow-up observations, but such an analysis is beyond the scope of this paper. However, we can comment on some of these objects. For Gaia DR3 5863544023161862144, the presence of eclipses allows us to classify it as an Algol system and to exclude the compact object companion hypothesis. The Gaia photometry of the source Gaia DR3 5857059996952633984 shows a light curve with eclipses of Algol type, albeit with a period of 1.17143 days, typical of Algol systems, in contrast to the period from the SB1 solution. By analysing the epoch radial velocities and the epoch photometry, we can exclude an aliasing in both the SB1 solution and the photometry. A possible solution is that this source is a triple system where the RV data are from the outer component, and the eclipses involve the two inner components.
A particularly interesting source is Gaia DR3 442992311418593664 (HIP 15429), a B5Ib star (Navarro et al. 2012) with f(ℳ) = 4.77 ℳ⊙. In order to validate the orbit, this source was observed with the HERMES spectrograph mounted on the 1.2 m Mercator telescope16 (Raskin et al. 2011) at the Roque de los Muchachos Observatory on La Palma Island. An RV of −47.2 ± 3.5 km s−1 at BJD 2459650.358 was obtained, which is compatible with the GaiaSB1 solution. The HERMES spectrum also confirms the spectral classification of Navarro et al. (2012). Using the 3D extinction map of Lallement et al. (2019), we estimate a dereddened absolute magnitude and colour, MG, 0 = −3.168 and GBP, 0 − GRP, 0 = 0.073, respectively. Comparing these values with the PARSEC evolutionary tracks (Bressan et al. 2012) for solar metallicity, we can interpret this source as being a 4.9 ± 0.3 ℳ⊙ star that has just left the main sequence. The resulting minimum mass for the companion would be 10.4 ℳ⊙. Under the hypothesis that this is a triple system, the secondary would then be a binary where at least one component should have a mass equal to or larger than 5.2 ℳ⊙. However, if all the stars in the system are coeval, this most massive star in the inner binary should be evolved too, and should therefore be brighter than the primary, refuting the triple-star hypothesis. Excluding HIP 15429 as an Algol system is more difficult because even a 12 ℳ⊙ companion on the main sequence would be fainter than the B5Ib primary. However, we note that the absorption lines in the HERMES spectrum do not show any clear double profile, despite the fact that the spectrum was obtained at the phase with maximum radial-velocity difference between the two components. Moreover, there are only a few known Algol systems with such a long period, ≈216 days, and consisting of early-type stars (e.g. μ Sgr). Another possibility is that this source may have a dormant BH companion. More observations and modelling will be needed to decide between the different hypotheses. We finally note that the astrometric ruwe parameter of this star is 2.10, which suggests that upon the next data release it will be possible to obtain an astrometric orbit.
We now move our attention to SB1 sources which can be classified as belonging to the main sequence, for which an estimate of the mass of the primary is provided by IsocLum. Restricting the search for compact object companions to main sequence primaries allows us to reduce the number of false detections where the secondary is a normal main sequence star outshined by an evolved primary. We then selected from the table presented in Sect. 5.1 the SB1 sources for which m2_lower > m1_upper and significance > 20. This results in 68 sources; among them 15 have m2_lower > 3 ℳ⊙ and 25 have 1.4 ℳ⊙ < m2_lower ≤ 3 ℳ⊙. Their position in the magnitude–colour diagram is shown in Fig. 45.
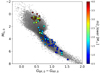 |
Fig. 45. Dereddened HRD of compact object companion candidates from SB1 solutions on the main sequence. Circle symbols are for sources with m2_lower ≤ 1.4 ℳ⊙, square symbols are for sources with 1.4 ℳ⊙ < m2_lower ≤ 3 ℳ⊙, and stars symbols are for sources with m2_lower > 3 ℳ⊙. The background grey scale shows the density distribution of all SB1 solutions classified as belonging to the main sequence by IsocLum. |
Source candidates with compact object companions with m2_lower > 3 ℳ⊙ and m2_lower > m1_upper from SB1 solutions with significance > 20.
It should be noted that the spectroscopic RVs of stars cooler than 3875 K were not processed by the NSS pipeline. This introduces a selection on the mass of the primary that means that almost no SB1s are present in the catalogue with a primary mass below 0.6 ℳ⊙. It is therefore not possible with this selection to obtain candidates with more massive companions belonging to the main population of white dwarfs.
Particularly interesting are sources with m2_lower > 3 ℳ⊙, which could have a dormant BH companion. We checked each of the candidates and found that, among sources with m2_lower > 3 ℳ⊙, the sources Gaia DR3 548272473920331136 and Gaia DR3 6000420920026118656 are known eclipsing binaries (Otero 2008; Avvakumova et al. 2013) classified as Algol type, while Gaia DR3 1850548988047789696 is an Algol-type eclipsing binary detected by Gaia.
We then checked the Gaia and TESS (Ricker et al. 2015) photometry for the other 11 sources, and all show a modulation of the flux that is in phase with the radial velocity, similar to that expected for an ellipsoidal star17, confirming the binary nature. However, this ellipsoidal behaviour suggests that these stars are rather evolved, but the small amplitude of the modulation (a few percents) tells us that the primaries do not fill their Roche lobe. Using the relation between the mass ratio and the effective radius of the Roche lobe provided by Eggleton (1983), we get that the mass required for the primary to fill the Roche lobe, given the radii estimated with the IsocLum code, would be always below 0.1 ℳ⊙, which is too low for an evolved star and for the observed effective temperature. A more detailed modelling of the light curve of these objects is out of the scope of this article.
 |
Fig. 46. Top panel: phase-folded radial velocity of Gaia DR3 2966694650501747328 (P = 10.398 d). Bottom panel: phase-folded TESS (black circles) and Gaia normalised flux (green, blue, and red circles: flux in G, GBP, and GRP bands respectively). |
 |
Fig. 47. HRD of sources with low astrometric mass functions (< 0.001 ℳ⊙; green dots); the grey background is the DR3 low-extinction HRD. A very large fraction are not stars with low-mass companions, but rather binaries with a mass ratio similar to their flux ratio. The two blue sources are HD 12800 and HD 3221, described in Sect. 8.7 while the four WDs are discussed in Sect. 8.8. |
The 17 known X-ray binaries with BH companions (Corral-Santana et al. 2016) have periods of 0.3−5 days. We expect the similar dormant binaries to have longer periods, and therefore the range we find here is consistent with the expected periods. Our sources are nevertheless only considered to be candidates, because other explanations are possible that do not invoke a compact companion. With the information that we have, we cannot rule out the possibility that these sources are Algol-type systems, but the bluest sources should be considered as more promising candidates of dormant BHs because they are nearer the main sequence than the redder sources, and therefore cannot easily outshine a MS companion. Finally, as mentioned above, we cannot exclude that the unseen companion is the inner binary composed of two MS stars. The periods of these 11 candidates range from 8.2 to 23.5 days, which is not short enough to exclude the triple system hypothesis.
The data for these 11 candidates are reported in Table 10. Figure 46 shows the phase-folded radial velocity of the source Gaia DR3 2966694650501747328, together with its phase-folded TESS and Gaia normalised flux.
8. Substellar companions
The two well-known categories of substellar companions, namely planets and brown dwarfs, have, for a few decades now, been the objective of long-term ground-based Doppler search programs in the solar neighbourhood (e.g. Cumming et al. 2008; Howard et al. 2010; Mayor et al. 2011; Bonfils et al. 2013; Butler et al. 2017; Rosenthal et al. 2021; Pinamonti et al. 2022). The Gaia DR3 astrometric performance levels reach the sensitivity to detect substellar companions around a statistically significant number of stars, enabling first-time measurements of their three-dimensional orbital architectures and true masses.
8.1. Astrometry: substellar companions
A naive search for substellar companions detected by Gaia astrometry might simply select solutions with low values of the astrometric mass function, say f(ℳ) < 0.001 ℳ⊙. However, inspection of Fig. 47 shows that a sizeable fraction of the companions of sources with low f(ℳ) do not have small secondary mass with a negligible flux ratio but rather have a flux ratio close to the mass ratio, leaving them clearly above the main sequence.
Keeping this in mind, we browsed the catalogue of masses presented in Sect. 5.1 to investigate the regime of astrometrically detected companions with lower mass bound ℳc (assuming they contribute no flux) in the substellar regime, operationally defined as having 20 ≤ ℳc ≤ 80 ℳJup and ℳc ≤ 20 ℳJup for brown dwarfs (BDs) and exoplanets (EPs), respectively. For a subset of sources with orbital solutions in the Gaia DR3 archive but without a companion mass estimate in our catalogue of masses, the information was derived based on primary mass estimates from the Starhorse catalogue (Anders et al. 2022).
A total of 1843 BDs and 72 EPs were identified in the catalogue of companion masses. This includes 20 sources with AstroSpectroSB1 solution type that have upper bounds to the companion mass < 80 ℳJup, that is, for which the assumption of negligible flux ratio is confirmed. A small subset of 10 BDs were already known, identified in ground-based RV surveys for planets (Ma & Ge 2014; Wilson et al. 2016; Kiefer et al. 2019; Dalal et al. 2021). Table 11 reports the basic comparison between period and eccentricity from Gaia and the literature, as well as minimum and true mass estimates. A total of 9 known EPs were also validated against literature sources, and we report the same information in Table 11. As an illustrative example, the astrometric orbital solution for HD 81040 b is shown online18. Additional plots of Gaia DR3 orbits of substellar companions can also be found in Holl et al. (2023b).
Known substellar companions with a confirmed mass in the planetary and brown dwarf regime, respectively.
8.2. Astrometric masses: transition regimes
The results of long-term Doppler surveys have allowed detailed studies of the shape of the mass distribution of relatively close-in (a ≲ 5 au or so) companions to solar-type (F-G-K-type) stars, particularly in the two transition regimes between EPs and BDs and between BDs and stars. The most notable feature is the so-called ‘brown dwarf desert’: the (minimum) mass distribution has a clear decline moving from the planetary-mass to the BD-mass regime, reaches an apparent plateau with a minimum at ∼40 − 50 ℳJup (0.04 − 0.05 ℳ⊙), and then rises again reaching the stellar-mass regime (e.g. Grether & Lineweaver 2006; Sahlmann et al. 2011; Ma & Ge 2014; Grieves et al. 2017).
Figure 48 shows the distribution of primary masses for sources with astrometrically detected substellar-mass companions for the cases of NSS solution types (Orbital and OrbitalTargetedSearch*). The medians of the two distributions are 0.42 ℳ⊙ and 0.91 ℳ⊙, respectively. The striking difference stems from the different ways in which the input lists for the two analysis channels were constructed (see Sects. 2.2.1 and 2.2.2, and references therein). In particular, the bulk of the sources with known solutions input to the alternative orbit determination algorithms are solar-type stars, and this is reflected in Fig. 48. The calibration levels in the bright-star regime are still suboptimal for Gaia DR3; consequently, it is expected that nearby, relatively faint low-mass stars might be the sample of primaries around which the chances of detecting substellar companions are maximised, and this is also reflected in Fig. 48.
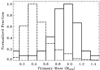 |
Fig. 48. Primary mass distributions for sources with astrometrically detected substellar companions with Orbital (long-dashed histogram) and OrbitalTargetedSearch* (solid-line histogram) solution types. |
The three panels of Fig. 49 show the distribution of substellar companion masses for three samples. The distribution for the OrbitalTargetedSearch* sample (top panel) corroborates the notion – already provided by Doppler surveys – of a minimum in the occurrence of ∼40 ℳJup close-in BDs around solar-type stars. For the first time, Gaia DR3 offers the opportunity to see the feature in the distribution based on true companion mass estimates, without the ambiguities inherent to studies of the population of substellar companions based on minimum mass values and/or simulation-driven upper mass limits (e.g. Kiefer et al. 2021, and references therein).
 |
Fig. 49. Top: substellar companion mass distribution for the OrbitalTargetedSearch* solution type. Centre: same as above, but for the Orbital solution type, with a cut-off in the primary mass ℳ⋆ < 0.6 ℳ⊙. Bottom: same again, but for the Orbital solution type, with a cut-off in the primary mass ℳ⋆ > 0.6 ℳ⊙. |
The centre and bottom panels of Fig. 49 show the equivalent distribution for the main NSS sample, split into two regimes of companions with substellar masses around M dwarfs (M⋆ < 0.6 ℳ⊙) and higher-mass primaries, respectively. The first notable feature is the difference in slope between the two samples rising towards the highest masses: a simple power-law fit returns 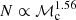 and
and 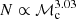 for companions around M dwarfs and higher mass stars, respectively. A Kolmogorov-Smirnov (K-S) test indicates that the two distributions of substellar companion masses around M dwarfs and higher mass stars in the centre and bottom panels of Fig. 49 have a p-value of ∼1 × 10−6, allowing us to reject the hypothesis that they are drawn from the same distributions. Secondly, the occurrence of detected companions around higher mass dwarfs appears roughly flat in the approximate range 0.04 ≲ ℳc ≲ 0.06 ℳ⊙. For M dwarf primaries, the distribution continues to show a declining trend towards the low-mass end (corresponding to super-Jupiter-mass objects with ℳc ≲ 0.01 ℳ⊙).
for companions around M dwarfs and higher mass stars, respectively. A Kolmogorov-Smirnov (K-S) test indicates that the two distributions of substellar companion masses around M dwarfs and higher mass stars in the centre and bottom panels of Fig. 49 have a p-value of ∼1 × 10−6, allowing us to reject the hypothesis that they are drawn from the same distributions. Secondly, the occurrence of detected companions around higher mass dwarfs appears roughly flat in the approximate range 0.04 ≲ ℳc ≲ 0.06 ℳ⊙. For M dwarf primaries, the distribution continues to show a declining trend towards the low-mass end (corresponding to super-Jupiter-mass objects with ℳc ≲ 0.01 ℳ⊙).
The above differences could in principle be mostly due to the not-yet-well-characterised sensitivity to substellar companions in different mass and orbital separation regimes of Gaia DR3 astrometry. However, a few considerations help to reinforce the idea that we are seeing, at least in part, intrinsic features in the distributions rather than effects due to the selection function. Most notably, (1) the flat shape of the distribution in the bottom panel of Fig. 49 is consistent with that of the substellar companion distribution derived from RV surveys (e.g. Kiefer et al. 2019), and (2) the declining trend in the distribution towards the lowest-mass end in the central panel of Fig. 49 is consistent with the well-established notion of a much lower frequency of giant planets around M dwarfs with respect to solar-type primaries (e.g. Endl et al. 2006; Cumming et al. 2008; Bonfils et al. 2013; Pinamonti et al. 2022). With Gaia DR3, we therefore achieve the first-ever characterisation of a conspicuous population of substellar companions with true mass estimates within typically 1−2 au of nearby M dwarfs.
8.3. Substellar companion frequency in the 100 pc sample
As low-mass stars provide the primary sample around which substellar companions have been detected with Gaia DR3 astrometry, we can attempt to derive a first-order estimate of their occurrence rate. Clearly, a detailed assessment of the Gaia sensitivity in terms of completeness (estimation of the number of missed companions) and reliability (estimate of the number of false detections) is warranted, but goes beyond the scope of this work, and will be presented elsewhere (Giacobbe et al., in prep.).
Gaia Collaboration (2021b) show that Gaia DR3 is complete down to the M7 spectral sub-type within 100 pc from the Sun, with an M dwarf sample amounting to 218 366 sources. The NSS sample encompasses 790 astrometrically detected companions with likely substellar masses around M dwarfs within 100 pc. Of these, the vast majority (∼94%) are BDs. Under the optimistic assumptions that (i) Gaia has homogeneous sensitivity to and is 100% complete for BD companions across the M dwarf 100-pc sample, (ii) none of the orbital solutions corresponding to BD companions around this sample are spurious, and (iii) the companion does not contribute light, we propose an initial value for the frequency of BDs around M dwarfs with P ≲ 1000 days of ∼0.3%.
Dieterich et al. (2012) report a BD companion frequency around M dwarfs of 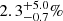 for separation in the range 10−70 au. Bowler et al. (2015) find that such companions in the 10−100 au orbital radius range have an occurrence rate of
for separation in the range 10−70 au. Bowler et al. (2015) find that such companions in the 10−100 au orbital radius range have an occurrence rate of 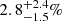 around M dwarfs in young moving groups. Susemiehl & Meyer (2022) find a similar frequency (
around M dwarfs in young moving groups. Susemiehl & Meyer (2022) find a similar frequency (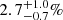 ) for field M dwarfs in the same separation interval. Winters et al. (2019) report a formally lower value of 1.3 ± 0.3% for the frequency for BDs around M dwarfs within 25 pc in the separation range out to ∼300″, but this is still compatible within the uncertainties.
) for field M dwarfs in the same separation interval. Winters et al. (2019) report a formally lower value of 1.3 ± 0.3% for the frequency for BDs around M dwarfs within 25 pc in the separation range out to ∼300″, but this is still compatible within the uncertainties.
Our occurrence rate estimate is likely an underestimate (pending detailed assessment of the numbers of missed companions versus those of spurious solutions and incorrectly classified objects), but nevertheless it is a clear example of the fact that Gaia DR3 provides critical constraints on the M dwarf binary fraction at close separations and very low mass ratios. Even with corrections for completeness and reliability still to be accounted for, the Gaia M dwarf sample in the solar neighbourhood with sensitivity to substellar companions within a few astronomical units is orders of magnitude larger than those of all other spectroscopic surveys combined.
8.4. Astrometric masses: trends with stellar metallicity
The number of new Gaia detections of substellar companions in the EP regime is still too small to provide an independent assessment of well-known trends of EP frequency with stellar properties, such as the strong dependence of giant planet occurrence with metallicity (e.g. Fischer & Valenti 2005; Sozzetti et al. 2009; Santos et al. 2011; Mortier et al. 2012; Adibekyan 2019, and references therein). The population of likely BD companions is instead conspicuous, and can be used to verify the outcome of recent statistical investigations.
As an example, Ma & Ge (2014) showed that, using the iron abundance relative to the Sun [Fe/H] as a proxy, the metallicity distribution of BD solar-type hosts has a median and standard deviation [Fe/H] = −0.04 ± 0.28. Using the most recent compilation of BD companions (based on Wilson et al. 2016; Kiefer et al. 2019; Dalal et al. 2021), the corresponding values are [Fe/H] = +0.01 ± 0.25. The stellar sample is therefore not particularly metal rich, as is the case of giant-planet hosts (median [Fe/H] ∼ +0.12, e.g. Adibekyan 2019), but is also not as metal deficient as the typical field stars in the solar neighbourhood, depending on stellar sample, with median [Fe/H] in the range [−0.10, −0.15] (see e.g. Nordström et al. 2004; Raghavan et al. 2010; Sousa et al. 2011; Adibekyan 2019).
Gaia Collaboration (2023a) outline recipes for selection of sources with global metallicity ([M/H]) of good and intermediate quality determined based on Gaia data. A total of 17 129 sources with an astrometric orbital solution were selected to have intermediate-quality [M/H] from the archive. Unsurprisingly, the overwhelming majority of [M/H] determinations is for the brighter solar-type stars, and therefore the typical M-dwarf primary with a substellar companion does not have a metallicity determination. However, we find [M/H] = −0.02 ± 0.29 for a sample of 143 F-G-K-type BD hosts. For reference, applying a more strict recipe for good-quality [M/H] returns a sample of 74 sources with [M/H] = +0.01 ± 0.27. Both estimates are in excellent agreement, and indeed indistinguishable, with literature results. If no quality constraints are used, 327 sources with a substellar companion and a Gaia-derived metallicity have [M/H] = −0.25 ± 0.49, which is indicative of the need to restrict ourselves to the regime of primaries with better-calibrated metallicities.
8.5. Known substellar objects: statistics and notable examples
The comparison between Gaia orbital solutions and companion mass estimates for known substellar companions and literature results, despite the small sample sizes, is interesting for a number of reasons.
First of all, a quick look at Table 11 allows us to underline how the angular orbit size for known BDs is always ≳0.5 mas, while the opposite, with a few exceptions, holds for the known EPs, HD 132406 b being the record holder with the smallest measured angular semi-major axis: a1 = 136 ± 40 μas. Overall, for both EPs and BDs there is a tendency to underestimate orbital periods longer than the time-span of Gaia observations. Not unexpectedly, orbital eccentricities are typically more loosely constrained by Gaia astrometry than by Doppler spectroscopy, and very high-eccentricity orbits (e ≳ 0.8) are typically underestimated. The loss of accuracy in the long-period and high-eccentricity regimes are known effects, already quantified via detailed simulations by Casertano et al. (2008), and further discussed in by Holl et al. (2023b), for example.
Inspection of Table 11 also shows that there is no simple mapping of ℳc sin i from literature into ℳc given the derived i value. For some objects (e.g. HD 132406 b, HD 81040 b, and HD 52756 b), the minimum mass estimate translates into a larger true mass, in agreement with the determined value of inclination, but in other cases (e.g. HD 164604 b, HR 810 b, and HD 142 b), ℳc is estimated to be much larger than if it were inferred from ℳc sin i together with the sin i value, or even lower (e.g. HD 30246 b and HD 82460 b) than ℳc sin i. When the parameter uncertainties are taken into account, the discrepancies are typically not very statistically significant, but the effect will nevertheless require elucidation. As both minimum and true mass estimates depend on the assumptions made for the mass of the primary, part of the reason for the discrepancy might be due to the heterogeneity of methods used to derive the latter. However, the more fundamental explanation is likely to be found in the overall limitations of Gaia DR3 detection sensitivity, including the selection effects and biases introduced by astrometric NSS processing, as discussed in Sect. 4.1 and Appendix C, particularly in the limit of relatively low astrometric S/Ns and suboptimal redundancy in the number of visibility periods with respect to the number of model parameters19.
Among the companions with a derived mass in the planetary regime, the case of GJ 876 b stands out. The planet constitutes one of the earliest radial-velocity discoveries in the field, first announced by Marcy et al. (1998) as a gas giant with ℳc sin i ∼ 2 ℳJup orbiting a mid-M dwarf in the backyard of the Sun (d = 4.67 pc). Benedict et al. (2002), using HST/FGS data, published the astrometric orbit of GJ 876 b (constrained by the RV solution), determining an orbit size of 0.25 ± 0.06 mas, an inclination of 84°, and a true mass very close to the minimum mass limit. The GJ 876 planetary system was subsequently found to host four planets: the hot super Earth GJ 876 d with period of ∼2 d, the two Jupiter-type planets GJ 876 c,b with periods of ∼30 and ∼61 d, respectively, and the Neptune-mass companion GJ 876 e with a period of ∼125 d. The three outermost companions are dynamically interacting, locked in a 1:2:4 Laplace mean-motion resonance, which has been the subject of many studies (e.g. Rivera et al. 2005, 2010; Correia et al. 2010; Nelson et al. 2016; Trifonov et al. 2018). The more recent investigations, based on dynamical considerations, infer a close-to-coplanar configuration for the three interacting planets, and a likely inclination of GJ 876 b ∼50 − 60°. This implies a true mass of ℳc ∼ 2.3 − 2.7 ℳJup. The amplitude of the astrometric perturbation determined with Gaia, 0.43 ± 0.05 mas, is larger than that measured by HST/FGS, and discrepant at the 2.3σ level. The inferred mass, 3.6 ℳJup, is correspondingly larger, and also in this case the derived inclination i = 101° does not allow for a simple mapping from the ℳc sin i value.
A number of known companions, which in the literature have minimum mass estimates in the planetary regime, appear in Table 3 with much higher true mass estimates from Gaia. These appear in the Gaia DR3 archive as validated orbital solutions of type OrbitalTargetedSearchValidated. A few cases of particular interest are discussed below.
HD 114762 (Gaia DR3 3937211745905473024): The first substellar companion candidate around a solar-type star with minimum mass ℳc sin i = 0.011 ± 0.001 ℳ⊙ was inferred from radial velocity variations by Latham et al. (1989). Gaia DR1 noise modelling resulted in a considerably higher companion mass estimate of 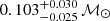 (Kiefer 2019). The Gaia DR3 orbital solution has a period of 83.73 ± 0.12 d in agreement with the radial-velocity orbit and an orbit size of a0 = 1.80 ± 0.07 mas. Using the primary mass estimate from Table 3 and standard linear propagation of the uncertainties, the inferred companion mass is ℳc = 0.21 ± 0.01 ℳ⊙. Gaia DR3 therefore establishes that the companion is a low-mass M dwarf and not a substellar object.
(Kiefer 2019). The Gaia DR3 orbital solution has a period of 83.73 ± 0.12 d in agreement with the radial-velocity orbit and an orbit size of a0 = 1.80 ± 0.07 mas. Using the primary mass estimate from Table 3 and standard linear propagation of the uncertainties, the inferred companion mass is ℳc = 0.21 ± 0.01 ℳ⊙. Gaia DR3 therefore establishes that the companion is a low-mass M dwarf and not a substellar object.
HD 164604 (Gaia DR3 4062446910648807168): Arriagada et al. (2010) announced a low-confidence detection of a ℳc sin i ∼ 2.7 ℳJup companion on a 606 ± 9 d orbit, whose parameters were then refined by Feng et al. (2019) who reported ℳc sin i = 1.99 ± 0.26 ℳJup and P = 641 ± 9 d. The Gaia DR3 orbital solution has P = 615 ± 12 d (in agreement at the 1.7σ and 0.6σ level with Feng et al. 2019 and Arriagada et al. 2010, respectively) and a0 = 0.56 ± 0.22 mas. The inferred companion mass is ℳc = 14.3 ± 5.5 ℳJup.
HD 162020 (Gaia DR3 5957920668132624256): Udry et al. (2002) published the discovery of slightly eccentric (e = 0.28) ℳc sin i ∼ 14 ℳJup companion with P = 8.428 d, whose minimum mass was recently updated to 9.8 ± 2.7 ℳJup by Stassun et al. (2017). The Gaia DR3 orbital solution has P = 8.429 ± 0.001 d, e = 0.23 ± 0.05, and a0 = 0.91 ± 0.03 mas. The detected companion is a low-mass star with ℳc = 0.39 ± 0.02 ℳ⊙.
KIC 7917485 (Gaia DR3 2075978592919858432): Murphy et al. 2016 published the detection of a 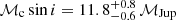 companion on a
companion on a 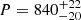 d orbit around the Delta Scuti, A-type star Kepler-1648, based on a pulsation timing variation technique. The Gaia DR3 orbital solution has P = 810 ± 28 d and a0 = 0.42 ± 0.02 mas. At a distance of 1.38 kpc, the companion turns out to be an M dwarf with ℳc = 0.55 ± 0.03 ℳ⊙.
d orbit around the Delta Scuti, A-type star Kepler-1648, based on a pulsation timing variation technique. The Gaia DR3 orbital solution has P = 810 ± 28 d and a0 = 0.42 ± 0.02 mas. At a distance of 1.38 kpc, the companion turns out to be an M dwarf with ℳc = 0.55 ± 0.03 ℳ⊙.
8.6. Validated orbital solutions that can imply new exoplanet discoveries
Two sources have validated astrometric orbital solutions (see Holl et al. 2023b, for details) that imply the presence of previously unpublished planetary-mass companions if a ‘binary scenario’ can be excluded. In such a scenario, the small apparent orbit size would be caused by a binary star with components of similar mass and brightness ratios. These two sources are discussed below.
HIP 66074 (Gaia DR3 1712614124767394816): The Gaia DR3 orbital solution has P = 297 ± 2.8 d, e = 0.46 ± 0.17, a0 = 0.21 ± 0.03 mas. Given the primary mass estimate corresponding to an M0 dwarf, the inferred companion mass in the exoplanet scenario is ℳc = 7.3 ± 1.1 ℳJup.
HIP 28193 (Gaia DR3 2884087104955208064): the orbital period, semi-major axis, and eccentricity of this new exoplanet are 827 ± 50 d, e = 0.07 ± 0.10, and a0 = 0.25 ± 0.02 mas, respectively. Using the K-dwarf primary mass from Table 3, the inferred companion in the exoplanet scenario is a super-Jupiter with a mass of 5.3 ± 0.6 ℳJup.
We note that, had we used Monte Carlo resampling, the semi-major axis distribution would have been asymmetric with larger uncertainties, and this would have been the case for the companion-mass distribution as well. This is an example of a solution with a poorly constrained eccentricity (e = 0.07 ± 0.10) for which the uncertainties in the Thiele-Innes coefficients are likely overestimated and Monte Carlo resampling is not advisable (cf. Babusiaux et al. 2023; Holl et al. 2023b).
A third source (Gaia DR3 1035000055055287680, HIP 40497) that initially also fell into this category has been identified as SB2 in the literature (Busà et al. 2007); see also the discussion in Holl et al. (2023b). This illustrates that the risk of confusing the binary and exoplanet scenarios is real when only considering the Gaia astrometric orbit.
For HIP 66074 and HIP 28193 on the other hand, we can make use of auxiliary radial-velocity information. To evaluate the binary scenario where the companion is a MS star, we used the mass–luminosity relationships of Henry & McCarthy (1993) to estimate that the two components must have masses that agree within a few percent to be compatible with both the orbital parameters and the photocentre orbit size. Consequently, the RV semi-amplitudes of the primary components of HIP 66074 and HIP 28193 would be K1 ∼ 20 km s−1 and K1 ∼ 9 km s−1, respectively, clearly incompatible with the high-precision RVs used for validating the orbital solution that have dispersions that are three orders of magnitude smaller (Butler et al. 2017; Holl et al. 2023b). Similarly, the Gaia DR3 radial_velocity_error computed from the dispersion of individual Gaia RV measurements is 0.15 km s−1 and 0.16 km s−1, respectively, which lies in the first percentile for sources with G < 12, and therefore also appears incompatible with the binary scenario. The blending of the SB2 spectra could possibly lead to such suppressed RV variability. In the case of HIP 28193, the small uncertainties in the ground-based RVs coupled with the estimated FWHM of the underlying cross-correlation functions of ≲9 km s−1 speak against this possibility20. In terms of absolute magnitudes of these systems, the difference between the exoplanet and binary scenario amounts to ∼0.8 mag, which, because of the width of the observed HRD, can also not be used to definitely rule out the binary scenario.
In the HIPPARCOS-Gaia catalogues of accelerations produced by Brandt (2021) and Kervella et al. (2022), no statistically significant PMa is reported for HIP 66074 (S/N ∼ 1), while a moderately high PMa (S/N ∼ 10) at the Gaia mean epoch is found for HIP 28193. For the relatively short-period orbit of the companion around HIP 66074, the inferred companion mass is approximately in line with a S/N ∼ 1 in the proper motion difference. In the case of the longer-period orbit of the companion around HIP 28193, the PMa value might point to a companion with a larger mass than the one inferred nominally. An alternative possibility would be that the Gaia orbit has significantly underestimated the true period.
In summary, the most likely scenario for both HIP 66074 and HIP 28193 is the presence of a newly discovered giant exoplanet. A more detailed analysis and probably more auxiliary data are needed to definitely rule out the binary scenario. When that is achieved, these are to be considered as the first Gaia astrometric planet detections and the first examples of confirmed exoplanet discoveries with the astrometry technique.
8.7. Candidates with substellar masses: statistics and notable examples
Among the substellar mass candidates with solution type OrbitalTargetedSearch, two are worth particular mention.
HD 12800 (Gaia DR3 522135261462534528): the Gaia DR3 orbital solution for this bright source (54 Cas) has P = 401 ± 12 d, a0 = 0.25 ± 0.05 mas, and ℳc = 5.6 ± 1.4 ℳJup. This is the only candidate companion around a MS solar-type star with a mass well within the planetary regime.
HD 3221 (Gaia DR3 4901802507993393664): the Gaia DR3 orbital solution for this bright solar-type star has P = 476 ± 5 d, a0 = 0.36 ± 0.01 mas, and ℳc = 14.2 ± 0.6 ℳJup. The primary is a fast-rotating (v sin i ∼ 70 km s−1), very young star with an estimated age of ∼10 − 30 Myr in the Tucana/Horologium association. The candidate companion, at the planet–brown dwarf mass boundary according to a classical definition (Burrows et al. 2001), if confirmed, would be the first of this type in an orbital separation regime virtually inaccessible to Doppler and direct imaging surveys.
As mentioned above, the population of substellar mass candidates with solution type OrbitalTargetedSearch* is typically found around solar-type primaries. It is interesting to note how the eccentricity distributions for EPs and BDs in this sample are marginally different based on a K-S test (p-value of 0.04), with the more massive BDs (ℳc ≳ 50 ℳJup) having a median of e ∼ 0.5, while EPs and lower-mass BDs (ℳc ≲ 40 ℳJup) have typically e ∼ 0.3. This is in agreement with Ma & Ge (2014), and with the notion that the former might correspond to the low-mass tail of objects formed in the same manner as stars while the latter sample would map the high-mass tail of objects formed in the same manner as planets.
The population of substellar mass candidates with solution type Orbital is instead predominantly found around low-mass M primaries. In this case, the eccentricity distributions of candidate EPs and BDs detected around this sample are indistinguishable, with typically e ∼ 0.4 in both cases. This might indicate that most of the detected companions might have formed in the same way, and that some of them are actually of intrinsically larger mass compared to the lower mass bounds adopted in this work as discussed in Sect. 8.1.
8.8. White dwarfs with a substellar companion candidate
The nss_two_body_orbit table contains 38 orbital solutions for sources on the WD sequence, and all of them correspond to astrometric orbits. Assuming a fixed mass of 0.6 M⊙ for the WD host and that the companion is dark, there are four sources with substellar companion candidates, namely Gaia DR3 2813020961166816512 (LP 522–46) with ℳc ∼ 34 ℳJup, Gaia DR3 2098419251579450880 with ℳc ∼ 34 ℳJup, Gaia DR3 6471102606408911360 (L 279–25) with ℳc ∼ 22 ℳJup, and Gaia DR3 4698424845771339520 (WD 0141–675), with this last one standing out as being part of the 10 pc sample and with a companion candidate in the planetary-mass range.
In Fig. 39 these four sources are marked with red symbols. Two sources (LP 522–46 and L 279–25) are located above the hydrogen sequence, which suggests that the companion could itself be degenerate and luminous enough to cause an excess in luminosity and at the same time dilute the astrometric orbit signal. The companions of these sources are therefore unlikely to be either dark or substellar. On the other hand, Gaia DR3 2098419251579450880 and WD 0141–675 lie within the hydrogen sequence and therefore Fig. 39 appears consistent with the interpretation that these sources have substellar companions.
WD 0141–675 in particular was included in the OrbitalTargetedSearch sample (Holl et al. 2023b) because it is nearby and metal-polluted (Debes & Kilic 2010), and therefore represents a promising target to search for the presence of an orbiting giant planet that could act as the much sought-after perturber of the circumstellar material (Debes et al. 2012). The Gaia DR3 orbital solution has a period of 33.65 ± 0.05 d and with a WD mass of 0.57 ± 0.03 M⊙ (Subasavage et al. 2017), the estimated planet mass is 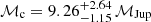 , where we accounted for all parameter covariances using Monte Carlo resampling. The resulting ℳc distribution is asymmetric with its mode at ∼8.3 ℳJup.
, where we accounted for all parameter covariances using Monte Carlo resampling. The resulting ℳc distribution is asymmetric with its mode at ∼8.3 ℳJup.
With only a handful of known giant planets orbiting white dwarfs (Veras 2021; Blackman et al. 2021), the Gaia discovery of a super-Jupiter candidate planet orbiting WD 0141–675 is remarkable. If the Gaia DR3 orbit is confirmed and other possible scenarios can be excluded – such as some kind of WD binary system with nearly equal-brightness components (WD 0141–675 is marked with an orange square in Fig. 39) –, this would represent the discovery of the most nearby planet-hosting WD and the first giant planet around a metal-enriched WD, which would make it an important test for our understanding of the fate of stars and their planetary systems.
 |
Fig. 50. Top: primary mass distribution for sources with SB1 solution type and inferred minimum companion masses in the substellar regime. Bottom: substellar companion mass distribution for the SB1 solution type. |
8.9. Radial velocity: Substellar companions
Out of 6 × 104 minimum mass estimates for SB1 solutions (see Table 3), about 10% (5723) have ℳc sin i < 0.08 ℳ⊙, and about 10% of these (437) have ℳc sin i < 0.02 ℳ⊙. Not unexpectedly, the mass distribution for the primaries (see Fig. 50, top panel) has a median of ∼1.0 ℳ⊙, similar to that of the primary mass distribution of OrbitalTargetedSearch* sources rather, but with a significantly larger contribution from bright, earlier type stars. The distribution of ℳc sin i shown in the lower panel of Fig. 50 contains an expected feature, namely a decline in numbers of companions at the low-mass end due to the intrinsic lack of sensitivity of Gaia RVS to RV amplitudes of signals typically induced by planetary-mass companions (significantly < 1 km s−1). On the other hand, the number of higher mass substellar companions appears constant all the way into the low-mass star regime, and independently of primary mass. This is unexpected, as an intrinsically lower frequency of intermediate-mass BDs is observed in RV surveys (Ma & Ge 2014), particularly in the short-period regime to which Gaia RVs are sensitive. The eccentricity distributions of SB1 companions with mass estimates in the EP and BD regimes appear entirely indistinguishable, independently of primary mass, and this is also not in agreement with the Ma & Ge (2014) analysis.
For more than 80% of the SB1 sample of close-in companions with ℳc sin i < 0.08 ℳ⊙, the orbital solutions have P < 10 days, and this fraction grows to > 90% for companions with ℳc sin i < 0.02 ℳ⊙. Such companions, which are detected with K1-values with significance of below 10, typically correspond to primaries with ruwe > 1.4, but they are not expected to be those responsible for high ruwe values, as the typical sizes of the induced astrometric perturbations would escape detection by Gaia (e.g. Belokurov et al. 2020). As discussed in Sect. 2.3, a sizeable fraction of these short-period orbits are rather a kind of alias of longer period orbits. For example, the companions reported around HIP 24329, HD 35956, and HD 8691 have ℳc sin i ∼ 3 ℳJup, ∼11 ℳJup, and ∼14 ℳJup, respectively, and P = 0.63 d, 3.02, and 3.77 d, respectively. However, these sources also have Orbital solutions with P = 1499 d, 1203 d, and 581 d. The latter P values very closely match the published periods of the spectroscopic orbits for the three stars reported by Wilson et al. (2016), Katoh et al. (2013), and Sperauskas et al. (2019), respectively.
The sample of short-period SB1 orbits with minimum masses corresponding to substellar companions should therefore be considered with caution, although not all solutions can be incorrect or spurious. For example, a cross-check with the NASA Exoplanet Archive shows that the spectroscopic orbit of WASP-18b (Gaia DR3 4955371367334610048), a transiting super-Jupiter with ℳc ∼ 10 ℳJup and P = 0.94 d discovered by Hellier et al. (2009) around the Hyades-age F6 dwarf HD 10069, is recovered as an SB1 with the correct period and RV semi-amplitude (K1 ∼ 1.8 km s−1). This source has also been detected in the Gaia photometry (Eyer et al. 2023) and is present in the vari_planetary_transit table.
The list of most exoplanet candidates detected by Gaia using either astrometry, transit, or radial velocities is published online21.
9. Multiple stars
Although the NSS pipeline in Gaia DR3 produces solutions of binary stars, the results can also be used to uncover higher multiplicity stars. Triple (and higher multiplicity) stars are of particular interest. The study of the architecture and dynamics of hierarchical stellar systems provides precious information on the mechanisms at work during star formation. For example, the fact that the orbits of a hierarchical system are coplanar would indicate that the stars are formed in a viscous accretion disc, while their mass ratios shed light on the disc fragmentation mechanism (see e.g. Tokovinin 2017).
 |
Fig. 51. Distribution of outer vs. inner periods for triple systems found by matching Orbital with SB1 (circles), SB2 (squares), and SB2C solutions (triangles), coloured by the ratio of spectroscopic to astrometric semi-amplitudes. The solid line shows the limit POrbital = 5 PSB. Top panel: integrated distribution of inner periods. |
9.1. Multiplicity from spectroscopic and astrometric solutions
A first way to find multiple stars is to look at the sources for which the pipeline produced an astrometric Orbital solution and an SB1/SB2 solution, which were not combined. Given that the astrometry is sensitive to long periods and larger orbits while the spectroscopy is sensitive to shorter periods, in the case of a triple star the astrometry would detect the outer period while the spectroscopy would unveil the inner period.
However, many of the sources for which the Orbital and SB1/SB1C solution was found but not combined by the pipeline are not triple stars. In many cases, they have similar periods but were not combined because of the inconsistency of the other orbital parameters. There are also many cases where the SB solution is actually some kind of alias of the astrometric period; these cases can be spotted noting that the semi-amplitude K0 of the astrometric motion (defined by Eq. (B.10), substituting a0/ϖ for a1) is similar to the semi-amplitude K1 of the radial velocity curve. These confusing cases typically have a significance of lower than 10. We then identify genuine triple stars by selecting those for which the significance of both the astrometric and the spectroscopic solution is larger than 10, K1 > 3 ⋅ K0 and POrbital > 5 ⋅ PSB. With this selection, we obtain 81 triple systems from matching Orbital with SB1 solutions, 55 from matching with SB2, 16 from matching with SB2C, and none from matching with SB1C. The distribution of the outer versus inner periods of these sources is reported in Fig. 51.
One can also find multiple stars by looking at the sources for which the pipeline produced an astrometric acceleration solution and an SB1/SB2 solution. In this case, the astrometric acceleration would detect outer periods which are similar to or longer than the length of Gaia observations (∼1000 days), while the SB solutions detect the inner periods.
In order to avoid the situation whereby the astrometric acceleration and the SB solutions are in reality of the same orbit, we selected only SB solutions with a period of < 300 days. We also restrain our search to SB solutions with significance > 20 to avoid pollution from some kind of aliasing.
The distribution of inner periods for triple systems found by matching astrometric acceleration and SB solutions is shown in Fig. 52. We can note that the mode of the distribution is at around 3 days.
 |
Fig. 52. Distribution of inner periods for triple systems found by comparing astrometric acceleration and SB solutions. |
9.2. Multiplicity in wide visual binaries
Another method to discover triple or higher multiplicity stars consists in using catalogues of wide visual binaries and checking whether or not one of the two components is detected as a binary. We started from the El-Badry et al. (2021) catalogue, and selected sources with ℛ < 0.01 (0.08% contamination from chance-alignment), cross-matched with nss_two_body_orbit solutions and spectroscopic trends, and we found 10 063 systems for which one of the two components is a non-single star and 52 systems where both components are non-single stars. For 10 of the first group, the non-single component is actually a triple star (Orbital+SB1/SB2, selected as in Sect. 9.1), making these quadruple systems.
 |
Fig. 53. Distribution of outer vs. inner periods for triple systems found in the El-Badry catalogue. Left scale: period. Right scale: separation. The line in the bottom right corner shows the limit Pout = 5 Pin. |
 |
Fig. 54. Distribution of inner periods for triple systems found in the El-Badry catalogue. |
Figure 53 shows the distribution of the outer versus inner periods for the triple systems found in the El-Badry catalogue, where the outer period Pout is computed from the separation s (provided in the El-Badry catalogue) as 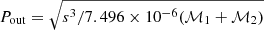 and assuming ℳ1 + ℳ2 = 1.5 ℳ⊙, while the inner period Pin is the period in the NSS solution.
and assuming ℳ1 + ℳ2 = 1.5 ℳ⊙, while the inner period Pin is the period in the NSS solution.
The drop in the distribution for separations below 200 au is certainly due to selection effects introduced by the blending of the two components in a large range of scanning angles. The cut at longer inner periods is dictated by the limited baseline of Gaia observations. The shortening of the maximum inner period with the increase in separation is due to the fact that sources at large separations are also at larger distances, where the astrometric signal of the internal orbit drops.
We note from Fig. 53 that the distribution of the inner period is multimodal. As shown in Fig. 54, this is in part due to the different methods of orbital detection (highlighted with different colours). However, if we compare the distribution of spectroscopic solutions in this sample with respect to the whole NSS solutions (Fig. 2), we can see that the overabundance of solutions with 2 days < Pin < 30 days is real. This overabundance is also visible in the Multiple Star catalogue by Tokovinin (2018); see their Fig. 7. Tokovinin (2004) attributed the overdensity he observed at Pin < 7 days to dynamical interaction between the orbits and consequent tidal interaction within the inner couple, as suggested by Kiseleva et al. (1998). This short analysis shows that the study of multiple systems will greatly benefit from the results of the NSS catalogue.
10. Conclusions
On 24 April 1610, Galileo brought his telescope to demonstrate its performances to his opponents and other scholars in Bologna. Martin Horký, a student of Kepler noted: “I tested the instrument of Galileo’s in a thousands ways”, ... , “below it works wonderfully; in the heavens, it deceives one as some fixed stars are seen double” (Feyerabend 1970). This is how the discovery of some of the first telescopic double stars failed and how easy it is to consider that facts can be contradicted by prejudice.
Over four centuries later, the validations and the results obtained so far suggest that NSS entries in Gaia DR3 are binaries and not Gaia telescope artefacts. Nevertheless, in fairness, this catalogue is expected to contain some spurious solutions. We therefore need to start this conclusion by stressing that the counterpart of such a large catalogue is some unavoidable contamination, which should be kept in mind when analysing the results.
In particular, the selection of distribution tails (e.g. small periods and small or large mass functions) is likely to preferentially select incorrect solutions, as we experienced in the course of this verification paper. The abundant partially resolved sources and their impact on the astrometry and epoch radial velocities conspire with the scanning law periodic motions to produce solutions that look like bona fide unresolved binaries. To cope with this, increasing the threshold on the significance of the solutions appears satisfactory but may well represent a Pyrrhic victory, as this decreases the sample sizes drastically.
The NSS catalogue is already the result of a drastic selection of sources. The impact of the total selection effects – due successively to the input list, the data processing, and the posterior source filtering – need to be taken into account, and statistical studies of the NSS sample will require dedicated efforts. This has not been attempted here, although the main points have probably been mentioned. There are subjects that are already known to represent pitfalls, such as the acceleration solutions, which should not be used for physical interpretations.
Although the main impact of the NSS catalogue originates from the simultaneous presence of the main kind of unresolved binaries, and consequently an impressive coverage of binary periods, the novelty is mainly brought by the exquisite astrometric precision, allowing the detection of many astrometric binaries. However, there is one strength and one weakness concerning astrometric orbits: if the astrometric and the photometric effects are not decoupled, the actual size of the orbit of the primary cannot be found. The decoupling here is difficult, but when it can be achieved, then both masses and luminosities of the components become available. We have tried to take this into account for the masses estimated here, but the combination with external data, as some examples show, will prove very useful if not sometimes mandatory.
The whole HRD can be studied with the abundant number of astrometric orbits, spectroscopic orbits, or both. Some analyses may be more interesting than others. Here, new ultracool dwarf binaries are found, and the small mass ratios can also be studied down to the substellar domain. True masses are found for substellar companions and two new super-Jupiter candidates may have been found. Twin degenerates and one WD hosting a super-Jupiter companion are also proposed. Concerning compact companions with larger masses, potential companions are present in the mass range of neutron stars or black holes, but these may also be Algol or triple systems: indeed, at this step, we stress that most findings here should be considered as tentative; although verifications have been done, further analyses are warranted. The eccentricity–period relation will also undoubtedly be under scrutiny although interesting substructures for giants are already shown here. The detection of ellipsoidal variables mistaken as long-period variables, or the detection of sources found in a rare evolutionary stage as in EL CVn, underlines the potential of acquiring both photometric and spectroscopic data. This is further testimony that Gaia is an impressively complete observatory in orbit.
Without any detailed content study or modelling, which will be tasks of the scientific exploitation to come, the multiple topics tackled in the sections above, while only a very preliminary and tentative exploration of the Gaia DR3 binaries, clearly demonstrate the great scientific potential of this catalogue. Paraphrasing Aaron Levenstein on the topic of statistics, what these analyses reveal is suggestive; what they conceal may be essential.
We coined the word ‘Gaiacenter’ in Kervella et al. (2022) by analogy with the ‘Hippacenter’ defining the actual pointing of the epoch HIPPARCOS observations of double stars (Martin et al. 1997).
This holds when neglecting complications with e.g. periods of around 1 yr due to crosstalk with parallax- or scan-angle-dependent effects (Holl et al. 2023a).
These Campbell elements were computed from the Thiele-Innes coefficients (A, B, F, G) – which are part of the archive table – using standard formulae (e.g. Halbwachs et al. 2023); software tools are available at https://www.cosmos.esa.int/web/gaia/dr3-software-tools
MK, RGB − tip = −6.49 as derived from Lebzelter et al. (2019) who find KRGB − tip = 12 for the LMC and considering its distance modulus 18.49 ± 0.09 mag (de Grijs et al. 2017).
The astrometric orbit figure was obtained on the basis of the pystrometry package (https://github.com/Johannes-Sahlmann/pystrometry, Sahlmann 2019). Other examples and a description are given in Holl et al. (2023b).
The sources Gaia DR3 2219809419798508544 and Gaia DR3 4514813786980451840 are also classified as eclipsing, but the light curve is clearly ellipsoidal. See Mowlavi et al. (2023) for more details about this type of misclassification.
The typical number of visibility periods is only twice the number of fitted parameters in an orbital model (see Appendix C, and also Holl et al. 2023b).
This two-dimensional case was formally derived with a random rotation of the frame per observation, which does not correspond to fixed-axis orientation CCD observation. In our toy model, the scan-angle integral takes care of considering the random (Ω-)orientation of the orbit since we assumed the rotation axis is aligned with α⋆. Alternatively the sky rotation angle reminiscent of Ω could be introduced and integrated over to achieve this averaging, and then there is no need to integrate over scan angle for a fixed orientation telescope. As long as ψ and/or Ω are assumed to be randomly oriented without range restriction, the simpler model used here is accurate.
There are three flavours: (1) the ‘binary pipeline’ (Halbwachs et al. 2023) (2) the Genetic Algorithm channel of the ‘exoplanet pipeline’ (Holl et al. 2023b) (3) the Markov Chain Monte Carlo channel of the ‘exoplanet pipeline’.
Acknowledgments
This work is dedicated to the memory of our late colleague Dimitri Pourbaix who suggested the title of this article. He had been for many years leader of the Gaia CU4 Coordination Unit and passed away before seeing the Gaia DR3 NSS outcome. This catalogue will remain in a large part the testimony of his involvement. We would like to thank the referee Andrei Tokovinin, and the DPAC reporter, Lennart Lindegren, for their useful suggestions. This work presents results from the European Space Agency (ESA) space mission Gaia. Gaia data are being processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC is provided by national institutions, in particular the institutions participating in the Gaia MultiLateral Agreement (MLA). The Gaia mission website is https://www.cosmos.esa.int/gaia. The Gaia archive website is https://archives.esac.esa.int/gaia. Further acknowledgements are given in Appendix A. This publication has also made use of observations collected with the SOPHIE spectrograph on the 1.93-m telescope at Observatoire de Haute-Provence (CNRS), France (program 21B.PNPS.AREN) using support by the French Programme National de Physique Stellaire (PNPS). We thank all the staff of Haute-Provence Observatory for their support at the 1.93 m telescope and on SOPHIE. Observations have also been obtained with the Mercator Telescope and the HERMES spectrograph, which is supported by the Research Foundation – Flanders (FWO), Belgium, the Research Council of KULeuven, Belgium, the Fonds National de la Recherche Scientifique (F.R.S.-FNRS), Belgium, the Royal Observatory of Belgium, the Observatoire de Genève, Switzerland and the Thüringer Landessternwarte Tautenburg, Germany. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. [951549]). Ts.M. research was supported by Grant No. 2016069 of the United States-Israel Binational Science Foundation (BSF) and by Grant No. I-1498-303.7/2019 of the German-Israeli Foundation for Scientific Research and Development (GIF). The full acknowledgements are available in Appendix A.
References
- Adibekyan, V. 2019, Geosciences, 9, 105 [Google Scholar]
- Ahn, C. P., Alexandroff, R., Allende Prieto, C., et al. 2012, ApJS, 203, 21 [Google Scholar]
- Albareti, F. D., Allende Prieto, C., Almeida, A., et al. 2017, ApJS, 233, 25 [Google Scholar]
- Alvarez, R., Jorissen, A., Plez, B., et al. 2001, A&A, 379, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anders, F., Khalatyan, A., Queiroz, A. B. A., et al. 2022, A&A, 658, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arenou, F., Halbwachs, J.-L., Mayor, M., Palasi, J., & Udry, S. 2000, IAU Symp., 200, 135 [Google Scholar]
- Arriagada, P., Butler, R. P., Minniti, D., et al. 2010, ApJ, 711, 1229 [CrossRef] [Google Scholar]
- Artigau, É., Gagné, J., Faherty, J., et al. 2015, ApJ, 806, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A., et al.) 2018, AJ, 156, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Avvakumova, E. A., Malkov, O. Y., & Kniazev, A. Y. 2013, Astron. Nachr., 334, 860 [Google Scholar]
- Babusiaux, C., Fabricius, C., Khanna, S., et al. 2023, A&A, 674, A32 (Gaia DR3 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bardalez Gagliuffi, D. C., Burgasser, A. J., Gelino, C. R., et al. 2014, ApJ, 794, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Barstow, M. A., Holberg, J. B., Fleming, T. A., et al. 1994, MNRAS, 270, 499 [NASA ADS] [Google Scholar]
- Barstow, M. A., Bond, H. E., Burleigh, M. R., & Holberg, J. B. 2001, MNRAS, 322, 891 [Google Scholar]
- Barstow, M. A., Bond, H. E., Holberg, J. B., et al. 2005, MNRAS, 362, 1134 [CrossRef] [Google Scholar]
- Belokurov, V., Penoyre, Z., Oh, S., et al. 2020, MNRAS, 496, 1922 [Google Scholar]
- Benedict, G. F., McArthur, B. E., Forveille, T., et al. 2002, ApJ, 581, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Bessel, F. W. 1844, MNRAS, 6, 136 [Google Scholar]
- Blackman, J. W., Beaulieu, J. P., Bennett, D. P., et al. 2021, Nature, 598, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, C. H., Charbonneau, D., White, R. J., et al. 2008, ApJ, 678, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, C. H., Charbonneau, D., & White, R. J. 2010, ApJ, 723, 684 [Google Scholar]
- Boch, T., & Fernique, P. 2014, ASP Conf. Ser., 485, 277 [Google Scholar]
- Bond, H. E., Schaefer, G. H., Gilliland, R. L., et al. 2017, ApJ, 840, 70 [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnarel, F., Fernique, P., Bienaymé, O., et al. 2000, A&AS, 143, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boubert, D., Strader, J., Aguado, D., et al. 2019, MNRAS, 486, 2618 [Google Scholar]
- Bouchy, F., Hébrard, G., Udry, S., et al. 2009, A&A, 505, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bowler, B. P., Liu, M. C., Shkolnik, E. L., & Tamura, M. 2015, ApJS, 216, 7 [Google Scholar]
- Brandt, T. D. 2021, ApJS, 254, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, T. D., Dupuy, T. J., Bowler, B. P., et al. 2020, AJ, 160, 196 [Google Scholar]
- Bransgrove, A., Levin, Y., & Beloborodov, A. 2018, MNRAS, 473, 2771 [CrossRef] [Google Scholar]
- Breddels, M. A., & Veljanoski, J. 2018, A&A, 618, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Breivik, K., Chatterjee, S., & Larson, S. L. 2017, ApJ, 850, L13 [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Breton, R. P., Rappaport, S. A., van Kerkwijk, M. H., & Carter, J. A. 2012, ApJ, 748, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Burgasser, A. J., & McElwain, M. W. 2006, AJ, 131, 1007 [Google Scholar]
- Burgasser, A. J., Reid, I. N., Siegler, N., et al. 2007, Protostars and Planets V (Tucson: University of Arizona Press), 427 [Google Scholar]
- Burrows, A., Hubbard, W. B., Lunine, J. I., & Liebert, J. 2001, Rev. Mod. Phys., 73, 719 [Google Scholar]
- Busà, I., Aznar Cuadrado, R., Terranegra, L., Andretta, V., & Gomez, M. T. 2007, A&A, 466, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butler, R. P., Wright, J. T., Marcy, G. W., et al. 2006, ApJ, 646, 505 [Google Scholar]
- Butler, R. P., Vogt, S. S., Laughlin, G., et al. 2017, AJ, 153, 208 [Google Scholar]
- Carter, J. A., Rappaport, S., & Fabrycky, D. 2011, ApJ, 728, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Casertano, S., Lattanzi, M. G., Sozzetti, A., et al. 2008, A&A, 482, 699 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G. 2001, ApJ, 554, 1274 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, ArXiv e-prints [arXiv:1612.05560] [Google Scholar]
- Corral-Santana, J. M., Casares, J., Muñoz-Darias, T., et al. 2016, A&A, 587, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Correia, A. C. M., Couetdic, J., Laskar, J., et al. 2010, A&A, 511, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Creevey, O. L., Sordo, R., Pailler, F., et al. 2023, A&A, 674, A26 (Gaia DR3 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cropper, M., Katz, D., Sartoretti, P., et al. 2018, A&A, 616, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cruzalèbes, P., Petrov, R. G., Robbe-Dubois, S., et al. 2019, MNRAS, 490, 3158 [Google Scholar]
- Cumming, A., Butler, R. P., Marcy, G. W., et al. 2008, PASP, 120, 531 [CrossRef] [Google Scholar]
- da Silva, R., Udry, S., Bouchy, F., et al. 2007, A&A, 473, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dahn, C. C., Harris, H. C., Levine, S. E., et al. 2008, ApJ, 686, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Dalal, S., Kiefer, F., Hébrard, G., et al. 2021, A&A, 651, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Angeli, F., Weiler, M., Montegriffo, P., et al. 2023, A&A, 674, A2 (Gaia DR3 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Grijs, R., Courbin, F., Martínez-Vázquez, C. E., et al. 2017, Space Sci. Rev., 212, 1743 [CrossRef] [Google Scholar]
- Debes, J. H., & Kilic, M. 2010, in American Institute of Physics Conference Series, eds. K. Werner, & T. Rauch, 1273, 488 [Google Scholar]
- Debes, J. H., Walsh, K. J., & Stark, C. 2012, ApJ, 747, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Decin, L., Montargès, M., Richards, A. M. S., et al. 2020, Science, 369, 1497 [Google Scholar]
- Dieterich, S. B., Henry, T. J., Golimowski, D. A., Krist, J. E., & Tanner, A. M. 2012, AJ, 144, 64 [Google Scholar]
- Dupuy, T. J., & Liu, M. C. 2011, ApJ, 733, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Dupuy, T. J., & Liu, M. C. 2017, ApJS, 231, 15 [Google Scholar]
- Dupuy, T. J., Liu, M. C., Best, W. M. J., et al. 2019, AJ, 158, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Eddington, A. S. 1913, MNRAS, 73, 359 [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [Google Scholar]
- El-Badry, K., & Rix, H.-W. 2018, MNRAS, 480, 4884 [Google Scholar]
- El-Badry, K., Rix, H.-W., & Heintz, T. M. 2021, MNRAS, 506, 2269 [NASA ADS] [CrossRef] [Google Scholar]
- El-Badry, K., Seeburger, R., Jayasinghe, T., et al. 2022, MNRAS, 512, 5620 [NASA ADS] [CrossRef] [Google Scholar]
- Endl, M., Cochran, W. D., Kürster, M., et al. 2006, ApJ, 649, 436 [Google Scholar]
- ESA 1997, in The HIPPARCOS and Tycho Catalogues. Astrometric and Photometric Star Catalogues Derived from the ESA HIPPARCOS Space Astrometry Mission (Noordwijk, Netherlands: ESA Publications Division), 1200 [Google Scholar]
- Escorza, A., Boffin, H. M. J., Jorissen, A., et al. 2019, A&A, 625, C3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eyer, L., Audard, M., Holl, B., et al. 2023, A&A, 674, A13 (Gaia DR3 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [Google Scholar]
- Fabricius, C., Høg, E., Makarov, V. V., et al. 2002, A&A, 384, 180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faigler, S., Kull, I., Mazeh, T., et al. 2015, ApJ, 815, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Faucher-Giguère, C.-A., & Kaspi, V. M. 2006, ApJ, 643, 332 [CrossRef] [Google Scholar]
- Feng, F., Crane, J. D., Xuesong Wang, S., et al. 2019, ApJS, 242, 25 [Google Scholar]
- Feyerabend, P. 1970, in The Nature and Function of Scientific Theories: Essays in Contemporary Science and Philosophy, ed. R. G. Colodny (Pittsburgh: University of Pittsburgh Press) [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Flewelling, H. A., Magnier, E. A., Chambers, K. C., et al. 2020, ApJS, 251, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Frankowski, A., Jancart, S., & Jorissen, A. 2007, A&A, 464, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A., et al.) 2016a, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016b, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Babusiaux, C., et al.) 2018a, A&A, 616, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018b, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021a, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Smart, R. L., et al.) 2021b, A&A, 649, A6 [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Recio-Blanco, A., et al.) 2023a, A&A, 674, A38 (Gaia DR3 SI) [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023b, A&A, 674, A1 (Gaia DR3 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia, E. V., Ammons, S. M., Salama, M., et al. 2017, ApJ, 846, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Gelino, C. R., & Burgasser, A. J. 2010, AJ, 140, 110 [Google Scholar]
- Gentile Fusillo, N. P., Tremblay, P.-E., Gänsicke, B. T., et al. 2019, MNRAS, 482, 4570 [Google Scholar]
- Gentile Fusillo, N. P., Tremblay, P. E., Cukanovaite, E., et al. 2021, MNRAS, 508, 3877 [NASA ADS] [CrossRef] [Google Scholar]
- Giammichele, N., Bergeron, P., & Dufour, P. 2012, ApJS, 199, 29 [Google Scholar]
- Gilmore, G., Randich, S., Worley, C. C., et al. 2022, A&A, 666, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González, G., & González, G. 1956, Boletin de los Observatorios Tonantzintla y Tacubaya, 2, 19 [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [Google Scholar]
- Grether, D., & Lineweaver, C. H. 2006, ApJ, 640, 1051 [Google Scholar]
- Grieves, N., Ge, J., Thomas, N., et al. 2017, MNRAS, 467, 4264 [Google Scholar]
- Groenewegen, M. A. T. 2013, A&A, 550, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guseinov, O. K., & Zel’dovich, Y. B. 1966, Sov. Astron., 10, 251 [Google Scholar]
- Halbwachs, J. L., Pourbaix, D., Arenou, F., et al. 2023, A&A, 674, A9 (Gaia DR3 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartkopf, W. I., Mason, B. D., & Worley, C. E. 2001, AJ, 122, 3472 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., Anderson, D. R., Collier Cameron, A., et al. 2009, Nature, 460, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Henden, A. A., Templeton, M., Terrell, D., et al. 2016, VizieR Online Data Catalogue: II/336 [Google Scholar]
- Henry, T. J., & McCarthy, D. W., Jr. 1993, AJ, 106, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Herald, D., Gault, D., Anderson, R., et al. 2020, MNRAS, 499, 4570 [Google Scholar]
- Hinkle, K. H., Lebzelter, T., Joyce, R. R., & Fekel, F. C. 2002, AJ, 123, 1002 [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [Google Scholar]
- Holl, B., Fabricius, C., Portell, J., et al. 2023a, A&A, 674, A25 (Gaia DR3 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holl, B., Sozzetti, A., Sahlmann, J., et al. 2023b, A&A, 674, A10 (Gaia DR3 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howard, A. W., Marcy, G. W., Johnson, J. A., et al. 2010, Science, 330, 653 [Google Scholar]
- Huber, D., Bryson, S. T., Haas, M. R., et al. 2016, ApJS, 224, 2 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Imbert, M. 1996, A&AS, 116, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open Source Scientific Tools for Python [Google Scholar]
- Jorissen, A. 2004, in Binary AGB Stars, eds. H. Habing, & H. Olofsson (New York: Springer-Verlag) [Google Scholar]
- Jorissen, A., & Frankowski, A. 2008, AIP Conf. Ser., 1057, 1 [Google Scholar]
- Jorissen, A., Frankowski, A., Famaey, B., & van Eck, S. 2009, A&A, 498, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jorissen, A., Van Eck, S., Merle, T., & Van Winckel, H. 2019, IAU Symp., 343, 431 [NASA ADS] [Google Scholar]
- Katoh, N., Itoh, Y., Toyota, E., & Sato, B. 2013, AJ, 145, 41 [Google Scholar]
- Katz, D., Sartoretti, P., Cropper, M., et al. 2019, A&A, 622, A205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katz, D., Sartoretti, P., Guerrier, A., et al. 2023, A&A, 674, A5 (Gaia DR3 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Arenou, F., Mignard, F., & Thévenin, F. 2019a, A&A, 623, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Gallenne, A., Remage Evans, N., et al. 2019b, A&A, 623, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Arenou, F., & Thévenin, F. 2022, A&A, 657, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kiefer, F. 2019, A&A, 632, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kiefer, F., Hébrard, G., Sahlmann, J., et al. 2019, A&A, 631, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kiefer, F., Hébrard, G., Lecavelier des Etangs, A., et al. 2021, A&A, 645, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kiseleva, L. G., Eggleton, P. P., & Mikkola, S. 1998, MNRAS, 300, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Klüter, J., Bastian, U., & Wambsganss, J. 2020, A&A, 640, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koren, S. C., Blake, C. H., Dahn, C. C., & Harris, H. C. 2016, AJ, 151, 57 [Google Scholar]
- Kounkel, M., Covey, K. R., Stassun, K. G., et al. 2021, AJ, 162, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Kürster, M., Endl, M., Els, S., et al. 2000, A&A, 353, L33 [Google Scholar]
- Lallement, R., Babusiaux, C., Vergely, J. L., et al. 2019, A&A, 625, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lasker, B. M., Lattanzi, M. G., McLean, B. J., et al. 2008, AJ, 136, 735 [Google Scholar]
- Latham, D. W., Stefanik, R. P., Mazeh, T., Mayor, M., & Burki, G. 1989, Nature, 339, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Lebzelter, T., Trabucchi, M., Mowlavi, N., et al. 2019, A&A, 631, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leverington, D. 1995, A History of Astronomy from 1890 to the Present (Berlin: Springer) [Google Scholar]
- Lindegren, L. 1997, in Hipparcos – Venice ’97, eds. R. M. Bonnet, E. Høg, P. L. Bernacca, et al., ESA Spec. Publ., 402, 13 [Google Scholar]
- Lindegren, L. 2022, Gaia Data Processing and Analysis Consortium (DPAC) Technical Note GAIA-C3-TN-LU-LL-136-01, http://www.cosmos.esa.int/web/gaia/public-dpac-documents [Google Scholar]
- Lindegren, L., Klioner, S., Hernández, J., et al. 2021, A&A, 649, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luo, A. L., Zhao, Y. H., Zhao, G., et al. 2015, Res. Astron. Astrophys., 15, 1095 [Google Scholar]
- Ma, B., & Ge, J. 2014, MNRAS, 439, 2781 [Google Scholar]
- Magnier, E. A., Chambers, K. C., Flewelling, H. A., et al. 2020a, ApJS, 251, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Magnier, E. A., Sweeney, W. E., Chambers, K. C., et al. 2020b, ApJS, 251, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Magnier, E. A., Schlafly, E. F., Finkbeiner, D. P., et al. 2020c, ApJS, 251, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, V. V., & Kaplan, G. H. 2005, AJ, 129, 2420 [Google Scholar]
- Marcy, G. W., Butler, R. P., Vogt, S. S., Fischer, D., & Lissauer, J. J. 1998, ApJ, 505, L147 [Google Scholar]
- Marcy, G. W., Butler, R. P., Fischer, D., et al. 2001, ApJ, 556, 296 [Google Scholar]
- Martin, C., Mignard, F., & Froeschle, M. 1997, A&AS, 122, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mashian, N., & Loeb, A. 2017, MNRAS, 470, 2611 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., Anderson, D. R., Burleigh, M. R., et al. 2011, MNRAS, 418, 1156 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., Bloemen, S., Heber, U., et al. 2014, MNRAS, 437, 1681 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Udry, S., Naef, D., et al. 2004, A&A, 415, 391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, ArXiv e-prints [arXiv:1109.2497] [Google Scholar]
- Mazeh, T. 2008, in EAS Publications Series, eds. M. J. Goupil, & J. P. Zahn, 29, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mowlavi, N., Holl, B., Lecoeur-Taïbi, I., et al. 2023, A&A, 674, A16 (Gaia DR3 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortier, A., Santos, N. C., Sozzetti, A., et al. 2012, A&A, 543, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moutou, C., Mayor, M., Lo Curto, G., et al. 2009, A&A, 496, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, S. J., Bedding, T. R., & Shibahashi, H. 2016, ApJ, 827, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Napiwotzki, R., Karl, C. A., Lisker, T., et al. 2020, A&A, 638, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Navarro, S. G., Corradi, R. L. M., & Mampaso, A. 2012, A&A, 538, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelson, B. E., Robertson, P. M., Payne, M. J., et al. 2016, MNRAS, 455, 2484 [NASA ADS] [CrossRef] [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [Google Scholar]
- Ochsenbein, F., Bauer, P., & Marcout, J. 2000, A&AS, 143, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oliphant, T. E. 2007, Comput. Sci. Eng., 9, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Onken, C. A., Wolf, C., Bessell, M. S., et al. 2019, PASA, 36, e033 [Google Scholar]
- Orosz, J. A., McClintock, J. E., Narayan, R., et al. 2007, Nature, 449, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz, R., & Guerrero, M. A. 2021, ApJ, 912, 93 [Google Scholar]
- Otero, S. A. 2008, Open Eur. J. Var. Stars, 0083, 1 [NASA ADS] [Google Scholar]
- Paczyński, B. 1971, ARA&A, 9, 183 [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [Google Scholar]
- Penoyre, Z., Belokurov, V., & Evans, N. W. 2022, MNRAS, 513, 2437 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
- Pietrzyński, G., Graczyk, D., Gallenne, A., et al. 2019, Nature, 567, 200 [Google Scholar]
- Pinamonti, M., Sozzetti, A., Maldonado, J., et al. 2022, A&A, 664, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pourbaix, D., Tokovinin, A. A., Batten, A. H., et al. 2004, A&A, 424, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pourbaix, D., Arenou, F., & Gavras, P. 2022, Gaia DR3 Documentation Chapter 7: Non-single Stars. Online at https://gea.esac.esa.int/archive/documentation/GDR3/index.html, 7 [Google Scholar]
- R Core Team 2013, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [Google Scholar]
- Randich, S., Gilmore, G., Magrini, L., et al. 2022, A&A, 666, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rappaport, S., Nelson, L., Levine, A., et al. 2015, ApJ, 803, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [CrossRef] [EDP Sciences] [Google Scholar]
- Reback, J., McKinney, W., Van den Bossche, J., et al. 2022, https://doi.org/10.5281/zenodo.6408044 [Google Scholar]
- Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rivera, E. J., Lissauer, J. J., Butler, R. P., et al. 2005, ApJ, 634, 625 [Google Scholar]
- Rivera, E. J., Laughlin, G., Butler, R. P., et al. 2010, ApJ, 719, 890 [Google Scholar]
- Robertson, T. H., & Jordan, T. M. 1989, AJ, 98, 1354 [Google Scholar]
- Roeser, S., Demleitner, M., & Schilbach, E. 2010, AJ, 139, 2440 [Google Scholar]
- Rosenthal, L. J., Fulton, B. J., Hirsch, L. A., et al. 2021, ApJS, 255, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Rousseau, J., Martin, N., Prévot, L., et al. 1978, A&AS, 31, 243 [NASA ADS] [Google Scholar]
- Sahai, R., Findeisen, K., Gil de Paz, A., & Sánchez Contreras, C. 2008, ApJ, 689, 1274 [NASA ADS] [CrossRef] [Google Scholar]
- Sahlmann, J. 2019, https://doi.org/10.5281/zenodo.3515526 [Google Scholar]
- Sahlmann, J., Ségransan, D., Queloz, D., et al. 2011, A&A, 525, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahlmann, J., Lazorenko, P. F., Ségransan, D., et al. 2013, A&A, 556, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahlmann, J., Lazorenko, P. F., Ségransan, D., et al. 2014a, A&A, 565, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahlmann, J., Lazorenko, P. F., Ségransan, D., et al. 2014b, Mem. Soc. Astron. It., 85, 674 [NASA ADS] [Google Scholar]
- Sahlmann, J., Burgasser, A. J., Martín, E. L., et al. 2015, A&A, 579, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahlmann, J., Burgasser, A. J., Bardalez Gagliuffi, D. C., et al. 2020, MNRAS, 495, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Sahlmann, J., Dupuy, T. J., Burgasser, A. J., et al. 2021, MNRAS, 500, 5453 [Google Scholar]
- Santos, N. C., Mayor, M., Bonfils, X., et al. 2011, A&A, 526, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Satō, I., Buie, M., Maley, P. D., et al. 2014, Int. J. Astron. Astrophys., 4, 91 [CrossRef] [Google Scholar]
- Seabroke, G. M., Fabricius, C., Teyssier, D., et al. 2021, A&A, 653, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shahaf, S., Mazeh, T., Faigler, S., & Holl, B. 2019, MNRAS, 487, 5610 [NASA ADS] [CrossRef] [Google Scholar]
- Shao, Y., & Li, X.-D. 2019, ApJ, 885, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Siebert, H. 2005, J. Hist. Astron., 36, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smart, R. L., Marocco, F., Sarro, L. M., et al. 2019, MNRAS, 485, 4423 [Google Scholar]
- Söderhjelm, S., Lindegren, L., & Perryman, M. A. C. 1997, ESA Spec. Publ., 402, 251 [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Udry, S. 2011, A&A, 533, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sozzetti, A., Udry, S., Zucker, S., et al. 2006, A&A, 449, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sozzetti, A., Torres, G., Latham, D. W., et al. 2009, ApJ, 697, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Sperauskas, J., Deveikis, V., & Tokovinin, A. 2019, A&A, 626, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stassun, K. G., & Torres, G. 2021, ApJ, 907, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Stassun, K. G., Collins, K. A., & Gaudi, B. S. 2017, AJ, 153, 136 [Google Scholar]
- Steinmetz, M., Guiglion, G., McMillan, P. J., et al. 2020a, AJ, 160, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Steinmetz, M., Matijevič, G., Enke, H., et al. 2020b, AJ, 160, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Subasavage, J. P., Jao, W.-C., Henry, T. J., et al. 2017, AJ, 154, 32 [Google Scholar]
- Susemiehl, N., & Meyer, M. R. 2022, A&A, 657, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, M. B. 2005, ASP Conf. Ser., 347, 29 [Google Scholar]
- Taylor, M. B. 2006, ASP Conf. Ser., 351, 666 [Google Scholar]
- Tinney, C. G., Butler, R. P., Marcy, G. W., et al. 2002, ApJ, 571, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A. 2004, Rev. Mex. Astron. Astrofis. Conf. Ser., 21, 7 [NASA ADS] [Google Scholar]
- Tokovinin, A. 2017, ApJ, 844, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A. 2018, ApJS, 235, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Trifonov, T., Kürster, M., Zechmeister, M., et al. 2018, A&A, 609, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trimble, V. L., & Thorne, K. S. 1969, ApJ, 156, 1013 [Google Scholar]
- Trumpler, R. J., & Weaver, H. F. 1953, Statistical Astronomy (New York: Dover Publication, Inc.) [CrossRef] [Google Scholar]
- Udry, S., Mayor, M., Naef, D., et al. 2002, A&A, 390, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Kerkwijk, M. H., Rappaport, S. A., Breton, R. P., et al. 2010, ApJ, 715, 51 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007a, Hipparcos, the New Reduction of the Raw Data, Astrophysics and Space Science Library (Springer), 350 [Google Scholar]
- van Leeuwen, F. 2007b, A&A, 474, 653 [CrossRef] [EDP Sciences] [Google Scholar]
- van Roestel, J., Kupfer, T., Ruiz-Carmona, R., et al. 2018, MNRAS, 475, 2560 [CrossRef] [Google Scholar]
- Veras, D. 2021, Oxford Research Encyclopedia of Planetary Science (Oxford: Oxford University Press) [Google Scholar]
- Verbunt, F., & Phinney, E. S. 1995, A&A, 296, 709 [NASA ADS] [Google Scholar]
- Waters, C. Z., Magnier, E. A., Price, P. A., et al. 2020, ApJS, 251, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wielen, R., Dettbarn, C., Jahreiß, H., Lenhardt, H., & Schwan, H. 1999, A&A, 346, 675 [NASA ADS] [Google Scholar]
- Wiktorowicz, G., Wyrzykowski, Ł., Chruslinska, M., et al. 2019, ApJ, 885, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, P. A., Hébrard, G., Santos, N. C., et al. 2016, A&A, 588, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winters, J. G., Irwin, J., Newton, E. R., et al. 2018, AJ, 155, 125 [Google Scholar]
- Winters, J. G., Henry, T. J., Jao, W.-C., et al. 2019, AJ, 157, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Wittenmyer, R. A., Horner, J., Tuomi, M., et al. 2012, ApJ, 753, 169 [CrossRef] [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2013, AJ, 145, 44 [Google Scholar]
- Zacharias, N., Finch, C., Subasavage, J., et al. 2015, AJ, 150, 101 [Google Scholar]
- Zahn, J. P., & Bouchet, L. 1989, A&A, 223, 112 [NASA ADS] [Google Scholar]
- Ziolkowski, J. 2014, MNRAS, 440, L61 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Acknowledgements
The Gaia mission and data processing have been financially supported by, in alphabetical order by country:
-
the Algerian Centre de Recherche en Astronomie, Astrophysique et Géophysique of Bouzareah Observatory;
-
the Austrian Fonds zur Förderung der wissenschaftlichen Forschung (FWF) Hertha Firnberg Programme through grants T359, P20046, and P23737;
-
the BELgian federal Science Policy Office (BELSPO) through various PROgramme de Développement d’Expériences scientifiques (PRODEX) grants, the Fonds Wetenschappelijk Onderzoek through grant VS.091.16N, the Fonds de la Recherche Scientifique (FNRS), and the Research Council of Katholieke Universiteit (KU) Leuven through grant C16/18/005 (Pushing AsteRoseismology to the next level with TESS, GaiA, and the Sloan DIgital Sky SurvEy – PARADISE);
-
the Brazil-France exchange programmes Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) and Coordenação de Aperfeicoamento de Pessoal de Nível Superior (CAPES) – Comité Français d’Evaluation de la Coopération Universitaire et Scientifique avec le Brésil (COFECUB);
-
the Chilean Agencia Nacional de Investigación y Desarrollo (ANID) through Fondo Nacional de Desarrollo Científico y Tecnológico (FONDECYT) Regular Project 1210992 (L. Chemin);
-
the National Natural Science Foundation of China (NSFC) through grants 11573054, 11703065, and 12173069, the China Scholarship Council through grant 201806040200, and the Natural Science Foundation of Shanghai through grant 21ZR1474100;
-
the Tenure Track Pilot Programme of the Croatian Science Foundation and the École Polytechnique Fédérale de Lausanne and the project TTP-2018-07-1171 ‘Mining the Variable Sky’, with the funds of the Croatian-Swiss Research Programme;
-
the Czech-Republic Ministry of Education, Youth, and Sports through grant LG 15010 and INTER-EXCELLENCE grant LTAUSA18093, and the Czech Space Office through ESA PECS contract 98058;
-
the Danish Ministry of Science;
-
the Estonian Ministry of Education and Research through grant IUT40-1;
-
the European Commission’s Sixth Framework Programme through the European Leadership in Space Astrometry (ELSA) Marie Curie Research Training Network (MRTN-CT-2006-033481), through Marie Curie project PIOF-GA-2009-255267 (Space AsteroSeismology & RR Lyrae stars, SAS-RRL), and through a Marie Curie Transfer-of-Knowledge (ToK) fellowship (MTKD-CT-2004-014188); the European Commission’s Seventh Framework Programme through grant FP7-606740 (FP7-SPACE-2013-1) for the Gaia European Network for Improved data User Services (GENIUS) and through grant 264895 for the Gaia Research for European Astronomy Training (GREAT-ITN) network;
-
the European Cooperation in Science and Technology (COST) through COST Action CA18104 ‘Revealing the Milky Way with Gaia (MW-Gaia)’;
-
the European Research Council (ERC) through grants 320360, 647208, and 834148 and through the European Union’s Horizon 2020 research and innovation and excellent science programmes through Marie Skłodowska-Curie grant 745617 (Our Galaxy at full HD – Gal-HD) and 895174 (The build-up and fate of self-gravitating systems in the Universe) as well as grants 687378 (Small Bodies: Near and Far), 682115 (Using the Magellanic Clouds to Understand the Interaction of Galaxies), 695099 (A sub-percent distance scale from binaries and Cepheids – CepBin), 716155 (Structured ACCREtion Disks – SACCRED), 951549 (Sub-percent calibration of the extragalactic distance scale in the era of big surveys – UniverScale), and 101004214 (Innovative Scientific Data Exploration and Exploitation Applications for Space Sciences – EXPLORE);
-
the European Science Foundation (ESF), in the framework of the Gaia Research for European Astronomy Training Research Network Programme (GREAT-ESF);
-
the European Space Agency (ESA) in the framework of the Gaia project, through the Plan for European Cooperating States (PECS) programme through contracts C98090 and 4000106398/12/NL/KML for Hungary, through contract 4000115263/15/NL/IB for Germany, and through PROgramme de Développement d’Expériences scientifiques (PRODEX) grant 4000127986 for Slovenia;
-
the Academy of Finland through grants 299543, 307157, 325805, 328654, 336546, and 345115 and the Magnus Ehrnrooth Foundation;
-
the French Centre National d’Études Spatiales (CNES), the Agence Nationale de la Recherche (ANR) through grant ANR-10-IDEX-0001-02 for the ‘Investissements d’avenir’ programme, through grant ANR-15-CE31-0007 for project ‘Modelling the Milky Way in the Gaia era’ (MOD4Gaia), through grant ANR-14-CE33-0014-01 for project ‘The Milky Way disc formation in the Gaia era’ (ARCHEOGAL), through grant ANR-15-CE31-0012-01 for project ‘Unlocking the potential of Cepheids as primary distance calibrators’ (UnlockCepheids), through grant ANR-19-CE31-0017 for project ‘Secular evolution of galaxies’ (SEGAL), and through grant ANR-18-CE31-0006 for project ‘Galactic Dark Matter’ (GaDaMa), the Centre National de la Recherche Scientifique (CNRS) and its SNO Gaia of the Institut des Sciences de l’Univers (INSU), its Programmes Nationaux: Cosmologie et Galaxies (PNCG), Gravitation Références Astronomie Métrologie (PNGRAM), Planétologie (PNP), Physique et Chimie du Milieu Interstellaire (PCMI), and Physique Stellaire (PNPS), the ‘Action Fédératrice Gaia’ of the Observatoire de Paris, the Région de Franche-Comté, the Institut National Polytechnique (INP) and the Institut National de Physique nucléaire et de Physique des Particules (IN2P3) co-funded by CNES;
-
the German Aerospace Agency (Deutsches Zentrum für Luft- und Raumfahrt e.V., DLR) through grants 50QG0501, 50QG0601, 50QG0602, 50QG0701, 50QG0901, 50QG1001, 50QG1101, 50QG1401, 50QG1402, 50QG1403, 50QG1404, 50QG1904, 50QG2101, 50QG2102, and 50QG2202, and the Centre for Information Services and High Performance Computing (ZIH) at the Technische Universität Dresden for generous allocations of computer time;
-
the Hungarian Academy of Sciences through the Lendület Programme grants LP2014-17 and LP2018-7 and the Hungarian National Research, Development, and Innovation Office (NKFIH) through grant KKP-137523 (‘SeismoLab’);
-
the Science Foundation Ireland (SFI) through a Royal Society – SFI University Research Fellowship (M. Fraser);
-
the Israel Ministry of Science and Technology through grant 3-18143 and the Tel Aviv University Center for Artificial Intelligence and Data Science (TAD) through a grant;
-
the Agenzia Spaziale Italiana (ASI) through contracts I/037/08/0, I/058/10/0, 2014-025-R.0, 2014-025-R.1.2015, and 2018-24-HH.0 to the Italian Istituto Nazionale di Astrofisica (INAF), contract 2014-049-R.0/1/2 to INAF for the Space Science Data Centre (SSDC, formerly known as the ASI Science Data Center, ASDC), contracts I/008/10/0, 2013/030/I.0, 2013-030-I.0.1-2015, and 2016-17-I.0 to the Aerospace Logistics Technology Engineering Company (ALTEC S.p.A.), INAF, and the Italian Ministry of Education, University, and Research (Ministero dell’Istruzione, dell’Università e della Ricerca) through the Premiale project ‘MIning The Cosmos Big Data and Innovative Italian Technology for Frontier Astrophysics and Cosmology’ (MITiC);
-
the Netherlands Organisation for Scientific Research (NWO) through grant NWO-M-614.061.414, through a VICI grant (A. Helmi), and through a Spinoza prize (A. Helmi), and the Netherlands Research School for Astronomy (NOVA);
-
the Polish National Science Centre through HARMONIA grant 2018/30/M/ST9/00311 and DAINA grant 2017/27/L/ST9/03221 and the Ministry of Science and Higher Education (MNiSW) through grant DIR/WK/2018/12;
-
the Portuguese Fundação para a Ciência e a Tecnologia (FCT) through national funds, grants SFRH/BD/128840/2017 and PTDC/FIS-AST/30389/2017, and work contract DL 57/2016/CP1364/CT0006, the Fundo Europeu de Desenvolvimento Regional (FEDER) through grant POCI-01-0145-FEDER-030389 and its Programa Operacional Competitividade e Internacionalização (COMPETE2020) through grants UIDB/04434/2020 and UIDP/04434/2020, and the Strategic Programme UIDB/00099/2020 for the Centro de Astrofísica e Gravitação (CENTRA);
-
the Slovenian Research Agency through grant P1-0188;
-
the Spanish Ministry of Economy (MINECO/FEDER, UE), the Spanish Ministry of Science and Innovation (MICIN), the Spanish Ministry of Education, Culture, and Sports, and the Spanish Government through grants BES-2016-078499, BES-2017-083126, BES-C-2017-0085, ESP2016-80079-C2-1-R, ESP2016-80079-C2-2-R, FPU16/03827, PDC2021-121059-C22, RTI2018-095076-B-C22, and TIN2015-65316-P (‘Computación de Altas Prestaciones VII’), the Juan de la Cierva Incorporación Programme (FJCI-2015-2671 and IJC2019-04862-I for F. Anders), the Severo Ochoa Centre of Excellence Programme (SEV2015-0493), and MICIN/AEI/10.13039/501100011033 (and the European Union through European Regional Development Fund ‘A way of making Europe’) through grant RTI2018-095076-B-C21, the Institute of Cosmos Sciences University of Barcelona (ICCUB, Unidad de Excelencia ‘María de Maeztu’) through grant CEX2019-000918-M, the University of Barcelona’s official doctoral programme for the development of an R+D+i project through an Ajuts de Personal Investigador en Formació (APIF) grant, the Spanish Virtual Observatory through project AyA2017-84089, the Galician Regional Government, Xunta de Galicia, through grants ED431B-2021/36, ED481A-2019/155, and ED481A-2021/296, the Centro de Investigación en Tecnologías de la Información y las Comunicaciones (CITIC), funded by the Xunta de Galicia and the European Union (European Regional Development Fund – Galicia 2014-2020 Programme), through grant ED431G-2019/01, the Red Española de Supercomputación (RES) computer resources at MareNostrum, the Barcelona Supercomputing Centre – Centro Nacional de Supercomputación (BSC-CNS) through activities AECT-2017-2-0002, AECT-2017-3-0006, AECT-2018-1-0017, AECT-2018-2-0013, AECT-2018-3-0011, AECT-2019-1-0010, AECT-2019-2-0014, AECT-2019-3-0003, AECT-2020-1-0004, and DATA-2020-1-0010, the Departament d’Innovació, Universitats i Empresa de la Generalitat de Catalunya through grant 2014-SGR-1051 for project ‘Models de Programació i Entorns d’Execució Parallels’ (MPEXPAR), and Ramon y Cajal Fellowship RYC2018-025968-I funded by MICIN/AEI/10.13039/501100011033 and the European Science Foundation (‘Investing in your future’);
-
the Swedish National Space Agency (SNSA/Rymdstyrelsen);
-
the Swiss State Secretariat for Education, Research, and Innovation through the Swiss Activités Nationales Complémentaires and the Swiss National Science Foundation through an Eccellenza Professorial Fellowship (award PCEFP2_194638 for R. Anderson);
-
the United Kingdom Particle Physics and Astronomy Research Council (PPARC), the United Kingdom Science and Technology Facilities Council (STFC), and the United Kingdom Space Agency (UKSA) through the following grants to the University of Bristol, the University of Cambridge, the University of Edinburgh, the University of Leicester, the Mullard Space Sciences Laboratory of University College London, and the United Kingdom Rutherford Appleton Laboratory (RAL): PP/D006511/1, PP/D006546/1, PP/D006570/1, ST/I000852/1, ST/J005045/1, ST/K00056X/1, ST/K000209/1, ST/K000756/1, ST/L006561/1, ST/N000595/1, ST/N000641/1, ST/N000978/1, ST/N001117/1, ST/S000089/1, ST/S000976/1, ST/S000984/1, ST/S001123/1, ST/S001948/1, ST/S001980/1, ST/S002103/1, ST/V000969/1, ST/W002469/1, ST/W002493/1, ST/W002671/1, ST/W002809/1, and EP/V520342/1.
The Gaia project and data processing have made use of:
-
the Set of Identifications, Measurements, and Bibliography for Astronomical Data (SIMBAD, Wenger et al. 2000), the ‘Aladin sky atlas’ (Bonnarel et al. 2000; Boch & Fernique 2014), and the VizieR catalogue access tool (Ochsenbein et al. 2000), all operated at the Centre de Données astronomiques de Strasbourg ((CDS);
-
the National Aeronautics and Space Administration (NASA) Astrophysics Data System (ADS);
-
the SPace ENVironment Information System (SPENVIS), initiated by the Space Environment and Effects Section (TEC-EES) of ESA and developed by the Belgian Institute for Space Aeronomy (BIRA-IASB) under ESA contract through ESA’s General Support Technologies Programme (GSTP), administered by the BELgian federal Science Policy Office (BELSPO);
-
the software products TOPCAT, STIL, and STILTS (Taylor 2005, 2006);
-
Matplotlib (Hunter 2007);
-
IPython (Pérez & Granger 2007);
-
Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2018);
-
SCIPY (Jones et al. 2001),
-
NUMPY (Oliphant 2007),
-
PANDAS (Reback et al. 2022),
-
R (R Core Team 2013);
-
Vaex (Breddels & Veljanoski 2018);
-
the HIPPARCOS-2 catalogue (van Leeuwen 2007b). The HIPPARCOS and Tycho catalogues were constructed under the responsibility of large scientific teams collaborating with ESA. The Consortia Leaders were Lennart Lindegren (Lund, Sweden: NDAC) and Jean Kovalevsky (Grasse, France: FAST), together responsible for the HIPPARCOS Catalogue; Erik Høg (Copenhagen, Denmark: TDAC) responsible for the Tycho Catalogue; and Catherine Turon (Meudon, France: INCA) responsible for the HIPPARCOS Input Catalogue (HIC);
-
the Tycho-2 catalogue (Høg et al. 2000), the construction of which was supported by the Velux Foundation of 1981 and the Danish Space Board;
-
The Tycho double star catalogue (TDSC, Fabricius et al. 2002), based on observations made with the ESA HIPPARCOS astrometry satellite, as supported by the Danish Space Board and the United States Naval Observatory through their double-star programme;
-
data products from the Two Micron All Sky Survey (2MASS, Skrutskie et al. 2006), which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center (IPAC)/California Institute of Technology, funded by the National Aeronautics and Space Administration (NASA) and the National Science Foundation (NSF) of the USA;
-
the ninth data release of the AAVSO Photometric All-Sky Survey (APASS, Henden et al. 2016), funded by the Robert Martin Ayers Sciences Fund;
-
the first data release of the Pan-STARRS survey (Chambers et al. 2016; Magnier et al. 2020a; Waters et al. 2020; Magnier et al. 2020b,c; Flewelling et al. 2020). The Pan-STARRS1 Surveys (PS1) and the PS1 public science archive have been made possible through contributions by the Institute for Astronomy, the University of Hawaii, the Pan-STARRS Project Office, the Max-Planck Society and its participating institutes, the Max Planck Institute for Astronomy, Heidelberg and the Max Planck Institute for Extraterrestrial Physics, Garching, The Johns Hopkins University, Durham University, the University of Edinburgh, the Queen’s University Belfast, the Harvard-Smithsonian Center for Astrophysics, the Las Cumbres Observatory Global Telescope Network Incorporated, the National Central University of Taiwan, the Space Telescope Science Institute, the National Aeronautics and Space Administration (NASA) through grant NNX08AR22G issued through the Planetary Science Division of the NASA Science Mission Directorate, the National Science Foundation through grant AST-1238877, the University of Maryland, Eotvos Lorand University (ELTE), the Los Alamos National Laboratory, and the Gordon and Betty Moore Foundation;
-
the second release of the Guide Star Catalogue (GSC2.3, Lasker et al. 2008). The Guide Star Catalogue II is a joint project of the Space Telescope Science Institute (STScI) and the Osservatorio Astrofisico di Torino (OATo). STScI is operated by the Association of Universities for Research in Astronomy (AURA), for the National Aeronautics and Space Administration (NASA) under contract NAS5-26555. OATo is operated by the Italian National Institute for Astrophysics (INAF). Additional support was provided by the European Southern Observatory (ESO), the Space Telescope European Coordinating Facility (STECF), the International GEMINI project, and the European Space Agency (ESA) Astrophysics Division (nowadays SCI-S);
-
the eXtended, Large (XL) version of the catalogue of Positions and Proper Motions (PPM-XL, Roeser et al. 2010);
-
data products from the Wide-field Infrared Survey Explorer (WISE), which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, and NEOWISE, which is a project of the Jet Propulsion Laboratory/California Institute of Technology. WISE and NEOWISE are funded by the National Aeronautics and Space Administration (NASA);
-
the first data release of the United States Naval Observatory (USNO) Robotic Astrometric Telescope (URAT-1, Zacharias et al. 2015);
-
the fourth data release of the United States Naval Observatory (USNO) CCD Astrograph Catalogue (UCAC-4, Zacharias et al. 2013);
-
the sixth and final data release of the Radial Velocity Experiment (RAVE DR6, Steinmetz et al. 2020a,b). Funding for RAVE has been provided by the Leibniz Institute for Astrophysics Potsdam (AIP), the Australian Astronomical Observatory, the Australian National University, the Australian Research Council, the French National Research Agency, the German Research Foundation (SPP 1177 and SFB 881), the European Research Council (ERC-StG 240271 Galactica), the Istituto Nazionale di Astrofisica at Padova, the Johns Hopkins University, the National Science Foundation of the USA (AST-0908326), the W.M. Keck foundation, the Macquarie University, the Netherlands Research School for Astronomy, the Natural Sciences and Engineering Research Council of Canada, the Slovenian Research Agency, the Swiss National Science Foundation, the Science & Technology Facilities Council of the UK, Opticon, Strasbourg Observatory, and the Universities of Basel, Groningen, Heidelberg, and Sydney. The RAVE website is at https://www.rave-survey.org/;
-
the first data release of the Large sky Area Multi-Object Fibre Spectroscopic Telescope (LAMOST DR1, Luo et al. 2015);
-
the K2 Ecliptic Plane Input Catalogue (EPIC, Huber et al. 2016);
-
the ninth data release of the Sloan Digitial Sky Survey (SDSS DR9, Ahn et al. 2012). Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the United States Department of Energy Office of Science. The SDSS-III website is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofísica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University;
-
the thirteenth release of the Sloan Digital Sky Survey (SDSS DR13, Albareti et al. 2017). Funding for SDSS-IV has been provided by the Alfred P. Sloan Foundation, the United States Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS website is https://www.sdss.org/. SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University;
-
the second release of the SkyMapper catalogue (SkyMapper DR2, Onken et al. 2019, Digital Object Identifier 10.25914/5ce60d31ce759). The national facility capability for SkyMapper has been funded through grant LE130100104 from the Australian Research Council (ARC) Linkage Infrastructure, Equipment, and Facilities (LIEF) programme, awarded to the University of Sydney, the Australian National University, Swinburne University of Technology, the University of Queensland, the University of Western Australia, the University of Melbourne, Curtin University of Technology, Monash University, and the Australian Astronomical Observatory. SkyMapper is owned and operated by The Australian National University’s Research School of Astronomy and Astrophysics. The survey data were processed and provided by the SkyMapper Team at the Australian National University. The SkyMapper node of the All-Sky Virtual Observatory (ASVO) is hosted at the National Computational Infrastructure (NCI). Development and support the SkyMapper node of the ASVO has been funded in part by Astronomy Australia Limited (AAL) and the Australian Government through the Commonwealth’s Education Investment Fund (EIF) and National Collaborative Research Infrastructure Strategy (NCRIS), particularly the National eResearch Collaboration Tools and Resources (NeCTAR) and the Australian National Data Service Projects (ANDS);
-
the Gaia-ESO Public Spectroscopic Survey (GES, Gilmore et al. 2022; Randich et al. 2022). The Gaia-ESO Survey is based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under programme ID 188.B-3002. Public data releases are available through the ESO Science Portal. The project has received funding from the Leverhulme Trust (project RPG-2012-541), the European Research Council (project ERC-2012-AdG 320360-Gaia-ESO-MW), and the Istituto Nazionale di Astrofisica, INAF (2012: CRA 1.05.01.09.16; 2013: CRA 1.05.06.02.07).
The GBOT programme uses observations collected at (i) the European Organisation for Astronomical Research in the Southern Hemisphere (ESO) with the VLT Survey Telescope (VST), under ESO programmes 092.B-0165, 093.B-0236, 094.B-0181, 095.B-0046, 096.B-0162, 097.B-0304, 098.B-0030, 099.B-0034, 0100.B-0131, 0101.B-0156, 0102.B-0174, and 0103.B-0165; and (ii) the Liverpool Telescope, which is operated on the island of La Palma by Liverpool John Moores University in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias with financial support from the United Kingdom Science and Technology Facilities Council, and (iii) telescopes of the Las Cumbres Observatory Global Telescope Network.
Appendix B: Parameters describing the orbital motion
The parameters relative to the orbital motion as presented in the nss_two_body_orbit are introduced in what follows. More details can be found in the online documentation and articles accompanying the data release Halbwachs et al. (2023); Holl et al. (2023b), Gosset et al. (in prep.), and Siopis (in prep.) for astrometric, spectroscopic, and eclipsing binaries respectively.
B.1. Astrometry
The Gaia AL astrometric measurement w (abscissa) for a binary system can be modelled by the combination of a single-source model wss, describing the standard astrometric motion of the system’s barycentre, and a Keplerian model wk1.
The single-source model can be written as
where Δα⋆ = Δα cos δ and Δδ are small offsets in equatorial coordinates from some fixed reference point, μα⋆, μδ are proper motions in these coordinates, t is time, ϖ is the parallax, fϖ is the parallax factor, and ψ is the scan angle. The astrometric motion corresponding to a Keplerian orbit of a binary system has generally seven independent parameters, namely the Campbell elements. These are the period P, the epoch of periastron passage T0, the eccentricity e, the inclination i, the ascending node Ω, the argument of periastron ω, and the semi-major axis of the photocentre a0. The Thiele-Innes coefficients A, B, F, and G are defined as
The elliptical rectangular coordinates X and Y are functions of eccentric anomaly E and eccentricity:
The single Keplerian model can then be written as
The combined model w(model) for the Gaia AL astrometry is
This model has been extensively used for modelling the HIPPARCOS epoch data of non-single stars (e.g. Sahlmann et al. 2011).
B.2. Spectroscopy
The radial motion of the primary is given by
with v(t) the true anomaly deriving from the eccentric anomaly E by
and with the semi-amplitude of the primary (resp. secondary)
where κ ∼ 10879 when Ki is expressed in km s−1, P in days and ai the semi-major axis of the primary (resp. secondary) in astronomical units (au).
This model has been used to produce the NSS solutions for SB1 and SB2. When astrometry and spectroscopy were combined (AstroSpectroSB1 solutions) in order to avoid correlations with the Campbell elements, it was easier to complete the Thiele-Innes elements with
and these parameters have been published instead.
Appendix C: Analytic orbit detection sensitivity as a function of orbit inclination
Our toy orbit model is shown in Fig. C.1. To keep the expressions simple, we aligned the ellipse major-axis a with α* and introduced the inclination as rotation around the α*-axis. The orbital-phase (ϕ)-dependent position (x(t),y(t)) is projected to the on-sky position α*, δ via:
The orbit signal in the AL (i.e. along ψ) and across-scan (AC, rotated 90 degrees counter-clockwise) directions is
To derive the RMS of dAL and dAC, we make the following simplifying assumptions: (a) the orbit is circular, i.e. a = b: The angular velocity  is constant and integration over ϕ is straightforward. (b) At each observation the orbital phase ϕ is random: the orbital-average value can be obtained by simply integrating over ϕ. (c) At each observation the scan-angle ψ is random. The mean square amplitude of dAL for a given scan angle ψ under assumptions (a) and (b) reduces to
is constant and integration over ϕ is straightforward. (b) At each observation the orbital phase ϕ is random: the orbital-average value can be obtained by simply integrating over ϕ. (c) At each observation the scan-angle ψ is random. The mean square amplitude of dAL for a given scan angle ψ under assumptions (a) and (b) reduces to
where we used the identity
Similarly, we obtain in the AC direction
Applying assumption (c) we get
and in AC
Assuming constant weights WAL and WAC for the AL and AC observations, respectively, the resulting RMS level is
It is instructive to examine the two extreme scenarios:
-
One-dimensional astrometry, i.e. WAL = 1 and WAC = 0, which approximates the Gaia DR3 astrometric solution: we obtain
which results in a
 reduction for edge-on systems compared to the face-on configuration.
reduction for edge-on systems compared to the face-on configuration. -
Two-dimensional astrometry with equal weights, i.e. WAL = WAC = 1, which approximates conventional CCD imaging:
i.e. same inclination-dependency as one-dimensional observations but with a
 boost in RMS because the number of observations is doubled22.
boost in RMS because the number of observations is doubled22.
 |
Fig. C.1. Left: Orbital plane ellipse with width a and height b (the circular case a = b = 1 is shown). Middle: Sky-projected plane with scan angle ψ and projected orbit due to inclination i shown in the right panel. |
Appendix D: Biases and uncertainties of Thiele-Innes parameters
D.1. Biases introduced by fitting Thiele-Innes parameters to noisy data
All Gaia processing pipelines for fitting astrometric orbits23 follow a similar parametrisation scheme (Sect. B.1; DR3 documentation; Halbwachs et al. 2023; Holl et al. 2023b): the three non-linear parameters P, e, and T0 are fitted using different algorithms but the four remaining parameters are represented by the Thiele-Innes coefficients A, B, F, G, which linearise part of the equations.
As the features in the distributions of DR3 orbit parameters hinted at signal-dependent effects, we simulated the A, B, F, G recovery performance as a function of noise level. We applied the same simulation approach as in Sect. 3.2 to compute the AL signal wk1 of the Keplerian orbit, Eq. (B.6), for an ensemble of binary systems with the same distance, period, and semi-major axis. We computed the rectangular coordinates X and Y according to the simulated parameters and then solved the linear equation
for the unknown A, B, F, G, where ϵw is a random noise term that we added to the noiseless simulated abscissa. For simplicity, we chose uniform abscissa uncertainties σw and zero covariances. We used a standard matrix-inversion solver24 to determine the solution.
For the noise term ϵw, we chose its amplitude relative to the simulated semi-major axis, which was the same for all simulated systems (a0 = 0.059 mas, see Sect. 3.2) but independent of the number of simulated observation epochs for a given source. For S/N=5, for example, a random noise term was added to w according to a normal distribution with dispersion ϵw, 5 = a0/5. This setup does intentionally not account for the inclination-dependent sensitivity (Sect. 3.2).
Figure show the simulated and recovered distributions of cos i for various levels of noise. At high S/N=100, the simulated distribution is recovered, but for progressively smaller S/N, a lack of face-on configurations starts to appear and the inclinations extracted from the fitted A, B, F, G are biased towards edge-on configurations. At very small S/N=0.01, where the A, B, F, G are essentially unconstrained except for their amplitude term dependent on a0, the cos i distribution is peaked at cos i = 0, i.e. edge-on configurations.
 |
Fig. D.1. Simulated (filled grey) and recovered (solid line) distributions of cos i for six levels of signal-to-noise as explained in the text. The vertical dashed line at i = 90° indicates the edge-on configurations. |
The apparent dearth of face-on configurations for Orbital solutions (Fig. 11) is therefore the consequence of extracting the Thiele-Innes parameters A, B, F, G from noisy data. The dependence on S/N expected from the simulations is observed in the actual data as well (Fig. 12). As the DR3 solutions contain a continuum of S/N levels, the corresponding cos i distribution is a superposition of the distributions for individual S/N levels.
Figure shows the recovered Ω distribution in the lowest S/N case we simulated. The suppression of orbits with Ω = 90° observed for Orbital solutions is reproduced by the simulation. This modulation becomes very weak for higher levels of S/N. We conclude that this feature can therefore also be attributed to a bias introduced by fitting the A, B, F, G coefficients.
 |
Fig. D.2. Simulated (filled grey) and recovered (solid line) distributions of Ω at S/N = 0.01. |
To simulate the effect on ω we simulated non-circular orbits with eccentricity e = 0.5, all other parameters remained the same. Figure shows a bimodal modulation of the recovered ω distribution. However, the minima at ω = 0° or 180° do not match the ones observed for Orbital solutions at ω = 90° or 270°. Instead, they reproduce the minima seen in the orb6 solutions shown in Fig. 11.
 |
Fig. D.3. Simulated (filled grey) and recovered (solid line) distributions of ω for non-circular orbits with e = 0.5 at S/N = 0.01. |
D.2. Selection effect causing the modulation in the ω distribution
The accepted Orbital solutions have to pass a period-dependent threshold on their significance, defined as the ratio between the semi-major axis and its uncertainty a0/σa0 (Halbwachs et al. 2023). Figure shows that there is a bimodal correlation between the published significance and ω with minima at ω = 90° or 270°. The application of an ω-independent significance threshold therefore leads to a suppression of solutions around these values. We argue that this is the explanation for the observed modulation in the ω distribution of GaiaOrbital solutions.
 |
Fig. D.4. Density histogram of published significance as a function of ω for DR3 Orbital solutions. The solid curve shows the running median value. The dashed curve shows the median of the Monte Carlo-resampled significance. |
D.3. Geometric element conversion from Thiele-Innes parameters in the presence of uncertainties
The archive tables list the fitted astrometric-orbit parameters P, e, T0, A, B, F, G with their formal uncertainties and the corr_vec field contains the correlation strengths between those parameters. When converting A, B, F, G to geometric orbit elements and determining their uncertainties we therefore have to account for their covariances. This can be done with classical error propagation using some form of linearisation of the parameter dependencies or by Monte Carlo simulations. As also pointed out in Babusiaux et al. (2023), the distributions of the geometric parameters are often non-Gaussian, which favours the latter approach.
We used Python implementations of both methods25 to investigate the value and uncertainty estimates of i, Ω, and ω for the non-circular Orbital solution in DR3. One finding is that the inclination uncertainty generally increases towards face-on configurations and that the linearised uncertainty estimate is usually comparable to the Monte Carlo estimate, except for large uncertainties ≳10° where the former is larger. There are only few cases where the discrepancy between the two different inclination estimates is larger than the linearised uncertainty.
The significance estimates using linearised error propagation can be different from alternative estimates that use Monte Carlo resampling for obtaining 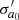 . These differences typically become important for solutions with poorly constrained eccentricities (i.e. e/σe < 1) for which Monte Carlo resampling is not recommended because of overestimated variances of the Thiele-Innes coefficients (Babusiaux et al. 2023; Holl et al. 2023b). In Fig. we see that the correlation between the Monte Carlo-resampled semi-major axis significance and ω is slightly weaker, i.e. has a smaller amplitude variation, than for the published significance.
. These differences typically become important for solutions with poorly constrained eccentricities (i.e. e/σe < 1) for which Monte Carlo resampling is not recommended because of overestimated variances of the Thiele-Innes coefficients (Babusiaux et al. 2023; Holl et al. 2023b). In Fig. we see that the correlation between the Monte Carlo-resampled semi-major axis significance and ω is slightly weaker, i.e. has a smaller amplitude variation, than for the published significance.
Appendix E: Primary mass computation
We use the PARSEC isochrones26 (Bressan et al. 2012) with ages τ by steps of 0.01 in log(τ) and metallicity [M/H] from −2 to 0.4 dex by steps of 0.05. Considering that the mass distribution of the isochrones is not uniform and that the age sampling is in log, weights need to be applied to each isochrone point i: P(i) = P(ℳ, τ, [M/H]) = P(ℳ)P(τ)P([M/H]). For P(ℳ) we use the Chabrier (2001) IMF, for P(τ) a flat star formation rate and for P([M/H]) a Gaussian centred on zero with a dispersion of 0.05 so that by default the solar isochrones will drive the mass determination. The default mass sampling being too sparse at the bottom of the main sequence, we interpolated the isochrones with finer mass steps. We removed the lowest mass stars which present a step feature in the isochrone HRD which is not observed in the Gaia DR3 HRD, so that the masses can only be derived for MG < 14.4 which corresponds to ℳ > 0.1 ℳ⊙. We also removed points outside a very crude age–metallicity relation that is [M/H]< − 0.4 − 0.05τ for τ > 10 or [M/H]> 0.5 − 0.05τ.
 |
Fig. E.1. Density plot of the comparison between the primary masses derived here with the FLAME ones for systems with fluxratio < 0.01. |
 |
Fig. E.2. HRD of the NSS astrometric solutions without a primary mass estimate. The grey background is the HRD of the full DR3 low-extinction stars (A0 < 0.05 according to Lallement et al. 2019), equivalent to Fig. 5 of Gaia Collaboration (2018a). The orange points are identified as giants. The red points do not have isochrone match. Violet + do not have an extinction estimate and uncorrected magnitude and colour are therefore used for those. Green points are the white dwarfs with a mass of 0.65 ± 0.16 ℳ⊙ assumed for Table 3. |
Our observables are the absolute magnitude MG and the colour (BP − RP)0, noted below 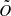 . Through Bayes’s theorem and considering that the isochrone point i contains the ℳ information, we have:
. Through Bayes’s theorem and considering that the isochrone point i contains the ℳ information, we have:
To allow for small systematic errors in the Gaia photometry, we quadratically add a 0.01 mag error to the G, GBP, GRP formal magnitude errors.
To avoid the presence of outliers in azero_gspphot, especially at the bottom of the MS (Babusiaux et al. 2023), we use the 3D extinction map of Lallement et al. (2019) to provide an estimate of the extinction A0. Most of the sources in the MS are within the completeness limit of this map. A 10% relative error on the extinction with a minimum error of 0.01 is assumed. We derive the extinction coefficients kG, kBP, kRP from the EDR3 extinction law27.
We know that the position on the HRD provides a direct estimate on the mass only for MS stars. We therefore remove all isochrone points with PARSEC label=0 (pre-MS stage) before applying Eq. and only provide a mass estimate for stars with more than half of the isochrone points at 3σ from the observables with PARSEC label=1 (main sequence stage). When several flux ratios are tested, the label of the smallest valid one is used for the MS star selection. Therefore no mass estimate is provided for giant stars and mass estimates for pre-MS stars will not be valid.
For each flux ratio F2/F1 tested, we obtain the absolute magnitude to be compared with the isochrones with:
and the colour simply with GBP − GRP − (kBP − kRP)A0. We note that we do not consider the change in colour induced by the presence of the secondary. The mass is then fully driven by MG. We consider that the resulting mass distribution obtained through Eq. is valid if we have more than five isochrone points within 3σ in both magnitude and colour to be compared with our star and if the closest isochrone point has a χ2 p-value larger than 0.01.
Our derived masses are compared with the FLAME ones for systems with a small flux ratio in Fig. E.1. As expected those are fully consistent within the errors quoted, with less than 1% of 5σ outliers. For the small masses, we see the overestimation trend of the FLAME masses due to the overestimation of the GSP-Phot extinction for stars with MG > 7 (Babusiaux et al. 2023), corresponding to ℳ < 0.7 ℳ⊙.
Figure shows the location in the HRD of the sources with an astrometric solution but no primary mass estimate obtained from our procedure. They have all been corrected by the extinction except those without an extinction estimate. Apart from giants, young stars above the main sequence are missed by construction as well as a few subdwarfs and sources too faint to have a reliable GBP.
Appendix F: Acronyms
List of acronyms used in this paper. Each acronym is also defined at its first occurrence in the paper.
All Tables
Comparison of the PMa and NSS astrometric detection rate on the common HIPPARCOS star sample.
Sizes of the SB1 sample involving RGB and AGB primaries for different filtering on the significance threshold.
A few illustrative examples of ellipsoidal variables (Plpv/Pnss = 0.5) mistaken as LPVs in the vari_long_period_variable table, LPVs with a pseudo SB1 orbit (Plpv/Pnss = 1, ΔG > 0.1 mag, Plpv > 180 d) in the nss_two_body_orbit table and short-period (Plpv < 100 d) ‘LPVs’ with Plpv/Pnss = 1.
Source candidates with compact object companions with m2_lower > 3 ℳ⊙ and m2_lower > m1_upper from SB1 solutions with significance > 20.
Known substellar companions with a confirmed mass in the planetary and brown dwarf regime, respectively.
List of acronyms used in this paper. Each acronym is also defined at its first occurrence in the paper.
All Figures
 |
Fig. 1. Magnitude distribution for each solution type in the nss_two_body_orbit table. |
| In the text | |
 |
Fig. 2. Number of solutions for each solution type in the nss_two_body_orbit table as a function of period. |
| In the text | |
 |
Fig. 3. G apparent magnitude vs. period in the nss_two_body_orbit table. |
| In the text | |
 |
Fig. 4. Gaia HRD, uncorrected for extinction, for all NSS solutions with a relative parallax error of better than 20%. No selection is done on the photometric quality. The colour scale represents the square root of the relative density of stars. Top: astrometric binaries, (a): allOrbital*solutions plusAstroSpectroSB1, (b): Acceleration solutions, (c): VIMF; bottom: Spectroscopic binaries with (d): SB* orbits and (e): NonLinearSpectro, (f): eclipsing binaries. |
| In the text | |
 |
Fig. 5. K1 semi-amplitude vs. period diagram of SB1 solutions, colour coded according to their astrometric_excess_noise. The diagram shows the presence of an overdensity of solutions at periods near the precession period (marked with a vertical line) with large astrometric excess noise. The histogram at the top shows the density of solutions with astrometric excess noise larger than 1 mas (blue line) and of those with ipd_frac_multi_peak > 20 (orange line). |
| In the text | |
 |
Fig. 6. Sky density factor (Galactic coordinates, healpix level 4, log scale, see text) illustrating the excess or deficit factors of NSS sources compared to their sky average value. Panel a: SB*, panel b: Acceleration, panel c: EclipsingBinary, panel d: Orbital*. |
| In the text | |
 |
Fig. 7. Ratio of the number of photometric observations over their median values for G < 18 (left) and the ratio of the number of visibility periods used in astrometry over their median values for G < 15 (right), with the same colour scale (from |
| In the text | |
 |
Fig. 8. Density histograms of simulated orbit signal dispersion as a function of cos i (top) and Ω (bottom). The black solid curve shows the running median value. Top panel: the empirical and analytic models are shown as dashed grey and black lines, respectively. Edge-on orbits have cos i = 0 and face-on configurations have |cos i |=1. |
| In the text | |
 |
Fig. 9. Fraction of NSS solutions among EDR3 sources vs. parallax (left) and fraction of NSS sources in GCNS (right). In both figures, we added AstroSpectroSB1 counts to Orbital counts and to SB*=SB1+SB2 counts in addition to counting them individually, and we restrict the ratios to GRVS < 12 sources only for SB* and NonLinearSpectro, to G < 19 for Orbital and Acceleration solutions, and to G < 20 for eclipsing binaries. |
| In the text | |
 |
Fig. 10. Fraction of NSS solutions among GCNS sources vs. G apparent magnitude (left) and vs. G GSP-Phot absolute magnitude (right). The same constraints as mentioned in Fig. 9 have been applied. |
| In the text | |
 |
Fig. 11. Normalised distributions of cos i (left), Ω (middle), and ω (right) parameters. Orbital (solid lines, 122 989 entries) and AstroSpectroSB1 (dashed lines, 29 770 entries) solutions with P < 1000 d are shown. The orb6 solutions from the literature (3405 entries, without filter on period) are shown in grey. Left panel: the dotted line shows the empirical model defined in Sect. 3.2, which was re-scaled on the five central histogram bins. Right panel: we have suppressed the circular solutions with ω = 0. |
| In the text | |
 |
Fig. 12. Normalised distributions of cos i within 200 pc for Orbital (solid line, 9106 entries) and AstroSpectroSB1 (grey-filled, 5735 entries) solutions with P < 1000 d and ϖ > 5 mas. The dashed line shows the empirical model defined in Sect. 3.2. |
| In the text | |
 |
Fig. 13. Normalised distributions of cos i for non-circular Orbital solutions with P < 1000 d (121 207 entries). The linearised and Monte Carlo estimates are shown as a solid line and a filled grey area, respectively. |
| In the text | |
 |
Fig. 14. Histogram of the number of NSS stars with different solution types that are present in the HIPPARCOS catalogue, as a function of the S/N of their Gaia DR3 proper motion anomaly from Kervella et al. (2022). The total number of targets N and the fraction of stars with a PMa S/N larger than 3 is displayed in each panel. |
| In the text | |
 |
Fig. 15. Proper motion anomaly S/N as a function of the NSS catalogue orbital period for the DR2 PMa (top panel) from Kervella et al. (2019a); and the EDR3 PMa (bottom panel) from Kervella et al. (2022). The horizontal dashed line indicates the PMa S/N = 3 significance limit. |
| In the text | |
 |
Fig. 16. Comparison of the long-term proper motions determined from the HIPPARCOS and Gaia DR3 positions μHG with the Gaia DR3 proper motions μNSS for NSS stars with acceleration solutions (left panel) and orbital solutions (right panel). We highlight the different scales. |
| In the text | |
 |
Fig. 17. Distribution of the secondary mass of astrometric solutions with fluxratio_upper = 0 in Table 3. |
| In the text | |
 |
Fig. 18. Eccentricity vs. period for most solutions with orbits. |
| In the text | |
 |
Fig. 19. Location in the dereddened HRD of the (GBP, 0 − GRP, 0) bins used in Fig. 20. Small blue dots correspond to the SB1s not selected by our selection criteria. The radius is the FLAME estimate. |
| In the text | |
 |
Fig. 20. The e − P diagram for SB1s along the main sequence, filtered according to significance factors larger than 10, 20, or 40 (from left to right), and for different (GBP, 0 − GRP, 0) spans (top to bottom). Filtering on the significance removes potentially spurious high-eccentricity solutions at small periods with the side effect of removing long period solutions. The drop in the number of systems at P = 0.5 yr due to insufficient sampling at this specific period. The color codes for the FLAME radius estimate. |
| In the text | |
 |
Fig. 21. Period–radius diagram for all SB1 solutions falling along the RGB and AGB according to criterion (5), and with a radius available from radius_flame. The dashed lines correspond to the threshold periods expressed by Eq. (7) for ℳ1 = 1.3 ℳ⊙ and ℳ2 = 1.0 ℳ⊙ (red dashed line) and ℳ1 = 1.3 ℳ⊙ and ℳ2 = 0.2 ℳ⊙ (cyan dashed line). Left (a): unfiltered, 44 706 SB1 solutions (among which 3056 unphysical, that is, below the cyan dashed line). Middle (b): filtered by significance K1/σK1 > 20, 27 404 solutions are rejected and 17 302 are kept (among which 214 unphysical). Right (c): filtered by significance > 40, 37 850 solutions are rejected and 6856 are kept (among which 21 unphysical). |
| In the text | |
 |
Fig. 22. e − P diagrams for all SB1 (left panel: unfiltered; adequately filtered e − P diagrams for SB1 with an RGB and AGB primary are presented in Fig. 24) and astrometric (right panel) solutions falling along the RGB and AGB according to criterion (5), and with a radius available from radius_flame. We highlight the restricted period scale of the astrometric binaries as compared to the SB1, and the lack of binaries with periods close to 1 yr among astrometric binaries. |
| In the text | |
 |
Fig. 23. P − f(ℳ) diagrams for SB1 along the RGB/AGB. Left (a): unfiltered. The yellow tail extending down to f(ℳ) ∼ 10−5 ℳ⊙ at periods in the range 300−800 d corresponds to pseudo-orbits associated to long-period pulsators (see Sect. 6.2.3). Middle (b): filtered by significance > 20 and > 40 (right (c)). |
| In the text | |
 |
Fig. 24. e − P diagram for SB1 systems along the giant branch, filtered according to significance factors larger than 40, for various radius spans. Top panel: is the full sample. The solid black lines correspond to the loci where P(1 − e)3 is constant (see text). The sample sizes are, from top to bottom, 1960, 2358, 1643, 737, and 40. The location in the HRD of the SB1 systems with 0.7 < log(R/R⊙)≤1.0 (second panel from top), 1.3 < log(R/R⊙)≤1.6 (fourth panel from top) and 1.9 < log(R/R⊙) (bottom panel) is shown in Fig. 25. |
| In the text | |
 |
Fig. 25. Location in the HRD of three among the samples displayed in Fig. 24, namely 0.7 < log(R/R⊙)≤1.0 (dots), 1.3 < log(R/R⊙)≤1.6 (plus symbols), and 1.9 < log(R/R⊙) (crosses). Small cyan dots correspond to the SB1 not selected by our selection criteria. See Table 5 for a full discussion of the properties of the yellow crosses. |
| In the text | |
 |
Fig. 26. Orbital period from the nss_two_body_orbit table vs. photometric period from the vari_long_period_variable table. Top, middle, and bottom panels: correspond to different filtering based on the SB1 significance (respectively, larger than 5, 20, and 40). The two sequences observed in all panels correspond to Plpv/Pnss = 0.5 (ellipsoidal variables; upper sequence) and Plpv/Pnss = 1 (LPVs or rotational modulation in a synchronised system; lower sequence). Top panel: crosses denote NSS solutions for which the Roche-lobe filling factor is above unity, and therefore unphysical. The filtering with significance larger than 40 makes these latter disappear almost entirely. |
| In the text | |
 |
Fig. 27. Location in the infrared colour–magnitude diagram of the stars with 0.45 ≤ Plpv/Pnss ≤ 0.55 (ellipsoidal variables) from Table 6 (dots). Stars with 0.95 ≤ Plpv/Pnss ≤ 1.05 are represented by crosses; they appear in two different locations, among LPVs with low orbital significance on one hand, and among less luminous giants with much larger orbital significance on the other, perhaps suggesting starspot modulation or short-period pulsators. The dots (Plpv/Pnss ∼ 0.5) fall in between these two groups, as they are located just below the tip of the RGB. |
| In the text | |
 |
Fig. 28. Folded Gaia G, GBP, and GRP photometry and RV data of HD 23692, together with TESS binned data. Top panel: Gaia RV data, while the second panel presents the Gaia G data. Third panel: Gaia GBP and GRP data, with medians shifted to the Gaia G median for clarity, and the bottom panel presents the TESS data binned to 200 phase bins. All plots were folded using the Gaia EB-model period and deeper-eclipse epoch as the folding period and phase zero, respectively. We note that the primary eclipse is at phase 0.5, while the secondary eclipse is at phase zero. Observed TESS-eclipse phase drift is due to the more than 1300 day delay from the last Gaia point to the first TESS point. For clarity, the three bottom panels use the same y-axis scale. |
| In the text | |
 |
Fig. 29. Histogram of phase difference between SB-model primary eclipse and EB-model deeper eclipse, for 1174 stars in our sample. |
| In the text | |
 |
Fig. 30. Gaia and TESS data of four new EL CVn candidates presented as in Fig. 28. We could not find TESS photometry for Gaia DR3 2048990809445098112, so its TESS panel was left empty. |
| In the text | |
 |
Fig. 31. Colour–magnitude diagram of 533 sources with OrbitalTargetedSearch* solutions (black circles). The larger grey circles indicate sources that are listed in the GUCD sample (Smart et al. 2019), the grey squares indicate red sources discussed in the text, and the diamond indicates the WD discussed in Sect. 8.8. |
| In the text | |
 |
Fig. 32. Orbital eccentricity as a function of period for the UCD systems listed in Table 8 (black symbols). The parameters of Orbital solutions within 200 pc are shown in grey. |
| In the text | |
 |
Fig. 33. Triage of the Gaia astrometric binaries, with classes I to III from bottom to top delineated by dotted and dashed lines respectively. Left: AMRF vs. mass of the primary for the astrometric solutions of this paper. The systems with a probable compact-object companion (class III) are presented as bold black points (see text). For reference, the rest of the sample is plotted as fine black points. Right: masses of the compact companions derived from the AMRF as a function of their primary mass. The remaining systems do not appear in this panel. The yellow star is the neutron star candidate Gaia DR3 5136025521527939072 discussed in Sect. 7.3. |
| In the text | |
 |
Fig. 34. Left: comparison between the minimum companion mass derived in Sect. 5.1, and the AMRF-derived masses for the compact-object candidates. The sources where the AMRF mass is smaller than the minimum mass are AstroSpectroSB1, which have a non-negligeable flux ratio. Right: comparison between semi-major axes derived for the AstroSpectroSB1 systems using the astrometric parameters (horizontal axis) and the spectroscopic parameters (vertical axis). The yellow star is Gaia DR3 5136025521527939072. |
| In the text | |
 |
Fig. 35. Class-III CMD. Black points show Orbital and AstroSpectro objects for reference. Red points are AMRF class-III. The yellow star is Gaia DR3 5136025521527939072. |
| In the text | |
 |
Fig. 36. A histogram of the companion masses for compact object candidates up to a mass of 2.1 ℳ⊙. |
| In the text | |
 |
Fig. 37. e − P diagram. Black points are Orbital and AstroSpectro objects for reference. Red points are AMRF class-III. The yellow star is Gaia DR3 5136025521527939072. |
| In the text | |
 |
Fig. 38. HRD of the candidate NSSs with WD components with a secondary mass solution below the Chandrasekhar limit (< 1.4 ℳ⊙, green data points). These are compared with the locus of stars in the GCNS (grey data points). |
| In the text | |
 |
Fig. 39. WD with orbital solutions (green points, corrected from extinction) overplotted on the Gaia DR3 low-extinction HRD. Most of the points lie above the hydrogen sequence. The red dots and WD 0141–675 (orange square) are discussed in Sect. 8.8. |
| In the text | |
 |
Fig. 40. G vs. GBP − GRP HRD showing the cross-match between the GALEX GR6+7 AIS catalogue with the GCNS (small symbols) and the candidate list of binaries with WD components with computed secondary star masses below the Chandrasekhar limit (< 1.4 ℳ⊙). The symbols are colour coded with the absolute NUV magnitude. |
| In the text | |
 |
Fig. 41. G vs. GBP − GRP HRD showing the cross-match between the GALEX GR6+7 AIS catalogue with the GCNS (small symbols) and the candidate list of binaries with WD components with computed secondary star masses below the Chandrasekhar limit (< 1.4 ℳ⊙). The symbols are colour coded with the absolute FUV magnitude. |
| In the text | |
 |
Fig. 42. G vs. GBP − GRP HRD showing the cross-match between the GALEX GR6+7 AIS catalogue and the full list of non-SB2 binaries selected here (large symbols). The symbols are colour coded according to absolute FUV magnitude as indicated by the side-bar. The small grey data points are the full list of non-SB2 binaries. |
| In the text | |
 |
Fig. 43. Top panel: phase-folded radial velocity data of Gaia DR3 5136025521527939072, together with the orbits using the astrometric (red dot-dashed line) and spectroscopic (blue solid line) orbital elements separately; the OHP/Sophie external measurement (green squared point) was not part of the fit. Bottom panel: along-scan residuals of the mean epoch astrometric measurements (black symbols) relative to the model positions (grey circles) and the astrometric orbit (red solid line) of the same source. The red cross marks the focus of the orbit and the grey square is the periastron location. |
| In the text | |
 |
Fig. 44. HRD of SB1 solutions with f(ℳ) > 1.4 ℳ⊙ and significance > 20. Squared symbols are for sources with 1.4 ℳ⊙ < f(ℳ)≤3 ℳ⊙, star symbols for sources with f(ℳ) > 3 ℳ⊙. The background grey scale shows the density distribution of all SB1 solutions. |
| In the text | |
 |
Fig. 45. Dereddened HRD of compact object companion candidates from SB1 solutions on the main sequence. Circle symbols are for sources with m2_lower ≤ 1.4 ℳ⊙, square symbols are for sources with 1.4 ℳ⊙ < m2_lower ≤ 3 ℳ⊙, and stars symbols are for sources with m2_lower > 3 ℳ⊙. The background grey scale shows the density distribution of all SB1 solutions classified as belonging to the main sequence by IsocLum. |
| In the text | |
 |
Fig. 46. Top panel: phase-folded radial velocity of Gaia DR3 2966694650501747328 (P = 10.398 d). Bottom panel: phase-folded TESS (black circles) and Gaia normalised flux (green, blue, and red circles: flux in G, GBP, and GRP bands respectively). |
| In the text | |
 |
Fig. 47. HRD of sources with low astrometric mass functions (< 0.001 ℳ⊙; green dots); the grey background is the DR3 low-extinction HRD. A very large fraction are not stars with low-mass companions, but rather binaries with a mass ratio similar to their flux ratio. The two blue sources are HD 12800 and HD 3221, described in Sect. 8.7 while the four WDs are discussed in Sect. 8.8. |
| In the text | |
 |
Fig. 48. Primary mass distributions for sources with astrometrically detected substellar companions with Orbital (long-dashed histogram) and OrbitalTargetedSearch* (solid-line histogram) solution types. |
| In the text | |
 |
Fig. 49. Top: substellar companion mass distribution for the OrbitalTargetedSearch* solution type. Centre: same as above, but for the Orbital solution type, with a cut-off in the primary mass ℳ⋆ < 0.6 ℳ⊙. Bottom: same again, but for the Orbital solution type, with a cut-off in the primary mass ℳ⋆ > 0.6 ℳ⊙. |
| In the text | |
 |
Fig. 50. Top: primary mass distribution for sources with SB1 solution type and inferred minimum companion masses in the substellar regime. Bottom: substellar companion mass distribution for the SB1 solution type. |
| In the text | |
 |
Fig. 51. Distribution of outer vs. inner periods for triple systems found by matching Orbital with SB1 (circles), SB2 (squares), and SB2C solutions (triangles), coloured by the ratio of spectroscopic to astrometric semi-amplitudes. The solid line shows the limit POrbital = 5 PSB. Top panel: integrated distribution of inner periods. |
| In the text | |
 |
Fig. 52. Distribution of inner periods for triple systems found by comparing astrometric acceleration and SB solutions. |
| In the text | |
 |
Fig. 53. Distribution of outer vs. inner periods for triple systems found in the El-Badry catalogue. Left scale: period. Right scale: separation. The line in the bottom right corner shows the limit Pout = 5 Pin. |
| In the text | |
 |
Fig. 54. Distribution of inner periods for triple systems found in the El-Badry catalogue. |
| In the text | |
 |
Fig. C.1. Left: Orbital plane ellipse with width a and height b (the circular case a = b = 1 is shown). Middle: Sky-projected plane with scan angle ψ and projected orbit due to inclination i shown in the right panel. |
| In the text | |
 |
Fig. D.1. Simulated (filled grey) and recovered (solid line) distributions of cos i for six levels of signal-to-noise as explained in the text. The vertical dashed line at i = 90° indicates the edge-on configurations. |
| In the text | |
 |
Fig. D.2. Simulated (filled grey) and recovered (solid line) distributions of Ω at S/N = 0.01. |
| In the text | |
 |
Fig. D.3. Simulated (filled grey) and recovered (solid line) distributions of ω for non-circular orbits with e = 0.5 at S/N = 0.01. |
| In the text | |
 |
Fig. D.4. Density histogram of published significance as a function of ω for DR3 Orbital solutions. The solid curve shows the running median value. The dashed curve shows the median of the Monte Carlo-resampled significance. |
| In the text | |
 |
Fig. E.1. Density plot of the comparison between the primary masses derived here with the FLAME ones for systems with fluxratio < 0.01. |
| In the text | |
 |
Fig. E.2. HRD of the NSS astrometric solutions without a primary mass estimate. The grey background is the HRD of the full DR3 low-extinction stars (A0 < 0.05 according to Lallement et al. 2019), equivalent to Fig. 5 of Gaia Collaboration (2018a). The orange points are identified as giants. The red points do not have isochrone match. Violet + do not have an extinction estimate and uncorrected magnitude and colour are therefore used for those. Green points are the white dwarfs with a mass of 0.65 ± 0.16 ℳ⊙ assumed for Table 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



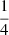
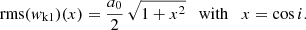
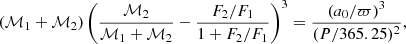
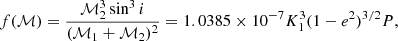
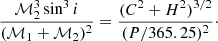
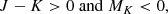
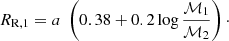
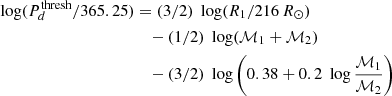
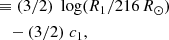
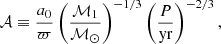
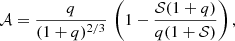
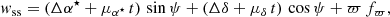
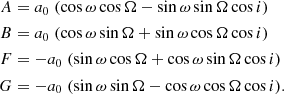

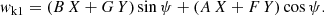
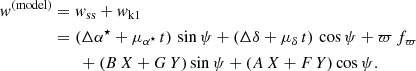
![$$ \begin{aligned} \mathrm{RV}_1(t) = \gamma \, + \, K_1 \left[\cos (v(t)+\omega ) + e \, \cos (\omega )\right], \end{aligned} $$](/articles/aa/full_html/2023/06/aa43782-22/aa43782-22-eq60.gif)