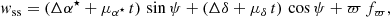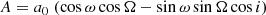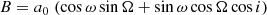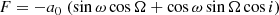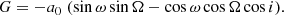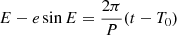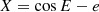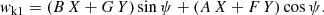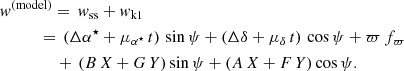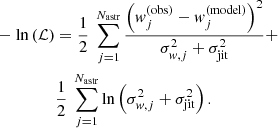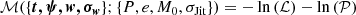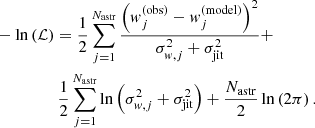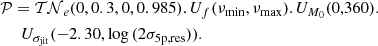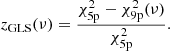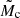| Issue |
A&A
Volume 674, June 2023
Gaia Data Release 3
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 27 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/202244161 | |
| Published online | 16 June 2023 | |
Gaia Data Release 3
Astrometric orbit determination with Markov chain Monte Carlo and genetic algorithms: Systems with stellar, sub-stellar, and planetary mass companions⋆
1
Department of Astronomy, University of Geneva, Chemin Pegasi 51, 1290 Versoix, Switzerland
e-mail: berry.holl@unige.ch
2
Department of Astronomy, University of Geneva, Ch. d’Ecogia 16, 1290 Versoix, Switzerland
3
INAF – Osservatorio Astrofisico di Torino, Via Osservaorio 20, 10025 Pino Torinese, Italy
4
RHEA Group for the European Space Agency (ESA), European Space Astronomy Centre (ESAC), Camino Bajo del Castillo s/n, 28692 Villanueva de la Cañada, Madrid, Spain
Received:
31
May
2022
Accepted:
1
October
2022
Context. The astrometric discovery of sub-stellar mass companions orbiting stars is exceedingly hard due to the required sub-milliarcsecond precision, limiting the application of this technique to only a few instruments on a target-per-target basis and to the global astrometry space missions HIPPARCOS and Gaia. The third Gaia data release (Gaia DR3) includes the first Gaia astrometric orbital solutions whose sensitivity in terms of estimated companion mass extends down to the planetary-mass regime.
Aims. We present the contribution of the exoplanet pipeline to the Gaia DR3 sample of astrometric orbital solutions by describing the methods used for fitting the orbits, the identification of significant solutions, and their validation. We then present an overview of the statistical properties of the solution parameters.
Methods. Using both a Markov chain Monte Carlo and a genetic algorithm, we fitted the 34 months of Gaia DR3 astrometric time series with a single Keplerian astrometric-orbit model that had 12 free parameters and an additional jitter term, and retained the solutions with the lowest χ2. Verification and validation steps were taken using significance tests, internal consistency checks using the Gaia radial velocity measurements (when available), as well as literature radial velocity and astrometric data, leading to a subset of candidates that were labelled “validated”.
Results. We determined astrometric-orbit solutions for 1162 sources, and 198 solutions were assigned the “Validated” label. Precise companion-mass estimates require external information and are presented elsewhere. To broadly categorise the different mass regimes in this paper, we use the pseudo-companion mass M̃c assuming a solar-mass host and define three solution groups: 17 (9 validated) solutions with companions in the planetary-mass regime (M̃c < 20 MJ), 52 (29 validated) in the brown dwarf regime (20 MJ ≤ M̃c ≤ 120 MJ), and 1093 (160 validated) in the low-mass stellar companion regime (M̃c > 120 MJ). From internal and external verification and validation, we estimate the level of spurious and incorrect solutions in our sample to be ∼5% and ∼10% in the ‘OrbitalAlternative’ and ‘OrbitalTargetedSearch’ candidate sample, respectively.
Conclusions. We demonstrate that Gaia is able to confirm and sometimes refine the orbits of known orbital companions and to identify new candidates, providing us with a positive outlook for the expected harvest from the full mission data in future data releases.
Key words: astrometry / planets and satellites: detection / techniques: radial velocities / catalogs / brown dwarfs / binaries: general
Tables refsols.dat, bd-18113.dat, 46_10046.dat, gj812a.dat, gj9732.dat, hd26596.dat, hd40503.dat, hd68638.dat, hd89010.dat, hd134237.dat, hd183162.dat, hip9095.dat, and toi-288.dat are only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/674/A10
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The third Gaia data release (Gaia DR3, Gaia Collaboration 2023b) is the first release that includes non-single star (NSS) solutions (Gaia Collaboration 2023a; Pourbaix et al. 2022). The main astrometric NSS processing, which we refer to as the “binary pipeline”, is described in Halbwachs et al. (2023). It analysed sources that failed a single-star model using a cascade of double-star models of increasing complexity, up to the determination of a full orbital solution for one companion. An alternative NSS processing module is the subject of this paper, which we call the “exoplanet pipeline”. It was designed with the twofold goal of a) modelling higher-complexity NSS signals, such as those produced by multiple companions, and b) providing further insight into the regime of low-amplitude signals, such as those produced by sub-stellar companions, that is, exoplanets and brown dwarfs, around nearby stars. In Gaia DR3, we do not provide results for multiple companions because only a limited number of observations is available to constrain the solution. The per-source computational effort is higher for the exoplanet pipeline, and the default channel for NSS processing is therefore the binary pipeline.
The design of the exoplanet pipeline takes advantage of some of the lessons learned from Doppler searches for planets. In particular, the modelling of complex, low-amplitude planetary signals can be prone to ambiguities in the interpretation of the results, with well-known cases in the recent literature of disagreement on the actual values of the orbital elements of a given companion or on the number of companions, also depending on the details of the treatment of noise sources in the radial velocity (RV) measurements. A non-exhaustive list of controversies in RV surveys includes the planetary systems around α Cen B (Dumusque et al. 2012; Hatzes 2013; Rajpaul et al. 2016), τ Ceti (Pepe et al. 2011; Tuomi et al. 2013; Feng et al. 2017b), GJ 667C (Anglada-Escudé et al. 2012, 2013; Delfosse et al. 2013; Feroz & Hobson 2014; Robertson & Mahadevan 2014), GJ 581 (Vogt et al. 2010; Baluev 2013; Robertson et al. 2014, 2015a; Anglada-Escudé & Tuomi 2015; Hatzes 2016; Trifonov et al. 2018), GJ 176 (Endl et al. 2008; Butler et al. 2009; Forveille et al. 2009), HD 41248 (Jenkins et al. 2013; Jenkins & Tuomi 2014; Santos et al. 2014; Feng et al. 2017a; Faria et al. 2020), Barnard’s Star (Ribas et al. 2018; Lubin et al. 2021), Kapteyn’s Star (Anglada-Escudé et al. 2014, 2016; Robertson et al. 2015b), GJ 3998 (Affer et al. 2016; Dodson-Robinson et al. 2022), Lalande 21185 (Butler et al. 2017; Díaz et al. 2019; Stock et al. 2020; Rosenthal et al. 2021; Hurt et al. 2022), BD −06° 1339 (Lo Curto et al. 2013; Simpson et al. 2022), and HD 219134 (Motalebi et al. 2015; Vogt et al. 2015; Gillon et al. 2017).
These considerations prompted us to adopt a methodological approach that implements two different algorithms for alternative orbit fitting of Gaia DR3 astrometry. The exoplanet pipeline was applied to process two datasets: the first contained a large number of sources for which none of the models attempted in the binary pipeline was able to successfully improve upon the single-star fit based on the adopted thresholds on goodness-of-fit and significance statistics. These are labelled either ‘OrbitalAlternative’ or ‘OrbitalAlternativeValidated’, and the combination of the two sets is labelled ‘OrbitalAlternative[Validated]’ (or ‘OrbitalAlternative*’ for short). The second dataset constituted a much smaller collection of high-visibility sources, either because of their intrinsic nature or because of already known sub-stellar and low-mass stellar companions around them. These are labelled either ‘OrbitalTargetedSearch’ or ‘OrbitalTargetedSearchValidated’, and the combination of the two sets is labelled ‘OrbitalTargetedSearch[Validated]’ (or ‘OrbitalTargetedSearch*’ for short).
In this paper we provide an overview of the exoplanet pipeline, describe the functioning of the two orbit-fitting algorithms in detail, and discuss the main characteristics of the orbital solution results obtained for the two processing experiments described above, which have been included in the Gaia DR3 archive of NSS solutions. It is important to point out that orbital solutions compatible with sub-stellar mass companions can also be found in the output of the binary pipeline (see Halbwachs et al. 2023; Gaia Collaboration 2023a).
Our paper is organised as follows: in Sects. 2 and 3 we briefly discuss the properties of the astrometric data and the model we fit to it. Section 4 describes the algorithms we used to derive the orbital solutions and the procedure to select the best solutions. The input-source selection and solution-filtering procedures are detailed in Sect. 5, and the results are verified and validated in Sect. 6. We conclude in Sect. 7 with additional details regarding the reference solution data and Gaia archive queries in Appendices A and B, respectively.
2. Properties of the astrometric data
The input data span about 34 months, as shown in Fig. 1. They consist of time series of along-scan abscissa measurements w with respect to the reference position (α0, δ0) derived in the Gaia EDR3 Astrometric Global Iterative Solution (AGIS; see Lindegren et al. 2021) together with the associated scan angles and parallax factors. Details as well as several pre-processing steps are described in Halbwachs et al. (2023) and in section 7.2.2 of the DR3 NSS documentation (Pourbaix et al. 2022), which includes per FoV1 CCD outlier rejection and modification of the measurements of stars with ϖ > 5 mas (i.e. within 200 pc) to take the perspective acceleration into account (to identify the latter, see flags in Sect. 3.3). Figure 2 shows the number of observations per source after outlier rejection. As expected, the minimum number of visibility periods2 is not smaller than about 13, that is, the number of parameters we solved for with a single-Keplerian orbit. Fitting for a second orbit would require an additional seven parameters and thus (at least) 20 visibility periods. For this and various other reasons, the general attempt to fit for more than one Keplerian was not made for Gaia DR3.
 |
Fig. 1. Histogram of the observation time spans. |
 |
Fig. 2. Histogram of the number of CCD observations and visibility periods. The number of CCD observations is divided by nine to provide the approximate number of FoV observations above the left panel. |
The mean and median of the per CCD uncertainties of each source are shown in Fig. 3. The outlier rejection applied in the binary pipeline pre-processing step did not remove all strong outliers in abscissa value and/or uncertainty, which generally is the reason for the difference between the mean and median. In the orbit figures that we show in Sect. 6.2.2, the persisting outliers are usually not displayed. We compare these data with the EDR3 median formal uncertainty ση of Lindegren et al. (2021, their Fig. A.1, red median line), here drawn as a grey line. To estimate the CCD AL-scan abscissa uncertainty σw in the astrometric NSS pipeline, the ση was first inflated by3fruwe(G, GBP − GRP), after which a (typical value of) 0.08 mas calibration noise was added in quadrature. The result is shown as the dotted line in Fig. 3. It matches the lower envelope of the median σw of our sources well.
 |
Fig. 3. Mean and median CCD AL-scan abscissa uncertainty σw per source. |
However, the abscissa data used for Gaia DR3 are generally affected by some level of under-/overestimation of uncertainties and potential biases, which can lead to unrealistic good or bad goodness-of-fit statistics. To mitigate the effects of these undefined noise contributions, we fitted for an additional jitter term similar to the AGIS astrometric_excess_noise, as explained in Sect. 3. It proved difficult to define general filtering criteria to distinguish a spurious from a significant solution. This task required additional procedures in which many sources were individually checked against literature data (in this release, leading to those labelled Validated; see Sect. 6).
3. Astrometric model
3.1. Mathematical description
As discussed in Sect. 2, the input data for the exoplanet pipeline are the Gaia along-scan abscissa measurements w. For a binary system and neglecting all noise considerations, these can be modelled by the combination of a single-source model wss, describing the standard astrometric motion of the system barycentre, and a Keplerian model wk1. The single-source model can be written as
where Δα⋆ = Δα cos δ and Δδ are small offsets in equatorial coordinates from some fixed reference point (α0, δ0), μα⋆ and μδ are proper motions in these coordinates, t is time since the reference time J2016.0, ϖ is the parallax, fϖ is the parallax factor, and ψ is the scan angle. The Gaia scan angle is defined as having a value of ψ = 0 when the field of view is moving towards local north, and ψ = 90° towards local east4. This is a different convention from the one used for HIPPARCOS (e.g., van Leeuwen 2007).
The astrometric motion corresponding to a Keplerian orbit of a binary system generally has seven independent parameters. These are the period P, the epoch of periastron passage T0, the eccentricity e, the inclination i, the ascending node Ω, the argument of periastron ω, and the semi-major axis of the photocentre a0. The Thiele-Innes coefficients A, B, F, and G, which linearise part of the equations, are defined as
The elliptical rectangular coordinates X and Y are functions of eccentric anomaly E and eccentricity,
The single-Keplerian model can then be written as
The combined model w(model) for the Gaia along-scan abscissa is
This model has been extensively used to model the HIPPARCOS epoch data of non-single stars (e.g., Sahlmann et al. 2011).
More details about the modelling of non-single star data in the Gaia pipelines can be found in the DR3 NSS documentation of Pourbaix et al. (2022) and in Halbwachs et al. (2023). In the latter, the instantaneous scan angle is described as the coordinate-derivative of the abscissa, that is 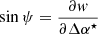 .
.
Finally, to account for potentially unmodelled signals or modelling errors, we additionally fit for a jitter term that was added in quadrature to the provided uncertainties of the along-scan abscissa, bringing the total number of fitted parameters to 13: five linear parameters for the single-source model wss, seven for the single-Keplerian model wk1 (of which the four A, B, F, and G parameters are linear), and one non-linear jitter term σjit.
Symmetric parameter uncertainty estimates were obtained by reconstructing the covariance matrix directly from the Jacobians of all parameters for all observations. No scaling of these formal covariances was performed, which might potentially suffer from over-/underestimations for example due to unmodelled signals (which might be partially absorbed by the jitter term).
3.2. Conversion of Thiele-Innes parameters into Campbell elements
The conversion of the Thiele-Innes parameters (A, B, F, G) into Campbell or geometric elements (a0, ω, Ω, i) is straightforward in principle (e.g., Halbwachs et al. 2023), but several caveats exist that are related to the amplitudes of the A, B, F, and G co-variance terms, which sometimes seem to be overestimated, in particular for solutions with poorly constrained eccentricities (see Gaia Collaboration 2023a; Babusiaux et al. 2023). In Sect. 6.1.6 we discuss some examples. Unless specifically mentioned, all figures with Campbell element values in this paper use the linear error propagation. Regarding the semi-major axis, in this work we always assume that the companion is sufficiently non-luminous for the semi-major axis of the photocentre and that of the observed host star to be the same, that is a1 = a0, and we only refer to a1.
3.3. Archive model parameter fields
Table 1 provides an overview of all solution parameters and additional fields populated for our sources in the nss_two_body_orbitGaia DR3 archive table. The goodness_of_fit is the F2, or so-called Gaussianised chi-square (Wilson & Hilferty 1931), which should approximately follow a normal distribution with zero mean value and unit standard deviation for good fits.
gaia_dr3.nss_two_body_orbit table fields filled for the 1162 sources from the exoplanet pipeline described in this paper.
The flags field only has integer values 0, 64, and 192. Value 0 means that no bit-flags were set. Value 64 means that bit 6 was set: this means that a mean RV value was available. Value 192 means that bits 6 and 7 were set, where bit 7 indicates that mean RV was used for a perspective acceleration correction of the local plane coordinates. Our published sample includes 164 sources with a flag value 0, 571 sources with a flag value 64, and 427 sources with a flag value 192 (see the result of the query provided in Appendix B for finer details).
The astrometric_n_obs_al provides the number of CCD observations that were available before outlier rejection. In the archive, the astrometric_n_good_obs_al should represent the number after outlier rejection, but erroneously, it reports the same value as astrometric_n_obs_al. Figure 2 shows the correct number of filtered (good) observations. For completeness, we document here that the number of rejected CCD observations varies between zero and 269. Zero to three observations are rejected for most, and fewer than 12 observations are rejected for even more.
We did not make use of the efficiency parameter in our verification, which incidentally is 0 for a large fraction of our sample.
Gaia photometric time series are available for 76 sources in our sample, that is sources in gaia_source with has_epoch_photometry=true. Of these, 75 overlap with the variable source catalogue (Eyer et al. 2023), and one source (367906215676634752) was released as part of the Gaia Andromeda Photometric Survey (Evans et al. 2023), which can be identified in gaia_source by phot_variable_flag=VARIABLE and in_andromeda_survey=true, respectively. In this Gaia DR3, no Gaia astrometric time series were made public.
4. Processing procedure
Astrometric orbit modelling requires solving a highly non-linear least-squares problem with a minimum of 12 parameters (Sect. 3). The orbital motion is usually seen as a small perturbation of the standard stellar motion, with a magnitude that can be orders of magnitude smaller than those of parallax and proper motion. This motivated the original design of the exoplanet element of the non-single-star (NSS) processing pipeline (see DR3 NSS documentation in Pourbaix et al. (2022) for the full NSS pipeline structure). In particular, it was recognised that orbit modelling in the limit of low signal amplitudes would benefit from a more in-depth (computationally expensive) parameter search. This meant the adoption of two independent orbit-fitting algorithms exploiting different philosophies, which we describe below in turn. Both algorithms are executed in parallel, and a standard recipe based on Bayesian model selection is used to select the best-fit solution, as further detailed below.
4.1. Differential evolution Markov chain Monte Carlo
The first orbit-fitting code is a hybrid implementation of a Bayesian analysis based on the differential evolution Markov chain Monte Carlo (DE-MCMC) method (Ter Braak 2006; Eastman et al. 2013). An earlier version of the code had been extensively tested in Casertano et al. (2008), while its upgrade has recently been used in Drimmel et al. (2021). In this scheme, we take advantage of the representation of the four (A, B, F, G) Thiele-Innes constants (see Sect. 3.1; see also e.g., Binnendijk 1960; Wright & Howard 2009) to partially linearise the problem. Within this dimensionality reduction scheme, only three non-linear orbital parameters must be effectively explored using the DE-MCMC algorithm (e.g., Casertano et al. 2008; Wright & Howard 2009; Mendez et al. 2017; Drimmel et al. 2021), namely P, T0, and e. The fourth model parameter that is explored in the DE-MCMC way is an uncorrelated astrometric jitter term σjit. At each step of the DE-MCMC analysis, the resulting linear system of equations is solved in terms of the Thiele-Innes constants using simple matrix algebra, QR decomposition being the method of choice. The final likelihood function used in the DE-MCMC analysis is then
The DE-MCMC analysis is carried out with a number of chains equal to twice the number of free parameters. A period search is first performed in order to identify statistically more probable periodicities. Because of the nature of the astrometric dataset, the direct application of publicly available tools for the periodogram analysis of unevenly sampled time-series (e.g., the generalised Lomb-Scargle periodogram; Zechmeister & Kürster 2009) is not possible. For any given source, the DE-MCMC module draws a large sample of initial trial periods for sinusoidal signals projected along the scan directions of the time series, based on a uniform grid that is up to twice as large as the observations time span. A sparsely sampled selection of periods corresponding to local χ2 minima becomes the seed for the P parameter initialisation of the DE-MCMC chains. Uniform priors in the ranges [−P/2,P/2] and Butler et al. (2001) mas are used for T0 and σjit, respectively. Finally, starting values for e are drawn from a Beta distribution following Kipping (2013).
Convergence and good mixing of the chains are checked based on the Gelman-Rubin statistics (e.g., Ford 2006). The medians of posterior distributions are taken as the final parameters. In order to comply with the choice of the main non-single-star processing chain (Halbwachs et al. 2023), we did not adopt the standard approach for computing the 1σ uncertainties on model parameters, that is evaluating the ±34.13 % intervals from the posterior distributions, which typically results in asymmetric error bars, but rather provided symmetric estimates of the uncertainties by reconstructing the covariance matrix directly from the Jacobians of all parameters for all observations.
4.2. Genetic algorithm
The implementation of the genetic algorithm for Gaia (MIKS-GA) is a direct adaptation of YORBIT, a tool used to search for exoplanets in radial velocity time series (Ségransan et al. 2011; Hébrard et al. 2016; Triaud et al. 2017, 2022; Kiefer et al. 2019). An implementation of the MIKS-GA algorithm has been successfully used to discover brown dwarf binaries from the orbital solutions identified in high-precision astrometric time series obtained with ground-based telescopes (Sahlmann et al. 2013, 2015a, 2020).
Genetic algorithms (GA) are a class of optimisation algorithms that are loosely based on Darwin’s theory of evolution by natural selection (Holland 1975; Jong 1988). In GA, a population of chromosomes is initialised and evolves by applying a set of genetic operators (e.g., crossover, recombination, mutation, and selection) until the best genotype dominates the population. These algorithms are particularly well suited for highly non-linear model with irregular sampling, provided that the genetic operators are fine-tuned to the specificity of the problem.
Here, a chromosome consists of the non-linear parameters needed to model a merit function ℳ defined as the sum of the log-likelihood and the log-prior. We further assume that the residuals of the astrometric data to the model are drawn from independent realisations of a normal distribution of zero mean with a variance composed of the astrometric uncertainty plus an additional jitter term that accounts for anything in the data that cannot be modelled by the analytical astrometric model. It results in the following expression of the merit function:
and in the log-likelihood
The prior expression is the product of uniform distributions for the mean anomaly M0 computed at J2016.0 (JD 2457388.5) in Gaia DR3 for the frequency (between 2.5 d and twice the observation time span) for the log of the jitter term (between [0.005, 2σ5p,res] mas, where σ5p,res is the standard deviation of the residuals of a five-parameter astrometric fit to the observations), and of a truncated normal distribution for the eccentricity (with μ = 0, σ = 0.3, truncated over [0, 0.985]) to penalise highly eccentric orbit solutions that commonly arise in time series with a low signal-to-noise ratio series with irregular sampling,
4.2.1. Initialisation phase
The initialisation phase of the chromosome population is based on a frequency analysis of the Gaia astrometric time series and on the analytical determination of orbital elements using Fourier analysis (Delisle & Ségransan 2022). To do this, a least-square periodogram (Lomb 1976; Scargle 1982) of the Gaia astrometric time series is built (Delisle & Ségransan 2022; see Eq. (15)), comparing for each frequency the chi-square of a circular orbit model plus the parallactic motion (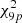 ) to the chi-square of the parallactic motion only (
) to the chi-square of the parallactic motion only (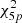 ),
),
The first step consists of drawing a set of frequencies from a log-uniform law log(𝒱) ∼ U(log(νmin), log(νmax, init)) (between 2.5 d and the observation time span), where frequencies with a lower significance according to the Signal Detection Efficiency statistic (SDE; see Alcock et al. 2000; Kovács et al. 2002) are redrawn until selected. This procedure discards periodic signals with lower probability from the initial population and in this way improves the efficiency of the GA.
The second step of the initialisation concerns the eccentricity and the mean anomaly. For 50% of the chromosomes, the eccentricity is drawn according to 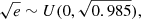 while the mean anomaly is uniformly drawn according to M0 ∼ U(0, 2π). For the remaining 50% of the chromosomes, the eccentricity and the mean anomaly are analytically derived using the signal frequency decomposition described in Delisle & Ségransan (2022) and drawn accordingly to
while the mean anomaly is uniformly drawn according to M0 ∼ U(0, 2π). For the remaining 50% of the chromosomes, the eccentricity and the mean anomaly are analytically derived using the signal frequency decomposition described in Delisle & Ségransan (2022) and drawn accordingly to 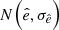 and
and 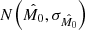 . Finally, the astrometric jitter σjit of each chromosome is drawn from a log-uniform distribution log(Σ0) ∼ U(log(0.005 mas), log(2σ5p,res)).
. Finally, the astrometric jitter σjit of each chromosome is drawn from a log-uniform distribution log(Σ0) ∼ U(log(0.005 mas), log(2σ5p,res)).
The last stage of the initialisation phase of the GA consists of evaluating the merit function ℳ of each chromosome in the population.
4.2.2. Evolution
The population is evolved by randomly drawing chromosomes from the population and by applying genetic operators. The efficiency of the GA is improved by applying the genetic operators on the non-linear parameters of the model alone, while the linear parameters are obtained through a linear regression.
Drawing process: The first step consists of drawing a local random sub-population of 5 × 5 to 7 × 7 chromosomes at most (from the 80 × 80 full population) over which several operators are applied. These four operators especially effective: a) Full crossover: Two chromosomes (mother and father) are drawn from the sub-population from which a child genome is bred with the frequency, mean anomaly, eccentricity, and astrometric jitter randomly drawn from the mother and father. The child chromosomes replace the worst chromosomes in a local sub-population according to the merit function; b) Harmony mutation: A chromosome is randomly drawn from the sub-population, and a new frequency is drawn among possible harmonics. The mutated chromosomes replace the worst chromosome in a local sub-population according to the merit function. This operator is efficient in finding the period of eccentric orbits, in which the fundamental frequency is not always dominant; c) Alias mutation: A chromosome is randomly drawn from the sub-population, and a new frequency is randomly drawn from the spectral window frequencies of the aliases. The mutated chromosomes replace the worst chromosome in a local sub-population according to the merit function. This operator is efficient in finding the true fundamental frequency of unevenly sampled data; d) Simplex mutation: The best chromosome is selected from the sub-population and is improved using a Nelder-Mead simplex algorithm. It replaces the worst chromosome in a local sub-population according to the merit function. This operator is efficient at the end of the evolution and allows reaching convergence towards the best merit function.
The computation time allocated to each genetic operator depends on its ability to improve the merit function at different stages of evolution. In order to avoid the population converging to a local maximum, a minimum computation time is assigned to all operators.
4.2.3. Termination
Termination is reached when 95% of the population has converged towards the maximum merit function or when the total computing time reaches 60 s.
4.3. Pipeline execution and best-solution choice
The sequential pipeline execution of the DE-MCMC and GA orbit-fitting modules is as follows: 1) Both modules are executed independently until convergence is achieved on an optimised best-fit configuration or for a maximum execution time of 60 sec. Each algorithm produces the best-fit parameter solution based on their internal likelihood merit functions: Eq. (11) for DE-MCMC and Eq. (13) for GA; 2) When both modules have obtained convergence, the selection of the statistically preferred solution is made based on the Bayesian information criterion (BIC; Schwarz 1978): BIC = kln(n)−2lnℒ (where k is the number of parameters estimated by the model, and n is the number of data points). The adopted best-fit model is the one with the lowest BIC. It is published if it passes the subsequent export filters (see Sect. 5). No information is published on which module provided a particular source solution. For the Gaia DR3 processing, the GA always provided the maximum likelihood, while the DE-MCMC provided the more conservative median of its posterior distribution around the best solution. This imbalanced solution comparison caused the vast majority of published solutions to be provided by GA. We intend to improve upon this in Gaia DR4.
5. Source selection and solution filtering
We describe here the steps involved in the solution filtering process. They were applied to the results obtained running the exoplanet pipeline on two separate input source lists.
5.1. Stochastic solutions: ‘OrbitalAlternative’
5.1.1. Input source list
The Gaia non-single-star (NSS) processing pipeline tested a variety of astrometric solution models (Halbwachs et al. 2023; Pourbaix et al. 2022), and if none fitted the data to a satisfactory degree, the single-star solution from Gaia EDR3 was retained, in which the excess noise will have absorbed any unmodelled (presumably stochastic) signal. Although the exoplanet pipeline is too computationally intensive to be run on all sources that pass through the NSS chain (see Sect. 4), it is run on this sample of 2 457 530 sources that are presumed to be stochastic to search for difficult-to-detect orbital signals with both the DE-MCMC and GA algorithms. This sample is mostly composed of faint and distant sources.
5.1.2. Solution filtering
Force-fitting the sample of sources for which a stochastic solution was found returned a vast majority of solutions of dubious quality, primarily due to known aliasing effects with scanning law periodicities (Holl et al. 2023). An aggressive filtering strategy was therefore applied to the output of the exoplanet pipeline in order to provide a sub-sample of candidate solutions for which the likelihood of retaining spurious solutions would be minimised. We filtered solutions using the following five constraints: a) fractional difference in parallax between the one fitted by the exoplanet pipeline and that in the original EDR3 single-star solution < 5%; b) statistical significance of the derived semi-major axis of the orbit a1/σa1 > 20 (uncertainty derived from the Thiele-Innes parameters using linear error propagation); c) ratio of the EDR3 astrometric excess noise to the uncorrelated jitter term fitted by the exoplanet pipeline > 20; d) number of individual FoV transits > 36; e) EDR3 parallax of the source > 0.1 mas.
Overall, the sample that survived the filtering process is composed of 629 orbital solutions. The period distribution of the selected solutions is mostly free of the doubtful spurious values, as discussed in Sect. 6.2.4. The filtered sample is published in Gaia DR3 with the nss_solution_type ‘OrbitalAlternative[Validated]’, and it was carefully inspected for verification and validation purposes, as described in Sect. 6).
5.2. Input source list: OrbitalTargetedSearch
5.2.1. Input source list
The modules of the exoplanet pipeline have been in development from a time before the launch of Gaia and were verified mostly with the help of simulated data. The number of epochs and calibration noise-level were sufficient to fit meaningful orbits with the exoplanet pipeline only with DR3. In order to test its performance with real data we compiled source lists that would serve the following two purposes: a) Pipeline testing, verification, and validation, for example to demonstrate that the orbits of known exoplanets can be detected; and b) Sample the properties of Gaia astrometric time series in different regimes, for example bright and faint, and investigate how this affects the pipeline performance.
As we progressed in understanding the performances of the non-single star pipelines and when the input source selection for the binary pipeline was finalised (Halbwachs et al. 2023), it was decided to perform a dedicated (additional) run of the exoplanet pipeline on a pre-defined source list, hence the orbital name suffix ‘OrbitalTargetedSearch’.
Starting from the previously defined list of test sources, we therefore compiled a more extensive sample for the targeted search. We identified sources for which information about the presence or absence of exoplanets and substellar companions was available in the literature. These typically were stars that were included in observational planet-search programs. The list included three sets of sources. First, sources in the Nasa Exoplanet Archive5. These are hosts of confirmed and candidate exoplanets that were discovered with various observation techniques. Second, sources in planet-search programmes, predominantly using spectrographs for precision radial-velocity measurements. This included the samples of, for example, HIRES (Butler et al. 2017), CORALIE (Udry et al. 2000), HARPS (Mayor et al. 2003), SOPHIE (Bouchy et al. 2009), and HARPS M dwarfs (Bonfils et al. 2013). Third, sources in known astrometric binaries from the HIPPARCOS binary solutions compiled in Table F1 of van Leeuwen (2007). All the sources in these three samples predominantly consist of bright stars (G ≲ 10). We complemented them with sources that promised compelling scientific outcomes in the case of orbit detection, and that would otherwise possibly not have been processed with an orbit-fitting pipeline. For example, the binary pipeline only processed sources with G < 19, regardless of distance. To probe fainter sources that yet remain within a distance horizon that in principle allows the detection of signals caused by sub-stellar companions, we included the ultra-cool dwarf sample of Smart et al. (2019) and metal-polluted white dwarfs within 20 pc from the Sion et al. (2014) and Giammichele et al. (2012) compilations. The total number of unique sources selected for the targeted search was 19 845.
We obtained Gaia DR2 source identifiers of these targets either directly from the respective catalogue, from Simbad (Wenger et al. 2000), or from a positional crossmatch with the Gaia DR2 catalogue. The corresponding Gaia DR3 identifiers where then submitted for the dedicated processing run.
5.2.2. Solution filtering
An in-depth scrutiny of the resulting solutions was performed on multiple levels in an attempt to retain the most sensible orbits. The different steps taken in order to filter out implausible solutions, which we detail below, have a high degree of heterogeneity, and our final choices translate into a complex selection function.
Our approach to solution filtering was threefold. We first defined various indicators of the statistical significance of the solutions, then we fine-tuned their threshold values with an iterative process, and we finally performed a selection of different sub-samples of solutions based on different choices of subsets of the indicators. The statistical filters included an extensive model comparison with alternative, less complex models to safeguard the detection of bona fide candidates, a distance-dependent threshold for the orbit significance, a relative agreement between the fitted parallax and the AGIS parallax, an upper limit to the derived value of the mass function, a constraint on closed orbits, and variable thresholds for the value of the ratio of the AGIS astrometric excess noise to the Keplerian jitter term in the solution.
We used two sets of statistical filters. In each set, the filters were applied in conjunction, and then the full list was constructed with the targets that passed the filters of either one or the other set.
Set 1:
-
BICKep − BIC5 < −30
-
BICKep − BIC7 < −30
-
ϖ > σjit
-
|Δϖ| < 0.5 a1
-
a1/σa1 > 2
-
P < ΔT
-
f(ℳ) < 0.02
-
σjit < max(0.1, 2σjit, agis)
-
σSTD < 1.5σMAD
Set 2:
-
|Δϖ| < 0.05 ϖ
-
a1/σa1 > 5
-
σjit, agis/σjit > 5,
where BICKep is the BIC for the Keplerian solution, and BIC5 and BIC7 are the BICs for the five- and seven-parameter solutions, respectively6. ϖ is the parallax from the Keplerian solution, |Δϖ| is the absolute difference between the parallax of the Keplerian solution and the AGIS parallax, a1 and σa1 are the semi-major axis and its uncertainty, respectively, P is the period of the companion, ΔT is the time span of observation for each target, f(ℳ) is the mass function of the primary and companion system and is calculated as 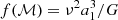 (where ν = 2π/P is the orbital frequency), σjit is the astrometric excess noise as calculated by the exoplanet pipeline, σjit, agis is the astrometric excess noise from the five-parameter AGIS solution, σSTD is the weighted standard deviation of the residuals of the Keplerian solution, and σMAD is 1.4826 times the median absolute deviation (MAD) of the residuals of the Keplerian solution.
(where ν = 2π/P is the orbital frequency), σjit is the astrometric excess noise as calculated by the exoplanet pipeline, σjit, agis is the astrometric excess noise from the five-parameter AGIS solution, σSTD is the weighted standard deviation of the residuals of the Keplerian solution, and σMAD is 1.4826 times the median absolute deviation (MAD) of the residuals of the Keplerian solution.
We complemented the statistical filtering approach with visual inspection of individual orbits (see Sect. 6.2.2). In this way, we searched for symptoms of spurious results due to, for example, important numbers of outliers and/or correlated residuals even for cases of statistically robust solutions. Finally, we used a threshold (10%) in the relative agreement between the fitted value of P and that from existing literature data and independent Gaia solutions as additional discriminant in an attempt to recover bona fide solutions that otherwise might have been discarded based on too stringent statistical filtering. The final number of sources with solutions accepted for publications in Gaia DR3 is 533. Of these, 188 were validated with the nss_solution_type ‘OrbitalTargetedSearchValidated’ (see Sect. 6.3).
The difficulties we faced in converging on a coherent approach for the identification of well-defined classes of robust solutions and spurious orbits are illustrative of the challenges inherent in the Gaia DR3 NSS processing, particularly in the limit of low astrometric signal-to-noise ratio (and correspondingly low companion mass) for bright stars, which are still affected by limitations in the error model and by the generally low number of visibility periods (see Sect. 2). We caution users against performing detailed statistical analyses with this sample of orbital solutions.
6. Results
In total, the exoplanet pipeline populates 1162 orbits in the Gaia DR3 table nss_two_body_orbit into four nss_solution_type: ‘OrbitalAlternative’ (619), ‘OrbitalAlternativeValidated’ (10), ‘OrbitalTargetedSearch’ (345), and ‘OrbitalTargetedSearchValidated’ (188).
Calibrated companion mass estimates require additional non-astrometric information and thus are beyond the scope of this paper. They are presented in Gaia Collaboration (2023a).
To facilitate interpretation of the ‘OrbitalAlternative[Validated]’ and ‘OrbitalTargetedSearch[Validated]’ sub-sample figures, they are always shown side by side: the first on the left, and the second on the right. For brevity, we refer in the text below to these two categories as ‘OrbitalAlternative*’ and ‘OrbitalTargetedSearch*’ to refer to the combined sample of the non-validated and validated solutions in both categories.
6.1. General overview
6.1.1. Sky distribution
The sky distribution of our solutions is shown in Fig. 4. Clearly, the filtering with ‘OrbitalAlternative*’ has selected sources in regions of the sky with sufficiently dense sampling, causing holes mainly around low ecliptic latitudes (|β|< 45°) that are generally less well sampled. In contrast, the external input catalogue-based ‘OrbitalTargetedSearch*’ has a much more uniform distribution.
 |
Fig. 4. Galactic sky distribution of our published solutions. The longitude increases to the left. We broadly categorise the different mass regimes using the pseudo-companion mass |
6.1.2. Estimating the signal-to-noise ratio
In Fig. 5 we explore the approximate signal-to-noise ratio of our results, where the fitted semi-major axis (a1 [mas]) is taken as a proxy for the signal level and the median abscissa uncertainty as the noise proxy. We compare two commonly used definitions: the top panels show the definition of Casertano et al. (2008) with its typical proposed threshold of 3, and the bottom panel shows the definition of Sahlmann et al. (2015b) with its proposed threshold of 20. Only three (0.3%; two validated) solutions fall below the threshold of Sahlmann et al. (2015b), whereas 515 (44%; 33 validated) solutions fall below the threshold of Casertano et al. (2008).
 |
Fig. 5. Signal-to-noise ratio of a1 with respect to the uncertainty on the median abscissa. Top panel: statistics used in Casertano et al. (2008) with its typical proposed threshold of 3. Bottom panel: statistics used in Sahlmann et al. (2015b) with its proposed threshold of 20. |
The majority of our sample has a reasonable to high signal-to-noise ratio, although targets with very low signal-to-noise ratio levels are generally the least massive companions, as expected.
On the ordinate axis, we plot the significance of the derived semi-major axis (a1/σa1), which shows the expected trend that a higher signal-to-noise ratio is associated with better constrained parameter estimates.
6.1.3. Goodness-of-fit statistics
In Fig. 6 we present the goodness-of-fit statistics that are available in the Gaia data archive (Sect. 3.3): χ2 (obj_func) and F2 (goodness_of_fit). While the first is difficult to interpret globally without compensating for the varying number of degrees of freedom (i.e. the 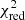 ), the second, F2, Gaussianized chi-square, is expected to follow a normal distribution with zero mean and unit standard deviation, as shown with the thin green line. Comparison to the histogram and a fit to it (thick black line) shows that the distribution is not completely symmetric, but is generally rather well-behaved. This can largely be subscribed to the inclusion of the non-linear jitter term σjit model parameter (see Sect. 3.1 and Figs. 9 and 17), however, which was meant to absorb any unmodelled variance in the data, and thus likely contributed to the normalisation of the expected goodness-of-fit statistics.
), the second, F2, Gaussianized chi-square, is expected to follow a normal distribution with zero mean and unit standard deviation, as shown with the thin green line. Comparison to the histogram and a fit to it (thick black line) shows that the distribution is not completely symmetric, but is generally rather well-behaved. This can largely be subscribed to the inclusion of the non-linear jitter term σjit model parameter (see Sect. 3.1 and Figs. 9 and 17), however, which was meant to absorb any unmodelled variance in the data, and thus likely contributed to the normalisation of the expected goodness-of-fit statistics.
 |
Fig. 6. Goodness-of-fit statistics. Left panel: χ2 (obj_func in Table 1). Right panel: F2 (goodness_of_fit in Table 1). |
6.1.4. Parameter distributions
In the top row panels of Fig. 7, the period eccentricity is well constrained by a 5-day circularisation period (formulation of Halbwachs et al. 2005) and our validated targets generally have medium to low eccentricities. Due to the aggressive filtering on the ‘OrbitalAlternative*’, mainly periods longer than 100 d and orbits with eccentricities lower than 0.4 were selected.
 |
Fig. 7. Parameter distributions of the published solutions: Period-eccentricity and period vs. semi-major axis (top panels), apparent magnitude vs. inverse parallax (third panel), and zero-extinction absolute magnitude vs. colour (bottom panel). See Sects. 6.1.4 and 6.2 for a discussion. |
The right panel in the second row shows that the different pseudo-mass groups roughly follow a a1 ∝ P2/3 relation with different offsets, which is expected from Kepler’s third law for the astrometric signal of systems with companions at similar distances and masses (mass ratios). The right panel in the third row shows that the sources are indeed roughly at a typical distance of about 50 pc. The left panel shows that the distance distribution is rather widely spread out and thus would not produce a nice relation in the period versus a1 plot above it. We note the excess of high semi-major axis solution for short periods in the left plot: these are likely spurious or incorrect period detections (see Gaia Collaboration 2023a).
The panels in the third row also illustrate that the blind-search ‘OrbitalAlternative*’ sample (left) is at much fainter magnitudes and larger distances than the ‘OrbitalTargetedSearch*’ (right). The second sample is mainly compiled from radial velocity sources in the literature and thus not surprisingly consists of mostly relatively bright targets.
The fourth row of panels shows the zero-extinction absolute magnitude estimate. It is based on parallax and G-band apparent magnitude; see the discussion in Sect. 6.2.1 for more details.
The discussed parallax-based distance and absolute magnitude estimates are meaningful because the uncertainty on the parallax is generally (much) smaller than 20% of the value; see the bottom panel of Fig. 8. This is further supported by the relative tightness of the Hertzsprung-Russell (HR) diagram in the bottom right panel.
 |
Fig. 8. Uncertainties for period (top panel), eccentricity (second panel), periastron epoch (third panel), and parallax (fourth panel) as a function of the parameter value itself. See Sect. 6.1.5 for a discussion. |
Figure 9 presents several parameters as function of a1. We start with the jitter term, which for most ‘OrbitalAlternative*’ is at about or lower than an insignificant 0.01 mas. For the ‘OrbitalTargetedSearch*’, the level is generally at about 0.1 mas, and for about a dozen of solutions the jitter level is above a1/2, that is an (unmodelled) noise of the same order as the orbital solution semi-major axis.
 |
Fig. 9. Parameter distributions as a function of (photocentre) semi-major axis a1: Jitter term (top panel), semi-major axis (second panel), cosine of the inclination (third panel), longitude of the ascending node (fourth panel), and argument of periastron (bottom panel). See Sect. 6.1.4 for a discussion. |
The second row of panels shows the significance of the semi-major axis (a1/σa1), which is about 20–30 for the ‘OrbitalAlternative*’ sample and spans several orders of magnitude for the ‘OrbitalTargetedSearch*’ sample. As expected, the validated samples generally have a relatively high significance in both cases.
The cosine inclination distribution on the third row of panels is rather flat for the ‘OrbitalAlternative*’, as expected for randomly oriented systems. For the ‘OrbitalTargetedSearch*’, we see an excess of edge-on systems, as expected because the input selection was mainly based on radial velocity targets. The bottom two rows show the longitude of the ascending node (Ω) and argument of periastron (ω), which both are relatively flat for both samples, as expected for randomly oriented orbits. A general discussion of the expected distributions and observed biases in the geometric orbital elements of astrometric orbits is given in Gaia Collaboration (2023a).
6.1.5. Parameter uncertainties
We systematically inspected the parameter uncertainties of all fitted parameters versus their value and did not see any unexpected trends or outliers. As noted in Sect. 3.1, we exported the formal uncertainties as provided from the covariance matrix of the best-solution least-squares solution without any scaling. As we know from the astrometric jitter term that there is some level of unmodelled noise left in the data, these values might not always give reliable estimates of the true uncertainties of these parameters. See also Sect. 3.2, which details the propagation of uncertainties on the derived parameters.
We plot the data shown in Fig. 8 for a few interesting parameters. The top panels show the period uncertainty versus period along with an observation time span (i.e. cycle-normalised) phase shift of 5%, below which almost all solutions lie, except for the longest periods, as expected because of the mild constrains on the period due to the very low cycle count.
The second row of panels show the eccentricity uncertainty versus their value, which is typically between 0.06–0.1 for the ‘OrbitalAlternative*’, but varies over a much wider range for the ‘OrbitalTargetedSearch*’. The majority of the latter still remains below a meaningful uncertainty of 0.2, however.
The epoch of periastron is distributed between −0.5 – 0.5 of the period around T0, as shown in the third row of panels, and is rather flatly distributed in this range, as expected. A relative uncertainty above 1 (solid line) clearly is non-informative, which fortunately only happens for a dozen objects in either category.
Finally, we also show the relative parallax uncertainty in the bottom row of panels, which shows that the majority of our sample has a relative precision better than 5%, and the precision of almost the entire sample is better than 10%. Because 20% is an absolute minimum when parallaxes are to be used as a distance estimator, we are confident that the distance and absolute magnitude estimates in the two bottom panel rows of Fig. 7 are meaningful.
6.1.6. Estimating the Campbell element
Figures 10 and 11 show the differences between using Monte Carlo resampling and linear propagation when the values and uncertainties of these geometric parameters are calculated. They also show their significance. The agreement is good in general, but for about ten solutions, the Monte Carlo estimate for the semi-major axis is much larger than the linearly estimated one. These cases typically correspond to solutions with poorly constrained eccentricities (i.e. e/σe < 1) for which Monte Carlo resampling is not recommended because of unrealistic variances of the Thiele-Innes coefficients (Babusiaux et al. 2023). This is also reflected in the comparison of the semi-major significance estimators (Fig. 11), which shows significant discrepancies predominantly for solutions with poorly constrained eccentricities.
 |
Fig. 10. Values and uncertainties for geometric elements. Estimates using linear error propagation and Monte Carlo resampling are shown on the x- and y-axes, respectively. In the latter case, the median value is adopted with a symmetric uncertainty computed as the mean of the upper and lower 1σ equivalent confidence interval. The dashed line indicates equality, and solutions with e/σe < 1 are marked with grey squares. Large discrepancies in ω at the 360°→0° boundary (e.g., the point in the bottom right corner) are of no major concern. |
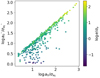 |
Fig. 11. Significance estimates (a over sigma_a). Density histogram of estimates using linear error propagation and Monte Carlo resampling on the x- and y-axes, respectively. The histogram bins are colour-coded by the average eccentricity significance e/σe. |
Four solutions have linearly propagated ω-uncertainties σω > 1000 deg, and they also have low or very low eccentricities. This shows that both Monte Carlo resampling and linear propagation can lead to unrealistic results for some almost-circular orbits.
6.2. Verification
In this verification section, the focus is on confirming bona fide companions based on internal consistency checks and expectations.
6.2.1. Position in the HR diagram
The bottom row of panels in Fig. 7 shows the zero-extinction absolute magnitude estimate (i.e. Gapparent + 5(log10(ϖ/1000) + 1), with ϖ in [mas]). Most of our host stars lie along the main sequence, but a small fraction are likely (sub-)giants. Interestingly, all ‘OrbitalAlternativeValidated’ sources (i.e., the filled dark orange diamonds) appear to belong to this class. The relative tightness of the HR diagram in the right panel reinforces that our parallaxes have high relative precision, and that extinction amongst most of these targets is likely low. A binary sequence is not clearly identifiable (in contrast to Fig. 47 of Gaia Collaboration 2023a), which further reinforces the expectation that the sample is not significantly polluted by impostors masquerading as systems with low-mass ratios and negligible flux ratios that are instead binaries with a flux ratio close to the mass ratio.
6.2.2. Astrometric orbit visualisation
We generated graphical representations of all ‘OrbitalTargetedSearch*’ solutions. These contain the modelled astrometric motion, the post-fit residuals, and auxiliary information describing the properties of the source data and fit quality metrics. These figures were used as an empirical tool to assess the quality of the solutions, but not to validate them. The visual discovery of a doubtful solution usually led to the identification or refinement of filter criteria. In other words, this visual inspection was most efficiently used to identify spurious solutions that should be rejected.
Figures 12–16 show examples of orbit visualisations that were obtained on the basis of the pystrometry package (Sahlmann 2019)7. An additional example that also demonstrated the solution validation with external RVs is the case of HD 81040, which was shown in a Gaia Image of the Week8.
 |
Fig. 12. Astrometric orbit of HD 114762 (i.e. Gaia DR3 3937211745905473024, bottom left panel) as determined by Gaia (G = 7.15 mag, P = 83.74 ± 0.12 day, e = 0.32 ± 0.04, and ϖ = 25.36 ± 0.04 mas). North is up, and east is left. The sky-projected orbit model about the system barycentre marked with a cross is shown in grey, and astrometric measurements and normal points after subtraction of parallax and proper motion are shown in grey and black, respectively. Only one-dimensional (along-scan) astrometry was used. The shown offsets are therefore projected along the instantaneous scan angle of Gaia, whose orientation is also indicated by the error bars. The modelled parallax and proper motion of the star are shown in the top left panel by the solid curve, where open circles indicate the times when the star crossed the Gaia field of view. The arrow indicates the direction of motion. The top right panel shows the normal points after subtraction of the parallax and proper motion as a function of time. The middle right and bottom right panels shows the post-fit residual normal points and individual CCD transit data, respectively. Normal points are computed at every field-of-view transit of the star from the approximately nine individual CCD transits and are only used for visualisation, whereas the data processing uses individual CCD transit data. |
 |
Fig. 13. Same as Fig. 12, but for Gl 876 (i.e. Gaia DR3 2603090003484152064, G = 8.88 mag, P = 61.36 ± 0.22 day, e = 0.16 ± 0.15, and ϖ = 213.79 ± 0.07 mas). |
 |
Fig. 14. Same as Fig. 12, but for WD0141-279 (i.e. Gaia DR3 4698424845771339520, G = 13.70 mag, P = 33.65 ± 0.05 day, e = 0.20 ± 0.15, and ϖ = 102.87 ± 0.01 mas). |
 |
Fig. 15. Same as Fig. 12, but for HD 40503 (i.e. Gaia DR3 2884087104955208064, G = 8.97 mag, P = 826.53 ± 49.89 day, e = 0.07 ± 0.10, and ϖ = 25.49 ± 0.01 mas). |
 |
Fig. 16. Same as Fig. 12, but for 2MASS J08053189+4812330 (i.e. Gaia DR3 933054951834436352, G = 20.01 mag, P = 735.91 ± 22.99 day, e = 0.42 ± 0.23, and ϖ = 43.77 ± 0.71 mas). |
These figures illustrate the different regimes in terms of sampling, source magnitude, measurement uncertainty, and orbit size in which our algorithms were successful in identifying significant solutions. The scientific implications of the orbital solutions we show are discussed in Gaia Collaboration (2023a).
6.2.3. Comparison with excess noise from the AGIS solution
A crude but generally effective indicator of improved modelling is to compare the excess noise level between the five-parameter AGIS solution and a Keplerian orbit solution (called jitter term in the latter). The top panels of Fig. 17 show that for the most massive companions, the decrease in the residuals noise level exceeds more than an order of magnitude, but for the less massive companions, this difference is reduced, as expected.
 |
Fig. 17. Comparison with the single-star AGIS excess noise. |
The second row of panels shows an interesting relation between the AGIS excess noise and the fitted semi-major axis: typically, the semi-major axis is about half the AGIS excess noise, which holds true for the wide range of masses and semi-major axis in our sample. A comparison of other parameters with those from AGIS does not present any unexpected deviations and is not shown.
6.2.4. Spurious orbits
Figure 18 shows an example of the period-eccentricity diagram from the sample of the unfiltered stochastic solution. The clear structure of period aliases corresponding for instance to one year, 6 months, or the 63-day precession period of the satellite, and their harmonics is further discussed in Holl et al. (2023). The filled green dots correspond to P and e values from ‘OrbitalAlternative’ solutions equivalent to the data in the top left panel of Fig. 7. This large number of spurious solutions was mostly filtered out by our aggressive filter criteria described in Sect. 5, at the cost of removing potentially good solution and thus overall low completeness.
 |
Fig. 18. Period-eccentricity diagram for a random sample of sources (black points) with orbits obtained by the DE-MCMC or GA algorithms from the processing the stochastic solution sample. The clear structure of period aliases is a symptom of incorrectly derived orbits and is further discussed in Holl et al. (2023). The filled green dots correspond to P and e values from ‘OrbitalAlternative’ solutions. The solid black curve indicates the maximum eccentricity attainable for an orbit that is not affected by tides, assuming a cut-off period of 5 days (see e.g., Halbwachs et al. 2005). |
The adopted solution-filtering procedure did not include constraints on the mass function. A few percent of unrealistically high values of f(ℳ) primarily with short orbital periods (P ≲ 100 days) are still present. As further discussed in Gaia Collaboration (2023a), these are likely to be spurious, and therefore, the level of contamination of the ‘OrbitalAlternative’ solutions is probably about 5%. Gaia Collaboration (2023a; see Sect. 5.1) offered a recipe for effectively excluding these spurious orbits based on constraints of the parallax significance as a function of the orbital period of the solution.
The identification of likely spurious solutions in the ‘OrbitalTargetedSearch’ sample and the corresponding estimate of the degree of contamination was performed as part of the validation analysis. This is described in the following sections.
6.3. Validation
Validation includes a comparison with available literature data of the radial velocity or astrometry and with Gaia radial velocity solutions. These were used to grant certain candidate orbits the status of Validated. They are identified by this suffix to their nss_solution_type.
6.3.1. Astrometric solutions from the literature
In the ‘OrbitalTargetedSearch’ category, astrometric orbits for two targets from the literature were available: DE0823−49 (Gaia DR3 5514929155583865216, Sahlmann et al. 2013) and 2M0805+48 (Gaia DR3 933054951834436352, Sahlmann et al. 2020). They are both consistent with the Gaia orbit and thus lead to their Validated suffix. They are listed in Appendix A.
6.3.2. Radial velocity solutions from the literature
When available, radial velocity data from the literature were used to vet the full subset of candidate companions with 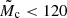 MJ (i.e., assuming 1 M⊙ host) and a subset with
MJ (i.e., assuming 1 M⊙ host) and a subset with 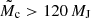 in the ‘OrbitalTargetedSearch’ candidate set. When the orbital parameters (typically the period and eccentricity) between the RV solution and the Gaia solution were found to be consistent, it resulted in the Validated suffix. All these parameters are listed in Appendix A.
in the ‘OrbitalTargetedSearch’ candidate set. When the orbital parameters (typically the period and eccentricity) between the RV solution and the Gaia solution were found to be consistent, it resulted in the Validated suffix. All these parameters are listed in Appendix A.
For several sources, the RV reference parameters are not given. This is to indicate that the RV data alone were insufficient to validate the orbit on their own (e.g., there were multiple significant peaks in the RV periodogram). In these cases, we validated the target when the RV data were consistent after constraining the period of the Keplerian to the Gaia orbital period.
If no literature RV solution was found, the source was kept without an additional suffix in the name, that is it stayed a candidate. When an astrometric orbit was found to be incompatible with RV data, it was removed from our publication list, thus making this validation step part of the filtering process (see Sect. 5.2.2).
While this step of the validation procedures was performed quite carefully, it is not entirely free from pitfalls. For example, a small number of sources with good matches between the fitted and literature P values where not flagged as Validated and are still listed in Table A.1 with the solution type ‘OrbitalTargetedSearch’. They include two known RV planet hosts, HR 810 (Gaia DR3 4745373133284418816) and HD 142 (Gaia DR3 4976894960284258048), as well as Gaia DR3 2133476355197071616 (Kepler-16 AB). This third source hosts the first circumbinary planet detected by the Kepler mission, with P = 105 d (Doyle et al. 2011; Triaud et al. 2022). In this case, Gaia detects a companion with P = 41 d and an almost edge-on orbit, which is in fact the low-mass stellar companion Kepler-16 B, which eclipses Kepler-16 A. In a few cases, inconsistencies between literature RV data and the Gaia solutions were overlooked. Two such examples are Gaia DR3 1748596020745038208 (WASP-2) and Gaia DR3 5656896924435896832 (HATS-26, TOI-574). The two known companions are hot Jupiters with orbital periods of 2.1 d (Collier Cameron et al. 2007; Knutson et al. 2014) and 3.3 d (Espinoza et al. 2016), respectively. The Gaia solutions have P = 38 d and P = 193 d, respectively. No additional RV trends or modulations are detected for WASP-2 and HATS-26, indicating that the Gaia detections might be spurious.
Another illustration of the challenges of the validation procedure is the case of GJ 812A (HIP 103393), for which nine HARPS measurement were taken between August 2011 and August 2012 that are publicly available on DACE (see Table A.1). The periodogram of the RV time series does not show any significant peak at the Gaia period (P = 23.926 ± 0.010 d), but a compatible RV orbit can be found when the period is fixed to the Gaia period. Furthermore, a close inspection of the HARPS CCFs shows that GJ 812A is a double-line spectroscopic binary. This rules out the presence of a brown dwarf companion to GJ 812A.
6.3.3. Other literature solutions
Of the literature solutions obtained with techniques other than astrometry and RVs, we report in Table A.1 the good agreement between the Gaia period and that obtained byMurphy et al. (2016) for the companion orbiting Gaia DR3 2075978592919858432 (KIC 7917485, Kepler-1648). The primary is a δ Scuti variable A-type star, and the companion was identified based on phase modulation of the pulsations of the host.
In the sample of Kepler-transiting planets that have been statistically validated, Kepler-1697b orbits a K-dwarf primary (Gaia DR3 2102991776844251264) with P = 33.5 d (Armstrong et al. 2021). The Gaia ‘OrbitalTargetedSearch’ solution has P = 98.5 d and i ≃ 65 deg, which might either indicate a spurious orbit or the presence of a third body in the system.
A small number of transiting planet candidates from the TESS mission (TESS Objects of Interest, TOIs) are worth mentioning. TOI-288 (Gaia DR3 6608926350294211328), TOI 289 (Gaia DR3 4919562197762515456), TOI-1104 (Gaia DR3 6345896578791113472), and TOI-2008 (Gaia DR3 5096613016130459136) are indicated as single-transit candidates, and the Gaia solutions of type ‘OrbitalTargetedSearchValidated’ have P = 79 d, P = 223 d, P = 170 d, and P = 52 d, respectively, and close to edge-on configurations, indicating these are likely to be the companions that cause the eclipses. In the case of TOI-355 (Gaia DR3 5013703860801457280), the transit candidate has P = 1.03 d, while the Gaia solution is validated with P = 297 d, indicating the presence of a third body in the system (not necessarily transiting). Similar conclusions could be drawn for TOI-614 (Gaia DR3 570355367386642611), TOI-746 (Gaia DR3 528033714422882547), TOI-946 (Gaia DR3 5549740136101187840), and TOI-1113 (Gaia DR3 6356417496318028928), all found to be hosting short-period transiting planet candidates and for which Gaia solutions of type ‘OrbitalTargetedSearch’ have much longer P values. Without additional external validation, however, they might also correspond to spurious solutions, as in the case of TOI-574, discussed in Sect 6.3.2. For TOI-933 (Gaia DR3 5499342375670742784), the period of the transit candidate is almost exactly twice that fitted in the Gaia astrometry. The latter solution is far from edge-on, which might be a symptom of a spurious solution.
Finally, the case of HD 185501 (Gaia DR3 2047188847334279424) is particularly instructive: the Gaia solution has P = 450 d and a1 = 0.48 mas, which at the distance of 32.75 pc (assuming a 1 − M⊙ primary) would imply the detection of a companion well in the substellar regime. However, speckle imaging data have revealed HD 185501 to be an equal-mass binary with ∼0.04 arcsec separation and P = 434 d (Horch et al. 2020, and references therein). To our knowledge, this is the only clear case in the ‘OrbitalTargetedSearch’ sample of a system that was incorrectly classified as having a low-mass companion with negligible flux ratio, but rather being one with two components having a flux ratio very close to the mass ratio (see Sect. 6.2.1).
6.3.4. Compatibility with independent Gaia solutions
The overlap with alternative solution published by the Gaia NSS pipeline includes a total of 230 cases: 213 in nss_two_body_orbit and 17 in nss_non_linear_spectro, as tabulated in Table 2. See Appendix B for the related queries. Our sample has no overlap with the nss_acceleration_astro and nss_vim_fl solution tables.
Overview of 213 source_ids with an alternative solution in either nss_two_body_orbit or nss_non_linear_spectro.
Generally, a given source can have solutions of different nss_solution_type in nss_two_body_orbit, except for solutions that were obtained from astrometric data alone, that is an ‘OrbitalTargetedSearch[Validated]’ solution would supersede an ‘Orbital’ solution. For the ten ‘OrbitalAlternativeValidated’ sources the alternative and completely independent SB1 solutions have compatible periods (to within 10%) and eccentricities with respect to the orbital solutions from our exoplanet pipeline, and thus were used to provide these sources with the Validated suffix. They are listed in Appendix A. Similarly, out of 147 ‘OrbitalAlternativeValidated’ sources with alternative Gaia solutions, 142 were found to have matching periods to within 10% with solutions of different nss_solution_type in nss_two_body_orbit.
The identification of discrepant orbital solutions for the same source_id in Gaia astrometry, spectroscopy, and/or photometry does not necessarily mean that either one is incorrect because their respective sensitivities largely do not overlap, especially for the lower mass regime. They may therefore correspond to effects induced by different components of the system. No sources were thus filtered out based on this Gaia internal comparison.
Five ‘OrbitalTargetedSearchValidated’ sources have orbital periods differing by more than 10% from those of other Gaia solutions. Gaia DR3 4748772376561143424, Gaia DR3 3309006602007842048, and Gaia DR3 276487905502478720 have AstroSpectroSB1 and SB1 (the latter two) long-period solutions, which appear compatible with the fitted values from astrometry. The SB1 solution for Gaia DR3 3550762648877966336 has P = 6.8 d, while the astrometric orbit has P = 1213 d. Based on criteria of significance of the semi-major axis and RV semi-amplitude of the astrometric and spectroscopic orbit and period ratios such as those listed in Gaia Collaboration (2023a), the system is robustly classified as a hierarchical triple. Gaia DR3 2370173652144123008 is discussed further in the following section.
A total of 57 sources have ‘OrbitalTargetedSearch’ solutions and another orbital solution of type: SB1, SB2, SB2C, EclipsingSpectro, or AstroSpectroSB1. Of these, 48 have period discrepancies in excess of 10%. For 22 of them, both periods are > 750 d, so they can be considered compatible on the grounds of the expectedly larger uncertainties as P is similar to or exceeds the DR3 observation time span. Seven sources with astrometric orbits with P > 330 d have additional short-period solutions (one EclipsingSpectro: Gaia DR3 5556931152602576000; three SB1: Gaia DR3 3537815929524205568, Gaia DR3 4975005999307397376, Gaia DR3 3775615766054509568; and three SB2: Gaia DR3 5963704000561744768, Gaia DR3 3304340751399786752, Gaia DR3 5549740136101187840). These might still be interpreted as triple systems. The remainder of the sources have two solutions with both periods ≲120 d. In a few cases (Gaia DR3 5294105439288288256, Gaia DR3 2729543564483732608, and Gaia DR3 6531037981670835584) the period ratio is approximately 2, but for the majority of the sources, the period values do not appear compatible. This indicates that a fraction of the solutions might be spurious.
For 15 sources with ‘OrbitalTargetedSearch’ orbits (and one ‘OrbitalTargetedSearchValidated’ orbit), the additional Gaia solution is of the type FirstDegreeTrendSB1 or SecondDegreeTrendSB1. With one exception, all astrometric orbits have P > 820 d, likely indicating that the fitted astrometric orbits have significantly underestimated the true periods of the companions. This is an expected feature of the orbit-fitting process in the limit of periods that are longer than the time span of the Gaia observations (e.g., Casertano et al. 2008). For Gaia DR3 5140730507877918592, the P ≃ 53 d orbit might be spurious.
Overall, based on the above consideration, we roughly estimate a degree of contamination from spurious solutions of ∼10% in the ‘OrbitalTargetedSearch’ sample.
6.3.5. Solutions of particular interest
Three ‘OrbitalTargetedSearch[Validated]’ solutions imply the discovery of previously unknown planetary-mass companions if a diluted binary scenario can be discarded. These refer to HIP 66074, HD 40503, and HD 68638A, whose properties are discussed in Gaia Collaboration (2023a).
HIP 66074 has 11 radial velocity measurements taken with the HIRES instrument (Butler et al. 2017), which show a significant dispersion (11 m s−1) compared to the measurement uncertainties (1.5 m s−1). Fitting the RV data with a constant model and a jitter term (σRVJit) results in a log(likelihood) = −37.82 and σRVJit = 10.5 ± 2.5 m s−1. A thorough frequency analysis of the radial velocity time series is not possible due to the limited number of measurements, but we can nevertheless assess whether the radial velocities are compatible with the Gaia orbit solution. To do this, we fitted a single-Keplerian model to the radial velocity with an additional jitter term while keeping the period, the eccentricity, and the argument of periastron fixed at the Gaia-derived values (i.e. P = 297.6 d; e = 0.46 and ω = 263.11 deg.). The adjustment converges to log(likelihood) = − 18.45, with σV = 0.4 ± 1.2 m s−1 and 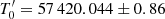 MJD, which is compatible within 1σ with the Gaia-derived value of T0 = 57 443.7 ± 31.4 MJD. The comparison between the two RV models based on ΔBIC favours the single-Keplerian model with a highly significant value of ΔBIC = −34. Assuming the exoplanet scenario is correct, Gaia Collaboration (2023a) reported a value of 7.3 ± 1.1 MJup for the companion.
MJD, which is compatible within 1σ with the Gaia-derived value of T0 = 57 443.7 ± 31.4 MJD. The comparison between the two RV models based on ΔBIC favours the single-Keplerian model with a highly significant value of ΔBIC = −34. Assuming the exoplanet scenario is correct, Gaia Collaboration (2023a) reported a value of 7.3 ± 1.1 MJup for the companion.
HD 40503 (HIP 28193) has four HARPS and 13 CORALIE radial velocity measurements taken between December 2003 and November 2021 that are publicly available on DACE (see Table A.1). With a chromospheric activity index of 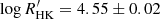 derived from the HARPS spectra, the K2 dwarf is considered as active, which makes the analysis of the few publicly available RV measurements challenging. The periodogram of the RV time series is also impacted by the sparsity of the data and the different instrumental offsets. It can nevertheless be used to validate the Gaia-orbit. Two dominant peaks at 748 d and 917 d are within 2σ of the Gaia-derived period (P = 826 ± 50 d). In addition, the corresponding Keplerian solutions both lead to a significant improvement of the ΔBIC = −52 compared to the constant model with an additional RV jitter term. However, due to the limited number of high-resolution spectra and RV measurements, we are not able to rule out the scenario of a blended double-line spectroscopic binary, which would require a better phase coverage of the orbital period.
derived from the HARPS spectra, the K2 dwarf is considered as active, which makes the analysis of the few publicly available RV measurements challenging. The periodogram of the RV time series is also impacted by the sparsity of the data and the different instrumental offsets. It can nevertheless be used to validate the Gaia-orbit. Two dominant peaks at 748 d and 917 d are within 2σ of the Gaia-derived period (P = 826 ± 50 d). In addition, the corresponding Keplerian solutions both lead to a significant improvement of the ΔBIC = −52 compared to the constant model with an additional RV jitter term. However, due to the limited number of high-resolution spectra and RV measurements, we are not able to rule out the scenario of a blended double-line spectroscopic binary, which would require a better phase coverage of the orbital period.
HD 68638A (HIP 40497) has 27 ELODIE radial velocity measurements taken between November 1997 and November 2003 that are publicly available on DACE (see Table A.1). The periodogram of the RV time series shows a significant peak at 243 days with a false-alarm probability lower than 0.01. The corresponding Keplerian solution derived using DACE leads to a significant improvement of the ΔBIC = −85 compared to the constant model with an additional RV jitter term and a period P = 240.85 ± 0.38 d that is compatible with the Gaia-derived period (241.6 ± 1.0 d). However, Busà et al. (2007) described the target as a double-line spectroscopic binary, which is confirmed by an inspection of the ELODIE’s CCFs available on the “Observatoire de Haute-Provence” archive and rules out the substellar nature of the companion.
6.3.6. Compatibility with reference data
For 194 sources (188 of which were validated), a reference period and eccentricity are available, as listed in Appendix A. Here we plot the period and eccentricity compatibility in Figs. 19 and 20, respectively. In the left panels (‘OrbitalAlternativeValidated’), the reference data are exclusively from the Gaia ‘SB1’ solutions.
 |
Fig. 19. Period vs. reference period of sources with available reference data. |
 |
Fig. 20. Eccentricity vs. reference eccentricity of sources with available reference data. |
In the bottom panels of each figure, we plot the uncertainly normalised absolute differences (assuming independent solutions and normal distributed uncertainties) to offer an idea of the X-sigma offset between the reference and fitted values. As shown, the vast majority lies within ±3 sigma, with only a dozen or so beyond it. The most notable outliers are the periods of HD21703 (5086152743542494592, pref = 4.0199 d) and BD-18113 (2370173652144123008, pref = 10.3 d), which are different by 0.04 and 7.3 d, respectively. Together with very small uncertainties in the astrometric and literature RV period, this causes the large divergence that we accepted in this case. Figure 21 shows that for the ‘OrbitalTargetedSearch[Validated]’ samples, the normalised p − pref distributions is reasonably well represented by the expected normal distribution centred on 0 with a standard deviation of 1, while the normalised e − eref distribution has a rather non-Gaussian shape with excesses and deficiencies on the positive and negative side, as is also clearly visible in Fig. 20. The median offset −0.22 indicates that overall, we tend to fit lower eccentricities.
 |
Fig. 21. Distribution of normalised reference value offsets for the 184 solutions in the ‘OrbitalTargetedSearch[Validated]’ sample. |
7. Conclusions
We presented a sample of 1162 orbital solutions of Gaia astrometric data produced by the exoplanet pipeline, spanning the planetary-mass regime up to low-mass stellar companions and probing a regime with a low astrometric signal-to-noise ratio. The host star distribution is dominated by main-sequence stars along with a small fraction of (sub-)giant stars spanning the apparent magnitude range of G ∼ 3 − 20. The vast majority of least massive (potentially brown dwarf and planetary mass) companions are confined to G ≲ 11. Semi-major axes range between a1 ∼ 0.1 − 10 mas with the majority of periods found between 100 − 2000 d and a noticeable tail down to ∼8 d. The least massive companions are detected out to ∼100 pc, with (sub-)stellar mass companions up to (several) kiloparsecs. The sky distribution is rather uniform for the (nearby) least massive companions and more confined to the Galactic plane for the more massive (farther out) ones.
The sample orbital solutions is subdivided in the Gaia DR3 nss_two_body_orbit archive table into four nss_solution_type: 629 ‘OrbitalAlternative[Validated]’, 10 of which are validated, and 533 ‘OrbitalTargetedSearch[Validated]’, 188 of which validated (Sect. 5).
Due to the rather short available time span of 34 months of data, the limited number of observations, and the error model that still has to be improved (in particular the calibrations) in the bright-star regime, we had to adopt a complex, inhomogeneous filtering procedure and a large variety of verification and validation steps (often on source-per-source basis) in order to present a sample with high reliability (i.e. low contamination from spurious solutions and incorrectly classified objects) at the cost of very low completeness and very uneven selection function. We estimate that the level of spurious and incorrect solutions in our sample is ∼5% and ∼10% in the ‘OrbitalAlternative’ and ‘OrbitalTargetedSearch’ sample, respectively.
Because of these difficulties, it is therefore no surprise that the Gaia DR3 sample of (known and new) exoplanets and brown dwarfs orbiting bright F-G-K dwarfs with reliable astrometric orbits is small9. Over the past two decades, estimates of the Gaia harvest of exoplanets and brown dwarfs (Lattanzi et al. 2000; Sozzetti et al. 2001, 2014; Casertano et al. 2008; Sozzetti 2014; Perryman et al. 2014; Sahlmann et al. 2015b; Holl et al. 2022) have converged on ballpark numbers of (tens of) thousands of new detections. These studies have always provided end-of-mission (nominal or extend) figures, which therefore cannot be directly compared with the DR3-level sensitivity of the Gaia survey. Gaia DR3 indeed provides the first ever full orbital solutions for a number of known exoplanets and brown dwarfs, and allows identifying a few previously unknown planetary-mass companions based on astrometric data alone. This should by no means be regarded a small feat, but rather a fundamental stepping stone for the expected improvements in future data releases.
One field-of-view (FoV) passage of a source across the Gaia focal plane generally produces eight or nine individual CCD transits, each corresponding to the passage of the source image across an astrometric field (AF) detector (Gaia Collaboration 2016).
A visibility period groups observations separated from other groups by at least four days which (usually) assures that scan angle and parallax factors have changed by a significant amount due to the evolution of the scanning law. It is therefore a better measure of independent epochs than simply counting CCD observations or FoV transits.
The renormalisation function value that transforms the AGIS unit weight error (uwe) into a renormalised unit weight error (ruwe); for details, see the definition of the Gaia archive ruwe parameter.
Ranalli et al. (2018) presented an independent approach in which they used the BIC for their model selection.
See Gaia Collaboration (2023a) for a different perspective on the sample of astrometrically detected substellar companions to low-mass M dwarfs.
Acknowledgments
We thank the anonymous referee for helpful feedback and suggestions that improved the quality of this paper. We also thank Marcus Marcussen for identifying a small error in an earlier version of this paper. This work has, in part, been carried out within the framework of the National Centre for Competence in Research PlanetS supported by SNSF. A.S., P.G., M.G.L., and R.M. gratefully acknowledge financial support of the Italian Space Agency (ASI) under contracts 2018-24-HH.0 and 2018-24-HH.1-2022 in support of the Italian participation to the Gaia mission. This work presents results from the European Space Agency (ESA) space mission Gaia. Gaia data are being processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC is provided by national institutions, in particular the institutions participating in the Gaia MultiLateral Agreement (MLA). The Gaia mission website is https://www.cosmos.esa.int/gaia. The Gaia archive website is https://archives.esac.esa.int/gaia. Full acknowledgements are given in Appendix C. This publication makes use of the Data & Analysis Center for Exoplanets (DACE), which is a facility based at the University of Geneva (CH) dedicated to extrasolar planets data visualisation, exchange and analysis. DACE is a platform of the Swiss National Centre of Competence in Research (NCCR) PlanetS, federating the Swiss expertise in Exoplanet research. The DACE platform is available at https://dace.unige.ch. This research has made use of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. The authors made use of DATAGRAPH (https://www.visualdatatools.com/DataGraph/), TOPCAT (Taylor 2005), ASTROPY (a community-developed core Python package for Astronomy; Astropy Collaboration 2013), SCIPY (Jones et al. 2001), NUMPY (Oliphant 2007), IPYTHON (Pérez & Granger 2007), PANDAS (Reback et al. 2022) and MATPLOTLIB (Hunter 2007).
References
- Affer, L., Micela, G., Damasso, M., et al. 2016, A&A, 593, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alcock, C., Allsman, R., Alves, D. R., et al. 2000, ApJ, 542, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada-Escudé, G., & Tuomi, M. 2015, Science, 347, 1080 [CrossRef] [Google Scholar]
- Anglada-Escudé, G., Arriagada, P., Vogt, S. S., et al. 2012, ApJ, 751, L16 [CrossRef] [Google Scholar]
- Anglada-Escudé, G., Tuomi, M., Gerlach, E., et al. 2013, A&A, 556, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anglada-Escudé, G., Arriagada, P., Tuomi, M., et al. 2014, MNRAS, 443, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada-Escudé, G., Tuomi, M., Arriagada, P., et al. 2016, ApJ, 830, 74 [CrossRef] [Google Scholar]
- Armstrong, D. J., Gamper, J., & Damoulas, T. 2021, MNRAS, 504, 5327 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Babusiaux, C., Fabricius, C., Khanna, S., et al. 2023, A&A, 674, A32 (Gaia DR3 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baluev, R. V. 2013, MNRAS, 429, 2052 [Google Scholar]
- Binnendijk, L. 1960, Properties of Double Stars; a Survey of Parallaxes and Orbits (University of Pennsylvania Press) [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Hébrard, G., Udry, S., et al. 2009, A&A, 505, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Busà, I., Aznar Cuadrado, R., Terranegra, L., Andretta, V., & Gomez, M. T. 2007, A&A, 466, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butler, R. P., Tinney, C. G., Marcy, G. W., et al. 2001, ApJ, 555, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Wright, J. T., Marcy, G. W., et al. 2006, ApJ, 646, 505 [Google Scholar]
- Butler, R. P., Howard, A. W., Vogt, S. S., & Wright, J. T. 2009, ApJ, 691, 1738 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Vogt, S. S., Laughlin, G., et al. 2017, AJ, 153, 208 [Google Scholar]
- Casertano, S., Lattanzi, M. G., Sozzetti, A., et al. 2008, A&A, 482, 699 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collier Cameron, A., Bouchy, F., Hébrard, G., et al. 2007, MNRAS, 375, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Dalal, S., Kiefer, F., Hébrard, G., et al. 2021, A&A, 651, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delfosse, X., Bonfils, X., Forveille, T., et al. 2013, A&A, 553, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delisle, J. B., & Ségransan, D. 2022, A&A, 667, A172 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz, R. F., Delfosse, X., Hobson, M. J., et al. 2019, A&A, 625, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dodson-Robinson, S. E., Delgado, V. R., Harrell, J., & Haley, C. L. 2022, AJ, 163, 169 [Google Scholar]
- Doyle, L. R., Carter, J. A., Fabrycky, D. C., et al. 2011, Science, 333, 1602 [NASA ADS] [CrossRef] [Google Scholar]
- Drimmel, R., Sozzetti, A., Schröder, K.-P., et al. 2021, MNRAS, 502, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Dumusque, X., Pepe, F., Lovis, C., et al. 2012, Nature, 491, 207 [Google Scholar]
- Eastman, J., Gaudi, B. S., & Agol, E. 2013, PASP, 125, 83 [Google Scholar]
- Endl, M., Cochran, W. D., Wittenmyer, R. A., & Boss, A. P. 2008, ApJ, 673, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Espinoza, N., Bayliss, D., Hartman, J. D., et al. 2016, AJ, 152, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, D. W., Eyer, L., Busso, G., et al. 2023, A&A, 674, A4 (Gaia DR3 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eyer, L., Audard, M., Holl, B., et al. 2023, A&A, 674, A13 (Gaia DR3 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faria, J. P., Adibekyan, V., Amazo-Gómez, E. M., et al. 2020, A&A, 635, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feng, F., Tuomi, M., & Jones, H. R. A. 2017a, MNRAS, 470, 4794 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, F., Tuomi, M., Jones, H. R. A., et al. 2017b, AJ, 154, 135 [Google Scholar]
- Feroz, F., & Hobson, M. P. 2014, MNRAS, 437, 3540 [Google Scholar]
- Ford, E. B. 2006, ApJ, 642, 505 [Google Scholar]
- Forveille, T., Bonfils, X., Delfosse, X., et al. 2009, A&A, 493, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Arenou, F., et al.) 2023a, A&A, 674, A34 (Gaia DR3 SI) [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023b, A&A, 674, A1 (Gaia DR3 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giammichele, N., Bergeron, P., & Dufour, P. 2012, ApJS, 199, 29 [Google Scholar]
- Gillon, M., Demory, B.-O., Van Grootel, V., et al. 2017, Nat. Astron., 1, 0056 [Google Scholar]
- Górski, K. M., Banday, A. J., Hivon, E., & Wandelt, B. D. 2002, ASP Conf. Ser., 281, 107 [Google Scholar]
- Halbwachs, J. L., Mayor, M., & Udry, S. 2005, A&A, 431, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Halbwachs, J.-L., Pourbaix, D., Arenou, F., et al. 2023, A&A, 674, A9 (Gaia DR3 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatzes, A. P. 2013, ApJ, 770, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Hatzes, A. P. 2016, A&A, 585, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hébrard, G., Arnold, L., Forveille, T., et al. 2016, A&A, 588, A145 [Google Scholar]
- Holl, B., Perryman, M., Lindegren, L., Ségransan, D., & Raimbault, M. 2022, A&A, 661, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holl, B., Fabricius, C., Portell, J., et al. 2023, A&A, 674, A25 (Gaia DR3 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holland, J. H. 1975, Adaptation in Natural and Artificial Systems (Ann Arbor, MI: University of Michigan Press) [Google Scholar]
- Horch, E. P., van Belle, G. T., Davidson, James W. J., et al. 2020, AJ, 159, 233 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Hurt, S. A., Fulton, B., Isaacson, H., et al. 2022, AJ, 163, 218 [Google Scholar]
- Jenkins, J. S., & Tuomi, M. 2014, ApJ, 794, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. S., Tuomi, M., Brasser, R., Ivanyuk, O., & Murgas, F. 2013, ApJ, 771, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open source scientific tools for Python [Google Scholar]
- Jong, K. D. 1988, Mach. Learn., 3, 123 [Google Scholar]
- Kiefer, F., Hébrard, G., Sahlmann, J., et al. 2019, A&A, 631, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 434, L51 [Google Scholar]
- Knutson, H. A., Fulton, B. J., Montet, B. T., et al. 2014, ApJ, 785, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Kovács, G., Zucker, S., & Mazeh, T. 2002, A&A, 391, 369 [Google Scholar]
- Lattanzi, M. G., Spagna, A., Sozzetti, A., & Casertano, S. 2000, MNRAS, 317, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Lo Curto, G., Mayor, M., Benz, W., et al. 2013, A&A, 551, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
- Lubin, J., Robertson, P., Stefansson, G., et al. 2021, AJ, 162, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mendez, R. A., Claveria, R. M., Orchard, M. E., & Silva, J. F. 2017, AJ, 154, 187 [Google Scholar]
- Motalebi, F., Udry, S., Gillon, M., et al. 2015, A&A, 584, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, S. J., Bedding, T. R., & Shibahashi, H. 2016, ApJ, 827, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Oliphant, T. E. 2007, Comput. Sci. Eng., 9, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Lovis, C., Ségransan, D., et al. 2011, A&A, 534, A58 [CrossRef] [EDP Sciences] [Google Scholar]
- Pérez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
- Perryman, M., Hartman, J., Bakos, G. Á., & Lindegren, L. 2014, ApJ, 797, 14 [Google Scholar]
- Pourbaix, D., Arenou, F., Gavras, P., et al. 2022, Gaia DR3 documentation Chapter 7: Non-single stars, Gaia DR3 documentation, European Space Agency; Gaia Data Processing and Analysis Consortium, https://gea.esac.esa.int/archive/documentation/GDR3/Data_analysis/chap_cu4nss/ [Google Scholar]
- Psaridi, A., Bouchy, F., Lendl, M., et al. 2022, A&A, 664, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rajpaul, V., Aigrain, S., & Roberts, S. 2016, MNRAS, 456, L6 [CrossRef] [Google Scholar]
- Ranalli, P., Hobbs, D., & Lindegren, L. 2018, A&A, 614, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reback, J., McKinney, W., Van den Bossche, J., et al. 2022, https://zenodo.org/record/6408044 [Google Scholar]
- Ribas, I., Tuomi, M., Reiners, A., et al. 2018, Nature, 563, 365 [Google Scholar]
- Robertson, P., & Mahadevan, S. 2014, ApJ, 793, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, P., Mahadevan, S., Endl, M., & Roy, A. 2014, Science, 345, 440 [Google Scholar]
- Robertson, P., Mahadevan, S., Endl, M., & Roy, A. 2015a, Science, 347, 1080 [CrossRef] [Google Scholar]
- Robertson, P., Roy, A., & Mahadevan, S. 2015b, ApJ, 805, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenthal, L. J., Fulton, B. J., Hirsch, L. A., et al. 2021, ApJS, 255, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Sahlmann, J. 2019, https://doi.org/10.5281/zenodo.3515526 [Google Scholar]
- Sahlmann, J., Ségransan, D., Queloz, D., et al. 2011, A&A, 525, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahlmann, J., Lazorenko, P. F., Ségransan, D., et al. 2013, A&A, 556, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahlmann, J., Lazorenko, P. F., Ségransan, D., et al. 2015a, A&A, 577, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahlmann, J., Triaud, A. H. M. J., & Martin, D. V. 2015b, MNRAS, 447, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Sahlmann, J., Burgasser, A. J., Bardalez Gagliuffi, D. C., et al. 2020, MNRAS, 495, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Mortier, A., Faria, J. P., et al. 2014, A&A, 566, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
- Schwarz, G. E. 1978, Ann. Stat., 6, 461 [CrossRef] [Google Scholar]
- Ségransan, D., Mayor, M., Udry, S., et al. 2011, A&A, 535, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simpson, E. R., Fetherolf, T., Kane, S. R., et al. 2022, AJ, 163, 215 [Google Scholar]
- Sion, E. M., Holberg, J. B., Oswalt, T. D., et al. 2014, AJ, 147, 129 [Google Scholar]
- Smart, R. L., Marocco, F., Sarro, L. M., et al. 2019, MNRAS, 485, 4423 [Google Scholar]
- Sozzetti, A. 2014, Mem. Soc. Astron. Ital., 85, 643 [Google Scholar]
- Sozzetti, A., Casertano, S., Lattanzi, M. G., & Spagna, A. 2001, A&A, 373, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sozzetti, A., Giacobbe, P., Lattanzi, M. G., et al. 2014, MNRAS, 437, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Stock, S., Nagel, E., Kemmer, J., et al. 2020, A&A, 643, A112 [EDP Sciences] [Google Scholar]
- Taylor, M. B. 2005, ASP Conf. Ser., 347, 29 [Google Scholar]
- Ter Braak, C. J. F. 2006, Stat. Comput., 16, 239 [Google Scholar]
- Triaud, A. H. M. J., Martin, D. V., Ségransan, D., et al. 2017, A&A, 608, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Triaud, A. H. M. J., Standing, M. R., Heidari, N., et al. 2022, MNRAS, 511, 3561 [NASA ADS] [CrossRef] [Google Scholar]
- Trifonov, T., Kürster, M., Zechmeister, M., et al. 2018, A&A, 609, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tuomi, M., Jones, H. R. A., Jenkins, J. S., et al. 2013, A&A, 551, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Udry, S., Mayor, M., Naef, D., et al. 2000, A&A, 356, 590 [NASA ADS] [Google Scholar]
- Unger, N., Ségransan, D., et al. 2022, A&A, submitted [Google Scholar]
- van Leeuwen, F. 2007, Hipparcos, the New Reduction of the Raw Data: Astrophysics and Space Science Library (Springer Science+Business Media B.V), 350 [CrossRef] [Google Scholar]
- Vogt, S. S., Butler, R. P., Rivera, E. J., et al. 2010, ApJ, 723, 954 [CrossRef] [Google Scholar]
- Vogt, S. S., Burt, J., Meschiari, S., et al. 2015, ApJ, 814, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, E. B., & Hilferty, M. M. 1931, Proc. Nat. Acad. Sci., 17, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, P. A., Hébrard, G., Santos, N. C., et al. 2016, A&A, 588, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, J. T., & Howard, A. W. 2009, ApJS, 182, 205 [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Reference solution parameters
The electronic table refsols.dat contains an overview of all sources we published into Gaia DR3 table nss_two_body_orbit for which we identified reference data. A sample is provided in Table A.1. The last column contains an index relating to our pseudo-companion mass estimate 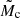 assuming a solar-mass host, with 0 = {
assuming a solar-mass host, with 0 = {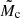 < 20 MJ},1 = {20 MJ ≤
< 20 MJ},1 = {20 MJ ≤ 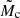 ≤ 120 MJ}, and 2 = {
≤ 120 MJ}, and 2 = {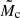 > 120 MJ}.
> 120 MJ}.
Conveniently formatted sample of the online refsols.dat table with reference solutions. Full numerical precision is available at the CDS.
For several sources, no non-Gaia RV reference parameters are provided. This is true for the sources mentioned in Sect. 6.3.2, for which the literature radial velocity by itself did not provide a constrained orbital solution, but the data are consistent with the astrometric orbital period. The three sources Gaia DR3 2185171578009765632 (HD193468), Gaia DR3 6678530491511225856, and Gaia DR3 6778413151435607680 were validated based on internal Gaia reference data that were in the end not published in Gaia DR3, therefore, no reference values are provided. All sources with an available period and eccentricity were used in the analyses of Sect. 6.3.6. Reference radial velocity data that are publicly available on the Data and Analysis Center for Exoplanets (DACE) platform10 can be directly queried online via the link provided in the ref_note column in the electronic table and are marked with a hyperlink asterisk in Table A.1. The reference radial velocity time series for these latter sources are also exported in the following electronic tables with this paper:
-
bd-18113.dat: CORALIE radial velocity time series for BD-18113, first published with this publication.
-
46_10046.dat: CORALIE radial velocity time series for CD-46 10046, first published with this publication.
-
gj812a.dat: HARPS03 radial velocity time series for GJ812A from the HARPS- ESO public archive program id: 183.C-0437(A) (Bonfils).
-
gj9732.dat: HARPS03 radial velocity time series for GJ9732 from the HARPS- ESO public archive program id: 180.C-0886(A) and 183.C-0437(A) (Bonfils).
-
hd26596.dat: radial velocity time series for HD26596 from the SOPHIE public archive11.
-
hd40503.dat: HARPS03 program id: 085.C-0019(A) (Lo Curto) and CORALIE radial velocity time series for HD40503, first published with this publication.
-
hd68638.dat: ELODIE radial velocity time series for HD68638 from the ELODIE public archive12.
-
hd89010.dat: ELODIE - SOPHIE - OHP radial velocity time series for HD89010 from the SOPHIE and ELODIE public archives.
-
hd134237.dat: CORALIE (prog. 703) radial velocity time series for HD134237 first published with this publication.
-
hd183162.dat: radial velocity time series for HD183162 from HIRES Butler et al. (2017), as well as SOPHIE public archive.
-
hip9095.dat: CORALIE (prog. 714) radial velocity time series for HIP9095 series first published with this publication.
-
toi-288.dat: CORALIE radial velocity time series for TOI-288 from Psaridi et al. (2022).
All observations are before JD 2459519.5 (1 Nov 2021), which is the time at which the validations for this paper were done.
Appendix B: Examples of Gaia archive queries
This section describes Gaia archive queries in the ADQL format that return the various selections and tables presented in this paper. These queries can be made online in the Gaia DR3 archive.
B.1. Sky source density and number of observations
Input data for HEALPix (Górski et al. 2002) plots of the source sky density and number of FoV observations in the lower two panels of Fig. 4:
select gaia_healpix_index(8, source_id) AS hpx8, round( count(*) / 0.052441, 0) as sources_per_sq_deg, round( avg(astrometric_matched_transits), 1) as mean_agis_fov, round( max(astrometric_matched_transits), 0) as max_agis_fov from gaiadr3.gaia_source group by hpx8
B.2. Flag counts
Counts of flags in nss_two_body_orbit for our nss_solution_type discussed in Sect. 3.3:
select flags, nss_solution_type, count(source_id) as counts from
gaiadr3.nss_two_body_orbit where nss_solution_type in
('OrbitalTargetedSearch','OrbitalAlternative', 'OrbitalTargetedSearchValidated','OrbitalAlternativeValidated')
group by nss_solution_type, flags
order by flags, counts
B.3. Table 2 counts
Counts of source_ids with alternative solutions in table nss_two_body_orbit:
select nss_solution_type_exopl, nonexopl.nss_solution_type as
nss_solution_type_other, count(source_id) as counts from ( select
source_id, cnt.num_solutions, orb.nss_solution_type as
nss_solution_type_exopl, period as period_exopl
from gaiadr3.nss_two_body_orbit orb join
( select source_id, count(source_id) as num_solutions from gaiadr3.nss_two_body_orbit group by source_id
) as cnt using (source_id)
where nss_solution_type in
('OrbitalTargetedSearch','OrbitalAlternative','OrbitalTargetedSearchValidated', 'OrbitalAlternativeValidated')
and cnt.num_solutions = 2 -- subset of source_id with two entries (there are none with >2)
) as exopl join gaiadr3.nss_two_body_orbit nonexopl using
(source_id) where nonexopl.nss_solution_type not in
('OrbitalTargetedSearch','OrbitalAlternative','OrbitalTargetedSearchValidated', 'OrbitalAlternativeValidated')
group by nss_solution_type_exopl,nss_solution_type order by
nss_solution_type_exopl asc, counts desc
Counts of source_ids with an alternative solution in table nss_non_linear_spectro: https://gea.esac.esa.int/archive/
select exopl.nss_solution_type as nss_solution_type_exopl,
nnls.nss_solution_type as nss_solution_type_other, count(source_id)
as counts from gaiadr3.nss_non_linear_spectro nnls join
gaiadr3.nss_two_body_orbit exopl using (source_id) where
exopl.nss_solution_type in
('OrbitalTargetedSearch','OrbitalAlternative','OrbitalTargetedSearchValidated', 'OrbitalAlternativeValidated')
group by exopl.nss_solution_type, nnls.nss_solution_type order by
exopl.nss_solution_type asc, counts desc
Appendix C: Full acknowledgements
This work presents results from the European Space Agency (ESA) space mission Gaia. Gaia data are being processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC is provided by national institutions, in particular the institutions participating in the Gaia MultiLateral Agreement (MLA). The Gaia mission website is https://www.cosmos.esa.int/gaia. The Gaia archive website is https://archives.esac.esa.int/gaia.
The Gaia mission and data processing have financially been supported by, in alphabetical order by country:
-
the Algerian Centre de Recherche en Astronomie, Astrophysique et Géophysique of Bouzareah Observatory;
-
the Austrian Fonds zur Förderung der wissenschaftlichen Forschung (FWF) Hertha Firnberg Programme through grants T359, P20046, and P23737;
-
the BELgian federal Science Policy Office (BELSPO) through various PROgramme de Développement d’Expériences scientifiques (PRODEX) grants and the Polish Academy of Sciences - Fonds Wetenschappelijk Onderzoek through grant VS.091.16N, and the Fonds de la Recherche Scientifique (FNRS), and the Research Council of Katholieke Universiteit (KU) Leuven through grant C16/18/005 (Pushing AsteRoseismology to the next level with TESS, GaiA, and the Sloan DIgital Sky SurvEy – PARADISE);
-
the Brazil-France exchange programmes Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) and Coordenação de Aperfeicoamento de Pessoal de Nível Superior (CAPES) - Comité Français d’Evaluation de la Coopération Universitaire et Scientifique avec le Brésil (COFECUB);
-
the Chilean Agencia Nacional de Investigación y Desarrollo (ANID) through Fondo Nacional de Desarrollo Científico y Tecnológico (FONDECYT) Regular Project 1210992 (L. Chemin);
-
the National Natural Science Foundation of China (NSFC) through grants 11573054, 11703065, and 12173069, the China Scholarship Council through grant 201806040200, and the Natural Science Foundation of Shanghai through grant 21ZR1474100;
-
the Tenure Track Pilot Programme of the Croatian Science Foundation and the École Polytechnique Fédérale de Lausanne and the project TTP-2018-07-1171 ‘Mining the Variable Sky’, with the funds of the Croatian-Swiss Research Programme;
-
the Czech-Republic Ministry of Education, Youth, and Sports through grant LG 15010 and INTER-EXCELLENCE grant LTAUSA18093, and the Czech Space Office through ESA PECS contract 98058;
-
the Danish Ministry of Science;
-
the Estonian Ministry of Education and Research through grant IUT40-1;
-
the European Commission’s Sixth Framework Programme through the European Leadership in Space Astrometry (ELSA) Marie Curie Research Training Network (MRTN-CT-2006-033481), through Marie Curie project PIOF-GA-2009-255267 (Space AsteroSeismology & RR Lyrae stars, SAS-RRL), and through a Marie Curie Transfer-of-Knowledge (ToK) fellowship (MTKD-CT-2004-014188); the European Commission’s Seventh Framework Programme through grant FP7-606740 (FP7-SPACE-2013-1) for the Gaia European Network for Improved data User Services (GENIUS) and through grant 264895 for the Gaia Research for European Astronomy Training (GREAT-ITN) network;
-
the European Cooperation in Science and Technology (COST) through COST Action CA18104 ‘Revealing the Milky Way with Gaia (MW-Gaia)’;
-
the European Research Council (ERC) through grants 320360, 647208, and 834148 and through the European Union’s Horizon 2020 research and innovation and excellent science programmes through Marie Skłodowska-Curie grant 745617 (Our Galaxy at full HD – Gal-HD) and 895174 (The build-up and fate of self-gravitating systems in the Universe) as well as grants 687378 (Small Bodies: Near and Far), 682115 (Using the Magellanic Clouds to Understand the Interaction of Galaxies), 695099 (A sub-percent distance scale from binaries and Cepheids – CepBin), 716155 (Structured ACCREtion Disks – SACCRED), 951549 (Sub-percent calibration of the extragalactic distance scale in the era of big surveys – UniverScale), and 101004214 (Innovative Scientific Data Exploration and Exploitation Applications for Space Sciences – EXPLORE);
-
the European Science Foundation (ESF), in the framework of the Gaia Research for European Astronomy Training Research Network Programme (GREAT-ESF);
-
the European Space Agency (ESA) in the framework of the Gaia project, through the Plan for European Cooperating States (PECS) programme through contracts C98090 and 4000106398/12/NL/KML for Hungary, through contract 4000115263/15/NL/IB for Germany, and through PROgramme de Développement d’Expériences scientifiques (PRODEX) grant 4000127986 for Slovenia;
-
the Academy of Finland through grants 299543, 307157, 325805, 328654, 336546, and 345115 and the Magnus Ehrnrooth Foundation;
-
the French Centre National d’Études Spatiales (CNES), the Agence Nationale de la Recherche (ANR) through grant ANR-10-IDEX-0001-02 for the ‘Investissements d’avenir’ programme, through grant ANR-15-CE31-0007 for project ‘Modelling the Milky Way in the Gaia era’ (MOD4Gaia), through grant ANR-14-CE33-0014-01 for project ‘The Milky Way disc formation in the Gaia era’ (ARCHEOGAL), through grant ANR-15-CE31-0012-01 for project ‘Unlocking the potential of Cepheids as primary distance calibrators’ (UnlockCepheids), through grant ANR-19-CE31-0017 for project ‘Secular evolution of galxies’ (SEGAL), and through grant ANR-18-CE31-0006 for project ‘Galactic Dark Matter’ (GaDaMa), the Centre National de la Recherche Scientifique (CNRS) and its SNO Gaia of the Institut des Sciences de l’Univers (INSU), its Programmes Nationaux: Cosmologie et Galaxies (PNCG), Gravitation Références Astronomie Métrologie (PNGRAM), Planétologie (PNP), Physique et Chimie du Milieu Interstellaire (PCMI), and Physique Stellaire (PNPS), the ‘Action Fédératrice Gaia’ of the Observatoire de Paris, the Région de Franche-Comté, the Institut National Polytechnique (INP) and the Institut National de Physique nucléaire et de Physique des Particules (IN2P3) co-funded by CNES;
-
the German Aerospace Agency (Deutsches Zentrum für Luft- und Raumfahrt e.V., DLR) through grants 50QG0501, 50QG0601, 50QG0602, 50QG0701, 50QG0901, 50QG1001, 50QG1101, 50QG1401, 50QG1402, 50QG1403, 50QG1404, 50QG1904, 50QG2101, 50QG2102, and 50QG2202, and the Centre for Information Services and High Performance Computing (ZIH) at the Technische Universität Dresden for generous allocations of computer time;
-
the Hungarian Academy of Sciences through the Lendület Programme grants LP2014-17 and LP2018-7 and the Hungarian National Research, Development, and Innovation Office (NKFIH) through grant KKP-137523 (‘SeismoLab’);
-
the Science Foundation Ireland (SFI) through a Royal Society - SFI University Research Fellowship (M. Fraser);
-
the Israel Ministry of Science and Technology through grant 3-18143 and the Tel Aviv University Center for Artificial Intelligence and Data Science (TAD) through a grant;
-
the Agenzia Spaziale Italiana (ASI) through contracts I/037/08/0, I/058/10/0, 2014-025-R.0, 2014-025-R.1.2015, and 2018-24-HH.0 to the Italian Istituto Nazionale di Astrofisica (INAF), contract 2014-049-R.0/1/2 to INAF for the Space Science Data Centre (SSDC, formerly known as the ASI Science Data Center, ASDC), contracts I/008/10/0, 2013/030/I.0, 2013-030-I.0.1-2015, and 2016-17-I.0 to the Aerospace Logistics Technology Engineering Company (ALTEC S.p.A.), INAF, and the Italian Ministry of Education, University, and Research (Ministero dell’Istruzione, dell’Università e della Ricerca) through the Premiale project ‘MIning The Cosmos Big Data and Innovative Italian Technology for Frontier Astrophysics and Cosmology’ (MITiC);
-
the Netherlands Organisation for Scientific Research (NWO) through grant NWO-M-614.061.414, through a VICI grant (A. Helmi), and through a Spinoza prize (A. Helmi), and the Netherlands Research School for Astronomy (NOVA);
-
the Polish National Science Centre through HARMONIA grant 2018/30/M/ST9/00311 and DAINA grant 2017/27/L/ST9/03221 and the Ministry of Science and Higher Education (MNiSW) through grant DIR/WK/2018/12;
-
the Portuguese Fundação para a Ciência e a Tecnologia (FCT) through national funds, grants SFRH/BD/128840/2017 and PTDC/FIS-AST/30389/2017, and work contract DL 57/2016/CP1364/CT0006, the Fundo Europeu de Desenvolvimento Regional (FEDER) through grant POCI-01-0145-FEDER-030389 and its Programa Operacional Competitividade e Internacionalização (COMPETE2020) through grants UIDB/04434/2020 and UIDP/04434/2020, and the Strategic Programme UIDB/00099/2020 for the Centro de Astrofísica e Gravitação (CENTRA);
-
the Slovenian Research Agency through grant P1-0188;
-
the Spanish Ministry of Economy (MINECO/FEDER, UE), the Spanish Ministry of Science and Innovation (MICIN), the Spanish Ministry of Education, Culture, and Sports, and the Spanish Government through grants BES-2016-078499, BES-2017-083126, BES-C-2017-0085, ESP2016-80079-C2-1-R, ESP2016-80079-C2-2-R, FPU16/03827, PDC2021-121059-C22, RTI2018-095076-B-C22, and TIN2015-65316-P (‘Computación de Altas Prestaciones VII’), the Juan de la Cierva Incorporación Programme (FJCI-2015-2671 and IJC2019-04862-I for F. Anders), the Severo Ochoa Centre of Excellence Programme (SEV2015-0493), and MICIN/AEI/10.13039/501100011033 (and the European Union through European Regional Development Fund ‘A way of making Europe’) through grant RTI2018-095076-B-C21, the Institute of Cosmos Sciences University of Barcelona (ICCUB, Unidad de Excelencia ‘María de Maeztu’) through grant CEX2019-000918-M, the University of Barcelona’s official doctoral programme for the development of an R+D+i project through an Ajuts de Personal Investigador en Formació (APIF) grant, the Spanish Virtual Observatory through project AyA2017-84089, the Galician Regional Government, Xunta de Galicia, through grants ED431B-2021/36, ED481A-2019/155, and ED481A-2021/296, the Centro de Investigación en Tecnologías de la Información y las Comunicaciones (CITIC), funded by the Xunta de Galicia and the European Union (European Regional Development Fund – Galicia 2014-2020 Programme), through grant ED431G-2019/01, the Red Española de Supercomputación (RES) computer resources at MareNostrum, the Barcelona Supercomputing Centre - Centro Nacional de Supercomputación (BSC-CNS) through activities AECT-2017-2-0002, AECT-2017-3-0006, AECT-2018-1-0017, AECT-2018-2-0013, AECT-2018-3-0011, AECT-2019-1-0010, AECT-2019-2-0014, AECT-2019-3-0003, AECT-2020-1-0004, and DATA-2020-1-0010, the Departament d’Innovació, Universitats i Empresa de la Generalitat de Catalunya through grant 2014-SGR-1051 for project ‘Models de Programació i Entorns d’Execució Parallels’ (MPEXPAR), and Ramon y Cajal Fellowship RYC2018-025968-I funded by MICIN/AEI/10.13039/501100011033 and the European Science Foundation (‘Investing in your future’);
-
the Swedish National Space Agency (SNSA/Rymdstyrelsen);
-
the Swiss State Secretariat for Education, Research, and Innovation through the Swiss Activités Nationales Complémentaires and the Swiss National Science Foundation through an Eccellenza Professorial Fellowship (award PCEFP2_194638 for R. Anderson);
-
the United Kingdom Particle Physics and Astronomy Research Council (PPARC), the United Kingdom Science and Technology Facilities Council (STFC), and the United Kingdom Space Agency (UKSA) through the following grants to the University of Bristol, the University of Cambridge, the University of Edinburgh, the University of Leicester, the Mullard Space Sciences Laboratory of University College London, and the United Kingdom Rutherford Appleton Laboratory (RAL): PP/D006511/1, PP/D006546/1, PP/D006570/1, ST/I000852/1, ST/J005045/1, ST/K00056X/1, ST/K000209/1, ST/K000756/1, ST/L006561/1, ST/N000595/1, ST/N000641/1, ST/N000978/1, ST/N001117/1, ST/S000089/1, ST/S000976/1, ST/S000984/1, ST/S001123/1, ST/S001948/1, ST/S001980/1, ST/S002103/1, ST/V000969/1, ST/W002469/1, ST/W002493/1, ST/W002671/1, ST/W002809/1, and EP/V520342/1.
The GBOT programme uses observations collected at (i) the European Organisation for Astronomical Research in the Southern Hemisphere (ESO) with the VLT Survey Telescope (VST), under ESO programmes 092.B-0165, 093.B-0236, 094.B-0181, 095.B-0046, 096.B-0162, 097.B-0304, 098.B-0030, 099.B-0034, 0100.B-0131, 0101.B-0156, 0102.B-0174, and 0103.B-0165; and (ii) the Liverpool Telescope, which is operated on the island of La Palma by Liverpool John Moores University in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias with financial support from the United Kingdom Science and Technology Facilities Council, and (iii) telescopes of the Las Cumbres Observatory Global Telescope Network.
All Tables
gaia_dr3.nss_two_body_orbit table fields filled for the 1162 sources from the exoplanet pipeline described in this paper.
Overview of 213 source_ids with an alternative solution in either nss_two_body_orbit or nss_non_linear_spectro.
Conveniently formatted sample of the online refsols.dat table with reference solutions. Full numerical precision is available at the CDS.
All Figures
 |
Fig. 1. Histogram of the observation time spans. |
| In the text | |
 |
Fig. 2. Histogram of the number of CCD observations and visibility periods. The number of CCD observations is divided by nine to provide the approximate number of FoV observations above the left panel. |
| In the text | |
 |
Fig. 3. Mean and median CCD AL-scan abscissa uncertainty σw per source. |
| In the text | |
 |
Fig. 4. Galactic sky distribution of our published solutions. The longitude increases to the left. We broadly categorise the different mass regimes using the pseudo-companion mass |
| In the text | |
 |
Fig. 5. Signal-to-noise ratio of a1 with respect to the uncertainty on the median abscissa. Top panel: statistics used in Casertano et al. (2008) with its typical proposed threshold of 3. Bottom panel: statistics used in Sahlmann et al. (2015b) with its proposed threshold of 20. |
| In the text | |
 |
Fig. 6. Goodness-of-fit statistics. Left panel: χ2 (obj_func in Table 1). Right panel: F2 (goodness_of_fit in Table 1). |
| In the text | |
 |
Fig. 7. Parameter distributions of the published solutions: Period-eccentricity and period vs. semi-major axis (top panels), apparent magnitude vs. inverse parallax (third panel), and zero-extinction absolute magnitude vs. colour (bottom panel). See Sects. 6.1.4 and 6.2 for a discussion. |
| In the text | |
 |
Fig. 8. Uncertainties for period (top panel), eccentricity (second panel), periastron epoch (third panel), and parallax (fourth panel) as a function of the parameter value itself. See Sect. 6.1.5 for a discussion. |
| In the text | |
 |
Fig. 9. Parameter distributions as a function of (photocentre) semi-major axis a1: Jitter term (top panel), semi-major axis (second panel), cosine of the inclination (third panel), longitude of the ascending node (fourth panel), and argument of periastron (bottom panel). See Sect. 6.1.4 for a discussion. |
| In the text | |
 |
Fig. 10. Values and uncertainties for geometric elements. Estimates using linear error propagation and Monte Carlo resampling are shown on the x- and y-axes, respectively. In the latter case, the median value is adopted with a symmetric uncertainty computed as the mean of the upper and lower 1σ equivalent confidence interval. The dashed line indicates equality, and solutions with e/σe < 1 are marked with grey squares. Large discrepancies in ω at the 360°→0° boundary (e.g., the point in the bottom right corner) are of no major concern. |
| In the text | |
 |
Fig. 11. Significance estimates (a over sigma_a). Density histogram of estimates using linear error propagation and Monte Carlo resampling on the x- and y-axes, respectively. The histogram bins are colour-coded by the average eccentricity significance e/σe. |
| In the text | |
 |
Fig. 12. Astrometric orbit of HD 114762 (i.e. Gaia DR3 3937211745905473024, bottom left panel) as determined by Gaia (G = 7.15 mag, P = 83.74 ± 0.12 day, e = 0.32 ± 0.04, and ϖ = 25.36 ± 0.04 mas). North is up, and east is left. The sky-projected orbit model about the system barycentre marked with a cross is shown in grey, and astrometric measurements and normal points after subtraction of parallax and proper motion are shown in grey and black, respectively. Only one-dimensional (along-scan) astrometry was used. The shown offsets are therefore projected along the instantaneous scan angle of Gaia, whose orientation is also indicated by the error bars. The modelled parallax and proper motion of the star are shown in the top left panel by the solid curve, where open circles indicate the times when the star crossed the Gaia field of view. The arrow indicates the direction of motion. The top right panel shows the normal points after subtraction of the parallax and proper motion as a function of time. The middle right and bottom right panels shows the post-fit residual normal points and individual CCD transit data, respectively. Normal points are computed at every field-of-view transit of the star from the approximately nine individual CCD transits and are only used for visualisation, whereas the data processing uses individual CCD transit data. |
| In the text | |
 |
Fig. 13. Same as Fig. 12, but for Gl 876 (i.e. Gaia DR3 2603090003484152064, G = 8.88 mag, P = 61.36 ± 0.22 day, e = 0.16 ± 0.15, and ϖ = 213.79 ± 0.07 mas). |
| In the text | |
 |
Fig. 14. Same as Fig. 12, but for WD0141-279 (i.e. Gaia DR3 4698424845771339520, G = 13.70 mag, P = 33.65 ± 0.05 day, e = 0.20 ± 0.15, and ϖ = 102.87 ± 0.01 mas). |
| In the text | |
 |
Fig. 15. Same as Fig. 12, but for HD 40503 (i.e. Gaia DR3 2884087104955208064, G = 8.97 mag, P = 826.53 ± 49.89 day, e = 0.07 ± 0.10, and ϖ = 25.49 ± 0.01 mas). |
| In the text | |
 |
Fig. 16. Same as Fig. 12, but for 2MASS J08053189+4812330 (i.e. Gaia DR3 933054951834436352, G = 20.01 mag, P = 735.91 ± 22.99 day, e = 0.42 ± 0.23, and ϖ = 43.77 ± 0.71 mas). |
| In the text | |
 |
Fig. 17. Comparison with the single-star AGIS excess noise. |
| In the text | |
 |
Fig. 18. Period-eccentricity diagram for a random sample of sources (black points) with orbits obtained by the DE-MCMC or GA algorithms from the processing the stochastic solution sample. The clear structure of period aliases is a symptom of incorrectly derived orbits and is further discussed in Holl et al. (2023). The filled green dots correspond to P and e values from ‘OrbitalAlternative’ solutions. The solid black curve indicates the maximum eccentricity attainable for an orbit that is not affected by tides, assuming a cut-off period of 5 days (see e.g., Halbwachs et al. 2005). |
| In the text | |
 |
Fig. 19. Period vs. reference period of sources with available reference data. |
| In the text | |
 |
Fig. 20. Eccentricity vs. reference eccentricity of sources with available reference data. |
| In the text | |
 |
Fig. 21. Distribution of normalised reference value offsets for the 184 solutions in the ‘OrbitalTargetedSearch[Validated]’ sample. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.