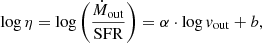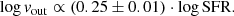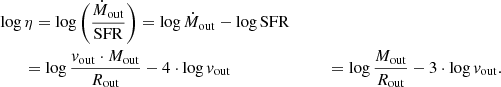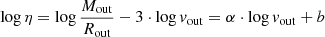| Issue |
A&A
Volume 668, December 2022
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 49 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202244054 | |
| Published online | 01 December 2022 | |
Physics of ULIRGs with MUSE and ALMA: The PUMA project
IV. No tight relation between cold molecular outflow rates and AGN luminosities
1
Centro de Astrobiología (CAB), CSIC-INTA, Ctra. de Ajalvir Km. 4, 28850 Torrejón de Ardoz, Madrid, Spain
e-mail: isabellalamperti@gmail.com
2
INAF – Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy
3
Observatorio Astronómico Nacional (OAN-IGN) – Observatorio de Madrid, Alfonso XII, 3, 28014 Madrid, Spain
4
Universidad de Alcalá, Departamento de Física y Matemáticas, Campus Universitario, 28871 Alcalá de Henares, Madrid, Spain
5
Department of Space, Earth and Environment, Division of Astronomy and Plasma Physics, 412 96 Gothenburg, Sweden
6
Centro de Astrobiología (CAB), CSIC-INTA, Camino Bajo del Castillo s/n, 28692 Villanueva de la Cañada, Madrid, Spain
7
LERMA, Obs. de Paris, PSL Univ., Collège de France, CNRS, Sorbonne Univ., Paris, France
8
Telespazio UK for ESA, ESAC, 28692 Villanueva de la Cañada, Madrid, Spain
9
Department of Physics, University of Oxford, Keble Road, Oxford OX1 3RH, UK
10
Leiden Observatory, Leiden University, PO Box 9513 2300 RA Leiden, The Netherlands
Received:
19
May
2022
Accepted:
15
August
2022
We study molecular outflows in a sample of 25 nearby (z < 0.17, d < 750 Mpc) ultra-luminous infrared galaxy (ULIRG) systems (38 individual nuclei) as part of the Physics of ULIRGs with MUSE and ALMA (PUMA) survey, using ∼400 pc (0.1–1.0″ beam FWHM) resolution ALMA CO(2–1) observations. We used a spectro-astrometry analysis to identify high-velocity (> 300 km s−1) molecular gas disconnected from the galaxy rotation, which we attribute to outflows. In 77% of the 26 nuclei with log LIR/L⊙ > 11.8, we identified molecular outflows with an average vout = 490 km s−1, outflow masses 1 − 35 × 107 M⊙, mass outflow rates Ṁout = 6 − 300 M⊙ yr−1, mass-loading factors η = Ṁout/SFR = 0.1 − 1, and an average outflow mass escape fraction of 45 ± 6%. The majority of these outflows (18/20) are spatially resolved with radii of 0.2 − 0.9 kpc and have short dynamical times (tdyn = Rout/vout) in the range 0.5 − 2.8 Myr. The outflow detection rate is higher in nuclei dominated by starbursts (SBs, 14/15 = 93%) than in active galactic nuclei (AGN, 6/11 = 55%). Outflows perpendicular to the kinematic major axis are mainly found in interacting SBs. We also find that our sample does not follow the Ṁout versus AGN luminosity relation reported in previous works. In our analysis, we include a sample of nearby main-sequence galaxies (SFR = 0.3 − 17 M⊙ yr−1) with detected molecular outflows from the PHANGS-ALMA survey to increase the LIR dynamic range. Using these two samples, we find a correlation between the outflow velocity and the star-formation rate (SFR), as traced by LIR (vout ∝ SFR0.25±0.01), which is consistent with what was found for the atomic ionised and neutral phases. Using this correlation, and the relation between Mout/Rout and vout, we conclude that these outflows are likely momentum-driven. Finally, we compare the CO outflow velocities with the ones derived from the OH 119 μm doublet. In 76% of the targets, the outflow is detected in both CO and OH, while in three targets (18%) the outflow is only detected in CO, and in one target the outflow is detected in OH but not in CO. The difference between the OH and CO outflow velocities could be due to the far-IR background source required by the OH absorption which makes these observations more dependent on the specific outflow geometry.
Key words: galaxies: evolution / galaxies: nuclei / galaxies: active / galaxies: starburst
© I. Lamperti et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Local ultraluminous infrared galaxies (ULIRGs) are extreme objects with infrared (IR, 8–1000 μm) luminosities LIR > 1012 L⊙. ULIRGs are mostly gas-rich major mergers (Lonsdale et al. 2006) and represent an important stage in galaxy evolution. The nuclei of ULIRGs host intense starbursts, and active galactic nuclei (AGN) can also account for a significant fraction of their IR luminosity (Farrah et al. 2003; Nardini et al. 2010). Nuclear outflows powered by starbursts and AGN are thought to play a significant role in the evolution of galaxies. They can influence star-formation by injecting energy into the interstellar medium (ISM), heating or expelling gas from the galaxy (e.g., Fabian 2012; Veilleux et al. 2020). In ULIRGs, outflows have been detected in different gas phases: atomic neutral (e.g., Rupke et al. 2005a; Cazzoli et al. 2016), atomic ionised (e.g., Westmoquette et al. 2012; Bellocchi et al. 2013; Arribas et al. 2014), hot molecular (e.g., Dasyra & Combes 2011; Dasyra et al. 2014; Emonts et al. 2017), and cold molecular (e.g., Fischer et al. 2010; Feruglio et al. 2010, 2015; Sturm et al. 2011; Cicone et al. 2014; Sakamoto et al. 2014; García-Burillo et al. 2015; Aalto et al. 2015; Pereira-Santaella et al. 2018; Fluetsch et al. 2019; Lutz et al. 2020).
In this work, we focus on the cold molecular phase, which is thought to account for most of the mass outflow rate (e.g., Rupke & Veilleux 2013; Carniani et al. 2015; Ramos Almeida et al. 2019; Fluetsch et al. 2021). The most common tracers of the cold molecular phase are the low-J transitions of CO (Feruglio et al. 2010; Chung et al. 2011; Cicone et al. 2014; Pereira-Santaella et al. 2018; Lutz et al. 2020), HCN (Aalto et al. 2012, 2015; Walter et al. 2017; Barcos-Muñoz et al. 2018), and FIR OH lines (e.g., Fischer et al. 2010; Sturm et al. 2011; Spoon et al. 2013; Veilleux et al. 2013; González-Alfonso et al. 2017).
To accurately measure the outflow properties, such as the mass outflow rate, outflow energy and momentum rate, it is necessary to know the distribution of the outflowing gas. Spatially resolved studies of molecular outflows in ULIRGs have only been performed on a few sources (e.g., García-Burillo et al. 2015; Saito et al. 2018; Barcos-Muñoz et al. 2018; Pereira-Santaella et al. 2018). In most cases, the targeted objects were selected based on the presence of an outflow, which was detected through previous low-resolution observations. This could introduce a bias in the samples, in which only ULIRGs with the most-extreme outflows are selected.
In this work, we present high spatial resolution (0.1–1.0″, ∼400 pc) ALMA observations of the CO(2–1) line for an unbiased sample of 25 ULIRGs, selected only based on their IR luminosity. This paper is part of the Physics of ULIRGs with MUSE and ALMA (PUMA) project. The main goals of PUMA are the following: (i) to study the prevalence of outflows in different gas phases (ionised, neutral, and molecular) as a function of the galaxy properties, (ii) to determine the driving mechanisms of the outflows (e.g., distinguish between starburst- and AGN-powered outflows), and (iii) to characterise the effects of outflow feedback on the host galaxies. The PUMA survey combines VLT/MUSE optical integrated field spectroscopy and ALMA CO(2–1) and continuum observations to study the multi-phase (ionised, neutral, and molecular) properties of outflows in ULIRGs. Perna et al. (2021) have presented the first results on the spatial distribution of the ionised gas and the resolved stellar kinematics derived from the MUSE data. A detailed analysis of the MUSE data for Arp 220 has been presented in Perna et al. (2020). Perna et al. (2022) studied the properties and incidence of the ionised gas disks in the PUMA ULIRGs, the associated velocity dispersion and its relation with the offset from the main sequence. Pereira-Santaella et al. (2021) analysed the ALMA 220 GHz continuum and provided evidence for the ubiquitous presence of deeply obscured AGN in ULIRGs, which could substantially contribute to their IR emission.
This paper is organised as follows. In Sect. 2, we describe the sample selection criteria and the general properties of the PUMA targets. Section 3 describes the ALMA observations and the data reduction. In Sect. 4, we present the CO(2–1) moment maps (Sect. 4.1), the spectro-astrometry analysis (Sect. 4.2), and the method used to derive the properties of the molecular outflows (Sects. 4.4–4.6), as well as the analysis of the OH 119 μm spectra (Sect. 4.7). The outflow properties, detection rate, energetics, and launching mechanisms are discussed in Sects. 5.1–5.3. In Sect. 5.4, we compare the outflow properties derived from the CO(2–1) data with the ones derived from the OH 119 μm doublet. The discussion is presented in Sect. 6. In Sect. 7, we summarise the main results and our conclusions. Throughout this work, we assume a cosmological model with Ωλ = 0.7, ΩM = 0.3, and H0 = 70 km s−1 Mpc−1.
2. Sample
The PUMA sample consists of 25 nearby (z < 0.165, d < 750 Mpc) ULIRG systems (38 individual nuclei) with IR luminosities (8 − 1000 μm) in the range log LIR/L⊙ = 11.9 − 12.7. The individual nuclei have luminosities from log LIR/L⊙ < 10.5 to log LIR/L⊙ = 12.7, based on the relative contribution of the nuclei to the total ALMA continuum fluxes (see Pereira-Santaella et al. 2021). The sample has been selected to cover a range of interacting phases: 12 systems are classified as advanced mergers (with distance between the nuclei dnuclei < 1 kpc) and 13 systems are classifies as interacting (with dnuclei = 1.8 − 8.3 kpc). The nuclei of the ULIRGs can be classified as AGN-dominated or starburst- (SB-) dominated based on the AGN contribution in the MIR (αAGN, see Perna et al. 2021): eight ULIRG systems are dominated by AGN (αAGN ≥ 0.5) and 17 by a SB (αAGN < 0.5). Based on the optical classification, our sample includes the following: nine Seyfert galaxies (two Seyfert 1 and seven Seyfert 2), eight HII and eight low ionisation nuclear emission regions (LINERs, Perna et al. 2021). In this paper we adopt a combined classification, in which we consider as AGN all nuclei classified as AGN either based on the MIR criterion (αAGN ≥ 0.5) or based on the optical classification (Seyfert 1 or Seyfert 2). According to this combined classification, 11/25 systems (14/38 individual nuclei) are classified as AGN, while the others are classified as SBs.
An overview of the sample properties is shown in Table 1. Figure 1 shows the IR luminosities and redshift of the sample.
 |
Fig. 1. Infrared luminosity (8–1000 μm) and redshift of the individual nuclei in the PUMA sample. AGN are shown in orange, while starburst (SB) dominated nuclei are in lightblue. Circles indicate interacting systems and squares indicate advanced mergers. The nuclei with log LIR/L⊙ < 12 are the fainter nuclei in interacting systems, where the IR luminosity is dominated by the other nucleus. |
Properties of the sample.
3. Observations and data reduction
In this work, we analyse ALMA 12-m array CO(2–1) 230.538 GHz observations of the 25 ULIRGs systems in the PUMA sample. Most of these observations were carried out as part of our programmes 2015.1.00263.S, 2016.1.00170.S, 2018.1.00486.S, and 2018.1.00699.S (PI: M. Pereira-Santaella). Additionally, we use archival data for 13120−5453 and 15327+2340 (Arp 220), from programmes 2016.1.00777.S (PI: K. Sliwa) and 2015.1.00113.S (PI: N. Scoville), respectively. The observations were taken between 2015 and 2021. We note that the analysis of the CO(2–1) observations of three of the PUMA ULIRGs (12112+0305, 14348−1447, and 22491−1808) has already been presented in Pereira-Santaella et al. (2018), but are included in this paper for completeness.
Depending on the redshift of the targets, the CO(2–1) transition falls in Band 5 or Band 6. The synthesised beam full-width at half-maximum (FWHM) has been selected for each target so that it corresponds to a similar physical spatial resolution for all targets (∼400 − 500 pc). As a result, the synthesised beam FWHM are in the range 0.13 − 1.05″. The maximum recoverable scales are ∼10 times the beam FWHM. Table 2 presents the details of the observations: the beam FWHM, line sensitivity and total CO(2–1) fluxes. The data-reduction is described in detail in the PUMA II paper (Pereira-Santaella et al. 2021). We note that two targets (12071−0444 and 13451+1232) are not presented in that work because the ALMA observations were not available at the time of publication, but they are included in this work. The ALMA observations of 12071−0444 have been reduced following the same procedure used for the other sources. The second target, 13451+1232 (4C+12.50), is a radio AGN with a strong 230 GHz continuum dominated by synchrotron radiation (Pereira-Santaella et al. 2021). Given that for this source the continuum is strong enough, we decide to apply self-calibration to these data in order to increase the signal-to-noise. We apply five rounds of phase self-calibration and one round of amplitude self-calibration. Due to the steep slope of its continuum, we use a first-order polynomial to subtract the continuum from the CO(2–1) spectral window in the uv plane. For the rest of the data-reduction, we follow the same procedure as presented in Pereira-Santaella et al. (2021).
Properties of the ALMA CO(2–1) observations.
4. Analysis
4.1. CO(2–1) moment maps
We produced the maps of the CO(2–1) intensity (moment 0), velocity (moment 1), and velocity dispersion (moment 2) for our sample. Before producing the moment maps, we masked pixels with low signal-to-noise ratio (S/N) in each velocity channel, where the noise was estimated using the median absolute deviation (MAD). Specifically, for each velocity channel, we masked spaxels with S/N < 3.5 − 5 depending on the overall S/N of the observations.
Moreover, we masked individual spaxels which show spurious emission applying the following procedure. For each spectral channel, we applied a Gaussian kernel with a size of three pixels to smooth the channel image and then we masked individual pixels with S/N < 0.4 in the smoothed image. In this way, for each velocity channel, we remove isolated pixels with spurious emission, which could bias the calculation of the moment maps. The moment 0, moment 1, and moment 2 maps were produced using the cubes obtained with this masking process, while the CO(2–1) peak map was obtained from the original data cubes. We define the zero velocity (and consequently the redshift) based on the moment 1 velocity at the position of the continuum peak. The CO(2–1) redshifts (reported in Table 2) are in good agreement with previously reported redshifts. Throughout this paper, we use the radio velocity definition.
Figure 2 shows the CO(2–1) moment 0, 1, and 2 maps, along with the CO(2–1) peak map and continuum map for four targets as an example. The maps of the full sample are shown in Fig. D.1. The CO(2–1) emission is detected with S/N > 3 in all individual nuclei but 16156+0146 SE. In the majority of the nuclei (32/37), the kinematic major axis is clearly visible in the moment 1 maps. The moment 1 maps of five nuclei show a less ordered motion (01572+0009, 05189−2524, 12112+0305 NE, 14348−1447 SW, 22491−1808 E+W). In 22/37 nuclei the moment 2 map shows an increase in the velocity dispersion close to the peak continuum position.
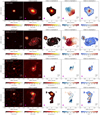 |
Fig. 2. Examples of the ALMA ∼220 − 250 GHz continuum and CO(2–1) moment maps (from left to right: peak map, moment 0, 1, and 2) for a merger (20087−0308) and an interacting (10190+1322) starburst-dominated system and for a merger (01572+0009) and an interacting (12071−0444) AGN-dominated system. The blue crosses mark the position of the nuclei (see Table 1). The magenta ellipse shows the FWHM and position angle of the ALMA beam . The contours in the maps are: continuum map: [0.3, 0.4, 0.6, 0. 8, 0.9] of the maximum; peak map: 1.5 × σ (where σ is the rms) and [0.1, 0. 2, 0.4, 0.6, 0.8] of the maximum; moment 0: [3, 6, 25, 50, 75] × σ (where σ is the rms), moment 1: every 50 km s−1 (every 25 km s−1 if the maximum value < 100 km s−1), moment 2: every 25 km s−1 (every 15 km s−1 if the maximum value < 150 km s−1). |
In 09022−3615, we detect an increase in velocity dispersion south of the nucleus (distance ∼1″, equivalent to ∼1 kpc), which corresponds to the most blue-shifted velocities in the moment 1 map. The spectrum in this location shows two peaks. This could be due to a blue-shifted outflow (or inflow) in this location, or a cloud pushed by an outflow. An alternative explanation is the presence of a second very obscured nucleus, which is not detected in the ALMA millimetre continuum. As we do not see evidence of rotation at the position of the putative second nucleus, we consider more likely the former explanations.
The CO(2–1) peak maps of 10/38 nuclei show a dip in the centre, corresponding roughly to the position of the continuum peak (e.g., 00188−0856, 12112+0305 NE, 13120−5453, 13451+1232 N). This drop in the centre is compatible with an extreme central optical depth. In a future work, we will present ongoing ALMA observations of the optically thin 13CO isotopologue to investigate this.
Figures F.1 and F.2 show the maps of the CO(2–1) emission integrated in 50 km s−1 channels for one target (00091−0738)1.
4.2. Spectro-astrometry
We perform a spectro-astrometry analysis to identify high-velocity molecular gas that is decoupled from the main rotation of the galaxy disk. This analysis consists in determining how the centroid position of the CO(2–1) emission changes as a function of velocity. We follow a similar methodology to the one used by García-Burillo et al. (2015) and Pereira-Santaella et al. (2018).
We binned together the velocity channels in order to achieve a minimum S/N of five, necessary to reliably determine the position of the peak of the emission. To determine the peak position in each binned channel, we first identify the spaxel with the highest flux. Then, we consider a region of 5 × 5 spaxels centred on the maximum spaxel and we perform a 2D Gaussian fit. In this way, we can determine the position at sub-pixel scales. In some targets, the CO(2–1) peak map presents a dip in the centre (see previous section) in the central velocity-channels. Thus, the position determined from the pixel with the maximum flux is not representative of the centroid of the emission. In these cases (07251−0248, 10190+1322, 13120−5453, 13451+1232, 19297−0406, 19542+1110, and 20414−1651), we determine the centroid emission by fitting a 2D Gaussian. The uncertainties on the centroids are calculated as Δx = FWHMbeam/(2 × S/N), where FWHMbeam is the beam size and S/N is the signal-to-noise ratio of the binned channel (Condon 1997). The spectro-astrometry analysis of 13120-5453 and 20100−4156 SE are shown in Figs. 3 and 4 as examples.
 |
Fig. 3. Example of spectro-astrometry and outflow maps for one target (20100−4156 SE) with outflow direction perpendicular to the kinematic major axis. Panel a: spectro-astrometry of the CO(2–1) emission line, i.e. centroid position of the CO(2–1) emission in the different velocity channels. The points are colour-coded by the channel velocity. The pink diamond indicates the peak ALMA millimetre continuum position. The dashed line is a linear fit to the low-velocity points (kinematic major axis) and the dotted line is a fit to the high-velocity points (indicating the outflow direction, if present). Panels b,c: moment 1 and moment 2 maps, where the green square indicate the field of view of panel a. The grey ellipse illustrates the ALMA beam FWHM. The grey contours on the moment 1 maps are every 50 km s−1 (every 25 km s−1 if the maximum value < 100 km s−1), and every 25 km s−1 (every 15 km s−1 if the maximum value < 150 km s−1) on the moment 2 map. In black are the CO(2–1) moment 0 contours ([3, 6, 25, 50, 75] × σ). Panel d: emission of the high-velocity channels, integrated over the velocity ranges indicated on the CO(2–1) spectrum (shown in panel e). Blue- and red-shifted channels are shown with blue and red contours, respectively (dashed lines indicate negative contour levels). The lowest contour corresponds to the 3σ level. The next contour levels are (0.5, 0.7, 0.9) of the peak of the emission, if these are above the 3σ level. The dashed circle shows the size of the outflow (Rout). Panel e: CO(2–1) continuum-subtracted spectrum extracted from a circle with radius equivalent to the outflow size (Rout). The lower panel shows an y-axis zoom-in to highlight the emission in the wings. The horizontal dashed line shows the 1σ noise level. The vertical dashed lines indicated the ‘flux-weighted’ velocity of the blue and red-shifted outflow (vout). Panel f: OH 119 μm spectrum (upper) compared with the nuclear CO(2–1) spectrum (bottom), convolved to the resolution of the OH spectrum (FWHM ∼ 270 km s−1). The total fit to the OH lines is shown with a magenta line, while the Gaussian components of the fit are shown in lightblue and brown. The orange lines show the 50 Monte Carlo iterations used to estimate the uncertainties on the fit (see Sect. 4.7). The vertical dotted, dashed and dot-dashed lines show the v50, v84, and v98 percentile velocities, respectively. The blue-shaded area in the upper panel shows the wavelength range between v84 and v98. Figures for the rest of the sample are in the appendix. |
 |
Fig. 4. Same as Fig. 3, but for 20087-0308, a target with outflow direction not perpendicular to the kinematic major axis. |
We perform a linear bisector fit of the centroids of the low-velocity channels, to determine the orientation of the kinematic major axis (see dashed line in Figs. 3, 4, and E.1). As low-velocity channels, we consider absolute velocities |v|< 300 km s−1. If there are channels at |v|< 300 km s−1 whose position deviates significantly from the direction described by the other low-velocity channels (e.g., 00091−0738 N), we do not include them in the fit of the kinematic major axis. To determine the direction of the high-velocity gas, we perform a bisector fit to the high-velocity centroids (see dotted line in Figs. 3, 4, and E.1). In general, we consider as high-velocity the channels with |v|> 300 km s−1, and we exclude channels that do not agree with the direction of the highest-velocity centroids or that follow the directions of the kinematic major axis. In some cases, the centroids of the blue-shifted and red-shifted high-velocity channels occupy a very similar region (e.g., 13451+1232 W or 14378−3651), which prevents us from determining the direction of the outflow axis. It is possible that the emission of the high-velocity gas is compact and unresolved, or that the outflow is pointing towards our line of sight, so that the blue- and red-sides overlap. In some cases, we observe some gas deviating from the kinematic major axis, however, because of its low relative velocity, ∼200 − 300 km s−1, it is more likely due to a tidal tail than to an outflow (e.g., 00091−0738 N, 01572+0009).
4.3. Comparison of position angles of the molecular gas, stellar and ionised gas disks
From the fit of the spectro-astrometry low-velocity channels, we derive the position angles (PAs) of the kinematic major axis of the molecular gas disk (listed in Table 2). We obtain the PA of the major axis on the receding half of the galaxy, measured east of north (anticlockwise). We compare these PAs with the ones of the stellar and ionised gas (traced by Hα) disks presented in Perna et al. (2022). Figure 5 shows the absolute differences between PA(CO) and the PA derived from the stellar and ionised gas kinematics.
 |
Fig. 5. Absolute difference between the position angles (PAs) of the kinematic major axis derived from CO and the PAs derived from the stellar kinematics (left), and the ionised gas kinematics (right). The PAs of the stars and ionised gas are taken from Perna et al. (2022). The dashed lines show a difference of 20°. The names of galaxies with large PA differences (≫20°) are shown on the figure. The colours and shapes of the symbols are as in Fig. 1. |
Overall, there is a general agreement between these measurements, with differences within ∼20°, hence it is consistent with what observed in non-interacting galaxies (see Perna et al. 2022). We identify only six outliers with PA differences ≫20° (01572+0009, 07251−0248 E, 09022−3615, 14348−1447 SW, 16090−0139, and 17208−0014). The PAs of CO are measured on smaller scales (∼1 kpc), compared to the scales used to derive the PAs of the stellar disk and ionised gas (∼5–10 kpc). Thus, we expect to see some differences between the PAs, especially considering the fact that our targets are mergers or interacting systems, many of which do not show regular rotating disk (only 27% and < 50% of nuclei in the PUMA sample show rotating disks in the ionised gas and stars, respectively, Perna et al. 2022). In summary, we find that in most of the targets the molecular gas disk has an orientation (PA) similar to the stellar and ionised gas disk.
4.4. Outflow velocity range definition
One of the main goals of this work is to identify and characterise high-velocity (> 300 km s−1) outflows of cold molecular gas, which produce broad wings in the line profile. Moreover, outflowing gas does not have to follow the disk rotation, thus it can be identified as high velocity gas that does not follow the main rotation pattern of the galaxy. For each nucleus, we define the velocity range where a potential outflow is located, using the spectro-astrometry analysis and the integrated CO(2–1) spectrum. We define the minimum (vmin) and maximum (vmax) velocities of the outflow (separately for the blue and red part of the outflow) and consider the emitting gas in the [vmin, vmax] velocity range as part of the outflow.
To define vmin and vmax for each nucleus, we perform the following procedure, separately for the blue-shifted and red-shifted emission. We used the spectro-astrometry plot to select the minimum velocity at which the centroid position of the gas starts to deviate from the direction of the major axis of rotation. In particular, we look for velocity channels whose centroid position deviates significantly from the direction of the kinematic major axis, or that does not follow the rotation pattern (from blue to red). The vmin values are in the range |vmin| = 180 − 450 km s−1. To define vmax, we started from the channel corresponding to vmin and we continued adding velocity channels to create the map of the high-velocity emission, until the peak S/N of the integrated map starts to decrease. We checked by looking at the integrated CO(2–1) spectrum that we are not missing significant emission at v > vmax due to a particular low S/N channel. The vmax values are in the range |vmax| = 300 − 800 km s−1. Figures 3, 4, and E.1 show the CO(2–1) spectra with the blue-shifted and red-shifted outflow velocity ranges highlighted with blue and red shaded areas. The integrated maps of the blue- and red-shifted outflow channels are shown as contours in the bottom-left panel of the figures.
One caveat of our analysis is that since we are observing projected velocities, we are not sensitive to high velocity gas in the plane of the sky. Additionally, with our method we are not considering outflowing gas with low projected velocities, that is with velocities v such that vmin(blue) < v < vmin(red), because it overlaps with the velocities of the rotating disk. In order to identify this gas, we would need to model the rotation of the system to identify non-rotating gas (e.g., Brusa et al. 2018; Gao et al. 2021; Ramos Almeida et al. 2022). We plan to investigate this in a future work.
4.5. Measurements of the outflow properties and energetics
In this section, we describe the method we use to measure the main outflow parameters: outflow radius (Rout), outflow velocity (vout), and molecular gas mass in the outflow (Mout). We use these parameters to derive the outflow energetics: mass outflow rate (Ṁout), mass-loading factor (η = Ṁout/SFR), outflow momentum rate (Ṗout), and kinetic luminosity (Lout). In the following, we explain how we measure the ‘projected’ Rout and vout. We discuss the inclination corrections in Sect. 4.5.1.
Different methods have been used in the literature to separate the outflow and rotating disk emission. A possible method (used for example by Pereira-Santaella et al. 2018) consists in subtracting the flux belonging to the rotating disk, by fitting the central velocity channels with one or two Gaussians and then considering only the flux in the residuals as part of the outflow. However, this method may underestimate the outflow mass as outflow flux with low (projected) velocities is generally assigned to the disk regardless of the actual position of the emission. An alternative method used in the literature consists in fitting the line profile using a systemic Gaussian component and a broader Gaussian component for the outflow (e.g., Fluetsch et al. 2019). This method may be overestimating the flux of the outflowing gas, since it considers that a large portion of the outflowing gas is at low velocities.
Since the resolution of the observations allows us to determine the position of the gas and to identify the gas that is not following the galaxy rotation, we prefer to consider only the gas with high velocities as part of the outflow. Moreover, most of the line profiles of our targets cannot be well fitted using a simple model with only one or two Gaussians (see Figs. 3, 4 and E.1). The line profiles are asymmetric and show multiple peaks, which could also include self-absorption (see Sect. 4.1). Thus, to measure the outflow gas mass, we consider the total flux in the high-velocity channels, highlighted in the blue and red shaded regions on the spectra (see Fig. 3, previous section), without subtracting the low-velocity Gaussian fit.
In Sect. 4.5.2, we discuss the systematic effects affecting the derived outflow quantities depending on the different methods. A comparison of our outflow parameters with the ones reported by Fluetsch et al. (2019) and Lutz et al. (2020) is shown in Sect. 4.6.
Outflow size: to measure the outflow radius, we fit a 2D Gaussian model to the high-velocity maps, obtained integrating the flux over the high-velocity channels (see bottom left panel in Fig. 3), separately for the blue and red part. To take into account the beam size and obtain the ‘intrinsic radius’, we convolve our model with a 2D Gaussian with the shape of the ALMA beam, and we fit this ‘convolved model’ to the maps. The radius of the blue (red) part of the outflow is defined as:
where 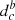 is the centroid distance from the nucleus and FWHMb is the average size (deconvolved from the beam) of the two axes of the 2D Gaussian fit.
is the centroid distance from the nucleus and FWHMb is the average size (deconvolved from the beam) of the two axes of the 2D Gaussian fit.
The outflow radius Rout is the mean of the radii of the blue- and red-shifted wings:
The outflow radii are shown in Fig. 3 as dashed circles (bottom left panel). This method is analogous to the method used by Lutz et al. (2020), although applied here to higher spatial resolution data (400 pc vs. 700 pc), which is enough to resolve the outflow structure. Due to the limited S/N of the single channels, it is not possible to measure the radius in each channel, which would give a more accurate measurement to derive the mass outflow rate.
We also measure the maximum extent of the outflow, by taking the maximum distance from the continuum position reached by the 3σ contour. We subtract the beam size in quadrature to obtain the ‘intrinsic’ distance. Then, we take the mean between the radius of the red- and blue-shifted channels as the representative maximum radius of the outflow (R3σ).
The outflow radii Rout measured from the 2D Gaussian fit are in the range 0.18 − 0.94 kpc (0.1 − 1.5″). The maximum outflow radii R3σ are in the range 0.1 − 2.1 kpc (0.05 − 2.5″). The ratio of the observed R3σ/Rout is in the range 1–3, with a mean of 1.45. We note that in some cases the R3σ values reported in Table 3 are smaller than Rout. This is due to the different way used to deconvolve the beam and to the uncertainty on the Gaussian fit. We calculate that > 50% of the outflow flux is within Rout, with a median of 76%. Given that most of the outflow flux is located within Rout, we decide to use Rout to compute the mass outflow rate and the energetics. If we were to use the outflow flux within R3σ instead of within Rout to calculate the outflow mass, Mout would increase on average by a factor of 1.3 (0.11 dex). The mass outflow rate is proportional to Mout/Rout, thus the larger molecular mass included within R3σ is counterbalanced by the larger radius. If we were to use R3σ and the outflow flux within this radius, we would obtain very similar values (less than 8% smaller, −0.04 dex) compared to the Ṁout estimated using Rout.
CO(2–1) observed outflow properties.
We do not attempt to correct the radii of the single targets for inclination, since information about the inclination is not available for the full sample (see discussion in Sect. 4.5.1).
Outflow mass: to derive the outflow mass, we extract the central spectrum from a radius equal to the observed Rout (not deconvolved from the beam) and we integrate the flux in the high-velocity channels between vmin and vmax, separately for the blue and the red part of the outflow. The central spectra are shown in Figs. 3, 4 and E.1 (bottom row, middle panel). Then, we sum the flux of the blue and red part of the outflow to obtain the total outflow flux (Fout).
We estimate the uncertainties on Fout by extracting a spectrum from a region away from the source and measuring the standard deviation of the flux density in the high-velocity channels (σ in units of mJy). The uncertainty on Fout is :
where Δvch is the width of a velocity channel in km s−1, and Nch is the number of velocity channels in the high-velocity windows. We transform the CO(2–1) flux into luminosity (in units of K km s−1 pc2) using the formula:
where SCO is the velocity-integrated CO line flux in Jy km s−1, νrest is the line rest-frequency in GHz, DL is the luminosity distance in Mpc, and z is the redshift (Solomon et al. 1997). We convert the CO(2–1) luminosity to CO(1–0) luminosity using 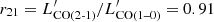 (Bolatto et al. 2013b). Then we multiply it by the ULIRGs-like CO-to-H2 conversion factor α = 0.78 M⊙/(K km s−1 pc2), to obtain the outflow molecular (H2) gas mass Mout. Although, we note that the cold molecular gas conditions in the outflow likely differ from those in the disk and, therefore, the CO-to-H2 outflow conversion factor is uncertain (see e.g., Pereira-Santaella et al. 2020).
(Bolatto et al. 2013b). Then we multiply it by the ULIRGs-like CO-to-H2 conversion factor α = 0.78 M⊙/(K km s−1 pc2), to obtain the outflow molecular (H2) gas mass Mout. Although, we note that the cold molecular gas conditions in the outflow likely differ from those in the disk and, therefore, the CO-to-H2 outflow conversion factor is uncertain (see e.g., Pereira-Santaella et al. 2020).
Mean outflow velocity: we calculate the mean velocity of the outflow separately for the blue- and red-shifted high-velocity wings, by taking the flux-weighted mean of the velocity in the channels identified as part of the blue-shifted (or red-shifted) emission (see Sect. 4.4, Fig. 3, middle panel of the bottom row):
where vi is the velocity of channel i and Fi is the CO(2-1) flux density in that channel.
Different methods have been used in the literature to estimate the outflow velocity (see Sect. 4.5.2). We decide to use this ‘flux-weighted velocity’ to calculate the mass outflow rate, because it is independent from the modelling of the emission line profile and it gives more weight to the velocities at which most of the emission takes place. We note that the outflow velocities measured with this method are sensitive to the choice of the velocity window defined as ‘high-velocity gas’. In Sects. 4.5.2 and 4.6 we explore this possible bias.
Mass outflow rate: for the red and blue part of the outflow separately, we calculate the mass outflow rate (in units of [M⊙ yr−1]) using the formula:
where Rout is the outflow radius, Mi is the H2 gas mass in the channel with velocity vi, and the sum is over the velocity channels identified as part of the blue-shifted (or red-shifted) emission (see Fig. 3). The total mass outflow rate is the sum of the blue and red Ṁout. We note that this formula corresponds to the assumption that the outflow has started at a point in the past (−t = −Rout/vout) and has continued with a constant Ṁout (Rupke et al. 2005b; Veilleux et al. 2005; Lutz et al. 2020). Under this assumption, the average volume density of the outflowing gas decreases with radius (∝R−2). Assuming that the outflowing gas fills a spherical or multi-conical volume with a constant average volume density, would increase Ṁout by a factor of three (e.g., Maiolino et al. 2012; Cicone et al. 2014; Lutz et al. 2020).
In the cases where the outflow is not detected, we estimate 3σ upper limits on Ṁout as:
where ⟨vout⟩ = 390 km s−1 and ⟨Rout⟩ = 0.52 kpc are the median outflow velocity and radius of our sample. Mout, err is calculated based on Fout, err (Eq. (3)), measured from the spectrum extracted from a radius ⟨Rout⟩. The mass outflow rates are in the range ∼5 to ∼300 M⊙ yr−1.
We compare the outflow properties (vout, Rout and Mout) measured from the blue and red-shifted wings. The vout, Rout and Mout measured from the red and blue parts are similar within a factor of 1.6, 2.4 and 1.2 respectively. The mean and corresponding standard deviation of the ratio of the red- and blue-shifted outflow quantities are: 0.97 ± 0.16, 1.05 ± 0.51, 0.99 ± 0.04, respectively.
4.5.1. Inclination corrections
We do not attempt to correct the outflow radii and velocities of the single targets for the inclination, since this information is not available for all objects. In order to apply an inclination correction to vout and Rout, we need to know the inclination of the outflow with respect to our line of sight. Even if we knew the inclination of the molecular gas disk, in order to use this information we would need to know the inclination of the outflow with respect to the disk. In Sect. 5.2 we discuss the projected angles between the outflow axis and the major kinematics axis. For a handful of targets (6), there is evidence that the outflow may be perpendicular to the major kinematics axis. However, only for one of them we have a measurement of the ionised gas (or stellar) disk inclination from Perna et al. (2022). Thus, we decide not to attempt to correct for inclination vout and Rout of the single targets, and all the quantities reported here are the ‘projected’ ones.
However, we derive an average inclination correction that we apply to the average outflow properties of the sample. To convert the observed (projected) mean outflow velocity to intrinsic velocity, we need to divide vout by sin(i), where i is the inclination. Analogously, the observed outflow radius needs to be divided by cos(i) to recover the intrinsic value. Following Law et al. (2009), who considered the average for a collection of objects oriented isotropically in space, the average correction for the velocities is 1/⟨sin(i)⟩ = 1/0.79 = 1.27. Analogously, we calculated the average correction for the radius: 1/⟨cos(i)⟩ = 2. We use these values to correct the mean outflow velocity and mean outflow radius reported in Table 3.
It is not possible to derive the average inclination correction for the mass outflow rate Ṁout in a similar way, since the calculation of the integral over the entire solid angle gives infinity. However, the average inclination correction for the dynamical time (tdyn = Rout/vout ∝ Mout/Ṁout) is unity (see Cicone et al. 2015).
4.5.2. Caveats: Methods to measure outflow parameters
In this section, we discuss how the outflow parameters (in particular vout, Mout and Ṁout) change depending on the method adopted for the measurements. Readers who are less interested in the details about the methodology and the comparison with previous works may wish to go directly to Sect. 4.7.
1) Low projected velocity (v < 300 km s−1) gas in the outflow: since we are not considering low projected velocities (|v|≲200 − 300 km s−1), it is possible that we are missing part of the outflow flux. If we were to consider also this low velocities, the outflow mass Mout would increase and the flux-weighted outflow velocity vout would decrease. Overall, we expect Ṁout to increase, but by a lower factor than Mout, because the increase in Mout is counterbalanced by the decrease of vout.
To test how much this effect could affect our measurements of the outflow properties, we consider 3D models of biconical outflows based on the models presented by Bae & Woo (2016). The outflow is a bicone with a half opening angle of 40°. We set the maximum velocity of the outflow to 750 km s−1. We consider several outflow radial velocity profiles, motivated by previous works in the literature (e.g., Förster Schreiber et al. 2014; Venturi et al. 2018; Meena et al. 2021), and different outflow inclinations with respect to the line of sight. More details on the simulations can be found in the Appendix A. We measure vout, Mout and Ṁout from the total simulated profile (outflow+systemic component) considering only |v|> 300 km s−1, to mimic the method we are using with our data. Then, we measure the outflow quantities (vout, Mout, and Ṁout) from the simulated outflow emission profile (without the systemic component) considering the full velocity range.
The Mout measured from |v|> 300 km s−1 are underestimated compared to the values measured from the entire velocity range by a factor of 0.2 − 1 (average 0.5), while the vout are overestimated by up to a factor of 2.2 (average of 1.6). Consequently, Ṁout would be underestimated by up to ∼0.45 dex (65%) for outflow inclinations close to the plane of the sky (90°). For an inclination of 10°, the measured Ṁout would be underestimated by up to 0.1 dex (see Fig. 6).
 |
Fig. 6. Simulated outflow profiles for outflow inclinations with respect to our line of sight of 10° (upper) and 90° (bottom). The outflow velocity in this particular simulation increases up to a turnover radius and then decreases. Up to four different velocity fields are considered in Appendix A. The magenta curve shows the outflow component, the grey curve the systemic component and the black curve the total profile. The vertical dashed lines show the flux-weighted vout measured from the total profile at |v|≥300 km s−1 (coloured in blue and red). The vertical solid lines show the flux-weighted vout measured from the outflow component over the full velocity range. For high outflow inclination (close to the plane of the sky), the contribution to the outflow flux by the gas at low projected velocities (|v|< 300 km s−1) increases. |
For targets with a wide CO(2–1) line core (large FWHM), the flux of the gas in the rotating disk can overlap with the outflow flux up to larger velocities. Indeed, there is a positive correlation between the velocity at which we start to consider the flux to be dominated by the outflow (vmin) and the FWHM of the line (Spearmann rank correlation coefficient r = 0.81, p-value < 0.1). We did a test to estimate how much flux we may be missing in our measurements of the outflow flux for the targets with large FWHM CO(2–1) line profiles. In particular, we consider the 13 targets with |vmin|> 300 km s−1 (either in the blue or red side). To estimate the amount of possible flux belonging to the outflow in the velocity range between |v| = 300 km s−1 and |vmin|, we assume the outflow flux density in this range to be equal to the value at vmin. Using this assumption, we estimate the outflow parameters (Mout, vout, and Ṁout) starting from vmin = 300 km s−1. We find that the value of Mout increases by 0.28 dex on average (maximum 0.67 dex), while vout decreases by a factor of −0.07 dex on average (minimum −0.11 dex). So, the Ṁout estimates increase by 0.2 dex on average (maximum 0.6 dex).
2) Possible overestimation of Ṁout due to the rotating disk contribution at |v| = 250−300 km s−1: since we do not model and subtract the disk rotation, it is possible that at low velocities (250 − 350 km s−1) we are including in the outflow flux some flux emitted by the gas in the rotating galaxy disk. To test how large this contribution could be, we subtract from the spectra the flux due to rotation estimated by modelling the core of the emission profile (with absolute velocities smaller than ∼300 km s−1) with one, two or three Gaussians (e.g., Pereira-Santaella et al. 2018). Then, we compute the outflow parameters (Mout, vout, Ṁout) from the residuals, considering the velocity range between vmax and the velocity (vmin) at which the residuals approach zero. The outflow masses vary in the range −1.0 dex to 0.5 dex (−0.12 dex on average). In some cases, the measured Mout increases because we can extend the outflow velocity range to smaller velocities, since there is no risk of including flux from the rotation. The outflow velocities vary by less than ±50 km s−1. The Ṁout vary between −0.82 dex and +0.45 dex (−0.11 dex on average).
3) Different methods to estimate the outflow velocity: in this work, we adopted the ‘flux-weighted’ outflow velocity definition to compute the mass outflow rate. Other works instead have used different definitions of ‘maximum outflow velocity’ (e.g., Fluetsch et al. 2019; Lutz et al. 2020). If we assume a biconical outflow with constant gas velocity within the outflow, the range of velocities observed in the broad wings of the CO profile would be solely due to different orientation angles of the outflow gas clouds with respect to our line of sight. The part of the outflow closer to our line of sight would have the highest observed velocity. Thus, one could assume that this maximum velocity is the closest to the true/intrinsic velocity. We do not know the true radial profile of the velocity or the geometry of the outflowing gas for our targets. However, we can estimate how much our ‘flux-weighted outflow velocity’ differ from the ‘maximum outflow velocity’ assumption in our sample. We consider two definition of the maximum velocity. Both definition require the fit of the line profile with multiple Gaussian components: a broad component for the outflow, and other components for the systemic emission. The first definition that we consider is the prescription from Rupke et al. (2005a), used for example by Fluetsch et al. (2019):
where |Δv| is the shift of the broad Gaussian outflow component with respect to systemic velocity and FWHMbroad its full width at a half maximum. The second definition, adopted for example by Lutz et al. (2020), is:
where FW10% is the full width of the broad component at a tenth of its peak. We measure vmax, FWHM and vmax, FW10 for our sample of galaxies with outflow detection. We use up to three Gaussian components to model the systemic emission. We stress that in most of the cases, the parameters of the Gaussian components are highly degenerate. Thus, the derived maximum velocity can vary depending on the assumptions used in the fit. In Fig. 7 we compare the flux-weighted vout with the maximum velocity vmax, FWHM and vmax, FW10 for our sample. The ratio vmax, FWHM/vout varies between 0.5 and 2.0, with a median 0.9. The ratio vmax, FW10/vout instead is almost always larger than one, with a maximum of 3.2 and a median of 1.6. Assuming that vmax is the closest measure of the ‘true’ outflow velocity, it does not need to be corrected for inclination, while the observed (projected) vout would need to be corrected by an average factor of 1.3 (see Sect. 4.5.1). This factor can account for most of the average difference between vmax, FW10 and vout.
 |
Fig. 7. Comparison of different methods for measuring the outflow velocity. Left: ratio between the maximum outflow velocity vmax, FWHM (Eq. (8)) and the flux-weighted outflow velocity (vout) in our sample. Right: ratio between vmax, FW10% (Eq. (9)) and vout. The horizontal lines show the 1-to-1 ratio. |
We decide to avoid the methods based on the fit of the emission line profile with multiple Gaussian components, because the components are degenerate and this will introduce further uncertainties in the measurements.
An additional caveat is related to the definition of vmax, which will impact the vout estimates. In selecting vmax based on the S/N of the integrated high-velocity maps, it is possible that we are excluding diffuse high-velocity flux which is below the 3σ level. In this way, we may underestimate vout, especially for cases in which the outflow velocity increases radially. Unfortunately, with our current data it is not possible to estimate the impact of this possible additional component. Higher sensitivity observations are needed for this purpose.
In Table 4, we summarise the average biases in the outflow properties (vout, Mout and Ṁout) due to the effects described in 1), 2) and 3). Since the two effects described in 1) and 2) go in opposite directions, they tend to compensate each other. Taking into account the two effects, we may be underestimating Mout ∼ 0.2 dex and Ṁout by ∼0.04 dex on average.
Possible biases in the outflow properties measured with our method, due to different issues.
Based on the variations of outflow quantities from the tests using different methods, we estimate the typical uncertainties on the outflow quantities. For the outflow velocity, we estimate a typical uncertainty of 0.1 dex, while for Mout and Ṁout we adopt a typical uncertainty of 0.3 dex. For Rout, we estimate a typical uncertainty of 0.2 dex, based on the difference between Rout and R3σ.
The uncertainties on Ṁout are dominated by the uncertainties on the αCO conversion factor, which can be up to 0.7 dex (Papadopoulos et al. 2012; Bolatto et al. 2013b; Pereira-Santaella et al. 2020), and on the outflow geometry. If the αCO is more similar to the Galactic value (αCO = 4.3 M⊙/(K km s−1 pc2)), it would imply that all our Mout and Ṁout measurements are underestimated by a factor of ∼5 (0.7 dex), while if the optically thin case applies (αCO = 0.35 M⊙/(K km s−1 pc2)), our measurements would be overestimated by a factor of ∼2 (Bolatto et al. 2013b).
4.6. Comparison with previous works
In this Section we compare the derived outflow parameters with previous works that study properties of molecular outflow in nearby ULIRGs using CO observations.
4.6.1. Comparison with Lutz et al. (2020)
Lutz et al. (2020) study the outflow properties in a sample of 54 nearby (z < 0.2) galaxies with CO(1–0), CO(2–1) or CO(3–2) observations, with a range of spatial resolutions (30 pc to 5 kpc; 0.5 − 5 arcsec beam FWHM). They collect 41 nearby galaxies with molecular outflow detections or upper limits from the literature. They also present new NOEMA and ALMA observations, with a spatial resolution of ∼700 pc (0.5–3.7 arcsec beam FWHM), for 13 compact far-infrared galaxies from the Lutz et al. (2016) sample. To derive the outflow velocity and flux, they fitted the line profile with two Gaussian components (systemic and broad (outflow) component). They defined the outflow velocity using Eq. (9). To derive the outflow flux, they integrated the broad component only over the velocity ranges for which it contributes at least 50% of the total flux density of the line profile. The outflow radius was defined similarly to our method: Rout = |ΔR|+FWHM/2, where |ΔR| is the distance of the outflow emission centroid from the continuum position and FWHM was derived from a Gaussian spatial fit in the uv-plane using a velocity range that is dominated by outflow, although, the spatial resolution is a factor of ∼2 lower than in our work. For the other 41 targets, they collect information about the outflow parameters (vout, Rout, Mout) from the data published in the literature, trying to be consistent with their adopted definition of these parameters and their adopted methodology to separate the flux of the line core and high velocity wings.
There are 12 objects in common with our sample, with data published by Cicone et al. (2014) Barcos-Muñoz et al. (2018), Gowardhan et al. (2018), Pereira-Santaella et al. (2018), and Lutz et al. (2020). We compare our measurements of the outflow parameters (vout, Rout, Mout, Ṁout) with these works in Fig. 8. There are some discrepancy between our measurements and the literature values. In particular for two galaxies (17208−0014 and 20100−4156) the literature vout is larger than 900 km s−1, while we measure vout < 500 km s−1. For 20100−4156, it is possible that the spectral range of our observations (v = [ − 1200, 1200] km s−1) is not wide enough to detect the emission at very high velocities (|vout|> 1000 km s−1). Additionally, this high-velocity outflow is detected in CO(1–0), while in CO(3–2) no outflow is detected (Gowardhan et al. 2018). Thus, it is possible that this difference also depends on the J-level observed. For 17208−0014, the S/N of the outflow component presented in Lutz et al. (2020) is not very high, thus the uncertainty on vout should be large (even though it is not reported in the paper). For four galaxies, Rout values from the literature are considerably higher than our measurements (∼2 − 6 times higher). For three of these galaxies, the difference is due to the different definition of Rout as the maximum radius at which the outflow is detected (see Rmax definition in Pereira-Santaella et al. 2018). For the other target (20100−4156), the difference could be due to the different spatial resolution (1.5 arcsec vs. 0.2 arcsec). For Arp 220 instead Rout from the literature is smaller than our measurement; also in this case the difference could be due to the different spatial resolution (0.09 arcsec vs. 1.0 arcsec). The Mout values agree within a factor of 2.5, with some of our values being smaller and other larger than the values from Lutz et al. (2020). Since Ṁout is proportional to vout and 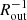 , the differences in Rout and vout tend to balance each other and lead to similar Ṁout (within a factor of 3).
, the differences in Rout and vout tend to balance each other and lead to similar Ṁout (within a factor of 3).
 |
Fig. 8. Comparison of outflow parameters measured in this work with values reported in Lutz et al. (2020). From left to right: outflow velocity, outflow radius, outflow mass and mass outflow rate. The dashed line marks the ratio of 1. Even though there are differences in outflow velocities and radii, the mass outflow rates agree within a factor of 3. |
4.6.2. Comparison with Fluetsch et al. (2019)
We also compared the Mout and Ṁout of our sample with the values reported by Fluetsch et al. (2019) for a sample of 45 local (z < 0.2) star-forming galaxies with CO(1–0), CO(2–1), or CO(3–2) ALMA observations. Fluetsch et al. (2019) used a different method to estimate the outflow mass: they measured the outflow flux by fitting the line profile with two Gaussians, one for the core of the line and one broad component for the outflow, and they considered the total flux of the broad component as the outflow flux. We expect that the outflow fluxes measured in this way will be higher than the ones measured with our method, since in addition to the flux in the wings, they are also considering the low-velocity emission of the broad component as part of the outflow. They measured the outflow velocity using Eq. (8). They fitted a 2D-Gaussian profile to the wing maps and used the beam-deconvolved major axis (FWHM) divided by two as the radius of the outflow. Compared to our methodology, they did not include the distance between the centroids of the blue-shifted and red-shifted emission in the calculation of Rout, thus their Rout estimates are expected to be smaller.
Figure 9 shows the comparison of the outflow parameters derived by Fluetsch et al. (2019) with our results for the five sources in common between the two samples. Their vout tend to be higher than ours (maximum by factor of 1.7), while their Rout tend to be smaller (maximum by a factor of 1/4). The largest difference is in the outflow masses, that are larger by up to a factor of 16 (1.2 dex). This difference can be attributed to the different method used to estimate the flux belonging to the outflowing gas. This difference in Mout propagates to the Ṁout.
 |
Fig. 9. Comparison of outflow parameters measured in this work with values reported in Fluetsch et al. (2019). From left to right: outflow velocity, outflow radius, outflow mass and mass outflow rate. Differences in Mout and Ṁout can be up to a factor of 16. |
Since the overlap between the two samples is small, we decide to also compare the outflow properties of the two samples at the same IR luminosity. Figure 10 shows Mout and Ṁout as a function of IR luminosity for the Fluetsch et al. (2019) sample and our sample. The diamond symbols with red borders show the average values of the two samples for different bins of IR luminosity (with bin width of 0.5 dex). For the same IR luminosity (in the range log LIR/L⊙ = 12.0 − 12.5), their average Mout and Ṁout are ∼0.6 − 0.8 dex higher than our measurements (factor of ×4 − 6).
 |
Fig. 10. Comparison of the outflow mass and mass outflow rate as a function of IR luminosity for our sample and the sample from Fluetsch et al. (2019, purple triangles). The red symbols show the average values (considering only the detections) in bins of log LIR for the Fluetsch et al. (2019) sample (triangles) and the PUMA sample (circles). The sources in common between the two samples are highlighted with black contours. Due to the different methods, the Mout and Ṁout values estimated by Fluetsch et al. (2019) are higher by a factor of ×5 − 8 compared with our measurements at the same infrared luminosity. |
Given the different methodology used to measure these parameters, the difference is not surprising. As discussed in Sect. 4.5.2, this comparison highlights the large effect that the choice of methodology can have on the measured outflow parameters. The approach used by Fluetsch et al. (2019) assumes that most of the outflow flux is at low projected velocity. Based on simulations of biconical outflows (e.g., Bae & Woo 2016), this scenario is possible when the outflow is oriented in a direction close to the plane of the sky, or if the outflow has low velocities. In general, this method would tend to over-estimate the outflow mass and it suffers from the degeneracy of the fit with multiple Guassian components. With our method on the other hand, we could be missing the outflow contribution at the low projected velocities, thus, we may be underestimating the outflow mass.
4.7. Analysis of the OH 119 μm spectra
Other lines that are often used as tracer of molecular outflows are the OH (hydroxyl) FIR lines (e.g., Fischer et al. 2010; Sturm et al. 2011; Spoon et al. 2013; Veilleux et al. 2013; González-Alfonso et al. 2014, 2017; Stone et al. 2016). We compare the outflow parameters derived from CO(2–1) with the ones derived from the OH 119 μm doublet, which is the strongest of the OH ground-state lines (e.g., González-Alfonso et al. 2017). We collect archival Herschel/PACS spectra of the OH 119 μm doublet transition (hereafter OH) for 22/25 of our ULIRGs systems (no data available for 00091−0738, 10190+1322, and 16156+0146). The majority of the spectra (20/22) were published in Veilleux et al. (2013), Spoon et al. (2013), and González-Alfonso et al. (2017); 11095-0238 and 13451+1232 are not presented in these works but were found in the Herschel archive.
We extract the spectra from the central 9.4″ × 9.4″ spaxel and apply the point source aperture correction. We fit the OH spectra to derive the velocity of the outflow. In particular, we want to compare the velocity ranges where the OH outflow is detected with the ones of the CO outflow. Outflow parameters were derived by Veilleux et al. (2013) for 14 of the ULIRGs in our sample, but we repeat the analysis in order to obtain consistent parameters for the full sample. We set the zero velocity of the OH spectra based on the redshift of CO (see Table 1), so that we can directly compare the outflow velocities of the two tracers.
We fit the line profile following the method used by Veilleux et al. (2013), and we check that our derived parameters are consistent with their results. We first perform a linear fit of the continuum around the OH line and normalise the spectra to the continuum level. The OH doublet can appear in absorption (11/22), emission (4/22) or as P-Cygni profile (7/22). The P-Cygni profile is considered a clear indication of the presence of an outflow (e.g., Prochaska et al. 2011; Fischer et al. 2010; Sturm et al. 2011; González-Alfonso et al. 2012, 2013; Veilleux et al. 2013). In our sample, emission and P-Cygni profiles are more common in AGN (73%) than in SB-dominated nuclei, which is consistent with previous findings (Veilleux et al. 2013; Stone et al. 2016; Runco et al. 2020).
For the absorption profiles, we fit a model with two Gaussians (one for the systemic and one for the outflow) for each line of the OH doublet. The separation between the two lines of the Λ-doublet is fixed to 0.208 μm (in rest-frame) and the amplitude and width of the two lines were tied to be the same in each component. We convolve our model with the Herschel/PACS instrumental resolution (FWHM ∼ 270 km s−1, Veilleux et al. 2013), to recover the intrinsic shape of the line. For profiles in emission, we fit a model with two Gaussians (one for the systemic and one for the outflow component) in emission for each OH line. For the P-Cygni profiles, we consider one component in absorption and one in emission for each line. Adding more components is not possible due to parameter degeneracy (Veilleux et al. 2013). We add as an additional constraint that the model absorption can not be deeper than the observed absorption (similar to Veilleux et al. 2013), to avoid a fitting result with unrealistically large amplitude of the emission and absorption components that cancel each other out.
We use the best-fit model to derive the characteristic velocity of the emission and absorption profiles, separately. For the absorption components, v50, v84 and v98 are the velocities corresponding to the 50th, 84th and 98th percentile of the absorption line profile, i.e. the velocities above which 50%, 84%, and 98% of the absorption takes place. Similarly, for the emission components, v50, v84 and v98 are the velocities corresponding to the 50th, 84th and 98th percentile of the emission line profile. Veilleux et al. (2013) consider v84 to be a more robust estimate of the outflow velocity compared to the ‘maximum outflow velocity’. We use v98 as an estimate of the maximum outflow velocity, keeping in mind that it may be more susceptible to noise variation than v84.
We apply a Monte Carlo (MC) approach to estimate the uncertainty on the derived parameters. We estimate the noise level on a region of the continuum away from the line (excluding also the region of the CH+(3-2) and 18OH 120 μm lines), then we add random Gaussian noise, proportional to the noise level, to the best-fit model and we run the line fitting on this artificial spectrum. We repeat this procedure 50 times and we use the 16th and 84th percentiles of the distribution of best-fit parameters to estimate the 1σ uncertainties on the derived parameters. The 50 MC realisations are shown as orange curves on Fig. 11. The velocities derived from the OH profiles are shown in Table 5. The properties of molecular outflows derived from OH will be discussed and compared with those derived from the CO tracer in Sect. 5.4.
 |
Fig. 11. Example of the fit of the OH 119 μm doublet with absorption (upper), emission (middle) and P-Cygni (bottom) profile. The velocity is relative to the blue component of the doublet (at 119.233 μm) at the systemic velocity inferred from the CO(2–1) line. The best-fit model is shown in magenta, while the orange models are the results of the 50 Monte Carlo realisations that illustrate the uncertainty of the fit. Solid lines show the model convolved with the instrumental resolution, while dashed lines indicate the intrinsic (deconvolved) model. Blue and red mark the two components of the fit. The vertical dotted, dashed and dot-dashed lines show the v50, v84 and v98 percentile velocities, respectively, derived from the absorption (blue) and/or emission (red) profiles. Grey dashed lines at ∼2000 km s−1 show the position of the 18OH 120 μm doublet and the CH+(3-2) absorption line. |
Velocities derived from the OH 119 μm profiles.
5. Results
5.1. Mean outflow properties
Here we summarise the ranges of outflow properties of our sample and their average values, corrected for inclination as described in Sect. 4.5.1. We measure projected outflow velocities of ∼260 − 490 km s−1, with a mean outflow velocity (corrected for inclination) of 485 ± 16 km s−1. Outflow radii are in the range 0.17–0.94 kpc and the mean inclination-corrected outflow radius is 1.1 ± 0.1 kpc. The outflow masses are between 1 − 35 × 107 M⊙, with an average of (10 ± 2)×107 M⊙. These outflow masses corresponds to 0.2–6.5% of the total molecular gas masses. The mass outflow rates are in the range 6 − 302 M⊙ yr−1, with an average outflow rate of 78 ± 16 M⊙ yr−1. The ranges and averages of the outflow parameters measured in this work are summarised in Table 6.
Mean cold molecular outflow properties in ULIRGs.
As a comparison, Ramos Almeida et al. (2022) find molecular gas mass outflow rate Ṁout = 8−16 M⊙ yr−1 in a sample of nearby type 2 quasars (log LAGN/[erg s−1] = 45.7−46.3). Lower Ṁout = 0.3−5 M⊙ yr−1 have been measured in lower luminosity (log LAGN/[erg s−1] = 43.2 − 44.2) Seyfert galaxies (Alonso-Herrero et al. 2019; Domínguez-Fernández et al. 2020; García-Bernete et al. 2021). Higher molecular gas mass outflow rates (Ṁout = 60−400 M⊙ yr−1) have been measured in ULIRGs hosting an AGN (Feruglio et al. 2010; Cicone et al. 2014). We note that, as discussed in Sect. 4.6, the method used to derive the mass outflow rates can introduce systematic differences (up to factor of ∼10) between different samples.
We also compare our measurements with the properties of the ionised outflows measured by Arribas et al. (2014) for a sample of nearby U/LIRGs. For ULIRGs, they find maximum outflow velocities in the range 100–1000 km s−1, with a mean 393 ± 38 km s−1 and mass outflow rates in the range 1 − 100 M⊙ yr−1 (from Fig. 13 in the paper), with an average 38 M⊙ yr−1. The average Ṁout of the ionised gas is about a factor of 2 smaller than the one of the molecular phase. For U/LIRGs, they find outflow masses in the range 0.14 − 28 × 107 M⊙, with a average of 6.7 × 107 M⊙, similar to the masses of the molecular phase (Table 6).
We find molecular outflow dynamical times (tdyn = Rout/vout) in the range 0.45 − 2.77 Myr. The mean tdyn, based on the mean observed Rout and vout, is 1.37 Myr, assuming a average inclination correction of unity (Cicone et al. 2015). This is similar to the outflow dynamical times 0.63–2.51 Myr reported in Pereira-Santaella et al. (2018). The outflow depletion times (tdep = M(H2)tot/Ṁout) in our sample are in the range 15 − 644 Myr, with a median of 75 Myr. These are a bit longer than the values reported for ULIRGs in Pereira-Santaella et al. (2018, 15 − 80 Myr) and Cicone et al. (2015, 1.2 − 50 Myr). For comparison, the star-formation depletion times (tdep = M(H2)tot/SFR) for targets with detected outflows in our sample are in the range 9–77 Myr (median 27 Myr).
5.2. Outflow characteristics for AGN/SB and interacting/mergers
5.2.1. Outflow detection rate and direction
In this Section, we present the statistics of the number of detected molecular outflows in our sample and we investigate whether there is any dependency of the outflow detection rate on the nuclear classification (AGN or SB) or on the merger stage (advanced mergers or interacting systems).
The top panel of Fig. 12 shows the percentage of nuclei in the sample belonging to each category: AGN, SB, merger (M), interacting (I), and the mixed categories (merger AGN, merger SB, interacting AGN, and interacting SB). For the interacting systems, we consider only the nuclei with log LIR/L⊙ > 11.8 in this statistical analysis. As shown in Pereira-Santaella et al. (2021), in most of our interacting systems the IR luminosity is dominated by one nucleus, thus by applying this luminosity threshold, we discard the fainter nuclei (with log LIR/L⊙ = 10.3 − 11.7) which would not be classified as ULIRGs. In this way, we avoid that the outflow detection rate in interacting nuclei is artificially lower only because of the ‘secondary’ faint nuclei.
 |
Fig. 12. Outflow detection statistics for different categories: AGN, starburst (SB), mergers (M, dnuclei < 1 kpc), interacting systems (I, dnuclei > 1 kpc), and mixed categories (mergers AGN, mergers SB, interacting AGN, interacting SB). Upper panel: fraction of individual galaxy nuclei in each category with respect to the total sample. The scale on the right axis shows the number of objects. Middle panel: outflow detections fractions. The percentages have been calculated with respect to the total number of nuclei in each category. Lower panel: outflow orientation statistics divided in three groups: outflow projected orientation perpendicular to the kinematic major axis of the disk (angle 90 ± 20°), outflow projected orientation non-perpendicular, or orientation could not be determined. The percentages have been calculated with respect to the number of outflow detection in each category. Error bars in middle and lower panel show the 90% binomial confidence interval. |
The second panel of Fig. 12 presents the percentage of outflow detections in each category. We detect an outflow, defined as high-velocity (|v|> 300 km s−1) CO(2–1) emission which deviates from the main rotation, in 20/26 of the nuclei with log LIR/L⊙ > 11.8 (77 ± 7%2). The nuclei with outflow detections are equally divided between mergers and interacting systems. The percentage of detections in SB (93 ± 4%, 14/15) is higher than in AGN (55 ± 14%, 6/11). A possible explanation for this difference is related to the outflow inclination: if AGN outflows are in the plane of the disk (contrary to SB outflows that tend to be perpendicular to the disk), they are more difficult to detect with our method, but by modelling and subtracting the disk rotation, it may be possible to identify them. Additionally, outflows in the plane of the disk may be braked and prevented from reaching high velocities, while outflows perpendicular to the disk can escape more freely, reaching higher velocities and being more easily detectable. Another possibility is that AGN outflows could be more collimated, and therefore more difficult to detect for some orientations (i.e. on the plane of the sky). A third possible explanation could be the different amount of molecular gas in the nucleus. AGN in our sample have on average lower nuclear molecular gas masses (log M(H2)/M⊙ = 9.2 ± 0.1), than SB nuclei (log M(H2)/M⊙ = 9.4 ± 0.1). The lower amount of material close to the nucleus may also be the reason that allows us to identify them as AGN, contrary to deeply buried nuclei. This is in agreement with an evolutionary scenario in which in a first merger phase the nuclei are more obscured and produced outflows, which expel gas and dust from the nuclear region; in a second phase, after some of the material has been removed, the nuclei are visible as AGN (e.g., Hopkins et al. 2008). Similarly, Stone et al. (2016) find a lower OH outflow detection fraction in X-ray selected AGN (24%) than in ULIRGs (∼70%) and suggest that outflow detection in ULIRGs may be easier due to their higher gas fraction.
With the spectro-astrometry analysis (see Sect. 4.2), we determine the outflow direction in 16/20 (80%) of the nuclei with outflow detection, while in the remaining four nuclei the outflow direction is not clear. This could be due to the fact that the outflow is unresolved, or to the fact that the outflow is pointing towards our line of sight, so that the blue and red-shifted sides of the outflow overlap. For the nuclei with a well determined outflow direction, we measure the angle between the outflow and the major axis of rotation (see Sect. 4.2). We qualitatively compare the direction of the high-velocity gas with the integrated maps of the blue and red-shifted high-velocity channels (see lower left panel in Figs. 3, 4 and E.1) to check that the direction is consistent with the position of the gas in the high-velocity channels. The bottom panel of Fig. 12 shows, for each category, the fraction of outflows with 1) direction perpendicular to the rotating disk (angle 90 ± 20°), 2) direction non-perpendicular, or 3) unclear direction. The percentages of outflow with determined direction in mergers (70 ± 12%, 7/10) is smaller than in interacting nuclei (90 ± 6%, 9/10). We could determine the outflow direction in 86 ± 7% (12/14) of SB nuclei with outflow detection, but only in 67 ± 15% (4/6) of AGN. If in AGN the outflow is oriented within the plane of the disk, it is possible that it can not travel very far, thus it appear very compact and unresolved. This could explain why we could not determine the outflow direction in many AGN.
We find that in six nuclei the outflow direction is nearly perpendicular (angle 90 ± 20°) to the kinematic major axis. These nuclei are 12112+0305 NE, 12112+0305 SW, 14348−1447 NE (already presented in Pereira-Santaella et al. 2018), 10190+1322 E, 19542+1110 and 20100−4156 SE. All these nuclei are SB dominated. This supports the idea that outflow powered by SB tend to be perpendicular to the disk, while AGN outflow can have any orientation (e.g., Pjanka et al. 2017). However, there are also many SB nuclei (50 ± 13%) for which the outflow direction is not perpendicular. This could be due to a hidden (deeply buried) AGN that is powering the outflow, even though it is not detected in the MIR or optical (see Pereira-Santaella et al. 2021). An alternative explanation is that in these SB the molecular gas is still strongly disturbed and has not yet settled into a galactic plane, and consequently also the path of least resistance is not well defined. We note that we measure the angle between outflow and major kinematic axis projected in the plane of the sky. Thus, there is the possibility that we measured a projected angle of 90° for an outflow that is not perpendicular to the plane if we observe it from a particular orientation. However, for SB it is more likely that the outflow escape from the path of least resistance (perpendicular to the disk) than from any other direction, where the outflow will encounter more material. The majority of the nuclei with perpendicular outflow (5/6) are interacting systems. Although the number statistics are small, this could be due to the poorly defined disk rotation axis in some of the more advanced mergers.
Our sample was selected to have a similar number of objects in each category (AGN/SB, interacting/mergers), thus it does not have the LIR distribution or AGN fraction of the general population of ULIRGs. We estimate the outflow detection fraction that would be measured in a sample of ULIRGs with the same AGN fraction as the local ULIRGs population. Veilleux et al. (2009) study the AGN contribution in a representative sample of 74 ULIRGs from the IRAS 1 Jy Survey (Kim & Sanders 1998) and find that 24% of their sample has an AGN contribution > 50% in the MIR. We use this AGN fraction to correct our outflow detection statistics and we find that the expected outflow detection fraction in local ULIRGs is 84% (compared to 77% measured in our sample).
5.2.2. Outflow quantities
In this Section, we investigate whether there are differences in the outflow properties depending on these categories. We calculate the mean outflow parameters (vout, Rout, Mout, Ṁout) for each category and we compare it with the mean of the total sample. We do not include upper limits in this comparison. Even though there are small differences, the mean quantities in all categories are consistent (within 2σ) with the sample mean (see Fig. 13).
 |
Fig. 13. Cumulative distribution function (CDF) of the outflow properties of AGN and starbursts (SB, top) and mergers (M) and interacting (I, bottom). The solid lines show the CDFs for the outflow detections only, while the dashed lines show the CDFs including upper limits (only for Mout, Ṁout and η). The shaded area mark the area between the CDFs with and without upper limits. The square symbols show the average values for the outflow detections in the two categories, the points with arrows show the upper limits (with arbitrary values on the y-axis). According to a survival analysis Two Sample test, the differences between AGN and SB and between interacting and mergers, are not statistically significant. |
Additionally, we compare the distribution of outflow properties for AGN vs. SB and mergers vs. interacting systems, taking into account also the upper limits on the non-detections. Figure 13 shows the cumulative distribution functions (CDF) of the outflow properties (vout, Rout, log Mout, log Ṁout, and log η = log(Ṁout/SFR)) for the AGN and SB categories (upper) and mergers and interacting (bottom) categories. To test whether two samples have different distributions, we perform a Two Sample test using the survival analysis package ASURV (Feigelson & Nelson 1985) which allows us to take into account upper limits. We find that the distributions of the outflow properties of AGN and SB are not significantly different according to the Gehan’s, Logrank and Peto-Prentice’s Two Sample Tests (p-value = 0.2–0.7). Similarly, we do not find significant differences between mergers and interacting systems (p-value = 0.2–0.9).
We also consider the mean outflow rate normalised by the total LIR (see Fig. 14), in order to remove the effect of the correlation between Ṁout and LIR (see Sect. 5.3). Also in this case there are no significant differences in the average Ṁout/LIR of the different categories. The average for the total sample is Ṁout/LIR = (3.8 ± 0.6)×10−11 M⊙ yr−1
 . In the right panel, we also plot the average outflow rates normalised by AGN luminosity Ṁout/LIR, AGN for the AGN categories. The average Ṁout/LIR, AGN for AGN are ∼3 − 6 times higher than the Ṁout/LIR for starbursts.
. In the right panel, we also plot the average outflow rates normalised by AGN luminosity Ṁout/LIR, AGN for the AGN categories. The average Ṁout/LIR, AGN for AGN are ∼3 − 6 times higher than the Ṁout/LIR for starbursts.
 |
Fig. 14. Left: mean values of the ratio of Ṁout and total LIR for different categories: AGN, starbursts (SB), mergers (M), interacting (I), and the mix categories mergers AGN, mergers SB, interacting AGN and interacting SB. The errorbars show the uncertainty on the mean. The grey diamond and horizontal band shows the mean of the total sample and the corresponding uncertainty. Right: for the AGN categories, mean ratios of Ṁout and LIR, AGN. |
5.3. Outflow properties and energetics
In this section, we investigate the relation between the outflow properties and the SFR, as well as with the AGN luminosity and AGN fraction.
5.3.1. Outflow and AGN properties
In this section, we look at trends between the outflow properties and the AGN luminosity and AGN fraction. We calculate the AGN luminosity (LIR, AGN) as the fraction of the total infrared luminosity LIR due to AGN, based on the MIR AGN fraction (αAGN, see Perna et al. 2021). For the interacting systems, αAGN is determined only for the IR brightest nucleus, thus, for the second faint nucleus we cannot estimate LIR, AGN and LIR, SF. Cicone et al. (2014) reported a trend for the mass-loading factor (η = Ṁout/SFR) to increase with AGN fraction (αAGN = LAGN/Lbol), while we do not find a correlation between these two quantities in our sample (Spearmann rank correlation coefficient for the detections r = 0.27, p-value = 0.28), as it is shown in Fig. 15. The correlation found in Cicone et al. (2014) is driven mostly by the objects with high AGN fraction (> 0.8), which have η > 10. Fluetsch et al. (2019) expand the Cicone et al. (2014) sample and find that the correlation between η and αAGN is only evident for αAGN > 0.7. They propose that the lack of correlation for αAGN < 0.7 could be due to i) the contribution from star-formation to the mass outflow rate for small AGN fractions or ii) to the short timescale of AGN variability (10 − 105 yr, Gilli et al. 2000; Schawinski et al. 2015), compared to the outflow timescales (106 yr). Since Cicone et al. (2014) included in the study objects with known molecular outflows, it is possible that they sample the upper end of the distribution of η at large αAGN. On the other hand, our sample was selected without a prior knowledge of the presence of outflows. The difference could be also due to the method used to estimate the AGN fraction. We use αAGN estimated from the MIR 30 μm to 15 μm flux ratio. Cicone et al. (2014) estimate the AGN fraction using different methods: from the 5–8 μm spectral range using the method from Nardini et al. (2010), from a combination of MIR and FIR diagnostics as described in Veilleux et al. (2009), by taking the fraction of LAGN (estimated from [OIII] or from the X-ray luminosity) and Lbol. If we were to use the method from Nardini et al. (2010), the αAGN for our sample would be lower (< 0.7 for all sources).
 |
Fig. 15. Mass-loading factor (η = Ṁout/SFR) versus AGN fraction (αAGN). Star symbols show the Cicone et al. (2014) sample (scaled down by a factor of three to match our outflow geometry definition). Symbols for the PUMA sample are as in Fig. 1. |
Cicone et al. (2014) also find a correlation between the molecular mass outflow rate and the AGN luminosity. A similar correlation was also reported in Fiore et al. (2017), who expanded the sample used by Cicone et al. (2014). Figure 16 shows Ṁout as a function of LAGN for our sample, together with the sample from Cicone et al. (2014), Lutz et al. (2020), the nearby (non-ULIRGs) AGN from Stuber et al. (2021), and the nearby (z < 0.13) type 2 AGN from Ramos Almeida et al. (2022). Ramos Almeida et al. (2022) find that their sample has Ṁout more than one order of magnitude below the relation derived by Cicone et al. (2014; dashed line on the Fig. 16). Our sample occupies the parameter space between the Ramos Almeida et al. (2022) objects and the Cicone et al. (2014) relation. Ramos Almeida et al. (2022) suggest that this scaling relation represents the upper boundary of the Ṁout versus AGN luminosity relation. Our sample confirms that for the same AGN luminosity, ULIRGs can have a wide range of Ṁout. We note that most of the objects in Cicone et al. (2014) were selected based on the presence of a molecular outflow (detected in CO or OH), while for our sample we do not apply this prior criterion. This may explain the fact that the sources in their sample have the highest Ṁout values for a given AGN luminosity.
 |
Fig. 16. Mass outflow rate versus AGN luminosity. Diamonds symbols show the sample from Cicone et al. (2014), for which Ṁout have been scaled down by a factor of three to match our outflow geometry definition. The sample of Ramos Almeida et al. (2022) is shown with triangles. Horizontal lines for the Ramos Almeida et al. (2022) sample indicate the position that they would occupy if we were to use the LAGN derived from SED fitting from Jarvis et al. (2019), instead of the one derived from the [O III] luminosity (see Ramos Almeida et al. 2022, for details). The Lutz et al. (2020) sample is shown with red pentagons. For the Stuber et al. (2021) sample (stars), the AGN luminosities have been derived from the 14–195 keV X-ray luminosity. Symbols for the PUMA sample are as in Fig. 1. The dashed and dotted lines show the relations presented by Cicone et al. (2014) and by Fiore et al. (2017), respectively, scaled down by a factor of three to match our outflow geometry definition. |
5.3.2. Outflow energetics
In Fig. 17 we show the outflow rate, momentum rate (Ṗout = Ṁout·vout), and kinetic luminosity (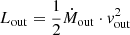 ) as a function of SFR. The SFR has been estimated from the IR luminosity, using the Kennicutt & Evans (2012) relation (with Kroupa & Weidner (2003) initial mass function (IMF)) after removing the fraction of luminosity associated with the AGN (αAGN).
) as a function of SFR. The SFR has been estimated from the IR luminosity, using the Kennicutt & Evans (2012) relation (with Kroupa & Weidner (2003) initial mass function (IMF)) after removing the fraction of luminosity associated with the AGN (αAGN).
 |
Fig. 17. Mass outflow rate (left), outflow momentum rate (middle), and outflow kinetic luminosity (right) as a function of SFR. Lightblue and orange symbols indicate SB- and AGN-dominated nuclei, respectively. Circles indicate interacting systems and squares indicate mergers from the PUMA sample (including nuclei with log LIR/L⊙ < 11.8). Stars show the PHANGS-ALMA targets from Stuber et al. (2021). A representative errorbar is shown on the lower right. Left panel: the black dotted-dashed lines show lines of constant mass-loading factors (η = Ṁout/SFR) of 0.1, 1 and 10. Middle panel: the dashed line indicates the total momentum injected by SNe as a function of SFR. The dotted line shows the LSFR/c ratio, where LSFR is the IR luminosity for a given SFR derived using the Kennicutt & Evans (2012) relation. Right panel: the lines show the 1%, 10% and 100% of the energy produced by SNe. The lightblue lines in the three panels are the best linear fit to the data, with the shaded area indicating the 1σ uncertainty. |
To increase the dynamic range of SFR, we include in this figure also the 20 galaxies with candidate outflows from the Physics at High Angular resolution in Nearby GalaxieS (PHANGS3) ALMA survey (Leroy et al. 2021; Stuber et al. 2021). The PHANGS-ALMA sample consists of 90 nearby (d < 24 Mpc) star-forming galaxies (logsSFR/yr−1 > −11) with stellar masses in the range 9.3 ≤ log M⋆/M⊙ ≤ 11.1. Stuber et al. (2021) use ALMA CO(2–1) observations with a resolution of ∼100 pc to look for molecular outflows in their sample and they find 20 (22%) outflow candidates, of which 16 are classified as ‘secure’ candidates. Half of the candidates are classified as AGN hosts based on Véron-Cetty & Véron (2010).
The outflow parameters of this sample have been measured using a method comparable to ours. They integrated the total flux within the defined outflow velocity range to derive the outflow mass and measure the flux-weighted outflow velocity. They also measured flux-weighted outflow radii. Because of the limited S/N, we did not attempt to derive flux-weighted Rout by measuring the outflow radii in each channel, but the Rout derived from the 2D Gaussian fit should be representative of the radius where most of the flux is located. To convert the CO(2–1) outflow flux to outflow mass, Stuber et al. (2021) use the conversion factor αCO = 0.8 M⊙/(K km s−1 pc2) (Bolatto et al. 2013b), similar to our assumption of αCO = 0.78 M⊙/(K km s−1 pc2), and r21 = 0.65 (Bolatto et al. 2013a; Leroy et al. 2013, 2021; den Brok et al. 2021) while we use the value of r21 = 0.91 measured in ULIRGs (Papadopoulos et al. 2012). The SFR for this sample are derived by Leroy et al. (2021) from the WISE band 4 photometry, with a calibration consistent with Kennicutt & Evans (2012), the one used for the PUMA targets. The molecular outflows detected in the PHANGS galaxies have weighted velocities vout = 65 − 238 km s−1, Mout = 0.35 − 102 × 106 M⊙ and Ṁout = 0.15−21 M⊙ yr−1. These outflow parameters are lower than the ones we measure for PUMA, as it is expected for galaxies with lower SFR compared to ULIRGs.
The left panel of Fig. 17 shows the relation between mass outflow rate and SFR. The dashed lines indicate constant mass-loading factors (η = Ṁout/SFR). The PUMA objects have η < 0.04 − 1. The PHANGS-ALMA galaxies have slightly higher η = 0.15 − 4. The dispersion in Ṁout for a given SFR is quite high (∼1 dex). Mass-loading factors in local starburst galaxies are typically lower than 2 − 3 (e.g., Bolatto et al. 2013b; Cicone et al. 2014; Salak et al. 2016), thus, the outflows of the PUMA sample are consistent with being powered by starburst. We note that the nuclei classified as AGN through MIR or optical diagnostics (orange symbols) do not show higher mass-loading factors compared with the rest of the sample. For the PUMA sample, the vertical errorbars are probably more extended towards higher values, given that with our method it is possible that we are underestimating Ṁout in some of the objects (see discussion in Sect. 4.5.2).
In Fig. 17 we also show the outflow momentum rate (Ṗout) as a function of SFR. We follow Pereira-Santaella et al. (2018) to calculate the total momentum injected by supernova explosions. We assume that the momentum per supernova is 1.3 × 105 M⊙ km s−1 ×(n0/100 cm−3)−0.17 (Kim & Ostriker 2015), where n0 = 100 cm−3 is the electron density; and that the supernova rate is 0.012 × SFR(M⊙ yr−1) for the adopted IMF (Leitherer et al. 1999). Since all the PUMA galaxies have Ṗout smaller than the total momentum injected by supernovae (SNe, see dashed line in the middle panel of Fig. 17), their outflow momentum rate could be explained entirely by SNe.
The outflow kinetic luminosity is shown in the right panel of Fig. 17. The dashed lines show fractions of the energy produced by SNe (1%, 10%, 100%). The kinetic energy injected by supernova explosions is calculated as LSNe [erg s−1] = 9 × 1041 × SFR [M⊙ yr−1] (Leitherer et al. 1999), adapted for a Kroupa (2001) IMF. For the PUMA ULIRGs, the outflow kinetic luminosity is 0.2 − 5.9% of the energy produced by SNe, for the PHANGS-ALMA sample it is slightly lower (0.1 − 2.4%). The linear fit to the two samples gives:
The slope is larger than one, meaning that, assuming that these outflows are driven by SNe, the coupling efficiency between ISM and SNe increases slightly with SFR. This slope is shallower than the value of 2 ± 0.2 found by Pereira-Santaella et al. (2018) using a smaller sample (15 objects). The difference could be partly explained by the different method used to derive the outflow parameters in Pereira-Santaella et al. (2018), which obtained higher mass outflow rates for ULIRGs (12–400 M⊙ yr−1).
5.3.3. Outflow launching mechanism
In this section we investigate the outflow launching mechanism. In particular, we investigate whether the detected molecular outflows are momentum-driven or energy-driven. For momentum-driven outflows, the mass-loading factor (η = Ṁout/SFR) is proportional to 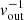 , while for energy driven outflows
, while for energy driven outflows 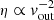 (e.g., Murray et al. 2005). It is possible to distinguish between the two scenarios by looking at the slope of the relation between log η and log vout:
(e.g., Murray et al. 2005). It is possible to distinguish between the two scenarios by looking at the slope of the relation between log η and log vout:
where α and b are the slope and intercept of the linear relation. In Fig. 18 we show log η as a function of log vout for the PUMA and PHANGS-ALMA samples. We fit a linear relation between these two quantities using the Monte Carlo Markov-Chain (MCMC) implementation PyStan4. The lightblue shaded region shows the 1σ uncertainty on the fit, obtained by sampling the posterior distribution. We assume a systematic error of 0.1 dex on vout and 0.3 dex on η. We also model the intrinsic scatter of the relation and we assume that the noise is normal distributed. We derive the best fit values and the corresponding 1σ uncertainties from the median and the 16th-84th percentiles, respectively, of the marginalised posterior distributions of the parameters (more details on the fitting procedure can be found in Appendix B).
 |
Fig. 18. Mass-loading factor versus outflow velocity for our sample (circles and square symbols) and the PHANGS-ALMA sample (stars). The lightblue line is the best linear bisector fit to the data and the shaded areas indicates the 1σ uncertainty on the fit with and without including the intrinsic scatter term (lighter and darker colour, respectively). The blue dashed line shows the predictions for a energy-driven outflow (α = −2) and the red dotted-dashed line for a momentum-driven outflow (α = −1). |
The best linear bisector fit gives a slope α = −1.43 ± 0.28 (σintr = 0.35). This slope is between the momentum-driven (α = −1) and energy-driven (α = −2) value. From Fig. 18, we can see that both slopes are included within the 1σ fit uncertainty (lightblue shaded area), and therefore we cannot distinguish between the two options on the basis of this figure.
In Fig. 19, we show the SFR as a function of vout. There is a strong positive correlation between these two quantities (r = 0.84, p-value < 0.01). The best linear fit gives:
 |
Fig. 19. Outflow velocity versus star-formation rate for our sample and the PHANGS-ALMA sample. The lightblue line is the best linear fit to the data (slope: 0.25 ± 0.01); the 1σ uncertainties on the fit (with and without including the intrinsic scatter term) are indicated with shaded areas (lighter and darker colour, respectively). Symbols as in Fig. 17. |
The slope of the relation is in agreement with the relation found for the ionised gas by Arribas et al. (2014, slope 0.24 ± 0.05) and for neutral gas by Rupke et al. (2005b, slope 0.21 ± 0.04). It is also in agreement with the theoretical prediction from Heckman et al. (2000) of the relation between velocity and starburst luminosity 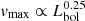 . This relation is derived under the assumption that starbursts have a maximum characteristic surface brightness (Lehnert & Heckman 1996; Meurer et al. 1997), and therefore their bolometric luminosity is proportional to their radius squared. We note that these relations consider vmax, not the mean outflow velocity. We cannot use vmax in our analysis, because it is not available for the PHANGS sample and we consider it less robust than vout. Nonetheless, for the PUMA sample we find a good correlation between vmax and vout (r = 0.58, p-value < 0.01).
. This relation is derived under the assumption that starbursts have a maximum characteristic surface brightness (Lehnert & Heckman 1996; Meurer et al. 1997), and therefore their bolometric luminosity is proportional to their radius squared. We note that these relations consider vmax, not the mean outflow velocity. We cannot use vmax in our analysis, because it is not available for the PHANGS sample and we consider it less robust than vout. Nonetheless, for the PUMA sample we find a good correlation between vmax and vout (r = 0.58, p-value < 0.01).
Using this relation, we can substitute logSFR with 4 ⋅ log vout in the expression of the mass-loading factor:
Substituting this in equation 11 gives:
Thus, by looking at the relation between Mout/Rout and vout, we can derive the value of α. For the fit, we assume a systematic error of 0.1 dex on log vout and 0.3 dex on log(Mout/Rout). Figure 20 shows log(Mout/Rout) as a function of log vout.
 |
Fig. 20. Outflow mass divided by outflow radius (Mout/Rout) versus outflow velocity. The lightblue line is the best linear fit to the data (slope = 2.61 ± 0.25). The shaded area indicates the 1σ uncertainty with and without including the intrinsic scatter term (lighter and darker colour, respectively). The blue dashed line shows the predictions for a energy-driven outflow (α = −2) and the red dotted-dashed line for a momentum-driven outflow (α = −1). Symbols as in Fig. 17. |
The best linear bisector fit relation has a slope of 2.61 ± 0.25, which implies α = −0.39. The α = −1 scenario (momentum-driven) is within the 1σ uncertainty (see shaded area in Fig. 20), while the α = −2 scenario does not agree with the fit. Therefore, our analysis favours the momentum-driven scenario as the primary launching mechanism for molecular outflows in ULIRGs. Previous works investigating the molecular outflows in ULIRGs also reach this conclusion. Cicone et al. (2014) find α = −1.0 ± 0.5 for a sample of five pure starburst galaxies, in agreement with the momentum-driven scenario. Pereira-Santaella et al. (2018) find α = −0.3 ± 0.2 combining a sample U/LIRGs and lower luminosity starbursts. We note that for this analysis we adopt a different r21 value for the Stuber et al. (2021) sample (r21 = 0.6) and for the PUMA sample (r21 = 0.91). If we were to use the same value for both samples, the fit would agree even more with the momentum-driven scenario.
5.3.4. Escape fractions
We estimate the average fraction of the outflowing gas that can potentially escape from the gravitation potential of the galaxies. To estimate the escape fraction, we compare the outflow velocity with the escape velocity derived from a gravitational model of the host galaxy, which is assumed to be a truncated isothermal sphere (e.g., Veilleux et al. 2005). We use Eq. (7) in Arribas et al. (2014) to estimate the average escape velocity for our sample at the average outflow radius r = 1 kpc. Since estimates of the dynamical masses have been obtained by Perna et al. (2022) only for a subset of our targets (eight objects), we use the mean dynamical mass of the PUMA sample for our calculation ⟨Mdyn⟩ = 3.9 × 1010 M⊙. The dynamical masses have been obtained from the modelling of the rotation of the ionised gas (see Perna et al. 2022, for more details). As truncating radius we assume two times the average effective radius ⟨Re⟩ = 2 kpc (Perna et al. 2022). We assume that the outflow velocity only has a radial component. With these assumptions, we estimate an average escape velocity of vesc = 486 ± 40 km s−1. We apply an inclination correction to determine the average ‘observed’ vesc, obs = vesc/1.27 = 382 km s−1 (see Sect. 4.5).
Integrating the CO(2–1) emission at velocities higher than vesc, obs, we find that between 4 − 100% of the high-velocity gas will escape to the circumgalactic medium, with mean escape fraction ⟨fesc⟩ = 45 ± 6%. This calculation depends on the assumption on the truncating radius. If we were to assume a larger truncating radius, the escape velocity would increase, and the escape fraction would decrease. For example, assuming a truncating radius larger by a factor of two (rmax = 4 × ⟨Re⟩ = 8 kpc), vesc would increase by 13%. The escape outflow rates are in the range 1–173 M⊙ yr−1, with an average ⟨Ṁesc⟩ = 40±10 M⊙ yr−1. We find that interacting systems tend to have lower fesc than mergers (mean fesc = 33 ± 6% vs. fesc = 60 ± 10%).
We also compare the escape molecular gas mass (M(H2)esc) with the total M(H2) of the galaxy (i.e. systemic and outflow). The escape M(H2)esc is < 5% of the total M(H2), with a mean of 1%. The mean depletion time based on the escape outflow rate (tdep = M(H2)/Ṁesc) is 158 Myr (range 23 − 3715 Myr).
5.4. OH vs. CO outflow properties
In this section we compare the molecular outflow properties derived from the CO(2–1) emission line with the ones derived from the OH 119 μm doublet, which is an alternative tracer used to identify molecular outflows.
We compare the OH and CO profile of each PUMA target in Figs. 3, 4, and E.1. The OH absorption is produced in front of the continuum emission, thus, we can assume that it is located in a region of the size of the continuum, which in most cases is equal or smaller than the beam size (Pereira-Santaella et al. 2021). Therefore, to have a fair comparison, we extract the nuclear CO spectrum from a region equal to the beam size. We also smooth the CO spectrum to the same spectral resolution of the OH spectrum. Qualitatively, it is evident from this comparison that there are some cases where a clear blue-shifted outflow is detected in OH but not in CO (e.g., 00188−0856), and vice-versa (e.g., 09022−3615, 17208−0014). In Fig. 21 we show four example cases: i) broad OH absorption reaching high negative velocities (v < −1000 km s−1), but no CO blue-shifted emission at v < −300 km s−1 (00188−0856); ii) CO outflow, but no sign of outflow in OH (22491−1808); iii) outflow detected in both OH and CO, but OH outflow maximum velocity (v98 = −1540 km s−1) much larger than CO outflow maximum velocity vmax = −800 km s−1 (20100−4156); iv) OH outflow maximum velocity (v98 = −360 km s−1) smaller than CO outflow maximum velocity vmax = −600 km s−1 (15327+2340).
 |
Fig. 21. Comparison of the OH 119 μm and CO(2–1) line profile. The CO(2–1) spectrum is extracted from a nuclear region corresponding to the ALMA beam size and is convolved to the resolution of the OH spectrum (FWHM ∼ 270 km s−1). We identified four different cases: (i) OH absorption reaching high velocity (|v|> 1000 km s−1), but no CO blue-shifted emission (00188−0856); (ii) CO outflow, but no sign of OH outflow (22491−1808); (iii) outflow detected in both OH and CO, but OH outflow maximum velocity (v98) larger than CO outflow maximum velocity (20100−4156); (iv) OH outflow maximum velocity (v98) smaller than CO outflow maximum velocity (15327+2340). |
In Fig. 22, we compare the OH and CO outflow velocities. In the upper row, we compare the OH v98 velocity of the absorption profile with the ‘weighted’ outflow velocity (vout, left) and maximum outflow velocity (vmax, right) of the blue-shifted wing of the CO profile. We show the objects with OH absorption or P-Cygni profile, for a total of 20 nuclei. For 12112+0305 and 14348−1447, we show both nuclei, since a CO outflow is detected around each nucleus and they have comparable continuum luminosity. For the other interacting systems, we consider only the nucleus with the brightest continuum, since the second nucleus does not have a CO outflow detection.
 |
Fig. 22. Comparison of the outflow velocities of OH and CO. Upper row: v98 derived from the OH absorption profile compared with the mean (vout(b), left) and maximum (vmax(b), right) velocities of the CO blue-shifted wing. The background colours highlight the three regions described in Sect. 5.4: (i) targets with v98 similar to vmax(b), (ii) targets with v98 > vmax(b), and (iii) targets v84 < vmax(b). Lower row: v98 derived from the OH emission profile compared with the mean (vout(r), left) and maximum (vmax(r), right) velocities of the CO red-shifted wing. The blue lines mark the outflow detection threshold of |v|> 300 km s−1. Black circles mark targets classified as compact obscured nuclei (CONs). Colour-code as in Fig. 1. |
We identify three groups: i) targets with comparable OH and CO outflow velocity, ii) targets with OH outflow velocity larger than the ones from CO, and iii) targets with CO outflow velocity larger than the OH outflow velocity. In 13 targets, both |v98(abs)(OH)| and |vmax(CO)| are > 300 km s−1. The |v98(abs)(OH)| values tend to be higher (on average by 170 km s−1) than the |vmax(CO)| values, but this is not surprising given that v98 and vmax are measured using different methods.
For 3/20 targets, |v98(abs)(OH)|< 300 km s−1, thus, there is no evidence of an outflow in the OH absorption profile, while a CO outflow is detected. This difference may be due to a collimated outflow in CO. In this case, the associated OH will absorb only a tiny fraction of the continuum behind the outflow and thus it will be undetectable. In Fig. 23 we compare the velocity difference |v98(abs)(OH) − vmax(CO)| with the CO outflow radius Rout. We find a weak anti-correlation between the Rout and the OH-CO velocity difference (r = −0.4, or r = −0.3 if we exclude the point with vmax(CO) = 0 kms−1), meaning that for more extended CO outflow, the CO velocity tend to be larger than the OH velocity. This is consistent with the scenario explained before, where for an outflow extending to a larger distance from the nucleus, a lower fraction of the outflowing gas may overlap with the background continuum, making the OH absorption weaker (Veilleux et al. 2020). Additionally, if the velocity of the outflow increases with distance from the nucleus, the part with the highest velocity is more likely to not overlap with the continuum and thus, will not be detected in the OH absorption. Indeed, a radial velocity gradient of ∼1 km s−1 pc−1 has been detected in the molecular outflows of two galaxies: in the nearby starburst galaxy NGC 253 by Walter et al. (2017) and in the LIRG ESO 320-G030 by Pereira-Santaella et al. (2020).
 |
Fig. 23. Comparison of the difference between the outflow velocities of OH (v98) and CO (vmax) with the CO outflow radius Rout (left) and the AGN fraction αAGN (right). Black circles mark targets classified as compact obscured nuclei (CONs). Colour-code as in Fig. 1. |
For one target (00188−0856), the OH spectrum shows a clear outflow signature with v98(abs)(OH) ∼ −1200 km s−1, but there is no outflow signature in the CO spectrum. The case of 00188−0856 can potentially be explained with extreme environments: if the ionisation fraction of the molecular gas is high, the abundance of CO would decrease while the abundance of OH remains high (González-Alfonso et al. 2018). This could be mostly associated with the highest-velocity gas. Alternatively, this difference may be explained by the geometry of the outflow.
Another factor that can explain part of the differences in outflow velocities is the difference in sensitivities of the CO and OH observations. Thus, the observation of one tracer may be more sensitive to weak outflow signatures at high velocities than the other.
We note that the AGN nuclei tend to have faster OH outflows than SB-dominated nuclei. Indeed, all AGN nuclei have |v98(OH)|> 300 km s−1. There is a positive correlation (r = 0.51) between the outflow velocity difference |v98(OH) − v(CO)| and the AGN fraction (see Fig. 23). Veilleux et al. (2013) find that AGN-dominated nuclei (αAGN > 0.5) tend to have more negative OH outflow velocities than SB-dominated nuclei. Their interpretation of this result is that once a significant fraction of the material has been pushed away from the nucleus by the outflow, the AGN is more likely to be identifiable. At the same time, the central high-velocity part of the outflow can be seen more easily.
To investigate the differences between the OH and CO outflow velocities, we consider the possibility that the presence of a compact obscured nucleus (CON) could influence the OH outflow velocities. Falstad et al. (2019) find that CONs with the most luminous HCN-vib line lack signatures of high velocity outflows in the OH 119 μm absorption lines, even though some of them have molecular outflows detected in the CO or HCN emission lines. We apply the method described in García-Bernete et al. (2022) to identify CONs in our sample, based on the ratios of the equivalent widths of different polycyclic aromatic hydrocarbons (PAHs) features from the literature (see Table 1). We find that CONs do not occupy a specific region of the v98(abs)(OH) vs. vmax(CO) diagram (see black circles in Fig. 22). We find that 6/7 CONs have |v98(abs)(OH)| > 300 km s−1, a sign of molecular outflows.
In Fig. 22, we also compared the velocities derived from the OH emission (v98(em)) with the velocities of the red-shifted CO outflow (vout(r) and vmax(r)). Most targets have v98(em) > 300 km s−1. For these targets, v98(em) generally agree, within the uncertainties, with the CO outflow velocities. The uncertainties on OH velocities derived from the emission profiles tend to be larger than the ones derived from the absorption, because the emission features are weaker.
One possible caveat of this analysis is the fact that the OH spectrum includes the nuclear region with a beam size ∼20 arcsec5. For the interacting systems, these include the two nuclei. To detect the OH absorption, it is necessary to have the continuum emission in the background. In the majority of interacting cases, the ALMA continuum emission is dominated by one nucleus (> 80% of the total emission for all but two cases, 11095−0238 (65%) and 14348−1447 (60%), see Table 7 in Pereira-Santaella et al. 2021), thus we can associate the OH absorption to the nucleus with the brightest continuum emission.
6. Discussion
In our sample, we find a lower molecular outflow detection rate in AGN (55 ± 14%) than in SB (93 ± 4%), for the nuclei with log LIR > 11.8 L⊙ (see Sect. 5.2). This finding is in contrast with the result of Stuber et al. (2021), who find higher molecular outflow detection rate in AGN (53%) compared to non-AGN (17%) in main-sequence galaxies from the PHANGS sample. A possible explanation is that the situation in ULIRGs is different than in main-sequence galaxies: in ULIRGs, SB-driven outflows are stronger and may be easier to detect than AGN-driven outflows. In main-sequence galaxies on the other hand, outflows driven by star-formation are weaker, and the AGN-outflows are more important.
Other than the detection rate, we do not find significant differences in the outflow properties (vout, Rout, Mout, Ṁout) in AGN and SB in the PUMA sample. Thus, molecular outflow in AGN-dominated nuclei seem to be as powerful as SB-driven outflows, contrary to what was found in previous works (Cicone et al. 2014; Fluetsch et al. 2019). Cicone et al. (2014) and Fiore et al. (2017) reported a positive correlation between Ṁout and AGN luminosity, while in the PUMA sample we do not see this correlation, in agreement with the findings of Ramos Almeida et al. (2022). The previous relations maybe trace the most efficient coupling between AGN and molecular gas, so that the objects with the most extreme outflows follow those relations. This implies that there are other factors that set the mass outflow rate other than the AGN luminosity, as for example the geometry of the outflow and the coupling between the outflow and the CO disk, the efficiency of the energy/momentum transfer between the AGN and the molecular gas, or the distribution of the gas around the AGN. Additionally, starbursts could contribute to powering the molecular outflows even in AGN-dominated nuclei.
In our sample, we find outflow dynamical times 0.5–2.8 Myr (see Sect. 5.1). These dynamical times are significantly shorter than the expected age of the star-formation burst in ULIRGs (∼60 − 100 Myr, Rodríguez Zaurín et al. 2010), the depletion times of star-formation (10 − 100 Myr for our sample) or the outflow depletion times (∼10 − 700 Myr, Cicone et al. 2015; Pereira-Santaella et al. 2018). These short dynamical times of the molecular outflows may be due to the survival time of the molecular gas in the hot outflow environment (e.g., Decataldo et al. 2017). An alternative explanation may be related to the geometry of the outflow. If the outflow has a bi-conical geometry, the area of the outflow increases with the squared of the radial distance from the nucleus (r2). Thus, the column density of the outflow decreases with radius, making the emission fainter and more difficult to detect at large radii (Pereira-Santaella et al. 2018).
In our sample, we find that between 4–100% of the outflow gas could escape from the gravitational potential of the galaxies into the circumgalactic medium (see Sect. 5.3.4). However, this represents only 1–5% of the total molecular gas reservoir of the galaxies. Thus, it is unlikely that these outflows are able to impact star-formation by removing gas from the molecular gas reservoir.
7. Summary and conclusions
In this work, we present ALMA CO(2–1) observations of 25 nearby (z < 0.165) ULIRG systems (38 individual nuclei) with a resolution of ∼400 pc. We have used these observations to study their molecular outflow properties. The main results of this work are as follows:
-
We detect molecular outflows in 20/26 (77%) nuclei with log LIR/L⊙ > 11.8. The molecular outflows have an average outflow velocity 485 ± 16 km s−1, outflow masses 1 − 35 × 107 M⊙, mass outflow rates Ṁout = 6−300 M⊙ yr−1, and mass-loading factors η = Ṁout/SFR = 0.1 − 1. The majority of the outflows (18/20) are spatially resolved with radii of 0.2 − 0.9 kpc and have short dynamical times (tdyn = Rout/vout) in the range 0.5 − 2.8 Myr. We estimate the average escape velocity for our sample vesc = 486 ± 40 km s−1. We find that, on average, 45 ± 6% of the high-velocity gas will escape to the circumgalactic medium, which represents less than 5% of the total molecular gas mass of the systems (see Sect. 4.5.)
-
We find that the outflow detection rate is higher in SBs (93 ± 4%, 14/15) than in AGN (55 ± 14%, 6/11) (see Sect. 5.2, Fig. 12). A possible interpretation is that SB outflows tend to be perpendicular to the disk, and thus they are easier to detect, while AGN outflow can have any inclination and/or can be more collimated. Indeed, we find that in 43% (6/14) of the SB nuclei with outflow detection, the projected position angle of the outflow is along the kinematic minor axis, which suggests that these outflows are perpendicular to the disk. This fraction is higher in early interacting SBs (50%) than in advanced merger SBs (17%). Outflows powered by AGN do not have a preferred orientation with respect to the disk. We do not find any significant difference in the mean outflow properties depending on the nuclear engine (AGN versus SBs) or on the merger stage (advanced mergers versus interacting systems, see Fig. 14).
-
We find that our sample does not follow a tight Ṁout versus AGN luminosity relation, as reported in previous works (see Fig. 16). For the same AGN luminosity, we find Ṁout spanning up to 1.2 dex. This suggests that other factors may contribute in determining Ṁout in AGN ULIRGs, such as the efficiency of the energy or momentum transfer between the AGN and the molecular gas, the outflow geometry, or the distribution of the gas around the AGN.
-
We investigate whether the molecular outflows are momentum-driven or energy-driven, using also the PHANGS-ALMA sample (Stuber et al. 2021) to extend the analysis to galaxies with lower SFR. Based on the slope (α = −1.43 ± 028) of the mass-loading factor versus outflow-velocity relation (Fig. 18), we cannot distinguish between the momentum-driven (α = −1) and energy-driven (α = −1) scenarios. However, using the relation between the SFR and the outflow velocity (log vout ∝ 0.25 ⋅ logSFR), we could derive the value of α by fitting the relation between Mout/Rout and vout. From this analysis, we derived a slope α = −0.39 ± 0.25, which is more consistent with the momentum-driven than with the energy-driven scenario (see Sect. 5.3.3, Fig. 20).
-
We compare the outflow velocities derived from CO (vout) with the ones derived from OH outflow (v98; see Sect. 5.4, Fig. 22). We find that for 13 targets, both the CO and OH velocities are above 300 km s−1, which is a sign of outflow, while in three targets the OH velocities are considerably lower than vout, and therefore there is no evidence of outflows. This could be explained if the outflow is highly collimated, and thus the outflowing OH covers a small region of the background continuum. In one case (00188−0856), the OH outflow velocity is very high, but no outflow is detected in CO. This situation could be explained by an extreme environment, where the high ionisation would decrease the CO abundance more than the OH abundance, by the outflow geometry or by the different sensitivities of the OH and CO observations.
The channel maps for the rest of the sample can be found at https://doi.org/10.5281/zenodo.7022665.
Acknowledgments
We thank the referee for the useful comments and suggestions which helped improve this manuscript. We thank Cristina Ramos Almeida for helpful discussion. We thank the staff of the European ALMA ARC for the support with the self-calibration of the data. This research has been funded by MDM-2017-0737 Unidad de Excelencia “María de Maeztu”- Centro de Astrobiología (INTA-CSIC) by the Spanish Ministry of Science and Innovation/State Agency of Research MCIN/AEI/ 10.13039/501100011033 and by “ERDF A way of making Europe”. IL and MPS acknowledge support from the Comunidad de Madrid through the Atracción de Talento Investigador Grant 2018-T1/TIC-11035 and PID2019-105423GA-I00 funded by MCIN/AEI/10.13039/501100011033. MP is supported by the Programa Atracción de Talento de la Comunidad de Madrid via grant 2018-T2/TIC-11715. MP and SA acknowledge support from the Spanish Ministerio de Economía y Competitividad through the grant ESP2017-83197-Py and PID2019-106280GB-I00. EG-A is a Research Associate at the Harvard-Smithsonian Center for Astrophysics, and thanks the Spanish Ministerio de Economía y Competitividad for support under projects ESP2017-86582-C4-1-R and PID2019-105552RB-C41. AAH and SGB acknowledge grant PGC2018-094671-B-I00 funded by MCIN/AEI/ 10.13039/501100011033 and by ERDF A way of making Europe. SGB acknowledges support from the research project PID2019-106027GA-C44 of the Spanish Ministerio de Ciencia e Innovación. SAa gratefully acknowledges support from an ERC Advanced Grant 789410, from the Swedish Research Council and from the Knut and Alice Wallenberg Foundation (KAW). DR acknowledges support from STFC through grant ST/S000488/1. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2015.1.00113.S, ADS/JAO.ALMA#2015.1.00263.S, ADS/JAO.ALMA#2016.1.00170.S, ADS/JAO.ALMA#2016.1.00777.S, ADS/JAO.ALMA#2018.1.00486.S, and ADS/JAO.ALMA#2018.1.00699.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013), Matplotlib (Hunter 2007), NumPy (Van Der Walt et al. 2011). This research used the TOPCAT tool for catalogue cross-matching (Taylor 2005) and the Stan interface for Python PyStan (Stan Development Team 2018).
References
- Aalto, S., Garcia-Burillo, S., Muller, S., et al. 2012, A&A, 537, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aalto, S., Garcia-Burillo, S., Muller, S., et al. 2015, A&A, 574, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso-Herrero, A., Esquej, P., Roche, P. F., et al. 2016, MNRAS, 455, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., García-Burillo, S., Pereira-Santaella, M., et al. 2019, A&A, 628, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arribas, S., Colina, L., Bellocchi, E., Maiolino, R., & Villar-Martín, M. 2014, A&A, 568, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bae, H.-J., & Woo, J.-H. 2016, ApJ, 828, 97 [Google Scholar]
- Barcos-Muñoz, L., Aalto, S., Thompson, T. A., et al. 2018, ApJ, 853, L28 [Google Scholar]
- Bellocchi, E., Arribas, S., Colina, L., & Miralles-Caballero, D. 2013, A&A, 557, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013a, ARA&A, 51, 207 [CrossRef] [Google Scholar]
- Bolatto, A. D., Warren, S. R., Leroy, A. K., et al. 2013b, Nature, 499, 450 [Google Scholar]
- Brusa, M., Cresci, G., Daddi, E., et al. 2018, A&A, 612, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carniani, S., Marconi, A., Maiolino, R., et al. 2015, A&A, 580, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cazzoli, S., Arribas, S., Maiolino, R., & Colina, L. 2016, A&A, 590, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chung, A., Yun, M. S., Naraynan, G., Heyer, M., & Erickson, N. R. 2011, ApJ, 732, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Cicone, C., Maiolino, R., Sturm, E., et al. 2014, A&A, 562, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cicone, C., Maiolino, R., Gallerani, S., et al. 2015, A&A, 574, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Condon, J. J. 1997, PASP, 109, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Dasyra, K. M., & Combes, F. 2011, A&A, 533, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dasyra, K. M., & Combes, F. 2012, A&A, 541, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dasyra, K. M., Combes, F., Novak, G. S., et al. 2014, A&A, 565, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decataldo, D., Ferrara, A., Pallottini, A., Gallerani, S., & Vallini, L. 2017, MNRAS, 471, 4476 [NASA ADS] [CrossRef] [Google Scholar]
- den Brok, J. S., Chatzigiannakis, D., Bigiel, F., et al. 2021, MNRAS, 504, 3221 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez-Fernández, A. J., Alonso-Herrero, A., García-Burillo, S., et al. 2020, A&A, 643, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Emonts, B. H. C., Colina, L., Piqueras-López, J., et al. 2017, A&A, 607, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C. 2012, ARA&A, 50, 455 [Google Scholar]
- Falstad, N., Hallqvist, F., Aalto, S., et al. 2019, A&A, 623, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farrah, D., Afonso, J., Efstathiou, A., et al. 2003, MNRAS, 343, 585 [Google Scholar]
- Feigelson, E. D., & Nelson, P. I. 1985, ApJ, 293, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Feruglio, C., Maiolino, R., Piconcelli, E., et al. 2010, A&A, 518, L155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feruglio, C., Fiore, F., Carniani, S., et al. 2015, A&A, 583, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fiore, F., Feruglio, C., Shankar, F., et al. 2017, A&A, 601, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, J., Sturm, E., González-Alfonso, E., et al. 2010, A&A, 518, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fluetsch, A., Maiolino, R., Carniani, S., et al. 2019, MNRAS, 483, 4586 [NASA ADS] [Google Scholar]
- Fluetsch, A., Maiolino, R., Carniani, S., et al. 2021, MNRAS, 505, 5753 [NASA ADS] [CrossRef] [Google Scholar]
- Förster Schreiber, N. M., Genzel, R., Newman, S. F., et al. 2014, ApJ, 787, 38 [Google Scholar]
- Gao, Y., Egusa, F., Liu, G., et al. 2021, ApJ, 913, 139 [NASA ADS] [CrossRef] [Google Scholar]
- García-Bernete, I., Alonso-Herrero, A., García-Burillo, S., et al. 2021, A&A, 645, A21 [EDP Sciences] [Google Scholar]
- García-Bernete, I., Rigopoulou, D., Aalto, S., et al. 2022, A&A, 663, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Combes, F., Usero, A., et al. 2015, A&A, 580, A35 [Google Scholar]
- Gelman, A., Carlin, J. B., Ster, H. S., et al. 2004, Bayesian Data Analysis (Chapman and Hall/CRC) [Google Scholar]
- Gilli, R., Maiolino, R., Marconi, A., et al. 2000, A&A, 355, 485 [NASA ADS] [Google Scholar]
- González-Alfonso, E., Fischer, J., Graciá-Carpio, J., et al. 2012, A&A, 541, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Alfonso, E., Fischer, J., Bruderer, S., et al. 2013, A&A, 550, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Alfonso, E., Fischer, J., Graciá-Carpio, J., et al. 2014, A&A, 561, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Alfonso, E., Fischer, J., Spoon, H. W. W., et al. 2017, ApJ, 836, 11 [Google Scholar]
- González-Alfonso, E., Fischer, J., Bruderer, S., et al. 2018, ApJ, 857, 66 [Google Scholar]
- Gowardhan, A., Spoon, H., Riechers, D. A., et al. 2018, ApJ, 859, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Lehnert, M. D., Strickland, D. K., & Armus, L. 2000, ApJS, 129, 493 [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., & Kereš, D. 2008, ApJS, 175, 356 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jarvis, M. E., Harrison, C. M., Thomson, A. P., et al. 2019, MNRAS, 485, 2710 [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, C.-G., & Ostriker, E. C. 2015, ApJ, 802, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D. C., & Sanders, D. B. 1998, ApJS, 119, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., & Weidner, C. 2003, ApJ, 598, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Law, D. R., Steidel, C. C., Erb, D. K., et al. 2009, ApJ, 697, 2057 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., & Heckman, T. M. 1996, ApJ, 472, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [Google Scholar]
- Leroy, A. K., Walter, F., Sandstrom, K., et al. 2013, AJ, 146, 19 [Google Scholar]
- Leroy, A. K., Schinnerer, E., Hughes, A., et al. 2021, ApJS, 257, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Lonsdale, C. J., Farrah, D., & Smith, H. E. 2006, in Astrophysics Update 2, ed. J. W. Mason, 285 [CrossRef] [Google Scholar]
- Lutz, D., Berta, S., Contursi, A., et al. 2016, A&A, 591, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lutz, D., Sturm, E., Janssen, A., et al. 2020, A&A, 633, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., Gallerani, S., Neri, R., et al. 2012, MNRAS, 425, L66 [Google Scholar]
- Meena, B., Crenshaw, D. M., Schmitt, H. R., et al. 2021, ApJ, 916, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Meurer, G. R., Heckman, T. M., Lehnert, M. D., Leitherer, C., & Lowenthal, J. 1997, AJ, 114, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, N., Quataert, E., & Thompson, T. A. 2005, ApJ, 618, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Nardini, E., Risaliti, G., Watabe, Y., Salvati, M., & Sani, E. 2010, MNRAS, 405, 2505 [NASA ADS] [Google Scholar]
- Papadopoulos, P. P., van der Werf, P. P., Xilouris, E. M., et al. 2012, MNRAS, 426, 2601 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira-Santaella, M., Colina, L., García-Burillo, S., et al. 2018, A&A, 616, A171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira-Santaella, M., Colina, L., García-Burillo, S., et al. 2020, A&A, 643, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira-Santaella, M., Colina, L., García-Burillo, S., et al. 2021, A&A, 651, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perna, M., Arribas, S., Catalan-Torrecilla, C., et al. 2020, A&A, 643, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perna, M., Arribas, S., Pereira Santaella, M., et al. 2021, A&A, 646, A101 [EDP Sciences] [Google Scholar]
- Perna, M., Arribas, S., Colina, L., et al. 2022, A&A, 662, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pjanka, P., Greene, J. E., Seth, A. C., et al. 2017, ApJ, 844, 165 [Google Scholar]
- Prochaska, J. X., Kasen, D., & Rubin, K. 2011, ApJ, 734, 24 [Google Scholar]
- Ramos Almeida, C., Acosta-Pulido, J. A., Tadhunter, C. N., et al. 2019, MNRAS, 487, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., Bischetti, M., García-Burillo, S., et al. 2022, A&A, 658, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez Zaurín, J., Tadhunter, C. N., & González Delgado, R. M. 2010, MNRAS, 403, 1317 [CrossRef] [Google Scholar]
- Runco, J. N., Malkan, M. A., Fernández-Ontiveros, J. A., Spinoglio, L., & Pereira-Santaella, M. 2020, ApJ, 905, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Rupke, D. S., Veilleux, S., & Sanders, D. B. 2005a, ApJ, 632, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Rupke, D. S., Veilleux, S., & Sanders, D. B. 2005b, ApJS, 160, 115 [Google Scholar]
- Rupke, D. S. N., & Veilleux, S. 2013, ApJ, 768, 75 [Google Scholar]
- Saito, T., Iono, D., Ueda, J., et al. 2018, MNRAS, 475, L52 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, K., Aalto, S., Combes, F., Evans, A., & Peck, A. 2014, ApJ, 797, 90 [Google Scholar]
- Salak, D., Nakai, N., Hatakeyama, T., & Miyamoto, Y. 2016, ApJ, 823, 68 [CrossRef] [Google Scholar]
- Schawinski, K., Koss, M., Berney, S., & Sartori, L. F. 2015, MNRAS, 451, 2517 [Google Scholar]
- Solomon, P. M., Downes, D., Radford, S. J. E., & Barrett, J. W. 1997, ApJ, 478, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Spoon, H. W. W., Farrah, D., Lebouteiller, V., et al. 2013, ApJ, 775, 127 [Google Scholar]
- Stan Development Team 2018, PyStan: the Python interface to Stan, Version 2.17.1.0 [Google Scholar]
- Stone, M., Veilleux, S., Meléndez, M., et al. 2016, ApJ, 826, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Stuber, S. K., Saito, T., Schinnerer, E., et al. 2021, A&A, 653, A172 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sturm, E., González-Alfonso, E., Veilleux, S., et al. 2011, ApJ, 733, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2005, Astronomical Data Analysis Software and Systems XIV, ASP Conf. Ser., 347, 29 [NASA ADS] [Google Scholar]
- Van Der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- Veilleux, S., Cecil, G., & Bland-Hawthorn, J. 2005, ARA&A, 43, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Rupke, D. S. N., Kim, D. C., et al. 2009, ApJS, 182, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Meléndez, M., Sturm, E., et al. 2013, ApJ, 776, 27 [Google Scholar]
- Veilleux, S., Maiolino, R., Bolatto, A. D., & Aalto, S. 2020, A&ARv, 28, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Venturi, G., Nardini, E., Marconi, A., et al. 2018, A&A, 619, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Véron-Cetty, M. P., & Véron, P. 2010, A&A, 518, A10 [Google Scholar]
- Walter, F., Bolatto, A. D., Leroy, A. K., et al. 2017, ApJ, 835, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Westmoquette, M. S., Clements, D. L., Bendo, G. J., & Khan, S. A. 2012, MNRAS, 424, 416 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Simulations of biconical outflows
In this section we provide some additional information about the simulations used to estimate the biases in the outflow properties measured with our method (see Sec. 4.5.2). We simulate a biconcal outflow with a half opening angle of 40°. The maximum velocity of the outflow is 750 km s−1 and the maximum outflow extension is Rout = 2 kpc. The outflow flux decreases with increasing radius (as it is expected in a scenario with constant mass outflow rate). We consider four distributions of the outflow velocity as a function of radius: 1) constant velocity, 2) velocity linearly decreasing with radius, 3) linear velocity law with an increasing velocity going from zero to vmax at a given turnover radius Rto = 0.5 × Rout, followed by a linearly decreasing trend with v(Rout) = 0 km s−1, 4) a radial velocity profile with turnover radius as in the previous case, but accounting for an initial velocity v(r = 0) = 400 km s−1. We consider four values for the inclination of the outflow with respect to our line of sight: 10°, 40°, 70°, and 90° (where an inclination i = 90° corresponds to the plane of the sky). The systemic component has a FWHM of 360 km s−1 and a flux ∼10 times the outflow flux. We measure vout, Mout and Ṁout from the total simulated profile (outflow+systemic component) considering only |v|> 300 km s−1, to mimic the method we are using with our data. Then, we measure the outflow quantities (vout,Mout and Ṁout) from the simulated outflow emission profile (without the systemic component) considering the full velocity range.
Figure A.1 shows the ratios of the outflow quantities measured with our method (|v|> 300 km s−1) and from the total outflow profile. The differences between the two methods increase with increasing outflow inclination.
 |
Fig. A.1. Ratios of the outflow properties (vout, Mout and Ṁout) measured with our method from the total profile (systemic+outflow) considering only the |v|> 300 km s−1 range and from only the outflow profile considering the full velocity range. The ratios are shown as a function of the outflow inclination with respect to our line of sight (where i = 90° is in the plane of the sky). The points are colour-coded according to outflow velocity radial distribution used in the simulation. The black lines show the one-to-one ratio. |
Appendix B: Bisector fit methodology
Here we explain in detail the methodology used for the bisector fit used in Figures 17, 18, 19, and 20. Considering two generic quantities x andy, we fit a linear relation between them using the Monte Carlo Markov-Chain (MCMC) implementation PyStan6. We assume that the noise is normal distributed. We fit for the parameter α and β that minimises the quantity:
where f(xi, α, β) = α ⋅ xi + β, yerr, i is the error on the quantity yi, σintr is the intrinsic scatter, and the sum is over the data points. The analogous expression can be defined with respect to the quantity xi and the error xerr, i:
We run the fitting algorithm to find the best parameters that minimise ϵy and ϵx, and then we perform a bisector fit. We run the algorithm for 2000 steps with 4 chains as ‘burn-in’ phase. We monitor the convergence by looking at the effective sample size (Neff), which is defined as the number of iterations divided by the integrated autocorrelation time Neff = Niter/τint. We check that the number of effective samples is > 10, which indicate that the algorithm has converged (Gelman et al. 2004).
We derive the best fit values and the corresponding 1σ uncertainties from the median and the 16th-84th percentiles, respectively, of the marginalised posterior distributions of the parameters. The intrisic scatter is obtained by adding in quadrature σintr, x and σintr, y. The lightblue shaded regions in the Figures shows the 1 σ uncertainty on the fit, obtained by sampling the posterior distribution.
Appendix C: CO outflow detection in absorption
We detect a blue-shifted absorption in the CO(2–1) spectrum of 07251-0248 E at velocities v = [ − 320, −500] km s−1 (see Fig. C.1). The absorption is compact, centred at the position of the continuum peak and nearly coincident with the position of the red-shifted outflow emission at v = [300, 550] km s−1. This absorption can be interpreted as an outflow located in front of the continuum source and moving towards us. Alternatively, it could be due to an extremely compact outflow. The redshifted part of the outflow, identified in emission, appears compact and moves away from us along a direction compatible with our line of sight.
 |
Fig. C.1. Left: CO(2–1) spectrum (with continuum) of 07251-0248 E, showing an absorption at velocities v = [ − 320, −500] km s−1. Middle: Emission of the blue- and red-shifted high-velocity channels of 07251-0248 E, shown with blue and red contours, respectively. The lowest contour corresponds to the 3σ level. The next contour levels are (0.5, 0.7, 0.9) of the peak of the emission. Dashed lines indicate negative contour levels ([-3, -4, -5, -6, -7]×σ). The dashed black circle shows the size of the outflow (Rout) and the grey cross the central position of the outflow. The black and green crosses shows the position of the continuum peaks of the E and W nuclei, respectively. Right: CO(2–1) spectrum (with continuum) of 13451+1232 W. No clear absorption is detected in this spectrum at the velocities of the an absorption detected in the CO(3–2) spectrum by Dasyra & Combes (2012) at v = [ − 700, −1200] km s−1 (see orange shaded region). |
This is the only target for which we could identify an absorption. Dasyra & Combes (2012) detected a blue-shifted absorption at −950 km s−1 in the CO(3–2) spectrum of 13451+1232 (4C+12.50), obtained with the IRAM 30m telescope. No absorption was detected in the CO(1–0) data observed with the IRAM Plateau de Bure Interferometer (PdBI) by Dasyra et al. (2014). We inspect the ALMA CO(2–1) spectrum of the west nucleus of 13451+1232 (shown in Fig. C.1), which is the nucleus dominating the FIR continuum emission and therefore, the nucleus where an absorption could be produced. We do not observe any significant absorption in the spectral channels on the blue-side of the CO(2–1) line in this target. Although, we note that the CO(3–2) absorption feature would be near the edge of the spectral window of our CO(2–1) spectrum.
Appendix D: CO(2-1) moment maps
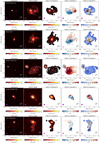 |
Fig. D.1. continued. |
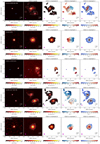 |
Fig. D.1. continued. |
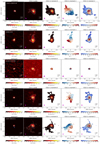 |
Fig. D.1. continued. |
 |
Fig. D.1. continued. |
Appendix E: CO(2-1) spectra and spectro-astrometry
 |
Fig. E.1. Spectro-astrometry and outflow maps for 00091-0738 S and 00091-0738 N. a) Spectro-astrometry of the CO(2-1) emission line, i.e. centroid position of the CO(2-1) emission in the different velocity channels. The points are colour-coded by the channel velocity. The dotted line is a linear fit to the low-velocity points (kinematic major axis) and the dashed line is a fit to the high-velocity points (indicating the outflow direction, if present). Panel b) and c) show the moment 1 and moment 2 maps, where the green square indicate the field of view of panel (a). The grey ellipse illustrates the ALMA beam FWHM. The grey contours on the moment 1 maps are every 50 km s−1 (every 25 km s−1 if the maximum value < 100 km s−1), and every 25 km s−1 (every 15 km s−1 if the maximum value < 150 km s−1) on the moment 2 map. In black are the CO(2-1) moment 0 contours ([3, 6, 25, 50, 75]×σ). d) Emission of the high-velocity channels(if detected), integrated over the velocity ranges indicated on the CO(2-1) spectrum (shown in panel e). Blue- and red-shifted channels are shown with blue and red contours, respectively (dashed lines indicate negative contour levels). The lowest contour corresponds to the 3σ level. The next contour levels are (0.5, 0.7, 0.9) of the peak of the emission, if these are above the 3σ level. The dashed circle shows the size of the outflow (Rout). e) CO(2-1) continuum-subtracted spectrum extracted from a circle with radius equivalent to the outflow size (Rout). The lower panel shows an y-axis zoom-in to highlight the emission in the wings. The horizontal dashed line show the 1σ noise level. The vertical dashed lines indicated the ‘flux-weighted’ velocity of the blue and red-shifted outflow (vout). f) OH 119 μm spectrum (upper, if available) compared with the nuclear CO spectrum (bottom), convolved to the resolution of the OH spectrum (FWHM∼270 km s−1). The total fit to the OH lines is shown with a magenta line, while the Gaussian components of the fit are shown in lightblue and brown. The orange lines show the 50 Monte Carlo iterations used to estimate the uncertainties on the fit (see Sec. 4.7). The vertical dotted, dashed and dot-dashed lines show the v50, v84, and v98 percentile velocities, respectively. The blue-shaded area in the upper panel shows the wavelength range between v84 and v98. |
 |
Fig. E.1. continued. |
 |
Fig. E.1. continued. |
 |
Fig. E.1. continued. |
 |
Fig. E.1. continued. |
 |
Fig. E.1. continued. |
 |
Fig. E.1. continued. |
 |
Fig. E.1. continued. |
 |
Fig. E.1. continued. |
 |
Fig. E.1. continued. |
 |
Fig. E.1. continued. |
 |
Fig. E.1. continued. |
 |
Fig. E.1. continued. |
Appendix F: Channel maps
 |
Fig. F.1. CO channel maps of 00091-0738 S showing the emission in channels of 50 km s−1 on the blue and red-shifted side with respect to the CO redshift (zCO). The lowest contour corresponds to 3×σ, where σ is the rms measured in each 50 km s−1 channel (in mJy), and the other contours correspond to 0.1, 0.2, 0.3, 0.5, 0.7, 0.9× maximum flux. Contours are shown only if they are above the 3×σ level. Dashed contours show negative -3, -4, -5 ...×σ levels. The σ values (in mJy) for the blue and red channels are indicated in the top-right corner. The dotted line shows the kinematic major axis, the dashed line shows the direction of the outflow (if present). The black cross shows the peak position of the ALMA continuum. The green cross shows the continuum position of the second nucleus in interacting systems. The CO channel maps for the rest of the sample can be found at bluehttps://doi.org/10.5281/zenodo.7022665. |
 |
Fig. F.2. 00091-0738 N. |
All Tables
Possible biases in the outflow properties measured with our method, due to different issues.
All Figures
 |
Fig. 1. Infrared luminosity (8–1000 μm) and redshift of the individual nuclei in the PUMA sample. AGN are shown in orange, while starburst (SB) dominated nuclei are in lightblue. Circles indicate interacting systems and squares indicate advanced mergers. The nuclei with log LIR/L⊙ < 12 are the fainter nuclei in interacting systems, where the IR luminosity is dominated by the other nucleus. |
| In the text | |
 |
Fig. 2. Examples of the ALMA ∼220 − 250 GHz continuum and CO(2–1) moment maps (from left to right: peak map, moment 0, 1, and 2) for a merger (20087−0308) and an interacting (10190+1322) starburst-dominated system and for a merger (01572+0009) and an interacting (12071−0444) AGN-dominated system. The blue crosses mark the position of the nuclei (see Table 1). The magenta ellipse shows the FWHM and position angle of the ALMA beam . The contours in the maps are: continuum map: [0.3, 0.4, 0.6, 0. 8, 0.9] of the maximum; peak map: 1.5 × σ (where σ is the rms) and [0.1, 0. 2, 0.4, 0.6, 0.8] of the maximum; moment 0: [3, 6, 25, 50, 75] × σ (where σ is the rms), moment 1: every 50 km s−1 (every 25 km s−1 if the maximum value < 100 km s−1), moment 2: every 25 km s−1 (every 15 km s−1 if the maximum value < 150 km s−1). |
| In the text | |
 |
Fig. 3. Example of spectro-astrometry and outflow maps for one target (20100−4156 SE) with outflow direction perpendicular to the kinematic major axis. Panel a: spectro-astrometry of the CO(2–1) emission line, i.e. centroid position of the CO(2–1) emission in the different velocity channels. The points are colour-coded by the channel velocity. The pink diamond indicates the peak ALMA millimetre continuum position. The dashed line is a linear fit to the low-velocity points (kinematic major axis) and the dotted line is a fit to the high-velocity points (indicating the outflow direction, if present). Panels b,c: moment 1 and moment 2 maps, where the green square indicate the field of view of panel a. The grey ellipse illustrates the ALMA beam FWHM. The grey contours on the moment 1 maps are every 50 km s−1 (every 25 km s−1 if the maximum value < 100 km s−1), and every 25 km s−1 (every 15 km s−1 if the maximum value < 150 km s−1) on the moment 2 map. In black are the CO(2–1) moment 0 contours ([3, 6, 25, 50, 75] × σ). Panel d: emission of the high-velocity channels, integrated over the velocity ranges indicated on the CO(2–1) spectrum (shown in panel e). Blue- and red-shifted channels are shown with blue and red contours, respectively (dashed lines indicate negative contour levels). The lowest contour corresponds to the 3σ level. The next contour levels are (0.5, 0.7, 0.9) of the peak of the emission, if these are above the 3σ level. The dashed circle shows the size of the outflow (Rout). Panel e: CO(2–1) continuum-subtracted spectrum extracted from a circle with radius equivalent to the outflow size (Rout). The lower panel shows an y-axis zoom-in to highlight the emission in the wings. The horizontal dashed line shows the 1σ noise level. The vertical dashed lines indicated the ‘flux-weighted’ velocity of the blue and red-shifted outflow (vout). Panel f: OH 119 μm spectrum (upper) compared with the nuclear CO(2–1) spectrum (bottom), convolved to the resolution of the OH spectrum (FWHM ∼ 270 km s−1). The total fit to the OH lines is shown with a magenta line, while the Gaussian components of the fit are shown in lightblue and brown. The orange lines show the 50 Monte Carlo iterations used to estimate the uncertainties on the fit (see Sect. 4.7). The vertical dotted, dashed and dot-dashed lines show the v50, v84, and v98 percentile velocities, respectively. The blue-shaded area in the upper panel shows the wavelength range between v84 and v98. Figures for the rest of the sample are in the appendix. |
| In the text | |
 |
Fig. 4. Same as Fig. 3, but for 20087-0308, a target with outflow direction not perpendicular to the kinematic major axis. |
| In the text | |
 |
Fig. 5. Absolute difference between the position angles (PAs) of the kinematic major axis derived from CO and the PAs derived from the stellar kinematics (left), and the ionised gas kinematics (right). The PAs of the stars and ionised gas are taken from Perna et al. (2022). The dashed lines show a difference of 20°. The names of galaxies with large PA differences (≫20°) are shown on the figure. The colours and shapes of the symbols are as in Fig. 1. |
| In the text | |
 |
Fig. 6. Simulated outflow profiles for outflow inclinations with respect to our line of sight of 10° (upper) and 90° (bottom). The outflow velocity in this particular simulation increases up to a turnover radius and then decreases. Up to four different velocity fields are considered in Appendix A. The magenta curve shows the outflow component, the grey curve the systemic component and the black curve the total profile. The vertical dashed lines show the flux-weighted vout measured from the total profile at |v|≥300 km s−1 (coloured in blue and red). The vertical solid lines show the flux-weighted vout measured from the outflow component over the full velocity range. For high outflow inclination (close to the plane of the sky), the contribution to the outflow flux by the gas at low projected velocities (|v|< 300 km s−1) increases. |
| In the text | |
 |
Fig. 7. Comparison of different methods for measuring the outflow velocity. Left: ratio between the maximum outflow velocity vmax, FWHM (Eq. (8)) and the flux-weighted outflow velocity (vout) in our sample. Right: ratio between vmax, FW10% (Eq. (9)) and vout. The horizontal lines show the 1-to-1 ratio. |
| In the text | |
 |
Fig. 8. Comparison of outflow parameters measured in this work with values reported in Lutz et al. (2020). From left to right: outflow velocity, outflow radius, outflow mass and mass outflow rate. The dashed line marks the ratio of 1. Even though there are differences in outflow velocities and radii, the mass outflow rates agree within a factor of 3. |
| In the text | |
 |
Fig. 9. Comparison of outflow parameters measured in this work with values reported in Fluetsch et al. (2019). From left to right: outflow velocity, outflow radius, outflow mass and mass outflow rate. Differences in Mout and Ṁout can be up to a factor of 16. |
| In the text | |
 |
Fig. 10. Comparison of the outflow mass and mass outflow rate as a function of IR luminosity for our sample and the sample from Fluetsch et al. (2019, purple triangles). The red symbols show the average values (considering only the detections) in bins of log LIR for the Fluetsch et al. (2019) sample (triangles) and the PUMA sample (circles). The sources in common between the two samples are highlighted with black contours. Due to the different methods, the Mout and Ṁout values estimated by Fluetsch et al. (2019) are higher by a factor of ×5 − 8 compared with our measurements at the same infrared luminosity. |
| In the text | |
 |
Fig. 11. Example of the fit of the OH 119 μm doublet with absorption (upper), emission (middle) and P-Cygni (bottom) profile. The velocity is relative to the blue component of the doublet (at 119.233 μm) at the systemic velocity inferred from the CO(2–1) line. The best-fit model is shown in magenta, while the orange models are the results of the 50 Monte Carlo realisations that illustrate the uncertainty of the fit. Solid lines show the model convolved with the instrumental resolution, while dashed lines indicate the intrinsic (deconvolved) model. Blue and red mark the two components of the fit. The vertical dotted, dashed and dot-dashed lines show the v50, v84 and v98 percentile velocities, respectively, derived from the absorption (blue) and/or emission (red) profiles. Grey dashed lines at ∼2000 km s−1 show the position of the 18OH 120 μm doublet and the CH+(3-2) absorption line. |
| In the text | |
 |
Fig. 12. Outflow detection statistics for different categories: AGN, starburst (SB), mergers (M, dnuclei < 1 kpc), interacting systems (I, dnuclei > 1 kpc), and mixed categories (mergers AGN, mergers SB, interacting AGN, interacting SB). Upper panel: fraction of individual galaxy nuclei in each category with respect to the total sample. The scale on the right axis shows the number of objects. Middle panel: outflow detections fractions. The percentages have been calculated with respect to the total number of nuclei in each category. Lower panel: outflow orientation statistics divided in three groups: outflow projected orientation perpendicular to the kinematic major axis of the disk (angle 90 ± 20°), outflow projected orientation non-perpendicular, or orientation could not be determined. The percentages have been calculated with respect to the number of outflow detection in each category. Error bars in middle and lower panel show the 90% binomial confidence interval. |
| In the text | |
 |
Fig. 13. Cumulative distribution function (CDF) of the outflow properties of AGN and starbursts (SB, top) and mergers (M) and interacting (I, bottom). The solid lines show the CDFs for the outflow detections only, while the dashed lines show the CDFs including upper limits (only for Mout, Ṁout and η). The shaded area mark the area between the CDFs with and without upper limits. The square symbols show the average values for the outflow detections in the two categories, the points with arrows show the upper limits (with arbitrary values on the y-axis). According to a survival analysis Two Sample test, the differences between AGN and SB and between interacting and mergers, are not statistically significant. |
| In the text | |
 |
Fig. 14. Left: mean values of the ratio of Ṁout and total LIR for different categories: AGN, starbursts (SB), mergers (M), interacting (I), and the mix categories mergers AGN, mergers SB, interacting AGN and interacting SB. The errorbars show the uncertainty on the mean. The grey diamond and horizontal band shows the mean of the total sample and the corresponding uncertainty. Right: for the AGN categories, mean ratios of Ṁout and LIR, AGN. |
| In the text | |
 |
Fig. 15. Mass-loading factor (η = Ṁout/SFR) versus AGN fraction (αAGN). Star symbols show the Cicone et al. (2014) sample (scaled down by a factor of three to match our outflow geometry definition). Symbols for the PUMA sample are as in Fig. 1. |
| In the text | |
 |
Fig. 16. Mass outflow rate versus AGN luminosity. Diamonds symbols show the sample from Cicone et al. (2014), for which Ṁout have been scaled down by a factor of three to match our outflow geometry definition. The sample of Ramos Almeida et al. (2022) is shown with triangles. Horizontal lines for the Ramos Almeida et al. (2022) sample indicate the position that they would occupy if we were to use the LAGN derived from SED fitting from Jarvis et al. (2019), instead of the one derived from the [O III] luminosity (see Ramos Almeida et al. 2022, for details). The Lutz et al. (2020) sample is shown with red pentagons. For the Stuber et al. (2021) sample (stars), the AGN luminosities have been derived from the 14–195 keV X-ray luminosity. Symbols for the PUMA sample are as in Fig. 1. The dashed and dotted lines show the relations presented by Cicone et al. (2014) and by Fiore et al. (2017), respectively, scaled down by a factor of three to match our outflow geometry definition. |
| In the text | |
 |
Fig. 17. Mass outflow rate (left), outflow momentum rate (middle), and outflow kinetic luminosity (right) as a function of SFR. Lightblue and orange symbols indicate SB- and AGN-dominated nuclei, respectively. Circles indicate interacting systems and squares indicate mergers from the PUMA sample (including nuclei with log LIR/L⊙ < 11.8). Stars show the PHANGS-ALMA targets from Stuber et al. (2021). A representative errorbar is shown on the lower right. Left panel: the black dotted-dashed lines show lines of constant mass-loading factors (η = Ṁout/SFR) of 0.1, 1 and 10. Middle panel: the dashed line indicates the total momentum injected by SNe as a function of SFR. The dotted line shows the LSFR/c ratio, where LSFR is the IR luminosity for a given SFR derived using the Kennicutt & Evans (2012) relation. Right panel: the lines show the 1%, 10% and 100% of the energy produced by SNe. The lightblue lines in the three panels are the best linear fit to the data, with the shaded area indicating the 1σ uncertainty. |
| In the text | |
 |
Fig. 18. Mass-loading factor versus outflow velocity for our sample (circles and square symbols) and the PHANGS-ALMA sample (stars). The lightblue line is the best linear bisector fit to the data and the shaded areas indicates the 1σ uncertainty on the fit with and without including the intrinsic scatter term (lighter and darker colour, respectively). The blue dashed line shows the predictions for a energy-driven outflow (α = −2) and the red dotted-dashed line for a momentum-driven outflow (α = −1). |
| In the text | |
 |
Fig. 19. Outflow velocity versus star-formation rate for our sample and the PHANGS-ALMA sample. The lightblue line is the best linear fit to the data (slope: 0.25 ± 0.01); the 1σ uncertainties on the fit (with and without including the intrinsic scatter term) are indicated with shaded areas (lighter and darker colour, respectively). Symbols as in Fig. 17. |
| In the text | |
 |
Fig. 20. Outflow mass divided by outflow radius (Mout/Rout) versus outflow velocity. The lightblue line is the best linear fit to the data (slope = 2.61 ± 0.25). The shaded area indicates the 1σ uncertainty with and without including the intrinsic scatter term (lighter and darker colour, respectively). The blue dashed line shows the predictions for a energy-driven outflow (α = −2) and the red dotted-dashed line for a momentum-driven outflow (α = −1). Symbols as in Fig. 17. |
| In the text | |
 |
Fig. 21. Comparison of the OH 119 μm and CO(2–1) line profile. The CO(2–1) spectrum is extracted from a nuclear region corresponding to the ALMA beam size and is convolved to the resolution of the OH spectrum (FWHM ∼ 270 km s−1). We identified four different cases: (i) OH absorption reaching high velocity (|v|> 1000 km s−1), but no CO blue-shifted emission (00188−0856); (ii) CO outflow, but no sign of OH outflow (22491−1808); (iii) outflow detected in both OH and CO, but OH outflow maximum velocity (v98) larger than CO outflow maximum velocity (20100−4156); (iv) OH outflow maximum velocity (v98) smaller than CO outflow maximum velocity (15327+2340). |
| In the text | |
 |
Fig. 22. Comparison of the outflow velocities of OH and CO. Upper row: v98 derived from the OH absorption profile compared with the mean (vout(b), left) and maximum (vmax(b), right) velocities of the CO blue-shifted wing. The background colours highlight the three regions described in Sect. 5.4: (i) targets with v98 similar to vmax(b), (ii) targets with v98 > vmax(b), and (iii) targets v84 < vmax(b). Lower row: v98 derived from the OH emission profile compared with the mean (vout(r), left) and maximum (vmax(r), right) velocities of the CO red-shifted wing. The blue lines mark the outflow detection threshold of |v|> 300 km s−1. Black circles mark targets classified as compact obscured nuclei (CONs). Colour-code as in Fig. 1. |
| In the text | |
 |
Fig. 23. Comparison of the difference between the outflow velocities of OH (v98) and CO (vmax) with the CO outflow radius Rout (left) and the AGN fraction αAGN (right). Black circles mark targets classified as compact obscured nuclei (CONs). Colour-code as in Fig. 1. |
| In the text | |
 |
Fig. A.1. Ratios of the outflow properties (vout, Mout and Ṁout) measured with our method from the total profile (systemic+outflow) considering only the |v|> 300 km s−1 range and from only the outflow profile considering the full velocity range. The ratios are shown as a function of the outflow inclination with respect to our line of sight (where i = 90° is in the plane of the sky). The points are colour-coded according to outflow velocity radial distribution used in the simulation. The black lines show the one-to-one ratio. |
| In the text | |
 |
Fig. C.1. Left: CO(2–1) spectrum (with continuum) of 07251-0248 E, showing an absorption at velocities v = [ − 320, −500] km s−1. Middle: Emission of the blue- and red-shifted high-velocity channels of 07251-0248 E, shown with blue and red contours, respectively. The lowest contour corresponds to the 3σ level. The next contour levels are (0.5, 0.7, 0.9) of the peak of the emission. Dashed lines indicate negative contour levels ([-3, -4, -5, -6, -7]×σ). The dashed black circle shows the size of the outflow (Rout) and the grey cross the central position of the outflow. The black and green crosses shows the position of the continuum peaks of the E and W nuclei, respectively. Right: CO(2–1) spectrum (with continuum) of 13451+1232 W. No clear absorption is detected in this spectrum at the velocities of the an absorption detected in the CO(3–2) spectrum by Dasyra & Combes (2012) at v = [ − 700, −1200] km s−1 (see orange shaded region). |
| In the text | |
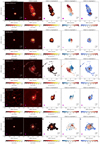 |
Fig. D.1. See caption of Figure 2 |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
 |
Fig. E.1. Spectro-astrometry and outflow maps for 00091-0738 S and 00091-0738 N. a) Spectro-astrometry of the CO(2-1) emission line, i.e. centroid position of the CO(2-1) emission in the different velocity channels. The points are colour-coded by the channel velocity. The dotted line is a linear fit to the low-velocity points (kinematic major axis) and the dashed line is a fit to the high-velocity points (indicating the outflow direction, if present). Panel b) and c) show the moment 1 and moment 2 maps, where the green square indicate the field of view of panel (a). The grey ellipse illustrates the ALMA beam FWHM. The grey contours on the moment 1 maps are every 50 km s−1 (every 25 km s−1 if the maximum value < 100 km s−1), and every 25 km s−1 (every 15 km s−1 if the maximum value < 150 km s−1) on the moment 2 map. In black are the CO(2-1) moment 0 contours ([3, 6, 25, 50, 75]×σ). d) Emission of the high-velocity channels(if detected), integrated over the velocity ranges indicated on the CO(2-1) spectrum (shown in panel e). Blue- and red-shifted channels are shown with blue and red contours, respectively (dashed lines indicate negative contour levels). The lowest contour corresponds to the 3σ level. The next contour levels are (0.5, 0.7, 0.9) of the peak of the emission, if these are above the 3σ level. The dashed circle shows the size of the outflow (Rout). e) CO(2-1) continuum-subtracted spectrum extracted from a circle with radius equivalent to the outflow size (Rout). The lower panel shows an y-axis zoom-in to highlight the emission in the wings. The horizontal dashed line show the 1σ noise level. The vertical dashed lines indicated the ‘flux-weighted’ velocity of the blue and red-shifted outflow (vout). f) OH 119 μm spectrum (upper, if available) compared with the nuclear CO spectrum (bottom), convolved to the resolution of the OH spectrum (FWHM∼270 km s−1). The total fit to the OH lines is shown with a magenta line, while the Gaussian components of the fit are shown in lightblue and brown. The orange lines show the 50 Monte Carlo iterations used to estimate the uncertainties on the fit (see Sec. 4.7). The vertical dotted, dashed and dot-dashed lines show the v50, v84, and v98 percentile velocities, respectively. The blue-shaded area in the upper panel shows the wavelength range between v84 and v98. |
| In the text | |
 |
Fig. E.1. continued. |
| In the text | |
 |
Fig. E.1. continued. |
| In the text | |
 |
Fig. E.1. continued. |
| In the text | |
 |
Fig. E.1. continued. |
| In the text | |
 |
Fig. E.1. continued. |
| In the text | |
 |
Fig. E.1. continued. |
| In the text | |
 |
Fig. E.1. continued. |
| In the text | |
 |
Fig. E.1. continued. |
| In the text | |
 |
Fig. E.1. continued. |
| In the text | |
 |
Fig. E.1. continued. |
| In the text | |
 |
Fig. E.1. continued. |
| In the text | |
 |
Fig. E.1. continued. |
| In the text | |
 |
Fig. F.1. CO channel maps of 00091-0738 S showing the emission in channels of 50 km s−1 on the blue and red-shifted side with respect to the CO redshift (zCO). The lowest contour corresponds to 3×σ, where σ is the rms measured in each 50 km s−1 channel (in mJy), and the other contours correspond to 0.1, 0.2, 0.3, 0.5, 0.7, 0.9× maximum flux. Contours are shown only if they are above the 3×σ level. Dashed contours show negative -3, -4, -5 ...×σ levels. The σ values (in mJy) for the blue and red channels are indicated in the top-right corner. The dotted line shows the kinematic major axis, the dashed line shows the direction of the outflow (if present). The black cross shows the peak position of the ALMA continuum. The green cross shows the continuum position of the second nucleus in interacting systems. The CO channel maps for the rest of the sample can be found at bluehttps://doi.org/10.5281/zenodo.7022665. |
| In the text | |
 |
Fig. F.2. 00091-0738 N. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



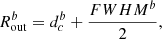
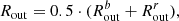
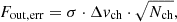
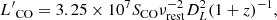
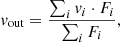
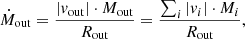
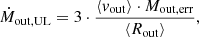
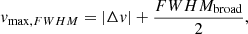
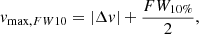
![$$ \begin{aligned} \log L_{\rm out}\, \text{[erg} \text{ s}^{-1}] = (39.4\pm 0.08)+(1.3\pm 0.05) \log \mathrm{SFR}\, [{M}_{\odot }\, \mathrm{yr}^{-1}]. \end{aligned} $$](/articles/aa/full_html/2022/12/aa44054-22/aa44054-22-eq19.gif)