| Issue |
A&A
Volume 667, November 2022
|
|
|---|---|---|
| Article Number | A156 | |
| Number of page(s) | 27 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202243888 | |
| Published online | 22 November 2022 | |
CONCERTO: High-fidelity simulation of millimeter line emissions of galaxies and [CII] intensity mapping
1
Aix-Marseille Univ., CNRS, CNES, LAM, Marseille, France
e-mail: matthieu.bethermin@lam.fr
2
Université de Strasbourg, CNRS, Observatoire astronomique de Strasbourg, UMR 7550, 67000 Strasbourg, France
3
Núcleo de Astronomía, Facultad de Ingeniería y Ciencias, Universidad Diego Portales, Av. Ejército 441, Santiago, Chile
4
Univ. Grenoble Alpes, CNRS, Grenoble INP, Institut Néel, 38000 Grenoble, France
5
Groupement d’Intérêt Scientifique KID, 38000 Grenoble and 38400 Saint-Martin-d’Hères, France
6
Univ. Grenoble Alpes, CNRS, LPSC/IN2P3, 38000 Grenoble, France
7
European Southern Observatory, Karl Schwarzschild Straße 2, 85748 Garching, Germany
8
Univ. Grenoble Alpes, CNRS, IPAG, 38400 Saint-Martin-d’Hères, France
9
Scuola Normale Superiore, Piazza dei Cavalieri 7, 56126 Pisa, Italy
10
Chalmers University of Technology, Department of Space, Earth and Environment, Onsala Space Observatory, 43992 Onsala, Sweden
11
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
12
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
Received:
27
April
2022
Accepted:
9
August
2022
The intensity mapping of the [CII] 158-μm line redshifted to the submillimeter window is a promising probe of the z > 4 star formation and its spatial distribution into large-scale structures. To prepare the first-generation experiments (e.g., CONCERTO), we need realistic simulations of the submillimeter extragalactic sky in spectroscopy. We present a new version of the simulated infrared dusty extragalactic sky (SIDES) model including the main submillimeter lines around 1 mm (CO, [CII], [CI]). This approach successfully reproduces the observed line luminosity functions. We then use our simulation to generate CONCERTO-like cubes (125–305 GHz) and forecast the power spectra of the fluctuations caused by the various astrophysical components at those frequencies. Depending on our assumptions on the relation between the star formation rate and [CII] luminosity, and the star formation history, our predictions of the z ∼ 6 [CII] power spectrum vary by two orders of magnitude. This highlights how uncertain the predictions are and how important future measurements will be to improve our understanding of this early epoch. SIDES can reproduce the CO shot noise recently measured at ∼100 GHz by the millimeter-wavelength intensity mapping experiment (mmIME). Finally, we compare the contribution of the different astrophysical components at various redshifts to the power spectra. The continuum is by far the brightest, by a factor of three to 100, depending on the frequency. At 300 GHz, the CO foreground power spectrum is higher than the [CII] one for our base scenario. At lower frequencies, the contrast between [CII] and extragalactic foregrounds is even worse. Masking the known galaxies from deep surveys should allow us to reduce the foregrounds to 20% of the [CII] power spectrum up to z ∼ 6.5. However, this masking method will not be sufficient at higher redshifts. The code and the products of our simulation are released publicly, and can be used for both intensity mapping experiments and submillimeter continuum and line surveys.
Key words: cosmic background radiation / galaxies: ISM / galaxies: star formation / galaxies: high-redshift / large-scale structure of Universe
© M. Béthermin et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Our understanding of star formation history in the Universe has dramatically evolved during the last two decades (see Madau & Dickinson 2014 for a review). We now have access to the rest-frame UV light from young massive stars escaping galaxies up to z ∼ 10 (e.g., Schenker et al. 2013; Bouwens et al. 2015; Ishigaki et al. 2018) and to the UV energy absorbed by dust and reprocessed into the far-infrared up to z ∼ 7 (e.g., Gruppioni et al. 2020; Khusanova et al. 2021; Fudamoto et al. 2021; Zavala et al. 2021; Wang et al. 2021), even if there are still significant discrepancies between authors’ findings in the far-infrared (see Sect. 2.7). The combination of these two pieces of information allows us to reconstruct the full evolution of the star formation rate density (SFRD), namely the total mass of stars formed per time unit in a comoving volume of Universe over about 13 Gyr.
In contrast, we know much less about the spatial distribution of star formation in large-scale structures at z ≳ 2. Most studies use the stellar mass function and abundance matching (sometimes combined with clustering measurements) to measure the relation between stellar mass and halo mass (e.g., Behroozi et al. 2013, 2019; Moster et al. 2013, 2018; McCracken et al. 2015; Cowley et al. 2018; Legrand et al. 2019). These studies showed that star formation is most efficient in dark-matter halos of ∼1012 M⊙. However, this only provides information about the integrated star formation history of the halo. The link between the star formation rate (SFR) and the halo mass has been less extensively analyzed and the works are mostly focused on z ∼ 2 (e.g., Magliocchetti et al. 2011; Lin et al. 2012; Béthermin et al. 2012, 2014; Wang et al. 2013; Ishikawa et al. 2016). These studies are usually based on the angular clustering of galaxies selected in the optical and/or the far-infrared regimes. At higher redshifts, the studies are limited to the clustering of Lyman break galaxies (e.g., Kashikawa et al. 2006; Lee et al. 2009; Ishikawa et al. 2017), which are biased toward unobscured star formation. Measurements of dusty galaxies selected in the submillimeter domain remain difficult because of the small samples and the large beam (> 10″) of single-dish instruments (Cowley et al. 2017; Wilkinson et al. 2017).
The cosmic infrared background (CIB) anisotropies (i.e., the integrated emission of dust in galaxies across cosmic times), provide an alternative probe of the spatial distribution of the SFR in the high-redshift Universe (e.g., Lagache et al. 2007; Viero et al. 2009; Planck Collaboration XVIII 2011; Planck Collaboration XXX 2014; Amblard et al. 2011). The modeling of these anisotropies at various frequencies can thus provide constraints on both the SFRD evolution and the host halos of the dust-obscured star formation (Pénin et al. 2012; Shang et al. 2012; Viero et al. 2013; Béthermin et al. 2013; Maniyar et al. 2018, 2021). However, the CIB comes from a large redshift range and significant degeneracies between redshift slices exist. Depending on the emission redshift, the observed peak of the dust emission is located at different frequencies. Consequently, lower frequencies have a higher contribution from higher redshifts. The degeneracies between redshift slices can thus be broken by modeling several frequencies simultaneoulsy. However, this becomes extremely difficult at z > 4.
These degeneracies no longer exist if we use a line emission and spectroscopy instead of the continuum and broad-band photometry. Indeed, spectroscopy naturally isolates a thin redshift slice, while the photometric signal is the sum of galaxy emissions at all redshifts. Intensity mapping experiments aim to detect the large-scale collective line emission from galaxies using wide-field spectral mapping. The [CII] line at 158 μm is one of the main cooling lines of the interstellar medium (e.g., Tielens & Hollenbach 1985; Wolfire et al. 2022). Observational studies at low redshifts (e.g., De Looze et al. 2014; Herrera-Camus et al. 2015) and high redshifts (e.g., Capak et al. 2015; Schaerer et al. 2020; Carniani et al. 2020) found a non-evolving and nearly linear empirical correlation between [CII] luminosity and the SFR. Both numerical simulations (Vallini et al. 2015; Olsen et al. 2017; Lupi & Bovino 2020; Pallottini et al. 2022) and semi-analytical models (Lagache et al. 2018; Popping et al. 2019; Yang et al. 2021) predict a weakly evolving relation with redshift. The [CII] line is thus a suitable tracer of high-z star formation at large scales. Several intensity mapping experiments (see Kovetz et al. 2017 for a review) aim to probe the [CII] emission from z > 4 galaxies redshifted in the submillimeter domain: the Carbon [CII] line in post-reionization and reionization epoch project (CONCERTO, Concerto & Ade 2020), the instrumentation for the tomographic ionized-carbon intensity mapping experiment (TIME, Crites et al. 2014), and the Fred Young submillimeter telescope (FYST, formerly CCAT-prime, Stacey et al. 2018). Since they aim to target large scales, these experiments are all installed on single-dish telescopes with a limited angular resolution (≳20″) but a large field of view (≳10′), and have an intermediate spectral resolution (R ≳ 100).
The interpretation of this new type of data brings new challenges, such as characterizing the transfer function from the astrophysical signal to the data cubes through the instrument and the analysis pipeline, and separating the [CII] line from other astrophysical components, such as the dust continuum or lower-z CO lines (e.g., Sun et al. 2018; Cheng et al. 2020). To prepare our analysis pipelines, we need realistic simulations of the submillimeter extragalactic sky in spectroscopy. Predictions from hydrodynamical simulations are limited to small volumes (Pallottini et al. 2015; Hernandez-Monteagudo et al. 2017), and thus the current forecasts are thus based either on analytical approaches, based in turn on halo occupation distribution models (Gong et al. 2012; Yue & Ferrara 2019; Yang et al. 2022), or empirical recipes to predict the [CII] emission of galaxies hosted by dark-matter halo simulations (Silva et al. 2015; Yue et al. 2015; Chung et al. 2020). There are huge differences between these models. For instance, there are more than two orders of magnitude between the amplitudes of the [CII] power spectrum at z ∼ 6 predicted by the various models (see Sect. 4). It is crucial to use the latest measurements of these empirical relations in order to obtain reliable forecasts.
In this paper, we present a new simulation dedicated to submillimeter intensity mapping, which was calibrated and tested using the latest observational data from (sub)millimeter observatories, such as the Atacama Large Millimeter/submillimeter Array (ALMA) and the NOrthern Extended Millimeter Array (NOEMA). This simulation is an extension of the simulated infrared dusty extragalactic sky (SIDES) model, which starts from dark-matter halo light cones and uses an empirical prescription to accurately reproduce a large set of mid-infrared to millimeter statistical properties of galaxies in continuum as number counts, redshift distribution, pixel histograms, or power spectra (Béthermin et al. 2017). The [CII] line and its two main lower-z contaminants (CO and [CI]) are included using new empirically based recipes. The codes and products of this new simulation are publicly available1 and can be used to prepare or interpret intensity mapping experiments, deep spectral scans with interferometers, or photometric surveys.
In Sect. 2 we describe the new version of the SIDES simulation and, in particular, the implementation of the emission lines in the model. We then compare our results with the latest constraints from deep (sub)millimeter spectroscopic surveys in Sect. 3. In Sect. 4 we compare the intensity-mapping forecasts of our simulations with other models. Finally, we discuss the contribution of the various astrophysical components ([CII], dust, continuum, CO, and [CI]) to the intensity mapping signal as a function of frequency and the effect of the masking of known galaxies in Sect. 5. We assume a Planck Collaboration XIII (2016) cosmology and a Chabrier (2003) initial mass function (IMF) throughout the paper.
2. Modeling of the lines in SIDES
The intensity mapping simulations presented in this paper are based on SIDES, presented in Béthermin et al. (2017, see Sect. 2.1 for a short description). This new version of the simulation now includes the main high-redshift lines observed in the millimeter domain: CO, [CII], and [CI] (see Sects. 2.3–2.5, respectively). In addition, the new version of the code contains a spectral cube generator, described in Sect. 2.6. Contrary to the 2017 version, which was coded in IDL, the new pySIDES code is entirely written in Python and is publicly available2 (see Appendix A).
2.1. The SIDES simulation
The SIDES simulation is based on the Bolshoi-Planck simulation (Rodríguez-Puebla et al. 2016), from which a light cone of 1.4 × 1.4 deg2 was produced. For each halo and sub-halo, we generated a stellar mass using an abundance matching technique tuned to reproduce observed stellar mass functions (e.g., Ilbert et al. 2013; Davidzon et al. 2017; Grazian et al. 2015). We then randomly split this sample into star-forming and passive galaxies, with a probability depending on their redshift and stellar mass.
For the star-forming population, we generated SFRs by distributing galaxies on the so-called main sequence of star-forming galaxies, following the observational constraints of Schreiber et al. (2015). A small fraction of this population (3% at z > 1) are located on the starburst sequence and exhibit an SFR excess. We then derived dust continuum properties using the evolving main-sequence and starburst observed spectral energy distribution (SED) up to z = 4 from Béthermin et al. (2017). As shown in Béthermin et al. (2020), these SEDs are also compatible with the most recent measurements between z = 4 and z = 6.
All the details are provided in Béthermin et al. (2017). This model is compatible with the observed continuum number counts from the mid-infrared to the millimeter domain after taking into account the angular resolution effects, the source redshift distribution, and the pixel histograms and power spectra of the Herschel maps. The results presented in this paper are based on a new Python implementation called pySIDES using a pandas data structure (pandas development team 2020) for the catalogs. We carefully verified that the results are fully compatible with the Béthermin et al. (2017) version based on an IDL code by comparing the stellar masses, SFR, and continuum flux distributions in a large set of redshift slices.
2.2. Philosophy of this extension of SIDES
To prepare the data analysis and the interpretation of future submillimeter intensity mapping experiments, we need simulations with galaxy properties as accurate as possible. Semi-analytical models (e.g., Lagache et al. 2018; Popping et al. 2019; Yang et al. 2021) can produce physically motivated forecasts, but they are usually limited in volume and can be expensive in terms of computing time. Simpler approaches use relations between the halo masses and the line intensity. The intensity mapping signal is then derived by either applying such relations to dark-matter simulations (e.g. Yue et al. 2015; Chung et al. 2020) or deriving the expected signal analytically using halo occupation distribution models (e.g., Yue & Ferrara 2019; Yang et al. 2022). These approaches allow us to rapidly process large-volume dark matter simulations, but the galaxy properties are usually simplified. For instance, they have the same continuum SEDs or fixed CO line ratios for all galaxies, or there is no scatter in the relations used to generate the galaxy properties.
Our new SIDES simulation aims to propose an intermediate solution between these two approaches, as it produces realistic galaxy properties and can be very efficiently applied to large dark-matter light cones. It will also model both the [CII] emission and its foregrounds (continuum, CO, and [CI]) in a consistent manner at all redshifts. At its core the model is semiempirical, meaning it is more physically motivated than a completely empirical model and it accurately describes the various galaxy properties that are relevant for intensity mapping. The previous version of the model produces continuum properties with a scatter in dust temperature and for the relation between stellar mass and the SFR, together with different SEDs, depending on the type of galaxy. All of these recipes evolve with redshift.
In this new version of SIDES, we implemented the lines following the same philosophy. We focused on the three main lines relevant for submillimeter intensity mapping: [CII], CO, and [CI]. For [CII] we used two different empirical relations to test how our results depend on it. For CO we used spectral line energy distribution (SLED) templates, which are linked to the intensity of the UV radiation field that is used to derive the dust continuum. This allowed us to have diverse CO line ratios and an overall evolution with redshift. This feature is particularly important in order to test component separation methods (e.g., Cheng et al. 2016, 2020; Sun et al. 2018), whose formalism assumes implicitly fixed line ratios. For [CI], we had fewer constraints and we propose new empirical recipes based on a recent observational compilation.
The new SIDES code is modular and can be easily modified to include new observational results. The version presented in this paper is a compromise between simplicity and being realistic. It was not fine-tuned, since the observational constraints were well reproduced overall on the first try. Since the code is public, documented, and modular, different methods can easily be implemented by other users, based on their preferences and access to new observational data. The code has been optimized to be able to produce a catalog or data cube on a laptop in a few tens of minutes, which is ideal for performing tests and exploring the impact of the various parameters.
2.3. [CII] emission
The [CII] line at 158 μm (1900.54 GHz) is one of the brightest lines emitted by galaxies and is shifted to the millimeter domain for high-z galaxies. CONCERTO will be sensitive to [CII] at z > 5.2. Before ALMA, there were very few constraints on [CII] at these early times, but important results were obtained in recent years. Initially, the [CII] detection rate of high-redshift targets was low (e.g., Ouchi et al. 2013; Ota et al. 2014; Maiolino et al. 2015; Willott et al. 2015) and theoretical explanations were proposed to explain this [CII] deficit. For instance, Vallini et al. (2015) suggested that it could be due to extremely low metallicities, while Katz et al. (2017) pointed out the high ionized gas filling factors as a possible explanation. However, using a small sample, Capak et al. (2015) showed that 5 < z < 6 galaxies still follow the L[CII]-SFR relation observed in the local Universe (HII/starburst relation from De Looze et al. 2014, hereafter DL14):
This result was confirmed by the ALPINE large program (Le Fèvre et al. 2020; Béthermin et al. 2020; Faisst et al. 2020), which targeted 118 normal galaxies at 4.4 < z < 5.9, and Schaerer et al. (2020) confirmed that the DL14 relation remains valid at high-redshifts. Carniani et al. (2020) found a similar result after reanalyzing archival data and correcting for the flux loss caused by the excessively extended configuration used in the early observations. We thus used the DL14 relation (Eq. (1)) to derive [CII] luminosities from the SFR in the SIDES simulation.
As pointed out by Ferrara et al. (2019), massive high-redshift galaxies correspond to much higher [CII] surface brightness regimes than the initial low-redshift DL14 observations and it is almost surprising that this relation remains valid under these physical conditions. While numerical simulations (Arata et al. 2020; Pallottini et al. 2019, 2022) predict that the local relation is respected also for M⋆ < 109 M⊙ galaxies, we currently have no strong observational support for this and we cannot guarantee that a [CII]-deficit does not appear at low mass (M⋆ < 109.5 M⊙) or at higher redshifts (z > 6), where the metallicity is expected to be much lower. To test this scenario, we also implemented the Lagache et al. (2018, hereafter L18) relation, predicted by a semi-analytical model, which produces a lower [CII] luminosity at higher redshifts and lower SFRs:
This relation predicts a lower [CII] luminosity at higher redshifts caused by the high intensity of the radiation field and the cosmic microwave background (CMB) effect (e.g., da Cunha et al. 2013).
We do not expect all the galaxies to exactly follow these relations. In the local Universe, DL14 measured a scatter of 0.27 dex, while Schaerer et al. (2020) found 0.28 dex after correcting SFR estimates from dust attenuation using Fudamoto et al. (2020) IRX-β corrections. However, the intrinsic scatter on the observed L[CII]-SFR relation is difficult to estimate observationally because of the uncertainties on the SFR estimators. The SFR uncertainties are not well known at high redshifts, but they are usually estimated to be around 0.2 dex. If we combine this 0.2 dex scatter quadratically with another 0.2 dex scatter, we obtain 0.28 dex, which is compatible with the observed scatter. We thus assume an intrinsic scatter of 0.2 dex to generate [CII] luminosities from the SFR in our simulation.
Finally, the line flux in Jy km s−1 (I[CII]) is then derived from the L[CII] using the standard formula provided in Carilli & Walter (2013) – see also Solomon et al. (1997) and Solomon & Vanden Bout (2005):
where μ is the lensing magnification provided by SIDES, DL is the luminosity distance in Mpc, and νobs is the observed frequency in GHz. The same formula is also used to convert L[CI] into I[CI] in Sect. 2.5.
2.4. CO emission
The CO rotational transitions result in emissions at frequencies that are multiples of 115.27 GHz, and they dominate the rest-frame millimeter spectra of star-forming galaxies. This molecule is the most popular tracer of molecular gas (e.g., Solomon & Vanden Bout 2005; Carilli & Walter 2013). The evolution of galaxy CO emissions from the local to the high-redshift Universe has been widely explored (e.g., Magdis et al. 2012; Tacconi et al. 2013, 2020; Saintonge et al. 2013; Daddi et al. 2015; Dessauges-Zavadsky et al. 2015; Genzel et al. 2015; Aravena et al. 2016b; Freundlich et al. 2019). These studies have shown that, at fixed stellar masses, galaxies at higher redshifts have higher CO luminosities, and the gas fraction is higher in high-redshift galaxies.
Main-sequence galaxies at various redshifts follow the same correlation between the luminosity of the ground transition of CO (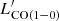 ) and the bolometric infrared luminosity (LIR, integrated between 8 and 1000 μm), which is directly proportional to the SFR in the context of our model. Here, we use the L′ pseudo luminosities expressed in K km s−1 pc2. We chose to derive
) and the bolometric infrared luminosity (LIR, integrated between 8 and 1000 μm), which is directly proportional to the SFR in the context of our model. Here, we use the L′ pseudo luminosities expressed in K km s−1 pc2. We chose to derive 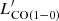 directly from LIR for simplicity. In our model, we use the relation calibrated by Sargent et al. (2014) for main-sequence galaxies:
directly from LIR for simplicity. In our model, we use the relation calibrated by Sargent et al. (2014) for main-sequence galaxies:
Similarly to [CII], we assume an intrinsic scatter of 0.2 dex, since Greve et al. (2014) measured a scatter of 0.26 dex on the 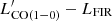 . The line flux in Jy km s−1 (ICO) is then computed from
. The line flux in Jy km s−1 (ICO) is then computed from 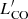 in K km s−1 pc2 using a formula similar to Eq. (3) (Carilli & Walter 2013):
in K km s−1 pc2 using a formula similar to Eq. (3) (Carilli & Walter 2013):
Starbursting systems3 do not follow this correlation. This may be caused by two phenomena: (i) starbursts have a higher SFR for a similar gas mass (e.g., Genzel et al. 2010; Daddi et al. 2010), and (ii) the conversion factor from 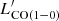 to gas mass is different in starbursts (Downes & Solomon 1998). Because of these effects, Sargent et al. (2014) found that their
to gas mass is different in starbursts (Downes & Solomon 1998). Because of these effects, Sargent et al. (2014) found that their 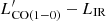 correlation lies below the main-sequence correlation, with an offset of −0.46 dex. We apply the same offset to galaxies labeled as starburst in the SIDES simulation.
correlation lies below the main-sequence correlation, with an offset of −0.46 dex. We apply the same offset to galaxies labeled as starburst in the SIDES simulation.
To produce the flux of the other transitions, we assume a SLED for each object. Both low-redshift (e.g., Rosenberg et al. 2015; Kamenetzky et al. 2016) and high-redshift objects (e.g., Yang et al. 2017; Cañameras et al. 2018; Valentino et al. 2020a; Boogaard et al. 2020) exhibit a large variety of SLEDs. Our simulation does not aim to encompass all the complexity of the gas physics in high-redshift galaxies. For main sequence galaxies, we thus use an empirical approach based on Daddi et al. (2015), who found a correlation between the CO(5–4)/CO(2–1) flux ratio and the mean intensity of the UV radiation field ⟨U⟩4:
We note that Rosenberg et al. (2015) also found a similar relation between the CO excitation and the 60-μm versus 100-μm color. In our simulation, the dust continuum SEDs are already parametrized using this ⟨U⟩ parameter, which is also linked to the dust temperature and increases with increasing redshift for main-sequence galaxies (see details in Béthermin et al. 2017). Our simulated galaxies will thus have a higher CO excitation at higher redshifts. In addition, a scatter on ⟨U⟩ of 0.2 dex is already included, and there will thus be naturally diverse SLEDs for a given galaxy type and redshift.
To generate all the transitions, we need to produce the full SLED. We use a linear combination of the clump and the diffuse templates from Bournaud et al. (2015), noted as Tclump and Tdiff, respectively, and normalize them to unity for the 1–0 transition. These templates are computed only up to the 8–7 transition. However, Decarli et al. (2020) showed that higher transitions have a negligible contribution at CONCERTO frequencies. The flux of the CO transition between the Jup and the Jup − 1 levels, ICO(Jup, Jup − 1), is computed using:
where fclump is the contribution of the clump component to the 1–0 transition. We chose fclump to obtain a CO(5–4)/CO(2–1) ratio corresponding to the Daddi et al. (2015) relation. This constraint implies that:
Because of the scatter on ⟨U⟩, some objects have extreme values for this parameter and the ICO(5 − 4)/ICO(2 − 1) ratio cannot be reproduced using a combination of these two templates with 0 < fclump < 1. For these objects, we use a pure diffuse (low ⟨U⟩) or pure clump template (high ⟨U⟩). Because of the increasing ⟨U⟩ with increasing redshift, the main-sequence galaxies at higher redshifts are more excited, which agrees with the conclusion of, for example, Daddi et al. (2015) and Boogaard et al. (2020). At z > 4, their excitation is close to the average SLED of the submillimeter galaxies (SMGs) reported in Carilli & Walter (2013) or Birkin et al. (2021).
The method described in the two previous paragraphs is mainly based on observations of main-sequence galaxies. For the starburst galaxies, we produced an alternative version of the simulation, in which we used the same mean SMG (≳3 mJy at 870 μm) SLED template of Birkin et al. (2021) for all galaxies labeled as starburst. The 8–7 transition was not provided and we assumed that it had the same flux as the 7–6 transition. We compared the two approaches and found no significant difference because of the small relative contribution of starbursts to the observables related to intensity mapping. In the rest of the paper, we use the version of the model that uses the Birkin et al. (2021) SLED.
2.5. [CI] emission
The [CI](3P1−3P0) transition at 492.16 GHz rest-frame and the [CI](3P2−3P1) transition at 809.344 GHz rest-frame (hereafter shortened to [CI](1–0) and [CI](2–1), respectively, for simplicity) are also non-negligible contributors to the millimeter sky. The [CI](2–1) transition is often as bright as its CO(7–6) neighbor at 806.65 GHz rest-frame (Valentino et al. 2020b) and can be much brighter in some objects (Gullberg et al. 2016). It can potentially contaminate the CO(7–6) signal and be a problem for CO-decontamination methods assuming a constant CO SLED. The [CI](1–0) transition is usually a factor of roughly two fainter than the CO(4–3) line (Alaghband-Zadeh et al. 2013; Bothwell et al. 2016; Valentino et al. 2020b; Bisbas et al. 2021).
For the SIDES simulation, we calibrated empirical relations using the compilation of [CI] data from Valentino et al. (2020b). After exploring various correlations, we found two reasonably tight relations (< 0.2 dex of scatter) presented in Fig. 1. In this section and contrary to Eq. (4), all luminosities are expressed in normal power units (i.e., in multiples of watts), such as solar luminosities5.
We found that the ratio between the [CI](1–0) line luminosity (L[CI](1 − 0)) and the total infrared luminosity (LIR), and the ratio between LCO(4 − 3) and LIR, are correlated with a dispersion of 0.2 dex (see Fig. 1 upper panel):
 |
Fig. 1. Empirical relations used to produce the [CI] line fluxes. Upper panel: relation between the L[CI](1 − 0)/LIR and LCO(4 − 3)/LIR ratios. The filled blue circles and the red filled squares are, respectively, the low-z and high-z galaxies compiled by Valentino et al. (2020b). The solid line is our best-fit of this correlation used to generate [CI](1–0) fluxes in our simulation. Lower panel: same figure for the relation between the L[CI](2 − 1)/L[CI](1 − 0) and LCO(7 − 6)/LCO(4 − 3) ratios. |
We used the CO(4–3) transition instead of a lower-energy one because of the larger high-z observational dataset available to calibrate our relation. For the typical range of values of LCO(4 − 3)/LIR in the Valentino et al. (2020b) study (10−6–10−4), the mean L[CI](1 − 0)/LCO(4 − 3) is in the range between 0.5 and 0.7. The slightly superlinear slope suggests that [CI](1–0) is fainter than CO(4–3) in objects with a low line-to-continuum ratio, such as starbursts or main-sequence galaxies with higher star formation efficiencies than the average. This is expected, since [CI](1–0) traces more diffuse gas than CO(4–3), and thus tends to be relatively brighter in less extreme objects. We thus generated [CI](1–0) luminosities and fluxes in our simulation using this relation and the CO(4–3) derived using the method described in Sect. 2.4. We added a 0.2 dex scatter following the observational constraints.
The ratio between the [CI](2–1) and the [CI](1–0) luminosity is directly linked to the kinematic temperature of the gas (Papadopoulos & Greve 2004). This parameter was not included in our simulation. We thus used the CO excitation as a proxy for it. Using the Valentino et al. (2020b) compilation, we found the following correlation (see Fig. 1 lower panel):
This relation has a scatter of 0.19 dex. In the simulation, we generated the [CI](2–1) luminosities from the [CI](1–0) luminosities using this relation and its scatter.
The two [CI] line fluxes in Jy km s−1 (I[CI]) were finally derived from the [CI] luminosities. To perform this computation, we used Eq. (3).
2.6. Data cubes
From the line and continuum properties produced in the simulated catalog, we built simulated CONCERTO cubes. The simulated cubes covers the frequency range between 125 GHz and 305 GHz. The width of the spectral elements is fixed to 1 GHz over the entire bandpass. We set the cube pixel size to 5 arcsec to properly sample the beam. The pySIDES cube generator can be easily adapted to produce simulated observations for other instruments from a few tens of GHz to a few THz.
We first produced the cubes associated with each line. These first cubes were not smoothed by the instrumental beam. They are used in this paper to derive the intrinsic power spectra of the simulation (see Sect. 5). We first computed the flux density associated to all the sources in a given voxel. We neglected the width of the line and placed the entire flux of a line in the spectral element, where its central observed frequency 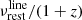 is located. The surface brightness density of a voxel
is located. The surface brightness density of a voxel 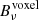 expressed in Jy/sr is then:
expressed in Jy/sr is then:
where c is the speed of light and Ωpixel is the solid angle of a pixel in steradians. Δυelement, νelement, and Δνelement are the velocity width, the central frequency, and the frequency width of the voxel, respectively6. 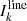 is the flux in Jy km s−1 of the kth source in the voxel. We remark that the 1/Δνelement is compensated by the number of sources in the voxel proportional to Δνelement. In practice, we first converted the spatial and spectral sky coordinates of the lines into cube coordinates using the astropy (Astropy Collaboration 2013, 2018) world coordinate system (WCS) package. We then used the histogramdd 3D histogram routine of the numpy package (Harris et al. 2020) that used the line fluxes as weights to generate the cube and normalize each of its frequency slices using Eq. (11). This operation was performed for each transition of each line.
is the flux in Jy km s−1 of the kth source in the voxel. We remark that the 1/Δνelement is compensated by the number of sources in the voxel proportional to Δνelement. In practice, we first converted the spatial and spectral sky coordinates of the lines into cube coordinates using the astropy (Astropy Collaboration 2013, 2018) world coordinate system (WCS) package. We then used the histogramdd 3D histogram routine of the numpy package (Harris et al. 2020) that used the line fluxes as weights to generate the cube and normalize each of its frequency slices using Eq. (11). This operation was performed for each transition of each line.
To produce the continuum cube, we computed the flux density of each galaxy at the central frequency of each spectral element using a parallelized code. For each frequency, we then produced a map using the histogram2d histogram routine, applying the flux density at this frequency as weight. The maps corresponding to all the frequency slices were then stacked to produce the cube. The final cube was created by summing the line cubes and the continuum cube.
We then produced cubes including the instrumental beam by convolving them by the beam. Each frequency slice was treated separately, since the beam size varies with frequency. For simplicity, we assumed Gaussian beams with a full width at half maximum (FWHM) of 1.22 λ/D, where λ is the wavelength and D is the diameter of the telescope. Since CONCERTO is installed on APEX, we use D = 12 m in this paper.
In Fig. 2, we show various frequency slices of the cubes. In the total cube, including both the lines and the continuum (top panels), the large-scale structures are not obviously visible, even if a trained eye can see that the source distribution is not Poissonian. We also remark that the slices at various frequencies are remarkably similar. This is not surprising, since these maps are dominated by the continuum and most of the sources at these frequencies are in the Rayleigh-Jean regime.
 |
Fig. 2. Slices of simulated CONCERTO data cubes. These cubes are produced using a Gaussian beam and have no instrumental noise. Each slice has a 1 GHz width. The four columns, from the left to the right, correspond to 305 GHz (z[CII] = 5.23, Δz[CII] = 0.020), 275 GHz (z[CII] = 5.91, Δz[CII] = 0.025), 245 GHz (z[CII] = 6.75, Δz[CII] = 0.032), and 215 GHz (z[CII] = 7.83, Δz[CII] = 0.041). Five rows, from top to bottom: the cubes containing all the components, including the continuum, all the lines, the CO lines only, the [CI] lines, and the [CII] line. To make comparisons easier, the color scale of the four panels with continuum (top row) is the same. All the other panels share another common color scale. We assume the DL14 [CII]-SFR relation in this figure. |
In the cube containing only the lines (second row), we start to see the filamentary structures, while they appear more clearly in the cubes containing a single species (third to fifth rows). The CO is widely distributed over the map and the [CII] emission is located in a couple of dense regions. This is expected, since star formation at high-redshifts where [CII] is emitted is more clustered than at lower redshifts where the CO comes from (e.g., Béthermin et al. 2013; Maniyar et al. 2018). We can also note that there is much less [CII] emission at lower frequencies, while CO is stronger. The power spectrum from each component and the implication for CONCERTO will be discussed in details in Sect. 5.
2.7. Alternative model with a higher star formation rate density at z > 4
The Hubble space telescope (HST) deep surveys provided constraints on the z > 4 SFRD (e.g., Bouwens et al. 2007, 2012; Schenker et al. 2013) using dust-corrected UV data. They found that the SFRD decreases with increasing redshift at z > 3. This is compatible with the predictions of the latest semi-analytical models (e.g., Lagos et al. 2020) and hydrodynamical simulations (e.g., Pillepich et al. 2018). However, the discovery of a dusty galaxy population without any counterparts seen by the Hubble space telescope (e.g., Wang et al. 2019b; Talia et al. 2021; Fudamoto et al. 2021) showed how important long-wavelength data are to obtain the full picture of star formation. Based on a combination of aggressively deblended Herschel data and modeling, Rowan-Robinson et al. (2016) claimed that SFRD is flat even above z = 3 (see also the discussion in Casey et al. 2018), but another analysis using a similar approach found results more compatible with the UV-corrected estimates (Wang et al. 2019a).
In Fig. 3 we compare the SFRD from our simulation (solid gray line) with the various observations. Below z = 4, our simulation is inside the cloud of observational points. Up to z ∼ 7, our model is compatible with the dust-corrected UV measurements. In contrast, the SFRD from SIDES is systematically lower than the recent constraints from ALPINE (Gruppioni et al. 2020; Loiacono et al. 2021; Khusanova et al. 2021) and the radio (Novak et al. 2017), but it remains compatible at the 1.5σ level. At z ∼ 7, the SFRD in SIDES is a factor of roughlt two above the estimate of the obscured SFRD from REBELS, based on their two serendipitous detections (Fudamoto et al. 2021). Considering that they applied a correction of roughly a factor of four for the clustering and that there are only two objects, this factor of two difference cannot be considered as significant.
 |
Fig. 3. Evolution of the star formation rate density. The solid gray line is derived from the SIDES simulation and the solid brown line is an alternative model at z > 4 for which we boosted the SFRs to obtain a flat SFRD at high-redshifts (“high SFRD” model, see Sect. 2.7). The SFR boosting factor to obtain a flat SFRD is computed from the fit of the z > 4 original model (dotted line). The compilations of UV-derived and infrared-derived measurements by Madau & Dickinson (2014) are represented by blue crosses and filled orange circles, respectively. We also show the measurement from the ALPINE survey based on the luminosity function of serendipitous continuum detections (Gruppioni et al. 2020, red upward-pointing triangles), the [CII] luminosity function of serendipitous detection (Loiacono et al. 2021, purple downward-pointing triangles), and an indirect method using the stacking of the target sample (Khusanova et al. 2021, dark orange squares). The dark red left-pointing triangles are the estimates of the obscured SFRD from REBELS by Fudamoto et al. (2021), using the continuum (low value) and the [CII] (high value). The constraints from the radio from Novak et al. (2017) are shown using green right-pointing triangles. As discussed in Sect. 4.4, the SFRD at z > 7 could be underestimated by our simulation because of its halo mass limit, and thus a paler color is used. |
To study the impact of an extreme scenario with a flat SFRD at z > 4, we produced a version of the SIDES model with a flat SFRD by multiplying all the SFRs in the SIDES simulation by a factor, CSFR, varying with redshift. To compute this factor, we fitted the decimal logarithm of the SIDES SFRD versus z by a fourth-order polynomial, considering only the z > 4 points (dotted line in Fig. 3) and obtained the following correction:
This version of the simulation is compatible with the ALPINE and radio data, but is one order of magnitude higher than the UV constraints at z = 7. Using this model with the DL14 relation, we can thus derive an optimistic upper limit on our intensity mapping predictions, hereafter called the “high SFRD” model.
3. Comparison with observations from deep surveys
In order to validate our model, we checked if we reproduce basic statistical observables. In this section, we discuss the line versus dust luminosities (Sect. 3.1), the line luminosity functions (Sects. 3.2–3.5), and the measured average line ratios (Sect. 3.3).
3.1. Relation between the CO luminosity and the infrared luminosity
The relation between the dust luminosity and the CO luminosity of the various transitions is one of the most basic tests to check the reliability of the model. In the literature, the total infrared luminosity between 8 and 1000 μm (LIR) is rarely used, and instead authors prefer the far-infrared luminosity LFIR. Using our SED templates, we precomputed the ratio between LIR and LFIR for the various values of ⟨U⟩. The wavelength range integrated to derive LFIR varies marginally depending on the authors and we chose to use 40–400 μm in this paper.
In Fig. 4, we compare the relations found in SIDES and from the literature. We obviously expect to recover the relation between the CO(1–0) and the far-infrared luminosities, since we used it to build our model. In contrast, the other transitions are produced from SLED templates and comparing our results with the observations allows us to test our model. There is an overall excellent agreement between the results of Kamenetzky et al. (2016) and Liu et al. (2015), based on Herschel observations of low-z galaxies. However, for the 4–3 and 5–4 transitions, the center of the SIDES relation is a factor of approximately two below the observed relation at low CO luminosity (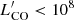 K km s−1 pc2), although still in the scatter. At these luminosities, observational constraints come only from the local Universe. If we consider only the z < 0.2 objects in SIDES, the results agree with the observed relations (see Appendix B). Thus, there might be a small selection bias, but the nature of these data compilations do not produce a clear selection function that can be applied to our simulation. Contrary to the two previous studies, Greve et al. (2014) used mainly local (ultra)luminous infrared galaxies ((U)LIRGs) and high-z dusty star-forming galaxies, including lensed ones. The SIDES simulation agrees overall with their relation probing higher luminosities. However, they found a much flatter slope for the 8–7 transition. In this case, the difference could be due to the low number of objects used in the study of Greve et al. (2014).
K km s−1 pc2), although still in the scatter. At these luminosities, observational constraints come only from the local Universe. If we consider only the z < 0.2 objects in SIDES, the results agree with the observed relations (see Appendix B). Thus, there might be a small selection bias, but the nature of these data compilations do not produce a clear selection function that can be applied to our simulation. Contrary to the two previous studies, Greve et al. (2014) used mainly local (ultra)luminous infrared galaxies ((U)LIRGs) and high-z dusty star-forming galaxies, including lensed ones. The SIDES simulation agrees overall with their relation probing higher luminosities. However, they found a much flatter slope for the 8–7 transition. In this case, the difference could be due to the low number of objects used in the study of Greve et al. (2014).
 |
Fig. 4. Relation between the CO and the far-infrared luminosity integrated between 40 and 400 μm. The number of density of SIDES galaxies is coded using a gray scale. The best-fit observed relations of Greve et al. (2014, local and high-z (U)LIRGs), Liu et al. (2015, low-z sample), and Kamenetzky et al. (2016, low-z sample) are represented by a solid red, a dotted green, and a dashed blue line, respectively. These relations are plotted only in the luminosity range in which they were measured. It should be noted that the Liu et al. (2015) study does not include the three lowest rotationnal transitions of CO. |
3.2. CO luminosity functions
The CO luminosity functions (i.e., the comoving volume density of galaxies at a given redshift as a function of their CO luminosity) also provide important constraints to test simulations and they have already been used extensively to test theoretical models (e.g., Lagos et al. 2012; Popping et al. 2014; Vallini et al. 2016). A new generation of deep spectral scans with the Jansky Very Large Array (JVLA) and ALMA have provided important measurements at high redshifts. The CO(1–0) luminosity at z ∼ 2.4 has been measured by Riechers et al. (2019) using the JVLA COLDz survey (51 arcmin2 in GOODS-N and 9 arcmin2 in COSMOS). As shown in Fig. 5, SIDES reproduces these observations very well.
 |
Fig. 5. CO(1–0) luminosity function at z ∼ 2.4. The solid black line is computed using SIDES and the filled blue rectangles are the measurements of Riechers et al. (2019, 51+9 arcmin2) using the JVLA COLDz survey. The width of the rectangles indicates the bin size and the height shows the 1-σ confidence region. |
We have much richer constraints on the higher-J transitions thanks to millimeter interferometers. A pilot deep survey has been performed by Walter et al. (2014) using the Plateau de Bure interferometer. This survey covered a single pointing (∼1 arcmin diameter) in the 79–115 GHz range. The ALMA spectroscopic survey (ASPECS) started by a first pilot survey with a similar size, covering band 3 (84–115 GHz) and band 6 (212–272 GHz) with an improved depth (Walter et al. 2016; Decarli et al. 2016). Finally, a large program extended the coverage to a 4.6 arcmin2 region (Decarli et al. 2019, 2020). In Fig. 6 we compare the luminosity function in our simulation with the measurements from these various surveys.
 |
Fig. 6. Comparison between CO luminosity from the SIDES simulations (solid black lines) and the observations for various transitions and redshifts (see details above each panel). Observational data are represented by filled rectangles, whose width indicates the bin size and whose height shows the 1-σ confidence region. The PdBI HDFM program of Walter et al. (2016, 1 arcmin2) is in green. The ALMA/ASPECS pilot program is in blue (1 arcmin2 Decarli et al. 2016) and the large program is in red (4.6 arcmin2Decarli et al. 2019, 2020). |
The band 3 and the band 6 windows correspond to a different redshift range for each line. This offers a wide variety of constraints on the various transitions and redshifts. The SIDES luminosity functions are derived from the simulated catalog using a volume corresponding to a [zcen − 0.1, zcen + 0.1] redshift range, where zcen is the central redshift of the ASPECS measurement. We used the apparent luminosity in this computation for consistency, since the observations have not been corrected for lensing magnification. However, this effect is negligible in the luminosity regime probed by the observation. The SIDES simulation is always in the 1-σ range of the observations. However, for the higher-J transitions (Jupper ≥ 4), the simulation tends to be systematically on the lower end of the confidence interval. This could be due to a field-to-field variance effect, since the field covered by the ASPECS large program was only 4.6 arcmin2. A companion paper will demonstrate that the field-to-field variance caused by large-scale structures is non-negligible (Gkogkou et al., in prep.).
3.3. Comparison with CO line stacking
We can also check if our simulation agrees with the results obtained using stacking, which usually probe fainter flux regimes. Inami et al. (2020) stacked MUSE-selected galaxies with known spectroscopic redshifts and detected CO(2–1) in several stellar mass bins. Higher transitions were not detected. For their main-sequence sample, they measured the mean line flux in four stellar mass bins. To compare with our simulation, we computed the mean flux of the CO(2–1) in the same redshift range (1 < z < 1.7) and using the same stellar mass bins. Since they stacked a rather small number of objects (3–38, depending on the bin), we estimated the sample variance by drawing 10 000 samples that were the same size as the samples in Inami et al. (2020). The results are presented in Table 1. Apart from the 9 < log(M⋆/M⊙) < 10 bin, the simulation agrees with the observations. The disagreement in the 9 < log(M⋆/M⊙) < 10 bin could come from a small underestimation of this upper limit, since Inami et al. (2020) explicitly assume that their stacked galaxies are point sources to compute their upper limits, but they could be marginally resolved.
Comparison between the measured ALMA stacked fluxes of CO(2–1) of MUSE-selected 1 < z < 1.7 galaxies by Inami et al. (2020) and our results from SIDES (see a description of the computation method in Sect. 3.3).
To measure the CO SLED of galaxies in the ASPECS field, Boogaard et al. (2020) selected objects for which at least one line was detected and stacked the other transitions to measure their mean flux. In Fig. 7, we show their SLED for CO(2–1)-selected galaxies at z ∼ 1.2 and CO(3–2)-selected galaxies at z ∼ 2.5. To compare their results with our simulation, we performed a similar selection in our simulation.
 |
Fig. 7. Comparison between the stacked SLEDs of Boogaard et al. (2020) and the results from SIDES. The filled blue and red circles represent the SLED of z ∼ 1.2 objects detected in CO(2–1). The red filled squares correspond to the z ∼ 2.5 objects detected in CO(3–2). The SLED is normalized to unity for the transition used to select the sample to stack. The light and dark shaded areas show, respectively, the 1 and 2σ confidence region of the mean SLED in our simulation, taking into account the sample variance (see Sect. 3.3). |
Simulating the full process of selecting sources from single-line detections in the noisy cubes and then stacking the other transitions is beyond the scope of this paper. We thus used a simplified selection, which should be roughly equivalent. We selected sources with redshifts corresponding to the frequency range probed by ASPECS and with ICO> 0.2 Jy km s−1, corresponding typical flux of their faintest detections. We then computed the ratio between the mean line flux of a given transition and the reference transition (CO(2–1) or CO(3–2)) to obtain the same normalization. Boogaard et al. (2020) samples are small and only five objects are stacked to derive some ratios. We estimated the sample variance from our simulation by drawing 10 000 samples of the same size in our simulation and recomputing the mean SLED. In our simulation, the variance comes only from the scatter on ⟨U⟩, which correlates with the CO excitation by construction and the presence of a few starbursts with a different SLED. We cannot exclude that the actual scatter is larger and our confidence region is too small.
The SLEDs derived from the simulation are shown in Fig. 7. Apart from the CO(1–0) at z ∼ 2.5, the observations are systematically in the 2-σ region of the simulation. We can note that both CO(4–3) and CO(5–4) at z ∼ 1.2 in our simulation are systematically lower than the observations, and both CO(7–6) and CO(8–7) at z ∼ 2.5 are higher. However, using our 10 000 samples from the simulation, we determined that two consecutive transitions are strongly correlated with a Pearson correlation coefficient of 0.94 for CO(4–3) and CO(5–4), and 0.98 for CO(7–6) and CO(8–7). Thus, they are not independent. In contrast, the CO(1–0) deficit at z ∼ 2.5 seems significant. However, it is hard to reconcile with the fact that both the CO(1–0) and CO(3–2) luminosity functions at z ∼ 2.5 are well reproduced (see Figs. 5 and 6).
3.4. [CI] luminosity functions
Since there are fewer transitions of [CI] and they are usually slightly fainter than CO, making them harder to detect, we have much fewer constraints on the [CI] luminosity functions. However, the ASPECS survey obtained first constraints around the knee of the luminosity function (Decarli et al. 2020), where the bulk of the [CI] integrated emission comes from. In Fig. 8, we compare our simulation with their results. The simulation is always in the 1σ range of the observations. The method used to generate [CI] line fluxes, presented in Sect. 2.5, is thus sufficient to reproduce the current observational constraints.
 |
Fig. 8. Comparison between the [CI] luminosity functions from the SIDES simulation (solid black line) and the ASPECS survey (red areas, Decarli et al. 2020, 4.6 arcmin2). |
3.5. [CII] luminosity function
The [CII] luminosity function is more difficult to measure. Contrary to CO and [CI] sources, which are mainly below z = 3, [CII] sources observables at ALMA frequencies are at higher redshifts. Consequently, they rarely have a good photometric coverage to firmly identify the line using a photometric redshift and the follow-up of another line can be very difficult. Aravena et al. (2016a) performed a first attempt of measurement at z > 6 with the ASPECS pilot survey. However, most of their detections were not found by deeper observations and were likely caused by noise. The most recent analysis of the full ASPECS survey provides only upper limits (Uzgil et al. 2021). The ALPINE survey (Le Fèvre et al. 2020; Béthermin et al. 2020; Faisst et al. 2020) targeted the [CII] line with ALMA in 118 4.4 < z < 5.9 normal star-forming galaxies. Constraints on the [CII] luminosity function were obtained using two different methods. The first methods use the sideband where the ALPINE targets are not located (12 GHz appart) to get 118 small blank fields (Loiacono et al. 2021). The second method is more indirect and uses both the properties of ALPINE sources (UV luminosity, redshift, and [CII] luminosity) and the luminosity function of the UV parent sample Yan et al. (2020).
In Fig. 9 we compare the SIDES [CII] luminosity function with the ALPINE constraints. To compare with the Yan et al. (2020) results, we computed the SIDES luminosity functions in the same 4.4 < z < 4.6 (upper panel) and 5.1 < z < 5.9 (lower panel) redshift bins as them. The SIDES results agree at ∼1σ with these measurements at z ∼ 4.5 (in blue), independently of whether the DL14 or L18 relation is used to derive [CII]. The agreement is not as good at z ∼ 5.5 (in red). While we found an overall agreement between 108 and 109 L⊙ using the DL14 relation, the highest- and the lowest-luminosity points are lower than the simulation by 2σ. However, as discussed in Yan et al. (2020), the faintest point could be affected by incompleteness of the detection. They propose a robust upper limit (downward arrow), which agrees with our simulation. In contrast, the simulation using the L18 relation is systematically low in the 108 and 109 L⊙ range at z ∼ 5.5, and the one using the flat high-z SFRD and DL14 is too high. Finally, our simulation agrees at ∼1σ with the Loiacono et al. (2021) measurement, which is less precise but also less sensitive to assumptions or systematic effects.
 |
Fig. 9. Current constraints on the [CII] luminosity function at z ∼ 4.5 (upper panel) and z ∼ 5.5 (lower panel), and comparison with our SIDES simulation. The filled blue (z ∼ 4.5) and red (z ∼ 5.5) rectangles show the reconstruction of the luminosity function from the ALPINE sample (Yan et al. 2020). The two data points at the lowest luminosities could be impacted by non-detections and the upper limits estimated by Yan et al. (2020) are shown as downward arrows. The constraint at z ∼ 5 using the other sideband of ALPINE is shown with green rectangles (Loiacono et al. 2021). The solid red lines and the dashed orange lines are the SIDES results, assuming the DL14 or the L18 relation, respectively. The long-dashed brown line is the flat high-z SFRD version of SIDES. |
Thus, our simulation roughly agrees with the early measurements of the [CII] luminosity function. While there are minor discrepancies with the indirect measurement of Yan et al. (2020), it is hard to know if this is really a problem in the simulation or a problem with the measurement, since the discrepancy between Loiacono et al. (2021) and Yan et al. (2020) at z ∼ 5.5 suggests that some significant systematic effects may impact these early measurements.
4. Comparison with other models
As shown in Sect. 3, our new version of the SIDES simulation is compatible with the current constraints from the observations. In this section, we compare the results of this approach with other recent (≥2018) models7. We study the [CII] luminosity function (Sect. 4.1), the cosmic [CII] background (Sect. 4.2), and the [CII] power spectrum at z = 6 (Sect. 4.3). Finally, we discuss the difference between the models, and the strengths and weaknesses of the different approaches (Sect. 4.4). We compare our predictions with the three following models: Yue & Ferrara (2019), Chung et al. (2020), and Yang et al. (2022).
The Yue & Ferrara (2019) model starts from the UV luminosity function and uses various empirical scaling relations to produce the [CII] luminosity. The UV luminosity is connected to the halo mass through abundance matching. All the observables are derived from an analytical formulae. The [CII] power spectrum is derived using a halo model.
The Chung et al. (2020) model starts from dark-matter simulation. The dark-matter halos are populated by galaxies using the UNIVERSEMACHINE (Behroozi et al. 2019) approach. The [CII] luminosity is derived from the SFR using the Lagache et al. (2018) relation. The observables, such as background and power spectra, are derived from the simulated cubes.
Yang et al. (2022) calibrated the relation between the [CII] luminosity and the halo mass using the Popping et al. (2019) semi-analytical model. The intensity mapping observables are derived using an analytical halo model.
4.1. [CII] luminosity functions at z ∼ 6
The [CII] luminosity function is one of the most basic observables for comparing models. The [CII] background (see Sect. 4.2 and Appendix C) and the shot noise of the [CII] power spectrum (see Sect. 4.3 and Appendix D) are dertived directly from it. The link with the correlated fluctuations is less direct, since they also depends on the relation between the halo properties and the [CII] luminosity. In this paper, we chose to focus on the luminosity function at z ∼ 6, which is the aim of most of the first generation experiments (CONCERTO, TIME, and FYST) and has been studied by all the models in our compilation.
In Fig. 10 we show the [CII] luminosity function predicted by these various models. The version of SIDES using the L18 relation and the Chung et al. (2020) model using the same relation have quite similar [CII] luminosity functions. However, we note that SIDES has a slightly shallower slope. Chung et al. (2020) is really close to the full semi-analytical L18 model, which indicates that their SFR distributions are very similar, since they use the same SFR-L[CII] relation. They are both very close to a power law, while the L18 version of SIDES has a knee around 109 L⊙. The DL14 version of SIDES is higher than the L18 version by a factor of ∼1.5 around 107 L⊙, and a factor of roughly three around 109 L⊙. It also has an even shallower slope than the previous models. This can be explained by the higher [CII] luminosity predicted by the DL14 and the nonlinear slope of the L18 relation. Overall, these four models (SIDES L18, SIDES L14, Chung et al. 2020, and the original L18) have relatively similar luminosity functions with a significantly higher luminous end for the DL14 SIDES.
 |
Fig. 10. Comparison between the luminosity functions produced by various models at z = 6. The solid red lines and the dashed orange lines represent the SIDES luminosity function using the DL14 or the L18 relation, respectively. The long-dashed brown line is the high SFRD version of SIDES. The models shown for comparison are Lagache et al. (2018, two-dot-dashed turquoise line), Yang et al. (2022, dotted blue line), Yue & Ferrara (2019, short-dash-long-dashed purple line), and Chung et al. (2020, dot-dashed green line). |
The Yue & Ferrara (2019), Yang et al. (2022), and high-SFRD versions of SIDES have much higher luminosity functions overall than the previously discussed models. Below 108.5 L⊙, these models are factor of approximately three higher than SIDES assuming the DL14 relation. We can also note that the Yang et al. (2022) model has a steep slope around 108.5 L⊙, while the two other high-luminosity-function models exhibit a more discrete knee.
We remark that the high-SFRD version of SIDES has a sharp cutoff below 107 L⊙, which is caused by the halo mass limit of our underlying dark-matter simulation (see Sect. 4.4). Since this model has a higher SFR and [CII] luminosity at a fixed halo mass, this cutoff is at a higher luminosity than in the other versions of the model. This cutoff is around 106 L⊙ for the DL14 version of SIDES.
4.2. Cosmic [CII] background
One of the most simple global quantities that we can derive from the simulated cubes is the line background, namely the total surface brightness density from all the lines emitted by all the galaxies. Each galaxy contributes to a couple of specific observed frequencies that correspond to its various redshifted lines, but the total background is smooth since galaxies are distributed continuously over a wide range of redshift. While this quantity is very useful for comparing models, it is very hard to measure it in practice, since it would require an absolute photometer and an extremely accurate subtraction of the CIB and the CMB, which are much brighter. For instance, the CIB is ∼100 times brighter than the [CII] background at 300 GHz (see below). However, lower limits could be obtained from deep line spectral scans such as ASPECS, but a direct comparison with the luminosity functions is then more informative (see Sect. 4).
The [CII] background at a frequency νobs is directly connected to the [CII] luminosity function (![$ \frac{d^2 N}{\mathrm{d}L_{\mathrm{[CII]}} \mathrm{d}V} $](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq23.gif) ) at the associated redshift (z = νrest/νobs − 1) by the following equation:
) at the associated redshift (z = νrest/νobs − 1) by the following equation:
where C is a constant conversion factor and H(z) is the Hubble parameter at a redshift z (see Appendix C for the full computation).
To check the consistency between our input catalogs and cubes, we derived the background using two different methods. The first approach uses the catalogs. We defined small bins in frequencies and summed the flux (in Jy km s−1) of all the lines falling in each bin. We then divided this quantity by the solid angle in the sky associated with the catalog and the width of the velocity associated with each bin (cΔνobs/νobs). For the second approach, we averaged the cubes in the two spatial dimensions and obtained the mean spectra of the sky, which is exactly the line background. This task was performed on the cubes corresponding to each line to obtain their individual contribution. The results of the two methods agree at better than the percent demonstrating that no major artifact is created during the cube making.
In Fig. 11, we present the line background derived from SIDES. The CIB (continuum) is always brighter than the lines. It is a factor of five higher than the line background at 100 GHz and a factor of 200 higher at 1000 GHz. If we consider only the lines, the [CII] background dominates at high frequencies, while CO dominates at low frequencies. The crossing frequency slightly varies depending on the version of the [CII] model: 365 GHz for the DL14 relation, 371 GHz for the L18 relation, and 345 GHz for the high-SFDR scenario (see Sect. 2.7). The [CI] background is never dominant.
 |
Fig. 11. Cosmic line background as a function of frequency. The solid red line, the dashed yellow line, and the long-dashed brown line, show the predictions of our simulation assuming the DL14 relation, the L18 relation, and the flat z > 4 SFRD (see Sect. 2.7), respectively. The CO, [CI], and continuum background predicted by SIDES are shown as a dot-dashed blue line, a two-dot-dashed dark blue line, and a solid gray line, respectively. The dot-dashed green line, the short-dash-long-dashed purple line, and the dotted blue line are the [CII] forecast from the Chung et al. (2020) model, the Yue & Ferrara (2019) model, and the Yang et al. (2022) model, respectively. |
We can also compare our predictions with other models. The L18 version of our simulation agrees well with the Chung et al. (2020) work based on the same SFR-L[CII] relation but using the UNIVERSEMACHINEBehroozi et al. (2019) approach to populate dark-matter halos. The other versions of our model produce stronger [CII] background. The Yue & Ferrara (2019) model is much higher than the standard versions of our model whatever the assumed SFR-L[CII] relation, but it is similar to our high-SFRD model. Their model is higher than SIDES (DL14 version) at z ∼ 6 by a factor of roughly three, (see Sect. 4.1 and Fig. 10) around 109 L⊙ and exhibits an even stronger excess at fainter fluxes. Thus, it is not surprising that this model produces a stronger background. Finally, the Yang et al. (2022) model is higher than SIDES between 250 GHz and 1 THz without being as extreme as the Yue & Ferrara (2019) model. This is consistent with their luminosity function being higher overall than SIDES (except at the very bright end), but having a shallower faint-end slope and a sharper high-luminosity cutoff than the Yue & Ferrara (2019) model.
4.3. Computation of the [CII] 3D power spectrum at z ∼ 6 and comparison with other models
While our simulation produced spectral cubes, most of the theoretical models forecasted only the 3D power spectra at some specific redshift. To perform a more direct comparison, we also produced a 3D cube from our catalog. We first defined a 3D grid in comoving units centered on z = 6 (DC = 8435 Mpc) and the middle of the SIDES field. This grid has 512 elements of 0.4 Mpc in each direction to cover the full simulated field. For each of these voxels, we can associate a central redshift and redshift width by converting the depth coordinate into a redshift. Our cube covers the 5.76 < z < 6.24 range (8332 Mpc < DC < 8538 Mpc). Each source in this redshift range is associated with a voxel based on its redshift and sky coordinates. To derive the surface brightness density in Jy/sr of a voxel (Sν), we computed the sum of the [CII] line fluxes from all the sources associated with a given voxel and divided it by the velocity width Δυvoxel and the solid angle associated with the voxel 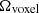 (
(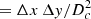 ):
):
where zvoxel and Δzvoxel are the center and the width of the voxel, respectively, after converting the radial distances into redshifts. I[CII] is the line flux in Jy km/s. Finally, we computed the 3D power spectrum of this cube. This quantity is independent from the choice of the voxel size (see Appendix D).
Our results are presented in Fig.12. At small scales (high k), we can see a plateau corresponding to the shot noise (also called the Poisson component), which we would still have in the absence of any clustering, and which depends only on the luminosity functions (see Appendix D). At large scales (k ≲ 0.5 arcmin−1), we can observe an excess compared to the shot noise corresponding to the clustering of [CII]-emitting galaxies. This behavior is similar to what has already been observed for the CIB (Lagache et al. 2007; Viero et al. 2009, 2013; Planck Collaboration XVIII 2011; Planck Collaboration XXX 2014; Amblard et al. 2011; Pénin et al. 2012; Béthermin et al. 2013).
 |
Fig. 12. Comparison of the 3D [CII] power spectra at z = 6 from various models. The lengths are in comoving units. We also indicate the corresponding projected angular wavenumber at z = 6 as the upper x-axis. The x-axis range corresponds approximately to the scales, which will be probed by CONCERTO. The solid red and dashed orange dashed lines are from the SIDES simulation assuming the DL14 and L18 relations, respectively. The long-dashed brown line is the high-SFRD version of SIDES (see Sect. 2.7). We also compare with the models of Yue & Ferrara (2019, two-dot-dashed purple line), Chung et al. (2020, dot-dashed green line), and Yang et al. (2022, dotted blue line). |
The various versions of SIDES produce power spectra with similar shapes but very different normalizations. The version using the L18 relation is lower than the one using the DL14 relation by a factor of about five. The difference is stronger than for the cosmic [CII] background. This is expected, since the power spectrum is proportional to the emissivity squared. In addition, because of the different shapes of the L[CII]-SFR relation, there are more luminous objects in the DL14 version. These rare luminous sources have a stronger relative contribution to the shot noise than the background (proportional to the luminosity squared instead of the luminosity, see Appendices C and D). They also contribute more to correlated anisotropies at larger scales relatively to their flux, since they tend to live in more massive halos, which are also more clustered. Finally, the high-SFRD version corresponds to a simple rescaling of the [CII] fluxes from the DL14 version by a constant, which leads to a power spectrum higher by this constant squared.
The Chung et al. (2020) model has a lower shot noise at small scales than the DL14 version of SIDES, but a steeper slope at large scales where the clustering dominates. The Yang et al. (2022) model has a lower shot noise than the DL14 SIDES and a similar one as the Chung et al. (2020) model, but a much stronger correlated signal. While their luminosity function is relatively high compared to the DL14 SIDES (Sect. 4.1), Yang et al. (2022) have fewer objects than SIDES at the luminous end, which dominate the shot noise and cause their shot noise to be higher. In contrast, the larger amount of correlated signal likely comes from the excess of 107–108 L⊙ emitters by a factor of roughly three, compared to the DL14 SIDES. Finally, the Yue & Ferrara (2019) model, which has the highest luminosity function at all luminosities, has naturally a higher power spectrum than all the previously cited models by at least an order of magnitude. It has a similar shot noise to the SIDES high-SFRD model, but a stronger correlated signal.
4.4. Discussion about the different models
The z ∼ 6 [CII] luminosity functions forecast from the various models discussed in this section vary by an order of magnitude, and the power spectra vary by more than two orders of magnitude. These models are all built on very reasonable assumptions and these disagreements demonstrate that it is still hard to predict the number density of [CII] galaxies and how they are distributed in the dark-matter halos, even in the ALMA era. On the positive side, the availability of all these models allows us to know in which range we can expect the real Universe to be, and thus better prepare ongoing and future experiments. They will be key to better understanding this early phase of galaxy evolution.
The shot-noise level can vary strongly from one model to another. It is really sensitive to the bright end of the luminosity function. There is no systematic difference between the family of models using a halo model (Yue & Ferrara 2019; Yang et al. 2022) and those using simulated cubes (Chung et al. 2020, SIDES). As discussed by Murmu et al. (2021), the scatter on the L[CII] can significantly impact the shot noise. However, it is hard to compare the various models since they do not connect quantities in the same way. Yue & Ferrara (2019) connect the UV to the [CII] luminosity assuming a scatter, Chung et al. (2020) assume a scatter on the SFR-[CII] relation, and finally Yang et al. (2022) directly parameterize the scatter in the relation between the halo mass and the [CII] luminosity. In our model, we have a cascade of the scatters, when we connect the halo mass to the stellar mass, then the stellar mass to the SFR, and then the SFR to the [CII] luminosity.
The relative level of the large-scale correlated fluctuations compared to the shot noise can also vary between models. Overall, the models based on simulations tend to have a lower ratio of correlated fluctuations versus Poisson fluctuations (see Fig. 12). The Yang et al. (2022) model has the largest ratio. This is not surprising, since this model has a large number of faint sources, but very few bright sources (L[CII] > 109 L⊙, see Fig. 10). The bright sources have a strong contribution to the Poisson term, since the contribution to it is proportional to the luminosity squared (see Appendix D). In contrast, the contribution to the correlated fluctuations is linked to the luminosity weighted by the linear bias of the host halos (see, e.g., Eq. (17) of Yue & Ferrara 2019 or Eqs. (6) and (7) of Yang et al. 2022). Even if the low-luminosity sources are usually hosted by lower-mass halos with a lower bias, this usually does not compensate for the fact that they are much more numerous than the very bright objects.
A potential explanation for the lowest power spectra of the models based on dark-matter simulation could come from their halo mass limit. Since the very low-mass halos are missing in the simulation, a significant fraction of the signal coming from the hosted galaxies may be lacking. Chung et al. (2020) discussed this effect and estimated that it could have an impact up to a factor of three.
To estimate the actual effect of the halo mass limit on the prediction of our simulation, we computed the relative contribution of galaxies to various observables as a function of their host halo mass. We divided our simulated catalog into halo bins with widths of 0.1 dex. We then computed the number density, the sum of the [CII] luminosities, the sum of the [CII] luminosities squared, and the sum of the [CII] luminosities weighted by the bias of the host halo from Tinker et al. (2010). We normalized all the results, since we are only interested in the relative contribution. The results are shown in Fig. 13. We see a strong turnover in the number density (solid gray line) at 1010.5 M⊙, which corresponds to the halo mass limit of the dark-matter simulation.
 |
Fig. 13. Effect of the halo mass limit on various [CII] observables (see Sect. 4.4). The curves show the total contribution of galaxies to these observables per logarithmic interval of host halo masses (dex). All the curves are normalized to have their maximum equal to one. Top, central, and bottom panels: correspond to z ∼ 5, z ∼ 6, and z ∼ 7, respectively. Left panels: have a y-axis in linear units, allowing us to naturally visualize the area under the curves, and the right panels are in logarithmic scale to better visualize the behavior at low masses. The gray curve is the number density of the halos and the vertical dotted line shows the halo mass limit of 1010.5 M⊙. The dashed blue line shows the contribution of galaxies to the [CII] background, which is directly derived from the integral of the [CII] line luminosities (see Appendix C). The dot-dashed green line is the contribution to the shot noise, which is directly connected to the integral of the [CII] luminosity squared (see Appendix D). Finally, the solid red curve presents the integral of the luminosity of the galaxies multiplied by the linear bias corresponding to their halo mass. This term is directly connected to the amplitude of the correlated fluctuation of the [CII] background (see Sect. 4.4). |
We first looked at the sum of the [CII] luminosities (dashed blue line), which is proportional to the contribution to the [CII] background (see Appendix C). We can already visually notice that the contribution at the mass limit is small. To quantify more accurately the missing background, we fitted the curve between 1010.5 M⊙ and 1011 M⊙ by a power law. This function was used to extrapolate the contributions of the low-mass halos. We then integrated the curve above the limit and compared it with the integral down to 105 M⊙ using our power-law extrapolation below the mass limit. We found that the halos in our simulation contribute to 96% of the total background at z ∼ 5 and z ∼ 6, but only 81% at z ∼ 7.
As shown in Appendix D, the contribution to the shot noise is proportional to the luminosity squared (dot-dashed green line). Thus, massive halos hosting luminous galaxies have a stronger contribution. Consequently, at z ∼ 5, the signal is mainly coming from galaxies hosted by ∼1012 M⊙ halos. At higher redshifts, these halos are rarer and the maximal contribution drifts to slightly lower masses. However, we estimated the contribution of the halos below the mass cut to be below 1%.
Finally, we estimated the contribution of the various halos to the correlated fluctuations from the product of the luminosity by the linear bias (solid red line). We find a peak contribution around 1012 M⊙ at z ∼ 5, and 2 × 1011 M⊙ at z ∼ 7. This agrees with the estimate of Yue et al. (2015) at z ∼ 5 using a similar approach. At z = 5 and z = 6, we estimated that 98% of the integral is coming from halos above the mass limit, but only 92% at z = 7. These values have to be squared to evaluate the impact on the power spectra. Our simulation should therefore be reliable at a 20% level up to z = 7. At z > 7, the results of our simulation should be taken with caution, since the mass resolution of the underlying dark-matter simulation may be not sufficient to be reliable at the very early stages of the structure formation. The sharp drop in the SFRD at z > 7 (see Fig. 3) could be caused by the same problem. In contrast, our simulation could overestimate the correlated [CII] fluctuations, if the SFR-L[CII] breaks in low-mass galaxies due to the low metallicity. So far, the observations of lensed low-SFR galaxies have given contrasting results on this question. Some studies found a clear deficit (Knudsen et al. 2016; Bradač et al. 2017), while Fujimoto et al. (2021) did not find any evidence for it.
5. Contribution of the various astrophysical components to CONCERTO power spectra
Our simulation reproduces the observed line luminosity functions (Sect. 3), the observed dust continuum statistical properties (Béthermin et al. 2017), and the CIB anisotropies (Béthermin et al. 2017; Gkogkou et al., in prep.). We can thus use it to forecast the power spectra of the various lines at various redshifts.
5.1. Computation of power spectra per frequency slices and link with 3D power spectra
In Sect. 4.3, we compared the 3D power spectra of various models. In this section, we instead use angular power spectra of 1 GHz frequency slices. We simply calculated the angular power spectrum of each 1 GHz spectral cube slice using the powspec package8. Working in angular wavenumber and frequency is closer to the data that the instruments produce. It also allows us to produce figures that are independent of the choice of a reference line for the projection into the 3D physical space. Finally, the low spectral resolution of CONCERTO will not allow us to probe the small scales in the radial direction. Projected to the physical space, the angular resolution (22 arcsec at 305 GHz) and the frequency resolution are very different. For instance, for [CII] at z = 6, the transverse resolution is 0.9 comoving Mpc, while it is only 11 comoving Mpc in the radial direction.
However, we note that formalisms were developed to reproject another line acting as a contaminant on the 3D physical power spectrum of a given reference line (Gong et al. 2014; Lidz & Taylor 2016; Breysse et al. 2022). For two different lines, the same frequency interval corresponds to different widths in the radial direction. Similarly, the same angular scale is associated with different physical scales in the transverse direction. However, for the interlopers, the radial and transverse distorsions have no reason to be the same, and thus the power spectrum is anisotropic. This effect could be used to separate the signal from line interlopers from the targeted line. However, Lidz & Taylor (2016) showed that this decomposition requires high signal-to-noise ratios, which will not be achieved by first-generation experiments such as CONCERTO. For simplicity, we do not consider anisotropies in this paper focused on CONCERTO.
In practice, the angular power spectrum P2D is approximately linked to the 3D power spectrum P3D by the following formula (Neben et al. 2017; Yue & Ferrara 2019):
where P2D(kθ) is the angular power spectrum of the frequency slice, DC is the distance to the slice in comoving units, 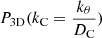 is the 3D power spectrum at the redshift associated with the frequency slice, and ΔDC is the thickness of the slice in the same units:
is the 3D power spectrum at the redshift associated with the frequency slice, and ΔDC is the thickness of the slice in the same units:
where H(z) is the Hubble parameter at a redshift z. Using this formula, we implicitly assume that ΔDC ≪ DC and that P3D does not vary significantly across the slice. To evaluate the accuracy of this approximation, we compared the 3D power spectrum derived at z = 6 from the comoving cubes (see Sect. 4.3) with the angular power spectrum derived from the simulated observed cubes. We found a maximal difference of 10%, which is negligible compared to the various calibration uncertainties on the model (e.g., CO and [CII] scaling relations, stellar mass function, evolution of the main sequence and its scatter).
5.2. Power spectra at various frequencies
We computed the angular power spectrum of various astrophysical components at 305 GHz, 270 GHz, 240 GHz, and 210 GHz, which correspond to [CII] at a redshift of 5.2, 6.0, 6.9, and 8.1, respectively. At 210 GHz, the [CII] forecast from our model should be taken with caution, as discussed in Sect. 4.4. The results are presented in Fig. 14. Similarly to the 3D power spectra (Sect. 4.3), for all the components, we can see a Poisson plateau at small scales (large k) and an excess of power at large scales (small k), coming from the galaxy clustering. However, the relative contribution from the clustering decreases with increasing z for [CII] and is very weak at z = 8.1 (210 GHz).
 |
Fig. 14. Contribution of the various extragalactic components to the CONCERTO angular power spectra at 305 GHz (upper left panel), 270 GHz (upper right panel), 240 GHz (lower left panel), and 210 GHz (lower right panel) predicted by SIDES. As discussed in Sect. 4.4, the [CII] power spectra at 210 GHz (z = 8.1) could be significantly underestimated by our model. To minimize the effect of the field-to-field variance, we computed the average of the 11 power spectra corresponding to the 1 GHz-wide slices placed between 5 GHz below and above the central slice (except at 305 GHz, for which we have no slice at a higher frequency). The continuum is represented by the dotted line. The solid red lines and the dashed orange lines show the [CII] contribution in SIDES assuming the DL14 and the L18 relations, respectively. The long-dashed brown lines represent the high-SFRD variant of the model (see Sect. 2.7). The black and gray lines show the contribution from both CO and [CI] before and after removing the known galaxies from surveys (see Sect. 5.4). |
At all frequencies, the continuum (CIB) is the dominant component by more than one order of magnitude. However, this component should not be too serious a problem for intensity mapping experiments, since it should be easy to subtract due to its smooth dependence on frequency. Techniques were already developed for the 21-cm survey (e.g., Wang & Hu 2006; Jelić et al. 2008; Alonso et al. 2014) and could be adapted to [CII] intensity mapping. To analyze the results of the mmIME (see Sect. 5.7), Keating et al. (2020) ignored the modes affected by the continuum, since the continuum has a very different behavior in the radial and traverse directions because of its smooth frequency dependence. The continuum can also be subtracted directly in the coordinate-frequency cubes, also taking advantage of its smoothness as function of frequency (Van Cuyck et al., in prep.). The continuum component thus has thus very convenient properties, which should allow us to subtract it with minimal residuals. However, because of its intrinsic brightness, any systematic effects or residuals in its subtraction could have a significant impact on the line measurements.
At 305 GHz (the highest frequency reachable by CONCERTO), the power spectrum of CO and [CI] combined (solid black line) is slightly higher than the DL14 version of [CII]. The L18 version is lower than the DL14 version by a factor of roughly two, and the high-SFRD model is higher by a factor of roughly 5. At lower frequencies (higher [CII] redshifts), the level of the [CII] power spectrum is lower than the sum of the CO and [CI] contributions. The level of the L18 version decreases quicker with increasing redshift, since the normalization of the L[CII]-SFR relation from L18 decreases with increasing redshift.
To visualize the variation in frequency of each of these contributions, for each slice we computed the mean level of the power spectra between 0.15 and 0.35 arcmin−1 for the large scales, and between 5 and 7 arcmin−1 for the Poisson term. These results are interpreted in Sects. 5.3, 5.5, and 5.6. The angular power spectrum is dependent on the choice of the spectral resolution (see Appendix D). In the following sections, we normalize the Poisson component by the frequency width of the slice following Eq. (D.3) to make it independent of the spectral grid. The corresponding unit is the Jy2 sr−1 GHz. This does not apply to large scales, since we cannot assume that several frequency slices are fully independent due to the large-scale clustering.
5.3. Contribution of the main extragalactic lines as a function of frequency
In Fig. 15 we present the contribution of the various astrophysical components as a function of frequency. Because of the small comoving volume associated with a frequency slice (∼603 Mpc3), there are large fluctuations between neighboring spectral slices. To obtain a better visualization, we smoothed the curves by a Gaussian kernel with a σ of 3 GHz. As expected, the continuum dominates at all frequencies, except if there is an unlikely flat SFRD scenario up to z ∼ 8 (high-SFRD model). However, the continuum should not be too difficult to subtract from the cubes because of its smoothness as a function of frequencies (e.g., Yue et al. 2015). The CO-versus-continuum ratio varies with frequency, with a higher ratio at a lower frequency. This is expected, since the continuum increases strongly with increasing frequency, while the CO line flux does not increase as much from low-J to high-J transitions.
 |
Fig. 15. Level of the power spectrum of the various components in SIDES as a function of the frequency. Left panel: the small scales dominated by the shot noise and the right panel shows the large scales. The dotted black line is the continuum computed using the standard model (low SFRD). The solid red line, the long-dashed brown line, and the short-dashed orange lines are the SIDES predictions for [CII] using the DL18, high-SFRD, and L18 versions, respectively. As discussed in Sect. 4.4, the [CII] power spectra at z > 7 may be underestimated. We thus used a paler color to illustrate it. The dot-dashed light-blue line and the dash-dot-dot dark-blue lines correspond to all the CO and [CI] lines, respectively. The solid black line shows the total contribution of all the CO and [CI] lines, while the solid gray line is the same after masking galaxies known from galaxy surveys (see Sect. 5.4). For a better visualization, we smoothed the curves by a Gaussian kernel with a σ of 3 GHz. |
The contribution from [CI] to the power spectra is five to ten times less than the contribution from CO. This is not a surprise, since there are fewer [CI] transitions and they are usually slightly fainter. Both species have a shallow frequency dependence, with more contribution at higher frequencies. Finally, we can observe a strong spike for CO just below 230 GHz. These frequencies correspond to low-z galaxies seen in CO(2–1) (see Sect. 5.5). Since the Poisson fluctuations are proportional to the flux squared (see Appendix D), a couple of bright nearby sources can have a major contribution to the power spectrum at this frequency. We can also observe a weaker ∼230 GHz bump at large scales, where we observe the sum of the correlated fluctuations and the Poisson fluctuations. Its amplitude compared to the baseline (in linear units) is similar to what is observed for the Poisson fluctuations, suggesting that it comes mainly from the shot noise.
The [CII] forecast depends strongly on the assumptions of the simulation. For the DL14 and L18 prescriptions, the signal increases strongly with frequencies, while it is rather flat for the high-SFRD version assuming a flat SFRD at z > 4. There is virtually no signal below ∼200 GHz, since this corresponds to z > 8.5, and thus very small SFRDs in the standard version of our model. However, these results should be taken with caution, since the halo mass limit of our simulation can have a strong impact on our results, as discussed in Sect. 4.4. At 305 GHz (z = 5.2), the three versions diverge by less than a factor of ten. In contrast, at z = 8, there are already four orders of magnitude between the L18 and the high-SFRD models. This illustrates how uncertain the [CII] intensity mapping is at the highest redshift, and how important observational constraints will be.
At 305 GHz, for the DL14 version of SIDES, the [CII] is a factor of two lower than the sum of CO and [CI] at both small (Poisson) and large scales. The [CII] amplitude is about a factor of five lower than the sum of CO and [CI] for the L18 version. The [CI] is always an order of magnitude lower than the two other species. Below 270 GHz (above z = 6.0), the [CII] decreases rapidly with decreasing frequency (or increasing redshift). At 250 GHz (z = 6.6), the [CII] is already an order of magnitude below the CO in the DL14 version of the model. This is low but more optimistic for intensity mapping experiments than the < 1% contribution of [CII] to the line background at 250 GHz, estimated empirically by Decarli et al. (2020). These results demonstrate how crucial the accurate cleaning of the CO contribution is if the SFRD is not flat at high redshifts.
5.4. Effect of masking known sources
Yue et al. (2015) and Sun et al. (2018) showed that the masking of the voxels associated with known galaxies from optical and near-infrared surveys could allow us to isolate the contribution of [CII]. To evaluate how powerful this technique could be, we produced new cubes injecting only galaxies, which would not be found by surveys at z < 4. We used the stellar mass limits of the COSMOS catalog from Laigle et al. (2016) and considered that any galaxy above this stellar mass could be properly masked. This mass limit varies with redshift and we removed sources down to much lower masses at lower redshifts. This is indeed an approximation and it assumes that the redshift of the sources will be accurate enough to mask only the associated voxels, and that no signal beyond the mask (e.g., PSF wings or map making artifacts) will contaminate the power spectra measured outside of the masked area. Our approach thus provides an upper limit on the efficiency of the CO and [CI] masking technique. Detailed simulations of the full process will be presented in a future paper (Van Cuyck et al., in prep.).
As illustrated by Fig. 15, the masking reduces the level of the CO and [CI] contribution by more than one order of magnitude. At 305 GHz (z = 5.2), the residuals of CO and [CI] are a factor ∼25 below the [CII] signal predicted by the DL14 version of SIDES (factor of about ten for the L18 version). The impact of these residuals increases rapidly with decreasing frequency. For the DL14 version, the CO and [CI] residuals reach 20% of the [CII] signal at 260 GHz (z = 6.3). The equality between [CII] and the residuals is reached at 230 GHz (z = 7.3). This suggests that the masking will not be sufficient beyond z ∼ 6.5, as already mentioned by Yue et al. (2015), and more advanced techniques of decontamination will be necessary (e.g., Cheng et al. 2020; Concerto & Ade 2020).
5.5. Contribution of the different CO transitions
The CO is thus the main contaminant for [CII] intensity mapping. However, all the transitions do not contribute equally. In Fig. 16 we show the contribution of each CO transition to the power spectrum at various frequencies. As discussed in Sect. 5.3, there is a large spike just below 230 GHz. This figure confirms that it is caused by CO(2–1) at low redshifts. If we do not mask the known galaxy populations, the CO power spectrum is dominated by the 2–1, 3–2, 4–3, and 5–4 transition above 230 GHz. Between 200 and 230 GHz, the signal comes mainly from CO(2–1) at low redshifts. Below 200 GHz, all the transitions between 2–1 and 5–4 have similar contributions. The contribution of higher-J transitions decreases strongly with increasing J.
 |
Fig. 16. Contribution of the various CO lines to the Poisson term (left panels) and the large-scale power spectrum (right panels) before (upper panels) and after (lower panels) masking the known galaxies from surveys. Together with the total CO (solid black line), we show the contribution of CO(2–1) (long-dashed red line), CO(3–2) (short-dashed orange line), CO(4–3) (dotted green line), CO(5–4) (long-dash-dot turquoise line), CO(6–5) (two-dot-dash light-blue line), CO(7–6) (dot-two-dash dark-blue line), and CO(8–7) (two-dash-two-dot purple line). For a better visualization, we smoothed the curves by a Gaussian kernel with a σ of 3 GHz. |
The results are very different after masking. The main contributors are then the 5–4 and 6–5 transitions. Since the galaxy catalogs reach lower masses at lower redshifts, most of the low-z signal is removed, while high-z intermediate mass galaxies still contribute. The low-z CO(2–1) peak also has a much lower amplitude relative to the other transition and does not significantly impact the total CO power spectra. We can also notice a small spike in CO(6–5) at 155 GHz, CO(7–6) at 180 GHz, and CO(8–7) at 210 GHz. This is likely caused by the same overdensity around z ∼ 4.4 in the SIDES cube.
Finally, we can notice that the CO(8–7) transition has a non-negligible contribution at high frequencies after masking. High-J transitions could thus play an important role after masking. These transitions are less known, especially in low-mass galaxies at high redshifts, and a hypothetical population of low-mass galaxies with a particularly high CO excitation could have a significant impact on the CO residuals. However, this is disfavored by theoretical models, which predict a turnover of the SLED around J = 7 for normal high-z galaxies (e.g., Vallini et al. 2018).
5.6. Contribution of the [CI] lines
The two [CI] transitions also contribute to the power spectrum. In Fig. 17 we present [CI] power spectra levels as a function of frequency. Before masking, the [CI]1–0 and 2–1 transitions have similar contributions above 270 GHz. Between 180 and 270 GHz, the ratio between [CI](2–1) and [CI](1–0) decreases mildly with decreasing frequency (increasing redshift). This is expected, since [CI]2–1 is probed between z = 2 and z = 3.5, where the SFRD is almost flat, while [CI]1–0 is probed between z = 0.8 and 1.7, where it has a mild increase. Below 180 GHz, [CI]2–1 drops sharply, since it corresponds to z > 3.5, where the SFRD decreases quickly with increasing redshift.
 |
Fig. 17. Contribution of the two [CI] transitions to the Poisson term (left panels) and large-scale power spectrum (right panels) before (upper panels) and after (lower panels) masking the known galaxies from surveys. The solid black line represents the total, while the dotted red line and the dashed blue line correspond to the [CI](1–0) and [CI](2–1) transitions, respectively. For a better visualization, we smoothed the curves by a Gaussian kernel with a σ of 3 GHz. |
Similarly with the CO, the relative contribution of the various transitions is strongly affected by the masking. The [CI]2–1 transition is dominant down to 150 GHz. This can be easily explained by [CI]2–1 being emitted at higher redshifts, and thus less affected by the masking.
5.7. Comparison with the mmIME measurements
Millimeter intensity mapping is an emerging technique and so far very few measurements have been obtained. The first pioneering results have been obtained by the mmIME (Keating et al. 2020) using both the results of the ASPECS survey and a dedicated Atacama Compact Array (ACA) survey. They managed to obtain a 2.5σ tentative detection of the shot noise around 100 GHz. They subtracted the continuum signal from galaxies (CIB) by discarding the modes corresponding to smooth components on the spectral axis. They found 770 μK2 Hz sr correcting only for the instrumental noise and 1010
μK2 Hz sr correcting only for the instrumental noise and 1010 μK2 Hz sr using a more complex maximum likelihood estimation (MLE). Since the SIDES simulation is in Jy units, we converted the mmIME results to a more convenient unit (see Appendix E). We obtained 0.07
μK2 Hz sr using a more complex maximum likelihood estimation (MLE). Since the SIDES simulation is in Jy units, we converted the mmIME results to a more convenient unit (see Appendix E). We obtained 0.07 Jy2 sr−1 GHz−1 for the simple noise correction and 0.09
Jy2 sr−1 GHz−1 for the simple noise correction and 0.09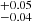 Jy2 sr−1 GHz−1 for the MLE.
Jy2 sr−1 GHz−1 for the MLE.
To compare SIDES with mmIME, we produced simulated cubes using the method described in Sect. 2.6 between 84 and 115 GHz (the frequency range probed by mmIME). For each 1 GHz element, we then computed the angular power spectrum of the slice using the powspec package. The Poisson level is estimated averaging the k > 5 arcmin−1 scales. The results are presented in Fig. 18.
 |
Fig. 18. Shot-noise level predicted by SIDES as a function of frequency and a comparison with the mmIME measurements (Keating et al. 2020, total area of 20 arcmin2, horizontal dark gray line and associated 1σ area for the MLE method, dark blue line and area for the simpler instrumental noise correction). The frequency range shown in this figure corresponds to the mmIME used. The filled black circle is the average shot noise predicted by SIDES in this range. The solid black line is the total of CO and [CI]. The various colored lines captioned directly in the figures indicate the contribution of each CO transition. |
Above 100 GHz, the shot noise is dominated by CO(1–0) at low redshifts. This is not surprising, since the flux of low-z sources can be very high and the shot noise is particularly impacted by bright sources, contrary to the mean background (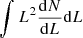 instead of
instead of 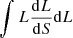 , see Appendices C and D). A similar behavior has already been identified for the redshift distribution of the CIB shot noise with both a low-redshift and a z ∼ 2 peak (e.g., Béthermin et al. 2013, Fig. 12). In Keating et al. (2020), they computed the CO(1–0) shot noise predicted by their model only up to ∼ 75 GHz and did not investigate the possibility of a low-z second peak. Below 100 GHz, there is a similar contribution from the four lowest CO transitions.
, see Appendices C and D). A similar behavior has already been identified for the redshift distribution of the CIB shot noise with both a low-redshift and a z ∼ 2 peak (e.g., Béthermin et al. 2013, Fig. 12). In Keating et al. (2020), they computed the CO(1–0) shot noise predicted by their model only up to ∼ 75 GHz and did not investigate the possibility of a low-z second peak. Below 100 GHz, there is a similar contribution from the four lowest CO transitions.
The total contribution of the CO and [CI] averaged over the mmIME frequency range (filled circle in Fig. 18) is 0.059 Jy2 sr−1 GHz−1, which agrees with the mmIME measurements. Only four lines contribute to 10% or more of the total shot noise: CO(1–0) with 33%, CO(2–1) with 19%, CO(3–2) with 12%, and CO(4–3) with 17%. Thus, the signal mainly comes from CO emitters below z = 4. Only 7.4% of the total shot noise is produced by the two [CI] lines, and most of this (98%) comes from [CI](1–0). Since the CO(1–0) contributes only to approximately one third of the signal, the model presented in Keating et al. (2020) should remain in the 1-σ confidence region of their measurements if they add this contribution.
6. Conclusion
We have presented a new model and its associated public code to generate submillimeter and millimeter intensity mapping simulated cubes from dark-matter light cones. This new model produces realistic dust continuum SEDs that evolve with redshift and with an intrinsic scatter in radiation-field intensity, and thus temperature. The various CO transitions are generated using the combination of two SLEDs (a clump and a diffuse medium). The fraction of each component is also linked to the radiation field. The CO SLEDs of galaxies thus evolve with z and have an intrinsic scatter. [CI] is generated using empirical relations. Finally, [CII] is generated using several prescriptions based on recent [CII] studies and includes a scatter. Our model thus includes a certain level of complexity to test future analysis methods without being too computationally demanding.
Our model successfully reproduces the various observed line luminosity functions of CO and [CI] at z < 4. It also correctly reproduces the CO-dominated shot-noise signal measured around 100 GHz by the mmIME precursor program. Finally, the version of our model using the DL14 prescription for the SFR-[CII] relation is compatible with the first constraints on the [CII] luminosity function at z > 4 from ALPINE.
The forecast of the [CII] power spectra at z = 6 can vary significantly depending on the model. We compiled recent models and found differences of up to 2.5 orders of magnitude between them. These differences can mainly be explained by the very different luminosity functions. Models with high number densities of bright sources have high shot-noise levels, while models with numerous faint populations tend to produce higher levels of correlated fluctuations. However, these discrepancies between models highlight how uncertain the emissivity and the spatial distribution of [CII] are in the high-redshift Universe. The first generation of experiments will therefore have a key role in either confirming or ruling out the optimistic models.
In addition, our new simulation provides a detailed view of the contribution of the various extragalactic components as a function of frequency. The continuum is by far the dominant component and will have to be subtracted with a precision better than one percent. At 305 GHz (z = 5.2), the CO is higher than [CII] in the versions of our model with a standard star formation history at high redshifts.
However, by subtracting the known galaxies from surveys, this contribution becomes lower than 20% of the [CII]. The masking method could thus be suitable at z ≲ 6.5. At higher redshifts (lower frequencies), the [CII] level drops sharply, while CO is almost constant. We will need to develop more advanced methods to isolate [CII]. Our simulation will be ideal to test these future methods, since it does not contain the classic but simplified assumption of component separation methods as fixed CO SLED or dust continuum templates. With our simulation in input, we will be able to perform end-to-end simulations of the full process, and identify and correct the main biases of the analysis pipelines.
The new version of the SIDES simulation is thus a powerful tool for preparing and interpreting future intensity mapping experiments. It can also be used for interferometric spectral scans and photometric surveys (e.g., to forecast the number of detections, properties of the detections, and end-to-end simulations). A companion paper (Gkogkou et al., in prep.) will present a larger simulation and discuss the field-to-field variance on these various probes of galaxy evolution. The code and its products are publicly available9. The code has been developed to be flexible and easily modifiable to adapt to the needs of the community.
As described in Béthermin et al. (2017), starbursts in SIDES are treated as a separate population. Their SFRs are drawn from a relation offset by a factor of approximately six above the main sequence. Because of the scatter around both the main and the starburst sequences, there is no clear border between the two populations in the SFR-M⋆ plane.
We use the same definition of the mean UV radiation field as Magdis et al. (2012), which itself is based on Draine & Li (2007). The unity corresponds to the solar neighborhood.
The study of Karoumpis et al. (2022) was published after most of our analysis was completed, and therefore it is not included here.
Public code by Alexandre Beelen hosted at https://zenodo.org/record/4507624
Acknowledgments
We thank the referee for their insightful comments. We warmly thank Bin Yue, Dongwoo Chung, Marco Viero, Gergö Popping, and Shengqi Yang for sharing their model predictions and discussing them. We thank Gareth Keating for suggesting to test our simulation on the mmIME results and his explanations. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No 788212) and from the Excellence Initiative of Aix-Marseille University-A*Midex, a French “Investissements d’Avenir” program. M.A. acknowledges support from FONDECYT grant 1211951, ANID+PCI+INSTITUTO MAX PLANCK DE ASTRONOMIA MPG 190030, ANID+PCI+REDES 190194 and ANID BASAL project FB210003. A.P. acknowledges support from the ERC Advanced Grant INTERSTELLAR H2020/740120.
References
- Alaghband-Zadeh, S., Chapman, S. C., Swinbank, A. M., et al. 2013, MNRAS, 435, 1493 [Google Scholar]
- Alonso, D., Ferreira, P. G., & Santos, M. G. 2014, MNRAS, 444, 3183 [NASA ADS] [CrossRef] [Google Scholar]
- Amblard, A., Cooray, A., Serra, P., et al. 2011, Nature, 470, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Arata, S., Yajima, H., Nagamine, K., Abe, M., & Khochfar, S. 2020, MNRAS, 498, 5541 [NASA ADS] [CrossRef] [Google Scholar]
- Aravena, M., Decarli, R., Walter, F., et al. 2016a, ApJ, 833, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Aravena, M., Spilker, J. S., Bethermin, M., et al. 2016b, MNRAS, 457, 4406 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., & Conroy, C. 2013, ApJ, 770, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., Hearin, A. P., & Conroy, C. 2019, MNRAS, 488, 3143 [NASA ADS] [CrossRef] [Google Scholar]
- Béthermin, M., Doré, O., & Lagache, G. 2012, A&A, 537, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Wang, L., Doré, O., et al. 2013, A&A, 557, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Kilbinger, M., Daddi, E., et al. 2014, A&A, 567, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Wu, H.-Y., Lagache, G., et al. 2017, A&A, 607, A89 [Google Scholar]
- Béthermin, M., Fudamoto, Y., Ginolfi, M., et al. 2020, A&A, 643, A2 [Google Scholar]
- Birkin, J. E., Weiss, A., Wardlow, J. L., et al. 2021, MNRAS, 501, 3926 [Google Scholar]
- Bisbas, T. G., Tan, J. C., & Tanaka, K. E. I. 2021, MNRAS, 502, 2701 [CrossRef] [Google Scholar]
- Boogaard, L. A., van der Werf, P., Weiss, A., et al. 2020, ApJ, 902, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Bothwell, M. S., Maiolino, R., Peng, Y., et al. 2016, MNRAS, 455, 1156 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Daddi, E., Weiß, A., et al. 2015, A&A, 575, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Franx, M., & Ford, H. 2007, ApJ, 670, 928 [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2012, ApJ, 752, L5 [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2015, ApJ, 803, 34 [Google Scholar]
- Bradač, M., Garcia-Appadoo, D., Huang, K.-H., et al. 2017, ApJ, 836, L2 [Google Scholar]
- Breysse, P. C., Chung, D. T., Cleary, K. A., et al. 2022, ApJ, 933, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Cañameras, R., Yang, C., Nesvadba, N. P. H., et al. 2018, A&A, 620, A61 [Google Scholar]
- Capak, P. L., Carilli, C., Jones, G., et al. 2015, Nature, 522, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Carniani, S., Ferrara, A., Maiolino, R., et al. 2020, MNRAS, 499, 5136 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M., Zavala, J. A., Spilker, J., et al. 2018, ApJ, 862, 77 [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Cheng, Y.-T., Chang, T.-C., Bock, J. J., Bradford, C. M., & Cooray, A. 2016, ApJ, 832, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, Y.-T., Chang, T.-C., & Bock, J. J. 2020, ApJ, 901, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Chung, D. T., Viero, M. P., Church, S. E., & Wechsler, R. H. 2020, ApJ, 892, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Concerto, C., Ade, P., et al. 2020, A&A, 642, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowley, W. I., Lacey, C. G., Baugh, C. M., Cole, S., & Wilkinson, A. 2017, MNRAS, 469, 3396 [NASA ADS] [CrossRef] [Google Scholar]
- Cowley, W. I., Caputi, K. I., Deshmukh, S., et al. 2018, ApJ, 853, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Crites, A. T., Bock, J. J., & Bradford, C. M. 2014, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VII, eds. W. S. Holland, & J. Zmuidzinas, SPIE Conf. Ser., 9153, 91531W [NASA ADS] [CrossRef] [Google Scholar]
- da Cunha, E., Groves, B., Walter, F., et al. 2013, ApJ, 766, 13 [Google Scholar]
- Daddi, E., Elbaz, D., Walter, F., et al. 2010, ApJ, 714, L118 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Dannerbauer, H., Liu, D., et al. 2015, A&A, 577, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davidzon, I., Ilbert, O., Laigle, C., et al. 2017, A&A, 605, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Looze, I., Cormier, D., Lebouteiller, V., et al. 2014, A&A, 568, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decarli, R., Walter, F., Aravena, M., et al. 2016, ApJ, 833, 69 [Google Scholar]
- Decarli, R., Walter, F., Gónzalez-López, J., et al. 2019, ApJ, 882, 138 [Google Scholar]
- Decarli, R., Aravena, M., Boogaard, L., et al. 2020, ApJ, 902, 110 [Google Scholar]
- Dessauges-Zavadsky, M., Zamojski, M., Schaerer, D., et al. 2015, A&A, 577, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Downes, D., & Solomon, P. M. 1998, ApJ, 507, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [CrossRef] [Google Scholar]
- Faisst, A. L., Schaerer, D., Lemaux, B. C., et al. 2020, ApJS, 247, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrara, A., Vallini, L., Pallottini, A., et al. 2019, MNRAS, 489, 1 [Google Scholar]
- Freundlich, J., Combes, F., Tacconi, L. J., et al. 2019, A&A, 622, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fudamoto, Y., Oesch, P. A., Faisst, A., et al. 2020, A&A, 643, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fudamoto, Y., Oesch, P. A., Schouws, S., et al. 2021, Nature, 597, 489 [CrossRef] [Google Scholar]
- Fujimoto, S., Oguri, M., Brammer, G., et al. 2021, ApJ, 911, 99 [Google Scholar]
- Genzel, R., Tacconi, L. J., Gracia-Carpio, J., et al. 2010, MNRAS, 407, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Tacconi, L. J., Lutz, D., et al. 2015, ApJ, 800, 20 [Google Scholar]
- Gong, Y., Cooray, A., Silva, M., et al. 2012, ApJ, 745, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Gong, Y., Silva, M., Cooray, A., & Santos, M. G. 2014, ApJ, 785, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Grazian, A., Fontana, A., Santini, P., et al. 2015, A&A, 575, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greve, T. R., Leonidaki, I., Xilouris, E. M., et al. 2014, ApJ, 794, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Gruppioni, C., Béthermin, M., Loiacono, F., et al. 2020, A&A, 643, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gullberg, B., Lehnert, M. D., De Breuck, C., et al. 2016, A&A, 591, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hernandez-Monteagudo, C., Maio, U., Ciardi, B., & Sunyaev, R. A. 2017, arXiv e-prints [arXiv:1707.01910] [Google Scholar]
- Herrera-Camus, R., Bolatto, A. D., Wolfire, M. G., et al. 2015, ApJ, 800, 1 [Google Scholar]
- Hogg, D. W. 1999, arXiv e-prints [arXiv:astro-ph/9905116] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inami, H., Decarli, R., Walter, F., et al. 2020, ApJ, 902, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Ishigaki, M., Kawamata, R., Ouchi, M., et al. 2018, ApJ, 854, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Ishikawa, S., Kashikawa, N., Hamana, T., Toshikawa, J., & Onoue, M. 2016, MNRAS, 458, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Ishikawa, S., Kashikawa, N., Toshikawa, J., et al. 2017, ApJ, 841, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Jelić, V., Zaroubi, S., Labropoulos, P., et al. 2008, MNRAS, 389, 1319 [CrossRef] [Google Scholar]
- Kamenetzky, J., Rangwala, N., Glenn, J., Maloney, P. R., & Conley, A. 2016, ApJ, 829, 93 [Google Scholar]
- Karoumpis, C., Magnelli, B., Romano-Díaz, E., Haslbauer, M., & Bertoldi, F. 2022, A&A, 659, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kashikawa, N., Yoshida, M., Shimasaku, K., et al. 2006, ApJ, 637, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, H., Kimm, T., Sijacki, D., & Haehnelt, M. G. 2017, MNRAS, 468, 4831 [Google Scholar]
- Keating, G. K., Marrone, D. P., Bower, G. C., & Keenan, R. P. 2020, ApJ, 901, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Khusanova, Y., Bethermin, M., Le Fèvre, O., et al. 2021, A&A, 649, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knudsen, K. K., Richard, J., Kneib, J.-P., et al. 2016, MNRAS, 462, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Kovetz, E. D., Viero, M. P., Lidz, A., et al. 2017, arXiv e-prints [arXiv:1709.09066] [Google Scholar]
- Lagache, G., Dole, H., & Puget, J.-L. 2003, MNRAS, 338, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Bavouzet, N., Fernandez-Conde, N., et al. 2007, ApJ, 665, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Cousin, M., & Chatzikos, M. 2018, A&A, 609, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagos, C. D. P., Bayet, E., Baugh, C. M., et al. 2012, MNRAS, 426, 2142 [Google Scholar]
- Lagos, C. D. P., da Cunha, E., Robotham, A. S. G., et al. 2020, MNRAS, 499, 1948 [CrossRef] [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [Google Scholar]
- Le Fèvre, O., Béthermin, M., Faisst, A., et al. 2020, A&A, 643, A1 [Google Scholar]
- Lee, K.-S., Giavalisco, M., Conroy, C., et al. 2009, ApJ, 695, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Legrand, L., McCracken, H. J., Davidzon, I., et al. 2019, MNRAS, 486, 5468 [NASA ADS] [CrossRef] [Google Scholar]
- Lidz, A., & Taylor, J. 2016, ApJ, 825, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, L., Dickinson, M., Jian, H.-Y., et al. 2012, ApJ, 756, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, D., Gao, Y., Isaak, K., et al. 2015, ApJ, 810, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Loiacono, F., Decarli, R., Gruppioni, C., et al. 2021, A&A, 646, A76 [EDP Sciences] [Google Scholar]
- Lupi, A., & Bovino, S. 2020, MNRAS, 492, 2818 [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [Google Scholar]
- Magdis, G. E., Daddi, E., Béthermin, M., et al. 2012, ApJ, 760, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Magliocchetti, M., Santini, P., Rodighiero, G., et al. 2011, MNRAS, 416, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Carniani, S., Fontana, A., et al. 2015, MNRAS, 452, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Maniyar, A. S., Béthermin, M., & Lagache, G. 2018, A&A, 614, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maniyar, A. S., Béthermin, M., & Lagache, G. 2021, A&A, 645, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCracken, H. J., Wolk, M., Colombi, S., et al. 2015, MNRAS, 449, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. M. 2013, MNRAS, 428, 3121 [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. M. 2018, MNRAS, 477, 1822 [Google Scholar]
- Murmu, C. S., Majumdar, S., & Datta, K. K. 2021, MNRAS, 507, 2500 [NASA ADS] [CrossRef] [Google Scholar]
- Neben, A. R., Stalder, B., Hewitt, J. N., & Tonry, J. L. 2017, ApJ, 849, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Novak, M., Smolčić, V., Delhaize, J., et al. 2017, A&A, 602, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olsen, K., Greve, T. R., Narayanan, D., et al. 2017, ApJ, 846, 105 [Google Scholar]
- Ota, K., Walter, F., Ohta, K., et al. 2014, ApJ, 792, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Ellis, R., Ono, Y., et al. 2013, ApJ, 778, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Pallottini, A., Gallerani, S., Ferrara, A., et al. 2015, MNRAS, 453, 1898 [NASA ADS] [CrossRef] [Google Scholar]
- Pallottini, A., Ferrara, A., Decataldo, D., et al. 2019, MNRAS, 487, 1689 [Google Scholar]
- Pallottini, A., Ferrara, A., Gallerani, S., et al. 2022, MNRAS, 513, 5621 [NASA ADS] [Google Scholar]
- pandas development team 2020, https://doi.org/10.5281/zenodo.3509134 [Google Scholar]
- Papadopoulos, P. P., & Greve, T. R. 2004, ApJ, 615, L29 [Google Scholar]
- Pénin, A., Doré, O., Lagache, G., & Béthermin, M. 2012, A&A, 537, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pillepich, A., Springel, V., Nelson, D., et al. 2018, MNRAS, 473, 4077 [Google Scholar]
- Planck Collaboration XVIII. 2011, A&A, 536, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXX. 2014, A&A, 571, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popping, G., Somerville, R. S., & Trager, S. C. 2014, MNRAS, 442, 2398 [NASA ADS] [CrossRef] [Google Scholar]
- Popping, G., Narayanan, D., Somerville, R. S., Faisst, A. L., & Krumholz, M. R. 2019, MNRAS, 482, 4906 [Google Scholar]
- Riechers, D. A., Pavesi, R., Sharon, C. E., et al. 2019, ApJ, 872, 7 [Google Scholar]
- Rodríguez-Puebla, A., Behroozi, P., Primack, J., et al. 2016, MNRAS, 462, 893 [CrossRef] [Google Scholar]
- Rosenberg, M. J. F., van der Werf, P. P., Aalto, S., et al. 2015, ApJ, 801, 72 [Google Scholar]
- Rowan-Robinson, M., Oliver, S., Wang, L., et al. 2016, MNRAS, 461, 1100 [Google Scholar]
- Saintonge, A., Lutz, D., Genzel, R., et al. 2013, ApJ, 778, 2 [Google Scholar]
- Sargent, M. T., Daddi, E., Béthermin, M., et al. 2014, ApJ, 793, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D., Ginolfi, M., Béthermin, M., et al. 2020, A&A, 643, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schenker, M. A., Robertson, B. E., Ellis, R. S., et al. 2013, ApJ, 768, 196 [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shang, C., Haiman, Z., Knox, L., & Oh, S. P. 2012, MNRAS, 421, 2832 [NASA ADS] [CrossRef] [Google Scholar]
- Silva, M., Santos, M. G., Cooray, A., & Gong, Y. 2015, ApJ, 806, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., Downes, D., Radford, S. J. E., & Barrett, J. W. 1997, ApJ, 478, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., & Vanden Bout, P. A. 2005, ARA&A, 43, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Stacey, G. J., Aravena, M., Basu, K., et al. 2018, in Ground-based and Airborne Telescopes VII, eds. H. K. Marshall, & J. Spyromilio, SPIE Conf. Ser., 10700, 107001M [NASA ADS] [Google Scholar]
- Sun, G., Moncelsi, L., Viero, M. P., et al. 2018, ApJ, 856, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Neri, R., Genzel, R., et al. 2013, ApJ, 768, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., & Sternberg, A. 2020, ARA&A, 58, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Talia, M., Cimatti, A., Giulietti, M., et al. 2021, ApJ, 909, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., & Hollenbach, D. 1985, ApJ, 291, 722 [Google Scholar]
- Tinker, J. L., Robertson, B. E., Kravtsov, A. V., et al. 2010, ApJ, 724, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Uzgil, B. D., Oesch, P. A., Walter, F., et al. 2021, ApJ, 912, 67 [Google Scholar]
- Valentino, F., Daddi, E., Puglisi, A., et al. 2020a, A&A, 641, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valentino, F., Magdis, G. E., Daddi, E., et al. 2020b, ApJ, 890, 24 [Google Scholar]
- Vallini, L., Gallerani, S., Ferrara, A., Pallottini, A., & Yue, B. 2015, ApJ, 813, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Vallini, L., Gruppioni, C., Pozzi, F., Vignali, C., & Zamorani, G. 2016, MNRAS, 456, L40 [Google Scholar]
- Vallini, L., Pallottini, A., Ferrara, A., et al. 2018, MNRAS, 473, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Viero, M. P., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 707, 1766 [NASA ADS] [CrossRef] [Google Scholar]
- Viero, M. P., Wang, L., Zemcov, M., et al. 2013, ApJ, 772, 77 [Google Scholar]
- Walter, F., Decarli, R., Sargent, M., et al. 2014, ApJ, 782, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, F., Decarli, R., Aravena, M., et al. 2016, ApJ, 833, 67 [Google Scholar]
- Wang, X., & Hu, W. 2006, ApJ, 643, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., Farrah, D., Oliver, S. J., et al. 2013, MNRAS, 431, 648 [Google Scholar]
- Wang, L., Pearson, W. J., Cowley, W., et al. 2019a, A&A, 624, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, T., Schreiber, C., Elbaz, D., et al. 2019b, Nature, 572, 211 [Google Scholar]
- Wang, L., Gao, F., Best, P. N., et al. 2021, A&A, 648, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilkinson, A., Almaini, O., Chen, C.-C., et al. 2017, MNRAS, 464, 1380 [NASA ADS] [CrossRef] [Google Scholar]
- Willott, C. J., Carilli, C. L., Wagg, J., & Wang, R. 2015, ApJ, 807, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., Vallini, L., & Chevance, M. 2022, ARA&A, 60, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, L., Sajina, A., Loiacono, F., et al. 2020, ApJ, 905, 147 [Google Scholar]
- Yang, C., Omont, A., Beelen, A., et al. 2017, A&A, 608, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, S., Somerville, R. S., Pullen, A. R., et al. 2021, ApJ, 911, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, S., Popping, G., Somerville, R. S., et al. 2022, ApJ, 929, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Yue, B., & Ferrara, A. 2019, MNRAS, 490, 1928 [NASA ADS] [CrossRef] [Google Scholar]
- Yue, B., Ferrara, A., Pallottini, A., Gallerani, S., & Vallini, L. 2015, MNRAS, 450, 3829 [NASA ADS] [CrossRef] [Google Scholar]
- Zavala, J. A., Casey, C. M., Manning, S. M., et al. 2021, ApJ, 909, 165 [CrossRef] [Google Scholar]
Appendix A: Description of the release
The code and a set of products are released together with this paper. The Python code is released publicly10. It contains the routines used to generate the catalogs, the cubes, and the maps used in this paper. The jupyter notebooks used to produce the plots are also released. We also release the simulated catalog used in this paper11. The columns are described in Table A.1. Finally, the cubes are available at the same address.
Description of the columns of the simulated catalog released together with this paper.
Appendix B: Relation between the CO and infrared luminosity at low redshifts
As we discussed in Sect. 3.1, there is a small offset between the observed 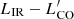 relations and SIDES. However, these relations are measured in the local Universe. As shown by Fig. B.1, there is no offset if we consider only z < 0.2 objects in SIDES. The 0.2 redshift limit was chosen as a compromise between keeping the lowest possible redshift and having a sufficiently large volume in order to have statistics.
relations and SIDES. However, these relations are measured in the local Universe. As shown by Fig. B.1, there is no offset if we consider only z < 0.2 objects in SIDES. The 0.2 redshift limit was chosen as a compromise between keeping the lowest possible redshift and having a sufficiently large volume in order to have statistics.
Appendix C: Analytical computation of the [CII] background from the luminosity function
The [CII] background at a frequency νobs is directly connected to the [CII] luminosity function at a redshift z = (ν[CII],rest/νobs)−1 through the equation:
where ![$ B_\nu^{\rm [CII]} $](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq40.gif) is the surface brightness density of the [CII] background,
is the surface brightness density of the [CII] background, ![$ S_\nu^{\rm [CII]} $](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq41.gif) is flux density corresponding to a line with a luminosity L[CII] at a redshift z, and
is flux density corresponding to a line with a luminosity L[CII] at a redshift z, and ![$ \frac{d^2 N}{dL_{\mathrm{[CII]}} dV} $](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq42.gif) is the [CII] luminosity function, and
is the [CII] luminosity function, and 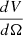 is the differential comoving volume associated with a solid angle dΩ and a small frequency interval dνobs.
is the differential comoving volume associated with a solid angle dΩ and a small frequency interval dνobs.
The [CII] flux density depends on the frequency interval dν and can be obtained using the Carilli & Walter (2013) formula to convert luminosities into fluxes:
where ![$ S_\nu^{\rm [CII]} $](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq45.gif) , L[CII], and DL are expressed in Jy, L⊙, and Mpc, respectively. Velocities c and dυ are expressed in km/s and frequencies are expressed in GHz. The C value is constant and equal to 1.04 × 10−3 L⊙ (Jy km s−1 GHz Mpc2)−1.12
, L[CII], and DL are expressed in Jy, L⊙, and Mpc, respectively. Velocities c and dυ are expressed in km/s and frequencies are expressed in GHz. The C value is constant and equal to 1.04 × 10−3 L⊙ (Jy km s−1 GHz Mpc2)−1.12
The differential comoving volume element 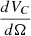 is (see, e.g., Hogg 1999):
is (see, e.g., Hogg 1999):
where H(z) is the Hubble parameter at a redshift z (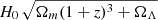 for a flat cosmology).
for a flat cosmology).
By combining Eq. C.1, C.2, and C.3, we obtain:
The result is in Jy/sr if the units mentioned previously are used. We can remark that the two terms in dν from the previous equation cancel each other. This is normal, since the background does not depend on the resolution.
The exact same computation can be performed for the various CO and [CI] transitions.
Appendix D: Analytical computation of the [CII] shot noise from the luminosity function
The Poisson part of the 2D power spectrum of the [CII] (![$ P_{\mathrm{Poi}}^{\mathrm{[CII]}} $](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq50.gif) ) from a thin frequency slice with a center νobs and a width Δν can be computed using a similar approach as in Sect. C:
) from a thin frequency slice with a center νobs and a width Δν can be computed using a similar approach as in Sect. C:
The flux density squared term is similar to the one in the computation of the CIB shot noise (e.g., Lagache et al. 2003).
We then combine the Eq. D.1, C.2, and C.3 and obtain:
We remark that the terms in dν do not simplify and the Poisson term is inversely proportional to Δν. This behavior is expected, since doubling the frequency width dilutes the line fluxes by a factor of two, and the power spectrum by a factor of four, while the power spectra of two independent redshift slices sum linearly (factor of two). However we can define a quantity independent of the spectral resolution:
This quantity is used, for instance, by Keating et al. (2020) to report the CO shot noise measured around 100 GHz. This normalization applies only to the shot-noise component and not to the large-scale clustering term, since the frequency slices are no longer independent in the presence of clustering.
The 3D power spectrum can be derived using Eq. 15:
We note that the 3D power spectrum is independent of the spectral resolution.
Appendix E: Conversion of the shot noise from μK2 Hz sr to Jy2 sr−1 GHz
The shot noise measured by the mmIME (Keating et al. 2020) is expressed in μK2 Hz sr, while we use Jy2 sr−1 GHz in our simulation. We detail here the conversion from one unit to the other.
The conversion from sky temperature T at a given observed frequency νobs and surface brightness density Bν expressed in SI units:
where kB is the Boltzmann constant and c is the speed of light. The conversion from μK to Jy2/sr involves two extra factors: 10−6 (from μK to K) and 1026 (from SI to Jy). An additional factor of (109)2 must be applied if we want to use GHz instead of Hz. We thus get:
This conversion factor must be squared for the power spectrum units. We also have to convert the bandwidth normalization from Hz to GHz. We finally obtain:
where 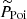 is the shot noise, normalized to be bandwidth independent (see Appendix D).
is the shot noise, normalized to be bandwidth independent (see Appendix D).
All Tables
Comparison between the measured ALMA stacked fluxes of CO(2–1) of MUSE-selected 1 < z < 1.7 galaxies by Inami et al. (2020) and our results from SIDES (see a description of the computation method in Sect. 3.3).
Description of the columns of the simulated catalog released together with this paper.
All Figures
 |
Fig. 1. Empirical relations used to produce the [CI] line fluxes. Upper panel: relation between the L[CI](1 − 0)/LIR and LCO(4 − 3)/LIR ratios. The filled blue circles and the red filled squares are, respectively, the low-z and high-z galaxies compiled by Valentino et al. (2020b). The solid line is our best-fit of this correlation used to generate [CI](1–0) fluxes in our simulation. Lower panel: same figure for the relation between the L[CI](2 − 1)/L[CI](1 − 0) and LCO(7 − 6)/LCO(4 − 3) ratios. |
| In the text | |
 |
Fig. 2. Slices of simulated CONCERTO data cubes. These cubes are produced using a Gaussian beam and have no instrumental noise. Each slice has a 1 GHz width. The four columns, from the left to the right, correspond to 305 GHz (z[CII] = 5.23, Δz[CII] = 0.020), 275 GHz (z[CII] = 5.91, Δz[CII] = 0.025), 245 GHz (z[CII] = 6.75, Δz[CII] = 0.032), and 215 GHz (z[CII] = 7.83, Δz[CII] = 0.041). Five rows, from top to bottom: the cubes containing all the components, including the continuum, all the lines, the CO lines only, the [CI] lines, and the [CII] line. To make comparisons easier, the color scale of the four panels with continuum (top row) is the same. All the other panels share another common color scale. We assume the DL14 [CII]-SFR relation in this figure. |
| In the text | |
 |
Fig. 3. Evolution of the star formation rate density. The solid gray line is derived from the SIDES simulation and the solid brown line is an alternative model at z > 4 for which we boosted the SFRs to obtain a flat SFRD at high-redshifts (“high SFRD” model, see Sect. 2.7). The SFR boosting factor to obtain a flat SFRD is computed from the fit of the z > 4 original model (dotted line). The compilations of UV-derived and infrared-derived measurements by Madau & Dickinson (2014) are represented by blue crosses and filled orange circles, respectively. We also show the measurement from the ALPINE survey based on the luminosity function of serendipitous continuum detections (Gruppioni et al. 2020, red upward-pointing triangles), the [CII] luminosity function of serendipitous detection (Loiacono et al. 2021, purple downward-pointing triangles), and an indirect method using the stacking of the target sample (Khusanova et al. 2021, dark orange squares). The dark red left-pointing triangles are the estimates of the obscured SFRD from REBELS by Fudamoto et al. (2021), using the continuum (low value) and the [CII] (high value). The constraints from the radio from Novak et al. (2017) are shown using green right-pointing triangles. As discussed in Sect. 4.4, the SFRD at z > 7 could be underestimated by our simulation because of its halo mass limit, and thus a paler color is used. |
| In the text | |
 |
Fig. 4. Relation between the CO and the far-infrared luminosity integrated between 40 and 400 μm. The number of density of SIDES galaxies is coded using a gray scale. The best-fit observed relations of Greve et al. (2014, local and high-z (U)LIRGs), Liu et al. (2015, low-z sample), and Kamenetzky et al. (2016, low-z sample) are represented by a solid red, a dotted green, and a dashed blue line, respectively. These relations are plotted only in the luminosity range in which they were measured. It should be noted that the Liu et al. (2015) study does not include the three lowest rotationnal transitions of CO. |
| In the text | |
 |
Fig. 5. CO(1–0) luminosity function at z ∼ 2.4. The solid black line is computed using SIDES and the filled blue rectangles are the measurements of Riechers et al. (2019, 51+9 arcmin2) using the JVLA COLDz survey. The width of the rectangles indicates the bin size and the height shows the 1-σ confidence region. |
| In the text | |
 |
Fig. 6. Comparison between CO luminosity from the SIDES simulations (solid black lines) and the observations for various transitions and redshifts (see details above each panel). Observational data are represented by filled rectangles, whose width indicates the bin size and whose height shows the 1-σ confidence region. The PdBI HDFM program of Walter et al. (2016, 1 arcmin2) is in green. The ALMA/ASPECS pilot program is in blue (1 arcmin2 Decarli et al. 2016) and the large program is in red (4.6 arcmin2Decarli et al. 2019, 2020). |
| In the text | |
 |
Fig. 7. Comparison between the stacked SLEDs of Boogaard et al. (2020) and the results from SIDES. The filled blue and red circles represent the SLED of z ∼ 1.2 objects detected in CO(2–1). The red filled squares correspond to the z ∼ 2.5 objects detected in CO(3–2). The SLED is normalized to unity for the transition used to select the sample to stack. The light and dark shaded areas show, respectively, the 1 and 2σ confidence region of the mean SLED in our simulation, taking into account the sample variance (see Sect. 3.3). |
| In the text | |
 |
Fig. 8. Comparison between the [CI] luminosity functions from the SIDES simulation (solid black line) and the ASPECS survey (red areas, Decarli et al. 2020, 4.6 arcmin2). |
| In the text | |
 |
Fig. 9. Current constraints on the [CII] luminosity function at z ∼ 4.5 (upper panel) and z ∼ 5.5 (lower panel), and comparison with our SIDES simulation. The filled blue (z ∼ 4.5) and red (z ∼ 5.5) rectangles show the reconstruction of the luminosity function from the ALPINE sample (Yan et al. 2020). The two data points at the lowest luminosities could be impacted by non-detections and the upper limits estimated by Yan et al. (2020) are shown as downward arrows. The constraint at z ∼ 5 using the other sideband of ALPINE is shown with green rectangles (Loiacono et al. 2021). The solid red lines and the dashed orange lines are the SIDES results, assuming the DL14 or the L18 relation, respectively. The long-dashed brown line is the flat high-z SFRD version of SIDES. |
| In the text | |
 |
Fig. 10. Comparison between the luminosity functions produced by various models at z = 6. The solid red lines and the dashed orange lines represent the SIDES luminosity function using the DL14 or the L18 relation, respectively. The long-dashed brown line is the high SFRD version of SIDES. The models shown for comparison are Lagache et al. (2018, two-dot-dashed turquoise line), Yang et al. (2022, dotted blue line), Yue & Ferrara (2019, short-dash-long-dashed purple line), and Chung et al. (2020, dot-dashed green line). |
| In the text | |
 |
Fig. 11. Cosmic line background as a function of frequency. The solid red line, the dashed yellow line, and the long-dashed brown line, show the predictions of our simulation assuming the DL14 relation, the L18 relation, and the flat z > 4 SFRD (see Sect. 2.7), respectively. The CO, [CI], and continuum background predicted by SIDES are shown as a dot-dashed blue line, a two-dot-dashed dark blue line, and a solid gray line, respectively. The dot-dashed green line, the short-dash-long-dashed purple line, and the dotted blue line are the [CII] forecast from the Chung et al. (2020) model, the Yue & Ferrara (2019) model, and the Yang et al. (2022) model, respectively. |
| In the text | |
 |
Fig. 12. Comparison of the 3D [CII] power spectra at z = 6 from various models. The lengths are in comoving units. We also indicate the corresponding projected angular wavenumber at z = 6 as the upper x-axis. The x-axis range corresponds approximately to the scales, which will be probed by CONCERTO. The solid red and dashed orange dashed lines are from the SIDES simulation assuming the DL14 and L18 relations, respectively. The long-dashed brown line is the high-SFRD version of SIDES (see Sect. 2.7). We also compare with the models of Yue & Ferrara (2019, two-dot-dashed purple line), Chung et al. (2020, dot-dashed green line), and Yang et al. (2022, dotted blue line). |
| In the text | |
 |
Fig. 13. Effect of the halo mass limit on various [CII] observables (see Sect. 4.4). The curves show the total contribution of galaxies to these observables per logarithmic interval of host halo masses (dex). All the curves are normalized to have their maximum equal to one. Top, central, and bottom panels: correspond to z ∼ 5, z ∼ 6, and z ∼ 7, respectively. Left panels: have a y-axis in linear units, allowing us to naturally visualize the area under the curves, and the right panels are in logarithmic scale to better visualize the behavior at low masses. The gray curve is the number density of the halos and the vertical dotted line shows the halo mass limit of 1010.5 M⊙. The dashed blue line shows the contribution of galaxies to the [CII] background, which is directly derived from the integral of the [CII] line luminosities (see Appendix C). The dot-dashed green line is the contribution to the shot noise, which is directly connected to the integral of the [CII] luminosity squared (see Appendix D). Finally, the solid red curve presents the integral of the luminosity of the galaxies multiplied by the linear bias corresponding to their halo mass. This term is directly connected to the amplitude of the correlated fluctuation of the [CII] background (see Sect. 4.4). |
| In the text | |
 |
Fig. 14. Contribution of the various extragalactic components to the CONCERTO angular power spectra at 305 GHz (upper left panel), 270 GHz (upper right panel), 240 GHz (lower left panel), and 210 GHz (lower right panel) predicted by SIDES. As discussed in Sect. 4.4, the [CII] power spectra at 210 GHz (z = 8.1) could be significantly underestimated by our model. To minimize the effect of the field-to-field variance, we computed the average of the 11 power spectra corresponding to the 1 GHz-wide slices placed between 5 GHz below and above the central slice (except at 305 GHz, for which we have no slice at a higher frequency). The continuum is represented by the dotted line. The solid red lines and the dashed orange lines show the [CII] contribution in SIDES assuming the DL14 and the L18 relations, respectively. The long-dashed brown lines represent the high-SFRD variant of the model (see Sect. 2.7). The black and gray lines show the contribution from both CO and [CI] before and after removing the known galaxies from surveys (see Sect. 5.4). |
| In the text | |
 |
Fig. 15. Level of the power spectrum of the various components in SIDES as a function of the frequency. Left panel: the small scales dominated by the shot noise and the right panel shows the large scales. The dotted black line is the continuum computed using the standard model (low SFRD). The solid red line, the long-dashed brown line, and the short-dashed orange lines are the SIDES predictions for [CII] using the DL18, high-SFRD, and L18 versions, respectively. As discussed in Sect. 4.4, the [CII] power spectra at z > 7 may be underestimated. We thus used a paler color to illustrate it. The dot-dashed light-blue line and the dash-dot-dot dark-blue lines correspond to all the CO and [CI] lines, respectively. The solid black line shows the total contribution of all the CO and [CI] lines, while the solid gray line is the same after masking galaxies known from galaxy surveys (see Sect. 5.4). For a better visualization, we smoothed the curves by a Gaussian kernel with a σ of 3 GHz. |
| In the text | |
 |
Fig. 16. Contribution of the various CO lines to the Poisson term (left panels) and the large-scale power spectrum (right panels) before (upper panels) and after (lower panels) masking the known galaxies from surveys. Together with the total CO (solid black line), we show the contribution of CO(2–1) (long-dashed red line), CO(3–2) (short-dashed orange line), CO(4–3) (dotted green line), CO(5–4) (long-dash-dot turquoise line), CO(6–5) (two-dot-dash light-blue line), CO(7–6) (dot-two-dash dark-blue line), and CO(8–7) (two-dash-two-dot purple line). For a better visualization, we smoothed the curves by a Gaussian kernel with a σ of 3 GHz. |
| In the text | |
 |
Fig. 17. Contribution of the two [CI] transitions to the Poisson term (left panels) and large-scale power spectrum (right panels) before (upper panels) and after (lower panels) masking the known galaxies from surveys. The solid black line represents the total, while the dotted red line and the dashed blue line correspond to the [CI](1–0) and [CI](2–1) transitions, respectively. For a better visualization, we smoothed the curves by a Gaussian kernel with a σ of 3 GHz. |
| In the text | |
 |
Fig. 18. Shot-noise level predicted by SIDES as a function of frequency and a comparison with the mmIME measurements (Keating et al. 2020, total area of 20 arcmin2, horizontal dark gray line and associated 1σ area for the MLE method, dark blue line and area for the simpler instrumental noise correction). The frequency range shown in this figure corresponds to the mmIME used. The filled black circle is the average shot noise predicted by SIDES in this range. The solid black line is the total of CO and [CI]. The various colored lines captioned directly in the figures indicate the contribution of each CO transition. |
| In the text | |
 |
Fig. B.1. Same plot as for Fig. 4, but considering the z< 0.2 objects in SIDES. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \log _{10} \left( \frac{L_{\rm [CII]}^{\mathrm{DL14}}}{L_\odot } \right) = 7.06 + \log _{10} \left( \frac{\mathrm{SFR}}{M_\odot \, \mathrm{yr}^{-1}} \right)\!. \end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq1.gif)
![$$ \begin{aligned} \log _{10} \left( \frac{L_{\rm [CII]}^{L18}}{L_\odot } \right) = (1.4 - 0.07 { z}) \log _{10} \left( \frac{\mathrm{SFR}}{{M_\odot \, \mathrm{yr}^{-1}}} \right) + 7.1 - 0.07 { z}. \end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq2.gif)
![$$ \begin{aligned} I_{\rm [CII]} = \mu \, \frac{1}{1.04 \times 10^{-3} \, D_{\rm L}^2 \, \nu _{\rm obs}} \, L_{\rm [CII]}, \end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq3.gif)
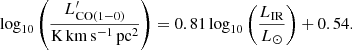
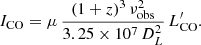
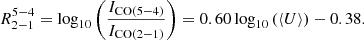
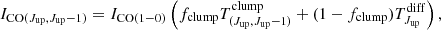
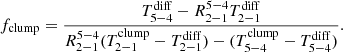
}}{L_{\rm IR}} \right) = 1.07 \, \log _{10} \left( \frac{L_{\rm CO(4-3)}}{L_{\rm IR}} \right) + 0.14. \end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq15.gif)
}}{L_{\rm [CI](1-0)}} \right) = 0.63 \, \log _{10} \left( \frac{L_{\rm CO(7-6)}}{L_{\rm CO(4-3)}} \right) + 0.17. \end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq16.gif)
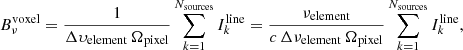
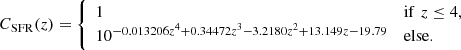
![$$ \begin{aligned} B_\nu ^\mathrm{[CII]} (\nu _{\rm obs}) = \frac{1}{C \, (1+{ z}) \, \nu _{\rm obs} \, H({ z})} \int L_{\rm [CII]} \, \frac{d^2 N}{\mathrm{d}L_{\rm [CII]} \mathrm{d}V} \, \mathrm{d}L_{\rm [CII]}, \end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq24.gif)
![$$ \begin{aligned} S_\nu = \frac{ \sum _{\rm sources} I_{\rm [CII]}}{\Omega _{\rm voxel} \, \Delta \upsilon _{\rm voxel}} = \frac{(1+{ z}_{\rm voxel}) \, \sum _{\rm sources} I_{\rm [CII]}}{\Omega _{\rm voxel} \, \Delta { z}_{\rm voxel} \,c}, \end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq27.gif)
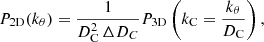
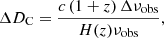
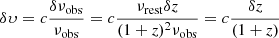
![$$ \begin{aligned} B_\nu ^\mathrm{[CII]} (\nu _{\rm obs}) = \int S_\nu ^\mathrm{[CII]} \frac{d^2 N}{dL_{\rm [CII]} dV_C} \frac{d V_C}{d \Omega } \, dL_{\rm [CII]} , \end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq39.gif)
![$$ \begin{aligned} S_\nu ^\mathrm{[CII]} = \frac{L_{\rm [CII]}}{C d \upsilon \, \nu _{\rm obs} \, D_L^2} = \frac{L_{\rm [CII]}}{C \, c \, d \nu _{\rm obs} \, D_L^2}, \end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq44.gif)
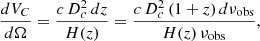
![$$ \begin{aligned} B_\nu ^\mathrm{[CII]} (\nu _{\rm obs}) = \frac{1}{C \, (1+{ z}) \, \nu _{\rm obs} \, H({ z})} \int L_{\rm [CII]} \, \frac{d^2 N}{dL_{\rm [CII]} dV_C} \, dL_{\rm [CII]}. \end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq49.gif)
![$$ \begin{aligned} P_{\rm Poi}^\mathrm{[CII]} (\nu _{\rm obs}) = \int \left( S_\nu ^\mathrm{[CII]} \right)^2 \frac{d^2 N}{dL_{\rm [CII]} dV_C} \frac{d V_C}{d \Omega } \, dL_{\rm [CII]}. \end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq51.gif)
![$$ \begin{aligned} P_{\rm Poi}^\mathrm{[CII]} (\nu _{\rm obs}) = \frac{1}{C^2 \, c \, D_L^2 \, (1+{ z}) \, H({ z}) \, \nu _{\rm obs} \Delta \nu _{\rm obs}} \int L_{\rm [CII]}^2 \, \frac{d^2 N}{dL_{\rm [CII]} dV_C} \, dL_{\rm [CII]}. \end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq52.gif)
![$$ \begin{aligned} \widetilde{P}_{\rm Poi}^\mathrm{[CII]} = {P}_{\rm Poi}^\mathrm{[CII]} \times \Delta \nu _{\rm obs}. \end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq53.gif)
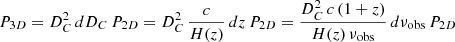
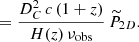
![$$ \begin{aligned} B_\nu [\mathrm{W m^{-2} sr^{-1} Hz^{-1}}]&= 2 k_B \left( \frac{\nu _{\rm obs} [\mathrm{Hz]}}{c} \right)^2 T[K] \nonumber \\&= 2 \times 1.38 \times 10^{-23} \left( \frac{\nu _{\rm obs} [\mathrm{Hz}]}{3 \times 10^{8}} \right)^2\,T[\mathrm{K}]\end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq56.gif)
![$$ \begin{aligned}&= 3.07 \times 10^{-40} \nu _{\rm obs}^2 [\mathrm{Hz^2}] T[\mathrm{K}], \end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq57.gif)
![$$ \begin{aligned} B_\nu [\mathrm{Jy\,sr^{-1}}] = 0.0307 \, \nu _{\rm obs}^2 [\mathrm{GHz^2}] \, T[ \mu \mathrm{K}]. \end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq58.gif)
![$$ \begin{aligned} \widetilde{P}_{\rm Poi} [ \mathrm{Jy^2 \, sr^{-1} \, GHz}]&= 0.0307^2 \times 10^{-9}\, \nu ^4 [\mathrm{GHz^4}] \, \widetilde{P}_{\rm Poi} [ \mathrm{\mu K^2 \,Hz\,sr} ]\end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq59.gif)
![$$ \begin{aligned}&= 9.44 \times 10^{-13} \, \nu _{\rm obs}^4 [\mathrm{GHz}] \, \widetilde{P}_{\rm Poi} \, [ \mathrm{\mu K^2 \,Hz\,sr} ], \end{aligned} $$](/articles/aa/full_html/2022/11/aa43888-22/aa43888-22-eq60.gif)