| Issue |
A&A
Volume 656, December 2021
|
|
|---|---|---|
| Article Number | A147 | |
| Number of page(s) | 24 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202142168 | |
| Published online | 15 December 2021 | |
CLASH-VLT: Abell S1063
Cluster assembly history and spectroscopic catalogue
1
INAF-Osservatorio Astronomico di Capodimonte, Via Moiariello 16, 80131 Napoli, Italy
e-mail: amata.mercurio@inaf.it
2
Dipartimento di Fisica e Scienze della Terra, Università di Ferrara, Via Saragat 1, 44122 Ferrara, Italy
3
INAF – OAS, Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Gobetti 93/3, 40129 Bologna, Italy
4
INAF-Osservatorio Astronomico di Trieste, Via G. B. Tiepolo 11, 34143 Trieste, Italy
5
IFPU – Institute for Fundamental Physics of the Universe, Via Beirut 2, 34014 Trieste, Italy
6
Centro de Astrobiología, Instituto Nacional de Técnica Aeroespacial, Ctra de Torrejón a Ajalvir, km 4, 28850 Torrejón de Ardoz, Madrid, Spain
7
Dipartimento di Fisica, Univ. degli Studi di Trieste, Via Tiepolo 11, 34143 Trieste, Italy
8
Dipartimento di Fisica, Università degli Studi di Milano, Via Celoria 16, 20133 Milano, Italy
9
INAF – IASF Milano, Via A. Corti 12, 20133 Milano, Italy
10
OmegaLambdaTec GmbH, Lichtenbergstrasse 8, 85748 Garching bei Munchen, Germany
11
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85748 Garching, Germany
12
Instituto de Física, Pontificia Universidad Católica de Valparaíso, Casilla, 4059 Valparaíso, Chile
13
Max Planck Institute for Extraterrestrial Physics, Giessenbachstrasse, 85748 Garching, Germany
14
Universitäts-Sternwarte, Fakultät für Physik, Ludwig-Maximilians Universität München, Scheinerstr. 1, 81679 München, Germany
15
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi, 50125 Firenze, Italy
16
INFN–Sezione di Trieste, Trieste, Italy
17
Departamento de Astronomía, Facultad de Ciencias Físicas y Matemáticas, Universidad de Concepción, Concepción, Chile
18
INAF – Osservatorio Astronomico di Brera, Via Brera 28, 20121 Milano, Italy
19
Institute for Particle Physics and Astrophysics, ETH Zürich, Wolfgang-Pauli-Str. 27, 8093 Zürich, Switzerland
20
Academia Sinica Institute of Astronomy and Astrophysics (ASIAA), No. 1, Section 4, Roosevelt Road, Taipei 10617, Taiwan
21
Carnegie Observatories, 813 Santa Barbara Street, Pasadena, California 91101, USA
22
University of Vienna, Department of Astrophysics, Tuerkenschanzstrasse 17, 1180 Vienna, Austria
23
Space Telescope Science Institute, 3700 San Martin Dr., Baltimore, MD 21218, USA
24
Dipartimento di Fisica e Astronomia, Universitá degli Studi di Padova, Padova, Italy
Received:
7
September
2021
Accepted:
30
October
2021
Context. The processes responsible for galaxy evolution in different environments as a function of galaxy mass remain heavily debated. Rich galaxy clusters are ideal laboratories in which to distinguish the role of environmental versus mass quenching because they consist of a full range of galaxies and environments.
Aims. Using the CLASH-VLT survey, we assembled an unprecedentedly large sample of 1234 spectroscopically confirmed members in Abell S1063. We found a dynamically complex structure at ⟨zcl⟩ = 0.3457 with a velocity dispersion σv = 1380−32+26 km s−1. We investigated cluster environmental and dynamical effects by analysing the projected phase-space diagram and the orbits as a function of galaxy spectral properties.
Methods. We classified cluster galaxies according to the presence and strength of the [OII] emission line, the strength of the Hδ absorption line, and colours. We investigated the relation between the spectral classes of galaxies and their position in the projected phase-space diagram. We separately analysed red and blue galaxy orbits. By correlating the observed positions and velocities with the projected phase-space constructed from simulations, we constrained the accretion redshift of galaxies with different spectral types.
Results. Passive galaxies are mainly located in the virialised region, while emission-line galaxies lie beyond r200 and are accreted into the cluster at a later time. Emission-line and post-starburst galaxies show an asymmetric distribution in projected phase-space within r200; emission-line galaxies are prominent at Δv/σ ≲ −1.5 and post-starburst galaxies at Δv/σ ≳ 1.5, suggesting that backsplash galaxies lie at high positive velocities. We find that low-mass passive galaxies are accreted into the cluster before high-mass galaxies. This suggests that we observe as passives only the low-mass galaxies that are accreted early into the cluster as blue galaxies. They had the time to quench their star formation. We also find that red galaxies move on more radial orbits than blue galaxies. This can be explained if infalling galaxies can remain blue by moving on tangential orbits.
Key words: galaxies: clusters: general / galaxies: clusters: individual: A S1063 / galaxies: kinematics and dynamics / galaxies: stellar content / galaxies: evolution
© ESO 2018
1. Introduction
Massive galaxy clusters at intermediate redshifts represent ideal test-beds in which to study the impact of hierarchical cluster assembly on galaxy evolution. The galaxy population in clusters has evolved rapidly over the last 5 Gyr (Butcher & Oemler 1978, 1984). Star-forming spiral galaxies found at z ∼ 0.2–0.4 are mainly replaced by the S0 galaxies in local clusters (Dressler et al. 1997; Treu et al. 2003). This suggests that clusters accrete blue gas-rich star-forming spirals at z ≳ 0.5 − 1. Then these galaxies are transformed into the passive S0s that are found in the local clusters. This transformation is due to the depletion of their gas reservoir by one or more cluster-related mechanisms, such as ram pressure (see Sheen et al. 2017; Foltz et al. 2018 for an example) and/or strangulation, tidal stripping, harassment, mergers, and group-cluster collisions (see Boselli & Gavazzi 2006).
Observational evidence reveals that at least at z < 1, the current properties and past evolution of galaxies are strongly dependent on the environment (e.g., Blanton et al. 2005; Tanaka et al. 2005; Peng et al. 2010; Nantais et al. 2016; Lemaux et al. 2019). Moreover, the fraction of quenched galaxies strongly depends on galaxy mass (e.g., van der Burg et al. 2020). For massive galaxies, the star formation histories and morphologies seem to be determined by their build-up through mergers and the probable consequent feedback from Supernovae (SN) and Active Galactic Nuclei (AGN) (e.g., Gómez et al. 2003; Tanaka et al. 2004; Haines et al. 2006; Fritz et al. 2009). Dwarf galaxies, instead, are more strongly affected by environmental effects. Passive dEs are found as satellites within massive halos, whether that is a cluster, group, or massive galaxy (Haines et al. 2006, 2007; Boselli & Gavazzi 2014; Fritz et al. 2014; Roberts et al. 2019).
Despite decades of work (e.g., Dressler 1980; Kauffmann et al. 2004; Balogh et al. 2004; Postman et al. 2005; Smith et al. 2005; Mercurio et al. 2010; Moresco et al. 2010; Kovač et al. 2014; Just et al. 2015; Annunziatella et al. 2014, 2016; Jaffé et al. 2015; Boselli et al. 2016; Rhee et al. 2017, 2020; Oemler et al. 2017; Owers et al. 2019), the evolutionary pathways and the relative importance of the processes that govern galaxy transformations as a function of mass (mass quenching, e.g., AGN or SN feedback) and environment (environmental quenching, e.g., ram-pressure and/or tidal stripping, harassment, group-cluster collisions, and starvation) remain heavily debated. To properly address this issue, it is necessary to observe a large sample of infalling galaxies all the way from the cluster centre out to the field, in halos of different masses and at epochs when the galaxy population is still rapidly evolving.
Spectroscopic information is needed to identify the infalling population from the background and foreground galaxies. In this case, a useful tool for investigating the quenching of star formation in cluster galaxies is the study of their velocities and positions in the projected phase-space diagram. Cosmological simulations have confirmed that cluster galaxies tend to follow a common path in the 3D phase-space diagram (see Fig. 1 in Rhee et al. 2017). Thus, it is possible to trace back the accretion histories of galaxies in clusters, associating different populations with different phase-space locations (virialised, infalling, or backsplash; e.g. Pasquali et al. 2019).
In this context, we present a detailed study of the galaxy population of the galaxy cluster Abell S1063 (hereafter A S1063; Abell et al. 1989), a very massive cluster at z = 0.348 (Karman et al. 2015) with a total mass of (2.9±0.3)×1015 M⊙ (Sartoris et al. 2020). The cluster was also catalogued as RXJ2248.7−4431 because it was detected in the ROSAT All-Sky Survey (De Grandi et al. 1999; Guzzo et al. 1999). It has a high X-ray luminosity (LX ≈ 8 × 1045 erg s−1) and high X-ray temperature, TX ≈ 13 KeV (Gómez et al. 2012). An SZ signal is also detected with high significance in the Planck data (Planck Collaboration VIII 2011; Plagge et al. 2010).
Gómez et al. (2012) proposed that A S1063 hosts a recent merger event close to the plane of sky along the NE–SW direction. They derived their conclusion as based on the spectroscopic GMOS data for 51 members and X-ray Chandra data. This NE–SW elongation is also visible in X-ray and in the dark matter (DM) distribution as reconstructed by the strong-lensing analysis (see Fig. 2 in Bonamigo et al. 2018). However, the DM and hot-gas mass distributions have different shapes and centres because their physical properties are intrinsically different. While the DM component is roughly centred on the brightest cluster galaxy (BCG), the hot-gas mass distribution is skewed towards the northeast and is rounder than the DM distribution. Moreover, Xie et al. (2020) found a giant radio halo with a size of ∼1.2 Mpc and an integrated spectral index that steepens between 1.5 and 3.0 GHz.
Sartoris et al. (2020) performed a full dynamical reconstruction of the mass density profile from the very centre (∼1 Kpc) out to the virial radius. They separted the DM profile from the total mass profile and showed the different contributions of the stellar mass profile of cluster members, BCG, and of the intra-cluster gas mass profile. They found the inner slope of the DM density profile modelled as a gNFW, γDM = 0.99 ± 0.04, in agreement with the predictions from the ΛCDM model.
Other previous studies of this cluster include the weak-lensing (WL) analysis presented in Gruen et al. (2013), the detection of ultra-diffuse galaxies in Lee et al. (2017), the analysis of the Kormendy relation in Tortorelli et al. (2018), the analysis of the enhancement in (O/H) in Ciocan et al. (2020), and the analysis of Chandra X-ray observations and 325 MHz Giant Metre Radio Telescope observations in Rahaman et al. (2021).
The cluster A S1063 was part of the HST treasury program CLASH (Postman et al. 2012) and of the Frontier Field initiative1 (Lotz et al. 2017, hereafter FF). In this paper, we exploit and make public the extensive CLASH-VLT spectroscopic campaign (Rosati et al. 2014, and in prep.) of the A S1063 field with the VIMOS spectrograph, augmented with MUSE integral-field spectroscopy in the cluster core (Caminha et al. 2017).
This paper specifically presents the analysis of low- and medium-resolution VIMOS spectroscopic data, combined with multi-band photometry from HST/FF and the WFI at the ESO 2.2 m telescope. The purpose of this study is to explore the dominant quenching processes by focusing on the accretion histories of cluster galaxies through the analysis of the projected phase-space diagram enabled by the available unique spectroscopic sample. The structure of this paper is the following. Observations and catalogues are described in Sect. 2 and in Appendix A. The member selection, the dynamical analysis, and the substructures are discussed in Sects. 3–5 and in Appendix B. We describe the spectroscopic classification of galaxies in Sect. 6. In Sect. 7 we discuss the accretion history of galaxies in the cluster, using the location in the phase-space diagram as a diagnostic of the accretion redshift, and also for the comparison with simulations and the analysis of the orbits. Finally, in Sects. 8, we discuss and summarise our results.
Throughout the paper we adopt a cosmology with Ωm = 0.3, ΩΛ = 0.7, and H0 = 70 km s−1 Mpc−1. According to this cosmology, 1 arcmin corresponds to 0.294 Mpc at z = 0.3457. Unless otherwise specified, figures are oriented with north at the top and east to the left, magnitudes are in the AB system, and stellar masses are obtained using a Salpeter IMF (Salpeter 1955).
2. Observations and catalogues
In this paper, we examine the spectro-photometric dataset of A S1063. It provides a unique combination of photometric coverage over a wide wavelength range [0.2–1.6] μm, from HST, ground-based WFI observations, and wide-field VLT-VIMOS spectroscopy. This is further complemented with the integral-field VLT-MUSE spectroscopy in the central 0.3 Mpc region. The photometric data and catalogues are presented in Appendix A, while in this section, we describe the spectroscopy. Figure 1 summarises the data we used.
 |
Fig. 1. Ground-based and HST color image of the galaxy cluster Abell S1063 with the wedge redshift diagram from the CLASH-VLT survey. Right panel: WFI colour-composite image of A S1063 (UBVRIz, 30 × 30 arcmin2). The cyan square indicates the VIMOS spectroscopic survey area (28.9 × 22.7 arcmin2), and the white and green polygons indicate the HST FF colour-composite image (F435W, F606W, and F814W) and the footprint of MUSE observations (two pointings, 2 × 1 arcmin2) enlarged in the inset. The dotted and dashed circles have radii R = 1 Mpc and R = r200, respectively. Left panel: 3D spatial distribution of all measured redshifts at 0.2 < z < 0.6, where cluster members are marked in red. |
2.1. Spectroscopy
The analysis presented here is based on low- and medium-resolution VIMOS spectroscopic data obtained in 25 × 25 arcmin2. Moreover, we use MUSE integral-field spectroscopy in the cluster core that we published in Caminha et al. (2017) and additional redshifts from other sources (see Sect. 2.2).
2.1.1. VIMOS data
The cluster A S1063 was observed with VIMOS as part of the ESO Large Programme 186.A-0798 “Dark Matter Mass Distributions of Hubble Treasury Clusters and the Foundations of ΛCDM Structure Formation Models” (PI: P. Rosati, Rosati et al. 2014, hereafter CLASH-VLT). This programme performed a panoramic spectroscopic survey of the 13 CLASH clusters visible from ESO-Paranal.
The VIMOS observations were designed in sets of four separate pointings, each with a different quadrant centred on the cluster core (see Fig. 2), for a total of 16 masks. We used the low-resolution blue grism (LRb) for 12 of these masks, covering the spectral range 3700–6700 Å with a resolution of R = 180. For the remaining 4 masks, we used the medium-resolution grism (MR) in the range 4800–10 000 Å with a resolution of R = 580. The pointings overlap on the cluster centre to achieve longer integration times on faint arcs and other interesting strong-lensing (SL) features. They have the largest possible number of slits on candidate cluster members in the crowded central region of the cluster. The resulting exposure map of the 16 VIMOS pointings footprint is shown in Fig. 2, and the number of exposures and the integration time are reported in Table 1.
 |
Fig. 2. Exposure map of the 16 VIMOS pointings in the field of A S1063. The red circles are centred on the BCG and have radii of r200 = 2.63 Mpc (see Sect. 4). The cross marks the position of the BCG. |
VIMOS observations of A S1063.
We selected spectroscopic targets through specifically defined cuts in the colour-to-colour space using the WFI photometry. These cuts were set to include both blue and red galaxies at the cluster redshift, according to the expected colours. Figure 3 shows the selection box in the V–I versus B–R diagram.
 |
Fig. 3. WFI V − I vs. B − R colours for all of the extracted sources with R magnitudes ≤ 24. The dashed blue and black lines show the colour cuts defining the box we used for target selection. Small black and green dots are the sources classified as galaxies and stars in the WFI photometric catalogue, respectively. Larger data points mark cluster member galaxies in black and non-members in red that belong to our CLASH-VLT spectroscopic catalogue. |
We reduced the data using the VIMOS interactive pipeline graphical interface (VIPGI, Scodeggio et al. 2005), which performs bias subtraction, flat-field correction, bad-pixel cleaning, sky subtraction, fringing correction, and wavelength calibration.
The redshift determination follows the procedure described in Balestra et al. (2016). First, we ran the EZ software (Garilli et al. 2010) for a cross-correlation with template spectra. Then, we visually inspected redshift solutions obtained in the first step. During the visual check, we also assigned a quality flag (QF) to each redshift, according to four classes “secure” (QF = 3), several emission lines and/or strong absorption features are identified, 100% reliability; “emission-line” (QF = 9), redshift based on one or more emission lines, > 90% reliability; “likely”(QF = 2), intermediate-quality spectra with at least two well-identified spectral features, ∼80% reliability; and “uncertain” (QF = 1), spectra with a low signal-to-noise ratio, that is, with spectral features that are less clearly identified, 20–40% reliability.
We extracted 6477 spectra and measured 4199 redshifts with QF ≥ 1, corresponding to a success rate of ∼65%. When we considered repeated observations of the same objects, we obtained 3607 redshifts of different objects. We used repeated observations to confirm the redshift uncertainties as a function of the spectral resolution and the assigned quality flag. We found that the uncertainties vary between 75 and 150 km s−1 for MR and LRb observations, respectively (consistent with our previous estimates; see Biviano et al. 2013).
2.1.2. MUSE data
The source A S1063 was observed with the MUSE integral-field spectrograph (Karman et al. 2015, 2017; Caminha et al. 2016) as part of ESO Programme IDs 60.A-9345(A) (P.I. Caputi & Grillo) and 095.A-0653(A) (P.I. Caputi). Two pointings, covering the NE and SW sides of the cluster core, were observed (see the bottom right panel in Fig. 1). The SW pointing has a total exposure time of 3.1 h, with a seeing of ∼1.1″, while the NE pointing has a coadded exposure time of 4.8 h with 0.9″ seeing. Data reduction and redshift measurements are fully described in Karman et al. (2015, 2017), and the catalogues of cluster members and multiply lensed images, together with the first SL model, in the ∼2 × 1 arcmin2 central region, were presented in Caminha et al. (2016). The MUSE data provided 175 additional redshifts.
2.2. Spectroscopic catalogue
The final spectroscopic catalogue contains 3850 redshifts with QF ≥ 2, where a single entry2 is preserved in duplicate observations of the same object. We measured 3607 redshifts from VIMOS spectra, 175 redshifts from MUSE data, 21 redshifts from Gómez et al. (2012), 30 redshifts from the Grism Lens-Amplified Survey from Space (GLASS, GO-13459, PI: Treu; Treu & GLASS Team 2016), and 17 unpublished redshifts from Magellan observations (D. Kelson, priv. comm.). We measured and visually verified the redshifts for VIMOS, MUSE, and GLASS data and assigned the QF as explained in Sect. 2.1.1. Thus, for these 3812 sources, we obtained 3005 secure, 183 emission-line, and 624 likely redshifts. Figure 4 shows the redshift distribution of all the 3850 sources. The 175 MUSE objects are highlighted in red. The inset shows a zoom-in around the mean cluster redshift (⟨zcl⟩ = 0.3457, see below). The redshift catalogue is publicly available at the CLASH-VLT website3. We determined the spectroscopic sample completeness as a function of position on the sky and magnitude. We defined completeness as the ratio of the galaxies with measured redshifts and the number of galaxies in the colour-colour box we used to select targets (see Fig. 3), down to the fiducial limiting magnitude of R = 24. Figure 5 shows the spectroscopic completeness as a function of the distance from the BCG ([RA = 22h48m44.0s, Dec. = −44d31m51s (J2000.0)]), adopted as the cluster centre. This plot shows that the completeness is approximately 1 in the central 0.25 Mpc based on the MUSE coverage, then it decreases to 0.8 out to 1.25 Mpc, down to 0.7 from 1.25 Mpc to 2.75 Mpc.
 |
Fig. 4. Spectroscopic redshift distribution of 3850 sources in A S1063 from the CLASH-VLT catalogue, including 175 MUSE redshifts. The inset shows a zoom-in around the mean cluster redshift ⟨zcl⟩ = 0.3457 (red histogram for MUSE galaxies) of the 1234 cluster members found from the kinematic analysis. |
 |
Fig. 5. Completeness of the spectroscopic sample as a function of the custercentric distance. The shaded area indicates the 68% confidence regions according the algorithm of Gehrels (Gehrels 1986). The dashed line indicates r200 = 2.63 Mpc (see Sect. 4). |
3. Selection of cluster members
In order to select cluster members, we applied the two-step method called “peak+gap” (P+G) that has been applied in Girardi et al. (2015, see also refs. therein). The method is a combination of the 1D adaptive-kernel method DEDICA (Pisani 1993) and the “shifting gapper”, which uses both position and velocity information (Fadda et al. 1996; Girardi et al. 1996). In the first step, the 1D DEDICA method detects A S1063 as two overlapping peaks of 590 and 715 galaxies at z = 0.3424 and z = 0.3467, respectively, in the range 0.30905 ≤ z ≤ 0.3716 (see Fig. 6) for a total of 1305 candidate members.
 |
Fig. 6. Redshift distribution of the 1234 cluster members found in the kinematical analysis of the members in A S1063. The two dashed lines show the two overlapping peaks of 590 and 715 galaxies at z = 0.3424 and z = 0.3467 detected with 1D DEDICA. |
The second step in the member selection procedure combines galaxy positions and velocities to reject sources that are too far in velocity from the main body of galaxies within a fixed radial bin that is shifted along with the clustercentric distance. The procedure is iterated until the number of cluster members converges to a stable value. We used a velocity gap of 800 km s−1 in the cluster rest frame and a bin of 0.6 h−1 Mpc, or a bin that was large enough to include 15 galaxies. For the centre of A S1063, we adopted the position of the BCG. The shifting gapper procedure rejected another 71 interlopers that survived the first step of our member selection procedure. Thus, we obtained a sample of 1234 fiducial members (see Fig. 6), whose spatial distribution is shown in Fig. 7. MUSE members are highlighted in red.
 |
Fig. 7. 2D spatial distribution of VIMOS (blue circles) and MUSE (red circles) spectroscopically confirmed members. The large black circle has a radius equal to r200 = 2.63 Mpc (see Sect. 4). |
By applying the biweight estimator (Beers et al. 1990, ROSTAT software) to the 1234 cluster members, we computed a mean cluster line-of-sight (LOS) velocity ⟨V⟩ = ⟨cz⟩ = (103 640 ± 39) km s−1. This corresponds to a mean cluster redshift ⟨zcl⟩ = 0.3457±0.0001.
The positions of cluster members in the (projected) phase-space are shown in Fig. 8. This figure suggests that escape velocities (blue lines; we refer to the following section for how they were computed) are adequate to describe the position of the A S1063 galaxies in the phase-space. This can also be considered as an a posteriori validation of our member selection procedure (see Sect. 4).
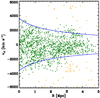 |
Fig. 8. Phase-space diagram including 1305 galaxies from the spectroscopic sample, where rest-frame velocities are plotted vs. the clustercentric distance. Green circles highlight the 1234 cluster members. Yellow circles indicate galaxies that lie in the selected cluster redshift range, but are rejected in the second step of our member selection procedure. The escape velocity curves are also shown (blue lines). |
4. Dynamical analysis
We used the mass model derived from Sartoris et al. (2020) to compute the escape velocity profile, and we briefly summarise the results presented in Sartoris et al. (2020) to compute the total mass profile of A S1063, using the same spectroscopic dataset as presented here. This analysis is based on the combined constraints obtained from the velocity dispersion profile of the stellar component of the BCG and the velocity distribution of cluster member galaxies. Sartoris et al. (2020) used an extension of the MAMPOSSt technique (Mamon et al. 2013) to solve the Jeans equation of dynamical equilibrium. Sartoris et al. (2020) determined a value γDM = 0.99 ± 0.04 for the inner slope of the gNFW profile, in agreement with the expectation from the CDM model. They also derived the contributions of the stellar mass component of cluster members and of the intra-cluster gas and of the DM profile to the cluster total mass profile. Their study also showed an excellent agreement among the projected total mass profiles obtained from a combined SL plus WL analysis, hydrostatic X-ray analysis, and their dynamical analysis, thus indicating a negligible hydrostatic mass bias.
We used the total mass profile of A S1063 derived by Sartoris et al. (2020) and adopted a simple NFW parametrisation. The best-fit parameters are rs = 0.84 ± 0.18 Mpc, r200, c = 2.63 ± 0.09 Mpc, and M = 2.9 ± 0.3 × 1015 M⊙.
This mass model was used to compute the projected escape velocity profile in Fig. 8, which is directly related to the potential well as 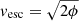 and, thus, to the cluster total mass. To derive the vesc profile, we followed the procedure described in Stark et al. (2016, and references therein). According to Nandra et al. (2012) and Stark et al. (2016), a massive particle in the vicinity of a galaxy cluster with gravitational potential
and, thus, to the cluster total mass. To derive the vesc profile, we followed the procedure described in Stark et al. (2016, and references therein). According to Nandra et al. (2012) and Stark et al. (2016), a massive particle in the vicinity of a galaxy cluster with gravitational potential 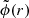 experiences an effective potential, ϕ(r), that is the sum of the cluster potential and a second term related to the expansion of the universe that can be thought of as a repulsive force that opposes the inward pull of the cluster mass distribution:
experiences an effective potential, ϕ(r), that is the sum of the cluster potential and a second term related to the expansion of the universe that can be thought of as a repulsive force that opposes the inward pull of the cluster mass distribution: 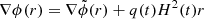 . We integrated this equation between a given r and the equivalent radius (req), that is, where the acceleration due to the cluster gravitational potential and the acceleration of the expanding universe are equivalent (Behroozi et al. 2013). Following Łokas & Mamon (2001), we calculated the cluster potential
. We integrated this equation between a given r and the equivalent radius (req), that is, where the acceleration due to the cluster gravitational potential and the acceleration of the expanding universe are equivalent (Behroozi et al. 2013). Following Łokas & Mamon (2001), we calculated the cluster potential 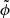 for an NFW mass density profile. This potential is a function of the NFW mass profile parameters r200, and rs that we obtained from the MAMPOSSt analysis. Finally, we projected the 3D escape velocity profile by rescaling it with a function of the velocity anisotropy according to the formulation presented in Diaferio & Geller (1997) and Diaferio (1999). The values of the velocity anisotropy profile parameters were also measured in the MAMPOSSt analysis.
for an NFW mass density profile. This potential is a function of the NFW mass profile parameters r200, and rs that we obtained from the MAMPOSSt analysis. Finally, we projected the 3D escape velocity profile by rescaling it with a function of the velocity anisotropy according to the formulation presented in Diaferio & Geller (1997) and Diaferio (1999). The values of the velocity anisotropy profile parameters were also measured in the MAMPOSSt analysis.
5. Substructures
We estimated the cluster LOS velocity dispersion, σV, using the biweight estimator and applying the cosmological correction and the standard correction for velocity errors (Danese et al. 1980). We obtained 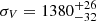 km s−1, where errors were estimated through a bootstrap technique.
km s−1, where errors were estimated through a bootstrap technique.
The BCG velocity is VBCG = (104 088 ± 40) km s−1, and its rest-frame relative velocity with respect to the mean velocity is ΔV = (VBCG − ⟨V⟩)/(1 + z) = 333 km s−1. The corresponding value of |ΔV|/σV = 0.24 is a rather typical velocity offset for BCGs (Lauer et al. 2014), as was also confirmed by Gebhardt & Beers (1991).
When galaxies with R < 20 are selected (120 galaxies, hereafter indicated as “bright galaxies”), they show a bimodality in the velocity distribution (left panel of Fig. 9), with the BCG in the middle (the arrow in the figure). The secondary peak is at velocities higher than that of the BCG. We applied the 1d KMM algorithm (cf. Ashman et al. 1994; Girardi et al. 2008) to the velocity distribution of the R < 20 galaxy subsample, and we find that the superposition of two Gaussians with n1 = 96 and n2 = 24 members at mean redshifts z1 = 0.3413 (102 617 km s−1) and z2 = 0.3555 (106 565 km s−1) is a better description of the velocity distribution than a single Gaussian with a probability of 94.9%.
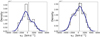 |
Fig. 9. Rest-frame velocity distribution relative to the mean cluster velocity of the 120 galaxies having R < 20 (left panel), and of the 395 galaxies within 1 Mpc from the cluster centre (right panel). The smooth curve is the probability density function obtained with a kernel density estimator. In both panels, the dashed line indicates the rest-frame velocity of the BCG: (VBCG − ⟨V⟩)/(1 + z) = 333 km s−1. |
An asymmetry in the velocity distribution is also evident by selecting the 395 member galaxies in the cluster inner 1 Mpc (right panel of Fig. 9). In this subsample, the secondary peak is at lower velocities than that of the BCG, with the BCG lying in the main peak. In this case, by applying the 1d KMM algorithm, we also find a very high probability (99.3%) that a mixture of two Gaussians, with n1 = 135 and n2 = 260 members at mean redshifts z1 = 0.3377 (101 245 km s−1) and z2 = 0.3501 (105 955 km s−1) is a better description of the velocity distribution than a single Gaussian.
We furthermore tested for the presence of substructures by considering the velocity and spatial distributions of cluster galaxies at the same time by using the 3D DEDICA method described in Appendix B and the test of Dressler & Shectman (1988) that we discuss below. The test of Dressler & Shectman (1988) compares the local mean velocity and velocity dispersion as computed around each galaxy with the global cluster values. We used the modification of the method introduced by Girardi et al. (1997, 2010), which considers only the more useful and immediate kinematical indicator based on the local mean. Following the method of Girardi et al. (2010, hereafter DSv-test), the kinematical indicator is based on the deviation of the local mean, ![$ \delta_{\mathrm{v},i}^2= [(N_{\mathrm{nn}}+1)/\sigma_{\mathrm{v}}^2][(\overline {\mathit{v}_{\mathrm{l}}} - \overline {v})^2] $](/articles/aa/full_html/2021/12/aa42168-21/aa42168-21-eq7.gif) , where the subscript l denotes the local quantity computed over the group formed by the galaxy i itself and its Nnn = 10 neighbours. The value Δ (i.e., the sum of the δv, i of the individual N galaxies) gives the cumulative deviation of the local mean velocities from the global cluster mean velocity. The significance of Δ, that is, how far away the system is from dynamical equilibrium, was determined by running 1000 Monte Carlo simulations, for which the galaxy velocities were randomly shuffled.
, where the subscript l denotes the local quantity computed over the group formed by the galaxy i itself and its Nnn = 10 neighbours. The value Δ (i.e., the sum of the δv, i of the individual N galaxies) gives the cumulative deviation of the local mean velocities from the global cluster mean velocity. The significance of Δ, that is, how far away the system is from dynamical equilibrium, was determined by running 1000 Monte Carlo simulations, for which the galaxy velocities were randomly shuffled.
The DSv-test reveals that A S1063 is not relaxed, at the > 99.9% confidence level, as also suggested by Gómez et al. (2012) from the analysis of the X-ray emission, the optical imaging, and the spectroscopy of 51 cluster members. In particular, within r200, a high-velocity region lies in the NE (X = −0.5 Mpc Y = 0.5 Mpc in Fig. 10) and a low-velocity region in the SW (X = 1.0 Mpc Y = −1.0 Mpc in Fig. 10). This peak is similar to the NE peak reported in Fig. 15 (right panel) of Gruen et al. (2013), from the photometric redshift information and the WL analysis. A small group with a high velocity is located in the South, outside r200 (X = 1.0 Mpc Y = −3.2 Mpc in Fig. 10), and considering the whole spatial distribution of the 1234 members (see Fig. 7 and Fig. 10), there is also an elongation NE–SW.
 |
Fig. 10. 2D spatial distribution of the 1234 member galaxies colour-coded according to the local mean velocity deviations δv, i. The circle has a radius equal to r200 = 2.63 Mpc. |
When only bright galaxies are considered (see Fig. 11), the NE-SW elongation is more evident. The δv, i/σV parameter shows that within r200, at least two groups are populated by bright galaxies, one of which is a low-velocity region in the SW of the cluster centre (at ∼X = 1.0 Mpc Y = −1.0 Mpc) mentioned above. As expected, bright galaxies serve as signposts for the substructures (e.g., Girardi et al. 2008 and see also below). These results agree with those of Rahaman et al. (2021), who identified the merger axis along the same direction as we obtained from the dynamical analysis using Chandra X-ray observations and 325 MHz Giant Metre Radio Telescope observations.
 |
Fig. 11. 2D spatial distribution of the 120 member galaxies with R < 20, colour-coded as in Fig. 10. The circle has a radius equal to r200 = 2.63 Mpc. |
6. Galaxy classification
We classified galaxies according to the presence of emission lines and the strength of the Hδ absorption line. Out of a total of 1234 members, we classified 960 members after inspection of the spectra, excluding 256 galaxies whose S/N was too low and 18 galaxies for which no colours were available. In Fig. 12, we show that unclassified galaxies are uniformly distributed at faint magnitudes in the colour-magnitude diagram. Within r200, we spectroscopically classify 700 members. We measured the equivalent widths (EWs) for the emission lines [OII], [OIII], and when available, Hα, and the EW of the Hδ line (see Mercurio et al. 2004 for the definition of wavelength ranges).
 |
Fig. 12. Colour-magnitude diagram of the spectroscopic members in A S1063. Black circles mark the 960 galaxies with robust spectral classification, and filled grey circles indicate galaxies with reliable colours and a spectral S/N that is too low to be classified. |
We detect 459 galaxies with evidence of emission lines. These were divided into four subclasses depending on the strength of the [OII] emission line: faint (EW[OII] > −7 Å, hereafter wELG, 158 galaxies), medium (−15Å< EW[OII] ≤ −7Å, hereafter mELG, 69 galaxies), strong (−40Å< EW[OII] ≤ −15 Å, hereafter ELGs15, 172 galaxies), and very strong (EW[OII] ≤ −40 Å, hereafter ELGs40, 65 galaxies) emission-line galaxies (ELGs). Very strong emission lines (EW[OII] ≤ −40 Å) are generally taken as a significant indication of starburst (e.g., Dressler et al. 1999), while weaker lines can also be due to continuous star formation (e.g., Oemler et al. 2009). Among the non-emission line galaxies, the 70 galaxies with EW(Hδ) > 3 Å are classified as strong Hδ absorption galaxies (HDS sample, or post-starburst), interpreted as post-starburst galaxies or galaxies with truncated star formation (e.g., Oemler et al. 2009). However, bluer galaxies require a larger EW(Hδ) to be identified as HDS galaxies. Thus, a more precise way to classify strong Hδ galaxies uses the diagram of EW(Hδ) versus the B − R colour or versus the strength of the 4000 Å break, which correlates with colour (Couch & Sharples 1987; Barger et al. 1996; Balogh et al. 1999). In this separation, we followed Mercurio et al. (2004). First, we fit the colour-magnitude relation of spectroscopic members,
where the B − R colour is obtained from aperture magnitudes, and R are Kron magnitudes. Then, we calculated the corrected colours as (B − R)corr = [(B − R)obs − (B − R)], and we used the same threshold as Mercurio et al. (2004), (B − R)corr = −0.5. In their original study, Mercurio et al. (2004) based their scheme directly on the strength of the 4000 Å break, while we used the corresponding colour4. In Fig. 13 we separately show the spectroscopic completeness of red and blue galaxies as a function of their radial position. They are consistent within 1σ uncertainties. As a result, we adopted the same completeness function to correct different galaxy types.
 |
Fig. 13. Completeness of the spectroscopic sample of blue and red galaxies as a function of custercentric distance. The shaded regions indicate the 68% confidence intervals, following the algorithm of Gehrels (Gehrels 1986). The dashed line indicates r200 = 2.63 Mpc. |
Thus, according to the criteria mentioned above, we find 47 strong Hδ galaxies with red colours and EW(Hδ) > 3 Å (hereafter, rHDS, red HDS, or red post-starburst) and 23 strong Hδ galaxies with blue colours and EW(Hδ) > 5 Å (hereafter, bHDS, blue HDS, or blue post-starburst). The remaining 431 galaxies are classified as passive (hereafter P).
Finally, among the 960 members with spectroscopic classification, we find 44.9% are P, 4.9%/2.4% rHDS/bHDS; 16.4% wELG; 6.7% mELG, and 17.9%/6.8% ELGs15/s40. Moreover, the y-axis histograms in Fig. 14 show that the spectral sequence P, rHDS, bHDS, wELG, mELG, ELGs corresponds to a colour sequence from red to blue. Red HDS follow the colour distribution of P galaxies, lying on the red sequence, although at magnitudes fainter than R = 19.5, while bHDS galaxies have intermediate colours, lying in a region between the red P galaxies and the blue ELGs. The spectral sequence also roughly corresponds to a magnitude sequence at the bright end; only P galaxies are brighter than R = 18.5, and all ELGs are fainter than R = 20.5 (see x-axis histograms in Fig. 14).
 |
Fig. 14. Colour-magnitude relation of 960 spectroscopic members in A S1063 with reliable spectral classification. The best-fit of the CM is indicated by the black line, and 68% and 99% limits are marked as dashed and dotted red lines, respectively. The red empty circle highlights the BCG. |
7. Accretion history of different galaxy populations in the cluster
This section investigates the accretion history of galaxies in the cluster and the possible differences among different galaxy populations, as classified above. More specifically, (i) we analyse the 2D distribution as well as the position of galaxies of different spectral classes in the projected phase-space diagram (Sect. 7.1), (ii) we use a semi-analytical model to investigate the relation between the position of the different spectral classes and the accretion redshift (Sect. 7.2), and (iii) we calculate the orbits of cluster galaxies (Sect. 7.3).
7.1. Projected phase-space diagram
The top panels of Fig. 15 show the 2D distribution of galaxies with different spectral types. Passive and red HDS galaxies (top left panel) trace the NE-SW elongation of the cluster. They are concentrated in the centre, and only 18% of these galaxies lie outside r200. A similar elongation is traced by blue HDS and wELG galaxies (top central panel). However, these populations are less concentrated in the centre, and the fraction of galaxies outside r200 is slightly higher (25%). When the three populations of ELGs with larger EWs are considered (mELG, ELGs15, and ELGs40; top right panel), the 2D distribution shows that these galaxies avoid the centre, and almost half (44%) of these galaxies are located outside r200.
 |
Fig. 15. Spatial distribution and projected phase-space diagram of the spectroscopic members. Top panels: 2D spatial distribution of the 960 spectroscopic member galaxies, classified according to their spectral properties. The circle has a radius equal to r200 = 2.63 Mpc. Bottom panels: phase-space diagram of the spectroscopic members, according to their spectral types. The underlying greyscale image in the top and bottom panels shows the galaxy number density distribution in 2D and in the phase-space, respectively, considering the whole population. |
The bottom panels in Fig. 15 show the projected phase-space diagrams as a function of galaxy spectral properties. In all the panels, the x-axis shows the projected distance from the cluster centre, normalised by r200, while the y-axis shows the rest-frame line-of-sight velocity. By comparing the three panels, it is evident that passive and red HDS populations are concentrated at low clustercentric distances in a region that all the remaining spectral classes mostly avoid; blue HDS and wELGs trace the projected phase-space diagram at a greater distance from the centre; and, as expected, galaxies with stronger emission lines occupy the outer regions of the projected phase-space.
To increase the statistics, we merge some of the spectral classes defined in Sect. 6: (1) P and red HDS (hereafter P+red HDS or P+rHDS), (2) blue HDS and wELG (hereafter blue HDS+wELG or bHDS+wELG), and (3) mELG, ELGs15, and ELGs40 (hereafter mELG+ELGs15+ELGs40). We confirm, according to the two-dimensional Kolmogorov-Smirnov test (Fasano & Franceschini 1987), that the classes we merge have similar spatial distributions. Moreover, a 2D Kolmogorov-Smirnov test confirms the visual impression obtained in the bottom panels of Fig. 15, namely that the phase-space distributions of the three samples defined above are all different from one another with a probability > 0.99.
To quantify this difference, we considered the spatial and velocity distributions of the different sub-populations separately. We fit the incompleteness-corrected number density profiles of the three samples with an NFW model (Navarro et al. 1997). We used a universal completeness correction for different galaxy types, as discussed Sect. 6 (see Fig. 13).
The number density profiles and their best fits are shown in Fig. 16. We find that the best-fit concentrations (c ≡ r200/rs where rs is the scale radius of the NFW model) are 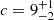 for passive+red HDS, c = 5 ± 1 for blue HDS+wELG, and
for passive+red HDS, c = 5 ± 1 for blue HDS+wELG, and 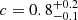 for mELG+ELGs15+ELGs40. Therefore, the passive+red HDS and the blue HDS+wELG populations are only marginally different from one another (see red and green best-fit curves in Fig. 16), whereas the profile of the blue population (mELG+ELGs15+ELGs40) appears to be significantly different from the other two samples. The velocity dispersion profiles of the three samples are shown in Fig. 17. We compare the three profiles two by two using the χ2 distribution,
for mELG+ELGs15+ELGs40. Therefore, the passive+red HDS and the blue HDS+wELG populations are only marginally different from one another (see red and green best-fit curves in Fig. 16), whereas the profile of the blue population (mELG+ELGs15+ELGs40) appears to be significantly different from the other two samples. The velocity dispersion profiles of the three samples are shown in Fig. 17. We compare the three profiles two by two using the χ2 distribution,
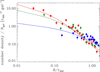 |
Fig. 16. Number density profiles (normalised by the total number of galaxies in each sample, Ngal) of the passive and red HDS (red points and lines), blue HDS, and wELG (green), and mELG, ELGs15, and ELGs40 (blue) populations. Error bars are 1 σ. Solid lines are best-fit NFW models for each population. |
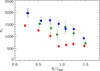 |
Fig. 17. Velocity dispersion profiles of the passive and red HDS (red points), blue HDS and wELG (green), and mELG, ELGs15, and ELGs40 (blue) populations. Error bars correspond to 1σ. Velocity dispersions are in km s−1. |
where the sum runs over the seven radial bins, j, k identify the two samples compared, σi, j is the value of the velocity dispersion of sample j at the radial bin i, and δi, j is its error. We find that the population of passive P+red HDS galaxies has a systematically lower velocity dispersion profile than the other two populations of blue HDS+wELG and mELG+ELGs15+ELGs40, which instead show consistent velocity dispersion profiles. We then conclude that most of the difference we see in the projected phase-space distribution of the different populations is due to their different velocity distributions.
We explored the accretion histories of these three classes of galaxies by dividing the projected phase-space diagram into the regions inside and outside r200 (Fig. 18). We found that 75% of the cluster members located inside r200 are passive. This agrees with the results of Bakels et al. (2021), who used a high-resolution cosmological dark matter-only simulation and found that 79% of the galaxies, in projection, inside r200 have passed their orbital pericenter at least once. Moreover, the black lines in Fig. 18 show the lines corresponding to constant values of (R/r200)×(vrf/σ) in projected phase-space, which corresponds to caustic profiles (Noble et al. 2013), and can be used to identify regions in projected phase-space containing infalling, backsplash, and virialised galaxy populations. The relation between caustic and the observed spectral properties of member galaxies can shed light on the importance of a dynamically defined environment and the cluster accretion scenario.
 |
Fig. 18. Projected phase-space distribution and fraction of galaxies with different spectral types. Main panel: projected phase-space distribution of galaxies with different spectral types. The two lines of constant (vrf/σ)×(R/r200) = 0.1, 0.4 are plotted as in Noble et al. (2013) to delineate the separation into regions of virialised (within the inner caustic), backsplash (between caustics), and infall galaxies (along and outside caustics). The dashed black line delimits the regions inside and outside r200. We indicate as regions A and B the two areas with R < r200 outside the virialised region. Top panel: fraction of P+red HDS (orange circles), blue HDS+wELG (green triangles), and mELG+ELGs15+EGs40 (blue stars) as a function of the clustercentric distance. Left and right panels: velocity distribution of the three corresponding samples inside and outside r200, respectively. The smoothed curves are the probability density functions obtained with a kernel density estimator. |
Noble et al. (2013) defined (i) as virialised the region within the caustic lines of constant (R/r200) × (vrf/σ) equal to 0.1 (the inner caustic in Fig. 18), (ii) the backsplash region as the one between caustic equal to 0.1 and to 0.4, and (iii) the infall region along and outside the caustic equal to 0.4. Galaxies located at R ≤ r200 and low rest-frame velocities (|Δv|/σ ≲ 1.5 (Jaffé et al. 2015; Mahajan et al. 2011, i.e. within the virialised region) may have experienced many pericentric passages and were accreted when the cluster core was forming. At R < r200 and intermediate values of (R/r200) × (vrf/σ), we expect a mix of all galaxy types, but backsplash galaxies are most likely present (Mahajan et al. 2011; Haines et al. 2012; Noble et al. 2013). Galaxies falling into the cluster for the first time can be found outside the caustic equal to 0.4 within r200 and at R > r200 (Mamon et al. 2004; Dünner et al. 2007; Mahajan et al. 2011; Haines et al. 2012, 2015).
Our data confirm this scenario. The top panel of Fig. 18 shows the fraction of the different spectral types as a function of the clustercentric distance. As discussed above, ELGs are mainly located outside r200 and avoid the cluster centre. The fraction of blue post-starburst galaxies and galaxies with weak emission lines is almost constant with the clustercentric distance (see also the discussion below of post-starburst galaxies alone). The fraction of P+rHDS decreases as the clustercentric distance increases.
We also indicate as A and B the two regions within r200, with high radial velocities that have uncertain accretion histories. Jaffé et al. (2015) suggested that in the projected phase-space region R ≤ r200 and |Δv|/σ ≳ 1.5, ram-pressure stripping could play an important role in quenching galaxy star formation because of the high density of the intra-cluster gas near the centre and the high galaxy velocities. Ciocan et al. (2020) showed an enhancement of metallicities for galaxies with 9.2 < Log(M*/M⊙) < 10.2 in A S1063 compared to the field galaxies (see their Fig. 8). This was interpreted as a scenario in which only the hot halo gas of these cluster galaxies is removed due to strangulation, leading to an increase in their gas-phase metallicity (because dilution of the interstellar-medium with pristine inflowing gas no longer occurs). However, the galaxies continue to form stars using the available cold gas in the disk, which is not stripped. Thus, strangulation could be another mechanism affecting infalling galaxies at R ≤ r200. Rhee et al. (2017), using a schematic galaxy trajectory after infalling into the cluster, showed that after the first pericenter passage, the galaxy is found as backsplash in this region as well. Then, the galaxy may settle into the virialised area.
Our data suggest a different mix of post-starburst and star-forming galaxies in the two regions A (R ≤ r200 and (vrf/σ)≥0) and B (R ≤ r200 and (vrf/σ)≤0), outside the virialised region. We find that post-starburst galaxies are approximately 20% (±3%) of the total sample of galaxies in regions A and B, while star-forming galaxies are 27% (±4%) in region A and 33% (±4%) in region B. By considering only the galaxies with |Δv|/σ ≲ 1.5, we find that there are 19 post-starburst galaxies out of a total of 61 (31%) galaxies and 16 emission-line galaxies out of a total of 64 galaxies with Δv/σ ≥ 1.5, while there are 18 post-starburst galaxies out of a total of 74 (24%) galaxies and 34 emission-line galaxies out of a total of 107 (32%) galaxies at Δv/σ ≤ −1.5. This is also shown in the left panel of Fig. 18, where we plot the smoothed velocity distribution of galaxies with different spectral types obtained with a kernel density estimator. The green curve indicating the velocity distribution of post-starburst galaxies is higher than that of star-forming galaxies in region A, while this is the opposite in region B. This suggests a different accretion scenario of galaxies in the two regions, with galaxies that have already experienced the first pericenter passage located mainly in region A, while galaxies falling into the cluster for the first time mainly lie in region B. As shown in the right panel of Fig. 18, star-forming and post-starburst galaxies have a similar distribution outside the virial radius.
It is also interesting to note that red and blue post-starburst galaxies mainly lie in the region between caustic parameter 0.1 and 0.4 (see Fig. 19) or along the outer caustic. Blue post-starburst galaxies seem to prefer regions where vrf/σ ≤ 0, where Fig. 18 also shows an excess of star-forming galaxies with respect to the region in which vrf/σ ≥ 0. The top panel of Fig. 19 shows that the fraction of post-starburst galaxies decreases as a function of the clustercentric distance. The asymmetry of the distribution of blue HDS in projected phase-space is striking. Muzzin et al. (2014) found a similar asymmetry in the projected phase-space distribution of post-starburst galaxies in a sample of z 1 clusters (see their Fig. 1), although the asymmetry in Muzzin et al. and our asymmetry are opposite in velocity sign.
 |
Fig. 19. Projected phase-space distribution and fraction of post-starburst galaxies. Bottom panel: projected phase-space distribution of red (magenta) and blue (cyan) post-starburst galaxies. The lines are the same as those in Fig. 18. Top panel: fraction of post-starburst galaxies with respect to all classified members as a function of the clustercentric distance. |
7.2. Accretion redshift from simulations
To interpret the results obtained in the previous section in the context of the cluster assembly history, we compared the observed distribution of galaxies in the projected phase-space diagram with the distribution predicted from a simulated cluster with a mass similar to that of A S1063. The projected phase-space distribution of galaxies is an important tool for constraining the epoch of their accretion from their location in the diagram. We used the semi-analytical model of De Lucia & Blaizot (2007, hereafter DLB07) to investigate the relation between the location of galaxies in the pseudo-phase-space diagram and the redshift at which they are accreted into the cluster. This model was run on the Millennium Simulation (Springel 2005), which assumes a WMAP1 cosmology with ΩΛ = 0.75, Ωm = 0.25, Ωb = 0.045, σ8 = 0.9, and h = 0.73. The semi-analytical model includes physical ingredients that were first introduced by White & Frenk (1991) and later refined by Springel et al. (2001), De Lucia et al. (2004) and De Lucia & Blaizot (2007). In particular, it includes prescriptions for gas accretion and cooling, star formation, feedback, galaxy mergers, the formation of supermassive black holes, and treatment of the radio-mode feedback from galaxies located at the centres of groups or clusters of galaxies. The accretion redshift is defined as the first time when galaxies that reside in the cluster today are accreted onto its main progenitor.
To compare observations to the SAM predictions, we selected the only halo available in the simulations with 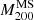 similar to A S1063 at z = 0.3.
similar to A S1063 at z = 0.3. 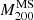 masses were computed from the N-body simulation as the mass enclosed within
masses were computed from the N-body simulation as the mass enclosed within 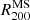 , the radius of a sphere that is centred on the most strongly bound particle of the group and has an overdensity of 200 with respect to the critical density of the Universe at the redshift of interest. We considered galaxies within a cylinder with a radius of 2 r200 and height of 2r200 to approximately match the data coverage, and with masses greater than Log(M*/M⊙) = 9.5, which is also the mass limit used for the analysis of the orbits described in Sect. 7.3.
, the radius of a sphere that is centred on the most strongly bound particle of the group and has an overdensity of 200 with respect to the critical density of the Universe at the redshift of interest. We considered galaxies within a cylinder with a radius of 2 r200 and height of 2r200 to approximately match the data coverage, and with masses greater than Log(M*/M⊙) = 9.5, which is also the mass limit used for the analysis of the orbits described in Sect. 7.3.
Using the sample of simulated galaxies selected as described above, we constructed the three phase-space diagrams using three different projections (xy, xz, and yz). From these three diagrams and the accretion redshift of each simulated galaxy, zi, we interpolated three different functions, zi(R/r200, Vrf/σ), one for each projection. The final accretion redshift we obtained for each position in the projected simulated phase-space diagram results from the mean among the three adopted projections of the simulated cluster.
First, we compared the mean accretion redshift of galaxies belonging to the three populations defined in the previous section. The accretion redshift, zi, was assigned to each observed galaxy corresponding to its position in the projected phase-space diagram. We show in the upper panel of Fig. 20 the cumulative distribution for the three galaxy classes. It shows that galaxies with increasing star-formation rate are progressively accreted at lower redhift. According to the 1D Kolmogorov-Smirnov test (KS-1D), we find that the distributions of the accretion redshifts of the three different spectroscopic populations are not drawn from the same parent distribution at more than 99% confidence level. Then, we investigated whether there is a difference in the accretion redshift distributions of galaxies with different stellar masses (see Appendix C for the derivation of galaxies stellar mass). According to the KS-1D, there is no significant dependence of the HDS+wELG and mELG+ELGs15+ELGs40 samples on the galaxy stellar masses. On the other hand, the mean accretion redshift distribution of P+red HDS galaxies with Log(M*/M⊙) ≥ 10.4 is different from that of galaxies with Log(M*/M⊙) < 10.4 at a probability > 0.99. As shown in the upper right panel of Fig. 20, the cumulative distribution of the mean accretion redshift of low-mass (Log(M*/M⊙) < 10.4) galaxies moves towards higher accretion redshifts than the distribution of high-mass (Log(M*/M⊙) ≥ 10.4) galaxies. This result is discussed in Sect. 8.
 |
Fig. 20. Cumulative distribution of the accretion redshift. Upper left panel: cumulative distribution of the accretion redshift, zaccretion, for galaxies with different spectral types: passive + red post-starbursts (orange), blue post-starburst galaxies + weak emission-line galaxies (green), and strong emission-line galaxies (blue). Other three panels: same distribution separated into high- and low-mass bins (using as a threshold Log(M*/M⊙) = 10.4) for the corresponding (colour-coded) galaxy spectral types. |
7.3. Orbits
Many of the physical processes that can affect the properties of cluster galaxies are likely to be related to their orbits (Tonnesen 2019; Joshi et al. 2020). Thus, to better investigate the physical mechanisms that cause galaxy transformations, we derived orbits for red and blue cluster galaxies separately (see Sect. 6 for the definition of red and blue galaxies), following the procedure explained in Biviano et al. (2013). Our procedure is almost fully non-parametric when the mass profile is specified. We follow Solanes & Salvador-Sole (1990) to invert the Jeans equation, assuming spherical symmetry, and using the projected number density and velocity dispersion profile of red and blue galaxies separately and the total mass profile either from Sartoris et al. (2020) or from the joint WL and SL analysis of Umetsu et al. (2016). We then inverted the Jeans equation and obtained a non-parametric form of the 3D velocity anisotropy profile, β(r)≡1 − (σt/σr)2, where σt, σr are the tangential and radial components of the velocity dispersion tensor (we adopted the common assumption of two identical tangential components). The uncertainties on β(r) were evaluated via a bootstrap procedure on the spectroscopic members. At each new bootstrap sampling, the number density and the line-of-sight velocity dispersion profiles were recomputed, and the inversion procedure was carried out.
In Fig. 21 we show β(r) of the red (top panel) and blue (bottom panel) galaxies separately. We considered only objects with a stellar mass Log(M*/M⊙) ≥ 9.5 (see Appendix C for the derivation of stellar masses) to reduce the completeness correction factor that is applied in the estimate of the number density profiles. We also show the solution obtained by Sartoris et al. (2020) using MAMPOSSt (Mamon et al. 2013), assuming a Tiret et al. (2007) model for β(r) (magenta shaded region). This solution agrees very well with the Jeans inversion solution for the red galaxies, the dominant sample.
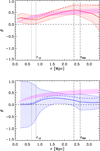 |
Fig. 21. Velocity anisotropy profiles of the red and blue cluster members in the upper and lower panels, respectively. The solid (dashed) coloured lines represent the solutions of the inversion of the Jeans equation adopting the mass profile from Sartoris et al. (2020) (Umetsu et al. 2016). The coloured area indicates the 68% confidence region around the solution. The magenta shading indicates the 68% confidence region around the MAMPOSSt best-fit solution for a Tiret model (Sartoris et al. 2020). In both panels we use the same Tiret model, which was computed considering the full sample of member galaxies. The vertical dotted and dash-dotted black lines mark r−2 (which corresponds to rs for an NFW model) and r200 obtained from Umetsu et al. (2016) and the MAMPOSSt analysis of Sartoris et al. (2020), respectively. |
Red galaxies in A S1063 have radial orbits that are characterised by small pericenters (this result is also discussed in Sect. 8). Hence, they may have experienced denser environments than galaxies on more tangential orbits. This can lead to more rapid transformations or to a more efficient gas stripping, as suggested by Solanes et al. (2001) by analysing galaxies in the Virgo cluster. We could also expect a difference in the orbits of high- and low-mass galaxies because the more massive galaxies may be better able to survive the passage through small pericenters, that is, the very hostile and dense environment of the central cluster region. However, dynamical friction acting on the more massive galaxies would have the opposite effect of reducing the radial anisotropy of these galaxies. To this end, we compared the orbits of red galaxies in different mass ranges, but we do not see any significant difference in the galaxy orbits at varying masses.
The blue population has a systematically lower velocity anisotropy than the red population, at least at r > 0.7Rvir. This means that red galaxies seem to move on more radially biased orbits than the blue counterparts (see Fig. 21), although the difference is not statistically significant.
8. Discussion and conclusions
Our analysis of the Frontier Fields cluster A S1063 is based on an unprecedentedly large sample of 1234 spectroscopic member galaxies out to 1.7 × r200 (or R ≈ 4.5 Mpc). Using the whole spectroscopic sample, we estimated the mean cluster redshift ⟨zcl⟩ = 0.3457±0.0001 and the LOS velocity dispersion of galaxies 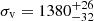 . Our estimate of σv is significantly smaller than that presented by Gómez et al. (2012,
. Our estimate of σv is significantly smaller than that presented by Gómez et al. (2012, 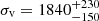 ). This difference is likely due to the significantly larger size of our sample (≃24× larger), which allows us to measure the σv radial profile, which declines with radius (see Fig. 15 and Sartoris et al. 2020), and also to obtain a better rejection of non-member galaxies.
). This difference is likely due to the significantly larger size of our sample (≃24× larger), which allows us to measure the σv radial profile, which declines with radius (see Fig. 15 and Sartoris et al. 2020), and also to obtain a better rejection of non-member galaxies.
Based on the spectroscopic classification of 960 galaxies of our sample with high S/N spectra, we find that 50% of cluster members are passive and red post-starburst galaxies, 18% are blue post-starbursts and weak emission-line galaxies, and 32% are medium, strong, and very strong emission-line galaxies. To compare our results with the study of Dressler et al. (2013), who considered five rich clusters at 0.31 < z < 0.54, we recomputed the fractions per spectral class within 1.5 × r200 and R < 22.3. We find that 59% of all galaxies are either passive or post-starburst galaxies, and, among the members with no emission lines, 15% are post-starburst galaxies. These values are to be compared to those of Dressler et al. 2013 (2013, see their Fig. 16 and Table 4), who found values in the range 50–80% for a fraction of P and HDS galaxies among all members and 10–20% for a fraction of post-starburst galaxies among passive members. We infer that A S1063 shows a typical distribution of spectral types across its galaxy population.
On the basis of 51 member galaxies, Gómez et al. (2012) detected substructure at the 90% confidence level according to the DS test, and their Fig. 10 suggested a bimodal galaxy distribution. Our analysis adds several pieces of observational evidence that A S1063 is far from being dynamically relaxed. We find two peaks in the velocity distribution, the strong NE–SW elongation in the galaxy distribution, and evidence of substructure at > 99.9% according to the DSv test (see Sect. 5 and Figs. 9–11). Although this study is not focused on the cluster structure, we also present a more refined analysis in Appendix B, which finds five subclumps. We conclude that A S1063 is far from being dynamically relaxed, and we suggest that two or more subclumps have merged in the NE-SW direction.
To further investigate the merging scenario and related timescales, we used the high-resolution set of adiabatic binary galaxy cluster merger simulations of ZuHone (2011). The qualitative comparison between the X-ray emissivity of simulations and the X-ray contours published in Bonamigo et al. (2018) suggests that a merger with a mass ratio of 1:3 between the two sub-clusters best represents the X-ray observations. This scenario also agrees with the radio halo found by Xie et al. (2020). Radio halos are interpreted as transient components due to the turbulent reacceleration of relativistic electrons generated (and then dissipated) in cluster mergers (e.g. Brunetti 2009). The acceleration timescale of the emitting electrons is ∼0.1–0.2 Gyr.
Our spectral galaxy classification allowed us to obtain new insight into the merging scenario for A S1063. Figure 15 shows that the NE-SW direction is well traced by passive and red post-starburst galaxies, but not by medium, strong, or very strong emission-line galaxies. Similar evidence that the cluster elongation is traced by passive and red post-starburst galaxies but not by galaxies with strong emission lines has already been found in the massive cluster MACS J1206.2-0847 (Girardi et al. 2015). A plausible interpretation is that passive galaxies trace the main accretion filament during the cluster formation and/or the last important cluster merger. On the other hand, emission-line galaxies trace more recent infall through several small groups or eventually randomly backsplash galaxies.
We then explored the accretion histories of the different sub-populations of galaxies by dividing the projected phase-space diagram into infalling, backsplash, and virialised regions inside and outside r200, guided also by studies based on simulations. We found that 75% of the galaxies within r200 are passive or post-starburst galaxies. This result suggests that they passed through the cluster at least once, in agreement with Bakels et al. (2021), who found that roughly 21% of the subhaloes within the viral radius of a host are currently on first infall and have not yet reached their first orbital pericentre.
Moreover, we studied how galaxies with different spectral properties populate these pre-defined phase-space regions: the virialised region is dominated by passive galaxies, that is, it contains galaxies that have passed through the cluster at least once; the region of galaxies with negative high radial velocities (Δv/σ ≲ −1.5) within r ≤ r200 is mainly dominated by galaxies with medium or strong emission lines that have not yet passed through the cluster centre; the region with positive radial velocities (Δv/σ ≳ 1.5) at r ≤ r200 is populated primarily by weak emission-line or post-starburst galaxies, suggesting that these galaxies after passing the pericenter may lie along the top edge of the projected phase-space diagram at positive radial velocities, showing signs of quenching of star formation. Inside r200, the fraction of passive galaxies decreases as a function of the cluster radius, while the fraction of strong emission-line galaxies increases. Outside r200, the fraction of strong emission-line galaxies reaches half of the whole population.
By analysing the position of post-starbursts in the phase-space diagram depending on their colours, we find that blue post-starburst galaxies have negative velocities. We can speculate that blue post-starburst galaxies result from the quenching (or the truncation) of star formation in star-forming galaxies during the infall (ELG⇒bHDS⇒P). In this case, ram-pressure stripping or strangulation could play an important role in quenching star formation. On the other hand, red post-starbursts may be the result of an evolutionary path of the type P⇒rHDS⇒P (e.g. Dressler et al. 2013). In this case, the infall onto the cluster, or the merging of substructures, may trigger the starburst in P galaxies, and we observe these galaxies 1−2 Gyr after the burst (e.g. Girardi et al. 2015). This timescale is comparable with the crossing time of A S1063 (r200/σ ∼ 1.9 Gyr). The evolutionary scenario, in which rHDS galaxies could be the remnant of the core of an infalling clump of galaxies that have experienced a merger with the main cluster and bHDS could be the result of an ICM-related phenomenon, has also been suggested by Mercurio et al. (2004) in the cluster Abell 209. Mercurio et al. (2004) also found that bHDS and ELG galaxies are blue disks, while P and rHDS are spheroids.
By correlating the projected phase-space diagram obtained from the DLB07 simulations of massive cluster assembly with the distribution of different spectral classes in the observed projected phase-space diagram, we were able to estimate the accretion redshift for different galaxy populations (Fig. 20). According to the KS-1D test, the accretion redshifts of the three populations are not drawn from the same parent distribution at a confidence level > 99%. Thus, we find a strong correlation between the infall times and the galaxy spectral properties. Galaxies with higher star formation rates are accreted later into the cluster.
Moreover, high-mass (Log(M*/M⊙) ≥ 10.4) passive and red post-starburst galaxies appear to have a different distribution of mean accretion redshift with respect to low-mass (Log(M*/M⊙) < 10.4) passive galaxies (with a probability > 0.99 based on the KS-1D test). The accretion redshift distribution of low-mass galaxies moves towards higher redshifts than the distribution of high-mass galaxies. This result may seem at odds with the expectation that more massive galaxies are accreted at earlier epochs as a natural consequence of hierarchical structure growth (De Lucia et al. 2012). However, we should consider that we observe this difference in the accretion redshift among galaxies that are passive at the time of observation, but we do not know whether they were passive at the time of accretion as well. Mass-quenching processes could explain our result when the time needed to quench star formation as a function of the galaxy stellar mass is considered. If the quenching time is longer for low-mass galaxies than for high-mass galaxies, we will observe as low-mass passive galaxies only those galaxies that are accreted early onto the cluster (when they were star forming) and that had the time to quench their star formation.
By analysing the orbits of member galaxies, we find that red galaxies move on more radial orbits than blue galaxies. Using a semi-analytical model applied to the Millennium Simulation, Iannuzzi & Dolag (2012) found that blue galaxies move on less radial orbits than red galaxies in clusters at any redshift from 0 to 0.7. They predicted β ≈ 0.4 (0.2) for red (blue) galaxies in clusters at z ≈ 0.3, in agreement with our result. This orbital difference was attributed by Iannuzzi & Dolag (2012) to the fact that infalling galaxies can remain blue only if they move on tangential orbits.
On the other hand, the cosmological hydrodynamical simulation analysis by Lotz et al. (2019) reached the opposite conclusion. Blue galaxies move on more radial orbits than red galaxies, a difference that the authors interpreted as blue galaxies being more infall dominated than red galaxies. The difference between the results of Iannuzzi & Dolag (2012) and those of Lotz et al. (2019) seems to point towards a different quenching timescale in the two simulations. If blue galaxies are more infall dominated than red galaxies, they would appear on more radial orbits than red galaxies only if they can survive quenching for at least an orbital time.
Another possible explanation for the more radial orbits of red galaxies is that at least part of them have been pre-processed before their infall and are in fact recent infallers. Thus, they show radial orbits because they still retain part of their original infalling trajectories before reaching the cluster centre for the first time. However, in this case, it is not clear why we should expect that red pre-processed galaxies infall on more radial orbits than blue galaxies that were not pre-processed.
From the observational point of view, our finding that red galaxies move on more radial orbits than blue galaxies is not generally confirmed in other clusters. Although the error bars are large, the opposite trend is seen in clusters at any redshift (Biviano & Katgert 2004; Biviano et al. 2013, 2016; Munari et al. 2014; Mamon et al. 2019). However, most of the existing results are based on stack samples so that a large spread may exist in the β(r) of red and blue galaxies in different clusters. Aguerri et al. (2017) reported that in the nearby cluster Abell 85, red galaxies have more radially elongated orbits than blue galaxies, as we find here. The spread in the β(r) of red and blue galaxies in different clusters may be due to different accretion histories, different current accretion rates, or a different quenching efficiency. Thus, we plan to extend our analysis to quantify the spread in the β(r) of red and blue galaxies by analysing the full sample of CLASH-VLT clusters in the near future.
Our analysis shows that extensive spectroscopic information on large samples of cluster members, extending well beyond the virial radius, allows new insights to be obtained on the assembly history of cluster galaxies in relation to their star formation histories via a direct comparison of observed (projected) phase-space diagrams with those derived from cosmological simulations.
In order to further investigate the accretion history of cluster galaxies, as well as the mechanisms and timescales of star-formation quenching, we plan to extend our analysis to the full sample of CLASH-VLT clusters in the near future.
Currently located at https://sites.google.com/site/vltclashpublic/.
We use the threshold (B − R)corr = −0.5 to also separate blue and red galaxies in the analysis of the orbits described in Sect. 7.3.
Available at http://www.astromatic.net/software/psfex.
Acknowledgments
The authors thank the anonymous referee for the very useful comments, that improved the manuscript. We acknowledge financial contributions by PRIN-MIUR 2017WSCC32 “Zooming into dark matter and proto-galaxies with massive lensing clusters” (P.I.: P.Rosati), INAF “main-stream” 1.05.01.86.20: “Deep and wide view of galaxy clusters (P.I.: M. Nonino)” and INAF “main-stream” 1.05.01.86.31 “The deepest view of high-redshift galaxies and globular cluster precursors in the early Universe” (P.I.: E. Vanzella). M.B. acknowledges financial contributions from the agreement ASI/INAF 2018-23-HH.0, Euclid ESA mission - Phase D and with AM the INAF PRIN-SKA 2017 program 1.05.01.88.04. C.G. acknowledges support through grant no. 10123 of the VILLUM FONDEN Young Investigator Programme. G.B.C. acknowledges the Max Planck Society for financial support through the Max Planck Research Group for S. H. Suyu and the academic support from the German Centre for Cosmological Lensing. P.B. acknowledges financial support from ASI through the agreement ASI-INAF n. 2018-29-HH.0. R.D. gratefully acknowledges support from the Chilean Centro de Excelencia en Astrofísica y Tecnologías Afines (CATA) BASAL grant AFB-170002".
References
- Abell, G. O., Corwin, H. G., Jr, & Olowin, R. P. 1989, ApJS, 70, 1 [Google Scholar]
- Aguerri, J. A. L., Agulli, I., Diaferio, A., & Dalla Vecchia, C. 2017, MNRAS, 468, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, J., & Ogaz, S. 2014, hst2galign: an Automated Galaxy-based Alignment Routine, Instrument Science Report ACS 2014-03, Instrument Science Report WFC/UVIS 2014-23 [Google Scholar]
- Annunziatella, M., Mercurio, A., Brescia, M., Cavuoti, S., & Longo, G. 2013, PASP, 125, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Annunziatella, M., Biviano, A., Mercurio, A., et al. 2014, A&A, 571, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Annunziatella, M., Mercurio, A., Biviano, A., et al. 2016, A&A, 585, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Armstrong, B., Mohr, J., Adams, D., et al. 2010, Am. Astron. Soc. Meeting Abstracts, 215, 438.07 [NASA ADS] [Google Scholar]
- Ashman, K. M., Bird, C. M., & Zepf, S. E. 1994, AJ, 108, 2348 [Google Scholar]
- Bakels, L., Ludlow, A. D., & Power, C. 2021, MNRAS, 501, 5948 [NASA ADS] [CrossRef] [Google Scholar]
- Balestra, I., Mercurio, A., Sartoris, B., et al. 2016, ApJS, 224, 33 [Google Scholar]
- Balogh, M. L., Morris, S. L., Yee, H. K. C., Carlberg, R. G., & Ellingson, E. 1999, ApJ, 527, 54 [Google Scholar]
- Balogh, M. L., Baldry, I. K., Nichol, R., et al. 2004, ApJ, 615, L101 [Google Scholar]
- Barger, A. J., Aragon-Salamanca, A., Ellis, R. S., et al. 1996, MNRAS, 279, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., Wu, H.-Y., et al. 2013, ApJ, 763, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E. 2011, in Automated Morphometry with SExtractor and PSFEx, eds. I. N. Evans, A. Accomazzi, D. J. Mink, & A. H. Rots, ASP Conf. Ser., 442, 435 [NASA ADS] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biviano, A., & Katgert, P. 2004, A&A, 424, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biviano, A., Rosati, P., Balestra, I., et al. 2013, A&A, 558, A1 [Google Scholar]
- Biviano, A., van der Burg, R. F. J., Muzzin, A., et al. 2016, A&A, 594, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanton, M. R., Eisenstein, D., Hogg, D. W., Schlegel, D. J., & Brinkmann, J. 2005, ApJ, 629, 143 [Google Scholar]
- Bonamigo, M., Grillo, C., Ettori, S., et al. 2018, ApJ, 864, 98 [Google Scholar]
- Boselli, A., & Gavazzi, G. 2006, PASP, 118, 517 [Google Scholar]
- Boselli, A., & Gavazzi, G. 2014, A&A Rv., 22, 74 [NASA ADS] [Google Scholar]
- Boselli, A., Roehlly, Y., Fossati, M., et al. 2016, A&A, 596, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouy, H., Bertin, E., Moraux, E., et al. 2013, A&A, 554, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brunetti, G. 2009, Rev. Mex. Astron. Astrofis. Conf. Ser., 36, 208 [NASA ADS] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Butcher, H., & Oemler, A., Jr. 1978, ApJ, 226, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Butcher, H., & Oemler, A., Jr. 1984, ApJ, 285, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Caldwell, J. A. R., McIntosh, D. H., Rix, H.-W., et al. 2008, ApJS, 174, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Tremonti, C. A., Heckman, T. M., & Leitherer, C. 2000, in The Evolution of the Interstellar Medium Around Young Stellar Clusters, eds. A. Lançon, & C. M. Boily, ASP Conf. Ser., 211, 25 [NASA ADS] [Google Scholar]
- Caminha, G. B., Grillo, C., Rosati, P., et al. 2016, A&A, 587, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caminha, G. B., Grillo, C., Rosati, P., et al. 2017, A&A, 600, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ciocan, B. I., Maier, C., Ziegler, B. L., & Verdugo, M. 2020, A&A, 633, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Couch, W. J., & Sharples, R. M. 1987, MNRAS, 229, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Danese, L., de Zotti, G., & di Tullio, G. 1980, A&A, 82, 322 [NASA ADS] [Google Scholar]
- De Grandi, S., Böhringer, H., Guzzo, L., et al. 1999, ApJ, 514, 148 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [Google Scholar]
- De Lucia, G., Kauffmann, G., Springel, V., et al. 2004, MNRAS, 348, 333 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Weinmann, S., Poggianti, B. M., Aragón-Salamanca, A., & Zaritsky, D. 2012, MNRAS, 423, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Diaferio, A. 1999, MNRAS, 309, 610 [CrossRef] [Google Scholar]
- Diaferio, A., & Geller, M. J. 1997, ApJ, 481, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [Google Scholar]
- Dressler, A., & Shectman, S. A. 1988, AJ, 95, 985 [Google Scholar]
- Dressler, A., Oemler, A. J., Couch, W. J., et al. 1997, ApJ, 490, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Smail, I., Poggianti, B. M., et al. 1999, ApJS, 122, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Oemler, A. J., Poggianti, B. M., et al. 2013, ApJ, 770, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Dünner, R., Reisenegger, A., Meza, A., Araya, P. A., & Quintana, H. 2007, MNRAS, 376, 1577 [CrossRef] [Google Scholar]
- Fadda, D., Girardi, M., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1996, ApJ, 473, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Fasano, G., & Franceschini, A. 1987, MNRAS, 225, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Foltz, R., Wilson, G., Muzzin, A., et al. 2018, ApJ, 866, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, A., Böhm, A., & Ziegler, B. L. 2009, MNRAS, 393, 1467 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, A., Scodeggio, M., Ilbert, O., et al. 2014, A&A, 563, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garilli, B., Maccagni, D., & Andreon, S. 1999, A&A, 342, 408 [NASA ADS] [Google Scholar]
- Garilli, B., Fumana, M., Franzetti, P., et al. 2010, PASP, 122, 827 [Google Scholar]
- Gebhardt, K., & Beers, T. C. 1991, ApJ, 383, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [Google Scholar]
- Girardi, M., Fadda, D., Giuricin, G., et al. 1996, in The Galaxy Velocity Dispersion - X-ray Temperature Helation in Galaxy Clusters, eds. P. Coles, V. Martinez, & M. J. Pons-Borderia, ASP Conf. Ser., 94, 221 [NASA ADS] [Google Scholar]
- Girardi, M., Escalera, E., Fadda, D., et al. 1997, ApJ, 482, 41 [Google Scholar]
- Girardi, M., Barrena, R., Boschin, W., & Ellingson, E. 2008, A&A, 491, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, M., Boschin, W., & Barrena, R. 2010, A&A, 517, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, M., Mercurio, A., Balestra, I., et al. 2015, A&A, 579, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gómez, P. L., Nichol, R. C., Miller, C. J., et al. 2003, ApJ, 584, 210 [Google Scholar]
- Gómez, P. L., Valkonen, L. E., Romer, A. K., et al. 2012, AJ, 144, 79 [CrossRef] [Google Scholar]
- Gruen, D., Brimioulle, F., Seitz, S., et al. 2013, MNRAS, 432, 1455 [NASA ADS] [CrossRef] [Google Scholar]
- Guzzo, L., Böhringer, H., Schuecker, P., et al. 1999, The Messenger, 95, 27 [NASA ADS] [Google Scholar]
- Haines, C. P., La Barbera, F., Mercurio, A., Merluzzi, P., & Busarello, G. 2006, ApJ, 647, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Haines, C. P., Gargiulo, A., La Barbera, F., et al. 2007, MNRAS, 381, 7 [Google Scholar]
- Haines, C. P., Pereira, M. J., Sanderson, A. J. R., et al. 2012, ApJ, 754, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Haines, C. P., Pereira, M. J., Smith, G. P., et al. 2015, ApJ, 806, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Iannuzzi, F., & Dolag, K. 2012, MNRAS, 427, 1024 [Google Scholar]
- Jaffé, Y. L., Smith, R., Candlish, G. N., et al. 2015, MNRAS, 448, 1715 [Google Scholar]
- Joshi, G. D., Pillepich, A., Nelson, D., et al. 2020, MNRAS, 496, 2673 [Google Scholar]
- Just, A., Fuchs, B., Jahreiß, H., et al. 2015, MNRAS, 451, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Karman, W., Caputi, K. I., Grillo, C., et al. 2015, A&A, 574, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karman, W., Caputi, K. I., Caminha, G. B., et al. 2017, A&A, 599, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kauffmann, G., White, S. D. M., Heckman, T. M., et al. 2004, MNRAS, 353, 713 [Google Scholar]
- Koekemoer, A., Fruchter, A., & Hack, W. 2003, Space Telescope Eur. Coordinating Facility Newsletter, 33, 10 [NASA ADS] [Google Scholar]
- Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Kovač, K., Lilly, S. J., Knobel, C., et al. 2014, MNRAS, 438, 717 [CrossRef] [Google Scholar]
- Kron, R. G. 1980, ApJS, 43, 305 [Google Scholar]
- Lauer, T. R., Postman, M., Strauss, M. A., Graves, G. J., & Chisari, N. E. 2014, ApJ, 797, 82 [Google Scholar]
- Lee, M. G., Kang, J., Lee, J. H., & Jang, I. S. 2017, ApJ, 844, 157 [CrossRef] [Google Scholar]
- Lemaux, B. C., Tomczak, A. R., Lubin, L. M., et al. 2019, MNRAS, 490, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Łokas, E. L., & Mamon, G. A. 2001, MNRAS, 321, 155 [CrossRef] [Google Scholar]
- Lotz, J. M., Koekemoer, A., Coe, D., et al. 2017, ApJ, 837, 97 [Google Scholar]
- Lotz, M., Remus, R.-S., Dolag, K., Biviano, A., & Burkert, A. 2019, MNRAS, 488, 5370 [NASA ADS] [CrossRef] [Google Scholar]
- Mahajan, S., Mamon, G. A., & Raychaudhury, S. 2011, MNRAS, 416, 2882 [NASA ADS] [CrossRef] [Google Scholar]
- Mamon, G. A., Sanchis, T., Salvador-Solé, E., & Solanes, J. M. 2004, A&A, 414, 445 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mamon, G. A., Biviano, A., & Boué, G. 2013, MNRAS, 429, 3079 [Google Scholar]
- Mamon, G. A., Cava, A., Biviano, A., et al. 2019, A&A, 631, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mercurio, A., Busarello, G., Merluzzi, P., et al. 2004, A&A, 424, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mercurio, A., Haines, C. P., Gargiulo, A., et al. 2010, ArXiv e-prints [arXiv:1006.5001] [Google Scholar]
- Mercurio, A., Merluzzi, P., Busarello, G., et al. 2015, MNRAS, 453, 3685 [Google Scholar]
- Mohr, J. J., Armstrong, R., Bertin, E., et al. 2012, in The Dark Energy Survey Data Processing and Calibration System, SPIE Conf. Ser., 8451, 84510D [NASA ADS] [Google Scholar]
- Molino, A., Benítez, N., Ascaso, B., et al. 2017, MNRAS, 470, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Moresco, M., Pozzetti, L., Cimatti, A., et al. 2010, A&A, 524, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Munari, E., Biviano, A., & Mamon, G. A. 2014, A&A, 566, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muzzin, A., van der Burg, R. F. J., McGee, S. L., et al. 2014, ApJ, 796, 65 [Google Scholar]
- Nandra, R., Lasenby, A. N., & Hobson, M. P. 2012, MNRAS, 422, 2931 [NASA ADS] [CrossRef] [Google Scholar]
- Nantais, J. B., van der Burg, R. F. J., Lidman, C., et al. 2016, A&A, 592, A161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [Google Scholar]
- Noble, A. G., Webb, T. M. A., Muzzin, A., et al. 2013, ApJ, 768, 118 [Google Scholar]
- Oemler, A. J., Abramson, L. E., Gladders, M. D., et al. 2017, ApJ, 844, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Oemler, A. J., Dressler, A., Kelson, D., et al. 2009, ApJ, 693, 153 [Google Scholar]
- Owers, M. S., Hudson, M. J., Oman, K. A., et al. 2019, ApJ, 873, 52 [Google Scholar]
- Pasquali, A., Smith, R., Gallazzi, A., et al. 2019, MNRAS, 484, 1702 [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [Google Scholar]
- Pisani, A. 1993, MNRAS, 265, 706 [NASA ADS] [Google Scholar]
- Pisani, A. 1996, MNRAS, 278, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Plagge, T. J., Bonamente, M., & South Pole Telescope Collaboration 2010, AAS/High Energy Astrophys Div., 11, 31.06 [NASA ADS] [Google Scholar]
- Planck Collaboration VIII. 2011, A&A, 536, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Postman, M., Franx, M., Cross, N. J. G., et al. 2005, ApJ, 623, 721 [Google Scholar]
- Postman, M., Coe, D., Benítez, N., et al. 2012, ApJS, 199, 25 [Google Scholar]
- Rahaman, M., Raja, R., Datta, A., et al. 2021, MNRAS, 505, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Rhee, J., Smith, R., Choi, H., et al. 2017, ApJ, 843, 128 [Google Scholar]
- Rhee, J., Smith, R., Choi, H., et al. 2020, ApJS, 247, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Rix, H.-W., Barden, M., Beckwith, S. V. W., et al. 2004, ApJS, 152, 163 [CrossRef] [Google Scholar]
- Roberts, I. D., Parker, L. C., Brown, T., et al. 2019, ApJ, 873, 42 [CrossRef] [Google Scholar]
- Rosati, P., Balestra, I., Grillo, C., et al. 2014, The Messenger, 158, 48 [NASA ADS] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sartoris, B., Biviano, A., Rosati, P., et al. 2020, A&A, 637, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scodeggio, M., Franzetti, P., Garilli, B., et al. 2005, PASP, 117, 1284 [NASA ADS] [CrossRef] [Google Scholar]
- Sheen, Y.-K., Smith, R., Jaffé, Y., et al. 2017, ApJ, 840, L7 [Google Scholar]
- Silverman, B. W. 1986, Density Estimation for Statistics and Data Analysis [Google Scholar]
- Smith, G. P., Treu, T., Ellis, R. S., Moran, S. M., & Dressler, A. 2005, ApJ, 620, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Solanes, J. M., & Salvador-Sole, E. 1990, A&A, 234, 93 [Google Scholar]
- Solanes, J. M., Manrique, A., García-Gómez, C., et al. 2001, ApJ, 548, 97 [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [Google Scholar]
- Springel, V., White, S. D. M., Tormen, G., & Kauffmann, G. 2001, MNRAS, 328, 726 [Google Scholar]
- Stark, A., Miller, C. J., & Gifford, D. 2016, ApJ, 830, 109 [CrossRef] [Google Scholar]
- Tanaka, M., Goto, T., Okamura, S., Shimasaku, K., & Brinkmann, J. 2004, AJ, 128, 2677 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, M., Kodama, T., Arimoto, N., et al. 2005, MNRAS, 362, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2006, in STILTS - A Package for Command-Line Processing of Tabular Data, eds. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, ASP Conf. Ser., 351, 666 [NASA ADS] [Google Scholar]
- Tiret, O., Combes, F., Angus, G. W., Famaey, B., & Zhao, H. S. 2007, A&A, 476, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tonnesen, S. 2019, ApJ, 874, 161 [Google Scholar]
- Tortorelli, L., Mercurio, A., Paolillo, M., et al. 2018, MNRAS, 477, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., & GLASS Team 2016, Am. Astron. Soc. Meeting Abstracts, 227, 324.04 [NASA ADS] [Google Scholar]
- Treu, T., Ellis, R. S., Kneib, J.-P., et al. 2003, ApJ, 591, 53 [Google Scholar]
- Umetsu, K., Zitrin, A., Gruen, D., et al. 2016, ApJ, 821, 116 [Google Scholar]
- van der Burg, R. F. J., Rudnick, G., Balogh, M. L., et al. 2020, A&A, 638, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, S. D. M., & Frenk, C. S. 1991, ApJ, 379, 52 [Google Scholar]
- Xie, C., van Weeren, R. J., Lovisari, L., et al. 2020, A&A, 636, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- ZuHone, J. A. 2011, ApJ, 728, 54 [Google Scholar]
Appendix A: Photometry
The photometric data include ground-based wide-field observations in B, V, R, i, and z band carried out with the wide-field imager (WFI) at the MPG/ESO 2.2-meter telescope at the La Silla Observatory 2.2, giving a field of view of 34′ × 33′, and HST data in 16 broad-band filters, from the UV to the near-IR, as part of the CLASH multi-cycle treasury program (see Postman et al. 2012). Moreover, as part of the FF program, A S1063 was also imaged with the HST for a total of 140 orbits, divided over seven optical/near-infrared bands (F435W, F606W, F814W, F105W, F125W, F140W, and F160W).
A.1. WFI data
The ground-based photometric observations were carried out with the WFI5 under programme 085.A-9002(A), P.I. S. Seitz. In this paper we analysed B-, V-, R-, i-, and z-band images with total exposure times of 20297.6137 s, 23696.685 s, 34195.3103 s, 29391.937 s, and 11537.7814 s and FWHMs of ∼1.25, ∼0.95, ∼0.76, ∼1.18, and ∼1.04, respectively, sampled at 0.20 arcsec per pixel.
The photometric catalogues were produced using the software SExtractor (Bertin & Arnouts 1996) in conjunction with PSFEx6 (Bertin 2011), which performs PSF fitting photometry. We extracted independent catalogues in each band that were then matched across the four wavebands using STILTS (Taylor 2006). We used a two-step approach in the catalogue extraction as in Mercurio et al. (2015). First, we ran SExtractor in the so-called cold mode, in which the brightest and most extended sources are properly deblended; then, in a second step, we set configuration parameters in the so-called hot mode in order to detect fainter objects and to split close sources properly (e.g. Rix et al. 2004; Caldwell et al. 2008). Finally, we combined the two catalogues by replacing extended objects, properly deblended in cold mode, in the catalogue of sources detected in the hot mode, and by deleting multiple detections of these extended sources. Among the photometric quantities, we measured aperture magnitudes (MAG_APER) in nine circular apertures with diameters of 1.5, 3.0, 4.0, 5.0, 8.0, 16.0, 30.0, and 3*FWHM, 8*FWHM, isophotal magnitudes (MAG_ISO), computed by considering the threshold value as the lowest isophote and the Kron magnitude (MAG_AUTO, which is estimated through an adaptive elliptical aperture (Kron 1980).
Using PSFEx, we modelled the PSF of the images (see Armstrong et al. 2010; Bertin 2011; Mohr et al. 2012; Bouy et al. 2013 for details). Thus, we ran SExtractor taking the PSF models as input to measure the PSF-corrected model-fitting photometry for all sources in the image. In this case, we extracted magnitudes from (i) the PSF fitting (MAG_PSF) and (ii) the sum of the bulge and the disk components, centred on the same position, convolved with the local PSF model (MAG_MODEL).
To separate galaxies and point-like sources, we adopted a progressive approach analogous to the approaches described in Annunziatella et al. (2013) and Mercurio et al. (2015), using i) the stellarity index (CLASS_STAR), ii) the half-light radius (FLUX_RADIUS), iii) the new SExtractor-classifier SPREAD_MODEL, iv) the peak of the surface brightness above the background (μmax), and v) a final visual inspection for objects that were classified as galaxies but had edge values of the stellarity index (CLASS_STAR≥0.9, see below).
In the top panel of Fig. A.1, CLASS_STAR is plotted as a function of the Kron magnitude for the R band. The sequence of unsaturated stars (R> 16.8 mag) is separated from galaxies by selecting a CLASS_STAR value above 0.98 only down to R = 21.5 mag. For magnitudes fainter than this value, lowering the established limit to separate stars and galaxies causes an increase in the star sub-sample contamination from galaxies. We classified sources fainter than R = 21.5 mag using FLUX_RADIUS as a measure of source concentration. The top right panel of Figure A.1 shows that the locus of stars, defined according to the relation between half-light radius and Kron magnitude. It is reliable down to R = 23.0 mag. Finally, to obtain a reliable star and galaxy classification for sources fainter than this limit, we used the new SExtractor classifier, SPREAD_MODEL, which takes the difference between the model of the source and the model of the local PSF into account (Mohr et al. 2012). By construction, this parameter is close to zero for point sources, positive for extended sources (galaxies), and negative for detections smaller than the PSF, such as cosmic rays. The bottom left panel of Figure A.1 shows that stars and galaxies tend to arrange themselves in two different loci in the distribution of the SPREAD_MODEL as a function of Kron magnitude. Based on this diagram, we classified as galaxies all sources with SPREAD_MODEL > 0.003 and 23.0< R< 25.0 mag. The plot of μmax as a function of the Kron magnitude was used in order to select saturated stars (vertical dashed line Fig. A.1), as shown in the bottom right panel. We also performed a visual inspection of the objects that were classified as galaxies but had CLASS_STAR> 0.9. Because the R band is the deepest band of the survey and is conducted in the best seeing conditions, it was used to classify sources in the cross-correlated catalogue of the five bands. Finally, the catalogues in all bands were visually inspected in the images to confirm the residual presence of spurious or misclassified objects, such as traces of satellites or effects of bad columns.
 |
Fig. A.1. Two-dimensional histogram of SExtractor stellarity index (top left panel), half-light radius (top right panel), spread model (bottom left panel), and μmax (bottom right panel) as a function of the Kron magnitudes for sources in the R-band image. The vertical dashed line in all panels is the magnitude limit we adopted for saturated objects. The points are colour-coded according to their number counts as reported in the vertical colour bars. |
The photometric limiting magnitude of the extracted catalogue for galaxies is defined as the magnitude limit below which the completeness drops from 95%. Following the method of Garilli et al. (1999) that was also adopted in Mercurio et al. (2015), we estimated the completeness magnitude limit as the magnitude at which we begin to lose galaxies because they are fainter than the brightness threshold inside a detection aperture of 1.5″ diameter7 for all the optical bands. In all panels of Fig. A.2, the vertical dashed blue lines represent the detection limit, while the continuous red lines are the linear empirical relation between the magnitude within a 8.0″ diameter aperture and the magnitude within the detection aperture. The relation between the two magnitudes shows a scatter that essentially depends on the galaxy profiles. Taking this scatter (see dashed red lines in Fig. A.2) into account, we fixed as a completeness magnitude limit (dashed blue horizontal line) the intersection between the lower 2.6*σ limit of the relation and the detection limit.
 |
Fig. A.2. Completeness magnitude limits for ground-based imaging. Left panels: Distribution of the SExtractor magnitude inside an 8.0″ diameter as a function of the magnitude inside a detection aperture of 1.5″ diameter for BVRiz bands. The horizontal and vertical dashed blue lines indicate the detection and completeness limits, respectively. The continuous red lines are the linear relation between the magnitude within the 8.0″ diameter aperture and the magnitude within the detection aperture, minus/plus 1σ (dashed red lines). Right panels: Number counts of galaxies for each band. The dashed blue lines mark the completeness magnitudes. |
The catalogues are 95% complete at total magnitudes of 24.7, 24.4, 24.5, 23.2, and 20.5 in the B, V, R, i, and z bands, respectively. The final photometric catalogue contains ∼ 34 000 (33 879) objects down to RAB = 24.6 mag.
A.2. HST data
The cluster A S1063 is one of the six clusters that were imaged in seven optical/near-infrared bands, F435W, F606W, F814W, F105W, F125W, F140W, and dF160W, with the FF program (P.I.: J. Lotz). This program combines the power of HST with the natural gravitational telescopes of high-magnification clusters of galaxies, producing the deepest observations of clusters and their lensed galaxies ever obtained. These images allow (1) studying distant galaxy populations ∼10-100 times fainter than any previously observed, (2) improving the statistical understanding of galaxies during the epoch of reionisation, and (3) providing unprecedented measurements of the dark matter within massive clusters. We analysed the public HST photometric data available at the STScI MAST Archive8. We used the v1.0 release of epoch 1 images, processed with the new self-calibration approach (Anderson & Ogaz 2014) to reduce low-level dark current artefacts across the detector (Tortorelli et al. 2018). A S1063 is also one of the 25 massive (virial mass Mvir 5-30 × 1014 M⊙) galaxy clusters observed with The Cluster Lensing And Supernova survey with Hubble (CLASH, P.I.: M. Postman). This survey was awarded 524 orbits of HST to observe a sample of clusters, spanning the redshift range z = 0.18-0.90 in 16 broad-band filters: four filters from WFC3/UVIS, five from WFC3/IR, and seven from ACS/WFC, ranging from approximately 2000 to 17000 Å. The sample was carefully chosen to be largely free of lensing bias and representative of relaxed clusters, based on their symmetric and smooth X-ray emission profiles (for a thorough overview, see Postman et al. 2012). CLASH has four main scientific goals: (1) measuring the cluster total mass profiles over a wide radial range through SL and WL analyses, (2) detecting new type Ia supernovae out to redshift z ∼ 2.5 to improve the constraints on the dark energy equation of state, (3) discovering and studying some of the first galaxies that formed after the Big Bang, and (4) performing galaxy evolution analyses of cluster members and background galaxies. Ancillary science that can indeed be carried out with the superb data set of CLASH is the analysis of several new SL systems on the galaxy scale. With an averaged exposure time of ∼2500 s (one to two orbits) per image (or 20 orbits per cluster if all filters are included), the CLASH observations reach a typical photometric depth of F814W = 28.0 or F160W = 26.5 (S/N> 3) (see Molino et al. 2017 for details). Image reduction, alignment, and co-adding were made using the MosaicDrizzle pipeline (Koekemoer et al. 2003, 2011), where a final scale of 0.065 arcsec pixel1 was chosen for all the fields. The reduced images and weight maps are available at the Mikulski Archive for Space Telescopes (MAST)9.
We extracted the catalogues for each of the 16 CLASH bands in dual mode using as detection image the deep image obtained combining all the optical plus NIR images. For ground-based catalogues, we used a two-step approach in the catalogue extraction using cold and hot mode (see above) in order to detect fainter objects and to properly split close sources (e.g. Rix et al. 2004; Caldwell et al. 2008). We finally combined the two catalogues by replacing extended objects, properly deblended in cold mode in the catalogue of sources detected in the hot mode and by deleting multiple detections of these extended sources. Finally, we visually inspected the catalogues to clean them from spurious detections, and we placed magnitudes equalling -99.0 (i.e. no magnitude measurement) in the bands where objects were detected in the combined image but had a value equal to zero in the weight map of these bands. Finally, we obtained a multi-band catalogue of ∼ 4300 sources with ∼ 1500 sources down to the 95% limiting magnitude of F814W = 25.5 mag (see the vertical green line in Fig. A.3).
 |
Fig. A.3. Magnitude distribution of HST sources for 12 wavebands from F435W to F160W in the field of A S1063. The dashed line indicates the 95% limiting magnitude in F814W band. |
Appendix B: 3D dynamical analysis with DEDICA
We applied the 3D-DEDICA method (Pisani 1993, 1996) to the full spectroscopic sample. As in Balestra et al. (2016), we used a simplified version of the 3D-DEDICA method based on the same definition of the adaptive kernel estimate as in Pisani (Pisani 1993, 1996), with the same computation of the local bandwidth factor λi (see Equations (26) and (27) in Pisani 1993), but using the size parameter of the kernel proposed by Silverman (1986). This simplified procedure is optimised to mainly race the large-scale structure of the cluster. This procedure identified five sub-clumps with a significance > 99.9%, whose properties are described in Table B.1.
Results for the detection of 3D substructures with a significance > 99.9% in the whole sample of cluster members of A S1063. Columns list the following information: (1) id of the sub-clump, (2) number of assigned members, (3) peak velocity in km s−1, and (4) coordinates.
Figure B.1 shows the velocity (left panel) and 2D (right panel) distributions of the five sub-clumps detected with 3D-DEDICA. Sub-clumps 1 (red) and 2 (purple) follow the NE-SW elongation of the cluster (right panel of Fig. B.1) and show different velocity distributions (left panel of Fig. B.1). Sub-clump 1 has a broader distribution and a higher velocity peak than sub-clump 2, also producing the two peaks visible in the right panel of fig 9. Sub-clump 3 (blue) is concentrated inside r200, while sub-clumps 4 (orange) and 5 (green) lie outside r200. Galaxies in the small high-velocity group detected by the DSv-test at X = 1.0 Mpc and Y=−3.2 Mpc in Fig. 10 belong to substructure 4. On the other hand, the SW low-velocity region (X = 1.0 Mpc and Y=−1.0 Mpc in Figs. 10 and 11) detected by the DSv test is composed mainly of galaxies belonging to sub-clump 3. The BCG, whose velocity is indicated by the arrow in the left panel of Fig. B.1, belongs to sub-clump 1.
 |
Fig. B.1. Velocity (left panel) and 2D (right panel) distributions of the five substructures detected with 3D-DEDICA. The arrow indicates the velocity of the BCG. The colour code, velocity peak, and the centre for each substructure are reported in Tab. B.1. In the right panel, the circle has a radius equal to r200 = 2.63 Mpc. |
We also examined the fraction of different spectral types in each identified sub-clump (Fig. B.2 and Tab. B.2). Sub-clumps 1 and 2 are composed mainly of P+red HDS, which belong to the virialised region in the projected phase-space diagram. Sub-clump 3 shows similar fractions of P+red and mELG+ELGs15+ELGs40, which belong to the virialised region and region inside r200 with negative high-velocity dispersion (Δv/σ< -1.5) in the projected phase-space diagram. Sub-clump 5 is located outside r200 (i.e. belonging to the infalling region) and is composed mainly of galaxies with velocities lower than the mean cluster LOS velocity (⟨V⟩ = 103 640 ± 39 km s−1, see Fig. B.1). It shows, as expected, a high fraction of mELG+ELGs15+ELGs40. On the other hand, sub-clump 4 is located outside r200 and is composed of galaxies with velocities higher than the mean cluster LOS velocity (see Fig. B.1). We found a lower fraction of mELG+ELGs15+ELGs40 and the higher fraction of P+red HDS in sub-clump 4 than in sub-clump 5, indicating a different spectral composition of galaxies outside r200, but velocities higher and lower than the mean cluster LOS velocity.
 |
Fig. B.2. Fraction of galaxies with different spectral types inside each sub-clump. |
Finally, we compared the accretion redshift distributions of the five sub-clumps (see Fig. B.3). According to the KS-1D, the accretion redshift distributions of sub-clumps 1, 2, and 3 differ from those of sub-clumps 4 and 5. The latter are accreted later on average, as expected, because sub-clumps 4 and 5 are more external and composed mainly of SF galaxies.
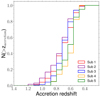 |
Fig. B.3. Cumulative distribution of accretion redshift for galaxies belonging to the five sub-clumps. |
Fraction of different spectral classes inside each of the 3D substructures detected in Sect. 5. Columns list the following information: (1) id of the sub-clump, (2)-(3)-(4) fractions of [P+red HDS], [blue HDS+wELG] and [mELG+ELGs15+ELGs40] for each substructure, respectively.
Appendix C: Stellar masses
The available HST photometry from the CLASH survey plus the MUSE spectra were used to determine the stellar mass values of a subsample of 81 spectroscopic members in the centre of the cluster. MUSE spectra plus HST photometry were used to fit the spectral energy distributions (SEDs) of these galaxies. The SED fitting was performed using composite stellar population models based on Bruzual & Charlot (2003) templates, with delayed exponential star formation histories, solar metallicity, and a Salpeter (Salpeter 1955) stellar IMF. The presence of dust was taken into account following Calzetti et al. (2000). For each galaxy, the best-fit (Mbest) and 1σ lower (Mlow) and upper limit (Mhigh) values of the stellar mass were measured. An example of an SED is shown in Fig. C.1.
 |
Fig. C.1. Example of the composite stellar population modelling of the 12 OPT/NIR HST bands (left panel, open blue symbols) plus MUSE spectra (right panel, black line) of the BCG. The best fit is shown in red in both panels. In the left panel, blue empty circles and bars are the observed fluxes with 1σ errors, and filled yellow circles are model-predicted HST fluxes. In the right panel, blue areas indicate the masked regions. |
Then we used the stellar masses obtained from the HST+MUSE data to cross-calibrate the stellar mass of each member galaxy, which has only the four optical WFI photometric magnitudes available for the majority of members. We obtained that the Salpeter stellar masses follow the relations
or, if the I band is not available,
with an average scatter of 0.155 and 0.175, respectively.
All Tables
Results for the detection of 3D substructures with a significance > 99.9% in the whole sample of cluster members of A S1063. Columns list the following information: (1) id of the sub-clump, (2) number of assigned members, (3) peak velocity in km s−1, and (4) coordinates.
Fraction of different spectral classes inside each of the 3D substructures detected in Sect. 5. Columns list the following information: (1) id of the sub-clump, (2)-(3)-(4) fractions of [P+red HDS], [blue HDS+wELG] and [mELG+ELGs15+ELGs40] for each substructure, respectively.
All Figures
 |
Fig. 1. Ground-based and HST color image of the galaxy cluster Abell S1063 with the wedge redshift diagram from the CLASH-VLT survey. Right panel: WFI colour-composite image of A S1063 (UBVRIz, 30 × 30 arcmin2). The cyan square indicates the VIMOS spectroscopic survey area (28.9 × 22.7 arcmin2), and the white and green polygons indicate the HST FF colour-composite image (F435W, F606W, and F814W) and the footprint of MUSE observations (two pointings, 2 × 1 arcmin2) enlarged in the inset. The dotted and dashed circles have radii R = 1 Mpc and R = r200, respectively. Left panel: 3D spatial distribution of all measured redshifts at 0.2 < z < 0.6, where cluster members are marked in red. |
| In the text | |
 |
Fig. 2. Exposure map of the 16 VIMOS pointings in the field of A S1063. The red circles are centred on the BCG and have radii of r200 = 2.63 Mpc (see Sect. 4). The cross marks the position of the BCG. |
| In the text | |
 |
Fig. 3. WFI V − I vs. B − R colours for all of the extracted sources with R magnitudes ≤ 24. The dashed blue and black lines show the colour cuts defining the box we used for target selection. Small black and green dots are the sources classified as galaxies and stars in the WFI photometric catalogue, respectively. Larger data points mark cluster member galaxies in black and non-members in red that belong to our CLASH-VLT spectroscopic catalogue. |
| In the text | |
 |
Fig. 4. Spectroscopic redshift distribution of 3850 sources in A S1063 from the CLASH-VLT catalogue, including 175 MUSE redshifts. The inset shows a zoom-in around the mean cluster redshift ⟨zcl⟩ = 0.3457 (red histogram for MUSE galaxies) of the 1234 cluster members found from the kinematic analysis. |
| In the text | |
 |
Fig. 5. Completeness of the spectroscopic sample as a function of the custercentric distance. The shaded area indicates the 68% confidence regions according the algorithm of Gehrels (Gehrels 1986). The dashed line indicates r200 = 2.63 Mpc (see Sect. 4). |
| In the text | |
 |
Fig. 6. Redshift distribution of the 1234 cluster members found in the kinematical analysis of the members in A S1063. The two dashed lines show the two overlapping peaks of 590 and 715 galaxies at z = 0.3424 and z = 0.3467 detected with 1D DEDICA. |
| In the text | |
 |
Fig. 7. 2D spatial distribution of VIMOS (blue circles) and MUSE (red circles) spectroscopically confirmed members. The large black circle has a radius equal to r200 = 2.63 Mpc (see Sect. 4). |
| In the text | |
 |
Fig. 8. Phase-space diagram including 1305 galaxies from the spectroscopic sample, where rest-frame velocities are plotted vs. the clustercentric distance. Green circles highlight the 1234 cluster members. Yellow circles indicate galaxies that lie in the selected cluster redshift range, but are rejected in the second step of our member selection procedure. The escape velocity curves are also shown (blue lines). |
| In the text | |
 |
Fig. 9. Rest-frame velocity distribution relative to the mean cluster velocity of the 120 galaxies having R < 20 (left panel), and of the 395 galaxies within 1 Mpc from the cluster centre (right panel). The smooth curve is the probability density function obtained with a kernel density estimator. In both panels, the dashed line indicates the rest-frame velocity of the BCG: (VBCG − ⟨V⟩)/(1 + z) = 333 km s−1. |
| In the text | |
 |
Fig. 10. 2D spatial distribution of the 1234 member galaxies colour-coded according to the local mean velocity deviations δv, i. The circle has a radius equal to r200 = 2.63 Mpc. |
| In the text | |
 |
Fig. 11. 2D spatial distribution of the 120 member galaxies with R < 20, colour-coded as in Fig. 10. The circle has a radius equal to r200 = 2.63 Mpc. |
| In the text | |
 |
Fig. 12. Colour-magnitude diagram of the spectroscopic members in A S1063. Black circles mark the 960 galaxies with robust spectral classification, and filled grey circles indicate galaxies with reliable colours and a spectral S/N that is too low to be classified. |
| In the text | |
 |
Fig. 13. Completeness of the spectroscopic sample of blue and red galaxies as a function of custercentric distance. The shaded regions indicate the 68% confidence intervals, following the algorithm of Gehrels (Gehrels 1986). The dashed line indicates r200 = 2.63 Mpc. |
| In the text | |
 |
Fig. 14. Colour-magnitude relation of 960 spectroscopic members in A S1063 with reliable spectral classification. The best-fit of the CM is indicated by the black line, and 68% and 99% limits are marked as dashed and dotted red lines, respectively. The red empty circle highlights the BCG. |
| In the text | |
 |
Fig. 15. Spatial distribution and projected phase-space diagram of the spectroscopic members. Top panels: 2D spatial distribution of the 960 spectroscopic member galaxies, classified according to their spectral properties. The circle has a radius equal to r200 = 2.63 Mpc. Bottom panels: phase-space diagram of the spectroscopic members, according to their spectral types. The underlying greyscale image in the top and bottom panels shows the galaxy number density distribution in 2D and in the phase-space, respectively, considering the whole population. |
| In the text | |
 |
Fig. 16. Number density profiles (normalised by the total number of galaxies in each sample, Ngal) of the passive and red HDS (red points and lines), blue HDS, and wELG (green), and mELG, ELGs15, and ELGs40 (blue) populations. Error bars are 1 σ. Solid lines are best-fit NFW models for each population. |
| In the text | |
 |
Fig. 17. Velocity dispersion profiles of the passive and red HDS (red points), blue HDS and wELG (green), and mELG, ELGs15, and ELGs40 (blue) populations. Error bars correspond to 1σ. Velocity dispersions are in km s−1. |
| In the text | |
 |
Fig. 18. Projected phase-space distribution and fraction of galaxies with different spectral types. Main panel: projected phase-space distribution of galaxies with different spectral types. The two lines of constant (vrf/σ)×(R/r200) = 0.1, 0.4 are plotted as in Noble et al. (2013) to delineate the separation into regions of virialised (within the inner caustic), backsplash (between caustics), and infall galaxies (along and outside caustics). The dashed black line delimits the regions inside and outside r200. We indicate as regions A and B the two areas with R < r200 outside the virialised region. Top panel: fraction of P+red HDS (orange circles), blue HDS+wELG (green triangles), and mELG+ELGs15+EGs40 (blue stars) as a function of the clustercentric distance. Left and right panels: velocity distribution of the three corresponding samples inside and outside r200, respectively. The smoothed curves are the probability density functions obtained with a kernel density estimator. |
| In the text | |
 |
Fig. 19. Projected phase-space distribution and fraction of post-starburst galaxies. Bottom panel: projected phase-space distribution of red (magenta) and blue (cyan) post-starburst galaxies. The lines are the same as those in Fig. 18. Top panel: fraction of post-starburst galaxies with respect to all classified members as a function of the clustercentric distance. |
| In the text | |
 |
Fig. 20. Cumulative distribution of the accretion redshift. Upper left panel: cumulative distribution of the accretion redshift, zaccretion, for galaxies with different spectral types: passive + red post-starbursts (orange), blue post-starburst galaxies + weak emission-line galaxies (green), and strong emission-line galaxies (blue). Other three panels: same distribution separated into high- and low-mass bins (using as a threshold Log(M*/M⊙) = 10.4) for the corresponding (colour-coded) galaxy spectral types. |
| In the text | |
 |
Fig. 21. Velocity anisotropy profiles of the red and blue cluster members in the upper and lower panels, respectively. The solid (dashed) coloured lines represent the solutions of the inversion of the Jeans equation adopting the mass profile from Sartoris et al. (2020) (Umetsu et al. 2016). The coloured area indicates the 68% confidence region around the solution. The magenta shading indicates the 68% confidence region around the MAMPOSSt best-fit solution for a Tiret model (Sartoris et al. 2020). In both panels we use the same Tiret model, which was computed considering the full sample of member galaxies. The vertical dotted and dash-dotted black lines mark r−2 (which corresponds to rs for an NFW model) and r200 obtained from Umetsu et al. (2016) and the MAMPOSSt analysis of Sartoris et al. (2020), respectively. |
| In the text | |
 |
Fig. A.1. Two-dimensional histogram of SExtractor stellarity index (top left panel), half-light radius (top right panel), spread model (bottom left panel), and μmax (bottom right panel) as a function of the Kron magnitudes for sources in the R-band image. The vertical dashed line in all panels is the magnitude limit we adopted for saturated objects. The points are colour-coded according to their number counts as reported in the vertical colour bars. |
| In the text | |
 |
Fig. A.2. Completeness magnitude limits for ground-based imaging. Left panels: Distribution of the SExtractor magnitude inside an 8.0″ diameter as a function of the magnitude inside a detection aperture of 1.5″ diameter for BVRiz bands. The horizontal and vertical dashed blue lines indicate the detection and completeness limits, respectively. The continuous red lines are the linear relation between the magnitude within the 8.0″ diameter aperture and the magnitude within the detection aperture, minus/plus 1σ (dashed red lines). Right panels: Number counts of galaxies for each band. The dashed blue lines mark the completeness magnitudes. |
| In the text | |
 |
Fig. A.3. Magnitude distribution of HST sources for 12 wavebands from F435W to F160W in the field of A S1063. The dashed line indicates the 95% limiting magnitude in F814W band. |
| In the text | |
 |
Fig. B.1. Velocity (left panel) and 2D (right panel) distributions of the five substructures detected with 3D-DEDICA. The arrow indicates the velocity of the BCG. The colour code, velocity peak, and the centre for each substructure are reported in Tab. B.1. In the right panel, the circle has a radius equal to r200 = 2.63 Mpc. |
| In the text | |
 |
Fig. B.2. Fraction of galaxies with different spectral types inside each sub-clump. |
| In the text | |
 |
Fig. B.3. Cumulative distribution of accretion redshift for galaxies belonging to the five sub-clumps. |
| In the text | |
 |
Fig. C.1. Example of the composite stellar population modelling of the 12 OPT/NIR HST bands (left panel, open blue symbols) plus MUSE spectra (right panel, black line) of the BCG. The best fit is shown in red in both panels. In the left panel, blue empty circles and bars are the observed fluxes with 1σ errors, and filled yellow circles are model-predicted HST fluxes. In the right panel, blue areas indicate the masked regions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.