| Issue |
A&A
Volume 628, August 2019
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 32 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201935623 | |
| Published online | 26 July 2019 | |
Atmospheric characterization of the ultra-hot Jupiter MASCARA-2b/KELT-20b
Detection of CaII, FeII, NaI, and the Balmer series of H (Hα, Hβ, and Hγ) with high-dispersion transit spectroscopy★
1
Instituto de Astrofísica de Canarias,
Vía Láctea s/n,
38205 La
Laguna,
Tenerife, Spain
e-mail: nuriacb@iac.es
2
Departamento de Astrofísica, Universidad de La Laguna,
La Laguna,
Spain
3
Institut für Astrophysik, Georg-August-Universität,
Friedrich-Hund-Platz 1,
37077
Göttingen,
Germany
4
Key Laboratory of Planetary Sciences, Purple Mountain Observatory, Chinese Academy of Sciences,
Nanjing
210008, PR China
5
Hamburger Sternwarte, Universität Hamburg,
Gojenbergsweg 112,
21029
Hamburg, Germany
6
Centre for Exoplanet Science, University of St Andrews,
St Andrews, UK
7
SUPA, School of Physics & Astronomy, University of St Andrews,
St Andrews,
KY16 9SS, UK
8
SRON Netherlands Institute for Space Research,
Sorbonnelaan 2,
3584 CA
Utrecht,
The Netherlands
9
National Astronomical Observatory of Japan,
2-21-1 Osawa,
Mitaka,
Tokyo
181-8588, Japan
10
SOKENDAI (The Graduate University of Advanced Studies),
2-21-1 Osawa,
Mitaka,
Tokyo
181-8588, Japan
11
Astrobiology Center,
2-21-1 Osawa,
Mitaka,
Tokyo
181-8588, Japan
12
JST, PRESTO,
2-21-1 Osawa,
Mitaka,
Tokyo
181-8588, Japan
13
Centro de Astrobiología (CSIC-INTA),
Carretera de Ajalvir km 4,
28850
Torrejón de Ardoz,
Madrid,
Spain
14
Department of Earth and Planetary Science, Graduate School of Science, The University of Tokyo,
7-3-1 Hongo,
Bunkyo-ku,
Tokyo
113-0033, Japan
Received:
4
April
2019
Accepted:
29
May
2019
Ultra-hot Jupiters orbit very close to their host star and consequently receive strong irradiation, causing their atmospheric chemistry to be different from the common gas giants. Here, we have studied the atmosphere of one of these particular hot planets, MASCARA-2b/KELT-20b, using four transit observations with high resolution spectroscopy facilities. Three of these observations were performed with HARPS-N and one with CARMENES. Additionally, we simultaneously observed one of the transits with MuSCAT2 to monitor possible spots in the stellar surface. At high resolution, the transmission residuals show the effects of Rossiter-McLaughlin and centre-to-limb variations from the stellar lines profiles, which we have corrected to finally extract the transmission spectra of the planet. We clearly observe the absorption features of CaII, FeII, NaI, Hα, and Hβ in the atmosphere of MASCARA-2b, and indications of Hγ and MgI at low signal-to-noise ratio. In the case of NaI, the true absorption is difficult to disentangle from the strong telluric and interstellar contamination. The results obtained with CARMENES and HARPS-N are consistent, measuring an Hα absorption depth of 0.68 ± 0.05 and 0.59 ± 0.07%, and NaI absorption of 0.11 ± 0.04 and 0.09 ± 0.05% for a 0.75 Å passband, in the two instruments respectively. The Hα absorption corresponds to ~1.2 Rp, which implies an expanded atmosphere, as a result of the gas heating caused by the irradiation received from the host star. For Hβ and Hγ only HARPS-N covers this wavelength range, measuring an absorption depth of 0.28 ± 0.06 and 0.21 ± 0.07%, respectively. For CaII, only CARMENES covers this wavelength range measuring an absorption depth of 0.28 ± 0.05, 0.41 ± 0.05 and 0.27 ± 0.06% for CaII λ8498Å, λ8542Å and λ8662Å lines, respectively. Three additional absorption lines of FeII are observed in the transmission spectrum by HARPS-N (partially covered by CARMENES), measuring an average absorption depth of 0.08 ± 0.04% (0.75 Å passband). The results presented here are consistent with theoretical models of ultra-hot Jupiters atmospheres, suggesting the emergence of an ionised gas on the day-side of such planets. Calcium and iron, together with other elements, are expected to be singly ionised at these temperatures and be more numerous than its neutral state. The Calcium triplet lines are detected here for the first time in transmission in an exoplanet atmosphere.
Key words: planets and satellites: atmospheres / planetary systems / methods: observational / techniques: spectroscopic / planets and satellites: individual: MASCARA-2b / planets and satellites: individual: KELT-20b
Reduced spectra are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/628/A9
© ESO 2019
1 Introduction
The study of hot Jupiters atmospheres has revealed a broad composition and structural diversity in gas-rich planets (Jensen et al. 2012; Sing et al. 2012; Crossfield 2015; Deming & Seager 2017; Madhusudhan et al. 2016). When these planets are under extreme conditions, in particular, located very close to their host stars and consequently being strongly irradiated, their temperatures increase and lead to different atmospheric chemistry between the day and night-sides of atmosphere (Arcangeli et al. 2018; Bell & Cowan 2018; Helling & Rimmer 2019) in comparison with cooler planets. This creates a new type of exoplanet called ultra-hot Jupiters (hereafter UHJ).
We define UHJs as planets with day-side temperatures higher than 2200 K (Parmentier et al. 2018). One of the most significant differences between hot and ultra-hot Jupiters is perhaps the presence of water vapour in their atmospheres. Water has become a common species in hot Jupiters but is missing in the day-side of ultra-hot Jupiters, even though the ingredients to form water vapor are present. The high irradiation received by the day-side of such UHJs causes the atmospheric gas temperature to increase to further more than 3000 K, as for example demonstrated for WASP-18b (Helling et al. 2019). The dominating gas species in the upper, day-side atmosphere is therefore atomic hydrogen (HI) instead of molecular hydrogen (H2). Water (H2O) is approximately five orders of magnitude less abundant on the day-side than on the night-side. Such high day-side gas temperatures further result in an increased number of H− compared to cooler giant gas planets like HD 189733b. In the case of WASP-18b, in the upper low-pressure atmosphere, the day-side has more than ten orders of magnitude more H− and H+ than the night-side. Therefore, H− opacity at the day-side plays an important role (Lothringer et al. 2018).
Several ultra-hot Jupiters have been studied: WASP-33b (Haynes et al. 2015), WASP-121b (Evans et al. 2017), WASP-103b (Kreidberg et al. 2018), WASP-18b (Sheppard et al. 2017; Arcangeli et al. 2018; Helling et al. 2019), HAT-P-7b (Armstrong et al. 2016), most of them presenting thermal inversions. Focusing on transmission spectroscopy at high resolution, a study of the atmosphere of KELT-9b, the hottest planet known to date (Teq = 4050 K and day-side temperature of 4600 K), by Yan & Henning (2018) shows a detection of an extended atmosphere of Hα produced by irradiation. On the other hand, Hoeijmakers et al. (2018) study the atmosphere of this same planet, detecting Fe, Fe+, and Ti+ and concluding that at such these high temperatures metals are predominantly in their ionic forms. Cauley et al. (2019) further report the detection of Hβ and the optical MgI triplet, and find that planetary rotational broadening is needed to reproduce the Balmer line transmission profile shapes.
Here, we present the study of the atmosphere of MASCARA-2b (Talens et al. 2018), also known as KELT-20b (Lund et al. 2017), using four transit observations, three of them observed with the HARPS-North spectrograph and one observed with the CARMENES spectrograph. MASCARA-2b is an ultra-hot Jupiter with an equilibrium temperature of 2260 K, located in a 3.5 day orbit around an A-type star (mV = 7.6) with an effective temperature (Teff) of 8980 K and a rotation (vsini) of 114 km s−1. MASCARA-2b orbits very close to its host star (a = 0.057 AU) and is strongly irradiated. Its mass, because radial-velocity measurements of rapid-rotators are very challenging, has not been measured, and only an upper limit is available: Mp < 3.510 MJ. The details of the system are summarised in Table 1. In Fig. 1 our target can be contextualised among the other known ultra-hot Jupiters. MASCARA-2b orbits around the second hottest host star of the UHJ population, although its equilibrium temperature is typical for UHJs. Given that the effective temperature of MASCARA-2 is larger than WASP-18, the effect of thermal ionisation of the day-side can be expected to be stronger for MASCARA-2b/KELT-20b due to a stronger irradiation by the host star.
Due to its brightness and the fast rotation of the host star, MASCARA-2b is an ideal target for transmission spectroscopy. Its atmosphere is previously studied in Casasayas-Barris et al. (2018), where only the first HARPS-North transit on 16 August 2017 was analysed, finding evidence of Hα and NaI absorption features and noisy features at Hβ position. Here, combining four transits, we achieve higher signal-to-noise ratio (S/N) as we are able to clearly distinguish the centre-to-limb variation (CLV) and the Rossiter-McLaughlin effect (RME), whose treatment will become very important for atmospheric studies of this kind of planets when observing with ESPRESSO-like facilities.
This paper is organised in seven sections. In Sect. 1 we present a general introduction of transmission spectroscopy and ultra-hot Jupiters. In Sect. 2 we detail the observations. Methods to extract the colour-photometry light curves and high resolution transmission spectra are explained in Sect. 3. In Sect. 4 we explain how the CLV and RME are modelled. In Sect. 5 we present the results obtained in the analysis of high resolution transmission spectra. The analysis of the systematic effects are presented in Sect. 6 and the conclusions in Sect. 5.
Physical and orbital parameters of MASCARA-2b.
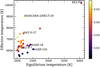 |
Fig. 1 Ultra-hot Jupiters sample from exoplanets.eu. This sample corresponds to all confirmed planets with equilibrium temperatures larger than 2000 K, which have been detected via radial-velocity or transits methods. In the horizontal axis we show the equilibrium temperatureof the planet, and in the vertical axis the stellar effective temperature. The semi-major axes of the systems are colour-coded in the side bar (in AU). Some names of UHJs’ host stars mentioned in this paper are shown as reference. |
2 Observations
We observed a total of four transits of MASCARA-2b using the HARPS-N and CARMENES high resolution spectrographs. One of these transits was simultaneously observed with the Multicolour Simultaneous Camera for studying Atmospheres of Transiting exoplanets 2 (MuSCAT2), a four-colour simultaneous imager, in order to monitor possible stellar activity. One additional epoch was observed with MuSCAT2 to reproduce the results of the first observation. Details of the observations can be found in Table 2 and Fig. 3.
2.1 HARPS-N observations
We observed three transits of MASCARA-2b using the HARPS-North spectrograph mounted on the 3.58-m TNG telescope, located at the Observatorio del Roque de los Muchachos (ORM, La Palma). The observations were on 16 August 2017, 12 and 19 July 2018. For the two last observations we used the GIARPS mode, which permits simultaneous high resolution spectroscopy observations in the near-infrared and in the optical wavelength regions, using GIANO-B and HARPS-North, respectively.
We exposed continuously before, during and after the transit, using the fibre A on the target and fibre B on the sky in order to monitor possible sky emissions. For the first and second night we used an exposure time of 200 s while in the third night we increased it to 300 s, to obtain a higher S/N.
2.2 CARMENES observations
One more transit was observed with Calar Alto high-Resolution search for M dwarfs with Exoearths with Near-infrared and optical Echelle Spectrographs (CARMENES) spectrograph located at the Calar Alto Observatory, on 23 August 2017. The strategy of these observations was the same as with HARPS-North. For these observations an exposure time of 192 s was used, obtaining a S/N of around 100 near the Hα line.
2.3 Photometric observations with MuSCAT2
The transit of MASCARA-2b on 12 July 2018 was observed simultaneously using MuSCAT2 (Narita et al. 2019) located at the 1.52 m Carlos Sánchez Telescope (TCS) at the Teide Observatory. Another transit on 30 September 2018 was observed using MuSCAT2 only. Both observations were heavily defocussed to avoid saturation. While the first observation covered the whole transit event, the second observation had to stop at ~43 min after the mid-transit point due to low elevation of the target. Both nights were mostly clear. Although defocussed, the profile of point spread function (PSF) was not stable for either of the two observations. The observing log is presented in Table 2.
3 Methods
In this section we present the data processing applied to extract the four colour light curves observed with MuSCAT2 (photometry) and the transmission spectra using the high resolution observations (spectroscopy).
3.1 Photometry
Two independent approaches were used for the MuSCAT2 photometry, light curve detrending, and transit modelling to search for possible spot-crossing events. The first approach uses the dedicated MuSCAT2 photometry and transit modelling pipeline: the photometry follows the standard aperture photometry practices, the transit modelling is carried out with PyTransit (Parviainen 2015) and the priors for the quadratic limb darkening coefficients are calculated using LDTk (Parviainen & Aigrain 2015). The final transit light curve modelling was carried out jointly for the two nights and all passbands, using a Gaussian process (GP) based systematics model calculated with george (Ambikasaran et al. 2015) with the sky level, airmass, seeing, and CCD centroid shifts as co-variates.
Our second approach followed closely the approach described in Chen et al. (2014). The photometry was carried out with the DAOPHOT package in the NASA IDL Astronomy User’s Library, the transit modelling was done with batman (Kreidberg 2015), Celerite (Foreman-Mackey et al. 2017) was used to implement a Gaussian process-based systematics model, and the method by Espinoza & Jordán (2015) was used to obtain priors on the quadratic limb darkening coefficients.
In both cases, emcee (Foreman-Mackey et al. 2013) was used to estimate the model parameter posteriors. The parameter posterior estimates are presented in Table 3, and the MuSCAT2 light curves are shown in Fig. 2. The transit light curves do not feature evident spot-crossing events, nor do they show significant colour-dependent depth variations.
3.2 Spectroscopy
The observations were reduced with the HARPS-North Data reduction Software (DRS), version 3.7. The DRS extracts the spectra order-by-order, which are then flat-fielded using the daily calibration set. A blaze correction and the wavelength calibration are applied to each spectral order and, finally, all the spectral orders from each two-dimensional echelle spectrum are combined and resampled into a one-dimensional spectrum. The resulting one-dimensional spectra cover the optical range between 3800 and 6900 Å and has a wavelength step of 0.01 Å. The spectra are referred to the Baricentric rest frame and the wavelengths are given in the air.
All nights present stable seeing at ~1 arcsec with the Moon at more than 90 deg from our target. HARPS-N Night 1 and CARMENES observations are observed to be very stable in terms of S/N during the night. For Night 2 and 3, however, we noticed variable S/N and variations of the continuum similar to a bad blaze function correction. This was caused by a problem with the Atmospheric Dispersion Corrector (ADC) of the telescope, that causes PSF distortions and variations of the continuum. For both these nights, re-reducing the data with the DRS did not produce any improvement. Our method for correcting this variation is discussed in detail in Sect. 5.1. On the other hand, during the Night 2 we observe a drop in the S/N of some spectra before the transit, possibly caused by the presence of a cloud. We discarded the spectra from 22:58 UT until 23:24 UT (eight spectra), where the S/N is lower than 35 (around 6600 Å). Additionally, for consistency with the S/N established for the cloud region, for this night we also removed the spectra taken at 01:28UT which also present S/N smaller than 35 (i.e. a total of nine spectra are discarded).
CARMENES observations are processed with the CARMENES pipeline CARACAL (CARMENES Reduction And Calibration; Caballero et al. 2016), which considers bias, flat-relative optimal extraction (Zechmeister et al. 2014), cosmic ray correction, and a wavelength calibration described in Bauer et al. (2015). The reduced spectra are referred to the terrestrial rest frame and the wavelengths are given in the vacuum. At the beginning of the night some technical problems lead to some very short time exposures with very low S/N which are directly discarded. The spectra, S/N and airmass evolution of each night can be observed in Fig. 3.
Observing log of the MASCARA-2b transit observations.
Best-fit parameters from MuSCAT2 transit light curve.
 |
Fig. 2 MASCARA-2b transit light curves obtained with MuSCAT2. The data have been binned to 7.2 min intervals for display clarity. |
3.2.1 Telluric correction
Taking advantage of the fact that the observations were carried out using fibre B monitoring the sky, we checked for possible atmospheric emissions features during the night. We observed no telluric emission feature needing to be corrected, and since subtracting the sky to the target spectra introduces additional noise, we did not apply this correction.
Following Allart et al. (2017), we corrected the telluric absorption contamination using version 1.2.0 of Molecfit (Smette et al. 2015 and Kausch et al. 2015). Molecfit is an ESO tool built to correct Earth atmospheric features in ground-based spectra, which uses a line-by-line radiative transfer model (LBLRTM). HARPS-North spectra are given in the solar system baricentric rest frame, while Molecfit models are computed in the terrestrial rest frame. For this reason, before fitting the telluric contamination we shifted the spectra to the terrestrial rest frame using the baricentric Earth radial velocity (BERV) information. We shifted the spectra using the IRAF (Tody 1986) routine dopcor. The parameters used to compute the high-resolution telluric spectrum are detailed in Allart et al. (2017), and the wavelength regions with strong lines used here are very similar to those used in that paper, but considering only those regions out of stellar features.
In the case of CARMENES data, the spectra after CARACAL reduction are already given in the terrestrial rest frame. The Molecfit correction applied is slightly different, and follows the method discussed in Nortmann et al. (2018) and Salz et al. (2018). The telluric uncorrected and corrected spectra in the atomic sodium (NaI) region for Night 4 obtained with CARMENES are shown in Fig. 4.
 |
Fig. 3 Observed spectra around the Hα line (left column), for Night 1 (first row), Night 2 (second row), Night 3 (third row) and Night 4 (fourth row). The three first nights were observed with HARPS-N and the last night, with CARMENES. The spectra are normalised to the same continuum level (see colour bar) and moved to the stellar rest frame. In the y-axis we show the spectrum number starting from zero and in the x-axis the velocity in km s−1. The narrow lines correspond to telluric contamination and the deepest central line (at 0 km s −1) corresponds to the centre of the Hα line core. Second and third columns: S/N and the airmass variation during the night, respectively. The S/N per pixel is extracted in the continuum near the Hα line, specifically around 6600 Å as the Hα line for this target is very broad due to its rapid rotation. The red S/N values correspond to the spectra which are not considered in our analysis. In particular, we observe a stable S/N during Night 1. Night 2 shows a drop in the S/N for the presence of a cloud around spectrum number 25 and two stops of the instrument around spectrum number 50 and 100 because GIANO-B suddenly aborted itself and it was necessary to restart the exposure with both the HARPS-N and GIANO-B instruments. |
3.2.2 General transmission spectrum extraction
Once the telluric correction has been applied, we cut the spectra in the wavelength region we want to study and normalise them by the continuum. This is done recursively over the whole spectral range covered by both spectrographs to screen for all possible planetary signals. Then, as the spectra after the Molecfit correction isreferred to the terrestrial rest frame, we shifted them to the stellar rest frame considering the system velocity (γ) and the BERV information. The stellar reflex motion is not considered because the mass of the planet (Mp) has not yet been determined, and the radial velocity measurements in rapid-rotating stars are difficult to determine. If we assume Ks = 322.51 m s−1 (i.e. the mass upper limit Mp= 3.510 MJ; Lund et al. 2017), the maximum stellar radial-velocity change is ~ ± 0.3 km s−1. Since one pixel in HARPS is around 0.8 km s−1 and the stellar lines present a large broadening caused by the fast stellar rotation, considering or not considering this reflex motion contributionto the radial velocity correction does not have any significant impact to the results, as presented in Casasayas-Barris et al. (2018). In addition, the spectra could be also affected by stellar activity and instrumental radial-velocity drifts. However, an A-type star like MASCARA-2 is not expected to be active, and the instrumental effects would similarly affect to all spectra, resulting in global wavelength offsets from the rest frame position (which after the daily calibration are expected to be of the order of 10 m s−1 for the instruments used here). For CARMENES observations, when shifting the spectra to the stellar rest frame, we rebinned the data to the same wavelength grid using the IDL routine rebinw from the PINTofALE package, which ensures flux conservation (Drake & Kashyap 2010).
For the next steps, we followed Wyttenbach et al. (2015): we computed the out-of-transit master spectrum (combination of all the stellar spectra taken when the planet is not transiting) and we then divided each spectrum by this master spectrum to remove the stellar lines. The resulting residuals contain the variations of the stellar lines profile produced by the presence of the planet and additional systematic effects. These variations include the absorption produced by the exoplanet atmosphere, the CLV and the RME. At this step we find the best-fit model of the absorption, CLV and RME, and the resulting best-fit parameters are used to compute the best-fit CLV and RME model, which is then removed from the residuals (see Sect. 4 for a detailed explanation of the models). Once these effects had been corrected, we shifted the remaining residuals to the planet rest frame and we then combined the in-transit residuals to find the transmission spectrum for each night.
HARPS-N Night 2 and Night 3 are affected by an ADC problem, presenting weird continuum variations similar to a bad blaze function correction. In order to solve this problem, we tried to re-reduce the raw data with the DRS pipeline, without any improvement. This effect introduces differences in the line wings changing in time, and which are more significant in very broad spectral lines, specially in the Hα line. These differences become very important after dividing the spectra by the out-of-transit master spectrum, as the resulting spectra present broad variations that partially hide the narrow residuals we are looking for behind this broad effect. For this reason, after computing the spectra of residuals we applied a very broad median filter using medfilt from scipy library with a kernel size of 1505 to protect the planetary signals from being diluted and remove only the low frequency variations produced by the variation of the continuum, and the final transmission spectrum was normalised with UnivariateSplines from scipy in order to remove remaining undulations. This additional correction is only applied to HARPS-N Night 2 and Night 3. Finally, we note that the parameters used during the whole process are those presented in Table 1 except for the epoch (T0), orbital period (P), and inclination (i), which are from the recalculated parameters of Table 3.
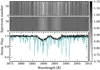 |
Fig. 4 Telluric correction of CARMENES observations (Night 4) of MASCARA-2b in the NaI doublet region. Top panel: observed spectra before the telluric correction; second panel: spectra after correcting the telluric contamination with Molecfit. For these two panels the y-axis corresponds to the spectrum number, the x-axis to wavelength in Å, and the normalised flux is shown in the colour bar. Third panel: one single spectrum before (blue) and after (black) the telluric correction. The narrow lines observed in the first and third panels are telluric lines, while the broad lines centred at 5890 and 5896 Å are the stellar sodium lines. In the second panel, where the telluric lines have been subtracted, we observe the interstellar sodium in the centre of the stellar lines and, additionally, the planetary shadow (Rossiter–McLaughlin effect) as a trail moving into the lines. The spectra are presented in the terrestrial rest frame. |
4 Modelling and fitting the CLV and RME
The Rossiter–McLaughlin effect (RME) strongly affects the stellar lines profile of a fast-rotating star such as MASCARA-2b, which has a v sini = 114 km s−1. As the transit progresses, the light from different regions of the stellar disc is blocked by the planet, producing a lack of flux in different parts of the stellar lines which depends on the geometry of the system. On the other hand, the centre-to-limb variation (CLV) also affects the stellar lines profile (Czesla et al. 2015), which becomes broader and/or deeper than the integrated flux spectrum depending on the stellar properties of the region obscured by the planet.
The stellar spectrum is modelled using VALD3 (Ryabchikova et al. 2015) line lists and Kurucz ATLAS9 models, computed with Spectroscopy Made Easy tool (SME; Valenti & Piskunov 1996). As presented in Yan et al. (2017), using SME we computed the stellar spectrum at 21 different limb-darkening angles (μ) without considering the rotation broadening. For the stellar model computation we used the local thermodynamic equilibrium (LTE) and solar abundance for the hydrogen lines. For the NaI, the solar abundance model strongly differs from the data. For this reason, we fitted the NaI abundance using the SME tool. In this process, the spectra used to fit the abundance is the combination of all the out-of-transit data of Night 4 with CARMENES, which have higher S/N. After checking the fitted [Na/H] results for a range of [Fe/H] values from literature ([Fe/H] = −0.02 ± 0.07 in Talens et al. 2018) we noticed that the NaI abundance changes significantly when varying the [Fe/H] value (see below). The most reasonable NaI abundance is obtained in the 1 − σ upper limit value, that is, assuming [Fe/H] = + 0.05 finding [Na/H] = 0.98. As we do not consider non-LTE effects that could be important in this stellar type (Kubát & Korcáková 2004). These [Fe/H], [Na/H] values together with the parameters given in Table 1 are those used to compute the stellar models. We note here that for our computation of these models, we need a good description of the line profile and the actual abundance value is not the focus of our analysis. The maximum relative difference obtained between models when assuming [Fe/H] = −0.29 (Lund et al. 2017) (for which we obtain the [Na/H] = 1.39) or [Fe/H] = +0.05 ([Na/H] = 0.98) is ~ 0.08%.
We divide, then, the stellar disc in cells of size 0.01 R⋆ × 0.01 R⋆. Each of these cells contain its own properties, such as the rotation velocity due to v sin i, which depends on its distance to the stellar rotation axis (i.e. the spin-orbit angle, λ), its μ angle value, and could be obscured by the planet at a given time. At the time of each exposure it is possible to compute the position of the planet in the stellar disc using EXOFAST (Eastman et al. 2013) and compute the integrated stellar disc flux considering the obscured cells, their proper radial velocity shift caused by the rotation and the correspondent μ spectrum (which are linearly interpolated using the 21 μ angle reference spectra). The only difference between the HARPS-N and CARMENES modelled spectra is the spectral resolution, 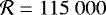 and
and 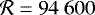 , respectively.
, respectively.
The modelled stellar spectra at different orbital phases depend on the geometry of the system but also the planetary radius, Rp. For a particular wavelength, and depending on the amount of material, the atmosphere becomes opaque at a given pressure level or radius of the planet, Rλ. In order to consider this radius change when fitting the data, the modelled stellar spectra is computed for a grid of Rλ, increasing from 0.7 Rp (1 Rp = 1.83 RJ; Talens et al. 2018) to 2.5 Rp in steps of 0.1 Rp. For a given Rλ, we then calculated the stellar spectrum by linearly interpolating these grid of models. Finally, the modelled residuals were computed dividing all the modelled stellar spectra by the out-of-transit model.
Finally, and similarly to Yan & Henning (2018), in the modelled in-transit residuals we add a Gaussian profile to describe the absorption of the planet. This profile, depends on the centre of the Gaussian (v0), the full width at half maximum (FWHM) and constrast (h). The centre position is defined as v0 = vp + vwind where vp = Kp sin(2πφ) is the planet radial velocity in each in-transit exposure time (φ is the orbital phase) and vwind is the radial velocity of the atmospheric wind.
With this, we performed a Markov chain Monte Carlo (MCMC) analysis to fit the observed residuals using emcee (Foreman-Mackey et al. 2013) code. The free parameters are Rλ, h, vwind, Kp, and FWHM. We used 14 walkers and 1 × 105 steps. The best-fit Rλ value was used to compute the CLV and RME model, which was then subtracted from the data, leaving only the true planetary absorption remaining. Before combining the data residuals, this absorption was shifted to the planet rest frame using the best-fit Kp value. The MCMC analysis is based on binned spectra (0.05 Å and 0.002 orbital phase bins) and only applied to the fully in-transit data (i.e. excluding the ingress and egress). The planetary absorption spectrum in the ingress and in the egress could present different geometries (Yan & Henning 2018), as shown in Salz et al. (2018).
During the modelling, we observed that in some cases the best-fit value of Rλ is smaller than 1 Rp. This is possibly due to the intrinsic error of the stellar models, which are computed considering LTE and solar abundance in case of the hydrogen lines (the NaI abundance is fitted). The non-LTE effects in these stellar-typescan become strong (Kubát & Korcáková 2004) and, as calculated previously, the abundance of the lines also influences the final model. For two different values of [Fe/H] inside the error bars presented in Lund et al. (2017) and Talens et al. (2018), we can obtain the same intensity of the RME for two different Rλ. Additionally, if we compare two models computed with the same abundance, one calculated for 0.85 Rp and one for 1.0 Rp, in the mid-transit time their relative difference in the RME centre is ~0.2%. Thus, there are different assumptions that can produce variations of the final Rp values. However, our main goal here with the model fitting is to remove the strong RME and CLV effects, which are easily observed in the residuals. For this reason, considering the Rp change permits us to find the best model that reproduces the effects, even if the best-fit Rλ value is not exactly that expected. This is one of the reasons we have not linked the increase of radius (Rλ) with the absorption that we measured (h) in the models, and we left both free, independently. We do not expect these Rλ values to have any effect on our results and we used the models as a tool to discard the RME and CLV effects from the absorption signatures. When comparing models, we observe that in the mid-transit time the RME is more constraining for the Rλ parameter. In the ingress and egress regions, where the CLV becomes important, both the CLV and RME are constraining Rλ. However, we stress that only the fully in-transit data is used in the fitting procedure, in other words, the location at which the RME most constrains the Rλ parameter.
5 Results
We present here the results obtained in the different wavelength regions. In all cases, we have analysed each individual night separately and, additionally, the three HARPS-N data together, sorting the spectra in time from the mid-transit centre. We note that in this latter case all the spectra were telluric-corrected first.
Here, we show the 2D maps of the final residuals obtained after applying the differential spectroscopy, the final transmission spectrum and the transmission light curves around several spectral lines detectable in MASCARA-2b’s transmission spectrum. The 2D maps of individual nights are presented in the Appendix A (Figs. A.1–A.5), their best-fit values in Table B.1 and MCMC correlation diagrams in Appendix D (Figs. D.1–D.7). All light curves are also presented in Appendix C (Figs. C.1–C.6). The absorption depth values measured in the transmission spectra and light curves can be found in Table B.2.
The transmission light curves were obtained by calculating the equivalent width of the residuals after dividing each spectrum by the master out-of-transit spectrum, and then moved to the planet rest frame. The integration to obtain the equivalent width was computed using the scipy library (Jones et al. 2001) from Python2.7.
In tables and figures hereafter, we refer to the different nights as HARPS-N 1 (Night 1), HARPS-N 2 (Night 2), HARPS-N 3 (Night 3) and CARMENES 1 (Night 4) to avoid confusion between instruments. The combined results of all three HARPS-N nights are presented as HARPS-Nx3.
5.1 Hα
The residuals after computing the ratios of each spectra respectively to the master out-of-transit spectrum, the best-fit models and the transmission spectra around Hα (6562.81 Å) of each individual night can be observed in Fig. 5. The best-fit values and the 1-σ error bars obtained with the MCMC analysis are presented in Table 4.
In Fig. 5 we can see that the three nights observed with the HARPS-N are, in general, more noisy than the night observed with CARMENES, with residuals showing larger standard deviation. No obvious reason for this fact can be derived from checking the weather or seeing logs, only the ADC problem in HARPS-N Nights 2 and 3 are noticeable. During the transit, the RME is observed as a red trail (positive relative flux) moving in the ± 114 km s−1 (v sini) range of velocities and the absorption as a blue trail (negative relative flux) around ± 24 km s−1, approximately.
Due to the noise, specially for Nights 2 and 3 for which it increases during the transit, we are not able to totally fit the planetary absorption for the HARPS-N nights, which becomes underestimated by the model, and cannot be recovered in the region were it intersects with the RME around mid-transit. However, for Night 4 where the S/N is higher, the absorption during the whole transit is recovered. In particular, this underestimation of the absorption can be observed in the residuals of the Gaussian profiles derived from the best-fit model, which seem to present smaller contrast (h) than the absorption observed in the transmission spectrum of HARPS-N (see fourth and fifth row of Fig. 5). When we fit all HARPS-N data together (see Fig. 6), the central absorption still remains within the noise level and the absorption is slightly underestimated. This is possibly caused by the decrease in S/N during the transit. We also analysed the HARPS-N data considering only Nights 1 and 3, with results closer to those obtained for CARMENES in Night 4 but the mid-transit region still remains within the noise level. The final transmission spectra of CARMENES 1 and the analysis combining all three HARPS-N nights, together with the Gaussian profiles derived from the best-fit parameters, can be observed in Fig. 7.
The observed transmission light curves before and after correcting the CLV and RME effects can be observed in Fig. 8. The models are also obtained with the best-fit parameters from the general fitting shown in Fig. 5. In these light curves the RME effect and the time regions where the noise is higher can be clearly observed. The error bars are obtained by the error propagation from the photon noise. In order to include the ingress and egress shape of the transmission model we used the PyLDTk (Parviainen & Aigrain 2015) and the PyTransit (Parviainen 2015) Python packages. The PyLDTk estimates the limb-darkening coefficients for a given filter and stellar properties using the library of PHOENIX stellar atmospheres(Husser et al. 2013). Then, PyTransit allows us to obtain the transit shape with the same absorption (h) measured during the fitting procedure and the limb-darkening coefficients assumed from PyLDTk.
The absorption that we measure from the best-fit model in the line core is 0.85 ± 0.03% for CARMENES data and 0.68 ± 0.06% for HARPS-N data combined, meaning an effective radius (Rλ(h)) of ~ 1.20 Rp as presented inCasasayas-Barris et al. (2018) where only HARPS-N Night 1 was available. We measure a mean standard deviation of 1.3 and 2.3% in the residuals and a S/N of ~350 and ~300 around the Hα position (±180 km s−1) for CARMENES and HARPS-Nx3 analysis, respectively. We note that the results from both instruments are not totally consistent, as explained above. HARPS-N Night 1 and CARMENES observations are the most stable nights, with consistent values, while HARPS-N Nights 2 and 3 present S/N variations during the transit that are then propagated to the final result when combining all three HARPS-N nights. These two nights, especially Night 3, present strong S/N variations during the observation due to the ADC problem. Although this effect is mainly removed during the analysis, in this process we apply additional steps that could introduce small over-corrections and cause variation of the final absorption level in these two nights. On the other hand, for these nights, the RME is not totally removed (see transmission light curves in Fig. 8), and when combining the mid-transit signals we were averaging regions with RME residuals that decrease the absorption depth.
The differences observed in the effective radius values obtained when fitting the CLV and RME models (Rλ) to the 2D residual maps and those derived from the absorption in the core of the lines (Rλ (h)) are possibly caused by intrinsic errors of the models. In particular, in the case of hydrogen atoms, we considered solar abundance and LTE, but for MASCARA2 stellar-type we expected the non-LTE effects to become significant (Kubát & Korcáková 2004). There is also the low and variable S/N difficulty added when fitting the data. We can observe that for CARMENES data, which have higher S/N, the RME measurement is better.
We measure, in all cases, a shift of the absorption line with respect to the theoretical position of Hα, which could be indicative of planetary winds. However, as discussed in Sect. 3.2, we did not use the radial-velocity information from the instrument pipeline, and consequently we do not consider possible instrumental offsets in radial-velocity. For this reason, the winds measured here can be influenced by this effect. In all cases, before combining the residuals to obtain the transmission spectrum, we shift these residuals to the planet rest frame using the best-fit Kp parameter of each night. This value has large error bars for the noisiest nights, thus, we checked the differences when combining the spectra with different Kp values within these 1-σ error bars, but only differences inside the noise level are noticeable. From Lund et al. (2017) we estimate that Kp should be about 170 ± 7 km s−1. We expect all nights and lines present consistent values (within the error bars) close to this estimation, however, caused by irregularities in the maps due to small residuals and the low S/N that makes difficult for the model to distinguish between CLV, RME and absorption regions, the measured Kp values can be far from the expectation for a single night but become consistent after the combination of more nights. Small deviations of these measurements are introduced by the non-corrected reflex motion from the host star.
The absorption depths measured for 1.5 Å passband in the final transmission spectra and light curves are presented in Table 5. We can observe that the results of CARMENES data and the combined HARPS-N nights are consistent, while individual HARPS-N nights give more dispersed values. We also note the slightly different results obtained in the analysis presented here and in Casasayas-Barris et al. (2018) for HARPS-N Night 1. The difference comes because here we are only considering the spectra fully in-transit (the ingress and egress files are not considered when computing the in-transit sample). Additionally, we used different methods of telluric correction, Kp values used when shifting the spectra to the planet rest-frame, and slightly improved corrections of the CLV and RME effects.
 |
Fig. 5 Results of the Hα line analysis of MASCARA-2b. Each column corresponds to one night. First row,top: residuals after dividing each spectrum by the master-out spectrum. Second row: best-fit model describing the first panel residuals, including absorption, CLV and RME. Third row: residuals after subtracting the best-fit model (second row) to the data (first row). Fourth row: transmission spectrum obtained when combining the in-transit residuals from fourth row in the planetary rest frame. The black dots show the transmission spectrum binned in 0.2 Å intervals and the propagated errors from the photon noise. Light blue shows the standard deviation of the residuals from fourth row. The red lines show the Gaussian profile derived from the best-fit parameters of second row. Fifth row: residuals after subtracting the Gaussian profile to the transmission spectrum. In all cases the residuals (rows from 1st to 3rd) are binned in intervals of 0.002 in orbital phase and 0.05 Å in wavelength. The relative flux (Fin /Fout −1) in % is shown in the colour bar. In white we show the time regions for which we have no information. The horizontal lines show the first and last contact times of the transit. |
Best-fit parameters and 1-σ error bars from the MCMC analysis of the Hα line for each individual night and combined HARPS-N observations.
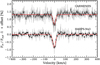 |
Fig. 7 Transmission spectra around Hα line obtained with all nights of HARPS-N combined and CARMENES data (Night 4), with an offsetfor a better visualisation. The best-fit Gaussian profiles are shown in red. In grey we show the original transmission spectrum and the black dots show the data binned in 0.2 Å intervals. |
 |
Fig. 8 Hα transmissionlight curves for 1.5 Å bandwidth. Each column correspond to one night, and the last column (right) to the analysis of all HARPS-N nights together. First row, top: observed transmission light curves. These light curves contain the contribution of the CLV, RME and absorption of the planet. The red dashed line shows the best-fit model derived from the fitting procedure of the residuals from Fig. 5. Second row: Hα transmission light curve after removing the CLV and RME. In red we show the best-fit absorption model. Third row: residuals between the model and the data. In all cases the grey dots are the original data points, in black we show the data binned by 0.003 orbital phase. We note the different x-scale of the different columns, as different nights present different time extension. |
5.2 Hβ and Hγ
The method applied to study the Hβ (4861.28 Å) and Hγ (4340.46 Å) lines is exactly the same as for Hα. In Fig. 9 we present the results for the joint analysis of all nights observed with HARPS-N. The best-fit values are shown in Table 5. We note that CARMENES data do notcover this wavelength range, and thus only HARPS-N data are presented. Same as the Hα line, the models were computed for a grid of [0.7 − 2.5] Rp with 0.1 Rp step.
In Casasayas-Barris et al. (2018) we observe noisy features in the transmission spectrum around the Hβ line analysing only Night 1. Here, with three transits and after correcting the strong CLV and RME, we observe absorption centred at the Hβ laboratory value. We note that some CLV and RME residuals remain after removing the best-fit model (see the residuals in Fig. 9). The absorption is observable in the analysis of the individual nights, except for Night 1 where the MCMC fitting is notable to distinguish between the noise and the absorption, in other words the parameters related to the absorption profile (h, Kp and FWHM) are not well determined. However, when combining all three transits the absorption is well recovered. The absorption measured in this case corresponds to − 0.45 ± 0.05% in the line core, which is consistent with the value measured in the transmission light curves during the transit (see Table 5). It is noticeable that the Rλ values that we obtain in the fitting procedure are lower than 1 Rp in some cases.
On the other hand, we find a Hγ absorption of − 0.4 ± 0.1% in the line core when combining all nights. However, the in-transit trail in the 2D maps is not clear, possibly because the signal is less intense and remains partially hidden in the noise. This absorption is only observed when combining all data and in Night 2 when analysing each individual night. Additionally, the final transmission spectrum presents some residuals near the line.
In Table 5 we give the absorption depth values measured in the spectra and the transmission light curves of Hβ and Hγ for 1.5 Å passband. The results of each individual night and light curves are presented in Appendices A and C.
 |
Fig. 9 As Fig. 5, but for Hβ and Hγ lines. The colour bar indicates the flux relative to the continuum (Fin/Fout −1) in %. |
Summary of the results obtained in the analysis presented here, for the different species and instruments.
5.3 The CaII triplet
The CaII triplet lines are located at 8498.02 , 8542.09 and 8662.14 Å. Only the transit observed with CARMENES (Night 4) was used to analyse these lines, as HARPS-N data do not cover this wavelength range. The telluric contamination observed in this region is low. The second and third lines (ordered in wavelength) are in the limit of two orders meaning that both lines are covered by two different CARMENES orders. The analysis shown here is performed using the orders where these lines are located in a most central region of the order. Although the detection of the lines, at lower S/N, is also possible in the other orders.
In Fig. 10 we show the 2D maps of these lines, where the planetary absorption trail is clear, specially for the second line (λ8542 Å) which is the strongest of the triplet. We measured absorption of 0.52 ± 0.05, 0.60 ± 0.04 and 0.55 ± 0.06% in the lines core, respectively, which correspond to an effective radius of ~ 1.2 RP. The transmission spectrum around λ8662 Å show a smaller second absorption peak in the right side of the main absorption feature. Even the telluric contamination is low in this region, it can be caused by a small telluric residual. The transmission light curves of each individual CaII line and the transmission light curve after combining of all three lines (see Appendix C) present consistent absorption depth values in comparison with those measured in the transmission spectra (see Table 5). The transmission light curves and MCMC correlation diagrams can be observed in Appendices C and D.
As absorption residuals are observed at the CaII triplet lines, we also checked the CaII H & K lines, which are only covered with HARPS-N observations. Unfortunately, these lines are located at the beginning of the first echelle order of the CCD and the spectra are too noisy in that region to be of any value. These lines are chromospherically sensitive lines, which could present variations caused by the contrast between different regions of the stellar disc (Cauley et al. 2018). However, as expected for this stellar type, we notice no variations or emissions in the line cores that could be produced by stellar activity.
5.4 Na I doublet
Due to the rotational broadening, the NaI stellar lines expand over a large wavelength range, and a large number of telluric lines fall into the NaI lines, as we showed in Fig. 4. Additionally, interstellar medium (ISM) NaI absorption at the stellar lines core is observed for all nights, affecting the region where we would expect the planetary signal. We used the LISM Kinematic Calculator (Redfield & Linsky 2008) in order to determine the origin of the interstellar NaI lines, which gives us information about the interstellar medium clouds that our line-of-sight traverses while observing a target. Although we expect this ISM NaI absorption at the same spectral position and to be stable during the night, any small variation of this absorption during the transit could mimic a planetary atmospheric absorption. As a first approximation, assuming that the ISM remains totally stable, and not correcting by the stellar reflex motion around the Barycentre of the system, the ISM effects would be removed when dividing each spectrum by the master-out spectrum.
Because of the large telluric contamination of the NaI stellar lines, we included an additional correction. After computing the ratio between each spectrum and the out-of-transit master spectrum, similarly to Snellen et al. (2010), we removed the remaining telluric residuals by fitting the time variation in each pixel by, in this case, linear splines using the UnivariateSpline class from scipy to refuse outliers. The resulting fit is compared to the data, and those points differing more than 5% from the fit values are set to 1.0 (we note that the residuals spectra are normalised to the unit). This would not affect the possible planetary signals, as they are expected to be smaller than5%, as observed in Casasayas-Barris et al. (2018).
As explained in Sect. 4, the stellar models computed with SME in the NaI lines region assuming solar abundance were observed to be very different compared with the observational data in the same region. For this reason, we fitted the abundance, and the final models were computed using the resulting NaI abundance value ([Na/H] = 0.98). We then fit the residuals after dividing each spectrum by the master out spectrum as we did for the Hα in Sect. 5.1. The MCMC fitting procedure is applied to each NaI D2 and D1 lines separately (for which we take reference positions at 5889.95 and 5895.92 Å, respectively) and the grid of models is computed for [0.7–2.5] Rp with steps of 0.1 Rp. The results for CARMENES and combined HARPS-N data analysis are shown in Fig. 10, and the best-fit parameters are given in Table 5.
In the 2D maps, the in-transit trail seems to be observable for both D2 and D1 lines and both CARMENES and HARPS-N analysis (see Fig. 10), being clearer in HARPS-N. The MCMCanalysis is able to distinguish and characterise the absorption, finding a consistent value of Kp with the one theoretically predicted. When we analysed the nights separately, the D2 line absorption can be reproduced every night except for HARPS-N Night 2, and the D1 line can be reproduced in Night 1, CARMENES data, and when all HARPS-N data are combined. The measured absorption in the line core (h) is consistent for both analysis, with approximately − 0.30%, which corresponds to an effective radius of ~1.1 Rp of absorption in both lines of the NaI doublet. These results are also consistent with the results obtained for Night 1 in Casasayas-Barris et al. (2018), who apply a different analysis.
The light curves and transmission spectra present consistent absorption depth (see values in Table 5). See 2D maps of each night and light curves in Appendices A and C. The transmission light curves are computed for each line of the doublet separately and are then combined using the weighted mean.
 |
Fig. 10 As Fig. 5, but for CaII (top) and NaI lines (bottom). The name of the line is indicated in each top-left panel and the titles indicate the instrument used to retrieve the data. The transmission spectra are binned by 0.1 Å (black dots). The colour bar indicates the flux relative to the continuum (Fin /Fout −1) in %. |
 |
Fig. 11 As Fig. 5, but for FeII and MgI lines. The name of the line is indicated in each top-left panel. The transmission spectra are binned by 0.1 Å (black dots). The colour bar indicates the flux relative to the continuum (Fin /Fout −1) in %. |
5.5 FeII
Three other transmission signals are observed when scanning the residuals in the wavelength range covered by both spectrographs. The position of these lines are 5018.38 ± 0.01 , 5168.96 ± 0.01, and 5316.57 ± 0.01 Å, which we attribute to FeII λ5018.43, λ5169.03 and λ5316.61, respectively. However, we note that due to the large rotation velocity of the star, it is difficult to distinguish a single line within the blended stellar lines. The FeII λ5316 Å line is also covered by CARMENES at very low S/N (the mean S/N of this order is around 10). The transmission spectrum obtained shows absorption in the same place as HARPS-N (5316.61 ± 0.02 Å), but we also observe additional features that are not observed in HARPS-N results, and whose origin is not clear, possibly caused by the low S/N (see this results in Appendix A).
In the same way as for the other lines, we removed the RM and CLV, and find the best-fit parameters (see Fig. 11 and Table 5). A faint trail during the transit is observed for each line 2D map, but stronger for FeII λ5169 line, which presents an absorption of 0.47 ± 0.05 in the core. We note that near this line, we observe a second and fainter residual at 5172.66 ± 0.02. The unique specie that overlaps this position is MgI at 5172.68, but the significance of this absorption signal is very low (1.7σ) with an absorption depth of 0.07 ± 0.04% in the transmission spectrum for a 0.75Å passband, and approximately −0.2% of absorption in the line core (see the results for this MgI residual in Fig. 11).
We computed the transmission light curves of each FeII and MgI lines, and the FeII combined transmission light curve (see Appendix C). We then measured the absorption depth in the transmission spectra and light curves, with values presented in Table 5. The results from the transmission spectra and light curves are consistent.
6 Systematic effects
As presented in Redfield et al. (2008), we were able to measure the stability of the individual observations by quantifying the systematic effects with the empirical Monte Carlo (EMC) or bootstrapping diagnostic. The EMC analysis helps us to quantify the systematic errors, since the absorption depth measurements error bars come from the propagation of the random photon noise from Poisson statistics through the process. This analysis involves the random selection of a number of individual exposures to build the “in-transit” sample and another random selection for the “out-of-transit” sample. With these two samples we then extracted the transmission spectrum and we measure the absorption depth of this result. This process is applied 10 000 times with different random samples in order to have statistical significance. With this, we were able to check how likely it is that the signal we are observing has planetary origin, or is caused by a random combination of the data.
We assumed three different scenarios, as presented in Redfield et al. (2008) and other recentstudies such as Wyttenbach et al. (2015, 2017). The first scenario is called “out–out” where we randomly split the out-of-transit observations in two samples with the same number of individual observations; one of these two samples will be used as the in-transit sample and the other as the out-of-transit sample. The second scenario is called “in–in” and constructed in the same way, but now splitting the in-transit observations. The final scenario is the “in–out” and represent the atmospheric absorption case. Here, the in-transit and out-of-transit samples were built with the in- and out-of-transit observations, respectively. For the in–in and out–out scenarios, we selected the same number of exposures included in the in-transit and in the out-of-transit samples. This means that in the in–in scenario this value is half the total number of real in-transit observations and in the out-out is half the real out-of-transit observations. For the in–out scenario the number of exposures included in each sample changes randomly, never being less than half the total number of real in- or out-of-transit exposures and always accomplishing the number ratio of real in-transit to the out-of-transit observations. We note that each sample including in-transit data is corrected by the CLV and RME effects, computed considering the best-fit parameters of each line presented in Sect. 7.
This analysis is applied to each line analysed here. The distributions for a 1.5 Å passband can be observed in Fig. E.1. In all cases the out–out and in–in scenarios show distributions centred to 0% absorption while the in–out scenario is centred to a different position. The clearest case is the Hα line, where the absorption scenario is centred to 0.36 ± 0.14 and 0.40 ± 0.14% (the error corresponds to the standard deviation of the distribution) for HARPS-N and CARMENES analysis, respectively, consistent with the absorption depth measured from the final transmission spectrum (see Table 5). In case of the CaII we observed the in–out samples centred on 0.10 ± 0.08, 0.12 ± 0.11 and 0.11 ± 0.09 absorption, for the λ8498 , λ8542 and λ8662 Å lines, respectively.
For the NaI doublet case, the in–out scenario distributions clearly present different characteristics in comparison with the other scenarios for HARPS-N analysis. Both D2 and D1 distributions are centred to 0.07 ± 0.05%. In the case of CARMENES, the three different scenarios give closer results; in this case, the distributions are centred on 0.05 ± 0.09% for the D2 line and 0.12 ± 0.08% for the D1 line. The absorption scenario of Hβ presents a distribution centred to 0.14 ± 0.08%. Finally, for Hγ the scenarios for all three distribution overlapped, being the in–out distribution centred on 0.04 ± 0.09% absorption.
The FeII lines obtained with HARPS-N data show in–out distributions centred to 0.03 ± 0.03, 0.04 ± 0.04 and 0.04 ± 0.03, for the λ5018, λ5169 and λ5316, respectively, close to the in–in and out–out scenarios. Similarly to Hγ, the in–out scenario distributions obtained for FeII λ5316 using CARMENES data and MgI λ5173 using HARPS-N data, show mainly indistinguishable distributions with respect in–in and out–out scenarios, centred to 0.09 ± 0.15 and 0.03 ± 0.05, respectively.
7 Discussion and conclusions
Casasayas-Barris et al. (2018) present the analysis of one HARPS-N transit observation of MASCARA-2b, Night 1 in this paper, and reported the detection of Hα and NaI in its atmosphere, and a hint of Hβ detection. Here we have repeated the analysis after combining two more transit observations of MASCARA-2b with HARPS-N and one more with the CARMENES spectrograph. After analysing the 2D residual transit maps, the transmission spectra, the transmission light curves and EMC results, we conclude that we have detected a hint to the presence of a possible ionosphere around MASCARA2-b, including the detection of CaII, FeII, NaI, Hα, Hβ, and Hγ transitions. We note that, with respect to the previous study, we are using here different telluric correction and only the spectra taken in the fully in-transit time are combined when computing the transmission spectra (the ingress and egress data are excluded from this sample). We summarise the results obtained in Table 5 and Fig. 12.
Focusing on the Balmer lines, the Hα absorption by the planetary atmosphere can be observed by eye in the residuals of each single night, appearing during the transit and ranging different radial-velocities than the RME, which is also clearly observed. The planet orbital radial-velocity semi-amplitude (Kp) values measured are consistent (considering the error bars) with those from the literature. For Hβ, on the otherhand, the absorption by the planetary atmosphere is not clear if we do not combine the three transits observed with HARPS-N. But when doing so, the absorption in the transmission spectrum and the light curves is statistically significant (5σ and 6σ, respectively, for a 0.75 Å passband). Finally, the Hγ analysis of each individual night show mainly flat transmission spectra and light curves, but a faint Hγ signal moving at the planetary speed for MASCARA-2b results when combining all the HARPS-N data (3σ for a 0.75 Å passband).
Yan & Henning (2018) detect Hα in the atmosphere of KELT-9b, the ultra-hot Jupiter with highest day-side temperature (4600 K). They measure 1.15 ± 0.05% of absorption which corresponds to a hydrogen atmosphere around 1.64 times the radius of the planet, close to the Roche Lobe (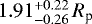 ), and an estimated mass loss rate of ~1012 g s−1. In extreme cases, photo-evaporation causes a transonic planetary wind and the mass loss rate could affect the planetary evolution (Salz et al. 2015). Cauley et al. (2019) reproduced the Hα detection in KELT-9b and also reported significant absorption in Hβ. Here, for MASCARA-2b, the measurement of the Hα absorption is ~ 0.7%, which corresponds to an atmospheric extension of 1.2 Rp. Considering that the lower-limit of the scale height (H) is 281 km (calculated with μ = 2.3 and the gravity upper-limit from Lund et al. 2017), the atmosphere is extended by 545 H. The atmosphere is expanded due to the gas heating caused by the irradiation received from the host star. For Hβ, on the other hand, the 0.45% of absorption corresponds to 1.15 Rp (525 H). Considering the mass upper-limit from Lund et al. (2017), we estimate that the Roche Lobe radius (Eggleton 1983) of MASCARA-2b is < 3.6 Rp. If we now assume a mass of 2 MJ this radius decreases to 3 Rp. The effective radius measured for the different atoms/ions do not reach the Roche Lobe in any of those cases. The measured FWHM of Hα line is ~ 20 km s−1 which is significantly lower than that of KELT-9b (~ 51 km s−1). The large FWHM of Hα in KELT-9b is a result of high density of excited hydrogen atoms that causes the absorption to be optically thick at the line centre (τ ≈ 57). According to our estimation using the analytic Eq. (3) in Huang et al. (2017), the optical depth at the Hα line centre of MASCARA-2b is small (τ ≈ 2), indicating that the density of excited hydrogen is much lower than in KELT-9b. Such a lower density also explains why the effective radius of Hα line does not reach a high altitude like in KELT-9b. Thus, we conclude the Balmer lines absorption in MASCARA-2b are from relatively low altitude atmosphere which is far away from the Roche Lobe and therefore cannot be used to estimate the mass loss rate.
), and an estimated mass loss rate of ~1012 g s−1. In extreme cases, photo-evaporation causes a transonic planetary wind and the mass loss rate could affect the planetary evolution (Salz et al. 2015). Cauley et al. (2019) reproduced the Hα detection in KELT-9b and also reported significant absorption in Hβ. Here, for MASCARA-2b, the measurement of the Hα absorption is ~ 0.7%, which corresponds to an atmospheric extension of 1.2 Rp. Considering that the lower-limit of the scale height (H) is 281 km (calculated with μ = 2.3 and the gravity upper-limit from Lund et al. 2017), the atmosphere is extended by 545 H. The atmosphere is expanded due to the gas heating caused by the irradiation received from the host star. For Hβ, on the other hand, the 0.45% of absorption corresponds to 1.15 Rp (525 H). Considering the mass upper-limit from Lund et al. (2017), we estimate that the Roche Lobe radius (Eggleton 1983) of MASCARA-2b is < 3.6 Rp. If we now assume a mass of 2 MJ this radius decreases to 3 Rp. The effective radius measured for the different atoms/ions do not reach the Roche Lobe in any of those cases. The measured FWHM of Hα line is ~ 20 km s−1 which is significantly lower than that of KELT-9b (~ 51 km s−1). The large FWHM of Hα in KELT-9b is a result of high density of excited hydrogen atoms that causes the absorption to be optically thick at the line centre (τ ≈ 57). According to our estimation using the analytic Eq. (3) in Huang et al. (2017), the optical depth at the Hα line centre of MASCARA-2b is small (τ ≈ 2), indicating that the density of excited hydrogen is much lower than in KELT-9b. Such a lower density also explains why the effective radius of Hα line does not reach a high altitude like in KELT-9b. Thus, we conclude the Balmer lines absorption in MASCARA-2b are from relatively low altitude atmosphere which is far away from the Roche Lobe and therefore cannot be used to estimate the mass loss rate.
For CaII, the individual lines of the triplet are clearly detected in the CARMENES night that covers this wavelength range. The trail of the strongest line (8σ of absorption significance for 0.75 Å) at λ8542 Å can be observed in the 2D maps tracing the radial-velocity change of the planet during the transit, while the other two lines of the triplet are also significant but fainter (around 5σ). We note that this results from the analysis of only one transit. Using the combination of three HARPS-N nights, we also observe the presence of FeII ions in MASCARA-2b atmosphere at the 2σ level measured in the absorption depth for 0.75 Å passband, and an averaged significance around 7σ in the lines core. Finally, the traces of NaI planetary absorption are observable in each individual night, although the true absorption values retrieved here could be affected by the strong telluric and interstellar contamination in this region of the spectrum. The significance of these lines is around 7σ in the lines core and 2–3σ when averaging the absorption in a 0.75 Å passband, for both instruments.
Absorption excess in neutral Ca lines was firstly reported by Astudillo-Defru & Rojo (2013) in HD 209458b atmosphere, and the Ca+ triplet lines variation during a transit was studied for the first time by Khalafinejad et al. (2018) as indicator of stellar activity. Hoeijmakers et al. (2018) detected Fe, Fe+, and Ti+ atoms in the KELT-9b atmosphere, using the cross-correlation technique. For MASCARA-2b, we are able to resolve individual lines of Ca+ and Fe+ in transmission. The individual Fe+ lines and neutral Mg at λ5173 observed here were also observed in the atmosphere of KELT-9b by Cauley et al. (2019). Fe+, together with Ti+, Ca+, is expected to be more abundant than its neutral form (Helling et al. 2019) due to thermal ionisation. In the high altitude atmosphere of MASCARA-2b, the temperature could be very high causing the Fe+ more abundant than neutral Fe. Our detection of these species, in a planet with equilibrium temperature almost 2000 K colder that KELT-9b, could indicate that either a large difference between actual and equilibrium temperatures or that there are strong mechanisms of transport to move atmospheric species from day-side to the planet’s terminator. Our detection of neutral Na falls in line also with the recent detection of this species in the atmosphere of WASP-76b, a hot planet with equilibrium temperature similar to MASCARA-2b (Seidel et al. 2019).
For all species, the resulting absorption signatures are blueshifted with respect their reference values, with velocities larger than 1 km s−1, while the instrumental drifts for the spectrographs used here are expected to be around 10 m s−1. These blueshifts can be associated to atmospheric winds. For Hα and NaI, the blueshift measured in CARMENES and HARPS-N data are consistent. For the Hβ and Hγ lines, the significance is low (<0.9σ) to determine if the measured blueshift is real. On the other hand, the FWHMs measured for the different lines are consistent for those measured with HARPS-N and CARMENES. The Balmer lines are measured to be broader than CaII, NaI and FeII lines. The line spread function of HARPS-N is 2.7 km s−1 while for CARMENES is 3.5 km s−1. In all cases, the FWHM measurements are larger than the resolution element of those instruments, and are probably associated to kinematic and/or thermal broadening. In Fig. 13 we relate the velocity shifts (vwind) and FWHM measurements with respect the absorption (Rλ(h)). In the vwind versus absorption relation no obvious correlation is observed, with a mean vwind value around − 2.4 ± 1.0 km s−1. For FWHM versus Rλ(h), however, each element relation could be explained by a linear regression. Koll & Komacek (2018) studied the magnitude of the wind speeds expected in hot Jupiters, as a result of the incident flux that they receive and tidally locked spin states. Considering this study, the average wind measurement of − 2.4 ± 1.0 km s−1 is in agreement with the estimated values, for a planet with the equilibrium temperature of MASCARA-2b, assuming that the dissipation is caused by shear instabilities (Eq. (15)).
Ultra-hot Jupiters lie in the temperature transition region between gas-giants and stars, some of them having very similar temperatures as the coldest stars. As such they are useful tests cases to study the atmospheric chemistry, understand planetary mass loss and provide constrains for planetary theories of formation and evolution. As presented in several studies (Parmentier et al. 2018; Arcangeli et al. 2018 and Bell & Cowan 2018), we expect these extremely hot planets to present close to stellar-like atmospherictemperatures. The stellar radiation heats the atmospheric gas to temperatures considerably higher than 3000 K causing the day-side atmosphere to be composed of atoms rather than molecules in addition to an increased fraction of ions (see discussion in Helling &Rimmer 2019. Such a high irradiation leads to large day-night temperature differences and therefore we expect these planets to present hot days and cold nights, in particular for those planets with short orbital periods. For WASP-18b, for example, a planet with an effective temperature very close to MASCARA-2b, detailed theoretical studies show that we expect two very different sides, a cloudy night-side depleted of elements (which are then left to form atoms, ions, molecules and will make up the atmosphere of the planet) and a cloud-free day-side that forms a thermal ionosphere (Helling et al. 2019). As the day-side is ≈ 2500 K hotter than the night-side on WASP-18b, hydrogen is present in its atomic form (HI) such that n(HI) > n(H2) ≫ n(H2O) in the low-pressure, upper atmospheric regions. The same pattern holds for most atoms, including Na, K, Ca, Ti, Al, Fe, Mg, and Si. Only at higher pressures, molecule like H2, SiO, AlH are the dominating species of their element. Na, K, Ca, Ti, Al, Fe, Mg, and Si are singly ionised, with Na+, Ca+, K+, Al+, and Ti+ being more abundant than their neutral atomic or ionic form. On the night-side, the thermal ionisation is smaller and the elements remain in their neutral state of ionization or are bound in molecules. The detection of HI, NaI, Ca+ (CaII), and Fe+ (FeII) in MASCARA-2b using transmission spectroscopy data from the planet’s terminator is consistent with this theoretical works. We note, however, that transmission spectroscopy does not probe the day-side directly but rather indirectly through the observation of the terminator regions. The terminator regions are transition regions between theday- and the night-side where the temperature differences will not be as large as between the day- and night-side. The effect on the chemistry will therefore also be less pronounced. The observation of HI, NaI, Ca+, and Fe+ is therefore indicative for rather warm terminator regions. The blueshifted HI, NaI, Ca+, and Fe+ absorption suggests that strong winds emerge from the day-side transporting hot and considerably ionised material into the respective terminator region, hence, providing us with information about the chemistry on the day-side, too. We would therefore expect the evening terminator to be geometrically more extended than the cooler morning terminator of MASCARA-2b. We note, however, that with the observations presented here we cannot conclude if the heat is coming from the day-side or we are observing at very high altitudes where the atmosphere is hotter.
Thus, the theoretical picture of UHJs possessing extended ionospheres and two differentiated day-side and night-side chemistries is consistent with our MASCARA-2b results. However, more observational evidence is desirable to underpin this hypothesis such as CCF studies. For this planet the detection of several species at the same time has become possible with 3–4 m class telescopes. UHJs present an exciting opportunity to study their detailed composition, with state-of-the-art spectrographs such as ESPRESSO, which will be able to characterise the Hγ features observed in MASCARA-2b and possibly other fainter elements predicted by the theoretical models. In the near future high-resolution spectrographs, such as HIRES for the ELT, will be able to disentangle the complex picture of UHJ atmospheres through the simultaneous detection of multiple species in their atmospheres.
 |
Fig. 12 Summary of the 2D maps with the remaining absorption after the CLV and RM correction (left column) and final transmission spectra (right column) of all species analysed. Each row corresponds to one line, whose name is indicated inside each transmission spectrum figure. The residual maps data is presented binned by 0.05 Å and 0.002 in orbital phase in order to have better contrast. The transmission spectrum of Balmer lines are shown binned by 0.2 Å and the remaining lines by 0.1 Å (black dots). The colour bar indicates the flux relative to the continuum (Fin /Fout −1) in %. |
 |
Fig. 12 continued. |
 |
Fig. 13 Top: FWHM values versus Rλ(h). Bottom: vwind values versus Rλ(h). The measurements obtained with HARPS-N data are shown in dots while those obtained with CARMENES data are marked with stars. The horizontal blue dashed line shows the mean vwind value at − 2.4 ± 1.0 km s−1. All values are extracted from Table 5. |
Acknowledgements
The authors would like to thank Dr Sven Buder for his useful comments and discussion about Na abundances. Based on observations made with the Italian Telescopio Nazionale Galileo (TNG) operated on the island of La Palma by the Fundación Galileo Galilei of the INAF (Istituto Nazionale di Astrofisica) at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias. CARMENES is an instrument for the Centro Astronómico Hispano-Alemán de Calar Alto (CAHA, Almería, Spain) funded by the German Max-Planck-Gesellschaft (MPG), the Spanish Consejo Superior de Investigaciones Científicas (CSIC), the European Union through FEDER/ERF FICTS-2011-02 funds, and the members of the CARMENES Consortium. This work is partly financed by the Spanish Ministry of Economics and Competitiveness through project ESP2016-80 435-C2-2-R. G.C. acknowledges the support by the National Natural Science Foundation of China (Grant No. 11503088, 11573073, 11573075) and by the project “Technology of Space Telescope Detecting Exoplanet and Life” from National Defense Science and Engineering Bureau civil spaceflight advanced research project (D030201). F.Y. acknowledges the support of the DFG priority programme SPP 1992 “Exploring the Diversity of Extrasolar Planets (RE 1664/16-1)”. A.F. acknowledges the support from JSPS KAKENHI Grant Number JP17H04574. This work is partly supported by JSPS KAKENHI Grant Numbers JP18H01265 and 18H05439, and JST PRESTO Grant Number JPMJPR1775. This article is based on observations made with the MuSCAT2 instrument, developed by ABC, at Telescopio Carlos Sánchez operated on the island of Tenerife by the IAC in the Spanish Observatorio del Teide. This work made use of PyAstronomy and of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna.
Appendix A Individual transmission spectra
We present here the transmission spectra obtained for each individual night.
A.1 Hβ
 |
Fig. A.1 Results around the Hβ of Night 1 (left column), Night 2 (middle column), and Night 3 (right column). First row (top): results after dividing each spectrum by the out-of-transit master spectrum. Second row: best-fit model of the residuals. The RME is observed in red colour (see colour bar) and the absorption and CLV in blue (negative relative flux). Third row: residuals when subtracting the best-fit model (second row) to the data (first row). Fourth row: absorption signature remaining after correcting the CLV and RME effects from first row residuals. Fifth row: transmission spectrum. Sixth row: residuals of removing the Gaussian profile model to the data in fourth row. Black dots show the result binned by 0.2 Å, the light blue region is the standard deviation of the residuals and the red line is the Gaussian computed with the best-fit parameters. In all panels, except for the last two rows, the data is shown with 0.05 Å bins in wavelength and 0.002 in orbital phase. |
A.2 Hγ
A.3 NaI D2
 |
Fig. A.3 Results around the NaI D2 of HARPS-N Night 1 (first column starting from left), Night 2 (second column), Night 3 (third column) and CARMENES data (fourth column). The different panels are explained in Fig. A.1. In the last two rows (starting from top) in black dots we show the result binned by 0.1 Å. |
A.4 NaI D1
A.5 FeII
 |
Fig. A.5 As Fig. A.3 but for the FeII λ5316 Å analysis obtained with the night observed with CARMENES. We note the strong residual observed close to the FeII line position. |
Appendix B Best-fit parameters and absorption depth values
We present here the best-fit parameters obtained with the MCMC fitting procedure and the absorption depth values measured in the transmission spectra and light curves.
B.1 MCMC best-fit parameters
Best-fit parameters and 1-σ error bars from the MCMC analysis.
B.2 Absorption depth values
Absorption depth (in %) measured for 0.75 and 1.5 Å bandwidths calculated in the final transmission spectra (TS) and transmission light curves (TLC).
Appendix C Individual transmission light curves
We present here the transmission light curves obtained for each species analysed in this work.
C.1 Hβ
 |
Fig. C.1 Hβ transmission light curves of HARPS-N Night 1 (first column, left), Night 2 (second column), Night 3 (third column) and join analysis of all HARPS-N observations (fourth column, right) computed for 1.5 Å passband. First row, top: observed transmission light curve. Second row: after correcting for theCLV and RME. Third row, bottom: residuals when subtracting the model to the data. The grey dots are the original data, the black dots is the data binned 0.003 in orbital phase. The red dashed line of the first row is the best-fit model containing the CLV, RME and absorption. The red dashed line of the second row corresponds to the model containing only absorption. In the third row, the red line is a reference showing the null flux level. |
C.2 Hγ
C.3 CaII triplet
 |
Fig. C.3 CaII transmission light curves obtained with CARMENES data. Left: as Fig. C.1 but for the CaII triplet lines. The analysis of each line is shown in one column. Right: combined light curve (using the weighted mean) of the three individual light curves of CaII triplet lines observed in the left panel. These are the results for a 0.75 Å passband analysis. Data binned 0.002 in orbital phase. |
C.4 NaI doublet
 |
Fig. C.4 As Fig. C.1 but for both NaI D2 and D1 lines. This is the result of computing the weighted mean of both individual NaI D lines transmission light curves for a 0.75 Å passband. Data binned 0.002 in orbital phase. |
C.5 FeII
 |
Fig. C.5 FeII transmission light curves obtained combining the three nights of HARPS-N data. Left: as Fig. C.3 but for three individual FeII lines and using a 0.75 Å passband. We note the asymmetry of the observed transmission light curve (first row) of the FeIIλ5169 line, caused by the RM effect from the closest line crossing the position of the FeII for times close to the egress. Right: transmission light curve after combining the three individual FeII lines. The data is binned by 0.002 in orbital phase. |
C.6 MgI
 |
Fig. C.6 As Fig. C.5 right but for the MgI λ5173 Å. We note the asymmetry of the observed transmission light curve (first row) caused by a second RM effect from the closest line crossing the position (see Fig. 11). |
Appendix D Correlation diagrams of the best-fit models
We present here the correlation diagrams of the best-fit CLV, RME and absorption model for the different nights and wavelength regions.
D.1 Hα
 |
Fig. D.1 Correlation diagrams of MCMC analysis of the Hα line of CARMENES (left) and HARPS-N data analysis (right). |
D.2 Hβ and Hγ
 |
Fig. D.2 Correlation diagrams of MCMC analysis of the Hβ (left) and Hγ (right) lines obtained with the HARPS-N data analysis. |
D.3 CaII
 |
Fig. D.3 Correlation diagrams of MCMC analysis of the CaII triplet lines of CARMENES. Top left panel: CaII λ8498 Å, top right: CaII λ8542 Å, bottom panel: λ8662 Å. |
D.4 NaI
 |
Fig. D.4 Correlation diagrams of MCMC analysis of the NaI D2 line of CARMENES (left) and HARPS-N data analysis (right). |
 |
Fig. D.5 Correlation diagrams of MCMC analysis of the NaI D1 line of CARMENES (left) and HARPS-N data analysis (right). |
D.5 FeII
 |
Fig. D.6 Correlation diagrams of MCMC analysis of the FeII triplet lines. The FeII λ5018 Å diagram is shown on top left and the FeII λ5169 Å in top right, both result from the HARPS-N combined data analysis. The FeII λ5316 Å diagrams are shown in the bottom panels: the HARPS-N analysis on the left and CARMENES on the right. |
D.6 MgI
 |
Fig. D.7 Correlation diagrams of MCMC analysis of the MgI line at 5173 Å. |
Appendix E Empirical Monte-Carlo distributions
 |
Fig. E.1 Distributions of the empirical Monte-Carlo analysis of the different lines, for a 1.5 Å passband. Each individual panel corresponds to the analysis of one line and one instrument, which are detailed in text. In violet wepresent the “out–out” scenario, in cyan the “in–in” scenario and in black the “in–out” scenario. The blue dashed vertical line shows the null absorption level. The CARMENES and HARPS-N analysis have different number of spectra, which means that the distributions will have different number of counts. This is also the case for the three scenarios in which the number of spectra considered is also different. |
References
- Allart, R., Lovis, C., Pino, L., et al. 2017, A&A, 606, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ambikasaran, S., Foreman-Mackey, D., Greengard, L., Hogg, D. W., & O’Neil, M. 2015, IEEE Trans. Pattern Anal. Mach. Intell., 38, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Arcangeli, J., Désert, J.-M., Line, M. R., et al. 2018, ApJ, 855, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Armstrong, D. J., de Mooij, E., Barstow, J., et al. 2016, Nat. Astron., 1, 0004 [NASA ADS] [CrossRef] [Google Scholar]
- Astudillo-Defru, N., & Rojo, P. 2013, A&A, 557, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bauer, F. F., Zechmeister, M., & Reiners, A. 2015, A&A, 581, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, T. J., & Cowan, N. B. 2018, ApJ, 857, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero, J. A., Guàrdia, J., López del Fresno, M., et al. 2016, Proc. SPIE, 9910, 99100E [Google Scholar]
- Casasayas-Barris, N., Pallé, E., Yan, F., et al. 2018, A&A, 616, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cauley, P. W., Shkolnik, E. L., Llama, J., Bourrier, V., & Moutou, C. 2018, AJ, 156, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Cauley, P. W., Shkolnik, E. L., Ilyin, I., et al. 2019, AJ, 157, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, G., van Boekel, R., Wang, H., et al. 2014, A&A, 563, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crossfield, I. J. M. 2015, PASP, 127, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Czesla, S., Klocová, T., Khalafinejad, S., Wolter, U., & Schmitt, J. H. M. M. 2015, A&A, 582, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deming, L. D., & Seager, S. 2017, J. Geophys. Res. Planets, 122, 53 [Google Scholar]
- Drake, J. J., & Kashyap, V. L. 2010, Astrophysics Source Code Library [record ascl:1007.001] [Google Scholar]
- Eastman, J., Gaudi, B. S., & Agol, E. 2013, PASP, 125, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Espinoza, N., & Jordán, A. 2015, MNRAS, 450, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, T. M., Sing, D. K., Kataria, T., et al. 2017, Nature, 548, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Agol, E., Ambikasaran, S., & Angus, R. 2017, AJ, 154, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Haynes, K., Mandell, A. M., Madhusudhan, N., Deming, D., & Knutson, H. 2015, ApJ, 806, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Helling, C., & Rimmer, P. B. 2019, Philos. Trans. A R. Soc., in press [arXiv:1903.04565] [Google Scholar]
- Helling, C., Gourbin, P., Woitke, P., & Parmentier, V. 2019, A&A, 626, A133 [CrossRef] [Google Scholar]
- Hoeijmakers, H. J., Ehrenreich, D., Heng, K., et al. 2018, Nature, 560, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, C., Arras, P., Christie, D., & Li, Z.-Y. 2017, ApJ, 851, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jensen, A. G., Redfield, S., Endl, M., et al. 2012, ApJ, 751, 86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open source scientific tools for Python [Google Scholar]
- Kausch, W., Noll, S., Smette, A., et al. 2015, A&A, 576, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khalafinejad, S., Salz, M., Cubillos, P. E., et al. 2018, A&A, 618, A98 [Google Scholar]
- Koll, D. D. B., & Komacek, T. D. 2018, ApJ, 853, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Kreidberg, L. 2015, PASP, 127, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Kreidberg, L., Line, M. R., Parmentier, V., et al. 2018, AJ, 156, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Kubát, J., & Korcáková, D. 2004, in The A-Star Puzzle, eds. J. Zverko, J. Ziznovsky, S. J. Adelman, & W. W. Weiss, IAU Symp., 224, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Lothringer, J. D., Barman, T., & Koskinen, T. 2018, ApJ, 866, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Lund, M. B., Rodriguez, J. E., Zhou, G., et al. 2017, AJ, 154, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N., Agúndez, M., Moses, J. I., & Hu, Y. 2016, Space Sci. Rev., 205, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Narita, N., Fukui, A., Kusakabe, N., et al. 2019, J. Astron. Telesc. Instrum., Syst., 5, 015001 [Google Scholar]
- Nortmann, L., Pallé, E., Salz, M., et al. 2018, Science, 362, 1388 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parmentier, V., Line, M. R., Bean, J. L., et al. 2018, A&A, 617, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parviainen, H. 2015, MNRAS, 450, 3233 [NASA ADS] [CrossRef] [Google Scholar]
- Parviainen, H., & Aigrain, S. 2015, MNRAS, 453, 3821 [Google Scholar]
- Redfield, S., & Linsky, J. L. 2008, ApJ, 673, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Redfield, S., Endl, M., Cochran, W. D., & Koesterke, L. 2008, ApJ, 673, L87 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr., 90, 054005 [NASA ADS] [CrossRef] [Google Scholar]
- Salz, M., Schneider, P. C., Czesla, S., & Schmitt, J. H. M. M. 2015, A&A, 576, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salz, M., Czesla, S., Schneider, P. C., et al. 2018, A&A, 620, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seidel, J. V., Ehrenreich, D., Wyttenbach, A., et al. 2019, A&A, 623, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sheppard, K. B., Mandell, A. M., Tamburo, P., et al. 2017, ApJ, 850, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K., Huitson, C. M., Lopez-Morales, M., et al. 2012, MNRAS, 426, 1663 [NASA ADS] [CrossRef] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snellen, I. A. G., de Kok, R. J., de Mooij, E. J. W., & Albrecht, S. 2010, Nature, 465, 1049 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Talens, G. J. J., Justesen, A. B., Albrecht, S., et al. 2018, A&A, 612, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tody, D. 1986, Proc. SPIE, 627, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyttenbach, A., Ehrenreich, D., Lovis, C., Udry, S., & Pepe, F. 2015, A&A, 577, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyttenbach, A., Lovis, C., Ehrenreich, D., et al. 2017, A&A, 602, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, F., & Henning, T. 2018, Nat. Astron., 2, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, F., Pallé, E., Fosbury, R. A. E., Petr-Gotzens, M. G., & Henning, T. 2017, A&A, 603, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Anglada-Escudé, G., & Reiners, A. 2014, A&A, 561, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Best-fit parameters and 1-σ error bars from the MCMC analysis of the Hα line for each individual night and combined HARPS-N observations.
Summary of the results obtained in the analysis presented here, for the different species and instruments.
Absorption depth (in %) measured for 0.75 and 1.5 Å bandwidths calculated in the final transmission spectra (TS) and transmission light curves (TLC).
All Figures
 |
Fig. 1 Ultra-hot Jupiters sample from exoplanets.eu. This sample corresponds to all confirmed planets with equilibrium temperatures larger than 2000 K, which have been detected via radial-velocity or transits methods. In the horizontal axis we show the equilibrium temperatureof the planet, and in the vertical axis the stellar effective temperature. The semi-major axes of the systems are colour-coded in the side bar (in AU). Some names of UHJs’ host stars mentioned in this paper are shown as reference. |
| In the text | |
 |
Fig. 2 MASCARA-2b transit light curves obtained with MuSCAT2. The data have been binned to 7.2 min intervals for display clarity. |
| In the text | |
 |
Fig. 3 Observed spectra around the Hα line (left column), for Night 1 (first row), Night 2 (second row), Night 3 (third row) and Night 4 (fourth row). The three first nights were observed with HARPS-N and the last night, with CARMENES. The spectra are normalised to the same continuum level (see colour bar) and moved to the stellar rest frame. In the y-axis we show the spectrum number starting from zero and in the x-axis the velocity in km s−1. The narrow lines correspond to telluric contamination and the deepest central line (at 0 km s −1) corresponds to the centre of the Hα line core. Second and third columns: S/N and the airmass variation during the night, respectively. The S/N per pixel is extracted in the continuum near the Hα line, specifically around 6600 Å as the Hα line for this target is very broad due to its rapid rotation. The red S/N values correspond to the spectra which are not considered in our analysis. In particular, we observe a stable S/N during Night 1. Night 2 shows a drop in the S/N for the presence of a cloud around spectrum number 25 and two stops of the instrument around spectrum number 50 and 100 because GIANO-B suddenly aborted itself and it was necessary to restart the exposure with both the HARPS-N and GIANO-B instruments. |
| In the text | |
 |
Fig. 4 Telluric correction of CARMENES observations (Night 4) of MASCARA-2b in the NaI doublet region. Top panel: observed spectra before the telluric correction; second panel: spectra after correcting the telluric contamination with Molecfit. For these two panels the y-axis corresponds to the spectrum number, the x-axis to wavelength in Å, and the normalised flux is shown in the colour bar. Third panel: one single spectrum before (blue) and after (black) the telluric correction. The narrow lines observed in the first and third panels are telluric lines, while the broad lines centred at 5890 and 5896 Å are the stellar sodium lines. In the second panel, where the telluric lines have been subtracted, we observe the interstellar sodium in the centre of the stellar lines and, additionally, the planetary shadow (Rossiter–McLaughlin effect) as a trail moving into the lines. The spectra are presented in the terrestrial rest frame. |
| In the text | |
 |
Fig. 5 Results of the Hα line analysis of MASCARA-2b. Each column corresponds to one night. First row,top: residuals after dividing each spectrum by the master-out spectrum. Second row: best-fit model describing the first panel residuals, including absorption, CLV and RME. Third row: residuals after subtracting the best-fit model (second row) to the data (first row). Fourth row: transmission spectrum obtained when combining the in-transit residuals from fourth row in the planetary rest frame. The black dots show the transmission spectrum binned in 0.2 Å intervals and the propagated errors from the photon noise. Light blue shows the standard deviation of the residuals from fourth row. The red lines show the Gaussian profile derived from the best-fit parameters of second row. Fifth row: residuals after subtracting the Gaussian profile to the transmission spectrum. In all cases the residuals (rows from 1st to 3rd) are binned in intervals of 0.002 in orbital phase and 0.05 Å in wavelength. The relative flux (Fin /Fout −1) in % is shown in the colour bar. In white we show the time regions for which we have no information. The horizontal lines show the first and last contact times of the transit. |
| In the text | |
 |
Fig. 6 As Fig. 5 but combining the three nights observed with HARPS-N. |
| In the text | |
 |
Fig. 7 Transmission spectra around Hα line obtained with all nights of HARPS-N combined and CARMENES data (Night 4), with an offsetfor a better visualisation. The best-fit Gaussian profiles are shown in red. In grey we show the original transmission spectrum and the black dots show the data binned in 0.2 Å intervals. |
| In the text | |
 |
Fig. 8 Hα transmissionlight curves for 1.5 Å bandwidth. Each column correspond to one night, and the last column (right) to the analysis of all HARPS-N nights together. First row, top: observed transmission light curves. These light curves contain the contribution of the CLV, RME and absorption of the planet. The red dashed line shows the best-fit model derived from the fitting procedure of the residuals from Fig. 5. Second row: Hα transmission light curve after removing the CLV and RME. In red we show the best-fit absorption model. Third row: residuals between the model and the data. In all cases the grey dots are the original data points, in black we show the data binned by 0.003 orbital phase. We note the different x-scale of the different columns, as different nights present different time extension. |
| In the text | |
 |
Fig. 9 As Fig. 5, but for Hβ and Hγ lines. The colour bar indicates the flux relative to the continuum (Fin/Fout −1) in %. |
| In the text | |
 |
Fig. 10 As Fig. 5, but for CaII (top) and NaI lines (bottom). The name of the line is indicated in each top-left panel and the titles indicate the instrument used to retrieve the data. The transmission spectra are binned by 0.1 Å (black dots). The colour bar indicates the flux relative to the continuum (Fin /Fout −1) in %. |
| In the text | |
 |
Fig. 11 As Fig. 5, but for FeII and MgI lines. The name of the line is indicated in each top-left panel. The transmission spectra are binned by 0.1 Å (black dots). The colour bar indicates the flux relative to the continuum (Fin /Fout −1) in %. |
| In the text | |
 |
Fig. 12 Summary of the 2D maps with the remaining absorption after the CLV and RM correction (left column) and final transmission spectra (right column) of all species analysed. Each row corresponds to one line, whose name is indicated inside each transmission spectrum figure. The residual maps data is presented binned by 0.05 Å and 0.002 in orbital phase in order to have better contrast. The transmission spectrum of Balmer lines are shown binned by 0.2 Å and the remaining lines by 0.1 Å (black dots). The colour bar indicates the flux relative to the continuum (Fin /Fout −1) in %. |
| In the text | |
 |
Fig. 12 continued. |
| In the text | |
 |
Fig. 13 Top: FWHM values versus Rλ(h). Bottom: vwind values versus Rλ(h). The measurements obtained with HARPS-N data are shown in dots while those obtained with CARMENES data are marked with stars. The horizontal blue dashed line shows the mean vwind value at − 2.4 ± 1.0 km s−1. All values are extracted from Table 5. |
| In the text | |
 |
Fig. A.1 Results around the Hβ of Night 1 (left column), Night 2 (middle column), and Night 3 (right column). First row (top): results after dividing each spectrum by the out-of-transit master spectrum. Second row: best-fit model of the residuals. The RME is observed in red colour (see colour bar) and the absorption and CLV in blue (negative relative flux). Third row: residuals when subtracting the best-fit model (second row) to the data (first row). Fourth row: absorption signature remaining after correcting the CLV and RME effects from first row residuals. Fifth row: transmission spectrum. Sixth row: residuals of removing the Gaussian profile model to the data in fourth row. Black dots show the result binned by 0.2 Å, the light blue region is the standard deviation of the residuals and the red line is the Gaussian computed with the best-fit parameters. In all panels, except for the last two rows, the data is shown with 0.05 Å bins in wavelength and 0.002 in orbital phase. |
| In the text | |
 |
Fig. A.2 As Fig. A.1 but for the Hγ line. |
| In the text | |
 |
Fig. A.3 Results around the NaI D2 of HARPS-N Night 1 (first column starting from left), Night 2 (second column), Night 3 (third column) and CARMENES data (fourth column). The different panels are explained in Fig. A.1. In the last two rows (starting from top) in black dots we show the result binned by 0.1 Å. |
| In the text | |
 |
Fig. A.4 As Fig. A.3 but for the Na D1 line. |
| In the text | |
 |
Fig. A.5 As Fig. A.3 but for the FeII λ5316 Å analysis obtained with the night observed with CARMENES. We note the strong residual observed close to the FeII line position. |
| In the text | |
 |
Fig. C.1 Hβ transmission light curves of HARPS-N Night 1 (first column, left), Night 2 (second column), Night 3 (third column) and join analysis of all HARPS-N observations (fourth column, right) computed for 1.5 Å passband. First row, top: observed transmission light curve. Second row: after correcting for theCLV and RME. Third row, bottom: residuals when subtracting the model to the data. The grey dots are the original data, the black dots is the data binned 0.003 in orbital phase. The red dashed line of the first row is the best-fit model containing the CLV, RME and absorption. The red dashed line of the second row corresponds to the model containing only absorption. In the third row, the red line is a reference showing the null flux level. |
| In the text | |
 |
Fig. C.2 As Fig. C.1 but for the Hγ line. |
| In the text | |
 |
Fig. C.3 CaII transmission light curves obtained with CARMENES data. Left: as Fig. C.1 but for the CaII triplet lines. The analysis of each line is shown in one column. Right: combined light curve (using the weighted mean) of the three individual light curves of CaII triplet lines observed in the left panel. These are the results for a 0.75 Å passband analysis. Data binned 0.002 in orbital phase. |
| In the text | |
 |
Fig. C.4 As Fig. C.1 but for both NaI D2 and D1 lines. This is the result of computing the weighted mean of both individual NaI D lines transmission light curves for a 0.75 Å passband. Data binned 0.002 in orbital phase. |
| In the text | |
 |
Fig. C.5 FeII transmission light curves obtained combining the three nights of HARPS-N data. Left: as Fig. C.3 but for three individual FeII lines and using a 0.75 Å passband. We note the asymmetry of the observed transmission light curve (first row) of the FeIIλ5169 line, caused by the RM effect from the closest line crossing the position of the FeII for times close to the egress. Right: transmission light curve after combining the three individual FeII lines. The data is binned by 0.002 in orbital phase. |
| In the text | |
 |
Fig. C.6 As Fig. C.5 right but for the MgI λ5173 Å. We note the asymmetry of the observed transmission light curve (first row) caused by a second RM effect from the closest line crossing the position (see Fig. 11). |
| In the text | |
 |
Fig. D.1 Correlation diagrams of MCMC analysis of the Hα line of CARMENES (left) and HARPS-N data analysis (right). |
| In the text | |
 |
Fig. D.2 Correlation diagrams of MCMC analysis of the Hβ (left) and Hγ (right) lines obtained with the HARPS-N data analysis. |
| In the text | |
 |
Fig. D.3 Correlation diagrams of MCMC analysis of the CaII triplet lines of CARMENES. Top left panel: CaII λ8498 Å, top right: CaII λ8542 Å, bottom panel: λ8662 Å. |
| In the text | |
 |
Fig. D.4 Correlation diagrams of MCMC analysis of the NaI D2 line of CARMENES (left) and HARPS-N data analysis (right). |
| In the text | |
 |
Fig. D.5 Correlation diagrams of MCMC analysis of the NaI D1 line of CARMENES (left) and HARPS-N data analysis (right). |
| In the text | |
 |
Fig. D.6 Correlation diagrams of MCMC analysis of the FeII triplet lines. The FeII λ5018 Å diagram is shown on top left and the FeII λ5169 Å in top right, both result from the HARPS-N combined data analysis. The FeII λ5316 Å diagrams are shown in the bottom panels: the HARPS-N analysis on the left and CARMENES on the right. |
| In the text | |
 |
Fig. D.7 Correlation diagrams of MCMC analysis of the MgI line at 5173 Å. |
| In the text | |
 |
Fig. E.1 Distributions of the empirical Monte-Carlo analysis of the different lines, for a 1.5 Å passband. Each individual panel corresponds to the analysis of one line and one instrument, which are detailed in text. In violet wepresent the “out–out” scenario, in cyan the “in–in” scenario and in black the “in–out” scenario. The blue dashed vertical line shows the null absorption level. The CARMENES and HARPS-N analysis have different number of spectra, which means that the distributions will have different number of counts. This is also the case for the three scenarios in which the number of spectra considered is also different. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


