| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 28 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201833944 | |
| Published online | 07 February 2019 | |
Galaxy populations in the most distant SPT-SZ clusters
I. Environmental quenching in massive clusters at 1.4 ≲ z ≲ 1.7
1
Faculty of Physics, Ludwig-Maximilians-Universität, Scheinerstr. 1, 81679 Munich, Germany
e-mail: vstrazz@usm.lmu.de
2
Max Planck Institute for Extraterrestrial Physics, Giessenbachstr. 1, 85748 Garching, Germany
3
Excellence Cluster Universe, Boltzmannstr. 2, 85748 Garching, Germany
4
INAF-Osservatorio Astronomico di Trieste, Via G. B. Tiepolo 11, 34143 Trieste, Italy
5
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
6
Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
7
Kavli Institute for Cosmological Physics, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA
8
Department of Astronomy and Astrophysics, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA
9
Kavli Institute for Particle Astrophysics and Cosmology, Stanford University, 452 Lomita Mall, Stanford, CA 94305, USA
10
Department of Physics, Stanford University, 382 Via Pueblo Mall, Stanford, CA 94305, USA
11
Physics Department, University of California, Davis, CA 95616, USA
12
Fermi National Accelerator Laboratory, Batavia, IL 60510-0500, USA
13
Argonne National Laboratory, High-Energy Physics Division, 9700 S. Cass Avenue, Argonne, IL 60439, USA
14
Department of Physics and Astronomy, University of Missouri, 5110 Rockhill Road, Kansas City, MO 64110, USA
15
Academia Sinica Institute of Astronomy and Astrophysics, 11F of AS/NTU Astronomy-Mathematics Building, No.1, Sec. 4, Roosevelt Rd, Taipei 10617, Taiwan
16
Department of Astronomy, University of Florida, Gainesville, FL 32611, USA
17
School of Physics, University of Melbourne, Parkville, VIC 3010, Australia
18
Department of Physics, University of Montreal, Montreal, QC H3C 3J7, Canada
19
Center for Astrophysics and Space Astronomy, Department of Astrophysical and Planetary Science, University of Colorado, Boulder, CO 80309, USA
20
NASA Ames Research Center, Moffett Field, CA 94035, USA
21
Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
22
Department of Physics, University of Michigan, 450 Church Street, Ann Arbor, MI 48109, USA
23
LSST, 950 North Cherry Avenue, Tucson, AZ 85719, USA
Received:
24
July
2018
Accepted:
18
December
2018
We present the first results from a galaxy population study in the highest redshift galaxy clusters identified in the 2500 deg2 South Pole Telescope Sunyaev Zel’dovich effect (SPT-SZ) survey, which is sensitive to M500 ≳ 3 × 1014 M⊙ clusters from z ∼ 0.2 out to the highest redshifts where such massive structures exist. The cluster selection is to first order independent of galaxy properties, making the SPT-SZ sample particularly well suited for cluster galaxy population studies. We carried out a four-band imaging campaign with the Hubble and Spitzer Space Telescopes of the five z ≳ 1.4, S/NSZE > 5 clusters, that are among the rarest most massive clusters known at this redshift. All five clusters show clear overdensities of red galaxies whose colors agree with the initial cluster redshift estimates, although one (SPT-CLJ0607–4448) shows a galaxy concentration much less prominent than the others. The highest redshift cluster in this sample, SPT-CLJ0459–4947 at z ∼ 1.72, is the most distant M500 > 1014 M⊙ cluster discovered thus far through its intracluster medium, and is one of only three known clusters in this mass range at z ≳ 1.7, regardless of selection. Based on UVJ-like photometric classification of quiescent and star-forming galaxies, we find that the quiescent fraction in the cluster central regions (r/r500 < 0.7) is higher than in the field at the same redshift, with corresponding environmental quenching efficiencies typically in the range ∼0.5 − 0.8 for stellar masses log(M/M⊙) > 10.85. We have explored the impact of emission from star formation on the selection of this sample, concluding that all five clusters studied here would still have been detected with S/NSZE> 5, even if they had the same quiescent fraction as measured in the field. Our results thus point towards an efficient suppression of star formation in the central regions of the most massive clusters, occurring already earlier than z ∼ 1.5.
Key words: galaxies: general / galaxies: clusters: general / galaxies: evolution / galaxies: high-redshift
© ESO 2019
1. Introduction
The long-known environmental influences on galaxy population properties observed at low and intermediate redshifts have often motivated the study of galaxy evolution in galaxy clusters. Commonly observed features – such as the color-density and morphology-density relations – suggest a faster evolution of galaxies towards quiescent, bulge-dominated systems in denser environments (e.g., Dressler 1980; Tanaka et al. 2004; Postman et al. 2005; Cooper et al. 2006; Poggianti et al. 2008; Pannella et al. 2009; Peng et al. 2010; Muzzin et al. 2012; Mok et al. 2013; Woo et al. 2013; Kovač et al. 2014). At the center of the most massive haloes, cluster cores turn out to be the most extreme regions of the Universe, where the evolution of galaxies and thus their resulting properties are most biased by a range of environmental effects (e.g., Moran et al. 2007).
Indeed, cluster cores in the nearby Universe host the most massive early-type galaxies, containing stars nearly as old as the Universe, and producing the tight red sequence in the color-magnitude diagram of cluster galaxies (Visvanathan & Sandage 1977; Bower et al. 1992; Kodama & Arimoto 1997) that is often considered to be a defining signature of high-density environments at low and intermediate redshifts. Most studies of the evolution of the red sequence and of the cluster galaxy luminosity function up to z ∼ 1 − 1.3 largely agree on a broad-brush picture where the high-mass end of the cluster galaxy population is largely in place even before redshift one, with the bulk of its stars formed in a massive star formation event in the cluster progenitor environments at z ∼ 2 or higher (e.g., De Propris et al. 1999, 2007; Andreon 2006, 2013; Strazzullo et al. 2006, 2010; Lin et al. 2006; Lidman et al. 2008; Mei et al. 2009; Mancone et al. 2010; Wylezalek et al. 2014; Foltz et al. 2015), followed by efficient suppression of star formation in a major part of the massive galaxy population, creating a first red sequence (e.g., Kodama et al. 2007; Zirm et al. 2008; Strazzullo et al. 2016). Direct observations of the star formation suppression in high-redshift clusters add important constraints to this broad-brush picture (e.g., Muzzin et al. 2014; Balogh et al. 2016; Noble et al. 2016; Rudnick et al. 2017) concerning time scales, relevance, and actual nature of environmental effects (e.g., Wetzel et al. 2012, 2013; Hirschmann et al. 2014; Bahé et al. 2017, and references therein). In this respect, observations of the onset of star formation suppression in very distant clusters clearly provide a strong leverage on the environmental effects most relevant at early times.
Over the last decade, cluster surveys have pushed the high-redshift cluster frontier well beyond z ∼ 1 and into the z ∼ 2 regime, bridging the cluster and proto-cluster realms (e.g., Andreon et al. 2009; Henry et al. 2010; Gobat et al. 2011; Spitler et al. 2012; Stanford et al. 2012; Zeimann et al. 2012; Yuan et al. 2014; Newman et al. 2014; Wang et al. 2016; Mantz et al. 2018). Cluster galaxy studies have thus started approaching the expected main epoch of star formation, and indeed have revealed significant star formation, nuclear and merging activity in clusters at z ≳ 1.4, with star-forming galaxy fractions sometimes approaching or even exceeding the field levels, suggesting a rapidly decreasing impact of environmental quenching at this cosmic time (e.g., Hilton et al. 2010; Tran et al. 2010, 2015; Hayashi et al. 2010, 2011; Santos et al. 2011, 2015; Stanford et al. 2012; Zeimann et al. 2012; Brodwin et al. 2013; Bayliss et al. 2014; Wang et al. 2016; Alberts et al. 2016; Wagner et al. 2017; Nantais et al. 2017).
On the other hand, passively evolving galaxies with typically early-type morphology are often found in z ≳ 1.4 clusters and even up to z ∼ 2 (e.g., Kurk et al. 2009; Papovich et al. 2010; Strazzullo et al. 2010, 2013; Tanaka et al. 2013a,b; Snyder et al. 2012; Spitler et al. 2012; Newman et al. 2014; Cooke et al. 2016), although their predominance, even at high stellar masses, is not necessarily as high as at lower redshifts. The highest redshift clusters in particular, close to z ∼ 2, often host a mixed massive galaxy population including both very active and quenching or quiescent systems (e.g., Kurk et al. 2009; Tanaka et al. 2013b; Strazzullo et al. 2016; Hatch et al. 2017), although in some cases quiescent galaxies already heavily dominate the massive population, forming a tight, well defined red sequence even at very early times (e.g., Andreon & Huertas-Company 2011; Andreon et al. 2014; Newman et al. 2014). Even considering only the most massive among the very distant clusters, which may be expected to also host the most evolved galaxy populations, a complex picture has emerged, where star formation is already efficiently suppressed in the central regions of some clusters (Strazzullo et al. 2010; Newman et al. 2014), while it is still ongoing at significant rates in others (Santos et al. 2015, see more detailed discussion in Sect. 6).
The variety of results described above occur at a redshift where cluster-to-cluster variations likely start to become significant, cluster samples are usually of very small size and are selected with a variety of different methods, and the study of cluster galaxies is complicated by observational difficulties and selection effects. Depending on galaxy sample selection and observations, one may highlight different characteristics of galaxy populations (e.g., Tran et al. 2010, 2015; Smail et al. 2014). Furthermore, galaxy population properties might possibly exhibit a dependence on cluster mass or assembly history. Therefore, galaxy- vs. intracluster medium (ICM)-selected cluster samples might, for instance, suggest seemingly inconsistent results, which are in fact due to specific aspects of galaxy evolution in dense environments, to first order related to the different cluster masses typical of the differently selected samples (e.g., Culverhouse et al. 2010). Poor statistics and concerns about possible biases associated with cluster selection thus still challenge our understanding of cluster galaxy populations at these redshifts.
Historically, X-ray cluster searches have provided the optimal selection of cluster samples with a well-understood cluster selection function, no direct bias with respect to the properties of cluster galaxies, and the availability of cluster mass estimates. Such mass estimates also crucially provide cluster scale radii for proper comparison of properties with a radial dependence, such as galaxy population properties. However, z ∼ 1.5 is close to the limit where current X-ray satellites are able to detect clusters. Only a few of the known z ≳ 1.4 clusters are X-ray selected (Mullis et al. 2005; Stanford et al. 2006; Henry et al. 2010; Fassbender et al. 2011; Santos et al. 2011; Mantz et al. 2018); most of the very distant clusters have been identified instead through their galaxies. However, cluster selection based on galaxies is by definition biased with respect to galaxy population studies, to a greater (e.g., Andreon et al. 2009; Spitler et al. 2012) or lesser extent (e.g., Eisenhardt et al. 2004, 2008; Papovich 2008; Papovich et al. 2010; Gobat et al. 2011; Stanford et al. 2012; Zeimann et al. 2012; Muzzin et al. 2013a) depending on the actual selection criteria adopted. This is especially true at a redshift where galaxy population properties may more significantly depend on the dynamical state and/or mass of the host halo.
In this work, we carry out an investigation of early environmental effects on galaxy populations in a sample of the most massive clusters at z ∼ 1.5, selected through the Sunyaev Zel’dovich effect (SZE; Sunyaev & Zeldovich 1972) in the South Pole Telescope (SPT; Carlstrom et al. 2011) mm-wave survey over 2500 deg2 (SPT-SZ; Bleem et al. 2015). The cluster SZE signature or signal-to-noise (S/N) is related to the total thermal energy in the ICM, resulting in a relatively low scatter (∼20%) in cluster mass at fixed SZE signature and redshift (Andersson et al. 2011; Bocquet et al. 2015). Moreover, the mapping from SZE signature to mass has only a weak redshift dependence (e.g., de Haan et al. 2016). Therefore, the SPT-SZ cluster sample can be considered to a first approximation to be a mass-selected sample, whose selection is independent of both the redshift and the properties of the cluster galaxy population.
For this analysis, we start with the optically confirmed cluster sample from the SPT-SZ survey associated with SZE detections having S/N > 4.5. These clusters have measured photometric redshifts accurate to δz/(1 + z) ≲ 0.02 − 0.04 up to z ∼ 1.5 (Bleem et al. 2015). The purity of the original SZE–only candidate catalog, as estimated through simulations and confirmed by optical/NIR follow-up observations, is 95% for the S/N > 5 sample, and 75% for the S/N > 4.5 sample (Song et al. 2012). Confirmation through optical/NIR follow-up effectively removes the noise fluctuations responsible for the contamination in the candidate cluster catalog. About 40 optically confirmed SPT-SZ clusters lie at z > 1, and a tail of five S/N > 5 systems are at z > 1.4. We focus here on this highest redshift tail, a representative sample of the most massive, collapsed structures at z ≳ 1.4 selected over 2500 deg2.
The (negative) SZE signatures of our cluster sample are contaminated at some level by mm-wave emission from galaxies and AGN. Because we empirically calibrate this observed signature directly to halo mass, the effects of this contamination are already reflected in the resulting mass–observable relation, which is characterized by an amplitude, power law trends in mass and redshift, and the amplitude of the intrinsic scatter in the observable at fixed mass and redshift. This empirically calibrated mass–observable relation indicates that the cluster mass threshold of the SPT-SZ sample is M500 ∼ 3 × 1014 M⊙ from z ∼ 0.2 out to the highest redshifts where such massive structures exist (Bleem et al. 2015; Bocquet et al. 2015; de Haan et al. 2016). We estimate the completeness of the z ≳ 1.4, S/N > 5 cluster sample studied here to be 70% above the mass of our least massive cluster (M500 = 2.74 × 1014 M⊙). The completeness above the mass corresponding to S/N = 5 at z = 1.4 (M500 = 2.65 × 1014 M⊙) is 63%.
Individual clusters with higher contamination from galaxy and/or AGN emission and that lie close to the selection threshold could drop out of the sample. However, high frequency cluster radio AGN are rare (Lin & Mohr 2007). Although studies of the cluster radio AGN population out to redshifts z ∼ 1 are ongoing, Gupta et al. (2017a) have already characterized the high frequency cluster radio AGN population in an X-ray selected local cluster sample. Assuming a relatively strong redshift evolution scenario, they estimate that no more than ∼10% of SZE selected clusters at z ∼ 1.5 would fall out of a pristine S/N > 4.5 sample due to cluster radio AGN contamination. Similarly, strong emission from star formation could impact the SZE detection, making it more difficult to select clusters characterized by higher star formation rates. We explore this effect in Sect. 5.4, and we conclude that the cluster sample studied here would not be significantly impacted even if the star-forming galaxy fraction and star formation rates of cluster galaxies were the same as in the field at the cluster redshift (i.e., even if the environmental quenching efficiency were negligible).
We present the main properties of this cluster sample in Sect. 2 (see Table 1). These five M500 ∼ 3 × 1014 M⊙ (M200 ∼ 5 × 1014 M⊙) SPT-SZ clusters that we study here are among the few known examples of the rarest, first massive clusters to have formed (Mullis et al. 2005; Rosati et al. 2009; Andreon et al. 2009; Stanford et al. 2012; Brodwin et al. 2012; Bayliss et al. 2014; Tozzi et al. 2015). They are thus the likely progenitors of the most massive clusters in the nearby Universe.
The cluster sample studied in this work.
In this paper we focus on cluster redshift constraints, the red galaxy population, and quiescent galaxy fractions in the central cluster regions within r5001, as determined from new observations from a dedicated, homogeneous imaging follow-up of the full sample with the Hubble (HST) and Spitzer Space Telescopes. This follow-up program was designed to meaningfully constrain main galaxy population properties with a minimum observational effort, acquiring imaging in only four passbands chosen to enable the selection of a candidate member sample, to allow a broad statistical separation of quiescent and star-forming sources, to provide measurements of galaxy stellar masses and structural properties, and to constrain the cluster redshift. Forthcoming papers based on the cluster sample and data set used here will present the investigation of structural vs. stellar population properties of cluster vs. field galaxies and their structural evolution, mergers in massive cluster vs. field environments at z ∼ 1.5, galaxy stellar mass functions (on 3.6 μm-selected samples), galaxy number density profiles, cluster stellar mass fractions and the halo occupation distribution.
We adopt a flat ΛCDM cosmological model with ΩM = 0.3, and H0 = 70 km s−1 Mpc−1. A Salpeter (1955) initial mass function (IMF) is assumed throughout. Magnitudes are quoted in the AB system.
2. Data, photometry, and measurements
We selected the cluster sample used in this work from the Bleem et al. (2015) SPT-SZ cluster catalog, taking all clusters with a photometric (except for SPT-CLJ2040, see Table 1) redshift z > 1.4 and an SZE significance S/N > 5. Table 1 summarizes the main properties of the clusters. Cluster names are shortened to SPT-CLJxxxx hereafter.
Because of the photometric redshift uncertainties, our z > 1.4 selected cluster sample had some associated ambiguities. Indeed, out of the seven S/N > 5 clusters in the Bleem et al. (2015) catalog at 1.2 ≤ z ≤ 1.42, five are now spectroscopically confirmed, and one turns out to be at z ≥ 1.4 (Stalder et al. 2013; Khullar et al. 2019). The two remaining clusters have photometric redshifts of 1.23 and 1.30. Therefore, the sample studied in this work contains five of the six S/N > 5 SPT-SZ clusters deemed to be at z ≥ 1.4, and the possibility that we are missing any significant number of other z > 1.4 clusters is small, given the results of the recent spectroscopic follow-up (Khullar et al. 2019). We thus consider the sample studied here to be representative of the z ≥ 1.4 massive cluster population as selected from the SPT-SZ S/N > 5 catalog.
In Table 1 we present masses M500 and associated radii r500 for each cluster, derived from the cluster SPT-SZ observable and redshift using the latest empirical calibration of the SPT-SZ mass–observable relation. For this purpose, we adopt the best fit scaling relation parameters from de Haan et al. (2016, see their Table 3). Specifically, we consider the SPTCL+H0+BBN data set, a combination of the SPT-SZ S/N > 5 cluster sample, X-ray YX based mass estimates for 82 of those clusters calibrated externally through weak lensing (Vikhlinin et al. 2009; Hoekstra et al. 2015), and external priors on H0 (Riess et al. 2011) and Ωbh2 (Cooke et al. 2014). Our mass estimates include corrections for the Eddington bias, and the mass uncertainties that we present correspond to the sum in quadrature of two components. The first “systematic” component, corresponding to a ∼15% uncertainty, reflects the current uncertainty on the mass-observable scaling relation parameters, which is due to cosmological parameter uncertainties and the limitations of the current direct mass calibration dataset. The second “statistical” component, corresponding to ∼20% for a S/N = 5 cluster, is the combination of the measurement uncertainty of the SZE S/N and the intrinsic scatter of the underlying SZE signature at fixed mass and redshift. For a more complete discussion of the mass calibration of the SPT-SZ sample and of its impact on individual cluster mass estimates, we refer the reader to recent studies of the baryonic components and X-ray properties of SPT-SZ clusters (Chiu et al. 2018; Bulbul et al. 2019). As alluded to previously, the cluster masses M500 ranging from 2.7 to 3.4 × 1014 M⊙ (with corresponding M200 ranging from 4.5 to 5.6 × 1014 M⊙) make these clusters among the most massive systems identified to date at z ∼ 1.5.
All clusters in this sample have been homogeneously observed in a dedicated follow-up program with HST and Spitzer. We describe below these data, their reduction and the derived photometric measurements, as well as data from part of the GOODS-S survey used as a control field.
2.1. HST observations, data reduction and photometry
HST observations with the Advanced Camera for Surveys (ACS) in the F814W band (∼4800 s for each cluster), and with the Wide Field Camera 3 (WFC3) in the F140W band (∼2400 s per cluster) were acquired in Cycle 23 (GO 14252, PI: Strazzullo). The exception is the F140W band imaging of cluster SPT-CLJ2040, for which we used observations (∼9200 s) taken as part of program GO-14327 (hereafter See Change, PI: Perlmutter). We used the DrizzlePac release 2.1.0 to produce science ready images with standard procedures from the preprocessed flat-fielded single exposure frames retrieved from the STScI archive. More specifically we used AstroDrizzle (v. 2.1.11) to subtract the background, perform cosmic-ray removal and drizzle all frames to a common astrometric solution, with a square kernel and a PIXFRAC=0.8, before combining them in a final stacked image with a pixel scale of 0.06″. The tasks Tweakreg and Tweakback were used to register images in the different bands to the same sky coordinates and remove some residual astrometric offsets.
Source extraction and photometry were carried out with SExtractor (Bertin & Arnouts 1996) in double image mode with detection performed on the F140W image. With the aim of removing stars, point-like sources identified from SExtractor’s MAG_AUTO vs. FLUX_RADIUS sequence were removed down to a F140W band magnitude m140 = 22 AB mag. This selection is purely based on a morphological criterion, thus unresolved non-stellar sources, like very bright AGNs or very compact galaxies, might be selected as point-like sources as well. Out of a total of 120 point-like sources removed across all five cluster fields, the colors of 116 sources (∼97%) are not compatible with those of m140 < 22 galaxies at any redshift z > 0.6. The stellar nature is potentially dubious for only ∼3% of the removed sources. We thus estimate that the contamination of our point-like source sample from non-stellar objects is at the few percent level at most.
Galactic extinction correction for each field was applied according to Schlafly & Finkbeiner (2011). We adopted SExtractor MAG_AUTO as an estimate of total magnitude, while m814–m140 colors were measured from 1″ (diameter) aperture magnitudes in the F814W and F140W bands, applying an aperture correction for the different PSF between the two bands determined using growth curves of bright unsaturated point like sources in the image. Realistic depths and errors on the aperture magnitudes were estimated by measuring the flux rms in 1″ apertures placed at random locations in the image. We also empirically estimated the completeness of the F140W band data by comparing number counts and unmatched sources between the full-depth (∼9200 s) F140W band image of the cluster SPT-CLJ2040 from the See Change program, and a reduced-depth image obtained by coadding exposures to the same exposure time of the other clusters observed in our PID 14252 program. Based on this estimate, F140W band catalogs are > 95% complete in the magnitude range used in this work (m140 < 24 AB mag for all clusters).
2.2. Spitzer observations, data reduction and photometry
Spitzer observations with the Infrared Array Camera (IRAC, Fazio et al. 2004) were carried out in Cycle 12 (PID 12030, PI: Strazzullo). Each cluster was observed for 5500 s in both the 3.6 and 4.5 μm bands, except SPT-CLJ2040, which lies in a region of higher background. SPT-CLJ2040 was therefore observed with a total integration time of 7500 s in each IRAC band. All integrations consisted of overlapping full-array exposures with 100 s frame times, dithered using a cycling pattern with a medium throw. The resulting coverage pattern generated by the 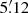 -wide IRAC field of view combined with the dithering was sufficient to completely cover all the observed clusters.
-wide IRAC field of view combined with the dithering was sufficient to completely cover all the observed clusters.
The IRAC exposures were reduced using standard procedures following steps adopted for other similar science targets (Bleem et al. 2015; Paterno-Mahler et al. 2017), adjusting for the relatively high sensitivity of the PID 12030 observations. The reduction was based on the IRAC corrected basic calibrated data (cBCD). Median stacks for all cBCD frames in each IRAC band and field were made after masking bright sources. These median stacks were subtracted from the individual cBCD frames to eliminate residual images from prior observations of bright sources, and to compensate for gradients in the backgrounds of each field. A custom column-pulldown corrector was applied to fix the ubiquitous low-lying array columns that result from observing sources close to saturation. The resulting modified cBCD frames were then combined into spatially registered mosaics using the wrapper IRACproc (Schuster et al. 2006). With the high redundancy of these IRAC observations (typically 55 overlapping exposures per pixel), cosmic rays were automatically removed by outlier rejection during mosaicking. The final mosaics were generated with 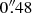 pixels and a tangent-plane projection set to match that of the HST/WFC3 F140W mosaics, in order to facilitate subsequent use of the latter as priors for source extraction and to optimize coordinated photometric measurements.
pixels and a tangent-plane projection set to match that of the HST/WFC3 F140W mosaics, in order to facilitate subsequent use of the latter as priors for source extraction and to optimize coordinated photometric measurements.
For the purpose of the work presented here, photometry was carried out on the IRAC mosaics with T_PHOT (see Merlin et al. 2015, 2016a, for a detailed description). We used priors from the WFC3 F140W band imaging down to m140 = 25.5 AB mag, and IRAC point spread functions generated separately for each field by stacking a few tens of bright unsaturated stars. Given the relatively small fields studied here, we adopted a “single image mode” fitting (fitting the entire input catalog at once), providing the most robust results especially in terms of uncertainty estimates and covariance between close neighbors. We also tested a second pass “dance” run allowing refinements of the input source centroid positions by approximately one third of the IRAC point spread function, but the retrieved fluxes, uncertainties and estimated covariances were essentially unaffected with respect to the main run. The estimated effective sensitivity was very similar for all clusters, with an estimated S/N ∼ 3 for point-like sources at ∼25.2 AB mag in both the 3.6 and 4.5 μm mosaics. In the following we consider that with this approach and observations we are not able to measure reliable photometry for sources fainter than 25.2 AB mag, as well as for those with a T_PHOT covariance index > 0.85 (potentially contaminated by nearby sources to a significant level, see Merlin et al. 2016b). This has a marginal effect on the subsequent analysis, as discussed in Sects. 3, 5.2, 6. At z ∼ 1.5, a 3.6 μm magnitude of [3.6] ∼ 25.2 AB corresponds to stellar masses well below ∼1010 M⊙; given the mass completeness limits set by the F140W-band selection as discussed in Sects. 2.3.1 and 5, our sources of interest are expected to be generally detected at high S/N in the IRAC mosaics.
2.3. Stellar mass estimates and control field
For the purpose of comparing cluster galaxy properties with field counterparts, defining a control field for statistical background subtraction, and estimating stellar masses for galaxies in our cluster fields, we used photometry and derived properties of galaxies in the CANDELS GOODS-S field (Grogin et al. 2011). We used multiwavelength photometry from Guo et al. (2013) and photo-z’s and stellar masses from spectral energy distribution (SED) fitting from Pannella et al. (2015) and Schreiber et al. (2015). Because the available F140W imaging of the GOODS-S field (Skelton et al. 2014) is shallower than that used in this work, we opted for measuring a synthetic m140 magnitude for all sources in the Guo et al. (2013) catalog, by convolving the best-fit SED of each source from Schreiber et al. (2015) with the response curve of the F140W filter (see Strazzullo et al. 2016). From the internal comparison of analogously derived F160W synthetic magnitudes with the observed ones, and the external comparison of our synthetic m140 magnitudes with the F140W photometry published in Skelton et al. (2014), we estimate the uncertainty on our synthetic m140 magnitudes, in the magnitude range of interest for this work, to be ≲0.1 mag, with an essentially negligible impact on the analyses presented here.
2.3.1. Stellar masses
This work is largely based on deep photometry in just four bands. Since such photometric coverage is not ideally suited for a full-fledged SED fitting approach, we estimated stellar masses by converting 3.6 μm flux to stellar mass with a mass-to-light ratio (M/L) based on the m814–m140 color. We calibrated the M/L vs. color relation on galaxies in the GOODS-S field at a redshift within ±0.15 from each cluster redshift, and in the same magnitude range of our sample. Based on the scatter around the median M/L vs. color relation for the selected GOODS-S galaxies, we estimate a typical error on our stellar mass estimates of ∼20 − 30%. This is the internal uncertainty of the empirical mass calibration against the stellar masses in the control field sample. It thus relies on the assumptions adopted in estimating stellar masses for the control field sample, and it does not represent an uncertainty on stellar mass on an absolute scale.
In a minority of cases (see details in Sect. 3.1 below) we were not able to measure reliable 3.6 μm fluxes (as noted in Sect. 2.2 above), thus we estimated stellar masses from the F140W band flux with a M/L calibrated on the m814–m140 color (with a typical stellar mass uncertainty of ∼30 − 40% estimated as described above). We need to resort to these F140W-scaled mass estimates for only a very small fraction of the mass complete samples discussed below, and we have verified that any small systematics of these F140W-scaled mass estimates with respect to our default 3.6 μm-scaled ones do not produce any appreciable effect on the results presented in this work.
For the purpose of the analysis described in the following, the stellar mass completeness limit adopted for each cluster is defined as the stellar mass of a solar-metallicity, unattenuated Bruzual & Charlot (2003) simple stellar population (SSP) with a formation redshift zf ∼ 8, having at the cluster redshift a F140W-band magnitude equal to the limiting m140 adopted for the given cluster, as detailed in Sect. 3.
2.3.2. Control field
The GOODS-S field catalogs described above (photometry, photometric redshifts, SED fitting results including stellar masses and restframe photometry) were also used for comparison with galaxy population properties in the field at the cluster redshifts, and for the purpose of statistical background subtraction. In fact, given the small field probed by our observations (in particular the HST/WFC3 imaging), we could not adopt a local control field for background estimation in the vicinity of each cluster. As mentioned in Sect. 2.3, the GOODS-S observations at the core of these measurements are not exactly the same as those in the cluster fields. However, both the cluster and field samples are used in a regime where the adopted catalogs are complete and photometric errors are small (typically < 0.1 mag, or at most 0.2 mag for F814W magnitudes for the faintest red sources in our samples of interest). The resulting small differences in the photometric and stellar population parameter measurements used here are estimated to be negligible with respect to the uncertainties involved, and thus not relevant for the way these measurements are used in this work.
3. Galaxies in the cluster fields
In this Section we describe the definition of the galaxy samples used in this work. Figure 1 (panels a, hereafter Fig. 1a) shows, for each cluster, the m140 vs. m814–m140 (approximately V vs. U-V restframe) color-magnitude diagram of galaxies in the cluster central region. The details of our imaging data (in particular the ∼2 × 2 arcmin2 WFC3 field of view) limit our analysis to a homogeneously covered region reaching out to r ≲ r500 ∼ 1′∼500 kpc (proper, for this cluster sample). Given the cluster position in the HST images (as well as the occurrence of masked areas for some of the clusters), this r ≲ r500 region is not fully and homogeneously covered by our data (see Fig. 4). Given the assumption of spherical symmetry of galaxy distribution and population properties, in the following we will correct for this by introducing a coverage weight factor for each galaxy, given by the fraction of covered area in a thin (5″) annulus at the galaxy’s clustercentric distance. For this reason, we limit our analysis to a clustercentric distance3 r < 0.7r500, so that the maximum coverage weight factor that we need to apply is ≤2 for all clusters, and the fraction of uncovered area is typically small (≲10% at the outskirts of the r < 0.7r500 area, with the exception of SPT-CLJ2040 for which it is ∼20%). For each cluster, we thus start by considering a sample of galaxies within a clustercentric distance r < 0.7r500.
 |
Fig. 1. Color-magnitude diagrams and derived properties within the r < 0.7r500 region of each cluster are shown in subfigures, each with three panels. Panel a: visualization of the background-subtracted color-magnitude diagram, where size and color of each galaxy point scale according to its statistical background subtraction weight (see color bar in legend) determined in Sect. 3.2. All galaxies are shown, but color-rejected interlopers (see Sect. 3.1) are shown as crosses. Gray lines show Kodama & Arimoto (1997) red-sequence (RS) models with formation redshifts zf = 2, 3, 5. The color range is the same for all clusters to facilitate direct comparison of RS colors. Panel b: color distribution of background-subtracted and area-corrected cluster members (red points with error bars) down to the indicated m140 limit. The orange shaded area shows an estimate of the impact of cosmic variance on the scale of the cluster core field, as detailed in Sect. 5.1. The blue histograms show the color distribution (rescaled by total number of galaxies) in the control-field sample, using the same color selection as for cluster candidate members (light blue), or a photometric redshift selection within ±0.2 of the cluster redshift (darker blue). All clusters show a clear excess of red galaxies with respect to the field distribution. Panel c: estimated fraction of interlopers in the color-selected candidate member sample as a function of color (down to the indicated m140 limit), based on the weights in panel a. Contamination is low for RS galaxies but significant for blue galaxies. Error bars show binomial confidence intervals (1σ) computed following Cameron et al. (2011). |
Furthermore, we focus in this work on the bright F140W-selected galaxy sample down to m140 ∼ 23.5 AB mag. More specifically, for each cluster we limit ourselves to the m140 magnitude range where we can measure the F814W-band aperture magnitudes for red sequence (RS) galaxies (see Fig. 1a) with a S/N > 5. The adopted m140 magnitude limits range from m140 = 23.2 to 23.5, as reported in Fig. 1b.
Figure 1a thus shows the color-magnitude diagrams of galaxies in cluster fields within r < 0.7r500 of the cluster center, and down to m140 ∼ 23.5 AB mag. All galaxies in the probed field are shown, with different symbols referring to a visualization of the background-subtracted color-magnitude diagram that is discussed in Sect. 3.2.
We describe in the following the definition of the candidate cluster member samples at the core of all the analyses reported in this work. A description of Fig. 1 in the context of cluster galaxy population properties is given instead in Sect. 5. Given the very limited spectroscopic follow-up available for these clusters, we cannot rely on spectroscopic redshifts for membership determination of a representative sample of cluster galaxies. Furthermore, this work is based on deep photometric coverage in only a small number of bands, resulting in limited photometric redshift (photo-z) accuracy. We thus adopt a color selection to identify candidate cluster members (Sect. 3.1), plus a subsequent statistical background subtraction (Sect. 3.2) to account for the residual fore-/background contamination.
3.1. Color-selected candidate member samples
For each cluster, we defined a color selection to identify a sample of candidate cluster members. The m814–m140 vs. [3.6]–[4.5] color-color diagram in Fig. 2 shows an example of this selection, illustrating the main points of this approach for the two clusters at the lowest and highest redshift in our sample, as described in detail here below.
-
Initial m140-selected sample: Colored squares in Fig. 2 show all galaxies in the inital m140-selected sample with a measured [3.6]–[4.5] color (see Sect. 2.2). For the galaxy samples we are interested in, that is at a clustercentric distance within 0.7r500 (or 0.45r500 in part of the analysis) and down to m140 = 23.2 to 23.5 AB mag (depending on the cluster, see Sect. 3), we have at least one retained measured IRAC flux (3.6 or 4.5 μm) for on average 90% (ranging from 84% to 95% for the different clusters) of the initial sample, with both IRAC fluxes missing for typically ≲5% (or 8% in the worse case) of the initial samples. To favor completeness (and at the expense of purity) all galaxies for which we do not have a [3.6]–[4.5] color measurement were initially retained in the candidate member sample.
-
Selection of a high-purity red-sequence candidate member sample: As can be seen in Fig. 1a, all clusters in this sample show a clear red (in the m814–m140 color, ∼U-V restframe) galaxy population, with high contrast over the background. We can thus easily identify a sample of red candidate cluster members with low contamination from interlopers. For this purpose, we consider here only RS galaxies within < 2σ from the red peak in the galaxy color distribution (see, e.g., Fig. 1b). From our analysis of statistically background-subtracted samples in Sect. 3.2, the overall fore-/background contamination for RS galaxies in the probed region is estimated to be typically at the 10% level (Fig. 1c). We note that this RS sample used here is not meant to be a complete sample of RS galaxies, but rather to be a sample of cluster members with the lowest possible contamination by interlopers. We thus select galaxies in the m814–m140 color range where the contrast of the cluster vs. background galaxy population is highest. In both panels of Fig. 2, the concentration of sources at the RS color (see for comparison Fig. 1a) is clearly visible. The vertical light gray lines show the adopted selection of the RS sample described above.
-
First definition of IRAC color selection for candidate cluster members: The [3.6]–[4.5] color (or also “IRAC color” hereafter) at this redshift has a relatively weak dependence on stellar population properties (see Fig. 2, and Sect. 4 below) as compared to optical colors spanning the 4000 Å break. In fact, the similar IRAC colors of galaxies in a cluster result in a “stellar bump sequence” whose color mainly depends on the cluster redshift (e.g., Muzzin et al. 2013a). We can thus tune, for each cluster, the IRAC color selection based on the high-purity RS sample, and then use it to identify a sample of candidate members including all galaxy types. In fact, to ensure the high completeness of such a sample, we will later adapt this first IRAC color selection (based on the RS sample alone) by considering a plausible IRAC color range for galaxies at the same redshift but with different stellar population properties, as detailed below. For each cluster, we thus initially defined a first IRAC color selection as the ±3σ range of [3.6]–[4.5] color of the RS sample. This [3.6]–[4.5] color range is much larger than the color uncertainty of individual galaxies (see Fig. 2), which was thus not considered to define this color selection. As shown in Fig. 2, these RS galaxies have indeed very similar IRAC colors – as expected, given the low background contamination of the selected RS sample and the uniformity of IRAC colors for galaxies at the same redshift, and in this case also of very similar stellar population properties. We also note in Fig. 2 the clear concentration of galaxies with m814–m140 colors corresponding to the peak of the blue cloud (see Fig. 1a and b) and with IRAC colors very similar to those of the RS sample. The resulting first IRAC color selection of candidate cluster members is shown by the horizontal light gray lines in Fig. 2.
-
Refined definition of IRAC color selection for candidate cluster members, accounting for galaxy populations bluer than the red sequence: To extend this selection to the full sample of cluster galaxies, we need to account for the possible color difference between galaxies hosting different stellar populations. Using Bruzual & Charlot (2003) models, we thus increased the IRAC color selection range by the estimated difference between the color of passive galaxies (nominally an SSP with a formation redshift zf = 3, but the difference between plausible passive galaxy colors is very small, see Fig. 2) and the color of a stellar population at the same redshift forming stars at a constant rate for 100 Myr (different ages in a reasonable range do not increase further the color range of our selection), with solar metallicity and a dust attenuation ranging from Av = 0 to 3 mag (see Fig. 2). This procedure yields the final adopted color selection, shown by dark gray lines in Fig. 2. The red and blue sets of tracks in Fig. 2 show the color evolution of the adopted passive (SSPs with zf = 2, 3, 5) and star-forming (with Av = 0, 1, 3) models, respectively, in the redshift range 1 < z < 2, with small solid points indicating z = 1.3, 1.6, 1.9 and the large circle indicating the cluster redshift. In order to be representative of a passive population, the zf = 2 SSP track is only shown up to z = 1.7.
-
Final definition of candidate member samples: All galaxies (except those with unmeasured or unreliable IRAC fluxes, as discussed above) outside of the adopted color selection were discarded as interlopers. The rest of the galaxies were retained to form the candidate cluster member sample. Finally, given the redshift dependence of the [3.6]–[4.5] color, we expect that across the redshift range of interest here (z ∼ 1.4 − 1.8), the IRAC color-selected candidate member samples defined as above are affected by some (variable level of) contamination from interlopers at redshifts similar to the cluster, as well as contamination from low-redshift sources (e.g., Muzzin et al. 2013a; Papovich 2008). To remove sources which are most likely low-redshift interlopers, we further cleaned the candidate member sample by requiring that m140–[3.6] ≥ 0, m814–[3.6] ≥ 0.4, m140–[4.5] ≥ −0.5, m814–[4.5] ≥ 0, and m814–m140 > 0, as calibrated on galaxies in the GOODS-S field sample described in Sect. 2.3. This is the candidate member sample used in the following analysis. In the example Fig. 2, this sample is shown with orange squares, while rejected interlopers are shown with blue squares. We deal with the residual contamination from interlopers at redshifts broadly similar to the cluster in Sect. 3.2.
 |
Fig. 2. Two examples of the selection of candidate cluster members (see Sect. 3.1). Vertical gray lines bound the m814–m140 RS sample used for the initial definition of the IRAC color selection range, shown by the horizontal light-gray lines. Groups of red and blue tracks show, respectively, the colors as a function of redshift in the range 1 < z < 2 of quiescent (SSPs with zf = 2, 3, 5) and actively star-forming (100 Myr old constant star formation, Av = 0, 1, 3) stellar populations, used to obtain the final adopted IRAC color selection range (dark-gray lines, see Sect. 3.1 for full details). Small solid points along the tracks indicate z = 1.3, 1.6, 1.9; the large circle indicates the cluster redshift. Orange and blue squares mark the galaxies in the cluster field classified as candidate members or interlopers, respectively, with the full IRAC+HST color selection criteria described in Sect. 3.1. |
3.2. Statistical subtraction of residual background contamination
Although the color selection applied to this point removes obvious interlopers, the large IRAC color range used in the selection to ensure a high completeness of the sample, and the intrinsically small variation in IRAC color spanned by different populations in a relatively broad redshift range, result in an expected significant residual contamination from sources at redshifts broadly similar to the cluster (see tracks in Fig. 2, as well as Fig. 5 below). This was accounted for by applying a residual statistical background subtraction using a ∼60 arcmin2 control field in the CANDELS GOODS-S field discussed in Sect. 2.3, where we applied exactly the same color selections as we do for our candidate cluster member samples.
Figure 1a shows for each cluster a visualization of the resulting background-subtracted color-magnitude diagram, produced with an approach similar to that of van der Burg et al. (2016). Specifically, we subtracted the residual background contamination as follows: 1) We start from a candidate cluster member sample obtained as discussed in Sect. 3.1, and a control field sample from the GOODS-S field (see Sect. 2.3) that is selected in the same manner. 2) For each galaxy in the candidate member sample, we calculate a “weight” that corresponds to the statistical excess of the candidate member sample over the control field density at the magnitude and colors of the given galaxy. Weights are calculated as follows (see van der Burg et al. 2016, for a more detailed description): first, all candidate member weights are initially set to 1. Then, for each galaxy in the control field sample we subtract the corresponding “background contamination” from the candidate member sample by appropriately reducing the weights of all candidate members that lie within a distance in the color (m814–m140) – color (m140–[3.6]) – magnitude (m140) space given by their photometric uncertainties (1σ), with a minimum distance of 0.3 mag, effectively resulting in a smoothing of galaxy densities in the color-color-magnitude space. If no galaxies are found within this distance, we double the search distance, and then if necessary increase the search distance to 1.3 times the distance to the closest galaxy. This criterion allows the full subtraction of the background contamination estimated from all galaxies in the control field sample, while reducing the weights of those candidate members that are more similar to the galaxies in the control field. For each considered control-field galaxy, the weights of all selected candidate members identified with the above criterion are reduced so that the contribution of the considered field galaxy (normalized by the areas of the probed cluster region and of the control field) is removed. At the end of this procedure, the contributions of all galaxies from the field sample have been subtracted from the candidate member sample.
This approach effectively follows the procedure adopted in previous analyses (e.g., van der Burg et al. 2016; Strazzullo et al. 2016), except that we apply the statistical background subtraction in magnitude-color-color rather than in magnitude-color space, and that we equally de-weight candidate members with similar color-color-magnitude rather than de-weighting the single candidate member closest in color-color-magnitude space to the given field galaxy. The reason why we perform the statistical background subtraction in magnitude-color-color space, is that by adopting colors close to the restframe U-V, V-J we expect to account for differences in specific star formation activity and dust attenuation (and thus also mass-to-light ratio) across galaxy populations better than with a subtraction in color-magnitude space (see e.g., Sect. 5.2).
The result of this procedure is that in regions of the color-color-magnitude space that are more densely populated in the control field sample, the weights of candidate cluster members are more significantly reduced. At the end of the procedure, each galaxy in the candidate member sample has an associated weight corresponding to its statistical excess probability over the galaxy density in the control field at that location in color-color-magnitude space. We stress that, as this excess probability results from a statistical background subtraction, it does not translate into a membership probability on a single galaxy basis, and it is only meant to describe the contribution of cluster galaxies as a population across the color-color-magnitude space. We also note that the determination of the statistical background subtraction weight does not include any dependence on clustercentric distance. In Fig. 1a, candidate cluster members are shown as filled circles whose size scales with this weight.
3.3. Completeness and contamination of candidate member samples
Given the statistical background subtraction weights calculated in Sect. 3.2, we can further examine the color-selected candidate member samples defined in Sect. 3.1, that are the basis of all the following analyses.
Based on these weights, we show in Fig. 1c the expected fraction of interlopers in the candidate member sample as a function of m814–m140 color. We estimate a very low contamination (as expected) from fore-/background galaxies in the red candidate member sample, but a non-negligible contamination for blue galaxies. The background subtraction weights allow us to account for this contamination in the analyses described below.
In Fig. 3 we show the projected densities of cluster candidate members and interlopers resulting from the procedure in Sect. 3.1. The figure shows projected densities for the two regions in each cluster used in the following analyses, the inner core region r < 0.45r500, and a larger region out to r < 0.7r500. (Because the r < 0.45r500 region is included in the r < 0.7r500 one, the respective measured densities shown in Fig. 3 are not independent.) For comparison, we also show the region corresponding to the annulus 0.45 < r/r500 < 0.7, although given the expected more significant background contamination this annulus is not investigated in detail in the following. We note that both the r < 0.7r500 and the outer annulus regions are not completely covered by our homogeneous catalogs, and that the inner r < 0.45r500 region is affected by masked areas for SPT-CLJ2040 and SPT-CLJ0607 (Fig. 4). In the analysis below we will correct for the uncovered portions of the probed regions assuming spherical symmetry (see Sect. 3), but for the purpose of this figure we use densities computed in the actual covered area. The red- and blue-shade squares show, respectively, the galaxy projected number density for the samples of candidate members and interlopers as determined with the color selection described in Sect 3.1.
 |
Fig. 3. Projected number density of candidate cluster members (shades of red) and interlopers (blue) in the five clusters as measured in three cluster regions, as indicated. Empty squares show densities for color-selected samples (see Sect. 3.1), and filled circles show how member number density decreases – and interloper density increases – after applying the statistical subtraction of residual background contamination described in Sect. 3.2. The blue line shows the average density of control field galaxies in the same magnitude range adopted for the cluster, with the light-blue shaded areas showing the density variation (16th–84th percentiles) in apertures corresponding to the three probed regions. The relative flatness of the interloper density profiles constrains the cluster member sample incompleteness due to member misclassification (see Sect. 3.3). |
 |
Fig. 4. Projected density maps (see color bar) of candidate cluster members for the five clusters. Gray empty symbols show the position of individual candidate members, where symbol size scales with the galaxy statistical background subtraction weight (Sect. 3.2), and symbol shape reflects galaxy morphology. The cross marks the coordinates of the SPT-SZ detection, with the cross size showing the estimated positional uncertainty (1σ, see Sect. 3.4). The position of the adopted brightest central galaxy, defining the cluster center in the subsequent analysis, is indicated by a star. The circle is centered at the median coordinates of the 5% highest-density points in the map, and has a radius of 250 kpc at the cluster redshift (for comparison r500 ∼ 70″ ∼ 600 kpc for these clusters). Masked areas are blanked out and white gridding marks areas affected by edge effects. |
Because, as discussed in Sects. 3.1 and 3.2, the candidate member samples are affected by residual background contamination, the projected number densities of both candidate members and interlopers will also be affected. In particular, the number density of candidate cluster members will be an overestimate of the actual density of cluster members, while the density of color-selected interlopers will be an underestimate of the actual interloper density. By applying the statistical residual background subtraction weights from Sect. 3.2, we can estimate the actual (background corrected) projected densities of cluster members and interlopers. These are shown as filled circles in Fig. 3.
The blue line in Fig. 3 shows the average density of galaxies in the selected m140 range in the GOODS-S control field, where the thickness of the line shows the uncertainty on this average value. The light-blue shaded areas show, as an estimate of the variance on the scales of the considered cluster regions, the 16th–84th percentile range of projected densities obtained at 100 random positions in the control field, within apertures of the same angular size as the adopted cluster regions.
The estimated density of interlopers for each cluster is consistent with being flat across the three (partially overlapping) samples at different clustercentric distances, with a marginal increase of the estimated interloper density towards the cluster center for SPT-CLJ0607 and SPT-CLJ2040 that is nevertheless still consistent with the outer value. In particular for SPT-CLJ2040, the interloper density tends to also be marginally higher than the typical expectations from the control field (Fig. 3). An interloper density higher than expected and, in particular, rising towards the cluster center, might indicate a misclassification of a fraction of candidate members as interlopers, possibly due to inaccurate IRAC fluxes because of contamination from bright neighbors, or biased color selection. Other explanations such as weak gravitational lensing magnification that is stronger in this cluster or a truly higher density of fore-background sources are also possible. In this respect, we note that a very bright and extended foreground source lies along the line of sight very close to the center of SPT-CLJ2040.
If misclassification of candidate members as interlopers is indeed occurring, Fig. 3 provides an estimate of the incompleteness of the member sample. Assuming that the interloper density in the outer annulus is actually correct4, and that the interloper density is flat across the probed cluster field, we can estimate the expected number of interlopers in the cluster central fields (r/r500 < 0.45, 0.7) from the interloper density in the outer annulus and the projected area of the central fields. By comparing this number to the number of actually identified interlopers in the central fields we can estimate how many cluster members were possibly misclassified as interlopers. This calculation yields an estimate of the completeness for the member sample in the r < 0.7r500 region of 88% for SPT-CLJ0607, 93% for SPT-CLJ0446, 88% for SPT-CLJ2040, and 100% for SPT-CLJ0421 and SPT-CLJ0459. Because of the low number statistics affecting these completeness estimates, these percentages are affected by significant uncertanties, with errors of ±40%. In the central r < 0.45r500 region, the estimated completeness would be 83% for SPT-CLJ0607, 87% for SPT-CLJ0446, 82% for SPT-CLJ2040, and 100% for SPT-CLJ0421 and SPT-CLJ0459 (with errors of ±30%). Given the significant uncertainties (Fig. 3), all samples are consistent with being formally 100% complete (meaning that the number of cluster members that we estimate might be misclassified as interlopers is always consistent with zero).
3.4. Projected galaxy density maps and cluster center definition
Figure 4 shows for all clusters the 5th nearest neighbour density map of candidate cluster members, down to the m140 limit indicated in each panel. Individual candidate members are also shown with gray symbols, with symbol shape reflecting galaxy morphology (Strazzullo et al., in prep.) as indicated, and symbol size scaling with the galaxy statistical background subtraction weight. Because clustercentric distance is not considered in the weight determination (Sect. 3.2), these density maps are based on the full color-selected candidate member sample, and thus include residual background contamination.
Figure 4 shows the very prominent concentrations of massive galaxies associated with the clusters, with the exception of SPT-CLJ0607 that seems to exhibit a milder or less concentrated galaxy overdensity at least in the magnitude range probed here (see also Fig. 1). We note that Khullar et al. (2019) suggest the possible presence of a background structure close to the line of sight of SPT-CLJ0607 and at slightly higher (spectroscopic) redshift z = 1.48. Given the redshift difference, it is possible that this background structure contaminates our candidate member sample, and thus also the projected density distribution in Fig. 4. On the other hand, the X-ray based (Fe-K emission line) redshift estimate for SPT-CLJ0607, z ∼ 1.37 ± 0.02 (Bulbul et al., in prep.), is consistent with the z = 1.40 redshift from Khullar et al. (2019), suggesting that the z ∼ 1.48 background structure is likely sub-dominant with respect to the more massive z = 1.40 cluster.
In this work, we adopt as the cluster center the position of the brightest red galaxy (based on the observed color-magnitude diagram in Fig. 1a; hereafter referred to as the brightest central galaxy, BCG) within 100 kpc (proper) of the projected number density peak of candidate members (Fig. 4). The adopted BCG is the brightest red (and most massive) galaxy lying at the center of the red galaxy concentration associated with the cluster. It is generally also the brightest red galaxy in the cluster core (at least out to r ∼ 250 kpc), and the most massive galaxy of the whole candidate member sample (Sect. 3.1), with the exception of SPT-CLJ0459 for which the brightest red galaxy is ∼120 kpc away from the galaxy overdensity peak, and six massive sources formally more massive (by a factor ranging from 5% to 70%) than the adopted BCG are spread along the overdensity described by the full candidate member population. Interestingly, despite the less prominent galaxy overdensity of SPT-CLJ0607, its adopted BCG is instead the largest, most massive central galaxy across the cluster sample (see e.g., Figs. 1a, 7).
In Fig. 4 the position of the adopted cluster center (BCG; marked by a star) is compared to the candidate member overdensity, and to the original cluster coordinates from the position of the SZE detection (marked by a cross; the cross size shows the SPT beam FWHM divided by the S/N of the cluster SZE detection, as an indication of the positional uncertainty).
The distance between the adopted BCG and the center of the candidate member overdensity ranges from ∼10 kpc (∼1% of the virial radius r200; SPT-CLJ0421, SPT-CLJ0459, SPT-CLJ0446) to ∼60 kpc (∼6% of the virial radius; SPT-CLJ0607, SPT-CLJ2040). In this respect, we note that for SPT-CLJ2040 the center of the candidate member overdensity may be biased by the masked area close to the cluster center (see Fig. 4), while for SPT-CLJ0607 it could be affected by other structure close to the line of sight as mentioned above.
The distance between the adopted BCG and the centroid of the SZE detection ranges instead from ∼80–110 kpc (∼10% of r200; SPT-CLJ0421, SPT-CLJ0607, SPT-CLJ0446) to ∼200 kpc (∼20% of r200; SPT-CLJ0459, SPT-CLJ2040). Given the S/N of the SZE detection for these clusters (Table 1), and the SPT beam FWHM (∼1.1′ at 150 GHz), the formal positional uncertainty (1σ) of the SZE centroid would correspond to ∼35 − 40 kpc. This suggests that the distribution of positional offsets between the adopted BCG and the SZE center cannot be attributed to positional uncertainties alone. With a larger sample of SPT-SZ clusters spanning the range 0.1 ≲ z ≲ 1.3 (median redshift ∼0.6), Song et al. (2012) indeed concluded that 68% (95%) of these clusters show a BCG vs. SZE centroid offset of < 0.17r200 (< 0.43r200, respectively), suggesting an intrinsic positional offset of BCGs from the ICM based cluster centroid similar to what has been estimated using X-ray selected samples of low-redshift clusters (e.g. Lin et al. 2004). For higher redshift clusters, significantly larger BCG offsets from the X-ray centroid (up to ∼300 kpc, with a median offset of ∼50 kpc) have been suggested (Fassbender et al. 2011).
Adopting the BCG position defined as described above as the cluster center, implicitly focuses the analysis presented in this work on the cluster region with the highest galaxy density. Nonetheless, this choice of the cluster center has a limited relevance with respect to our results, given the density maps shown in Fig. 4 and the relatively small BCG vs. SZE centroid distances of ≲100 kpc for SPT-CLJ0421, SPT-CLJ0607, SPT-CLJ0446. Concerning the two clusters with more significant offsets of ∼200 kpc (SPT-CLJ0459, SPT-CLJ2040), in both cases X-ray imaging is available and the centroid of the X-ray emission (Bulbul et al., in prep., Mantz et al., in prep.) is closer to the adopted BCG than to the SZE centroid, with BCG vs. X-ray centroid offsets of ∼30 and 90 kpc for the two clusters, respectively. A more detailed investigation of the X-ray vs. SZE vs. galaxy overdensity center offsets is beyond the scope of this work. As we only have X-ray data on three clusters (SPT-CLJ0607, SPT-CLJ0459, SPT-CLJ2040) we conclude in the interests of homogeneity that adopting the BCG position as the cluster center is the most reasonable choice for this work.
4. Cluster redshift constraints
Out of five clusters in our sample, spectroscopic redshifts have been obtained for SPT-CLJ2040 and more recently for SPT-CLJ0607 (Bayliss et al. 2014; Khullar et al. 2019). Future spectroscopic campaigns are planned for the remaining three clusters. The new observations presented in this work allow us to improve upon the originally published (Bleem et al. 2015) photometric redshifts of these systems, which were used for our sample definition. We employ both the RS color m814–m140, and the IRAC color [3.6]–[4.5], each offering a handle on the cluster redshift with different limitations.
The zeropoint and slope of the red sequence can be used to constrain the cluster redshift with fairly good accuracy up to z ∼ 1, and indeed this is the primary approach used for SPT clusters (Song et al. 2012; Bleem et al. 2015). However, given the high redshifts of the clusters studied here, we need to consider the effect of different formation redshifts or formation histories, as shown for instance in Fig. 5.
 |
Fig. 5. Photometric redshift constraints for all clusters (black points with 1σ errorbars reported in both panels) as determined with the simultaneous modeling of the red sequence (RS) and [3.6]–[4.5] color in Sect. 4. Red stars show the spectroscopic redshifts for SPT-CLJ2040 and SPT-CLJ0607, as well as the best current constraint for SPT-CLJ0459 (see Sect. 4). Bottom panel: adopted model RS m814–m140 color at M* vs. redshift, for formation redshifts 2 < zf < 5 (orange lines). Light blue bars show the 1σ constraints from modeling only the RS color (dark blue assuming zf = 3). Light green bars show constraints from the [3.6]–[4.5] color alone. Top panel: adopted model [3.6]–[4.5] color vs. redshift, for 2 < zf < 5 as in the bottom panel. The shaded area shows for reference the 16th–84th percentile range of [3.6]–[4.5] color vs. redshift for field galaxies in the magnitude range of our samples (m140 ≲ 23.5). Dark green (bottom panel) and white (top panel) bars show the impact on the best-fit redshift (from IRAC color alone and RS + IRAC color, respectively) of a ± 0.03 AB mag systematic offset on the [3.6]–[4.5] color. |
The [3.6]–[4.5] color used as a probe of the 1.6 μm “stellar bump” (e.g., Sawicki 2002) is much less sensitive to star formation history, which is an advantage for use as a photometric redshift indicator (e.g., Sawicki 2002; Papovich 2008). In spite of the small color range spanned by galaxy populations in [3.6]–[4.5] color with respect to colors probing the 4000 Å break (see also Fig. 5), the “stellar bump sequence” due to the very similar [3.6]–[4.5] colors of galaxies in a cluster has indeed been shown to be a potentially effective redshift indicator for distant clusters where the observed [3.6]–[4.5] color uniquely maps onto redshift (0.7 < z < 1.7 e.g., Muzzin et al. 2013a). On the other hand, the small [3.6]–[4.5] color range makes this approach more sensitive to even small systematics in the color measurement (see Fig. 5), and the flattening of the [3.6]–[4.5] color vs. redshift at z ∼ 1.6 reduces its usefulness at the high-redshift end of our sample.
To estimate cluster photometric redshifts, we identify a red galaxy sample by modeling the red peak in the color distribution with a Gaussian and selecting all galaxies within 3σ of the peak. As mentioned in Sect. 3, here we only consider a F140W magnitude range where we can still measure the 1″ aperture magnitude in the F814W band with a S/N ≳ 5. This criterion, together with the high contrast of the red sequence over the field, makes our selection of the RS sample largely insensitive to the details in the adopted criteria, as well as to background contamination.
Although not necessarily required for a redshift estimate based on the [3.6]–[4.5] color, adopting the RS sample allows us to use a cleaner, low-contamination sample of cluster galaxies, and to simultaneously model both the RS (m814–m140 vs. m140) and [3.6]–[4.5] colors as a function of redshift in a consistent way (that is, the RS and stellar bump sequence colors correspond to the same galaxy population, and are thus modeled for the same formation redshift). For the RS color, we use RS models by Kodama & Arimoto (1997). IRAC colors are derived using Bruzual & Charlot (2003) solar-metallicity SSP models. In our modeling, we account for photometric uncertainties and allow for a variable intrinsic scatter in both the red sequence and stellar bump sequence. Color uncertainties of individual galaxies and the intrinsic scatter – modeled as a free parameter – are summed in quadrature to give a total observed scatter both for the red sequence and stellar bump sequence. We account for uncertainties associated with the formation redshift zf of stellar populations in the red sample by adopting a flat prior on the formation time tf (the age of the Universe at redshift zf) corresponding to the range 2 < zf < 5. The parameter space is explored with an MCMC approach. The free parameters are the cluster redshift, the formation time tf, and the intrinsic scatters in the red sequence and in the stellar bump sequence. For each cluster, uncertainties on the estimated photometric redshift (1σ) are quoted after marginalization over all the other parameters.
Figure 5 shows the derived redshift constraints from the full modeling of the RS and IRAC color simultaneously (black points and error bars reported in both panels) together with the models used for the redshift estimation. The bottom panel of Fig. 5 shows the expected (Kodama & Arimoto 1997) RS color at the characteristic magnitude M* for different formation redshifts, while the top panel shows the adopted model [3.6]–[4.5] color vs. redshift for the same formation redshifts. As discussed above and as shown in the top panel of Fig. 5, the expected [3.6]–[4.5] color range of the red sample for the different assumed formation redshifts is very small as compared to the corresponding expected range of RS colors. Considering the expected size of possible systematics on the IRAC zero-point, as well as the color difference between plausible models for RS galaxies with different zf, and the fact that stellar population models are expected to have larger uncertainties in the restframe NIR, we also estimate the impact of a ±0.03 AB mag systematic bias on the expected (model) IRAC color. The resulting effect on the redshift estimates is also shown in Fig. 5 (white error bars in the top panel). For reference, the top panel also shows (shaded area) the 16th–84th percentile range of [3.6]–[4.5] color vs. redshift for galaxies in the GOODS-S control field in the same m140 magnitude range adopted for the cluster samples (m140 ≲ 23.5).
The bottom panel of Fig. 5 also shows for reference the constraints derived using only the RS or IRAC colors, respectively (blue and green symbols, as indicated). In particular, following results from previous investigations of the formation epoch of bright RS galaxies in massive clusters in this redshift range (e.g., Strazzullo et al. 2010; Andreon et al. 2014; Cooke et al. 2016; Beifiori et al. 2017; Prichard et al. 2017), the RS-only redshift estimate obtained assuming a formation redshift zf = 3 as typically suggested by such studies is explicitly marked in the figure. Finally, in both panels we also show (red stars) the available spectroscopic redshifts for the clusters SPT-CLJ2040 (z = 1.478; Bayliss et al. 2014) and SPT-CLJ0607 (z = 1.401; Khullar et al. 2019), and the current best redshift constraint for SPT-CLJ0459 (see discussion below).
Overall, Fig. 5 clearly shows the discussed limitations of the RS and IRAC colors as cluster redshift indicators in this redshift range, and in particular the redshift – formation epoch degeneracy for the RS color, and the lack of redshift sensitivity at z ≳ 1.6 for the IRAC color. At the same time, Fig. 5 shows to what extent we may improve cluster photometric redshift constraints by combining both indicators in our simultaneous modeling of the RS and stellar bump sequence colors. Up to z ∼ 1.5, the combined modeling effectively reduces the impact of the degeneracy between cluster redshift and formation redshift that otherwise significantly affects redshift estimates from the RS color only. However, at z > 1.5 the flattening of the IRAC color vs. redshift relation significantly limits such improvement.
All clusters’ estimated redshifts are consistent with our initial z > 1.4 selection (Bleem et al. 2015). As expected given the redshift distribution of massive clusters, most clusters lie at the low end of the probed z ≳ 1.4 range. The highest-redshift cluster is SPT-CLJ0459, with a photometric redshift 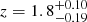 from the combined RS+IRAC color modeling. Modeling the RS and stellar bump colors independently yields two completely consistent redshift estimates placing SPT-CLJ0459 at 1.6 ≲ z ≲ 1.9 (Fig. 5,
from the combined RS+IRAC color modeling. Modeling the RS and stellar bump colors independently yields two completely consistent redshift estimates placing SPT-CLJ0459 at 1.6 ≲ z ≲ 1.9 (Fig. 5, 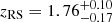 ,
, 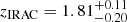 ). Given the mentioned limitations of the redshift estimates from RS and stellar bump colors in this redshift range (which indeed reflect in the quoted redshift uncertainties), we also note that modeling the RS color limiting the formation redshift range by plausibility arguments5 to 2.5 ≤ zf ≤ 4 yields a redshift of
). Given the mentioned limitations of the redshift estimates from RS and stellar bump colors in this redshift range (which indeed reflect in the quoted redshift uncertainties), we also note that modeling the RS color limiting the formation redshift range by plausibility arguments5 to 2.5 ≤ zf ≤ 4 yields a redshift of 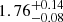 . An independent and fully consistent redshift estimate for SPT-CLJ0459 was also derived from the modeling of the 6.7 keV Fe-K emission line complex from Chandra observations (z = 1.84 ± 0.12, A. Mantz priv. comm., see also McDonald et al. 2017), and has very recently been refined with new XMM observations to z = 1.72 ± 0.02 (preliminary, Mantz et al., in prep.). The agreement between these independent estimates strongly suggests that SPT-CLJ0459 is not only the most distant cluster in the SPT-SZ survey, but also likely the most distant massive (M500 > 1014 M⊙) ICM-selected cluster discovered thus far, and one of only three known such massive systems at z > 1.7, irrespective of selection (Andreon et al. 2009, 2014; Stanford et al. 2012; Newman et al. 2014). Given that the much tighter constraints derived from the XMM observations are fully consistent with results from our modeling, in the following we adopt for SPT-CLJ0459 a redshift of z = 1.72.
. An independent and fully consistent redshift estimate for SPT-CLJ0459 was also derived from the modeling of the 6.7 keV Fe-K emission line complex from Chandra observations (z = 1.84 ± 0.12, A. Mantz priv. comm., see also McDonald et al. 2017), and has very recently been refined with new XMM observations to z = 1.72 ± 0.02 (preliminary, Mantz et al., in prep.). The agreement between these independent estimates strongly suggests that SPT-CLJ0459 is not only the most distant cluster in the SPT-SZ survey, but also likely the most distant massive (M500 > 1014 M⊙) ICM-selected cluster discovered thus far, and one of only three known such massive systems at z > 1.7, irrespective of selection (Andreon et al. 2009, 2014; Stanford et al. 2012; Newman et al. 2014). Given that the much tighter constraints derived from the XMM observations are fully consistent with results from our modeling, in the following we adopt for SPT-CLJ0459 a redshift of z = 1.72.
As shown in Fig. 5 and Table 1, for the two (or three, including SPT-CLJ0459) clusters for which a spectroscopic redshift is known, the photometric redshifts derived above are fully consistent (≤1σ with uncertainties from the default combined modeling) with the spectroscopic determination, suggesting a likely minor impact of the possible systematics on the redshifts of the two remaining clusters as well.
5. Galaxy populations in the central cluster region
Studies of (massive) galaxy populations in the field observe a significant drop in the fraction of quiescent galaxies beyond z ∼ 1.5 (e.g., Muzzin et al. 2013b; Ilbert et al. 2013). As discussed in Sect. 1, the evolution of quiescent and star-forming galaxy populations in dense environments and in particular massive clusters is still debated. In this section we focus on the prevalence of massive quiescent galaxies in the central cluster regions. We first investigate the predominance of (optically) red galaxies in the cluster vs. control fields (Sect. 5.1). Because optical colors of massive star-forming galaxies are also significantly dust-reddened, it is important to investigate the nature of the stellar populations in massive red galaxies (Sect. 5.2), to properly estimate the relevance of the quiescent (vs. star-forming) population and to quantify the role of the cluster environment in suppressing star formation (Sects. 5.3 and 6).
5.1. The red population
Figure 1a shows the candidate member sample at r < 0.7r500 in the color-magnitude diagram for each cluster (as described in Sect. 3). As a reference, the expected location of the red sequence (according to Kodama & Arimoto 1997) at the cluster redshifts derived in Sect. 4 is also shown, for different formation redshifts in the range 2 ≤ zf ≤ 5 (the zf = 2 model is not shown for SPT-CLJ0459 as it would correspond to a stellar population younger than ∼0.5 Gyr at the cluster redshift). The colors and slopes of the observed red sequences are in line with the expectations for a formation redshift around z ∼ 3 as often found in previous studies of similar systems (see Sect. 4). When comparing the color-magnitude diagrams in Fig. 1a, we stress that because of our choice of the m140 limit described in Sect. 3, different clusters are probed in this Figure down to different depths ranging from ∼M*+2 at z ∼ 1.4 to ∼M*+1.3 at z ∼ 1.7. In terms of galaxy stellar mass, the adopted m140 limits translate into stellar mass completeness limits for the red population ranging from log(M/M⊙) ∼ 10.55 at z ∼ 1.4 to log(M/M⊙) ∼ 10.85 at z ∼ 1.72. For this reason, the appearance of the color-magnitude diagrams in Fig. 1a is bound to be different because at lower redshifts we reach fainter, lower mass galaxies. Nonetheless, even the color-magnitude diagrams of clusters at very similar redshifts show some noticeable differences. For instance, SPT-CLJ0421 and SPT-CLJ0607 at z ∼ 1.4 show an overall different galaxy overdensity in their color-magnitude diagram (see related discussion in Sect. 3.4), and in particular a different population of the red sequence and a different color distribution (see also Fig. 1b). Similarly, there are noticeable differences between the color-magnitude diagrams of SPT-CLJ2040 and SPT-CLJ0446, that are also estimated to be at similar redshift z ∼ 1.5. SPT-CLJ2040 shows a stronger overall galaxy overdensity, and in particular a well populated red sequence, but at the same time also exhibits a significant overdensity of blue galaxies. These differences are discussed further below.
For each cluster, Fig. 1b also shows the color distribution of cluster galaxies (red symbols), where candidate members are weighted according to the residual statistical background subtraction discussed in Sect. 3.2, as well as by the area coverage weight factor discussed in Sect. 3. To the extent that the control field is representative of the local cluster background and that there are no strong asymmetries around the cluster in galaxy population properties, the background and area coverage corrected color distributions in Fig. 1 will be representative of the actual cluster galaxy population within r < 0.7r500. As an estimate of the impact of cosmic variance on the scale of the probed cluster core field, the orange shaded area shows the 16th–84th percentile range of color distributions obtained by performing the residual statistical background subtraction (Sect. 3.2) considering, rather than the full control field, 100 fields of size r = 0.7r500 located at random positions in the GOODS-S field (see Sect. 3.3).
For comparison, the figure also shows the color distribution of galaxies in the control field at similar redshift (blue histograms, scaled to the total number of galaxies in the background and area coverage corrected cluster sample). The darker blue histogram refers to a field sample selected by photometric redshifts within a range ±0.2 from the cluster redshift, and in the same m140 magnitude range as the candidate member sample. The lighter blue histogram refers instead to a field sample obtained with the same magnitude and color criteria as the candidate member sample.
For each cluster in our sample, a marked excess of red galaxies, typically in a tight color range (the intrinsic scatter in the observed m814–m140 color, as derived from the MCMC modeling in Sect. 4, is in the ranges from 0.10 ± 0.02 to 0.15 ± 0.04), makes the color distribution of cluster galaxies in the probed magnitude range clearly different from that of the field analogs.
As mentioned above, there are differences between the color-magnitude diagrams of different clusters, and in particular their color distributions and red galaxy fractions. Figure A.1 (bottom panel) shows the red galaxy fraction estimated to a common limit of ∼M*+1.3 for all clusters6, highlighting in a more direct, quantitative way the more significant blue population in SPT-CLJ0607 and SPT-CLJ2040 that can already be seen in Fig. 1. While such differences in galaxy population properties can obviously be due to cluster-to-cluster variation, in principle they could also be artificially produced, at least to some extent, by differences in the local background of the different clusters. In Appendix A, we redetermine the red galaxy fraction adopting as control fields the random sub-fields described above for the estimation of the effect of small-scale cosmic variance. Figure A.1 shows that the red galaxy fraction is affected by at most 10% even considering sub-fields with a galaxy density at the 10th and 90th percentile level across the default control field. As further discussed in Appendix A, we do not have any significant evidence from the data studied here that differences in the local background density are the actual cause of differences in the estimated galaxy population properties among these clusters, although we have already noted that SPT-CLJ0607 could be affected by the presence of a background structure close to the line of sight (Sect. 3.4), and that the inferred background density for SPT-CLJ2040 tends to be marginally higher than the typical expectations from the control field (Sect. 3.3). Nonetheless, we present in Fig. A.1 our current best estimates of the possible systematics on the red galaxy fraction (which then translate to the quiescent galaxy fraction) coming from differences in the background densities of the cluster and adopted control fields. According to these estimates, the cluster that could be, potentially, more significantly affected is SPT-CLJ2040, for which our default red fraction measurement might in principle underestimate by up to ∼30% the actual value. We note once again, though, that Appendix A presents these results for completeness, and we currently have no significant evidence to suggest that differences in the local cluster background densities may be the main source of differences in their observed galaxy population properties.
Differences in galaxy population properties of clusters in this sample are discussed further in the following Sections.
5.2. The quiescent population
Figure 7 (bottom panel of each subfigure) shows the stellar mass vs. m814–m140 color diagram for candidate members of the five clusters, with the same symbol size and color coding as the color-magnitude diagrams in Fig. 1. The massive cluster galaxy population is dominated by red sources, which may be due to older stellar populations of mostly quiescent galaxies, but also to higher dust attenuation of more massive star-forming galaxies (e.g., Garn & Best 2010; Pannella et al. 2015).
To disentangle quiescent vs. dusty star-forming populations, we adopt an approximate version of the restframe U-V vs. V-J (hereafrer UVJ) color–color diagram (e.g., Labbé et al. 2005; Williams et al. 2009), which has been routinely used over the last decade for studying star-forming vs. quiescent populations up to high redshift. In Fig. 6 we show the m814–m140 vs. m140–[3.6] colors of candidate cluster members in all cluster fields. In the probed redshift range 1.4 ≲ z ≲ 1.8 the F814W, F140W and 3.6 μm bands probe, respectively, the rest-frame ranges ∼2900 − 3400 Å ∼5000 − 6000 Å and ∼13 000 − 15 000 Å. In fact, these passbands were explicitly selected to approximate the restframe UVJ color diagram.
 |
Fig. 6. Adopted quiescent vs. star-forming galaxy classification. The observed m814–m140 vs. m140–[3.6] color–color diagram of candidate members (green points) is shown for all clusters in the r/r500 < 0.7 region (the effective area covered for each cluster is indicated). Upper set of panels: m140-selected (not mass complete) candidate member samples (the mass completeness limit for each cluster is indicated). Lower set of panels: galaxies down to the common stellar mass completeness limit for all clusters, log(M/M⊙) = 10.85. Symbol size of green points scales with the statistical background-subtraction weights as in Fig. 1. Symbol color scales with stellar mass as shown by the color bar. Empty symbols show points for which a m140–[3.6] color was inferred using the 4.5 μm flux (see Sect. 5.2). Light red and blue squares show, respectively, UVJ-quiescent and UVJ-starforming galaxies from the control field sample with the same magnitude (top panels) or mass (bottom panels) threshold as candidate cluster members, and with a photometric redshift within ±0.1 from the cluster redshift. The thick light-gray line shows the adopted quiescent vs. star-forming separation in the observed m814–m140 vs. m140–[3.6] color plane. For clusters without a final spectroscopic redshift confirmation (see Sect. 4), the thin dark-gray lines show the separation that would be adopted if assuming a redshift at the edges of the black+white error bars in Fig. 5 (top). |
Green points in Fig. 6 show all candidate members, color-coded by their estimated stellar mass, with point size scaling according to the statistical background subtraction weight determined in Sect. 3.2. As discussed in Sect. 3.2, although these weights do not directly translate into membership likelihood on a galaxy-by-galaxy basis, the distribution of weights across the m814–m140–[3.6] diagram is expected to be representative of the cluster galaxy population.
All panels in Fig. 6 refer to the r < 0.7r500 region. The (m140-selected) galaxy samples shown in the upper set of panels are not mass complete – the mass completeness limit is indicated in each panel. In the lower set of panels we only show cluster candidate members above a common mass completeness limit of log(M/M⊙) > 10.85, which is reached in the most distant cluster. Therefore, although most of the star-forming population (by number) falls below this mass threshold, the bottom panels show a more proper comparison of the relevance of the quiescent and star-forming components of massive galaxy populations across the different clusters in our sample, and with respect to the field, which is discussed in detail in Sects. 5.3 and 6.
Figure 6 also shows the color-color criterion adopted to separate quiescent from star-forming galaxies (thick gray line), which was determined based on Bruzual & Charlot (2003) stellar population models as described in Strazzullo et al. (2016). The thin dark-gray lines show how the quiescent vs. star-forming separation would be displaced if the cluster redshift were moved at the edges of the white+black error bar range shown in the top panel of Fig. 5. For reference, we show with light red (blue) squares field galaxies from the GOODS-S sample at similar redshift as the cluster, with the same magnitude (top panels) or mass (bottom panels) selection as candidate cluster members, and classified as quiescent (star-forming, respectively) based on their restframe UVJ colors. This confirms that our adopted color-color criterion is analogous to the usual UVJ classification in terms of selecting the same quiescent and star-forming sub-samples, and also visually confirms the locations in the color-color diagram of the quiescent and star-forming galaxy populations in the cluster fields with respect to a reference (field) population at the same redshift. A quiescent clump and a star-forming sequence consistent with the expected colors are indeed clearly visible in the color-color diagrams of all clusters.
In the following analysis, we classify as quiescent (star-forming) sources those falling in the upper-left (bottom-right, respectively) part of the diagram according to the color criterion shown in Fig. 6. Due to unreliable IRAC flux measurements for some sources (Sects. 2.2 and 3.1), the m140–[3.6] color is not available for the full candidate member samples. The small fraction of sources for which we miss both IRAC fluxes (see Sect. 3.1) are not shown in this figure. However, we still show the very few sources for which we only have a 4.5 μm flux measurement (empty circles), translating it to a 3.6 μm magnitude using the average color of the IRAC sequence for the cluster’s red galaxy sample (Sect. 3.1). Furthermore, even where a 3.6 μm flux measurement is not available, we classify as star-forming all galaxies having a m814–m140 color bluer than the blue color-selection cutoff. All sources that, after this procedure, still lack a quiescent vs. star-forming color classification, are conservatively considered as star-forming in the following. Depending on the cluster, these amount to 0–6% of the candidate member sample above the individual cluster mass completeness limit over the r < 0.7r500 area. The effect of these unclassified sources on the main results of this work is shown in Table 2 and Figs. 7 and 10.
 |
Fig. 7. For each cluster: Bottom panel: m814–m140 color vs. stellar mass of candidate cluster members within r < 0.7r500. Symbol size and color reflect the statistical background subtraction weight as in Fig. 1. The light-gray shading shows the stellar mass range below the mass completeness limit. Top panel: quiescent fraction within r < 0.7r500 at masses above the individual mass completeness limit of the cluster (red symbols; error bars show the width of the stellar mass bin and the 1σ binomial confidence intervals, see Sect. 5.2). Where applicable, red triangles show quiescent fractions assuming that all unclassified galaxies are quiescent (rather than all star-forming, see Sect. 5.2). Blue symbols show the quiescent fraction in the same stellar mass bins for photo-z and color-selected field samples as in Fig. 1, as indicated. All symbols are plotted at the median mass of the given sample. |
The quiescent fraction (corrected for area coverage and background contamination) estimated for each cluster in the r < 0.45r500 and r < 0.7r500 regions, for stellar masses above the individual cluster mass completeness limit as well as the common limit of log(M/M⊙) = 10.85.
According to this color classification, the bulk of the RS population in the probed cluster central regions is indeed made of quiescent sources rather than very dusty star-forming galaxies, as shown more specifically in Fig. 8. This is consistent with other studies in massive clusters at similar redshifts (e.g., Strazzullo et al. 2010; Newman et al. 2014; Andreon et al. 2014; Cooke et al. 2016).
 |
Fig. 8. Quiescent fraction vs. m814–m140 color for red (m814–m140 > 1.5) galaxies in all five clusters. Galaxies bluer than m814–m140 = 1.5 are not shown as they are always classified as star-forming (thus 0% quiescent fraction, see Fig. 6). Shaded histograms represent the color distribution of cluster galaxies as in Fig. 1, arbitrarily rescaled. Empty and solid symbols show, respectively, quiescent fractions for the m140-selected and for the log(M/M⊙) > 10.85 (common) mass complete samples. Error bars show binomial confidence intervals (1σ). Color bins with < 2 galaxies are not shown. |
Figure 9 shows the projected distribution of candidate members in the cluster fields, summarizing their estimated properties as derived above, and highlighting the spatial concentration of massive red and quiescent galaxies.
 |
Fig. 9. Projected distribution of candidate cluster members. All candidate members are shown regardless of their statistical background subtraction weight. Each symbol has two colors. The color of the symbol boundary scales with the m814–m140 color of each galaxy relative to the cluster RS color (see insert). The internal symbol color, in red or blue shade according to the galaxy classification as quiescent or starforming, scales with the reliability of this classification only accounting for the distance of the galaxy colors from the adopted selection dividing line and the relevant photometric errors. Symbol shape reflects the estimated Sersic index as indicated. Masked areas and regions deemed to be outside of our uniform coverage are gray shaded. The two circles show the limiting radii of the adopted cluster regions (r < 0.45r500, r < 0.7r500). |
For each cluster, we then compute the quiescent galaxy fraction in different stellar mass ranges (above the stellar mass completeness limit) by adopting for each candidate cluster member the quiescent vs. star-forming classification discussed above. More specifically, from the statistical background subtraction and area coverage weights of all (and quiescent, respectively) candidate members in a given stellar mass range, we compute the background-corrected number of all (and quiescent) cluster galaxies in that mass range, giving the corresponding background-corrected quiescent fraction.
In Fig. 7 (top panels), these fractions are shown for each cluster down to its individual mass completeness limit, dividing the mass-complete candidate member sample in two mass bins with approximately the same number of galaxies (stellar mass bins are not the same for different clusters). The quiescent fraction of the matched field control sample (photo-z or color-selected, analogous to Fig. 1) is also shown.
Figure 7 thus clearly shows that the massive population is in fact dominated by quiescent galaxies rather than very dusty star-forming sources, and generally especially so at higher stellar masses, as expected from previous work up to this redshift in both clusters and average density fields. Figure 7 also shows that the quiescent fraction in the probed cluster region is typically higher than in the field at the same redshift for all clusters and in all stellar mass bins shown, although there are variations across different clusters and different mass bins.
Table 2 summarizes the quiescent fraction measurements described above, presenting the quiescent fraction down to the common (log(M/M⊙) > 10.85) and individual stellar mass completeness limits, for both the r < 0.45r500 and r < 0.7r500 regions. The quiescent fraction of field galaxies at the cluster redshift to the same stellar mass limits is also listed. With the (mild) exception of cluster SPT-CLJ2040 (whose central region is affected by the masking of a significant area very close to the cluster center, see Fig. 4), the quiescent fraction of massive galaxies within r < 0.45r500 is higher than within r < 0.7r500, as observed in lower redshift clusters as well as at least in most massive clusters at z ∼ 1.5 (e.g., Strazzullo et al. 2010; Newman et al. 2014; Andreon et al. 2014; Cooke et al. 2016, and more references in Sect. 1 also for lower-mass systems).
5.3. The environmental quenching efficiency in the most massive distant cluster cores
The comparison of the quiescent fraction in the cluster (fq, cl) and control field (fq, fld) can be directly translated into the so-called environmental quenching efficiency (fq, cl − fq, fld)/(1 − fq, fld), which is the fraction of galaxies that would be star-forming in the field and that instead have had their star formation suppressed by the cluster environment (e.g., van den Bosch et al. 2008; Peng et al. 2012; Wetzel et al. 2012; Balogh et al. 2016; Nantais et al. 2017). This conversion is shown in Fig. 10, where the top panel shows the quiescent fraction for the five clusters and their matched photo-z selected field samples, and the bottom panel shows the corresponding environmental quenching efficiencies. Filled red circles show the quiescent fractions and quenching efficiencies within r < 0.45r500 and r < 0.7r500 computed down to the common stellar mass completeness limit of the full sample. For reference, we also show the corresponding measurements down to the individual mass completeness limit of each cluster in Fig. B.1 (these cannot be properly compared across different clusters due to the different stellar mass limits). In contrast with Fig. 7 and Table 2, the error bars reported in Fig. 10 show the impact on the estimated quiescent fraction of uncertainties in the source photometry and in the definition of the quiescent color selection region. The quoted cluster quiescent fractions and related uncertainties in Fig. 10 correspond to the median and 16th–84th percentile range of 1000 realizations obtained by randomly shifting the m814, m140, [3.6] photometry of each candidate member according to a Gaussian with σ given by the source photometric uncertainties, and randomly offsetting the borders of the color selection by ±0.1 mag (see for comparison Fig. 6). The quoted quiescent fractions and uncertainties for the corresponding field samples are the median and 16th–84th percentile range of 1000 bootstraps on the photo-z and mass selected field samples. Correspondingly, the quoted values and uncertainties for the environmental quenching efficiency in the bottom panel show the median and 16th–84th percentile range of environmental quenching efficiencies obtained for each cluster from the different 1000 realizations for both cluster and field samples. In the top panel of Fig. 10, large empty blue squares show for comparison the quiescent fraction in the ∼1.6 deg2 COSMOS/UltraVISTA field, estimated for log(M/M⊙) > 10.85 galaxies with photo-z within ±0.15 from the clusters’ redshift, based on the Muzzin et al. (2013c) catalogs and the Williams et al. (2009) UVJ classification. Although, due to differences in the available data, we cannot reproduce the analysis as described in this work on the COSMOS field, the quiescent fractions estimated in the smaller GOODS-S field are still representative of analogous measurements in the significantly larger COSMOS survey.
 |
Fig. 10. Top panel: quiescent fraction of cluster galaxies within r < 0.45r500 (dark red) and r < 0.7r500 (light red) above the common mass completeness limit log(M/M⊙) > 10.85. Error bars account for uncertainties in the quiescent vs. star-forming classification as described in Sect. 5.3. Blue symbols show the quiescent fraction in corresponding photo-z selected control field samples (see Sect. 5.3). Large empty blue squares show values from the COSMOS field (see text). Bottom panel: environmental quenching efficiency as derived from cluster and field quiescent fractions in the top panel. Color coding reflects the top panel. In both panels empty triangles show, where applicable, the quiescent fraction and derived quenching efficiency assuming that galaxies lacking a quiescent vs. star-forming classification are all quiescent (rather than all star-forming, see Sect. 5.2, Table 2). |
5.4. Is this sample really unbiased with respect to galaxy population properties?
As mentioned in Sect. 1, the SZE cluster selection is approximately a halo mass selection with no a-priori dependence on cluster galaxy properties. However, given the high star formation rates observed in some clusters in this redshift range, we need to examine the possibility that mm-wave emission produced by high levels of star formation may offset the SZE decrement, thus effectively resulting in a biased cluster sample disfavoring systems with low quiescent fractions. A general modeling of the effect of increased star formation rates at high redshift on cluster SZE detection will be presented elsewhere. We focus here on the potential impact of mm-wave emission from star formation on the SZE selection of the five clusters studied here. In particular, we seek to quantify the potential selection bias that could impact our conclusions about quiescent fractions and environmental quenching efficiencies for the broader, massive cluster populations in this redshift range.
We start from the measured quiescent fractions within r < 0.45r500, and consider whether these five clusters (or more generally clusters of similar mass and richness as those in this sample) would still be in our sample if their quiescent fractions were lower than we observe. We describe our modeling in full detail in Appendix C, summarizing here the adopted approach, assumptions and results.
For each cluster, we start from our mass complete sample of cluster members within r < 0.45r500 and their quiescent vs. star-forming classification, and assume that all star-forming cluster galaxies form stars at the same Main Sequence (MS, e.g., Elbaz et al. 2011) rate of their field analogs (and that quiescent galaxies have a negligible star formation rate, SFR). This gives an estimate of the total SFR of cluster galaxies above mass completeness at r < 0.45r500 (see Appendix C). To account for the contribution of galaxies below our mass completeness limit, we further assume that (see Appendix C.1): 1) the cluster galaxy stellar mass function is to first order the same as in the field at the cluster redshift; and 2) the quiescent fraction vs. stellar mass of cluster galaxies can be modeled starting from our measured quiescent fraction at high stellar masses and the quiescent fraction vs. stellar mass observed in the field at the cluster redshift.
For each cluster in our sample, we thus obtain an estimate of the total SFR within r < 0.45r500. We finally estimate the SFR contribution from cluster galaxies at r > 0.45r500 by assuming an NFW (Navarro et al. 1997) galaxy number density profile, and a quiescent fraction vs. clustercentric radius profile determined based on the measured quiescent fraction at r < 0.45r500 and on the corresponding field value at the cluster redshift (see Appendix C.2).
In practice, for the adopted assumptions and given a quiescent fraction at r < 0.45r500 above the mass completeness limit, our modeling yields a SFR density profile of cluster galaxies (see Appendix C.3) that can be translated into flux density maps at 95 and 150 GHz assuming an appropriate flux density to SFR conversion (see Appendix C.4). If we consider the actually measured quiescent fraction at r < 0.45r500, such modeling provides an estimate of the contamination of the observed SZE signal from mm-wave emission of star-forming cluster galaxies. If instead we consider a lower quiescent fraction at r < 0.45r500, such modeling yields an estimate of the additional contamination from mm-wave emission that would be further reducing the SZE signal if the star-forming galaxy fraction were higher than actually measured.
We estimate such additional contamination as a function of the r < 0.45r500 quiescent fraction above mass completeness, for such quiescent fraction values down to 10% (see Appendix C.3). We then add the derived additional flux density profile at 95 and 150 GHz to the observed 95 and 150 GHz maps of the cluster, and estimate the S/N of the resulting SZE detection (see Appendix C.4). Figure 11 shows this retrieved S/N for all five clusters as a function of the assumed r < 0.45r500 quiescent fraction above mass completeness, from the actual measured value down to 10%. We note that a quiescent fraction of 10% is significantly lower than the field value appropriate for the cluster redshift and mass completeness limit. In Fig. 11, solid lines show our S/N estimates for r < 0.45r500 quiescent fractions down to the relevant field level, while dotted lines show the S/N for central quiescent fractions below the field level. Although there is no evidence from this work that quiescent fractions below the field level are common in these massive cluster cores at the probed stellar masses, we show our S/N estimates down to very low quiescent fractions below the field in the context of the studies reporting a possible reversal of the star formation vs. density relation in clusters at z ≳ 1.3, as discussed in Sect. 1.
 |
Fig. 11. Retrieved S/N of the cluster SZE detection obtained as a function of the r < 0.45r500 quiescent fraction, from the observed value down to the field level (solid lines) at the cluster redshift and mass completeness limit (see Sect. 5.4). Dotted lines show for completeness the retrieved S/N for central quiescent fractions down to 10%. For each cluster, the S/N is shown for both MS SEDs adopted to convert SFRs to 95, 150 GHz fluxes, as indicated. The gray line marks the S/N > 5 limit of our original sample selection. According to the modeling in Sect. 5.4, all five clusters would have been included in our S/N > 5 sample even if environmental quenching were negligible. |
To show the approximate sensitivity of the results in Fig. 11 to the assumed conversion from SFR to 95 and 150 GHz flux density, the figure shows the S/N obtained with both of the adopted MS SEDs (Béthermin et al. 2015; Schreiber et al. 2018) used to convert the SFR density profile into 95 and 150 GHz flux density maps. On the other hand, the figure shows the most conservative result (that is, producing lower S/N ratios) with respect to the modeling of the quiescent fraction vs. stellar mass (see Appendix C.4).
In summary, Fig. 11 shows that, as expected, the lower the quiescent fraction the lower the S/N with which we retrieve the cluster SZE detection. However, although this modeling clearly relies on the several assumptions discussed above and in full detail in Appendix C, it shows that at face value all five clusters would have still been included in our S/N > 5 sample even if their central quiescent fractions were significantly lower than what we observe, and at least down to the field level (that is, even if the environmental quenching efficiency were actually zero). In fact, according to Fig. 11 most clusters in this sample would still have been detected at S/N > 5 even if 90% of their central massive galaxy population were still forming stars at the MS level.
A full modeling of the impact of star formation in cluster galaxies on cluster SZE detection for a range of cluster masses and as a function of redshift, also considering in particular the possibility of a bias on inferred galaxy population properties coming from cluster selection, will be discussed in a future work. Nonetheless, from the modeling presented here we conclude that this sample is not significantly biased by cluster selection in terms of galaxy population properties, and that thus the high quiescent fractions observed in these clusters should be considered as representative of the properties of galaxy clusters in this mass and redshift range.
6. Discussion and conclusions
This work presents first results from a study of galaxy populations in the five highest redshift (1.35 ≲ z ≲ 1.75) massive clusters that were selected from the 2500 deg2 SPT-SZ survey via their SZE signatures. As has been shown in previous work (e.g., Bleem et al. 2015; de Haan et al. 2016), the SPT-SZ selection produces a roughly mass limited sample of clusters over the (z ≳ 0.2) redshift range where these systems exist. Importantly, the selection is based on the integrated pressure within the ICM, and therefore – to first order– is not impacted by the galaxy populations. For the specific clusters studied here, based on the analysis discussed in Sect. 5.4, even a quiescent fraction as low as that measured in the field at these redshifts would not have impacted their selection.
Furthermore, as discussed in Sect. 1, our z ≳ 1.4, S/N > 5 sample is expected to probe the M500 > 2.74 × 1014 M⊙, z > 1.4 galaxy cluster population with a completeness of ∼70%. Sample incompleteness is caused by scatter in the SZE observable–mass relation, and this comes from both the measurement noise in the extraction of the SZE observable from the mm-wave maps (20% for a S/N = 5 cluster) and the intrinsic scatter in the noise-free SZE observable at fixed mass (empirically estimated to be 20 ± 7%; de Haan et al. 2016). These two sources of scatter combine to ∼28%, which in combination with the mass trend parameter BSZ ∼ 1.6 of the SZE observable mass relation results in a ∼20% mass scatter at fixed observable and redshift. Interesting for our study is to understand the significance of the contribution of contaminating flux from star formation to this scatter. With a large volume hydrodynamical simulation, Gupta et al. (2017b) estimate a scatter in SZE integrated Compton Y500 at fixed mass of ∼13.5% at M500 = 3 × 1014 M⊙. This scatter, due to variation in cluster morphology and large scale structure projected onto the cluster line of sight, is the dominant source of intrinsic scatter in the SZE observable–mass relation. The contribution to the scatter due to high frequency cluster radio galaxies is estimated to be marginal (∼3%; Gupta et al. 2017a). When added in quadrature, these components of the scatter correspond roughly to 24% scatter in the observable at fixed mass. From Fig. 11 we can estimate the scatter due to contamination from star forming cluster galaxies at these cluster masses and redshifts to be < 5% (< 10% with the more conservative assumption on the mm-wave SED) even if assuming zero environmental quenching in the cluster core (Sect. 5.4). The scatter would be larger (up to < 15% in the worse case considered in Sect. 5.4) if a relevant part of the cluster population at these masses had quiescent fractions below the field level, but as discussed in Sect. 5.4 there is no evidence for this from our current results. At these levels, the contaminating flux from star formation is expected to play a lesser role in comparison to the dominant sources of scatter. Therefore, with our current estimates, the expected 30% incompleteness in our sample can be no more than marginally correlated with the star formation properties of cluster galaxies. Following the discussions above, we conclude that the galaxy population properties we report here should be representative of the populations in massive clusters in this redshift range.
This study is based on deep imaging follow-up of the clusters in four broad bands (F814W and F140W from HST, 3.6 μm and 4.5 μm from Spitzer). Additional imaging has been acquired on part of this sample (in particular with HST, within the See Change program, and Cycle 24 GO-14677 program (PI Schrabback) for weak lensing analyses), and will be used in future investigations. However, the work presented here completely relies on homogeneous, four band photometry across the full sample, and may be considered as a field-test of the minimal requirements adopted in designing our follow-up program to study cluster galaxy populations at this redshift.
Clusters in this mass and redshift range are exceedingly rare. Thus, although the current sample is very small for statistical purposes, this work is still the first “sample study” of quiescent fractions and environmental quenching efficiency in such massive, distant clusters.
The cluster redshifts estimated from RS and IRAC colors (Sect. 4) are consistent with the original redshift selection (z > 1.4) of this sample from the Bleem et al. (2015) catalog, and with the existing spectroscopic redshift determinations (Bayliss et al. 2014; Khullar et al. 2019). Cluster SPT-CLJ0459 seems to be not only the most distant cluster found in the SPT-SZ survey but likely the most distant ICM-selected massive cluster found to date, and among the very few extremely massive systems known near z ∼ 2, irrespective of their selection (Andreon et al. 2009; Newman et al. 2014; Stanford et al. 2012; Brodwin et al. 2016).
6.1. Derived galaxy population properties and comparison with previous work
All clusters in this sample show a very strong galaxy concentration near the position of the SPT detection (Fig. 4), with the exception of SPT-CLJ0607, which has a seemingly milder, less concentrated galaxy overdensity at least in the probed magnitude range. All clusters show an excess of red galaxies with respect to similarly selected field galaxy samples at the same redshift, with colors consistent with evolved stellar populations formed at z > 2 (Sect. 5.1).
According to the adopted UVJ-like color classification, the bulk of the massive red galaxy population within r < 0.7r500 consists of quiescent galaxies rather than very dusty star-forming sources. Quiescent fractions above the common mass completeness limit log(M/M⊙) > 10.85 are in the range ∼60 − 90% (≳80% within r < 0.45r500), compared to field levels of ∼50 − 60% above the same stellar mass limit and across the probed redshift range (Sects. 5.2 and 5.3). The higher quiescent fractions in clusters relative to the field translate into environmental quenching efficiencies of typically ∼0.50 − 0.70 at r < 0.7r500 with the exception of SPT-CLJ0607, and ∼0.5 − 0.9 at r < 0.45r500. This level of environmental quenching efficiency is comparable to that observed in cluster cores at z ∼ 1 (for a similar stellar mass threshold, e.g., Muzzin et al. 2012), and already close to that observed in the densest environments in the nearby Universe (e.g., Peng et al. 2012; Raichoor & Andreon 2014). The observed variations between clusters (see Figs. 7 and 10, and Table 2), particularly with reference to SPT-CL0607, may suggest a possibly non negligible range of quiescent fractions and environmental quenching efficiencies even among clusters of similar halo mass and redshift (see also related findings from Nantais et al. 2017, as also discussed below). However, given the small cluster sample size and the uncertainties on the environmental quenching efficiency of individual clusters, it is not possible to draw firm conclusions.
SPT-CLJ0459, in spite of being the most distant cluster in the sample, still shows a quiescent fraction of ≳0.8 in the probed mass range and cluster region, close to the striking value observed in JKCS 041 at z = 1.8 (Newman et al. 2014; Andreon et al. 2014). As already discussed above, cluster selection bias – that could be considered in the case of JKCS 041, which was indeed selected as an overdensity of red sources – is not relevant for this sample. Finally, as described in Sect. 5.2, the quoted quiescent fractions are formally lower limits in the sense that galaxies redder than the color selection blue cutoff without a reliable IRAC flux measurement cannot be classified as quiescent or star-forming based on our criteria, and are conservatively considered as star-forming. In the case of SPT-CLJ0459, the fraction of candidate members without a quiescent vs. star-forming classification and above the mass completeness limit is 5% at r < 0.7r500, and 10% at r < 0.45r500. Figures 7 and 10 and Table 2 also show for reference the impact of unclassified galaxies on the measured quiescent fractions, when assuming they are all quiescent rather than all star-forming.
Although high quiescent fractions in cluster central regions are the obvious expectation at z ≲ 1, several studies (see Sect. 1) have reported high fractions of star forming galaxies even in cluster cores at z ≳ 1.4. Some mid-IR and far-IR based studies of IR-selected cluster samples (Brodwin et al. 2013; Alberts et al. 2016) have shown a star-forming fraction for z ≳ 1.4 clusters at clustercentric radii < 0.5 Mpc consistent with or even higher than field levels. Although our probed r < 0.7r500 areas are comparable to r < 0.5 Mpc (our corresponding clustercentric radius is on average 430 kpc, ranging from 390 to 460 kpc), given the high mass of our clusters compared to the typically lower masses (≈1014 M⊙) of clusters in the IR-selected samples, the area we probe corresponds to a more central region with respect to the cluster virial radius. In addition, the selection of the galaxy samples in our work differs from that in the mentioned studies. Nevertheless, the results of our analysis do not generally lend support to the view that z ≳ 1.4 corresponds to an era before significant quenching in cluster cores, at least for clusters as massive as those studied here.
It is also conceivable – perhaps even expected – that galaxy population properties depend on cluster mass and assembly history (see e.g., discussion in Nantais et al. 2017, and references therein), with more massive clusters typically hosting more evolved populations (see e.g., Balogh et al. 2016, for a study of clusters and groups at z ∼ 1). Indeed, JKCS 041 at z = 1.8 (as mentioned above, Andreon et al. 2009, 2014; Newman et al. 2014) and XMMU J2235–2557 at z = 1.39 (Mullis et al. 2005; Rosati et al. 2009; Strazzullo et al. 2010) are two examples of very massive clusters bracketing the redshift range probed here, and both show strongly suppressed star formation in their core. On the other hand, the far-IR based work of Santos et al. (2015) indicates significant star formation activity in the inner r < 250 kpc core of the very massive cluster XDCP J0044.0–2033 at z = 1.58 (Santos et al. 2011; Tozzi et al. 2015), with a star formation rate approaching 2000 M⊙/yr just accounting for three Herschel-detected ULIRGs associated with massive cluster members. Thus, it is not clear that what we are seeing is a simple cluster mass dependence of the quiescent fraction.
In the recent work by Nantais et al. (2017), the evolution of the environmental quenching efficiency at z ∼ 0.9 to 1.6 was investigated with a sample of RS selected (SpARCS, Wilson et al. 2009) clusters. They measure quiescent fractions within a clustercentric radius of 1 Mpc which are very close to the field level, resulting in an environmental quenching efficiency consistent with zero, although the authors note that there is considerable dispersion in environmental quenching efficiencies of different clusters in their z ∼ 1.6 sample (three clusters), larger than in any of their lower-redshift samples. For reference, tentative masses from velocity dispersions of the z ∼ 1.6 clusters in Nantais et al. (2017) are estimated to be of order 0.4 − 2.4 × 1014 M⊙ (Lidman et al. 2012). The very low quenching efficiency they measure at z ∼ 1.6 makes for a significant drop from the ∼0.6 and 0.7 values measured at z∼1.3 and 0.9, respectively, from which Nantais et al. (2017) conclude that environmental quenching in clusters is a relatively subdominant process earlier than z ∼ 1.5, and then rapidly rises, increasing its relevance up to z ∼ 1. The clustercentric radius of our probed region is significantly smaller than 1 Mpc (∼r200 for our clusters), and we clearly expect quiescent fractions to decrease at increasing clustercentric distance. This complicates any quantitative comparison of our current results with Nantais et al. (2017). Nonetheless, we must conclude that environmental quenching efficiency seems to be significantly larger than zero in the cluster central regions, at least in the approximately halo mass selected z ≳ 1.4 sample we have studied here.
6.2. Future directions
Obvious future directions for this study involve at least two aspects. First, obtaining an accurate measurement of the star formation rate in the cluster core with tracers not biased by dust attenuation remains critical. Our current data do not allow us to estimate star formation rates – especially for red sources – with any reasonable accuracy. Although the classification of quiescent and star-forming galaxies based on the adopted color criterion seems to be well-behaved with respect to separation of the quiescent and star-forming sequences, and to match well with expectations based on equivalent galaxy samples in the control field, the ultimate confirmation that these environments are already so efficiently quenched remains with direct dust-unbiased star formation rate measurements, especially given the mid-/far-IR based results mentioned above. The cluster sky locations and needed sensitivity place limits on the possible choice of instruments for such observations to JWST, ALMA, or SKA pathfinders.
Second, an extension of this analysis out to the virial radius and even beyond would allow us to probe the relevance and timescales of environmental effects in suppressing star formation as galaxies are accreted by the clusters. We stress again that the accurate knowledge of cluster masses, and thus of their virial radii, allows us to consider meaningful apertures for comparing quenching efficiencies across different clusters. This is obviously crucial when studying any property that exhibits a radial dependence.
Ultimately, larger well-defined cluster samples at redshifts well beyond z ∼ 1 and up to z ≳ 2 over a range of halo masses still remain a critical missing piece in defining a quantitative picture of early-time environmental effects on galaxy evolution in the first clusters. New and upcoming surveys, notably SPTpol (Austermann et al. 2012), SPT-3G (Benson et al. 2014), Advanced ACTPOL (Thornton et al. 2016) and eROSITA (Merloni et al. 2012), will contribute to shaping our view in the near future, in preparation for the next generation of distant cluster surveys.
See Sect. 3.4 for the adopted definition of cluster center.
We recall that for all clusters the interloper density in the outer annulus is consistent with expectations from the average density in the control field. For SPT-CLJ2040, which has the highest interloper density in the outer annulus and also the highest difference with respect to the control field, the completeness levels of the r < 0.7r500 and r < 0.45r500 member samples would be 78% and 76%, respectively, if assuming the control field average value for the reference interloper density rather than the measured value in the outer annulus.
Given its RS and IRAC colors, SPT-CLJ0459 may be reasonably expected to be at a redshift at least higher – and likely significantly so – than SPT-CLJ2040 which is confirmed at z = 1.48. A zf = 2, though still potentially appropriate for galaxies more recently accreted onto the red sequence, is thus very likely too low for the bulk of the established RS population in this cluster. Furthermore, as already discussed earlier in this section, most studies of the RS population in massive clusters at 1.4 ≲ z ≲ 1.8 generally favor formation redshifts around zf ∼ 3. Even in the most distant such massive cluster studied thus far (Andreon et al. 2014), the formation redshift of RS galaxies is rarely exceeding zf = 3.5. Therefore, a range 2.5 ≤ zf ≤ 4 is plausibly appropriate for a cluster like SPT-CLJ0459. On the other hand, the bulk of our analysis in this section purposedly avoids assumptions on formation redshifts, to minimize any bias on our conclusions and to account for the largely unexplored potential diversity of cluster galaxy populations at this redshift (see e.g. the higher zf estimated by Zeimann et al. 2012).
By density we mean here the galaxy density in the control field after applying the magnitude and color selection criteria as described in Sect. 3.2.
We note that the Ngal/Mhalo uncertainties in Fig. A.1 are, if anything, somewhat underestimated, as they only account for Poisson error on the estimated total number of cluster galaxies, and for the error on M500.
The galaxy number density profile is obviously normalized by the total galaxy number at r < 0.45r500 estimated from the (weighted) candidate members above mass completeness, but we check that the total stellar mass and SFR above the mass completeness limit predicted by our modeling at r < 0.45r500 are indeed in agreement (on average within ∼10 − 15%, or < 20 − 25% at worst) with those estimated from the adopted stellar masses and SFRs of the individual (weighted) candidate members.
Acknowledgments
We thank Emiliano Merlin for helpful suggestions on the use of T_PHOT, and Corentin Schreiber for discussions and clarifications on the MS SED model adopted in Sect. 5.4. We thank the anonymous referee for a constructive report that improved the presentation of this work. M.P., N.G., R.C. and V.S. acknowledge support from the German Space Agency (DLR) through Verbundforschung project ID 50OR1603. We acknowledge the support by the DFG Cluster of Excellence “Origin and Structure of the Universe”, the Ludwig-Maximilians-Universität (LMU-Munich), and the Transregio program TR33 “The Dark Universe”. A.S. is supported by the ERC-StG “ClustersXCosmo”, grant agreement 71676. B.B. is supported by the Fermi Research Alliance LLC under contract no. De-AC02-07CH11359 with the U.S. Department of Energy. T.S. acknowledges support from the German Federal Ministry of Economics and Technology (BMWi) provided through DLR under projects 50 OR 1407, 50 OR 1610, and 50 OR 1803. D.R. is supported by a NASA Postdoctoral Program Senior Fellowship at the NASA Ames Research Center, administered by the Universities Space Research Association under contract with NASA. C.L.R. acknowledges support from Australian Research Council’s Discovery Projects scheme (DP150103208). The South Pole Telescope is supported by the National Science Foundation through grant PLR-1248097. Based on observations made with the NASA/ESA Hubble Space Telescope under program GO-14252, obtained from the Data Archive at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555. Based on observations made with the Spitzer Space Telescope (program ID 12030) which is operated by the Jet Propulsion Laboratory, California Institute of Technology under NASA contract.
References
- Alberts, S., Pope, A., Brodwin, M., et al. 2016, ApJ, 825, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, K., Benson, B. A., Ade, P. A. R., et al. 2011, ApJ, 738, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S. 2006, A&A, 448, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S. 2013, A&A, 554, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S., & Huertas-Company, M. 2011, A&A, 526, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S., Maughan, B., Trinchieri, G., & Kurk, J. 2009, A&A, 507, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S., Newman, A. B., Trinchieri, G., et al. 2014, A&A, 565, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Austermann, J. E., Aird, K. A., Beall, J. A., et al. 2012, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VI, Proc. SPIE, 8452, 84521E [CrossRef] [Google Scholar]
- Bahé, Y. M., Barnes, D. J., Dalla Vecchia, C., et al. 2017, MNRAS, 470, 4186 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, M. L., McGee, S. L., Mok, A., et al. 2016, MNRAS, 456, 4364 [NASA ADS] [CrossRef] [Google Scholar]
- Bayliss, M. B., Ashby, M. L. N., Ruel, J., et al. 2014, ApJ, 794, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Beifiori, A., Mendel, J. T., Chan, J. C. C., et al. 2017, ApJ, 846, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, B., Ade, P., Ahmed, Z., et al. 2014, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VII, Proc. SPIE, 9153, 91531P [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Daddi, E., Magdis, G., et al. 2012, ApJ, 757, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Béthermin, M., Daddi, E., Magdis, G., et al. 2015, A&A, 573, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bleem, L. E., Stalder, B., de Haan, T., et al. 2015, ApJS, 216, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Bocquet, S., Saro, A., Mohr, J. J., et al. 2015, ApJ, 799, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Lucey, J. R., & Ellis, R. S. 1992, MNRAS, 254, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Brodwin, M., Gonzalez, A. H., Stanford, S. A., et al. 2012, ApJ, 753, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Brodwin, M., Stanford, S. A., Gonzalez, A. H., et al. 2013, ApJ, 779, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Brodwin, M., McDonald, M., Gonzalez, A. H., et al. 2016, ApJ, 817, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Bulbul, E., Chiu, I., Mohr, J. J., et al. 2019, ApJ, 871, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, E., Carollo, C. M., Oesch, P. A., et al. 2011, ApJ, 743, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Carlstrom, J. E., Ade, P. A. R., Aird, K. A., et al. 2011, PASP, 123, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Chiu, I., Mohr, J. J., McDonald, M., et al. 2018, MNRAS, 478, 3072 [NASA ADS] [CrossRef] [Google Scholar]
- Cooke, R. J., Pettini, M., Jorgenson, R. A., Murphy, M. T., & Steidel, C. C. 2014, Mem. Soc. Astron. It., 85, 192 [NASA ADS] [Google Scholar]
- Cooke, E. A., Hatch, N. A., Stern, D., et al. 2016, ApJ, 816, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, M. C., Newman, J. A., Croton, D. J., et al. 2006, MNRAS, 370, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Culverhouse, T. L., Bonamente, M., Bulbul, E., et al. 2010, ApJ, 723, L78 [NASA ADS] [CrossRef] [Google Scholar]
- de Haan, T., Benson, B., Bleem, L., et al. 2016, ApJ, 832, 95 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Stanford, S. A., Eisenhardt, P. R., Dickinson, M., & Elston, R. 1999, AJ, 118, 719 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Stanford, S. A., Eisenhardt, P. R., Holden, B. P., & Rosati, P. 2007, AJ, 133, 2209 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Duffy, A. R., Schaye, J., Kay, S. T., & Dalla Vecchia, C. 2008, MNRAS, 390, L64 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenhardt, P. R., Stern, D., Brodwin, M., et al. 2004, ApJS, 154, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenhardt, P. R. M., Brodwin, M., Gonzalez, A. H., et al. 2008, ApJ, 684, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Dickinson, M., Hwang, H. S., et al. 2011, A&A, 533, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fassbender, R., Nastasi, A., Böhringer, H., et al. 2011, A&A, 527, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Foltz, R., Rettura, A., Wilson, G., et al. 2015, ApJ, 812, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Garn, T., & Best, P. N. 2010, MNRAS, 409, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Gobat, R., Daddi, E., Onodera, M., et al. 2011, A&A, 526, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Ferguson, H. C., Giavalisco, M., et al. 2013, ApJS, 207, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, N., Saro, A., Mohr, J. J., et al. 2017a, MNRAS, 467, 3737 [NASA ADS] [Google Scholar]
- Gupta, N., Saro, A., Mohr, J. J., Dolag, K., & Liu, J. 2017b, MNRAS, 469, 3069 [NASA ADS] [CrossRef] [Google Scholar]
- Hatch, N. A., Cooke, E. A., Muldrew, S. I., et al. 2017, MNRAS, 464, 876 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, M., Kodama, T., Koyama, Y., et al. 2010, MNRAS, 402, 1980 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, M., Kodama, T., Koyama, Y., Tadaki, K.-I., & Tanaka, I. 2011, MNRAS, 415, 2670 [NASA ADS] [CrossRef] [Google Scholar]
- Hennig, C., Mohr, J. J., Zenteno, A., et al. 2017, MNRAS, 467, 4015 [NASA ADS] [Google Scholar]
- Henry, J. P., Salvato, M., Finoguenov, A., et al. 2010, ApJ, 725, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Hilton, M., Lloyd-Davies, E., Stanford, S. A., et al. 2010, ApJ, 718, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschmann, M., De Lucia, G., Wilman, D., et al. 2014, MNRAS, 444, 2938 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Herbonnet, R., Muzzin, A., et al. 2015, MNRAS, 449, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kawinwanichakij, L., Papovich, C., Quadri, R. F., et al. 2017, ApJ, 847, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Khullar, G., Bleem, L. E., Bayliss, M. B., et al. 2019, ApJ, 870, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Kodama, T., & Arimoto, N. 1997, A&A, 320, 41 [NASA ADS] [Google Scholar]
- Kodama, T., Tanaka, I., Kajisawa, M., et al. 2007, MNRAS, 377, 1717 [NASA ADS] [CrossRef] [Google Scholar]
- Kovač, K., Lilly, S. J., Knobel, C., et al. 2014, MNRAS, 438, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Kurk, J., Cimatti, A., Zamorani, G., et al. 2009, A&A, 504, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Labbé, I., Huang, J., Franx, M., et al. 2005, ApJ, 624, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Lidman, C., Rosati, P., Tanaka, M., et al. 2008, A&A, 489, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lidman, C., Suherli, J., Muzzin, A., et al. 2012, MNRAS, 427, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y.-T., & Mohr, J. J. 2007, ApJS, 170, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Mohr, J. J., & Stanford, S. A. 2004, ApJ, 610, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y.-T., Mohr, J. J., Gonzalez, A. H., & Stanford, S. A. 2006, ApJ, 650, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Mancone, C. L., Gonzalez, A. H., Brodwin, M., et al. 2010, ApJ, 720, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Mantz, A. B., Abdulla, Z., Allen, S. W., et al. 2018, A&A, 620, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McDonald, M., Allen, S. W., Bayliss, M., et al. 2017, ApJ, 843, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Mei, S., Holden, B. P., Blakeslee, J. P., et al. 2009, ApJ, 690, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Merlin, E., Fontana, A., Ferguson, H. C., et al. 2015, A&A, 582, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merlin, E., Bourne, N., Castellano, M., et al. 2016a, A&A, 595, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merlin, E., Amorín, R., Castellano, M., et al. 2016b, A&A, 590, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merloni, A., Predehl, P., Becker, W., et al. 2012, ArXiv e-prints [arXiv:1209.3114] [Google Scholar]
- Mok, A., Balogh, M. L., McGee, S. L., et al. 2013, MNRAS, 431, 1090 [NASA ADS] [CrossRef] [Google Scholar]
- Moran, S. M., Ellis, R. S., Treu, T., et al. 2007, ApJ, 671, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Mullis, C. R., Rosati, P., Lamer, G., et al. 2005, ApJ, 623, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Muzzin, A., Wilson, G., Yee, H. K. C., et al. 2012, ApJ, 746, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Muzzin, A., Wilson, G., Demarco, R., et al. 2013a, ApJ, 767, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Muzzin, A., Marchesini, D., Stefanon, M., et al. 2013b, ApJ, 777, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Muzzin, A., Marchesini, D., Stefanon, M., et al. 2013c, ApJS, 206, 8 [Google Scholar]
- Muzzin, A., van der Burg, R. F. J., McGee, S. L., et al. 2014, ApJ, 796, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Nantais, J. B., Muzzin, A., van der Burg, R. F. J., et al. 2017, MNRAS, 465, L104 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Ellis, R. S., Andreon, S., et al. 2014, ApJ, 788, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Noble, A. G., Webb, T. M. A., Yee, H. K. C., et al. 2016, ApJ, 816, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Pannella, M., Gabasch, A., Goranova, Y., et al. 2009, ApJ, 701, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Pannella, M., Elbaz, D., Daddi, E., et al. 2015, ApJ, 807, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Papovich, C. 2008, ApJ, 676, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Papovich, C., Momcheva, I., Willmer, C. N. A., et al. 2010, ApJ, 716, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Paterno-Mahler, R., Blanton, E. L., Brodwin, M., et al. 2017, ApJ, 844, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Renzini, A., & Carollo, M. 2012, ApJ, 757, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., Desai, V., Finn, R., et al. 2008, ApJ, 684, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Postman, M., Franx, M., Cross, N. J. G., et al. 2005, ApJ, 623, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Prichard, L. J., Davies, R. L., Beifiori, A., et al. 2017, ApJ, 850, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Raichoor, A., & Andreon, S. 2014, A&A, 570, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riess, A. G., Macri, L., Casertano, S., et al. 2011, ApJ, 732, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Rodighiero, G., Daddi, E., Baronchelli, I., et al. 2011, ApJ, 739, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Rosati, P., Tozzi, P., Gobat, R., et al. 2009, A&A, 508, 583 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rudnick, G., Jablonka, P., Moustakas, J., et al. 2017, ApJ, 850, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Santos, J. S., Fassbender, R., Nastasi, A., et al. 2011, A&A, 531, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, J. S., Altieri, B., Valtchanov, I., et al. 2015, MNRAS, 447, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, M. T., Béthermin, M., Daddi, E., & Elbaz, D. 2012, ApJ, 747, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, M. T., Daddi, E., Béthermin, M., et al. 2014, ApJ, 793, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Sawicki, M. 2002, AJ, 124, 3050 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, C., Elbaz, D., Pannella, M., et al. 2018, A&A, 609, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuster, M. T., Marengo, M., & Patten, B. M. 2006, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Proc. SPIE, 6270, 627020 [Google Scholar]
- Skelton, R. E., Whitaker, K. E., Momcheva, I. G., et al. 2014, ApJS, 214, 24 [Google Scholar]
- Smail, I., Geach, J. E., Swinbank, A. M., et al. 2014, ApJ, 782, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Snyder, G. F., Brodwin, M., Mancone, C. M., et al. 2012, ApJ, 756, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Song, J., Zenteno, A., Stalder, B., et al. 2012, ApJ, 761, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Spitler, L. R., Labbé, I., Glazebrook, K., et al. 2012, ApJ, 748, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Stalder, B., Ruel, J., Šuhada, R., et al. 2013, ApJ, 763, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Stanford, S. A., Romer, A. K., Sabirli, K., et al. 2006, ApJ, 646, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Stanford, S. A., Brodwin, M., Gonzalez, A. H., et al. 2012, ApJ, 753, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Strazzullo, V., Rosati, P., Stanford, S. A., et al. 2006, A&A, 450, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strazzullo, V., Rosati, P., Pannella, M., et al. 2010, A&A, 524, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strazzullo, V., Gobat, R., Daddi, E., et al. 2013, ApJ, 772, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Strazzullo, V., Daddi, E., Gobat, R., et al. 2016, ApJ, 833, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comments Astrophys. Space Phys., 4, 173 [NASA ADS] [EDP Sciences] [Google Scholar]
- Tanaka, M., Goto, T., Okamura, S., Shimasaku, K., & Brinkmann, J. 2004, AJ, 128, 2677 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, M., Finoguenov, A., Mirkazemi, M., et al. 2013a, PASJ, 65, 17 [NASA ADS] [Google Scholar]
- Tanaka, M., Toft, S., Marchesini, D., et al. 2013b, ApJ, 772, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Thornton, R. J., Ade, P. A. R., Aiola, S., et al. 2016, ApJS, 227, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Tozzi, P., Santos, J. S., Jee, M. J., et al. 2015, ApJ, 799, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Tran, K., Papovich, C., Saintonge, A., et al. 2010, ApJ, 719, L126 [CrossRef] [Google Scholar]
- Tran, K.-V. H., Nanayakkara, T., Yuan, T., et al. 2015, ApJ, 811, 28 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, F. C., Aquino, D., Yang, X., et al. 2008, MNRAS, 387, 79 [Google Scholar]
- van der Burg, R. F. J., Muzzin, A., Hoekstra, H., et al. 2013, A&A, 557, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Burg, R. F. J., Muzzin, A., & Hoekstra, H. 2016, A&A, 590, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vikhlinin, A., Burenin, R. A., Ebeling, H., et al. 2009, ApJ, 692, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Visvanathan, N., & Sandage, A. 1977, ApJ, 216, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, C. R., Courteau, S., Brodwin, M., et al. 2017, ApJ, 834, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T., Elbaz, D., Daddi, E., et al. 2016, ApJ, 828, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Wetzel, A. R., Tinker, J. L., & Conroy, C. 2012, MNRAS, 424, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Wetzel, A. R., Tinker, J. L., Conroy, C., & van den Bosch, F. C. 2013, MNRAS, 432, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, R. J., Quadri, R. F., Franx, M., et al. 2009, ApJ, 691, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, G., Muzzin, A., Yee, H. K. C., et al. 2009, ApJ, 698, 1943 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J., Dekel, A., Faber, S. M., et al. 2013, MNRAS, 428, 3306 [NASA ADS] [CrossRef] [Google Scholar]
- Wylezalek, D., Vernet, J., De Breuck, C., et al. 2014, ApJ, 786, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, T., Nanayakkara, T., Kacprzak, G. G., et al. 2014, ApJ, 795, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Zeimann, G. R., Stanford, S. A., Brodwin, M., et al. 2012, ApJ, 756, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zirm, A. W., Stanford, S. A., Postman, M., et al. 2008, ApJ, 680, 224 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Effect of the background estimation on the red galaxy fraction in relation to different red fractions across clusters in this sample
As mentioned in Sect. 5.1, different clusters in this sample exhibit different color distributions in their color-magnitude diagram, resulting in a range of red galaxy fractions, with SPT-CLJ0607 and SPT-CLJ2040 showing a more significant blue population. Figure A.1 (bottom panel) shows the red fraction of all clusters down to a same limit of m140 < M* + 1.3, making for a more proper comparison than what can be done on Fig. 1, that reaches different depths ranging from ∼M* + 2 to ∼M* + 1.3 depending on the cluster redshift (see Sect. 5.1). We note that, in contrast with the quiescent fractions discussed in Sects. 5.2–5.4, 6, the red fractions discussed here are based on flux limited, not mass complete galaxy samples. For the purpose of Fig. A.1, we define as “red” those galaxies with a m814–m140 color redder than 0.4 mag below the RS model with zf = 3 (see Fig. 1).
Black symbols with error bars show the red fraction estimated based on the statistical background subtraction weights calculated in Sect. 3.2 on the full control field. Similarly to what can be inferred from Fig. 1, clusters SPT-CLJ0421, SPT-CLJ0446, and SPT-CLJ0459 have a higher red fraction (∼70% at m140 < M* + 1.3) than SPT-CLJ0607 and SPT-CLJ2040 (< 50%). We then redetermine the statistical background subtraction weights using 100 sub-fields at random positions in the control field of the same area as the probed cluster region (see Sect. 3.3), estimating each time the corresponding red galaxy fraction. As expected, the red fraction depends on the assumed control field, so that for each given cluster we obtain a higher red fraction when using a higher density7 control field. The dark gray bars in Fig. A.1 (bottom) show the variation of the estimated red fraction when assuming control fields with densities spanning from the 10th to the 90th percentile of the density distribution across the 100 random sub-fields. As the figure shows cosmic variance on small scales, as can be probed with this approach, results in a relatively minor impact (10% at most) on the estimated red fraction. On the other hand, we do not probe with this approach cosmic variance on large scales.
 |
Fig. A.1. Top panel: black points show for all clusters the estimated total number of background-subtracted cluster members at m140 < M* + 1.3 and within r < 0.7r500 divided by the total projected halo mass within the same region (Ngal/Mhalo). The solid gray line shows the median value for this cluster sample. The dashed lines show an estimate of the intrinsic scatter of Ngal/Mhalo. See text for details. Bottom panel: estimate of the effect of differences in the background density along the line of sight of the clusters on the estimated red fraction of cluster galaxies. Black points show the red fraction for all clusters as estimated adopting the default control field for the statistical residual background subtraction (Sect. 3.2). Dark gray bars show the effect on the estimated red fraction of adopting control sub-fields with densities in the 10th to 90th percentile range across the default control field. Light gray bars show the effect of considering the background-subtracted cluster member samples contaminated or incomplete according to the face-value Ngal/Mhalo of each cluster with respect to the median Ngal/Mhalo of the sample. See text for details. For comparison, light gray empty circles show the red fraction in field galaxies in the same m140 magnitude range, and with a photo-z within ±0.15 of the cluster redshift. |
The top panel of Fig. A.1 shows the number of background-subtracted cluster galaxies at m140 < M* + 1.3 and r < 0.7r500 as estimated with our default background subtraction weights (Sect. 3.2) divided by the projected halo mass at r < 0.7r500 (calculated based on the cluster mass M500 and redshift assuming a concentration according to Duffy et al. 2008). This number of galaxies per halo mass (hereafter, Ngal/Mhalo) is similar across our sample, as can be expected given the small cluster mass range. Most values of Ngal/Mhalo are indeed consistent within the uncertainties8. The solid gray line shows the median Ngal/Mhalo across the sample, with the dashed gray lines showing an intrinsic scatter on Ngal/Mhalo based on the estimates of Hennig et al. (2017). Based on Fig. A.1 all clusters are thus consistent with having similar Ngal/Mhalo according to our expectations. This suggests that there is no evidence for large variations in the local background (corresponding to the redshift range resulting from our color selections) of the individual clusters, because such large variations would affect the estimated Ngal (and thus Ngal/Mhalo) if using the same control field for all clusters. The largest deviation of Ngal/Mhalo with respect to the median of the sample occurs for SPT-CLJ2040. Although given the uncertainties we cannot take this as actual evidence, we consider here the possibility that the higher face-value Ngal/Mhalo of SPT-CLJ2040 results from an higher local background density (than in our control field) which is not accounted for by our statistical background subtraction. That is, we assume that the excess of SPT-CLJ2040’s Ngal/Mhalo with respect to the median value is due to unaccounted interlopers contaminating the number of background-subtracted cluster members. In this assumption, we can estimate the number of such unaccounted interlopers assuming that SPT-CLJ2040 has intrinsically the median Ngal/Mhalo of the sample. This would result in 29 of the estimated 71 background-subtracted cluster members within r < 0.7r500 being actually interlopers. Given our initial color and magnitude selection (Sect. 3), we can reasonably assume (see e.g. Figs. 2 and 5) that the bulk of the background contaminating the color-selected candidate member sample is roughly at 1.2 ≲ z ≲ 2. Therefore, we can estimate the fraction of galaxies in the control field at these redshifts and within our magnitude limit that would appear as “red” with the m814–m140 color threshold applied for SPT-CLJ2040. This is about 25% over the full 1.2 ≲ z ≲ 2 redshift range, ranging from ∼20% to ∼40% across the range when calculated in Δz = 0.2 redshift bins. We thus consider a minimum and maximum “red fraction” of the unaccounted interlopers of 20% and 40%, respectively. We can thus estimate a “corrected” red fraction for SPT-CLJ2040 as:
“corrected red fraction” = ![$ \frac{N_{\mathrm{red,bkgsub}} - [0.2,0.4] N_{\mathrm{interlopers}}}{N_{\mathrm{total,bkgsub}}-N_{\mathrm{interlopers}}} $](/articles/aa/full_html/2019/02/aa33944-18/aa33944-18-eq56.gif)
where Nred, bkgsub and Ntotal, bkgsub are our default estimates of the number of red and all background-subtracted candidate members (with standard background subtraction from Sect. 3.2), respectively, while Ninterlopers is the estimated number of interlopers contaminating Ntotal, bkgsub in the assumptions described above. The adopted 0.2–0.4 “red fraction” range of the unacconted interlopers corresponds to the minimum and maximum values estimated above, and results in a “corrected red fraction” ranging from 41% to 54%, as shown by the light gray band for SPT-CLJ2040 in the bottom panel of Fig. A.1.
We estimate in an analogous way the “corrected red fractions” shown by light gray bands in Fig. A.1 for all other clusters. The deviation from the median Ngal/Mhalo for the other clusters is more marginal than for SPT-CLJ2040 (all being consistent at < 1σ with the median value, even not accounting for the intrinsic scatter). Therefore, as mentioned above, there is no evidence for significant cluster-to-cluster background variations. We show nonetheless for completeness the “corrected red fractions” as a reference. We note that assuming a local background density significantly lower (rather than higher) than our default control field (e.g. in particular for SPT-CLJ0459) has the effect of reducing (rather than increasing) the estimated red fraction (due to the observed color distribution of field galaxies in the magnitude and redshift range considered).
Appendix B: Environmental quenching efficiency down to the individual mass completeness limit of each cluster
Figure B.1 shows the quiescent fraction for the five clusters and their matched photo-z selected field samples (top panel) and the corresponding environmental quenching efficiencies (bottom panel) down to the individual stellar mass completeness limit of each cluster. Because the individual mass completeness limits differ, in contrast with the results shown in Fig. 10 those in Fig. B.1 cannot be properly compared across different clusters.
 |
Fig. B.1. Top panel: quiescent fraction of cluster galaxies within r < 0.45r500 (dark red) and r < 0.7r500 (light red) above the mass completeness limit of each cluster as reported in the bottom panel. Error bars account for uncertainties in the quiescent vs. star-forming classification as described in Sect. 5.3. Blue symbols show the quiescent fraction in corresponding photo-z selected control field samples (see Sect. 5.3). Bottom panel: environmental quenching efficiency as derived from cluster and field quiescent fractions in the top panel. Color coding reflects the top panel. In both panels empty triangles show, where applicable, the quiescent fraction and derived quenching efficiency assuming that galaxies lacking a quiescent vs. star-forming classification are all quiescent (rather than all star-forming, see Sect. 5.2, Table 2). |
Appendix C: Modeling of mm-wave emission from star-forming cluster galaxies and its effect on SZE detection and completeness of this cluster sample
We describe here in detail the modeling outlined in Sect. 5.4, devised to investigate a possible bias of this cluster sample against clusters with higher star-forming galaxy fractions.
 |
Fig. C.1. Example illustration of the modeling of the quiescent fraction vs. stellar mass. Top panels: assumed radial profile of the quiescent fraction above mass completeness. In the three panels a green circle highlights a given clustercentric distance, and thus quiescent fraction value. Based on these values, the corresponding middle panels show the quiescent fraction vs. stellar mass as estimated with both approaches described in Sect. 5.4 (red, orange lines). The blue line shows the quiescent fraction vs. mass in the field at the cluster redshift. The corresponding bottom panels show the overall contribution of galaxies above a given stellar masses to the total SFR density at the given clustercentric distance assuming the quiescent fraction vs. mass from the middle panels (see Sect. 5.4). |
For each cluster, from the background subtracted and area weighted mass complete sample of cluster members we first estimate the total SFR in the r < 0.45r500 region above the mass completeness limit, by assuming that all galaxies classified as star forming with our color criterion (Sect. 5.2) are forming stars at the Main Sequence (MS, e.g., Elbaz et al. 2011) rate. We adopt the MS modeling of Schreiber et al. (2015), which includes bending at high stellar masses; adopting a straight MS modeling as from e.g., Sargent et al. (2014) would produce here only marginal differences. No contribution to the SFR is considered from galaxies classified as quiescent.
C.1. Contribution of cluster galaxies below the mass completeness limit
We then estimate the star formation rate contribution from cluster galaxies below the mass completeness limit and down to M = 108 M⊙ by assuming:
-
That the shape of the galaxy stellar mass function in clusters is to first order the same as in the field at the same redshift (but see e.g., van der Burg et al. 2013). We adopt the Muzzin et al. (2013b) stellar mass functions.
-
The Schreiber et al. (2015) MS SFR for all star-forming galaxies depending only on their stellar mass. We neglect here (as above for the total SFR estimate of the mass complete sample) modeling the intrinsic scatter of the MS as we are averaging over the full star-forming galaxy population to obtain total star formation rates for the whole cluster galaxy sample. On the other hand, we also neglect to model non-MS populations: all galaxies classified as quiescent are assumed to have a negligible SFR, and we neglect the minority population (∼2% by number) of starbursts, estimated to contribute < 10 − 15% of the star formation rate density (in the field, at this redshift) (e.g., Rodighiero et al. 2011; Sargent et al. 2012). In this respect, we note though that the possible relevance to the mm-wave emission contamination of the higher SFRs of the small fraction of starburst galaxies is reduced by their different SED: according to Béthermin et al. (2012,2015) SEDs, the 150 GHz (95 GHz) flux of a starburst galaxy with a SFR six times greater than the MS SFR, is within a factor 2–3 (≲3 − 4) of the flux of a MS galaxy of the same stellar mass.
-
That the quiescent fraction at stellar masses below our mass completeness limit can be estimated from our measured quiescent fraction with the following approach. We start from the Muzzin et al. (2013b) estimate of the quiescent fraction as a function of stellar mass in the field at the cluster redshift. Since above the mass completeness limit we observe higher quiescent fractions than in the field, we model the quiescent fraction vs. stellar mass for cluster galaxies in two ways, both sketched in Fig. C.1. The first approach assumes that mass and environmental quenching are separable, and following Peng et al. (2010) we estimate the quiescent fraction vs. stellar mass as fq = ϵm + ϵρ − ϵm × ϵρ, with ϵm and ϵρ the mass and environmental quenching efficiencies, respectively. As an estimate of ϵm, we take the field quiescent fraction of Muzzin et al. (2013b which indeed drops to very low values at low masses at the clusters’ redshift, so that it can be interpreted to first approximation as a mass quenching efficiency if considering the “reference” mass where no mass quenching occurs below 109 M⊙). As an estimate of ϵρ we adopt the environmental quenching efficiency measured for each given cluster in Sect. 5.3 (again, this assumes that mass and environmental quenching are completely separable and thus that the environmental quenching efficiency is independent of stellar mass, but see e.g., Kawinwanichakij et al. 2017, for contrasting results on this assumption at this redshift). This gives us the adopted quiescent fraction vs. mass from the first approach, labeled as (1) in Fig. C.1.
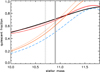 |
Fig. C.2. Test of the quiescent fraction vs. stellar mass modeling discussed in Sect. 5.4. The black line shows the observed quiescent fraction vs. stellar mass in z ∼ 1 clusters from van der Burg et al. (2013). The red and orange solid (dotted) lines (color coding as in Fig. C.1) show the estimated quiescent fraction vs. mass using the two approaches shown in Fig. C.1, starting from the observed quiescent fraction in a mass complete sample with log(M/M⊙) > 10.9 (10.7, respectively, as shown by vertical gray lines). Blue dashed line shows the field quiescent fractions vs. mass at the same redshift. |
The second approach just rescales the field quiescent fraction vs. stellar mass by multiplying it by the ratio of the measured quiescent fraction in the cluster (from Sect. 5.3) and in the field (from Muzzin et al. 2013b) above the mass completeness limit of the given cluster. This second approach produces by definition the same quiescent fraction above mass completeness, but considerably lower quiescent fractions at lower stellar masses, quickly approaching the field levels rather than reaching the quiescent fraction plateau determined by the assumed environmental quenching efficiency in the first approach. This second approach is labeled (2) in Fig. C.1. By definition, both approaches reproduce the assumed field quiescent fraction vs. stellar mass when the quiescent fraction in the mass complete sample of cluster galaxies is taken to be the same as in the field.
We believe that these two approaches reasonably bracket the plausible range of quiescent fraction vs. stellar mass. Figure C.2 presents a test of both approaches against the quiescent fraction vs. stellar mass observed in z ∼ 1 clusters from van der Burg et al. (2013). We simulate our modeling by considering from these data the quiescent fraction in two mass complete samples with log(M/M⊙) > 10.7,10.9, and estimating the quiescent fraction at lower masses with the two approaches described above. As Fig. C.2 shows, the first approach (1) based on the separable environmental and mass quenching efficiencies reproduces a quiescent fraction vs. mass in much better agreement with the observed trend than the second approach. We thus mostly focus in the following analysis on the quiescent fraction vs. stellar mass from the first aproach. We also stress that, for the purpose of this section, this is a conservative choice as explained below.
 |
Fig. C.3. Example illustration of the modeling of the SFR density profiles described in Sect. 5.4, see text for full details. Left, middle and right panel: three different values assumed for the r < r500 quiescent fraction above mass completeness, as indicated. Top panels: radial profile of quiescent fraction above mass completeness (black, the field value is shown in gray). The dotted red line shows the quiescent fraction of the full mass complete sample out to the given clustercentric radius. Middle panels: projected galaxy number density profile above mass completeness (black), and the derived profiles of star-forming and quiescent galaxies (blue and red) given the quiescent fraction profile in the corresponding top panel. Bottom panels: corresponding projected SFR density profiles, derived with the two models of quiescent fraction vs. stellar mass as indicated (solid lines). Dashed and dotted lines show the additional SFR density profile over the prediction for the actually observed quiescent fraction (see text). Inserts show the corresponding cumulative SFR as a function of clustercentric radius. |
For each cluster in our sample, we thus obtain an approximate estimate of the total SFR within the r < 0.45r500 region by adding up the estimated MS SFRs of all (background subtraction and area coverage weighted) candidate members classified as star forming, and the estimated SFR of cluster galaxies below the mass completeness limit described above.
C.2. Contribution of cluster galaxies at r > 0.45r500
We estimate the total SFR density profile of the cluster beyond r = 0.45r500 by assuming a NFW (Navarro et al. 1997) galaxy number density profile (normalized to the r < 0.45r500 region9) with concentration according to Duffy et al. (2008), and a quiescent fraction profile determined as follows.
We start from a red fraction profile determined from the stacked total and red galaxy projected number density profiles of 0 < z < 1 clusters from Hennig et al. (2017). This red fraction profile is then distorted to force a match with the central cluster quiescent fraction above mass completeness at r < 0.45r500, and with the corresponding field quiescent fraction at r = 2r500 (Fig. C.3, top panels). The assumed total (NFW) projected galaxy number density profile, and the described quiescent fraction profile above mass completeness, together yield a projected number density profile of star-forming cluster galaxies (Fig. C.3, middle panels). In the assumption that the galaxy stellar mass function and MS SFR do not depend on clustercentric radius, and that the quiescent fraction vs. stellar mass can be determined as described above at each clustercentric distance given the adopted quiescent fraction profile above mass completeness, we thus derive for each cluster a SFR projected density profile (Fig. C.3, bottom panels).
C.3. Modeling of the total cluster SFR vs. quiescent fraction
To carry out a first-order investigation of how much the cluster SZE detection would be affected by a quiescent fraction lower than what observed, we then reduce in the modeling above the quiescent fraction above mass completeness in the r < 0.45r500 region, to progressively lower values down to a quiescent fraction of 10%, and compute the SFR density profile of the cluster for the given r < 0.45r500 quiescent fraction. As discussed in Sect. 5.4, the smallest adopted value of 10% for the central quiescent fraction is well below the field value at the cluster redshift for the considered stellar mass range.
Figures C.1 and C.3 show an actual example of the overall derivation based on the cluster SPT-CLJ0459. The top panels of Fig. C.1 show the adopted radial profile of the quiescent fraction above mass completeness for the measured value of the r < r500 quiescent fraction (black line). The green circles highlight three radii – and thus three values of the quiescent fraction above mass completeness – for which the middle and bottom panels present, respectively, the modeling of the quiescent fraction vs. stellar mass with both approaches described above, and the corresponding inferred contribution of galaxies of different stellar mass to the total SFR density at the given clustercentric distance. Figure C.3 shows instead the modeling of the SFR density profile for three different values assumed for the r < 0.45r500 quiescent fraction above mass completeness: the actually observed one (left panels), the field quiescent fraction (right), and an intermediate value (middle). For each of these, the top panels show the radial profile of the quiescent fraction above mass completeness derived as described above (black line). For comparison, the red dotted line shows the predicted quiescent fraction of the whole cluster galaxy population above mass completeness out to a given clustercentric distance. The middle panels show, for the assumed total projected galaxy number density profile above mass completeness (black), the star-forming galaxy projected density profile (blue, also at M > Mcompl) obtained for the quiescent fraction profile in the corresponding top panel. Finally, the bottom panels show the corresponding predicted SFR projected density profile obtained with the described modeling for both estimated of the quiescent fraction vs. stellar mass (solid lines, color coding as in Fig. C.1). We note that in fact we consider that the actual SZE measurement of the cluster is indeed affected by some amount of contamination from star formation in cluster galaxies, corresponding to the star forming galaxy fraction actually observed. Decreasing the r < 0.45r500 quiescent fraction increases the contamination of the cluster SZE signal from mm-wave emission due to star formation, and we estimate this additional contamination (dashed and dotted lines, labeled as “additional SFR density profile” in the bottom panels of Fig. C.3) as the difference between the SFR density profiles estimated with the assumed quiescent fraction and with the actually measured one.
C.4. Modeling of the S/N of the SZE detection vs. quiescent fraction
We translate this additional SFR projected density profile into flux density maps at 95 and 150 GHz assuming the MS SEDs from either Béthermin et al. (2015) or Schreiber et al. (2018). We then add these additional flux density maps to the observed 95 and 150 GHz maps of the cluster and reanalyze the resulting maps with the same filtering procedure used to detect clusters in the SPT-SZ survey (Bleem et al. 2015), estimating a S/N for the resulting SZE detection. Figure 11 shows this retrieved S/N as a function of the assumed r < 0.45r500 quiescent fraction above mass completeness down to a value of 10%. The figure shows the S/N obtained with both the adopted MS SEDs, and for the main adopted approach (1) for estimating the quiescent fraction vs. stellar mass below the mass completeness limit. The other approach (2) resulting in comparatively higher star-forming fractions below the mass completeness limit (Fig. C.1), produces even higher predicted S/N due to the smaller difference in SFR between the observed and reduced quiescent fraction cases. Further discussion of Fig. 11 and derived conclusions are presented in Sect. 5.4.
All Tables
The quiescent fraction (corrected for area coverage and background contamination) estimated for each cluster in the r < 0.45r500 and r < 0.7r500 regions, for stellar masses above the individual cluster mass completeness limit as well as the common limit of log(M/M⊙) = 10.85.
All Figures
 |
Fig. 1. Color-magnitude diagrams and derived properties within the r < 0.7r500 region of each cluster are shown in subfigures, each with three panels. Panel a: visualization of the background-subtracted color-magnitude diagram, where size and color of each galaxy point scale according to its statistical background subtraction weight (see color bar in legend) determined in Sect. 3.2. All galaxies are shown, but color-rejected interlopers (see Sect. 3.1) are shown as crosses. Gray lines show Kodama & Arimoto (1997) red-sequence (RS) models with formation redshifts zf = 2, 3, 5. The color range is the same for all clusters to facilitate direct comparison of RS colors. Panel b: color distribution of background-subtracted and area-corrected cluster members (red points with error bars) down to the indicated m140 limit. The orange shaded area shows an estimate of the impact of cosmic variance on the scale of the cluster core field, as detailed in Sect. 5.1. The blue histograms show the color distribution (rescaled by total number of galaxies) in the control-field sample, using the same color selection as for cluster candidate members (light blue), or a photometric redshift selection within ±0.2 of the cluster redshift (darker blue). All clusters show a clear excess of red galaxies with respect to the field distribution. Panel c: estimated fraction of interlopers in the color-selected candidate member sample as a function of color (down to the indicated m140 limit), based on the weights in panel a. Contamination is low for RS galaxies but significant for blue galaxies. Error bars show binomial confidence intervals (1σ) computed following Cameron et al. (2011). |
| In the text | |
 |
Fig. 2. Two examples of the selection of candidate cluster members (see Sect. 3.1). Vertical gray lines bound the m814–m140 RS sample used for the initial definition of the IRAC color selection range, shown by the horizontal light-gray lines. Groups of red and blue tracks show, respectively, the colors as a function of redshift in the range 1 < z < 2 of quiescent (SSPs with zf = 2, 3, 5) and actively star-forming (100 Myr old constant star formation, Av = 0, 1, 3) stellar populations, used to obtain the final adopted IRAC color selection range (dark-gray lines, see Sect. 3.1 for full details). Small solid points along the tracks indicate z = 1.3, 1.6, 1.9; the large circle indicates the cluster redshift. Orange and blue squares mark the galaxies in the cluster field classified as candidate members or interlopers, respectively, with the full IRAC+HST color selection criteria described in Sect. 3.1. |
| In the text | |
 |
Fig. 3. Projected number density of candidate cluster members (shades of red) and interlopers (blue) in the five clusters as measured in three cluster regions, as indicated. Empty squares show densities for color-selected samples (see Sect. 3.1), and filled circles show how member number density decreases – and interloper density increases – after applying the statistical subtraction of residual background contamination described in Sect. 3.2. The blue line shows the average density of control field galaxies in the same magnitude range adopted for the cluster, with the light-blue shaded areas showing the density variation (16th–84th percentiles) in apertures corresponding to the three probed regions. The relative flatness of the interloper density profiles constrains the cluster member sample incompleteness due to member misclassification (see Sect. 3.3). |
| In the text | |
 |
Fig. 4. Projected density maps (see color bar) of candidate cluster members for the five clusters. Gray empty symbols show the position of individual candidate members, where symbol size scales with the galaxy statistical background subtraction weight (Sect. 3.2), and symbol shape reflects galaxy morphology. The cross marks the coordinates of the SPT-SZ detection, with the cross size showing the estimated positional uncertainty (1σ, see Sect. 3.4). The position of the adopted brightest central galaxy, defining the cluster center in the subsequent analysis, is indicated by a star. The circle is centered at the median coordinates of the 5% highest-density points in the map, and has a radius of 250 kpc at the cluster redshift (for comparison r500 ∼ 70″ ∼ 600 kpc for these clusters). Masked areas are blanked out and white gridding marks areas affected by edge effects. |
| In the text | |
 |
Fig. 5. Photometric redshift constraints for all clusters (black points with 1σ errorbars reported in both panels) as determined with the simultaneous modeling of the red sequence (RS) and [3.6]–[4.5] color in Sect. 4. Red stars show the spectroscopic redshifts for SPT-CLJ2040 and SPT-CLJ0607, as well as the best current constraint for SPT-CLJ0459 (see Sect. 4). Bottom panel: adopted model RS m814–m140 color at M* vs. redshift, for formation redshifts 2 < zf < 5 (orange lines). Light blue bars show the 1σ constraints from modeling only the RS color (dark blue assuming zf = 3). Light green bars show constraints from the [3.6]–[4.5] color alone. Top panel: adopted model [3.6]–[4.5] color vs. redshift, for 2 < zf < 5 as in the bottom panel. The shaded area shows for reference the 16th–84th percentile range of [3.6]–[4.5] color vs. redshift for field galaxies in the magnitude range of our samples (m140 ≲ 23.5). Dark green (bottom panel) and white (top panel) bars show the impact on the best-fit redshift (from IRAC color alone and RS + IRAC color, respectively) of a ± 0.03 AB mag systematic offset on the [3.6]–[4.5] color. |
| In the text | |
 |
Fig. 6. Adopted quiescent vs. star-forming galaxy classification. The observed m814–m140 vs. m140–[3.6] color–color diagram of candidate members (green points) is shown for all clusters in the r/r500 < 0.7 region (the effective area covered for each cluster is indicated). Upper set of panels: m140-selected (not mass complete) candidate member samples (the mass completeness limit for each cluster is indicated). Lower set of panels: galaxies down to the common stellar mass completeness limit for all clusters, log(M/M⊙) = 10.85. Symbol size of green points scales with the statistical background-subtraction weights as in Fig. 1. Symbol color scales with stellar mass as shown by the color bar. Empty symbols show points for which a m140–[3.6] color was inferred using the 4.5 μm flux (see Sect. 5.2). Light red and blue squares show, respectively, UVJ-quiescent and UVJ-starforming galaxies from the control field sample with the same magnitude (top panels) or mass (bottom panels) threshold as candidate cluster members, and with a photometric redshift within ±0.1 from the cluster redshift. The thick light-gray line shows the adopted quiescent vs. star-forming separation in the observed m814–m140 vs. m140–[3.6] color plane. For clusters without a final spectroscopic redshift confirmation (see Sect. 4), the thin dark-gray lines show the separation that would be adopted if assuming a redshift at the edges of the black+white error bars in Fig. 5 (top). |
| In the text | |
 |
Fig. 7. For each cluster: Bottom panel: m814–m140 color vs. stellar mass of candidate cluster members within r < 0.7r500. Symbol size and color reflect the statistical background subtraction weight as in Fig. 1. The light-gray shading shows the stellar mass range below the mass completeness limit. Top panel: quiescent fraction within r < 0.7r500 at masses above the individual mass completeness limit of the cluster (red symbols; error bars show the width of the stellar mass bin and the 1σ binomial confidence intervals, see Sect. 5.2). Where applicable, red triangles show quiescent fractions assuming that all unclassified galaxies are quiescent (rather than all star-forming, see Sect. 5.2). Blue symbols show the quiescent fraction in the same stellar mass bins for photo-z and color-selected field samples as in Fig. 1, as indicated. All symbols are plotted at the median mass of the given sample. |
| In the text | |
 |
Fig. 8. Quiescent fraction vs. m814–m140 color for red (m814–m140 > 1.5) galaxies in all five clusters. Galaxies bluer than m814–m140 = 1.5 are not shown as they are always classified as star-forming (thus 0% quiescent fraction, see Fig. 6). Shaded histograms represent the color distribution of cluster galaxies as in Fig. 1, arbitrarily rescaled. Empty and solid symbols show, respectively, quiescent fractions for the m140-selected and for the log(M/M⊙) > 10.85 (common) mass complete samples. Error bars show binomial confidence intervals (1σ). Color bins with < 2 galaxies are not shown. |
| In the text | |
 |
Fig. 9. Projected distribution of candidate cluster members. All candidate members are shown regardless of their statistical background subtraction weight. Each symbol has two colors. The color of the symbol boundary scales with the m814–m140 color of each galaxy relative to the cluster RS color (see insert). The internal symbol color, in red or blue shade according to the galaxy classification as quiescent or starforming, scales with the reliability of this classification only accounting for the distance of the galaxy colors from the adopted selection dividing line and the relevant photometric errors. Symbol shape reflects the estimated Sersic index as indicated. Masked areas and regions deemed to be outside of our uniform coverage are gray shaded. The two circles show the limiting radii of the adopted cluster regions (r < 0.45r500, r < 0.7r500). |
| In the text | |
 |
Fig. 10. Top panel: quiescent fraction of cluster galaxies within r < 0.45r500 (dark red) and r < 0.7r500 (light red) above the common mass completeness limit log(M/M⊙) > 10.85. Error bars account for uncertainties in the quiescent vs. star-forming classification as described in Sect. 5.3. Blue symbols show the quiescent fraction in corresponding photo-z selected control field samples (see Sect. 5.3). Large empty blue squares show values from the COSMOS field (see text). Bottom panel: environmental quenching efficiency as derived from cluster and field quiescent fractions in the top panel. Color coding reflects the top panel. In both panels empty triangles show, where applicable, the quiescent fraction and derived quenching efficiency assuming that galaxies lacking a quiescent vs. star-forming classification are all quiescent (rather than all star-forming, see Sect. 5.2, Table 2). |
| In the text | |
 |
Fig. 11. Retrieved S/N of the cluster SZE detection obtained as a function of the r < 0.45r500 quiescent fraction, from the observed value down to the field level (solid lines) at the cluster redshift and mass completeness limit (see Sect. 5.4). Dotted lines show for completeness the retrieved S/N for central quiescent fractions down to 10%. For each cluster, the S/N is shown for both MS SEDs adopted to convert SFRs to 95, 150 GHz fluxes, as indicated. The gray line marks the S/N > 5 limit of our original sample selection. According to the modeling in Sect. 5.4, all five clusters would have been included in our S/N > 5 sample even if environmental quenching were negligible. |
| In the text | |
 |
Fig. A.1. Top panel: black points show for all clusters the estimated total number of background-subtracted cluster members at m140 < M* + 1.3 and within r < 0.7r500 divided by the total projected halo mass within the same region (Ngal/Mhalo). The solid gray line shows the median value for this cluster sample. The dashed lines show an estimate of the intrinsic scatter of Ngal/Mhalo. See text for details. Bottom panel: estimate of the effect of differences in the background density along the line of sight of the clusters on the estimated red fraction of cluster galaxies. Black points show the red fraction for all clusters as estimated adopting the default control field for the statistical residual background subtraction (Sect. 3.2). Dark gray bars show the effect on the estimated red fraction of adopting control sub-fields with densities in the 10th to 90th percentile range across the default control field. Light gray bars show the effect of considering the background-subtracted cluster member samples contaminated or incomplete according to the face-value Ngal/Mhalo of each cluster with respect to the median Ngal/Mhalo of the sample. See text for details. For comparison, light gray empty circles show the red fraction in field galaxies in the same m140 magnitude range, and with a photo-z within ±0.15 of the cluster redshift. |
| In the text | |
 |
Fig. B.1. Top panel: quiescent fraction of cluster galaxies within r < 0.45r500 (dark red) and r < 0.7r500 (light red) above the mass completeness limit of each cluster as reported in the bottom panel. Error bars account for uncertainties in the quiescent vs. star-forming classification as described in Sect. 5.3. Blue symbols show the quiescent fraction in corresponding photo-z selected control field samples (see Sect. 5.3). Bottom panel: environmental quenching efficiency as derived from cluster and field quiescent fractions in the top panel. Color coding reflects the top panel. In both panels empty triangles show, where applicable, the quiescent fraction and derived quenching efficiency assuming that galaxies lacking a quiescent vs. star-forming classification are all quiescent (rather than all star-forming, see Sect. 5.2, Table 2). |
| In the text | |
 |
Fig. C.1. Example illustration of the modeling of the quiescent fraction vs. stellar mass. Top panels: assumed radial profile of the quiescent fraction above mass completeness. In the three panels a green circle highlights a given clustercentric distance, and thus quiescent fraction value. Based on these values, the corresponding middle panels show the quiescent fraction vs. stellar mass as estimated with both approaches described in Sect. 5.4 (red, orange lines). The blue line shows the quiescent fraction vs. mass in the field at the cluster redshift. The corresponding bottom panels show the overall contribution of galaxies above a given stellar masses to the total SFR density at the given clustercentric distance assuming the quiescent fraction vs. mass from the middle panels (see Sect. 5.4). |
| In the text | |
 |
Fig. C.2. Test of the quiescent fraction vs. stellar mass modeling discussed in Sect. 5.4. The black line shows the observed quiescent fraction vs. stellar mass in z ∼ 1 clusters from van der Burg et al. (2013). The red and orange solid (dotted) lines (color coding as in Fig. C.1) show the estimated quiescent fraction vs. mass using the two approaches shown in Fig. C.1, starting from the observed quiescent fraction in a mass complete sample with log(M/M⊙) > 10.9 (10.7, respectively, as shown by vertical gray lines). Blue dashed line shows the field quiescent fractions vs. mass at the same redshift. |
| In the text | |
 |
Fig. C.3. Example illustration of the modeling of the SFR density profiles described in Sect. 5.4, see text for full details. Left, middle and right panel: three different values assumed for the r < r500 quiescent fraction above mass completeness, as indicated. Top panels: radial profile of quiescent fraction above mass completeness (black, the field value is shown in gray). The dotted red line shows the quiescent fraction of the full mass complete sample out to the given clustercentric radius. Middle panels: projected galaxy number density profile above mass completeness (black), and the derived profiles of star-forming and quiescent galaxies (blue and red) given the quiescent fraction profile in the corresponding top panel. Bottom panels: corresponding projected SFR density profiles, derived with the two models of quiescent fraction vs. stellar mass as indicated (solid lines). Dashed and dotted lines show the additional SFR density profile over the prediction for the actually observed quiescent fraction (see text). Inserts show the corresponding cumulative SFR as a function of clustercentric radius. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


