| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A162 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202348055 | |
| Published online | 19 February 2024 | |
The history of star-forming regions in the tails of six GASP jellyfish galaxies observed with the Hubble Space Telescope⋆
1
INAF – Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
e-mail: ariel.werle@inaf.it
2
Dipartimento di Fisica e Astronomia, Università di Padova, Vicolo Osservatorio 3, 35122 Padova, Italy
3
Flatiron Institute, CCA, 162 5th Avenue, New York, NY 10010, USA
4
Instituto de Radioastronomía y Astrofísica, Universidad Nacional Autónoma de México, Morelia, Michoacán 58089, Mexico
5
Department of Physics, Faculty of Science, University of Zagreb, Bijenička 32, 10 000 Zagreb, Croatia
6
Departamento de Física, Universidad Técnica Federico Santa María, Avenida Vicuña Mackenna 3939, San Joaquín, Santiago, Chile
7
INAF – Osservatorio Astronomico di Brera, Via Brera 28, 20121 Milano, Italy
Received:
24
September
2023
Accepted:
10
December
2023
Aims. In this work, we aim to characterize the stellar populations of star-forming regions detached from the stellar disks of galaxies undergoing ram-pressure stripping.
Methods. Using images collected with the WFC3 camera on board of the Hubble Space Telescope, we detected stellar clumps in continuum-subtracted Hα and the ultraviolet (F275W filter); such clumps are often embedded in larger regions (star-forming complexes) detected in the optical (F606W filter). Our sample includes 347 Hα clumps, 851 F275W clumps, and 296 star-forming complexes. We modeled the photometry of these objects in five bands using BAGPIPES to obtain their stellar population parameters.
Results. The median mass-weighted stellar ages are 27 Myr for Hα clumps and 39 Myr for F275W clumps and star-forming complexes, but the oldest stars in the complexes can be older than ∼300 Myr which indicates that star formation is sustained for long periods of time. Stellar masses vary from 103.5 to 107.1 M⊙, with star-forming complexes being more massive objects in the sample. Clumps and complexes found further away from the host galaxy are on average younger, less massive, and less obscured by dust. We interpret these trends as due to the effect of ram pressure in different phases of the interstellar medium. Hα clumps form a well-defined sequence in the stellar mass–SFR plane with a slope of 0.73. Some F275W clumps and star-forming complexes follow the same sequence while others stray away from it and passively age. The difference in mean stellar age between a complex and its youngest embedded clump scales with the distance between the clump and the center of the optical emission of the complex, with the most displaced clumps being hosted by the most elongated complexes. This is consistent with a fireball-like morphology, where star formation proceeds in a small portion of the complex while older stars are left behind producing a linear stellar population gradient. The stellar masses of star-forming complexes are consistent with the ones of globular clusters, but their stellar mass surface densities are lower by 2 dex, and their properties are more consistent with the population of dwarf galaxies in clusters.
Key words: galaxies: clusters: general / galaxies: evolution / galaxies: ISM / galaxies: star formation
The catalog of physical properties is available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/682/A162
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The interaction with the hot gas of the intracluster medium (ICM) may remove gas from the interstellar medium (ISM) of galaxies falling into a galaxy cluster. This interaction is known as ram-pressure-stripping (RPS; Gunn et al. 1972). The most extreme examples of RPS are showcased by jellyfish galaxies, objects in the peak phase of stripping that display long tails of stripped gas. Jellyfish galaxies can be identified in a variety of wavelengths, from X-rays to cold gas (Poggianti et al. 2019b; Moretti et al. 2020; Roberts et al. 2021; Boselli et al. 2022; Rohr et al. 2023). In many cases, the tails of jellyfish galaxies can harbor star-forming regions (see simulations by Kapferer et al. 2009; Tonnesen & Bryan 2012) and are thus detectable in ionized gas and in the ultraviolet (UV; e.g, Fritz et al. 2017; George et al. 2018, 2023). However, there is no consensus on how frequently star formation is present in these tails, either in simulations (Bekki 2014; Steinhauser et al. 2016) or in observations (Laudari et al. 2022).
One of the largest samples of confirmed jellyfish galaxies is that of the GASP survey (GAs Stripping Phenomena in galaxies with MUSE; Poggianti et al. 2017). GASP observed 114 galaxies with the MUSE (Multi Unit Spectroscopic Explorer, Bacon et al. 2010) integral field spectrograph on the Very Large Telescope with the goal of clarifying how, where, and when gas is removed from galaxies. The sample includes several galaxies that are undergoing RPS, some of which are textbook examples of jellyfish galaxies, while others have less prominent features. The MUSE data provided by GASP reveal a clumpy structure in the Hα images of the tails. Emission line diagnostic diagrams confirm these Hα clumps as star-forming regions originating from the stripped gas, with median star formation rates (SFRs) of 0.00 M⊙ yr−1, compatible with the low end of the SFR distribution for Hα clumps in the disks of the same galaxies. Their stellar masses typically vary between ∼104 and ∼107 M⊙, which is comparable to globular clusters and dwarf galaxies (Poggianti et al. 2019a; Vulcani et al. 2020). The Hα clumps in ram-pressure-stripped tails observed by GASP are surrounded by a diffuse ionized gas (DIG) component where ionization is at least partially powered by a nonstellar source, possibly the mixing of the ISM and ICM gas (Tomičić et al. 2021).
High spatial resolution observations of nearby galaxies using the Hubble Space Telescope (HST) such as the ones provided by the Legacy ExtraGalactic UV Survey (LEGUS; Calzetti et al. 2015) and the Physics at High Angular resolution in Nearby GalaxieS (PHANGS; Schinnerer et al. 2019) projects allow for very detailed studies of the structure of extragalactic star-forming regions that cannot be performed with ground-based instruments such as MUSE. For example, these studies have shown that star formation is a hierarchical process (Elmegreen et al. 2006; Gouliermis et al. 2015, 2017) in both space and time, with young structures being highly clustered and becoming less spatially correlated as they age (e.g, Grasha et al. 2017a,b). High resolution studies using HST have also been performed for galaxies undergoing RPS, most notably in the Coma and Virgo clusters. These works highlight the decoupling of dense gas from the surrounding ISM in the disk (Abramson & Kenney 2014; Kenney et al. 2015) and constrain the sizes and stellar populations of stellar sources in the stripped tails (e.g, Cramer et al. 2019; Waldron et al. 2023).
Recently, Gullieuszik et al. (2023) obtained HST images of six jellyfish galaxies from the GASP survey, allowing a statistical study of star-forming regions in the tails and disks of these objects at sub-kiloparsec resolution. The observations were made in five filters, from the UV to the I band, including a narrow-band filter around the Hα emission line. Giunchi et al. (2023a) used the ASTRODENDRO software to identify star-forming clumps in the Hα and F275W images of these galaxies; these clumps are shown to be embedded in larger structures detected in the F606W filter, called star-forming complexes. The authors find that these clumps have enhanced Hα luminosity at a given size, falling in a luminosity-size relation that is more similar to the one observed for starburst galaxies than that of normal star-forming galaxies. In the following paper of the series (Giunchi et al. 2023b), the authors focus on the morphological properties of the clumps and complexes, finding that they have slightly elongated structures, with clumps being displaced by 0.1 to 1 kpc from the center of the star-forming complex in which they are embedded. These results, confirmed by the visual inspection of the images, show that these objects are organized in structures known as “fireballs” (Cortese et al. 2007; Yoshida et al. 2008; Kenney et al. 2014; Jáchym et al. 2017; Waldron et al. 2023).
For this study, we modeled the spectral energy distribution (SED) of the clumps detected by Giunchi et al. (2023a) in order to determine their ages, masses, SFRs and other properties, extending previous studies of stellar populations of clumps in these galaxies to the sub-kiloparsec regime. The dataset is presented in Sect. 2 and the SED fitting procedure is described in Sect. 3. In Sects. 4 and 5, we present results of the SED fitting and explore applications to several science cases.
We assume a standard Λ cold dark matter cosmology with ΩM = 0.3, ΩΛ = 0.7, and h = 0.7. The chosen epoch for right ascension and declination (RA and Dec) is J2000.
2. Observations and clump detection
This paper relies on data from Gullieuszik et al. (2023) and the clump detection method of Giunchi et al. (2023a). All procedures are described in detail in the respective papers, but we summarize the main aspects of the data and methodology in this section.
2.1. The data
Our work is based on images obtained using the UVIS channel of the WFC3 camera on board of HST for six jellyfish galaxies in the GASP sample: JO175, JO201, JO204, JO206, JW39, and JW100. These galaxies were observed in five filters: F275W, F336W, F606W, F680N and F814W, sampling the wavelength range from ∼ 2475 Å to ∼ 9560 Å, with F680N covering the Hα emission line in the redshift range of the targeted galaxies (0.042–0.066). The FWHM of the PSF of the observations in this redshift range corresponds to ∼70 pc.
The data are available in the Mikulski Archive for Space Telescopes (MAST)1. The ID of the project is GO-16223; PI Gullieuszik.
2.2. Clump detection
Clump candidates are detected using ASTRODENDRO2, a Python package designed to define bright regions and brighter subregions inside them. The algorithm builds a tree structure formed by trunks (the ground levels), branches (the intermediate levels), and leaves (the top levels, containing no subregions).
The clumps analyzed in this work are located in two subregions of the galaxies: (i) extraplanar, the region where clumps show clear signs of disturbance due to ram pressure but still overlap (at least in projection) with the outskirts of the stellar disk (as defined by Giunchi et al. 2023a); and (ii) tails, where clumps do not overlap with the disks.
ASTRODENDRO was run independently in the Hα (continuum subtracted) and F275W images, and set to detect structures where at least five adjacent pixels have fluxes 2σ above the background level in the detection filter. To avoid spurious detection due to background objects, in the tails we kept only candidates either (i) matched with MUSE clumps (Poggianti et al. 2019a; ii) with a redshift consistent with the one of the galaxy in the corresponding region of its MUSE data cube or (iii) emitting in all the filters and with a positive Hα flux. We refer to Giunchi et al. (2023a) for a flowchart that illustrates the aforementioned selection criteria. To ensure that the physical properties derived from the SED fitting can be adequately constrained, we further select only ASTRODENDRO trunks and leaves that have a signal-to-noise ratio S/N > 2 in all of the five filters; these are the only criteria in our selection that differ from Giunchi et al. (2023a). This leads to an initial sample of 409 Hα clumps and 1208 F275W clumps (combining tail and extraplanar regions).
In order to trace the emission of older stellar population and recover the whole stellar mass formed from stripped gas in the tails, we ran ASTRODENDRO also on the F606W filter. Throughout the paper, these larger structures detected in the F606W filter are referred to as star-forming complexes, or just “complexes”. In order to avoid the diffuse emission of the galactic stellar disk, which is very bright in the F606W filter, the detection of these star-forming complexes was performed only in the tails (not in extraplanar regions), and the detection threshold was increased to 3σ. Further selection criteria require the candidate to be an ASTRODENDRO trunk matched to at least one F275W or Hα clump3. The total number of star-forming complexes is 338.
From these samples, we selected a subsample of spatially resolved clumps and complexes. The size of a clump is defined as 2RC, where RC is the PSF-corrected core radius, that is, the geometric mean of the semi-major and semi-minor axes of the clumps, computed as the standard deviations of the clump surface brightness distribution along and perpendicular to the direction of maximum elongation. We define a clump or a complex as resolved if its size is larger than 2FWHMPSF (∼140 pc). The median sizes of resolved Hα clumps, F275W clumps and star-forming complexes are ∼201 pc, ∼214 pc and ∼251 pc, respectively. Typically, 15 − 20% of Hα and F275W clumps and about half of the star-forming complexes are resolved. Throughout the paper, morphological quantities such as size, axial ratio and stellar mass surface density are reported only for resolved objects.
We anticipate that some of the clumps and complexes that were detected will not be used in this work, as some quality control cuts are applied based on the results of the stellar population modeling. These additional cuts are discussed in Sect. 3.2, where we present our final sample.
3. Deriving physical properties
We modeled the stellar populations of clumps and complexes in our sample by fitting all five observed fluxes with the SED fitting code BAGPIPES (Bayesian Analysis of Galaxies for Physical Inference and Parameter EStimation; Carnall et al. 2018). For each band, these fluxes are measured as the sum of the fluxes of all pixels belonging to a given clump or complex as defined by ASTRODENDRO. We adopt the 2016 update of the simple stellar population (SSP) models from Bruzual & Charlot (2003) with a Kroupa (2001) initial mass function; the solar metallicity in these models is Z⊙ = 0.017. BAGPIPES returns posterior probability distributions (PDFs) for each of the measured properties; throughout the paper we use the median of the PDFs when referring to the value of a physical property of an object.
3.1. Model description
Star formation histories (SFHs) of clumps and star-forming complexes are parameterized as a single delayed exponential (see Carnall et al. 2019) following
where t is the time since the Big Bang, t0 the time when star formation starts and τ is the timescale of the decline of star formation. This parametrization can be quite flexible as it reduces to a single burst for τ ∼ 0.
We also tested two other models for the SFHs: (i) instantaneous bursts (or single SSPs) and (ii) square bursts (constant star formation during a certain period of time). In general, both models perform somewhat similarly to the delayed exponential. However, single SSPs are not flexible enough to reproduce some of the observed colors (see Sect. 3.3). Square bursts yield very similar fits to delayed exponentials, with just slightly higher residuals.
Dust is modeled using the Milky Way extinction curve from Cardelli et al. (1989) with RV = 3.1 and two foreground dust screens with different V-band extinction AV, for stellar populations older and younger than 20 Myr. We have also experimented with the possibility of setting the AV priors according to the Balmer decrement of star-forming regions detected in Hα maps obtained from the MUSE data cubes available for these galaxies. However, for Hα clumps we found that better fits are usually achieved with slightly lower AV (∼0.3 mag on average) and due to the substructure of HST clumps the same idea doesn’t apply for F275W clumps and star-forming complexes, which is why we chose to keep AV as a free parameter. Emission lines and nebular continuum emission (derived using CLOUDY; Ferland et al. 2017) are included in the models for stellar populations as old as 20 Myr.
Priors on the parameters fitted by BAGPIPES are set according to the expected properties for these recently formed objects. Ages are allowed to vary between 0 and 500 Myr and the total mass assembled into stars is left to vary from 0 to 1010 M⊙. Stellar metallicity follows a Gaussian prior with mean μ = Z⊙ and standard deviation σ = 0.25 Z⊙. The τ parameter in the delayed exponential varies from 10−3 to 500 Myr according to a logarithmic prior; this prior was adopted to allow τ to converge to very low values when necessary, eventually reducing the delayed exponential to a single burst of star formation. AV varies from 0 to 1.25 magnitudes and the ratio between the AV of the young and the old populations varies from 1 and 2.5. The ionization parameter log U varies from −3.5 to −2 and gas metallicity is the same as the stellar metallicity. Redshift is fixed at the galaxy redshift measured from the MUSE datacubes (Gullieuszik et al. 2020), as variations within a single galaxy have a negligible effect on the photometry.
Examples of BAGPIPES fits for a star-forming complex and two embedded clumps (one detected in Hα and one in F275W) are shown in Fig. 1. Corner plots showing the covariance between the main derived parameters are shown in Appendix A.
 |
Fig. 1. Examples of BAGPIPES fits for clumps selected from Hα, F275W, and F606W images. On the left: F275W image of a region in the tail of JO201; regions in golden yellow, pink and purple indicate an Hα clump, a UV clump and a star-forming complex, respectively. On the right: Examples of BAGPIPES fits to the photometry of the regions indicated on the image to the left; shaded region corresponds to the full range of the model spectra PDF and are plotted with the same color as the corresponding region in the image; black points with errorbars (generally too small to be seen) indicate the observed photometric fluxes in the five HST bands used in this work. Rectangles show the region between the 1% and 99% percentiles of the photometric fluxes fitted by BAGPIPES. Inset plots in the right panels show the posterior PDFs of mass-weighted ages (⟨t⋆⟩), stellar masses (log M⋆/M⊙), SFRs, and AV derived for each object. |
3.2. Quality control cuts and final sample
To evaluate how the underlying stellar populations in the galaxy disk might affect our results, we tested a star formation history with two components: one with the same configuration described above, and an older one representing the underlying stellar population of the disk. This is expected to be an issue especially in the extraplanar regions (which overlap with the disk), but also for tail clumps near the stellar disk contour delimited by Giunchi et al. (2023a). Star-forming complexes are less prone to this effect as they are detected in the F606W filter and by selection are well detached from the disk. This test showed that the stellar mass contribution of the old components was generally very low (≲1%) and the properties (ages, dust content, stellar masses and SFRs) derived for the clumps were unaffected. However, in some cases this experiment has revealed non-negligible old components, which leads to unconstrained ages (∼flat PDFs) for the young components. This happens for 29 Hα clumps (7.0%) and 204 F275W clumps (15.7%), all of which are removed from the final sample. Of these, 21 Hα clumps and 123 F275W clumps are in the extraplanar region of JW100.
In some cases, the fluxes of our models are outside the 2σ error bars of the observations for one or more filters, thus the fit cannot be considered satisfactory. This happens mostly for clumps detected in F275W: due to the slightly lower signal to noise of this filter, the detection sometimes misses some of the faint pixels that are below the background level in F275W but still contribute to F336W. In these cases, the F275W flux tends to be slightly under predicted, and F336W slightly over predicted. To ensure data quality, we have discarded objects for which either the median of the model flux PDF is outside error bars of the observed photometry for more than one filter or the interquartile region of the model flux PDF does not intersect with the observed flux error bar for one of the filters. These criteria further remove 33 (8.6%) Hα clumps, 243 (22.2%) F275W clumps, and 42 (12%) star-forming complexes. Examples of fits that failed the quality control are provided in Appendix B.
After these cuts, our final sample contains 347 Hα clumps, 851 F275W clumps, and 296 star-forming complexes. The final number of clumps and complexes in each galaxy and the number of resolved objects according to the criterion described in Sect. 2.2 are shown in Table 1. For information on our galaxy sample and their host clusters, we refer to Giunchi et al. (2023a).
Number of objects in each galaxy (and in total) that are included in our final sample.
3.3. 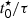 and SFH complexity
and SFH complexity
As mentioned in Sect. 3.1, our delayed exponential model can reproduce both burst-like and slowly decaying SFHs, but it is worthwhile (and wise) to ask if such complexity is needed to reproduce the observations. To verify that, we use the ratio between the age of the oldest stars in the model (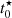 4) and τ (see Eq. (1)) as a normalized proxy of the SFR evolution, as this ratio effectively measures how much the SFR has declined from its maximum value. Histograms of
4) and τ (see Eq. (1)) as a normalized proxy of the SFR evolution, as this ratio effectively measures how much the SFR has declined from its maximum value. Histograms of 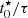 for our sample of clumps and complexes are shown in the top panel of Fig. 2. Hα clumps have typically low
for our sample of clumps and complexes are shown in the top panel of Fig. 2. Hα clumps have typically low 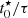 indicative of SFHs that have not declined significantly (consistent with constant SFR), while F275W clumps and star-forming complexes show bimodal distributions; we refer to these two distinct populations as early (high
indicative of SFHs that have not declined significantly (consistent with constant SFR), while F275W clumps and star-forming complexes show bimodal distributions; we refer to these two distinct populations as early (high 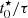 ) and late (low
) and late (low 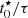 ) decliners. To separate these classes, we have used a Gaussian mixture model with three clusters: one for each population and a third one to account for intermediate objects. The model was trained in the combined sample of clumps and complexes and then applied for the classification of each subsample. We classify 90% of Hα clumps, 49% of F275W clumps, and 61% of star-forming complexes as late decliners, while 30% of F275W clumps, 22% of star-forming complexes, and none of the Hα clumps are early decliners according to the Gaussian Mixture model.
) decliners. To separate these classes, we have used a Gaussian mixture model with three clusters: one for each population and a third one to account for intermediate objects. The model was trained in the combined sample of clumps and complexes and then applied for the classification of each subsample. We classify 90% of Hα clumps, 49% of F275W clumps, and 61% of star-forming complexes as late decliners, while 30% of F275W clumps, 22% of star-forming complexes, and none of the Hα clumps are early decliners according to the Gaussian Mixture model.
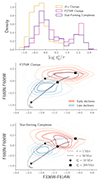 |
Fig. 2. Early and late decliners and their observed properties. Top: Histograms tracing the distributions of the SFH decay proxy |
We found that early and late decliners occupy well-defined loci in color-color diagrams, and are especially well separated in F680N–F606W, which is a color that traces the strength of Hα emission compared to the underlying continuum (similarly to an equivalent width, with stronger Hα corresponding to bluer color). In the central and bottom panels of Fig. 2 we show the F680N–F606W vs. F336W–F814W color-color diagram for F275W clumps and star-forming complexes, respectively; with contours tracing the distribution of fast and slow decliners. The population of clumps and complexes that is intermediate in  is also intermediate in the color-color diagrams, but was omitted from the figure to improve visualization. We compare the colors of early and late decliners with two model tracks generated with BAGPIPES (according to Eq. (1)) for ages between 1 and 300 Myr and τ between 1 and 50 Myr. Other parameters are kept constant: Z = Z⊙, log U = −2.75, and AV = 0.1 for stars of all ages.
is also intermediate in the color-color diagrams, but was omitted from the figure to improve visualization. We compare the colors of early and late decliners with two model tracks generated with BAGPIPES (according to Eq. (1)) for ages between 1 and 300 Myr and τ between 1 and 50 Myr. Other parameters are kept constant: Z = Z⊙, log U = −2.75, and AV = 0.1 for stars of all ages.
The two model tracks start indistinguishable from each other at 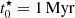 , but quickly diverge to different trajectories in the diagram. The τ = 1 Myr models cross the threshold between late and early decliners at
, but quickly diverge to different trajectories in the diagram. The τ = 1 Myr models cross the threshold between late and early decliners at 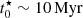 (corresponding to log
(corresponding to log 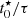 ∼ 1) and evolve to redder F336W–F814W with little change in F680N–F606W after that. On the other hand, models with τ = 50 Myr retain blue F680N–F606W for a long time (up to
∼ 1) and evolve to redder F336W–F814W with little change in F680N–F606W after that. On the other hand, models with τ = 50 Myr retain blue F680N–F606W for a long time (up to 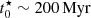 ) because they keep generating strong Hα emission as they become older and their broad-band colors redden.
) because they keep generating strong Hα emission as they become older and their broad-band colors redden.
This indicates that some level of complexity in the SFH models is indeed required to reproduce the mixture of Hα-strong and Hα-weak objects with a variety of broad-band colors. We also note that although our analysis is able to distinguish between two broad ranges of log 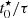 and we show why these two regimes are necessary to reproduce the data, we lack the constraining power to obtain precise estimates for this parameter.
and we show why these two regimes are necessary to reproduce the data, we lack the constraining power to obtain precise estimates for this parameter.
4. Properties of clumps and complexes
The main quantities of interest for this paper are the stellar ages, stellar masses, SFRs (calculated in the past 10 Myr) and AV of the clumps and complexes. Here and throughout most of the paper we use mass-weighted stellar ages (⟨ t⋆⟩M). These are very similar to luminosity-weighted ages for these objects as the mass-to-light ratios do not vary widely in these age ranges (see Cid Fernandes et al. 2005 for a discussion on age definitions). The reported AV values correspond to the attenuation affecting stars younger than 20 Myr, and to ensure meaningful measurements we analyze this quantity only for objects classified as late decliners in Sect. 3.3, that is, objects with significant amounts of young (< 20 Myr) stars.
4.1. Distributions of measured properties
The distributions of ⟨ t⋆⟩M, log M⋆, SFR, and AV for our sample of clumps and complexes in tails and extraplanar regions are shown in Fig. 3. As expected, Hα-detected clumps are the youngest, as these regions contain mostly very young stars still enclosed in their birth clouds. Considering the whole sample of Hα clumps, the median mass-weighted age is 27 Myr. The ages vary between subsamples: tail clumps have a median mass-weighted age of 16 Myr, while extraplanar clumps are relatively older (median ⟨ t⋆ ⟩M = 46 Myr). In comparison, clumps detected in F275W are slightly older, with median ⟨ t⋆ ⟩M of 39 Myr for the whole sample, 27 Myr in tails and 58 Myr in the extraplanar regions. This confirms the observational interpretation that these regions include stars that have just left their birth clouds and have slightly older ages than the ones in Hα-emitting regions. Star-forming complexes also have a median ⟨ t⋆ ⟩M of 39 Myr, but we remind the reader that these objects are only detected in the tails, where both clump samples are younger. When masking out the Hα and F275W clumps inside the complex and leaving only the flux of the region detected in F606W, we obtain a much older median ⟨ t⋆ ⟩M of 84 Myr. This shows that the diffuse emission detected in the F606W filter is really associated with an older stellar population, and not just a fainter region of the F275W clump that is not detected due to the lower S/N of this filter.
 |
Fig. 3. Distributions of (from top to bottom) mass-weighted ages, stellar masses, SFRs, and dust attenuation of clumps detected in Hα (in gold) and F275W (in dark pink), and star-forming complexes (in purple). We limit the histograms to the 95th percentiles of ⟨ t⋆⟩M and AV, and to the 15th percentile of SFR. These percentiles are calculated for the combined (all clumps and complexes) samples and the ranges are kept the same in all histograms of the same variable. Left panels show the general samples, tail clumps and complexes are in the middle panels and extraplanar clumps are on the right. Histograms are normalized to have the same area. |
The median stellar mass of Hα clumps is 104.8 M⊙ for the whole sample, 104.4 M⊙ in the tails and 105.1 M⊙ in extraplanar regions. For F275W clumps the median stellar masses are very similar: 104.7 M⊙ for the whole sample, 104.4 M⊙ for tail clumps and 105 M⊙ for extraplanar clumps. On the other hand, star-forming complexes are more massive, with median log M⋆/M⊙ = 5.2. The full stellar mass range of our sample is from 103.5 to 107.1 M⊙, similar to the one of globular clusters and dwarf galaxies.
Recent works in the literature also derive ages and masses for stellar clumps in the tails of jellyfish galaxies based on HST photometry. These works report stellar masses similar to the ones we obtain, but ages that are relatively younger: 1–35 Myr for D100 (Cramer et al. 2019) and < 10 Myr for ESO 137-001 (Waldron et al. 2023). Although these are different galaxies and the values might indeed differ, differences in methodology and data certainly play a role in producing this discrepancy. Both Cramer et al. (2019) and Waldron et al. (2023) use Starburst99 and Cloudy to model colors, magnitudes, and/or the equivalent width of Hα of the clumps. These models are based on single bursts and therefore not comparable to the model used in this work. When limiting our SFHs to a single burst, we obtain median ages of 6 Myr to Hα clumps and 15 Myr for F275W clumps, which is closer to the literature values.
Another important quantity for understanding the structure of star-forming regions is the average stellar mass surface density ΣM⋆. With the diffraction limited images provided by HST, we are able to constrain ΣM⋆ for a significant fraction of clumps and complexes, although many remain unresolved (see Sect. 5). We note that in this work ΣM⋆ is obtained by dividing the stellar mass of the object by its total physical area (the sum of the area of all pixels, converted to kiloparsec2 according to the galaxy redshift), which is slightly different from what is done in some works in the literature where ΣM⋆ is calculated within an effective radius. Histograms of log ΣM⋆ are shown as an inset in the stellar mass histogram for the whole sample. Hα clumps are denser in stellar mass than F275W clumps, which in turn are denser than star-forming complexes, even though the median values are very similar: log ΣM⋆/M⊙ kpc−2 = 6.6 for Hα clumps, 6.4 for F275W clumps and 6.3 for star-forming complexes.
As expected, Hα clumps represent regions of ongoing star formation and thus are all characterized by significant SFRs (median SFR of 10−2.9 M⊙ yr−1 for the whole sample, 10−3 M⊙ yr−1 for tail clumps and 10−2.8 M⊙ yr−1 for extraplanar clumps). For F275W clumps and star-forming complexes, the distributions of log SFR show a tail toward low values (log SFR/M⊙ yr−1 < −4.5), these tails contain 26% of F275W clumps and 18% of star-forming complexes. This happens because some of these objects do not display any star formation in the past 10 Myr, but since we used a delayed exponential model for the SFH, we still measure SFR > 0, although very low. When considering only star-forming complexes with SFR > 10−4.5 M⊙ yr−1 (i.e neglecting the tail of the distribution) the median SFR is 10−2.75 M⊙ yr−1, very similar to (and slightly higher than) the one of Hα clumps in the tails, which can be understood as star-forming complexes may contain one or more Hα clump(s). On the other hand, F275W clumps have lower SFRs when compared to Hα clumps or star-forming complexes even when neglecting the tails of the distribution, their median SFR for clumps with SFR > 10−4.5 M⊙ yr−1 is ∼10−3.15 M⊙ yr−1 for both subsamples. We note that a substantial fraction of the objects in our sample have SFR < 10−3 M⊙ yr−1, which corresponds to a mass formed in the past 10 Myr that is smaller than 104 M⊙, which is the typical value required for a fully sampled IMF (da Silva et al. 2012); despite this relevant caveat, we find no indication that objects with SFRs below this threshold behave in any peculiar way. The SFRs of objects in our sample will be further explored in Sect. 4.2.
When considering the whole sample or the tail regions, the distribution of AV for Hα clumps is slightly skewed toward larger values when compared to F275W clumps. However, all distributions are concentrated at low AV, except for the population of Hα clumps in extraplanar regions. Furthermore, F275W clumps in extraplanar regions are slightly more attenuated than their tail counterparts. We do expect Hα clumps to be more strongly attenuated by dust, in the same way that star-forming regions in galaxy disks are more attenuated than the older stellar populations (Charlot & Fall 2000). What is unclear is why the most attenuated clumps are in extraplanar regions. We see two possible explanations for this: (i) the extra AV might actually be due to diffuse (possibly stripped) dust in and around the galaxy disk; (ii) alternatively, this might be a consequence of the fact that extraplanar clumps are typically the oldest and thus had more time to form dust grains in-situ. The two explanations are not mutually exclusive, and both effects might contribute to the observed AV differences. However, both of these interpretations would point to the conclusion that dust has not been stripped out to large distances.
The distributions presented in Fig. 3 remain fairly similar in all galaxies of our sample. Box plots showing the medians, interquartile regions and 15% and 85% percentiles of the distributions in individual galaxies are shown in Fig. 4. The distinction between tail and extraplanar clumps is neglected for simplicity, but also because some galaxies do not have enough clumps to produce meaningful distributions when making the distinction.
 |
Fig. 4. Box plots showing galaxy-to-galaxy variations of the distributions shown in Fig. 3. As before, clumps detected in Hα and F275W are shown in gold and in dark pink, respectively, and star-forming complexes are shown in purple. Boxes span the interquartile regions, horizontal lines in the boxes indicate the median and whiskers mark the 15% and 85% percentiles of the distributions. |
4.2. Stellar mass – SFR relation
A widely studied characteristic of the population of star-forming galaxies is the star-forming main sequence in the stellar mass–SFR plane. This relation is also studied for star-forming clumps, which are shown to follow similar (but not equal) trends (Mehta et al. 2021). We show the log M⋆–log SFR relation for our sample of clumps and complexes in Fig. 5.
 |
Fig. 5. Stellar mass–SFR relation for clumps and complexes in our sample. Panels from top to bottom show the relations for Hα clumps, F275W clumps and star-forming complexes, respectively. Points are colored according to ⟨ t⋆ ⟩M, truncating at 10 Myr and 150 Myr, clumps containing only stars younger than 10 Myr form a relation by definition and are shown as white circles. The gray band indicates a ±1 dex range around a linear fit to the Hα relation, the dashed line shows a fit to the relation for star-forming galaxies in the Sloan Digital Sky Survey from Renzini & Peng (2015). For F275W clumps and star-forming complexes we set the lower limit of the y-axis to the 1% percentile of the SFR distribution. |
Hα clumps (top panel in Fig. 5) form a well defined sequence in the stellar mass–SFR plane, akin to the one observed for normal star-forming galaxies, with all points lying within ±1 dex from a linear fit to the relation (log SFR/M⊙ yr−1 = 0.73 × log M⋆/M⊙ − 6.4). White points with black edges in the figure represent clumps containing only stars younger than 10 Myr and are not considered in the linear fit as they form a perfect correlation by definition, marking the maximum possible specific SFR. At fixed SFR, age increases toward more massive clumps. This can be partially attributed to the SFH parametrization used in this work (see Sect. 3.1), but we note that Zanella et al. (2019) have also found (at z ∼ 2) that more massive clumps tend to be older, and a comparable behavior was observed by Zanella et al. (2015) for simulated clumps in the Schmidt-Kennicutt plane (Kennicutt 1989).
Differences in methodology limit our ability to make strict comparisons with the literature; however, comparisons can be made to some extent as long as their limitations are kept in mind. It is interesting that the slope of the relation obtained by Renzini & Peng (2015) for the global (galaxy-wide) relation of star-forming galaxies in the Sloan Digital Sky Survey (SDSS; York et al. 2000) is remarkably similar (0.76 ± 0.01) to the one of our linear fit (0.73). Although the slopes are similar, the relation from Renzini & Peng (2015) lies close to −1 dex from our relation in the log M⋆ range of interest. It is indeed expected for star-forming clumps to be above galaxies in this relation (e.g, Mehta et al. 2021), as those represent isolated actively star-forming regions, while for whole galaxies these regions are averaged out with non star-forming regions, decreasing the specific SFR. We note that the difference in SFR indicators between this work and Renzini & Peng (2015; SED fitting and Hα luminosity) should not be affecting the comparisons, as the SFRs obtained from BAGPIPES with a 10 Myr timescale are very similar (median absolute difference ⪅0.1 dex) to those obtained by applying the Kennicutt (1998) conversion from Hα luminosity (LHα) to SFR (SFR/M⊙ yr−1 = 10−41.28 LHα/erg s−1 for a Kroupa IMF as in Brinchmann et al. 2004) to either the Hα luminosity of the BAGPIPES model spectra or the continuum subtracted photometric Hα luminosity from Giunchi et al. (2023a), corrected by dust using a Calzetti attenuation law and the AV value for young stellar populations obtained from the BAGPIPES fit.
For F275W clumps and star-forming complexes (middle and bottom panels in Fig. 5) the behavior in the log M⋆–log SFR plane is more complex, with some clumps/complexes lying around the same correlation found for Hα clumps, and other straying away toward lower SFRs. 29.6% of F275W clumps and 20.8% of star-forming complexes are below 1 dex from the relation found for Hα clumps. For these objects, mass-weighted ages increase with the distance from the relation, indicating passive aging of stellar population reminiscent of the process of star formation quenching observed in galaxies. All objects falling away from the relation are classified as early decliners according to their SFHs (see Sect. 3.3), but the youngest early decliners are still within ±1 dex of the relation. On the other hand, clumps and complexes along the sequence have mass-weighted ages that increase toward higher stellar masses and SFRs similarly to what is observed for Hα clumps.
This same relation was studied by Vulcani et al. (2020) for the entire sample of stripped galaxies in GASP (which includes the 6 galaxies in our sample), where clumps are detected from the Hα emission in the MUSE data cubes. The authors find a much steeper slope of 1.63. We acknowledge that the results presented here are in tension with the ones of Vulcani et al. (2020), which can most likely be ascribed to differences in spatial and spectral resolution, wavelength range and methodology. Understanding how these methodological differences and selection effects work on shaping these difference is an open issue that we defer to future work.
4.3. Trends with galactocentric distance
The properties of star-forming regions at different distances from the stripped galaxy can give us hints about the process of star formation itself, and also about how stripping occurs in a galaxy. In Fig. 6 we plot ⟨ t⋆ ⟩M, log M⋆, SFR and AV of clumps and complexes in our sample against the log projected distance to the center of the host galaxy, normalized by its effective radius (log d/Re). We use effective radii measured by Franchetto et al. (2020) using MUSE data. Not normalizing the radius or using the distance to the edge of the galaxy disk yields very similar (and qualitatively equivalent) trends.
 |
Fig. 6. Trends (or lack thereof) of the measured properties with galactocentric distance. ⟨ t⋆ ⟩M (top), log M⋆ (second row), SFR (third row) and AV (bottom) of clumps and complexes are plotted against the normalized log distance log d/Re to the center of the host galaxy. The different panels show clumps selected from Hα (left) and F275W (middle), as well as star-forming complexes (right). Black points trace the median values of physical properties in bins of log d/Re and vertical lines indicate interquartile regions, points are plotted in the center of each bin. In the third row of panels, only objects within ±1 dex of the sequence shown in Fig. 5 are included as points, histograms show the distribution of objects below (dashed line) and within (solid line) ±1 dex of the sequence. In the bottom row we show only objects that formed a significant fraction of their stellar mass in the past 20 Myr (classified as late decliners in Sect. 3.3). |
We observe a clear5 anti correlation of ⟨ t⋆ ⟩M with distance for all subclasses of objects, which is stronger in Hα clumps, and slightly weaker for F275W clumps and star-forming complexes; thus, mass-weighted ages get on average younger with increasing distance from the disk. This is in line with previous works that find similar trends (Fumagalli et al. 2011; Kenney et al. 2014; Bellhouse et al. 2019). We interpret this anti-correlation as due to the effect of ram pressure on different gas phases. When the multiphase gas is stripped, atomic gas is easily moved out to large distances from the disk. On the other hand, the molecular gas, closer to the conditions necessary for star formation, is less efficiently stripped (see Bacchini et al. 2023). However, RPS tails are known to host a large amount of diffuse molecular gas (Jáchym et al. 2019; Moretti et al. 2020). The age trend that we find suggests that the denser component of the molecular gas is not able to travel long distances before it is turned into stars, which are not susceptible to ram pressure. This locks these early star-forming regions to the vicinity of the disk, while atomic gas continues to be stripped away until it forms new molecular clouds (as the ones observed by Moretti et al. 2020) and eventually reaches the conditions for star formation at large distances from the disk. This interpretation is in line with the results of simulations (see Tonnesen & Bryan 2012).
We also observe a anti correlation6 of stellar mass and distance from the host galaxy, which we interpret as a consequence of the trend with ⟨ t⋆ ⟩M. Under the assumption that star formation rate does not drop significantly over the SFH, the older objects have been forming stars for a longer time, and thus have assembled more mass. This assumption is valid for Hα clumps as they are mostly late decliners (see Sect. 3.3), but less so for F275W clumps and star-forming complexes, for which the SFHs are more diverse. Moreover, under the interpretation that star-forming regions near the disk originated from the dense molecular gas component of the ISM, these regions would also have a larger supply of gas to turn into stars. Cloud crushing simulations also show that as gas is being stripped and cooled it might also be fragmenting into lower mass clumps, which would also lead to lower stellar masses at larger distances (e.g, Abruzzo et al. 2023).
In the third row of panels in Fig. 6, we plot the SFR vs. log d/Re for objects within ±1 dex of the fit to the stellar mass–SFR relation of Hα clumps (see Fig. 5). The SFR values of these objects do not vary significantly with d/Re. The log d/Re distribution for objects below (by at least 1 dex) a linear fit to Hα sequence is traced by the dashed histograms in the same panels, and we also include the log d/Re distribution of objects within the sequence for comparison. We also find that there is no striking difference between the log d/Re distributions of objects that are within or below the sequence defined by Hα clumps; indicating that the quenched fraction of F275W clumps and star-forming complexes does not vary with galactocentric distance.
Large values of AV are observed only in clumps close to the stellar disk, as already seen from the difference between the AV distributions of tail and extraplanar clumps in Fig. 3. This supports the idea that dust is not efficiently stripped to large distances from the disk, and that the AV measured in the BAGPIPES fit might be due to dust that is formed in situ, or diffuse dust surrounding the galaxy disk. Another interesting possibility is that dust might be destroyed via sputtering due to the interaction with the ICM (Draine & Salpeter 1979; Gutiérrez & López-Corredoira 2017; Vogelsberger et al. 2019).
The number of clumps per galaxy is not sufficient to allow meaningful interpretations of all trends (or lack thereof) in a galaxy-by-galaxy basis. Nevertheless, we include a version of Fig. 6 showing data of individual galaxies in Appendix C for reference.
4.4. Onset of star formation
Another interesting parameter when studying jellyfish galaxies is the age of the oldest stars in the tails. Under the assumption that star formation starts immediately after stripping and stars remain detectable for long enough, the age of the oldest stars in the tails would correspond to the stripping timescale. Since star formation can take some time to occur and stellar associations fade, the age of the onset of star formation in the clumps serves as a lower (younger) limit for the onset of stripping. As introduced in Sect. 3.3, the age of the oldest stars in our SFH models corresponds to the value of 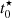 (related to t0 in Eq. (1)). We note that
(related to t0 in Eq. (1)). We note that 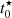 can be degenerate with τ and is typically not as well constrained as ⟨ t⋆ ⟩M.
can be degenerate with τ and is typically not as well constrained as ⟨ t⋆ ⟩M.
A similar analysis has been performed for JO201 by Bellhouse et al. (2019) using MUSE data from the GASP project and the SINOPSIS spectral synthesis code (Fritz et al. 2017). The authors find that the star-forming regions detected in Hα with MUSE in the tail that galaxy are typically younger than 800 Myr (with two outliers as old as 2 Gyr).
We probe the timescale of the onset of star formation using the 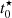 value of the star forming complexes. These regions are the oldest in our sample, and also the largest ones which makes them more comparable to the MUSE regions studied by Bellhouse et al. (2019) at a lower spatial resolution. In Fig. 7, we show box plots tracing the distributions of
value of the star forming complexes. These regions are the oldest in our sample, and also the largest ones which makes them more comparable to the MUSE regions studied by Bellhouse et al. (2019) at a lower spatial resolution. In Fig. 7, we show box plots tracing the distributions of 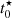 for each galaxy in our sample, with whiskers indicating the 1% and 99% percentiles. The 99% percentiles of
for each galaxy in our sample, with whiskers indicating the 1% and 99% percentiles. The 99% percentiles of 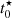 are very similar between galaxies, varying from 284 Myr for JO204 to 383 Myr for JO206. These values are comparable to that of Fumagalli et al. (2011), who constrain the ages of blobs in the tail of IC 3418 to be younger than 400 Myr.
are very similar between galaxies, varying from 284 Myr for JO204 to 383 Myr for JO206. These values are comparable to that of Fumagalli et al. (2011), who constrain the ages of blobs in the tail of IC 3418 to be younger than 400 Myr.
 |
Fig. 7. Box plots tracing the distribution of the age of the oldest stars in star-forming complexes. Boxes span the interquartile regions, horizontal lines in the boxes indicate the median and whiskers mark the 1% and 99% percentiles of the distributions. |
Taken at face value, the similarity of the maximum 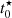 in different galaxies points to a scenario where the stripping timescales do not strongly depend on galaxy properties and surrounding environment. However, it likely that the
in different galaxies points to a scenario where the stripping timescales do not strongly depend on galaxy properties and surrounding environment. However, it likely that the 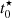 distributions are limited by our ability to detect the oldest complexes, as very old stellar associations that quenched star formation long (∼300 Myr) ago may not be detectable in either F275W or Hα and thus would not be included in our sample. Moreover, galaxies in our sample were selected because all of them show strong stripping features, and the similar timescales might be a consequence of this selection.
distributions are limited by our ability to detect the oldest complexes, as very old stellar associations that quenched star formation long (∼300 Myr) ago may not be detectable in either F275W or Hα and thus would not be included in our sample. Moreover, galaxies in our sample were selected because all of them show strong stripping features, and the similar timescales might be a consequence of this selection.
5. Structure and evolution of star-forming complexes
The star-forming clumps studied in this work are rarely found in isolation, and are usually part of larger structures (star-forming complexes). In this section, we focus on the morphology and evolution of star-forming complexes as a whole. We stress that the present section focuses only on complexes that are considered resolved (see section for details).
5.1. No conspicuous evidence for morphological evolution
Star-forming regions under ram pressure are often observed to be organized in structures called fireballs, where stellar populations of different ages are linearly displaced from one another (Kenney et al. 2014; Giunchi et al. 2023b). Fireballs take shape as ram pressure acts in regions that are continuously forming new stars, shaping their morphology into elongated structures. Thus, we expect some degree of morphological evolution for clumps and complexes in our sample. These morphological changes can be traced by the axial ratio (the ratio b/a between the lengths of the minor and the major axes) of the best-fitting ellipse of each resolved clump or complex. A perfectly round object will have b/a = 1, and values get closer to zero for more elongated objects. We note that Giunchi et al. (2023b) have already shown that many of the star-forming complexes in our sample of galaxies are organized in fireball-like configurations. However, it is interesting to revisit this analysis using the information obtained in this work and verify if clumps and complexes undergo any morphological changes as they age and assemble stellar mass.
However, when probing this idea (Fig. 8), we do not find any significant trend of b/a with stellar mass and ⟨ t⋆ ⟩M for clumps or complexes. We note that the correlations might be stronger than we are able to assess due to the resolution of the observations. Small complexes, that are unresolved in our observations, are less massive and also more likely to be rounder. Higher spatial resolution could potentially populate the lower-right portions of Fig. 8 and possibly reveal stronger trends, although we are unable to extrapolate to which extent this would happen. Also, projection effects strongly bias this analysis, as objects that are elongated along the line of sight are seen as round. Furthermore, star-forming clumps come in a variety of shapes even in the absence of ram pressure (see simulations from Mandelker et al. 2017) so it is possible that these trends are intrinsically weak.
 |
Fig. 8. Axial ratio (b/a) against stellar mass (top) and ⟨ t⋆ ⟩M (bottom) for Hα clumps (gold), F275W clumps (pink), and star-forming complexes (purple). Median lines are color-coded as the points and error bars represent interquartile regions for each b/a bin. |
5.2. A trace of fireballs
To look further into the structure of star-forming complexes, we investigate how the displacement of clumps within a complex correlates with the difference in mass weighted age between clumps and their host complexes (Δlog⟨ t⋆ ⟩M). To obtain the measurement of clump displacement, we isolate the region of the complex that is detected only in the F606W filter, that is, the region not covered by any clumps, and calculate the physical distance between the center of this region and the center of each embedded clump. For this analysis, we consider only the youngest clump inside each resolved complex, as these are the ones expected to be more displaced. The results of this experiment are shown in Fig. 9. To aid interpretation we have made the size of the points proportional to the radius of the complexes and colored them according to the area of the complex that is devoid of clumps. We note that several complexes lack either Hα or F275W clumps, which is why the number of points in each panel is different.
 |
Fig. 9. Clump displacement as a function of the difference between the log ⟨ t⋆ ⟩M of a star-forming complex and the one of the youngest Hα (left) and F275W (right) clump embedded in it. Color indicates the fraction of the star-forming complex that is covered by optical-only emission, and the size of the points is proportional to the radius of the complex. Squares indicate the median position of the 20% most elongated (black) and the 20% least elongated (white) complexes, with error bars showing the interquartile regions of the distributions. |
We observe reasonable linear correlations between clump displacement and Δlog⟨ t⋆ ⟩M for both Hα (Pearson R = 0.44) and F275W (Pearson R = 0.41) clumps. The clumps that contain younger stars (when compared to the age of the complex) tend to be further away from the center of the complex, as expected in a fireball-like structure. Furthermore, displacement (as well as age difference) is larger in the largest complexes (larger points in the figure), which also typically have a smaller fraction of their area covered with clumps.
Changes in clump elongation are traced by the black and white squares in Fig. 9, which represent the median position of the 20% most elongated (black) and least elongated (white) complexes, with error bars spanning from the 25th to the 75th percentile of the distributions of Δlog⟨ t⋆ ⟩M and displacement. Although the variation in b/a along the plane of Fig. 9 is small, the difference between these two extreme populations shows that the most displaced clumps are typically in the most elongated complexes.
We note that the increase in Δlog⟨ t⋆ ⟩M shown in Fig. 9 occurs despite the fact that the clumps in older complexes are also older themselves. We illustrate this in Fig. 10, where the age of the clumps is plotted against the age of their respective complex for the same objects as in Fig. 9. As complexes get older, so do their embedded clumps, but as a sublinear function of the log⟨ t⋆ ⟩M of the complex, leading Δlog⟨ t⋆ ⟩M to increase as clumps deviate more and more from the identity function (dashed black line in the figure). Moreover, it is noticeable that some clumps are above the dashed line in the figure, being older than their host complex (which can also be seen in Fig. 9). For Hα clumps this is simply due to uncertainties in the age measurement, while for F275W the difference might also be due to Hα clumps in the same complex shifting the overall log⟨ t⋆ ⟩M to younger ages.
 |
Fig. 10. log⟨ t⋆ ⟩M of star-forming complexes against log⟨ t⋆ ⟩M of the youngest Hα (golden) and F275W (pink) clumps inside them. An y = x function is represented by a dashed black line. Solid lines color-coded as the points are linear fits to the relation for the two subsamples of clumps. |
5.3. Comparisons with similar objects
Having established the properties of star-forming complexes in the tails of jellyfish galaxies in our sample, we may speculate on possible connections with other objects in the same mass range. We note that these comparisons are made under the assumption that star-forming complexes are gravitationally bound structures, which we are not able to confirm with the available data.
In Fig. 11 we show the relation between stellar mass and stellar mass surface density for our sample of star-forming complexes, comparing them to objects at similar stellar mass ranges, namely globular clusters, ultra-compact dwarfs and local dwarf spheroidals from Norris et al. (2014), as well as dwarf galaxies in the Fornax cluster (Venhola et al. 2018, 2022). Note that the public catalog from Norris et al. (2014) does not provide a separation between globular Clusters, ultra-compact dwarfs and compact ellipticals, but we exclude the latter by applying a mass cut for log M⋆/M⊙ < 8. The catalog includes additional data from many sources, the relevant references for the objects included in the figure are Brodie et al. (2011), Norris & Kannappan (2011), Strader et al. (2011), Norris et al. (2012), Forbes et al. (2013) and Mieske et al. (2013) for globular clusters and ultra-compact dwarfs, and Walker et al. (2009), McConnachie (2012) and Tollerud et al. (2012, 2013) for local dwarf spheroidals. For objects in the Norris et al. (2014) sample, we use the stellar masses provided in the catalog, while for the Fornax dwarfs we use the empirical relation between g − i color and mass-to-light ratio derived by Taylor et al. (2011), neglecting the difference between observed and rest-frame colors (k-correction), which is very small for broad bands at the Fornax redshift.
 |
Fig. 11. log M⋆ – log ΣM⋆ relation for star-forming complexes (purple). Dashed line traces the 5% percentile of log ΣM⋆ for globular clusters and ultra-compact dwarfs. Red and black contours trace the distributions of local dwarf spheroidals from Norris et al. (2014) Fornax dwarf galaxies from Venhola et al. (2018, 2022). |
Globular clusters and ultra-compact dwarf galaxies lie in a mass range quite similar to the one of star-forming complexes. However, these objects have effective radii of up to ∼10 pc (e.g, Misgeld & Hilker 2011), while our star-forming complexes have sizes of up to ∼1 kpc. This difference in size leads to a large difference in stellar-mass surface density. The dashed line in Fig. 11 shows the 5% percentile of the ΣM⋆ distribution for globular clusters and ultra-compact dwarfs, which is 2 dex above the 95% percentile of ΣM⋆ for our complexes. This difference is much larger than what can be accounted for by methodological differences, and thus star-forming complexes are unlikely to be progenitors of these objects, unless significant morphological evolution takes place.
The position of star-forming complexes in Fig. 11 is consistent with the distributions traced by both dwarf galaxy samples being considered. However, the local dwarf spheroidals from Norris et al. (2014) reside in widely different environments and are dark matter dominated, while star-forming complexes are expected to remain dark matter free. On the other hand, the Fornax dwarfs are in an environment consistent with the one of star-forming complexes, and their dark matter content is a topic of ongoing debate (Eftekhari et al. 2022; Asencio et al. 2022).
To further compare our star-forming complexes to the Fornax dwarfs, we have placed them at the redshift of the Fornax cluster and extrapolated their SFHs to obtain their expected properties up to 6 Gyr after the observation (note that the magnitudes change very little after 6 Gyr). To ensure relatively stable results, this experiment is performed only for the 121 resolved complexes that are older (in terms of 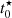 ) than 50 Myr. In Fig. 12 we show the extrapolated evolution of the r-band apparent magnitude (at the Fornax redshift) of star-forming complexes and compare it with the magnitude distribution of Fornax dwarfs. The expected magnitudes of star-forming complexes remain consistent with Fornax dwarfs at all simulated time steps, but are mostly situated in the faint end at 6 Gyr. This indicates that the remnants of star-forming complexes would stay detectable in nearby clusters such as Fornax for several billion years, possibly contributing to form a population of (dark matter free) cluster dwarf galaxies.
) than 50 Myr. In Fig. 12 we show the extrapolated evolution of the r-band apparent magnitude (at the Fornax redshift) of star-forming complexes and compare it with the magnitude distribution of Fornax dwarfs. The expected magnitudes of star-forming complexes remain consistent with Fornax dwarfs at all simulated time steps, but are mostly situated in the faint end at 6 Gyr. This indicates that the remnants of star-forming complexes would stay detectable in nearby clusters such as Fornax for several billion years, possibly contributing to form a population of (dark matter free) cluster dwarf galaxies.
 |
Fig. 12. Extrapolated r-band apparent magnitude evolution in of star-forming complexes in the next 6 Gyr, placing them at the redshift of the Fornax cluster. The solid line shows the median extrapolated magnitude in each time step and the shaded region traces the 25th and 75th percentiles. Projected histograms show the magnitude distribution for Fornax dwarfs (pink), current magnitude distribution of star-forming complexes (solid purple) and the expected distribution in 3 and 6 Gyr (dashed and dotted purple, respectively). Only complexes older than 50 Myr are included. |
6. Summary and conclusions
In this work, we have applied the BAGPIPES SED modeling code to a sample of star-forming clumps and complexes detected by Giunchi et al. (2023a) in the tails and extraplanar regions of 6 GASP jellyfish galaxies observed with HST. This allowed us to retrace their star formation histories and measure their ages, stellar masses, star formation rates and dust attenuation.
The typical (median) ⟨ t⋆ ⟩M are ∼27 Myr for Hα clumps and ∼39 Myr for F275W clumps and star-forming complexes. When masking out the clumps inside the complex and leaving only the flux of the region detected in F606W, the median ⟨ t⋆ ⟩M is 84 Myr, and in some cases these objects may include stars older than 300 Myr. This, combined with the evidence for a diversity of star formation histories in the sample, indicates that star formation can sustained for a long period of time in the tails of jellyfish galaxies.
As expected, Hα clumps also have higher star formation rates when compared to F275W clumps, and their typical SFR is very similar to the one of star-forming complexes if the low SFR tail of the distribution for complexes is excluded. Hα clumps form a well defined sequence in the stellar mass–SFR plane, with a similar slope to (but systematically above) the main sequence of star-forming galaxies. This is not always true for F275W clumps and star-forming complexes. We find that 66% of F275W clumps and 79% of star-forming complexes are within ±1 dex from a linear fit to the relation of Hα clumps, while the remainder appear to have recently ceased their star formation activity and are found below 1 dex from the relation.
The stellar masses of objects in our sample vary from ∼103.5 to ∼107.1 M⊙, with median values of 104.8 for Hα clumps, 104.7 for F275W clumps and, 107.1 for star-forming complexes. Although the stellar masses of star-forming complexes are consistent with the ones of globular clusters, their stellar mass surface densities are lower by 2 dex, which makes it unlikely that the objects studied in this paper may evolve into a population of globular clusters. On the other hand, their stellar masses and surface densities are compatible with that of dwarf galaxies. By extrapolating the star formation histories obtained with BAGPIPES for star-forming complexes, we obtain a r-band magnitude distribution that matches the one of dwarf galaxies in the Fornax cluster and show that these objects may remain detectable in nearby clusters for several billion years. Despite the tentative nature of this approach, it serves as indication that the objects formed in the tails of jellyfish galaxies may evolve into a population of dark matter free dwarf galaxies in clusters.
We observe trends of ⟨ t⋆ ⟩M and stellar mass with the distance from the center of the host galaxy. Clumps and complexes further away from the galaxy center have younger stellar populations and are less massive. This can be ascribed to the effect of ram pressure in different ISM phases, and indicates that the denser component of the molecular gas in the ISM is not able to travel out to long distances from the stellar disk before it is turned into stars, which tend to stay near the stellar disk as they are not susceptible to ram pressure. In the meantime, atomic gas continues to be stripped away until it forms new molecular clouds and ultimately lead to the young, low-mass star-forming regions found far away from the galactic disks. Clumps further away from the galaxy disk are also less attenuated by dust, and the distributions of AV are all concentrated at low (< 0.5 mag) values, except for the population of Hα clumps in extraplanar regions. This indicates that dust is not efficiently stripped to large distances from the host galaxies, or is destroyed in the process.
The difference in the mean age of the stellar populations between the complex and its youngest embedded clump scales with the distance between the clump and the center of the optical emission of the complex. Although the variation in b/a in our sample is small, it is possible to show that the most displaced clumps are hosted by the most elongated complexes. This is consistent with a fireball-like morphology, where the cumulative effect of ram pressure moves the star-forming region away from the galaxy disk, leaving behind a trail of slightly older stars. We also show that clump displacement (and age difference) is smaller for complexes that have young stellar populations overall, and that have a large fraction of their area covered by clumps. These results show how fireball-like morphologies take shape over time, allowing us to interpret the non-fireball complexes (or the ones with less prominent features) as more recently formed objects that are yet to develop their structure.
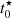 corresponds to the time spanned between t0 in Eq. (1) and the age of the universe at the observed redshift.
corresponds to the time spanned between t0 in Eq. (1) and the age of the universe at the observed redshift.
Acknowledgments
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 833824, GASP project). B.V. and M.G. also acknowledge the Italian PRIN-Miur 2017 (PI A. Cimatti). J.F. acknowledges financial support from the UNAM- DGAPA-PAPIIT IN110723 grant, México.
References
- Abramson, A., & Kenney, J. D. P. 2014, AJ, 147, 63 [Google Scholar]
- Abruzzo, M. W., Fielding, D. B., & Bryan, G. L. 2023, ApJL, submitted [arXiv:2307.03228] [Google Scholar]
- Asencio, E., Banik, I., Mieske, S., et al. 2022, MNRAS, 515, 2981 [CrossRef] [Google Scholar]
- Bacchini, C., Mingozzi, M., Poggianti, B. M., et al. 2023, ApJ, 950, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2010, in Ground-based and Airborne Instrumentation for Astronomy III, eds. I. S. McLean, S. K. Ramsay, & H. Takami, SPIE Conf. Ser., 7735, 773508 [Google Scholar]
- Bekki, K. 2014, MNRAS, 438, 444 [Google Scholar]
- Bellhouse, C., Jaffé, Y. L., McGee, S. L., et al. 2019, MNRAS, 485, 1157 [Google Scholar]
- Boselli, A., Fossati, M., & Sun, M. 2022, A&ARv, 30, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [Google Scholar]
- Brodie, J. P., Romanowsky, A. J., Strader, J., & Forbes, D. A. 2011, AJ, 142, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Lee, J. C., Sabbi, E., et al. 2015, AJ, 149, 51 [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Carnall, A. C., McLure, R. J., Dunlop, J. S., & Davé, R. 2018, MNRAS, 480, 4379 [Google Scholar]
- Carnall, A. C., Leja, J., Johnson, B. D., et al. 2019, ApJ, 873, 44 [Google Scholar]
- Charlot, S., & Fall, S. M. 2000, ApJ, 539, 718 [Google Scholar]
- Cid Fernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [Google Scholar]
- Cortese, L., Marcillac, D., Richard, J., et al. 2007, MNRAS, 376, 157 [Google Scholar]
- Cramer, W. J., Kenney, J. D. P., Sun, M., et al. 2019, ApJ, 870, 63 [Google Scholar]
- da Silva, R. L., Fumagalli, M., & Krumholz, M. 2012, ApJ, 745, 145 [CrossRef] [Google Scholar]
- Draine, B. T., & Salpeter, E. E. 1979, ApJ, 231, 438 [Google Scholar]
- Eftekhari, F. S., Peletier, R. F., Scott, N., et al. 2022, MNRAS, 517, 4714 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Elmegreen, D. M., Chandar, R., Whitmore, B., & Regan, M. 2006, ApJ, 644, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mex. Astron. Astrofis., 53, 385 [NASA ADS] [Google Scholar]
- Forbes, D. A., Pota, V., Usher, C., et al. 2013, MNRAS, 435, L6 [Google Scholar]
- Franchetto, A., Vulcani, B., Poggianti, B. M., et al. 2020, ApJ, 895, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, J., Moretti, A., Gullieuszik, M., et al. 2017, ApJ, 848, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Fumagalli, M., Gavazzi, G., Scaramella, R., & Franzetti, P. 2011, A&A, 528, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- George, K., Poggianti, B. M., Gullieuszik, M., et al. 2018, MNRAS, 479, 4126 [Google Scholar]
- George, K., Poggianti, B. M., Tomičić, N., et al. 2023, MNRAS, 519, 2426 [Google Scholar]
- Giunchi, E., Gullieuszik, M., Poggianti, B. M., et al. 2023a, ApJ, 949, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Giunchi, E., Poggianti, B. M., Gullieuszik, M., et al. 2023b, ApJ, 958, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Gouliermis, D. A., Thilker, D., Elmegreen, B. G., et al. 2015, MNRAS, 452, 3508 [NASA ADS] [CrossRef] [Google Scholar]
- Gouliermis, D. A., Elmegreen, B. G., Elmegreen, D. M., et al. 2017, MNRAS, 468, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Grasha, K., Calzetti, D., Adamo, A., et al. 2017a, ApJ, 840, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Grasha, K., Elmegreen, B. G., Calzetti, D., et al. 2017b, ApJ, 842, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Gullieuszik, M., Poggianti, B. M., McGee, S. L., et al. 2020, ApJ, 899, 13 [Google Scholar]
- Gullieuszik, M., Giunchi, E., Poggianti, B. M., et al. 2023, ApJ, 945, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Gott, J., & Richard, I. 1972, ApJ, 176, 1 [Google Scholar]
- Gutiérrez, C. M., & López-Corredoira, M. 2017, ApJ, 835, 111 [CrossRef] [Google Scholar]
- Jáchym, P., Sun, M., Kenney, J. D. P., et al. 2017, ApJ, 839, 114 [Google Scholar]
- Jáchym, P., Kenney, J. D. P., Sun, M., et al. 2019, ApJ, 883, 145 [Google Scholar]
- Kapferer, W., Sluka, C., Schindler, S., Ferrari, C., & Ziegler, B. 2009, A&A, 499, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kenney, J. D. P., Geha, M., Jáchym, P., et al. 2014, ApJ, 780, 119 [Google Scholar]
- Kenney, J. D. P., Abramson, A., & Bravo-Alfaro, H. 2015, AJ, 150, 59 [Google Scholar]
- Kennicutt, R. C., Jr 1989, ApJ, 344, 685 [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr 1998, ARA&A, 36, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Laudari, S., Jáchym, P., Sun, M., et al. 2022, MNRAS, 509, 3938 [Google Scholar]
- Mandelker, N., Dekel, A., Ceverino, D., et al. 2017, MNRAS, 464, 635 [NASA ADS] [CrossRef] [Google Scholar]
- McConnachie, A. W. 2012, AJ, 144, 4 [Google Scholar]
- Mehta, V., Scarlata, C., Fortson, L., et al. 2021, ApJ, 912, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Mieske, S., Frank, M. J., Baumgardt, H., et al. 2013, A&A, 558, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Misgeld, I., & Hilker, M. 2011, MNRAS, 414, 3699 [Google Scholar]
- Moretti, A., Paladino, R., Poggianti, B. M., et al. 2020, ApJ, 889, 9 [Google Scholar]
- Norris, M. A., & Kannappan, S. J. 2011, MNRAS, 414, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, M. A., Gebhardt, K., Sharples, R. M., et al. 2012, MNRAS, 421, 1485 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, M. A., Kannappan, S. J., Forbes, D. A., et al. 2014, MNRAS, 443, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., Jaffé, Y. L., Moretti, A., et al. 2017, Nature, 548, 304 [Google Scholar]
- Poggianti, B. M., Gullieuszik, M., Tonnesen, S., et al. 2019a, MNRAS, 482, 4466 [Google Scholar]
- Poggianti, B. M., Ignesti, A., Gitti, M., et al. 2019b, ApJ, 887, 155 [Google Scholar]
- Renzini, A., & Peng, Y.-J. 2015, ApJ, 801, L29 [Google Scholar]
- Roberts, I. D., van Weeren, R. J., McGee, S. L., et al. 2021, A&A, 650, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rohr, E., Pillepich, A., Nelson, D., et al. 2023, MNRAS, 524, 3502 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E., Leroy, A., Blanc, G., et al. 2019, The Messenger, 177, 36 [NASA ADS] [Google Scholar]
- Steinhauser, D., Schindler, S., & Springel, V. 2016, A&A, 591, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strader, J., Caldwell, N., & Seth, A. C. 2011, AJ, 142, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, E. N., Hopkins, A. M., Baldry, I. K., et al. 2011, MNRAS, 418, 1587 [Google Scholar]
- Tollerud, E. J., Beaton, R. L., Geha, M. C., et al. 2012, ApJ, 752, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Tollerud, E. J., Geha, M. C., Vargas, L. C., & Bullock, J. S. 2013, ApJ, 768, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Tomičić, N., Vulcani, B., Poggianti, B. M., et al. 2021, ApJ, 922, 131 [CrossRef] [Google Scholar]
- Tonnesen, S., & Bryan, G. L. 2012, MNRAS, 422, 1609 [CrossRef] [Google Scholar]
- Venhola, A., Peletier, R., Laurikainen, E., et al. 2018, A&A, 620, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venhola, A., Peletier, R. F., Salo, H., et al. 2022, A&AS, 662, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vogelsberger, M., McKinnon, R., O’Neil, S., et al. 2019, MNRAS, 487, 4870 [NASA ADS] [CrossRef] [Google Scholar]
- Vulcani, B., Poggianti, B. M., Tonnesen, S., et al. 2020, ApJ, 899, 98 [Google Scholar]
- Waldron, W., Sun, M., Luo, R., et al. 2023, MNRAS, 522, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2009, ApJ, 704, 1274 [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., Jr, et al. 2000, AJ, 120, 1579 [Google Scholar]
- Yoshida, M., Yagi, M., Komiyama, Y., et al. 2008, ApJ, 688, 918 [Google Scholar]
- Zanella, A., Daddi, E., Le Floc’h, E., et al. 2015, Nature, 521, 54 [Google Scholar]
- Zanella, A., Le Floc’h, E., Harrison, C. M., et al. 2019, MNRAS, 489, 2792 [Google Scholar]
Appendix A: Covarainces between derived parameters
Fig. A.1 shows corner plots of the main parameters analyzed in this paper for the three example fits shown in Fig. 1. As expected, there is covariance between the PDFs of parameters derived from the star formation history, such as age, stellar mass and star formation rate. However, this covariance is restricted to very small ranges of values and does not diminish the reliability of the method.
 |
Fig. A.1. Corner plots showing 2D projections of the fitted parameter space for the three example fits shown in Fig. 1. The Hα clump in the top left, the F275W clump in the top right, and the star-forming complex at the bottom are color-coded as in Fig. 1. We include the four main variables used in our analysis: ⟨ t⋆ ⟩M, log M⋆, log SFR, and AV. |
Appendix B: Examples of fits rejected in the quality control
In section 3.2 we have presented two quality control criteria that were used to remove objects with unsatisfactory fits from our sample. These are: (a) the median of the model flux PDF is outside of the error bars of the observations in two or more filters; or (b) the interquartile range of the model flux PDF is fully outside of the error bars of the observation (i.e more than 50% of the generated models are outside error bars) in one or more filters.
In Fig. B.1, we provide examples of F275W clumps in JO201 that were rejected according one of the quality control criteria, and also of a fit considered good (although not perfect). Note that the criteria are somewhat intertwined, and work together to establish some degree of tolerance. If one of the median model fluxes is outside error bars but the interquartile range still intersects with the error bar and all others filters are well fitted, the fit is accepted; this case is exemplified in the top panel of Fig. B.1. In the examples, the filters that lead the object to fail the quality control are the two bluest ones, which is the most common case.
 |
Fig. B.1. Examples of BAGPIPES fits accepted (top) and rejected according to quality control criteria a and b (middle and bottom, see text for details). Black points with errorbars show observed photometric fluxes in the five HST bands used in this work. Blue lines show the median of all models generated in the fit, and the shaded regions indicate interquartile ranges. Rectangles show the interquartile ranges of the modeled photometric fluxes, with horizontal lines indicating their median. |
Appendix C: Trends (or lack thereof) of properties with galactocentric distance for individual galaxies
In section 4.3, we have explored trends of the properties derived in this work with the distance from the clumps and complexes to the center of the host galaxy. For reference, we show the same trends for individual galaxies in Fig. C.1.
 |
Fig. C.1. ⟨ t⋆ ⟩M, log M⋆, SFR, and AV of clumps and complexes plotted against the normalized log distance log d/Re to the center of the host galaxy. Each column of panels corresponds to a different galaxy. Top panels show data for Hα clumps (gold), middle panels show F275W clumps (pink) and bottom panels show star-forming complexes (purple). Black dashed lines show linear fits to the relations. For SFR and AV we use the same selection as in Fig. 6. |
All Tables
Number of objects in each galaxy (and in total) that are included in our final sample.
All Figures
 |
Fig. 1. Examples of BAGPIPES fits for clumps selected from Hα, F275W, and F606W images. On the left: F275W image of a region in the tail of JO201; regions in golden yellow, pink and purple indicate an Hα clump, a UV clump and a star-forming complex, respectively. On the right: Examples of BAGPIPES fits to the photometry of the regions indicated on the image to the left; shaded region corresponds to the full range of the model spectra PDF and are plotted with the same color as the corresponding region in the image; black points with errorbars (generally too small to be seen) indicate the observed photometric fluxes in the five HST bands used in this work. Rectangles show the region between the 1% and 99% percentiles of the photometric fluxes fitted by BAGPIPES. Inset plots in the right panels show the posterior PDFs of mass-weighted ages (⟨t⋆⟩), stellar masses (log M⋆/M⊙), SFRs, and AV derived for each object. |
| In the text | |
 |
Fig. 2. Early and late decliners and their observed properties. Top: Histograms tracing the distributions of the SFH decay proxy |
| In the text | |
 |
Fig. 3. Distributions of (from top to bottom) mass-weighted ages, stellar masses, SFRs, and dust attenuation of clumps detected in Hα (in gold) and F275W (in dark pink), and star-forming complexes (in purple). We limit the histograms to the 95th percentiles of ⟨ t⋆⟩M and AV, and to the 15th percentile of SFR. These percentiles are calculated for the combined (all clumps and complexes) samples and the ranges are kept the same in all histograms of the same variable. Left panels show the general samples, tail clumps and complexes are in the middle panels and extraplanar clumps are on the right. Histograms are normalized to have the same area. |
| In the text | |
 |
Fig. 4. Box plots showing galaxy-to-galaxy variations of the distributions shown in Fig. 3. As before, clumps detected in Hα and F275W are shown in gold and in dark pink, respectively, and star-forming complexes are shown in purple. Boxes span the interquartile regions, horizontal lines in the boxes indicate the median and whiskers mark the 15% and 85% percentiles of the distributions. |
| In the text | |
 |
Fig. 5. Stellar mass–SFR relation for clumps and complexes in our sample. Panels from top to bottom show the relations for Hα clumps, F275W clumps and star-forming complexes, respectively. Points are colored according to ⟨ t⋆ ⟩M, truncating at 10 Myr and 150 Myr, clumps containing only stars younger than 10 Myr form a relation by definition and are shown as white circles. The gray band indicates a ±1 dex range around a linear fit to the Hα relation, the dashed line shows a fit to the relation for star-forming galaxies in the Sloan Digital Sky Survey from Renzini & Peng (2015). For F275W clumps and star-forming complexes we set the lower limit of the y-axis to the 1% percentile of the SFR distribution. |
| In the text | |
 |
Fig. 6. Trends (or lack thereof) of the measured properties with galactocentric distance. ⟨ t⋆ ⟩M (top), log M⋆ (second row), SFR (third row) and AV (bottom) of clumps and complexes are plotted against the normalized log distance log d/Re to the center of the host galaxy. The different panels show clumps selected from Hα (left) and F275W (middle), as well as star-forming complexes (right). Black points trace the median values of physical properties in bins of log d/Re and vertical lines indicate interquartile regions, points are plotted in the center of each bin. In the third row of panels, only objects within ±1 dex of the sequence shown in Fig. 5 are included as points, histograms show the distribution of objects below (dashed line) and within (solid line) ±1 dex of the sequence. In the bottom row we show only objects that formed a significant fraction of their stellar mass in the past 20 Myr (classified as late decliners in Sect. 3.3). |
| In the text | |
 |
Fig. 7. Box plots tracing the distribution of the age of the oldest stars in star-forming complexes. Boxes span the interquartile regions, horizontal lines in the boxes indicate the median and whiskers mark the 1% and 99% percentiles of the distributions. |
| In the text | |
 |
Fig. 8. Axial ratio (b/a) against stellar mass (top) and ⟨ t⋆ ⟩M (bottom) for Hα clumps (gold), F275W clumps (pink), and star-forming complexes (purple). Median lines are color-coded as the points and error bars represent interquartile regions for each b/a bin. |
| In the text | |
 |
Fig. 9. Clump displacement as a function of the difference between the log ⟨ t⋆ ⟩M of a star-forming complex and the one of the youngest Hα (left) and F275W (right) clump embedded in it. Color indicates the fraction of the star-forming complex that is covered by optical-only emission, and the size of the points is proportional to the radius of the complex. Squares indicate the median position of the 20% most elongated (black) and the 20% least elongated (white) complexes, with error bars showing the interquartile regions of the distributions. |
| In the text | |
 |
Fig. 10. log⟨ t⋆ ⟩M of star-forming complexes against log⟨ t⋆ ⟩M of the youngest Hα (golden) and F275W (pink) clumps inside them. An y = x function is represented by a dashed black line. Solid lines color-coded as the points are linear fits to the relation for the two subsamples of clumps. |
| In the text | |
 |
Fig. 11. log M⋆ – log ΣM⋆ relation for star-forming complexes (purple). Dashed line traces the 5% percentile of log ΣM⋆ for globular clusters and ultra-compact dwarfs. Red and black contours trace the distributions of local dwarf spheroidals from Norris et al. (2014) Fornax dwarf galaxies from Venhola et al. (2018, 2022). |
| In the text | |
 |
Fig. 12. Extrapolated r-band apparent magnitude evolution in of star-forming complexes in the next 6 Gyr, placing them at the redshift of the Fornax cluster. The solid line shows the median extrapolated magnitude in each time step and the shaded region traces the 25th and 75th percentiles. Projected histograms show the magnitude distribution for Fornax dwarfs (pink), current magnitude distribution of star-forming complexes (solid purple) and the expected distribution in 3 and 6 Gyr (dashed and dotted purple, respectively). Only complexes older than 50 Myr are included. |
| In the text | |
 |
Fig. A.1. Corner plots showing 2D projections of the fitted parameter space for the three example fits shown in Fig. 1. The Hα clump in the top left, the F275W clump in the top right, and the star-forming complex at the bottom are color-coded as in Fig. 1. We include the four main variables used in our analysis: ⟨ t⋆ ⟩M, log M⋆, log SFR, and AV. |
| In the text | |
 |
Fig. B.1. Examples of BAGPIPES fits accepted (top) and rejected according to quality control criteria a and b (middle and bottom, see text for details). Black points with errorbars show observed photometric fluxes in the five HST bands used in this work. Blue lines show the median of all models generated in the fit, and the shaded regions indicate interquartile ranges. Rectangles show the interquartile ranges of the modeled photometric fluxes, with horizontal lines indicating their median. |
| In the text | |
 |
Fig. C.1. ⟨ t⋆ ⟩M, log M⋆, SFR, and AV of clumps and complexes plotted against the normalized log distance log d/Re to the center of the host galaxy. Each column of panels corresponds to a different galaxy. Top panels show data for Hα clumps (gold), middle panels show F275W clumps (pink) and bottom panels show star-forming complexes (purple). Black dashed lines show linear fits to the relations. For SFR and AV we use the same selection as in Fig. 6. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.