| Issue |
A&A
Volume 646, February 2021
|
|
|---|---|---|
| Article Number | A108 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202038877 | |
| Published online | 16 February 2021 | |
Down-the-barrel observations of a multi-phase quasar outflow at high redshift
VLT/X-shooter spectroscopy of the proximate molecular absorber at z = 2.631 towards SDSS J001514+184212⋆
1
Institut d’Astrophysique de Paris, CNRS-SU, UMR 7095, 98bis bd Arago, 75014 Paris, France
e-mail: noterdaeme@iap.fr
2
Ioffe Institute, Polyteknicheskaya 26, 194021 Saint-Petersburg, Russia
3
Institute of Theoretical Astrophysics, University of Oslo, PO Box 1029 Blindern, 0315 Oslo, Norway
4
Cosmic Dawn Center (DAWN), University of Copenhagen, Jagtvej 128, 2200 Copenhagen N, Denmark
5
Inter-University Centre for Astronomy and Astrophysics, Pune University Campus, Ganeshkhind, Pune 411007, India
6
Niels Bohr Institute, University of Copenhagen, Jagtvej 128, 2200 Copenhagen N, Denmark
Received:
8
July
2020
Accepted:
3
December
2020
We present ultraviolet to near infrared spectroscopic observations of the quasar SDSS J001514+184212 and its proximate molecular absorber at z = 2.631. The [O III] emission line of the quasar is composed of a broad (FWHM ∼ 1600 km s−1), spatially unresolved component, blueshifted by about 600 km s−1 from a narrow, spatially-resolved component (FWHM ∼ 650 km s−1). The wide, blueshifted, unresolved component is consistent with the presence of outflowing gas in the nuclear region. The narrow component can be further decomposed into a blue and a red blob with a velocity width of several hundred km s−1 each, seen ∼5 pkpc on opposite spatial locations from the nuclear continuum emission, indicating outflows on galactic scales. The presence of ionised gas on kpc scales is also seen from a weak C IV emission component, detected in the trough of a saturated C IV absorption that removes the strong nuclear emission from the quasar. Towards the nuclear emission, we observe absorption lines from atomic species in various ionisation and excitation stages and confirm the presence of strong H2 lines originally detected in the SDSS spectrum. The overall absorption profile is very wide, spread over ∼600 km s−1, and it roughly matches the velocities of the narrow blue [O III] blob. From a detailed investigation of the chemical and physical conditions in the absorbing gas, we infer densities of about nH ∼ 104 − 105 cm−3 in the cold (T ∼ 100 K) H2-bearing gas, which we find to be located at ∼10 kpc distances from the central UV source. We conjecture that we are witnessing different manifestations of a same AGN-driven multi-phase outflow, where approaching gas is intercepted by the line of sight to the nucleus. We corroborate this picture by modelling the scattering of Ly-α photons from the central source through the outflowing gas, reproducing the peculiar Ly-α absorption-emission profile, with a damped Ly-α absorption in which red-peaked, spatially offset, and extended Ly-α emission is seen. Our observations open up a new way to investigate quasar outflows at high redshift and shed light on the complex issue of AGN feedback.
Key words: quasars: emission lines / quasars: absorption lines / quasars: individual: SDSS J001514.82+184212.34
© P. Noterdaeme et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Feedback from active galactic nuclei (AGN) is an essential element in modern models of galaxy formation and evolution (e.g., Silk & Rees 1998). It may quench star formation (e.g., Zubovas & King 2012; Pontzen et al. 2017; Terrazas et al. 2020), impact galaxy morphology (Dubois et al. 2016), regulate the growth of the supermassive black holes (Volonteri et al. 2016), and so on. It may also have positive feedback on star formation through compression of the gas (e.g., Zubovas et al. 2013; Richings & Faucher-Giguère 2018). The most supportive evidence for AGN feedback is the presence of kiloparsec-scale outflows, which result from the propagation of energy and momentum from accretion disc winds to the host galaxy interstellar medium (e.g., Fabian 2012; Costa et al. 2015). At low and intermediate redshifts, such outflows have been observed in ionised and molecular phases, with many studies focusing on Type 2 quasars, where the obscuration of the nuclear emission facilitates the observations (e.g., Sun et al. 2017). Outflows have also been observed in unobscured, luminous AGN (Type 1 quasars), but mostly at low redshift, such as the well-known Mrk 231 at z = 0.04 (Rupke & Veilleux 2011; Feruglio et al. 2015). Naturally, observational constraints on hot and cold outflows in high-redshift Type 1 quasars are much harder to obtain, not only because of the dimming of the light, but also because the coarser angular resolution impedes observations close to the bright nucleus.
In turn, the cosmological distances and high luminosity of the nuclear emission of high-z quasars make them excellent background sources against which gas in any phase can be studied in absorption. This includes not only gas at any place along the line of sight (from the intergalactic medium, giving rise to the Ly-α forest or closer to intervening galaxies, producing damped Ly-α systems (DLAs) in the quasar spectrum), but also gas close to the supermassive black hole, in the quasar host galaxy or in galaxies belonging to the quasar group environment. While broad absorption lines have long been associated with gas flows close to the central engine (e.g., Weymann et al. 1991; Arav et al. 2018), large-scale outflows, when intercepted by the line of sight to the nucleus, should also produce a detectable signature in absorption.
Absorption spectroscopy has proven to provide very detailed information about the kinematics, chemical composition, and physical conditions in the absorbing gas, in particular when molecules are detected. Indeed, the formation, survival, and excitation of molecules is very sensitive to the prevailing physical conditions, such as abundance of dust, temperature, density, and ambient UV field (e.g., Reimers et al. 2003; Srianand et al. 2005; Cui et al. 2005; Guillard et al. 2009; Balashev et al. 2017; Wakelam et al. 2017, among many others).
Combining information from both emission and absorption line measurements could hence provide us with a fresh view of quasar outflows and feedback at high redshift. We recently embarked on a search for damped molecular hydrogen (H2) absorption lines at the quasar redshift in low-resolution spectra from the Sloan Digital Sky Survey (SDSS) III (BOSS) Data Release 14. Through this targeted search, we discovered a population of strong proximate H2 absorption systems at z > 2.5 with log N(H2) > 19 (Noterdaeme et al. 2019). Detailed follow-up observations are currently on-going using the multi-wavelength spectrograph X-shooter on the Very Large Telescope (VLT).
In this paper, we report on the observations of the first object in our sample, the quasar SDSS J001514.82+184212.34 (hereafter J0015+1842) at z = 2.63. We interpret the observations as evidence of kilo-parsec scale, multi-phase, biconical outflows that are mainly orientated along the line of sight and also probed in absorption against the nucleus. We present the observations and data reduction in Sect. 2, the analysis of spatially-resolved emission lines in Sect. 3, and that of absorption lines and dust extinction towards the nucleus in Sect. 4. We discuss our results in Sect. 5, along with the derivation of the chemical and physical conditions in the absorbing clouds and the modelling of leaking Ly-α emission. We summarise our findings in Sect. 6. Throughout this paper, we assume a flat ΛCDM cosmology with H0 = 68 km s−1 Mpc−1, ΩΛ = 0.69, and Ωm = 0.31 (Planck Collaboration XIII 2016).
2. Observations and data reduction
J0015+1842 was observed in stare mode with the X-shooter spectrograph at the VLT at the Paranal Observatory in Chile between July and September 2019. The log of observations is provided in Table 1.
Log of observations and atmospheric parameters.
The X-shooter spectrograph simultaneously covers the wavelength range from 0.3 to 2.5 μm in three separate spectrographs, which are the so-called arms: UVB ranging from 0.3 to 0.6 μm; VIS ranging from 0.6 to 1.0 μm; and NIR ranging from 1.0 to 2.5 μm. For all observations, slit widths of 1.0, 0.9, and 1.2 arcsec were used for the UVB, VIS, and NIR arms, respectively. The slit was aligned to the parallactic angle at the start to minimise slit losses of the exposure, and it was kept fixed on sky during the ∼1 h long exposure (see Fig. 1). The observation from August 30 failed due to an error in the atmospheric dispersion corrector (ADC), and exposures from this date were therefore not included in the analysis. For one other observation (July 29), we noted a strong chromatic suppression of flux in the UVB arm1, hence the UVB spectrum from this observation has been discarded from our analysis. As the loss of flux in the VIS and NIR arms is much less severe, we used these spectra in our analysis but weighted them appropriately (using the inverse variance) when combining the individual spectra.
 |
Fig. 1. Layout of 1.2″-wide X-shooter slits in the NIR. The small dotted circle represents a projected area of radius 5 kpc (at the redshift of the quasar) with 100% coverage by all our X-shooter slit positions, and the larger dashed circle represents the BOSS fibre aperture. |
The raw spectra were processed using the official esorex pipeline for X-shooter version 2.6.8. Before passing the raw spectra through the pipeline, we corrected cosmic ray hits using the code ASTROSCRAPPY (McCully et al. 2018), which is a Python implementation of the algorithm by van Dokkum (2001). The pipeline then performed subtraction of bias and dark levels on the CCD, spectral flat fielding, tracing of the curved echelle orders, and computation of the wavelength solution. The individual curved 2D orders were then rectified onto a straightened grid. The sky background was subsequently subtracted before the individual orders were combined. The full spectrum was flux-calibrated using a sensitivity function calculated for each observation using a spectroscopic standard star observed during the same night. The three spectra (UVB, VIS, NIR) were stitched together in the overlapping regions, correcting for any small offsets between the absolute flux calibration of the individual arms. Lastly, in order to correct for possible slit loss, we scaled the calibrated spectra to match the SDSS i band photometry. Because of the possible variation of the quasar brightness between the time of observation for the SDSS photometry and our data, the absolute flux calibration has a systematic uncertainty of order 20%, which corresponds to the typical long-term variability of quasars (Hook et al. 1994).
From the 2D spectra produced by the pipeline, we performed an optimal extraction (Horne 1986) to obtain 1D spectra. The 1D and 2D spectra were subsequently corrected to vacuum wavelengths and shifted to the heliocentric reference frame before being corrected for Galactic extinction using the maps by Schlafly & Finkbeiner (2011). Lastly, we combined the individual observations for each arm into final 1D spectra using a weighted mean.
Telluric correction. The NIR spectra were corrected for telluric absorption using the software tool molecfit (Smette et al. 2015; Kausch et al. 2015). The code fits a synthetic absorption profile to the telluric absorption features in the data. For the NIR spectra, the dominant molecular species giving strong telluric absorption lines are H2O and CO2. The relative abundances of these two species were fitted together with a fifth-order polynomial model for the intrinsic spectrum in order to reproduce the shape of the wings of the quasar emission lines. We fitted the telluric model using seven narrow bands of the spectra dominated by telluric absorption features only. These seven regions were chosen to encompass regions of interest, that is, the regions around the quasar emission lines from oxygen. The wavelength intervals used were as follows: 1.13–1.14, 1.37–1.39, 1.44–1.45, 1.75–1.76, 1.82–1.83, 1.94–1.97, and 2.02–2.03 μm. For each region, we iteratively masked out pixels affected by skyline residuals or bad pixels. The optimal parameters for each spectrum are given in Table 1. The optimised telluric absorption model for each spectrum was then used to correct the corresponding 1D and 2D spectra.
3. Emission line analysis
We analysed the 1D and 2D together spectra to extract information about the spatial and spectral properties of the various emission lines of interest. In addition to the 1D spectrum obtained through the optimal extraction method, which mostly samples the unresolved nuclear emission (due to the weighting profile), we also constructed a total 1D NIR spectrum directly extracted from the combined 2D data over a wider spatial range of ±9 pixels (or equivalently 1.9 arcsec) around the quasar trace without weighting. This is specifically constructed for the analysis of spatially extended emission lines such as [O III]. In summary, we therefore consider three kinds of 1D spectra in the following: (i) the on-trace spectrum, which is obtained from the trace by optimal extraction; (ii) the overall spectrum, which is extracted within wide spatial range; and (iii) the off-trace spectrum, which is the difference between the two others.
3.1. [O II]
The [O II]λλ3727, 3729 doublet is redshifted into a strong telluric band and not directly visible in the original data. However, applying the telluric correction described in Sect. 2 allowed us to recover the lines, which, given their large velocity width, are strongly blended and appear as a single line in Fig. 2. To estimate the intrinsic line width we fitted the [O II] doublet using the sum of two Gaussians plus a linear continuum in that region. The relative positions of the Gaussians were kept fixed to the doublet wavelength ratio, and their widths were forced to be the same. In principle, the amplitude ratio for the [O II] doublet can vary between 0.35 and 1.5, depending on the kinetic temperature of the gas and the electron density (e.g., Kisielius et al. 2009). However, because this region of the spectrum is quite noisy, we assumed a fixed ratio of 1.3. This assumption has almost no influence on the total line flux and width. The obtained parameters are given in Table 2. We measured the [O II] emission redshift to be z = 2.631.
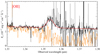 |
Fig. 2. Portion of combined 1D NIR spectrum around the [O II] doublet emission line. The 1D spectrum with (without) telluric correction is shown in black (orange) together with the fitted profile in red. |
Emission line parameters.
3.2. [O III] and H β
We analysed the H β and [O III]λλ4960,5008 lines simultaneously, since these lines are located in the same region from 1.74 to 1.84 μm. Both the Hβ and the [O III] profiles are found to be non-Gaussian and spread over about 2000 km s−1. The forbidden [O III]λλ4960, 5008 emission lines are clearly asymmetric, and composed of a broad and ‘narrow’ component separated by about 600 km s−1. We found that the overall Hβ+[O III] complex can be well modelled by the sum of a smooth continuum component (green line in Fig. 3) and six Gaussian profiles, two for each spectral line (purple and brown for Hβ; orange and blue for the [O III] doublet). Because [O III] lines can only be deexcited radiatively and since their upper energy levels are only slightly different, the [O III] line ratio remains constant. Therefore, to fit these lines we tied the redshifts and line widths for the two [O III] lines and imposed their amplitude to follow the theoretical 1:3 ratio (e.g., Storey & Zeippen 2000; Dimitrijević et al. 2007). Since the narrow [O III] component is spatially resolved (see Sect. 3.4), we considered the overall 1D spectrum instead of the on-trace spectrum when fitting this line. We also used the off-trace spectrum to obtain an initial guess for the parameters of the narrow component free from contamination by the broad nuclear component (top panel of Fig. 3). We then fitted the overall spectral profile relaxing all parameters and rejecting deviating pixels iteratively. The corresponding line parameters are given in Table 2.
 |
Fig. 3. Portion of combined 1D NIR spectrum around Hβ and [O III] emission lines. Top panel: contribution from the off-trace spatially extended emission, which is apparent in both [O III] lines. Bottom panel: spectrum collapsed over its full spatial extent at wavelengths 1.790 < λ(μm) < 1.825 and the optimal extraction elsewhere, for presentation purposes. The green line shows our estimate of featureless continuum emission. Individual Gaussians constrained during the fit are shown in different colours, with the total fitted profile shown in red. |
The peak of the narrow [O III] emission provides us with an estimate of the quasar host’s systemic redshift, which also matches that obtained from [O II]. Given the associated uncertainty of about 100 km s−1, we rounded the value to z = 2.631, which we take as a convenient reference redshift to define the zero point of our velocity scale throughout this work.
3.3. C IV emission
The region of 1D spectrum around the C IV emission line is shown in Fig. 4. Strong absorption from the proximate DLA (PDLA) is observed in the red wing of the emission line. We fitted the emission line using the sum of two Gaussians plus a linear continuum in that region, excluding the region affected by absorption. The C IV emission peaks at ∼5611 Å, while the C IV absorption is centred at ∼5625 Å. Furthermore, the C IV emission is shifted by about 700 km s−1 bluewards of the systemic redshift but matches the location of the broad [O III] component well. Interestingly, while the shape and strength of the C IV absorption profile indicate strong saturation, a residual emission is seen in the trough, with a possible peak at the systemic velocity. Even though the value for each pixel remains relatively close to the noise level, the residual emission is consistently seen above zero for almost all pixels, with integrated flux Fresi ∼ (1.3 ± 0.1) × 10−17 erg s−1 cm−2, that is, 13σ significance. In principle, we cannot rule out that this is due to the absorption profile being composed of a blend of many narrow unsaturated components. We note, however, that reproducing the sharp edges and the width of the profile while keeping the non-zero absorption in the centre is very difficult, even more so with the condition that the C IV column density be bounded by the metallicity. A more likely explanation is that the C IV emission is not fully covered by the C IV absorbing gas. This is corroborated by the spatial extent of the residual emission, which is discussed in the following sub-section.
 |
Fig. 4. Bottom: portion of 1D X-shooter spectrum around the C IV emission line, median-smoothed using a 5-pixel sliding window for presentation purposes (black, with 1σ error level in green). The inset shows an unsmoothed zoom-in on the C IV absorption, with the blue region highlighting the residual emission. The best-fit model is shown by the red solid line and the individual Gaussians as red dotted lines. The downwards arrow indicates the systemic redshift. Top: 2D spectrum in the region featuring the C IV absorption line as well as residual C IV emission in the trough. |
3.4. Spatial extent of line-emitting regions
The spatial profiles of the [O II], [O III], Hβ and C IV emission lines are compared to that of the continuum in Fig. 5. These were obtained by collapsing the combined 2D spectrum along the wavelength axis around each line, while rejecting outlying pixels (due to telluric residuals or bad pixels). The regions for collapsing the data were chosen as follows. For [O II] and Hβ, we collapsed the data in a region centred at the peak of each line using a width matching the measured FWHM. Since the [O III] profile is very asymmetric, we considered two regions representative of the broad and narrow components separately. To investigate the spatial profile around the narrow [O III] component, we again used a region centred at the peak position within one FWHM. However, to assess whether the photons from the broad component come from compact (unresolved) or spatially extended regions, we restricted the region to 1.805−1.815 μm. This avoids contamination by the narrow component. In the case of C IV, we collapsed the data over the 5580−5650 Å region, which roughly corresponds to the FWHM centred at the line peak. We also collapsed the data in the 5619−5628 Å region, corresponding to the region of the C IV absorption trough where some residual emission is seen (Fig. 4).
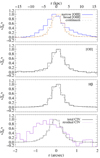 |
Fig. 5. Average observed spatial profiles at the location of different emission lines. In each panel, the dashed curve shows the spatial point spread function obtained from the quasar continuum in a nearby region. We note that the profile around the narrow [O III] emission still contains a contribution from the continuum and the broad [O III] emission. For the sake of easy comparison, each profile is normalised by its maximum value. |
We found that the spatial profiles of [O II], H β the broad [O III], and the overall C IV emission are unresolved, perfectly matching the spatial profile of the continuum and hence mostly originating from the nuclear region. In turn, the narrow [O III] line is significantly extended, over several kpc, on both sides of the trace of the continuum. The C IV absorption trough acts like a natural coronagraph, removing the bright quasar glow at these wavelengths. This provides easier access to extended but fainter C IV emission. While it is hard to appreciate the spatial profile of the residual (weak) C IV emission from the 2D data (top panel of Fig. 4), when collapsing along the wavelength axis, and albeit still noisy, this profile clearly presents a spatial kpc-scale extension below the trace.
In order to further characterise the extension of the narrow [O III] emission line, we show the individual 2D spectra in Fig. 6, with and without subtraction of the smooth continuum and broad emission. The extended narrow [O III] emission appears as blobs both above and below the quasar trace, with very similar locations and extents for all position angles (PA). This is not very surprising given the small differences in PAs (due to the observations always being taken with the slit aligned to parallactic angle; see Fig. 1). However, we noticed that the observed fluxes are higher for PA = +177 deg and PA = −164 deg than for the other position angles. This suggests that slit losses could be at play for PA = 155 deg and +166 deg, and hence the extended emission is oriented close to the north-south direction.
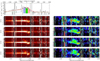 |
Fig. 6. Individual 2D spectra around the [O III]λ5008 region (from top to bottom: PA = −155 deg, −164 deg, +177 deg, and +166 deg east of north, i.e. in these figures, north is down and south is up). The total observed emission is shown in the left panels, while the unresolved emission (continuum+broad component) has been subtracted in the right panels to better highlight the spatially-extended narrow [O III] emission alone. Each panel is 4000 km s−1 wide. The main skyline residuals are masked out by a white hashed grid. Top-left panel: total extracted 1D spectrum, with the corresponding Gaussian fits. The coloured regions show the velocity bins used in Fig. 7. |
In Fig. 7, we show the average spatial profile in three velocity bins around our reference redshift (v (km s−1) = [−300, −100]; [−100, +100]; [+100, +300]) after removing the unresolved continuum+broad [O III] emission. The centroids of the both blue and red blobs are at projected distances ∼4−6 pkpc from the nuclear emission. In addition, the centre and the blue wing of the narrow [O III] emission extend from the nucleus up to large distances. While part of these spatial extents are due to the smearing effect of the seeing, it clearly indicates that [O III] emission extends over at least ∼10 pkpc from the central engine. We remark that the [O III] emission extends above and below the trace for roughly negative and positive velocities (according to our reference redshift), respectively.
 |
Fig. 7. Total spatial profile of narrow [O III] emission (black) and in three velocity bins (with colours indicated in the legend) after subtracting the unresolved broad [O III] and continuum emission. The dotted line shows the spectral PSF obtained from the trace of the quasar continuum. |
3.5. The Ly-α emission
The spectrum of J0015+1842 in the Ly-α region is the sum of the quasar emission absorbed by the proximate DLA and the leaking Ly-α emission superimposed on the DLA trough, as already mentioned in our discovery work (Noterdaeme et al. 2019). One difficulty with the low-resolution, low signal-to-noise ratio (S/N) BOSS fibre spectrum was to ascertain the combined model of absorption and emission since the quasar redshift was not easily determined and the wings of the DLA were not clearly detected. The higher quality X-shooter spectrum confirms our previous decomposition (see Fig. 8). The absorption profile is well constrained by the damping wings of the DLA as well as other lines from the Lyman series, which were fitted simultaneously with H2 lines (Fig. 10). The intrinsic quasar emission profile was reconstructed simultaneously using a smooth spline profile, aided by the quasar template matching (see Sect. 4.5); however, the exact shape of the peak is highly uncertain since it is positioned at the same place as the DLA trough. Nonetheless, we note that the exact shape and strength of the intrinsic, broad Ly-α emission line has little influence on the analysis presented in this paper.
 |
Fig. 8. Decomposition of rest-frame Ly-α region. The observed on-trace X-shooter spectrum is shown in black with uncertainties as grey error bars. The reconstructed unabsorbed quasar emission line is shown as the dashed purple curve. The red curve is the combination of this unabsorbed emission together with the modelled DLA absorption profile with log N(H I) = 20.71. Subtracting the absorption profile from the intrinsic emission profile provides us with the residual emission shown in blue, over the 4400−4440 Å wavelength interval. The BOSS fibre spectrum is shown in green. |
In Fig. 8, we also show the original BOSS spectrum. The residual Ly-α emission appears nearly two times stronger in the BOSS spectrum than in the X-shooter spectrum. The reason is that the optimal extraction method used for the X-shooter spectrum gives lower weight to the extended and spatially offset Ly-α emission. Instead, the 2D spectra clearly show that the residual Ly-α emission is spatially offset and extended (Fig. 9), and the overall (non-optimal) X-shooter extraction does match the SDSS data (top-right panel of that figure) much better. This will be discussed in the following.
 |
Fig. 9. Ly-α emission in PDLA core before (left) and after (right) subtraction of the unresolved quasar continuum emission. From top to bottom: PAs = −155, −164 and +177 deg. Top-right panel: spectral profile of the extended Ly-α emission for each position angle as well as their average, collapsing over the full spatial range shown in the 2D panels (hence an aperture of 6 × 1 arcsec). The SDSS-III/BOSS spectrum is shown in green. The small side panels show the spatial profiles of the unresolved quasar continuum emission (red) and the extended Ly-α emission (black). |
Since the system was identified through its H2 absorption lines imprinted on the quasar continuum, the absorbing gas intercepts the line of sight to the central engine, removing the unresolved emission and leaving us with a perfect PSF subtraction of the nuclear emission over the saturated region (∼4405−4420 Å observed) of the DLA trough. In other words, the DLA acts as a natural coronagraph (see e.g., Finley et al. 2013; Jiang et al. 2016). However, the leaking Ly-α emission remains partly blended with light from the quasar nucleus in the wings of the DLA (mostly in the red wing, λobs ∼ 4420−4430 Å). We therefore subtracted the nuclear emission over a wider region in order to isolate the extended emission. For this purpose, we constructed a 2D model of the nuclear emission using a Moffat profile to describe the spatial point spread function (SPSF). The shape and position of the SPSF is constrained by the continuum emission far from the Ly-α region. The amplitude of the spatial profile is then multiplied by the combined 1D spectral model for the nuclear emission and Ly-α absorption (i.e. the red line in Fig. 8). The resulting core-subtracted 2D spectra are shown in the right-hand panels of Fig. 9. The right-most panels indicate the corresponding spatial profiles for the nuclear (red) and residual (black) emission.
In the top-right panel of Fig. 9, we show the collapsed 1D spectra of the extended Ly-α emission over the full spatial range presented in the 2D panels (i.e. ∼6 arcsec). The individual spectra for the different position angles are all consistent with one another, indicating that differential slit losses are negligible. Given the observed north-south extension of the emission, the narrow slit width (1 arcsec in UVB), and the position angles of the slits (see Fig. 1), this suggests that most of the extended Ly-α emission falls within the region covered by all three slits, with an offset of ∼0.7 arcsec from the nuclear emission, as seen from the side panels of Fig. 9. Most of the extended Ly-α emission then corresponds to the same location as the red component of the narrow [O III] emission. However, the Ly-α flux remains slightly higher in the BOSS spectrum (2 arcsec diameter fibre), in particular bluewards of the Ly-α peak. We note that shifts in the zero level have been observed in BOSS spectra, but on much lower levels. Furthermore, other saturated lines in the BOSS spectrum do not show any residual flux. This means that the excess emission at ∼4400−4420 Å in the BOSS spectrum compared to the X-shooter one is likely real, suggesting that some extended emission is not covered by the X-shooter slits. The emission could then extend beyond 5 kpc from the nucleus in the direction perpendicular to the slits.
4. Absorption line analysis
We analysed the absorption lines using standard multi-component Voigt profile fitting and vpfit v10.3 (Carswell & Webb 2014) to obtain redshifts, Doppler parameters, and column densities of different species. We used both the UVB and VIS spectra with resolving powers of about 5400 and 8900, respectively. While we fitted all absorption lines simultaneously, the description of the analysis is split into sub-sections for convenience.
4.1. Neutral atomic hydrogen
The total H I column density was obtained not only from fitting the damped Ly-α absorption together with the unabsorbed quasar continuum (see Sect. 3.5), but also by including other lines from the Lyman series, the central redshift of the overall H I absorption also being constrained by the metal lines. We obtained a total column density log N(H I) = 20.71 ± 0.02, consistent with the previously estimated value from the low-resolution, low-S/N BOSS data. The region where extended emission is seen was ignored during the fitting process. The result of the fit is shown in Fig. 8.
4.2. Molecular hydrogen content
Bluewards of λobs = 4100 Å, the spectrum is crowded with numerous H2 lines from different rotational levels (Fig. 10), confirming the detection from Noterdaeme et al. (2019) based on a low-resolution, low-S/N BOSS spectrum. We modelled the H2 absorption profile using three components (which we label A, B, and C from blue to red). The strongest two components (B and C) are located close to each other in velocity space, so their respective absorption lines are strongly blended. Notwithstanding, these two components are also seen in the neutral chlorine profile (with total log N(Cl I) ≈ 13.4 ± 0.1, see Fig. 11), which is known to be chemically linked to H2 (see e.g., Balashev et al. 2015 and references therein).
 |
Fig. 10. Portion of X-shooter UVB spectrum of J0015+1842 (black, with uncertainties in grey). Horizontal blue segments connect rotational levels (short tick marks) from a given Lyman (L) or Werner (W) band of H2 for the central H2 component. The same is shown in grey for the two other components, but they are not labelled for visibility. The overall model (MCMC-based) spectrum is over-plotted in red, with contribution from non-H2 lines (H I and metal lines) shown as a dotted purple line. |
 |
Fig. 11. Fit to neutral chlorine absorption line. The observed data are shown in black, with the best-fit profile shown in red. Top panel: residuals (black) and 1σ error level (orange). The short tick marks show the location of the H2 components, while long dashed blue lines show those of other metal lines. As for all similar figures in this work, the origin of the velocity scale is set to zref = 2.631. |
We first used standard multi-component fitting using vpfit, including rotational levels up to J = 5. Because of the decreasing S/N and increasing line blending towards the blue, only the data at λ > 3600 Å was used to constrain the fit of the molecular hydrogen lines. We tied together the redshifts and Doppler parameters between rotational levels for a given component. This implicitly assumes that H2 in different rotational levels is well mixed, which is not necessarily the case. Indeed, an increase of b with J has been observed with VLT/UVES in a few cases of relatively low H2 column densities (e.g., Noterdaeme et al. 2007; Balashev et al. 2009; Albornoz Vásquez et al. 2014). However, in this work, the fit to the lower rotational levels is independent of the exact b value since the lines are damped.
Given the complexity of the H2 absorption spectrum and to account for the possibility of different Doppler parameters, which can have an effect on the high-J levels, we also fitted the H2 lines with a Markov chain Monte Carlo (MCMC) procedure. During this fit, we again tied the Doppler parameters of J = 0 and J = 1, as these levels are mostly co-spatial, but those from other rotational levels were allowed to vary independently. However, we added a penalty function to the likelihood function to favour the solutions where Doppler parameters increase with J. We also included the H2 absorption from J = 6 and J = 7 levels: these are albeit marginally detected. To get posteriors on fitting parameters, we used an affine sampler (Goodman & Weare 2010) with a flat prior on log N, b, and z. The result from the MCMC fit is shown in Fig. 10, but we note that the standard vpfit procedure provides a visually almost indistinguishable profile. Indeed, higher spectral resolution remains necessary to ascertain the velocity structure and widths of the lines. Hence, we provide the best-fit parameters from both fitting methods in Table 3.
Result of Voigt profile fitting to molecular hydrogen lines.
In all three components, the column densities of high rotational levels (J ≳ 2) are significantly enhanced compared to what is seen in typical H2-bearing DLAs at high redshifts. The observed T01 temperatures (∼100 K for components B and C and closer to ∼200 K for component A) remain consistent with what is seen for intervening systems, albeit with a small tendency to be in the upper range for the observed column densities (e.g., Balashev et al. 2019). This could result from an enhanced heating of the gas through photoelectric effect of UV photons on dust grains. We discuss the observed H2 excitation diagrams quantitatively in Sect. 5.2.
4.3. Chemical enrichment
Metal absorption lines are seen spread over 600 km s−1 mostly bluewards of the systemic redshift. Since the H I column density is large enough for self-shielding from ionising photons, we focused our analysis on the low-ionisation species in order to estimate the gas phase metallicity, since these are in their dominant ionisation stage in the neutral gas.
The initial guess for the velocity decomposition was obtained from the absorption lines of singly ionised silicon and iron that have several transitions with a wide range of oscillator strengths. Singly ionised sulphur and zinc were subsequently added to the model, and finally, all parameters were fitted simultaneously under the usual assumption that Zn II, S II, Si II, and Fe II are located in the same gas (i.e. we tied their Doppler parameters and redshifts). Since Zn IIλ2026 is blended with Mg Iλ2026, we also included this line in the fit with an independent Doppler parameter and redshift. We note that Si IIλ1526 is detected in the overlap between the UVB and VIS spectra. We therefore included both these spectral regions to constrain the fit.
The result of the fits are shown in Fig. 12 and the corresponding parameters are provided in Table 4. The total column densities are log N(cm−2) = 15.52 ± 0.03 (Si II), 14.46 ± 0.02 (Fe II), 15.39 ± 0.08 (S II), and 13.34 ± 0.07 (Zn II). Using the total H (H I + H2) column density, log N(H) = 20.75 ± 0.02, these values translate to overall gas-phase abundances of [Si/H] = −0.74 ± 0.04, [Fe/H] = −1.77 ± 0.03, [S/H] = −0.49 ± 0.08, and [Zn/H] = −0.39 ± 0.05, where ionisation corrections were assumed to be negligible, and the solar reference values were taken from Asplund et al. (2009) following the recommendation of Lodders et al. (2009) on whether to use photospheric, meteoritic, or average values. Both zinc and sulphur are known to be volatile species and hence provide a good estimate of the metallicity, which is about 40% solar. In turn, silicon and iron tend to deplete more onto dust grains (e.g., De Cia et al. 2016). Indeed, we measured depletion by a factor of two for silicon, while 96% of iron is locked into dust grains.
 |
Fig. 12. Fit to metal absorption lines. The observed data are shown in black with the synthetic profile for each given species overplotted in red. In case of several lines contributing to the observed profile (see e.g., S IIλ1259 and Si IIλ1260), the contribution for the labelled line alone is shown in red, while the total synthetic profile is shown in orange. Residuals are shown in the small panel above each line, with the orange line showing the 1σ error level. The location of the different components of the model are indicated by blue vertical dashed lines, with short red marks showing the position of H2 components. The zero of the velocity scale is set to zref = 2.631. |
Result of Voigt profile fitting to singly ionised metal lines.
4.4. Excited carbon and silicon
Neutral carbon absorption lines are detected in the spectrum of J0015+1842. This is not surprising given the presence of H2 and the high metallicity of the system (Noterdaeme et al. 2018). Three components are detected, matching those seen in H2, and we detect all three fine structure levels of the ground state triplet (2s22p23PJ = 0, 1, 2). All C I (J = 0), C I* (J = 1), and C I** (J = 2) lines were first fitted together using the bands at 1277, 1280, 1328, 1560, and 1656 Å, avoiding regions affected by blends (in particular for the 1328 Å band) and tying the redshifts and Doppler parameters for each component. The result of the fit is shown in Fig. 13, and the corresponding parameters are summarised in Table 5. The Doppler parameters are found to be as small as 1 km s−1. While such small values are similar to what is seen in H2, and not uncommon for C I-absorbers (e.g., Noterdaeme et al. 2017), here they are observed far below the spectral resolution, implying large uncertainties on the column densities. We therefore repeated the fit using the MCMC method, which suggested that the uncertainties on the b-values provided by vpfit were likely underestimated. Finally, we performed a final test assuming a fixed, somehow higher b = 3.5 km s−1 value. The column densities obtained from the different methods remain similar, although differing in some cases by up to ∼0.5 dex. Nevertheless, all results indicate higher excited-to-ground, fine-structure level ratios than usually seen in intervening systems. We caution, however, that high spectral resolution observations remain vital to accurately measuring the corresponding column densities.
 |
Fig. 13. Fit to C I absorption lines. The data are shown in black with the best-fit over-plotted in red. The contribution from individual fine-structure levels are shown in orange (C I), green (C I*), and purple (C I**). Top panels: residuals. |
Result of Voigt profile fitting to neutral carbon lines.
Singly ionised carbon and silicon are also detected in excited fine-structure states (C II* and Si II*, respectively). While C II* is in principle useful in estimating the cooling rate of the gas through [C II]158 μm emission (Pottasch et al. 1979), the corresponding absorption lines here are saturated, impeding the measurement of the C II* column density.
The Si II* absorption is in turn much weaker but clearly detected in its strongest line at 1264 Å. We identify three main components that correspond to those seen in the metal lines. We also used the weaker 1309 Å line to ascertain the detection and constrain the fit, shown in Fig. 14. The corresponding parameters are given in Table 4.
 |
Fig. 14. Same as Fig. 12 for the absorption lines from excited fine-structure of singly-ionised silicon. |
4.5. Dust extinction
We fitted the dust reddening using the formalism by Fitzpatrick & Massa (2007) assuming various fixed extinction laws (Gordon et al. 2003) to identify the overall shape of the dust reddening law applied to the composite X-shooter spectrum from Selsing et al. (2016). The details of the method are presented by Noterdaeme et al. (2017). We found a best match using a rather shallow extinction curve like the one observed towards the Large Magellanic super-shell (LMC2). However, we needed to vary the strength of the extinction bump at 2175 Å in order to properly match the observed spectrum. The spectrum exhibits significant variations of the iron emission lines in the region between the C IV and Mg II lines. We included a model of these iron lines using the template given by Vestergaard & Wilkes (2001). While this template improves the overall fit, the exact variations of the myriad of iron lines cannot be captured by a fixed line template. Taking systematic uncertainties due to variations in the intrinsic quasar shape into account, we found a best-fit solution of A(V) = 0.4 ± 0.1 mag, Fe2 = 0.5 ± 0.2, Fe3 = −1.5 ± 0.5, c3 = 0.7 ± 0.1, where A(V) is the amount of extinction and Fe2 and Fe3 multiplicative factors parametrising the strengths of the Fe II and Fe III lines with respect to the template. The inferred strength of the 2175 Å bump is Abump = πc3/(2γ) = 1.2 ± 0.2, where γ = 0.95 is the width of the bump (Gordon et al. 2003). The best-fit solution is shown in Fig. 15. Based on the inferred extinction law from the spectral fitting, we constructed a dust model to reproduce this extinction law by varying the dust-grain size distribution and the ratio of silicate to graphite grains (Si/C). The grain size distribution was assumed to be a power-law distribution with a slope of −3.5 and a maximum grain size of 0.25 μm similar to the standard ISM size distribution (e.g., Nozawa & Fukugita 2013). The best match to the extinction law was found for a minimum dust grain size of 0.01 μm (compared to 0.005 μm for standard ISM dust grains) and a silicate-to-graphite ratio of Si/C = 2 relative to the standard ISM abundance ratio.
 |
Fig. 15. Combined X-shooter spectrum of J0015+1842 in black with best-fit SED corrected for dust extinction shown in red. For visual purposes, the data have been filtered (rejecting 4-σ outliers; light grey) and smoothed (black) in order to remove the strong skyline residuals in the NIR data. The position of the 2175 Å extinction feature is indicated by an arrow, and the best-fit model without the 2175 Å feature is indicated by the purple line. The unreddened quasar template is shown in blue. Photometric data from SDSS (u, g, r, i, and z bands) and WISE (band 1) are shown as orange squares. |
5. Results and discussions
In this section, we first discuss the implications of the emission line properties and why this suggests that we are observing galactic-scale outflows, and we show that the absorbing gas is likely a different manifestation of the same galactic-scale outflows, intercepted by the line of sight to the nucleus. We then derive the physical conditions in the absorbing gas and its distance to the central engine. Finally, we substantiate the overall picture by modelling the Ly-α absorption-emission profile both spatially and spectrally.
5.1. Evidence of galactic-scale outflows
5.1.1. The extended emission from ionised gas
According to the standard paradigm of AGN, the broad emission lines of quasars arise from dense regions with high velocities close to the central engine. Since these regions are far too small (∼1 pc, e.g., Kaspi et al. 2007) to be resolved at cosmological distances, information about their sizes is generally obtained through reverberation mapping (Blandford & McKee 1982). However, valuable constraints can also be obtained from partial coverage by a foreground absorber (e.g., Balashev et al. 2011).
The narrow emission lines are in turn expected to arise further away from the obscuring torus, from gas at sufficiently low density where the emission is dominated by forbidden-line transitions. While initially thought to be less than kpc-sized, evidence of the presence of extended narrow line regions (NLR) around diverse types of AGN has increased. This is particularly evident for low redshift Type 2 AGN, where the observations are facilitated by larger angular sizes and obscuration of the nucleus emission (e.g., Sun et al. 2017). However, evidence for kpc-scale emission is also seen in high-redshift quasars (e.g., Rupke et al. 2017). This also includes the ubiquity of giant (≳100 kpc) Lyα nebulae around luminous quasars at 3 < z < 4 (Borisova et al. 2016). The narrow emission lines therefore contain important information for the study of ionised gas on large scales.
If the energy from accretion disc winds propagates to the host galaxy ISM, then we expect to observe some connection between the properties of the different types of emission lines. For example, Coatman et al. (2019) observed a correlation between the blueshifts of the overall C IV and [O III] emissions, as well as an anti-correlation between [O III] equivalent width and C IV blueshift. This suggests that high-velocity accretion disc winds, arising in a compact region very close (< 1 pc) to the supermassive black hole (Netzer 2015) can influence the host-galaxy on kpc-scales, assuming [O III] is extended over such scales2. While our observation here concerns a single object, the observed kinematics and equivalent width are in agreement with those observed by these authors. More importantly, we also confirm that most of the C IV emission arises from the broad nuclear region, but we observe a weak C IV emission at least as extended as the narrow [O III] emission, supporting the above picture. Finally, Tombesi et al. (2015) found evidence for accretion-disc winds driving galactic-scale molecular outflows, as later confirmed by Veilleux et al. (2017). Taken together, these works suggest that the H2 absorption system observed here could be linked to the same outflow process.
The commonly-used Baldwin et al. (1981, BPT) diagram provides a useful diagnostic to discriminate between photoionisation by AGN or star formation. While we do not have access to the [N II] or Hα lines, the fact that [O III] is detected outside the unresolved nuclear region while Hβ is not (see Figs. 3 and 5) suggests a very high [O III]/Hβ ratio, as expected in the case of ionisation by AGN (e.g., Kewley et al. 2001; Kauffmann et al. 2003). This ionisation mechanism is further supported by the large velocity dispersion, FWHM ∼ 600 km s−1, of the extended [O III] emission (see e.g., Zhang & Hao 2018).
As shown in Sect. 3.4, the narrow [O III] emission presents two blobs on both sides of the nucleus (at a distance of ∼5 kpc projected on the plane of the sky) and with opposite line-of-sight velocities with respect to our reference redshift. The bulk velocities of the emission are of several hundred km s−1. These are at the limit between what is expected from rotational and non-gravitational velocities (e.g., Comerford et al. 2018). However, the emission is well detached from the nucleus (in particular the red lobe, see Fig. 7) which is better explained by an outflow. This is also consistent with the presence of blueshifted broad [O III] emission closer to the nucleus, following the picture of energy propagation from the inner to the outer regions (e.g., Fabian 2012). Since the [O III] emissivity scales with the square of the density, the observed [O III] emission traces the densest ionised gas clouds, which, being detached, could indicate compressed regions at the front of the outflow. Furthermore, a careful look at Fig. 6 reveals that as the distance from the nuclear emission increases, the line width of the narrow emission decreases, and the centroid of the emission approaches the systemic velocity (see right panels of that figure). These kinematic signatures are consistent with a decelerating outflow and a possible compression at the front of the outflow. However, this interpretation remains tentative and requires confirmation through deeper observations with higher spatial resolution, ideally using integral field spectroscopy.
5.1.2. Kinematics: Absorption and emission as different manifestations of the same wind
While the velocity profile of neutral hydrogen seen in absorption is not directly accessible because of saturation of H I lines, from Fig. 16 it is clear that the profiles of low-ionisation and high-ionisation metal species share the same overall structure, with several components spread over about 600 km s−1, almost completely blueshifted with respect to the assumed systemic redshift. Such a broad, blueshifted structure is consistent with the expected signature of outflowing gas. The kinematics contrast what is usually seen in intervening DLAs, where the velocity spread of low-ionisation metals are generally much smaller (Ledoux et al. 2006) and systematically less extended than more ionised species (see Fig. 4 of Fox et al. 2007). The profiles observed here suggest that ionised and neutral phases could be well mixed up within the gross structure of the outflowing gas.
 |
Fig. 16. Velocity profile of thrice-ionised silicon (top and middle panels), compared to that of singly-ionised silicon (bottom panel). Short tick marks indicate the position of H2 components. The zero of the velocity scale is set to zref = 2.631. |
The absorption line kinematics observed in the spectrum of J0015+1842 also corresponds well to the kinematics of the blueshifted, extended, ionised gas seen in emission (the blue component of the extended [O III] emission), indicating that we are looking at the same phenomenon both in emission and absorption and that the kpc-scale outflowing gas likely contains a mixture of different phases. A similar interpretation has recently been put forward by Xu et al. (2020). Based on the kinematics of [O III] emission and C IV absorption in seven quasars, the authors suggest that outflows seen in emission and absorption are likely different manifestations of the same wind.
5.2. Physical conditions in the absorbing gas
If the absorbing gas is also part of the outflow, which can typically span around a few tens of kpc from the AGN, then we expect to see effects of the quasar proximity on the physical conditions. The presence and excitation of atomic and molecular species provides a unique opportunity to investigate these physical conditions.
Singly-ionised silicon is an interesting species since its excited fine-structure level has been detected in only a few high-z intervening DLAs to date (e.g., Kulkarni et al. 2012; Noterdaeme et al. 2015) and most likely in regions of high pressure (Neeleman et al. 2015). However, it appears to be more conspicuous in proximate DLAs, where the excitation of silicon fine structure could be enhanced by both high densities and strong UV flux (e.g., Ellison et al. 2010; Fathivavsari et al. 2018). Hence, its presence may indicate close proximity to the quasar central engine. However, in the absence of other information, it is hard to discriminate between the case of high density or high UV flux.
Molecular hydrogen can provide important information, since both the presence of H2 and the excitation of its rotational levels depend on the strength of the UV field, the gas density and its temperature (e.g., Balashev et al. 2019). Owing to formation on dust grains and destruction through line absorption in the Lyman and Werner bands, the presence of molecular hydrogen mainly depends on the ratio between the UV intensity and the gas density (e.g., Sternberg et al. 2014). This implies that the density required for an atomic-to-molecular transition to occur follows n ∝ d−2, where d is the distance to the central UV source. For the H I column density and metallicity (or equivalently dust-to-gas ratio) observed for J0015+1842, the normalisation of this relation3 is about log n (cm−3) ∼ 4 at d ∼ 10 kpc distances from the nucleus (Noterdaeme et al. 2019).
Combining the information from Si II* and H2, as well as other species sensitive to the density and UV radiation (e.g., C I fine structure, whether CO molecules are present or not), can therefore provide constraints on the physical state of the gas and its distance to the central UV source. In Fig. 17, we compare the apparent optical depths of the Si IIλ1808 and Si II*λ1264 lines4, which are both optically thin. The ground state and excited profiles of singly-ionised silicon have similar velocity profiles with three main clumps, two of which coincide with the positions of H2 absorption components. Yet, the strongest bulk component of Si II* does not align with the H2 components. In the top panel of Fig. 17, we show the ratio of Si II*/Si II. This ratio is not enhanced at the position of H2 absorption, where instead it tends to be consistently lower than average over several pixels. Since molecular hydrogen traces the high-density regions in the absorbing gas, this may suggest that the high excitation of Si II* is not due to high density but rather due to strong UV irradiation.
 |
Fig. 17. Bottom: pixel optical depths of Si IIλ1808 and Si II*λ1264 lines. Top: apparent column density ratio per unit velocity bin (i.e. the ratios of τ/(fλ0)). The location of H2 components is marked by the red dashed lines. The horizontal dashed line shows the overall column density ratio as derived from the Voigt-profile fitting. Values for which the optical depth of either line is below 0.03 lead to large errors and are not plotted. The zero point of the velocity scale is set to zref = 2.631. |
5.2.1. Modelling warm and cold gas as successive slabs
Since the quasar itself is likely the dominant source of photons striking the medium at distances ≲ few tens of kpc, the UV field received by each slab of gas (absorption component) actually depends on the transmitted field through the previous slab of gas on the line of sight. While understanding successive filtering slabs of gas makes the study of proximate systems significantly more complex than intervening ones (where the components can generally be treated independently), advantages are that the observed column densities correspond to the actual layers through which UV photons propagate, and we have prior knowledge about the shape of this field5. However, the large number of components and their unknown respective physical locations along the line of sight does not allow for a full modelling of the system, which would have far too many parameters to vary.
We simplified the problem by considering two successive slabs of gas along the line of sight to get an idea of the physical conditions in the different phases. In this picture, one slab of warm gas, directly illuminated by the quasar, is likely responsible for most of the Si II*, while the second slab, for which the incident field contains no more H-ionising photons, is in a cold state and contains the H2.
We used the photoionisation code Cloudy v17.1 (Ferland et al. 2017), running grids of constant density models with plane-parallel geometry illuminated on one side by the built-in cloudy AGN spectral energy distribution. The cosmic microwave and cosmic ray backgrounds were included. The gas phase abundances were set to match the observed ones, and we included dust using the grain mixture and size distribution described in Sect. 4.5. In the first runs, the abundance of dust was scaled to self-consistently (i.e. conserving mass) match the observed depletion factors of iron and silicon. This in turn implies depletion factors of about 50% and 25% for carbon and oxygen, respectively. We tested and found that the results concerning the first layer are actually little sensitive to the abundance of dust, except, naturally, for the calculated extinction, which tends to strongly exceed the observed one due to the large total column density in the model. However, as we see below, the first layer contains mostly ionised gas, as well as neutral gas with high temperatures (> 104 K), so it is most likely that grains, in particular small ones, are destroyed. We then assumed no grains in that phase – but these are kept in the second (cold) slab.
The results concerning the excitation of silicon in the first slab are shown in Fig. 18, where the UV flux is converted into distance to the source using the observed quasar luminosity. These show that the observed excitation of Si II* can be reproduced by gas with densities of the order of ∼10 cm−3 at any distance less than ∼50 kpc from the source. Exciting Si II at the observed level, if located further, would require higher densities. However, this would also push the second slab further out, where the cold slab of gas containing H2 would become too cold and little excited compared to observations, as we discuss later. We note that the two slabs need not have the same velocities since the ionising cross-section is wide.
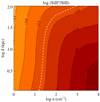 |
Fig. 18. Excitation of ionised silicon fine-structure level as a function of density and distance to the quasar. The dashed white line corresponds to the observed integrated ratio (i.e. N(Si II*)/N(Si II)). |
In Fig. 19, we show the variation of number densities of neutral hydrogen, electrons, and singly- and thrice-ionised silicon, as well as the excitation of silicon and the electron temperature as a function of the cumulative H I column density for an example model with n = 10 cm−3 and d = 10 kpc. In the ionised gas, the excitation of Si II is high owing to efficient collisions with electrons. The local Si II*/Si II ratio then drops by about a factor of ten after crossing the dissociation front, when the gas becomes neutral and both the electron density and the temperature decrease. The Si II*/Si II ratio then remains constant afterwards, as do ne and T. However, since singly-ionised silicon is not the main ionisation stage upstream, the overall column density ratio, N(Si II*)/N(Si II) (which is what we observe), is actually N(H I)-weighted, explaining the slow dependence on the stopping H I column, as shown by the cumulative N(Si II*)/N(Si II) ratio6 (dashed-dotted curve) in the middle panel.
 |
Fig. 19. Abundances of various species (top) and variation of Si II*/Si II ratio (middle) and temperature (bottom) as a function of cumulative H I column density for a constant density model with log n/cm−3 = 1 at d = 10 kpc. The dashed-dotted line in the middle panel shows the cumulative N(Si II*)/N(Si II) ratio. |
Changing the UV field affects the depth of the dissociation front (i.e. the column density of upstream ionised gas), but the results remain almost unchanged with respect to the cumulative H I column density. This explains the low dependence of the N(Si II*)/N(Si II) ratio on the distance to the UV source. It is interesting, however, to note that the range spread by Si II*/Si II at different depths (from about 0.01 in the ionised gas to 0.001 in the neutral gas) corresponds roughly to that seen in Fig. 14, which is consistent with the fact that the absorption system also contains ionised gas. The main effect of increasing the volumic density is an upwards shift of the Si II*/Si II curve, as collisional excitation of Si II increases both in the ionised gas (collisions with electrons) and in the neutral gas (collisions with H I), so Si II*/Si II is roughly proportional to n in the UV-independent regime. At much higher densities, the increasing dependence of Si II* on the distance to the AGN is mostly due to the dependence of the gas temperature and ionisation fraction on the strength of the UV field. Finally, we note that H2 is not yet produced in the first slab, which is consistent with the non-detection of H2 in the strongest Si II* component.
We modelled the second slab of gas again using constant density models at various distances from the quasar. However, the striking radiation field is now the transmitted field through the first slab. The main effect of the first slab on the incident field is a removal of hydrogen-ionising photons. This means that the assumed parameters for the first slab actually have little effect on the second slab. We stopped the calculations of this second slab when reaching log N(H2) = 19.3, as a representative value for individual H2 components. The results are shown in Fig. 20.
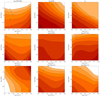 |
Fig. 20. Cloudy model predictions for the second slab of gas, with log N(H2) = 19.3. |
The excitation of Si II* is now significantly lower compared to the first slab for a given distance and density as the temperature decreases considerably. The Si II*-to-Si II ratio reaches the same level as in the first layer for distances of only a few kpc, for densities up to log n ∼ 5, and it increases at higher densities. However, there is also indication that the excitation of silicon is less at the velocities of H2 components, with log(Si II*/Si II) between roughly −3 and −2.5, than at other velocities (where, as we showed above, the high excitation is easily explained by the high pressure in the first layer). In that case, the distance is slightly larger, between 5 and 12 kpc.
The T01 excitation temperature strongly depends on the UV flux, but more weakly on the density. The observed value of about 100 K corresponds to distances of the order of 5–15 kpc. At such distances, the high rotational levels are highly populated, even though they remain lower than what is observed for the total column in the model (equating that of component C). This is a common situation in the modelling of static slabs and depends much on the actual geometry and turbulence, so we do not consider the 0.5 dex as a strong mismatch between the data and model.
The excitation of neutral-carbon fine-structure levels has also proved to be a useful probe of the physical conditions in H2-bearing DLAs (e.g., Silva & Viegas 2002), in which it is usually detected (e.g., Srianand et al. 2005; Noterdaeme et al. 2018). Here, the C I*/C I ratio is notably high in all three components, reaching the limit of a statistical weight ratio, and it appears to be mostly populated by UV pumping. The C I*/C I favours distances smaller than the above 10 kpc, it but remains consistent within the large uncertainties of the observations over most of the parameter space probed. For component C, where the constraints are slightly better, the excitation of C I rejects distances larger than about 10 kpc at ∼2σ.
The strict upper limit on the H I column density is consistent with these distances as long as the density is as high as log n ∼ 4.5 or more. The dust extinction is then also within the allowed range. Finally, the absence of CO at a detectable level (log N(CO) < 13.4 (3σ) following the procedure presented by Noterdaeme et al. 2018) rejects the high density, large distance corner of the plot.
Our model is of course very simplified, as the actual system presents numerous components at various velocities and unknown respective spatial location along the line-of-sight. The chemical properties, gas-phase metal abundances, and dust grain properties can also vary from one component to another. We also explored a number of varying parameters, like turbulence, shape of incident radiation field, column density of the first layer, and the use of the simple removal of H-ionising photons instead of a full transfer calculation. All this typically affects the distances and densities further by a factor of two. We thus conclude that within a factor of a few, the distances of the clouds are of the order of ∼10 kpc, and H2 is produced in clouds with densities as high as n ∼ 104.5 cm−3, located downstream, after H-ionising photons have been removed by a warm atomic layer. The latter is also responsible for most of the Si II fine-structure excitation, while C I is only present in the denser molecular gas.
5.2.2. Modelling the excitation of H2 components individually using Meudon PDR
In order to further test our results on the molecular phase, we used the MEUDON PDR code (Le Petit et al. 2006) to model the population of all detected H2 rotational levels in the different individual components separately. We ran grids of isobaric cloud models, with thermal pressure from 104 to 108kB K cm−3 and illuminated by a UV field with intensity from 1 to 3 × 104 times the Mathis field (Mathis et al. 1983), corresponding to distances of ∼160 to 1 kpc from the central engine7.
We modelled each H2 component independently, that is, we did not take into account shielding in H2 UV lines of one component by another component located closer to AGN. The column densities in the different rotational levels are all compared to the data using a simple least-square likelihood function. The constraints on the thermal pressure, P, and distance to AGN, d for all three H2 components are shown in Fig. 21. The constraints are similar for vpfit and MCMC H2 fitting methods. The most likely values correspond to high pressures P/kB ∼ 106 − 107 K cm−3 located at distances of 10−20 kpc for all three components. The corresponding modelled excitation diagram is shown in Fig. 22. The typical kinetic temperatures in the H2 dominated cores of the clouds is then ∼200−300 K, which is slightly higher than the observed T01. The number density in the H2-dominated medium is in the range of 104 − 105 cm−3, which is in agreement with the results using Cloudy. We also ran isochoric models and found that while isobaric models reproduce the observed H2 excitation diagram slightly better, the constrained values of d, P, and n remain very similar. We note that the derived distances are also consistent with the limits predicted by the static H2-H I transition theory from Sternberg et al. (2014), shown as a black line in Fig. 21: below these lines, the predicted H I columns in the envelope of H2 clouds would be higher than the total N(H I) observed.
 |
Fig. 21. Constraints on thermal pressure, P, and distance from cloud to AGN, d, obtained by modelling the excitation of H2 rotational levels with the PDR MEUDON code. The contours show formal regions that contain 0.683 probability distribution functions. The solid and dashed lines correspond to the estimates based on MCMC and vpfit result of H2 fit (see Table 3), respectively. The marginalised probability distribution functions (along right and top axes) and the best-fit values (stars) are shown for MCMC results only for the sake of clarity. The black line with upwards arrows show the constraints from the H2-H I transition, assuming the kinetic temperature is T ∼ 100 K, which is consistent with the observations. |
 |
Fig. 22. Comparison of model and observed excitation diagram of H2 rotational levels. The filled and open circles represent the measurements using vpfit and a MCMC method (see Sect. 4.2), respectively. The dashed lines show the best fit of the excitation diagram (corresponding parameters d and P marked by stars in Fig. 21). The data points are artificially shifted on the x-axis to ease representation. |
 |
Fig. 23. Comparison between simulated 2D spectrum of photons escaping in the particular direction of the observer looking down the barrel of the jet (bottom) with the actual observed X-shooter 2D spectrum (top). The distance along slit is taken from the unresolved quasar continuum emission. We note that the observed spectrum is also affected by unrelated absorption, which we do not model here (e.g., at 4396 Å). |
While the distances are constrained to be of the order of 10 kpc, these do not allow us to determine which component is located closer to the AGN. In any case, since cold clumps can drop out from the bulk motion (see e.g., Wu et al. 2020), the information of the respective locations of H2 clouds would not likely tell us whether the bulk outflow is decelerating or not.
Interestingly, the high density derived in the H2-bearing medium implies very small longitudinal sizes, of the order of ∼100 AU only. This is actually comparable to the size of the accretion disc, assuming the relation from Morgan et al. (2010) and the black hole mass of log MBH/M⊙ = 8.6 derived from width of the C IV line (FWHM ∼ 3000 km s−1) and the rest-frame continuum luminosity at 1350 Å using the calibration from Vestergaard & Peterson (2006). However, we do not see any partial coverage of the background source by H2. This could be due to the nuclear emission arising from a smaller area than expected, or the transverse extent of H2-bearing gas being larger than the longitudinal one. The latter could be effectively reproduced by a large covering factor of H2-bearing clumps around the component velocity. Given the typical (longitudinal) velocities of the components of ∼400 km s−1 future observations on timescales of a few years could reveal a variability of the H2 absorption lines, if the transverse velocities are of the same order.
5.3. The leaking Lyα emission
Sensitive integral field spectrographs, in particular MUSE at the VLT (Bacon et al. 2010), have revealed a near ubiquity of Ly-α nebulae around high-redshift quasars (e.g., Borisova et al. 2016; Arrigoni Battaia et al. 2018). Extended Ly-α emission has been observed up to hundreds of kpc in some cases, and routinely over several tens of kpc. In turn, the strong glare from the quasar itself complicates the observations of the Ly-α emission at the small distances from the nucleus. In the case of J0015+1842, the presence of the DLA removes the nuclear emission, leaving us with free access to the Ly-α emission as soon as it is outside the BLR.
To verify if the conjectured configuration of clumpy, gaseous outflows from J0015+1842 is a likely representation of the system (see cartoon in Fig. 24), we constructed a 3D model in an adaptively refined mesh and carried out Ly-α radiative transfer (RT). The model is based upon our observational constraints, as discussed below; where we have no constraints, we assumed plausible values (in particular concerning the properties of the inter-cloud medium). In both cases, we then varied the physical parameters in certain ranges to get a feeling for the importance and degeneracies of these parameters.
 |
Fig. 24. Cartoon of inferred configuration of the system. The emission properties of the unresolved active nucleus (e.g., blueshifted broad [O III]) are not shown to avoid overcrowding the figure. Ly-α photons can be more easily scattered out from the cones towards the observer from the receding outflow and appear red peaked. |
The Ly-α RT was conducted using the Monte Carlo code MOCALATA8 (Laursen et al. 2009a,b). Given a grid of cells containing thephysical parameters of the gas (densities, temperature, and velocity field), the code traces the paths of individual photons, producing a 3D (two spatial + one frequential) cube that can be compared to our observation. Given the large number of unknowns, rather than performing a stringent fit to the observed spectrum (as has sometimes been done, see e.g., Verhamme et al. 2008; Gronke 2017), we aimed to construct a model that would at the same time be consistent with our various observational constraints, and – most importantly – roughly reproduce both the observed Ly-α spatial and spectral shapes.
The gas is assumed to have been expelled in a biconical outflow down through one of which we observe the quasar nucleus. Given the similar transverse and longitudinal length, we set the opening angle of the cone to θ ≃ 45°. The number of low-ionisation absorption lines seen along the line of sight (covering factor fc ∼ 10) can then be reproduced distributing Ncl ≃ 750 000 effective clouds in the outflows, each of radii rcl ≃ 40 pc, Tcl = 104 K and nHI, cl = 0.25 cm−3. These are located between inner and outer radii of 16 and 20 kpc, respectively9 and immersed into a mostly ionised inter-cloud medium with TICM = 105 K and a residual neutral gas nHI, ICM = 0.005 cm−3. Both phases have metallicity Z = 0.5 Z⊙. With these numbers, the covering factor is 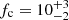 H I column density is
H I column density is 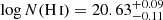 . The gas follows a velocity profile decreasing linearly from 250 km s−1 to 0 at the end of the jet. In addition to this, the clouds have a velocity dispersion of σv, cl = 10 km s−1. Finally, photons are emitted from the centre with an intrinsic spectrum given by the reconstructed unabsorbed emission (see Fig. 8).
. The gas follows a velocity profile decreasing linearly from 250 km s−1 to 0 at the end of the jet. In addition to this, the clouds have a velocity dispersion of σv, cl = 10 km s−1. Finally, photons are emitted from the centre with an intrinsic spectrum given by the reconstructed unabsorbed emission (see Fig. 8).
We generated a 2D spectrum of the photons escaping (in the particular direction of the observer looking down the barrel of the jet) as would be seen with X-shooter, that is, with the same slit parameters, resolution, and seeing as observed. This is compared to the observed spectrum in Fig. 23. While far from a perfect match, our model reproduces (i) the damped absorption line towards the nucleus, (ii) the red-peaked leaking Ly-α emission, and (iii) the spatial offset of this emission down the trace. We note that Ly-α photons are also likely to be produced from recombination in the outflow as well as in the host galayx, hence contributing to the overall observed profile.
6. Conclusion
Active galactic nucleus feedback is a very complex issue that motivates significant efforts from the community in terms of theory, simulations, and observations. While progress in understanding galactic-scale outflows as the main observable evidence of feedback is being made quickly, Cicone et al. (2018) recently noted that these remain largely unconstrained as they imply various scales and different gas phases. Furthermore, the observation of outflows, especially at high redshift, is notoriously difficult.
Our VLT/X-shooter observations of the proximate molecular absorber towards J0015+1842 suggest that spatially resolved emission of ionised gas and kinematically wide absorption in various phases towards the nucleus are different manifestations of a single outflowing process. From detailed investigation of the physical conditions in the cold phase of the absorbing gas, we derived a distance to the central engine of the order of 10 kpc. This, together with the similar kinematics and transverse extent of the ionised gas seen in emission, indicates a picture of a multi-phase quasar outflow, down the barrel, that is, intercepted by the line of sight to the bright nucleus. This configuration is corroborated by modelling of the resonant Ly-α emission-absorption spectral and spatial profiles.
Of course, it may be reasonable to recall that this is likely an extremely simplified version of the actual geometry. It is, for example, well possible that the ISM in the quasar host is disrupted by the ionised outflow, giving rise to a much more complex structure of the various phases in the outflow. While the present observations open up a new way to study outflow properties, they do not yet tell us what the effect of these outflows on the host galaxy are. Understanding how much molecular outflows affect the host galaxy’s reservoir, and hence whether outflows are effectively quenching star formation, could be addressed from spatially resolved observations of CO emission lines (e.g., Carniani et al. 2017).
Since the present analysis includes only a single object, it is legitimate to ask whether the prevalence of (multi-phase) outflowing gas is larger in quasars with proximate H2 absorbers than in the overall population. By spreading out H2 gas, outflows may contribute to increasing the H2 absorption cross-section, and hence proximate H2 absorbers could represent an effective way of pre-selecting these. If, as shown here, outflowing gas facilitates the scattering of Ly-α photons on galactic scales, then the presence of leaking Ly-α emission in a fraction of them could be an additional effective criterion. Finally, the presence of excited atomic species could indicate proximity of the gas to the central engine. Outflowing gas being responsible for a fraction of proximate H2 absorbers could provide an explanation to the at least five-fold enhancement of the incidence rate of H2-selected proximate DLAs compared to intervening statistics (Noterdaeme et al. 2019) when H I-selected proximate DLA show only marginal enhancement (Prochaska et al. 2008) and likely missed systems with strong Ly-α leakage. Of course, a fraction of proximate H2 absorbers could also originate from galaxies in the quasar group.
We note that a correlation between a fraction of leaking Ly-α photons (not absorbed by the foreground cloud) and the strength of Si II* in metal-selected proximate DLAs (without information of H2) has been observed by Fathivavsari (2020). The author interprets this as a decrease of the covering fraction of the background Ly-α emission by clouds with increasing compactness (i.e. of higher density for a given column density). However, there may be no causality between the density inside individual (sub)-pc-scaled clouds and the fraction of leaking Ly-α photons (over kpc-scales) throughout the whole system. Instead, the prevalence of dense clouds and the Ly-α leaking fraction may both depend on the gas flow configuration, including the outflow viewing angle (see e.g., Gupta & Saikia 2006 for a similar discussion on the detectability of H I 21 cm absorption) and quasar properties. Similarly, den Brok et al. (2020) recently suggested that the morphologies of extended Ly-α nebulae can be used to understand the geometry of high-redshift AGN on circumnuclear scales. Nevertheless, the interpretation of single clouds partially covering the nucleus may still be valid for extreme cases where the Ly-α appears completely unabsorbed.
This was actually not constrained by the data obtained by Coatman et al. (2019).
In turn, modelling of intervening DLAs is generally intended to reproduce the observed column densities, but the actual incident flux intensity and shape is not known (for example, whether it is attenuated or not before striking the cloud) and there is no reason for its direction to match that of the line of sight.
Assuming the UV field is dominated by the AGN. We note that there is no option to set the external radiation field shape to AGN in the PDR Meudon code. However, in the UV range, the shape of the Mathis field is quite similar to that of typical AGN, so that uncertainties related to the shape of the field are negligible compared to those arising from the unknown geometry of the clouds.
These values are taken to be representative of the distances derived from the physical conditions and the fact that clouds are more easily ionised close to the quasar. As we aim at a global agreement between the model and actual data and still have many unknowns, we chose to fix them instead of considering these radii as free parameters.
Acknowledgments
We thank the anonymous referee for thorough reading of the paper and constructive comments. We are grateful to ESO and Paranal observatory staff for carrying out the observations in service mode. We acknowledge support from the French Agence Nationale de la Recherche under ANR grant 17-CE31-0011-01/project “HIH2” (PI: Noterdaeme) as well as from the Russian-French collaborative programme (PRC). SB is supported by RSF grant 18-12-00301. PL acknowledges the warm and welcoming atmosphere of IAP during his visit. The Cosmic Dawn Center (DAWN) is funded by the Danish National Research Foundation under grant no. 140. JPUF acknowledges support from the Carlsberg foundation. We all thank our close relatives for facilitating good working conditions during the covid-19 confinement.
References
- Albornoz Vásquez, D., Rahmani, H., Noterdaeme, P., et al. 2014, A&A, 562, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arav, N., Liu, G., Xu, X., et al. 2018, ApJ, 857, 60 [Google Scholar]
- Arrigoni Battaia, F., Prochaska, J. X., Hennawi, J. F., et al. 2018, MNRAS, 473, 3907 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2010, Proc. SPIE, 7735, 773508 [Google Scholar]
- Balashev, S. A., Varshalovich, D. A., & Ivanchik, A. V. 2009, Astron. Lett., 35, 150 [Google Scholar]
- Balashev, S. A., Petitjean, P., Ivanchik, A. V., et al. 2011, MNRAS, 418, 357 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Balashev, S. A., Noterdaeme, P., Klimenko, V. V., et al. 2015, A&A, 575, L8 [Google Scholar]
- Balashev, S. A., Noterdaeme, P., Rahmani, H., et al. 2017, MNRAS, 470, 2890 [NASA ADS] [CrossRef] [Google Scholar]
- Balashev, S. A., Klimenko, V. V., Noterdaeme, P., et al. 2019, MNRAS, 490, 2668 [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R. D., & McKee, C. F. 1982, ApJ, 255, 419 [Google Scholar]
- Borisova, E., Cantalupo, S., Lilly, S. J., et al. 2016, ApJ, 831, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Carniani, S., Marconi, A., Maiolino, R., et al. 2017, A&A, 605, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carswell, R. F., & Webb, J. K. 2014, Astrophysics Source Code Library [record ascl:1408.015] [Google Scholar]
- Cicone, C., Brusa, M., Ramos Almeida, C., et al. 2018, Nat. Astron., 2, 176 [Google Scholar]
- Coatman, L., Hewett, P. C., Banerji, M., et al. 2019, MNRAS, 486, 5335 [NASA ADS] [CrossRef] [Google Scholar]
- Comerford, J. M., Nevin, R., Stemo, A., et al. 2018, ApJ, 867, 66 [Google Scholar]
- Costa, T., Sijacki, D., & Haehnelt, M. G. 2015, MNRAS, 448, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, J., Bechtold, J., Ge, J., & Meyer, D. M. 2005, ApJ, 633, 649 [Google Scholar]
- De Cia, A., Ledoux, C., Mattsson, L., et al. 2016, A&A, 596, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- den Brok, J. S., Cantalupo, S., Mackenzie, R., et al. 2020, MNRAS, 495, 1874 [CrossRef] [Google Scholar]
- Dimitrijević, M. S., Popović, L. Č., Kovačević, J., Dačić, M., & Ilić, D. 2007, MNRAS, 374, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Dubois, Y., Peirani, S., Pichon, C., et al. 2016, MNRAS, 463, 3948 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, S. L., Prochaska, J. X., Hennawi, J., et al. 2010, MNRAS, 406, 1435 [NASA ADS] [Google Scholar]
- Fabian, A. C. 2012, ARA&A, 50, 455 [Google Scholar]
- Fathivavsari, H. 2020, ApJ, 888, 85 [Google Scholar]
- Fathivavsari, H., Petitjean, P., Jamialahmadi, N., et al. 2018, MNRAS, 477, 5625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mex. Astron. Astrofis., 53, 385 [NASA ADS] [Google Scholar]
- Feruglio, C., Fiore, F., Carniani, S., et al. 2015, A&A, 583, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finley, H., Petitjean, P., Pâris, I., et al. 2013, A&A, 558, A111 [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2007, ApJ, 663, 320 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fox, A. J., Ledoux, C., Petitjean, P., & Srianand, R. 2007, A&A, 473, 791 [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
- Gordon, K. D., Clayton, G. C., Misselt, K. A., Landolt, A. U., & Wolff, M. J. 2003, ApJ, 594, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gronke, M. 2017, A&A, 608, A139 [Google Scholar]
- Guillard, P., Boulanger, F., Pineau Des Forêts, G., & Appleton, P. N. 2009, A&A, 502, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gupta, N., & Saikia, D. J. 2006, MNRAS, 370, 738 [Google Scholar]
- Hook, I. M., McMahon, R. G., Boyle, B. J., & Irwin, M. J. 1994, MNRAS, 268, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiang, P., Zhou, H., Pan, X., et al. 2016, ApJ, 821, 1 [Google Scholar]
- Kaspi, S., Brandt, W. N., Maoz, D., et al. 2007, ApJ, 659, 997 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kausch, W., Noll, S., Smette, A., et al. 2015, A&A, 576, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Kisielius, R., Storey, P. J., Ferland, G. J., & Keenan, F. P. 2009, MNRAS, 397, 903 [Google Scholar]
- Kulkarni, V. P., Meiring, J., Som, D., et al. 2012, ApJ, 749, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Laursen, P., Razoumov, A. O., & Sommer-Larsen, J. 2009a, ApJ, 696, 853 [Google Scholar]
- Laursen, P., Sommer-Larsen, J., & Andersen, A. C. 2009b, ApJ, 704, 1640 [NASA ADS] [CrossRef] [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ledoux, C., Petitjean, P., Fynbo, J. P. U., Møller, P., & Srianand, R. 2006, A&A, 457, 71 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H. P. 2009, Landolt Börnstein, 4B, 712 [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 500, 259 [NASA ADS] [Google Scholar]
- McCully, C., Crawford, S., Kovacs, G., et al. 2018, https://doi.org/10.5281/zenodo.1482019 [Google Scholar]
- Morgan, C. W., Kochanek, C. S., Morgan, N. D., & Falco, E. E. 2010, ApJ, 712, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Neeleman, M., Prochaska, J. X., & Wolfe, A. M. 2015, ApJ, 800, 7 [Google Scholar]
- Netzer, H. 2015, ARA&A, 53, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Noterdaeme, P., Ledoux, C., Petitjean, P., et al. 2007, A&A, 474, 393 [Google Scholar]
- Noterdaeme, P., Srianand, R., Rahmani, H., et al. 2015, A&A, 577, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Krogager, J.-K., Balashev, S., et al. 2017, A&A, 597, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Ledoux, C., Zou, S., et al. 2018, A&A, 612, A58 [Google Scholar]
- Noterdaeme, P., Balashev, S., Krogager, J. K., et al. 2019, A&A, 627, A32 [CrossRef] [EDP Sciences] [Google Scholar]
- Nozawa, T., & Fukugita, M. 2013, ApJ, 770, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pontzen, A., Tremmel, M., Roth, N., et al. 2017, MNRAS, 465, 547 [Google Scholar]
- Pottasch, S. R., Wesselius, P. R., & van Duinen, R. J. 1979, A&A, 74, L15 [NASA ADS] [Google Scholar]
- Prochaska, J. X., Hennawi, J. F., & Herbert-Fort, S. 2008, ApJ, 675, 1002 [Google Scholar]
- Reimers, D., Baade, R., Quast, R., & Levshakov, S. A. 2003, A&A, 410, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richings, A. J., & Faucher-Giguère, C.-A. 2018, MNRAS, 474, 3673 [Google Scholar]
- Rupke, D. S. N., & Veilleux, S. 2011, ApJ, 729, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Rupke, D. S. N., Gültekin, K., & Veilleux, S. 2017, ApJ, 850, 40 [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Selsing, J., Fynbo, J. P. U., Christensen, L., & Krogager, J.-K. 2016, A&A, 585, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silk, J., & Rees, M. J. 1998, A&A, 331, L1 [NASA ADS] [Google Scholar]
- Silva, A. I., & Viegas, S. M. 2002, MNRAS, 329, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Srianand, R., Petitjean, P., Ledoux, C., Ferland, G., & Shaw, G. 2005, MNRAS, 362, 549 [Google Scholar]
- Sternberg, A., Le Petit, F., Roueff, E., & Le Bourlot, J. 2014, ApJ, 790, 10 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Storey, P. J., & Zeippen, C. J. 2000, MNRAS, 312, 813 [Google Scholar]
- Sun, A.-L., Greene, J. E., & Zakamska, N. L. 2017, ApJ, 835, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Terrazas, B. A., Bell, E. F., Pillepich, A., et al. 2020, MNRAS, 493, 1888 [Google Scholar]
- Tombesi, F., Meléndez, M., Veilleux, S., et al. 2015, Nature, 519, 436 [Google Scholar]
- van Dokkum, P. G. 2001, PASP, 113, 1420 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Bolatto, A., Tombesi, F., et al. 2017, ApJ, 843, 18 [Google Scholar]
- Verhamme, A., Schaerer, D., Atek, H., & Tapken, C. 2008, A&A, 491, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vestergaard, M., & Peterson, B. M. 2006, ApJ, 641, 689 [Google Scholar]
- Vestergaard, M., & Wilkes, B. J. 2001, ApJS, 134, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Volonteri, M., Dubois, Y., Pichon, C., & Devriendt, J. 2016, MNRAS, 460, 2979 [Google Scholar]
- Wakelam, V., Bron, E., Cazaux, S., et al. 2017, Mol. Astrophys., 9, 1 [Google Scholar]
- Weymann, R. J., Morris, S. L., Foltz, C. B., & Hewett, P. C. 1991, ApJ, 373, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, K., Li, K. J., Owen, E. R., et al. 2020, MNRAS, 491, 5621 [Google Scholar]
- Xu, X., Zakamska, N. L., Arav, N., Miller, T., & Benn, C. 2020, MNRAS, 495, 305 [Google Scholar]
- Zhang, K., & Hao, L. 2018, ApJ, 856, 171 [Google Scholar]
- Zubovas, K., & King, A. 2012, ApJ, 745, L34 [Google Scholar]
- Zubovas, K., Nayakshin, S., King, A., & Wilkinson, M. 2013, MNRAS, 433, 3079 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Layout of 1.2″-wide X-shooter slits in the NIR. The small dotted circle represents a projected area of radius 5 kpc (at the redshift of the quasar) with 100% coverage by all our X-shooter slit positions, and the larger dashed circle represents the BOSS fibre aperture. |
| In the text | |
 |
Fig. 2. Portion of combined 1D NIR spectrum around the [O II] doublet emission line. The 1D spectrum with (without) telluric correction is shown in black (orange) together with the fitted profile in red. |
| In the text | |
 |
Fig. 3. Portion of combined 1D NIR spectrum around Hβ and [O III] emission lines. Top panel: contribution from the off-trace spatially extended emission, which is apparent in both [O III] lines. Bottom panel: spectrum collapsed over its full spatial extent at wavelengths 1.790 < λ(μm) < 1.825 and the optimal extraction elsewhere, for presentation purposes. The green line shows our estimate of featureless continuum emission. Individual Gaussians constrained during the fit are shown in different colours, with the total fitted profile shown in red. |
| In the text | |
 |
Fig. 4. Bottom: portion of 1D X-shooter spectrum around the C IV emission line, median-smoothed using a 5-pixel sliding window for presentation purposes (black, with 1σ error level in green). The inset shows an unsmoothed zoom-in on the C IV absorption, with the blue region highlighting the residual emission. The best-fit model is shown by the red solid line and the individual Gaussians as red dotted lines. The downwards arrow indicates the systemic redshift. Top: 2D spectrum in the region featuring the C IV absorption line as well as residual C IV emission in the trough. |
| In the text | |
 |
Fig. 5. Average observed spatial profiles at the location of different emission lines. In each panel, the dashed curve shows the spatial point spread function obtained from the quasar continuum in a nearby region. We note that the profile around the narrow [O III] emission still contains a contribution from the continuum and the broad [O III] emission. For the sake of easy comparison, each profile is normalised by its maximum value. |
| In the text | |
 |
Fig. 6. Individual 2D spectra around the [O III]λ5008 region (from top to bottom: PA = −155 deg, −164 deg, +177 deg, and +166 deg east of north, i.e. in these figures, north is down and south is up). The total observed emission is shown in the left panels, while the unresolved emission (continuum+broad component) has been subtracted in the right panels to better highlight the spatially-extended narrow [O III] emission alone. Each panel is 4000 km s−1 wide. The main skyline residuals are masked out by a white hashed grid. Top-left panel: total extracted 1D spectrum, with the corresponding Gaussian fits. The coloured regions show the velocity bins used in Fig. 7. |
| In the text | |
 |
Fig. 7. Total spatial profile of narrow [O III] emission (black) and in three velocity bins (with colours indicated in the legend) after subtracting the unresolved broad [O III] and continuum emission. The dotted line shows the spectral PSF obtained from the trace of the quasar continuum. |
| In the text | |
 |
Fig. 8. Decomposition of rest-frame Ly-α region. The observed on-trace X-shooter spectrum is shown in black with uncertainties as grey error bars. The reconstructed unabsorbed quasar emission line is shown as the dashed purple curve. The red curve is the combination of this unabsorbed emission together with the modelled DLA absorption profile with log N(H I) = 20.71. Subtracting the absorption profile from the intrinsic emission profile provides us with the residual emission shown in blue, over the 4400−4440 Å wavelength interval. The BOSS fibre spectrum is shown in green. |
| In the text | |
 |
Fig. 9. Ly-α emission in PDLA core before (left) and after (right) subtraction of the unresolved quasar continuum emission. From top to bottom: PAs = −155, −164 and +177 deg. Top-right panel: spectral profile of the extended Ly-α emission for each position angle as well as their average, collapsing over the full spatial range shown in the 2D panels (hence an aperture of 6 × 1 arcsec). The SDSS-III/BOSS spectrum is shown in green. The small side panels show the spatial profiles of the unresolved quasar continuum emission (red) and the extended Ly-α emission (black). |
| In the text | |
 |
Fig. 10. Portion of X-shooter UVB spectrum of J0015+1842 (black, with uncertainties in grey). Horizontal blue segments connect rotational levels (short tick marks) from a given Lyman (L) or Werner (W) band of H2 for the central H2 component. The same is shown in grey for the two other components, but they are not labelled for visibility. The overall model (MCMC-based) spectrum is over-plotted in red, with contribution from non-H2 lines (H I and metal lines) shown as a dotted purple line. |
| In the text | |
 |
Fig. 11. Fit to neutral chlorine absorption line. The observed data are shown in black, with the best-fit profile shown in red. Top panel: residuals (black) and 1σ error level (orange). The short tick marks show the location of the H2 components, while long dashed blue lines show those of other metal lines. As for all similar figures in this work, the origin of the velocity scale is set to zref = 2.631. |
| In the text | |
 |
Fig. 12. Fit to metal absorption lines. The observed data are shown in black with the synthetic profile for each given species overplotted in red. In case of several lines contributing to the observed profile (see e.g., S IIλ1259 and Si IIλ1260), the contribution for the labelled line alone is shown in red, while the total synthetic profile is shown in orange. Residuals are shown in the small panel above each line, with the orange line showing the 1σ error level. The location of the different components of the model are indicated by blue vertical dashed lines, with short red marks showing the position of H2 components. The zero of the velocity scale is set to zref = 2.631. |
| In the text | |
 |
Fig. 13. Fit to C I absorption lines. The data are shown in black with the best-fit over-plotted in red. The contribution from individual fine-structure levels are shown in orange (C I), green (C I*), and purple (C I**). Top panels: residuals. |
| In the text | |
 |
Fig. 14. Same as Fig. 12 for the absorption lines from excited fine-structure of singly-ionised silicon. |
| In the text | |
 |
Fig. 15. Combined X-shooter spectrum of J0015+1842 in black with best-fit SED corrected for dust extinction shown in red. For visual purposes, the data have been filtered (rejecting 4-σ outliers; light grey) and smoothed (black) in order to remove the strong skyline residuals in the NIR data. The position of the 2175 Å extinction feature is indicated by an arrow, and the best-fit model without the 2175 Å feature is indicated by the purple line. The unreddened quasar template is shown in blue. Photometric data from SDSS (u, g, r, i, and z bands) and WISE (band 1) are shown as orange squares. |
| In the text | |
 |
Fig. 16. Velocity profile of thrice-ionised silicon (top and middle panels), compared to that of singly-ionised silicon (bottom panel). Short tick marks indicate the position of H2 components. The zero of the velocity scale is set to zref = 2.631. |
| In the text | |
 |
Fig. 17. Bottom: pixel optical depths of Si IIλ1808 and Si II*λ1264 lines. Top: apparent column density ratio per unit velocity bin (i.e. the ratios of τ/(fλ0)). The location of H2 components is marked by the red dashed lines. The horizontal dashed line shows the overall column density ratio as derived from the Voigt-profile fitting. Values for which the optical depth of either line is below 0.03 lead to large errors and are not plotted. The zero point of the velocity scale is set to zref = 2.631. |
| In the text | |
 |
Fig. 18. Excitation of ionised silicon fine-structure level as a function of density and distance to the quasar. The dashed white line corresponds to the observed integrated ratio (i.e. N(Si II*)/N(Si II)). |
| In the text | |
 |
Fig. 19. Abundances of various species (top) and variation of Si II*/Si II ratio (middle) and temperature (bottom) as a function of cumulative H I column density for a constant density model with log n/cm−3 = 1 at d = 10 kpc. The dashed-dotted line in the middle panel shows the cumulative N(Si II*)/N(Si II) ratio. |
| In the text | |
 |
Fig. 20. Cloudy model predictions for the second slab of gas, with log N(H2) = 19.3. |
| In the text | |
 |
Fig. 21. Constraints on thermal pressure, P, and distance from cloud to AGN, d, obtained by modelling the excitation of H2 rotational levels with the PDR MEUDON code. The contours show formal regions that contain 0.683 probability distribution functions. The solid and dashed lines correspond to the estimates based on MCMC and vpfit result of H2 fit (see Table 3), respectively. The marginalised probability distribution functions (along right and top axes) and the best-fit values (stars) are shown for MCMC results only for the sake of clarity. The black line with upwards arrows show the constraints from the H2-H I transition, assuming the kinetic temperature is T ∼ 100 K, which is consistent with the observations. |
| In the text | |
 |
Fig. 22. Comparison of model and observed excitation diagram of H2 rotational levels. The filled and open circles represent the measurements using vpfit and a MCMC method (see Sect. 4.2), respectively. The dashed lines show the best fit of the excitation diagram (corresponding parameters d and P marked by stars in Fig. 21). The data points are artificially shifted on the x-axis to ease representation. |
| In the text | |
 |
Fig. 23. Comparison between simulated 2D spectrum of photons escaping in the particular direction of the observer looking down the barrel of the jet (bottom) with the actual observed X-shooter 2D spectrum (top). The distance along slit is taken from the unresolved quasar continuum emission. We note that the observed spectrum is also affected by unrelated absorption, which we do not model here (e.g., at 4396 Å). |
| In the text | |
 |
Fig. 24. Cartoon of inferred configuration of the system. The emission properties of the unresolved active nucleus (e.g., blueshifted broad [O III]) are not shown to avoid overcrowding the figure. Ly-α photons can be more easily scattered out from the cones towards the observer from the receding outflow and appear red peaked. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


