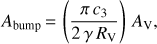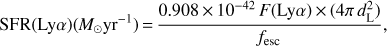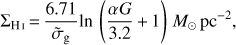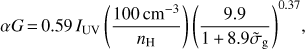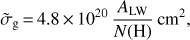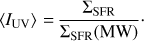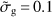| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A184 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201833446 | |
| Published online | 01 November 2018 | |
Molecular gas and star formation in an absorption-selected galaxy: Hitting the bull’s eye at z ≃ 2.46⋆,⋆⋆
1 Institut d’astrophysique de Paris, UMR 7095, CNRS-SU, 98bis bd Arago, 75014 Paris, France
e-mail: adarsh.ranjan@iap.fr
2 Ioffe Institute of RAS, Polytekhnicheskaya 26, 194021 Saint-Petersburg, Russia
3 Raymond and Beverly Sackler School of Physics & Astronomy, Tel Aviv University, 69978 Ramat Aviv, Israel
4 Inter-University Centre for Astronomy and Astrophysics, Post Bag 4, Ganeshkhind, 411 007 Pune, India
5 Cosmic Dawn Center, Niels Bohr Institute, Copenhagen University, Juliane Maries Vej 30, 2100 Copenhagen Ø, Denmark
6 European Southern Observatory, Alonso de Córdova 3107, Casilla 19001, Vitacura, Santiago, Chile
7 Oskar Klein Centre, Dept. of Astronomy, Stockholm University, AlbaNova, 10691 Stockholm, Sweden
Received:
17
May
2018
Accepted:
19
June
2018
We present the detection and detailed analysis of a diffuse molecular cloud at zabs = 2.4636 towards the quasar SDSS J 1513+0352 (zem ≃ 2.68) observed with the X-shooter spectrograph at the Very Large Telescope. We measured very high column densities of atomic and molecular hydrogen with log N(H I, H2) ≃ 21.8, 21.3. This is the highest H2 column density ever measured in an intervening damped Lyman-α system but we did not detect CO, implying log N(CO)/N(H2) < −7.8, which could be due to a low metallicity of the cloud. From the metal absorption lines, we derived the metallicity to be Z ≃ 0.15 Z⊙ and determined the amount of dust by measuring the induced extinction of the background quasar light, AV ≃ 0.4. We simultaneously detected Lyman-α emission at the same redshift with a centroid located at a most probable impact parameter of only ρ ≃ 1.4 kpc. We argue that the line of sight is therefore likely passing through the interstellar medium (ISM), as opposed to the circumgalactic medium (CGM), of a galaxy. The relation between the surface density of gas and that of star formation seems to follow the global empirical relation derived in the nearby Universe although our constraints on the star formation rate (SFR) and the galaxy extent remain too loose to be conclusive. We study the transition from atomic to molecular hydrogen using a theoretical description based on the microphysics of molecular hydrogen. We use the derived chemical properties of the cloud and physical conditions (Tk ≃ 90 K and n ≃ 250 cm−3) derived through the excitation of H2 rotational levels and neutral carbon fine structure transitions to constrain the fundamental parameters that govern this transition. By comparing the theoretical and observed H I column densities, we are able to bring an independent constraint on the incident ultra-violet (UV) flux, which we find to be in agreement with that estimated from the observed SFR.
Key words: quasars: absorption lines / galaxies: high-redshift / galaxies: ISM
Based on observations performed with the Very Large Telescope of the European Southern Observatory under Prog. ID 095.A-0224(A).
The final reduced spectrum (FITS file) is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/618/A184
© ESO 2018
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Stars are known to form from the gravitational collapse of cold dense gas clumps in the interstellar medium (ISM; see Leroy et al. 2008). Observations in our own Galaxy and in the nearby Universe have further shown that this dense gas is in molecular form (H2). It is well known that gas giving birth to stars is molecular. Although the exact reason for this is not trivial since H2 is not a good coolant of the ISM. However, it is energetically favoured compared to atomic hydrogen. In fact, the molecular state of the gas is more the consequence of physical conditions favouring both the conversion of atomic into molecular gas and the formation of stars, than a true pre-requisite for star formation (see discussions in Glover & Clark 2012). Indeed, it may also be possible that, below a certain metallicity, the gas collapses into stars on a timescale shorter than needed to form H2 (e.g. Krumholz 2012; Michałowski et al. 2015).
Therefore, while investigating globally the relations between atomic gas, molecular gas, and star formation at different epochs should bring important clues to understand the formation and evolution of galaxies, it is equally important to understand the micro-physics at play in the gas (i.e. at a small scale) for a complete theory of star formation.
An empirical relation between the surface density of neutral gas and that of star formation is well established over galactic scales in the nearby Universe (see Kennicutt & Evans 2012). It seems that this relation actually implicitly results from a strong relation between H2 and star formation seen on kiloparsec (kpc) or sub-kiloparsec (sub-kpc) scales (e.g. Schruba et al. 2011) and a conversion from H I to H2. This conversion can be described phenomenologically as a relation between molecular fraction and hydrostatic pressure at galactic mid-plane (Blitz & Rosolowsky 2006), but also from the first principles as an equilibrium between the formation and destruction of the molecule. This has been intensively studied theoretically and observationally in the local ISM (see review by Wakelam et al. 2017). In short, the formation of H2 in cold neutral medium is dominated by three-body reactions on the surface of dust grains (e.g. Hollenbach et al. 1971), even at relatively low metallicities. The gas-phase production of H2 is not efficient although it is the only route to form H2 in pristine gas (e.g. Black & van Dishoeck 1987). H2 is destroyed primarily through absorption of ultraviolet (UV) photons in the Lyman–Werner (LW) bands of H2, followed by a radiative decay onto a dissociative state in approximately 12% of the cases (Abgrall et al. 1992). Therefore, shielding of H2 occurs both as self-shielding (in these LW bands) and shielding from dust that absorbs the incident UV radiation over an extended wavelength range.
Large and deep surveys now permit the study of star formation properties of galaxies in the distant Universe (see e.g. Madau & Dickinson 2014). Furthermore, thanks to the advances of submillimeter (sub-mm) astronomy, it is also possible to detect large molecular reservoirs traced by CO emission lines (see Carilli & Walter 2013, and references therein). Finally, the forthcoming Square Kilometer Array (Huynh & Lazio 2013) will open the possibility to study the atomic gas in emission beyond the local Universe.
Currently the only way to study the small-scale chemical and physical properties of neutral gas is by observing the absorption lines imprinted by the gas on the spectra of background sources, such as quasars. Absorption spectroscopy indeed allows the study of several gas phases simultaneously while probing the associated galaxy irrespective of its brightness. Hence, this technique efficiently traces the overall population of galaxies.
However, gas-phase studies remain very disconnected from that of the star formation and macroscopic properties of galaxies.
This is not only due to the difficulty in detecting in emission the galaxy counterpart of the absorbing gas (or finding background sources behind emission-selected galaxies), but also because the cross-section selection makes most lines of sight only probe the very outskirts of these galaxies. For the highest column density absorbers (the so-called damped Lyman-α absorbers [DLAs], see Wolfe et al. 2005), the typical impact parameters are of the order ρ ∼ 10 kpc or less (Rahmati & Schaye 2014; Rubin et al. 2015; Krogager et al. 2017). Improved observational strategies and new powerful instruments have now permitted the detection of the host galaxies responsible for an increasing number of DLAs (e.g. Fynbo et al. 2010, 2011; Noterdaeme et al. 2012; Krogager et al. 2013; Hartoog et al. 2015; Srianand et al. 2016; Ma et al. 2018; Neeleman et al. 2018). Statistical relations start to emerge, such as a relation between the metallicity of the gas probed in absorption and the impact parameter and luminosity of the host galaxy (Krogager et al. 2017). However, the number of detections remains low and, it is crucial to study lines of sight that pass through the ISM of high-redshift galaxies which, as its name indicates, refers to the gas collocated with stars in galaxies. Since the gas falls in the gravitational potential of galaxies, it is naturally expected that higher column densities of gas trace more central regions, where stars are found. This results in an anti-correlation between H I column density and the impact parameter that is predicted by simulations (e.g. Pontzen et al. 2008) and observed over a wide range of redshifts (Zwaan et al. 2005; Rao et al. 2011; Krogager et al. 2012).
Based on these considerations, Noterdaeme et al. (2014) searched for extremely strong DLAs (ESDLAs; with log N(H I) > 21.7) in the Sloan Digital Sky Survey (SDSS) (York et al. 2000). They statistically showed that these systems are connected to the population of Lyman-α emitters (LAEs) and that the impact parameters are likely small. Simulations furthermore show that the high end of the N(H I) distribution is sensitive to the stellar feedback and the formation of molecules (e.g. Altay et al. 2013; Bird et al. 2014). We have, therefore, initiated an observational campaign to search not only for the associated galaxies in emission but also for the molecular gas in absorption. We note two interesting cases in this work: the ESDLAs at zabs = 2.207 and zabs = 2.786 towards SDSS J1135−0010 and SDSS J0843+0221, respectively. In the former case, a star-forming galaxy is detected with its centroid located at a very small impact parameter ρ < 1 kpc, directly showing that the line of sight passes through the main star-forming region of the galaxy (Noterdaeme et al. 2012). Unfortunately, because of a higher redshift Lyman limit system, H2 cannot be detected. In the second case, extremely strong H2 lines are detected (Balashev et al. 2017) but the galaxy emission remains undetected. Owing to the low metallicity in the latter case, we can expect the host galaxy to be of low mass and low luminosity (e.g. Fynbo et al. 2008; Krogager et al. 2017). We present the simultaneous detection of molecular gas with very high H2 column density and star formation activity from a galaxy at z ≈ 2.46 aligned with the background quasar SDSS J 151349.52+035211.68 (hereafter J 1513+0352).
Standard ΛCDM flat cosmology is used for the paper with H0 = 67.8 ± 0.9 km s−1 Mpc−1, ΩΛ = 0.692 ± 0.012 and Ωm = 0.308 ± 0.012 (Planck Collaboration XIII 2016). The details of the observations and data reduction are presented in Sect. 2. The analysis of the chemical properties of the gas and dust content are described in Sect. 3. The detection and properties of the associated galaxy are presented in Sect. 4. We discuss and compare our results with global relationships between gas and star formation and discuss the gas microphysics in Sect. 5 before finally summarizing our findings and concluding in Sect. 6.
2. Observations and data reduction
The quasar J 1513+0352 was observed on four different nights in service mode, on 15−16 Apr 2015 and 14−15 May 2015 under ESO programme ID 095.A-0224(A) with the multiwavelength, medium-resolution spectrograph X-shooter (Vernet et al. 2011) mounted at the Cassegrain focus of the Very Large Telescope UT2. The observations were performed under good conditions (average seeing ∼0.69 and airmass ∼1.15). Each time, the target was observed in a nodding sequence totalling 2960 s (2 × 1480 s) in the UV-Blue (UVB), 2860 s (2 × 1430 s) in the Visible (VIS) and 2880 s (2 × 3 × 480 s) in the Near-Infrared (NIR). The slit widths used were 1.6, 0.9 and 1.2 arcsec for the UVB, VIS, and NIR arms, respectively.
All observations were performed with the slit aligned with the parallactic angle, which changed little between the observations (±10°). The log of the observations is summarised in Table 1. We reduced the data using the X-shooter pipeline (Modigliani et al. 2010) and combined individual exposures weighting each pixel by the inverse of its variance to obtain the final 2D and 1D spectra used in this paper. The typical signal-to-noise (per pixel) ratios achieved are S/N ≃ 25, 23 and 15 at 4700, 6500 and 12 400 Å, respectively. Since the seeing was significantly smaller than the slit width, in particular in the UVB, the spectral resolution achieved is higher than the nominal resolution for the given slit widths. This is in agreement with the resolution expected in cases in which the seeing is significantly smaller than the slit width as in Fynbo et al. (2011). Moreover, we checked the actual spectral resolution directly from the combined spectra by first fitting the numerous Fe II lines in the VIS part of the spectra that was obtained with a narrower slit using a multicomponent model with the column density, Doppler parameter, redshift, and resolution as free parameters. We found a spectral resolution of R = 9300, which is consistently slightly higher than the nominal resolution for the given slit width. We then used this model to derive the resolution in the UVB region using the Fe II λ 1608 and Fe II λ 1611 lines and obtain R = 7300. This was confirmed by fitting the Si II lines along with the Fe II lines.
Journal of observations.
3. Absorption analysis
The DLA at zabs = 2.4636 towards the quasar SDSS J 1513+0352 presents extremely strong absorption lines from atomic (H I) and molecular (H2) hydrogen and absorption lines from metals in different ionisation stages. The kinematic profiles of selected species tracing different phases are illustrated in Fig. 1. As in the overall population of DLAs, singly ionised metal species are seen and are expected to be in their dominant ionisation stage in the neutral gas, where only photons with energies less than 13.6 eV can penetrate. The corresponding profile is compact with a main central component that likely contains the bulk of the atomic gas. A single component of neutral carbon is seen at the velocity of this main metal component. Since the first ionisation potential of carbon is lower than the energy of photons that destroy H2 (see e.g. Noterdaeme et al. 2017), this component also likely contains most of the molecular hydrogen. In turn, high ionisation species trace ionised gas and have a very different kinematic profile. Indeed, the C IV profile is strongest where there is no component seen in the neutral or low ionisation species, which is possibly indicative of outflowing material (Fox et al. 2007). Since this ionised phase is, apparently, physically and kinematically disconnected from the neutral and molecular phases, it is not considered further in this paper, as we concentrate on the properties of the neutral and molecular gas.
 |
Fig. 1. Velocity profiles of selected species associated with the DLA system at z = 2.4636 towards J 1513+0352, tracing the ionised gas (C IV), neutral atomic gas (Fe II), and molecular gas (C I). Despite the apparent complexity, the C I profile is actually characterised by a single component (shown in blue) and other absorption seen in the panel arise from excited fine-structure levels (J = 1 and J = 2 in cyan and green, respectively; the total profile is in red). The blue line in the Fe II panel shows the contribution from the ν = 0 component. |
We analysed the absorption line profiles of H I, H2 and low-ionisation metals using standard multiple Voigt profile fitting using VPFIT v10.2 (Carswell & Webb 2014). The gas-phase abundances are expressed relative to the solar values as
where N(Htot) = N(H I) + 2N(H2) is the total hydrogen column density, X denotes the metal species, and (X/H)⊙ is the solar metal abundance. We adopted the same solar abundances as in De Cia et al. (2016), i.e. from Asplund et al. (2009), following the recommendations of Lodders et al. (2009) about the choice of photospheric, meteoritic, or average values.
3.1. Neutral carbon
Neutral carbon is detected in the fine-structure levels of the electronic ground state denoted here C I (J = 0), C I* (J = 1), and C I** (J = 2). We derived the column density in each fine-structure level by simultaneously fitting the C I bands located at λ = 1280, 1328, 1560, and 1656 Å in the DLA rest frame (see Fig. 2). The single component is fitted assuming the same redshift and Doppler parameter for all fine-structure levels. We obtain a Doppler parameter b = 3.9 ± 0.3 km s−1 and column densities of log N(C I, J = 0, 1, 2) = 14.82 ± 0.18, 14.60 ± 0.06 and 14.03 ± 0.06, respectively1 The best-fit synthetic profile is over-plotted on the data in Fig. 2. We note that the bluer C I bands are detected in the UVB but not used to constrain the fit since they are partly blended with the Lyman-α forest. We, however, checked that the calculated profile using our derived best-fit parameter values is consistent with the data in these regions as well. For the remaining figures in the paper, where we show the absorption profile as a function of relative velocity, the zero point of the velocity scale (ν = 0 km s−1) corresponds to the C I component at z = 2.46362.
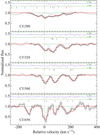 |
Fig. 2. Fit to the C I lines associated with the DLA. The panels show the 4 lines used for fitting. The data is represented in black and the best-fit synthetic profile in red with residuals in a ± 2σ-scale on the top of each panel. The individual contributions from J = 0 (C I), J = 1 (C I*), and J = 2 (C I**) are shown with cyan, magenta, and green lines, respectively. |
3.2. Neutral and molecular hydrogen
Figure 3 shows the portion of the UVB spectrum with absorption originating from the Lyman series of H I and the Lyman and Werner bands of H2 associated with the DLA. The blending of numerous molecular hydrogen lines with each other significantly decreases the apparent continuum. In order to retrieve the true unabsorbed quasar continuum, we used the same approach as in Balashev et al. (2017). We first, simultaneously, fitted the damped H I and H2 lines together with the continuum using the full wavelength range from 3200 to 4500 Å. We found that the first ten Chebyshev polynomials were sufficient to model the unabsorbed continuum. We then used this derived continuum to perform the complete fit of H I and H2 lines using VPFIT and removing the regions apparently contaminated by unrelated absorption (e.g. Ly α forest).
 |
Fig. 3. Portion of the X-shooter spectrum of J 1513+0352 covering the absorption lines of H I (Lyman-α shown in the bottom panel) and H2 (top three panels) from the DLA at z = 2.4636. The normalised data are shown in black and the synthetic profile is overplotted in red. We note the very strong flux suppression at the bluest wavelengths due to the increased overlapping of H2 lines. Horizontal blue segments connect rotational levels (short tick marks) from a given Lyman (L) or Werner (W) band, as labelled above. |
We obtain a total H I column density of log N(H I) = 21.83 ± 0.01, which confirms the value derived by Noterdaeme et al. (2014) from the low S/N and low-resolution SDSS spectrum (log N(H I) ≃ 21.80). The total H2 column density is found to be log N(H2) = 21.31 ± 0.01. This is the highest value reported to date in an intervening DLA, much above typical H2 columns (log N(H2) ∼ 18.2) seen in other DLAs (Noterdaeme et al. 2008) although only slightly higher than the recent detection associated with another extremely strong DLA recently reported by Balashev et al. (2017). The total hydrogen column density is then also amongst the highest seen in DLAs, i.e. log N(Htot) = 22.04 ± 0.01, with a very significant overall molecular fraction of f = 2N(H2)/(2N(H2) + N(H I)) = 0.38 ± 0.02. Since low-ionisation metals suggest that atomic gas is present in various components, this represents a lower limit to the molecular fraction in the H2 bearing cloud (likely present in a single component, as suggested from the C I profile). Furthermore, at such high hydrogen column density, the gas is likely to be fully molecular in the cloud core with the atomic gas corresponding to its external layers. We discuss this in detail in Sect. 5.3.
As for other known H2 systems, most of the total H2 is found in the first two rotational levels (see Table 2), for which the column densities are very well constrained thanks to the damping wings. We detect rotational levels up to J = 6 (and possibly J = 7); the spectral resolution does not allow us to obtain trustable column densities beyond J = 4. In particular, the saturated nature of many H2 lines together with the medium spectral resolution of X-shooter does not allow us to consider independent Doppler parameters for each rotational level when a possible increase of b with J has been shown to exist in different environments at low (Lacour et al. 2005) and high redshift (Noterdaeme et al. 2007). Still the measurement of the first five rotational levels contains interesting information, which we discuss below.
Column densities of H2 in various rotational levels at zabs = 2.4636 towards J1513+0352.
3.3. Rotational levels of H2
Figure 4 presents the excitation diagram of H2, i.e. the relative population of H2 rotational levels as a function of their energy with respect to the ground state. We find that both the J = 1 and J = 2 levels are consistent with a single excitation temperature, T012 = 92 ± 3 K. Since these low rotational levels are thermalised, their excitation temperature is known to be a good measurement of the kinetic temperature of the gas (see Roy et al. 2006), meaning that Tk ≈ T012. This temperature is only slightly higher than what is observed towards nearby stars (T01 ∼ 77 K; Savage et al. 1977) but lower than what is typically seen in other high-z H2-bearing DLAs (T ∼ 150 K; Srianand et al. 2005), although there is also dispersion between the measurements, which may also reflect the dispersion in metallicity, with a trend of lower temperatures with higher metallicities. In addition, most previous measurements were derived from lower column-density systems and the lower temperature measured is consistent with the trend of decreasing Tk with increasing N(H2) (see e.g. Muzahid et al. 2015; Balashev et al. 2017).
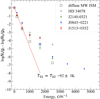 |
Fig. 4. H2 excitation diagram of the diffuse molecular cloud towards J1513+0352 (red) compared with other environments (typical diffuse ISM in the Milky Way (MW) shown as empty squares, the high-excitation case next to the bright star HD 34078 shown with a plus sign; and two other ESDLAs, towards J0843+0221 (blue) and J2140−0321 (green)). The red line shows the best fit to the J = 0,1 and 2 rotational levels towards J1513+0352, indicating Tk = 92 ± 3 K. |
Higher rotational levels (i.e. J ≥ 3) in turn have higher excitation temperatures. Such deviations from the Boltzman distribution is ubiquitous in the diffuse gas and generally explained by UV pumping and the fact that H2 is produced in excited states at the surface of dust grains. A comparison between different diagrams in different environments is then useful to get at least a qualitative estimate of the UV field. In Fig. 4, the excitation of H2 rotational levels towards J1513+0352 is compared with typical excitation seen in the Galactic disc (Gry et al. 2002) and in a molecular cloud illuminated by a high UV field near a O 9.5V star (Boissé et al. 2005). We also show the excitation diagrams for the high-redshift systems towards J0843+0221 (Balashev et al. 2017) and J2140−0321 (Noterdaeme et al. 2015) that also have very large H I column densities. The excitation of the DLA studied in this work is higher than the typical Milky Way (MW) environment and is suggestive of a relatively strong UV field. An accurate measurement of the H2 population in the high-rotational levels would be highly desirable, together with a measurement of the corresponding Doppler parameters. This should be possible with high-resolution spectroscopy. Nevertheless, the high-excitation inferred in this work suggests that the system towards J1513+0352 may represent gas in the star-forming disc of its associated galaxy.
3.4. CO content
Carbon monoxide (CO) can only survive in cold H2 gas. However, in spite of the very high H2 column density observed here, CO lines are not detected. Using the procedure described in Noterdaeme et al. (2018), we derive an upper limit of log N(CO) < 13.60 cm−2 at the 3σ confidence level. This translates to an upper limit on the CO/H2 ratio of log(N(CO)/N(H2)) of <−7.8, which is about two to three orders of magnitude lower than the typical value seen in the MW at the same H2 column density (e.g. Federman et al. 1990; Sheffer et al. 2008; Burgh et al. 2010). As discussed by Balashev et al. (2017), such an extremely low value is likely due to low metallicity of the gas. We indeed note that all CO detections to date at high redshift have been obtained in high-metallicity gas (Z ∼ Z⊙, Noterdaeme et al. 2018), although with low total hydrogen column densities. While high metallicities certainly favour the production of CO, through increased abundance of carbon and oxygen, but also an increased dust content, the low total column densities in turn most likely reflect a bias against high dust column densities that preclude the background quasars from being selected in optical surveys, as evidenced by several authors (see e.g. Fynbo et al. 2013, 2017; Krogager et al. 2016; Heintz et al. 2018).
The low CO/H2 ratio perhaps hints towards higher than Galactic cosmic-ray or X-ray ionisation rates (see Figs. 16 and 17 of Bialy & Sternberg 2015). However, a qualitative conclusion would require a detailed modelling that takes into account cloud geometry, covering factor, radiative transfer models etc., which are beyond the scope of this paper. The CO/C I ratio is also low, with log N(CO)/N(C I) < −1.3, which, in addition to the low metallicity, can also be explained by a high UV field to density ratio, as shown by Burgh et al. (2010). This is actually what we find from the physical conditions analysed in Sect. 5.3.
Interestingly enough, we remark that the system studied in this work is further evidence for the existence of CO-dark molecular gas at high redshift. Deriving the properties of a larger sample of such systems, together with determining a global census of strong H2 systems would be highly desirable to provide an independent look at the molecular gas content of high-z galaxies (see also Balashev & Noterdaeme 2018).
3.5. Metallicity and depletion
We derive the metal abundances in the neutral gas from measuring the column densities of low-ionisation species. We fitted the absorption lines from Si II, Ni II, Fe II, Zn II, Cr II, and Mn II assuming the same kinematic profile; i.e. we tied the redshifts and Doppler parameters, b, for each component. O I and Mg II are also detected in the DLA, but the observed lines (specifically O I λ 1302, Mg II λ 2796, and Mg II λ 2803) are saturated, so that we cannot get meaningful constraints on the corresponding column densities. We found that the metal absorption profiles are well reproduced using a four components model, one of which is narrow and corresponds to the C I absorption. We also checked that using more components does not provide any improvement in the fit and results in the same total column densities within errors. In order to take into account the contribution of Mg I λ2026 to the Zn II λ 2026 profile, we also included Mg I lines (Mg I λ1747, Mg I λ1827, and Mg I λ2852) while fitting the metals. The velocity profiles of the metal lines are shown in Fig. 5 together with the best-fit multicomponent Voigt profile. The total column densities, gas-phase abundances and abundance relative to zinc are summarised in Table 3.
 |
Fig. 5. Absorption profiles of Si II, Ni II, Fe II, Zn II, Cr II, Mn II, and Mg I. The grey line represents the data with parts used to constrain the fit shown in black. The red line represents the synthetic profile. The black tick marks on top of the profile show the position of individual velocity components. The top box represents the residuals in the ±2σ range. The individual contributions from Mg I and Cr II in the box showing Zn II(λ = 2026 and 2062) profiles are shown in cyan and magenta respectively. |
Summary of column densities and abundances.
We use the abundance of zinc, which is a non-refractory element, as an estimate for the DLA metallicity, [Zn/H] = −0.84 ± 0.23, where the relatively large uncertainty is due to the observations of the main narrow component at medium spectral resolution. The abundance of silicon is apparently possibly higher than that of zinc albeit consistent within errors, which would be surprising since silicon tends to be mildly depleted. Indeed, De Cia et al. (2016) showed that silicon should be depleted by a factor of two compared to zinc at the estimated metallicity. However, because the Si II lines are intrinsically saturated and the narrow component is hidden within a broad component, we caution its column density may be overestimated and hence, we prefer not to rely on Si II. We also detect P II and S II in the system. However, we do not use these lines to constrain the fit as all S II lines are located in the Lyman-α forest. The strongest P II line is also located in the Lyman-α forest and another line, which is outside the forest, is close to the noise level. Still, these species provide a nice consistency check, in particular, since they are little or not depleted. We calculated the S II and P II profiles assuming a solar abundance relative to zinc and found a very good match between the expected profile and the data; see Fig. 6. This further confirms our metallicity measurement. The derived metallicity is typical of DLAs at that redshift, although slightly higher than the cosmological mean metallicity value (Rafelski et al. 2014; De Cia et al. 2018). It is in turn significantly higher than the metallicity in the system towards J 0843+0221 (Balashev et al. 2017), which has similar H I and H2 content.
 |
Fig. 6. Expected velocity profiles of P II and S II lines (red) overplotted on the observed spectrum (black). We emphasise that this is not a fit, but the scaling of the derived zinc profile assuming solar phosphorus-to-zinc and sulphur-to-zinc ratios. |
3.6. Dust extinction of the background quasar’s light
The wide wavelength range and good flux calibration of the X-Shooter spectrum allow us to measure the reddening of the light of the background quasar due to dust associated with the ESDLA. We use the template-matching technique as used in several studies of quasar absorbers (see e.g. Srianand et al. 2008; Noterdaeme et al. 2009; Ma et al. 2015). We allow for intrinsic quasar shape variation directly from fitting, as in Krogager et al. (2016), instead of correcting the observed values using a control sample. More specifically, the observed quasar spectrum is matched by a quasar template taken from Selsing et al. (2016), reddened using extinction laws applied at the DLA redshift. The extinction laws are described using the standard parametrisation by Fitzpatrick & Massa (2007) and the parameters obtained for different environments by Gordon et al. (2003). We then fitted the model T (λ) to the observed spectrum using
where TQSO denotes the unreddened quasar template at the quasar redshift and ε(λ) is the wavelength-dependent reddening law. The parameters we vary are E(B − V), the colour excess at the DLA redshift, Δβ, the power-law slope relative to the intrinsic slope of the quasar template, and f0, which is a constant scaling of the intrinsic quasar brightness.
We found that the best fit was obtained using the “LMC Average” extinction curve with an AV ≈ 0.43; see Fig. 7. The statistical error from the fit is only of 0.01 mag, but this does not represent the systematic error due to the spread of intrinsic quasar spectral slopes. A more realistic estimate of the uncertainty is of the order of 0.1 mag (e.g. Noterdaeme et al. 2017), which is consistent with the dispersion in intrinsic quasar spectral slope observed in the literature (Vanden Berk et al. 2001; Krawczyk et al. 2015).
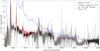 |
Fig. 7. Measurement of the extinction of the background quasar by dust in the DLA. The X-shooter spectrum is shown in grey with the continuum regions used to constrain the fit highlighted in black. The blue spectrum shows the scaled but unreddened quasar composite from Selsing et al. (2016). The thick red line shows the composite reddened by a LMC average extinction law with AV(DLA) = 0.43. The shaded region represents the strength of the 2175 Å bump (Abump(DLA) = 0.58 ± 0.003), that is the area between the reddened composite and the same reddened composite where the bump component (c3) has been set to zero. |
The absorption bump that exists in the LMC dust law is clearly visible at 2175 Å in the DLA rest frame. We quantified the strength of the bump following the prescription of Gordon et al. (2003) by following the parametrisation from Fitzpatrick & Massa, keeping c3 and the other parameters fixed to the LMC value. The bump strength, which corresponds to the shaded area in Fig. 7, is then given by
where, c3 and γ correspond to the amplitude and width of the 2175 Å bump. We obtain Abump ≃ 0.58, which is among the high values seen in other quasar absorption systems such as C I systems (Ledoux et al. 2015), which are also known to have high metallicities (Zou et al. 2018) and high molecular content (Noterdaeme et al. 2018). However, the high AV and Abump observed are mostly due to the very large column density of the system.
Indeed, the dust-to-gas ratio, AV/N(H) ≃ 4 × 10−23 mag cm2 remains modest and similar to the average value of typical DLAs (∼2−4 × 10−23 mag cm2; Vladilo et al. 2008) yet much smaller than the local ISM (0.45 × 10−21 mag cm2, Watson 2011) or C I-selected high-metallicity DLA systems at high-z (∼10−21 mag cm2; see Ledoux et al. 2015 and Zou et al. 2018). We note that the dust-to-gas ratio, relative to the MW, is about 0.09 when the metallicity is about 0.14 Solar. While the uncertainty on our measurement remains large, it may also indicate a non-linear relation between dust-to-gas ratio and metallicity, as seen by Rémy-Ruyer et al. (2013).
4. Detection of the associated galaxy
4.1. Ly-α emission
A faint Lyman-α emission is detected at the bottom of the DLA trough that is already seen as a non-zero flux in the unbinned 1D data (see Fig. 3). The same excess appears clearer in Fig. 8, where we rebinned the data by 6 pixels in a flux-conservative manner. The emission is also seen in the combined 2D data as a blob at around 1216 Å in the DLA rest frame and a possible peak at 1214 Å, both well aligned with the quasar trace (top panel of Fig. 8). We note that all three observed position angles used for the observations differ by no more than ±10°, allowing us to use the combined 2D spectrum for the measurement. From this 2D spectrum, we measured a flux of 2.2 ± 0.5 × 10−18 erg s−1 cm−2 in an aperture of ±400 km s−1 in the wavelength direction and ±0.8 arcsec in the spatial direction relative to the centre of emission (corresponding to about twice the Full width at half maximum (FWHM) of the trace). Figure 9 shows the distribution of fluxes in apertures of the same size, randomly located in the fully absorbed part of the DLA trough (excluding the region near the emission) on either side of the quasar trace. In the spatial direction, the apertures extended roughly to about ±2.5 arcsec. We find that the zero flux level is slightly offset by 0.3 × 10−18 erg s−1 cm−2, which we subtract from the measured Lyα flux. The rms dispersion of the random aperture flux distribution additionally gives a more appropriate estimate on the Lyα flux uncertainty of σ(FLyα) = 0.7 × 10−18 erg s−1 cm−2. Therefore, the corrected estimate of the observed Ly-α flux is FLyα = 1.9 ± 0.7 × 10−18 erg s−1 cm− and the detection is significant at the 2.7σ level.
 |
Fig. 8. Lyα emission in the DLA absorption trough shown in 1D (bottom, using a flux-conservative re-binning) and the 2D spectrum (top). The 2D data have been further smoothed by a Gaussian filter with σ of 1.8 pixel. The extracted flux is ∼1.9 ± 0.7 × 10−18 erg s−1 cm−2. |
 |
Fig. 9. Histogram shows the distribution of fluxes measured in apertures randomly located around the detected emission. The apertures have the same size as that used for the Lyα measurement. The mean of the distribution (vertical dotted line) provides an estimate of the zero flux level and the dispersion provides a more conservative estimate of the noise in the aperture. The red dashed vertical line shows the measured value of Lyα emission associated with the DLA. |
Considering the standard relation between Hα and star formation rate (SFR) from Kennicutt (1998), case-B recombination theory (Brocklehurst 1971) for the conversion of Lyα flux into Hα and introducing the escape fraction of Lyα photons, fesc, we obtain a constraint on the SFR as follows:
where, dL = 6.3 × 1028 cm is the luminosity distance for z = 2.46. For fesc = 1, Eq. (4) provides a lower limit on the SFR of SFR > 0.09 M⊙ yr−1.
4.2. Impact parameter
While the similar position angles of each exposure allowed us to use the combined 2D spectrum to detect the emission, it is not possible to triangulate the emission as done when position angles differ by a larger amount (see e.g. Møller et al. 2004; Fynbo et al. 2010; Noterdaeme et al. 2012; Srianand et al. 2016; Krogager et al. 2017). We can still estimate the impact parameter along the direction of the slit, ρ‖ from the spatial offset between the centroid of the Lyman-α emission and location of the quasar trace. We fitted Gaussian functions to the Ly-α and quasar spatial profiles collapsed along the wavelength dimension in the Ly-α region and quasar continuum near to the DLA, respectively; we obtain ρ‖ = 0.15 ± 0.06 arcsec, which corresponds to 1.24 ± 0.5 kpc at the DLA redshift (see Fig. 10). Since the Lyα emission is detected, we can further constrain its impact parameter in the direction perpendicular to the slit, ρ⊥, to be less than half the slit width, i.e. ρ⊥ < 0.8 arcsec, or equivalently ρ⊥ < 6.6 kpc in physical projected distance at the DLA redshift. This is a strict upper limit since there is no particular reason for the impact parameter perpendicular to the slit to be much larger than that along the slit length since the position angles were chosen without any prior. Indeed, assuming a uniformly distributed random angle of the quasar to Lyα emission direction with respect to the direction of the slit, we obtain the most probable value of the impact parameter to be ρ ≃ 0.17 ± 0.11 arcsec, or 1.4 ± 0.9 kpc (see Fig. 11). In the following, we assume this to be the true impact parameter of the galaxy. We caution that it is still possible that the Lyα emission arises only from the outskirts of a galaxy that would be located mostly outside of the slit, although the probability distribution function shown on Fig. 11 suggests this is highly unlikely.
 |
Fig. 10. Spatial profile of the Lyα emission (top) and quasar continuum (bottom) along the slit. The Lyα profile has been averaged over 10 pixels centred at the Lyα position (4211.8 Å). The quasar continuum profile has been averaged over the wavelength range free of strong absorption (4135−4150 Å). In each panel, we show the best-fit Gaussian model to the data. The vertical dashed lines indicate the centres of the profiles. |
 |
Fig. 11. Left: layout of the 1.6″-wide slit (white region) with the position of the quasar marked as red cross. The dashed line represents our measured constraint on ρ‖. The value ρ⊥ is constrained to be within the slit width. The black points show the distribution of possible locations of the emission, taking into account a normally distributed uncertainty on ρ‖ and a uniformly distributed random angle between quasar-galaxy and slit directions. Right: probability distribution function of the impact parameter. |
4.3. Near-infrared emission
Since the NIR arm of X-shooter covers the expected position of the redshifted oxygen and Balmer emission lines, we performed a subtraction of the spectral trace of the quasar to search for [O II], [O III] doublet, Hβ, and Hα. We do not detect any emission line, but we are able to put 3σ upper limits on the Hα and [O II] fluxes of < 2.6 × 10−17 erg s−1 cm−2 and <1.3 × 10−17 erg s−1 cm−2, respectively. The aperture used for the emission lines in the NIR is ±200 km s−1 along the wavelength axis and ±0.6 arcsec (corresponding to twice the FWHM of the trace) in the spatial direction. Using Kennicutt (1998), we can convert these line fluxes into dust-uncorrected SFRs SFR < 6.6 Myr−1 and SFR < 5.9 Myr−1 for Hα and [O II ], respectively. These limits on the SFR are consistent with the lower limit inferred from Lyα and it also places a lower limit on the escape fraction, fesc > 1.5%.
5. Discussion
5.1. Does the line of sight pass through the main disc of the associated galaxy?
There has been growing evidence that the column density observed along a given line of sight is anti-correlated with the impact parameter between this line of sight and the centroid of the associated galaxy. More specifically, low column densities are found over a wide range of impact parameters, while large column densities are restricted to the inner regions of galaxies (see Fig. 8 of Krogager et al. 2017). This is not only evident from 21 cm maps of atomic hydrogen in well-formed nearby galaxies (Zwaan et al. 2005; Braun 2012), but also in hydrodynamical simulations of gas at high redshift (e.g. Pontzen et al. 2008; Yajima et al. 2012; Altay et al. 2013; Rahmati & Schaye 2014) and direct detection of high-z galaxies responsible for DLA absorption (Krogager et al. 2017). In addition, Noterdaeme et al. (2014) have statistically shown that ESDLAs, with column densities in excess of N(H I) > 5 × 1021 cm−2, are located on average at impact parameters less than 2.5 kpc from Lyman-α emitters; however this value may be much larger in a fraction of systems (see Srianand et al. 2016). In our case, the small impact parameter and the large hydrogen column density fits well within this picture. Indeed, Rahmati & Schaye (2014) predicted a 1σ range of 1 ≲ ρ ≲ 6 kpc for the observed log N(H I) = 21.83 and we observed a most probable value of ρ ∼ 1.4 kpc. With such a small impact parameter, it is reasonable to think that the line of sight passes through the main disc of the associated galaxy2. Paulino-Afonso et al. (2018) estimated that the effective radius, reff of Lyman-α emitting galaxies at the DLA redshift (z ∼ 2.5) is reff ∼ 1 kpc, which is consistent with our measured impact parameter since the effective radius is defined such that it covers half of the total stellar light emitted from the galaxy, which then drops down exponentially. This suggests that the line of sight still could pass through the light-emitting region of the associated galaxy. We can also get a constraint on the spatial extent of the Lyα emission of our DLA galaxy from the 2D data. The unresolved emission suggests that the radius of the Lyα emission is smaller than the physical projected size corresponding to the seeing, i.e. r < 2.85 kpc, which remains consistent with our above picture.
In conclusion, the typical properties of LAEs at high-z, the measured small impact parameter, and the large hydrogen column density suggest that the line of sight passes through the main galactic disc. We caution again that we cannot exclude the possibility that the slit covers only part of the extended Lyα emission from a galaxy that would be located outside the slit. However, this would require an ad hoc configuration, putting the galaxy at a peculiar position such that the centroid of the covered Ly-α emission falls at the edge of the slit almost perpendicularly to the slit direction. This is unlikely given the small value of ρ∥ and the large slit width, as estimated in Fig. 11. It still remains possible that the detected Lyα emission corresponds to a star-forming region that is disconnected from a large galaxy, in which case we can consider the star-forming region to be a galaxy on its own (possibly part of a group) and our discussion, then, still stands. Considering the impact parameter between the quasar and the observed Lyα emission as a lower limit to the galaxy extent and the unresolved 2D emission as an upper limit, we then constrain the radius of the galaxy to be in the range (1.4 kpc < r < 2.85 kpc).
5.2. Relation between gas surface density and star formation rate
In this section, we discuss how our observations compares with the relation between the surface densities of gas and SFR as observed in the nearby Universe, i.e. the Kennicutt–Schmidt relation. This is valid over galactic scales and expressed as 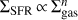 with n ∼ 1.4 (Kennicutt & Evans 2012). Absorption line measurements do not provide the disc-averaged surface densities but the column density along a single line of sight such that we have to assume that this column density is representative of the value over the galaxy extent.
with n ∼ 1.4 (Kennicutt & Evans 2012). Absorption line measurements do not provide the disc-averaged surface densities but the column density along a single line of sight such that we have to assume that this column density is representative of the value over the galaxy extent.
The total (H I + H2) column density we observe then corresponds to Σgas ≃ 86 M⊙ pc−2.
From the detection of the Lyman-α emission and the 3σ upper limit from the non-detection of [O II], we obtain a conservative range on the SFR to be 0.1 < SFR < 5.9 M⊙ yr−1. This range actually corresponds to an escape fraction ranging from 100% (if SFR = 0.1 M⊙ yr−1) to 1.5% (if SFR = 5.9 M⊙ yr−1). However, the typical escape fraction for the overall population of emission-selected galaxies at this redshift has been estimated to be more around 5% (Hayes et al. 2011) but can be much larger in low mass (Fernandez & Shull 2011)) and compact (Paulino-Afonso et al. 2018) galaxies. Indeed, for typical Lyman-α emitters, the escape fraction is found to be about fesc ∼ 30% (Finkelstein et al. 2011; Nakajima et al. 2012; Nestor et al. 2013). A more realistic range for the SFR can then be estimated considering fesc ∼ 5−30%, from which we get 0.2 < SFR < 2.4 M⊙ yr−1. Combining these constraints with those on the galaxy extent, this translates to a surface density of SFR in the range −2.1 < log ΣSFR (M⊙ yr−1 kpc−2) < −0.4, assuming disc-like geometry and ignoring projection effects (i.e. taking the surface of the galaxy to be πr2). The estimated surface SFR and the observed column density are therefore consistent with the observations in the nearby Universe (see e.g. Fig. 11 of Kennicutt & Evans 2012).
Narrowing down the constraint on the surface SFR through deep observations at high spatial resolution together with assembling a large sample of such high column density systems may provide very unique information concerning the relations between total gas and star formation in normal galaxies in the distant Universe, when current observations mostly consider only the molecular reservoirs (estimated indirectly through CO emission) and in emission-selected galaxies.
5.3. H I–H2 transition
A key process in the conversion of gas into stars in galaxies is the transition from the atomic to the molecular phase, i.e. the H I–H2 transition. While it is not absolutely clear whether the change in chemical state of the gas (atomic to molecular) is required for stars to form or if this transition is simply the consequence of a change in the physical state of the gas that also leads to star formation, it remains one of the most fascinating processes that occur in the ISM and so far has not been studied in depth at high redshift, despite important recent progress (Noterdaeme et al. 2017; Balashev et al. 2017; Balashev & Noterdaeme 2018). The transition from H I-to-H2 is however well studied theoretically and understood as a balance between the formation process of H2 onto dust grains and its destruction by UV photons. Detailed microphysics models link the column density above which the gas in a cloud turns molecular mostly with the metallicity, which acts as a proxy for the amount of dust in the gas and assuming a priori conditions of a cold neutral medium (see e.g. Krumholz et al. 2009; Sternberg et al. 2014; Bialy & Sternberg 2016). More recently, Bialy et al. (2017) have related the total atomic column density in the cloud external layer to the density in the cloud, the average absorption cross section of dust grains and the intensity of the UV field, based on the theoretical work by Sternberg et al. (2014).
The H I surface mass density (ΣHI) of an optically thick, uniformly dense, two-sided slab irradiated by a far-UV flux is given as
where 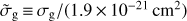 is the dust grain LW (LW = 11.2–13.6 eV, 911.6 Å–1107 Å) photon absorption cross section per hydrogen nucleon normalised to the fiducial Galactic value, α is the ratio of the unshielded H2 dissociation rate to H2 formation rate, and G is an average H2 self-shielding factor in dusty clouds (see Bialy & Sternberg 2016 for details on each parameter). The product αG is expressed as
is the dust grain LW (LW = 11.2–13.6 eV, 911.6 Å–1107 Å) photon absorption cross section per hydrogen nucleon normalised to the fiducial Galactic value, α is the ratio of the unshielded H2 dissociation rate to H2 formation rate, and G is an average H2 self-shielding factor in dusty clouds (see Bialy & Sternberg 2016 for details on each parameter). The product αG is expressed as
where nH is the cloud hydrogen density and IUV is the intensity of radiation field expressed in units of the Draine field (Habing 1968).
This theoretical model has been successfully used to interpret the observations of molecular clouds in our galaxy (Bialy et al. 2015), but not yet to interpret absorption-line systems in the distant Universe. Doing so is of particular interest since the available observables are very different locally in emission and at high redshift in absorption. For example, in the study of the molecular cloud complex W43 by Bialy et al. (2017), the H I column density has been obtained from 21 cm emission map by Bihr et al. (2015), corrected for continuum emission and optical depth effects; the UV field in W43 is estimated from dust emission maps assuming thermal equilibrium of dust grains, the density is estimated from typical values predicted for pressure equilibrium between cold neutral medium and warm neutral medium or from taking the averaged observed H I surface density and dividing by an estimate of the radius of the molecular complex. Finally, a fiducial value is taken for the dust-grain absorption cross section. We discuss the derivation of the three parameters 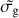 , IUV, and nH entering Eq. (5) using our observables measured in Sect. 3.
, IUV, and nH entering Eq. (5) using our observables measured in Sect. 3.
Dust-to-gas ratio, 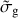
The LW dust absorption cross section per hydrogen nucleon, relative to the Galactic value, can be expressed as
where N(H) = N(H I) + 2N(H2) is the total hydrogen column density, ALW is the extinction in the Lyman and Werner band, which is the wavelength range of interest for the shielding of H2. We derive ALW at the centre of the band (λLW(rest) = 1010 Å, λLW(DLA) = 3496 Å) using AV = 0.43 (from dust reddening, Sect. 3.6) using the best-fit extinction law, which we found to be that of the Large Magellanic Cloud. We obtain ALW = 2.1 and hence 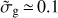 with a statistical uncertainty of about 25%. However, to take into account possible systematics intrinsic to the derivation of AV, we consider a factor of 2 range on
with a statistical uncertainty of about 25%. However, to take into account possible systematics intrinsic to the derivation of AV, we consider a factor of 2 range on 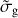 . We finally note that this value is also consistent with the expected approximate scaling with metallicity.
. We finally note that this value is also consistent with the expected approximate scaling with metallicity.
Hydrogen density (nH) and UV field density (IUV)
We used measured excitation of fine-structure levels of C I to estimate the physical conditions in the medium. The fine-structure levels of C I can be excited by collisions, UV pumping, and direct excitation by photons from the cosmic microwave background (CMB) (see Silva & Viegas 2002). The CMB radiation is fixed at any redshift following the adiabatic expression TCMB(z) = (1 + z)TCMB(z = 0), as predicted by standard Big Bang theory and constrained by observations (e.g. Noterdaeme et al. 2011). The UV radiation field corresponds to the metagalactic background (taken from Khaire & Srianand 2018) plus the additional UV field, which corresponds to the galaxy. Collision rates depend on the number density of the medium and the temperature, which we fixed to be T = 92 K, based on the excitation of lower rotational levels of H2. Therefore, we are left with two parameters, nH and IUV that are constrained simultaneously from the observed population ratio of C I fine structure levels. We also assume a local molecular fraction f = 1, which is expected at such high H2 column density.
In any case, using the overall molecular fraction 〈f〉 = 0.38 does not change the result significantly and would actually make little sense since this molecular fraction implies a perfectly uniform mixing of atomic and molecular hydrogen, i.e. no transition.
We calculated the relative ratio of C I fine-structure levels using our own Python code, described in Balashev et al. (2017), and similar to the P OPR ATIO code from Silva & Viegas (2002). We varied the density and UV field intensity over a 100 × 100 grid with nH and IUV ranging on a log-linear scale from 1 to 1000 cm−3 and 0.1 to 100 G⊙, respectively, where G⊙ represents the average UV radiation field of Draine (1978). We then compared the calculated values with those observed. Assuming the uncertainty on the observed log N(C I *)/N(C I) and log N(C I * *)/N(C I) are Gaussian, we obtain the probability distribution in the (nH − IUV) plane shown on Fig. 12.
 |
Fig. 12. Constraints on the hydrogen density–UV field plane from the excitation of C I fine-structure levels. The probability density is represented by the colour intensity, and the 68% and 30% confidence level contours are shown as solid and dashed green lines, respectively. The extragalactic UV background sets a lower limit to IUV as shown by the horizontal black line with upward arrows. Attenuation effects are not taken into account and the actual incident UV field can be a few times higher. |
The C I population ratio indicates a high hydrogen density, of the order of 250 cm−3, in which case the excitation is dominated by collision and becomes insensitive to the UV field for a wide range of values. However, a lower hydrogen density is also allowed provided the UV field is high, around 20 times the Draine field, but this is less probable, as can be seen from the contours in Fig. 12. We note that this remains a simple diagnostic and that the calculation does not include radiative transfer. In other words, the estimated UV flux corresponds to an unattenuated value due to shielding by dust and does not include effects of line saturation. Since C I is found only in the cloud interior, with some amount of shielding, the IUV values derived from the excitation of this species should be considered as a lower limit to the actual UV field incident to the cloud, which could be up to a factor of a few higher, considering the measured dust extinction (see Fig. 7).
We finally note that while the effect of cosmic rays is not taken into account here nor in the used transition theory, it is possible that cosmic rays maintain the molecular fraction to a value less than unity, even deeper than the H I–H2 transition layer (e.g. Noterdaeme et al. 2017). Assuming only cosmic rays are responsible for the destruction of H2, the equilibrium between formation and destruction of H2 gives N(H I)/N(H2) = ζ(H2)/(Rn) ≃ 3.3. Then, assuming a formation rate on dust grains R = 3 × 10−18 (a factor of roughly 10 smaller than in the MW), and for density obtained (at IUV = 0) we get and upper limit on the H2 ionisation rate by cosmic rays to be about ζ(H2) = 2.5 × 10−15 s−1.
An independent and alternative way to estimate the incident radiation field is to scale it to the surface SFR, assuming that the field is uniform and isotropic, i.e.
Using the observed ΣSFR in the DLA in the range 0.01–0.4 M⊙ yr−1 kpc−2 and the average MW value of ΣSFR(MW) ∼ 0.003 M⊙ yr−1 kpc−2 (Kennicutt & Evans 2012), the intensity of the mean radiation field in the DLA galaxy should be of the order of IUV ∼ 2.5–100. We emphasise that this range is loose because of the uncertainties on the size and SFR of the galaxy and that this range represents only an average intensity field in the DLA galaxy, meaning that the local field incident to the cloud can actually be different. On the other hand, the H2 high rotational levels actually also suggest a UV field higher than the average MW value.
Comparing observations to theory
By propagating our constraints in the UV field – density plane as shown in Fig. 13, we obtain the probability distribution function of αG, as shown in the top panel of Fig. 13. We note that the dependence of αG on the dust is very small so that we simply used the value from the best-fit extinction, i.e. 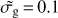 The allowed αG range remains very wide around a central value of about unity.
The allowed αG range remains very wide around a central value of about unity.
 |
Fig. 13. Comparison of H I–H2 transition theory predictions with observations. Top panel: derived probability distribution function of αG from excitation of C I fine-structure levels. The green shaded region shows the interval estimate on αG corresponding to 0.683 confidence level. Bottom panel: theoretical H I surface density of a single H I–H2 transition layer as a function of αG Eq. (5) for |
The bottom panel of Fig. 13 shows the theoretical dependence of the atomic hydrogen surface density as a function of αG. In this figure, the dependence on the dust-to-gas ratio is linear. We illustrate the theoretical expectations for a factor of two around 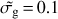 as well. The horizontal line corresponds to the observed total H I column density integrated in the system. This should actually be considered as an upper limit since it may well contain atomic gas that does not belong to the envelope of the molecular cloud. Indeed, several components were seen in the low-ionisation metal lines. Assuming uniform metallicity, the atomic gas column density associated with the molecular component decreases to 85% of the overall value. Remarkably, the observed column density corresponds to a value of αG that falls in the middle of our allowed range. In turn, it appears that the high end of our derived αG range is inconsistent with the theoretical expectations. Similarly, the low end of our allowed range on αG would indicate a very small H I column density, when the observed value is very high. This would only be possible if almost all of the H I is not associated with the H2 component, and in which case the metallicity of the narrow component would become unrealistically high. This shows that we can actually use the theoretical ΣHI to constrain the UV field to density ratio. For the observed dust grain abundance, Eq. (6) simplifies as IUV/(nH/100 cm−2) ≈ αG. Using H I column density from the simple redistribution of H I in the different components assuming uniform metallicity, we obtain αG ≈ 2.
as well. The horizontal line corresponds to the observed total H I column density integrated in the system. This should actually be considered as an upper limit since it may well contain atomic gas that does not belong to the envelope of the molecular cloud. Indeed, several components were seen in the low-ionisation metal lines. Assuming uniform metallicity, the atomic gas column density associated with the molecular component decreases to 85% of the overall value. Remarkably, the observed column density corresponds to a value of αG that falls in the middle of our allowed range. In turn, it appears that the high end of our derived αG range is inconsistent with the theoretical expectations. Similarly, the low end of our allowed range on αG would indicate a very small H I column density, when the observed value is very high. This would only be possible if almost all of the H I is not associated with the H2 component, and in which case the metallicity of the narrow component would become unrealistically high. This shows that we can actually use the theoretical ΣHI to constrain the UV field to density ratio. For the observed dust grain abundance, Eq. (6) simplifies as IUV/(nH/100 cm−2) ≈ αG. Using H I column density from the simple redistribution of H I in the different components assuming uniform metallicity, we obtain αG ≈ 2.
This, together with the constraint on the (IUV,nH) plane from C I excitation implies that the density is about nH ≃ 250 cm−3 and the UV field is several times higher than the Draine field and possibly even an order of magnitude higher when taking into account the fact that C I excitation provides a constraint on the attenuated flux (see previous section). This is also consistent with the observed SFR and with the high excitation of H2.
6. Conclusions
We have presented the simultaneous detection of atomic and molecular gas and star formation activity in an absorption-selected galaxy. This allows us to study the global relationship between the gas phase and galactic properties on one side, and to investigate the physical conditions and microphysics of the H I–H2 transition on the other side. In particular, we find that the measured extremely high column densities of hydrogen (for both atomic and molecular form, log N(cm−2) = 21.83 ± 0.01 and log N(cm−2) = 21.31 ± 0.01, respectively) are consistent with the very small impact parameter on the centroid of the galaxy (ρ ∼ 1.4 kpc) and that the observed constraints on the SFR are consistent with the local Kennicutt-Schmidt law, although we note that our constraints remain very loose. Using the abundances and excitation of atomic and molecular species together with the dust extinction, we derive the chemical and physical conditions in the molecular cloud. Based on the measured zinc column density, we measure the average metallicity of this ESDLA to be about 15% of the solar value. Thanks to the long wavelength range of the X-shooter spectrum we measure associated extinction to be AV ≈ 0.43 (assuming LMC average extinction curve). Using the relative population of C I fine-structure levels we estimate the number density in the molecular cloud to be nH ≈ 250 cm−3, although a solution with high UV field and low density is also allowed. Unfortunately, independent constraints on the mean UV field in the galaxy from the observed SFR are not very stringent. The observed H I column density is, in turn, consistent with the prediction from H I-to-H2 transition theory for a narrower range of physical conditions. This provides a constraint on the ratio of UV radiation intensity to hydrogen density, G ≈ 2. This constraint complements that from C I excitation in the UV intensity–hydrogen density plane and implies that the UV field is several times that of our Galaxy, which is consistent with the average UV field estimated from the observed SFR and qualitatively consistent with the high excitation of H2 in the cloud. In other words, we show that the observed H I column density together with a measurement of dust abundance are able to provide important constraints on the physical conditions in a molecular cloud by comparing with the H I–H2 transition theory.
Obtaining high-resolution data is desirable to ascertain the column densities, in particular of the high rotational levels of H2, get better constraints on the absorption-line kinematics, and possibly detect excited levels of more species, such as Si II* and O I*, as seen in other ESDLAs (Kulkarni et al. 2012; Noterdaeme et al. 2015). Detailed modelling of the cloud would then certainly help to further understand the physical conditions. Obtaining tighter constraints on the SFR through deep observations of nebular emission lines and on the macroscopic properties of the galaxy (in particular its extent) would also be of great value to further link the local chemical and physical conditions of the molecular cloud to those of star formation. Deep, spatially resolved observations of the Lyα emission together with radiative transfer modelling should also provide very useful information about the gas kinematics. Finally, our single system suggests that absorption and emission observations of a sample of ESDLAs are a promising way to link star formation to the properties of the ISM in normal, high-redshift galaxies.
Acknowledgments
We thank the referee for useful comments and suggestions. The authors are very grateful to ESO and in particular to the staff of Paranal observatory for carrying out our observations in service mode. AR, PN, PPJ, NG, and RS gratefully acknowledge the support of the Indo-French Centre for the Promotion of Advanced Research (Centre Franco-Indien pour la Promotion de la Recherche Avancée) under contract no. 5504-2. The research leading to these results has received funding from the French Agence Nationale de la Recherche under grant no ANR-17-CE31-0011-01 (project “HIH2” – PI Noterdaeme). SAB thanks the Institut d’Astrophysique de Paris for hospitality and the Institut Lagrange de Paris for financial support during the time part of this work was done. SAB is supported by RFBR (grant No. 18-02-00596). JPUF thanks the DNRF for supporting research at the Cosmic Dawn Center, Niels Bohr Institute, Copenhagen University.
References
- Abgrall, H., Le Bourlot, J., Pineau Des Forets, G., et al. 1992, A&A, 253, 525 [Google Scholar]
- Altay, G., Theuns, T., Schaye, J., Booth, C. M., & Dalla Vecchia, C. 2013, MNRAS, 436, 2689 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Balashev, S. A., & Noterdaeme, P. 2018, MNRAS, 478, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Balashev, S. A., Noterdaeme, P., Rahmani, H., et al. 2017, MNRAS, 470, 2890 [NASA ADS] [CrossRef] [Google Scholar]
- Bialy, S., & Sternberg, A. 2015, MNRAS, 450, 4424 [NASA ADS] [CrossRef] [Google Scholar]
- Bialy, S., & Sternberg, A. 2016, ApJ, 822, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Bialy, S., Sternberg, A., Lee, M.-Y., Le Petit, F., & Roueff, E. 2015, ApJ, 809, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Bialy, S., Bihr, S., Beuther, H., Henning, T., & Sternberg, A. 2017, ApJ, 835, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Bihr, S., Beuther, H., Ott, J., et al. 2015, A&A, 580, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bird, S., Vogelsberger, M., Haehnelt, M., et al. 2014, MNRAS, 445, 2313 [NASA ADS] [CrossRef] [Google Scholar]
- Black, J. H., & van Dishoeck, E. F. 1987, ApJ, 322, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Blitz, L., & Rosolowsky, E. 2006, ApJ, 650, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Boissé, P., Le Petit, F., Rollinde, E., et al. 2005, A&A, 429, 509 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braun, R. 2012, ApJ, 749, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Brocklehurst, M. 1971, MNRAS, 153, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Burgh, E. B., France, K., & Jenkins, E. B. 2010, ApJ, 708, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carswell, R. F., & Webb, J. K. 2014, VPFIT: Voigt Profile Fitting Program, Astrophysics Source Code Library [record ascl:1408.015] [Google Scholar]
- De Cia, A., Ledoux, C., Mattsson, L., et al. 2016, A&A, 596, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Cia, A., Ledoux, C., Petitjean, P., & Savaglio, S. 2018, A&A, 611, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Federman, S. R., Huntress, Jr., W. T., & Prasad, S. S. 1990, ApJ, 354, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Fernandez, E. R., & Shull, J. M. 2011, ApJ, 731, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Finkelstein, S. L., Hill, G. J., Gebhardt, K., et al. 2011, ApJ, 729, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2007, ApJ, 663, 320 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fox, A. J., Ledoux, C., Petitjean, P., & Srianand, R. 2007, A&A, 473, 791 [Google Scholar]
- Fynbo, J. P. U., Prochaska, J. X., Sommer-Larsen, J., Dessauges-Zavadsky, M., & Møller, P. 2008, ApJ, 683, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. P. U., Laursen, P., Ledoux, C., et al. 2010, MNRAS, 408, 2128 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. P. U., Ledoux, C., Noterdaeme, P., et al. 2011, MNRAS, 413, 2481 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. P. U., Krogager, J.-K., Venemans, B., et al. 2013, ApJS, 204, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. P. U., Krogager, J.-K., Heintz, K. E., et al. 2017, A&A, 606, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glover, S. C. O., & Clark, P. C. 2012, MNRAS, 421, 9 [NASA ADS] [Google Scholar]
- Gordon, K. D., Clayton, G. C., Misselt, K. A., Landolt, A. U., & Wolff, M. J. 2003, ApJ, 594, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gry, C., Boulanger, F., Nehmé, C., et al. 2002, A&A, 391, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habing, H. J. 1968, Bull. Astron. Inst. Neth., 19, 421 [Google Scholar]
- Hartoog, O. E., Fynbo, J. P. U., Kaper, L., De Cia, A., & Bagdonaite, J. 2015, MNRAS, 447, 2738 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, M., Schaerer, D., Östlin, G., et al. 2011, ApJ, 730, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Heintz, K. E., Fynbo, J. P. U., Ledoux, C., et al. 2018, A&A, 615, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hollenbach, D. J., Werner, M. W., & Salpeter, E. E. 1971, ApJ, 163, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Huynh, M., & Lazio, J. 2013, ArXiv e-prints [arXiv:1311.4288] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Khaire, V., & Srianand, R. 2018, MNRAS, submitted [arXiv:1801.09693] [Google Scholar]
- Krawczyk, C. M., Richards, G. T., Gallagher, S. C., et al. 2015, AJ, 149, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Krogager, J.-K., Fynbo, J. P. U., Møller, P., et al. 2012, MNRAS, 424, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Krogager, J.-K., Fynbo, J. P. U., Ledoux, C., et al. 2013, MNRAS, 433, 3091 [NASA ADS] [CrossRef] [Google Scholar]
- Krogager, J.-K., Fynbo, J. P. U., Heintz, K. E., et al. 2016, ApJ, 832, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Krogager, J.-K., Møller, P., Fynbo, J. P. U., & Noterdaeme, P. 2017, MNRAS, 469, 2959 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R. 2012, ApJ, 759, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Tumlinson, J. 2009, ApJ, 693, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, V. P., Meiring, J., Som, D., et al. 2012, ApJ, 749, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Lacour, S., Ziskin, V., Hébrard, G., et al. 2005, ApJ, 627, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Ledoux, C., Noterdaeme, P., Petitjean, P., & Srianand, R. 2015, A&A, 580, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [Google Scholar]
- Lodders, K., Palme, H., & Gail, H. 2009, JE Trümper, 4, 44 [Google Scholar]
- Ma, J., Caucal, P., Noterdaeme, P., et al. 2015, MNRAS, 454, 1751 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, J., Ge, J., Prochaska, J. X., et al. 2018, MNRAS, 474, 4870 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Michałowski, M. J., Gentile, G., Hjorth, J., et al. 2015, A&A, 582, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Modigliani, A., Goldoni, P., Royer, F., et al. 2010, in Observatory Operations: Strategies, Processes, and Systems III, Proc. SPIE, 7737, 773728 [CrossRef] [Google Scholar]
- Møller, P., Fynbo, J. P. U., & Fall, S. M. 2004, A&A, 422, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muzahid, S., Srianand, R., & Charlton, J. 2015, MNRAS, 448, 2840 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, K., Ouchi, M., Shimasaku, K., et al. 2012, ApJ, 745, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Neeleman, M., Kanekar, N., Prochaska, J. X., et al. 2018, ApJ, 856, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Nestor, D. B., Shapley, A. E., Kornei, K. A., Steidel, C. C., & Siana, B. 2013, ApJ, 765, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Noterdaeme, P., Ledoux, C., Petitjean, P., et al. 2007, A&A, 474, 393 [Google Scholar]
- Noterdaeme, P., Ledoux, C., Petitjean, P., & Srianand, R. 2008, A&A, 481, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Ledoux, C., Srianand, R., Petitjean, P., & Lopez, S. 2009, A&A, 503, 765 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Petitjean, P., Srianand, R., Ledoux, C., & López, S. 2011, A&A, 526, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Laursen, P., Petitjean, P., et al. 2012, A&A, 540, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Petitjean, P., Pâris, I., et al. 2014, A&A, 566, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Srianand, R., Rahmani, H., et al. 2015, A&A, 577, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Krogager, J.-K., Balashev, S., et al. 2017, A&A, 597, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Ledoux, C., Zou, S., et al. 2018, A&A, 612, A58 [Google Scholar]
- Paulino-Afonso, A., Sobral, D., Ribeiro, B., et al. 2018, MNRAS, 476, 5479 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pontzen, A., Governato, F., Pettini, M., et al. 2008, MNRAS, 390, 1349 [NASA ADS] [Google Scholar]
- Rafelski, M., Neeleman, M., Fumagalli, M., Wolfe, A. M., & Prochaska, J. X. 2014, ApJ, 782, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Rahmati, A., & Schaye, J. 2014, MNRAS, 438, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Rao, S. M., Belfort-Mihalyi, M., Turnshek, D. A., et al. 2011, MNRAS, 416, 1215 [NASA ADS] [CrossRef] [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2013, A&A, 557, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roy, N., Chengalur, J. N., & Srianand, R. 2006, MNRAS, 365, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, K. H. R., Hennawi, J. F., Prochaska, J. X., et al. 2015, ApJ, 808, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., Bohlin, R. C., Drake, J. F., & Budich, W. 1977, ApJ, 216, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Schruba, A., Leroy, A. K., Walter, F., et al. 2011, AJ, 142, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Selsing, J., Fynbo, J. P. U., Christensen, L., & Krogager, J.-K. 2016, A&A, 585, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sheffer, Y., Rogers, M., Federman, S. R., et al. 2008, ApJ, 687, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Silva, A. I., & Viegas, S. M. 2002, MNRAS, 329, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Srianand, R., Petitjean, P., Ledoux, C., Ferland, G., & Shaw, G. 2005, MNRAS, 362, 549 [Google Scholar]
- Srianand, R., Gupta, N., Petitjean, P., Noterdaeme, P., & Saikia, D. J. 2008, MNRAS, 391, L69 [NASA ADS] [Google Scholar]
- Srianand, R., Hussain, T., Noterdaeme, P., et al. 2016, MNRAS, 460, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Sternberg, A., Le Petit, F., Roueff, E., & Le Bourlot, J. 2014, ApJ, 790, 10 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Vanden Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vladilo, G., Prochaska, J. X., & Wolfe, A. M. 2008, A&A, 478, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Bron, E., Cazaux, S., et al. 2017, Mol. Astrophys., 9, 1 [Google Scholar]
- Watson, D. 2011, A&A, 533, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolfe, A. M., Gawiser, E., & Prochaska, J. X. 2005, ARA&A, 43, 861 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Yajima, H., Choi, J.-H., & Nagamine, K. 2012, MNRAS, 427, 2889 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
- Zou, S., Petitjean, P., Noterdaeme, P., et al. 2018, A&A, 616, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwaan, M. A., van der Hulst, J. M., Briggs, F. H., Verheijen, M. A. W., & Ryan-Weber, E. V. 2005, MNRAS, 364, 1467 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Column densities of H2 in various rotational levels at zabs = 2.4636 towards J1513+0352.
All Figures
 |
Fig. 1. Velocity profiles of selected species associated with the DLA system at z = 2.4636 towards J 1513+0352, tracing the ionised gas (C IV), neutral atomic gas (Fe II), and molecular gas (C I). Despite the apparent complexity, the C I profile is actually characterised by a single component (shown in blue) and other absorption seen in the panel arise from excited fine-structure levels (J = 1 and J = 2 in cyan and green, respectively; the total profile is in red). The blue line in the Fe II panel shows the contribution from the ν = 0 component. |
| In the text | |
 |
Fig. 2. Fit to the C I lines associated with the DLA. The panels show the 4 lines used for fitting. The data is represented in black and the best-fit synthetic profile in red with residuals in a ± 2σ-scale on the top of each panel. The individual contributions from J = 0 (C I), J = 1 (C I*), and J = 2 (C I**) are shown with cyan, magenta, and green lines, respectively. |
| In the text | |
 |
Fig. 3. Portion of the X-shooter spectrum of J 1513+0352 covering the absorption lines of H I (Lyman-α shown in the bottom panel) and H2 (top three panels) from the DLA at z = 2.4636. The normalised data are shown in black and the synthetic profile is overplotted in red. We note the very strong flux suppression at the bluest wavelengths due to the increased overlapping of H2 lines. Horizontal blue segments connect rotational levels (short tick marks) from a given Lyman (L) or Werner (W) band, as labelled above. |
| In the text | |
 |
Fig. 4. H2 excitation diagram of the diffuse molecular cloud towards J1513+0352 (red) compared with other environments (typical diffuse ISM in the Milky Way (MW) shown as empty squares, the high-excitation case next to the bright star HD 34078 shown with a plus sign; and two other ESDLAs, towards J0843+0221 (blue) and J2140−0321 (green)). The red line shows the best fit to the J = 0,1 and 2 rotational levels towards J1513+0352, indicating Tk = 92 ± 3 K. |
| In the text | |
 |
Fig. 5. Absorption profiles of Si II, Ni II, Fe II, Zn II, Cr II, Mn II, and Mg I. The grey line represents the data with parts used to constrain the fit shown in black. The red line represents the synthetic profile. The black tick marks on top of the profile show the position of individual velocity components. The top box represents the residuals in the ±2σ range. The individual contributions from Mg I and Cr II in the box showing Zn II(λ = 2026 and 2062) profiles are shown in cyan and magenta respectively. |
| In the text | |
 |
Fig. 6. Expected velocity profiles of P II and S II lines (red) overplotted on the observed spectrum (black). We emphasise that this is not a fit, but the scaling of the derived zinc profile assuming solar phosphorus-to-zinc and sulphur-to-zinc ratios. |
| In the text | |
 |
Fig. 7. Measurement of the extinction of the background quasar by dust in the DLA. The X-shooter spectrum is shown in grey with the continuum regions used to constrain the fit highlighted in black. The blue spectrum shows the scaled but unreddened quasar composite from Selsing et al. (2016). The thick red line shows the composite reddened by a LMC average extinction law with AV(DLA) = 0.43. The shaded region represents the strength of the 2175 Å bump (Abump(DLA) = 0.58 ± 0.003), that is the area between the reddened composite and the same reddened composite where the bump component (c3) has been set to zero. |
| In the text | |
 |
Fig. 8. Lyα emission in the DLA absorption trough shown in 1D (bottom, using a flux-conservative re-binning) and the 2D spectrum (top). The 2D data have been further smoothed by a Gaussian filter with σ of 1.8 pixel. The extracted flux is ∼1.9 ± 0.7 × 10−18 erg s−1 cm−2. |
| In the text | |
 |
Fig. 9. Histogram shows the distribution of fluxes measured in apertures randomly located around the detected emission. The apertures have the same size as that used for the Lyα measurement. The mean of the distribution (vertical dotted line) provides an estimate of the zero flux level and the dispersion provides a more conservative estimate of the noise in the aperture. The red dashed vertical line shows the measured value of Lyα emission associated with the DLA. |
| In the text | |
 |
Fig. 10. Spatial profile of the Lyα emission (top) and quasar continuum (bottom) along the slit. The Lyα profile has been averaged over 10 pixels centred at the Lyα position (4211.8 Å). The quasar continuum profile has been averaged over the wavelength range free of strong absorption (4135−4150 Å). In each panel, we show the best-fit Gaussian model to the data. The vertical dashed lines indicate the centres of the profiles. |
| In the text | |
 |
Fig. 11. Left: layout of the 1.6″-wide slit (white region) with the position of the quasar marked as red cross. The dashed line represents our measured constraint on ρ‖. The value ρ⊥ is constrained to be within the slit width. The black points show the distribution of possible locations of the emission, taking into account a normally distributed uncertainty on ρ‖ and a uniformly distributed random angle between quasar-galaxy and slit directions. Right: probability distribution function of the impact parameter. |
| In the text | |
 |
Fig. 12. Constraints on the hydrogen density–UV field plane from the excitation of C I fine-structure levels. The probability density is represented by the colour intensity, and the 68% and 30% confidence level contours are shown as solid and dashed green lines, respectively. The extragalactic UV background sets a lower limit to IUV as shown by the horizontal black line with upward arrows. Attenuation effects are not taken into account and the actual incident UV field can be a few times higher. |
| In the text | |
 |
Fig. 13. Comparison of H I–H2 transition theory predictions with observations. Top panel: derived probability distribution function of αG from excitation of C I fine-structure levels. The green shaded region shows the interval estimate on αG corresponding to 0.683 confidence level. Bottom panel: theoretical H I surface density of a single H I–H2 transition layer as a function of αG Eq. (5) for |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$\left[ {{\rm{X/H}}} \right] = \log \left( {{{N\left( {\rm{X}} \right)} \over {N\left( {{{\rm{H}}_{{\rm{tot}}}}} \right)}}} \right) - \log {\left( {{{\rm{X}} \over {\rm{H}}}} \right)_ \odot },$$](/articles/aa/full_html/2018/10/aa33446-18/aa33446-18-eq1.gif)
![$$T\left( \lambda \right) = {f_0} \times {T_{{\rm{QSO}}}}{\left( {{\lambda \over {{\lambda _0}}}} \right)^{\Delta \beta }} \times \exp \left[ { - 0.92\; \in \left( \lambda \right)E\left( {B - V} \right)} \right],$$](/articles/aa/full_html/2018/10/aa33446-18/aa33446-18-eq2.gif)