| Issue |
A&A
Volume 643, November 2020
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 25 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202038487 | |
| Published online | 27 October 2020 | |
The ALPINE-ALMA [CII] survey
The nature, luminosity function, and star formation history of dusty galaxies up to z ≃ 6
1
Istituto Nazionale di Astrofisica: Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Gobetti 93/3, 40129 Bologna, Italy
e-mail: carlotta.gruppioni@inaf.it
2
Aix Marseille University, CNRS, LAM, Laboratoire d’Astrophysique de Marseille, Marseille, France
3
Dipartimento di Fisica e Astronomia, Università of Bologna, Via Gobetti 93/2, 40129 Bologna, Italy
4
Infrared Processing and Analysis Center, California Institute of Technology, Pasadena, CA 91125, USA
5
Dipartimento di Fisica e Astronomia, Università di Padova, Vicolo Osservatorio 3, 35122 Padova, Italy
6
Istituto Nazionale di Astrofisica: Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
7
Observatoire de Genève, Université de Genève, 51 Ch. des Maillettes, 1290 Versoix, Switzerland
8
Kavli Institute for the Physics and Mathematics of the Universe, The University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa-shi, Chiba 277-8583, Japan
9
The Caltech Optical Observatories, California Institute of Technology, Pasadena, CA 91125, USA
10
Centro de Astronomía (CITEVA), Universidad de Antofagasta, Avenida Angamos 601, Antofagasta, Chile
11
Instituto de Física y Astronomía, Universidad de Valparaíso, Gran Bretaña 1111, Playa Ancha, Valparaíso, Chile
12
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
13
Cosmic Dawn Center (DAWN), Copenhagen, Denmark
14
Niels Bohr Institute, University of Copenhagen, Lyngbyvej 2, 2100 Copenhagen, Denmark
15
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
16
Cavendish Laboratory, University of Cambridge, 19 J. J. Thomson Ave., Cambridge CB3 0HE, UK
17
Kavli Institute for Cosmology, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
18
Department of Physics, University of California, Davis, One Shields Ave., Davis, CA 95616, USA
19
Department of Astronomy, Cornell University, Space Sciences Building, Ithaca, NY 14853, USA
20
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
21
Leiden Observatory, PO Box 9513 2300 RA, The Netherlands
Received:
25
May
2020
Accepted:
14
September
2020
Aims. We present the detailed characterisation of a sample of 56 sources serendipitously detected in ALMA band 7 as part of the ALMA Large Program to INvestigate CII at Early Times (ALPINE). These sources, detected in COSMOS and ECDFS, have been used to derive the total infrared luminosity function (LF) and to estimate the cosmic star formation rate density (SFRD) up to z ≃ 6.
Methods. We looked for counterparts of the ALMA sources in all the available multi-wavelength (from HST to VLA) and photometric redshift catalogues. We also made use of deeper UltraVISTA and Spitzer source lists and maps to identify optically dark sources with no matches in the public catalogues. We used the sources with estimated redshifts to derive the 250 μm rest-frame and total infrared (8–1000 μm) LFs from z ≃ 0.5 to 6.
Results. Our ALMA blind survey (860 μm flux density range: ∼0.3–12.5 mJy) allows us to further push the study of the nature and evolution of dusty galaxies at high-z, identifying luminous and massive sources to redshifts and faint luminosities never probed before by any far-infrared surveys. The ALPINE data are the first ones to sample the faint end of the infrared LF, showing little evolution from z ≃ 2.5 to z ≃ 6, and a “flat” slope up to the highest redshifts (i.e. 4.5 < z < 6). The SFRD obtained by integrating the luminosity function remains almost constant between z ≃ 2 and z ≃ 6, and significantly higher than the optical or ultra-violet derivations, showing a significant contribution of dusty galaxies and obscured star formation at high-z. About 14% of all the ALPINE serendipitous continuum sources are found to be optically and near-infrared (near-IR) dark (to a depth Ks ∼ 24.9 mag). Six show a counterpart only in the mid-IR and no HST or near-IR identification, while two are detected as [C II] emitters at z ≃ 5. The six HST+near-IR dark galaxies with mid-IR counterparts are found to contribute about 17% of the total SFRD at z ≃ 5 and to dominate the high-mass end of the stellar mass function at z > 3.
Key words: galaxies: evolution / galaxies: high-redshift / galaxies: luminosity function / mass function / cosmology: observations / submillimeter: galaxies
© ESO 2020
1. Introduction
Our current knowledge of the cosmic star formation rate density (SFRD) at high redshift (z > 3) is based mostly on galaxy samples selected in the ultra-violet (UV) rest frame (e.g. Bouwens et al. 2015 and Oesch et al. 2018), whose bolometric star formation rates (SFRs) are not measured, but rather inferred through uncertain dust-correction techniques, and which are not necessarily representative of the whole galaxy population (e.g. missing strongly obscured massive systems with high dust content).
Since the discovery of the cosmic infrared background (CIB; representing the cumulative emission reprocessed by dust from all the galaxies throughout the cosmic history of the Universe; e.g. Lagache et al. 2005) at the end of the 1990s by the COBE satellite (Puget et al. 1996; Hauser et al. 1998), and its resolution into discrete, rapidly evolving, far-infrared (far-IR) and sub-millimetre (sub-mm) sources by deep extragalactic surveys performed with the Infrared Space Observatory (ISO) and the Submillimetre Common-User Bolometer Array (SCUBA) on the James Clerk Maxwell Telescope (JCMT), many searches have focused on deriving how much star formation activity in the early Universe is obscured by dust. These dusty star-forming galaxies, also called “sub-millimetre galaxies” (SMGs; e.g. Smail et al. 1997 and Hughes et al. 1998; Barger et al. 1998; Blain et al. 2002), are characterised by large far-IR luminosities (≳1012 L⊙) and stellar masses (M ≳ 7 × 1010 M⊙; e.g. Chapman et al. 2005, Simpson et al. 2014), extremely high star formation rates (SFRs, ≳100 M⊙ yr−1; e.g. Swinbank et al. 2014), and large gas reservoirs (≳1010 M⊙; e.g. Bothwell et al. 2013; Béthermin et al. 2015). Despite them being rare and luminous objects, typically located around z ∼ 2–2.5 (e.g. Chapman et al. 2003; Wardlow et al. 2011), their tremendous SFRs make them substantial contributors to the SFRD at Cosmic Noon, that is, 1 < z < 3 (e.g. Casey et al. 2013). However, the fraction of dust-obscured star formation, which is traced by Spitzer and AKARI up to z ≃ 2 (e.g. Rodighiero et al. 2010, Goto et al. 2019), and by Herschel up to z ≃ 3 (e.g. Gruppioni et al. 2013, Magnelli et al. 2013), is still unknown at higher redshifts.
One of the problems is the difficulty in identifying the SMGs because of the coarse angular resolution of single-dish telescopes and the faintness of the optical/UV counterparts. The few SMGs that have been identified at z > 4 trace only the bright tail of the SFR distribution (e.g. Capak et al. 2011; Walter et al. 2012; Riechers et al. 2011, 2013, 2017; Marrone et al. 2018) and are unlikely to represent the bulk of the population. Moreover, most of the SMGs have photometric or spectroscopic observations that likely place them at z < 3 (Brisbin et al. 2017).
The Atacama Large Millimetre/submillimetre Array (ALMA) has now opened a gap in the wall, allowing us to refine our understanding of dusty galaxies at high redshifts by unveiling less extreme galaxies, between massive SMGs and normal star-forming galaxies, through superb sensitivity and high spatial resolution surveys in the sub-mm/mm domain. This can be achieved thanks to the recently explored ability of ALMA to reveal serendipitously detected galaxies in blind extragalactic surveys.
The ALMA deep surveys performed by Dunlop et al. (2017), Walter et al. (2016), and Aravena et al. (2016), probing very faint fluxes over small areas (< 5 arcmin2), as well as the wider (covering few tens of arcmin2) and shallower (to ∼0.2–0.7 mJy) surveys by Hatsukade et al. (2018) and Franco et al. (2018), have enabled us to uncover faint (sub-)mm populations at z> 4, with infrared luminosities (LIR, between 8 and 1000 μm) ≲1012 L⊙ (e.g. Yamaguchi et al. 2019). An important product of these surveys is the discovery of a population of faint ALMA galaxies that are undetected even in the deepest optical and near-infrared (near-IR; i.e. ≃1–3 μm) images with the Hubble Space Telescope (HST). These “HST-dark” galaxies are often identified in the mid-infrared (mid-IR), in deep Spitzer-IRAC 3.6 or 4.5 μm images (e.g. Franco et al. 2018; Wang et al. 2019; Yamaguchi et al. 2019), although, despite them being unlikely spurious ALMA detections (e.g. Williams et al. 2019; Romano et al. 2020), some remain undetected even in IRAC maps.
Indeed, ALMA follow-up studies of “classical” SMGs (e.g. Simpson et al. 2014; Dudzevičiūtė et al. 2020) have found that a fraction of these objects are invisible in deep optical/near-IR images; in particular, Dudzevičiūtė et al. (2020) found that ∼17% of the SCUBA-2 SMGs in the UKIDSS/UDS field (AS2UDS survey) are undetected in the optical/near-IR down to Ks = 25.7 mag. Already in the pre-ALMA studies there were cases of bright SMGs, such as the source GOODS 850-5 (also known as GN10), undetected in very deep optical/near-IR images (e.g. Wang et al. 2009), while the existence of dusty star-forming systems at z > 5 was already discussed by Dey et al. (1999) in the late 90s as a realistic expectation.
The HST-dark galaxies also tend to be serendipitously found in CO line scan surveys (see e.g. Riechers et al. 2020, who found two of them at z > 5), possibly with space densities higher than expected even at the bright end of the CO luminosity functions (LFs). These results indicate the existence of a prominent population of dusty star-forming galaxies at z > 4, which is fainter than the confusion limit of the single-dish sub-mm surveys that discovered the SMGs, but with much larger space densities, providing a significant contribution to the SFRD at high-z, even higher than that of the UV-bright galaxies at the same redshifts (e.g. Rodighiero et al. 2007; Williams et al. 2019; Wang et al. 2019).
Very faint ALMA fluxes were also reached by surveys of serendipitously detected sources in targeted observations (i.e. non-pure-blind surveys), which were able to constrain the faint end of the sub-mm/mm galaxy source counts, estimate their contribution to extragalactic background light, study their nature, and possibly detect dark galaxies (e.g. Hatsukade et al. 2013; Ono et al. 2014; Carniani et al. 2015; Oteo et al. 2016; Fujimoto et al. 2016).
Here, we present the identification, multi-wavelength characterisation, and luminosity function of a sample of 56 sources, serendipitously detected in continuum at ∼860 and ∼1000 μm (ALMA band 7), within the ALMA Large Program to INvestigate CII at Early Times (ALPINE, PI: Le Fèvre; see Le Fèvre et al. 2020; Faisst et al. 2020; Béthermin et al. 2020)1 survey fields. Firstly, ALPINE is a 70 h ALMA survey in band 7, specifically designed to measure singly ionised carbon ([C II] at 158 μm) emission and any associated far-IR continuum for 118 main-sequence galaxies at 4.4 < z < 5.9 (representative in stellar mass and SFR of the star-forming population at z ≃ 5; see Le Fèvre et al. 2020; Faisst et al. 2020). The programme, completed in February 2019, allows us to build a coherent picture of the baryon cycle in galaxies at z > 4 for the first time, by connecting the internal ISM properties to their well-characterised stellar masses and SFRs (from a wealth of ancillary photometric and spectroscopic data, which is already in hand). All the ALPINE pointings are located in the Extended Chandra Deep Field South (ECDFS; Giacconi et al. 2002) and Cosmic Evolution Survey (COSMOS; Scoville et al. 2007), thus benefitting from a wealth of ancillary multi-wavelength photometric data (from UV to far-IR), making ALPINE currently one of the largest panchromatic samples to study the physical properties of normal galaxies at high-z.
Besides the main targets, in the ALPINE pointings a blind search for serendipitous line and/or continuum emitters has been performed in a total area of 24.9 arcmin2 providing two independent catalogues of emission-line (Loiacono et al. 2020) and continuum (Béthermin et al. 2020) detections. This work focuses on the continuum sample of serendipitous detections. For these sources, we performed identifications in all the catalogues and deep images available in the COSMOS and ECDFS fields. We also constructed spectral energy distributions (SEDs), estimated photometric redshifts when they were unavailable in the literature, and derived the 250 μm rest-frame and total IR (8–1000 μm) luminosity functions and the contribution of dusty galaxies to the cosmic SFRD up to z ≃ 6.
The ALPINE sample of serendipitous continuum galaxies is briefly described in Sect. 2, the identification process and results are presented in Sect. 3, while the luminosity function results are discussed in Sect. 4. In Sect. 5, we derive the contribution of our sources to the cosmic SFRD, and in Sect. 6 we present our conclusions. Throughout the paper, we use a Chabrier (2003) stellar initial mass function (IMF) and adopt a ΛCDM cosmology with H0 = 70 km s−1 Mpc−1, Ωm = 0.3, and ΩΛ = 0.7.
2. The ALPINE serendipitous continuum detections
The ALMA ALPINE observations were carried out in band 7 during Cycle 5 and Cycle 6, and were completed in February 2019. Each target was observed for ∼30 min of on-source integration time, with the phase centre pointed at the UV position of the sources. One spectral window was centred on the [C II] expected frequencies, according to the spectroscopic redshifts extracted from the UV spectra, while the other side bands were used for continuum measurements only. The data were calibrated using the Common Astronomy Software Applications package (CASA; McMullin et al. 2007), version 5.4.0, and the continuum maps were obtained by collapsing the line-free channels in all the spectral windows (see Béthermin et al. 2020).
The ALMA observational strategy/setup, the details of the data reduction and the method adopted to extract continuum flux density information from ALPINE data and to select a complete sample of serendipitous sources, are comprehensively discussed in Béthermin et al. (2020). In the following paragraphs we summarise the main steps. The data cubes were imaged using the tclean CASA routine down to a flux threshold of 3σ (σ being the standard deviation measured in a non-primary-beam-corrected map after masking the sources). A natural weighting of the visibilities was applied in order to maximise the point-source sensitivity and to optimise the measurement of the integrated properties of the ALPINE targets. The continuum maps were obtained by excluding the channels contaminated target source lines and those of a few off-centre, serendipitously detected continuum sources with lines. In fact, in order to avoid possible contamination of the continuum flux by line flux, spectra were extracted for all the non-target sources and new tailored continuum maps were produced by masking the potentially line-contaminated channels and then remeasuring the continuum flux (correction varying from 58% to a negligible fraction of the flux density).
The average synthesized beam size is 1.13 × 0.85 arcsec2 (size varies with frequency and array configuration, i.e. between 5.2 and 6 kpc at 4.4 < z < 6). The continuum sensitivity also varies with the frequency, and for this reason the continuum sources have been extracted on signal-to-noise ratio (S/N) maps, by searching for local maxima above a given threshold using the find_peak routine of astropy. As revealed from simulations shown in Béthermin et al. (2020), the threshold above which we obtain a purity of 95% corresponds to an S/N = 5 outside the central region of 1 arcsec radius (expected to contain the ALMA continuum flux of the ALPINE targets). The sources extracted in the 1 arcsec central regions are referred to as “target”, and the objects found outside of this area are referred to as “non-target”. In this paper, we focus only on the non-target sources.
The final sample of non-target sources detected in continuum at S/N > 5 in ALMA band 7 consists of 56 sources, of which three are in the ECDFS and 53 are in COSMOS, and which were extracted over a total area of 24.92 arcmin2 (excluding the circle of 1 arcsec radius around the central ALPINE targets). The number of expected spurious sources in this sample is ≤3, while the completeness is a function of the flux density and the size of each source (see Béthermin et al. 2020), as discussed in Sect. 4. One of the ECDFS sources has been detected in two different (slightly overlapping) ALPINE pointings, therefore it has a flux measurement in both channels, that is, 860 μm and 1000 μm. Details on the flux measurement and uncertainties are provided in Béthermin et al. (2020).
3. The nature of the ALPINE serendipitous sources
We took advantage of the great wealth of multi-wavelength ancillary data, catalogues, spectroscopic and photometric redshifts, and deep images that are available in the ALPINE fields (ECDFS and COSMOS; see e.g. Faisst et al. 2020) to investigate the nature of the serendipitous sources detected in continuum by ALMA.
The ground-based photometry available in the ECDFS includes U38, b, v, Rc, and I broad-band filters from the Wide Field Imager on the ESO/2.2-m telescope; U and R bands from VIMOS on the ESO VLT; near-IR filters J, H, and Ks from ISAAC on the ESO VLT; J and Ks data from WIRCam on the CFHT; and 14 intermediate-band filters from the Suprime-Cam on the Subaru telescope. In addition, a wealth of HST observations are available in the ECDFS field.
The photometric data available in the COSMOS field include u-band observations from MegaCam on CFHT; B, V, r+, i+, z++, as well as 12 intermediate-band and two narrow-band filters from the Suprime-Cam on Subaru; YHSC-band from the Hyper Suprime-Cam on Subaru; as well as near-IR bands H and Ks from WIRCam on CFHT; and Y, J, H, and Ks from VIRCAM on the ESO-VISTA telescope. In terms of HST data, all but one ALPINE pointing in COSMOS are covered by ACS F814W observations (Koekemoer et al. 2007; Scoville et al. 2007). This is also the case for CANDELS data in ACS and WFC3 bands (Grogin et al. 2011; Koekemoer et al. 2011) and several additional pointings in ACS and WFC3 bands. The space-based photometry in both fields includes Spitzer data in the four IRAC bands (3.6, 4.5, 5.8, and 8.0 μm) and in the MIPS 24 μm band, and Herschel data in the PACS (100 and 160 μm) and SPIRE bands (250, 350, and 500 μm). A detailed summary and references of the different ground- and space-based data available in the two fields are presented in Faisst et al. (2020).
In the identification process, we first matched the ALMA non-target list with the 3D-HST catalogues (Brammer et al. 2012; Skelton et al. 2014; Momcheva et al. 2016) in both ECDFS and COSMOS, and with the COSMOS2015 (Laigle et al. 2016) in COSMOS. Then, for the COSMOS sources, we looked for counterparts in the super-deblended (Jin et al. 2018) and the DR4 UltraVISTA catalogues (McCracken et al. 2012; Moneti et al. 2019). Moreover, in COSMOS we considered the IRAC catalogue based on the Spitzer Large Area Survey with Hyper-Suprime-Cam data (SPLASH; Capak et al. 2012; Steinhardt et al. 2014)2. In the following sections, we describe in detail the identification process of the ALPINE non-target continuum sources and the results obtained.
3.1. Source identification
3.1.1. Catalogue match
As a first step in the identification process of the ALPINE non-target sources, we cross-matched the ALMA list with the multi-wavelength catalogues available from the literature in COSMOS and ECDFS. We found a counterpart within 1 arcsec of the source position for all three GOODS-S galaxies in the 3D-HST catalogue, and for 38 of the COSMOS sources in the Laigle et al. (2016) catalogue. We then found one additional COSMOS source in the 3D-HST catalogue (three in total, but two in common with Laigle et al. 2016), while other three (39 in total, but 36 already in the COSMOS2015 catalogue) were identified with galaxies in the super-deblended catalogue (at λ ≥ 24 μm, as well as two also in the UltraVISTA DR4 catalogue) by Jin et al. (2018), plus another three only with IRAC/SPLASH objects (the fluxes were provided by M. Giulietti, priv. comm.). By running Monte Carlo random shifts of the COSMOS15 catalogue, we find an average number of spurious matches ≲2, at an average distance of ∼0.7″ from the ALMA sources. Since the great majority of the positional offsets between the ALMA sources and the catalogue counterparts are < 0.4″, with just six sources with an offset in the range of 0.4″–0.6″, we can consider that the false match rate is negligible. Moreover, as we discuss later, we visually inspected the ALMA contours over-plotted onto the images in all the available bands and for all the sources, in order to validate the match. We were therefore able to photometrically identify 48 sources out of 56 (3/3 in ECDFS and 45/53 in COSMOS), leaving us with a sample of eight galaxies with no counterpart in any of the available catalogues. Of these eight sources, two were identified as line emitters in the blind-lines catalogue by Loiacono et al. (2020). Because the two serendipitously detected lines associated with unidentified continuum sources are in the same side band as the [C II] 158 μm emission of the ALPINE targets in the same pointings, they are likely [C II] as well (see e.g. Jones et al. 2020; Romano et al. 2020). This provided us with a spectroscopic redshift estimate for two sources without any catalogue counterparts, leaving us with six sources with neither catalogue matches nor redshift estimates.
3.1.2. Image visual inspection
In a second step, we inspected the images – from UV to sub-mm and radio – at the position of the ALMA sources, finding a likely faint counterpart (i.e. below the threshold imposed by the catalogues, at 2.5–4.5σ) in the IRAC/SPLASH maps (at 4.5 μm) for two of the unidentified sources. By inspecting the images, we also found two sources for which the optical counterpart from Laigle et al. (2016) – though within 1 arcsec from the ALMA position – was slightly offset and likely not the true identification. This is because at longer wavelengths (i.e. Ks and IRAC bands) another source appeared at the exact position of the ALMA galaxy. For these sources, only the long wavelength photometric data (≳2 μm, assumed to represent the true identification) were considered for constructing the spectral energy distribution (SED).
In the end, the number of sources with no obvious identification (either photometric nor spectroscopic) is four, which is more or less consistent with the number of expected spurious detections estimated through inverted map analysis: 2.8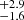 (see Béthermin et al. 2020). The S/Ns of these four unidentified sources are 9.3, 6.7, 5.5, and 5.1: while the latter two are likely spurious detections, for the other two, this conclusion is not so obvious, since they were detected at a significantly high S/N. They could be dark galaxies with a mid-IR counterpart just below the detection threshold. To summarise, among the 56 continuum sources, 44 were identified in the optical and/or near-IR (38 COSMOS2015, four 3D-HST, two UltraVISTA DR4), six only in the mid-IR (three SPLASH, one super-deblended, two IRAC images), two in [C II] line (with no photometric counterpart), and four remained unidentified (two of which could be spurious). The results of our identification process are summarised in Table 1.
(see Béthermin et al. 2020). The S/Ns of these four unidentified sources are 9.3, 6.7, 5.5, and 5.1: while the latter two are likely spurious detections, for the other two, this conclusion is not so obvious, since they were detected at a significantly high S/N. They could be dark galaxies with a mid-IR counterpart just below the detection threshold. To summarise, among the 56 continuum sources, 44 were identified in the optical and/or near-IR (38 COSMOS2015, four 3D-HST, two UltraVISTA DR4), six only in the mid-IR (three SPLASH, one super-deblended, two IRAC images), two in [C II] line (with no photometric counterpart), and four remained unidentified (two of which could be spurious). The results of our identification process are summarised in Table 1.
Summary of continuum source identification.
In Figs. 1–4 we show some examples of different cases resulting from the identification process of the ALPINE continuum non-target sources: from top left to bottom right, we plot the ALMA > 3σ contours superimposed to the ALMA, HST/ACS-i (5σ = 27.5 mag in COSMOS; Koekemoer et al. 2007), Subaru (IA484(5σ) = 25.9 mag in COSMOS; Taniguchi et al. 2015), UltraVISTA (Ks(5σ) = 24.9 mag in COSMOS; McCracken et al. 2012; Moneti et al. 2019), IRAC (S4.5(5σ)≃1.67 μJy in COSMOS; Capak et al. 2012; Steinhardt et al. 2014), MIPS (S24(5σ) = 71 μJy in COSMOS; Le Floc’h et al. 2009), and radio VLA-1.4 GHz images (5σ = 10.5 μJy in COSMOS; Schinnerer et al. 2010). Figure 1 shows an object with multi-wavelength counterparts in all bands and photo-z from Laigle et al. (2016). Figure 2 shows an object with near-IR to sub-mm identification and photo-z. Figure 3 shows an optically+near-IR dark galaxy detected only in the SPLASH/IRAC-3.6/4.5 μm images. Figure 4 shows an unidentified source.
 |
Fig. 1. Example of identification of ALPINE non-target continuum source: the postage stamps (from top left to bottom right) show the ALMA band 7 continuum map and the ALMA ≥ 3σ contours over-plotted on images from HST/ACS-i to radio VLA-1.4 GHz (band specified in the top-right corner). Object with multi-wavelength counterparts in all bands and photo-z from Laigle et al. (2016). The plotted contour levels are at 3, 5, 7, 9, 11, 13, and 15σ, corresponding to 0.32, 0.53, 0.74, 0.95, 1.16, 1.37, and 1.58 mJy. The ALMA 1-mm flux density of this source (SC_1_DEIMOS_COSMOS_910650) is 4.22 mJy, the RMS (1σ) of this pointing is ∼0.11 mJy. |
 |
Fig. 2. Object with no optical counterpart, but with multi-wavelength counterparts from near-IR to sub-mm and photo-z (from Laigle et al. 2016). The plotted contour levels are at 3, 5, 7, 9, 11, 13, and 15σ, corresponding to 0.26, 0.44, 0.62, 0.79, 0.97, 1.15, and 1.32 mJy. The ALMA 860 μm flux density of this source (SC_1_DEIMOS_COSMOS_680104) is 3.54 mJy, the RMS (1σ) of this pointing ∼0.088 mJy. |
 |
Fig. 3. Optically dark galaxy detected only in deep IRAC-SPLASH 4.5 μm catalogue. The photo-z has been derived with LE PHARE using ALMA and IRAC data only. The plotted contour levels are at 3, 5σ, corresponding to 0.14, 0.23 mJy. The ALMA 1 mm flux density of this source (SC_1_DEIMOS_COSMOS_224751) is 0.25 mJy, the RMS (1σ) of this pointing is ∼0.046 mJy. |
 |
Fig. 4. ALPINE serendipitous source with no obvious identification in any bands. The plotted contour levels are at 3, 5, and 6.5σ, corresponding to 0.47, 0.79, and 1.02 mJy. The ALMA 1 mm flux density of this source (SC_1_DEIMOS_COSMOS_471063) is 1.06 mJy, the RMS (1σ) of this pointing is ∼0.16 mJy. |
In Fig. 5, we show the Ks magnitude versus 860 μm flux for the ALPINE sources with a Ks-band counterpart; the arrows show the locus of the six sources identified only in the mid-IR (plotted at the 5σ limit of the UltraVISTA survey in COSMOS, i.e. Ks = 24.9). The ALMA flux and Ks magnitude distribution of our sample are shown on the top and right axes, respectively. We show the ALMA flux and Ks-magnitude limits as vertical and horizontal dashed lines (limiting an orange coloured area), and, for comparison, those of the AS2UDS survey of SMGs (Dudzevičiūtė et al. 2020) as dotted lines (surrounding a green coloured area): while the 860 μm flux of our sample is significantly fainter than that of the AS2UDS survey, our Ks-magnitude limit is shallower. Our HST+near-IR dark sources (shown in orange) span about the whole range in flux, but – by definition – are all below the Ks-band limit (downward-pointing arrows). Only half of them are below the AS2UDS flux limit, the other three could also have been detected in that survey.
 |
Fig. 5. Distribution of observed Ks-band magnitude and 860 μm ALMA fluxes of ALPINE serendipitous continuum sources with a Ks counterpart. The horizontal dashed line shows the UltraVISTA Ks-band 5σ limit of 24.9, while the vertical one shows the minimum 860 μm (5σ) flux density reached by the ALMA sample (the orange coloured area shows the region covered by our data). For comparison, the dotted lines (green filled area) indicate the Ks magnitude and 870 μm flux limits of the AS2UDS sample of SMGs reported by Dudzevičiūtė et al. (2020). The downward-pointing arrows shown at the Ks-band limit are the six sources detected only at mid-IR wavelengths. The histograms show the Ks-band magnitude distribution on the right axis, and the 860 μm flux density distribution is on the top axis of the plot (orange histogram showing the fluxes of the mid-IR detected sources). |
3.2. Spectral energy distributions and source properties
Using all the available photometric data in COSMOS and ECDFS, we constructed the SEDs of all the ALPINE non-target sources with at least one photometric detection in addition to the ALMA one. In order to also obtain the complete mid- and far-IR coverage for our sources, the ALMA sample was cross-matched with the Spitzer and Herschel catalogues in both the ECDFS and COSMOS fields (i.e. the PACS Extragalactic Probe Survey, PEP, Lutz et al. 2011, the Herschel-GOODS, H-GOODS, Elbaz et al. 2011, the Herschel Multi-tiered Extragalactic Survey, HerMES, Oliver et al. 2012, the super-deblended catalogue by Jin et al. 2018). In the COSMOS15 and super-deblended catalogues, the Herschel fluxes are already reported: we chose the values from the super-deblended catalogue, when available. No additional Herschel matches for sources not identified in these two catalogues have been found. In H-GOODS, the Herschel fluxes were obtained from IRAC priors, thus source blending should not be an issue.
For two sources for which a faint counterpart (below the catalogue threshold) is detected only in the IRAC maps, we obtained a magnitude measurement by performing aperture photometry directly on the images. We remind the reader that the depth of the IRAC/SPLASH observations in COSMOS is 1.67 μJy (5σ) at 4.5 μm. Thus, for two sources we obtained IRAC flux densities at 3.6 and 4.5 μm (S4.5 ≃ 1.25 and 1.61 μJy, corresponding to ∼3.7 and 4.8σ). For six sources (two with just a line identification and no photometric counterparts and four with no counterpart at all – two of which are likely spurious detections), we could not construct any SEDs.
3.2.1. SED fitting
We made use of all the available multi-wavelength information (either detections or upper limits) to fit the SEDs of our sources using the LE PHARE software (i.e., Arnouts et al. 2002; Ilbert et al. 2006), which performs an χ2 fit to the data by considering different templates. We considered the semi-empirical template library of Polletta et al. (2007), representative of different classes of IR galaxies and AGN, to which we added some templates modified in their far-IR part to better reproduce the observed Herschel data (see Gruppioni et al. 2010, 2013), and three starburst templates from Rieke et al. (2009). The final set of templates (32 in total) included SEDs of different types of galaxies, from ellipticals to starbursts, and AGN and composite ultra-luminous infrared galaxies (ULIRGs; containing both AGN and star-forming galaxies) in the rest-frame wavelength interval, 0.1–1000 μm. We allowed the code to apply different extinction values (E(B − V) from 0.0 to 5) and extinction curves to the templates in order to improve the fit. This increased the real number of possible templates. When performing the fit, the redshifts were fixed to the spectroscopic or photometric values from the literature, or from [C II] line detection, when available. In most cases, we found good consistency between the photo-z from the literature and the best fit SED obtained with our SED fitting by fixing the redshift at that value. For the six sources with only a mid-IR counterpart, we attempted a photo-z estimate with LE PHARE, obtaining values of 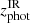 in the 2.2–6 range (with an average value
in the 2.2–6 range (with an average value 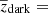 3.5; see Sect. 3.3). In order to obtain a better determination of the total IR luminosity, we simultaneously fitted only the rest frame’s 8–1000 μm range with additional far-IR template libraries included in LE PHARE (e.g. Chary & Elbaz 2001; Dale & Helou 2002; Lagache et al. 2004; Rieke et al. 2009; Siebenmorgen & Krügel 2007). We thus best fitted the far-IR bump rather than constraining the whole SED from UV to mm (where optical/near-IR data always dominate the χ2, because of their smaller errors than those affecting the longer wavelength bands).
3.5; see Sect. 3.3). In order to obtain a better determination of the total IR luminosity, we simultaneously fitted only the rest frame’s 8–1000 μm range with additional far-IR template libraries included in LE PHARE (e.g. Chary & Elbaz 2001; Dale & Helou 2002; Lagache et al. 2004; Rieke et al. 2009; Siebenmorgen & Krügel 2007). We thus best fitted the far-IR bump rather than constraining the whole SED from UV to mm (where optical/near-IR data always dominate the χ2, because of their smaller errors than those affecting the longer wavelength bands).
For most of the continuum non-target ALPINE galaxies we could obtain a good fit to all the data points and a SED estimate: the majority (75%) are best reproduced by star-forming galaxy templates (though 55% of them are composite, i.e. star-forming galaxies containing an obscured or low-luminosity AGN), while the remaining 25% are fitted by type 1 or 2 AGN templates. We checked for signal by stacking on the X-ray images (Chandra) at the positions of the AGN and non-AGN samples, but measured no significant signal for either of the samples. Although, for the AGN-SED sources, a 1.5σ positive signal was detected, against a negative signal for the non-AGN SEDs. We stress that for the six sources detected only in the mid-IR (i.e. IRAC bands), the SED type and redshift are very uncertain, and the relative results have to be taken only as indications.
In Fig. 6, we show some examples of the observed SEDs and their best fitting templates obtained from our analysis. The redshift distribution of the whole sample, including the spectroscopic and photometric redshifts from the literature, those from [C II] detection, and those obtained with LE PHARE for the sources not in the COSMOS2015, super-deblended, or 3D-HST catalogues, is shown in Fig. 7. The five redshifts from [C II] are in a different colour, since we treated those sources separately in the LF analysis because (being at the same redshifts of the ALPINE targets at the centre of the ALMA pointing) they might be part of an overdensity, or in any case associated to the target. Indeed, at z ≃ 4.57, a massive proto-cluster of galaxies located in the COSMOS field has been identified by Lemaux et al. (2018), therefore some of our [C II] emitters might be part of it. Considering them as blindly detected sources might bias the LF calculation (see Loiacono et al. 2020). These possible effects are discussed in Sect. 4.3.
 |
Fig. 6. Example of observed SEDs of ALPINE continuum non-target sources with an identification and a photo-z in the available catalogues. The observed SEDs have been fitted with LE PHARE by fixing the redshift at the catalogue value: the best fit template to all the data is shown in black, while the template best reproducing the IR data (i.e. from 8 to 1000 μm rest frame, used to derive LIR) is shown in red. |
3.2.2. Redshifts
In the paper by Béthermin et al. (2020), the redshift distribution is presented and discussed only for the “secure” identifications, that is, the 38 sources with a counterpart in the catalogues. In this work, we used all the redshifts, including the more uncertain ones, considering a total of 52 out of 56 sources. The redshift distribution obtained for the whole sample of 52 sources is shown in Fig. 7 (green-filled and empty black histogram in the top and bottom panels, respectively). We note that the total redshift distribution has a broad peak in the z ≃ 1.5–3.5 range (with a low-significance dip at z ∼ 2), followed by a secondary peak at z ∼ 5. The secondary peak at z≃5 is partially due to the sources “associated” with the ALPINE targets (i.e. with a line in the same ALMA side band; deep-pink histogram in the top panel), although it is also occupied by sources apparently not related to the targets.
 |
Fig. 7. Redshift distribution of ALPINE non-target sources detected in continuum with an identification (green-filled black histogram in the top panel, empty in the bottom panel). Top panel: the deep-pink histogram shows the five sources detected in [C II] at the same redshift of the ALPINE central targets, while the blue-dashed histogram shows the redshifts of the 47 sources considered for the unbiased LF calculation (i.e. excluding the five [C II] emitters). Bottom panel: the latter distribution is shown in blue, while the best fit photometric redshifts of the six HST+near-IR dark galaxies are shown as a red and orange-filled histogram. |
The median redshift of the total distribution is zmed ≃ 2.84 ± 0.18 (zmed ≃ 2.53 ± 0.17 if we exclude the sources at the same z of the targets; blue-dashed and blue-filled distribution in the upper and lower panel, respectively), which is similar to that found by Franco et al. (2018) in a 2–3× larger (69 arcmin2) and shallower (to 0.7 mJy) ALMA survey at 1.1 mm in GOODS-S (zmed ≃ 2.9), although the number of blindly detected objects in our ALPINE pointings is larger (56 compared to 20). The size of our continuum survey is similar to that of the ALMA twenty-six arcmin2 Survey of GOODS-S at One-millimeter (ASAGAO; Hatsukade et al. 2018), which is 26 arcmin2, although our number of detections is more than double (i.e. we detect 56 sources above 5σ compared to 25 in ASAGAO). However, we must note that our sources are selected in two different side bands, and the 1.1 mm one goes about a factor of 1.5–2 deeper than the ASAGAO survey at the same wavelength.
In panel b of Fig. 8, the redshift distribution of the 47 identified sources of our sample (excluding the [C II] emitters) is compared to those from other ALMA surveys, such as GOODS-ALMA, ASAGAO, the ALMA Spectroscopic Survey in the Hubble Ultra Deep Field (ASPECS; Aravena et al. 2016, 2020) and AS2UDS. While the ASPECS distribution (magenta) peaks at lower redshift, and the GOODS-ALMA (red) at slightly higher redshift than ours (blue filled), we notice that the ALPINE continuum survey peaks at redshifts similar to those of the ASAGAO (green dashed) and AS2UDS (orange dashed) surveys. However, the secondary peak at z ∼ 5 of our distribution does not seem to be present in the other two. We refer the reader to Béthermin et al. (2020) for a more detailed discussion about the redshift distribution of the ALPINE continuum non-target sources and the comparison with other ALMA survey works.
 |
Fig. 8. Distribution of 860 μm flux density of all 56 ALMA continuum serendipitous detections (a), redshift (b), total IR luminosity (c), and stellar mass distribution (d) of the 47 sources with measured redshift that were not associated with the ALPINE targets (i.e. blue histogram in Fig. 7). The four distributions are compared with previous results from the literature, either from blind ALMA surveys like GOODS-ALMA, ASAGAO, and ASPECS (Franco et al. 2018; Hatsukade et al. 2018; Aravena et al. 2020, respectively), or from ALMA surveys of pre-selected SMGs such as the AS2UDS (i.e. Dudzevičiūtė et al. 2020; the AS2UDS distributions have been rescaled, i.e. divided by 100, for comparison purposes). The ASAGAO masses are from Table 1 of Yamaguchi et al. (2020): the plotted values are the ZFOURGE ones (those derived with MAGPHYS are significantly higher). The different colours and shadings of the histograms associated with each survey are shown in the legend. The yellow histograms show the distribution of the six HST+near-IR dark galaxies. We note that the flux densities reported in panel a from different surveys are at different wavelengths, therefore not directly comparable, meaning the 860/870 μm fluxes would correspond to about a factor of ∼2 fainter values if translated to 1.1/1.2 mm. |
3.2.3. Total IR luminosity
We derived the total IR luminosities (LIR = L[8–1000 μm]) for all the ALPINE sources with at least one detection in addition to the ALMA one, that is, for 50 galaxies (47+3 [C II] emitters). In order to obtain the total IR luminosities, we integrate the best fit SED of each source over the range 8 ≤ λrest ≤ 1000 μm. This integration for most of our sources has been performed on well constrained SEDs covered by data in several bands (see Fig. 6), while for few sources an extrapolation of the SED with no data constraining the far-IR peak was required (thus reflecting in large uncertainties in LIR). In Fig. 8, we show the distribution of the 860 μm flux density of all the 56 ALMA continuum serendipitous detections (panel a), and the redshift (panel b), LIR (panel c) and stellar mass (panel d) distributions of the 47 sources with spectroscopic or photometric redshift measurements not associated with the ALPINE targets (i.e. blue histogram in Fig. 7), compared to other samples from the literature. The total IR luminosity distribution of our sources (blue) peaks at LIR ≃ 1012 L⊙, similarly to ASAGAO (green; Hatsukade et al. 2018), although we cover a larger range, from ∼1011–1013 L⊙. The ASPECS survey (Aravena et al. 2020) peaks at significantly fainter luminosities (LIR ≃ 3 × 1011 L⊙), while the AS2UDS (Dudzevičiūtė et al. 2020) at brighter ones (LIR ≃ 4 × 1012 L⊙). This is a direct consequence of the combination of the flux (panel a) and redshift (panel b) histograms. The AS2UDS survey, though covering the same redshift range of ALPINE, extends to and peaks at much larger fluxes, while the ASPECS survey covers much fainter fluxes and lower redshifts, resulting in fainter luminosities. Also, ASAGAO seems to sample fainter fluxes than ALPINE, but similar redshifts (though it misses a low-z peak present in our distribution), while their LIR are similar to ours (with a narrower distribution, but similar peak). The similar luminosity distribution derived from similar redshifts but fainter fluxes might appear puzzling: however, we must note that the flux densities reported in panel a of Fig. 8 are at different wavelengths, as made clear in the legend, and are therefore not directly comparable. This means that the 860/870 μm fluxes would correspond to about a factor of ∼2–3 fainter values if translated to 1.1/1.2 mm. Indeed, our 1 mm channel (here, all the ALPINE flux densities are converted to 860 μm for simplicity) reaches fluxes 1.5–2× fainter than ASAGAO. This could likely reconcile our results with the ASAGAO ones.
3.2.4. Stellar mass
We used the Le PHARE code and the Bruzual & Charlot (2003) libraries to estimate the stellar masses of our sources. We stress that the stellar masses derived for the HST and near-IR dark galaxies are extremely uncertain, given the few photometric points available (although we made use of all the 3σ upper limits to constrain the masses). Therefore, we can only take the results as an indication. In panel d of Fig. 8, we show the mass distribution of our sources (blue) compared to those from GOODS-ALMA (red), ASAGAO (green), ASPECS (magenta) and AS2UDS (orange). We find that our galaxies are massive (our mass distribution extends up to masses as high as 2.5 × 1011 M⊙; see also Fig. 9), but slightly less extreme than those detected by Franco et al. (2018) and by Dudzevičiūtė et al. (2020). In fact, the median stellar mass of our distribution is M* = (4.1 ± 0.7) × 1010 M⊙, while for GOODS-ALMA is 1.1 × 1011 M⊙ and for AS2UDS (1.26 ± 0.05) × 1011 M⊙. The stellar mass distribution of the ASPECS sample is similar to ours, both in peak position and mass coverage. The ASAGAO masses have been derived by Yamaguchi et al. (2020) with MAGPHYS (da Cunha et al. 2008) and also by Straatman et al. (2016) in the FourStar galaxy evolution survey (ZFOURGE) using FAST (Kriek et al. 2009). In the figure we plot the latter ones, which are well consistent with ours (while the MAGPHYS masses are significantly higher by ≳0.2–0.5 dex, as also noted by Yamaguchi et al. 2020).
 |
Fig. 9. Stellar mass versus redshift (left) and stellar mass histogram (right) for ALPINE continuum non-target detections. The black filled circles and blue filled histogram show the distribution of the whole sample, while the orange circles and histogram show the locus occupied by the HST+near-IR dark sources. The cyan open squares and dashed-histogram show, for comparison, the locus of the sources identified with [C II] emitters at the same redshift of the ALPINE targets (we note that the two without photometric counterparts are missing, since for them a mass estimate was impossible). |
3.3. Optically and near-IR dark galaxies
As mentioned in the previous section, of the 56 galaxies detected in our main catalogue, 12 (21%) do not present any obvious HST or near-IR (UltraVISTA, to Ks ≃ 24.9; see McCracken et al. 2012, DR4; Moneti et al. 2019) counterparts. Six of these sources have been identified in the IRAC 3.6 or 4.5 μm bands (one also in the MIPS 24 μm and Herschel bands), while six have no photometric counterpart at all. Two of these unidentified sources have been detected as line (likely [C II]) emitters by Loiacono et al. (2020), while four remain unidentified (compatible with the number of expected spurious sources based on simulations, though two are at significantly high S/N; see Béthermin et al. 2020). If we exclude the four sources without identification, we end up with a ≃14% fraction of HST+near-IR dark galaxies among the ALPINE non-target continuum detections (six with a mid-IR counterpart + two [C II] emitters). The observed SEDs of the six dark galaxies with an IRAC (or far-IR) counterpart, and their best fit template found by LE PHARE, are shown in Fig. 10. Their photometric redshifts are in the 2.23–5.85 range, with an average value of 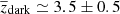 . We stress again that the estimated redshifts for five of these sources are extremely uncertain (while for the reminder the photo-z is better constrained by the available IRAC, MIPS and Herschel data); the width of the probability distribution function (PDF) can be as large as ∼1–1.5. Moreover, with few photometric data, the best fitting solutions can degenerate in the photo-z/AV space (i.e. Caputi et al. 2012). However, in our case the ALMA detection and the absence of optical and near-IR counterparts come to our aid, as they ruled out the low-z solutions and better constrained the photometric redshift.
. We stress again that the estimated redshifts for five of these sources are extremely uncertain (while for the reminder the photo-z is better constrained by the available IRAC, MIPS and Herschel data); the width of the probability distribution function (PDF) can be as large as ∼1–1.5. Moreover, with few photometric data, the best fitting solutions can degenerate in the photo-z/AV space (i.e. Caputi et al. 2012). However, in our case the ALMA detection and the absence of optical and near-IR counterparts come to our aid, as they ruled out the low-z solutions and better constrained the photometric redshift.
 |
Fig. 10. Observed SEDs for HST+near-IR-dark galaxies, with their tentative best fitting templates (black for the broad-band SED and red for the far-IR SED, as in Fig. 6) and photometric redshifts found with LE PHARE. For all but one source, the fits are based only on the IRAC and ALMA data points, combined with the 3σ UV, optical, near- and far-IR 3σ upper limits. |
In order to check whether we can detect and eventually measure an average flux in the optical and near-IR bands for these dark sources, we performed stacking at their positions in the HST-ACS band and in all four Subaru, Ultra-VISTA, and IRAC bands. We note that in the Subaru, Ultra-VISTA, and IRAC bands, we co-added images at different wavelengths. We thus applied average corrections to the fluxes when required (i.e. we multiplied the 2″ aperture photometry value of the IRAC stacked flux by a factor 1.22). In fact, the aim of our stacking analysis was not to measure accurate values, but just to validate our conclusions by detecting and estimating an average flux density for the ALPINE galaxies undetected in the optical and near-IR. In Fig. 11, we show the results of our stacking analysis for the six HST+near-IR dark galaxies (top row) in the ACS-I, Subaru (g + i + z + y), UltraVISTA (Y + J + H + Ks), and IRAC (ch1 + ch2 + ch3 + ch4) bands (from left to right, respectively). We compared to the results obtained for the two [C II] emitters without any counterparts (middle row) and for the four unidentified sources (bottom row). A positive signal comes up clearly in the UltraVISTA and IRAC bands for the six HST+near-IR dark galaxies, providing an average flux of ∼(1.21 ± 0.03) and (1.7 ± 0.3) μJy, respectively. In the ACS and Subaru images, we detect only the background. The images co-added at the positions of the two [C II] emitters without counterparts show a faint signal only in the UltraVISTA bands, and maybe in the IRAC ones, but nothing in the ACS and Subaru bands. The four unidentified galaxies do not show any signal in the stacked images, at any wavelengths. In a future paper (Gruppioni et al., in prep.), we intend to investigate and discuss in more detail the nature and average properties of the ALPINE optical and near-IR dark sources (detected both in continuum and [C II]).
 |
Fig. 11. Stacked images (10 arcmin size) resulting from co-addition of ACS-I, Subaru g + i + z + y, Ultra-VISTA Y + J + H + Ks, and IRAC ch1 + ch2 + ch3 + ch4 bands (from left to right, respectively) at the positions of the six HST+near-IR dark galaxies (top), of the two [C II] emitters without photometric counterparts (middle), and of the four unidentified sources (bottom). |
Previous studies have found faint ALMA galaxies completely missed at optical and near-IR wavelengths (Franco et al. 2018; Wang et al. 2019; Yamaguchi et al. 2019), even in the deepest surveys in GOODS. The fraction of HST-dark sources discovered in the GOODS-ALMA survey by Franco et al. (2018) is 20% of their sample, which is similar to the fraction found for the ASAGAO survey by Yamaguchi et al. (2019), and similar to the fraction that we find in our sample if we consider all the sources not detected in the HST and near-IR bands (∼21%). However, if we exclude the four sources without any counterparts, but keep the two sources with [C II] lines, we find a more realistic percentage of 14%. If we also exclude the two [C II] emitters, likely associated with the ALPINE targets, we find a conservative percentage of 11% of serendipitous HST+near-IR dark galaxies in our sample. However, for a fair comparison, we must note that the HST-dark galaxies found by Franco et al. (2018) are undetected in GOODS-S, whose photometry is deeper than in COSMOS. Therefore, some of our HST-galaxies could have been detected in optical or near-IR images as deep as the ones covering the GOODS-S field. Indeed, this would further reduce our fraction of HST-dark sources, increasing the difference with the previous results. For a more direct comparison of the results, in Table 2 we report the size and depth of ALPINE, GOODS-ALMA, and ASAGAO.
ALMA selected HST-dark sources.
While the depth and size of the GOODS-ALMA survey are different to ours (it is about 2.5× the size and 2–3× shallower), the ASAGAO survey is similar to ALPINE, both in size and sensitivity. However, our detections are either at 860 or 1000 μm, while the two mentioned surveys in GOODS-S are at 1100–1200 μm. A similar depth but in two different selection bands, in a range where the galaxy SEDs are steep, makes our survey about 2× deeper than the ASAGAO survey. Given all these factors (ALPINE deeper in ALMA, but shallower in the counterpart identification), we would have expected to find a larger fraction of galaxies undetected in the HST and/or UltraVISTA bands in ALPINE (COSMOS) than in GOODS-ALMA or ASAGAO. However, we must note that, considering the shot noise, the uncertainties in equivalence of detection and matching methodology, the data quality and depth in various bands, we cannot take this as a really significant difference.
The stellar masses estimated for the HST+near-IR dark galaxies in our sample (shown in orange in Fig. 9 and as a yellow histogram in panel d of Fig. 8) span about an order of magnitude in stellar mass, from 1.1 × 1010 to 9.5 × 1010 M⊙, and are not necessarily the most massive of the sample. For the purpose of the luminosity function calculation, we considered the HST-dark galaxies, although with large uncertainties in their redshifts and 8–1000 μm integrated luminosities (accounted for in our simulations).
4. Luminosity function
The size and depth of our sample allow us to derive the far-IR LF in more than one redshift bin, spanning from z ≃ 0.5 up to z ∼ 6. Because of the redshift range covered by our continuum sample, we would need to make significant wavelength extrapolations when computing the rest-frame LFs at any chosen wavelength. In order to apply the smallest extrapolations for the majority of our sources, we chose to derive the far-IR LF at the rest-frame wavelength corresponding to the median redshift of the sample (∼3): we therefore derive the rest-frame LF at 250 μm. Given the excellent multi-wavelength coverage of our fields, the SEDs of most of our sources are very well determined from the UV to the sub-mm. The extrapolations are therefore well constrained by accurately defined SEDs, even at redshifts lower and higher than the median value. However, there are few sources for which the photometric redshift is based only on the ALMA and one or two mid-IR fluxes, therefore the redshift itself is very uncertain and the SED not well sampled. The extrapolation for these sources is thus not very accurate and the luminosity is derived with a high level of indeterminateness (i.e. it may vary by a factor of 2–3). We took into account these uncertainties in the error bars associated with the LF values (as discussed in detail in Sect. 4.3).
4.1. Method
We derived the LFs using the 1/Vmax method (Schmidt 1968). This method is non-parametric and does not require any assumptions on the LF shape, but derives the LF directly from the data. In order to derive the monochromatic and total IR LFs, we used all the sources with a spectroscopic or photometric redshift, with the exception of two sources (SC_1_DEIMOS_COSMOS_787780, SC_1_vuds_cosmos_5101210235) that were also excluded from the continuum number counts by Béthermin et al. (2020) because their flux density was found to be boosted by an emission line (CO(7-6) at z = 1.28 and [C II] at z = 4.51, respectively). At z ≃ 5, we computed (and compared) two different LFs by either excluding or including the three [C II] emitters with optical/near-IR identification likely associated with the ALPINE targets. In the case of the former, we used 46 sources (out of 47, one was excluded because it was boosted by a CO line), and for the latter we used 48 (two [C II] emitters could not be used because they had no counterpart, one was excluded because it was boosted by the line). We divided the sample into five different redshift bins (over the 0.5 ≲ z ≲ 6 range), which we selected to be similarly populated. In each redshift bin, we computed the co-moving volume available to each source belonging to that bin, defined as
where zmax is the minimum between the maximum redshift at which a source would still be included in the sample – given the limiting flux of the survey – and the upper boundary of the considered redshift bin. Analogously, zmin is the maximum between the minimum redshift above which the source will be detected in the survey and the lower boundary of the redshift bin. The quantity dV/(dΩdz) is the co-moving volume element per unit solid angle and unit redshift, while Ωeff, i is the effective area of the i-th galaxy and depends on both the flux density (i.e. the total area covered by the survey, 24.92 arcmin2, at bright fluxes, since only the brightest sources can be detected when distant from the centre of the pointing) and the size of each source (e.g. compact sources show better completeness than extended ones at a given flux density). We note that to calculate the areal coverage of the serendipitous detections, we excluded the 1 arcsec central area where the target source was extracted. The effective area is derived from the completeness Compl(S850,θi,xi, yi) at the position (xi,yi) of the i-th source:
where the sum is over the 118 pointings. The completenesses were derived through accurate simulations by Béthermin et al. (2020). Their Fig. 8 shows the effective area as a function of the 850 μm flux for different source sizes.
For each luminosity and redshift bin, the LF is given by
where Δ log L is the size of the logarithmic luminosity bin, incompl(z) is the correction for redshift incompleteness (i.e. sources without redshift), and Vmax, i is the maximum co-moving volume over which the i-th galaxy could be observed given its luminosity and redshift (Equation 1). We adopted incompl(z) = 1 for z ≤ 6, under the assumption that the unidentified sources are all at z > 6 or spurious. In any case, whether or not we consider the redshift incompleteness (e.g. assuming that the three unidentified sources are at z > 3) will not affect our conclusions.
Uncertainties in the infrared LF values depend on the number of sources in the luminosity bin (i.e. Poissonian error) and on the photometric redshift uncertainties. In particular, significant errors on the redshift estimate can shift a low redshift galaxy to higher redshifts and vice versa, thus modifying the number density of sources in a given redshift bin. To study the impact of these uncertainties on the inferred IR LF, we performed Monte Carlo simulations, as described in Sect. 4.3.
4.2. The rest-frame 250 μm luminosity function
Following the method described above, we derived the 250 μm LF of the ALMA ALPINE sources. We divided the sample into five redshift bins: 0.5 < z ≤ 1.5, 1.5 < z ≤ 2.5, 2.5 < z ≤ 3.5, 3.5 < z ≤ 4.5, and 4.5 < z ≤ 6. We considered luminosity bins of 0.5 dex, covering the whole luminosity range by overlapping by 0.25 dex. In this way, the luminosity bins are not statistically independent (they are “alternately” independent), but we can better observe the “shape” of the LF and the position of the sources within the bin (e.g. if the bin is uniformly populated or the sources are grouped at the edge of a bin). To study the possible bias introduced by the sources with spectroscopic redshifts (from [C II] 158 μm line emission) very close to that of the ALPINE targets, we derived two LFs at 4.5 < z < 6: one by excluding and another by including the two [C II] emitters with identification from/in the calculation. The comparison between the two LFs (excluding and including the two sources) is presented and discussed only in Sect. 4.3, in order to avoid repetitions.
The results of the computation of our rest-frame 250 μm LFs are reported in Table 3; the errors were computed through Monte Carlo simulations in order to study the impact of redshift uncertainties on the LFs. We refer the reader to the next section for a detailed description of the simulation. Given the area covered by our survey and the number of independent pointings, the contribution due to cosmic variance (from Driver & Robotham 2010) is always negligible with respect to the uncertainties due to photo-z and luminosity.
ALPINE rest-frame 250 μm LF.
Our 250 μm LFs are shown in Fig. 12. The completeness limits, shown as vertical dotted lines, were computed by considering the nominal 860 μm limiting flux of our survey, that is, 0.3 mJy (see Béthermin et al. 2020), and the template, among those of the library reproducing our SEDs, which provided the brightest luminosity at the redshift of the bin. For comparison, we over-plotted previous results from the literature at 250 μm, specifically the LFs derived by Koprowski et al. (2017) from the SCUBA-2 S2CLS survey and by Lapi et al. (2011) from the Herschel-ATLAS survey.
 |
Fig. 12. Rest-frame 250 μm LF estimated with 1/Vmax method from ALPINE continuum sample (green boxes and black filled circles). The luminosity bins have a width of 0.5 dex in L250 μm, and step through the luminosity range in stages of 0.25 dex. For this reason, the individual bins are not statistically independent. The error bars in the data points represent the uncertainties obtained from the simulations (as described in Sect. 4.3). The deep-pink triangles and dashed curves are the SCUBA-2 250 μm LFs by Koprowski et al. (2017), while the blue filled squares are the Herschel ATLAS 250 μm LFs by Lapi et al. (2011), the latter being in slightly different redshift intervals. The vertical dotted line shows the completeness limit of our continuum survey, estimated as described in the text by considering the nominal 860 μm limiting flux of 0.3 mJy (Béthermin et al. 2020). |
In the common redshift intervals, our data are almost complementary to the literature data, mostly covering the faint end of the LFs (below the knee), while LF data from both Koprowski et al. (2017) and Lapi et al. (2011) cover the bright end (above the knee). In three of the four redshift intervals in common with Koprowski et al. (2017) (i.e. 0.5–1.5, 1.5–2.5, and 3.5–4.5), in the very limited common range of luminosity our 250 μm LFs are consistent with the SCUBA-2 one around the knee (at z = 2.5–3.5, our knee is at brighter luminosities). Our LFs at the faint end are flatter than the extrapolation of the Koprowski et al. (2017) fit at low z, consistent at z ∼ 3, and higher at z∼4. In fact, in the higher redshift bin in common (3.5 < z < 4.5), our data, which reach an order of magnitude fainter luminosities, are slightly higher than the faint-L extrapolation of their Schechter fit. We note that Koprowski et al. (2017) can constrain the Schechter curve with data (from Dunlop et al. 2017) at L250μm < 1011 L⊙ only in the 1.5 < z < 2.5 redshift interval.
Given the error bars of our LFs, in the overlapping redshift range (i.e. at z < 3.5) we are fully consistent with the Herschel LFs by Lapi et al. (2011), although only our highest luminosity bin is in common with their faintest one. However, in the redshift bin where our redshift distribution peaks and our data cover a wider luminosity range (i.e. 2.5 < z < 3.5), our LF is higher than the S2CLS one at bright luminosities (e.g. at L250 > 1011 L⊙), while it shows good agreement with the Lapi et al. (2011) H-ATLAS derivation (although it is almost complementary and was calculated in somewhat different redshift bins). Both our LFs and the Herschel ones indicate a more prominent bright end (i.e. more luminous sources) than derived from SCUBA-2. The consistency between our 250 μm LFs and the Lapi et al. (2011) ones (derived from a different sample and instrument, using a different template SED to fit the data and a far-IR based method to derive photometric redshifts) gives us confidence that, at least in the common redshift intervals, the photo-z uncertainties do not significantly affect our computation.
On the other hand, the underestimated bright end by the Koprowski et al. (2017) S2CLS LF had previously been noted by Gruppioni & Pozzi (2019) regarding the total IR LF (obtained with the same SCUBA-2 data used for the 250 μm derivation) at z = 2–3, and likely ascribed to the use of different template SEDs (i.e. they considered a low temperature SED, T ≃ 35 K) to compute the 8–1000 μm luminosity as well as to incompleteness issues. A similar difference is now also observed with our monochromatic derivation at similar redshifts, although these are the redshifts at which our data are less affected by SED extrapolations. Therefore, it is likely that incompleteness issue in S2CLS data are the principal cause of the observed discrepancy.
At z > 4.5 no comparison data from the literature are available, with our derivation providing the first ever determination of the luminosity and density distribution of dusty galaxies at such high redshifts. What is really surprising is that, even excluding the two sources at the same redshifts of the ALPINE targets, and despite the large uncertainties, at 4.5 < z < 6 there are no hints of a significant decrease in the volume density of dusty galaxies (i.e. in the LF normalisation) with respect to the epoch commonly considered to have experienced major galaxy activity (i.e. cosmic noon, z ∼ 1–3). A comparison between the LFs obtained with and without the two sources is shown in the next section for the total IR LF.
4.3. The total infrared luminosity function
In order to derive the total IR luminosities (and LFs), we integrated the best fit SED of each source over the 8 ≤ λrest ≤ 1000 μm (LIR = L[8–1000 μm]) range. This integration for most of our sources was performed on well-constrained SEDs covered by data in several bands (see Fig. 6), while for a few sources, an extrapolation of the SED with no data constraining the far-IR peak was required (thus reflecting large uncertainties in LIR). We computed the total IR LFs in the same redshift bins considered for the monochromatic LFs at 250 μm (i.e. 0.5 < z < 1.5, 1.5 < z < 2.5, 2.5 < z < 3.5, 3.5 < z < 4.5, and 4.5 < z < 6), and we used the same method (1/Vmax) described in the previous section.
As already mentioned, we studied the impact of redshift uncertainties on the total IR LFs by performing a set of Monte Carlo simulations. We iterated the computation of the monochromatic and total IR LFs 100 times, each time varying the photometric redshift of each source (i.e. assigning a randomly selected value, according to the probability density function, PDF, associated with each redshift). Each time, we then recomputed the monochromatic and total IR luminosities, as well as the Vmax, but keeping the previously found best fitting template for each object (i.e. we did not perform the SED fitting again, since the effect of the k-correction is not significant in the sub-mm wavelength range). For the total uncertainty in each luminosity bin, we assumed the larger dispersion between that provided by the Monte Carlo simulations and the Poissonian one (following Gehrels 1986), although the effect of the photometric redshift uncertainty on the error bars is larger than the simple Poissonian value in the majority of cases.
The values of our ALPINE total IR LFs in each redshift and luminosity bin, with their total uncertainties, are reported in Table 4. The alternately independent luminosity bins are shown in italics and bold face, as in Table 3.
ALPINE total IR LF.
4.3.1. Comparison with previous results from the literature
In Fig. 13, the total IR LFs obtained from the ALPINE sample are shown and compared with other derivations available in the literature at similar redshifts. The Herschel (e.g. Gruppioni et al. 2013), SCUBA-2 (e.g. Koprowski et al. 2017), and ALMA (e.g. Hatsukade et al. 2018) LFs are reported in the common or similar redshift ranges.
 |
Fig. 13. Total IR LF of ALPINE non-target continuum detections (red boxes and black filled circles). The luminosity bins have a width of 0.5 dex in LIR, and step through the luminosity range in steps of 0.25 dex. For this reason, the individual bins are not statistically independent. The red filled boxes and error bars indicate the 1σ errors derived through simulations (taking into account the photometric redshift uncertainties). The red solid curve is the best fit modified Schechter function derived through the MCMC analysis (see Sect. 4.3.3), while the grey long-dashed curve represents the best fit (modified Schechter function) to the Herschel PEP+HerMES total IR LF by Gruppioni et al. (2013) (interpolated to the redshift bins considered in this work). The Herschel PEP+HerMES 1/Vmax data and error bars (at slightly different redshift intervals) are plotted as grey symbols. The green short-dashed curves represent the SCUBA-2 S2CLS derivation by Koprowski et al. (2017). The blue open squares show the ALMA ASAGAO LFs by Hatsukade et al. (2018). The dark green dashed boxes and downward-pointing arrows are the COLDz CO(2-1) and CO(1-0) LFs and limits by Riechers et al. (2019) at z = 2.4 and 5.8, respectively, converted to LIR as described in the text. The vertical dotted line shows the ALPINE continuum survey completeness limit in LIR, computed by considering the nominal 860 μm limiting flux of our survey (0.3 mJy; Béthermin et al. 2020) and the template, among those of the library fitting our SEDs, which provided the brightest luminosity at the redshift of the bin. |
We stress that this is the first total IR LF derivation reaching such faint luminosities and high redshifts: thanks to ALMA and the depth reached by the ALPINE survey, we are finally able to sample IR luminosities typical of “normal” (i.e., main-sequence) star-forming galaxies, rather than only those of extreme starbursts. We are therefore able to shape the LFs over a large luminosity range, by joining the ALMA data to the somewhat complementary Herschel and SCUBA-2 ones, at least up to z ≃ 4. Globally, data from different surveys and wavelengths agree relatively well over the common z-range (up to z ≲ 4–4.5): despite the large redshift and SED extrapolation uncertainties, the total IR LF derived from the ALPINE data is in broad agreement with those obtained in previous works. No continuum survey data are available for comparison at z > 4.5, since our IR LF is the first at such high redshifts. We can only compare our data with line LFs at those redshifts.
We observe a difference with previous data in the lower redshift bin, 0.5–1.5, where both the Herschel and SCUBA-2 LFs are higher at the faint end and lower at the bright end, with their knee occurring at slightly fainter LIR. Indeed, the low-LIR discrepancy (i.e. at < 1011.5 L⊙) with Herschel is mostly determined by a single Herschel data point below the completeness limit of the ALPINE survey. The Herschel data beyond that limit are consistent within the errors with the ALPINE derivation. The SCUBA-2 curve is a low-luminosity extrapolation, if we consider Fig. 3 of Koprowski et al. (2017).
The faint-end extrapolations of the Herschel and SCUBA-2 LFs are still slightly steeper (and higher) than ours (at 1.5 < z < 2.5), though at those redshifts the inconsistency is also observed mostly below the ALPINE completeness limit, in a range where no Herschel (and probably also SCUBA-2, if we judge from the 250 μm data points in their Fig. 3) data are available to constrain the slope.
In the luminosity range 11.5 < log(LIR/L⊙) < 12.5, the agreement between Herschel and ALPINE is reasonably good, while at larger luminosities the ALPINE LF seems to remain higher (at least in the two brighter bins). The ALMA LFs from the ASAGAO survey (Hatsukade et al. 2018) agrees within the errors with our derivation (in the common luminosity range, around the knee L*), at all redshifts (from z = 0.5 to z = 3.5).
At log(LIR/L⊙) > 12.5, the S2CLS LF (Koprowski et al. 2017) shows an even steeper and lower bright end than the Herschel one, although we can only compare it to the best fit curve, with no data values available to check whether the agreement could have been better if we had limited our comparison to the luminosity range sampled by the SCUBA-2 data. The discrepancy with the S2CLS LF at the bright end is observed in all the common redshift bins, up to the 3.5 < z < 4.5 interval.
On the contrary, the agreement between ALPINE and the Herschel LF derivation increases with increasing redshifts, with the Herschel data being almost complementary in luminosity, but consistent with our data within the errors in most of the common LIR bins. We note that at 2.5 < z < 3.5, which is the redshift range corresponding to the peak of our z-distribution, the ALPINE LF seems to remain slightly higher at the bright end than the Herschel one, while the faint end is in good agreement with the Herschel best fit extrapolation.
At 3.5 < z < 4.5, the ALPINE data are totally complementary to the Herschel ones, the former covering the faint end and the latter the bright end of the LF, in a sort of continuity and agreement between the two derivations. The S2CLS LF, instead, is lower than the ALPINE and Herschel ones, not only at the bright-end, but also in normalisation and over the whole luminosity range. The underestimation of the bright end and normalisation of the total IR LF by the S2CLS data could be attributed to the method of deriving LIR by Koprowski et al. (2017) and to an incompleteness issue due to the SCUBA-2 data sensitivity, as discussed by Gruppioni & Pozzi (2019).
The occurance of the bright end remaining significantly high, and even up to brighter luminosities than those sampled by our data, is also observed in the CO LFs by Riechers et al. (2019) and Decarli et al. (2019), which are shown in Fig. 13 by the dark green dashed boxes and downward-pointing arrows (upper limits), and by the empty purple boxes, respectively. These CO LFs were obtained from the blind CO surveys, CO Luminosity Density at High Redshift (COLDz; Riechers et al. 2019) and Wide ASPECS (Decarli et al. 2019), at z ≃ 2.4, 5.8 and z = 1.43, 2.61, 3.80, respectively. In order to allow a direct comparison with our data, the CO luminosities (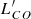 , in K km s−1 pc2) were converted to IR luminosities (in L⊙) by following Carilli & Walter (2013) to pass from
, in K km s−1 pc2) were converted to IR luminosities (in L⊙) by following Carilli & Walter (2013) to pass from 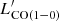 to LIR (i.e.
to LIR (i.e. 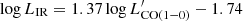 ), and Decarli et al. (2016) to convert
), and Decarli et al. (2016) to convert 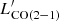 to
to 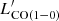 (i.e.,
(i.e., 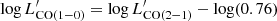 ). We note that in the common luminosity bins, the COLDz derivation is in very good agreement with our estimate, with the CO LFs extending the high bright end to even higher luminosities. Indeed, the recent finding that in the COLDz survey there may be an overdensity at z ∼ 5 capturing three bright dusty starbursts (Riechers et al. 2020) could partially explain such a high CO LF at 4.5 < z < 6 (see e.g. our LF obtained by including the two [C II] emitters likely associated with the ALPINE targets shown in Fig. 14 and discussed in the next section). The ASPECS LF is also in agreement with our estimate, especially at 2.5 < z < 3.5, while at 3.5 < z < 4.5 it extends the bright end to higher luminosities than are sampled by our data. At low redshift (i.e. 0.5 < z < 1.5), it is well consistent with our LF at the bright end, while it is higher at fainter luminosities (i.e. < 1012 L⊙). Overall, the good consistency with these completely independent derivations validate the existence of a prominent bright end in the dusty galaxies’ LFs, which has so far been highly debated in the literature and often attributed to source blending due to low resolution in far-IR/sub-mm data.
). We note that in the common luminosity bins, the COLDz derivation is in very good agreement with our estimate, with the CO LFs extending the high bright end to even higher luminosities. Indeed, the recent finding that in the COLDz survey there may be an overdensity at z ∼ 5 capturing three bright dusty starbursts (Riechers et al. 2020) could partially explain such a high CO LF at 4.5 < z < 6 (see e.g. our LF obtained by including the two [C II] emitters likely associated with the ALPINE targets shown in Fig. 14 and discussed in the next section). The ASPECS LF is also in agreement with our estimate, especially at 2.5 < z < 3.5, while at 3.5 < z < 4.5 it extends the bright end to higher luminosities than are sampled by our data. At low redshift (i.e. 0.5 < z < 1.5), it is well consistent with our LF at the bright end, while it is higher at fainter luminosities (i.e. < 1012 L⊙). Overall, the good consistency with these completely independent derivations validate the existence of a prominent bright end in the dusty galaxies’ LFs, which has so far been highly debated in the literature and often attributed to source blending due to low resolution in far-IR/sub-mm data.
 |
Fig. 14. Total IR LF of ALPINE non-target continuum detections in redshift interval 4.5 < z < 6: the results shown in Fig. 13 (red boxes and black filled circles, red solid curve) – obtained by excluding the sources with spectroscopic redshift equal to that of the ALPINE target at the centre of the pointing (i.e. two sources with optical/near-IR identification) – are compared to those obtained by also including these objects (yellow boxes and brown open squares). The brown dashed line is the MCMC modified Schechter fit to the latter LF derivation. The cyan dashed boxes show the LF recomputed after excluding the source with more uncertain photo-z (the one at z = 5.85). This test was performed to check the robustness of our result at these critical redshifts. The error bars in all the LFs show the 1σ errors obtained by combining the Poissonian errors with those derived with simulations, the latter considering the photometric redshift uncertainties. The vertical dotted line shows the ALPINE continuum survey completeness limit in this redshift interval. For comparison, we report the ALPINE [C II]158 μm LFs (converted to total IR LFs as described in the text) at similar redshifts, obtained by Yan et al. (2020) for the UV-selected ALPINE targets detected in [C II] (z ≃ 4.5: blue filled squares, z ≃ 5.5: red filled circles), and by Loiacono et al. (2020) for the serendipitous [C II] detections at 4.5 < z < 6.0 (lines falling in the same spectral window of the targets, that is, “clustered”: violet filled triangles; lines separated by that of the targets by > 2000 km s−1, that is, “field”: green upside-down triangles). The [C II] LF model predictions by Lagache et al. (2018) at z = 4.7–5.9 are reported via the light blue coloured area (z = 4.7 upper boundary, z = 5.9 lower), while the ASPECS derivation of the [C II] LFs at z = 6–8 by Aravena et al. (2020) are shown as dark blue open symbols (squares with downward-pointing arrows show upper limits, and the diamond shows the lower limit assuming that only one source is real). |
4.3.2. Luminosity function at z ≃ 5
In the highest redshift bin covered by our survey (4.5 < z < 6), we find no comparison data in the IR from the literature, but only constraints from the CO emission (Riechers et al. 2019). The hints provided by our LF in the z = 4.5–6 redshift range, in good agreement with those by Riechers et al. (2019), are that the volume density of dusty sources remains high (almost as much as at z ≃ 2–3), with no significant drop in normalisation at z > 2.5–3. The global shape of the LF does not change significantly from low to high redshift. The faint end of the LF does not show any evident steepening, and the LF knee, though barely constrained by data, seems to fall at bright luminosities, similarly to those found at lower redshifts.
In Fig. 14, we compare the total IR LF at 4.5 < z < 6 obtained by excluding the sources found at the same redshift of the ALPINE targets (the same is shown in Fig. 13: red boxes and black filled circles) to that obtained by also including two of these galaxies (i.e. those with an optical/near-IR identification, which are shown by yellow dashed boxes and brown open squares). We note that the inclusion of the two [C II] emitters does not alter the shape of the LF in the common luminosity range. What actually happens is that these sources populate the higher luminosity bins, extending the bright end of the LF to higher LIR. The reason why these sources (associated with the ALPINE central targets) have luminosities higher than the other sources at similar redshifts is not clear: however, this investigation is beyond the scope of this work and will be considered in a future paper.
We also performed a further check to test the robustness of our result in this redshift bin by recomputing the LF after excluding the source with more uncertain photo-z, meaning the one at z = 5.85. The result is shown in Fig. 14 with cyan dashed boxes. The luminosity range covered by the LF is smaller (i.e. the excluded source was populating the lower luminosity bin, that was partially affected by incompleteness), but the normalisation remains exactly the same and also the best fit curve passes through the data well. We therefore find that even if this source were at a smaller than estimated redshift, our high-z LF derivation and our conclusions would not be affected.
For comparison, in the figure we plot also the [C II] LFs obtained at similar redshifts by Yan et al. (2020) for the UV-selected ALPINE targets detected in [C II] (z ≃ 4.5: blue filled squares, z ≃ 5.5: red filled circles), and by Loiacono et al. (2020) for the serendipitous [C II] detections in the ALPINE pointings (at 4.5 < z < 6.0). The latter LF is divided in two derivations: one considers the lines in the same ALMA spectral window of the targets (i.e. “clustered”: violet filled triangles), and the other the lines spectrally distant from the targets by > 2000 km s−1 (i.e. “field”: green upside-down triangles). To allow the comparison with our continuum data, we converted the [C II] luminosities (L[C II]) to LIR by following the recipe of Hemmati et al. (2017) by adopting log10(LFIR/L[C II]) = 2.69 (value from Zanella et al. 2018), then a ratio LIR/LFIR(=L[8 − 1000 μm]/L[42 − 122 μm]) = 1.3. The results do not change if we convert L[C II] to SFR using the De Looze et al. (2014) relation, then the SFR to LIR through the Kennicutt (1998) calibration.
The [C II] LFs of the ALPINE targets (UV-selected; Yan et al. 2020) at both z ∼ 4.5 and 5.5 are lower and steeper than our best fit curve, although the high-L data point at z ∼ 4.5, at log10(LIR/L⊙) = 12.5, rises again and reaches our values. The fact that the ALPINE targets were selected in the UV rest frame can explain the steeper bright end, because the UV selection can miss the dustier sources.
On the other hand, the [C II] LF of the field serendipitous detections (Loiacono et al. 2020) is in perfect agreement with our data. The [C II] LF of the clustered serendipitous detections instead is slightly higher than our derivation (though consistent within the uncertainties), especially below our completeness limit. Similarly to our LF obtained by including the two sources at the redshift of the ALPINE targets, the [C II] clustered LF also extends to higher luminosities than the field one. This seems to imply that sources belonging to an overdensity are more luminous than the field ones.
The model prediction of [C II] LF by Lagache et al. (2018) at z = 4.7–5.9 is also reported (as a light blue coloured area: z = 4.7 upper boundary, z = 5.9 lower) in Fig. 14: it is generally steeper than our LF, slightly lower at bright luminosities, and consistent at low LIR (though we are likely affected by incompleteness in the first two luminosity bins). The ASPECS [C II] LF at z = 6–8 by Aravena et al. (2020), converted to LIR by means of the same method used for Loiacono et al. (2020) and Yan et al. (2020) LFs, is shown with dark blue open symbols (the squares with downward-pointing arrows show the upper limits, and the diamond shows the conservative value obtained by assuming that only the source with an optical counterpart is real). The “conservative” ASPECS data point is in very good agreement with our LF, with the latter never exceeding their upper limits.
4.3.3. Evolution
In order to facilitate the comparison between the LFs at different redshifts, in the top panel of Fig. 15 we plot the total IR LFs at all redshifts with their ±1σ uncertainty regions (different colours for different z-intervals). The errors are large, therefore it is difficult to detect any significant evolution of the LF with z; it is however surprising to note that there does not seem to be any appreciable evolution from z ∼ 0.5 to z ∼ 6, both in shape and normalisation.
 |
Fig. 15. Total IR LF shown in the different panels of Fig. 13 plotted at all the different redshift intervals considered in this study, from z ∼ 0.5 to z ∼ 6. Top: the different coloured areas represent the ±1σ uncertainty regions at different redshifts obtained from the Monte Carlo simulations. We note that for the highest redshift interval (4.5 < z < 6.0), in both panels the LF is shown for both derivations. This was obtained by excluding (blue) and including (green) the sources at the same redshifts of the ALPINE targets (see legend). Bottom: median value of the LFs in each luminosity bin at all the redshift intervals, each scaled by a factor of 0.5 relatively to the previous one, from the lowest to the highest redshift. The different colours show the different redshift intervals, with the same colours of the top panel. |
However, we must stress that with ALPINE we are mostly covering the faint end of the total IR LF over the whole redshift range, with the exception of the 2.5 < z < 3.5 interval, where we span a slightly larger range of luminosities and we are also able to reach luminosities above the knee. Therefore, the apparent non-evolution of the LF found in this work is not inconsistent with previous results (i.e. based on Herschel data) claiming a strong luminosity evolution up to z ≃ 2–3 (e.g. Gruppioni et al. 2013). This is because the evolution in the Herschel LFs is observed principally at its bright end, where ALPINE has limited constraining power.
In the bottom panel of Fig. 15, we show only the median values of the LFs in each luminosity bin at all the redshift intervals, each scaled by a factor of 0.5 relatively to the previous one, from the lowest to the highest redshift, in order to facilitate the shape comparison. From the figure, we note that in general the LFs seem to present two “bumps”, one at lower and the other at higher luminosities, though at very low significance (i.e. 1.5σ). The two bumps are noticeable in particular where our sample covers the wider range of luminosities, that is, at z = 0.5–1.5 and 2.5–3.5 (dark green and red dashed areas – top – and curves – bottom). In the lowest redshift bin, the bump at brighter luminosities has a lower normalisation than the one peaking at fainter LIR. At z = 1.5–2.5 and 3.5–4.5 our LFs sample only the fainter luminosities (and perhaps the fainter bump), while at 4.5–6 a sort of double-peaked distribution is observed only when we consider all the serendipitous detections (i.e. without excluding the sources at the same redshift of the ALPINE targets; bright green). If the two bumps were real and maybe due to two different populations, the one responsible for the higher LIR bump will become more dominant with increasing z. We would need more data to confirm these hints: with the current data we can only make speculations.
In general, the ALPINE total IR LFs seem to confirm the “flat” shape already found by Herschel, at both its faint and bright ends. In particular, the bright end remains significantly high even in the higher redshift interval, where the volume density of ultra-/hyper-luminous IR galaxies equals that of more “normal” galaxies. The presence of such (and so many) bright IR galaxies at high-z is a real challenge for galaxy formation models (already at z ∼ 2–3, even worse at higher z), with no current model being able to explain the existence of massive, dusty, and actively star-forming galaxies at such early epochs.
On the other hand, the flat faint end implies a minor contribution from low-luminosity and/or low-mass galaxies to the dust emission, while a main contribution from high-luminosity and/or high-mass systems, up to the highest redshifts, is required by the bright end. The increasing number of low-mass systems with increasing redshift predicted by the hierarchical structure formation scenario is not observed in our data. It might however be that low-mass and/or low-dust-mass systems become more important or numerous at higher redshifts, but do not produce (heat) enough far-IR emission (dust) to be detected in far-IR/mm surveys. In order to study the evolution of the total IR LF and of the SFRD with z, we obtained a parametric estimate of the luminosity function at different redshifts. Although the ALPINE LFs may have a more complex shape (i.e. a double-peaked distribution), for simplicity and to better compare the values of the parameters with previous results, we assumed a modified Schechter function (i.e. Saunders et al. 1990), with ϕ(L) given by
behaving as a power law for L ≪ L⋆ and as a Gaussian in log L for L ≫ L⋆. The adopted LF parametric shape depends on four parameters (α, σ, L⋆ and ϕ⋆), whose best fitting values and uncertainties were derived using a Markov chain Monte Carlo (MCMC) procedure. Since the ALPINE data do not sample the bright luminosities, the slope of the bright end is almost unconstrained: we therefore fixed the value of σ (the parameter shaping the bright-end slope) to that found for the Herschel LFs (σ = 0.5). We considered flat priors for the other three parameters (α, L⋆ and ϕ⋆), limiting the MCMC exploration to a reasonably wide range of values (i.e. log(L⋆/L⊙): [10,13], log(ϕ⋆/Mpc−3 dex−1): [−2,−5], α: [−1,2]). The result of the MCMC analysis is shown in Figs. 13 (red solid curve) and 14 (red solid and brown dashed curves) and presented in Table 5.
MCMC best fitting parameters.
5. Contribution to the cosmic SFRD
We derived the evolution of the co-moving luminosity density (ρIR) of the ALPINE continuum non-target sources by integrating the total IR LF in the different redshift bins, from z ≃ 0.5–1.5 to z ≃ 4.5–6 (i.e. ρIR(z) = ∫ϕ(log LIR, z) LIR dlog LIR). In order to do this, we extrapolated the modified Schechter functions that best reproduce our data down to log(LIR/L⊙) = 8. If the overall contribution to the IR luminosity density from the AGN components of galaxies is small, ρIR can be considered as a proxy of the co-moving SFRD (ρSFR(z)), assuming the Kennicutt (1998) relation that connects the SFR and LIR. For the majority of our SEDs, we cannot reliably disentangle the AGN from the star formation contribution, since we do not have enough data in the mid-/far-IR. However, although we cannot exclude the presence of an AGN inside our galaxies, we notice that the large majority of the ALPINE SEDs are best fitted by star-forming or composite templates rather than by AGN-dominated ones. Indeed, the best fit templates that reproduce the ALPINE SEDs are similar to those found to reproduce the majority of the Herschel PEP+HerMES galaxies at z ≃ 2–3 (Gruppioni et al. 2013). Furthermore, their decomposition and separation into AGN and SF contributions (performed by Delvecchio et al. 2014) showed a negligible contribution to LIR (< 10 per cent) from the AGN and an SF component dominating the far-IR, even in the SEDs fitted by more powerful AGN templates (see also Lemaux et al. 2014). Since in ALPINE we found very few AGN-dominated templates, we do not expect that contamination related to accretion activity can significantly affect the results in terms of ρSFR. We therefore used the relation found by Kennicutt (1998) to convert LIR to SFR, then ρIR(z) to ρSFR(z), for a Chabrier (2003) IMF:
In Fig. 16, we show ρSFR(z) estimated from our total IR LF (values presented in Table 6) and compare it with results obtained from previous surveys in different bands, from the optical/UV to the radio (see references in the figure legend and caption). Since our lower redshift bin is centred at z = 1, our co-moving SFRD does not show the rapid rise from z ∼ 0 to z ∼ 1 observed in other surveys. It does, however, show a very flat distribution from z = 0.5 to z = 6, with no significant decrease beyond the cosmic noon (z ≃ 1–3), as is observed from optical/UV surveys. Other SFRD derivations from the ALPINE collaboration are shown for comparison: from the serendipitous [C II] LF (blue box; Loiacono et al. 2020) and from the UV+IR SFR of the ALPINE targets (yellow filled hexagons; Khusanova et al. 2020), highlighted in the top-right corner of the plot. The [C II] result agrees well with our z≃5 value, and also the UV+IR target data are consistent with ours within the uncertainties, though the higher redshift one is slightly lower (possibly due to the UV selection missing highly obscured galaxies).
 |
Fig. 16. Redshift evolution of co-moving star formation rate density (ρSFR), obtained by integrating the modified Schechter function that best reproduces the ALPINE total IR LF of the continuum non-target detections (excluding the [C II] emitters): black circles. The error bars and the red boxes around our data points show the 1σ uncertainty range derived through the MCMC analysis of the LF. The SFRD estimates from ALPINE (legend in the top-right corner of the plot) are also shown for comparison: the blue box with blue open triangle represents the result obtained from the [C II] LF of the serendipitous line emitters by Loiacono et al. (2020), while the yellow filled hexagons with error bars are the values obtained by Khusanova et al. (2020) from the UV+IR emission of the ALPINE targets. For comparison, estimates from other surveys (UV: Schiminovich et al. 2005; Dahlen et al. 2007; Reddy & Steidel 2009; Cucciati et al. 2012; Schenker et al. 2013; Bouwens et al. 2015; Oesch et al. 2018; optical/near-IR: Driver et al. 2018; Merlin et al. 2019; far-IR: Sanders et al. 2003; Takeuchi et al. 2003; Magnelli et al. 2011, 2013; Gruppioni et al. 2013, 2015; Rowan-Robinson et al. 2016; mm: Dunlop et al. 2017; radio: Novak et al. 2017; gamma-ray bursts: Kistler et al. 2009) are also shown (grey shaded areas and open or filled symbols), as described in the legend at the bottom of the plot. The models by Madau & Dickinson (2014) and Béthermin et al. (2017) are shown as black dashed and orange dot-dashed curves, respectively, while the prediction of the IllustrisTNG simulation (Pillepich et al. 2018) is shown as a dark green solid curve. Also shown are the measurements derived from the cross-correlation between the lensing map of the CMB and the CIB (light blue crosses with error bars, Planck Collaboration XVIII 2014) and the prediction by Lagache (2018) obtained by modelling the CIB (violet triple-dot-dashed curves, showing the pessimistic and optimistic cases). |
Star formation rate density.
Our data are also in very good agreement with the far-IR results (from Spitzer and Herschel) over the common redshift range (e.g. 1–3: Rodighiero et al. 2010; Magnelli et al. 2011, 2013; Gruppioni et al. 2013), and in particular with the sub-mm results of Rowan-Robinson et al. (2016) (highly debated because they are based on exceptional Herschel SPIRE 500 μm galaxies) over the whole redshift range. In addition, we find a good agreement with the results of Kistler et al. (2009) from gamma-ray bursts at z> 4, with the measurements derived from the cross-correlation between the lensing map of the CMB and the CIB by the Planck Collaboration XVIII 2014, and with the ρSFR(z) derived by Novak et al. (2017) from radio surveys at z ≃ 1–5.
On the other hand, the SFRD derived from optical/UV surveys, although extending to higher redshifts (i.e. z ≃ 10), are always significantly lower than our estimates at z > 3. The difference increases with redshift, reaching a factor of about 10 at z∼6. When performing this comparison, we must note that, while we integrated the IR LF down to 108 L⊙ (i.e. an SFR of ≃10−2 M⊙ yr−1) to derive the SFRD, the SFRD estimates for UV-selected galaxies are always integrated down to the detection limits of the highest redshift LF (e.g. to an SFR limit of 0.3 M⊙ yr−1 at z = 10; Oesch et al. 2018). This is done because the faint-end slope of the UV LF at high redshift is found to be very steep, leading the UV LF integration to diverge. However, given the very flat faint end of our IR LF, integrating it to SFR limits similar to those of the UV works would not significantly modify our results.
The models by Madau & Dickinson (2014), Béthermin et al. (2017), and Pillepich et al. (2018) are also reported as black dashed, orange dot-dashed, and dark green solid curves, respectively. We notice that the more recent galaxy formation simulations (e.g. IllustrisTNG, Pillepich et al. 2018) and the model by Béthermin et al. (2017) are consistent with the ALPINE 1σ lower error up to z ∼ 4 (excluding the z = 3 bin, where our data are always higher), but significantly lower than the ALPINE ρSFR(z) at z ≳ 4, with the difference becoming a factor of ≳5–6 at z ∼ 6. The predictions by Lagache (2018) obtained by modelling the CIB are plotted as violet triple-dot-dashed curves (showing both pessimistic and optimistic cases), and show good consistency with our data. In Fig. 17, which is less crowded by data, we report the four models again for a better comparison with our results, and we also add the prediction by Maniyar et al. (2018) obtained by modelling the CIB (light yellow dashed area). This latter prediction, similarly to the Madau & Dickinson (2014) model, is lower than our data at z ≳ 2.5.
 |
Fig. 17. Comparison between SFRD obtained by excluding the two [C II] emitters with optical/near-IR counterparts (red boxes and black circles, same as in Fig. 16) and that estimated by integrating the best fit curve to the 4.5 < z < 6 LF obtained from all the continuum detections, including the two [C II] emitters (yellow boxes and brown open square). For comparison, we also report the results obtained by Loiacono et al. (2020) by integrating the [C II] LF of the serendipitous line emitters for field (i.e. lines separated by that of the ALPINE targets by > 2000 km s−1: blue box and open up-side down triangle) and clustered sources (i.e. lines falling in the same spectral window of the ALPINE targets: green box and open triangle). The models by Madau & Dickinson (2014), Béthermin et al. (2017), and Pillepich et al. (2018) are also reported as black dashed, orange dot-dashed, and dark green solid curves, respectively. In addition, we plot the predictions obtained by modelling the CIB of Maniyar et al. (2018), as a light yellow dashed area, and by Lagache (2018) as violet triple-dot-dashed lines (pessimistic and optimistic cases). |
From the comparison of all the data shown in Fig. 16, we can conclude that a significant amount of SF activity at high-z is still missed by surveys sampling the UV rest frame of galaxy emission. Indeed, all the far-IR/sub-mm and radio estimates agree within the uncertainties in showing an almost constant SFRD distribution from z ∼ 1 to 6, implying a significant and increasing contribution of dust-obscured activity, which, starting from z > 3–4, cannot be recovered by the dust-extinction corrected UV data. A similar discrepancy is observed with the predictions of galaxy formation simulations, that are not able to predict such a high amount of SFR in galaxies as we observe from z ∼ 3–4 to higher redshifts. As discussed also by Rowan-Robinson et al. (2016), this result implies a significantly earlier start of the epoch of high SFRD than assumed by galaxy formation models and by UV-based works. Therefore, the epoch of major activity in galaxies, corresponding to the rapid heavy element formation, extended at least from redshift 6 to redshift 1, which is at odds with the predictions of the semi-analytic models for galaxy formation (e.g. Henriques et al. 2015), which set the epoch of intense star formation at z ≃ 1–2. Our result strengthens the debated result of Rowan-Robinson et al. (2016), but also the previous conclusion of Gruppioni et al. (2015) showing that the semi-analytic models under-predict the high SFRs observed in the Herschel galaxies already at z ≳ 1.5–2.
5.1. Comparison with the SFRD derived from the ALPINE [C II] luminosity functions
In Fig. 17, we compare the SFRD obtained by excluding the [C II] emitters (red boxes and black circles: same as in Fig. 16) to that estimated by integrating the best fit curve to the 4.5 < z< 6 LF obtained from all the continuum detections, including the two [C II] emitters (yellow dashed boxes and brown open squares). The inclusion of the two [C II] emitters enhances our SFRD in the highest redshift bin, causing a discontinuity with respect to the SFRD at lower redshifts, due to the overdensity associated with the ALPINE targets to which these sources likely belong. A similar – and even more pronounced – effect is observed with the [C II] SFRD by Loiacono et al. (2020) (also shown in the figure for comparison), where the SFRD derived for the detected [C II] lines in the same side band of the ALPINE targets (i.e. clustered: green box and open triangle) is about an order of magnitude higher than the SFRD of the [C II] emitters not associated with the targets (i.e. field: blue box and upside-down triangle). Therefore, we can conclude that by also including the sources detected because they were associated with the primary targets of the ALMA observation, we would have likely introduced a bias (overestimate) in our SFRD derivations.
5.2. Contribution of the optically and near-IR dark galaxies to the SFRD
In Fig. 18, we show the estimated contribution to the SFRD at z ≃ 3 and 5 from the ALPINE optically+near-IR dark galaxies. Our result, obtained by summing the SFR contribution of the HST+near-IR sources in the two redshift intervals 2.2–4.0 and 4.0–6.0 (i.e. four and two sources, respectively, if we exclude the [C II] emitters in the latter bin) is compared to previous estimates from the literature, obtained either through ALMA selection (e.g. Yamaguchi et al. 2019; Williams et al. 2019) or with different techniques (e.g. H-dropouts; Wang et al. 2019). Despite the large uncertainties, our estimates are significantly higher than the SFRD contribution of the HST-dark galaxies selected by Wang et al. (2019) as H-dropouts, and of those selected by Yamaguchi et al. (2019) from the ASAGAO ALMA survey. However, our result is consistent with the estimate based on a single sub-mm galaxy published by Williams et al. (2019) (i.e. 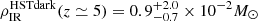 yr−1 Mpc−3), while we find (1.5 ± 0.9) × 10−2 and (0.9 ± 0.7) × 10−2 M⊙ yr−1 Mpc−3 at z≃3 and 5, respectively. From Fig. 18, we note that the contribution to the co-moving SFRD of the HST+near-IR dark galaxies in ALPINE at z ≃ 5 is almost equal to the extinction-corrected contribution from all the known UV-selected galaxies at similar redshifts. This means that the dust-obscured star formation also continues to contribute a significant fraction of the total SFRD beyond z > 3, and at least up to z ≃ 6, where the available IR and mm estimates are still scanty. Previous works, such as the detailed “super-deblending” analysis of Herschel fluxes in the GOODS-N field performed by Liu et al. (2018), found that z > 3 dusty galaxies missed by optical-to-near-IR colour selection can significantly contribute to the SFRD at 3 < z < 6, and that far-IR+mm-derived SFRD are mostly independent of or complementary to those derived from optical and UV measurements. We note, however, that the contribution at z = 5 from the HST+near-IR dark galaxies is only ∼1/6 of the total (i.e. from all the sources), therefore the bulk of the difference between the corrected-UV and the total SFRD is not due to the dark galaxies, but more likely the dust correction of the UV samples that is too difficult to estimate from optical data.
yr−1 Mpc−3), while we find (1.5 ± 0.9) × 10−2 and (0.9 ± 0.7) × 10−2 M⊙ yr−1 Mpc−3 at z≃3 and 5, respectively. From Fig. 18, we note that the contribution to the co-moving SFRD of the HST+near-IR dark galaxies in ALPINE at z ≃ 5 is almost equal to the extinction-corrected contribution from all the known UV-selected galaxies at similar redshifts. This means that the dust-obscured star formation also continues to contribute a significant fraction of the total SFRD beyond z > 3, and at least up to z ≃ 6, where the available IR and mm estimates are still scanty. Previous works, such as the detailed “super-deblending” analysis of Herschel fluxes in the GOODS-N field performed by Liu et al. (2018), found that z > 3 dusty galaxies missed by optical-to-near-IR colour selection can significantly contribute to the SFRD at 3 < z < 6, and that far-IR+mm-derived SFRD are mostly independent of or complementary to those derived from optical and UV measurements. We note, however, that the contribution at z = 5 from the HST+near-IR dark galaxies is only ∼1/6 of the total (i.e. from all the sources), therefore the bulk of the difference between the corrected-UV and the total SFRD is not due to the dark galaxies, but more likely the dust correction of the UV samples that is too difficult to estimate from optical data.
 |
Fig. 18. Contribution of HST+near-IR dark galaxies to ρSFR(z): the derivation from this work (ALMA selection) in two redshift intervals (i.e. z = 2.2–4.0 and 4.0–6.0) is shown via the magenta filled area and the black stars, and is compared to the derivation by Wang et al. (2019) from H-dropout selection (blue open squares and line), by Yamaguchi et al. (2019) from ASAGAO (purple filled area), and by Williams et al. (2019) from the ALMA selection (green diamond). The red boxes with black circles and the violet filled pentagons (the same as in Fig. 16) represent the obscured and unobscured SFRD from this work and from Bouwens et al. (2015), respectively. |
The fact that we identified six dark galaxies in a survey of 24.9 arcmin2 implies a source density of about 0.24 arcmin−2, of the same order of that derived by Williams et al. (2019) (0.13 arcmin−2), which is about a factor of three higher than the density of near-IR dark galaxies in ASAGAO (e.g. two sources in 26 arcmin2: ∼8 × 10−2 arcmin−2; Yamaguchi et al. 2019). At z> 3, our dark galaxies have a density of ∼0.12 arcmin−2, which is ∼10× higher than that of z> 4 SMGs (1–2 × 10−2 arcmin−2; e.g. Danielson et al. 2017; Marrone et al. 2018). Similar densities, such as (0.042 ± 0.028) arcmin−2, are reported by Riechers et al. (2020) for optically dark CO emitters at z > 5 detected down to an equivalent 870 μm flux density of ∼5 mJy.
By considering the volumes corresponding to each source in our survey, we derive a space density of HST+near-IR dark galaxies in ALPINE of ∼(1.2 ± 0.7) × 10−4 and (5.0 ± 3.8) × 10−5 Mpc−3 at z ≃ 3 and 5, respectively. The value found in the highest redshift interval is higher (though consistent within the uncertainties) than the source density of dark galaxies estimated by Williams et al. (2019) at z ≃ 4.1–5.7 (2.9 × 10−5 Mpc−3) and by Riechers et al. (2020) at z > 5 (i.e. (1.0 ± 0.7) × 10−5 Mpc−3).
5.3. Contribution of the optically and near-IR dark galaxies to the stellar mass density
Although the mass estimates for the ALPINE-detected, HST+near-R dark galaxies are very uncertain (given the paucity of photometric points available), these sources are likely to contribute significantly to the cosmic stellar mass density (SMD or ρ*) at high redshifts. Indeed, by summing up the volume-weighted masses of our dark galaxies, we find that they might represent a fraction of the total SMD (as derived by Davidzon et al. 2017 for the COSMOS15 galaxies) as high as ∼20%, and > 50% at z ≃ 3 and 5, respectively. They could even dominate the high-mass end of the stellar mass function at z > 3 (see also Rodighiero et al. 2007). In fact, we find that the number density of the ALPINE dark galaxies with M* > 1010.7 M⊙ is ∼(5.1 ± 3.7) × 10−5 Mpc−3, which is comparable to that of the more massive quiescent galaxies at z≳3–4 (e.g. ∼2 × 10−5 Mpc−3; Gobat et al. 2012; Straatman et al. 2014; Song et al. 2016; Glazebrook et al. 2017). The early formation of such a large number of massive, dusty galaxies is not predicted by the current semi-analytical models (e.g. Henriques et al. 2015) and hydrodynamic simulations (e.g. Pillepich et al. 2018), which largely underestimate the density of massive galaxies at high redshifts (see e.g. Alcalde Pampliega et al. 2019; Wang et al. 2019). Similarly, the galaxy formation models and simulations are also not able to explain the observed large density of IR luminous galaxies at z > 2 (e.g. Gruppioni et al. 2015; Rowan-Robinson et al. 2016). The direct implication of these large abundances of massive and IR luminous (dusty) galaxies in the early Universe (not predicted by the up-to-date state-of-the-art models) is that our current knowledge of the formation and evolution of massive/luminous galaxies is still far from being complete, and the relative theories might need important revisions.
In the near future, further investigations of the nature and physical parameters of the HST+near-IR dark galaxies will be necessary to consolidate our results and conclusions. In particular, follow-up studies in the mid-IR (photometry and/or spectroscopy) with the James Webb Space Telescope, and in the sub-mm/mm (continuum and/or spectral-scanning) with ALMA or NOEMA will be the foreseen key observations.
6. Conclusions
We used the 56 sources blindly detected in continuum (ALMA band 7, i.e. at 860 or 1000 μm) within the ALPINE survey to investigate the nature, evolution, and main properties of the dusty galaxy population across the 0.5 ≲ z ≲ 6 redshift range. The main points of our work can be summarised as follows:
-
We performed a detailed identification analysis, either by matching the positions of the ALPINE continuum sources with the available multi-wavelength and photo-z catalogues, or by looking for counterparts in the deep photometric images, then performing ad-hoc photometry and deriving photometric redshifts. Six of the continuum sources showed a faint counterpart only in the mid-IR, with no HST or near-IR matches. Five (two with no counterparts at all) have been identified with [C II] emitters at z ∼ 5 (same z as the ALPINE targets at the centre of the pointings). For four sources, no counterpart was found in any of the available catalogues or images, though two are detected at significantly high S/N (6.7 and 9.3).
-
We fully characterised the multi-wavelength SEDs of the ALPINE non-target sources by performing a detailed SED-fitting analysis and comparison with known template libraries of IR populations. The SED-fitting analysis provided the main physical parameters of the sources, which are LIR, SFR, M*, galaxy class, k-correction and, if needed, a photo-z estimate. The median redshift of the whole ALPINE non-target, continuum-detected sub-mm galaxy population is
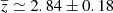 (2.53 ± 0.17 if we exclude the five sources at the same z of the ALPINE targets), while for the HST and near-IR dark galaxies it is
(2.53 ± 0.17 if we exclude the five sources at the same z of the ALPINE targets), while for the HST and near-IR dark galaxies it is 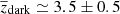 (although their z-distribution shows two peaks around z ∼ 3 and 5). The ALPINE continuum sources on average resulted to be massive galaxies, with stellar masses in the 1010–1011 M⊙ range (
(although their z-distribution shows two peaks around z ∼ 3 and 5). The ALPINE continuum sources on average resulted to be massive galaxies, with stellar masses in the 1010–1011 M⊙ range (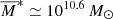 for the HST+near-IR dark galaxies), though not as extreme as what was found in previous works.
for the HST+near-IR dark galaxies), though not as extreme as what was found in previous works. -
We computed the rest-frame LFs at 250 μm in different redshift bins, from 0.5 < z < 1.5 up to 4.5 < z < 6 and compared them with the Herschel and SCUBA-2 LFs at the same wavelength available in the literature. The ALPINE LF is almost complementary to the previous ones, the former mostly sampling the faint end, and the latter the bright end. In the common redshift and luminosity range, our results are more consistent with the Herschel ones.
-
We integrated the SEDs over λrest = 8–1000 μm, computed the total IR LFs in different redshift intervals (from z ≃ 0.5 up to z ∼ 6), and studied its evolution with z. Although ALPINE mostly covers the faint end of the LFs, the global shape appears flat, with a low faint-end slope and a high bright end, not dropping at bright LIR. There are no signs of a significant decrease in the normalisation nor of a change in shape from z = 0.5 to z = 6. Our results are in very good agreement with those from CO LFs by Riechers et al. (2019) and Decarli et al. (2016, 2019).
-
We derived the co-moving SFRD over the z ≃ 0.5–6 redshift range and the contribution of HST and near-IR dark galaxies at z ≃ 3 and 5. The SFRD shows a flat distribution over the whole z-range, with no significant decrease beyond the cosmic noon (z ≃ 1–3). Our result is in agreement with those from previous far-IR and radio surveys, but higher than that found by optical/UV surveys at z > 3. The difference between our results and the optical/UV ones increases with redshift, reaching a factor of about 10 at z ∼ 6. The HST+near-IR dark galaxies contribute a significant fraction (about 17%) of the total SFRD at high-z (> 3). We can conclude that a considerable amount of SF activity at high-z is still missed by surveys sampling the UV rest frame (most of it not due to dark galaxies), with a significant and increasing contribution of dust-obscured activity that cannot be recovered even by correcting the UV data for dust extinction. Similarly, the current galaxy formation models and simulations are not able to predict such a high amount of SFR in dusty galaxies as is observed beyond cosmic noon.
-
We derived the contribution of the ALPINE HST+near-IR dark galaxies to the cosmic mass density, notably finding that the number density of M* > 1010.7 M⊙ dark galaxies is comparable to that of the more massive quiescent galaxies at z ≳ 3. Given that neither the current semi-analytical models nor the more recent hydrodynamic simulations can explain the early formation of such a large number of massive dusty galaxies, we will need to revise our current understanding of the formation of massive/luminous galaxies.
The SPLASH maps are available, upon request, at http://splash.caltech.edu/
Acknowledgments
This paper is dedicated to the memory of Olivier Le Fèvre, PI of the ALPINE survey. We are grateful to the anonymous referee, whose constructive comments helped us to improve the manuscript. CG acknowledges financial support from the Italian Space Agency under the ASI-INAF contract n. 2018-31-HH.0. CG, FP, MT, AC, GR acknowledge the support from grant PRIN MIUR 2017−20173ML3WW_001. GL acknowledges support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (project CONCERTO, grant agreement No 788212) and from the Excellence Initiative of Aix-Marseille University-A*Midex, a French “Investissements d’Avenir” programme. SF acknowledge support from the European Research Council (ERC) Consolidator Grant funding scheme (project ConTExt, grant No. 648179). The Cosmic Dawn Center is funded by the Danish National Research Foundation under grant No. 140. D.R. acknowledges support from the National Science Foundation under grant numbers AST-1614213 and AST-1910107. D.R. also acknowledges support from the Alexander von Humboldt Foundation through a Humboldt Research Fellowship for Experienced Researchers. This work is based on observations taken by the 3D-HST Treasury Program (GO 12177 and 12328) with the NASA/ESA HST, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5−26555. Based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under ESO programme ID 179.A-2005 and on data products produced by CALET and the Cambridge Astronomy Survey Unit on behalf of the UltraVISTA consortium.
References
- Alcalde Pampliega, B., Pérez-González, P. G., Barro, G., et al. 2019, ApJ, 876, 135 [CrossRef] [Google Scholar]
- Aravena, M., Decarli, R., Walter, F., et al. 2016, ApJ, 833, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Aravena, M., Boogaard, L., Gónzalez-López, J., et al. 2020, ApJ, 901, 79 [CrossRef] [Google Scholar]
- Arnouts, S., Moscardini, L., Vanzella, E., et al. 2002, MNRAS, 329, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Barger, A. J., Cowie, L. L., Sanders, D. B., et al. 1998, Nature, 394, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Béthermin, M., Daddi, E., Magdis, G., et al. 2015, A&A, 573, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Wu, H.-Y., Lagache, G., et al. 2017, A&A, 607, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Fudamoto, Y., Ginolfi, M., et al. 2020, A&A, 643, A2 [CrossRef] [EDP Sciences] [Google Scholar]
- Blain, A. W., Smail, I., Ivison, R. J., Kneib, J. P., & Frayer, D. T. 2002, Phys. Rep., 369, 111 [Google Scholar]
- Bothwell, M. S., Smail, I., Chapman, S. C., et al. 2013, MNRAS, 429, 3047 [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2015, ApJ, 811, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., Franx, M., et al. 2012, ApJS, 200, 13 [Google Scholar]
- Brisbin, D., Miettinen, O., Aravena, M., et al. 2017, A&A, 608, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P. L., Riechers, D., Scoville, N. Z., et al. 2011, Nature, 470, 233 [Google Scholar]
- Capak, P., Aussel, H., Bundy, K., et al. 2012, SPLASH: Spitzer Large Area Survey with Hyper-Suprime-Cam (Spitzer Proposal) [Google Scholar]
- Caputi, K. I., Dunlop, J. S., McLure, R. J., et al. 2012, ApJ, 750, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carniani, S., Maiolino, R., De Zotti, G., et al. 2015, A&A, 584, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casey, C. M., Chen, C.-C., Cowie, L. L., et al. 2013, MNRAS, 436, 1919 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Chapman, S. C., Windhorst, R., Odewahn, S., Yan, H., & Conselice, C. 2003, ApJ, 599, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, S. C., Blain, A. W., Smail, I., & Ivison, R. J. 2005, ApJ, 622, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Chary, R., & Elbaz, D. 2001, ApJ, 556, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Cucciati, O., Tresse, L., Ilbert, O., et al. 2012, A&A, 539, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- da Cunha, E., Charlot, S., & Elbaz, D. 2008, MNRAS, 388, 1595 [Google Scholar]
- Dahlen, T., Mobasher, B., Dickinson, M., et al. 2007, ApJ, 654, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., & Helou, G. 2002, ApJ, 576, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Danielson, A. L. R., Swinbank, A. M., Smail, I., et al. 2017, ApJ, 840, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Davidzon, I., Ilbert, O., Laigle, C., et al. 2017, A&A, 605, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decarli, R., Walter, F., Aravena, M., et al. 2016, ApJ, 833, 69 [Google Scholar]
- Decarli, R., Walter, F., Gónzalez-López, J., et al. 2019, ApJ, 882, 138 [Google Scholar]
- De Looze, I., Cormier, D., Lebouteiller, V., et al. 2014, A&A, 568, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delvecchio, I., Gruppioni, C., Pozzi, F., et al. 2014, MNRAS, 439, 2736 [NASA ADS] [CrossRef] [Google Scholar]
- Dey, A., Graham, J. R., Ivison, R. J., et al. 1999, ApJ, 519, 610 [Google Scholar]
- Driver, S. P., & Robotham, A. S. G. 2010, MNRAS, 407, 2131 [NASA ADS] [CrossRef] [Google Scholar]
- Driver, S. P., Andrews, S. K., da Cunha, E., et al. 2018, MNRAS, 475, 2891 [NASA ADS] [CrossRef] [Google Scholar]
- Dudzevičiūtė, U., Smail, I., Swinbank, A. M., et al. 2020, MNRAS, 494, 3828 [Google Scholar]
- Dunlop, J. S., McLure, R. J., Biggs, A. D., et al. 2017, MNRAS, 466, 861 [Google Scholar]
- Elbaz, D., Dickinson, M., Hwang, H. S., et al. 2011, A&A, 533, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faisst, A. L., Schaerer, D., Lemaux, B. C., et al. 2020, ApJS, 247, 61 [Google Scholar]
- Franco, M., Elbaz, D., Béthermin, M., et al. 2018, A&A, 620, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fujimoto, S., Ouchi, M., Ono, Y., et al. 2016, ApJS, 222, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Giacconi, R., Zirm, A., Wang, J., et al. 2002, ApJS, 139, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Glazebrook, K., Schreiber, C., Labbé, I., et al. 2017, Nature, 544, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Gobat, R., Strazzullo, V., Daddi, E., et al. 2012, ApJ, 759, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, T., Oi, N., Utsumi, Y., et al. 2019, PASJ, 71, 30 [CrossRef] [Google Scholar]
- Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Gruppioni, C., & Pozzi, F. 2019, MNRAS, 483, 1993 [NASA ADS] [CrossRef] [Google Scholar]
- Gruppioni, C., Pozzi, F., Andreani, P., et al. 2010, A&A, 518, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gruppioni, C., Pozzi, F., Rodighiero, G., et al. 2013, MNRAS, 432, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Gruppioni, C., Calura, F., Pozzi, F., et al. 2015, MNRAS, 451, 3419 [NASA ADS] [CrossRef] [Google Scholar]
- Hatsukade, B., Ohta, K., Seko, A., Yabe, K., & Akiyama, M. 2013, ApJ, 769, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Hatsukade, B., Kohno, K., Yamaguchi, Y., et al. 2018, PASJ, 70, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Hauser, M. G., Arendt, R. G., Kelsall, T., et al. 1998, ApJ, 508, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Hemmati, S., Yan, L., Diaz-Santos, T., et al. 2017, ApJ, 834, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Henriques, B. M. B., White, S. D. M., Thomas, P. A., et al. 2015, MNRAS, 451, 2663 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, D. H., Serjeant, S., Dunlop, J., et al. 1998, Nature, 394, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jin, S., Daddi, E., Liu, D., et al. 2018, ApJ, 864, 56 [Google Scholar]
- Jones, G. C., Béthermin, M., Fudamoto, Y., et al. 2020, MNRAS, 491, L18 [Google Scholar]
- Kennicutt, R. C., Jr 1998, ARA&A, 36, 189 [Google Scholar]
- Khusanova, Y., Béthermin, M., Le Fèvre, O., et al. 2020, A&A, submitted [arXiv:2007.08384] [Google Scholar]
- Kistler, M. D., Yüksel, H., Beacom, J. F., Hopkins, A. M., & Wyithe, J. S. B. 2009, ApJ, 705, L104 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Aussel, H., Calzetti, D., et al. 2007, ApJS, 172, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Koprowski, M. P., Dunlop, J. S., Michałowski, M. J., et al. 2017, MNRAS, 471, 4155 [NASA ADS] [CrossRef] [Google Scholar]
- Kriek, M., van Dokkum, P. G., Labbé, I., et al. 2009, ApJ, 700, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G. 2018, in Peering towards Cosmic Dawn, eds. V. Jelić, & T. van der Hulst, IAU Symp., 333, 228 [NASA ADS] [Google Scholar]
- Lagache, G., Dole, H., Puget, J. L., et al. 2004, ApJS, 154, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Puget, J.-L., & Dole, H. 2005, ARA&A, 43, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Cousin, M., & Chatzikos, M. 2018, A&A, 609, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Lapi, A., González-Nuevo, J., Fan, L., et al. 2011, ApJ, 742, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Béthermin, M., Faisst, A., et al. 2020, A&A, 643, A1 [CrossRef] [EDP Sciences] [Google Scholar]
- Le Floc’h, E., Aussel, H., Ilbert, O., et al. 2009, ApJ, 703, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Lemaux, B. C., Le Floc’h, E., Le Fèvre, O., et al. 2014, A&A, 572, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemaux, B. C., Le Fèvre, O., Cucciati, O., et al. 2018, A&A, 615, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, D., Daddi, E., Dickinson, M., et al. 2018, ApJ, 853, 172 [Google Scholar]
- Loiacono, F., Decarli, R., Gruppioni, C., et al. 2020, A&A, submitted [arXiv:2006.04837] [Google Scholar]
- Lutz, D., Poglitsch, A., Altieri, B., et al. 2011, A&A, 532, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Magnelli, B., Elbaz, D., Chary, R. R., et al. 2011, A&A, 528, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnelli, B., Popesso, P., Berta, S., et al. 2013, A&A, 553, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maniyar, A. S., Béthermin, M., & Lagache, G. 2018, A&A, 614, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marrone, D. P., Spilker, J. S., Hayward, C. C., et al. 2018, Nature, 553, 51 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, H. J., Milvang-Jensen, B., Dunlop, J., et al. 2012, A&A, 544, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [Google Scholar]
- Merlin, E., Fortuni, F., Torelli, M., et al. 2019, MNRAS, 490, 3309 [NASA ADS] [CrossRef] [Google Scholar]
- Momcheva, I. G., Brammer, G. B., van Dokkum, P. G., et al. 2016, ApJS, 225, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Moneti, A., McCracken, H. J., Hudelot, P., et al. 2019, ESO Science Archive Facility - Phase 3 Data Release Description http://ultravista.org/release4/dr4_release.pdf [Google Scholar]
- Novak, M., Smolčić, V., Delhaize, J., et al. 2017, A&A, 602, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oesch, P. A., Bouwens, R. J., Illingworth, G. D., Labbé, I., & Stefanon, M. 2018, ApJ, 855, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, S. J., Bock, J., Altieri, B., et al. 2012, MNRAS, 424, 1614 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ono, Y., Ouchi, M., Kurono, Y., & Momose, R. 2014, ApJ, 795, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Oteo, I., Zwaan, M. A., Ivison, R. J., Smail, I., & Biggs, A. D. 2016, ApJ, 822, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Pillepich, A., Springel, V., Nelson, D., et al. 2018, MNRAS, 473, 4077 [Google Scholar]
- Planck Collaboration XVIII. 2014, A&A, 571, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polletta, M., Tajer, M., Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Puget, J. L., Abergel, A., Bernard, J. P., et al. 1996, A&A, 308, L5 [Google Scholar]
- Reddy, N. A., & Steidel, C. C. 2009, ApJ, 692, 778 [NASA ADS] [CrossRef] [Google Scholar]
- Riechers, D. A., Hodge, J., Walter, F., Carilli, C. L., & Bertoldi, F. 2011, ApJ, 739, L31 [Google Scholar]
- Riechers, D. A., Bradford, C. M., Clements, D. L., et al. 2013, Nature, 496, 329 [Google Scholar]
- Riechers, D. A., Leung, T. K. D., Ivison, R. J., et al. 2017, ApJ, 850, 1 [Google Scholar]
- Riechers, D. A., Pavesi, R., Sharon, C. E., et al. 2019, ApJ, 872, 7 [Google Scholar]
- Riechers, D. A., Hodge, J. A., Pavesi, R., et al. 2020, ApJ, 895, 81 [Google Scholar]
- Rieke, G. H., Alonso-Herrero, A., Weiner, B. J., et al. 2009, ApJ, 692, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Rodighiero, G., Cimatti, A., Franceschini, A., et al. 2007, A&A, 470, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodighiero, G., Vaccari, M., Franceschini, A., et al. 2010, A&A, 515, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romano, M., Cassata, P., Morselli, L., et al. 2020, MNRAS, 496, 875 [CrossRef] [Google Scholar]
- Rowan-Robinson, M., Oliver, S., Wang, L., et al. 2016, MNRAS, 461, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Mazzarella, J. M., Kim, D. C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [Google Scholar]
- Saunders, W., Rowan-Robinson, M., Lawrence, A., et al. 1990, MNRAS, 242, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Schenker, M. A., Robertson, B. E., Ellis, R. S., et al. 2013, ApJ, 768, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Schiminovich, D., Ilbert, O., Arnouts, S., et al. 2005, ApJ, 619, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E., Sargent, M. T., Bondi, M., et al. 2010, ApJS, 188, 384 [Google Scholar]
- Schmidt, M. 1968, ApJ, 151, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Siebenmorgen, R., & Krügel, E. 2007, A&A, 461, 445 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simpson, J. M., Swinbank, A. M., Smail, I., et al. 2014, ApJ, 788, 125 [Google Scholar]
- Skelton, R. E., Whitaker, K. E., Momcheva, I. G., et al. 2014, ApJS, 214, 24 [Google Scholar]
- Smail, I., Ivison, R. J., & Blain, A. W. 1997, ApJ, 490, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Song, M., Finkelstein, S. L., Ashby, M. L. N., et al. 2016, ApJ, 825, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Steinhardt, C. L., Speagle, J. S., Capak, P., et al. 2014, ApJ, 791, L25 [Google Scholar]
- Straatman, C. M. S., Labbé, I., Spitler, L. R., et al. 2014, ApJ, 783, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Straatman, C. M. S., Spitler, L. R., Quadri, R. F., et al. 2016, ApJ, 830, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M., Simpson, J. M., Smail, I., et al. 2014, MNRAS, 438, 1267 [Google Scholar]
- Takeuchi, T. T., Yoshikawa, K., & Ishii, T. T. 2003, ApJ, 587, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Taniguchi, Y., Kajisawa, M., Kobayashi, M. A. R., et al. 2015, PASJ, 67, 104 [NASA ADS] [Google Scholar]
- Walter, F., Decarli, R., Carilli, C., et al. 2012, Nature, 486, 233 [Google Scholar]
- Walter, F., Decarli, R., Aravena, M., et al. 2016, ApJ, 833, 67 [Google Scholar]
- Wang, W.-H., Barger, A. J., & Cowie, L. L. 2009, ApJ, 690, 319 [Google Scholar]
- Wang, T., Schreiber, C., Elbaz, C., et al. 2019, Nature, 572, 211 [CrossRef] [Google Scholar]
- Wardlow, J. L., Smail, I., Coppin, K. E. K., et al. 2011, MNRAS, 415, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, C. C., Labbe, I., Spilker, J., et al. 2019, ApJ, 884, 154 [CrossRef] [Google Scholar]
- Yamaguchi, Y., Kohno, K., Hatsukade, B., et al. 2019, ApJ, 878, 73 [Google Scholar]
- Yamaguchi, Y., Kohno, K., Hatsukade, B., et al. 2020, PASJ, 72, 69 [CrossRef] [Google Scholar]
- Yan, L., Sajina, A., Loiacono, F., et al. 2020, ApJ, submitted [arXiv:2006.04835] [Google Scholar]
- Zanella, A., Daddi, E., Magdis, G., et al. 2018, MNRAS, 481, 1976 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Example of identification of ALPINE non-target continuum source: the postage stamps (from top left to bottom right) show the ALMA band 7 continuum map and the ALMA ≥ 3σ contours over-plotted on images from HST/ACS-i to radio VLA-1.4 GHz (band specified in the top-right corner). Object with multi-wavelength counterparts in all bands and photo-z from Laigle et al. (2016). The plotted contour levels are at 3, 5, 7, 9, 11, 13, and 15σ, corresponding to 0.32, 0.53, 0.74, 0.95, 1.16, 1.37, and 1.58 mJy. The ALMA 1-mm flux density of this source (SC_1_DEIMOS_COSMOS_910650) is 4.22 mJy, the RMS (1σ) of this pointing is ∼0.11 mJy. |
| In the text | |
 |
Fig. 2. Object with no optical counterpart, but with multi-wavelength counterparts from near-IR to sub-mm and photo-z (from Laigle et al. 2016). The plotted contour levels are at 3, 5, 7, 9, 11, 13, and 15σ, corresponding to 0.26, 0.44, 0.62, 0.79, 0.97, 1.15, and 1.32 mJy. The ALMA 860 μm flux density of this source (SC_1_DEIMOS_COSMOS_680104) is 3.54 mJy, the RMS (1σ) of this pointing ∼0.088 mJy. |
| In the text | |
 |
Fig. 3. Optically dark galaxy detected only in deep IRAC-SPLASH 4.5 μm catalogue. The photo-z has been derived with LE PHARE using ALMA and IRAC data only. The plotted contour levels are at 3, 5σ, corresponding to 0.14, 0.23 mJy. The ALMA 1 mm flux density of this source (SC_1_DEIMOS_COSMOS_224751) is 0.25 mJy, the RMS (1σ) of this pointing is ∼0.046 mJy. |
| In the text | |
 |
Fig. 4. ALPINE serendipitous source with no obvious identification in any bands. The plotted contour levels are at 3, 5, and 6.5σ, corresponding to 0.47, 0.79, and 1.02 mJy. The ALMA 1 mm flux density of this source (SC_1_DEIMOS_COSMOS_471063) is 1.06 mJy, the RMS (1σ) of this pointing is ∼0.16 mJy. |
| In the text | |
 |
Fig. 5. Distribution of observed Ks-band magnitude and 860 μm ALMA fluxes of ALPINE serendipitous continuum sources with a Ks counterpart. The horizontal dashed line shows the UltraVISTA Ks-band 5σ limit of 24.9, while the vertical one shows the minimum 860 μm (5σ) flux density reached by the ALMA sample (the orange coloured area shows the region covered by our data). For comparison, the dotted lines (green filled area) indicate the Ks magnitude and 870 μm flux limits of the AS2UDS sample of SMGs reported by Dudzevičiūtė et al. (2020). The downward-pointing arrows shown at the Ks-band limit are the six sources detected only at mid-IR wavelengths. The histograms show the Ks-band magnitude distribution on the right axis, and the 860 μm flux density distribution is on the top axis of the plot (orange histogram showing the fluxes of the mid-IR detected sources). |
| In the text | |
 |
Fig. 6. Example of observed SEDs of ALPINE continuum non-target sources with an identification and a photo-z in the available catalogues. The observed SEDs have been fitted with LE PHARE by fixing the redshift at the catalogue value: the best fit template to all the data is shown in black, while the template best reproducing the IR data (i.e. from 8 to 1000 μm rest frame, used to derive LIR) is shown in red. |
| In the text | |
 |
Fig. 7. Redshift distribution of ALPINE non-target sources detected in continuum with an identification (green-filled black histogram in the top panel, empty in the bottom panel). Top panel: the deep-pink histogram shows the five sources detected in [C II] at the same redshift of the ALPINE central targets, while the blue-dashed histogram shows the redshifts of the 47 sources considered for the unbiased LF calculation (i.e. excluding the five [C II] emitters). Bottom panel: the latter distribution is shown in blue, while the best fit photometric redshifts of the six HST+near-IR dark galaxies are shown as a red and orange-filled histogram. |
| In the text | |
 |
Fig. 8. Distribution of 860 μm flux density of all 56 ALMA continuum serendipitous detections (a), redshift (b), total IR luminosity (c), and stellar mass distribution (d) of the 47 sources with measured redshift that were not associated with the ALPINE targets (i.e. blue histogram in Fig. 7). The four distributions are compared with previous results from the literature, either from blind ALMA surveys like GOODS-ALMA, ASAGAO, and ASPECS (Franco et al. 2018; Hatsukade et al. 2018; Aravena et al. 2020, respectively), or from ALMA surveys of pre-selected SMGs such as the AS2UDS (i.e. Dudzevičiūtė et al. 2020; the AS2UDS distributions have been rescaled, i.e. divided by 100, for comparison purposes). The ASAGAO masses are from Table 1 of Yamaguchi et al. (2020): the plotted values are the ZFOURGE ones (those derived with MAGPHYS are significantly higher). The different colours and shadings of the histograms associated with each survey are shown in the legend. The yellow histograms show the distribution of the six HST+near-IR dark galaxies. We note that the flux densities reported in panel a from different surveys are at different wavelengths, therefore not directly comparable, meaning the 860/870 μm fluxes would correspond to about a factor of ∼2 fainter values if translated to 1.1/1.2 mm. |
| In the text | |
 |
Fig. 9. Stellar mass versus redshift (left) and stellar mass histogram (right) for ALPINE continuum non-target detections. The black filled circles and blue filled histogram show the distribution of the whole sample, while the orange circles and histogram show the locus occupied by the HST+near-IR dark sources. The cyan open squares and dashed-histogram show, for comparison, the locus of the sources identified with [C II] emitters at the same redshift of the ALPINE targets (we note that the two without photometric counterparts are missing, since for them a mass estimate was impossible). |
| In the text | |
 |
Fig. 10. Observed SEDs for HST+near-IR-dark galaxies, with their tentative best fitting templates (black for the broad-band SED and red for the far-IR SED, as in Fig. 6) and photometric redshifts found with LE PHARE. For all but one source, the fits are based only on the IRAC and ALMA data points, combined with the 3σ UV, optical, near- and far-IR 3σ upper limits. |
| In the text | |
 |
Fig. 11. Stacked images (10 arcmin size) resulting from co-addition of ACS-I, Subaru g + i + z + y, Ultra-VISTA Y + J + H + Ks, and IRAC ch1 + ch2 + ch3 + ch4 bands (from left to right, respectively) at the positions of the six HST+near-IR dark galaxies (top), of the two [C II] emitters without photometric counterparts (middle), and of the four unidentified sources (bottom). |
| In the text | |
 |
Fig. 12. Rest-frame 250 μm LF estimated with 1/Vmax method from ALPINE continuum sample (green boxes and black filled circles). The luminosity bins have a width of 0.5 dex in L250 μm, and step through the luminosity range in stages of 0.25 dex. For this reason, the individual bins are not statistically independent. The error bars in the data points represent the uncertainties obtained from the simulations (as described in Sect. 4.3). The deep-pink triangles and dashed curves are the SCUBA-2 250 μm LFs by Koprowski et al. (2017), while the blue filled squares are the Herschel ATLAS 250 μm LFs by Lapi et al. (2011), the latter being in slightly different redshift intervals. The vertical dotted line shows the completeness limit of our continuum survey, estimated as described in the text by considering the nominal 860 μm limiting flux of 0.3 mJy (Béthermin et al. 2020). |
| In the text | |
 |
Fig. 13. Total IR LF of ALPINE non-target continuum detections (red boxes and black filled circles). The luminosity bins have a width of 0.5 dex in LIR, and step through the luminosity range in steps of 0.25 dex. For this reason, the individual bins are not statistically independent. The red filled boxes and error bars indicate the 1σ errors derived through simulations (taking into account the photometric redshift uncertainties). The red solid curve is the best fit modified Schechter function derived through the MCMC analysis (see Sect. 4.3.3), while the grey long-dashed curve represents the best fit (modified Schechter function) to the Herschel PEP+HerMES total IR LF by Gruppioni et al. (2013) (interpolated to the redshift bins considered in this work). The Herschel PEP+HerMES 1/Vmax data and error bars (at slightly different redshift intervals) are plotted as grey symbols. The green short-dashed curves represent the SCUBA-2 S2CLS derivation by Koprowski et al. (2017). The blue open squares show the ALMA ASAGAO LFs by Hatsukade et al. (2018). The dark green dashed boxes and downward-pointing arrows are the COLDz CO(2-1) and CO(1-0) LFs and limits by Riechers et al. (2019) at z = 2.4 and 5.8, respectively, converted to LIR as described in the text. The vertical dotted line shows the ALPINE continuum survey completeness limit in LIR, computed by considering the nominal 860 μm limiting flux of our survey (0.3 mJy; Béthermin et al. 2020) and the template, among those of the library fitting our SEDs, which provided the brightest luminosity at the redshift of the bin. |
| In the text | |
 |
Fig. 14. Total IR LF of ALPINE non-target continuum detections in redshift interval 4.5 < z < 6: the results shown in Fig. 13 (red boxes and black filled circles, red solid curve) – obtained by excluding the sources with spectroscopic redshift equal to that of the ALPINE target at the centre of the pointing (i.e. two sources with optical/near-IR identification) – are compared to those obtained by also including these objects (yellow boxes and brown open squares). The brown dashed line is the MCMC modified Schechter fit to the latter LF derivation. The cyan dashed boxes show the LF recomputed after excluding the source with more uncertain photo-z (the one at z = 5.85). This test was performed to check the robustness of our result at these critical redshifts. The error bars in all the LFs show the 1σ errors obtained by combining the Poissonian errors with those derived with simulations, the latter considering the photometric redshift uncertainties. The vertical dotted line shows the ALPINE continuum survey completeness limit in this redshift interval. For comparison, we report the ALPINE [C II]158 μm LFs (converted to total IR LFs as described in the text) at similar redshifts, obtained by Yan et al. (2020) for the UV-selected ALPINE targets detected in [C II] (z ≃ 4.5: blue filled squares, z ≃ 5.5: red filled circles), and by Loiacono et al. (2020) for the serendipitous [C II] detections at 4.5 < z < 6.0 (lines falling in the same spectral window of the targets, that is, “clustered”: violet filled triangles; lines separated by that of the targets by > 2000 km s−1, that is, “field”: green upside-down triangles). The [C II] LF model predictions by Lagache et al. (2018) at z = 4.7–5.9 are reported via the light blue coloured area (z = 4.7 upper boundary, z = 5.9 lower), while the ASPECS derivation of the [C II] LFs at z = 6–8 by Aravena et al. (2020) are shown as dark blue open symbols (squares with downward-pointing arrows show upper limits, and the diamond shows the lower limit assuming that only one source is real). |
| In the text | |
 |
Fig. 15. Total IR LF shown in the different panels of Fig. 13 plotted at all the different redshift intervals considered in this study, from z ∼ 0.5 to z ∼ 6. Top: the different coloured areas represent the ±1σ uncertainty regions at different redshifts obtained from the Monte Carlo simulations. We note that for the highest redshift interval (4.5 < z < 6.0), in both panels the LF is shown for both derivations. This was obtained by excluding (blue) and including (green) the sources at the same redshifts of the ALPINE targets (see legend). Bottom: median value of the LFs in each luminosity bin at all the redshift intervals, each scaled by a factor of 0.5 relatively to the previous one, from the lowest to the highest redshift. The different colours show the different redshift intervals, with the same colours of the top panel. |
| In the text | |
 |
Fig. 16. Redshift evolution of co-moving star formation rate density (ρSFR), obtained by integrating the modified Schechter function that best reproduces the ALPINE total IR LF of the continuum non-target detections (excluding the [C II] emitters): black circles. The error bars and the red boxes around our data points show the 1σ uncertainty range derived through the MCMC analysis of the LF. The SFRD estimates from ALPINE (legend in the top-right corner of the plot) are also shown for comparison: the blue box with blue open triangle represents the result obtained from the [C II] LF of the serendipitous line emitters by Loiacono et al. (2020), while the yellow filled hexagons with error bars are the values obtained by Khusanova et al. (2020) from the UV+IR emission of the ALPINE targets. For comparison, estimates from other surveys (UV: Schiminovich et al. 2005; Dahlen et al. 2007; Reddy & Steidel 2009; Cucciati et al. 2012; Schenker et al. 2013; Bouwens et al. 2015; Oesch et al. 2018; optical/near-IR: Driver et al. 2018; Merlin et al. 2019; far-IR: Sanders et al. 2003; Takeuchi et al. 2003; Magnelli et al. 2011, 2013; Gruppioni et al. 2013, 2015; Rowan-Robinson et al. 2016; mm: Dunlop et al. 2017; radio: Novak et al. 2017; gamma-ray bursts: Kistler et al. 2009) are also shown (grey shaded areas and open or filled symbols), as described in the legend at the bottom of the plot. The models by Madau & Dickinson (2014) and Béthermin et al. (2017) are shown as black dashed and orange dot-dashed curves, respectively, while the prediction of the IllustrisTNG simulation (Pillepich et al. 2018) is shown as a dark green solid curve. Also shown are the measurements derived from the cross-correlation between the lensing map of the CMB and the CIB (light blue crosses with error bars, Planck Collaboration XVIII 2014) and the prediction by Lagache (2018) obtained by modelling the CIB (violet triple-dot-dashed curves, showing the pessimistic and optimistic cases). |
| In the text | |
 |
Fig. 17. Comparison between SFRD obtained by excluding the two [C II] emitters with optical/near-IR counterparts (red boxes and black circles, same as in Fig. 16) and that estimated by integrating the best fit curve to the 4.5 < z < 6 LF obtained from all the continuum detections, including the two [C II] emitters (yellow boxes and brown open square). For comparison, we also report the results obtained by Loiacono et al. (2020) by integrating the [C II] LF of the serendipitous line emitters for field (i.e. lines separated by that of the ALPINE targets by > 2000 km s−1: blue box and open up-side down triangle) and clustered sources (i.e. lines falling in the same spectral window of the ALPINE targets: green box and open triangle). The models by Madau & Dickinson (2014), Béthermin et al. (2017), and Pillepich et al. (2018) are also reported as black dashed, orange dot-dashed, and dark green solid curves, respectively. In addition, we plot the predictions obtained by modelling the CIB of Maniyar et al. (2018), as a light yellow dashed area, and by Lagache (2018) as violet triple-dot-dashed lines (pessimistic and optimistic cases). |
| In the text | |
 |
Fig. 18. Contribution of HST+near-IR dark galaxies to ρSFR(z): the derivation from this work (ALMA selection) in two redshift intervals (i.e. z = 2.2–4.0 and 4.0–6.0) is shown via the magenta filled area and the black stars, and is compared to the derivation by Wang et al. (2019) from H-dropout selection (blue open squares and line), by Yamaguchi et al. (2019) from ASAGAO (purple filled area), and by Williams et al. (2019) from the ALMA selection (green diamond). The red boxes with black circles and the violet filled pentagons (the same as in Fig. 16) represent the obscured and unobscured SFRD from this work and from Bouwens et al. (2015), respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



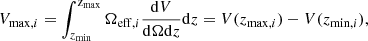
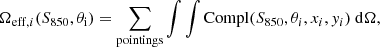
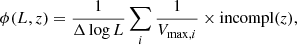
![$$ \begin{aligned} \phi (L)~\mathrm{dlog}L=\phi ^{\star }\left(\frac{L}{L^{\star }}\right)^{1-\alpha } \exp \left[-\frac{1}{2\sigma ^2}\log _{10}^2\left(1+\frac{L}{L^{\star }}\right)\right]\mathrm{dlog}L, \end{aligned} $$](/articles/aa/full_html/2020/11/aa38487-20/aa38487-20-eq90.gif)