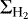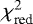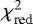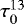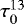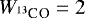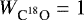| Issue |
A&A
Volume 633, January 2020
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 25 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201936814 | |
| Published online | 24 December 2019 | |
Autonomous Gaussian decomposition of the Galactic Ring Survey
I. Global statistics and properties of the 13CO emission data★
1
Max-Planck Institute for Astronomy,
Königstuhl 17,
69117 Heidelberg, Germany
e-mail: riener@mpia.de
2
Department of Space, Chalmers University of Technology, Earth and Environment,
412 93 Gothenburg, Sweden
Received:
30
September
2019
Accepted:
14
November
2019
The analysis of large molecular line surveys of the Galactic plane is essential for our understanding of the gas kinematics on Galactic scales and, in particular, its link with the formation and evolution of dense structures in the interstellar medium. An approximation of the emission peaks with Gaussian functions allows for an efficient and straightforward extraction of useful physical information contained in the shape and Doppler-shifted frequency of the emission lines contained in these enormous data sets. In this work, we present an overview and the first results of a Gaussian decomposition of the entire Galactic Ring Survey (GRS) 13CO (1–0) data that consists of about 2.3 million spectra. We performed the decomposition with the fully automated GAUSSPY+ algorithm and fitted about 4.6 million Gaussian components to the GRS spectra. These decomposition results enable novel and unexplored ways to interpret and study the gas velocity structure. We discuss the statistics of the fit components and relations between the fitted intensities, velocity centroids, and velocity dispersions. We find that the magnitude of the velocity dispersion values increase towards the inner Galaxy and around the Galactic midplane, which we speculate is partly due to the influence of the Galactic bar and regions with higher non-thermal motions located in the midplane, respectively. We also used our decomposition results to infer global properties of the gas emission and find that the number of fit components used per spectrum is indicative of the amount of structure along the line of sight. We find that the emission lines from regions located on the far side of the Galaxy show increased velocity dispersion values, which are likely due to beam averaging effects. We demonstrate how this trend has the potential to aid in characterising Galactic structure by disentangling emission that belongs to the nearby Aquila Rift molecular cloud from emission that is more likely associated with the Perseus and Outer spiral arms. With this work, we also make our entire decomposition results available.
Key words: methods: data analysis / radio lines: general / ISM: kinematics and dynamics / ISM: lines and bands
Full Table 1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/633/A14
© M. Riener et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1 Introduction
The study of the velocity structure of molecular gas is of vital importance for understanding the origin and evolution of structures in the interstellar medium (ISM). Carbon monoxyde (CO), which is the most abundant molecule in the ISM after molecular hydrogen (H2), has multiple transitions that are excited at the low temperatures prevalent in the molecular part of the ISM and can be observed in the radio and sub-mm part of the electromagnetic spectrum. Thus CO is often used as a tracer of H2 (for a review see Bolatto et al. 2013), whose observation at the typical temperatures (~10−30 K) of molecular clouds and clumps are challenging or effectively impossible. Moreover, the CO emission lines contain useful velocity information: The Doppler shift of the centroid frequency of the line, compared to the rest frequency in the local standard of rest (LSR), comes from the bulk motion of the gas, which is mostly due to Galactic dynamics; and the width of the line beyond the natural line broadening is caused by thermal (or Doppler) and non-thermal contributions, for which the line shape is usually well-described by a Gaussian shape.
Given the relative ease of observation and the plethora of information they encode, the rotational transitions of the most abundant isotopologues of CO – 12CO, 13CO, and C18O – have thus been prime targets for large mapping surveys of the Milky Way’s disk for a long time. Examples of Galactic plane surveys from the last two decades that are already published or currently in preparation are as follows: the Galactic Ring Survey (GRS; Jackson et al. 2006); the CO (3–2) High-resolution Survey of the Galactic Plane (COHRS; Dempsey et al. 2013); the Mopra Southern Galactic Plane CO Survey (MGPS; Burton et al. 2013; Braiding et al. 2018); the Three-mm Ultimate Mopra Milky Way Survey (ThrUMMS, Barnes et al. 2015); the 13CO/C18O (J = 3–2) Heterodyne Inner Milky Way Plane Survey (CHIMPS; Rigby et al. 2016); the FOREST unbiased Galactic plane imaging survey with the Nobeyama 45 m telescope (FUGIN; Umemoto et al. 2017); the Structure, Excitation, and Dynamics of the Inner Galactic Interstellar Medium survey (SEDIGISM, Schuller et al. 2017); and the Milky Way Imaging Scroll Painting survey (MWISP, Su et al. 2019). See also Fig. 2 in Heyer & Dame (2015) for an exhaustive overview of large CO surveys of the Galactic plane up until 2015.
These data sets have provided and continue to provide invaluable information about the CO content and kinematics for individual case studies or samples of molecular clouds (e.g. Heyer & Dame 2015; Miville-Deschênes et al. 2017), infrared dark clouds (IRDCs) (e.g. Simon et al. 2006; Kainulainen & Tan 2013; Barnes et al. 2018; Zhou et al. 2019), molecular clumps (e.g. Urquhart et al. 2018), or filaments (e.g. Zucker et al. 2018; Zhang et al. 2019) covered by these surveys. While for many works the average kinematic properties of their objects have been of prime interest, some studies have further analysed the detailed velocity structure of their objects by exploiting the full spatial and spectral resolution of one or more of these surveys (e.g. Barnes et al. 2018).
There are also studies that used the entire data set of one of the Galactic plane surveys; so far, these have mostly focussed on either the global properties of the gas emission at larger scales to obtain information about the Galactic structure (e.g. Dame et al. 2001; Nakanishi & Sofue 2006; Rigby et al. 2016; Roman-Duval et al. 2016) or they have concentrated on segmenting the observed gas emission into molecular clouds, clumps, or filaments (e.g. Solomon et al. 1987; Rathborne et al. 2009; Rice et al. 2016; Miville-Deschênes et al. 2017; Colombo et al. 2019) to infer useful average physical properties of the gas emission on the scales of these objects and to try to put them into the context of their location within our Galaxy (e.g. Roman-Duval et al. 2010; Heyer & Dame 2015; Miville-Deschênes et al. 2017).
We currently still lack a study of the detailed velocity structure of the molecular gas on Galactic scales, with sufficient spatial resolution to resolve the inner structure of molecular clouds (≲ 1′) and sufficient spectral resolution to resolve the thermal linewidth of the cold molecular gas (~ 0.2 km s−1). Such a study requires analysing the entire data set of one of the more recent large Galactic plane surveys in its native spatial and spectral resolution. Presently, we do not know what this velocity structure looks like on Galactic scales and its study could reveal systematic trends linked to physical processes, for instance, the effects spiral arms have on the kinematics of the gas in the context of star formation.
However, a study of the detailed velocity structure of any of these Galactic plane surveys requires a reduction of the complexity of these data sets. One possible approach is the decomposition of the emission lines of each spectrum into individual (velocity) components. In case of CO emission of Galactic plane surveys, these velocity components can be associated with different structures along the line of sight. This association is non-trivial and complicated due to multiple physical and observational effects, such as velocity crowding (mixing of emission along the line of sight), velocity gradients, optical depth, and difficulties in transforming vLSR velocities to physical distances. The main problem in the decomposition itself is how to correctly identify the (sometimes blended) emission lines so that we can determine the shape of the individual lines and subsequently infer the correct physical properties producing these line shapes.
Riener et al. (2019) recently presented the Gaussian decomposition package GAUSSPY+, which was designed for the fully automated and efficient decomposition of large data sets of emission lines, such as Galactic plane surveys, by fitting multi-Gaussian models to the spectra. In Riener et al. (2019), GAUSSPY+ was already applied on a challenging test field of the GRS data set, for which it performed well in terms of recovered flux and spatial coherence of the fit results.
In this work, we present decomposition results with GAUSSPY+ for the entire GRS data set. We mostly focus on the global properties of the gas emission and discuss distributions of and correlations between the fit parameters. We provide a characterisation of the complexity of gas emission along the line of sight and try to combine it with information about the dust emission from the Herschel infrared Galactic Plane Survey (Hi-GAL; Molinari et al. 2016). We also present a way in which the simplification of the data set via the Gaussian decomposition may allow one to narrow down the location of the emitting gas within our Galaxy. In a forthcoming work (Riener et al., in prep.), we aim to present distance estimates to the Gaussian fit components. This will enable discussion about the Galactic distribution of the gas emission and variations with Galactocentric distance of the kinematic properties of the gas, and this will foster synergies with other ISM tracers, such as the upcoming large-scale dust extinction map from the PROMISE project (Kainulainen et al., in prep.).
2 Observational data and decomposition method
2.1 Galactic Ring Survey
In this work we use data from the Boston University-Five College Radio Astronomy Observatory GRS (Jackson et al. 2006). This survey covers a longitude range of ℓ = 18°−55.7° and a latitude range of 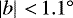 with an angular resolution of 46′′ and a pixel sampling of 22′′. The velocity coverage of the survey is − 5 to 135 km s−1 for ℓ ≤ 40° and − 5 to 85 km s−1 for ℓ > 40°. We also used the additional limited data from ℓ = 14°−18° that does not cover the full latitude range of the rest of the data; the velocity range of this additional data is again − 5 to 135 km s−1. The GRS data set has a velocity resolution of 0.21 km s−1. We used SWARP1 (Bertin et al. 2002) to combine the original data cubes of the GRS2 into a single mosaicked cube (see Appendix A.1). The values in the GRS data set are given in terms of antenna temperatures (
with an angular resolution of 46′′ and a pixel sampling of 22′′. The velocity coverage of the survey is − 5 to 135 km s−1 for ℓ ≤ 40° and − 5 to 85 km s−1 for ℓ > 40°. We also used the additional limited data from ℓ = 14°−18° that does not cover the full latitude range of the rest of the data; the velocity range of this additional data is again − 5 to 135 km s−1. The GRS data set has a velocity resolution of 0.21 km s−1. We used SWARP1 (Bertin et al. 2002) to combine the original data cubes of the GRS2 into a single mosaicked cube (see Appendix A.1). The values in the GRS data set are given in terms of antenna temperatures (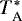 ) that we converted to main beam temperatures (TMB) by dividing by the main beam efficiency1 of ηMB = 0.48.
) that we converted to main beam temperatures (TMB) by dividing by the main beam efficiency1 of ηMB = 0.48.
2.2 Hi-GAL
We use maps of mean dust temperatures and H2 column densities from Marsh et al. (2017)3 that are based on dust emission observations from Hi-GAL (Molinari et al. 2016). The maps from Marsh et al. (2017) combine continuum data spanning a wavelength range of 70− 500 μm at a spatial resolution of 12′′. We used SWARP2 to combine 21 PPMAP fields overlapping with the GRS coverage. We spatially smoothed the mosaicked maps of mean dust temperatures and H2 column densities to the GRS resolution and regridded the smoothed maps so that the pixels aligned with the GRS mosaic.
2.3 The GAUSSPY+ algorithm
For the decomposition of the GRS data set we used GAUSSPY+4 (Riener et al. 2019), a fully automated Gaussian decomposition package that is based on GAUSSPY5 (Lindner et al. 2015). The GAUSSPY algorithm uses derivative spectroscopy to automatically decide on the number of fit components and the initial guesses for their parameters. The GAUSSPY+ package enhances the performance of GAUSSPY by introducing an improved fitting routine that tries to refit decomposition results that failed in-built and optional user-selected quality criteria. Moreover, GAUSSPY+ includes spatially coherent refitting routines that aim to improve spatial consistency of the decomposition results. In addition, GAUSSPY+ offers many convenience functions and automated preparatory steps, such as a reliable noise estimation, signal identification, and masking of instrumental artefacts. For further details about the GAUSSPY+ algorithm, such as an in-depth explanation of its functionality and discussion about its performance for decompositions of synthetic spectra and a GRS test field, see Riener et al. (2019).
Our main aim in this work is to present a homogeneous decomposition and analysis of the GRS data set in its native spatial and spectralresolution. We used the same parameter settings in GAUSSPY+ throughout the entire survey region to guarantee a comparable analysis of the data set. This means that we did not finetune our settings to individual regions and the decomposition results with GAUSSPY+ thus might show differences in their performance, given the non-uniform noise coverage of the GRS that can show significant variation (see Fig. B.1). The variations in the noise values between different regions of the survey means that the signal-to-noise ratio (S/N) based thresholds of GAUSSPY+ could extract more signal peaks in the spectra that showed reduced noise values. Some of the emission peaks may also have a non-Gaussian shape due to, for example, line blending or optical depth effects and will thus likely not be well fit by GAUSSPY+ (see Appendix C for a discussion about the impact of optical depth on our fitting results).
Decomposition results.
3 Gaussian decomposition of the GRS data
In this section, we present results of the Gaussian decomposition with GAUSSPY+ for the entire GRS data set. The appendix contains further, more technical discussions about the decomposition. Details about the data preparation, parameter settings, and decomposition runs can be found in Appendix A; we also present quality assurance metrics for the fit results in Appendix B. Furthermore, we give a detailed discussion about the effects of optical depth on our decomposition in Appendix C. We find that issues due to optical depth only affect the densest regions in the GRS and should not be a problem for the vast majority of the decomposition results presented in this work.
The whole GRS data set contains in total 2 283 920 spectra. Of these, we excluded 1188 spectra (0.05%) that showed extremely high noise values (see Appendix B.1). In the data preparation step (see Appendix A), GAUSSPY+ identified signal peaks in 75.3% of all spectra; ~96% of these were fitted with one or multiple components in the decomposition.
The final decomposition contains 4 648 985 fitted Gaussian components. The best fit solutions include fit components with S/Ns as low as 1.5 (it is beneficial to allow fit components with amplitudes below S∕N < 3, cf., Riener et al. 2019). We highlight the ~75% of the fit components with S∕N >3 in our discussion of the fit parameter statistics in Sects. 4.1–4.4, since the components with lower S/N can already be severely affected by the noise. Depending on what the decomposition results are used for, it may thus be beneficial to only select more reliable fit components with S∕N > 3 or amplitude values above a specific TMB threshold.
3.1 Catalogue description
With this work we also make a catalogue of all our decomposition results for the GRS available. In this section we describe the entries of the catalogue, which include quality flags that can be useful in identifying fit solutions that might have problems or are inconsistent with neighbouring decomposition results.
We show a subset of the decomposition results in Table 1. Each row corresponds to a single Gaussian fit component; a spectrum fitted with eight Gaussian components will occupy eight consecutive rows in the table.
Columns (1) and (2) show the pixel position of the spectrum in the mosaicked cube of the GRS with the corresponding Galactic coordinate values given in Cols. (3) and (4). The next columns list the parameters and associated errors of the Gaussian fit parameters: peak main beam brightness temperature or amplitude value TMB (5) and its error ΔTMB (6); mean position vLSR (7) and its error ΔvLSR (8); and line of sight velocity dispersion σv (9) and its error Δσv (10). Column (11) gives the root-mean-square value of the estimated noise of the spectrum σrms given in TMB values. The remaining columns list quality metrics that can indicate problems with the fit solutions, such as inconsistencies with neighbouring fit results. Column (12) gives the resulting p-value of a normality test for normally distributed residual values (see Appendix B.2 for more details); Col. (13) shows the value of the corrected Akaike information criterion (AICc; Akaike 1973) for the best fit solution; and Col. (14) gives the reduced chi-squared (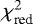 ) values (see Appendix B.2 for more details). The next three columns can be used to identify fit solutions whose number of fit components is inconsistent with neighbouring fit solutions. Columns (15)–(17) give the number of fit components Ncomp, the weighted median number of fit components Nmed determined from the fit solutions of the direct neighbours, and the number of component jumps Njump > 2 towards directly neighbouring fit solutions (see Sect. 3.2.2 in Riener et al. 2019 for more information on the last two parameters). Finally, the last four columns indicate whether the fit component was flagged with one of the remaining optional quality flagging criteria described in Sect. 3.2.2 of Riener et al. 2019, with “1” indicating that the component was flagged with the respective criterion. The flagging criteria are as follows: F1 (18) indicates whether the fit component was strongly blended with another component; F2 (19) indicates whether the fit component caused a negative feature in the residual; F3 (20) indicates whether the fit component was flagged as comparatively broad; and F4 (21) indicates whether the fit component was part of a region in the spectrum, which was flagged in phase 2 of the spatially coherent refitting routine in GAUSSPY+, which aims at identifying inconsistencies between the centroid values of the fit components of neighbouring fit solutions (see Sect. 3.3.2 in Riener et al. 2019 for more details).
) values (see Appendix B.2 for more details). The next three columns can be used to identify fit solutions whose number of fit components is inconsistent with neighbouring fit solutions. Columns (15)–(17) give the number of fit components Ncomp, the weighted median number of fit components Nmed determined from the fit solutions of the direct neighbours, and the number of component jumps Njump > 2 towards directly neighbouring fit solutions (see Sect. 3.2.2 in Riener et al. 2019 for more information on the last two parameters). Finally, the last four columns indicate whether the fit component was flagged with one of the remaining optional quality flagging criteria described in Sect. 3.2.2 of Riener et al. 2019, with “1” indicating that the component was flagged with the respective criterion. The flagging criteria are as follows: F1 (18) indicates whether the fit component was strongly blended with another component; F2 (19) indicates whether the fit component caused a negative feature in the residual; F3 (20) indicates whether the fit component was flagged as comparatively broad; and F4 (21) indicates whether the fit component was part of a region in the spectrum, which was flagged in phase 2 of the spatially coherent refitting routine in GAUSSPY+, which aims at identifying inconsistencies between the centroid values of the fit components of neighbouring fit solutions (see Sect. 3.3.2 in Riener et al. 2019 for more details).
The criteria for the quality flags are very strict in the default settings of GAUSSPY+. To catch the majority of potential problems with the fit solutions, these criteria were designed to be biased towards producing false positives rather than false negatives. It is thus likely that a significant fraction of flagged components, in particular those flagged as blended (F1) or broad (F3), will be good fits.
 |
Fig. 1 Average spectra of the full GRS data set (grey lines) and our final Gaussian decomposition results (blue lines). The three panels show different ways the average spectra were created: in (a) we use all voxels, in (b) we use only the voxels retained from moment masking, and in (c) we use only voxels whose intensity value is above a S/N threshold of 3. The red line in panel c shows an average of high negative values throughout the GRS data set that was obtained by using only voxels with a value below − 3 × S∕N. The inset inthe right panel shows a zoom-in of the red line to better display the individual smaller negative peaks. See Sect. 3.2 for more details. |
3.2 Flux recovery
In this section we discuss the quality of our decomposition results in terms of recovered flux. We start by comparing the average spectrum of the original GRS data set to that of the decomposition. Figure 1 shows this comparison for spectra obtained using three different averaging methods. In Fig. 1a, we use all available voxels; in Fig. 1b, we use the moment masking technique as outlined in Dame (2011); and in Fig. 1c, we only use voxels that have a value above 3 × σrms. By comparing the average spectra of the original data and the decomposition, we can estimate the recovered flux in our decomposition, which is 84.3, 87.5, and 92.1% for the three respective cases. The moment masking technique provides the most accurate comparison, as it recovers most of the emission, while still being relatively unaffected by noise contributions (Riener et al. 2019).
We can partly understand the missing flux by the fact that the moment masking technique recovers flux that is buried deep within the noise and will thus likely not be recovered in our decomposition. The clipped average spectra in Fig. 1c neglect all of the smaller intensity contributions below a S/N threshold of 3. As expected, the fraction of recovered flux in our decomposition is higher for these high S/N regions. A comparison of Fig. 1b with Fig. 1c shows that about a third of the total flux is coming from voxels with amplitude values below a S/N threshold of 3.
Next, we discuss the average spectrum of negative values to show that the GRS data set contains significant negative spectral features. The red line in Fig. 1c shows an average spectrum of all voxels from the original data set with values smaller than − 3 × σrms. The inset in Fig. 1c shows a zoomed-in version of the average spectrum of negative values. Most values of this average negative spectrum are due to random noise fluctuations that exceed a threshold of − 3 × σrms and cause the general offset (the jump occurring at vLSR ~ 35 km s−1 is due to a change in the observing mode that resulted in lower noise values; see Jackson et al. 2006). However, on top of this general offset are also many individual negative spikes located at specific vLSR values. The most prominent negative peak is situated at a velocity range of vLSR = 11 − 17 km s−1 and reaches its lowest value at vLSR ~ 12.5 km s−1. This artefact is due to the presence of 13CO emission in one of the “off” positions used in the subtraction of sky emission (Jackson et al. 2006). The negative spikes at this position affect a significant number of spectra. We suspect that the remaining smaller negative spikes are likely also due to contaminating 13CO emission in other off positions used in the sky subtraction.
In the default settings of GAUSSPY+, all negative peaks smaller than − 5 × σrms are automatically masked for the decomposition, which led to the identification and masking of negative spectral features for about 1.6% of all spectra from the GRS data set. The vast majority of identified negative spikes are located in the region within 32.8° ≤ ℓ ≤ 38.1° and − 0.7° ≤ b ≤ 1.1°. Another region containing many negative spikes is located at 32.2° ≤ ℓ ≤ 32.7° and − 1.1° ≤ b ≤−0.7°. Not excluding these negative spikes leads to incorrect comparisons if all spectral channels are summed up, since the average spectrum from the original data set is substantially reduced at the spectral range where the largest negative peaks are located (cf. Fig. 1a).
We now shift our comparison to the examination of the spatial distribution of the integrated intensity, that means the zeroth moment maps of the data and decomposition results (Fig. 2). These maps were obtained with the moment masking technique outlined in Dame (2011), that means for the decomposition results we used the same unmasked spectral channels that were also used for the original data set. The similarity of the two maps gives us already a qualitative confirmation that the decomposition manages to reproduce the data set well. We provide a normalised residual map to better quantify this similarity (bottom part of Fig. 2). Positive and negative values can indicate spectra for which emission features were left unfit and spectra for which the final fit solution might fit a single component over multiple emission peaks, respectively. The empty spaces correspond to unobserved regions and regions where the moment masking technique identified no signal. The positions of high positive values in the normalised residual map are predominantly associated with diffuse emission in the original data set. This diffuse emission was likely too buried within the noise to be identified in the decomposition. More quantitatively, the 19.4% of the spectra with normalised residual values of one are responsible for 21% of the residual emission but only account for 2.6% of the totalflux in the zeroth moment map of the original data set. For 4.1% of the spectra, the value in the zeroth moment map of the decomposed data set is higher than for the original data set; this could indicate that noise was fitted or that a single component was incorrectly fitted over multiple signal peaks. However, since for these spectra the emission from the decomposed data set is on average only higher by about 1% than the emission in the original data set, we conclude that this is only a minor issue.
Features of high values in the normalised residual map can also be traced back to elevated noise levels (cf. Fig. B.1). This correlation is expected, given that we use the same S/N thresholds over the entire survey region and the noise properties do vary significantly throughout the map. We try to quantify this correlation by splitting the data set in two parts, using the median of the noise distribution (σ(TMB) = 0.25 K) as the threshold. We find that the50% of spectra with noise values >0.25 K contribute 62.8% to the residual, confirming that the regions with higher noise are indeed correlated with higher residual values.
Next, we discuss the recovered flux in terms of the position-velocity (PV) map of the GRS (Fig. 3). We obtained these PV maps by integrating the moment masked data over the full Galactic latitude range. The positions of spiral arms, spurs, and local Galactic features from Reid et al. (2016) are also shown. The GRS covers both the near and far sides of the Scutum and Sagittarius spiral arms, which is why they make a turn in the PV map with the near sides having the lower velocity values.
The similarity of the PV maps of the original and decomposed data sets is another reassurance that our fits managed to reproduce all main features of the GRS data set, which is also confirmed in the normalised residuals (bottom part of Fig. 3). More quantitatively, the 12.5% of the data points in the normalised residual map with positive values of one – so the positions where none of the features of the original PV map could be recreated in the decomposed version – areresponsible for 17.9% of the residual flux but are associated with positions in the PV map that account for only 3.5% of the total emission in the GRS. These percentages again confirm that positions with the highest normalised residual values are correlated with weak or diffuse emission in the original data set that was difficult to fit.
 |
Fig. 2 Top: zeroth moment map of the GRS data set recreated from the Gaussian fit components and integrated over the entire velocity range (− 5 ≲ vLSR ≲ 135 km s−1). When displayed in Adobe Acrobat, it is possible to switch to the map of the original data set. Bottom: map of the normalised residual values. |
 |
Fig. 3 Top: PV map of the decomposed GRS data set. The emission was integrated over the full Galactic latitude range (± 1.1°). When displayed in Adobe Acrobat, it is possible to switch to the map of the original data set. Bottom: map of the normalised residual values. Overplotted on both panels are positions of spiral arms, spurs, and local Galactic features from Reid et al. (2016). |
4 Statistics of the Gaussian components
In this section, we present the distributions of the Gaussian fit parameters, namely the amplitude or intensity TMB, velocity dispersion σv, and mean position vLSR. We also examine the relationships between the fit parameters and discuss some general properties of the GRS emission line data.
 |
Fig. 4 Map of the number of fitted Gaussian components per spectrum. |
 |
Fig. 5 Histogram of the number of fitted Gaussian components per spectrum across the whole GRS data set for the full decomposition results (black line) and the fit components with S∕N > 3 (blue). The inset shows the same distribution on a logarithmic scale. |
4.1 Number of fitted components
The number of fitted Gaussian components per spectrum (Ncomp) is an interesting quantity because it is a measure for the complexity of the CO emission along the line of sight. For most of the GRS, we can assume that emission peaks in a spectrum that are well separated in vLSR will be associated with different Galactic orbits and will thus originate from different structures along the line of sight. Figure 4, which shows the Ncomp values for the entire GRS coverage, is then a proxy for how many structures there are along the line of sight. Especially near the Galactic midplane, multiple Gaussian components are required to fit the spectra.
We show a histogram of the number of fitted Gaussian components for the entire decomposition in Fig. 5. For about 27.3% of the spectra, we could fit no Gaussian components and for about 24.7% of the spectra, only one Gaussian component was fitted. The percentage of GRS spectra that have at least one or more fit components (72.7%) is close to the percentage of spectra for which GAUSSPY+ identified signal peaks (75.3%). If we assume all signal peaks identified by GAUSSPY+ are correct, we get that for 2.6% of the spectra from the GRS data set we do not fit valid signal peaks in our decomposition. Most of these unfit signal peakslikely did not satisfy the minimum requirements for fit components in the GAUSSPY+ decomposition run.
We considered whether the ~0.1% of GRS spectra with best-fit solutions that use a high number of components (Ncomp > 10) are indeed connected with very complex lines of sight or whether they result from artefacts or problems in the decomposition. Most of the spectra that were fitted with a large number of components do occur in groups near the mid-plane, where complex spectra are expected (cf. Fig. 4). We can use the information contained in Table 1 to gauge to first order whether these complex fit solutions are significantly different from their neighbours. We can use the number of component jumps Njump and the difference between Ncomp and Nmed (with Nmed being the weighted median number of components calculated from the immediate neighbours) as good first indicators for whether the fit solution is similar to its neighbours. In the default settings of GAUSSPY+, spectra get flagged if Njump > 1 or ΔNmax = comp − Nmed| > 1. With these criteria ~71% of the 4884 fit solutions using more than 10 components get flagged. Relaxing the criteria to ΔNmax > 2 and Njump > 2, to factor in uncertainties in the neighbouring fit solutions, and requiring that both of these criteria are fulfilled reduces the percentage of flagged fit solutions to ~31%. Based on this analysis, we conclude that for about a third, but possibly the majority of the spectra with a high number of components (Ncomp > 10), the fit solutions could be (partly) inconsistent with their neighbouring fit solutions.
There are multiple possible explanations for these inconsistencies, for example: (i) spectra that show instrumental artefacts (e.g. regions of the spectrum that fluctuate to very high and low values causing the decomposition algorithm to fit many of the high positive peaks), (ii) spectra for which the estimated noise value was too low, causing the decomposition algorithm to mistake noise peaks for signal peaks with high S/N, (iii) spectra that show leftover continuum emission that was fitted with many individual components, or (iv) spectra that contained emission features deviating from a Gaussian shape that could not be fitted well with Gaussian components. We return to the question of complexity along the line of sight in Sect. 5.2, where we compare the number of fit components with the integrated CO emission and molecular gas surface densities derived from dust emission.
 |
Fig. 6 Histogram of intensity values for all fit components (black line) and fit components with S∕N > 3 (blue). The inset shows the same distribution on a logarithmic scale. The dotted vertical line shows the 3 × S∕N limit for thepeak value of the noise distribution (shown in Fig. B.2). The hatched areas mark the IQRs of the two distributions. The bin width is 0.05 K. |
4.2 Intensity values
The distribution of the fitted amplitude values for the entire GRS data set (Fig. 6) peaks at about TMB = 0.68 K and the interquartile range (IQR) is 0.71−1.71 K. For the subset of components with S∕N > 3, the distribution peaks at a value of about 0.88 K and the IQRis 0.95−1.98 K. The dashed vertical line at TMB = 0.6 K shows the typical sensitivity limit of 3 × S∕N based on the peak value from the noise distribution shown in Fig. B.2 (σ(TMB) = 0.2 K), which is very close to the peak value of the distribution of intensity values. The drop in the intensity distribution below the indicated sensitivity limit is thus likely not a physical effect but a result of the noise properties preventing the extraction of weaker signal peaks. When viewed logarithmically, the distribution shows an almost linear decrease between TMB ~ 1−6 K, after which it flattens. We checked the spatial distribution of the fit components with high amplitude values of TMB > 6 K. The vast majority of these components form separate connected structures on scales of individual molecular clouds, with TMB values ≳ 10 K concentrated at their centres. We thus conclude that most of the components with high TMB values are not due to instrumental artefacts, but come from high column density regions.
4.3 Centroid velocity values
The distribution of the vLSR positions of the Gaussian fit parameters (Fig. 7) shows that we do fit components across the entire velocity range (− 5 to 135 km s−1) spanned by the GRS. Some of the peaks in the distribution can be attributed to inferred positions of spiral arms, spurs, or local Galactic features (cf. the PV map in Fig. 3), for example, the Aquila Rift cloud at centroid velocities of about 10 km s−1 and the far and near portion of the Sagittarius and Scutum spiral arm, respectively, at around 60 km s−1. As expected, the shape of the distribution is very similar to the average spectra from Fig. 1. A comparison between those two figures shows that even though the number of fit components with vLSR values of 0− 20 km s−1 is high, their average intensity values are much lower than for the vLSR range between ~ 40 and 70 km s−1. This is likely due to a larger contribution of diffuse, faint emission from local gas at low vLSR values. For regions close to the sun that are spatially well resolved, we can have only diffuse emission in the beam, which causes comparatively weak emission lines. At larger distances, where much larger physical areas are covered in the beam, this diffuse emission will likely be diluted and merged with stronger emission peaks, so that diffuse and strong emission is detected simultaneously in the beam. Moreover, the moderate spatial resolution of the GRS can cause stronger emission lines for molecular clouds observed at larger distances (if the beam filling factor is still approximately unity).
 |
Fig. 7 Histogram of centroid velocity values for all fit components (black) and fit components with S∕N > 3 (blue). The bin width is 1 km s−1. |
4.4 Velocity dispersion values
The distribution of the σv values of the Gaussian fit components (Fig. 8) is interesting, as it allows us to already estimate to first order upper limitsfor the turbulent Mach number associated with the emission lines. The peak for the distribution of σv values for all fit components is at σv ~ 0.6 km s−1 and the IQR is 0.68< σv < 1.89 km s−1. For the subset of fit components with S∕N > 3, the peak is shifted towards a lower value of 0.45 km s−1 and the IQR is 0.59−1.58 km s−1. About 0.6% of all fitted components have a velocity dispersion value below the resolution limit. In the default settings of GAUSSPY+, the minimum allowed value for the full width at half maximum (FWHM) is set to the width of a single spectral channel, which yields σv values below the resolution limit.
When plotted logarithmically, the distribution has a linear dropoff from about 1− 4 km s−1, after which it flattens and has a shallower decline; it also shows that most of the fit components with very broad FWHM values have S∕N < 3. It is likely that most of these broad components were fit over multiple low S/N peaks that could not be correctly deblended. A visual inspection of some of the GRS spectra showed that a small fraction also suffers from what seems to be an incorrect or insufficient baseline subtraction, which could lead to broad spectral features with low S/N.
We can get upper limits for the turbulent Mach number 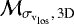 by assuming that all non-thermal contributions to the velocity dispersion σv are due to turbulence:
by assuming that all non-thermal contributions to the velocity dispersion σv are due to turbulence:
![\begin{equation*} {\cal{M}}_{\sigma_{v_{los}}, 3\text{D}} \approx \sqrt{3} \dfrac{\sigma_{v_{\text{turb},\,1\text{D}}}}{c_{\textrm{S}}} = \sqrt{3}\left[\left(\dfrac{\sigma_{v}}{c_{\textrm{S}}}\right)^{2} - \left(\dfrac{\bar{\mu}_{\text{p}}}{\mu_{\text{obs}}}\right)\right]^{1/2},\end{equation*}](/articles/aa/full_html/2020/01/aa36814-19/aa36814-19-eq5.png) (1)
(1)
where σv is the velocity dispersion along the line of sight, cS is the isothermal sound speed, 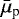 is the mean molecular mass (
is the mean molecular mass (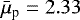 amu), and μobs is the molecular mass of the observed molecule (29 amu for 13CO). We estimate the isothermal sound speed cS with
amu), and μobs is the molecular mass of the observed molecule (29 amu for 13CO). We estimate the isothermal sound speed cS with
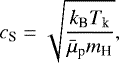 (2)
(2)
where Tk is the kinetic temperature of the gas, kB is the Boltzmann constant, and mH is the mass of atomic hydrogen. For Tk, we assume a uniform value of 18 K throughout the survey, which corresponds to the average of the mean line of sight dust temperature values for the HiGAL data overlapping with the GRS as estimated by Marsh et al. (2017).
The upper abscissa in Fig. 8 shows the resulting Mach number axis. The peak of the distribution corresponds to a Mach number of about 4. About 36.7% of all fit components and 28.6% of the fit components with S∕N > 3 are associated with turbulent Mach number values >10. About 3% of the fit components have σv values > 5 km s−1, resulting in associated high Mach numbers that are greater than 34. To put these large σv values into perspective, we can compare them to typical line width values found on cloud scales. For their catalogue of molecular clouds in the GRS, Rathborne et al. (2009) found average and maximum values for the line width of 3.6 and 9.8 km s−1, which translate to σv values of 1.5 and 4.2 km s−1, respectively. Given these values, it seems unlikely that the fit components with large σv values trace regions of extreme turbulence; it seems more likely they are: (i) due to non-random ordered motion, for example, velocity gradients along the line of sight; (ii) incorrect fits of multiple signal peaks with a single component; (iii) fits of artefacts in the spectrum, introduced, for example, by insufficient or incorrect baseline subtraction; (iv) associated with warmer gas temperatures (that increase the thermal linewidth and decrease the non-thermal contribution).
 |
Fig. 8 Histogram of velocity dispersion values for all fit components (black) and fit components with S∕N > 3 (blue). The upper abscissa indicates corresponding upper limits for turbulent Mach number values. The inset shows the same distribution on a logarithmic scale. The dotted vertical line indicates the velocity resolution of 0.21 km s−1. The hatched areas mark the IQRs of the two distributions. The bin width is 0.05 km s−1. |
 |
Fig. 9 2D histogram of intensity and velocity dispersion values for all fit components. The dashed line shows the lower limit for a chosen significance value of |
4.5 Relationships between the parameters
In this section we describe the relationships between the fit parameters using two-dimensional (2D) histograms. This will allow us to better characterise our population of fit components, for example, the typical shape of the fitted lines. We also look at trends of TMB and σv values with vLSR position, which we can use to infer to first order properties of the gas emission at different Galactic distances.
Figure 9 shows the 2D distribution of the intensity and velocity dispersion values of all Gaussian fit components. The majority of components show both moderate intensity and velocity dispersion values (0.5≲ TMB ≲ 1.5 K, 0.25≲ σv ≲ 1.5 km s−1). Beyond this concentration of most data points, the distribution shows a bifurcation, with the components having either high intensity and small velocity dispersion values or low intensity and high velocity dispersion values. That components with high σv values are predominantly connected with low TMB values is an indication that these are likely fits to artefacts in the spectrum, as discussed in Sect. 4.4.
The absence of components with both low intensity and low velocity dispersion values is due to a selection effect in our decomposition. We only retain Gaussian components above a chosen significance value 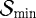 (see Sect. 3.2.1 in Riener et al. 2019), which excludes components with low intensity and low velocity dispersion values, because they are indistinguishable from individual random noise peaks. In Fig. 9, we indicate the expected lower limit for a significance limit of
(see Sect. 3.2.1 in Riener et al. 2019), which excludes components with low intensity and low velocity dispersion values, because they are indistinguishable from individual random noise peaks. In Fig. 9, we indicate the expected lower limit for a significance limit of 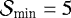 , the spectral resolution limit of the GRS (0.21 km s−1), and a typical noise value of σ(TMB) = 0.2 K (corresponding to the peak of the noise distribution shown in Fig. B.2). This lower limit corresponds very well to the shape of the distribution, with velocity dispersion values being clearly limited by the spectral resolution. Thus, Fig. 9 also serves as a good indicator of the sensitivity limit of our decomposition.
, the spectral resolution limit of the GRS (0.21 km s−1), and a typical noise value of σ(TMB) = 0.2 K (corresponding to the peak of the noise distribution shown in Fig. B.2). This lower limit corresponds very well to the shape of the distribution, with velocity dispersion values being clearly limited by the spectral resolution. Thus, Fig. 9 also serves as a good indicator of the sensitivity limit of our decomposition.
Only about 4% of all fit components have both high values of TMB (> 2 K) and σv (> 2 km s−1). Moreover, the IQR of the vLSR values of these strong fit components stretches from 57.3 to 94.5 km s−1 and is thus clearly shifted towards higher values compared to the IQR of the full distribution (30.5−78.1 km s−1).
We can see a similar trend of increasing line widths at higher vLSR values in the relation between the fitted vLSR and σv values (Fig. 10). In contrast, the distribution of fitted intensity values with vLSR position (Fig. 11) is on average very constant at a value of about 1.5 K, which is expected from the distance-independence of the surface brightness. However, Fig. 11 also shows very bright intensity peaks, in particular from components located at velocities of ~ 10 km s−1, most of which also have narrow line widths (Fig. 10). This emission at velocities of ~ 10 km s−1 predominantly originates from the very nearby Aquila Rift cloud and is thus spatially and spectrally well resolved in the GRS observations, which explains the narrow and bright emission peaks. For regions farther away, beam averaging effects will cause broader emission lines, which will be reflected in the shape of the fit components. We discuss these trends further in Sect. 6, where we put them into the context of a size-linewidth relationship.
 |
Fig. 10 2D histogram of centroid velocity and velocity dispersion values for all fit components. The dashed horizontal line indicates the velocity resolution of 0.21 km s−1. The blue line shows the mean σv value per centroid velocity bin. The number of bins in either direction is 300. The data points with very low σv values located at ~63 < vLSR < 66 km s−1 are due to an instrumental artefact. |
 |
Fig. 11 2D histogram of centroid velocity and intensity values for all fit components. The dashed horizontal line indicates a S/N limit of 3 for σ(TMB) = 0.12 K, which corresponds to the 0.1st percentile of the noise distribution shown in Fig. B.2. The blue line shows the mean intensity value per centroid velocity bin. The number of bins in either direction is 300. |
 |
Fig. 12 2D histogram of the velocity dispersion values against their Galactic latitude positions for all fit components with S∕N > 3. The dashed horizontal line indicates the velocity resolution of 0.21 km s−1. The blue line shows the mean σv value per Galactic latitude bin. The number of bins used in either direction is 358. |
5 Global properties of the gas emission
In this section we focus on the global properties of our decomposition. We first look at the distribution of the velocity dispersion values with Galactic coordinates and then use the number of fit components per spectrum to gauge the complexity of the gas emission along the line of sight.
5.1 Distribution of velocity dispersion values as a function of Galactic coordinates
Here we examine how the velocity dispersion values of the fit components are distributed as a function of the Galactic coordinates. We search for global trends and outlying regions, such as regions with above-average non-thermal motion, within the Galactic disk. We focus on fit components with S∕N > 3 in this analysis, since the line shape of components with a lower S/N could be significantly impacted by noise. We again use the σv values to estimate upper limits for the turbulent Mach numbers assuming isothermal gas temperatures of 18 K (see Sect. 4.4).
We first focus on the distribution of the σv values as a function of Galactic latitude (Fig. 12). The number of high velocity dispersions (and Mach numbers) increase towards the Galactic midplane, which is likely due to the following three effects. First, most substantial star-forming regions are concentrated in the midplane (e.g. Beuther et al. 2012). These star-formingregions are associated with warmer molecular gas and plenty of high-velocity dispersion events (such as protostellar jets, outflows, shells, and supernova remnants), which will cause broader emission lines and higher σv values of the associated fit components. Second, we would expect more confusion along the line of sight towards the midplane, where multiple individual velocity components could be blended together and would thus be observed as a single broad component at the moderate resolution of the GRS. Third, to maintain a stable disk, the gas pressure of the Galacticdisk must balance the imposed pressure created by the weight of the vertical layers of gas and stars. This pressure will be higher towards the midplane and will accordingly increase the velocity dispersion in the gas.
We also detect a clear asymmetry, with higher mean velocity dispersions at negative Galactic latitude values. This can be partly explained by a vertical offset of the sun from the physical Galactic midplane (e.g. Goodman et al. 2014, however, see also Sect. 6.2).
Next, we look at the distribution of the σv values as a function of Galactic longitude (Fig. 13). The distribution shows that the number of components with very high σv values increases towards the inner Galaxy. The mean of the σv distribution shows multiple peaks, some of which are likely associated with large HII region complexes, for example, W51 at ℓ ~ 49.5°, and W39 at ℓ ~ 19°. Apart from these individual peaks and even though the velocity coverage is reduced for ℓ > 40°, the general offset of the mean σv curve is remarkably constant at a value of ~ 1 km s−1 from the outermost coverage in Galactic longitude up until ℓ ~ 32°. For the GRS coverage with ℓ < 32° the offset of the mean σv curve is shifted to higher values of ~ 1.2−1.3 km s−1, in agreement with recent studies that also found increased molecular gas velocity dispersion towards the inner part of the Milky Way (Miville-Deschênes et al. 2017). The giant HII region complex W43 is located at a Galactic longitude range of about 30° < ℓ < 31.5° and is close to the near end of the Galactic bar (Zhang et al. 2014). Recent simulations of barred galaxies showed that gas within the central regions dominated by the Galactic bar can reach high gas velocity dispersion values (Khoperskov et al. 2018). We thus speculate that the increase in the offset of the mean σv curve is at least partly due to increased turbulence introduced by the Galactic bar. Another reason for the increased non-thermal motions could be that there is more feedback from star formation towards the inner part of the Galaxy, as evidenced, for example, by the increased HII region density (see Fig. 3 in Anderson et al. 2017) and an increase in the fraction of clumps that show signs of embedded star formation (Ragan et al. 2018).
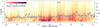 |
Fig. 13 2D histogram of velocity dispersion values against their Galactic longitude positions for all fit components with S∕N > 3. The dashed horizontal line indicates the velocity resolution of 0.21 km s−1. In the horizontal and vertical direction we use 3415 and 200 bins, respectively. The blue line indicates the mean velocity dispersion value per Galactic longitude bin. The grey solid line is a smoothed version of the mean σv curve using a median filter with a kernel of ~3°. Dashed vertical lines show the approximate location of the giant HII region complex W43. |
5.2 Complexity along the line of sight
In this section we discuss the relation between the integrated intensity (WCO) of 13CO emission, H2 column densities inferred from dust emission, and complexity along the line of sight as measured by the number of fit components. We want to determine if the 13CO emission preferentially originates from a few strong components or a larger number of smaller components, possibly spread wide along the spectrum. We test this by comparing the WCO values of the moment masked GRS data (shown in Fig. 2) with the number of fit components per spectrum (Fig. 4). We illustrate the results in form of a ridge plot (left panel of Fig. 14). In this plot, each row shows the probability distribution functions (PDFs) of WCO values for all spectra fitted with Ncomp components. For better visibility, we chose upper limits of WCO = 85 K km s−1 and Ncomp = 10. Figure 14 shows that the integrated intensity of 13CO correlates with the number of emission peaks. The spread of the distributions increases with the number of components, and the distributions overlap in the WCO range. However, based on Fig. 14 we can say that, for example, lines of sight with WCO values of 20 K km s−1 are predominantly associated with four to six fit components.
A similar analysis can provide insight into interpreting dust continuum emission features in the Galactic plane; for such data, there is otherwise no straightforward way to estimate how complex a line of sight is. This comparison is interesting, because it immediatelyshows us how well the gas and dust are mixed. If the dust column density is independent from the number of 13CO fit components, it could indicate differences in the distribution of dust and 13CO gas. The right panel of Fig. 14 shows a ridge plot constructed from H2 column density values derived from dust emission (Sect. 2.2). We can see the same trend with dust as with 13CO: the dust-derivedcolumn densities correlate with the number of fit components. To first order, this confirms that the 13CO gas and dust are indeed well mixed and thus largely originate from the same structures along the line of sight. Moreover, this analysis indicates that high dust column densities (leading to inferred H2 column density values > 200 × 1021 cm−2) arise from a composite of many dust components along the line of sight, rather than a single very dense structure.
Morover, Fig. 14 shows that dust emission is present along lines of sight for which no components could be fit in the 13CO spectra. This implies that the dust emission traces also a more diffuse gas component that shows little to no 13CO emission. This is in agreement with previous studies that have established that 13CO mostly traces the denser parts of molecular clouds, with surface densities exceeding ~ 25 M⊙ pc−2 (e.g. Roman-Duval et al. 2016).
6 Example application: disentangling emission from the near and far side of the Galaxy
Determining the exact location of molecular gas emission, and hence the Galactic distribution of it, is a major problem for understanding the structure of the Milky Way. The location of the emitting gas is usually determined using the kinematic distance method (Clemens et al. 1988; Reid et al. 2014), which yields two distance solutions (near and far) for the lines of sight within the solar orbit. This distance ambiguity can only be resolved with additional information, for example, using HI self-absorption features (e.g. Roman-Duval et al. 2009). In this section, we discuss how our decomposition results can be useful in solving the distance ambiguity of features at low vLSR values, specifically between − 5 and 20 km s−1. We use the fact that beam averaging effects for regions at larger distances to the sun will cause broader emission lines and thus higher σv values of the fit components. The general principle of using the σv value of the fit components to help resolve the kinematic distance ambiguity should also be applicable to other vLSR values, albeit with less accuracy. In Sect. 6.1, we first recall the relationship between the Galactic structure and radial velocities of − 5 to 20 km s−1. We then discuss the expected location and width of the physical midplane for this vLSR regime (Sect. 6.2) and how we would expect the linewidths to differ between emission coming from nearby and far away regions (Sect. 6.3). We then use these three discussions in Sect. 6.4 to argue how our decomposition results can give useful prior information in solving kinematic distance ambiguities.
 |
Fig. 14 Ridge plots showing PDFs of integrated 13CO emission (left panel) and H2 surface density values inferred from dust emission (right panel). For the left panel, each row shows the PDF of the WCO values of all spectra fitted with Ncomp components (indicated with the number to the left and the colour-shading of the PDF). For the right panel, each row shows the PDF of the |
6.1 Considerations based on Galactic kinematics
The observed line of sight radial velocity vLSR of a point along Galactic longitude ℓ can be calculated as
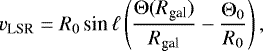 (3)
(3)
where Rgal is the Galactocentric radius to the point along the line of sight, Θ(Rgal) is the value of the rotation curve for Rgal, and R0 and Θ0 are the radius of the solar circle and the corresponding rotational speed of that orbit. We use values of R0 = 8.15 kpc and Θ0 = 236 km s−1 as estimated by Reid et al. (2019). For simplicity, we assume a flat rotation curve (i.e. Θ(Rgal) = const.) and we do not correct for effects of non-circular motions towards the Galactic centre or the direction of Galactic rotation. We also do not correct for solar peculiar motions used by the telescope. For a given value of vLSR, Eq. (3) can be solved for Rgal and rewritten as a function of ℓ. We can then use the relation
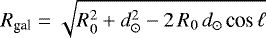 (4)
(4)
to solve for d⊙, the distance to the point along the line of sight associated with the vLSR value:
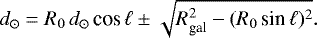 (5)
(5)
For lines of sight inside the solar orbit, Eq. (5) always yields two distance solutions, corresponding to points on the near and far side of the Galaxy that would be observed as having the same vLSR value.
In Fig. 15 we show estimated lines of constant projected vLSR values of − 5 and 20 km s−1 in a face-on view of the first quadrant of the Milky Way. Given the assumptions listed above, emission peaks observed in GRS with − 5 < vLSR < 20 km s−1 are thus expected to come from regions between those two curves of constant vLSR. On the near side, this corresponds to the regions in the GRS that are located closest to the sun, with distances mostly ≲ 1 kpc. On the far side, this area overlaps with the inferred locations of the Perseus and Outer spiral arms (Reid et al. 2019), with emission at lower longitude values expected to come from regions that can be located up to ~ 15 kpc away.
 |
Fig. 15 Face-on view of the Galactic plane. The black solid lines show constant projected vLSR values of − 5 and 20 km s−1. The orange-shaded area indicates the coverage of the GRS. Inferred positions and estimated widths for the Perseus and Outer spiral arm from Reid et al. (2019) are shown with the shaded green and blue areas, respectively. The central positions of the spiral arms are marked with solid and dashed lines depending on whether the majority of the arm is visible in the selected velocity range of − 5 < vLSR < 20 km s−1. The position of the Galactic centre and the sun are indicated with a black dot and the sun symbol, respectively. Dotted grey lines indicate distances to the sun in 2.5 kpc intervals. The black dash-dotted line shows the distances used to estimate the FWHM extent of the molecular gas disk. See Sects. 6.1 and 6.2 for more details. |
6.2 Expected location and extent of the Galactic disk
Recent studies by Anderson et al. (2019) and Reid et al. (2019) found a good correspondence of the vertical position of the sun with the IAU definition of the Galactic midplane, which is in contrast to past studies that determined vertical offset positions of z0 = 25 ± 5 pc (Bland-Hawthorn & Gerhard 2016). Even a larger offset of z0 = 25 pc would only have strong implications for the most nearby emission from the Galactic midplane, which would be shifted towards negative Galactic latitudes. We would nevertheless expect the midplane to be centred at about b = −0.1° to 0° for GRS emission with vLSR values of − 5 to 20 km s−1 originating from the far side of the Galaxy. However, previous studies of the Milky Way HI and molecular gas disk showed that the first quadrant of the Galactic disk is warped towards positive Galactic latitude values at the larger distances (≳ 8 kpc) probed by GRS (e.g. Kalberla & Kerp 2009; Roman-Duval et al. 2016; Miville-Deschênes et al. 2017). Assuming a moderate warp of the Galactic midplane of 50–100 pc at a distance of about 10 kpc would translate to positive shifts in Galactic latitude of ~ 0.3−0.6°. Factoring in a warp of the Galactic disk, we would thus expect the physical midplane to be shifted towards positive Galactic latitude values. The FWHM extent of the molecular gas disk in the outer Galaxy (Rgal ≳ 8.5 kpc) is on average about 200 pc (Roman-Duval et al. 2016), which at distances of 8 and 15 kpc (the typical distances of GRS emission with − 5 < vLSR < 20 km s−1 at the far side of the disk) corresponds to a range in Galactic latitude of about 0.7° and 0.4°, respectively.
Expected velocity dispersion values based on a size-linewidth relationship for different physical extents of the beam size at different distances.
6.3 Expected velocity dispersion values
The physical beam size (dbeam) of the GRS varies significantly for distances to gas emission on the near and far side of our Galaxy: dbeam is about 0.06 pc at the distance of 250 pc and 3.35 pc at 15 kpc (Table 2). The larger beam for regions farther away can be argued to result in broader linewidths; the widths of emission lines have been shown to exhibit scale dependency (Solomon et al. 1987)6:
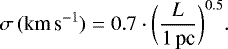 (6)
(6)
Table 2 shows the linewidths predicted by this scaling. For the scales probed by the GRS data at near distances (~ 250−500 pc), the size-linewidth relation predicts narrow velocity dispersions of about 0.2 km s−1. For distances beyond 8.5 kpc, the relation predicts velocity dispersions > 1 km s−1.
6.4 Information contained in the velocity dispersion values
In Sects. 6.1–6.3 we discuss what we would expect for the origin, extent, and shape of velocity components with vLSR values of − 5 to 20 km s−1. Now we demonstrate how this applies to our decomposition results and how the σv values of the fit components can give us an indication of whether the emission line originates from regions close to the sun or farther away.
The upper part of Fig. 16 shows the moment masked version of the decomposed GRS data set integrated within a velocity range of − 5< vLSR < 20 km s−1 (if fit components extended beyond this range we only included the emission within these limits). As already discussed in the previous sections, this channel map contains a combination of emission features that originate either from regions very close to the sun or as far away as 15 kpc. We also show the positions of the Perseus and Outer spiral arms as inferred by Reid et al. (2019), which indicates where we would expect emission from the far side of the disk to appear in the channel map. In the Galactic longitude range from about 17–43°, Fig. 16 is dominated by emission from the Aquila Rift cloud (see Fig. 3 and the schematic map in Fig. 9 of Dame & Thaddeus 1985), which is located at a distance to the sun of about 250–500 pc (Straižys et al. 2003; Zucker et al. 2019). Due to this close distance, emission from the Aquila Rift is spread out and extends over the full survey coverage in Galactic latitude.
With the predictions from Sects. 6.1 to 6.3 in hand, we can now try to understand the spatial distribution of the observed velocity dispersions. The bottom part of Fig. 16 shows for each line of sight the σv values and corresponding upper limits for the turbulent Mach number of the narrowest fit components (with centroid position values within − 5< vLSR < 20 km s−1). The region dominated by the Aquila Rift shows overall much lower σv values. The distribution of all σv values contained in the bottom part of Fig. 16 peaks at a value of 0.35 km s−1, matching the low σv values we would expect for the physical extent of the GRS beam at 250−500 pc derived from the size-linewidth relation in Sect. 6.3. Towards higher Galactic longitude values (ℓ ≳ 40°), where confusion with emission from the Aquila Rift cloud is expected to be less severe, we can see a strip of increased σv values that seems confined in Galactic latitude to ~1° in extent. If these velocity components also originate from regions close to the sun, these must be regions with increased non-thermal motions. However interestingly, fit components with higher σv values are less spread out in Galactic latitude than components with lower velocity dispersion values, which agrees with what we would expect from emission lines coming from regions farther away. We thus speculate that this emission with high σv values is coming mostly from the Perseus and Outer arm on the far side of the Galactic disk (cf. Fig. 15).
Based on our arguments from a size-linewidth relationship, we expect the emission lines originating from far distances to show increased σv values > 1 km s−1 (cf. Table 2). Using this prediction as a threshold, we fitted a polynomial of the third order to all σv values > 1 km s−1 in the lower part of Fig. 16, which is indicated with the dash-dotted black line. For the polynomial fit we first calculated the average Galactic latitude position per Galactic longitude bin for all σv values > 1 km s−1. We also overplot the expected scale height of the molecular gas disk with dashed black lines, which we calculated for the average distance to emission lines with vLSR values of − 5 to 20 km s−1 on the far side of the disk (indicated with dashed black lines in Fig. 15). This estimated range for the scale height of the molecular gas disk well matches the height of the strip with increased σv values. Assuming that the indicated strip of high σv values indeed corresponds to the Galactic midplane at the far distance, its position at positive Galactic latitude values would also be consistent with the shift expected from a contribution of the warp of the Galactic disk towards positive heights in the first quadrant (Sect. 6.2). If our conjecture is true, this would point to an increase in the warp of the Galactic disk at Galactic longitude values ≳ 42° at distances of ~ 10 to 12 kpc (cf. Fig. 15). Moreover, it would suggest that the majority of the increased σv values in Fig. 16 are caused by effects of resolution, beam averaging, or turbulent motion on the scale of clouds (macroturbulence) rather than being introduced by highly turbulent subregions within nearby local clouds (microturbulence).
The Gaussian decomposition results can thus be useful in disentangling near and far emission for characterising and constraining Galactic structure. In a follow-up work (Riener et al., in prep.) we concentrate on establishing distances to the Gaussian fit components, for which the considerations from this section can serve as useful prior information on solving the kinematic distance ambiguity.
 |
Fig. 16 Top: zeroth moment map of the decomposed data set integrated within − 5 < vLSR < 20 km s−1. Bottom: velocity dispersion values for the narrowest fit component within the same vLSR range as used in the top panel. The second scaling on the colourbar indicates corresponding estimates for upper limits of the turbulent Mach number. In both panels we show: the position of the Perseus and Outer spiral arms as inferred by Reid et al. (2019) (green and blue lines, respectively, cf. Fig. 15); black contours indicating a WCO value of 0.5 K km s−1; a fit to the positions with σv values >1 km s−1 (dash-dotted black line); and the estimated FWHM extent of the molecular gas disk on the far side of the Milky Way (dashed black lines). See Sect. 6.4 for more details. When displayed in Adobe Acrobat, it is possible to switch to the channel map of the original data set, show only the positions with σv values > 1 km s−1, hide the contours, hide the fit to the positions with σv values > 1 km s−1 and estimated FWHM extent of the gas disk, and hide the positions of the Perseus arm and Outer arm. |
7 Summary
In this work we present Gaussian decomposition results obtained with GAUSSPY+ (Riener et al. 2019) for the entire GRS data set at its full spatial and spectral resolution. In total, we fitted ~ 4.6 million Gaussian components to the ~2.3 million 13CO emission line spectra of the GRS. Especially spectra from lines of sight near the Galactic midplane showed great complexity, requiring 10 or more fit components for a good decomposition.
The decomposition recovers 87.5% of the flux contained in the GRS (92.1% of emission with S∕N > 3). Most of the non-recovered flux is due to diffuse or weak 13CO emission that could not be identified in the decomposition due to varying noise properties and our use of a single S/N threshold for the entire data set.
Assuming a uniform gas temperature of 18 K, we determined upper limits for the turbulent Mach number. We estimate from the velocity dispersion of our fit components with S∕N > 3 that about 28.6% are associated with turbulent Mach number values >10. We see a clear trend of higher velocity dispersion values for fit components with higher vLSR values, which is likely due to the effect of beam averaging of emission lines originating at larger distances to the sun.
We studied the distribution of velocity dispersion values along the Galactic coordinates and find that velocity dispersions increase towards the Galactic midplane, likely due to the concentration of star forming regions in the Galactic plane. We also find an increase in the σv values towards the inner Galaxy, which we speculate could be due to the influence of the Galactic bar.
The integrated intensities of 13CO correlate with the number of Gaussian fit components along the line of sight, indicating that larger integrated intensity values are associated with more complexity in the spectra. We also compared the number of fitted components to H2 surface density values inferred from dust emission by Marsh et al. (2017) and find a similar trend of higher 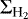 values being associated with more fit components in the corresponding 13CO spectra. This indicates that 13CO gas and dust emission is originating from the same structures along the line of sight.
values being associated with more fit components in the corresponding 13CO spectra. This indicates that 13CO gas and dust emission is originating from the same structures along the line of sight.
We also demonstrated how the decomposition results can aid in resolving confusion from kinematic distance ambiguities. We use arguments based on Galactic structure and the Galactic rotation curve to disentangle emission from the nearby Aquila Rift molecular cloud and gas emission at distances ≳ 8.5 kpc that is likely associated with the Perseus and Outer spiral arms. Our fitting results thus may be useful as prior information in determining kinematic distances.
In a forthcoming work we will present distance estimates to all the fit components presented in this paper, which will enable us to better associate emission peaks to locations in the Galaxy. This will allow us to discuss the Galactic distribution of the gas emission and to infer how physical quantities vary with Galactocentric distance.
Acknowledgements
This project received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 639459 (PROMISE). This publication makes use of molecular line data from the Boston University-FCRAO Galactic Ring Survey (GRS). The GRS is a joint project of Boston University and Five College Radio Astronomy Observatory, funded by the National Science Foundation under grants AST-9800334, AST-0098562, & AST-0100793. H.B. acknowledges support from the European Research Council under the European Community’s Horizon 2020 framework program (2014-2020) via the ERC Consolidator Grant “From Cloud to Star Formation (CSF)” (project number 648505). H.B. also acknowledges support from the Deutsche Forschungsgemeinschaft in the Collaborative Research Center (SFB 881) “The Milky Way System” (subproject B1). We would like to thank the MWISP collaboration for generously sharing the data of the G24 region with us. We would also like to thank the referee, Mark Heyer, for constructive and useful suggestions that helped to improve the paper. Code bibliography. This research made use of MATPLOTLIB (Hunter 2007), a suite of open-source python modules that provides a framework for creating scientific plots; ASTROPY, a community-developed core Python package for Astronomy (Astropy Collaboration 2013); APLPY, an open-source plotting package for Python (Robitaille & Bressert 2012); and SEABORN (Waskom et al. 2018).
Appendix A Chosen parameters, data preparation, and decomposition runs for the GRS survey
In this appendix we describe the settings we used for the decomposition runs with GAUSSPY+. Where not specified otherwise, we used the default settings of GAUSSPY+ as described in Riener et al. (2019).
A.1 Preparatory steps
The cubes of the original GRS data set7 are centred on integer Galactic longitude values, with each cube overlapping by one degree with the following cube. For the mosaicking we only used the cubes centred on odd integer values in Galactic longitude. Since the mosaicked cube of the entire GRS data set was too large fora decomposition with GAUSSPY+, we split it again along the Galactic longitude axis into 23 individual, non-overlapping subcubes8. We performed all preparatory and decomposition steps with GAUSSPY+ on these individual subcubes; this also included the spatially coherent refitting phases, which means that the decomposition results might show discontinuities at the borders of the individual subcubes. We checked for such an effect on the map showing the number of fit components (Fig. 4) but did not find any obvious problems.
Especially close to the borders of the coverage in Galactic latitude and longitude, the GRS data set contains spectra with instrumental artefacts, such as strongly amplified noise fluctuations. We thus masked out all spectra with extremely high noise values (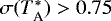 K; see Appendix B.1 for more details).
K; see Appendix B.1 for more details).
The GAUSSPY+ package includes preparatory steps for the decomposition, such as the identification of regions in the spectrum estimated to contain signal and the automated masking of negative features that are likely noise spikes or artefacts (see Sect. 3.1 in Riener et al. 2019 for more details). We found that about 1.6% of the spectra from the GRS data set contained significant negative features in the spectrum (see Sect. 3.2 for more details).
A.2 Choice of the GAUSSPY smoothing parameters
The GAUSSPY algorithm needs to be supplied with a training set consisting of a couple of hundred well-fit spectra, so that it can infer optimal smoothing parameters for the respective data set via its in-built supervised machine learning method (see Lindner et al. 2015 for more details). The GAUSSPY algorithm uses higher derivatives of a spectrum to automatically decide on initial guesses for the number and shape of fit components. To suppress negative impacts of noise fluctuations, the spectrum needs to be smoothed before derivatives are taken. For the decomposition of HI and CO spectra, a two-phase approach using two different smoothing parameters α1 and α2 (corresponding to the size of two different Gaussian smoothing kernels) was found to be beneficial (Lindner et al. 2015; Riener et al. 2019). In the training step of GAUSSPY, the algorithm essentially iterates in a controlled manner through different values for the two smoothing parameters and compares the resulting decompositions of the training set with the user-provided corresponding best fit solutions for the spectra. The GAUSSPY algorithm evaluates the accuracy of the decomposition results via the F1 score:
Smoothing parameters (in units of spectral channels) obtained for the GAUSSPY+ training sets.
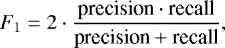 (A.1)
(A.1)
where precision is defined as the comparison of the fraction of correctly fitted components to the number of total fitted components and recall is defined as the fraction of components from the provided best fit solutions that had matching counterparts in the decomposition with the tested smoothing parameters.
The GAUSSPY+ package includes a routine that automatically creates a training set of high-quality decompositions that lead to values forthe smoothing parameters that are close to the optimal ones (see Appendix B.5 in Riener et al. 2019). For the GRS data set, we used the default settings of GAUSSPY+ to create nine different training sets, each containing 500 spectra. The spectra for each training set were randomly sampled from the entire GRS coverage and were then automatically decomposed with GAUSSPY+ (see Sect. 3.1.4 in Riener et al. 2019 for more details about the decomposition method that is used to create training sets).
In Table A.1 we list the value for the smoothing parameters α1 and α2 and the corresponding F1 score we obtained with the machine learning functionality of GAUSSPY for these nine training sets. In general, the resulting inferred smoothing parameter values are similar and compare well to each other. We expect small to moderate deviations between the samples such as they are present in Table A.1, since we randomly chose the spectra for the training sets from the entire GRS coverage, which contains spectra with significantly different noise values (Fig. B.1). As discussed in Appendix B.5 of Riener et al. (2019), such small deviations of the smoothing parameters only have a limited impact on the decomposition results. Moreover, with gausspy+ the fitting is not that dependent anymore on the exact values of the smoothing parameters, since it includes an improved fitting routine that aims to improve decompositions obtained with GAUSSPY that did not yield a good fit.
The training set decomposition method in GAUSSPY+ only includes fit solutions that have a 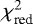 value below a chosen threshold (in our case 1.2). As discussed by Andrae et al. (2010), a threshold based on a fixed value of
value below a chosen threshold (in our case 1.2). As discussed by Andrae et al. (2010), a threshold based on a fixed value of 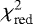 can be problematic, since for non-linear functions, such as Gaussian fit components, the degrees of freedom cannot be exactly determined and may vary substantially. To check whether this
can be problematic, since for non-linear functions, such as Gaussian fit components, the degrees of freedom cannot be exactly determined and may vary substantially. To check whether this 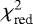 threshold might have biased the training samples produced with GAUSSPY+, we also tried a different approach to create training sets by using the semi-automated spectral line fitting package SCOUSEPY (Henshaw et al. 2016, 2019).
threshold might have biased the training samples produced with GAUSSPY+, we also tried a different approach to create training sets by using the semi-automated spectral line fitting package SCOUSEPY (Henshaw et al. 2016, 2019).
Smoothing parameters (in units of spectral channels) obtained for training set decompositions with SCOUSEPY and GAUSSPY+.
In SCOUSEPY, the data set is first divided into spectral averaging areas (SAAs). All spectra contained in an individual SAA are then averaged and the user manually fits the resulting spectrum by deciding on the number of fit components and their shape. The fit results from the SAA then help to inform the automated decomposition of the individual spectra contained in the SAA, which moreover leads to spatial coherence between the fit results of neighbouring spectra.
To create training sets with SCOUSEPY, we split the mosaicked GRS data set along the Galactic longitude axis into 23 individual subcubes and randomly placed nine spectral averaging areas (SAAs) with 3 × 3 pixels in each subcube for a total of 207 SAAs and 1863 individual spectra. We then proceeded with the suggested workflow for SCOUSEPY: First we manually fitted the averaged spectrum of each SAA, which informed the automated decomposition step for each individual spectrum contained in the SAA. Then we visually inspected the best fit solutions for all individual spectra and refitted them manually if the best fit results were not satisfactory, that means if they showed unfit peaks, strongly blended components, or fit components with very broad line widths, or if the fit solution was not spatially coherent with its neighbours.
For the selection of good-quality decompositions for the training set, we checked the final SCOUSEPY best fit results of all 1863 decomposed spectra with their corresponding residuals again by eye, which left us with a working sample of 1639 individual spectra. We then created three training sets, each of which contained 500 randomly chosen spectra and decomposition results from our final selection (we drew the spectra without replacement, which means an individual spectrum could only appear in one training set).
Table A.2 shows the resulting smoothing parameter values for these three training sets as determined by the machine learning routine of GAUSSPY. A comparison with Table A.1 demonstrates that the inferred values for α1 and α2 cover the same range of values. Table A.2 also shows the results obtained if we instead used the training set decomposition technique of GAUSSPY+ to produce best fit solutions for GAUSSPY for the same three training sets. The obtained values for the smoothing parameters are again similar to the values obtained with SCOUSEPY and the values obtained forthe GAUSSPY+ training sets in Table A.1. The larger spread of the obtained values for α1 is due to the presence of emission lines with low S/N and non-Gaussian shapes in the random selection of spectra in the SCOUSEPY training sets. Spectra containing such challenging spectral features can lead to increased 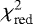 values for the fit solution, which would usually cause their exclusion from the GAUSSPY+ training set selection. The similarity of the obtained smoothing parameter values is thus a reassuring confirmation that both GAUSSPY+ and SCOUSEPY produce good training set decompositions.
values for the fit solution, which would usually cause their exclusion from the GAUSSPY+ training set selection. The similarity of the obtained smoothing parameter values is thus a reassuring confirmation that both GAUSSPY+ and SCOUSEPY produce good training set decompositions.
Given this similarity, we thus decided to use the median values for α1 and α2 obtained from the nine training sets created with GAUSSPY+ as our chosen parameters for the decomposition of the GRS data set. This yielded values of α1 = 1.97 and α2 = 4.15, which also compare well with the values inferred from the three training sets listed in Table A.2. Given the highly non-uniformnoise coverage of the GRS (see Fig. B.1), it is clear that our chosen values for the smoothing parameters will not be the optimal ones for all regions of the GRS data set. For example, Riener et al. (2019) inferred higher smoothing parameters of α1 = 2.89 and α2 = 6.65 for a small GRS test field that showed a strong noise gradient. However, as discussed in Riener et al. (2019), the improved fitting and spatially coherent refitting routines of GAUSSPY+ should be able to salvage or mitigate negative effects introduced by the choice of non-optimal smoothing parameters.
A.3 Decomposition parameters and steps
The GAUSSPY+ decomposition proceeds in three stages (see Riener et al. 2019 for more details). In Stage 1, GAUSSPY+ fits each spectrum individually, with the AICc serving as decision criterion between different fit solutions for the same spectrum. In Stage 2, fit solutions from Stage 1 can be flagged based on different user-selected criteria. Neighbouring fit solutions are then used for refitting attempts of the flagged spectra, which already introduces local spatial coherence between the fit solutions. Finally, in Stage 3 all fit solutions are checked for spatial coherence of the centroid position values of the fit components, with the aim of introducing spatial coherence more globally. Neighbouring fit solutions again serve as refit templates for decomposition results that have deviating centroid position values.
By default, GAUSSPY+ does not include flagged spectra as possible refit solutions in Stage 1. This was problematic for the GRS data set, as with our chosen flagging criteria there were regions near the Galactic midplane where almost all spectra were flagged and thus no refit solutions were available. We thus introduced the new parameter use_all_neighbors to GAUSSPY+, with which users can allow flagged spectra to serve as templates in case no unflagged spectra are available or refit attempts using only the unflagged spectra were not successful. In case flagged neighbouring spectra are used as refit templates, the flagged spectra are ranked according to their total flag values 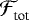 and the fit solution with the lowest
and the fit solution with the lowest 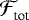 value is used first. Otherwise, we used the default settings of GAUSSPY+ as described in Riener et al. (2019), with the exception of relaxing the Δμmax9 parameter from its default value of 2 to 4 channels in phase 2 of the spatially coherent refitting, as it was done for the decomposition of the GRS test field in Riener et al. (2019). We also increased the minimum weight threshold
value is used first. Otherwise, we used the default settings of GAUSSPY+ as described in Riener et al. (2019), with the exception of relaxing the Δμmax9 parameter from its default value of 2 to 4 channels in phase 2 of the spatially coherent refitting, as it was done for the decomposition of the GRS test field in Riener et al. (2019). We also increased the minimum weight threshold  from its default value of 3∕6 to 4 ∕6, which means that in Stage 3 we only had two iterations with subsequent weight thresholds of
from its default value of 3∕6 to 4 ∕6, which means that in Stage 3 we only had two iterations with subsequent weight thresholds of 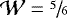 and
and 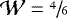 (see Sect. 3.3.2 in Riener et al. 2019 for more details). We tested the decomposition for one of the most complex regions in the GRS (with 10 or more emission peaks per spectrum) and found that a
(see Sect. 3.3.2 in Riener et al. 2019 for more details). We tested the decomposition for one of the most complex regions in the GRS (with 10 or more emission peaks per spectrum) and found that a 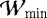 value of 0.5 was less beneficial, as it sometimes resulted in overly complex best fit solutions, especially for heavily blended structures.
value of 0.5 was less beneficial, as it sometimes resulted in overly complex best fit solutions, especially for heavily blended structures.
Percentages of refitted spectra, added and subtracted fit components, and flagged spectra after each stage of GAUSSPY+.
Table A.3 gives an overview of the percentage of spectra refitted in each stage and the percentage of spectra flagged after each stage. The Nrefit parameter gives the percentage of spectra that obtained a new best fit solution in the spatially coherent refitting phases. In Stage 2, almost 59% of the spectra were successfully refit based on a neighbouring fit solution, whereas in Stage 3 only about 6% of the spectra were refit based on the neighbouring centroid position values. Based on this high fraction of refitted spectra, it is reasonable to assume that Stage 2 of GAUSSPY+ already managed to introduce a large amount of spatial coherence. The Ncomp (+) and Ncomp (-) parameters give the percentage of added and removed fit components from the total number of fit components used for the entire decomposition in Stages 2 and 3 of GAUSSPY+. Similar as for the decomposition of the GRS test field in Riener et al. (2019), we find that the spatially coherent refitting stages tend to add more components to the fit solution. This is expected, as the fit solutions in Stage 1 are guided by the AICc, which aims at a good trade-off between the number of fit components and the resulting goodness of fit of the model (see Sects. 3.2.1 and 3.2.3 in Riener et al. 2019 for more information). Stages 2 and 3 are designed to improve the fit solutions of spectra that were flagged by user-selected criteria. For the decomposition of the GRS we use the default flags of GAUSSPY+, which flag spectra with: blended fit components (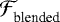 ); negative residual peaks (
); negative residual peaks (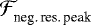 ); broad fit components (
); broad fit components (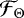 ); non-normally distributed residual values (
); non-normally distributed residual values (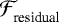 ); the numberof fit components not compatible with neighbouring fits (
); the numberof fit components not compatible with neighbouring fits (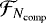 ). The
). The 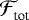 value gives the percentage of spectra that were flagged by any of these flagging criteria. The
value gives the percentage of spectra that were flagged by any of these flagging criteria. The 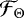 criterion only flags spectra that contain fit components that are broad compared to other fit components in the spectrum or broad compared tocomponents in the fit solutions of directly neighbouring spectra. However, it is also interesting to see whether the decomposition managed to reduce the fraction of fit components with very high absolute values for the linewidth. We thus also give the percentage of spectra that contain fit components with FWHM values that are higher than 50 spectral channels or about 10.5 km s−1 (
criterion only flags spectra that contain fit components that are broad compared to other fit components in the spectrum or broad compared tocomponents in the fit solutions of directly neighbouring spectra. However, it is also interesting to see whether the decomposition managed to reduce the fraction of fit components with very high absolute values for the linewidth. We thus also give the percentage of spectra that contain fit components with FWHM values that are higher than 50 spectral channels or about 10.5 km s−1 (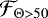 ), even though this was not a flagging criterion used in the GAUSSPY+ decomposition. We chose this upper limit for the FWHM as it is close to the maximum line widths of 9.8 and 8.3 km s−1 that Rathborne et al. (2009) found in their catalogue of GRS clouds and clumps, respectively. Table A.3 shows that in Stage 2 we are able to significantly reduce the percentage of flagged spectra for all flagging criteria. Since in Stage 3 we are more concerned with enforcing spatial coherence based on the centroid velocity values of neighbouring fit components, the number of spectra flagged as having blended and broad fit components increases again slightly.
), even though this was not a flagging criterion used in the GAUSSPY+ decomposition. We chose this upper limit for the FWHM as it is close to the maximum line widths of 9.8 and 8.3 km s−1 that Rathborne et al. (2009) found in their catalogue of GRS clouds and clumps, respectively. Table A.3 shows that in Stage 2 we are able to significantly reduce the percentage of flagged spectra for all flagging criteria. Since in Stage 3 we are more concerned with enforcing spatial coherence based on the centroid velocity values of neighbouring fit components, the number of spectra flagged as having blended and broad fit components increases again slightly.
A.4 Additional remarks on the decomposition results
Some of the original GRS subcubes we used to produce a big mosaic of the entire data set (Appendix A.1) overlapped with each other. This overlap caused an averaging of the columns at the edges of the respective subcubes at even integer values in Galactic longitude (ℓ = 16, 18, …, 54°). This averaging produced lower noise values and higher S/N ratios of peaks in the spectrum, which led to a large number of fit components. We include these averaged columns in the best fit solutions presented in Tables 1 and A.3, but we note that these fit solutions should be treated with caution.
There is an instrumental artefact present at vLSR values of 63.3−66.1 km s−1 and ranges in Galactic coordinates of 32.2° < ℓ < 32.7° and − 1.1° < b < −0.7°, which causes very narrow positive and negative high amplitude spikes, whose effect is especially visible in Figs. 3 and 10. The final decomposition results still contain the fit components of the positive spikes for this region.
Appendix B Quality assurance metrics
In this appendix we present different quality assurance metrics for our decomposition results. We discuss the distributions of our calculated noise values, goodness of fit values, and measures for the distribution of the residual values.
B.1 Noise values
Vital parameters of the GAUSSPY+ algorithm are based on S/N thresholds, which is why a reliable noise estimate is an essential basis for obtaining good decomposition results (Riener et al. 2019). Figure B.1 shows the noise map of the entire coverage of the GRS data set that was obtained with the automated noise estimation routine of GAUSSPY+ (see Sect. 3.1.1 in Riener et al. 2019 for more details on the noise estimation). A comparison with the noise map published in the GRS overview paper (Fig. 7 from Jackson et al. 2006) shows that our noise map reproduces the overall large-scale patterns; however, the individual noise values on a line of sight scale are more accurate and can show significant differences (see Sect. 5.2 in Riener et al. 2019 for more details).
We show a histogram of the σrms values (given in antenna temperatures) estimated by GAUSSPY+ in Fig. B.2. The noise distribution peaks at a value of 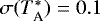 K and shows a clear second bump after the IQR indicated with the hatched grey area. This bimodal noise distribution was already discussed in Jackson et al. (2006) and is explained by different observing modes used for the GRS (cf. their Fig. 8, but we note that they do not include positions of ℓ < 18° and |b| > 1°). We decided to mask out 1188 spectrawith
K and shows a clear second bump after the IQR indicated with the hatched grey area. This bimodal noise distribution was already discussed in Jackson et al. (2006) and is explained by different observing modes used for the GRS (cf. their Fig. 8, but we note that they do not include positions of ℓ < 18° and |b| > 1°). We decided to mask out 1188 spectrawith 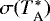 values > 0.75 K, which corresponds to the top 0.05% of the noise distribution. We found that such high
values > 0.75 K, which corresponds to the top 0.05% of the noise distribution. We found that such high 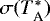 values can be indicative of instrumental artefacts. The inset in Fig. B.2 shows the noise distribution plotted on a logarithmic scale, and the
values can be indicative of instrumental artefacts. The inset in Fig. B.2 shows the noise distribution plotted on a logarithmic scale, and the 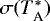 values of the masked spectra with high noise values are indicated in red.
values of the masked spectra with high noise values are indicated in red.
B.2 Goodness of fit statistics
One of the goodness-of-fit estimates employed by GAUSSPY+ is a check of whether the normalised residuals of the spectra show a normal distribution and are thus consistent with Gaussian or white noise (see Sect. 3.2.1 in Riener et al. 2019 for more details). This check yields a p-value for the null hypothesis that the residuals are consistent with white noise. Figure B.3 shows the distribution of p-values for all spectra (blue line) and spectra that were fit by at least one component in the final decomposition results (black line). The inset gives the same distribution for a logarithmically scaled ordinate. In the default settings of GAUSSPY+, a p-value of < 1% serves as anindication that the residual contains features inconsistent with Gaussian noise, which is used to initiate refit attempts or decide between alternative fit solutions. This threshold for the p-value is indicated with the vertical dashed line and we can see a clear jump in the distribution at this value.
 |
Fig. B.1 Map of determined rms noise (given in antenna temperature values). |
 |
Fig. B.2 Histogram of determined rms noise (given in antenna temperature values) for all spectra in the GRS. Theinset shows the same distribution on a logarithmic scale. The red line in the inset indicates masked out spectra with high noise values. The grey-shaded area marks the IQR, ranging from about 0.1− 0.16 K. The bin width is 0.005 K. |
Another goodness-of-fit statistic that is often used to report the quality of fit results is the  value that isdefined as
value that isdefined as
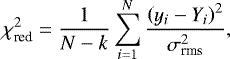 (B.1)
(B.1)
 |
Fig. B.3 Histogram of p-values from normality tests for the distribution of residual values for all GRS spectra (blue) and GRS spectra that have at least one fit component (black). The inset shows the same distribution on a logarithmic scale. The dashed vertical line marks the default p-value limit, below which GAUSSPY+ tries to refit spectra if possible. The grey-shaded area marks the IQR for the distribution of spectra with fitted components, ranging from about 0.03−0.3. The bin width is 0.02 dex. |
where in the case of the Gaussian decomposition N corresponds to the number of spectral channels, k correspondsto the number of free parameters used in the fit solution, and yi and Y i are the data and fit value at channel position i. Since for non-linear models the 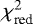 estimate can suffer from large uncertainties (Andrae et al. 2010), it is not the best goodness-of-fit metric for the Gaussian decomposition results. As discussed in Riener et al. (2019), another problem of
estimate can suffer from large uncertainties (Andrae et al. 2010), it is not the best goodness-of-fit metric for the Gaussian decomposition results. As discussed in Riener et al. (2019), another problem of 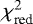 estimates is that the inclusion of a large number of spectral channels containing only noise can mask bad fit results. Given these caveats, our reported
estimates is that the inclusion of a large number of spectral channels containing only noise can mask bad fit results. Given these caveats, our reported 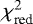 values for our fit results should be taken with caution. If GAUSSPY+ identified signal intervals in a spectrum, we only include the spectral channels from those identified intervals for the
values for our fit results should be taken with caution. If GAUSSPY+ identified signal intervals in a spectrum, we only include the spectral channels from those identified intervals for the 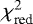 estimate, which increases its ability to identify potentially incorrect or insufficient fit results.
estimate, which increases its ability to identify potentially incorrect or insufficient fit results.
 |
Fig. B.4 Histogram of |
The distribution of the 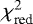 values for the spectra from the GRS is shown in Fig. B.4. The distribution marked with the blue line contains all spectra of the GRS data set, irrespective of whether they were fitted in the decomposition. The black line shows the distribution of the
values for the spectra from the GRS is shown in Fig. B.4. The distribution marked with the blue line contains all spectra of the GRS data set, irrespective of whether they were fitted in the decomposition. The black line shows the distribution of the 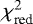 values for spectra that have at least one fitted Gaussian component. Both of the distributions peak at a value of 1. Spectra with no fitted Gaussian components are expected to have a
values for spectra that have at least one fitted Gaussian component. Both of the distributions peak at a value of 1. Spectra with no fitted Gaussian components are expected to have a 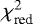 value close to 1 if they only contain noise and the σrms value was estimated correctly. Increased
value close to 1 if they only contain noise and the σrms value was estimated correctly. Increased 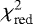 values for these unfitted spectra can thus indicate spectra with valid signal that could not be fit, an incorrect noise estimation, or artefacts in the spectrum such as insufficient baseline subtraction.
values for these unfitted spectra can thus indicate spectra with valid signal that could not be fit, an incorrect noise estimation, or artefacts in the spectrum such as insufficient baseline subtraction.
About 35% of the spectra with fitted Gaussian components have 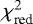 values below1; about 0.4% of the spectra with fitted Gaussian components have
values below1; about 0.4% of the spectra with fitted Gaussian components have 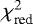 values above 2. Since we aimed to mostly include channels that contain signal in the calculation of the goodness of fit criterion, for most of the spectra low
values above 2. Since we aimed to mostly include channels that contain signal in the calculation of the goodness of fit criterion, for most of the spectra low 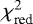 values do very likely not indicate an overfitting of the data, but rather reflect a smaller amount of spectral channels that were used for the
values do very likely not indicate an overfitting of the data, but rather reflect a smaller amount of spectral channels that were used for the 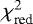 calculation.
calculation.
Figure B.5 shows a map of the 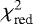 values for the entire GRS data set. This map does not show any obvious correlations with the maps showing the normalised residuals (Fig. 2), noise values (Fig. B.1), and number of fit components (Fig. 4). However, we can see regions of increased
values for the entire GRS data set. This map does not show any obvious correlations with the maps showing the normalised residuals (Fig. 2), noise values (Fig. B.1), and number of fit components (Fig. 4). However, we can see regions of increased 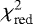 values (e.g. around ℓ ~ 51.5° and b ~ 1°), which could indicate problems with the decomposition, such as missed or incorrectly fitted signal peaks, or problems in the original data, such as insufficient baseline corrections.
values (e.g. around ℓ ~ 51.5° and b ~ 1°), which could indicate problems with the decomposition, such as missed or incorrectly fitted signal peaks, or problems in the original data, such as insufficient baseline corrections.
 |
Fig. B.5 Map of |
Appendix C Effects of optical depth on the decomposition results
Interpretation of the Gaussian decomposition data can potentially be affected by optical depth effects; we examine in this section how severe such effects may be. Moderate optical depth effects can lead to a broadening of the emission lines, which affects the line widths (and further, estimated Mach numbers; e.g. Hacar et al. 2016). Increased optical depth effects can cause flat-topped or self-absorbed emission lines, which can yield two-component fits that are unphysical. The version of GAUSSPY+ used in this work does not account for any possible optical depth effects. If an emission line is affected by self-absorption, GAUSSPY+ will likely fit it with multiple Gaussian components. Our aim here is to establish in which regions, or for which spectra in the GRS, optical depth effects may impact the decomposition results. We start by recalling previous results about optical depth effects, depletion, and freeze out on the 13CO isotopologue. We then present two methods of calculating the optical depth 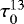 for 13CO (1– 0). Subsequently, we apply these methods to observations from the MWISP survey of a dense molecular cloud, to establish how severe the optical depth effects are and how we can apply these results to the GRS decomposition.
for 13CO (1– 0). Subsequently, we apply these methods to observations from the MWISP survey of a dense molecular cloud, to establish how severe the optical depth effects are and how we can apply these results to the GRS decomposition.
C.1 Depletion, freeze-out, and self-absorption of 13CO
Evidence for depletion or freeze-out of CO isotopologues is already well-documented for IRDCs and clumps contained in the GRS data set (e.g. Hernandez et al. 2011; Pitann et al. 2013; Giannetti et al. 2014; Pon et al. 2016; Barnes et al. 2018), albeit for observations at spatial and spectral resolutions that are typically at least a factor of two better than for the GRS. For clumps, the depletions are usually most severe for their densest and coldest parts (Hernandez et al. 2011; Giannetti et al. 2014). In the GRS data set, such small regions are only resolved for gas emission that is located within ~ 3 kpc of the sun, which is only a small fraction of the emission contained in the GRS. We thus conclude that freeze-out and depletion effects will not be a problem at the scales probed by the GRS.
Optical depth values have already been calculated for the GRS, albeit only on scales of molecular clouds and for spatially and spectrally smoothed versions of the data set. For their catalogue of molecular clouds in the GRS, Rathborne et al. (2009) found the 13CO emission to be optically thin with averageand maximum 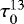 values of 0.13 and 0.5, respectively. Roman-Duval et al. (2010) repeated the
values of 0.13 and 0.5, respectively. Roman-Duval et al. (2010) repeated the 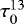 estimation for 583 molecular clouds from Rathborne et al. (2009), but performed the calculation on a voxel-by-voxel basis first before averaging; this resulted in a higher mean optical depth value of 1.46, indicating that the GRS data set includes optically thick emission. Rigby et al. (2016) also found indications for self-absorption in the GRS data set, by comparing it to 13CO (3–2) and C 18 O (3–2) transitions of the CHIMPS survey (that has a spatial resolution about 3 times better than GRS).
estimation for 583 molecular clouds from Rathborne et al. (2009), but performed the calculation on a voxel-by-voxel basis first before averaging; this resulted in a higher mean optical depth value of 1.46, indicating that the GRS data set includes optically thick emission. Rigby et al. (2016) also found indications for self-absorption in the GRS data set, by comparing it to 13CO (3–2) and C 18 O (3–2) transitions of the CHIMPS survey (that has a spatial resolution about 3 times better than GRS).
However, there are also counterexamples that indicate that 13CO (1– 0) stays mostly optically thin even in dense regions. For example, Beuther & Sridharan (2007) studied a sample of 43 IRDCs and found that the peaks in 13CO (1– 0) correspond very well with peaks of the high density tracer H13CO+ (1–0), even for regions in the spectrum where 12CO (2–1) seems to get optically thick. Since these were IRAM-30 m observations at about half the spatial resolution of GRS, one would conclude that for a larger physical beam such effects should be even more reduced due to beam averaging.
C.2 Calculation of optical depth values
Here we review two common ways of estimating the optical depth of 13CO, which we later apply in Appendix C.3 to assess the importance of optical depth effects on the decomposition results. The first method for calculating 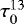 requires information about the excitation temperature Tex, obtained from 12CO (1–0) emission that is assumed to be optically thick. The second method for calculating
requires information about the excitation temperature Tex, obtained from 12CO (1–0) emission that is assumed to be optically thick. The second method for calculating 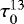 is based on the relative abundance of 13CO to another isotopologue that traces higher column densities and is assumed to be optically thin; in our case this is the C18O (1– 0) emission line. This method is thus best applicable to dense regions of molecular clouds, such as IRDCs, filaments, clumps, and cores.
is based on the relative abundance of 13CO to another isotopologue that traces higher column densities and is assumed to be optically thin; in our case this is the C18O (1– 0) emission line. This method is thus best applicable to dense regions of molecular clouds, such as IRDCs, filaments, clumps, and cores.
C.2.1 Method 1: estimating 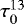 with additional 12CO(1–0) observations
with additional 12CO(1–0) observations
Under the condition of local thermodynamic equilibrium and the assumption that the 12CO (1– 0) line is optically thick, the excitation temperature Tex can be determined as (Wilson et al. 2014):
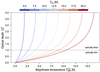 |
Fig. C.1 Optical depth of 13CO as a function of main beam brightness temperature for different excitation temperature (Tex) values. The dotted horizontal line marks the threshold between the regimes where 13CO is optically thin or thick. |
Threshold between optically thin and thick emission for given excitation temperature values.
![\begin{equation*} T_{\textrm{ex}} = T_{0}^{12} \cdot \left( \text{{\textrm{ln}}}\left[ 1 + \dfrac{T_{0}^{12}}{T_{\textrm{MB}}^{12} + 0.82} \right] \right)^{-1},\end{equation*}](/articles/aa/full_html/2020/01/aa36814-19/aa36814-19-eq63.png) (C.1)
(C.1)
where 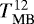 is the maximum main beam brightness temperature of the 12CO (1–0) line and
is the maximum main beam brightness temperature of the 12CO (1–0) line and 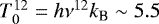 K at the rest frequency of 12CO (ν12 = 115.271 GHz). Assuming that Tex is the same for the 12CO (1–0) and 13 C O (1–0) transitions, the optical depth for the 13CO (1–0) line is then given by (Wilson et al. 2014):
K at the rest frequency of 12CO (ν12 = 115.271 GHz). Assuming that Tex is the same for the 12CO (1–0) and 13 C O (1–0) transitions, the optical depth for the 13CO (1–0) line is then given by (Wilson et al. 2014):
![\begin{equation*} {\tau_{0}^{13}} = -\text{{\textrm{ln}}} \left[ 1 - \dfrac{T_{\textrm{MB}}^{13}}{T_{0}^{13}} \left( \dfrac{1}{e^{T_{0}^{13} / T_{\textrm{ex}}} - 1} - 0.16\right)^{-1} \right],\end{equation*}](/articles/aa/full_html/2020/01/aa36814-19/aa36814-19-eq66.png) (C.2)
(C.2)
where 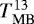 is the maximum main beam brightness temperature of the 13CO (1–0) line and
is the maximum main beam brightness temperature of the 13CO (1–0) line and 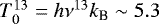 K at the rest frequency of 13CO (ν13 = 110.201 GHz).
K at the rest frequency of 13CO (ν13 = 110.201 GHz).
Figure C.1 shows how  increases as a function of
increases as a function of  for different fixed values of Tex. Table C.1 gives the
for different fixed values of Tex. Table C.1 gives the  values for which we expect the 13CO emission to get optically thick for a given Tex value. The table also shows the percentage of fit components from the GRS decomposition that have amplitude values greater than this
values for which we expect the 13CO emission to get optically thick for a given Tex value. The table also shows the percentage of fit components from the GRS decomposition that have amplitude values greater than this 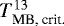 value. For example, for an assumed fixed value of Tex = 10 K, about 1.8% of all Gaussian fit components in the GRS decomposition would pass the threshold between optically thin and optically thick gas. A comparison with Fig. 6 also confirms that optical depth effects get important for our decomposition results if the excitation temperature values are ≲10 K.
value. For example, for an assumed fixed value of Tex = 10 K, about 1.8% of all Gaussian fit components in the GRS decomposition would pass the threshold between optically thin and optically thick gas. A comparison with Fig. 6 also confirms that optical depth effects get important for our decomposition results if the excitation temperature values are ≲10 K.
C.2.2 Method 2: estimating 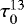 with additional C18O (1–0) observations
with additional C18O (1–0) observations
In case additional C18O (1–0) observations are available, 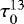 can be determined based on the expected relative abundance of 13CO to C 18 O. Under the assumption that the C18O emission is optically thin, a comparison of the integrated emission WCO of 13 C O and C18O can be put in direct relation to their opacities
can be determined based on the expected relative abundance of 13CO to C 18 O. Under the assumption that the C18O emission is optically thin, a comparison of the integrated emission WCO of 13 C O and C18O can be put in direct relation to their opacities 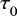 :
:
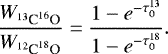 (C.3)
(C.3)
We can use information about the isotopic ratios of carbon and oxygen to rewrite 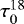 in terms of
in terms of 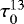 :
:
![\begin{equation*} {\tau_{0}^{18}} = \dfrac{[^{12}\text{C}]/[^{13}\text{C}]}{[^{16}\text{O}]/[^{18}\text{O}]} \cdot {\tau_{0}^{13}}.\end{equation*}](/articles/aa/full_html/2020/01/aa36814-19/aa36814-19-eq79.png) (C.4)
(C.4)
Giannetti et al. (2014) determined that these isotope ratios vary with Galactocentric distance Rgal as ![$[^{12}\text{C}]/[^{13}\text{C}] = 6.1\times {R}_{\text{gal}}~\text{[kpc]} + 14.3$](/articles/aa/full_html/2020/01/aa36814-19/aa36814-19-eq80.png) and
and ![$[^{16}\text{O}]/[^{18}\text{O}] = 58.8\times {R}_{\text{gal}}~\text{[kpc]} + 37.1$](/articles/aa/full_html/2020/01/aa36814-19/aa36814-19-eq81.png) . Substituting Eq. (C.4) in Eq. (C.3) thus allows to solve for
. Substituting Eq. (C.4) in Eq. (C.3) thus allows to solve for 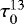 .
.
C.3 Optical depth effects in the G24 region
In this section we study the effects of optical depth on the decomposition with the help of a dense, elongated giant molecular cloud. The cloud, G24, has been identified by Wang et al. (2015) from the HiGAL and GRS data sets. G24 is located at the Galactic coordinates ℓ = 24°, b = +0.48°, and spans vLSR values of 93– 99 km s−1 (Wang et al. 2015). The total mass of G24 has been estimated to be about 105 M⊙, the length about 100 pc, and the distance about 5.8 kpc (Zucker et al. 2018; Zhang et al. 2019). The cloud is star-forming and its star formation rate and efficiency are typical for similar clouds in the Milky Way (Zhang et al. 2019). G24 overlaps with the molecular cloud GRSMC G024.09+00.44 identified by Rathborne et al. (2009), whose total mass was estimated to be 2.8 × 105 M⊙ (Roman-Duval et al. 2010).
There are two reasons that make G24 a good example to test if optical depth effects impact our decomposition. First, G24 is located in one of the most complex regions of the GRS data set, judging by the number of fitted components along the line of sight (Fig. 4). The decomposition is most challenging for such complex lines of sight. Second, G24 is among the most massive structures identified from GRS as distinct clouds, with a gas surface density of ~ 105 M⊙ pc−2 (Zhang et al. 2019). As a result, if optical depth effects hamper the GRS decomposition in general, we should definitely see the effects in G24.
C.3.1 Observations
We used data of the G24 region from the MWISP project (Su et al. 2019), which is an ongoing CO survey for the northern Galactic plane (ℓ = −10 to 250°, |b| ≤ 5.2°) using the PMO-13.7 m single-dish telescope located at Delingha in China. We obtained observations of 12CO (1– 0), 13CO (1– 0), and C18O (1– 0) covering a 2.5° × 1° field centred at Galactic coordinates ℓ = 23.75° and b = 0.5°. The angular resolution of the data is 54.8′′ with a pixel sampling of 30′′. The covered velocity range is from −500 to +500 km s−1 with a velocity resolution of ~0.16 km s−1 and 0.17 km s−1 for the 12CO and 13CO/C18O observations, respectively. The data was already supplied in main beam temperatures.
 |
Fig. C.2 Maps for the region containing the elongated molecular cloud G24. (a) Zeroth moment map of the 13CO emission.(b) Map of determined excitation temperature values. (c) Map of determined |
Figure C.2a shows a zeroth moment map for the G24 region, which was obtained from the 13CO MWISP data integrated between 93 < vLSR < 99 km s−1 using the moment masking technique described in Dame (2011). The very good correspondence of the 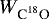 contour defined on the corresponding C18O data with the zeroth moment map of 13CO confirms that C18O emission is coming from areas with increased 13CO emission and thus increased column density. The
contour defined on the corresponding C18O data with the zeroth moment map of 13CO confirms that C18O emission is coming from areas with increased 13CO emission and thus increased column density. The 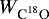 contour shown in Fig. C.2a corresponds to a
contour shown in Fig. C.2a corresponds to a 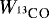 contour of ~ 10 K km s−1.
contour of ~ 10 K km s−1.
Smoothing parameters (in units of spectral channels) obtained for decompositions of the GAUSSPY+ training sets for the 13CO and C18O MWISP datasets.
 |
Fig. C.3 Distributions of fit parameters for the decomposition of the GRS (left), MWISP (middle), and the difference between the two data sets (right). The rows show normalised 2D histograms of: peak main beam brightness temperature and velocity dispersion values (top), centroid velocity and peak main beam brightness temperature values (middle), centroid velocity and velocity dispersion values (bottom). Colourbars in all panels indicate the values of the normalised 2D distributions. |
C.3.2 GAUSSPY+ decomposition
For the decomposition of the MWISP data set we reduced the velocity axis to a range of − 50 to +150 km s−1, which corresponds to 1207 and 1202 spectral channels for 13CO and C 18 O, respectively. Similar as in Appendix A.2, we used the default settings of GAUSSPY+ to create training sets with 500 decomposed spectra for both isotopologues. In Table C.2, we list the determined smoothing parameters and corresponding F1 score for both training sets. The C18O data has a much lower S/N and noise properties can thus affect the line shape already significantly, so the data neededto be smoothed more to yield a good decomposition performance. Apart from the different smoothing parameter values, we used the same GAUSSPY+ settings to prepare and decompose the MWISP 13CO and C18O spectra as for the GRS data set (described in Appendices A.1 and A.3).
C.3.3 Comparison of the decomposition results between the GRS and MWISP
We now compare the GAUSSPY+ decomposition results obtained for the GRS and MWISP data sets. If the fit results for the two data sets are comparable, we can conclude that also our following results about the optical depth effects derived for the MWISP data will apply similarly to the GRS. We cannot perform a straightforward spectrum-per-spectrum comparison, since the spectral channel widths and pixel scales of the data sets are not identical. We thus opted for a simpler approach of comparing the fit parameter statistics.
 |
Fig. C.4 2D distribution of determined Tex and |
For this comparison we used all fit components within 22.5° ≲ ℓ ≲ 25°, 0° ≲ b ≲ 1°, and − 5≲ vLSR ≲ 135 km s−1. Due to the different spatial resolutions and pixel scales this selection included 58 635 spectra with 271 896 fit components in the GRS data set and 32 153 spectra with 144 555 fit components in the MWISP data set. Figure C.3 shows normalised 2D histograms for all possible combinations of the Gaussian fit parameters for the GRS (left panels) and MWISP (middle panels) data sets. The shapes of the 2D distributions of the GRS and MWISP match very well, which already demonstrates that the two decompositions yielded similar results. To better quantify how similar the 2D distributions are, we show the difference between their distributions in the right panels, where red and blue indicate higher values in the GRS and MWISP distributions, respectively. The GRS data set includes regions with very low σrms values, which led to fitted components with low TMB values that could not be detected in the MWISP data set. Otherwise these distributions do not show any noticeable biases; there are individual small differences, but these can be explained by the variation in the resolution elements and the noise coverage.
We thus conclude that the GRS and MWISP decomposition results are sufficiently similar. Thus, we expect that the following results about optical depth effects derived from the MWISP data can be applied to the GRS.
C.3.4 Estimated 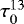 values with Method 1
values with Method 1
With the 12CO and 13 C O MWISP observations of the G24 region and Eqs. (C.1) and (C.2) we can estimate values for Tex and 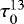 , respectively. For the Tex and
, respectively. For the Tex and 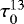 calculation we only considered data points within 93 < vLSR < 99 km s−1. We show theresulting maps for Tex and
calculation we only considered data points within 93 < vLSR < 99 km s−1. We show theresulting maps for Tex and 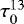 in panels b and c of Fig. C.2, which already shows that the densest part of G24 is associated with higher
in panels b and c of Fig. C.2, which already shows that the densest part of G24 is associated with higher 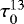 values. To better quantify how the optical depth varies with density and excitation temperature, we show 2D distributions of the Tex and
values. To better quantify how the optical depth varies with density and excitation temperature, we show 2D distributions of the Tex and 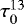 values in Fig. C.4. Inside the contour defined by
values in Fig. C.4. Inside the contour defined by 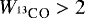 K km s−1, the Tex values range from about 6 to 23.5 K and the
K km s−1, the Tex values range from about 6 to 23.5 K and the 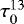 values range from 0.12 to 1.04, with a median
values range from 0.12 to 1.04, with a median 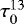 value of 0.32. The area of G24 within a contour of
value of 0.32. The area of G24 within a contour of 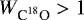 K km s−1 is also associated with the highest Tex values (fromabout 8.5 to 23.5 K), as can be clearly seen in the respective marginal distribution shown in red in Fig. C.4. The corresponding
K km s−1 is also associated with the highest Tex values (fromabout 8.5 to 23.5 K), as can be clearly seen in the respective marginal distribution shown in red in Fig. C.4. The corresponding  values in this area range from 0.3 to 0.92, and the median
values in this area range from 0.3 to 0.92, and the median  value is 0.54. While the densest regions of G24 definitely show increased values for
value is 0.54. While the densest regions of G24 definitely show increased values for  , the 13CO (1– 0) transition isfor most lines of sight still well below optical depth values of 1. Based on the calculation of
, the 13CO (1– 0) transition isfor most lines of sight still well below optical depth values of 1. Based on the calculation of 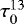 with Method 1, we conclude that optical depth effects do not play a significant role in the GRS data set.
with Method 1, we conclude that optical depth effects do not play a significant role in the GRS data set.
C.3.5 Estimated 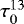 values with Method 2
values with Method 2
With the 13CO and C 18 O MWISP observations of the G24 region and Eq. (C.3), we can give an independent estimate for 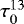 . We took values for the integrated intensity from our GAUSSPY+ decomposition of the MWISP 13CO and C18O data sets (Appendix C.3.2)10. We selected all C18O fit components in the region whose centroid positions were within 93 ≲ vLSR ≲ 99 km s−1. For each of these fitted C18O components, we associated 13CO fit components along the same line of sight, whose centroid position was contained within the FWHM interval (vLSR ± FWHM) of the C18O fit component. Thus a single C18O fit component could be associated with multiple 13CO fit components.
. We took values for the integrated intensity from our GAUSSPY+ decomposition of the MWISP 13CO and C18O data sets (Appendix C.3.2)10. We selected all C18O fit components in the region whose centroid positions were within 93 ≲ vLSR ≲ 99 km s−1. For each of these fitted C18O components, we associated 13CO fit components along the same line of sight, whose centroid position was contained within the FWHM interval (vLSR ± FWHM) of the C18O fit component. Thus a single C18O fit component could be associated with multiple 13CO fit components.
For a calculated Galactocentric distance of G24 of about 3.8 kpc, we expect isotope ratios of ![$[^{12}\text{C}]/[^{13}\text{C}] \sim 38$](/articles/aa/full_html/2020/01/aa36814-19/aa36814-19-eq102.png) and
and ![$[^{16}\text{O}]/[^{18}\text{O}] \sim 263$](/articles/aa/full_html/2020/01/aa36814-19/aa36814-19-eq103.png) (based on the work of Giannetti et al. 2014). Using these isotope ratios to rewrite
(based on the work of Giannetti et al. 2014). Using these isotope ratios to rewrite 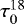 in terms of
in terms of 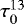 together with the integrated emission inferred from the 13CO and C18O fit components, we can solve for
together with the integrated emission inferred from the 13CO and C18O fit components, we can solve for 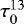 in Eq. (C.3). We show the resulting map of
in Eq. (C.3). We show the resulting map of 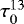 values estimated with Method 2 in Fig. C.2d. The IQR of the
values estimated with Method 2 in Fig. C.2d. The IQR of the 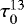 values goes from 0.29 to 0.96, with a median value of 0.57. So even though the median
values goes from 0.29 to 0.96, with a median value of 0.57. So even though the median 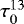 value is comparable to what was obtained with Method 1 for the same region, individual
value is comparable to what was obtained with Method 1 for the same region, individual 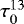 values can be much higher for Method 2. However, the median S/N for the fit components in C18O is only ~ 2.8, which means that the uncertainty on their fit parameters due to impacts of the noise and thus also the uncertainty on the
values can be much higher for Method 2. However, the median S/N for the fit components in C18O is only ~ 2.8, which means that the uncertainty on their fit parameters due to impacts of the noise and thus also the uncertainty on the 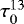 calculation will be increased. These increased uncertainties might also explain the surprising lack of correlation we find between the two independent results for
calculation will be increased. These increased uncertainties might also explain the surprising lack of correlation we find between the two independent results for 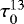 obtained for471 positions with Method 1 and 2 (with a Pearson correlation coefficient of 0.1 and corresponding p-value of 1.2%). Based on the
obtained for471 positions with Method 1 and 2 (with a Pearson correlation coefficient of 0.1 and corresponding p-value of 1.2%). Based on the 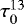 calculation with Method 2, we thus conclude that optical depth effects can get important for the densest structures in the GRS, but still seem to not be an overwhelming issue even for these most problematic regions.
calculation with Method 2, we thus conclude that optical depth effects can get important for the densest structures in the GRS, but still seem to not be an overwhelming issue even for these most problematic regions.
C.4 Effects on the decomposition
Our main concern is whether  values are high enough to impact the decomposition, so that the underlying emission lines get fitted by multiple components instead of a single one. We saw in the last two sections that we find increased optical depth values in the densest regions of G24 (panels c and d in Fig. C.2), where we also detect the C18O line. For these dense regions, we can thus compare the position of the fit component(s) of the 13CO emission to the position of the fitted C18O line. If multiple fit components in 13CO are associated with a single C18O fit component, it can serve as an indication that the 13CO emission might suffer from optical depth effects that could have led to the fitting of multiple components. We associate a fit component in 13 C O with a fit component in C18O if the centroid position of the former is contained within the FWHM interval of the latter.
values are high enough to impact the decomposition, so that the underlying emission lines get fitted by multiple components instead of a single one. We saw in the last two sections that we find increased optical depth values in the densest regions of G24 (panels c and d in Fig. C.2), where we also detect the C18O line. For these dense regions, we can thus compare the position of the fit component(s) of the 13CO emission to the position of the fitted C18O line. If multiple fit components in 13CO are associated with a single C18O fit component, it can serve as an indication that the 13CO emission might suffer from optical depth effects that could have led to the fitting of multiple components. We associate a fit component in 13 C O with a fit component in C18O if the centroid position of the former is contained within the FWHM interval of the latter.
We show a map of the number of 13CO fit components associated with a single C18O fit component in Fig. C.2e. Within the 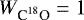 K km s−1 contour, that means the densest part of the G24 region, 71.8% of the C 18O fit components are associated with a single 13CO component; 25.5% of the C18O components are associated with two 13CO components, and the remaining 2.8% are associated with three 13CO components. Based on these results, we conclude that for about a third of the positions in the most dense region of G24 the decomposition may fit two or three components for what may be a single 13CO emission line, whose shape is non-Gaussian due to optical depth effects. Another possibility is that complex line structure is detected in 13CO, but not in C 18 O, due to differences in sensitivity.
K km s−1 contour, that means the densest part of the G24 region, 71.8% of the C 18O fit components are associated with a single 13CO component; 25.5% of the C18O components are associated with two 13CO components, and the remaining 2.8% are associated with three 13CO components. Based on these results, we conclude that for about a third of the positions in the most dense region of G24 the decomposition may fit two or three components for what may be a single 13CO emission line, whose shape is non-Gaussian due to optical depth effects. Another possibility is that complex line structure is detected in 13CO, but not in C 18 O, due to differences in sensitivity.
However, the low S/N of the C18O components makes this analysis rather uncertain. We checked whether the association of a single C18O component with multiple 13CO fit components could be due to broader σv values of theC18O component. The median σv value for C18O components associated with one, two, or three 13CO fit components is 1.0, 1.4, and 2.4 km s−1, respectively, and the respective S/N of the C18O componentsis 3.2, 3.0, and 2.3. It thus seems likely that the association of multiple 13CO fit components with a single C18O component is at least partly affected by the low S/N of the C18O components.
Finally, we calculate 13CO column densities for the densest region in G24, which can serve as a guideline for when optical depth effects may impact the fitting results. We can calculate 13CO column densities including a correction for optical depth effects via (Wilson et al. 2014):
![\begin{equation*} N_{\text{CO}}^{13} \left[\text{cm}^{-2} \right] = 3\times 10^{14} \cdot \left(1 - e^{T_{0}^{13} / T_{\textrm{ex}}}\right)^{-1} \cdot \dfrac{{\tau_{0}^{13}}}{1 - e^{-{\tau_{0}^{13}}}}\cdot W_{{^{13}\textrm{C}^{}\textrm{O}}},\end{equation*}](/articles/aa/full_html/2020/01/aa36814-19/aa36814-19-eq116.png) (C.5)
(C.5)
where we plug in the values for 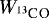 , Tex, and
, Tex, and 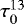 shown in Fig. C.2a–c. The region within the
shown in Fig. C.2a–c. The region within the 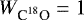 K km s−1 contour has a mean
K km s−1 contour has a mean 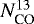 value of 1.4 × 1016 cm−2 (with minimum and maximum
value of 1.4 × 1016 cm−2 (with minimum and maximum 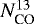 values of 5.0 × 1015 and 5.1 × 1016 cm−2, respectively). We compared the
values of 5.0 × 1015 and 5.1 × 1016 cm−2, respectively). We compared the 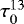 values calculated with Method 2 (Fig. C.2 d) with the corresponding
values calculated with Method 2 (Fig. C.2 d) with the corresponding 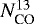 values but did not find any correlation. However, based on the discussion in this section, we infer that optical depth effects might have an impact on the decomposition if 13CO column densities exceed values of
values but did not find any correlation. However, based on the discussion in this section, we infer that optical depth effects might have an impact on the decomposition if 13CO column densities exceed values of 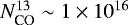 cm−2.
cm−2.
References
- Akaike, H. 1973, in, Proceedings of the 2nd International Symposium on Information Theory, 267 [Google Scholar]
- Anderson, L. D., Wang, Y., Bihr, S., et al. 2017, A&A, 605, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, L. D., Wenger, T. V., Armentrout, W. P., Balser, D. S., & Bania, T. M. 2019, ApJ, 871, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Andrae, R., Schulze-Hartung, T., & Melchior, P. 2010, ArXiv e-prints [arXiv:1012.3754] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnes, A. T., Henshaw, J. D., Caselli, P., et al. 2018, MNRAS, 475, 5268 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, P. J., Muller, E., Indermuehle, B., et al. 2015, ApJ, 812, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., Mellier, Y., Radovich, M., et al. 2002, ASP Conf. Ser., 281, 228 [Google Scholar]
- Beuther, H., & Sridharan, T. K. 2007, ApJ, 668, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Tackenberg, J., Linz, H., et al. 2012, ApJ, 747, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Bland-Hawthorn, J., & Gerhard, O. 2016, ARA&A, 54, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
- Braiding, C., Wong, G. F., Maxted, N. I., et al. 2018, PASA, 35, e029 [NASA ADS] [CrossRef] [Google Scholar]
- Burton, M. G., Braiding, C., Glueck, C., et al. 2013, PASA, 30, e044 [NASA ADS] [CrossRef] [Google Scholar]
- Clemens, D. P., Sanders, D. B., & Scoville, N. Z. 1988, ApJ, 327, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Colombo, D., Rosolowsky, E., Duarte-Cabral, A., et al. 2019, MNRAS, 483, 4291 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M. 2011, ArXiv e-prints [arXiv:1101.1499] [Google Scholar]
- Dame, T. M., & Thaddeus, P. 1985, ApJ, 297, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Dempsey, J. T., Thomas, H. S., & Currie, M. J. 2013, ApJS, 209, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Giannetti, A., Wyrowski, F., Brand, J., et al. 2014, A&A, 570, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodman, A. A., Alves, J., Beaumont, C. N., et al. 2014, ApJ, 797, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Hacar, A., Alves, J., Burkert, A., & Goldsmith, P. 2016, A&A, 591, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henshaw, J. D., Longmore, S. N., Kruijssen, J. M. D., et al. 2016, MNRAS, 457, 2675 [NASA ADS] [CrossRef] [Google Scholar]
- Henshaw, J. D., Ginsburg, A., Haworth, T. J., et al. 2019, MNRAS, 485, 2457 [NASA ADS] [CrossRef] [Google Scholar]
- Hernandez, A. K., Tan, J. C., Caselli, P., et al. 2011, ApJ, 738, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Heyer, M., & Dame, T. M. 2015, ARA&A, 53, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, J. M., Rathborne, J. M., Shah, R. Y., et al. 2006, ApJ, 163, 145 [Google Scholar]
- Kainulainen, J., & Tan, J. C. 2013, A&A, 549, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., & Kerp, J. 2009, ARA&A, 47, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Khoperskov, S., Haywood, M., Di Matteo, P., Lehnert, M. D., & Combes, F. 2018, A&A, 609, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindner, R. R., Vera-Ciro, C., Murray, C. E., et al. 2015, AJ, 149, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, K. A., Whitworth, A. P., Lomax, O., et al. 2017, MNRAS, 471, 2730 [Google Scholar]
- Miville-Deschênes, M.-A., Murray, N., & Lee, E. J. 2017, ApJ, 834, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Schisano, E., Elia, D., et al. 2016, A&A, 591, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakanishi, H., & Sofue, Y. 2006, PASJ, 58, 847 [NASA ADS] [Google Scholar]
- Pitann, J., Linz, H., Ragan, S., et al. 2013, ApJ, 766, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Pon, A., Johnstone, D., Caselli, P., et al. 2016, A&A, 587, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ragan, S. E., Moore, T. J. T., Eden, D. J., et al. 2018, MNRAS, 479, 2361 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Johnson, A. M., Jackson, J. M., Shah, R. Y., & Simon, R. 2009, ApJS, 182, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
- Reid, M. J., Dame, T. M., Menten, K. M., & Brunthaler, A. 2016, ApJ, 823, 1 [CrossRef] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2019, ArXiv e-prints [arXiv:1910.03357] [Google Scholar]
- Rice, T. S., Goodman, A. A., Bergin, E. A., Beaumont, C., & Dame, T. M. 2016, ApJ, 822, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Riener, M., Kainulainen, J., Henshaw, J. D., et al. 2019, A&A, 628, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rigby, A. J., Moore, T. J. T., Plume, R., et al. 2016, MNRAS, 456, 2885 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T., & Bressert, E. 2012, Astrophysics Source Code Library [record ascl:1208.017] [Google Scholar]
- Roman-Duval, J., Jackson, J. M., Heyer, M., et al. 2009, ApJ, 699, 1153 [NASA ADS] [CrossRef] [Google Scholar]
- Roman-Duval, J., Jackson, J. M., Heyer, M., Rathborne, J., & Simon, R. 2010, ApJ, 723, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Roman-Duval, J., Heyer, M., Brunt, C. M., et al. 2016, ApJ, 818, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Schuller, F., Csengeri, T., Urquhart, J. S., et al. 2017, A&A, 601, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, R., Rathborne, J. M., Shah, R. Y., Jackson, J. M., & Chambers, E. T. 2006, ApJ, 653, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., Rivolo, A. R., Barrett, J., & Yahil, A. 1987, ApJ, 319, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Straižys, V., Černis, K., & Bartašiūtė, S. 2003, A&A, 405, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Su, Y., Yang, J., Zhang, S., et al. 2019, ApJS, 240, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Umemoto, T., Minamidani, T., Kuno, N., et al. 2017, PASJ, 69, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Urquhart, J. S., König, C., Giannetti, A., et al. 2018, MNRAS, 473, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, K., Testi, L., Ginsburg, A., et al. 2015, MNRAS, 450, 4043 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Waskom, M., Botvinnik, O., O’Kane, D., et al. 2018, mwaskom/seaborn: v0.9.0 [Google Scholar]
- Wilson, T. L., Rohlfs, K., & Hüttemeister, S. 2014, Tools of Radio Astronomy (Berlin: Springer-Verlag) [Google Scholar]
- Zhang, B., Moscadelli, L., Sato, M., et al. 2014, ApJ, 781, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, M., Kainulainen, J., Mattern, M., Fang, M., & Henning, T. 2019, A&A, 622, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhou, C., Zhu, M., Yuan, J., et al. 2019, MNRAS, 485, 3334 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, C., Battersby, C., & Goodman, A. 2018, ApJ, 864, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, C., Speagle, J. S., Schlafly, E. F., et al. 2019, ApJ, 879, 125 [NASA ADS] [CrossRef] [Google Scholar]
The normalisation factor of 0.7 corrects for the different distance to the Galactic centre of R0 = 10 kpc used by Solomon et al. (1987).
See Sect. 3.3.1 in Riener et al. (2019) for more details.
All Tables
Expected velocity dispersion values based on a size-linewidth relationship for different physical extents of the beam size at different distances.
Smoothing parameters (in units of spectral channels) obtained for the GAUSSPY+ training sets.
Smoothing parameters (in units of spectral channels) obtained for training set decompositions with SCOUSEPY and GAUSSPY+.
Percentages of refitted spectra, added and subtracted fit components, and flagged spectra after each stage of GAUSSPY+.
Threshold between optically thin and thick emission for given excitation temperature values.
Smoothing parameters (in units of spectral channels) obtained for decompositions of the GAUSSPY+ training sets for the 13CO and C18O MWISP datasets.
All Figures
 |
Fig. 1 Average spectra of the full GRS data set (grey lines) and our final Gaussian decomposition results (blue lines). The three panels show different ways the average spectra were created: in (a) we use all voxels, in (b) we use only the voxels retained from moment masking, and in (c) we use only voxels whose intensity value is above a S/N threshold of 3. The red line in panel c shows an average of high negative values throughout the GRS data set that was obtained by using only voxels with a value below − 3 × S∕N. The inset inthe right panel shows a zoom-in of the red line to better display the individual smaller negative peaks. See Sect. 3.2 for more details. |
| In the text | |
 |
Fig. 2 Top: zeroth moment map of the GRS data set recreated from the Gaussian fit components and integrated over the entire velocity range (− 5 ≲ vLSR ≲ 135 km s−1). When displayed in Adobe Acrobat, it is possible to switch to the map of the original data set. Bottom: map of the normalised residual values. |
| In the text | |
 |
Fig. 3 Top: PV map of the decomposed GRS data set. The emission was integrated over the full Galactic latitude range (± 1.1°). When displayed in Adobe Acrobat, it is possible to switch to the map of the original data set. Bottom: map of the normalised residual values. Overplotted on both panels are positions of spiral arms, spurs, and local Galactic features from Reid et al. (2016). |
| In the text | |
 |
Fig. 4 Map of the number of fitted Gaussian components per spectrum. |
| In the text | |
 |
Fig. 5 Histogram of the number of fitted Gaussian components per spectrum across the whole GRS data set for the full decomposition results (black line) and the fit components with S∕N > 3 (blue). The inset shows the same distribution on a logarithmic scale. |
| In the text | |
 |
Fig. 6 Histogram of intensity values for all fit components (black line) and fit components with S∕N > 3 (blue). The inset shows the same distribution on a logarithmic scale. The dotted vertical line shows the 3 × S∕N limit for thepeak value of the noise distribution (shown in Fig. B.2). The hatched areas mark the IQRs of the two distributions. The bin width is 0.05 K. |
| In the text | |
 |
Fig. 7 Histogram of centroid velocity values for all fit components (black) and fit components with S∕N > 3 (blue). The bin width is 1 km s−1. |
| In the text | |
 |
Fig. 8 Histogram of velocity dispersion values for all fit components (black) and fit components with S∕N > 3 (blue). The upper abscissa indicates corresponding upper limits for turbulent Mach number values. The inset shows the same distribution on a logarithmic scale. The dotted vertical line indicates the velocity resolution of 0.21 km s−1. The hatched areas mark the IQRs of the two distributions. The bin width is 0.05 km s−1. |
| In the text | |
 |
Fig. 9 2D histogram of intensity and velocity dispersion values for all fit components. The dashed line shows the lower limit for a chosen significance value of |
| In the text | |
 |
Fig. 10 2D histogram of centroid velocity and velocity dispersion values for all fit components. The dashed horizontal line indicates the velocity resolution of 0.21 km s−1. The blue line shows the mean σv value per centroid velocity bin. The number of bins in either direction is 300. The data points with very low σv values located at ~63 < vLSR < 66 km s−1 are due to an instrumental artefact. |
| In the text | |
 |
Fig. 11 2D histogram of centroid velocity and intensity values for all fit components. The dashed horizontal line indicates a S/N limit of 3 for σ(TMB) = 0.12 K, which corresponds to the 0.1st percentile of the noise distribution shown in Fig. B.2. The blue line shows the mean intensity value per centroid velocity bin. The number of bins in either direction is 300. |
| In the text | |
 |
Fig. 12 2D histogram of the velocity dispersion values against their Galactic latitude positions for all fit components with S∕N > 3. The dashed horizontal line indicates the velocity resolution of 0.21 km s−1. The blue line shows the mean σv value per Galactic latitude bin. The number of bins used in either direction is 358. |
| In the text | |
 |
Fig. 13 2D histogram of velocity dispersion values against their Galactic longitude positions for all fit components with S∕N > 3. The dashed horizontal line indicates the velocity resolution of 0.21 km s−1. In the horizontal and vertical direction we use 3415 and 200 bins, respectively. The blue line indicates the mean velocity dispersion value per Galactic longitude bin. The grey solid line is a smoothed version of the mean σv curve using a median filter with a kernel of ~3°. Dashed vertical lines show the approximate location of the giant HII region complex W43. |
| In the text | |
 |
Fig. 14 Ridge plots showing PDFs of integrated 13CO emission (left panel) and H2 surface density values inferred from dust emission (right panel). For the left panel, each row shows the PDF of the WCO values of all spectra fitted with Ncomp components (indicated with the number to the left and the colour-shading of the PDF). For the right panel, each row shows the PDF of the |
| In the text | |
 |
Fig. 15 Face-on view of the Galactic plane. The black solid lines show constant projected vLSR values of − 5 and 20 km s−1. The orange-shaded area indicates the coverage of the GRS. Inferred positions and estimated widths for the Perseus and Outer spiral arm from Reid et al. (2019) are shown with the shaded green and blue areas, respectively. The central positions of the spiral arms are marked with solid and dashed lines depending on whether the majority of the arm is visible in the selected velocity range of − 5 < vLSR < 20 km s−1. The position of the Galactic centre and the sun are indicated with a black dot and the sun symbol, respectively. Dotted grey lines indicate distances to the sun in 2.5 kpc intervals. The black dash-dotted line shows the distances used to estimate the FWHM extent of the molecular gas disk. See Sects. 6.1 and 6.2 for more details. |
| In the text | |
 |
Fig. 16 Top: zeroth moment map of the decomposed data set integrated within − 5 < vLSR < 20 km s−1. Bottom: velocity dispersion values for the narrowest fit component within the same vLSR range as used in the top panel. The second scaling on the colourbar indicates corresponding estimates for upper limits of the turbulent Mach number. In both panels we show: the position of the Perseus and Outer spiral arms as inferred by Reid et al. (2019) (green and blue lines, respectively, cf. Fig. 15); black contours indicating a WCO value of 0.5 K km s−1; a fit to the positions with σv values >1 km s−1 (dash-dotted black line); and the estimated FWHM extent of the molecular gas disk on the far side of the Milky Way (dashed black lines). See Sect. 6.4 for more details. When displayed in Adobe Acrobat, it is possible to switch to the channel map of the original data set, show only the positions with σv values > 1 km s−1, hide the contours, hide the fit to the positions with σv values > 1 km s−1 and estimated FWHM extent of the gas disk, and hide the positions of the Perseus arm and Outer arm. |
| In the text | |
 |
Fig. B.1 Map of determined rms noise (given in antenna temperature values). |
| In the text | |
 |
Fig. B.2 Histogram of determined rms noise (given in antenna temperature values) for all spectra in the GRS. Theinset shows the same distribution on a logarithmic scale. The red line in the inset indicates masked out spectra with high noise values. The grey-shaded area marks the IQR, ranging from about 0.1− 0.16 K. The bin width is 0.005 K. |
| In the text | |
 |
Fig. B.3 Histogram of p-values from normality tests for the distribution of residual values for all GRS spectra (blue) and GRS spectra that have at least one fit component (black). The inset shows the same distribution on a logarithmic scale. The dashed vertical line marks the default p-value limit, below which GAUSSPY+ tries to refit spectra if possible. The grey-shaded area marks the IQR for the distribution of spectra with fitted components, ranging from about 0.03−0.3. The bin width is 0.02 dex. |
| In the text | |
 |
Fig. B.4 Histogram of |
| In the text | |
 |
Fig. B.5 Map of |
| In the text | |
 |
Fig. C.1 Optical depth of 13CO as a function of main beam brightness temperature for different excitation temperature (Tex) values. The dotted horizontal line marks the threshold between the regimes where 13CO is optically thin or thick. |
| In the text | |
 |
Fig. C.2 Maps for the region containing the elongated molecular cloud G24. (a) Zeroth moment map of the 13CO emission.(b) Map of determined excitation temperature values. (c) Map of determined |
| In the text | |
 |
Fig. C.3 Distributions of fit parameters for the decomposition of the GRS (left), MWISP (middle), and the difference between the two data sets (right). The rows show normalised 2D histograms of: peak main beam brightness temperature and velocity dispersion values (top), centroid velocity and peak main beam brightness temperature values (middle), centroid velocity and velocity dispersion values (bottom). Colourbars in all panels indicate the values of the normalised 2D distributions. |
| In the text | |
 |
Fig. C.4 2D distribution of determined Tex and |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.