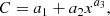| Issue |
A&A
Volume 626, June 2019
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 17 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201935131 | |
| Published online | 21 June 2019 | |
Recovering the unsigned photospheric magnetic field from Ca II K observations
1
Max Planck Institute for Solar System Research, Justus-von-Liebig-weg 3, 37077 Göttingen, Germany
e-mail: chatzistergos@mps.mpg.de, theodosios.chatzistergos@inaf.it
2
INAF Osservatorio Astronomico di Roma, Via Frascati 33, 00078 Monte Porzio Catone, Italy
3
School of Space Research, Kyung Hee University, Yongin, Gyeonggi 446-701, Republic of Korea
Received:
25
January
2019
Accepted:
9
May
2019
Context. A number of studies have aimed at defining the exact form of the relation between magnetic field strength and Ca II H and K core brightness. All previous studies have however been restricted to isolated regions on the solar disc or to a limited set of observations.
Aims. We reassess the relationship between the photospheric magnetic field strength and the Ca II K intensity for a variety of surface features as a function of the position on the disc and the solar activity level. This relationship can be used to recover the unsigned photospheric magnetic field from images recorded in the core of Ca II K line.
Methods. We have analysed 131 pairs of high-quality, full-disc, near-co-temporal observations from the Helioseismic and Magnetic Imager (SDO/HMI) and Precision Solar Photometric Telescope (Rome/PSPT) spanning half a solar cycle. To analytically describe the observationally determined relation, we considered three different functions: a power law with an offset, a logarithmic function, and a power-law function of the logarithm of the magnetic flux density. We used the obtained relations to reconstruct maps of the line-of-sight component of the unsigned magnetic field (unsigned magnetograms) from Ca II K observations, which were then compared to the original magnetograms.
Results. We find that both power-law functions represent the data well, while the logarithmic function is good only for quiet periods. We see no significant variation over the solar cycle or over the disc in the derived fit parameters, independently of the function used. We find that errors in the independent variable, which are usually not accounted for, introduce attenuation bias. To address this, we binned the data with respect to the magnetic field strength and Ca II K contrast separately and derived the relation for the bisector of the two binned curves. The reconstructed unsigned magnetograms show good agreement with the original ones. Root mean square differences are less than 90 G. The results were unaffected by the stray-light correction of the SDO/HMI and Rome/PSPT data.
Conclusions. Our results imply that accurately processed and calibrated Ca II K observations can be used to reconstruct unsigned magnetograms by using the relations derived in our study.
Key words: Sun: activity / Sun: photosphere / Sun: chromosphere / Sun: faculae, plages / Sun: magnetic fields
© T. Chatzistergos et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
Babcock & Babcock (1955) noticed a “one-to-one correspondence” between bright regions in Mt Wilson Ca II K spectroheliograms and magnetic regions in magnetograms. This reported association, which was promptly confirmed by Howard (1959) and Leighton (1959), initiated numerous studies of solar and stellar Ca II data. Since then, considerable efforts have been devoted to understanding the relation between the magnetic field strength and the Ca II K intensity for different solar magnetic regions on the Sun (e.g. Frazier 1971; Skumanich et al. 1975; Schrijver et al. 1989; Nindos & Zirin 1998; Harvey & White 1999; Vogler et al. 2005; Rast 2003a; Ortiz & Rast 2005; Rezaei et al. 2007; Loukitcheva et al. 2009; Pevtsov et al. 2016; Kahil et al. 2017, 2019). Table 1 summarises the main features and results of the earlier studies compared with the results of this one. All previous works were based on analysis of small data samples (with the possible exception of Vogler et al. 2005), mainly considering regions at the disc centre and using data with a spatial resolution lower than ≈2″. Most earlier studies reported that the link between the magnetic field strength and Ca II K intensity is best described by a power-law function with an exponent in the range 0.3−0.6. However, Skumanich et al. (1975) and Nindos & Zirin (1998) found that their data were best represented by a linear relation, while Kahil et al. (2017, 2019) found a logarithmic function to fit their data best. It is worth noting that the latter authors analysed Ca II H observations taken with the Sunrise balloon-borne telescope (Solanki et al. 2010, 2017; Barthol et al. 2011), which have a higher spatial resolution than in previous studies. These (and other similar) studies are discussed in detail in Sect. 3.7.
Previously published results on the relation between magnetic flux and Ca II intensity along with our results.
Major efforts have also been invested to measure the disc-integrated Ca II H and K emission of many other stars. Such measurements have regularly been carried out for example within the synoptic ground-based programs at Mt Wilson (1966–2003, Wilson 1978; Duncan et al. 1991; Baliunas et al. 1995) and Lowell Observatories (1994–present, Hall et al. 2007), as well as by the space-born photometer on-board the CoRoT mission (Michel et al. 2008; Auvergne et al. 2009; Gondoin et al. 2012). Ca II H and K emission is an indicator of the strength of, and the area covered by, magnetic fields on the Sun (Leighton 1959). Since the Ca II H and K variations due to magnetic regions are of the order of a few tens of percent, they can be easily detected for many active stars. Hence, the Ca II H and K measurements have been used to trace long-term changes in surface activity of stars caused by for example the activity cycle, rotation, and convection (e.g. Sheeley 1967; White & Livingston 1978; Keil & Worden 1984; Baliunas et al. 1985, etc.). These studies have led to an improved knowledge of stellar rotation and activity, and of the degree to which the Sun and other stars share similar dynamical properties (for reviews, see e.g. Lockwood et al. 2007, 2013; Hall 2008; Reiners 2012). It is worth noting that stellar Ca II observations are per force integrated over the whole stellar disc. However, except for the studies of Harvey & White (1999), Vogler et al. (2005), and Pevtsov et al. (2016), restricted to a few images, no other previous investigation has determined the relation between Ca II brightness and magnetic field strength covering the full solar disc.
Furthermore, many studies require long data sets of the solar surface magnetic field, for example to derive information on the structure, activity, and variability of the Sun, or for related applications such as the climate response of Earth to solar irradiance variability. Regular magnetograms are however available only for the last four solar cycles, while synoptic Ca II K solar observations have been carried out for more than 120 years (Chatzistergos 2017; Chatzistergos et al. 2019a). In recent years, following the availability of a number of digitized series of historical Ca II K observations, attempts have been made to reconstruct magnetograms from Ca II K observations based on the relation between the Ca II K intensity and the magnetic field strength. In particular, Pevtsov et al. (2016) reconstructed magnetograms from Ca II K synoptic charts made from Mt Wilson observatory images. For their reconstruction they used sunspot records to get information about the polarity and assigned each plage area with a single magnetic field strength value based on the area of the plage. The areas and locations of plage regions were derived from photometrically uncalibrated Ca II K images. Besides that, Sheeley et al. (2011) and Chatterjee et al. (2016) constructed Carrington maps with Ca II K images from the Mt Wilson and Kodaikanal observatories, respectively. These maps can be used to trace the evolution of the plage regions. Nevertheless, they provide Ca II K contrast and need to be converted into magnetic field strength for any application based on magnetic field measurements.
In this paper, we study the relationship between the magnetic field strength and the Ca II K intensity using data from two archives of high-quality full-disc solar observations. We use significantly more data of higher quality than in previous studies, which allows a more detailed and accurate assessment of this relationship over the whole disc and at different levels of solar activity during cycle 24. We test the accuracy of our results by applying the derived relationship to reconstruct unsigned magnetograms and then comparing them with the actual ones.
This paper is organised as follows. Section 2 describes the data and methods employed for our analysis. In Sect. 3 we study the relation between the magnetic field strength and the Ca II K excess intensity. In Sect. 4 we use our results to reconstruct magnetograms from the Ca II K images and to test the accuracy of our method. Finally we draw our conclusions in Sect. 5.
2. Data and methods
2.1. Data
We analysed full-disc photospheric longitudinal magnetograms and continuum intensity images from the space-borne Helioseismic and Magnetic Imager (HMI, Scherrer et al. 2012; Schou et al. 2012) aboard the Solar Dynamics Observatory (SDO, Pesnell et al. 2012), and full-disc filtergrams taken at the Ca II K line and red continuum from the Precision Solar Photometric Telescope at the Rome Observatory (Rome/PSPT, Ermolli et al. 1998, 2007). Figure 1 shows examples of the analysed SDO/HMI and Rome/PSPT images.
 |
Fig. 1. Examples of the observations analysed in this study taken on 01 April 2011 at 09:06:00 UT. Panel a: SDO/HMI unsigned BLOS magnetogram. Panel b: SDO/HMI continuum contrast image (i.e. compensated for intensity CLV). Panel c: Rome/PSPT Ca II K. Panel d: red continuum contrast images. The grey-scale bars on the right-hand side of each panel show magnetic signal in G and contrast, respectively. The squares indicate the insets shown in Fig. A.1. |
Rome/PSPT, in operation since 1996, is a 15 cm telescope designed for photometric solar observations characterised by 0.1% pixel-to-pixel relative photometric precision (Coulter & Kuhn 1994). The images1 were acquired with narrow-band interference filters by single exposure of a 2048 × 2048 CCD array. The filters employed for the observations analysed here are centred at the Ca II K line core (393.3 nm) with a bandwidth of 0.25 nm, and in the red continuum at 607.2 nm with a bandwidth of 0.5 nm. The Ca II K and red continuum images were taken within 3 min of each other. At the acquisition, the data were reduced to a pixel scale of 2″ to account for typical conditions of local seeing. Standard instrumental calibration has been applied to the data (Ermolli et al. 1998, 2010).
In operation since April 2010, SDO/HMI takes full-disc 4096 × 4096 pixel filtergrams at six wavelength positions across the Fe I 617.3 nm line at 1.875 s intervals. The filtergrams are combined to form simultaneous continuum intensity images and longitudinal magnetograms with a pixel scale of 0.505″ and 45 s cadence. For each Rome/PSPT image pair, we took the 360 s average of the SDO/HMI images and magnetograms taken close in time (on average less than 2 min apart and no more than 8 min). The averaging was done to suppress intensity and magnetogram signal fluctuations from noise and p-mode oscillations.
For our analysis, we have selected data with the highest spatial resolution (for Rome/PSPT), closest time between SDO/HMI and Rome/PSPT observations, and highest signal-to-noise ratio. We avoided winter periods and kept observations mostly during summer months, when the seeing-induced degradation in Rome/PSPT data is lower. Our data sample consists of 131 sets of near-simultaneous observations. These observations cover the period between 18 May 2010 and 29 August 2016.
We have ignored the pixels in SDO/HMI magnetograms with flux density below 20 G. The value of 20 G corresponds roughly to three times the noise level as evaluated by Yeo et al. (2013, 2014a). Since the magnetic flux tubes making up network and plage tend towards an orientation normal to the surface, while magnetograms measure the line-of-sight (LOS) component of it (BLOS), we divided the pixel signal by the corresponding μ (cosine of the heliocentric azimuthal angle) to get the intrinsic magnetic field strength. We also removed the polarity information from the SDO/HMI data, and only considered the absolute value of the magnetic flux density, |BLOS|/μ (i.e. the magnetic field strength averaged over the effective pixel).
The Rome/PSPT images were first rescaled to match the size of SDO/HMI so that we could align both observations with highest accuracy. The Rome/PSPT images were then rotated and aligned to the SDO/HMI observations, by applying compensations for ephemeris. All observations were then re-scaled to the original dimensions of Rome/PSPT. To further reduce effects due to seeing, we also reduced the resolution of the SDO/HMI data to that of the Rome/PSPT by smoothing them with a low-pass filter with a 2 × 2 pixel running window width. In the following, we refer to the thus-obtained SDO/HMI data as SDO/HMI degraded magnetograms.
For each analysed intensity image (Rome/PSPT and SDO/HMI) we removed the limb darkening and obtained a contrast map. In particular, for each image pixel i, we defined its contrast Ci as 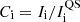 , where Ii is the measured intensity of pixel i, and
, where Ii is the measured intensity of pixel i, and 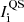 is the intensity of the quiet Sun (QS) at the same position. The latter was derived with the iterative procedure described by Chatzistergos et al. (2018a), which returns contrast images with an average error in contrast values lower than 0.6% (see Chatzistergos et al. 2018a, for more details).
is the intensity of the quiet Sun (QS) at the same position. The latter was derived with the iterative procedure described by Chatzistergos et al. (2018a), which returns contrast images with an average error in contrast values lower than 0.6% (see Chatzistergos et al. 2018a, for more details).
Since our aim here was a study of the relation between the magnetic field strength and Ca II K brightness in bright magnetic regions, we masked out sunspots in the magnetograms and in Ca II K observations. Sunspots were identified in SDO/HMI continuum intensity as regions having intensity contrast lower than 0.89 (following Yeo et al. 2013) and in Rome/PSPT red continuum images lower than 0.95. The above thresholds were derived as the average value of C̄ − 3σ, where C̄ is the average value of contrast over the disc and σ is the standard deviation of contrast values, from all Rome/PSPT red continuum and SDO/HMI continuum images separately. The plage regions immediately surrounding sunspots were excluded as well, as they could be affected by stray-light and by extended low-lying sunspot canopies (e.g. Giovanelli & Jones 1982; Solanki et al. 1994, 1999), as was shown by Yeo et al. (2013). This was done by expanding the sunspot regions with a varying size kernel, corresponding to 10 × 10 and 30 × 30 pixel2 at disc centre and limb, respectively. The excluded regions have areas on average 0.001 in fraction of the disc, while the maximum value is 0.005. These regions amount on average to 13 ± 9% of the total flux in the original magnetograms, which appears to be roughly constant in time for the analysed data.
2.2. Stray-light removal
To investigate whether our results depend on the removal of stray-light from the analysed images, we restored 51 pairs of the SDO/HMI and Rome/PSPT images following Yeo et al. (2014b) and Criscuoli & Ermolli (2008), respectively. We also analysed a sample of ten SDO/HMI magnetograms from our dataset which were restored with the method employed by Criscuoli et al. (2017). Employment of different methods helps us to assess the potential errors in the relation between the Ca II K contrast and the magnetic field strength due to the stray-light degradation.
For the SDO/HMI observations, the point-spread function (PSF) of the instrument was deconvolved from Stokes I and V observables, which were then used to produce the stray-light corrected magnetograms. The PSF derived by Yeo et al. (2014b) has the form of the sum of five Gaussian functions. The PSF parameters were determined from the Venus transit data by performing a fit over the shaded areas.
The PSF applied by Criscuoli et al. (2017) instead has the form of an Airy function convolved with a Lorentzian. The parameters of the PSF were derived using pre-launch testing data as well as post-launch off-limb data taken during a partial lunar eclipse and the transit of Venus. According to Criscuoli et al. (2017), the PSF employed by Yeo et al. (2014b) does not account for large-angle or long-distance scattering, thus affecting results from analyses of data concerning large spatial scales on the solar disc such as in the present study.
The Rome/PSPT data were deconvolved using analytical functions defined from modelling the centre-to-limb variation of intensity in the data and instrumental PSF (Criscuoli & Ermolli 2008). The PSF here is modelled as the sum of three Gaussian functions and one Lorentzian function, following Walton & Preminger (1999).
2.3. Segmentation
For our analysis we selected pixels that correspond to magnetic regions in magnetograms and bright regions in Ca II K images. We identified features of interest with two methods.
Method 1. We distinguished between two different types of bright magnetic features: plage and the network. These are differentiated with single-contrast and |BLOS|/μ thresholds in Ca II K and magnetograms, respectively. The thresholds are 20 G ≤ |BLOS|/μ < 60 G and 1.12 ≤ C < 1.21 for network and |BLOS|/μ ≥ 60 G and C ≥ 1.21 for plage. The thresholds given above for plage in the magnetograms, as well as for the network in Ca II K images, were acquired by minimising the differences between the average disc fractions calculated in the magnetograms and the Ca II K images.
Method 2. We used this method to isolate individual activity clusters which may be composed of multiple close or overlapping active regions (ARs). In this way we can study how the relation between the magnetic field strength and the Ca II K contrast varies among features of different sizes and locations on the disc. We applied a low-pass filter with a 50 pixel window width to the degraded magnetograms and a constant threshold of |BLOS|/μ = 15 G to isolate individual magnetic regions. Contiguous pixels were grouped together, and all isolated regions were considered as separate clusters. We also applied a size threshold of 50 pixels to the clusters. Pixels not assigned to any cluster were categorised as QS, though they include the network as well. This method is similar to that used by Harvey & White (1999).
In our analysis we excluded all pixels with μ < 0.14 (outermost 1% of the solar radius) to restrict errors due to projection effects. Finally, the sunspot regions were also excluded from all masks as described in Sect. 2.1.
Figures 2a and b show the masks derived from the SDO/HMI magnetogram and the Rome/PSPT Ca II K image using Method 1 on the images shown in Figs. 1a and c, respectively. Figure 2c shows the mask derived with Method 2 on the Ca II K image shown in Fig. 1a.
 |
Fig. 2. Segmentation masks of bright magnetic features derived from the observations shown in Fig. 1 by applying the two methods described in Sect. 2.3. Panel a: mask of magnetogram and panel b: mask of Ca II K image derived with Method 1, showing plage (red), network (green), and QS (blue). Panel c: mask of magnetogram derived with Method 2, showing individual activity clusters with different colours (the QS is in dark blue). The masks are shown prior to the exclusion of the sunspot regions. |
3. Results
3.1. Pixel-by-pixel relationship
We first considered the data without the corrections for stray-light and without performing any segmentation other than excluding the sunspot regions. Figure 3 shows the relation between the Ca II K brightness and |BLOS|/μ for all pairs of the degraded magnetograms and corresponding Ca II K images considered in our study. Each colour-coded pixel represents the logarithm of the number density within bins of 1 G and 0.01 in contrast. The sources of the scatter seen in Fig. 3 are discussed in more detail in Appendix A. Briefly, one reason for the scatter of values is the projection effect. The SDO/HMI and Rome/PSPT observations sample different formation heights, which introduces changes in the distribution and shape of flux elements over space. Due to the expansion of the flux tubes with height, the magnetic features at the two heights have different sizes, which leads to a size mismatch between the same feature seen in a magnetogram and in the corresponding Ca II K data and therefore also contributes to the scatter. Another source of scatter is the diverse spatial and spectral resolution of the compared data. In Appendix A we discuss the spatial correspondence between the features in the magnetograms and the Ca II K observations and show close-ups of a quiet and an active region to demonstrate the smearing of the features in the Ca II K observations compared to the magnetograms.
 |
Fig. 3. Ca II K contrast plotted against the unsigned LOS magnetic flux density divided by μ (|BLOS|/μ) for all pixel pairs (excluding sunspots) in all available images. The pixels are colour-coded denoting the logarithm of the number density within bins of 1 G and 0.01 in contrast. The contour lines give the logarithm of the pixel number density in intervals of 0.5. Curves show 5000-point running means (over |BLOS|/μ in yellow, over contrast in light blue, and their bisector in purple), as well as PF (red), PFL (blue), and LFL (green) fits on the binned curve over |BLOS|/μ (yellow curve). The vertical grey dashed line denotes the 20 G threshold in |BLOS|/μ. A magnified section for low |BLOS|/μ is shown at the lower right corner of the figure to illustrate the differences of the different fits over that region. Also shown are histograms of |BLOS|/μ within 3 ranges of contrast values (right) and histograms of Ca II K contrast for 4 ranges of |BLOS|/μ (top). The ranges used for the histograms are shown on the upper part of the corresponding sub-plot. |
The Spearman correlation coefficient between |BLOS|/μ and Ca II K contrast supports a monotonous relationship. The coefficient obtained for individual images is on average ρ = 0.60, while it is ρ = 0.98 for all pixels from all data. The significance level is zero with double-precision accuracy, implying a highly significant correlation.
Figure 3 shows that the Ca II K contrast increases with increasing magnetic field strength, but tends to saturate at high |BLOS|/μ (see e.g. Saar & Schrijver 1987; Schrijver et al. 1989). The yellow curve in Fig. 3 is a running mean over |BLOS|/μ values. Fitting the points of this binned curve has been the most common approach in the literature when studying the relation between Ca II K contrast and magnetic field strength (e.g. Rast 2003a; Ortiz & Rast 2005; Rezaei et al. 2007; Loukitcheva et al. 2009; Pevtsov et al. 2016; Kahil et al. 2017, 2019). This binning suggests that the relation saturates at around 400 G. However, binning the data over the Ca II K contrast values suggests a somewhat different relation. We found that the choice of the quantity over which the binning is performed affects the exact form of the relation between the magnetic field strength and the Ca II K intensity. Attenuation bias due to errors in the independent variable in each case can cause these relations to skew compared to the true relationship. This result, not yet reported in the literature, also needs to be considered when comparing outcomes from different studies. We note that the histograms shown in Fig. 3 illustrate that the distribution of contrast values is, to a good approximation, symmetric around the mean value for 150 G < |BLOS|/μ < 450 G. The distribution for high and low |BLOS|/μ is skewed with a tail for high and low contrasts, respectively.
To find the best relation describing the data, we considered three different functions: a) a power law with an offset (PF) as commonly used in the literature (e.g. Schrijver et al. 1989; Harvey & White 1999; Ortiz & Rast 2005; Rezaei et al. 2007; Loukitcheva et al. 2009); b) a logarithm (LFL) as proposed by Kahil et al. (2017, 2019); and c) a power-law function of the logarithm of |BLOS|/μ (PFL). These three functions can be described by the following equation:
where x = |BLOS|/μ for PF, and x = log(|BLOS|/μ) for PFL and LFL (with a3 = 1 for LFL). We perform these fits on the curve that resulted by averaging contrast values over |BLOS|/μ values (yellow curve in Fig. 3), based on all selected pixel pairs from all images where |BLOS|/μ ≥ 20 G. However, for comparison we also performed the fits on the curve after binning over contrast values and on the bisector of the two running means (these sets of fits will be referred to as PF*, PFL*, and LFL*).
The fits with the three tested functions for the |BLOS|/μ binning (yellow solid line in Fig. 3) are shown in Fig. 3, with red dashed line (PF), blue dotted line (PFL), and green dashed line (LFL). Table 2 lists the derived parameters.
Results of fitting.
Both PF and PFL give low values for χ2, namely ≃0.16 and ≃0.1, respectively. The fitted curve for both PF and PFL does not follow the binned curve for high |BLOS|/μ, lying above it. The curves for PF and PFL closely follow each other up to about 400 G, but slightly diverge at higher magnetic field strengths, with PFL following the binned curve more closely; they also differ for |BLOS|/μ < 20 G (which were not included in the fit, so that the curves are extrapolated there), with PFL giving higher contrasts. However, the differences between the two curves are minute. We found that the exponents for PF and PFL increase when the fit is performed on the curves binned over contrast values or on the bisector (see Table 2), while the χ2 is reduced, being 0.03 and 0.01, respectively. The LFL fails to reproduce the binned curve over |BLOS|/μ, but follows the trend of the curve for |BLOS|/μ > 400 G slightly better than PF or PFL. However, the fit of LFL gives high values for χ2 (2.24), showing that LFL does not describe the data well.
The analysis described in the following was performed by applying all functions and binning curves described above to the available data. However, due to the similarity of the results obtained from the PF and PFL fits and the lower accuracy of the LFL fit compared to both PF and PFL fits, for the sake of clarity we present only the results for PFL* and PF. Our analysis suggests that the PFL* fit is more accurate and stable (see Sect. 4) than the other considered functions, while those derived with the PF fit allow for comparison with previous results in the literature. We note however that due to the scatter in Fig. 3 we cannot rule out the aptness of PF to describe the relation between the magnetic field strength and the Ca II K brightness. The results derived with PF* and LFL* fits can be found in Chatzistergos (2017).
3.2. Effects of the |BLOS|/μ threshold on the derived exponents
To better understand the sources of differences with other results, we have studied how our findings depend on the |BLOS|/μ threshold applied. Figure 4 shows the parameters derived by applying PF and PFL to the data shown in Fig. 3 and varying the threshold in |BLOS|/μ between 1 G and 50 G, that is 0.15 to 7 times the noise level. We show only the exponents, though the other parameters of the tested functions are affected as well. We show the results of performing the fit to all three binned curves as shown in Fig. 3. For the binning over |BLOS|/μ, the exponent for PF constantly decreases, while for PFL it reaches a plateau for magnetic field strengths in the range of ∼5–20 G and then slightly decreases. When the fit is performed on the bisector, the exponents for PF* and PFL* reach a plateau after a threshold of ∼8 G and ∼18 G, respectively, and after that they tend to slightly decrease. The exponent we derived for PFL* (Table 2) lies within the 1σ interval of all derived exponents with thresholds greater than 18 G. For the binning over contrast values, the exponents of PF and PFL show an almost constant increase for |BLOS|/μ > 10 G.
 |
Fig. 4. Parameters of the fits (Eq. (1)) as a function of the threshold in |BLOS|/μ for PF (panel a) and PFL (panel b) fits. The fits are performed on the curves derived by binning over |BLOS|/μ (blue), contrast values (yellow), and the bisector (red). The dotted line in each panel is the best fit parameter derived with the threshold of |BLOS|/μ = 20 G for the blue points. |
The threshold seems to play a more important role if the fit is performed by binning over contrast values or |BLOS|/μ compared to the results of the fit on the bisector. Overall, the curves derived with PFL* are more stable against the choice of the |BLOS|/μ threshold. In Fig. 5 we show the results of fitting PF to the binned curve over |BLOS|/μ by varying the threshold between 1 G and 50 G. All of the derived curves agree very well for the interval 50–350 G, but they diverge for higher and lower values. This is expected since the low |BLOS|/μ regions dominate the relation and by increasing the threshold it shifts the weight for the fit to higher |BLOS|/μ.
 |
Fig. 5. As in Fig. 3 but showing only the results of PF on the binned curve over |BLOS|/μ (yellow curve) by varying the |BLOS|/μ threshold, i.e. the magnetogram noise cut-off (dotted coloured curves). The threshold is 1 G for the black curve and rises to 50 G for the red curve. The curve corresponding to the 20 G threshold adopted in this study is shown with the light-blue solid curve. The thick yellow curve shows 5000-point running mean over |BLOS|/μ. The vertical grey dashed line denotes the 20 G threshold in |BLOS|/μ. |
3.3. Exponents over time and different μ positions
We also studied if the exponents of the fits change with the activity level. To understand the change with time we performed the fits on every image separately, first for all pixels with μ > 0.14, and then for the plage and network regions separately. The differentiation between the various types of features was done with Method 1 applied to Rome/PSPT images, but keeping only the regions that also have |BLOS|/μ > 20 G in the magnetograms. To study the variation of the exponent we fixed a1 and a2 for the PF and PFL fits to the values derived in Sect. 3.1 (listed in Table 2).
Figure 6 shows the coefficients of the fits to the curve binned over |BLOS|/μ as a function of time. The resulting exponents for PF and PFL depend on the type of feature and are slightly higher for plage than for the network. The uncertainty in the derived parameters (not shown in Fig. 6 due to their low values) is less than 0.001 for a3 in PF and 0.014 for a3 in PFL*. Performing the fit to all pixels on the disc with μ > 0.14 and each image separately, we found an average exponent of 0.52 ± 0.02 and 3.9 ± 0.1 for PF and PFL*, respectively. The errors are the 1σ intervals among all the daily calculated values. These values agree within the 1σ uncertainty level with those we derived in Sect. 3.1 for all three functions. As seen in Fig. 6 the scatter of the resulting exponents is such that within the limits of the current analysis, we found no evidence that the relationship between |BLOS|/μ and Ca II K intensity varies over the solar cycle. We noticed exactly the same behaviour for the plage component for PF and PFL*. We found some changes in the network component that result in higher exponents for the low activity period in 2010 for PF and PFL*, but the derived exponents are still constant in time within the uncertainties.
 |
Fig. 6. Parameters of the fits (Eq. (1)) as a function of time, derived for all bright features (black), as well as for the network (blue), and plage (red) separately, for PF (panel a) and PFL* (panel b) fits. The dashed lines connect the median values obtained from all analysed images within a given year, while the dotted lines mark the values of the parameters of the best fit derived in Sect. 3.1. The shaded grey surface in panel (b) shows the plage areas determined with Method 1 from the Rome/PSPT images. The areas were scaled to have a maximum value of 4.2 and minimum value 2.8 in order to match the range of values shown in panel (b); they indicate the level of solar activity at the considered times. |
We have also studied how the exponents of the fits change for different positions of the disc. Figure 7 shows the coefficients of the various features as a function of their position on the solar disc in terms of μ. The segmentation was done with Method 1, identifying plage and network regions. We considered ten concentric annuli of equal area covering the solar disc up to μ = 0.14. The mean values of the exponents computed over the various annuli slightly decrease towards the limb, but their standard deviation increases so that the exponents do not show any significant variation with the position on the disc (within the 1σ uncertainty). In particular, the relative difference between the average value of the exponents within the innermost and outermost annuli for PF (PFL*) is 4% (10%). The same behaviour is seen also when network and plage regions are considered separately.
 |
Fig. 7. Parameters of the fits (Eq. (1)) as a function of μ, derived for ten annuli of equal area for all bright features (black), as well as for the network (blue), and plage (red) separately, for PF (panel a) and PFL* (panel b). The values shown are the means over the entire sample of data, while the error bars denote the 1σ interval. Results for the network are shown in the middle of the μ interval they represent, while the others are slightly shifted in μ to improve the clarity of the plot. The dotted lines mark the values of the best fit parameters derived in Sect. 3.1. |
3.4. Exponents for individual activity clusters
We also tested how different the exponents of the fits are when applied to the data from individual activity clusters. The images were segmented with Method 2. We performed the fit with PFL* to each individual cluster, while we also considered the QS (including the network) separately. Figure 8 shows a scatter plot for the images shown in Fig. 1, but now including only the pixels corresponding to activity clusters and QS. The binned curves and the result of the fits from different activity clusters are in agreement with each other, with the exception of one cluster. However, this cluster is very small in size and the statistics are worse than for the other clusters. The relation derived from QS regions shows a smaller slope than the one obtained for active regions. However, this is probably due to a much lower number of QS and network pixels with strong resolved magnetic fields in the analysed SDO/HMI degraded data.
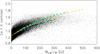 |
Fig. 8. Ca II K contrast plotted against |BLOS|/μ for all activity clusters identified with Method 2 in observations shown in Fig. 1 (black dots). The coloured curves are the result of the PFL* fit to the individual clusters, shown with the same colours as in Fig. 2c. |
Results for different clusters agree well with each other within the accuracy of the fit. Averaging all exponents derived for clusters (QS and network) from all images gave on average the values of 0.54 ± 0.03 (0.50 ± 0.01), and 3.9 ± 0.2 (3.7 ± 0.1), for PF and PFL*, respectively. The exponents derived here are in agreement with those presented in the previous subsections. We find no dependence on μ for the derived exponents with this segmentation method either.
Figure 9 shows the exponents derived with PF (red) and PFL* (blue) as a function of the area of the clusters expressed in fractions of the disc. We found no dependence of the exponent on the cluster size, however the uncertainty of the derived parameters was obviously higher for smaller features, because of poorer statistics. Also, effects of potential misalignment between SDO/HMI and Rome/PSPT data become more significant in this case. Find more information in Sect. 3.5.
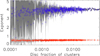 |
Fig. 9. Exponents of the PF (red) and PFL* (blue) fits as a function of size for individual activity clusters. The light grey and dark grey shaded areas denote the 1σ error in the fit parameters for PF and PFL*, respectively. |
3.5. Effects of potential misalignment
To test the sensitivity of our results to potential misalignment of the images, we repeated our analysis using Rome/PSPT images shifted by a random number of pixels, in both the x and y direction and compared the results with those from the original Rome/PSPT images. The test was done ten times, whereby the possible maximum offset varied between 1 and 10 pixels (2″ and 20″) in any direction. Each time, we performed 1000 computations with a random offset for each image lying in the range between zero and the maximum allowed value. The choice of a maximum offset of 10 pixels is extreme considering that the alignment with the data employed in this study is considerably more precise. However, it is useful to test such a high value in order to have an estimate of the errors when applying the relationships on lower resolution data or with greater temporal difference than the images analysed here, such as the magnetograms from Kitt Peak and Ca II K spectroheliograms from Kodaikanal observatory, which are taken on average more than 12 h apart. Figure 10 shows the relative difference of the derived exponents on each offset image from the original ones. Shown are the average values over the 1000 realisations on each image (abscissa) for each maximum possible offset (ordinate). We show the errors for the exponents derived for PF and PFL* in different panels. We notice that the errors are significant for PF, but they are considerably lower for PFL*. The errors in the derived parameters with PF reach 50%, while they are less than 8% for offsets of 1 pixel. With offsets up to 10 pixels (20″), the errors for the derived parameters with PFL* remain below 24%, while they are less than 13% and 2% for offsets of 5 and 1 pixels (10″ and 2″), respectively. We noticed that errors due to the offsets are higher during periods of low activity with all tested functions. This may be due to the smaller size of individual magnetic features when activity is low, so that an offset quickly leads to a substantial mismatch between the magnetic features in SDO/HMI and the brightness features in Rome/PSPT images.
 |
Fig. 10. Colour-coded relative errors in the exponent derived with PF (panel a) and PFL* (panel b) due to misalignment of the analysed images. Each Ca II K image was randomly shifted in both x and y directions by up to 10 pixels. The boxes give the average error after 1000 realisations. The y axis gives the value of the maximum possible offset in any direction. The x axis indicates the analysed images ordered by date covering the period 2010–2016. Colour bars show the relative errors in the computed exponents. Over-plotted with white are the plage areas derived from the Ca II K images. The areas were scaled in the range [0,9] and are shown to indicate the activity level. |
3.6. Effects of stray-light
We studied the effect of the stray-light on our results. For this, we repeated the same analysis on images corrected for stray light (as described in Sect. 2.2). Since the Ca II K stray-light-corrected images have higher contrast values, the segmentation parameters for different features had to be adapted (increased by 0.02 in contrast and 10 G). Otherwise the methods that we applied were exactly the same. Figure 11 is similar to Fig. 3, but now for the stray-light corrected data. The scatter in Ca II K contrast is higher compared to that from the Ca II K images affected by stray light. However, our results remain unchanged with almost constant exponents over the disc and time, and values of the exponents close to those reported above. The best-fit parameters from images corrected for stray light are 0.51 ± 0.02 and 3.89 ± 0.08 for PF and PFL*, respectively. Furthermore, there are no significant differences from the results obtained from analysis of the data corrected with the method of Criscuoli et al. (2017), thus supporting the assumptions of the correction method by Yeo et al. (2014b). Our previous conclusions of weak CLV of the exponents and time independence are also valid with these data. The values of the exponents are slightly lower than in the rest of our analysis, with best-fit parameters 0.50 ± 0.03 and 3.88 ± 0.05 for PF and PFL*, respectively. These results are still within the 1σ interval of our main results based on data uncorrected for stray light.
 |
Fig. 11. As in Fig. 3 but for stray-light corrected magnetograms and Ca II K observations with the methods by Yeo et al. (2014b) and Criscuoli & Ermolli (2008), respectively. |
3.7. Comparison with results from the literature
The exponent derived for PF (0.53 ± 0.01) is lower than those obtained by Schrijver et al. (1989), Harvey & White (1999), and Ortiz & Rast (2005), who favoured exponents of 0.6, 0.69, and 0.65, respectively, for all bright features considered. However, it is higher than those derived by Rezaei et al. (2007), Loukitcheva et al. (2009) and Vogler et al. (2005), ranging from 0.31 to 0.51. The difference between our results and those of Loukitcheva et al. (2009, exponent of 0.31) can potentially be explained by the different threshold in the magnetic field strength used by the two studies. Rezaei et al. (2007) found the exponent to increase to 0.51 when the threshold was 20 G, which is consistent with our results. The same stands for Loukitcheva et al. (2009) who used a threshold of 1.5 G and showed that the exponent increases to roughly 0.53 if a threshold of 20 G is used. It is worth noting however that Loukitcheva et al. (2009) analysed lower-resolution magnetograms from the Solar and Heliospheric Observatory Michelson Doppler Imager magnetograms (SOHO/MDI Scherrer et al. 1995), while we analysed SDO/HMI magnetograms and hence the magnetic field strengths reported by the various instruments are not necessarily directly comparable (cf. Yeo et al. 2014a). We note that the exponents derived by Schrijver et al. (1989), Harvey & White (1999), and Ortiz & Rast (2005) are consistent with the one we derive here by performing the fit on the bisector (PF*).
Our results for LFL differ from those presented by Kahil et al. (2017, 2019). For the LFL, Kahil et al. (2017, 2019) reported the best-fit parameters a1 = 0.29 ± 0.003 and a2 = 0.51 ± 0.004 for |BLOS| > 50 G, and a1 = 0.456 ± 0.003 and a2 = 0.512 ± 0.001 for |BLOS| > 100 G for a QS and an AR in Ca II H data, respectively. The differences can be due to different atmospheric heights sampled in the analysed data, as well as due to the lower spatial resolution of the observations used here compared to those used by Kahil et al. (2017, 2019). Thus, LFL might not be an appropriate function for analysis of full-disc data like those used in our study.
Harvey & White (1999) analysed data from three observatories, specifically the Big Bear, Sacramento Peak, and Kitt Peak observatories, and segmented the features into four sub-categories. In addition to the categories we use, they also have a feature class that they termed “enhanced network”. Our results are close to those of Harvey & White (1999) for the Big Bear data (0.52 and 0.58 for plage and network, respectively), but are slightly higher than those from Sacramento Peak (0.47–0.48 and 0.47–0.56 for plage and network, respectively) and are lower than those of Kitt Peat (0.62 and 0.64 for plage and network, respectively) measurements. This can potentially be explained by the different bandwidth of the observations made at the different observatories. Indeed, the Big Bear data have a bandwidth of 3 Å being the closest to the one of the Rome/PSPT (2.5 Å). The bandwidth used for the Sacramento Peak data is narrower (0.5 Å), while for the Kitt Peak data it is broader (10 Å). Another difference is that Harvey & White (1999) found lower (or equal) exponents for the active regions than for the network, while in our study we found the opposite. We note that the exponent obtained for the enhanced network component by Harvey & White (1999) is higher than the one we derived here for network and plage. Our finding of small to no dependence of the exponents to μ is in agreement with the results of Harvey & White (1999).
Pevtsov et al. (2016) analysed the pairs of Kitt Peak magnetograms and uncalibrated Mt Wilson Ca II K spectroheliograms after converting them to Carrington maps, as well as SOLIS/VSM observations in Ca II 854.2 nm and magnetograms. They concluded that Ca II brightness is an unreliable proxy for the magnetic field strength because of the large scatter between Ca II K brightness and the magnetic flux and that they saw a reversal of the relationship at high magnetic fluxes. It should be noted however that the data they analysed were of significantly lower quality than those used here. This is manifested by the number of pixel pairs and years analysed: ∼62 000 over 12 years in Pevtsov et al. (2016) and ∼103 000 000 over 6 years of Ca II K data. The issue of the low spatial resolution of the Ca 854.2 nm line was mentioned by Pevtsov et al. (2016) based on the findings of Leenaarts et al. (2006). The reported reversal of the relation at high magnetic fluxes with the Ca II K data, as well as the lack of correlation for the Ca II infrared data considered by Pevtsov et al. (2016), is perfectly consistent with the inclusion of sunspots in their analysis. The large scatter is possibly due to the narrower nominal bandwidth of Mt Wilson data (0.35 Å) compared to that of the Rome/PSPT (2.5 Å). This means that Mt Wilson is sampling greater atmospheric heights than Rome/PSPT, where the flux tubes are more expanded and hence the spatial agreement between the Ca II K data and the magnetograms should be reduced. In addition, at greater height, the emitted radiation is more strongly affected by shock waves and local heating events, which reduce the agreement even more. Lack of photometric calibration of the historical images and potential not very accurate methods applied for processing can also distort the relation (see Chatzistergos 2017; Chatzistergos et al. 2018a, 2019a).
4. Reconstructing unsigned magnetograms from Ca II K images
In the previous section we showed that the exponents of the functions tested in our study remained independent of time and μ. This allows us to reconstruct unsigned magnetograms or pseudo-magnetograms from the full-disc Ca II K observations using the parameters derived in Sect. 3.1.
For this, we apply the three tested relationships with the best-fit parameters listed in Table 2 on the Ca II K observations. We used the parameters from all three different binning approaches. However, we noticed that using the bisector fit produced magnetograms with the lowest differences from the original ones. We also found that parameters derived from the |BLOS|/μ binning tend to result in magnetograms with overestimated bright regions compared to the original magnetograms. This is also found in magnetograms reconstructed with the fits to the bisector, however to a lesser degree. The magnetograms reconstructed with the parameters from the binning over contrast values tend to underestimate the magnetogram signal in large parts of the bright regions. Based on this, in the following we present the results for magnetograms obtained with the parameters for PFL* applied to the bisector. However, for comparison, we also show in Appendix B the results of PF*, LFL*, and PF.
The pixels with contrast ≤1 were set to 0 G. Figure 12 shows examples of reconstructed magnetograms for both an active and a quiet day by applying the best fit PFL* relationship on the Rome/PSPT Ca II K image (panels a and d) and the corresponding SDO/HMI magnetogram (panels b and e). The pixel-by-pixel absolute differences between the reconstructed and the original magnetograms are shown in Fig. 12 (panels c and f). Prior to obtaining the differences, the original and reconstructed magnetograms were multiplied with μ, so that the compared quantity is |BLOS|. In this reconstruction we only made use of the information on the Ca II K image to identify the regions on which we applied the relationships obtained in Sect. 3.1. This means that sunspots were not identified accurately and their immediate surroundings were the regions with the highest errors, reaching differences of up to ∼1000 G. These regions were masked out in Fig. 12 and the errors reported in the plots do not include sunspots.
 |
Fig. 12. Unsigned magnetograms reconstructed from the Ca II K images taken on 01 April 2011 (top) and 07 June 2010 (bottom) using the average parameters for PFL* (left), SDO/HMI unsigned magnetograms (middle) co-temporal to the Ca II K images, and difference between the reconstructed unsigned magnetogram (simulated) from Ca II K data and the original (true) SDO/HMI unsigned magnetogram (right). The rms, mean, mean absolute, and maximum absolute differences are listed under each panel. The colour bars show the ranges of |BLOS| in G. All images are saturated at 100 G to improve the visibility of the regions with low magnetic field strength. |
Comparing the errors between the reconstructed and the original magnetograms we obtained rms differences of ≃30 G and ≃20 G for the active and quiet days, respectively. The differences for the quiet day show that we slightly underestimated the weak fields.
Figure 13 shows scatter plots between the reconstructed magnetograms and the original ones for the observations shown in Fig. 12. Figure 14 shows the pixel-by-pixel rms differences between the original and the reconstructed unsigned magnetograms obtained using the derived best-fit parameters of PFL* without masking the surroundings of the sunspots this time. Figure 14 reveals that the rms differences remain less than 88 G for all 131 reconstructed unsigned magnetograms with an average value of 50 G. This is approximately 20 G lower than the standard deviation of the magnetic field strength of the original unsigned magnetograms. The rms differences decrease on overage by 9 G if the sunspots are masked out.
 |
Fig. 13. Scatter plots between original (degraded) magnetogram and the reconstructed from the Ca II K image taken on 07/06/2010 (panel a) and 01/04/2011 (panel b) using the average parameters for PFL*. The yellow line has a slope of unity. The axes are shown in the range from the original magnetogram. |
 |
Fig. 14. rms pixel by pixel differences in G between the original unsigned magnetograms and the reconstructed ones using the parameters (listed in Table 2) derived from the PFL* fits for the whole disc (blue downward triangles) and by masking out the sunspot regions (green rhombuses). Also shown is the standard deviation of the original unsigned magnetograms (black squares). The dashed lines connect annual median values. The shaded grey surface shows the plage areas determined with Method 1 from the Rome/PSPT images. The areas were scaled to have a maximum value of 120 and are included to indicate the level of solar activity. |
We also evaluated how well the regions with strong magnetic fields in the reconstructed unsigned magnetograms correspond to magnetic regions and network in the original magnetograms. For this, we derived the disc fractions covered by features with Method 1 (i.e. applying constant thresholds on contrast in the Rome/PSPT and on |BLOS|/μ in the original SDO/HMI and reconstructed images). The residual disc fractions between the ones derived from the degraded unsigned magnetograms and the reconstructed ones with PFL* are shown in Fig. 15. We also show separately the disc fractions derived from the original-size SDO/HMI magnetograms. When doing so we used the same segmentation parameters for all cases. For all feature classes the difference of the disc fractions derived from degraded SDO/HMI magnetograms and Rome/PSPT are on average 0.3% and are always below 1.3%. We notice that the area of the features in the degraded SDO/HMI magnetograms increase in disc fraction on average by 0.8% (and up to 1.8%) compared to the original-sized magnetograms. The differences between the degraded magnetograms and the reconstructed ones with PFL* are on average 0.8% and are always below 2.0%. We noticed that the reconstructed magnetograms exhibit higher disc fractions for network by ∼1%.
 |
Fig. 15. Left: difference between the disc fraction of magnetic features derived from SDO/HMI observations with reduced spatial resolution and Rome/PSPT (black downward triangles), SDO/HMI with original spatial resolution (yellow circles), and reconstructed magnetograms with PFL* (blue rhombuses). Each of the upper two panels corresponds to a different feature (as marked in each panel) identified with Method 1, while the bottom panel is for all features together. The dashed lines connect annual median values, while the dotted horizontal lines are for a difference of zero. The shaded grey surface in the lower panel shows the plage areas determined with Method 1 from the Rome/PSPT images. The areas were scaled to match the range of the plot and are included to indicate the level of solar activity. Right: distribution functions of the residual disc fractions. |
Finally, we calculated the total unsigned magnetic flux from the reconstructed and the original unsigned magnetograms. The results are plotted in Fig. 16 for the same |BLOS|/μ ranges as in Fig. 15. The day-by-day correlation coefficient between the total flux in the original and the reconstructed magnetograms with the PFL* fit is 0.98 for all bright features and is similar for plage and network. We noticed that the slightly higher network disc fractions result in an almost constant offset in the total unsigned magnetic flux of the network component. The total unsigned magnetic flux in the degraded magnetograms is reduced compared to that from the original-sized magnetograms due to the smoothing applied on the magnetograms to match the Rome/PSPT resolution (see Sect. 2.1).
 |
Fig. 16. Total unsigned magnetic flux in Mx of AR derived from the magnetograms (yellow circles for the original and black plus signs for the reduced spatial resolution ones) and from the unsigned magnetograms reconstructed from Ca II K observations with PFL* (blue rhombuses). Each of the upper two panels corresponds to a different type of features (as listed in the panels) identified with Method 1, while the bottom panel is for all features together. The dashed lines connect the annual median values. The shaded surface in the lower panel is as in Fig. 15. |
5. Summary and conclusions
We analysed the relationship between the excess Ca II K emission and the magnetic field strength. For this, we used 131 sets of co-aligned near-co-temporal SDO/HMI magnetogram and continuum observations and Rome/PSPT filtergrams taken in the core of the Ca II K line and in the red continuum. We confirm the existence of a consistent relation between the excess Ca II K emission and the magnetic field strength. We fit the relation between the Ca II K intensity and the vertical component of the magnetic field (|BLOS|/μ) with a power-law function of the logarithm of |BLOS|/μ with an offset, and test it against a power-law function and a logarithmic function of |BLOS|/μ that have been presented in the literature. The parameters we derived for the power-law function are consistent with those from previous studies. The results for a power-law function of |BLOS|/μ are also very similar to those derived with a power-law function of the logarithm of |BLOS|/μ. The logarithmic function recently employed in the analysis of high-resolution Sunrise data in the Ca II H line is found to be unrepresentative of bright features in the full-disc Ca II K images analysed in our study. We note that in previous studies the data were binned in terms of |BLOS|/μ before performing the fit. However, results obtained by such fits suffer from attenuation bias due to errors in the independent variable, which are not taken into account. For that reason we decided to bin the data both in |BLOS|/μ and Ca II K contrast values and perform the fits on the bisector of the two binned curves.
The observations analysed here greatly extend the sample of studied data with respect to previous works. In particular, we examined a greater amount and in many ways higher-quality data than has been done before for such studies. The data span half a solar cycle, and for this timescale we report no significant variation with time of the obtained power-law exponents. Moreover, we find no variation of the exponents over the disc positions between μ = 1 and μ = 0.14. Finally, the numerical values of the exponents remain nearly the same if stray light is taken into account. We found no significant differences between results derived from images corrected with the methods by Yeo et al. (2014b) and by Criscuoli et al. (2017). The fact that we studied this relation for almost the entire disc, up to μ = 0.14 or 0.99R, makes this analysis more applicable to stellar studies than most earlier investigations.
The exponents being independent of time and μ suggests that maps of the unsigned LOS magnetic field can be reconstructed from Ca II K observations with merely the knowledge of the exponent derived here. We tested the reconstruction of unsigned magnetograms from available Ca II K observations and compared our results to co-temporal directly measured magnetograms. The total magnetic flux calculated for the series of the original and reconstructed magnetograms agrees well with the correlation factor of 0.98. This means that historical Ca II K spectroheliograms, when properly processed and calibrated (e.g. Chatzistergos et al. 2016, 2018b, 2019b,a), can be used to extend the series of magnetograms throughout the whole of the twentieth century. This approach suffers from the limitation that it does not allow the polarity of the magnetic field to be recovered. However, this is not a problem for a number of studies and applications; for example for irradiance reconstructions, where the models do not require the polarity of the bright features. Furthermore, if other data are also used, for instance sunspot measurements, it might be possible to recover the polarity of the ARs as well.
Available at http://www.oa-roma.inaf.it/fisica-solare/
Acknowledgments
We are grateful to Yang Liu, Aimee Norton, and Phil Scherrer for the helpful and fruitful discussions and for providing the stray-light-corrected SDO/HMI data. T.C. acknowledges a postgraduate fellowship of the International Max Planck Research School on Physical Processes in the Solar System and Beyond. I.E. acknowledges support by grants PRIN-INAF-2014 and PRIN/MIUR 2012P2HRCR “Il Sole attivo” and FP7 SOLID. The work was also partly supported by COST Action ES1005 “TOSCA”, and by the BK21 plus program through the National Research Foundation (NRF) funded by the Ministry of Education of Korea. This research has made use of NASA’s Astrophysics Data System.
References
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Babcock, H. W., & Babcock, H. D. 1955, ApJ, 121, 349 [Google Scholar]
- Baliunas, S. L., Horne, J. H., Porter, A., et al. 1985, ApJ, 294, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Barthol, P., Gandorfer, A., Solanki, S. K., et al. 2011, Sol. Phys., 268, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, S., Banerjee, D., & Ravindra, B. 2016, ApJ, 827, 87 [Google Scholar]
- Chatzistergos, T., Ermolli, I., Solanki, S. K., & Krivova, N. A. 2016, in Coimbra Solar Physics Meeting: Ground-based Solar Observations in the Space Instrumentation Era, eds. I. Dorotovic, C. E. Fischer, & M. Temmer (San Francisco: Astronomical Society of the Pacific), ASP Conf. Ser., 504, 227 [NASA ADS] [Google Scholar]
- Chatzistergos, T. 2017, Analysis of Historical Solar Observations and Long-term Changes in Solar Irradiance, PhD Thesis (Uni-edition) [Google Scholar]
- Chatzistergos, T., Ermolli, I., Solanki, S. K., & Krivova, N. A. 2018a, A&A, 609, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chatzistergos, T., Ermolli, I., Krivova, N. A., & Solanki, S. K. 2018b, in IAU Symposium, eds. D. Banerjee, J. Jiang, K. Kusano, & S. Solanki, 340, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Chatzistergos, T., Ermolli, I., Krivova, N. A., & Solanki, S. K. 2019a, A&A, 625, A69 [Google Scholar]
- Chatzistergos, T., Ermolli, I., Falco, M., et al. 2019b, il nuovo cimento, 42C, 5 [NASA ADS] [Google Scholar]
- Chitta, L. P., Peter, H., Solanki, S. K., et al. 2017, ApJS, 229, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Coulter, R. L., & Kuhn, J. R. 1994, in Solar Active Region Evolution: Comparing Models with Observations, (San Francisco: ASP), ASP Conf. Ser., 68, 37 [NASA ADS] [Google Scholar]
- Criscuoli, S., & Ermolli, I. 2008, A&A, 484, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Criscuoli, S., Norton, A., & Whitney, T. 2017, ApJ, 847, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, D. K., Vaughan, A. H., Wilson, O. C., et al. 1991, ApJS, 76, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Ermolli, I., Fofi, M., Bernacchia, C., et al. 1998, Sol. Phys., 177, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ermolli, I., Criscuoli, S., Centrone, M., Giorgi, F., & Penza, V. 2007, A&A, 465, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ermolli, I., Criscuoli, S., Uitenbroek, H., et al. 2010, A&A, 523, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frazier, E. N. 1971, Sol. Phys., 21, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Giovanelli, R. G., & Jones, H. P. 1982, Sol. Phys., 79, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Gondoin, P., Gandolfi, D., Fridlund, M., et al. 2012, A&A, 548, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hall, J. C. 2008, Living Rev. Sol. Phys., 5, 53 [CrossRef] [Google Scholar]
- Hall, J. C., Lockwood, G. W., & Skiff, B. A. 2007, AJ, 133, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, K. L., & White, O. R. 1999, ApJ, 515, 812 [Google Scholar]
- Howard, R. 1959, ApJ, 130, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Kahil, F., Riethmüller, T. L., & Solanki, S. K. 2017, ApJS, 229, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Kahil, F., Riethmüller, T. L., & Solanki, S. K. 2019, A&A, 621, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keil, S. L., & Worden, S. P. 1984, ApJ, 276, 766 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., Rutten, R. J., Carlsson, M., & Uitenbroek, H. 2006, A&A, 452, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leighton, R. B. 1959, ApJ, 130, 366 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, G. W., Skiff, B. A., Henry, G. W., et al. 2007, ApJS, 171, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, G. W., Henry, G. W., Hall, J. C., & Radick, R. R. 2013, in New Quests in Stellar Astrophysics III: A Panchromatic View of Solar-like Stars, With and Without Planets, ed. M. Chavez, ASP Conf. Ser., 472, 203 [NASA ADS] [Google Scholar]
- Loukitcheva, M., Solanki, S. K., & White, S. M. 2009, A&A, 497, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michel, E., Baglin, A., Weiss, W. W., et al. 2008, Commun. Asteroseismol., 157, 69 [NASA ADS] [Google Scholar]
- Nindos, A., & Zirin, H. 1998, Sol. Phys., 179, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz, A., & Rast, M. 2005, Mem. Soc. Astron. It., 76, 1018 [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Pevtsov, A. A., Virtanen, I., Mursula, K., Tlatov, A., & Bertello, L. 2016, A&A, 585, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pietarila, A., Hirzberger, J., Zakharov, V., & Solanki, S. K. 2009, A&A, 502, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rast, M. P. 2003a, ApJ, 597, 1200 [NASA ADS] [CrossRef] [Google Scholar]
- Rast, M. P. 2003b, in GONG+ 2002. Local and Global Helioseismology: The Present and Future, ESA SP, 517, 163 [NASA ADS] [Google Scholar]
- Reiners, A. 2012, Living Rev. Sol. Phys., 9, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Rezaei, R., Schlichenmaier, R., Beck, C. A. R., Bruls, J. H. M. J., & Schmidt, W. 2007, A&A, 466, 1131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saar, S. H., & Schrijver, C. J. 1987, in Cool Stars, Stellar Systems, and the Sun, eds. J. L. Linsky, & R. E. Stencel, Proceedings of the Fifth Cambridge Workshop held in Boulder, Colorado, 291, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
- Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Schrijver, C. J., Cote, J., Zwaan, C., & Saar, S. H. 1989, ApJ, 337, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., Shine, R. A., Hagenaar, H. J., et al. 1996, ApJ, 468, 921 [NASA ADS] [CrossRef] [Google Scholar]
- Sheeley, N. R. 1967, ApJ, 147, 1106 [NASA ADS] [CrossRef] [Google Scholar]
- Sheeley, Jr., N. R., Cooper, T. J., & Anderson, J. R. L. 2011, ApJ, 730, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Skumanich, A., Smythe, C., & Frazier, E. N. 1975, ApJ, 200, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., Montavon, C. A. P., & Livingston, W. 1994, A&A, 283, 221 [NASA ADS] [Google Scholar]
- Solanki, S. K., Finsterle, W., Rüedi, I., & Livingston, W. 1999, A&A, 347, L27 [NASA ADS] [Google Scholar]
- Solanki, S. K., Barthol, P., Danilovic, S., et al. 2010, ApJ, 723, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., Riethmüller, T. L., Barthol, P., et al. 2017, ApJS, 229, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Vogler, F. L., Brandt, P. N., Otruba, W., & Hanslmeier, A. 2005, Hvar Obs. Bull., 29, 79 [NASA ADS] [Google Scholar]
- Walton, S. R., & Preminger, D. G. 1999, ApJ, 514, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H. 1988, Sol. Phys., 117, 343 [NASA ADS] [CrossRef] [Google Scholar]
- White, O. R., & Livingston, W. 1978, ApJ, 226, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, O. C. 1978, ApJ, 226, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Yeo, K. L., Solanki, S. K., & Krivova, N. A. 2013, A&A, 550, A95 [Google Scholar]
- Yeo, K. L., Krivova, N. A., Solanki, S. K., & Glassmeier, K. H. 2014a, A&A, 570, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yeo, K. L., Feller, A., Solanki, S. K., et al. 2014b, A&A, 561, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Spatial agreement between magnetograms and Ca II K images
Figure A.1 displays examples of close-ups of one active and one quiet region from the observations shown in Fig. 1 to illustrate the good spatial agreement between the SDO/HMI and Rome/PSPT images. Figure A.1 (e–h) displays the corresponding masks of plage and network combined for the close-ups shown in Fig. A.1 (a–d) derived with method 1 (see Sect. 2.3). Figure A.1 illustrates the well-known fact that the bright features in the Ca II K images belong to magnetic regions and network in the magnetograms. The ARs appear slightly smaller and show smaller-scale features in the magnetograms than in the Ca II K data. This can occur for a variety of reasons. The flux tubes comprising ARs expand with height in the solar atmosphere, therefore ARs are expected to be more extended in Ca II K images. Furthermore, if the flux tubes are inclined then they can appear more broadened in the Ca II K data as well. Other possible reasons include lower spatial resolution and seeing effects due to the atmosphere of the Earth that smear the features in the Ca II K observations. Some contribution will be provided by cancellation of magnetograph signal between opposite polarities within the same resolution element (see e.g. Chitta et al. 2017, for hidden opposite polarities at SDO/HMI resolution that appear at the higher resolution of Sunrise observations). However, these effects should be minimised after the spatial degradation we applied to the magnetograms. Finally, the choice of the segmentation thresholds has an effect as well, if they are not consistent between the magnetograms and Ca II K images. We evaluated a variety of threshold combinations, but were unable to better match the AR areas in the two observations without introducing even smaller-scale features in the magnetograms. Therefore, we assumed that the differences are to a significant extent due to the expansion of the flux tubes, in particular by the fibrils spreading out at the edges of ARs, as found by Pietarila et al. (2009), for example.
 |
Fig. A.1. Magnified 400 × 400 arcsec2 sub-arrays of the images shown in Fig. 1 for a network (left) and a plage region (right). From top to bottom: (panels a and b) SDO/HMI unsigned (and spatially degraded) magnetogram; (panels c and d) Rome/PSPT Ca II K; the corresponding segmentation masks derived with Method 1, i.e. constant thresholds, from (panels e and f) the magnetograms and (panels g and h) the Ca II K images. The magnetograms are saturated in the range [−300,300] G (the negative value was chosen merely to improve visibility of the pixels), and Ca II K observations in the range [0.5,1.6] (the QS has an average value of 1). |
Appendix B: Reconstructed magnetograms with different functions
Here we use the parameters derived for PF, PF*, and LFL* to reconstruct unsigned magnetograms and compare the results with those derived with PFL*. Figure B.1 shows the pixel by pixel absolute differences between the reconstructed and the original magnetograms by using PF* (panels a and e), PFL* (panels b and f), LFL* (panels c and g), and PF (panels d and h).
Comparing the errors between the reconstructed and the original magnetograms we got similar uncertainties for both PF* and PFL*. In particular we found rms differences of ≃30 G and ≃20 G for the active and quiet days, respectively, for both PF* and PFL*. We discern no significant difference between these two reconstructed magnetograms, although a careful comparison reveals many differences at small scales. The differences for the quiet day show that we slightly underestimated the weak fields. The differences for the LFL reach up to 2500 G in plage regions. These high errors arise due to the large pixel-to-pixel scatter in the relationship between Ca II K contrast and |BLOS|/μ. Consequently, there are numerous very bright pixels in the Ca II K observations that would correspond to very strong fields in this case, as the fitted curve increases very slowly. This problem is somewhat more acute for reconstructions that use the PF and PFL relationships (i.e. those derived from a fit to data binned in |BLOS|/μ). We also show the differences for PF, which has been commonly used in the literature. In this case, the errors are slightly higher than for PF* or PFL* for times with high activity.
 |
Fig. B.1. Difference between the reconstructed unsigned magnetogram (simulated) from Ca II K data and original (true) SDO/HMI unsigned magnetogram taken on 01 April 2011 (top) and 07 June 2010 (bottom). The reconstruction was done with the parameters derived in Sect. 3.1 for PF* (panels a and e), PFL* (panels b and f), LFL* (panels c and g), and PF (panels d and h). The rms, mean, mean absolute, and maximum absolute differences are listed under each panel. The colour bars show the ranges of B in G. |
Figure B.2 shows scatter plots between the four reconstructed magnetograms and the original one for the observation taken on 01 April 2011 (the active day shown in Fig. B.1). The unsigned magnetograms reconstructed with PF* and PFL* show the best correspondence, while the ones with LFL* and PF tend to overestimate the magnetic field. Figure B.3 shows the pixel-by-pixel rms differences between the original and the reconstructed unsigned magnetograms obtained using the derived best fit parameters of the three functions we tested, without masking the surroundings of the sunspots this time. Figure B.3 reveals that the rms differences remain less than 88 G for all 131 unsigned magnetograms reconstructed with the PF* and PFL*, but reach 100 G for PF and 7500 G for LFL*.
 |
Fig. B.2. Scatter plots between original (degraded) magnetograms and those reconstructed from the Ca II K image taken on 01 April 2011 using the average parameters for PF* (panel a), PFL* (panel b), LFL* (panel c), and PF (panel d). The yellow line has a slope of unity. The axes are shown in the range from the original magnetogram. |
 |
Fig. B.3. rms pixel-by-pixel differences in G between the original magnetograms and the reconstructed ones using the parameters (listed in Table 2) derived from the PF* (red), PFL* (blue), LFL* (green), and PF (yellow) fits. The dashed lines connect annual median values. The shaded surface is as in Fig. 15. |
Figure B.4 shows the residual disc fractions between the ones derived from the degraded unsigned magnetograms and the reconstructed ones with the PF*, PFL*, LFL*, and PF fits. The results for PF* follow very closely those for PFL*, though giving minutely (on average by 0.3%) higher differences. The differences between the degraded magnetograms and the reconstructed ones with PF* fits are on average 1.0% and are always below 2.3%. The disc fractions in the magnetograms reconstructed with LFL* are on average 6% higher than in the original magnetograms when all features are considered, however the difference remains less than 0.1% when only the plage regions are considered. The errors in the disc fractions slightly increase when the magnetograms are reconstructed with PF, being ∼4% for all features.
 |
Fig. B.4. Left: difference between the disc fraction of magnetic features derived from SDO/HMI observations with reduced spatial resolution and reconstructed magnetograms with PF* (red upward triangles), PFL* (blue rhombuses), LFL* (green squares), and PF (light blue downward triangles). Each of the upper two panels corresponds to a different feature (as marked in each panel) identified with Method 1, while the bottom panel is for all features together. The dashed lines connect annual median values, while the dotted horizontal lines are for a difference of zero. The shaded surface in the lower panel is as in Fig. 15. Right: distribution functions of the residual disc fractions. |
The total unsigned magnetic flux is plotted in Fig. B.5 for the same |BLOS|/μ ranges as in Fig. B.4. The day-by-day correlation coefficient between the total flux in the original and the reconstructed magnetograms with both PF* and PFL* fits is 0.98 for all bright features and is similar for plage and network. The differences between the results for PF* and PFL* are minute, with the latter giving slightly higher values. The total flux derived from the reconstructed unsigned magnetograms with PF and LFL* give consistently higher values.
 |
Fig. B.5. Total unsigned magnetic flux in Mx of AR derived from the magnetograms (yellow circles for the original and black plus signs for the reduced spatial resolution ones) and from the unsigned magnetograms reconstructed from Ca II K observations with PF* (red upward triangles), PFL* (blue rhombuses), LFL* (green squares), and PF (light blue downward triangles). Each of the upper two panels corresponds to a different type of features (as listed in the panels) identified with Method 1, while the bottom panel is for all features together. The dashed lines connect the annual median values. The shaded surface in the lower panel is as in Fig. 15. |
All Tables
Previously published results on the relation between magnetic flux and Ca II intensity along with our results.
All Figures
 |
Fig. 1. Examples of the observations analysed in this study taken on 01 April 2011 at 09:06:00 UT. Panel a: SDO/HMI unsigned BLOS magnetogram. Panel b: SDO/HMI continuum contrast image (i.e. compensated for intensity CLV). Panel c: Rome/PSPT Ca II K. Panel d: red continuum contrast images. The grey-scale bars on the right-hand side of each panel show magnetic signal in G and contrast, respectively. The squares indicate the insets shown in Fig. A.1. |
| In the text | |
 |
Fig. 2. Segmentation masks of bright magnetic features derived from the observations shown in Fig. 1 by applying the two methods described in Sect. 2.3. Panel a: mask of magnetogram and panel b: mask of Ca II K image derived with Method 1, showing plage (red), network (green), and QS (blue). Panel c: mask of magnetogram derived with Method 2, showing individual activity clusters with different colours (the QS is in dark blue). The masks are shown prior to the exclusion of the sunspot regions. |
| In the text | |
 |
Fig. 3. Ca II K contrast plotted against the unsigned LOS magnetic flux density divided by μ (|BLOS|/μ) for all pixel pairs (excluding sunspots) in all available images. The pixels are colour-coded denoting the logarithm of the number density within bins of 1 G and 0.01 in contrast. The contour lines give the logarithm of the pixel number density in intervals of 0.5. Curves show 5000-point running means (over |BLOS|/μ in yellow, over contrast in light blue, and their bisector in purple), as well as PF (red), PFL (blue), and LFL (green) fits on the binned curve over |BLOS|/μ (yellow curve). The vertical grey dashed line denotes the 20 G threshold in |BLOS|/μ. A magnified section for low |BLOS|/μ is shown at the lower right corner of the figure to illustrate the differences of the different fits over that region. Also shown are histograms of |BLOS|/μ within 3 ranges of contrast values (right) and histograms of Ca II K contrast for 4 ranges of |BLOS|/μ (top). The ranges used for the histograms are shown on the upper part of the corresponding sub-plot. |
| In the text | |
 |
Fig. 4. Parameters of the fits (Eq. (1)) as a function of the threshold in |BLOS|/μ for PF (panel a) and PFL (panel b) fits. The fits are performed on the curves derived by binning over |BLOS|/μ (blue), contrast values (yellow), and the bisector (red). The dotted line in each panel is the best fit parameter derived with the threshold of |BLOS|/μ = 20 G for the blue points. |
| In the text | |
 |
Fig. 5. As in Fig. 3 but showing only the results of PF on the binned curve over |BLOS|/μ (yellow curve) by varying the |BLOS|/μ threshold, i.e. the magnetogram noise cut-off (dotted coloured curves). The threshold is 1 G for the black curve and rises to 50 G for the red curve. The curve corresponding to the 20 G threshold adopted in this study is shown with the light-blue solid curve. The thick yellow curve shows 5000-point running mean over |BLOS|/μ. The vertical grey dashed line denotes the 20 G threshold in |BLOS|/μ. |
| In the text | |
 |
Fig. 6. Parameters of the fits (Eq. (1)) as a function of time, derived for all bright features (black), as well as for the network (blue), and plage (red) separately, for PF (panel a) and PFL* (panel b) fits. The dashed lines connect the median values obtained from all analysed images within a given year, while the dotted lines mark the values of the parameters of the best fit derived in Sect. 3.1. The shaded grey surface in panel (b) shows the plage areas determined with Method 1 from the Rome/PSPT images. The areas were scaled to have a maximum value of 4.2 and minimum value 2.8 in order to match the range of values shown in panel (b); they indicate the level of solar activity at the considered times. |
| In the text | |
 |
Fig. 7. Parameters of the fits (Eq. (1)) as a function of μ, derived for ten annuli of equal area for all bright features (black), as well as for the network (blue), and plage (red) separately, for PF (panel a) and PFL* (panel b). The values shown are the means over the entire sample of data, while the error bars denote the 1σ interval. Results for the network are shown in the middle of the μ interval they represent, while the others are slightly shifted in μ to improve the clarity of the plot. The dotted lines mark the values of the best fit parameters derived in Sect. 3.1. |
| In the text | |
 |
Fig. 8. Ca II K contrast plotted against |BLOS|/μ for all activity clusters identified with Method 2 in observations shown in Fig. 1 (black dots). The coloured curves are the result of the PFL* fit to the individual clusters, shown with the same colours as in Fig. 2c. |
| In the text | |
 |
Fig. 9. Exponents of the PF (red) and PFL* (blue) fits as a function of size for individual activity clusters. The light grey and dark grey shaded areas denote the 1σ error in the fit parameters for PF and PFL*, respectively. |
| In the text | |
 |
Fig. 10. Colour-coded relative errors in the exponent derived with PF (panel a) and PFL* (panel b) due to misalignment of the analysed images. Each Ca II K image was randomly shifted in both x and y directions by up to 10 pixels. The boxes give the average error after 1000 realisations. The y axis gives the value of the maximum possible offset in any direction. The x axis indicates the analysed images ordered by date covering the period 2010–2016. Colour bars show the relative errors in the computed exponents. Over-plotted with white are the plage areas derived from the Ca II K images. The areas were scaled in the range [0,9] and are shown to indicate the activity level. |
| In the text | |
 |
Fig. 11. As in Fig. 3 but for stray-light corrected magnetograms and Ca II K observations with the methods by Yeo et al. (2014b) and Criscuoli & Ermolli (2008), respectively. |
| In the text | |
 |
Fig. 12. Unsigned magnetograms reconstructed from the Ca II K images taken on 01 April 2011 (top) and 07 June 2010 (bottom) using the average parameters for PFL* (left), SDO/HMI unsigned magnetograms (middle) co-temporal to the Ca II K images, and difference between the reconstructed unsigned magnetogram (simulated) from Ca II K data and the original (true) SDO/HMI unsigned magnetogram (right). The rms, mean, mean absolute, and maximum absolute differences are listed under each panel. The colour bars show the ranges of |BLOS| in G. All images are saturated at 100 G to improve the visibility of the regions with low magnetic field strength. |
| In the text | |
 |
Fig. 13. Scatter plots between original (degraded) magnetogram and the reconstructed from the Ca II K image taken on 07/06/2010 (panel a) and 01/04/2011 (panel b) using the average parameters for PFL*. The yellow line has a slope of unity. The axes are shown in the range from the original magnetogram. |
| In the text | |
 |
Fig. 14. rms pixel by pixel differences in G between the original unsigned magnetograms and the reconstructed ones using the parameters (listed in Table 2) derived from the PFL* fits for the whole disc (blue downward triangles) and by masking out the sunspot regions (green rhombuses). Also shown is the standard deviation of the original unsigned magnetograms (black squares). The dashed lines connect annual median values. The shaded grey surface shows the plage areas determined with Method 1 from the Rome/PSPT images. The areas were scaled to have a maximum value of 120 and are included to indicate the level of solar activity. |
| In the text | |
 |
Fig. 15. Left: difference between the disc fraction of magnetic features derived from SDO/HMI observations with reduced spatial resolution and Rome/PSPT (black downward triangles), SDO/HMI with original spatial resolution (yellow circles), and reconstructed magnetograms with PFL* (blue rhombuses). Each of the upper two panels corresponds to a different feature (as marked in each panel) identified with Method 1, while the bottom panel is for all features together. The dashed lines connect annual median values, while the dotted horizontal lines are for a difference of zero. The shaded grey surface in the lower panel shows the plage areas determined with Method 1 from the Rome/PSPT images. The areas were scaled to match the range of the plot and are included to indicate the level of solar activity. Right: distribution functions of the residual disc fractions. |
| In the text | |
 |
Fig. 16. Total unsigned magnetic flux in Mx of AR derived from the magnetograms (yellow circles for the original and black plus signs for the reduced spatial resolution ones) and from the unsigned magnetograms reconstructed from Ca II K observations with PFL* (blue rhombuses). Each of the upper two panels corresponds to a different type of features (as listed in the panels) identified with Method 1, while the bottom panel is for all features together. The dashed lines connect the annual median values. The shaded surface in the lower panel is as in Fig. 15. |
| In the text | |
 |
Fig. A.1. Magnified 400 × 400 arcsec2 sub-arrays of the images shown in Fig. 1 for a network (left) and a plage region (right). From top to bottom: (panels a and b) SDO/HMI unsigned (and spatially degraded) magnetogram; (panels c and d) Rome/PSPT Ca II K; the corresponding segmentation masks derived with Method 1, i.e. constant thresholds, from (panels e and f) the magnetograms and (panels g and h) the Ca II K images. The magnetograms are saturated in the range [−300,300] G (the negative value was chosen merely to improve visibility of the pixels), and Ca II K observations in the range [0.5,1.6] (the QS has an average value of 1). |
| In the text | |
 |
Fig. B.1. Difference between the reconstructed unsigned magnetogram (simulated) from Ca II K data and original (true) SDO/HMI unsigned magnetogram taken on 01 April 2011 (top) and 07 June 2010 (bottom). The reconstruction was done with the parameters derived in Sect. 3.1 for PF* (panels a and e), PFL* (panels b and f), LFL* (panels c and g), and PF (panels d and h). The rms, mean, mean absolute, and maximum absolute differences are listed under each panel. The colour bars show the ranges of B in G. |
| In the text | |
 |
Fig. B.2. Scatter plots between original (degraded) magnetograms and those reconstructed from the Ca II K image taken on 01 April 2011 using the average parameters for PF* (panel a), PFL* (panel b), LFL* (panel c), and PF (panel d). The yellow line has a slope of unity. The axes are shown in the range from the original magnetogram. |
| In the text | |
 |
Fig. B.3. rms pixel-by-pixel differences in G between the original magnetograms and the reconstructed ones using the parameters (listed in Table 2) derived from the PF* (red), PFL* (blue), LFL* (green), and PF (yellow) fits. The dashed lines connect annual median values. The shaded surface is as in Fig. 15. |
| In the text | |
 |
Fig. B.4. Left: difference between the disc fraction of magnetic features derived from SDO/HMI observations with reduced spatial resolution and reconstructed magnetograms with PF* (red upward triangles), PFL* (blue rhombuses), LFL* (green squares), and PF (light blue downward triangles). Each of the upper two panels corresponds to a different feature (as marked in each panel) identified with Method 1, while the bottom panel is for all features together. The dashed lines connect annual median values, while the dotted horizontal lines are for a difference of zero. The shaded surface in the lower panel is as in Fig. 15. Right: distribution functions of the residual disc fractions. |
| In the text | |
 |
Fig. B.5. Total unsigned magnetic flux in Mx of AR derived from the magnetograms (yellow circles for the original and black plus signs for the reduced spatial resolution ones) and from the unsigned magnetograms reconstructed from Ca II K observations with PF* (red upward triangles), PFL* (blue rhombuses), LFL* (green squares), and PF (light blue downward triangles). Each of the upper two panels corresponds to a different type of features (as listed in the panels) identified with Method 1, while the bottom panel is for all features together. The dashed lines connect the annual median values. The shaded surface in the lower panel is as in Fig. 15. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.