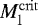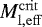| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | A113 | |
| Number of page(s) | 22 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201833410 | |
| Published online | 22 April 2019 | |
A dynamically young, gravitationally stable network of filaments in Orion B★
1
Université Grenoble Alpes, IRAM,
38000 Grenoble, France
e-mail: jan.orkisz@chalmers.se
2
IRAM,
300 rue de la Piscine,
38406 Saint Martin d’Hères, France
3
Observatoire de Paris, Sorbonne Université, École normale supérieure, CNRS, LERMA, Université PSL,
75005 Paris, France
4
School of Physics and Astronomy, Cardiff University,
Queen’s buildings, Cardiff CF24 3AA, UK
5
Observatoire de Paris, Sorbonne Université, CNRS, LERMA, Université PSL,
92190 Meudon, France
6
Grupo de Astrofísica Molecular, IFF-CSIC,
Calle Serrano 121-123,
28006 Madrid, Spain
7
Laboratoire d’astrophysique de Bordeaux, Université de Bordeaux, CNRS, B18N, allée Geoffroy Saint-Hilaire,
33615 Pessac, France
8
Instituto de Astrofísica, Ponticia Universidad Católica de Chile,
Avenida Vicuña Mackenna 4860,
7820436 Macul, Santiago, Chile
9
CNRS, IRAP,
9 avenue colonel Roche,
BP 44346,
31028 Toulouse Cedex 4, France
10
National Radio Astronomy Observatory,
520 Edgemont Road,
Charlottesville,
VA 22903, USA
11
Harvard-Smithsonian Center for Astrophysics,
60 Garden Street,
Cambridge,
MA 02138, USA
12
IRAM,
Avenida Divina Pastora, 7,
Núcleo Central,
18012 Granada, España
13
Maison de la Simulation, CEA-CNRS-INRIA-UPS-UVSQ, USR 3441, Centre d’étude de Saclay,
91191 Gif-Sur-Yvette, France
Received:
11
May
2018
Accepted:
6
February
2019
Context. Filaments are a key step on the path that leads from molecular clouds to star formation. However, their characteristics, for instance their width, are heavily debated and the exact processes that lead to their formation and fragmentation into dense cores still remain to be fully understood.
Aims. We aim at characterising the mass, kinematics, and stability against gravitational collapse of a statistically significant sample of filaments in the Orion B molecular cloud, which is renown for its very low star formation efficiency.
Methods. We characterised the gas column densities and kinematics over a field of 1.9 deg2, using C18O (J = 1−0) data from the IRAM 30 m large programme ORION-B at angular and spectral resolutions of 23.5″ and 49.5 kHz, respectively. Using two different Hessian-based filters, we extracted and compared two filamentary networks, each containing over 100 filaments.
Results. Independent of the extraction method, the filament networks have consistent characteristics. The filaments have widths of ~0.12 ± 0.04 pc and show a wide range of linear (~1−100 M⊙ pc−1) and volume densities (~2 × 103−2 × 105 cm−3). Compared to previous studies, the filament population is dominated by low-density, thermally sub-critical structures, suggesting that most of the identified filaments are not collapsing to form stars. In fact, only ~1% of the Orion B cloud mass covered by our observations can be found in super-critical, star-forming filaments, explaining the low star formation efficiency of the region. The velocity profiles observed across the filaments show quiescence in the centre and coherency in the plane of the sky, even though these profiles are mostly supersonic.
Conclusions. The filaments in Orion B apparently belong to a continuum which contains a few elements comparable to already studied star-forming filaments, for example in the IC 5146, Aquila or Taurus regions, as well as many lower density, gravitationally unbound structures. This comprehensive study of the Orion B filaments shows that the mass fraction in super-critical filaments is a key factor in determining star formation efficiency.
Key words: ISM: clouds / ISM: structure / ISM: kinematics and dynamics / methods: data analysis / radio lines: ISM / ISM: individual objects: Orion B
© J. H. Orkisz et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
For decades, filaments of interstellar dust and molecular gas have been known to represent an important structural element of star-forming regions in the Galaxy (e.g. Schneider & Elmegreen 1979). The possible mechanisms leading to the formation of interstellar filaments are numerous, and can involve turbulence, gravity, magnetic fields, or any combination of these (e.g. Padoan et al. 2001; Burkert & Hartmann 2004; Hennebelle 2013; Smith et al. 2014; Federrath 2016). The presence of filaments in non-self-gravitating clouds (e.g. Ward-Thompson et al. 2010) suggests that turbulence plays a major role in filament formation. It has been proposed that filaments result from the intersection of sheet-like shock structures in supersonic turbulence (Pety & Falgarone 2000; Padoan et al. 2001). Recently, Hennebelle (2013) showed that in fact if compression is necessary toaccumulate gas in the first place, shear is the main driver behind clump elongation, and magnetic fields help confinefilamentary structures and therefore make them more long-lived. Compression from winds of OB associations are also believed to have formed some of the Pipe Nebula filaments (Peretto et al. 2012). External ram pressure is not the only process leading to the formation of filaments; in particular in self-gravitating gas, self-gravity also has the effect of enhancing density anisotropies, and thus clump elongation (e.g. Hartmann & Burkert 2007; Peretto et al. 2007). Nagai et al. (1998) showed how gas sheets in hydrostatic equilibrium threaded by a magnetic field can fragment into filaments that are parallel or perpendicular to the field lines, depending on the gas density.
Lately, far-infrared and submillimetre observations of the sky made with the Herschel space observatory revealed the tight link between the presenceand properties of interstellar filaments and their ability to form stars (e.g. André et al. 2010; Molinari et al. 2010). It has been shown that more than 70% of gravitationally bound cores lie within thermally super-critical filaments, where the linear density Ml is larger than a critical value 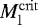 above whichthe filaments become gravitationally unstable (Polychroni et al. 2013; Könyves et al. 2015). This suggests that most star-formingcores form as the result of gravitational instabilities occurring within unstable filaments (André et al. 2014). Another key proposition that has emerged from Herschel observations of star-formingclouds in the Gould Belt is the potential universality of the width of interstellar filaments at ~ 0.1 pc (Arzoumanian et al. 2011). This width seems to be relatively independent of the central column density of the filaments, which is surprising as the densest filaments would be expected to collapse quickly and radially into thin spindles. Arzoumanian et al. (2013) proposed that accretion onto super-critical filaments could maintain a constant filament diameter during the contraction of the filament. However, using velocity-resolved maps of the filament gas emission, Hacar et al. (2013, 2018) proposed that the filament width is actually not universal; but the filament width depends on environment and has broader filaments in low-mass, star-forming regions and narrower filaments in massive star-forming regions. In this picture, all filaments have a linear density that is about critical, close to hydrostatic equilibrium, explaining why they would not collapse into spindles. The so-called universality of the filament width would then be an observational bias of dust continuum emission maps that would merge narrower, velocity coherent filaments (called “fibres” by Hacar et al. 2013) into one, non-velocitycoherent elongated structure. Filaments formed in numerical simulations that involve the three key elements (turbulence, gravity, and magnetic fields) discussed above seem to agree with Herschel results regarding the proposed universality of filament widths (e.g. Kirk et al. 2015; Federrath 2016), possibly linked to the scale at which the gas becomes subsonic, as first proposed by André et al. (2010). However, the predicted decrease of the velocity dispersion towards the inner parts of filaments is not always observed (Williams et al. 2018). This question of the (non-)universality of filament widths is still very much debated (e.g. Panopoulou et al. 2017).
above whichthe filaments become gravitationally unstable (Polychroni et al. 2013; Könyves et al. 2015). This suggests that most star-formingcores form as the result of gravitational instabilities occurring within unstable filaments (André et al. 2014). Another key proposition that has emerged from Herschel observations of star-formingclouds in the Gould Belt is the potential universality of the width of interstellar filaments at ~ 0.1 pc (Arzoumanian et al. 2011). This width seems to be relatively independent of the central column density of the filaments, which is surprising as the densest filaments would be expected to collapse quickly and radially into thin spindles. Arzoumanian et al. (2013) proposed that accretion onto super-critical filaments could maintain a constant filament diameter during the contraction of the filament. However, using velocity-resolved maps of the filament gas emission, Hacar et al. (2013, 2018) proposed that the filament width is actually not universal; but the filament width depends on environment and has broader filaments in low-mass, star-forming regions and narrower filaments in massive star-forming regions. In this picture, all filaments have a linear density that is about critical, close to hydrostatic equilibrium, explaining why they would not collapse into spindles. The so-called universality of the filament width would then be an observational bias of dust continuum emission maps that would merge narrower, velocity coherent filaments (called “fibres” by Hacar et al. 2013) into one, non-velocitycoherent elongated structure. Filaments formed in numerical simulations that involve the three key elements (turbulence, gravity, and magnetic fields) discussed above seem to agree with Herschel results regarding the proposed universality of filament widths (e.g. Kirk et al. 2015; Federrath 2016), possibly linked to the scale at which the gas becomes subsonic, as first proposed by André et al. (2010). However, the predicted decrease of the velocity dispersion towards the inner parts of filaments is not always observed (Williams et al. 2018). This question of the (non-)universality of filament widths is still very much debated (e.g. Panopoulou et al. 2017).
Observationally, the statistical characterisation of filament kinematics is a difficult task because it requires a large amount of telescope time. Until recently, only studies dedicated to a few individual filaments have been performed (Busquet et al. 2013; Hacar et al. 2013, 2016; Kirk et al. 2013; Peretto et al. 2013, 2014; Williams et al. 2018). Only in the last few years, large surveys such as the Green Bank Ammonia Survey (GAS; Friesen et al. 2017) and the CARMA-NRO Orion Survey (Kong et al. 2018) have started to observe Gould Belt clouds in molecular lines over several square degrees. Such large datasets are required to build statistically significant samples of filaments and characterise their dynamical properties. However, none of these large surveys have yet looked in detail at the filament population. We propose to use observations from the IRAM 30 m large programme Outstanding Imaging of OrioN-B (ORION-B) to analyse the properties of the Orion B filaments over an area of 1.9 deg2. This study will provide, for the first time, a complete picture of the filament population in the region and shed light on the origin of the low star formation efficiency (SFE) observed in Orion B.
This paper is organised as follows. In Sect. 2, we present the IRAM 30 m, Herschel, and Planck data used in this study, and the data processing to which the IRAM 30 m position–position-velocity (PPV) cubes were submitted. Section 3 introduces the filamentary network in the molecular cloud, and briefly explains how it is detected; methodological details on the filament identification procedures can be found in Appendix B. A statistical analysis of the physical properties that characterise these filaments is presented in Sect. 4, while the implications of these properties for the structure and evolution of the filaments are discussed in Sect. 5. Section 6 summarises the results and provides outlooks for this work.
2 Observational data and data processing
We aim at studying the structure and dynamics of the filaments in the south-western part the Orion B cloud. To do this, we need to constrain the mass, temperature, kinematics, and magnetic field in this region. We use Planck data to constrain the geometry of the source; we use the map of the C18O (J = 1−0) line observed as part of the ORION-B large programme, combined with a dust temperature map deduced from Herschel Gould Belt Survey (HGBS) observations, to derive the other quantities. This section presents the datasets and steps applied to obtain an accurate map of the molecular hydrogen column density.
2.1 Molecular lines from the IRAM 30 m ORION-B large programme
The ORION-B project (Outstanding Radio-Imaging of OrioN B; co-PIs: Jérôme Pety and Maryvonne Gerin) aims at mapping about 5 deg2 of the southern part of the Orion B molecular cloud over most of the 3 mm band in about 850 h of IRAM 30 m telescope time. The observing strategy and data reduction are discussed in detail in Pety et al. (2017), and we recall just a few key numbers. The observations cover a bandwidth of 40 GHz, from 72 to 80 and from 84 to 116 GHz, in three tunings of the EMIR receivers. The angular resolution ranges from 36′′ to 22.5′′ for these frequencies. The median sensitivity of the Fast Fourier Transform Spectrometer (FTS) spectra ranges from 0.1 to 0.5 K in main beam temperature depending on the frequency at a spectral channel spacing of 195 kHz. The J = 1−0 lines of the 13CO and C18O isotopologues are observed with a median noise of 0.12 K and a spatial resolution of 23′′. At the typical distance of ~400 pc of the Orion B cloud (Menten et al. 2007; Schlafly et al. 2014; Schaefer et al. 2016), this corresponds to a resolution of about 45 mpc. The higher spectral resolution but narrower bandwidth VESPA auto-correlator was used simultaneously to observe several lines, including 13CO and C18O (J = 1−0). The median noise for these data is 0.34 K (Tmb) for a spectral channel spacing of 40 kHz. The PPV cubes of all identified molecular lines are all smoothed to a 29′′ (60 mpc) resolution by convolution with a Gaussian kernel, and resampled onto identical grids with a resolution of 9′′ × 9′′× 0.5 km s−1 (or 0.1 km s−1 for VESPA). The spatial coordinates of the data cubes are centred onto the photodissociation region (PDR) of the Horsehead Nebula and rotated by 14° anti-clockwise with respect to RA–Dec (J2000) coordinates, so that the edge of the IC 434 PDR, from which the famous Horsehead Nebula emerges, is vertical in the maps.
As the data are still being acquired, the field presented in this paper covers 99′ by 68′, which corresponds to about 11.5 by 7.9 pc at the distance of Orion B (Fig. 1). It features objects such as the Horsehead pillar, the NGC 2023 and NGC 2024 (a.k.a. Flame Nebula) star-forming regions, and the PDRs IC 434 (illuminated by the multiple system σ Ori) and IC 435 (illuminated by HD 38087).
In this work we make use of the VESPA data because it provides a better spectral resolution while still retaining a good sensitivity, similar to the FTS sensitivity when smoothing the data to the same spectral resolution1. Most of the analysis focusses on the C18O (J = 1−0) data cube, which is our best available molecular tracer for the medium at high visual extinctions typical of filamentary structures. As Pety et al. (2017) have shown, the 12CO but also the 13CO (J = 1−0) lines are saturated at high visual extinctions, while the C17 O (J = 1−0) line is only detected around dense cores. In situations in which we compare the filaments with the more diffuse surrounding medium, we complement the C18O (J = 1−0) data with 13CO (J = 1−0).
Figure 1 shows a RGB representation of the complex velocity structure of the denser parts of Orion B, deduced from the C18O (J = 1−0) PPV cube. A map of its peak temperature can also be seen in Fig. B.1 (panel 1).
2.2 Modelling the data cube as a sum of Gaussian profiles
The maximum value of the peak signal-to-noise ratio (S/N) over the entire field of view in C18O (J = 1−0) is 63, while its median value is 2.8. It means that many lines of sight over the studied field of view are measured at a relatively low S/N. The first step of our analysis is thus to transform the noisy observational data into a model cube. For that purpose, we performed a multi-Gaussian fit of the spectra for each individual line of sight. This provides a model data cube at a final spatial resolution ofabout 60 mpc (see Appendix A). The resulting model cube allows us to have a clean and easily exploitable representation of the noisy signal without the problematic windowing effects that may occur when S/N masks are applied to the data.
2.3 Independent column density and temperature estimate from the Herschel Gould Belt Survey
By fitting a composite spectral energy distribution built from HGBS (André et al. 2010; Schneider et al. 2013) and Planck satellite (Planck Collaboration XIX 2011) continuum observations, Lombardi et al. (2014) derived a dust temperature map Tdust and a dust opacity map at 850 μm, τ850. These maps have a resolution of36′′, where HGBS coverage is available, and 5′ otherwise.
We converted the opacity map to a map of total hydrogen column density NH using the following conversion factors:
![\begin{equation*} \begin{array}{r@{\,}c@{\,}l} &&\hspace*{-7pt} {{N_{\mathrm{H}}}}/{A_{\mathrm{V}}} = 1.8\times 10^{21} \,\textrm{cm}^{-2}\,\textrm{mag}^{-1},\\[4pt] &&\hspace*{-7pt} {A_{\mathrm{V}}}/\tau_{850} = 2.7 \times 10^4. \end{array} \end{equation*}](/articles/aa/full_html/2019/04/aa33410-18/aa33410-18-eq2.png) (1)
(1)
These factors are based on Bohlin et al. (1978) and Liszt (2014), and on Rieke & Lebofsky (1985) and Cardelli et al. (1989), respectively (see Pety et al. 2017, for detailed explanations).
The C18O (J = 1−0) line traces relatively dense (nH ~ 103−104 cm−3) material with low far-ultraviolet (FUV) illumination (Pety et al. 2017; Gratier et al. 2017; Bron et al. 2018). Although the dust-to-gas coupling is completely established only above 105 cm−3 (Goldsmith 2001), the dust temperature should still be a better proxy for the gas temperature of this relatively cold medium than the excitation temperature of 12 CO (J = 1−0), which traces the warmer, more diffuse envelope of the cloud (Bron et al. 2018). The dust temperature map is shown in Fig. 2 (right).
 |
Fig. 1 Composite image representing the velocity structure present in the C18O (J = 1−0) cube. Each velocity channel is directly encoded as a hue, and the final image is obtained by additive colour synthesis. The brightest points correspond to 4 K in main beam temperature. The labels indicate, (1) the Horsehead Nebula, (2) NGC 2023, (3) NGC 2024 (the Flame Nebula), (4) the Flame filament, and (5) the Hummingbird filament. The spatial and kinematic complexity of the cloud appear clearly in particular in regions such as the north-eastern part of the cloud or around NGC 2023. |
2.4 C18O-derived column density
Using the integrated intensities from the modelled C18O (J = 1− 0) cube, an estimate of the column density of C18O was computed assuming local thermodynamic equilibrium (LTE) and an optically thin medium in this line, and using the dust temperaturefrom Lombardi et al. (2014). We followed the standard equations described in Mangum & Shirley (2015), using spectroscopic data from the Cologne Database for Molecular Spectroscopy (CDMS; Müller et al. 2005). The C18O column density was converted toNH via 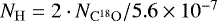 . This assumes that all the available carbon is locked in gas-phase CO and has a C/H2 abundance of ~2.8 × 10−4 (Sofia et al. 2004; Parvathi et al. 2012; Gerin et al. 2015) and a 18 O/16O isotopic ratio of ~1∕500 (Wilson & Rood 1994).
. This assumes that all the available carbon is locked in gas-phase CO and has a C/H2 abundance of ~2.8 × 10−4 (Sofia et al. 2004; Parvathi et al. 2012; Gerin et al. 2015) and a 18 O/16O isotopic ratio of ~1∕500 (Wilson & Rood 1994).
The obtained column densities are not expected to trace the totality of the matter present along the line of sight, as there can be both atomic and molecular C18O-dark gas in the fore- or background of the molecular emission region. When comparing this molecular emission and the dust extinction AV derived from Herschel data, Pety et al. (2017) showed that the C18O emission starts to be detected at AV ~ 3. We therefore compared the obtained C18O -traced column densities to the dust-traced column density above 1 magnitude of AV, rather than to the total dust-traced column density. The comparison of these tracers in the filamentary regions identified and analysed in this work is shown in Fig. 3. We see a good consistency of the resulting column densities. The ratio of NH [C18O]∕NH[AV − 3 mag] has a mean value of 1.02, a median of 0.83, and has a standard deviation of 1.19.
The middle panel of Fig. 2 shows the spatial distribution of the ![${{N_{\mathrm{H}}}}[{\mathrm{C}{^{18}}\mathrm{O}}]/{{N_{\mathrm{H}}}}\left[{A_{\mathrm{V}}}-3\,\textrm{mag}\right]$](/articles/aa/full_html/2019/04/aa33410-18/aa33410-18-eq4.png) ratio, which is close to one in a large fraction of the map. It is significantly smaller than 1 on the western edge of the cloud, and in particular at the base of the Horsehead pillar. This might be an effect of selective photodissociation: at the edge of the IC 434 PDR, the self-shielding of C18O is too weak to prevent its destruction by FUV radiation. The ratio is also much smaller than 1 in a region to the north-east, which is the coldest in the current field of view and is known to harbour dense cores. In that case, C18O depletion is the most probable explanation because the dust is cold enough for CO to freeze out on grain surfaces. The NH [C18O]∕NH[AV − 3 mag] ratio is conversely significantly larger than 1 in several low-density regions lying to the east. In these regions, away from the sources of photodissociating radiation, AV ranges from 3.0 to 5.4, with an average of 3.5, close to the chosen extinction threshold of 3 magnitudes. In this region the column density ratio becomes very sensitive to the choice of the extinction threshold, leading to higher uncertainties. The extinction threshold may vary across the field of view and reach somewhat lower values in regions away from the interface with IC 434. The ratio is also larger than 1 around NGC 2024, which is mostly likely due to a layering effect with a significant temperaturegradient along the line of sight, poorly rendered by a single value of effective dust temperature. As a consequence, the dust-traced column density is underestimated and the CO-traced column density is overestimated (Pety et al. 2017).
ratio, which is close to one in a large fraction of the map. It is significantly smaller than 1 on the western edge of the cloud, and in particular at the base of the Horsehead pillar. This might be an effect of selective photodissociation: at the edge of the IC 434 PDR, the self-shielding of C18O is too weak to prevent its destruction by FUV radiation. The ratio is also much smaller than 1 in a region to the north-east, which is the coldest in the current field of view and is known to harbour dense cores. In that case, C18O depletion is the most probable explanation because the dust is cold enough for CO to freeze out on grain surfaces. The NH [C18O]∕NH[AV − 3 mag] ratio is conversely significantly larger than 1 in several low-density regions lying to the east. In these regions, away from the sources of photodissociating radiation, AV ranges from 3.0 to 5.4, with an average of 3.5, close to the chosen extinction threshold of 3 magnitudes. In this region the column density ratio becomes very sensitive to the choice of the extinction threshold, leading to higher uncertainties. The extinction threshold may vary across the field of view and reach somewhat lower values in regions away from the interface with IC 434. The ratio is also larger than 1 around NGC 2024, which is mostly likely due to a layering effect with a significant temperaturegradient along the line of sight, poorly rendered by a single value of effective dust temperature. As a consequence, the dust-traced column density is underestimated and the CO-traced column density is overestimated (Pety et al. 2017).
The question of depletion by freeze-out is important when studying filaments because they are expected to be dense and cold, and CO is known to freeze out at temperatures < 20 K. We therefore compared the NH[C18O]∕NH[AV − 3] ratio to the temperature (Fig. 4) to search for potential signs of such a systematic depletion effect in the regions identified asfilamentary (see Sect. 3.2). A tail, corresponding to both a lower temperature and a lower column density ratio, exists in the distribution. However, the lines of sight where CO is probably depleted (lines of sight with a temperature below 20 K and a column density ratio 50% below its average value) amount to less than 8% of the filamentary regions. Moreover, they almost exclusively lie in the north-eastern cold core region, which does not host major filaments (see Figs. 1 and 2). For the most part, C18O (J = 1−0) is therefore a tracer well suited to recover the gas column densities in the density and temperature regimes of the filamentary regions of the Orion B cloud.
 |
Fig. 2 Left: NH column density map derived from the C18O (J = 1−0) integrated intensity (multi-Gaussian model). The orientation of the magnetic field, derived from Planck polarimetric data, is shown by the black segments. The spacing of the segments corresponds to the 5′ beam of Planck. Middle: map of the ratio of the C18O-traced NH to the dust-traced NH above 3 magnitudes of AV in Orion B. Superimposed are contours of the C18O (J = 1−0) integrated intensity at 0.75, 2.5 and 7.5 K km s−1. Right: effective dust temperature map computed by Lombardi et al. (2014). The black segments again show the orientation of the magnetic field. |
 |
Fig. 3 Joint distributions of the NH column densities as traced by C18O (J = 1−0) against those inferred from AV with an offsets of 3 magnitudes. This threshold corresponds to the extinctions at which the molecular tracers starts to be detected according to Pety et al. (2017). The distribution is computed in the identified filamentary regions. The 1:1 relation is overplotted as a black line. |
 |
Fig. 4 Joint distribution of the ratio of C18O-traced vs. dust-traced NH column density (Fig. 2 middle) against the dust temperature (Fig. 2 right), taken only in the identified filamentary regions. |
2.5 Magnetic field orientation from the Planck all-sky survey
We also used Planck polarisation data2 at 353 GHz to estimate the orientation of the magnetic field in Orion B. The Stokes I, Q, U maps were used at their native resolution of5′ to derive the polarisation angle χ and the magnetic field angle ψ, which is rotated by 90° with respect to χ in the International Astronomical Union convention. These angles were rotated to match the custom north-south axis of our projection; i.e. 0° points to the top of the presented field, not to the standard north in J2000 equatorial coordinates. The orientation of the magnetic field ψ is presented in the left and right panels of Fig. 2 superimposed on the column density map and temperature map, respectively.
3 Detection and characterisation of the filamentary network
3.1 Qualitative description of the filaments
Figures 1 and 2 suggest that observations of C18O (J = 1−0) bring out a complex molecular filamentary network. At the very centre of the observed field, the star-forming region NGC 2024 shines brightly. This spot has both the warmest temperature and highest column density in this area. The molecular emission comes from a dense filament, seen in the optical as a dark dusty lane in the foreground of the young H II region, with a characteristic shape that earned the Flame Nebula its name. This large Flame filament can be clearly seen in C18O (J = 1−0), as it flows diagonally from NGC 2024 to the south-east. In its more diffuse part, it is clearly sub-structured, made of parallel strands of molecular gas.
At the south-west of our field lies the Horsehead Nebula, with its characteristic shape. This nebula is a pillar carved in the Orion molecular cloud by the IC 434 H II region. Between NGC 2024 and the Horsehead lies the quieter star-forming region NGC 2023. The kinematics of the gas surrounding NGC 2023 is complex; this region has at least two velocity components (visible in green and orange colours in Fig. 1), and the filaments this medium might host are less obviously distinguishable by eye.
Just north of the Flame Nebula lies a filamentary region exposed to the influence of the NGC 2024 H II region. Further north, the round shape of the H II bubble becomes less visible (δx; δy ≈−20′;−40′). At the northern edge of our field lies another long filament, which we dub the Hummingbird filament. By eye, it is the second longest filament in the cloud after the Flame filament, and it stands out as an isolated structure, which makes it a perfect subject to study for example gravitational fragmentation. Finally, to the north-east lies a blue-shifted turbulent region containing dense cores within a complex velocity structure. Here again, the filaments are not easy to identify by eye.
3.2 Identifying the filaments
Visual inspection is insufficient to locate precisely and objectively and thus study filaments, in particular in the most entangled regions. Therefore, we implemented several algorithms to identify filamentary structures in a map. These algorithms are presented in detail in Appendix B. We describe the concepts we use and we briefly summarise the algorithms that we apply to the NH map derived from the C18O (J = 1−0) integrated intensity.
3.2.1 Morphological definition and extraction algorithms
From an observational point of view, we can qualitatively define filaments as elongated, over-dense structures in the molecular interstellar medium (ISM). We thus expect to see these as bright structures with high aspect ratios. If we were looking at the altitude map of a mountainous region, where the altitude would correspond to the brightness of molecular emission, the filaments would correspond to the main mountain ranges of this region. The ridge lines of these mountain ranges would correspond in turn to the filamentary skeleton. These mountain ranges, and these ridge lines, can be simply defined in terms of topography, that is in terms of differential properties of the studied map.
The filaments are characterised by the properties of the Hessian matrix, the second derivative of the map (Schisano et al. 2014): the main directions of variation are identified and ridges appear as local maxima along one direction, while the perpendicular direction shows negligible, or at least smaller, variation (Table B.1). The first filament extraction procedure was meant to be as straightforward as possible, and simply applied a threshold on the eigenvalues of the Hessian matrix yielding the skeleton S1. The second procedure aimed at introducing several refinements:the data were rescaled with an arcsinh function prior to the computation of the Hessian matrix, then the eigenvalues were used to compute the local aspect ratio of the structures in the column density map, and the gradient was also used to refine the ridge detection. The whole analysis was performed in a multi-scale fashion, andyielded the skeleton S2. The details of both approaches are described in Appendix B.
3.2.2 Skeletons, bones, nodes, and filamentary network
To avoid confusion between the different filamentary objects that are discussed in this paper, we define them as follows. The filament identification process yields a set of 1-pixel wide curves, which constitute a graph called the “skeleton” (or “filamentary skeleton”). These lines have endpoints and intersections, which are called “nodes”; the branches of the graph between two nodes are “bones” (as in Panopoulou et al. 2014). The bones can be fleshed out by attributing some of the surrounding gas to each 1-pixel wide curve, thus yielding “individual filaments”. Taken together, these individual filaments form a “filamentary network” (i.e. a fleshed-out skeleton). Some objects visible in the field and spontaneously referred to as filaments can be made of several individual filaments (e.g. the Flame filament); to avoid confusion these are therefore referred to as “filamentary structures”. Finally, the term “filamentary regions” refers to the regions identified as bright and structured during the filament identification process, regardless of any attribution of the gas to a specific individual filament (binary masks shown in panel 5 of Figs. B.1 and B.2).
3.2.3 Skeleton analysis
The two methods show disparities. Some structures can be identified by one method and not the other, or vice versa. To assess the similarities and differences quantitatively, we superimpose both skeletons (Fig. 5). The different filtering approaches can lead to differences of the order of one or two pixels in the position of the identified structures. But as this does not have much impact on the further analysis of the filaments, such neighbouring points are considered as matching points, up to a distance of two pixels. While there are some structures that are exclusive to one skeleton or the other, this criterion shows that a large portion (about 68% of S1, 83% of S2) of the skeletons is common to both methods.
Rather than choosing between the two possible skeletons, our approach is to keep both and study them and their statistical properties to assess the variability in the physical properties that can result from a variability in filament identification method. Therefore, four skeletons in total are compared throughout this work: the skeleton S1 obtained by simple thresholding; the skeleton S2 obtained by the adaptive method with ridge-detection; the “robust skeleton”, which is made of the common or neighbouring points of S1 and S2, and thus corresponds to the intersection S1∩S2; and the “composite skeleton”, which is made of all the points of S1 and S2, and thus corresponds to the union S1∪S2. Since the robust skeleton has, by construction, a thickness of two or three pixels because neighbouring points are taken into account, it needs to be thinned again (see Appendix B.1) to a single-pixel width. The first three skeletons are used for statistical comparisons, while the last is useful for displaying simple maps of the physical quantities.
Once the skeletons are extracted from the observational data, we still need to identify the bones. This sorting of the skeleton into bones and nodes allows us to analyse the local properties of the filamentary skeleton. It also enables us to “clean” (Appendix B.2) the skeleton by removing isolated nodes and short bones (under 0.22 pc long), and those that do not match the definition of what a filament should be: curvature (Appendix B.2.2) and contrast (Appendix B.2.3) can show that some structures are not over-dense, narrow, or elongated enough to be regarded as filaments. With the exception of the Appendix, the figures and statistics presented in this paper are therefore obtained using the cleaned skeletons.
 |
Fig. 5 Comparison of the skeletons obtained with the two different methods. The S1 skeleton denotes the skeleton obtained by simple thresholding, and S2 is obtained by the adaptive method with ridge detection. The structures only identified by one method appear in red or blue, the structures common to both methods appear in green if they perfectly match, and in yellow in the cases where the morphological thinning led to small position offsets (see Appendix B). |
3.3 Transverse profile fitting
The Hessianidentification of filaments provides us with their position angles. We can thus study the cross-sections (or transverse profiles) of the individual filaments, by plotting the variations of a physical quantity of interest perpendicular to the bone’s local major axis – in particular using the hydrogen column density map.
For the sake of simplicity and robustness (see Arzoumanian et al. 2011 and Panopoulou et al. 2014 for a discussion), the column density profiles of the individual filaments were considered to be Gaussian peaks superimposed on a linear baseline. Such a profile is therefore constrained by five parameters: the position x0 of the Gaussian with respect to the reference pixel in the skeleton, the amplitude and width of the Gaussian, A and w, and the slope and offset of the baseline, α and β as follows:
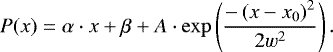 (2)
(2)
The range over which the profile is fitted, on either side of the skeleton ridge, can have a strong influence on the resulting model profile (Panopoulou et al. 2014). Therefore, we tried to use a spatial range as wide as possible, but we were limited by the density of the filamentary network: a very wide range can intersect several individual filaments, which leads to incorrect fitting results. As a compromise between these limitations, we set the fitting range to six pixels on each side of the ridge (or about 1.9′) to limit this effect. We thus avoid getting a secondary bump in the outer parts of the profile, which would be due to a neighbouring individual filament. However, even with this fitting range, the same pixel in the column density map can be attributed to several profiles, either of the same individual filament (e.g. after a turn) or of neighbouring individual filaments.
We started by fitting the transverse profiles individually (i.e. for each pixel of the skeleton). However, this led to strong degeneracies between the various parameters when the baseline deviates from the assumed straight line, which required human supervision to be overcome. As we wanted to avoid this in a semi-automated, statistical analysis of the filamentary network, we set the individual filament width w as a semi-fixed parameter. To determine its value, we fit the mean profile of each individual filament with all five free parameters, since this mean profile has a better S/N and a more Gaussian shape than the profiles for individual pixels. The obtained value of w is then kept for the transverse profile of each pixel in the individual filament.
We have also taken into account the fact that the skeleton is not always perfectly aligned with the physical ridge lines of the filaments: as shown in Fig. 5, the thinning of the skeletons can lead to positional uncertainties of about one or two pixels. For a given transverse profile, this means that the peak of the profile is off-centred, and that x0 ≠ 0. Such offsets can artificially broaden the mean profile. Therefore, a recursive approach is used: after a first fit of the mean individual filament profile which results in a given individual filament width, we fit each individual profile using that width as a fixed parameter. This individual fit yields in turn the position offset of the profile peaks, which allows us to re-align the profiles before recomputing an updated, centred mean profile. This centred mean profile is then fitted (with five free parameters) and yields a better (usually narrower) estimate of the average profile width in the individual filament. This filament is then used to perform a better fitting, with only α, β, A and x0 as free parameters, of the individual profiles.
The fit results give us access directly to such quantities as the filament width (Sect. 4.1.1) and contrast (Appendix B.2.3) and to quantities more closely linked to star formation, such as the mass and gravitational stability of the filaments (Sect. 4.1.2).
4 Physical properties of the filaments
4.1 Profile and mass
4.1.1 Filament width
The characteristic width of filaments is a direct output of column density profile fitting, and it is the most commonly measured and discussed quantity for filaments in the ISM (see e.g. Arzoumanian et al. 2011, 2013; Kainulainen et al. 2016; Panopoulou et al. 2014, 2017). The filament width is measured on the global profile of each individual filament (as described above), using a non-weighted average; i.e. all profiles in the individual filament are normalised to the same amplitude. The obtained result is deconvolved from the synthetic Gaussian beam of the fitted IRAM 30 m observations, which corresponds to 29′′ or about 60 mpc. The final width is thus given by 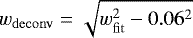 pc.
pc.
The results are shown in Fig. 6. The typical widths for each skeleton, in terms of mean, median, or most probable value are listed in Table 1. Except for a few individual filaments, mostly short filaments for which the fit does not converge or yields oddly high values (which is the sign of filaments with low contrast, see Appendix B.2.3), the spread of widths is rather small.
 |
Fig. 6 Top: map of the FWHM of the mean profiles of the individual filaments (combined skeleton). Bottom: histograms of the filament width for the S1, S2, and robust skeletons. |
4.1.2 Linear density and gravitational stability
The next physical quantity derived from the profile fitting is the linear density of the filaments. The linear density Ml of a filamentshould take into account only the matter in the filament itself, not its foreground or background. This is why the linear baseline of Eq. (2) is subtracted from the fitted profile. The linear density for a given line of sight is then simply the integral of the corresponding Gaussian transverse profile of surface density.
Knowing the linear density of the individual filaments and having a proxy for their kinetic temperature TK thanks to the dust temperature map, we can also estimate the stability of Orion B’s filaments against gravitational collapse. The criterion for balance between thermal pressure and gravity is given by 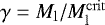 , where
, where 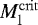 is determined by Ostriker (1964) as
is determined by Ostriker (1964) as
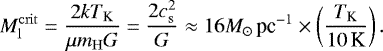 (3)
(3)
The resulting gravitational instability criterion γ of the filaments is presented in Fig. 7 (left).
However, with this approach, the critical linear density 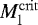 is a lower limit because it only takes into account the thermal (kinetic) pressure. In order to account for support against gravity from both thermal and non-thermal motions of the gas, we need to compute an effective temperature
is a lower limit because it only takes into account the thermal (kinetic) pressure. In order to account for support against gravity from both thermal and non-thermal motions of the gas, we need to compute an effective temperature 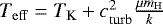 , where cturb is the observed non-thermal velocity dispersion (Arzoumanian et al. 2013; Peretto et al. 2014; Kainulainen et al. 2016). We could have access to the turbulent velocity dispersion cturb = Δv thanks to the velocity-weighted moments of the C18O (J = 1−0) spectra. However this would not take into account the fact that spectra can contain several velocity components. The spectral signature of the turbulence providing support in the form of an effective pressure is expected to be found in line broadening rather than in the multiplicity of spectral components, which rather trace the presence of physical substructures. Therefore, when computing Teff, the velocity dispersion Δv that we use is rather the typical full width at half maximum (FWHM) of the Gaussian velocity components identified by the multi-Gaussian fit (Sect. 3.3). The corresponding effective critical linear density
, where cturb is the observed non-thermal velocity dispersion (Arzoumanian et al. 2013; Peretto et al. 2014; Kainulainen et al. 2016). We could have access to the turbulent velocity dispersion cturb = Δv thanks to the velocity-weighted moments of the C18O (J = 1−0) spectra. However this would not take into account the fact that spectra can contain several velocity components. The spectral signature of the turbulence providing support in the form of an effective pressure is expected to be found in line broadening rather than in the multiplicity of spectral components, which rather trace the presence of physical substructures. Therefore, when computing Teff, the velocity dispersion Δv that we use is rather the typical full width at half maximum (FWHM) of the Gaussian velocity components identified by the multi-Gaussian fit (Sect. 3.3). The corresponding effective critical linear density 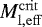 is an upper limit this time. This is because of the implicit assumption that all the non-thermal spectral broadening arises from turbulent motions, which might not necessarily be the case; for example. accretion or gravitational collapse can also contribute to line broadening. From that, we derive the effective gravitational instability criterion γeff (Fig. 7, right).
is an upper limit this time. This is because of the implicit assumption that all the non-thermal spectral broadening arises from turbulent motions, which might not necessarily be the case; for example. accretion or gravitational collapse can also contribute to line broadening. From that, we derive the effective gravitational instability criterion γeff (Fig. 7, right).
Both thelower limit of the instability criterion, γeff, and its upper limit, γ, show that the filaments in Orion B are mostly stable against gravitational collapse. This is further discussed in Sect. 5.2.
Since unstable filaments undergoing gravitational collapse are likely to lead to star formation (Arzoumanian et al. 2011; Hacar et al. 2013), we also compare the spatial distribution of the gravitational instability criteria γ and γeff in the filamentary network with the positions of the youngest among the young stellar objects (YSOs) identified by Megeath et al. (2016) and by the Herschel Orion Protostar Survey (HOPS, Fischer et al. 2013; Furlan et al. 2016). We can see indeed on Fig. 7 that the positions of YSOs, in dense clusters (NGC 2024), in looser groups (between NGC 2023 and the Horsehead) or isolated, tend to correspond to local maxima of the instability criterion γ or γeff, i.e. regions where the filaments are closest to radially collapsing under the effect of self-gravity.
Mean, median, and most probable FWHM of filaments for the three studied skeletons, resulting from mean profile fitting of the C18O-derived NH column density.
4.2 Relative alignment of the magnetic field and filaments
The relativeorientation of filaments with respect to the magnetic field is an important element of their dynamical evolution: sub-critical structures are expected to be parallel to the magnetic field, and super-critical structures perpendicular to it (Nagai et al. 1998). As we have access to an estimate of the magnetic field orientation thanks to Planck data (Fig. 2), it is straightforward to compare this orientation with the position angle of bones, which is obtained as a by-product of the Hessian filament extraction as mentioned in Sect. 3.3. Given that both the filament position angle and the orientation of the magnetic field are defined as only modulo 180°, their relative orientation is between 0° and 90° (Fig. 8). However, the major caveat is that the resolution of Planck data does not match that of the IRAM 30 m observations (5′ and 31′′ respectively). We thus smoothed the IRAM 30 m data to the resolution of the Planck magnetic field data, i.e. 5′, and performed the filament extraction on that smoothed data, before comparing it to the magnetic field map. The distribution of this relative orientation is compared to what it would have been if the two orientations were uncorrelated. The uncorrelated distribution and corresponding error margins are obtained by a Monte Carlo sampling, which randomly associates one value from the observed filament position angle distribution with one value from the observed magnetic field orientation distribution (Fig. 8).
The distribution obtained for uncorrelated quantities is not flat, which is a result of the anisotropy of both the magnetic field (Fig. 2) and the large-scale structures of the gas. The actual distribution of relative orientation shows a modest peak around 20° and a major peak, which lies between 40 and 60°. The latter corresponds to the large filamentary structures with a position angle of roughly ±45° (the north-eastern extension, part of the Flame filament, and mostly the NGC 2023-Horsehead complex). However, as the resolution of Planck data does not resolve the actual filamentary structures in the cloud, beam-averaging makes the distribution of relative orientation difficult to interpret. Polarimetry measurements at higher angular resolution are thus required to better understand how the magnetic field interacts with gas structures on the ~ 0.1 pc scale. Measurements of the dust continuum polarisation using the NIKA-2 (Catalano et al. 2018; Adam et al. 2018) camera at the IRAM 30 m telescope could provide a major improvement in that regard.
4.3 Velocity field around filaments
Compared to Herschel photometric images, the high spectral resolution of the molecular line data provides access to the motions of the gas inthe filaments and their immediate surroundings.
4.3.1 Line-of-sight velocity dispersion
As mentioned in Sect. 4.1.2, we computed the line-of-sight FWHM velocity dispersion Δv using the typical width of a Gaussian component identified by the multi-Gaussian fit. From this velocity dispersion we derived the Mach number, by comparing it with the sound speed 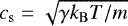 , where T is the gas temperature (assumed equal to the effective dust temperature) and m is the average molecular mass. The average transverse profiles of the Mach number in the filaments as probed by C18O (J = 1−0) are shown in Fig. 9 (top). For comparison, we also plotted the transverse profiles of the Mach number as probed by 13CO (J = 1−0) in Fig. 9 (bottom). In that case, the gas temperature used to compute the sound speed was the composite temperature obtained using the effective dust temperature and the 12 CO(J = 1−0) peak temperature. This takes into account the fact that 13CO is present in regions of lower density than C18O, where the gas and dust are not so well coupled. Under the assumption of LTE, the peak temperature of the (often strongly saturated) 12 CO(J = 1−0) line can thus offer a better proxy for the kinetic temperature of the gas in the moderately dense envelope of the cloud. The details of the derivation of this composite temperature are found in Orkisz et al. (2017).
, where T is the gas temperature (assumed equal to the effective dust temperature) and m is the average molecular mass. The average transverse profiles of the Mach number in the filaments as probed by C18O (J = 1−0) are shown in Fig. 9 (top). For comparison, we also plotted the transverse profiles of the Mach number as probed by 13CO (J = 1−0) in Fig. 9 (bottom). In that case, the gas temperature used to compute the sound speed was the composite temperature obtained using the effective dust temperature and the 12 CO(J = 1−0) peak temperature. This takes into account the fact that 13CO is present in regions of lower density than C18O, where the gas and dust are not so well coupled. Under the assumption of LTE, the peak temperature of the (often strongly saturated) 12 CO(J = 1−0) line can thus offer a better proxy for the kinetic temperature of the gas in the moderately dense envelope of the cloud. The details of the derivation of this composite temperature are found in Orkisz et al. (2017).
The 13CO (J = 1−0) profiles display significantly higher Mach numbers than C18O (J = 1−0), but show no significant feature whatsoever. On the other hand, the C18O (J = 1−0) profiles show a pronounced decrease in Mach number towards the centre of the filaments. The width of this feature is similar to the measured filament width.
 |
Fig. 7 Gravitational instability criterion of the filaments (combined skeleton). This criterion is derived from the C18O-traced linear density estimation and either the thermal pressure (γ, left) or the effective pressure, which also takes into account the C18O (J = 1−0) velocity dispersion (γeff, right). Overlaid are the positions of protostars from Megeath et al. (2016) in white, and class 0 YSOs from HOPS (Furlan et al. 2016) in green. |
4.3.2 Centroid velocity gradient
While the velocity dispersion gives access to the kinematics along the line of sight, there is no direct way to observe velocity effects in the plane of the sky. As a proxy for such observations, we used the gradient of centroid velocity. Its amplitude measures the variations of the velocity field in the plane of the sky, in contrast to the linewidth, which probes the velocity dispersion along the line of sight.
Figure 10 shows the average transverse profiles of the amplitude of the centroid velocity gradient observed in C18O (J = 1−0) (top) and in 13CO (J = 1−0) (bottom). The gradient amplitude is almost constant across the filaments in C18O (J = 1−0) with no particular visible trend. The 13CO (J = 1−0) profiles, on the other hand, exhibit slightly higher amplitudes of the gradient, with a pronounced minimum towards the centre of the filaments, which brings the centroid velocity gradient amplitudes of 13CO (J = 1−0) down to the average value observed for C18O (J = 1−0).
5 Discussion
5.1 Width of the filaments
5.1.1 On the robustness of our width estimation
Panopoulou et al. (2017) suggested that the narrow distribution of filament widths with a typical scale of 0.1 pc can be an artefact resulting from the analysis method, in particular the measure of the width of the mean profile of a filament rather than the widths of its individual profiles and the spatial range used for the profile fitting. The use of average filament profiles results in a narrower distribution of widths, but does not modify its peak significantly. In our case, the high spatial density of detected filaments and thus the number of intersections fragments the largest filamentary structures (such as the Flame filament) into shorter individual filaments, reducing the amount of averaging. The obtained distribution of filament widths, and in particular its dispersion, appears as an intermediate between the broad distributions obtained for individual profile widths and the very narrow distributions obtained for average filament profiles, as shown in Panopoulou et al. (2017, their Fig. 2). The comparison with measurements on filaments in the Polaris Flare by Panopoulou et al. (2017) suggests that the absence of filaments with widths larger than 0.2 pc in Orion B can be a result of the fitting window, which is 1.9′, or 0.21 pc on each side of the filament ridge. However, the median and most likely widths in Fig. 6 and Table 1 are small enough to be confidently measured, but large enough not to be due to the telescope beam. We can therefore say that, even though the spread of widths of the filaments is probably underestimated in this work, the median and most probable value of the filament width, of the order of 0.12 pc, are reliable.
In addition to this first caveat, we should also stress that a Hessian detection filter behaves to some extent like a wavelet filter, bringing out structures matching the scale of the Gaussian derivative used for the calculation. However, the skeleton S2, thanks to its adaptive nature, can overcome this bias, since the data dictate the scales at which the filter has its strongest response (see Appendix B.1). For the skeleton S1, the use of a single smoothing scale could induce a stronger bias, but the robustness of the results was checked by studying skeletons obtained in the same way as S1, but with a halved or doubled smoothing scale. The distribution of the obtained filament widths however was slightly shifted towards smaller or larger scales, respectively, owing to the inability of a very narrow filter to pick up very broad structures and the excessive smoothing by a very wide filter that blurs out very small structures. The peak of this skeleton remained unchanged, thus proving that the main detected structures do not strongly depend on the filter and that they correspond indeed to filaments with a mean width of the order of 0.12 pc (Table 1).
Finally, the average Mach number profiles derived from the C18O (J = 1−0) velocity dispersion show a feature of similar width (Fig. 9). The width of the feature seen in the average profiles of the 13CO (J = 1−0) centroid velocity gradient norm is also of the order of 0.1 – 0.2 pc. These measurements, completely independent from spatial distribution of the column density, argue in favour of the robustness of our estimate for the FWHM of filaments.
 |
Fig. 8 Top: map of the angle between the magnetic field and filaments detected in Orion B at a 5′ resolution. The filaments are red when they are parallel to the magnetic field and blue when perpendicular to it. Bottom: distribution of the relative orientation of the filaments and the magnetic field for the S1, S2, and robust skeletons. The dotted lines (and the shaded areas) present the distribution (and the corresponding ± 1σ uncertainties) that we would get if the two quantities were uncorrelated. The uncorrelated distribution is obtained by a Monte Carlo sampling of the magnetic field and filament position angles. |
 |
Fig. 9 Top: average transverse profiles of the line-of-sight FWHM velocity dispersion of the filaments. These profiles are computed for the S1, S2, and robust skeletons via the modelled C18O (J = 1−0) linewidth; the shaded areas show the standard error for each profile. Bottom: same as above, but using the 13CO (J = 1−0) data cube for comparison. |
 |
Fig. 10 Top: average transverse profiles of the amplitude of the centroid velocity gradient of the filaments. These profiles are computed for the S1, S2, and robust skeletons via the C18O (J = 1−0) data cube; the shaded areas show the standard error for each profile. Bottom: same as above, but using the 13CO (J = 1−0) data cube for comparison. |
5.1.2 Universal filament width?
The distribution of mean filament widths that we obtain in Orion B, no matter which skeleton we consider, is very similar to that presented by Arzoumanian et al. (2011) for the IC 5146, Polaris, and Aquila regions, where a 0.1 pc “typical” width with a 0.03 pc spread was reported, and to simulations results by for example Federrath (2016).
In contrast, our statistics of the filament widths are different from what is observed in the Taurus molecular cloud by Panopoulou et al. (2014), based on 13CO (J = 1−0) observations(Narayanan et al. 2008) that have a typical filament width of 0.4 pc. This discrepancy results at least partly from the chosen molecular tracer, which is less adapted for tracing the filamentary material, as discussed in Sect. 2.1. 13CO is susceptible to become optically thick and therefore to better trace the extended, power-law-like envelope of the filament rather than its tubular, central part (Arzoumanian et al. 2011), which can result in wider FWHM estimations. In the case of Orion B, the measurement of filament widths applied to the 13CO-derived NH column density yields filament widths of 0.18 ± 0.04 pc, which are wider than the 0.12 ± 0.04 pc measured with C18O.
5.2 Gravitational stability and star formation
5.2.1 Low linear and volume densities
The linear densities of the filaments that we detected range from a few M⊙ ∕ pc to about 100 M⊙∕pc, with a median linear density of ~5 M⊙∕pc for all skeletons (Fig. 11, top). This apparently log-normal distribution matches the usual linear densities of interstellar filaments rather well, as observed for example in IC 5146 (Arzoumanian et al. 2011), Taurus (Panopoulou et al. 2014), or Musca (Kainulainen et al. 2016). This distribution is of course lower than what is observed for high linear-density filaments such as the Integral-Shaped Filament (Stutz & Kainulainen 2015; Kainulainen et al. 2017), for which the linear density is of the order of several 102 M⊙∕pc. More precisely, while the upper end of our distribution reaches the typical order of magnitude for linear densities (in the range of a few tens or hundreds of M⊙∕pc), a large fraction of the filamentary network have rather low linear densities.
This is also visible when looking at the typical volume densities of the filaments, which are estimated by assigning the linear density to a uniformcylinder, the diameter of which would be the FWHM of the individual filament profile. These volume densities range from 104 to 105 cm−3, again with a distribution close to a log-normal one, with a median value of ~ 2 × 104 cm−3 (Fig. 11, bottom). This is consistent with the upper end of the volume density distribution in the whole western edge of the Orion B molecular cloud, as presented in Bron et al. (2018). These typical densities are however lower by an order of magnitude than those measured by Teixeira et al. (2016; and references therein) or Kirk et al. (2015), based on observations of filaments or hydrodynamical simulations, respectively.
These distributions of linear densities and volume densities can be affected by completeness effects. The chosen molecular tracer, C18O, has a broad sensitivity range (Pety et al. 2017), but it still has its limits,; this implies that faint structures lying below ~ 2 × 1021 cm−2 can be missed, while the densest filaments can have their density underestimated due to CO freeze-out or line saturation (Sect. 2.4). In addition, the filament identification process removes a number of low-contrast individual filaments (Appendix B.2.3) which would have fallen into the lower end of the density distributions. In total, completeness effects might affect low-density filaments more than high-density filaments.
We therefore have a set of filaments which contains a few objects matching the usual linear or volume densities found in the literature, but with an excess of low-density elements. There are several possibilities to explain this effect. First, André et al. (2010) and Arzoumanian et al. (2011) noted that fitting filament profiles with a Gaussian rather than a Plummer profile can lead to an underestimation of their density by about 20%. However, this does not increase the densities we measured by an order of magnitude, and many studies cited above also used Gaussians to fit the transverse profiles. A more important factor is the detection scheme used in this work. Most studies focus on a small number of well-identified and carefully selected filaments, for example by setting high persistence levels when detecting filaments with DisPerSE (Sousbie 2011). In contrast, we use a lax definition of the filaments, resulting in a number of rather faint, but still contrasting and elongated objects to be part of the analysed skeletons. In certain cases, this is desirable, for example in the case of the south-eastern extension of the Flame filament, which clearly divides into many substructures that we do not want to miss. In other cases, structures that would usually not classify as filaments are retained, such as lower density striations; i.e. strands of more diffuse gas that is accreting onto a main filament.
 |
Fig. 11 Top: distribution of the linear density of the filaments. The vertical dashed lines show the most probable critical linear densities corresponding to |
5.2.2 No signs of gravitational collapse
The filaments in Orion B are striking owing to their exceptional stability against gravitational collapse, even when looking at the higher limit of their instability criterion (Fig. 7, left). While the denser filaments in our skeletons match rather well the sample in Arzoumanian et al. (2013), this exceptional stability of the filaments can be explained by several factors.
First, the western edge of Orion B is a warm environment, heated by the large amount of FUV radiation coming both from outside (σ Ori) and inside (NGC 2024) the cloud. These high temperatures (Fig. 2, right) lead to high thermal pressures and therefore high critical masses (Eq. (3)). Arzoumanian et al. (2013) simply assumed a constant temperature of 10 K in the filaments, Teixeira et al. (2016) a constant temperature of 15 K, while the dust temperature in Orion B rarely drops below 20 K. These warm temperatures could either be a layering effect or an actual specificity of this region of Orion B; in the layering effect, the filaments are actually cold but the dust temperature is dominated by the warmer surrounding medium. In any case, an overestimated or genuinely higher temperature of the gas leads to higher critical linear densities.
Second, turbulence also plays a role in stabilising the filaments against gravity. Kainulainen et al. (2016) showed that taking turbulence into account brings the Musca filament from a super-critical to trans-critical state. In the case of Orion B, this corresponds to the dramatic difference between the left and right panels of Fig. 7, although, as mentioned, γeff is a lower limit, as some of the velocity dispersion might come, for example from infall/collapse (Arzoumanian et al. 2013), and not from rotation or turbulent motions that would support the filaments against gravity. Table 2 summarises by how much the fraction of the filamentary network prone to gravitational instability would have increased if we had assumed no turbulent support or a lower gas temperature. It shows how important velocity-resolved observations of molecular lines are when trying to determine the stability of filaments.
This overall lack of gravitationally unstable filaments in Orion B correlates well with its known low SFE (Lada 1992; Carpenter 2000; Federrath & Klessen 2013; Megeath et al. 2016; Orkisz et al. 2017). Moreover, the NGC 2023 and NGC 2024 star-formingregions are among the few regions containing super-critical or trans-critical filaments. This is consistent with the fact that these regions also show the most compressive motions, as measured by Orkisz et al. (2017).
Fraction of super-critical (γ > 1) or at least trans-critical (γ > 0.5) filaments depending on the assumptions on their internal pressure computed for the S1, S2, and robust skeletons.
5.2.3 Star formation efficiency
Measurement of the filament masses also enables us to check what fraction of the mass of the molecular cloud is contained in the filamentary network, and, in particular, in the gravitationally unstable filaments, as this last fraction directly relates to the SFE of the cloud. Using the 12 CO (J = 1−0) line and following Solomon et al. (1987) and Bolatto et al. (2013) in the same way as in Pety et al. (2017), we obtain a total virial mass of the cloud (for the considered field of view and accounting for the CO-empty IC 434 PDR) comprised between 8400 M⊙ and 13 900 M⊙. For simplicity, we use the average of these values, at 11 100 M⊙. This yields a fraction of mass in the filamentary network of about 4.3 ± 1.1% (474 ± 28 M⊙) in the case of the S1 skeleton, 3.6 ± 0.9% (405 ± 22 M⊙) in the case of S2, and 3.2 ± 0.8% (357 ± 21 M⊙) for the robust skeleton. It is significantly less than the fraction of mass derived for the “environment of filaments” in Pety et al. (2017; about 40%), which is mostly explained by the sparse character of the filamentary network, compared to an AV extinction mask, and also less than the total mass traced by C18O (about 1200 M⊙, or 11 ± 3% of the mass of the cloud). Thus, only about one-third of the C18O-traced mass is found in filaments.
The fraction of mass in gravitationally super-critical or trans-critical filaments depends on the definition of the instability criterion. When using γ, we have 266 ± 17 M⊙, or 2.4 ± 0.6% of the mass of the cloud in trans-critical filaments, and 111 ± 7 M⊙, or 1.0 ± 0.3% of the mass in super-critical filaments. When using γeff, the fraction of the mass of the cloud in trans-critical filaments is 0.9 ± 0.2% (95 ± 6 M⊙), with only 0.1% of the mass (21 ± 1 M⊙) in super-critical filaments. To first order, the fraction of the mass of a molecular cloud contained in gravitationally unstable structures can be directly related to the SFE of that cloud, as we can roughly assume that this mass is going to collapse into cores and into stars. Among the fractions mentioned above, the fraction of the mass of the cloud in the trans-critical filaments using the gravitational instability criterion γ can be considered as the upper limit for the SFE. Such a value of 2.4 ± 0.6% is consistent with previous measurements of the SFE by Lada (1992), Carpenter (2000), Federrath & Klessen (2013), or Megeath et al. (2016), which range from 0.4 to 3%.
Lada et al. (2010) proposed that the star formation rate of molecular clouds is proportional to the mass above a threshold of 0.8 AK, which corresponds approximately to 6 magnitudes of AV, or 1.1 × 1022 cm−2, while André et al. (2014) find prestellar cores only in regions with column densities higher than 1.4 × 1022 cm−2 (i.e. AV ≈ 8 mag). These thresholds are higher than the detection limit of C18O (J = 1−0) (about 3 magnitudes of AV, as mentioned in Sect. 2.1, which corresponds to ≈ 0.4 magnitudes of AK), and exclude part of the filamentary regions (Fig. 2 left and Fig. 3). They delimit a star-forming mass of the cloud of ~ 540 M⊙; this mass is less than the total of the C18O-traced mass, but much more than what is contained in trans-critical or super-critical filaments. The typical volume density threshold that we obtain for gravitationally unstable filaments, using a typical value of the critical linear density of 30–60 M⊙∕ pc (Fig. 11, Eq. (3)) and assuming a filament diameter of 0.12 pc, is about 5 × 105 cm−2. It corresponds to a column density of ~4 × 1022 cm−2, which is significantly higher than the threshold column densities proposed by Lada et al. (2010) and André et al. (2014). The ~ 1.1 × 1022 cm−2 threshold can thus be seen as a general absolute minimum under which the gas contained in molecular clouds does not contribute to star formation, but the actual column density threshold over which star formation is likely to occur in a given cloud can depend on intrinsic properties of the cloud, such as its age or kinematics. In the case of Orion B, in which strong solenoidal motions lower the SFE (Orkisz et al. 2017), this actual threshold is particularly high.
5.2.4 One clear example of longitudinal fragmentation
When trying to identify mechanisms of star formation in the filamentary network, it is difficult to conclude in favour of radial collapse, or longitudinal collapse leading to star formation via accretion onto hubs (Peretto et al. 2014) based on the relative positions of the YSOs and the filamentary skeleton (Fig. 7). However, another widely observed phenomenon leading to the formation of prestellar cores is longitudinal fragmentation (Hacar et al. 2013, 2018; Teixeira et al. 2016; Kainulainen et al. 2016). Filaments that are above the gravitational instability limit are expected to collapse radially. But when they come close to their gravitational stability limit (γ ≲ 1), filaments are mostly susceptible to fragment longitudinally on scales close to their Jeans length (Takahashi et al. 2013; Teixeira et al. 2016) or to four times their FWHM (Inutsuka & Miyama 1992).
Signs of such fragmentation are visible in at least one individual filament in our field, the Hummingbird filament, which, interestingly, does not harbour any known YSO. Oscillations of the linear density are visible along this filament, forming evenly spaced “beads”. Following the recommendations of Schulz-Dubois & Rehberg (1981), we computed the two-point auto-structure function of the linear density along the curvilinear abscissa of the filament’s bone. It is defined as follows:
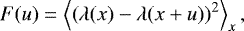 (4)
(4)
where λ is the linear density, x a position along the bone, and u the separation between the considered points. The resulting function is plotted in Fig. 12.
The oscillating pattern highlights the presence of evenly spaced structures with sizes of the order of 0.4 pc. Given that we have a FWHM of 0.11 pc for that individual filament, such a fragmentation length matches well the analytical prediction of Inutsuka & Miyama (1992) for collapsing isothermal filaments, and the simulation results of Clarke et al. (2016) for accreting filaments, since both predict a fragmentation with separations of about four times the diameter.
Following Spitzer (1998), Takahashi et al. (2013) and Teixeira et al. (2016), we computed the Jeans length of the filament, 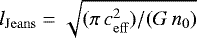 , where ceff is the effective sound speed, corresponding to the effective temperature, and ρ0 is the volume density. The mean volume density n0 = 1.5 × 104 cm−3 of the individual filament, derived for the case of a uniform cylinder, combined with an effective temperature Teff= 43 K (while TK = 18 K) yields a Jeans lengthof 0.54 pc, which is slightly higher than the observed characteristic scale in Fig. 12. We obtain a Jeans length of 0.38 pc if we replace this average density by an estimate of the maximum density that is obtained by comparing the average value of a Gaussian over its FWHM to its peak value and correcting for the transition from two to three dimensions as follows:
, where ceff is the effective sound speed, corresponding to the effective temperature, and ρ0 is the volume density. The mean volume density n0 = 1.5 × 104 cm−3 of the individual filament, derived for the case of a uniform cylinder, combined with an effective temperature Teff= 43 K (while TK = 18 K) yields a Jeans lengthof 0.54 pc, which is slightly higher than the observed characteristic scale in Fig. 12. We obtain a Jeans length of 0.38 pc if we replace this average density by an estimate of the maximum density that is obtained by comparing the average value of a Gaussian over its FWHM to its peak value and correcting for the transition from two to three dimensions as follows: 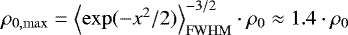 . The observed fragmentation length is therefore close to the scales expected from both a cylindrical or a spherical instability.
. The observed fragmentation length is therefore close to the scales expected from both a cylindrical or a spherical instability.
In summary, filaments in Orion B show no signs of radial collapse, no clear evidence (at this stage of the analysis) of longitudinal collapse onto hubs, but at least one good example of longitudinal fragmentation.
5.3 Kinematics
The 13CO (J = 1−0) line traces the moderately dense gas that forms the bulk of molecular clouds and surrounds the filamentary network. Towards filament ridges, a substantial fraction of the 13CO (J = 1−0) emission can start to originate from the filaments, traced by the C18O (J = 1−0) emission. The kinematics of 13CO could thus trace the transition between the turbulent environment and the quiescent inner part of filaments (e.g. Hatchell et al. 2005; Federrath 2016). Towards the centre of the filaments, the norm of the centroid velocity gradient decreases, reaching at its minimum the same value as for C18O (J = 1−0). We would expect the Mach number to decrease as well, but it shows flat profiles instead. This could be explained by the fact that the optical depth of 13CO (J = 1−0) increases towards the centre of the filaments, resulting in a non-negligible opacity broadening which compensates for the decrease in linewidth due to a lower velocity dispersion. Indeed, Orkisz et al. (2017) have shown that the 13CO (J = 1−0) opacity broadening is negligible except in the dense regions in which we are interested. For the column densities of 13CO typical of the densest filaments ( ), the opacity can reach
), the opacity can reach 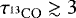 and lead to a line broadening by a factor ~1.5; this is consistent with the absence of variation of the FWHM across the filaments because the decrease in velocity dispersion is compensated by an increase in opacity broadening. The rather low Mach number traced by 13CO (J = 1−0) compared to the average of ~6 given in Orkisz et al. (2017) is because we only take into account one of the multiple spectral components along the line of sight, which can significantly reduce the measured velocity dispersion.
and lead to a line broadening by a factor ~1.5; this is consistent with the absence of variation of the FWHM across the filaments because the decrease in velocity dispersion is compensated by an increase in opacity broadening. The rather low Mach number traced by 13CO (J = 1−0) compared to the average of ~6 given in Orkisz et al. (2017) is because we only take into account one of the multiple spectral components along the line of sight, which can significantly reduce the measured velocity dispersion.
The C18O (J = 1−0) results contrast with 13CO (J = 1−0). The velocity dispersion along the line of sight is supersonic, however the Mach number decreases significantly inside the filaments, down to almost transonic values, as it is usually observed or predicted (e.g. Arzoumanian et al. 2013; Federrath 2016). This can be a sign of the dissipation of turbulence (Hennebelle 2013). The norm of the centroid velocity gradient possibly shows a similar, but far less pronounced decrease towards the centre of the filaments. We also notice that with filament widths of the order of 0.1 pc and centroid velocity gradients of < 2 km s−1∕pc, the centroidvelocity variations in the plane of the sky are subsonic, given typical sound speeds of the order of 0.3–0.7 km s−1. This is reminiscent of the results of Smith et al. (2016), who show that filaments are structures which move coherently on large scales (and thus have near-constant centroid velocities), regardless of the small-scale turbulence.
In the context of the velocity field of filaments, one element often discussed in the presence of fibres (Hacar et al. 2013, 2018; Panopoulou et al. 2014). We would expect from the possible presence of unresolved fibres that there would be multiple spectral components detected in many lines of sight in the filaments. However, it appears to be rarely the case. Only the part of the Flame filament closest to the NGC 2024 star-forming region displays a long portion that consistently has two or more identified spectral components. This calls into question the presence of fibres since it would mean that they are not only unresolved spatially, but also spectrally, since in most cases their presence would merely broaden the C18O (J = 1−0) line instead of showing more spectral peaks. Their presence could then possibly explain partly the supersonic Mach numbers even at the centre of the filaments.
A further understanding of the dynamics of these filaments using the ORION-B dataset would require performing a three-dimensional identification of the structures, which would improve the understanding of the spectral multiplicity of the filaments and provide a better view of their crossings and hubs. Further research on the velocity not only across but also along the filaments, studying their position-velocity diagrams in a fashion similar to for example Peretto et al. (2014), would also benefit our understanding of these filaments. For example, the observed longitudinal fragmentation in the Hummingbird filament appears to be associated with a specific velocity pattern that will be explored in detail in a future paper.
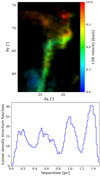 |
Fig. 12 Top: same as Fig. 1, but with the field and velocity range zoomed in on the Hummingbird filament, showing beads in the rectilinear tail of the Hummingbird. Bottom: two-point structure function of the linear density in the Hummingbird filament (following the robust skeleton), in (M⊙/pc)2, showing a periodic pattern which suggests longitudinal fragmentation with a period of 0.4 pc. |
5.4 Statistical influence of the filament extraction method
The study presented in this work shows that the difference between the statistical results of the different skeletons are modest, if not negligible. This could be expected from the significant overlap of the skeletons, which is in turn related to the consistent manner in which the tuning of the detection parameters was done, be it for the initial extraction (Appendix B.1) or during the cleaning process (Appendix B.2), for both the S1 and S2 skeletons.
When comparing Figs. 5 and 7, we can see that most of the individual filaments that are exclusive to either S1 or S2 are particularly stable, i.e. they are among the least dense structures in the field of view. The only significant structures that are not in common are the Horsehead PDR and a small portion of the Flame filament in NGC 2024. This last point can explain the difference in percentage of mass in super-critical or trans-critical filaments observed between S1, S2, and the robust skeleton, as the missing fragment of NGC 2024 in S1 contains a significant amount of mass above the gravitational instability threshold. The similarity of the results obtained with the robust skeleton compared to those with the S1 and S2 skeletons is also important, because it shows that the structures not detected by either S1 or S2 do not play a major role in the statistical properties of the filamentary network.
Provided that the definition of a filament is consistent with what was used in this paper (in particular in terms of density or length requirement) it is safe to assume that filament detection schemes do not play a significant role in the difference between different studies of interstellar filaments.
6 Conclusions
In this paper, we have used velocity-resolved line maps obtained through IRAM 30 m observations in the context of the ORION-B project to trace the dense, filamentary matter in the Orion B molecular cloud with the C18O (J = 1−0) line. Using two different extraction methods, we identified the network of filaments in the cloud and used both extracted skeletons as well as their intersection to compare the statistical properties of the filaments they contain.
The main results regarding these filaments are the following:
- 1.
Given the very coherent filament detection criteria between the two extraction methods (and despite the technical disparities) the statistical properties of the detected structures in any skeleton can be considered as quasi-identical.
- 2.
The filaments display a typical width of ~0.12 pc and have a narrow spread of ± 0.04 pc (Fig. 6). This value seems to be free from detection bias and is supported by the width of the variations in the velocity field (Figs. 4 and 10);
- 3.
The upper ends of the distributions of linear densities and volume densities of the filaments are consistent with observations and simulations of interstellar filaments. However, many extracted filaments have lower densities. This suggests that the criteria generally used to identify filaments are too restrictive.
- 4.
The filaments in Orion B are stable against gravitational collapse because of their relatively lukewarm temperatures and their moderately supersonic velocity dispersions. This is consistent with the very low SFE of Orion B, at about 1%;
- 5.
At least one filament (the Hummingbird filament, lying north of NGC 2024) shows visible signs of periodic longitudinal fragmentation, despite being clearly gravitationally sub-critical.
- 6.
In the vicinity of the filaments, the velocity dispersion is larger in 13CO (J = 1−0) than in C18O (J = 1−0). The surroundings of the filaments are thus more turbulent than their inner part. In addition to that, the C18O (J = 1−0) velocity dispersion decreases significantly towards the centre of the filaments, almost reaching transonic values. This suggests that turbulence is being dissipated in the filaments although they are not gravitationally bound.
These results speak in favour of the filamentary structures in Orion B being in a young evolutionary stage, meaning that the cloud might eventually evolve into a more active environment like its neighbour Orion A. This is consistent with the relatively young age of the H II regions within the cloud, estimated at ~ 100 000 and 200 000 yr for NGC 2023 and NGC 2024, respectively (Tremblin 2014, priv. comm.), and also with the fact that the fraction of very young protostars among all YSOs is significantly larger in the south-western part of Orion B than in Orion A (24 vs. 1.5%, Stutz et al. 2013)
This paper mostly focussed on the transverse properties of the filaments. The longitudinal properties were preliminarily tackled in the specific case of the Hummingbird filament, but these properties deserve an in-depth study as well, because signs of longitudinal fragmentation are suspected at other locations in the cloud and are apparently accompanied by longitudinal velocity patterns. The Hummingbird filament itself will be the object of a follow-up study at higher angular resolution, which will shed light onto the entire filamentary network of Orion B.
From a methodological point of view, the Hessian approach (Appendix B.1) can be easily extended to perform the filament detection in three dimensions. Such a three-dimensional detection making full use of the velocity information would facilitate the analysis of the longitudinal velocity structure of the filaments, and possibly enable the detection of fibres (Hacar et al. 2013).
Thanks to the multi-tracer nature of the ORION-B project, the filamentary skeletons could be used to stack the observed spectra to reveal faint molecular lines and characterise the molecular signature of filamentary regions, in a manner similar to Gratier et al. (2017) and Bron et al. (2018). Conversely, classification tools such as the clustering used by Bron et al. (2018) could possibly reveal the presence of different families of filaments, based on their properties derived in this paper, which could point to different evolutionary stages or scenarios for the filaments in Orion B.
Acknowledgements
We thank Pr. Maciej Orkisz for pointing us to the work of Frangi et al. (1998) and helping us with the understanding and implementation in an astrophysical context of this analysis method coming from the field of medical imaging. We also thank Pr. Jouni Kainulainen for stimulating discussions and helpful remarks. This research has made use of data from the Herschel Gould Belt Survey (HGBS) project (http://gouldbelt-herschel.cea.fr). The HGBS is a Herschel Key Programme jointly carried out by SPIRE Specialist Astronomy Group 3 (SAG 3), scientists of several institutes in the PACS Consortium (CEA Saclay, INAF-IFSI Rome and INAF-Arcetri, KU Leuven, MPIA Heidelberg), and scientists of the Herschel Science Center (HSC). This work was supported by the CNRS/CNES programme “Physique et Chimie du Milieu Interstellaire” (PCMI). We thank the CIAS for its hospitality during the three workshops devoted to this project. N.P. wishes to acknowledge support from STFC under grant number ST/N000706/1. P.G. thanks ERC starting grant (3DICE, grant agreement 336474) for funding during this work. J.R.G. thanks the Spanish MINECO for funding support under grant AYA2017-85111-P.
Appendix A Multi-Gaussian fitting of the molecular spectra
In order to transform the noisy observational data into a model cube, we first perform a Gaussian smoothing the C18O (J = 1−0) VESPA spectra with a width of 3 velocity channels to improve the peak detection. Significant peaks in the spectrum, above a threshold of 4σ, are detected, and then a multi-Gaussian fit is performed on the spectrum with one Gaussian component per identified peak. After that, the reduced χ2 is computedover 6 channels on either side of the peak (13 channels in total), and compared to the noise level of the spectrum.
 |
Fig. A.1 Examples of spectra fitted with multiple Gaussians, at signal-to-noise levels of about 15 (top) and 5 (bottom). The individual Gaussian components are indicated in dashed, dotted, or dash-dotted lines. |
If the χ2 is lower than 0.5σ, an unnecessary Gaussian component is removed. When it is larger than a threshold of 2σ, an extra Gaussian component is added in the corresponding velocity range. Our initial determination of the number of significant peaks tends to be overestimated. For that reason, during the iterative process, only one extra component can be added. Conversely, the number of components can decrease to a minimum of one. This allows the fitting process to take into account, for example components separated by less than their average velocity dispersion, which do not present one separate peak per component. But it also prevents over-fitting, whereby a single spectral component would be reproduced by many Gaussian peaks. Finally, we visually inspect the residual cube to check that no obvious signal feature remains unfitted. Figure A.1 shows two examples of the fit of multicomponent spectra.
Spatial correlations between neighbouring pixels are not taken into account during the fit. However, the retrieved moment maps, and in particular the integrated intensity, do not show any significant incoherence (Fig. 2, left).
Appendix B Structural detection of the filaments: methodological details
B.1 Step by step extraction of the filaments
After obtaining from the raw observational data a modelled cube and a column density estimate (Fig. B.1, panels 1, 2 and 3), we use this column density map to identify the filamentary structures in Orion B. This section details the extraction of the skeletons used throughout this paper. We restrict ourselves to study filamentary structures in a two-dimensional map but the concepts and implementations can be generalised to a PPV cube.
Topography of a two-dimensional dataset depending on the eigenvalues of its Hessian matrix ε1 and ε2.
B.1.1 Hessian approach
We have qualitatively and observationally defined filaments as elongated, over-dense structures in the molecular ISM. Their identification can be compared with that of mountain ranges in an altitude map. These mountain ranges and their ridge lines can be simply defined in terms of topography, that is in terms of differential properties of the studied map.
The Hessian matrix (i.e. the matrix of the second order partial derivatives) provides the most useful insight into the topography: it measures the variations of the slopes, and therefore enables us to locate the valleys, summits, and ridges. The eigenvectors of the Hessian indicate the main directions of variations of the slope, and the eigenvalues (ε1 and ε2 in our two-dimensional case) whether the terrain is passing through a minimum or a maximum in these two directions. In the case of filaments or ridges, we expect the altitude to vary very little in one direction, and to reach a local maximum in the other direction. We therefore expect a second derivative with a value close to zero along the ridge and a strongly negative derivative perpendicular to the ridge; if we were working with absorption data, the reasoning would remain the same, albeit with reversed signs. We can summarise the behaviours of ε1 and ε2 in terms of characteristic structures in Table B.1.
The computation of the Hessian itself makes use of the concepts of linear scale space theory (Florack et al. 1992; Koenderink 1984), as advised by Frangi et al. (1998). Differentiation is thus performed by convolving the field with derivatives of n-dimensional Gaussians, which allows us to smooth out simultaneously the noise and adapt to the typical spatial scale of searched structures (Frangi et al. 1998; Salji et al. 2015); in our case, as no initial assumption is made on the length of filaments, the only relevant scale is their width. Once the smooth Hessian is obtained and diagonalised, we can use the eigenvalues as a filter to extract filamentary regions from the map. In this work two implementations of such filters are used.
B.1.2 Filamentextraction by thresholding
The first approach is meant to be as simple as possible, and is similar to that presented in Planck Collaboration Int. XXXII (2016). The Hessian is directly computed for the map of C18O-derived column density (Fig. B.1, panel 4), and the analysis focussed on a single spatial scale set to 0.13 pc (corresponding to 0.11 pc after deconvolution). This choice of scale is the result of an iterative approach. The first guess for the size of the filaments was assumed to be 0.1 pc, following Arzoumanian et al. (2011). The distribution of filament widths yielded a peak consistent with this initial guess, which could have been a detection bias. The analysis was therefore repeated with a Hessian smoothing scale of 0.05 and 0.2 pc, and in both cases the peak of the filament width distribution was of 0.11 ± 0.01 pc. Therefore the final choice of detection scale is set to match as well as possible the scale properties of the dataset.
 |
Fig. B.1 From left to right and top to bottom: (1) peak temperature of the raw C18O (J = 1−0) data; (2)integrated intensity of the multi-Gaussian fit result; (3) column density estimate derived from this integrated intensity and the dust temperature; (4) largest (in absolute value) eigenvalue ε2 of the Hessian matrix computed at each point of the column density map; (5) regions identified as filamentary, by applying a threshold onto the ε2 map; and (6) skeleton obtained by morphological thinning of these regions. The filaments that are eliminated at some point in the cleaning process are indicated in red. |
We then threshold the eigenvalues. This is a quantitative way to transcribe the characteristics of a filament in terms of eigenvalues, as seen in Table B.1. If the eigenvalues are first sorted so that |ε1 | < |ε2|, then selecting the pixels where ε2 < τ < 0 (τ being a global threshold) ensures that we are in the vicinity of a local maximum in the direction perpendicular to the filament. No condition is set on the smaller eigenvalue, so that we allow any kind of peak or saddle point, as long as the relief is not steeper along the ridge than perpendicular to the ridge (Fig. B.1, panel 5). We find the best value of the threshold τ to be 4% of the lowest (negative) eigenvalue in the map, based on visual inspection (Fig. B.1 left).
B.1.3 Adaptive filament extraction with ridge detection
For the second approach, several additional features refine the filament detection method. Koch & Rosolowsky (2015) applied an arctan transform to the intensities to suppress bright point sources (e.g. dense cores) that can dominate the fainter filamentary structures which are being searched for. In our case, we find it better to use the asinh transform used in Gratier et al. (2017) (Fig. B.2, panel 1), which is linear at small intensities and logarithmic at high intensities. The asymptotic behaviour of the arctan transform would flatten the bright regions and thus render the Hessian approach ineffective. We therefore use
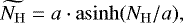 (B.1)
(B.1)
as an input for filament detection with the parameter a set to a = 5.18 × 1021 cm−2, i.e. the median of non-zero values of the C18O-derived column density.
This second filament extraction method takes into account the local aspect ratio of the studied field. The concepts behind this method were first described in the field of medical imaging for the purpose of identifying blood vessels in magnetic resonance imaging (MRI) or computer tomography (CT) images (Frangi et al. 1998). These concepts have been adapted to astrophysical data and extensively illustrated by Salji et al. (2015). The map of Hessian eigenvalues computed from 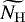 is filtered withthe following function:
is filtered withthe following function:
 |
Fig. B.2 From left to right and top to bottom: (1) column density (Fig. B.1, panel 3) after an asinh transform (colour scale is linear, not logarithmic); (2) structures resulting from the aspect-ratio filter of Frangi et al. (1998) applied to the Hessian eigenvalues of the transformed column density, with a single detection scale of 0.14 pc; (3) the samestructures after applying a gradient-based ridge-detection filter, with the same detection scale; (4) the result of the multi-scale (0.06–0.3 pc) filtering; (5) regions identified as filamentary, by applying a threshold onto the multi-scale filtered map; and (6) skeleton obtained by morphological thinning of these regions. The filaments that end up being eliminated at some point in the cleaning process are indicated in red. |
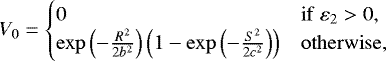 (B.2)
(B.2)
where R = ε1∕ε2 is the local aspect ratio (here again |ε1| < |ε2|), and 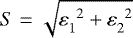 is the local amplitude of the second derivative. In other terms, the filter function emphasises pixels where the signal varies significantly (S > c), and the local aspect ratio is large (R < b).
is the local amplitude of the second derivative. In other terms, the filter function emphasises pixels where the signal varies significantly (S > c), and the local aspect ratio is large (R < b).
Following the recommendations of Frangi et al. (1998), the parameter b was set to b = 0.5, and c was set to half the maximum value of the Hessian norm S over the field of view. The resulting filtered map can be seen on Fig. B.2 (panel 2).
An extra step is added by implementing a ridge-detection function, which is, as far as we know, a novel addition, but can be compared tothe centreline extraction method of Aylward & Bullitt (2002). The goal is to narrow down the response of the filter, so that the obtained structures are as close as possible to the ridge lines (i.e. the skeleton) of the filaments, rather than being broad filamentary regions. This function makes use of the fact that the component of the gradient perpendicular to the filament should go through zero at the ridge line, hence the norm of the gradient should reach a local minimum also close to zero if the variations along the ridge line are negligible. We therefore compute the norm of the gradient of our map,  , again through convolution with Gaussian derivatives. The final filter is
, again through convolution with Gaussian derivatives. The final filter is
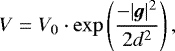 (B.3)
(B.3)
where the parameter d ensures that the slope |g| is close enough to zero. This parameter was set to 10% of the maximum value of |g| over the field of view (Fig. B.2, panel 3).
To avoid favouring a single scale, we perform this structure extraction in a multi-scale fashion, as advised by Frangi et al. (1998). We run the detection algorithm to obtain the filtered map V (s) with smoothing scales s from 0.06 to 0.32 pc in steps of 0.02 pc, and for each pixel we pick up the maximal response among these filters to achieve a scale-adapted filament detection. Thus, the wider structures are detected strongly and stand out well, while the narrower objects in the field are still picked up (Fig. B.2, panel 4). Once again the choice of scales is the result of an iterative approach. A first computation was performed with a 0.1 pc scale only, yielding filaments widths ranging from 0.06 pc (our resolution limit) to about 0.3 pc. Although the widest filaments were rather poorly identified, we kept a 0.06–0.32 pc detection range to avoid as much as possible a detection bias, while keeping the scale range reasonably limited.
After that, a global threshold τf is applied on the resulting scale-adapted filtered map (which now has values ranging from 0 to 1) to select regions which are close enough to the ridge lines of filaments. By visual inspection, τf was set to 0.03 (Fig. B.2, panel 5).
B.1.4 Skeletonisation
Once binary masks that identify the filamentary regions have been obtained, they are thinned down until we are left with single-pixel wide skeletons. One of the most common methods of skeletonisation is known as morphological thinning, which we perform following the algorithm of Zhang & Suen (1984), as implemented in the Python module scikit-image (van der Walt et al. 2014). The resulting skeletons are shown in the last panels of Figs. B.1 and B.2. As this step of the analysis only makes use of the geometry of the binary masks and does not take into account the underlying physical map, the extracted centrelines do not necessarily match the ridge lines of the filaments, especially if they do not have a cylindrical geometry. It is therefore all the more useful to try and narrow down the mask as accurately as possible before the skeletonisation, as done with the gradient filter in Appendix B.1.3.
B.2 Cleaningthe skeleton
Separating a filamentary skeleton into individual filaments enables us to clean it by checking if each individual filament matches the assumeddefinition. For that purpose, a geometrical analysis allows us to distinguish between regular points and nodes (or vertices). The regular points have exactly two neighbours, while the nodes have fewer (if they are endpoints) or more (if they are intersections) than two. The individual filaments are therefore strings of points belonging to the skeleton and linking two nodes. The cleaning process relies on the following criteria: skeleton geometry, curvature radius, relative contrast, and width of the individual filaments.
B.2.1 Geometrical cleaning
The first stage of geometrical cleaning is applied immediately after the first extraction of the filamentary skeleton. It consists in removing isolated nodes (i.e. single pixels) and very short filaments: to be able to distinguish between clumps and filaments, we require an aspect ratio of at least 2 and therefore we set a lower length limit at 0.22 pc, i.e. twice the typical filament width. As a dense skeleton can contain many short individual filaments owing to the frequency of the intersections, the length selection criterion is only applied to individual filaments that are either isolated or that are so-called spurious branches; i.e. filaments that stick out off the side of a structure and for which only one of their extremity is an intersection as the other is an endpoint.
This stage of cleaning is also reapplied after each of the other stages of cleaning, usually twice in a row to take into account the structure differences that can result from the elimination of spurious branches. Experience shows that two repetitions of this geometrical cleaning are enough to converge to a stable cleaned skeleton; the second repetition is even often superfluous.
B.2.2 Curvature radius
One of the first possible characterisations of the individual filaments is a quantitative analysis of their shape, namely whether the individual filaments are rather straight or very curvy. Several methods are possible to measure how straight or curvy a filament is. A simple approach is the measurement of the ratio of the distance between the extremities of the filament and its curvilinear length, but this does not discriminate between a large smooth loop and a jagged structure that is more likely to be an artefact of skeletonisation. Another approach is to compute the circular variance of the filament position angles. But again a large smooth loop might be discarded as its position angles are spread around 360°, while a poorly identified filament with a position angle varying wildly from − 70 to +70° might have a lower circular variance and could be retained. The chosen approach was thus to use the mean curvature radius of the filament, which would discard structures with rapid position angle variation, while keeping large-scale loops.
To that purpose, the first step is estimating the position angle of the filaments at each position. Two possible approaches are possible: either the position angle is directly deduced from the eigenvectors output by the Hessian matrix diagonalisation, or it can be geometrically computed on a pixel-by-pixel basis, by comparing the position of each point in the filaments with its nearest neighbours. The first option has the advantage of yielding continuous angles, whereas the second yields angles in steps of 22.5°. We use the Hessian angle in the entire paper, and in particular for curvature measurements, because this first approach is reasonably reliable despite some misalignments of the skeletons and position angle map.
The curvature radius is then simply defined as the inverse of the derivative of the position angle computed along the filament. This curvature radius Rc is then averaged over the individual filament, and is compared to the width w of the individual filament (Sect. 4.1.1). The individual filaments are rejected if they have a Rc ∕w ratio lower than 1.5, thus ensuring that the transverse profiles of the filament are not contaminated by a further part of the filament after a sharp turn. This selection affects a large number of individual filaments, mostly short ones, as can be see in Table B.2.
B.2.3 Contrast
The value of the baseline at the peak of the filament profile, obtained from the Gaussian fit (Eq. (2)), gives us an estimate of the surface density of the underlying background. An instinctive way to estimate the “contrast” of the filaments, i.e. how much they stand out from the background, is to take the ratio of the linear density of the filament to the surface density of the background for each line of sight. The resulting quantity has the dimension of a length, and can be interpreted as the distance from the filament needed to accumulate as much mass from the surrounding medium as there is in the filament. We can make this contrast dimensionless by defining the “relative contrast”, which is the ratio of the contrast to the filament width. To summarise,
Evolution of the skeletons S1 and S2 after successive stages of cleaning in terms of number of pixels (Pix) and filaments (Fil).
 (B.4)
(B.4)
The relative contrast measures how many times denser the filament is relative to its surrounding medium: for instance, a relative contrast of ten indicates that a region about ten times broader than the filament is needed to accumulate as much mass as contained in the corresponding portion of filament. This accumulation of mass might be interesting when studying the power-law-like extension of the profile of an isolated filament, but in skeletons as crowded as those studied in this paper, we are mostly concerned by the presence of a clearly visible inner part of the filaments – hence a lower limit imposed on the relative contrast at ~ 1. The distribution of relative contrasts in the non-cleaned filamentary skeletons featured a gap at a relative ratio of 0.6, which we thus chose as a limit under which filaments were rejected. As can be seen in Table B.2, this criterion only had a moderate impact on the cleaning of the skeleton.
B.2.4 Final selection and summary
In addition to the selection criteria described above, the widths of the filaments are also taken into account to reject filaments that we deem not reliably detected. Two limits are set. First, the lower limit at 0.06 pc, which corresponds to the resolution of the data; structures of this width or less are unresolved and thus cannot be characterised reliably. Second, an upper limit of 0.22 pc, which corresponds to a gap in the filament width distribution. The few wider individual filaments are considered as outliers. The lower limit mostly affects the smallest scale structures detected in the S2 skeleton. These narrow rejected objects are numerous. Indeed, the Hessian filter is a derivative, which by essence enhances small-scale, noisy structures, and when the Gaussian smoothing scale comes down to the 0.06 pc spatial resolution of the data, it stops preventing this noise enhancement, and thus many noisy structures at very low column densities are picked up by the filter. The upper limit, on the other hand, mostly affects “bridges” between two neighbouring filaments, which are artefacts of the skeletonisation process and are perpendicular to the orientation of well-detected filaments running close to each other.
Table B.2 summarises all stages of the cleaning process. After the first detection step, the geometrical cleaning is run twice and the resulting skeletons are used as a starting point (initial state) for the first analysis. This step starts by measuring the width and curvature of the filaments, leading to the rejection of a large amount of structures, some of which can be rejected by more than one criterion. After this, the geometrical cleaning is reapplied twice, yielding intermediate skeletons which then undergo the contrast cleaning. This is the last stage of cleaning because of the relative contrast computation is very sensitive to the quality of the transverse profile fitting, and therefore can lead to results too extreme to be analysed for some of the poorly defined structures that get eliminated in the previous stages of cleaning. After this, two last passes of geometrical cleaning yield the final skeletons, which are then used for the rest of the analysis in this paper. We note that the numbers of pixels and filaments in Table B.2 do not always add up properly. This is because some structures can be eliminated based on several criteria and because of geometrical cleaning, which removes some isolated nodes left out by other cleaning stage and can reduce the number of filaments either by removing the smallest or by merging these into larger filements when a spurious branch (and thus an intersection) is eliminated.
B.3 Qualities and limitations of the filament detection methods
Having used in parallel skeletons obtained with two different methods, we need to compare the relative merits of each with respect to the implementation, detection quality, and physical implications.
The first method (which yields the skeleton S1) presents the major advantage of being very straightforward in its implementation, providing a simple yet efficient way to identify filamentary regions in a molecular cloud. However, it is not very specific in its geometric requirements when identifying filaments. This means that regions with strong spatial features that are not filamentary are detected, only to be later rejected during the cleaning process (see the filaments indicated in red in Fig. B.1, panel 6), and that the identified filamentary regions are broad. This broadness is an advantage in terms of completeness, for example if we want to use the mask of Fig. B.1 (panel 5) to obtain molecular line ratios inside and outside the filaments, but it is a disadvantage during the skeletonisation, as the position of the skeleton is less precise. This uncertainty on the position of the skeleton can be a problem when measuring the properties of the filament profiles, in particular their widths (Sect. 4.1.1). The binary aspect of the detection method achieved with a single threshold also makes the method unsuitable for a multi-scale approach.
The second method, which yields the skeleton S2, is much more demanding as far as the properties of the identified structures are concerned, which also comes with its lot of pros and cons. The rescaling of the data, which could easily be transposed to the first method, makes the whole detection process less sensitive to the brightest/densest regions, allowing for a better tuning of the filtering parameters. The first stage of filtering achieves a better distinction between filament-like and blob-like structures using the local aspect ratio. Together with the second stage of filtering, it yields much thinner filamentary regions (Fig. B.2, panel 5), enabling a more accurate skeletonisation. The use of a continuous filter (with values ranging from 0 to 1) before thresholding makes the method suitable for a multi-scale approach, which reduces possible detection biases. However, as can be seen from the filaments indicated in red in Fig. B.2 (panel 6), this approach also yields a large amount of small-scale structures that end up being rejected during the cleaning; there is 19% of rejection in the first geometrical cleaning stage, compared to only 12% in the case of the S1 skeleton. The multi-stage filtering process also requires more parameters to be adjusted by hand (at least two, d and τf) than the first method. Another issue arises from the smoothing that occurs during the computation of the gradient. The gradient can be distorted in the vicinity of intersections of filaments, which can result in a distorted (misaligned) skeleton, but more often the filter simply misses the intersections, thereby truncating the filaments.
In summary, we can consider to first order that S1 is an upper limit for filament detection and S2 is a lower limit. This would be completely true if S2 were nested in S1 (i.e. if we had S2 = robust ⊂ S1). However, Fig. 5 shows that this is not the case, but that nonetheless filaments exclusive to S2 are far less numerous than those exclusive to S1.
It is important to note that the final quality of the obtained skeletons does not only depend on the initial detection method, but also on the cleaning process. In that respect, we can see that a larger proportion of the S2 skeleton (44%) is rejected than in the S1 skeleton (37%). In both cases it is a significant fraction, which shows that the skeletons should not be used without cleaning, lest the statistical results be contaminated by many unwanted structures. We can also add a qualitative remark on the rejected fraction of the skeletons: although the fraction rejected in S1 is smaller, the filaments rejected in S2 seem to be mostly very small structures, while the longer ones are retained. It can be a sign that the multi-scale detection has a drawback tightly linked to its main quality. Because this detection is unbiased, it picks up many small features that, on closer inspection, end up not matching the requirements that we set on bona fide filaments. Itis thus not easy to rule in favour of one or the other detection scheme – at least not in their current state.
We can also question the nature of the detected structures, regarding their geometry and their origin. Filaments are most often described as elongated, almost unidimensional condensations in the three-dimensional turbulent medium, but this mechanism is not the only one that can form elongated structures in the molecular ISM. Geometry and projection effects are an important issue. For example, it is possible that some detected filaments are actually two-dimensional structures seen edge-on. This is mostprobably the case for at least one filamentary structure detected in Orion B, namely the vertical filament at the base of the Horsehead Nebula. Rather than a unidimensional structure, this filament is the edge of the IC 434 ionisation front, a wall seen edge-on. Thus, its high observed density is the result of a larger dimension along the line of sight than for other filaments. Another structure can raise the question of its evolutionary scenario: the Horsehead Nebula itself. Rather than a condensation in a three-dimensional turbulent medium, it is rather a pillar carved by the IC 434 ionisation front.
There are two reasons to keep all structures in the filamentary network, even when the knowledge of the region points to the fact that they might not match the usual definition of filaments. First, this a priori knowledge of the structure can be absent when studying another filamentary region, and it is important to treat the skeleton statistically in an unbiased way, to see whether and how the physical properties of the filaments can distinguish different populations. The results of this paper suggest thatall the above-mentioned structures should be treated in the same way. Second, mostly in the case of the Horsehead Nebula, the fact that an elongated structure had one formation scenario or another does not necessarily determine its further evolution, hence the necessity of keeping the entire variety of structures in the sample.
References
- Adam, R., Adane, A., Ade, P. A. R., et al. 2018, A&A, 609, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, Protostars and Planets VI (Tucson: University of Arizona Press), 27 [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Arzoumanian, D., André, P., Peretto, N., & Könyves, V. 2013, A&A, 553, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aylward, S. R., & Bullitt, E. 2002, IEEE Trans. Med. Imaging, 21, 61 [CrossRef] [PubMed] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
- Bron, E., Daudon, C., Pety, J., et al. 2018, A&A, 610, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burkert, A., & Hartmann, L. 2004, ApJ, 616, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Busquet, G., Zhang, Q., Palau, A., et al. 2013, ApJ, 764, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M. 2000, AJ, 120, 3139 [NASA ADS] [CrossRef] [Google Scholar]
- Catalano, A., Adam, R., Ade, P. A. R., et al. 2018, J. Low Temp. Phys., 193, 916 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, S. D., Whitworth, A. P., & Hubber, D. A. 2016, MNRAS, 458, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C. 2016, MNRAS, 457, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., & Klessen, R. S. 2013, ApJ, 763, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, W. J., Megeath, S. T., Stutz, A. M., et al. 2013, Astron. Nachr., 334, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Florack, L. M., ter Haar Romeny, B. M., Koenderink, J. J., & Viergever, M. A. 1992, Image Vis. Comput., 10, 376 [CrossRef] [Google Scholar]
- Frangi, A. F., Niessen, W. J., Vincken, K. L., & Viergever, M. A. 1998, Medical Image Computing and Computer-Assisted Intervention (Berlin: Springer), 130 [Google Scholar]
- Friesen, R. K., Pineda, J. E., co-PIs, et al. 2017, ApJ, 843, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Furlan, E., Fischer, W. J., Ali, B., et al. 2016, ApJS, 224, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Gerin, M., Ruaud, M., Goicoechea, J. R., et al. 2015, A&A, 573, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F. 2001, ApJ, 557, 736 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gratier, P., Bron, E., Gerin, M., et al. 2017, A&A, 599, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., Tafalla, M., Kauffmann, J., & Kovács, A. 2013, A&A, 554, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., Kainulainen, J., Tafalla, M., Beuther, H., & Alves, J. 2016, A&A, 587, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., Tafalla, M., Forbrich, J., et al. 2018, A&A, 610, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L.,& Burkert, A. 2007, ApJ, 654, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Hatchell, J., Richer, J. S., Fuller, G. A., et al. 2005, A&A, 440, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P. 2013, A&A, 556, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inutsuka, S.-I., & Miyama, S. M. 1992, ApJ, 388, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Kainulainen, J., Hacar, A., Alves, J., et al. 2016, A&A, 586, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Stutz, A. M., Stanke, T., et al. 2017, A&A, 600, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirk, H., Myers, P. C., Bourke, T. L., et al. 2013, ApJ, 766, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, H., Klassen, M., Pudritz, R., & Pillsworth, S. 2015, ApJ, 802, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, E. W., & Rosolowsky, E. W. 2015, MNRAS, 452, 3435 [NASA ADS] [CrossRef] [Google Scholar]
- Koenderink, J. J. 1984, Biol. Cybern., 50, 363 [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Kong, S., Arce, H. G., Feddersen, J. R., et al. 2018, ApJS, 236, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Könyves, V., André, P., Men’shchikov, A., et al. 2015, A&A, 584, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lada, E. A. 1992, ApJ, 393, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., & Alves, J. F. 2010, ApJ, 724, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Liszt, H. 2014, ApJ, 783, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., Bouy, H., Alves, J., & Lada, C. J. 2014, A&A, 566, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mangum, J. G., & Shirley, Y. L. 2015, PASP, 127, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Megeath, S. T., Gutermuth, R., Muzerolle, J., et al. 2016, AJ, 151, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, T., Inutsuka, S.-i., & Miyama, S. M. 1998, ApJ, 506, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Narayanan, G., Heyer, M. H., Brunt, C., et al. 2008, ApJS, 177, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Orkisz, J. H., Pety, J., Gerin, M., et al. 2017, A&A, 599, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Padoan, P., Juvela, M., Goodman, A. A., & Nordlund, Å. 2001, ApJ, 553, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Panopoulou, G. V., Tassis, K., Goldsmith, P. F., & Heyer, M. H. 2014, MNRAS, 444, 2507 [NASA ADS] [CrossRef] [Google Scholar]
- Panopoulou, G. V., Psaradaki, I., Skalidis, R., Tassis, K., & Andrews, J. J. 2017, MNRAS, 466, 2529 [NASA ADS] [CrossRef] [Google Scholar]
- Parvathi, V. S., Sofia, U. J., Murthy, J., & Babu, B. R. S. 2012, ApJ, 760, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Peretto, N., Hennebelle, P., & André, P. 2007, A&A, 464, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peretto, N., André, P., Könyves, V., et al. 2012, A&A, 541, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peretto, N., Fuller, G. A., Duarte-Cabral, A., et al. 2013, A&A, 555, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peretto, N., Fuller, G. A., André, P., et al. 2014, A&A, 561, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J., & Falgarone, É. 2000, A&A, 356, 279 [NASA ADS] [Google Scholar]
- Pety, J., Guzmán, V. V., Orkisz, J. H., et al. 2017, A&A, 599, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIX. 2011, A&A, 536, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXXII. 2016, A&A, 586, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polychroni, D., Schisano, E., Elia, D., et al. 2013, ApJ, 777, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Salji, C. J., Richer, J. S., Buckle, J. V., et al. 2015, MNRAS, 449, 1782 [NASA ADS] [CrossRef] [Google Scholar]
- Schaefer, G. H., Hummel, C. A., Gies, D. R., et al. 2016, AJ, 152, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Schisano, E., Rygl, K. L. J., Molinari, S., et al. 2014, ApJ, 791, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., Green, G., Finkbeiner, D. P., et al. 2014, ApJ, 786, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, S., & Elmegreen, B. G. 1979, ApJS, 41, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., André, P., Könyves, V., et al. 2013, ApJ, 766, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Schulz-Dubois, E. O., & Rehberg, I. 1981, Appl. Phys., 24, 323 [Google Scholar]
- Smith, R. J., Glover, S. C. O., & Klessen, R. S. 2014, MNRAS, 445, 2900 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., Glover, S. C. O., Klessen, R. S., & Fuller, G. A. 2016, MNRAS, 455, 3640 [NASA ADS] [CrossRef] [Google Scholar]
- Sofia, U. J., Lauroesch, J. T., Meyer, D. M., & Cartledge, S. I. B. 2004, ApJ, 605, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., Rivolo, A. R., Barrett, J., & Yahil, A. 1987, ApJ, 319, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Sousbie, T. 2011, MNRAS, 414, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1998, Physical Processes in the Interstellar Medium (Hoboken, NJ: John Wiley & Sons), 335 [Google Scholar]
- Stutz, A. M., & Kainulainen, J. 2015, A&A, 577, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stutz, A. M., Tobin, J. J., Stanke, T., et al. 2013, ApJ, 767, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, S., Ho, P. T. P., Teixeira, P. S., Zapata, L. A., & Su, Y.-N. 2013, ApJ, 763, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Teixeira, P. S., Takahashi, S., Zapata, L. A., & Ho, P. T. P. 2016, A&A, 587, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Walt, S., Schönberger, J. L., Nunez-Iglesias, J., et al. 2014, PeerJ, 2, e453 [Google Scholar]
- Ward-Thompson, D., Kirk, J. M., André, P., et al. 2010, A&A, 518, L92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, G. M., Peretto, N., Avison, A., Duarte-Cabral, A., & Fuller, G. A. 2018, A&A, 613, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, T. Y., & Suen, C. Y. 1984, Commun. ACM, 27, 236 [CrossRef] [Google Scholar]
The data products associated with this paper are available at http://www.iram.fr/~pety/ORION-B
Based on observations obtained with Planck (http://www.esa.int/Planck), an ESA science mission with instruments and contributions directly funded by ESA Member States, NASA, and Canada.
All Tables
Mean, median, and most probable FWHM of filaments for the three studied skeletons, resulting from mean profile fitting of the C18O-derived NH column density.
Fraction of super-critical (γ > 1) or at least trans-critical (γ > 0.5) filaments depending on the assumptions on their internal pressure computed for the S1, S2, and robust skeletons.
Topography of a two-dimensional dataset depending on the eigenvalues of its Hessian matrix ε1 and ε2.
Evolution of the skeletons S1 and S2 after successive stages of cleaning in terms of number of pixels (Pix) and filaments (Fil).
All Figures
 |
Fig. 1 Composite image representing the velocity structure present in the C18O (J = 1−0) cube. Each velocity channel is directly encoded as a hue, and the final image is obtained by additive colour synthesis. The brightest points correspond to 4 K in main beam temperature. The labels indicate, (1) the Horsehead Nebula, (2) NGC 2023, (3) NGC 2024 (the Flame Nebula), (4) the Flame filament, and (5) the Hummingbird filament. The spatial and kinematic complexity of the cloud appear clearly in particular in regions such as the north-eastern part of the cloud or around NGC 2023. |
| In the text | |
 |
Fig. 2 Left: NH column density map derived from the C18O (J = 1−0) integrated intensity (multi-Gaussian model). The orientation of the magnetic field, derived from Planck polarimetric data, is shown by the black segments. The spacing of the segments corresponds to the 5′ beam of Planck. Middle: map of the ratio of the C18O-traced NH to the dust-traced NH above 3 magnitudes of AV in Orion B. Superimposed are contours of the C18O (J = 1−0) integrated intensity at 0.75, 2.5 and 7.5 K km s−1. Right: effective dust temperature map computed by Lombardi et al. (2014). The black segments again show the orientation of the magnetic field. |
| In the text | |
 |
Fig. 3 Joint distributions of the NH column densities as traced by C18O (J = 1−0) against those inferred from AV with an offsets of 3 magnitudes. This threshold corresponds to the extinctions at which the molecular tracers starts to be detected according to Pety et al. (2017). The distribution is computed in the identified filamentary regions. The 1:1 relation is overplotted as a black line. |
| In the text | |
 |
Fig. 4 Joint distribution of the ratio of C18O-traced vs. dust-traced NH column density (Fig. 2 middle) against the dust temperature (Fig. 2 right), taken only in the identified filamentary regions. |
| In the text | |
 |
Fig. 5 Comparison of the skeletons obtained with the two different methods. The S1 skeleton denotes the skeleton obtained by simple thresholding, and S2 is obtained by the adaptive method with ridge detection. The structures only identified by one method appear in red or blue, the structures common to both methods appear in green if they perfectly match, and in yellow in the cases where the morphological thinning led to small position offsets (see Appendix B). |
| In the text | |
 |
Fig. 6 Top: map of the FWHM of the mean profiles of the individual filaments (combined skeleton). Bottom: histograms of the filament width for the S1, S2, and robust skeletons. |
| In the text | |
 |
Fig. 7 Gravitational instability criterion of the filaments (combined skeleton). This criterion is derived from the C18O-traced linear density estimation and either the thermal pressure (γ, left) or the effective pressure, which also takes into account the C18O (J = 1−0) velocity dispersion (γeff, right). Overlaid are the positions of protostars from Megeath et al. (2016) in white, and class 0 YSOs from HOPS (Furlan et al. 2016) in green. |
| In the text | |
 |
Fig. 8 Top: map of the angle between the magnetic field and filaments detected in Orion B at a 5′ resolution. The filaments are red when they are parallel to the magnetic field and blue when perpendicular to it. Bottom: distribution of the relative orientation of the filaments and the magnetic field for the S1, S2, and robust skeletons. The dotted lines (and the shaded areas) present the distribution (and the corresponding ± 1σ uncertainties) that we would get if the two quantities were uncorrelated. The uncorrelated distribution is obtained by a Monte Carlo sampling of the magnetic field and filament position angles. |
| In the text | |
 |
Fig. 9 Top: average transverse profiles of the line-of-sight FWHM velocity dispersion of the filaments. These profiles are computed for the S1, S2, and robust skeletons via the modelled C18O (J = 1−0) linewidth; the shaded areas show the standard error for each profile. Bottom: same as above, but using the 13CO (J = 1−0) data cube for comparison. |
| In the text | |
 |
Fig. 10 Top: average transverse profiles of the amplitude of the centroid velocity gradient of the filaments. These profiles are computed for the S1, S2, and robust skeletons via the C18O (J = 1−0) data cube; the shaded areas show the standard error for each profile. Bottom: same as above, but using the 13CO (J = 1−0) data cube for comparison. |
| In the text | |
 |
Fig. 11 Top: distribution of the linear density of the filaments. The vertical dashed lines show the most probable critical linear densities corresponding to |
| In the text | |
 |
Fig. 12 Top: same as Fig. 1, but with the field and velocity range zoomed in on the Hummingbird filament, showing beads in the rectilinear tail of the Hummingbird. Bottom: two-point structure function of the linear density in the Hummingbird filament (following the robust skeleton), in (M⊙/pc)2, showing a periodic pattern which suggests longitudinal fragmentation with a period of 0.4 pc. |
| In the text | |
 |
Fig. A.1 Examples of spectra fitted with multiple Gaussians, at signal-to-noise levels of about 15 (top) and 5 (bottom). The individual Gaussian components are indicated in dashed, dotted, or dash-dotted lines. |
| In the text | |
 |
Fig. B.1 From left to right and top to bottom: (1) peak temperature of the raw C18O (J = 1−0) data; (2)integrated intensity of the multi-Gaussian fit result; (3) column density estimate derived from this integrated intensity and the dust temperature; (4) largest (in absolute value) eigenvalue ε2 of the Hessian matrix computed at each point of the column density map; (5) regions identified as filamentary, by applying a threshold onto the ε2 map; and (6) skeleton obtained by morphological thinning of these regions. The filaments that are eliminated at some point in the cleaning process are indicated in red. |
| In the text | |
 |
Fig. B.2 From left to right and top to bottom: (1) column density (Fig. B.1, panel 3) after an asinh transform (colour scale is linear, not logarithmic); (2) structures resulting from the aspect-ratio filter of Frangi et al. (1998) applied to the Hessian eigenvalues of the transformed column density, with a single detection scale of 0.14 pc; (3) the samestructures after applying a gradient-based ridge-detection filter, with the same detection scale; (4) the result of the multi-scale (0.06–0.3 pc) filtering; (5) regions identified as filamentary, by applying a threshold onto the multi-scale filtered map; and (6) skeleton obtained by morphological thinning of these regions. The filaments that end up being eliminated at some point in the cleaning process are indicated in red. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.