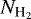| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 19 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201833583 | |
| Published online | 28 November 2018 | |
The Serpens filament at the onset of slightly supercritical collapse★
1
Max-Planck Institute für Radioastronomy,
Auf dem Hügel 69,
53121 Bonn,
Germany
e-mail: ygong@mpifr-bonn.mpg.de; gongyan2444@gmail.com
2
Purple Mountain Observatory & Key Laboratory for Radio Astronomy, Chinese Academy of Sciences,
2 West Beijing Road,
210008 Nanjing,
PR China
3
University Observatory Munich,
Scheinerstrasse 1,
81679 München, Germany
4
South-Western Institute for Astronomy Research, Yunnan University,
Kunming,
Yunnan 650500, PR China
5
Astronomy Department, Faculty of Science, King Abdulaziz University,
PO Box 80203,
Jeddah 21589, Saudi Arabia
6
Xinjiang Astronomical Observatory, Chinese Academy of Sciences,
830011 Urumqi,
PR China
7
Department of Astronomy, University of Arizona,
933 North Cherry Avenue,
Tucson,
AZ 85721, USA
Received:
6
June
2018
Accepted:
13
September
2018
The Serpens filament, as one of the nearest infrared dark clouds, is regarded as a pristine filament at a very early evolutionary stage of star formation. In order to study its molecular content and dynamical state, we mapped this filament in seven species: C18O, HCO+, HNC, HCN, N2H+, CS, and CH3OH. Among them, HCO+, HNC, HCN, and CS show self-absorption, while C18O is most sensitive to the filamentary structure. A kinematic analysis demonstrates that this filament forms a velocity-coherent (trans)sonic structure, a large part of which is one of the most quiescent regions in the Serpens cloud. Widespread C18O depletion is found throughout the Serpens filament. Based on the Herschel dust-derived H2 column density map, the line mass of the filament is 36–41 M⊙ pc−1, and its full width at half maximum is 0.17 ± 0.01 pc, while its length is ≈1.6 pc. The inner radial column density profile of this filament can be well fitted with a Plummer profile with an exponent of 2.2 ± 0.1, a scale radius of 0.018 ± 0.003 pc, and a central density of (4.0 ± 0.8) × 104 cm−3. The Serpens filament appears to be slightly supercritical. The widespread blue-skewed HNC and CS line profiles and HCN hyperfine line anomalies across this filament indicate radial infall in parts of the Serpens filament. C18O velocity gradients also indicate accretion flows along the filament. The velocity and density structures suggest that such accretion flows are likely due to a longitudinal collapse parallel to the filament’s long axis. Both the radial infall rate (~72 M⊙ Myr−1, inferred from HNC and CS blue-skewed profiles) and the longitudinal accretion rate (~10 M⊙ Myr−1, inferred from C18O velocity gradients) along the Serpens filament are lower than all previously reported values in other filaments. This indicates that the Serpens filament lies at an early evolutionary stage when collapse has just begun, or that thermal and nonthermal support are effective in providing support against gravity.
Key words: ISM: clouds / ISM: molecules / radio lines: ISM / line: profiles / ISM: kinematics and dynamics
The reduced datacubes (FITS files) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/620/A62
© ESO 2018
1 Introduction
For many decades filamentary structures have been known to exist in molecular clouds (e.g., Schneider & Elmegreen 1979; Bally et al. 1987; Loren 1989). More recently, the prevalence of filamentary structures was emphasized by Herschel observations of nearby molecular clouds, suggesting that filaments serve as a fundamental stage in star-forming processes, and could also play an important role in the evolution of molecular clouds (André et al. 2010, 2014; André 2017). Substantial observations of dust extinction, dust continuum emission, and molecular lines have demonstrated that filaments are ubiquitous in star-forming, translucent, and even diffuse molecular clouds (e.g., Myers 2009; André et al. 2010; Miville-Deschênes et al. 2010; Wang et al. 2015; Li et al. 2016a; Xiong et al. 2017; Gong et al. 2017; Mattern et al. 2018). However, the formation and evolution of filaments are still not fully understood. Identifying and characterizing isolated filaments at the earliest evolutionary stage of star formation is of great importance to this question.
The Serpens filament, named by Enoch et al. (2007), is also known as the “starless cores” region in Burleigh et al. (2013) and Filament 9 in Roccatagliata et al. (2015). This filament resides in the Serpens cloud, at a distance of about 440 pc, as deduced from the trigonometric parallax measured with the Very Long Baseline Array (VLBA; Ortiz-León et al. 2017). Figure 1a presents the distribution of 12 μm radiation in the region of interest here, observed by the Wide-Field Infrared Explorer (WISE). The filament appears in absorption against a diffuse background, making it an infrared dark cloud (IRDC). IRDCs are known to be the cold and dense part of molecular clouds (e.g., Carey et al. 1998; Pillai et al. 2006; Zhang et al. 2011) and represent a very early evolutionary stage harboring no embedded protostars, or only a limited number (e.g., Menten et al. 2005; Bergin & Tafalla 2007). IRDCs, which predominantly have filamentary structures, can serve as ideal targets for the study of the initial conditions of dense molecular cloud regions prior to star formation. This IRDC was not included in previous IRDC catalogs, because its location is not fully covered by previous mid-infrared surveys, many of which have been restricted to the Galactic plane. In contrast to most IRDCs, this IRDC is characterized by a particularly low mass (see results given below) and its extreme proximity. The Serpens filament, similar to its well-known sibling – Serpens South (e.g., Gutermuth et al. 2008), is one of the nearest IRDCs, but has much less substructure (e.g., subfilaments, fibres) than Serpens South. Furthermore, the Serpens filament was found to contain seven dust cores (Enoch et al. 2007) and three class I young stellar objects (YSOs; Enoch et al. 2009): emb10 (also known as IRAS 18262+0050), emb16, and emb28 (see Fig. 1a). On the other hand, its southeastern part is free of YSOs, i.e., starless. Burleigh et al. (2013) argued that this region will be the next site of star formation in Serpens.
Based on the Herschel observations, the Serpens filament is estimated to have a size of ~0.3 pc × 1.7 pc, and a position angle of 147° east of north (Roccatagliata et al. 2015). The highly rectilinear morphology of the Serpens filament is clearly seen in dust emission which matches the 12 μm absorption very well (see Fig. 1), but is invisible in either 12CO (2–1) or 13CO (2–1) maps (see Fig. 15 in Burleigh et al. 2013). More molecular line observations are crucial in order to study its molecular content and dynamical state.
 |
Fig. 1 Panel a: WISE 11.2 μm image of the Serpens filament that shows up in absorption. Panel b: Herschel 250 μm image of the Serpens filament. The contours start at 0.5 Jy beam−1, and increase by 0.5 Jy beam−1. In both panels, the three blue circles mark the embedded YSOs emb10, emb16, and emb28 (Enoch et al. 2009), while the white and cyan circles give the selected positions of Source A and Source B (see Sect. 2.1 and Table 1). The beam size is shown in the lower right of each panel. |
2 Observations and data reduction
2.1 PMO-13.7 m observations
We carried out multiple molecular line observations (project code: 17A004) toward the Serpens filament with the Purple Mountain Observatory 13.7 m (PMO-13.7 m) telescope from 2017 May 12 to 17. The 3 × 3 beam sideband separation Superconducting Spectroscopic Array Receiver (Shan et al. 2012) was employed as front-end, while a set of 18 fast Fourier transform spectrometers (FFTSs) was used as a back-end to analyze signals from both sidebands. During the observations, we used two different FFTS modes which provided instantaneous bandwidths of 1 and 200 MHz, respectively. Each FFTS consists of 16384 channels, resulting in channel spacings of 61.0 kHz and 12.2 kHz (corresponding velocity spacings are given in Table 1) for the two FFTS modes. The filament was observed in the on-the-fly mode (Sun et al. 2018) at a scanning rate of 50′′ s−1 and a dump time of 0.3 s. In order to minimize the overheads, the map was solely scanned along the long axis of this filament. The parameters of the observed transitions are given in Table 1. Follow-up single-point on–off observations with the 200 MHz FFTS mode were performed toward two peaks of the F = 0–1 line of HCN (1–0), source A (αJ2000 = 18h28m47.s62, δJ2000 = 00°50′55. ′′8) and source B (αJ2000 = 18h28m57.s70, δJ2000 = 00°48′02. ′′0) (see Fig. 1a) to obtain higher quality HCN (1–0) line profiles. Furthermore, we also performed single-point on-off observations toward source A to observe less abundant species and to confirm the observed self-absorption. For all the single-point on–off observations, only spectra obtained with the central beam are analyzed in this work. The observations encompass a total of ~34 observing hours.
The standard chopper-wheel method was used to calibrate the antenna temperature (Ulich & Haas 1976). The relationship 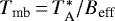 was used to convert antenna temperature,
was used to convert antenna temperature, 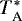 , to main-beam brightness temperature, Tmb, where Beff is the main beam efficiency. The half-power beam widths, θb, at different frequencies were found to be
, to main-beam brightness temperature, Tmb, where Beff is the main beam efficiency. The half-power beam widths, θb, at different frequencies were found to be 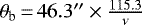 , where ν is the observed frequency in units of GHz. Two standard sources (W51D and S140) were used as spectral calibrators that were regularly observed with the same setups as for our scientific observations. A dispersion of ~5% in the peaks of observed lines toward these two standard sources indicate that the uncertainty on the temperature scale is better than the 10% given in the telescope status report. Typical system temperatures were 121–142 K on a
, where ν is the observed frequency in units of GHz. Two standard sources (W51D and S140) were used as spectral calibrators that were regularly observed with the same setups as for our scientific observations. A dispersion of ~5% in the peaks of observed lines toward these two standard sources indicate that the uncertainty on the temperature scale is better than the 10% given in the telescope status report. Typical system temperatures were 121–142 K on a 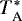 scale. The Pointing was found to be accurate to within ~5′′. Throughout this paper, velocities are given with respect to the local standard of rest (LSR).
scale. The Pointing was found to be accurate to within ~5′′. Throughout this paper, velocities are given with respect to the local standard of rest (LSR).
Data reduction was performed with the GILDAS1 software including CLASS and GREG (Pety 2005). Since the half-power beam widths are slightly different for each observed spectral line, all spectral maps have been convolved to an effective angular resolution of 1′ (corresponding to a linear scale of 0.13 pc at a distance of 440 pc) for direct comparison between different tracers. In these maps, a single pixel size is 20′′ × 20′′.
Observed parameters of the molecular lines used in the work.
2.2 Archival data
We also make use of mid-infrared data from WISE which mapped the full sky at 3.4, 4.6, 12, and 22 μm with angular resolutions of 6.1′′, 6.4′′, 6.5′′, and 12.0′′ in the four bands (Wright et al. 2010). Additional ancillary data include level 2.5 processed Herschel2 images observed at 70/160 μm with the PACS instrument (Poglitsch et al. 2010) and at 250/350/500 μm with the SPIRE instrument (Griffin et al. 2010). Their angular resolutions range from 6′′ to 37′′. The H2 column density map of this region is derived from the spectral energy distribution (SED) fitting from 160–500 μm, and is obtained from the Herschel Gould Belt (GB) Survey3 (André et al. 2010; Könyves et al. 2015; Fiorellino et al. 2017). The comparison with the extinction map from 2MASS on the same grid suggests that the derived H2 column densities have an uncertainty of ~10% (Könyves et al. 2015).
3 Results
3.1 Molecular gas distributions
Figure 2a shows the Herschel H2 column density image of the Serpens filament. In this panel, the two white dashed lines roughly divide the observed area into three individual regions that are labeled as NW (northwest), SE (southeast), and EX (extended), respectively.NW and SE represent the northwest and southeast part of the filamentary structure, while EX stands for the extended emission to the south and outside the filamentary structure. NW and SE have stronger 12 μm absorption than the EX region. Both500 μm emission and absorption at 12 μm show that NW is wider than SE (see Figs. 1 and 2a). The two YSOs emb10 and emb28 are seen projected near the center of NW, while emb16 is seen projected at the northeastern edge of NW. In NW, emb28 is located at the filament’s narrowest place, from which it extends in two opposite directions.
The Serpens filament has been mapped by our PMO-13.7 m observations in lines from seven different species, C18 O, HCO+, HNC, HCN, N2 H+, CS, and CH3OH, the integrated intensity maps of which are presented in Figs. 2b–h. All but two of the detected lines have upper energy levels (Eu∕k) lower than 7 K (see Table 1), and typical spectra toward source A are shown in Fig. 3. The observed properties and beam-averaged molecular column densities of source A are given in Table 2, and further details about source A are presented in Appendix A. Among these detected lines, C18 O (1–0) is the brightest. It is worth noting that none of the three YSOs has associated peaks in the distribution of detected species. The distribution of different species is discussed in the following.
C18O. The whole filamentary structure is well detected in C18O emission, which resembles the distribution of the Herschel H2 column density image. However, such a structure is not found in either 12CO (2–1) or 13 CO (2–1) maps (Burleigh et al. 2013). This is likely because there is significant 12CO and 13CO self-absorption in the filament and the bulk of optically thick CO/13CO gas in the outer region blocks the view to the filamentary structure. Meanwhile, EX shows stronger C18 O (1–0) integrated intensities than NW and SE, which is opposite to that in the Herschel H2 column density image. This is likely because the depletion of C18O molecules in the innermost region of the filament is more significant than that in EX (see Sect. 3.3).
HCO+. HCO+ (1–0) – This shows the weakest emission and is only marginally detected in NW and EX (see Fig. 2c). However, H13 CO (1–0) is detected by our single-point observations toward source A. Its peak intensity (0.56 K) is much stronger than that of HCO+ (1–0), suggesting that significant self-absorption plays an important role.
HNC. In Fig. 2d, the filament is clearly seen in HNC (1–0) with stronger emission in NW than in SE. Meanwhile, EX displays HNC (1–0) emission, which is not as extended as C18 O (1–0). Toward source A, HNC (1–0) shows self-absorption with a dip observed at the peak velocity of its 13C substitution HN13C.
HCN. In Fig. 2e, the integrated velocity range includes the three hyperfine structure (hfs) components of HCN (1–0) which are mostly weaker than HNC (1–0). HCN (1–0) is detected in NW and SE, and marginally detected in EX. The strongest emission is found in NW. However, the emission bridging NW and SE is not detected in HCN (1–0). This filament also shows widespread HCN (1–0) hyperfine line anomalies which are discussed in Sect. 3.4.
N2H+. Figure 2f gives the integrated intensity map of the three main hfs components of N2 H+ (1–0). This transition is detected in NW and SE but not in EX. Both NW and SE are elongated, and the emission is stronger in NW than in SE. Assuming that self-absorption is not present in N2 H+ (1–0), we can use the hfs line fitting subroutine in CLASS to determine the optical depth of N2 H+ (1–0), which gives an optical depth of 0.32 ± 0.15 for the mainhfs line in source A (see Fig. 3). This implies that this line is optically thin.
CS. As demonstrated in Fig. 2g, CS (2–1) is the second widespread tracer after C18 O (1–0) in the Serpens filament, but the CS (2–1) morphology is not as rectilinear as C18 O (1–0). Similar to HNC (1–0), CS (2–1) also displays self-absorption (see Fig. 3). On the other hand, CS (2–1) is more widespread than HNC (1–0), although their critical densities, where radiative decay rates match collisional de-excitation rates, are comparable (Shirley 2015). CH3OH. CH3OH is the only complex organic molecule observed by this study. CH3OH (Jk = 20–10 A) and CH3OH (2−1–1−1 E) are detected. CH3OH (20 –10 E) and CH3OH (21 –11 E) are also covered by our observations, but remain undetected, i.e., Tmb < 0.21 K. CH3OH (2−1–1−1 E) is also not shown in Fig. 2, because its distribution is similar to that of CH3OH (20 –10 A) and its dynamical range is lower. Figure 2h shows that CH3OH emission appears in NW, SE, and EX. The CH3OH emission peaks in SE, a starless region. This is reminiscent of CH3OH in other starless cores, e.g., TMC-1 (Friberg et al. 1988) and L1544 (Vastel et al. 2014).
Overall, different molecular species show noticeable differences in their distributions. Among them, HCO+, HNC, HCN, and CS are found to be affected by self-absorption. On the other hand, C18 O (1–0) is more sensitive for tracing the filamentary structure than the other tracers. Nearly all dense tracers (HNC, HCN, N2 H+, and CH3OH) are not detected in EX, indicating that EX is a less dense region than NW and SE.
 |
Fig. 2 Spatial distributions of different molecular species, labeled in the lower right of each panel, over the Serpens filament. Panel a: Herschel H2 column density image. The contours are H2 column densities of 4 × 1021 cm−2 and 6 × 1021 cm−2. This region is divided by the two white dashed lines into three individual regions which are labeled NW (northwest), SE (southeast), and EX (extended). Panel b: C18 O (1–0) intensity map integrated from 7.4 to 8.7 km s−1. The contours start at 0.30 K km s−1 (5σ), and increase by 0.18 K km s−1 (3σ). Panel c: HCO+ (1–0) intensity map integrated from 6.5 to 9.5 km s−1. The contours start at 0.27 K km s−1, and increase by 0.27 K km s−1. Panel d: HNC (1–0) intensity map integrated from 7.0 to 9.0 km s−1. The contours start at 0.24 K km s−1, and increase by 0.24 K km s−1. Panel e: HCN (1–0) intensity map integrated from 0 to 1.6 km s−1, from 7.0 to 8.6 km s−1, and from 11.8 to 13.4 km s−1 relative to the frequency of the F = 2–1 hyperfine structure component. The contours start at 0.27 K km s−1, and increase by 0.27 K km s−1. Panel f: N2H+ (1–0) intensity map integrated from 6.5 to 9.5 km s−1. The contours start at 0.30 K km s−1, and increase by 0.30 K km s−1. Panel g: CS (2–1) intensity map integrated from 7.0 to 9.5 km s−1. The contours start at 0.18 K km s−1, and increase by 0.18 K km s−1. Panel h: CH3OH (20 –10) intensity map integrated from 7.5 to 8.8 km s−1. The contours start at 0.12 K km s−1, and increase by 0.12 K km s−1. In all panels, the (0, 0) offset corresponds to αJ2000 = 18h28m49.s642, δJ2000 = 00°50′01.′′08, and the three blue crosses give the positions of the three embedded YSOs (see also Fig. 1). The beam size is shown in the lower right of each panel. |
 |
Fig. 3 Single-pixel spectra (black lines) of all detected molecules toward Source A. Species are given in the upper left of each panel. In all panels, the vertical blue dashed lines represent the systemic velocity obtained from C18 O (1–0). Single-peaked spectra are modeled with a Gaussian fit. The blue-skewed line profiles of CS (2–1), HCN (1–0), and HNC (1–0) are fitted with the Hill5 model (De Vries & Myers 2005). For H13 CN (1–0) and N2H+ (1–0), the spectra are fitted with the hyperfine structure fitting subroutine in GILDAS. All fitted results are shown in red lines. The velocities of the N2 H+ (1–0) hyperfine structure components are indicated by vertical red lines. In the CH3 OH panel where the velocity is given with respect to the rest frequency (96.74138 GHz) of CH3 OH (20 − 10 A+), the CH3OH triplet around 96.74 GHz is also indicated by three vertical red lines. |
Observed and physical properties of source A.
3.2 Properties of the Serpens filament derived from C18 O (1–0)
As shown in Sect. 3.1, C18O (1–0) data not only trace the distribution and velocity information of the filament, but also have the best signal-to-noise ratio of all the mapped lines. Furthermore, the difference between the systemic velocities derived by C18 O (1–0) and the other optically thin lines is less than 0.1 km s−1 (see Fig. 3), demonstrating that the velocity information derived from C18 O (1–0) will not be significantly affected by differences in molecular chemistry. Therefore, we simply apply Gaussian decomposition to the C18 O (1–0) data to study the kinematics of the Serpens filament. Before the fitting procedure, the rms noise level, σ, of each pixel is estimated from emission-free channels. We then create a mask that includes at least three adjacent channels with intensities higher than 3σ. Only spectra within this mask are used for the following analysis. Visual inspection of the spectra within this mask confirms that a single Gaussian component is a good approximation, so a single Gaussian component is assumed to obtain observed parameters after these spectra are binned to a channel width of 0.1 km s−1 to improve the signal-to-noise ratios of the resulting effective channels.
Figure 4 presents the overall distribution of peak intensities, LSR velocities, and linewidths derived from the single-component Gaussian decomposition of C18O (1–0) data. In Fig. 4a, NW, SE, and EX are clearly seen, but in SE the line shows brighter peak intensities than in NW, which is opposite to what is found in its integrated intensity map (see Fig. 2b). This is due to the linewidth variations. Meanwhile, the peak intensities of C18 O (1–0) range from 0.66 to 2.60 K with a mean uncertainty of 0.19 K on a main beam brightness temperature scale. These peak intensities correspond to optical depths of 0.10–0.49 at an assumed C18 O (1–0) excitation temperature of 10 K which is a typical value of IRDCs (e.g., Du & Yang 2008). The low opacities imply that opacity broadening is negligible in the obtained linewidths derived below (e.g., Hacar et al. 2016a). Assuming local thermodynamic equilibrium (LTE) and a constant excitation temperature of 10 K and following equation (80) of Mangum & Shirley (2015), the C18 O column densities are estimated to be (0.1–1.7) × 1015 cm−2 in NW, (0.2–1.6) × 1015 cm−2 in SE, and (0.2–2.3) × 1015 cm−2 in EX. Figure 4b shows that the determined centroid LSR velocities fall in the range from 7.85 to 8.56 km s−1 with Gaussian fitting uncertainties of 0.01–0.06 km s−1. The whole filament appears to be blueshifted with respect to the ambient molecular gas (vlsr ~ 8.4 km s−1). The maximum velocity difference is about 0.7 km s−1 across the whole region. A continuous velocity distribution is seen across the Serpens filament, suggesting that this filament is velocity-coherent (see also Sect. 3.5). At an offset of (3.′5, −7. ′5) in Fig. 4b, there is a clump whose velocity is blueshifted with respect to the bulk emission of EX. This blueshifted clump is seen in the C18O (1–0) and HNC (1–0) integrated intensity map (see Figs. 2b and d). Velocity gradients both parallel and perpendicular to the filament’s long axis are present in the Serpens filament. The velocity gradients parallel to the filament’s long axis are indicated by four black arrows in Fig. 4b. The associated four regions are found to show the largest velocity gradients. The four parallel velocity gradients are estimated to be ∇v∥,1 = 0.40 ± 0.05 km s−1 pc−1, ∇v∥,2 = 0.30 ± 0.09 km s−1 pc−1, ∇v∥,3 = 0.53 ± 0.06 km s−1 pc−1, and ∇v∥,4 = 0.55 ± 0.14 km s−1 pc−1 over a length of about 3.′9, 2.′ 2, 3.′ 9, and 2.′ 5, respectively, suggesting that the velocity gradients in NW are slightly larger than those in SE. The velocity gradients perpendicular to the major axis around emb28 are indicated by red arrows in Fig. 4b. These gradients are estimated to be 1.31 ± 0.78 km s−1 pc−1 and 1.34 ± 0.62 km s−1 pc−1 both over a length of about 1′, but keep in mind that the values have large uncertainties due to a small number of pixels.
Figure 4c shows that the derived linewidths, Δv, range from 0.33 to 1.11 km s−1. The mean error in the fitted linewidths is 0.06 km s−1. More than 70% of the pixels have linewidths of <0.7 km s−1. In this plot, an enhanced line broadening (Δv > 0.7 km s−1) is clearly found around emb10 and emb28, toward which the four velocity gradients are converging (see Fig. 4b). Both thermal and nonthermal motions contribute to the observed line broadening, so we can extract the nonthermal velocity dispersion, σNT, by subtracting the thermal velocity dispersion, σth, from the observed linewidths:
 (1)
(1)
where 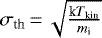 is the thermal velocity dispersion of C18O; mi is the mass weight of a C18O molecule, which is 30; k is the Boltzmann constant; and Tkin is the kinetic temperature. Following the method of Hacar et al. (2016b), we express the derived σNT in terms of the H2 sound speed, cs; in other words, the observed Mach number
is the thermal velocity dispersion of C18O; mi is the mass weight of a C18O molecule, which is 30; k is the Boltzmann constant; and Tkin is the kinetic temperature. Following the method of Hacar et al. (2016b), we express the derived σNT in terms of the H2 sound speed, cs; in other words, the observed Mach number 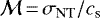 , where cs is derived by adopting a mean molecular weight of 2.33 (Kauffmann et al. 2008). Although the dust temperature is found to be 12–15 K in this region according to the dust temperature map4, gas kinetic temperature is found be lower than dust temperature in IRDCs (Sokolov et al. 2017; Wang 2018), which is likely due to the background/foreground contributions of the dust emission. Thus, we assume a constant kinetic temperature of 10 K (Benson & Myers 1989) to derive the H2 sound speed and thermal velocity dispersion, which gives cs = 0.19 km s−1 and σth = 0.05 km s−1. Using Equation (1), we obtain the
, where cs is derived by adopting a mean molecular weight of 2.33 (Kauffmann et al. 2008). Although the dust temperature is found to be 12–15 K in this region according to the dust temperature map4, gas kinetic temperature is found be lower than dust temperature in IRDCs (Sokolov et al. 2017; Wang 2018), which is likely due to the background/foreground contributions of the dust emission. Thus, we assume a constant kinetic temperature of 10 K (Benson & Myers 1989) to derive the H2 sound speed and thermal velocity dispersion, which gives cs = 0.19 km s−1 and σth = 0.05 km s−1. Using Equation (1), we obtain the 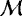 distribution of the Serpens filament which is displayed in Fig. 4d. Except cloud edges and regions where the three YSOs are located, the filament is found to have a mean
distribution of the Serpens filament which is displayed in Fig. 4d. Except cloud edges and regions where the three YSOs are located, the filament is found to have a mean 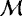 of <1, which suggests that this filament is a velocity-coherent and (trans)sonic filament. If the kinetic temperature were higher than 10 K, the nonthermal velocity dispersions would become even lower, so that it still would remain (trans)sonic. Compared with other regions in the Serpens cloud (Burleigh et al. 2013; Dhabal et al. 2018), the Serpens filament haslower nonthermal velocity dispersions, which makes it one of the most quiescent regions in the Serpens cloud. The kinematic properties of this filament are analogous to velocity-coherent fibers in L1495/B213, NGC 1333, and the Orion integral filament (Hacar et al. 2013, 2017, 2018), the Musca cloud (Hacar et al. 2016b), filaments in Barnard 5 (Pineda et al. 2011), dense filaments in OMC1 (Monsch et al. 2018), filaments with H2 column densities ≤8 × 1021 cm−2 in nearby molecular clouds (Arzoumanian et al. 2013), and more distant filaments in IRDCs (Sokolov et al. 2017; Wang 2018). Meanwhile, the Serpens filament, similar to the Musca cloud, appears to have much less substructure than the other filaments mentioned above, but this needs to be confirmed with higher angular resolution observations.
of <1, which suggests that this filament is a velocity-coherent and (trans)sonic filament. If the kinetic temperature were higher than 10 K, the nonthermal velocity dispersions would become even lower, so that it still would remain (trans)sonic. Compared with other regions in the Serpens cloud (Burleigh et al. 2013; Dhabal et al. 2018), the Serpens filament haslower nonthermal velocity dispersions, which makes it one of the most quiescent regions in the Serpens cloud. The kinematic properties of this filament are analogous to velocity-coherent fibers in L1495/B213, NGC 1333, and the Orion integral filament (Hacar et al. 2013, 2017, 2018), the Musca cloud (Hacar et al. 2016b), filaments in Barnard 5 (Pineda et al. 2011), dense filaments in OMC1 (Monsch et al. 2018), filaments with H2 column densities ≤8 × 1021 cm−2 in nearby molecular clouds (Arzoumanian et al. 2013), and more distant filaments in IRDCs (Sokolov et al. 2017; Wang 2018). Meanwhile, the Serpens filament, similar to the Musca cloud, appears to have much less substructure than the other filaments mentioned above, but this needs to be confirmed with higher angular resolution observations.
 |
Fig. 4 Maps of peak intensities (panel a), LSR velocities (panel b), linewidths (panel c), and Mach numbers (panel d) derived from single-component Gaussian fits to our C18 O (1–0) data. The color bars represent main beam brightness temperatures in units of K in panel a, LSR velocities in units of km s−1 in panel b, and linewidths in units of km s−1 in panel c. Velocity gradients along the filament and perpendicular to the filament are indicated by the blackand red arrows in panel b, respectively. In all panels, the (0, 0) offset corresponds to αJ2000 = 18h28m49.s642, δJ2000 = 00°50′01.′′08, and the three black crosses give the positions of the three embedded YSOs (see Fig. 1). The mean uncertainties in derived peak intensities, LSR velocities, linewidths, and Mach numbers are 0.19 K, 0.02 km s−1, 0.06 km s−1, and 0.1, respectively. The beam size is shown in the lower right of each panel. |
3.3 C18O and N2 H+ fractional abundances relative to H2
Among all mapped lines, C18O (1–0) and N2 H+ (1–0) are likely optically thin and have significant signal-to-noise ratios, so we only estimate their fractional abundances relative to H2 in the Serpens filament. The column densities of C18O and N2 H+ are calculated by assuming optically thin emission and an excitation temperature of 10 K. Under the optical thin assumption, the different excitation temperatures within the range of 5–15 K only lead to deviations of <15% in column densities. In order to match the angular resolution of molecular lines, the Herschel H2 column density map was convolved to an angular resolution of 1′ with a Gaussian kernel size of 47.′′2, and then was linearly interpolated to the same grid as our molecular line data. The fractional abundances are directly derived from the ratios of molecular column densities and H2 column densities. In the following analysis, only the C18O and N2 H+ data with signal-to-noise ratios higher than 5 are taken into account.
Figure 5a presents a pixel-by-pixel comparison between C18 O column densities and H2 column densities within the H2 column density range of (0.3–1.8) × 1022 cm−2. We clearly see two different groups whose column densities are roughly linearly correlated. The two groups are found to arise from EX and the Serpens filament including NW and SE (see Fig. 6a). Figure 5b demonstrates that the C18O fractional abundances in the Serpens filament tend to be lower than those in EX. As shown in Figs. 5b and 6a, the C18 O fractional abundances are found to be (0.7–1.5) × 10−7 with a median value of 1.1 × 10−7 in EX, and (3.4–7.0) × 10−8 with a median value of 5.6 × 108 in the Serpens filament. The C18O fractional abundances in the Serpens filament are lower than those in EX by roughly a factor of 2 (see Fig. 6a), which cannot be explained by the deviations caused by the different excitation temperatures. Rather, it is natural to assume that the gas-phase C18 O molecules have frozen out onto dust grain surfaces in cold dense regions (e.g., Bergin et al. 2002; Bergin & Tafalla 2007). The low C18 O fractional abundances suggest the presence of widespread C18O depletion throughout the Serpens filament. Meanwhile, this depletion is more significant in higher H2 column density regions (see Fig. 5b), consistent with the predictions of previous chemical models (see, e.g., Fig. 3 in Bergin et al. 2002).
Figure 5c shows that the N2 H+ column densities are linearly correlated with H2 column densities with a high Pearson correlation coefficient of 0.86. Figure 5d indicates that the N2 H+ fractional abundances tend to increase with increasing H2 column densities but with a lower Pearson correlation coefficient of 0.51. The N2 H+ fractional abundances also peak in dense regions (see Fig. 6b), better tracing dense cores. This trend is different from that observed for C18O in Fig. 5b. This is mainly due to selective freeze-out in the sense that C18 O molecules are more easily depleted than N2 H+ (Bergin & Tafalla 2007). Meanwhile, N2 H+ depletion has also been found in B68 (Bergin et al. 2002), but is not evident in the Serpens filament. This is mainly due to our lower linear resolution of 0.13 pc versus 0.01 pc in the case of B68. Within the H2 column density range of (0.8–1.8) × 1022 cm−2, the N2 H+ abundances are found to be (0.8–2.3) × 10−10 with a median value of 1.3 × 10−10. Figure 5e shows that fractional abundances of C18 O and N2 H+ are anticorrelated. This is similar to what has been found in a sample of low-mass protostellar objects (see Fig. 15 in Jørgensen et al. (2004)) and caused by the destruction of N2 H+ ions via the reaction N2 H+ + CO →HCO+ + N2 (e.g., Mauersberger & Henkel 1991; Jørgensen et al. 2004). Figure 5f shows that the N2 H+/C18O abundance ratios increase with increasing H2 column densities, which is also evident in the N2 H+/C18O abundance ratio map (see Fig. 6c). This is due to the above-mentioned selective freeze-out effect that causes C18 O molecules to become more significantly depleted in denser regions, whereas most N2 H+ ions remainstill in the gas phase. Meanwhile, the depletion of C18 O makes the removal mechanism for N2 H+ more inefficient, reinforcing such a trend.
3.4 Widespread HCN (1–0) hyperfine line anomalies
Rotational transitions of HCN exhibit hfs which can be used to estimate their optical depths from the intensity ratios between individual components. Under local thermodynamic equilibrium (LTE) conditions, the ratios R(I[F = 1−1]∕I[F = 2−1]) and R(I[F = 0−1]∕I[F = 2−1]) (R12 and R02 hereafter) are expected to be 0.6 < R12 < 1.0 and 0.2 < R02 < 1 for HCN (1–0), depending on different optical depths (e.g., Loughnane et al. 2012). However, HCN hyperfine line anomalies, in which case the observed ratios R12 and R02 deviate from the LTE ranges, make the HCN hyperfine lines less useful for optical depth and thus column density estimates.
Figure 7 shows the integrated intensity maps of the three individual hfs lines. Surprisingly, the F = 0−1 line is found to be stronger than the F = 2−1 line, i.e., R02 > 1, which demonstrates the presence of HCN (1–0) hyperfine line anomalies. On the other hand, the obtained R12 values lie in the expected LTE range. For positions in NW, toward which both the F = 0−1 and F = 2−1 hfs lines are detected with at least 5σ, R02 ranges from 0.6 to 1.7. The higher velocity resolution spectrum toward source A in NW reveals that all three individual hfs components show self-absorption (see Fig. 3). In SE, the integrated intensities of the F = 0−1 line are higher than those of the F = 2−1 line which is barely detected. This clearly shows that the entire SE region exhibits HCN (1–0) hyperfine line anomalies that are even more pronounced than those in NW. In SE, we can constrain the lower limits (3σ) to R02 which are found in the range of ~1.0–2.0 for different pixels. The lower limit of ~2.0 toward the F = 0−1 peak of SE surpasses all reported R02 values found in other sources (e.g., Loughnane et al. 2012). Such an extreme HCN (1–0) hyperfine line anomaly is confirmed by our deeper integration toward source B (see Fig. 8) which is found to have a R02 value of ~2.6.
3.5 Widespread blue-skewed profiles
As shown in Fig. 3, three optically thick lines, HCN (1–0), HNC (1–0), and CS (2–1), are double-peaked with a stronger component on the blueshifted side, while their corresponding rare isotopologs including H13 CN (1–0), HN13C (1–0), and 13CS (2–1) peak at the dips of the self-absorbed lines. Such blue-skewed profiles are known to be an indication of inward motion (e.g., Zhou et al. 1993; Myers et al. 1996). Figure 9 presents position-velocity (PV) diagrams across the crest of the filament in C18 O (1–0), HNC (1–0), and CS (2–1). In Fig. 9b, only a single velocity component is seen in C18 O (1–0), confirming that the Serpens filament is velocity-coherent. In Figs. 9c and d, two main velocity components are found in HNC (1–0) and CS (2–1), while C18O (1–0) lies between the two main velocity components. This structure, seen in HNC and CS, is more tentative in HCN (1–0) (see Fig. B.1a), but this is mainly due to this line’s coarser spectral resolution (0.21 km s−1). Generally, the blueshifted component is stronger than the redshifted component in HNC (1–0) and CS (2–1), indicating the presence of widespread blue-skewed profiles across the filament. This strongly suggests that the Serpens filament is undergoing radial gravitational collapse. Our observations demonstrate that the two velocity components identified in optically thick tracers can also arise from the same spectral component, so characterizing filaments and their velocity structures in optically thin tracers is more reliable.
4 Discussion
4.1 Density structure
In order to study the radial column density profile of the Serpens filament, we use the H2 column density maps from the Herschel Gould Belt Survey to constrain our physical model of filaments. We first extract the crest of the Serpens filament with the discrete persistent structure extractor (DisPerSe5) algorithm (Sousbie 2011). Based on the discrete Morse theory, this algorithm can be used to extract filamentary structures in 2D and 3D datasets. The extracted skeletons are representative of the crest of the filaments. There are two important parameters, the persistence and robustness thresholds, in this algorithm. The persistence threshold describes the column density difference of a pair of critical points where the gradient is null. This value is set to be 4.0 × 1020 cm−2 to isolate the filamentary structure. The robustness threshold is defined as a local measure of how contrasted the critical points and filaments are with respect to their background. The robustness threshold is set to be 6 × 1021 cm−2. In order to make the structure as long as possible, we also assemble pieces of filaments that form an angle smaller than 70°. These parameters are adopted to identify the skeleton in the H2 column density map without smoothing. Since we are only interested in the dense crest of the Serpens filament, the structures with column densities lower than 1 × 1022 cm−2 were trimmed to better visualize its crest. The resulting crest is shown as the blue line in Fig. 10a. The spatial separation between every pixel and the crest is calculated as the radial distance. The width in NW is apparently broader than in SE, because NW is likely affected by the feedback of the three YSOs. SE is more pristine, so SE is used to derive the radial H2 column density profile here. The radial column density profile of this filament is estimated within the white box in Fig. 10a. The western part is contaminated by the emission of EX, leading to the asymmetry of the radial column density profile in Figs. 10b and c. In order to avoid the errors caused by the contamination, we employ Gaussian functions to fit only the eastern part of SE. The fitted FWHM width is 0.19 ± 0.01 pc, corresponding to a deconvolved width of 0.17 ± 0.01 pc. Assuming a cylindrical geometry with a radius of 0.17 pc and a length of 1.6 pc, we estimate the average number density to be about 6.5 × 103 cm−3.
Based on theoretical predictions of infinitely long filaments (e.g., Ostriker 1964; Arzoumanian et al. 2011; Kainulainen et al. 2016), their radial column density profiles can be expressed in a Plummer-like function as
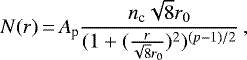 (2)
(2)
where 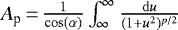 . Here the inclination, α, is set to 0, nc is the number density at the center of thefilament, and r0 is the scale radius. We note that the so-called characteristic radius, Rflat, was also used in previous studies (e.g., Arzoumanian et al. 2011). According to their definitions, Rflat is simply
. Here the inclination, α, is set to 0, nc is the number density at the center of thefilament, and r0 is the scale radius. We note that the so-called characteristic radius, Rflat, was also used in previous studies (e.g., Arzoumanian et al. 2011). According to their definitions, Rflat is simply 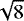 times r0, i.e.,
times r0, i.e., 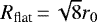 . During the fitting process, we first convolve Eq. (2) with a Gaussian function with a FWHM = 37′′ (~0.08 pc) to take the contribution of the beam into account. In the fitting processes, the modeled p varies from 1.0 to 4.0 with a step size of 0.1, the modeled nc varies from 1 × 103 to 1 × 105 cm−3 with a step size of 1 × 103 cm−3, and the modeled r0 varies from 0.001 to 0.030 pc with a step of 0.001 pc. The goodness of the fit is estimated from the chi-square (χ2) analysis, and we minimize χ2 between data points and models. Figure 10c gives the best fits to the observed radial column density of the regions east and west of the crest lines (as defined by the rectangles in Fig. 10a) within a radius range of r < 0.2 pc. The best fit to the east leads to p = 2.2 ± 0.1, nc = (4.0 ± 0.8) × 104 cm−3, and r0 = 0.018 ± 0.003 pc, while the best fit to the west results in p = 2.0 ± 0.3, nc = (2.5 ± 1.8) × 104 cm−3, and r0 = 0.023 ± 0.011 pc. The given errors are the one-sigma uncertainties of the fit. Since the asymmetry of the radial column density profile is likely due to the contamination by EX, only the derived parameters of the east are used for the following discussions. When adopting different inclinations, nc changes by a factor of 1∕cos(α). On the other hand, the p value is dependent on the selected radius range. When the range extends out to 0.25 pc toward the east, this leads to a much higher χ2, e.g., a poorer fit. On the other hand, the derived p-value (2.2 ± 0.1) of the east indicates that the profile is similar those found in IC 5146 (p, ~ 2; Arzoumanian et al. 2011) and other filaments in nearby molecular clouds (see Table 3), but is shallower than that of an isolated isothermal filament in hydrostatic equilibrium (p = 4; Ostriker 1964). Comparing other filaments in nearby molecular clouds (see Table 3), the physical properties of the Serpens filament are similar to those of Musca. At larger radial range (r ≳ 0.2 pc), the observed radial column density profiles of both the east and west significantly deviate from the Plummer-like function. When fitting the tail within the radial range of 0.2–0.35 pc with a power law, the H2 column density is found to decrease as NH2 ~ r−0.3 in the east profile and NH2 ~ r−0.5 in the west profile. At a radial range of >0.35 pc, the column densities of both the east and west stay nearly constant with mean values of 2.7 × 1021 and 5.1 × 1021 cm−2, respectively.
. During the fitting process, we first convolve Eq. (2) with a Gaussian function with a FWHM = 37′′ (~0.08 pc) to take the contribution of the beam into account. In the fitting processes, the modeled p varies from 1.0 to 4.0 with a step size of 0.1, the modeled nc varies from 1 × 103 to 1 × 105 cm−3 with a step size of 1 × 103 cm−3, and the modeled r0 varies from 0.001 to 0.030 pc with a step of 0.001 pc. The goodness of the fit is estimated from the chi-square (χ2) analysis, and we minimize χ2 between data points and models. Figure 10c gives the best fits to the observed radial column density of the regions east and west of the crest lines (as defined by the rectangles in Fig. 10a) within a radius range of r < 0.2 pc. The best fit to the east leads to p = 2.2 ± 0.1, nc = (4.0 ± 0.8) × 104 cm−3, and r0 = 0.018 ± 0.003 pc, while the best fit to the west results in p = 2.0 ± 0.3, nc = (2.5 ± 1.8) × 104 cm−3, and r0 = 0.023 ± 0.011 pc. The given errors are the one-sigma uncertainties of the fit. Since the asymmetry of the radial column density profile is likely due to the contamination by EX, only the derived parameters of the east are used for the following discussions. When adopting different inclinations, nc changes by a factor of 1∕cos(α). On the other hand, the p value is dependent on the selected radius range. When the range extends out to 0.25 pc toward the east, this leads to a much higher χ2, e.g., a poorer fit. On the other hand, the derived p-value (2.2 ± 0.1) of the east indicates that the profile is similar those found in IC 5146 (p, ~ 2; Arzoumanian et al. 2011) and other filaments in nearby molecular clouds (see Table 3), but is shallower than that of an isolated isothermal filament in hydrostatic equilibrium (p = 4; Ostriker 1964). Comparing other filaments in nearby molecular clouds (see Table 3), the physical properties of the Serpens filament are similar to those of Musca. At larger radial range (r ≳ 0.2 pc), the observed radial column density profiles of both the east and west significantly deviate from the Plummer-like function. When fitting the tail within the radial range of 0.2–0.35 pc with a power law, the H2 column density is found to decrease as NH2 ~ r−0.3 in the east profile and NH2 ~ r−0.5 in the west profile. At a radial range of >0.35 pc, the column densities of both the east and west stay nearly constant with mean values of 2.7 × 1021 and 5.1 × 1021 cm−2, respectively.
Figure 11b shows the column density profile along the crest of the Serpens filament. There are only three maxima across the ~1.5 pc long crest in this profile. In addition, this filament appears to have a separation at a projected scale of ~0.85 pc indicatedby the orange line in Fig. 11b, while a smaller separation at a projected scale of ~0.26 pc is found in NW (indicated by the red line in Fig. 11b). Since little is known about the inclination, we should keep in mind that these scales can only be taken as lower limits. The larger separation of ~0.85 pc is nearly five times the fitted FWHM width of the filament derived above. This is roughly consistent with the prediction that fragmentation is expected with separations of about four times the diameter of the filament in equilibrium or a dynamical system with the observed line mass (mass per unit length) close to the critical line mass (Chandrasekhar & Fermi 1953; Larson 1985; Inutsuka & Miyama 1992). On the other hand, the smaller separation of ~0.26 pc in NW is close to the thermal Jeans length (~0.26 pc) of a spherical cloud (Jeans 1902) by assuming a number density of 6.5 × 103 cm−3 averaged over the entire length of the filament and a kinetic temperature of 10 K. Alternatively, the smaller separation is also possibly caused by the feedback of emb28 observed at the dip of the H2 column density profile (see Fig. 11b).
 |
Fig. 5 Panel a: C18O column densities as a function of H2 column densities. Panel b: C18O fractional abundances as a function of H2 column densities. Panel c: similar to Fig. 5a but for N2H+ column densities. Panel d: similar to Fig. 5b, but for N2H+ fractional abundances. Panel e: C18O fractional abundances as a function of N2H+ fractional abundances. Panel f: N2H+/C18O abundance ratios as a function of H2 column densities. In all panels, the values of NW, SE, and EX are shown with red, green, and blue symbols, respectively. In panels c–f, only data from NW and SE are presented. |
 |
Fig. 6 Distributions of C18O (panel a) fractional abundances, N2H+ fractional abundances (panel b), and N2H+/C18O abundance ratios (panel c). The (0, 0) offset corresponds to αJ2000 = 18h28m49.s642, δJ2000 = 00°50′01.′′08. The beam size is shown in the lower right of each panel. |
 |
Fig. 7 HCN (1–0) intensity maps of the Serpens filament integrated from 0.0 to 1.6 km s−1 (panel a), integrated from 7.0 to 8.6 km s−1 (panel b), and integrated from 11.7 to 13.6 km s−1 (panel c) with respect to the frequency of the F = 2–1 hyperfine structure component. The three ranges correspond to the F = 0−1, F = 2− 1, and F = 1−1 hyperfine structure components, respectively. The color bar represents the integrated intensities in units of K km s−1. In all panels, the overlaid black contours denote H2 column densities of 6 × 1021 cm−2, while the two open circles give the observed positions of sources A and B. In all panels, the (0, 0) offset corresponds to αJ2000 = 18h28m49.s642, δJ2000 = 00°50′01.′′08. The beam size is shown in the lower right of each panel. |
 |
Fig. 8 Observed HCN (1–0) hyperfine line anomaly (black lines) toward source B. The three hyperfine structure components are indicated by vertical red lines. |
4.2 Gravitational collapse observed in a (trans)sonic filament
The stability of the Serpens filament can be assessed by comparing the observed line mass, Ml, with the critical line mass, Ml,crit, predicted by theoretical models. Based on the H2 column density map from the Herschel Gould Belt Survey, we calculate the mass of the Serpens filament by integrating the column densities inside the contour of NH2 = {6, 8, 10} × 1021 cm−2 (see Fig. 10a for the contours)s. The resulting total mass is {66, 50, 36} M⊙ within a length of {1.6, 1.3, 1.0} pc, which gives a line mass, Ml, of {41, 38, 36} M⊙ pc−1. We note that these values are about three times as high as the value of 13 M⊙ pc−1 reported by Roccatagliata et al. (2015), in which the number of bands, dust spectral indices, and color corrections adopted for SED fitting and the H2 column density map is different from that of the Herschel GB team (Könyves et al. 2015; Fiorellino et al. 2017). Detailed discussions about the differences are presented in Appendix C. The H2 column density map derived by the Herschel GB team is more appropriate and therefore used for this work. The critical line mass of an infinite filament in hydrostatic equilibrium is expected to be 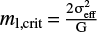 (e.g., Ostriker 1964; Inutsuka & Miyama 1992). When σeff is taken to be the sound speed, i.e., gravity is only balanced by thermal support, the critical line mass is 8–17 M⊙ pc−1 at a kinetic temperature of 5–10 K. As pointed out by previous studies (e.g., Hacar et al. 2017), the calculation of ml,crit should include the contributionfrom nonthermal motions in practice. When the equilibrium is achieved by the support from both the thermal and nonthermal motions, σeff should be taken to be the total velocity dispersion, σt, which can be calculated as
(e.g., Ostriker 1964; Inutsuka & Miyama 1992). When σeff is taken to be the sound speed, i.e., gravity is only balanced by thermal support, the critical line mass is 8–17 M⊙ pc−1 at a kinetic temperature of 5–10 K. As pointed out by previous studies (e.g., Hacar et al. 2017), the calculation of ml,crit should include the contributionfrom nonthermal motions in practice. When the equilibrium is achieved by the support from both the thermal and nonthermal motions, σeff should be taken to be the total velocity dispersion, σt, which can be calculated as
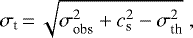 (3)
(3)
where σobs is the observed velocity dispersion. Because SE is more pristine, the properties of SE are more representative of the initial conditions, and σobs is thus taken to be the median velocity dispersion (0.20 km s−1) of SE. This leads to a critical line mass of 25–34 M⊙ pc−1 within a kinetic temperature range of 5–10 K. The observed line mass appears to be higher than the critical line mass, but does not exceed the critical value greatly, suggesting that the Serpens filament is slightly supercritical.
As predicted previously by theoretical models (e.g., Inutsuka & Miyama 1992), such slightly supercritical infinite filaments are able to collapse. Due to the gravitational focusing effect (Burkert & Hartmann 2004; Pon et al. 2011), finite filaments are more prone to collapse at the ends of a filament even when such filaments are subcritical. Blue-skewed line profiles are known to be a signature of infall motions (e.g., Zhou et al. 1993; Myers et al. 1996; Wyrowski et al. 2016). Recently, Mullins et al. (2016) pointed out that HCN (1–0) hyperfine line anomalies could also be ascribable to gravitational infall. The observed widespread blue-skewed line profiles and HCN (1–0) hyperfine line anomalies across the Serpens filament suggest that the filament is undergoing radial collapse (i.e., perpendicular to the major axis). Therefore, our observations indicate that such radial collapse is present in a (trans)sonic filament. This collapse has been observed in other supersonic filaments (e.g., Schneider et al. 2010; Kirk et al. 2013), but evidence for radial collapse in a (trans)sonic filament like the Serpens filament remains sparse.
 |
Fig. 9 Panel a: C18O (1–0) integrated intensity map similar to Fig. 2b but overlaid with a PV cut indicated by the white dashed line. Panel b: PV diagram of C18 O (1–0) along the PV cut in panel a. The channel width of C18O (1–0) spectra has been binned to 0.1 km s−1 to achieve a higher dynamical range. Panel c: similar to panel b but for HNC (1–0). Panel d: similar to panel b but for CS (2–1). In panels b–d, the color bars represent main beam brightness temperatures in units of K, and the black contours represent the C18 O (1–0) emission starting at 1.5 K (5σ) with increments of 0.9 K (3σ). The offsets are given with respect to the center of the PV cut (αJ2000 = 18h28m50.s865, δJ2000 = 00°50′21. ′′799, also indicated by the white filled circle in panel a), and increase from southeast to northwest. The resolution element is shown in the lower right of each panel. |
 |
Fig. 10 Panel a: H2 column density image of the Serpens filament obtained from the Herschel Gould belt survey. The contours correspond to column densities of 6 × 1021 cm−2, 8 × 1021 cm−2, and 1 × 1022 cm−2. The extracted crest of the Serpens filament is shown with the blue line. The emission within the white box is used to derive the radial profile of H2 column density. The three black crosses give the positions of the three embedded YSOs. The beam size is shown in the lower right. Panel b: mean radial profile of H2 column densities within the white box in panel a. The offsets increase from east to west. A Gaussian fit is indicated by the red line. Panel c: mean radial H2 column density profile on the west (yellow) and east (orange) sides of the crest. The red and blue dashed lines represent Plummer-like fits to the east and west (see panel a) within a radius range of <0.2 pc, while the cyan and black lines represent the beam-convolved radial profile of Musca-West (Kainulainen et al. 2016) and the Serpens South filament (Kirk et al. 2013). In both panels a and b, the beam size is shown by the brown line. |
Comparison between the Serpens filament and other filaments in nearby clouds.
 |
Fig. 11 Panel a: LSR velocity map similar to Fig. 4b but overlaid with the H2 column density contours which represent 4 × 1021 cm−2 and 6 × 1021 cm−2. Source B is marked with the red circle, and the three black crosses give the positions of the three embedded YSOs, em10, em28, and em16. Panel b: column density profile along the crest of the Serpens filament indicated by the blue line in panel a. The spatial resolution is ~0.08 pc. The offset increases from south to north. The red line represents a sinusoidal fit to the profile within the offset range of 1.0–1.4 pc. A sinusoidal orange line is created to better visualize the variation at a large scale. Panel c: similar to panel b, but for the C18 O (1–0) velocity. The four red arrows correspond to the velocity gradients in Fig. 4b, indicated there by black arrows. Panel d: similar to panel c, but for the C18 O (1–0) linewidths. In panels b–d, the red dashed lines indicate the positions of Source B and the YSO emb28. |
4.3 Radial collapse
Due to the greater gravitational potential in the central filament, ambient molecular material will collapse onto the center of the filament. As pointed out by previous studies (e.g., Kirk et al. 2013), the infall rate, Ṁ⊥, can be estimated with
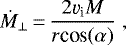 (4)
(4)
where vi is the infall velocity, M is the mass of the filament, r is the radius of the filament, and α is the inclination used to correct projection effects. In order to estimate the infall velocity, we use the Hill5 model (De Vries & Myers 2005) in the pyspeckit package (Ginsburg & Mirocha 2011). The Hill5 model employs an excitation temperature profile increasing linearly toward the center, rather than the two-slab model of Myers et al. (1996), so the Hill5 model is thought to provide a better fit of infall motions (De Vries &Myers 2005). In the Hill5 model, five physical parameters, including the opacity, τ0, the systemic LSR velocity, vs, the infall velocity, vi, the velocity dispersion, σ0, and the peak excitation temperature, Te, can be fitted. As shown in Figs. 3 and 9, both HNC (1–0) and CS (2–1) display widespread blue-skewed profiles, andare thus used as input in the Hill5 model. Spectra in NW and SE are averaged to improve the signal-to-noise ratios, and the averaged spectra are fitted with the Hill5 model to derive the infall velocity. The fitted results are shown in Fig. 12 and given in Table 4. These results suggest that both CS (2–1) and HNC (1–0) have high opacities (τ0 > 1). The fitted LSR velocities and velocity dispersions and the values derived from C18 O (1–0) agree within 0.1 km s−1. The fitted infall velocities of NW and SE are found to be 0.05 to 0.13 km s−1 with an average value of 0.09 km s−1. The fitted peak excitation temperatures are very low, i.e., Te ~ 5 K. Meanwhile, the HNC (1–0) and CS (2–1) spectra of source A are also fitted with the Hill5 model, and the results are shown in Fig. 3. The fitted parameters are consistent with the values derived with the average spectra.
Assuming that the whole filament is collapsing with a mean infall velocity of 0.09 km s−1, we use Eq. (4) to estimate its infall rate to be 72 M⊙ Myr−1 when the inclination is set to be 0°. This infall rate is likely to be lower than that found in Serpens South (130 M⊙ Myr−1 under the same assumption; Kirk et al. 2013) and in the much more massive DR21 filament (a few 103 M⊙ Myr−1; Schneider et al. 2010). We also note that the derived infall rate onto the filament is a lower limit, because cos(α) is very likely to be <1 in reality. With this current infall rate, it needs about 0.9 Myr to double the mass of the Serpens filament. This timescale is comparable to the age (~1 Myr) to form class I YSOs (Evans et al. 2009) which are found in the filament. On the other hand, this timescale is roughly twice the free-fall time (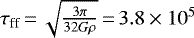 yr) at an average number density of 6.5 × 103 cm−3. The low rate could be due to its relatively early evolutionary stage. This is also supported by the derived infall velocities which are less than 10% of the free-fall velocity (
yr) at an average number density of 6.5 × 103 cm−3. The low rate could be due to its relatively early evolutionary stage. This is also supported by the derived infall velocities which are less than 10% of the free-fall velocity (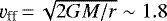 km s−1). As pointed out by Tan et al. (2014), such a low infall velocity indicates that collapse has just begun. Alternatively, both thermal and nonthermal support are effective in providing support against gravity, leading to the low rate.
km s−1). As pointed out by Tan et al. (2014), such a low infall velocity indicates that collapse has just begun. Alternatively, both thermal and nonthermal support are effective in providing support against gravity, leading to the low rate.
The mass of the Serpens filament (36–66 M⊙) is similar to that of the Serpens South filament (52 M⊙) (Kirk et al. 2013), but the radial column density profile is different for the two filaments. The Serpens filament has 10 times lower central density and 3 times higher scale radius than the Serpens South filament. As collapse goes on, the central density will become higher and the scale radius will become smaller (e.g., Inutsuka & Miyama 1992). This suggests that the Serpens filament may lie at an earlier evolutionary stage, prior to the Serpens South filament. This is reinforced by the fact that the Serpens filament contains fewer YSOs.
 |
Fig. 12 Panel a: HNC (1–0) spectrum averaged over 3 × 3 pixels centered at an offset of (−40′′, 40′′) in Fig. 2 to increase the signal-to-noise level. Panel b: similar to panel a, but for an offset of (100′′, −120′′). Panel c: similar to panel a, but for CS (2–1). Panel d: similar to panel b, but for CS (2–1). All these lines are modeled with the Hill5 model (De Vries & Myers 2005; see Sect. 4.3). These offsets are given with respect to αJ2000 = 18h28m49.s642, δJ2000 = 00°50′01.′′08. The fitted parameters and their uncertainties are given in the upper right of each panel. |
Fitted parameters of the Hill5 model for the average spectra and source A.
4.4 Longitudinal collapse
Accretion flows along filaments are important for the growth of dense cores and protostars. A few observational studies indicate that accretion flow occurring along a filament’s long axis feeds nascent stars or the dense cores (e.g., Kirk et al. 2013; Peretto et al. 2014; Liu et al. 2015; Lu et al. 2018; Yuan et al. 2018). As described in Sect. 3.2 (see also Fig. 4b), velocity gradients, ∇v∥, are also observed along the filament’s long axis, which could be due to such accretion flows. The accretion rate along the filament, Ṁ∥, can be estimated with the following equation (Kirk et al. 2013):
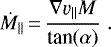 (5)
(5)
As mentioned in Sect. 3.2, ∇v∥,1, ∇v∥,2, ∇v∥,3, and ∇v∥,4 are 0.40 ± 0.05, 0.30 ± 0.09, 0.53 ± 0.06, and 0.55 ± 0.14 km s−1 pc−1. The regions showing the four velocity gradients are found to have masses of ~20, ~10, ~18, and ~16 M⊙ according to the H2 column densities derived from dust emission (see Fig. 10a). Assuming an inclination of 45°, we estimate the accretion rates to be ~8 M⊙ Myr−1, ~3 M⊙ Myr−1, ~10 M⊙ Myr−1, and ~9 M⊙ Myr−1. These values are lower than all reported accretion rates (≳50 M⊙ Myr−1) along filaments under the same assumption of an inclination of 45° (Kirk et al. 2013; Yuan et al. 2018; Lu et al. 2018). If these low values are due to the earlier evolutionary stage of the Serpens filament, this may indicate that gas accretion can be accelerated during its evolution. The accretion rate per unit length, Ṁ∥ ∕L, is found to be ~20 M⊙ Myr−1 pc−1, which is also lower than that (~90 M⊙ Myr−1 pc−1) of Serpens South (see Table 3). The low values of Ṁ∥ and Ṁ∥ ∕L may be the reason why star formation in the Serpens filament is not as active as that in Serpens South.
As shown in Figs. 4b and 11c, the two velocity gradients ∇v∥,1 and ∇v∥,2 converge to source B in SE, while the other two velocity gradients ∇v∥,3 and ∇v∥,4 converge to emb28 in NW. Furthermore, the two velocity converging positions roughly coincide with the enhancements of H2 column densities in Fig. 11b. In addition, the velocities change as a nearly linear function of offsets from the two converging positions (indicated by the arrows in Fig. 11c), which is roughly consistent with the velocity profiles expected in homologous free-fall collapse of filaments (see Fig. 5 in both Peretto et al. 2007, 2014 and Fig. 1 in Myers 2005). This suggests that such accretion flows are likely due to the longitudinal collapse of the Serpens filament. Toward the velocity converging place in NW, the linewidths are apparently higher (see Fig. 11d), which may also result from the collision of the longitudinal collapsing gas indicated by arrows in Fig. 4b or the feedback of the YSOs. Together with the velocity gradients perpendicular to the filament’s long axis and the widespread blue-skewed profiles (see Sects. 3.2 and 4.3), this implies that radial and longitudinal collapse occur simultaneously in the Serpens filament.
5 Summary and conclusion
We have mapped the Serpens filament (one of the nearest infrared dark clouds) in seven different species (C18O, HCO+, HNC, HCN, N2 H+, CS, and CH3OH) near λ = 3 mm with the PMO-13.7 m telescope, and have studied its physical properties and dynamical state. The main results are as follows:
- (1)
Among the seven species, HCO+, HNC, HCN, and CS are found to show self-absorption, while C18 O is most sensitive to the filamentary structure. Based on the C18O data, the Serpens filament is found to be a velocity-coherent (trans)sonic filament that is one of the most quiescent regions in the Serpens cloud. Widespread C18 O depletion is found throughout the Serpens filament where the C18O fractional abundances are (3.4–7.0) × 10−8, a factor of ~2 lower than those in ambient regions. N2 H+ has fractional abundances of (0.8–2.3) × 10−10. The N2 H+/C18O abundance ratios are found to increase with increasing H2 column densities, suggesting that N2 H+ is less depleted than C18O in dense regions. Furthermore, blue-skewed HNC and CS line profiles and HCN hyperfine line anomalies are widespread across this filament.
- (2)
The filament has a total gas mass of ~66 M⊙ within a length of ~1.6 pc, and its FWHM width is 0.17 ± 0.01 pc. The radial column density profile is asymmetric in the Serpens filament. Within a radius range of <0.2 pc, the radial H2 column density profile is well described as a Plummer-like profile. Our fit leads to an exponent (p) of 2.2 ± 0.1, scale radius (r0) of 0.018 ± 0.003 pc, and central density (nc) of (4.0 ± 0.8) × 104 cm−3 for the east profile which is similar to Musca but shallower than that of an infinite hydrostatic filament. In the outer part (r > 0.2 pc), the H2 column densities fall as a power-law profile to a nearly constant column density. The column density profile across the filament crest presents two characteristic fragmentation scales of ~0.85 pc and ~0.26 pc. The former roughly agrees with the filament fragmentation scale, while the latter could be due to the thermal Jeans instability or the feedback of young stellar objects.
- (3)
The Serpens filament is found to be slightly supercritical with an observed line mass (mass per unit length) of 36–41 M⊙ pc−1. The widespread blue-skewed HNC and CS line profiles and HCN hyperfine line anomalies across this filament imply that radial collapse is present in a (trans)sonic filament. This is consistent with the theoretical prediction that slightly supercritical filaments are prone tocollapse.
- (4)
Based on the HNC and CS blue-skewed profiles, the radial infall velocities of the Serpens filament are found to be less than 10% of the free-fall velocity, and the resulting infall rate of radial collapse is found to be ~72 M⊙ Myr−1, which implies that it needs about 0.9 Myr (roughly twice the free-fall time) to double the mass of the Serpens filament. The timescale is also comparable to the age (~1 Myr) needed to form class I young stellar objects. C18O velocity gradients along the filament’s long axis are indicative of gas accretion within this filament. This leads to an accretion rate of ~10 M⊙ Myr−1 along this filament. Its velocity and density structures suggest that such accretion flows are likely due to the filament’s longitudinal collapse. Both the infall rate and the accretion rate along the Serpens filament are lower than all previously reported values in other filaments. This indicates that the Serpens filament lies at an early evolutionary stage when collapse has just begun, or that thermal and nonthermal support are effective in providing support against gravity.
Acknowledgements
We appreciate the assistance of the PMO-13.7 m staff during the observations. We are grateful to the FFTS team who made the special 200 MHz FFTS mode available to the community. Y.G. also acknowledges the organizers of the treasure hunt around Yardangs in the Tsaidam Desert which triggered the idea of this paper. Stefano Pezzuto is acknowledged for providing information on the H2 column density map. Shaobo Zhang is acknowledged for providing his AICer6 plotting code. Xing Lu is acknowledged for introducing the pyspeckit package. This work was supported by the National Key Research & Development Program of China under grant 2017YFA0402702, the National Natural Science Foundation of China (NSFC) under grant 11127903, and the Chinese Academy of Sciences under grant QYZDJ-SSW-SLH047. J.X.S. was supported by NSFC under grant U1531103. This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration. This research has made use of data from the Herschel Gould Belt survey (HGBS) project (http://gouldbelt-Herschel.cea.fr). This research made use of NASA’s Astrophysics Data System. This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013). The authors thank the anonymous referee for the useful comments on the manuscript.
Appendix A More comments on Source A in the Serpens filament
Benefiting from a longer integration on source A which represents the peak of the F = 0–1 line of HCN(1–0) (see Fig. 7), our single-point observations have led to the detection of 13 transitions which can be assigned to eight different molecules and their isotopologs (see Fig. 3 and Table 2). As mentioned in Sect. 3.1, self-absorption is observed in HCO+ (1–0), CS (2–1) s, HCN (1–0), and HNC (1–0), which is analogous to those observed in Serpens South (Kirk et al. 2013). The hfs components of H13CN (1–0) are detected toward source A. The fit to its hfs lines gives an optical depth of ~0.70 for the F = 2−1 line of H13 CN (1–0). This implies a very high optical depth of ~50 for the corresponding line of HCN (1–0) with a typical isotopic ratio [12 C/13C] = 70 in nearby clouds (Gong et al. 2015; Li et al. 2016b). Furthermore, our measured H13 CN (1–0) and HN13C (1–0) brightness temperatures are comparable to those in TMC-1 (Hirota et al. 1998) and higher than those in Serpens South (Kirk et al. 2013), which were obtained with larger telescopes (Nobeyama 45m and Mopra 22m), neglecting beam dilution effects. The detection of CCS (87 –76) also points out that Source A is chemically young since this molecule tends to be abundant in early phases of star-forming cores (Suzuki et al. 1992). Furthermore, the peak intensity of HN13C (1–0) is about four times that of H13CN (1–0), indicative of an extremely cold kinetic temperature (Schilke et al. 1992). Based on the derived column densities in Table 2, the CH3OH A/E abundance ratio is estimated to be 1.7 ± 0.2, indicating an over-abundance of A type methanol. This could be the result of CH3OH that formedfrom hydrogenation of solid CO on interstellar grain surfaces and then released into the gas phase via reactive desorption (e.g., Wirström et al. 2011; Vasyunin & Herbst 2013). The frequency of SiO (2–1) has also been observed, but the line remains undetected, which suggests that the 3σ upper limit of the peak intensity is 0.06 K.
Appendix B Position-velocity diagrams of HCN (1–0), N2 H+ (1–0), and the CH3OH lines
In addition to Fig. 9, Fig. B.1 also presents the position-velocity diagrams of HCN (1–0), N2 H+ (1–0), and the CH3OH lines. In Fig. B.1a, we see that the F = 1–0 component of HCN (1–0) is brighter than the other two components in most of the observed regions, confirming the presence of the HCN hyperfine line anomalies.
 |
Fig. B.1 PV diagrams similar to Fig. 9b but for HCN (1–0) (panel a), N2 H+ (1–0) (panel b), and two CH3OH lines (panel c). In panel a, the three hyperfine structure components are labeled next to their respective emission. In panel b, the channel width of the N2H+ (1–0) spectra has been binned to 0.16 km s−1 to achieve a higher dynamical range in individual channels. In panel c, the two transitions are labeled next to their respective emission. In all panels, the color bars represent main beam brightness temperatures in units of K. The offsets are given with respect to the center of the PV cut (αJ2000 = 18h28m50.s865, δJ2000 = 00°50′21. ′′799, also indicated by the white filled circle in Fig. 9a), and increase from southeast to northwest. In all panels, the vertical dashed lines mark the systemic velocity of −8.11 km s−1 for corresponding lines. |
Appendix C Comments on H2 column densities
 |
Fig. C.1 Panel a: Spitzer c2d visual extinction map overlaid with the Herschel H2 column density contours. The contours increase from 4 × 1021 cm−2 to 1.2 × 1022 cm−2 by 4 × 1021 cm−2. The color bar represents the visual extinction in units of magnitude. Panel b: map of the ratios (NH_2,av/ |
H2 column densities derived from the Herschel GB team are nearly three times higher than those derived by Roccatagliata et al. (2015) in the Serpens filament. The differences may arise for one of three reasons given below. First, Roccatagliata et al. (2015) fitted the SED with data from all five Herschel bands (70–500 μm), while the Herschel GB team only used observed data points from 160 to 500 μm (Fiorellino et al. 2017). Since the 70 μm emission might trace a hotter dust population, including 70 μm data in the SED fitting may cause larger uncertainties in deriving the properties of molecular clouds. Second, the two teams used different dust spectral indices, which leads to a difference in the dust mass absorption coefficient by a factor of 1.2–1.5 for the five Herschel bands. Third, the color correction seems different. Although they both use the same model, the added offset values of the Herschel GB team (Könyves et al. 2015) are a factor of 1.5–2.6 higher than those used in Roccatagliata et al. (2015), leading to different absolute flux densities.
Here, we present a comparison between the Herschel H2 column density map used in this work and the visual extinction map that is obtained from the c2d Spitzer Legacy project7 (Evans et al. 2003, 2009). This project has provided visual extinction maps with angular resolutions of 90′′–300′′, and we chose the visual extinction map with the highest angular resolution of 90′′ for the comparison (see Fig. C.1a). The visual extinction (AV) was converted to the H2 column density by assumingN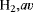 (cm−2) = 9.4 × 1020 AV (mag) (Bohlin et al. 1978). Meanwhile, the Herschel H2 column density map was also convolved to an angular resolution of 90′′ with a Gaussian kernal size of 82′′, and then was linearly interpolated to the same grid as the visual extinction map. Figure C.1b presents the ratio (
(cm−2) = 9.4 × 1020 AV (mag) (Bohlin et al. 1978). Meanwhile, the Herschel H2 column density map was also convolved to an angular resolution of 90′′ with a Gaussian kernal size of 82′′, and then was linearly interpolated to the same grid as the visual extinction map. Figure C.1b presents the ratio (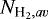 /
/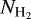 ) between the H2 column densities derived from the visual extinction and the Herschel SED. We find that the ratios are 0.8–1.5 in NW and SE, and 1.7–2.0 in EX. This suggests that the H2 column densities derived from the two methods agree with each other in NW and SE, and that the variations may mainly arisefrom the uncertainties in the Herschel column density map and the visual extinction map. In EX, the H2 column densities based on the extinction map are nearly twice the H2 column densities derived from the Herschel SED. This is probably because the conversion factor from AV to H2 column density and the dust spectral index (β) in EX are different from those in NW and SE.
) between the H2 column densities derived from the visual extinction and the Herschel SED. We find that the ratios are 0.8–1.5 in NW and SE, and 1.7–2.0 in EX. This suggests that the H2 column densities derived from the two methods agree with each other in NW and SE, and that the variations may mainly arisefrom the uncertainties in the Herschel column density map and the visual extinction map. In EX, the H2 column densities based on the extinction map are nearly twice the H2 column densities derived from the Herschel SED. This is probably because the conversion factor from AV to H2 column density and the dust spectral index (β) in EX are different from those in NW and SE.
Roccatagliata et al. (2015) also compared their results with other observations in other regions in Serpens. Their calculated mass of Serpens Core (i.e., Cluster A) is seven times less massive than the mass derived by C18O (scaled to the same distance, White et al. 1995), and their calculated masses of core B and C are also three times less massive than the masses derived with 3 mm continuum emission (scaled to the same distance, Testi & Sargent 1998; Testi et al. 2000). Given these values, the H2 column density map derived from the Herschel GB team is used for this work.
References
- André, P. 2017, C R Geosci., 349, 187 [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, Protostars and Planets VI, 27 [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Arzoumanian, D., André, P., Peretto, N., & Könyves, V. 2013, A&A, 553, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bally, J., Langer, W. D., Stark, A. A., & Wilson, R. W. 1987, ApJ, 312, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, P. J., & Myers, P. C. 1989, ApJS, 71, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Alves, J., Huard, T., & Lada, C. J. 2002, ApJ, 570, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Burkert, A., & Hartmann, L. 2004, ApJ, 616, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Burleigh, K. J., Bieging, J. H., Chromey, A., Kulesa, C., & Peters, W. L. 2013, ApJS, 209, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Clark, F. O., Egan, M. P., et al. 1998, ApJ, 508, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S., & Fermi, E. 1953, ApJ, 118, 116 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- De Vries, C. H., & Myers, P. C. 2005, ApJ, 620, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Dhabal, A., Mundy, L. G., Rizzo, M. J., Storm, S., & Teuben, P. 2018, ApJ, 853, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Du, F., & Yang, J. 2008, ApJ, 686, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Glenn, J., Evans, II, N. J., et al. 2007, ApJ, 666, 982 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Evans, II, N. J., Sargent, A. I., & Glenn, J. 2009, ApJ, 692, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, II, N. J., Allen, L. E., Blake, G. A., et al. 2003, PASP, 115, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, II, N. J., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fiorellino, E., Pezzuto, S., Liu, S. J., et al. 2017, Mem. Soc. Astron. It., 88, 783 [NASA ADS] [Google Scholar]
- Friberg, P., Hjalmarson, A., Madden, S. C., & Irvine, W. M. 1988, A&A, 195, 281 [Google Scholar]
- Ginsburg, A., & Mirocha, J. 2011, Astrophysics Source Code Library [record ascl:1109.001] [Google Scholar]
- Gong, Y., Henkel, C., Thorwirth, S., et al. 2015, A&A, 581, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gong, Y., Fang, M., Mao, R., et al. 2017, ApJ, 835, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Gutermuth, R. A., Bourke, T. L., Allen, L. E., et al. 2008, ApJ, 673, L151 [NASA ADS] [CrossRef] [Google Scholar]
- Hacar, A., Tafalla, M., Kauffmann, J., & Kovács, A. 2013, A&A, 554, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., Alves, J., Burkert, A., & Goldsmith, P. 2016a, A&A, 591, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., Kainulainen, J., Tafalla, M., Beuther, H., & Alves, J. 2016b, A&A, 587, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., Tafalla, M., & Alves, J. 2017, A&A, 606, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., Tafalla, M., Forbrich, J., et al. 2018, A&A, 610, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirota, T., Yamamoto, S., Mikami, H., & Ohishi, M. 1998, ApJ, 503, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Inutsuka, S.-I., & Miyama, S. M. 1992, ApJ, 388, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Jeans, J. H. 1902, Phil. Trans. R. Soc. London, Ser. A, 199, 1 [Google Scholar]
- Jørgensen, J. K., Schöier, F. L., & van Dishoeck E. F. 2004, A&A, 416, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Hacar, A., Alves, J., et al. 2016, A&A, 586, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kauffmann, J., Bertoldi, F., Bourke, T. L., Evans, II, N. J., & Lee, C. W. 2008, A&A, 487, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirk, H., Myers, P. C., Bourke, T. L., et al. 2013, ApJ, 766, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Könyves, V., André, P., Men’shchikov, A., et al. 2015, A&A, 584, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, R. B. 1985, MNRAS, 214, 379 [NASA ADS] [Google Scholar]
- Li, G.-X., Urquhart, J. S., Leurini, S., et al. 2016a, A&A, 591, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, J., Shen, Z.-Q., Wang, J., et al. 2016b, ApJ, 824, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H. B., Galván-Madrid, R., Jiménez-Serra, I., et al. 2015, ApJ, 804, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Loren, R. B. 1989, ApJ, 338, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Loughnane, R. M., Redman, M. P., Thompson, M. A., et al. 2012, MNRAS, 420, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, X., Zhang, Q., Liu, H. B., et al. 2018, ApJ, 855, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Malinen, J., Juvela, M., Rawlings, M. G., et al. 2012, A&A, 544, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mangum, J. G., & Shirley, Y. L. 2015, PASP, 127, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Mattern, M., Kauffmann, J., Csengeri, T., et al. 2018, A&A, 619, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mauersberger, R., & Henkel, C. 1991, A&A, 245, 457 [NASA ADS] [Google Scholar]
- Menten, K. M., Pillai, T., & Wyrowski, F. 2005, in Massive Star Birth: A Crossroads of Astrophysics, eds. R. Cesaroni, M. Felli, E. Churchwell, & M. Walmsley, IAU Symp., 227, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Miville-Deschênes, M.-A., Martin, P. G., Abergel, A., et al. 2010, A&A, 518, L104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monsch, K., Pineda, J. E., Liu, H. B., et al. 2018, ApJ, 861, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Mullins, A. M., Loughnane, R. M., Redman, M. P., et al. 2016, MNRAS, 459, 2882 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C. 2005, ApJ, 623, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C. 2009, ApJ, 700, 1609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Myers, P. C., Mardones, D., Tafalla, M., Williams, J. P., & Wilner, D. J. 1996, ApJ, 465, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz-León, G. N., Dzib, S. A., Kounkel, M. A., et al. 2017, ApJ, 834, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Peretto, N., Hennebelle, P., & André, P. 2007, A&A, 464, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peretto, N., Fuller, G. A., André, P., et al. 2014, A&A, 561, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J. 2005, in SF2A-2005: Semaine de l’ Astrophysique Francaise, eds. F. Casoli, T. Contini, J. M. Hameury, & L. Pagani, 721 [Google Scholar]
- Pillai, T., Wyrowski, F., Carey, S. J., & Menten, K. M. 2006, A&A, 450, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pineda, J. E., Goodman, A. A., Arce, H. G., et al. 2011, ApJ, 739, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pon, A., Johnstone, D., & Heitsch, F. 2011, ApJ, 740, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Roccatagliata, V., Dale, J. E., Ratzka, T., et al. 2015, A&A, 584, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schilke, P., Walmsley, C. M., Pineau Des Forets, G., et al. 1992, A&A, 256, 595 [Google Scholar]
- Schneider, S., & Elmegreen, B. G. 1979, ApJS, 41, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Csengeri, T., Bontemps, S., et al. 2010, A&A, 520, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shan, W., Yang, J., Shi, S., et al. 2012, IEEE Trans. Terahertz Sci. Technol., 2, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Shirley, Y. L. 2015, PASP, 127, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Sokolov, V., Wang, K., Pineda, J. E., et al. 2017, A&A, 606, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousbie, T. 2011, MNRAS, 414, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, J. X., Lu, D. R., Yang, J., et al. 2018, Acta Astron. Sin., 59, 3 [NASA ADS] [Google Scholar]
- Suzuki, H., Yamamoto, S., Ohishi, M., et al. 1992, ApJ, 392, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, J. C., Beltrán, M. T., Caselli, P., et al. 2014, Protostars and Planets VI, 149 [Google Scholar]
- Testi, L., & Sargent, A. I. 1998, ApJ, 508, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., Sargent, A. I., Olmi, L., & Onello, J. S. 2000, ApJ, 540, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Ulich, B. L., & Haas, R. W. 1976, ApJS, 30, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Vastel, C., Ceccarelli, C., Lefloch, B., & Bachiller, R. 2014, ApJ, 795, L2 [Google Scholar]
- Vasyunin, A. I., & Herbst, E. 2013, ApJ, 769, 34 [Google Scholar]
- Wang, K. 2018, Res. Notes Am. Astron. Soc., 2, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, K., Testi, L., Ginsburg, A., et al. 2015, MNRAS, 450, 4043 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- White, G. J., Casali, M. M., & Eiroa, C. 1995, A&A, 298, 594 [NASA ADS] [Google Scholar]
- Wirström, E. S., Geppert, W. D., Hjalmarson, Å., et al. 2011, A&A, 533, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Wyrowski, F., Güsten, R., Menten, K. M., et al. 2016, A&A, 585, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xiong, F., Chen, X., Yang, J., et al. 2017, ApJ, 838, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, J., Li, J.-Z., Wu, Y., et al. 2018, ApJ, 852, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, S. B., Yang, J., Xu, Y., et al. 2011, ApJS, 193, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, S., Evans, II, N. J., Koempe, C., & Walmsley, C. M. 1993, ApJ, 404, 232 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Panel a: WISE 11.2 μm image of the Serpens filament that shows up in absorption. Panel b: Herschel 250 μm image of the Serpens filament. The contours start at 0.5 Jy beam−1, and increase by 0.5 Jy beam−1. In both panels, the three blue circles mark the embedded YSOs emb10, emb16, and emb28 (Enoch et al. 2009), while the white and cyan circles give the selected positions of Source A and Source B (see Sect. 2.1 and Table 1). The beam size is shown in the lower right of each panel. |
| In the text | |
 |
Fig. 2 Spatial distributions of different molecular species, labeled in the lower right of each panel, over the Serpens filament. Panel a: Herschel H2 column density image. The contours are H2 column densities of 4 × 1021 cm−2 and 6 × 1021 cm−2. This region is divided by the two white dashed lines into three individual regions which are labeled NW (northwest), SE (southeast), and EX (extended). Panel b: C18 O (1–0) intensity map integrated from 7.4 to 8.7 km s−1. The contours start at 0.30 K km s−1 (5σ), and increase by 0.18 K km s−1 (3σ). Panel c: HCO+ (1–0) intensity map integrated from 6.5 to 9.5 km s−1. The contours start at 0.27 K km s−1, and increase by 0.27 K km s−1. Panel d: HNC (1–0) intensity map integrated from 7.0 to 9.0 km s−1. The contours start at 0.24 K km s−1, and increase by 0.24 K km s−1. Panel e: HCN (1–0) intensity map integrated from 0 to 1.6 km s−1, from 7.0 to 8.6 km s−1, and from 11.8 to 13.4 km s−1 relative to the frequency of the F = 2–1 hyperfine structure component. The contours start at 0.27 K km s−1, and increase by 0.27 K km s−1. Panel f: N2H+ (1–0) intensity map integrated from 6.5 to 9.5 km s−1. The contours start at 0.30 K km s−1, and increase by 0.30 K km s−1. Panel g: CS (2–1) intensity map integrated from 7.0 to 9.5 km s−1. The contours start at 0.18 K km s−1, and increase by 0.18 K km s−1. Panel h: CH3OH (20 –10) intensity map integrated from 7.5 to 8.8 km s−1. The contours start at 0.12 K km s−1, and increase by 0.12 K km s−1. In all panels, the (0, 0) offset corresponds to αJ2000 = 18h28m49.s642, δJ2000 = 00°50′01.′′08, and the three blue crosses give the positions of the three embedded YSOs (see also Fig. 1). The beam size is shown in the lower right of each panel. |
| In the text | |
 |
Fig. 3 Single-pixel spectra (black lines) of all detected molecules toward Source A. Species are given in the upper left of each panel. In all panels, the vertical blue dashed lines represent the systemic velocity obtained from C18 O (1–0). Single-peaked spectra are modeled with a Gaussian fit. The blue-skewed line profiles of CS (2–1), HCN (1–0), and HNC (1–0) are fitted with the Hill5 model (De Vries & Myers 2005). For H13 CN (1–0) and N2H+ (1–0), the spectra are fitted with the hyperfine structure fitting subroutine in GILDAS. All fitted results are shown in red lines. The velocities of the N2 H+ (1–0) hyperfine structure components are indicated by vertical red lines. In the CH3 OH panel where the velocity is given with respect to the rest frequency (96.74138 GHz) of CH3 OH (20 − 10 A+), the CH3OH triplet around 96.74 GHz is also indicated by three vertical red lines. |
| In the text | |
 |
Fig. 4 Maps of peak intensities (panel a), LSR velocities (panel b), linewidths (panel c), and Mach numbers (panel d) derived from single-component Gaussian fits to our C18 O (1–0) data. The color bars represent main beam brightness temperatures in units of K in panel a, LSR velocities in units of km s−1 in panel b, and linewidths in units of km s−1 in panel c. Velocity gradients along the filament and perpendicular to the filament are indicated by the blackand red arrows in panel b, respectively. In all panels, the (0, 0) offset corresponds to αJ2000 = 18h28m49.s642, δJ2000 = 00°50′01.′′08, and the three black crosses give the positions of the three embedded YSOs (see Fig. 1). The mean uncertainties in derived peak intensities, LSR velocities, linewidths, and Mach numbers are 0.19 K, 0.02 km s−1, 0.06 km s−1, and 0.1, respectively. The beam size is shown in the lower right of each panel. |
| In the text | |
 |
Fig. 5 Panel a: C18O column densities as a function of H2 column densities. Panel b: C18O fractional abundances as a function of H2 column densities. Panel c: similar to Fig. 5a but for N2H+ column densities. Panel d: similar to Fig. 5b, but for N2H+ fractional abundances. Panel e: C18O fractional abundances as a function of N2H+ fractional abundances. Panel f: N2H+/C18O abundance ratios as a function of H2 column densities. In all panels, the values of NW, SE, and EX are shown with red, green, and blue symbols, respectively. In panels c–f, only data from NW and SE are presented. |
| In the text | |
 |
Fig. 6 Distributions of C18O (panel a) fractional abundances, N2H+ fractional abundances (panel b), and N2H+/C18O abundance ratios (panel c). The (0, 0) offset corresponds to αJ2000 = 18h28m49.s642, δJ2000 = 00°50′01.′′08. The beam size is shown in the lower right of each panel. |
| In the text | |
 |
Fig. 7 HCN (1–0) intensity maps of the Serpens filament integrated from 0.0 to 1.6 km s−1 (panel a), integrated from 7.0 to 8.6 km s−1 (panel b), and integrated from 11.7 to 13.6 km s−1 (panel c) with respect to the frequency of the F = 2–1 hyperfine structure component. The three ranges correspond to the F = 0−1, F = 2− 1, and F = 1−1 hyperfine structure components, respectively. The color bar represents the integrated intensities in units of K km s−1. In all panels, the overlaid black contours denote H2 column densities of 6 × 1021 cm−2, while the two open circles give the observed positions of sources A and B. In all panels, the (0, 0) offset corresponds to αJ2000 = 18h28m49.s642, δJ2000 = 00°50′01.′′08. The beam size is shown in the lower right of each panel. |
| In the text | |
 |
Fig. 8 Observed HCN (1–0) hyperfine line anomaly (black lines) toward source B. The three hyperfine structure components are indicated by vertical red lines. |
| In the text | |
 |
Fig. 9 Panel a: C18O (1–0) integrated intensity map similar to Fig. 2b but overlaid with a PV cut indicated by the white dashed line. Panel b: PV diagram of C18 O (1–0) along the PV cut in panel a. The channel width of C18O (1–0) spectra has been binned to 0.1 km s−1 to achieve a higher dynamical range. Panel c: similar to panel b but for HNC (1–0). Panel d: similar to panel b but for CS (2–1). In panels b–d, the color bars represent main beam brightness temperatures in units of K, and the black contours represent the C18 O (1–0) emission starting at 1.5 K (5σ) with increments of 0.9 K (3σ). The offsets are given with respect to the center of the PV cut (αJ2000 = 18h28m50.s865, δJ2000 = 00°50′21. ′′799, also indicated by the white filled circle in panel a), and increase from southeast to northwest. The resolution element is shown in the lower right of each panel. |
| In the text | |
 |
Fig. 10 Panel a: H2 column density image of the Serpens filament obtained from the Herschel Gould belt survey. The contours correspond to column densities of 6 × 1021 cm−2, 8 × 1021 cm−2, and 1 × 1022 cm−2. The extracted crest of the Serpens filament is shown with the blue line. The emission within the white box is used to derive the radial profile of H2 column density. The three black crosses give the positions of the three embedded YSOs. The beam size is shown in the lower right. Panel b: mean radial profile of H2 column densities within the white box in panel a. The offsets increase from east to west. A Gaussian fit is indicated by the red line. Panel c: mean radial H2 column density profile on the west (yellow) and east (orange) sides of the crest. The red and blue dashed lines represent Plummer-like fits to the east and west (see panel a) within a radius range of <0.2 pc, while the cyan and black lines represent the beam-convolved radial profile of Musca-West (Kainulainen et al. 2016) and the Serpens South filament (Kirk et al. 2013). In both panels a and b, the beam size is shown by the brown line. |
| In the text | |
 |
Fig. 11 Panel a: LSR velocity map similar to Fig. 4b but overlaid with the H2 column density contours which represent 4 × 1021 cm−2 and 6 × 1021 cm−2. Source B is marked with the red circle, and the three black crosses give the positions of the three embedded YSOs, em10, em28, and em16. Panel b: column density profile along the crest of the Serpens filament indicated by the blue line in panel a. The spatial resolution is ~0.08 pc. The offset increases from south to north. The red line represents a sinusoidal fit to the profile within the offset range of 1.0–1.4 pc. A sinusoidal orange line is created to better visualize the variation at a large scale. Panel c: similar to panel b, but for the C18 O (1–0) velocity. The four red arrows correspond to the velocity gradients in Fig. 4b, indicated there by black arrows. Panel d: similar to panel c, but for the C18 O (1–0) linewidths. In panels b–d, the red dashed lines indicate the positions of Source B and the YSO emb28. |
| In the text | |
 |
Fig. 12 Panel a: HNC (1–0) spectrum averaged over 3 × 3 pixels centered at an offset of (−40′′, 40′′) in Fig. 2 to increase the signal-to-noise level. Panel b: similar to panel a, but for an offset of (100′′, −120′′). Panel c: similar to panel a, but for CS (2–1). Panel d: similar to panel b, but for CS (2–1). All these lines are modeled with the Hill5 model (De Vries & Myers 2005; see Sect. 4.3). These offsets are given with respect to αJ2000 = 18h28m49.s642, δJ2000 = 00°50′01.′′08. The fitted parameters and their uncertainties are given in the upper right of each panel. |
| In the text | |
 |
Fig. B.1 PV diagrams similar to Fig. 9b but for HCN (1–0) (panel a), N2 H+ (1–0) (panel b), and two CH3OH lines (panel c). In panel a, the three hyperfine structure components are labeled next to their respective emission. In panel b, the channel width of the N2H+ (1–0) spectra has been binned to 0.16 km s−1 to achieve a higher dynamical range in individual channels. In panel c, the two transitions are labeled next to their respective emission. In all panels, the color bars represent main beam brightness temperatures in units of K. The offsets are given with respect to the center of the PV cut (αJ2000 = 18h28m50.s865, δJ2000 = 00°50′21. ′′799, also indicated by the white filled circle in Fig. 9a), and increase from southeast to northwest. In all panels, the vertical dashed lines mark the systemic velocity of −8.11 km s−1 for corresponding lines. |
| In the text | |
 |
Fig. C.1 Panel a: Spitzer c2d visual extinction map overlaid with the Herschel H2 column density contours. The contours increase from 4 × 1021 cm−2 to 1.2 × 1022 cm−2 by 4 × 1021 cm−2. The color bar represents the visual extinction in units of magnitude. Panel b: map of the ratios (NH_2,av/ |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.