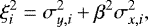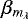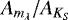| Issue |
A&A
Volume 614, June 2018
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 21 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201731396 | |
| Published online | 15 June 2018 | |
VISION - Vienna Survey in Orion
II. Infrared extinction in Orion A★
1
Department of Astrophysics, University of Vienna,
Türkenschanzstrasse 17,
1180
Wien,
Austria
e-mail: stefan.meingast@univie.ac.at
2
University of Milan, Department of Physics,
via Celoria 16,
20133
Milan,
Italy
Received:
19
June
2017
Accepted:
17
February
2018
We have investigated the shape of the extinction curve in the infrared up to ~25μm for the Orion A star-forming complex. The basis of this work is near-infrared data acquired with the Visual and Infrared Survey Telescope for Astronomy, in combination with Pan-STARRS and mid-infrared Spitzer photometry. We obtain colour excess ratios for eight passbands by fitting a series of colour-colour diagrams. The fits are performed using Markov chain Monte Carlo methods, together with a linear model under a Bayesian formalism. The resulting colour excess ratios are directly interpreted as a measure of the extinction law. We show that the Orion A molecular cloud is characterized by flat mid-infrared extinction, similar to many other recently studied sightlines. Moreover, we find statistically significant evidence that the extinction law from ~1μm to at least ~6μm varies across the cloud. In particular, we find a gradient along galactic longitude, where regions near the Orion Nebula Cluster show a different extinction law compared to L1641 and L1647, the low-mass star-forming sites in the cloud complex. These variations are of the order of only 3% and are most likely caused by the influence of the massive stars on their surrounding medium. While the observed general trends in our measurements are in agreement with model predictions, both well-established and new dust grain models are not able to fully reproduce our infrared extinction curve. We also present a new extinction map featuring a resolution of 1′ and revisit the correlation between extinction and dust optical depth. This analysis shows that cloud substructure, which is not sampled by background sources, affects the conversion factor between these two measures. In conclusion, we argue that specific characteristics of the infrared extinction law are still not well understood, but Orion A can serve as an unbiased template for future studies.
Key words: ISM: clouds / ISM: structure / dust, extinction / methods: data analysis / methods: statistical
The extinction map (FITS file) is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/614/A65
© ESO 2018
1 Introduction
Extinction is the attenuation of electromagnetic radiation by gas and dust. The term extinction combines the effects of absorption and scattering processes which lead to a loss in the measured intensity of a light-emitting source. This effect is generally much stronger for shorter wavelengths, often obscuring sightlines associated with large amounts of dust. Including the fact that much of the absorbed energy is re-radiated thermally in the infrared, it is generally understood that these processes play a fundamental role in the determination of the radiation field of galaxies at both small and large scales. It therefore has long been recognized that measuring and understanding extinction is crucial for a large variety of astrophysical problems (e.g. Lada et al. 1994). At the smallest scales, measuring extinction allows to constrain dust properties, such as grain sizes and element abundances (e.g. based on models from Weingartner & Draine 2001; Draine 2003). In star-forming regions, dust extinction shields pre-stellar cores from the surrounding UV radiation. On galactic scales, dust converts a large fraction of the absorbed starlight into thermal radiation (Bernstein et al. 2002) and at the largest scales the extra-galactic distance ladder critically depends on our understanding of the extinction law (e.g. Nataf 2015).
The shape of the extinction curve (i.e. how extinction varies with wavelength) has been the topic of many studies in the last few decades. Almost 30 yr ago, Cardelli et al. (1989) provided the framework for the characterization of extinction curves based on the fundamental work by Rieke & Lebofsky (1985), Fitzpatrick & Massa (1986), and Fitzpatrick & Massa (1988). They introduced a parameter family to describe the shape of the extinction curve and furthermore showed that an approximation is possible by using just one quantity: RV ≡ AV∕EB−V, with AV as the extinction in V band and EB−V as the colour excess in B − V. This parameter is nowadays widely used to describe extinction characteristics in general, and in particular also to probe variations in the extinction law across large spatial scales. To this day, several key characteristics of the extinction curve remain a controversial topic. For example, at UV to optical wavelengths, the extinction curve is relatively featureless with the exception of the prominent bump at 2175 Å of which the origin still remains under debate (e.g. Fitzpatrick & Massa 1986; Mathis 1994; Bradley et al. 2005).
While in the UV and optical spectral range the extinction law is generally found to vary by a large degree for different sightlines, the near-infrared (NIR) extinction law is widely believed to show little to no variation at all. Even though there are studies reporting different extinction parameters for the three NIR bands J, H, and KS, conclusive evidence of variations depending on dust characteristics is still missing. Numerous examples on the determination of the NIR extinction law can be found in the literature. Most of these are based on the Two Micron All Sky Survey (2MASS; Skrutskie et al. 2006) where some results indicate variability of the law (e.g. Nishiyama et al. 2006; Zasowski et al. 2009; Gosling et al. 2009; Wang et al. 2013; Nataf et al. 2016), while others do not (e.g. Stead & Hoare 2009; Majaess et al. 2016).
Investigating an often-used power-law parametrization in the NIR (Aλ ∝ λ−γ), Stead & Hoare (2009) further complicate the situation by claiming, that the value of the power law index is critically dependent on the choice of the filter wavelength. They also continue to show that previously found variations can be explained by systematic errors. Only recently, Wang & Jiang (2014) used APOGEE (Eisenstein et al. 2011) data to select K-type giants scattered across the galactic plane and presented convincing evidence that the NIR extinction law does not vary with colour excess. As a result, and in contrast to their previous work (Wang et al. 2013), this result indicates that the NIR extinction law is constant from diffuse to dense environments.
In the mid-infrared (MIR), this picture drastically changes. Here, many different absorption features – the most prominent ones at ~9.7 and ~ 18μm are caused by silicates – depend on environmental conditions. This has led to a variety of results, where some sightlines are well explained by the standard silicate-graphite model (Draine & Lee 1984; Draine 1989, 2003; Weingartner & Draine 2001), while other regions (including the galactic centre) show a particularly flat distribution between 4 and 8 μm. The origin of this flat extinction law between the NIR bands and silicate features is still not well understood (e.g. Wang et al. 2013, 2015; Voshchinnikov et al. 2017, and references therein).
By far the most popular targets for extinction studies in the NIR and MIR spectrum are found in the galactic plane, and in particular also near the galactic centre. Sightlines in these directions naturally provide many advantages when studying extinction in the infrared. Not only are there orders of magnitudes more sources compared to regions far away from the plane, but also distinct stellar populations can aid in the determination of the extinction law. Moreover, in recent year, the Spitzer Space Telescope (Werner et al. 2004), and in particular the GLIMPSE programme (Benjamin et al. 2003; Churchwell et al. 2009), have provided a large MIR database of the these regions.
There are many examples of studies inferring the MIR extinction law from Spitzer data. Most prominently, Indebetouw et al. (2005) used the well-known intrinsic magnitudes of red clump giants in the galactic plane for two different sightlines to determine the absolute extinction law for the NIR JHKS and the Spitzer/IRAC passbands. Furthermore, the regions near the galactic centre have been particularly popular to investigate the origins of the often-observed flat MIR extinction law (e.g. Lutz et al. 1996; Lutz 1999; Nishiyama et al. 2009; Fritz et al. 2011). Variations in the MIR extinction law have been detected in the Coalsack Nebula (l ~ 301, b ~ −1) by Wang et al. (2013). They find decreasing MIR extinction relative to KS band extinction 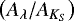 from diffuse to dense environments. In contrast, Ascenso et al. (2013) studied the dense cores B59 and FeSt 1-457 in the Pipe Nebula and do not find statistically significant evidence for a dependency of the MIR extinction law on local gas density.
from diffuse to dense environments. In contrast, Ascenso et al. (2013) studied the dense cores B59 and FeSt 1-457 in the Pipe Nebula and do not find statistically significant evidence for a dependency of the MIR extinction law on local gas density.
In light of these often-contradicting findings, it is rather challenging to draw final conclusions about the infrared extinction law and the origin of potential variability. Most of the above mentioned studies concentrate on regions in the galactic plane and use one or another combination of photometric passbands to determine colour excess ratios as a proxy for the extinction law. In the galactic plane, however, physical conditions of the interstellar environment are rarely well-known and measured colour excesses can be influenced by multiple, physically separate, stacked regions along the line-of-sight. To reach a full understanding of the extinction law and its characteristics in the infrared, it is therefore crucial to provide observational data for regions where environmental conditions are well-known and can be factored into the result.
In the spirit of this series of papers, we will base our investigation on the Orion A giant molecular cloud (Fig. 1; for an overview see the first paper in this series and references therein: Meingast et al. 2016, hereafter Paper I). Orion A is located at a distance of 414 pc (Menten et al. 2007) towards the direction of the galactic anti-centre, and far below the plane. Since the region harbors many isolated star-forming events, as well as the massive young Orion Nebula Cluster (ONC), it provides a unique opportunity to study different physical conditions in a self-consistent way. Moreover, the cloud is relatively well-isolated from other star-forming regions in the vicinity. This isolation assures that any characteristics with respect to extinction are only originating from the gas and dust associated with one single molecular cloud.
In this manuscript we will investigate the extinction law in the infrared from just below 1 μm up to about 25 μm. Based on statistically significant variations of the colour excess ratios in several passbands, we will show that the extinction law in the infrared varies with environmental conditions. In particular we will show that the most likely explanation for these variations is the influence of the massive stars in the ONC on the surrounding ISM. Their intense radiative feedback seems to impact the general dustcomposition and changes the overall extinction law for both NIR and MIR passbands. Comparing our findings to model predictions, we furthermore conclude, that popular dust models do not sufficiently explain the global infrared extinction law in Orion A. Based on these findings we will construct a new extinction map of the region and demonstrate that cross-calibration with Herschel dust optical depth data can be biased by cloud substructure that is not sampled by background sources.
To arrive at these conclusions, we first introduce our data sample in Sect. 2 before continuing to give an in-depth overview of the applied methods in this manuscript (Sect. 3). Following this technical overview, we separate ourresults into two major parts. We first investigate the characteristics of the infrared extinction law in Sect. 4, followed by the results with respect to our new extinction map in Sect. 5. Finally, we summarize our findings in Sect. 6.
2 Data
This sectionstarts with an overview of our data sources and a general description of their properties. Subsequently, we will describe how the data sets were matched, filtered, and finally combined into a master catalogue.
2.1 Overview
To study extinction in Orion A, we include a variety of passbands at infrared wavelengths. To this end, we combined several different sets of photometric data. The bluest bands under investigation are z and y, supplied by the Panoramic Survey Telescope and Rapid Response System (Pan-STARRS DR1; Chambers & Pan-STAARS Team 2018; Magnier et al. 2016; Flewelling et al. 2016), for which the observations cover the entire molecular cloud. The bulk of the NIR photometry is based on our work presented in Paper I. In this study, we introduced a large-scale imaging survey of Orion A with the Visible and Infrared Survey Telescope for Astronomy (VISTA; Dalton et al. 2006; Emerson et al. 2006) which encompasses observations in the J, H, and KS passbands. The survey covers an on-sky area of ~ 18.3deg2 with average 90% completeness limits of 20.4, 19.9, and 19.0 mag in J, H, and KS, respectively. These data are supplemented by the observations of Drass et al. (2016), who used HAWK-I (Kissler-Patig et al. 2008) to study the ONC and its immediate surroundings. With a coverage of ~ 0.17deg2, they only observed a small area of the entire cloud complex. The completeness limits for these data are 18 mag in J and H, and 17.5 mag KS in the innermost parts of the surveyed area (the estimated VISTA completeness limits in the same area are a few tenths of a magnitude brighter). Our analysis also covers the MIR bands as observed by Spitzer in the four channels of the InfraRed Array Camera (IRAC; Fazio et al. 2004) and the first channel of the Multiband Imaging Photometer for Spitzer (MIPS; Rieke et al. 2004). These Spitzer data for the Orion star-forming region were provided by Megeath et al. (2012) and cover most parts of Orion A which are associated with large gas column-densities (~ 5.86deg2 with IRACand ~ 11.4 deg2 with MIPS).The survey borders of the JHKS and IRAC data are shown in Fig. 1.
Since we include a total of 10 different passbands in the infrared we will use a consistent convention when referring to them throughout this manuscript. While for the bands z through KS we will simply use the original filter name, the four IRAC channels will be referred to as I1, I2, I3, and, I4. Furthermore, we only have access to the first MIPS channel, which will be denoted M1. In Table 1 we list effective wavelength and width for each passband. We will also make use of the first two WISE bands (Wright et al. 2010) for calibration purposes, which will be denoted W1 and W2. Furthermore, we associate the passbands z through KS (~ 0.9–2.2 μm) with the NIR region of the electromagnetic spectrum, while the Spitzer channels I1 through M1 (~ 3.5–24 μm) are placed in the MIR range. An overview of our wavelength coverage is given in Fig. 2, where the relative spectral response (RSR) curves of all passbands are displayed. The figure also shows the typical effects of extinction on a 3000 K black body.
 |
Fig. 1 Region under investigation in this work: the Orion A molecular cloud is visualized in green with the dust optical depth map from Lombardi et al. (2014b) blended with optical image data (deepskycolors.com; © Roberto Bernal Andreo). The solid lines indicate the coverage of the various surveys used to investigate the properties of dust extinction in the cloud, where the IRAC contour outlines the region covered by either of the first two IRAC channels. We also make use of MIPSdata, for which the covered region generally encompasses the IRAC contour. toggle labels |
 |
Fig. 2 Passbands used in our analysis cover the infrared wavelength range from just below 1 μm to about 25 μm utilizing the Pan-STARRS (z, y), VISTA (J, H, KS; calibrated against 2MASS), and Spitzer (I1, I2, I3, I4, M1) photometric systems. The filter curves have each been normalized to their maximum transmission and their relative spectral response (RSR) is shown as a function of wavelength. The two solid grey lines are 3000 K black bodies with a normalized intensity (Inorm). Here, the upper line is the unmodified black body, whereas the line at the bottom shows the resulting spectral energy distribution with 5 mag extinction in the KS band and using the RV = 3.1 Draine (2003) extinction law. |
2.2 Cross-matching and cleaning
All catalogues were combined with TOPCAT (Taylor 2005) using a 1′′ cross-matching radius where we only kept sources within the survey boundaries of the VISTA data (see Fig. 1). All detected sources in any band of either the JHKS or the MIR catalogues were retained, independent of whether a match in another passband was found. Only for the Pan-STARRS data we required a match in any of the other catalogues due a large number of detections of nebulosity in regions withextended emission. With these criteria, the mean separation between VISTA and Spitzer sources was 0.3′′ and between VISTA and Pan-STARRS sources 0.14′′. For sources which were detected in multiple catalogues, we averaged their coordinates.
The JHKS catalogues from Paper I and Drass et al. (2016) did not require photometric transformations between each other, as they are both calibrated towards the 2MASS photometric system. To minimize systematic errors, cross-matched sources between the VISTA and HAWK-I data were only retained if the magnitude difference was smaller than 0.5 mag. For sources which are in agreement with this criterion, we calculated average magnitudes weighted by their measurement errors. For a total of 4340 sources in the HAWK-I catalogue, we find 3827 cross-matches with the VISTA catalogue (~88%), thus 513 new sources. About 5% of the matched sources were then removed based on their magnitude differences. Interestingly, most of the new sources are found in a rim around the core of the ONC and are also quite easily distinguishable from the background in the VISTA image data. The fact that they were not detected in these data can be explained by the source detection procedure: While for the HAWK-I data, the entire mosaic has been searched for sources by eye, for Paper I we only cleaned the very central region (11′ × 11′) by hand. This also agrees well with the similar completeness limits stated above. Figure 3 shows a comparison of all matched sources in J band (the distributions for H and KS look almost identical). In general, we find negligible systematic offsets between the two JHKS data sets (Δ mag ~ –0.02 mag). The magnitude difference between the two catalogues shows a standard deviation of ~0.15 mag across all three bands. The measurement errors, on the other hand, show discontinuities for bright sources due to different criteria on how 2MASS data was incorporated in the catalogues. As expected, for faint sources, the HAWK-I photometry features smaller errors.
As our objective was to explore characteristics of dust extinction in the molecular cloud, we are furthermore primarily interested inbackground sources as probes of the gas distribution. Therefore, we removed foreground stars near NGC 1980, as identifiedby Bouy et al. (2014), and Young Stellar Objects (YSOs) in the cloud as classified by Megeath et al. (2012) and Großschedl et al. (in prep.). Furthermore, upon creating the final extinction map, we found that several sources produced artefacts on the resulting map. Essentially all of these were associated with very bright stars (KS ≲ 8 mag), or their point spread function halos in the VISTA images and therefore were also removed from our master catalogue in an iterative procedure.
 |
Fig. 3 Comparison of VISTA and HAWK-I photometry in J band. The panel at the top shows the difference in photometric errors as a function of the apparent VISTA magnitude. Similarly, the bottom plot displays the difference in the measured source magnitudes. The histogram to the right shows the distribution of the magnitude difference as a kernel density. Assuming a Gaussian distribution, the differently shaded areas under the curve represent the 1, 2, and 3-σ limits. |
Basic properties for all photometric bands used in this work, as well as corresponding source counts in our master catalogue for both the Orion A region and the control field.
 |
Fig. 4 Correlation between W1 and I1. The top panel shows the difference in photometric errors, while at the bottom the difference in source magnitudes is displayed. The orange line is our linear transformation between the two systems, which maps the two bands in almost a 1:1 relation. Similar to Fig. 3, the histogram to the right represents the kernel density of the magnitude differences. |
2.3 Control field data
For statistical comparisons of source populations we also required photometry in the same bands for an extinction-free field at approximately the same galactic latitude. JHKS photometry for a suitable control field (l = 233.3, b = −19.4) is available in our data release from Paper I. Pan-STARRS data for the z and y bands was acquired and cross-matched in the same way as for the Orion A science field. Only Spitzer photometry was not available in this field. Fortunately, the first two channels of IRAC share very similar transmission curves when compared to the two bluest WISE bands which enabled us to calculate a simple linear transformation between them. Due to the lower resolution of the WISE image data, we relaxed our cross-matching radius to 2′′ between theNIR sources and WISE, but required a detection with VISTA. In addition we required a photometric error smaller than 0.5 mag in each band. For the fit, we obtained AllWISE photometry (Cutri et al. 2013) in the corresponding bands and derived the linear transformation equations using the method later described in Sect. 3.1. Using the profile-fitting photometry in the catalogue (columns w1mpro, w2mpro and their associated errors), we find an almost perfect 1:1 correlation for both bands, for which the transformation equations read

As an example of the well-behaved fit between the two systems, we show the correlation between I1 and W1 in Fig. 4 (the correlation between I2 and W2 looks almost identical).
2.4 Master catalogue
With the criteria listed above we constructed our final master catalogues for both the Orion A, as well as the control field. Number counts and basic passband properties of all bands under consideration are tabulated in Table 1. Furthermore, a selection of colour-colour combinations is displayed in Fig. 5 for both the Orion A region (left-hand panels) and the control field (right-hand panels). Clearly, the Orion A field is affected by a significant amount of reddening when compared to the extinction-free control field. In almost all diagrams a clear distinction between extragalactic sources and main sequence stars is visible (e.g. J − H ~ 1, H − KS ~ 0.8, KS − I1 ~ 1.2). Another interesting feature in the Orion A diagrams is the clearly discernible changing extinction vector: the slope in the diagrams gets significantly steeper from H − KS to I1 − I2 indicating decreasing extinction differences in the two bands constituting each colour. For example, in the diagrams including I1 − I2, the extinction vector is almost vertical.
A closerlook at the control field diagrams, including the transformed Spitzer photometry, reveals a non-negligible amount of additional noise compared to the original Spitzer Orion A photometry. Most prominently, the stellar main sequence at I1 − I2 ~ 0 is significantly broader in the control field. Quantifying this additional noise component is difficult since the control field sample is not affected by extinction, whereas the Spitzer observations mostly cover areas associated with the molecular cloud. Limiting both samples to J − H < 0.5 mag and applying various magnitude cuts from I1 = 15 to 17 mag effectively removes many sources affected by extinction, as well as galaxies. Comparing the resulting distributions for the I1 − I2 colour, we find an about 50% broader stellar main sequence for the control field data and directly interpret this increase as an estimate for the additional noise. This presents a problem for statistical comparisons and will examine this issue further in Sect. 5 where these diagrams are used to construct an extinction map. For the remainder of this article, all further analysis is based on this master-catalogue and throughout the individual sections we will refer to various subsets on multiple occasions.
3 Methods
In this section we will give an in-depth overview of all methods used in this manuscripts. In particular, this includes mathematical background on how we fit observed noisy data with linear relations (Sect. 3.1), how to derive an infrared extinction law (Sect. 3.2.1), and how to measure extinction for point-sources (Sect. 3.2.2). Finally, we will also describe how to use these point-source measurements to construct the smooth gas distribution in the interstellar medium (ISM) in the plane of the sky with extinction mapping procedures (Sect. 3.2.3).
3.1 Linear fitting
Many results derived in this manuscript depend on reliable linear fitting procedures. Moreover, our interpretations and analysis also depend on the statistical significance of the resulting fit. For this purpose, we develop in this section a robust Bayesian framework which takes errors in both dimensions into account and ultimately enables us to derive reliable model parameters. The resulting framework is then employed in combination with a Markov chain Monte Carlo (MCMC) ensemble sampler. Specifically, we define a likelihood function which can be numerically optimized and also can, in principle, take any form, but must be an appropriate choice for the given data characteristics. The MCMC algorithm derives suitable model parameters by sampling the parameter space in a so-called chain. Individual positions in the chain are chosen based on the used samplers (e.g. Metropolis; Mackay 2003) and at each position in the chain, the posterior probability is evaluated. The probabilities at each step constitute a trace and these traces allow statistical evaluations for each parameter. Here, we always choose to use the mean and the standard deviation of the traces to describe the model parameters and its uncertainties. For reasons of simplicity and reproducibility we chose the emcee2 MCMC ensemble sampler (Foreman-Mackey et al. 2013; Hogg et al. 2010). This implementation allows to optimize model parameters with respect to a given pre-defined model likelihood. Details on how emcee constructs the chains are given in Foreman-Mackey et al. (2013).
The MCMC approach requires to define a model for our data and an associated likelihood. We start by defining a simple linear relation between generic values on the abscissa and the ordinate in a Euclidean space, which is given by
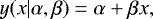 (3)
(3)
where α is the intercept, and β the slope3 . Furthermore, we define our generic observed dataset as
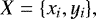 (4)
(4)
where the xi and yi are the measurements with corresponding errors σx,i and σy,i. We also define the unknown true values 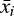 and
and 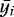 , which are connected to the above set via
, which are connected to the above set via
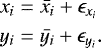 (5) (6)
(5) (6)
Here we a adopt a normal distribution for the errors ϵ in both coordinates such that
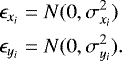 (7) (8)
(7) (8)
Given these assumptions and our data set, we can derive a model likelihood, for which the dispersions in x and y along the linear relation are described by normal distributions, which in turn are characterized by the measurement errors. Thus, the probability for each data point, given α and β defining a model as in Eq. (3), is
![\begin{align*} \begin{split}P(x_i, y_i | \alpha, \beta, \bar{x_i}, \sigma_{x,i}, \sigma_{y,i}) =& \,\frac{1}{\sqrt{2\pi} \sigma_{y_i}} \mathrm{exp} \left[ -\frac{\left( y_i - \alpha - \beta \bar{x_i} \right)^2}{2\sigma_{y_i}^2} \right] \\ & \times \frac{1}{\sqrt{2\pi} \sigma_{x_i}} \mathrm{exp} \left[ -\frac{\left( x_i - \bar{x_i} \right)^2}{2\sigma_{x_i}^2} \right], \end{split} \end{align*}](/articles/aa/full_html/2018/06/aa31396-17/aa31396-17-eq9.png) (9)
(9)
where we already take the linear relation, described by the intercept α and slope β, into account to eliminate the true values 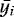 . We note here that Eq. (9) assumes uncorrelated errors for xi and yi . Strictly speaking, in many of our applications of the linear fitting technique in this manuscript, we do have correlated errors in both dimensions (e.g. in colour-colour diagrams where a given passband occurs in both colours). However, a generalization of the probability and resulting likelihood to account for correlated errors is far from trivial and is beyond the scope of this paper. Given the excellent results of the technique, we do not expect the assumption of uncorrelated errors to have a major impact on our results.
. We note here that Eq. (9) assumes uncorrelated errors for xi and yi . Strictly speaking, in many of our applications of the linear fitting technique in this manuscript, we do have correlated errors in both dimensions (e.g. in colour-colour diagrams where a given passband occurs in both colours). However, a generalization of the probability and resulting likelihood to account for correlated errors is far from trivial and is beyond the scope of this paper. Given the excellent results of the technique, we do not expect the assumption of uncorrelated errors to have a major impact on our results.
The above given definition in Eq. (9), still includes the unknown true values of xi, 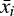 . For our application we therefore need to find a way to eliminate them as well. In the following lines we will derive our final model likelihood along which we will also deal with this issue. The full posterior probability distribution of the model parameters α and β, given the set of measurements X can be rewritten to include the true values
. For our application we therefore need to find a way to eliminate them as well. In the following lines we will derive our final model likelihood along which we will also deal with this issue. The full posterior probability distribution of the model parameters α and β, given the set of measurements X can be rewritten to include the true values 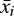 .
.
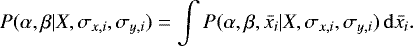 (10)
(10)
Following Bayes’ theorem, the term in the integral can be written as
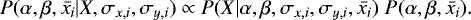 (11)
(11)
The right-hand side of this relation splits up into the likelihood function 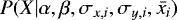 and the so-called prior function
and the so-called prior function 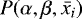 . For simplicity, we assume a flat prior on
. For simplicity, we assume a flat prior on 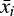 , i.e.
, i.e. 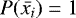 . Also, the normalization (the denominator in Bayes’ theorem) can be ignored in our case since it is a constant and would only become important if we attempted to compare different model definitions. Thus, Eq. (10) becomes
. Also, the normalization (the denominator in Bayes’ theorem) can be ignored in our case since it is a constant and would only become important if we attempted to compare different model definitions. Thus, Eq. (10) becomes
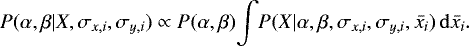 (12)
(12)
The likelihood function for the data ensemble X, given by 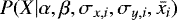 , can be constructed by multiplying over all i
, can be constructed by multiplying over all i
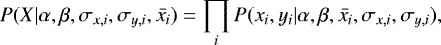 (13)
(13)
which, together with Eq. (9) can be inserted into Eq. (12), giving
![\begin{eqnarray*} P(\alpha, \beta | X, \sigma_{x,i}, \sigma_{y,i}) &\propto& \, P(\alpha, \beta)\\ && \times \prod_{i} \int\! \frac{1}{\sqrt{2\pi} \sigma_{y_i}} \mathrm{exp} \left[ -\frac{\left( y_i - \alpha - \beta \bar{x_i} \right)^2}{2\sigma_{y_i}^2} \right]\nonumber \\ &&\times \,\frac{1}{\sqrt{2\pi} \sigma_{x_i}} \mathrm{exp} \left[ -\frac{\left( x_i - \bar{x_i} \right)^2}{2\sigma_{x_i}^2} \right] \, \mathrm{d}\bar{x_i}.\nonumber\end{eqnarray*}](/articles/aa/full_html/2018/06/aa31396-17/aa31396-17-eq22.png) (14)
(14)
This relation contains an integral over the product of two Gaussians, that is, a convolution, and thus can be rewritten as a single normal distribution. Furthermore, by rearranging the argument of the exponential term in the first Gaussian function, we are also able to eliminate 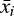 during this process. The integral in the above equation then evaluates to
during this process. The integral in the above equation then evaluates to
![\begin{equation*} \int P(X) \, \mathrm{d}\bar{x_i} = \frac{1}{\sqrt{2 \pi (\sigma_{y_i}^2 + \beta^2 \sigma_{x_i}^2)}} \mathrm{exp}\left[ -\frac{(y_i - \alpha - \beta x_i)^2}{2 (\sigma_{y_i}^2 + \beta^2 \sigma_{x_i}^2)} \right]. \end{equation*}](/articles/aa/full_html/2018/06/aa31396-17/aa31396-17-eq23.png) (15)
(15)
allows to rewrite our likelihood function which finally reads in logarithmic form
![\begin{equation*} \ln P \left(X | \alpha, \beta, \xi_{i} \right) \propto -\frac{1}{2} \sum_i \left[ \ln \,(2\pi \xi_{i}^2) + \frac{\left( y_i - \alpha - \beta x_i \right)^2}{\xi_{i}^2} \right].\end{equation*}](/articles/aa/full_html/2018/06/aa31396-17/aa31396-17-eq26.png) (17)
(17)
This likelihood allows to efficiently derive optimized linear fitting parameters, taking measurement errors in both dimensions into account. Interestingly, Clutton-Brock (1967) also investigated this issue and arrive at the same final likelihood definition, using a more traditional approach.
For the posterior probability defined in Eq. (11) we also need the prior function P(α, β). Here, we chose a uniform prior for our application and write the logarithmic prior for the intercept α and the slope β in the form of a piecewise function:
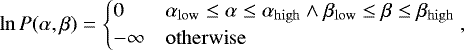 (18)
(18)
where αlow, αhigh, βlow, and βhigh are reasonable choices for the given application. For instance, when fitting colour-colour diagrams, we know that the intercept must be close to 0. We will, however, be very conservative with the choice of our priors, which mostly are needed for faster convergence of the numerical optimization process. Finally, with the prior given in Eq. (18) and the likelihood given in Eq. (17) we can calculate the posterior probabilities of the model parameters α and β from Eq. (12) as
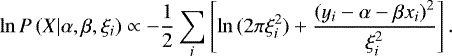 (19)
(19)
We want to close this section on our linear fitting algorithm by acknowledging that we are fully aware that our choice of a Gaussian distribution is not always strictly true. However, for most problems it is extremely challenging to define accurate likelihood functions. For instance, when fitting colour-colour diagrams, the intrinsic distribution of stellar colours and the dependence of this distribution on extinction (faint low-mass stars have different colours than bright high-mass stars) produce a highly complex spread in colours along the extinction vector, which is very difficult to model without prior information on the intrinsicsource characteristics. Therefore, choosing a Gaussian likelihood presents a very good compromise between theactual distribution and neglecting these errors in the first place, as is usually done when facing such problems.
3.2 Measuring extinction
In the following sections we discuss our procedures to derive an extinction law from photometric data, to extinction for single sources, andto construct the smooth column-density distribution from these measurements.
3.2.1 Deriving an extinction law
Many previous studies have derived extinction laws for a variety of different sightlines. In general, methods relying on spectroscopic data have proven to be very effective for determining the line-of-sight extinction as a function of wavelength for individual sources. For these, the underlying procedure relies on comparing spectra of the target of interest to an extinction-free source. On the other hand, the availability of photometric surveys, covering large spectral and spatial ranges, has also led to the development of techniques to derive extinction laws for the various available photometric passbands.
In general, these methods can be split into absolute determinations of the extinction law with respect to wavelength, and relative measurements. In the case of absolute determinations, a direct calibrator is required. Noteworthy examples of such calibrations can be found in Indebetouw et al. (2005), Schlafly et al. (2010), and Schlafly & Finkbeiner (2011). Indebetouw et al. (2005) parametrized the apparent magnitudes of red clump giants to determine the interstellar reddening as a function of distance. Schlafly et al. (2010) measured the main-sequence turnoff at the blue edge for various SDSS colours and then fitted this “blue tip” with a reddening-dependent relation, whereas Schlafly & Finkbeiner (2011) compared measured SDSS colours to model-predicted source colours.
In contrast, studies determining only a relative dependence of the extinction law require a zero-point to calibrate their results (e.g. Flaherty et al. 2007; Ascenso et al. 2013). In our case, we will also only determine a relative extinction dependence, mainly because it is very challenging to establish an absolute law for the specific case of the Orion A molecular cloud based on photometry. One can easily imagine that techniques relying on a distinct population of red giant stars can not be applied here due to the location of the cloud near the galactic anti-centre and ~ 20° below the plane. Also, our limited field-of-view which, to a large extent, is heavily affected by dust-extinction, makes statistical determinations of features in colour space (e.g. the blue edge) unreliable without prior assumptions on the dust distribution. Another reason for our choice of a relative calibration is that the interpretation of our findings does not depend on a direct calibration.
Here, we will derive a wavelength-dependent extinction law for a variety of photometric passbands based on the source distribution in a set of colour-colour diagrams. The basis for this method lies in the definition of a source’s colour excess

where 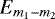 is the notation for the colour excess measured in the passbands m1 and m2 (e.g. J and H). This excess is simply the difference between the measured apparent colour (m1− m2) and the intrinsic colour
is the notation for the colour excess measured in the passbands m1 and m2 (e.g. J and H). This excess is simply the difference between the measured apparent colour (m1− m2) and the intrinsic colour 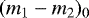 of the samesource, or the difference in extinction in the two passbands (
of the samesource, or the difference in extinction in the two passbands ( ). Using two colour excesses in differently combined passbands the colour excess ratio
). Using two colour excesses in differently combined passbands the colour excess ratio 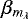 is defined as
is defined as
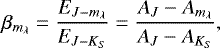 (22)
(22)
and represents the slope in the diagram plotting the two parameters against each other. Here, mλ denotes oneof the several passbands we investigate in this manuscript and 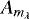 refers to the extinction in this particular band. Furthermore, for all applications we will use J − KS as the baseline of this parameter. This choice offers both a large range in measured colours (Δ (J − KS) > 8 for many areas) and superior number statistics.
refers to the extinction in this particular band. Furthermore, for all applications we will use J − KS as the baseline of this parameter. This choice offers both a large range in measured colours (Δ (J − KS) > 8 for many areas) and superior number statistics.
Upon extending the total extinction ratio 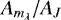 and substituting with a rearranged Eq. (22) we find
and substituting with a rearranged Eq. (22) we find
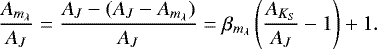 (23)
(23)
Using this equation, we see that the total extinction ratio for any passband can be determined by measuring the slope 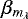 and assuming a value of
and assuming a value of 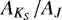 . For the remainder of this manuscript we adopt
. For the remainder of this manuscript we adopt 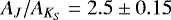
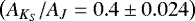 as published by Indebetouw et al. (2005). However, since this conversion necessarily includes further systematic errors, we prefer to make any comparisons directly with the fitted colour excess ratio.
as published by Indebetouw et al. (2005). However, since this conversion necessarily includes further systematic errors, we prefer to make any comparisons directly with the fitted colour excess ratio.
A closer examination of the Eqs. (20)–(22) reveals that the determination of 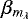 requires knowledge about the intrinsic source colours. It is, however, possible to bypass this requirement. Ignoring differences across the filter bandpasses due to varying spectral energy distributions, all sources in a colour-colour diagram are pushed in the same direction along the extinction vector in a diagram plotting the apparent colours of the sources. Thus, the slope in the distribution of apparent source colours equals the colour excess ratio in Eq. (22).
requires knowledge about the intrinsic source colours. It is, however, possible to bypass this requirement. Ignoring differences across the filter bandpasses due to varying spectral energy distributions, all sources in a colour-colour diagram are pushed in the same direction along the extinction vector in a diagram plotting the apparent colours of the sources. Thus, the slope in the distribution of apparent source colours equals the colour excess ratio in Eq. (22).
One caveat of this assumption is tied to the intrinsic source colour distribution in colour-colour diagrams. That is to say that the intrinsic colour distribution of the stellar main sequence is not parallel to the extinction vector which can introduce a bias in the measured slope. Ascenso et al. (2012) developed a technique to fit colour-colour diagrams taking this effect into consideration. However, preliminary tests with our data showed that the application of this method is unreliable in our case because the intrinsic source colour distribution rapidly changes for fields with variable extinction. In other words, for large amounts of reddening, only intrinsically bright background sources are visible through the cloud, while for regions with low extinction, the full stellar main sequence along with a set of galaxies are sampled in the diagram. For example, when searching for a spatially variable extinction law, this difference in the sampled source population introduces a bias in the fitting results, because the intrinsic colour distribution will be different for the individual fields. In contrast, when dealing with a spatially limited field with a well defined background source population, this method minimizes the bias introduced by the distribution of intrinsic source colours (for an application, see Ascenso et al. 2013).
In our case, the influence of the intrinsic source colour distribution is minimal in the first place, since the fields we investigate show a very large range of apparent source colours. Typically we find Δ (J− KS) > 8 mag for our fields, whereas changes in intrinsic stellar colours are mostly limited to Δ (J− KS) < 1 mag. Thus, the slope difference between intrinsic source colours and the distribution generated by pushing sources along the extinction vector only leads to a broadening of the source distribution along the extinction vector. Using our linear model defined in Sect. 3.1 this broadening will be taken into account when fitting the various colour-colour diagrams by introducing a systematic noise term which will later be discussed in the relevant sections.
3.2.2 Estimating line-of-sight extinction with photometry
Over the last decades a number of methods have been developed to derive extinction from point-source measurements including the well-established techniques relying on measured stellar colours (e.g., Lada et al. 1994; Alves et al. 1998; Lombardi & Alves 2001; Majewski et al. 2011; Juvela & Montillaud 2016). In this work, we use the recently published PNICER method (Meingast et al. 2017) to derive the extinction towards point sources using their measured colours with a given extinction law. Briefly summarized, PNICER builds on and extends some of the above mentioned methods. The routine applies machine learning techniques to photometric measurements of extincted sources, in combination with reddening-free control field data, to determine the extinction along the line of sight. In particular, PNICER fits Gaussian Mixture Models along the extinction vector in arbitrary numbers of dimensions to derive probability densities describing the extinction for each source. This process also effectively bypasses often-used simplifications of the reddening-free source distribution. In this way, PNICER circumvents many issues related to the more traditional methods mentioned above when highly sensitive photometric data are used. For example, the bias introduced by comparing the source population of highly extincted regions with extinction-free control field data can be eliminated by choosing a large number of dimensions (see Fig. 4 in Meingast et al. 2017). PNICER does neither require any prior knowledge of the projected gas density distribution, nor does it rely on any model predictions. The method is strictly data-driven and outperforms the above mentioned techniques when the observed source population includes a significant amount of late-type stars and galaxies which can introduce a complex pattern in the colour distribution of the observed sources. Furthermore, PNICER also is capable of reproducing results derived with the established methods for more simple setups (e.g. when using 2MASS data) and is therefore applicable in a multitude of setups.
3.2.3 Extinction mapping
As with determining the line-of-sight extinction towards single sources, there are also a number of mapping techniques available to construct the smooth projected gas surface density from photometric measurements. Traditionally, methods relying on the number density of sources have been used as a proxy for the density-distribution of gas in the ISM (e.g., Bok & Cordwell 1973; Cambrésy 1999; Dobashi et al. 2005) and these continue to be useful to this day (e.g. Beitia-Antero & Gómez de Castro 2017). Extinction measurements based on stellar colours have also been widely used in the past. Based on the work of Lada et al. (1994), Lombardi & Alves (2001) introduced the multi-band technique NICER which uses a weighted average smoothing process to calculate an extinction map (see also Alves et al. 2001). The pixel values in such extinction maps are weighted averages derived from line-of-sight “pencil-beam” measurements towards single sources. To combine this method with PNICER, we convert the derived extinction probability densities to discretized values with the expected value of the distribution (see Sect. 3.3 in Meingast et al. 2017).
Extinction mapping techniques based on discrete measurements of line-of-sight extinctions all suffer from unresolved substructure in the cloud: A given set of stars in a defined region (e.g. a pixel of an extinction map) only provides a limited number of samples of the (presumably smooth) column-density distribution of a molecular cloud. Moreover, the measured background sources have a higher probability to sample the low-column density parts of a cloud because larger extinctions push more background sources beyond the sensitivity limit of the observations. To counter this effect, Cambrésy et al. (2002) introduced a method which combines colour-based reddening calculations with star counts. Later, Dobashi et al. (2008) introduced a percentile-based method to minimize this bias and finally Lombardi (2009) published the so-called NICEST method which has already found many applications in recent years (e.g. Lombardi et al. 2011; Alves et al. 2014). NICEST adds an additional weighting factor –  – to the spatial smoothing process which attempts to correct for the unresolved cloud substructure. Here, αnicest refers to the slope in the expected number counts and the factor
– to the spatial smoothing process which attempts to correct for the unresolved cloud substructure. Here, αnicest refers to the slope in the expected number counts and the factor 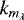 represents the extinction law in the passband mλ. When combining higher numbers of dimensions, however, these coefficients are not straight-forward to determine. We will therefore derive the best-fitting value in an iterative procedure.
represents the extinction law in the passband mλ. When combining higher numbers of dimensions, however, these coefficients are not straight-forward to determine. We will therefore derive the best-fitting value in an iterative procedure.
4 Infrared extinction law in Orion A
In this section we present, discuss, and interpret our findings with respect to the infrared extinction law in Orion A. Firstly, we will derive an average extinction law for the entire survey region. Subsequently, we continue to investigate spatial variations in our sample, by separately exploring the effects of the local environment, as well as a potential dependence on gas (column-)density.
4.1 Fitting colour-colour diagrams
As outlined in Sect. 3.2, we use a series of colour-colour diagrams with various passband combinations to determine colour excess ratios as a proxy for the extinction law. By investigating Fig. 5 in more detail, it becomes apparent that all such combinations show a rather complex distribution in the multivariate colour spaces. Since we are interested only in the effects of reddening, ideally only a well defined subset with sources of similar intrinsic colours should be used to fit the relation (e.g. Wang & Jiang 2014). As we do not have thorough source classifications for the entire sample, we start by reducing the amount of contamination with various filtering steps. To this end, subsets for each band have been defined to reduce the dispersion, resulting from intrinsic source colours, as well as the contamination by galaxies, nebulosity, and other spurious detections. Each band was treated separately with the following conditions:
-
Only sources with photometric errors smaller than 10% were considered.
-
For the Pan-STARRS bands, each source had to have at least ten independent detections (nz, ny > 10). This criterion significantly reduced the amount of nebulous detections.
-
For Spitzer data we only considered sources brighter than (14, 13, 13) mag in (I1, I2, I3). The main purpose here was also to reduce the amount of false detections (for I4, the error criterion above was enough to create a clean subset).
-
To effectively remove extended sources, which in general have significantly different intrinsic colours compared to stars, we used the flags from the catalogue in Paper I (Class_cog = 1 ∧ Class_sex > 0.9).
-
In addition to the criteria listed above, a few dozen remaining contaminating sources were removed by hand.
Applying the above criteria to our master-catalogue resulted in a remarkably clean selection of bright main sequence stars. Nevertheless, this reduced set still contained sources of different intrinsic colours. Intrinsic colours of stars show natural broad sequences, which are, in general, not parallel to the extinction vector. Thus, an additional systematic noise term is present in these data and as a consequence, the dispersion in both axes along the extinction vector is not fully described by the photometric measurement errors anymore. Due to these characteristics, extincted sources along the reddening vector are affected by a systematic broadening in addition to their photometric errors. For accurate linear fitting, however, this term needs to be accounted for.
To include the above mentioned additional dispersion factor, we measure the natural width of the main sequence in the extinction-free control field for each colour. Here, we use the previously defined filtering criteria (the list above) on the control field data and add the variances accounting for the natural broadening to the corresponding squared photometric errors before running the fitting procedure. The variances of our dataset, 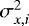 and
and 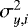 (Eq. (4)), therefore become
(Eq. (4)), therefore become
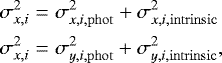 (24) (25)
(24) (25)
where the subscript “phot” refers to the measured errors of the photometry and “intrinsic” to the width of the intrinsic colour distribution as measured in the control field. The resulting total variances become rather large due to this additional systematic term, which, however, is well balanced by the large amount of available data points.
In addition to these modifications, we furthermore only include sources satisfying J − KS > 1 mag in the fit. This value represents the typical red limit in this colour for unextincted late-type main sequence stars and therefore ensures that only sources which are at least minimally affected by extinction are included in the fit. Furthermore, we define the prior function (Eq. (18)) with generous limits for the slope and the intercept as
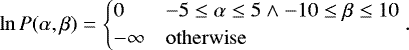 (26)
(26)
This definition allows very large ranges in both parameters and at the same time helps to speed up the convergence in the Markov chain.
We notehere, that in our case for accurate determinations of the colour excess ratios, we also need to allow the intercept 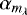 to be a free parameter in the fit. This is necessary since each colour is characterized by a different intrinsic mean, leading to asymmetric offsets in the colour-colour diagrams. Furthermore, we also note that the actual dispersion along the reddening vector is also a function of extinction: only intrinsically bright background sources (early spectral types) will be visible in regions of high column-density, thus reducing this systematic dispersion for increasingly redder colours. However, instead of introducing more systematic errors by adding an additional model component, we chose to be conservative and use the same intrinsic colour dispersion for all sources in a given colour combination.
to be a free parameter in the fit. This is necessary since each colour is characterized by a different intrinsic mean, leading to asymmetric offsets in the colour-colour diagrams. Furthermore, we also note that the actual dispersion along the reddening vector is also a function of extinction: only intrinsically bright background sources (early spectral types) will be visible in regions of high column-density, thus reducing this systematic dispersion for increasingly redder colours. However, instead of introducing more systematic errors by adding an additional model component, we chose to be conservative and use the same intrinsic colour dispersion for all sources in a given colour combination.
 |
Fig. 5 Various colour-colour diagrams constructed from our master-catalogue. The left-hand panels show data for the Orion A region, while the right-hand panels show the same combinations for the extinction free control field. Evidently, the Orion A field is heavily affected by reddening due to dust in the molecular cloud. The Spitzer photometry for the control fieldwas derived with a linear transformation from WISE data and therefore shows a larger dispersion when compared to the high-sensitivity data of the Spitzer Orion programme. |
Fitting results for the colour excess ratio 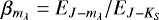 and the intercept
and the intercept 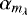 .
.
4.2 The average extinction law
After applying the filtering steps as listed above to the data collection, we first derived an average extinction law for the entire Orion A molecular cloud by fitting all available data in each band. The results of this procedure are (among others) tabulated in Table 2 for each band, where the measured colour excess ratios 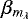 are also converted to total extinction ratios
are also converted to total extinction ratios 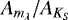 using Eq. (23) and
using Eq. (23) and 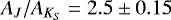 mag adopted from Indebetouw et al. (2005). With this equation it also becomes trivial to convert the measured slopes into total extinction ratios, in case a different zero-point is desired. As a representation for all bands, Fig. 6 shows the fitting results for the H band. Also displayed are the posterior probability distributions of the colour excess ratio βH (the slope) and the intercept αH. In the specific of case of H, we find ⟨βH ⟩ = 0.636 ± 0.002, thus a statistical error well below 1%. Upon converting this value to the total extinction ratio, we also take the errors from Indebetouw et al. (2005) into account. We then find
mag adopted from Indebetouw et al. (2005). With this equation it also becomes trivial to convert the measured slopes into total extinction ratios, in case a different zero-point is desired. As a representation for all bands, Fig. 6 shows the fitting results for the H band. Also displayed are the posterior probability distributions of the colour excess ratio βH (the slope) and the intercept αH. In the specific of case of H, we find ⟨βH ⟩ = 0.636 ± 0.002, thus a statistical error well below 1%. Upon converting this value to the total extinction ratio, we also take the errors from Indebetouw et al. (2005) into account. We then find 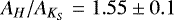 .
.
Due to the introduction of this additional error component when converting the fitted slope to total extinction ratios, it is far better to directly compare the colour excess ratios 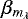 to results available in the literature. For the Pan-STARRS bands z and y, we convert the results of Schlafly & Finkbeiner (2011) to βz,lit = −1.56 and βy,lit = −0.92. Compared to our values of βz = −1.371 and βy = −0.925, only y band matches, while for z we find a clear deviation. This, however, can be caused by the different normalization as Schlafly & Finkbeiner (2011) list the extinction for the other NIR bands in the UKIRT photometric system. In contrast to our data, the UKIRT K band is slightly different compared to VISTA KS.
to results available in the literature. For the Pan-STARRS bands z and y, we convert the results of Schlafly & Finkbeiner (2011) to βz,lit = −1.56 and βy,lit = −0.92. Compared to our values of βz = −1.371 and βy = −0.925, only y band matches, while for z we find a clear deviation. This, however, can be caused by the different normalization as Schlafly & Finkbeiner (2011) list the extinction for the other NIR bands in the UKIRT photometric system. In contrast to our data, the UKIRT K band is slightly different compared to VISTA KS.
In the NIR, literature results generally agree very well with our value. Most prominently, the often-cited work by Indebetouw et al. (2005) and Wang & Jiang (2014) both find βH,lit = 0.64. Other results for this specific value are from Martin & Whittet (1990): 0.63; Nishiyama et al. (2006): 0.64; Stead & Hoare (2009): 0.65; Wang et al. (2013): 0.65. All of these are in excellent agreement with our findings and reinforce our conviction that the chosen fitting model and the filtering procedure accurately describe the colour excess ratios. Also, we emphasize here that the calibration towards total extinction ratios with the results from Indebetouw et al. (2005) is not in conflict with these findings, because we derive the slope β prior to the conversion.
Flaherty et al. (2007) already derived the total extinction ratios for Orion A in the IRAC bands with data from the Spitzer Orion programme. In contrast to our study, they used the less sensitive 2MASS observations to fit the colour excess ratios and therefore have fewer data points for their analysis. Nevertheless, also here, our values are in excellent agreement with their result of  ,
,  ,
,  , and
, and  . For M1, they did not derive the extinction for Orion A, but find
. For M1, they did not derive the extinction for Orion A, but find 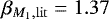 and 1.32 for Serpens and NGC 2068/2071, respectively, which also agrees very well with our findings.
and 1.32 for Serpens and NGC 2068/2071, respectively, which also agrees very well with our findings.
 |
Fig. 6 Fitting results for the colour excess ratio in H band. Left-hand side panels: filtered source distribution in a greyscale scatter plot, where the greyscale is proportional to the number density in this parameter space. The thin blue contours refer to 0.5, 10, 40, and 80% of the maximum source density. Also plotted is the resulting fit as the orange dashed line. Right-hand side panels: posterior probability distribution for the intercept αH and the slope βH (the colour excess ratio). The ellipses are the 1-, 2-, and 3-sigma covariances of the distribution. Projected to the top and to the right are normalized kernel densities of the resulting distribution for each parameter. The differently shaded filled areas under the curve highlight the 1-, 2-, and 3-σ ranges. |
4.3 Spatial variations across the cloud
The results presented in this section are split into two parts. Firstly, we investigate how the extinction law varies across the projected surface of the molecular cloud and, in particular, between regions which are affected by the intense radiation from the massive stars in the ONC. Secondly, we test whether the extinction law is constant when fitting regions with variable gas densities.
 |
Fig. 7 Similar to Fig. 6, we here show the fitting results for H when splitting the survey region in east-west direction along l = 210°. Our MCMC fitting method determines a significant difference in the colour excess ratios for the two sub-regions, indicating a variable extinction law across the molecular cloud. |
4.3.1 Dependence on environment
Among all nearby star-forming regions, the Orion A molecular cloud presents a unique opportunityto study variations in the extinction law across different environments. While the western4 parts of the cloud are affected by feedback from the hot, ionizing radiation of the massive stars, located in or near the ONC, to the east we find much more quiescent regions with smaller groups of YSOs and isolated star-forming events. Thanks to the supreme sensitivity of the VISTA observations, it becomes possible to systematically study changes in the colour excess ratios for individual regions. With about ten times more detected sources than previous surveys, the new JHKS data are generally a much better match in sensitivity to the Spitzer data compared to 2MASS, enabling us to cross-validate our findings with multiple bands.
Despite sharing a visually very similar distribution, the MCMC procedure finds a statistically significant difference for the colour excess ratio, implying a variable extinction law. For H, we find a 3-σ significance in the differences of the two slopes, while for z, y, I1, and I2 we find 1-σ differences. The other bands (I3, I4, M1), unfortunately, do have the necessary sample sizes to infer a significant difference within the errors. Taking a closer look at the left-hand side panel of Fig. 7, at first glance, it seems that there is very little difference in the distribution.Looking closer, however, it is possible to see a small difference in the distribution. Even to the eye, the l > 210° sample (orange) shows a trend towards larger J − H values with increasing J − KS as the data systematically envelope the other sample at the upper edge of the distribution (e.g. at J − KS ≈ 3, J − H ≈ 2 mag).
The right-hand side panel of Fig. 7 shows the posterior probability distributions of the linear fit parameters for both sub-regions. Interestingly, both results are found close to the edge or partially outside the average distribution of Fig. 6. In other words, the average distribution assigns 0 probability to many possible parameter combinations derived for each sub-region individually, which seems to lead to inconsistent results at first. However, this can be explained in the nature of the linear fits. The MC algorithm randomly samples the parameters space (α and β) for all data points and does not randomly sample the data space. In contrast, the two fits in Fig. 7 refer to two distinct subsets in data space. The fact that 0 probability is assigned in Fig. 6 to both high and low values from Fig. 7 is therefore a natural consequence of fitting all data points simultaneously.
Nevertheless, even though our linear fitting setup is already very conservative regarding statistical and systematic errors, at this point one can still be very skeptical about our findings. Therefore, as verification of this result, we compared the fitted colour excess ratios for allbands to a variety of model predictions. For optimal comparison, we converted all model values to our slope convention, 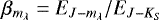 , by integrating the available tables over the filter transmission curves.
, by integrating the available tables over the filter transmission curves.
Figure 9 shows our fitted slopes as a function of wavelength on top of the models from Weingartner & Draine (2001, hereinafter WD01), Draine (2003, D03)5, and Voshchinnikov et al. (2017, model 25; V17), as well as the data from Rosenthal et al. (2000). These models represent a mixture of dust particle characteristics and size distributions. The D03 models are based on case A of Weingartner& Draine (2001) which consists of carbonaceous and silicate grains with sizes ranging from a few Å to several μm. D03 adjusted the size distribution for these models where for RV = 3.1 the grain abundance was reduced, while for RV = 5.5 the abundance was increased. The WD01 RV = 5.5 model in Fig. 9 refers to case B in their work case B contains a significant fraction of very large carbonaceous dust grains (1–10 μm), while case A stops at around 1 μm. The work by V17 is based on laboratory measurements of optical properties of three-layered spheres with the specific aim to understand the widely observed flat MIR extinction law. The comparison to Rosenthal et al. (2000) is especially interesting as they measure an infrared extinction curve towards OMC-1 which lies very close to the ONC.
One particularly interesting observation of our results refers to the difference in the colour excess ratio between the east and west regions, which we also list in Table. 2 (Δ β). Here, we find that for the east-west split, all passbands up to I3 show a deviation of ~3%. For the passbands z, y, I1, I2, and I3 we find a positive difference, while for H this difference is negative. More specifically, for the region including the ONC and its surroundings (l < 210°), we see larger 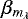 values for the Pan-STARRS and the Spitzer MIR bands, while in H
values for the Pan-STARRS and the Spitzer MIR bands, while in H 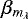 is smaller. In reference to Fig. 9, we note that the same characteristic is also present in the dust models. Considering for the moment only the models of WD01 and D03, we can see a different behaviour of
is smaller. In reference to Fig. 9, we note that the same characteristic is also present in the dust models. Considering for the moment only the models of WD01 and D03, we can see a different behaviour of 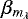 when comparing the RV = 3.1 to the RV = 5.5 models. While for z, y, and the MIR Spitzer bands,
when comparing the RV = 3.1 to the RV = 5.5 models. While for z, y, and the MIR Spitzer bands, 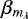 is systematically smaller for RV = 5.5 compared to the 3.1 models, in H this trend is reversed (we note that due to our colour excess ratio definition we have fixed values of
is systematically smaller for RV = 5.5 compared to the 3.1 models, in H this trend is reversed (we note that due to our colour excess ratio definition we have fixed values of 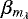 for J and KS . Only for H band we derive an independent estimate of the slope). Excluding the I4 and M1 channel with their much larger uncertainties, we see the exact same behaviour in our fitted colour excess ratios. This comparison therefore serves as a critical reinforcing argument with respect to the statistical significance of our linear fits. If our derived values were to be affected by an additional systematic noise component (e.g. biased photometry near the ONC due to extended emission), we would not expect to see such an agreement in the trends, but rather a random distribution. The slopes would also remain the same if, for instance, only the H band was affected by a systematic offset in the photometry. Such an offset in one band only leads to a shift in the colour-colour diagram and therefore would not affect the slope.
for J and KS . Only for H band we derive an independent estimate of the slope). Excluding the I4 and M1 channel with their much larger uncertainties, we see the exact same behaviour in our fitted colour excess ratios. This comparison therefore serves as a critical reinforcing argument with respect to the statistical significance of our linear fits. If our derived values were to be affected by an additional systematic noise component (e.g. biased photometry near the ONC due to extended emission), we would not expect to see such an agreement in the trends, but rather a random distribution. The slopes would also remain the same if, for instance, only the H band was affected by a systematic offset in the photometry. Such an offset in one band only leads to a shift in the colour-colour diagram and therefore would not affect the slope.
To investigate the origin of these variations in more detail, we divided our dataset into even smaller sub-regions. These definitions are shown in Fig. 8 and are adjusted so that (a) regional variations can be mapped and (b) there were still a reasonably significant amount of sources available. Due to the latter criterion, it was only possible to get reliable fits for H, I1, and I2 . The other bands did not have the necessary amount of measured sources to support such an analysis. Also here we repeatedthe fitting procedure for each sub-region with the same setup as before. The resulting colour excess ratios for the three passbands are displayed in Fig. 10. The order of the regions in the figure is organized in such way that the galactic longitude overall decreases from left to right. In H band there is a clearly visible trend towards smaller β for decreasing longitude. Starting with the ONC-S region and continuing towards the western parts, the values of β are systematically smaller than the average value for the cloud (the dashed horizontal line). Furthermore, the values for the L1641 regions are fairly constant and are near or slightly above the average. Within the error bars this is also true for L1647. The regions near the ONC, on the other hand, can be associated with value of βH smaller than the average (with the exception of ONC-NE).
For I1 and I2, three regions (ONC-NE, ONC-S, and ONC-East) had to be omitted in this analysis, because these were only partly covered by the Spitzer survey and did not include the necessary number of sources to produce a reliable fit. Even though the results for these two bands are not as convincing as for H, the general trend persists. Moreover, in agreement with model predictions, also here β increases for the regions near the ONC, while for H the colour excess ratio decreases. In light of all these findings, we finally conclude, that our results are indeed reliable and significant, which show that the infrared extinction law varies across the cloud. These variations are only of the order of 3%, but this value is consistent across the six passbands z through I3.
 |
Fig. 8 Our sub-region layout to study variations in the colour excess ratio. The top panel shows a dust optical depth map, the bottom panel the dust temperature derived by fitting a modified black-body to Herschel and Planck far-infrared data (Lombardi et al. 2014a,b). The analysis for the sub-regions is split into two parts: First, we study variations of the colour excess ratio by splitting the cloud in east-west direction at l = 210° (dashed line). Subsequently, the entire cloud is split into multiple sub-regions, outlined here by the boxes drawn with solid lines. Regions are labelled only in the top panel and the Spitzer survey contours for I1 and I2 are also drawn. toggle labels. |
4.3.2 Dependence on column-density
Due to external environmental effects on local dust characteristics, it is also reasonable to assume that embedded regions (i.e. regions with large extinction) harbor different dust grains compared to more exposed parts of a molecular cloud. To test this dependency, we repeated the fitting procedure once again, but this time on samples with variable amounts of extinction. As extinction is directly proportional to a source’s colour, we performed this test by restricting our samples with a series of colour thresholds in J − KS. Because of our previous result on the variable infrared extinction law in east-west direction across the survey region, we need to take extra precautions here. Therefore, for an unbiased result, we performed this test only for the sub-region defined by l > 210° (L1641/1647), which shows a relatively constant behaviour in the colour excess ratio. The results of the fit are visualized for H in Fig. 11, where the posterior probabilities for the intercept and the slope are shown. The distributions for I1 and I2 look almost identical with the exception of larger errors.
Across all passbands and sub-regions, and within the statistical significance of our fits, we are not able to determine a variation in the colour excess ratio as a function of J − KS colour. However, the regional variations determined above are of the order of only a few percent. The smaller sample sizes with increasing colour threshold lead to increasingly large errors in this determination for high extinction thresholds. Therefore, our sample size may not be large enough to make a final assessment on an extinction-dependent colour excess ratio in Orion A. Nevertheless, these results agree with the findings of Wang & Jiang (2014) who also concluded that the NIR extinction law does not vary with gas density.
 |
Fig. 9 Infrared extinction curve of Orion A in terms of the colour excess ratio |
 |
Fig. 10 Colour excess ratios |
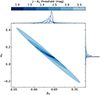 |
Fig. 11 Posterior probability distributions for the colours excess ratio βH and the intercept of the linear fit in the L1641/L1647 region (l > 210°) when restricting the sample to various J − KS colour thresholds. For example, for the J − KS = 1 mag threshold only source above this limit are fitted. The different thresholds are shown in increasingly dark blue colours and, similar to Fig. 6, the ellipses represent 3-sigma covariances of the parameter distribution. The histograms represent kernel densities for each parameter of the fit. |
4.3.3 Systematic error sources
In light of our findings of a spatially variable extinction law across the Orion A molecular cloud, it is worthwhile to discuss potential sources for systematic errors. Such errors could be attributed to, for example, source confusion, changes in the stellar populations across the field (along with variations in intrinsic colours), variable noise properties arising from differently calibrated data, or unaccounted foreground populations.
Source confusion mostly affects the region near the ONC and possibly other groups of stars with above-average spatial densities (i.e. groups of young stars). To minimize this impact, we removed all known YSOs prior to the linear fitting (see Sect. 2.2). Additionally, we verified our results by excluding sources in the ONC region (20′ around the given centre in the SIMBAD database). Doing so changes the derived 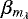 values only by about 1%, but the conclusions derived from Fig. 9 and Table 2 are unaltered. Moreover, observations of a variable colour-excess-ratio also persists in the ONC-East region where source confusion is not expected to be of any significance.
values only by about 1%, but the conclusions derived from Fig. 9 and Table 2 are unaltered. Moreover, observations of a variable colour-excess-ratio also persists in the ONC-East region where source confusion is not expected to be of any significance.
Another possible systematic error source could originate from changing stellar populations across the field. We do not expect this to be significant given the fact, that the Orion A molecular cloud is located towards the galactic anti-centre and 20° below the galactic plane. Even our control field data, located at the same galactic latitude, but 20° further east, does not show a significant change in stellar colours, when compared to the Orion A field. An observable signature of changing stellar populations, for instance, would be a shift in intrinsic colours. We tested this hypothesis by deriving intrinsic colours in bins of 2° in galactic longitude with PNICER for the colours J − H and H − KS. We find a standard deviation of only 2 mmag (0.5%) and 3 mmag (2%) for the mean intrinsic colour in these two passbands, respectively.However, we have to add here that the derived errors of individual intrinsic source colours are much larger (>0.1 mag).
In Paper I, we also highlighted other potential stellar groups in the foreground of the cloud. Since they lie in the foreground, they do not trace extinction through the molecular cloud and therefore should be removed prior to determining colour-excess ratios. In this work, however, we only removed the sources associated with NGC 1980 from our data, because the determination of the other groups was based on an entirely statistical analysis. Thus, we do not have a source list which can be removed from our sample. In any case, any foreground objects show negligible extinction and are therefore irrelevant for the fitting procedure, where we generally rely on a large spread in colour-space (see e.g. Fig. 6).
We alsochecked whether the data we used show a gradient along galactic longitude in terms of observing date, which could hint at differences in their calibration. Also here, no significant discernible pattern was visible with respectto our findings. To test for further systematic errors and to validate the robustness of our results we investiagted whether the results are invariant with respect to magnitude cuts. To this end, we created additional subsets, where we restricted the selected sources to increasingly rigorous magnitude limits (e.g. z < 17 mag, y < 17 mag, H < 16 mag, I1 < 12 mag). The changes in individual 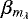 values are found consistently below 1% when when applying these magnitude cuts and consequently also the trends visible in Fig. 9 persist.
values are found consistently below 1% when when applying these magnitude cuts and consequently also the trends visible in Fig. 9 persist.
4.4 The shape of the Orion A infrared extinction curve
Studying Fig. 9 in more detail reveals several interesting findings with respect to the general trend in the infrared extinction. Overall, we find that our fitted colour-excess ratios are well traced by the various models. In particular, we see a flat MIR extinction curve, very similar to the ones that have been observed towards the galactic centre (e.g. Wang et al. 2015, and references therein). This contrasts to the findings of Rosenthal et al. (2000) for the OMC-1 region. Compared to our measurements of a relatively flat MIR extinction law in the IRAC channels, their data suggests a continued decline in the extinction towards the 9.7 μm feature. The same trend is seen in both D03 models. Our interpretation of this discrepancy is, that the work by Rosenthal et al. (2000) traces only very local conditions within OMC-1, which are not representative for the extinction law on larger scales in this region. However, they also state, that their derived extinction minimum at 6.5 μm is not very well constrained. On the other hand, the WD01 RV = 5.5 (case B) model along with the new results from V17 are a much better match to our results in the MIR.
Agreements between a measured flat MIR extinction and the WD01 RV = 5.5 case B model are often interpreted as an indicator of the presence of very large grain sizes (up to 10 μm). The comparison to the model by V17, however, shows, that this must not necessarily be the case. The V17 size distribution is based on work by Hirashita & Voshchinnikov (2014), who investigate dust grain growth over several hundred Myrs. Their initial distribution is taken from case A of WD01, thus only featuring smaller grain sizes. Even after a few Myrs, dust particle sizes do not exceed 1 μm, yet the new models of V17 are able to explain the flat MIR extinction curve.
In H, the situation is reversed. Here, the Rosenthal et al. (2000) and D03 RV = 3.1 models fit much better to our colour excess ratios and the models that fit best to our MIR findings (V17 and WD01) are by far the worst matches for this passband. Even worse, for both M1 and the Pan-STARRS bands z and y, yet another set of models seems to reproduce our findings better. It therefore seems, that these dust models are not able to fully reproduce the infrared extinction law from ~1 to ~ 25 μm, but are tuned to fit a narrower range. In conclusion for the overall infrared extinction law in Orion A, we argue that grain sizes are not the only necessary factor to explain variations, but more sophisticated models are required.
Our analysis also revealed a variable extinction law in east-west direction across the survey region: towards the east of the ONC we find a systematically different extinction law as in regions near the cluster. Because of the above mentioned caveats when comparing our colour excess ratios to dust models, it is almost impossible to arrive at a conclusion with respect to a variation in specific dustcharacteristics. As disappointing as it is, for the moment we can only conclude that the grain population in general changes across the cloud. Whether this is due to grain sizes, different particle structures, or abundances, we can not say.
We can however, speculate on the origin of these variations. The bottom panel of Fig. 8 highlights the dust temperaturederived with modified black body fits to Herschel and Planck dust emission measurements. In this figure it is clearly visible that the L1641/L1647 regions have a significantly lower dust temperature (10–15 K), while the other parts are apparently heated by the hot stars in the cluster. Even in the ONC-East region, which is spatially clearly separated from the cluster region, it seems that cold dust is surrounded by a layer of much warmer material. In contrast, the L1641W region, which is (in this projected view) closer to the cluster, does not have such an apparent layer of warm dust. It therefore seems, as if L1641 sits in the shadow of the cloud and is shielded from the intense radiation originating in the massive cluster stars. Therefore, the conclusion here is, that the radiative feedback from the hot stars significantly impacts the dust grain population.
Considering that we found variations in the colour excess ratio of the order of only 3%, we furthermore argue that research into variations of the infrared extinction law (in particular for the NIR) should be carried out in environments where systematic errors, or external effects can be controlled to at least some extent. For instance, when determining the extinction law for various sightlines near the galactic centre or in the plane, it becomes very difficult to control the influence of physically separate regions along the line of sight, potentially diluting signals of the order of only a few percent. Thus, such studies should ideally be carried out in isolated environments, such as the Orion A molecular cloud.
 |
Fig. 12 Comparison of source densities for consecutive passbands. The individual panels show the ratio of source densities for two particular passbands (e.g. J and y in the topmost panel) evaluated with a 1′ Epanechnikov kernel. The colour scale indicates the gain (or loss) of the redder band over the bluer. Clearly, the JHKS VISTA observations show overall the best sampling of sources in the region and even redder bands include more extincted sources in the cloud. Due to the small difference in the extinction between I1 and I2, the source density gain is negligible for I2. The apparent large-scale pattern for the second and third panel from the top is caused by the variable completeness of the VISTA observations. |
5 Orion A extinction map
Following the determination and discussion on the extinction law in the previous sections, this section concentrates on creating a new extinction map for Orion A. We start by describing several required preparatory steps, followed by a detailed description of the extinction map. We close this sections by comparing our new extinction map to dust emission measurements made with Herschel.
5.1 Preparations
From our analysis of the variability of the colour excess ratio it is not entirely clear which regions exactly are characterized by a given infrared extinction law. We were able to determine a trend in east–west direction which is most likely caused by the feedback from the massive cluster stars. However, drawing an exact border is not possible. For this reason we construct an extinction map for the entire survey region with the average extinction law determined in Sect. 4.2 (see Table 2).
To calculate the individual colour excesses for each source in our catalogue, we use the PNICER method (see Sect. 3.2.2 for details) which is able to combine photometric measurements in arbitrary numbers of passbands. Usually, including more passbands helps to decrease the statistical noise in the extinction calculations. However, the more bands included, the more susceptible the method becomes to systematic errors. For example, in our case the Pan-STARRS photometry is often affected by extended emission, leading to systematic offsets in the measured magnitudes which are not accounted for by the statistical error from the photometry. Furthermore, in the case of our combined photometric master catalogue, it may not even be necessary to include some bands due to very different sensitivity limits and the number of available sources in general.
To find an optimal compromise, we investigated the source densities across the survey area for each band. The results for a subset of these is shown in Fig. 12, where the gain in number density is plotted for consecutive passbands. Easily visible is the tremendous source density gain between the Pan-STARRS y and the VISTA H band. Not only do the NIR VISTA bands suffer much less from extinction (Fig. 2), but also the survey in general is tuned to observe much fainter objects. Another significant gain in the entire region is achieved when using H over J band. For KS over H and I1 over KS we find significantly more sources in the highly extincted regions. From the first to the second IRAC channel there is almost no gain due to the very small difference in extinction in these two bands (see Fig. 9).
In light of these findings, we chose to include only the NIR bands J, H, and KS, as well as I1 in the MIR. We specifically chose to not include I2 due to the small length of the extinction vector in I1 − I2, which can lead to large systematic errors when determining the colour excess with just these two bands. Moreover, I2 does not add sources to the highly extincted regions compared to I1. The Pan-STARRS bands are omitted, because they include significantly fewer sources than the VISTA observations and do not sample the high column-densities in the first place.
PNICER relies on intrinsic colour determinations in a control field. As outlined in Sect. 2, we do not have access to suitable Spitzer control fields data and therefore use transformed WISE photometry (Eqs. (1) and (2)) . However, as the WISE data are associated with larger uncertainties, the intrinsic colour distribution is expected to be significantly broader compared to Spitzer data. This is readily visible in the comparison of the Orion A data to the control field in Fig. 5. Furthermore, it would also be beneficial to reduce the scatter in the NIR data due to photometric errors for a better description (i.e. narrower sequences) of the intrinsic colours.
For this purpose we fit Gaussian Mixture Models to the density distributions in the three-dimensional colour space (J − H, H − KS, KS − I1) incorporating the measurement errors. In Bayesian statistics in astronomy, this process is commonly referred to as extreme deconvolution (Bovy et al. 2011). We use the astroML6 Python implementation (Vanderplas et al. 2012; Ivezić et al. 2014) of this method and apply it to the control field data in all three dimensions simultaneously. The number of model components (Gaussians) is chosen by minimizing the Bayesian Information Criterion (BIC; Schwarz 1978)
 (27)
(27)
where k is the number of model parameters, N the number of sources, and L the likelihood of the data under the given model. This is necessary because, one common caveat of such methods is that in principle it is possible to artificially increase the likelihood of models by increasing the number of components. The BIC definition attempts to correct for this fact by introducing a penalty term which includes this number (k). In our case the BIC showed a very flat distribution starting with about 5–10 Gaussians. However, by visually inspecting the fitting results we found that some features of the distribution were only reproduced by relatively high numbers of Gaussians (20–30). The fitting results of our final choice of 25 Gaussians is shown in Fig. 13. The cloned distribution of the XD resampling provides a very clean sample of the colour space. Moreover, the resampling process of the data space successfully produced a distribution which reduces the influence of photometric errors in the control field. We used this resampled distribution of the colour space to draw 106 randomly selected sources to construct a model control field. Using PNICER we then calculated line-of-sight extinctions for all sources which had independent measurements in at least two bands.
 |
Fig. 13 Extreme deconvolution (XD) resampling process of the three-dimensional control field data space (J − H, H − KS, KS − I1). Leftmost set of panels: original data distribution as projected views. The three panels in thecentre show the same set of combinations for the resampled data with 105 randomly drawn sources. Rightmost panels: locations of the individual three-dimensional Gaussians. For these, the opacity of the ellipses is an indicator of their respective weight in the model. |
5.2 Extinction map
Before creating an extinction map one further complication was to select the correct density correction scaling factor αnicest (Sect. 3.2.3). This parameter represents the slope of the luminosity function and depends on the used bands. For NIR JHKS data this value typically is 1/3 (Lombardi 2009). Here, however, we also include the Spitzer I1 channel which complicates the situation. Instead of trying to empirically derive the correct factor, we created a series of preliminary extinction maps with variable correction factors (αnicest = [0, 1] in steps of 10−2). The goal of this exercise was to calculate the extinction-corrected source density map and minimize the dispersion therein. The minimum value was found at αnicest = 0.25.
One major disadvantage of extinction mapping with discrete line-of-sight samples is the method’s dependency on the number of available background sources. The number density of the sources in highly extincted regions ultimately restricts the resolution of the map. Here, the case of the Orion A molecular cloud is one of the more difficult regions with respect to extinction mapping. This is because the cloud is located towards the galactic anti-centre and also well below the galactic plane, thus offering intrinsically very few background sources. For essentially all other nearby molecular clouds (e.g. the Ophiuchus molecular cloud or the Pipe Nebula) many more background sources are available, since they are projected against the galactic bulge. For these regions it is rather common to achieve much better extinction map resolutions compared to Herschel dust emission maps. To determine this limit for the given data, we created a series of extinction maps with a variety of resolutions following the method described in Sect. 3.2.3. We found that the limit in resolution lies at about 1′ . With this value only very few pixels could not be sampled in the high density regions of the cloud due to a lack of background sources. Well-sampled pixels are only achieved at lower resolutions of about 1.5′ –2′. We therefore provide a series of extinction maps calculated at different resolutions which will be made available to the community via CDS.
Figure 14 shows the final Orion A extinction map at 1′ resolution in units of KS band extinction. In particular, we used a Gaussian kernel with FWHM = 1′ which was truncated at 5 standard deviations and a pixel size of 0.5′ for sufficient sampling. The figure also includes further statistics for each pixel: the extinction error (1-σ), the number of sources (N), and the corrected sources densities resulting from NICEST (ρ). The extinction map offers a large dynamic range at much better resolutions than the previously available map of Lombardi et al. (2011) and traces the dense gas structure of the cloud very well. The map tracing the number of the used sources for each pixel (N) clearly outlines the regions of high extinction. In contrast, the source kernel density map displayed in panel d does not highlight the molecular cloud’s structure. This is because the kernel density in this panel incorporates the NICEST correction. In addition, the fact that the cloud is barely visible in this map is a direct indicator for the successful application of the NICEST algorithm. Only very localized prominent features are visible which are caused by parts in the VISTA image and the source catalogue where the correction factor is not applicable. This can be either due to extremely bright stars with halos on the images (ρnorm ~ 0), or due to stellar clusters in cloud (ρnorm ≳ 0.2). For such regions a density correction based on the expected number of sources not valid and leads to the residual pattern across the density map.
 |
Fig. 14 Orion A extinction map constructed with VISTA and Spitzer data. At the top, panel a shows the extinction map in KS magnitudes with a resolution of 1′. Panel b displays the associated 1-σ errors and panel c the number of sources used for each pixel to calculate the average extinction. The bottom panel d shows the source kernel density when adjusted with the NICEST technique, which applies a correction factor to account for a bias in the measured extinction due to cloud substructure. Due to this correction, the cloud structure mostly disappears when compared to panel c. The kernel density values shown in the bottom panel are normalized to the maximum density. |
5.3 Herschel–Planck re-calibration
The final maximum resolution of our extinction map of 1′ is still well above the resolution of the dust emission measurements by Herschel (~ 36′′). Thus, for the case of Orion A, it is practical to use the higher-resolution Herschel dust thermal emission measurements and convert them to column-density estimates. This procedure has been performed a number of times in the recent past for various cloud complexes (e.g. Stutz et al. 2010), but here we will use the method introduced by Lombardi et al. (2014b). To convert the far-infrared dust emission to column-density estimates, the authors used Herschel and Planck data to estimate the dust optical depth at 850 μm (τ850) in the cloud byfitting modified black bodies to each pixel in the various channel maps. In a subsequent step, the resulting map of dust optical depth was converted to extinction (and therefore column-density) by cross-calibration with an extinction map. Here, the assumption was made that the dust optical depth and extinction share a linear correlation described by
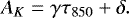 (28)
(28)
For a reliable fit, an upper limit in the parameters is necessary, because a linear correlation is expected to be only valid up to the point where the extinction map is unbiased. With typical 2MASS extinction maps this limit can be set to τ850 = 2 × 104 (Lombardi et al. 2014b; Zari et al. 2016). With our new extinction map, which features a much larger dynamic range, this limit is expected to be pushed to higher values.
For fitting the relation we also use the MCMC-based method outlined in Sect. 3.1. In this case our prior function (Eq. (18)) takes the form
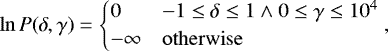 (29)
(29)
where now δ is the intercept, and γ the slope. In this case, however, we are not able to estimate additional systematic uncertainties in the correlation and rely only on the statistical errors derived for the extinction map and the dust optical depth. For this reason, the error in our fit is severely underestimated.
In Fig. 15 we plot the relation between extinction in the KS band against the dust optical depth at 850 μm along with our fitting result. Clearly, the linearity of the relation seems to persist beyond the previously adopted value and we fit the entire range up to τ850 = 105. We find a slope of γ = 3042 mag, which is about 15% steeper when compared to the previous fit of Lombardi et al. (2014b), who derived γ = 2640 mag. In light of additional unknown systematic errors, we round this value to γ = 3050 mag.
We now continue to investigate and discuss the origin of the discrepancy in the correlation of dust optical depth and extinction between the results of Lombardi et al. (2014b) and our fit. A detailed comparison of the extinction maps from 2MASS (Lombardi et al. 2011) and our new map reveals the reason. Figure 16 shows a comparison of the pixel values for 3′ extinction maps (the resolution of the 2MASS map) created from 2MASS and VISTA data, respectively. This comparison is shown for three different magnitude limits, in the sense of only including sources brighter than the given limit to create the map. For the typical 2MASS sensitivity limit of 14.5 mag in KS, the map values share a 1:1 correlation. However, when including more sources in the VISTA map (2MASS tops out at ~14.5 mag), a clear trend to higher extinctions in each pixel becomes visible. The most likely reason for this is that individual pixels have significant cloud substructure which only gets sampled when enough background sources are available. In the case of the typical 2MASS magnitude limit, only relatively few background sources are available per pixel. Thus, structure with a size smaller than the resolution of the map is partly not being sampled. In contrast, the VISTA data offer an order of magnitude more background sources which significantly increase the sampled area.
The maps, for which we display the pixel values in Fig. 16 have been created using the NICEST substructure correction (Sect. 3.2.3). This correction is in principal designed to minimize such an effect, however, a certain bias will still remain if structures are not sampled by background sources in the first place. It therefore seems likely, that the 2MASS observationswere apparently not sensitive enough to provide a full sampling of the cloud substructure. This trend continues for even higher magnitude limits but changes become less significant when approaching the sensitivity limit of the VISTA data (KS ~ 19 mag). Still, we cannot say with absolute confidence that the new data sample the substructure up to a point where no more improvements could be found by including even more background sources.
Other values for γ between extinction and dust optical depth in the literature are published for Orion B (~3460 mag; Lombardi et al. 2014b) and for the Perseus cloud complex (~3900 mag; Zari et al. 2016). Also here the authors used 2MASS extinction maps, and both clouds share a similar unfavourable position compared to Orion A with respect to the number of available background sources. Orion B lies at about the same distance as Orion A but is closer to the galactic plane. The Perseus cloud, on the other hand lies significantly closer (240 pc), which reduces the problem with structure not being sampled by background sources. Nevertheless, for these clouds it seems reasonable to assume that they are also affected by this problem to a certain extent. Furthermore, we also can not exclude the possibility that the different calibrations of the Herschel dust optical depth measurements are also affecting this relation.
The value of γ, in principle, can be correlated with physical conditions of the dust since it is proportional to the ratio of the opacity at 850 μm and the extinction coefficient in the KS passband (~2.2 μm). In light of our findings with respect to cloud substructure and the consequential introduced bias in the slope, we conclude, that at the moment it is difficult to make decisive physical interpretations, given a particular value of γ. More studies in regions, where extinction maps convincingly sample the entire cloud structure are necessary to arrive at a better understanding of the slope γ. Similar to what we found with the new VISTA data for Orion A, future observations will provide better insight into this problem. In particular, the VISTA Star Formation Atlas7 will performs high-sensitivity, wide-field JHKS observations of major nearby star-forming complexes. The NIR photometry will enable the construction of high resolution extinction maps, with well-sampled pixels and therefore will provide further insight into this problem.
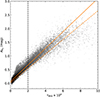 |
Fig. 15 Relation between Herschel–Planck dust optical depth at 850 μm (τ850) and dust extinction in KS. The orange solid line is our linear fit with the slope γ = 3042 mag. The dashed orange line is the previous fit of Lombardi et al. (2014b, γ = 2640 mag) who used an extinction map based on 2MASS data. They also limited their fit to τ850 < 2 × 104, as indicated by the vertical dashed line, while we use the entire range displayed in this figure. We find a ~ 15% larger slope in the relation due to much better sampling of the cloud’s substructure. |
 |
Fig. 16 Comparison of the pixel values for extinction maps created with 2MASS and VISTA data (sensitivity limits: ~14.5 mag and ~19 mag, respectively). Each of the three panel groups shows a different magnitude limit. The leftmost plot shows a comparison for extinction maps where all source brighter than 14.5 mag in KS are used. The panel in the centre and to the right display the same comparison, but with sources brighter than 16.5 and 18.5 mag in KS, respectively. While the bottom figures directly compare the two measures, we plot their difference ( |
6 Summary
In this second publication in the context of the Vienna Survey in Orion, we have investigated infrared extinction properties in the Orion A molecular cloud complex. The main results of this paper are as follows:
- 1.
We combined several large-scale photometric databases, covering a wavelength range from just below 1 μm to about 25 μm. Our master catalogue includes NIR data from Pan-STARRS, as well as HAWK-I and the VISTA observations presented in Paper I. The MIR is covered by Spitzer IRAC and MIPS photometry. A detailed description of our final catalogue is given in Sect. 2.
- 2.
Our results critically depend on the reliability of linear fitting procedures. For this reason, we have developed a two-dimensional Bayesian framework which is used together with a MCMC algorithm. Specifically, we have derived a model likelihood which takes measurement errors in both dimensions into account. This framework can be adapted to include more complex models and therefore can be used in a multitude of additional aspects far beyond the general scope of this publication. The final model likelihood is given in Eq. (17), for which a detailed derivation can be found in Sect. 3.1.
- 3.
We derived the infrared extinction law in Orion A by fitting colour excess ratios in a variety of colour-colour diagrams. Here, we first measured the average extinction law (Sect. 4.2), and continued to investigate spatial variations across the molecular cloud complex (Sect. 4.3). Fitting results and the total extinction ratios for all included passbands are available in Table 2. The results for the fitting procedures are visualized for the H passband in Figs. 6 and 7. For the average extinction law we find excellent agreement compared to results in the literature.
- 4.
For the passbands up to about 6 μm we find statistically significant spatial variations in the colour excess ratios of the order of 3%. We investigated the origin ofthese variations by splitting the survey into distinct sub-regions (Fig. 8). Here, we find a clear signature, that those regions, which seem to be affected by radiative feedback from the massive stars in the ONC, show a different extinction law when compared to other star-forming sites in the cloud (Fig. 10).
- 5.
To support and interpret our results on the spatial variations from the linear fitting procedure, we compared our findings to various model predictions (Fig. 9). Here, we found that the general trends can be reproduced by the models, reinforcing our claim with respect to a variable extinction law. However, a more detailed analysis revealed that these models are not able to fully explain all details of our findings across the entire infrared spectral range.
- 6.
The Orion A MIR extinction law is characteristically flat, similar to many other recently investigated sightlines (Fig. 9). This result contradicts previous investigations in the Orion A region. Furthermore, flat MIR extinction is oftentimes associated with extraordinary large dust grains (~10 μm). However, a comparison with recently published dust grain models shows that this must not necessarily be the case (Sect. 4.4).
- 7.
Based on the derived average extinction law, we constructed a new extinction map of Orion A with a resolution of 1′ (Fig. 14). We compared this map to Herschel dust optical depth measurements (Sect. 5.3) and derived a new calibration to convert these data to extinction (Fig. 15). However, we also found alarming evidence, that the conversion of dust optical depth, as derived from Herschel data, to column densities is likely biased by cloud substructure which is not sampled by background sources (Fig. 16). Another source of systematic uncertainty in this correlation may be the conversion of the dust emission measurements to dust optical depth itself.
Finally, we want to highlight that Orion A presents a unique opportunity to study the extinction law in an unbiased way. Many well-known results in the literature are based on measurements in the galactic plane and specifically towards the galactic centre. In these regions, however, it is difficult to interpret the extinction law and its variations, since many physically separate layers of interstellar material can overlap along the line of sight. Therefore, and in light of our findings on the variations in the extinction law, we argue that it is extremely difficult to find such small deviations (3%) in these regions. Moreover, since Orion A hosts the nearest massive star-forming region, it is the ideal location for detailed investigations into dust grain populations and their generic properties under the influence of radiative feedback.
Acknowledgements
We want to thank the anonymous referee for the very detailed and useful comments that helped to improve the quality of this publication. Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere. under ESO programmes 082.C-0032(A) and 090.C-0797(A). This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration et al. 2013). This research has made use of “Aladin sky atlas” developed at CDS, Strasbourg Observatory, France (Bonnarel et al. 2000). This research has made use of the SVO Filter Profile Service (http://svo2.cab.inta-csic.es/theory/fps/) supported from the Spanish MINECO through grant AyA2014-55216. We also acknowledge the various Python packages that were used in the data analysis of this work, including NumPy (Van Der Walt et al. 2011), SciPy (Jones et al. 2001), scikit-learn (Pedregosa et al. 2011), and Matplotlib (Hunter 2007). This research has made use of the SIMBAD database operated at CDS, Strasbourg, France (Wenger et al. 2000).
References
- Alves, J., Lada, C. J., Lada, E. A., Kenyon, S. J., & Phelps, R. 1998, ApJ, 506, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Alves, J. F., Lada, C. J., & Lada, E. A. 2001, Nature, 409, 159 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Alves, J., Lombardi, M., & Lada, C. J. 2014, A&A, 565, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ascenso, J., Lombardi, M., Lada, C. J., & Alves, J. 2012, A&A, 540, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ascenso, J., Lada, C. J., Alves, J., [Google Scholar]
- Astropy Collaboration, Robitaille, T. P., Tollerud, E. J., et al. 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beitia-Antero, L., & Gómez de Castro, A. I. 2017, MNRAS, 469, 2531 [NASA ADS] [CrossRef] [Google Scholar]
- Benjamin, R. A., Churchwell, E., Babler, B. L., et al. 2003, PASP, 115, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Bernstein, R. A., Freedman, W. L., & Madore, B. F. 2002, ApJ, 571, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Bok, B. J., & Cordwell, C. S. 1973, in Molecules in the Galactic Environment, eds. M. A. Gordon, & L. E. Snyder, 54 [Google Scholar]
- Bonnarel, F., Fernique, P., Bienaymé, O., et al. 2000, A&AS, 143, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouy, H., Alves, J., Bertin, E., Sarro, L. M., & Barrado, D. 2014, A&A, 564, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bovy, J., Hogg, D. W., & Roweis, S. T. 2011, Ann. Appl. Stat., 5, 1657 [NASA ADS] [CrossRef] [Google Scholar]
- Bradley, J., Dai, Z. R., Erni, R., et al. 2005, Science, 307, 244 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cambrésy, L. 1999, A&A, 345, 965 [NASA ADS] [Google Scholar]
- Cambrésy, L., Beichman, C. A., Jarrett, T. H., & Cutri, R. M. 2002, AJ, 123, 2559 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, K., & Pan-STARRS Team 2018, AAS Meet., 231, 102.01 [Google Scholar]
- Churchwell, E., Babler, B. L., Meade, M. R., et al. 2009, PASP, 121, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Clutton-Brock, M. 1967, Technometrics, 9, 261 [CrossRef] [Google Scholar]
- Cutri, R. M., Wright, E. L., Conrow, T., et al. 2013, VizieR Online Data Catalog: II/328 [Google Scholar]
- Dalton, G. B., Caldwell, M., Ward, A. K., et al. 2006, in Proc. SPIE, 6269, 62690X [Google Scholar]
- Dobashi, K., Uehara, H., Kandori, R., et al. 2005, PASJ, 57, S1 [NASA ADS] [CrossRef] [Google Scholar]
- Dobashi, K., Bernard, J.-P., Hughes, A., et al. 2008, A&A, 484, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 1989, in Infrared Spectroscopy in Astronomy, ed. E. Böhm-Vitense, ESA SP, 290 [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Drass, H., Haas, M., Chini, R., et al. 2016, MNRAS, 461, 1734 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Weinberg, D. H., Agol, E., et al. 2011, AJ, 142, 72 [Google Scholar]
- Emerson, J., McPherson, A., & Sutherland, W. 2006, The Messenger, 126, 41 [NASA ADS] [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 1986, ApJ, 307, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 1988, ApJ, 328, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Flaherty, K. M., Pipher, J. L., Megeath, S. T., et al. 2007, ApJ, 663, 1069 [CrossRef] [Google Scholar]
- Flewelling, H. A., Magnier, E. A., Chambers, K. C., et al. 2016, ArXiv e-prints [arXiv:1612.05243] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Fritz, T. K., Gillessen, S., Dodds-Eden, K., et al. 2011, ApJ, 737, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Gosling, A. J., Bandyopadhyay, R. M., & Blundell, K. M. 2009, MNRAS, 394, 2247 [NASA ADS] [CrossRef] [Google Scholar]
- Hirashita, H., & Voshchinnikov, N. V. 2014, MNRAS, 437, 1636 [NASA ADS] [CrossRef] [Google Scholar]
- Hogg, D. W., Bovy, J., & Lang, D. 2010, ArXiv e-prints [arXiv:1008.4686] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
- Indebetouw, R., Mathis, J. S., Babler, B. L., et al. 2005, ApJ, 619, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Connelly, A. J., VanderPlas, J. T., & Gray, A. 2014, Statistics, Data Mining, and Machine Learning in Astronomy (Princeton University Press) [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open source scientific tools for Python [Google Scholar]
- Juvela, M., & Montillaud, J. 2016, A&A, 585, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kissler-Patig, M., Pirard, J.-F., Casali, M., et al. 2008, A&A, 491, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lada, C. J., Lada, E. A., Clemens, D. P., & Bally, J. 1994, ApJ, 429, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M. 2009, A&A, 493, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M.,& Alves, J. 2001, A&A, 377, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. J. 2011, A&A, 535, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Bouy, H., Alves, J., & Lada, C. J. 2014a, A&A, 568, C1 [Google Scholar]
- Lombardi, M., Bouy, H., Alves, J., & Lada, C. J. 2014b, A&A, 566, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lutz, D. 1999,in The Universe as Seen by ISO, eds. P. Cox, & M. Kessler, ESA SP, 427, 623 [NASA ADS] [Google Scholar]
- Lutz, D., Feuchtgruber, H., Genzel, R., et al. 1996, A&A, 315, L269 [NASA ADS] [Google Scholar]
- Mackay, D. J. C. 2003, Information Theory, Inference and Learning Algorithms (Cambridge University Press), 640 [Google Scholar]
- Magnier, E. A., Schlafly, E. F., Finkbeiner, D. P., et al. 2016, ArXiv e-prints [arXiv:1612.05242] [Google Scholar]
- Majaess, D., Turner, D., Dékány, I., Minniti, D., & Gieren, W. 2016, A&A, 593, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Majewski, S. R., Zasowski, G., & Nidever, D. L. 2011, ApJ, 739, 25 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Martin, P. G., & Whittet, D. C. B. 1990, ApJ, 357, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S. 1994, ApJ, 422, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Megeath, S. T., Gutermuth, R., Muzerolle, J., et al. 2012, AJ, 144, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Meingast, S., Alves, J., Mardones, D., et al. 2016, A&A, 587, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meingast, S., Lombardi, M., & Alves, J. 2017, A&A, 601, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nataf, D. M. 2015, MNRAS, 449, 1171 [NASA ADS] [CrossRef] [Google Scholar]
- Nataf, D. M., Gonzalez, O. A., Casagrande, L., et al. 2016, MNRAS, 456, 2692 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Nagata, T., Kusakabe, N., et al. 2006, ApJ, 638, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Tamura, M., Hatano, H., et al. 2009, ApJ, 696, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., Young, E. T., Engelbracht, C. W., et al. 2004, ApJS, 154, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenthal, D., Bertoldi, F., & Drapatz, S. 2000, A&A, 356, 705 [NASA ADS] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., Finkbeiner, D. P., Schlegel, D. J., et al. 2010, ApJ, 725, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, G. 1978, Ann. Stat., 6, 461 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Stead, J. J., & Hoare, M. G. 2009, MNRAS, 400, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Stutz, A., Launhardt, R., Linz, H., et al. 2010, A&A, 518, L87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, M. B. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, ASP Conf. Ser., 347, 29 [Google Scholar]
- Vanderplas, J., Connolly, A., Ivezić, Ž., & Gray, A. 2012, in Conference on Intelligent Data Understanding (CIDU), 47 [Google Scholar]
- Van Der Walt,S., Colbert, S. C., & Varoquaux, G. 2011, ArXiv e-prints [arXiv:1102.1523] [Google Scholar]
- Voshchinnikov, N. V., Henning, T., & Il’in, V. B. 2017, ApJ, 837, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S., & Jiang, B. W. 2014, ApJ, 788, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S., Gao, J., Jiang, B. W., Li, A., & Chen, Y. 2013, ApJ, 773, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S., Li, A., & Jiang, B. W. 2015, ApJ, 811, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Zari, E., Lombardi, M., Alves, J., Lada, C. J., & Bouy, H. 2016, A&A, 587, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zasowski, G., Majewski, S. R., Indebetouw, R., et al. 2009, ApJ, 707, 510 [NASA ADS] [CrossRef] [Google Scholar]
Description, documentation, and source code are available at http://dan.iel.fm/emcee/current/
The models from WD01 and D03 are available for download at https://www.astro.princeton.edu/~draine/dust/dustmix.html
Source code and description available at http://www.astroml.org and https://github.com/astroML/astroML
VISIONS - The VISTA Star Formation Atlas is an ongoing ESO public survey and is based on this paper series. More information is available at http://visions.univie.ac.at
All Tables
Basic properties for all photometric bands used in this work, as well as corresponding source counts in our master catalogue for both the Orion A region and the control field.
All Figures
 |
Fig. 1 Region under investigation in this work: the Orion A molecular cloud is visualized in green with the dust optical depth map from Lombardi et al. (2014b) blended with optical image data (deepskycolors.com; © Roberto Bernal Andreo). The solid lines indicate the coverage of the various surveys used to investigate the properties of dust extinction in the cloud, where the IRAC contour outlines the region covered by either of the first two IRAC channels. We also make use of MIPSdata, for which the covered region generally encompasses the IRAC contour. toggle labels |
| In the text | |
 |
Fig. 2 Passbands used in our analysis cover the infrared wavelength range from just below 1 μm to about 25 μm utilizing the Pan-STARRS (z, y), VISTA (J, H, KS; calibrated against 2MASS), and Spitzer (I1, I2, I3, I4, M1) photometric systems. The filter curves have each been normalized to their maximum transmission and their relative spectral response (RSR) is shown as a function of wavelength. The two solid grey lines are 3000 K black bodies with a normalized intensity (Inorm). Here, the upper line is the unmodified black body, whereas the line at the bottom shows the resulting spectral energy distribution with 5 mag extinction in the KS band and using the RV = 3.1 Draine (2003) extinction law. |
| In the text | |
 |
Fig. 3 Comparison of VISTA and HAWK-I photometry in J band. The panel at the top shows the difference in photometric errors as a function of the apparent VISTA magnitude. Similarly, the bottom plot displays the difference in the measured source magnitudes. The histogram to the right shows the distribution of the magnitude difference as a kernel density. Assuming a Gaussian distribution, the differently shaded areas under the curve represent the 1, 2, and 3-σ limits. |
| In the text | |
 |
Fig. 4 Correlation between W1 and I1. The top panel shows the difference in photometric errors, while at the bottom the difference in source magnitudes is displayed. The orange line is our linear transformation between the two systems, which maps the two bands in almost a 1:1 relation. Similar to Fig. 3, the histogram to the right represents the kernel density of the magnitude differences. |
| In the text | |
 |
Fig. 5 Various colour-colour diagrams constructed from our master-catalogue. The left-hand panels show data for the Orion A region, while the right-hand panels show the same combinations for the extinction free control field. Evidently, the Orion A field is heavily affected by reddening due to dust in the molecular cloud. The Spitzer photometry for the control fieldwas derived with a linear transformation from WISE data and therefore shows a larger dispersion when compared to the high-sensitivity data of the Spitzer Orion programme. |
| In the text | |
 |
Fig. 6 Fitting results for the colour excess ratio in H band. Left-hand side panels: filtered source distribution in a greyscale scatter plot, where the greyscale is proportional to the number density in this parameter space. The thin blue contours refer to 0.5, 10, 40, and 80% of the maximum source density. Also plotted is the resulting fit as the orange dashed line. Right-hand side panels: posterior probability distribution for the intercept αH and the slope βH (the colour excess ratio). The ellipses are the 1-, 2-, and 3-sigma covariances of the distribution. Projected to the top and to the right are normalized kernel densities of the resulting distribution for each parameter. The differently shaded filled areas under the curve highlight the 1-, 2-, and 3-σ ranges. |
| In the text | |
 |
Fig. 7 Similar to Fig. 6, we here show the fitting results for H when splitting the survey region in east-west direction along l = 210°. Our MCMC fitting method determines a significant difference in the colour excess ratios for the two sub-regions, indicating a variable extinction law across the molecular cloud. |
| In the text | |
 |
Fig. 8 Our sub-region layout to study variations in the colour excess ratio. The top panel shows a dust optical depth map, the bottom panel the dust temperature derived by fitting a modified black-body to Herschel and Planck far-infrared data (Lombardi et al. 2014a,b). The analysis for the sub-regions is split into two parts: First, we study variations of the colour excess ratio by splitting the cloud in east-west direction at l = 210° (dashed line). Subsequently, the entire cloud is split into multiple sub-regions, outlined here by the boxes drawn with solid lines. Regions are labelled only in the top panel and the Spitzer survey contours for I1 and I2 are also drawn. toggle labels. |
| In the text | |
 |
Fig. 9 Infrared extinction curve of Orion A in terms of the colour excess ratio |
| In the text | |
 |
Fig. 10 Colour excess ratios |
| In the text | |
 |
Fig. 11 Posterior probability distributions for the colours excess ratio βH and the intercept of the linear fit in the L1641/L1647 region (l > 210°) when restricting the sample to various J − KS colour thresholds. For example, for the J − KS = 1 mag threshold only source above this limit are fitted. The different thresholds are shown in increasingly dark blue colours and, similar to Fig. 6, the ellipses represent 3-sigma covariances of the parameter distribution. The histograms represent kernel densities for each parameter of the fit. |
| In the text | |
 |
Fig. 12 Comparison of source densities for consecutive passbands. The individual panels show the ratio of source densities for two particular passbands (e.g. J and y in the topmost panel) evaluated with a 1′ Epanechnikov kernel. The colour scale indicates the gain (or loss) of the redder band over the bluer. Clearly, the JHKS VISTA observations show overall the best sampling of sources in the region and even redder bands include more extincted sources in the cloud. Due to the small difference in the extinction between I1 and I2, the source density gain is negligible for I2. The apparent large-scale pattern for the second and third panel from the top is caused by the variable completeness of the VISTA observations. |
| In the text | |
 |
Fig. 13 Extreme deconvolution (XD) resampling process of the three-dimensional control field data space (J − H, H − KS, KS − I1). Leftmost set of panels: original data distribution as projected views. The three panels in thecentre show the same set of combinations for the resampled data with 105 randomly drawn sources. Rightmost panels: locations of the individual three-dimensional Gaussians. For these, the opacity of the ellipses is an indicator of their respective weight in the model. |
| In the text | |
 |
Fig. 14 Orion A extinction map constructed with VISTA and Spitzer data. At the top, panel a shows the extinction map in KS magnitudes with a resolution of 1′. Panel b displays the associated 1-σ errors and panel c the number of sources used for each pixel to calculate the average extinction. The bottom panel d shows the source kernel density when adjusted with the NICEST technique, which applies a correction factor to account for a bias in the measured extinction due to cloud substructure. Due to this correction, the cloud structure mostly disappears when compared to panel c. The kernel density values shown in the bottom panel are normalized to the maximum density. |
| In the text | |
 |
Fig. 15 Relation between Herschel–Planck dust optical depth at 850 μm (τ850) and dust extinction in KS. The orange solid line is our linear fit with the slope γ = 3042 mag. The dashed orange line is the previous fit of Lombardi et al. (2014b, γ = 2640 mag) who used an extinction map based on 2MASS data. They also limited their fit to τ850 < 2 × 104, as indicated by the vertical dashed line, while we use the entire range displayed in this figure. We find a ~ 15% larger slope in the relation due to much better sampling of the cloud’s substructure. |
| In the text | |
 |
Fig. 16 Comparison of the pixel values for extinction maps created with 2MASS and VISTA data (sensitivity limits: ~14.5 mag and ~19 mag, respectively). Each of the three panel groups shows a different magnitude limit. The leftmost plot shows a comparison for extinction maps where all source brighter than 14.5 mag in KS are used. The panel in the centre and to the right display the same comparison, but with sources brighter than 16.5 and 18.5 mag in KS, respectively. While the bottom figures directly compare the two measures, we plot their difference ( |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.