| Issue |
A&A
Volume 607, November 2017
|
|
|---|---|---|
| Article Number | A122 | |
| Number of page(s) | 20 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201630311 | |
| Published online | 27 November 2017 | |
Planck intermediate results
LII. Planet flux densities
1 APC, AstroParticule et Cosmologie, Université Paris Diderot, CNRS/IN2P3, CEA/lrfu, Observatoire de Paris, Sorbonne Paris Cité, 10 rue Alice Domon et Léonie Duquet, 75205 Paris Cedex 13, France
2 African Institute for Mathematical Sciences, 6–8 Melrose Road, Muizenberg, 7950 Cape Town, South Africa
3 Agenzia Spaziale Italiana Science Data Center, via del Politecnico snc, 00133 Roma, Italy
4 Aix Marseille Univ, CNRS, LAM, Laboratoire d’Astrophysique de Marseille, 13013 Marseille, France
5 Astrophysics Group, Cavendish Laboratory, University of Cambridge, J J Thomson Avenue, Cambridge CB3 0HE, UK
6 Astrophysics & Cosmology Research Unit, School of Mathematics, Statistics & Computer Science, University of KwaZulu-Natal, Westville Campus, Private Bag X54001, 4000 Durban, South Africa
7 CITA, University of Toronto, 60 St. George St., Toronto, ON M5S 3H8, Canada
8 CNRS, IRAP, 9 Av. colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
9 California Institute of Technology, Pasadena, CA 91125, California, USA
10 Computational Cosmology Center, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, California, USA
11 DTU Space, National Space Institute, Technical University of Denmark, Elektrovej 327, 2800 Kgs. Lyngby, Denmark
12 Département de Physique Théorique, Université de Genève, 24 Quai E. Ansermet, 1211 Genève 4, Switzerland
13 Departamento de Astrofísica, Universidad de La Laguna (ULL), 38206 La Laguna, Tenerife, Spain
14 Departamento de Física, Universidad de Oviedo, Avda. Calvo Sotelo s/n, 33003 Oviedo, Spain
15 Department of Astrophysics/IMAPP, Radboud University, PO Box 9010, 6500 GL Nijmegen, The Netherlands
16 Department of Physics & Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, British Columbia, Canada
17 Department of Physics and Astronomy, Dana and David Dornsife College of Letter, Arts and Sciences, University of Southern California, Los Angeles, CA 90089, USA
18 Department of Physics and Astronomy, University College London, London WC1E 6BT, UK
19 Department of Physics and Astronomy, University of Sussex, Brighton BN1 9QH, UK
20 Department of Physics, Gustaf Hällströmin katu 2a, University of Helsinki, 00100 Helsinki, Finland
21 Department of Physics, Princeton University, Princeton, 08544 New Jersey, USA
22 Dipartimento di Fisica e Astronomia G. Galilei, Università degli Studi di Padova, via Marzolo 8, 35131 Padova, Italy
23 Dipartimento di Fisica e Astronomia, Alma Mater Studiorum, Università degli Studi di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
24 Dipartimento di Fisica e Scienze della Terra, Università di Ferrara, via Saragat 1, 44122 Ferrara, Italy
25 Dipartimento di Fisica, Università La Sapienza, P. le A. Moro 2, 00185 Roma, Italy
26 Dipartimento di Fisica, Università degli Studi di Milano, via Celoria, 16, 20122 Milano, Italy
27 Dipartimento di Fisica, Università degli Studi di Trieste, via A. Valerio 2, 34127 Trieste, Italy
28 Dipartimento di Matematica, Università di Roma Tor Vergata, via della Ricerca Scientifica, 1, 00163 Roma, Italy
29 European Space Agency, ESAC, Planck Science Office, Camino bajo del Castillo, s/n, Urbanización Villafranca del Castillo, Villanueva de la Cañada, 28692 Madrid, Spain
30 European Space Agency, ESTEC, Keplerlaan 1, 2201 AZNoordwijk, The Netherlands
31 Gran Sasso Science Institute, INFN, viale F. Crispi 7, 67100 L’ Aquila, Italy
32 Haverford College Astronomy Department, 370 Lancaster Avenue, Haverford, PA 19041 Pennsylvania, USA
33 Helsinki Institute of Physics, Gustaf Hällströmin katu 2, University of Helsinki, 00100 Helsinki, Finland
34 INAF–Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
35 INAF–Osservatorio Astronomico di Roma, via di Frascati 33, 00185 Monte Porzio Catone, Italy
36 INAF–Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, 34127 Trieste, Italy
37 INAF/IASF Bologna, via Gobetti 101, 40129 Bologna, Italy
38 INAF/IASF Milano, via E. Bassini 15, 20133 Milano, Italy
39 INFN–CNAF, viale Berti Pichat 6/2, 40127 Bologna, Italy
40 INFN, Sezione di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
41 INFN, Sezione di Ferrara, via Saragat 1, 44122 Ferrara, Italy
42 INFN, Sezione di Roma 1, Università di Roma Sapienza, Piazzale Aldo Moro 2, 00185 Roma, Italy
43 INFN, Sezione di Roma 2, Università di Roma Tor Vergata, via della Ricerca Scientifica, 1, 00173 Roma, Italy
44 Imperial College London, Astrophysics group, Blackett Laboratory, Prince Consort Road, London, SW7 2AZ, UK
45 Institut d’Astrophysique Spatiale, CNRS, Univ. Paris-Sud, Université Paris-Saclay, Bât. 121, 91405 Orsay Cedex, France
46 Institut d’Astrophysique de Paris, CNRS (UMR7095), 98bis Boulevard Arago, 75014 Paris, France
47 Institute of Theoretical Astrophysics, University of Oslo, Blindern, 0313 Oslo, Norway
48 Instituto de Astrofísica de Canarias, C/Vía Láctea s/n, La Laguna, 38205 Tenerife, Spain
49 Instituto de Física de Cantabria (CSIC-Universidad de Cantabria), Avda. de los Castros s/n, 39005 Santander, Spain
50 Istituto Nazionale di Fisica Nucleare, Sezione di Padova, via Marzolo 8, 35131 Padova, Italy
51 Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, California, USA
52 Jodrell Bank Centre for Astrophysics, Alan Turing Building, School of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK
53 Kavli Institute for Cosmological Physics, University of Chicago, Chicago, 60637, USA
54 Kavli Institute for Cosmology Cambridge, Madingley Road, Cambridge, CB3 0HA, UK
55 LAL, Université Paris-Sud, CNRS/IN2P3, 91400 Orsay, France
56 LERMA, CNRS, Observatoire de Paris, 61 Avenue de l’Observatoire, 75014 Paris, France
57 LESIA, Observatoire de Paris, CNRS, UPMC, Université Paris-Diderot, 5 place J. Janssen, 92195 Meudon, France
58 Laboratoire Traitement et Communication de l’Information, CNRS (UMR 5141) and Télécom ParisTech, 46 rue Barrault, 75634 Paris Cedex 13, France
59 Laboratoire de Physique Subatomique et Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, 53 rue des Martyrs, 38026 Grenoble Cedex, France
60 Laboratoire de Physique Théorique, Université Paris-Sud 11 & CNRS, Bâtiment 210, 91405 Orsay, France
61 Lawrence Berkeley National Laboratory, Berkeley, California, USA
62 Low Temperature Laboratory, Department of Applied Physics, Aalto University, Espoo, 00076 Aalto, Finland
63 Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
64 Mullard Space Science Laboratory, University College London, Surrey RH5 6NT, UK
65 Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warsaw, Poland
66 Nordita (Nordic Institute for Theoretical Physics), Roslagstullsbacken 23, 106 91 Stockholm, Sweden
67 SISSA, Astrophysics Sector, via Bonomea 265, 34136 Trieste, Italy
68 School of Chemistry and Physics, University of KwaZulu-Natal, Westville Campus, Private Bag X54001, 4000 Durban, South Africa
69 School of Physics and Astronomy, Cardiff University, Queens Buildings, The Parade, Cardiff, CF24 3AA, UK
70 Simon Fraser University, Department of Physics, 8888 University Drive, Burnaby BC, Canada
71 Sorbonne Université-UPMC, UMR7095, Institut d’Astrophysique de Paris, 98bis Boulevard Arago, 75014 Paris, France
72 Space Sciences Laboratory, University of California, Berkeley, CA 94607 California, USA
73 Sub-Department of Astrophysics, University of Oxford, Keble Road, Oxford OX1 3RH, UK
74 The Oskar Klein Centre for Cosmoparticle Physics, Department of Physics, Stockholm University, AlbaNova, 106 91 Stockholm, Sweden
75 UPMC Univ Paris 06, UMR7095, 98bis Boulevard Arago, 75014 Paris, France
76 Université de Toulouse, UPS-OMP, IRAP, 31028 Toulouse Cedex 4, France
77 University of Granada, Departamento de Física Teórica y del Cosmos, Facultad de Ciencias, 18010 Granada, Spain
78 University of Heidelberg, Institute for Theoretical Physics, Philosophenweg 16, 69120 Heidelberg, Germany
79 Warsaw University Observatory, Aleje Ujazdowskie 4, 00-478 Warszawa, Poland
⋆
Jon E. Gudmundsson, e-mail: jon.gudmundsson@fysik.su.se;jegudmunds@gmail.com
Received: 21 December 2016
Accepted: 30 March 2017
Measurements of flux density are described for five planets, Mars, Jupiter, Saturn, Uranus, and Neptune, across the six Planck High Frequency Instrument frequency bands (100–857 GHz) and these are then compared with models and existing data. In our analysis, we have also included estimates of the brightness of Jupiter and Saturn at the three frequencies of the Planck Low Frequency Instrument (30, 44, and 70 GHz). The results provide constraints on the intrinsic brightness and the brightness time-variability of these planets. The majority of the planet flux density estimates are limited by systematic errors, but still yield better than 1% measurements in many cases. Applying data from Planck HFI, the Wilkinson Microwave Anisotropy Probe (WMAP), and the Atacama Cosmology Telescope (ACT) to a model that incorporates contributions from Saturn’s rings to the planet’s total flux density suggests a best fit value for the spectral index of Saturn’s ring system of βring = 2.30 ± 0.03 over the 30–1000 GHz frequency range. Estimates of the polarization amplitude of the planets have also been made in the four bands that have polarization-sensitive detectors (100–353 GHz); this analysis provides a 95% confidence level upper limit on Mars’s polarization of 1.8, 1.7, 1.2, and 1.7% at 100, 143, 217, and 353 GHz, respectively. The average ratio between the Planck-HFI measurements and the adopted model predictions for all five planets (excluding Jupiter observations for 353 GHz) is 1.004, 1.002, 1.021, and 1.033 for 100, 143, 217, and 353 GHz, respectively. Model predictions for planet thermodynamic temperatures are therefore consistent with the absolute calibration of Planck-HFI detectors at about the three-percent level. We compare our measurements with published results from recent cosmic microwave background experiments. In particular, we observe that the flux densities measured by Planck HFI and WMAP agree to within 2%. These results allow experiments operating in the mm-wavelength range to cross-calibrate against Planck and improve models of radiative transport used in planetary science.
Key words: cosmic background radiation / cosmology: observations / planets and satellites: general
© ESO, 2017
1. Introduction
This paper presents Planck High Frequency Instrument (HFI) measurements of the flux densities of Mars, Jupiter, Saturn, Uranus, and Neptune at mm and sub-mm wavelengths1. The HFI beam does not resolve the planets and thus the flux densities reported here are whole-disc averages. These observations were performed over a 27-month period during the 30-month operational lifetime of the Planck HFI, spanning August 2009 to January 2012. As part of the nominal raster-scan strategy, approximately 20 planet observations were made, each lasting roughly a week.
This paper also reports on Jupiter and Saturn brightness measurements from the Planck Low Frequency Instrument (LFI). For Jupiter, those brightness estimates are based on data accumulated over the entire operational lifetime of Planck LFI, whereas the Saturn brightness estimates are based only on data from the first year of LFI observations. Future analysis of LFI planet flux densities is expected to incorporate all available data.
Observations of the microwave flux density of planets help to inform radiative transfer modelling, which in turn constrains a combination of atmospheric thermal structure, chemical abundances, surface, and subsurface temperature distributions and emissivity properties. Planet observations can also be used to cross-calibrate other experiments with Planck, providing a test of the absolute calibration of both instruments. Importantly, point source flux density reconstruction offers one of the few viable checks on the beam solid angle contained within far sidelobes, since a significant sidelobe contribution dilutes the perceived flux density. Finally, sufficiently precise planet models can be used to bracket the absolute calibration of Planck detectors.
The primary goals of this paper are: (1) to accurately report on the planet flux densities; (2) compare results with existing models and most relevant data sets in order to constrain instrument properties, including absolute calibration; and (3) to quantify the limitations of these measurements.
Planck orbits L2, the Earth-Sun Lagrange point outside Earth’s orbit that has an identical sidereal period. The colocation of the Earth and the Sun on the sky as viewed from L2 make it an optimal location for satellites conducting full-sky surveys. Planck essentially rotated around its symmetry axis at 1 rpm while stepping azimuthally (or in the ecliptic plane) by 2.5′ every hour. This ensured that the satellite’s solar panels were pointed directly at the Sun at all times, therefore, maintaining a stable thermal environment and minimizing stray radiation (Dupac & Tauber 2005). In the time between these azimuthal steps, the satellite would trace out approximately 60 circles on the sky. Additionally, the spin axis precessed with a 7.̊5 amplitude over the duration of a “survey” to cover the poles and smooth out the pixel hits (Tauber et al. 2010). Residual drifts and nutations were minimal and were accounted for in pointing reconstruction (Planck Collaboration I 2011). With this scan strategy, Planck observed the whole sky (including the five planets outside Earth’s orbit) in approximately 6 months per survey.
For a small patch of the sky, it is common to define a Cartesian coordinate system with axis aligned parallel and perpendicular to the primary scan direction of the satellite. In this system, the axes are usually referred to as the co- and cross-scan directions (Planck Collaboration VII 2014). Using this terminology, we can make the following statement regarding Planck’s scan strategy: samples separated in the cross-scan direction by more than 2–3′ will be separated temporally by at least one hour. Therefore, given the size of the Planck beams, all planet observations spanned many hours. Note that the full field of view of the HFI focal plane in the cross-scan direction is just under 4deg.
The absolute calibration of the HFI 100–353 GHz bands is derived from the cosmic microwave background dipole induced by the orbit of the Planck spacecraft around the Sun, and is known to much better than 1%; however as we will see, systematic errors prevent us from reaching this level of precision in some of the planetary flux densities. The calibration of the HFI 545 and 857 GHz channels, on the other hand, uses Uranus and Neptune observations (Planck Collaboration VIII 2016; Bertincourt et al. 2016).
The Second Planck Catalogue of Compact Sources (PCCS2, Planck Collaboration XXVI 2016) describes flux density reconstruction for Galactic and extragalactic objects seen in Planck maps. In the standard HFI processing pipeline, planets and other moving solar system objects are masked from subsequent analysis in the time-ordered data, and therefore do not appear in the sky maps. Of the sources described in the PCCS2, only a handful illuminate the Planck reflectors with flux density that exceeds that of Neptune and Uranus. Mars, Jupiter, and Saturn, on the other hand, are the brightest compact objects observed by Planck, and the two gas giants outshine any PCCS2 object by at least an order of magnitude.
At 143 GHz, the five planets appear in timelines with a signal-to-noise ratio ranging from 3 (Neptune) to 1200 (Jupiter). The average sample density of each observation spans approximately 9–16 samples per arcmin2, with variations caused by a combination of scan strategy and the apparent motion of the planets. Table 1 describes some properties of the planet observations for a single 143-GHz channel. Figure 1 shows a histogram of the 217-GHz flux densities of sources from the PCCS2, as well as our estimates for the flux density of the five planets. From this figure it is clear that the planets offer a unique view of the instrument, allowing us to constrain its temporal, spatial, and frequency response.
 |
Fig. 1 Histogram of the flux density of all 217-GHz PCCS2 sources together with vertical lines indicating the flux of the five planets discussed in this paper. It is clear that at 217 GHz, Mars, Saturn, and especially Jupiter, are much brighter than any of the PCCS2 sources. Here the Mars data point corresponds to best estimates for the 22 December 2011 flux density. The majority of the 217-GHz PCCS2 sources have flux densities in the 0.1–1.0 Jy range. Both axes are logarithmic on this figure. |
This paper is organized as follows. In Sect. 2 we describe the details of the flux density analysis, including statistical and systematic uncertainty estimates. In Sect. 3 we provide results on flux densities for Mars, Jupiter, Saturn, Uranus, and Neptune. We also investigate the contribution of Saturn’s rings to the planet’s total flux density and search for indications of diurnal variations in flux density for both Mars and Uranus. In Sect. 4 we compare the planet flux density results with public results from the Wilkinson Microwave Anisotropy Probe (WMAP) and the Atacama Cosmology Telescope (ACT) and look at the overall agreement between our measurements and model predictions. This section also discusses limits on polarization fraction of the five planets determined using Planck-HFI measurements at 100–353 GHz. We provide our final conclusions in Sect. 5.
2. Planet flux density measurements
Properties of the Planck HFI planet observations specifically for detector 1b at 143 GHz.
In this section, we describe the Planck HFI reconstruction of planet flux densities using a time-domain fit of the scanning-beam shape to the detector response from individual planet crossings. The peak of the reconstructed planet signal is then combined with information about the detector spectral response, planet ephemeris, and beam size to estimate the planet thermodynamic temperature, an intrinsic property of the planet. The detailed description of the algorithm used for the planet flux density analysis that is presented in the following subsections is meant to leave as little room for ambiguity as possible.
According to the International System of Units (SI) and International Astronomical Union (IAU) conventions, radiance has SI derived units W m-2 sr-1. Similarly, spectral radiance has SI derived units W m-2 sr-1 Hz-1 (Thompson & Taylor 1989; Wilkins 1989). The IAU states that flux density, Jy (or 10-26 W m-2 Hz-1), can also be reported in the appropriate context. In this paper, we use flux density to refer to quantities with units W m-2 Hz-1. The flux density of a source is obtained by calculating the product of the solid angle extended by the source on the sky and the spectral radiance of the source.
The planets are often used for calibration and general instrument characterization of cosmic microwave background (CMB) experiments. For example, planet flux densities measured by WMAP are described in Weiland et al. (2011) and Bennett et al. (2013) and those measured by ACT in Hasselfield et al. (2013) and Louis et al. (2014). Many other CMB observatories have also reported, or calibrated against, planet flux densities (e.g., Goldin et al. 1997; Mauskopf et al. 2000; Runyan et al. 2003).
Planck LFI reports on planet brightness and calibration in Planck Collaboration V (2014, 2016). In this paper, we include estimates of Jupiter’s thermodynamic temperatures at LFI frequencies, as reported in Planck Collaboration V (2016). The work presented in that paper does not consider planets other than Jupiter, since the main purpose of that work was to use Jupiter’s high S/N ratio to compare LFI and WMAP absolute calibrations. For Saturn’s thermodynamic temperature at LFI frequencies we use earlier results presented in Planck Collaboration V (2014), but correct them by approximately 10% to account for Saturn’s oblateness, an effect not considered in the LFI analysis. The Saturn results only include data extending through the end of LFI’s first full year of observations (2010), approximately 2.5 full sky surveys. The LFI Saturn brightness estimates will improve with the inclusion of more data. We choose not to use estimates provided in Planck Collaboration V (2014) for Mars, Uranus or Neptune, because of either low S/N (Uranus and Neptune) or systematic effects possibly related to pointing and beam reconstruction (in the case of Mars). Although the preliminary flux density results from LFI are discussed in this new paper, it is important to note that our main emphasis is HFI analysis of planet brightness.
In this paper we use the terms thermodynamic (blackbody) temperature and Rayleigh-Jeans (RJ) temperature, both of which can be used to estimate the effective temperature of a source over some frequency range. There is, however, a significant difference between how these two quantities are used to derive spectral radiance (see Sect. 2.1.1). In radio astronomy, the term brightness temperature is normally used to indicate RJ temperature and this term has also been used to indicate RJ temperature in the context of planet spectral radiance at mm-wavelengths (Page et al. 2003; Weiland et al. 2011; Bennett et al. 2013; Hasselfield et al. 2013). However, some authors use brightness temperature to indicate thermodynamic (blackbody) temperature at mm-wavelengths (Rather et al. 1974; Gibson et al. 2005). We choose not to use the term brightness temperature in this paper to reduce chances of confusion.
2.1. General analysis description
The Planck-HFI scanning beams are derived from a combination of Jupiter and Saturn observations and then extended using a diffraction model where the signal-to-noise ratio is low (Planck Collaboration VII 2016). In this paper, we use the acronym “PSF” (which stands for point spread function) to refer to the Planck-HFI scanning beams. The PSF fit to planet timelines returns a signal peak amplitude, ΔTp, which is used to estimate thermodynamic temperatures and spectral radiance. A PSF-fit method is preferred because the poor sampling in the cross-scan direction for individual planet observations does not allow a straightforward application of aperture photometry. For an experiment like Planck, it is important to distinguish between the so-called optical, scanning, and effective beams. The distinction is made clear in Sect. 1 of Planck Collaboration VII (2014) and also described in the Planck Explanatory Supplement Planck Collaboration (2015).
 |
Fig. 2 Composite diagram showing four planets as viewed from the centre of Earth around the turn of the year 2010; the view from L2 would have been similar. From left to right, the figure shows Uranus, Mars, Saturn, and Jupiter. The planets are drawn on the same scale and the numbers to the right of each planet represent the approxiate apparent diameter (in arcmin) of the planets at this particular epoch. A fraction of a typical 143 GHz beam is shown by the black line and large grey region, the diameter of this circle corresponds to the FWHM of the beam. This suggests that the planets are point sources relative to the spatial response of the instrument. The planet diagrams have been extracted from Showalter (2014). |
In this section, we present a quantitative description of the analysis. Together, the pipeline description and tabulated results allow independent verification of the derived fluxes, up to an accurate estimate of signal peak amplitude, ΔTp, a quantity that we extract from signal timelines. The Planck-HFI scanning-beam solid angles, spectral response, and planet flux density estimates can be accessed on the Planck Legacy Archive (PLA), the Planck Explanatory Supplement, and on servers maintained by the Infrared Processing and Analysis Center (IPAC)2.
2.1.1. Description of PSF fit and function definitions
Within a region centred on the planet crossing, the PSF fit is a time-domain minimization of ![\begin{equation} \chi ^{2}= \sum _{i}\left( s_i - D (\theta _i,\phi _i) -\DeltaT_{\rm p} \left[P (\theta _i,\phi _i) + g_{{\rm NL}} P( \theta _i, \phi _i)^2 \right]\right)^{2}/\sigma_i^{2}, \label{eq:fit} \end{equation}](/articles/aa/full_html/2017/11/aa30311-16/aa30311-16-eq14.png) (1)where D(θ,φ) and P(θ,φ) are functional descriptions of the astrophysical background (everything except the planet) and the Planck-HFI scanning beam, respectively, and si represents the signal timeline, with i indicating the sample index. The scanning beam is assumed to be constant throughout the mission, since no evidence to the contrary has been found.
(1)where D(θ,φ) and P(θ,φ) are functional descriptions of the astrophysical background (everything except the planet) and the Planck-HFI scanning beam, respectively, and si represents the signal timeline, with i indicating the sample index. The scanning beam is assumed to be constant throughout the mission, since no evidence to the contrary has been found.
The signal timelines used here have been processed in the same way as the scanning-beam planet data described in Appendix B of Planck Collaboration VII (2016). The key differences from the main science timelines are a second deglitcher and baseline removal at 60 s intervals in the timelines. Since the satellite scans with one full revolution per minute, the baseline removal corresponds to the removal of a constant offset over the 360deg circle. The term gNL is a nonlinear gain term describing the response of the bolometer, necessary for observations of Jupiter above 217 GHz. We assume that gNL = 0 for all planet observations except Jupiter. The error term 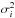 is an estimate of the uncertainty in each time-ordered data sample, derived from the rms of the background-subtracted data more than a degree away from the planet. Because of nonlinearity and possible detector saturation during Jupiter observations, we mask parts of the timelines that fall within some minimum radius to the planet centre. This minimum radius is 10, 8, 5, 5, 5, and 5′ at 100, 143, 217, 353, 545, and 857 GHz, respectively. The fit is performed using the Levenberg-Marquardt algorithm implemented in the scipy package (Jones et al. 2001).
is an estimate of the uncertainty in each time-ordered data sample, derived from the rms of the background-subtracted data more than a degree away from the planet. Because of nonlinearity and possible detector saturation during Jupiter observations, we mask parts of the timelines that fall within some minimum radius to the planet centre. This minimum radius is 10, 8, 5, 5, 5, and 5′ at 100, 143, 217, 353, 545, and 857 GHz, respectively. The fit is performed using the Levenberg-Marquardt algorithm implemented in the scipy package (Jones et al. 2001).
The signal timeline is calibrated in units of KCMB and MJy sr-1 for 100–353 and 545–857 GHz, respectively (Planck Collaboration VIII 2014, 2016). Implicit in these two units, both of which can be related to signal intensity (W m-2), are assumptions about the spectral energy distribution (SED) of the calibration source.
The calibration to units of KCMB, which is derived from comparing to a model of the CMB orbital dipole, assumes an SED for ∂B(ν,T) /∂T | T = TCMB, where ![\begin{equation} B(\nu,T) \equiv \frac{2h\nu ^3}{c^2}\frac{1}{{\rm e}^{h\nu /kT}-1} \qquad\left[ {\rm W\, m^{-2}\,sr^{-1}\,Hz^{-1}} \right] \label{eq:Bnu} \end{equation}](/articles/aa/full_html/2017/11/aa30311-16/aa30311-16-eq27.png) (2)is the Planck blackbody function, h, k, and c represent the Planck and Boltzmann constants and the speed of light in vacuum, respectively, and TCMB ≡ 2.7255 K is the temperature of the CMB monopole (Fixsen et al. 1994; Fixsen 2009). In this paper, we refer to the parameter T as thermodynamic temperature. Thermodynamic temperature should be distinguished from Rayleigh-Jeans temperature, TRJ, which can also be used to calculate spectral radiance through the equation
(2)is the Planck blackbody function, h, k, and c represent the Planck and Boltzmann constants and the speed of light in vacuum, respectively, and TCMB ≡ 2.7255 K is the temperature of the CMB monopole (Fixsen et al. 1994; Fixsen 2009). In this paper, we refer to the parameter T as thermodynamic temperature. Thermodynamic temperature should be distinguished from Rayleigh-Jeans temperature, TRJ, which can also be used to calculate spectral radiance through the equation ![\begin{equation} \tilde{B}(\nu,T_{\rm RJ}) \equiv \frac{2k\nu ^2}{c^2} T_{\rm RJ}, \qquad\left[ {\rm W\, m^{-2}\,sr^{-1}\,Hz^{-1}} \right]. \label{eq:Brj} \end{equation}](/articles/aa/full_html/2017/11/aa30311-16/aa30311-16-eq34.png) (3)The partial temperature derivative of the Planck blackbody function is
(3)The partial temperature derivative of the Planck blackbody function is 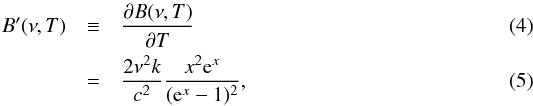 where x ≡ hν/kT and we define
where x ≡ hν/kT and we define 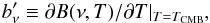 (6)for consistency with Planck Collaboration VI (2014) and Planck Collaboration IX (2014). Spectral radiance (in units of W m-2 sr-1 Hz-1) can be obtained by calculating the product
(6)for consistency with Planck Collaboration VI (2014) and Planck Collaboration IX (2014). Spectral radiance (in units of W m-2 sr-1 Hz-1) can be obtained by calculating the product 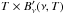 , where T is the perceived source temperature relative to a TCMB blackbody. Section 2.1.4 gives the expression that can be used to convert between KCMB and W m-2 sr-1.
, where T is the perceived source temperature relative to a TCMB blackbody. Section 2.1.4 gives the expression that can be used to convert between KCMB and W m-2 sr-1.
The 545- and 857-GHz frequency bands were calibrated against models of Uranus and Neptune thermodynamic temperature (Planck Collaboration VIII 2016; Bertincourt et al. 2016). The calibration adapted a reference in which the spectral radiance of a fiducial source, S(ν), follows νS(ν) = constant (discussed further in Sect. 2.1.4). This particular approach to calibration of the sub-mm bands was chosen to be analogous to that of the SPIRE instrument on the Herschel satellite (Bendo et al. 2013; Swinyard et al. 2014).
The 545- and 857-GHz beams are multi-moded in order to increase the throughput, and therefore increase the signal-to-noise ratio of those detectors at the cost of limiting the resolution (Murphy et al. 2002, 2010). Neither scan strategy nor sample rate justify finer resolution at those frequencies. Unfortunately, the multi-moded nature of the sub-mm beams seriously complicates any analytical description of their spatial response (Murphy & Padman 1991). In particular, a function basis with a Gaussian envelope does not easily capture the main-beam shape.
As part of the PSF fit to the planet timelines, we subtract best estimates for the astrophysical background, D(θ,φ). Depending on the frequency, this background can have contributions from the CMB, dust, as well as synchrotron, and other Galactic emission (Planck Collaboration X 2016). The background estimate is derived from a bilinear interpolation of the 2015 release maps at each frequency.
In the following analysis, it is assumed that the correction, gNL, captures, to first order, the large signal nonlinearity of the bolometers. Due to the wide dynamic range of the devices, this correction is only significant for observations of Jupiter at frequencies above 217 GHz; the gNL correction is therefore only applied for these observations. The validity of this correction is corroborated by a significant improvement in fit quality for these observations.
We note that the ADC nonlinearity correction, which is discussed in detail in Planck Collaboration VII (2016) and Planck Collaboration VIII (2016), and required due to the limited range of the sampling of the ADC, is applied to all detector timelines and across all HFI frequency bands used in this analysis. This ADC correction reduces time variation in the gain down to the 2 × 10-3 level (Planck Collaboration Int. XLVI 2016). After implementing this correction, we assume that the calibration is constant in time.
2.1.2. Calibration of sub-mm channels
Calibration of the sub-mm channels uses the planet time-ordered-data processed for beam reconstruction in the 2015 public data release (Planck Collaboration VII 2016)3 which adds an improved planet timeline despiking algorithm and baseline drift removal compared to that used in Bertincourt et al. (2016) and Planck Collaboration VIII (2016)4. Because of this, and due to differences in algorithms, the 545- and 857-GHz flux density for Uranus and Neptune described in this paper is not expected to agree perfectly with model predictions (see Sect. 3.4). However, large discrepancies between the results presented here and the results found in Planck Collaboration VIII (2016) would hint at poorly understood errors (and are not seen).
2.1.3. Signal estimates
The maximum planet signal amplitude, ΔTp, is influenced by a number of instrument and source-specific properties. Assuming an infinitely fast time response, a detector observing a point-like blackbody head-on should measure a background-removed signal, si, according to (Kraus 1950; Page et al. 2003) ![\begin{eqnarray} s_i &=& \iint \d\Omega\d\nu \tau^{\prime}(\nu) P(\theta_i,\phi_i) A_{\rm eff} (\nu) B (\nu,T) \nonumber\\ &=& \frac{c^{2}}{\Omega _{\rm b}} \iint \d\Omega\d\nu N \tau^{\prime}(\nu) P (\theta_i,\phi_i) B(\nu,T) / \nu^{2}\nonumber\\ &{ \approx}& \frac{\Omega_{{\rm p},i}}{\Omega _{\rm b}}\int {\rm d}\nu \tau (\nu) B (\nu,T) \qquad \left[ {\rm W\, m^{-2}\,sr^{-1}} \right]. \label{eq:P} \end{eqnarray}](/articles/aa/full_html/2017/11/aa30311-16/aa30311-16-eq47.png) (7)Here τ(ν) is the étendue-normalized detector spectral response function (SRF), (Pajot et al. 2010; Ade et al. 2010; Planck Collaboration IX 2014), P(θ,φ) is the instrument scanning beam, normalized to unity at its peak, Ωp,i is the time-varying planetary solid angle as seen by the detector, and Ωb is the scanning-beam solid angle, Ωb = ∫dΩP(θ,φ). The first and second integrals are over solid angle covered by the planet disc and over frequency, respectively. The above derivation adopts the well known relationship between effective telescope area, number of radiation modes, frequency, and beam solid angle, namely Aeff(ν) = Nc2/ (ν2Ωb) (Hudson 1974; Hodara & Slemon 1984). We note that in cases where the number of radiation modes, N, is not identically equal to unity, Aeff(ν) can be a strong function of frequency. Finally, the SRF incorporates the detector throughput, such that
(7)Here τ(ν) is the étendue-normalized detector spectral response function (SRF), (Pajot et al. 2010; Ade et al. 2010; Planck Collaboration IX 2014), P(θ,φ) is the instrument scanning beam, normalized to unity at its peak, Ωp,i is the time-varying planetary solid angle as seen by the detector, and Ωb is the scanning-beam solid angle, Ωb = ∫dΩP(θ,φ). The first and second integrals are over solid angle covered by the planet disc and over frequency, respectively. The above derivation adopts the well known relationship between effective telescope area, number of radiation modes, frequency, and beam solid angle, namely Aeff(ν) = Nc2/ (ν2Ωb) (Hudson 1974; Hodara & Slemon 1984). We note that in cases where the number of radiation modes, N, is not identically equal to unity, Aeff(ν) can be a strong function of frequency. Finally, the SRF incorporates the detector throughput, such that 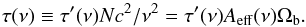 (8)The last step of the derivation presented in Eq. (7) is obtained by assuming that P(θ,φ) ≃ 1 over the planet disc area so that the integral over solid angle simply yields Ωp5. This is a good approximation for all planets observed by Planck, with the exception of Jupiter (see Fig. 2). We do not make this simplifying correction when estimating planet brightness, instead we implement the full integral over the planet area. The ratio Ωp/ Ωb is the beam correction factor often discussed in relation to flux estimates (Ulich & Haas 1976; Griffin et al. 2013; Swinyard et al. 2014). Finally, we note that the signal amplitude obtained from viewing the planet off axis relative to the peak scanning-beam amplitude is simply the peak signal amplitude scaled by the relative change in scanning-beam response, P(θ,φ) /P(0,0), where P(0,0) = 1 is the normalized peak response of the scanning beam and P(θ,φ) is the off-axis response. Equation (7) can be modified to incorporate the nonlinearity correction, gNL, by replacing P(θi,φi) with P(θi,φi) + gNLP(θi,φi)2.
(8)The last step of the derivation presented in Eq. (7) is obtained by assuming that P(θ,φ) ≃ 1 over the planet disc area so that the integral over solid angle simply yields Ωp5. This is a good approximation for all planets observed by Planck, with the exception of Jupiter (see Fig. 2). We do not make this simplifying correction when estimating planet brightness, instead we implement the full integral over the planet area. The ratio Ωp/ Ωb is the beam correction factor often discussed in relation to flux estimates (Ulich & Haas 1976; Griffin et al. 2013; Swinyard et al. 2014). Finally, we note that the signal amplitude obtained from viewing the planet off axis relative to the peak scanning-beam amplitude is simply the peak signal amplitude scaled by the relative change in scanning-beam response, P(θ,φ) /P(0,0), where P(0,0) = 1 is the normalized peak response of the scanning beam and P(θ,φ) is the off-axis response. Equation (7) can be modified to incorporate the nonlinearity correction, gNL, by replacing P(θi,φi) with P(θi,φi) + gNLP(θi,φi)2.
In deriving Eq. (7), we made the simplifying assumption that the beam response P(θ,φ), and therefore beam solid angle, Ωb, would not vary with frequency. This is certainly incorrect (see e.g., Maffei et al. 2010). However, as the Planck HFI scanning beam is calibrated using a combination of Jupiter and Saturn observations, whose SED closely resembles that of the Rayleigh-Jeans spectrum, it is reasonable to assume that the estimated scanning-beam solid angle, Ωb, properly represents a beam solid angle with frequency weighting appropriate for analysis of planet brightness (see Planck Collaboration VII 2016, for a discussion of beam colour corrections).
So far, our notation has adopted a source thermodynamic temperature, T, that is frequency independent. However, models of planet thermodynamic temperature show significant variation over a typical 30% frequency bandwidth of a Planck-HFI detector (Planck Collaboration IX 2014). To remedy this, we can allow the source thermodynamic temperature to be frequency-dependent. We define the frequency dependent thermodynamic temperature as the temperature T(ν) that is required to describe the source spectral radiance (defined by the Planck blackbody function): ![\begin{equation} B (\nu,T(\nu)) = \frac{2h\nu ^3}{c^2}\frac{1}{{\rm e}^{h\nu /kT(\nu)}-1} \qquad\left[ {\rm W\, m^{-2}\,sr^{-1}\,Hz^{-1}} \right]. \label{eq:brightness_temperature} \end{equation}](/articles/aa/full_html/2017/11/aa30311-16/aa30311-16-eq65.png) (9)In this paper, we choose to report monochromatic thermodynamic temperatures at a standard reference frequency, νc, where νc ∈ {100, 143, 217, 353, 545, 857} GHz. A colour correction is required to report the thermodynamic temperature at these reference frequencies (see Sect. 2.1.4).
(9)In this paper, we choose to report monochromatic thermodynamic temperatures at a standard reference frequency, νc, where νc ∈ {100, 143, 217, 353, 545, 857} GHz. A colour correction is required to report the thermodynamic temperature at these reference frequencies (see Sect. 2.1.4).
An estimate for the CMB monopole has already been subtracted from the Planck HFI timelines. As the planets block the CMB monopole, this signal subtraction will lead to an underestimate for the absolute brightness of the planets (see e.g., Page et al. 2003). This will cause an approximately 1 K bias in thermodynamic temperature estimates at 100 GHz and successively lower bias at higher frequencies. We choose to report thermodynamic temperature before correcting for this effect, since this simplifies comparison with Weiland et al. (2011). The absolute thermodynamic temperature Tabs can be calculated from the uncorrected thermodynamic temperatures, T, by solving the following transcendental equation 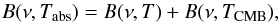 (10)where B represents Planck’s blackbody function and TCMB = 2.7255 K. We note that thermodynamic temperatures reported in this paper correspond to T, not Tabs. We also note that the sum of two blackbody functions is not a blackbody function.
(10)where B represents Planck’s blackbody function and TCMB = 2.7255 K. We note that thermodynamic temperatures reported in this paper correspond to T, not Tabs. We also note that the sum of two blackbody functions is not a blackbody function.
The solid angle of the projected oblate spheroid face of each planet is derived as 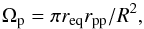 (11)where req is the equatorial radius of the planet, rpp is the projected polar radius of the planet, and R is the distance between the Planck spacecraft and the planet. The projected polar radius is given by:
(11)where req is the equatorial radius of the planet, rpp is the projected polar radius of the planet, and R is the distance between the Planck spacecraft and the planet. The projected polar radius is given by: 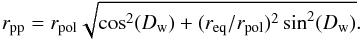 (12)Here Dw is the latitude of the planet coordinate system relative to Planck (needed for this projection) and rpol is the true polar radius of the planet.
(12)Here Dw is the latitude of the planet coordinate system relative to Planck (needed for this projection) and rpol is the true polar radius of the planet.
For a given detector, a single planet observation spans a few hours, during which the planet solid angle can vary by a non-negligible amount. Additionally, in the case of Mars, the observed thermodynamic temperature distribution varies with time, both on diurnal (Mars rotation) and seasonal timescales (see Sect. 3.1). Variations in planet disc size are accounted for by dividing the signal amplitude with an estimate of time-variations in the planet solid angle 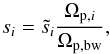 (13)where
(13)where 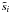 is the uncorrected signal timeline, Ωp,i is an estimate for the planet solid angle at time i, and Ωp,bw is an estimate for the planet solid angle at the beam-weighted average time of observation. Due to proximity, this effect is largest for Mars, with the planet solid angle changing by up to 0.07% in an hour. We implement this correction in our analysis. For Mars, it can also be important to account for time-varying albedo by calculating
is the uncorrected signal timeline, Ωp,i is an estimate for the planet solid angle at time i, and Ωp,bw is an estimate for the planet solid angle at the beam-weighted average time of observation. Due to proximity, this effect is largest for Mars, with the planet solid angle changing by up to 0.07% in an hour. We implement this correction in our analysis. For Mars, it can also be important to account for time-varying albedo by calculating 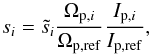 (14)where Ωp,ref and Ip,ref are, respectively, the predicted planet solid angle and flux density at a fixed reference time, and Ωp,i and Ip,i are the corresponding time-varying model predictions. We will provide results with and without this additional percent-level correction (see Sect. 3.1). However, all Mars brightness measurements discussed in this paper include this correction.
(14)where Ωp,ref and Ip,ref are, respectively, the predicted planet solid angle and flux density at a fixed reference time, and Ωp,i and Ip,i are the corresponding time-varying model predictions. We will provide results with and without this additional percent-level correction (see Sect. 3.1). However, all Mars brightness measurements discussed in this paper include this correction.
2.1.4. Unit and colour conversion
Unit conversion can be obtained by combining estimates for spectral response, τ(ν), with assumptions about the signal spectral energy distribution (see Planck Collaboration IX 2014, for a general discussion of unit conversions). The unit conversion factor, UC, that can be used to convert from the SI-unit for radiance W m-2 sr-1 to units of KCMB is ![\begin{equation} U_{\rm C} \equiv \int \d\nu \tau(\nu) b_\nu^{\prime} \qquad \left[ {\rm W\, m^{-2}\,sr^{-1}}\,{\rm K_{CMB}^{-1}} \right], \end{equation}](/articles/aa/full_html/2017/11/aa30311-16/aa30311-16-eq95.png) (15)where we have used the
(15)where we have used the  definition from Eq. (6). We can use this to convert our estimate for the KCMB peak signal amplitude, ΔTp, to the corresponding peak in radiance:
definition from Eq. (6). We can use this to convert our estimate for the KCMB peak signal amplitude, ΔTp, to the corresponding peak in radiance: ![\begin{equation} \Delta L_{\rm p} = U_{\rm C} \Delta T_{\rm p} \qquad \left[ {\rm W\, m^{-2}\,sr^{-1}} \right]. \label{eq:uc} \end{equation}](/articles/aa/full_html/2017/11/aa30311-16/aa30311-16-eq97.png) (16)We use colour corrections so that we can report flux density or spectral radiance, Sc, at a particular reference frequency, νc. The colour correction incorporates the spectral response function of the detector in question as well as an assumption about the spectral energy distribution of the source. Assuming Mp(ν) is a model that accurately represents the spectral radiance of a planet at any frequency, the spectral radiance at a standard reference frequency is
(16)We use colour corrections so that we can report flux density or spectral radiance, Sc, at a particular reference frequency, νc. The colour correction incorporates the spectral response function of the detector in question as well as an assumption about the spectral energy distribution of the source. Assuming Mp(ν) is a model that accurately represents the spectral radiance of a planet at any frequency, the spectral radiance at a standard reference frequency is 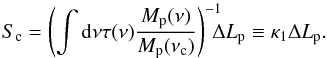 (17)Despite being calibrated on Uranus and Neptune, this type of correction is also necessary for the 545 and 857 GHz bands, since the official calibration included a colour correction appropriate for a flat spectrum. However, because the 545 and 857 GHz bands implemented a calibration that differs from the rest of the Planck-HFI bands, an additional correction is required
(17)Despite being calibrated on Uranus and Neptune, this type of correction is also necessary for the 545 and 857 GHz bands, since the official calibration included a colour correction appropriate for a flat spectrum. However, because the 545 and 857 GHz bands implemented a calibration that differs from the rest of the Planck-HFI bands, an additional correction is required 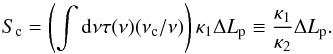 (18)The band-average values for the colour correction described here are shown in Table 2.
(18)The band-average values for the colour correction described here are shown in Table 2.
Because of our non-negligible detector bandpass, estimates of planet spectral radiance, flux density, or thermodynamic temperature at a particular frequency are model dependent. Since we focus on comparing our flux density estimates with ESA model predictions, we report planet thermodynamic temperatures that can include some deviations from a perfect Rayleigh-Jeans like spectrum (Sects. 3.1–3.4 describe models that are used for calculating these colour corrections). Other experiments, however, including WMAP and ACT (Weiland et al. 2011; Hasselfield et al. 2013), report an intrinsic temperature assuming that the planets SED can be approximated with a Rayleigh-Jeans-like spectrum. This essentially means that Mp(ν) ∝ ν2 is imposed in their estimates of planet temperature. Because no statement is made to the contrary, we also conclude that WMAP and ACT assume a fixed RJ temperature across the bandpass. When comparing our results with measurements from WMAP and ACT, we make sure to account for this discrepancy (see Sect. 4.2). This approximation, although quite valid in the high-temperature or low-frequency limit, can for example induce a 1% shift in the estimated flux density at 217 GHz for some of the colder planets.
2.1.5. Summary of adopted methods
For each planet observation we estimate the peak amplitude ΔTp by minimizing the residual in Eq. (1). We then use derivations from Sects. 2.1.3–2.1.4 to express ΔTp in terms of instrument properties as well as planet thermodynamic temperature and size.
 |
Fig. 3 Relative amplitude in derived flux density from observations of Jupiter, Saturn, and Mars at 100–353 GHz (Mars is limited by statistical error at 100 GHz). The flux density has been normalized to the band-mean. A clear correlation in relative flux amplitudes between planet observation periods is seen. Lines are used to guide the eye between flux values within a planet observation. For the top panel (100 GHz), the average standard deviation of the data is approximately 0.4%. |
For the 100–353 GHz bands, we can now combine Eqs. (7), (16), and (17) to write 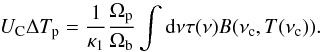 (19)No unit conversion is required for the 545 and 857 GHz bands, and the expression becomes
(19)No unit conversion is required for the 545 and 857 GHz bands, and the expression becomes 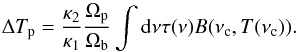 (20)Equations (19) and (20) allow us to estimate the planet thermodynamic temperature at a standard reference frequency, T(νc), by solving these transcendental equations. The corresponding flux density, Ip, can then be found by calculating
(20)Equations (19) and (20) allow us to estimate the planet thermodynamic temperature at a standard reference frequency, T(νc), by solving these transcendental equations. The corresponding flux density, Ip, can then be found by calculating ![\begin{equation} I_{\rm p} = \Omega _{\rm p} B (\nu _{\rm c},T(\nu _{\rm c})) \qquad \left[{\rm W\, m^{-2}\,Hz^{-1}} \right]. \label{eq:flux_eq} \end{equation}](/articles/aa/full_html/2017/11/aa30311-16/aa30311-16-eq108.png) (21)
(21)
2.2. Comparison with other fit methods
The determination of the peak signal amplitude, ΔTp, is based on a least squares fit to the data (see Eq. (1)). This method of determining the maximum likelihood value for the peak signal is by no means unique (see for example the algorithm described in Planck Collaboration VIII 2016).
We have compared our results with a Gauss-Hermite (GH) reconstruction of the peak amplitude and found that the two methods agree quite well on average. Descriptions of the Gauss-Hermite reconstruction method can be found for example in Hill et al. (2009), Huffenberger et al. (2010), Monsalve (2010). Even with the elliptical Gaussian base parameters of the Gauss-Hermite functions fixed, the functions offer a versatile basis for deconstructing the signal independently of the PSF definition. Unfortunately, simulations have shown that a Gauss-Hermite reconstruction of the multi-moded sub-mm beam responses is significantly biased. We therefore limit the comparison between flux density estimates from PSF and GH peak reconstruction to 100–353 GHz.
After decomposing the Gauss-Hermite coefficients in the time-domain, a map of the planet is reconstructed at an arbitrarily high resolution to produce an estimate for ΔTp,GH. We compare the ratio of the nominal peak amplitude estimate and the one derived using the GH decomposition, rpeak = ΔTp/ ΔTp,GH, over 100–353 GHz for all planet observations and find that the distribution has a mean and standard deviation of μr = 1.0000 and σr = 0.0056, respectively. Limiting that statistic to Mars, Jupiter, and Saturn, where the peak determination is not significantly affected by statistical noise, the mean and standard deviation of the distribution is 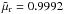 and
and 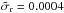 , respectively. Since all planet flux density estimates are derived from ΔTp, we take this as evidence that the analysis does not suffer from significant representation bias.
, respectively. Since all planet flux density estimates are derived from ΔTp, we take this as evidence that the analysis does not suffer from significant representation bias.
2.3. Statistical error estimates
The Planck-HFI planet flux estimates are affected by a number of telescope and detector properties, including spectral response, beam solid angle, and absolute calibration. Known error sources and their estimated amplitudes are described below. All estimates of statistical error are input into a simple Monte Carlo routine that propagates these errors through to a determination of the planet thermodynamic temperatures and flux densities. These statistical errors are then combined with estimates for systematic errors (see Sect. 2.4).
 |
Fig. 4 Maps of the normalized and background-subtracted timeline residuals, (si − D(θi,φi) − ΔTpP(θi,φi)) / ΔTp, combining all available observations and detectors within a frequency band. The number shown in the top left corner of each panel represents the extent of the colour scale, e.g., a value of 0.01 means that the darkest colour corresponds to a 0.01 deviation from the peak response ΔTp, with red (blue) corresponding to positive (negative) deviation. For Jupiter, we present two versions of the same plot. In one of the two versions, we have masked out the centres of the Jupiter observations, since nonlinearity and saturation lead to a large residual, especially at high frequencies. Each panel is 30′× 30′, and the co-scan direction is vertical on these plots (see discussion in Sect. 1). |
Band-average planet thermodynamic temperature, T, as measured by Planck LFI and reported in Planck Collaboration V (2014, 2016).
Band-average planet thermodynamic temperature and corresponding statistical uncertainty as measured by Planck HFI (survey 1–5).
2.3.1. Planet solid angle
The planet solid angles, Ωp, are estimated from the JPL ephemerides software (HORIZONS 2014) and subsequently corrected for planet oblateness (see Sect. 2.1.3). The signal timestream is used to estimate the time at which each channel is centred on the planet. This corresponds to the time at which the peak signal is observed. Due to the raster-like scan-strategy of the Planck satellite, a centred observation lasts for approximately one hour. Over this time, the solid angle extended by Mars as seen from L2 can change by up to 0.07%. We account for this variation in our analysis (see Sect. 2.1.3). For the error analysis, we conservatively assume a constant ΔΩp = 0.05% fractional error in the planet solid angle estimate; this is conservative because JPL ephemerides are known with much greater accuracy. This source of error is likely negligible compared to other contributions.
2.3.2. Absolute calibration and beam solid angle
For detectors in the 100–353 GHz bands, the absolute calibration is based on a fit to the orbital dipole of the CMB. For the 545 and 857 GHz bands, however, the absolute calibration is referenced to ESA models of Uranus and Neptune thermodynamic temperature (see discussion in Sect. 2.1). The absolute calibration of the instrument is described in detail in Planck Collaboration VII (2016). The band-average statistical calibration error is found to be 0.09, 0.07, 0.16, 0.78, 1.1, and 1.4% at 100, 143, 217, 353, 545, and 857 GHz, respectively. For the 545 and 857 GHz bands, an additional 5% systematic calibration error is attributed to the planet flux models.
 |
Fig. 5 Normalized single-detector statistical and systematic uncertainties for Mars, Jupiter, Saturn, and Uranus at all six Planck-HFI frequencies. The first six rows show the relative contribution of the different error terms described in Sects. 2.3 and 2.4. From top to bottom, these six rows describe uncertainties related to: detector noise and astrophysical confusion; scanning-beam solid angle; planet-disc solid angle; absolute calibration; spectral response function; and an unknown systematic term described in Sect. 2.4. The sum of the first six rows equals unity, but when combining errors, different terms are summed in quadrature. The last two rows show the total statistical uncertainty (in percent) and the total uncertainty in flux determination (in percent) appropriate for band-average flux density calculations, respectively. The total uncertainty is obtained by summing the total statistical and the total systematic uncertainties in quadrature. Finally, we note that statistical uncertainties (the first five rows) average down when we calculate band-averaged flux density estimates. |
The absolute calibration of the sub-mm bands was recently discussed in Planck Collaboration Int. XLVI (2016). This paper states that the 545 GHz planet model calibrations have been compared with the absolute calibration obtained from observing the solar dipole and the first two peaks in the CMB angular power spectrum and that this analysis suggests 1.5% agreement between the two calibration methods. Furthermore, the paper shows that the planet calibration agrees with the CMB calibration at the 1.5 and 2.5% level for the 545 and 857 GHz bands, respectively. That analysis provides a crucial link between the CMB power and planet model predictions.
The cross-calibration of Planck HFI and the SPIRE instrument on Herschel is discussed in Bertincourt et al. (2016). The relative calibration between SPIRE and Planck-HFI is found to be 1.045 ± 0.0085 and 1.000 ± 0.0080 at 545 and 857 GHz, respectively.
Errors in determination of the scanning-beam solid angle, Ωb, are determined from Monte Carlo simulations of the hybrid B-spline beam. The band-average fractional scanning-beam errors are found to be 0.13, 0.07, 0.13, 0.09, 0.08, and 0.08% at 100, 143, 217, 353, 545, and 857 GHz, respectively (Planck Collaboration VI 2016).
2.3.3. Spectral bandpass
The spectral bandpass of the entire HFI focal plane was estimated using a Fourier-transform spectrometer at Institut d’Astrophysique Spatiale (IAS) laboratory in Orsay, France (Planck Collaboration IX 2014). By combining data from roughly 100 interferograms, those measurements obtained sub-percent accuracy at a resolution of approximately 0.5 GHz. With these per-frequency-bin spectral response measurements, Monte Carlo simulations can be used to obtain statistical errors in the derivation of unit or colour corrections. To perform these simulations, for each realization and frequency bin, the spectral response is modified by a Gaussian random variate before integrating over the spectral bandpass.
2.4. Systematic uncertainties
The uncertainties described above are largely expected to be random and uncorrelated. However, intra-frequency correlations display clear signs of systematic errors. Figure 3 shows the relative amplitude of Mars, Jupiter, and Saturn derived from individual detectors within the 100–353 GHz bands. The 545 and 857 GHz intra-frequency correlations are omitted from Fig. 3; these can be reconstructed using the data accompanying this paper. If the flux determination was dominated by random uncorrelated errors, the relative planet flux densities would not be correlated between individual observations. Instead, a clear and repeatable pattern is observed for most planet observations shown.
Such a systematic effect could be caused by a number of sources, including an error in absolute calibration or scanning-beam solid angle. For the 100–353 GHz bands, a pure calibration error is ruled out as the sole cause of this effect by a number of intra-calibration checks (see discussion in Planck Collaboration VIII 2016). Simulations of beam reconstruction suggest that the scanning beams are determined with high fidelity (Planck Collaboration VII 2016). From arguments presented in these papers, we are confident that a pure beam- or calibration-related systematic cannot be the sole cause of this effect.
The significant temporal separation between planet observations also suggests that the systematic effect is stable in time, which argues against ADC nonlinearity (see Planck Collaboration VII 2016, for more discussion on ADC nonlinearity) as well as Galactic sidelobe pickup. It is peculiar, however, to see that at 217 and 353 GHz, the in-band correlation for Jupiter is somewhat different than that of Mars or Saturn. This might hint at an inadequate determination of spectral response. Other possible contributions to this systematic effect include, but are not limited to: transfer function deconvolution residuals causing a mismatch in dipole and point source calibration; dynamical nonlinearity; beam effects; and calibration errors. It is interesting to see a similar effect in the Planck-LFI observations of Jupiter (see e.g., Fig. 16 in Planck Collaboration V 2016). This might hint at a common cause of this systematic effect for both LFI and HFI.
We have tried to probe this effect by looking at differences in the relative scaling of detectors as a function of source SED. This can be done by comparing the in-band variations derived from the relatively thermal spectrum of the planets (S ∝ νβ with β ≈ 2) to that which is obtained by looking at objects in the PCCS2 that have a softer spectrum (β< 2). This procedure has provided some limits on the amplitude of this effect, but results are not conclusive enough to warrant a correction.
Figure 4 shows maps of the normalized and background subtracted timeline residuals, (si − D(θi,φi) − ΔTpP(θi,φi)) / ΔTp, for each planet and frequency band. These maps help quantify any discrepancy between the PSF fit and the raw data, since any residual amplitude that is not consistent with noise hints at a systematic difference. From these results it is clear that the Uranus and Neptune observations are noise-limited, except possibly at 545 and 857 GHz, whereas low-amplitude structure is apparent at all frequencies in residual maps for the other three planets. The relatively low amplitude of the residuals, however, suggests that the fits are accurate at the sub-percent level. The systematic effect that is shown in Fig. 3 is not evident from the residual maps in Fig. 4.
This systematic effect is comparable in amplitude to the combined statistical uncertainties described in the preceding sections. In view of our lack of understanding of the distribution of systematic errors, we are compelled to assign a systematic uncertainty corresponding to the standard deviation of the in-band variation. As an example, for Jupiter and Saturn, the mean standard deviation of the relative amplitude difference within the 100 GHz band is observed to be 0.42%. We implement this value as an estimate for the 1σ systematic uncertainty. Using this method, the systematic uncertainty that we assign to each determination of ΔTp is 0.42, 0.54, 0.63, 0.76, 1.93, and 3.08% for detectors in the six HFI frequency bands 100, 143, 217, 353, 545, and 857 GHz, respectively. This uncertainty is shown in the last column of Table 4.
Although we have found in this work an apparent systematic effect in the determination of point source brightness, there is no reason to suspect that this effect propagates to analysis pertaining to the CMB. This is because of Planck’s use of the orbital dipole for calibrating the channels used for analysis of the CMB signals (Planck Collaboration VIII 2016). Based on the analysis presented in this paper, however, we believe that the calibration of compact sources in the 100–353 GHz frequency bands needs to incorporate a fractional systematic error of about 0.4–3.1%.
2.5. Combined error budget
Figure 5 shows the relative contributions of different statistical and systematic uncertainties to the total error budget of a single detector within a given band. Apart from the systematic uncertainties described in Sect. 2.3, all error terms are assumed to be statistical. These terms therefore average down when we calculate band-averaged quantities. Figure 5 also shows the fractional (as percentages) total uncertainty contributions to flux density. It is clear that for all planets, flux density estimates at high frequencies (545 and 857 GHz) are limited by the systematic uncertainties. Detector noise and background confusion only limit flux density estimates of Uranus and Neptune and only at 100 and 143 GHz. From the figure it is also clear that uncertainties on scanning-beam solid angle and planet disc size are negligible compared to other error terms, whereas uncertainty in absolute calibration becomes relevant at frequencies above 217 GHz.
3. Planet flux density results
We now describe the general planet flux and thermodynamic temperature results and compare them with existing models. Tables 3 and 4 highlight the main results of this paper. The LFI measurements are referenced to 28.4, 44.1, and 70.4 GHz (Planck Collaboration V 2014, 2016). For Planck HFI, the average bandwidths used to derive these measurements are 32.9, 45.8, 64.5, 101, 171, and 246 GHz at 100, 143, 217, 353, 545, and 857 GHz, respectively (Planck Collaboration IX 2014).
 |
Fig. 6 Estimates of the thermodynamic temperature of Mars compared to a model for diurnal variations. The panel columns correspond to the first two Mars observations while the rows represent estimates at 100, 143, and 217 GHz. The model output has been scaled by ζP = 0.982 (dashed line) and a variable best-fit scale (solid line), which is annotated in each panel. The horizontal axis shows time relative to the mean observation time for that frequency band. Error bars show systematic and statistical uncertainties summed in quadrature. |
 |
Fig. 7 Measured thermodynamic temperature for the three Planck HFI observations of Mars. Black points represent band averages and corresponding error estimates. The thermodynamic temperature predictions of the Lellouch & Amri (2008) model (solid lines), scaled by ζP = 0.982, and the corresponding 5% absolute errors (coloured regions) are also shown. Both data and model results presented in this figure have been scaled to correspond to a single reference time (see discussion in Sect. 3.1). The grey region is meant to remind the reader that the sub-mm bands are calibrated on models of Uranus and Neptune brightness (see Sect. 2.1.2). The absolute thermodynamic temperature of Mars can be obtained by adding the spectral radiance from an occulted CMB monopole (see Sect. 2.1.3). |
The ESA planet brightness models that are mentioned in the following sections have been used for calibration of a number of astronomy experiments operating in the microwave range to the near-infrared. We reference publicly available discussions of these models as they are mentioned in the text (see Sects. 3.2–3.4). Digits following the “ESA” designation are used to indicate model revision numbers. Band-averages are calculated with uniform detector weights.
3.1. Mars
The Martian orbital period corresponds to 687 Earth days and the planet spins around its axis approximately once every 24.6 h (HORIZONS 2014). The 25.̊2 axial tilt is comparable to Earth’s 23.̊4 value, but the relatively large orbital eccentricity makes the southern hemisphere experience greater seasonal variations. The perceived thermodynamic temperature is highly dependent on viewing location, since the Martian surface is far from homogeneous. Finally, dynamical factors such as dust storms can also affect the planet’s surface temperature (Zurek 1982).
A number of models predicting Mars thermodynamic temperature exist (e.g., Golden 1979; Rudy et al. 1987). We have primarily considered the models of Lellouch & Amri (2008) and Weiland et al. (2011). The Lellouch and Amri model uses surface and subsurface temperatures taken from the European Martian General Circulation Model (Forget et al. 1999; Millour et al. 2015) and Martian ephemerides from IMCCE6. A standard dust scenario (“Climatology”) is used. For each user-provided date, the model first computes the aspect of Mars. The disc is then split on a 100 × 100 grid, each of them having its own latitude, longitude, and local time. On each point of the grid, the usual radiative transfer equation (e.g., Eq. (5) of Rudy et al. 1987) is used. Radiative transfer in the surface and subsurface includes an absorption coefficient corresponding to a radio absorption length equal to 12 times the wavelength. In addition, the thermal emission of the surface includes an emissivity term, calculated from a Fresnel reflection model with a dielectric constant of 2.25 and for the relevant emission angle. The latter is calculated taking into account a surface roughness of 12deg. Local fluxes calculated in this manner are finally convolved with a Gaussian beam to obtain beam-averaged fluxes and the corresponding Planck thermodynamic temperature.
The Weiland model is an alternative version of a model that was originally constructed by Edward Wright (Wright 2007; Weiland et al. 2011). This updated version was used by the WMAP team and incorporates L2 viewing angles, as well as extending the spectral coverage down to WMAP frequencies.
Parameters used in the fit to a ring system model of Saturn.
The radio and microwave brightness of Mars has been estimated by a number of experiments. The following papers discuss the brightness of the planet, either as an absolute measurement or one that is relative to another planet or a model: Wright (1976), Rather et al. (1974), Rudy et al. (1987), Muhleman & Berge (1991), Goldin et al. (1997), Sidher et al. (2000), Runyan et al. (2003), Swinyard et al. (2010), Perley & Butler (2013), and Müller et al. (2016). The polarization properties of Mars are described in Perley & Butler (2013).
Because of Planck’s scan strategy, detectors on the HFI focal plane observe a fixed point on the sky over the span of a week. Using the Lellouch & Amri (2008) model for comparison, we appear to detect rotational variations in Mars brightness with high significance; Fig. 6 shows estimates for thermodynamic temperature as a function of time spanning approximately one Martian day. These diurnal variations have been reported before and are consistent with predictions from models (e.g., Sidher et al. 2000). We correct for this in analysis, scaling measured values to a common observation time. These times correspond to unix time 1 256 545 807, 1 271 109 507, and 1 324 607 821 for Mars observations 1–3, respectively, and roughly represent the time when detectors in the 353 GHz band were observing the planet head on7. The corresponding Julian date (MJD) is 2 455 130.854, 2 455 299.416, and 2 455 918.609. Our estimates for the planet solid angle at those times are 45.616, 54.471, and 54.678 arcsec2, respectively. This rescaling changes the in-band standard deviation in measured thermodynamic temperature of the second Mars observation at 217 GHz from 2.5 to 1.0 K.
Figure 7 compares the measured thermodynamic temperature of Mars with predictions of the Lellouch & Amri (2008) model for the reference times stated previously. The Lellouch & Amri (2008) model has been scaled by a constant factor, ζP = 0.982, in order to improve consistency with Planck-HFI measurements. This scale factor was found by minimizing the 100–353 GHz residuals between model predictions for the three reference times with the corresponding diurnal-variation-corrected Planck thermodynamic temperature results. The greyed out region in Fig. 7 is there to remind the reader that the sub-mm bands are calibrated on models of the brightness of Uranus and Neptune (see Sect. 2.1.2).
Figures 6 and 7 indicate that once the Lellouch and Amri model is rescaled downwards by about 1.8%, it provides a good match of the absolute and relative (i.e., variations on diurnal and seasonal scales, and spectral dependence) Mars thermodynamic temperature as measured by HFI. This is consistent with the claimed 5% absolute accuracy of the model.
A series of HFI end-of-life tests were undertaken in December 2011 (see Planck Collaboration VII 2016). During these scans, the 100-, 143-, 217-, and 353-GHz frequency bands observed Mars at two different spin rates, the nominal 1.0 rpm and a faster 1.4 rpm. Although these tests were useful in further constraining the bolometer time-response functions, we have not considered these data in this paper.
3.2. Jupiter
There exists a rich literature on the mm and sub-mm flux densities of the Jovian planets (Goldin et al. 1997; Weisstein 1996; Weisstein & Serabyn 1996; Burgdorf et al. 2004; Gibson et al. 2005; Désert et al. 2008).
Despite having significantly lower millimetre wavelength thermodynamic temperature than Mars, Jupiter’s apparent size makes it the brightest planet on the sky as seen by Planck. Although high-frequency detectors are driven to saturation, in particular at 545 and 857 GHz, we attempt to estimate the planet brightness across all frequencies by masking the centre of the planet crossing. For frequencies above 217 GHz we also apply a nonlinearity correction (see discussion in Sects. 2.1.1 and 2.1.3). Fig. 8 shows the thermodynamic temperature at all Planck-HFI frequencies derived from the five Jupiter observations available and compares them with the ESA1 model predictions.
 |
Fig. 8 Measured thermodynamic temperature for the five Planck-HFI observations of Jupiter as well as Planck-LFI results (Planck Collaboration V 2016). Points and error bars represent average (maximum likelihood) thermodynamic temperature and associated errors (including systematic error). The orange line and region represent the ESA1 model predictions and the estimated absolute uncertainties. We note the ammonia absorption line at 572.5 GHz. Emission lines are due to stratospheric emission from H2O, CO, CS, and HCN. WMAP measurements are included for comparison (Bennett et al. 2013). The grey region is there to remind the reader that the sub-mm bands are calibrated on models of the brightness of Uranus and Neptune (see Sect. 2.1.2). |
The act of masking the planet centre dramatically reduces the statistical power in the Jupiter data set, but we also see that it significantly affects the flux density estimate. The masking radius was chosen so that the signal amplitude outside the masked region would be comparable to the signal amplitude seen in Saturn observations. Although we have not attempted to estimate the amplitude of any nonlinearity and saturation biases, we expect some increase in error, especially at 545 and 857 GHz, because of this effect. We do not account for any contamination in flux density determination due to Jupiter’s rings and moons.
In order to improve consistency between the ESA1 model predictions and the WMAP and Planck measurements at frequencies below 353 GHz, a roughly 3% upwards scaling of the model is required. If this model rescaling is necessary, we note an interesting discrepancy between Planck-HFI measurements and model predictions at 353 and 545 GHz (see Fig. 8). We further note that the 353 GHz thermodynamic temperature measurement of approximately (167.4 ± 1.4) K is quite stable in time (see Table 4).
3.3. Saturn
Saturn’s flux determination is complicated by the presence of extended rings. High resolution images of Saturn and its rings at 1- and 3-mm wavelength are provided in Dunn et al. (2005).
As is evident from Fig. 2, Planck HFI (4.́5 minimum resolution) does not resolve Saturn (radius approximately 8.̋), meaning that the flux seen from Saturn is an integrated, whole-disc signal. However, the four Planck-HFI observations of Saturn occurred at different ring inclination angles, B, making it possible to separate emission from the planetary disc and emission from the rings (see Table 5).
During the four Planck observations of the planet, Saturn’s ring inclination angle spanned +3 to + 13deg as viewed from L2. Saturn’s equinox was in August 2009, so the first two observations were nearly edge on. All Planck observations of Saturn are during northern spring, whereas WMAP observed Saturn during its northern winter, corresponding to primarily negative inclination angles. Together, WMAP and Planck measured the 100 GHz brightness of Saturn over a 39deg range of inclination angles, from –26 to + 13deg.
Following the notation of Weiland et al. (2011) we construct a model for the frequency and viewing-angle dependent Rayleigh-Jeans temperature that incorporates contributions from both the planet disc and the rings: ![\begin{eqnarray} T_{\rm RJ}(\nu,B) &=& \frac{T_{{\rm disc}(\nu)}}{\Omega _{\rm P}} \left[ \Omega_{{\rm ud}} + \textstyle \sum_{i=1}^{7} {\rm e}^{-\tau_i |\csc B|} \Omega_{{\rm od},i}\right] \nonumber \\ &&+ \frac{T_{{\rm ring}(\nu)}}{\Omega _{\rm P}} \textstyle \sum_{i=1}^{7} \Omega_{{\rm r},i}, \end{eqnarray}](/articles/aa/full_html/2017/11/aa30311-16/aa30311-16-eq143.png) (22)where ΩP is the solid angle of the planet disc and Tdisc and Tring are the planetary disc and ring Rayleigh-Jeans (RJ) temperatures, respectively. We use RJ temperature instead of thermodynamic temperature in this section for ease of comparison with WMAP and ACT results and for simplified modelling. The index i refers to one of the seven ring components used at microwave wavelengths (we use the value in table 10 of Weiland et al. 2011, following Dunn et al. 2002). Here, τi is the optical depth of the ring component, Ωud is the planetary disc solid angle unobscured by rings, Ωod,i is the solid angle of the disc that is obscured by the ith ring component and Ωr,i is the solid angle of the ith ring component. The portion of the disc solid angle obscured by the rings is
(22)where ΩP is the solid angle of the planet disc and Tdisc and Tring are the planetary disc and ring Rayleigh-Jeans (RJ) temperatures, respectively. We use RJ temperature instead of thermodynamic temperature in this section for ease of comparison with WMAP and ACT results and for simplified modelling. The index i refers to one of the seven ring components used at microwave wavelengths (we use the value in table 10 of Weiland et al. 2011, following Dunn et al. 2002). Here, τi is the optical depth of the ring component, Ωud is the planetary disc solid angle unobscured by rings, Ωod,i is the solid angle of the disc that is obscured by the ith ring component and Ωr,i is the solid angle of the ith ring component. The portion of the disc solid angle obscured by the rings is 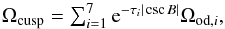 (23)and the total ring area is
(23)and the total ring area is 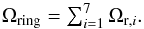 (24)In this model, all rings are assumed to have the same RJ temperature and the opacity of the rings is fixed a priori (Dunn et al. 2002). We do not explore models where these properties are allowed to vary.
(24)In this model, all rings are assumed to have the same RJ temperature and the opacity of the rings is fixed a priori (Dunn et al. 2002). We do not explore models where these properties are allowed to vary.
Best-fit parameters of two models for the Rayleigh-Jeans temperature of Saturn and its rings.
 |
Fig. 9 Rayleigh-Jeans temperature of the combined Saturn ring-disc system at 100 GHz with the WMAP measurements scaled from 94 GHz to match Planck (0.1% upwards scaling). The best-fit ring-disc models for the two data sets are also shown. We use RJ temperature instead of thermodynamic temperature for the Saturn ring-disc system for ease of comparison with WMAP and ACT results. The HFI error bars represent a combination of statistical and systematic error. The systematic error is expected to be strongly correlated between observations. We note that the third Planck-HFI observation of Saturn, corresponding to an inclination angle of + 12.6deg, appears somewhat anomalous. |
 |
Fig. 10 Rayleigh-Jeans temperature of Saturn’s ring as a function of frequency, as estimated by WMAP, ACT, and Planck HFI, plotted together with a power-law model fit to all measurements. The best-fit model (solid line) suggests a spectral index of βring = 2.30 ± 0.03 compared to a spectral index of β = 2 for a perfect RJ source. The grey region is there to remind the reader that the sub-mm bands are calibrated on models of the brightness of Uranus and Neptune (see Sect. 2.1.2). |
Figure 9 compares the 100-GHz Saturn RJ temperatures measured by WMAP and Planck and the best-fit models to the two independent data sets, as well as the combined data set (WMAP data are extracted from table 8 in Bennett et al. 2013). The WMAP results have been scaled up from 94 to 100 GHz using the ESA2 Saturn thermodynamic temperature model, corresponding to a 0.1% increase in RJ temperature.
The best-fit two-component model is listed in Table 6. The two-component model significantly improves the fit to the data over a simpler single-disc model that neglects effects from the ring geometry. We note, however, that the systematic uncertainty that we expect to be strongly correlated between observations dominates the statistical uncertainty in flux determination of Saturn at 100 GHz. Table 6 reports a goodness of fit parameter, χ2, as well as the corresponding degrees of freedom assuming that the errors are uncorrelated. If we instead account for the correlated error in our model comparison the two-component model is still significantly favoured over the simpler single component model, however, in that scenario the third (January 2011) observation of Saturn becomes significantly at odds with the other three (see the discrepant HFI data point in Fig. 9).
On 5 December 2010, a planetary-scale disturbance erupted in Saturn’s northern hemisphere, leading to large temperature perturbations (up to 50 K at 0.5 mbar) in Saturn’s stratosphere (e.g., Fletcher et al. 2012). Perturbations in the troposphere were much more subdued, although Achterberg et al. (2014) reported an increase of about 3 K in the far-IR (20–200 μm, probing the upper troposphere near 400 mbar) thermodynamic temperature at the storm’s latitude. In addition, 2.2-cm thermodynamic temperatures measured by the Cassini spacecraft three months into the storm were observed to increase more significantly (from 148 K to 166 K) at the storm latitude, likely due to a strong reduction in the relative humidity of ammonia there (Laraia et al. 2013). Although this information is not quite sufficient to quantitatively estimate the change of the disc-averaged continuum thermodynamic temperature at the storm’s epoch, it seems clear that if anything, the effect of the storm would be an increase in these continuum temperatures.
 |
Fig. 11 Thermodynamic temperature of Saturn’s disc as calculated from the four Planck-HFI observations compared with the ESA2 model output. The LFI data at 28, 44, and 70 GHz are taken from Planck Collaboration V (2014), but corrected for disc oblateness and ring contributions. The three prominent absorption lines, including the one at 530 GHz, are phosphine (PH3) related (Weisstein 1996). Emission lines are due to stratospheric emission from H2O. WMAP and ACT measurements are included here for comparison (Bennett et al. 2013; Hasselfield et al. 2013; Louis et al. 2014). |
The third HFI observation of Saturn took place in early January 2011, shortly after this disturbance is thought to have begun. The fourth observation took place in late June and early July that same year. Given our expectations for the thermal effects of the storm, and since our measurement uncertainty is dominated by systematic error which we expect to be strongly correlated between observations, we are surprised to see that the fourth Saturn observation appears more consistent with the two-component model than the third observation.
Figure 10 shows determinations of the Rayleigh-Jeans ring temperature as a function of frequency as estimated by WMAP, ACT, and Planck HFI. Here, all three experiments have employed the same two-component model described in Weiland et al. (2011). We adopt the following model to describe the Rayleigh-Jeans temperature as a function of frequency: 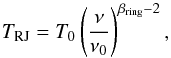 (25)with ν0 ≡ 23 GHz, and the data being used to fit for T0 and βring. The RJ-temperature can be used to calculate the spectral radiance of Saturn’s rings according to Eq. (3). The best-fit model, assuming errors are uncorrelated, suggests a spectral index of βring = 2.30 ± 0.03, with T0 = (11.3 ± 0.6) K. The goodness of fit for this models is χ2/ d.o.f. = 13.4 / 11.
(25)with ν0 ≡ 23 GHz, and the data being used to fit for T0 and βring. The RJ-temperature can be used to calculate the spectral radiance of Saturn’s rings according to Eq. (3). The best-fit model, assuming errors are uncorrelated, suggests a spectral index of βring = 2.30 ± 0.03, with T0 = (11.3 ± 0.6) K. The goodness of fit for this models is χ2/ d.o.f. = 13.4 / 11.
Figure 11 shows the observation-averaged Saturn thermodynamic temperature as a function of frequency using the disc contribution from the two-component ring-disc model, and compares those results with the ESA2 model. In order to accommodate Planck-LFI measurements of Saturn’s total system brightness, we have used the best-fit ring-disc model to subtract contributions from the planet’s rings from the Planck-LFI total system brightness measurements. The LFI data points presented in Figure 11 therefore represent best estimates for disc brightness only. The LFI measurements can be improved by incorporating data that extend past the first 2.5 surveys; however, we note that these preliminary LFI measurements appear to be in excellent agreement with the Planck-HFI measurements.
The WMAP and Planck measurements of Saturn’s disc brightness in the 100–353 GHz frequency range seem to suggest that a roughly 5% upward scaling, or other adjustment at 100–353 GHz, of the ESA2 model is necessary. If this overall absolute scaling is needed, the Planck-HFI results at 545 and 857 GHz become somewhat discrepant with model predictions. The dip in thermodynamic temperature near 545 GHz, observed in both Jupiter and Saturn, is understood, and is due to absorption features from PH3 and to a lesser extent NH3. It is worth noting that the 545-GHz observations of Saturn are subject to significant colour corrections (see Table 2).
3.4. Uranus and Neptune
The dimmest of the Jovian planets, Uranus and Neptune are often used as calibrators for CMB experiments that probe relatively small angular scales. The thermodynamic temperature of Uranus and Neptune at millimetre wavelengths is discussed in Muhleman & Berge (1991), Griffin & Orton (1993), Serabyn & Weisstein (1996), Sayers et al. (2012), and Dempsey et al. (2013).
The calibration of the sub-mm channels was initially performed using results from FIRAS (Planck HFI Core Team 2011). Peculiar discrepancies with planet models and other inconsistencies in the FIRAS calibration, however, caused the Planck HFI collaboration to decide in favour of a calibration using planet models (Planck Collaboration VIII 2014). A detailed description of the calibration approach for the 545- and 857-GHz bands can be found in Planck Collaboration VIII (2016) and Bertincourt et al. (2016). This new calibration procedure has the advantage of being similar to that used by instruments on-board Planck’s sister experiment, Herschel. Since the sub-mm channels are calibrated using models of Uranus and Neptune, the planet flux density results at these frequencies can only be used to check for self-consistency in flux reconstruction and relative differences between models of different planets.
Approximately 30-K variation in Uranus thermodynamic temperature at 3.5-cm wavelengths, spanning a 36 yr period, is reported in Klein & Hofstadter (2006). The evidence for brightness variations at 90 and 150 GHz is discussed in Kramer et al. (2008) and Hasselfield et al. (2013). Like ACT, we see no evidence for variation in the thermodynamic temperature of Uranus and Neptune over the five Planck-HFI observations that span a 750-day period (see Table 4). Instead, we find that our results for the thermodynamic temperature of these two ice giants are remarkably stable across observations.
A model of Uranus flux, attributed to Griffin and Orton (Griffin & Orton 1993), has recently been incorporated into the set of available ESA models (Moreno 2014). This model is discussed in the ACT analysis of Uranus’s flux (Hasselfield et al. 2013). The Griffin and Orton model of Uranus is referred to as “ESA5” by scientists working on the calibration of SPIRE, an instrument on the Herschel satellite (Moreno 2014).
The two ice giants are quite dim at 100 and 143 GHz (see Table 1 and Fig. 4). Unlike Mars, Jupiter, and Saturn, where instrument calibration dominates uncertainty, statistical error is significant in the flux determination of Uranus and Neptune. Figures 12 and 13 show a comparison of the predicted thermodynamic temperatures of these planets with the most up-to-date ESA models at the time of writing, namely ESA2 for Uranus and ESA5 for Neptune. We note an interesting discrepancy between the Planck-HFI measurements and model predictions for Uranus and Neptune at 100 and 143 GHz. This might be due to increased atmospheric absorption in the two planets at those frequencies.
4. Comparative tests and polarization limits
4.1. Comparison with Planck-HFI calibration
 |
Fig. 12 Top: measured Uranus thermodynamic temperature derived from five Planck-HFI observations, compared to predictions of the ESA2 model. Emission lines are due to stratospheric emission from H2O. We also show data from WMAP (Bennett et al. 2013) and ACT (Hasselfield et al. 2013; Louis et al. 2014). Bottom: difference (residuals) between the ESA2 model and the measurements. |
 |
Fig. 13 Top: measured thermodynamic temperature for the four Planck-HFI observations of Neptune compared to the ESA5 model. Emission lines are due to stratospheric emission from H2O, CO, and HCN. We also show results from WMAP (Bennett et al. 2013). Bottom: difference (residuals) between the ESA5 model and the measurements. |
 |
Fig. 14 Average ratio of measured flux (numerator) and model predicted flux (denominator) as a function of frequency for all five planets and all Planck-HFI frequencies. For Mars, the predicted thermodynamic temperature has been scaled by ζP = 0.982. The thin solid line is the estimated flux density, combining data from all planet observations, while the larger coloured region indicates the combined systematic and statistical uncertainties. Dashed horizontal lines represent the absolute 5% model error envelopes. We note that relative model errors between different frequencies are expected to be less than 5%. |
Figure 14 compares the ratio between measured spectral flux density and what is predicted by the adopted models for the five planets. We note that, unlike the thermodynamic temperature, this ratio is linearly dependent on parameters that commonly affect the calibration, such as the beam solid angle, gain, and colour correction. The dashed horizontal lines represent the 5% absolute model errors and the coloured region represents the statistical and systematic measurement uncertainty summed in quadrature.
The average ratio between the Planck-HFI measurements and the model predictions for all five planets (excluding Jupiter observations for frequencies above 217 GHz) is 1.004, 1.002, 1.021, 1.033, 1.009, and 1.007, for 100, 143, 217, 353, 545, and 857 GHz, respectively. Since the 545 and 857 GHz frequency bands derived their absolute calibration from models of the thermodynamic temperature of Uranus and Neptune, it is more appropriate to exclude those planets from such a comparison. However, since Jupiter observations at the highest frequencies are possibly affected by poorly captured detector nonlinearities and because the Lellouch & Amri (2008) model for Mars likely requires a 2–4% overall scaling, we are left with only the Saturn model for such a comparison. We observe a 1.1% and 1.2% agreement with the Saturn model at 545 and 857 GHz, respectively.
4.2. Comparison with WMAP and ACT
Assuming constant brightness, planet observations provide an approach for cross-calibrating millimetre-wavelength observatories that is independent of the CMB. We compare the absolute calibration of Planck HFI with WMAP at 100 GHz using Mars, Saturn, and Jupiter. The uncertainties on the Uranus and Neptune thermodynamic temperatures reported by WMAP are too large to provide a useful constraint (Bennett et al. 2013). Extensive comparison of Planck-LFI and WMAP absolute calibration using Jupiter is presented in Planck Collaboration V (2016). This analysis suggests sub-percent level agreement in the absolute calibration of the two experiments.
Jupiter is an ideal candidate for transferring WMAP’s dipole calibration to other instruments (Hill et al. 2009). Assuming the intrinsic brightness of the planet is stable in time, we use our estimate for the 100-GHz observation-averaged thermodynamic temperature to compare with the WMAP brightness estimates at 94 GHz. The seasonally averaged Jupiter thermodynamic temperature at 94 GHz, as reported by WMAP, is TW = (175.1 ± 0.9) K (Bennett et al. 2013). The HFI measurement at 100 GHz is 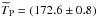 K, combining statistical and systematic 1σ error estimates. Using the ESA1 model to scale HFI predictions down to 94 GHz, we obtain TP = (172.3 ± 0.8) K. The ratio is TP/TW = 0.984 ± 0.007, where we have summed the errors from different experiments in quadrature. Calculating the corresponding ratio in predicted spectral radiance using the Planck blackbody function yields the same result. This suggests some tension between the two experiments at the 2.3σ level.
K, combining statistical and systematic 1σ error estimates. Using the ESA1 model to scale HFI predictions down to 94 GHz, we obtain TP = (172.3 ± 0.8) K. The ratio is TP/TW = 0.984 ± 0.007, where we have summed the errors from different experiments in quadrature. Calculating the corresponding ratio in predicted spectral radiance using the Planck blackbody function yields the same result. This suggests some tension between the two experiments at the 2.3σ level.
Unlike Jupiter, Mars displays both seasonal and diurnal variations in brightness. To correct for this, we use the time-dependent model from Lellouch & Amri (2008) to provide a temporal link between the WMAP and Planck-HFI observations. For the 100–353 GHz channels, we find that a global rescaling of the Lellouch and Amri model predictions by ζP = 0.982 minimizes the residual between the model predictions and the three available HFI measurements of Mars thermodynamic temperature. This same procedure suggests that a ζW = 0.970 rescaling of the Lellouch and Amri model minimizes the residual between model predictions and WMAP results (Weiland et al. 2011). The ratio of scaling factors, ζP/ζW = 1.012, suggests that WMAP and Planck HFI are consistent in their absolute calibration at the percent-level. Of course, this cross-calibration procedure puts stringent requirements on the temporal stability of the validity of the Lellouch and Amri model. It is worth noting that if we fit the Lellouch and Amri model only to the 100 GHz results from Planck HFI, we find 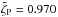 , which suggest even better agreement with WMAP. The five percent planet flux density modelling uncertainty dominates the error in this consistency check.
, which suggest even better agreement with WMAP. The five percent planet flux density modelling uncertainty dominates the error in this consistency check.
Saturn flux determinations are complicated by the presence of rings that can affect the effective thermodynamic temperature of the planet. From all four Planck-HFI observations of Saturn at 100 GHz, the estimate for the Rayleigh-Jeans temperature of the Saturn disc component is ΥP = (148.6 ± 0.8) K. The WMAP estimate for the disc RJ temperature at 94 GHz is 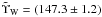 K, which we can scale up to 100 GHz using the ESA2 model to find ΥW = (147.5 ± 1.2) K. The ratio is therefore ΥP/ ΥW = 1.007 ± 0.010 suggesting the two experiments are in good agreement.
K, which we can scale up to 100 GHz using the ESA2 model to find ΥW = (147.5 ± 1.2) K. The ratio is therefore ΥP/ ΥW = 1.007 ± 0.010 suggesting the two experiments are in good agreement.
These comparisons suggest that at 100 GHz, WMAP and Planck HFI agree at the 0.984, 0.996, and 1.007 level for Jupiter, Mars, and Saturn, respectively. It is important to note that these calibration comparisons are performed using sources that have quite different spectra from that of the CMB. Comparison between the calibrations of the two satellites on the CMB dipole yield sub-percent agreement (Planck Collaboration I 2016; Planck Collaboration VIII 2016).
A measurement by the ACT collaboration (Hasselfield et al. 2013; Louis et al. 2014), quotes an average thermodynamic temperature for Uranus of TA,148 = (105.7 ± 2.2) K and TA,218 = (97.6 ± 2.8) K at 148 and 218 GHz, respectively. These estimates are derived assuming that the planet SEDs can be well approximated by a Rayleigh-Jeans form. If we apply the same approximation to the Planck-HFI results at those frequencies we find TP,148 = (107.9 ± 0.8) K and TP,218 = (97.3 ± 1.2) K at 147 and 217 GHz, respectively. These results are clearly consistent.
On the other hand, the ACT collaboration also provides an estimate of Saturn’s thermodynamic temperature using the model originally described in Weiland et al. (2011). These measurements suggest 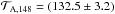 K and
K and 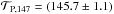 K at 148 and 218 GHz, respectively. The Planck-HFI estimate for the disc RJ temperature is
K at 148 and 218 GHz, respectively. The Planck-HFI estimate for the disc RJ temperature is 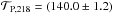 K and
K and 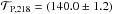 K at 147 and 217 GHz, respectively. Summing errors in quadrature suggest 3.9σ and 2.2σ difference between the results at 147 and 217 GHz, respectively.
K at 147 and 217 GHz, respectively. Summing errors in quadrature suggest 3.9σ and 2.2σ difference between the results at 147 and 217 GHz, respectively.
4.3. Polarized flux density of planets
HFI’s bands at 100, 143, 217, and 353 GHz include polarization-sensitive detectors. To search for polarized flux from the planets, we decompose the total flux from the planet into the I, Q, and U Stokes parameters for each individual observation within a band. We then use estimates for polarization sensitivities, efficiencies, and the measured flux from each polarization-sensitive detector to obtain the best fit Stokes parameters. The parametrization is 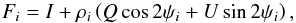 (26)where the quantities Fi are the total flux density measured for bolometer i, and ψi and ρi are the angles of polarization sensitivity and polarization efficiencies of the bolometers, respectively (Rosset et al. 2010). For the majority of the planet observations, the degree of polarization (defined as
(26)where the quantities Fi are the total flux density measured for bolometer i, and ψi and ρi are the angles of polarization sensitivity and polarization efficiencies of the bolometers, respectively (Rosset et al. 2010). For the majority of the planet observations, the degree of polarization (defined as 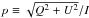 ) is consistent with zero to within the errors in the total flux measurements. The systematic relative calibration factor between detectors (see discussion in Sect. 2.4) represents the largest limitation to this analysis.
) is consistent with zero to within the errors in the total flux measurements. The systematic relative calibration factor between detectors (see discussion in Sect. 2.4) represents the largest limitation to this analysis.
68 and 95% confidence limits on polarization fraction, p (in percent), as derived using the approach of Simmons & Stewart (1985).
Uncertainties in the determination of Q and U inevitably bias estimates of the polarization fraction 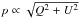 . To combat this, we use the formalism of Simmons & Stewart (1985) and Montier et al. (2015) to construct 95% confidence upper limits of the degree of polarization of the planets. We do not specifically assess possible bias in our determination of polarization fraction due to the relative calibration errors. Instead, both statistical and systematic errors are propagated into the estimation of the Q and U covariance matrix. Table 7 lists the 68 and 95% upper confidence levels on the polarization fraction for the four polarization-sensitive frequency bands.
. To combat this, we use the formalism of Simmons & Stewart (1985) and Montier et al. (2015) to construct 95% confidence upper limits of the degree of polarization of the planets. We do not specifically assess possible bias in our determination of polarization fraction due to the relative calibration errors. Instead, both statistical and systematic errors are propagated into the estimation of the Q and U covariance matrix. Table 7 lists the 68 and 95% upper confidence levels on the polarization fraction for the four polarization-sensitive frequency bands.
5. Conclusions
We have provided measurements of the flux densities and thermodynamic temperatures of Mars, Jupiter, Saturn, Uranus, and Neptune. These measurements span a decade in frequency, from 30–857 GHz, allowing for improved constraints on models of planetary thermodynamic temperature. We report on the data reduction scheme, as well as statistical and systematic error characterization. We detect time-variation in the thermodynamic temperature of Mars at high significance. Overall, we observe acceptable agreement with the ESA models for planet thermodynamic temperatures, however, below 545 GHz we do in some cases observe frequency scaling that deviates from model predictions at a significant level. Finally, comparisons with WMAP measurements show agreement in point source calibration at the two-percent-level. The largest discrepancy between WMAP and Planck HFI is in the brightness determination of Jupiter.
The planet flux density measurements are limited by systematic uncertainties and these are expected to affect the brightness determination of all Planck-HFI compact sources at the 0.4−3.1% level. These systematic uncertainties do not affect the calibration of CMB diffuse emission at the same level of significance, since that uses the cosmological dipole as primary calibrator, resulting in much lower uncertainties.
These results shed light on the fidelity of the Planck-HFI instrument characterization. We hope that current and future ground based CMB experiments that use planets to characterize their instruments will benefit from these results.
Planck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states and led by Principal Investigators from France and Italy, telescope reflectors provided through a collaboration between ESA and a scientific consortium led and funded by Denmark, and additional contributions from NASA (USA).
See http://pla.esac.esa.int/pla/, https://wiki.cosmos.esa.int/planckpla2015/ and http://irsa.ipac.caltech.edu/Missions/planck.html. The planet data will be made available at the time of publication.
Acknowledgments
The Planck Collaboration acknowledges the support of: ESA; CNES, and CNRS/INSUIN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MINECO, JA, and RES (Spain); Tekes, AoF, and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); ERC and PRACE (EU). A description of the Planck Collaboration and a list of its members, indicating which technical or scientific activities they have been involved in, can be found at http://www.cosmos.esa.int/web/planck/planck-collaboration. The authors thank Lyman Page for useful discussion. J.E. Gudmundsson acknowledges support through a grant from the Swedish Research Council (Contract No. 638-2013-8993).
References
- Achterberg, R. K., Gierasch, P. J., Conrath, B. J., et al. 2014, ApJ, 786, 92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ade, P. A. R., Savini, G., Sudiwala, R., et al. 2010, A&A, 520, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bendo, G. J., Griffin, M. J., Bock, J. J., et al. 2013, MNRAS, 433, 3062 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Larson, D., Weiland, J. L., et al. 2013, ApJS, 208, 20 [Google Scholar]
- Bertincourt, B., Lagache, G., Martin, P. G., et al. 2016, A&A, 588, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burgdorf, M. J., Orton, G. S., Encrenaz, T., et al. 2004, Planet. Space Sci., 52, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Dempsey, J. T., Friberg, P., Jenness, T., et al. 2013, MNRAS, 430, 2534 [Google Scholar]
- Désert, F.-X., Macías-Pérez, J. F., Mayet, F., et al. 2008, A&A, 481, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dunn, D. E., Molnar, L. A., & Fix, J. D. 2002, Icarus, 160, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Dunn, D. E., de Pater, I., Wright, M., Hogerheijde, M. R., & Molnar, L. A. 2005, AJ, 129, 1109 [Google Scholar]
- Dupac, X., & Tauber, J. 2005, A&A, 430, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fixsen, D. J. 2009, ApJ, 707, 916 [Google Scholar]
- Fixsen, D. J., Cheng, E. S., Cottingham, D. A., et al. 1994, ApJ, 420, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L. N., Hesman, B. E., Achterberg, R. K., et al. 2012, Icarus, 221, 560 [Google Scholar]
- Forget, F., Hourdin, F., Fournier, R., et al. 1999, J. Geophys. Res., 104, 24155 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, J., Welch, W. J., & de Pater, I. 2005, Icarus, 173, 439 [Google Scholar]
- Golden, L. M. 1979, Icarus, 38, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Goldin, A. B., Kowitt, M. S., Cheng, E. S., et al. 1997, ApJ, 488, L161 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M., & Orton, G. 1993, Icarus, 105, 537 [Google Scholar]
- Griffin, M. J., North, C. E., Schulz, B., et al. 2013, MNRAS, 434, 992 [NASA ADS] [CrossRef] [Google Scholar]
- Hasselfield, M., Moodley, K., Bond, J. R., et al. 2013, ApJS, 209, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, R. S., Weiland, J. L., Odegard, N., et al. 2009, ApJS, 180, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Hodara, H., & Slemon, C. 1984, Applied Scientific Research, 41, 203 [CrossRef] [Google Scholar]
- HORIZONS 2014, HORIZONS Web-Interface (JPL), http://ssd.jpl.nasa.gov/?ephemerides [Google Scholar]
- Hudson, M. C. 1974, Appl. Opt., 13, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huffenberger, K. M., Crill, B. P., Lange, A. E., Górski, K. M., & Lawrence, C. R. 2010, A&A, 510, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open source scientific tools for Python [Google Scholar]
- Klein, M. J., & Hofstadter, M. D. 2006, Icarus, 184, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Kramer, C., Moreno, R., & Greve, A. 2008, A&A, 482, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, J. D. 1950, Antennas, 1st edn. (McGraw-Hill) [Google Scholar]
- Laraia, A. L., Ingersoll, A. P., Janssen, M. A., et al. 2013, Icarus, 226, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Lellouch, E., & Amri, H. 2008, Mars Brightness Model, http://www.lesia.obspm.fr/perso/emmanuel-lellouch/mars/ [Google Scholar]
- Louis, T., Addison, G. E., Hasselfield, M., et al. 2014,J. Cosmol. Astropart. Phys., 7, 016 [Google Scholar]
- Maffei, B., Noviello, F., Murphy, J. A., et al. 2010, A&A, 520, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mauskopf, P. D., Ade, P. A. R., de Bernardis, P., et al. 2000, ApJ, 536, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Millour, E., Forget, F., Montabone, L., et al. 2015, Icarus, 251, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Monsalve, R. A. 2010, SPIE Conf. Ser., 7741 [Google Scholar]
- Montier, L., Plaszczynski, S., Levrier, F., et al. 2015, A&A, 574, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moreno, R. 2014, Neptune and Uranus planetary brightness temperature tabulation. Tech. Rep., ESA Herschel Science Center [Google Scholar]
- Muhleman, D. O., & Berge, G. L. 1991, Icarus, 92, 263 [Google Scholar]
- Müller, T. G., Balog, Z., Nielbock, M., et al. 2016, A&A, 588, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, J. A., & Padman, R. 1991, Infrared Physics, 31, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, J. A., Colgan, R., Gleeson, E., et al. 2002, in Experimental Cosmology at Millimetre Wavelengths, eds. M. de Petris, & M. Gervasi, AIP Conf. Ser., 616, 282 [Google Scholar]
- Murphy, J. A., Peacocke, T., Maffei, B., et al. 2010, J. Instr., 5, 4001 [Google Scholar]
- Page, L., Barnes, C., Hinshaw, G., et al. 2003, ApJS, 148, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Pajot, F., Ade, P. A. R., Beney, J., et al. 2010, A&A, 520, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perley, R. A., & Butler, B. J. 2013, ApJSS, 206, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration I. 2011, A&A, 536, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration V. 2014, A&A, 571, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VI. 2014, A&A, 571, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VII. 2014, A&A, 571, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VIII. 2014, A&A, 571, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IX. 2014, A&A, 571, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2015, The Explanatory Supplement to the Planck 2015 results, http://wiki.cosmos.esa.int/planckpla/index.php/Main_Page (ESA) [Google Scholar]
- Planck Collaboration I. 2016, A&A, 594, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration V. 2016, A&A, 594, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VI. 2016, A&A, 594, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VII. 2016, A&A, 594, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VIII. 2016, A&A, 594, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration X. 2016, A&A, 594, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVI. 2016, A&A, 594, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLVI. 2016, A&A, 596, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck HFI Core Team 2011, A&A, 536, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rather, J. D. G., Ulich, B. L., & Ade, P. A. R. 1974, Icarus, 22, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Rosset, C., Tristram, M., Ponthieu, N., et al. 2010, A&A, 520, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rudy, D. J., Muhleman, D. O., Berge, G. L., Jakosky, B. M., & Christensen, P. R. 1987, Icarus, 71, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Runyan, M. C., Ade, P. A. R., Bhatia, R. S., et al. 2003, ApJS, 149, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Sayers, J., Czakon, N. G., & Golwala, S. R. 2012, ApJ, 744, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Serabyn, E., & Weisstein, E. W. 1996, Appl. Opt., 35, 2752 [NASA ADS] [CrossRef] [Google Scholar]
- Showalter, M. 2014, Planet Viewers, http://pds-rings.seti.org/tools/index.html [Google Scholar]
- Sidher, S. D., Griffin, M. J., Davis, G. R., et al. 2000, Icarus, 147, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Simmons, J. F. L., & Stewart, B. G. 1985, A&A, 142, 100 [NASA ADS] [Google Scholar]
- Swinyard, B. M., Hartogh, P., Sidher, S., et al. 2010, A&A, 518, L151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Swinyard, B. M., Polehampton, E. T., Hopwood, R., et al. 2014, MNRAS, 440, 3658 [Google Scholar]
- Tauber, J. A., Mandolesi, N., Puget, J., et al. 2010, A&A, 520, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, A., & Taylor, B. N. 1989, Guide for the Use of the International System of Units (SI) (National Institute of Standards and Technology) [Google Scholar]
- Ulich, B. L., & Haas, R. W. 1976, ApJS, 30, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Weiland, J. L., Odegard, N., Hill, R. S., et al. 2011, ApJS, 192, 19 [Google Scholar]
- Weisstein, E. W. 1996, PhD thesis, California Institute of Technology [Google Scholar]
- Weisstein, E. W., & Serabyn, E. 1996, Icarus, 123, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkins, G. A. 1989, The IAU Style Manual, Vistas Astron., 39, 277 [Google Scholar]
- Wright, E. L. 1976, ApJ, 210, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L. 2007, ArXiv e-prints [arXiv:astro-ph/0703640] [Google Scholar]
- Zurek, R. W. 1982, Icarus, 50, 288 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Properties of the Planck HFI planet observations specifically for detector 1b at 143 GHz.
Band-average planet thermodynamic temperature, T, as measured by Planck LFI and reported in Planck Collaboration V (2014, 2016).
Band-average planet thermodynamic temperature and corresponding statistical uncertainty as measured by Planck HFI (survey 1–5).
Best-fit parameters of two models for the Rayleigh-Jeans temperature of Saturn and its rings.
68 and 95% confidence limits on polarization fraction, p (in percent), as derived using the approach of Simmons & Stewart (1985).
All Figures
 |
Fig. 1 Histogram of the flux density of all 217-GHz PCCS2 sources together with vertical lines indicating the flux of the five planets discussed in this paper. It is clear that at 217 GHz, Mars, Saturn, and especially Jupiter, are much brighter than any of the PCCS2 sources. Here the Mars data point corresponds to best estimates for the 22 December 2011 flux density. The majority of the 217-GHz PCCS2 sources have flux densities in the 0.1–1.0 Jy range. Both axes are logarithmic on this figure. |
| In the text | |
 |
Fig. 2 Composite diagram showing four planets as viewed from the centre of Earth around the turn of the year 2010; the view from L2 would have been similar. From left to right, the figure shows Uranus, Mars, Saturn, and Jupiter. The planets are drawn on the same scale and the numbers to the right of each planet represent the approxiate apparent diameter (in arcmin) of the planets at this particular epoch. A fraction of a typical 143 GHz beam is shown by the black line and large grey region, the diameter of this circle corresponds to the FWHM of the beam. This suggests that the planets are point sources relative to the spatial response of the instrument. The planet diagrams have been extracted from Showalter (2014). |
| In the text | |
 |
Fig. 3 Relative amplitude in derived flux density from observations of Jupiter, Saturn, and Mars at 100–353 GHz (Mars is limited by statistical error at 100 GHz). The flux density has been normalized to the band-mean. A clear correlation in relative flux amplitudes between planet observation periods is seen. Lines are used to guide the eye between flux values within a planet observation. For the top panel (100 GHz), the average standard deviation of the data is approximately 0.4%. |
| In the text | |
 |
Fig. 4 Maps of the normalized and background-subtracted timeline residuals, (si − D(θi,φi) − ΔTpP(θi,φi)) / ΔTp, combining all available observations and detectors within a frequency band. The number shown in the top left corner of each panel represents the extent of the colour scale, e.g., a value of 0.01 means that the darkest colour corresponds to a 0.01 deviation from the peak response ΔTp, with red (blue) corresponding to positive (negative) deviation. For Jupiter, we present two versions of the same plot. In one of the two versions, we have masked out the centres of the Jupiter observations, since nonlinearity and saturation lead to a large residual, especially at high frequencies. Each panel is 30′× 30′, and the co-scan direction is vertical on these plots (see discussion in Sect. 1). |
| In the text | |
 |
Fig. 5 Normalized single-detector statistical and systematic uncertainties for Mars, Jupiter, Saturn, and Uranus at all six Planck-HFI frequencies. The first six rows show the relative contribution of the different error terms described in Sects. 2.3 and 2.4. From top to bottom, these six rows describe uncertainties related to: detector noise and astrophysical confusion; scanning-beam solid angle; planet-disc solid angle; absolute calibration; spectral response function; and an unknown systematic term described in Sect. 2.4. The sum of the first six rows equals unity, but when combining errors, different terms are summed in quadrature. The last two rows show the total statistical uncertainty (in percent) and the total uncertainty in flux determination (in percent) appropriate for band-average flux density calculations, respectively. The total uncertainty is obtained by summing the total statistical and the total systematic uncertainties in quadrature. Finally, we note that statistical uncertainties (the first five rows) average down when we calculate band-averaged flux density estimates. |
| In the text | |
 |
Fig. 6 Estimates of the thermodynamic temperature of Mars compared to a model for diurnal variations. The panel columns correspond to the first two Mars observations while the rows represent estimates at 100, 143, and 217 GHz. The model output has been scaled by ζP = 0.982 (dashed line) and a variable best-fit scale (solid line), which is annotated in each panel. The horizontal axis shows time relative to the mean observation time for that frequency band. Error bars show systematic and statistical uncertainties summed in quadrature. |
| In the text | |
 |
Fig. 7 Measured thermodynamic temperature for the three Planck HFI observations of Mars. Black points represent band averages and corresponding error estimates. The thermodynamic temperature predictions of the Lellouch & Amri (2008) model (solid lines), scaled by ζP = 0.982, and the corresponding 5% absolute errors (coloured regions) are also shown. Both data and model results presented in this figure have been scaled to correspond to a single reference time (see discussion in Sect. 3.1). The grey region is meant to remind the reader that the sub-mm bands are calibrated on models of Uranus and Neptune brightness (see Sect. 2.1.2). The absolute thermodynamic temperature of Mars can be obtained by adding the spectral radiance from an occulted CMB monopole (see Sect. 2.1.3). |
| In the text | |
 |
Fig. 8 Measured thermodynamic temperature for the five Planck-HFI observations of Jupiter as well as Planck-LFI results (Planck Collaboration V 2016). Points and error bars represent average (maximum likelihood) thermodynamic temperature and associated errors (including systematic error). The orange line and region represent the ESA1 model predictions and the estimated absolute uncertainties. We note the ammonia absorption line at 572.5 GHz. Emission lines are due to stratospheric emission from H2O, CO, CS, and HCN. WMAP measurements are included for comparison (Bennett et al. 2013). The grey region is there to remind the reader that the sub-mm bands are calibrated on models of the brightness of Uranus and Neptune (see Sect. 2.1.2). |
| In the text | |
 |
Fig. 9 Rayleigh-Jeans temperature of the combined Saturn ring-disc system at 100 GHz with the WMAP measurements scaled from 94 GHz to match Planck (0.1% upwards scaling). The best-fit ring-disc models for the two data sets are also shown. We use RJ temperature instead of thermodynamic temperature for the Saturn ring-disc system for ease of comparison with WMAP and ACT results. The HFI error bars represent a combination of statistical and systematic error. The systematic error is expected to be strongly correlated between observations. We note that the third Planck-HFI observation of Saturn, corresponding to an inclination angle of + 12.6deg, appears somewhat anomalous. |
| In the text | |
 |
Fig. 10 Rayleigh-Jeans temperature of Saturn’s ring as a function of frequency, as estimated by WMAP, ACT, and Planck HFI, plotted together with a power-law model fit to all measurements. The best-fit model (solid line) suggests a spectral index of βring = 2.30 ± 0.03 compared to a spectral index of β = 2 for a perfect RJ source. The grey region is there to remind the reader that the sub-mm bands are calibrated on models of the brightness of Uranus and Neptune (see Sect. 2.1.2). |
| In the text | |
 |
Fig. 11 Thermodynamic temperature of Saturn’s disc as calculated from the four Planck-HFI observations compared with the ESA2 model output. The LFI data at 28, 44, and 70 GHz are taken from Planck Collaboration V (2014), but corrected for disc oblateness and ring contributions. The three prominent absorption lines, including the one at 530 GHz, are phosphine (PH3) related (Weisstein 1996). Emission lines are due to stratospheric emission from H2O. WMAP and ACT measurements are included here for comparison (Bennett et al. 2013; Hasselfield et al. 2013; Louis et al. 2014). |
| In the text | |
 |
Fig. 12 Top: measured Uranus thermodynamic temperature derived from five Planck-HFI observations, compared to predictions of the ESA2 model. Emission lines are due to stratospheric emission from H2O. We also show data from WMAP (Bennett et al. 2013) and ACT (Hasselfield et al. 2013; Louis et al. 2014). Bottom: difference (residuals) between the ESA2 model and the measurements. |
| In the text | |
 |
Fig. 13 Top: measured thermodynamic temperature for the four Planck-HFI observations of Neptune compared to the ESA5 model. Emission lines are due to stratospheric emission from H2O, CO, and HCN. We also show results from WMAP (Bennett et al. 2013). Bottom: difference (residuals) between the ESA5 model and the measurements. |
| In the text | |
 |
Fig. 14 Average ratio of measured flux (numerator) and model predicted flux (denominator) as a function of frequency for all five planets and all Planck-HFI frequencies. For Mars, the predicted thermodynamic temperature has been scaled by ζP = 0.982. The thin solid line is the estimated flux density, combining data from all planet observations, while the larger coloured region indicates the combined systematic and statistical uncertainties. Dashed horizontal lines represent the absolute 5% model error envelopes. We note that relative model errors between different frequencies are expected to be less than 5%. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


