| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 23 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201323270 | |
| Published online | 11 June 2014 | |
Planck intermediate results
XVII. Emission of dust in the diffuse interstellar medium from the far-infrared to microwave frequencies⋆
1
APC, AstroParticule et Cosmologie, Université Paris Diderot, CNRS/IN2P3,
CEA/lrfu, Observatoire de Paris, Sorbonne Paris Cité, 10 rue Alice Domon et Léonie Duquet,
75205
Paris Cedex 13,
France
2
Aalto University Metsähovi Radio Observatory and Dept of Radio
Science and Engineering, PO Box
13000, 00076
Aalto,
Finland
3
African Institute for Mathematical Sciences,
6-8 Melrose Road, Muizenberg,
7945
Cape Town, South
Africa
4
Agenzia Spaziale Italiana Science Data Center,
via del Politecnico snc,
00133
Roma,
Italy
5
Agenzia Spaziale Italiana, Viale Liegi 26, 00198
Roma,
Italy
6
Argelander-Institut für Astronomie, Universität Bonn,
Auf dem Hügel 71, 53121
Bonn,
Germany
7
Astrophysics Group, Cavendish Laboratory, University of
Cambridge, J J Thomson
Avenue, Cambridge
CB3 0HE,
UK
8
Astrophysics & Cosmology Research Unit, School of Mathematics,
Statistics & Computer Science, University of KwaZulu-Natal,
Westville Campus, Private Bag
X54001, 4000
Durban, South
Africa
9
Atacama Large Millimeter/submillimeter Array, ALMA Santiago Central
Offices, Alonso de Cordova 3107, Vitacura, 763 0355
Casilla Santiago,
Chile
10
CITA, University of Toronto, 60 St. George St., Toronto ON
M5S 3H8,
Canada
11
CNRS, IRAP, 9 Av.
colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
12
California Institute of Technology, Pasadena, California, USA
13
Centro de Estudios de Física del Cosmos de Aragón
(CEFCA), plaza San Juan, 1, planta
2, 44001
Teruel,
Spain
14
Computational Cosmology Center, Lawrence Berkeley National
Laboratory, Berkeley,
California,
USA
15
Consejo Superior de Investigaciones Científicas
(CSIC), 28006
Madrid,
Spain
16
DSM/Irfu/SPP, CEA-Saclay, 91191
Gif-sur-Yvette Cedex,
France
17
DTU Space, National Space Institute, Technical University of
Denmark, Elektrovej
327, 2800
Kgs. Lyngby,
Denmark
18
Département de Physique Théorique, Université de
Genève, 24, Quai E.
Ansermet, 1211
Genève 4,
Switzerland
19
Département de physique, de génie physique et d’optique, Université
Laval, Québec,
Canada
20
Departamento de Física, Universidad de Oviedo,
Avda. Calvo Sotelo s/n,
33007
Oviedo,
Spain
21
Department of Astrophysics/IMAPP, Radboud University
Nijmegen, PO Box
9010, 6500 GL
Nijmegen, The
Netherlands
22
Department of Electrical Engineering and Computer Sciences,
University of California, Berkeley, California, USA
23
Department of Physics and Astronomy, Dana and David Dornsife College
of Letter, Arts and Sciences, University of Southern California,
Los Angeles
CA
90089,
USA
24
Department of Physics and Astronomy, University College
London, London
WC1E 6BT,
UK
25
Department of Physics, Florida State University,
Keen Physics Building, 77 Chieftan
Way, Tallahassee,
Florida,
USA
26
Department of Physics, Gustaf Hällströmin katu 2a, University of
Helsinki, 00014
Helsinki,
Finland
27
Department of Physics, Princeton University,
Princeton, New Jersey, USA
28
Department of Physics, University of California,
Santa Barbara, California, USA
29
Department of Physics, University of Illinois at
Urbana-Champaign, 1110 West Green
Street, Urbana,
Illinois,
USA
30
Dipartimento di Fisica e Astronomia G. Galilei, Università degli
Studi di Padova, via Marzolo
8, 35131
Padova,
Italy
31
Dipartimento di Fisica e Scienze della Terra, Università di
Ferrara, via Saragat
1, 44122
Ferrara,
Italy
32
Dipartimento di Fisica, Università La Sapienza,
P. le A. Moro 2, 00185
Roma,
Italy
33
Dipartimento di Fisica, Università degli Studi di
Milano, via Celoria,
16, 20133
Milano,
Italy
34
Dipartimento di Fisica, Università degli Studi di
Trieste, via A. Valerio
2, 34127
Trieste,
Italy
35
Dipartimento di Fisica, Università di Roma Tor
Vergata, via della Ricerca Scientifica,
1, 00133
Roma,
Italy
36
Discovery Center, Niels Bohr Institute, Blegdamsvej 17, 2100
Copenhagen,
Denmark
37
Dpto. Astrofísica, Universidad de La Laguna (ULL),
38206, La Laguna, Tenerife,
Spain
38
European Southern Observatory, ESO Vitacura, Alonso de Cordova 3107, Vitacura,
Casilla
19001, Santiago, Chile
39
European Space Agency, ESAC, Planck Science Office, Camino bajo del
Castillo, s/n, Urbanización
Villafranca del Castillo, Villanueva de la Cañada, 28692
Madrid,
Spain
40
European Space Agency, ESTEC, Keplerlaan 1, 2201 AZ
Noordwijk, The
Netherlands
41
Helsinki Institute of Physics, Gustaf Hällströmin katu 2, University
of Helsinki, 00014
Helsinki,
Finland
42
INAF – Osservatorio Astrofisico di Catania,
via S. Sofia 78, 95123
Catania,
Italy
43
INAF – Osservatorio Astronomico di Padova,
Vicolo dell’Osservatorio 5,
35122
Padova,
Italy
44
INAF – Osservatorio Astronomico di Roma,
via di Frascati 33, 00040
Monte Porzio Catone,
Italy
45
INAF – Osservatorio Astronomico di Trieste,
via G.B. Tiepolo 11, 34143
Trieste,
Italy
46
INAF Istituto di Radioastronomia, via P. Gobetti 101, 40129
Bologna,
Italy
47
INAF/IASF Bologna, via Gobetti 101, 40129
Bologna,
Italy
48
INAF/IASF Milano, via E. Bassini 15, 20133
Milano,
Italy
49
INFN, Sezione di Bologna, via Irnerio 46, 40126
Bologna,
Italy
50
INFN, Sezione di Roma 1, Università di Roma Sapienza,
Piazzale Aldo Moro 2,
00185
Roma,
Italy
51
IPAG: Institut de Planétologie et d’Astrophysique de Grenoble,
Université Joseph Fourier, Grenoble 1/CNRS-INSU, UMR 5274, 38041
Grenoble,
France
52
IUCAA, Post Bag 4, Ganeshkhind, Pune University
Campus, 411007
Pune,
India
53
Imperial College London, Astrophysics group, Blackett
Laboratory, Prince Consort
Road, London,
SW7 2AZ,
UK
54
Infrared Processing and Analysis Center, California Institute of
Technology, Pasadena
CA
91125,
USA
55
Institut Universitaire de France, 103, bd Saint-Michel, 75005
Paris,
France
56
Institut d’Astrophysique Spatiale, CNRS (UMR8617) Université
Paris-Sud 11, Bâtiment
121, 91405
Orsay,
France
57
Institut d’Astrophysique de Paris, CNRS (UMR7095),
98 bis Boulevard Arago,
75014
Paris,
France
58
Institute for Space Sciences, Bucharest-Magurale,
Romania
59
Institute of Astronomy, University of Cambridge,
Madingley Road, Cambridge
CB3 0HA,
UK
60 Institute of Theoretical
Astrophysics, University of Oslo, Blindern, Oslo,
Norway
61
Instituto de Astrofísica de Canarias, C/Vía Láctea s/n, La Laguna, 38205
Tenerife,
Spain
62
Instituto de Física de Cantabria (CSIC-Universidad de
Cantabria), Avda. de los Castros
s/n, 39005
Santander,
Spain
63
Jet Propulsion Laboratory, California Institute of
Technology, 4800 Oak Grove
Drive, Pasadena,
California,
USA
64
Jodrell Bank Centre for Astrophysics, Alan Turing Building, School
of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester, M13
9PL, UK
65
Kavli Institute for Cosmology Cambridge,
Madingley Road, Cambridge, CB3 0HA, UK
66
LAL, Université Paris-Sud, CNRS/IN2P3, 91405
Orsay,
France
67
LERMA, CNRS, Observatoire de Paris, 61 Avenue de
l’Observatoire, 75014
Paris,
France
68
Laboratoire AIM, IRFU/Service d’Astrophysique – CEA/DSM – CNRS –
Université Paris Diderot, Bât. 709, CEA-Saclay, 91191
Gif-sur-Yvette Cedex,
France
69
Laboratoire Traitement et Communication de l’Information, CNRS (UMR
5141) and Télécom ParisTech, 46 rue
Barrault, 75634
Paris Cedex 13,
France
70
Laboratoire de Physique Subatomique et de Cosmologie, Université
Joseph Fourier Grenoble I, CNRS/IN2P3, Institut National Polytechnique de
Grenoble, 53 rue des
Martyrs, 38026
Grenoble Cedex,
France
71
Laboratoire de Physique Théorique, Université Paris-Sud 11 &
CNRS, Bâtiment 210,
91405
Orsay,
France
72
Lawrence Berkeley National Laboratory, Berkeley, California, USA
73
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741
Garching,
Germany
74
National University of Ireland, Department of Experimental
Physics, 12 Maynooth,
Co. Kildare,
Ireland
75
Niels Bohr Institute, Blegdamsvej 17, 2100
Copenhagen,
Denmark
76
Observational Cosmology, Mail Stop 367-17, California Institute of
Technology, Pasadena
CA
91125,
USA
77
Optical Science Laboratory, University College London,
Gower Street, London, UK
78
SISSA, Astrophysics Sector, via Bonomea 265, 34136
Trieste,
Italy
79
School of Physics and Astronomy, Cardiff University,
Queens Buildings, The Parade,
Cardiff, CF24 3AA, UK
80
UPMC Univ Paris 06, UMR7095, 98 bis Boulevard Arago, 75014
Paris,
France
81
Université de Toulouse, UPS-OMP, IRAP, 31028
Toulouse Cedex 4,
France
82
Universities Space Research Association, Stratospheric Observatory
for Infrared Astronomy, MS
232-11, Moffett Field
CA
94035,
USA
83
University of Granada, Departamento de Física Teórica y del Cosmos,
Facultad de Ciencias, 411007
Granada,
Spain
84
Warsaw University Observatory, Aleje Ujazdowskie 4, 00-478
Warszawa,
Poland
Received:
18
December
2013
Accepted:
29
January
2014
The dust-Hi correlation is used to characterize the emission properties of dust in the diffuse interstellar medium (ISM) from far infrared wavelengths to microwave frequencies. The field of this investigation encompasses the part of the southern sky best suited to study the cosmic infrared and microwave backgrounds. We cross-correlate sky maps from Planck, the Wilkinson Microwave Anisotropy Probe (WMAP), and the diffuse infrared background experiment (DIRBE), at 17 frequencies from 23 to 3000 GHz, with the Parkes survey of the 21 cm line emission of neutral atomic hydrogen, over a contiguous area of 7500 deg2 centred on the southern Galactic pole. We present a general methodology to study the dust-Hi correlation over the sky, including simulations to quantify uncertainties. Our analysis yields four specific results. (1) We map the temperature, submillimetre emissivity, and opacity of the dust per H-atom. The dust temperature is observed to be anti-correlated with the dust emissivity and opacity. We interpret this result as evidence of dust evolution within the diffuse ISM. The mean dust opacity is measured to be (7.1 ± 0.6) × 10-27 cm2 H-1 × (ν/ 353 GHz)1.53 ± 0.03 for 100 ≤ ν ≤ 353 GHz. This is a reference value to estimate hydrogen column densities from dust emission at submillimetre and millimetre wavelengths. (2) We map the spectral index βmm of dust emission at millimetre wavelengths (defined here as ν ≤ 353 GHz), and find it to be remarkably constant at βmm = 1.51 ± 0.13. We compare it with the far infrared spectral index βFIR derived from greybody fits at higher frequencies, and find a systematic difference, βmm − βFIR = − 0.15, which suggests that the dust spectral energy distribution (SED) flattens at ν ≤ 353 GHz. (3) We present spectral fits of the microwave emission correlated with Hi from 23 to 353 GHz, which separate dust and anomalous microwave emission (AME). We show that the flattening of the dust SED can be accounted for with an additional component with a blackbody spectrum. This additional component, which accounts for (26 ± 6)% of the dust emission at 100 GHz, could represent magnetic dipole emission. Alternatively, it could account for an increasing contribution of carbon dust, or a flattening of the emissivity of amorphous silicates, at millimetre wavelengths. These interpretations make different predictions for the dust polarization SED. (4) We analyse the residuals of the dust-Hi correlation. We identify a Galactic contribution to these residuals, which we model with variations of the dust emissivity on angular scales smaller than that of our correlation analysis. This model of the residuals is used to quantify uncertainties of the CIB power spectrum in a companion Planck paper.
Key words: dust, extinction / submillimeter: ISM / local insterstellar matter / infrared: diffuse background / cosmic background radiation
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Understanding interstellar dust is a major challenge in astrophysics related to physical and chemical processes in interstellar space. The composition of interstellar dust reflects the processes that contribute to breaking down and rebuilding grains over timescales much shorter than that of the injection of newly formed circumstellar or supernova dust. While there is wide consensus on this view, the composition of interstellar dust and the processes that drive its evolution are still poorly understood (Zhukovska et al. 2008; Draine 2009; Jones & Nuth 2011). Observations of dust emission are essential in constraining the nature of interstellar grains and their size distribution.
The Planck footnotePlanck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states (in particular the lead countries France and Italy), with contributions from NASA (USA) and telescope reflectors provided by a collaboration between ESA and a scientific consortium led and funded by Denmark. all-sky survey has opened a new era in dust studies by extending to submillimetre wavelengths and microwave frequencies the detailed mapping of the interstellar dust emission provided by past infrared space missions. For the first time we have the sensitivity to map the long wavelength emission of dust in the diffuse interstellar medium (ISM). Large dust grains (size >10 nm) dominate the dust mass. Far from luminous stars, the grains are cold (10–20 K) so that a significant fraction of their emission is over the Planck frequency range. Dipolar emission from small, rapidly spinning, dust particles is an additional emission component accounting for the so-called anomalous microwave emission (AME) revealed by observations of the cosmic microwave background (CMB) (e.g. Leitch et al. 1997; Banday et al. 2003; Davies et al. 2006; Ghosh et al. 2012; Planck Collaboration XX 2011). Magnetic dipole radiation from thermal fluctuations in magnetic nano-particles may also be a significant emission component over the frequency range relevant to CMB studies (Draine & Lazarian 1999; Draine & Hensley 2013), a possibility that has yet to be tested.
The separation of the dust emission from anisotropies of the cosmic infrared background (CIB) and the CMB is a difficulty for both dust and background studies. The dust-gas correlation provides a means to separate these emission components from an astrophysics perspective, complementary to mathematical component separation methods (Planck Collaboration XII 2014). At high Galactic latitudes, the dust emission is known to be correlated with the 21 cm line emission from neutral atomic hydrogen (Boulanger & Perault 1988). This correlation has been used to separate the dust emission from CIB anisotropies and characterize the emission properties of dust in the diffuse ISM using data from the cosmic background explorer (COBE, Boulanger et al. 1996; Dwek et al. 1997; Arendt et al. 1998), the Wilkinson Microwave Anisotropy Probe (WMAP, Lagache 2003), and Planck (Planck Collaboration XXIV 2011). The residual maps obtained after subtraction of the dust emission correlated with Hi have been used successfully to study CIB anisotropies (Puget et al. 1996; Fixsen et al. 1998; Hauser et al. 1998; Planck Collaboration XVIII 2011). The correlation analysis also yields the spectral energy distribution (SED) of the dust emission normalized per unit hydrogen column density, which is an essential input to dust models, and a prerequisite for determining the dust temperature and opacity (i.e. the optical depth per hydrogen atom).
The COBE satellite provided the first data on the thermal emission from large dust grains at long wavelengths. These data were used to define the dust models of Draine & Li (2007), Compiègne et al. (2011) and Siebenmorgen et al. (2014), and the analytical fit proposed by Finkbeiner et al. (1999), which has been widely used by the CMB community to extrapolate the IRAS all-sky survey to microwave frequencies. Today the Planck data allow us to characterize the dust emission at millimetre wavelengths directly from observations. A first analysis of the correlation between Planck and Hi observations was presented in Planck Collaboration XXIV (2011). In that study, the IRAS 100 μm and the 857, 545, and 353 GHz Planck maps were correlated with Hi observations made with the Green Bank Telescope (GBT) for a set of fields sampling a range of Hi column densities. We extend this early work to microwave frequencies, and to a total sky area more than an order of magnitude higher.
The goal of this paper is to characterize the emission properties of dust in the diffuse ISM, from far infrared to microwave frequencies, for dust, CIB, and CMB studies. We achieve this by cross-correlating the Planck data with atomic hydrogen emission surveyed over the southern sky with the Parkes telescope (the Galactic All Sky Survey, hereafter GASS; McClure-Griffiths et al. 2009; Kalberla et al. 2010). We focus on the southern Galactic polar cap (b < −25°) where the dust-gas correlation is most easily characterized using Hi data because the fraction of the sky with significant H2 column density is low (Gillmon et al. 2006). This is also the cleanest part of the southern sky for CIB and CMB studies.
The paper is organized as follows. We start by presenting the Planck and the ancillary data from the COBE diffuse infrared background experiment (DIRBE) and WMAP that we are correlating with the Hi GASS survey (Sect. 2). The methodology we follow to quantify the dust-gas correlation is described in Sect. 3. We use the results from the correlation analysis to characterize the variations of the dust emission properties across the southern Galactic polar cap in Sect. 4 and determine the spectral index of the thermal dust emission from submm to millimetre wavelengths in Sect. 5. In Sect. 6, we present the mean SED of dust from far infrared to millimetre wavelengths, and a comparison with models of the thermal dust emission. Section 7 focuses on the SED of the Hi correlated emission at microwave frequencies, which we quantify and model over the full spectral range relevant to CMB studies from 23 to 353 GHz. The main results of the paper are summarized in Sect. 8. The paper contains four appendices where we detail specific aspects of the data analysis. In Appendix A, we describe how maps of dust emission are built from the results of the Hi correlation analysis. We explain how we separate dust and CMB emission at microwave frequencies in Appendix B. We detail how we quantify the uncertainties of the results of the dust-Hi correlation in Appendix C. Appendix D presents simulations of the dust emission that we use to quantify uncertainties.
 |
Fig. 1 Left: Planck map at 857 GHz over the area where we have Hi data from the GASS survey. The center of the orthographic projection is the southern Galactic pole. Galactic longitudes and latitudes are marked by lines and circles, respectively. The Planck image has been smoothed to the 16′ resolution of the GASS NHI map. Right: GASS NHI map of Galactic disk emission, obtained by integrating over the velocity range defined by Galactic rotation (Sect. 2.2.2). |
2. Data sets
In this section, we introduce the Planck, Hi, and ancillary sky maps we use in the paper.
2.1. Planck data
Planck is the third generation space mission to characterize the anisotropies of the CMB. It observed the sky in nine frequency bands from 30 to 857 GHz with an angular resolution from 33′ to 5′ (Planck Collaboration I 2014). The Low Frequency Instrument (LFI, Mandolesi et al. 2010; Bersanelli et al. 2010; Mennella et al. 2010) observed the 30, 44, and 70 GHz bands with amplifiers cooled to 20 K. The High Frequency Instrument (HFI, Lamarre et al. 2010) observed the 100, 143, 217, 353, 545, and 857 GHz bands with bolometers cooled to 0.1 K. In this paper, we use the nine Planck frequency maps made from the first 15.5 months of the mission (Planck Collaboration I 2014) in HEALPix format1. Maps at 70 GHz and below are at Nside = 1024 (pixel size 3.′4); those at 100 GHz and above are at Nside = 2048 (1.′7). We refer to previous Planck publications for the data processing, map-making, photometric calibration, and photometric uncertainties (Planck Collaboration II 2014; Planck Collaboration VI 2014; Planck Collaboration V 2014; Planck Collaboration VIII 2014). At HFI frequencies, we analyse maps produced both with and without subtraction of the zodiacal emission (Planck Collaboration XIV 2014). To quantify uncertainties associated with noise, we use maps made from the first and second halves of each stable pointing period (Planck Collaboration VI 2014).
As an example, Fig. 1 shows the 857 GHz map for the area of the Hi GASS survey.
2.2. The GASS H I survey
In this section we explain how we produce the column density map of Galactic Hi gas that we will use as a spatial template in our dust-gas correlation analysis.
2.2.1. H I observations
We make use of data from the GASS Hi survey obtained with the Parkes telescope (McClure-Griffiths et al. 2009). The 21 cm line emission was mapped over the southern sky (δ < 1°) with FWHM angular resolution and a velocity resolution of 1 km s-1. At high Galactic latitudes, the average noise for individual emission-free channel maps is 50 mK (1σ). GASS is the most sensitive, highest angular resolution survey of Galactic Hi emission over the southern sky. We use data corrected for instrumental effects, stray radiation, and radio-frequency interference from Kalberla et al. (2010).
Maps of Hi emission integrated over velocities were generated from spectra in the 3D data cube. To minimize uncertainties from instrumental noise and to eliminate residual instrumental problems we do not integrate the emission over all velocities. The problem is that weak systematic biases over a large number of channels can add up to a significant error. We select the channels on a smoothed data cube to ensure that weak emission around Hi clouds is not affected. Specifically, we calculate a second data cube smoothed to angular and velocity resolutions of 30′ and 8 km s-1. Velocity channels where the emission in this smoothed data cube is below a 5σ level of 30 mK are not used in the integration. This brightness threshold is applied to each smoothed spectrum to define the velocity ranges, not necessarily contiguous, over which to integrate the signal in the full-resolution data cube. The impact on the HI column density map of the selection of channels is small and noticeable only in the regions of lowest column densities. The magnitude of the difference between maps produced with and without the 5σ selection of the channels is a few 1018 H cm-2. This small difference is not critical for our analysis.
2.2.2. Separation of H I emission from the Galaxy and Magellanic Stream
The southern polar cap contains Galactic Hi emission with typical column densities NHI from one to a few times 1020 cm-2, plus a significant contribution from the Magellanic Stream (MS; Nidever et al. 2008). We need to separate the Galactic and MS gas because the dust-to-gas mass ratio of the low metallicity MS gas is lower than that of the Galactic Hi.
 |
Fig. 2 NHI maps corresponding to the IVC (left) and HVC (right) velocity ranges as defined in Sect. 2.2.3. We show the data at Galactic latitudes b < −25° that we use in our correlation analysis. |
The velocity information permits a separation of the Galactic and MS emission over most of the sky (Venzmer et al. 2012). To distinguish the two components, we use a 3D model of the Galactic Hi emission presented in Kalberla & Dedes (2008). The model matches the velocity distribution of the observed emission. We produce a 3D data cube with the model that we use to distinguish parts of the GASS data cube that have emission likely to be associated with the MS from those associated with the Galaxy. Specifically, the emission in a given velocity channel is ascribed to the MS where Tmodel < 60 mK, and to the Galaxy where Tmodel ≥ 60 mK (see Fig. A.1 in Planck Collaboration XXX 2014). This defines the MS and Galactic maps used in the paper. The MS and Galactic emissions are clearly separated except in a circular area of 20° diameter centred at Magellanic longitudes and latitudes2lMS = − 50° and bMS = 0°, where the radial velocity of gas in the MS merges with Galactic velocities (Nidever et al. 2010). We do not use this area in our dust-gas correlation analysis.
2.2.3. The IVC and HVC contributions to the Magellanic Stream component
Our method to identify the emission from the local Hi differs from that used for the GBT fields in Planck Collaboration XXIV (2011), where the low velocity gas and intermediate and high velocity clouds (IVCs and HVCs) have been distinguished based on the specific spectral features present in each of the fields. Such a solution is not available across the much more extended GASS field, but our MS map may be expressed as the sum of IVC and HVC maps.
HVCs and IVCs are distinguished from gas in the Galactic disk by their deviation velocities vdev, defined as the difference between the observed radial velocity and that expected in a given direction from the Galactic rotation. Clouds with | vdev | > 90 km s-1 are usually considered as HVCs, while IVCs correspond to the velocity range 35 < | vdev | < 90 km s-1 (Wakker 2004). At high Galactic latitudes, our threshold of 60 mK for the Hi model corresponds to about | vdev | ≤ 45 km s-1; a threshold of Tmodel ≥ 16 mK corresponds to | vdev | ≤ 90 km s-1. To separate the MS emission into its IVC and HVC contributions, therefore, we make a second separation using the 16 mK threshold. The lower threshold allows us to identify the part of the MS emission with deviation velocities in the HVC range, and the difference between the two MS maps produced with 60 and 16 mK thresholds identifies the part of the MS map with deviation velocities in the IVC range.
We note that the HVC map could contain HVC gas not associated with the MS, but also of low dust content. The IVC map might contain Galactic gas with more normal dust content like in Galactic IVCs (Planck Collaboration XXIV 2011). In addition, the Galactic gas as defined might also contain Galactic IVCs, which often have a depleted dust content, typically by a factor two (Planck Collaboration XXIV 2011). However, anomalous lines of sight are removed by our masking process (Sect. 3.3).
2.2.4. Column density maps
The Galactic and the MS Hi emission maps, as well as the division of the MS map into its IVC and HVC contributions, are projected on a HEALPix grid with a resolution parameter Nside = 1024 using the nearest HEALPix pixel to each GASS position, before reducing the map to Nside = 512 (pixel size ) with the ud_grade HEALPix procedure. After interpolation onto the HEALPix grid, the angular resolution is . For all maps, the Hi emission is converted to Hi column density NHI assuming that the 21 cm line emission is optically thin. For the column densities of one to a few 1020H cm-2 relevant to this study, the opacity correction correction is expected to be less than 5% (see Fig. 4 in Elvis et al. 1989). The Galactic NHI map is presented in Fig. 1. Figure 2 shows the NHI maps corresponding to the IVC and HVC velocity ranges.
We use the Galactic NHI map as a spatial template in our dust-gas correlation analysis. The IVC and HVC maps are used to quantify how the separation of the Hi emission into its Galactic and MS contributions affects the results of our analysis.
2.3. Ancillary sky maps
In addition to the Planck maps, we use the DIRBE sky maps at 100, 140, and 240 μm (Hauser et al. 1998), and the WMAP 9-year sky maps at frequencies 23, 33, 41, 61, and 94 GHz (Bennett et al. 2013). The DIRBE maps allow us to extend our Hi correlation analysis to the peak of the dust SED in the far infrared. The WMAP maps complement the LFI data, giving finer frequency sampling of the SED at microwave frequencies. We also use the 408 MHz map of Haslam et al. (1982) to correct our dust-gas correlation for chance correlations of the Hi template with synchrotron emission. These chance correlations are non-negligible for the lowest Planck and WMAP frequencies.
The DIRBE, WMAP, and 408 MHz data are available from the Legacy Archive for Microwave Background Data3. We use the DIRBE data corrected for zodiacal emission. We project the data on a HEALPix grid at Nside = 512 with a Gaussian interpolation kernel that reduces the angular resolution to 50′. We compute maps of uncertainties that take into account this slight smoothing of the data. The photometric uncertainties of the DIRBE maps at 100, 140, and 240 μm are 13.6, 10.6, and 11.6%, respectively (Hauser et al. 1998).
3. The dust-gas correlation
Figure 1 illustrates the general correlation between the dust emission and Hi column density over the southern Galactic cap. In this section we describe how we quantify this correspondence by cross correlating locally the spatial structure in the dust and Hi maps. Section 3.1 describes the method that we use to cross correlate maps; Sects. 3.2 and 3.3 describe its implementation. Residuals to the dust-Hi correlation are discussed in Sect. 3.4.
3.1. Methodology
We follow the early Planck study (Planck
Collaboration XXIV 2011) in cross correlating spatially the Planck maps with the
Galactic Hi map (Sect. 2.2). For a set of sky
positions, we perform a linear fit between the data and the Hi template. We compute the
slope (αν) and offset
(ων) of the fit
minimizing the χ2![\begin{equation} \chi^2 = \sum_{i=1}^{N} [T_\nu (i) - \alpha_\nu ~ I_{\rm HI}(i) - \omega_\nu]^2, \label{eq:1} \end{equation}](/articles/aa/full_html/2014/06/aa23270-13/aa23270-13-eq59.png) (1)where Tν and IHI are the data
and template values from maps at a common resolution. The sum is computed over
N pixels
within sky patches centred on the positions at which the correlation is performed. The
minimization yields the following expressions for αν and ων
(1)where Tν and IHI are the data
and template values from maps at a common resolution. The sum is computed over
N pixels
within sky patches centred on the positions at which the correlation is performed. The
minimization yields the following expressions for αν and ων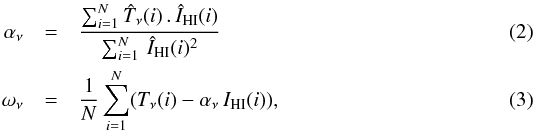 where
where 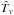 and
and
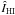 are the data and Hi template vectors with
mean values, computed over the N pixels, subtracted. The slope of the linear regression
αν, hereafter referred
to as the correlation measure, is used to compute the dust emission at frequency
ν per unit
NHI. The offset of the linear regression
ων is used in building
a model of the dust emission that is correlated with the Hi template in Appendix A.
are the data and Hi template vectors with
mean values, computed over the N pixels, subtracted. The slope of the linear regression
αν, hereafter referred
to as the correlation measure, is used to compute the dust emission at frequency
ν per unit
NHI. The offset of the linear regression
ων is used in building
a model of the dust emission that is correlated with the Hi template in Appendix A.
We write the sky emission as the sum of five contributions 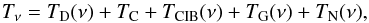 (4)where TD(ν) is the map of dust
emission associated with the Galactic Hi emission, TC and
TCIB(ν) are the cosmic
microwave and infrared backgrounds, TG(ν) represents
Galactic emission components unrelated to Hi emission (dust associated with
H2 and Hii gas,
synchrotron emission, and free-free), and TN(ν) is the data
noise. These five terms are expressed in units of thermodynamic CMB temperature.
(4)where TD(ν) is the map of dust
emission associated with the Galactic Hi emission, TC and
TCIB(ν) are the cosmic
microwave and infrared backgrounds, TG(ν) represents
Galactic emission components unrelated to Hi emission (dust associated with
H2 and Hii gas,
synchrotron emission, and free-free), and TN(ν) is the data
noise. These five terms are expressed in units of thermodynamic CMB temperature.
Combining Eqs. (2) and (4), we write the cross-correlation measure as
the sum of five contributions ![\begin{eqnarray} \alpha_\nu &=& \left(\frac{1}{\sum_{i=1}^{N}~ \vtHI (i)^2 }\right) ~ \sum_{i=1}^{N} [\hat{T}_{\rm D} (\nu,i) + \hat{T}_{\rm C} (i) + \hat{T}_{\rm CIB} (\nu,i) \nonumber \\ \label{eq:5} && \quad + \hat{T}_{\rm G} (\nu,i) + \hat{T}_{\rm N}(\nu,i)]. ~ \vtHI (i) \\ \label{eq:6} \alpha_\nu &=& \alpha_\nu(D_{\rm HI}) + \alpha (C_{\rm HI}) + \alpha_\nu({\rm CIB}_{\rm HI}) + \alpha_\nu(G_{\rm HI}) + \alpha_\nu(N), \end{eqnarray}](/articles/aa/full_html/2014/06/aa23270-13/aa23270-13-eq74.png) where the subscript HI refers to the Hi
template used in this paper. The first term αν(DHI)
is the dust emission at frequency ν per unit NHI, hereafter
referred to as the dust emissivity ϵH(ν). The second term
α(CHI) is the chance
correlation between the CMB and the Hi template. It is independent of the frequency
ν because
Eqs. (4) and (5) are written in units of thermodynamic CMB temperature. The last
terms in Eq. (6) represent the
cross-correlation of the Hi map with the CIB, the Galactic emission components unrelated
with Hi emission, and the data noise. We take these terms as uncertainties on
ϵH(ν). In Appendix
B, we detail how we estimate α(CHI) to get
ϵH(ν) from
αν. For part of our
analysis, we circumvent the calculation of α(CHI) by computing the
difference
where the subscript HI refers to the Hi
template used in this paper. The first term αν(DHI)
is the dust emission at frequency ν per unit NHI, hereafter
referred to as the dust emissivity ϵH(ν). The second term
α(CHI) is the chance
correlation between the CMB and the Hi template. It is independent of the frequency
ν because
Eqs. (4) and (5) are written in units of thermodynamic CMB temperature. The last
terms in Eq. (6) represent the
cross-correlation of the Hi map with the CIB, the Galactic emission components unrelated
with Hi emission, and the data noise. We take these terms as uncertainties on
ϵH(ν). In Appendix
B, we detail how we estimate α(CHI) to get
ϵH(ν) from
αν. For part of our
analysis, we circumvent the calculation of α(CHI) by computing the
difference 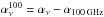 .
.
We write the standard deviation on the dust emissivity ϵH(ν) as 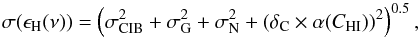 (7)where the first three terms represent the
contributions from CIB anisotropies, the Galactic residuals, and the data noise. Here and
subsequently, Galactic residuals refer to the difference between the dust emission and the
model derived from the correlation analysis (Appendix A). They arise from Galactic emission unrelated with Hi (TG(ν) in Eq. (4)), and also from variations of the dust
emissivity on angular scales smaller than the size of the sky patch used in computing the
correlation measure. The last term in Eq. (7) is the uncertainty associated with the subtraction of the CMB, quantified by
an uncertainty factor δCMB that we estimate in Appendix B to be 3%. For
(7)where the first three terms represent the
contributions from CIB anisotropies, the Galactic residuals, and the data noise. Here and
subsequently, Galactic residuals refer to the difference between the dust emission and the
model derived from the correlation analysis (Appendix A). They arise from Galactic emission unrelated with Hi (TG(ν) in Eq. (4)), and also from variations of the dust
emissivity on angular scales smaller than the size of the sky patch used in computing the
correlation measure. The last term in Eq. (7) is the uncertainty associated with the subtraction of the CMB, quantified by
an uncertainty factor δCMB that we estimate in Appendix B to be 3%. For 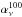 and a given experiment, the CMB
subtraction is limited only by the relative uncertainty of the photometric calibration,
which is 0.2–0.3% at microwave frequencies for both Planck and
WMAP (Planck Collaboration I
2014; Bennett et al. 2013).
and a given experiment, the CMB
subtraction is limited only by the relative uncertainty of the photometric calibration,
which is 0.2–0.3% at microwave frequencies for both Planck and
WMAP (Planck Collaboration I
2014; Bennett et al. 2013).
3.2. Implementation
We perform the cross-correlation analysis at two angular resolutions. First, we correlate the Hi template with the seven Planck maps at frequencies of 70 GHz and greater and the 94 GHz channel of WMAP, all smoothed to the 16′ resolution of the Hi map, i.e. Nside = 512, with pixels. The map smoothing uses a Gaussian approximation for the Planck beams. The cross-correlation with the DIRBE maps is done at a single 50′ resolution. Second, to extend our analysis to frequencies lower than 70 GHz, we also perform the data analysis using all of the Planck and WMAP maps smoothed to a common 60′ Gaussian beam (Planck Collaboration VI 2014) at a HEALPix resolution Nside = 128 ( pixels), combined with a smoothed and reprojected Hi template. At frequencies ν ≤ 353 GHz, we also perform a simultaneous linear correlation of the Planck and WMAP maps with two templates, the GASS Hi map and the 408 MHz map of Haslam et al. (1982). This corrects the results of the dust-Hi correlation for any chance correlation of the Hi spatial template with synchrotron emission. Peel et al. (2012) have shown that, at high Galactic latitudes, the level of the dust-correlated emission in the WMAP bands does not depend significantly on the frequency of the synchrotron template.
We perform the cross-correlation over circular sky patches 15° in diameter centred on HEALPix pixels. The analysis of sky simulations presented in Appendix C shows that the size of the sky patches is not critical. We require the number of unmasked pixels used to compute the correlation measure and the offset to be higher than one third of the total number of pixels within a sky patch. For input maps at 16′ angular resolution projected on HEALPix grid with Nside = 512, this corresponds to a threshold of 4500 pixels.
We compute the correlation measure αν and offset ων at positions corresponding to pixel centres on HEALPix grids with Nside = 32 and 8 (pixel size and , respectively). The higher resolution grid, which more finely samples variations of the dust emissivity on the sky, is used to produce images for display, for example the dust emissivity at 353 GHz presented in Fig. 3, and the dust model in Appendix A. For statistical studies, we use the lower resolution grid, for which we obtain a correlation measure for 135 sky patches. Because of the sampling of the 15° patches at Nside = 8, each pixel in the input data is part of three sky patches, and these correlation measures are not independent.
 |
Fig. 3 Map of the dust emissivity at 353 GHz, i.e. the correlation measure α353 with the CMB contribution α(CHI) subtracted (see Eq. (6)). The correlation measure is computed in each pixel correlating the Planck map with the Hi template over a sky patch with 15° diameter centred on it. |
We detail how we quantify the various contributions to the uncertainty of the dust emissivity in Appendix C, including those associated with the separation of the Hi emission between its Galactic and MS contributions (Sect. 2.2.2), which is the main source of uncertainty on the Hi template used as independent variable in the correlation analysis. As in Planck Collaboration XXIV (2011), we do not include any noise weighting in Eq. (1) because data noise is not the main source of uncertainty. For most HFI frequencies, the noise is much lower than either CIB anisotropies or the differences between the dust emission and the model we fit.
3.3. Sky masking
In applying Eqs. (2) and ( 3), we use a sky mask that defines the overall part of the sky where we characterize the correlation of Hi and dust, and within this large area the pixels that are used to compute the correlation measures. We describe in this section how we make this mask.
We focus our analysis on low column density gas around the southern Galactic pole, specifically, Hi column densities NHI ≤ 6 × 1020 cm-2 at Galactic latitudes b ≤ −25°. Within this sky area we mask a 20°-diameter circle centred at Magellanic longitude and latitude lMS = −50° and bMS = 0°, where the radial velocity of gas in the MS merges with Galactic velocities so that a Galactic Hi template cannot be separated.
To characterize the dust signal associated with the Hi gas, we also need to mask sky pixels where the dust and Hi emission are not correlated. As in Planck Collaboration XXIV (2011), we need to identify the sky pixels where there is significant dust emission from H2 gas. This is relatively easy to do at high Galactic latitudes where the gas column density is the lowest, and the surface filling factor of H2 gas is small. UV observations (Savage et al. 1977; Gillmon et al. 2006) and the early Planck study (Planck Collaboration XXIV 2011) show that the fraction of H2 gas can become significant for some sight lines where NHI exceeds 3 × 1020cm-2 or so. We also need to mask pixels where there is Galactic Hi gas with little or no far infrared counterpart, and bright extragalactic sources.
Following Planck Collaboration XXIV (2011), we build our mask by iterating the correlation analysis. At each step, we build a model of the dust emission associated with the Galactic Hi gas from the results of the IR-Hi correlation (Appendix A). We obtain a map of residuals by subtracting this model from the input data. At each iteration, we then compute the standard deviation of the Gaussian core of the residuals over unmasked pixels. The mask for the next iteration is set by masking all pixels where the absolute value of the residual is higher than 3σ. The choice of this threshold is not critical. For a 5σ cut, we obtain a mean dust emissivity at 857 GHz higher by only 1% than the value for a 3σ cut. The standard deviation of the fractional differences between the two sets of dust emissivities computed patch by patch is 3%. We use the highest Planck frequency, 857 GHz, to identify bright far infrared sources and pixels where the dust emission departs from the model emission estimated from the Hi map. The iteration rapidly converges to a stable mask. Once we have converged for the 857 GHz frequency channel, we look for outliers at other frequencies. This is necessary to mask a few infrared galaxies at 100 μm and bright radio sources at microwave frequencies. We perform this procedure with the maps at 16′, 50′, and 60′ resolution, obtaining a separate mask for each resolution.
Figure 4 presents the histogram of the residual map at 857 GHz with 16′ resolution. The mask discards the positive and negative tails that depart from the Gaussian fit of the central core of the histogram. These tails amount to 9% of the total area of the residual map.
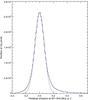 |
Fig. 4 Histogram of residual emission at 857 GHz after subtraction of the dust emission associated with HI gas. The blue solid line is a Gaussian fit to the core of the histogram, with dispersion σ = 0.07 MJy sr-1. We mask pixels where the absolute value of the residual emission is higher than 3σ. The positve (negative) wing of the histogram beyond this threshold represents 7% (2%) of the data. |
A sky image of the mask used in the analysis of HFI maps at 16′ resolution is shown in Fig. 5. The total area not masked is 7500 deg2 (18% of the sky). The median NHI is 2.1 × 1020 H cm-2, and NHI < 3 × 1020 H cm-2 for 74% of the unmasked pixels.
 |
Fig. 5 Mask for our analysis of the Planck-Hi correlation. The coloured area that is not blue defines the data used to compute the correlation measures. Within this area, the median NHI is 2.1 × 1020 H cm-2, and NHI < 3 × 1020 H cm-2 for 74% of the pixels. The blue patches correspond to regions where the absolute value of the residual emission is higher than 3σ at 857 GHz (Fig. 4). The circular hole near the Southern Galactic pole corresponds to the area where Hi gas in the Galaxy cannot be well separated because the mean radial velocity of the gas in the MS is within the Galactic range of velocities. |
3.4. Galactic residuals with respect to the dust-H I correlation
In this section, we describe the Galactic residuals with respect to the dust-Hi correlation. A power spectrum analysis of the CIB anisotropies over the cleanest part of the southern Galactic cap is presented in Planck Collaboration XXX (2014).
Figure 6 shows the map of residual emission at 857 GHz together with the map of Hi emission in the MS. The first striking result from Fig. 6 is that the residual map shows no evidence of dust emission from the MS. This result indicates that the MS is dust poor; it will be detailed in a dedicated paper.
 |
Fig. 6 Left: image of the residual emission at 857 GHz obtained by subtracting the Hi-based model of the dust emission from the input Planck map. Right: image of NHI from the Magellanic Stream (see Sect. 2.2.2), the sum of the IVC and HVC maps in Fig. 2. |
The residual map shows localized regions, both positive and negative, that produce the non-Gaussian wings of the histogram in Fig. 4. The positive residuals are likely to trace dust emission associated with molecular gas (Desert et al. 1988; Reach et al. 1998; Planck Collaboration XXIV 2011). In addition, some positive residuals may be from dust emission associated with Galactic IVC gas not in the Galactic Hi template.
The non-Gaussian tail toward negative residuals was not significant in the earlier higher resolution Planck study that analysed a much smaller sky area at low Hi column densities. However, that analysis deduced emissivities for low velocity gas and IVC gas independently, and did find many examples of IVCs with less than half the typical emissivity. If such gas were included in the Galactic Hi template for | vdev | ≤ 45 km s-1, then negative residuals could arise. Another interesting possible interpretation, which needs to be tested, is that negative residuals correspond to Hi gas at Galactic velocities with no or deficient dust emission, akin to the MS, or to typical HVC gas (Peek et al. 2009; Planck Collaboration XXIV 2011). We do not discuss further these regions that are masked in our data analysis. Instead, we focus our analysis on the fainter residuals of Galactic emission that together with CIB anisotropies make the Gaussian core of the histogram in Fig. 4.
 |
Fig. 7 Standard deviation σ857 of the residuals with respect to the Planck-Hi correlation at 857 GHz versus the mean NHI, both computed within circular sky patches with 5° diameter and over unmasked pixels. The red hatched strip marks the contribution of CIB anisotropies to the residuals at 16′ resolution, computed from the CIB model in Planck Collaboration XXX (2014). The width of the strip represents the expected scatter (± 1σ) of this contribution. Both the scattered distribution of data points above CIB anisotropies strip and the increase in the mean σ857 with NHI arise from residuals with a Galactic origin (Appendix D). |
To characterize the Gaussian component of the residuals with respect to the dust-Hi correlation, we compute the standard deviation σ857 of the residual map at 857 GHz within circular apertures of 5° diameter centred on Nside = 16 pixels. We choose this aperture size to be smaller than the sky patches used to compute the dust emissivity so as to sample more finely σ857. Within each 5° aperture, we compute the standard deviation of the residual 857 GHz map and the mean NHI over unmasked pixels, requiring at least 1000 of the maximum 1500 pixels available at Nside = 512. In Fig. 7, σ857 is plotted versus the mean NHI. The hatched strip in the figure indicates the contribution to σ857 from CIB anisotropies at 16′ resolution, as computed using the model power spectrum in Planck Collaboration XXX (2014). Most values of σ857 are above the strip. Since the contribution of noise to σ857 is negligible, there is a significant contribution to σ857 from residuals with a Galactic origin. The statistical properties of σ857 – the mean trend with increasing NHI and the large scatter around this trend in Fig. 7 – can be accounted for by a simple model where the Galactic residuals arise from variations of the dust emissivity on scales lower than the 15° diameter of the patches in our correlation analysis. In Appendix D, we quantify this interpretation with simulations.
The ratio of the dispersions from Galactic residuals and from CIB anisotropies increases towards higher frequencies, but it decreases with decreasing patch size used in the underlying correlation analysis and with better angular resolution of the Hi template map (Appendix C). Thereby an obvious Galactic contribution in the faintest fields was not noticed in the earlier study with the GBT of Planck Collaboration XXIV (2011), but they did find an increase in the standard deviation of the residuals with the mean column density (see their Fig. 12).
Unlike the localized features that make the non-Gaussian part of the histogram in Fig. 4, the Gaussian contribution cannot be masked out. As discussed in Planck Collaboration XXX (2014), it significantly biases the power spectrum of CIB anisotropies at ℓ < 100, depending on the range of NHI within the part of the sky used for the analysis.
 |
Fig. 8 Left: map of the dust opacity σH(353 GHz) in Eq. (9). Right: colour temperature map inferred from the ratio between the dust emissivities at 100 μm from DIRBE and 857 GHz from Planck, with a spectral index of the dust emissivity βFIR = 1.65. This figure reveals that the temperature and submillimetre opacity of dust are anti-correlated. |
 |
Fig. 9 Top: dust colour temperature Td versus dust emissivity at 353 GHz, two independent observables (Fig. 3), with typical error bars at the top right. The dashed line represents the expected dependency of Td on the dust emissivity for a fixed emitted power of 3.4 × 10-31 W H-1. The blue dots identify data for sky patches centred at Galactic latitudes b ≤ −60°. Bottom: Td versus dust opacity at 353 GHz, re-expressing the same data in the form plotted by Planck Collaboration XXIV (2011) and Martin et al. (2012). |
 |
Fig. 10 Map of the specific power radiated by dust at far infrared wavelengths per H. This figure displays spatial variations of the specific dust power, which may be decomposed as the sum of two parts correlated with the opacity and temperature maps (see Fig. 8), respectively. |
4. Dust emission properties across the southern Galactic cap
In this section, we use the results from our analysis of the dust-Hi correlation to describe how dust emission properties vary across the southern Galactic cap.
4.1. Dust temperature and opacity
At frequencies higher than 353 GHz, our analysis extends that of Planck Collaboration XXIV (2011) to a wider area. The dust emissivities are consistent with earlier values, once we correct them for the change in calibration of the 857 and 545 GHz data that occurred after the publication of the Planck Early Papers (Planck Collaboration VIII 2014). The dust emissivity is observed to vary over the sky in a correlated way between contiguous frequencies4. In units of MJy sr-1 per 1020 H cm-2, the dust emissivity at 857 GHz ranges from 0.20 to 0.57 with a mean 0.435. The emissivity also varies by nearly a factor of three at 353 GHz (see Fig. 3), and by a factor of four at 100 μm. The fact that we work on a large contiguous sky area allows us to map these variations over the sky and assess their nature.
Figure 8 displays maps of the dust temperature and
submillimetre opacity. The map of colour temperature Td is derived
from the ratio between the dust emissivities at 100 μm from DIRBE and at 857 GHz
from Planck, R(3000,857). We do not use the dust emissivities
from the 140 and 240
μm DIRBE bands because these maps are
noiser (see Fig. C.1). The colour ratio is converted
into a colour temperature assuming a greybody spectrum 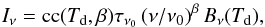 (8)where cc is the colour-correction (Planck Collaboration IX 2014), Bν is the Planck
function, Td is the dust temperature, and
β is the
dust spectral index. In the far infrared, we adopt βFIR = 1.65, the
value found fitting a greybody to the mean dust SED at ν ≥ 353 GHz. The reference
frequency ν0 and the optical depth there
τν0,
divide out in the colour ratio. The mean colour temperature is 19.8 K, in good agreement with what is
reported for the same part of the sky in Planck
Collaboration XI (2014) for the same βFIR. The dust opacity is computed from
the dust emissivity and colour temperature:
(8)where cc is the colour-correction (Planck Collaboration IX 2014), Bν is the Planck
function, Td is the dust temperature, and
β is the
dust spectral index. In the far infrared, we adopt βFIR = 1.65, the
value found fitting a greybody to the mean dust SED at ν ≥ 353 GHz. The reference
frequency ν0 and the optical depth there
τν0,
divide out in the colour ratio. The mean colour temperature is 19.8 K, in good agreement with what is
reported for the same part of the sky in Planck
Collaboration XI (2014) for the same βFIR. The dust opacity is computed from
the dust emissivity and colour temperature: 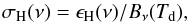 (9)the equivalent of the optical depth divided
by NHI.
(9)the equivalent of the optical depth divided
by NHI.
The two maps in Fig. 8 illustrate an anti-correlation between the dust opacity and the colour temperature, first reported in Planck Collaboration XXIV (2011). Our analysis confirms their result over a wider sky area. The anti-correlation is at odds with the expected increase in the dust emissivity with dust temperature. It suggests that the temperature is a response to variations in dust emission properties and not in the heating rate of dust. To support this interpretation, in Fig. 9 we plot the dust temperature versus the dust emissivity and opacity at 353 GHz. As in earlier studies where different data sets and sky regions have been analysed (Planck Collaboration XXIV 2011; Martin et al. 2012; Roy et al. 2013), we find that the dust temperature is anti-correlated with the dust emissivity and opacity in such a way that the far infrared specific dust power (i.e. the thermal emission integrated over the far infrared SED, per H) is constant. The dashed line in each panel corresponds to the mean value of the far infrared power, 3.4 × 10-31 W H-1, as also found by Planck Collaboration XI (2014) for high latitude dust.
To check that the anti-correlation does not depend on our assumption of a fixed βFIR used to compute the colour temperatures, we repeat our analysis with dust temperatures and opacities derived from a greybody fit to the dust emissivities at 100 μm and the Planck 353, 545 and 857 GHz frequencies, for each sky patch. The dust temperatures from these fits are closely correlated to the colour temperatures determined from the 100 μm and 857 GHz colour ratio. The mean temperature is 19.8 K for both sets of dust temperatures because the βFIR, 1.65, used in the calculation of colour temperatures is the mean of the values derived from the greybody fits. We find that variations of the dust spectral index do not change the anti-correlation between dust opacity and temperature, but they increase the scatter of the data points by about 20%.
The far infrared power emitted by dust equals that absorbed from the interstellar radiation field (ISRF) and so, as discussed by Planck Collaboration XXIV (2011) and Martin et al. (2012), the fact that the power is quite constant has two implications. (1) Increases (decreases) in the equilibrium value of Td are a response to decreases (increases) in the dust far infrared opacity (the ability of the dust to emit and thus cool). (2) The optical/UV absorption opacity of dust must be relatively unchanged, given that variations in the strength of the ISRF are probably small within the local ISM. Thus, an observational constraint to be understood in grain modeling is that the ratio of far infrared to optical/UV opacity changes within the diffuse ISM.
The anti-correlation between Td and σH(353 GHz) at constant power does not fully characterize the spatial variations of the dust emission properties. The scatter of the data points in Fig. 9 around the line of constant power is not noise. Figure 10 displays variations over the southern polar cap of the specific power radiated by dust at far-IR wavelengths per H (Fig. 8). They could result from variations in the dust-to-gas ratio, the dust absorption cross section per H of star light, and/or the ISRF intensity. The dust-to-H mass ratio is inferred from spectroscopic measurements of elements depletions to vary in the local ISM from 0.4% in warm gas to 1% in cold neutral medium (Jenkins 2009).
4.2. Dust evolution within the diffuse ISM
Our analysis provides evidence of a varying ratio between the dust opacity at far infrared and visible/UV wavelengths, strengthening the early results from Planck Collaboration XXIV (2011). These two Planck papers extend to the diffuse atomic ISM results reported in many studies for the translucent sections of molecular clouds (Cambrésy et al. 2001; Stepnik et al. 2003; Planck Collaboration XXV 2011; Martin et al. 2012; Roy et al. 2013). Evidence of dust evolution in the diffuse ISM from far-IR observations of large dust grains was first reported by Bot et al. (2009).
The observations of dust evolution in molecular clouds are often related to grain growth associated with mantle formation or grain coagulation/aggregation. Model calculations do indeed show that the variations in the far infrared dust opacity per unit Av may be accounted for by grain coagulation (Köhler et al. 2012). The fact that such variations are now observed in Hi gas, where densities are not high enough for coagulation to occur, challenges this interpretation. It would be more satisfactory to propose an interpretation that would account for opacity variations in both the diffuse ISM and molecular clouds. Jones (2012) and Jones et al. (2013) take steps in this direction by introducing evolution of carbon dust composition and properties into their dust model. A quantitative modeling of the data has yet to be done within this new framework, but the results presented by Jones et al. (2013) are encouraging. The variations in the far infrared opacity and temperature of dust could trace the degree of processing by UV photons of hydrocarbon dust formed within the ISM.
Alternatively, the variations of the far infrared dust opacity could result from changes in the composition and structure of silicate dust. At the temperature of interstellar dust grains in the diffuse ISM, low energy transitions, associated with disorder in the structure of amorphous solids on atomic scales, contribute to the far infrared dust opacity. This contribution depends on the dust temperature and on the composition and structure of the grains (Meny et al. 2007). The dust opacity of silicates is observed in laboratory experiments (Coupeaud et al. 2011) to depend on parameters describing the amorphous structure of the grains, which may evolve in interstellar space through, for example, exposure to cosmic rays.
A different perspective is considered in Martin et al. (2012). Dust evolution might not be ongoing now within the diffuse ISM. Instead, the observations might reflect the varying composition of interstellar dust after evolution both within molecular clouds and while recyling back to the diffuse ISM, reaching different end points.
5. The dust spectral index from submillimetre to millimetre wavelengths
Our analysis of the Planck data allows us to measure the spectral index of the thermal dust emission from submillimetre to millimetre wavelengths βmm. This complements measurements of the spectral index at far infrared wavelengths βFIR in Planck Collaboration XI (2014) and many earlier studies (e.g. Dupac et al. 2003).
5.1. Measuring the spectral index
For each circular sky patch, we compute the colour ratio
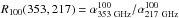 , where
, where
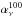 is the correlation measure at frequency
ν corrected
for the CMB contribution by subtracting the correlation measure at 100 GHz (Sect. 3.1). The colour ratio is converted into a spectral index using a
greybody spectrum (Eq. (8)). We compute
R100(353,217) for a grid of values of
βmm and Td. For each sky
patch, adopting the colour temperature determined above independently from the
R(3000,857)
colour ratio, we find the value of βmm that gives a match with the observed
R100(353,217). We obtain the
βmm map presented in Fig. 11.
is the correlation measure at frequency
ν corrected
for the CMB contribution by subtracting the correlation measure at 100 GHz (Sect. 3.1). The colour ratio is converted into a spectral index using a
greybody spectrum (Eq. (8)). We compute
R100(353,217) for a grid of values of
βmm and Td. For each sky
patch, adopting the colour temperature determined above independently from the
R(3000,857)
colour ratio, we find the value of βmm that gives a match with the observed
R100(353,217). We obtain the
βmm map presented in Fig. 11.
 |
Fig. 11 Spectral index βmm of the dust emission derived from the ratio between correlation measures at 353 and 217 GHz (both corrected for the CMB contribution by subtracting the correlation measure at 100 GHz) and the colour temperature map in Fig. 8. |
The mean value and standard deviation (dispersion) of βmm are 1.51 and 0.13 for Planck maps without subtraction of the model of zodiacal emission, and 1.51 and 0.16 for maps with the model subtracted. The standard deviation of the patch by patch difference between these two βmm values is 0.10, only slightly lower than the dispersion of each. The mean βmm is in good agreement with the value of 1.53 estimated for the more diffuse atomic regions of the Galactic disk by Planck Collaboration Int. XIV (2014), but it is lower than values close to 2 derived from the analysis of COBE data at higher frequencies (Boulanger et al. 1996; Finkbeiner et al. 1999). For comparison, we computed a value of βFIR for each sky patch by fitting a greybody to the dust emissivities at the high frequency Planck channels (ν ≥ 353 GHz) and at 100 μm. The difference βFIR − βmm has a median value of 0.15, and shows no systematic dependence on the colour temperature Td.
For the derivation of βmm, we have assumed that the dust emission at 100 GHz is well approximated by a greybody extrapolation from 353 to 100 GHz. To check that this assumption does not introduce a bias, we repeat the data analysis on Planck maps in which the CMB anisotropies have been subtracted using the CMB map obtained with SMICA (Planck Collaboration XII 2014). This allows us to compute the spectral index βmm(SMICA) directly from the ratio between the 353 and 217 GHz correlation measures. The mean value of the differences βmm − βmm(SMICA) is negligible, i.e. there is no bias.
5.2. Variations with dust temperature
Many studies, starting with the early work of Dupac et al. (2003), have reported an anti-correlation between βFIR and dust temperature. Laboratory data on amorphous silicates indicate that, at the temperature of dust grains in the diffuse ISM, it is at millimetre wavelengths that the variations of the spectral index may be the largest (Coupeaud et al. 2011). These laboratory results and astronomical data, have been interpreted within a model where variations in the dust spectral index stem from the contribution of low energy transitions, associated with disorder in the structure of amorphous solids on atomic scales, to the dust opacity (Meny et al. 2007; Paradis et al. 2011). Variations of βmm are also predicted to be possible signatures of the evolution of carbon dust (Jones et al. 2013).
 |
Fig. 12 Spectral index βmm versus Td for the 135 sky patches. The blue dots distinguish patches centred at Galactic latitude b ≤ − 60°. The uncertainties are derived from simulations. The dashed line is a linear regression of βmm on Td, slope (− 0.043 ± 0.009) K-1. |
Our analysis allows us to look for such variations over a frequency range where the determination of the spectral index is to a large extent decoupled from that of the dust temperature. We determine the dust colour temperature Td and the spectral index βmm from two independent colour ratios, whereas in far infrared studies the spectral index βFIR and temperature Td are determined simultaneously from a spectral fit of the SED (Shetty et al. 2009; Planck Collaboration XI 2014). Althought Td is used in the conversion of R100(353,217) into βmm, the uncertainty of Td has a marginal impact. Furthermore, the photometric uncertainty of far infrared data is higher than that at ν ≤ 353 GHz, where the data calibration is done on the CMB dipole.
We start quantifying the uncertainties of βmm using the numerical simulations presented in the companion Planck paper (Planck Collaboration Int. XXI 2014) that extends this work to dust polarization. These simulations include Hi correlated dust emission with a fixed spectral index 1.5, dust emission uncorrelated with Hi with a spectral index of 2, noise, CIB anisotropies, and free-free emission. We analyse 800 realizations of simulated maps at 100, 143, 217, and 353 GHz with the same procedure as used on the Planck data. For each sky patch, we obtain 800 values of βmm. The additional components do not bias the estimate of βmm, but introduce scatter around the mean input value of 1.5. We use the standard deviation of the extracted βmm values as a noise estimate σβ for each sky patch.
The noise on βmm shows a systematic increase towards low NHI, something that we also observe for the Planck analysis. We also measure the standard deviation of βmm over sky patches for each simulation. We find a value of 0.079 ± 0.01, lower than the dispersion 0.13 measured on the Planck data. If the simulations provide a good estimate of the uncertainties, the higher dispersion for the data shows that βmm has some variance. This can be appreciated in Fig. 12, where the values of βmm with their uncertainties are plotted versus the dust temperature Td. The plot also displays the result of a linear regression, which has a slope of (−0.043 ± 0.009) K-1. Using the set of temperatures obtained from the greybody fits increases the spread of the data points in Fig. 12. The slope is changed to (− 0.053 ± 0.007) K-1. The non-zero slope implies some variation of βmm, and also suggests that βmm and Td are anti-correlated. This would extend to the millimetre range a result that has been reported in many studies for βFIR versus Td, but the variations here are small and perhaps only marginally significant. The constancy of βmm is an observational constraint on the nature of the process at the origin of variations of the far-IR dust opacity (Sect. 4.2). We note that Planck Collaboration Int. XIV (2014) do not find evidence of an anti-correlation in their analysis of Planck observations of the diffuse emission in the Galactic disk.
6. The spectral energy distribution of Galactic dust in the diffuse ISM
At the Planck-LFI and WMAP frequencies, the signal-to-noise ratio on the dust emissivity for a given sky patch is very low because the signal is very faint compared to CMB anisotropies and noise. However, by averaging the emissivities over sky patches, we obtain an SED of dust emission spanning the full spectral range and computed consistently at all frequencies (Sect. 6.1). We present greybody fits of the thermal emission of dust at ν ≥ 100 GHz in Sect. 6.2. The SED is compared with existing models in Sect. 6.3.
Mean SED of dust emissivity from Hi correlation.
Mean microwave SED from Hi correlation.
6.1. The SED of the mean dust emissivity
We produce a mean SED of dust in the diffuse ISM by averaging the correlation measures, after correction for the CMB contribution as described in Appendix B, over the 135 sky patches on our lower resolution grid (Sect. 3.2). This SED characterizes the mean emission properties of dust in atomic gas in the local ISM. The statistical uncertainty of the mean SED is computed from the standard deviation of individual measurements divided by the square root of the number of independent sky patches (135/3) used. On average, each pixel of the images is part of 3 sky patches. This is why we consider that the number of independent sky patches is the total number divided by 3. This standard estimate is appropriate for the noisier low frequency data. For the emissivities at higher frequencies, we observe large variations over the sky (Sect. 4.1). However, analysis of our simulations (Appendix C) shows that the uncertainties, including the variations of the emission properties over the sky, average out when we compute the mean dust emissivity over sky patches. Mean emissivities with statistical and photometric uncertainties are listed in Table 1 for the 16′ resolution maps at ν ≥ 70 GHz.
Parameters from greybody fits of the mean dust SED.
6.2. Greybody fits
We characterize the dust SED with greybody fits. The mean emissivities are weighted using uncertainties that are the quadratic combination of the statistical and photometric uncertainties. We map the χ2 for greybody spectra over the parameter space to determine the best fit parameters listed in Table 3. We report parameters from data without and with subtraction of the zodiacal emission model (Planck Collaboration XIV 2014). The differences in fit parameters are within the uncertainties. This is to be expected because the zodiacal emission is a slowly varying function uncorrelated with the spatial fluctuations of the Hi template within the 15° patches.
All of the best fits have χ2 per degree of freedom much lower than 1, because the statistical and photometric uncertainties are correlated across frequencies. To test our fits and to estimate error bars on the parameters, we run a Monte-Carlo simulation that takes these correlations into account. We assume that the photometric uncertainties are correlated for the three DIRBE frequencies, for the two highest HFI frequencies calibrated on planets, and for the four lowest HFI frequencies calibrated on the CMB dipole. For the statistical errors, we use the frequency-dependent decomposition into Galactic, CMB, CIB, and noise contributions inferred from the sky simulations in Appendix C. The sky simulations ignore the decorrelation from far infrared to microwave frequencies of CIB anisotropies (Planck Collaboration XXX 2014) and of Galactic residuals due to variations in dust temperature. These two shortcomings are not an issue, because they mainly impact the modeling of the statistical uncertainties at far infrared frequencies where the photometric uncertainties are dominant. We apply our fits to a greybody spectrum with βFIR = βmm = 1.55 and Td = 19.8 K, combined with 1000 realizations of the statistical and photometric uncertainties. For each realization, we obtain a set of values for the parameters of the fit. For each of the three fits in Table 3, we compute the average and standard deviation of the parameters. The average values match the input values, showing that correlated uncertainties do not bias the fit. We list the standard deviations from the Monte Carlo simulation as error bars for the fit parameters in Table 3. We are confident about this estimate of the errors because the χ2 values obtained for the data fits are in the core of the χ2 distribution for the Monte Carlo simulation. In other words, the simulation accounts for the low values of the χ2 per degree of freedom in Table 3.
The first fit is for frequencies ν ≥ 353 GHz. It is directly comparable to the fits presented in the all-sky analysis of Planck Collaboration XI (2014). The spectral index that we find, β = 1.65 ± 0.10, agrees with the mean value used in Sect. 4 to compute colour temperatures, but it is greater than the values of βmm = 1.51 ± 0.13 derived from the R100(353,217) ratio in Sect. 5. The second fit extends the greybody fit with a single spectral index down to 100 GHz. This fit yields a spectral index of 1.52 ± 0.03 in agreement with the mean value inferred from the above R100(353,217) ratio. For the latter, the dispersion about the mean is higher than the uncertainty from the fit, which is more like an uncertainty of the mean.
The third fit, again from 100 to 3000 GHz, uses separate spectral indices for frequencies higher and lower than 353 GHz. With this extra parameter, a significantly lower χ2 per degree of freedom is achieved, and systematic departures from the fit (Fig. 13) are removed. The best fit is obtained for a higher spectral index at high frequency. The difference between the two spectral indices, βFIR − βmm, is 0.13 for the data not corrected for zodiacal emission. We use our Monte Carlo simulations to test whether the reduction of the χ2 per degree of freedom between the fits with one and two spectral indices (factors 3.7 and 5.4 for the SEDs with and without subtraction of the zodiacal light model) is statistically significant. We obtain a reduction of the χ2 by a factor greater than 3.5 for less than 5% of the realizations. Based on this test, we consider that the variation of the spectral index between far infrared and millimetre wavelengths, quantified by the third fit is statistically significant. Planck Collaboration Int. XIV (2014) reach the same conclusion for the diffuse dust emission in the inner Galactic plane.
The values of the opacity σH(353 GHz) for all fits listed in Table 3 are consistent with a mean value of (7.1 ± 0.6) × 10-27 cm2 H-1, as obtained for the first fit using data with the zodiacal emission subtracted. This mean value agrees with that of Planck Collaboration XI (2014) for low column density. For an dust-to-H mass ratio of 1% (Jenkins 2009), the specific absorption coefficient per unit dust mass is κν = 0.43 ± 0.04 cm2 g-1 at 850 μm.
Residuals of the first two greybody fits are plotted in Fig. 13. The top panel shows that the extrapolation to ν < 353 GHz of the first fit departs progressively from the data points toward lower frequencies. The bottom panel shows the residuals of the second fit of the SED from 100 to 3000 GHz with a single spectral index. The 3000 and 857GHz data points depart from the fit by more than the statistical uncertainties. The differences are within the photometric uncertainties listed in Table 3, but in opposite directions for the DIRBE 100 μm and the Planck 857 GHz emissivities. The residuals do not show the ~10% excess emission at 500 μm with respect to greybody fits that has been reported for the Large Magellanic Cloud (Gordon et al. 2010). We also point out that the residuals to the fits do not show any excess emission in the 100 and 217 GHz spectral bands, which could be coming from the CO(1−0) and CO(2−1) lines (Planck Collaboration XIII 2014).
 |
Fig. 13 Top: residuals from a greybody fit of the mean dust SED at ν ≥ 353 GHz, using one spectral index. Dashed error bars are the quadratic sum of the statistical error (solid) and the photometric uncertainty. The photometric uncertainty is dominant at ν ≥ 545 GHz and negligible for the lower frequencies. Bottom: residuals from a greybody fit to all data points down to 100 GHz, again using a single spectral index. |
 |
Fig. 14 Same as Fig. 13, but for residuals from fits of the mean dust SED with the DUSTEM (top panel) and DL07 (bottom panel) dust models. |
6.3. Comparison with dust models
In this section, we compare the mean SED from Planck with two models of the thermal dust emission. We fit the mean SED in Table 1 with the dust models presented in Compiègne et al. (2011) and Draine & Li (2007), hereafter the DUSTEM and DL07 models. For both models, we fit the scaling factor G0 of the mean interstellar radiation field in the Solar Neighbourhood from Mathis et al. (1983), and another scaling parameter, fSED, that allows for differences in the normalization of the dust emission per unit gas mass. The two parameters of the fit are quite independent. The value of fSED is constrained by the submillimetre data points, while G0 is constrained by the peak of the SED. For the DUSTEM model, the best fit is obtained for G0 = 1.0 and fSED = 1.05, whereas for the DL07 model we find G0 = 0.7 and fSED = 1.45. The residuals from these two fits are shown in Fig. 14. Both models fit the data within 5% at ν ≥ 353 GHz. They depart from the data at lower frequencies by 5 to 15%. We note that both models use the same optical properties for silicates from Li & Draine (2001), who introduced a flattening of the emissivity law at λ ≥ 250 μm to match the SED of Finkbeiner et al. (1999). They differ in their modeling of carbon dust.
This comparison shows that none of the models provides a fully satisfactory fit of the Planck SED. For the DL07 model, it also shows that there is a significant difference in the dust emission per unit gas mass, which is higher than what may be accounted for by dust within the diffuse ionized gas (Gaensler et al. 2008), even in the most favourable hypothesis where its spatial distribution is highly correlated with Hi emission.
7. Microwave dust emission
We extend our analysis of the thermal dust emission by analyzing the microwave SED of dust that combines the Planck and WMAP spectral channels. We present the SED and discuss several spectral decompositions.
7.1. Microwave SED of dust emission
The microwave SED of dust emission in the diffuse ISM at 23 ≤ ν ≤ 353 GHz, obtained by averaging the correlation measures for the 60′ resolution maps over the 135 sky patches on our lower resolution grid (Sect. 3.2), is listed in Table 2. The statistical uncertainty of the mean SED is computed from the standard deviation of individual measurements, after correction for the CMB contribution as described in Appendix B, divided by the square root of the number of independent sky patches (135/3) used. These error-bars include variations of the dust SED across the southern polar cap and uncertainties in the CMB subtraction. The mean difference between the two independent estimates of the CMB presented in Appendix B is one order of magnitude lower than the minimum of the dust SED at 60–70 GHz.
Table 2 lists two SEDs. In this section, we use
the SED, 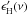 , computed from emissivities corrected for
the chance correlation of the Hi template with synchrotron emission by fitting the
Planck and WMAP data simultaneously with two templates
(Sect. 3.2). The synchrotron template impacts the
dust SED only at the lowest frequencies.
, computed from emissivities corrected for
the chance correlation of the Hi template with synchrotron emission by fitting the
Planck and WMAP data simultaneously with two templates
(Sect. 3.2). The synchrotron template impacts the
dust SED only at the lowest frequencies.
The microwave SED is displayed in Fig. 15. We check in two ways that this SED is not contaminated by free-free emission correlated with the Hi map. First, we find that the 70 GHz emission is not reduced if we compute the mean dust SED after masking the southern extension of the Orion-Eridanus super-bubble to high Galactic latitudes, the area of brightest Hα emission at b < − 30°. Second, we check that the correlation between the Hα emission and the Hi column density has a negligible impact on the dust SED by doing a three template fit, over the part of the southern Galactic cap covered by the survey of WHAM (Wisconsin H-Alpha Mapper) survey (Haffner et al. 2003). The photometry of diffuse Hα emission in the all-sky map of Dickinson et al. (2003) is not reliable on degrees scale outside of this area.
 |
Fig. 15 Mean microwave dust SED obtained by cross-correlating the Planck and WMAP data with the Hi and 408 MHz templates (blacks dots for Planck and blue squares for WMAP). Top: model 1 in Table 4, with two emission components combining AME and greybody thermal dust emission with β = 1.52. The AME is fitted with the analytical model in Eq. (10). Bottom: spectral fit for model 3, where the AME is fitted with two SPDUST spectra peaking at different frequencies. |
7.2. Separation of the thermal emission of dust from AME
The SED in Fig. 15 is dominated by thermal dust emission at the high frequencies and AME at low frequencies. We perform several spectral fits to separate the two emission components. The model parameters are listed in Table 4. In this section we present the fits with models 1 and 3 displayed in Fig. 15. Both models use a greybody spectrum at a fixed temperature of 19.8 K for the dust thermal emission, but they differ in the way the AME is fitted.
Spectral fits of the mean microwave dust SED.
In model 1, we fit the AME with the analytical model introduced by Bonaldi et al. (2007), which in the log(Brightness)-log(ν) plane is a parabola
parametrized by peak frequency νp6
and slope −
m60 at 60 GHz. Thus ![\begin{equation} \log \left (\frac{T_{\rm b}(\nu)}{T_{\rm b}(\nu_{\rm p})} \right )= -2 ~ \log(\nu/\nu_{\rm p}) +m_{60}~ \frac{\left[\log(\nu/\nu_{\rm p})\right]^2}{2~ \log(\nu_{\rm p}/60~{\rm GHz})}, \label{eq:Bonaldi} \end{equation}](/articles/aa/full_html/2014/06/aa23270-13/aa23270-13-eq272.png) (10)where Tb is the AME
brightness (Rayleigh-Jeans) temperature and ν is the frequency in gigahertz. Planck Collaboration Int. XII (2013) show that this
analytical function provides a good fit to the AME spectra derived from their analysis of
the Planck and WMAP maps along a section of the Gould
Belt at intermediate Galactic latitudes. In model 3, we fit the AME combining two spectra
labeled WNM and CNM, which were computed with the physical SPDUST
model (Ali-Haïmoud et al. 2009; Silsbee et al. 2011) using standard parameters for the
warm and cold neutral medium from Table 1 in Draine &
Lazarian (1999). This model allows us to check whether our determination of the
microwave emission from dust depends on the spectral template used for the AME. We do not
aim at proposing and discussing a physical fit of the AME.
(10)where Tb is the AME
brightness (Rayleigh-Jeans) temperature and ν is the frequency in gigahertz. Planck Collaboration Int. XII (2013) show that this
analytical function provides a good fit to the AME spectra derived from their analysis of
the Planck and WMAP maps along a section of the Gould
Belt at intermediate Galactic latitudes. In model 3, we fit the AME combining two spectra
labeled WNM and CNM, which were computed with the physical SPDUST
model (Ali-Haïmoud et al. 2009; Silsbee et al. 2011) using standard parameters for the
warm and cold neutral medium from Table 1 in Draine &
Lazarian (1999). This model allows us to check whether our determination of the
microwave emission from dust depends on the spectral template used for the AME. We do not
aim at proposing and discussing a physical fit of the AME.
 |
Fig. 16 Top: same microwave dust SED as in Fig. 15 with the spectral fit for model 2 in Table 4. The spectral index of the greybody is fixed to the value βFIR = 1.65 inferred from the fit of the dust SED at ν ≥ 353 GHz (Table 3). The AME is fitted with the analytical model in Eq. (10). This fit includes a third component represented by a blackbody spectrum at the same temperature (19.8 K) as that of the greybody. Bottom: blackbody component in model 2 as a fractional residual after subtraction of the AME and greybody emission from the total, compared to the data residuals. |
In model 1, we fit the 12 data points of the SED from 23 to 353 GHz with five free parameters: the specific opacity σH(353 GHz); the spectral index βmm for the greybody; νp; m60; and the AME brightness temperature Tb(23 GHz). In model 3, we also fit five free parameters. The AME parameters are the amplitudes of the two AME spectra, AWNM(23 GHz) and ACNM(41 GHz), plus a frequency shift νshift of the CNM SPDUST spectrum. This shift is an empirical means to account for the dependency of the peak frequency of the AME emission on physical parameters such as the gas density and the minimum grain size (Ysard et al. 2011; Hoang et al. 2011). Hoang et al. (2011) present a fit of the AME SED determined with WMAP data by Miville-Deschênes et al. (2008) with two AME spectra that have clearly distinct peak frequencies. The peak frequencies of the WNM and CNM SPDUST spectra we use are 24.3 and 30 GHz in flux units. We find that we need to introduce a positive shift of 25 GHz of the CNM spectrum to obtain a good fit. This shift moves the peak of the CNM SPDUST spectrum to 55 GHz in flux units (51 GHz in brightness temperature, Fig. 15).
The two models provide a very good fit of all data points. They yield similar results for the greybody parameters that characterize the dust thermal emission. These parameters match the corresponding ones derived from the fit of the data at ν ≥ 70 GHz in Sect. 6.2. They do not depend on the way the AME is modelled. The χ2 per degree of freedom of all fits is lower than unity. As for the greybody fits in Sect. 6.2, this results from the significant correlation of uncertainties across frequencies. To take this correlation into account, we run a Monte-Carlo simulation of each fit. We use each of the models in Table 4 as the input SED. We compute 1000 realizations of the data uncertainties using the results of a Principal Component Analysis of the 135 SEDs measured on the individual sky patches to parametrize the correlation across frequencies. We perform the spectral fits on each realization. The simulations show that the fit results are not biased, and provide the errors-bars in Table 4. We also find that the large errors-bars on the AME parameters for model 1 are highly correlated.
7.3. Spectral fit with an additional emission component
In this section, we discuss models 2 and 4 in Table 4, where we fix the spectral index of the greybody to the value βFIR = 1.65 inferred from the fit of the SED at ν ≥ 353 GHz. To account for the flattening of the dust SED at lower frequencies, we add a third emission component to the AME and the greybody. This additional component is assumed to have a blackbody spectrum with the same temperature 19.8 K as that of the thermal dust emission. We refer to this as the blackbody (BB) component. For the frequency range over which this component is significant, the blackbody spectrum is a good approximation of magnetic dipole emission from ferro-magnetic particles or magnetic inclusions in dust grains, as modelled by Draine & Hensley (2013). Model 2 uses the same analytical model for the AME as model 1; model 4 uses the same two SPDUST spectra as model 3. As in models 1 and 3, we fit for five parameters since the amplitude of the BB component replaces the spectral index of the greybody as a free parameter.
The three components model provides a good fit to all 12 data points (top panel in Fig.15). In particular, when added to the greybody component, the blackbody component accounts for the flattening of the spectral index of the thermal dust emission towards microwave frequencies. The specific opacity we find for the BB component is the same for both models. At 100 GHz, the blackbody component amounts to (26 ± 6)% of the greybody dust emission. This fraction is within the range of plausible values for dipolar magnetic emission within the model of Draine & Hensley (2013), and somewhat lower than the value reported by Draine & Hensley (2012) to fit the SED of dust emission from the Small Magellanic Cloud (Bot et al. 2010; Israel et al. 2010; Planck Collaboration XVII 2011).
Magnetic dipole emission is not a unique way to account for the flattening of the dust SED at ν ≤ 353 GHz. We cannot exclude alternative interpretations. First, the blackbody component may be a phenomenological way to introduce the progressive flattening of the thermal dust emission at long wavelengths observed in laboratory experiments on amorphous silicate particles (Coupeaud et al. 2011). Within this interpretation it would represent the contribution from low energy transitions to the opacity of interstellar silicates (Meny et al. 2007). Second, the flattening of the dust SED could be due to an increasing contribution of carbon dust towards millimetre wavelengths. In the dust model of Jones et al. (2013), the emission from amorphous carbon grains becomes dominant at λ> 1 mm for a spectral index at microwave frequencies in agreement with that measured on the data.
The physical interpretation of the additional emission component that would account for the flattening of the dust SED at microwave frequencies is further discussed in Planck Collaboration Int. XXI (2014), where the SED of the polarized dust emission is presented. The three interpretations proposed here make different predictions for the dust polarization SED. Dipole magnetic emission from iron inclusions would decrease the polarization of the thermal dust emission from silicate grains because the two polarization angles are 90° apart (Draine & Hensley 2013). Polarization may also allow us to distinguish between the carbon and silicate contributions to the SED flattening, if only the emission from silicates is polarized.
8. Summary
In a 7500 deg2 cap around the southern Galactic pole, we characterize the correlation between far infrared and microwave Planck emisison and NHI from the Hi GASS survey. This study covers the part of the southern sky best suited to study the structure of the CMB and CIB. We characterize the correlation between dust and gas and the SED of the dust emission. The data analysis yields four main scientific results.
-
(1)
The Hi correlation analysis allows us to separate the dust emission from the CIB and CMB anisotropies, and to map the emission properties of dust at high Galactic latitudes. We map the dust temperature, and its submillimetre emissivity and opacity. The variations of the dust emissivity at 353 GHz are surprisingly large, ranging over a factor close to three. The dust temperature is observed to be anti-correlated with the dust opacity. We interpret these results as evidence of dust evolution within the diffuse ISM, and discuss them within the context of existing models of dust. The mean dust opacity is measured to be (7.1 ± 0.6) × 10-27 cm2 H-1 × (ν/ 353 GHz)1.53 ± 0.03, for 100 ≤ ν ≤ 353 GHz. This is a reference value to estimate hydrogen masses from dust emission at submillimetre and millimetre wavelengths.
-
(2)
Using a colour ratio between 353 and 217 GHz that is free from CMB, we determine the spectral index βmm of the dust emission. We find a mean value of 1.51 that is remarkably constant over the field of our investigation; the standard deviation is 0.13. Variations of βmm show no clear trend with the 353 GHz dust emissivity, nor with the dust temperature. We compare βmm with the spectral index βFIR derived from greybody fits at ν ≥ 353 GHz. We find a systematic difference of βmm − βFIR = 0.15.
-
(3)
We fit the SED of the microwave emission correlated with Hi from 23 to 353 GHz with two components, a parametric model or SPDUST spectra for AME, and a greybody for the thermal dust emission. We show that the flattening of the dust SED at ν ≤ 353 GHz can be accounted for with an additional blackbody component. This additional component, which accounts for (26 ± 6)% of the dust emission at 100 GHz, could represent magnetic dipole emission. Alternatively, it could represent the contribution from low energy transitions in amorphous solids to the opacity of interstellar silicates, or an increasing contribution from carbon dust. These interpretations make different predictions for the dust polarization SED measured by Planck.
-
(4)
We analyse the residuals with respect to the dust-Hi correlation. We identify a Galactic contribution to these residuals, which we model with variations of the dust emissivity on angular scales smaller than the 15° patches of our correlation analysis. This model of the residuals is used to quantify uncertainties of the CIB power spectrum in a companion Planck paper (Planck Collaboration XXX 2014).
This paper opens the way to additional studies of the dust-Hi correlation. The methodology introduced in this paper is of general use to studies of the dust-Hi correlation with diverse science objectives. We have focused our scientific analysis on the emission properties of Galactic dust, leaving for further studies several aspects of the dust-gas correlation. In a future paper we will use the same data and method to quantify an upper limit on the dust-to-gas mass ratio in the MS gas, and to characterize Hi gas at Galactic velocities with no or only a faint counterpart in the Planck maps. The clouds of excess dust emission with respect to the Hi model also deserve further attention, to investigate where H2 forms within the diffuse ISM.
Online material
Appendix A: Model of the dust emission
We detail how we construct a map of the model of the dust emission that is spatially
correlated with the Hi emission. The model of the dust emission M is written as
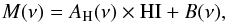 (A.1)where AH is a map at
resolution Nside
= 512 built from the correlation measure αν in Eq. (2), B is an offset map built
from ων in Eq. (3), and HI is the NHI template
for the Hi GASS data.
(A.1)where AH is a map at
resolution Nside
= 512 built from the correlation measure αν in Eq. (2), B is an offset map built
from ων in Eq. (3), and HI is the NHI template
for the Hi GASS data.
The AH and B maps are computed from the results of the dust-Hi correlation analysis over 15° diameter patches, sampled on HEALPix pixels with a resolution Nside = 32.
Specifically, at each frequency, AH and B maps are derived from the correlation measure and the offset maps (Sect. 3.1). Next we correct the correlation measures and the offsets for the CMB contributions, following the procedure presented in Appendix B. The offset map is also corrected for the CIB monopole using the values determined in Planck Collaboration XI (2014). Subsequently, we obtain the desired AH map by interpolating the map of correlation measures from Nside = 32 to 512 of the original data using a Gaussian kernel with a standard deviation equal to the 1.°8 pixel size at Nside = 32. This final AH map is a slightly smoothed version of the initial map of the correlation measures. We follow the same procedure to interpolate the map of offsets ων and get the desired B map.
The CMB anisotropies and the noise increase the uncertainty of the dust emissivity and dust model for ν ≤ 217 GHz. To reduce these uncertainties at these low frequencies, in Planck Collaboration XXX (2014) but not in this paper for which this is not necessary, we choose to extrapolate the 353 GHz model using the greybody function in Eq. (8) for the mean temperature of 19.8 K and the map of spectral indices from Sect. 5.
Appendix B: CMB contribution to correlation measures
Here is how we proceed to find the CMB contribution to the correlation measures, i.e. the α(CHI) term in Eq. (6) in units of thermodynamic (CMB) temperature. The correlation measures corrected for the CMB contributions are used in Sect. 6 to compute the mean SED averaged over all sky patches, and in Appendix A for the dust model.
We assume that the dust SED at 100 ≤ ν ≤ 353 GHz is well approximated by a greybody spectrum with the spectral indices βmm determined in Sect. 5 and the mean dust temperature of 19.8 K. For each sky patch, we perform a linear fit between the correlation measures at 100, 143, 217, and 353 GHz and the greybody SED normalized to unity at 353 GHz, with weights taking into account the uncertainties of the correlation measures. The slope of the fit is the dust emissivity at 353 GHz, while the offset is our estimate of α(CHI).
For comparison, we also quantify the cross-correlation between the CMB and the Hi map using the SMICA map presented in the Planck component separation paper (Planck Collaboration XII 2014). A histogram of the difference between the two values of α(CHI) for the 135 sky patches at Nside = 8 is presented in Fig. B.1. The standard deviation 0.7 μK per 1020 H cm-2 represents only 3% of the standard deviation of the α(CHI) values. We consider this percentage as our uncertainty factor δCMB on the CMB correction in Eq. (7). The mean difference (− 0.15 μK per 1020 H cm-2) is within the expected statistical error.
 |
Fig. B.1 Histogram of the difference between two estimates of α(CHI) (the correlation measure between the CMB and the Hi template), found assuming a greybody spectrum for the dust emissivity or calculated with the SMICA CMB map. The standard deviation of the difference, 0.7 μK per 1020 H cm-2, is 3% of the standard deviation of α(CHI). |
Appendix C: Uncertainty of the dust emissivity
In this Appendix, we quantify the uncertainty of the dust emissivity. In the first subsection, we quantify the uncertainties from the correlation analysis. In the second, we assess the uncertainties associated with the definition of the Galactic Hi template that depends on the separation between Galactic and MS emission (see Sect. 2.2). Finally, we discuss uncertainties associated with subtraction of the zodiacal emission.
Appendix C.1: Correlation analysis
We describe how we estimate each of the contributions to σ(ϵH) (Eq. (7)), the uncertainty of the dust emissivity. At each Planck frequency, we obtain a noise map by computing and dividing by two the difference of the two maps made out of the first and second halves of each stable pointing period (Planck Collaboration VI 2014). For the DIRBE frequencies, we compute one Gaussian realization of the noise using the maps of data uncertainty. The noise maps are cross-correlated with the Hi template using the same mask and over the same sky patches. The standard deviation of the correlation measures over all the sky patches yields the noise contribution to σ(ϵH) at each of the Planck and DIRBE frequencies.
To estimate the additional contributions to σ(ϵH), we use sky simulations of the Galactic emission and CMB and CIB anisotropies. For the Galactic maps, we consider only dust emission. We compute dust maps by multiplying the Hi template with a Gaussian realization of the dust emissivity map as described in Appendix D. For the CMB and CIB anisotropies, we compute Gaussian realizations using the power spectra of the Planck best-fit CMB model in Planck Collaboration XV (2014), and of the CIB model at 857 GHz in Planck Collaboration XXX (2014). We scale CIB anisotropy simulations at 857 GHz to the full set of Planck-HFI and DIRBE frequencies using a mean SED of CIB anisotropies. This SED is a greybody fit to the Cℓ values at ℓ = 500 in Planck Collaboration XXX (2014). The spectral index is β = 1 and the temperature 18.3 K. We use 100 realizations of each of the Galactic, CIB and CMB maps. We cross-correlate each of the simulated maps with the Hi template using the same circular sky patches with 15° diameter as for the data analysis.
Each component is analysed separately from the others to estimate its specific contribution to the error budget. The uncertainty of the dust emissivity is quantified by comparing the emissivity derived from the correlation analysis with the mean value of the input emissivity map for each sky patch and each realization. For the CMB contribution, we use a fractional error δCMB of 3% from Appendix B. In Fig. C.1, the four contributions to the fractional error σ(ϵH) /ϵH are plotted versus frequency. The total uncertainty is the top solid line. We find that the Galactic residual contribution is dominant at ν> 217 GHz, and the CMB contribution is dominant at lower frequencies. The noise is significant for the 140 and 240 μm bands and for the lowest HFI frequencies.
 |
Fig. C.1 Fractional uncertainty (solid line) of the dust emissivities ϵH, normalized to the mean dust SED in Table 1. This total consists of contributions from Galactic residuals (black dashed line), noise (red dashed line with stars), CIB anisotropies (blue dotted line), and the CMB correction (black dash-dotted line). The Galactic residual contribution is dominant at ν> 217 GHz, and the CMB contribution is dominant at lower frequencies. |
These results depend on the size of the sky patches and on the angular resolution. To quantify this dependence, we repeat the analysis of the simulations for sky patches with diameters of 5° and . We find that the contributions from noise and CIB anisotropies scale with the inverse of the diameter, while the Galactic contribution remains roughly constant. The ratio between the CIB and Galactic contributions also increases when we use a template with higher angular resolution. These two effects contribute to make the CIB contribution to the uncertainties more important for the low column density fields in Planck Collaboration XXIV (2011) than in our study.
The simulations show that the uncertainties do not bias our estimates of the dust emissivity. At all frequencies, the mean emissivity averaged over all sky patches and all simulated maps is equal to the mean input value within statistical errors. We also find that the uncertainty of the mean emissivity is roughly independent of the size of the sky patches. The diameter that we use is thus not a critical aspect of our data analysis.
The Galactic and CIB contributions to the uncertainty of the dust emissivity are correlated between frequencies because variations of the SED of dust and CIB anisotropies are not taken into account. This reason is a simplification, but the data analysis does show that the residual maps, obtained after subtracting the dust model (Appendix A) from the data, are highly correlated between frequencies.
Appendix C.2: Galactic H I template
To assess the uncertainties associated with the separation of the Hi emission into Galactic and MS components (Sect. 2.2.2), we follow Planck Collaboration XXIV (2011) in correlating the Planck maps with three Hi maps for the low velocity gas (the original single tempate), and for the IVC and HVC components (Sect. 2.2.3). We perform this analysis over the same sky patches, using the same mask, as in our cross-correlation with a single Galactic Hi template (Sect. 3.3). We obtain dust emissivities for each of the three Hi velocity components. The emissivities for the low velocity component are very close to those reported in the paper for our analysis with a single template. For example, at 857 GHz the fractional difference between the two sets of values (the ratio between the difference and the mean value computed for each sky patch) has a 1σ dispersion of 1.1%, which is small compared to the main uncertainties in Fig. C.1. The mean difference between the two sets of values is negligible.
Appendix C.3: Subtraction of the zodiacal emission
We end this Appendix by comparing dust emissivities obtained from the analysis of Planck maps with and without subtraction of the zodiacal emission. We find that the differences are minor. For example, at 857 GHz, the fractional difference in correlation measures has a mean of zero and a standard deviation of 1.4%, which is one order of magnitude lower than the total uncertainty in Fig. C.1. The differences are highest, but still small (up to 5%), in sky patches near the southern Galactic pole that are close to the zodiacal bands and where the Galactic emission is faint.
Appendix D: Simulations of Galactic residuals to the dust- H I correlation
A histogram of the residuals with respect to the dust-Hi correlation is shown in Fig. 4. This Appendix describes how we simulate the Galactic contribution to the Gaussian part of this histogram. These simulations are used in Appendix C to estimate the contribution of Galactic residuals to the uncertainty of the dust emissivities, and in Planck Collaboration XXX (2014) to assess the associated contamination of the CIB power spectra.
It is beyond the scope of this appendix to explore fully the origin and nature of the Galactic residuals. We briefly discuss and quantify two possible contributions. (1) The residual Galactic emission could trace dust associated with diffuse ionized gas that is not spatially correlated with the Hi template. The column density of this warm ionized medium is known to account for ~20% of the total gas column density over the high latitude sky (Gaensler et al. 2008). (2) The Galactic residuals could arise from variations of the dust emissivity on angular scales smaller than the 15° diameter of the sky patches used in our correlation analysis. These variations would be the extension to small scales of the variations mapped by our correlation analysis (Fig. 3). These two contributions are not mutually exclusive: it is possible that each contributes. We do not consider residual emission from molecular gas, however, because the molecular fraction of the gas is known from UV observations to be low at column densities lower than 3 × 1020 H cm-2 (Savage et al. 1977; Gillmon et al. 2006).
We produce sky simulations including each of these hypothetical contributions to the Galactic residuals and realizations of the CIB power spectrum. We process these simulated maps through the same correlation analysis as used on the Planck 857 GHz map. The simulations show that for each hypothesis we can match the amplitude and scatter of the values of σ857 in Fig. 7; however, it is only when the simulated maps include significant variations in the dust emissivity that the simulations match the systematic trend of σ857 growing with increasing NHI. We find that simulations can account for the main statistical properties of the Galactic residuals at 857 GHz when the map of variable dust emissivty is a Gaussian realization of a k-2.8 power spectrum, without needing any contribution from the warm ionized medium. The map of the dust emissivity is normalized to
reproduce the mean value and the standard deviation measured from the correlation of the 857 GHz map and the Hi template. We make multiple realizations of this specific model that are used in Appendix C and Planck Collaboration XXX (2014). The simulated maps at 857 GHz are scaled to other frequencies using the mean SED in Table 1. The simulations do not take into account the anti-correlation between the dust temperature and opacity.
Defined in Nidever et al. (2008). Magellanic latitude is along the MS. The trailing section of the MS has negative longitudes.
Planck Collaboration XXIV (2011) reported a systematic difference between the dust emissivities measured for local velocity gas and IVCs. This is difficult to confirm in our field where much of the gas in the IVC velocity range is low metallicity gas that belongs to the MS.
This range is much higher than the fractional uncertainty of 13% on the emissivity. See Appendix C.
Acknowledgments
The development of Planck has been supported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN, JA and RES (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and PRACE (EU). A description of the Planck Collaboration and a list of its members, including the technical or scientific activities in which they have been involved, can be found at http://www.sciops.esa.int/index.php?project=planck&page=Planck_Collaboration. The Parkes Radio Telescope is part of the Australia Telescope, which is funded by the Commonwealth of Australia for operation as a National Facility managed by CSIRO. The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement n° 267934.
References
- Ali-Haïmoud, Y., Hirata, C. M., & Dickinson, C. 2009, MNRAS, 395, 1055 [NASA ADS] [CrossRef] [Google Scholar]
- Arendt, R. G., Odegard, N., Weiland, J. L., et al. 1998, ApJ, 508, 74 [Google Scholar]
- Banday, A. J., Dickinson, C., Davies, R. D., Davis, R. J., & Górski, K. M. 2003, MNRAS, 345, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Larson, D., Weiland, J. L., et al. 2013, ApJS, 208, 20 [Google Scholar]
- Bersanelli, M., Mandolesi, N., Butler, R. C., et al. 2010, A&A, 520, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonaldi, A., Ricciardi, S., Leach, S., et al. 2007, MNRAS, 382, 1791 [NASA ADS] [Google Scholar]
- Bot, C., Helou, G., Boulanger, F., et al. 2009, ApJ, 695, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Bot, C., Ysard, N., Paradis, D., et al. 2010, A&A, 523, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boulanger, F., & Perault, M. 1988, ApJ, 330, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Boulanger, F., Abergel, A., Bernard, J.-P., et al. 1996, A&A, 312, 256 [NASA ADS] [Google Scholar]
- Cambrésy, L., Boulanger, F., Lagache, G., & Stepnik, B. 2001, A&A, 375, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Compiègne, M., Verstraete, L., Jones, A., et al. 2011, A&A, 525, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coupeaud, A., Demyk, K., Meny, C., et al. 2011, A&A, 535, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davies, R. D., Dickinson, C., Banday, A. J., et al. 2006, MNRAS, 370, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Desert, F. X., Bazell, D., & Boulanger, F. 1988, ApJ, 334, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, C., Davies, R. D., & Davis, R. J. 2003, MNRAS, 341, 369 [Google Scholar]
- Draine, B. T. 2009, in Cosmic Dust – Near and Far, eds. T. Henning, E. Grün, & J. Steinacker, ASP Conf. Ser., 414, 453 [Google Scholar]
- Draine, B. T., & Hensley, B. 2012, ApJ, 757, 103 [CrossRef] [Google Scholar]
- Draine, B. T., & Hensley, B. 2013, ApJ, 765, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lazarian, A. 1999, ApJ, 512, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Dupac, X., Bernard, J.-P., Boudet, N., et al. 2003, A&A, 404, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dwek, E., Arendt, R. G., Fixsen, D. J., et al. 1997, ApJ, 475, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Wilkes, B. J., & Lockman, F. J. 1989, AJ, 97, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P., Davis, M., & Schlegel, D. J. 1999, ApJ, 524, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Fixsen, D. J., Dwek, E., Mather, J. C., Bennett, C. L., & Shafer, R. A. 1998, ApJ, 508, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B. M., Madsen, G. J., Chatterjee, S., & Mao, S. A. 2008, PASA, 25, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, T., Banday, A. J., Jaffe, T., et al. 2012, MNRAS, 422, 3617 [NASA ADS] [CrossRef] [Google Scholar]
- Gillmon, K., Shull, J. M., Tumlinson, J., & Danforth, C. 2006, ApJ, 636, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Galliano, F., Hony, S., et al. 2010, A&A, 518, L89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Haffner, L. M., Reynolds, R. J., Tufte, S. L., et al. 2003, ApJS, 149, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Haslam, C. G. T., Salter, C. J., Stoffel, H., & Wilson, W. E. 1982, A&AS, 47, 1 [NASA ADS] [Google Scholar]
- Hauser, M. G., Arendt, R. G., Kelsall, T., et al. 1998, ApJ, 508, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Hoang, T., Lazarian, A., & Draine, B. T. 2011, ApJ, 741, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, F. P., Wall, W. F., Raban, D., et al. 2010, A&A, 519, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P. 2012, A&A, 542, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P., & Nuth, J. A. 2011, A&A, 530, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P., Fanciullo, L., Köhler, M., et al. 2013, A&A, 558, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., & Dedes, L. 2008, A&A, 487, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., McClure-Griffiths, N. M., Pisano, D. J., et al. 2010, A&A, 521, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Köhler, M., Stepnik, B., Jones, A. P., et al. 2012, A&A, 548, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagache, G. 2003, A&A, 405, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamarre, J.-M., Puget, J.-L., Ade, P. A. R., et al. 2010, A&A, 520, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitch, E. M., Readhead, A. C. S., Pearson, T. J., & Myers, S. T. 1997, ApJ, 486, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
- Mandolesi, N., Bersanelli, M., Butler, R. C., et al. 2010, A&A, 520, A3 [Google Scholar]
- Martin, P. G., Roy, A., Bontemps, S., et al. 2012, ApJ, 751, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- McClure-Griffiths, N. M., Pisano, D. J., Calabretta, M. R., et al. 2009, ApJS, 181, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Mennella, A., Bersanelli, M., Butler, R. C., et al. 2010, A&A, 520, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meny, C., Gromov, V., Boudet, N., et al. 2007, A&A, 468, 171 [Google Scholar]
- Miville-Deschênes, M.-A., Ysard, N., Lavabre, A., et al. 2008, A&A, 490, 1093 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nidever, D. L., Majewski, S. R., & Burton, W. B. 2008, ApJ, 679, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Nidever, D. L., Majewski, S. R., Butler Burton, W., & Nigra, L. 2010, ApJ, 723, 1618 [NASA ADS] [CrossRef] [Google Scholar]
- Paradis, D., Bernard, J.-P., Mény, C., & Gromov, V. 2011, A&A, 534, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peek, J. E. G., Heiles, C., Putman, M. E., & Douglas, K. 2009, ApJ, 692, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Peel, M. W., Dickinson, C., Davies, R. D., et al. 2012, MNRAS, 424, 2676 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XVII. 2011, A&A, 536, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVIII. 2011, A&A, 536, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2011, A&A, 536, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIV. 2011, A&A, 536, A24 [Google Scholar]
- Planck Collaboration XXV. 2011, A&A, 536, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XII. 2013, A&A, 557, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XIV. 2014, A&A, 564, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXI. 2014, A&A, submitted [Google Scholar]
- Planck Collaboration I. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321529 [Google Scholar]
- Planck Collaboration II. 2014, A&A, in press, DOI:10.1051/0004-6361/201321550 [Google Scholar]
- Planck Collaboration V. 2014, A&A, submitted [arXiv:1303.5066] [Google Scholar]
- Planck Collaboration VI. 2014, A&A, submitted [arXiv:1303.5067] [Google Scholar]
- Planck Collaboration VIII. 2014, A&A, in press, DOI:10.1051/0004-6361/201321538 [Google Scholar]
- Planck Collaboration IX. 2014, A&A, in press, DOI:10.1051/0004-6361/201321531 [Google Scholar]
- Planck Collaboration XI. 2014, A&A, submitted [arXiv:1312.1300] [Google Scholar]
- Planck Collaboration XII. 2014, A&A, in press, DOI:10.1051/0004-6361/201321580 [Google Scholar]
- Planck Collaboration XIII. 2014, A&A, in press, DOI:10.1051/0004-6361/201321553 [Google Scholar]
- Planck Collaboration XIV. 2014, A&A, in press, DOI:10.1051/0004-6361/201321562 [Google Scholar]
- Planck Collaboration XV. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321573 [Google Scholar]
- Planck Collaboration XXX. 2014, A&A, in press, DOI:10.1051/0004-6361/201322093 [Google Scholar]
- Puget, J.-L., Abergel, A., Bernard, J.-P., et al. 1996, A&A, 308, L5 [NASA ADS] [Google Scholar]
- Reach, W. T., Wall, W. F., & Odegard, N. 1998, ApJ, 507, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, A., Martin, P. G., Polychroni, D., et al. 2013, ApJ, 763, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., Bohlin, R. C., Drake, J. F., & Budich, W. 1977, ApJ, 216, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Shetty, R., Kauffmann, J., Schnee, S., Goodman, A. A., & Ercolano, B. 2009, ApJ, 696, 2234 [NASA ADS] [CrossRef] [Google Scholar]
- Siebenmorgen, R., Voshchinnikov, N. V., & Bagnulo, S. 2014, A&A, 561, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silsbee, K., Ali-Haïmoud, Y., & Hirata, C. M. 2011, MNRAS, 411, 2750 [NASA ADS] [CrossRef] [Google Scholar]
- Stepnik, B., Abergel, A., Bernard, J.-P., et al. 2003, A&A, 398, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venzmer, M. S., Kerp, J., & Kalberla, P. M. W. 2012, A&A, 547, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakker, B. P. 2004, in Recycling Intergalactic and Interstellar Matter, eds. P.-A. Duc, J. Braine, & E. Brinks, IAU Symp., 217, 2 [Google Scholar]
- Ysard, N., Juvela, M., & Verstraete, L. 2011, A&A, 535, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhukovska, S., Gail, H.-P., & Trieloff, M. 2008, A&A, 479, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left: Planck map at 857 GHz over the area where we have Hi data from the GASS survey. The center of the orthographic projection is the southern Galactic pole. Galactic longitudes and latitudes are marked by lines and circles, respectively. The Planck image has been smoothed to the 16′ resolution of the GASS NHI map. Right: GASS NHI map of Galactic disk emission, obtained by integrating over the velocity range defined by Galactic rotation (Sect. 2.2.2). |
| In the text | |
 |
Fig. 2 NHI maps corresponding to the IVC (left) and HVC (right) velocity ranges as defined in Sect. 2.2.3. We show the data at Galactic latitudes b < −25° that we use in our correlation analysis. |
| In the text | |
 |
Fig. 3 Map of the dust emissivity at 353 GHz, i.e. the correlation measure α353 with the CMB contribution α(CHI) subtracted (see Eq. (6)). The correlation measure is computed in each pixel correlating the Planck map with the Hi template over a sky patch with 15° diameter centred on it. |
| In the text | |
 |
Fig. 4 Histogram of residual emission at 857 GHz after subtraction of the dust emission associated with HI gas. The blue solid line is a Gaussian fit to the core of the histogram, with dispersion σ = 0.07 MJy sr-1. We mask pixels where the absolute value of the residual emission is higher than 3σ. The positve (negative) wing of the histogram beyond this threshold represents 7% (2%) of the data. |
| In the text | |
 |
Fig. 5 Mask for our analysis of the Planck-Hi correlation. The coloured area that is not blue defines the data used to compute the correlation measures. Within this area, the median NHI is 2.1 × 1020 H cm-2, and NHI < 3 × 1020 H cm-2 for 74% of the pixels. The blue patches correspond to regions where the absolute value of the residual emission is higher than 3σ at 857 GHz (Fig. 4). The circular hole near the Southern Galactic pole corresponds to the area where Hi gas in the Galaxy cannot be well separated because the mean radial velocity of the gas in the MS is within the Galactic range of velocities. |
| In the text | |
 |
Fig. 6 Left: image of the residual emission at 857 GHz obtained by subtracting the Hi-based model of the dust emission from the input Planck map. Right: image of NHI from the Magellanic Stream (see Sect. 2.2.2), the sum of the IVC and HVC maps in Fig. 2. |
| In the text | |
 |
Fig. 7 Standard deviation σ857 of the residuals with respect to the Planck-Hi correlation at 857 GHz versus the mean NHI, both computed within circular sky patches with 5° diameter and over unmasked pixels. The red hatched strip marks the contribution of CIB anisotropies to the residuals at 16′ resolution, computed from the CIB model in Planck Collaboration XXX (2014). The width of the strip represents the expected scatter (± 1σ) of this contribution. Both the scattered distribution of data points above CIB anisotropies strip and the increase in the mean σ857 with NHI arise from residuals with a Galactic origin (Appendix D). |
| In the text | |
 |
Fig. 8 Left: map of the dust opacity σH(353 GHz) in Eq. (9). Right: colour temperature map inferred from the ratio between the dust emissivities at 100 μm from DIRBE and 857 GHz from Planck, with a spectral index of the dust emissivity βFIR = 1.65. This figure reveals that the temperature and submillimetre opacity of dust are anti-correlated. |
| In the text | |
 |
Fig. 9 Top: dust colour temperature Td versus dust emissivity at 353 GHz, two independent observables (Fig. 3), with typical error bars at the top right. The dashed line represents the expected dependency of Td on the dust emissivity for a fixed emitted power of 3.4 × 10-31 W H-1. The blue dots identify data for sky patches centred at Galactic latitudes b ≤ −60°. Bottom: Td versus dust opacity at 353 GHz, re-expressing the same data in the form plotted by Planck Collaboration XXIV (2011) and Martin et al. (2012). |
| In the text | |
 |
Fig. 10 Map of the specific power radiated by dust at far infrared wavelengths per H. This figure displays spatial variations of the specific dust power, which may be decomposed as the sum of two parts correlated with the opacity and temperature maps (see Fig. 8), respectively. |
| In the text | |
 |
Fig. 11 Spectral index βmm of the dust emission derived from the ratio between correlation measures at 353 and 217 GHz (both corrected for the CMB contribution by subtracting the correlation measure at 100 GHz) and the colour temperature map in Fig. 8. |
| In the text | |
 |
Fig. 12 Spectral index βmm versus Td for the 135 sky patches. The blue dots distinguish patches centred at Galactic latitude b ≤ − 60°. The uncertainties are derived from simulations. The dashed line is a linear regression of βmm on Td, slope (− 0.043 ± 0.009) K-1. |
| In the text | |
 |
Fig. 13 Top: residuals from a greybody fit of the mean dust SED at ν ≥ 353 GHz, using one spectral index. Dashed error bars are the quadratic sum of the statistical error (solid) and the photometric uncertainty. The photometric uncertainty is dominant at ν ≥ 545 GHz and negligible for the lower frequencies. Bottom: residuals from a greybody fit to all data points down to 100 GHz, again using a single spectral index. |
| In the text | |
 |
Fig. 14 Same as Fig. 13, but for residuals from fits of the mean dust SED with the DUSTEM (top panel) and DL07 (bottom panel) dust models. |
| In the text | |
 |
Fig. 15 Mean microwave dust SED obtained by cross-correlating the Planck and WMAP data with the Hi and 408 MHz templates (blacks dots for Planck and blue squares for WMAP). Top: model 1 in Table 4, with two emission components combining AME and greybody thermal dust emission with β = 1.52. The AME is fitted with the analytical model in Eq. (10). Bottom: spectral fit for model 3, where the AME is fitted with two SPDUST spectra peaking at different frequencies. |
| In the text | |
 |
Fig. 16 Top: same microwave dust SED as in Fig. 15 with the spectral fit for model 2 in Table 4. The spectral index of the greybody is fixed to the value βFIR = 1.65 inferred from the fit of the dust SED at ν ≥ 353 GHz (Table 3). The AME is fitted with the analytical model in Eq. (10). This fit includes a third component represented by a blackbody spectrum at the same temperature (19.8 K) as that of the greybody. Bottom: blackbody component in model 2 as a fractional residual after subtraction of the AME and greybody emission from the total, compared to the data residuals. |
| In the text | |
 |
Fig. B.1 Histogram of the difference between two estimates of α(CHI) (the correlation measure between the CMB and the Hi template), found assuming a greybody spectrum for the dust emissivity or calculated with the SMICA CMB map. The standard deviation of the difference, 0.7 μK per 1020 H cm-2, is 3% of the standard deviation of α(CHI). |
| In the text | |
 |
Fig. C.1 Fractional uncertainty (solid line) of the dust emissivities ϵH, normalized to the mean dust SED in Table 1. This total consists of contributions from Galactic residuals (black dashed line), noise (red dashed line with stars), CIB anisotropies (blue dotted line), and the CMB correction (black dash-dotted line). The Galactic residual contribution is dominant at ν> 217 GHz, and the CMB contribution is dominant at lower frequencies. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


