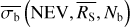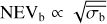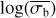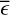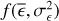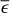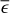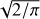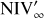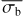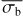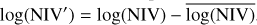| Issue |
A&A
Volume 687, July 2024
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 24 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202346368 | |
| Published online | 28 June 2024 | |
Characterising X-ray variability in light curves with complex sampling patterns: Application to the eROSITA south ecliptic pole survey
1
Max Planck Institute für Extraterrestrische Physik,
Gießenbachstraße 1,
85748
Garching bei München,
Germany
2
Department of Astronomy, The University of Michigan,
1085 South University Avenue,
Ann Arbor,
MI
48103,
USA
e-mail: dbogen@umich.edu
Received:
10
March
2023
Accepted:
1
March
2024
Aims. During its all-sky survey phase, the extended ROentgen Survey with an Imaging Telescope Array (eROSITA) X-ray telescope on board the Spectrum-Roentgen-Gamma (SRG) spacecraft scans through the ecliptic poles every 4 h. This extensive data set of long-duration, frequent, and consistent observations of thousands of X-ray sources is ideal for a detailed long-term X-ray-variability analysis. However, individual observations are short, are separated by long but consistent gaps, and have varying exposure times. Therefore, the identification of variable sources and the characterisation and quantification of their variability requires a unique methodology. We aim to develop and evaluate variability analysis methods for eROSITA observations, focusing on sources close to the survey poles. We also aim to detect intrinsically variable sources at any count rate and quantify the variability of low-count-rate sources.
Methods. We simulate eROSITA-like light curves to evaluate and quantify the effect of survey mode observations on the measured periodogram and normalised excess variance. We introduce a new method for estimating the normalised intrinsic variance of a source based on the Bayesian excess variance (bexvar) method.
Results. We determine thresholds for identifying likely variable sources while minimising the false-positive rate, as a function of the number of bins, and the average count rate in the light curve. The bexvar normalised intrinsic variance estimate is significantly more accurate than the normalised excess variance method in the Poisson regime. At high count rates, the two methods are comparable. We quantify the scatter in the intrinsic variance of a stationary pink-noise process, and investigate how to reduce it. Finally, we determine a description of the excess noise in a periodogram caused by varying exposure times throughout a light curve. Although most of these methods were developed specifically for analysing variable active galactic nuclei in the eROSITA all-sky survey, they can also be used for the variability analysis of other datasets from other telescopes, with slight modifications.
Key words: black hole physics / methods: numerical / methods: statistical / time / galaxies: active
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open Access funding provided by Max Planck Society.
1 Introduction
The X-ray luminosity of active galactic nuclei (AGNs), X-ray binaries (XRBs), and stars has been observed to vary strongly over a wide range of timescales. Analysing their light-curve variability can reveal information about their source properties and indicate various unique phenomena. This variability can be of a persistent or transient nature, depending on the source and the cause of the variability.
For instance, a measurement of the shortest timescale over which continuous brightness changes are detected can be used to estimate an upper bound on the size of the light-emitting region of a persistently variable source. This is done by equating it to the light-crossing timescale. This kind of variability analysis provided one of the first indications of the true nature of various bright astronomical objects that we now collectively group under the term AGN (Matthews & Sandage 1963). Despite the gigantic average luminosities of AGNs, they are observed to vary within hundreds of seconds. This indicates that they are incredibly compact and have radii on the subparsec scale (Woltjer 1959). The AGN variability studies also revealed a myriad of other intriguing properties. For example, the AGN X-ray variability has been found to anticorrelate with the AGN luminosity (Nandra et al. 1997; Yang et al. 2016; Zheng et al. 2017) and the mass of the supermassive black hole powering the AGN (Lu & Yu 2001; O’Neill et al. 2005; Paolillo et al. 2017; Arévalo et al. 2023). This means that the variability of an AGN can be used to estimate the BH mass when other methods are unavailable (Ponti et al. 2012). In addition, Vagnetti et al. (2011, 2016) used ensembles of AGNs to determine more correlated X-ray-variability scaling relations.
X-ray binaries are similar to AGNs in many of their properties but vary on much shorter timescales due to the smaller size of the compact object powering their X-ray emission. The X-ray variability in AGNs and XRBs is produced in the innermost part of the accretion disc and the corona (Uttley et al. 2002; McHardy 2010). Therefore, studies of the X-ray variability of AGNs and XRBs can determine the physical mechanisms at work there. Variability analysis of XRB light curves can also be used to distinguish between various states (Belloni et al. 2011). In addition, XRB variability studies often identify particular frequencies that dominate the light-curve evolution, known as quasi-periodic oscillations (Ingram & Motta 2019). These have also been detected in a few AGNs (e.g. Gierliński et al. 2008; Zhou et al. 2018; Smith et al. 2018; Ashton & Middleton 2021).
Many stars also exhibit X-ray variability, typically in the form of flares. These are generated by particle acceleration in the stellar corona, which in turn is due to chromospheric evaporation (Antonucci et al. 1984). X-ray-variability studies of stars can provide constraints on these processes. Young stellar objects are known to be particularly variable X-ray sources (Forbrich et al. 2006, 2017).
The extended ROentgen Survey with an Imaging Telescope Array (eROSITA; Predehl et al. 2021; Sunyaev et al. 2021) aimed to perform a four-year-long detailed survey of the entire sky in X-rays. The eROSITA instrument is mounted on the Spectrum-Roentgen-Gamma (SRG; Sunyaev et al. 2021) spacecraft, which rotates about itself at a constant angular velocity of 2.5 × 10−2 deg s−1, completing one rotation, referred to as an eroday, every 4 h. Its angular momentum also shifts direction by an average of 10″ per eroday, along the ecliptic plane. This observing pattern ensures that the entire sky is observed within six months. Eight eROSITA All-Sky Surveys (eRASSs) are planned.
During the eRASSs, the angular momentum vector of eROSITA’s rotation about itself always lies in the ecliptic plane. Therefore, the south and north ecliptic poles (SEP and NEP, respectively) are observed on every eroday. This means that sources lying close to the ecliptic poles are observed consistently every 4 h for most of the duration of the eRASSs. These observations enable a detailed investigation of the medium- to long-term X-ray-variability properties of the sources in these fields.
However, a variability analysis of eROSITA data faces various challenges, including varying exposure times, low count rates, and long gaps between short observations. In this paper, we describe various variability methods that can be used to characterise the intrinsic variability. We also analyse how these can be modified to minimise the detrimental effects of survey mode observations. In addition, we discuss ways to improve upon previous methods, for both eROSITA and other missions. We particularly focus on AGN variability, and pink-noise light curves expected for them in the frequency space probed by eROSITA. We also predominantly consider the field near the ecliptic poles, in which there are many more individual observations than for most sources in the sky. However, many results presented here can also be applied to other regions of the sky as observed by eROSITA, or in variability studies using entirely different instruments.
This paper is structured as follows. In Sect. 2, we discuss the properties of the eROSITA observations and the challenges faced by the variability analysis of eROSITA data. In Sect. 3, we describe the variability quantifiers used and explain how we simulated light curves for testing and optimising the variability methodology. In Sect. 4, we determine thresholds for selecting variable sources as a function of the count rate and the number of bins. We introduce a new method for estimating the normalised intrinsic variance of a light curve in Sect. 5. In Sect. 6, we describe the aliasing and red-noise leakage, which offset the measured variability from the band-limited power. We also investigate the intrinsic scatter due to the stochastic nature of the variability, and how to reduce it by averaging over multiple segments. Section 7 describes how to compute the periodograms of eROSITA light curves and calculate the excess noise level due to varying fractional exposures. Finally, in Sect. 8, we discuss our main findings and describe their applicability to eROSITA and other variability analyses.
2 eROSITA light curves
2.1 Properties of observations
While most eRASS sources are observed a handful of times, near the eRASS survey poles, sources receive very dense, more continuous sampling with up to 1080 observations per eRASS. The survey poles nearly coincide with the ecliptic poles, with a variable offset of a few arcminutes. The frequent observations make the regions of the sky close to the ecliptic poles the most interesting for long-term variability analysis. The German eROSITA consortium has the rights to the southern ecliptic hemisphere. Therefore, we focused primarily on the properties of the eRASS SEP field. However, this field comes with additional data analysis challenges.
Firstly, the total exposure time drops rapidly with an increasing angle from the ecliptic poles. For example, sources located 5° away from the poles are observed on an average of 70 erodays per eRASS, but sources within 0.5° of the poles are observed on 1080 erodays per eRASS. These large exposure gradients affect the source detection and result in a data set featuring a wide range of depths.
Secondly, for most sources, the sensitivity varies in complex patterns. We refer to all the data collected about the brightness of a source within a single eroday period as one observation of the source. eROSITA has a large field of view (FoV, 1.03°, Predehl et al. 2021), but individual observations of sources are short and have very different effective exposure times. When a source passes through the centre of the FoV, its exposure is 41.2 s, while sources at the border can have exposure times of a fraction of a second. The effective area drops rapidly with off-axis angle, with 80% at 10′ and 40% at 25′ (for 0.2-1.5 keV; Predehl et al. 2021, Fig. 8). Vignetting is even more pronounced at higher energies. Because of survey progression combined with small survey pole variations, the effective exposure time varies strongly over time for each source, with complex patterns.
The fractional exposure (є) quantifies the combination of the source crossing the FoV and experiencing variable vignetting. During an observation of duration ∆t, the effective exposure time є∆t describes the amount of time it would have had to have been observed on-axis to obtain the same exposure depth. By keeping ∆t constant, є fully describes the variation in effective exposure. We set ∆t = 40 s, the approximate maximum duration of a single eRASS observation of a source. Within 3° of the SEP, є is approximately uniformly distributed between 0.05 and 0.45, with a peak towards 0 and a rapid drop above 0.5.
The eROSITA effective area peaks between 0.2–5.0 keV (Predehl et al. 2021). There, most count rates range between 10−3–101 cts s−1 for detected sources. The deep pole exposure enables detecting sources fainter than 10−3 cts s−1. However, neither the brightest nor the faintest sources are relevant to this variability analysis. The brightest sources suffer from pileup, and there is too little information on the faintest sources to analyse their variability. This variability analysis instead focuses on the vast majority of sources with sources roughly within the range of 10−3–101 cts s−1.
We follow previous eROSITA analyses (Liu et al. 2022; Buchner et al. 2022; Boller et al. 2022), in extracting background count rates from much larger background than source extraction regions. The typical background region near the SEP is 112 times larger than the source region, with typical count rates of 0.71 cts s−1.
We seek to evaluate the variability of the X-ray source flux. As the effective area varies from observation to observation, the count rate found by dividing the measured number of source counts by the observation duration is not proportional to the source flux in different observations. Instead, we use an exposure-corrected count rate as a proxy of the source flux. Brunner et al. (2022) estimated the exposure-corrected count rate of an eRASS source in observation i, performed at time ti, as:
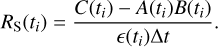 (1)
(1)
In this equation, RS is the exposure-corrected source count rate, C and B are the number of counts measured in the source and background extraction regions, respectively, and A is the background ratio. This equation is applicable to high-count observations, but problematic in low-count observations.
Buchner et al. (2022) presented a method for calculating the exposure-corrected count rate that accounts for Poisson uncertainties in both the source and background count rates. A probability density function (PDF) can be constructed based on the inverse incomplete Gamma function, as described by Knoetig (2014). We extract the median and 1σ equivalent quantiles from this PDF, as the exposure-corrected count rate, and its uncertainty. This method is less affected by the varying fractional exposure in the eRASS light curve, and more accurate in the Poisson regime, compared to Eq. (1). Throughout this paper, we use the term ‘count rate’ to refer to the exposure-corrected source count rate found using this methodology.
 |
Fig. 1 Simulated eROSITA-like light curves of a source lying close to either of the two ecliptic poles. These light curves are computed using a typical є evolution, as observed in actual eROSITA light curves. The top panel shows an intrinsically constant source, and the lower panel depicts an intrinsically-variable pink-noise source, both with an average count rate of ≈0.3 cts s−1. The variability class describes how the value of SCATT_LO and AMPL_SIG compares to the variability thresholds computed in Sect. 4. The pink-noise variable source is identified to have a SCATT_LO value above the 3σ threshold but an AMPL_SIG value only above the corresponding 1σ threshold. |
2.2 Challenges for eRASS light-curve variability analysis
One of the main challenges faced when analysing the variability properties of eROSITA light curves, and the key feature that differentiates an eROSITA variability analysis from many other variability analyses, is the varying fractional exposure in the light curves. Visually, the light curve appears to bend upwards when the fractional exposure decreases, due to the low number of detected counts coupled with a large fractional exposure correction. Commonly, this appears at the edges of the eROSITA observations for sources further than 0.5° from the poles, leading to ‘U’ shaped light curves. This is illustrated by the two simulated light curves shown in Fig. 1, one of which is intrinsically constant and the other highly variable.
The ‘U’-like shape of the light curves can be reduced by coarse rebinning, to several erodays. This is done by summing the counts and exposures from the bins to be merged, and then recomputing the count rate as described above. This eases visual inspection of long term variability, but loses information on eroday-to-eroday variability. To bridge this gap, we develop and characterise new methods.
Another challenge in analysing eROSITA light curves is posed by the gaps between observations. Short observation times (of 41.2 s or less) are separated by long but consistent gaps (4 h). The gaps are at least 350 times longer than the duration of each bin. Sources further than 0.5° from the poles also have gaps on 6-month timescales. Variability during the gaps will go undetected.
The SEP eROSITA observations are an unparalleled opportunity for variability analysis. Observations of tens of thousands of X-ray sources close to the ecliptic poles occur frequently and consistently over several years. eROSITA observations enable a long-term X-ray-variability analysis of a large, unbiased sample of AGNs, XRBs, and stars. For this purpose, we first need to decide on the variability quantifiers most useful for an eROSITA variability analysis.
3 Methods
3.1 Variability quantifiers
3.1.1 Normalised excess variance
A frequently used parameter for quantifying the degree of variability of X-ray light curves of AGNs and XRBs is the normalised excess variance (NEV; Edelson et al. 1990; Nandra et al. 1997):
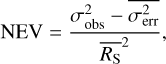 (2)
(2)
where the excess variance, 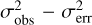 , describes how much the observed variance in the source count rates,
, describes how much the observed variance in the source count rates, 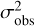 , exceeds the expected variance due to the measurement errors,
, exceeds the expected variance due to the measurement errors, 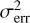 . The excess variance is then normalised by the square of the average source count rate,
. The excess variance is then normalised by the square of the average source count rate, 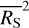 , to form the NEV. The normalisation removes a scaling with the source flux, and makes the NEV comparable across instruments of different sensitivities.
, to form the NEV. The normalisation removes a scaling with the source flux, and makes the NEV comparable across instruments of different sensitivities.
The NEV measures the excess variance within a time window, from the observed over-dispersion within the set of bins at hand. We refer to the intrinsic variability of the source at the particular times when it was observed as the normalised intrinsic variance (NIV). The NEV is an estimator of the NIV, but differs from it due to measurement errors. The NIV is equal to the NEV that would be calculated if the observations were obtained with infinite accuracy and negligible Poisson noise. The NIV is unaffected by Poisson noise, or measurement uncertainties, but does depend on the timing of the observations: the start time, the bin size, and the separation of the bins.
The NIV of variable sources varies stochastically even if the process causing the variability is stationary. The NIV of AGN light curves can therefore be described as ‘weakly non-stationary’ (Press & Rybicki 1997). We define the geometric mean of the NIV of an infinite number of light curves, all covering the same frequency interval and caused by a stationary variability process, as NIV∞. The NIV of any finite light-curve segment varies around the NIV∞.
For Nb bins of a variable source at times ti, where i ∈ {1,2,…, Nb}, with a measured, background subtracted, exposure-corrected source count rate of RS (ti), and associated measurement uncertainties of σerr (ti), the quantities in Eq. (2) are defined by:
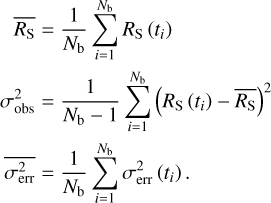 (3)
(3)
The lowest NIV that a source can have is 0. This occurs when its flux does not change at all during the observing window, so  . The highest value that the NIV can have occurs when the flux of a variable source is 0 in all bins, except one. For such a light curve,
. The highest value that the NIV can have occurs when the flux of a variable source is 0 in all bins, except one. For such a light curve, 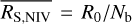 , where R0 is the only non-zero count rate of the source. Therefore, the variance of this light curve is
, where R0 is the only non-zero count rate of the source. Therefore, the variance of this light curve is 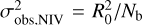 , so NIV = Nb. Hence, the NIV can only have values within the [0, Nb] range.
, so NIV = Nb. Hence, the NIV can only have values within the [0, Nb] range.
In contrast, the NEV can be measured to lie outside of this range. The NEV works well for estimating the NIV of sources with light curves consisting of many bins, each containing many source counts above the background level. Although it can still be used, the NEV faces challenges when applied to light curves of low-count-rate sources. For instance, it is not unlikely to measure a negative excess variance at low count rates (Paolillo et al. 2017). The NEV is most useful for investigating the variability of light curves consisting of ≳20 bins (Turner et al. 1999). For more discussion on the NEV, and its uses, see Vaughan et al. (2003); Paolillo et al. (2004, 2017, 2023); Vagnetti et al. (2011, 2016); Allevato et al. (2013); Zheng et al. (2017); Arévalo et al. (2023).
Special care needs to be taken when using the NEV to analyse eROSITA light curves. Firstly, the varying fractional exposures varies the information gained from each bin. However, the parameters of the NEV, as described by Eq. (3) depend equally on all bins. Therefore, in light curves where the fractional exposures varies, the NEV is biased by, and depends too strongly on the bins with the lowest fractional exposures. To reduce the impact of this, throughout this paper we only keep well-exposed time bins, with є > 0.1. Secondly, most bins have low counts. The NEV relies on accurate estimates of the variance in the measured count rates. The measured counts follow a Poisson distribution, which is asymmetric. To account for the resulting asymmetric uncertainty in the inferred net count rates, we chose σerr in Eq. (3) to be equal to the size of the uncertainty in the direction of the mean. However, this may cause the NEV be over-, or underestimated.
3.1.2 Maximum amplitude variation
The maximum amplitude variation significance (AMPL_SIG; Boller et al. 2016) is another method for detecting and quantifying source variability. The standard definition of the maximum amplitude variation (AMPL_MAX) uses the bins in which the highest and lowest count rates were measured, which we denote to have occurred at times tmax, and tmin, respectively. Then AMPL_MAX, and its significance, AMPL_SIG, are defined as:
![$\matrix{ {{\rm{AMPL\_AX = }}\left[ {{{\rm{R}}_{\rm{S}}}\left( {{{\rm{t}}_{\max }}} \right){\rm{ - }}{\sigma _{{\rm{err}}}}\left( {{{\rm{t}}_{\max }}} \right)} \right]{\rm{ - }}\left[ {{{\rm{R}}_{\rm{S}}}\left( {{{\rm{t}}_{\min }}} \right){\rm{ + }}{\sigma _{{\rm{err}}}}\left( {{{\rm{t}}_{\min }}} \right)} \right]} \cr {{\rm{AMPL\_IG = }}{{{\rm{AMPL\_AX}}} \over {\sqrt {\sigma _{{\rm{err}}}^{\rm{2}}\left( {{{\rm{t}}_{\max }}} \right){\rm{ + }}\sigma _{{\rm{err}}}^{\rm{2}}\left( {{{\rm{t}}_{\min }}} \right)} }}.} \cr } $](/articles/aa/full_html/2024/07/aa46368-23/aa46368-23-eq11.png) (4)
(4)
The advantage of AMPL_SIG is that it can quickly determine significant differences in the count rate observed within a light curve. The AMPL_MAX parameter only considers the two most extreme points of a light curve, making it suitable for short light curves, and optimal flare detection (see Buchner et al. 2022). However, it is less sensitive to milder stochastic variations, especially in the Poisson regime. In eROSITA, the highest and lowest count rates measured often occur in bins with the lowest fractional exposures and the largest uncertainties. These cause the AMPL_SIG to underestimate the actual significance (see calibrated thresholds in Buchner et al. 2022).
Therefore, we enhanced Eq. (4) for investigating light curves featuring varying exposure times. Rather than comparing the two bins with the highest and lowest measured count rates, we instead used the two bins with the highest lower bound and the lowest upper bound confidence interval for the count rate. Therefore, we redefined tmax, tmin, AMPL_MAX, and its significance, AMPL_SIG, as follows:
![$\matrix{ {{R_{\rm{S}}}\left( {{t_{\max }}} \right) - {\sigma _{ - {\rm{err}}}}\left( {{t_{\max }}} \right) = \max \left[ {{R_{\rm{S}}}\left( {{t_i}} \right) - {\sigma _{ - {\rm{err}}}}\left( {{t_i}} \right)} \right]} \cr {{R_{\rm{S}}}\left( {{t_{\min }}} \right) + {\sigma _{ + {\rm{err}}}}\left( {{t_{\min }}} \right) = \min \left[ {{R_{\rm{S}}}\left( {{t_i}} \right) + {\sigma _{{\rm{ + err }}}}\left( {{t_i}} \right)} \right]} \cr {{\rm{AMPL\_AX = }}\left[ {{R_S}\left( {{t_{\max }}} \right){\rm{ - }}{\sigma _{{\rm{ - err}}}}\left( {{t_{\max }}} \right)} \right]{\rm{ - }}\left[ {{{\rm{R}}_{\rm{S}}}\left( {{t_{\min }}} \right){\rm{ + }}{\sigma _{{\rm{ + err}}}}\left( {{t_{\min }}} \right)} \right]} \cr {{\rm{AMPL\_IG = }}{{{\rm{AMP}}{{\rm{L}}_{\rm{M}}}{\rm{AX}}} \over {\sqrt {\sigma _{{\rm{ - err}}}^{\rm{2}}\left( {{{\rm{t}}_{\max }}} \right){\rm{ + }}\sigma _{{\rm{ + err}}}^{\rm{2}}\left( {{{\rm{t}}_{\min }}} \right)} }},} \cr } $](/articles/aa/full_html/2024/07/aa46368-23/aa46368-23-eq12.png) (5)
(5)
where σ+err, and σ−err denote the 1σ errors of the measured count rates in the positive and negative directions, respectively. We used this modified definition of AMPL_SIG throughout the rest of the paper.
The AMPL_SIG can be calculated for all eROSITA detected sources, regardless of how often they were observed. However, the more bins there are in a light curve, the more efficient AMPL_SIG is at detecting variability. Therefore, we did not rebin any light curves for the AMPL_SIG variability detection and analysis. In Sect. 4, we defined significance thresholds on AMPL_SIG to identify variable sources.
3.1.3 Bayesian excess variance
A third method we used to quantify the variability is the Bayesian excess variance1 (bexvar; Buchner et al. 2022). It uses a hierarchical Bayesian model to determine a posterior probability distribution for the mean and standard deviation of the net count rate, assuming it to follow a log-normal distribution. Background, instrument, and Poisson variability are modelled out. The bexvar method models the variability intrinsic to the source, in addition to Poisson variability, background and instrument sensitivity variations with a hierarchical Bayesian model. We refer to samples from the posterior probability distribution of the standard deviation in the log count rate as σb. Buchner et al. (2022) also introduced the quantity SCATT_LO, the 10% quan-tile of the distribution of the σb samples, which is useful for distinguishing between variable and non-variable sources. The standard deviation of the log count rate is estimated by calculating the geometric mean of the samples, which we denote as 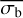 . We chose the 15.87% and 84.13% quantiles of the σb distribution as estimates of the uncertainty in the measurement.
. We chose the 15.87% and 84.13% quantiles of the σb distribution as estimates of the uncertainty in the measurement.
Similar to the NIV, we define the quantity σI to refer to the standard deviation that would be found by bexvar if all count rates were measured with infinite accuracy. Both the NIV and the σI are independent quantifiers of the intrinsic variability of a source, unaffected by Poisson noise or measurement uncertainties but dependent on the timing of the observations. Although σI is not normalised, as the NIV is, it is also invariable to a multiplicative scaling of the flux, due to the fact that it is defined on a logarithmic scale. The NIV describes a variance, and σI describes a standard deviation. Nevertheless, as the NIV is defined for a linear count rate, and σI is defined for a logarithmic count rate, the two quantities are not related by a square; 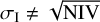 .
.
The strength of bexvar lies in the self-consistent Bayesian handling, modelling the observed counts with a Poisson distribution and propagating the probability distributions. Unlike the NEV, σb and 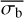 can never be negative. The bexvar method uses the Poisson probability distributions of the measured count rate in each bin, rather than a single value for the uncertainty in the count rate, as used by the NEV and AMPL_SIG.
can never be negative. The bexvar method uses the Poisson probability distributions of the measured count rate in each bin, rather than a single value for the uncertainty in the count rate, as used by the NEV and AMPL_SIG.
The bexvar method estimates the excess variability power on the timescale of the binning, assuming that each bin has an independently drawn count rate. We used a uniform prior within the [−2,2] interval for log (σb), as this is the range of values we expect to be able to measure for it. Smaller degrees of variability are possible but are unlikely to be distinguished from non-variability in eRASS light curves.
Unlike the standard NEV methodology, bexvar does not weigh all bins identically. It also uses Poisson probability distributions for the count rate in each bin to determine the degree of variability. These two features enable bexvar to estimate σI and the error in the measurement accurately, for a log-normal white-noise (P ∝ v0) light curve, with variable fractional exposures, over a wide range of count rates (Buchner et al. 2022, Fig. A.1)
Rebinning the light curves of very faint sources, which consist mostly of bins with 0 source counts, can be beneficial for a bexvar analysis. It is more computationally expensive than other variability estimators, and its computation time increases linearly with the number of bins in the light curve. Rebinning should not affect the measured variability as long as most of the variability power contained within the frequency interval of the original light curve is maintained below the Nyquist frequency of the rebinned light curve. Unless a very faint source exhibits brief, large flares, it is difficult to determine a precise or accurate estimate of its variability at the timescale of the separation of the eROSITA bins, even with bexvar. Therefore, rebinning the light curves of very faint sources usually does not reduce the ability to investigate their variability, but reduces the computation time.
Hence, we chose to rebin light curves of faint sources until an average of at least one source count was contained in every two bins, for detecting variability with bexvar. We also required that the rebinned light curve still consisted of at least 20 bins. For flaring sources, it is preferable to use AMPL_SIG to detect and characterise their variability, but only with the calibrated thresholds on AMPL_SIG defined by Buchner et al. (2022).
The bexvar parameter is most informative when calculated for light curves consisting of 20 bins or more. It can be used to quantify the variability of all eROSITA sources observed for 4 eRASSs or more. Fewer eRASSs of observation are required closer to either of the two ecliptic poles.
While σb is much more suitable for quantifying variability in the low count Poisson regime, it may be useful to convert this quantity into one equivalent to the NEV for comparison. We call this quantity NEVb. In Sect. 5, we derive an empirical conversion factor between σb and NEVb, and evaluate how it compares to the NEV in Appendix A.
3.1.4 Power spectral density and periodograms
The power spectral density (PSD; for a review see van der Klis 1989) describes the distribution of variability power as a function of frequency. A periodogram is an estimate of the PSD of a variable source, between the frequencies (Nbτ)−1, and (2τ)−1. The quantity τ represents the separation between one bin and the next. The periodogram is calculated as the modulus square of the Fourier transform. It depends on the time ordering of bins, and describes the correlation of individual measured count rates as a function of their temporal separation.
We normalised periodograms using the fractional rms normalisation (Belloni & Hasinger 1990). It has the useful feature that the NEV is equal to the integral of the rms-normalised and noise-subtracted periodogram.
The periodograms of variable sources are often dominated by a power-law shape: P(ν) ∝ v−α, where α is the power-law index. A power-law PSD with α = 0 is known as white noise and corresponds to a light curve in which the count rate in every bin is independent of the count rate in any other bin. A red-noise PSD is described by a power-law with α = 2 and is associated with a light curve dominated by long-term trends, in which the count rate in each bin is strongly correlated to that in adjacent bins. A pink-noise PSD lies between the two, and has α = 1.
The light curves of AGNs and XRBs are typically observed to have periodograms which can be described by a red-noise power-law of α ≈ 2 at high frequencies, and a pink-noise power-law of α ≈ 1 at lower frequencies (Edelson & Nandra 1999; Papadakis et al. 2002; Markowitz et al. 2003; Papadakis 2004; González-Martín & Vaughan 2012; Zheng et al. 2017). The transition from α ≈ 2 to α ≈ 1 is usually described by a sharp break, but has also been modelled as a gradual bend in the PSD (McHardy et al. 2004; González-Martín & Vaughan 2012). This break or bend occurs somewhere between about 10−6.4–10−3.3 Hz (González-Martín & Vaughan 2012).
Similar power-laws have been identified in the periodograms of XRBs, at much lower frequencies. For those, a low frequency break from α ≈ 1 to α ≈ 0 can be observed (Belloni & Hasinger 1990) as well. This has not yet been observed for AGNs. The timescales for XRB variability are on the order of seconds or less. Important features in XRB periodograms typically occur in the 0.01–100 Hz range (Wijnands & van der Klis 1999; Ingram & Motta 2019). Therefore, light curves binned into single eroday bins can only detect the long-term evolution of an XRB. Periodograms of such light curves are mainly useful for investigating AGNs.
To accurately estimate the PSD by computing a periodogram requires more information on the source flux at different times than is required to estimate the NIV, the σI, or for measuring AMPL_SIG. Therefore, for eROSITA observations, this detailed analysis will only be possible for bright variable sources close to either of the two ecliptic poles.
Periodograms of light curves were computed with the Stingray2 timing package (Huppenkothen et al. 2016). We particularly used the Stingray Powerspectrum function, which computes periodograms using a fast Fourier transform algorithm.
These four variability measures; the NEV, AMPL_MAX, 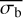 , and the periodogram, each quantify the degree of variability of a source in different ways. In the rest of the paper, we describe how they are best used for analysing eROSITA-like variable light curves.
, and the periodogram, each quantify the degree of variability of a source in different ways. In the rest of the paper, we describe how they are best used for analysing eROSITA-like variable light curves.
3.1.5 Band-limited power
We assume a stationary process causing the observed variability. In such a case, this process can be associated with a fixed PSD describing the source variability at all times. The constant value of the integral of such a PSD between two frequencies is the band-limited power, which describes how variable a source is within the selected frequency range. It does not depend on any properties of the observations, and is identical for different sets of observations.
The band-limited power is similar to the NIV∞, which is the geometrically averaged NIV over an assumed infinitely many time intervals. The NIV∞ is also a constant for a stationary process. The difference between them is that the NIV∞ overestimates the band-limited power due to power leakage (see e.g. van der Klis 1989; Vaughan et al. 2003). The properties of the observations can induce variability power at both lower (red noise leak) and higher frequencies (aliasing) than those being investigated, to leak into the [(Nbτ)−1, (2τ)−1] frequency space, and increase the power measured within it. This is discussed in more detail in Sect. 6.1.
The NIV varies around the NIV∞ due to the intrinsic scatter of the NIV, caused by the stochastic nature of the variability within a limited set of observations (Vaughan et al. 2003; Allevato et al. 2013). Finally, the NEV varies around the NIV due to measurement errors. The variance of the NEV is larger than its measurement error due to the intrinsic scatter in the NIV.
We prefer to use estimates of constant quantities, such as the band-limited power, or the NIV∞ when comparing the variability of different sources, when considering the scaling of the variability with other properties, such as the BH mass or the AGN luminosity, or when investigating whether the variability of an individual source changed over time. Even if the variability process is stationary, the NEV, AMPL_SIG, 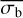 , and periodogram of two different sets of observations are likely to differ by more than their measurement errors would indicate. Without accounting for the intrinsic scatter, differences in variability measurements are likely to be overestimated. The intrinsic scatter is calculated based on an assumed PSD shape in the observed frequency interval, which may bias the result. Nevertheless, the intrinsic scatter cannot be assumed to be zero.
, and periodogram of two different sets of observations are likely to differ by more than their measurement errors would indicate. Without accounting for the intrinsic scatter, differences in variability measurements are likely to be overestimated. The intrinsic scatter is calculated based on an assumed PSD shape in the observed frequency interval, which may bias the result. Nevertheless, the intrinsic scatter cannot be assumed to be zero.
The first step to calculate the band-limited power is to estimate the NIV. This could be done by calculating the NEV, integrating the periodogram, or using 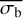 , along with the conversion from σI to the NIV, which is described in Sect. 5. The NIV∞ can then be estimated by including the intrinsic scatter in the NIV as an additional error. This is discussed in more detail in Sects. 6.2 and 6.3. Finally, the NIV∞ can be converted into an estimate of the band-limited power, by quantifying the strength of the power leakage from higher and lower frequencies into the [(Nbτ)−1, (2τ)−1] frequency space, and subtracting that from the estimate. This final step requires several assumptions about the shape of the source PSD in the frequency space not investigated. That can introduce additional uncertainty in the estimate of the band-limited power. Therefore, unless the strength of the power leakage can be reliably estimated without bias, it can be preferable to compare estimates of the NIV∞ instead.
, along with the conversion from σI to the NIV, which is described in Sect. 5. The NIV∞ can then be estimated by including the intrinsic scatter in the NIV as an additional error. This is discussed in more detail in Sects. 6.2 and 6.3. Finally, the NIV∞ can be converted into an estimate of the band-limited power, by quantifying the strength of the power leakage from higher and lower frequencies into the [(Nbτ)−1, (2τ)−1] frequency space, and subtracting that from the estimate. This final step requires several assumptions about the shape of the source PSD in the frequency space not investigated. That can introduce additional uncertainty in the estimate of the band-limited power. Therefore, unless the strength of the power leakage can be reliably estimated without bias, it can be preferable to compare estimates of the NIV∞ instead.
3.2 Simulations
We performed a variety of different types of simulations throughout this paper, to understand the statistical behaviour of each estimator when applied to eROSITA light curves. The true flux of simulated variable sources was determined by selecting the PSD of the source, and then using the Timmer & Koenig (1995) method to generate a light curve from it. We typically selected pink-noise PSDs for this purpose. The break in AGN PSDs, from an α ≈ 1 power-law, to an α ≈ 2 power-law has been observed to often occur within, or above, the frequency range probed by eROSITA (3.96 × 10−9–3.47 × 10−5 Hz; González-Martín & Vaughan 2012). The aliasing effect often counteracts the steeper power-law at high frequencies, and flattens the PSD (see Sect. 6.1). Therefore, the PSDs of typical eROSITA observed AGNs could, to first order, be assumed to approximately follow an α = 1 power-law. The accuracy of this first order assumption is also supported by the periodograms of actual eROSITA observations of AGNs (Bogensberger et al. 2024). We also simulated power-law PSDs with α = 0 (white noise) and α = 2 (red noise) for comparison, to determine how strongly the variability methods depend on the PSD shape. For the purpose of identifying significance thresholds for variability detection, we simulated constant light curves, in which the true flux did not vary.
From the simulated light curves of the true flux, we selected intervals of 1050 bins. That length approximately matches the upper limit on the number of observations of a source that can be made per eRASS. To simulate the red noise leak, we selected input PSDs that extended with the same power-law to frequencies at least one order of magnitude below the inverse of the total light-curve duration. We simulated light curves with at least one order of magnitude more bins than we needed for the analysis, and randomly selected starting points within that interval for the selected portion to be used for further analysis.
The true flux of the simulated light curves was shifted, and scaled such that the mean average source flux matched the desired source count rate at the detector, and there were no bins with a negative true flux. Increasing or decreasing the flux at all points by a constant amount only affects the value of the PSD associated with it at v = 0, which is not relevant to this analysis. Scaling the amplitude of the flux variation affects the NIV. This is how we generated light curves with a wide range of different NIVs. The light curves produced in this way do not contain any background or Poisson noise yet. Therefore, we refer to them as the true light curves of the simulated sources. The NIVs of these light curves were computed directly from the mean and variance of the true light curves, using Eqs. (2) and (3), with 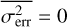 .
.
To investigate the ability to identify variable sources, and the reliability of estimating the NIV from a light curve (Sects. 4 and 5), we used the true light curves as a basis for generating simulated observed light curves, with properties as similar as possible to those detected by eROSITA. For this purpose, we selected a background count rate of 0.71 cts s−1 and a background area of 0.0089, which are equal to the mean value of both parameters found for sources detected by eROSITA close to the SEP. Next, we randomly selected a fractional exposure for each bin from the distribution observed for sources in the SEP field, assuming ∆t = 40 s. We cropped this distribution to avoid fractional exposures below 0.1, as is also done for the actual data. The light curves simulated in this way look similar to those in Fig. 1, except that they feature a random assortment of fractional exposures. These simulated light curves were only used in conjunction with the SCATT_LO, and AMPL_SIG methods, which do not depend on the time ordering of bins.
For each bin of the simulated true light curves, we randomly selected a measured number of source counts from the Pois-son distribution with a mean of (RS,t(ti) + RB,t(ti)A(ti)є∆t. In this equation, RS,t(ti), and RB,t(ti) are the true source and background count rates at time ti. We, similarly, selected a measured number of background counts from the Poisson distribution of RB,t(ti)є∆t. We computed source count rates from the simulated number of source and background counts, the background area, and the fractional exposure, as outlined in Sect. 2.1. These types of simulated light curves are referred to as being eROSITA-like.
We also simulated light curves with fractional exposure distributions that were not based on any observed distribution. This was done to investigate the dependence of the noise level in a periodogram on the mean 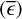 and variance
and variance 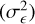 of the fractional exposure distribution in the light curve (Sect. 7). To span a large parameter space in both parameters, we first selected a minimum and maximum fractional exposure, drawn from a grid of 40 equally spaced points between 0.1 and 1.0, covering all possible combinations.
of the fractional exposure distribution in the light curve (Sect. 7). To span a large parameter space in both parameters, we first selected a minimum and maximum fractional exposure, drawn from a grid of 40 equally spaced points between 0.1 and 1.0, covering all possible combinations.
We generated scenarios for a maximum, minimum, and intermediate 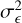 for each range of fractional exposures, at a fixed
for each range of fractional exposures, at a fixed 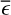 . For the maximum
. For the maximum 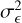 scenario, we assigned half of all bins to the maximum fractional exposure, and half to the minimum fractional exposure of the selected range. The ordering of the fractional exposures does not influence the periodogram noise level. For the minimum
scenario, we assigned half of all bins to the maximum fractional exposure, and half to the minimum fractional exposure of the selected range. The ordering of the fractional exposures does not influence the periodogram noise level. For the minimum 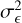 scenario, we assigned one randomly chosen bin with the maximum fractional exposure, one bin with the minimum fractional exposure, and kept the rest at the value halfway between the two. For the intermediate
scenario, we assigned one randomly chosen bin with the maximum fractional exposure, one bin with the minimum fractional exposure, and kept the rest at the value halfway between the two. For the intermediate 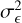 scenario, we selected fractional exposures to cover the interval with a constant incremental increase from minimum to maximum. We refer to the simulated true light curves created in this way as the patterned fractional exposure light curves.
scenario, we selected fractional exposures to cover the interval with a constant incremental increase from minimum to maximum. We refer to the simulated true light curves created in this way as the patterned fractional exposure light curves.
Throughout this paper, we investigated various analytical models, to characterise the use of variability quantifiers for eROSITA light curves. These were fitted with the nested sampling Monte Carlo algorithm MLFriends (Buchner 2016, 2019) through the UltraNest3 package (Buchner 2021).
4 Methods for identifying varying sources
Out of the millions of X-ray sources detected by eROSITA (Predehl et al. 2021), we intended to select a much smaller set of sources whose count rate changes significantly throughout the observing interval. These can subsequently be investigated individually in more detail. As described in Sect. 2.1, eRASS observations of X-ray sources feature a large variety of different properties. We aimed to have the capacity to detect significantly variable sources throughout the observed parameter space, even ones with low count rates. This method can be used to detect variable sources in the eRASS dataset, but may also be applicable to other surveys.
We did not seek to optimally divide the sample into likely variable and likely non-variable sources. Instead, we aimed to have the capacity to select variable sources at a low false-positive rate. In addition, we intended the variability thresholds to not be biased towards any particular type of variability, and be able to identify unexpected variability as well.
Buchner et al. (2022) investigated the ability of the AMPL_SIG, NEV, SCATT_LO, and Bayesian block methods to detect flaring, white noise (P ∝v0), and red noise (P ∝ ν−2) variability, for the eROSITA Final Equatorial-Depth Survey (eFEDS). Of the four methods, Buchner et al. (2022) found that SCATT_LO is almost always the most sensitive to detecting variability, regardless of its type. However, these authors also found that AMPL_SIG is slightly better at detecting flaring sources at high count rates than SCATT_LO. Both AMPL_MAX and SCATT_LO were designed to quantify variability, rather than to distinguish variable from non-variable sources. Nevertheless, they can both be used for that purpose as well. Following the conclusions of Buchner et al. (2022), we decided to use both SCATT_LO, and AMPL_SIG to distinguish likely variable from likely non-variable sources in eRASS data sets as well.
To use SCATT_LO and AMPL_SIG for variability detection in the eRASSs, we decided to define variability significance thresholds. Buchner et al. (2022) defined thresholds on both parameters for detecting variable sources in eFEDS. However, these are not necessarily applicable to eRASS observations, especially not for the regions close to the ecliptic poles, for which there is a large range of different number of bins, and an enhanced sensitivity to detect faint sources. Buchner et al. (2022) defined the thresholds as a function of count rate, but did not investigate the dependence on the number of bins. Therefore, we sought to define thresholds as a function of both parameters, and specific to the eRASSs.
For this purpose, we simulated 4 × 105 eROSITA-like light curves of intrinsically non-variable sources, as discussed in Sect. 3.2. We simulated 104 iterations of light curves for 40 sets of combinations of intrinsic source count rates of {0.001,0.003,0.01,0.03,0.1,0.3,1.0,3.0,10,30} cts s−1, and number of erodays of observation with є > 0.1, of {50, 135, 370, 1000}. This range of count rates and number of bins was selected to be most useful in selecting variable eRASS sources. For a single eRASS, sources within ≈7° of the ecliptic poles are observed between 50 and 1080 erodays per eRASS. When combining eight eRASSs, all sources in the sky will have been observed on at least 48 different erodays.
For each simulated light curve, we computed the SCATT_LO and AMPL_SIG parameters. From the resulting distribution of values, we determined one-tailed 1σ (84.13%), 2σ (97.72%), and 3σ (99.865%) equivalent quantiles for each input count rate and number of bins. These are displayed in Figs. 2 and 3, for SCATT_LO, and AMPL_SIG, respectively. They show that the variability significance thresholds of SCATT_LO, and AMPL_SIG depend on both the count rate and the number of bins. Variable sources may be selected at different significances, with differing purities, and false-positive rates.
The SCATT_LO thresholds have low values at a low count rates, due to the shape of the posterior distribution of the σb samples for light curves with very few counts. The thresholds then rise with an increasing count rate, until they reach a peak at 0.01–0.03 cts s−1, before gradually declining again. The peak is most prominent for the 3σ threshold, and occurs at a lower count rate for longer light curves. The 1σ threshold only has a very weak peak and does not change much as a function of the count rate or the number of bins. At high count rates above the peak, the three thresholds converge to one another, and towards SCATT_LO = 10−2. This is a consequence of the choice of prior for log (σb), which has a minimum value of −2.
The decline of the 3σ thresholds above 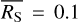 cts s−1 approximately follows a power-law of SCATT_LO
cts s−1 approximately follows a power-law of SCATT_LO 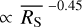 which is shown via the grey lines for light curves of 50 and 1000 bins in Fig. 2. Above the peak, the SCATT_LO thresholds also show a more simple dependence on the number of bins that can be approximated by
which is shown via the grey lines for light curves of 50 and 1000 bins in Fig. 2. Above the peak, the SCATT_LO thresholds also show a more simple dependence on the number of bins that can be approximated by 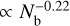 . Both of these trends reflect the increased sensitivity of SCATT_LO to detect lower degrees of variability when there are a greater number of source counts.
. Both of these trends reflect the increased sensitivity of SCATT_LO to detect lower degrees of variability when there are a greater number of source counts.
The AMPL_SIG thresholds have a very different dependence on the count rate and the number of bins. The three thresholds are much closer together than the SCATT_LO thresholds are. This makes it more challenging to distinguish between sources at different variability significances. The AMPL_SIG thresholds are dominated by a gradual rise with an increasing count rate until a shallow peak is reached at 1.0 cts s−1. The thresholds decrease slightly at higher count rates, before plateauing towards the highest count rates we investigated. This general shape of the thresholds can be understood to be a consequence of the accuracy of the assumptions of normal probability distributions on the measured count rate per bin.
The dependence of the AMPL_SIG thresholds on the number of bins is the opposite of what was observed for the SCATT_LO thresholds. The more bins there are, the higher the thresholds are. The reason for this is that it is more likely to find outliers in the count rate of longer light curves.
These results are qualitatively similar to those of Buchner et al. (2022). Their thresholds were calculated for a different number of bins, and for the eFEDS, rather than the eRASS dataset, so the exact values are not directly comparable. Nevertheless, we found the SCATT_LO thresholds to have a similar dependence on the count rate. However, whereas Buchner et al. (2022) found the AMPL_SIG thresholds to continuously increase with the count rate, we detected these to reach a plateau above 1.0 cts s−1. The likely reason for these differences is that the two thresholds use different definitions of AMPL_SIG.
We applied the two variability identification methodologies to the intrinsically non-variable and variable simulated eROSITA-like light curves of Fig. 1. Both methods correctly located the non-variable simulated source, shown in the top panel, in the <1σ variability class. In contrast, the intrinsically variable source exhibiting pink-noise variability, shown in the lower panel, was identified as variable above the 3σ threshold by SCATT_LO. However, AMPL_SIG placed its variability significance between the 1 and 2σ thresholds. This is a consequence of SCATT_LO being more sensitive to detecting pink-noise variability (Buchner et al. 2022).
The higher significance thresholds are based on smaller fractions of simulated light curves. To establish more accurate dependencies of the thresholds on the number of bins and the count rate, would require significantly more simulations.
 |
Fig. 2 1, 2, and 3σ thresholds on SCATT_LO for identifying variable sources. The thresholds are displayed as a function of the count rate. The dependence on the number of bins is illustrated by using different line styles. The grey lines indicate the best fit power-law relationship to the decreasing thresholds with increasing count rate, above the peak. |
 |
Fig. 3 1, 2, and 3σ thresholds on AMPL_SIG for identifying variable sources. The colours and line styles are the same as those in Fig. 2. |
5 Intrinsic variance estimation
The thresholds on SCATT_LO and AMPL_SIG were set up principally to identify variable sources at a given false-positive rate. They do not necessarily indicate the strength of the variability of a given source within a set of observations. In this section, we investigate the correlation between σb, and the NIV, such that a measurement of the former can be used to estimate the latter.
A successful method for estimating the NIV should be relatively unaffected by the features of eRASS light curves that could create issues for variability analysis (as outlined in Sect. 2.2), and remain accurate at both low and high count rates. The method presented in this section was derived for the assumption of eROSITA-like pink-noise light curves, but is applicable more generally to low-count-rate light curves with power-law PSDs.
The bexvar methodology allows a more accurate estimate of σI to be made, than the NEV is at estimating the NIV, especially at low count rates and for eROSITA light curves (see Appendix A). However, it is unclear how σI relates to other measures of the intrinsic variability of a source, such as the NIV or the PSD.
In contrast, the NIV is more easily interpretable, as it can be associated with the integral of the PSD, and is a measure of the variance of the linear flux distribution. It has been frequently used, and is tied to physical models. There are methods for converting estimates of the NIV into estimates of the constant band-limited power, which is intrinsic to the source, and not dependent on any properties of the observation. However, at the moment, there is no established quantity equivalent to the band-limited power for the σI. Furthermore, the impact of the red noise leak and the aliasing effect on σI are still unknown. It could be useful to combine the strengths of the NEV and bexvar methodologies, by using the Bayesian framework of bexvar to estimate the NIV.
Therefore, we investigated the possibility of converting the bexvar 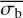 estimate of σI into an estimate of the NIV of a light curve. If such a function can be found, it could be used in both directions, and could allow the variability found by one parameter to be compared to that found by the other. It could also be used to explore the influence that power leakage has on σI, and help determine a stationary parameter equivalent to the band-limited power for
estimate of σI into an estimate of the NIV of a light curve. If such a function can be found, it could be used in both directions, and could allow the variability found by one parameter to be compared to that found by the other. It could also be used to explore the influence that power leakage has on σI, and help determine a stationary parameter equivalent to the band-limited power for 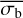 . We denote the NIV estimate based on a
. We denote the NIV estimate based on a 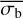 measurement, using the function relating it to the NIV, as the NEVb.
measurement, using the function relating it to the NIV, as the NEVb.
For this purpose, we simulated eROSITA-like light curves of intrinsically variable sources exhibiting pink-noise variability, as described in Sect. 3.2, in order to investigate the ability of 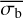 to accurately estimate the σI for these types of sources. We investigated light curves consisting of {20,75,150,400,1050} bins, with mean input count rates of {0.015,0.15,1.5,15} cts s−1. This range of count rates and number of bins was chosen to cover the parameter space of eRASS light curves, and is the same as those used to compare different methods of estimating the NIV, in Appendix A.
to accurately estimate the σI for these types of sources. We investigated light curves consisting of {20,75,150,400,1050} bins, with mean input count rates of {0.015,0.15,1.5,15} cts s−1. This range of count rates and number of bins was chosen to cover the parameter space of eRASS light curves, and is the same as those used to compare different methods of estimating the NIV, in Appendix A.
The results of these simulations are shown in Fig. 4. The σI was determined from the true light curve, before adding Pois-son noise and a background count rate. The 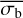 was calculated for the simulated measured source and background count rates. Buchner et al. (2022) showed that
was calculated for the simulated measured source and background count rates. Buchner et al. (2022) showed that 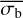 is an accurate estimator of σI for light curves with a log-normal distribution of count rates. Figure 4 shows that
is an accurate estimator of σI for light curves with a log-normal distribution of count rates. Figure 4 shows that 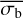 is also mostly accurate at estimating σI for sources exhibiting pink-noise variability. For very low-count-rate light curves,
is also mostly accurate at estimating σI for sources exhibiting pink-noise variability. For very low-count-rate light curves, 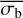 is very uncertain, but bexvar still estimates a reasonable error range within which σI is most likely to be found. This is very different to the ability of the NEV methodology to estimate the NIV (see Appendix A). However, this figure also shows that
is very uncertain, but bexvar still estimates a reasonable error range within which σI is most likely to be found. This is very different to the ability of the NEV methodology to estimate the NIV (see Appendix A). However, this figure also shows that 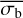 appears to systematically underestimate large σI values for pink-noise light curves, even at high count rates. As
appears to systematically underestimate large σI values for pink-noise light curves, even at high count rates. As 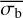 is a mostly accurate estimator of σI, it could potentially also be used to estimate the NIV, when using a function relating the two variability parameters. Therefore, we subsequently investigated the dependence of the measured
is a mostly accurate estimator of σI, it could potentially also be used to estimate the NIV, when using a function relating the two variability parameters. Therefore, we subsequently investigated the dependence of the measured 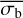 on the NIV of the true light curve.
on the NIV of the true light curve.
While a light curve with a larger NIV also tends to have a larger σI, the exact relationship between those two parameters is significantly more complex than the first-order estimate of 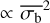 . To investigate the nature of the relationship, we simulated 3 × 104 eROSITA-like pink-noise light curves. These consist of 600 light curves for all combinations of the number of bins within the set {20,50,135,370,1000}, and count rates of {0.001,0.003,0.01,0.03,0.1,0.3,1.0,3.0,10.0,30.0} cts s−1 (see Sect. 3.2). As discussed in Appendix A, the resulting correlation remains accurate even for different PSDs.
. To investigate the nature of the relationship, we simulated 3 × 104 eROSITA-like pink-noise light curves. These consist of 600 light curves for all combinations of the number of bins within the set {20,50,135,370,1000}, and count rates of {0.001,0.003,0.01,0.03,0.1,0.3,1.0,3.0,10.0,30.0} cts s−1 (see Sect. 3.2). As discussed in Appendix A, the resulting correlation remains accurate even for different PSDs.
At the lowest count rates, and the smallest number of bins, the simulations produce so few source counts that it is not meaningful even to use the measured 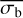 as an estimator of the degree of variability of the source. Nevertheless, we still included these instances, to investigate the ability to use the measured σb distribution to determine uncertainties and upper limits on an estimate of the NIV.
as an estimator of the degree of variability of the source. Nevertheless, we still included these instances, to investigate the ability to use the measured σb distribution to determine uncertainties and upper limits on an estimate of the NIV.
Figure 5 shows the relationship between 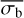 and the NIV in several simulated light curves for two particular average source count rates and number of bins. For bright sources observed in many bins, there is little scatter between
and the NIV in several simulated light curves for two particular average source count rates and number of bins. For bright sources observed in many bins, there is little scatter between 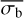 and the NIV. However, many more variable eRASS sources in the SEP field have count rates and number of bins similar to the values used for the simulations shown in the lower panel (RS = 0.3 cts s−1, Nb = 135). This indicates that there will still be significant uncertainty in the NEVb estimate of the NIV, for most sources.
and the NIV. However, many more variable eRASS sources in the SEP field have count rates and number of bins similar to the values used for the simulations shown in the lower panel (RS = 0.3 cts s−1, Nb = 135). This indicates that there will still be significant uncertainty in the NEVb estimate of the NIV, for most sources.
At low variabilities, low count rates, and a small number of bins, 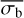 reaches a lower limit plateau, at the minimum value of σI that bexvar can measure. Whenever this level of
reaches a lower limit plateau, at the minimum value of σI that bexvar can measure. Whenever this level of 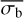 is measured, it should be treated as an upper limit measurement of the source variability. The minimum variability that can be detected by bexvar depends on both the number of bins, and the average count rate. This is indicated via a horizontal line in Fig. 5.
is measured, it should be treated as an upper limit measurement of the source variability. The minimum variability that can be detected by bexvar depends on both the number of bins, and the average count rate. This is indicated via a horizontal line in Fig. 5.
At greater degrees of variability, there is an approximately linear relationship between 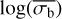 , and log(NIV), which has a gradient of approximately 0.5, and does not strongly depend on either the count rate or the number of bins. This is expected from the first order estimate of the relationship between the two parameters.
, and log(NIV), which has a gradient of approximately 0.5, and does not strongly depend on either the count rate or the number of bins. This is expected from the first order estimate of the relationship between the two parameters.
However, the top panel of Fig. 5 shows that a linear relationship underestimates 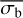 at both small and large values of the NIV. The gradient between
at both small and large values of the NIV. The gradient between 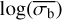 and log(NIV) increases at large values of the NIV for high count rate sources. This effect can also be seen in the underestimation of large values of σI by
and log(NIV) increases at large values of the NIV for high count rate sources. This effect can also be seen in the underestimation of large values of σI by 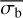 , in Fig. 4. Therefore, as a linear equation is insufficient to describe the relationship between the two parameters, we considered a quadratic equation instead. We found that the fits strongly preferred the parameters of this equation to depend on both the logarithm of the average count rate and number of bins. Therefore, we fitted the relationship between
, in Fig. 4. Therefore, as a linear equation is insufficient to describe the relationship between the two parameters, we considered a quadratic equation instead. We found that the fits strongly preferred the parameters of this equation to depend on both the logarithm of the average count rate and number of bins. Therefore, we fitted the relationship between 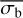 and the NIV with:
and the NIV with:
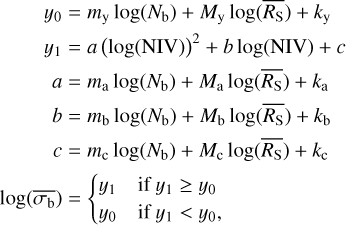 (6)
(6)
where y0 denotes the value of 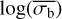 at the lower limit plateau, and y1 is the main function relating
at the lower limit plateau, and y1 is the main function relating 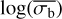 to log(NIV) above the plateau. We fitted for the best fit values of the parameters my, My, ky, ma, Ma, ka, mb, Mb, kb, mc, Mc, and kc. We defined the lower limit plateau as a level in
to log(NIV) above the plateau. We fitted for the best fit values of the parameters my, My, ky, ma, Ma, ka, mb, Mb, kb, mc, Mc, and kc. We defined the lower limit plateau as a level in 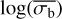 , rather than as a function of log(NIV), to reduce the degeneracy of the fit parameters.
, rather than as a function of log(NIV), to reduce the degeneracy of the fit parameters.
Table 1 lists the best parameters when using Eq. (6) to fit the relationship between 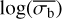 and log(NIV). To reduce degeneracy and improve the fit, we rescaled the NIV as:
and log(NIV). To reduce degeneracy and improve the fit, we rescaled the NIV as: 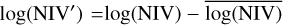 , where
, where 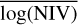 is the average NIV over all simulations. The parameter values presented in the table have been rescaled back, to describe the dependence of
is the average NIV over all simulations. The parameter values presented in the table have been rescaled back, to describe the dependence of 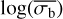 on log(NIV).
on log(NIV).
The amplitude of the quadratic term, a, is close to zero, and even changes sign within the parameter space we investigated. It is positive for light curves with a large source count rate, and few bins, and negative for low count rates and many bins. The linear and the constant terms, whose strength is defined by parameters b and c, respectively, depend more strongly on both the count rate and the number of bins. These three parameters all decrease with an increasing number of bins and increase with an increasing count rate. There is a similar dependence of parameters b and c on both the count rate and the number of bins.
Figure B.3 is the corner plot of the best fit of Eq. (6) to all the simulated data relating 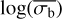 to the rescaled NIV in the light curve, log(NIV′). There are some degeneracies, most notably between my and ky and between other m and k parameters. This is probably because the number of bins does not change as much as the count rate within the sample of simulated light curves, so the m parameters can often act similarly to the constant k terms. There is also a slight negative degeneracy between Ma and Mb, as well as between some parameters of a and c. Nevertheless, the fitting parameters are otherwise well constrained. We tried to keep the degeneracies between parameters as minimal as possible, and only maintained parameters necessary to the fit. However, there might be the possibility of simplifying Eq. (6) by setting mb = mc and kb = kc.
to the rescaled NIV in the light curve, log(NIV′). There are some degeneracies, most notably between my and ky and between other m and k parameters. This is probably because the number of bins does not change as much as the count rate within the sample of simulated light curves, so the m parameters can often act similarly to the constant k terms. There is also a slight negative degeneracy between Ma and Mb, as well as between some parameters of a and c. Nevertheless, the fitting parameters are otherwise well constrained. We tried to keep the degeneracies between parameters as minimal as possible, and only maintained parameters necessary to the fit. However, there might be the possibility of simplifying Eq. (6) by setting mb = mc and kb = kc.
The ability of Eq. (6) to fit the relationship between 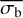 and the NIV within the parameter space we investigated, is shown via the solid black lines in Fig. 5. Equation (6) can be rearranged to determine the bexvar estimate of the NIV, NEVb, from the measurement of
and the NIV within the parameter space we investigated, is shown via the solid black lines in Fig. 5. Equation (6) can be rearranged to determine the bexvar estimate of the NIV, NEVb, from the measurement of 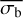 as follows:
as follows:
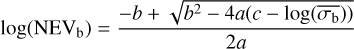 (7)
(7)
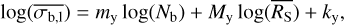 (8)
(8)
where 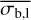 is the approximate value of the lower limit of
is the approximate value of the lower limit of 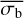 that is measurable at that particular count rate and number of bins. The equation for NEVb should only be considered as an upper limit estimate of the NIV if
that is measurable at that particular count rate and number of bins. The equation for NEVb should only be considered as an upper limit estimate of the NIV if 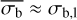 .
.
The above function can fail in two particular instances. Firstly, it is undefined when a = 0. In that case, Eq. (6) is solved as a simple linear equation. Secondly, it fails when 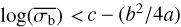 if a > 0, or
if a > 0, or 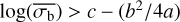 if a < 0. However, within the parameter space we investigated, this would require incredibly small or incredibly large degrees of variability, neither of which is likely to be found for a pink-noise light curve with a significant degree of variability, detected using the methods of Sect. 4.
if a < 0. However, within the parameter space we investigated, this would require incredibly small or incredibly large degrees of variability, neither of which is likely to be found for a pink-noise light curve with a significant degree of variability, detected using the methods of Sect. 4.
Finally, we tested how well this methodology would allow us to estimate the NIV with NEVb. Just as for Fig. 4, we simulated eROSITA-like light curves of pink-noise variable sources, consisting of {20, 75, 150, 400, 1050} bins, and average count rates of {0.015,0.15,1.5,15} cts s−1. We specifically selected different values for the number of bins and the average count rate than in the simulations used for determining the relationship between 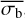 , and the NIV. In this way, we could independently verify the usefulness of this method, for other parameters not previously investigated. However, we used light curves of 20 bins both for defining the method and testing it, as that is the lower limit we chose for this type of variability analysis.
, and the NIV. In this way, we could independently verify the usefulness of this method, for other parameters not previously investigated. However, we used light curves of 20 bins both for defining the method and testing it, as that is the lower limit we chose for this type of variability analysis.
Figure 6 shows that NEVb can accurately estimate the NIV for this parameter space. We note that there is no apparent discrepancy between the two variability measures at high degrees of variability, as there was for 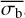 and σI. The uncertainties of NEVb depicted in this figure are determined by converting the upper and lower bounds of the 1σ confidence interval of
and σI. The uncertainties of NEVb depicted in this figure are determined by converting the upper and lower bounds of the 1σ confidence interval of 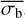 into NEVb values, using Eq. (6), and the parameters of Table 1. Whenever the lower bound error on
into NEVb values, using Eq. (6), and the parameters of Table 1. Whenever the lower bound error on 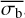 extends below
extends below 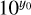 , the lower bound error on NEVb is extended to a value of 0. This is due to the inability to determine lower degrees of variability for those particular light curves. At very low count rates, when there is insufficient information available to properly constrain the NIV of a light curve, NEVb is still able to provide an accurate confidence interval within which the NIV of the light curve is likely to be.
, the lower bound error on NEVb is extended to a value of 0. This is due to the inability to determine lower degrees of variability for those particular light curves. At very low count rates, when there is insufficient information available to properly constrain the NIV of a light curve, NEVb is still able to provide an accurate confidence interval within which the NIV of the light curve is likely to be.
In Appendix A, we compared the NEVb against other estimators of the NIV. We also investigated to what extent the NEVb estimate of the NIV remains accurate for PSDs that differ from the assumed pink-noise shape. We found that NEVb provides the most accurate estimate of the NIV and the most accurate boundaries on the estimate, for eROSITA-like light curves with count rates below 1.5 cts s−1, for pink-, white-, and red-noise variable sources. At a count rate of 0.015 cts s−1, the average difference ratio between the estimated value and the NIV, is two orders of magnitude lower for NEVb, than it is for the NEV. Above 1.5 cts s−1, the NEVb is comparable to other methods. The NEVb was defined for eROSITA-like light curves, but can be used to estimate the NIV of any source observed with Nb ≤ 1000, and a power-law PSD with indices between 0 < α < 2. It may also be applicable to light curves with other properties, but we have not tested that yet. Due to its higher accuracy as compared to other methods, we decided to subsequently only use NEVb for estimating the NIV.
 |
Fig. 4 Ability of |
 |
Fig. 5 Relationship between |
 |
Fig. 6 Comparison of the NEVb measurements with the NIV of the light curve that it seeks to estimate, for pink-noise light curves, using Eq. (6), and the values listed in Table 1. The orange dashed line indicates the 1:1 relationship between NEVb, and the NIV. |
6 Power leakage and the intrinsic scatter in the NIV
We have developed and evaluated methods for accurately estimating the NIV of variable sources. However, the NIV is non-stationary, and varies stochastically, as outlined in Sects. 3.1.1 and 3.1.5. In this section, we discuss these effects, and introduce a new way to estimate the size of the intrinsic scatter of the NIV of a single, or multiple segments of a light curve. The results presented in this section are not specific to eROSITA, but apply to any variability analysis of approximately pink-noise light curves.
6.1 Aliasing and the red noise leak
All the variability power contained at frequencies above the inverse of the bin duration is integrated out within each bin. If the bins of a light curve are adjacent, having no gaps in between, the average count rate in each bin is not affected by power above the sampling frequency, so there is no aliasing effect. However, for light curves consisting of gaps of a constant duration between bins, power at frequencies between the inverse of the separation of bins, τ−1, and the inverse of the bin duration, ∆t−1, increases the flux difference from one bin to the next. This affects both the NIV and the periodogram. It is known as the aliasing effect (see van der Klis 1989; Kirchner 2005), and it is particularly strong for eROSITA light curves, as the gaps between observations are at least 360 times as long as the observations themselves.
If individual bins are substantially shorter than the gaps between them, and if there is negligible power at frequencies larger than the inverse of the duration of each bin, the timing of the observations can be mathematically described as delta functions. In that case, which applies to eROSITA light curves, we can simplify the mathematical description of the impact that aliasing has on a PSD, to:
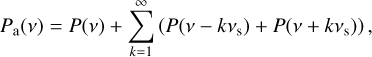 (9)
(9)
where Pa(v) is the observed periodogram affected by aliasing, P(v) is the true PSD that we want to determine accurately, and vs is the sampling frequency. For a derivation of this equation, see Kirchner (2005).
For AGN PSDs described by power-laws, in which variability power decreases with increasing frequency, aliasing predominantly affects the periodogram shape close to the Nyquist frequency. It causes the power-law slope to flatten at the highest frequencies observed. Figure 7 depicts various effects that afflict a measured periodogram and offset it from the source PSD.
Aliased periodograms can be fitted using Eq. (9) to determine an estimate of the intrinsic shape of the PSD of the variable source, if there were no aliasing. However, this requires some assumptions about the shape of the PSD above the Nyquist frequency, for which no data are available. Fortunately, we can rely on previous analyses of AGN periodograms at higher frequencies to inform this assumption (Papadakis et al. 2002; González-Martín & Vaughan 2012).
Another effect causes variability power at lower frequencies to leak into the observed frequency space, enhancing the measured degree of variability. This is known as the red noise leak. However, whereas the aliasing of α > 0 power-laws predominantly affects the variability measured at the highest frequencies, the red noise leak increases the power at all frequencies. For power-law PSDs, the red noise leak mainly increases their normalisation, but does not affect the power-law slopes (Zhu & Xue 2016).
Even without removing the impact that the red noise leak and aliasing have on the periodograms of light curves of a set of variable sources, it is still possible to compare their estimates of NIV∞, if it can be assumed that the combination of the two effects has a similar impact on the sources being compared. However, to compare NIV∞ estimates, it is first necessary to determine the intrinsic scatter in the NIV.
 |
Fig. 7 Comparison of a typical AGN PSD, and how a measured peri-odogram differs from it, within the frequency space that can be explored by eROSITA for sources lying close to the ecliptic poles. The intrinsic PSD is depicted as following a broken power-law of P ∝ v−1 at v < vb, and P ∝ v−2 at v ≥ vb, and continues beyond the frequency range probed by the observations. The measured periodogram is offset from the intrinsic PSD by the Poisson noise, the є noise, aliasing, and the red noise leak. The є noise (Eq. (16)) is often significantly larger than the Poisson noise (Eq. (15)). The flattening of the Poisson and є subtracted periodogram at the highest frequencies is due to aliasing. The red noise leak increases the amplitude of the power-laws. The relative strength of the Poisson, fractional-exposure noise, aliasing, and the red noise leak depicted in this figure are illustrative, and depend on the shape of the PSD, the average count rate, and the mean, and variance of the fractional exposure. Periodogram noise is not depicted. |
6.2 The intrinsic scatter of the NIV
The NIV is the intrinsic source variability at the time of the observations. It is unaffected by Poisson statistics and measurement errors. Nevertheless, it varies over time in a stochastic way, even if the process causing the variability is stationary. This has previously been discussed by Vaughan et al. (2003) and Allevato et al. (2013).
Figure 8 demonstrates how strongly the NIV can vary between light curves observed at different times, even if they are generated by the same PSD with the same band-limited power. In this particular example, a 5 × 103 bin pink-noise light curve was simulated, of which a 500 bin segment is shown. The NIV was computed for a sliding window interval of 50 bins each. The NIV was spread out over more than one order of magnitude between its maximal (0.21) and minimal (0.015) value in just this 500 bin segment. For steeper power-laws, the scatter of the NIV is even more pronounced (Vaughan et al. 2003).
In this simulation, the band-limited power, for the frequency range corresponding to a 50 bin light curve, has a value of 0.035. The NIV∞ is offset from the band-limited power by the red noise leak, to a value of 0.043. Aliasing was not included in this simulation. If it was, it would have caused an even larger difference between NIV∞ and the band-limited power. Figure 8 also shows that log(NIV) follows a normal distribution with a mean of NIV∞.
Vaughan et al. (2003) provided a table of the scatter to expect in the log variance of the count rate in light curves for a few different PSD slopes, for a few different number of bins.
Allevato et al. (2013) further investigated the mean, variance, and skewness of the distribution of the NEV for a sample of 5000 simulated light curves, with continuous, or sparse sampling, and different PSD slopes.
In this section, we instead focused on determining a more general description of the scatter in the NIV, rather than the variance, of a stationary pink-noise process. We aimed to provide a means to estimate the intrinsic scatter in the NIV for any number of bins in the light curve. We also investigated the dependence of the scatter on other parameters besides the number of bins. The following results are based on 20 times more simulated light curves for each selected number of bins, than those used by Vaughan et al. (2003) provided a table of the scatter to expect in the log variance of the count rate in light curves for a few different PSD slopes, for a few different number of bins.
The intrinsic scatter found in this way can be directly used alongside any NIV estimate, analogously to a sampling error, to estimate how much the NIV can be expected to vary between two different sets of observations. In so doing, the NEVb (or similar) measurement can also be used as an estimator of NIV∞. None of this section is specific to eROSITA, and the results can be used for any approximately pink-noise light curve.
We label the intrinsic scatter of the NIV in log-space as ∆s. It is equivalent to the standard deviation of the distribution of log(NIV), which can be seen in Fig. 8.
We simulated 3.2 × 105 pink-noise light curves like the one shown in Fig. 8 to determine the standard deviation of the distribution of NIVs for light curves consisting of {5, 10, 20, 30, 40, 50, 60, 75, 90, 100, 120, 140, 170, 200, 500, 1000} bins. We mainly focused on the range of bins most useful for an eRASS variability analysis. We extended the range somewhat, to better determine the dependence of the intrinsic scatter of the NIV on the number of bins of the light curve. We simulated 105 bins for each instance of a pink-noise light curve, to ensure that the NIV in each randomly selected segment was part of the same distribution about a fixed NIV∞. Unlike previous simulations, we did not include Poisson noise, a background count rate, or a fractional exposure, as this analysis seeks to only determine the intrinsic scatter of the NIV.
We randomly selected starting positions within the simulated light curves and calculated the NIV for each selected interval. We investigated different degrees of intrinsic variability by scaling the range of fluxes in the simulated light curves, while keeping the mean flux constant. A lower range at a constant mean, results in a lower NIV∞. For each set of 2000 such simulated light-curve intervals, which all have the same number of bins, and were generated from the same PSD, with the same NIV∞, we determined the standard deviation of the log(NIV) distribution (∆s). We subsequently investigated the dependence of ∆s on various parameters.
We found that the intrinsic scatter depends on both the number of bins, and NIV∞. Previously, Vaughan et al. (2003) and Allevato et al. (2013) investigated the dependence of it on the slope of the PSD, and the number of bins in the light curve, but not the dependence on NIV∞. The parameters NIV∞ and Nb are correlated with one another, for a stationary process, if α > 0. Nevertheless, we still treat them as mostly independent, as the NIV∞ can also vary across a wide range at a fixed number of bins of the light curve.
Figure 9 depicts the dependence of ∆s on the number of bins and the NIV∞. For a fixed Nb, the intrinsic scatter depends on the NIV∞ with an approximately quadratic relationship: ∆s(NIV∞) = a (log(NIV∞))2 + b log(NIV∞) + γ. We further analysed the dependence of a, b, and γ on the number of bins of the light curve. Only γ had a dependence on it, which could be approximately described by γ(Nb) = (c/Nb)d + f. Therefore, we fit the results of our simulations using:
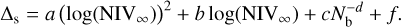 (10)
(10)
As Fig. 9 shows, the range of ∆s values at a fixed number of bins does not change significantly with an increasing number of bins in the light curve. That is why we modeled the dependence of ∆s on NIV∞ and Nb as additive, rather than multiplicative.
The largest value of NIV∞ is limited by the number of bins of the light curve. Very short light curves cannot have the same maximum value of NIV∞ as significantly longer light curves do. This prevents the low Nb, high log(NIV∞) corner of this figure from being populated with data points. The intrinsic scatter depends more strongly on the number of bins of the light curve, but the dependence on NIV∞ cannot be ignored, especially not for large variabilities of NIV∞ > 10−2.
To reduce the degeneracy between the two parameters a and b in the fit, the NIV was rescaled, so that Eq. (10) was instead fitted as a function of 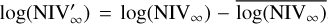 , where
, where  denotes the average log(NIV∞) over all simulations. When fitting Eq. (10) to all the values of
denotes the average log(NIV∞) over all simulations. When fitting Eq. (10) to all the values of 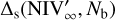 that had been obtained from the simulations, we obtained the corner plot for the best fit parameters a′, b′, c, d, and f′, which is shown in Fig. B.1. Table 2 lists the non-rescaled best fit parameters of ∆s(NIV∞, Nb).
that had been obtained from the simulations, we obtained the corner plot for the best fit parameters a′, b′, c, d, and f′, which is shown in Fig. B.1. Table 2 lists the non-rescaled best fit parameters of ∆s(NIV∞, Nb).
We expected ∆s to approximately depend on 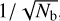 , and indeed we find d to be close to 0.5. There is some degeneracy between c and d, and between d and f. Nevertheless, all five parameters were essential to fit the dependence of ∆s on Nb and log(NIV∞).
, and indeed we find d to be close to 0.5. There is some degeneracy between c and d, and between d and f. Nevertheless, all five parameters were essential to fit the dependence of ∆s on Nb and log(NIV∞).
The best estimate of NIV∞ is NEVb, but with according upper and lower limits. The 1σ upper limit on the NIV∞ estimate based on a single measurement of the NEVb, is finally found using:
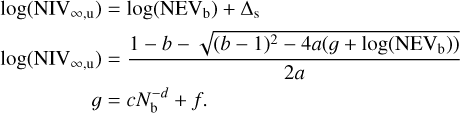 (11)
(11)
Similarly, the lower limit is calculated by:
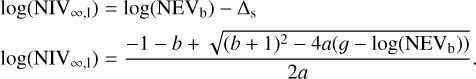 (12)
(12)
The content of the square root in these two equations is not likely to ever be negative. We only recommend using these equations for pink-noise light curves with fewer than 1000 bins, and −4 < log(NIV∞,l) < −1. The full error of the estimate of NIV∞ is found by combining the measurement error of NEVb with the intrinsic scatter found using Eqs. (11) and (12).
Our results are comparable to those of Vaughan et al. (2003), for the five different number of bins in the light curve discussed by them. When converting their 90% interval on the scatter in the variance for pink-noise light curves to a 1σ range in the NIV, we found values within the range of ∆s values we found, for differing NIV∞. We found a similar dependence on the number of bins as can be deduced from the results provided by Vaughan et al. (2003). In contrast, Eqs. (11) and (12), provide the intrinsic scatter in the NIV for any number of bins between 5 and 1000, based on 67 times more simulations. We also investigated, and quantified the dependence of ∆s on NIV∞, and found it to be non-negligible. Our results are also comparable to those of Allevato et al. (2013), for α = 1.
 |
Fig. 8 Simulated light curve demonstrating how the NIV of a variable source can change over time, even if the PSD and the band-limited power remain unchanged. Panel a: 500-bin segment of a simulated pink-noise light curve without measurement errors or Poisson noise. Panel b: Normalised intrinsic variance of a sliding window interval of 50 bins from the light curve in panel a. Each NIV data point is placed at the time of centre of the selected interval. The maximum and minimum NIV of this interval is indicated, and the parts of the light curve for which they were obtained are highlighted. Panel c: Geometric mean NIV of 10 adjoined segments, each consisting of 50 bins. Each value is placed at the center of the segments used. Panels b and c use data from the light curve outside of the interval shown in panel a. The panels on the right show the distribution of these parameters, throughout the entire 5 × 103 bin simulated light curve. |
 |
Fig. 9 Dependence of ∆s on the number of bins, and the NIV∞. Each data point represents the intrinsic scatter in the NIV, determined from 2000 light curves, randomly selected from a 105 bin simulated pink-noise light curve produced from a constant input PSD. The curves show the best fit relation of ∆s(Nb), at fixed levels of NIV∞, using Eq. (10) with parameter values as contained in Table 2. There is a significant scatter among the data points due to the probabilistic nature of this estimate. |
6.3 Reducing the intrinsic scatter in the NIV by averaging over multiple segments
The intrinsic scatter is best reduced by observing the source again at a different time. Without additional observations, the scatter can instead be reduced by splitting the total observed light curve into several segments. Instead of computing one NIV estimate for the entire frequency range, a more precise estimate over a smaller frequency range can be found by computing the geometric mean of the NIV estimates found in Nseg segments of Nb bins each. In choosing how to split a light curve into individual segments, a balance needs to be found between reducing the intrinsic scatter, by increasing the number of segments, and maximising the frequency space investigated, by having as many bins in each segment as possible.
Vaughan et al. (2003), and Allevato et al. (2013) also describe the use of such an ensemble average to reduce the intrinsic scatter of the NIV. In contrast to our approach, they use an arithmetic, rather than a geometric ensemble average of the NEV. If the distribution of the NIV is log-normal, a geometric mean provides a more accurate estimate of the NIV∞. Furthermore, a linear ensemble average NEV will tend to overestimate the NIV∞, if it does not follow a linear distribution. This difference in methodology makes our results not directly comparable to those of Vaughan et al. (2003) and Allevato et al. (2013) in regards to ensemble averages.
Calculating a geometric mean NEV is not possible if the NEV of any segment is negative. As the NEVb is never negative, its geometric mean,  , can always be computed, regardless of the mean count rate, or degree of variability in different segments.
, can always be computed, regardless of the mean count rate, or degree of variability in different segments.
The intrinsic scatter is affected by the placement of the segments in relation to each other. If all the segments used to compute  are spaced randomly, such that there are long, and inconsistent gaps between each of them, then the NIV in each segment is independent of the NIV of any of the other segments. In that case, the logarithmic intrinsic variance of
are spaced randomly, such that there are long, and inconsistent gaps between each of them, then the NIV in each segment is independent of the NIV of any of the other segments. In that case, the logarithmic intrinsic variance of 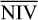 , which we refer to as ∆s,n, is:
, which we refer to as ∆s,n, is:
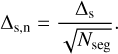 (13)
(13)
In this equation, ∆s is described by Eq. (10), with parameter values as listed in Table 2. The parameter Nb in Eq. (10) now refers to the number of bins in each of the segments of the light curve. The best estimate of NIV∞ is now  . The upper and lower limits of that estimate are still found by Eqs. (11) and (12), but using
. The upper and lower limits of that estimate are still found by Eqs. (11) and (12), but using 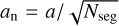 instead of a, and bn, cn, and ƒn, which are all adjusted from their values in Table 2 in the same way. This is also found by Vaughan et al. (2003) and Allevato et al. (2013).
instead of a, and bn, cn, and ƒn, which are all adjusted from their values in Table 2 in the same way. This is also found by Vaughan et al. (2003) and Allevato et al. (2013).
However, most cases are more complex. For example, the NIV in one segment is not independent of the NIV of directly neighbouring segments. In such cases, the intrinsic scatter of the NIV cannot be reduced linearly following Eq. (13), but decreases more gradually with an increasing number of segments. The geometric mean NIV of ten adjoined segments consisting of 50 bins each is illustrated in Fig. 8c. The range of values of the average NIV, computed over ten adjoined segments of 50 bins, is smaller than the range of the NIV in 50 bins, but not by a factor of 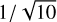 .
.
For eROSITA observations of sources spanning multiple eRASSs, there is a natural way to separate the light curve into segments during which the source was observed every eroday, separated by intervals with no observation. The gaps between the segments are not random, but are, in mostcases, considerably longer than the segments, so Eq. (13) is applicable. However, this does not apply to sources close to the ecliptic poles.
The reduction of the intrinsic scatter of the NIV in adjoined segments is studied with more simulations, identical in number and methodology as those described in Sect. 6.2. Figure 10 plots the trade-off between the number of bins per segment and the number of segments, restricted to combinations of Nb × Nseg ≤ 1000. The dashed curves in Fig. 10 decline steeper than the solid curves, demonstrating that the intrinsic scatter is reduced more quickly for randomly positioned segments, than adjacent ones. At the lowest NIV∞ values we simulated, ∆s,n approximately follows Eq. (13). For higher variabilities, the decline is more gradual. There is a significant scatter in the data points. Increasing the precision would have required a significantly greater number of simulations than were used.
Based on the form of Eq. (13), we investigated a power-law dependence of ∆s,n on Nseg. Visual inspection suggests that the exponent of Nseg changes linearly with log(NIV∞), and is independent of Nb:
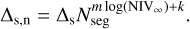 (14)
(14)
We fitted this equation and obtained the parameters listed in Table 3. Since NIV∞ is not known, it can be approximated by 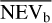 .
.
This relationship has only been derived for simulated pink-noise light curves. Equation (14) only applies to the interval 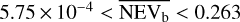 , for which the exponent in Eq. (14) is between 0 and −0.5. Pink-noise light curves of significantly variable sources with Nb ≤ 1000, should have log
, for which the exponent in Eq. (14) is between 0 and −0.5. Pink-noise light curves of significantly variable sources with Nb ≤ 1000, should have log 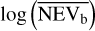 values well within these limits.
values well within these limits.
Best-fitting parameters describing the intrinsic scatter of the NIV, as a function of Nseg and NIV∞, if the segments are adjoined.
 |
Fig. 10 Reducing the intrinsic scatter by computing the geometric mean NIV for Nseg distant or adjoined segments of Nb bins each. The data points indicate the results of individual simulations for adjoined segments. The lines depict the best fits to the simulations, using Eqs. (14) and (10), and the parameter values in Tables 2, and 3. The solid lines show the dependence of ∆s,n on Nseg for adjoined segments, and the dotted lines for distant, randomly placed segments. |
7 Periodogram analysis
The shape of the power spectrum is a diagnostic of the variability process. Estimating the source PSD based on a periodogram requires understanding the biases introduced by the characteristics of the observation. For eRASS, the long but consistent gaps between observations lead to aliasing, described in Sect. 6.1. In addition, Poisson noise and the varying fractional exposures generate additional noise that affect the periodogram. These effects are discussed in turn in this section. The results presented here apply to all variability analyses, and are not specific to eROSITA.
Poisson noise in the count rate measurements affects the observed periodogram by increasing all powers by a constant value of 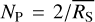 , in the fractional rms normalisation (Belloni & Hasinger 1990). However, while the eROSITA count rates are estimated from bins of effective duration є∆t, the PSD frequencies are based on the bin separation, τ. Therefore, the Poisson-noise level for light curves with regularly spaced gaps between bins is:
, in the fractional rms normalisation (Belloni & Hasinger 1990). However, while the eROSITA count rates are estimated from bins of effective duration є∆t, the PSD frequencies are based on the bin separation, τ. Therefore, the Poisson-noise level for light curves with regularly spaced gaps between bins is:
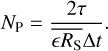 (15)
(15)
The varying fractional exposures in a light curve generate additional noise, which acts similar to the Poisson noise, by increasing the PSD power at all frequencies. The excess noise has the same dependence on the count rate, but also depends on the mean  , and variance
, and variance  of the fractional exposure. Therefore, we describe the total Poisson and fractional-exposure noise in the PSD as:
of the fractional exposure. Therefore, we describe the total Poisson and fractional-exposure noise in the PSD as:
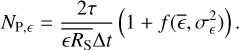 (16)
(16)
For other periodogram normalisations, the above equation is modified by replacing 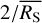 with the corresponding term.
with the corresponding term.
In the case of a constant fractional exposure, 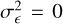 , we define f = 0, and the equation simplifies to Eq. (15). Besides that, we quantified f with simulations. We did not find a dependence of f on the count rate, the number of bins, or the time-ordering of the fractional exposures.
, we define f = 0, and the equation simplifies to Eq. (15). Besides that, we quantified f with simulations. We did not find a dependence of f on the count rate, the number of bins, or the time-ordering of the fractional exposures.
We simulated 2 × 106 instances of 1000 bin, high count rate (30 cts s−1) patterned fractional exposure light curves (see Sect. 3.2), of intrinsically constant sources with a negligible background. This corresponds to 1000 simulated light curves for each combination of 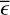 and
and 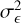 ). We determined the fractional-exposure-noise level, and averaged it over the simulations. The results of this are shown in Fig. 11. The range of
). We determined the fractional-exposure-noise level, and averaged it over the simulations. The results of this are shown in Fig. 11. The range of 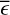 and
and 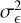 ) values we investigated encompasses the entire parameter space these parameters can have. Therefore, the results found here apply to any light curve with variable fractional exposures, observed by any instrument, and are not merely applicable to eROSITA.
) values we investigated encompasses the entire parameter space these parameters can have. Therefore, the results found here apply to any light curve with variable fractional exposures, observed by any instrument, and are not merely applicable to eROSITA.
We approximated the trends depicted in Fig. 11 with a functional form. At a fixed 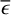 , we adopted the quadratic equation
, we adopted the quadratic equation 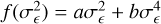 , fulfilling
, fulfilling 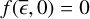 . At fixed
. At fixed 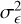 , we found that
, we found that 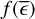 can be fitted with an exponential and a constant. Therefore, we chose the following fitting function for the results of these simulations:
can be fitted with an exponential and a constant. Therefore, we chose the following fitting function for the results of these simulations:
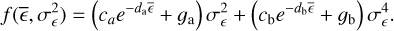 (17)
(17)
To reduce the degeneracy between the fitting parameters, we fitted f as a function of 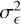 , and
, and 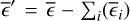 , where
, where 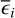 is the mean fractional exposure of simulation i. The best-fitting parameter values are described in Table 4, for the non-rescaled parameters
is the mean fractional exposure of simulation i. The best-fitting parameter values are described in Table 4, for the non-rescaled parameters 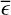 , and
, and 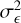 . Figure B.2 depicts the correlation between the parameters in the fit. There is a degeneracy between ca and da, and between cb and db, as these pairs of parameters increase the effect of the exponential functions involved.
. Figure B.2 depicts the correlation between the parameters in the fit. There is a degeneracy between ca and da, and between cb and db, as these pairs of parameters increase the effect of the exponential functions involved.
The fit slightly underestimates the excess fractional-exposure noise at the highest values of 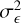 , and overestimates it at the lowest values. However, neither of these regimes is relevant for eRASS light curves. Therefore, we consider the accuracy of this approximation as sufficient for analysing eROSITA periodograms.
, and overestimates it at the lowest values. However, neither of these regimes is relevant for eRASS light curves. Therefore, we consider the accuracy of this approximation as sufficient for analysing eROSITA periodograms.
Importantly, the varying fractional exposures noise can be much larger than the standard Poisson noise. This is illustrated in Fig. 7 for typical values of 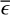 , and
, and 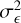 in eROSITA observations. Finally, estimating the NIV by integrating a periodogram of an eRASS source, after removing the Poisson and varying fractional-exposure noise, is validated in Appendix A.1. There, we demonstrate the impact of the excess noise and the accuracy of our analytic estimate.
in eROSITA observations. Finally, estimating the NIV by integrating a periodogram of an eRASS source, after removing the Poisson and varying fractional-exposure noise, is validated in Appendix A.1. There, we demonstrate the impact of the excess noise and the accuracy of our analytic estimate.
 |
Fig. 11 Dependence of the excess noise in a periodogram caused by varying fractional exposures, as a function of |
8 Discussion
For optimal variability analysis of eRASS observations, we recommend first reducing the extensive data set to a more manageable size of significantly variable sources, using the methods detailed in Sect. 4. After that, we recommend using the NEVb methodology to estimate the NIV of all significantly variable sources. The light curve might be split into individual segments to reduce the intrinsic scatter of the NIV. For comparison with other sources, the NIV∞ is estimated by computing the geometric mean NEVb of all segments. The error in the NIV∞ estimate is found by adding the measurement error with the intrinsic scatter in quadrature.
The thresholds for identifying variable sources using the two variability quantifiers SCATT_LO and AMPL_SIG were determined specifically for applicability to eROSITA observations of sources close to the SEP. They apply to light curves of between 50 and 1000 bins, for average count rates of between 0.001 and 30 cts s−1. As neither of the two variability quantifiers uses the timing of the observations, it is possible to combine data collected over multiple eRASSs. The greater the number of bins of the light curve, at a constant bin duration, the easier it is to identify intrinsically variable sources. Therefore, it is recommended to combine as many measures of the source flux as possible. For eROSITA, this means combining all observations of the same source obtained over multiple eRASSs. After eRASS:8, all X-ray sources in the sky will have been observed on ≳48 erodays. Therefore, the thresholds described in Sect. 4 can be used to identify likely variable sources throughout the entire sky, as observed by eROSITA. A caveat is that the thresholds might need to be adjusted for regions of the sky with significantly stronger background count rates, especially for faint sources.
Selecting variable sources in observations by other instruments may require these thresholds to be modified. They will be impacted by the properties of the observation, the fractional exposure distribution of the light curve bins, and the strength of the background count rate, which varies across the sky. It is unclear to what extent a variable background could affect these results. However, the eROSITA background is very stable (Predehl et al. 2021), so we do not expect it to have a significant impact on any of the results discussed here. The thresholds for variability detection are based on the specific fractional exposure distribution of eROSITA light curves. Variability thresholds for other surveys might differ to some extent from the ones presented here, and will likely require separate simulations.
The NEVb method is the most accurate way to estimate the NIV of a variable source. We encourage its use in future variability analyses of light curves with at least a few bins in the Poisson regime. This is of particular relevance for eROSITA variability analysis. However, the NEV is still the preferred method for high count rate sources. The conversion from 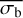 to NEVb (Sect. 5), was made with the assumption of a pink-noise PSD, and for typical source and background count rates, and fractional exposures of eRASS observations of SEP sources. However, the function relating the two parameters can also be used for light curves obtained by other instruments. We only expect potential slight differences in the lower limit of
to NEVb (Sect. 5), was made with the assumption of a pink-noise PSD, and for typical source and background count rates, and fractional exposures of eRASS observations of SEP sources. However, the function relating the two parameters can also be used for light curves obtained by other instruments. We only expect potential slight differences in the lower limit of 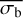 for different background count rates. A similar set of simulations can also be performed to improve the accuracy of a similar NEVb estimate for different types of PSDs generating the variability. However, as discussed in Appendix A, NEVb also works well for white- and red-noise variability. Even without any modification to the function relating
for different background count rates. A similar set of simulations can also be performed to improve the accuracy of a similar NEVb estimate for different types of PSDs generating the variability. However, as discussed in Appendix A, NEVb also works well for white- and red-noise variability. Even without any modification to the function relating 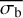 to the NIV, the NEVb provides the most accurate estimate of the NIV of a variable source for these types of variability. The NEVb has been tested to work for all eROSITA light curves with between 20 and 1000 consecutive bins. That corresponds to sources within ≈17° of the ecliptic poles. We recommend using AMPL_MAX as a variability measure for shorter light curves instead.
to the NIV, the NEVb provides the most accurate estimate of the NIV of a variable source for these types of variability. The NEVb has been tested to work for all eROSITA light curves with between 20 and 1000 consecutive bins. That corresponds to sources within ≈17° of the ecliptic poles. We recommend using AMPL_MAX as a variability measure for shorter light curves instead.
The NEVb estimate of the NIV can also be calculated for light curves of other instruments, and for other types of variability. To do so, the count rates can be converted to an average number of source counts per bin. The conversion is: 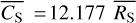 , where
, where 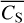 is the average number of source counts per bin. This is a consequence of the choice of bin size of 40 s, and the mean of the fractional exposure distribution above 0.1, of
is the average number of source counts per bin. This is a consequence of the choice of bin size of 40 s, and the mean of the fractional exposure distribution above 0.1, of 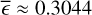 (Bogensberger et al. 2024).
(Bogensberger et al. 2024).
In order to compare the NIV estimate of different sources, the relevant light curves should cover the same frequency interval. This can be achieved by cropping longer light curves to be the same length as shorter ones. Alternatively, all light curves can be split into smaller segments of the same length. Then the geometric mean NEVb can be computed for all segments of the same source, and these quantities can then be compared. This method also helps to reduce the intrinsic scatter of the NIV, which corresponds to a smaller error on the estimate of the NIV∞.
The equations that were determined for the intrinsic scatter of the NIV in Sects. 6.2 and 6.3, apply to light curves of sources with approximately pink-noise PSDs. They are not specific to eROSITA and can be used to analyse pink light curves found by any instrument.
The description of the excess noise in the periodogram in Sect. 7, applies to all light curves from any single instrument or collection of instruments. It is not specific to eROSITA, or the fields closest to the ecliptic poles.
Periodograms can only reliably be computed for the brightest variable sources observed for the longest continuous intervals by eROSITA. In order to analyse the periodograms of eROSITA sources, it is first necessary to subtract the Poisson and fractional-exposure noise from them (Sect. 7), and consider the effects of aliasing (Sect. 6.1).
9 Summary and conclusions
In this paper, we investigated and described how to best perform an eRASS light-curve variability analysis. We also improved previously determined variability methodologies, particularly for low-count-rate sources, and light curves with varying exposure times.
We established a method for selecting significantly variable eRASS sources from a large sample with a wide range of different count rates and exposure times. We also determined reliable thresholds on the two variability quantifiers SCATT_LO and AMPL_SIG. These thresholds determine the significance of the detected variability and minimise the rate of false positives. They are defined as functions of both the count rate and the number of bins of eROSITA-like light curves.
The NIV quantifies the intrinsic degree of variability of a source within the duration of the observations and is usually estimated by the NEV. However, the NEV methodology faces challenges at low count rates and when faced with varying fractional exposures. We present a new method for estimating the NIV that remains accurate even in the Poisson regime, and is not biased by varying fractional exposures. This method uses the Bayesian excess variance (bexvar) and a function that converts that into an estimate of the NIV. This method is based on simulations of a pink-noise PSD but remains more accurate than the NEV for both red- and pink-noise PSDs at low count rates. Above 1.5 cts s−1 , the methods are comparably accurate.
The NIV of one light curve can substantially differ from the NIV in another light curve covering the same frequency interval, even if the process generating the variability is stationary. Therefore, the intrinsic scatter of the NIV must be determined in order to compare the variability of different sources or the same source at different times. The best way to reduce the scatter is to split a light curve into shorter segments of equal length, and compute the geometric mean of the NEVb measurements of individual segments. We found analytic expressions for the size of the intrinsic scatter for pink-noise variability as a function of the number of bins in each segment, the number of segments, and the intrinsic variability of the source. The intrinsic scatter also depends on whether the individual segments are adjacent, or randomly placed and far apart. It decreases more rapidly with an increasing number of segments in the latter case, especially for strongly variable sources.
Additionally, we investigated how to analyse the periodograms of variable sources observed by eROSITA. If a regularly sampled light curve consists of bins with differing exposure times, its periodogram will feature an additional noise component above the Poisson noise. We determined the dependence of this fractional-exposure noise on its mean and variance throughout the light curve.
The code that we developed and used throughout this study is available online4. Further instructions can be found at this address, detailing when and how these methods can be used, how to interpret the results, and when to consider modifying them for use in other areas of the sky, or other instruments.
The methods presented here are used to analyse the variability of X-ray sources detected within 3° of the SEP in the first three eRASSs, in Bogensberger et al. (2024).
Acknowledgements
This work is based on data from eROSITA, the soft X-ray instrument aboard SRG, a joint Russian-German science mission supported by the Russian Space Agency (Roskosmos), in the interests of the Russian Academy of Sciences represented by its Space Research Institute (IKI), and the Deutsches Zentrum für Luft- und Raumfahrt (DLR). The SRG spacecraft was built by Lav-ochkin Association (NPOL) and its subcontractors and is operated by NPOL with support from the Max Planck Institute for Extraterrestrial Physics (MPE). The development and construction of the eROSITA X-ray instrument was led by MPE, with contributions from the Dr. Karl Remeis Observatory Bamberg & ECAP (FAU Erlangen-Nuernberg), the University of Hamburg Observatory, the Leibniz Institute for Astrophysics Potsdam (AIP), and the Institute for Astronomy and Astrophysics of the University of Tübingen, with the support of DLR and the Max Planck Society. The Argelander Institute for Astronomy of the University of Bonn and the Ludwig Maximilians Universität Munich also participated in the science preparation for eROSITA. This work made use of the software packages astropy (https://www.astropy.org/; Astropy Collaboration 2013, 2018), bexvar (https://github.com/JohannesBuchner/bexvar; Buchner et al. 2022), numpy (https://www.numpy.org/; Harris et al. 2020), matplotlib (https://matplotlib.org/; Hunter 2007), scipy (https://scipy.org/; Virtanen et al. 2020), Stingray (https://docs.stingray.science/; Huppenkothen et al. 2016), and Ultranest (https://johannesbuchner.github.io/UltraNest/; Buchner 2021). We thank the anonymous referee for their helpful comments.
Appendix A Comparing methods for NIV estimation
In this appendix, we considered two other methods that could be used to estimate the NIV of the light curve of a variable source, and compared them against the NEVb method. The first of these methods estimates the NIV by integrating the periodogram of the light curve, and we label it NEVi. The second methodology is based on using Eqs. 2 and 3, but with an adjustment for reducing the effect of the lowest exposure bins on the estimate. We denote this estimate of the NIV as NEVeq. Finally, we evaluated the strengths and weaknesses of these three methods.
Appendix A.1 NEVi
Parseval’s theorem states that in the high count rate limit, when the assumption of a normal probability distribution of the measured count rate in every bin is true, the definition of the NEV as shown in Eq. 2, corresponds to the integral of the Poisson noise subtracted, rms normalised periodogram (van der Klis 1989):
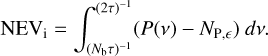 (A.1)
(A.1)
Therefore, it is also possible to estimate the NIV of the light curve of a variable source in this way. The Poisson noise of a light curve with variable fractional exposures is discussed in more detail in Section 7.
This method is more computationally expensive than calculating NEVeq. Nevertheless, it can be useful for estimating the NIV for a different frequency range.
Fig. A.1 shows the ability of NEVi to estimate the NIV in simulated pink-noise light curves, when subtracting the standard Poisson noise (Eq. 15) from the periodogram. It can be compared against Fig. 6, to see the different accuracies of the two methods. This shows that NEVi is only a good estimator of the NIV at the highest count rates and the greatest NIVs. At lower count rates and NIVs, NEVi levels off, diverging from the 1:1 line that the data points should ideally be distributed around. The minimum level of NEVi decreases with an increasing count rate. However, it seems largely independent of the number of bins in the light curve. At the lowest count rates considered for this figure, this plateau level even lies above the maximum NIV of the simulated light curves. The plateaus are caused by varying fractional exposures, and the excess noise they cause in the peri-odograms, which has not been subtracted in this example. This shows how important it is to subtract the fractional-exposure noise, as discussed in Section 7. The properties of the plateaus helped motivate the expression of the fractional-exposure noise of Eq. 16.
When subtracting the combined Poisson and fractional-exposure noise from the periodograms of the simulated light curves, using Eqs. 16, and 17, as well as the parameters listed in Table 4 in Section 7, the plateaus disappear, and NEVi becomes a much more accurate estimator of the NIV, as is shown in Fig. A.2. Henceforth, we use NEVi to refer to the Poisson and fractional-exposure noise subtracted integral of the periodogram.
At high count rates (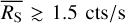 ), NEVi is an accurate estimator of the NIV for the entire range of values of the NIV, and for the number of bins in the light curve that we investigated. However, its accuracy decreases rapidly at lower count rates. At
), NEVi is an accurate estimator of the NIV for the entire range of values of the NIV, and for the number of bins in the light curve that we investigated. However, its accuracy decreases rapidly at lower count rates. At 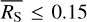 cts/s, the NEVi often differs significantly from the NIV, and is frequently underestimated. 87% of the light curves we simulated at a count rate of 0.015 cts/s had a negative NEVi. At 0.15 cts/s, 34% of the light curves are still found at a negative NEVi, and even at 1 .5 cts/s, 7% of light curves were found to have a negative NEVi. Possible reasons for this is that the periodogram weighs all bins equally, regardless of their fractional exposure, and the challenges of computing a periodogram from a very small number of counts.
cts/s, the NEVi often differs significantly from the NIV, and is frequently underestimated. 87% of the light curves we simulated at a count rate of 0.015 cts/s had a negative NEVi. At 0.15 cts/s, 34% of the light curves are still found at a negative NEVi, and even at 1 .5 cts/s, 7% of light curves were found to have a negative NEVi. Possible reasons for this is that the periodogram weighs all bins equally, regardless of their fractional exposure, and the challenges of computing a periodogram from a very small number of counts.
 |
Fig. A.1 Ability to estimate the NIV by integrating the periodograms of simulated eROSITA-like pink-noise light curves. Each data point indicates the result of a single simulation. The closer a data point lies to the orange dashed 1:1 line, the better the estimate of the NIV is. For this plot, only the standard Poisson noise (Eq. 15) was subtracted from the periodograms. |
Appendix A.2 NEVeq
The standard NEV, as defined in Eqs. 2 and 3 works well for normal probability distributions for the count rate in each bin. When the components used to calculate the NEV (Eq. 2) are defined as in Eq. 3, the NEV treats every bin identically, regardless of their fractional exposure. This might cause a significant portion of the excess variance detected in an eROSITA-like light curve to originate from the bins with the smallest exposure times.
One way of reducing the effect that the lowest exposure bins have on the measured NEV, is to weight each of the terms of the NEV by the fractional exposure itself. Rather than using the definitions described in Eq. 3, we would use:
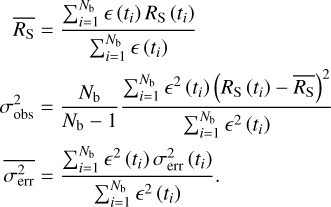 (A.2)
(A.2)
If the background area and count rate are constant, then the first equation of Eq. A.2 is identical to Eq. 1. These equations are applicable to instances of varying fractional exposures, unlike those of Eq. 3. By weighting the terms, the equations effectively deal with the individually measured source counts, rather than count rates.
Since the uncertainties in the measured count rates are asymmetric, it is worth considering which error to use for  .
.
 |
Fig. A.2 Accuracy of estimating the NIV by integrating periodograms of simulated eROSITA-like pink-noise light curves. Unlike in Fig. A.1, the NIV is estimated here by subtracting both the Poisson and fractional-exposure noise, using Eqs. 16, and 17, with parameters listed in Table 4 from the periodograms. This figure shows the relationship on both a logarithmic (top panel) and a symmetric logarithmic (lower panel) scale, to showcase how close the individual NEVi measurements are to the NIV, as well as the complete range of values measured for NEVi. |
The excess variance compares the difference between the contribution of each measured count rate to the total variance, with the error of that measurement. Therefore, we decided to use the error in the direction of the mean count rate, similar to the definition of the modified AMPL_SIG in Section 3.1.2. So if RS(ti)≤RS, we set σerr (ti) = σ+err (ti), and if RS(ti)>RS, we set σerr (ti) = σ−err (ti) in Eq. A.2. We label the NIV estimate found by using these modification to the NEV method, as NEVeq. Its value is still found from Eq. 2, but with the updated parameters of Eq. A.2.
These modifications allow NEVeq to not be as biased by varying fractional exposures. However, they do not deal with the inherent problems with these equations in Poisson regime, as discussed in Section 3.1.1.
Figure A.3 shows the performance of using NEVeq as an estimator of the NIV, using Eq. 2, and the weighted parameters of Eq. A.2. This method works well at high count rates. However, 95% of the simulated light curves at a count rate of 0.015 cts/s, and 29% of the light curves with a count rate of 0.15 cts/s were found to have a negative NEVeq, some at extremely negative values. At a count rate of 1.5 cts/s, 3% of simulated light curves still have a negative NEVeq. Negative NEVeq values are not necessarily a problem, given the proper statistical approaches, but can indicate a systematic offset from the NIV, and will prevent a geometric mean NEV to be calculated, for estimating NIV∞. At low count rates, NEVeq is less likely to significantly overestimate the NIV than NEVi, but is more likely to significantly underestimate it.
We used the results of Vaughan et al. (2003), their Equation 11, to determine the uncertainties in the individual measurements of the NEVeq, which we plot in Fig. A.3. However, this equation might not be accurate for light curves with varying fractional exposures or for the modifications to the standard method discussed above. It also does not reliably estimate the uncertainty in the measured NEVeq when it is less than 0, as can be seen by the lower panel in Fig. A.3. Accurate error bars should extend to above 0 in most instances.
Figures 4, A.1, A.2, and A.3, which depict the ability of various methods to estimate the NIV, are all based on the same set of simulated light curves. These were generated to have {20,75,150,400,1050} bins, and mean input count rates of {0.015,0.15,1.5,15} cts/s. Comparing Fig. 4 to Figs. A.2 and A.3, shows that NEVb is significantly more accurate at estimating the NIV in the light curve at low count rates, than NEVi or NEVeq are.
 |
Fig. A.3 Comparison of the NEVeq obtained by using the weighted parameters of Eq. A.2 in Eq. 2, with the NIV. This figure uses the same structure as Fig. A.2. |
Appendix A.3 Comparison
In this section, we compare the ability of the three methods previously discussed (NEVb, NEVi, and NEVeq), to provide an accurate estimate of the NIV in the light curve. We compared the accuracies as a function of the count rate, the number of bins, the degree of variability, and the type of variability observed. Figure A.4 depicts the absolute magnitude of the difference between the measured NIV estimate (which we label as NEVm to refer to the three methods), and the actual NIV, normalised by the NIV of the simulated light curves: |NEVm – NIV| /NIV = |Dm|. The figure shows the dependence of |Dm| on the NIV in each plot, as the ability to estimate the NIV strongly depends on its value. The three methods were applied to the same simulated light curves for a fair comparison. Three different types of variability were considered; white noise (P ∝ v0), pink noise (P ∝ v−1 ), and red noise (P ∝ v−2). We again selected mean count rates of {0.015,0.15,1.5,15.0} cts/s, and a number of bins of {20,75,150,400,1050} for the construction of the simulated light curves used in this analysis.
 |
Fig. A.4 Comparison of the ability of the integral of the periodogram (NEVi), the modified NEV equation (NEVeq), and the bexvar NIV estimate (NEVb), to accurately estimate the NIV of eROSITA-like light curves. This figure plots the absolute value of the difference between the measured value, NEVm (which refers to either NEVi, NEVeq, or NEVb), and the NIV (NIV), normalised by the NIV, as a function of the NIV. The lower the value of this parameter, the more accurate the estimate of the NIV is. Each data point represents one instance of a simulated light curve. The same light curves were used for computing NEVi, NEVeq, and NEVb. Each panel represents a different count rate. The dependence on the number of bins is showcased via different symbols. Figure (a), (b), (c): Accuracy of the NIV estimates for white-, pink-, and red-noise light curves, respectively. Solid lines are plotted on top of the distribution of points, corresponding to the geometric mean of the distribution of log (|NEVm – NIV|/NIV) as a function of log(NIV). Transparent areas indicate the part of the distribution corresponding to one standard deviation from the mean, in either direction. |
The results of these simulations are shown in Fig. A.4. As expected, the ability to estimate the NIV improves with an increasing number of bins, for all three methods. Figure A.4 shows that NEVb is more accurate at estimating the NIV than NEVi and NEVeq at low count rates, and low degrees of variability. Even though the conversion from  to NEVb was determined specifically for pink-noise PSDs, NEVb is still significantly more accurate than NEVi, or NEVeq for white- and red-noise light curves at low count rates and low degrees of variability. At the lowest count rates we investigated, of 0.015 cts/s, NEVb is always the most accurate NIV estimate, for the three types of PSDs, for all values of the NIV, and the entire range of the number of bins that we investigated. At this count rate, NEVb is often 2 orders of magnitude more accurate than the other two methods.
to NEVb was determined specifically for pink-noise PSDs, NEVb is still significantly more accurate than NEVi, or NEVeq for white- and red-noise light curves at low count rates and low degrees of variability. At the lowest count rates we investigated, of 0.015 cts/s, NEVb is always the most accurate NIV estimate, for the three types of PSDs, for all values of the NIV, and the entire range of the number of bins that we investigated. At this count rate, NEVb is often 2 orders of magnitude more accurate than the other two methods.
At 0.15 cts/s, NEVb is more accurate at low variabilities than either NEVi or NEVeq, but all three methods are approximately equally accurate at high degrees of variability. For count rates of 1.5 cts/s and 15 cts/s, the measured number of source counts per bin can reasonably accurately be assumed to have a normal probability distribution for most, or all erodays. As a result, all three methods have similar accuracies at these count rates, across the entire range of simulated NIVs. However, NEVb provides a slightly less accurate estimate of the NIV of high count rate sources (15 cts/s) exhibiting red-noise variability of NIV ≳5 × 10−2), as compared to NEVi or NEVeq.
 |
Fig. A.5 Accuracy of the uncertainties of NEVeq and NEVb, for a range of different count rates, number of bins, and types of PSDs. This figure used the results of the same simulated light curves as are displayed in Fig. A.4. The parameter NEVm denotes a NIV estimate, which is either NEVb, or NEVeq. The parameter σm denotes the uncertainty in the measurement. The black dashed line at a value of |
The NEVi and NEVeq methods estimate the NIV with similar accuracy. The |Dm| parameter follows a similar anticorrelation as a function of the NIV, for both NEVi and NEVeq. In contrast, the mean difference between the NEVb estimate, and the NIV, are maintained at an almost constant ratio of the NIV. The anticorrelation is predominantly caused by the normalisation of |Dm|. The existence of such an anticorrelation indicates that the average difference between the estimate, and the true value of the NIV is mainly independent of the NIV. Therefore, this also shows that the NEVb is a more reliable estimate of the NIV.
Another relevant feature to consider when comparing different methods of estimating the NIV in a light curve is the ability to estimate the uncertainty in the estimate accurately. To determine how accurate the NEVeq, and NEVb errors are, we investigated the ratio of the absolute value of the difference between the estimate, and the real value of the NIV, to the estimated error: |NEVm – NIV|/σNEV,m = |Zm|. Here, σNEV,m represents the error in NEVeq, or NEVb. Figure A.5 shows how this parameter varies as a function of the NIV, the mean count rate, the number of bins, and the type of variability (white noise, pink noise, and red noise). The figure display |Zm| for the two NIV estimators NEVeq, and NEVb. The NEVi is not considered here, as we found the computation of its error to be unreliable.
Assuming that the individual NIV estimates are distributed normally, with a mean equal to the NIV, and a standard deviation equal to the measurement uncertainty, 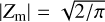 (Geary 1935). This is the value we compare the two methods against, indicated in Fig. A.5 as a dashed black line. If the mean value of |Zm| for either method is below
(Geary 1935). This is the value we compare the two methods against, indicated in Fig. A.5 as a dashed black line. If the mean value of |Zm| for either method is below 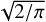 , then the uncertainties in the measurement are overestimated. If, instead the mean of |Zm| is less than
, then the uncertainties in the measurement are overestimated. If, instead the mean of |Zm| is less than 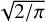 , then either the mean NIV estimate differs significantly from its actual value, or the uncertainties are underestimated. The closer the average value of |Zm| lies to
, then either the mean NIV estimate differs significantly from its actual value, or the uncertainties are underestimated. The closer the average value of |Zm| lies to 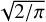 , the better the method is at correctly estimating the measurement uncertainties.
, the better the method is at correctly estimating the measurement uncertainties.
At low count rates, the errors in NEVb are slightly overestimated, which can be seen in the panels on the far left of Fig. A.5. This may be due to the decision to increase the size of the lower bound errors on NEVb, which extended below the lower limit of variability detectable by bexvar (see Section 5).
In contrast, the NEVeq uncertainties are significantly underestimated at 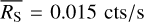 . There are even some instances, when
. There are even some instances, when 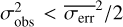 , such that
, such that 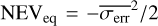 . When this happens, the error in NEVeq cannot be calculated. The figure does not include light curves with these properties as data points. The NEVeq errors based on Vaughan et al. (2003) are inaccurate whenever NEVeq < 0, which frequently occurs at low count rates.
. When this happens, the error in NEVeq cannot be calculated. The figure does not include light curves with these properties as data points. The NEVeq errors based on Vaughan et al. (2003) are inaccurate whenever NEVeq < 0, which frequently occurs at low count rates.
The accuracy of the errors on both NIV estimators improves with an increasing average source count rate, and they are reasonably reliable for 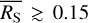 cts/s, for both methods. This can be seen in the second, third, and fourth panels from the left in Fig. A.5. At
cts/s, for both methods. This can be seen in the second, third, and fourth panels from the left in Fig. A.5. At 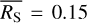 cts/s, the NEVeq uncertainties more accurately represent the error in the measurement than the NEVb ones. At
cts/s, the NEVeq uncertainties more accurately represent the error in the measurement than the NEVb ones. At
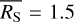 cts/s, and
cts/s, and 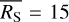 cts/s, both sets of errors perform about equally well, for all three different types of variability investigated here. Neverthless, the NEVb errors are still more likely to be slightly overestimated, and the NEVeq are still more likely to be slightly underestimated. The NEVb errors are also reasonably reliable for red and white-noise variability, even though they are based on the assumption of pink-noise variability. These errors only depict the measurement errors of estimating the NIV for the selected set of observations. They do not contain the intrinsic scatter in the NIV, which is discussed in Sections 6.2, and 6.3.
cts/s, both sets of errors perform about equally well, for all three different types of variability investigated here. Neverthless, the NEVb errors are still more likely to be slightly overestimated, and the NEVeq are still more likely to be slightly underestimated. The NEVb errors are also reasonably reliable for red and white-noise variability, even though they are based on the assumption of pink-noise variability. These errors only depict the measurement errors of estimating the NIV for the selected set of observations. They do not contain the intrinsic scatter in the NIV, which is discussed in Sections 6.2, and 6.3.
We note that NEVb is the best method for estimating the NIV of eROSITA-like light curves. Its estimates are reliable across a wide range of degrees of variability, count rates, number of bins, and types of variability. It never estimates the NIV to be negative, as NEVi, and NEVeq do, so it can always be used to estimate NIV∞, by computing its geometric mean,  . It can identify when an estimate of the NIV is merely an upper limit. The uncertainties of NEVb are well-defined and close to the size they should be, but are overestimated at low count rates. The downside to NEVb is that it is more computationally expensive than NEVi, and NEVeq. We recommend using NEVb to estimate the NIV in all light curves, except when a source has ≳ 20 source counts in every bin, or when it shows non-power-law variability.
. It can identify when an estimate of the NIV is merely an upper limit. The uncertainties of NEVb are well-defined and close to the size they should be, but are overestimated at low count rates. The downside to NEVb is that it is more computationally expensive than NEVi, and NEVeq. We recommend using NEVb to estimate the NIV in all light curves, except when a source has ≳ 20 source counts in every bin, or when it shows non-power-law variability.
The methods for computing NEVi and NEVeq, as they are described in Sections A.1 and A.2 can be used for any other instrument, as they were not explicitly developed for eROSITA. The modifications to the standard version of these estimates of the NIV are necessary whenever a light curve consists of varying fractional exposures.
Appendix B Corner plots
The corner plot of the best fit of Eq. 10 to the simulated data is shown in Fig. B.1. This best fit describes the dependence of the intrinsic scatter on the number of bins, and the intrinsic variability, for pink-noise light curves, which was computed in Section 6.2.
Figure B.2 shows the corner plot of the best fit to Eq. 17. It relates the fractional-exposure noise in a periodogram to the mean and variance of the fractional exposure, and was calculated in Section 7.
Figure B.3 is the corner plot of the best fit of Eq. 6 to the simulated data for the relationship between the 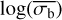 and log(NIV′). This best fit was used to define NEVb in Section 5.
and log(NIV′). This best fit was used to define NEVb in Section 5.
 |
Fig. B.1 Corner plot for the best-fitting parameters of a, b′, c, d, and ƒ′, for fitting ∆s as a function of Nb, and log( |
 |
Fig. B.2 Corner plot for the best-fitting parameters of ca, da, 𝑔a, cb, db, and 𝑔b for fitting the excess periodogram noise due to variable fractional exposures with Eq. 17. |
 |
Fig. B.3 The corner plot of the best-fitting parameters of Eq. 6, for fitting log( |
References
- Allevato, V., Paolillo, M., Papadakis, I., & Pinto, C. 2013, ApJ, 771, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, E., Gabriel, A. H., & Dennis, B. R. 1984, ApJ, 287, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Arévalo, P., Lira, P., Sánchez-Sáez, P., et al. 2023, MNRAS, 526, 6078 [CrossRef] [Google Scholar]
- Ashton, D. I., & Middleton, M. J. 2021, MNRAS, 501, 5478 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Belloni, T., & Hasinger, G. 1990, A&A, 227, L33 [NASA ADS] [Google Scholar]
- Belloni, T. M., Motta, S. E., & Muñoz-Darias, T. 2011, Bull. Astron. Soc. India, 39, 409 [Google Scholar]
- Bogensberger, D., Nandra, K., Salvato, M., et al. 2024, arXiv e-prints [arXiv: 1509.06851] [Google Scholar]
- Boller, T., Freyberg, M. J., Trümper, J., et al. 2016, A&A, 588, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boller, T., Schmitt, J. H. M. M., Buchner, J., et al. 2022, A&A, 661, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brunner, H., Liu, T., Lamer, G., et al. 2022, A&A, 661, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buchner, J. 2016, Statist. Comput., 26, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J. 2019, PASP, 131, 108005 [Google Scholar]
- Buchner, J. 2021, J. Open Source Softw., 6, 3001 [CrossRef] [Google Scholar]
- Buchner, J., Boller, T., Bogensberger, D., et al. 2022, A&A, 661, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edelson, R., & Nandra, K. 1999, ApJ, 514, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R. A., Krolik, J. H., & Pike, G. F. 1990, ApJ, 359, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Forbrich, J., Preibisch, T., & Menten, K. M. 2006, A&A, 446, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Forbrich, J., Reid, M. J., Menten, K. M., et al. 2017, ApJ, 844, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Geary, R. C. 1935, Biometrika, 27, 310 [CrossRef] [Google Scholar]
- Gierlinski, M., Middleton, M., Ward, M., & Done, C. 2008, Nature, 455, 369 [CrossRef] [Google Scholar]
- González-Martín, O., & Vaughan, S. 2012, A&A, 544, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Huppenkothen, D., Bachetti, M., Stevens, A. L., Migliari, S., & Balm, P. 2016, Astrophysics Source Code Library [record ascl:1608.001] [Google Scholar]
- Ingram, A. R., & Motta, S. E. 2019, New A Rev., 85, 101524 [NASA ADS] [CrossRef] [Google Scholar]
- Kirchner, J. W. 2005, Phys. Rev. E, 71, 066110 [CrossRef] [Google Scholar]
- Knoetig, M. L. 2014, ApJ, 790, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, T., Merloni, A., Comparat, J., et al. 2022, A&A, 661, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lu, Y., & Yu, Q. 2001, MNRAS, 324, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Markowitz, A., Edelson, R., Vaughan, S., et al. 2003, ApJ, 593, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, T. A., & Sandage, A. R. 1963, ApJ, 138, 30 [CrossRef] [Google Scholar]
- McHardy, I. 2010, in Lect. Notes Phys., 794 (Berlin: Springer Verlag), ed. T. Belloni, 203 [NASA ADS] [CrossRef] [Google Scholar]
- McHardy, I. M., Papadakis, I. E., Uttley, P., Page, M. J., & Mason, K. O. 2004, MNRAS, 348, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., George, I. M., Mushotzky, R. F., Turner, T. J., & Yaqoob, T. 1997, ApJ, 476, 70 [Google Scholar]
- O’Neill, P. M., Nandra, K., Papadakis, I. E., & Turner, T. J. 2005, MNRAS, 358, 1405 [CrossRef] [Google Scholar]
- Paolillo, M., Schreier, E. J., Giacconi, R., Koekemoer, A. M., & Grogin, N. A. 2004, ApJ, 611, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Paolillo, M., Papadakis, I., Brandt, W. N., et al. 2017, MNRAS, 471, 4398 [Google Scholar]
- Paolillo, M., Papadakis, I. E., Brandt, W. N., et al. 2023, A&A, 673, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papadakis, I. E. 2004, MNRAS, 348, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Papadakis, I. E., Brinkmann, W., Negoro, H., & Gliozzi, M. 2002, A&A, 382, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ponti, G., Papadakis, I., Bianchi, S., et al. 2012, A&A, 542, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Predehl, P., Andritschke, R., Arefiev, V., et al. 2021, A&A, 647, A1 [EDP Sciences] [Google Scholar]
- Press, W. H., & Rybicki, G. B. 1997, in Astrophys. Space Sci. Lib., 218, Astronomical Time Series, eds. D. Maoz, A. Sternberg, & E. M. Leibowitz, 61 [CrossRef] [Google Scholar]
- Smith, K. L., Mushotzky, R. F., Boyd, P. T., & Wagoner, R. V. 2018, ApJ, 860, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R., Arefiev, V., Babyshkin, V., et al. 2021, A&A, 656, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Timmer, J., & Koenig, M. 1995, A&A, 300, 707 [NASA ADS] [Google Scholar]
- Turner, T. J., George, I. M., Nandra, K., & Turcan, D. 1999, ApJ, 524, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Uttley, P., McHardy, I. M., & Papadakis, I. E. 2002, MNRAS, 332, 231 [Google Scholar]
- Vagnetti, F., Turriziani, S., & Trevese, D. 2011, A&A, 536, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vagnetti, F., Middei, R., Antonucci, M., Paolillo, M., & Serafinelli, R. 2016, A&A, 593, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Klis, M. 1989, in NATO Advanced Study Institute (ASI) Series C, 262, Timing Neutron Stars, eds. H. Ögelman, & E. P. J. van den Heuvel, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, S., Edelson, R., Warwick, R. S., & Uttley, P. 2003, MNRAS, 345, 1271 [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Wijnands, R., & van der Klis, M. 1999, ApJ, 514, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Woltjer, L. 1959, ApJ, 130, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, G., Brandt, W. N., Luo, B., et al. 2016, ApJ, 831, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, X. C., Xue, Y. Q., Brandt, W. N., et al. 2017, ApJ, 849, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, J., Wang, Z., Chen, L., et al. 2018, Nat. Commun., 9, 4599 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, S. F., & Xue, Y. Q. 2016, ApJ, 825, 56 [CrossRef] [Google Scholar]
All Tables
Best-fitting parameters describing the intrinsic scatter of the NIV, as a function of Nseg and NIV∞, if the segments are adjoined.
All Figures
 |
Fig. 1 Simulated eROSITA-like light curves of a source lying close to either of the two ecliptic poles. These light curves are computed using a typical є evolution, as observed in actual eROSITA light curves. The top panel shows an intrinsically constant source, and the lower panel depicts an intrinsically-variable pink-noise source, both with an average count rate of ≈0.3 cts s−1. The variability class describes how the value of SCATT_LO and AMPL_SIG compares to the variability thresholds computed in Sect. 4. The pink-noise variable source is identified to have a SCATT_LO value above the 3σ threshold but an AMPL_SIG value only above the corresponding 1σ threshold. |
| In the text | |
 |
Fig. 2 1, 2, and 3σ thresholds on SCATT_LO for identifying variable sources. The thresholds are displayed as a function of the count rate. The dependence on the number of bins is illustrated by using different line styles. The grey lines indicate the best fit power-law relationship to the decreasing thresholds with increasing count rate, above the peak. |
| In the text | |
 |
Fig. 3 1, 2, and 3σ thresholds on AMPL_SIG for identifying variable sources. The colours and line styles are the same as those in Fig. 2. |
| In the text | |
 |
Fig. 4 Ability of |
| In the text | |
 |
Fig. 5 Relationship between |
| In the text | |
 |
Fig. 6 Comparison of the NEVb measurements with the NIV of the light curve that it seeks to estimate, for pink-noise light curves, using Eq. (6), and the values listed in Table 1. The orange dashed line indicates the 1:1 relationship between NEVb, and the NIV. |
| In the text | |
 |
Fig. 7 Comparison of a typical AGN PSD, and how a measured peri-odogram differs from it, within the frequency space that can be explored by eROSITA for sources lying close to the ecliptic poles. The intrinsic PSD is depicted as following a broken power-law of P ∝ v−1 at v < vb, and P ∝ v−2 at v ≥ vb, and continues beyond the frequency range probed by the observations. The measured periodogram is offset from the intrinsic PSD by the Poisson noise, the є noise, aliasing, and the red noise leak. The є noise (Eq. (16)) is often significantly larger than the Poisson noise (Eq. (15)). The flattening of the Poisson and є subtracted periodogram at the highest frequencies is due to aliasing. The red noise leak increases the amplitude of the power-laws. The relative strength of the Poisson, fractional-exposure noise, aliasing, and the red noise leak depicted in this figure are illustrative, and depend on the shape of the PSD, the average count rate, and the mean, and variance of the fractional exposure. Periodogram noise is not depicted. |
| In the text | |
 |
Fig. 8 Simulated light curve demonstrating how the NIV of a variable source can change over time, even if the PSD and the band-limited power remain unchanged. Panel a: 500-bin segment of a simulated pink-noise light curve without measurement errors or Poisson noise. Panel b: Normalised intrinsic variance of a sliding window interval of 50 bins from the light curve in panel a. Each NIV data point is placed at the time of centre of the selected interval. The maximum and minimum NIV of this interval is indicated, and the parts of the light curve for which they were obtained are highlighted. Panel c: Geometric mean NIV of 10 adjoined segments, each consisting of 50 bins. Each value is placed at the center of the segments used. Panels b and c use data from the light curve outside of the interval shown in panel a. The panels on the right show the distribution of these parameters, throughout the entire 5 × 103 bin simulated light curve. |
| In the text | |
 |
Fig. 9 Dependence of ∆s on the number of bins, and the NIV∞. Each data point represents the intrinsic scatter in the NIV, determined from 2000 light curves, randomly selected from a 105 bin simulated pink-noise light curve produced from a constant input PSD. The curves show the best fit relation of ∆s(Nb), at fixed levels of NIV∞, using Eq. (10) with parameter values as contained in Table 2. There is a significant scatter among the data points due to the probabilistic nature of this estimate. |
| In the text | |
 |
Fig. 10 Reducing the intrinsic scatter by computing the geometric mean NIV for Nseg distant or adjoined segments of Nb bins each. The data points indicate the results of individual simulations for adjoined segments. The lines depict the best fits to the simulations, using Eqs. (14) and (10), and the parameter values in Tables 2, and 3. The solid lines show the dependence of ∆s,n on Nseg for adjoined segments, and the dotted lines for distant, randomly placed segments. |
| In the text | |
 |
Fig. 11 Dependence of the excess noise in a periodogram caused by varying fractional exposures, as a function of |
| In the text | |
 |
Fig. A.1 Ability to estimate the NIV by integrating the periodograms of simulated eROSITA-like pink-noise light curves. Each data point indicates the result of a single simulation. The closer a data point lies to the orange dashed 1:1 line, the better the estimate of the NIV is. For this plot, only the standard Poisson noise (Eq. 15) was subtracted from the periodograms. |
| In the text | |
 |
Fig. A.2 Accuracy of estimating the NIV by integrating periodograms of simulated eROSITA-like pink-noise light curves. Unlike in Fig. A.1, the NIV is estimated here by subtracting both the Poisson and fractional-exposure noise, using Eqs. 16, and 17, with parameters listed in Table 4 from the periodograms. This figure shows the relationship on both a logarithmic (top panel) and a symmetric logarithmic (lower panel) scale, to showcase how close the individual NEVi measurements are to the NIV, as well as the complete range of values measured for NEVi. |
| In the text | |
 |
Fig. A.3 Comparison of the NEVeq obtained by using the weighted parameters of Eq. A.2 in Eq. 2, with the NIV. This figure uses the same structure as Fig. A.2. |
| In the text | |
 |
Fig. A.4 Comparison of the ability of the integral of the periodogram (NEVi), the modified NEV equation (NEVeq), and the bexvar NIV estimate (NEVb), to accurately estimate the NIV of eROSITA-like light curves. This figure plots the absolute value of the difference between the measured value, NEVm (which refers to either NEVi, NEVeq, or NEVb), and the NIV (NIV), normalised by the NIV, as a function of the NIV. The lower the value of this parameter, the more accurate the estimate of the NIV is. Each data point represents one instance of a simulated light curve. The same light curves were used for computing NEVi, NEVeq, and NEVb. Each panel represents a different count rate. The dependence on the number of bins is showcased via different symbols. Figure (a), (b), (c): Accuracy of the NIV estimates for white-, pink-, and red-noise light curves, respectively. Solid lines are plotted on top of the distribution of points, corresponding to the geometric mean of the distribution of log (|NEVm – NIV|/NIV) as a function of log(NIV). Transparent areas indicate the part of the distribution corresponding to one standard deviation from the mean, in either direction. |
| In the text | |
 |
Fig. A.5 Accuracy of the uncertainties of NEVeq and NEVb, for a range of different count rates, number of bins, and types of PSDs. This figure used the results of the same simulated light curves as are displayed in Fig. A.4. The parameter NEVm denotes a NIV estimate, which is either NEVb, or NEVeq. The parameter σm denotes the uncertainty in the measurement. The black dashed line at a value of |
| In the text | |
 |
Fig. B.1 Corner plot for the best-fitting parameters of a, b′, c, d, and ƒ′, for fitting ∆s as a function of Nb, and log( |
| In the text | |
 |
Fig. B.2 Corner plot for the best-fitting parameters of ca, da, 𝑔a, cb, db, and 𝑔b for fitting the excess periodogram noise due to variable fractional exposures with Eq. 17. |
| In the text | |
 |
Fig. B.3 The corner plot of the best-fitting parameters of Eq. 6, for fitting log( |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.