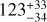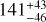| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A1 | |
| Number of page(s) | 25 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202347533 | |
| Published online | 29 February 2024 | |
CHEOPS observations of KELT-20 b/MASCARA-2 b: An aligned orbit and signs of variability from a reflective day side★,★★
1
INAF, Osservatorio Astrofisico di Catania, Via S. Sofia 78, 95123 Catania, Italy
e-mail: vikash.singh@inaf.it
2
Institute of Planetary Research, German Aerospace Center (DLR), Rutherfordstrasse 2, 12489 Berlin, Germany
3
INAF, Osservatorio Astrofisico di Torino, Via Osservatorio, 20, 10025 Pino Torinese To, Italy
4
Space Research Institute, Austrian Academy of Sciences, Schmiedlstrasse 6, 8042 Graz, Austria
5
Observatoire astronomique de l’Université de Genève, Chemin Pegasi 51, 1290 Versoix, Switzerland
6
Weltraumforschung und Planetologie, Physikalisches Institut, University of Bern, Gesellschaftsstrasse 6, 3012 Bern, Switzerland
7
Center for Space and Habitability, University of Bern, Gesellschaftsstrasse 6, 3012 Bern, Switzerland
8
ETH Zurich, Department of Physics, Wolfgang-Pauli-Strasse 2, 8093 Zurich, Switzerland
9
Cavendish Laboratory, JJ Thomson Avenue, Cambridge CB3 0HE, UK
10
Instituto de Astrofisica e Ciencias do Espaco, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762 Porto, Portugal
11
Department of Astronomy, Stockholm University, AlbaNova University Center, 10691 Stockholm, Sweden
12
Department of Physics, University of Warwick, Gibbet Hill Road, Coventry CV4 7AL, UK
13
Departamento de Fisica e Astronomia, Faculdade de Ciencias, Universidade do Porto, Rua do Campo Alegre, 4169-007 Porto, Portugal
14
Instituto de Astrofisica de Canarias, Via Lactea s/n, 38200 La Laguna, Tenerife, Spain
15
Departamento de Astrofisica, Universidad de La Laguna, Astrofisico Francisco Sanchez s/n, 38206 La Laguna, Tenerife, Spain
16
European Space Agency (ESA), European Space Research and Technology Centre (ESTEC), Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
17
Admatis, 5. Kandó Kálmán Street, 3534 Miskolc, Hungary
18
Depto. de Astrofisica, Centro de Astrobiologia (CSIC-INTA), ESAC campus, 28692 Villanueva de la Canada (Madrid), Spain
19
INAF, Osservatorio Astronomico di Padova, Vicolo dell'Osservatorio 5, 35122 Padova, Italy
20
Université Grenoble-Alpes, CNRS, IPAG, 38000 Grenoble, France
21
Université de Paris-Cité, Institut de physique du globe de Paris, CNRS, 1 Rue Jussieu, 75005 Paris, France
22
Centre for Exoplanet Science, SUPA School of Physics and Astronomy, University of St Andrews, North Haugh, St Andrews KY16 9SS, UK
23
Centre for Mathematical Sciences, Lund University, Box 118, 221 00 Lund, Sweden
24
Aix-Marseille Univ., CNRS, CNES, LAM, 38 rue Frédéric Joliot-Curie, 13388 Marseille, France
25
Astrobiology Research Unit, Université de Liège, Allée du 6 Août 19C, 4000 Liège, Belgium
26
Space sciences, Technologies and Astrophysics Research (STAR) Institute, Université de Liège, Allée du 6 Août 19C, 4000 Liège, Belgium
27
Centre Vie dans l’Univers, Faculté des sciences, Université de Genève, Quai Ernest-Ansermet 30, 1211 Genève 4, Switzerland
28
Leiden Observatory, University of Leiden, PO Box 9513, 2300 RA Leiden, The Netherlands
29
Department of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory, 439 92 Onsala, Sweden
30
Dipartimento di Fisica, Università degli Studi di Torino, via Pietro Giuria 1, 10125, Torino, Italy
31
Department of Astrophysics, University of Vienna, Türkenschanzstrasse 17, 1180 Vienna, Austria
32
Institute for Theoretical Physics and Computational Physics, Graz University of Technology, Petersgasse 16, 8010 Graz, Austria
33
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences, 1121 Budapest, Konkoly Thege Miklós út 15–17, Hungary
34
ELTE Eötvös Loránd University, Institute of Physics, Pázmány Péter sétány 1/A, 1117 Budapest, Hungary
35
IMCCE, UMR8028 CNRS, Observatoire de Paris, PSL Univ., Sorbonne Univ., 77 av. Denfert-Rochereau, 75014 Paris, France
36
Institut d’astrophysique de Paris, UMR7095 CNRS, Université Pierre & Marie Curie, 98bis blvd. Arago, 75014 Paris, France
37
Astrophysics Group, Lennard Jones Building, Keele University, Staffordshire ST5 5BG, UK
38
Physikalisches Institut, University of Bern, Gesellschaftsstrasse 6, 3012 Bern, Switzerland
39
Institute of Optical Sensor Systems, German Aerospace Center (DLR), Rutherfordstrasse 2, 12489 Berlin, Germany
40
Dipartimento di Fisica e Astronomia “Galileo Galilei”, Università degli Studi di Padova, Vicolo dell'Osservatorio 3, 35122 Padova, Italy
41
Zentrum für Astronomie und Astrophysik, Technische Universität Berlin, Hardenbergstr. 36, 10623 Berlin, Germany
42
Institut fuer Geologische Wissenschaften, Freie Universitaet Berlin, Maltheserstrasse 74-100, 12249 Berlin, Germany
43
Institut de Ciencies de l’Espai (ICE, CSIC), Campus UAB, Can Magrans s/n, 08193 Bellaterra, Spain
44
Institut d’Estudis Espacials de Catalunya (IEEC), Gran Capità 2-4, 08034 Barcelona, Spain
45
ELTE Eötvös Loránd University, Gothard Astrophysical Observatory, 9700 Szombathely, Szent Imre h. u. 112, Hungary
46
HUN-REN–ELTE Exoplanet Research Group, Szent Imre h. u. 112., Szombathely, 9700, Hungary
47
Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
Received:
21
July
2023
Accepted:
30
October
2023
Context. Occultations are windows of opportunity to indirectly peek into the dayside atmosphere of exoplanets. High-precision transit events provide information on the spin-orbit alignment of exoplanets around fast-rotating hosts.
Aims. We aim to precisely measure the planetary radius and geometric albedo of the ultra-hot Jupiter (UHJ) KELT-20 b along with the spin-orbit alignment of the system.
Methods. We obtained optical high-precision transits and occultations of KELT-20 b using CHEOPS observations in conjunction with simultaneous TESS observations. We interpreted the occultation measurements together with archival infrared observations to measure the planetary geometric albedo and dayside temperatures. We further used the host star’s gravity-darkened nature to measure the system’s obliquity.
Results. We present a time-averaged precise occultation depth of 82 ± 6 ppm measured with seven CHEOPS visits and 131−7+8 from the analysis of all available TESS photometry. Using these measurements, we precisely constrain the geometric albedo of KELT-20 b to 0.26 ± 0.04 and the brightness temperature of the dayside hemisphere to 2566−80+77 K. Assuming Lambertian scattering law, we constrain the Bond albedo to 0.36−0.05+0.04 along with a minimal heat transfer to the night side (ϵ = 0.14−0.10+0.13). Furthermore, using five transit observations we provide stricter constraints of 3 9 ± 1 1 deg on the sky-projected obliquity of the system.
Conclusions. The aligned orbit of KELT-20 b is in contrast to previous CHEOPS studies that have found strongly inclined orbits for planets orbiting other A-type stars. The comparably high planetary geometric albedo of KELT-20 b corroborates a known trend of strongly irradiated planets being more reflective. Finally, we tentatively detect signs of temporal variability in the occultation depths, which might indicate variable cloud cover advecting onto the planetary day side.
Key words: techniques: photometric / planets and satellites: atmospheres / planets and satellites: gaseous planets / planets and satellites: individual: KELT-20 b / planets and satellites: individual: MASCARA-2 b
The CHEOPS detrended photometry discussed in this article is available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (138.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/683/A1
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Occultations (or secondary eclipses) are windows of opportunity to study exoplanetary atmospheres. An occultation depth is a measure of the planet’s brightness that manifests in a subtle decrease in the observed flux as it goes behind (is occulted by) the star. This brightness consists of two components: the stellar light reflected off the planet’s visible hemisphere and its thermal emission. For ultra-hot Jupiters (UHJs) observed in optical passbands, the contribution of the planet’s thermal emission to its brightness is comparable to the predominant reflection contribution. Consequently, the measured occultation depth is a degenerate combination of the two, making it difficult to disentangle their respective contributions. This degeneracy can be broken with additional information, such as occultation depth measurements in different passbands.
KELT-20 b (Lund et al. 2017) or MASCARA-2b (Talens et al. 2018) was first reported simultaneously in the two discovery papers from the KELT (Pepper et al. 2018) and MASCARA (Snellen et al. 2012) transit surveys, respectively. Both surveys use dedicated ground-based telescopes for exoplanet discoveries, particularly the brightest transiting exoplanet systems. KELT-20b is a transiting UHJ that orbits one of the hottest (Teff ~9000K) fast-rotating (υ sin i⋆ ~ 116 km s−1) stars in a ~3.5 day orbit. This leads to an equilibrium temperature of Teq ~2300K (see Table 1 for details on stellar parameters).
By virtue of many follow-up observations in the form of high-resolution transmission spectroscopy, the atmosphere of KELT-20 b has been well characterised with the detection of the following species: Na, Hα, Mg, Fe, Fe I, Fe II, Ca+, Cr II, Si (Casasayas-Barris et al. 2018, 2020; Stangret et al. 2020; Hoeijmakers et al. 2020a; Nugroho et al. 2020; Cont et al. 2022). The day side of KELT-20 b is hotter than the theoretical equilibrium temperature because of the intense far-ultraviolet (FUV) and ultraviolet (UV) radiation received from its host A2 star, which heats up the upper layers of the atmosphere, leading to the expansion and abrasion of species between different layers (Fu et al. 2022). The FUV/UV radiation also facilitates the presence of a strong thermal inversion in the underlying layers, which is evident from the additional detection of neutral and atomic iron in the emission lines (Yan et al. 2022; Borsa et al. 2022). Consequently, the atmosphere is inflated enough to show strong absorption in the transmission spectrum, and the host star is sufficiently hot to strengthen the atomic/molecular spectral signatures in the emission spectrum leading to a plethora of species discoveries, including the likes of CO and H2O (Fu et al. 2022). Furthermore, Rainer et al. (2021) observed both the classical and the atmospheric Rossiter–McLaughlin (RM) effect by studying the Fe I feature in transmission. This detection of the blue-shift in the atmospheric signal during the transit along with the well-resolved double peak of the Fe I spectral feature in the emission spectrum (Nugroho et al. 2020) provides possible indications of atmospheric variability.
The study of exoplanet atmospheres, particularly hot Jupiters, has already benefited from the high-precision occul-tation measurements with CHEOPS (Lendl et al. 2020; Hooton et al. 2022; Deline et al. 2022; Brandeker et al. 2022; Scandariato et al. 2022; Jones et al. 2022; Parviainen et al. 2022; Krenn et al. 2023). One of the new frontiers in exoplanetology is the detection of atmospheric variability measured as variations in the occultation depth and the phase curve’s peak offset over time. Previous studies of atmospheric variability with Spitzer in the canonical hot Jupiters HD 209458b and HD 189733b did not show any variability with robust statistical significance (Kilpatrick et al. 2020). The first claim of atmospheric variability was announced for HAT-P-7 b (Armstrong et al. 2016) using the Kepler phase curves and later in Kepler-76 b (Jackson et al. 2019). Both of these studies found strong variations in the longitude of the brightest point in the planets’ atmospheres, although the former was recently attributed to photometric variability due to super-granulation in the host star (Lally & Vanderburg 2022). With increasing photometric precision and multi-epoch observations, more reports of exoplanet variability become prevalent (Hooton et al. 2019; Wilson et al. 2021; Parviainen et al. 2022).
In this paper, we present precise transit and occultation depths of KELT-20b using the data from its observation with the CHaracterising ExOplanet Satellite (CHEOPS; Benz et al. 2021) and the Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2014). We present all the datasets in Sect. 2 together with the description of the data reduction. In Sect. 3 we describe the planetary light curve fitting algorithms used in this article. In Sect. 4, we present the results of our analysis, and discuss the outcomes in Sect. 5. Finally in Sect. 6, we draw our conclusions.
Stellar parameters from SWEET-CAT catalogue used in this work.
2 Observations and data reduction
2.1 CHEOPS observations
CHEOPS observed the KELT-20 system in the consecutive summers of 2021 and 2022. The first set of observations include four secondary eclipses and four primary transits of the planet KELT-20 b extended over a period of two months starting from June 25 to September 1, 2021, while the second includes three additional secondary eclipses and one more primary transit that were observed from July 2 to August 9, 2022 (Fig. A.1). Each visit was centred around either the secondary eclipse or the primary transit using the ephemerides from Lund et al. (2017), with the total observation time equal to three times the eclipse or transit duration. Consequently, each visit spanned an average of 10 to 11 h where a time series was acquired with a cadence of 36 s. Due to interruptions from Earth occultations and crossings over the South Atlantic Anomaly (SAA) and to data flagging by the data reduction pipeline (DRP), the efficiency (i.e. the fraction of the visit time leading to scientifically valuable observations) was ~67%. All the information about the individual observations, which were part of two different CHEOPS Guaranteed Time Observation (GTO) subprogrammes, is summarised in Table 2.
Logbook of the CHEOPS observations of KELT-20.
2.2 Data reduction pipeline
Each CHEOPS observation was reduced by version 13.1.0 of the CHEOPS Data reduction pipeline (DRP; Hoyer et al. 2020). The processing summary of the pipeline includes standard calibration steps such as bias, gain, non-linearity, dark-current, and flat fielding, and the correction for the environmental affects such as cosmic rays, smearing trails from nearby stars, and the sky background. Following the corrections, the photometric extraction was performed over four aperture sizes, three predefined and one optimised aperture size corresponding to the best signal-to-noise ratio (S/N). The default S/N (25 pixels) is comparable to that of the optimal aperture size that varies between 15 and 19 pixels for different observations. The dispersion of the photometric light curve is lower with the former, and therefore we used the photometric extraction done with the default aperture radius instead of the optimal one. The field of view (FoV) of KELT-20 is populated with a few nearby background stars. The DRP estimated the contamination of these nearby objects by simulating the CHEOPS FoV based on the Gaia DR2 star catalogue (Gaia Collaboration 2021) and a template of the extended CHEOPS point spread function (PSF). To further analyse the DRP data, we used the PyCHEOPS software package developed specifically for the analysis of CHEOPS light curves (Maxted et al. 2022).
2.3 Detrending using point spread function
Due to the nature of the CHEOPS orbit, the presence of nearby background stars within the FoV can cause repeating flux variations on the timescales of the spacecraft’s orbital period. These variations are in correlation with the roll angle of the telescope. Therefore, to account for such systematic changes, we need to simultaneously use sinusoidal detrending vectors to the DRP light curve during model fitting. These features are already present in the PyCHEOPS package, and we used them in our DRP light curve analysis. Additionally, it has been observed that such flux variations lead to subtle modifications to the target PSF (e.g. Lendl et al. 2020; Bonfanti et al. 2021; Wilson et al. 2022). Upon closer inspection of our KELT-20 data, we found this characteristic systematic, and thus applied the PSF-SCALPELS algorithm (Wilson et al. 2022) to the DRP photometry. In brief, PSF-SCALPELS corrects flux modulations due to PSF shape changes by conducting a principal component analysis on the auto-correlation function of the photometric frames. This set of principal components traces variations in the PSF from the images, and is used in a linear noise model to detrend light curve fluxes. A more detailed explanation can be found in Wilson et al. (2022) with further examples of use shown in Hoyer et al. (2022), Parviainen et al. (2022), Hawthorn et al. (2023), and Ehrenreich et al. (2023).
While PSF-SCALPELS is a PSF-based correction to the DRP photometry, we also performed an independent photometric extraction using the PSF Imagette Photometric Extraction (PIPE) pipeline package1 (Morris et al. 2021; Brandeker et al. 2022). We found that the dispersion in the reduced light curves are compatible with that of the other extraction techniques. They vary around a median absolute deviation (MAD) of 150 ppm at the raw cadence of 36 s. The light curves with PIPE extraction are free from roll angle variations and do not require additional detrending. Consequently, the error bars on the resultant fit parameters are smaller compared to those obtained via other techniques. We therefore chose to use the PIPE extracted photometry for further light curve analysis. Nevertheless, we show a comparative measurement of the occultation depths analysed using the three data extraction pipelines in Fig. A.2. This exercise demonstrates the robustness of the extraction techniques, and further enhances confidence in the final outcome.
2.4 Outlier removal
Prior to the light curve analysis, we first filtered out the generic outliers flagged by PIPE that could have originated from cosmic ray encounters, centroid shifts far away from the median cen-troid, noisy bad pixels, or a poor PSF fit2. The data points in the light curve corresponding to these images were masked out from further analysis. In addition, we also discarded data points where the flux is far above or below the median flux by setting a limit of five times the MAD value.
During each CHEOPS orbit, the observations are interrupted by Earth occultations. In proximity to the occultations, the background flux is drastically pushed up by scattered light from the Earth, leading to increased scatter in the light curve as it closes to the Earth’s occultation. We decided to remove the data points whose corresponding background flux exceeds the median value by more than three times the median absolute deviation. We proceeded with the leftover good data points and fitted them with the planetary model discussed in the next section.
2.5 TESS observations
TESS observed the KELT-20 system in Sector 14 (July 18 to August 14, 2019), Sectors 40–41 (June 25 to August 20, 2021), and in Sector 54 (July 9 to August 5, 2022). We downloaded the 2 min cadence pre-searched data conditioning single aperture photometry (PDC-SAP) light curves (Jenkins et al. 2016) using the lightkurve package (Lightkurve Collaboration 2018). The light curves were corrected for instrumental systematics following Smith et al. (2012) and Stumpe et al. (2012, 2014). We also experimented with single aperture photometry (SAP) light curves. We found conflicting results between the PDC-SAP and the SAP detrended light curve analysis; the results of the former are consistent with the CHEOPS results, and therefore we present only the PDC-SAP light curve analysis.
3 Light curve analysis
3.1 Planetary model
Our light curve model F(ϕ) is defined as the sum of the contributions from several independent submodels related to planetary and stellar flux variations. These include a primary transit Ftr(ϕ) and an occultation Focc(ϕ) model with a flat out-of-eclipse baseline; a phase variation Fday(ϕ) model corresponding to the flux from the planetary day side and a similar nightside phase variation term Fnt(ϕ), an ellipsoidal variation (Morris 1985; Mislis et al. 2012) term FEV(ϕ), and a Doppler boosting (Loeb & Gaudi 2003; Barbier & López 2021) term FDB(ϕ) corresponding to the changes in stellar flux. For KELT-20 b the combined amplitude of FEV(ϕ) and FDB(ϕ) are of the order of unity (~2 ppm), which stands below the measured uncertainties, while the phase amplitude corresponding to the planetary brightness is of the order of tens of ppm, and therefore we excluded the former from our phase curve modelling. The final model constitutes the following:
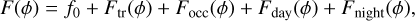 (1)
(1)
where ϕ is the planet’s orbital phase and f0 is an arbitrary additive offset to align the light curve such that the base of the eclipse is at a relative flux value equal to one. The complete mathematical description can be found in Esteves et al. (2013) and references therein. Our model assumes a tidally locked circular orbit for KELT-20b following Wong et al. (2021). We used the Mandel & Agol (2002) transit model of a circular disc passing over a spherical stellar disc with the following parametrisation:
mid-transit epoch T0;
orbital frequency νorb (inverse of the orbital period Porb);
stellar density ρ⋆;
planet to star radius ratio Rp/R⋆;
impact parameter b;
the re-parametrised quadratic limb darkening coefficients q1 and q2 (Kipping 2013).
The occultation model follows a similar description, with the difference that the smaller disc is passing behind the larger one and without any limb darkening law. This description was applied in previous works (Singh et al. 2022; Scandariato et al. 2022). The planetary brightness at superior conjunction is parametrised by an occultation depth δocc. The phase variation term Fday(ϕ) models the changing planetary flux emanating from the day side during its orbital motion, which is parametrised by an amplitude term Aday and a brightness variation term defined by the reflected light phase function (Esteves et al. 2015; Singh et al. 2022). The dayside phase variation is a consequence of Lam-bertian radiation from both reflection and thermal emission. A dayside phase offset Δϕ is included to account for the asymmetry in the phase variation (Scandariato et al. 2022). We followed the convention where positive Δϕ implies an eastward phase shift, while negative is for westward shift. We also incorporate a similar but inverted phase function for thermal emission from the night side, which is parametrised by Anight. No phase offset term is included, and therefore it peaks at mid-transit, while the minima is at mid-eclipse. The minima of the dayside flux is at mid-transit, while the minima of the nightside flux is at mid-occultation. The eclipse depth from these three parameters is obtained by the following equation:
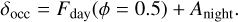 (2)
(2)
We followed this description along with the transit parameters while fitting the full phase curve. Phase curves are only available for the TESS light curves; the CHEOPS observations do not have phase information, and therefore we followed a simpler description with Fnight = 0. To take into account that white noise is not included in the formal photometric uncertainties, we added an independent jitter term to our model.
We fitted the data with the combined model and searched for the simultaneous convergence of the free parameters by maximising the log-likelihood function in the parameter space. We sampled the posterior probability distribution of the free model parameters in a Bayesian MCMC framework using the emcee package version 3.0.2 (Foreman-Mackey et al. 2013). We followed the base line criterion of convergence following the methods described in Goodman & Weare (2010). Under the situations where we had to choose among a set of different models, we followed the Akaike information criterion (AIC, Burnham & Anderson 1998) because of its robustness in information extraction without strongly penalising any additional model parameters. Given the complexity and demand of resources, we performed all our model fitting on the AMONRA computing infrastructure (Bertocco et al. 2020; Taffoni et al. 2020).
3.2 Transit model with gravity darkening
KELT-20 is an A2V star with a v sin i⋆ of 116 km s−1 and a radius of 1.6 R⊙ resulting in a rotation period of ~ 1 day and is therefore categorised as a fast-rotator. The centrifugal force at the surface of fast-rotating stars is non-negligible compared to the stellar gravitational force. Consequently, the stellar gravity is highest at the poles and lowest at the equators, creating an oblate star. According to the von Zeipel theorem, the radiative flux at a given latitude of a fast-rotating star is proportional to the local effective gravity (von Zeipel 1924). The flux radiated at equatorial stellar latitudes is significantly lower compared to the poles. This effect is referred to as gravity darkening (GD). During a transit, when a planet passes over and hides the varying brightness of the stellar surface, it generates an asymmetric transit curve, especially when the orbit is misaligned. The greater the projected orbital obliquity λp, the larger the asymmetry (Lendl et al. 2020; Deline et al. 2022; Hooton et al. 2022). In addition, high-precision transit analysis is the preferred technique in measuring the true obliquity (Ψ) of a planetary system. Using the stellar and orbital inclinations, it is computed by the following relation
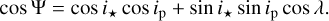 (3)
(3)
We model the GD transits of KELT-20 using the Transit Light Curve Modeler (TLCM; Csizmadia 2020, Csizmadia et al. 2023), which was used to model GD in the WASP-189 (Lendl et al. 2020), MASCARA-1 (Hooton et al. 2022), and WASP-33 (Kálmán et al. 2022) systems. The fitted GD parameters in TLCM are the inclination of the stellar rotation axis, i⋆, and the longitude of the node of the stellar rotation axis, Ω⋆, which is directly related to the sky-projected spin-orbit obliquity, λ, via cos λ = ± cos(Ωp − Ω⋆), where Ωp is the planetary rotational axis and is set to 90°. The GD exponent, β, is typically set to its theoretically expected value of 0.25 following von Zeipel’s law (von Zeipel 1924). Along with the GD parameters, the model describes the transits using the following fitted parameters: the scaled orbital semi-major axis, a/R⋆; the planet-to-star radius ratio, Rp/R⋆; the transit impact parameter, b; the epoch of mid-transit; the orbital period, P; and the limb-darkening parameters, u+ and u-, related to the quadratic limb-darkening parameters, u1 and u2, via u+ = u1 + u2 and u− = u1 − u2. Two additional parameters, σw and σr, describe respectively the levels of white and red (correlated) noise present in the light curves, determined using the wavelet formulation of Carter & Winn (2009).
4 Results
In this section, we present the outcomes of several of our analyses that include seven occultation and five transit observations of KELT-20 b with CHEOPS spanning over more than a year. Additionally, we also analysed the four TESS sectors of observations of KELT-20 that spanned over three years. We first present the results of the CHEOPS transit analysis with and without GD. We then present the results of only the occultation fits of both the telescopes followed by the results of the TESS phase curves.
4.1 Transits
4.1.1 Without gravity darkening
We fitted the five CHEOPS transit light curves individually following the model described in Sect. 3.1, where all the component models except for the transit (Ftr) are set to zero. The best-fit parameters of the individual transit fits are reported in Table A.1, while the same for the combined fit of all the transits are reported in Table 3. We present the best-fit transit model plotted over the phase folded photometry of all five transits in Fig. 1 (on the left). We also present the individual transit fits in Fig. A.1.
All the transits appear symmetrical with converging limb darkening coefficients, thereby implying an equatorial orbit for the hot Jupiter around the fast-rotator host. We compare the best-fit limb darkening coefficients (q1 and q2) reported in Table 3 with the theoretical estimates of q1 = 0.250 ± 0.001 and q2 = 0.288 ± 0.001, computed using the LDTk Python package (Parviainen & Aigrain 2015)3, and found that their agreement is close to 1σ. This description is fairly consistent with that obtained with Doppler tomography (Hoeijmakers et al. 2020b). The transit parameters observed by CHEOPS agree with the measurements of the TESS photometry described later in Sect. 4.3. Figure 2 shows the best-fit plot of the TESS transits. The outcome of the TESS photometry agrees with previously reported literature values (Patel & Espinoza 2022; Wong et al. 2021).
4.1.2 With gravity darkening
With the aim of better constraining the obliquity of the KELT-20 system, we fitted the CHEOPS transit light curves with a GD model as described in Sect. 3.2. We placed a uniform prior 𝒰(80°, 110°) on Ω⋆, corresponding to −10° < λ < 10°, based on Doppler tomography measurements of λ, which indicate that the KELT-20 system has an obliquity (sky-projected) close to zero (Hoeijmakers et al. 2020a). Without this prior, the obliquity is poorly constrained by the transit photometry alone. We report our sky-projected (λ) and true obliquity (Ψ) values along with the other gravity darkening parameters in Table 3. The measured sky-projected obliquity in TESS differs from the same measured with CHEOPS. This could be due to some unaccounted for noise sources or degeneracy in the fitting the TESS light curve. We present and compare our best-fit λ along with the literature values in Sect. 5.4. The flattening parameter (ƒ) is 0.03, which gives the planet’s polar-to-equatorial radius ratio Rpol/Req at 0.97. Consequently, the planet-to-star radius ratio differs by more than 3σ with and without GD model considerations. However, using the geometric mean as the stellar radius (i.e. 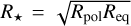 ) we reached an agreement between the two radius ratios.
) we reached an agreement between the two radius ratios.
We performed a similar analysis over the combined transits of the TESS photometry, and present it in Table 3. The fitting algorithm returns quite different outcomes compared to the CHEOPS transit fits. It returns a significantly inconsistent orientation of the KELT-20 system with a much lower radius ratio. This could be primarily attributed to the lower precision of the TESS light curves, and therefore a non-GD model best describes the transit light curve. Each sector’s individual TESS transits are shown in Figs. B.1 and B.2.
4.2 Occultations
CHEOPS observed a total of seven occultations of KELT-20 b, which we analysed individually and jointly. For these analyses we fitted the model as defined in Eq. (1), where the only free parameter is the occultation depth. We fixed the transit ephemerides following the TESS phase curve analysis described later in Sect. 4.3. We first fitted the data of only the occulta-tion model along with a jitter term. Following which we found a correlation with the time, x and y pixel centroids, and the roll angle, and therefore we decided to include them as a co-detrending term. We obtain a clear detection of the occultation depth in all the visits with a precision of more than 3 σ for the first and the last visit, and more than 5 σ for the rest. The best-fit occultation depths of the individual visits are 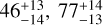 ,
, 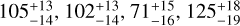 , and 51 ± 15 ppm. They are shown in Fig. 3 along with their posterior distributions in the side panel. The scatter of these measurements points towards a possible variability in the occultation depth of KELT-20b. The individual measurements are up to 2.8 σ discrepant from their weighted mean, with the two most extreme measurements disagreeing by 3.4σ. Conscious that the small sample size complicates a thorough statistical evaluation, we nevertheless attempted to quantify its significance. To do so, we created 104 mock datasets assuming a constant occultation depth and measurements scattered around it following a Gaussian distribution with a width equal to the measurements’ uncertainties. From this distribution, we find a 0.3% probability (i.e. a p-value of 0.0033, or a 2.9 σ significance) that measurements at least as discrepant as those observed are created randomly. While encouraging, this value hinges on the exact placement and uncertainty of each individual measurement, which hinges on the analysis approach (see Fig. A.2), and the treatment of stellar and instrumental correlated noise. The leftover correlated noise in the best-fit residuals contributes ~20% to the uncertainty levels, the rest being the white noise. Considering this non-negligible red noise to some extent could contribute to the observed discrepancies in the occultation depth. On the other hand, it is noteworthy that the simultaneous TESS data (averaged in each sector) show a similar behaviour at lower significance, tentatively supporting the variability. Using all the visits, we obtain a mean occultation depth of 82 ± 6 ppm, as shown by its posterior in the right plot of Fig. 1. We also present the individual occultation best-fits in the right panel of Fig. A.1.
, and 51 ± 15 ppm. They are shown in Fig. 3 along with their posterior distributions in the side panel. The scatter of these measurements points towards a possible variability in the occultation depth of KELT-20b. The individual measurements are up to 2.8 σ discrepant from their weighted mean, with the two most extreme measurements disagreeing by 3.4σ. Conscious that the small sample size complicates a thorough statistical evaluation, we nevertheless attempted to quantify its significance. To do so, we created 104 mock datasets assuming a constant occultation depth and measurements scattered around it following a Gaussian distribution with a width equal to the measurements’ uncertainties. From this distribution, we find a 0.3% probability (i.e. a p-value of 0.0033, or a 2.9 σ significance) that measurements at least as discrepant as those observed are created randomly. While encouraging, this value hinges on the exact placement and uncertainty of each individual measurement, which hinges on the analysis approach (see Fig. A.2), and the treatment of stellar and instrumental correlated noise. The leftover correlated noise in the best-fit residuals contributes ~20% to the uncertainty levels, the rest being the white noise. Considering this non-negligible red noise to some extent could contribute to the observed discrepancies in the occultation depth. On the other hand, it is noteworthy that the simultaneous TESS data (averaged in each sector) show a similar behaviour at lower significance, tentatively supporting the variability. Using all the visits, we obtain a mean occultation depth of 82 ± 6 ppm, as shown by its posterior in the right plot of Fig. 1. We also present the individual occultation best-fits in the right panel of Fig. A.1.
After finding the variability in the CHEOPS occultation depths, we looked for signs of variability in the TESS observations, which simultaneously observed the target during its Sector 40 and 41 orbits. The phase curve analysis from the second year of TESS has already been studied by Wong et al. (2021), and based on the four occultations in Sector 14, they report a depth of 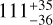 ppm. Fu et al. (2022) has analysed the occultation cuts from the three sectors observed at the time, and reports an average occultation depth of 139 ± 8 ppm. Following the same approach, we eliminated the data points centred at the individual occultations that span over three times the duration. We then fitted the data with the occultation model along with a linear detrending term. Upon respective sector-wise analysis, we obtained occultation depths of 123 ± 36, 105 ± 23, 196 ± 32, and 169 ± 29 ppm. Consequently, we observe a 2 σ difference in the measured depths between Sectors 40 and 41. This approach is convenient for obtaining an average measurement. However, a sector-wise comparison would need a complete planetary model with a better characterisation of the systematics present in the light curve.
ppm. Fu et al. (2022) has analysed the occultation cuts from the three sectors observed at the time, and reports an average occultation depth of 139 ± 8 ppm. Following the same approach, we eliminated the data points centred at the individual occultations that span over three times the duration. We then fitted the data with the occultation model along with a linear detrending term. Upon respective sector-wise analysis, we obtained occultation depths of 123 ± 36, 105 ± 23, 196 ± 32, and 169 ± 29 ppm. Consequently, we observe a 2 σ difference in the measured depths between Sectors 40 and 41. This approach is convenient for obtaining an average measurement. However, a sector-wise comparison would need a complete planetary model with a better characterisation of the systematics present in the light curve.
Best-fit model and derived parameters of the transit, occultation, and phase curve fit.
 |
Fig. 1 CHEOPS light curve. Left: detrended and phase-folded planetary transits. The solid red line is the best-fit model, while the blue dots represent the phase-folded and binned photometry (interval: 2.25 min for transit, 7.5 min for occultation). The residuals are shown in the bottom panel. Right: same as in the left panel, but centred at the occultations. |
 |
Fig. 2 TESS light curve. Left: detrended and phase-folded planetary transits from Sectors 14, 40, 41, and 54. The solid red line is the best-fit model, while the blue dots represent the phase-folded and binned photometry (Interval: 2.25 min for transit, 25 min for phase curve). The residuals are shown in the bottom panel. Right: combined phase curve using photometry from all four sectors. |
 |
Fig. 3 Best-fit occultation depths of individual CHEOPS visits (blue) along with their posteriors in the right panel. The horizontal solid and dashed lines represent the mean occultation depth of 82.4 ± 5.6 ppm. The green shaded regions indicate the span of the TESS Sectors 40, 41, and 54, while the brown points indicate the sector-wise occultation depths. |
4.3 TESS phase curves
We re-analysed the TESS light curves and fitted them with the complete model described in Sect. 3.1. We first fitted the model without any red noise correction term, and as a result we found strong short frequency trends in the residuals. To account for these low-frequency signals we simultaneously fitted the model with a Gaussian process (GP) model using a Matérn 3/2 kernel (Rasmussen & Williams 2006; Gibson et al. 2012). The Matérn 3/2 kernel defines the covariance between two observations at times 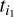 and
and 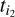 as
as
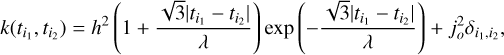 (4)
(4)
where h is the amplitude of the GP and λ is its timescale. In order to take into account any additional white noise not included in the uncertainties, either instrumental or astrophysical, we added the diagonal terms 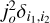 to the Matérn 3/2 kernel, where o denotes the TESS Sectors 14, 40, 41, and 54. Unfortunately, the precision in the TESS light curves is insufficient to provide precise constraints on the sector-wise phase offset and nightside flux. Phase offset and nightside flux convergence was reached only in the case of Sector 40 with values consistent with zero (i.e. −11 ± 32 deg; see Fig. B.4). Prior constraints on these parameters from the analysis of the Sector 14 phase curves were also consistent with zero (Wong et al. 2021). Hence, to reduce the dimensionality of the fit, we set these two parameters to zero. The parameters of the individual sector fits are presented in Table B.1. The occultation depths measured with this approach are in agreement with the value measured in the previous section, although these depths lie towards the shallow end of the 1σ distribution obtained using the previous approach.
to the Matérn 3/2 kernel, where o denotes the TESS Sectors 14, 40, 41, and 54. Unfortunately, the precision in the TESS light curves is insufficient to provide precise constraints on the sector-wise phase offset and nightside flux. Phase offset and nightside flux convergence was reached only in the case of Sector 40 with values consistent with zero (i.e. −11 ± 32 deg; see Fig. B.4). Prior constraints on these parameters from the analysis of the Sector 14 phase curves were also consistent with zero (Wong et al. 2021). Hence, to reduce the dimensionality of the fit, we set these two parameters to zero. The parameters of the individual sector fits are presented in Table B.1. The occultation depths measured with this approach are in agreement with the value measured in the previous section, although these depths lie towards the shallow end of the 1σ distribution obtained using the previous approach.
We fitted all four sectors, first independently and then simultaneously, with the same overall model parameters except the GP model hyper-parameters h and λ, which are specific to correlated trends in individual sectors, although we kept a separate jitter term to account for the white noise. All the model parameters described in Sect. 3.1 were kept free. The results of the best-fit parameters are presented in Table 3. The occultation depth is consistent with the previous analysis and literature values (Sect. 4.2). The best-fit model is shown in Fig. 2 and the sector-wise independent model plots are shown in Fig. B.3. We did not detect any significant nightside emission as Anight is consistent with zero within 1σ. We report a 99.9% upper limit on Anight of 29 ppm, which corresponds to an upper limit to the nightside temperature at 2280 K. We also did not find any significant phase offsets as Δϕ is consistent with zero.
5 Discussion
5.1 Atmospheric modelling
Given the bulk properties of KELT-20 b, we expect that thermal emission and stellar reflected signals both contribute to the planetary flux at the optical wavelengths probed by CHEOPS and TESS.
To provide a physical interpretation of the observed occultation depths, we modelled the planet’s emission spectrum using the open-source PYRAT BAY framework4 (Cubillos & Blecic 2021). This package employs parametric models of the planetary atmosphere (1D pressure profiles of the temperature, composition, and altitude), from which we then generate the thermal emission spectra. Using a Bayesian retrieval approach, the code constructs posterior distributions for the atmospheric parameters by fitting the emission models to observed occultation depth, using a differential-evolution MCMC (Cubillos et al. 2017). Since the PYRAT BAY code does not account for reflected light, we opted to constrain the thermal-emission models only by the infrared observations, which are largely dominated by the thermal component. We then computed the predicted thermal emission in the CHEOPS and TESS bands, and considered the reflected component as the difference between the observed and modelled fluxes.
We modelled the atmosphere from 100 to 10−9 bar, adopting a configuration similar to that of Fu et al. (2022). For the temperature profile we used the model of Guillot (2010), parametrised by the mean thermal opacity log10(κ′), the ratio of visible and thermal opacities log10(γ) to the irradiation temperature Tirr. We assumed an atmospheric composition in chemical equilibrium, including the main species that dominate the chemistry for the molecules expected to be probed by the observations. These include H2, He, H2O, CH4, CO, CO2, N2, HCN, NH3, C2H2, C2H4, TiO, VO, TiO2, VO2, S2, SH, SiO, H2S, SO, and SO2, as well as atomic and ionic species. To vary the atmospheric composition in the retrieval models, we used as parameters the abundance of metals [M/H], carbon [C/H], and oxygen [O/H], all relative to solar abundances in logarithmic scale. For these parameters we used a uniform prior ranging from 0.01 to 100 times solar (Table 4).
We computed the emission spectra for each atmospheric model with a line-by-line radiative transfer routine sampling between 0.3 and 5.5 µm at a constant resolving power of R = λ/∆λ = 15 000. For the molecular opacities we used the data from HITEMP for CO, CO2, and CH4 (Rothman et al. 2010; Li et al. 2015; Hargreaves et al. 2020), and from Exo-Mol for H2O, NH3, HCN, TiO, and VO (Harris et al. 2006, 2008; Polyansky et al. 2018; Coles et al. 2019; Yurchenko 2015; McKemmish et al. 2016, 2019). Prior to the retrieval we pre-processed these large data files, first using the REPACK algorithm to extract the dominant line transitions (Cubillos 2017), and then tabulating the opacities over a fixed pressure, temperature, and wavelength grid. In addition, the model included Na and K resonant-line opacities (Burrows et al. 2000); collision-induced opacities for H2–H2 (Borysow et al. 2001; Borysow 2002); Rayleigh-scattering opacity for H, H2, and He (Kurucz 1970); and a grey cloud deck model.
Figures 4 and C.1 and Table 4 summarise our atmospheric retrieval results. To account for the unknown impact of reflected emission in the optical, we considered two retrieval scenarios: one fitting only the HST/WFC3 and Spitzer/IRAC near-infrared (NIR) occultation depths of Fu et al. (2022), and another that fits the NIR data and TESS occultation depth reported in this work.
The retrieval models fit the occultation data well, with the HST data dominating the thermal structure constraints. The higher emission seen in the longer wavelengths 1.3–1.6 µm, where H2O absorbs more strongly, drives the retrieval towards inverted temperature profiles. In terms of composition, both fits (with and without the TESS constraint) find a strong correlation between the carbon and oxygen abundances (Fig. C.1). This results in broad carbon and oxygen posteriors, but a well-defined C/O ratio of less than one: 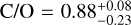 (NIR retrieval) and
(NIR retrieval) and 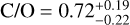 (NIR+TESS retrieval). Including the TESS constraint has the largest impact on the [M/H] parameters, which accounts for the metallicity of all other species (most affected by the TESS constraint) and which narrows down to solar values from an otherwise largely unconstrained posterior. This occurs because the TESS band probes the absorption from species such as TiO, VO, Na, and K, which were previously unconstrained. The relatively high value of the TESS occultation depth drives the [M/H] constraint towards the upper values given the non-inverted thermal profile (higher emission from the hotter, upper layers of the atmosphere). Our results are generally consistent with those of Fu et al. (2022); both analyses find a clear thermally inverted temperature profile that quickly increases from ~2300 K to ~3400K and C/O ratios close to the solar value (C/O⊙ = 0 55). In one additional test we explored cases excluding the absorption from TiO and VO, which are molecules that tend to condense out of planetary atmospheres (e.g., Hoeijmakers et al. 2020b). For these runs we found no significant variations in the retrieved properties (results consistent at the 1σ level).
(NIR+TESS retrieval). Including the TESS constraint has the largest impact on the [M/H] parameters, which accounts for the metallicity of all other species (most affected by the TESS constraint) and which narrows down to solar values from an otherwise largely unconstrained posterior. This occurs because the TESS band probes the absorption from species such as TiO, VO, Na, and K, which were previously unconstrained. The relatively high value of the TESS occultation depth drives the [M/H] constraint towards the upper values given the non-inverted thermal profile (higher emission from the hotter, upper layers of the atmosphere). Our results are generally consistent with those of Fu et al. (2022); both analyses find a clear thermally inverted temperature profile that quickly increases from ~2300 K to ~3400K and C/O ratios close to the solar value (C/O⊙ = 0 55). In one additional test we explored cases excluding the absorption from TiO and VO, which are molecules that tend to condense out of planetary atmospheres (e.g., Hoeijmakers et al. 2020b). For these runs we found no significant variations in the retrieved properties (results consistent at the 1σ level).
In terms of thermal-light versus reflected-light flux, our NIR retrieval underestimates the TESS and CHEOPS occultation depths (Fig. 4), indicating that there must be a non-negligible reflected-light component. By including the TESS measurement in the fit, the model matches the TESS occultation depth, but still underestimates the CHEOPS occultation depth, again suggesting that there should be some fraction of reflected light in that band, although we note that this fit makes the implicit assumption that the TESS occultation depth is purely due to thermal emission. Therefore, these two scenarios model the planetary optical emission under two extreme cases: no prior assumption of reflected or thermal contribution (NIR retrieval) versus maximum thermal contribution (NIR+TESS retrieval). Our contribution functions indicate that TESS and Spitzer probe higher layers in the atmospheres than HST. In each scenario, the CHEOPS contribution functions coincide fairly well with that of TESS, suggesting that they probe a similar region in the atmosphere (Fig. 4).
 |
Fig. 4 Left: KELT-20 b observed occultation depths (grey markers). The curve at the bottom shows the through-puts for each data point. The solid curves show the median of the retrieved model distributions when fitting the NIR HST and Spitzer occultations (blue) and the NIR+TESS occultations (red). The shaded areas (in corresponding colours) denote the span of the 68% central percentile of the distributions. The dashed grey curves show spectra for two black-body planetary model spectra at 2300 and 3200 K. Top right: retrieved temperature profiles (same colour-coding as before). The curves at the left edge show the contribution functions for selected bands (see legend). Bottom right: contribution functions integrated over the CHEOPS and TESS bands for the two cases shown in the left panel and for retrievals without TiO and VO opacity (same colour-coding as above). The band-integrated thermal flux in CHEOPS and TESS bands are (36 ± 18 ppm) and (85 ± 38 ppm), respectively (coloured markers). |
KELT-20 b atmospheric retrieval.
5.2 Albedo
5.2.1 Geometric albedo and brightness temperature
A geometric albedo (Ag(λ) or Ag,λ) is defined as the spherical albedo at full phase or phase angle α = 0 (superior conjunction, Seager 2010). It is defined as the ratio of the planet’s brightness to that of an idealised, flat, fully reflecting Lambertian disc with an identical cross-section. The brightness temperature (Tday(λ)) of the planetary day side is the temperature of a black-body that emits the same amount of radiation within a specific passband. The T–P profile from Fig. 4 suggests that CHEOPS and TESS practically probe the same layer of the atmosphere that irradiates at similar temperatures, which are computed to be 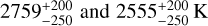 , respectively. Alternatively, following the HST/WFC3 + Spitzer/IRAC (NIR) model, we computed the band-integrated emission flux for both CHEOPS and TESS at 36 ± 18 ppm and 85 ± 38 ppm, respectively. As the resultant occultation depth is the sum of the two theoretical depths (i.e. (δocc = δref + δthm). Subtracting the emission flux from the observed depths listed in Table 3, we obtain the reflected flux and using Eq. (5) (Seager 2010), we obtain the band-integrated geometric albedos in the CHEOPS and TESS bands as Ag,CHEOPS = 0.19 ± 0.08 and Ag,TESS = 0.19 ± 0.16, respectively:
, respectively. Alternatively, following the HST/WFC3 + Spitzer/IRAC (NIR) model, we computed the band-integrated emission flux for both CHEOPS and TESS at 36 ± 18 ppm and 85 ± 38 ppm, respectively. As the resultant occultation depth is the sum of the two theoretical depths (i.e. (δocc = δref + δthm). Subtracting the emission flux from the observed depths listed in Table 3, we obtain the reflected flux and using Eq. (5) (Seager 2010), we obtain the band-integrated geometric albedos in the CHEOPS and TESS bands as Ag,CHEOPS = 0.19 ± 0.08 and Ag,TESS = 0.19 ± 0.16, respectively:
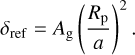 (5)
(5)
The geometric albedos in the two passbands are consistent with each other, as are the brightness temperatures from the T–P profile. Moreover, the retrieval model does not include scattering. In the absence of a detailed occultation spectrum at optical wavelengths, it is difficult to precisely predict the exact contribution of thermal emission or reflection to the planetary brightness. Therefore, to solve this degeneracy problem and to obtain stricter constraints on the dayside brightness temperature and the geometric albedo, we explored an alternate approach. Following the definition, we express the dayside emission in terms of the brightness temperature as Eq. (6) (Santerne et al. 2011; Singh et al. 2022):
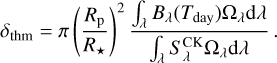 (6)
(6)
Here Bλ(Tday) is the Planck distribution for temperature Tday, 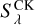 is the stellar Kurucz flux (Castelli & Kurucz 2003) for the nearest Teff, log 𝑔, and [Fe/H]. The stellar flux and the planetary black-body flux is integrated over the telescope’s passband λ with the corresponding response function Ωλ5. We use the measured value of δocc from observations together with Eqs. (5) and (6) to create a parametric relationship between the geometric albedo and the brightness temperature as
is the stellar Kurucz flux (Castelli & Kurucz 2003) for the nearest Teff, log 𝑔, and [Fe/H]. The stellar flux and the planetary black-body flux is integrated over the telescope’s passband λ with the corresponding response function Ωλ5. We use the measured value of δocc from observations together with Eqs. (5) and (6) to create a parametric relationship between the geometric albedo and the brightness temperature as
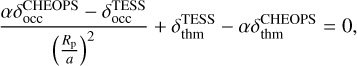 (7)
(7)
where α denotes the ratio of the two geometric albedos 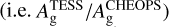 . Assuming identical band-integrated geometric albedos (or α = 1 ) and the same brightness temperatures in the two passbands, we can precisely constrain the two Ag–Tday pairs. Figure 5 shows the Ag versus Tday relation for the occultation depths measured in the CHEOPS and TESS passbands. The brightness temperature is the independent parameter that varies from 1200 K to 3500 K. We do not expect negative values for the geometric albedo and are therefore truncated in the plot.
. Assuming identical band-integrated geometric albedos (or α = 1 ) and the same brightness temperatures in the two passbands, we can precisely constrain the two Ag–Tday pairs. Figure 5 shows the Ag versus Tday relation for the occultation depths measured in the CHEOPS and TESS passbands. The brightness temperature is the independent parameter that varies from 1200 K to 3500 K. We do not expect negative values for the geometric albedo and are therefore truncated in the plot.
Being a wavelength-dependent property, Ag might, in principle, vary between the TESS and CHEOPS bands (i.e. α ≠ 1); however, to constrain the Tday–Ag pair, we assume this variation to be below the precision of our data. This corresponds to one of two scenarios: (1) a grey-sky reflective atmosphere (i.e. a flat reflection spectrum) or (2) if the albedo spectrum happens to be non-monotonic and gets averaged out to produce an identical band-integrated Ag for the two passbands. Following this methodology we obtained precisely constrained values of Ag and Tday at 0.26 ± 0.04 and 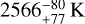 , respectively. We obtain a dayside temperature similar to that measured in Sect. 5.1. Furthermore, we derive the respective contributions of reflection (δref) and emission (δthm) to the occultation depth and are shown in the subfigure in Fig. 5. In the CHEOPS band, the reflection-emission contribution is almost 80–20%, while in the TESS band, they are equally distributed. The derived brightness temperature and albedo posteriors along with the posteriors of the fitted parameters used in their computation are shown in Fig. C.2. Ag and is more precisely constrained compared to the previous approach. Ag correlates with the occultation depth in CHEOPS as visible in the posterior distribution. The agreement between the Ag values determined with the two approaches is within 1 σ. On the other hand the brightness temperature correlates with the occultation depth measured in TESS.
, respectively. We obtain a dayside temperature similar to that measured in Sect. 5.1. Furthermore, we derive the respective contributions of reflection (δref) and emission (δthm) to the occultation depth and are shown in the subfigure in Fig. 5. In the CHEOPS band, the reflection-emission contribution is almost 80–20%, while in the TESS band, they are equally distributed. The derived brightness temperature and albedo posteriors along with the posteriors of the fitted parameters used in their computation are shown in Fig. C.2. Ag and is more precisely constrained compared to the previous approach. Ag correlates with the occultation depth in CHEOPS as visible in the posterior distribution. The agreement between the Ag values determined with the two approaches is within 1 σ. On the other hand the brightness temperature correlates with the occultation depth measured in TESS.
Additionally, the same dataset can also be explained with alternative scenarios. If we break the identical Ag assumption, but keep the same Tday, then the maximum brightness temperature is 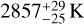 , which is equal to the maximum Tday associated with δocc of TESS. This would imply Ag,TESS = 0 and Ag,CHEOPS = 0.17 ± 0.03 (i.e. entirely absorbing atmosphere in TESS band, and yet significantly reflective in the CHEOPS band). Furthermore, if we assume no reflection contribution whatsoever, then we need to give up the black-body assumption. This leads to maximum Tday associated with the observed δocc of CHEOPS,
, which is equal to the maximum Tday associated with δocc of TESS. This would imply Ag,TESS = 0 and Ag,CHEOPS = 0.17 ± 0.03 (i.e. entirely absorbing atmosphere in TESS band, and yet significantly reflective in the CHEOPS band). Furthermore, if we assume no reflection contribution whatsoever, then we need to give up the black-body assumption. This leads to maximum Tday associated with the observed δocc of CHEOPS, 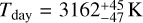 . Nevertheless, this scenario is less likely following Sect. 5.1.
. Nevertheless, this scenario is less likely following Sect. 5.1.
Following Wong et al. (2021), we re-plotted the Ag versus Tday for the sample of the hot Jupiters discussed in their paper along with the published CHEOPS results in Fig. 6. It is quite clear that there is a positive correlation between Ag and Tday for HJ to UHJ in their work, with the exception of a few outliers like WASP-18b and WASP-33b. We observed a similar trend within the CHEOPS sample, thereby corroborating that UHJs tend to be more reflective compared to HJs. Although in comparison with the entire sample, the addition of the CHEOPS sample suggests a flattening of Ag for higher temperatures.
 |
Fig. 5 Dayside reflection and emission brightness contributions. Left: geometric albedo (Ag) as a function of the dayside brightness temperature for the estimated occultation depths in CHEOPS (blue) and TESS (red). The decreasing intensity of the colour shades corresponds to the 1 σ, 2 σ, and 3 σ uncertainties in the computation of Ag for each Tday. The overlapping region provides the true constraints on the two parameters represented by the posterior distribution in grey. The individual posteriors of (Ag) and (Tday) are presented in the side panels. The resultant values are reported in the text. Subpanel: reflection and emission contributions to the occultation depth of the CHEOPS and TESS passbands. The identical height of the reflection component reflects the assumption of α = 1. Right: Kurucz stellar model [Teff = 9000, [Fe/H] = 0 and log = 4.5] along with the CHEOPS and TESS passband responses. The dayside planetary black-body flux (×100) is also plotted for a comparison with the stellar flux. Tday = 2600 K. |
 |
Fig. 6 Ag–Tday of several hot Jupiters following Wong et al. (2021). The black circles (Kepler–CoRoT) and the green squares (TESS) are taken directly from their sample. The blue diamonds correspond to the published values of the CHEOPS hot Jupiters (Krenn et al. 2023; Brandeker et al. 2022; Scandariato et al. 2022; Pagano et al. 2024; Hooton et al. 2022; Deline et al. 2022). The red diamond is from this work on KELT-20 b. |
 |
Fig. 7 Parameters determining planetary energy distribution under radiative equilibrium. Top right: Bond albedo plotted as a function of the heat re-circulation efficiency for the effective dayside temperature Td. Bottom left: respective posteriors of AB and ϵ from the overlapping region, which are then used to compute the nightside temperature. The values in the label correspond to the orange posteriors, while the light blue posteriors are shown only for comparison. |
5.2.2 Bond albedo
The Bond albedo (AB, Bond 1861) or the spherical bolometric albedo (Mallama 2017) is a measurement of the fraction of the total power of the incident radiation that is scattered back at all wavelengths and all phase angles. It provides a measure of a planet’s energy budget that further provides information about its atmospheric composition and the overall thermal properties (Schwartz & Cowan 2015). To convert a geometric albedo into a Bond albedo, we need information about the planet’s reflectance spectrum, scattering phase function, and spatial inhomogeneity (Hanel et al. 2003). In practice, the geometric albedo is related to the spherical albedo through the phase integral q (i.e. the integral of the scattering phase function), which gets translated to the Bond albedo through the relation
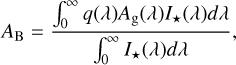 (8)
(8)
where I★ is the wavelength-dependent stellar intensity. For a Lambert sphere, q = 2/3, and assuming a geometric albedo independent of wavelengths (i.e. a flat albedo spectrum), we obtain AB = 3/2Ag. This formalism has been the norm during the Kepler and the Spitzer era.
Following Cowan & Agol (2011), the effective dayside (Td)6 and nightside temperatures (Tn) can be expressed in terms of the bond albedo AB and the heat re-circulation efficiency ϵ that parametrises the heat flow from the day side to the night side (Eqs. (9) and (10)):
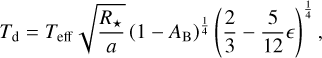 (9)
(9)
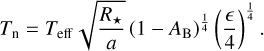 (10)
(10)
Here ϵ = 0 indicates instantaneous re-radiation or no recirculation of heat from the day side to the night side, while ϵ = 1 means perfect heat re-circulation. In the previous section we estimated the observed brightness temperature of the planet Tday within the CHEOPS-TESS passband. The best-fit planetary spectral energy distribution (SED) obtained from Sect. 5.1 equates to a thermal flux with an irradiation temperature of 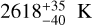 . We use this as the effective temperature of the planetary day side Td. We therefore invert Eq. (9) to provide constraints on the associated bond albedo AB with varying ϵ, as shown in Fig. 7. The solid black line represents the AB value with varying ϵ, while the dashed grey lines are the 16th and 84th percentiles. The orange and light blue span represents the constraints on the bond albedo following the Lambertian scattering law (i.e. q = 3/2) and the 100% back-scattering law (i.e. q = 1), respectively. These estimates are computed using the Ag value derived in Sect. 5.2.1.
. We use this as the effective temperature of the planetary day side Td. We therefore invert Eq. (9) to provide constraints on the associated bond albedo AB with varying ϵ, as shown in Fig. 7. The solid black line represents the AB value with varying ϵ, while the dashed grey lines are the 16th and 84th percentiles. The orange and light blue span represents the constraints on the bond albedo following the Lambertian scattering law (i.e. q = 3/2) and the 100% back-scattering law (i.e. q = 1), respectively. These estimates are computed using the Ag value derived in Sect. 5.2.1.
For the extreme case of inefficient heat re-circulation (i.e. ϵ = 0), we derive an upper limit on the bond albedo of 0.45 ± 0.07. We note that this does not make any assumptions regarding the phase integral (q), which relates the geometric albedo to the Bond albedo. We can however use our derived value of Ag within the CHEOPS–TESS passbands to further constrain the limits on AB and ϵ. Following the same approach as Schwartz & Cowan (2015), we use Eq. (8) and consider the two limits on the phase integral (i.e. q = 3/2, Lambert scattering, and q = 1, 100% back-scattering). As we have no information of the geometric albedo in the UV/FUV wavelength ranges, we assume a constant Ag equal to that measured in the optical. Figure 7 shows the posterior distribution of the AB, ϵ along with the dayside and nightside temperatures for the two limiting scenarios.
We report the values corresponding to the flat Ag with the planet following Lambertian scattering, which gives 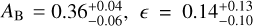 and the nightside temperature
and the nightside temperature 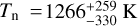 . The uncertainties are propagated from the error estimates on the stellar effective temperature from Table 1 and the semi-major axis from Table 3. The low value of e indicates weak heat re-circulation, while the average nightside temperature will result in emission signatures that too low to be detectable in the TESS phase curves, which corroborates well with the nightside emission estimates that is consistent with zero. If a more asymmetric scattering law is assumed (q < 3/2), a combination of smaller AB and higher ϵ would also be possible. In the limiting case of q = 1 or AB = Ag, we obtain ϵ as
. The uncertainties are propagated from the error estimates on the stellar effective temperature from Table 1 and the semi-major axis from Table 3. The low value of e indicates weak heat re-circulation, while the average nightside temperature will result in emission signatures that too low to be detectable in the TESS phase curves, which corroborates well with the nightside emission estimates that is consistent with zero. If a more asymmetric scattering law is assumed (q < 3/2), a combination of smaller AB and higher ϵ would also be possible. In the limiting case of q = 1 or AB = Ag, we obtain ϵ as 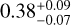 , while the nightside temperature Tn is
, while the nightside temperature Tn is 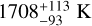 .
.
5.3 Atmospheric variability
In addition to a precisely constrained geometric albedo of the day side of KELT-20b, our data also shows a tentative detection of temporal variability in the occultation depth (see Sect. 4.2), which most plausibly can be attributed to the varying flux from the planetary day side. Prior reports of variability in a hot-Jupiter atmosphere were announced for HAT-P-7 b (Armstrong et al. 2016) and WASP-12 b (Wong et al. 2022). For HAT-P-7 b, variability was observed in the phase curve shape, interpreted as changes in the location of the brightest point. Although this interpretation was later challenged and attributed to stellar super-granulation (Lally & Vanderburg 2022). The behaviour of KELT-20 appears to differ, showing changes in the occultation depth itself which can be best illustrated when we analyse its variability within the first four visits of CHEOPS in conjunction with the simultaneous TESS Sector 40 and 41 occultations.
If we only consider the TESS Sector 40 observations combined with the first two simultaneous occultation observations of CHEOPS, we obtained the respective depths of 102 ± 22 and 62 ± 9 ppm for TESS and CHEOPS. Following the method described in Sect. 5.2.1, these values yield a grey-sky geometric albedo of 0.16 ± 0.1. Conversely, if we consider only TESS Sector 41 and the latter two occultations of CHEOPS (i.e. visits 3 and 4), then the respective depths are 149 ± 34 and 103 ± 10 ppm. This scenario yields a higher grey-sky geometric albedo of 0.31 ± 0.1. Driven by the less discrepant TESS measurements, the derived average dayside temperatures remain compatible within 1 σ. This suggests that a brightness variability through reflectivity, as expected from varying cloud cover, rather than temperature, is at play.
Understanding the cloud coverage and variability requires understanding the underlying 3D cloud coverage. Recently, Helling et al. (2023) provided an extensive grid of 3D cloudy models for warm to ultra-hot Jupiters. KELT-20 b is an ultra-hot Jupiter that corresponds best to the 2200 K hot 3D case around an F-type star in their Fig. 5. Such a planet is expected to have a partly cloudy morning terminator because the relatively slow rotation of the tidally locked planet of 3.5 days still promotes the formation of a strong super-rotating jet, which carries cloud particles from the night side towards the day side, that can cover up to 30 deg of the morning terminator with thick clouds in the steady-state climate. Therefore, the cloud coverage on the day-side limbs on such ultra-hot Jupiters is mostly determined by the strength of the super-rotating wind jet.
The location of the hot spot shift is also highly sensitive to the strength of the super-rotating wind jet. We note, however, that compared to hot Jupiters like HD 209458 b with an effective dayside temperature Td = 1500 K, the hot spot shift is very much reduced for an ultra-hot Jupiter with Td > 2000 K because the radiative timescales are proportional to ∝T−3, and thus become very short compared to the dynamical timescale. In other words, the hot air on the day side cools off faster as it is transported eastwards towards the night side.
It has been pointed out again by Helling et al. (2023) that such a planet is also highly thermally ionised at the day side (their Fig. 14). Several authors (Komacek & Showman 2020; Beltz et al. 2022; Hindle et al. 2021) suggest that the coupling of ionised flow with the planetary magnetic fields can then lead to drastic changes in the 3D wind structure, sometimes entirely suppressing the super-rotating wind jet. A suppressed super-rotating wind jet results in a reduction of the cloud influx towards the dayside hemisphere and a disappearance of any hot-spot offset on such a highly irradiated planet.
Additionally, changes in the interior heat flux can also lead to fluctuations in the strength of the super-rotating wind jet and thus the morning cloud and hot spot shift (Carone et al. 2020; Schneider et al. 2022; Komacek et al. 2022). Thus, a combination of magnetic field interactions and possible interior effects can lead to variations in the occultation depth, as the hot spot is shifted more or less away from the substellar point, and in the planet’s albedo, due to the accompanying morning cloud variability.
Next to the low S/N, distinguishing between reflection and emission in the TESS band is difficult as it is impractical to incorporate two degenerate phase amplitude terms to account for reflection and emission separately. Therefore, a single phase offset term would have to account for both the individual phase variations. A phase offset consistent with zero can still involve super-rotating jets accompanied by morning cloud because of the complementarity of the reflection bright spot and the emissive hot spot in the phase curve. Compared to TESS, the CHEOPS occultations are more sensitive towards the reflected stellar light that accounts for around three-fourths of the total planetary optical dayside flux (Fig. 5 inset). While CHEOPS data cover occultations only and are thus not well suited to deriving phase curve peak offsets, the object might possess a phase offset in the optical due to enhanced reflection from clouds near the dayside terminator. Future high-precision phase curves of KELT-20 b at bluer wavelengths can shed more light onto this aspect.
Unlike HAT-P-7 b (Armstrong et al. 2016), the variability in the occultation depth cannot be attributed to super-granulation in the host-star (Lally & Vanderburg 2022). Because KELT-20 is an A dwarf star, it does not possess a convective layer, and as a result it is less likely that it exhibits granulation signatures. Thus, KELT-20 b is ideally amenable to study 3D weather and variability due to interactions between a highly ionised day side and the planetary magnetic field.
5.4 Spin–orbit alignment
Our gravity-darkening analysis (Sect. 3.2, Table 3) confirms the previous Doppler tomography measurements (Table 5) that KELT-20 b orbits in a plane that is misaligned from the stellar equatorial plane by at most a few degrees. As Barnes et al. (2011) point out, there is a four-way degeneracy in the value of λ obtained from gravity-darkened transits; we must rely on the Doppler tomography results to exclude the retrograde solutions.
We see no evidence for nodal precession in KELT-20 unlike in the Kepler-13 (Szabó et al. 2012, 2020) and WASP-33 (Johnson et al. 2015; Watanabe et al. 2022; Stephan et al. 2022) systems, for instance, where the nodal precession is fast enough to cause measurable changes in the impact parameter of the transits over a relatively short baseline. This is in line with theoretical expectations (Iorio 2011) given that the KELT-20 system has a near-zero obliquity.
Comparison of the sky-projected obliquity values.
6 Conclusion
In this work, we present a detailed optical picture of the KELT-20 system. Using CHEOPS observations of five transits and seven occultations of KELT-20 b, as well as four Sectors worth of TESS data, we obtained a precise planetary radius along with a more than 3 σ detection of the planet’s obliquity and constraints on the star–planet alignment. The CHEOPS photometry found an aligned orbit for KELT-20 b, which is in contrast to previous CHEOPS studies that have found strongly inclined orbits for planets orbiting other A-type stars (Lendl et al. 2020; Hooton et al. 2022; Deline et al. 2022). At the same time, we also probed the atmospheric properties of this UHJ.
We used the emission spectrum obtained with HST and Spitzer from the literature to provide a picture of the UHJ dayside thermal profile. We confirmed the observation of temperature inversion in the atmosphere of KELT-20 b. Additionally, with the help of TESS photometry in synergy with CHEOPS we provide strong constraints on the geometric albedo at 0.26 ± 0.04 and the dayside brightness temperature at 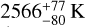 . The high geometric albedo corroborates a known trend of strongly irradiated planets being more reflective. Such a combination of the Ag − Tday pair results in a reflection emission contribution of 3:1 and 1:1 to the occultation depth for CHEOPS and TESS, respectively. This further leads to informative constraints on the planetary bond albedo and the heat re-circulation efficiency. The day side is too hot to form clouds, and therefore the precise nature of the high geometric albedo could either be attributed to strong scattering by atoms or ions on the day side or by reflective clouds around the planet’s terminator. We explored the possible scenarios of cloud reflections.
. The high geometric albedo corroborates a known trend of strongly irradiated planets being more reflective. Such a combination of the Ag − Tday pair results in a reflection emission contribution of 3:1 and 1:1 to the occultation depth for CHEOPS and TESS, respectively. This further leads to informative constraints on the planetary bond albedo and the heat re-circulation efficiency. The day side is too hot to form clouds, and therefore the precise nature of the high geometric albedo could either be attributed to strong scattering by atoms or ions on the day side or by reflective clouds around the planet’s terminator. We explored the possible scenarios of cloud reflections.
The high precision of the CHEOPS occultations also reveals signs of variability in the occultation depth, suggesting variable brightness of the planetary day side. As CHEOPS measurements are dominated by reflected light, the temporal variability in occultation depth could be attributed to variations in the extent of advected nightside clouds onto the planetary limbs (see e.g. Helling et al. 2021; Adams et al. 2022 for a discussion on the impact of clouds at the limbs of hot Jupiters and how these may affect dayside albedos). These authors note, however, that their simple model cannot address the variations seen to date. Thus, clearly more work is needed to investigate the precise origin of the variations that our CHEOPS measurements revealed. A combination of magnetic field interactions and possible interior feedback can also lead to such a variation. Spectroscopic occultation or phase curve observations of KELT-20 b especially in the UV/FUV will shed more light on the magnitude and nature of reflective sources in this UHJ. While spectroscopic observations in the infrared can shed more light on the energy budget and the physical processes governing this planet, making it ideally suited for follow-up observations with HST, JWST, and eventually Ariel.
Acknowledgments
Acknowledgements.
CHEOPS is an ESA mission in partnership with Switzerland with important contributions to the payload and the ground segment from Austria, Belgium, France, Germany, Hungary, Italy, Portugal, Spain, Sweden, and the UK. The CHEOPS Consortium would like to gratefully acknowledge the support received by all the agencies, offices, universities, and industries involved. Their flexibility and willingness to explore new approaches were essential to the success of this mission. CHEOPS data analysed in this article will be made available in the CHEOPS mission archive (https://cheops.unige.ch/archive_browser/). V.Si., G.Sc., G.Br., I.Pa., L.Bo., V.Na., G.Pi., R.Ra., and T.Zi. acknowledge support from CHEOPS ASI-INAF agreement no. 2019-29-HH.0. The author acknowledges the support of Prof. Kevin Heng for his comprehensive discussions on atmospheres of exoplanets during the early days of CHEOPS. P.E.C. is funded by the Austrian Science Fund (FWF) Erwin Schroedinger Fellowship, program J4595-N. M.L. acknowledges support of the Swiss National Science Foundation under grant number PCEFP2_194576. This work was also partially supported by a grant from the Simons Foundation (PI Queloz, grant number 327127). S.G.S. acknowledges support from FCT through FCT contract no. CEECIND/00826/2018 and POPH/FSE (EC). A.Br. was supported by the SNSA. L.Ca. and C.He. acknowledge support from the European Union H2020-MSCA-ITN-2019 under Grant Agreement no. 860470 (CHAMELEON). T.Wi. acknowledges support from the UKSA and the University of Warwick. This work was supported by FCT – Fundação para a Ciência e a Tecnologia through national funds and by FEDER through COMPETE2020 through the research grants UIDB/04434/2020, UIDP/04434/2020, 2022.06962.PTDC. O.D.S.D. is supported in the form of work contract (DL 57/2016/CP1364/CT0004) funded by national funds through FCT. N.C.Sa. acknowledges funding by the European Union (ERC, FIERCE, 101052347). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. Y.Al. acknowledges support from the Swiss National Science Foundation (SNSF) under grant 200020_192038. R.Al., D.Ba., E.Pa., and I.Ri. acknowledge financial support from the Agencia Estatal de Investigación of the Ministerio de Ciencia e Innovación MCIN/AEI/10.13039/501100011033 and the ERDF “A way of making Europe” through projects PID2019-107061GB-C61, PID2019-107061GB-C66, PID2021-125627OB-C31, and PID2021-125627OB-C32, from the Centre of Excellence “Severo Ochoa” award to the Instituto de Astrofísica de Canarias (CEX2019-000920-S), from the Centre of Excellence “María de Maeztu” award to the Institut de Ciències de l’Espai (CEX2020-001058-M), and from the Generalitat de Catalunya/CERCA programme. S.C.C.B. acknowledges support from FCT through FCT contracts nr. IF/01312/2014/CP1215/CT0004. X.B., S.C., D.G., M.F. and J.L. acknowledge their role as ESA-appointed CHEOPS science team members. C.Br. and A.Si. acknowledge support from the Swiss Space Office through the ESA PRODEX program. A.C.C. acknowledges support from STFC consolidated grant numbers ST/R000824/1 and ST/V000861/1, and UKSA grant number ST/R003203/1. This project was supported by the CNES. The Belgian participation to CHEOPS has been supported by the Belgian Federal Science Policy Office (BELSPO) in the framework of the PRODEX Program, and by the University of Liège through an ARC grant for Concerted Research Actions financed by the Wallonia-Brussels Federation. L.D. is an F.R.S.-FNRS Postdoctoral Researcher. B.-O.D. acknowledges support from the Swiss State Secretariat for Education, Research and Innovation (SERI) under contract number MB22.00046. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (project FOUR ACES. grant agreement no. 724427). It has also been carried out in the frame of the National Centre for Competence in Research PlanetS supported by the Swiss National Science Foundation (SNSF). D.E. acknowledges financial support from the Swiss National Science Foundation for project 200021_200726. M.F. and C.M.P. gratefully acknowledge the support of the Swedish National Space Agency (DNR 65/19, 174/18). D.G. gratefully acknowledges financial support from the CRT foundation under Grant No. 2018.2323 “Gaseousor rocky? Unveiling the nature of small worlds”. M.G. is an F.R.S.-FNRS Senior Research Associate. M.N.G. is the ESA CHEOPS Project Scientist and Mission Representative, and as such also responsible for the Guest Observers (GO) Programme. M.N.G. does not relay proprietary information between the GO and Guaranteed Time Observation (GTO) Programmes, and does not decide on the definition and target selection of the GTO Programme. S.H. gratefully acknowledges CNES funding through the grant 837319. K.G.I. is the ESA CHEOPS Project Scientist and is responsible for the ESA CHEOPS Guest Observers Programme. She does not participate in, or contribute to, the definition of the Guaranteed Time Programme of the CHEOPS mission through which observations described in this paper have been taken, nor to any aspect of target selection for the programme. K.W.F.L. was supported by Deutsche Forschungsgemeinschaft grants RA714/14-1 within the DFG Schwerpunkt SPP 1992, Exploring the Diversity of Extrasolar Planets. This work was granted access to the HPC resources of MesoPSL financed by the Region Ile de France and the project Equip@Meso (reference ANR-10-EQPX-29-01) of the programme Investissements d’Avenir supervised by the Agence Nationale pour la Recherche. P.M. acknowledges support from STFC research grant number ST/M001040/1. Gy.M.Sz. acknowledges the support of the Hungarian National Research, Development and Innovation Office (NKFIH) grant K-125015, a PRODEX Experiment Agreement No. 4000137122, the Lendület LP2018-7/2021 grant of the Hungarian Academy of Science and the support of the city of Szombathely. V.V.G. is an F.R.S-FNRS Research Associate. N.A.W. acknowledges UKSA grant ST/R004838/1. This paper includes data collected by the TESS mission. Funding for the TESS mission is provided by the NASA’s Science Mission Directorate.
Appendix A CHEOPS observations of KELT-20 b
 |
Fig. A.1 Individual CHEOPS transits (left) and occultations (right) of KELT-20 b. The solid red line is the best-fit model, while the blue and light blue points represent the binned and unbinned light curves, respectively. The numbers in the figure represent the BJD time stamp of individual transit epochs. The residuals are shown in the bottom panel. |
 |
Fig. A.2 Occultation depth measurements of KELT-20 b of the seven CHEOPS observations. The three sets of measurements correspond to the three data extraction techniques discussed in Sect. 2 |
Best-fit parameters of the individual transit fits of KELT-20 b
Appendix B TESS observations of KELT-20b
TESS: Best-fit transit and phase curve free parameters of KELT-20 b.
 |
Fig. B.1 Individual transits of KELT-20 b observed with TESS. The solid red line is the best-fit model, while the blue and light blue points represent the binned and unbinned light curves respectively. The numbers represent the BJD time stamp of individual transit epochs. The residuals are shown in the bottom panel. Left: All transits of sectors 14. Right: All transits of sector 40. |
 |
Fig. B.3 Individual sector-wise TESS phase curves of KELT-20b. The variation in the occultation depth is somewhat apparent between Sectors 40 and 41. The sector-wise occultation depths are |
 |
Fig. B.4 Posteriors of the model that includes the phase offset and the nightside flux as free parameters for TESS Sector 40. Δϕ varies between 0 and 1 (360°). Both Anight and Δϕ are consistent with zero, and the occultation depth measurement is the same as that measured when they are fixed to zero (see Table B.1). |
Appendix C Derived parameters
 |
Fig. C.1 Posterior distributions for our KELT-20b atmospheric retrievals constrained by the NIR occultations (HST and Spitzer, blue) and the NIR+TESS occultations (red). The reported values at the top of each marginal posterior denote the median of the distribution and the boundaries of the central 68% percentile (i.e. the 1σ credible intervals). The shaded areas in the marginal histograms denote the span of the credible intervals. |
 |
Fig. C.2 Posterior distribution of the CHEOPS and TESS eclipse depths in ppm along with the planetary fit parameters Rp/R★ [%] and a/R★ from the light curve fitting are used to create the posteriors on the dayside brightness temperature and geometric albedo (for reference, see Sect. 5). |
References
- Adams, D. J., Kataria, T., Batalha, N. E., Gao, P., & Knutson, H. A. 2022, ApJ, 9r26, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Armstrong, D. J., de Mooij, E., Barstow, J., et al. 2016, Nat. Astron., 1, 0004 [Google Scholar]
- Barbier, H., & López, E. 2021, Rev. Mex. Astron. Astrofis., 57, 123 [NASA ADS] [Google Scholar]
- Barnes, J. W., Linscott, E., & Shporer, A. 2011, ApJS, 197, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Beltz, H., Rauscher, E., Roman, M. T., & Guilliat, A. 2022, AJ, 163, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W., Broeg, C., Fortier, A., et al. 2021, Exp. Astron., 51, 109 [Google Scholar]
- Bertocco, S., Goz, D., Tornatore, L., et al. 2020, ASP Conf. Ser., 527, 303 [NASA ADS] [Google Scholar]
- Bond, G. P. 1861, MNRAS, 21, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfanti, A., Delrez, L., Hooton, M. J., et al. 2021, A&A, 646, A157 [EDP Sciences] [Google Scholar]
- Borsa, F., Giacobbe, P., Bonomo, A. S., et al. 2022, A&A, 663, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borysow, A. 2002, A&A, 390, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borysow, A., Jorgensen, U. G., & Fu, Y. 2001, J. Quant. Spec. Radiat. Transf., 68, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Brandeker, A., Heng, K., Lendl, M., et al. 2022, A&A, 659, A4 [Google Scholar]
- Burnham, K. P., & Anderson, D. R. 1998, in Model Selection and Inference (Springer), 75 [CrossRef] [Google Scholar]
- Burrows, A., Marley, M. S., & Sharp, C. M. 2000, ApJ, 531, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Carone, L., Baeyens, R., Mollière, P., et al. 2020, MNRAS, 496, 3582 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, J. A., & Winn, J. N. 2009, ApJ, 704, 51 [Google Scholar]
- Casasayas-Barris, N., Pallé, E., Yan, F., et al. 2018, A&A, 616, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casasayas-Barris, N., Pallé, E., Yan, F., et al. 2019, A&A, 628, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casasayas-Barris, N., Pallé, E., Yan, F., et al. 2020, A&A, 640, C6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, IAU Symp., 210, A20 [Google Scholar]
- Coles, P. A., Yurchenko, S. N., & Tennyson, J. 2019, MNRAS, 490, 4638 [CrossRef] [Google Scholar]
- Cont, D., Yan, F., Reiners, A., et al. 2022, A&A, 657, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowan, N. B., & Agol, E. 2011, ApJ, 729, 54 [Google Scholar]
- Csizmadia, S. 2020, MNRAS, 496, 4442 [Google Scholar]
- Csizmadia, S., Smith, A. M. S., Kálmán, S., et al. 2023, A&A, 675, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cubillos, P. E. 2017, ApJ, 850, 32 [CrossRef] [Google Scholar]
- Cubillos, P. E., & Blecic, J. 2021, MNRAS, 505, 2675 [NASA ADS] [CrossRef] [Google Scholar]
- Cubillos, P., Harrington, J., Loredo, T. J., et al. 2017, AJ, 153, 3 [Google Scholar]
- Deline, A., Hooton, M. J., Lendl, M., et al. 2022, A&A, 659, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ehrenreich, D., Delrez, L., Akinsanmi, B., et al. 2023, A&A, 671, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Esteves, L. J., De Mooij, E. J. W., & Jayawardhana, R. 2013, ApJ, 772, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Esteves, L. J., De Mooij, E. J. W., & Jayawardhana, R. 2015, ApJ, 804, 150 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Fu, G., Sing, D. K., Lothringer, J. D., et al. 2022, ApJ, 925, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gibson, N. P., Aigrain, S., Roberts, S., et al. 2012, MNRAS, 419, 2683 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
- Guillot, T. 2010, A&A, 520, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanel, R. A., Conrath, B. J., Jennings, D. E., & Samuelson, R. E. 2003, Exploration of the Solar System by Infrared Remote Sensing: Second Edition (Cambridge University Press) [CrossRef] [Google Scholar]
- Hargreaves, R. J., Gordon, I. E., Rey, M., et al. 2020, ApJS, 247, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, G. J., Tennyson, J., Kaminsky, B. M., Pavlenko, Y. V., & Jones, H. R. A. 2006, MNRAS, 367, 400 [Google Scholar]
- Harris, G. J., Larner, F. C., Tennyson, J., et al. 2008, MNRAS, 390, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Hawthorn, F., Bayliss, D., Wilson, T. G., et al. 2023, MNRAS, 520, 3649 [NASA ADS] [CrossRef] [Google Scholar]
- Helling, C., Lewis, D., Samra, D., et al. 2021, A&A, 649, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helling, C., Samra, D., Lewis, D., et al. 2023, A&A, 671, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hindle, A. W., Bushby, P. J., & Rogers, T. M. 2021, ApJ, 916, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeijmakers, H. J., Cabot, S. H. C., Zhao, L., et al. 2020a, A&A, 641, A120 [EDP Sciences] [Google Scholar]
- Hoeijmakers, H. J., Seidel, J. V., Pino, L., et al. 2020b, A&A, 641, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hooton, M. J., de Mooij, E. J. W., Watson, C. A., et al. 2019, MNRAS, 486, 2397 [NASA ADS] [CrossRef] [Google Scholar]
- Hooton, M. J., Hoyer, S., Kitzmann, D., et al. 2022, A&A, 658, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoyer, S., Guterman, P., Demangeon, O., et al. 2020, A&A, 635, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoyer, S., Bonfanti, A., Leleu, A., et al. 2022, A&A, 668, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iorio, L. 2011, MNRAS, 411, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, B., Adams, E., Sandidge, W., Kreyche, S., & Briggs, J. 2019, AJ, 157, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, SPIE Conf. Ser., 9913, 99133E [Google Scholar]
- Johnson, M. C., Cochran, W. D., Collier Cameron, A., & Bayliss, D. 2015, ApJ, 810, L23 [Google Scholar]
- Jones, K., Morris, B. M., Demory, B. O., et al. 2022, A&A, 666, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kálmán, S., Bokon, A., Derekas, A., et al. 2022, A&A, 660, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kilpatrick, B. M., Kataria, T., Lewis, N. K., et al. 2020, AJ, 159, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 435, 2152 [Google Scholar]
- Komacek, T. D., & Showman, A. P. 2020, ApJ, 888, 2 [Google Scholar]
- Komacek, T. D., Gao, P., Thorngren, D. P., May, E. M., & Tan, X. 2022, ApJ, 941, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Krenn, A. F., Lendl, M., Patel, J. A., et al. 2023, A&A, 672, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. L. 1970, SAO Special Report, 309 [Google Scholar]
- Lally, M., & Vanderburg, A. 2022, AJ, 163, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Lendl, M., Csizmadia, S., Deline, A., et al. 2020, A&A, 643, A94 [EDP Sciences] [Google Scholar]
- Li, G., Gordon, I. E., Rothman, L. S., et al. 2015, ApJS, 216, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Lightkurve Collaboration (Cardoso, J. V. d. M., et al.) 2018, Astrophysics Source Code Library [record ascl:1812.813] [Google Scholar]
- Loeb, A., & Gaudi, B. S. 2003, ApJ, 588, L117 [Google Scholar]
- Lund, M. B., Rodriguez, J. E., Zhou, G., et al. 2017, AJ, 154, 194 [Google Scholar]
- Mallama, A. 2017, ArXiv e-prints [arXiv:1783.82678] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [Google Scholar]
- Maxted, P. F. L., Ehrenreich, D., Wilson, T. G., et al. 2022, MNRAS, 514, 77 [NASA ADS] [CrossRef] [Google Scholar]
- McKemmish, L. K., Yurchenko, S. N., & Tennyson, J. 2016, MNRAS, 463, 771 [NASA ADS] [CrossRef] [Google Scholar]
- McKemmish, L. K., Masseron, T., Hoeijmakers, H. J., et al. 2019, MNRAS, 488, 2836 [Google Scholar]
- Mislis, D., Heller, R., Schmitt, J. H. M. M., & Hodgkin, S. 2012, A&A, 538, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morris, S. L. 1985, ApJ, 295, 143 [Google Scholar]
- Morris, B. M., Delrez, L., Brandeker, A., et al. 2021, A&A, 653, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nugroho, S. K., Gibson, N. P., de Mooij, E. J. W., et al. 2020, MNRAS, 496, 504 [Google Scholar]
- Pagano, I., Scandariato, G., Singh, V., et al. 2024, A&A, 682, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parviainen, H., & Aigrain, S. 2015, MNRAS, 453, 3821 [Google Scholar]
- Parviainen, H., Wilson, T. G., Lendl, M., et al. 2022, A&A, 668, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patel, J. A., & Espinoza, N. 2022, AJ, 163, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Pepper, J., Stassun, K. G., & Gaudi, B. S. 2018, in Handbook of Exoplanets, eds. H. J. Deeg, & J. A. Belmonte (Berlin: Springer), 128 [Google Scholar]
- Polyansky, O. L., Kyuberis, A. A., Zobov, N. F., et al. 2018, MNRAS, 480, 2597 [NASA ADS] [CrossRef] [Google Scholar]
- Rainer, M., Borsa, F., Pino, L., et al. 2021, A&A, 649, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rasmussen, C. E., & Williams, C. K. I. 2006, Gaussian Processes for Machine Learning (The MIT Press) [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, SPIE Conf. Ser., 9143, 914320 [Google Scholar]
- Rothman, L. S., Gordon, I. E., Barber, R. J., et al. 2010, J. Quant. Spec. Radiat. Transf., 111, 2139 [NASA ADS] [CrossRef] [Google Scholar]
- Santerne, A., Bonomo, A. S., Hébrard, G., et al. 2011, A&A, 536, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scandariato, G., Singh, V., Kitzmann, D., et al. 2022, A&A, 668, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, A. D., Carone, L., Decin, L., Jørgensen, U. G., & Helling, C. 2022, A&A, 666, A11 [Google Scholar]
- Schwartz, J. C., & Cowan, N. B. 2015, MNRAS, 449, 4192 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S. 2010, Exoplanets (Tucson, AZ: University of Arizona Press) [Google Scholar]
- Singh, V., Bonomo, A. S., Scandariato, G., et al. 2022, A&A, 658, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, J. C., Stumpe, M. C., Van Cleve, J. E., et al. 2012, PASP, 124, 1000 [Google Scholar]
- Snellen, I. A. G., Stuik, R., Navarro, R., et al. 2012, SPIE Conf. Ser., 8444, 84440I [NASA ADS] [Google Scholar]
- Stangret, M., Casasayas-Barris, N., Pallé, E., et al. 2020, A&A, 638, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stephan, A. P., Wang, J., Cauley, P. W., et al. 2022, ApJ, 931, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Stumpe, M. C., Smith, J. C., Van Cleve, J. E., et al. 2012, PASP, 124, 985 [Google Scholar]
- Stumpe, M. C., Smith, J. C., Catanzarite, J. H., et al. 2014, PASP, 126, 100 [Google Scholar]
- Szabó, G. M., Pal, A., Derekas, A., et al. 2012, MNRAS, 421, L122 [CrossRef] [Google Scholar]
- Szabó, G. M., Pribulla, T., Pál, A., et al. 2020, MNRAS, 492, L17 [CrossRef] [Google Scholar]
- Taffoni, G., Becciani, U., Garilli, B., et al. 2020, ASP Conf. Ser., 527, 307 [NASA ADS] [Google Scholar]
- Talens, G. J. J., Justesen, A. B., Albrecht, S., et al. 2018, A&A, 612, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, N., Narita, N., Palle, E., et al. 2022, MNRAS, 512, 4404 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, J., Gibson, N. P., Lothringer, J. D., et al. 2021, MNRAS, 503, 4787 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. G., Goffo, E., Alibert, Y., et al. 2022, MNRAS, 511, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, I., Kitzmann, D., Shporer, A., et al. 2021, AJ, 162, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, I., Shporer, A., Vissapragada, S., et al. 2022, AJ, 163, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, F., Reiners, A., Pallé, E., et al. 2022, A&A, 659, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yurchenko, S. N. 2015, J. Quant. Spec. Radiat. Transf., 152, 28 [NASA ADS] [CrossRef] [Google Scholar]
Telescope response functions were obtained from the SVO filter profile service: http://svo2.cab.inta-csic.es/theory/fps/
Seager (2010) uses the same formulation for the equilibrium temperature of the day side. The effective temperature is the equilibrium temperature if the heat flux from the planet’s interior is negligible. They are used interchangeably in the literature.
All Tables
Best-fit model and derived parameters of the transit, occultation, and phase curve fit.
All Figures
 |
Fig. 1 CHEOPS light curve. Left: detrended and phase-folded planetary transits. The solid red line is the best-fit model, while the blue dots represent the phase-folded and binned photometry (interval: 2.25 min for transit, 7.5 min for occultation). The residuals are shown in the bottom panel. Right: same as in the left panel, but centred at the occultations. |
| In the text | |
 |
Fig. 2 TESS light curve. Left: detrended and phase-folded planetary transits from Sectors 14, 40, 41, and 54. The solid red line is the best-fit model, while the blue dots represent the phase-folded and binned photometry (Interval: 2.25 min for transit, 25 min for phase curve). The residuals are shown in the bottom panel. Right: combined phase curve using photometry from all four sectors. |
| In the text | |
 |
Fig. 3 Best-fit occultation depths of individual CHEOPS visits (blue) along with their posteriors in the right panel. The horizontal solid and dashed lines represent the mean occultation depth of 82.4 ± 5.6 ppm. The green shaded regions indicate the span of the TESS Sectors 40, 41, and 54, while the brown points indicate the sector-wise occultation depths. |
| In the text | |
 |
Fig. 4 Left: KELT-20 b observed occultation depths (grey markers). The curve at the bottom shows the through-puts for each data point. The solid curves show the median of the retrieved model distributions when fitting the NIR HST and Spitzer occultations (blue) and the NIR+TESS occultations (red). The shaded areas (in corresponding colours) denote the span of the 68% central percentile of the distributions. The dashed grey curves show spectra for two black-body planetary model spectra at 2300 and 3200 K. Top right: retrieved temperature profiles (same colour-coding as before). The curves at the left edge show the contribution functions for selected bands (see legend). Bottom right: contribution functions integrated over the CHEOPS and TESS bands for the two cases shown in the left panel and for retrievals without TiO and VO opacity (same colour-coding as above). The band-integrated thermal flux in CHEOPS and TESS bands are (36 ± 18 ppm) and (85 ± 38 ppm), respectively (coloured markers). |
| In the text | |
 |
Fig. 5 Dayside reflection and emission brightness contributions. Left: geometric albedo (Ag) as a function of the dayside brightness temperature for the estimated occultation depths in CHEOPS (blue) and TESS (red). The decreasing intensity of the colour shades corresponds to the 1 σ, 2 σ, and 3 σ uncertainties in the computation of Ag for each Tday. The overlapping region provides the true constraints on the two parameters represented by the posterior distribution in grey. The individual posteriors of (Ag) and (Tday) are presented in the side panels. The resultant values are reported in the text. Subpanel: reflection and emission contributions to the occultation depth of the CHEOPS and TESS passbands. The identical height of the reflection component reflects the assumption of α = 1. Right: Kurucz stellar model [Teff = 9000, [Fe/H] = 0 and log = 4.5] along with the CHEOPS and TESS passband responses. The dayside planetary black-body flux (×100) is also plotted for a comparison with the stellar flux. Tday = 2600 K. |
| In the text | |
 |
Fig. 6 Ag–Tday of several hot Jupiters following Wong et al. (2021). The black circles (Kepler–CoRoT) and the green squares (TESS) are taken directly from their sample. The blue diamonds correspond to the published values of the CHEOPS hot Jupiters (Krenn et al. 2023; Brandeker et al. 2022; Scandariato et al. 2022; Pagano et al. 2024; Hooton et al. 2022; Deline et al. 2022). The red diamond is from this work on KELT-20 b. |
| In the text | |
 |
Fig. 7 Parameters determining planetary energy distribution under radiative equilibrium. Top right: Bond albedo plotted as a function of the heat re-circulation efficiency for the effective dayside temperature Td. Bottom left: respective posteriors of AB and ϵ from the overlapping region, which are then used to compute the nightside temperature. The values in the label correspond to the orange posteriors, while the light blue posteriors are shown only for comparison. |
| In the text | |
 |
Fig. A.1 Individual CHEOPS transits (left) and occultations (right) of KELT-20 b. The solid red line is the best-fit model, while the blue and light blue points represent the binned and unbinned light curves, respectively. The numbers in the figure represent the BJD time stamp of individual transit epochs. The residuals are shown in the bottom panel. |
| In the text | |
 |
Fig. A.2 Occultation depth measurements of KELT-20 b of the seven CHEOPS observations. The three sets of measurements correspond to the three data extraction techniques discussed in Sect. 2 |
| In the text | |
 |
Fig. B.1 Individual transits of KELT-20 b observed with TESS. The solid red line is the best-fit model, while the blue and light blue points represent the binned and unbinned light curves respectively. The numbers represent the BJD time stamp of individual transit epochs. The residuals are shown in the bottom panel. Left: All transits of sectors 14. Right: All transits of sector 40. |
| In the text | |
 |
Fig. B.2 Same as in Fig. B.1, but for sectors 41 and 54. |
| In the text | |
 |
Fig. B.3 Individual sector-wise TESS phase curves of KELT-20b. The variation in the occultation depth is somewhat apparent between Sectors 40 and 41. The sector-wise occultation depths are |
| In the text | |
 |
Fig. B.4 Posteriors of the model that includes the phase offset and the nightside flux as free parameters for TESS Sector 40. Δϕ varies between 0 and 1 (360°). Both Anight and Δϕ are consistent with zero, and the occultation depth measurement is the same as that measured when they are fixed to zero (see Table B.1). |
| In the text | |
 |
Fig. C.1 Posterior distributions for our KELT-20b atmospheric retrievals constrained by the NIR occultations (HST and Spitzer, blue) and the NIR+TESS occultations (red). The reported values at the top of each marginal posterior denote the median of the distribution and the boundaries of the central 68% percentile (i.e. the 1σ credible intervals). The shaded areas in the marginal histograms denote the span of the credible intervals. |
| In the text | |
 |
Fig. C.2 Posterior distribution of the CHEOPS and TESS eclipse depths in ppm along with the planetary fit parameters Rp/R★ [%] and a/R★ from the light curve fitting are used to create the posteriors on the dayside brightness temperature and geometric albedo (for reference, see Sect. 5). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.