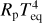EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 682 (February 2024) A&A, 682 (2024) A66 Full HTML
Open Access
Issue
A&A
Volume 682, February 2024
Article Number A66
Number of page(s) 28
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202348180
Published online 06 February 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

M dwarfs are the most common stars in the Universe (e.g. Bastian et al. 2010). Because of their low mass and small radius, they are quite attractive in the domain of exoplanetology: it is easier to detect low-mass planets with the transit method (e.g. Winn 2010) and the radial velocity (RV) technique (e.g. Hatzes 2016). In addition, the habitable zone (HZ; Kasting et al. 1993; Kopparapu et al. 2013) around M dwarfs is located closer to the host star than in stars of earlier spectral type, and therefore, it is more likely that planets in the habitable zone (HZ) of M dwarfs are found because both the transit method and the RV technique preferentially detect close-in planets.

A few mechanisms may act against the possibility that M dwarfs harbour life, such as their strong magnetic activity (e.g. Saar & Linsky 1985; Reiners et al. 2009; Shulyak et al. 2019), accompanied by flares and high-energy emission that induce atmospheric escape (e.g. Luger & Barnes 2015; Tilley et al. 2019), or the likely scenario of tidally locked close-in exoplanets that lead to extreme surface temperature gradients (e.g. Barnes 2017). However, different works highlighted ways in which planets might be able to become and remain habitable despite the unfavourable stellar environment (Kay et al. 2016; Sergeev et al. 2020; Childs et al. 2022; Ojha et al. 2022; Lobo et al. 2023).

The first exoplanet discovered around an M dwarf is GJ 876 b. This Jovian-mass planet was independently detected via the RV technique by Delfosse et al. (1998) and Marcy et al. (1998). Subsequent studies have also revealed smaller exoplanets (e.g. GJ 436 b; Butler et al. 2004; Gillon et al. 2007) or multiplanet systems containing Neptune-sized planets and super-Earths, such as GJ 581 (Bonfils et al. 2005; Udry et al. 2007). Since then, the search for exoplanets orbiting M dwarfs has been rather prolific; the community has never lost interest in M-dwarf exoplanets, as proven by several recent discoveries, such as TOI-244 b (Castro-Gonzalez et al. 2023), TOI-715 b (Dransfield et al. 2024), K2-416 b and K2-417 b (Incha et al. 2023), TOI-3785 b (Powers et al. 2023), TOI-3984 A b and TOI-5293 A b (Cañas et al. 2023), TOI-1680 b (Ghachoui et al. 2023), and TOI-2084 b and TOI-4184 b (Barkaoui et al. 2023).

In this work, we characterise TOI-732. This M dwarf is orbited by an ultrashort-period planet (TOI-732 b, P ~ 0.77 day) and an outer planet (TOI-732 c, P ~ 12.25 d). The system has been studied by Cloutier et al. (2020, hereafter C20), Nowak et al. (2020, hereafter N20), and Luque & Pallé (2022, hereafter L22). We add a new TESS (Transiting Exoplanet Survey Satellite; Ricker et al. 2015) sector, 25 novel space-based light curves (LCs) observed by CHEOPS (Characterising Exoplanet Satellite; Benz et al. 2021), and 39 RV data points taken with the high-precision echelle spectrograph MAROON-X (Seifahrt et al. 2018, 2022) to the already published data. Even with respect to the most recent analysis by L22, we almost doubled the number of space-based transit events, and we significantly increased the number of RV data points, which allowed us to significantly reduce the uncertainties in the planetary parameters.

From the point of view of planet formation and evolution, TOI-732 is an interesting system because the planets are located on the two opposite sides of the radius valley (Fulton et al. 2017). The paucity of exoplanets with orbital periods P < 100 days in the Rp 1.5–2.0 R⊕ radius range determines a bimodal Rp distribution that peaks at ~1.3 and ~2.4 R⊕ (e.g. Fulton et al. 2017; Fulton & Petigura 2018; Van Eylen et al. 2018). One interpretation of this distribution suggests that sub-Neptunes likely form with rocky cores with sizes 1.5 R⊕ or smaller, surrounded by an envelope with a low mean molecular weight that is subject to photo-evaporation (e.g. Lammer et al. 2003; Lopez & Fortney 2013; Owen & Wu 2013; Chen & Rogers 2016). However, atmospheric erosion may also be driven by cooling of rocky cores (core-powered mass loss; e.g. Ginzburg et al. 2018; Gupta & Schlichting 2019) and by energy release following cohesive giant impacts during proto-planet formation (impact erosion; e.g. Kegerreis et al. 2020). Finally, the smallest sub-Neptunes might also be the result of late formation within gas-depleted discs (gas-poor formation; e.g. Lee et al. 2014; Lee & Connors 2021; Lee et al. 2022).

These mechanisms that account for the radius valley assume that super-Earths and sub-Neptunes assembled from the same underlying population of dry rocky cores, which might or might not retain a H-He atmosphere. However, global planet formation models show that migration is a key mechanism delivering water-rich sub-Neptunes at short orbital periods (e.g. Alibert et al. 2013; Venturini et al. 2020; Emsenhuber et al. 2021), especially for low-mass planets around M dwarfs (Alibert 2017; Miguel et al. 2020; Burn et al. 2021). In particular, Venturini et al. (2020) showed that the radius valley emerges from a combination of formation and evolution processes that separate small rocky from larger water-rich- planets that formed beyond the ice line. Observational support for this scenario was recently found by L22, who studied a sub-sample of M-dwarf exoplanets and reported a clear density gap that separated super-Earths (identified as rocky planets) from mini-Neptunes (identified as water-ice-rich worlds and not as rocky cores surrounded by H-He). They also concluded that the radius dispersion, especially among puffy exoplanets, may be the consequence of the different accretion histories of H-He envelopes and not of the atmospheric mass loss.

Obtaining observational data is key to investigating the relative importance of the different formation and evolution scenarios. So far, most of the studies have investigated the nature of the radius valley by focusing on FGK stars (e.g. Van Eylen et al. 2018; MacDonald 2019; Martinez et al. 2019; Ho & Van Eylen 2023), while only a few works specifically drew attention to low-mass stars (Cloutier & Menou 2020; Van Eylen et al. 2021; Luque & Pallé 2022). The discoveries of M-dwarf systems in which planets straddle the radius gap have steadily increased. They comprise, for example, TOI-776 (Luque et al. 2021; Fridlund et al. 2024), TOI-1634 (Cloutier et al. 2021b; Hirano et al. 2021), TOI-270 (Van Eylen et al. 2021), TOI-1468 (Chaturvedi et al. 2022), K2-3 (Diamond-Lowe et al. 2022), TOI-2096 (Pozuelos et al. 2023), and LHS 1903 (Wilson et al. 2023). More generally, the parameters of planets orbiting low-mass stars are progressively known with increasingly better precision. This work therefore also aims at describing the characteristics of the radius valley better for planets orbiting M dwarfs.

This paper is organised as follows. Section 2 presents the stellar properties, Sects. 3 and 4 describe the photometric and RV data, that were used to characterise the system as explained in Sect. 5. Section 6 investigates the radius and density valleys of M-dwarf exoplanets from a quantitative perspective by using the most precise collection of planetary parameters available so far. Finally, Sect. 7 gathers our conclusions.

2 Host star properties

TOI-732 is an M4 V star (Scholz et al. 2005) located ~22 pc away from us (Gaia Collaboration 2023), with magnitudes V = 13.14 ± 0.04 (Zacharias et al. 2012) and K = 8.204 ± 0.021 (Cutri et al. 2003). It is part of a visual binary system, and its companion is known as LP 729-55 and is located at an angular separation θ = 15.81 ± 0.15″, which implies a projected orbital distance of 348 ± 3 AU (N20). LP 729-55 is fainter by ~2 K-band mag than TOI-732, and its spectral type has been estimated by N20 asM5.0 V.

To estimate the stellar effective temperature Teff and metal-licity [Fe/H] of TOI-732, we used the ODUSSEAS1 code (Antoniadis-Karnavas et al. 2020), and we input spectroscopic data taken from the ESO archive. Although we were able to combine data from ESPRESSO (Pepe et al. 2021) and HARPS (Mayor et al. 2003), we used the latter because it provided a higher signal-to-noise ratio (S/N) of the combined spectrum. ODUSSEAS uses the ridge regression (Hoerl & Kennard 1970) implemented via the machine-learning PYTHON package scikit-learn (Pedregosa et al. 2011), which is trained to measure the pseudo-equivalent widths of more than 4000 stellar absorption lines. Using a library of HARPS spectra for several M stars with well-defined reference parameters from interferometric calibrations (Antoniadis-Karnavas et al. in prep.), ODUSSEAS derived Teff = 3358 ± 92 K and [Fe/H] = 0.06 ± 0.11 dex. The trigonometric surface gravity was estimated using Teff and [Fe/H] in combination with the Gaia parallax (Gaia Collaboration 2023) and photometry, following the same procedure as described in Sousa et al. (2021), which yields log 𝑔 = 4.85 ± 0.11.

Because of the heavy line blending, the determination of the individual elemental abundances of M dwarfs from visible spectra is challenging (e.g. Maldonado et al. 2020). In this work, we estimated the abundance of Mg and Si following the procedure presented in Demangeon et al. (2021). In brief, we used the systemic radial velocity (RVsys), parallax (π), right ascension (α), declination (δ), and proper motions (µα and µδ) from Gaia DR3 (Gaia Collaboration 2023) to derive the Galactic space velocity UVW of TOI-732 via the GalVel_Pop.py routine2. We obtained U = 4.0 ± 0.1 km s−1, V = −10.3 ± 0.3 km s−1, and W = −27.5 ± 0.2 km s−1 with respect to the local standard of rest (LSR), adopting the solar peculiar motion from Schönrich et al. (2010). Based on these velocities, adopting the characteristic parameters of Galactic stellar populations from Reddy et al. (2006), and following Adibekyan et al. (2012), we estimated that the star belongs to the Galactic thin disc with a 97% probability. Then, from the APOGEE DR17 (Abdurro’uf et al. 2022), we selected cool stars with metallicities similar to that of TOI-732 that belong to the chemically defined Galactic thin disc. We obtained a sample of several thousand stars, for which we calculated the mean abundance of Mg and Si, and their standard deviation (star-to-star scatter). After taking the stellar metallic-ity into account, we obtained [Mg/H] = 0.04 ± 0.20 dex and [Si/H] = 0.02 ± 0.21 dex.

We computed the infrared flux method (IRFM; Blackwell & Shallis 1977) radius of TOI-732 using a modified Markov chain Monte Carlo (MCMC) approach (Schanche et al. 2020). We constructed spectral energy distributions (SEDs) by constraining stellar atmospheric models from three catalogues (Kurucz 1993; Castelli & Kurucz 2003; Allard 2014) with the results of our spectral analysis. From these, we calculated the stellar bolometric flux via comparison of synthetic and observed broadband photometry in the following bandpasses: Gaia G, GBP, and GRP, 2MASS J, H, and K, and WISE W1 and W2 (Gaia Collaboration 2023; Skrutskie et al. 2006; Wright et al. 2010). The bolometric flux was first converted into effective temperature and angular diameter and then into stellar radius using the offset-corrected Gaia parallax (Lindegren et al. 2021). The stellar atmospheric modelling uncertainties were accounted for by using a Bayesian modelling that averaged the radius posterior distributions. The complex spectral features of M-dwarfs can cause degeneracies in the strengths of molecular lines and thus in the bolometric flux computation within the MCMC when using different atmospheric models. This propagates to large errors on M-dwarf IRFM radii compared to using empirical relations (see C20 and N20). The consistency between our estimate and the outcomes in both C20 and N20 is well below 1 σ and therefore, we attributed the typical uncertainty to R★ as derived from empirical relations. We obtained R★ = 0.380 ± 0.012 R⊙.

We used Teff, [Fe/H], and R★ along with their error bars to then derive the stellar mass M★ from two different evolutionary models. In detail, we applied the isochrone placement algorithm (Bonfanti et al. 2015, 2016), which is designed to interpolate the set of input parameters within pre-computed grids of PARSEC3 v1.2S (Marigo et al. 2017) isochrones and tracks, and we obtained a first estimate for the mass. A second estimate was instead obtained via the Code Liègeois d’Évolution Stellaire (CLES; Scuflaire et al. 2008), which builds the best-fit evolutionary tracks on the fly following the Levenberg-Marquadt minimisation scheme (Salmon et al. 2021). As outlined in Bonfanti et al. (2021), the consistency of the two results is checked through a χ2-based criterion, after which the mass distributions inferred from the two different evolutionary models are merged together. We finally obtained 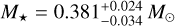M⋆=0.381−0.034+0.024M⊙${M_ \star } = 0.381_{ - 0.034}^{ + 0.024}{M_ \odot }$.

Both C20 and N20 have derived the stellar mass and obtained M★, C20 = 0.401 ± 0.012 M⊙ and M★, N20 = 0.379 ± 0.016 M⊙. These estimates are consistent with ours, but are more precise by a factor of ~2, but the uncertainties appear to be underestimated. In detail, C20 used the mass-luminosity relation from Benedict et al. (2016). Even considering the K-band luminosity, which yields the most satisfactory fit, the average root mean square (rms) of the residuals is 0.014 M⊙, which is larger than the reported estimate. Furthermore, the mass residuals in the neighbourhood of the TOI-732 absolute stellar magnitude (i.e. MK = 6.494 ± 0.021 mag) as displayed in Benedict et al. (2016, Fig. 23, right panel) are higher than the average value by about a factor of two. Instead, N20 used the mass-radius relation from Schweitzer et al. (2019), whose rms inherent to the fit is 0.02 M⊙. When the fit-related source of errors is accounted for, the uncertainties on M★ from both C20 and N20 become similar to ours. Therefore, our mass uncertainty is probably genuine and robust, also considering that it comes from evolutionary models employing different physical ingredients and was inferred using different derivation algorithms (see Bonfanti et al. 2021, for further details).

As is well known, M dwarfs evolve very slowly. Any age inference via isochrone fitting is therefore inconclusive. However, due to stellar interactions that manifest themselves as kinematic disturbances over the lifetimes of stars, we can estimate the stellar age based on kinematics alone (Wielen 1977; Nordström et al. 2004; Casagrande et al. 2011; Maciel et al. 2011). We used the method of Almeida-Fernandes & Rocha-Pinto (2018), which allows for age estimates based on kinematic-age probability distributions that were formalised and bench-marked using a sample of 9000 stars in the Geneva-Copenhagen Survey whose isochronal ages are known. For this study, we computed the age of TOI-732 using the Galactic U, V, and W velocities and Gaia DR3 Galactic reference coordinates (Gaia Collaboration 2023), and we obtained an age of 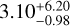3.10−0.98+6.20$3.10_{ - 0.98}^{ + 6.20}$ Gyr. All the relevant stellar parameters are reported in Table 1.

We further investigated the evolutionary stage of TOI-732 by computing the equivalent width (EW) of the Hα emission component, which has been related to the age of M dwarfs by Kiman et al. (2021). To this end, we used the HARPS and ESPRESSO combined spectra. Following the procedure described in Schmidt et al. (2015) and West et al. (2011), we calculated a Hα EW of 0.64 Å from the HARPS spectra and 0.52 Å from the ESPRESSO spectra.

Kiman et al. (2021) defined a boundary that separates active from inactive M dwarfs, which latter have an Hα EW below a colour-dependent threshold value. Given the G − GRP = 1.197 colour (Gaia Collaboration 2023) of TOI-732, the corresponding activity boundary is Hα-EWbound = 0.85 Å. Because both our Hα-EW estimates derived from HARPS and ESPRESSO are below the threshold value, TOI-732 can be categorised as inactive. Kiman et al. (2021) pointed out that inactive stars can be found at different evolutionary stages, and their age therefore cannot be well constrained in this way. However, they noted an increasing number of stars with low Hα EW as age increases. In particular, mid-M-type stars show a strong Hα decline after 1 Gyr, and TOI-732 is therefore likely to be older than one billion years, which is consistent with our kinematic age estimate.

A further indication for the evolutionary stage of TOI-732 may come from M-dwarf gyrochronology. Pass et al. (2022) found that M dwarfs usually start spinning down at about 2–3 Gyr. Given the Hα-based inactivity of TOI-732, it is likely that the star is older than the turning-point age of 2–3 Gyr, which again agrees with the stellar evolutionary stage we inferred from kinematics.

Table 1

Stellar properties.

3 Photometric data

Both C20 and N20 have performed a photometric analysis of the system based on one TESS sector and several observations taken with ground-based facilities (see Table 2). L22 used exclusively space-based observations instead, but added a second TESS sector for the photometric characterisation. In addition to using all the ground- and space-based data that were published in the literature, we added a significant number of space-based data as we benefited from a further TESS sector and collected 25 CHEOPS visits, 17 of which contain transit events, while the remaining 8 are short observations that were not time constrained (fillers) with the aim of monitoring stellar activity (see Table 3). Therefore, our photometric analysis is based on a total of ~140 transit events (spread over 132 different LCs), which enabled us to considerably improve the photometric properties of the system. All details of the available LCs are given below.

Table 2

Photometric observations from ground-based facilities.

3.1 TESS observations

The Transiting Exoplanet Survey Satellite (TESS, Ricker et al. 2015) observed the system in cycle 1 (Sector 8; from 28 February to 26 March 2019) in cycle 3 (Sector 35; from 9 February to 7 March 2021), and in cycle 5 (Sector 62; from 12 February to 10 March 2023). The data were downloaded from the Mikulski Archive for Space Telescopes (MAST)4, and we used the pre-search data conditioned simple aperture photometry (PDCSAP) LCs, as processed by the Science Processing Operation Center (SPOC; Jenkins et al. 2016).

After rejecting data with a poor-quality flag and performing a five median-absolute-deviation (MAD) clipping on the flux values to discard the outliers, we extracted the temporal windows that were centred on each transit event containing ~4 h of out-of-transit data both before and after the transit for detrending purposes. Following this procedure, we obtained 81 TESS LCs, 5 of which contain the transits of both planets because their transits are very close in time. Each LC lists the epoch of observation (t), the normalised PDCSAP flux with its uncertainty, and other parameters that are available from the TESS data products, such as MOM_CENTR 1, MOM_CENTR2 (hereafter denoted with x and y, respectively), and POS_CORR 1 and POS_CORR2 (hereafter denoted with dx and dy, respectively)5.

3.2 CHEOPS observations

The Characterising Exoplanet Satellite (CHEOPS, Benz et al. 2021) collected 25 LCs of TOI-732 from 8 January to 10 April 2022. Because nearby bright background stars strongly contaminate the aperture photometry, we opted to extract point-spread function (PSF) photometry using the PIPE package6 (Morris et al. 2021; Brandeker et al. 2022). The raw CHEOPS LCs are shown in Appendix A.

In addition to the parameters given by PIPE (i.e. the stellar flux and the x- and y-location of the target PSF centroid on the detector), we added a few more vectors to the information comprising the CHEOPS LCs that were to be used for the following data detrending. In detail, these vectors are produced by the default data reduction pipeline (DRP, Hoyer et al. 2020) v.13.1, and they are the spacecraft roll angle (roll), the flux due to contaminating background stars (conta), the smearing effect that is seen as trails on the CCD (smear), and the background flux (bg) due to zodiacal light, for example.

Among these data products, the stellar flux measured by CHEOPS usually exhibits a highly variable pattern against the roll angle (see e.g. Bonfanti et al. 2021, for a broader discussion about this topic). As our global LC+RV modelling (see Sect. 5.1) only accounts for polynomials when the time series is decorrelated, it would be hard to model the flux versus roll pattern. Therefore, after masking out the in-transit data points, we preliminary detrended the PIPE flux against roll angle via Gaussian processes (GPs; Rasmussen & Williams 2005) using a Matérn 3/2 kernel (Foreman-Mackey et al. 2017). We duly increased the error bars of the flux by adding the standard deviation of the GP model in quadrature.

Table 3

Details of the CHEOPS visits.

3.3 Ground-based observations

Several LCs taken with ground-based facilities from 2019 up to 2020 are available on the EXOFOP webpage7. In particular, we downloaded the data obtained with the following one-meter-class telescopes that are part of the Las Cumbres Observatory Global Telescope (LCOGT) network (Brown et al. 2013), which are located at the Cerro Tololo Inter-American Observatory (CTIO), the South Africa Astronomical Observatory (SAAO), and the Siding Spring Observatory (SSO). In addition, we downloaded LCs acquired with: (i) the 60 cm Trappist-North telescope (Jehin et al. 2011; Barkaoui et al. 2019) at Oukaimeden Observatory in Morocco; (ii) the 150 cm (T150) telescope at the Observatorio de Sierra Nevada (OSN)8 in Granada, Spain; (iii) the 40 cm telescope at the Observatori Astronomic Albanyà (OAA)9 in Catalonia, Spain; (iv) the 40cm telescope array at the Fred Lawrence Whipple Observatory (FLWO) in Arizona (MEarth project; Charbonneau et al. 2008).

We also retrieved four transit LCs of TOI-732 b and two transit LCs of TOI-732 c each observed in four different filters with the MuSCAT2 multi-colour imager (Narita et al. 2019) installed on the 1.5 m Telescopio Carlos Sanchez (TCS) at the Teide Observatory in Tenerife, Spain. MuSCAT2 is equipped with four CCDs, each of which has 1024 × 1024 pixels with a field of view of 7.4 × 7.4 square arcmin. The instrument is capable of obtaining simultaneous images in the 𝑔′, r′, i′, and zs bandpasses. The basic data reduction (i.e. dark and flat-field calibrations) was performed by the MuSCAT2 pipeline (Parviainen et al. 2019). This pipeline is also capable of fitting a transit model including instrumental systematics and a photometric aperture optimised to reduce the light-curve scatter. For all the transits of planets b and c observed by MuSCAT2, we found an optimal aperture for the target star of 13.92 arcsec.

Finally, all LCs that were taken with a time cadence shorter than one minute were downsampled by binning the data to a one-minute cadence. Further details about the telescope properties and the observational setups can be found in C20 and N20.

Table 4

RV data employed in the combined analysis.

4 Radial velocity data

Both C20 and N20 combined photometric and RV data. In particular, C20 analysed the RV time series obtained with HARPS and HARPS-N (Cosentino et al. 2012), while N20 separately analysed the RV time series obtained with CARMENES (Quirrenbach et al. 2014, 2018), IRD (Kotani et al. 2018), and iSHELL (Rayner et al. 2016, 2022). L22 performed an RV analysis using the data points coming from these five spectrographs together, while in our case, we further added MAROON-X observations as detailed below for a total of 165 data points. A summary of the RV data employed in our global analysis is given in Table 4.

4.1 Literature radial velocity data

The RV measurements available in the literature were retrieved directly from C20 and N20, who also provided a detailed description of the RV data reduction. We briefly recall here that C20 obtained 33 spectra with the HARPS echelle spectrograph mounted at the ESO 3.6 m telescope at the La Silla Observatory in Chile and 30 spectra with the HARPS-N echelle spectrograph mounted at Telescopio Nazionale Galileo (TNG; Cosentino et al. 2000; Oliva 2006) in the Canary Islands, Spain. The corresponding RV measurements along with their error bars were extracted using the TERRA reduction pipeline (Anglada-Escudé & Butler 2012).

Instead, N20 obtained 52 spectra with the CARMENES spectrograph mounted on the 3.5 m Calar Alto Observatory in Almería, Spain. They obtained the RV measurements using the serval code (Zechmeister et al. 2018) and applied the necessary corrections following Trifonov et al. (2018) and Kaminski et al. (2018). N20 also took five spectra with the IRD instrument mounted on the Subaru 8.2 m telescope in Mauna Kea, Hawaii. After discarding one low-quality observation, they reduced the spectra using iraf (Tody 1986, 1993) and extracted the RV measurements through the Subaru/IRD dedicated pipeline (Hirano et al. 2020). Using the iSHELL spectrometer mounted on the NASA Infrared Facility (IRTF) in Mauna Kea, Hawaii, N20 further collected eight RV measurements by applying the spectral reduction method presented in Cale et al. (2019).

Each of the five instruments is characterised by its own offset and is affected by a different jitter term. We therefore organised these RV time series as five independent data sets. These five RV time series contain the vectors of epochs, RV measurements, and RV error bars as found in the literature.

4.2 MAROON-X

We observed TOI-732 with MAROON-X, which is a high-precision echelle spectrograph installed on the 8.1 m telescope Gemini-North (Seifahrt et al. 2018, 2022), 19 times between February and June 2021. The MAROON-X data were reduced with a python3 pipeline based on the pipeline originally used for the CRIRES instrument (Bean et al. 2010), and the RVs were calculated with a version of serval (Zechmeister et al. 2020) modified to work on MAROON-X data. serval calculates RVs by least-squares fitting each individual spectrum to a template created by co-adding all spectra together. The serval routine also extracts the chromatic index (crx), the differential line width (dlw), and the Hα index, which may be useful for data detrending. The wavelength calibration is accomplished by simultaneously observing the science target with an etalon spectra, and the etalons themselves are calibrated using a ThAr lamp.

MAROON-X has two separate CCDs, each with slightly different wavelength coverages, which are exposed simultaneously. The blue channel (500–670 nm) and the red channel (650–920 nm) were treated as two separate instruments for the purposes of this analysis because they have a different wavelength coverage and thus capture different stellar signals. We achieved a median S/N of 200 in the red channel and 77 in the blue channel, which corresponded to median RV uncertainties of 0.5 m s−1 in the red channel and 1 m s−1 in the blue channel. The higher signal in the red channel is expected for the late stellar spectral type.

MAROON-X is a visitor instrument on Gemini-North, and it is thus connected and disconnected multiple times over the course of a semester. It organises its data into discretised runs. In particular, the TOI-732 data were collected over the course of three runs in 2021 (one in February, one in April, and one in May). Combined with the roughly 2.5 cm s−1 day−1 RV drift of the etalon calibrations, this results in small offsets between the RVs of MAROON-X data taken in separate runs. We therefore treated each run of the MAROON-X data as an independent RV time series and further distinguished the data taken via the red and blue channel. That is, we fit six independent MAROON-X RV time series. Accounting for the five RV time series described in Sect. 4.1, we analysed a total of 11 RV time series.

5 Methods and results

5.1 Global light-curve and radial-velocity modelling

We jointly analysed the 132 LCs and 11 RV time series using the MCMCI code (Bonfanti & Gillon 2020), where we switched off the interaction with stellar evolutionary models to avoid a dramatic increase in computational time due to the large data sets. In short, the code fit the LCs against the photometric model of Mandel & Agol (2002) and the RV data against a Keplerian model using an MCMC approach.

On the stellar side, we adopted Teff, [Fe/H], M★, and R★ as jump parameters that were subject to Gaussian priors based on the values reported in Table 1. The reason for this choice is twofold. On the one hand, both M★ and R★ induce a prior on the mean stellar density ρ★, which better constrains the transit fitting. On the other hand, stellar parameters are the starting point for interpolating within ATLAS910 grids of quadratic limb-darkening (LD) coefficients (u1, u2), which were set up for each of the 11 photometric filters using the code by Espinoza & Jordán (2015). Gaussian priors were then imposed on the 11 interpolated pairs (u1, u2) as summarised in Table C.1, but the actual LD-related jump parameters were derived from a linear combination of (u1, u2) following Holman et al. (2006) to reduce their mutual correlation.

For each planet, the jump parameters were the transit depth 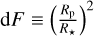dF≡(RpR⋆)2${\rm{d}}F \equiv {\left( {{{{R_{\rm{p}}}} \over {{R_ \star }}}} \right)^2}$, the impact parameter b, the mid-transit time T0, the orbital period P, and the RV semi-amplitude K. We assumed a circular orbit for TOI-732 b as its ultrashort orbital period implies a tide-induced circularisation timescale of ~15 Myr (Matsumura et al. 2008). We instead fit for the eccentricity of TOI-732 c using the parametrisation 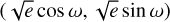(ecosω,esinω)$(\sqrt e \cos \omega ,\sqrt e \sin \omega )$, where e is the eccentricity and ω is the argument of periastron. In the case of TESS observations, N20 noted that a close-in star, namely TIC 36724077, was located within the aperture mask. We therefore fitted for a dilution factor following their estimate. All planetary jump parameters were subject to uniform unbounded priors (except for the physical limits). For details about the adopted parametrisations, we refer to Bonfanti & Gillon (2020, Sect. 2.1.2) and references therein.

The MCMCI tool is able to detrend data against time and the ancillary vectors of the LC and RV time series along the MCMC process via polynomial interpolation. To find the best polynomial order for each detrending parameter of each LC and RV time series, we launched several preliminary MCMC runs and changed the polynomial order of one detrending parameter at a time. We finally selected the best detrending polynomial baseline (see Table C.2) according to the Bayesian information criterion (BIC; Schwarz 1978).

We then launched a first MCMC run of 200 000 steps (burn-in: 40 000 steps) to evaluate the impact of the white and red noise as detailed in Pont et al. (2006) and Bonfanti & Gillon (2020) to properly rescale the photometric errors and provide reliable uncertainties on the fitted parameters. After this, we performed the final MCMCI analysis made of two independent runs (each comprising 200 000 steps with a burn-in of 40 000 steps) to check the posterior distribution convergence through the Gelman-Rubin (GR) test (Gelman & Rubin 1992).

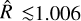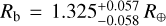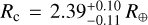The chains converged according to the GR statistic (R^≲1.006$\hat R \mathbin{\lower.3ex\hbox{$\buildrel<\over {\smash{\scriptstyle\sim}\vphantom{_x}}$}} 1.006$ for all the jump parameters), and we obtained planetary radii of Rb=1.325−0.058+0.057R⊕${R_{\rm{b}}} = 1.325_{ - 0.058}^{ + 0.057}{R_ \oplus }$ and Rc=2.39−0.11+0.10R⊕${R_{\rm{c}}} = 2.39_{ - 0.11}^{ + 0.10}{R_ \oplus }$, masses of Mb = 2.46 ± 0.19 M⊕ and 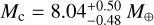Mc=8.04−0.48+0.50M⊕${M_{\rm{c}}} = 8.04_{ - 0.48}^{ + 0.50}{M_ \oplus }$, and thus densities of 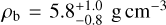ρb=5.8−0.8+1.0 g cm−3${\rho _{\rm{b}}} = 5.8_{ - 0.8}^{ + 1.0}{\rm{g}}{\rm{c}}{{\rm{m}}^{ - 3}}$ and ρc=3.24−0.43+0.55 g cm−3${\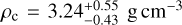rho _{\rm{c}}} = 3.24_{ - 0.43}^{ + 0.55}{\rm{g}}{\rm{c}}{{\rm{m}}^{ - 3}}$. All relevant system parameters as derived from our MCMC global analysis are listed in Tables 5, C.1, and C.3. The phase-folded and detrended LCs of both TOI-732 b and c, as observed by both TESS and CHEOPS, are shown in Fig. 1, while the LCs taken by ground-based facilities are shown in Appendix B. Finally, the phase-folded and detrended RV time-series of both TOI-732 b and c are displayed in Fig. 2.

The bulk densities obtained for both planets are at the ~15% precision level, and only ~20% of all known planets orbiting M dwarfs have been characterised to a similar or better precision11. This is a consequence of the precision we reached on both the transit depths of TOI-732 b and TOI-732 c (4.4% and 4.0%, respectively) and the radial velocity semi-amplitudes (6.2% and 3.8%, respectively), which marks a significant improvement over what was reported so far in the literature, as summarised in Table 6.

Based on the large amount of available data and the broad temporal baseline spanning four years, we were able to reduce the uncertainties on the orbital periods of both planets by more than two orders of magnitude with respect to what was reported by C20. Even comparing our results with those of L22, who derived the most precise ephemerides so far, we improved the uncertainty on the planetary orbital periods by a factor of ~1.3 and ~2.7 for planets b and c, respectively (see Table 6). By propagating our ephemerides, we computed that the 1σ uncertainties on the transit timings of the two planets are comparable to the respective transit durations after ~170 years from now.

Table 5

Parameters of the TOI-732 system.

Table 6

Comparison between literature uncertainties and those derived in this work on the orbital periods P, the transit depths dF, and the RV semi-amplitudes K of the planets.

thumbnail Fig. 1

Phase-folded and detrended LCs showing the transit of TOI-732 b (first column) and TOI-732 c (second column) as observed by CHEOPS (first row) and TESS (second row). The original data points are shown in blue, the binned data points are shown in black (binning of 10 min), and the transit model is displayed in red.

5.2 Internal structure of the planets

We modelled the internal structure of both TOI-732 b and c using a neural-network-based Bayesian inference scheme following the method that was described in detail in Leleu et al. (2021) and is based on Dorn et al. (2017). As input parameters, we used transit depths, periods, and the mass relative to that of the star for both planets, as well as some of the stellar parameters, namely mass, radius, age, effective temperature, [Si/H], [Mg/H], and [Fe/H]. We modelled both planets simultaneously, assuming that they consist of four fully distinct layers that we modelled according to the equations of state of Hakim et al. (2018; an inner iron core with up to 19% sulphur), Sotin et al. (2007; a silicate mantle consisting of Si, Mg, and Fe) and Haldemann et al. (2020; a condensed water layer), with a H-He envelope modelled following (Lopez & Fortney 2014) on top. Furthermore, we assumed that the Si, Mg, and Fe ratios of both planets match those of the star (Thiabaud et al. 2015), even if we note that despite an expected trend between stellar and planetary composition, the correlation might not necessarily be strict (Adibekyan et al. 2021).

As the problem of determining the internal structure of a planet is highly degenerate, the results of our analysis depend on our choice of prior. For the mass fractions of the inner iron core (i.e. the mantle layer and the water layer), all calculated with respect to the inner part of the planet without the H-He layer, we sampled from a prior that is uniform on the simplex on which they all add up to 1. Furthermore, we implemented an upper limit for the water-mass fraction of 0.5, in accordance with Thiabaud et al. (2014) and Marboeuf et al. (2014). We also used a prior that is log-uniform for the mass of the H-He envelope.

The results of our analysis are summarised in Figs. 3 and 4. The derived posteriors of the internal structure parameters show us that TOI-732 b is unlikely to host a H-He layer given its density. Meanwhile, the presence of a water layer is possible, but not necessary, as the derived mass and radius values also agree with a purely rocky structure. For TOI-732 c, the posterior distribution of the gas mass is instead quite well constrained, with a median of 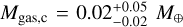Mgas,c=0.02−0.02+0.05M⊕${M_{{\rm{gas}},{\rm{c}}}} = 0.02_{ - 0.02}^{ + 0.05}{M_ \oplus }$, which corresponds to a thickness of 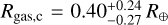Rgas,c=0.40−0.27+0.24R⊕${R_{{\rm{gas,c}}}} = 0.40_{ - 0.27}^{ + 0.24}{R_ \oplus }$ (errors are the 5th and 95th percentile of the distribution). However, the presence of a water layer is completely unconstrained.

Figure 5 locates TOI-732 b and TOI-732 c on the mass-radius (MR) diagram along with M-dwarf planets with Rp < 4 R⊕ and Mp < 30 M⊕ whose precision on the radius and mass are better than 8% and 25%, respectively. When TOI-732b and c are included, this exoplanet sample (hereafter denoted as Msample12) is made of 45 well-characterised planets (a mean planetary bulk density above the 3 σ level). The main parameters of the Msample are listed in Table C.4. Along with the planets belonging to the Msample, Fig. 5 also displays two sets of theoretical models for a planet composition that correspond to Teq = Teq,b = 900 K (solid lines) and Teq = Teq,c = 360 K (dashed lines) using the BICEPS model (Haldemann et al. 2024). In addition, we further collected the MR model as computed by Aguichine et al. (2021) for steam worlds made of 50% water + 50% rocks with Teq = 400 K ≈ Teq,c (the dashed cyan line). Theoretical models of rocky and/or iron worlds do not depend upon Teq, but differences become noticeable when water and/or H-He envelopes are added to the planet structure. The MR diagram confirms that TOI-732 b is likely rocky with a possible iron core, while TOI-732 c is likely rich in volatiles. As shown above, inferring the internal planet structure from observables is a degenerate problem and other mixtures of silicates, gas, and water (which is indeed unconstrained according to our modelling of TOI-732 c) may produce a (Mp, Rp) pair consistent with the observations. For example, we note that the MR location of TOI-732 c is compatible with either a rocky planet surrounded by a H-He envelope (1% by mass) or a steam world consisting of water and rocks in the same proportion by mass.

thumbnail Fig. 2

Phase-folded and detrended RV time series of TOI-732 b (top) and TOI-732 c (bottom), obtained after subtracting the signal of the other planet. The corresponding Keplerian model is superimposed in red. The different colours mark different instruments, namely HARPS (black), IRD (light green), HARPS-N (blue), CARMENES (magenta), iSHELL (cyan), MAROON-X (yellow, orange, and deep green for observations taken in February, April, and May 2021, respectively). As MAROON-X has two different channels, full and empty symbols represent data acquired using the blue and red channel, respectively (see text for further details).
thumbnail Fig. 3

Corner plot showing the posteriors of the main parameters of our internal structure analysis for TOI-732 b. The titles of each column correspond to the median of the distribution, with the 5th and 95th percentiles as the uncertainty values. From left to right, the depicted internal structure parameters are the mass fractions of the inner iron core and of the water layer (both calculated with respect to the condensed part of the planet without the H-He layer), the molar fractions of Si and Mg in the mantle, the molar fraction of Fe in the inner core, and the total mass of H-He in Earth masses on a logarithmic scale. The mass fractions of the inner core and the water layer add up to one, with the mass fraction of the mantle layer (not shown) by construction.
thumbnail Fig. 4

Same as Fig. 3, but for TOI-732 c.
thumbnail Fig. 5

Mass-radius diagram of M-dwarf planets with Rp < 4 R⊕ and Mp < 30 M⊕ whose Rp and Mp precision is better than 8% and 25%, respectively. All planets are colour-coded with respect to their equilibrium temperature (Teq) and in particular, TOI-732 b and TOI-732 c are marked by a star. Following the colour scheme given in the legend, two different sets of planet composition models generated with BICEPS (Haldemann et al. 2024) are displayed. The solid and dashed lines are obtained for Teq = Teq,b = 900 K and Teq = Teq,c = 360 K, respectively. The 50% steam + 50% Earth-like line corresponds to the model of Aguichine et al. (2021) for Teq = 400 K. An Earth-like composition implies a mixture of 32.5% iron and 67.5% silicates. The dotted black lines correspond to the loci of constant density, that is, 0.5, 1, 3, 5, and 10 g cm−3 (from top to bottom).

6 Radius valley of M-dwarf planets

According to their radii, TOI-732 b and TOI-732 c are located on the two opposite sides of the radius valley. Although some degeneracy is expected when modelling the internal structures of planets, we concluded in Sect. 5.2 that TOI-732 b is not likely to hold any gaseous envelope, while TOI-732 c cannot be just purely rocky. When we also consider the mean planetary densities, ρb > ρc, which can lead to a classification of the inner planet as a super-Earth and of the outer one as a mini-Neptune, the TOI-732 system has a quite common architecture (e.g. Ciardi et al. 2013; Weiss et al. 2018; Mishra et al. 2023).

6.1 Radius valley dependence on orbital period

Taking a step further, we studied the radius valley Rp, valley for M dwarfs as a function of planet orbital period P by using our Msample. Several theoretical studies (e.g. Owen & Wu 2017; Lopez & Rice 2018; Gupta & Schlichting 2019; Wyatt et al. 2020; Lee & Connors 2021; Rogers et al. 2021; Affolter et al. 2023) have quantified different d log Rp,valley/d log P slopes characterising the radius valley depending on the specific formation and evolution mechanisms causing it (e.g. impact erosion, photo-evaporation, core-powered mass loss, or late planet formation in either gas-poor or even gas-empty discs). It is worth emphasising that planets formed in a gas-poor environment may also be subject to thermally driven mechanisms (i.e. photo-evaporation and core-powered mass loss). Hereafter, the discussion of thermally driven mechanisms is intended to involve planets that have not formed in a gas-poor environment, unless stated otherwise.

As summarised in Table 7, a negative slope is theoretically expected for both impact erosion and thermally driven mass-loss mechanisms, with the slope becoming milder when passing from the former to the latter. Furthermore, in the case of late-time planet formation within a gas-poor environment, the slope is even shallower (but still negative) when photo-evaporation is considered to be at play afterwards. As emphasised by Lee & Connors (2021), a positive d log Rp,valley/d log P is sometimes incorrectly associated to late-time planet formation, according to the work by Lopez & Rice (2018). However, Lopez & Rice (2018) computed the expected scaling between Rp and P assuming a gas-empty scenario, and the positive slope line they derived therefore just corresponds to the maximum radius that can be reached by a purely rocky planet. Therefore, this locus of points does not trace the radius valley dividing rocky planets from sub-Neptune simply because no sub-Neptunes may form in a gas-empty environment. Nonetheless, we kept the d log Rp,valley/d log PL18 = +0.11 in Table 7 because it sets the upper limit of the radius valley slope for a sample of heterogeneous exoplanets in the Rp-P plane. On the one hand, the purely rocky exoplanets that are born in a gas-empty disc would be distributed following a positive trend, whose upper limit is given by d log Rp,valley/d log PL18. On the other hand, from a disc with gas, both super-Earth and sub-Neptunes would be generated, and they would appear on the two opposite sides of a descending radius valley. The full picture that we would see a posteriori in the Rp-P plane would be the overlap of these two groups of exo-planets, which would show a radius valley with an intermediate slope, possibly even positive, depending on the weights of the formation mechanisms at play.

To study the dependence of the radius valley on planetary orbital period, we followed the same approach as in Van Eylen et al. (2018) and Ho & Van Eylen (2023), but focused on M-dwarf hosts (M★ ≲ 0.6 M⊙). This complements the stellar mass range spanned by the F, G, and K type stars investigated by Ho & Van Eylen (2023). In detail, we first clustered our M-dwarf exoplanets into two different groups, according to their location with respect to the radius valley (above or below), by performing a Gaussian mixture model selection (e.g. Huang et al. 2017; Fruhwirth-Schnatter et al. 2018). To this end, we employed the PYTHON sklearn GridSearchCV() class, which allows specifying four different covariance types to define the clustering. After rescaling the period P by a factor of five to avoid misclassification (Ho & Van Eylen 2023), we fit the selection model within the log Rp–log P plane, and we finally selected the model inferred from the spherical covariance type, which has the lowest associated BIC.

After this, we followed a support vector machine (SVM) procedure (e.g. Cortes & Vapnik 1995; Ben-Hur et al. 2002) implemented via the sklearn SVC() class. After we set a linear kernel and a penalty parameter C = 10 (see Van Eylen et al. 2018), the fit method of SVC() was able to compute the best-fit line separating the two groups of exoplanets in any desired space of covariates. In particular, we obtained 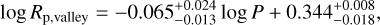logRp, valley =−0.065−0.013+0.024logP+0.344−0.018+0.008,$\log {R_{{\rm{p}},{\rm{ valley }}}} = - 0.065_{ - 0.013}^{ + 0.024}\log P + 0.344_{ - 0.018}^{ + 0.008},$(1)

where the uncertainties (at the 1 σ level) were computed by bootstrapping the Msample 10 000 times and repeating the algorithm outlined above.

When compared to the outcome obtained by Ho & Van Eylen (2023, d log Rp,valley/d log PH23 = −0.11 ± 0.02), the slope value we obtained differs by almost a factor of two (tension at the 2 σ level), which may suggest that formation and evolution mechanisms enter with different weights in the case of exoplanets orbiting M dwarfs or FGK stars. Instead, when we performed a homogeneous comparison with other works targeting the Rp,valley slope of exoplanets around low-mass stars, our d log Rp,valley/d log P value is consistent within 1 σ with the estimate from L22 (d log Rp,valley/d log PL22 = −0.02 ± 0.05), it is milder than the slope found by Van Eylen et al. (2021, 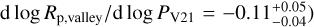dlogRp, valley /dlogPV21=−0.11−0.04+0.05${\rm{d}}\log {R_{{\rm{p}},{\rm{ valley }}}}/{\rm{d}}\log {P_{{\rm{V}}21}} = - 0.11_{ - 0.04}^{ + 0.05}$), but still consistent at the ~ 1 σ level, and it differs from the outcome of Cloutier & Menou (2020, d log Rp,valley/d log PC20 = +0.058 ± 0.022). The sample of Cloutier & Menou (2020) also comprises planets orbiting K dwarfs (with a spectral type later than K3.5V, i.e. M★ ≲ 0.8 M⊙), and the reason for the difference in slope may be that the Rp precision for half of the planets they analysed is lower than our 8% threshold (the 99th-quantile of their Rp relative uncertainties is ~26%). Instead, both Van Eylen et al. (2021) and L22 focused on planets orbiting M dwarfs alone, and the difference with our d log Rp,valley/d log P value decreases as the selection threshold for the sample is set to a lower Rp uncertainty (below 20% for Van Eylen et al. 2018 and below 8% for L22). Only the sample by L22 reaches the same precision level as our Msample (because we adopted the same selection criteria), but our sample contains 30% more planets (45 versus 34 planets).

A visual synthesis of our results is given in Fig. 6, where the best-fit line marking the radius valley (solid grey line) is compared with the theoretical slopes expected from a thermally driven mass-loss model (solid red line; Affolter et al. 2023) and a gas-empty formation model (dashed red line; Lopez & Rice 2018). When compared with the theoretical slope expected from a mixed scenario, where both photo-evaporation and core-powered mass loss are at play (that is −0.10; Affolter et al. 2023), the negative d log Rp,valley/d log P slope we computed (i.e. 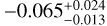−0.065−0.013+0.024$ - 0.065_{ - 0.013}^{ + 0.024}$) is shallower by a factor of ~1.5 (tension at the ~3 sigma level). Slopes milder than −0.10 possibly tending towards positive values indicate a stronger impact of gas-poor formation according to Lopez & Rice (2018); Lee & Connors (2021). Therefore, we may conclude that although thermally driven mechanisms appear to be statistically prevalent, the currently observed properties of some of the planets orbiting M dwarfs may be caused by late formation in gas-depleted discs. This scenario has indeed been proposed for a few M-dwarf systems, such as TOI-1634 (Cloutier et al. 2021b), where the composition of the close-in USP TOI-1634 b is inconsistent with that of the Earth, or LHS 1903 (Wilson et al. 2023), where the outermost planet at P ~ 29.3 days lacks any gaseous envelope, in contrast to some of the inner planets. An alternative scenario explaining our d log Rp,valley/d log P findings is investigated in Sect. 6.3.

As the strength of core-powered mass-loss experienced by a planet scales proportionally to 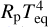RpTeq4${R_{\rm{p}}}T_{{\rm{eq}}}^4$ (Gupta & Schlichting 2019), the colour-coding in Fig. C.1 is an attempt of investigating the impact of core-powered mass loss in shaping the radius valley. However, the colour gradient from the bottom right to top left just reflects the increase in 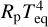RpTeq4${R_{\rm{p}}}T_{{\rm{eq}}}^4$ at greater radii and lower orbital period (hotter planets). The radii of billion-year-old planets dominating the Msample are thought to have significantly shrunk during their evolution due to planetary cooling and evaporation, which effect is correlated to the strength of the atmospheric escape (Lopez & Fortney 2014; Chen & Rogers 2016; Kubyshkina & Fossati 2022; Affolter et al. 2023). Thus, the present-day radii cannot unambiguously define the strength of core-powered mass loss because they are not indicative of the escape rates during the early evolution phases, when core-powered mass loss can dominate. In addition, the equilibrium temperature strongly correlates with the (poorly constrained) amount of XUV radiation received by the planet because both Teq and XUV radiation scale with the planet distance. Thus, the Teq dependence does not allow us to distinguish the inputs from the core-powered and XUV-driven escape mechanisms sufficiently well.

On the other hand, we know from hydrodynamic modeling that core-powered mass loss dominates the atmospheric escape completely if the atmospheric density is sufficiently high in the upper atmospheric layers to prevent the penetration of XUV radiation inside the planetary Roche lobe (Kubyshkina et al. 2018; Kubyshkina 2023). This situation occurs most likely for planets with low masses and small Roche radii (comprising a few Rp at young ages); of these two parameters, the Roche radius carries more information than the planetary mass alone. Along this line, the two panels of Fig. 7 still represent the planets of our Msample in the Rp-P plane, but with a specific focus on the role of the core-powered mass-loss mechanism by tracing the size of the planetary Roche radius. We computed the Roche-lobe radius (Eggleton 1983) of each planet 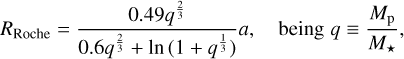RRoche =0.49q230.6q23+ln(1+q13)a,  being q≡MpM⋆, ${R_{{\rm{Roche }}}} = {{0.49{q^{{2 \over 3}}}} \over {0.6{q^{{2 \over 3}}} + \ln \left( {1 + {q^{{1 \over 3}}}} \right)}}a,\quad {\rm{ being }}q \equiv {{{M_{\rm{p}}}} \over {{M_ \star }}}{\rm{, }}$(2)

as a measure of the region within which a possible atmospheric envelope is bounded to the planet. The larger RRoche, the less effective the core-powered atmospheric escape. After normalisation to Rp (top panel), RRoche still maintains the linear dependence upon the semi-major axis a, and indeed, RRoche/Rp increases with the orbital period. On the one hand, while this trend is expected, this panel emphasises on the other hand, that planets on long-period orbits are less subject to core-powered mass loss. Therefore, a rocky planet (i.e. without a low mean-molecular weight envelope) farther away from its host is more likely to be born in a gas-depleted environment.

The bottom panel of Fig. 7 is similar to the top panel, but this time, the colour-coding follows RRoche normalised to a. In this way, we removed the linear dependence of the Roche radius on a, which means that RRoche depends solely on the Mp/M★ ratio. Now, RRoche/a increases as Rp increases, with the highest RRoche/a values clustering above the radius valley. The larger Roche radius of these planets enabled them to keep their atmospheric envelope, and they therefore appear to be more puffy than the planets below the radius valley.

Table 7

Radius valley slopes m ≡ d log Rp,valley/d log P as predicted from theory for different scenarios.

thumbnail Fig. 6

Rp vs P distribution representing the planets in our Msample. Planets classified above and below the radius valley are shown in blue and green, respectively, while the red star-shaped markers are for TOI-732 b and c. The radius valley inferred via the SVM-based method is marked by the solid grey line with the shaded region highlighting the 1 σ limits of the best-fit line. The two parallel dashed grey lines are the median boundaries passing through the supporting vectors that determine the location of the solid line. Finally, the red lines represent the theoretically expected Rp,valley boundary in case of a thermally-driven mass-loss scenario (solid line as computed from Affolter et al. 2023; negative slope) and the Rp upper limit of planets borned rocky in a gas-empty disc (dashed line as computed from Lopez & Rice 2018; positive slope).

6.2 Dependence of the radius valley on stellar mass

Considering the increasing interest in exploring the trend between the radius valley and the spectral type of the host star (e.g. Wu 2019; Gupta & Schlichting 2020; Rogers et al. 2021; Ho & Van Eylen 2023; Berger et al. 2023), we repeated the SVM analysis described above, but assuming the covariate pair (Rp, M★), and we derived 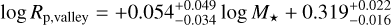logRp, valley =+0.054−0.034+0.049logM⋆+0.319−0.016+0.022$\log {R_{{\rm{p}},{\rm{ valley }}}} = + 0.054_{ - 0.034}^{ + 0.049}\log {M_ \star } + 0.319_{ - 0.016}^{ + 0.022}$(3)

(see Fig. 8). Estimates of the radius valley slope d log Rp,valley/d log M★ that are based on observational data as found in the literature (Berger et al. 2020; Petigura et al. 2022; Ho & Van Eylen 2023) are mainly the results of works focusing on FGK stars, which lead to steeper slopes (although the accompanying uncertainties are about 40% or higher). The only homogeneous comparison currently available is with the work by L22, who found d log Rp,valley/d log M★ = +0.08 ± 0.12 (consistent with our estimate), which may again suggest that planets orbiting M dwarfs differ from those orbiting FGK stars in the context of the radius valley.

However, from a theoretical perspective, it is hard to draw firm conclusions about the mechanisms underlying the formation and evolution of exoplanets when studying the radius valley within the Rp-M★ space. Rogers et al. (2021) cautioned that the Rp,valley-M★ slope shows several degeneracies. They theoretically derived that the expected slope does not only depend on M★, but also on the incident bolometric flux S, and it can be expressed as 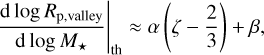dlogRp, valley dlogM⋆|th ≈α(ζ−23)+β,${\left. {{{{\rm{d}}\log {R_{{\rm{p}},{\rm{ valley }}}}} \over {{\rm{d}}\log {M_ \star }}}} \right|_{{\rm{th }}}} \approx \alpha \left( {\zeta - {2 \over 3}} \right) + \beta ,$(4)

where α ≡ ∂ log Rp,valley/∂ log S and β ≡ ∂ log Rp,valley/∂ log M★ are predicted, depending on the scenario at play (either photo-evaporation or core-powered mass loss), while ζ is the exponent entering the mass-luminosity relation, that is, 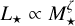L⋆∝M⋆ζ${L_ \star } \propto M_ \star ^\zeta $. Because ζ ≫ α and ζ ≫ |β| (Rogers et al. 2021), the slope value is mainly controlled by ζ, which needs to be properly estimated according to the stellar spectral type. Cuntz & Wang (2018) proposed the following expression for ζ = ζ(M★) for low-mass stars: 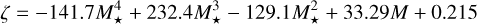ζ=−141.7M⋆4+232.4M⋆3−129.1M⋆2+33.29M+0.215$\zeta = - 141.7M_ \star ^4 + 232.4M_ \star ^3 - 129.1M_ \star ^2 + 33.29M + 0.215$(5)

and averaging out that function over our mass range of interest, we obtained ζM = 4.0. Plugging in the (α, β) predictions by Rogers et al. (2021) along with ζM in Eq. (4), we computed d log Rp,valley/d log M★th ≈ +0.23 and +0.27 for the photo-evaporation and core-powered mass-loss models, respectively. The difference with our observationally inferred estimate may suggest that other mechanisms shape the observed properties of planets orbiting M dwarfs (e.g. a significant role of gas-poor formation, for which Lee & Connors 2021 theoretically predicted a d log Rp,valley/d log M★ down to +0.11). However, Wu (2019) first remarked that the specific scaling relation between the planetary core mass and stellar mass further influences Eq. (4), and Rogers et al. (2021) indeed verified that the d log Rp,valley/d log M★ may be considerably altered when these scalings are accounted for.

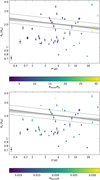thumbnail Fig. 7

Same as Fig. 6, but the markers are colour-coded against the Roche lobe of each planet normalised to the planetary radius (top) or to the orbital semi-major axis (bottom).
thumbnail Fig. 8

Same as Fig. 6, but this time, Rp is plotted against stellar mass.

6.3 Density valley

Finally, as L22 concluded that the demographics of exoplanets can be better visualised by considering the density valley, we repeated the SVM analysis in the 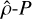ρ^-P$\hat \rho {\rm{ - }}P$ space, where the normalised density 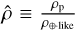ρ^≡ρpρ⊕⋅ like $\hat \rho \equiv {{{\rho _{\rm{p}}}} \over {{\rho _{ \oplus \cdot {\rm{ like }}}}}}$ and ρ⊕,like is the density that a planet of given mass would have if it had an Earth-like composition. As done by L22, we followed Zeng et al. (2019), who computed that an Earth-like planet of mass Mp has a radius 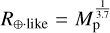R⊕ like =Mp13.7${R_{ \oplus {\rm{ like }}}} = M_{\rm{p}}^{{1 \over {3.7}}}$, where both the mass and the radius are expressed in Earth units. Therefore, according to Zeng et al. (2019), the density of an Earth-like planet scales as (Earth units) 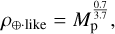ρ⊕⋅ like =Mp0.73.7, ${\rho _{ \oplus \cdot {\rm{ like }}}} = M_{\rm{p}}^{{{0.7} \over {3.7}}}{\rm{, }}$(6)

which is the normalisation factor to derive 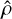ρ^$\hat \rho $ from ρp. The density valley is shown in Fig. 9 along with the SVM-based best-fit line, 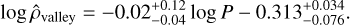logρ^valley =−0.02−0.04+0.12logP−0.313−0.076+0.034. $\log {\hat \rho _{{\rm{valley }}}} = - 0.02_{ - 0.04}^{ + 0.12}\log P - 0.313_{ - 0.076}^{ + 0.034}{\rm{. }}$(7)

Figure 9 confirms that the normalised density 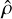ρ^$\hat \rho $ separates two different populations of exoplanets, as first pointed out by L22. Our quantitative characterisation of the valley yields a slope 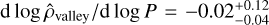dlogρ^valley /dlogP=−0.02−0.04+0.12${\rm{d}}\log {\hat \rho _{{\rm{valley }}}}/{\rm{d}}\log P = - 0.02_{ - 0.04}^{ + 0.12}$, which is well consistent with zero, similar to 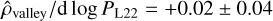dlogρ^valley /dlogPL22=+0.02±0.04${\rm{d}}\log {\hat \rho _{{\rm{valley }}}}/{\rm{d}}\log {P_{{\rm{L}}22}} = + 0.02 \pm 0.04$ estimated by L22.

The agreement of both our d log Rp,valley/d log P and 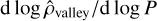dlogρ^valley /dlogP${\rm{d}}\log {\hat \rho _{{\rm{valley }}}}/{\rm{d}}\log P$ outcomes with the results from L22 may also suggest that the L22 interpretation of planet demographics may be followed. In detail, L22 identified that planets with Rp ≲ 1.6 R⊕ are rocky, planets with Rp ≳ 2.3 R⊕ are puffy sub-Neptunes, and planets with intermediate radii are water worlds, that is, planets with the same mass content of condensed water and rocks. L22 interpreted the density gap as a division between rocky planets and water worlds, which also agrees with the conclusions by Venturini et al. (2020), who find that the radius gap separates dry from wet planets.

At lower stellar mass, the minimum mass for a planet to undergo type I migration decreases (e.g. Burn et al. 2021). As a result, water worlds are more common around M dwarfs, and their abundance shapes the topology of the radius valley, which is then determined by the favoured inward migration of water worlds rather than by atmospheric loss processes (Venturini et al. in prep.). The migration causes an overlap between rocky planets and water worlds within the mass-radius and Rp−P space. Hence, the radius valley is partially filled (as also found by L22) and its slope becomes shallower than expected from thermally-driven atmospheric mass-loss mechanisms.

thumbnail Fig. 9

Normalised density as a function of orbital period. The normalised density is the mean density of the planet divided by the density the planet would have if it had an Earth-like composition (same variable as introduced in L22 to display the density valley). The grey line and its shaded area indicate the density valley with its corresponding error, as in Fig. 6.

7 Conclusions

The M4 V star TOI-732 hosts two transiting planets, namely a close-in USP planet at Pb ~ 0.77 days and an outer one at Pc ~ 12.25 days. They straddle the radius valley and have Rb ~ 1.3 R⊕ and Rc ~ 2.4 R⊕. The system has been analysed by C20, N20, and L22, but by collecting 25 CHEOPS LCs and benefiting from a further still unpublished TESS sector, we were able to double the number of space-based observations for a total of ~140 transit events observed with both ground- and space-based facilities. Furthermore, in addition to the 127 RV data points already available in the literature, we obtained 38 RV observations with the MAROON-X spectrograph.

We jointly analysed all the available LCs and RV time series using the MCMCI routine by Bonfanti & Gillon (2020), reaching a transit depth precision of 4.4% (resp. 4.0%) and an RV semi-amplitude precision of 6.2% (3.8%) for TOI-732b (TOI-732 c). Even with respect to the most recent parameters available in the literature, we were able to improve the precision on the transit and RV observables up to a factor ~2.4, with a remarkably positive impact on the mean densities of both planets. 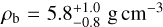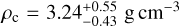We estimated ρb=5.8−0.8+1.0 g cm−3${\rho _{\rm{b}}} = 5.8_{ - 0.8}^{ + 1.0}{\rm{g}}{\rm{c}}{{\rm{m}}^{ - 3}}$ and ρc=3.24−0.43+0.55 g cm−3${\rho _{\rm{c}}} = 3.24_{ - 0.43}^{ + 0.55}{\rm{g}}{\rm{c}}{{\rm{m}}^{ - 3}}$ (hence ~15% uncertainty for both), and only ~20% of the currently known exoplanets around M dwarf are known with a comparable or better precision according to the NASA Exoplanet Archive.

Based on the internal structure modelling we performed, TOI-732 b probably does not host any gaseous envelope, but it is fully compatible with a rocky composition. Instead, TOI-732 c is compatible with having a volatile layer, with our interior structure model yielding a H-He envelope mass 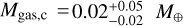Mgas,c=0.02−0.02+0.05 M⊕${M_{{\rm{gas,c}}}} = 0.02_{ - 0.02}^{ + 0.05}\,{M_ \oplus }$, which corresponds to a thickness of 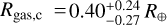Rgas,c=0.40−0.27+0.24 R⊕${R_{{\rm{gas,c}}}} = 0.40_{ - 0.27}^{ + 0.24}\,{R_ \oplus }$. However, based on the Aguichine et al. (2021) models, the mass and radius values of TOI-732 c are also compatible with an Earth-like core surrounded by a steam water layer. From the physical parameters of the planets, we then infer that the inner planet is a super-Earth, while the outer planet is a sub-Neptune. This constitutes a quite common system architecture in the exoplanet field.

We finally built a sample of well-characterised M-dwarf exo-planets (the Msample) with Rp < 4 R⊕ and whose radii and masses are known to better than 8% and 25%, respectively. After this, we investigated the slopes of the radius valley as a function of the planet orbital periods and of the host stellar mass because theoretical models predict different trends depending on the mechanisms that have underlain planet formation and evolution. Following an SVM approach (e.g. Cortes & Vapnik 1995), we determined a 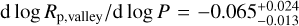dlogRp, valley /dlogP=−0.065−0.013+0.024${\rm{d}}\log {R_{{\rm{p}},{\rm{ valley }}}}/{\rm{d}}\log P = - 0.065_{ - 0.013}^{ + 0.024}$, differing by ~2σ from the d log Rp,valley/d log PH23 = −0.11 ± 0.02 slope derived by Ho & Van Eylen (2023) when targeting FGK stars, which may imply that formation and evolution mechanisms are at play with different weights in FGK and M-dwarf exoplanet systems.

Theoretical predictions would associate a d log Rp,valley/d log PTD = −0.10 with a thermally driven mass-loss scenario (Affolter et al. 2023), while Lopez & Rice (2018) computed an upper limit for the radius valley slope (d log Rp,valley/d log PL18 = +0.11) derived from gas-empty planet formation models. As our result falls in between, with a negative slope, we may argue that thermally driven mass-loss events can explain the evolution of the majority of M-dwarf exoplanets, but some of the planets in our Msample may be compatible with the gas-poor formation scenario. This type of formation mechanism has recently been invoked to justify the physical properties of some exoplanets hosted by M dwarfs, such as the cases of TOI-1634b (Cloutier et al. 2021b) or LHS 1903 e (Wilson et al. 2023).

An alternative explanation for the observed radius valley topology instead relies on the abundance of water worlds around low-mass stars. In particular, the favoured inward migration of water worlds suggested by simulations (Venturini et al. 2020; Burn et al. 2021) would cause a partial filling of the radius valley (L22; Venturini et al., in prep.). The radius-valley slope would then become flatter compared to what is theoretically expected if only thermally driven mass-loss mechanisms were at play; this agrees with our d log Rp,valley/d log P estimate. Following L22, we further confirm the presence of a density valley that better separates rocky and water-rich exoplanets.

By repeating the SVM analysis in the 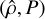(ρ^,P)$(\hat \rho ,P)$ plane, we computed a slope of 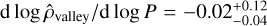dlogρ^valley /dlogP=−0.02−0.04+0.12${\rm{d}}\log {{\hat \rho }_{{\rm{valley }}}}/{\rm{d}}\log P = - 0.02_{ - 0.04}^{ + 0.12}$, which agrees well with the 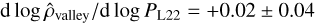dlogρ^valley /dlogPL22=+0.02±0.04${\rm{d}}\log {\hat \rho _{{\rm{valley }}}}/{\rm{d}}\log {P_{{\rm{L}}22}} = + 0.02 \pm 0.04$ value found by L22. Therefore, the interpretation of L22 in terms of planet demographics and formation can be adopted here as well. In summary, when comparing theoretical predictions of d log Rp,valley/d log P values (see Table 7) with our findings, our 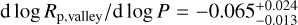dlogRp, valley /dlogP=−0.065−0.013+0.024${\rm{d}}\log {R_{{\rm{p}},{\rm{ valley }}}}/{\rm{d}}\log P = - 0.065_{ - 0.013}^{ + 0.024}$ estimate can be justified by invoking further mechanisms (e.g. gas-poor formation or inward migration) in addition to thermally driven mass-loss phenomena.

Acknowledgements

We thank the anonymous referee for the valuable comments, which improve the quality of the manuscript. CHEOPS is an ESA mission in partnership with Switzerland with important contributions to the payload and the ground segment from Austria, Belgium, France, Germany, Hungary, Italy, Portugal, Spain, Sweden, and the United Kingdom. The CHEOPS Consortium would like to gratefully acknowledge the support received by all the agencies, offices, universities, and industries involved. Their flexibility and willingness to explore new approaches were essential to the success of this mission. CHEOPS data analysed in this article will be made available in the CHEOPS mission archive (https://cheops.unige.ch/archive_browser/). T.Wi. acknowledges support from the UKSA and the University of Warwick. This work has been carried out within the framework of the NCCR PlanetS supported by the Swiss National Science Foundation under grants 51NF40_182901 and 51NF40_205606. A.Br. was supported by the SNSA. S.G.S. acknowledge support from FCT through FCT contract nr. CEECIND/00826/2018 and POPH/FSE (EC). M.L. acknowledges support of the Swiss National Science Foundation under grant number PCEFP2_194576. A.Si. and C.Br. acknowledge support from the Swiss Space Office through the ESA PRODEX program. This work was also partially supported by a grant from the Simons Foundation (PI Queloz, grant number 327127). Y.Al. acknowledges support from the Swiss National Science Foundation (SNSF) under grant 200020_192038. N.C.Sa. acknowledges funding by the European Union (ERC, FIERCE, 101052347). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. V.V.G. is an F.R.S-FNRS Research Associate. R.Al., D.Ba., E.Pa., and I.Ri. acknowledge financial support from the Agencia Estatal de Investigación of the Ministerio de Ciencia e Innovación MCIN/AEI/10.13039/501100011033 and the ERDF “A way of making Europe” through projects PID2019-107061GB-C61, PID2019-107061GB-C66, PID2021-125627OB-C31, and PID2021-125627OB-C32, from the Centre of Excellence “Severo Ochoa” award to the Instituto de Astrofísica de Canarias (CEX2019-000920-S), from the Centre of Excellence “María de Maeztu” award to the Institut de Ciències de l’Espai (CEX2020-001058-M), and from the Generalitat de Catalunya/CERCA programme. S.C.C.B. acknowledges support from FCT through FCT contracts nr. IF/01312/2014/CP1215/CT0004. L.Bo., V.Na., I.Pa., G.Pi., R.Ra., G.Sc., and T.Zi. acknowledge support from CHEOPS ASI-INAF agreement no. 2019-29-HH.0. A.C.C. acknowledges support from STFC consolidated grant numbers ST/R000824/1 and ST/V000861/1, and UKSA grant number ST/R003203/1. P.E.C. is funded by the Austrian Science Fund (FWF) Erwin Schroedinger Fellowship, program J4595-N. This project was supported by the CNES. The Belgian participation to CHEOPS has been supported by the Belgian Federal Science Policy Office (BELSPO) in the framework of the PRODEX Program, and by the University of Liège through an ARC grant for Concerted Research Actions financed by the Wallonia-Brussels Federation. L.D. is an F.R.S.-FNRS Postdoctoral Researcher. This work was supported by FCT – Fundação para a Ciência e a Tecnologia through national funds and by FEDER through COMPETE2020 through the research grants UIDB/04434/2020, UIDP/04434/2020, 2022.06962.PTDC. O.D.S.D. is supported in the form of work contract (DL 57/2016/CP1364/CT0004) funded by national funds through FCT. B.-O.D. acknowledges support from the Swiss State Secretariat for Education, Research and Innovation (SERI) under contract number MB22.00046. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (project FOUR ACES. grant agreement no. 724427). It has also been carried out in the frame of the National Centre for Competence in Research PlanetS supported by the Swiss National Science Foundation (SNSF). D.E. acknowledges financial support from the Swiss National Science Foundation for project 200021_200726. M.F. and C.M.P. gratefully acknowledge the support of the Swedish National Space Agency (DNR 65/19, 174/18). A.J.M. acknowledges support from the Swedish National Space Agency (120/19C). D.G. gratefully acknowledges financial support from the CRT foundation under Grant No. 2018.2323 “Gaseousor rocky? Unveiling the nature of small worlds”. M.G. is an F.R.S.-FNRS Senior Research Associate. M.N.G. is the ESA CHEOPS Project Scientist and Mission Representative, and as such also responsible for the Guest Observers (GO) Programme. M.N.G. does not relay proprietary information between the GO and Guaranteed Time Observation (GTO) Programmes, and does not decide on the definition and target selection of the GTO Programme. C.He. acknowledges support from the European Union H2020-MSCA-ITN-2019 under Grant Agreement no. 860470 (CHAMELEON). S.H. gratefully acknowledges CNES funding through the grant 837319. K.G.I. is the ESA CHEOPS Project Scientist and is responsible for the ESA CHEOPS Guest Observers Programme. She does not participate in, or contribute to, the definition of the Guaranteed Time Programme of the CHEOPS mission through which observations described in this paper have been taken, nor to any aspect of target selection for the programme. K.W.F.L. was supported by Deutsche Forschungsgemeinschaft grants RA714/14-1 within the DFG Schwerpunkt SPP 1992, Exploring the Diversity of Extrasolar Planets. This work was granted access to the HPC resources of MesoPSL financed by the Region Ile de France and the project Equip@Meso (reference ANR-10-EQPX-29-01) of the programme Investissements d’Avenir supervised by the Agence Nationale pour la Recherche. P.M. acknowledges support from STFC research grant number ST/M001040/1. G.S. acknowledges support provided by NASA through the NASA Hubble Fellowship grant HST-HF2-51519.001-A awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555. Gy.M.Sz. acknowledges the support of the Hungarian National Research, Development and Innovation Office (NKFIH) grant K-125015, a a PRODEX Experiment Agreement No. 4000137122, the Lendület LP2018-7/2021 grant of the Hungarian Academy of Science and the support of the city of Szombathely. N.A.W. acknowledges UKSA grant ST/R004838/1. R.L. acknowledges funding from University of La Laguna through the Margarita Salas Fellowship from the Spanish Ministry of Universities ref. UNI/551/2021-May 26, and under the EU Next Generation funds. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This article is based on observations made with the MuSCAT2 instrument, developed by ABC, at Telescopio Carlos Sánchez operated on the island of Tenerife by the IAC in the Spanish Observatorio del Teide. This work is partly financed by the Spanish Ministry of Economics and Competitiveness through grants PGC2018-098153-B-C31. This work is partly supported by JSPS KAKENHI Grant Numbers JP17H04574, JP18H01265, and JP18H05439, Grant-in-Aid for JSPS Fellows Grant Number JP20J21872, JST PRESTO Grant Number JPMJPR1775, and a University Research Support Grant from the National Astronomical Observatory of Japan (NAOJ). This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. DGE 1746045.

Appendix A CHEOPS raw light curves

thumbnail Fig. A.1

Raw CHEOPS LCs in chronological order of observations from CH 1 up to CH 6, as presented in Table 3. The main systematic affecting the LCs is due to the highly variable flux pattern correlating with the spacecraft roll angle.
thumbnail Fig. A.2

Same as Fig. A.1, but for CHEOPS LCs from CH 7 up to CH 12.
thumbnail Fig. A.3

Same as Fig. A.1, but for CHEOPS LCs from CH 13 up to CH 18.
thumbnail Fig. A.4

Same as Fig. A.1, but for CHEOPS LCs from CH 19 up to CH 24.
thumbnail Fig. A.5

Same as Fig. A.1, but for CHEOPS LCs CH 25.

Appendix B Ground-based facilities light curves

thumbnail Fig. B.1

Phase-folded LCs of TOI-732 b (first column) and TOI-732 c (second column) observed by ground-based facilities in the following filters: g’ (first row), r’ (second row), i’ (third row), and z’ (fourth row).
thumbnail Fig. B.2

LCs of TOI-732 c taken by ground-based facilities. From Top to Bottom going row wise the observation filters are B, V, R, and RG715.
thumbnail Fig. B.3

LC of TOI-732b as observed by OAA in the I filter.

Appendix C Additional tables and figures

Table C.1

Quadratic limb darkening (LD) coefficients (u1, u2) for each photo

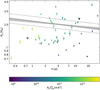thumbnail Fig. C.1

Same as Fig. 6, but with the markers colour-coded against RpTeq4${R_{\rm{p}}}T_{{\rm{eq}}}^4$, which correlates with the core-powered mass loss strength (Gupta & Schlichting 2019).
Table C.2

Polynomial detrending baselines applied to the space-based light curves within the MCMC scheme.

Table C.3

Radial velocity jitter for each RV time series as inferred from the MCMC global analysis, after applying the polynomial detrending as specified in the third column. c denotes a scalar offset; see text for further details

Table C.4

Main planetary parameters of the Msample.

References

  1. Abdurro’uf, Accetta, K., Aerts, C., et al. 2022, ApJS, 259, 35 [CrossRef] [Google Scholar]
  2. Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Adibekyan, V., Dorn, C., Sousa, S. G., et al. 2021, Science, 374, 330 [NASA ADS] [CrossRef] [Google Scholar]
  4. Affolter, L., Mordasini, C., Oza, A. V., Kubyshkina, D., & Fossati, L. 2023, A&A, 676, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Agol, E., Dorn, C., Grimm, S. L., et al. 2021, PSJ, 2, 1 [NASA ADS] [Google Scholar]
  6. Aguichine, A., Mousis, O., Deleuil, M., & Marcq, E. 2021, ApJ, 914, 84 [NASA ADS] [CrossRef] [Google Scholar]
  7. Alibert, Y. 2017, A&A, 606, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Alibert, Y., Carron, F., Fortier, A., et al. 2013, A&A, 558, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Allard, F. 2014, in Exploring the Formation and Evolution of Planetary Systems, 299, eds. M. Booth, B. C. Matthews, & J. R. Graham, 271 [NASA ADS] [Google Scholar]
  10. Almeida-Fernandes, F., & Rocha-Pinto, H. J. 2018, MNRAS, 476, 184 [Google Scholar]
  11. Almenara, J. M., Bonfils, X., Otegi, J. F., et al. 2022, A&A, 665, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Anglada-Escudé, G. & Butler, R. P. 2012, ApJS, 200, 15 [CrossRef] [Google Scholar]
  13. Antoniadis-Karnavas, A., Sousa, S. G., Delgado-Mena, E., et al. 2020, A&A, 636, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Astudillo-Defru, N., Cloutier, R., Wang, S. X., et al. 2020, A&A, 636, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Barkaoui, K., Burdanov, A., Hellier, C., et al. 2019, AJ, 157, 43 [NASA ADS] [CrossRef] [Google Scholar]
  16. Barkaoui, K., Timmermans, M., Soubkiou, A., et al. 2023, A&A, 677, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Barnes, R. 2017, Celest. Mech. Dyn. Astron., 129, 509 [Google Scholar]
  18. Bastian, N., Covey, K. R., & Meyer, M. R. 2010, ARA&A, 48, 339 [Google Scholar]
  19. Bean, J. L., Seifahrt, A., Hartman, H., et al. 2010, ApJ, 713, 410 [NASA ADS] [CrossRef] [Google Scholar]
  20. Ben-Hur, A., Horn, D., Siegelmann, H. T., & Vapnik, V. 2002, J. Mach. Learn. Res., 2, 125 [Google Scholar]
  21. Benedict, G. F., Henry, T. J., Franz, O. G., et al. 2016, AJ, 152, 141 [Google Scholar]
  22. Benneke, B., Wong, I., Piaulet, C., et al. 2019, ApJ, 887, L14 [Google Scholar]
  23. Benz, W., Broeg, C., Fortier, A., et al. 2021, Exp. Astron., 51, 109 [Google Scholar]
  24. Berger, T. A., Huber, D., Gaidos, E., van Saders, J. L., & Weiss, L. M. 2020, AJ, 160, 108 [NASA ADS] [CrossRef] [Google Scholar]
  25. Berger, T. A., Schlieder, J. E., Huber, D., & Barclay, T. 2023, ApJ, submitted [arXiv:2302.00009] [Google Scholar]
  26. Blackwell, D. E., & Shallis, M. J. 1977, MNRAS, 180, 177 [NASA ADS] [CrossRef] [Google Scholar]
  27. Bluhm, P., Luque, R., Espinoza, N., et al. 2020, A&A, 639, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Bonfanti, A., & Gillon, M. 2020, A&A, 635, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Bonfanti, A., Ortolani, S., Piotto, G., & Nascimbeni, V. 2015, A&A, 575, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Bonfanti, A., Ortolani, S., & Nascimbeni, V. 2016, A&A, 585, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Bonfanti, A., Delrez, L., Hooton, M. J., et al. 2021, A&A, 646, A157 [EDP Sciences] [Google Scholar]
  32. Bonfils, X., Forveille, T., Delfosse, X., et al. 2005, A&A, 443, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Bonfils, X., Almenara, J. M., Cloutier, R., et al. 2018, A&A, 618, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Brandeker, A., Heng, K., Lendl, M., et al. 2022, A&A, 659, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Brown, T. M., Baliber, N., Bianco, F. B., et al. 2013, PASP, 125, 1031 [Google Scholar]
  36. Burn, R., Schlecker, M., Mordasini, C., et al. 2021, A&A, 656, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Burt, J. A., Dragomir, D., Mollière, P., et al. 2021, AJ, 162, 87 [NASA ADS] [CrossRef] [Google Scholar]
  38. Butler, R. P., Vogt, S. S., Marcy, G. W., et al. 2004, ApJ, 617, 580 [NASA ADS] [CrossRef] [Google Scholar]
  39. Cale, B., Plavchan, P., LeBrun, D., et al. 2019, AJ, 158, 170 [Google Scholar]
  40. Cañas, C. I., Kanodia, S., Libby-Roberts, J., et al. 2023, AJ, 166, 30 [CrossRef] [Google Scholar]
  41. Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Castelli, F., & Kurucz, R. L. 2003, in IAU Symp., 210, Modelling of Stellar Atmospheres, eds. N. Piskunov, W. W. Weiss, & D. F. Gray, A20 [NASA ADS] [Google Scholar]
  43. Castro-González, A., Demangeon, O. D. S., Lillo-Box, J., et al. 2023, A&A, 675, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Charbonneau, D., Irwin, J., Nutzman, P., & Falco, E. E. 2008, in Am. Astron. Soc. Meeting Abstracts, 212, 44.02 [NASA ADS] [Google Scholar]
  45. Chaturvedi, P., Bluhm, P., Nagel, E., et al. 2022, A&A, 666, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Chen, H., & Rogers, L. A. 2016, ApJ, 831, 180 [Google Scholar]
  47. Cherubim, C., Cloutier, R., Charbonneau, D., et al. 2023, AJ, 165, 167 [NASA ADS] [CrossRef] [Google Scholar]
  48. Childs, A. C., Martin, R. G., & Livio, M. 2022, ApJ, 937, L41 [Google Scholar]
  49. Ciardi, D. R., Fabrycky, D. C., Ford, E. B., et al. 2013, ApJ, 763, 41 [CrossRef] [Google Scholar]
  50. Cloutier, R., & Menou, K. 2020, AJ, 159, 211 [NASA ADS] [CrossRef] [Google Scholar]
  51. Cloutier, R., Astudillo-Defru, N., Bonfils, X., et al. 2019, A&A, 629, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Cloutier, R., Eastman, J. D., Rodriguez, J. E., et al. 2020, AJ, 160, 3 [Google Scholar]
  53. Cloutier, R., Charbonneau, D., Deming, D., Bonfils, X., & Astudillo-Defru, N. 2021a, AJ, 162, 174 [NASA ADS] [CrossRef] [Google Scholar]
  54. Cloutier, R., Charbonneau, D., Stassun, K. G., et al. 2021b, AJ, 162, 79 [NASA ADS] [CrossRef] [Google Scholar]
  55. Cointepas, M., Almenara, J. M., Bonfils, X., et al. 2021, A&A, 650, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Cortes, C., & Vapnik, V. 1995, Mach. Learn., 20, 273 [Google Scholar]
  57. Cosentino, R., Bonanno, G., Bruno, P., et al. 2000, Mem. Soc. Astron. Italiana, 71, 393 [Google Scholar]
  58. Cosentino, R., Lovis, C., Pepe, F., et al. 2012, SPIE Conf. Ser., 8446, 84461V [Google Scholar]
  59. Crossfield, I. J. M., Malik, M., Hill, M. L., et al. 2022, ApJ, 937, L17 [NASA ADS] [CrossRef] [Google Scholar]
  60. Cuntz, M., & Wang, Z. 2018, RNAAS, 2, 19 [NASA ADS] [Google Scholar]
  61. Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog, II/246 [Google Scholar]
  62. Delfosse, X., Forveille, T., Mayor, M., et al. 1998, A&A, 338, L67 [Google Scholar]
  63. Demangeon, O. D. S., Zapatero Osorio, M. R., Alibert, Y., et al. 2021, A&A, 653, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Diamond-Lowe, H., Kreidberg, L., Harman, C. E., et al. 2022, AJ, 164, 172 [NASA ADS] [CrossRef] [Google Scholar]
  65. Dorn, C., Venturini, J., Khan, A., et al. 2017, A&A, 597, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Dransfield, G., Timmermans, M., Triaud, A. H. M. J., et al. 2024, MNRAS, 527, 35 [Google Scholar]
  67. Eggleton, P. P. 1983, ApJ, 268, 368 [Google Scholar]
  68. Emsenhuber, A., Mordasini, C., Burn, R., et al. 2021, A&A, 656, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Erkaev, N. V., Kulikov, Y. N., Lammer, H., et al. 2007, A&A, 472, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Espinoza, N., & Jordán, A. 2015, MNRAS, 450, 1879 [Google Scholar]
  71. Essack, Z., Shporer, A., Burt, J. A., et al. 2023, AJ, 165, 47 [NASA ADS] [CrossRef] [Google Scholar]
  72. Foreman-Mackey, D., Agol, E., Ambikasaran, S., & Angus, R. 2017, AJ, 154, 220 [Google Scholar]
  73. Fridlund, M., Georgieva, I. Y., Bonfanti, A., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202243838 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Fruhwirth-Schnatter, S., Celeux, G., & Robert, C. P. 2018, Handbook of Mixture Analysis, 1st edn. (Chapman and Hall/CRC) [Google Scholar]
  75. Fulton, B. J., & Petigura, E. A. 2018, AJ, 156, 264 [Google Scholar]
  76. Fulton, B. J., Petigura, E. A., Howard, A. W., et al. 2017, AJ, 154, 109 [Google Scholar]
  77. Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Gelman, A., & Rubin, D. B. 1992, Stat. Sci., 7, 457 [Google Scholar]
  79. Ghachoui, M., Soubkiou, A., Wells, R. D., et al. 2023, A&A, 677, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Gillon, M., Pont, F., Demory, B. O., et al. 2007, A&A, 472, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Ginzburg, S., Schlichting, H. E., & Sari, R. 2018, MNRAS, 476, 759 [Google Scholar]
  82. Gupta, A., & Schlichting, H. E. 2019, MNRAS, 487, 24 [Google Scholar]
  83. Gupta, A., & Schlichting, H. E. 2020, MNRAS, 493, 792 [Google Scholar]
  84. Hakim, K., Rivoldini, A., Van Hoolst, T., et al. 2018, Icarus, 313, 61 [Google Scholar]
  85. Haldemann, J., Alibert, Y., Mordasini, C., & Benz, W. 2020, A&A, 643, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Haldemann, J., Dorn, C., Venturini, J., et al. 2024, A&A, 681, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Hatzes, A. P. 2016, in Astrophys. Space Sci. Lib., 428, Methods of Detecting Exoplanets: 1st Advanced School on Exoplanetary Science, eds. V. Bozza, L. Mancini, & A. Sozzetti, 3 [NASA ADS] [CrossRef] [Google Scholar]
  88. Hirano, T., Gaidos, E., Winn, J. N., et al. 2020, ApJ, 890, L27 [NASA ADS] [CrossRef] [Google Scholar]
  89. Hirano, T., Livingston, J. H., Fukui, A., et al. 2021, AJ, 162, 161 [NASA ADS] [CrossRef] [Google Scholar]
  90. Ho, C. S. K., & Van Eylen, V. 2023, MNRAS, 519, 4056 [NASA ADS] [CrossRef] [Google Scholar]
  91. Hoerl, A. E., & Kennard, R. W. 1970, Technometrics, 12, 55 [Google Scholar]
  92. Holman, M. J., Winn, J. N., Latham, D. W., et al. 2006, ApJ, 652, 1715 [NASA ADS] [CrossRef] [Google Scholar]
  93. Hoyer, S., Guterman, P., Demangeon, O., et al. 2020, A&A, 635, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Huang, T., Peng, H., & Zhang, K. 2017, Statistica Sinica, 27, 147 [Google Scholar]
  95. Incha, E., Vanderburg, A., Jacobs, T., et al. 2023, MNRAS, 523, 474 [NASA ADS] [CrossRef] [Google Scholar]
  96. Jehin, E., Gillon, M., Queloz, D., et al. 2011, The Messenger, 145, 2 [NASA ADS] [Google Scholar]
  97. Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, SPIE Conf. Ser., 9913, 99133E [Google Scholar]
  98. Kaminski, A., Trifonov, T., Caballero, J. A., et al. 2018, A&A, 618, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [Google Scholar]
  100. Kay, C., Opher, M., & Kornbleuth, M. 2016, ApJ, 826, 195 [NASA ADS] [CrossRef] [Google Scholar]
  101. Kegerreis, J. A., Eke, V. R., Catling, D. C., et al. 2020, ApJ, 901, L31 [NASA ADS] [CrossRef] [Google Scholar]
  102. Kemmer, J., Stock, S., Kossakowski, D., et al. 2020, A&A, 642, A236 [EDP Sciences] [Google Scholar]
  103. Kiman, R., Faherty, J. K., Cruz, K. L., et al. 2021, AJ, 161, 277 [NASA ADS] [CrossRef] [Google Scholar]
  104. Kopparapu, R. K., Ramirez, R., Kasting, J. F., et al. 2013, ApJ, 765, 131 [NASA ADS] [CrossRef] [Google Scholar]
  105. Kossakowski, D., Kemmer, J., Bluhm, P., et al. 2021, A&A, 656, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  106. Kotani, T., Tamura, M., Nishikawa, J., et al. 2018, SPIE Conf. Ser., 10702, 1070211 [Google Scholar]
  107. Kubyshkina, D. 2023, IAU Symp., 370, 103 [NASA ADS] [Google Scholar]
  108. Kubyshkina, D., & Fossati, L. 2022, A&A, 668, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Kubyshkina, D., Fossati, L., Erkaev, N. V., et al. 2018, ApJ, 866, L18 [NASA ADS] [CrossRef] [Google Scholar]
  110. Kurucz, R. L. 1993, SYNTHE spectrum synthesis programs and line data (Cambridge, Mass.: Smithsonian, Astrophysical Observatory) [Google Scholar]
  111. Lam, K. W. F., Korth, J., Masuda, K., et al. 2020, AJ, 159, 120 [NASA ADS] [CrossRef] [Google Scholar]
  112. Lam, K. W. F., Csizmadia, S., Astudillo-Defru, N., et al. 2021, Science, 374, 1271 [NASA ADS] [CrossRef] [Google Scholar]
  113. Lammer, H., Selsis, F., Ribas, I., et al. 2003, ApJ, 598, L121 [Google Scholar]
  114. Lee, E. J., & Connors, N. J. 2021, ApJ, 908, 32 [NASA ADS] [CrossRef] [Google Scholar]
  115. Lee, E. J., Chiang, E., & Ormel, C. W. 2014, ApJ, 797, 95 [Google Scholar]
  116. Lee, E. J., Karalis, A., & Thorngren, D. P. 2022, ApJ, 941, 186 [NASA ADS] [CrossRef] [Google Scholar]
  117. Leleu, A., Alibert, Y., Hara, N. C., et al. 2021, A&A, 649, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  118. Lillo-Box, J., Figueira, P., Leleu, A., et al. 2020, A&A, 642, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  119. Lindegren, L., Bastian, U., Biermann, M., et al. 2021, A&A, 649, A4 [EDP Sciences] [Google Scholar]
  120. Lobo, A. H., Shields, A. L., Palubski, I. Z., & Wolf, E. 2023, ApJ, 945, 161 [NASA ADS] [CrossRef] [Google Scholar]
  121. Lopez, E. D., & Fortney, J. J. 2013, ApJ, 776, 2 [Google Scholar]
  122. Lopez, E. D., & Fortney, J. J. 2014, ApJ, 792, 1 [Google Scholar]
  123. Lopez, E. D., & Rice, K. 2018, MNRAS, 479, 5303 [NASA ADS] [CrossRef] [Google Scholar]
  124. Luger, R., & Barnes, R. 2015, Astrobiology, 15, 119 [Google Scholar]
  125. Luque, R., & Pallé, E. 2022, Science, 377, 1211 [NASA ADS] [CrossRef] [Google Scholar]
  126. Luque, R., Palle, E., Kossakowski, D., et al. 2019, A&A, 628, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. Luque, R., Serrano, L. M., Molaverdikhani, K., et al. 2021, A&A, 645, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  128. Luque, R., Fulton, B. J., Kunimoto, M., et al. 2022, A&A, 664, A199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  129. MacDonald, M. G. 2019, MNRAS, 487, 5062 [NASA ADS] [CrossRef] [Google Scholar]
  130. Maciel, W. J., Rodrigues, T. S., & Costa, R. D. D. 2011, Rev. Mex. Astron. Astrofis., 47, 401 [Google Scholar]
  131. Maldonado, J., Micela, G., Baratella, M., et al. 2020, A&A, 644, A68 [EDP Sciences] [Google Scholar]
  132. Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [Google Scholar]
  133. Marboeuf, U., Thiabaud, A., Alibert, Y., Cabral, N., & Benz, W. 2014, A&A, 570, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  134. Marcy, G. W., Butler, R. P., Vogt, S. S., Fischer, D., & Lissauer, J. J. 1998, ApJ, 505, L147 [Google Scholar]
  135. Marigo, P., Girardi, L., Bressan, A., et al. 2017, ApJ, 835, 77 [Google Scholar]
  136. Martinez, C. F., Cunha, K., Ghezzi, L., & Smith, V. V. 2019, ApJ, 875, 29 [Google Scholar]
  137. Matsumura, S., Takeda, G., & Rasio, F. A. 2008, ApJ, 686, L29 [Google Scholar]
  138. Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
  139. Miguel, Y., Cridland, A., Ormel, C. W., Fortney, J. J., & Ida, S. 2020, MNRAS, 491, 1998 [NASA ADS] [Google Scholar]
  140. Mishra, L., Alibert, Y., Udry, S., & Mordasini, C. 2023, A&A, 670, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  141. Morris, B. M., Delrez, L., Brandeker, A., et al. 2021, A&A, 653, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  142. Narita, N., Fukui, A., Kusakabe, N., et al. 2019, J. Astron. Telescopes Instrum. Syst., 5, 015001 [Google Scholar]
  143. Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [Google Scholar]
  144. Nowak, G., Luque, R., Parviainen, H., et al. 2020, A&A, 642, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  145. Ojha, L., Troncone, B., Buffo, J., Journaux, B., & McDonald, G. 2022, Nat. Commun., 13, 7521 [NASA ADS] [CrossRef] [Google Scholar]
  146. Oliva, E. 2006, Mem. Soc. Astron. Ital. Suppl., 9, 409 [Google Scholar]
  147. Owen, J. E., & Wu, Y. 2013, ApJ, 775, 105 [Google Scholar]
  148. Owen, J. E., & Wu, Y. 2017, ApJ, 847, 29 [Google Scholar]
  149. Parviainen, H., Tingley, B., Deeg, H. J., et al. 2019, A&A, 630, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  150. Pass, E. K., Charbonneau, D., Irwin, J. M., & Winters, J. G. 2022, ApJ, 936, 109 [NASA ADS] [CrossRef] [Google Scholar]
  151. Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
  152. Pepe, F., Cristiani, S., Rebolo, R., et al. 2021, A&A, 645, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  153. Peterson, M. S., Benneke, B., Collins, K., et al. 2023, Nature, 617, 701 [NASA ADS] [CrossRef] [Google Scholar]
  154. Petigura, E. A., Rogers, J. G., Isaacson, H., et al. 2022, AJ, 163, 179 [NASA ADS] [CrossRef] [Google Scholar]
  155. Piaulet, C., Benneke, B., Almenara, J. M., et al. 2023, Nat. Astron., 7, 206 [Google Scholar]
  156. Pont, F., Zucker, S., & Queloz, D. 2006, MNRAS, 373, 231 [NASA ADS] [CrossRef] [Google Scholar]
  157. Powers, L. C., Libby-Roberts, J., Lin, A. S. J., et al. 2023, AJ, 166, 44 [NASA ADS] [CrossRef] [Google Scholar]
  158. Pozuelos, F. J., Timmermans, M., Rackham, B. V., et al. 2023, A&A, 672, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  159. Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2014, SPIE Conf. Ser., 9147, 91471F [Google Scholar]
  160. Quirrenbach, A., Amado, P. J., Ribas, I., et al. 2018, SPIE Conf. Ser., 10702, 107020W [Google Scholar]
  161. Rasmussen, C. E., & Williams, C. K. I. 2005, Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning) (The MIT Press) [Google Scholar]
  162. Rayner, J., Tokunaga, A., Jaffe, D., et al. 2016, SPIE Conf. Ser., 9908, 990884 [Google Scholar]
  163. Rayner, J., Tokunaga, A., Jaffe, D., et al. 2022, PASP, 134, 015002 [NASA ADS] [CrossRef] [Google Scholar]
  164. Reddy, B. E., Lambert, D. L., & Allende Prieto, C. 2006, MNRAS, 367, 1329 [Google Scholar]
  165. Reiners, A., Basri, G., & Browning, M. 2009, ApJ, 692, 538 [NASA ADS] [CrossRef] [Google Scholar]
  166. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telescopes Instrum. Syst., 1, 014003 [Google Scholar]
  167. Rogers, J. G., Gupta, A., Owen, J. E., & Schlichting, H. E. 2021, MNRAS, 508, 5886 [NASA ADS] [CrossRef] [Google Scholar]
  168. Saar, S. H., & Linsky, J. L. 1985, ApJ, 299, L47 [Google Scholar]
  169. Salmon, S. J. A. J., Van Grootel, V., Buldgen, G., Dupret, M. A., & Eggenberger, P. 2021, A&A, 646, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  170. Schanche, N., Hébrard, G., Collier Cameron, A., et al. 2020, MNRAS, 499, 428 [NASA ADS] [CrossRef] [Google Scholar]
  171. Schmidt, S. J., Hawley, S. L., West, A. A., et al. 2015, AJ, 149, 158 [NASA ADS] [CrossRef] [Google Scholar]
  172. Scholz, R. D., Meusinger, H., & Jahreiß, H. 2005, A&A, 442, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  173. Schönrich, R., Binney, J., & Dehnen, W. 2010, MNRAS, 403, 1829 [Google Scholar]
  174. Schwarz, G. 1978, Ann. Stati., 6, 461 [NASA ADS] [CrossRef] [Google Scholar]
  175. Schweitzer, A., Passegger, V. M., Cifuentes, C., et al. 2019, A&A, 625, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  176. Scuflaire, R., Théado, S., Montalbán, J., et al. 2008, Ap&SS, 316, 83 [Google Scholar]
  177. Seifahrt, A., Stürmer, J., Bean, J. L., & Schwab, C. 2018, SPIE Conf. Ser., 10702, 107026D [NASA ADS] [Google Scholar]
  178. Seifahrt, A., Bean, J. L., Kasper, D., et al. 2022, SPIE Conf. Ser., 12184, 121841G [Google Scholar]
  179. Sergeev, D. E., Lambert, F. H., Mayne, N. J., et al. 2020, ApJ, 894, 84 [NASA ADS] [CrossRef] [Google Scholar]
  180. Shulyak, D., Reiners, A., Nagel, E., et al. 2019, A&A, 626, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  181. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [Google Scholar]
  182. Sotin, C., Grasset, O., & Mocquet, A. 2007, Icarus, 191, 337 [Google Scholar]
  183. Soto, M. G., Anglada-Escudé, G., Dreizler, S., et al. 2021, A&A, 649, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  184. Sousa, S. G., Adibekyan, V., Delgado-Mena, E., et al. 2021, A&A, 656, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  185. Stefansson, G., Mahadevan, S., Maney, M., et al. 2020, AJ, 160, 192 [NASA ADS] [CrossRef] [Google Scholar]
  186. Thiabaud, A., Marboeuf, U., Alibert, Y., et al. 2014, A&A, 562, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  187. Thiabaud, A., Marboeuf, U., Alibert, Y., Leya, I., & Mezger, K. 2015, A&A, 574, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  188. Tilley, M. A., Segura, A., Meadows, V., Hawley, S., & Davenport, J. 2019, Astrobiology, 19, 64 [Google Scholar]
  189. Tody, D. 1986, SPIE Conf. Ser., 627, 733 [Google Scholar]
  190. Tody, D. 1993, in ASP Conf. Ser., 52, Astronomical Data Analysis Software and Systems II, eds. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, 173 [NASA ADS] [Google Scholar]
  191. Trifonov, T., Kürster, M., Zechmeister, M., et al. 2018, A&A, 609, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  192. Trifonov, T., Caballero, J. A., Morales, J. C., et al. 2021, Science, 371, 1038 [Google Scholar]
  193. Udry, S., Bonfils, X., Delfosse, X., et al. 2007, A&A, 469, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  194. Van Eylen, V., Agentoft, C., Lundkvist, M. S., et al. 2018, MNRAS, 479, 4786 [Google Scholar]
  195. Van Eylen, V., Astudillo-Defru, N., Bonfils, X., et al. 2021, MNRAS, 507, 2154 [NASA ADS] [Google Scholar]
  196. Venturini, J., Guilera, O. M., Haldemann, J., Ronco, M. P., & Mordasini, C. 2020, A&A, 643, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  197. Watson, A. J., Donahue, T. M., & Walker, J. C. G. 1981, Icarus, 48, 150 [NASA ADS] [CrossRef] [Google Scholar]
  198. Weiss, L. M., Marcy, G. W., Petigura, E. A., et al. 2018, AJ, 155, 48 [Google Scholar]
  199. West, A. A., Morgan, D. P., Bochanski, J. J., et al. 2011, AJ, 141, 97 [NASA ADS] [CrossRef] [Google Scholar]
  200. Wielen, R. 1977, A&A, 60, 263 [NASA ADS] [Google Scholar]
  201. Wilson, T. G., Simpson, A. M., Collier Cameron, A., et al. 2023, Science, submitted [Google Scholar]
  202. Winn, J. N. 2010, in Exoplanets, ed. S. Seager (Tucson: University of Arizona Press), 55 [Google Scholar]
  203. Winters, J. G., Cloutier, R., Medina, A. A., et al. 2022, AJ, 163, 168 [NASA ADS] [CrossRef] [Google Scholar]
  204. Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
  205. Wu, Y. 2019, ApJ, 874, 91 [NASA ADS] [CrossRef] [Google Scholar]
  206. Wyatt, M. C., Kral, Q., & Sinclair, C. A. 2020, MNRAS, 491, 782 [NASA ADS] [Google Scholar]
  207. Zacharias, N., Finch, C. T., Girard, T. M., et al. 2012, VizieR Online Data Catalog, I/322A [Google Scholar]
  208. Zechmeister, M., Reiners, A., Amado, P. J., et al. 2018, A&A, 609, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  209. Zechmeister, M., Reiners, A., Amado, P. J., et al. 2020, Astrophysics Source Code Library [record ascl:2886.811] [Google Scholar]
  210. Zeng, L., Jacobsen, S. B., Sasselov, D. D., et al. 2019, PNAS, 116, 9723 [Google Scholar]
3

PAdova and TRieste Stellar Evolutionary Code: http://stev.oapd.inaf.it/cgi-bin/cmd

5

See https://tasoc.dk/docs/EXP-TESS-ARC-ICD-TM-8814-Rev-F.pdf for further details about the TESS Science Data Products.

11

Source: Nasa Exoplanet Archive, https://exoplanetarchive.ipac.caltech.edu/

12

Planetary data of M dwarfs (that is stars with Teff < 4000 K) were properly filtered and downloaded from the NASA Exoplanet Archive https://exoplanetarchive.ipac.caltech.edu/ as of 27 July 2023.

All Tables

Table 1

Stellar properties.

In the text
Table 2

Photometric observations from ground-based facilities.

In the text
Table 3

Details of the CHEOPS visits.

In the text
Table 4

RV data employed in the combined analysis.

In the text
Table 5

Parameters of the TOI-732 system.

In the text
Table 6

Comparison between literature uncertainties and those derived in this work on the orbital periods P, the transit depths dF, and the RV semi-amplitudes K of the planets.

In the text
Table 7

Radius valley slopes m ≡ d log Rp,valley/d log P as predicted from theory for different scenarios.

In the text
Table C.1

Quadratic limb darkening (LD) coefficients (u1, u2) for each photo

In the text
Table C.2

Polynomial detrending baselines applied to the space-based light curves within the MCMC scheme.

In the text
Table C.3

Radial velocity jitter for each RV time series as inferred from the MCMC global analysis, after applying the polynomial detrending as specified in the third column. c denotes a scalar offset; see text for further details

In the text
Table C.4

Main planetary parameters of the Msample.

In the text

All Figures

thumbnail Fig. 1

Phase-folded and detrended LCs showing the transit of TOI-732 b (first column) and TOI-732 c (second column) as observed by CHEOPS (first row) and TESS (second row). The original data points are shown in blue, the binned data points are shown in black (binning of 10 min), and the transit model is displayed in red.
In the text
thumbnail Fig. 2

Phase-folded and detrended RV time series of TOI-732 b (top) and TOI-732 c (bottom), obtained after subtracting the signal of the other planet. The corresponding Keplerian model is superimposed in red. The different colours mark different instruments, namely HARPS (black), IRD (light green), HARPS-N (blue), CARMENES (magenta), iSHELL (cyan), MAROON-X (yellow, orange, and deep green for observations taken in February, April, and May 2021, respectively). As MAROON-X has two different channels, full and empty symbols represent data acquired using the blue and red channel, respectively (see text for further details).
In the text
thumbnail Fig. 3

Corner plot showing the posteriors of the main parameters of our internal structure analysis for TOI-732 b. The titles of each column correspond to the median of the distribution, with the 5th and 95th percentiles as the uncertainty values. From left to right, the depicted internal structure parameters are the mass fractions of the inner iron core and of the water layer (both calculated with respect to the condensed part of the planet without the H-He layer), the molar fractions of Si and Mg in the mantle, the molar fraction of Fe in the inner core, and the total mass of H-He in Earth masses on a logarithmic scale. The mass fractions of the inner core and the water layer add up to one, with the mass fraction of the mantle layer (not shown) by construction.
In the text
thumbnail Fig. 4

Same as Fig. 3, but for TOI-732 c.
In the text
thumbnail Fig. 5

Mass-radius diagram of M-dwarf planets with Rp < 4 R⊕ and Mp < 30 M⊕ whose Rp and Mp precision is better than 8% and 25%, respectively. All planets are colour-coded with respect to their equilibrium temperature (Teq) and in particular, TOI-732 b and TOI-732 c are marked by a star. Following the colour scheme given in the legend, two different sets of planet composition models generated with BICEPS (Haldemann et al. 2024) are displayed. The solid and dashed lines are obtained for Teq = Teq,b = 900 K and Teq = Teq,c = 360 K, respectively. The 50% steam + 50% Earth-like line corresponds to the model of Aguichine et al. (2021) for Teq = 400 K. An Earth-like composition implies a mixture of 32.5% iron and 67.5% silicates. The dotted black lines correspond to the loci of constant density, that is, 0.5, 1, 3, 5, and 10 g cm−3 (from top to bottom).
In the text
thumbnail Fig. 6

Rp vs P distribution representing the planets in our Msample. Planets classified above and below the radius valley are shown in blue and green, respectively, while the red star-shaped markers are for TOI-732 b and c. The radius valley inferred via the SVM-based method is marked by the solid grey line with the shaded region highlighting the 1 σ limits of the best-fit line. The two parallel dashed grey lines are the median boundaries passing through the supporting vectors that determine the location of the solid line. Finally, the red lines represent the theoretically expected Rp,valley boundary in case of a thermally-driven mass-loss scenario (solid line as computed from Affolter et al. 2023; negative slope) and the Rp upper limit of planets borned rocky in a gas-empty disc (dashed line as computed from Lopez & Rice 2018; positive slope).
In the text
thumbnail Fig. 7

Same as Fig. 6, but the markers are colour-coded against the Roche lobe of each planet normalised to the planetary radius (top) or to the orbital semi-major axis (bottom).
In the text
thumbnail Fig. 8

Same as Fig. 6, but this time, Rp is plotted against stellar mass.
In the text
thumbnail Fig. 9

Normalised density as a function of orbital period. The normalised density is the mean density of the planet divided by the density the planet would have if it had an Earth-like composition (same variable as introduced in L22 to display the density valley). The grey line and its shaded area indicate the density valley with its corresponding error, as in Fig. 6.
In the text
thumbnail Fig. A.1

Raw CHEOPS LCs in chronological order of observations from CH 1 up to CH 6, as presented in Table 3. The main systematic affecting the LCs is due to the highly variable flux pattern correlating with the spacecraft roll angle.
In the text
thumbnail Fig. A.2

Same as Fig. A.1, but for CHEOPS LCs from CH 7 up to CH 12.
In the text
thumbnail Fig. A.3

Same as Fig. A.1, but for CHEOPS LCs from CH 13 up to CH 18.
In the text
thumbnail Fig. A.4

Same as Fig. A.1, but for CHEOPS LCs from CH 19 up to CH 24.
In the text
thumbnail Fig. A.5

Same as Fig. A.1, but for CHEOPS LCs CH 25.
In the text
thumbnail Fig. B.1

Phase-folded LCs of TOI-732 b (first column) and TOI-732 c (second column) observed by ground-based facilities in the following filters: g’ (first row), r’ (second row), i’ (third row), and z’ (fourth row).
In the text
thumbnail Fig. B.2

LCs of TOI-732 c taken by ground-based facilities. From Top to Bottom going row wise the observation filters are B, V, R, and RG715.
In the text
thumbnail Fig. B.3

LC of TOI-732b as observed by OAA in the I filter.
In the text
thumbnail Fig. C.1

Same as Fig. 6, but with the markers colour-coded against RpTeq4${R_{\rm{p}}}T_{{\rm{eq}}}^4$, which correlates with the core-powered mass loss strength (Gupta & Schlichting 2019).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.