EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 683 (March 2024) A&A, 683 (2024) A170 Full HTML
Open Access
Issue
A&A
Volume 683, March 2024
Article Number A170
Number of page(s) 13
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202347431
Published online 19 March 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

The radius distribution for Earth-to-Neptune-sized exoplanets on short-period orbits around M dwarfs is bimodal, seeming to imply the existence of two planet populations with distinct physical properties (Cherubim et al. 2023; Luque et al. 2022, 2021; Cloutier et al. 2021, 2020a,b; Van Eylen et al. 2021; Cloutier & Menou 2020). This bimodality is similar to what has been observed for planets orbiting FGK-stars (Mayo et al. 2018; Fulton & Petigura 2018; Fulton et al. 2017), but the minimum between the two modes, also known as the radius valley, is located at 1.4–1.7 R⊕ for M dwarfs, a somewhat smaller radius than observed for the FGK-star radius valley (1.7–2.0 R⊕).

The smaller-radius population of planets is expected to consist of rocky planets with negligible atmospheres (sub-Earths, Earths, and super-Earths), while the larger-radius population has been considered to consist of Neptune-like ice giants with extended H/He envelopes (sub-Neptunes). Water-rich planets (water worlds) with a water-to-rock ratio close to unity but lacking a significant H/He envelope have also been suggested as a third major population between rocky planets and sub-Neptunes (Zeng et al. 2019), but observational evidence supporting this was limited until recent work by Luque & Pallé (2022).

In their study, Luque & Pallé focused on a set of small planets orbiting M dwarfs on periods shorter than 35 days with masses and radii estimated to a precision of 25% and 8% or better, respectively. They found that the density distribution for small planets features three modes agreeing with the densities predicted for rocky planets, water worlds, and sub-Neptunes by Zeng et al. (2019). From this perspective, the bimodal radius distribution would correspond to a projection of the density distribution blending the water worlds and sub-Neptunes together.

The result by Luque & Pallé (2022) is based on a small number of well-characterised planets, and the statistical significance of the hypothesis of three main planet-type populations can be improved by discovering more Earth-to-Neptune-sized planets around M dwarfs. The Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2014) has identified several hundred planet candidates fitting the period and radius criteria used by Luque & Pallé (2022)1, but some of these candidates are false positives, and instruments capable of carrying out radial velocity (RV) mass estimation of small planets around M dwarfs are few and in high demand. Consequently, the first step in the process of identifying the main small-planet population types is to validate and characterise planet candidates amenable to RV mass estimation.

The planets used to study the small-planet populations can also be used to probe how small planets form around M dwarfs (Burn et al. 2021; Stefánsson et al. 2020; Lopez & Rice 2018). The formation of short-period non-rocky planets (water worlds and sub-Neptunes) is roughly understood since these planets are expected to have formed originally beyond the protoplanetary disk ice line to accrete the water and gases that make them what they are, after which they have migrated inwards to their current orbits. However, the formation of rocky planets is still an open question with two proposed main competing formation pathways: gas-depleted formation or formation through thermally-driven mass loss. The gas-depleted formation proposes that rocky planets and water- and gas-rich planets consist of two separate planet populations that formed at different times. In contrast, the thermally-driven mass loss scenario proposes that rocky planets are basically sub-Neptune cores stripped of their H/He envelopes. These formation scenarios (discussed in more detail later in Sect. 5) lead to conflicting predictions on how the upper limit of the rocky planet size (that is, the centre of the radius valley) depends on the orbital period of the planet. Planets that are located in the area in the period-radius plane where the predictions from the two formation scenarios disagree (named ‘keystone planets’ by Cloutier et al. 2021) can be used to probe which of the pathways is the dominant one.

Here we report the validation and characterisation of TOI-2266 b, a small transiting planet (1.54 ± 0.09 R⊕), orbiting a faint M5 dwarf (TIC 8348911, see Table 1) on a 2.33 d orbit. The Science Processing Operations Center (SPOC) located at NASA Ames Research Center conducted a transit search of Sector 24 on 2020 August 2 with an adaptive, noise-compensating matched filter (Jenkins 2002; Jenkins et al. 2010, 2016) producing a Threshold Crossing Event (TCE) for which an initial limb-darkened transit model was fitted (Li et al. 2019) and a suite of diagnostic tests were conducted to help make or break the planetary nature of the signal (Twicken et al. 2018). The TESS Science Office (TSO) reviewed the vetting information and issued an alert on 30 September 2020 (Guerrero et al. 2021). The transit signature passed all the diagnostic tests presented in the Data Validation reports. The host star is located within 1.95 ± 3.90 arcsec of the source of the transit signal. The planet candidate was later followed up from the ground using multicolour transit photometry and low-resolution spectroscopy. The validation is carried out using the multicolour transit validation approach described in Parviainen et al. (2019) and applied later in Parviainen et al. (2020, 2021), Esparza-Borges et al. (2022), and Morello et al. (2023). The analyses and data discussed in this paper are publicly available from GitHub2.

Table 1

TOI-2266 identifiers, coordinates, properties, and magnitudes.

2 Stellar characterisation

We obtained an optical low-resolution spectrum of TOI-2266 with the Alhambra Faint Object Spectrograph and Camera (ALFOSC) mounted at the 2.56 m Nordic Optical Telescope (NOT) on the Roque de los Muchachos Observatory (ORM) on 2021 July 1 UT. ALFOSC is equipped with a 2048 × 2064 CCD detector with a pixel scale of 0.2138″pixel−1. We used grism number 5 and an horizontal long slit with a width of 1.0″, which yield a nominal spectral dispersion of 3.53 Å pixel−1 and a usable wavelength space coverage between 5000 and 9400 Å. Two spectra of 900 s each were acquired at parallactic angle and airmass of 1.03. We also observed a spectrophotometric standard star BD+17 4708 with the same instrumental setup as TOI-2266, with an exposure time of 15 s, and at an airmass of 1.02. Raw images were reduced following standard procedures at optical wavelengths: bias subtraction, flat-fielding using dome flats, and optimal extraction using appropriate packages within the IRAF3 environment. Wavelength calibration was performed with a precision of 0.65 Å using He I and Ne I arc lines observed on the same night. The instrumental response was corrected using observations of the standard star. Because the primary target and the standard star were observed close in time and at a similar airmass, we corrected for telluric lines absorption by dividing the target data by the spectrum of the standard normalised to the continuum.

The estimation of the stellar parameters (spectral type, effective temperature, and stellar mass and radius) was carried out as in Parviainen et al. (2021); Parviainen (2020) based on tabulations by Schweitzer et al. (2019) and Mann et al. (2019), and the parameters are listed in Table 1. We used the reference spectra of Kesseli et al. (2017) for the spectral classification, and the spectrum is compatible with solar metallicity. Further, the astrometry of TOI-2266 is incompatible with membership in young stellar moving groups independently of its radial velocity, so the star is likely not young (age >300 Myr). This is also evident from the strength of the atomic lines (particularly K I and Na I) from the ALFOSC spectrum.

thumbnail Fig. 1

Contrast with its 1-σ uncertainties as a function of separation and angular separation in Brgamma, J and Ks (left) and a high-resolution PHARO image (right).

3 High-resolution imaging

3.1 Palomar observations

As part of our standard process for validating transiting exoplanets to assess the possible contamination of bound or unbound companions on the derived planetary radii (Ciardi et al. 2015), we observed TOI-2266 with high-resolution near-infrared adaptive optics (AO) imaging at Lick and Palomar Observatories. While the Palomar observations provided higher resolution and sensitivity, the Lick observations provided multiple filters. Neither set of observations detected additional stars; additionally, the Gaia DR3 astrometry is consistent with the star being single with an astrometric excess noise value of <1.4 (RUWE = 1.03).

The Palomar Observatory observations were made with the PHARO instrument (Hayward et al. 2001) behind the natural guide star AO system P3K (Dekany et al. 2013) on 2021 February 24 UT in a standard 5-point quincunx dither pattern with steps of 5″ in the narrow-band Br – γ filter (λ0 = 2.1686; Δλ = 0.0326 μm). Each dither position was observed three times, offset in position from each other by 0.5″ for a total of 15 frames; with an integration time of 10 s per frame, the total on-source time was 150 s. PHARO has a pixel scale of 0.025″ per pixel for a total field of view of ~25″.

The AO data were processed and analysed with a custom set of IDL tools. The science frames were flat-fielded and sky-subtracted. The flat fields were generated from a median average of dark subtracted flats taken on the sky. The flats were normalised such that the median value of the flats was unity. The sky frames were generated from the median average of the 15 dithered science frames; each science image was then sky-subtracted and flat-fielded. The reduced science frames were combined into a single combined image using an intra-pixel interpolation that conserves flux, shifts the individual dithered frames by the appropriate fractional pixels, and median-adds the frames. The final resolution of the combined dithers was determined from the full-width half-maximum of the point spread function: 0.108″. The sensitivities of the final combined AO image were determined by injecting simulated sources azimuthally around the primary target every 20° at separations of integer multiples of the central source's FWHM (Furlan et al. 2017). The brightness of each injected source was scaled until standard aperture photometry detected it with 5σ significance. The resulting brightness of the injected sources relative to TOI-2266 set the contrast limits at that injection location. The final 5σ limit at each separation was determined from the average of all of the determined limits at that separation, and the uncertainty on the limit was set by the rms dispersion of the azimuthal slices at a given radial distance (Fig. 1).

3.2 Lick observations

We observed TIC 8348911 on 2021 March 28 UT using the ShARCS camera on the Shane 3-m telescope at Lick Observatory (Kupke et al. 2012; Gavel et al. 2014; McGurk et al. 2014). The observation was taken with the Shane adaptive optics system in natural guide star mode. The final images were constructed using sequences of images taken in a 4-point dither pattern with a separation of 4″ between each dither position. Two image sequences were taken of this star: one with a K s filter (λ0 = 2.150 μm, Δλ = 0.320 μm) and one with a J filter (λ0 = 1.238 μm, Δλ = 0.271 μm), both of which used an exposure time of 60 s at each dither position. A more detailed description of the observing strategy and reduction procedure can be found in Savel et al. (2020). The contrast curves extracted from these observations are shown in Fig. 1. We find no nearby stellar companions within our detection limits.

4 Transit light curve analysis

4.1 Observations

4.1.1 TESS photometry

TESS observed 31 full transits of TOI-2266 b during Sectors 24, 25, 51, and 52 with a two-minute cadence. We chose to use the Presearch Data Conditioning (PDC) light curves (Stumpe et al. 2014, 2012; Smith et al. 2012) produced by the SPOC pipeline, but, as in Parviainen et al. (2020, 2021), we add back the crowding correction (‘CROWDSAP’) removed by the SPOC pipeline since the crowding correction could introduce a bias into our parameter estimation if the crowding were to be overestimated by the SPOC pipeline. The final TESS photometry used in the transit analysis consists of 31 7.2 h-long windows centred around each transit based on the linear ephemeris, and each window was normalised to its median out-of-transit level assuming a transit duration of 2.4 h. The photometry has an average point-to-point (ptp) scatter of 11.5 parts per thousand.

4.1.2 MuSCAT2 photometry

We observed five full transits of TOI-2266 b simultaneously in g, r, i, and zs bands with the MuSCAT2 multicolour imager (Narita et al. 2019) installed at the 1.52 m Telescopio Carlos Sánchez (TCS) in the Teide Observatory, Spain, on the nights of 2021 February 9, 2021 March 3, 2021 June 24, 2021 July 8, and 2021 July 15. The exposure times were optimised for each night and CCD and varied from 30 to 120 s. The observing conditions were mostly good through all the nights, but we decided to discard the g band photometry because of the low signal-to-noise ratio (S/N), and we also discarded the r band photometry observed on a night with anomalously bad seeing. The photometry was carried out using standard aperture photometry calibration and reduction steps with a dedicated MuSCAT2 photometry pipeline, as described in Parviainen et al. (2020). Values for x- and y- centroid shifts, airmass, and PSF width were also extracted and stored to be used in the analysis as baseline model components.

4.1.3 LCOGT 1 m and TRAPPIST photometry

We observed three transits of TOI-2266 b in Sloan i' band from the Las Cumbres Observatory Global Telescope (LCOGT; Brown et al. 2013) 1.0 m network. A full transit was observed on 2021 March 5 from the McDonald Observatory node, and near-full and full transits were observed on 2021 March 26 and 2021 April 16, respectively, from the Cerro Tololo Inter-American Observatory node. We used the TESS Transit Finder, which is a customised version of the Tapir software package (Jensen 2013), to schedule our transit observations. The 4096 × 4096 LCOGT SINISTRO cameras have an image scale of 0.″389 per pixel, resulting in a 26′ × 26′ field of view. The images were calibrated by the standard LCOGT BANZAI pipeline (McCully et al. 2018), and photometric data were extracted with AstroImageJ (Collins et al. 2017). The images were focused and have typical stellar point-spread-functions with a full-width-half-maximum (FWHM) of roughly 2″, and circular apertures with radius 4″ were used to extract the differential photometry.

Several transits of TOI-2266 b were also observed with the TRAPPIST-South and TRAPPIST-North telescopes. However, the S/Ns from these observations were too low to include in the analysis.

4.1.4 LCOGT MuSCAT3 photometry

A full transit of TOI-2266 b was observed simultaneously in Sloan g, r, i, and Pan-STARRS z-short bands on 2021 May 23 using the LCOGT 2 m Faulkes Telescope North at Haleakala Observatory on Maui, Hawai'i. The telescope is equipped with the MuSCAT3 multi-band imager (Narita et al. 2020). The images were calibrated using the standard LCOGT BANZAI pipeline, and photometric data were extracted using AstroImageJ. The images were mildly defocused and had typical stellar point spread functions (PSFs) with FWHM of ~2″.5, and circular apertures with radius 4″ were used to extract the differential photometry.

4.1.5 HiPERCAM photometry

A full transit of TOI-2266 b was observed simultaneously in u, g, r, i, and z with the High PERformance CAMera (HiPERCAM, Dhillon et al. 2021) mounted on the 10.4 m Gran Telescopio Canarias (GTC) on ORM on 2021 August 5. HiPERCAM is a multicolour imager composed of 5 CCD cameras capable of obtaining simultaneous observations in u, g, r, i, and z. Each camera has a field of view of 2.8′ × 1.4′ with a pixel scale of 0.081″ pixel−1. The exposure time was set to 1.69 s for all bands, and the data acquisition started at ~22:20 UT (airmass 1.10) and ended at ~01:00 UT (airmass 1.88).

4.2 Multicolour planet candidate validation and system characterisation

We modelled the TESS light curves simultaneously with the MuSCAT2, HiPERCAM, and LCOGT light curves following the approach described in Parviainen et al. (2019) and used in Parviainen et al. (2020, 2021), Esparza-Borges et al. (2022), and Morello et al. (2023). Briefly, multicolour planet candidate validation works by estimating the maximum radius for the planet candidate when accounting for third-light contamination from possible unresolved stars. If this upper radius limit is below the theoretical radius limit of a brown dwarf (~0.8 RJup, Burrows et al. 2011), the candidate can be securely treated as a planet.

Without contamination, a planet candidate's radius, Rp, is directly related to the planet-star radius ratio, k, and stellar radius, R*, as Rp = k R*. The radius ratio is related to the area ratio, k2, and transit depth, ΔF, as 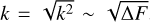k=k2~ΔF$k = \sqrt {{k^2}} \~\sqrt {{\rm{\Delta }}F} $, and can be estimated with the help of a transit model that also accounts for the effects from the stellar limb darkening and the planet's orbital geometry.

Third-light contamination from unresolved sources inside a photometric aperture dilutes a transit signal, making a transit with a ‘true’ depth, ΔFtrue, to appear to have an ‘apparent’ depth of 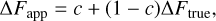ΔFapp =c+(1−c) ΔFtrue ,${\rm{\Delta }}{F_{{\rm{app}}}} = c + (1 - c)\,{\rm{\Delta }}{F_{{\rm{true}}}},$(1)

where c is the contamination, c = Fc/(Fc + Fh), Fc is the flux from the contaminants, and Fh is the flux from the candidate host. The diluted transit depth results in an underestimated radius ratio, and, consequently, an underestimated planet candidate's radius. In an extreme case, a strongly contaminated eclipsing binary can appear as a small planet when observed in a single passband.

Contamination depends on the spectral type of the contaminating stars, observation passband, instrument pixel size and point spread function (PSF), and photometry aperture. Consequently, the apparent transit depth also varies between instruments and passbands.

The passband dependency allows for estimating contamination within an aperture centred around the host star using multicolour transit observations. Our multicolour contamination analysis integrates a physical contamination model with a transit model. The physical contamination model, parameterised by the effective temperatures of the planet candidate host star and the contaminating stars, and the contamination factor in some reference passband, calculates the passband-integrated contamination factors based on theoretical stellar spectra by Husser et al. (2013). These factors are then used to dilute the transits created by the transit model. Marginalising over all the host and contaminant star temperatures and reference contamination levels allowed by the photometry gives us a robust estimate for the planet-star radius ratio.

Unlike in our previous papers (Parviainen et al. 2019, 2020, 2021; Esparza-Borges et al. 2022; Morello et al. 2023), in this paper, we distinguish the ‘robust’ radius and area ratio estimates from the ‘true’ ratios. The ‘robust’ ratios refer to the estimates inferred from the observations when using a model that accounts for the contamination; the ‘apparent’ ratios refer to the estimates that would be inferred with a model that does not account for possible contamination; and the ‘true’ ratios refer to the actual, unknown, true geometric ratios. The apparent ratio posteriors contain the true ones if no contamination is present (and the systematics are modelled correctly) but will be biased in the presence of contamination. The robust ratio estimates have significantly larger uncertainties than the apparent ones, but their posteriors will contain the true ratios in the presence of contamination.

The apparent radius ratio in passband i is related to the true are ratio as 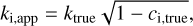ki, app =ktrue 1−ci, true ,${k_{{\rm{i}},{\rm{app}}}} = {k_{{\rm{true}}}}\sqrt {1 - {c_{{\rm{i}},{\rm{true}}}}} ,$(2)

where ci,true is the actual contamination in the passband, and the robust radius ratio is related to the apparent one as 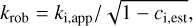krob =ki, app /1−ci, est ,${k_{{\rm{rob}}}} = {k_{{\rm{i}},{\rm{app}}}}/\sqrt {1 - {c_{{\rm{i}},{\rm{est}}}}} ,$(3)

where ci,est is the contamination estimate in the passband. The robust and true radius ratios do not depend on the passband or the instrument, but the apparent radius ratios and contamination factors do.

While the passband-specific variation can be explained using a physical model, the instrumental variation cannot. However, this is not a major issue because the ground-based observations generally have a similar spatial resolution. The only major difference is between the ground-based instruments and TESS because the TESS photometry has significantly lower spatial resolution than the ground-based photometry due to TESS's large pixel size. This means that the TESS photometry cannot generally be modelled using the same physical model as the ground-based photometry. Instead, we include it in the analysis parameterised by an independent apparent area ratio parameter.

The final multicolour photometry dataset consists of the 55 transit light curves observed with TESS, HiPERCAM, MuSCAT2, MuSCAT3, and LCOGT 1 m telescopes. We calculate priors on the limb darkening coefficients using LDTK (Parviainen & Aigrain 2015). Further, we have assumed zero eccentricity in all the analyses given the short circularisation time scales for short-period planets (Dawson & Johnson 2018).

We deviate from the analyses in Parviainen et al. (2019, 2020, 2021) by using a transit model following the power-2 limb darkening law (Morello et al. 2017; Maxted 2018; Maxted & Gill 2019) implemented by the RoadRunner transit model in PYTRANSIT (Parviainen 2015, 2020). Otherwise, the analysis follows the steps described in these previous papers. The posterior estimation begins with a global optimisation run using the Differential Evolution global optimisation method (Storn & Price 1997; Price et al. 2005) that results in a population of parameter vectors clumped close to the global posterior mode. This parameter vector population is then used as a starting population for the MCMC sampling with EMCEE, and the sampling is carried out until a suitable posterior sample has been obtained (Parviainen 2018). The model parametrisation, priors, and the construction of the posterior function follow directly Parviainen et al. (2020), and are listed in Table 2.

The analyses were carried out with a custom Python code based on PYTRANSIT v24 (Parviainen 2015, 2020; Parviainen et al. 2019), which includes a physics-based contamination model based on the PHOENIX-calculated stellar spectrum library by Husser et al. (2013). The limb darkening computations were carried out with LDTK5 (Parviainen & Aigrain 2015), and Markov chain Monte Carlo (MCMC) sampling was carried out with EMCEE (Foreman-Mackey et al. 2013; Goodman & Weare 2010). The code relies on the existing PYTHON packages for scientific computing and astrophysics: SCIPY, NUMPY (Van Der Walt et al. 2011), ASTROPY (Astropy Collaboration 2013, 2018), PHOTUTILS (Bradley et al. 2022), ASTROMETRY.NET (Lang et al. 2010), IPYTHON (Perez et al. 2007), PANDAS (McKinney 2010), XARRAY (Hoyer & Hamman 2017), MATPLOTLIB (Hunter 2007), and SEABORN. The code and the data are publicly available from GitHub6 as Jupyter notebooks.

4.3 Results from multicolour validation and system characterisation

We show the photometry used in the multicolour analysis with the posterior transit model in Fig. 2, and the posterior densities for the true radius ratio, the effective temperature of the contaminant, impact parameter, and stellar density in Fig. 3. The multicolour analysis robustly rejects any false positive scenarios where the transit signal would not be caused by a small transiting planet with a false alarm probability (FAP) equivalent to 0 (see Sect. 5.1 for more details about the multicolour validation results).

Since false positive scenarios affecting the planet candidate radius significantly can be rejected, we adopt the values from a separate uncontaminated light curve analysis as our final system characterisation results. The posterior estimates for the stellar and planetary parameters inferred from the analysis ignoring possible contamination are listed in Table 3.

Table 2

Transit light curve model parameters and priors.

4.4 Transit timing variations

We carried out an additional transit timing variation analysis where the transit centre times for each transit were free parameters in the model. The transit centres from the TESS observations were poorly constrained due to the low S/N for a single transit. Still, the ground-based observations reached up to 30-s 1σ transit centre precision and agreed with a linear period without signs of significant dynamical interactions with other possible bodies in the system.

5 Discussion

5.1 Validation summary

We validate TOI-2266 b as a small planet with a radius of 1.54 ± 0.09 R⊕ based on high-resolution imaging and multicolour transit photometry. Specifically,

  • high-resolution imaging rules out significant blending from sources with angular separation ≳0.25″

  • and multicolour transit photometry rules out significant contamination from stars of different spectral type than the host.

The analysis rules out any contamination from sources dissimilar to the host star that would significantly affect the radius of the transiting object (see the ΔΤEff vs robust radius ratio posterior in Fig. 3). This applies equally to scenarios where the transit signal would occur in a faint background star (in which case our spectroscopic characterisation of the host star would be incorrect) or where the signal would occur in the assumed host star but would be blended with fainter contaminant stars.

For ΔΤEff ≈ the true radius ratio and contamination are constrained by the achromatic transit geometry: radius ratios larger than the inferred upper limit cannot produce the observed flat-bottomed transit with relatively short ingress and egress durations. The multicolour analysis yields a true radius ratio 99th percentile posterior upper limit of 0.19. Since the host star needs to be similar to the assumed host star, the upper radius ratio limit corresponds to a contamination factor of 90% and a planetary radius of 5 R⊕ that is well below the brown dwarf radius limit of 0.8 RJup. However, a contamination level this high is physically implausible because the scenario would require ~10 M dwarfs with Teff ~ 3200 K (one being orbited by the transiting object) residing within angular separations ≲0.5″ of each other (see Fig. 1).

The only realistic contamination scenario not rejected by the analysis would be that the transiting object orbits a component of an equal-mass binary. This would lead to a contamination factor of 50% and a planet radius of 2R⊕.

5.2 Radius uncertainty

Our radius ratio estimate for TOI-2266 b has a relative uncertainty of 2%, while the absolute radius estimate has a relative uncertainty of 4.3%. The high precision in radius ratio is largely thanks to the transit observed with HiPERCAM, while the significantly lower precision in the absolute radius is due to the 3.8% relative uncertainty in the stellar radius. M dwarf radii and masses are notoriously challenging to estimate reliably, and the uncertainty in the stellar radius impedes any attempts to improve the absolute planet radius estimate by observing additional transits.

5.3 TOI-2266 b and the M dwarf radius valley

TOI-2266 b's period and radius make it a welcome addition to a relatively small sample of known planets that can be used to study planet formation around M dwarfs and, especially, probe the transition zone between rocky and water-rich planets.

First, considering the recent work by Luque & Pallé (2022), with a radius of 1.54 ± 0.09 R⊕, TOI-2266 b falls inside a transition zone where we find both rocky and water-rich planets, as shown in Fig. 4. This transition zone corresponds to the M dwarf radius valley in planet radius space (Cloutier & Menou 2020; Van Eylen et al. 2021), but its extent is poorly defined due to the small number of known planets inside it. If we take the zone to span from 1.5 to 1.8 R⊕ (roughly corresponding to the radius of the smallest known water world and the largest known Earth-like planet) and consider the planets with masses and radii estimated to a precision of 25% and 8% or better7, the zone encompasses three rocky planets, four water worlds, and one planet with an intermediate composition. This is insufficient to constrain the extent of the zone or study its physics, but more planets with accurately measured masses are needed. Mass measurement of TOI-2266 b should be within reach of the current instruments (see discussion below), and even an upper mass limit measured to an RV semi-amplitude precision of 4 m s−1 suffice to determine whether the planet is rocky or water-rich.

Second, considering the M dwarf radius valley (Cloutier & Menou 2020) and rocky planet formation, TOI-2266 b is located in a sparsely populated region in the period-radius plane (Fig. 5) inside the ‘keystone planet’ wedge where rocky planet formation scenarios make disagreeing predictions on how the radius valley location depends on the planet's orbital period (Cherubim et al. 2023; Cloutier et al. 2021 ; Van Eylen et al. 2021 ; Cloutier & Menou 2020). Simplistically, the thermally-driven mass loss scenario proposes that rocky planets are stripped cores of planets that accreted a significant atmosphere during their birth but lost it due to core-powered mass loss, photoevaporation, or one of several other physical processes that can strip a planet of its atmosphere, while the gas-depleted formation scenario proposes that the rocky planets formed later than the planets with significant H/He envelopes after the gas in the protoplanetary disk had dissipated. The thermally-driven mass loss scenario predicts that the upper limit of rocky-planet radii decreases with the orbital period because the process can strip a larger planet of its atmosphere the closer to the star the planet migrates. The gas-depleted scenario predicts an opposite trend where the upper limit for the rocky-planet radius increases slightly with the orbital period because the forming planets can accrete more mass the longer their period is.

Notes. The estimates correspond to the posterior median (P50) with 1σ uncertainty estimate based on the 16th and 84th posterior percentiles (P16 and P84 respectively) for symmetric, approximately normal posteriors. For asymmetric, unimodal posteriors, the estimates are 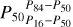P50P84−P50P16−P50${P_{50}}\matrix{ {{P_{84}} - {P_{50}}} \cr {{P_{16}} - {P_{50}}} \cr } $. (a)The semi-major axis and planet candidate radius are based on the scaled semi-major axis and apparent radius ratio samples, and the stellar radius estimate shown in Table 1. (b)The equilibrium temperature of the planet candidate is calculated using the stellar Teff estimate, scaled semi-major axis distribution, heat redistribution factor distributed uniformly between 0.25 and 0.5, and planet's Bond albedo distributed uniformly between 0 and 0.4.

TOI-2266 b is located at the lower end of the ‘keystone planet’ wedge in the period-radius plane, so estimating its density via RV mass measurements can help shed light on the dominant small-planet formation pathway for M dwarfs. Were TOI-2266 b to be water-rich (or a sub-Neptune), it would further contribute to the growing evidence that small planets are mainly formed through the gas-depleted formation scenario (Cherubim et al. 2023).

thumbnail Fig. 2

TESS, LCO 1m, MuSCAT2, MuSCAT3, and HiPERCAM light curves together with the posterior median models. The median posterior baseline model has been removed from the observed photometry, and the observations have been combined, phase folded and binned to 10 min for each instrument and passband for visualisation.
thumbnail Fig. 3

Marginal and joint posterior distributions for the robust radius ratio, apparent radius ratio, difference between the host and contaminant effective temperatures, impact parameter, and stellar density from the multicolour contamination analysis.
Table 3

Relative and absolute estimates for the stellar and companion parameters derived from the multicolour transit analysis.

thumbnail Fig. 4

TOI-2266 b's location in the plane of radius and relative density (black vertical line and shading) with well-characterised small planets orbiting M dwarfs with periods shorter than 32 days by Luque & Pallé (2022). The colour shading corresponds to rocky planets (brown), water worlds (blue), and sub-Neptunes (yellow).
thumbnail Fig. 5

TOI-2266 b's location in the period-radius plane with the currently known planets orbiting M dwarfs. The planets without sufficiently precise density estimates are shown as grey crosses (from exoplanet. eu), while the planets with well-constrained densities from the catalogue by Luque & Pallé (2022) are separated by their likely type: rocky planets are shown as black dots, water worlds as blue circles, and sub-Neptunes as green circles. The upper radius limits for rocky planets for the gas-depleted formation and thermally-driven mass loss scenarios are drawn as dashed lines.

5.4 Possible photometric signal related to stellar rotation

A Lomb-Scargle analysis (LS; Lomb 1976; Scargle 1982) of the TESS photometry divided by the best-fitting transit model using the Generalized Lomb–Scargle (GLS) periodogram by Zechmeister & Kürster (2009) shows evidence for a periodic variability with a period of 4.54 d and a semi-amplitude of 1300 + 100 ppm. The signal is loosely sinusoidal in shape and its period is close to being twice the planet's orbital period (2P = 4.65 days). It is unlikely that the signal would be caused by the planet, and we consider it more likely that it is indicative of a stellar rotation period of ≈4.5 days. This would agree well with the results by Popinchalk et al. (2021), who measured relatively rapid stellar rotation periods of 0.3–10 days for M5 dwarfs of all ages.

5.5 Prospects for RV follow-up

We use a numerical radius-mass relation provided by the SPRIGHT package8 (Parviainen et al. 2024) to predict TOI-2266 b's mass and RV semi-amplitude distributions (Fig. 6) and composition class given the planet's radius (Fig. 7). SPRICHT is a novel probabilistic mass-density-radius relation for small planets that represents the joint planetary radius and bulk density probability distribution as a mean posterior predictive distribution of an analytical three-component mixture model. The three components represent rocky planets, water-rich planets, and sub-Neptunes, and the final numerical probability model is obtained by marginalising over all analytical model solutions allowed by observations. The approach allows for solutions where the water-rich planet component does not exist, and so the final SPRICHT mass-radius model is agnostic to the existence of water-rich planets as a separate population on their own.

For TOI-2266 b, SPRICHT predicts an RV semi-amplitude, K, of 1.9–8.3 m s−1 (95% central posterior limits, Fig. 6). If the planet is rocky, we expect a Κ value of 5.4 + 1.3 m s−1, while for water-rich planets and sub-Neptunes we expect Κ values of 2.8 + 0.8 and 3.3 + 0.7 m s−1, respectively.

The RV semi-amplitudes are large enough that the planet's mass can be expected to be measurable using RV observations with the currently available red-sensitive instruments. Due to TOI-2266's high declination, it makes a poor target for telescopes in the southern hemisphere. However, the star is observable from telescopes located in Mauna Kea, Hawaii, during the summer period, reaching a minimum airmass of 1.02 in late May. Thus, TOI-2266 b would be amenable to mass measurements using MAROON-X (Seifahrt et al. 2018), KPF (Gibson et al. 2016), or SPIRou (Donati et al. 2020).

Assuming good observing conditions and exposure times of one hour, the instrument-specific exposure time calculators9 predict RV observation uncertainties of 1 m s−1 for MAROON-X, 2 m s−1 for KPF, and 6–11 m s−1 for SPIRou. We carried out numerical RV mass measurement simulations to study the precision and significance of a mass measurement achieved by 4, 6, 8, and 10 one-hour exposures with these three instruments considering five composition scenarios corresponding to the 2.5% and 97.5% SPRICHT posterior percentiles, and the Κ posterior median values for the rocky, water-rich and (puffy) sub-Neptune compositions. For a single simulation, we created a set of Nobs simulated RV observations with observation phases clustered randomly close to the RV signal minima and maxima, Κ following from a given composition scenario, and noise following the instrument-specific noise estimate for a one-hour exposure. After this, we estimated the posterior distribution for Κ given the simulated measurements using PYTRANSIT'S RVLPF class. We repeated the simulation 10 times for each combination of the composition classes, instruments, and number of exposures, and summarise the average mass measurement significances and precisions10 in Table 4.

The results in Table 4 are optimistic because they consider only photon noise and ignore correlated noise from stellar granulation and variability, but they nevertheless allow us to conclude that TOI-2266 b's mass can likely be estimated with a relatively small number of MAROON-X or KPF observations. MAROON-X observations of bright M1.5V star GJ 806 (Palle et al. 2023) and M3.5 V star Gl 486 (Caballero et al. 2022) have led to additional RV jitter estimates for the MAROON-X red arm RV observations up to 1 m s−1, while stellar variability and star spots can lead to quasi-periodic RV signals with amplitudes up to 10–20 m s−1 (Kossakowski et al. 2022; Cortés-Zuleta et al. 2023). The short-time-scale jitter should not form a major obstacle for MAROON-X observations since additional noise of 1 m s−1 leads to KPF-like performance. However, the larger-amplitude RV signals related to stellar variability have periods matching the stellar rotation period, and if the periodic photometric signal of 4.54 days identified in Sect. 5.4 corresponds to the stellar rotation period, a significantly larger number of observations may be required to ensure that the RV signal caused by the planet can be disentangled from the one cause by stellar variability.

thumbnail Fig. 6

TOI-2266 b's bulk density, mass, and radial velocity semi-amplitude probability distributions given a posterior radius estimate of 1.54 ± 0.09 R⊕ predicted by the SPRIGHT package. The complete probability distribution is marked by a thick black line and gray shading, and the individual contributions from the three SPRIGHT model components (rocky planets, water-rich planets, and sub-Neptunes) are plotted in light brown, light blue, and yellow. The blue shading in the background shows the 68% and 95% central posterior intervals for the distributions.
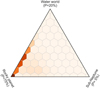thumbnail Fig. 7

TOI-2266 b's composition class based on its radius predicted by the SPRIGHT package.

6 Conclusions

We have validated TOI-2266 b as a small planet (most likely a super-Earth or a water world) using multicolour transit photometry and high-resolution imaging. The planet is amenable to ground-based RV mass estimation with MAROON-X and KPF, and a mass measurement combined with our radius estimate precision of 4% will make the planet a valuable addition in studying small-planet populations and planet formation scenarios.

Considering the planet's radius, TOI-2266 b is a welcome addition to a small population of planets located inside a transition zone where Luque & Pallé (2022) find both rocky planets and water worlds, and measuring the planet's density may allow us to understand better the differences in the formation histories of these two populations. Further, considering rocky planet formation scenarios, the planet occupies a currently sparsely populated region in the period-radius plane, the so-called ‘keystone’ wedge as defined by Cloutier & Menou (2020). Were TOI-2266 b to be identified as a water world or a sub-Neptune, this would increase support for the gas-depleted formation scenario.

Table 4

Simulated ideal RV mass measurement significances and precisions for MAROON-X, KPF, and SPIRou.

Acknowledgements

We thank the anonymous referee for their extremely helpful comments and suggestions. We acknowledge financial support from the Agencia Estatal de Investigacion of the Ministerio de Ciencia, Innovacion y Universidades and the European FEDER/ERF funds through projects ESP2013-48391-C4-2-R, AYA2016-79425-C3-2-P, AYA2015-69350-C3-2-P, and PID2019-109522GB-C53, and PGC2018-098153-B-C31. This work is partly financed by the Spanish Ministry of Economics and Competitiveness through project ESP2016-80435-C2-2-R. Funding from the University of La Laguna and the Spanish Ministry of Universities is acknowledged. H.P. acknowledges support by the Spanish Ministry of Science and Innovation with the Ramon y Cajal fellowship number RYC2021-031798-I. This work is partly supported by JSPS KAKENHI Grant Numbers JP15H02063, JP17H04574, JP18H05442, JP18H05439, JP20K14521, JP21K13975, JP21K13955, JP21K20376, JP22000005, JST CREST Grant Number JPMJCR1761, and Astrobiology Center SATELLITE Research project AB022006. R.L. acknowledges funding from the University of La Laguna through the Margarita Salas Fellowship from the Spanish Ministry of Universities ref. UNI/551/2021-May 26, and under the EU Next Generation funds. J. K. gratefully acknowledges the support of the Swedish National Space Agency (SNSA; DNR 2020-00104) and of the Swedish Research Council (VR: Etableringsbidrag 2017-04945). G.N. thanks for the research funding from the Ministry of Education and Science programme the ‘Excellence Initiative - Research University’ conducted at the Centre of Excellence in Astrophysics and Astro-chemistry of the Nicolaus Copernicus University in Torun, Poland. This article is partly based on observations made with the MuSCAT2 instrument, developed by ABC, at Telescopio Carlos Sánchez operated on the island of Tenerife by the IAC in the Spanish Observatorio del Teide. Based on observations made with the Nordic Optical Telescope, owned in collaboration by the University of Turku and Aarhus University, and operated jointly by Aarhus University, the University of Turku and the University of Oslo, representing Denmark, Finland and Norway, the University of Iceland and Stockholm University at the Observatorio del Roque de los Muchachos, La Palma, Spain, of the Instituto de Astrofisica de Canarias. The data presented here were obtained in part with ALFOSC, which is provided by the Instituto de Astrofisica de Andalucia (IAA) under a joint agreement with the University of Copenhagen and NOT. We acknowledge the use of public TESS Alert data from pipelines at the TESS Science Office and at the TESS Science Processing Operations Center. This work makes use of observations from the LCOGT network. Part of the LCOGT telescope time was granted by NOIRLab through the Mid-Scale Innovations Program (MSIP). MSIP is funded by NSF. This paper is based on observations made with the MuSCAT3 instrument, developed by the Astrobiology Center and under financial supports by JSPS KAKENHI (JP18H05439) and JST PRESTO (JPMJPR1775), at Faulkes Telescope North on Maui, HI, operated by the Las Cumbres Observatory. This paper made use of data collected by the TESS mission and are publicly available from the Mikulski Archive for Space Telescopes (MAST) operated by the Space Telescope Science Institute (STScI). Funding for the TESS mission is provided by NASA's Science Mission Directorate. Resources supporting this work were provided by the NASA HighEnd Computing (HEC) Program through the NASA Advanced Supercomputing (NAS) Division at Ames Research Center for the production of the SPOC data products. This work made use of tpfplotter by J. Lillo-Box (publicly available in www.github.com/jlillo/tpfplotter), which also made use of the Python packages astropy, lightkurve, matplotlib and numpy. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. The postdoctoral fellowship of K.B. is funded by F.R.S.-FNRS grant T.0109.20 and by the Francqui Foundation. This publication benefits from the support of the French Community of Belgium in the context of the FRIA Doctoral Grant awarded to MT.

References

  1. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A & A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
  3. Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
  4. Bradley, L., Sipőcz, B., Robitaille, T., et. al. 2022, https://doi.org/18.5281/zenodo.682 5892 [Google Scholar]
  5. Brown, T. M., Baliber, N., Bianco, F. B., et. al. 2013, PASP, 125, 1031 [Google Scholar]
  6. Burn, R., Schlecker, M., Mordasini, C., et. al. 2021, A & A, 656, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Burrows, A. S., Heng, K., & Nampaisarn, T. 2011, ApJ, 736, 47 [NASA ADS] [CrossRef] [Google Scholar]
  8. Caballero, J. A., González-Álvarez, E., Brady, M., et. al. 2022, A & A, 665, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Cherubim, C., Cloutier, R., Charbonneau, D., et. al. 2023, AJ, 165, 167 [NASA ADS] [CrossRef] [Google Scholar]
  10. Ciardi, D. R., Beichman, C. A., Horch, E. P., & Howell, S. B. 2015, ApJ, 805, 16 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cloutier, R., & Menou, K. 2020, AJ, 159, 211 [NASA ADS] [CrossRef] [Google Scholar]
  12. Cloutier, R., Eastman, J. D., Rodriguez, J. E., et. al. 2020a, AJ, 160, 3 [Google Scholar]
  13. Cloutier, R., Rodriguez, J. E., Irwin, J., et. al. 2020b, AJ, 160, 22 [NASA ADS] [CrossRef] [Google Scholar]
  14. Cloutier, R., Charbonneau, D., Stassun, K. G., et. al. 2021, AJ, 162, 79 [NASA ADS] [CrossRef] [Google Scholar]
  15. Collins, K. A., Kielkopf, J. F., Stassun, K. G., & Hessman, F. V. 2017, AJ, 153, 77 [Google Scholar]
  16. Cortés-Zuleta, P., Boisse, I., Klein, B., et. al. 2023, A & A, 673, A14 [CrossRef] [EDP Sciences] [Google Scholar]
  17. Dawson, R. I., & Johnson, J. A. 2018, ARA & A, 56, 175 [CrossRef] [Google Scholar]
  18. Dekany, R., Roberts, J., Burruss, R., et. al. 2013, ApJ, 776, 130 [CrossRef] [Google Scholar]
  19. Dhillon, V. S., Bezawada, N., Black, M., et. al. 2021, MNRAS, 507, 350 [NASA ADS] [CrossRef] [Google Scholar]
  20. Donati, J.-F., Kouach, D., Moutou, C., et. al. 2020, MNRAS, 498, 5684 [NASA ADS] [CrossRef] [Google Scholar]
  21. Esparza-Borges, E., Parviainen, H., Murgas, F., et. al. 2022, A & A, 666, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  23. Fulton, B. J., & Petigura, E. A. 2018, AJ, 156, 264 [Google Scholar]
  24. Fulton, B. J., Petigura, E. A., Howard, A. W., et. al. 2017, AJ, 154, 109 [Google Scholar]
  25. Furlan, E., Ciardi, D. R., Everett, M. E., et. al. 2017, AJ, 153, 71 [NASA ADS] [CrossRef] [Google Scholar]
  26. Gavel, D., Kupke, R., Dillon, D., et. al. 2014, in Adaptive Optics Systems IV, 9148, eds. E. Marchetti, L. M. Close, & J.-P. Vran, 914805 [NASA ADS] [CrossRef] [Google Scholar]
  27. Gibson, S. R., Howard, A. W., Marcy, G. W., et. al. 2016, Proc. SPIE, 9908, 990870 [NASA ADS] [CrossRef] [Google Scholar]
  28. Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
  29. Guerrero, N. M., Seager, S., Huang, C. X., et. al. 2021, ApJS, 254, 39 [NASA ADS] [CrossRef] [Google Scholar]
  30. Hayward, T. L., Brandl, B., Pirger, B., et. al. 2001, PASP, 113, 105 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hoyer, S., & Hamman, J. J. 2017, J. Open Res. Softw., 5, 1 [Google Scholar]
  32. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  33. Husser, T. O., Wende-Von Berg, S., Dreizler, S., et. al. 2013, A & A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Jenkins, J. M. 2002, ApJ, 575, 493 [Google Scholar]
  35. Jenkins, J. M. A., Caldwell, D., Chandrasekaran, H., et. al. 2010, ApJ, 713, L87 [NASA ADS] [CrossRef] [Google Scholar]
  36. Jenkins, J. M., Twicken, J. D., McCauliff, S., et. al. 2016, in Software and Cyber-infrastructure for Astronomy IV, 9913, eds. G. Chiozzi, & J. C. Guzman, 99133E [NASA ADS] [CrossRef] [Google Scholar]
  37. Jensen, E. 2013, Astrophysics Source Code Library, [record ascl:1306.007] [Google Scholar]
  38. Kesseli, A. Y., West, A. A., Veyette, M., et. al. 2017, ApJS, 230, 16 [NASA ADS] [CrossRef] [Google Scholar]
  39. Kossakowski' D., Kürster, M., Henning, T., et. al. 2022, A & A, 666, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Kupke, R., Gavel, D., Roskosi, C., et. al. 2012, in Adaptive Optics Systems III, 8447, eds. B. L. Ellerbroek, E. Marchetti, & J.-P. Véran, 84473G [NASA ADS] [CrossRef] [Google Scholar]
  41. Lang, D., Hogg, D. W., Mierle, K., Blanton, M., & Roweis, S. 2010, AJ, 139, 1782 [Google Scholar]
  42. Li, J., Tenenbaum, P., Twicken, J. D., et. al. 2019, PASP, 131, 024506 [NASA ADS] [CrossRef] [Google Scholar]
  43. Lomb N. R. 1976 Astrophys. Space Sci. 39 447 [NASA ADS] [CrossRef] [Google Scholar]
  44. Lopez, E. D., & Rice, K. 2018, MNRAS, 479, 5303 [NASA ADS] [CrossRef] [Google Scholar]
  45. Luque, R., & Pallé, E. 2022, Science, 377, 1211 [NASA ADS] [CrossRef] [Google Scholar]
  46. Luque, R., Serrano, L. M., Molaverdikhani, K., et. al. 2021, A & A, 645, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Luque, R., Nowak, G., Hirano, T., et. al. 2022, A & A, 666, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Mann, A. W., Dupuy, T., Kraus, A. L., et. al. 2019, ApJ, 871, 63 [Google Scholar]
  49. Maxted, P. F. 2018, A & A, 616, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Maxted, P. F., & Gill, S. 2019, A & A, 622, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Mayo, A. W., Vanderburg, A., Latham, D. W., et. al. 2018, AJ, 155, 136 [Google Scholar]
  52. McCully, C., Volgenau, N. H., Harbeck, D.-R., et. al. 2018, Proc. SPIE, 10707, 107070K [Google Scholar]
  53. McGurk, R., Rockosi, C., Gavel, D., et. al. 2014, in Adaptive Optics Systems IV, 9148, eds. E. Marchetti, L. M. Close, & J.-P. Vran, 91483A [NASA ADS] [Google Scholar]
  54. McKinney, W. 2010, Proceedings of the 9th Python in Science Conference, 41, 56 [CrossRef] [Google Scholar]
  55. Morello, G., Tsiaras, A., Howarth, I. D., & Homeier, D. 2017, AJ, 154, 111 [NASA ADS] [CrossRef] [Google Scholar]
  56. Morello, G., Parviainen, H., Murgas, F., et. al. 2023, A & A, 673, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Narita, N., Fukui, A., Kusakabe, N., et. al. 2019, J. Astron. Telesc. Instrum. Syst., 5, 015001 [NASA ADS] [Google Scholar]
  58. Narita, N., Fukui, A., Yamamuro, T., et. al. 2020, SPIE Conf. Ser., 11447, 29 [Google Scholar]
  59. Palle E. Orell-Miquel J. Brady M. et. al. 2023 A & A 678 A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Parviainen, H. 2015, MNRAS, 450, 3233 [Google Scholar]
  61. Parviainen, H. 2018, in Handbook of Exoplanets (Cham: Springer International Publishing), 1 [Google Scholar]
  62. Parviainen, H. 2020, MNRAS, 499, 1633 [NASA ADS] [CrossRef] [Google Scholar]
  63. Parviainen, H., & Aigrain, S. 2015, MNRAS, 453, 3821 [Google Scholar]
  64. Parviainen, H., Tingley, B., Deeg, H. J., et. al. 2019, A & A, 630, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Parviainen, H., Palle, E., Zapatero-Osorio, M. R., et. al. 2020, A & A, 633, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Parviainen, H., Palle, E., Zapatero-Osorio, M. R., et. al. 2021, A & A, 645, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Parviainen, H., Luque, R., & Palle, E. 2024, MNRAS, 527, 5693 [Google Scholar]
  68. Perez, F., Granger, B. B. E., Pérez, F., & Granger, B. B. E. 2007, Comput. Sci. Eng., 9, 21 [CrossRef] [Google Scholar]
  69. Popinchalk, M., Faherty, J. K., Kiman, R., et. al. 2021, ApJ, 916, 77 [NASA ADS] [CrossRef] [Google Scholar]
  70. Price, K., Storn, R., & Lampinen, J. 2005, Differential Evolution (Berlin: Springer) [Google Scholar]
  71. Ricker, G. R., Winn, J. N., Vanderspek, R., et. al. 2014, J. Astron. Telescopes Instrum. Syst., 1, 014003 [NASA ADS] [CrossRef] [Google Scholar]
  72. Savel, A. B., Dressing, C. D., Hirsch, L. A., et. al. 2020, AJ, 160, 287 [NASA ADS] [CrossRef] [Google Scholar]
  73. Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
  74. Schweitzer, A., Passegger, V. M., Cifuentes, C., et. al. 2019, A & A, 625, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Seifahrt, A., Stürmer, J., Bean, J. L., & Schwab, C. 2018, Proc. SPIE, 10702, 107026D [NASA ADS] [Google Scholar]
  76. Smith, J. C., Stumpe, M. C., Van Cleve, J. E., et. al. 2012, PASP, 124, 1000 [Google Scholar]
  77. Stefánsson, G., Kopparapu, R., Lin, A., et. al. 2020, AJ, 160, 259 [CrossRef] [Google Scholar]
  78. Storn, R., & Price, K. 1997, JGOpt, 11, 341 [NASA ADS] [Google Scholar]
  79. Stumpe, M. C., Smith, J. C., Van Cleve, J. E., et. al. 2012, PASP, 124, 985 [Google Scholar]
  80. Stumpe, M. C., Smith, J. C., Catanzarite, J. H., et. al. 2014, PASP, 126, 100 [Google Scholar]
  81. Twicken, J. D., Catanzarite, J. H., Clarke, B. D., et. al. 2018, PASP, 130, 064502 [Google Scholar]
  82. Van Der Walt, S. S., Colbert, S. C., & Varoquaux, G. G. 2011, Comput. Sci. Eng., 13, 22 [NASA ADS] [CrossRef] [Google Scholar]
  83. Van Eylen, V., Astudillo-Defru, N., Bonfils, X., et. al. 2021, MNRAS, 507, 2154 [NASA ADS] [Google Scholar]
  84. Zechmeister, M., & Kürster, M. 2009, A & A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Zeng, L., Jacobsen, S. B., Sasselov, D. D., et. al. 2019, PNAS, 116, 9723 [Google Scholar]
1

The TESS Project Candidate table in the NASA Exoplanet Archive contains 172 open candidates (disposition PC) around M dwarfs with periods shorter than 35 d and radii smaller than 5 R⊕ at the time of writing (2022 October 21).

3

Image Reduction and Analysis Facility (IRAF) is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, Inc., under contract with the National Science Foundation.

7

Based on an updated catalogue by R. Luque (priv. comm.).

8

The analysis used SPRIGHT version 23.11.01 (10.5281/zenodo.10082653); the SPRIGHT package is available from https://github.com/hpparvi/spright and PyPI.

10

We define the ‘mass measurement significance’ here as the Κ posterior median divided by the posterior's standard deviation, that is, the distance of the posterior median from zero in units of standard deviation.

All Tables

Table 1

TOI-2266 identifiers, coordinates, properties, and magnitudes.

In the text
Table 2

Transit light curve model parameters and priors.

In the text
Table 3

Relative and absolute estimates for the stellar and companion parameters derived from the multicolour transit analysis.

In the text
Table 4

Simulated ideal RV mass measurement significances and precisions for MAROON-X, KPF, and SPIRou.

In the text

All Figures

thumbnail Fig. 1

Contrast with its 1-σ uncertainties as a function of separation and angular separation in Brgamma, J and Ks (left) and a high-resolution PHARO image (right).
In the text
thumbnail Fig. 2

TESS, LCO 1m, MuSCAT2, MuSCAT3, and HiPERCAM light curves together with the posterior median models. The median posterior baseline model has been removed from the observed photometry, and the observations have been combined, phase folded and binned to 10 min for each instrument and passband for visualisation.
In the text
thumbnail Fig. 3

Marginal and joint posterior distributions for the robust radius ratio, apparent radius ratio, difference between the host and contaminant effective temperatures, impact parameter, and stellar density from the multicolour contamination analysis.
In the text
thumbnail Fig. 4

TOI-2266 b's location in the plane of radius and relative density (black vertical line and shading) with well-characterised small planets orbiting M dwarfs with periods shorter than 32 days by Luque & Pallé (2022). The colour shading corresponds to rocky planets (brown), water worlds (blue), and sub-Neptunes (yellow).
In the text
thumbnail Fig. 5

TOI-2266 b's location in the period-radius plane with the currently known planets orbiting M dwarfs. The planets without sufficiently precise density estimates are shown as grey crosses (from exoplanet. eu), while the planets with well-constrained densities from the catalogue by Luque & Pallé (2022) are separated by their likely type: rocky planets are shown as black dots, water worlds as blue circles, and sub-Neptunes as green circles. The upper radius limits for rocky planets for the gas-depleted formation and thermally-driven mass loss scenarios are drawn as dashed lines.
In the text
thumbnail Fig. 6

TOI-2266 b's bulk density, mass, and radial velocity semi-amplitude probability distributions given a posterior radius estimate of 1.54 ± 0.09 R⊕ predicted by the SPRIGHT package. The complete probability distribution is marked by a thick black line and gray shading, and the individual contributions from the three SPRIGHT model components (rocky planets, water-rich planets, and sub-Neptunes) are plotted in light brown, light blue, and yellow. The blue shading in the background shows the 68% and 95% central posterior intervals for the distributions.
In the text
thumbnail Fig. 7

TOI-2266 b's composition class based on its radius predicted by the SPRIGHT package.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.