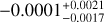| Issue |
A&A
Volume 679, November 2023
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 22 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202347240 | |
| Published online | 01 November 2023 | |
A compact multi-planet system transiting HIP 29442 (TOI-469) discovered by TESS and ESPRESSO
Radial velocities lead to the detection of transits with low signal-to-noise ratio★
1
INAF – Osservatorio Astrofisico di Torino,
Via Osservatorio 20,
10025
Pino Torinese, Italy
e-mail: mario.damasso@inaf.it
2
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP,
Rua das Estrelas,
4150-762
Porto, Portugal
3
Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto,
Rua do Campo Alegre,
4169-007
Porto, Portugal
4
Centro de Astrobiología (CAB,CSIC-INTA), Dep. de Astrofísica,
ESAC campus, Villanueva de la Cañada,
28692
Madrid, Spain
5
Département d’Astronomie, Université de Genève,
Chemin Pegasi 51,
1290
Versoix, Switzerland
6
Center for Space and Habitability, University of Bern,
Gesellschaftsstrasse 6,
3012
Bern, Switzerland
7
Physics Institute of University of Bern,
Gesellschaftsstrasse 6,
3012
Bern, Switzerland
8
Centro de Astrobiología (CSIC-INTA),
Carretera de Ajalvir km 4,
28850
Torrejón de Ardoz, Madrid, Spain
9
School of Physics, H.H. Wills Physics Laboratory, University of Bristol,
Tyndall Avenue,
Bristol
BS8 1TL, UK
10
Astrophysics Group, Department of Physics, Imperial College London,
Prince Consort Rd,
London,
SW7 2AZ, UK
11
Institute of Geochemistry and Petrology, ETH Zürich,
Clausiusstrasse 25,
8092
Zürich, Switzerland
12
Department of Physics, Engineering and Astronomy, Stephen F. Austin State University,
1936 North St,
Nacogdoches, TX
75962, USA
13
NASA Exoplanet Science Institute-Caltech/IPAC,
1200 East California Blvd.,
Pasadena, CA
91125, USA
14
Max Planck Institute for Astronomy,
Königstuhl 17,
69117
Heidelberg, Germany
15
Instituto de Astrofisica de Canarias,
Via Lactea,
38200
La Laguna, Tenerife, Spain
16
Universidad de La Laguna, Departamento de Astrofísica,
Avda. Astrofisico Francisco Sánchez s/n,
38206
La Laguna, Tenerife, Spain
17
INAF – Osservatorio Astronomico di Trieste,
Via Tiepolo 11,
34143
Trieste, Italy
18
Institute for Fundamental Physics of the Universe, IFPU,
Via Beirut 2,
34151
Grignano, Trieste, Italy
19
Consejo Superior de Investigaciones Científicas,
C. de Serrano 117,
28006
Madrid, Spain
20
INAF – Osservatorio Astronomico di Palermo,
Piazza del Parlamento 1,
90134
Palermo, Italy
21
Cerro Tololo Inter-American Observatory/NSF’s NOIRLab,
Casilla 603,
La Serena, Chile
22
Department of Astronomy and Astrophysics, University of California,
1156 High Street,
Santa Cruz, CA
95064, USA
23
Department of Physics and Astronomy, The University of North Carolina at Chapel Hill,
120 E. Cameron Ave., Phillips Hall CB3255,
Chapel Hill, NC
27599, USA
24
ESO, European Southern Observatory,
Alonso de Cordova 3107,
Vitacura, Santiago, Chile
25
Centro de Astrofísica da Universidade do Porto,
Rua das Estrelas,
4150-762
Porto, Portugal
26
Instituto de Astrofísica e Ciências do Espaço, Faculdade de Ciências da Universidade de Lisboa,
Campo Grande,
PT1749-016
Lisboa, Portugal
27
INAF – Osservatorio Astronomico di Brera,
Via Bianchi 46,
23807
Merate, Italy
28
Exoplanets and Stellar Astrophysics Laboratory, NASA Goddard Space Flight Center,
8800 Greenbelt Road,
Greenbelt, MD
20771, USA
Received:
20
June
2023
Accepted:
12
August
2023
Context. One of the goals of the Echelle Spectrograph for Rocky Exoplanets and Stable Spectroscopic Observations (ESPRESSO) Guaranteed Time Observations (GTO) consortium is the precise characterisation of a selected sample of planetary systems discovered by TESS. One such target is the K0V star HIP 29442 (TOI-469), already known to host a validated sub-Neptune companion TOI-469.01, which we followed-up with ESPRESSO.
Aims. We aim to verify the planetary nature of TOI-469.01 by obtaining precise mass, radius, and ephemeris, and constraining its bulk physical structure and composition.
Methods. Following a Bayesian approach, we modelled radial velocity and photometric time series to measure the dynamical mass, radius, and ephemeris, and to characterise the internal structure and composition of TOI-469.01.
Results. We confirmed the planetary nature of TOI-469.01 (now renamed HIP 29442 b), and thanks to the ESPRESSO radial velocities we discovered two additional close-in companions. Through an in-depth analysis of the TESS light curve, we could also detect their low signal-to-noise transit signals. We characterised the additional companions, and conclude that HIP 29442 is a compact multi-planet system. The three planets have orbital periods Porb,b = 13.63083 ± 0.00003, Porb,c = 3.53796 ± 0.00003, and Porb,d = 6.42975−0.00010+0.00009 days, and we measured their masses with high precision: mp,b = 9.6 ± 0.8 M⊕, mp,c = 4.5 ± 0.3 M⊕, and mp,d = 5.1 ± 0.4 M⊕. We measured radii and bulk densities of all the planets (the 3σ confidence intervals are shown in parentheses): Rp,b = 3.48−0.08(−0.28)+0.07(+0.19) R⊕ and ρp,b = 1.3 ± 0.2(0.3)g cm−3; Rp,c = 1.58−0.11(−0.34)+0.10(+0.30) R⊕ and ρp,c = 6.3−1.3(−2.7)+1.7(+6.0)g cm−3; Rp,d = 1.37 ± 0.11(−0.43)(+0.32) R⊕ and ρp,d = 11.0−2.4(−6.3)+3.4(+21.0)g cm−3. Due to noisy light curves, we used the more conservative 3σ confidence intervals for the radii as input to the interior structure modelling. We find that HIP 29442 b appears as a typical sub-Neptune, likely surrounded by a gas layer of pure H-He with amass of 0.27−0.17+0.24 M⊕ and a thickness of 1.4 ± 0.5 R⊕. For the innermost companions HIP 29442 c and HIP 29442 d, the model supports an Earth-like composition.
Conclusions. The compact multi-planet system orbiting HIP 29442 offers the opportunity to study simultaneously planets straddling the gap in the observed radius distribution of close-in small-size exoplanets. High-precision photometric follow-up is required to obtain more accurate and precise radius measurements, especially for planets c and d. This, together with our determined high-precision masses, will provide the accurate and precise bulk structure of the planets, and enable an accurate investigation of the system’s evolution.
Key words: stars: individual: HIP29442 / stars: individual: TOI-469 / planetary systems / techniques: photometric / techniques: radial velocities / planets and satellites: interiors
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
After starting operations in October 2018, the Echelle Spectrograph for Rocky Exoplanets and Stable Spectroscopic Observations (ESPRESSO) high-resolution spectrograph (Pepe et al. 2021) at the ESO Very Large Telescope (VLT) has demonstrated its unprecedented capabilities to reach radial velocity (RV) precision at a level of a few tens of cm s−1, and to guarantee stability over several months. ESPRESSO observations have allowed the mean densities of transiting exoplanets detected by TESS to be precisely measured (Ricker et al. 2016), and their fundamental physical properties to be closely constrained, as demonstrated by the spectroscopic follow-up of several planetary systems (e.g. Demangeon et al. 2021; Leleu et al. 2021; Sozzetti et al. 2021; Van Eylen et al. 2021; Barros et al. 2022; Lavie et al. 2023).
The radial velocity follow-up of known transiting planets holds surprises in some cases. For instance, ESPRESSO allowed the discovery of additional candidate planets in multi-planet systems (e.g. Lillo-Box et al. 2020a; Sozzetti et al. 2021; Barros et al. 2022), and in the case of LTT 1445A (TOI-455) the spectroscopic detection of LTT 1445A c triggered a thorough analysis of the TESS photometry, which revealed previously undetected transits for this planet (Lavie et al. 2023). Undetected transits in systems with known sub-Neptunes (here defined as planets with a radius 2 ≲ R ≲ 4 R⊕) are particularly interesting because such shallow transits could be likely produced by smaller-size Earths or super-Earths (with radii 1 ≲ R ≲ 2 R⊕). Such a system would host planets residing in different locations on the well-known bi-modal radius distribution of small-size (R < 4R⊕, i.e. from Earth- to Neptune-size), close-in planets that emerged from the population of transiting planets discovered by Kepler (Fulton et al. 2017). The observed distribution shows two distinct peaks at ~1.3 and ~2.4 R⊕, with a scarcity of planets found between ~ 1.5–2 R⊕ (an interval thus known as the ‘radius gap’), suggesting the existence of two well-defined families of planets, usually identified as super-Earths and sub-Neptunes, respectively. A mechanism able to predict the existence of the gap for close-in planets is the atmospheric mass-loss due to photo-evaporation driven by the high-energy irradiation of the hosts (e.g. Owen & Wu 2013, 2017; Jin et al. 2014), but whether this is the dominant process or the only process at play to explain the transition from super-Earths to sub-Neptunes is still being debated (e.g. core-powered atmospheric mass loss models have also been proposed, such as Ginzburg et al. 2018; Gupta & Schlichting 2019).
A first and critical step in understanding the processes that determine the current location of a planet within the radius distribution is an accurate and precise determination of its physical properties, such as mass and bulk density, that allow us to determine its average composition, and whether a planet is surrounded or not by a significant gaseous envelope. Multiplanet systems where transiting close-in planets cross over the radius distribution offer the fascinating opportunity to investigate the planets’ evolution within the same environment, and to constrain the models of the radius valley over some of the system parameters. These planets formed from the same proto-planetary disk, and their evolution has been taking place under the influence of the same stellar high-energy irradiation field. Examples of systems with planets that straddle the radius valley are Kepler-36 (Carter et al. 2012; Owen & Morton 2016), K2-3 (Damasso et al. 2018; Diamond-Lowe et al. 2022), K2-36 (Damasso et al. 2019), L231-32 (Günther et al. 2019; Van Eylen et al. 2021), LTT 3780 (Cloutier et al. 2020), TOI-1266 (Stefánsson et al. 2020), K2-32 and K2-233 (Lillo-Box et al. 2020b), and TOI-1468 (Chaturvedi et al. 2022), just to mention some. They represent very interesting targets to explore the role and relevance of evolutionary processes, such as the above-mentioned photo-evaporation and core-powered mass loss, in shaping the system, and to also test alternative hypotheses, such as those that connect the emergence of the radius gap with the location of small-size planets within the system at the time of birth. These models attribute the existence of the radius valley primarily to the differences in the bulk composition of the planets, identifying the super-Earths as rocky planets that form within the snow line and sub-Neptunes as mostly water-ice-rich worlds that form outside the snow line and later migrate inward (e.g. Zeng et al. 2019; Izidoro et al. 2022; Luque & Pallé 2022). Moreover, the cases of the planets Kepler-138 d (Piaulet et al. 2023) and TOI-244b (Castro-González et al. 2023), which are low-density super-Earths skimming the radius gap (Rp = 1.51 ± 0.04 R⊕ and Rp = 1.52 ± 0.12 R⊕, respectively) whose compositions are consistent with that of a volatile-rich water world, show that we should not expect all super-Earth-sized planets to have an Earth-like composition.
That is the setting where our story takes place. In this work, we present the detection and a characterisation of a packed multi-planet system, with close-in planets that occupy different locations in the bi-modal radius distribution. They orbit the star HIP 29442 (TIC 33692729, TOI-469, where TIC and TOI stand for TESS Input Catalogue and TESS Object of Interest, respectively), and have been detected using data from TESS and ESPRESSO, which are described in Sect. 2. This K-type main sequence star (characterised in Sects. 3 and 4), was originally included in the Exoplanet Follow-up Observing Program (ExoFOP) database1 as it hosts a planet candidate TOI-469.01 (orbital period 13.6 days; radius 3.3 R⊕), later validated by Giacalone et al. (2020). Recently, a mass measurement has been obtained by Akana Murphy et al. (2023) thanks to Keck-HIRES RVs (5.8 ± 2.4 M⊕). This short-period sub-Neptune-sized planet was deemed interesting for follow-up characterisation with ESPRESSO within the Guaranteed Time Observations (GTO) Consortium. Thanks to ESPRESSO RVs, we confirmed the planetary nature of TOI-469.01, and detected the presence of two additional periodic signals. Through a detailed analysis of the TESS data, we discovered transit signals with periods that correspond to those detected in the RV time series. We describe the system’s detection and analysis in Sect. 5. The newly detected pair of signals are due to small-size planets that orbit their host with periods shorter than that of TOI-469.01. Thus, HIP 29442 turns out to be a compact multi-planet system. The results of a first internal structure modelling of the three planets is presented in Sect. 6. We draw conclusions in Sect. 7, exploring the role of photo-evaporation in the system’s evolution, based on the current properties of the planets.
2 Materials and methods
2.1 TESS light curve
HIP 29442 was observed by TESS during Sector 6 (hereafter S6; 11 December 2018-7 January 2019) and Sector 33 (hereafter S33; 17 December 2020–13 January 2021) on Camera 2, in short-cadence mode (texp = 2 min). The observations were processed using the Science Processing Operations Center (SPOC) pipeline (Jenkins et al. 2016). For our analysis, we used the Presearch Data Conditioning Simple Aperture Photometry (PDCSAP) flux (Stumpe et al. 2012, 2014; Smith et al. 2012), which has common trends removed and is corrected for crowding from known nearby stars. Observations flagged by the pipeline as low quality were removed. Figure B.1 shows the TESS Target Pixel Files (TPF) centred on HIP 29442, with sources cross-matched with the Gaia DR3 catalogue overplotted (Gaia Collaboration 2021). There are no bright sources falling within the TESS aperture that can significantly contaminate the light curve and dilute the transits, or additional widely separated companions with similar parallaxes and proper motions (Mugrauer & Michel 2020, 2021) identified by Gaia. Moreover, HIP 29442 has a Gaia DR3 Renormalised Unit Weight Error (RUWE) of 1.11, consistent with the single-star model. The possibility of contamination by closer stars (within 3″ from HIP 29442) has also been investigated in more detail through speckle and adaptive optics imaging, as discussed in Sect. 2.2.
2.2 Imaging observations
As part of the standard process for validating transiting exo-planets, high angular resolution imaging is needed to search for nearby sources that can contaminate the TESS photometry, resulting in an underestimated planetary radius, or can be the source of astrophysical false positives, such as background eclipsing binaries (e.g. Lillo-Box et al. 2014; Ciardi et al. 2015). HIP 29442 was observed with infrared high-resolution adaptive optics (AO) imaging at Keck Observatory with the NIRC2 instrument on Keck-II behind the natural guide star AO system (Wizinowich et al. 2000; Schlieder et al. 2021). The observations were made on 25 March 2019 in the standard three-point dither pattern that is used with NIRC2 to avoid the left lower quadrant of the detector, which is typically noisier than the other three quadrants. The dither pattern step size was 3″ and was repeated twice, with each dither offset from the previous dither by 0.5″. The camera was in the narrow-angle mode with a full field of view of ~10″ and a pixel scale of approximately 0.0099442″ per pixel. The observations were made in the narrow-band Br-γ filter (λo = 2.1686; Δλ = 0.0326 µm) with an integration time of 30 s with one coadd per frame, for a total of 270 s on target. The final resolution of the combined dithers was determined from the full width at half maximum (FWHM) of the point spread function 0.057″. The sensitivities of the final combined AO image were determined by injecting simulated sources azimuthally around the primary target every 20° at separations of integer multiples of the central source’s FWHM (Furlan et al. 2017). The brightness of each injected source was scaled until standard aperture photometry detected it with 5σ significance. The resulting brightness of the injected sources relative to the target set the contrast limits at that injection location. The final 5σ limit at each separation was determined from the average of all of the determined limits at that separation and the uncertainty on the limit was set by the rms dispersion of the azimuthal slices at a given radial distance. The final sensitivity curve for the Keck data is shown in the upper panel of Fig. 1). We reached a contrast upper limit of ~8 mag at 0.5″ from the target star.
We vet for visual companions also with Gemini/NIRI AO imaging. We collected nine science images, each with an integration time of 1.5 s, on 5 April 2019, and offset the telescope by ~2″ in a grid-like dither pattern between each image. These science images were reduced following standard data reduction practices: we removed bad pixels, applied flat-field and sky background corrections (using a sky background reconstructed from the dithered science images themselves), aligned the images based on fitting the stellar position, and then co-added the data. No candidates were identified within the field of view, and we reach a contrast of 7.85 magnitudes in the background limited regime, and are sensitive to companions within 5 mag of the host beyond 250 mas. The contrast and a thumbnail image of the target are shown in the middle panel of Fig. 1.
We also used speckle imaging to search for stellar companions to HIP 29442 with the 4.1 m Southern Astrophysical Research (SOAR) telescope (Tokovinin 2018). We observed the star on 17 March 2019 in the Cousins I-band, which is a visible bandpass similar to that for TESS. This observation was sensitive to a 5.5-magnitude fainter star at an angular distance of 1″ from the target. More details of the observations within the SOAR TESS survey are available in Ziegler et al. (2020). The 5σ detection sensitivity and speckle autocorrelation functions from the observations are shown in the bottom panel of Fig. 1. No nearby stars were detected within 3″ of HIP 29442 in the SOAR observations. No additional stellar companions were detected, in agreement with the AO observations.
 |
Fig. 1 Imaging observations. Upper panel: Keck near-IR AO imaging and sensitivity curves for HIP 29442 taken in the Br-γ filter on 25 March 2019. The image reaches a contrast of ~8 magnitudes fainter than the host star within 0.5″. Middle panel: Gemini/NIRI AO imaging of HIP 29442. Observation taken on 5 April 2019 in the Br-γ filter. Lower panel: speckle imaging of HIP 29442 taken with the SOAR telescope on 17 March 2019. No nearby stars were detected within 3″ of the target. Insets: image of the central portion of the data, centred on the star. |
2.3 Spectroscopic follow-up with ESPRESSO
We observed HIP 29442 with the ESPRESSO spectrograph installed at the Very Large Telescope (VLT) at the Paranal Observatory in Chile (Pepe et al. 2021) between 9 October 2019 and 24 March 2022 (time span of 897 d). We collected 83 spectra in high-resolution (HR) single-telescope mode, with an exposure time of 900 s; the spectra were reduced with the data reduction software (DRS) v.3.0.0, using a G9 mask. The observations were executed with fibre B illuminated by a Fabry-Pérot light as a spectral reference to measure the instrument’s internal drift (Pepe et al. 2021). The RVs, bisector inverse slope (BIS), and FWHM were calculated from the cross-correlation function (CCF). The RVs have a median photon noise precision of 0.31 m s−1and an rms of 3.53 m s−1, and are listed in Table A.1. Due to the COVID-19 pandemic, ESPRESSO was in downtime for nine months between 24 March and 24 December 2020. Therefore, in our modelling we considered the possible presence of a relative offset between data obtained before and after the interruption of the observations (Sect. 5).
3 Fundamental stellar parameters
We compiled a list of astrometric, photometric, and spec-troscopic parameters of HIP 29442 (Table 1). The stellar atmospheric parameters (Teff, log g, microturbulence, [Fe/H]) were derived from a combined ESPRESSO spectrum using ARES+MOOG, following the same methodology described in Sousa et al. (2021), Sousa (2014), and Santos et al. (2013). The latest version of ARES2 (Sousa et al. 2007, 2015) was used to consistently measure the equivalent widths (EWs) of selected iron lines based on the line list presented in Sousa et al. (2008). We used a minimisation process to find ionisation and excitation equilibrium and to converge to the best set of spectro-scopic parameters. This process makes use of a grid of Kurucz model atmospheres (Kurucz 1993) and the radiative transfer code MOOG (Sneden 1973). The trigonometric surface gravity was also derived using eDR3 Gaia data following the same methodology as described in Sousa et al. (2021). The age, mass, and radius were determined using the Bayesian code PARAM3 (da Silva et al. 2006; Rodrigues et al. 2014, 2017) v1.4. The derived values are 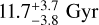 (>4.07 Gyr at 95% of confidence level; we note that here we report the 68% confidence interval derived from the posterior distribution, without constraining its upper limit to be 13.78 Gyr),
(>4.07 Gyr at 95% of confidence level; we note that here we report the 68% confidence interval derived from the posterior distribution, without constraining its upper limit to be 13.78 Gyr), 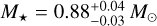 , and
, and 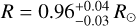 , respectively. The code followed a grid-based approach where a well-sampled grid of stellar evolutionary tracks is matched to the observed quantities Teff, [Fe/H], and luminosity. The derivation of the errors on the mass and radius were calculated from the PDF of the posteriors, in which we took the median as the central value and the 16th and 84th percentiles (1σ confidence interval). The grid of stellar evolutionary isochrones was taken from the code PARSEC4 v2.1 (Bressan et al. 2012). The mass and radius derived with PARAM are the values adopted in our work. The luminosity was computed by converting the bolo-metric magnitude, calculated from the Ks 2MASS magnitude (Skrutskie et al. 2006) corrected for the corresponding bolometric correction and for the distance. The bolometric correction was estimated through the online tool YBC5 (PARSEC Bolometric Correction; Chen et al. 2019) with the input quantities Teff, [Fe/H], log g). The distance was calculated by the inverse of the Gaia eDR3 parallax (Gaia Collaboration 2021). The interstellar absorption was neglected, assuming that our target has low reddening due to its proximity to the Sun and taking into account that the contribution of the reddening in the band Ks is generally lower than or comparable to the photometric error. We derived a bolometric luminosity L = 0.70 ± 0.03 L⊙.
, respectively. The code followed a grid-based approach where a well-sampled grid of stellar evolutionary tracks is matched to the observed quantities Teff, [Fe/H], and luminosity. The derivation of the errors on the mass and radius were calculated from the PDF of the posteriors, in which we took the median as the central value and the 16th and 84th percentiles (1σ confidence interval). The grid of stellar evolutionary isochrones was taken from the code PARSEC4 v2.1 (Bressan et al. 2012). The mass and radius derived with PARAM are the values adopted in our work. The luminosity was computed by converting the bolo-metric magnitude, calculated from the Ks 2MASS magnitude (Skrutskie et al. 2006) corrected for the corresponding bolometric correction and for the distance. The bolometric correction was estimated through the online tool YBC5 (PARSEC Bolometric Correction; Chen et al. 2019) with the input quantities Teff, [Fe/H], log g). The distance was calculated by the inverse of the Gaia eDR3 parallax (Gaia Collaboration 2021). The interstellar absorption was neglected, assuming that our target has low reddening due to its proximity to the Sun and taking into account that the contribution of the reddening in the band Ks is generally lower than or comparable to the photometric error. We derived a bolometric luminosity L = 0.70 ± 0.03 L⊙.
We calculated a model-independent bolometric luminosity by fitting the spectral energy distribution (SED) of TOI-469, taking advantage of the precise photometry available in several bands in the range ~0.3–25 µm and the Gaia EDR3 parallax (Fig. B.2). We find L = 0.695 ± 0.011 L⊙. The best-fit black-body curve for Teff = 5289 ± 69 K shows that there is no infrared-flux excesses from the star up to 25 µm. From the SED-derived bolometric luminosity and Teff, we determined the stellar radius by applying the Stefan–Boltzmann equation. We obtain 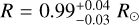 , in agreement with the radius calculated using stellar evolutionary models.
, in agreement with the radius calculated using stellar evolutionary models.
We also performed a chemical abundance analysis of HIP 29442, using the combined ESPRESSO spectrum. Under the assumption of local thermodynamic equilibrium, the classical curve-of-growth analysis technique was used (e.g. Nissen 2015; Casali et al. 2020; da Silva et al. 2012; Bensby et al. 2014). The stellar abundances of the elements were also determined, using the same methods and models used to determine the stellar parameters. For the derivation of chemical abundances of the refractory elements we closely followed the methods described in Adibekyan et al. (2012, 2015), among others. Although the EWs of the spectral lines were measured automatically with ARES, we undertook a detailed visual review of the EWs for the elements Na, Al, and Mg with only two or three lines available. Abundances of the volatile elements C and O were derived following the method of Delgado Mena et al. (2021) and Bertran de Lis et al. (2015). Since the two spectral lines of oxygen are usually weak, the EWs of these lines were manually measured with the task splot in IRAF. In addition, a careful inspection of the individual spectra was done to remove the spectra contaminated by telluric lines or the oxygen airglow at 6300 Å. The abundance values of oxygen from different line indicators tend to show dissimilar values. In particular, for relatively cool stars (as is the case for HIP 29442), the oxygen line at 6300 Å tends to provide lower abundances that usually translate into higher C/O ratios (Delgado Mena et al. 2021). Therefore, we only used the oxygen abundance from the O I line at 6158 Å, which is not dependent on Teff. All the [X/H] ratios are obtained by doing a differential analysis with respect to a high signal-to-noise ratio (S/N) solar (Vesta) spectrum. The results are shown in Table 1. Overall, the chemical pattern of HIP 29442 resembles that of a typical Galactic thin disk star in the solar neighbourhood (e.g. Adibekyan et al. 2012).
We computed the Galactic space velocity (U, V, W) of HIP 29442 based on its coordinates, proper motion, parallax, and systemic RV extracted from Gaia DR3. Considering the solar peculiar motion from Robin et al. (2003), we obtain U = 87.10 ± 0.10 km s−1, V = −2.71 ± 0.10 km s−1, and W = −16.75 ± 0.04 km s−1 with respect to the local standard of rest. We used these velocities to estimate the probability that HIP 29442 belongs to the thin disk (D), the thick disk (TD), and the halo (H), based on the kinematic approach from Bensby et al. (2003) and the kinematic characteristics for the stellar components in the solar neighbourhood from Robin et al. (2003). We obtain D = 96.376%, TD = 3.610%, and H = 0.014%. Thus, it is very likely that HIP 29442 is a member of the Galactic thin-disk population, which is a conclusion in agreement with its chemical pattern.
Stellar properties of HIP 29442 (HD 42813; TOI-469).
4 Stellar activity characterisation
HIP 29442 appears to be a chromospherically quiet star over the timespan of the observations, with the log R′HK index, calculated by the DRS v.3.0.0 pipeline using the calcium (Ca) H&K lines, first deriving the well-known Mount Wilson chromospheric S-index, then converting it to log R′HK following Noyes et al. (1984). The log R′HK index has an average of −5.25 dex and rms of 0.12 dex. We investigated the frequency content of the log R′HK index, and of the spectral FWHM and BIS calculated from the CCF. The analysis consisted of the calculation of the maximum likelihood periodograms (MLPs; Zechmeister et al. 2019), using the implementation of the MLP code included in the EXO-STRIKER package6 (version 0.65). Differently from the generalised Lomb-Scargle periodogram (GLS; Zechmeister et al. 2009), the y-axis of the MLP represents the difference Δ(ln L) between the logarithm of the likelihood function corresponding to the bestfit sine function for each tested frequency, and that of a constant function. The levels of false alarm probability (FAP) are calculated analytically. The MLP algorithm includes zero points as free parameters if datasets from different instruments, as well as instrumental uncorrelated jitter terms. In our case we treated the data collected pre- and post-COVID interruption as two independent datasets. The MLPs are shown in Fig. 2. The periodogram of the FWHM shows a significant peak at 760 days, which is close to the time span of the dataset, and a second peak at 37 days, which is also detected in the MLPs of the RV residuals (see Sect. 5.1). The origin of the first and lower frequency signal is unclear. The periodograms of the log R′HK and BIS activity diagnostics do not show significant peaks around 37 days. That of log R′HK shows 1% significant peaks at 173 and 411 days, the latter also appearing with low significance in the periodogram of the RV residuals. We interpret the 37 d signal as the signature of the stellar rotation period. Using our derived values of the projected rotation velocity υ sin i⋆ (1.94 ± 0.45 km s−1) and stellar radius 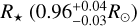 , we can assess the maximum stellar rotation period. We find
, we can assess the maximum stellar rotation period. We find 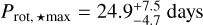 . This value is compatible within 2σ with the periods detected in the activity diagnostics and RVs. This inconsistency between Prot,⋆max and the period detected in the data can be justified; taking into account that HIP 29442 is a slow rotator, it is difficult to measure a value of υ sin i⋆ lower than that we determined (i.e. we cannot reach a sensitivity to longer Prot,⋆max) because we are limited by the width of the instrument profile.
. This value is compatible within 2σ with the periods detected in the activity diagnostics and RVs. This inconsistency between Prot,⋆max and the period detected in the data can be justified; taking into account that HIP 29442 is a slow rotator, it is difficult to measure a value of υ sin i⋆ lower than that we determined (i.e. we cannot reach a sensitivity to longer Prot,⋆max) because we are limited by the width of the instrument profile.
We note that there is no evidence for a clear rotational modulation in the TESS light curve. We searched for a possible rotation modulation within the ASAS-SN public data7 (Shappee et al. 2014; Kochanek et al. 2017). HIP 29442 has been observed with six cameras since 2013 (five facilities used a g-band filter, one employed a V-band filter), making a total of 1313 photometric data points to date. We shifted the photometric aperture on a yearly basis to correct for the target proper motion, in order to ensure a proper centring of the star, hence avoiding flux loss from the aperture. Data from the six cameras are shown in Fig. B.3. Observations in V-band were collected up to 2019. Observations in g-band appear to be quite different from camera to camera. Data from camera bE are particularly affected by large systematics, and there is a clear jump visible in the last part of the data that we cannot explain. Therefore, we discarded data from camera bE. We applied a 3σ clipping to the data and performed a frequency analysis to the photometric time series, exploring frequencies up to 1/100 c/d, in order to be sensitive to a rotational modulation. Given the limited time coverage of the data and that the g-band time series do not show consistent long-term trends, although they cover a similar time span, we cannot draw conclusions about the presence of real long-term photometric modulations. We calculated Lomb–Scargle periodograms, without finding significant peaks, concluding that ASAS-SN data do not allow us to detect the stellar rotation period.
 |
Fig. 2 Maximum likelihood periodograms of spectroscopic activity diagnostics of HIP 29442. The window function of the data is shown in the lower panel. The periodograms include levels of analytical FAR |
5 RV and light curve analysis
5.1 Frequency content analysis of the RVs
The time series of the ESPRESSO RVs is shown in Fig. 3. Using MLPs, we determined the frequency content of the original RV dataset and of the residuals, after subtracting the best-fit sinusoidal signal with the highest peak frequency recursively (Fig. 4). The MLP of the original data shows the main peak very closely compatible with the orbital period of TOI-469.01 (~13.55 days), and two additional peaks at 3.54 and 6.44 days. They are still present in the MLP after a first pre-whitening (i.e. after removing the best-fit sinusoid with a period corresponding to the peak with the highest power in the MLP) and with higher significance (second panel of Fig. 4). A further pre-whitening increases the significance of the 6.44-day period, and also that of a 37-day signal, that was detected in the previous MLPs with low power. A peak at 37 days is also present in the periodograms of the FWHM with a FAP lower than 1 % (Sect. 4), and we attribute the corresponding signal to stellar magnetic activity, which is likely the rotational frequency of HIP 29442. The MLP of the RV residuals, labelled O-C #3 and #4 in Fig. 4, show a peak at 411 days that was not significant in the previous periodograms. This signal has a counterpart in the periodogram of the log R′HK (Sect. 4), and could be induced by some form of stellar activity.
The preliminary results provided by the MLP show that the signal at ~13.55 days has a semi-amplitude of ~2.6 ± 0.5 m s−1, which allows us to label TOI-469.01 as a planet (minimum mass m sin i ≅ 9 M⊕), thoroughly characterised in Sect. 5.4. Therefore, hereafter we refer to TOI-469.01 as HIP 29442 b. Following the detection in the MLP of the lower-amplitude signals at 3.54 and 6.44 days (K = 2.2 ± 0.4 and 1.9 ± 0.3 m s−1, respectively, both corresponding to ~5 M⊕), we performed an in-depth analysis of the TESS light curve to search for transits at such periods that remained undetected and have not been reported in the ExoFOP website.
 |
Fig. 3 ESPRESSO RVs. Blue circles: pre-COVID dataset; red circles: post-COVID dataset. The mean value of the full dataset has been subtracted from the original data. No offset has been subtracted from the two subsamples. The error bars represent the formal RV uncertainties derived by the DRS pipeline. |
 |
Fig. 4 Maximum likelihood periodograms of the original RVs (top panel) and of the RV residuals O-C after subtracting recursively the best-fit sinusoidal signal with the highest peak frequency. The periodograms include levels of analytical FAP. The window function of the data is the same as in Fig. 2. |
5.2 Search for additional transits in the TESS light curve
The discovery of two additional signals in the RVs triggered a careful analysis of the light curve in order to reveal shallow transits not detected in previous analyses. In the beginning we used a first version of the detrended light curve. We modelled the variability with a Gaussian process (GP) regression, using a covariance matrix obtained by combining two SHOTerm kernels into a RotationTerm kernel as implemented in Celerite2 (Foreman-Mackey et al. 2017; Foreman-Mackey 2018). The SHOTerm represents a stochastically driven, damped harmonic oscillator (SHO), with a power spectrum that can be written as
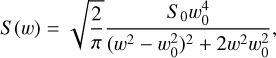 (1)
(1)
where S0 is the amplitude and w0 is the angular frequency corresponding to the break point in the power spectral density of the kernel. A mixture of two SHO terms (i.e. the Rotation Term kernel) can be used to model stellar rotation. The model was trained on a light curve consisting of 44 min binned PDCSAP data to avoid fitting short-term variations. The parameters were optimised to find the maximum a posteriori parameters values, and then the model was sampled using the PyMC3-Extras (Salvatier et al. 2016) library and the exoplanet package (Foreman-Mackey et al. 2021), using two chains with 2500 tuning steps and another 2500 steps each. The corresponding trend was then interpolated and removed from the original light curve. We also flagged and removed observations that were more than five times the standard deviation above the mean of the corrected flux. A similar approach was used for observations more than five times the standard deviation under the mean corrected flux, with the difference that each observation oi whose two neighbours oi–1, oi+1 were considered outliers as well were considered of probable physical origin, and therefore not removed from the light curve. As this is a blind analysis to search for additional transits, the model does not include transit signals in addition to the GP signal; therefore, transits that are still undetected could be removed or their profiles altered. For these reasons, we did not adopt this light curve as our final dataset. We adopted a more thorough model to extract the final detrended light curve, as described in Sect. 5.3. We searched for transit signals through the Transit Least–Squares (TLS) periodogram (Hippke & Heller 2019), which easily recovered the HIP 29442 b signal with a high signal detection efficiency (SDE). We used starry (Luger et al. 2019) to model the light curve, and adopted a quadratic limb darkening law (Kipping 2013). For a quicker fit we used a subsample of data centred around the mid-transit times spanning 0.25 days before and after each transit, and considered a circular orbit. Using the period, time of transit centre and duration resulting from this fit, we masked the transits of HIP 29442 b in the light curve, and ran the TLS search again. The second TLS search reveals a signal with a SDE of 12.31 at ~3.54 days. The same methodology was applied once again to mask these additional transits. The third iteration with TLS resulted in the identification of a peak with SDE = 7.06 at ~6.43 days. Different SDE thresholds have been proposed in the literature to claim a detection. Dressing & Charbonneau (2015) consider SDE > 6 to be a sufficient threshold, while other authors suggest fixing the threshold at SDE > 7 (Siverd et al. 2012; Hippke & Heller 2019). According to the TLS documentation8, an SDE = 7 corresponds to a FAP of 1%, and SDE = 8.3 to a FAP of 0.1%. A further iteration with TLS resulted in peaks that are not significant and that do not have a counterpart in the RVs. In the end, we detected 4 transits of HIP 29442 b (2 in S6 and 2 in S33), 12 transits of HIP 29442 c (6 in S6 and 6 in S33), and 7 transits of HIP 29442 d (3 in S6 and 4 in S33). We note that one transit of HIP 29442 c is almost overlapped by a transit of HIP 29442 b (around BJD 2459 210.7).
After this first analysis with TLS, all the transits were masked in the PDCSAP light curve, and the stellar activity was modelled again using the same approach as described above, interpolating the best-fit model to correct the masked data points. We analysed this new version of the light curve again with TLS to re-assess the SDE of the transit signals. The final TLS periodograms are shown in Fig. 5. The SDE of the signals at P = 3.54 and P = 6.43 increased to 18.4 and 8.9, respectively. The transits correspond to a R ~ 3.6 R⊕ (HIP 29442b) and to two Earth-sized companions on innermost orbits. The orbital periods of these two innermost companions derived from TESS photometry are perfectly in agreement with the results of the RV frequency analysis. Therefore, we conclude that photometry and RVs both significantly reveal the presence of two additional companions that, taking into account their preliminary mass and size, can be confirmed as planets. Hereafter, we label HIP 29442 c and HIP 29442 d the planets with the shortest and intermediate orbital periods, respectively.
5.3 Modelling of the TESS data
We found low S/N transits of HIP 29442 c and HIP 29442 d in the TESS data, which is the reason why they have low SDE and have gone undetected so far. This also implies that the detrending of the light curve has to be performed with special care in order to minimise the distortion of the transit profiles, which would hamper a correct retrieval of the transit parameters and the planetary radii. To this end, we took a step further with respect to the preliminary analysis described in Sect. 5.2 by fitting the TESS PDCSAP curve through a model composed of two components: the transit signals and a GP regression to model photometrically correlated signals. Modelling these two components jointly proved to be very successful in preserving the transit shapes (e.g. Luque et al. 2021; Soto et al. 2021; Lillo-Box et al. 2023), especially for transits with low S/N, such as those of HIP 29442 c and HIP 29442 d (e.g. Dransfield et al. 2022; Cacciapuoti et al. 2022). In addition, this approach ensures a correct propagation of the uncertainties of the model parameters (Leleu et al. 2021). We used the batman implementation (Kreidberg 2015) of the quadratic limb darkened transit model formulated by Mandel & Agol (2002). The model is described by the orbital period (Porb), the time of inferior conjunction (Tconj), the orbital inclination angle (ip), and the radius (Rp) of the transiting planets (in units of stellar radii), and by the stellar quadratic limb darkening (LD) coefficients u1 and u2. We used the adopted stellar mass and radius to calculate the stellar density, and used it to better constrain the model parameters a(b, c, d)/R* (Sozzetti et al. 2007).
We modelled the TESS correlated noise through a GP with an approximate Matérn-3/2 kernel (Foreman-Mackey et al. 2017), which has been widely used to model TESS PDCSAP (e.g. Mori et al. 2022; Morello et al. 2023; Murgas et al. 2023). We chose this kernel because it has covariance properties that are very well matched to short-term instrumental red-noise structures (e.g. Pepper et al. 2017; Stefánsson et al. 2020). Hence, it is appropriate for modelling TESS data, such as that of TOI-469, in which the stellar rotation is not detectable and instead residual systematics dominate the correlated noise (Castro-González et al. 2023).
The approximate Matérn-3/2 kernel can be written in terms of the temporal separation between two data points τ = ti – tj as
![${K_{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} = \eta _\sigma ^2\,\left[ {\left( {1 + {1 \over }} \right)\,{e^{ - \left( {1 - } \right)\,{{\sqrt {3\tau } } \mathord{\left/ {\vphantom {{\sqrt {3\tau } } {{\eta _\rho }}}} \right. \kern-\nulldelimiterspace} {{\eta _\rho }}}}} \cdot \left( {1 - {1 \over }} \right)\,{e^{ - \left( {1 + } \right)\,{{\sqrt {3\tau } } \mathord{\left/ {\vphantom {{\sqrt {3\tau } } {{\eta _\rho }}}} \right. \kern-\nulldelimiterspace} {{\eta _\rho }}}}}\,} \right],$](/articles/aa/full_html/2023/11/aa47240-23/aa47240-23-eq20.png) (2)
(2)
where the hyperparameters ησ and ηρ, are the characteristic amplitude and timescale of the correlated variations, respectively. The parameter ϵ controls the approximation to the exact Matérn-3/2 kernel, and we fixed it to its default value of 10−2 (Foreman-Mackey et al. 2017). Given that both the amplitudes and frequencies of TESS sytematics might change between sectors, we fitted those parameters independently. In addition, we added ajitter term σTESS in quadrature to the flux uncertainties in order to account for the white noise not considered in our model. In order to ensure that our computed planetary parameters are independent of the kernel choice, we also tested a GP with the simple harmonic oscillator kernel described in Eq. (1), which we used for a blind transit search, and it has been designed to model smooth modulations related to the stellar rotation. We found no differences in the derived model parameters.
We sampled the posterior probability density function of the parameters in our model through a Markov chain Monte Carlo (MCMC) affine-invariant ensemble sampler (Goodman & Weare 2010), as implemented in emcee (Foreman-Mackey et al. 2013). We performed a first run with 200 000 iterations, and then reset the sampler and performed a second run with 100 000 iterations starting from the maxima of the posterior probabilities as computed from the last iteration of the first run. For each run we used four times as many walkers as the number of parameters. Once the process was finished, we estimated the autocorrelation time for each fitted parameter and verified that it is at least 30 times less than the chain length, hence ensuring the convergence.
We ran the MCMC fit on the full S6+S33 dataset. We summarise the priors and best-fit values of the free parameters in Table 2. We show in Fig. 6 the full TESS light curve with the best-fit GP and transit models, and in Fig. 7 the transit light curves of the three planets phase-folded using their best-fit transit ephemeris. The transit depths, expressed as 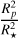 , are
, are 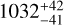 ,
, 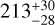 , and
, and 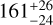 , respectively. As a comparison, the rms of the detrended and normalised light curve, after masking the transits, is 581 ppm and 604 ppm for Sectors S6 and S33, respectively. The individual transits of all the planets in the system are shown in Fig. 8, which emphasises that the transits of HIP 29442 c and HIP 29442 d are so shallow that some of them can be barely detected, or not at all, by eye (e.g. see transits 1, 8, and 10 of planet c, and transits 1, 3, and 6 of planet d). The observed high variability in the S/N of the individual transits brings us to the conclusion that the 1σ error bars for the radii of planets c and d derived through the MCMC simulations are likely too optimistic. Thus, in order to provide more conservative results, it seems appropriate to also adopt the 3σ confidence interval especially, but not exclusively, for the transit-derived parameters of the two innermost planets. This has important implications for the accuracy and precision of the interior structure modelling that we describe in Sect. 6. From the results with TESS data, it is clear that a high-precision photometric follow-up is needed to measure an accurate transit depth and radius of HIP 29442 c and HIP 29442 d, and to determine their bulk structure more precisely.
, respectively. As a comparison, the rms of the detrended and normalised light curve, after masking the transits, is 581 ppm and 604 ppm for Sectors S6 and S33, respectively. The individual transits of all the planets in the system are shown in Fig. 8, which emphasises that the transits of HIP 29442 c and HIP 29442 d are so shallow that some of them can be barely detected, or not at all, by eye (e.g. see transits 1, 8, and 10 of planet c, and transits 1, 3, and 6 of planet d). The observed high variability in the S/N of the individual transits brings us to the conclusion that the 1σ error bars for the radii of planets c and d derived through the MCMC simulations are likely too optimistic. Thus, in order to provide more conservative results, it seems appropriate to also adopt the 3σ confidence interval especially, but not exclusively, for the transit-derived parameters of the two innermost planets. This has important implications for the accuracy and precision of the interior structure modelling that we describe in Sect. 6. From the results with TESS data, it is clear that a high-precision photometric follow-up is needed to measure an accurate transit depth and radius of HIP 29442 c and HIP 29442 d, and to determine their bulk structure more precisely.
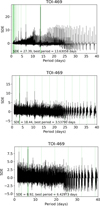 |
Fig. 5 TLS periodograms of the detrended TESS light curve (see Sect. 2.1) showing peaks of the three transiting planets. The periodogram in the second panel was obtained after masking the transits of planet b, and that in the third panel was calculated after masking the transits of planets b and c. The dashed lines correspond to the harmonics of the orbital periods. Planets c and b were identified first in the ESPRESSO RV time series; their presence was confirmed by the transit signals detected in the TESS data. |
5.4 Monte Carlo RV fitting
We used the results of the transit modelling to constrain the orbital periods and time of inferior conjunction by using Gaussian priors, based on the analysis of the S6+S33 dataset (see Table 2). Given the low S/N of the transits, a joint RV+light curve analysis would not help to better constraining the system’s parameters, at a higher cost in terms of computing resources when different RV models are tested, as happens in our case. We modelled the orbits of all the transiting planets with Keplerians, and adopted the parametrisation 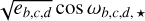 and
and 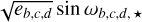 , where eb,c,d and ωb,c,d,⋆ are free parameters for the eccentricities and arguments of periastron. We also tested models with eb,c,d fixed to zero to assess the statistical significance of the fitted eccentricities. To investigate the existence of an additional planetary-like signal, we also tested models including a fourth Keplerian (or sinusoid), that we labelled ‘signal x’, with period Px sampled uniformly between 15 and 1000 days. By treating pre- and post-COVID data as independent RV subsamples (labelled ESP19 and ESP21, respectively), the models include the pair of offsets γESP, 19 and γESP, 21, and two white noise jitters σjitt.ESP, 19 and σjitt.ESP, 219.
, where eb,c,d and ωb,c,d,⋆ are free parameters for the eccentricities and arguments of periastron. We also tested models with eb,c,d fixed to zero to assess the statistical significance of the fitted eccentricities. To investigate the existence of an additional planetary-like signal, we also tested models including a fourth Keplerian (or sinusoid), that we labelled ‘signal x’, with period Px sampled uniformly between 15 and 1000 days. By treating pre- and post-COVID data as independent RV subsamples (labelled ESP19 and ESP21, respectively), the models include the pair of offsets γESP, 19 and γESP, 21, and two white noise jitters σjitt.ESP, 19 and σjitt.ESP, 219.
We tested models including a Gaussian process (GP) regression, to model a correlated signal induced by the stellar variability and modulated over the stellar rotation with a periodicity of ~37 days, which is present in the data, as shown by the results of the frequency analysis (Sect. 5.1), and similarly in the FWHM time series (Sect. 4). To this end, we adopted the frequently used and highly functional quasi-periodic (QP) kernel (e.g. Haywood et al. 2014). The elements of the QP covariance matrix are defined as follows:
![$\matrix{ {{k_{QP}}\left( {t,t\prime } \right) = {h^2} \cdot {\rm{exp}}\,\left[ { - {{\left( {t - t\prime } \right)} \over {2{\lambda ^2}}} - {{{\rm{si}}{{\rm{n}}^2}\,\left( {\pi {{\left( {t - t\prime } \right)} \mathord{\left/ {\vphantom {{\left( {t - t\prime } \right)} \theta }} \right. \kern-\nulldelimiterspace} \theta }} \right)} \over {2{w^2}}}} \right]} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \left( {\sigma _{{\rm{RV}}}^2\left( t \right) + \sigma _{{\rm{jitt,ESP}}}^2} \right) \cdot {\delta _{t,t\prime }}.} \hfill \cr }$](/articles/aa/full_html/2023/11/aa47240-23/aa47240-23-eq27.png) (3)
(3)
Here t and t′ denote two different epochs of observations, σRV(t) represents the radial velocity uncertainty at the observing epoch t, and δt,t′ is the Kronecker delta. The GP hyper-parameters are h, which denotes the amplitude scale of the correlated signal; θ, which represents the periodic time-scale of the modelled signal, and corresponds to the stellar rotation period; w, which describes the ‘weight’ of the rotation period harmonic content within a complete stellar rotation (i.e. a low value of w indicates that the periodic variations contain a significant contribution from the harmonics of the rotation periods); and λ, which represents the decay timescale of the correlations, and is related to the temporal evolution of the magnetically active regions responsible for the correlated signal observed in the RVs.
We explored the full (hyper-)parameter space using the publicly available Monte Carlo (MC) nested sampler and Bayesian inference tool MUlTINEST v3.10 (e.g. Feroz et al. 2019), through the PYMULTINEST wrapper (Buchner et al. 2014). Our MC set-up included 300 live points and we adopted a sampling efficiency of 0.5 and a tolerance on the Bayesian evidence calculation of 0.3. To perform the GP regression, we used the publicly available PHTHON module GEORGE v0.2.1 (Ambikasaran et al. 2015), integrated within the MultiNest framework.
We summarise all the tested models in Table 3, providing their Bayesian evidence ln 𝒵. For the Bayesian model comparison analysis, we adopt the conventional scale used for the interpretation of model probabilities presented in Table 1 of Feroz et al. (2011), according to which ∆ ln 𝒵 ~ 2.5 and ∆ ln 𝒵 > 5 respectively denote moderate and strong evidence in favour of the model with the higher value of ln 𝒵. We note that we also tested models that do not include a GP term, and in all cases we found that they are statistically strongly penalised. Table 3 includes two test models that incorporate the FWHM time series. In these cases we modelled the RVs and FWHM with the same GP QP kernel, with three out of four hyper-parameters in common between the two time series (namely, θ, w, and λ), while different scale amplitudes were used. With this approach, we make use of the information about the stellar activity contained in the FWHM data to constrain the activity-related correlated signal in the RVs. Due to the different datasets analysed in these cases, the Bayesian evidence of these two models cannot be compared with that of the other models in Table 3.
From the results listed in Table 3 we can draw some conclusions. The three transiting planets are well described by assuming circular orbits, because the model with Keplerians (M1) is strongly penalised with respect to M2 (eccentricities of model M1 are all consistent with zero). Models M3 and M4, which include a fourth signal x, are not statistically favoured over the simpler three-planet model M2. In M3, the semi-amplitude Kx appears significant at a ≳2σ level, the period is not well constrained (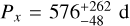 ), and the signal has a high eccentricity (ex = 0.6 ± 0.2). We note for model M2 that we found no significant relative offset. For other targets followed up by the ESPRESSO GTO collaboration we found very small RV offsets between the ESP19 and ESP21 subsamples, and we expect the same for HIP 29442. Moreover, we found that using the FWHM to constrain the stellar activity term in the RVs (models MFWHM, 1 and MFWHM, 2) does not affect the planetary parameters for HIP 29442 b, c, and d, but affects the posteriors of the parameters of signal x: the semi-amplitude Kx is lower and less significant than for models M3 and M4. From these considerations we conclude that our data do not support the existence of a periodic signal x that can be attributed to a fourth planet on an external orbit. We elect model M2 as our reference model, and summarise the best-fit values (the median of the marginalised posteriors, and 1σ confidence intervals) for all the free parameters in Table 4, together with the priors adopted in the analysis. The best-fit spectroscopic orbits and the quasi-periodic stellar activity induced signal are shown in Fig. 9. We note that the best-fit values found for the planetary parameters are consistent for all the test models, and they are recovered with very high significance. Thus, we consider the GP QP regression a successful and sufficient approach, and we do not deem it necessary to test alternative models for the stellar activity component.
), and the signal has a high eccentricity (ex = 0.6 ± 0.2). We note for model M2 that we found no significant relative offset. For other targets followed up by the ESPRESSO GTO collaboration we found very small RV offsets between the ESP19 and ESP21 subsamples, and we expect the same for HIP 29442. Moreover, we found that using the FWHM to constrain the stellar activity term in the RVs (models MFWHM, 1 and MFWHM, 2) does not affect the planetary parameters for HIP 29442 b, c, and d, but affects the posteriors of the parameters of signal x: the semi-amplitude Kx is lower and less significant than for models M3 and M4. From these considerations we conclude that our data do not support the existence of a periodic signal x that can be attributed to a fourth planet on an external orbit. We elect model M2 as our reference model, and summarise the best-fit values (the median of the marginalised posteriors, and 1σ confidence intervals) for all the free parameters in Table 4, together with the priors adopted in the analysis. The best-fit spectroscopic orbits and the quasi-periodic stellar activity induced signal are shown in Fig. 9. We note that the best-fit values found for the planetary parameters are consistent for all the test models, and they are recovered with very high significance. Thus, we consider the GP QP regression a successful and sufficient approach, and we do not deem it necessary to test alternative models for the stellar activity component.
Prior and posterior distributions of the transit+GP model parameters used to analyse the TESS PDCSAP (sectors S6+S33).
 |
Fig. 6 TESS photometry of HIP 29442 (TOI-469) with the median posterior model (transits + GP) overplotted, showing the different locations of the transit events for the three planets over the low-frequency photometric modulation. The light grey data points correspond to the SPOC two-minute cadence PDCSAP photometry. |
 |
Fig. 7 TESS PDCSAP light curve with the GP component subtracted, and phase-folded to the orbital periods of HIP 29442 b (first panel), HIP 29442 c (second panel), and HIP 29442 d (third panel). The solid lines indicate the models calculated using the median of the posteriors. Residuals of the best-fit model are shown at the bottom of each phase-folded plot. |
 |
Fig. 8 Individual transits of HIP 29442 b, HIP 29442 c, and HIP 29442 d within the PDCSAP together with the best-fit transit+GP model overplotted. |
GP-based ESPRESSO RV models tested in this work, and the corresponding best-fit values of RV semi-amplitudes for the three transiting planets b, c, and d.
6 Modelling the planetary internal structure and composition
Following the discussion in Sect. 5.3, we modelled the internal structure and composition of the planets, adopting the 3σ confidence intervals for the planet-to-star ratio (Table 2). Before entering the details of the analysis, we show in Fig. 10 the location of the HIP 29442 planets on a mass-radius diagram for a selected sample of planets with precise mass and radius measurements. HIP 29442 b appears as a typical sub-Neptune, with a structure and composition consistent with an Earth-like rocky core covered by a massive H2O layer, plus a small amount of gaseous envelope. We note that our mass measurement significantly differs from that obtained by Akana Murphy et al. (2023; 5.8 ± 2.4 M⊕), likely mainly due to undetected planets c and d in their work. The composition of planets c and d is very uncertain, as expected if one adopts the 3σ error bars for the radii. The two planets could share a similar Earth-like rocky composition, and it cannot be ruled out that HIP 29442 d is a high-density iron-dominated core.
We performed a quantitative Bayesian analysis of the internal structure of the three planets, with the purpose of improving the results that can be extrapolated from Fig. 10 by using tighter constraints. The method is described in detail in Dorn et al. (2015, 2017) and has already been used to study systems such as L98-59 (Demangeon et al. 2021), TOI-178 (Leleu et al. 2021), and v2 Lupi (Delrez et al. 2021). The model of planetary interiors assumes four layers: an inner core made of iron and sulphur, a mantle of silicates (Si, Mg, and Fe), a water layer, and a gaseous envelope of pure H-He. For the iron core we used the equation of state from Hakim et al. (2018); the equation of state for the silicate mantle comes from Sotin et al. (2007); and for the water layer we adopted the equation of state from (Haldemann et al. 2020). These three layers constitute the ‘solid’ part of a planet; the thickness of the gaseous envelope depends on its mass and radius and on the stellar age and irradiation (Lopez & Fortney 2014).
For the Bayesian analysis we followed two steps. First, we generated 8000 synthetic stars, taking randomly their masses, radii, effective temperatures, ages, and Mg/Si bulk molar ratios within the range of the stellar parameters derived in Sect. 3. Then, for each simulated star, we generated 6000 planetary systems, varying the internal structure parameters of all planets, and assuming that the bulk Fe/Si/Mg molar ratios are equal to the stellar ones. The transit depth and RV semi-amplitude are then computed for each of the planets, and we retained the models that fitted at 2σ the observed data within the error bars. By generating planetary systems around each simulated star, we include the fact that all synthetic planets orbit a star with exactly the same parameters since transit depth and RV semi-amplitude depend on the stellar radius and mass. The modelled planetary parameters are the mass fraction of each layer, the iron molar fraction in the core, the silicon and magnesium molar fraction in the mantle, the equilibrium temperature, and the age of the planet (equal to the age of the star). Uniform priors are used for these parameters, except for the mass of the gas layer which is assumed to follow a uniform-in-log prior, with the water mass fraction having an upper boundary of 0.5 (Thiabaud et al. 2014; Marboeuf et al. 2014). For more details related to the link between observed data and derived parameters, we refer to Leleu et al. (2021).
The results of the internal structure modelling of the planets b, c, and d are shown in Table 5. The corner plots with the marginalised posteriors of the model free parameters are shown in Fig. B.4. As for HIP 29442 b, they are consistent with a planet having a core with a mass fraction of ~0.14, and a mantle with a mass fraction of ~0.61 surrounded by a water layer representing 24% of the mass of the solid part of the planet. The planet could be surrounded by a gas layer of pure H-He with a mass of 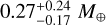 , and a thickness of
, and a thickness of 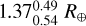 . For HIP 29442 c and d the model suggests an internal structure consistent with that of planet b and likely an Earth-like composition: ~15–16% of their mass could be concentrated in an iron core, and ~66–68% of the mass in the mantle. The amount of mass in the form of a water layer surrounding the mantle is found to be compatible with zero for both planets (Fig. B.4), and in Table 5 we report the upper limits at a 95% level of confidence. According to our results, neither HIP 29442 c nor d is expected to harbour a H-He dominated atmosphere. The model uses a scientific approach to analyse all possible configurations of planets based on their given characteristics, such as mass and radii, while considering the associated error bars. The resulting modelled planets generally exhibit lower densities compared to those estimated using the median values provided in Table 2. This tendency towards lower density allows for compositions that are more similar to Earth-like planets, especially for planet d in this case. A more accurate and precise radius determination will allow us to verify the model prediction.
. For HIP 29442 c and d the model suggests an internal structure consistent with that of planet b and likely an Earth-like composition: ~15–16% of their mass could be concentrated in an iron core, and ~66–68% of the mass in the mantle. The amount of mass in the form of a water layer surrounding the mantle is found to be compatible with zero for both planets (Fig. B.4), and in Table 5 we report the upper limits at a 95% level of confidence. According to our results, neither HIP 29442 c nor d is expected to harbour a H-He dominated atmosphere. The model uses a scientific approach to analyse all possible configurations of planets based on their given characteristics, such as mass and radii, while considering the associated error bars. The resulting modelled planets generally exhibit lower densities compared to those estimated using the median values provided in Table 2. This tendency towards lower density allows for compositions that are more similar to Earth-like planets, especially for planet d in this case. A more accurate and precise radius determination will allow us to verify the model prediction.
7 Conclusions
The main achievements of this work are the discovery and the characterisation of a compact multi-planet system orbiting the evolved K0V star HIP 29442 (TOI-469), based on data collected with the TESS space telescope and the ESPRESSO spectrograph. Thanks to the RVs collected with ESPRESSO, we first detected the Doppler signals due to the companions HIP 29442 c and d. The results from the RV analysis allowed us to uncover the shallow transit signals in the TESS light curve. Using the ESPRESSO RVs we measured the dynamical masses of the planets with the very high precision of 6.7%, 7.8%, and 8.3% for planets c, d, and b, respectively. The low S/N of the transit signals of HIP 29442 c and d, which has, to date, made their blind detection in the TESS data elusive, compelled us to adopt the more conservative 3σ error bars for their radii (including planet b) when performing the internal structure analysis (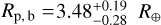 ,
, 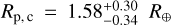 , and
, and 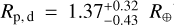 ). Photometric follow-up is indeed necessary to determine more accurate and precise radii, and consequently more accurate and precise bulk densities, which will enable us to better constrain the planets’ internal structure and composition. A similar follow-up was being conducted with CHEOPS at the time of writing (paper in preparation).
). Photometric follow-up is indeed necessary to determine more accurate and precise radii, and consequently more accurate and precise bulk densities, which will enable us to better constrain the planets’ internal structure and composition. A similar follow-up was being conducted with CHEOPS at the time of writing (paper in preparation).
Despite the uncertainty on the radii, nonetheless we can draw interesting conclusions about the system. It is composed of planets that span the bi-modal radius distribution, with the outermost planet b being a sub-Neptune, possibly surrounded by a water layer for more than 20% of the total mass, and by a gaseous envelope with ~30% of the Earth’s mass and a thickness of nearly 1.5 R⊕. The innermost companions c and d could reside on the rocky planet–super-Earth side of the distribution, but they could be located within the radius gap. Their composition is likely Earth-like, and they are not expected to have a H-He gaseous envelope. Our results with the TESS light curve do not exclude the possibility that they are high-density cores, especially planet d, which could be a pure iron core. This would make HIP 29442 d a potential member of the now emerging family of super-Mercuries (i.e. higher-mass analogues of Mercury; e.g. Adibekyan et al. 2021).
HIP 29442 represents an interesting system to explore the role of photo-evaporation during its evolution. It provides an excellent test of the photo-evaporation scenario as uncertainty in the history of the star’s high-energy output can be overcome by scaling the planet’s relative to each other (Owen & Campos Estrada 2020). To check consistency with the photo-evaporation scenario, we apply the test described in Owen & Campos Estrada (2020), and we estimate the mass that planet b must have to retain a hydrogen-dominated atmosphere given planet c and d have lost their atmosphere. We use the updated version of EVAPMASS10, where mass-loss efficiencies from hydrodynamic simulations are used instead of the original power-law scaling (see Rogers et al. 2023). In doing this calculation we find that planet b must have a mass of ≳2.6 M⊕ at the 95% confidence level, consistent with its measured mass. We also made a reverse test to that performed above, asking: assuming that planet b has retained a hydrogen-dominated atmosphere against photo-evaporation, how massive both planets c and d have originally been and still have lost their atmospheres? Due to the possibility of dynamical changes in the planet’s orbit triggered by mass-loss (e.g. Boué et al. 2012; Teyssandier et al. 2015; Fujita et al. 2022), we did this calculation assuming planet b originally had an orbital period of 8 days, 13.63 days or 18 days before any dynamical re-arrangement took place. We calculated the maximum planet mass any interior planet (in this case either c or d) could have had as a function of different original periods. Namely, if we assume planet b at an original period of 8 days and the interior planet had an original period of 2 days, we ask how massive could the interior planet has been such that it could have lost its atmosphere while b retained it. This calculation is then repeated for a range of possible initial periods for the interior planets. The results of this analysis are shown in Fig. 11. They show that the inner planets (c and d) could have been considerably more massive than currently, and are still consistent with a system that underwent photo-evaporation while leaving planet b with a H-He-dominated atmosphere.
Our analysis indicates that the architecture of the HIP 29442 system is consistent with a picture in which all planets accreted a primordial hydrogen dominated atmosphere, which the inner two planets then lost due to their high irradiation levels. We leave to a future work a more detailed investigation of the possible formation and evolutionary histories of the system HIP 29442, once the planets’ size and bulk physical structure will be pinned down more precisely.
 |
Fig. 9 RV Doppler signals due to three transiting planets orbiting HIP 29442 (TOI-469) (panels a, b, and c), and the RV activity term, as fitted through a GP QP regression (panel d; blue curve: best-fit model; grey area: 1σ confidence interval). The RV error bars include a jitter term added in quadrature to the measurement uncertainties. |
 |
Fig. 10 Mass-radius diagram for planets with mass <20 M⊕ and radius <4 R⊕, selected from the TEPCAT sample, available at https://www.astro.keele.ac.uk/jkt/tepcat/ (updated to 22 March 2023; Southworth 2011). The grey dots represent planets with mass and radius measured with a relative precision lower than 20% and 10%, respectively. The planets of the HIP 29442 system are indicated by black triangles. The 1σ confidence intervals for the radius measurements are shown as black lines, while the red dashed lines indicate the 3σ confidence intervals. The overplotted theoretical curves are derived by assuming equations of state detailed in Leleu et al. (2021). |
Results of the internal structure modelling of the planets orbiting HIP 29442.
 |
Fig. 11 Maximum initial planet mass an interior planet (to planet b) could have had and be consistent with photo-evaporation, assuming planet b retained its atmosphere against photo-evaporation. Given the possibility that dynamical re-arrangement within the system might have occurred, we performed this calculation assuming that planet b had an initial period identical to its current period (orange), a shorter initial orbital period of 8 days (blue), or a longer initial orbital period of 18 days (green). The shaded region encompasses the 1 σ error bars, mainly arising from uncertainties in the properties of planet b. The current architecture of the system is shown by the blue points. The two interior planets to b lie below the curves, which indicates the system is consistent with photo-evaporation sculpting the system before any dynamical re-arrangement. |
Acknowledgements
The INAF authors acknowledge financial support of the Italian Ministry of Education, University, and Research through PRIN 201278X4FL and the “Progetti Premiali” funding scheme. J.D. and Y.A. acknowledge support from the Swiss National Science Foundation (SNSF) under grant 200020_192038. Part of this work has been carried out within the framework of the NCCR PlanetS supported by the Swiss National Science Foundation under grants 51NF40_182901 and 51NF40_205606. J.L.-B. and A.C.-G. are partly funded by grants LCF/BQ/PI20/11760023, Ramón y Cajal fellowship with code RYC2021-031640-I, and the Spanish MCIN/AEI/10.13039/501100011033 grant PID2019-107061GB-C61. J.Dou. would like to acknowledge the funding support from the Chinese Scholarship Council (nr. 202008610218,). The giant impact simulations were carried out using the computational facilities of the Advanced Computing Research Centre, University of Bristol (https://www.bristol.ac.uk/acrc/). F.P.E. and C.L.O. would like to acknowledge the Swiss National Science Foundation (SNSF) for supporting research with ESPRESSO through the SNSF grants nr. 140649, 152721, 166227 and 184618. The ESPRESSO Instrument Project was partially funded through SNSF’s FLARE Programme for large infrastructures. This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement SCORE No 851555). This study was funded/co-funded by the European Union (ERC, FIERCE, 101052347). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. The team of the Universidade do Porto acknowledge the support from FCT-Fundação para a Ciência e a Tecnologia through national funds and by FEDER through COMPETE2020-Programa Operacional Competitividade e Internacionalização by these grants: UIDB/04434/2020; UIDP/04434/2020; 2022.04048.PTDC. E.D.M. acknowledges the support from FCT through Stimulus FCT contract 2021.01294.CEECIND. C.J.M. also acknowledges FCT and POCH/FSE (EC) support through Investigador. FCT Contract 2021.01214.CEECIND/CP1658/CT0001. J.I.G.H. and A.S.M. acknowledge financial support from the Spanish Ministry of Science and Innovation (MICINN) project PID2020-117493GB-I00, and also from the Government of the Canary Islands project ProID2020010129. This work is based in part on observations obtained at the Southern Astrophysical Research (SOAR) telescope, which is a joint project of the Ministério da Ciência, Tecnologia e Inovações (MCTI/LNA) do Brasil, the US National Science Foundation’s NOIRLab, the University of North Carolina at Chapel Hill (UNC), and Michigan State University (MSU). This research has made use of the Exoplanet Follow-up Observation Program (ExoFOP; DOI: 10.26134/ExoFOP5) website, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.
Appendix A Dataset
ESPRESSO RVs and activity diagnostics.
Appendix B Additional plots
 |
Fig. B.1 TESS Target Pixel Files for sectors 6 and 33 obtained with TPFPLOTTER (Aller et al. 2020; the code is publicly available at www.github.com/jlillo/tpfplotter). The orange squares identify the aperture masks used to extract the light curve. The sources cross-matched with the Gaia DR3 catalogue are indicated by red dots; the size is scaled with their relative magnitude compared to that of HIP 29442 (TOI-469). Proper motions are indicated by arrows. The pixel scale is 21″ pixel−1. |
 |
Fig. B.2 Spectral energy distribution in the range ~0.3−25 µm, used to derive the bolometric luminosity and the stellar radius through the Stefan–Boltzmann equation. The adopted stellar distance is the trigonometric parallax from the Gaia EDR3. |
 |
Fig. B.3 ASAS-SN photometry of HIP 29442. For a better visualisation, offsets have been applied to the original magnitudes, as indicated in the legend. |
 |
Fig. B.4 Corner plots showing the posteriors of the free parameters adopted for the planetary internal structure modelling described in Sect. 6. From top to bottom, the plots refer to HIP 29442 b, HIP 29442 c, and HIP 29442 d. |
References
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A & A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V., Figueira, P., Santos, N. C., et al. 2015, A & A, 583, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V., Dorn, C., Sousa, S. G., et al. 2021, Science, 374, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Akana Murphy, J. M., Batalha, N. M., Scarsdale, N., et al. 2023, AJ, 166, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Aller, A., Lillo-Box, J., Jones, D., Miranda, L. F., & Barceló Forteza, S. 2020, A & A, 635, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ambikasaran, S., Foreman-Mackey, D., Greengard, L., Hogg, D. W., & O’Neil, M. 2015, IEEE Transactions on Pattern Analysis and Machine Intelligence, 38 [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
- Barros, S. C. C., Demangeon, O. D. S., Alibert, Y., et al. 2022, A & A, 665, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2003, A & A, 410, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., & Oey, M. S. 2014, A & A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertran de Lis, S., Delgado Mena, E., Adibekyan, V. Z., Santos, N. C., & Sousa, S. G. 2015, A & A, 576, A89 [Google Scholar]
- Boué, G., Figueira, P., Correia, A. C. M., & Santos, N. C. 2012, A & A, 537, L3 [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A & A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cacciapuoti, L., Inno, L., Covone, G., et al. 2022, A & A, 668, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carter, J. A., Agol, E., Chaplin, W. J., et al. 2012, Science, 337, 556 [Google Scholar]
- Casali, G., Magrini, L., Frasca, A., et al. 2020, A & A, 643, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castro-González, A., Demangeon, O. D. S., Lillo-Box, J., et al. 2023, A & A, 675, A52 [CrossRef] [EDP Sciences] [Google Scholar]
- Chaturvedi, P., Bluhm, P., Nagel, E., et al. 2022, A & A, 666, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Y., Girardi, L., Fu, X., et al. 2019, A & A, 632, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ciardi, D. R., Beichman, C. A., Horch, E. P., & Howell, S. B. 2015, ApJ, 805, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Cloutier, R., Eastman, J. D., Rodriguez, J. E., et al. 2020, AJ, 160, 3 [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Damasso, M., Bonomo, A. S., Astudillo-Defru, N., et al. 2018, A & A, 615, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Damasso, M., Zeng, L., Malavolta, L., et al. 2019, A & A, 624, A38 [CrossRef] [EDP Sciences] [Google Scholar]
- da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A & A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- da Silva, R., Porto de Mello, G. F., Milone, A. C., et al. 2012, A & A, 542, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delgado Mena, E., Adibekyan, V., Santos, N. C., et al. 2021, A & A, 655, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delrez, L., Ehrenreich, D., Alibert, Y., et al. 2021, Nat. Astron., 5, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Demangeon, O. D. S., Zapatero Osorio, M. R., Alibert, Y., et al. 2021, A & A, 653, A41 [CrossRef] [EDP Sciences] [Google Scholar]
- Diamond-Lowe, H., Kreidberg, L., Harman, C. E., et al. 2022, AJ, 164, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Dorn, C., Khan, A., Heng, K., et al. 2015, A & A, 577, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorn, C., Venturini, J., Khan, A., et al. 2017, A & A, 597, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dransfield, G., Triaud, A. H. M. J., Guillot, T., et al. 2022, MNRAS, 515, 1328 [NASA ADS] [CrossRef] [Google Scholar]
- Dressing, C. D. & Charbonneau, D. 2015, ApJ, 807, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., Balan, S. T., & Hobson, M. P. 2011, MNRAS, 415, 3462 [Google Scholar]
- Feroz, F., Hobson, M. P., Cameron, E., & Pettitt, A. N. 2019, ApJ, 2, 10 [Google Scholar]
- Foreman-Mackey, D. 2018, RNAAS, 2, 31 [NASA ADS] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Foreman-Mackey, D., Agol, E., Ambikasaran, S., & Angus, R. 2017, AJ, 154, 220 [Google Scholar]
- Foreman-Mackey, D., Luger, R., Agol, E., et al. 2021, J. open source softw., 6, 3285 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, N., Hori, Y., & Sasaki, T. 2022, ApJ, 928, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Fulton, B. J., Petigura, E. A., Howard, A. W., et al. 2017, AJ, 154, 109 [Google Scholar]
- Furlan, E., Ciardi, D. R., Everett, M. E., et al. 2017, AJ, 153, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration, (Prusti, T., et al.) 2016, A & A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration, (Brown, A. G. A., et al.) 2021, A & A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration, (Vallenari, A., et al.) 2023, A & A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giacalone, S., Dressing, C. D., Jensen, E. L. N., et al. 2020, AJ, 161, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, S., Schlichting, H. E., & Sari, R. 2018, MNRAS, 476, 759 [Google Scholar]
- Goodman, J., & Weare, J. 2010, Comm. App. Math. Comp. Sci., 5, 65 [Google Scholar]
- Günther, M. N., Pozuelos, F. J., Dittmann, J. A., et al. 2019, Nat. Astron., 3, 1099 [Google Scholar]
- Gupta, A., & Schlichting, H. E. 2019, MNRAS, 487, 24 [Google Scholar]
- Hakim, K., Rivoldini, A., Van Hoolst, T., et al. 2018, Icarus, 313, 61 [Google Scholar]
- Haldemann, J., Alibert, Y., Mordasini, C., & Benz, W. 2020, A & A, 643, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, R. D., Collier Cameron, A., Queloz, D., et al. 2014, MNRAS, 443, 2517 [Google Scholar]
- Hippke, M., & Heller, R. 2019, A & A, 623, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izidoro, A., Schlichting, H. E., Isella, A., et al. 2022, ApJ, 939, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 9913, Software and Cyberinfrastructure for Astronomy IV, eds. G. Chiozzi, & J. C. Guzman, 99133E [Google Scholar]
- Jin, S., Mordasini, C., Parmentier, V., et al. 2014, ApJ, 795, 65 [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 435, 2152 [Google Scholar]
- Kochanek, C. S., Shappee, B. J., Stanek, K. Z., et al. 2017, PASP, 129, 104502 [Google Scholar]
- Kreidberg, L. 2015, PASP, 127, 1161 [Google Scholar]
- Kurucz, R. L. 1993, SYNTHE Spectrum Synthesis Programs and Line Data (Cambridge, Mass.: Smithsonian Astrophysical Observatory) [Google Scholar]
- Lavie, B., Bouchy, F., Lovis, C., et al. 2023, A & A, 673, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leleu, A., Alibert, Y., Hara, N. C., et al. 2021, A & A, 649, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lillo-Box, J., Barrado, D., & Bouy, H. 2014, A & A, 566, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lillo-Box, J., Figueira, P., Leleu, A., et al. 2020a, A & A, 642, A121 [CrossRef] [EDP Sciences] [Google Scholar]
- Lillo-Box, J., Lopez, T. A., Santerne, A., et al. 2020b, A & A, 640, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lillo-Box, J., Gandolfi, D., Armstrong, D. J., et al. 2023, A & A, 669, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lopez, E. D., & Fortney, J. J. 2014, ApJ, 792, 1 [Google Scholar]
- Luger, R., Agol, E., Foreman-Mackey, D., et al. 2019, AJ, 157, 64 [Google Scholar]
- Luque, R., & Pallé, E. 2022, Science, 377, 1211 [NASA ADS] [CrossRef] [Google Scholar]
- Luque, R., Serrano, L. M., Molaverdikhani, K., et al. 2021, A & A, 645, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [Google Scholar]
- Marboeuf, U., Thiabaud, A., Alibert, Y., Cabral, N., & Benz, W. 2014, A & A, 570, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morello, G., Parviainen, H., Murgas, F., et al. 2023, A & A, 673, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mori, M., Livingston, J. H., Leon, J. d., et al. 2022, AJ, 163, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Mugrauer, M., & Michel, K.-U. 2020, Astron. Nachr., 341, 996 [NASA ADS] [CrossRef] [Google Scholar]
- Mugrauer, M., & Michel, K.-U. 2021, Astron. Nachr., 342, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Murgas, F., Castro-González, A., Pallé, E., et al. 2023, A & A, 677, A182 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nissen, P. E. 2015, A & A, 579, A52 [CrossRef] [EDP Sciences] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [Google Scholar]
- Owen, J. E., & Campos Estrada, B. 2020, MNRAS, 491, 5287 [Google Scholar]
- Owen, J. E., & Morton, T. D. 2016, ApJ, 819, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, J. E., & Wu, Y. 2013, ApJ, 775, 105 [Google Scholar]
- Owen, J. E., & Wu, Y. 2017, ApJ, 847, 29 [Google Scholar]
- Pepe, F., Cristiani, S., Rebolo, R., et al. 2021, A & A, 645, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepper, J., Gillen, E., Parviainen, H., et al. 2017, AJ, 153, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Piaulet, C., Benneke, B., Almenara, J. M., et al. 2023, Nat. Astron., 7, 206 [Google Scholar]
- Ricker, G. R., Vanderspek, R., Winn, J., et al. 2016, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 9904, Space Telescopes and Instrumentation 2016: Optical, Infrared, and Millimeter Wave, eds. H. A. MacEwen, G. G. Fazio, M. Lystrup, et al., 99042B [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A & A, 409, 523 [CrossRef] [EDP Sciences] [Google Scholar]
- Rodrigues, T. S., Girardi, L., Miglio, A., et al. 2014, MNRAS, 445, 2758 [Google Scholar]
- Rodrigues, T. S., Bossini, D., Miglio, A., et al. 2017, MNRAS, 467, 1433 [NASA ADS] [Google Scholar]
- Rogers, J. G., Janó Muñoz, C., Owen, J. E., & Makinen, T. L. 2023, MNRAS, 519, 6028 [NASA ADS] [CrossRef] [Google Scholar]
- Salvatier, J., Wiecki, T. V., & Fonnesbeck, C. 2016, PeerJ Comput. Sci., 2, e55 [Google Scholar]
- Santos, N. C., Sousa, S. G., Mortier, A., et al. 2013, A & A, 556, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlieder, J. E., Gonzales, E. J., Ciardi, D. R., et al. 2021, Front. Astron. Space Sci., 8, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Shappee, B. J., Prieto, J. L., Grupe, D., et al. 2014, ApJ, 788, 48 [Google Scholar]
- Siverd, R. J., Beatty, T. G., Pepper, J., et al. 2012, ApJ, 761, 123 [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. C., Stumpe, M. C., Van Cleve, J. E., et al. 2012, PASP, 124, 1000 [Google Scholar]
- Sneden, C. A. 1973, PhD thesis, The University of Texas at Austin, USA Sotin, C., Grasset, O., & Mocquet, A. 2007, Icarus, 191, 337 [Google Scholar]
- Soto, M. G., Anglada-Escudé, G., Dreizler, S., et al. 2021, A & A, 649, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G. 2014, in Determination of Atmospheric Parameters of B, A, F and G Type Stars, 297 [CrossRef] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A & A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A & A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Adibekyan, V., Delgado-Mena, E., & Israelian, G. 2015, A & A, 577, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Adibekyan, V., Delgado-Mena, E., et al. 2021, A & A, 656, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J. 2011, MNRAS, 417, 2166 [Google Scholar]
- Sozzetti, A., Torres, G., Charbonneau, D., et al. 2007, ApJ, 664, 1190 [Google Scholar]
- Sozzetti, A., Damasso, M., Bonomo, A. S., et al. 2021, A & A, 648, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stefánsson, G., Kopparapu, R., Lin, A., et al. 2020, AJ, 160, 259 [CrossRef] [Google Scholar]
- Stumpe, M. C., Smith, J. C., Van Cleve, J. E., et al. 2012, PASP, 124, 985 [Google Scholar]
- Stumpe, M. C., Smith, J. C., Catanzarite, J. H., et al. 2014, PASP, 126, 100 [Google Scholar]
- Teyssandier, J., Owen, J. E., Adams, F. C., & Quillen, A. C. 2015, MNRAS, 452, 1743 [NASA ADS] [CrossRef] [Google Scholar]
- Thiabaud, A., Marboeuf, U., Alibert, Y., et al. 2014, A & A, 562, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tokovinin, A. 2018, PASP, 130, 035002 [Google Scholar]
- Van Eylen, V., Astudillo-Defru, N., Bonfils, X., et al. 2021, MNRAS, 507, 2154 [NASA ADS] [Google Scholar]
- Wizinowich, P., Acton, D. S., Shelton, C., et al. 2000, PASP, 112, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2012, VizieR Online Data Catalog: I/322A [Google Scholar]
- Zechmeister, M., Kürster, M., & Endl, M. 2009, A & A, 505, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Dreizler, S., Ribas, I., et al. 2019, A & A, 627, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zeng, L., Jacobsen, S. B., Sasselov, D. D., et al. 2019, PNAS, 116, 9723 [Google Scholar]
- Ziegler, C., Tokovinin, A., Briceño, C., et al. 2020, AJ, 159, 19 [Google Scholar]
The latest version of the code ARES V2 can be downloaded at https://github.com/sousasag/ARES
All Tables
Prior and posterior distributions of the transit+GP model parameters used to analyse the TESS PDCSAP (sectors S6+S33).
GP-based ESPRESSO RV models tested in this work, and the corresponding best-fit values of RV semi-amplitudes for the three transiting planets b, c, and d.
All Figures
 |
Fig. 1 Imaging observations. Upper panel: Keck near-IR AO imaging and sensitivity curves for HIP 29442 taken in the Br-γ filter on 25 March 2019. The image reaches a contrast of ~8 magnitudes fainter than the host star within 0.5″. Middle panel: Gemini/NIRI AO imaging of HIP 29442. Observation taken on 5 April 2019 in the Br-γ filter. Lower panel: speckle imaging of HIP 29442 taken with the SOAR telescope on 17 March 2019. No nearby stars were detected within 3″ of the target. Insets: image of the central portion of the data, centred on the star. |
| In the text | |
 |
Fig. 2 Maximum likelihood periodograms of spectroscopic activity diagnostics of HIP 29442. The window function of the data is shown in the lower panel. The periodograms include levels of analytical FAR |
| In the text | |
 |
Fig. 3 ESPRESSO RVs. Blue circles: pre-COVID dataset; red circles: post-COVID dataset. The mean value of the full dataset has been subtracted from the original data. No offset has been subtracted from the two subsamples. The error bars represent the formal RV uncertainties derived by the DRS pipeline. |
| In the text | |
 |
Fig. 4 Maximum likelihood periodograms of the original RVs (top panel) and of the RV residuals O-C after subtracting recursively the best-fit sinusoidal signal with the highest peak frequency. The periodograms include levels of analytical FAP. The window function of the data is the same as in Fig. 2. |
| In the text | |
 |
Fig. 5 TLS periodograms of the detrended TESS light curve (see Sect. 2.1) showing peaks of the three transiting planets. The periodogram in the second panel was obtained after masking the transits of planet b, and that in the third panel was calculated after masking the transits of planets b and c. The dashed lines correspond to the harmonics of the orbital periods. Planets c and b were identified first in the ESPRESSO RV time series; their presence was confirmed by the transit signals detected in the TESS data. |
| In the text | |
 |
Fig. 6 TESS photometry of HIP 29442 (TOI-469) with the median posterior model (transits + GP) overplotted, showing the different locations of the transit events for the three planets over the low-frequency photometric modulation. The light grey data points correspond to the SPOC two-minute cadence PDCSAP photometry. |
| In the text | |
 |
Fig. 7 TESS PDCSAP light curve with the GP component subtracted, and phase-folded to the orbital periods of HIP 29442 b (first panel), HIP 29442 c (second panel), and HIP 29442 d (third panel). The solid lines indicate the models calculated using the median of the posteriors. Residuals of the best-fit model are shown at the bottom of each phase-folded plot. |
| In the text | |
 |
Fig. 8 Individual transits of HIP 29442 b, HIP 29442 c, and HIP 29442 d within the PDCSAP together with the best-fit transit+GP model overplotted. |
| In the text | |
 |
Fig. 9 RV Doppler signals due to three transiting planets orbiting HIP 29442 (TOI-469) (panels a, b, and c), and the RV activity term, as fitted through a GP QP regression (panel d; blue curve: best-fit model; grey area: 1σ confidence interval). The RV error bars include a jitter term added in quadrature to the measurement uncertainties. |
| In the text | |
 |
Fig. 10 Mass-radius diagram for planets with mass <20 M⊕ and radius <4 R⊕, selected from the TEPCAT sample, available at https://www.astro.keele.ac.uk/jkt/tepcat/ (updated to 22 March 2023; Southworth 2011). The grey dots represent planets with mass and radius measured with a relative precision lower than 20% and 10%, respectively. The planets of the HIP 29442 system are indicated by black triangles. The 1σ confidence intervals for the radius measurements are shown as black lines, while the red dashed lines indicate the 3σ confidence intervals. The overplotted theoretical curves are derived by assuming equations of state detailed in Leleu et al. (2021). |
| In the text | |
 |
Fig. 11 Maximum initial planet mass an interior planet (to planet b) could have had and be consistent with photo-evaporation, assuming planet b retained its atmosphere against photo-evaporation. Given the possibility that dynamical re-arrangement within the system might have occurred, we performed this calculation assuming that planet b had an initial period identical to its current period (orange), a shorter initial orbital period of 8 days (blue), or a longer initial orbital period of 18 days (green). The shaded region encompasses the 1 σ error bars, mainly arising from uncertainties in the properties of planet b. The current architecture of the system is shown by the blue points. The two interior planets to b lie below the curves, which indicates the system is consistent with photo-evaporation sculpting the system before any dynamical re-arrangement. |
| In the text | |
 |
Fig. B.1 TESS Target Pixel Files for sectors 6 and 33 obtained with TPFPLOTTER (Aller et al. 2020; the code is publicly available at www.github.com/jlillo/tpfplotter). The orange squares identify the aperture masks used to extract the light curve. The sources cross-matched with the Gaia DR3 catalogue are indicated by red dots; the size is scaled with their relative magnitude compared to that of HIP 29442 (TOI-469). Proper motions are indicated by arrows. The pixel scale is 21″ pixel−1. |
| In the text | |
 |
Fig. B.2 Spectral energy distribution in the range ~0.3−25 µm, used to derive the bolometric luminosity and the stellar radius through the Stefan–Boltzmann equation. The adopted stellar distance is the trigonometric parallax from the Gaia EDR3. |
| In the text | |
 |
Fig. B.3 ASAS-SN photometry of HIP 29442. For a better visualisation, offsets have been applied to the original magnitudes, as indicated in the legend. |
| In the text | |
 |
Fig. B.4 Corner plots showing the posteriors of the free parameters adopted for the planetary internal structure modelling described in Sect. 6. From top to bottom, the plots refer to HIP 29442 b, HIP 29442 c, and HIP 29442 d. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.