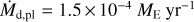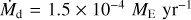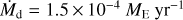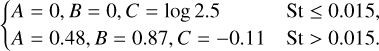| Issue |
A&A
Volume 678, October 2023
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 17 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202346126 | |
| Published online | 11 October 2023 | |
Planetesimal formation at the gas pressure bump following a migrating planet
II. Effects of dust growth
Space Research and Planetary Sciences, Physics Institute & NCCR PlanetS, University of Bern,
3012
Bern, Switzerland
e-mail: yuhito.shibaike@unibe.ch
Received:
12
February
2023
Accepted:
20
June
2023
Context. Planetesimal formation is still mysterious. One of the ways to form planetesimals is to invoke a gas pressure bump in a protoplanetary disc. In our previous paper, we proposed a new scenario in which the piled-up dust at a gas pressure bump created by a migrating planet forms planetesimals by streaming instability in a wide region of the disc as the planet migrates inwards.
Aims. In the present work, we consider the global time evolution of dust and investigate the detailed conditions and results of the planetesimal formation in our scenario.
Methods. We used a 1D grid single-sized dust evolution model, which can follow the growth of the particles in terms of their mutual collision and their radial drift and diffusion. We calculated the time-evolution of the radial distribution of the peak mass and surface density of the dust in a gas disc perturbed by an embedded migrating planet and investigated whether or not the dust satisfies the condition for planetesimal formation.
Results. We find that planetesimals form in a belt-like region between the snowline and the position where the planet reaches its pebble-isolation mass when the strength of turbulence is 10−4 ≤ α ≤ 10−3, which is broadly consistent with the observed value of α. Whether the mechanism of the formation is streaming instability or mutual collision depends on the timescale of the streaming instability. The total mass of planetesimals formed in this scenario also depends on α; it is about 30–100 ME if the planetary core already exists at the beginning of the simulation and grows by gas accretion, but decreases as the timing of the formation of the planetary core gets later. We also provide simple approximate expressions for the surface density and total mass of the planetesimals and find that the total planetesimal mass strongly depends on the dust mass.
Conclusions. We show that planetesimals form in a belt-like region by a combination of dust pile-up at the gas pressure bump formed by a planet and its inward migration.
Key words: planets and satellites: formation / protoplanetary disks / planet-disk interactions / methods: numerical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The formation of planetesimals, that is, the kilometre-sized building blocks of planets, has been investigated for a long time, but many problems remain unsolved. One such problem is the so-called ‘drift barrier’. Planetesimals were considered to form by mutual collisions of dust particles in protoplanetary discs. However, the particles suffer head wind from the gas disc rotating with a sub-Kepler speed due to the gas pressure gradient and lose their angular momentum, which forces the particles to drift toward the central star before they grow to planetesimals (e.g. Whipple 1972).
One of the solutions to avoid the loss of the particles by inward drift is to invoke the gas pressure bump at some location in the disc. The gas pressure gradient is null at the bump, and drifting particles pile up there (e.g. Zhu et al. 2012). Many observations of the millimetre continuum emission from protoplanetary discs show ring and gap structures (e.g. ALMA Partnership 2015; Andrews et al. 2018; Segura-Cox et al. 2020), which are considered as the evidence of the dust pile-up at gas pressure bumps (Dullemond et al. 2018). One of the most popular mechanisms to form the ring and gap structures is gravitational interaction with embedded planets (e.g. Paardekooper & Mellema 2004), and some observations of pro-toplanets in the gaps support this mechanism (e.g. Keppler et al. 2018; Pinte et al. 2019; Currie et al. 2022). Such locations of concentrated dust are suitable for planetesimal formation by gravitational instabilities or by mutual sticking (collision) of the dust (e.g. Sekiya 1998). In particular, streaming instability occurs by the accumulation of dust and makes clumps of dust, which triggers further gravitational instability and the formation of planetesimals (e.g. Youdin & Goodman 2005). Stammler et al. (2019) show that if dust particles at the gas pressure bump form planetesimals by streaming instability, the dust rings in multiple protoplanetary discs observed as part of the Disk Substructures at High Angular Resolution Project (DSHARP; Andrews et al. 2018) are better explained. Many previous works also argued that planetesimals can form at the gas pressure bump created by an embedded planet (e.g. Lyra et al. 2009; Ayliffe et al. 2012; Chatterjee & Tan 2013; Drazkowska et al. 2019; Eriksson et al. 2020). The planetesimals formed at the bump grow larger and parts of them are captured or scattered by the planet (Kobayashi et al. 2012; Eriksson et al. 2020, 2021).
In our previous paper, Shibaike & Alibert (2020, hereafter Paper I), we proposed a new scenario in which planetesimals form by streaming instability at the gas pressure bump created by a migrating planet, resulting in planetesimal formation in a wide region of the protoplanetary disc. We developed a simple 1D Lagrangian particle model, which can follow the radial distribution of fixed-sized dust in a gas disc perturbed by a migrating planet. We showed that planetesimals form in a wide region of the disc, and their total mass and formation region depend on the dust mass flux and the strength of turbulence in the disc. We also found that the surface density of formed planetesimals can be approximated by a simple equation. Miller et al. (2021) reproduced the observed exoKuiper belts (i.e. planetesimal belts in extrasolar systems) by this scenario with a simple grid model of the global dust evolution. The surface density profiles of the formed planetesimals in Miller et al. (2021) are consistent with the approximate expression in our Paper I.
In the present paper, we investigate the detailed conditions and results for our planetesimal formation scenario by considering global dust evolution. We do not use the Lagrangian model developed in Paper I but use a grid model, which can follow the time evolution of the radial profiles of the peak mass and surface density of dust particles. We assume the existence of a migrating planet (or a planetary core) carving the gas disc and investigate when and where the planetesimals form by streaming instability or by mutual collision by changing the strength of turbulence and the (poorly known) condition for streaming instability. Although this work is similar to Miller et al. (2021), we do not focus on the reproduction of observations but on the detailed investigation of the phenomena of planetesimal formation. Also, we consider an earlier stage of planet formation, when the planet does not migrate in Type II migration but in Type I migration.
In Sect. 2, we explain the methods used in this work. We then show the results of the calculation depending on the timescale of streaming instability in Sect. 3. We also explain a case where the properties of streaming instability depend on the Stokes number of dust. In Sect. 4, we investigate the effects of changes to the disc properties. Furthermore, we investigate the effects of planetary growth by gas accretion and the later formation of the planetary cores considering the shift of the migration type from Type I to Type II and the time evolution of the disc. We also discuss the effects of the back reaction from dust to gas and the dust leak from gas pressure bumps. Finally, we conclude this work in Sect. 5.
2 Methods
2.1 Gas disc model
First, we set a gas disc model. The unperturbed (i.e. not perturbed by a planet) gas surface density is assumed to follow a power law:
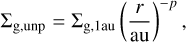 (1)
(1)
where r is the distance to the star, and Σg,1au and p are constants. The disc temperature (in the midplane) is
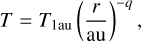 (2)
(2)
where T1au and q are constants. We assume the constants as Σg,1au = 500 g cm−2, T1au = 280 K, p = 1, and q = 1/2. This set of assumptions is consistent with ‘Model A’ of Paper I. The slope of the gas surface density is consistent with the observations of protoplanetary discs under the assumption that the dust-to-gas surface density ratio is uniform throughout the entire disc in each case (Andrews et al. 2010). We set the snowline at the orbit where T = 160 K, which is rSL = 3.06 au in this disc model.
We note that when the disc temperature is dominated by the viscous heating, the temperature increases as the turbulence is stronger. However, in this paper, we fix the gas surface density and temperature while changing the strength of turbulence. We investigate the cases with a hotter disc in Sect. 4.1 and with a time-evolving gas disc in Sect. 4.2.
2.2 Gap formation by a migrating planet
Planets embedded in gas discs influence the discs and change the gas structure. We assume the presence of a single planet with fixed mass Mpl = 20 ME, migrating inwards from r = 50 au. In Sect. 4.2, we consider the growth of the planet by gas accretion and its later formation. The subscript ‘pl’ indicates the properties of the planet and/or its location. The surface density of the local perturbed gas disc has been modeled by many previous works. We use a model provided by Duffell (2015) in order to compare our results with the pebble-isolation mass provided by Ataiee et al. (2018; see following paragraph), which also uses the model of Duffell (2015)1. The perturbed gas surface density profiles is
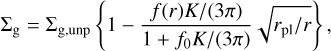 (3)
(3)
where rpl is the orbital radius of the embedded planet, and the parameter f0 is fixed as 0.45. The factor K is defined as
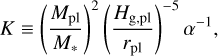 (4)
(4)
where M* = 1 M⊙ is the mass of the star, and α is the strength of turbulence of the gas (Kanagawa et al. 2015). We treat α as a constant (in space and time) and change the value as a parameter. The gas scale height (at rpl) is Hg,pl = cs,pl/ΩK,pl, where the sound speed and the Kepler frequency are 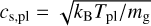 and
and 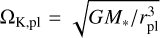 , respectively2. The Boltzmann constant and the gravitational constant are kB and G, respectively. The mean molecular mass is mg = 3.9 × 10−24 g. The function f(r), the scaled-out angular momentum flux by the shocking of the planetary wake, is
, respectively2. The Boltzmann constant and the gravitational constant are kB and G, respectively. The mean molecular mass is mg = 3.9 × 10−24 g. The function f(r), the scaled-out angular momentum flux by the shocking of the planetary wake, is
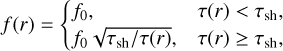 (5)
(5)
where the shock position, τsh, is given as (Goodman & Rafikov 2001)
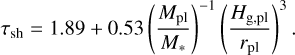 (6)
(6)
The parameter τ(r), representing an appropriately scaled distance from the planet, is
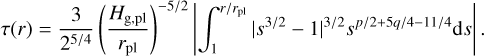 (7)
(7)
Once a gap forms around a planet, the dust particles start to pile up at the gas pressure bump, and their accretion onto the planet stops. The planet mass where the dust (pebble) accretion stops is called the ‘pebble-isolation mass’ (e.g. Lambrechts et al. 2014). Ataiee et al. (2018) found that this latter depends on the planet mass and the strength of turbulence,
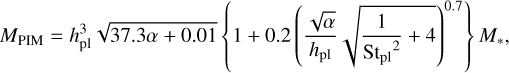 (8)
(8)
where hpl = Hg,pl/rpl is the aspect ratio of the disc at the orbital position of the planet. We define rPIM as the orbital position where the planet mass Mpl (we fix it as 20ME) is equal to MPIM. The planet crosses the orbital position of r = rPIM during its inward migration outside the snowline when α ≤ 10−2.6 (see Sect. 3.1.2 for details).
The ratio of the pressure gradient to the gravity of the central star, η, is important, because it determines the direction and speed of the drift of the particles (see Eq. (13)). We calculate the ratio as
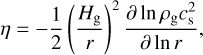 (9)
(9)
where 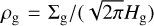 is the (local) gas density in the mid-plane. We here define rη0 as the orbital position where η is zero (due to the cavity of the gas disc by the planet) when the planet is at r = rPIM.
is the (local) gas density in the mid-plane. We here define rη0 as the orbital position where η is zero (due to the cavity of the gas disc by the planet) when the planet is at r = rPIM.
We consider the Type I migration of the planet. The migration timescale depends on the planet mass and the structures of the gas and temperature of the disc (Tanaka et al. 2002; Ida & Lin 2008),
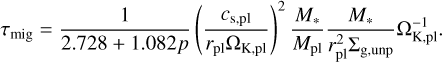 (10)
(10)
We assume the planet is at r = 50 au at t = 0 and migrates inwards with a velocity equal to υpl = −rpl/τmig. We consider the reduction in migration speed and the shift from Type I to Type II migration to be due to the deep gap formation with the planetary growth by gas accretion in Sect. 4.2. In the same section, we also investigate the cases where the planet forms later.
2.3 Dust evolution
We include in our model the evolution of dust particles in the gas disc model. We use a single-sized dust-evolution model proposed by Sato et al. (2016), which assumes that md singly peaks the mass distribution of dust at each orbit r. We calculate the radial distribution of the surface density of dust particles, Σd, and their peak mass, md, by solving Eqs. (11) and (15) simultaneously. The subscript ‘d’ indicates the properties of the dust particles.
We consider the evolution of compact and spherical dust particles, the mass of a single particle being 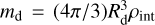 , where Rd is the radius of the particles, and ρint = 1.4 and 3.0 g cm−3 are the internal density of the icy and rocky particles, respectively. Here, we assume that the particles are icy and rocky outside and inside the snowline, respectively.
, where Rd is the radius of the particles, and ρint = 1.4 and 3.0 g cm−3 are the internal density of the icy and rocky particles, respectively. Here, we assume that the particles are icy and rocky outside and inside the snowline, respectively.
The continuity equation of the dust particles is,
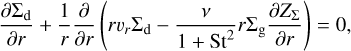 (11)
(11)
where Σd is the dust surface density, υr is the radial velocity of dust, ν = αcsHg is the gas viscosity, and Zς = Σd/Σg is the dust-to-gas surface density ratio. The Stokes number (stopping time normalized by Kepler time), St = tstopΩK, determines the motion of the particles. The first and second terms in the parentheses represent the drift and diffusion of the particles, respectively.
The Stokes number of the dust particles is
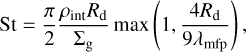 (12)
(12)
where λmfp = mg/(σmolρg) is the mean free path of the gas molecules. Their collisional cross section is σmol = 2 × 10−15cm2.
The radial drift velocity of the particles is calculated by (Whipple 1972; Adachi et al. 1976; Weidenschilling 1977)
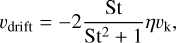 (13)
(13)
where υk = rΩk is the Kepler velocity. The radial velocity of the particles due to their diffusion is
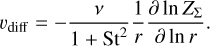 (14)
(14)
The total radial velocity of the particles is υr = υdrift + υdiff. We reduce the inward flux of dust mass, 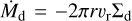 , just inside the snowline to be half of that just outside when υr < 0 and increase the flux outside the snowline to double that just inside when υr > 0 in order to express the evaporation and re-condensation of the icy material of the particles.
, just inside the snowline to be half of that just outside when υr < 0 and increase the flux outside the snowline to double that just inside when υr > 0 in order to express the evaporation and re-condensation of the icy material of the particles.
The growth of the particles due to their mutual collision is (Sato et al. 2016)
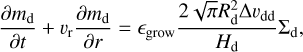 (15)
(15)
where ϵgrow, Δυdd, and Hd are the sticking efficiency, collision velocity, and dust scale height, respectively.
The particles break up rather than merge when the collision speed is too high. We model the sticking efficiency as (Okuzumi et al. 2016)
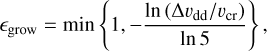 (16)
(16)
where the critical fragmentation velocities for the collision of rocky and icy particles are υcr = 1 and 10 m s−1, respectively (e.g. Blum & Wurm 2000; Wada et al. 2009)3.
The collision velocity between the dust particles is
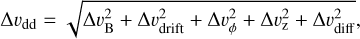 (17)
(17)
where ΔυB, Δυdrift, Δυϕ, Δυz, and Δυdiff are the relative velocities induced by their Brownian motion, radial drift, azimuthal drift, vertical sedimentation, and diffusion, respectively (Okuzumi et al. 2012). The relative velocity induced by Brownian-motion between the particles with the same mass is 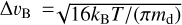 . The relative velocity induced by the radial drift is Δυdrift = |υdrift(St1) - υdrift(St2)|, where St1 and St2 are the Stokes numbers of the two colliding particles. The relative velocity induced by the azimuthal drift is Δυϕ = |υϕ(St1) − υϕ(St2)|, where υϕ = −ηυK/(1 + St2), and that by the vertical motion is Δυz = |υz(St1) − υz(St2)|, where υz = −ΩKStHd/(1 + St). We assume St2 = 0.5St1, because the single-size simulation reproduces the results by a full-size simulation very well with that assumption (Sato et al. 2016). For the relative velocity induced by diffusion, we use the following three limiting expressions derived from Ormel & Cuzzi (2007):
. The relative velocity induced by the radial drift is Δυdrift = |υdrift(St1) - υdrift(St2)|, where St1 and St2 are the Stokes numbers of the two colliding particles. The relative velocity induced by the azimuthal drift is Δυϕ = |υϕ(St1) − υϕ(St2)|, where υϕ = −ηυK/(1 + St2), and that by the vertical motion is Δυz = |υz(St1) − υz(St2)|, where υz = −ΩKStHd/(1 + St). We assume St2 = 0.5St1, because the single-size simulation reproduces the results by a full-size simulation very well with that assumption (Sato et al. 2016). For the relative velocity induced by diffusion, we use the following three limiting expressions derived from Ormel & Cuzzi (2007):
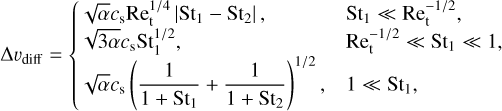 (18)
(18)
where Ret = ν/νmol is the turbulence Reynolds number. The molecular viscosity is νmol = υthλmfp/2, where 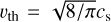 is the thermal gas velocity.
is the thermal gas velocity.
The dust scale height is given by (Youdin & Lithwick 2007),
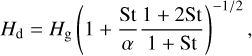 (19)
(19)
and the midplane dust density is 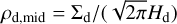 .
.
2.4 Planetesimal formation
We calculate when, where, and how many planetesimals form in our scenario. In this work, we consider two mechanisms of planetesimal formation: streaming instability and mutual collision of particles. First, we consider the condition for plan-etesimal formation by streaming instability. Streaming instability can enhance the accumulation of dust particles, which helps the condition for gravitational instability be reached, namely 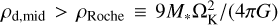 . We define the condition for planetesimal formation as the dust-to-gas density ratio on the midplane, Zρ ≡ ρd,mid/ρd,gas, is larger than the critical density ratio ϵcrit = 1 (Youdin & Goodman 2005; Johansen & Youdin 2007; Drazkowska & Dullemond 2014). We also consider the case in which ϵcrit depends on St in Sect. 3.3. We assume that planetesimal formation only occurs outside the orbit of the migrating planet in order to focus on the planetesimal formation at the gas pressure bump created by the planet4.
. We define the condition for planetesimal formation as the dust-to-gas density ratio on the midplane, Zρ ≡ ρd,mid/ρd,gas, is larger than the critical density ratio ϵcrit = 1 (Youdin & Goodman 2005; Johansen & Youdin 2007; Drazkowska & Dullemond 2014). We also consider the case in which ϵcrit depends on St in Sect. 3.3. We assume that planetesimal formation only occurs outside the orbit of the migrating planet in order to focus on the planetesimal formation at the gas pressure bump created by the planet4.
The change of the planetesimal surface density due to streaming instability is
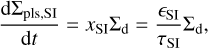 (20)
(20)
where the efficiency of streaming instability is assumed to be ϵSI = 0.1 (Schoonenberg et al. 2018)5. The timescale of streaming instability, τSI, is an important parameter of this work. We consider the cases with short timescale (τSI = 10 years; Youdin & Goodman 2005; Johansen & Youdin 2007, in Sect. 3.1) and long timescale (τSI = 103TK, where TK = 2π/ΩK is the orbital period; Drążkowska et al. 2016, in Sect. 3.2). We also investigate the cases where the timescale depends on St in Sect. 3.3.
We also consider planetesimal formation due to mutual collision of particles. When the dust radius Rd is larger than Rd,max = 1 m, we define that the particles become planetesimals. This is a valid definition, because the rapid growth of particles starts when the particles are smaller than 1 m (see the third column of Fig. 7)6. In every time step, we check this condition after checking the condition for streaming instability.
Although we use a single-sized dust evolution model in this work, the particles follow a size frequency distribution (SFD) at each r in reality. We therefore assume an ‘imaginary’ SFD and regard the mass of the particles larger than Rd,max in the SFD as the mass of newly formed planetesimals due to mutual collision. We assume the SFD to be 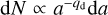 , where N is the number of the particles larger than a, and the minimum radius to be Rd,min. In that case, the change of the planetesimal surface density due to mutual collision is
, where N is the number of the particles larger than a, and the minimum radius to be Rd,min. In that case, the change of the planetesimal surface density due to mutual collision is
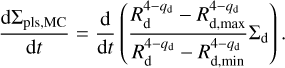 (21)
(21)
Here, we assume that Rd,min = 0.1 µm and qd = 3.5.
The total planetesimal formation rate is
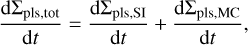 (22)
(22)
where the total planetesimal surface density is Σpls,tot = Σpls,SI + Σpls,MC. At the same time, the dust surface density is reduced by planetesimal formation,
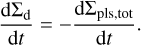 (23)
(23)
3 Results
3.1 Short streaming instability timescale
3.1.1 Evolution of gas and solids
Figure 1 shows the results with the short streaming instability (SI) timescale (τSI = 10 yr). The figure represents the evolution of the surface densities of the gas, dust, and planetesimals with α = 10−3.4 = 4 × 10−4. The embedded planet carves a deeper gap in the gas as it migrates inwards (the sky-blue curves). Therefore, the dust particles accumulate more at the outer edge of the gap as the planet migrates inwards (blue curves). The figure also shows that the pebble front, the orbital position where the drift timescale of dust becomes shorter than the growth timescale, and dust (pebbles) starts to drift towards the central star (Lambrechts & Johansen 2014), moves outward (the bold curves around 100 au). This phenomenon is not related to the embedded planet. Figure 1 also shows that planetesimals form by streaming instability between the snowline and the orbital position where the inward drift of dust starts to be halted (red curves). The formed planetesimal surface density is about 2 g cm−2 at the inner edge and about 0.6 g cm−2 at the outer edge of the formation region.
Figure 2 shows the detailed evolution of the dust. The first column shows that the radius is smaller than Rd,max = 1 m, meaning that all planetesimals should be formed by streaming instability. The Stokes number of dust is smaller than 0.1 when the dust drifts inwards, but it increases when the dust is accumulated (the second column). The Stokes number in the accumulation is about 0.1 when the accumulation starts (t = 0.35 Myr) and is larger than 0.1 in the full accumulation (t = 0.53 and 0.63 Myr). The accumulation of dust is insufficient for planetesimal formation (Zρ ≥ 1) in the beginning of the accumulation (t = 0.35 Myr), but reaches a sufficient level when the drift of dust is stopped (t = 0.53 Myr) (the third column). After that, the particles disappear inside the outer edge of the gap, and the inward flux of drifting dust mass is zero (the fourth column). This condition for the rapid accumulation of dust is consistent with that proposed by Taki et al. (2021), 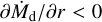 (Eq. (30) in that paper). The inward mass flux is uniform, almost constant, and equal to
(Eq. (30) in that paper). The inward mass flux is uniform, almost constant, and equal to 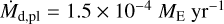 outside the gap.
outside the gap.
Once the planet (and the gas pressure bump) crosses the snowline, the midplane dust-to-gas density ratio decreases and planetesimals cannot form. This is because the Stokes number of the dust becomes smaller because of the fragile rocky particles (the second column), which makes the vertical diffusion of dust more efficient and lowers ρd,mid (the third column). The dust mass flux is about half of that outside the snowline (the fourth column), which is another reason why planetesimals cannot form.
We proposed an approximate expression of the planetesimal surface density in Paper I,
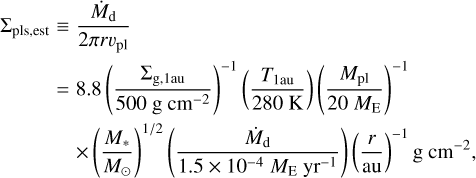 (24)
(24)
where 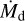 is the inward flux of dust mass (see Appendix B for more general expressions). Figure 1 shows that our results are very well approximated when we substitute
is the inward flux of dust mass (see Appendix B for more general expressions). Figure 1 shows that our results are very well approximated when we substitute 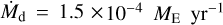 – which is obtained from our results (see the fourth column of Fig. 2) – into Eq. (24). This means that all dust drifting into the formation place (around where η = 0) is converted immediately to planetesimals once the formation starts. This is also shown in Fig. 3, where the planetesimal mass (red solid curve) increases linearly along with the slope of the cumulative dust mass drifting into the formation place with
– which is obtained from our results (see the fourth column of Fig. 2) – into Eq. (24). This means that all dust drifting into the formation place (around where η = 0) is converted immediately to planetesimals once the formation starts. This is also shown in Fig. 3, where the planetesimal mass (red solid curve) increases linearly along with the slope of the cumulative dust mass drifting into the formation place with 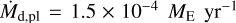 (red dashed line). The dust mass (blue solid curve) also decreases linearly before the beginning of planetesimal formation along with the slope of the dust mass-assuming constant loss with the same mass flux with
(red dashed line). The dust mass (blue solid curve) also decreases linearly before the beginning of planetesimal formation along with the slope of the dust mass-assuming constant loss with the same mass flux with 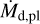 (blue dashed line)–but it decreases more once the planetesimals start to form (0.53 ≤ t ≤ 0.6 Myr). This is because, although the rate of mass conversion from dust to planetesimals is the same as the rate of mass loss from the disc before the planetesimal formation starts, the dust existing inside the gas pressure bump continues to disappear gradually also after the formation starts (see Fig. 1). This is also the reason why the slope of the solid (sum of the dust and planetesimals) mass profile in Fig. 3 gradually becomes zero. Once the gas pressure bump crosses the snowline, the planetesimal formation stops, and the increase in planetesimal mass also stops (t = 0.66 Myr).
(blue dashed line)–but it decreases more once the planetesimals start to form (0.53 ≤ t ≤ 0.6 Myr). This is because, although the rate of mass conversion from dust to planetesimals is the same as the rate of mass loss from the disc before the planetesimal formation starts, the dust existing inside the gas pressure bump continues to disappear gradually also after the formation starts (see Fig. 1). This is also the reason why the slope of the solid (sum of the dust and planetesimals) mass profile in Fig. 3 gradually becomes zero. Once the gas pressure bump crosses the snowline, the planetesimal formation stops, and the increase in planetesimal mass also stops (t = 0.66 Myr).
 |
Fig. 1 Time evolution of the surface density of gas, dust, and formed planetesimals, with α = 10−3.4. The sky-blue, blue, and red curves represent the profiles of gas, dust, and planetesimals, respectively. All planetesimals form by streaming instability. The black dashed lines represent the approximation of the planetesimal surface density by Eq. (24) with |
3.1.2 Planetesimal formation regions
We then investigate the formation regions of planetesimals by changing the value of a. Figure 4 shows that planetesimals form when 10−4 ≤ α ≤ 103, which is broadly consistent with the measured value of a in a lot of observed protoplanetary discs (Pinte et al. 2022). The figure also shows that the mechanism of the planetesimal formation is streaming instability in all cases. This is because the dust being piled up at the bump is converted to planetesimals with the instability before they grow to planetesimals by mutual collision. We find that belt-like planetesimal formation regions exist between the snowline and the position where the planet reaches its pebble-isolation mass (Eq. (8)), rPIM. Planetesimals do not form inside the snowline, as explain in Sect. 3.1.1. The pebble-isolation mass is the mass the planet needs in order to make the gap deep enough to stop the dust (pebble) accretion, meaning that all of the dust drifting into the region piles up, which in turn triggers streaming instability. For the calculation of rPIM in this work, we fix the Stokes number to St = 0.1.
When α < 10−3.4, the outer edge of the formation region is slightly outside rPIM, and the smaller the value of α, the larger the distance between the two orbital positions. On the other hand, when α > 10−3.4, the outer edge is inwards of rPIM, and the larger the value of α, the larger the distance between the two orbital positions. This is because Zρ needs to increase beyond unity against the turbulence in order to meet the condition for planetesimal formation. In other words, it is the diffusion of the particles, that prevents the accumulation of dust. Figure 5 shows that the orbital position where the largest Zρ outside the planetary orbit reaches unity is outside r = rPIM when α = 10−4. The position is on r = rPIM when α = 10−3.4 and is inside when α = 10−3. This result is consistent with Fig. 4. The profiles in Fig. 5 wander at their outer parts because the pebble front has the largest value of Zρ until the rapid accumulation of dust begins at the gas pressure bump, and the pebble front also makes waves in the dust profiles when it crosses the gap created by the planet (especially when α = 10−4).
Figure 6 shows that the smaller the value of α, the larger the total mass of the formed planetesimals, which is due to the α dependence of the outer edge of the formation region. When α = 10−4, the total mass reaches about 60 ME. We estimate the total mass of the planetesimals as
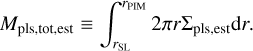 (25)
(25)
The figure shows this estimate roughly reproduces the results of our calculations. The difference at the high and low α is due to the fact that the precise location of the outer edge of the planetesimal formation region is different from rPIM, as explained above.
 |
Fig. 2 Time evolution of the detailed profiles of dust with α = 10−3.4. The first to fourth columns from the left represent the radial profiles of the radius, Stokes number, midplane dust-to-gas density ratio, and inward flux of mass, respectively. The first to fifth rows from the top represent the profiles at t = 0, 0.35, 0.53, 0.63, and 0.75 Myr, respectively. The horizontal lines represent the critical or important values of each profile. The vertical lines represent the position of the snowline. The circles represent the orbital positions of the planet. |
 |
Fig. 3 Time evolution of the dust, planetesimal, and solid (sum of the dust and planetesimals) mass with τSI = 10 yr and α = 10−34. The blue, red, and purple curves represent the profiles of the dust, planetesimal, and solid, respectively. The dashed blue line represents the slope of the dust mass assuming constant loss with |
 |
Fig. 4 Planetesimal formation regions with τSI = 10 yr and various a. The colour represents the planetesimal surface density. The solid and dotted curves represent rPIM and rη0, respectively. The vertical dashed line is the snowline. |
 |
Fig. 5 Trajectory of the largest Zρ outside the orbit of the planet with τSI = 10 yr. The red, purple, and blue curves represent the cases with α = 10−4, 10−34, and 10−3, respectively. The solid and dotted vertical lines represent rPIM and rη0 with each α, respectively. |
3.2 Long streaming instability timescale
We then investigated the planetesimal formation with the long SI timescale (τSI = 103TK). In the case of the short SI timescale, all planetesimals form with streaming instability independent of the strength of the turbulence. On the other hand, in the case of the long SI timescale, the formation mechanism depends on the turbulence strength.
Figures 7 and 8 represent the profiles of the dust evolution and the planetesimal surface density with the long SI timescale, respectively. The first column of Fig. 7 shows that the dust radius is smaller than Rd,max = 1m, meaning that the planetesimals are formed by streaming instability as in the case of the short SI timescale. However, the left panel of Fig. 8 shows that the radial profile of the planetesimal surface density is lower than the approximation (Eq. (24)) in the outer part of the planetesimal formation region. This means that only part of the drifting dust entering the formation place of planetesimals is converted to planetesimals, because the approximation Eq. (24) assumes that all dust converts to planetesimals immediately. The rest of the dust piles up there and makes Zρ larger than ϵcrit = 1, the local condition for planetesimal formation (the second column of Fig. 7). These interpretations are consistent with the time evolution of the dust and planetesimal mass shown in the left panel of Fig. 9. The panel shows that the slope of the planetesimal mass with the long SI timescale (red solid curve) is much shallower than that with the short SI timescale (dotted red curve; i.e. the case where all dust mass is converted to planetesimals) especially at the begging of the planetesimal formation (0.55 < t < 0.6 Myr). The profiles of the solid mass (solid and dotted purple curves) are the same irrespective of the SI timescale, but the dust mass assuming the long SI timescale (blue solid) does not decrease like the case assuming the short SI timescale (blue dotted). This also means that dust particles not converted to planetesimals pile up at the gas pressure bump when the long SI timescale is assumed. The sharp decrease in dust (and solid) mass at t = 0.65 Myr is because the piled-up dust evaporates when it crosses the snowline.
On the other hand, the third column of Fig. 7 shows that the radius reaches Rd,max = 1m when α = 10−4. At the same time, the density ratio Zρ is larger than ϵcrit = 1 (the fourth column). This means that the planetesimals are formed by both streaming instability and mutual collision. The right panel of Fig. 8 shows that planetesimals are formed by both mechanisms but mainly by mutual collision when the turbulence is weak. The surface density of planetesimals formed by mutual collision is about 100 times larger than that of planetesimals formed by streaming instability. The panel also shows that the surface density of planetesimals formed by mutual collision is very well approximated by Eq. (24). However, dust also piles up at the formation place with Zρ larger than ϵcrit = 1 (the fourth column of Fig. 7), because Zρ easily becomes large, with α = 10−4 (i.e. weak diffusion) compared to α = 10−3.4. The right panel of Fig. 9 shows that all of the dust mass drifting into the formation place is converted to planetesimal mass (mainly) by mutual collision once the planetesimals start to form (t = 0.3 Myr). As a result, the solid mass (i.e. total mass of the dust and planetesimals) is conserved after that.
Figure 10 shows that the planetesimal formation region is between r = rSL and rPIM, which is the same as with the short SI timescale case, which includes the deviation of the outer edge from r = rPIM. The figure also shows that all planetesimals form by streaming instability when α ≥ 10−3.5, but most of the planetesimals form by mutual collision when α ≤ 10−3.6. The left panel also shows that the planetesimal surface density of the outer part of the formation region is smaller than that with the short SI timescale when α ≥ 10−3.5. This is because only part of the dust drifting into the formation place (i.e. the gas pressure bump) is converted to planetesimals, as explained above. Except for these cases, the surface density of the planetesimals (formed by both mechanisms) is well approximated by Eq. (24) for any strength of turbulence. Figure 11 also shows that the dominant planetesimal formation mechanism is streaming instability when α ≥ 10−3.5 and is mutual collision when α ≤ 10−3.6. When α ≥ 10−3.5, the total mass is much smaller than the approximation by Eq. (25), because the planetesimal surface density of the outer part of the formation region is smaller than the approximation by Eq. (24).
 |
Fig. 6 Total mass of the formed planetesimals with τSI = 10 yr and various α. The solid and dashed curves represent the results of our calculations and the approximation by Eq. (25), respectively. |
 |
Fig. 7 Same as the first and third columns of Fig. 2 but with τSI = 103TK. The first and second columns represent the profiles with α = 10−3.4, and the third and fourth columns represent those with 10−4. |
 |
Fig. 8 Final profiles of the planetesimal surface density with τSI = 103TK. The red and green curves represent the surface density of the planetesimals formed by streaming instability and mutual collision, respectively. The left and right panels represent the profiles with α = 10−3.4 and 10−4, respectively. |
 |
Fig. 9 Same as Fig. 3 but with τSI = 103TK. The left and right panels represent the profiles with α = 10−3.4 and 10−4, respectively. In the left panel, the profiles with τSI = 10 yr are also plotted as the dotted curves. All planetesimals form by streaming instability when α = 10 −3.4. In the right panel, we plot the mass of the planetesimals formed by streaming instability (red) and by mutual collision (green). The blue dashed line represents the slope of the dust mass assuming constant loss with |
 |
Fig. 10 Same as Fig. 4 but with τSI = 103TK. The left and right panels represent the formation regions of the planetesimals formed by streaming instability and mutual collision, respectively. |
3.3 Effects of the Stokes number dependence of streaming instability
Previous 3D hydrodynamical simulations have shown that the condition and timescale of streaming instability depend on the Stokes number of dust particles. We consider such a case according to the results of Li & Youdin (2021). In this case, the logarithm of the critical density ratio is
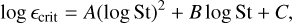 (26)
(26)
The streaming instability timescale depends on the Stokes number of the particles,
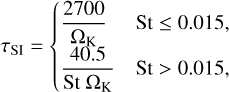 (27)
(27)
as shown by the approximation of the results of Li & Youdin (2021; see Appendix A).
Figure 12 represents the surface density and formation regions of planetesimals when streaming instability depends on the Stokes number. The figure shows that the profiles of planetesimals are similar to the case with the short SI timescale (see Fig. 4). All planetesimals form by streaming instability, and the planetesimal surface density is well approximated by Eq. (24). The planetesimal formation region lies between rSL and rPIM, as in the cases shown in Sects. 3.1 and 3.2. Planetesimals form even when α = 10−2.9, and the outer edge of the formation region for each α is slightly larger than that with short τSI. This is because ϵcrit is smaller than unity when 0.015 < St(< 1) (Eq. (26)), which is the case for the drifting dust (see the second column of Fig. 2).
 |
Fig. 11 Same as Fig. 6 but with τSI = 103TK. The red dotted and green dashed-and-dotted curves represent the mass of the planetesimals formed by streaming instability and mutual collision, respectively. The black solid curve represents their total mass. |
Disc properties.
4 Discussion
4.1 Disc properties dependence
We investigate the effects of changes to the disc properties. We consider cases with various initial dust-to-gas surface density ratios, gas surface densities, and disc temperatures as described in Table 1. In this section, the condition for planetesimal formation by streaming instability is the same as that used in Sect. 3.3. We then find that planetesimals form perfectly or mainly by streaming instability in all cases. Figure 13 represents the surface density and total mass of the planetesimals (including both planetesimals formed by streaming instability and formed by mutual collision) with various disc properties.
The left panel of Fig. 13 shows the dependence of the planetesimal surface density on the disc properties. Surface density depends on dust mass, depends only weakly on disc temperature, and not at all on the mass of the gas disc. This dependence can be explained by updating the approximation of planetesimal surface density in Eq. (24). According to Lambrechts & Johansen (2014), the inward dust mass flux is estimated by the following equation:
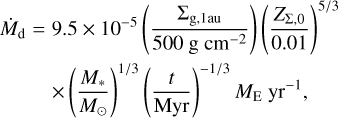 (28)
(28)
and this is consistent with our result, 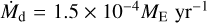 , when we substitute t = 0.25 Myr into Eq. (28) (see Appendix B for more general expressions). Then, by substituting Eq. (28) with Eq. (24), we get the general expression:
, when we substitute t = 0.25 Myr into Eq. (28) (see Appendix B for more general expressions). Then, by substituting Eq. (28) with Eq. (24), we get the general expression:
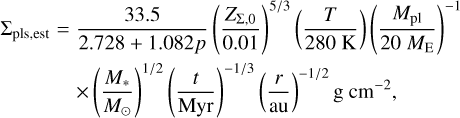 (29)
(29)
which depends on the dust mass, the disc temperature, and the slope of the gas surface density but not on the disc mass (see also Appendix B for detailed derivation). In the case of our simulations,
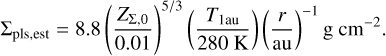 (30)
(30)
The left panel of Fig. 13 shows that the obtained planetesimal surface density with various parameters fits the approximation lines (Eq. (30), dotted lines with corresponding colours) very well. The surface density is 25/3 = 3.2 times higher than that of the fiducial case when Zς,0 is two times higher (green) and is slightly higher when T1au is 1.25 times higher (orange). On the other hand, the surface density is the same as that of the fiducial case when Σg,1au is two times higher (light blue).
We also plot the positions of the snowline (rSL) and where the planet reaches its pebble-isolation mass (rPIM) in the left panel of Fig. 13. When the disc is hot, rPIM is small (8.60 au), because the pebble-isolation mass depends on the sound speed (see Eq. (8)). On the other hand, rPIM is at the same position as it is for the fiducial case (13.4 au) when the dust or disc mass is changed (black lines). The position of the snowline (where the temperature is 160 K) is changed from the fiducial case (3.06 au) to 4.78 au only when the disc temperature is higher.
The right panel of Fig. 13 shows that the total planetesimal mass also depends on the disc properties, and it fits well with the approximation by Eq. (25) (dotted curves). When Zς,0 is changed, the total mass is in proportion to Σpls,est, because the positions of the inner and outer edges of the planetesimal formation region are fixed (see Eq. (25)). Hence, the total mass is 25/3 = 3.2 times greater when Zς,0 is two times higher (green). As a result, the total planetesimal mass could be about 200 Me when Zς,0 = 0.02 and α = 10−4. When Σg,1au is large, the total planetesimal mass is the same as that of the fiducial case, because both the surface density and the formation region of planetesimals do not depend on the gas surface density (light blue). When T1au is 1.25 times higher, the planetesimal surface density is higher in proportion to the temperature (see Eq. (30)), but the formation region is much narrower (orange). As a result, the total planetesimal mass is smaller than that of the fiducial case.
 |
Fig. 13 Surface density and total mass of planetesimals with various disc properties. The left panel shows the surface density of the planetesimals (solid lines) and the corresponding approximations by Eq. (30) (dotted lines). The vertical solid and dotted lines represent rSL and rPIM, respectively. The vertical lines with different Zς,0 and Σg,1au overlap with those of the fiducial case. The right panel shows the total planetesimal mass (solid curves) and the corresponding approximations by Eqs. (25) and (30) (dashed curves). |
4.2 Effects of the planetary growth and the later formation of the planetary core
In the previous sections, we consider the cases with simple assumptions to understand how planetesimals form in belt-like regions. Here, we investigate a more realistic situation, considering the evolution of the gas disc, later formation of the embedded planet, growth of the planet by gas accretion, and Type II migration of the planet.
In this section, we improve the gas disc model used in the previous sections (Eq. (1)) to express the time and radial reduction of the gas surface density (Andrews et al. 2009),
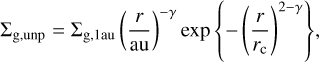 (31)
(31)
where Σg,1au = 500 exp (−t/τdisc) g cm−2 with τdisc = 3 Myr, γ = 1.5 − q = 1 (see Eq. (2)), and rc = 150 au. The outer edge of the disc (calculation region) is 300 au, which is assumed in the previous sections as well.
Planets grown to around the pebble isolation mass also begin to accrete gas. We consider the growth of the embedded planet by gas accretion as,
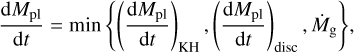 (32)
(32)
where the first, second, and third terms of the right-hand side represent the gas accretion by the Kelvin–Helmholtz-like contraction of the envelope, the accretion of gas from the protoplanetary disc into the Hill sphere, and the limit due to the global gas-accretion rate, respectively (Johansen et al. 2019). The first term is motivated by the findings of Ikoma et al. (2000):
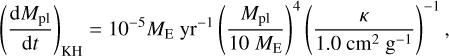 (33)
(33)
where we assume κ = 0.05 cm2 g−1 as the opacity of the envelope. The second term is given by
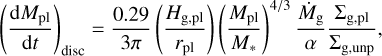 (34)
(34)
where Σg,pl is the gas surface density at the planetary orbit inside the gap (Tanigawa & Tanaka 2016). The global gas accretion rate is (Andrews et al. 2009)
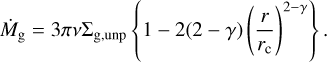 (35)
(35)
As the planet mass increases, the analytical gap model we used in the previous sections is not accurate (Duffell 2015). Therefore, in this section, we use the model described in Paper I (see Appendix C for the details).
The type of the planetary migration also shifts from Type I to Type II as the gap around the planet is deeper. In order to express the Type II migration as well, we adjust the migration timescale Eq. (10), as follows (Kanagawa et al. 2018b):
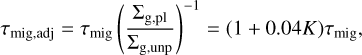 (36)
(36)
where the factor K is defined as Eq. (4).
The approximation of the planetesimal surface density, Eq. (29), is then improved:
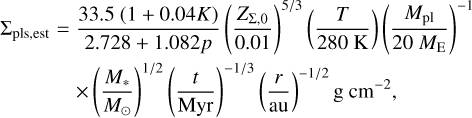 (37)
(37)
where we assume that the effect of the radial reduction of Σg,unp is negligible.
Figure 14 presents the cases where the above effects are included. In all cases, planets grow large and make deep and wide gas gaps during their inward migration. The positions where the planets start to grow are relatively far out as the strength of turbulence is small. After the accretion starts, the migration speed decreases because the type of migration shifts from Type I to Type II. Finally, the mass of the planets goes to ~1000 ME, and their migration stops. The migration speed before the start of the rapid planetary growth is slower than that of the simple Type I migration case. The migration speed is slower as α is smaller, because the gap is deeper (Eq. (36)). After the rapid growth starts, the migration speed no longer depends on α to the same extent, because the gas accretion rate is small as the turbulence is strong (Eq. (34)), which cancels out the above effect.
The first column shows that planetesimals form (by streaming instability) from the start of the calculation, where the planetary orbit is 50 au (see the top panel at t = 0.5 Myr). This outer edge of the formation region is farther than that in the previous sections, because the gap model used in this section is different from the model used in the other sections. The surface density of the formed planetesimals is well reproduced by the approximation updated with Eq. (37) (the black dashed curve) and continuously increases as the planet migrates inwards. Then, the pebble front reaches the outer edge of the disc by 1.0 Myr, and the inward flux of dust decreases, resulting in the rapid reduction in planetesimal surface density at 26 au (the second panel from the top in the first row), which is not expressed in the approximation. After that, planetesimal formation continues until the end of planet migration (2.0–10.0 Myr). A small number of planetesimals also form by mutual collision at this stage (green). As the planet stops before it reaches the snowline, the inner edge of the planetesimal formation region is at 9 au, which is further out than that of our previous results without the planetary growth and the Type II migration.
The second column shows the case where α = 10−3.4. Planetesimals start to form at 27 au, which is inwards from its location when α = 10−4 (the top panel). This trend seen for the position of the outer edge of the planetesimal formation region is the same with the cases without planetary growth and without Type II migration. At 13 au, the slope of the surface density of planetesimals starts to be steeper than that without the additional effects (Σpls ∝ r−1), because the planet starts the rapid growth, and so the migration speed becomes slow (the second top). This change of the slope is well reproduced by the approximation in Eq. (37), showing that the planetesimal surface density is proportional to Mplr−1 when K ≫ 25 and T ∝ r−1. However, the increase in planetesimal surface density stops at 8 au, because the inward flux of dust decreases after the pebble front reaches the outer edge of the disc. Finally, the planet crosses the snowline, but the outer edge of the gap (i.e. the gas pressure maximum) is still outside the snowline, and the inner edge of the planetesimal formation region is outside the snowline as well, although it is inwards from the case with α = 10−4.
The third column shows the profiles with α = 10−3. Planetesimal formation begins later than in the case with weaker turbulence. Here, the pebble front has already reached the outer edge of the disc and the inward flux of dust has decreased (the second panel from the top). As the planet rapidly grows by gas accretion and the migration speed decreases, the slope of the planetesimal surface density is steeper than it is in the case without planetary growth and without Type II migration, which is well reproduced by the approximation (Eq. (37)). The planet migrates inwards to 1 au, where the pressure maximum also reaches the snowline (the bottom panel). The inner edge of the planetesimal formation region is then at the snowline, as it is in the cases without the planetary growth and without Type II migration.
The fourth column shows the case where α = 10−3.4 and the planetary core forms at tpl,0 = 2.0 Myr. The top panel shows the properties when the time has already passed 2.5 Myr. As the amount of the gas and dust still existing in the disc is smaller than in the other cases, the planetary growth is less efficient and the inward flux of dust is smaller. As a result, the start position of the planetesimal formation (i.e. the outer edge of the planetesimal formation region) is inwards from the case with the earlier formation of the planetary core (the second column), and the planetesimal surface density is smaller. The planetesimal surface density is also smaller than the approximation, which does not consider the decrease in the inward flux of dust due to the pebble front reaching the outer edge of the disc. Also, the planet migrates to only just outside the snowline, resulting in the inner edge of the planetesimal formation region being further out than the earlier planetary core formation case.
Figure 15 shows the final distribution of the planetesimal surface density. As explained in the previous paragraphs, the growth of the planet makes its migration slower, which changes the profiles from those without the growth (the black curve). Due to the slower migration, the embedded planet stops at the point where the gas pressure bump has not yet reached the snowline, which moves the inner edge of the planetesimal formation region further out. The time when the pebble front reaches the outer edge of the disc (i.e. the inward dust mass flux decreases) is also an important factor for the profiles of the belt-like planetesimal formation region. Also, if the formation of the embedded planet is late, the inward flux of dust was small, resulting in a low planetesimal surface density and a narrow planetesimal formation region.
Figure 16 also shows that the belt-like planetesimal formation region is formed alongside planetary growth. In the case where the planet exists from the start of the calculation (the left panel), the planetesimal formation region spreads to outside rPIM, the orbital position where the planet reaches the pebble isolation mass (same as in the case in the previous section; the planet mass, the gas disc, and the Stokes number of the dust are fixed), which is farther out than in the fiducial case in the previous sections. This is simply because the gas gap model we use here is different from that used in the previous section. The inner edge of the planetesimal formation region is outside the snowline, because the migration speed of the planet decreases as the planet grows heavy, and the gas disc disappears before the outer edge of the gap reaches the snowline. The a dependence of the orbital position of the inner edge of the formed planetesimal belt reflects the a dependence of the migration speed, as discussed in the previous paragraphs. The panel also shows that the slope of the planetesimal surface density is gentle at the inner part of the belt, and even a peak is formed when α ≤ 10−3.4, which is because the pebble front reaches the outer edge of the disc and then the flux of dust mass flowing into the planetesimal formation region decreases.
The right panel of Fig. 16 shows that the planetesimal formation region with tpl,0 = 2 Myr has a similar a dependence to that with tpl,0 = 0 Myr (the left panel), but that the region is narrower, and the value of the planetesimal surface density is much lower. This is because the pebble front has already reached the outer edge of the disc, and the inward flux of dust mass has decreased, as was also interpreted from Figs. 14 and 15 in the previous sections.
Figure 17 shows that the total mass of the formed planetesimals can be 30–100 ME when the planet is formed at tpl,0 = 0 yr (the purple curve). This is higher than the cases without the planetary growth and without Type II migration (the black curve), because the planetesimal formation starts at more outward orbital positions than those in the previous section due to the change of the gas gap model. On the other hand, the total mass where the planet is formed at tpl,0 = 1 Myr (green) and 2 Myr (sky blue) is about 10 and 100 times smaller than that with tpl,0 = 0 yr, respectively. This is because the planetesimal surface density is smaller and the widths of the planetesimal formation regions are narrower, as discussed in the previous paragraph (Fig. 15). We note that Fig. 16 shows that the planetesimal formation region may spread farther than r = 50 au, and the planetesimal mass may be greater than 100 ME when α ≤ 10−3.7 and tpl,0 = 0 yr if the planet forms farther out than our assumption.
 |
Fig. 14 Same as Fig. 1 but considering the evolution of the gas disc, the growth of the embedded planet by gas accretion, and Type II migration of the planet. The red and green curves represent the surface density of the planetesimals formed by streaming instability and mutual collision, respectively. The mass and orbital position of the planet are also plotted (orange), where the large and small circles represent the mass at that time and the mass at every 2 Myr after t = tpl,0, respectively. The black dashed curves are the approximations of the planetesimal surface densities expressed by Eq. (37). The first to third columns from the left represent the evolution with α = 10−4, 10−3.4, and 10−3, respectively. The fourth column is the case with α = 10−3.4, and the planet is put at tpl,0 = 2 Myr. |
 |
Fig. 15 Final profiles of the total planetesimal surface density considering the evolution of the gas disc, the growth of the embedded planet by gas accretion, and Type II migration of the planet. The red, blue, and green solid blue curves represent the profiles with α = 10−4, 10−3.4, and 10−3, respectively. The solid, dashed, and dotted curves are the cases where the planet is put at tpl,0 = 0 Myr, 1 Myr, and 2 Myr, respectively, with α = 10−3.4. The black curve is the case without the additional effects when α = 10−3.4 (the same as the Fiducilal case in the left panel of Fig. 13). |
 |
Fig. 16 Same as Fig. 4 but considering the evolution of the gas disc, the growth of the embedded planet by gas accretion, and Type II migration of the planet. The left and right panels represent the cases where tpl,0 = 0 and 2 Myr, respectively. The black curves are the same as those in Fig. 4 assuming that the planet mass and gas disc are fixed. |
 |
Fig. 17 Same as Fig. 6 but considering the evolution of the gas disc, the growth of the embedded planet by gas accretion, and Type II migration of the planet. The vertical axis is in the logarithmic scale. The purple, green, and sky-blue curves represent the total planetesimals mass where the planet is put at tpl,0 = 0 yr, 1 Myr, and 2 Myr, respectively. The black curve is the case without the additional effects when α = 10−3.4 (the same as the Fiducilal case in the right panel of Fig. 13). |
4.3 Effects of the back-reaction from dust to gas
We do not consider the effects of the back-reaction from dust to gas, which could change the gas structure at the pressure bump and prevent the accumulation of dust. A gas and dust 2D (radial and vertical) hydrodynamical simulation by Taki et al. (2016) shows that the deformation of the gas pressure bump by the back-reaction prevents direct gravitational instability, and the size of the planetesimals formed by streaming instability becomes smaller even if they form. However, a 2D simulation including the stellar vertical gravity shows that gravitational instability occurs at the gas pressure bump (Onishi & Sekiya 2017). A gas and dust 2D (radial and azimuth) hydrodynamical simulation with a fixed-orbit planet including a simple dust growth model by Kanagawa et al. (2018a) shows that the back-reaction makes the gas pressure bump flatter, and extreme dust accumulation is suppressed. However, the dust-to-gas density ratio in the midplane Zρ is still about unity, which satisfies the condition for planetesimal formation by streaming instability. A similar simulation but with a migrating planet and a fixed size of dust by Kanagawa et al. (2021) shows that the gas pressure bump does not constantly follow the inward migration of the planet, and multiple dust rings form when α ≤ 3 × 10−4. If this occurs even when the dust growth and the planetesimal formation are considered, the radial profile of the planetesimal surface density inside the formation region will be different from our results. On the other hand, a recent gas and dust 3D hydrodynamical simulation with a fixed size of dust by Bi et al. (2023) shows that, although the accumulation is moderate when Zρ > 1, the dust ring is narrower rather than wider when Zρ < 1, which is different from the results of the simulations by Kanagawa et al. (2018a). Therefore, more precise 3D simulations considering dust growth with a migrating planet should be conducted in order to predict the precise formation process of planetesimals in the future.
4.4 Effects of the dust leak
We use a dust evolution model expressing the dust mass at each distance as single peak (largest) mass. This is consistent with full-size simulations because the mass is dominated by the peak (largest) mass. However, in reality the dust follows a mass distribution, and small dust is relatively easy to escape from the accumulation at the gas pressure bump because of diffusion. This is obvious from the condition for the accumulation of dust, which is determined by the ratio of the speeds of diffusion and drift (Zhu et al. 2012; see Eqs. (13) and (14)),
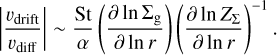 (38)
(38)
Therefore, if the fragmentation of the piled-up dust is efficient, and great many small dust particles are formed, the gas pressure bump may not be able to maintain the accumulation of dust.
However, a recent full-size simulation by Stammler et al. (2023) shows that small particles leak from the gas pressure bump, but the dust-to-gas surface density ratio maintains Zς ≳ 0.01 for ~1 Myr when the critical fragmentation speed is υcr = 10 m s−1, which is sufficient to trigger streaming instability outside the snowline (Li & Youdin 2021). Therefore, our scenario of planetesimal formation should still work even if the leak of small dust is considered. A recent 2D gas and fixed-sized dust shearing-box simulation by Lee et al. (2022) shows that dust particles smaller than St ~ 0.1 cannot pile up at the gas pressure bump, and the trap efficiency is about 80% even for the particles with St ≳ 0.1. This result suggests that the surface density and total mass of real planetesimals could be smaller than that suggested by our results, but a significant leak of dust should not happen given the quick growth of dust at the gas pressure bump predicted in our simulations.
4.5 Effects of the vertical stirring by the planet
Recent 3D simulations show that an embedded planet vertically stirs dust settling onto the midplane (e.g. Binkert et al. 2021). This effect can reach the outer region of the protoplanetary disc as the planet is heavy. Here, we briefly check how this vertical stirring changes our results by mimicking the situation.
We treat the strength of turbulence α in Eq. (19), dominating the vertical equilibrium distribution, as αvert = 10−2. We assume this value is spatially and temporally constant. Figure 18 shows that the final distribution of the planetesimal surface density is similar to the normal case. The total formed planetesimal mass is 59 ME, which is also similar to that of the normal case, 52 ME. However, in the case of the vertical stirring, the starting point of the planetesimal formation (i.e. the outer edge of the planetesimal formation region) is further inward than in the normal case. This is due to the fact that the dust density in the midplane is lower than that of the normal case because of the vertical stirring, which moves the point at which the condition for the streaming instability is satisfied to a later time. This trend is also shown in Fig. 5, where α is changed. At the inner part of the planetesimal distribution, the surface density of the vertical stirring case is higher than that of the normal case. This is because the time at which the pebble front reaches the disc outer edge is later than in the normal case because of the less efficient collisional growth of dust on the midplane. The vertical stirring lowers the midplane dust density, and the collision rate decreases. However, the vertical stirring is weaker as the distance to the planet is farther; the speed of the pebble front may not change significantly, especially when the planet (or planetary core) is not heavy. On the other hand, the difference between the starting points of the planetesimal formation will remain in the case of a lighter planet.
The presence of an embedded planet may also make the dust ring wider. This will change the starting position of the planetesimal formation and may make the planetesimal surface density lower if the planetesimal formation rate is also affected by the planet. However, the overall scenario of the planetesimal formation mechanism will not change, similar to the cases where the effects of the dust back reaction are considered (see Sect. 4.3).
5 Conclusions
A planet carves through the protoplanetary disc and creates a gas pressure bump. Dust drifting from the outer region of the disc piles up there and form planetesimals. As the planet migrates inwards, the planetesimal formation place also moves inwards, and the formation region spreads over the inner disc. As a result, planetesimals form in a wide belt-like region in the disc (Shibaike & Alibert 2020).
We investigated this scenario for planetesimal formation by additionally considering the global dust evolution in a protoplanetary disc with a wide range of values for turbulence strength, α. We show that the dust particles pile up at the bump and form planetesimals by streaming instability and mutual collision. As the planet migrates inward, the formation region lies roughly between the snowline and the orbital position where the planet reaches its pebble-isolation mass when 10−4 ≤ α ≤ 10−3, which is broadly consistent with the observed value of α (Pinte et al. 2022). As α is smaller, the planetesimal formation region is wider, and the total mass of the formed planetesimals is greater.
The formation mechanism depends on the SI (streaming instability) timescale. In the case of a short SI timescale, all planetesimals form by streaming instability regardless of the value of α. On the other hand, in the case of a long SI timescale, all planetesimals form by streaming instability when α ≥ 10−3.5, but most of them form by mutual collision when α ≤ 10−3.6. We also investigated the case where the condition for streaming instability and the SI timescale depend on the Stokes number of dust (Li & Youdin 2021). The results are almost the same as those with the short SI timescale, except that the outer edge of the planetesimal formation region is slightly farther out.
The planetesimal surface density is ~10 g cm−2 around the inner edge and ~0.1–1 g cm−2 around the outer edge of the formation region. This is consistent with the results of Shibaike & Alibert (2020), and means that almost all dust drifting into the formation place is converted immediately to planetesimals. The total planetesimal mass depends on α, and it reaches about 60 ME with α = 10−4 and a typical initial dust-to-gas surface density ratio (i.e. dust mass). Also, the total planetesimal mass strongly depends on the dust mass, and can be about 200 ME when the initial dust-to-gas surface density ratio is 0.02. We also show that the surface density and total mass of the planetesimals can be approximated with simple expressions.
Furthermore, when the growth of the embedded planet by gas accretion and the shift to Type II migration are considered, the profiles of the planetesimal surface density change from those with the simple assumptions. The slowdown of the migration of the planet makes the slopes of the profiles steeper at their inner regions, but it also reduces the surface density once the pebble front reaches the outer edge of the disc and the inward flux of dust (pebble) mass decreases. When 10−4 ≤ α ≤ 10−3, the total mass of the formed planetesimals is about 30–100 ME if the planetary core has already existed at t = 0 yr. However, the total mass is about 10 and 100 times smaller in the cases where the planetary core forms at t = 1 Myr and 2 Myr, respectively, because most of the dust (pebbles) has already fallen onto the star before the planetesimal formation starts.
 |
Fig. 18 Same as Fig. 15, but the orange curve is a vertically stirred situation, αvert = 10−2 and α = 10−3.4. The blue curve is the normal case with α = 10−3.4, and is the same as the blue curve in Fig. 15. |
Acknowledgements
We thank the referee, Joanna Drazkowska, for the very valuable comments. We also thank Christoph Mordasini and Takahiro Ueda for constrictive and useful discussion. This work has been carried out within the framework of the NCCR PlanetS supported by the Swiss National Science Foundation under grants 51NF40_182901 and 51NF40_205606.
Appendix A Clumping timescale of dust
Clumping timescale of dust (i.e. the SI timescale) depends on the Stokes number of dust particles. We approximate (by eye) the results of a recent vertically stratified gas and dust hydrodynamical simulation by Li & Youdin (2021). Figure A.1 shows the results of this latter work and our approximation of them; see Eq. (3.3).
 |
Fig. A.1 Clumping timescale of dust with various values of Stokes number. The circles represent the simulation results of Li & Youdin (2021; τs in Table 1 and tpre–cl in Table 2 of the paper). The solid curve represents our approximation of the results (Eq. (3.3)). |
Appendix B Analytical explanation of the approximate expressions
The analytical expression of the inward dust (pebble) flux provided by Lambrechts & Johansen (2014) can be expressed in a more general manner:
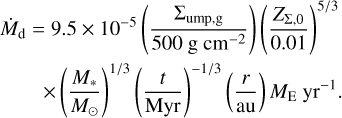 (B.1)
(B.1)
When Σump,g = Σg,1au(r/au)−p,
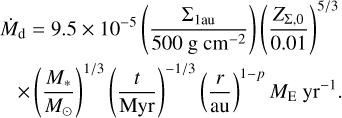 (B.2)
(B.2)
When p = 1, the r dependence is canceled out, and we get Eq. (28), which is exactly the same expression as Eq. (14) of Lambrechts & Johansen (2014). By this assumption (p = 1), the dust mass flux is uniform. When we also substitute t = 0.25 Myr into Eq. (28),
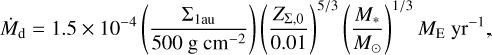 (B.3)
(B.3)
which is consistent with the results of our simulations.
By substituting Eq. (10) with the upper expression of Eq. (24), and combining it with Eqs. (1) and (2), we get general approximate expressions of the planetesimal surface density:
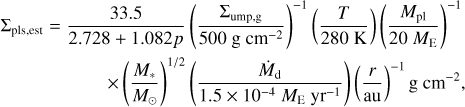 (B.4)
(B.4)
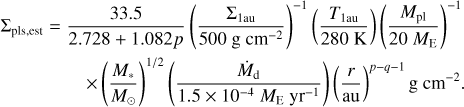 (B.5)
(B.5)
When we substitute p = 1 and q = 1/2 into Eq. (B.5), we get the lower expression of Eq. (24).
If we substitute Eq. (B.1) into Eqs. (B.4) and (B.5), we get Eq. (29) and
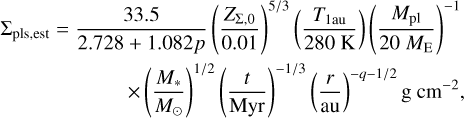 (B.6)
(B.6)
respectively. Here, Σpls,est does not depend on Σg,unp except for the week dependence in the coefficient 33.5/(2.728 + 1.082p), because it is canceled out. When p = 1 and q = 1/2,
 (B.7)
(B.7)
When we also substitute t = 0.25 Myr, Mpl = 20 ME, and M* = M⊙ into Eq. (B.7), we get Eq. (29).
Appendix C Gap model used in the cases with planetary growth
In Section 4.2, we use the gap model used in Paper I (Shibaike & Alibert 2020) to express the cases with planetary growth. This model is more accurate than that by Duffell (2015) when the planet is heavy. The perturbed gas surface density is
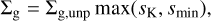 (C.1)
(C.1)
where sK = max(sKepler, sRayleigh). The factor sKepler is
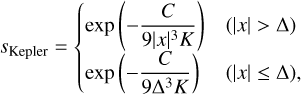 (C.2)
(C.2)
where C = 0.798, Δ = 1.3, and x = (r − rpl)/Hg,pl. The factor sRayleigh is
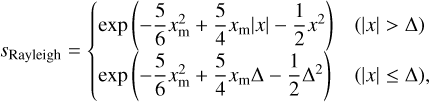 (C.3)
(C.3)
where xm = {(4/3)CK}1/5 is the outer edge of the marginal Rayleigh stable region (i.e. |x| < xm). The factor smin is given by (Kanagawa et al. 2015):
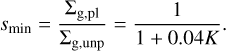 (C.4)
(C.4)
References
- Adachi, I., Hayashi, C., & Nakazawa, K. 1976, Progr. Theor. Phys., 56, 1756 [Google Scholar]
- ALMA Partnership (Brogan, C. L., et al.) 2015, ApJ, 808, L3 [Google Scholar]
- Andrews, S. M., Wilner, D., Hughes, A., Qi, C., & Dullemond, C. 2009, ApJ, 700, 1502 [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D., Hughes, A., Qi, C., & Dullemond, C. 2010, ApJ, 723, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Huang, J., Pérez, L. M., et al. 2018, ApJ, 869, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Ataiee, S., Baruteau, C., Alibert, Y., & Benz, W. 2018, A&A, 615, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ayliffe, B. A., Laibe, G., Price, D. J., & Bate, M. R. 2012, MNRAS, 423, 1450 [Google Scholar]
- Bi, J., Lin, M.-K., & Dong, R. 2023, ApJ, 942, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Binkert, F., Szulágyi, J., & Birnstiel, T. 2021, MNRAS, 506, 5969 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, J., & Wurm, G. 2000, Icarus, 143, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, S., & Tan, J. C. 2013, ApJ, 780, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Currie, T., Lawson, K., Schneider, G., et al. 2022, Nat. Astron., 6, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Drazkowska, J., & Dullemond, C. P. 2014, A&A, 572, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drążkowska, J., Alibert, Y., & Moore, B. 2016, A&A, 594, A105 [Google Scholar]
- Drazkowska, J., Li, S., Birnstiel, T., Stammler, S. M., & Li, H. 2019, ApJ, 885, 91 [CrossRef] [Google Scholar]
- Duffell, P. C. 2015, ApJ, 807, L11 [CrossRef] [Google Scholar]
- Dullemond, C. P., Birnstiel, T., Huang, J., et al. 2018, ApJ, 869, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksson, L. E., Johansen, A., & Liu, B. 2020, A&A, 635, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eriksson, L. E., Ronnet, T., & Johansen, A. 2021, A&A, 648, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodman, J., & Rafikov, R. 2001, ApJ, 552, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2008, ApJ, 673, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Ikoma, M., Nakazawa, K., & Emori, H. 2000, ApJ, 537, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., & Youdin, A. 2007, ApJ, 662, 627 [Google Scholar]
- Johansen, A., Ida, S., & Brasser, R. 2019, A&A, 622, A202 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kanagawa, K. D., Tanaka, H., Muto, T., Tanigawa, T., & Takeuchi, T. 2015, MNRAS, 448, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Kanagawa, K. D., Muto, T., Okuzumi, S., et al. 2018a, ApJ, 868, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Kanagawa, K. D., Tanaka, H., & Szuszkiewicz, E. 2018b, ApJ, 861, 140 [Google Scholar]
- Kanagawa, K. D., Muto, T., & Tanaka, H. 2021, ApJ, 921, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Keppler, M., Benisty, M., Müller, A., et al. 2018, A&A, 617, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kobayashi, H., Ormel, C. W., & Ida, S. 2012, ApJ, 756, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, E. J., Fuentes, J., & Hopkins, P. F. 2022, ApJ, 937, 95 [CrossRef] [Google Scholar]
- Li, R., & Youdin, A. N. 2021, ApJ, 919, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Lyra, W., Johansen, A., Klahr, H., & Piskunov, N. 2009, A&A, 493, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, E., Marino, S., Stammler, S., et al. 2021, MNRAS, 508, 5638 [NASA ADS] [CrossRef] [Google Scholar]
- Okuzumi, S., Tanaka, H., Kobayashi, H., & Wada, K. 2012, ApJ, 752, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Okuzumi, S., Momose, M., Sirono, S., Kobayashi, H., & Tanaka, H. 2016, ApJ, 821, 82 [Google Scholar]
- Onishi, I. K., & Sekiya, M. 2017, Earth Planets Space, 69, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C., & Cuzzi, J. 2007, A&A, 466, 413 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., & Mellema, G. 2004, A&A, 425, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., van der Plas, G., Ménard, F., et al. 2019, Nat. Astron., 3, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Pinte, C., Teague, R., Flaherty, K., et al. 2022, ArXiv e-prints [arXiv:2203.09528] [Google Scholar]
- Sato, T., Okuzumi, S., & Ida, S. 2016, A&A, 589, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schoonenberg, D., Ormel, C. W., & Krijt, S. 2018, A&A, 620, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Segura-Cox, D. M., Schmiedeke, A., Pineda, J. E., et al. 2020, Nature, 586, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Sekiya, M. 1998, Icarus, 133, 298 [CrossRef] [Google Scholar]
- Shibaike, Y., & Alibert, Y. 2020, A&A, 644, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stammler, S. M., Drazkowska, J., Birnstiel, T., et al. 2019, ApJ, 884, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Stammler, S. M., Lichtenberg, T., Drążkowska, J., & Birnstiel, T. 2023, A&A 670, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taki, T., Fujimoto, M., & Ida, S. 2016, A&A, 591, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taki, T., Kuwabara, K., Kobayashi, H., & Suzuki, T. K. 2021, ApJ, 909, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., Takeuchi, T., & Ward, W. R. 2002, ApJ, 565, 1257 [Google Scholar]
- Tanigawa, T., & Tanaka, H. 2016, ApJ, 823, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2009, ApJ, 702, 1490 [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [Google Scholar]
- Whipple, F. 1972, From Plasma to Planet, ed. A. Elvius (London: Wiley) [Google Scholar]
- Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [Google Scholar]
- Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Nelson, R. P., Dong, R., Espaillat, C., & Hartmann, L. 2012, ApJ, 755, 6 [Google Scholar]
In Sect. 4.2, we use the model described in Paper I, because the model by Duffell (2015) is not accurate when the planet is heavy.
This expression can be used even if dust grows to metre-size, because numerical simulations show that the fragmentation does not depend on the number of monomers of dust aggregates (Wada et al. 2009).
Although ϵSI has been treated as a free parameter in previous works (e.g. Drazkowska & Dullemond 2014), its variety is implicitly expressed together with the variety of τSI in this work.
All Tables
All Figures
 |
Fig. 1 Time evolution of the surface density of gas, dust, and formed planetesimals, with α = 10−3.4. The sky-blue, blue, and red curves represent the profiles of gas, dust, and planetesimals, respectively. All planetesimals form by streaming instability. The black dashed lines represent the approximation of the planetesimal surface density by Eq. (24) with |
| In the text | |
 |
Fig. 2 Time evolution of the detailed profiles of dust with α = 10−3.4. The first to fourth columns from the left represent the radial profiles of the radius, Stokes number, midplane dust-to-gas density ratio, and inward flux of mass, respectively. The first to fifth rows from the top represent the profiles at t = 0, 0.35, 0.53, 0.63, and 0.75 Myr, respectively. The horizontal lines represent the critical or important values of each profile. The vertical lines represent the position of the snowline. The circles represent the orbital positions of the planet. |
| In the text | |
 |
Fig. 3 Time evolution of the dust, planetesimal, and solid (sum of the dust and planetesimals) mass with τSI = 10 yr and α = 10−34. The blue, red, and purple curves represent the profiles of the dust, planetesimal, and solid, respectively. The dashed blue line represents the slope of the dust mass assuming constant loss with |
| In the text | |
 |
Fig. 4 Planetesimal formation regions with τSI = 10 yr and various a. The colour represents the planetesimal surface density. The solid and dotted curves represent rPIM and rη0, respectively. The vertical dashed line is the snowline. |
| In the text | |
 |
Fig. 5 Trajectory of the largest Zρ outside the orbit of the planet with τSI = 10 yr. The red, purple, and blue curves represent the cases with α = 10−4, 10−34, and 10−3, respectively. The solid and dotted vertical lines represent rPIM and rη0 with each α, respectively. |
| In the text | |
 |
Fig. 6 Total mass of the formed planetesimals with τSI = 10 yr and various α. The solid and dashed curves represent the results of our calculations and the approximation by Eq. (25), respectively. |
| In the text | |
 |
Fig. 7 Same as the first and third columns of Fig. 2 but with τSI = 103TK. The first and second columns represent the profiles with α = 10−3.4, and the third and fourth columns represent those with 10−4. |
| In the text | |
 |
Fig. 8 Final profiles of the planetesimal surface density with τSI = 103TK. The red and green curves represent the surface density of the planetesimals formed by streaming instability and mutual collision, respectively. The left and right panels represent the profiles with α = 10−3.4 and 10−4, respectively. |
| In the text | |
 |
Fig. 9 Same as Fig. 3 but with τSI = 103TK. The left and right panels represent the profiles with α = 10−3.4 and 10−4, respectively. In the left panel, the profiles with τSI = 10 yr are also plotted as the dotted curves. All planetesimals form by streaming instability when α = 10 −3.4. In the right panel, we plot the mass of the planetesimals formed by streaming instability (red) and by mutual collision (green). The blue dashed line represents the slope of the dust mass assuming constant loss with |
| In the text | |
 |
Fig. 10 Same as Fig. 4 but with τSI = 103TK. The left and right panels represent the formation regions of the planetesimals formed by streaming instability and mutual collision, respectively. |
| In the text | |
 |
Fig. 11 Same as Fig. 6 but with τSI = 103TK. The red dotted and green dashed-and-dotted curves represent the mass of the planetesimals formed by streaming instability and mutual collision, respectively. The black solid curve represents their total mass. |
| In the text | |
 |
Fig. 12 Same as Fig. 4, but ϵcrit and τSI depend on St as Eqs. (26) and (3.3), respectively. |
| In the text | |
 |
Fig. 13 Surface density and total mass of planetesimals with various disc properties. The left panel shows the surface density of the planetesimals (solid lines) and the corresponding approximations by Eq. (30) (dotted lines). The vertical solid and dotted lines represent rSL and rPIM, respectively. The vertical lines with different Zς,0 and Σg,1au overlap with those of the fiducial case. The right panel shows the total planetesimal mass (solid curves) and the corresponding approximations by Eqs. (25) and (30) (dashed curves). |
| In the text | |
 |
Fig. 14 Same as Fig. 1 but considering the evolution of the gas disc, the growth of the embedded planet by gas accretion, and Type II migration of the planet. The red and green curves represent the surface density of the planetesimals formed by streaming instability and mutual collision, respectively. The mass and orbital position of the planet are also plotted (orange), where the large and small circles represent the mass at that time and the mass at every 2 Myr after t = tpl,0, respectively. The black dashed curves are the approximations of the planetesimal surface densities expressed by Eq. (37). The first to third columns from the left represent the evolution with α = 10−4, 10−3.4, and 10−3, respectively. The fourth column is the case with α = 10−3.4, and the planet is put at tpl,0 = 2 Myr. |
| In the text | |
 |
Fig. 15 Final profiles of the total planetesimal surface density considering the evolution of the gas disc, the growth of the embedded planet by gas accretion, and Type II migration of the planet. The red, blue, and green solid blue curves represent the profiles with α = 10−4, 10−3.4, and 10−3, respectively. The solid, dashed, and dotted curves are the cases where the planet is put at tpl,0 = 0 Myr, 1 Myr, and 2 Myr, respectively, with α = 10−3.4. The black curve is the case without the additional effects when α = 10−3.4 (the same as the Fiducilal case in the left panel of Fig. 13). |
| In the text | |
 |
Fig. 16 Same as Fig. 4 but considering the evolution of the gas disc, the growth of the embedded planet by gas accretion, and Type II migration of the planet. The left and right panels represent the cases where tpl,0 = 0 and 2 Myr, respectively. The black curves are the same as those in Fig. 4 assuming that the planet mass and gas disc are fixed. |
| In the text | |
 |
Fig. 17 Same as Fig. 6 but considering the evolution of the gas disc, the growth of the embedded planet by gas accretion, and Type II migration of the planet. The vertical axis is in the logarithmic scale. The purple, green, and sky-blue curves represent the total planetesimals mass where the planet is put at tpl,0 = 0 yr, 1 Myr, and 2 Myr, respectively. The black curve is the case without the additional effects when α = 10−3.4 (the same as the Fiducilal case in the right panel of Fig. 13). |
| In the text | |
 |
Fig. 18 Same as Fig. 15, but the orange curve is a vertically stirred situation, αvert = 10−2 and α = 10−3.4. The blue curve is the normal case with α = 10−3.4, and is the same as the blue curve in Fig. 15. |
| In the text | |
 |
Fig. A.1 Clumping timescale of dust with various values of Stokes number. The circles represent the simulation results of Li & Youdin (2021; τs in Table 1 and tpre–cl in Table 2 of the paper). The solid curve represents our approximation of the results (Eq. (3.3)). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.