| Issue |
A&A
Volume 676, August 2023
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 20 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202345901 | |
| Published online | 08 August 2023 | |
The influence of planetesimal fragmentation on planet formation
Physikalisches Institut, Universität Bern,
Gesellschaftsstrasse 6,
3012
Bern, Switzerland
e-mail: nicolas.kaufmann@unibe.ch
Received:
11
January
2023
Accepted:
25
May
2023
Context. The effects of planetesimal fragmentation on planet formation have been studied via various models on single embryos, and have therefore mostly neglected concurrent effects in the outer disk. They show that planetesimal fragmentation can either hinder or aid planet formation, due to the introduction of competing effects, namely speeding up accretion and depleting the feeding zone of forming planets.
Aims. We investigate the influence of the collisional fragmentation of planetesimals on the planet formation process using a population synthesis approach. Our aim is to investigate its effects for a large set of initial conditions and also to explore the consequences on the formation of multiple embryos in the same disk.
Methods. We ran global planet formation simulations including fragmentation, drift, and an improved ice line description. To do this we used a fragmentation model in our code. The initial conditions for the simulations that are informed by observations are varied to generate synthetic exoplanet populations.
Results. Our synthetic populations show that depending on the typical size of solids generated in collisions, fragmentation in tandem with radial drift can either enhance or hinder planet formation. For larger fragments we see increased accretion throughout the populations especially beyond the ice line. However, the shorter drift timescale of smaller fragments, due to their stronger coupling to the gas, can hinder the formation process. Furthermore, beyond the ice line fragmentation promotes late growth when the damping by gas drag fades.
Conclusions. Fragmentation significantly affects the planet formation process in various ways for all types of planets and warrants further investigation.
Key words: Planets and satellites: formation / protoplanetary disks / methods: numerical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
In the classical core accretion scenario terrestrial planets and the cores of giant planets are formed in multiple steps. The first step is the formation of planetesimals from dust, for which multiple pathways are proposed. The two main proposed mechanisms are coagulation and gravitational collapse via streaming instability (Okuzumi et al. 2012; Kobayashi & Tanaka 2021; Yang et al. 2017). The first process describes the formation of planetesimals via the sticking of smaller dust grains in collisions. In the second process, streaming instability forms planetesimals through the gravitational collapse of chondrule-sized objects (Johansen et al. 2007, Johansen et al. 2014; Schäfer et al. 2017).
Planetary embryos form from these planetesimals via runaway growth as their accretion rate speeds up with increasing mass, and they separate themselves from the rest of the planetesimals (Ormel et al. 2010). As the embryos grow they start stirring up the remaining planetesimals, which reduces the rate at which embryos accrete planetesimals and allows other embryos (oligarchs) in neighbouring regions to catch up in mass (Ida & Makino 1993). The size distribution of the remaining planetesimals is quite important for the further growth of the embryos as the accretion rates depend strongly on their size and dynamical state (Fortier et al. 2012; Chambers 2006; Guilera et al. 2010). Furthermore, the size distribution of the planetesimals continues to evolve through their mutual collisions, which can lead to the coagulation or fragmentation of planetesimals, depending on their relative speeds (Kenyon & Bromley 2004). The relative speed between planetesimals is caused by their gravitational interaction with the embryos and other planetesimals and is influenced by the interactions with the gas disk. For higher relative speeds this results in the generation of smaller fragments that get removed from the disk via drift due to the sub-Keplerian headwind of the gas disk. In some models the initial size of the planetesimals is estimated to be ≈ 100 km (Morbidelli et al. 2009), but the typical size of accreted solids is still poorly constrained (Helled & Morbidelli 2021). In addition, the outcomes of collisions are also rather uncertain (Kobayashi & Tanaka 2010), which makes the further study of the collisional evolution important to improve our understanding of these processes and their imprint on planet formation as a whole.
There have been many studies of the collisional evolution and fragmentation of planetesimals (Kobayashi & Tanaka 2018; Chambers 2008, 2014; Guilera et al. 2014; San Sebastián et al. 2019; Inaba et al. 2003). These studies show that planetesimal fragmentation can both inhibit and/or enhance the formation of planets as it introduces competing effects. This especially affects the growth of the core of gas giants as their greater mass increases the random velocities of planetesimals more strongly, and therefore shortens collisonal timescales and reduces the typical size of solids (Guilera et al. 2014). These smaller solids are easier to accrete, but also lead to the removal of accretable material caused by their faster drift speeds.
Previous studies focused on single-planet systems, and often other parts of the planet formation process have to be simplified, for example migration and the calculation of the internal structure of the forming planets. Furthermore, studies on the impact of fragmentation in a population synthesis approach are valuable because they allow us to probe a larger part of the parameter space of planet formation; unfortunately, these studies were not performed previously. The study of multiple discrete interacting embryos has also been neglected in previous studies, but this consideration is important as it allows the investigation of features that may arise due to the presence of multiple planets.
In this work we therefore present a population level investigation into the influence of the size evolution of planetesimals on planet formation, more specifically the influence of the fragmentation of planetesimals. This was done by implementing a fragmentation model in the Bern model (Alibert et al. 2004, 2005, 2013; Mordasini et al. 2009, 2012; Emsenhuber et al. 2021b) and by improving the treatment of the solid disk. This was then used to run many global planet formation simulations varying the initial conditions in a population synthesis approach. We considered the formation of single embryos or multiple embryos simultaneously. This lets us create synthetic planet populations that show how collisions between the solids in the disks influence the formation of various types of planets. To do this, we ran the planet formation model for different model choices and parameters of our fragmentation model to explore its effects in different regimes.
In Sect. 2 we give an overview of the Bern model. We discuss the basic features of the code and the description of the solid disk, due to its importance to the investigated collisional processes (i.e. fragmentation). Furthermore, we describe the newly implemented features that build on previous iterations of the model, including drift and the calculation of the dynamical state. Then the addition of the fragmentation model that is introduced to the code is discussed. Finally, the population synthesis approach is presented. In Sect. 3 we test our calculations against other formation models that include fragmentation to ensure our model’s validity. Then we use the model to generate synthetic populations of planets in Sect. 4 to investigate the influence of fragmentation on the planet formation process. Finally, in Sect. 5 we present the discussion, summarise our results, and list our conclusions.
2 Planet formation model
The numerical code used to model the formation of planets (the Bern model) is an adaption of the code described in Emsenhuber et al. (2021b). The Bern model includes the formation and long-term evolution of planets in two stages. The planet formation is first tracked for a fixed time interval (20 Myr), and is derived from previous works (Alibert et al. 2004, 2005, 2013; Mordasini et al. 2009; Emsenhuber et al. 2021b). The gas disk is described as a viscous accretion disk. The turbulent viscosity is parametrised with the constant α parameter (Shakura & Sunyaev 1973). The formation phase additionally considers the interplay between the planet and the disk: migration, gas, and solid accretion. The gravitational interactions between planetary embryos are integrated with the mercury integrator (Chambers 1999). The gas accretion is calculated by solving the structure equations. When the planet becomes massive enough, runaway gas accretion occurs, the envelop contracts, and accretion is limited by the supply of the gas disk. We include core growth by accreting planetesimals in the oligarchic regime. For multiple planets, we consider up to 100 initial embryos of moon mass (10−2M⊕) and a mono-disperse swarm of planetesimals (when fragmentation is not considered) of a single size (typically 300 m).
After the formation phase we continue to evolve the planets individually to 10 Gyr, as described in Mordasini et al. (2012). This includes the solving of the internal structure equations, atmospheric escape (Jin et al. 2014), and tidal migration (Benítez-Llambay et al. 2011).
2.1 Solid disk
The planetesimals are not represented individually, but rather are described on a grid using a few key quantities, namely surface density (Σ), mean root squared eccentricity (e), inclination (i), typical size (s), and bulk density (ρ), along with the ice fraction of the planetesimals. The introduction of fragmentation adds objects of different typical sizes (fragments) to the solid disk. To treat this we have separate grids (with individual Σ and other quantities) for the fragments and planetesimals, which we also refer to as different swarms of solids in the rest of the paper.
The eccentricities and inclinations are assumed to be Rayleigh distributed which is motivated by N-body simulations (Salo 1985). Since we assume an azimuthally symmetrical disk we can describe the dynamical state (i.e. their random velocities) with just the mean root squared eccentricity and inclination of the swarm. The random velocities of the planetesimals, described by e and i, are increased due to the gravitational interactions among the planetesimals themselves and with the embryos, and are dampened by the gas drag. The stirring by density fluctuations in the gas is also considered. To calculate the dynamical state we follow the approach of Fortier et al. (2012) and solve the evolution equations for e and i at each time step given by
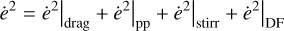 (1)
(1)
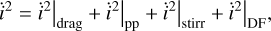 (2)
(2)
where the contributions on the right-hand side arise due to the gas drag, the planetesimal–planetesimal interaction, the stirring by the embryos, and the stirring by density fluctuations, in that order. The gas drag depends on the relative velocity between the planetesimals and the gas. We consider three regimes: Epstein, Stokes, and quadratic (Rafikov 2004). The regimes are separated by the size of the planetesimals and the relative velocity between the planetesimals and the gas: 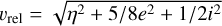 , where
, where 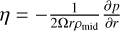 is the deviation of the gas from Keplerian speed. The Epstein drag is considered when the planetesimals are roughly smaller than the mean free path of the gas (i.e. s < 1.5 × λ = (nH2σH2)−1, where n is the number density of hydrogen, which is the main component of the gas disk and σ its cross-section). Otherwise the distinction between the two remaining cases is made with the Reynolds number Remol = υrels/vmol, where vmol = λcs/3 is the molecular viscosity and cs the sound speed. For a Reynolds number respectively above and below 27, the quadratic regime and the Stokes regime is considered. The drag expressions for the Epstein regime are
is the deviation of the gas from Keplerian speed. The Epstein drag is considered when the planetesimals are roughly smaller than the mean free path of the gas (i.e. s < 1.5 × λ = (nH2σH2)−1, where n is the number density of hydrogen, which is the main component of the gas disk and σ its cross-section). Otherwise the distinction between the two remaining cases is made with the Reynolds number Remol = υrels/vmol, where vmol = λcs/3 is the molecular viscosity and cs the sound speed. For a Reynolds number respectively above and below 27, the quadratic regime and the Stokes regime is considered. The drag expressions for the Epstein regime are
 (3)
(3)
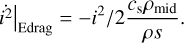 (4)
(4)
The formulas for the Stokes regime are
 (5)
(5)
 (6)
(6)
and in the quadratic regime they are
 (7)
(7)
 (8)
(8)
The second term in the dynamical evolution stems from the planetesimal–planetesimal interaction, and follows the description of Ohtsuki et al. (2002),
![$\matrix{ {{{\dot e}^2}\left| {_{{\rm{pp}}} = {a_0}{\rm{\Omega }}} \right.\,\,\sum\limits_j {\,\left[ {{N_j}{{h_{ij}^4{m_j}} \over {{{\left( {{m_i} + {m_j}} \right)}^2}}}*\left\{ {{m_j}{P_{{\rm{VS}}}}} \right.\left( {{{\tilde e}_i},{{\tilde i}_i},{{\tilde e}_j},{{\tilde i}_j}} \right)} \right.} } \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {{{m_j}e_j^2 - {m_i}e_i^2} \over {e_i^2 + e_j^2}}{P_{{\rm{DF}}}}\left. {\left. {\left( {{{\tilde e}_i},{{\tilde i}_i},{{\tilde e}_j},{{\tilde i}_j}} \right)} \right\}} \right],} \hfill \cr } $](/articles/aa/full_html/2023/08/aa45901-23/aa45901-23-eq11.png) (9)
(9)
![$\matrix{ {{{\dot i}^2}\left| {_{{\rm{pp}}} = {a_0}{\rm{\Omega }}} \right.\,\,\sum\limits_j {\,\left[ {{N_j}{{h_{ij}^4{m_j}} \over {{{\left( {{m_i} + {m_j}} \right)}^2}}}*\left\{ {{m_j}{Q_{{\rm{VS}}}}} \right.\left( {{{\tilde e}_i},{{\tilde i}_i},{{\tilde e}_j},{{\tilde i}_j}} \right)} \right.} } \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {{{m_j}i_j^2 - {m_i}i_i^2} \over {i_i^2 + i_j^2}}{Q_{{\rm{DF}}}}\left. {\left. {\left( {{{\tilde e}_i},{{\tilde i}_i},{{\tilde e}_j},{{\tilde i}_j}} \right)} \right\}} \right].} \hfill \cr } $](/articles/aa/full_html/2023/08/aa45901-23/aa45901-23-eq12.png) (10)
(10)
Here a0 is the semi-major axis, Ω is Kepler angular speed, and i and j refer to the different swarms, for example when we consider planetesimals and fragments. The viscous stirring is the first term in the curly brackets in Eqs. (9) and (10). The dynamical friction term is the second contribution, which vanishes for a single size of planetesimals (i.e. when no fragments are present). The functions QVS, PVS, QDF, and PDF are given by Ohtsuki et al. (2002). These functions along with the approximated stirring integral can be found in Appendix B.
A further contribution to the dynamical evolution stems from the stirring of the planetesimals by the embryos, which is given by
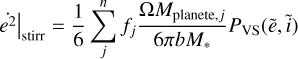 (11)
(11)
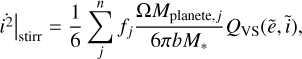 (12)
(12)
where QVS and PVS are the same functions as above (with the caveat that 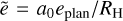 and
and 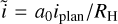 , where RH is the planet’s Hill radius). The distance modulation function f of the j′ th planet is given by
, where RH is the planet’s Hill radius). The distance modulation function f of the j′ th planet is given by
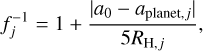 (13)
(13)
and describes the fall-off in stirring by the planet outside of its feeding zone. For the stirring from the density fluctuation, we follow the description of Ormel & Kobayashi (2012) and Kobayashi et al. (2016) which is given by
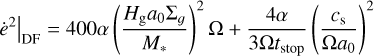 (14)
(14)
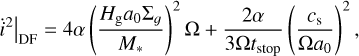 (15)
(15)
where Hg is the scale height of the gas disk and tstop is the same stopping time as for the damping given in Eq. (17).
As the gas disk is partially pressure supported, its orbital speed is sub-Keplerian, which means the planetesimals experience a headwind when orbiting around the star. Therefore, they lose angular momentum, which leads to the decay of their semimajor axis, referred to as drift. This radial motion depends on the same drag regimes (Guilera et al. 2014) as for the damping discussed before, and can be described as
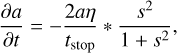 (16)
(16)
with s = 2π * tstop/P (where P is the period) and the stopping time is given by
 (17)
(17)
The consideration of drift is important as we can see the strong dependence of the drift speed on the size of the planetesimals. This becomes important as we reduce the typical size of solids via fragmentation.
As the planetesimals drift across the ice line, we expect their volatile components to evaporate reducing the typical mass and also the typical radius of the solids. To account for this we implemented a simple ablation model following the prescription of Burn et al. (2019). The ablation follows the theoretic kinetic expression for water ice,
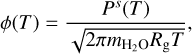 (18)
(18)
where Ps is the water vapour sublimation pressure, 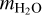 is the molecular mass of water, and Rg is the universal gas constant. The above equation assumes zero partial pressure of water in the vicinity of the planetesimals. From this formula, and assuming that the ice is removed from a layer with thickness δ ≪ rp, we calculate the water mass loss as:
is the molecular mass of water, and Rg is the universal gas constant. The above equation assumes zero partial pressure of water in the vicinity of the planetesimals. From this formula, and assuming that the ice is removed from a layer with thickness δ ≪ rp, we calculate the water mass loss as:
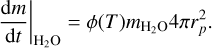 (19)
(19)
With the mass loss calculated we can calculate the change in other properties that result from it, for example their bulk density and radius, which is done by calculating the density according to the updated ice fraction and computing the new radius from it. This only affects planetesimals from beyond the initial ice line that have drifted across the dynamic ice line calculated from the structure of the gas disk. This only occurs for small planetesimal sizes (s <= 100 m) because the ice line moves towards the central star faster than the larger solids.
The gravitational interaction between planetesimals not only changes their dynamical state, but also leads to radial diffusion. To describe this behaviour we use the prescription of Tanaka et al. (2003). The associated viscosity of the diffusion process can be written as
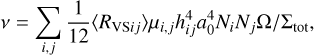 (20)
(20)
where 〈RVS,ij〉 = 4/3(〈QVS,ij〉 + 〈PVS,ij〉) and Ni is the number surface density of the i-th planetesimal swarms, µ is the reduced mass of the interacting planetesimals, and hij their mutual Hill radius. We then use the diffusion and the drift velocities to solve the advection diffusion equation for each swarm (including the fragments), which is described by the diffusion advection equation
![$\matrix{ {{\partial \over {\partial t}}\left( {{{\rm{\Sigma }}_i}} \right) - {1 \over r}{\partial \over {\partial r}}\left( {r{\upsilon _{{\rm{drift}}}}{{\rm{\Sigma }}_i}} \right) - {1 \over r}{\partial \over {\partial r}}\left[ {3{r^{0.5}}{\partial \over {\partial r}}\left( {{r^{0.5}}v{{\rm{\Sigma }}_i}} \right)} \right],} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{ = }}{{{\rm{\dot \Sigma }}}_{{\rm{accretion}}}} + {{{\rm{\dot \Sigma }}}_{{\rm{frag}}}} + {{{\rm{\dot \Sigma }}}_{{\rm{ablation}}}}} \hfill \cr } $](/articles/aa/full_html/2023/08/aa45901-23/aa45901-23-eq26.png) (21)
(21)
where, on the right-hand side, the sink terms describe the mass removal due to the accretion by the planetary embryos, the mass transferred between the swarms due to fragmentation, and the ablation of the ices when crossing the water ice line, as described above, each of which is treated in its own step. The initialisation of the solid disk is important because it dictates the speed of the early accretion. The initial solid surface density follows a power law with an exponential cutoff described by
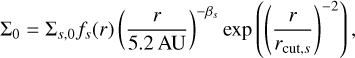 (22)
(22)
where the power law is chosen to be minimum mass solar nebula (MMSN)-like (Weidenschilling 1977) as βs = 1.5 and the outer radius rcut,s is given as a function of the cutoff radius of the gas rcut,g as rcut,s = 0.5rcut,g (Ansdell et al. 2018). The initial solid surface density Σ0,s is calculated by enforcing a specific dust-to-gas ratio in the protoplanetary disk. The factor fs accounts for the fact that not all elements are in the solid phase in all radial parts of the disk. This is calculated with the disk chemistry model of Thiabaud et al. (2014) and Marboeuf et al. (2014). The relative abundances are set according to the interstellar medium (for the volatiles we track H, O, C, and S atoms), and thus we calculate the fraction of material that is in its solid phase fs at each radial location in the disk. This factor becomes unity for large separations past all the ice lines. This also naturally sets the inner solid disk edge when fs = 0 (i.e. when the planetesimals sublimate completely). This sublimation radius is enforced, removing the solid mass interior to it throughout the formation stage depending on the temperature structure of the gas disk. The water ice line is calculated in the same way and is the biggest jump in surface density as it makes up ≈60% of the ice mass (Marboeuf et al. 2014). The bulk density ρ is also determined by the location of the ice line, meaning we consider rocky planetesimals with a bulk density of (3.2 g cm−3) inside the initial ice line and icy planetesimals outside with (ρ = 1 g cm−3).
The initialisation of the dynamical state of the solid disks is simply given by the equilibrium between the self stirring of the planetesimals and the gas drag by the gas disk (Fortier et al. 2012). We note that the initialisation does not change when considering fragmentation as at t = 0 no fragments are present in the disk, and therefore we do not have to consider the dynamic friction term. This results in
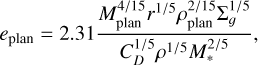 (23)
(23)
and the inclinations are simply given by β = i/e = 0.5.
2.2 Planet population synthesis
In order to probe the planet formation process for different initial conditions and to compare our theoretical results with the actual exoplanet population, we need to make use of population synthesis (Ida & Lin 2004; Mordasini et al. 2009, 2015; Emsenhuber et al. 2021a). The main idea is to run multiple global simulations with different initial conditions to capture the diversity of resulting planets and to account for the chaotic nature of the N-body interactions in planet formation (Mordasini 2018). For this we run many systems (typically ~1000) with the Bern model, as described above, where the initial conditions are generated from the following random variables:
Dust-to-gas ratio fD/G. To constrain the mass of gas in the disk we make use of the gas-to-solid mass ratio fD/G and assume the disks and their stars have the same metallicity, which leads to
![${{{f_{{D \mathord{\left/ {\vphantom {D G}} \right. \kern-\nulldelimiterspace} G}}}} \over {{f_{{D \mathord{\left/ {\vphantom {D {G, \odot }}} \right. \kern-\nulldelimiterspace} {G, \odot }}}}}} = {10^{\left[ {{{{\rm{Fe}}} \mathord{\left/ {\vphantom {{{\rm{Fe}}} {\rm{H}}}} \right. \kern-\nulldelimiterspace} {\rm{H}}}} \right]}},$](/articles/aa/full_html/2023/08/aa45901-23/aa45901-23-eq29.png) (24)
(24)
where the metallicities follow the distribution of Santos et al. (2005). The entire dust mass is assumed to be converted to planetesimals.
Initial gas disk Mass Mg and dust mass. The distribution of initial dust disk masses Mg reproduces the Class I disks reported in Tychoniec et al. (2018). The dust masses of the disks follow a log-normal distribution with log10(µ/M⊕) = 2.03 and σ = 0.35 dex. The gas mass is then obtained by dividing by the previously defined dust-to-gas ratio. The sampled gas disk mass range is limited from 0.004 M⊙ to 0.16 M⊙ to ensure self-gravitational stability.
Photo evaporation rate Ṁwind. Since the disk lifetimes are constrained by a combination of α and Ṁwind, and α is kept constant at a value of 2 × 10−3, we choose the evaporation such that the disk lifetimes fit observations (Emsenhuber et al. 2021a). This results in a log-normal distribution with log(µ/(M⊙ yr−1)) = −6 and σ = 0.5 dex.
Inner edge of the gas disk rin. The inner disk edge of the gas disk is chosen to be the co-rotation distance to the star (i.e. where the Kepler period matches the rotation period of the star). The stellar periods are sampled from Venuti et al. (2017).
Initial location of the embryos aembryos. The initial embryo locations are randomly chosen between the inner disk edge and 40 Au uniformly in logarithm. To reproduce the results from N-body simulations (Kokubo & Ida 2002), the embryos cannot be closer to another than 10 Hill radii if we consider multiple embryos.
In addition the remaining parameters can be found in Table A.3. We note that all of the systems are formed around solar mass stars. One particular parameter of interest is the chosen planetesimal size, which has great effect on the fragmentation model introduced in the next section. We consider two choices for the planetesimals size 100 and 1 km. The first choice is motivated by the size distribution of asteroids in the main belt (Morbidelli et al. 2009) and the results from streaming instability (Schäfer et al. 2017). The second choice lets us explore setting closer to the previous choice of Emsenhuber et al. (2021b), which is motivated by Schlichting et al. (2013), Arimatsu et al. (2019), Kenyon & Bromley (2012), and Weidenschilling (2011).
2.3 Fragmentation model
To study the influence of fragmentation on the population of exo-planets we have to use a simplified model that follows in parts the model described in Ormel & Kobayashi (2012) with a few notable differences. The model described in Ormel & Kobayashi (2012) is a local model and does not support multi-planet systems and migration. Furthermore, it takes a simplified approach to the calculation of the dynamical state and the effects of drift. Our model adds to the description of the solid disk a swarm of solids of a second variable size (known as fragments) that are created by the mutual collisions of planetesimals.
First, we take a look at the baseline description of the fragmentation model. In this case the fragments are modelled as an additional swarm of solids of a fixed size (sf) that is a parameter of the model. At each time step we calculate the fragmentation rates from the mutual collisions of the planetesimals (PPs) and, if there are any, the eroding collisions of planetesimals with fragments (PFs). At each radial bin we calculate first the collisional timescale among planetesimals which is given by
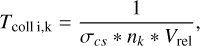 (25)
(25)
where Vrel is the relative velocity among the colliders. The number density nk of projectiles and the cross-section are given by
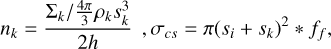 (26)
(26)
where ρ is the bulk density of the planetesimals, h = a * imax(i,k) is the scale height of the solid disk, and ff is the gravitational focus factor (Morbidelli et al. 2009). The subscripts i and k refer to the properties of the targets and projectiles, respectively. When we consider collisions among different swarms the scale height used is the highest one as it reflects the true number densities in the collisional volume. The gravitational focus factor describes the deviation of the collisonal cross-section from the geometric one (i.e. it accounts for the fact that the colliders have a gravitational field enhancing their cross-section). For this we follow the description of Morbidelli et al. (2009). We define the ratio of specific collision energy to the specific material strength as
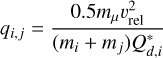 (27)
(27)
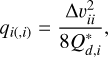 (28)
(28)
where mµ = (1/mi + 1/mj)−1 is the reduced mass. For the specific fragmentation energy 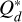 we use the value from the bigger collider (i), which is considered the target. The excavated mass of a collision mexc is then given by the collisional outcome model of Kobayashi et al. (2010):
we use the value from the bigger collider (i), which is considered the target. The excavated mass of a collision mexc is then given by the collisional outcome model of Kobayashi et al. (2010):
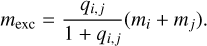 (29)
(29)
We assume that all of the mass that gets excavated flows instantaneously to the fragments. This is justified by the fact that the bodies in the gravity regime have lower material strength with reduced size, which should induce a collisional cascade and the size of the fragments represents its lower end (Ormel & Kobayashi 2012, and see our discussion in Sect. 4.3). In the nominal case we do not consider a change in the typical size of planetesimals due to these collisions for the planetesimals despite the mass that is excavated. This is ignored because outside of the feeding zone of embryos the collisional evolution is in the runaway regime due to the lack of added stirring by larger bodies. This, combined with the fact that we do not track individual bodies and only consider one size of planetesimals means we are not able to resolve the behaviour of the runaway bodies. This could then affect the growing embryo as it migrates. The resulting change in surface density from the collisions is then obtained by combining Eqs. (25) and (29) which results in
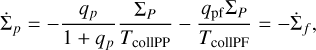 (30)
(30)
where the second term stems from the collisions with fragments. We note that because the impact energy of the fragments is significantly smaller qPF ≪ 1 we can use that qPF/(1 + qPF) ≈ qPF·
The description of the material strength is vital for the fragmentation model because it dictates the speed of fragmentation and the size distribution of fragments. We utilize the specific fragmentation energy 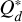 (i.e. the energy needed to disperse 50% of the target body) as it is used to determine the collisional outcomes as described above. For this model we consider two descriptions of
(i.e. the energy needed to disperse 50% of the target body) as it is used to determine the collisional outcomes as described above. For this model we consider two descriptions of 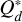 . The nominal case takes the results from Benz (1999) at υ = 3 km s−1 for basalt and ice, as described below,
. The nominal case takes the results from Benz (1999) at υ = 3 km s−1 for basalt and ice, as described below,
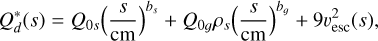 (31)
(31)
where s refers to the size of the planetesimals and υesc is their mutual escape velocity, and the remaining parameters can be found in Table A.2. The first term refers to the strength regime, the second term is the gravitational regime, and the last term is the gravitational potential (Stewart & Leinhardt 2009). A visualisation of the function can be seen in Fig. 1. We also consider another description of the fragmentation energy 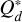 , which takes into account the effect of different impact velocities and the differences in strengths between icy and rocky planetesimals. Specifically, this means that we interpolate between the curves given by the parameters in Table A.2 according to the impact speed and ice fraction of the planetesimals. The parametrisations of
, which takes into account the effect of different impact velocities and the differences in strengths between icy and rocky planetesimals. Specifically, this means that we interpolate between the curves given by the parameters in Table A.2 according to the impact speed and ice fraction of the planetesimals. The parametrisations of 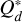 are described in Benz (1999, 2000), and the interpolation follows the approach of San Sebastián et al. (2019). For velocities above the maximum or below the minimum relative velocity covered by the parameters in Table A.2, we take the values of the closest curve (i.e. we do not extrapolate beyond the curves). This leads to a more accurate representation of the specific material strength, which mainly impacts the low-velocity regime where the material strength is considerably lower.
are described in Benz (1999, 2000), and the interpolation follows the approach of San Sebastián et al. (2019). For velocities above the maximum or below the minimum relative velocity covered by the parameters in Table A.2, we take the values of the closest curve (i.e. we do not extrapolate beyond the curves). This leads to a more accurate representation of the specific material strength, which mainly impacts the low-velocity regime where the material strength is considerably lower.
The fragment size can either be given as a parameter or can be calculated. When calculated by the model, the initial fragment size is given by the minimum in the specific fragmentation energy 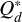 for the respective materials. This means icy and rocky planetesimals have different initial sizes. This leads (for an ice fraction of ≈0.6) to an initial fragment size of 105 m inside the ice line and a size of 147 m outside. The size of fragments is then only changed if the collisions between the fragments become destructive (i.e. if
for the respective materials. This means icy and rocky planetesimals have different initial sizes. This leads (for an ice fraction of ≈0.6) to an initial fragment size of 105 m inside the ice line and a size of 147 m outside. The size of fragments is then only changed if the collisions between the fragments become destructive (i.e. if 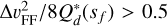 ) meaning the collisions between the equal-sized fragments excavate more mass than they add. In this case we reduce the size of fragments until the collision become non-destructive, meaning their size at each radial separation of the disk is then given by the implicit equation
) meaning the collisions between the equal-sized fragments excavate more mass than they add. In this case we reduce the size of fragments until the collision become non-destructive, meaning their size at each radial separation of the disk is then given by the implicit equation
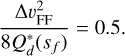 (32)
(32)
In this equation sf is the fragment size and ΔυFF is the relative velocity among fragments. Due to the negative slope in the strength regime of the 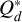 curve and the increased gas damping at lower sizes, we are able to find a stable size for the fragments (i.e. Eq. (32) has a solution).
curve and the increased gas damping at lower sizes, we are able to find a stable size for the fragments (i.e. Eq. (32) has a solution).
The fragments have short drift timescales, due to their strong coupling to the gas. As dictated by the pressure structure of the gas disk they drift towards the central star until they reach a pressure maximum. This leads to a significant pile-up of fragments at the global pressure maximum located at the inner disk edge (Guilera & Sándor 2017). For our gas disk structures and condensation model (Thiabaud et al. 2014) this pressure maximum is located outside of the dust sublimation line. The resulting pile-up of fragments can lead to very high solid-to-gas ratios at the pile-up which is not well described by our model as we do not account for the back reaction of solids onto the gas. Furthermore we expect mass to be removed from the inner disk edge through various processes (Li et al. 2022); however, the exact structure of the inner disk edge remains quite uncertain (Dullemond & Monnier 2010). As we are not able to resolve the full dust evolution and collisional evolution that comes with the pile-up, we use a heuristic simplified treatment of the solids at the global gas pressure maximum. We limit the solid surface density to the gas surface density when the gas surface density is above a certain threshold, which we chose to be 200 g cm−2. We ignore the limiting at lower gas surface densities because we do not expect solids in the entire disk to vanish when the gas disk dissipates, and because the drifting of solid slows down significantly as the gas disk dissipates. We discuss this simplified treatment and its effects in Sect. 5.
The code features an adaptive time step for the solid disk that ensures that the processes are treated consistently, which follows the approach of Morbidelli et al. (2009). The time step is chosen such that neither the surface density (Σ) nor the random velocities (e and i) change by more than 10% anywhere in the disk in a single time step. Another limit is that we ensure that the solids, especially the fragments, do not drift further than 1% of their semi-major axis, but there is a minimum time step of 1 yr. We note that these restrictions for the time step are in addition to those described in Emsenhuber et al. (2021b), which come from the planet’s internal structure and growth and the evolution of the gas disk.
 |
Fig. 1 Specific material strength for different ice (blue) and basalt (red) at different sizes and impact velocities. |
 |
Fig. 2 Fragmentation rates of planetesimals due to their mutual collisions in our model (solid) and from Eq. (33) (dashed) at different times. The dot indicates the location of the forming planet. |
3 Comparison with previous work
In order to ensure the validity of the fragmentation model introduced in the last section it is important to make a comparison to similar models presented in the literature, namely Chambers (2006) and Ormel & Kobayashi (2012). These models both operate with a similar three-component approximation to the solids in the disk (embryos, planetesimals, and fragments).
First, we wanted to compare the fragmentation rates of our planetesimal–planetesimal collisions to the ones from Chambers (2006) which are given by
![${{{\rm{d}}{{\rm{\Sigma }}_p}} \over {{\rm{d}}t}} = {{69.4{\rm{\Sigma }}_p^2a_0^2} \over {Pm}}*\min \,\left[ {{Q \over {2Q_d^*}},1} \right]\,,$](/articles/aa/full_html/2023/08/aa45901-23/aa45901-23-eq46.png) (33)
(33)
where Q is the specific impact energy (i.e. Q = 0.5 * mµ * υrel/mp). This formula is constructed under the assumption that β = i/e = 0.5, which does not hold throughout the entire disk in our simulations. The comparison of our fragmentation rates resulting from planetesimal–planetesimal collisions and theirs can be seen in Fig. 2. We tested this on a system with initial conditions that can be seen in Table A.4.
As can be seen, the rates are quite close to one another except on the outer edges of the feeding zone of the embryo, which is expected as this is where we get values of β that are significantly lower than the equilibrium value of β = 0.5. This arises due to the stirring of the planet that affects the eccentricities and inclinations with different strengths leading to a deviation from the equilibrium value of β = 0.5. Furthermore, Chambers (2006) assumes that all the collisions happen in the high-velocity regime, which might not hold far away from the embryo.
For the second comparison we constructed a test system with the initial conditions that can be seen in Table A.1. Additionally, to be consistent with the works of Ormel & Kobayashi (2012), for the profile of the disk we chose MMSN-like initial conditions of
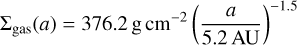 (34)
(34)
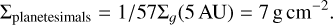 (35)
(35)
This corresponds to a MMSN model with an enhanced surface density of 2.65. Furthermore, we set the fragment size to a fixed size of 1 cm and planetesimals were set to a size of 106 cm so that the model could be compared to Fig. 6 from Ormel & Kobayashi (2012). Additionally, we disabled planet migration, the evolution of the gas disk, and the drift of solids and the gravitational focusing for the collisions as they do not consider these processes. For the description of the specific fragmentation energy we used the 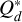 description of Benz (1999) for ices at 500 m s−1 (see Table A.2). For the relative velocity between solids for this comparison we also followed their simplified formula of ΔυPP = ΔυPF = 2eP * υk. To have a comparable treatment for the dynamical state we increased the integration time of Eq. (2) by a factor of 50, which ensures the dynamical state is always in equilibrium.
description of Benz (1999) for ices at 500 m s−1 (see Table A.2). For the relative velocity between solids for this comparison we also followed their simplified formula of ΔυPP = ΔυPF = 2eP * υk. To have a comparable treatment for the dynamical state we increased the integration time of Eq. (2) by a factor of 50, which ensures the dynamical state is always in equilibrium.
The resulting mass growth of the embryo is displayed in Fig. 3. The major difference between the two runs is in the initial stages of embryo growth, which is mainly due to the different ways the eccentricities and inclinations are calculated: they consider the balance between the two dominant timescales, whereas we integrate the dynamical evolution equation given in Eq. (2), which leads to different eccentricities and inclinations during the early stages. However, the end results are very close as the isolation mass is reached almost simultaneously.
In addition to the evolution of the forming planet we can compare the surface densities of planetesimals and fragments at the embryo’s location, which ultimately dictates the accretion rates. The surfaces densities at the embryos throughout the simulation can be seen in Fig. 4. The surface densities around the embryos compare rather well. The biggest differences are present in the early stages of the formation process, which can once again be explained by the different ways the dynamical state of the solids is calculated, which mostly comes into play at early times. As we can see, the outcome of our model is comparable to the results of different simplified models used to characterise fragmentation.
 |
Fig. 3 Core mass of the embryos in our simulation (red) and the reference simulation from Ormel & Kobayashi (2012), see their Fig. 6A (blue). |
4 Population synthesis
To get a more robust understanding of how our newly added fragmentation model affects the synthetic populations, we consider different set-ups for the treatment of the solid disk. To do this we ran single-embryo populations for three different models for two different sizes of planetesimals: 100 and 1 km. The three set-ups differ in their treatment of fragmentation. The first represents a reference case that includes the updated stirring, drift, and treatment of the ice line for the solid disk, but does not include fragmentation. The second includes fragmentation with a fixed fragment size of 100 m. The third set-up adds the dynamical calculation of the fragment size, as dictated by Eq. (32). To investigate the formation of multiple planets in the same disk, we completed a population with 20 embryos for both planetesimal sizes of 100 and 1 km that consider fragments of 100 m. We also considered the dynamical treatment of the fragment size for the 100 km planetesimals. As a comparison, we also ran non-fragmenting populations with 20 embryos for the 100 and the 1 km planetesimals. An overview of the populations with their abbreviations and their chosen model parameters can be seen in Table 1.
 |
Fig. 4 Surface densities of the planetesimals (solid) and fragments (dashed) at the embryo’s location for our model (red) and the Ormel & Kobayashi (2012) model (blue). |
Chosen settings for the different populations.
4.1 Single-embryo populations
In order to isolate the effects of fragmentation, it is useful to discuss the formation of single embryos in the disk as it allows us to prevent any chaotic noise stemming from the N-body interaction between the different forming planets. For this we investigated different settings for the fragmentation models L and Ldyn. Population L is the nominal case with 100 km planetesimals and a constant fragment size of 100 m. The fragment size was chosen to be close to the minimum in the 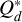 functions for ice and basalt from Benz (1999). In the second population, Ldyn, we also enable the dynamical calculation of the fragment size, as described in Sect. 2.3. We also ran a population without fragmentation to have a reference case to compare it to (Lno). As the effects of fragmentation strongly depend on the size of the initial planetesimals, we also ran simulations with smaller planetesimals of 1 km size in the set of populations Sno, S, and Sdyn, where we explore the same three settings of our fragmentation model.
functions for ice and basalt from Benz (1999). In the second population, Ldyn, we also enable the dynamical calculation of the fragment size, as described in Sect. 2.3. We also ran a population without fragmentation to have a reference case to compare it to (Lno). As the effects of fragmentation strongly depend on the size of the initial planetesimals, we also ran simulations with smaller planetesimals of 1 km size in the set of populations Sno, S, and Sdyn, where we explore the same three settings of our fragmentation model.
One of the main results of the population synthesis is the semi-major axis mass diagram, which allows us to see where the forming planets end up and the formation pathways to their final locations. To illustrate this we show the semi-major axis mass diagram for our different single-embryo populations in Fig. 5 we group the planets according to different properties: planets that have accreted more than 1% of volatile material are considered icy planets, planets that have a higher envelope than core mass are referred to as gas giants and The remaining planets are considered to be rocky. All of the following diagrams show their respective populations at a time of 5 Gyr.
In the left column of Fig. 5 (i.e. for the 100 km initial planetesimals) when comparing the population L with the reference case Lno we can see a few notable differences. Firstly, we can generally observe more massive planets when we consider the effects of fragmentation. This is especially visible for the icy planets where for the fragmenting population we see the vertical branch of inward-drifting icy planets at around ~10 M⊕, as described by Mordasini et al. (2012, 2009). Furthermore, we get significantly fewer very low-mass planets of around ~0.1 M⊕ in the inner regions of the disk. This feature mainly arises due to the transport of fragments to the inner disk where they pile up and enhance the growth rates. To illustrate this pile-up we show an example system where we omitted the limiting of the surface density described in Sect. 2.3 as this makes it easier to see the mass transported to the inner disk. This can be seen in Fig. 6 where we plot the surface density evolution of the fragments close to the star. As we can clearly see, there is a significant enhancement of the solid surface density of fragments at the inner disk edge when compared with the initial solid surface density. The initial disk profile represents the distribution of solids in the non-fragmenting case as the drift of 100 km planetesimals is negligible. We additionally see a void of Earth-mass planets at ~ 1 AU in population L, which we discuss below.
When we include the dynamic calculation of the fragment size in population Ldyn we similarly see that the growth in the outer disk is greatly enhanced. This holds true even further out in the disk when compared to population L. Additionally, we observe icy planets being formed closer to the star down to ~1 AU. This is true even for low-mass planets (M < M⊕) that experience little migration. This can be explained by the drift timescales of the smaller fragments that are significantly shorter leading to increased volatile transport to the inside of the initial ice line. The population in the inner disk is significantly less massive due to the short drift timescale of the solid material in the inner disk. This material is not entirely available to be accreted due to the limiting of the surface density at the inner disk edge, as described in Sect. 2.3.
When we look at the 1 km sized planetesimals in the right column of Fig. 5 (populations Sno, S, and Sdyn), the effects remain largely the same as before, but with the caveat that the planetary masses are already enhanced due to the faster accretion of the smaller planetesimals. This allows giant planets to be formed in the population with fragmentation, whereas they are absent in the reference simulation Sno. Additionally, we once again see the lack of planets forming at Earth’s location for the fragmenting population. When including the dynamical fragment size we once again see the same imprint as for the bigger planetesimals, mainly the halted growth for rocky planets and enhanced growth outside the ice line. Interestingly, we see a sharp transition in planet masses at ~ 10 AU separating embryos experiencing no growth with M ≈ 10−2M⊕ and the more massive ones.
When comparing the populations Sno to the previous populations computed with the previous iterations of the code shown in Emsenhuber et al. (2021a), we generally observe a significantly less massive population. Specifically, in the Sno populations no giant planets are formed. However, there are three main differences in the updated model that inhibit the formation of giant planets. The first two are the choice of planetesimal size, which is increased from 300 m to 1 km, and the inclusion of stirring of the planetesimals by density fluctuation, which both lead to higher eccentricities and inclinations for the planetesimals making them harder to accrete. The third is that we consider different distributions of the initial conditions, which results in the shorter lifetimes of the gas disks (see Sect. 2.2), leaving less time for gas giants to be formed.
A planet’s properties depend not only on its final location but also on its formation pathway. Therefore, we are also interested in the formation tracks for different types of planets forming in the populations. Tracks for different types of planets forming in the populations Lno and L can be seen in Fig. 7. This is done by plotting the formation pathways of a group of planets that have similar final properties (i.e. they end up at the same location in the distance–mass diagram). To determine what is close, we use the logarithmic distance in the semi-major axis mass plane 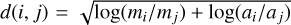 , where m[i,j] are the final planet masses and a[i,i] the semi-major axes.
, where m[i,j] are the final planet masses and a[i,i] the semi-major axes.
The groups that are not shown in either of the columns of Fig. 7 have no planet that is in close enough proximity (dmin > 2) to the group centre; in other words, these particular types of planets do not form in that population (e.g. the violet group in the bottom left panel). The formation tracks for the first row of Fig. 7 look quite similar for the two populations, except for the green group where the fragmenting population keeps accreting material during outward migration. The second row displays interesting differences when it comes to the red group, where in the fragmenting population the planets accrete a larger part of their mass closer to the star compared to their non-fragmenting counterparts. The planets growing further out (yellow and orange) form almost in situ, meaning they migrate very little during their formation. When comparing the orange and cyan groups, we see that for population L the planets show more migration close to their final mass, whereas for population Lno the planets migrate during the entire growth process, which implies a difference in timing of the accretion. The void of planets at Earth’s location seen in population L can be explained by the difference in migration; we see the yellow group experiencing little migration and the orange group migrating significantly more leaving this part of the diagram depleted. The migration becomes more significant when we get to ~10 Earth masses which is an expected result for type I migration (Ward 1997). When comparing the brown group we see a picture similar to that for the red group. The fragmenting population accretes more of its material closer to the star where the same type of planet migrating inwards forms further out in the disk in the non-fragmenting case. The purple and pink groups are absent from population Lno as the planets beyond the ice line do not grow massive enough to fill that part of the diagram (i.e. there are no planets forming with M > M⊕ beyond 1 AU for population Lno).
We can also probe the importance of the starting location of the embryo by running different simulations of the same initial disk (see parameters in Fig. A.4). To probe the importance of the initial location of the embryo we ran 100 single-embryo simulations with different starting locations. We did this with and without the fragmentation of planetesimals to be able to compare the two scenarios. This can be seen in Fig. 8; the embryos are equally spaced in log between the inner edge of the disk and 40 AU as this is also the range of semi-major axes allowed for the seeding of the initial embryo location for our populations, and it has the same spatial density distribution (uniform in log).
When we look at the non-fragmenting tracks of Fig. 8 we can see that all of the icy planets originate from beyond the initial ice line because the 100km planetesimals experience very little drift. For the rocky planets we see that most of them end up at the inner disk edge and that the more massive ones originate from further out in the disk, which is consistent with the brown group from Fig. 7. The tracks in the right panel of Fig. 8 illustrate similar features that can be seen for the most massive part of the entire population L. For the close-in planets we recover tracks similar to those of the brown group in Fig. 7. The outer tracks are similar to the purple, violet, and blue group, although with enhanced growth, which results from the massive disk of the system. We can clearly see that with the inclusion of fragmentation we are able to form icy planets from initial embryos that are well within the initial ice line, which is not the case without. This is due to the drift of fragments and the movement of the ice line during the simulation. As the ice line moves towards the star during the evolution of the gas disk (Burn et al. 2019), icy fragments drift past initial location of the ice line enriching the interior embryos in volatiles. This does not happen for the planetesimals as their drift timescales are significantly longer, meaning the icy planetesimals do not migrate far past the initial ice line. Additionally, we can see a distinct difference between the formation pathways of icy and rocky planets in these heavier disks where the growth of icy planets is greatly enhanced because of the drift pile-up at the ice line caused by the transition in drift speed due to the change in bulk density of solids (by a factor of ~3). This can be seen by the sharp transition between the furthest initial embryo that forms a rocky planet and the closest icy planet-forming embryo that differ in final mass by a factor of ≈5 (black crosses in Fig. 8). This also links to the previously discussed gap in planets around the Earth’s location seemingly being an effect of the sharp transition between icy and rocky planets. Additionally, the distribution of the rocky planets also changes significantly leading to the formation of more massive planets from embryos starting close to the inner disk edge, due to the increased access of accretable solids when compared to the non-fragmenting case. So we can clearly see that the addition of fragmentation affects the formation pathways of planets very differently depending on the starting location of the embryos.
The core mass budget in terms of fragments and planetesimals is an interesting statistic to look at as it allows us to directly see what the most dominant mode of accretion is (i.e. how much mass was accreted in the form of fragments or planetesimals for the different types of planets). Additionally, it lets us see the direct impact that fragmentation has on the formation of different types of planets. This is depicted in Fig. 9.
A general trend for all populations is that in the far outer disk (from ~10 AU outward) fragmentation seems to have less effect on the accretion mode of planets as the embryos in these regions accrete negligible amounts of fragments. This can be explained by the low surface densities and long collision timescales among planetesimals leading to few fragments being produced and explains why the fragmenting populations are very similar to their non-fragmenting counterparts beyond ~ 10–20 AU. However, this region is noticeably pushed outwards for the smaller planetesimals because, due to their smaller size, they have shorter collisional timescales. As a general trend in the populations with fixed fragment size, Fig. 9 shows that the closer we get to the star and the heavier the final planet is, the higher its mass fraction of accreted fragments is. When enabling the dynamic calculation of the fragment size we can see a similar trend, with the caveat that we get low-mass planets in the inner disk that accrete significantly fewer fragments and have a lower final mass of ≈10−1 Μ⊕. This shows that the inner disk gets depleted of fragments when we consider these smaller fragments that have very short drift timescales which halts the growth of these embryos. The right column of Fig. 9 shows that more fragments are being accreted on the planets when compared to their 100 km counterpart, which is true for both set-ups. This can be explained by the fact that the smaller planetesimal are much easier to fragment due to their lower material strength. In the end for the 1 km planetesimals the planets almost exclusively consist of fragments, which implies that the initial 1 km sized planetesimals are very weak with regard to collisions among themselves.
An additional important factor for planet formation is the timescale on which the planets form. This can be tracked by comparing the formation time of the core versus the lifetime of the gas disk. This largely dictates the amount of gas that can be accreted onto the planet for the heavier cores. This is especially important for the formation of giant planets as they have to accrete their gaseous envelop while the gas disk is still massive enough. To illustrate this, in Fig. 10 we plot the time in which the core grows by half of its final accreted core mass versus the disk lifetime.
Looking at the left column of Fig. 10 for the 100 km planetesimals we see a few key features. When we compare the formation times in the inner disk, we can see that planets at the inner disk edge with ~3–5 Μ⊕ have shorter formation times when considering fragmentation compared to the ones without. Specifically, we can see this quite clearly for the more massive planets (Mp > Μ⊕). Another interesting feature is the added late accretion for the planets further out (between 1 and 6 AU and masses between 0.5 and 5 Μ⊕), which all have formation timescales around the disk lifetime and slightly above. The planets forming further out in the disk have formation times longer than the disk lifetime; however, the fragmenting population L displays a significant reduction in formation times for these planets. Looking at the dynamic fragment size (Ldyn) we see and additional speed-up for the outer planets.
For the 1 km sized planetesimals we can see a significant reduction in the growth timescale when adding fragments of a fixed size, which is in line with what we see for the 100 km planetesimals. However, the formation times get shortened significantly more, so much that for population S virtually all planets form within the disk lifetime. For population S we can also see that the giant planets have shorter formation times than the intermediate-mass planets with ~1–100 Μ⊕. With the introduction of fragmentation we can observe an increase in occurrence rate of planets that grow to around ~ 1 Μ⊕ for population L and in the range 1–100 Μ⊕ for S beyond the ice line on the timescale of the disk lifetime. In order to illustrate what happens for these systems, we show the growth track along with surface densities of fragments and planetesimals around an example planet in Fig. 11.
As we can see for this type of forming planet, the generation of fragments occurs just before the dispersal of the gas disk. This means that the enhanced growth rate provided by the fragments only contributes during the later stages of planet formation. The fragments get generated during the end of the disk lifetime because with the removal of the disk the eccentricity damping from gas drag weakens and relative velocities are increased, leading to higher fragmentation rates. The generated fragments have much lower e and i than the planetesimals as long as the disk is still present and take some time to be stirred up as the disk vanishes. Which means they are accreted much more quickly. This leads to a significant accretion boost right around the time of disk dispersal that we can see in many simulations where the embryo is outside of ~3 AU. This is an interesting feature as it implies that the stirring by the planet can lead to the generation fragments, and that the dispersal of the gas disk also plays an important roll in the collisional evolution. This enhanced growth around the disk lifetime also has implications for the enrichment of heavy elements in the envelopes of these planets (Shibata & Helled 2022) as we expect a significant amount of the planetesimals accreted at later times when the planet has already accreted gas to be deposited in the envelop.
Another important quantity to compare the planet populations is the mass distribution of the formed planets, which is described by the planetary mass function (PMF). We show the PMF as a reversed cumulative distribution function for all our populations (including the multi-embryo populations discussed below), which can be seen in Fig. 12.
As we can clearly see, the addition of fragmentation leads to a significantly more massive population of planets when we consider a fixed size for the generated fragments. This is true for both the 100 and the 1 km planetesimals. However, when we consider the dynamical size calculation of the fragments, the picture changes quite drastically and we get an adverse effect across all mass ranges. As expected, the runs with smaller planetesimals yield enhanced growth across the spectrum when compared to their 100 km counterparts as the smaller planetesimals are more easily accreted. An interesting feature of population S when compared to previous works (Emsenhuber et al. 2021a) is that the occurrence rate gap of planets around 100 M⊕, is much less pronounced, which may be due to the late growing outer planets discussed above as they fit in the mass range of the gap.
With the introduction of the radial drift of solids, a significant amount of mass is transported to the global pressure maximum at the inner disk edge, which leads to a pile-up of solids (see Sect. 2.1). This happens because in our disk models this trapping of solids happens outside of the sublimation line for refractories. In order to approximately treat the unresolved complex physics at the inner disk edge, we limit the solid surface density to the gas surface density above a limit of 200 g cm−2. In Fig. 13 we display the mass removed by this limiting of surface density for the different populations during the formation stage of the planet formation. We do this by plotting the median mass removed along with the 10th–90th percentile interval for all systems. This serves as a good measure for the mass transport in the inner disk as it allows us to see how much additional material is transported to the inner disk edge.
As we can clearly see in Fig. 13 the addition of fragmentation leads to much earlier mass removal (i.e. increased mass transport to the inner disk). This is enhanced even further when we consider the dynamical calculation of the fragment size, which is expected as the smaller fragments have shorter drift timescales than the bigger fragments. Additionally, for the 1 km planetesimals we observe little difference (except populations Sno and Lno) when compared to their 100 km counterparts owing to the fact the mass transport is dominated by the fragments and not the planetesimals. We can see in Fig. 13 that this affects the populations without planetesimal fragmentation mostly on the timescale of lifetimes of the gas disks, which limits its imprint on the forming planets especially as the formation timescales are short in the inner disk (see Fig. 10). However, for the populations with planetesimal fragmentation we remove this mass quite early, meaning we experience a great deal of drift in the early stages depleting the inner disk of solid material. This is one of the main explanations why growth is halted for embryos in the inner disk when we consider the dynamical size of the fragments.
In order to investigate the radial extent of the mass removal in the inner disk and its impact on the forming planets, we ran an additional population with the same initial conditions as population Lno, but without limiting the surface density. We chose this population because the surface density profile steepens with shorter drift timescales, so population Lno is affected out to the greatest distance from the star when compared with the other populations. This makes it the most conservative choice showing an upper limit for the radial influence of this treatment. When we compare the final masses of the same planets forming in the two populations, we see that the differences are negligible outside of 0.4 AU with the maximum relative difference in mass being 7 × 10−3 and with an average of 3.5 × 10−4. However, we should be aware that it impacts the planets forming at the inner disk edge where we see an average mass deviation of 7% inside 0.4 AU. This means we have to be careful when interpreting the results of our simulations with forming planets close to the inner disk edge. However, we know that we underestimate the masses of these planets, and so the resulting final planet masses serve as a lower limit.
 |
Fig. 5 Distance–mass diagrams for the populations with a single embryo. The colour of the points refer to their bulk composition: red for Menv/Mcore > 1; blue for a volatile fraction >1%; green for the remaining points (i.e. rocky planets). |
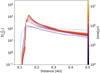 |
Fig. 6 Surface density evolution of the fragments of an example disk. The initial solid surface density is in blue and the disk lifetime is in white. The dashed lines mark the evolution after disk dispersal. |
 |
Fig. 7 Formation tracks (populations Lno (left) and L (right)) of nine groups of systems that form similar planets. The colour-coding (no physical meaning) is as follows: green (0.1,1), cyan (1,0.5), blue (10,0.5), red (0.05,3), orange (0.5,1), yellow (2,1),brown (0.05,7), pink (1,7), and violet (0.2,30). The groups are defined by the final distance and mass of the formed planets (AU, M⊕) and are explained in the text. Each row probes the formation of planet types with increasing final mass at different separations from the star. |
 |
Fig. 8 Tracks for 100 separately evolved embryos at different starting locations with the same initial conditions. Right: same model choice as population L. Left: same model choice as population Lno. The colour separates icy planets (blue > 1%volatiles) from rocky planets (green), and the initial water ice line is plotted in blue (dashed). The furthest initial embryo forming a rocky planet and the closest initial embryo forming an icy planet are indicated with a black cross (×). |
 |
Fig. 9 Distance–mass diagram for single-embryo populations (100 km (left) and 1 km (right)). The colour refers to the mass fraction of planetesimals that were accreted onto the core. |
 |
Fig. 10 Mass–distance diagram for single-embryo populations. The colour refers to the ratio of the time in which the embryos accrete half their final mass to the gas disk lifetime. |
 |
Fig. 11 Core growth (green right y-axis) for an example outer system (995 of L) with the surface densities (left y-axis) of planetesimals (blue) and fragments (red) and the time of the dispersal of the gas disk (black). |
 |
Fig. 12 The reversed cumulative planetary mass function for the populations. It is normalised to the number of systems for all populations. |
4.2 Multi-embryo population
It is also interesting to investigate the formation of multiple planets in the same disk because fragmentation and the other added processes open up further possibilities of interaction between planets, for example the accretion of the inward-drifting fragments generated by another planet further out. To investigate this we ran a population with the same parameters as Lno, L, Ldyn, Sno, and S (named MX where X is the single-embryo name) that include 20 initial embryos per system to see if there are any emerging imprints on the forming planets left by the interplay between the presence of multiple embryos per disk and planetesimal fragmentation. To investigate this we show in Figs. 14 and 15 the same quantities as in Figs. 9 and 10 for the multiplanet populations. We note that we did not plot the planetesimal mass fraction in the core for populations MLno and MSno as it adds no new information (cores are made up of planetesimals alone).
When we compare the final masses and positions of the planets in the reference simulation (MLno) to those in the fragmenting counterpart (ML), we recover effects of fragmentation on the population very similar to those in the single-embryo case. Specifically, the features we observe are significantly enhanced growth beyond the ice line and the increased occurrence rate of massive planets with formation times around the dispersal of the gas disk outside of the ice line. We also see the promoted growth at the inner disk edge where we do not have many planets remaining in the 10−2−10−1Μ⊕ mass range when considering fragmentation. When considering the dynamic treatment of the fragment size (MLdyn), we can see the significantly lower planet masses inside of 1 AU when compared to population ML along with the enhanced growth in the outer disk, which are both features we recovered from comparing the respective singe embryo populations. For the smaller planetesimals, when looking at the population MSno, we see that with the addition of multiple embryos giant planets form in the disks, which is not the case for Sno as giant impacts between the embryos lead to enhanced growth. For the population MS we see that the gas giants have a much wider distribution of semi-major axes when compared to their single-embryo counterparts, which is due to the n-body interactions between the growing embryos. By comparing the two (MSno and MS) we can see that the addition of fragmentation clearly enhances growth in the outer disk and shortens formation timescales beyond the ice line.
The fragment fractions displayed in the left column of Figs. 14 and 15 take into account the composition of the colliders for embryo mergers (i.e. the planetesimal fraction of the merged core is computed consistently from its colliders). When we compare the fragment fraction of the multi-embryo populations with their respective single-embryo counterparts we can see the same general trends of higher fragment fractions for closer-in and heavier planets. When we look at the simulations with bigger planetesimals (ML) the picture remains largely the same; however, due to the scatter introduced by the N-body interactions we have a less homogeneous picture. For example, we can see quite a few planets containing few fragments in the inner system. Additionally, for the MLdyn we see that most low-mass planets inside of 1 AU have higher planetesimal mass fractions in the core compared with the fixed size treatment. For the 1 km sized planetesimals we once again see that apart from the very low-mass planets all the mass gets accreted in the form of fragments. The right column of Figs. 14 and 15 depict the formation times, and also generally show the same trends as discussed in Sect. 4.1. In these plots we can nicely see the random scatter from the N-body interactions with the planets with very long formation times (dark blue) that are distributed throughout the populations including fragmentation. These planets grow from giant impacts, and therefore are not restricted by the lifetime of the gas disk nor can they be present in the single-embryo case. The remaining planets display the same distribution of formation times as their single-embryo counterparts.
The PMFs for the multi-embryo populations are already shown in Fig. 12. The y-intersect of the PMF is at less than the initial number of embryos because only the surviving planets at 5 Gyr are being counted for the statistic, which means that all the planets lost to collisions and the star are omitted. For the single-embryo case, the addition of fragmentation (i.e. comparing MLno and ML) with a fixed fragment size leads to significantly more massive planets. However, contrary to the single-embryo case, the dynamic fragments also produce more massive planets, which is due to the large number of planets with masses in the range 1–10 Μ⊕ outside of 1 AU. For the 100 km planetesimal populations ML and MLdyn we see that only very few planets get lost to collisions, which is due to their overall lower mass when compared to the simulations with 1 km sized planetesimals. When we look at the population MSno we clearly see the imprint of the giant planets on the PMF, which are not present in the single-embryo counterpart, leading to a much higher maximum mass. For the smaller planetesimals with fragmentation (MS) we see very similar results when compared to their single-embryo counterparts; however, the lack of planets around ~100 Μ⊕ is less pronounced than expected, but more pronounced than in the single-embryo case. The addition of fragments of a fixed size still seems to enhance the growth of the planets significantly, and also lead to more planets being lost (i.e. an increase in the embryo–embryo collisions that occur). The maximum masses appear to be almost the same for the single-embryo and the multi-embryo cases for the three simulations, which is in line with the results from Emsenhuber et al. (2021a) where the maximum mass shows only a slight dependence on the initial number of embryos.
When we look at the mass that was removed due to the limiting of the surface density in the inner disk displayed in Fig. 13, we see that there is less mass removed when we compare the multi-embryo populations to the single-embryo equivalents. This is to be expected: the more embryos there are in the disk, the higher the chance that one starts in the inner disk and accretes some of the material before it is lost to the removal. Additionally the mass flux to the inner disk edge gets reduced for a larger number of embryos as they accrete the fragments before they reach inner disk edge. This trend does not hold when we compare MSno with Sno, which can be explained by the added presence of giant planets that stir up the planetesimals, leading to increased drift speeds (see Eq. (16)).
In summary, we can see that the presence of multiple planets does not seem to break the imprint that planetesimal fragmentation has on planet formation; however, there are still a few changes that arise due to the multi-planet nature of these systems. This is in line with the results of Guilera et al. (2014), who find little change for two in situ forming planets in the same disk. However, in this work we explored the possible effects of multiple forming migrating planets on many different systems and planet pairs, leading to a more robust confirmation of the lack of or little influence of the interplay.
 |
Fig. 13 Median mass removed from all the disks in each population at different times along with the 10th–90th percentile interval (shaded) for the bigger planetesimals (left) and the smaller ones (right). |
4.3 Limitations of the model
Our model describes the size distribution of solids with two bins as opposed to treating the entire size range of solids. We do this to reduce the computational cost of the simulations and to have a conceptually simpler model. However, this means that we do not account for the fact that the fragments created by collisions have a size distribution rather than a characteristic size. This becomes important for the collisions among fragments in the typical size range we consider (~ 100 m) as they become super catastrophic (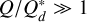 ), (Guilera et al. 2014) and lead to mass being transported to smaller sizes. This leads to a loss of accretable material (via drift or reduction to dust sizes), which is ignored in our model. The only way this is considered at the moment is when considering the dynamical size change by assigning a smaller typical size to the fragments for which the collisions are not super destructive anymore. In order to investigate the effect of the single size treatment of fragments, we can compare our results with the giant planet formation model of Guilera et al. (2010, 2014) and San Sebastián et al. (2019) that includes fragmentation and the full size distribution. We simulated the in situ formation of an initially 0.05 M⊕ mass embryo in a 10 MMSN disk, as described in the baseline case of San Sebastián et al. (2019). The growth was calculated until the crossover mass was reached. To be consistent with their results we use the fragmentation energy description of Benz (1999) for basalt at 3 km s−1 and assume a bulk density of 1.6 g cm−3 for the solids. We ran our model both with a fixed fragment size of 100 m (red) and the dynamical size calculation (magenta). The resulting growth tracks of the embryo computed with our model and theirs (blue) can be seen in Fig. 16. Their resulting formation times are considerably different as our simulations display shorter formation times in such a massive disk. One reason for this is that they only consider the generation of fragments once the collisions among planetesimals reaches
), (Guilera et al. 2014) and lead to mass being transported to smaller sizes. This leads to a loss of accretable material (via drift or reduction to dust sizes), which is ignored in our model. The only way this is considered at the moment is when considering the dynamical size change by assigning a smaller typical size to the fragments for which the collisions are not super destructive anymore. In order to investigate the effect of the single size treatment of fragments, we can compare our results with the giant planet formation model of Guilera et al. (2010, 2014) and San Sebastián et al. (2019) that includes fragmentation and the full size distribution. We simulated the in situ formation of an initially 0.05 M⊕ mass embryo in a 10 MMSN disk, as described in the baseline case of San Sebastián et al. (2019). The growth was calculated until the crossover mass was reached. To be consistent with their results we use the fragmentation energy description of Benz (1999) for basalt at 3 km s−1 and assume a bulk density of 1.6 g cm−3 for the solids. We ran our model both with a fixed fragment size of 100 m (red) and the dynamical size calculation (magenta). The resulting growth tracks of the embryo computed with our model and theirs (blue) can be seen in Fig. 16. Their resulting formation times are considerably different as our simulations display shorter formation times in such a massive disk. One reason for this is that they only consider the generation of fragments once the collisions among planetesimals reaches 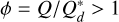 , where Q is the specific impact energy and
, where Q is the specific impact energy and  is the specific fragmentation energy (i.e. when collisions become fully fragmenting), which is not the case in our model. To account for this we ran a second set of simulations with our model (black 100 m, green dyn) also adopting that model choice. With these additional changes we see that the formation time and crossover mass of the forming planet lies between our different fragment size treatments, which illustrates nicely the influence the size distribution has on the formation of planets.
is the specific fragmentation energy (i.e. when collisions become fully fragmenting), which is not the case in our model. To account for this we ran a second set of simulations with our model (black 100 m, green dyn) also adopting that model choice. With these additional changes we see that the formation time and crossover mass of the forming planet lies between our different fragment size treatments, which illustrates nicely the influence the size distribution has on the formation of planets.
Additionally, we approximated treatment of the inner disk because without the full size range we lack the information to apply more sophisticated models for the mass loss and solid evolution at the global pressure maximum (Li et al. 2022). However, previous studies simply treated the inward-drifting material as direct mass loss, which can account for a significant amount of their mass budget (Chambers 2008). Furthermore, at the moment we only account for the sublimation of volatiles at the water ice line and do not add the sublimated material back to the gas disk. However, this is reasonable as water ice makes up a major part of the volatile mass fraction leading to the most significant change in planetesimal properties. We also assume local collision rates for the planetesimals; in other words, we do not account for the fact that planetesimals with high eccentricities collide with planetesimals in neighbouring radial bins (Morbidelli et al. 2009; Guilera et al. 2014).
 |
Fig. 14 Distance–mass diagram analogous to Figs. 9 (left) and 10 (right) for populations MLno (top), ML (middle), and MLdyn (bottom) with 20 embryos per disk where only the surviving planets are included. The mass limits of the figures vary for the different populations. |
 |
Fig. 15 Distance–mass diagram analogous to Figs. 9 (left) and 10 (right) for populations MSno (top) and MS (bottom) with 20 embryos per disk where only the surviving planets are included. |
 |
Fig. 16 Growth tracks of an in situ forming planet at 5 AU. Shown are a 10 MMSN disk calculated with the model of San Sebastián et al. (2019) (blue), our model with fixed size (red, black), and the dynamic size calculation (magenta, green), in the nominal case and when only considering collisions once ϕ > 1. The solid lines are core masses and the dashed lines are the envelope masses. |
5 Summary and conclusions
In this work we investigated the influence of planetesimal fragmentation on the planet formation process by adding planetesimal fragmentation to the Bern model along with an updated description of the solid disk. Using the population synthesis approach we probed its impact on the formation on the different types of exoplanets for different planetesimal sizes and model parameters. The main results of this analysis are as follows:
The addition of fragmentation does not allow for the formation of giant planets for 100 km planetesimals. However, it does promote the growth in the outer regions of the disk, which is enough to enhance or enable the giant planet formation for smaller 1 km sized planetesimals.
For smaller fragments we can expect a hindering effect of planetesimal fragmentation on the planet formation process, especially in the inner disk where the drift timescales are very short. For 100 km planetesimals, however, fragmentation can still promote the growth of planets outside a few AU both in single-embryo and in multiple-embryo simulations.
We find fragmentation promotes late growth beyond the ice line where we get a boost in accretion rate from fragments that are generated around the time of the gas disk dispersal as the damping by gas drag weakens.
The simulations highlight the significance of how the inner disk edge and its associated gas pressure maximum is treated for planet formation. In consequence our results in the inner disk (<0.4 AU) are to be treated as preliminary due to the shortcomings of the model.
The presence of multiple embryos in the disk does not significantly alter the imprint of fragmentation onto planet formation.
As we see significant changes for the populations when considering fragmentation, we discuss their implications on previous results obtained with the Bern model (Emsenhuber et al. 2021a,b; Voelkel et al. 2020). Voelkel et al. (2020) also performed single-embryo populations via the accretion of 100 km planetesimals. However, they investigated the influence of different surface density slopes for the planetesimals along with the dynamic formation of planetesimals. Due to the differing initial conditions in the two works, a quantitative comparison is not feasible so we discuss the emerging features from the investigated added physics. The effects of a steeper density slope and the addition of fragmentation for the nominal case show similar imprints on the populations in the inner disk where we get significantly enhanced growth. However, the results start to vary beyond the ice line where the steeper density profiles have little effect on the population, whereas fragmentation gives a significant boost to planetary growth as icy planetesimals fragment faster. With the consideration of the dynamic fragment size the picture changes quite a lot, and prevents most planets from forming within the ice line to grow beyond 0.5 Μ⊕. So the consideration of fragmentation can enhance or counteract the effects the dynamic embryo creation has on the forming planets, as found in the works of Voelkel et al. (2020), depending on the fragmentation model chosen. This would make it important to consider the effects in tandem in future works, especially since the consideration of both processes increase the self-consistency of the solid disk and both have a non-negligible effects on the formation of planets.
There are several improvements and follow-up questions we want to explore in future works. The single-size treatment of fragments is not ideal when considering a collisional outcome model with varying slope for the size distribution of fragments (Guilera et al. 2014). This means a more elaborate description of the full size distribution of solids should be added, incorporating a model for the dust evolution and planetesimal formation (Guilera et al. 2020; Voelkel et al. 2020). We showed the importance of this by comparing our results with the works of San Sebastián et al. (2019) leading to significant differences depending on the treatment of the fragment size. Additionally, the impact of different descriptions of the fragmentation energy is also of interest as it greatly impacts the timescale on which fragmentation operates along with the size distribution of the fragments generated. This may be especially important when considering rubble pile-like objects (Krivov et al. 2017) that may be present in the disk. Furthermore the treatment of the inner disk edge warrants further investigation as we expect many of the current model assumptions to not hold up in this environment.
Acknowledgements
We acknowledge the support from the Swiss National Science Foundation (SNSF) under grant 200020_192038. We would like to thank the anonymous referee for the valuable comments and suggestions that helped us improve the manuscript.
Appendix A Simulation details
Additional parameters for the test comparison vs Ormel & Kobayashi (2012)
Specific material strengths for ices and basalt at different relative velocities
Additional global parameters for all of the populations
Initial conditions of system 63 of population L
Appendix B Stirring functions
The stirring functions for the viscous stirring of planetesimals from Ohtsuki et al. (2002) are given by
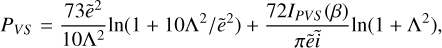 (B.1)
(B.1)
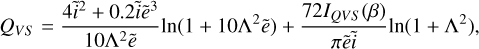 (B.2)
(B.2)
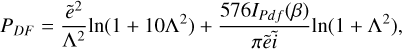 (B.3)
(B.3)
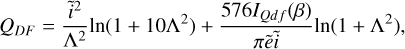 (B.4)
(B.4)
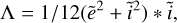 (B.5)
(B.5)
where 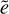 and
and 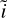 refer to the reduced eccentricity and inclination given by
refer to the reduced eccentricity and inclination given by 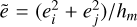 (where
(where 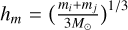 is the mutual Hill radius of swarms of solids i and j). Since it is impractical to calculate the elliptic integrals appearing in the in the equations above, we need approximations. The integrals I[P,Q],[VS,DF] are approximated in the range 0 < β = i/e < 1 as
is the mutual Hill radius of swarms of solids i and j). Since it is impractical to calculate the elliptic integrals appearing in the in the equations above, we need approximations. The integrals I[P,Q],[VS,DF] are approximated in the range 0 < β = i/e < 1 as
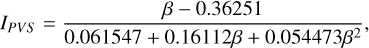 (B.6)
(B.6)
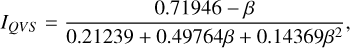 (B.7)
(B.7)
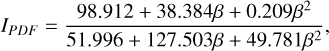 (B.8)
(B.8)
 (B.9)
(B.9)
The approximations of IPVS and IQVS are given by Chambers (2006) and IPDF and IQDF are obtained in the same way, and it can be checked that they match the approximated integrals from Ohtsuki et al. (2002) within 3% in the range 0 <β ≤ 1, which is the range of allowed values in the code.
References
- Alibert, Y., Mordasini, C., & Benz, W. 2004, A&A, 417, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alibert, Y., Mordasini, C., Benz, W., & Winisdoerffer, C. 2005, A&A, 434, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alibert, Y., Carron, F., Fortier, A., et al. 2013, A&A, 558, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ansdell, M., Williams, J. P., Trapman, L., et al. 2018, ApJ, 859, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Arimatsu, K., Tsumura, K., Usui, F., et al. 2019, Nat. Astron., 3, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez-Llambay, P., Masset, F., & Beaugé, C. 2011, A&A, 528, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benz, W. 1999, Icarus, 142, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W. 2000, in From Dust to Terrestrial Planets, eds. W. Benz, R. Kallenbach, & G. W. Lugmair (Dordrecht: Springer Netherlands), 279 [NASA ADS] [CrossRef] [Google Scholar]
- Burn, R., Marboeuf, U., Alibert, Y., & Benz, W. 2019, A&A, 629, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [Google Scholar]
- Chambers, J. 2006, Icarus, 180, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. 2008, Icarus, 198, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E. 2014, Icarus, 233, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C., & Monnier, J. 2010, ARA&A, 48, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Emsenhuber, A., Mordasini, C., Burn, R., et al. 2021a, A&A, 656, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Emsenhuber, A., Mordasini, C., Burn, R., et al. 2021b, A&A, 656, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fortier, A., Alibert, Y., Carron, F., Benz, W., & Dittkrist, K.-M. 2012, A&A, 549, A44 [Google Scholar]
- Guilera, O. M., & Sándor, Z. 2017, A&A, 604, A10 [Google Scholar]
- Guilera, O. M., Brunini, A., & Benvenuto, O. G. 2010, A&A, 521, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guilera, O. M., de Elía, G. C., Brunini, A., & Santamaría, P. J. 2014, A&A, 565, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guilera, O. M., Sándor, Z., Ronco, M. P., Venturini, J., & Miller Bertolami, M. M. 2020, A&A, 642, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helled, R., & Morbidelli, A. 2021, in ExoFrontiers; Big Questions in Exoplanetary Science, ed. N. Madhusudhan (UK: IOP Publishing), 12 [Google Scholar]
- Ida, S., & Lin, D. N. C. 2004, ApJ, 604, 388 [Google Scholar]
- Ida, S., & Makino, J. 1993, Icarus, 106, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Inaba, S., Wetherill, G. W., & Ikoma, M. 2003, Icarus, 166, 46 [Google Scholar]
- Jin, S., Mordasini, C., Parmentier, V., et al. 2014, ApJ, 795, 65 [Google Scholar]
- Johansen, A., Oishi, J. S., Low, M.-M. M., et al. 2007, Nature, 448, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Blum, J., Tanaka, H., et al. 2014, in Protostars and Planets VI (Tucson: University of Arizona Press) [Google Scholar]
- Kenyon, S. J., & Bromley, B. C. 2004, AJ, 127, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Bromley, B. C. 2012, AJ, 143, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, H., & Tanaka, H. 2010, Icarus, 206, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, H., & Tanaka, H. 2018, ApJ, 862, 127 [Google Scholar]
- Kobayashi, H., & Tanaka, H. 2021, ApJ, 922, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, H., Tanaka, H., Krivov, A. V., & Inaba, S. 2010, Icarus, 209, 836 [CrossRef] [Google Scholar]
- Kobayashi, H., Tanaka, H., & Okuzumi, S. 2016, ApJ, 817, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Kokubo, E., & Ida, S. 2002, ApJ, 581, 666 [Google Scholar]
- Krivov, A. V., Ide, A., Löhne, T., Johansen, A., & Blum, J. 2017, MNRAS, 474, 2564 [Google Scholar]
- Li, R., Chen, Y.-X., & Lin, D. N. C. 2022, MNRAS, 510, 5246 [NASA ADS] [CrossRef] [Google Scholar]
- Marboeuf, U., Thiabaud, A., Alibert, Y., Cabral, N., & Benz, W. 2014, A&A, 570, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morbidelli, A., Bottke, W. F., Nesvorný, D., & Levison, H. F. 2009, Icarus, 204, 558 [Google Scholar]
- Mordasini, C. 2018, Handbook of Exoplanets (Berlin: Springer International Publishing), 2425 [CrossRef] [Google Scholar]
- Mordasini, C., Alibert, Y., & Benz, W. 2009, A&A, 501, 1139 [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., Klahr, H., & Henning, T. 2012, A&A, 547, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Mollière, P., Dittkrist, K.-M., Jin, S., & Alibert, Y. 2015, Int. J. Astrobiol., 14, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Ohtsuki, K., Stewart, G. R., & Ida, S. 2002, Icarus, 155, 436 [Google Scholar]
- Okuzumi, S., Tanaka, H., Kobayashi, H., & Wada, K. 2012, ApJ, 752, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., & Kobayashi, H. 2012, ApJ, 747, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., Dullemond, C. P., & Spaans, M. 2010, ApJ, 714, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2004, AJ, 128, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Salo, H. 1985, Earth Moon Planets, 33, 189 [NASA ADS] [CrossRef] [Google Scholar]
- San Sebastián, I. L., Guilera, O. M., & Parisi, M. G. 2019, A&A, 625, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Israelian, G., Mayor, M., et al. 2005, A&A, 437, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schäfer, U., Yang, C.-C., & Johansen, A. 2017, A&A, 597, A69 [Google Scholar]
- Schlichting, H. E., Fuentes, C. I., & Trilling, D. E. 2013, AJ, 146, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shibata, S., & Helled, R. 2022, ApJ, 926, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Stewart, S. T., & Leinhardt, Z. M. 2009, ApJ, 691, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., Ohtsuki, K., & Daisaka, H. 2003, Icarus, 161, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Thiabaud, A., Marboeuf, U., Alibert, Y., et al. 2014, A&A, 562, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tychoniec, Ł., Tobin, J. J., Karska, A., et al. 2018, ApJS, 238, 19 [Google Scholar]
- Venuti, L., Bouvier, J., Cody, A. M., et al. 2017, A&A, 599, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voelkel, O., Klahr, H., Mordasini, C., Emsenhuber, A., & Lenz, C. 2020, A&A, 642, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ward, W. R. 1997, ApJ, 482, L211 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1977, Ap&SS, 51, 153 [Google Scholar]
- Weidenschilling, S. J. 2011, Icarus, 214, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, C.-C., Johansen, A., & Carrera, D. 2017, A&A, 606, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Specific material strengths for ices and basalt at different relative velocities
All Figures
 |
Fig. 1 Specific material strength for different ice (blue) and basalt (red) at different sizes and impact velocities. |
| In the text | |
 |
Fig. 2 Fragmentation rates of planetesimals due to their mutual collisions in our model (solid) and from Eq. (33) (dashed) at different times. The dot indicates the location of the forming planet. |
| In the text | |
 |
Fig. 3 Core mass of the embryos in our simulation (red) and the reference simulation from Ormel & Kobayashi (2012), see their Fig. 6A (blue). |
| In the text | |
 |
Fig. 4 Surface densities of the planetesimals (solid) and fragments (dashed) at the embryo’s location for our model (red) and the Ormel & Kobayashi (2012) model (blue). |
| In the text | |
 |
Fig. 5 Distance–mass diagrams for the populations with a single embryo. The colour of the points refer to their bulk composition: red for Menv/Mcore > 1; blue for a volatile fraction >1%; green for the remaining points (i.e. rocky planets). |
| In the text | |
 |
Fig. 6 Surface density evolution of the fragments of an example disk. The initial solid surface density is in blue and the disk lifetime is in white. The dashed lines mark the evolution after disk dispersal. |
| In the text | |
 |
Fig. 7 Formation tracks (populations Lno (left) and L (right)) of nine groups of systems that form similar planets. The colour-coding (no physical meaning) is as follows: green (0.1,1), cyan (1,0.5), blue (10,0.5), red (0.05,3), orange (0.5,1), yellow (2,1),brown (0.05,7), pink (1,7), and violet (0.2,30). The groups are defined by the final distance and mass of the formed planets (AU, M⊕) and are explained in the text. Each row probes the formation of planet types with increasing final mass at different separations from the star. |
| In the text | |
 |
Fig. 8 Tracks for 100 separately evolved embryos at different starting locations with the same initial conditions. Right: same model choice as population L. Left: same model choice as population Lno. The colour separates icy planets (blue > 1%volatiles) from rocky planets (green), and the initial water ice line is plotted in blue (dashed). The furthest initial embryo forming a rocky planet and the closest initial embryo forming an icy planet are indicated with a black cross (×). |
| In the text | |
 |
Fig. 9 Distance–mass diagram for single-embryo populations (100 km (left) and 1 km (right)). The colour refers to the mass fraction of planetesimals that were accreted onto the core. |
| In the text | |
 |
Fig. 10 Mass–distance diagram for single-embryo populations. The colour refers to the ratio of the time in which the embryos accrete half their final mass to the gas disk lifetime. |
| In the text | |
 |
Fig. 11 Core growth (green right y-axis) for an example outer system (995 of L) with the surface densities (left y-axis) of planetesimals (blue) and fragments (red) and the time of the dispersal of the gas disk (black). |
| In the text | |
 |
Fig. 12 The reversed cumulative planetary mass function for the populations. It is normalised to the number of systems for all populations. |
| In the text | |
 |
Fig. 13 Median mass removed from all the disks in each population at different times along with the 10th–90th percentile interval (shaded) for the bigger planetesimals (left) and the smaller ones (right). |
| In the text | |
 |
Fig. 14 Distance–mass diagram analogous to Figs. 9 (left) and 10 (right) for populations MLno (top), ML (middle), and MLdyn (bottom) with 20 embryos per disk where only the surviving planets are included. The mass limits of the figures vary for the different populations. |
| In the text | |
 |
Fig. 15 Distance–mass diagram analogous to Figs. 9 (left) and 10 (right) for populations MSno (top) and MS (bottom) with 20 embryos per disk where only the surviving planets are included. |
| In the text | |
 |
Fig. 16 Growth tracks of an in situ forming planet at 5 AU. Shown are a 10 MMSN disk calculated with the model of San Sebastián et al. (2019) (blue), our model with fixed size (red, black), and the dynamic size calculation (magenta, green), in the nominal case and when only considering collisions once ϕ > 1. The solid lines are core masses and the dashed lines are the envelope masses. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


