| Issue |
A&A
Volume 675, July 2023
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202346868 | |
| Published online | 04 July 2023 | |
In situ enrichment in heavy elements of hot Jupiters
1
Département Lagrange, CNRS, Université Côte d’Azur,
Observatoire de la Côte d’Azur,
Nice, France
e-mail: alessandro.morbidelli@oca.eu
2
Division of Geological and Planetary Sciences, California Institute of Technology,
Pasadena, CA, USA
Received:
11
May
2023
Accepted:
2
June
2023
Context. Radius and mass measurements of short-period giant planets reveal that many of these planets contain a large amount of heavy elements. Although the range of inferred metallicities is broad, planets with more than 100 M⊕ of heavy elements are not rare. This is in sharp contrast with the expectations of the conventional core-accretion model for the origin of giant planets.
Aims. The proposed explanations for the heavy-element enrichment of giant planets fall short of explaining the most enriched planets. We look for additional processes that can explain the full envelope of inferred enrichments.
Methods. We revisited the dynamics of pebbles and dust in the vicinity of giant planets using analytic estimates and published results on the profile of a gap opened by a giant planet, the radial velocity of the gas with respect to the planet, the Stokes number of particles in the different parts of the disk, and the consequent dust/gas ratio. Although our results are derived in the framework of a viscous α-disk, we also discuss the case of disks driven by angular momentum removal in magnetized winds.
Results. When giant planets are far from the star, dust and pebbles are confined to a pressure bump at the outer edge of the planet-induced gap. When the planets reach the inner part of the disk (rp ≪ 2 au), dust instead penetrates into the gap together with the gas. The dust/gas ratio can be enhanced by more than an order of magnitude if the radial drift of dust is not impeded farther out by other barriers. Thus, hot planets undergoing runaway gas accretion can swallow a large amount of dust, acquiring ~100 M⊕ of heavy elements by the time they reach Jupiter masses.
Conclusions. Whereas the gas accreted by giant planets in the outer disk is very dust-poor, that accreted by hot planets can be extremely dust-rich. Thus, provided that a large fraction of the atmosphere of hot Jupiters is accreted in situ, a large amount of dust can be accreted as well. We draw a distinction between this process and pebble accretion (i.e., the capture of dust without the accretion of gas), which is ineffective at small stellocentric radii, even for super-Earths. Giant planets farther out in the disk are extremely effective barriers against the flow of pebbles and dust across their gap. Saturn and Jupiter, after locking into a mutual mean motion resonance and reversing their migration, could have accreted small pebble debris.
Key words: planets and satellites: composition / planets and satellites: gaseous planets / planets and satellites: formation / protoplanetary disks
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The discovery and characterization of exoplanets over the course of the last 30 yr has brought about a seismic shift in our comprehension of planetary formation and evolution. Nonetheless, the first objects to be discovered in large numbers – hot Jupiters – continue to stand out as an enigmatic class of astrophysical bodies. These giants are close to their host stars (with orbital periods of less than 10 days) and, despite their unexpected nature, have attracted extensive scrutiny due to their distinctive features and relative ease of observation. In particular, precise mass and radius determinations are substantially more common within the presently known census of hot Jupiters than for other types of extrasolar planets.
Conventional giant planet structure theory holds that the mass-radius relation for degenerate Jovian planets is approximately flat (i.e., mass-independent; Stevenson 1982), meaning that their size is largely dictated by their composition. Within this framework, Jupiter’s radius in the first approximation corresponds to a roughly solar mixture of hydrogen and helium, meaning that any smaller radius is indicative of a substantially super-solar overall metallicity. The estimate of the total mass of heavy elements, here denoted as Mh, can be sharpened further through detailed modeling (which accounts for the corrections due to age, total mass, etc.). Guillot et al. (2006) were the first to carry out this analysis for a pool of nine well-characterized hot Jupiters. Intriguingly, they found that some objects have Mh on the order of ~ 100 M⊕, where M⊕ denotes the mass of Earth, and pointed out an apparent correlation between the planet’s Mh and the metallicity of the central star. This investigation was later extended and confirmed in Guillot (2008), Laughlin et al. (2011), and Moutou et al. (2013).
An important complication that arises within such analyses is that hot Jupiters experience substantial radius inflation, and, as such, their interiors are not in a fully degenerate state. Though a number of physical mechanisms – including tidal damping (Bodenheimer et al. 2003; Levrard et al. 2007), breaking gravity waves (Guillot & Showman 2002), impeded cooling due to enhanced atmospheric opacity (Burrows et al. 2007), double-diffusive convection (Chabrier & Baraffe 2007), turbulent burial of atmospheric entropy (Youdin & Mitchell 2010), and Ohmic dissipation (Batygin & Stevenson 2010) – have been proposed to explain this anomalous heating within the planets’ envelopes, statistical analyses (Thorngren & Fortney 2018) have shown that the strong dependence of the degree of inflation on stellar irradiation predicted by the Ohmic dissipation mechanism is indeed reflected in the data (see also Knierim et al. 2022). Consequently, the application of conventional giant planet evolution models to strongly irradiated planets can yield negative heavy element masses. In turn, this implies that the values of Mh reported in the aforementioned studies are lower bounds.
To circumvent this problem, Thorngren et al. (2016) considered a subset of 47 giant planets that are not strongly irradiated by their central star. Within this subset of objects, anomalous heating of the interior could be reasonably assumed to be negligible, meaning that the computed values of Mh likely represent the actual masses in heavy elements and not their lower bounds (indeed, no negative values of Mh appear in the Thorngren et al. calculations). We note that, strictly speaking, many of these planets fall into the “warm Jupiter” category because they have periods that exceed the nominal 10 day boundary, but for simplicity we still refer to them as hot Jupiters.
The main result of Thorngren et al. is reproduced in Fig. 1, which shows that many hot Jupiters are more enriched in heavy elements than Jupiter or Saturn. Some Jupiter-mass planets exceed 100 Earth masses in heavy elements. On average, the mass in heavy elements, Mh, is correlated to the total planet mass, Mp, as
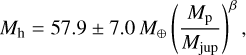 (1)
(1)
where Mjup is the mass of Jupiter. The exponent β of the Mh(Mp) correlation is 0.61 ± 0.08. Thorngren et al. also confirmed the correlation between Mh/Mp (the planet metallicity) and the stellar metallicity1. When this correlation is accounted for, the scatter of the data around the correlation law given by Eq. (1) is significantly reduced.
These results are surprising. According to the core-accretion theory of giant planet formation, giant planets are nucleated by the gradual accumulation of solid material into a ~15 M⊕ core, which then accretes a massive envelope of gas and small dust with approximately stellar metallicity. This process is expected to result in a range of solid-to-gas ratios for giant planets that is appreciably super-stellar but nonetheless much smaller than that given by Eq. (1). For instance, a Jupiter-mass planet would be expected to have ~18 M⊕ of heavy elements. This mismatch between expectations and observations suggests that the process of hot-Jupiter formation may be more complex than originally thought.
Thorngren et al. proposed an explanation for the surprising heavy element enrichment observed in hot Jupiters. They conjectured that planets accrete all planetesimals located within their feeding zone, an annulus with a radial width proportional to the planet’s Hill radius, RH = a(Mp/3Mstar)1/3, where a is the semi-major axis of the accreting planet. The exponent 1/3 is smaller than that of Eq. (1) but still not grossly inconsistent with the data. Venturini & Helled (2020) proposed a similar explanation for the enrichment in heavy elements in Jupiter and, through a more sophisticated planetesimal accretion model, predicted an exponent of 2/5 when the formation of a planetesimal gap is considered, which is a bit closer to the measured value of β than the estimate of Thorngren et al. The combination of accretion of gas with a 1% metallicity and the accretion of planetesimals with the 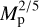 relationship gives the magenta curve in Fig. 1, which explains some of the planets, but clearly not the majority of them. Shibata et al. (2020, 2022) show that planet migration can enhance the efficiency of planetesimal accretion, due to a combination of resonant shepherding and gas drag. This is particularly efficient when the planet is migrating through specific locations of the disk (depending on the parameters). This may potentially make hot Jupiters more metal-rich than Jupiter itself.
relationship gives the magenta curve in Fig. 1, which explains some of the planets, but clearly not the majority of them. Shibata et al. (2020, 2022) show that planet migration can enhance the efficiency of planetesimal accretion, due to a combination of resonant shepherding and gas drag. This is particularly efficient when the planet is migrating through specific locations of the disk (depending on the parameters). This may potentially make hot Jupiters more metal-rich than Jupiter itself.
A radically different mechanism for the heavy element enrichment of giant planets has been proposed by Schneider & Bitsch (2021), elaborating on an original idea of Guillot & Hueso (2006). In their model, inward drifting dust particles (also known as pebbles) evaporate their volatile elements, each at a specific distance (the sublimation line of the corresponding volatile species). Therefore, the gas in the inner part of the disk gets enriched in volatile element vapor, and by a substantial amount for some disk parameters. Because a planet accretes H, He, and heavier element vapors indiscriminately, it can be enriched in heavy volatile elements through this process.
It is worth noting that this model is not restricted to hot Jupiters; it also applies to any planet accreting a substantial fraction of its gaseous envelope in the inner part of the protoplanetary disk, where volatile elements are in a vapor state. Nevertheless, this model falls a bit short of reproducing correlation (1). The Mh are typically below the value predicted by correlation (1) up to planets with Mp = 2 MJup and can reach the observed mean values only for more massive planets formed in the most metallic disks. Planets with Mh > 100 M⊕ are not expected in the Schneider and Bitsch model unless their total mass is larger than ~3 MJup.
Here we propose that the heavy element enrichment of hot Jupiters can be explained by the accretion of very dust-polluted gas in the inner part of the disk (essentially in situ; Bodenheimer et al. 2000; Batygin et al. 2016). This idea does not contradict the picture proposed by Schneider and Bitsch but introduces a previously overlooked effect. It can explain the enrichment in refractory elements, whereas Schneider and Bitsch predict an enrichment only in volatile elements.
It is generally expected that the gas accreted by a giant planet is metal-poor. This is because dust coagulation converts most of the solid mass into pebble-size objects, which are moderately coupled to the gas; pebbles cannot be accreted by planets exceeding ~ 20–40 Μ⊕ (the exact value depending on the disk’s viscosity and scale height; Lambrechts et al. 2014; Bitsch et al. 2018) because they remain trapped in the pressure bump produced at the outer edge of the planet-induced gap.
In this manuscript we show that, while this is true for giant planets in the central and outer parts of the disk, at small orbital radii pebbles readily permeate the gap of close-in giant planets due to two important factors: (1) the gas flows through the planet’s gap in the outside-in direction if the planet is sufficiently close to the star, whereas it flows through the gap in the inside-out direction if the planet is farther out (Dürmann & Kley 2015), and (2) pebbles have very low Stokes numbers in the inner part of the disk (Batygin & Morbidelli 2022) and therefore can be entrained into the gap by the radial flow of the gas despite the existence of a pressure bump at the gap’s outer edge. Pebbles are expected to fragment while flowing into the gap, thus maintaining a low Stokes number even inside the gap. The strong coupling with the gas then makes the accretion of solids possible only in conjunction with the accretion of gas. Nevertheless, this can considerably increase the planet’s heavy element budget because of the very high dust/gas density ratio that can be achieved in the inner disk due to the rapid drop in the dust/gas radial velocity ratio.
For simplicity, we elaborate on this process in Sect. 2 by adopting a viscous α-disk model, but we then discuss in Sect. 3 how the process is affected if the radial transport of gas is mostly due to angular momentum removal in disk winds and/or occurs only near the surface of the disk. Thus, we present a comprehensive revision of the problem of the interaction of a gap-opening planet with the flow of gas and dust or pebbles, hopefully correcting some misconceptions that are often found in the literature.
This manuscript ends with a discussion on super-Earths and the case of Jupiter and Saturn in Sect. 4, and we summarize our conclusions in Sect. 5.
 |
Fig. 1 Reproduction of Fig. 7 from Thorngren et al. (2016), showing the mass in heavy elements of weakly irradiated transiting giant planets as a function of the total planet mass. Relationship (1) is also illustrated. The magenta curve shows the expected enrichment if one considers the accretion of gas with 1% metallicity and the accretion of planetesimals following Venturini & Helled (2020). The green curve represents the case with a gas metallicity of 30%, the most favorable case expected from Sect. 2. |
2 Pebble dynamics in the vicinity of a giant planet in an α-disk model
The dynamics of a pebble in a protoplanetary disk is dictated by its coupling with the gas. Due to gas drag, the pebble’s velocity, v, relative to the gas velocity, u, is damped following the equation
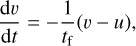 (2)
(2)
where tf is called the friction timescale. The Stokes number, St, of a pebble is the value of its friction timescale in units of the local orbital timescale:
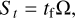 (3)
(3)
where Ω is the local orbital frequency.
The radial velocity of a pebble is given by
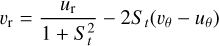 (4)
(4)
(Nakagawa et al. 1986; Takeuchi & Lin 2002), where the r and θ subscripts denote the radial and azimuthal components of the velocities. This formula does not account for the back-reaction of dust over gas (Dipierro et al. 2018). For a pebble on a circular orbit, the difference in azimuthal velocities νθ − uθ is a fraction η (depending on r) of the Keplerian velocity vK, where
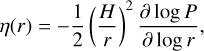 (5)
(5)
Η is the scale height of the disk, and 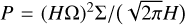 is the internal pressure of the gas. Assuming H ∝ r (i.e., neglecting disk flaring), Eq. (5) can be approximated as
is the internal pressure of the gas. Assuming H ∝ r (i.e., neglecting disk flaring), Eq. (5) can be approximated as
![$\eta \left( r \right) = - {1 \over 2}\,{\left( {{H \over r}} \right)^2}\,\left[ {{r \over {\rm{\Sigma }}}{{\partial {\rm{\Sigma }}} \over {\partial r}} - 2} \right],$](/articles/aa/full_html/2023/07/aa46868-23/aa46868-23-eq8.png) (6)
(6)
which is the equation we use in the rest of this paper.
Equation (6) reveals that, where Σ monotonically decays with r, η > 0. In this case, the azimuthal drag of the gas on the pebble leads to the star-ward radial drift of the pebble. However, where Σ has a sufficiently positive radial gradient, η < 0 and the drag is reversed. The location where η = 0 is called a pressure bump.
Giant planets open deep gaps in the gas distribution of the disk. Along the outer edge of the gap δΣ/∂r is positive and large, so that η < 0, whereas far from the planet’s orbit η > 0. So, a pressure bump is established whenever a giant planet forms. If the radial velocity of the gas ur > 0 then pebbles cannot drift into the gap, whatever their Stokes number. If instead ur < 0 only particles with St > min[ur(r)/2η(r)vK] do not penetrate the gap, where the minimum is computed for r ranging from one to multiple Hill radii beyond the planet’s orbit.
In most hydrodynamical studies on gap opening by giant planets published in the literature, the giant planet is kept on a fixed orbit. The gas is then observed to flow through the gap, from the outer part of the disk to the inner part (Bryden et al. 1999; Kley 1999; Lubow et al. 1999; Weber et al. 2018). Thus, Weber et al. computed that only particles with St > 10−3 do not penetrate a gap opened by a Jupiter-mass planet, for the disk parameters used in their nominal simulations. Consequently, it is often considered in the literature that the so-called planet barrier against the radial drift of pebbles is effective only for pebbles with a Stokes number larger than this order of magnitude (e.g., Stammler et al. 2023).
However, the situation is radically different if the planet is allowed to migrate, instead of being kept artificially on a fixed orbit. It has been shown (Duffell et al. 2014; Dürmann & Kley 2015; Robert et al. 2018) that, although the migration speed of giant planets is proportional to disk viscosity, giant planets migrate faster than the unperturbed radial velocity of the gas (which, in a viscous, disk is ur = −3/2(v/r), where ν is the disk’s viscosity, expressed as ν = αΗ2Ω in the so-called α-disks) when 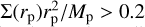 , where Σ(rp) is the gas’s unperturbed surface density at the radial distance of the planet rp. In this case, the gas flows through the gap in the inside-out direction (even if the radial motion of the gas in an absolute reference frame can remain negative). Instead, the planet migrates significantly slower than the radial motion of the gas, allowing gas to pass through the gap in the outside-in direction, if
, where Σ(rp) is the gas’s unperturbed surface density at the radial distance of the planet rp. In this case, the gas flows through the gap in the inside-out direction (even if the radial motion of the gas in an absolute reference frame can remain negative). Instead, the planet migrates significantly slower than the radial motion of the gas, allowing gas to pass through the gap in the outside-in direction, if
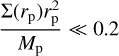 (7)
(7)
(Dürmann & Kley 2015). Because of the 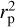 dependence of this formula and the typical weak radial decay of Σ (usually proportional to
dependence of this formula and the typical weak radial decay of Σ (usually proportional to 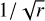 ) this happens only when the planet is in the very inner part of the disk. For a typical disk with surface density
) this happens only when the planet is in the very inner part of the disk. For a typical disk with surface density 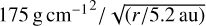 , (delivering a stellar accretion rate of ~4 × 10−8 M⊙ yr−1 for α = 3 × 10−3) and a Jupiter-mass planet, condition (7) translates to rp ≪ 2.5 au (Robert et al. 2018), which is well satisfied by the planets studied in Thorngren et al. (2016).
, (delivering a stellar accretion rate of ~4 × 10−8 M⊙ yr−1 for α = 3 × 10−3) and a Jupiter-mass planet, condition (7) translates to rp ≪ 2.5 au (Robert et al. 2018), which is well satisfied by the planets studied in Thorngren et al. (2016).
Obviously, in a reference frame co-moving radially with the planet, ur > 0 in the first case (inside-out flow through the gap) and ur < 0 in the second case. This means that the planet barrier is effective for particles of all sizes and Stokes numbers when a giant planet migrates in the central or outer parts of the disk2, whereas the barrier starts to be leaky when the planet reaches the vicinity of the star.
In the following, we present some quantitative estimates of the Stokes number of pebbles that can penetrate a gap opened by a giant planet, once the latter is close enough to the star for condition (7) to be true.
2.1 Searching for a dust trap: Are particles characterized by a size or a Stokes number?
Before computing the critical Stokes number below which pebbles can penetrate the gap, we need to determine whether particles should be characterized by a given size or a given Stokes number, whatever their position in the disk. In fact, if particles are characterized by a given St, we can apply Eq. (4), computing ur and η as a function of r and setting ![$S_t^{{\rm{crit}}} = \min \,\left[ {{{{u_{\rm{r}}}\left( r \right)} \mathord{\left/ {\vphantom {{{u_{\rm{r}}}\left( r \right)} {2\eta \left( r \right){\upsilon _K}}}} \right. \kern-\nulldelimiterspace} {2\eta \left( r \right){\upsilon _K}}}} \right] $](/articles/aa/full_html/2023/07/aa46868-23/aa46868-23-eq14.png) . If instead particles are characterized by a given size, the Stokes number depends on the gas surface density Σ as
. If instead particles are characterized by a given size, the Stokes number depends on the gas surface density Σ as 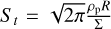 , where ρp is the bulk density of the pebble of radius R; thus, we need to set
, where ρp is the bulk density of the pebble of radius R; thus, we need to set 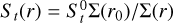 , where
, where 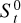 is the Stokes number of the pebble at a reference location r0 and Σ(r) is the actual density of the disk due to the presence of the gap, and solve Eq. (4) with respect to
is the Stokes number of the pebble at a reference location r0 and Σ(r) is the actual density of the disk due to the presence of the gap, and solve Eq. (4) with respect to 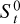 .
.
Particles continuously collide with each other, and break or coagulate depending of their collision speed. If the size of particles is limited by the fragmentation barrier, they achieve at collisional equilibrium a Stokes number given by (Birnstiel et al. 2009)
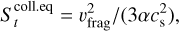 (8)
(8)
where ufrag is the velocity threshold for fragmentation and cs is the sound speed. Equation (8) is independent of the gas surface density, Σ, if not indirectly through cs ∝ Σ1/8, a weak dependence that we neglect in the following for simplicity3. Equation (8) applies if the timescale over which a particle experiences a change in Σ is longer than the collision timescale with other particles.
In the search for a dust trap at some location along the Σ-gradient characterizing the gap, it is correct to assume that the particle’s Stokes number is that given by Eq. (8). In fact, when a particle is trapped, it has the time to experience collisions and grind down until its Stokes decreases to 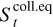 . Thus, the trapping can be permanent only if the condition vr = 0 in Eq. (4) holds for
. Thus, the trapping can be permanent only if the condition vr = 0 in Eq. (4) holds for 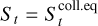 . Searching for a dust-trap location assuming a fixed dust size is not a valid approximation.
. Searching for a dust-trap location assuming a fixed dust size is not a valid approximation.
2.2 Evaluating the velocity of the gas
Having determined that St is roughly constant and that the critical Stokes number below which particles can penetrate into the gap is ![$S_t^{{\rm{crit}}} = \min \left[ {{{{u_{\rm{r}}}\left( r \right)} \mathord{\left/ {\vphantom {{{u_{\rm{r}}}\left( r \right)} {2\eta \left( r \right){\upsilon _K}}}} \right. \kern-\nulldelimiterspace} {2\eta \left( r \right){\upsilon _K}}}} \right] $](/articles/aa/full_html/2023/07/aa46868-23/aa46868-23-eq22.png) , we now proceed to evaluate η(r) and ur(r).
, we now proceed to evaluate η(r) and ur(r).
We started from the gap profile formula provided in Crida et al. (2006), which gives an expression for η as a function of Δ = (r − rp)/RH, α and q = Mp/Mstar:
![$\eta = - {1 \over 2}\,\left[ {{{0.4{q^2}r_{\rm{p}}^4\,{{\left( {{1 \over {{R_{\rm{h}}}{\rm{\Delta }}}}} \right)}^4}} \over {{3 \over 2}\alpha + {{{{{R_{\rm{h}}}} \mathord{\left/ {\vphantom {{{R_{\rm{h}}}} {{r_{\rm{p}}}}}} \right. \kern-\nulldelimiterspace} {{r_{\rm{p}}}}}} \over {8{\rm{\Delta }}}} + 200{{{{{R_{\rm{h}}}} \mathord{\left/ {\vphantom {{{R_{\rm{h}}}} {{r_{\rm{p}}}}}} \right. \kern-\nulldelimiterspace} {{r_{\rm{p}}}}}} \over {{{\rm{\Delta }}^{10}}}}}} - 2\,{{\left( {{H \over r}} \right)}^2}} \right], $](/articles/aa/full_html/2023/07/aa46868-23/aa46868-23-eq23.png) (9)
(9)
where, with respect to formula (14) in Crida et al., we have retained only the term corresponding to (6), assumed r ~ rp and retained only the dependence on Δ.
Formula (9) gives a minimum of η of −0.024 at Δ = 2.2 for q = 1 × 10−3, α = 3 × 10−3 and H/r = 0.05, in good agreement with the nominal hydrodynamical simulation of Weber et al. (2018, −0.03; see their Fig. 2). Instead, for q = 7.6 × 10−5, α = 10−3 and H/r = 0.05, formula (9) gives η = −0.009, whereas Bitsch et al. (2018) found η = 0. It is well known that the model of Crida et al. is not very accurate for planets of moderate mass. Thus, we introduce an empirical correction to formula (9) by dividing the first term in the [.] by 3.5(7.6 × 10−5/q + 0.2).
Concerning the radial velocity of the gas ur we remark that, due to the conservation of radial mass flow, one has 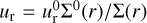 , where
, where 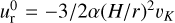 is the gas radial velocity in the unperturbed α-disk. We note that this implicitly assumes that the radial migration of the planet is much slower than −3/2α(Η/r)2υK, that is to say, that condition (7) holds true. Otherwise, we should use the relative velocity
is the gas radial velocity in the unperturbed α-disk. We note that this implicitly assumes that the radial migration of the planet is much slower than −3/2α(Η/r)2υK, that is to say, that condition (7) holds true. Otherwise, we should use the relative velocity 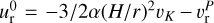 , where
, where 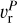 is the radial migration velocity of the planet. Again, if
is the radial migration velocity of the planet. Again, if 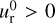 there is no possibility for particles with any St to penetrate into the gap.
there is no possibility for particles with any St to penetrate into the gap.
To evaluate Σ(r), and then ur, we turned again to the analytic gap model of Crida et al. (2006). From Eq. (6) one has
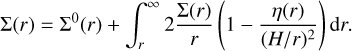 (10)
(10)
Equation (10) is implicit, but it can be solved iteratively, starting from r = ∞ and setting Σ(∞) = Σ0(∞). Of course, a physical approximation of infinity is 10RH or so, which is well beyond the planet’s gap.
Figure 2 shows St(r), solution of vr = 0 in (4) in the nominal case considered by Weber et al. (2018). The critical Stokes number  is the minimum of St (r) and is ~ 10−3, in good agreement with Weber et al. numerical results.
is the minimum of St (r) and is ~ 10−3, in good agreement with Weber et al. numerical results.
Figure 3 shows a map of the critical Stokes number as a function of q and α for H/r = 5% (top) and 3% (bottom). We remark that the two panels are quite similar, revealing a weak dependence on H/r. It is also worth noticing that, for a given value of α, the critical Stokes number does not monotonically decrease with increasing planet’s mass, as one could naively expect. This is due to the fact that, although the pressure bump becomes stronger with increasing q, −ur(r) increases at any value of r because the gap becomes wider and deeper. Consequently, the value 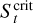 is achieved farther away from the planet and can result bigger than that computed for a smaller planet. According to Fig. 3, for H/r = 0.05 the planets that oppose the most severe barriers to pebble drift are those of approximately Saturn’s mass (log q ~ − 3.5).
is achieved farther away from the planet and can result bigger than that computed for a smaller planet. According to Fig. 3, for H/r = 0.05 the planets that oppose the most severe barriers to pebble drift are those of approximately Saturn’s mass (log q ~ − 3.5).
It is clear from Fig. 3 that, even for the least viscous (α ~ 10−4) and shallow (H/r = 0.03) disks, giant planets’ gaps are leaky for pebbles with St ≲ 10−4. This value is small, but it is the characteristic Stokes number of pebbles that reach the fragmentation limit (8) in the inner part of the protoplanetary disk, where condition (7) is fulfilled (Fig. 4). In particular, when planets approach the very inner part of the disk where the magneto-rotational instability (MRI) is active, the α parameter is expected to increase from 10−4 toward several times 10−3 (Flock et al. 2016). If α ~ 10−3, Fig. 4 shows that pebbles have St < 10−4, which is significantly smaller than 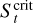 (Fig. 3).
(Fig. 3).
Thus, we conclude that when giant planets migrate near the central star, eventually pebble isolation disappears and planets can potentially feed from the full radial flow of solid (refractory) material. The efficiency of the accretion process is discussed next.
 |
Fig. 2 Value of the Stokes number of particles with zero radial velocity, as a function of the radial distance beyond the planet, normalized to the planet’s RH. The parameters used for the calculations are the same as those of the nominal simulation in Weber et al. (2018): q = 10−3, α = 3 × 10−3, and H/r = 0.05, so that the curve depicted here can be compared with the red curve in the bottom panel of Fig. 4 of Weber et al.. The critical Stokes number is the minimal value along the curve. |
2.3 Once in the gap: Accretion on the planet
Particles with 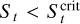 penetrate into the gap. For these particles, the evolution of the Stokes number is not obvious. In fact, it is important to remember that Eq. (8) only applies if the timescale over which a particle experiences a change in Σ is longer than the timescale of collisions with other particles. Because the particles radial speed increases as they go into the gap as Σ0(r)/Σ(r), where Σ0(r) is the unperturbed surface density and Σ(r) the actual density, it is possible that the migration timescale becomes shorter, so that particles preserve their sizes and increase in Stokes number. By comparing the timescale of the unperturbed radial motion of particles coupled to the gas (i.e., Tdrift = r/ur = 2/[3α(Η/r)2Ω]) with the particle collision timescale, Tcoll = 1/[fdustΩ], and adopting nominal parameters (α = 10−3, (H/r) = 0.05, and fdust = 0.01), we find that the drift timescale becomes shorter than the collision timescale only in gaps that are at least three orders of magnitude deep, namely for planets significantly more massive than Jupiter.
penetrate into the gap. For these particles, the evolution of the Stokes number is not obvious. In fact, it is important to remember that Eq. (8) only applies if the timescale over which a particle experiences a change in Σ is longer than the timescale of collisions with other particles. Because the particles radial speed increases as they go into the gap as Σ0(r)/Σ(r), where Σ0(r) is the unperturbed surface density and Σ(r) the actual density, it is possible that the migration timescale becomes shorter, so that particles preserve their sizes and increase in Stokes number. By comparing the timescale of the unperturbed radial motion of particles coupled to the gas (i.e., Tdrift = r/ur = 2/[3α(Η/r)2Ω]) with the particle collision timescale, Tcoll = 1/[fdustΩ], and adopting nominal parameters (α = 10−3, (H/r) = 0.05, and fdust = 0.01), we find that the drift timescale becomes shorter than the collision timescale only in gaps that are at least three orders of magnitude deep, namely for planets significantly more massive than Jupiter.
If the gas is very dust-rich, as argued below (Sect. 2.4), the particle collision timescale becomes even shorter. However, for large values of fdust the stirring of dust by turbulent diffusion in the gas is reduced by their collective inertia (see Schneider & Wurm 2019 for laboratory experiments and Sect. 4 of Batygin & Morbidelli 2020 for an analytic derivation). This lowers the impact velocity and raises the value of the Stokes number at the fragmentation threshold.
Nevertheless, we consider it unlikely that the Stokes number of particles can increase by orders of magnitude. Thus, particles should remain very coupled to the gas (e.g., St ~ 10−4−10−3). The usual formulæ for pebble accretion cannot be applied in our case because they are derived for small planets that do not accrete (nor perturb) the surrounding gas. Instead, the dynamics of gas in the vicinity of a giant planet is very perturbed. Hydrodynamical simulations (e.g., Lambrechts et al. 2019) show that part of the gas entering the planet’s Hill sphere is accreted into a bound atmosphere, while some merely passes through the Hill sphere with a residence timescale typically shorter than the Keplerian orbital period around the planet itself. Given the low Stokes number, particles coming with the accreted flow of gas will also be accreted in the envelope, whereas those carried by the unbound flow will not have enough time to decouple from the background flow and will be eventually transported away. Although solid particles can be accreted in this regime, they are accreted along with the gas. For this reason, it would be misleading refer to this process as pebble-accretion, since this term specifically refers to the selective accretion of dust over gas.
The accretion of dust together with gas may suggest that the overall planet metallicity cannot increase in this process. However, we show below that the gas in the inner part of a planetary disk can be very dust-rich, with ƒdust that can approach unity.
 |
Fig. 3 Critical Stokes number as a function of planetary mass, q (normalized to the stellar mass) and viscosity parameter, α, for H/r = 0.05 (top) and H/r = 0.03 (bottom). The dark red color in the top-left corner of the top panel denotes a region of parameter space where particles with any Stokes number penetrate into the gap. |
 |
Fig. 4 Reedition of Fig. of Batygin & Morbidelli (2022), re-centered in the region of interest, from 0.01 to 10 au. |
2.4 Metallicity of the inner part of the disk
In steady state, if dust drifts radially in the disk at the speed υr and gas at the speed ur, the dust/gas ratio ƒdust is given by
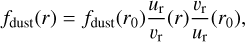 (11)
(11)
where r0 is a reference distance in the disk. Correspondingly, from Eq. (4) wehave
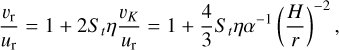 (12)
(12)
where for ur we have assumed the usual formula for an unflared α-disk.
As a standard assumption, we use H/r = 0.05 and η = 0.003 (Bitsch et al. 2015). Following Flock et al. (2016), we also assume
![$\alpha \left( r \right) = {{{{10}^{ - 2}} - {{10}^{ - 4}}} \over 2}\,\,\left[ {1 - \tanh \,\left( {10 - {1 \over r}} \right)} \right] + {10^{ - 4}},$](/articles/aa/full_html/2023/07/aa46868-23/aa46868-23-eq36.png) (13)
(13)
where we have adopted a 1/r dependence of the temperature and a critical temperature of TMRI ~ 1000 K to activate the MRI at 0.1 au. Finally, for St we used the value derived from a self-consistent description of an α-disk in Batygin & Morbidelli (2022):
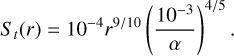 (14)
(14)
Using Eqs. (13) and (14), the resulting dust/gas radial velocity ratio given by Eq. (12) is illustrated in Fig. 5. We recall from Eq. (11) that the dust/gas ratio (i.e., the gas metallicity) is inversely proportional to Eq. (12). Thus, in the inner disk, the metallicity can be ~2.5 times higher than at 1 au and ~6 times higher than at 3 au.
To use this result, we need to anchor the dust/gas ratio somewhere in the disk. In a steady-state scenario, where the dust radial velocity is dominated by the −2StηυK term in Eq. (4), the dust to gas ratio is (Ida et al. 2016, formula 46)
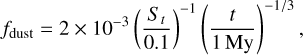 (15)
(15)
where t is the age of the disk. We recognize the inverse dependence on St (itself proportional to r9/10; see Eq. (14)) beyond ~0.3 au in Fig. 5. Formula (15) is valid only until the pebble formation front, rpƒ ~ 50 au(t/1 My)7/3 (Ida et al. 2016), reaches the outer edge of the disk. After this event, the dust flux drops and so drops also the dust/gas ratio. Even before that time, there may be obstacles to dust drift, due to gaps opened by distant giant planets (Weber et al. 2018) or the formation of dust-trapping rings due to nonideal magnetohydrodynamic effects (Riols et al. 2020). Until all these limitations become real, formula 15 predicts ƒdust = 0.2 at 1 au, where St ~ 10−3 and t ~ 1 Myr (i.e., enhanced by a factor of 50 with respect to solar metallicity). However, the enhancement has to be limited by planetesimal formation. For St > 10−3 the streaming instability converts dust into planetesimals when the dust/gas volume density ratio on the midplane is of order unity (Li & Youdin 2021). Depending on the disk viscosity and its ability to stir the vertical distribution of dust (usually encapsulated in the so-called Schmidt number Sc) the vertical scale height of the dust layer can be ~1/10 to ~1/3 that of the gas disk (i.e., for α = 10−4 and Sc = 10 ans 1, respectively); consequently, when ƒdust exceeds ~0.1–0.3 planetesimal formation is expected to convert the dust excess into macroscopic bodies. For this reason, we assume that ƒdust at 1 au cannot exceed these values. Therefore, we predict that, in the best case scenario, the ƒdust in the region of warm and hot Jupiters, where planetesimal formation is inhibited by the Stokes number being ≪10−3, can be 0.3 to 1, that is, enriched in metallicity by a factor of 30 to 100. The dust/gas ratio nevertheless remains smaller than one, which justifies the use of Eq. (4) for the dust velocity, even if it neglects the back-reaction of dust on gas.
The green curve in Fig. 1 shows the mass in heavy elements expected for giant planet accreting most of their atmosphere in the inner disk, from a gas enhanced in metallicity by a factor of 30. We note that we do not expect all planets to lie on this curve; the curve illustrates how metal-rich hot Jupiters can become under the most favorable conditions. Correspondingly, a large scatter of values are expected, depending on the actual metallicity of gas and the fraction of the planet’s atmosphere accreted in the inner disk.
 |
Fig. 5 Dust/gas radial velocity ratio, υr/ur, as given by Eq. (12) as a function of radial distance from the star. The validity of the curve extends to the location of the snow line (2–15 au, depending on the stellar accretion rate for the assumed α = 10−4; see Batygin & Morbidelli 2022), where St (and hence υr/ur) jumps by a factor equal to the square of the ratio of fragmentation velocity thresholds for icy and rocky particles. |
3 Wind-driven disks and layered accretion
One-dimensional α-disk models – of the type we have employed thus far – are routinely adopted for their simplicity and the ability to obtain analytical estimates. Their realism, however, is diminished in part by the fact that they do not account for other modes of angular momentum transfer within the system. In this section we address this drawback by describing what we expect to happen if the flow of gas toward the central star ensues due to angular momentum removal in disk winds, and if the transport of gas occurs predominantly on the surface layer of the disk. This is typical of disks where Ohmic diffusion dominates (Lesur 2021), namely in the inner disk region (0.1 < r < 1 au, Armitage 2011), but can also occur in viscous disks, due to the meridional circulation unveiled in Takeuchi & Lin (2002) or if there is a dead zone near the midplane (Bitsch et al. 2014).
We started with wind-driven disks. A main difference with the a-disk considered in the previous section is the radial dependence of the gas radial velocity ur. As we have seen above, in an α-disk ur scales with υK. Thus, the balance between radial drag and pressure bump (see Eq. (4)) is independent of the distance from the star and only depends on the particles’ Stokes number. Particles penetrate into the gap in the inner part of the disk because their Stokes number is smaller there. In a wind-driven disk, instead, ur scales as 1/r, which is to say it increases faster than υK as the gas approaches the star (Lega et al. 2022). This is because the wind removes angular momentum only from a sufficiently ionized layer and ionization depends on the amount of gas encountered by radiation as it penetrates from the surface of the disk toward the mid-plane. Thus, the vertically integrated column density of gas of the “active” layer of the disk, where the gas flows toward the central star, is independent of r. Then, conservation of mass-flow implies ur ∝ 1/r. In this case, it is even easier for particles to penetrate into a planet-carved gap in the inner disk, because the radial entrainment due to the gas radial velocity is stronger. For the same reason, the condition for outside-in flow of gas across the planet gap (a necessary condition for particles of any size to reach the planet) is no longer given by Eq. (7) and in general can be fulfilled farther out in the disk (Lega et al. 2022). To this end, Aoyama & Bai (2023) reported an acceleration of the gas radial velocity near the gap due to a concentration of magnetic field lines there. In other words, the scenario envisioned above appears even more favorable for efficient accretion of dust by hot Jupiters if the disk's evolution is driven by magnetized winds.
The fact that the flow of gas toward the star occurs near the surface in wind-driven disks (and also in some two-dimensional α-disks models, with or without dead zone) is not an obstacle to dust accretion. The small Stokes number of particles previously considered (St ~ 10−4) ensures that the dust is well coupled to the gas and uniformly distributed in the vertical direction of the disk, unless the turbulent vertical stirring is pathologically low (α/Sc ≪ 10−4), which is unlikely, particularly in the inner disk. Under these conditions, the flow of dust from a given disk layer into the gap prompts the vertical redistribution of the dust. This prevents the dust from accumulating indefinitely on the midplane, even if the pressure bump operates there.
This argument can be formalized. To fix ideas, we can imagine a disk of gas where ur = 0 everywhere but in a near-surface layer, where ur is large enough to transport the dust in that layer into the gap. The vertically integrated radial mass-flow of dust toward the pressure bump is
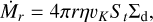 (16)
(16)
where η ~ 3 × 10−3 is the value of η beyond the pressure bump and Σd = ƒdust∑g is the surface density of the dust. The vertical flow of dust to restore a vertically uniform distribution of the dust/gas ratio is
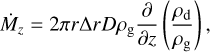 (17)
(17)
where ρd(z) and ρg(z) are the volume densities of dust and gas at height z and ∆r is the width of the ring where the dust tends to be concentrated due to the pressure bump on the mid-plane. The latter is 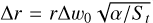 (Dullemond et al. 2018), where ∆w0 is the radial width of the pressure bump in normalized units. In Eq. (17) D = αH2Ω is the diffusion coefficient. Because on the surface layer of the disk the dust flows into the gap, ρd is reset to ƒdustρg there, and therefore we can approximate ∂/∂z (ρd/ρg) ~ 1/H[(ρd/ρg)z=0 − ƒdust].
(Dullemond et al. 2018), where ∆w0 is the radial width of the pressure bump in normalized units. In Eq. (17) D = αH2Ω is the diffusion coefficient. Because on the surface layer of the disk the dust flows into the gap, ρd is reset to ƒdustρg there, and therefore we can approximate ∂/∂z (ρd/ρg) ~ 1/H[(ρd/ρg)z=0 − ƒdust].
In a steady state, Eqs. (16) and (17) have to be equal. Approximating ρg ~ Σg/(2H), this gives
![${\left( {{{{\rho _{\rm{d}}}} \over {{\rho _{\rm{g}}}}}} \right)_{z = 0}} = \left[ {1 + 4\,{{\left( {{{{S_{\,t}}} \over \alpha }} \right)}^{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}}\,{\eta \over {{\rm{\Delta }}{w_0}}}} \right]\,{f_{{\rm{dust}}}}. $](/articles/aa/full_html/2023/07/aa46868-23/aa46868-23-eq42.png) (18)
(18)
The term St/α is of order unity, as required for a uniform vertical dust distribution. The ratio η/∆w0 is typically much smaller than 1/4, ∆w0 being ~0.1 for a pressure bump induced by a Jupitermass planet (Weber et al. 2018). Thus, the dust/gas ratio on the midplane at the pressure bump is only moderately increased, by a factor of (1 + 4η/∆w0) < 2 with respect to the local, vertically integrated disk metallicity ƒdust. Once this moderate enrichment is achieved, a steady state dust flux is set and all the net dust flow is carried into the gap, preventing any further accumulation of dust at the pressure bump in the midplane. In particular, it is unlikely that planetesimals would start to form in the midplane near a giant planet gap if they could not form in absence of the planet.
4 The case of super-Earths, and of Jupiter and Saturn in the Solar System
If giant planets cannot block the flux of dust in the inner part of the disk, the case is considerably more hopeless for super-Earths, as they open much shallower gaps. This does not imply that close-in super-Earth grew efficiently in situ by pebble accretion. The small Stokes number of the dust and their uniform vertical distribution in the disk makes pebble accretion an inefficient three-dimensional process (Batygin & Morbidelli 2022). Indeed, as we have seen above, even for giant planets the accretion of dust has to occur together with the accretion of gas. Given that super-Earths, by definition, accreted only moderate quantities of gas, we do not expect that the accretion of dust delivered a substantial fraction of a super-Earth's solid mass. Planets with Mp ~ Mh ~ 70 M⊕, as visible in Fig. 1, are not reproduced in our model starting from a 15 M⊕ core, as the green curve in the figure shows. Indeed, within the framework of our picture, these objects require the accretion of a large amount of planetesimals or mutual merging of multiple super-Earths of smaller masses.
Jupiter and Saturn are also enriched in heavy elements relative to solar metallicity. As individual planets in the outer disk, condition (7) would not be satisfied because the gas would flow through their gaps in the inside-out direction. However, Jupiter and Saturn have the tendency to lock in a mean motion resonance within the nebula, which halts or reverses their migration direction (Masset & Snellgrove 2001; Morbidelli & Crida 2007; Griveaud et al. 2023). Once this happens, the gas flows in the outside-in direction through their common gap, carrying small-enough dust with it. The typical Stokes number of particles at ~5 au should be much larger than the threshold of 10−4 − 10−3 for transport into the gap (Fig. 3 and Weber et al. 2018), but particle fragmentation at the pressure bump can produce a small-end tail in the particle size distribution with Stokes numbers smaller than this threshold (Stammler et al. 2023). These particles would be accreted by the planets with the same efficiency as gas (i.e., up to 90%; Lubow et al. 1999)4. However, it is unlikely that the presence of these particles would have made the metallicity of the accreted gas super-solar given that, as fragments, they do not represent the bulk of the solid mass and the outer disk metallicity is not expected to be substantially enriched, unlike in the inner disk (Sect. 2.4). Thus, we conclude that the enrichment in heavy elements of Jupiter and Saturn is likely due to accretion of planetesimals (Venturini & Helled 2020) and volatile-element vapors (Guillot & Hueso 2006).
5 Conclusions
In this work, we have analyzed the dynamics of particles near the outer edge of a gap opened by a giant planet in the gas radial distribution. The edge of a gap is a pressure bump, but it also enhances the radial velocity of the gas. In the outer part, giant planet Type-II migration toward the star is typically faster than the radial velocity of the disk gas, and slower in the inner part. Thus, in the outer disk, giant planets are effective barriers against the flow of dust of any size because both the positive radial motion of the gas relative to the planet and the pressure bump prevent particle drift into the gap. Instead, in the inner part of the disk the radial flow of gas relative to the planet is in the outside-in direction and can entrain particles with low Stokes numbers into the gap. We find that for the radial entraining to ensue despite the existence of a pressure bump, the particles’ Stokes number has to be lower than 10−4−10−3, depending on planet mass, disk viscosity, and scale height. For particles whose size is limited by the velocity fragmentation threshold, the Stokes number scales inversely with the square of the gas sound speed, and therefore it decreases rapidly in the inner disk. Thus, in the inner disk all conditions are met for typical particles to flow into the gaps opened by giant planets.
As an aside, this implies that the so-called inside-out planet formation model (Chatterjee & Tan 2014) is unlikely to be operational. That model relies on the ability of the first planet (either formed at or migrated to the inner edge of the disk) to create a pressure bump where drifting dust particles accumulate until forming a second planet, and so on. If even a giant planet is not able to block the drift of particles in the innermost part of the disk, this process should not promote the formation of super-Earth systems.
Returning to giant planet metal enrichment, we have shown that particles, once in the gap, can only be accreted by a planet together with the gas because of the low Stokes number. This does not, however, mean that the accreted material has a stellar metallicity. In fact, if the dust is allowed to freely drift toward the star (i.e., it is not blocked farther out by a dynamical barrier), it naturally piles up in the inner disk, enhancing the local metallicity by an order of magnitude or more. For this reason, if hot Jupiters accreted a substantial fraction of their envelope in situ (see Bodenheimer et al. 2000; Batygin et al. 2016, but these works should be updated to account for the high opacity of the dust-rich gas demonstrated in this paper), the large enrichments in heavy elements deduced from measurements of the planet’s mass and radius could have been achieved by this process.
Although we based our analysis on an α-disk model, we have shown that it also holds if the flow of gas in the disk is dominated by angular momentum removal in magnetized winds. We have also shown that, because of the low Stokes number, the transport of gas and dust into the gap in a surface layer of the disk is sufficient to prevent dust pileup at the outer edge of the gap and ensures that, in a steady state, the full dust flux crosses the orbit of the planet. To sum up, this study has explored the multi-faceted relationship between particles, gas flow, and giant planet migration near gap edges, contributing to a better understanding of the conditions under which particles can enter these gaps. Our findings may help inform future research on the heavy element enrichment observed in hot Jupiters.
Acknowledgments
A.M. is grateful for support from the ERC advanced grant HolyEarth N. 101019380 and to Caltech for the visiting professor program that he could benefit from. K. B. is grateful to Caltech’s center for comparative planetology, the David and Lucile Packard Foundation, and the National Science Foundation (grant number: AST 2109276) for their generous support.
References
- Armitage, P. J. 2011, ARA&A, 49, 195 [Google Scholar]
- Aoyama, Y., & Bai, X.-N. 2023, ApJ, 946, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., & Morbidelli, A. 2020, ApJ, 894, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., & Morbidelli, A. 2022, A&A, 666, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batygin, K., & Stevenson, D. J. 2010, ApJ, 714, L238 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., Bodenheimer, P. H., & Laughlin, G. P. 2016, ApJ, 829, 114 [Google Scholar]
- Birnstiel, T., Dullemond, C. P., & Brauer, F. 2009, A&A, 503, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Morbidelli, A., Lega, E., et al. 2014, A&A, 570, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Johansen, A., Lambrechts, M., et al. 2015, A&A, 575, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Morbidelli, A., Johansen, A., et al. 2018, A&A, 612, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bodenheimer, P., Hubickyj, O., & Lissauer, J. J. 2000, Icarus, 143, 2 [Google Scholar]
- Bodenheimer, P., Laughlin, G., & Lin, D. N. C. 2003, ApJ, 592, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Bryden, G., Chen, X., Lin, D. N. C., et al. 1999, ApJ, 514, 344 [CrossRef] [Google Scholar]
- Burrows, A., Hubeny, I., Budaj, J., et al. 2007, ApJ, 661, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Baraffe, I. 2007, ApJ, 661, L81 [Google Scholar]
- Chatterjee, S., & Tan, J. C. 2014, ApJ, 780, 53 [Google Scholar]
- Crida, A., Morbidelli, A., & Masset, F. 2006, Icarus, 181, 587 [Google Scholar]
- Dipierro, G., Laibe, G., Alexander, R., Hutchison, M. 2018. MNRAS, 479, 4187 [NASA ADS] [CrossRef] [Google Scholar]
- DraZkowska, J., Alibert, Y., & Moore, B. 2016, A&A, 594, A105 [CrossRef] [EDP Sciences] [Google Scholar]
- Duffell, P. C., Haiman, Z., MacFadyen, A. I., et al. 2014, ApJ, 792, L10 [Google Scholar]
- Dullemond, C. P., Birnstiel, T., Huang, J., et al. 2018, ApJ, 869, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Dürmann, C., & Kley, W. 2015, A&A, 574, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flock, M., Fromang, S., Turner, N. J., et al. 2016, ApJ, 827, 144 [CrossRef] [Google Scholar]
- Griveaud, P., Crida, A., & Lega, E. 2023, A&A, 672, A190 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T. 2008, Phys. Scr. T, 130, 014023 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T., & Hueso, R. 2006, MNRAS, 367, L47 [CrossRef] [Google Scholar]
- Guillot, T., & Showman, A. P. 2002, A&A, 385, 156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T., Santos, N. C., Pont, F., et al. 2006, A&A, 453, L21 [CrossRef] [EDP Sciences] [Google Scholar]
- Ida, S., Guillot, T., & Morbidelli, A. 2016, A&A, 591, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W. 1999, MNRAS, 303, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Knierim, H., Batygin, K., & Bitsch, B. 2022, A&A, 658, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kruijer, T. S., Burkhardt, C., Budde, G., et al. 2017, PNAS, 114, 6712 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Lega, E., Nelson, R. P., et al. 2019, A&A, 630, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laughlin, G., Crismani, M., & Adams, F. C. 2011, ApJ, 729, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Lega, E., Morbidelli, A., Nelson, R. P., et al. 2022, A&A, 658, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G. R. J. 2021, A&A, 650, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levrard, B., Correia, A. C. M., Chabrier, G., et al. 2007, A&A, 462, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, R., & Youdin, A. N. 2021, ApJ, 919, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Lubow, S. H., Seibert, M., & Artymowicz, P. 1999, ApJ, 526, 1001 [Google Scholar]
- Masset, F., & Snellgrove, M. 2001, MNRAS, 320, L55 [Google Scholar]
- Morbidelli, A., & Crida, A. 2007, Icarus, 191, 158 [Google Scholar]
- Moutou, C., Deleuil, M., Guillot, T., et al. 2013, Icarus, 226, 1625 [NASA ADS] [CrossRef] [Google Scholar]
- Nakagawa, Y., Sekiya, M., & Hayashi, C. 1986. Icarus, 67, 375 [Google Scholar]
- Riols, A., Lesur, G., & Menard, F. 2020, A&A, 639, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robert, C. M. T., Crida, A., Lega, E., et al. 2018, A&A, 617, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, A. D., & Bitsch, B. 2021, A&A, 654, A71 [Google Scholar]
- Schneider, N., & Wurm, G. 2019, ApJ, 886, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, S., Helled, R., & Ikoma, M. 2020, A&A, 633, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shibata, S., Helled, R., & Ikoma, M. 2022, A&A, 659, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stammler, S. M., Lichtenberg, T., DraZkowska, J., et al. 2023, A&A, 670, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stevenson, D. J. 1982, Annu. Rev. Earth Planet. Sci., 10, 257 [CrossRef] [Google Scholar]
- Takeuchi, T., & Lin, D. N. C. 2002, ApJ, 581, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Thorngren, D. P., & Fortney, J. J. 2018, AJ, 155, 214 [Google Scholar]
- Thorngren, D. P., Fortney, J. J., Murray-Clay, R. A., et al. 2016, ApJ, 831, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Venturini, J., & Helled, R. 2020, A&A, 634, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weber, P., BeníteZ-Llambay, P., Gressel, O., et al. 2018, ApJ, 854, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Mitchell, J. L. 2010, ApJ, 721, 1113 [NASA ADS] [CrossRef] [Google Scholar]
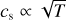 , where T is the gas temperature. The value of the temperature is dictated by the balance between the energy released by accretion of gas toward the star, which is constant through the gap by conservation of mass flow, and cooling, which is proportional to T4/(Σfdustκdust) where fdust is the dust/gas surface density ratio and κdust is the opacity of dust. Thus, T ∝ Σ1/4 and cs ∝ Σ1/8.
, where T is the gas temperature. The value of the temperature is dictated by the balance between the energy released by accretion of gas toward the star, which is constant through the gap by conservation of mass flow, and cooling, which is proportional to T4/(Σfdustκdust) where fdust is the dust/gas surface density ratio and κdust is the opacity of dust. Thus, T ∝ Σ1/4 and cs ∝ Σ1/8.
This implies that only a minority of these small particles reached the inner part of the disk and are thus unlikely to contaminate the so-called Solar System isotopic dichotomy (Kruijer et al. 2017).
All Figures
 |
Fig. 1 Reproduction of Fig. 7 from Thorngren et al. (2016), showing the mass in heavy elements of weakly irradiated transiting giant planets as a function of the total planet mass. Relationship (1) is also illustrated. The magenta curve shows the expected enrichment if one considers the accretion of gas with 1% metallicity and the accretion of planetesimals following Venturini & Helled (2020). The green curve represents the case with a gas metallicity of 30%, the most favorable case expected from Sect. 2. |
| In the text | |
 |
Fig. 2 Value of the Stokes number of particles with zero radial velocity, as a function of the radial distance beyond the planet, normalized to the planet’s RH. The parameters used for the calculations are the same as those of the nominal simulation in Weber et al. (2018): q = 10−3, α = 3 × 10−3, and H/r = 0.05, so that the curve depicted here can be compared with the red curve in the bottom panel of Fig. 4 of Weber et al.. The critical Stokes number is the minimal value along the curve. |
| In the text | |
 |
Fig. 3 Critical Stokes number as a function of planetary mass, q (normalized to the stellar mass) and viscosity parameter, α, for H/r = 0.05 (top) and H/r = 0.03 (bottom). The dark red color in the top-left corner of the top panel denotes a region of parameter space where particles with any Stokes number penetrate into the gap. |
| In the text | |
 |
Fig. 4 Reedition of Fig. of Batygin & Morbidelli (2022), re-centered in the region of interest, from 0.01 to 10 au. |
| In the text | |
 |
Fig. 5 Dust/gas radial velocity ratio, υr/ur, as given by Eq. (12) as a function of radial distance from the star. The validity of the curve extends to the location of the snow line (2–15 au, depending on the stellar accretion rate for the assumed α = 10−4; see Batygin & Morbidelli 2022), where St (and hence υr/ur) jumps by a factor equal to the square of the ratio of fragmentation velocity thresholds for icy and rocky particles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


